Как разложить число на множители: Разложение на множители, онлайн сервис для разложения чисел на простые множители — Детская игровая комната «Волшебный лес»

Posted on 17.03.197503.02.2022 by alexxlab

Содержание

Разложение чисел на простые множители

Онлайн-калькулятор «Разложение числа на простые множители» позволит вам разложить любое составное число на простые множители. Для этого вам нужно ввести число в поле и нажать кнопку «Вычислить». Особенностью данного калькулятора является то, что он не просто выдаст ответ, но и представит подробное решение. С помощью нашего калькулятора Вы сможете быстро получить результат, а подробное решение поможет вам разобраться, как был произведен расчет.

Введите число:

Вычислить

Все натуральные числа можно разделить на две группы чисел: простые и составные.

Простое число – это число, которые имеют только два делителя (единица и само это число), т.е. делится без остатка только на единицу и на само себя.

Принято считать, что единица (1) не является простым числом. Пример простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 и т.д. Простых чисел бесконечное множество, ниже в таблице представлены простые числа до 1000.

Составное число – это число, которые имеют более двух делителей. Любое составное число может быть представлено в виде произведенения простых чисел, например: 84 = 2 · 2 ·3 ·7.

Таблица простых чисел до 1000

2	3	5	7	11	13
17	19	23	29	31	37
41	43	47	53	59	61
67	71	73	79	83	89
97	101	103	107	109	113
127	131	137	139	149	151
157	163	167	173	179	181
191	193	197	199	211	223
227	229	233	239	241	251
257	263	269	271	277	281
283	293	307	311	313	317
331	337	347	349	353	359
367	373	379	383	389	397
401	409	419	421	431	433
439	443	449	457	461	463
467	479	487	491	499	503
509	521	523	541	547	557
563	569	571	577	587	593
599	601	607	613	617	619
631	641	643	647	653	659
661	673	677	683	691	701
709	719	727	733	739	743
751	757	761	769	773	787
797	809	811	821	823	827
829	839	853	857	859	863
877	881	883	887	907	911
919	929	937	941	947	953
967	971	977	983	991	997

Разложение на простые множители

Любое число, которое является составным, можно показать в виде произведения отдельных множителей.

150 = 2 × 3 × 5 × 5

225 = 3 × 3 × 5 × 5

1470 = 2 × 3 × 5 × 7 × 7

Небольшие числа можно легко разложить, используя таблицу умножения. Для больших же чисел, следует воспользоваться таблицей простых чисел.

В качестве примера разложим число 1463 на простые множители с помощью таблицы простых чисел:

2	23	61	103	151
3	29	67	107	157
4	31	71	109	163
5	37	73	113	167
7	41	79	127	173
11	43	83	131	179
13	47	89	137	181
17	53	97	139	191
19	59	101	149	193

Просматриваем простые числа данной таблицы и выбираем то число, которым можно разделить исходное число, например

7.

Число 1463 делим на 7, в результате получаем 209.

Далее повторяем процесс поиска простых чисел для 209 по признакам делимости, и выбираем число 11, которое представляет собой его делитель.

Делим число 209 на 11 и в результате получаем число 19, в свою очередь, являющееся простым числом, в соответствии таблицей простых чисел.

Таким образом, делителями для числа 1463 будут числа 7, 11 и 19.

1463 = 7 × 11 × 19

Описанную последовательность можно записать следующим образом:

Делимое	Делитель
1463	7
209	11
19	19

Разложение числа.

Разложение чисел на простые множители, способы и примеры разложения

Разложить на множители большое число – нелегкая задача. Большинство людей затрудняются раскладывать четырех- или пятизначные числа. Для упрощения процесса запишите число над двумя колонками.

Разложим на множители число 6552.

Разделите данное число на наименьший простой делитель (кроме 1), на который данное число делится без остатка. Запишите этот делитель в левой колонке, а в правой колонке запишите результат деления. Как отмечалось выше, четные числа легко раскладывать на множители, так как их наименьшим простым множителем всегда будет число 2 (у нечетных чисел наименьшие простые множители различны).

В нашем примере число 6552 – четное, поэтому 2 является его наименьшим простым множителем. 6552 ÷ 2 = 3276. В левой колонке запишите 2, а в правой — 3276.

Далее разделите число в правой колонке на наименьший простой делитель (кроме 1), на который данное число делится без остатка. Запишите этот делитель в левой колонке, а в правой колонке запишите результат деления (продолжите этот процесс до тех пор, пока в правой колонке не останется 1).

В нашем примере: 3276 ÷ 2 = 1638. В левой колонке запишите 2, а в правой — 1638. Далее: 1638 ÷ 2 = 819. В левой колонке запишите 2, а в правой — 819.

Вы получили нечетное число; для таких чисел найти наименьший простой делитель сложнее. Если вы получили нечетное число, попробуйте разделить его на наименьшие простые нечетные числа: 3, 5, 7, 11.

В нашем примере вы получили нечетное число 819. Разделите его на 3: 819 ÷ 3 = 273. В левой колонке запишите 3, а в правой — 273.
При подборе делителей опробуйте все простые числа вплоть до квадратного корня из наибольшего делителя, который вы нашли. Если ни один делитель не делит число нацело, то вы, скорее всего, получили простое число и можете прекратить вычисления.

Продолжите процесс деления чисел на простые делители до тех пор, пока в правой колонке не останется 1 (если в правой колонке вы получили простое число, разделите его само на себя, чтобы получить 1).

Продолжим вычисления в нашем примере:
- Разделите на 3: 273 ÷ 3 = 91. Остатка нет. В левой колонке запишите 3, а в правой — 91.
- Разделите на 3. 91 делится на 3 с остатком, поэтому разделите на 5. 91 делится на 5 с остатком, поэтому разделите на 7: 91 ÷ 7 = 13. Остатка нет. В левой колонке запишите 7, а в правой — 13.
- Разделите на 7. 13 делится на 7 с остатком, поэтому разделите на 11. 13 делится на 11 с остатком, поэтому разделите на 13: 13 ÷ 13 = 1. Остатка нет. В левой колонке запишите 13, а в правой — 1. Ваши вычисления закончены.

В левой колонке представлены простые множители исходного числа. Другими словами, при перемножении всех чисел из левой колонки вы получите число, записанное над колонками. Если один множитель появляется в списке множителей несколько раз, используйте показатели степени для его обозначения. В нашем примере в списке множителей 2 появляется 4 раза; запишите эти множители как 2 4 , а не как 2*2*2*2.

В нашем примере 6552 = 2 3 × 3 2 × 7 × 13. Вы разложили число 6552 на простые множители (порядок множителей в этой записи не имеет значения).

Что значит разложить на простые множители? Как это сделать? Что можно узнать по разложению числа на простые множители? Ответы на эти вопросы иллюстрируются конкретными примерами.

Определения:

Простым называют число, которое имеет ровно два различных делителя.

Составным называют число, которое имеет более двух делителей.

Разложить натуральное число на множители — значит представить его в виде произведения натуральных чисел.

Разложить натуральное число на простые множители — значит представить его в виде произведения простых чисел.

Замечания:

В разложении простого числа один из множителей равен единице, а другой — самому этому числу.
Говорить о разложении единицы на множители не имеет смысла.
Составное число можно разложить на множители, каждый из которых отличен от 1.

	Разложим число 150 на множители. Например, 150 — это 15 умножить на 10. 15 — это составное число. Его можно разложить на простые множители 5 и 3. 10 — это составное число. Его можно разложить на простые множители 5 и 2. Записав вместо 15 и 10 их разложения на простые множители, мы получили разложение числа 150.
	Число 150 можно по-другому разложить на множители. Например, 150 — это произведение чисел 5 и 30. 5 — число простое. 30 — это число составное. Его можно представить как произведение 10 и 3. 10 — число составное. Его можно разложить на простые множители 5 и 2. Мы получили разложение числа 150 на простые множители другим способом.
	Заметим, что первое и второе разложение одинаковы. Они отличаются только порядком следования множителей. Принято записывать множители в порядке возрастания.
Всякое составное число можно разложить на простые множители единственным образом с точностью до порядка множителей.

При разложении больших чисел на простые множители используют запись в столбик:

Наименьшее простое число, на которое делится 216 — это 2.

Разделим 216 на 2. Получим 108.

Полученное число 108 делится на 2.

Выполним деление. Получим в результате 54.

Согласно признаку делимости на 2 число 54 делится на 2.

Выполнив деление, получим 27.

Число 27 заканчивается на нечетную цифру 7 . Оно

Не делится на 2. Следующее простое число — это 3.

Разделим 27 на 3. Получим 9. Наименьшее простое

Число, на которое делится 9, — это 3. Три — само является простым числом, оно делится на себя и на единицу. Разделим 3 на себя. В итоге мы получили 1.

Число делится лишь на те простые числа, которые входят в состав его разложения.
Число делится лишь на те составные числа, разложение которых на простые множители полностью в нем содержится.

Рассмотрим примеры:

4900 делится на простые числа 2, 5 и 7. (они входят в разложение числа 4900), но не делится, например, на 13.

11 550 75. Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550.

В результате деления будет произведение множителей 2, 7 и 11.

11550 не делится на 4 потому, что в разложении четырех есть лишняя двойка.

Найти частное от деления числа a на число b, если эти числа раскладываются на простые множители следующим образом a=2∙2∙2∙3∙3∙3∙5∙5∙19; b=2∙2∙3∙3∙5∙19

Разложение числа b полностью содержится в разложении числа a.

Результат деления a на b — это произведение оставшихся в разложении числа a трех чисел.

Итак, ответ: 30.

Список литературы

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — М.: ЗШ МИФИ, 2011.
Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.

Интернет-портал Matematika-na.ru ().
Интернет-портал Math-portal. ru ().

Домашнее задание

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. № 127, № 129, № 141.
Другие задания: № 133, № 144.

Любое составное число можно разложить на простые множители. Способов разложения может быть несколько. При любом способе получается один и тот же результат.

Как разложить число на простые множители наиболее удобным способом? Рассмотрим, как это лучше сделать, на конкретных примерах.

Примеры. 1) Разложить число 1400 на простые множители.

1400 делится на 2. 2 — простое число, раскладывать его на множители не нужно. Получаем 700. Делим его на 2. Получаем 350. 350 тоже делим на 2. Полученное число 175 можно разделить на 5. Результат — з5 — еще раз делим на 5. Итого — 7. Его можно разделить только на 7. Получили 1, деление окончено.

Это же число можно разложить на простые множители иначе:

1400 удобно разделить на 10. 10 не является простым числом, поэтому его нужно разложить на простые множители: 10=2∙5. Результат — 140. Его снова делим на 10=2∙5. Получаем 14. Если 14 разделить на 14, то его тоже следует разложить на произведение простых множителей: 14=2∙7.

Таким образом, снова пришли к такому же, как и в первом случае, разложению, но быстрее.

Вывод: не обязательно при разложении числа делить его только на простые делители. Делим на то, что удобнее, например, на 10. Надо только составные делители не забыть разложить на простые множители.

2) Разложить число 1620 на простые множители.

Число 1620 удобнее всего разделить на 10. Поскольку 10 простым числом не является, представляем его в виде произведения простых множителей: 10=2∙5. Получили 162. Его удобно разделить на 2. Результат — 81. Число 81 можно разделить на 3, но на 9 — удобнее. Так как 9 — не простое число, раскладываем его как 9=3∙3. Получили 9. Его также делим на 9 и раскладываем на произведение простых множителей.

Каждое натуральное число, кроме единицы, имеет два или более делителей. Например, число 7, делится без остатка только на 1 и на 7, то есть имеет два делителя. А у числа 8, делители 1, 2, 4, 8, то есть аж 4 делителя сразу.

Чем отличаются простые и составные числа

Числа, которые имеют более двух делителей, называются составными. Числа, которые имеют только два делителя: единица и само это число, называются простыми числами.

Число 1 имеет только один делить, а именно само это число. Единица не относится ни к простым, ни к составным числам.

Например, число 7 простое, а число 8 составное.

Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Число 2 единственное четное простое число, все остальные простые числа нечетные.

Число 78 составное, так как помимо 1 и самого себя, оно делится еще и на 2. При делении на 2 получим 39. То есть 78= 2*39. В таких случаях говорят, что число разложили на множители 2 и 39.

Любое составное число можно разложить на два множителя, каждый из которых больше 1. С простым числом такой фокус не прокатит. Такие дела.

Разложение числа на простые множители

Как уже отмечалось выше, любое составное число, можно разложить на два множителя. Возьмем, к примеру, число 210. Это число можно разложить на два множителя 21 и 10. Но числа 21 и 10 тоже составные, разложим и их на два множителя. Получим 10 = 2*5, 21=3*7. И в итоге число 210 разложилось уже на 4 множителя: 2,3,5,7. Эти числа уже простые и их разложить нельзя. То есть мы разложили число 210 на простые множители.

При разложении составных чисел на простые множители, их обычно, записывают в порядке возрастания.

Следует запомнить, что любое составное число можно разложить на простые множители и причем единственным образом, с точностью до перестановки.

Обычно, при разложении числа на простые множители пользуются признаками делимости.

Разложим число 378 на простые множители

Будем записывать числа, разделяя их вертикальной чертой. Число 378 делится на 2, так как оканчивается на 8. При делении получим число 189. Сумма цифр числа 189 делится на 3, значит и само число 189 делится на 3. В результате получим 63.

Число 63 тоже делится на 3, по признаку делимости. Получаем 21, число 21 снова можно разделить на 3, получим 7. Семерка делится только на себя, получаем единицу. На этом закончено деление. Справа после черты получились простые множители, на которые раскладывается число 378.

378|2
189|3
63|3
21|3

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Простые и составные числа. Как разложить число на простые множители + калькулятор ⏳

Простое число — это натуральное число, которое делится только на 1 и на само себя, то есть имеет всего два делителя. Числа, имеющие более двух делителей, называются составными.

Пример. Найдите среди перечисленных чисел простые: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13?

Чтобы узнать, простое число или составное, нужно найти делители числа. Если получится только 2 делителя — 1 и само число, то число простое. Если более двух делителей — составное.

Д(1) = {1}
Д(2) = {1,2}
Д(3) = {1,3}
Д(4) = {1,2,4}
Д(5) = {1,5}
Д(6) = {1,2,3,6}
Д(7) = {1,7}
Д(8) = {1,2,4,8}
Д(9) = {1,3,9}
Д(10) = {1,2,5,10}
Д(11) = {1,11}
Д(12) = {1,2,3,6,12}
Д(13) = {1,13}

У чисел 2,3,5,7,11,13 по 2 делителя, значит это простые числа.

Что же делать с единицей, у которой только 1 делитель? Единица не входит ни в простые числа, ни в составные.

Натуральное число 1 не является ни простым, ни составным.

Как разложить составное число на простые множители

Любое составное число можно представить в виде произведения простых чисел.

Например, 50 = 5 * 10 = 5 * 2 * 5 = 2 * 5² 300 = 3 * 100 = 3 * 10 * 10 = 3 * 2 * 5 * 2 * 5 = 2² * 3 * 5² 36 = 6 * 6 = 2 * 3 * 2 * 3 = 2² * 3²

Но не всегда легко разложить на простые множители устно, как в предыдущих примерах. Тогда прибегают к разложению столбиком.

Чтобы разложить число на простые множители, нужно разделить его на наименьшее простое число, которое возможно, а полученный остаток снова разделить на наименьшее простое число, которое возможно, и так далее, пока остаток не станет равен 1.

Для этого воспользуемся признаками делимости на 2,3, 5.

Пример. Разложите на простые множители число 24.

24 — четное число, значит делится на 2. Записываем:

24 | 2

24 : 2 = 12, записываем число 12 под 24:

24 | 2
12 |

Работаем с числом 12. Оно четное, значит делится на 2, 12:2 = 6. Записываем:

24 | 2
12 | 2
6 |

Число 6 четное, делится на 2, 6 : 2 = 3, записываем:

24 | 2
12 | 2
6 | 2
3 |

Число 3 — простое, значит оно и есть простой множитель, 3 : 3 = 1:

24 | 2
12 | 2
6 | 2
3 | 3
1 |

Выписываем простые множители из правого столбца. Получаем разложение:

24 = 2 * 2 * 2 * 3 = 2³ * 3

Давайте потренируемся и разложим на простые множители число 129.

129 — нечетное, поэтому не делится на 2. Сумма его цифр = 12, 12 делится на 3, значит 129 делится на 3. 129 : 3 = 43

129 | 3
43 |

43 — нечетное, значит не делится на 2, не делится на 3, не делится на 5, 7,11. Может быть оно — простое число? Узнать это поможет таблица вверху страницы или наш калькулятор простых чисел. Вводим 43, получаем ответ, что 43 — простое число, значит это и есть наш второй простой множитель.

129 | 3
43 | 43
1 |

129 = 3 * 43

Разложите на простые множители число 2268.

2268 | 2
1134 | 2
567 | 3
189 | 3
63 | 3
21 | 3
7 | 7
1 |

2268 = 2·2·3·3·3·3·7 = 2² * 3⁴ * 7

Чтобы узнать простое число или составное, можно воспользоваться калькулятором.

Калькулятор простых чисел

Введите число до 99 991 и нажмите кнопку проверки.

Разложение на простые множители онлайн

А если совсем запутались и не можете разложить число или хотите себя проверить, воспользуйтесь нашим калькулятором.

Если что-либо осталось для вас непонятным, задавайте вопросы в комментариях.

Разложение чисел на простые множители, способы и примеры разложения. Разложение числа на множители

Что значит разложить на множители? Это значит найти числа, произведение которых равно исходному числу.

Чтобы понять, что значит разложить на множители, рассмотрим пример.

Пример разложения числа на множители

Разложить на множители число 8.

Число 8 можно представить в виде произведения 2 на 4:

Представление 8 в виде произведения 2 * 4 и значит разложение на множители.

Обратите внимание, что это не единственное разложение 8 на множители.

Ведь 4 разлагается на множители так:

Отсюда 8 можно представить:

8 = 2 * 2 * 2 = 2 3

Проверяем наш ответ. Найдем, чему равно разложение на множители:

То есть получили исходное число, ответ верный.

Разложите на простые множители число 24

Как разложить на простые множители число 24?

Простым называют число, если оно нацело делится только на единицу и на себя.

Число 8 можно представить в виде произведения 3 на 8:

Здесь число 24 разложено на множители. Но в задании сказано «разложить на простые множители число 24», т.е. нужны именно простые множители. А в нашем разложении 3 является простым множителем, а 8 не является простым множителем.

Что такое разложение на множители? Это способ превращения неудобного и сложного примера в простой и симпатичный.) Оч-ч-чень мощный приём! Встречается на каждом шагу и в элементарной математике, и в высшей.

Подобные превращения на математическом языке называются тождественными преобразованиями выражений. Кто не в теме — прогуляйтесь по ссылке. Там совсем немного, просто и полезно.) Смысл любого тождественного преобразования — это запись выражения в другом виде с сохранением его сути.

Смысл разложения на множители предельно прост и понятен. Прямо из самого названия. Можно забыть (или не знать), что такое множитель, но то, что это слово происходит от слова «умножить» сообразить-то можно?) Разложить на множители означает: представить выражение в виде умножения чего-то на чего-то. Да простят мне математика и русский язык…) И всё.

Например, надо разложить число 12. Можно смело записать:

Вот мы и представили число 12 в виде умножения 3 на 4. Прошу заметить, что циферки справа (3 и 4) совсем другие, чем слева (1 и 2). Но мы прекрасно понимаем, что 12 и 3·4 одно и то же. Суть числа 12 от преобразования не изменилась.

А можно разложить 12 по-другому? Легко!

12=3·4=2·6=3·2·2=0,5·24=……..

Вариантов разложения — бесконечное количество.

Разложение чисел на множители — штука полезная. Очень помогает, например, при действиях с корнями. Но разложение на множители алгебраических выражений вещь не то, что полезная, она — необходимая! Чисто для примера:

Упростить:

Кто не умеете раскладывать выражение на множители, отдыхает в сторонке. Кто умеет — упрощает и получает:

Эффект потрясающий, правда?) Кстати, решение достаточно простое. Ниже сами увидите. Или, например, такое задание:

Решить уравнение:

х 5 — x 4 = 0

Решается в уме, между прочим. С помощью разложения на множители. Ниже мы решим этот пример. Ответ: x 1 = 0; x 2 = 1 .

Или, то же самое, но для старшеньких):

Решить уравнение:

На этих примерах я показал основное назначение разложения на множители: упрощение дробных выражений и решение некоторых типов уравнений. Рекомендую запомнить практическое правило:

Если перед нами страшное дробное выражение, можно попробовать разложить на множители числитель и знаменатель. Очень часто дробь сокращается и упрощается.

Если перед нами уравнение, где справа — ноль, а слева — не пойми что, можно попробовать разложить левую часть на множители. Иногда помогает).

Основные способы разложения на множители.

Вот они, самые популярные способы:

4. Разложение квадратного трёхчлена.

Эти способы надо запомнить. Именно в таком порядке. Сложные примеры проверяются на все возможные способы разложения. И лучше уж проверять по порядочку, чтобы не запутаться. .. Вот по порядочку и начнём.)

1. Вынесение общего множителя за скобки.

Простой и надёжный способ. От него плохо не бывает! Бывает либо хорошо, либо никак.) Поэтому он и стоит первым. Разбираемся.

Все знают (я верю!)) правило:

a(b+c) = ab+ac

Или, в более общем виде:

a(b+c+d+…..) = ab+ac+ad+….

Все равенства работают как слева направо, так и наоборот, справа налево. Можно записать:

ab+ac = a(b+c)

ab+ac+ad+…. = a(b+c+d+…..)

Вот и вся суть вынесения общего множителя за скобки.

В левой части а — общий множитель для всех слагаемых. Умножается на всё, что есть). Справа это самое а находится уже за скобками.

Практическое применение способа рассмотрим на примерах. Сначала вариант простой, даже примитивный.) Но на этом варианте я отмечу (зелёным цветом) очень важные моменты для любого разложения на множители.

Разложить на множители:

ах+9х

Какой общий множитель сидит в обоих слагаемых? Икс, разумеется! Его и будем выносить за скобки. Делаем так. Сразу пишем икс за скобками:

ах+9х=х(

А в скобках пишем результат деления каждого слагаемого на этот самый икс. По порядочку:

Вот и всё. Конечно, так подробно расписывать не нужно, Это в уме делается. Но понимать, что к чему, желательно). Фиксируем в памяти:

Пишем общий множитель за скобками. В скобках записываем результаты деления всех слагаемых на этот самый общий множитель. По порядочку.

Вот мы и разложили выражение ах+9х на множители. Превратили его в умножение икса на (а+9). Замечу, что в исходном выражении тоже было умножение, даже два: а·х и 9·х. Но оно не было разложено на множители! Потому, что кроме умножения, в этом выражении было ещё и сложение, знак «+»! А в выражении х(а+9) кроме умножения ничего нет!

Как так!? — слышу возмущённый глас народа — А в скобках!?)

Да, внутри скобок есть сложение. Но фишка в том, что пока скобки не раскрыты, мы рассматриваем их как одну букву. И все действия со скобками делаем целиком, как с одной буквой. В этом смысле в выражении х(а+9) кроме умножения ничего нет. В этом вся суть разложения на множители.

Кстати, можно ли как-то проверить, всё ли правильно мы сделали? Запросто! Достаточно обратно умножить то, что вынесли (икс) на скобки и посмотреть — получилось ли исходное выражение? Если получилось, всё тип-топ!)

х(а+9)=ах+9х

Получилось.)

В этом примитивном примере проблем нет. Но если слагаемых несколько, да ещё с разными знаками… Короче, каждый третий ученик косячит). Посему:

При необходимости проверяем разложение на множители обратным умножением.

Разложить на множители:

3ах+9х

Ищем общий множитель. Ну, с иксом всё ясно, его можно вынести. А есть ли ещё общий множитель? Да! Это тройка. Можно же записать выражение вот так:

3ах+3·3х

Здесь сразу видно, что общий множителем будет 3х . Вот его и выносим:

3ах+3·3х=3х(а+3)

Разложили.

А что будет, если вынести только х? Да ничего особенного:

3ах+9х=х(3а+9)

Это тоже будет разложение на множители. Но в этом увлекательном процессе принято раскладывать всё до упора, пока есть возможность. Здесь в скобках есть возможность вынести тройку. Получится:

3ах+9х=х(3а+9)=3х(а+3)

То же самое, только с одним лишним действием.) Запоминаем:

При вынесении общего множителя за скобки, стараемся вынести максимальный общий множитель.

Продолжаем развлечение?)

Разложить на множители выражение:

3ах+9х-8а-24

Что будем выносить? Тройку, икс? Не-е-е… Нельзя. Напоминаю, выносить можно только общий множитель, который есть во всех слагаемых выражения. На то он и общий. Здесь такого множителя нету… Что, можно не раскладывать!? Ну да, обрадовались, как же… Знакомьтесь:

2.

Группировка.

Собственно, группировку трудно назвать самостоятельным способом разложения на множители. Это, скорее, способ выкрутиться в сложном примере.) Надо сгруппировать слагаемые так, чтобы всё получилось. Это только на примере показать можно. Итак, перед нами выражение:

3ах+9х-8а-24

Видно, что какие-то общие буквы и числа имеются. Но… Общего множителя, чтобы был во всех слагаемых — нет. Не падаем духом и разбиваем выражение на кусочки. Группируем. Так, чтобы в каждом кусочке был общий множитель, было чего вынести. Как разбиваем? Да просто ставим скобки.

Напомню, что скобки можно ставить где угодно и как угодно. Лишь бы суть примера не менялась. Например, можно так:

3ах+9х-8а-24 =(3ах+9х)-(8а+24 )

Прошу обратить внимание на вторые скобки! Перед ними стоит знак минус, а 8а и 24 стали положительными! Если, для проверки, обратно раскрыть скобки, знаки поменяются, и мы получим исходное выражение. Т.е. суть выражения от скобок не изменилась.

Но если вы просто воткнули скобки, не учитывая смену знака, например, вот так:

3ах+9х-8а-24 =(3ах+9х)-(8а-24 )

это будет ошибкой. Справа — уже другое выражение. Раскройте скобки и всё станет видно. Дальше можно не решать, да…)

Но возвращаемся к разложению на множители. Смотрим на первые скобки (3ах+9х) и соображаем, можно ли чего вынести? Ну, этот пример мы выше решали, можно вынести 3х:

(3ах+9х)=3х(а+3)

Изучаем вторые скобки, там можно вынести восьмёрку:

(8а+24)=8(а+3)

Всё наше выражение получится:

(3ах+9х)-(8а+24)=3х(а+3)-8(а+3)

Разложили на множители? Нет. В результате разложения должно получиться только умножение, а у нас знак минус всё портит. Но… В обоих слагаемых есть общий множитель! Это (а+3) . Я не зря говорил, что скобки целиком — это, как бы, одна буква. Значит, эти скобки можно вынести за скобки.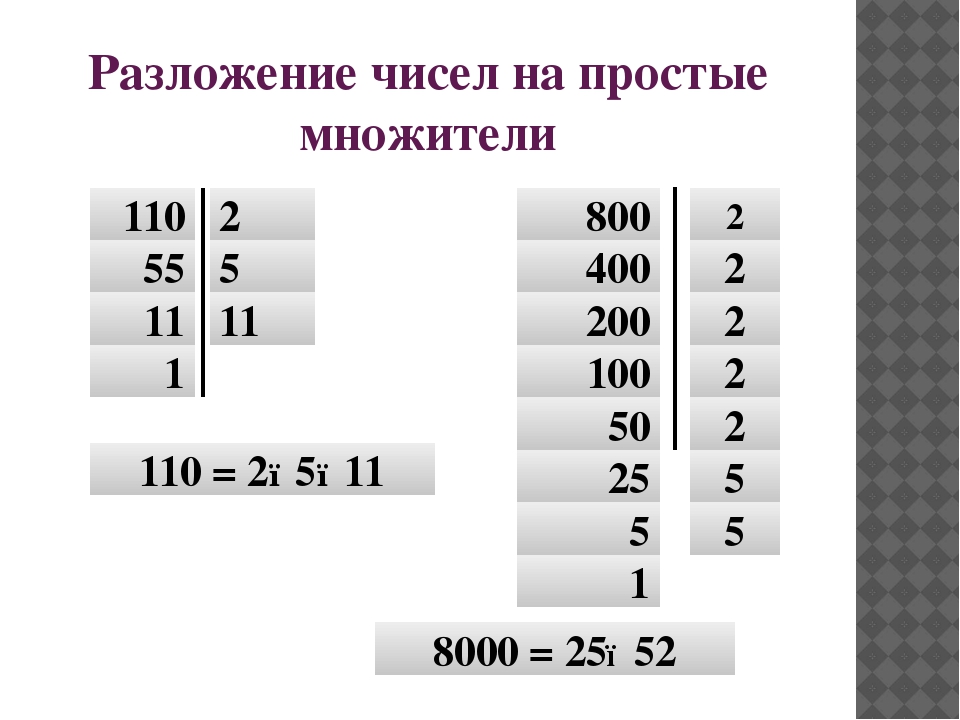 Да, именно так и звучит.)

Делаем, как было рассказано выше. Пишем общий множитель (а+3) , во вторых скобках записываем результаты деления слагаемых на (а+3) :

3х(а+3)-8(а+3)=(а+3)(3х-8)

Всё! Справа кроме умножения ничего нет! Значит, разложение на множители завершено успешно!) Вот оно:

3ах+9х-8а-24=(а+3)(3х-8)

Повторим кратенько суть группировки.

Если в выражении нет общего множителя для всех слагаемых, разбиваем выражение скобками так, чтобы внутри скобок общий множитель был. Выносим его и смотрим, что получилось. Если повезло, и в скобках остались совершенно одинаковые выражения, выносим эти скобки за скобки.

Добавлю, что группировка — процесс творческий). Не всегда с первого раза получается. Ничего страшного. Иногда приходится менять слагаемые местами, рассматривать разные варианты группировки, пока не найдётся удачный. Главное здесь — не падать духом!)

Примеры.

Сейчас, обогатившись знаниями, можно и хитрые примеры порешать. ) Была в начале урока тройка таких…

Упростить:

В сущности, этот пример мы уже решили. Незаметно для себя.) Напоминаю: если нам дана страшная дробь, пробуем разложить числитель и знаменатель на множители. Других вариантов упрощения просто нет.

Ну, знаменатель здесь не раскладывается, а числитель… Числитель мы уже разложили по ходу урока! Вот так:

3ах+9х-8а-24=(а+3)(3х-8)

Пишем результат разложения в числитель дроби:

По правилу сокращения дробей (основное свойство дроби), мы можем разделить (одновременно!) числитель и знаменатель на одно и то же число, или выражение. Дробь от этого не меняется. Вот и делим числитель и знаменатель на выражение (3х-8) . И там и там получим единички. Окончательный результат упрощения:

Особо подчеркну: сокращение дроби возможно тогда и только тогда, когда в числителе и знаменателе кроме умножения выражений ничего нет. Именно потому превращение суммы (разности) в умножение так важно для упрощения. Конечно, если выражения разные, то и не сократится ничего. Бывет. Но разложение на множители даёт шанс. Этого шанса без разложения — просто нет.

Пример с уравнением:

Решить уравнение:

х 5 — x 4 = 0

Выносим общий множитель х 4 за скобки. Получаем:

х 4 (x-1)=0

Соображаем, что произведение множителей равно нулю тогда и только тогда, когда какой-нибудь из них равен нулю. Если сомневаетесь, найдите мне парочку ненулевых чисел, которые при умножении ноль дадут.) Вот и пишем, сначала первый множитель:

При таком равенстве второй множитель нас не волнует. Любой может быть, всё равно в итоге ноль получится. А какое число в четвёртой степени ноль даст? Только ноль! И никакое другое… Стало быть:

С первым множителем разобрались, один корень нашли. Разбираемся со вторым множителем. Теперь нас не волнует уже первый множитель.):

Вот и нашли решение: x 1 = 0; x 2 = 1 . Любой из этих корней подходит к нашему уравнению.

Очень важное замечание. Обратите внимание, мы решали уравнение по кусочкам! Каждый множитель приравнивали к нулю, не обращая внимания на остальные множители. Кстати, если в подобном уравнении будет не два множителя, как у нас, а три, пять, сколько угодно — решать будем точно так же. По кусочкам. Например:

(х-1)(х+5)(х-3)(х+2)=0

Тот, кто раскроет скобки, перемножит всё, тот навсегда зависнет на этом уравнении.) Правильный ученик сразу увидит, что слева кроме умножения ничего нет, справа — ноль. И начнёт (в уме!) приравнивать к нулю все скобочки по порядочку. И получит (за 10 секунд!) верное решение: x 1 = 1; x 2 = -5; x 3 = 3; x 4 = -2.

Здорово, правда?) Такое элегантное решение возможно, если левая часть уравнения разложена на множители. Намёк понятен?)

Ну и, последний пример, для старшеньких):

Решить уравнение:

Чем-то он похож на предыдущий, не находите?) Конечно. Самое время вспомнить, что в алгебре седьмого класса под буквами могут скрываться и синусы, и логарифмы, и всё, что угодно! Разложение на множители работает во всей математике.

Выносим общий множитель lg 4 x за скобки. Получаем:

lg 4 x=0

Это один корень. Разбираемся со вторым множителем.

Вот и окончательный ответ: x 1 = 1; x 2 = 10 .

Надеюсь, вы осознали всю мощь разложения на множители в упрощении дробей и решении уравнений.)

В этом уроке мы познакомились с вынесением общего множителя и группировкой. Остаётся разобраться с формулами сокращённого умножения и квадратным трёхчленом.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Примеры. 1) Разложить число 1400 на простые множители.

Это же число можно разложить на простые множители иначе:

Таким образом, снова пришли к такому же, как и в первом случае, разложению, но быстрее.

2) Разложить число 1620 на простые множители.

Чем отличаются простые и составные числа

Например, число 7 простое, а число 8 составное.

Разложение числа на простые множители

При разложении составных чисел на простые множители, их обычно, записывают в порядке возрастания.

Обычно, при разложении числа на простые множители пользуются признаками делимости.

Разложим число 378 на простые множители

378|2
189|3
63|3
21|3

Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.

Yandex.RTB R-A-339285-1

Что значит разложить число на простые множители?

Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2 · 7 · 7 · 23 имеем, что у нас 4 простых множителя в виде 2 , 7 , 7 , 23 .

Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30 , тогда получим 2 , 3 , 5 . Запись примет вид 30 = 2 · 3 · 5 . Не исключено, что множители могут повторяться. Такое число как 144 имеет 144 = 2 · 2 · 2 · 2 · 3 · 3 .

Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.

При z , относящемуся к целым числам, представляется в виде произведения а и b , где z делится на а и на b . Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1 , то его разложение на множители p 1 , p 2 , … , p n принимает вид a = p 1 , p 2 , … , p n . Разложение предполагается в единственном варианте.

Каноническое разложение числа на простые множители

При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p 1 , который встречается s 1 раз и так далее p n – s n раз. Таким образом разложение примет вид a=p 1 s 1 · a = p 1 s 1 · p 2 s 2 · … · p n s n . Эта запись имеет название канонического разложения числа на простые множители.

При разложении числа 609840 получим, что 609 840 = 2 · 2 · 2 · 2 · 3 · 3 · 5 · 7 · 11 · 11 ,его канонический вид будет 609 840 = 2 4 · 3 2 · 5 · 7 · 11 2 . При помощи канонического разложения можно найти все делители числа и их количество.

Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p 1 , p 2 , … , p n чисел a , a 1 , a 2 , … , a n — 1 , это дает возможность получить a = p 1 · a 1 , где a 1 = a: p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , где a 2 = a 1: p 2 , … , a = p 1 · p 2 · … · p n · a n , где a n = a n — 1: p n . При получении a n = 1 , то равенство a = p 1 · p 2 · … · p n получим искомое разложение числа а на простые множители. Заметим, что p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n .

Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z . При взятии простых чисел 2 , 3 , 5 , 11 и так далее, причем на них делим число z . Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z . Видно, что не существуют делителей z , тогда понятно, что z является простым числом.

Пример 1

Рассмотрим на примере числа 87 . При его делении на 2 имеем, что 87: 2 = 43 с остатком равным 1 . Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87: 3 = 29 . Отсюда вывод – 3 является наименьшим простым делителем числа 87 .

При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a . При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000 .

Рассмотрим алгоритм разложения на простые множители:

нахождение наименьшего множителя при делителе p 1 числа a по формуле a 1 = a: p 1 , когда a 1 = 1 , тогда а является простым числом и включено в разложение на множители, когда не равняется 1 , тогда a = p 1 · a 1 и следуем к пункту, находящемуся ниже;
нахождение простого делителя p 2 числа a 1 при помощи последовательного перебора простых чисел, используя a 2 = a 1: p 2 , когда a 2 = 1 , тогда разложение примет вид a = p 1 · p 2 , когда a 2 = 1 , тогда a = p 1 · p 2 · a 2 , причем производим переход к следующему шагу;
перебор простых чисел и нахождение простого делителя p 3 числа a 2 по формуле a 3 = a 2: p 3 , когда a 3 = 1 , тогда получим, что a = p 1 · p 2 · p 3 , когда не равняется 1 , тогда a = p 1 · p 2 · p 3 · a 3 и производим переход к следующему шагу;
производится нахождение простого делителя p n числа a n — 1 при помощи перебора простых чисел с p n — 1 , а также a n = a n — 1: p n , где a n = 1 , шаг является завершающим, в итоге получаем, что a = p 1 · p 2 · … · p n .

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.

Полученный алгоритм можно применять при помощи разложения чисел на простые множители.

Во время разложения на простые множители следует придерживаться основного алгоритма.

Пример 2

Произвести разложение числа 78 на простые множители.

Решение

Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78 . То есть 78: 2 = 39 . Деление без остатка, значит это первый простой делитель, который обозначим как p 1 . Получаем, что a 1 = a: p 1 = 78: 2 = 39 . Пришли к равенству вида a = p 1 · a 1 , где 78 = 2 · 39 . Тогда a 1 = 39 , то есть следует перейти к следующему шагу.

Остановимся на нахождении простого делителя p 2 числа a 1 = 39 . Следует перебрать простые числа, то есть 39: 2 = 19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39: 3 = 13 . Значит, что p 2 = 3 является наименьшим простым делителем 39 по a 2 = a 1: p 2 = 39: 3 = 13 . Получим равенство вида a = p 1 · p 2 · a 2 в виде 78 = 2 · 3 · 13 . Имеем, что a 2 = 13 не равно 1 , тогда следует переходит дальше.

Наименьший простой делитель числа a 2 = 13 ищется при помощи перебора чисел, начиная с 3 . Получим, что 13: 3 = 4 (ост. 1). Отсюда видно, что 13 не делится на 5 , 7 , 11 , потому как 13: 5 = 2 (ост. 3), 13: 7 = 1 (ост. 6) и 13: 11 = 1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a 3 = a 2: p 3 = 13: 13 = 1 . Получили, что a 3 = 1 , что означает завершение алгоритма. Теперь множители записываются в виде 78 = 2 · 3 · 13 (a = p 1 · p 2 · p 3) .

Ответ: 78 = 2 · 3 · 13 .

Пример 3

Разложить число 83 006 на простые множители.

Решение

Первый шаг предусматривает разложение на простые множители p 1 = 2 и a 1 = a: p 1 = 83 006: 2 = 41 503 , где 83 006 = 2 · 41 503 .

Второй шаг предполагает, что 2 , 3 и 5 не простые делители для числа a 1 = 41 503 , а 7 простой делитель, потому как 41 503: 7 = 5 929 . Получаем, что p 2 = 7 , a 2 = a 1: p 2 = 41 503: 7 = 5 929 . Очевидно, что 83 006 = 2 · 7 · 5 929 .

Нахождение наименьшего простого делителя p 4 к числу a 3 = 847 равняется 7 . Видно, что a 4 = a 3: p 4 = 847: 7 = 121 , поэтому 83 006 = 2 · 7 · 7 · 7 · 121 .

Для нахождения простого делителя числа a 4 = 121 используем число 11 , то есть p 5 = 11 . Тогда получим выражение вида a 5 = a 4: p 5 = 121: 11 = 11 , и 83 006 = 2 · 7 · 7 · 7 · 11 · 11 .

Для числа a 5 = 11 число p 6 = 11 является наименьшим простым делителем. Отсюда a 6 = a 5: p 6 = 11: 11 = 1 . Тогда a 6 = 1 . Это указывает на завершение алгоритма. Множители запишутся в виде 83 006 = 2 · 7 · 7 · 7 · 11 · 11 .

Каноническая запись ответа примет вид 83 006 = 2 · 7 3 · 11 2 .

Ответ: 83 006 = 2 · 7 · 7 · 7 · 11 · 11 = 2 · 7 3 · 11 2 .

Пример 4

Произвести разложение числа 897 924 289 на множители.

Решение

Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2 . Конец перебора приходится на число 937 . Тогда p 1 = 937 , a 1 = a: p 1 = 897 924 289: 937 = 958 297 и 897 924 289 = 937 · 958 297 .

Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа 937 . Число 967 можно считать простым, потому как оно является простым делителем числа a 1 = 958 297 . Отсюда получаем, что p 2 = 967 , то a 2 = a 1: p 1 = 958 297: 967 = 991 и 897 924 289 = 937 · 967 · 991 .

Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991 . Примерное значение подкоренного выражения имеет вид 991 991 . Отсюда видно, что p 3 = 991 и a 3 = a 2: p 3 = 991: 991 = 1 . Получим, что разложение числа 897 924 289 на простые множители получается как 897 924 289 = 937 · 967 · 991 .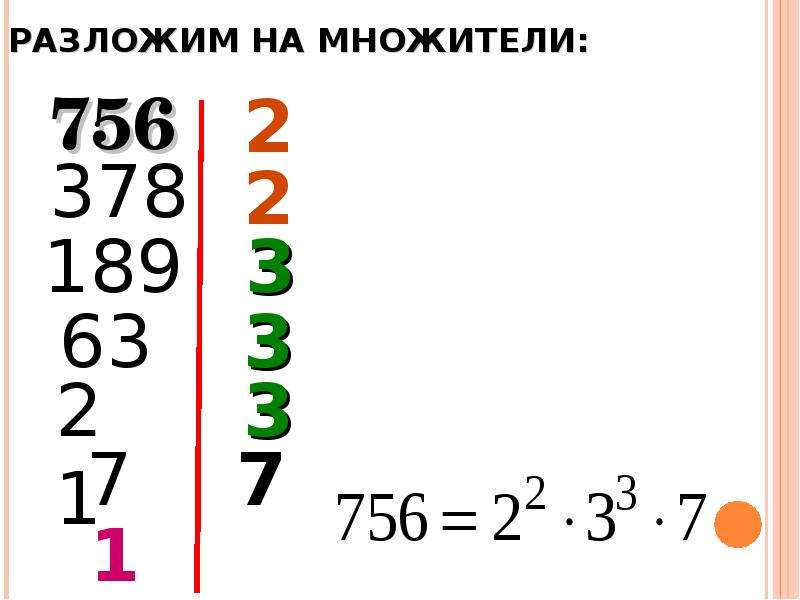

Ответ: 897 924 289 = 937 · 967 · 991 .

Использование признаков делимости для разложения на простые множители

Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.

Пример 5

Если необходимо произвести разложение на множители 10 , то по таблице видно: 2 · 5 = 10 . Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10 .

Пример 6

Если необходимо произвести разложение числа 48 , то по таблице видно: 48 = 6 · 8 . Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6 = 2 · 3 и 8 = 2 · 4 . Тогда полное разложение отсюда получается как 48 = 6 · 8 = 2 · 3 · 2 · 4 . Каноническая запись примет вид 48 = 2 4 · 3 .

Пример 7

При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100 . Отсюда получаем, что 3 400 = 34 · 100 , где 100 можно разделить на 10 , то есть записать в виде 100 = 10 · 10 , а значит, что 3 400 = 34 · 10 · 10 . Основываясь на признаке делимости получаем, что 3 400 = 34 · 10 · 10 = 2 · 17 · 2 · 5 · 2 · 5 . Все множители простые. Каноническое разложение принимает вид 3 400 = 2 3 · 5 2 · 17 .

Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5 . Получим, что 75 = 5 · 15 , причем 15 = 3 · 5 . То есть искомое разложение пример вид произведения 75 = 5 · 3 · 5 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

На какие множители раскладывается. Калькулятор разложения числа на простые множители. Вынесение общего множителя за скобки. Примеры

(кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются простыми числами .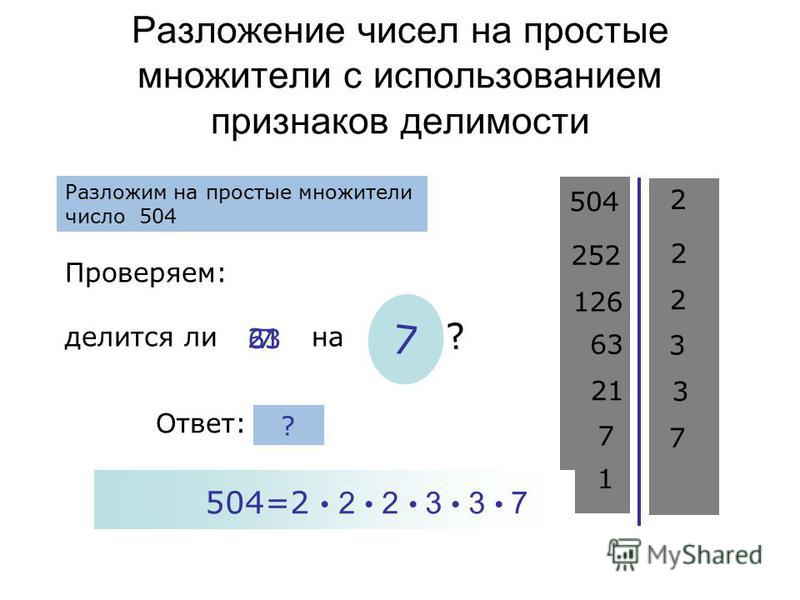 Числа, имеющие другие делители, называются составными (или сложными ) числами . Простых чисел — бесконечное множество. Ниже приведены простые числа, не превосходящие 200:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой. В арифметике под умножением понимают краткую запись сложения указанного количества одинаковых слагаемых.

Например , запись 5*3 обозначает «сложить три пятёрки», то есть 5+5+5. Результат умножения называется произведением , а умножаемые числа — множителями или сомножителями . Первый множитель иногда называется «множимое ».

Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.

Разложение числа на множители (Факторизация).

Разложение на множители (факторизация) — перебор делителей — алгоритм факторизации или тестирования простоты числа путем полного перебора всех возможных потенциальных делителей.

Т.е., простым языком, факторизация — это название процесса разложения чисел на множители, выраженное научным языком.

Последовательность действий при разложении на простые множители:

1. Проверяем, не является ли предложенное число простым.

2. Если нет, то подбираем, руководствуясь признаками деления делитель, из простых чисел начиная с наименьшего (2, 3, 5 …).

3. Повторяем это действие до тех пор, пока частное не окажется простым числом.

Чем отличаются простые и составные числа

Например, число 7 простое, а число 8 составное.

Разложение числа на простые множители

При разложении составных чисел на простые множители, их обычно, записывают в порядке возрастания.

Обычно, при разложении числа на простые множители пользуются признаками делимости.

Разложим число 378 на простые множители

378|2
189|3
63|3
21|3

Разложение числа на простые множители – это часто встречающаяся задача, которую нужно уметь решать. Разложение на простые множители может потребоваться при нахождении НОД (наибольший общий делитель) и НОК (наименьшее общее кратное), а также при проверке, являются ли числа взаимно простыми.

Все числа можно разделить на два основных типа:

Простое число – это число, которое делится только на само себя и на 1.
Составное число – это число, которое имеет другие делители, кроме самого себя и 1.

Чтобы проверить, является ли число простым или составным, можно воспользоваться специальной таблицей простых чисел.

Таблица простых чисел

Для удобства вычислений все простые числа были собраны в таблицу. Ниже приведена таблица простых чисел из диапазона от 1 до 1000.

2	3	5	7	11	13	17	19	23	29	31	37
41	43	47	53	59	61	67	71	73	79	83	89
97	101	103	107	109	113	127	131	137	139	149	151
157	163	167	173	179	181	191	193	197	199	211	223
227	229	233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409	419	421	431	433
439	443	449	457	461	463	467	479	487	491	499	503
509	521	523	541	547	557	563	569	571	577	587	593
599	601	607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733	739	743
751	757	761	769	773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881	883	887	907	911
919	929	937	941	947	953	967	971	977	983	991	997

Разложение на простые множители

Для разложения числа на простые множители можно использовать таблицу простых чисел и признаки делимости чисел . До тех пор, пока число не станет равно 1, нужно подбирать простое число, на которое делится текущее, и выполнять деление. Если не удалось подобрать ни одного множителя, не равного 1 и самому числу, то число простое. Рассмотрим, как это делается на примере.

Разложить на простые множители число 63140.

Чтобы не потерять множители, будем записывать их в столбик, как показано на картинке. Такое решение является достаточно компактным и удобным. Рассмотрим его подробнее.

Примеры. 1) Разложить число 1400 на простые множители.

Это же число можно разложить на простые множители иначе:

Таким образом, снова пришли к такому же, как и в первом случае, разложению, но быстрее.

2) Разложить число 1620 на простые множители.

Всякое составное число может быть единственным образом представлено в виде произведения простых множителей. Например,

48 = 2 · 2 · 2 · 2 · 3, 225 = 3 · 3 · 5 · 5, 1050 = 2 · 3 · 5 · 5 · 7 .

Для небольших чисел это разложение легко делается на основе таблицы умножения. Для больших чисел рекомендуем пользоваться следующим способом, который рассмотрим на конкретном примере. Разложим на простые множители число 1463. Для этого воспользуемся таблицей простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Перебираем числа по этой таблице и останавливаемся на том числе, которое является делителем данного числа. В нашем примере это 7. Делим 1463 на 7 и получаем 209. Теперь повторяем процесс перебора простых чисел для 209 и останавливаемся на числе 11, которое является его делителем (см. ). Делим 209 на 11 и получаем 19, которое в соответствии с этой же таблицей является простым числом. Таким образом, имеем:

Выполните 8 простых шагов, чтобы разложить число на множители

В этой статье мы собираемся объяснить, как шаг за шагом разложить или разложить число на его простые числа.

Прежде чем мы начнем что-либо, не стесняйтесь просмотреть эти записи, где мы объясняем, что означает «факторинг» и что такое простое число, чтобы вы могли освежить свою память.

Теперь давайте разложим числа на их простые числа.

Мы собираемся разложить на 12.

Шаг 1. Напишите число, которое мы хотим разложить, рядом с вертикальной линией.

Шаг 2. Найдите наименьший простой делитель числа 12. В нашем примере это будет 2.

Шаг 3. Разделите 12 на 2 и запишите ответ под числом 12.

Шаг 4. Теперь мы просто повторяем. Мы будем искать наименьший простой делитель 6. Это четное число, поэтому наименьшее простое число снова равно 2, и мы пишем его рядом с 6.

Шаг 5. Делим 6 на 2 и получаем 3, поэтому записываем под 6.

Шаг 6. Теперь нам нужно повторить шаги еще раз. Какое простое число является делителем 3? 3 сама.

Шаг 7. Продолжаем делить 3 на 3 и получаем 1.

Шаг 8. Процесс завершается, когда мы достигаем 1. Второй столбец — наш ответ.

Теперь мы можем выразить наше число как произведение простых множителей:

Просто, правда? Мы можем разбить любое число на его простые числа, следуя инструкциям, независимо от того, насколько оно велико.

Все числа могут быть выражены как произведение простых множителей, и разбивка каждого числа различна.

Помните, что в Smartick вы можете научиться вычислять числа и выполнять всевозможные математические задания для детей от 4 до 14 лет. Создайте учетную запись сейчас и попробуйте бесплатно.

Подробнее:

Веселье — любимый способ обучения нашего мозга

Дайан Акерман

Smartick — увлекательный способ изучения математики

15 минут веселья в день
Адаптируется к уровню вашего ребенка
Миллионы учеников с 2009 года

Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Калькулятор факторизации простых чисел

Использование калькулятора

Используйте этот калькулятор простых чисел, чтобы найти все простые делители заданного целого числа до 10 триллионов. В этом калькуляторе представлено:

Простые множители числа
Разложение простых чисел в экспоненциальной форме
CSV (значения, разделенные запятыми) список простых множителей
Факторизация в дереве простых множителей

Для первых 5000 простых чисел этот калькулятор указывает индекс простого числа. То n ^th Простое число обозначается как Prime[n], поэтому Prime[1] = 2, Prime[2] = 3, Prime[3] = 5 и так далее.

Ограничение на число, вводимое в фактор, меньше 10 000 000 000 000 (менее 10 триллионов или максимум 13 цифр).

Что такое простая факторизация?

Простая факторизация или целочисленная факторизация числа — это разбиение числа на набор простых чисел, которые умножаются вместе, чтобы получить исходное число. Это также известно как первичное разложение.

Как найти простую факторизацию числа

Мы рассмотрим два метода факторизации простых чисел: поиск простых чисел путем пробного деления и использование простых чисел для создания дерева простых множителей.

Факторизация простых чисел пробным отделом

Допустим, вы хотите найти простые множители числа 100 с помощью пробного деления. Начните с проверки каждого целого числа, чтобы увидеть, делится ли оно на 100 и последующие частные, и если да, то как часто. Результирующий набор множителей будет простым, поскольку, например, когда 2 исчерпано, все числа, кратные 2, также исчерпаны.

Найдите простые делители числа 100:

100 ÷ 2 = 50; сохранить 2
50 ÷ 2 = 25; сохранить 2
25 ÷ 2 = 12.5, неравномерно разделить на следующее наибольшее число, 3
25 ÷ 3 = 8,333, неравномерно, поэтому разделить на следующее наибольшее число, 4
Но 4 кратно 2, так что это уже проверено, поэтому разделите на следующее наибольшее число, 5
25 ÷ 5 = 5; сохранить 5
5 ÷ 5 = 1; сохранить 5

Перечислите получившиеся простые множители в виде последовательности кратных 2 x 2 x 5 x 5 или в виде множителей с показателями степени 2 ² x 5 ² .

Примеры простого разложения: множители и показатели

Простая факторизация 100 равна 2 x 2 x 5 x 5 или 2 ² x 5 ²
Простая факторизация числа 76 равна 2 x 2 x 19 или 2 ² x 19 ¹
Разложение числа 50 на простые множители равно 2 x 5 x 5 или 2 x 5 ²
Простая факторизация числа 48 равна 2 x 2 x 2 x 2 x 3 или 2 ⁴ x 3 ¹
Простая факторизация числа 36 равна 2 x 2 x 3 x 3 или 2 ² x 3 ²
Простая факторизация числа 20 равна 2 x 2 x 5 или 2 ² x 5 ¹
Простая факторизация числа 10 равна 2 x 5 или 2 ¹ x 5 ¹

Дерево основных факторов

Используя дерево простой факторизации, чтобы увидеть работу, простое разложение 100 = 2 x 2 x 5 x 5 выглядит следующим образом:

Связанные калькуляторы

Список первых 1000 простых чисел см. Таблица 1000 простых чисел.

Ссылки и дополнительная литература

Математика — это весело: Факторизация простых чисел.

Вайсштейн, Эрик В. «Простое число». Из MathWorld — веб-ресурса Wolfram.

Вайсштейн, Эрик В. «Факторизация прямого поиска». Из MathWorld — веб-ресурса Wolfram.

Вайсштейн, Эрик В. «Алгоритмы простой факторизации.» Из MathWorld — веб-ресурса Wolfram.

Колдуэлл, Крис К. Основные страницы.

Простая факторизация

Простые числа

Простое число:

целое число больше 1, которое можно не получить путем умножения других целых чисел

Первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19 и 23, и у нас есть диаграмма простых чисел, если вам нужно больше.

Если мы можем составить его путем умножения других целых чисел, то это составное число .

Вот так:

2 — Prime, 3 — Prime, 4 — Composite (=2×2), 5 — Prime и так далее…

Факторы

«Коэффициенты» — это числа, которые нужно перемножить, чтобы получить другой номер:

Факторизация простых чисел

«Факторизация простых чисел» находит , какие простые числа перемножаются, чтобы получить исходное число.

Вот несколько примеров:

Пример: Каковы простые делители числа 12?

Лучше всего начинать работу с наименьшего простого числа, которое равно 2, так что давайте проверим:

12 ÷ 2 = 6

Да, оно поделилось ровно на 2. Мы сделали первый шаг!

Но 6 не простое число, поэтому нужно идти дальше. Попробуем снова 2:

6 ÷ 2 = 3

Да, это тоже сработало. А 3 — это простое число, так что у нас есть ответ:

12 = 2 × 2 × 3

Как видите, каждый множитель является простым числом , поэтому ответ должен быть правильным.

Примечание: 12 = 2 × 2 × 3 можно также записать с использованием показателей степени как 12 = 2 ² × 3

Пример: Какова простая факторизация числа 147?

Можем ли мы разделить 147 точно на 2?

147 ÷ 2 = 73½

Нет, нельзя.Ответ должен быть целым числом, а 73½ — нет.

Давайте попробуем следующее простое число номер, 3:

147 ÷ 3 = 49

Сработало, теперь попробуем разложить на множители 49.

Следующее простое число 5 не работает. Но 7 подходит, поэтому мы получаем:

49 ÷ 7 = 7

И это все, что нам нужно сделать, потому что все факторы простые числа.

147 = 3 × 7 × 7

(или 147 = 3 × 7 ² с использованием показателей)

Пример: Какова простая факторизация числа 17?

Подожди… 17 — это простое число .

Вот и все, что мы можем сделать.

17 = 17

Другой метод

Мы показали вам, как разложить на множители, начав с наименьшего простого числа и продвигаясь вверх.

Но иногда проще разбить число на любые множители , которые вы можете … затем разложить эти множители на простые числа.

Пример: Каковы простые делители числа 90?

Разбить 90 на 9 × 10

Простые делители числа 9 равны 3 и 3
Простые делители числа 10 равны 2 и 5

Таким образом, простые делители числа 90 равны 3, 3, 2 и 5

Факторное дерево

И «Дерево множителей» может помочь: найти любые множители числа, затем множители этих чисел и т. д., пока мы не сможем больше множить.

Пример: 48

48 = 8 × 6 , поэтому запишем «8» и «6» ниже 48

Теперь мы продолжаем и делим 8 на 4 × 2

Затем 4 в 2 × 2

И, наконец, 6 в 3 × 2

Мы больше не можем разлагать, поэтому мы нашли простые множители.

Что показывает, что 48 = 2 × 2 × 2 × 2 × 3

(или 48 = 2 ⁴ × 3 с использованием показателей)

Зачем искать Prime Factors?

Простое число можно разделить только на 1 или само на себя, поэтому оно не может учитываться дальше!

Каждое второе целое число можно разбить на простые множители.

Это похоже на то, что простые числа являются основными строительными блоками всех чисел.

Эта идея может быть очень полезна при работе с большими числами, например, в криптографии.

Криптография

Криптография — это изучение секретных кодов. Прайм-факторизация очень важна для людей, которые пытаются создавать (или взламывать) секретные коды на основе чисел.

Это потому, что разложение очень больших чисел на множители очень сложно и может занять много времени у компьютеров.

Если вы хотите знать больше, предметом является «шифрование» или «криптография».

Уникальный

И вот еще что:

Для любого числа существует только один (уникальный!) набор простых множителей.

Пример: простые делители числа 330 равны 2, 3, 5 и 11

330 = 2 × 3 × 5 × 11

Не существует другого возможного набора простых чисел, которые можно умножить, чтобы получить 330.

На самом деле эта идея настолько важна, что ее называют Фундаментальной теоремой арифметики .

Инструмент простой факторизации

Хорошо, у нас есть еще один метод… используйте наш Инструмент факторизации простых чисел, который может вычислять простые множители для чисел до 4 294 967 296.

370, 1055, 1694, 1695, 1696, 1697

Факторизация простых чисел — значение, методы, приложения, примеры

Разложение на простые множители — это способ представить число как произведение его простых множителей.Простое число — это число, которое имеет ровно два делителя: 1 и само число. Например, если мы возьмем число 30. Мы знаем, что 30 = 5 × 6, но 6 не является простым числом. Число 6 можно разложить на множители как 2 × 3, где 2 и 3 — простые числа. Следовательно, простая факторизация числа 30 = 2 × 3 × 5, где все множители — простые числа.

Давайте узнаем больше о простой факторизации с различными математическими задачами, за которыми следуют решенные примеры и практические вопросы.

В чем смысл простой факторизации?

Процесс записи числа в виде произведения простых чисел называется простой факторизацией. Простые числа — это числа, которые имеют только два делителя: 1 и само число. Например, 2, 3, 5, 7, 11, 13, 17, 19 и так далее — простые числа. Разложение на простые множители любого числа означает представление этого числа как произведения простых чисел. Например, разложить число 40 на простые множители можно следующим образом:

Определение простой факторизации

Метод разложения числа на его простые числа, помогающие образовать число при умножении, называется простой факторизацией.Другими словами, когда простые числа умножаются, чтобы получить исходное число.

Простая факторизация числа

Давайте посмотрим на диаграмму простой факторизации еще нескольких чисел в таблице, приведенной ниже:

Номера	Простая факторизация
36	2 ² × 3 ²
24	2 ³ × 3
60	2 ² × 3 × 5
18	2 × 3 ²
72	2 ³ × 3 ²
45	3 ² × 5
40	2 ³ × 5
50	2 × 5 ²
48	2 ⁴ × 3
30	2 × 3 × 5
42	2 × 3 × 7

Что такое множители и простые множители?

Факторы числа — это числа, которые умножаются, чтобы получить исходное число. Например, 4 и 5 — это множители числа 20, т. е. 4 × 5 = 20, тогда как простых делителей числа — это простые числа, которые нужно умножить, чтобы получить исходное число. Например: 2, 2 и 5 — простые множители числа 20, т. е. 2 × 2 × 5 = 20,

Разложение на простые множители похоже на разложение числа на множители, но в качестве множителей рассматриваются только простые числа (2, 3, 5, 7, 11, 13, 17, 19 и т. д.). Следовательно, можно сказать, что множители, которые полностью делят исходное число и не могут быть разделены на большее количество множителей, называются простыми множителями данного числа.

Методы простой факторизации

Существуют различные методы простой факторизации числа. Наиболее распространенные методы, используемые для простой факторизации, приведены ниже:

Факторизация простых чисел с использованием метода факторного дерева
Разложение на простые множители методом деления

Факторизация простых чисел с использованием метода факторного дерева

В методе факторного дерева находятся делители числа, а затем эти числа разлагаются на множители, пока мы не достигнем простых чисел. Чтобы оценить простую факторизацию числа с использованием метода факторного дерева, мы используем шаги, указанные ниже:

Шаг 1: Поместите число в начало дерева факторов.
Шаг 2: Затем запишите соответствующую пару факторов как ветви дерева.
Шаг 3: Факторизируйте составные факторы, найденные на шаге 2, и запишите пару факторов в качестве следующих ветвей дерева.
Шаг 4: Повторяем шаг 3, пока не получим простые множители всех составных множителей.

Пример: Следуйте приведенному ниже рисунку, чтобы понять концепцию и выполнить разложение числа 850 на простые множители.

Факторизация простых чисел с использованием метода деления

Метод деления также можно использовать для нахождения простых множителей большого числа путем деления числа на простые числа. Выполните шаги, указанные ниже, чтобы найти простые делители числа с помощью метода деления:

Шаг 1: Разделите число на наименьшее простое число так, чтобы наименьшее простое число полностью делило число.
Шаг 2: Снова разделите частное шага 1 на наименьшее простое число.
Шаг 3: Повторяйте шаг 2, пока частное не станет равным 1.
Шаг 4: Наконец, перемножьте все простые множители, являющиеся делителями.

Пример: Выполним разложение числа 60 на простые множители методом деления, используя описанные выше шаги.

Разложение числа 60 на простые множители = 2 × 2 × 3 × 5
Таким образом, простые делители числа 60 равны 2, 3 и 5.

Применение простой факторизации

Факторизация простых чисел широко используется в реальном мире. Ниже приведены два наиболее важных применения простой факторизации.

Криптография и первичная факторизация
HCF и LCM с использованием простой факторизации

Криптография и первичная факторизация

Криптография — это метод защиты информации с помощью кодов. Факторизация простых чисел играет важную роль для кодеров, которые создают уникальный код, используя числа, которые не слишком сложны для компьютера, чтобы хранить или быстро обрабатывать.

HCF и LCM с использованием простой факторизации

Чтобы найти наибольший общий делитель (HCF) и наименьшее общее кратное (НОК) двух чисел, мы используем метод простой факторизации. Для этого мы сначала делаем простую факторизацию обоих чисел. Необходимо помнить о следующих моментах, связанных с HCF и LCM:

HCF является произведением наименьшей степени каждого общего простого множителя.
LCM является произведением наибольшей степени каждого общего простого множителя.

Пример: Что такое HCF и LCM для 850 и 680?

Решение: Сначала мы проведем разложение обоих чисел на простые множители. Простая факторизация числа 850: 850 = 2 × 5 ² × 17. Простая факторизация 680: 680 = 2 ³ × 5 × 17

HCF является произведением наименьшей степени каждого общего простого множителя. Следовательно, HCF (850, 680) = 2 ¹ × 5 ¹ × 17 ¹ = 170. НОК является произведением наибольшей степени каждого общего простого множителя.Следовательно, НОК (850, 680) = 2 ³ × 5 ² × 17 ¹ = 3400. Таким образом, НКМ (850, 680) = 170, НОК (850, 680) = 3400

☛ Похожие статьи

Часто задаваемые вопросы о простой факторизации

Что такое простая факторизация в математике?

Разложение любого числа на простые множители означает представление этого числа как произведения простых чисел. Простое число — это число, которое имеет ровно два делителя: 1 и само число.

Как провести простую факторизацию?

Разложение любого числа на простые множители можно выполнить двумя способами:

Метод деления — В этом методе заданное число делится на наименьшее простое число, на которое оно полностью делится. После этого частное снова делится на наименьшее простое число. Этот шаг повторяется до тех пор, пока частное не станет равным 1. Затем перемножаются все простые делители.
Метод факторного дерева — В этом методе заданное число помещается в верхнюю часть факторного дерева.Тогда соответствующие пары факторов записываются в виде ветвей дерева. После этого шага составные факторы снова факторизуются и записываются в виде следующих ветвей. Эта процедура повторяется до тех пор, пока мы не получим простые множители всех составных множителей.

Что такое простая факторизация чисел 72, 36 и 45?

Факторизация простых чисел — это способ записи числа как кратного их простых множителей. Первые несколько простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19 и так далее.Ниже показана простая факторизация чисел 72, 36 и 45.

Разложение числа 72 на простые множители = 2 ³ × 3 ²
Разложение числа 36 на простые множители = 2 ² × 3 ²
Разложение числа 45 на простые множители = 3 ² × 5

Как найти LCM с помощью простой факторизации?

Аббревиатура LCM означает «наименее распространенное кратное». Наименьшее общее кратное (НОК) числа — это наименьшее число, являющееся произведением двух или более чисел.НОК двух чисел можно узнать, сначала выяснив простые множители чисел. LCM является произведением наибольшей мощности каждого общего простого множителя.

Как найти HCF с помощью простой факторизации?

Аббревиатура HCF означает «наивысший общий фактор». Наивысший общий делитель (HCF) двух чисел — это максимально возможное число, которое полностью делит оба числа. HCF двух чисел можно узнать, сначала выяснив простые множители чисел.HCF является наибольшим общим множителем из простых множителей двух чисел.

Где полезна простая факторизация?

Факторизация простых чисел используется для нахождения HCF и LCM чисел. Он широко используется в криптографии, которая представляет собой метод защиты информации с помощью кодов. Простые числа используются для формирования или декодирования этих кодов.

Что такое простая факторизация числа 24?

Число 24 можно записать как 4 × 6. Теперь составные числа 4 и 6 можно разложить на множители как 4 = 2 × 2 и 6 = 2 × 3.Таким образом, простая факторизация числа 24 равна 24 = 2 × 2 × 2 × 3 = 2 ³ × 3

Как Prime Factorization используется в реальном мире?

Факторизация простых чисел широко используется в реальном мире. Например, если нам нужно разделить что-либо на равные части, или нам нужно обменять деньги, или рассчитать время в пути, мы используем простую факторизацию. Один из распространенных примеров: если у нас есть 21 конфета, и нам нужно разделить ее между 3 детьми, мы знаем множители 21 как 21 = 3 × 7.Это означает, что мы можем раздать каждому ребенку по 7 конфет.

Когда использовать прайм-факторизацию?

Факторизация простых чисел — это один из методов, используемых для нахождения наибольшего общего делителя (НОД) заданного набора чисел. GCF с помощью простой факторизации полезен для больших чисел, для которых перечисление всех факторов требует много времени.

Как найти простую факторизацию числа — видео и расшифровка урока

Простое число — это любое число, которое делится только на себя и на 1.Некоторые примеры простых чисел включают 2, 5 и 17. Такие числа, как 15 или 21, не являются простыми, потому что они делятся не только на себя, но и на 1.

Факторизация простых чисел число на более мелкие части. Чтобы найти

простую факторизацию числа, вам нужно разбить это число на его простые множители.

Как определить разложение числа на простые множители

Существует два основных способа определения простых делителей числа.Я продемонстрирую оба метода, а вы решите, какой вам больше нравится.

Оба метода начинаются с дерева факторов . Факторное дерево — это диаграмма, которая используется для разложения числа на его множители до тех пор, пока все оставшиеся числа не станут простыми.

Первый способ использовать дерево множителей для разложения числа на множители — это разделить только простые числа. Разложим 24, используя этот метод.

Поскольку 24 — четное число, первое простое число, которое можно разложить, — это 2.Это оставляет нас с 2 * 12. Опять же, 12 — четное число, поэтому мы можем вынести еще 2, оставив нам 2 * 2 * 6. Поскольку 6 четно, мы можем вынести третьи два, оставив 2 * 2. * 2 * 3.

Все эти числа простые, поэтому факторизация завершена.

Другой метод использования дерева множителей для нахождения разложения числа на простые множители состоит в том, чтобы просто извлечь первые попавшиеся множители, независимо от того, простые они или нет.Возвращаясь к нашему примеру сверху, давайте снова умножим на 24, используя этот метод.

Первое, что вы можете заметить, это то, что 6 * 4 равно 24, так что это один набор множителей для 24. Поскольку ни одно из этих чисел не является простым, мы можем продолжить множить их оба. 6 можно разложить на 2 * 3, а 4 можно разбить на 2 * 2. Теперь все наши делители простые, и разложение числа 24 на множители завершено, снова давая ответ 2 * 2 * 2 * 3.

Оба эти метода работают одинаково хорошо и могут использоваться взаимозаменяемо.Есть люди, которым нравится использовать определенные приемы, чтобы сначала извлечь простые числа, не решая, какие другие числа могут быть факторами исходного числа.

Уловки для нахождения некоторых простых чисел:

Любое четное число делится на 2.
Если сложить цифры большого числа и полученная сумма будет делиться на 3, то и число делится на 3.
Число, оканчивающееся на 5 или 0, делится на 5.

Эти маленькие хитрости могут помочь вам разложить на множители большие числа, когда не всегда понятно, с чего начать.

Попробуем другой пример.

Найдите простые делители числа 117.

Первое, что я замечаю в этом числе, это то, что если вы сложите цифры (1+1+7), вы получите 9. Это означает, что число делится на 3. Поскольку оно нечетно и не заканчивается на 5 или 0, оно не делится ни на 2, ни на 5, поэтому мы можем начать с 3.

117 разделить на 3 равно 39, поэтому наши первые два множителя — это 3 и 39. 39 также делится на три, потому что 3 + 9 = 12

39/3 равно 13

13 — простое число, поэтому наша факторизация завершена, и множители 117 равны 3 * 3 * 13.

Резюме урока

Простые делители числа — это все простые числа, которые при умножении дают исходное число. Вы можете найти простую факторизацию числа, используя факторное дерево и разделив число на более мелкие части. Вы можете начать с нахождения простого числа и разложения его на множители, а затем продолжить в том же духе. Или вы можете просто разделить число на любые два числа, даже если они не простые, и продолжать до тех пор, пока каждое число не станет простым.

Результат обучения

После просмотра этого урока вы сможете продемонстрировать нахождение разложения любого числа на простые множители с помощью двух описанных выше методов.

Факторы, простые числа, композиты и факторные деревья

Вам следует ознакомиться с определениями некоторых типов чисел и способами их нахождения.

Факторы

Числа, которые перемножаются для получения произведения, называются множителями .

Пример 1

Каковы делители числа 18?

коэффициент × коэффициент = 18

1 × 18 = 18

2 × 9 = 18

3 × 6 = 18

Итак, делители числа 18 равны 1, 2, 3, 6, 9 и 18. Эти числа также называются делителями 18. Делители числа также называются делителями того же числа.

Простые числа

простое число – натуральное число, большее 1, которое делится только на себя и на 1.Другое определение: простое число — это положительное целое число, имеющее ровно два разных делителя: само себя и 1.

.
Пример 2
Является ли 19 простым числом?
Да. Единственными делителями числа 19 являются 1 и 19, поэтому 19 — простое число. То есть 19 делится только на 1 и на 19, значит, оно простое.
Пример 3
Является ли 27 простым числом?
№ 27 делится на другие числа (3 и 9), поэтому оно не является простым. Делители числа 27 равны 1, 3, 9 и 27, поэтому оно не простое.
Единственное четное простое число — 2; после этого любое четное число можно разделить на 2. Числа 0 и 1 не являются простыми числами. Простые числа меньше 50: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 и 47.
Составные номера
Составное число – это натуральное число, которое делится более чем на 1 и само на себя. Другое определение: составное число — это положительное целое число, имеющее более двух различных делителей. Числа 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, … являются составными числами, потому что они «состоят» из других чисел. Числа 0 и 1 не являются составными числами. (Они не простые и не составные.)
Пример 4
Является ли 25 составным числом?
Да. 25 делится на 5, поэтому оно составное. Делители 25 равны 1, 5 и 25.
Факторные деревья
Каждое составное число можно представить в виде произведения простых множителей. Вы можете найти простых множителей , используя факторное дерево. Дерево факторов выглядит так.
Вы также можете сделать дерево, как показано на следующем дереве.
В любом случае, независимо от того, как разложено число 18, произведение простых чисел будет одним и тем же, хотя порядок может быть разным.
Пример 5
Используйте дерево множителей, чтобы выразить 60 как произведение простых множителей.
Таким образом, простая факторизация числа 60 равна 2 × 2 × 3 × 5, что можно записать как 2 ² × 3 × 5. Фактические простых делителей числа 60 равны 2, 3 и 5.
Факторизация и простые числа (предварительная алгебра, открытие дробей и множителей) – Mathplanet
Множитель — это число, которое делится на другое число и частное которого является целым числом.
Пример
$$\frac{18}{2}=9\коэффициент стрелки вправо$$
$$\frac{18}{4}=4.5\Стрелка вправо не\: a\: фактор$$
2 — это коэффициент 18, потому что ответ — целое число (9). 4 не является коэффициентом 18, потому что ответ равен 4 с остатком 5.
Существует несколько эмпирических правил, позволяющих легко определить, является ли число коэффициентом
.
2 — четное число всегда делится на два
3 — если сумма его цифр делится на 3
5 — если последняя цифра числителя 5 или 0, то число делится на 5
6 — если число делится на 2 и 3
10 — если последняя цифра числителя 0, то число делится на 10
Пример
Определить, делится ли число 256 на 2, 3, 4, 5, 6 или 10
$$\begin{matrix} 256\div 2=128\: \: \: \: & ({\color{green} yes})\\ 256\div 3=85.