Разложение многочлена на множители

Рассмотрим основные определения и теоремы о многочленах.

Определение 1

Функция

\[f(x)=A_{0} x^{n} +A_{1} x^{n-1} +…+A_{n} ,\]

где $n\in Z$, называется многочленом, число $n$ — степень многочлена. Коэффициенты $A_{0} ,A_{1} ,…,A_{n} $при переменных являются действительными или комплексными числами.

Определение 2

Корень многочлена — это значение переменной $x$, при котором заданный многочлен обращается в ноль.

Теорема 1

При делении многочлена $f(x)$ на $x-a$ получается остаток, который равен $f(a)$.

Следствие 1

Если $a$ есть корень заданного многочлена, т.е. $f(a)=0$, то заданный многочлен представляется в виде следующего произведения

\[f(x)=(x-a)\cdot f_{1} (x),\]

где $f_{1} (x)$ — многочлен.

Теорема 2

Любая целая рациональная функция $f(x)$ имеет хотя бы один корень, вещественный (действительный) или комплексный.

Теорема 3

Любой многочлен степени $n$ может быть представлен как разложение многочлена на $n$ линейных сомножителей вида $x-a$ и множитель, который равен коэффициенту при $x^{n} $:

\[f(x)=A_{0} \cdot (x-a_{1} )\cdot (x-a_{2} )\cdot …\cdot (x-a_{n} ),\]

где $a_{1} ,a_{2} ,…,a_{n} $ — корни многочлена.

Пример 1

Записать разложение заданного многочлена $f(x)=x^{3} -6x^{2} +11x-6$ на множители.

Решение:

При $x=1$ получаем $f(1)=0$. Следовательно, исходный многочлен делится на $x-1$ без остатка. После деления получаем разложение многочлена следующего вида:

\[x^{3} -6x^{2} +11x-6=(x-1)\cdot (x^{2} -5x+6).\]

Найдем корни второго сомножителя, который является квадратным многочленом:

\[x^{2} -5x+6=0\]\[D=(-5)^{2} -4\cdot 1\cdot 6=25-24=1\]\[x_{1} =\frac{5-1}{2} =2,x_{2} =\frac{5+1}{2} =3\]

Получим разложение многочлена:

\[x^{3} -6x^{2} +11x-6=(x-1)\cdot (x-2)\cdot (x-3).\]

Теорема 4

Если заданный многочлен тождественно равен нулю, то все коэффициенты этого многочлена равны нулю.

Теорема 5

Если два заданных многочлена тождественно равны друг другу, то коэффициенты одного из этих многочленов равны соответствующим коэффициентам другого.

Пример 2

Определить коэффициенты многочлена $ax^{3} +bx^{2} +cx+d$ тождественно равного многочлену $2x^{2} +3x$.

Решение:

На основании теоремы 5 получаем, что $a=0,\, \, b=2,\, \, c=3,\, \, d=0$.

Если в разложении многочлена степени $n$ на линейные множители

$f(x)=A_{0} \cdot (x-a_{1} )\cdot (x-a_{2} )\cdot …\cdot (x-a_{n} )$, (*)

некоторые линейные сомножители оказываются одинаковыми, то данные множители можно объединить, и тогда разложение данного многочлена на множители будет иметь следующий вид:

$f(x)=A_{0} \cdot (x-a_{1} )^{k_{1} } \cdot (x-a_{2} )^{k_{2} } \cdot …\cdot (x-a_{n} )^{k_{m} } $ ($k_{1} +k_{2} +…+k_{m} =n$).

В формуле (*) корни многочлена $a_{1} ,a_{2} ,…,a_{n} $ могут быть не только вещественными, но и комплексными числами.

Пример 3

Записать разложение на множители многочлена, имеющего корень $x=1$ кратности 2, корень $x=-3$ кратности 3.

Решение:

Искомое разложение запишется следующим образом:

\[f(x)=(x-1)^{2} \cdot (x+3)^{3} .\]

Определение 2

Многочленом $n$-ой степени называется функция

\[P_{n} (z)=a_{n} z^{n} +a_{n-1} z^{n-1} +a_{n-2} z^{n-2} +…+a_{1} z+a_{0} ,\]

где коэффициенты $a_{0} ,a_{1} ,a_{2} ,…,a_{n-1} ,a_{n} $ — постоянные комплексные числа, $a_{n} \ne 0$, $z\in Z$ — комплексная переменная. Число $z_{0} $, при котором многочлен принимает нулевое значение ($P_{n} (z_{0} )=0$), называется корнем многочлена.

Теорема 6

Любой многочлен, степень которого $n\ge 1$, имеет комплексный корень.

Пример 4

Найти корни заданного многочлена $P(z)=z^{2} +2z+2$ и разложить на множители.

Решение:

\[z^{2} +2z+2=0\]\[D=2^{2} -4\cdot 1\cdot 2=4-8=-4\]\[\begin{array}{l} {z_{1} =\frac{-2-\sqrt{-4} }{2} =\frac{-2-2\sqrt{-1} }{2} =\frac{-2-2i}{2} =-1-i,} \\ {z_{2} =\frac{-2+\sqrt{-4} }{2} =\frac{-2+2\sqrt{-1} }{2} =\frac{-2+2i}{2} =-1+i} \end{array}\]

$z_{1} =-1-i,z_{2} =-1+i$ — комплексные корни многочлена

Искомое разложение запишется следующим образом:

\[P(z)=z^{2} +2z+2=(z-(-1-i))\cdot (z-(-1+i)).\]

Многочлен $P_{n} (z)$ комплексной переменной $z$ с действительными коэффициентами $a_{0} ,a_{1} ,a_{2} ,…,a_{n-1} ,a_{n} $ обладает следующими свойствами:

• Если $\bar{z}$ — число, комплексно-сопряженное для числа $z$, то имеет место равенство $P_{n} (\bar{z})=\mathop{P_{n} (z)}\limits^{\_ \_ \_ \_ \_ } $.
• Если некоторое число $z_{1} =a+b\cdot i$ является корнем заданного многочлена $P_{n} (z)$, то число $z_{2} =\bar{z}_{1} =a-b\cdot i$ тоже является корнем заданного многочлена.
• Если некоторое число $z_{1} =a+b\cdot i$ является корнем заданного многочлена с действительными коэффициентами $P_{n} (z)$, то $P_{n} (z)$ без остатка делится на квадратный трехчлен $z^{2} +pz+q$, где $p=-2a,\; q=a^{2} +b^{2} $.
• Если некоторое число $z_{1} =a+b\cdot i$ является корнем заданного многочлена $P_{n} (z)$ кратности $k$, то число $z_{2} =\bar{z}_{1} =a-b\cdot i$ так же является корнем данного многочлена и той же кратности. В разложение заданного многочлена на множители наряду с линейными множителями $x-(a+bi)$ входит столько же линейных множителей $x-(a-bi)$.

Пример 5

Найти комплексные корни заданного многочлена $P(z)=z^{2} +2z+5$, используя свойства многочленов.

Решение:

\[z^{2} +2z+5=0\]\[D=2^{2} -4\cdot 1\cdot 5=4-20=-16\]

$z_{1} =\frac{-2-\sqrt{-16} }{2} =\frac{-2-4\sqrt{-1} }{2} =\frac{-2-4i}{2} =-1-2i$ — комплексный корень многочлена.

Следовательно, на основании свойств число $z_{2} =-1+2i$ является корнем заданного многочлена.

Пример 6

Проверить выполнимость свойства $P_{n} (\bar{z})=\mathop{P_{n} (z)}\limits^{\_ \_ \_ \_ \_ } $ для многочлена $P(z)=z^{2} +2z+5$ и комплексного числа $z=1+i$.

Решение:

\[P_{2} (z)=P(1+i)=(1+i)^{2} +2\cdot (1+i)+5=1+2i+i^{2} +2+2i+5=7+4i\]\[P_{2} (\overline{z})=P(1-i)=(1-i)^{2} +2\cdot (1-i)+5=1-2i+i^{2} +2-2i+5=7-4i\]\[\overline{P_{2} (z)}=7-4i\]

Следовательно, равенство $P_{2} (\bar{z})=\mathop{P_{2} (z)}\limits^{\_ \_ \_ \_ \_ } $ является верным.

Примечание

Для многочленов определены следующие операции: сложение, вычитание, умножение. Операция деления многочленов определена не для любых двух многочленов, однако, как и для целых чисел, имеется возможность выполнить деление с остатком.

Пример 7

Вычислить сумму и разность двух многочленов:

$f_{1} (z)=(1+i)z^{3} +3z^{2} +(1-i)\cdot z+5$ и $f_{2} (z)=(1-3i)\cdot z^{3} +2z^{2} +(1+2i)\cdot z+1$.

Решение:

\[\begin{array}{l} {f_{1} (z)+f_{2} (z)=\left((1+i)\cdot z^{3} +3z^{2} +(1-i)\cdot z+5\right)+\left((1-3i)\cdot z^{3} +2z^{2} +(1+2i)\cdot z+1\right)=} \\ {=(1+i+1-3i)\cdot z^{3} +(3+2)\cdot z^{2} +(1-i+1+2i)\cdot z+(5+1)=(2-2i)\cdot z^{3} +5\cdot z^{2} +(2+i)\cdot z+6} \end{array}\]\[\begin{array}{l} {f_{1} (z)-f_{2} (z)=\left((1+i)\cdot z^{3} +3z^{2} +(1-i)\cdot z+5\right)-\left((1-3i)\cdot z^{3} +2z^{2} +(1+2i)\cdot z+1\right)=} \\ {=(1+i-1+3i)\cdot z^{3} +(3-2)\cdot z^{2} +(1-i-1-2i)\cdot z+(5-1)=4i\cdot z^{3} +z^{2} +(-3i)\cdot z+4} \end{array}\]

Разложение многочлена на множители методом неопределенных коэффициентов

29 Авг 2016

АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ

Разложение многочлена на множители методом неопределенных коэффициентов

В этой статье мы рассмотрим решение уравнения четвертой степени с помощью разложения на множители методом неопределенных коэффициентов.

Решить уравнение:

Решение. показать

Перед нами уравнение четвертой степени.

Чтобы решить это уравнение, разложим левую часть уравнения на множители.

Многочлен четвертой степени можно разложить на произведение двух многочленов второй степени.

Воспользуемся методом неопределенных коэффициентов.

Пусть выполняется равенство:

Здесь -целые числа.

Перемножим две скобки справа и приведем подобные члены. Получим:

Два многочлена равны тогда и только тогда, когда равны их коэффициенты.

Приравняем коэффициенты при одинаковых степенях  и получим систему уравнений:

Без ограничения общности можем считать, что

, тогда пусть

, отсюда или .

Рассмотрим два случая:

1. , 

Получим систему уравнений:

Из второго и третьего уравнений получаем — что не удовлетворяет третьему уравнению. Система не имеет решений.

2. , 

Из второго и третьего уравнений получаем

— и эти значения удовлетворяет третьему уравнению.

Получили:

Тогда наше разложение имеет вид:

Осталось приравнять  квадратные трехчлены в скобках к нулю и найти корни:

Ответ: , 

И.В. Фельдман, репетитор по математике

Для вас другие записи этой рубрики:

3.1.2. Разложение выражений на множители

Глава 3. Решение уравнений и неравенств

3.1.

3.1.2.

Изучение приёмов преобразования уравнений начнём с обсуждения того, как можно разлагать на множители выражения, входящие в данное уравнение. Вообще представление уравнения f (x) = g (x) в виде

F1 (x) · F2 (x) · … · Fn (x) = 0,

(5)

где выражения F_k (x), k = 1, …, n «проще» функций f (x) и g (x), представляет собой несомненное продвижение в решении уравнения. В самом деле, представление вида (5) позволяет сразу приравнивать множители F

k (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель).

Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.

1. Вынесение общего множителя за скобку

В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена.

Пример 1

Разложить на множители многочлен x⁵ – 2x³ + x².

Каждое слагаемое этого многочлена содержит множитель x 2. Вынесем его за скобку и получим ответ: x5 – 2x3 + x2 = x2(x3 – 2x + 1).

2. Применение формул сокращённого умножения

Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы:

Пример 2

Разложить на множители многочлен (x – 2)⁴ – (3x + 1)⁴.

Разложим разность четвёртых степеней по формуле, приведённой выше:

3. Применение выделения полного квадрата

Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.

Пример 3

Разложить на множители многочлен x⁴ + 4x² – 1.

Имеем

4. Группировка

Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель.

5. Метод неопределённых коэффициентов

Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной.

Теоретической основой метода являются следующие утверждения.

• Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
• Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
• Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Для доказательства второго утверждения вспомним, как выглядит график степенной функции с нечетной целой степенью (§ 2.2.5). Действительно, из его вида следует, что значение многочлена имеет разные знаки при x → +∞ и x → –∞. Многочлен степени n – непрерывная функция, значит, найдется хотя бы одна точка, в которой график этой функции пересечет ось Ox.

Пример 4

Разложить на множители многочлен 3x³ – x² – 3x + 1.

Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax2 + bx  + c такие, что справедливо равенство 3x3 – x2 – 3x + 1 = (x – p)(ax2 + bx + c) = ax3 + (b – ap)x2 + (c – bp)x – pc. Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырёх уравнений для определения четырёх неизвестных коэффициентов: Решая эту систему, получаем: a = 3, p = –1,  b = 2, c = –1. Итак, многочлен 3x3 – x2 – 3x + 1 разлагается на множители: 3x3 – x2 – 3x + 1 = (x – 1)(3x2 + 2x – 1).

6. Теорема о корнях многочлена

Разложение многочлена на множители иногда удаётся провести, если один из его корней угадан с помощью теоремы о рациональных корнях, доказанной в § 2.1.4. После того, как корень x = α угадан, многочлен P_n (x) представим в виде P_n (x) = (x – α) · P_n – 1 (x), где P_n – 1 (x) − многочлен степени на 1 меньше, чем P_n (x).

Пример 5

Разложить на множители многочлен x³ – 5x² – 2x + 16.

Данный многочлен имеет целые коэффициенты. По следствию теоремы о рациональных корнях (см. § 2.1.4) если целое число является корнем этого многочлена, то оно является делителем числа 16, то есть если у данного многочлена есть целые корни, то это могут быть только числа ±1, ±2, ±4, ±8, ±16. Проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть x3 – 5x2 – 2x + 16 = (x – 2) · Q (x), где Q (x) − многочлен второй степени. Следовательно, исходный многочлен разлагается на множители, один из которых (x – 2).

7. Разложение относительно параметра

Суть этого метода легче всего понять на примере.

Пример 6

Разложить на множители многочлен x⁴ – 10x² – x + 20.

Преобразуем данный многочлен: x4 – 10x2 – x + 20 = x4 – 5 · 2x2 – x + 25 – 5 = 25 – 5(1 + 2x2) + x4 – x Рассмотрим теперь многочлен a2 – a(1 + 2x2) + x4 – x, который при a = 5 совпадает с данным. Полученный многочлен является квадратным, его корни легко найти по теореме Виета: a2 – a(1 + 2x2) + x4 – x = a2 – a(1 + 2x2) + x(x3 – 1) = a2 – a(1 + 2x2) + x(x – 1)(x2 + x + 1). Следовательно, a1 = x(x – 1), a2 = x2 + x + 1. Значит, исходный многочлен разлагается на множители a2 – a(1 + 2x2) + x4 – x = (a – (x2 – x))(a – (x2 + x + 1)). Вернемся к многочлену, данному в условии задачи, подставив a = 5. Получим: x4 – 10x2 + x + 20 = (5 – x2 + x)(5 – x2 – x – 1) = (x2 – x – 5)(x2 + x – 4).



Разложение на множители суммы и разности степеней

Для любого натурального числа 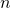верно равенство

   

Доказательство. Чтобы убедиться в справедливости этого равенства, раскроем скобки и приведём подобные члены. Получим

   

   

При раскрытии скобок вслед за произведением каждого слагаемого на мы записывали его произведение на 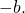После приведения подобных слагаемых в сумме останутся только первое и последнее слагаемое, то есть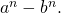

Если 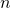— нечётное число (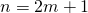), то после замены 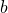на 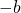в формуле разности степеней получим тождество