Как решать через виета: Теорема Виета: формула и примеры решений — Детская игровая комната «Волшебный лес»

Posted on 05.07.197021.12.2021 by alexxlab

{k} a_{k}$ равно сумме всех возможных произведений из $k$ корней.

Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни. Названы в честь французского математика Франсуа Виета (1540 — 1603).

Если старший коэффициент многочлена $a_{0} \neq 1$, то есть многочлен не является приведенным, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на $a_{0}$ (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

Содержание

Теорема Виета

Теорема Виета звучит так:

Теорема Виета широко используется при решении задач, в которых

не требуется найти корни квадратного уравнения, а лишь некоторое их соотношение;
нужно найти значение параметра, при котором значение корней удовлетворяет заданному соотношению.

С помощью теоремы Виета можно устно находить корни квадратного уравнения, а также проверять, являются ли заданные числа корнями уравнения.

Чтобы грамотно использовать теорему Виета, ее нужно хорошо понимать.

Остановимся подробнее на каждом слове этой теоремы. Сначала о коэффициентах квадратного уравнения:

Квадратное уравнение называется приведенным, если старший коэффициент равен 1, то есть если

В общем случае не каждое квадратное уравнение является приведенным, например, уравнение не является приведенным. В этом уравнении .

Но каждое квадратное уравнение можно сделать приведенным, для этого достаточно обе части уравнения вида разделить на :

В полученном уравнении старший коэффициент равен 1, второй коэффициент равен , свободный член равен .

То есть корни произвольного квадратного уравнения, согласно теоремы Виета, удовлетворяют системе:

Например корни уравнения

удовлетворяют системе

Обратная теорема Виета позволяет составить квадратное уравнение по значениям его корней:

Например, числа -7 и -2 являются корнями уравнения , или

Решим несколько задач с использованием теоремы Виета.

Задача 1. Составьте квадратное уравнение с рациональными коэффициентами, если известно, что один из корней равен

Так как произведение корней должно быть числом рациональным, второй корень может представлять выражение, сопряженное выражению , то есть дополняющее его до формулы разности квадратов. Это выражение :

Тогда ;

Отсюда получаем уравнение:

Задача 2. Найдите значения выражения , где и — корни уравнения .

Если в задаче не требуется найти значения корней квадратного уравнения, а только их соотношение, следовательно, нужно воспользоваться теоремой Виета.

Запишем теорему Виета для этого уравнения:

Теперь мы знаем, чему равны сумма и произведение корней. Представим выражение в виде комбинации суммы и произведения. Приведем дроби к общему знаменателю.

Ответ: -8

Задача 3. Найдите значение выражения , где и — корни уравнения .

Эта задача аналогична предыдущей, только в ней чуть сложнее преобразование выражения в комбинацию выражений и .

Вспомним формулу квадрата суммы: . Перенесем влево и получим соотношение (1)

Запишем теорему Виета для уравнения :

(по формуле 1)

Ответ: 20,5

Задача 4. Решите устно уравнение:

Теорем Виета позволяет в некоторых случаях легко находить корни квадратного уравнения.

Для этого удобно придерживаться такой последовательности шагов:

Выписываем теорему Виета для данного уравнения.
Определяем знаки корней.
Раскладываем на два множителя свободный член, и определяем, какая пара множителей в сумме дает второй коэффициент, взятый с противоположным знаком.

Для данного уравнения

2 Определим знаки корней.

Для определения знаков удобно пользоваться такой таблицей:

Так как в уравнении произведение корней отрицательно, корни имеют разные знаки. Сумма корней также отрицательна, следовательно, корень с большим модулем отрицателен.

3. Будем раскладывать на множители число 24, имея в виду, что множитель с большим модулем отрицателен, и выбираем пару чисел, сумма которых равна -2.

Очевидно, что это числа -6 и 4.

Ответ: -6; 4

Задача 5. Решите устно уравнение:

2 Определим знаки корней.

Так как в уравнении

произведение корней отрицательно, корни имеют разные знаки. Сумма корней отрицательна, следовательно, корень с большим модулем отрицателен.

В данном случае корни проще подобрать, зная их сумму: . Можно предположить, что . Проверим, чему равно произведение этих выражений:

Предположение верное.

Ответ:

Следствием из теоремы Виета являются такие полезные факты:

Задача 6. Найти корни уравнения:

Заметим, что , следовательно, .

Задача 7.

Найти корни уравнения:

Заметим, что , следовательно,

Как решать задачи с параметром с помощью теоремы Виета читайте здесь.

И.В. Фельдман, репетитор по математике.

Дискриминант. Теорема Виета

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. 2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..

Общая формула для нахождения корней квадратного уравнения:

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни

До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),

или парабола ветвями вниз (a<0).

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).

Неполные квадратные уравнения

Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах «+, -» или «-, +».
Неполное квадратное уравнение вида
одним из корней всегда имеет точку x=0.
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!

Внеклассный урок — Теорема Виета

Теорема Виета

Сумма корней приведенного квадратного уравнения равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену.

(Напомним: приведенное квадратное уравнение – это уравнение, где первый коэффициент равен 1).

Пояснение:

Пусть квадратное уравнение ax² + bx + c = 0 имеет корни х₁ и х₂. Тогда по теореме Виета:

b c
х₁ +

х₂ = – ——, х₁ · х₂ = ——
a a

Пример 1:

Приведенное уравнение x² – 7x + 10 = 0 имеет корни 2 и 5.

Сумма корней равна 7, а произведение равно 10.

А в нашем уравнении второй коэффициент равен -7, а свободный член 10.

Таким образом, сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней – свободному члену.

Довольно часто встречаются квадратные уравнения, которые можно легко вычислить с помощью теоремы Виета – больше того, с ее помощью их вычислять проще. В этом легко убедиться как на предыдущем примере, так и на следующем.

Пример 2. Решить квадратное уравнение

х² – 2х – 24 = 0.

Решение.

Применяем теорему Виета и записываем два тождества:

х₁ · х₂ = –24

х₁ + х₂ = 2

Подбираем такие множители для –24, чтобы их сумма была равна 2. После недолгих размышлений находим: 6 и –4. Проверим:

6 · (– 4) = –24.

6 + (– 4) = 6 – 4 = 2.

Как вы заметили, на практике суть теоремы Виета заключается в том, чтобы в приведенном квадратном уравнении свободный член разложить на такие множители, сумма которых равна второму коэффициенту с противопложным знаком. Эти множители и будут корнями.

Значит, корнями нашего квадратного уравнения являются 6 и –4.

Ответ: х₁ = 6, х₂ = –4.

Пример 3. Решим квадратное уравнение 3х² + 2х – 5 = 0.

Здесь мы имеем дело не с приведенным квадратным уравнением. Но и такие уравнения тоже можно решать с помощью теоремы Виета, если их коэффициенты уравновешены – например, если сумма первого и третьего коэффициентов равна второму с обратным знаком.

Решение.

Коэффициенты уравнения уравновешены: сумма первого и третьего членов равны второму с противоположным знаком:

3 + (–5) = –2.

В соответствии с теоремой Виета

х₁ + х₂ = –2/3
х₁ · х₂ = –5/3.

Нам надо найти такие два числа, сумма которых равна –2/3, а произведение –5/3. Эти числа и будут корнями уравнения.

Первое число угадывается сразу: это 1. Ведь при х = 1 уравнение превращается в простейшее сложение-вычитание:
3 + 2 – 5 = 0. Как найти второй корень?
Представим 1 в виде 3/3, чтобы все числа имели одинаковый знаменатель: так проще. И сразу напрашиваются дальнейшие действия. Если х

1 = 3/3, то:

3/3 + х₂ = –2/3.

Решаем простое уравнение:

х₂ = –2/3 – 3/3.

х₂ = –5/3.

Ответ: х₁ = 1; х₂ = –5/3

Пример 4: Решить квадратное уравнение 7x² – 6x – 1 = 0.

Решение:

Один корень обнаруживается сразу – он прямо в глаза бросается: х₁ = 1 (потому что получается простая арифметика: 7 – 6 – 1 = 0).

Ищем дальше.

Коэффициенты уравнения уравновешены: сумма первого и третьего равны второму с обратным знаком:
7 + (– 1) = 6.

В соответствии с теоремой Виета составляем два тождества (хотя в данном случае достаточно одного из них):

х₁ · х₂ = –1/7
х₁ + х₂ = 6/7

Подставляем значение х₁ в любое из этих двух выражений и находим х₂:

х₂ = –1/7 : 1 = –1/7

Ответ: х₁ = 1; х₂ = –1/7

Дискриминант приведенного квадратного уравнения.

Дискриминант приведенного квадратного уравнения можно вычислять как общей формуле, так и по упрощенной:

D = p² – 4q

где p – второй коэффициент квадратного уравнения, q – свободный член.

При D = 0 корни приведенного уравнения можно вычислять по формуле:

                                                                                   -p ± √D
                                                                            x = ————.
                                                                                        2

Если D < 0, то уравнение не имеет корней. 2-x-420=0`

Спустя пару лет после написания статьи появился сборник из 150 заданий для разложения квадратного многочлена по теореме Виета.

Ставьте лайки и задавайте вопросы в комментариях!

РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ — алгоритмы и примеры

Квадратным уравнением называется уравнение вида

где a, b, c — коэффициенты, причем a ≠ 0, а x – неизвестное, которое нужно найти.

Квадратное уравнение можно свести к приведенному виду – это вид, при котором коэффициент a = 1.

Решение квадратного уравнения через дискриминант

Решение квадратного уравнения через дискриминант выполняется по строго определенному алгоритму:

1. Вычислить дискриминант по формуле

2. Если D < 0 — уравнение не имеет корней

3. Если D > 0 — уравнение имеет 2 корня, которые вычисляются по формулам:

4. Если D = 0 — уравнение имеет ровно 1 корень, который вычисляется по формуле:

Теорема Виета для решения квадратного уравнения

Квадратное уравнение можно решить и с помощью теоремы Виета.

Теорема: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение – свободному члену этого уравнения.

То есть, чтобы решить квадратное уравнение с помощью теоремы Виета, достаточно подобрать такие x1 и x2, чтобы выполнялось:

Пример решения квадратного уравнения

Решим квадратное уравнение 2x² — 16x + 30 = 0 двумя способами.

Решение через дискриминант:

a = 2, b = -16, c = 30

D = (-16)² — 4 ⋅ 2 ⋅ 30 = 256 — 240 = 16

D > 0 => имеется 2 различных корня

x1 = (-(-16) + √16) / (2 ⋅ 2) = (16 + 4) / 4 = 5

x2 = (-(-16) — √16) / (2 ⋅ 2) = (16 — 4) / 4 = 3

Ответ: 3 и 5

Решение через теорему Виета:

a = 2, b = -16, c = 30

x1 + x2 = -(-16) / 2 = 8

x1 ⋅ x2 = 30 / 2 = 15

Разложим 15 на возможные пары множителей:

15 = 1 ⋅ 15 = (-1) ⋅ (-15) = 3 ⋅ 5 = (-3) ⋅ (-5)

И проверим, какие из них подойдут в качестве решения:

1 + 15 = 16 ≠ 8

-1 — 15 = -16 ≠ 8

3 + 5 = 8

-3 — 5 = -8 ≠ 8

Таким образом, в качестве корней подойдут только 3 и 5. {n-1} + \ cdots + a_0P (x) = xn + an − 1 xn − 1 + ⋯ + a0 такое, что ai = ± 1a_i = \ pm 1ai = ± 1 для всех 0≤i≤n − 10 \ leq i \ leq n-10 ≤i≤n − 1, удовлетворяющее условию вещественности всех корней P (x) P (x) P (x).2-3 \ times \ frac {7} {5} \ right] \\ & = — \ frac {49} {125}. \ _\квадратный \ end {array} r13 + r23 + r33 = 3r1 r2 r3 + (r1 + r2 + r3) [r12 + r22 + r32 — (r1 r2 + r2 r3 + r3 r1)] = 3r1 r2 r3 + (r1 + r2 + r3) [(r1 + r2 + r3) 2−3 (r1 r2 + r2 r3 + R3 r1)] = 3 × (−53) + (511) [(511) 2−3 × 57] = — 12549. □

кубических уравнений: красота алгебры | Автор Сухрид Саха | Cosmus Mathematicus

(Ниже представлена расширенная и неотредактированная версия моей статьи, опубликованной в моем школьном бюллетене по математике.)

Источник изображения: Shutter stock

Алгебра считается связующим звеном между большей частью математики и восходит к древним вавилонянам. и египтяне.Впервые она рассматривалась как формальная наука греками, из которых великий математик Диофант (3 век нашей эры) иногда называют «отцом алгебры». Позже исследование процветало в руках индейцев, китайцев, средневековых арабов, а позже и европейцев эпохи Возрождения и Нового времени.

Большая часть алгебры связана с выражениями, тождествами и уравнениями, и в настоящее время нас интересуют именно последние. Одной из специальных форм уравнений являются уравнения третьей степени, более известные как кубических уравнений. Ранние греки и индийцы добились больших успехов в решении этих проблем, но большая часть того, что мы знаем о кубических уравнениях, относится к 15 веку и позже, когда общее решение этих уравнений обсуждалось очень подробно. Наша работа состоит в том, чтобы найти как раз : попытаться решить кубическое уравнение любого вида.

Любое уравнение вида ax³ + bx² + cx + d = 0, где a, b, c, d — все действительные числа, такие, что a не равно нулю, рассматриваются как кубические уравнения. Таким образом, единственная разница между кубическим уравнением и квадратным уравнением (уравнениями 2-й степени) состоит в том, что дополнительный член ax³ действительно полностью меняет уравнение. Вы можете понять это из графиков кубических функций, которые мы изучим позже, и попробуем сравнить их с любой квадратичной функцией с помощью вашего графического калькулятора.

Что раньше математики находили странным, так это их неспособность решить эти уравнения, прежде всего потому, что их почти невозможно решить с помощью простой евклидовой геометрии, в отличие от квадратных уравнений, для которых персидский математик Аль-Хорезми нашел общее решение путем завершения квадратов. Его метод позже был использован Рене Декартом , чтобы прийти к:

Квадратичная формула.Источник изображения: Википедия

Однако, если кто-то пытается найти общее решение для кубики, он может зайти в тупик, потому что это требует предварительных знаний комплексных чисел. Удивительно, но персидский поэт Омар Хайям придумал метод решения кубического уравнения с использованием геометрического анализа, но только в 16 веке итальянский гений по имени Сципионе дель Ферро смог решить кубические уравнения особый тип, известный как вогнутых кубиков , который мы вскоре обсудим.

После смерти дель Ферро именно Никколо Тарталья продвинул вперед изучение кубических уравнений, придя к общему решению. Другой итальянец по имени Джироламо Кардано , как утверждается, заставил Тарталья раскрыть секретный метод (примерно в 1530 году) и пообещал ему, что он никогда не опубликует его. Увы, Кардано нарушил обещание, и хотя до сих пор остается спорным, чей это был метод, сегодня метод решения кубического уравнения известен как метод Кардано.

Рассмотрим общую кубическую форму ax³ + bx² + cx + d = 0. Чтобы решить эту проблему легко, попробуем убрать член bx². Преобразование левой части уравнения как функции на декартовой плоскости говорит нам, что второй и третий члены отвечают за горизонтальное преобразование графика. Если мы можем преобразовать это в форму x³ + 3Hx + g = 0, все станет намного проще. Эта форма кубики называется угнетенным кубическим уравнением .

Возможно, кто-то из Дель-Ферро, Кардано и Тарталья понял это и таким образом преобразовал кубику, заменив x координатой x точки перегиба кубики (показано ниже).

Если вы знакомы с дифференциальным исчислением, возможно, вы знаете, что это ноль второй производной любой кубики.

(Тот факт, что координата x была нулем второй производной, тогда не был известен ни одному из итальянцев, поскольку исчисление было разработано Исааком Ньютоном и Готфридом Лейбницем позже в 17 веке. я знаю исчисление, это совсем не проблема!)

Точка перегиба на графике кубической функции. Используемое приложение для построения графиков: Desmos

Таким образом, координата x оказалась равной x = (- b / 3a) для любого куба.Используя это, они заменили x: x = y- (b / 3a). Когда эта замена использовалась в ax³ + bx² + cx + d = 0, уравнение было преобразовано в: y³ + 3Hy + G = 0, где H и G равны: H = (c / 3a) — (b² / 9a²) и G = (d / a) + (2b³ / 27a³) — (bc / 3a²).

Пусть y = s-t для некоторых чисел s и t таких, что H = st. Это означает:

G = — (st) ³-3st (st) => G = t³-s³ + 3st (st) -3st (st) => G = t³-s³

Это может занять некоторое время, чтобы получить понимается, потому что шаг принятия y в качестве разницы между любыми двумя числами является просто произвольным. Возможно, кто-то заметил сходство между депрессивным кубическим уравнением и тождеством, используемым для нахождения (a + b) ³, и случайно подумал об этом. Следовательно, математики сами по себе художники!

Теперь H = st => s = H / t => G = t³- (H / t) ³ => t⁶-Gt³-H³ = 0

Это квадратное уравнение относительно t³, которое может быть решено с помощью квадратичного уравнения. формула:

Уравнение, написанное с использованием MS Word

Таким образом, из значений t³ и s³ мы можем найти s и t и решить для y. Следовательно, мы можем решить для x.

В описанном выше методе Кардано мы на самом деле не пошли дальше, чтобы найти формулу для поиска решений общей кубики, так как это требует понимания комплексных чисел (если вам известны примитивные корни из единицы, то предстоящий!). Однако это говорит нам о том, что кубическое уравнение должно иметь комплексные корни, в том числе потому, что не все кубические функции, построенные на декартовой плоскости, пересекают ось x.

Рассмотрим угнетенную кубику x³-3Hx-G = y

График x³-Hx (для некоторого x).Используемое приложение для построения графиков: Desmos

Таким образом, решения кубической формы можно найти, найдя точки пересечения кривой y = x³-Hx и линии y = 2Hx + G. Когда первый набросан, он будет выглядеть, как на графике справа.

Он может выглядеть как другие похожие кривые, но давайте остановимся на этой.

Кривая y = x³-Hx как C и линия y = 2Hx + G как L. C и L пересекаются хотя бы один раз, поэтому депрессивная кубика должна иметь как минимум один действительный корень.

Когда L проходит через одну из стационарных точек или вершин C, то есть точку максимума или минимума (посмотрите на точку, где C собирается повернуть или изменить направление на графике), кубика имеет повторяющийся корень.

Итак, когда:

Написано с использованием MS Word

(Если вы не понимаете обозначение, в котором используется дифференциальное исчисление, вам не о чем беспокоиться. Все это означает, что наклон касательной к кривой в неподвижной точке равен плюс или минус квадратный корень из H на 3. Если вы все еще не убеждены или кажетесь заинтересованным, вы можете изучить производные функций.)

Итак, если L встречается с C в одной из стационарных точек,

Написано с использованием MS Word

Это подразумевает что если депрессивная кубика имеет три действительных решения, L ограничена линиями, проходящими через две стационарные точки C.Таким образом,

Написано с использованием MS Word

И для того, чтобы C встретился с L в одной из стационарных точек, 64H³-27G² = 0

Следовательно, x³-3Hx-G = 0 имеет:

1) 1 действительный корень и 2 комплексных / мнимые корни, если Δ <0

2) 1 действительный корень и 2 действительных равных корня, если Δ = 0

3) 3 различных действительных корня, если Δ> 0

Где Δ = 64H³- 27G² — дискриминант. Поскольку природа корней общей кубики также зависит от природы корней депрессивной кубики, мы можем определить природу корней любого кубического уравнения, используя этот дискриминант. Этот метод, который мы использовали, относится к математической дисциплине под названием «Аналитическая геометрия ».

Можем ли мы представить кубическое выражение как сумму двух кубов? Эта мысль, возможно, пришла вам в голову после того, как вы заметили сходство между угнетенной кубикой и тождеством для (a + b) ³. Давай попробуем это выяснить.

Написано с использованием MS Word

Это означает, что: y = A (x- λ) ³ + B (x- μ) ³

Таким образом, мы представили кубическое выражение в виде суммы двух кубов. Кроме того,

Написано с использованием MS Word

Следовательно, мы также заключаем, что λ и μ являются корнями уравнения:

Контрольный вопрос:

Написано с использованием MS Word

Математика так же стара, как сама человеческая цивилизация.Человеческие существа встречали так много разных закономерностей в природе и при измерении величин в зарегистрированной истории. Кубические уравнения — лишь одна из многих прекрасных вещей, на которые мы наткнулись, и, к счастью, мы знаем, как решать такие типы уравнений.

Приятно осознавать, что метод Кардано — не единственный существующий метод, который можно использовать для решения кубического уравнения. Рафаэль Бомбелли, Франсуа Виет, Лодовико Феррари и многие другие открыли новые инновационные методы решения кубических уравнений.Поэтому всегда важно смотреть на одну и ту же задачу в более, чем на один вариант , чтобы математика изучалась строго. Мы обсудили здесь только несколько аспектов кубических уравнений. На самом деле существует так много исследовательских работ и статей по ним, что Интернет заполнен, но здесь важно то, сколько человек готов пройти, чтобы получить удовольствие от процессов, связанных с математикой.

Пожалуйста, поставьте лайк (или похлопайте), прокомментируйте и подпишитесь на эту страницу, если вы любите математику, как я. Также, если вам интересно, пожалуйста, ознакомьтесь с тригонометрическим решением Виета для определенных типов кубических уравнений, а также с решением Эйлера.(Они гении, не так ли?)

Решение кубических и четвертых уравнений | Марко Тавора, доктор философии

Мы все учимся решать квадратные уравнения в старшей школе. Квадратные уравнения — это полиномиальные уравнения второго порядка, включающие только одну переменную. Однако проблемы решения кубических и четвертых уравнений не преподаются в школе, хотя для этого требуются только базовые математические методы. В этой статье я покажу, как получить решения этих двух типов полиномиальных уравнений.Точные решения (или корни многочлена) могут быть найдены методами алгебры или тригонометрии (однако эта статья будет ограничена только алгебраическими методами).

Я начну с краткого обзора истории предмета.

Кубические уравнения

Кубические уравнения изучались веками, начиная с древних вавилонян, греков, китайцев, индийцев и египтян (подробнее см. Статью в Wiki). Самым старым кубическим уравнением, которое нужно было изучить, была алгебраическая версия знаменитой геометрической задачи удвоения куба, так называемой задачи Делиана (которая в алгебраических терминах эквивалентна решению уравнения x ³ = 2).

Рисунок 1: Леонардо да Винчи неудачные попытки решить проблему Делиана (источник).

Несколько известных математиков решили частные случаи кубических уравнений, но общее решение было найдено только в 1500-х годах. Это решение было впервые опубликовано итальянским эрудитом Джероламо Кардано в его важной книге по алгебре Ars Magna (1545 г.). Здесь можно найти версию книги на латыни.

Рисунок 2: Титульный лист Ars Magna ( , источник ).

Однако Кардано не был первым изобретателем этого результата.Первым, кто нашел решение кубического уравнения, был итальянский математик эпохи Возрождения Сципионе дель Ферро. Дель Ферро передал свою формулу своему ученику, математику Антонио Фьоре (когда он был на смертном одре).

Рис. 3: Сципионе дель Ферро, Никколо Тарталья и Джероламо Кардано слева направо.

Итальянский математик и инженер Никколо Тарталья также обнаружил решение (независимо). Позже Кардано убедил его раскрыть свой секрет (решение) при условии, что Кардано поклялся никогда не публиковать его.Однако, когда Кардано узнал, что дель Ферро независимо нашел решение до Тартальи, он решил включить его в свой Ars Magna (хотя Кардано признал как Тарталью, так и дель Ферро за оригинальное открытие, Тарталья не был доволен раскрытием его секрета! ).

Однако Кардано заметил, что решение Тартальи иногда включает в себя то, что мы теперь называем комплексными числами, поэтому он не осознавал всех последствий результата. Позднее итальянский математик Рафаэль Бомбелли подробно изучил этот вопрос.По этой причине многие считают Бомбелли первооткрывателем комплексных чисел.

Уравнения четвертой степени

Уравнение четвертой степени было решено в 1540 году математиком Людовико Феррари. Однако, как мы увидим, решение уравнений четвертой степени требует решения кубических уравнений. Следовательно, он был опубликован только позже, в Ars Magna Кардано.

Рисунок 4: Математик Людовико Феррари (источник).

Теперь мы покажем, как найти решения. Начнем с кубических уравнений, поскольку они нужны для решения квартик.

Наша цель — показать, как решить следующее кубическое уравнение:

Уравнение 1: Наша цель в этом разделе — решить кубическое уравнение.

Это уравнение называется депрессивной кубикой. Хотя они проще, чем общие кубические уравнения (которые имеют квадратичный член), любое кубическое уравнение может быть сведено к угнетенной кубике (с помощью замены переменных).

Рисунок 5: Пример кубического полинома (источник).

Левая часть уравнения. 1 является примером полиномиальной функции p ( z ), которая представляет собой выражение, включающее сумму степеней переменных, умноженную на коэффициенты.Уравнение 1 — полином , уравнение , соответствующее полиномиальной функции p ( z ). Как упоминалось ранее, нули уравнения называются корнями.

Чтобы найти z в уравнении. 1, мы сначала выбираем две вспомогательные переменные u и v , так что u + v = z , и подставляем это выражение в уравнение. 1. Удобная группировка терминов дает:

Уравнение 2: Результат подстановки u + v = z в уравнение.1.

Теперь, u и v могут иметь любые значения, если их сумма равна z . Наиболее очевидный выбор для u и v здесь должен подчиняться

Уравнение 3: Более очевидный выбор для u и v.

, поскольку при этом выборе средний член в формуле. 2 исчезает. Мы получаем систему из двух уравнений:

Уравнение 4: Подставив uv = — p /3 в уравнение. 2 средний член обращается в нуль, и мы получаем эту систему уравнений.

Теперь определите:

Уравнение 5: Определение z и w.

Система уравнений принимает следующий вид:

Уравнение 6: Система в уравнении. 4 с использованием уравнения. 5.

Ур. 6 представляет собой решение квадратного уравнения. Тогда переменные z и w равны:

Уравнение 7: квадратное уравнение, соответствующее решениям, которые подчиняются уравнению. 6.

Используя u + v = z , мы получаем искомые решения:

Уравнение 8: Решения уравнения1.

Напомним, что это решение предполагает уравнение. 3, которым нужно подчиняться. Давайте теперь посмотрим, как решать многочлены четвертой степени.

Стратегия, которой мы будем следовать здесь, состоит в том, чтобы получить решения уравнения четвертой степени в терминах решений кубического уравнения (которое мы знаем, как решать). Этот подход был разработан Леонардом Эйлером, одним из величайших математиков в истории. Поскольку уравнение четвертой степени без члена x ³, известное как сокращенное уравнение четвертой степени, может быть получено из общего уравнения четвертой степени с использованием только тривиальной замены переменных, нам нужно только решить первое (сокращенное уравнение).

Рисунок 6: Портрет Леонарда Эйлера работы Якоба Эмануэля Хандманна (источник).

Следуя Эйлеру, наша цель — доказать, что приведенное уравнение четвертой степени.

Уравнение 9: Пример уравнения четвертой степени.

имеет следующие корни:

Уравнение 10: Решения уравнения. 9.

при условии, что три θ s являются нулями следующего кубического полинома:

Уравнение 11: Уравнение, корни которого задаются θ s.

Как упоминалось ранее, это уравнение можно тривиально преобразовать в депрессивное кубическое уравнение, которое мы знаем, как решить (см. Раздел выше).

Рисунок 7: Пример полинома четвертой степени (источник).

Чтобы найти наше доказательство, поступим следующим образом. Суммируя четыре уравнения в формуле. 10 или используя одну из формул Виета (которые устанавливают связь между коэффициентами многочлена и его нулями), мы находим, что zs уравнения. 10 удовлетворяют:

Уравнение 12: Формула подчиняется zs уравнения. 10. Рисунок 8: Французский математик Франсуа Виет (источник).

Теперь мы сделаем следующие определения:

Уравнение 13: Определение θ₁, θ₂ и θ₃.

Решая четыре z s в этой системе уравнений, мы получаем уравнение. 10. Подставляя уравнение. 10 в уравнение. 9 получаем:

Уравнение 14: Полученные соотношения Подставляя уравнение. 13 в уравнение. 9.

Прямое применение формул Виета подразумевает, что θ с в уравнении. 12 являются корнями кубического многочлена

Уравнение 15: θ s являются корнями этого кубического многочлена.

, которую мы ранее научились решать. Это завершает наше доказательство.

Кубических уравнений

Общее кубическое уравнение

        А х ³ + В х ² + С х + D = 0

Коэффициенты A, B, C, D являются действительными или комплексными числами, где A не 0.После деления на A уравнение принимает вид

         х ³ + б х ² + с х + d = 0

Теперь мы хотим сократить последнее уравнение заменой

        х = у + г

Кубическое уравнение принимает следующий вид:

        (y + r) ³ + b (y + r) ² + c (y + r) + d = 0

        y ³ + (3 r + b) y ² + (3 r ² + 2 r b + c) y + r ³ + r ² b + r c + d = 0

Теперь выберем y так, чтобы квадратичный член исчезал.

        выберите r = -b / 3

Итак, при замене

                б
        х = у - -
                3
уравнение

         х ³ + б х ² + с х + d = 0

приходит в форме

        y ³ + e y + f = 0

Чтобы уменьшить последнее уравнение, воспользуемся заменой Виета

                  1
        у = г + с -
                  z

Константа s на данный момент не определена.

Уравнение

        y ³ + e y + f = 0
становится

             s
        (z + -) ³ + e (z + (s / z)) + f = 0
             z

расширяя и умножая на z ³, имеем

        z ⁶ + (3 s + e) z ⁴ + f z ³ + s (3 s + e) z ² + s ³ = 0

Теперь выбираем s = -e / 3.
Уравнение принимает вид

        z ⁶ + f z ³ - e ³/27 = 0

При z ³ = u

        u ² + f u -e ³/27 = 0

Это простое решение квадратного уравнения.
Общее кубическое уравнение

        А х ³ + В х ² + С х + D = 0

Коэффициенты A, B, C, D являются действительными или комплексными числами, где A не 0. После деления на A уравнение принимает вид

         х ³ + б х ² + с х + d = 0

С заменой

                б
        х = у - -
                3
приходит

        y ³ + e y + f = 0

Чтобы уменьшить последнее уравнение, воспользуемся заменой Виета

                  е
        у = г - ---
                 3 z

Уравнение становится

        z ⁶ + f z ³ - e ³/27 = 0

При z ³ = u

        u ² + f u - e ³/27 = 0

Это простое решение квадратного уравнения.

Пример

Решать

45 x ³ + 24 x ²-7 x - 2 = 0 3 8 2 7 2 х + - х - - х - - = 0 15 45 45 С заменой 8 х = у - --- 45 приходит 3 169 506 у - --- у - ----- = 0 675 Теперь оставим дробные обозначения г ³ - 0,25037037037 г - 5,55281207133e-3 = 0 Чтобы уменьшить последнее уравнение, воспользуемся заменой Виета 0.0834567

5 у = г + --------------- z Тогда у нас есть z ⁶ - 5.55281207133e-3 z ³ + 5.81279532442e-4 = 0 При z ³ = u u ² - 5.55281207133e-3 u + 5.81279532442e-4 = 0 Решения для u: u ₁ = 2,77640603567e-3 + 0,0239493444997 i и u ₂ = 2,77640603567e-3 - 0,0239493444997 i

Каждое решение дает три значения z. Чтобы вычислить эти значения, мы приводим значения u в полярной форме.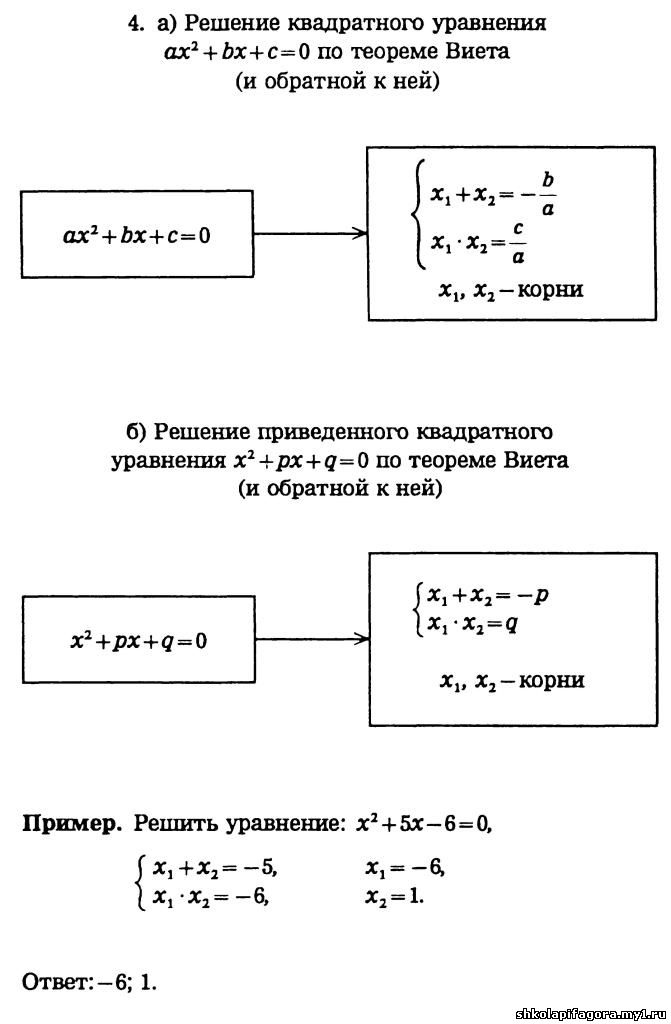

u ₁ = 0,024109739369 (cos (1.45538324457) + i sin (1.45538324457))

u ₂ = 0,024109739369 (cos (1.45538324457) - i sin (1.45538324457))

Шесть значений z представлены в полярной форме

z ₁ = 0,288888888889 (cos (0,48512774819) + i sin (0,48512774819))
z ₂ = 0,288888888889 (cos (2,57952285058) + i sin (2,57952285058))
z ₃ = 0,288888888889 (cos (-1,6092673542) + i sin (-1,6092673542))
z ₄ = 0,288888888889 (cos (0,48512774819) - i sin (0.48512774819))
z ₅ = 0,288888888889 (cos (2,57952285058) - i sin (2,57952285058))
z ₆ = 0,288888888889 (cos (-1,6092673542) - i sin (-1,6092673542))

С участием
                 0,08345675
        у = г + ---------------
                        z

мы находим три реальных значения y

        y ₁ = 0,511111111112
        у ₂ = - 0,488888888888
        у ₃ = - 0,022222222221

Наконец, с заменой

                 8
        х = у - ---
                 45

находим три корня данного уравнения
        х ₁ = 0. 333333333334

        х ₂ = -0,666666666666

        х ₃ = -0,199999999999

Точные корни

        х ₁ = 1/3

        х ₂ = -2/3

        х ₃ = 1/5

Если у вас есть первое приближение корней, все действительные корни кубических уравнений можно найти с помощью простого итерационного метода.

Используйте эту ссылку для теории , процедура оптимизации и примеры этого итерационного метода.

Пример 1

Опираясь на оптимизированную процедуру итерационного метода, решаем теперь уравнение
x ³ + 2 x ² + 3 x — 4 = 0.Соблюдаем процедуру буквально.

Построив x ³ + 2 x ² + 3 x — 4, мы видим, что 0,77 является приближением единственного действительного корня.
Пишем x = x + r (x ³ + 2 x ² + 3 x — 4)
Мы выбираем значение r так, чтобы 1 + r (3. (0,77) ² + 4. (0,77) +3) = 0. r _o = -0,13 — хорошее приближение.
Мы применяем итерацию для x = x — 0,13 (x ³ + 2 x ² + 3 x — 4), начиная с x = 0.77
Мы получаем очень хороший результат, используя всего 5 шагов.
```
0,77619671
0,776041122953
0,776045557563
0,776045431542
0,776045435125
 
```

Пример 2

Решаем уравнение x ³ — 2,7 x ² + 4,5 x — 6 = 0

Построив x ³ — 2,7 x ² + 4,5 x — 6, мы видим, что 2 является грубым приближением единственного настоящего корня.
Запишем x = x + r (x ³ — 2,7 x ² + 4,5 x — 6)
Опираясь на оптимизированную процедуру итерационного метода, мы выбираем r-значение так, чтобы
1 + r (3 * 4-5.4 * 2 + 4,5) = 0. r _o = -0,175 — хорошее приближение.
Применяем итерацию к x = x — 0,175 (x ³ — 2,7 x ² + 4,5 x — 6)
Начнем с x = 2. Мы находим очень хороший результат, используя всего 5 шагов.
```
1,96500000
1,96421257
1,96417892
1,96417747
1,96417741
 
```

Другие учебные пособия по той же теме

Кубические уравнения (pdf)
решение кубических уравнений с одним простым корнем; Использование графиков для решения кубических уравнений

Темы и проблемы

Домашняя страница MATH-изобилие — урок

Указатель MATH-учебника

Условия копирования

Все предложения, замечания и отчеты об ошибках отправляйте по адресу jcinfo @ telenet.быть Тема письма должна содержать фламандское слово wiskunde. потому что другие письма фильтруются в корзину

Аналитическое решение для нелинейной многомодовой вибрации луча с использованием модифицированного подхода гармонического баланса и замены Виета

В этой статье представлен модифицированный метод решения гармонического баланса, объединенный с методом замены Виета для нелинейной многомодовой демпфированной вибрации луча. Целью модификации процедур решения является разработка аналитических формулировок, которые используются для расчета амплитуд колебаний нелинейной многомодовой демпфированной балки без необходимости в решателе нелинейных уравнений для нелинейных алгебраических уравнений, генерируемых в процессах гармонического баланса.Результат, полученный с помощью предложенного метода, демонстрирует разумное согласие с результатом предыдущего метода численного интегрирования. В целом результаты могут показать сходимость и подтвердить точность предложенного метода.

1. Введение

За последние десятилетия было разработано множество методов решения различных задач инженерного моделирования (например, [1–4]). Два хорошо известных метода решения, метод возмущений и метод множественных масштабов (например, [5–7]), получили широкое распространение.В этих двух методах генерируются связанные нелинейные алгебраические уравнения, которые требуется решить с помощью решателя нелинейных уравнений. Также широко используются два метода гармонического баланса (т. е. метод полного гармонического баланса и метод приращения гармонического баланса, например, [8, 9]). Они также генерируют связанные нелинейные алгебраические уравнения в процессах гармонического баланса. В предыдущих работах [10, 11] метод многоуровневого остаточного гармонического баланса был модифицирован из метода полного гармонического баланса и разработан для нелинейных колебаний.Хотя точность этих решений была хорошей и подтверждена другими методами решения, разработка решателя нелинейных уравнений для тех нелинейных алгебраических уравнений, сгенерированных в процедурах решения, занимала довольно много времени. С другой стороны, было множество исследовательских проблем, связанных с балкой / пластиной, которые решались с использованием различных численных и классических методов (например, [12–15]). Это мотивация в данном исследовании для разработки аналитических формулировок для расчета вибрационных откликов нелинейной многомодовой балки без использования решателя нелинейных уравнений для нелинейных алгебраических уравнений, генерируемых в процедурах гармонического баланса. Предлагаемый метод является модифицированным по сравнению с предыдущим методом гармонического баланса и объединен с методом замещения Виета. Используя формулировки аналитических расчетов, результаты могут быть получены без необходимости решателя нелинейных уравнений.

2. Основное уравнение

Основное уравнение движения нелинейной вибрации теории Эйлера-Бернулли выглядит следующим образом [16]: где — продольная координата, а — поперечное смещение. ,, а — 1-я, 2-я и 4-я производные с соответственно; и являются 1-й и 2-й производными по времени,.длина, толщина, модуль Юнга × площадь поперечного сечения, плотность материала на единицу длины и внешнее гармоническое возбуждение. Для равномерно распределенного возбуждения,, = величина возбуждения, — безразмерный параметр возбуждения, мс ^-2., а — частота возбуждения.

Затем управляющее уравнение дискретизируется с использованием метода редукции мод, где — модальная амплитуда th моды, является структурной формой моды th и количеством используемых мод.

Рассмотрим замену (2) в (1), умножение на него и интегрирование по длине балки, где,,, и — модальная сила. Для равномерно распределенного возбуждения.

Если балка просто поддерживается, то и = для. Тогда (3) можно привести к следующему виду: где и — собственная частота -й моды.

3. Модифицированная процедура решения с использованием подстановки Виета

Форма решения модальных амплитуд определяется выражением [10, 17], где — параметр внедрения; « и — решения модальной амплитуды нулевого, 1-го и 2-го уровня.

Путем ввода (5) в (4) рассмотрите те члены, которые связаны с управляющими уравнениями нулевого уровня, и составьте их, где первый, второй и третий индексы в — это номер режима, нулевой уровень и номер 1-й гармоники; — остаток нулевого уровня.

Для простоты пусть тогда (7a) — (7b) в (6) Рассмотрим гармонический баланс в (7a): Когда учитывается затухающая вибрация, модальная амплитуда колебаний нулевого уровня переписывается из (9) и ее комплексная форма имеет вид Тогда (10a) можно переписать как Рассмотрим полиномиальную форму, где для простоты пусть,; — коэффициент демпфирования, а — нелинейная пиковая частота (обратите внимание, что в случае линейной вибрации,;;;;;.

Используя замену, (10c) можно упростить следующим образом: где; ; (т.е. замена Виеты [18]). Уравнение (10c) можно переписать как If рассматривается как независимая неизвестная, а (12) — это «модифицированное» квадратное уравнение. Следовательно, аналитическая формула для решений может быть получена без необходимости решателя нелинейных уравнений. Затем можно составить управляющее уравнение 1-го уровня, введя (5) в (4) и выбрав те члены, которые связаны с: где =.

Обратите внимание, что это было найдено из процедуры решения нулевого уровня.Таким образом, и в (13), которые находятся в терминах, известны. Следовательно, (13) — линейное уравнение.

Рассмотрим гармонические балансы и в (13), чтобы составить два алгебраических линейных уравнения Поскольку (14a) — (14b) являются линейными, неизвестные модальные амплитуды и могут быть найдены аналитически.

Опять же, управляющее уравнение 2-го уровня можно составить, введя (5) в (4) и выбрав те члены, которые связаны с: где.

Обратите внимание, что и были найдены из процедуры решения 1-го уровня.Таким образом, и в (15), которые находятся в терминах и, известны. Следовательно, (15) — линейное дифференциальное уравнение.

Рассмотрим гармонические балансы, и в (15), чтобы составить три алгебраических линейных уравнения: Поскольку (16a) — (16c) линейны, неизвестные модальные амплитуды, и могут быть найдены аналитически. Аналогичным образом, управляющие уравнения -го уровня могут быть составлены путем ввода (5) в (4) и выбора тех членов, которые связаны с формой решения более высокого уровня, и рассмотрения Затем, рассмотрите гармонические балансы, чтобы создать линейные алгебраические уравнения и решить для неизвестные модальные амплитуды.

Наконец, общая амплитуда и общая модальная амплитуда определяются как где — номер моды (т. Е.), — уровень решения (т. Е.) И — номер гармоники (т. Е.).

4. Результаты и обсуждения

В этом разделе свойства материала балок без опоры в численных случаях рассматриваются следующим образом: модуль Юнга = 71 × 10 ⁹ Н / м ², массовая плотность = 2700 кг / м ³, размеры балки = 0,5 м × 0,2 м × 5 мм, коэффициент Пуассона = 0. 3, а коэффициент демпфирования = 0,02. Таблицы 1 (a) -1 (b) показывают исследования сходимости нормированной амплитуды колебаний балки для различных величин и частот возбуждения. Применяется двухрежимный подход. Гармоническое возбуждение распределено равномерно. Решения 2-го уровня нормируются как сто. Показано, что решения 1-го уровня достаточно точны для диапазона частот возбуждения от 0,5 до 6 и параметра возбуждения от до 25. Различия между решениями нулевого уровня и 2-го уровня тем больше, чем выше уровень возбуждения или частота возбуждения.Подразумевается, что высшие гармонические составляющие в колебательных характеристиках более важны, когда уровень возбуждения или частота возбуждения выше. Таблицы 2 (a) -2 (b) показывают вклады первых трех симметричных мод для различных величин и частот возбуждения. Можно видеть, что решения для 2 мод достаточно точны для диапазона частот возбуждения от 0,5 до 6 и параметра возбуждения от = 1 до 25. Для частоты возбуждения, близкой или меньшей, чем 1-я резонансная частота, реакция 1-го режима является доминирующей. Подразумевается, что одномодовое решение достаточно точное. Когда частота возбуждения установлена выше и ближе ко 2-й резонансной частоте, вклад 2-й моды более значителен. На рисунках 1 (а) — 1 (б) показаны частотно-амплитудные кривые для двух случаев возбуждения (один равномерно распределен, другой есть. Видно, что модифицированные решения гармонического баланса хорошо согласуются с решениями, полученными путем численного интегрирования. Метод, использованный в [11], на первом пике можно увидеть хорошо известное явление скачка.Есть только небольшие отклонения наблюдений вокруг и. На рисунке 1 (а) 2-й резонансный пик выглядит более линейным (без явления скачка), потому что 2-я модальная сила довольно мала. Таким образом, это можно рассматривать как линейную вибрацию. На Рисунке 1 (b) вторая модальная сила установлена выше, чтобы вызвать явление скачка. На рис. 2 показан график зависимости общей амплитуды колебаний от частоты возбуждения для различных уровней возбуждения. Функция возбуждения есть. Явление скачка наблюдается на каждом пике из трех случаев возбуждения, кроме 2-го пика.Кроме того, вокруг наблюдается очень маленький затухающий нелинейный пик из-за высокого уровня возбуждения или высокой нелинейности. На рисунках 3 (a) –3 (c) показаны остатки 1-го уровня, оставшиеся в 1-м и 2-м модальных уравнениях для различных частот возбуждения. Видно, что остатки монотонно увеличиваются с увеличением параметра возбуждения; остатки в первом модальном уравнении больше, чем во втором модальном уравнении, и остатки являются самыми высокими среди трех случаев, в то время как остатки (частота возбуждения находится между двумя резонансными частотами) являются наименьшими.В целом результаты показали сходимость решений и доказали точность предложенного метода.

(a)

605 9068 9068


Нормализованная общая амплитуда	= 1	7,5	15	25
15	25
99,92	101,00	101,93	102,69
Решение 1-го уровня	100. 00	100,03	100,13	100,32
Решение 2-го уровня	100,00	100,00	100,00	100,00

9069


Нормализованная общая амплитуда

Решение нулевого уровня	99.79	100,44	96,43	79,43
Решение 1-го уровня	100,03	100,03	100,00	100,00
Решение 2-го уровня 100

0,05 9069

(a)


Нормализованный модальный вклад	= 1	15	25

1-й режим	99,94	99,88	99,67	99,54
99,67	99,54
2-ой режим
3-й режим	0,01	0,01	0,04	0,06

(b)

906

1-й режим

99.

99,78

96,03

78,20

2-й режим

0,36

0,19

3,56

20,25

3-й режим

0,05

5. Выводы
В этом исследовании были разработаны шаги аналитического решения для нелинейной многомодовой вибрации балки с использованием модифицированного подхода гармонического баланса и замены Виета.Используя предложенный метод, результаты нелинейной многомодовой вибрации балки могут быть получены без необходимости решения нелинейных уравнений. При моделировании был рассмотрен стандартный вариант балки с простой опорой. Проверены сходимости решений и модальные вклады. Теоретический результат, полученный с помощью предлагаемого метода, демонстрирует разумное согласие с результатами предыдущего метода численного интегрирования.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов относительно публикации данной статьи.
Благодарность
Работа, описанная в этой статье, была полностью поддержана грантом Городского университета Гонконга (проект № 7004362 / ACE).
(PDF) ОПРОС ОШИБОК УЧАЩИХСЯ 10 И 12 КЛАССА ПРИ ИСПОЛЬЗОВАНИИ ФОРМУЛ ВЬЕТЫ ДЛЯ РЕШЕНИЯ СООТВЕТСТВУЮЩИХ МАТЕМАТИЧЕСКИХ ЗАДАЧ ОШИБКИ УЧАЩИХСЯ 10 И 12 КЛАССОВ ПРИ ИСПОЛЬЗОВАНИИ ФОРМУЛ
VIETA ДЛЯ РЕШЕНИЯ СООТВЕТСТВУЮЩИХ МАТЕМАТИЧЕСКИХ ПРОБЛЕМ
European Journal of Education Studies — Volume 3 │ Issue 11│ 2017 305
Ссылки
1.Хао, Т. В. (2015). Алгебра 10 (Đại Số 10), Вьетнамское издательство
Образование.
2. Хао Т. В. (2015). Исчисление 12 (Giải tích 12), Вьетнамское издательство
Образование.
3. Херхольдт Р. и Сапире И. (2014). Анализ ошибок в младших классах
Математика — возможности обучения. Южноафриканский журнал детства
Education, Vol. 4, №1, 42-60.
4.Юпри, А. и Драйверс, П. (2016). Студенческие трудности при математизации слова
Задачи по алгебре. Евразийский журнал математики, науки и технологий
Образование, Том. 12, No. 9, 2481-2502.
5. Ньюман Н. А. (1977). Анализ ошибок школьников шестого класса при выполнении письменных
математических заданий. Бюллетень Викторианского института педагогических исследований, Vol. 39, 31-
43.
6. Поля Г. (1973). Как решить: новый аспект математического метода.Princeton,
N.J .: Princeton University Press. Пракитипонг.
7. Саварди, Х., Р., Х. и Шахрилл, М. (2014). Понимание математических
ошибок и заблуждений учащихся: случай повторных учащихся 11-го класса. Математика
Тенденции в образовании и исследования, Vol. 2014, 1-10.
8. Тхук П. Д. (2009). Методы преподавания математики в начальных школах, Ханой:
Издательство образования.
Условия лицензирования Creative Commons
Автор (ы) сохранят за собой авторские права на свои опубликованные статьи, согласившись с тем, что Creative Commons Attribution 4. 0 К их работе будут применяться условия Международной лицензии (CC BY 4.0)
. Согласно условиям этой лицензии, для членов сообщества
не требуется разрешения от автора или издателя на копирование, распространение, передачу или адаптацию содержания статьи с указанием надлежащей, заметной и недвусмысленной ссылки на авторов. таким образом, что
дает понять, что материалы используются повторно с разрешения Creative Commons License. Взгляды, мнения и выводы, выраженные в этой исследовательской статье
, являются взглядами, мнениями и выводами авторов.Издательская группа открытого доступа и Европейский журнал образовательных исследований
не несут ответственности за любые убытки, ущерб или обязательства, вызванные / возникшие в результате конфликта интересов, нарушений авторских прав и
неуместного или неточного использования любого рода. контент, связанный с исследовательской работой или интегрированный в нее. Все опубликованные работы соответствуют требованиям Open Access
Publishing и могут быть свободно доступны, распространяться, изменяться, распространяться и использоваться в образовательных, коммерческих и некоммерческих целях
под лицензией Creative Commons Attribution 4. 0 Международная лицензия (CC BY 4.0).
Формула Виета — Изучите формулу Виета для полиномов
Формулы Виета, иначе называемые законами Виэта, находят применение при связывании коэффициентов многочленов с суммами и произведениями их корней, а также с произведениями корней, взятых в группы. Его открыл Франсуа Вите. Простейшим применением формулы Вите является квадратичная формула Виете, которая используется специально в алгебре. Давайте подробно разберемся с формулой Виета в следующем разделе.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом в решении проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Забронируйте бесплатную пробную версию Класс
Что такое формула Виета?
Формулы Виета представляют собой набор уравнений, связывающих корни и коэффициенты многочленов. Различные формулы Виета для разных случаев представлены как,
Формула Виета для квадратичных вычислений: дано f (x) = ax ² + bx + c, если уравнение f (x) = 0 имеет корни f (x) = \ (r_1, r_2 \), то
\ (r_1 + r_2 = — \ frac {b} {a}, \ quad r_1 r_2 = \ frac {c} {a} \)
Формула Виета для обобщенных многочленов высшей степени: Пусть \ (P (x) = a_nx ^ n + a_ {n-1} x ^ {n-1} + \ cdots + a_0 \) будет многочленом с комплексными коэффициентами и степенью n , имеющие комплексные корни \ (r_n, r_ {n-1}, \ ldots, r_1 \). 2} \) = 22/1 = 22
Ответ: Сумма корней = 11; Произведение корней = 22
Пример 2: Сумма и произведение корней квадратного многочлена
p равны 9 и 20 соответственно.Также p (6) = 4. Определите многочлен p (x).
Решение:
Обратите внимание, что в этой задаче нам предоставили некоторую дополнительную информацию — значение полинома при конкретном значении x .
Используя формулу Виета, подставляя значения суммы и произведения, мы можем записать многочлен как p (x): k (x ² −9x + 20).
Теперь p (6) = 4 ⇒ k (6 ²-9 (6) + 20) = 4 ⇒ k (36-54 + 20) = 4 ⇒ 2k = 4 ⇒ k = 2.Примечание: как дополнительная информация позволила нам определить значение k . Следовательно, многочлен p (x): 2 (x ² — 9x + 20). Это означает, что p (x): 2x ² — 18x + 40.
Ответ: Многочлен p (x) = 2x ² — 18x + 40.

Теорема Виета

Дискриминант. Теорема Виета

Давайте попробуем разобраться,

Физический смысл дискриминанта:

Внеклассный урок — Теорема Виета

РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ — алгоритмы и примеры

Решение квадратного уравнения через дискриминант

Теорема Виета для решения квадратного уравнения

Пример решения квадратного уравнения

кубических уравнений: красота алгебры | Автор Сухрид Саха | Cosmus Mathematicus

Решение кубических и четвертых уравнений | Марко Тавора, доктор философии

Кубические уравнения

Уравнения четвертой степени

Кубических уравнений

Пример

Пример 1

Пример 2

Аналитическое решение для нелинейной многомодовой вибрации луча с использованием модифицированного подхода гармонического баланса и замены Виета

1. Введение

2. Основное уравнение

3. Модифицированная процедура решения с использованием подстановки Виета

4. Результаты и обсуждения

5. Выводы

Конфликт интересов

Благодарность

Формула Виета — Изучите формулу Виета для полиномов

Что такое формула Виета?

Пример 2: Сумма и произведение корней квадратного многочлена

Добавить комментарий Отменить ответ