уравнения Виета
Теорема Виета (точнее, теорема, обратная теореме Виета) позволяет сократить время на решение квадратных уравнений. Только надо уметь ею пользоваться. Как научиться решать квадратные уравнения по теореме Виета? Это несложно, если немного порассуждать.
Сейчас мы будем говорить только о решении по теореме Виета приведенного квадратного уравнения.Приведенное квадратное уравнение — это уравнение, в котором a, то есть коэффициент перед x², равен единице. Не приведенные квадратные уравнения решить по теореме Виета тоже можно, но там уже, как минимум, один из корней — не целое число. Их угадывать сложнее.
Теорема, обратная теореме Виета, гласит: если числа x1 и x2 таковы, что
то x1 и x2 — корни квадратного уравнения
При решении квадратного уравнения по теореме Виета возможны всего 4 варианта. Если запомнить ход рассуждений, находить целые корни можно научиться очень быстро.
I. Если q — положительное число,
это означает, что корни x1 и x2 — числа одинакового знака (поскольку только при умножении чисел с одинаковыми знаками получается положительное число).
I.a. Если -p — положительное число, (соответственно, p<0), то оба корня x1 и x2 — положительные числа (поскольку складывали числа одного знака и получили положительное число).
I.b. Если -p — отрицательное число, (соответственно, p>0), то оба корня — отрицательные числа (складывали числа одного знака, получили отрицательное число).
II. Если q — отрицательное число,
это значит, что корни x1 и x2 имеют разные знаки (при умножении чисел отрицательное число получается только в случае, когда знаки у множителей разные). В этом случае x1+x2 является уже не суммой, а разностью (ведь при сложении чисел с разными знаками мы вычитаем из большего по модулю меньшее). Поэтому x1+x2 показывает, на сколько одно отличаются корни x1 и x2, то есть, на сколько один корень больше другого (по модулю).
II.a. Если -p — положительное число, ( то есть p<0), то больший (по модулю) корень — положительное число.
II.b. Если -p — отрицательное число, (p>0), то больший (по модулю) корень — отрицательное число.
Рассмотрим решение квадратных уравнений по теореме Виета на примерах.
Решить приведенное квадратное уравнение по теореме Виета:
Здесь q=12>0, поэтому корни x1 и x2 — числа одного знака. Их сумма равна -p=7>0, поэтому оба корня — положительные числа. Подбираем целые числа, произведение которых равно 12. Это 1 и 12, 2 и 6, 3 и 4. Сумма равна 7 у пары 3 и 4. Значит, 3 и 4 — корни уравнения.
В данном примере q=16>0, значит, корни x1 и x2 — числа одного знака. Их сумма -p=-10<0, поэтому оба корня — отрицательные числа. Подбираем числа, произведение которых равно 16. Это 1 и 16, 2 и 8, 4 и 4. Сумма 2 и 8 равна 10, а раз нужны отрицательные числа, то искомые корни — это -2 и -8.
Здесь q=-15<0, что означает, что корни x1 и x2 — числа разных знаков. Поэтому 2 — это уже не их сумма, а разность, то есть числа отличаются на 2. Подбираем числа, произведение которых равно 15, отличающиеся на 2. Произведение равно 15 у 1 и 15, 3 и 5. Отличаются на 2 числа в паре 3 и 5. Поскольку -p=2>0, то бОльшее число положительно. Значит, корни 5 и -3.
q=-36<0, значит, корни x1 и x2 имеют разные знаки. Тогда 5 — это то, насколько отличаются x1 и x2 (по модулю, то есть пока что без учета знака). Среди чисел, произведение которых равно 36: 1 и 36, 2 и 18, 3 и 12, 4 и 9 — выбираем пару, в которой числа отличаются на 5. Это 4 и 9. Осталось определить их знаки. Поскольку -p=-5<0, бОльшее число имеет знак минус. Поэтому корни данного уравнения равны -9 и 4.
www.uznateshe.ru
«Теорема Виета. Применение теоремы Виета к решению квадратных уравнений общего вида»
Цель урока: Сформулировать приём, позволяющий свести решение уравнения общего вида к нахождению целых корней вспомогательного уравнения и решение с применением теоремы Виета.
Образовательные задачи урока: Обеспечить закрепление теоремы Виета. Научить учащихся решать квадратные уравнения общего вида, с использованием теоремы Виета. Привить навыки устного решения квадратных уравнений общего вида.
Воспитательные задачи урока: Способствовать выработке у школьников умения обобщать факты, содействовать стремлению к личностному росту учащихся; развивать самостоятельность путём использования ИКТ для выполнения упражнений, навыки групповой и парной работы, самооценку собственных достижений.
Формы работы на уроке:
- групповая работа
- индивидуальная работа
- фронтальная работа
- парная работа
Методы работы на уроке:
- компьютерное состязание (тренажёр на время)
- взаимопроверка
- беседа
- создание проблемной ситуации и открытие знаний в результате проблемного диалога.
- работа с электронными учебниками.
- поощрение
- работа в тетрадях
План урока:
|
№ |
Этап урока |
Содержание (цель) этапа |
Время (мин) |
Цоры |
|
1 |
Организационный момент (этап самоопределение деятельности). |
Поставлена цель урока. На этапе самоопределения к деятельности были созданы условия для возникновения внутренней потребности включения в деятельность. А также была обозначена содержательная область. В работу были включены принципы: деятельности, непрерывности, психологической комфортности. Созданы условия для успешной совместной деятельности (Работа на уроке оценивается бальной системой, ведётся электронный журнал). |
1 |
Презентация |
|
2 |
Проверка домашнего задания |
Фронтальная и индивидуальная проверка и коррекции знаний и умений учащихся. |
5 |
Проверка домашнего задания по электронному журналу |
|
Фронтальный опрос правил (парная работа) |
Презентация |
|||
|
3 |
Устный счёт по выбранным цветам (жёлтые и оранжевые по очереди) на ЭВМ (электронный тренажёр) и тест (Microsoft Office Excel, составленный учителем) |
Предварительная подготовка к восприятию новой темы на уроке |
5 |
Математика 5-11 (Практикум. Лаборатория. Тренажёр для устного счёта |
|
4 |
Создание проблемной ситуации. |
Этап актуализации знаний и постановки проблемы. Чётко были обозначены знания умения и навыки для построения нового способа действия. Учащиеся выявили и зафиксировали в речи причины затруднения. Поставили цель своей деятельности. Использовались такие принципы как, деятельности, вариативности, творчества. |
2 |
Листки с примером |
|
5 |
Проблемно-диалогическое обучение Объяснение новой темы |
Совместно с детьми «открывается» способ решение общего квадратного уравнения через вспомогательное уравнение. Открытие детьми “нового” знания происходило через проблемный диалог. Учащиеся подходили к выбору метода решения учебной задачи, выдвигали и обосновывали свои собственные гипотезы. Ярко выражены следующие принципы: минимакса, деятельности, вариативности, психологической комфортности. |
5 |
На доске |
|
6 |
Инструкция к решению |
Воспроизведение знаний учащимися, проговаривание в устной речи |
2 |
Презентация |
|
7 |
Разбор проблемной задачи |
Первичное закрепление знаний, фронтальная работа с классом по усвоению новой темы |
2 |
Презентация |
|
8 |
Решение примеров из учебника |
Разбор примера на доске учителем, Работа учащихся на доске, выявление затруднений. |
На доске |
|
|
9 |
Самостоятельная работа учащихся |
Закрепление знаний учащихся (индивидуальная работа учащихся). На данном этапе уч-ся выполняли задания на новый способ действия. Была создана ситуация успеха. Индивидуальная работа учащихся, самооценка и коррекция знаний. |
|
|
|
10 |
Рефлексия |
В заключение урока была организована самооценка собственной деятельности. На данном этапе были ярко выражены основные идеи урока, подведены итоги работы в группах и представлены вывода о значимости нового способа решения уравнений для дальнейшего обучения. |
2 |
|
|
11 |
Результаты работы учащихся |
Представление результатов по этапам урока в электронной таблице. Выставление оценок, распечатка результатов. |
Презентация. Электронный журнал |
Конспект урока:
Организационный момент. Обеспечение техники безопасности, постановка цели урока. Создание условий для успешной совместной деятельности (Работа на уроке оценивается бальной системой, ведётся электронный журнал).
Проверка домашнего задания (электронный журнал к уроку). ( Слайд №3 «ссылка на проверка домашнего задания»).
Домашнее задание было трёх уровней: А, В и С.
Задание на дом: §29
Задачи трёх уровней: (Решения задач даны в Microsoft office на компьютерах для сверки с домашним заданием учащихся)
Уровень А.
1. Найдите сумму и произведение корней уравнения:А)
Б)
Решение:
А) по теореме Виета:
Ответ: сумма корней равна 16, а произведение равно 28.
Б) по теореме Виета:
Ответ: сумма корней равна 12, а произведение равно -45.
2.Пользуясь теоремой обратной теореме Виета, составьте квадратное уравнение, корни которого равны 2 и 5.
Решение: -общий вид приведённого квадратного уравнения.
,
Уравнение имеет вид:
Если умножить обе части уравнения на какое-нибудь число, то получим новое равносильное уравнение. Например:
Уровень В.
1. Найдите сумму и произведение корней уравнения:
А)
Б)
Решение:
А) По теореме Виета
Б)
Приведём к виду . Для этого разделим обе части уравнения на 2, получим:
2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны и
Решение:
Уравнение имеет вид:
Уровень С. (2балла)
Пример.
При каких значениях параметра a сумма квадратов корней уравнения равна 4.
Разбор задания С. (Слайд №3 «ссылка на уровень С»).
Уровень С.
Пример.
При каких значениях параметра a сумма квадратов корней уравнения равна 4.
Решение: По условию задачи уравнение должно быть разрешимо, т.е. и где — корни уравнения.
Значит:
так как по теореме Виета
Тогда
Ответ: a=0
Устный опрос учащихся (взаимопроверка и выставление баллов в карточку учёта результатов, в ходе урока результаты заносятся в электронный журнал).
Учитель: (параллельно идёт слайд №4 с вопросом)
Какое уравнение называется квадратным.
Учащиеся:
Квадратным уравнением называется уравнение , где - заданные числа
Учитель (параллельно идёт слайд №4 с вопросом)
Какое квадратное уравнение называется приведённым.
Учащиеся:
Квадратным уравнение вида называется приведённым. В этом уравнении старший коэффициент равен единице.
Учитель (параллельно идёт слайд №4 с вопросом)
Как привести квадратное уравнение к приведённому виду.
Учащиеся:
Всякое квадратное уравнение может быть приведено к виду делением обеих частей уравнения на
Учитель (параллельно идёт слайд №4 с вопросом)
Сформулируйте теорему Виета
Учащиеся:
Если и - корни уравнения то справедливы формулы , , т.е сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Учитель (параллельно идёт слайд №4 с вопросом)
Сформулируйте теорему, обратную теореме Виета
Учащиеся:
Если числа таковы, что , , то и - корни уравнения
Учитель (параллельно идёт слайд №4 с вопросом)
Зачем нужна теорема Виета.
Учащиеся:
- Найти сумму и произведение корней квадратного уравнения, не решая его;
- Зная один корень, найти другой;
- Определить знаки корней уравнения;
- Подобрать корни уравнения, не решая его
Устный счёт с использованием электронного тренажёра (в начале оранжевые карточки, затем жёлтые, в ходе устного счёта «компьютерное тестирование» проходят все учащиеся класса). Математика 5-11 (Практикум. Лаборатория. Тренажёр для устного счёта).
(фиксируется время 2 мин. Решить приведённые квадратные уравнения, предложенные случайным образом компьютером, после работы компьютер выдаёт протокол результатов, и дети заносят их в карточку учёта результатов, в ходе урока результаты заносятся в электронный журнал). Учащиеся за партами работают с таблицей на карточках и проверяют совместно с учителем на электронной таблице, которая показывает правильность найденных ответов.
При выполнения первые выполняют 1-4 примеры, последующие 5-8 примеры: (Слайд№10 «ссылка переход к тесту»)
|
№ |
Уравнение |
p |
q |
x1 |
x2 |
|
1 |
х2+px+6=0 |
|
6 |
-2 |
|
|
2 |
х2+px+6=0 |
|
6 |
3 |
|
|
3 |
х2+3x+q=0 |
3 |
|
-4 |
|
|
4 |
х2+px+15=0 |
|
15 |
5 |
|
|
№ |
Уравнение |
p |
q |
x1 |
x2 |
|
5 |
х2+px-8=0 |
|
-8 |
-2 |
|
|
6 |
х2-3x+q=0 |
-3 |
|
1 |
|
|
7 |
х2+px-15=0 |
|
-15 |
-5 |
|
|
8 |
х2-3x+q=0 |
-3 |
|
-2 |
|
Проблемное задание (работа в группах), задания на красных листочках.
Учитель: Решите уравнение:
(Слайд№11)
Учащиеся решают разными способами, которые известны (через дискриминант, кто-то пытается через теорему Виета). Решая теоремой Виета, учащиеся получают .
Такие числа подобрать очень сложно (возникает проблема у учащихся).
Учитель:
Подобрать два числа, сумма которых равна (), а произведение корней равно () не так просто. Для преодоления возникающей трудности мы будем использовать приём, позволяющий свести задачу к нахождению целых корней вспомогательного уравнения.
Итак, открыли тетради, запишем дату и тему сегодняшнего урока. (Слайд№12)
(Объяснение нового материала на доске с использованием проблемно-диалогического метода).
Пусть требуется решить квадратное уравнение
(Для него ).
Умножив обе части данного уравнения на , перепишем его в виде
Обозначим , получим уравнение. Это приведённое квадратное уравнение. В полученном уравнении, т.е.
т.е. . Теперь видно, что для решения исходного уравнения достаточно решить вспомогательное квадратное уравнение и его корни разделить на . Показывается связь между уравнениями и
Для практического применения этого приёма мы формулируем его как инструкцию: «перебросить» коэффициент в свободный член, найти корни нового уравнения и разделить их на a.(Слайд№13)
Покажем это на конкретных примерах. (Слайд№14) Возьмём наше уравнение
Запишем вспомогательное уравнение , имеющее корни Следовательно, исходное уравнение имеет корни
Далее идёт решение №444 (1,3) с использованием теоремы Виета. Первый пример учитель решает у доски сам, далее у доски решают учащиеся 3 пример и пример из карточки. Решите уравнения:
У каждого на парте имеются карточки с заданиями.
Инструкция: «перебросить» коэффициент в свободный член, найти корни нового уравнения и разделить их на a.
Ребятам предлагается дополнительно работать с электронным учебником Алгебра 7-11. Электронный учебник справочник. Квадратные уравнения. Сильные учащиеся обычно сразу же обращаются к компьютерам.
Идёт самостоятельная работа за компьютерами и за партами. Индивидуальная работа учащихся, самооценка и коррекция знаний с использованием ИКТ.
Рефлексия: В заключение урока была организована самооценка собственной деятельности. На данном этапе были ярко выражены основные идеи урока, подведены итоги работы в группах и представлены вывода о значимости нового способа решения уравнений для дальнейшего обучения.
На уроке в качестве «яркого пятна» используется «Линия времени» электронного учебника «Математика 5-11. Практикум. Интерактивная линия жизни учёных математиков». (Слайд№15)
Подведение итогов урока:
Представление результатов по этапам урока в электронной форме: в виде таблиц и диаграмм.
Выставление оценок, распечатка результатов
Материалы к уроку
urok.1sept.ru
теорема Виета проект (разработка)
Муниципальное казенное образовательное учреждение
«Очкуровская средняя общеобразовательная школа»
Николаевского муниципального района Волгоградской области
Теорема Виета
Выполнила: Оноприенко Кристина,
обучающаяся 8 класса
МКОУ «Очкуровская СОШ»
Николаевского района
Руководитель: Е.А.Бульба
с. Очкуровка
2015
Оглавление
Введение……………………………………………………………………… ……3
Основная часть
1.Историческая справка……………………………………………………….4
2.Докозательство теоремы Виета……………………………………………..6
3.Состаление блока уравнений решаемых по теореме Виета……………….8
4.Составлеие тренажера………………………………………………………10
Заключение
Практическая значимость проекта………………………………………12
Выводы…………………………………………………………………….13
Список источников информации…………………….…………………………14
Приложение……………………………………………………………………..15
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — дробь уж готова!
В числителе с, в знаменателе а.
А сумма корней тоже дроби ровна.
Хоть с минусом дробь, что за беда!
В числителе b, в знаменателе а.
Введение
Актуальность темы проекта: Применение теоремы Виета является уникальным приемом для решения квадратных уравнений устно. В учебнике очень мало квадратных уравнений, решаемых по теореме Виета. Я и мои одноклассники допускаем ошибки.
Объектом исследования является теорема Виета , как неотъемлемая часть решения квадратных уравнений на уроках алгебры .
Предмет исследования – теорема Виета и составление блока уравнений для закрепления навыка решения квадратных уравнений.
Гипотеза: я предположила, что научиться безошибочно решать уравнения по теореме Виета можно, для этого нужен применяя тренажер.
Цель проекта: составить тренажер уравнений, решаемых по теореме Виета.
Задачи:
узнать историю открытия теоремы Виета;
провести исследование зависимости коэффициентов квадратного
уравнения и произведения и суммы его корней.
научиться доказывать теорему Виета;
самостоятельно составить уравнения, решаемые по теореме Виета
оформить блок уравнений на бумажном носителе и составить тренажер в электронном виде
предложить одноклассникам тренажер для решения уравнений по теореме Виета
Методы:
сравнение результатов самостоятельной работы до проекта и после тренировки решение квадратных уравнений применяя теорему Виета
изучение и анализ электронных источников и литературы
самостоятельная работа по составлению блока уравнений и тренажера

1.Исторические сведения
Франсуа Виет родился в 1540 году на юге Франции в небольшом городке Фантене-ле-Конт.
Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.
Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей и переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы. Он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вел дружескую переписку.
В 1571 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.
В 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.
В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Обретя покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи.
Виет изложил программу своих исследований и перечислил трактаты, объединенные общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом «Введение в аналитическое искусство». Основу своего подхода Виет называл видовой логистикой, он четко разграничивал числа, величины и отношения, собрав их в некую систему «видов». В эту систему входили, например, переменные, их корни, квадраты, кубы, квадрато-квадраты и т. д. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных — согласные.
Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.
Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: «Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D».
В трактате «Дополнения к геометрии» он стремился создать некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвертой степеней. Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.
Математиков столетиями интересовал вопрос решения треугольников, так как он диктовался нуждами астрономии, архитектуры, геодезии. Виет первым явно сформулировал в словесной форме теорему косинусов, хотя положения, эквивалентные ей, эпизодически применялись с первого века до нашей эры. Известный ранее своей трудностью случай решения треугольника по двум данным сторонам и одному из противолежащих им углов получил у Виета исчерпывающий разбор. Глубокое знание алгебры давало Виету большие преимущества. Причем интерес его к алгебре первоначально был вызван приложениями к тригонометрии и астрономии. Не только каждое новое применение алгебры давало импульс новым исследованиям по тригонометрии, но и полученные тригонометрические результаты являлись источником важных успехов алгебры. Виету, в частности, принадлежит вывод выражений для синусов (или хорд) и косинусов кратных дуг.
В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался сеньор де ла Биготье. В придворных новостях маркиз Летуаль писал: «…14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых ученых математиков века умер… в Париже. Ему было более шестидесяти лет».
2 .Доказательство теоремы Виета





3.Составление блока уравнений и электронного тренажера
х2 + 17х — 38 = 0,
х2 — 16х + 4 = 0,
3х2 + 8х — 15 = 0,
7х2 + 23х + 5 = 0,
х2 + 2х — 3 = 0,
х2 + 12х + 32 = 0,
х2 — 7х + 10 = 0,
х2 — 2х — 3= 0,
х2 + 12х + 32 = 0,
2х2 — 11х + 15 = 0,
3х2 + 3х — 18 = 0,
2х2 — 7х + 3 = 0,
х2 + 17х — 18 = 0,
х2 — 17х — 18 = 0,
х2 — 11х + 18 = 0,
х2 + 7х — 38 = 0,
х2 — 9х + 18 = 0,
х2 — 13х + 36 = 0,
х2 — 15х + 36 = 0,
х2 — 5х — 36 = 0.
х2 + х – 2 = 0
х2 + 2х – 3 =0
х2 — 3х + 2 =0
х2 — х – 2 = 0
х2 — 2х – 3 = 0
х2 — 3х – 4 = 0
x2 +17x -18=0
x2 + 23x – 24=0
x2 – 39x-40=0
x2 – 37x – 38=0
x2 – 3x – 10 = 0
x2 – 5x + 3 = 0
x2 + 8x – 11 = 0
x2 + 6х + 5 = 0
x2 – x – 12 = 0
x2 + 5x + 6 = 0
x2 + 3x – 10 = 0
x2 – 8x– 9 = 0
х 2 + х – 56 = 0
х 2 – 19х + 88 = 0
х 2 – 4х – 4 = 0
x 2 -15х+14=0
x 2 +8х+7=0
x2+9х+20=0
x2 +18х -11 = 0
x2 +27х – 24 = 0
5х2 +10х – 3 = 0
3х2 — 16х +9 = 0
x2 +18х -11 = 0
x2 +27х – 24 = 0
 -4х-21=0
-4х-21=0 -4х-21=0
-4х-21=0x2-15х+56=0
x2-4х-60=0
x2+5х+6=0
 +2х-3=0
+2х-3=0x2+18х+81=0
 -х-20=0
-х-20=0x2+4х+21=0
x2-10х-24=0
x2+х-56=0
x2-х-56=0
x2+3х+2=0
x2+5х-6=0
x2-18х+81=0
x2-9х+20=0
x2 -5х+6=0
x2-4х-21=0
-x2 -7х+6=0
x2-15х+56=0
х2 – 3х + 2 = 0
х2 – 4х + 3 = 0
х2 – 2х + 4 = 0
х2 – 2х + 5 = 0
х2 – 2х + 6 = 0
х2 – 11х + 24 = 0
х2 + 11х – 30 = 0
х2 + х – 12 = 0
x2 – 6х + 8 = 0
х2 – 15х + 14 = 0
x2 – 15x + 14 = 0
x2+ 4 х -21 =0
х2+ х – 42 =0
х2 – х – 20 =0
х2+ 4 х -32=0
х2— 2х – 35 =0
х2+ х — 20 =0
х2+ 7 х + 10 =0
х2— х — 6=0
х2+ 2 х +0=0
х2+ 6 х+0 =0
х2+ 3х — 18=0
х2+ 5 х -24=0
х2— 2 х — 24=0
х2 – 15х + 14 = 0
х2 + 8х + 7 =0
х2+ 9х – 20=0
х2 – 6х — 7 = 0
х2 + 3х — 10 = 0
х2 – х — 12 = 0
3.Тренажер
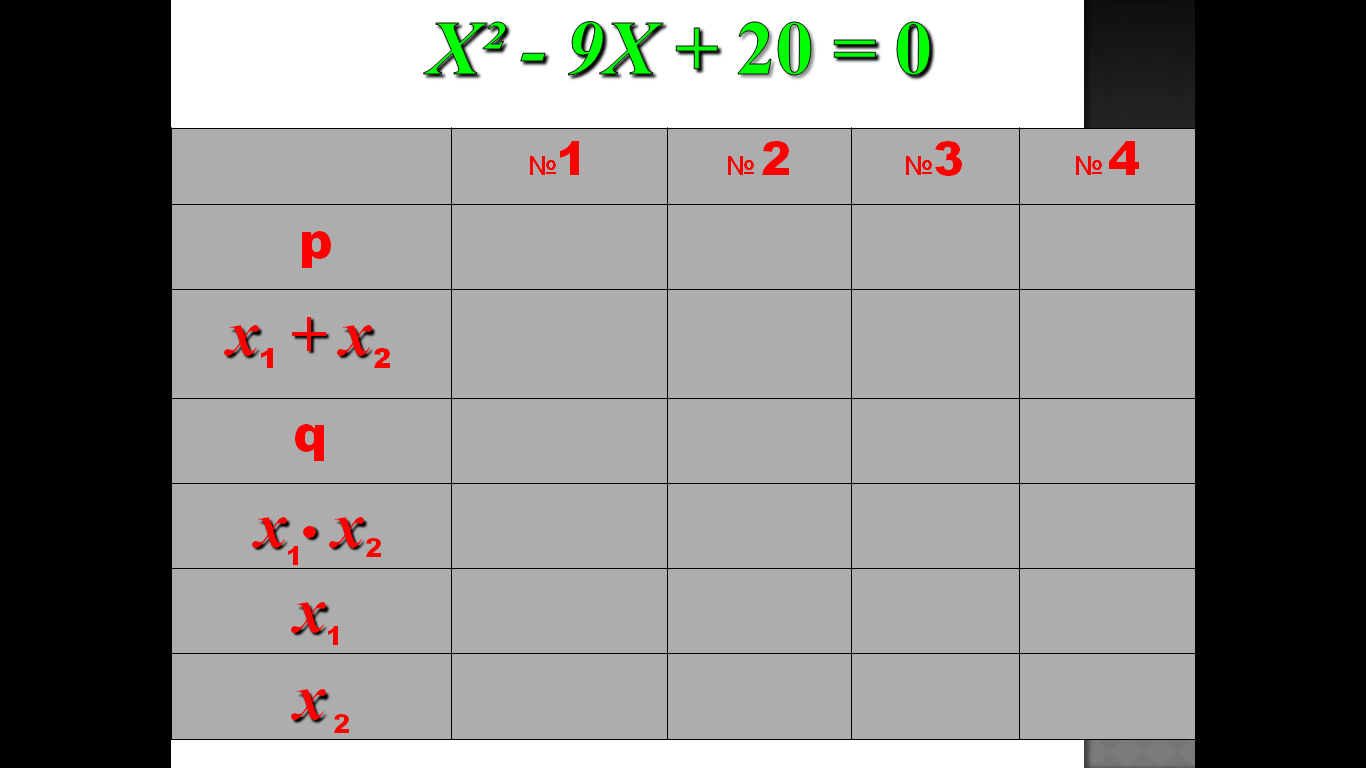
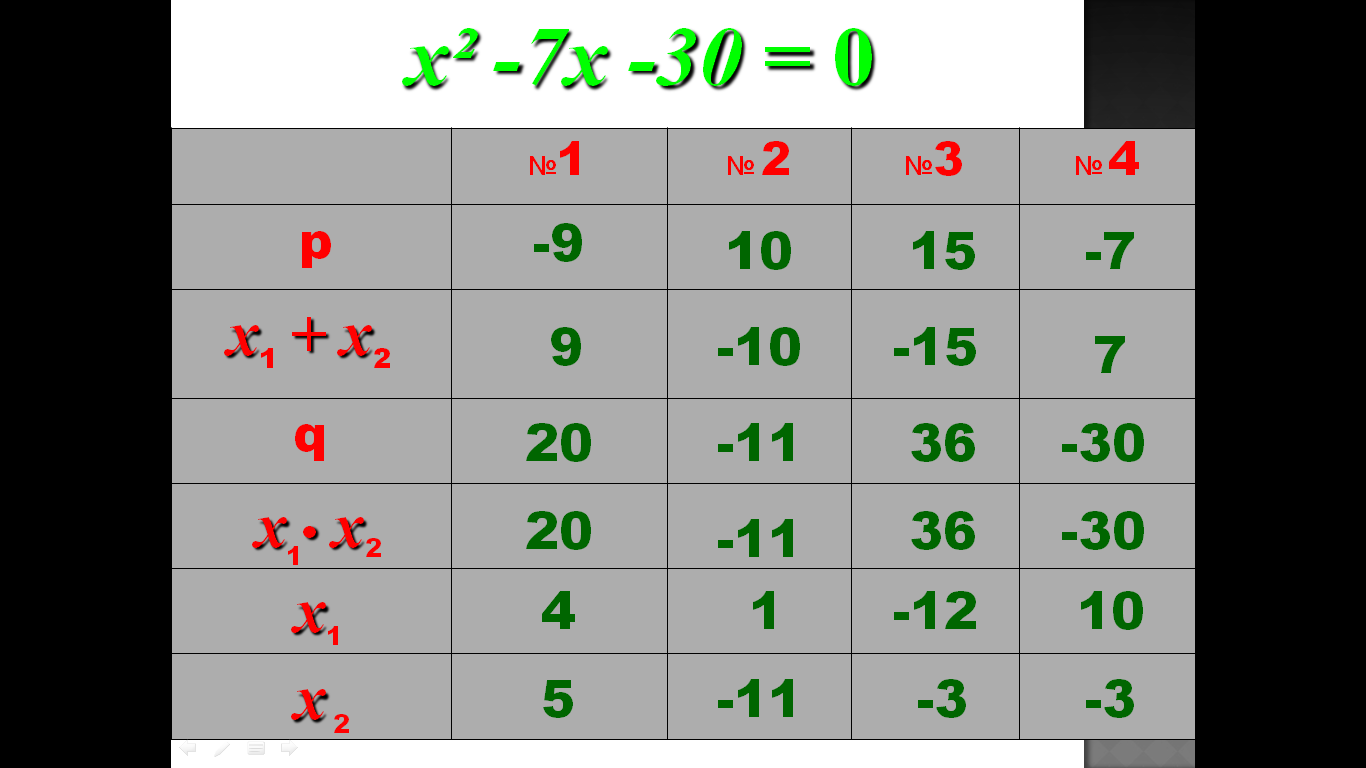
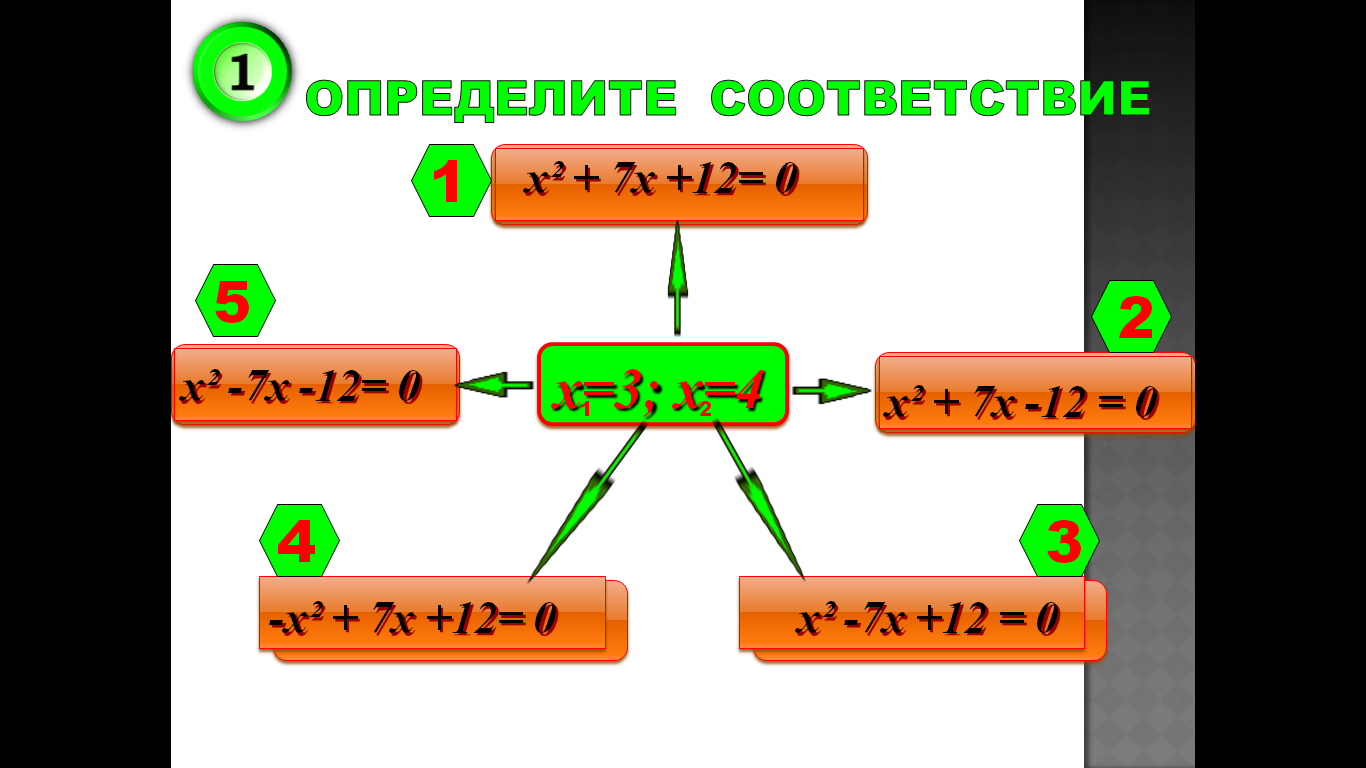
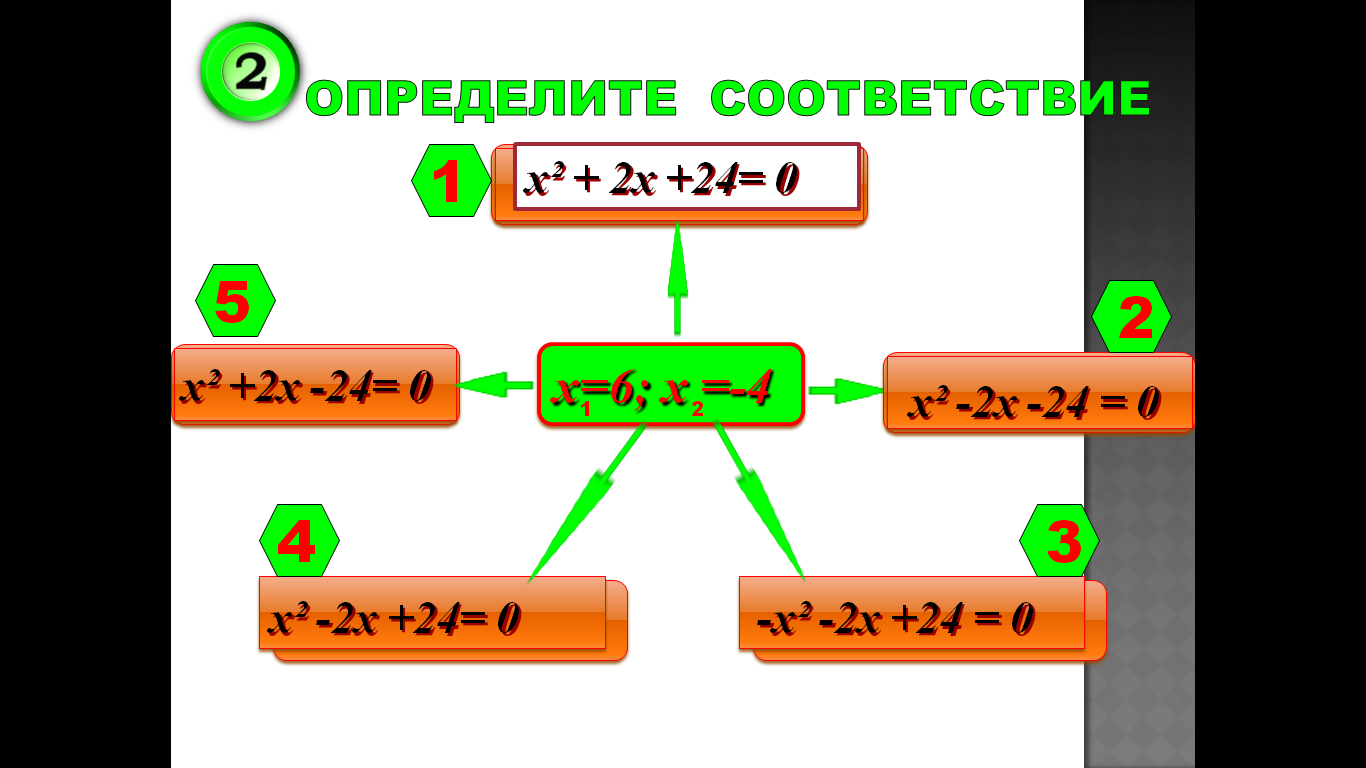
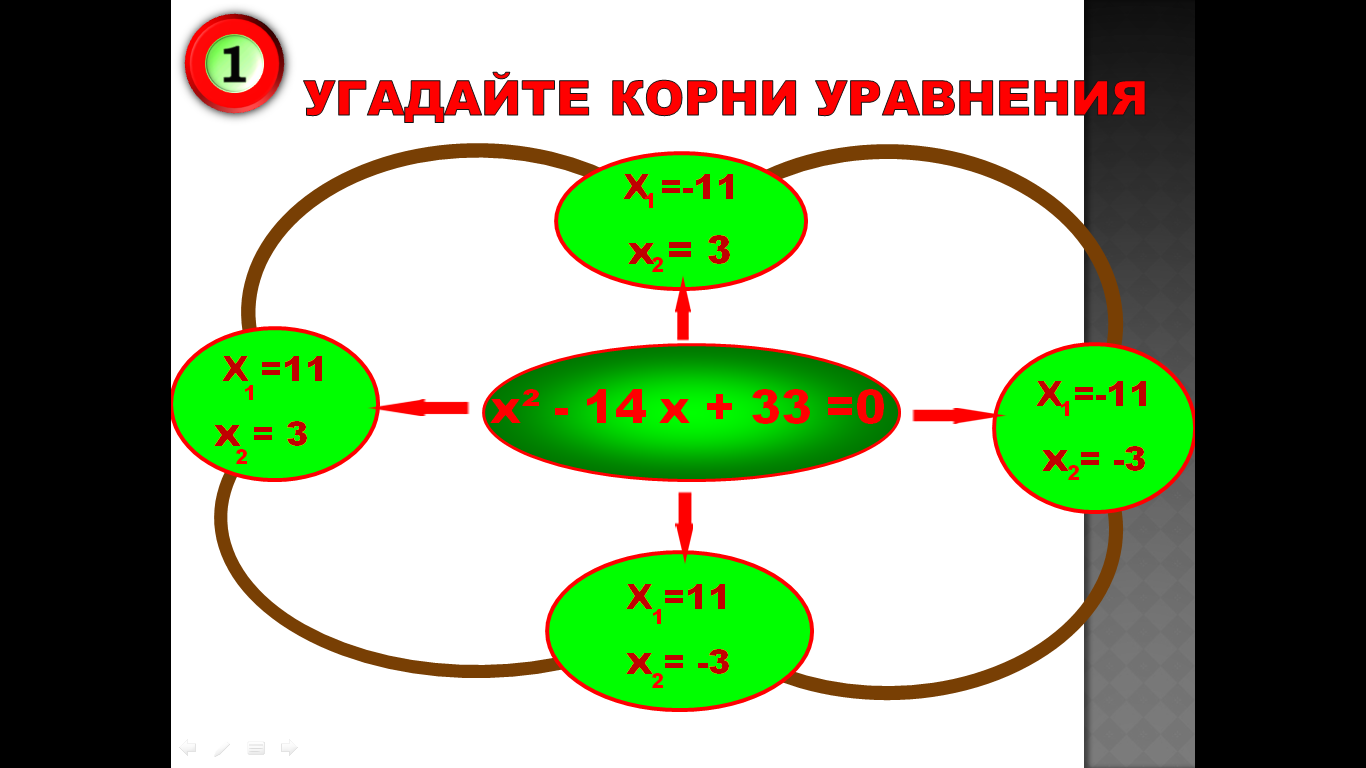
4.Практическая значимость проекта
Применение, а уроках алгебры 8 класса и при итоговом повторении ОГЭ
Выводы:
Результат моего труда – создан блок квадратных уравнений решаемых по теореме Виета.
Я увлеклась работой, проще всего было составить квадратные уравнения, в которых свободный член находится по таблице умножения. Теперь я не только безошибочно нахожу корни уравнения по теореме Виета, но и применяю ее при проверке решения любого квадратного уравнения.
Используя тренажер, я и мои одноклассники научилась решать квадратные уравнения, применяя теорему Виета.
Список источников информации:
Список литературы
Алгебра 8 класс: учебник для общеобразовательных учреждений. Г.В.Дорофеев, С.Б.Суворова
Дидактические материалы по алгебре для 8 класса. В.И.Жохов, Ю.Н.Макарычев, Н.Г.Миндюк. М.: Просвещение, 2000.
Математика. 8 класс: дидактические материалы к учебнику «Математика 8. Алгебра» / под ред. Г. В. Дорофеева. – М. : Дрофа, 2012г.\
Государственная итоговая аттестация. 9 класс. Математика. Тематические тестовые задания./Л.Д. Лаппо, М.А. Попов/-М.: Издательство « Экзамен », 2011
Интернет ресурсы
2.2 http://fcior.edu.ru/card/3726/kvadratnoe-uravnenie.html
2.3 http://kopilkaurokov.ru/matematika/uroki/107955
2.4 http://nsportal.ru/shkola/algebra/library/2012/12/10/razrabotki-urokov-po- teme-teorema-vieta
2.5 http://gigabaza.ru/doc/40685.html
Приложение
Этапы реализации проекта
Этапы
Методы исследования
Содержание работы
Планируемый результат
1.Информационный
Сбор информации, ее анализ
Изучение литературы
Материал для теоретической части проекта
2.Организационный
Анализ, обобщение
Разработка блока уравнений
Материал для работы
3. Технологический этап
Подбор уравнений
Составление тренажера
Тренажер
4. Заключительный
Обобщение опыта
Выводы о проделанной работе, оформление проекта
Проект. Оформление коллекции. Мастер-класс. Участие в конкурсе.
infourok.ru
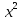 -4х-21=0
-4х-21=0