{3x}=1$.

Второй замечательный предел, следствия, примеры

Второй замечательный (особый) предел часто вызывает трудности у студентов, хотя сам предел довольно прост и понятен на практике. Он позволяет раскрывать неопределенности вида единица в степени бесконечность . Замечательный предел имеет следующий вид

где «е»-экспонента.

Следствия второго замечательного предела

1)

2)
3)
4)
5)
6)

На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в простой способ не решить.

Примеры на замечательный предел

Рассмотрим некоторые примеры из сборника А.В. Тевяшев, А.Г. Литвин, Г.М. Кривошеева и др.»Высшая математика в примерах и задачах. Ч.5 Тесты» (Харьков, 2007, ст. 99).

Пример 6.1. Найти предел функции
а)

Решение.
Преобразуем функцию к виду при котором возможно применить формулу замечательного предела

В результате можем применить правило замечательного предела

 

б)

Решение.
Подобно предыдущему примеру превращаем функцию в скобках чтобы применить замечательный предел

Нужно отметить, что в этом примере и во многих подобных константы в степенях, как правило вклада не несут. Функцию можно расписать следующим образом

Предел умышленно расписан в виде произведения двух множителей чтобы Вы убедились что константы в степенях вклада не несут. Их цель запутать Вас, если плохо знаете теоретический материал или сомневаетесь в правильности решения. Во всех последующих примерах мы не будем расписывать примеры на произведение двух границ, однако помните, что они не меняют конечного результата (вклад — множитель единица).

————————————

в)

Решение.
Выполняем преобразование заданной функции

Запись в таком виде сделана специально, потому что степень нужно свести к подобному виду

В такой простой способ получили искомый предел функции. В дальнейшем необходимые замены или подсказки будут выделены цветом из общего решения.

 

г)

Решение.
Выполним замену переменных в пределе

и определенные преобразования для нахождения предела

Бывают случаи, когда прямо применить правило второго замечательного предела довольно сложно, в таких ситуациях используйте простые замены которые Вам понятны и позволяют в быстрый способ найти предел.

 

Пример 6. 2 Вычислить предел функции

а)

Решение.
Сводим функцию к правилу замечательного предела

Подставляем и вычисляем, выполняя нужные манипуляции с показателями

 

в)

Решение.
За известным уже алгоритмом преобразуем функцию

Применяя определение второго важного предела находим

 

Пример 6. 3 Определить предел функции
б)

Решение.
Сведем функцию для применения замечательного предела

Подставляем в границу и упрощаем

 

г)

Решение.
«Как найти предел ? — скажете Вы, ведь переменная равна минус бесконечности.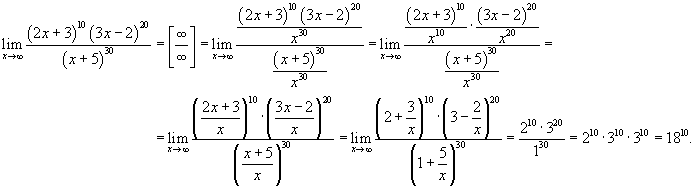
В этом примере видим что аргумент стремится к минус бесконечности, кроме того функция в скобках следует не до единицы, а до 2 при больших аргументах.

Учитывая что степень отрицательный получим следующее значение предела

Во всех примерах второго замечательного предела следует сначала проверять условие что выражение в скобках стремится к единице. Если нет, то предел функции в зависимости от степени будет равен или нулю или бесконечности. Те из Вас кто часто решает примеры такие проверки осуществляет автоматически. Остальные сводят границу в экспоненте в определенном степени, но все равно вылезает множителем или ноль или бесконечность. В конечном варианте правы все, однако в первом случае тратится гораздо меньше времени, которое так необходима на контрольных работах, тестах, ВНО. Поэтому выбирайте для себя простой путь и делайте в обучении правильные выводы.

 

Пример 6. 5 Найти предел функции
а)

Решение.
Заданный пример на вид отличается от предыдущих, однако решение получаем по такой же схеме. Выполняем преобразования функции в скобках под правило замечательного предела

Осталось в степени выделить обратный множитель

и подставить в границу

По такой схеме вычисляйте все подобные пределы, она проста и не требует дополнительных пояснений.

————————————

в)

Решение.
К рассматриваемому примеру великих преобразований делать не нужно. Он имеет достаточно простую запись и решение осуществляем в одну строку

Практикуйте с подобными пределами, используйте удобные для себя схемы сведения задач под необходимое правило. Не бойтесь делать ошибки — без них обучение не обходится!

Практика. Математика. Пределы (lim). Второй замечательный предел. | Vseznayka

Продолжаем цикл наших занятий по пределам. Сегодня у нас пойдёт речь о втором замечательном пределе. С первым они отличаются значительно, можно сказать что совсем ничего общего не имеют, кроме того что оба «замечательные». В плане решения он чуточку сложнее, это нас не должно останавливать, ведь знать и применять его действительно необходимо студентам имеющим дело с матаном. В общем нас сегодня ждёт интересный материал. Приступим…

Запишем, как выглядит второй замечательный предел математически.

Попробуйте пока что определить вид неопределённости которую он раскрывает, чуть позже мы это обговорим. Стоит упомянуть, что буковка «е» это иррациональное число. e=2,718…

Попробуйте пока что определить вид неопределённости которую он раскрывает, чуть позже мы это обговорим. Стоит упомянуть, что буковка «е» это иррациональное число. e=2,718…

Существует другой вид записи.

Вместо «икса» может находиться любая другая функция.

Вместо «икса» может находиться любая другая функция.

Запишем всё в виде равенства.

Так-то лучше.

Так-то лучше.

О следствиях думаю говорить не стоит, их как всегда великое множество. Стоит затронуть, какие всё же неопределённости он раскрывает. Это:

Приступим к решению примеров.

Логично будет рассмотреть второй вид неопределённости для начала (единица в степени бесконечность), так как разобраться с ним легче.

Анализируем. Сравниваем что наш пример с формулой, видим что в числителе у нас двойка вместо единицы, ничего, исправим, просто перекинем её в знаменатель знаменателя. А вот в степени нам нужна та же функция что и в знаменателе.

Анализируем. Сравниваем что наш пример с формулой, видим что в числителе у нас двойка вместо единицы, ничего, исправим, просто перекинем её в знаменатель знаменателя. А вот в степени нам нужна та же функция что и в знаменателе.

Распишем подробно.

Перекинули двойку, дальше наша задача подогнать под формулу, чтобы было похоже поэтому функцию находящуюся в знаменателе записываем в степень, для того чтобы в степени ничего не изменилось, умножим на функцию обратную знаменателю, все эти действия производятся в степени. Экспоненту получили, осталось разобраться со степенью нашей экспоненты, у нас там получается неопределённость, которую мы научились раскрывать (ссылка в конце урока). раскрыв эту неопределённость получили в степени единицу, следовательно ответ равен экспоненте.

Перекинули двойку, дальше наша задача подогнать под формулу, чтобы было похоже поэтому функцию находящуюся в знаменателе записываем в степень, для того чтобы в степени ничего не изменилось, умножим на функцию обратную знаменателю, все эти действия производятся в степени. Экспоненту получили, осталось разобраться со степенью нашей экспоненты, у нас там получается неопределённость, которую мы научились раскрывать (ссылка в конце урока). раскрыв эту неопределённость получили в степени единицу, следовательно ответ равен экспоненте.

При раскрытии неопределённости единицы в степени бесконечность, как правило использую такой ход решения. Желательно просто всё понять и запомнить примерную последовательность действий.

Закрепим на похожем примерчике.

Пятёрку перекинули в знаменатель знаменателя, дальше знаменатель записали в степень и умножили на обратную ей функцию. Получили экспоненту, осталось разобраться со степенью, расписали по формулам сокращённого умножения знаменатель, квадрат в числителе представили в виде произведения, сократили, там появилась неопределённость, мы пропустили этот момент, в итоге получили экспоненту в пятой степени.

Пятёрку перекинули в знаменатель знаменателя, дальше знаменатель записали в степень и умножили на обратную ей функцию. Получили экспоненту, осталось разобраться со степенью, расписали по формулам сокращённого умножения знаменатель, квадрат в числителе представили в виде произведения, сократили, там появилась неопределённость, мы пропустили этот момент, в итоге получили экспоненту в пятой степени.

Алгоритм вполне понятный, придерживаясь, таким образом решили два примера. Рассмотрим другой вид неопределённости.

А вот и она самая, бесконечность на бесконечность в степени бесконечность.

А вот и она самая, бесконечность на бесконечность в степени бесконечность.

Ход решения почти не отличается от стандартного, добавляется маленький дополнительный шаг. Вы правильно заметили. Нам не хватает единицы. Вот её мы сейчас и будем искать.

Таким образом мы выделили единичку, хитро, не правда ли?

Таким образом мы выделили единичку, хитро, не правда ли?

И полное решение будет выглядеть:

Формулу мы использовали другую, вот и трёхэтажные дроби пропали.

Формулу мы использовали другую, вот и трёхэтажные дроби пропали.

Ну что же, пора закрепить весь материал на 100%. Встречайте…

Ух, примерчик не маленький.

Ух, примерчик не маленький.

И решение будет не слабое.

Действовали обычным алгоритмом, добавили и отняли единичку, привели общему знаменателю минус единичку. Добавили в степень обратную функцию, домножили на обратную ей, получили экспоненту в основании. В степени расписали произведение двух функций как произведение пределов этих функций (по свойствам пределов разрешено), вот от одного из пределов мы получили ноль, в ответе в итоге единица.

Действовали обычным алгоритмом, добавили и отняли единичку, привели общему знаменателю минус единичку. Добавили в степень обратную функцию, домножили на обратную ей, получили экспоненту в основании. В степени расписали произведение двух функций как произведение пределов этих функций (по свойствам пределов разрешено), вот от одного из пределов мы получили ноль, в ответе в итоге единица.

Достаточно на сегодня примерчиков, мы и так многое познали. Разобрали ещё два вида неопределённости и методы её устранения. Спасибо за внимание.

Другие темы:

‎App Store: Photomath

Научитесь решать математические задачи, проверять домашние задания и готовиться к предстоящим экзаменам и экзаменам ACT / SAT с помощью самого популярного в мире учебного ресурса по математике. Более 100 миллионов загрузок и миллиарды решенных задач каждый месяц!

КАК ЭТО РАБОТАЕТ
С помощью камеры своего устройства мгновенно отсканируйте печатный текст И рукописные математические задачи или введите и отредактируйте уравнения в нашем научном калькуляторе. Каждую математическую задачу Photomath разбивает на простые, понятные шаги, чтобы Вы могли хорошо понять основные концепции и уверенно отвечать на вопросы.

КЛЮЧЕВЫЕ ОСОБЕННОСТИ
Сканирование (печатного) учебника И рукописных задач
Научный калькулятор
Пошаговые объяснения для каждого решения
Несколько методов решения

Поддержка более 30 языков
Интерактивные графики

МАТЕМИЧЕСКИЕ ТЕМЫ
Базовая математика / начала алгебры: арифметика, целые числа, дроби, десятичные числа, степени, корни, факторы
Алгебра: линейные уравнения / неравенства, квадратные уравнения, системы уравнений, логарифмы, функции, матрицы, графики, полиномы
Тригонометрия / начала математического анализа: тождества, конические сечения, векторы, матрицы, комплексные числа, последовательности и ряды, логарифмические функции
Исчисления (математический анализ): пределы, производные, интегралы, построение кривых
Статистика: комбинации, факториалы

Наша собственная команда ветеранов преподавателей математики также сотрудничает с учителями по всему миру, что дает возможность гарантировать использование наиболее эффективных методик обучения в наших математических системах.

Представлено в Huffington Post, Forbes, TIME, CNN, EdSurge, Guiding Tech, The Verge, TechCrunch и других.

Предложения, комментарии или вопросы? Напишите нам по адресу [email protected]

Подписывайтесь на нас!
Facebook: facebook.com/Photomathapp
Twitter: @Photomath

Photomath есть и всегда будет бесплатным, но Вы можете улучшить свое обучение, перейдя на Photomath Plus. Photomath Plus предлагает решения для всех задач и примеров из учебников! В настоящее время предложение действительно только для США и для конкретных учебников.

Оплата будет снята с Вашей учетной записи Apple ID при подтверждении покупки. Подписка продлевается автоматически, если она не отменена как минимум за 24 часа до окончания текущего периода. За 24 часа до окончания текущего периода с Вашего счета будет снята плата за продление. Вы можете управлять своими подписками и отменять их, перейдя в настройки своей учетной записи в App Store после покупки. Предложения и цены могут быть изменены без предварительного уведомления.

2

Иноземцев о повторении «империей Путина» судьбы СССР, войне на Украине, объединении РФ с Белоруссией

https://www.znak.com/2021-12-25/zhiznesposobna_li_imperiya_putina_i_spasut_li_ee_ot_uchasti_sssr_intervyu_s_inozemcevym

2021.12.25

Тридцать лет назад, 25 декабря 1991 года, Михаил Горбачев, попрощавшись с согражданами в прямом телевизионном обращении, «прекратил свою деятельность на посту президента СССР». Сразу после этого кумачовый советский флаг, развевавшийся над Кремлем, был спущен и заменен на российский триколор. Этому предшествовал провал многомесячных переговоров о переформатировании Советского Союза в конфедерацию суверенных государств, неожиданное для Горбачева отделение Украины, такие же внезапные Беловежские соглашения России, Украины и Белоруссии, ликвидировавшие СССР и учредившие Содружество Независимых Государств, присоединение к новому образованию еще восьми республик. 

«Горбачев-фонд»

Так завершилась и 69-летняя биография «советской империи», воссоздавшей 200-летнюю Российскую, и короткая, но революционная эпоха Перестройки, итоги которой оказались противоположными стремлениям оживить «союз нерушимый».

Но через какой-то десяток лет империя начала постепенно возрождаться в управленческих практиках путинского Кремля. Какими были основные причины гибели «единого, могучего» Советского Союза и жизнеспособна ли «империя Путина»? Обсуждаем с известным экономистом, соавтором книги «Бесконечная империя. Россия в поисках себя» Владиславом Иноземцевым. 

«Перестройка должна была начаться с создания устойчивой конфедерации»

— Владислав Леонидович, в конце 1991 года вам было 23 года, вы были аспирантом МГУ. Как вы восприняли факт распада СССР? Какие были ощущения, переживания?

— Я не ощущал особой трагедии. Хотя я никогда не был фанатом «демократов» и, когда Ельцин избирался народным депутатом СССР, оказался в числе тех 8%, кто голосовал за его оппонента, директора ЗИЛа Евгения Бракова, но к концу 1991 года стало ясно, что система мертва, Советский Союз нежизнеспособен, что пора поставить точку в его истории и переходить к чему-то новому.

Помню, как 25 декабря я хотел пойти посмотреть на спуск советского флага над Кремлем. Но моя ныне уже покойная мама, которая в детстве эвакуировалась из блокадного Ленинграда в одном из самых последних эшелонов и была убежденным советским человеком, отнеслась к этому событию и вообще к распаду СССР с очевидной грустью, и мы не пошли. Да и эмоции к тому времени перегорели, мое восприятие происходящего было спокойным.

— Однажды Владимир Путин попенял Владимиру Ленину за то, что тот наделил советские республики правом свободного выхода из состава СССР. Как напоминает «Бесконечная империя», этот принцип был подтвержден и в брежневской Конституции 1977 года. На ваш взгляд, если бы в начале 1920-х годов верх взяла концепция Сталина и республики — учредители СССР вошли в состав РСФСР, Союз бы выжил?

— Прежде всего отмечу, что главу в «Бесконечной империи», посвященную Советскому Союзу, писал мой соавтор — заслуженный учитель Москвы, кандидат исторических наук Александр Абалов, и он наверняка более компетентен в этой теме. Мой взгляд таков: думаю, других вариантов в то время просто не было. Когда к окончанию Гражданской войны большевики сплачивали советские республики, они исходили из того, что СССР — временная конструкция, по ходу мировой революции он расширится до всемирного масштаба за счет вхождения в него всех прочих народов и государств. Причем в качестве равноправных республик, ведь с самого начала было понятно, что включить в состав СССР, например, Баварскую советскую республику на условиях автономии не очень реально. А норма о праве выхода из Союза могла подчеркивать привлекательность этой структуры и, таким образом, служить дополнительным инструментом идеологической экспансии большевиков. Так что в данном случае следует говорить не об опрометчивости и недальновидности ленинского подхода, а, наоборот, о его прагматизме в тех условиях, когда он был применен.

Сайт Кремля

Если бы победила концепция Сталина, полагаю, «развод» России с другими республиками в начале 90-х (а в том, что к тому времени большинство из них созрело для обретения независимости, сомневаться не приходилось) проходил бы гораздо более конфликтно, войн по нашим границам было бы больше и в результате территория России оказалась бы меньше, чем сегодня.

— «Бесконечная империя» дает широкую панораму подходов советских вождей к «национальному вопросу»: это и сталинское «возвращение к имперским практикам управления», и русский национализм и иерархия народов и этносов, и хрущевская ограниченная децентрализация наряду с идеями «полного слияния всех наций в единое целое» и «ликвидации национальностей», и брежневская концепция «многонационального советского народа» вкупе с «жестким преследованием любых проявлений национализма». Но лично мое внимание больше всего привлекло упоминание о планах Андропова: «Была начата разработка нескольких проектов упразднения национально-территориальных образований в составе СССР, планировалось переформатировать Советский Союз в своего рода совокупность «штатов» на основе численности населения и производственной целесообразности, с «погашением» образующей нации». Как вы полагаете, Владислав Леонидович, удалось бы впоследствии избежать межнациональных конфликтов, кровопролития и дезинтеграции при реализации такого проекта?

— С моей точки зрения, в подходе Андропова было рациональное зерно. Но дело в том, что такие коренные изменения нужно осуществлять в революционные эпохи. Например, те же 1920-е годы, когда большевики предрекали всемирное торжество интернационализма и упразднение наций, были подходящим моментом для реализации этой концепции. Тем более что ей соответствовало административное устройство Российской империи, разумное и достаточно современное. Но ведь большевики считали империю «тюрьмой народов», достойной только одного — чтобы не оставить от нее камня на камне.

Следующим благоприятным периодом было хрущевское десятилетие ренессанса идеалов коммунизма и интернационализма, стремительного технического прогресса и космических побед СССР, беспощадного искоренения религии, большого энтузиазма и исторического оптимизма. Но в то же время в мире разворачивалось национально-освободительное движение, появлялись новые национальные государства, и Советский Союз не только поддерживал эти процессы, но и претендовал на то, чтобы вдохновлять их и руководить ими. На этом фоне упразднение организации собственной страны, «собранной» с учетом национального принципа, было идеологически и политически несвоевременным и, значит, неприемлемым.  

К периоду правления Андропова любые искры мечтаний о мировой революции и всемирной «семье народов» окончательно потухли. Страна ощущала, что вступила в период кризиса. На мой взгляд, в этом состоянии система столкнулась с дилеммой: менять хоть что-нибудь или не менять ничего. Я глубоко убежден, что если бы Советский Союз, — неэффективный, но при этом еще достаточно прочный, — пошел по второму пути, он прожил бы намного дольше. Неслучайно андроповская программа «реформ» носила довольно ограниченный характер: ужесточение трудовой дисциплины, борьба с пьянством и прогулами, казнокрадством, «повышение роли трудовых коллективов в управлении предприятиями», привязка зарплат к показателям производительности труда и тому подобное. Приступать к капитальному административному переустройству «советской империи» тоже уже было поздно. Это стало бы таким же смертельным ударом по системе, как и перестройка. 

— Что, с вашей точки зрения, добило советскую систему в период горбачевской перестройки: гласность (разоблачившая пакт Риббентропа — Молотова, со всеми вытекающими в виде прибалтийского «сепаратизма»), демократизация, экономические проблемы?

— По моему мнению, лидеры перестройки, и в первую очередь Горбачев, допустили две фундаментальные ошибки. Во-первых, они считали Советский Союз обычным государством с правовым режимом, оформленным в системе законов и кодексов. На самом же деле ничего правового в советской юридической системе не было. Вместо разделения властей — засилье партийного аппарата, вместо открытой состязательности в судебном процессе — «телефонное право», и так далее. Ни демократии, ни рыночной экономики на этой базе построить было невозможно. А новые законы, которые, по мысли руководства, должны были оздоровить систему, в действительности разрушили ее.

Почему Михаил Горбачев возглавил Советский Союз и начал Перестройку

Во-вторых, Горбачев и его соратники были убеждены, что в Советском Союзе не существует «национального вопроса», они даже не подозревали, что в СССР возможны межнациональные конфликты. При этом, повторю, советские коммунисты всегда активно поддерживали национально-освободительные движения и распад империй, совершенно не принимая в расчет того, что их собственное государство тоже представляло собой империю, как оказалось, практически готовую к распаду.

Я напомню, что еще за несколько месяцев до официального объявления политики гласности и за два года до начала полномасштабного экономического кризиса — в декабре 1986 года в Алма-Ате вспыхнули беспорядки, которые были спровоцированы отставкой Динмухамеда Кунаева (на протяжении более 30 лет возглавлявшего правительство и Компартию Казахстана. — Прим. ред.) и назначением на его место Геннадия Колбина. Возмущение казахов, которое завершилось кровопролитием и человеческими жертвами, было вызвано исключительно «национальным вопросом». Потом последовательно вспыхнули Азербайджан, Грузия, Прибалтика, Узбекистан, Армения, Киргизия…

Если бы кремлевские обитатели были более осведомленными и дальновидными, они бы немедленно отреагировали на алма-атинский конфликт (а еще лучше — предотвратили бы его) серьезными размышлениями о переформатировании Союза и выстроили бы перестройку вокруг конфедерализации страны.

Вспомним, почему по итогам референдума о независимости в 2014 году Шотландия осталась в составе Великобритании. По одной простой причине: потому что, придя к власти в 1997 году, лейбористский премьер Тони Блэр провел впечатляющую реформу, в итоге которой с благословения Лондона Шотландия и Уэльс обрели собственные парламенты и правительства, наделенные достаточно широкими полномочиями, которые через полтора десятилетия стали еще больше. Сегодня шотландский язык имеет официальный статус, Банк Шотландии имеет право эмиссии фунта стерлингов и так далее.

Точно так же еще в первые годы перестройки нужно было поступать и советскому руководству. Обновление советского государства должно было начаться с перезапуска системы отношений Центра и республик, с создания устойчивой конфедерации с высокой степенью самоуправления (делегирование ответственности только укрепило бы репутацию и положение Центра). И лишь осуществив все это, можно было выводить войска из Афганистана, заниматься разоружением и собирать дивиденды от миролюбивой внешней политики, провозглашать демократию и гласность, проводить экономические преобразования (которые в этом случае начались бы «снизу», с муниципалитетов, регионов и республик, и не с раздачи общесоюзной собственности, а, по китайскому варианту, с приватизации мелких предприятий или, например, с роспуска колхозов и решения «продовольственной проблемы»).

Да, даже в этом случае Прибалтика скорее всего стремилась бы к независимости и воссоединению с Европой, потому что обнародование деталей пакта Риббентропа — Молотова подтвердило тот мало кем отрицавшийся факт, что перед войной прибалтийские республики были попросту захвачены. Но эту проблему можно было решать в контексте и на общих принципах отношений с Восточной Европой. Если бы уже на первом этапе перестройки произошло переформатирование Советского Союза, Прибалтику можно было спокойно отпустить сначала в сообщество «братских стран социализма», а потом, вместе с ГДР, Польшей и другими восточноевропейскими странами — и из «социалистического лагеря». Тогда идущая от Прибалтики угроза взрыва Советского Союза изнутри была бы пресечена и вся остальная территория страны была бы гораздо более консолидированной.

Но пленум ЦК КПСС по «национальному вопросу» состоялся только осенью 1989 года, когда кровь пролилась уже не только в Алма-Ате, но и в Сумгаите, Баку, Тбилиси, Фергане. А предметное обсуждение нового Союзного договора началось лишь за восемь месяцев до распада СССР, и в нем не принимали участие Молдавия, Армения, Грузия и три прибалтийские республики.

— В «Бесконечной империи» справедливо говорится, что «приводным ремнем» всесилия Кремля, «мощнейшим инструментом централизации управления» в советскую эпоху была ВКП(б) — КПСС. Значит ли это, что отправной точкой распада СССР была отмена в марте 1990 года пресловутой 6-й статьи брежневской  Конституции о «руководящей и направляющей» роли Компартии?

— Думаю, что отмена 6-й статьи советской Конституции не имела принципиального значения. На протяжении многих лет КПСС действительно служила и главным управленческим механизмом, и идеологическим «кормчим», и основным карьерным и социальным лифтом. Но к 1990 году ее авторитет и влиятельность сошли на нет. Снова стал актуальным лозунг «Вся власть Советам!», в 1989 году впервые прошли альтернативные выборы депутатов I Съезда народных депутатов СССР, началось формирование оппозиции, стала оформляться мысль о том, что дальнейшее развитие страны может идти без диктата коммунистов.

«Вторжение в Украину будет означать конец сегодняшнего российского режима»

— Владислав Леонидович, незадолго до распада СССР Борис Ельцин размышлял о проекте создания содружества трех славянских республик: России, Украины и Белоруссии. И это было во вкусе позднесоветского руководства: как отмечает «Бесконечная империя», к концу правления Брежнева доля славян в ЦК КПСС составляла 85%, славянами были все секретари ЦК, а представительство славян среди генералов, избранных в ЦК и Верховный Совет СССР, приближалось к 100%. Геополитические помыслы Владимира Путина тоже накрепко связаны с Киевом и Минском. В «Бесконечной империи» приводятся его высказывания о том, что «русские и украинцы — это вообще один народ, по сути, одна нация… русский и белорусский народы — то же самое, что украинский и русский, почти одно и то же». Допускаю, что Владимир Владимирович искренне переживает из-за того, что именно провозглашение Украиной своей независимости 1 декабря 1991 года привело к тому, что «великая империя распалась». Как вы думаете, Владислав Леонидович, «панславянское содружество» еще возможно?

— Сейчас — нет. Впрочем, об этом было поздно думать и при распаде Советского Союза. Как я уже сказал, создать новую структуру из старой можно, только действуя на опережение. Если бы в 1988–1989 годах возникло видение, что Советский Союз придется распускать, славянскому ядру СССР было бы совершенно разумным начать дрейфовать от Закавказья и Средней Азии — территорий, присоединенных лишь в XIX веке, и создавать союз трех славянских республик, где были сконцентрированы население, природные богатства, промышленность, в том числе на тот момент высокотехнологичная. Но для этого нужно было обладать невиданным даром исторического предвидения.

При этом межнациональные противоречия давали бы знать о себе и внутри этого союза. Ведь Украина стремилась к независимости не только в 1991 году, но и после распада Российской империи в 1917-м. Это стремление было вызвано достаточно долгой историей дискриминации и угнетения малороссов, которая не могла быть просто «забыта».

— Вы, авторы «Бесконечной империи», отмечаете: «Любые имперские предприятия исключительно рискованны». Как вы думаете, пойдет ли Путин на риск дальнейшей эскалации взаимоотношений с Украиной и Западом по вопросу расширения НАТО? На пресс-конференции он заявил, что «дальнейшее движение НАТО на Восток неприемлемо», и потребовал от «западных партнеров» немедленных гарантий.

— По-моему, полномасштабная война невозможна, для этого нет и не предвидится веских поводов. К тому же нет ощущения, что российская армия способна решить в Украине серьезные стратегические задачи.

Мы что, собираемся штурмовать многотысячные города авиацией и танками? Мы готовы на сопутствующие потери?

Но даже если российская армия пройдет территорию от границы с Украиной до Киева и хоть до Львова, как будет ее потом контролировать? В то же время реакция Запада на прямую агрессию против Украины будет стоит нам чрезвычайно дорого. Уверен: вторжение в Украину будет означать конец сегодняшнего российского режима, и вероятность такого исхода куда больше, чем риски падения Дома Романовых при вступлении Российской империи в Первую мировую войну. 

Путин слишком осторожен, чтобы пойти на это, и как Верховный главнокомандующий не возьмет на себя персональную ответственность за приказ о нападении на соседнюю «братскую» страну. Да и в 2014 году, если бы верный долгу и присяге украинский полк обезвредил в Крыму сотню-другую «зеленых человечков», Путин бы под камеры заявил, что вообще не знает, кто они такие, и вскоре радостно обнимался бы с Порошенко.  

Global Look Press

Так что будет вялотекущая конфронтация, долгосрочное и глубокое ухудшение отношений между Россией и Западом, Россией и Украиной как фактически состоявшейся частью Запада, и основательной перезагрузки отношений на этом фоне не произойдет.

— А полноценное Союзное российско-белорусское государство может стать «геополитической реальностью»?

— Я считаю, что у Кремля есть большое желание присоединить Белоруссию. И с точки зрения задачи продления сроков полномочий Путина, и из-за желания контролировать территорию, в которую Россия вкладывает колоссальные средства и, видимо, готова вкладывать еще. Но так же очевидно, что у белорусов стремления объединяться нет. В последние два года для 90% граждан понятия «Москва» и Кремль» соединились с понятием «Лукашенко» и вызывают страшную изжогу.

Любая попытка присоединить Белоруссию к России приведет к социальному взрыву, вплоть до выступлений, которые будут гораздо более массовыми и решительными, чем в августе прошлого года. Поэтому все ограничится, как описал на своей пресс-конференции российский президент, попытками углубить экономическое сотрудничество, синхронизировать таможенное и налоговое законодательство, создать единую валюту, одновременно потихоньку вышибая рычаги власти из рук Лукашенко. Процесс будет долгим, потому что его активизация приведет к тому, что ситуация в Белоруссии станет непредсказуемой.

— Как вы оцениваете эффективность и перспективность для России того, что возникло на месте СССР, вместо несостоявшейся конфедерации? Я имею в виду, например, Евразийский экономический союз, куда, помимо России и Белоруссии, входят Армения, Казахстан и Киргизия. Насколько устойчиво это образование? Насколько в этой компании сильна и авторитетна Россия? (В «Бесконечной империи» говорится, что она обеспечивает почти 87% суммарного валового продукта ЕАЭС). Возможна ли российская имперская экспансия на базе этой организации?

— Евразийский экономический союз достаточно устойчив, и у него есть будущее, прежде всего из-за отсутствия больших амбиций. Когда Путин говорит, что в ЕАЭС нет признаков имперского ренессанса, это правда: этот союз — не более чем экономическое объединение.

Другое дело, что в той же Белоруссии оно воспринимается позитивно, потому что в рамках ЕАЭС небольшие государства получают преимущества доступа на большой российский рынок. Для граждан Киргизии, например, это создает хорошие  возможности работы, заработка и содержания семей. А вот у более мощного Казахстана насчет ЕАЭС определенные сомнения, потому что Россия свои действия с партнерами по Евразийскому союзу не согласовывает. В результате «продуктовые» санкции, которые Россия ввела в ответ на ограничительные меры Запада, сильно затруднили доставку в Казахстан товаров из Европы (я уж не говорю про удар по торговле между Казахстаном и Украиной). Россия в нынешней ситуации является «железным занавесом», через который очень сложно пробиться. Вдобавок она навязывает свои принципы и стандарты в области мобильной связи, производства автомобилей по иностранным лицензиям. И таких вопросов, по которым Россия продавила свои интересы, вызвав недовольство партнеров по ЕАЭС, достаточно много.

«Любая попытка присоединить Белоруссию к России приведет к социальному взрыву»Сайт президента РФ

В Казахстане это недовольство накладывается на болезненный для казахской независимости «русский вопрос». Поэтому там наблюдается определенное давление на русскоязычное население, которое, замечу, за постсоветские годы сократилось больше, чем в постоянно обсуждаемой российскими политиками Прибалтике: до распада СССР русские, украинцы и белорусы составляли 44% населения Казахстана и 34% населения Латвии, сейчас — соответственно 18% и 26%. С другой стороны, Назарбаев с самого начала был большим сторонником создания и развития постсоветских интеграционных структур, высказавшись за это еще в первой половине 1990-х, и одним из первых в 2014 году подписал договор о создании ЕАЭС. Одно другому не помешало и не мешает.

Одним словом, я не вижу большого смысла в этой организации, потому что политического измерения этот инструмент очень мягкой интеграции не имеет, а восторги Кремля по поводу того, что создание единого рынка даст толчок росту ВВП, себя не оправдали. Но и вызовов, из-за которых ЕАЭС может прекратить свое существование, я тоже не усматриваю.

— Путинизм как фиктивная империя с ее «комичным», как определяет «Бесконечная империя», «собиранием земель», безусловно, не вечен. Каким вы видите будущее таких «спорных территорий», как Донбасс, Приднестровье, Абхазия, Южная Осетия?

— Их сегодняшнее положение довольно печально. И когда власть в России поменяется, они окажутся ей не нужны. Справедливости ради отмечу, что Владимир Владимирович не несет всей полноты ответственности за появление этих непризнанных образований, потому что сепаратизм Приднестровья, Абхазии и Южной Осетии активно поддерживался и Борисом Николаевичем. Несмотря на то что, по словам [первого президента Украины. — Прим. ред.] Леонида Кравчука, именно принятие в 1990 году Декларации о суверенитете РСФСР подтолкнуло Украину к провозглашению независимости и выходу из состава СССР, Россия всегда была уязвлена распадом Советского Союза, и потому создание проблем для бывших советских республик является для Кремля «национальным видом спорта» еще с ельцинской поры.

Полагаю, что в конечном счете при отсутствии российской поддержки Донбасс, Приднестровье и Южная Осетия будут достаточно быстро реинтегрированы в состав тех государств, частями которых они являлись.

В Приднестровье не менее половины взрослых граждан обзавелись молдавским паспортом в течение первых двух лет после установления безвизового режима между Молдовой и Евросоюзом (сегодня, думаю, молдавские документы имеют 75-80% приднестровцев), приднестровский экспорт идет через молдавскую таможню, сильны социальные и культурные связи. От прежнего противостояния мало что осталось, и если Молдова войдет в ЕС (а это вполне вероятно), приднестровцы незамедлительно и охотно проголосуют за возвращение к Кишиневу. Это будет чувствительным щелчком по носу Кремлю, ведь Европа покажет, что способна довольно легко завершить многолетний сепаратистский конфликт на постсоветском пространстве, которое Москва считает зоной своего приоритетного влияния.

Исключение, может быть, составит только Абхазия: во-первых, у нее давняя история противостояния с Грузией; во-вторых, она обладает некоторыми признаками жизнеспособного государства, имея выход к морю и ряд конкурентных преимуществ, способных привлечь внешних инвесторов.  

«Не вижу угрозы распада страны, но возможность отделения отдельных территорий допускаю»

— Отдельный вопрос, конечно, о Крыме. Возможно ли такое, что впоследствии «крымский вопрос» во весь рост будет поставлен перед Россией? Так что, как говорится, «не отвертеться»? И если да, какое решение этого вопроса вы бы предложили?

— Вопрос о Крыме будет поставлен однозначно. Крым, по юридическому статусу и возможным последствиям, — то же самое, чем в составе Советского Союза была Прибалтика. Ясно, что решение этой проблемы возможно только с приходом нового президента и при сближении с Западом.

Я бы на месте нового президента на вопросы о будущем Крыма ответил, что операцию по его присоединению не поддерживаю, но прошу понять, что в 2014 году российское руководство действовало исходя из того, что к власти в Киеве приходят националистические силы, а в Крыму большое число русскоязычных граждан, которым угрожали межнациональные конфликты и репрессии, поэтому российская сторона предприняла упреждающую гуманитарную интервенцию. А вот присоединение Крыма к России было ошибкой, но теперь, после многолетнего и тяжелого конфликта с Украиной, вернуть его не представляется возможным. В Украине действуют законы, серьезно ущемляющие права не только русского меньшинства, но и многих других (можно вспомнить про галицийских венгров), и есть большие опасения, что точно так же пострадают те крымчане, которые сотрудничали с Россией. К тому же в Крыму проживают и владеют собственностью многие приезжие граждане России, и непонятно, как будут защищены их права. 

Я бы занял такую позицию: мы не верим Украине, но верим Европейскому Союзу, в его добросовестное отношение к правам человека и правам собственности. Поэтому мы согласны вернуть Крым Украине как члену Евросоюза. И готовы заключить договор о передаче Крыма на следующий же день после того, как Украина станет полноправным членом ЕС. А когда это случится и случится ли вообще, решайте между собой.

— Владислав Леонидович, следующий вопрос — в контексте недавнего наделавшего шуму спора Александра Сокурова с Владимиром Путиным. В «Бесконечной империи» присутствуют красноречивые данные: русские составляют этническое меньшинство в 14 субъектах Российской Федерации, среди которых преобладают кавказские республики: Карачаево-Черкесия, Кабардино-Балкария, Северная Осетия, Ингушетия, Чечня, Дагестан. Вместе с тем в книге есть яркая формулировка: «основная функция имперского распада — четкое отделение метрополии от колоний, как политическое, так и ментальное — не выполнена даже в малейшей степени… распад империи не запустил процесса национального самоопределения метрополии… дальнейшая дезинтеграция части бывшего имперского организма остается вполне реальной». Значит ли все это, что при федерализации России сохранение перечисленных регионов в ее составе может быть поставлено под вопрос?

— Позиция Сокурова мне абсолютно ясна, и я считаю, что он прав. Если кавказские республики пожелают уйти, удерживать их не стоит, несмотря на отсутствие юридического права выхода из состава Российской Федерации. Повторение того кровопролития, какое мы видели в связи с войной в Чечне, не нужно никому. Вместе с тем от себя добавлю: если они не пожелают отделиться от России, выгонять их, как предлагают те, кто говорит «хватит кормить Кавказ», нельзя.

Сокуров извинился за свою перепалку с президентомстраница Фонда Александра Сокурова «Пример интонации» / Facebook

 — В начале 1990-х годов особой «головной болью» Бориса Ельцина были национальные республики Поволжья. Именно в Татарстане он произнес знаменитое «берите суверенитета, сколько сможете проглотить». Но при Владимире Путине Москва вернулась к жестким имперским практикам управления страной. В «Бесконечной империи» неоднократно подчеркивается, что, например, к Сибири и Дальнему Востоку она, как и в XVI веке, относится как к поселенческой колонии, «далеким туземным территориям», источнику экспортируемого сырья. Притом что «в последние годы федеральный бюджет более чем наполовину обеспечивался налогами и сборами с «колониальных товаров»». Можно ли быть уверенными в том, что и Татарстан, и Сибирь с Дальним Востоком навсегда останутся синонимами и тождествами России?

— Мое мнение таково: у жителей этих регионов есть понятное желание подчеркнуть собственную значимость и особость. Но я не вижу у них стремления порвать с Россией. На Дальнем Востоке и в Сибири есть четкое понимание того, что если выйти из России, то рано или поздно окажешься под властью Китая. Ни у кого эта перспектива восторга не вызывает. Видя, что происходит в Китае, особенно в «автономиях» типа Синьцзяна, наши люди совершенно не стремятся стать подданными «китайской империи». И если в Европе живут не менее 3 млн россиян, сохраняющих свое российское гражданство, в Китае таких совсем не много, может, несколько десятков тысяч. Суждения о том, что Владивосток включен в азиатскую экономику больше, чем в российскую, неверны. Никакие гигантские инвестиции из Азии туда не приходят. А то, что приморцам проще поехать на отдых в Таиланд, чем в Сочи, к политике отношения не имеет. Отсюда мое ощущение, что дальневосточный и сибирский сепаратизмы России не грозят.

И каких-то больших проблем с Татарстаном я тоже не вижу. Татарстан — немного «мятежная» республика.

Но с другой стороны, это очень многонациональный субъект, а вовсе не моноэтничный. А сепаратизм в обществе с таким многообразным населением, где большинство браков — смешанные, опасная затея, и это прекрасно понимают не только в Москве, но и в Казани. Думаю, что жители Татарстана вполне осознают, какими последствиями лично для них обернется попытка республики отделиться от России.

Вообще угроза сепаратизма у нас невероятно раздута. Нормальные требования признать официальный статус национальных языков, разрешить преподавание на них, позволить руководителям субъектов именоваться президентами и так далее — все это к сепаратизму не имеет никакого отношения. Наоборот, чем больше будет национального и территориального многообразия, чем выразительнее будут внешние атрибуты, подчеркивающие своеобразие регионов, и чем адекватнее будут возможности территорий отвечать задачам их полноценного развития, тем меньше у них будет желания перейти к политике и практике сепаратизма.

Понятно, что рассчитывать на федерализацию страны при авторитарном режиме не приходится. Но и зуд, с которым Москва настырно ведет к отмене президентства в Татарстане, ничего, кроме вреда, не несет. Оставьте как есть. Зачем накалять обстановку, раздражать и настраивать против себя большую республику? Что вам неймется, других проблем нет?

— Еще одно многозначительное высказывание из «Бесконечной империи»: «Долгосрочные источники экономического роста и повышения качества жизни уже сейчас выглядят исчерпанными, а в перспективе ситуация станет еще более драматичной. Все это говорит о том, что нынешний политический режим и нынешняя экономическая система, сформировавшиеся в России, не являются некой конечной точкой постсоветского (и тем более постимперского) транзита. Впереди нас ждет неминуемая дестабилизация с непредсказуемыми результатами». С какими событиями, вызовами вы связываете такую перспективу?

— Триггером может стать, например, переход во второй половине 2030-х годов к возобновляемым источникам энергии и «зеленой экономике». Но я надеюсь, что еще до того, как энергопереход станет свершившимся фактом, в России начнутся перемены, связанные с транзитом президентской власти.

Любое переформатирование и тем более ослабление сегодняшней власти вызовет серьезную дестабилизацию и в федеративном устройстве России, и во всех других сферах, которые мы сейчас обсуждаем. Поэтому, по-хорошему, готовиться к этим испытаниям, в том числе постепенно развивая федерализм, нужно уже сегодня. Однако никаких предпосылок к этому нет, и, хоть я не вижу угрозы распада страны, возможность отделения от нее отдельных территорий тем не менее допускаю.

— С одной стороны, как пишите вы, авторы «Бесконечной империи», «переродиться в подлинное современное национальное государство постимперского типа Россия не имеет ни желания, ни, вероятно, возможности».  С другой — «следование России в имперской парадигме является однозначно тупиковым». Это похоже на состояние невротика: сущее бесперспективно, а перспективное невозможно. Каким вам видится выход?

— Чтобы Россия перешла в качество национального государства, как это ни печально, потребуются довольно радикальные испытания. Сегодняшние трескучие речи о патриотизме, переписывание истории в угоду политической конъюнктуре и второсортные фильмы о войне — совсем не те инструменты, которые необходимы для формирования гражданской нации. Если мы все-таки окажемся за пределами зоны комфорта, в которой находимся сейчас, то есть столкнемся с разрушением вертикали власти и исчерпанием источника основных доходов, – вот тогда, возможно, как уже бывало, гражданское общество придет в движение, возникнут какие-то низовые формы самоорганизации. И осознав, что наиболее короткий и эффективный путь к благополучию лежит не через возрождение империи и не через ее раздробление, а через создание добровольной договорной федерации, население наконец возьмется за создание современного общества европейского типа.

Но относиться к этому процессу как к проекту и заранее «рисовать» план его реализации бессмысленно. Если он и начнется, то как стихийное движение. Это сравнимо с тем, как, чтобы научить плавать, бросают в воду. Что из этого выйдет, предсказать нельзя. Мы в «Бессмертной империи» только зафиксировали, что формат империи безнадежно устарел. Россия — последняя империя, все остальные вымерли. И если наша страна не хочет закончить тем же, ее выбор очевиден и однозначен: перестать быть империей. В этом смысле я согласен с Путиным, который сказал, что «Россию нельзя победить, ее можно только развалить изнутри».

ЛИНДА ГОТЛИБ. ТЕРАПИЯ ВОССОЕДИНЕНИЯ (TPFF) ПРИ ТЯЖЕЛОМ РОДИТЕЛЬСКОМ ОТЧУЖДЕНИИ (2): vm_pas — LiveJournal

Предпочитаемый или отчуждающий родитель

 

            В книге 2013 года Американской ассоциации юристов (АВА) под названием «Дети-заложники» (выявление детей с промытыми мозгами, представление дела и выработка решений) авторы Клавар и Ривлин проследили за 1000 детьми родительского конфликта или развода. Они пришли к выводу, что процент родителей, которые программировали/«промывали  мозги» своим детям по крайней мере один раз в неделю составил 86% , а процент тех, кто занимается программированием /«промыванием мозгов» детям  более чем один раз в сутки — 23%. (Стр. 420) Это очень тревожная статистика, указывающая на широко распространенные страдания и травмы детей.

            Клавар и Ривлин всесторонне описали характеристики и поведение детей в  средних и тяжелых случаях отчуждения. Их тревожные открытия об этих отчужденных детях дают основания судебной системе серьезно относиться к делам о родительском отчуждении, признавая, что это жестокое обращение с детьми, и применять максимально быстрое рассмотрение этих дел.

            Некоторые авторские оценки среднетяжелых и тяжелых случаев родительского отчуждения следующие:

Родители, занимающиеся программированием и промыванием мозгов, привыкли к конфликтам. Это означает, что они провоцируют, способствуют конфликту, а некоторые живут этими конфликтами (как говорил доктор Ричард Гарднер, это их modus vivendi, образ жизни). Они  становятся более напряженными и возбужденными по мере роста социальной и правовой напряженности вокруг детей. Существует почти привыкание, как качество в их реакции на конфликт — чем больше конфликтов, тем больше они стимулируют этих родителей; тем больше они нуждаются в конфликтах, и порог увеличивается . … Это происходит потому, что они получают психологические и социальные бонусы от конфликта. Их конфликт часто планируется (стр.288).

            Родители, занимающиеся программированием и промыванием мозгов, усугубляют социальные конфликтные ситуации … Это ими используется, чтобы вызвать выгорание, отчаяние  и, в конечном итоге, психологическое истощение противника, т.е другой стороны, втянутой в  конфликт (стр. 274-275).

            Вышеупомянутые родители, занимающиеся программированием и «промыванием мозгов», используют «ковровую бомбардировку» против своих противников. Для этих родителей характерно нападать на всех без исключения людей, которые как им кажется, поддерживает целевого родителя (стр.275). Такой эффект приводит  к большим расходам денег, времени, энергии и беспокойству у всех сторон. Это часть их социального насилия, социопатического [жирный шрифт мой] стиля поведения. Такое поведение обычно устойчиво к внешним воздействиям и обычно не прекращается, пока не появятся мощные санкции (финансовые и юридические) за необоснованный судебный процесс и/или передачу опеки целевому родителю. Даже тогда они не могут остановиться. (стр.275).

            Эскалация психологического насилия принимает разные формы. Усиление давления на детей, возбуждение нового судебного процесса, распространение клеветы  и усиление обвинений — лишь несколько примеров того, что может иметь место. (стр.276).

            Следовательно, лечение тяжелых случаев родительского отчуждения требует очень сложного вмешательства, требующего специальных навыков и знаний. Обширные исследования пришли к выводу, что у серьезных отчуждателей есть глубокая психопатология и одно или более расстройств личности кластера B. Расстройства личности кластера B включают: пограничное, нарциссическое и антисоциальное.             Нормальные родители не совершают отчуждения своих детей от другого родителя; нормальные родители не будут эгоистично держать ребенка в рабстве  у  себя; нормальные родители не изгонят из жизни своего ребенка его второго  родителя; нормальные родители не претендуют на роль единственного родителя, в котором нуждается ребенок; нормальные родители не убедят своих детей поверить в ложь того, что они подверглись насилию со стороны другого родителя; нормальные родители не нарушают закон, препятствуя общению с детьми другого родителя, и не требуют от  своих детей отказаться от своего родителя; нормальные родители не манипулируют своими детьми для того, чтобы они оскорбляли  и отвергали другого родителя. Нормальные родители просто не делают всего этого со своими детьми. В Диагностическом  и статистическом Руководстве по психическим расстройствам (DSM-5) расстройство личности определяется следующим образом:

            «Устойчивый паттерн внутреннего опыта и поведения, который заметно отличается от ожиданий культуры человека». Паттерн «негибкий и распространяются в широком диапазоне личных и социальных ситуаций ». Паттерн проявляется в сферах познания, аффективности, межличностного взаимодействия, и импульсивных действий» (DSM 5, с. 646).

            Учитывая все вышесказанное, самостоятельное изменение поведения со стороны серьезных отчуждателей крайне редко происходит добровольно и быстро — и часто даже терапия бессильна.

            Серьезные отчуждатели обычно меняют свое поведение  только перед лицом значимых юридических последствий — например, потери контакта с детьми.

 

Отвергнутый / отчужденный родитель

 

            Нередко психиатр или судебно-медицинский эксперт, не являющийся специалистом по родительскому отчуждению, неправильно диагностирует отвергнутого родителя как предрасположенного к психическому расстройству  или с наличием тяжелого психического состояния. Это происходит потому, что профессионалу не удалось оценить, является ли симптоматическое поведение целевого родителя ситуативным, в результате  травмы отчуждения от детей, а не внутренней характерной чертой поведения. Приписывая проблемы последнему и исключая ситуационные факторы, профессионал совершает ошибку, известную как «фундаментальная ошибка атрибуции».  Прежде чем прийти к выводу, что проблемное  поведение является характерологическим, необходимо установить не  является ли такое поведение связанным с отчуждением- то есть по времени  связано или предшествует отчуждению.

            Если проблемное поведение является реакцией на отказ детей от родителя, то оно обусловлено ситуацией, психологической травмой. Отчужденные родители — жертвы психологических травм; они реагируют на неприятие, унижение и жестокое обращение со стороны своих любимых детей. Конечно, это пример обвинения жертвы, когда профессионалы критикуют и находят психическую патологию у  отвергнутого родителя из-за того, что у него была нормальная человеческая реакция, такая как гнев, страх, беспокойство, или любой другой симптом, связанный с психической травмой.

 

Семейное исцеление

 

            TPFF стремится к содержательному и уважительному совместному воспитанию детей и достижения уверенности в том, что оба родителя серьезно вовлечены в воспитание  ребенка. Оно основано на том, что любимый родитель поощряет  ребенка поддерживать  воссоединение и постоянные отношения с отвергнутым родителем.

            Когда любимый (отчуждающий ранее) родитель искренне поддерживает отношения между другим  родителем  и их  ребенком, ребенок знает и переживает это и реагирует соответственно, быстро обнимая отвергнутого родителя. Разумные родители признают, что родительская компетентность включает в себя способность заставить ребенка делать то, что родитель искренне хочет, чтобы ребенок делал. Родитель не может претендовать на наличие  искренней  поддержки и своей компетентности, когда заявляет, что всегда поддерживал отношения ребенка с другим родителем, но ребенок не хочет  подчиниться. Это отсутствие искренности (ложь) или некомпетентность: выбирайте!

            TPFF попытается привлечь предпочитаемого  родителя к устранению препятствий на пути оперативного прекращения периода изоляции целевого родителя от ребенка. Это осуществляется с помощью  ежедневного телефонного общения во время 4-дневного вмешательства, чтобы предоставить родителям образовательные услуги, обращая  внимание на  ответственность родителей за содействие и гарантию отношений между другим  родителем и ребенком, а также для устранения очень пагубных последствий для детей из-за того, что любящий родитель был изгнан из их жизни. Важно, чтобы предпочитаемый родитель обратился  к психотерапевту для решения проблем, которые возникли из-за  отчуждающего воздействия на ребенка и для помощи из-за неспособности этого родителя проявлять инициативу, требуя от ребенка восстановления отношений с отвергнутым родителем – точно так же, как компетентный родитель требует, чтобы ребенок посещал школу и ходил  на прием к врачу. Цель терапии состоит в преодолении препятствий для общения целевого родителя и ребенка. Благодаря этим совместным усилиям, будут даны рекомендации суду на основе усилий родителей по изменению ситуации.

 

Своевременная передача ребенка  на попечение отчужденного родителя

 

            Как правило, лучше всего передать ребенка на попечение отчужденного родителя в момент судебного постановления о вмешательстве  TPFF. Учитывая исследования, которые имеются у нас  о глубокой психологической нестабильности серьезных отчуждателей — и особенно если отчуждающий родитель имел историю суицидальных мыслей, попыток и / или угроз, или если есть другие важные признаки нестабильности — серьезным риском для ребенка будет  оставление его  под опекой отчуждающего родителя до начала вмешательства.

            Были ситуации, когда отчуждающий родитель скрывался с ребенком  после решения суда о назначении лечения. И в некоторых редких случаях отчуждающий родитель совершал акт убийства ребенка, а затем совершал самоубийство.

            Еще одна важная причина скорейшего перехода ребенка под опеку отчужденного родителя состоит в том, что отчуждающий родитель воспользуется временем между постановлением суда  и терапевтическим вмешательством для эскалации процесса «промывания мозгов»,  как это описали Клавар и Ривлин. TPFF вмешательство должно в идеале начинаться  сразу после вынесения постановления суда. Альтернативное размещение ребенка в расширенной семье отчужденного родителя может быть вариантом, если отчужденный родитель не может  быть доступен сразу после вынесения постановления суда.

 

Месторасположение

 

            Семья должна будет поехать в Нью-Йорк и обеспечить размещение в отеле или путем краткосрочной аренды дома. TPFF не предоставляет жилье.

            Я договариваюсь о встрече в Нью-Йорке для сеансов терапии, а послеобеденные мероприятия выбираются семьей из списка близлежащих достопримечательностей. Место в Нью-Йорке для проведения терапии  выбирается на основе семейного удобства и интересов.

 

Требования:

 

            TPFF принимает и полагается на выводы Суда, который заслушал показания и получил доказательства относительно семейной динамики. Таким образом, TPFF работает на основе следующих судебных заключений: 1) ребенок находится в безопасности на попечении отвергнутого  родителя, и 2) предпочитаемый родитель, как минимум, вмешался в отношения между другим родителем и их ребенком.

            TPFF не подходит и не принимает направления при наличии  законных причин для отказа ребенка от родителя (т.е. насилия, пренебрежения, психических расстройств и пр.) .

            Учитывая все вышесказанное, следующие положения постановления суда должны включать следующее: 1) ребенок должен находиться в сопровождении  отвергнутого родителя в Нью-Йорке для участия в 4-дневной терапевтической интервенции  TPFF; 2) наличие временного  или постоянного  постановления суда  о передаче единоличной физической и юридической  опеки отвергнутому родителю; 3) 90-дневный период отсутствия контактов между ребенком и отчуждающим  родителем; это должно включать все телефонные и электронные сообщения, а также физический контакт; 4) требование участия  отчуждающего  родителя в  образовательных  услугах с TPFF; 5) любимый (отчуждающий) родитель должен написать ребенку письмо-указание на важность наличия отвергнутого родителя в жизни ребенка и что она / он поддерживает воссоединение ребенка с целевым родителем и объяснить почему. Это письмо должно быть одобрено специалистом TPFF перед передачей ребенку 5) предпочитаемый родитель должен предоставить отчужденному родителю  любые сувениры, видео, фотографии и другие материалы, свидетельствующими о семейной жизни, семейной истории и участии отчужденного родителя в воспитании  своего  ребенка для использования в процессе терапевтического вмешательства; 6) положение о бессрочном продлении периода изоляции,  если предпочитаемый родитель (отчуждатель) не сможет поддерживать отношения отвергнутого родителя с их ребенком. TPFF будет сотрудничать с терапевтом предпочитаемого  родителя, чтобы провести оценку поддержки отношений ребенка с целевым родителем со стороны предпочитаемого  родителя и уведомить суд по запросу; 7) предпочитаемый  родитель должен участвовать в утвержденной TPFF -психотерапии, чтобы исключить  поведение, которое не поддерживало отношения между целевым родителем и их ребенком, чтобы понять, что отчуждение — это форма психологического насилия над детьми, и признать, что в интересах ребенка другой родитель должен быть значимым в жизни ребенка. До периода изоляции психотерапия может  быть отменена, терапевт должен получить письменное согласие от  предпочтительного родителя о том, что он готов, желает и способен поддерживать отношения между другим родителем и своим  ребенком  и будет воздерживаться от отчуждающего поведения.

            TPFF не устанавливает минимального или максимального возраста ребенка. у меня есть случаи с детьми в возрасте 12 месяцев при их  отказе от объятий любящего родителя путем подстрекательства со стороны другого родителя. TPFF также не имеет верхнего возрастного ограничения.

            Совершеннолетние дети могут участвовать на добровольных началах.

TPFF, по запросу, предоставит суду резюме вмешательства, разработки, рекомендации по дальнейшему уходу и ответит на другие вопросы, вызывающие озабоченность у суда.

По запросу суда также даются показания в судебном заседании.

 

Путешествие в TPFF

 

            Есть два реальных варианта поездки в TPFF. Но предпочтительный вариант – для ребенка путешествие под присмотром и опекой отвергнутого родителя.

Учитывая мой опыт экспертизы и/или лечения случаев родительского отчуждения — включая непосредственное лечение более 550 отчужденных детей и с участием еще 250 детей, которых я оценила как отчужденных на основании клинических исследований  — я могу с высокой степенью клинической уверенности заявить, что отчужденный ребенок тайно жаждет воссоединения, даже если это желание было подавлено. Когда тайная тяга ребенка к отчужденному родителю сочетается с постановлением суда о проведении терапии, это является лучшим вариантом. Отвергнутый родитель может воспользоваться помощью семьи и друзей, с которыми ребенок имел предыдущие отношения. Отчужденные дети искренне не будут сопротивляться этому варианту путешествия и лечебному вмешательству, как только они поймут, что 1) решение о терапии принято  профессионалами; 2) цель лечения — сохранить здоровые отношения ребенка с обоими родителями; 3) быстрое разрешение этого семейного кризиса и восстановление отношений целевого родителя с  ребенком  зависит от сотрудничества предпочитаемого родителя; 4) выражение одобрения  ребенку и искренней поддержки со стороны предпочитаемого родителя для воссоединения полезно, но не обязательно для участия в программе.

            Помощь родственников или значимых друзей отчужденного родителя, у которых ранее были положительные отношения с ребенком приветствуется, ценится и будет далее включаться в терапию воссоединения.

            В качестве альтернативы предпочтитаемый родитель может сопроводить ребенка в TPFF и передать ребенка на попечение отвергнутого родителя в моем присутствии. Это полезно для ребенка и еще раз свидетельствует об искренней поддержке воссоединения ребенка с отчужденным родителем со стороны любимого родителя, ранее обсужденное и одобренное письмо можно прочитать вслух в присутствии всех сторон. После перехода ребенка предпочитаемый родитель незамедлительно покидает  TPFF и не должен  оставаться в пределах 60 миль от места лечебного вмешательства.

            Несмотря на то, что для этого вида путешествий существуют наши профессиональные транспортные услуги, вовсе не обязательно полагаться на такие услуги.

            В ответ на комментарии небольшого числа профессионалов, которые не имели опыта лечения тяжелого отчуждения — я верю, что следующая информация снимает опасения, что это вмешательство, включая поездку в TPFF, является травматичной для ребенка: все данные о результатах на основе фактических данных и исследования, проведенные в Family Bridges и Family Reflections окончательно оспаривают  это. Ни один ребенок не был травмирован и не высказывал  какую-либо угрозу  причинения себе вреда или побега — даже если некоторые дети ранее этим угрожали. Детям нравится активная часть вмешательства, а терапевтические сеансы не отличаются от проведения других методов  психотерапии.

            Обеспокоенность коллег психотравмой детей основана на чистом предположении, они не изучили клиническую литературу, чтобы подтвердить это предположение. Клиническая литература поддерживает прямо противоположное: восстановление детско-родительских отношений является  наилучшими интересами  ребенка и приветствуется  ребенком.

 

Оплата

 

            Стоимость лечения будет предоставлена по письменному запросу и считается разумной для такого рода вмешательства. Для наиболее эффективных и быстрых результатов отчуждающий родитель должен нести основную ответственность за вознаграждение — если у отчуждающего  родителя есть для этого средства. Терапия прогрессирует значительно быстрее и сохраняет результаты, если отчуждающий родитель несет финансовые затраты  за терапевтический  процесс — это просто человеческая природа. Но хоть какие-то финансовые вложения со стороны предпочтительного  родителя настоятельно рекомендуется, хотя и не требуется.

 

Резюме программы

 

            Сеансы терапии проводится ежедневно в каждый из 4-х дней и длятся 3-4 часа. В распорядке  дня используется также как средство терапии,  возможно, даже в большей степени; когда  отвергнутый родитель и ребенок будут участвовать в постоянных новых корректирующих событиях друг с другом, поскольку они будут  изучать местные достопримечательности и совершать взаимно приятные  действия. Они могут посетить  музеи, парки развлечений, сады, плавательный бассейн, покататься  на лодках, поиграть в боулинг, покататься  на коньках, использовать скалолазание, батуты и, конечно же, магазины игрушек и электроники. В результате опеки над ребенком в это время со стороны отчужденного родителя  восстанавливается родительская власть над ребенком, забота и поддержка, оказываемая  в течение четырех дней. Я сопровождаю семью в этих мероприятиях,  вмешиваясь при необходимости и осуществляю наблюдение за развитием событий. По завершении повседневной деятельности семья удаляется в выбранные ими  помещения.

            Я на связи 24 часа в сутки, 7 дней в неделю, если мои услуги понадобятся в экстренных случаях, что никогда, кстати, не случалось!

 

СТАТЬИ ПО ТЕМЕ

 

ЛИНДА ГОТЛИБ. РАЗМЫШЛЕНИЯ  СЕМЕЙНОГО ТЕРАПЕВТА О РОДИТЕЛЬСКОМ ОТЧУЖДЕНИИ

 

ДЖЕНИФЕР ХАРМАН И ДР. ЭКСПЕРТИЗА, ПРОФИЛАКТИКА И ВМЕШАТЕЛЬСТВО ПРИ РОДИТЕЛЬСКОМ ОТЧУЖДЕНИИ

 

ДОКТОР РИЧАРД ВАРШАК. СУДЕБНАЯ ЭКСПЕРТИЗА И ЛЕЧЕНИЕ РОДИТЕЛЬСКОГО ОТЧУЖДЕНИЯ

 

 

 

ДОКТОР ДУГЛАС ДАРНАЛЛ. ПСИХОСОЦИАЛЬНОЕ ЛЕЧЕНИЕ РОДИТЕЛЬСКОГО ОТЧУЖДЕНИЯ

 

КЕЙТ ТЕМПЛЕР И ДР. ОБЗОР СОВРЕМЕННОЙ ПРАКТИКИ ЛЕЧЕНИЯ РОДИТЕЛЬСКОГО ОТЧУЖДЕНИЯ

Пределы

— Оценка

Вы должны сначала прочитать Limits (An Introduction)

Краткое описание лимитов

Иногда мы не можем что-то придумать напрямую . .. но мы можем видеть, что это должно быть, когда мы приближаемся все ближе и ближе!

Пример:

(х ² — 1) (х — 1)

Давайте разберемся для x = 1:

(1 ² — 1) (1–1) знак равно (1–1) (1–1) знак равно 0 0

Теперь 0/0 — это сложность! Мы действительно не знаем значение 0/0 (оно «неопределенное»), поэтому нам нужен другой способ ответить на этот вопрос.

Итак, вместо того, чтобы пытаться вычислить это для x = 1, давайте попробуем

, приближаясь к , это все ближе и ближе:

Продолжение примера:

x		(х 2 — 1) (х — 1)
0,5		1.50000
0,9		1.
0,99		1,99000
0,999		1. 99900
0,9999		1.99990
0,99999		1,99999
…		…

Теперь мы видим, что когда x приближается к 1, то (х ² -1) (х − 1) получает близко к 2

Мы столкнулись с интересной ситуацией:

• Когда x = 1, мы не знаем ответа (это неопределенно )
• Но мы видим, что будет 2

Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»

Предел из (х ² -1) (х − 1) когда x приближается к 1, будет 2

И записывается символами как:

предм x → 1 x ² −1 x − 1 = 2

Так что это особый способ сказать «», игнорируя то, что происходит, когда мы приближаемся, но по мере того, как мы приближаемся, ответ становится все ближе и ближе к 2 »

В виде графика это выглядит так: Итак, по правде говоря, мы не можем сказать, каково значение при x = 1. Но мы можем сказать, что по мере приближения к 1, предел равен 2.

Оценка пределов

«Оценка» означает нахождение значения ( думаю, е- « значение» -значение )

В приведенном выше примере мы сказали, что предел равен 2, потому что выглядело так, как будто это будет . Но этого недостаточно!

На самом деле существует способов получить точный ответ.Давайте посмотрим на некоторые:

1. Просто введите значение

Первое, что нужно попробовать, это просто ввести значение лимита и посмотреть, работает ли оно (другими словами, подстановка).

Пример:

lim x → 10 x 2

10 2 = 5

Легко!

Пример:

lim x → 1 x 2 −1 x − 1

(1−1) (1−1) = 0 0

Не повезло. Нужно попробовать что-нибудь еще.

2. Факторы

Можем попробовать факторинг.

Пример:

lim x → 1 x ² −1 x − 1

Разлагая (x ² −1) на (x − 1) (x + 1), получаем:

lim x → 1 x ² −1 x − 1 = lim x → 1 (x − 1) (x + 1) (x − 1)

= лим x → 1 (x + 1)

Теперь мы можем просто подставить x = 1, чтобы получить предел:

предм x → 1 (x + 1) = 1 + 1 = 2

3.Конъюгат

Для некоторых дробей может помочь умножение верха и низа на конъюгат.

Сопряжение — это то, где мы меняем знак в середине двух членов следующим образом:

Вот пример, где это поможет нам найти предел:

lim x → 4 2 − √x 4 − x

Оценка этого при x = 4 дает 0/0, что не является хорошим ответом!

Итак, попробуем переставить:

Умножить верхнюю и нижнюю части на конъюгат верха:		2 − √x 4 − x × 2 + √x 2 + √x
Упростите верх, используя (a + b) (a − b) = a 2 — b 2 :		2 2 — (√x) 2 (4 − x) (2 + √x)
Дальнейшее упрощение верха:		4 − x (4 − x) (2 + √x)
Отмена (4-x) сверху и снизу:		1 2 + √x

Итак, теперь у нас:

lim x → 4 2 − √x 4 − x = lim x → 4 1 2 + √x = 1 2 + √4 = 1 4

Готово!

4.

Бесконечные пределы и рациональные функции

Рациональная функция — это функция, которая представляет собой отношение двух полиномов:		f (x) = P (x) Q (x)
Например, здесь P (x) = x 3 + 2x — 1 и Q (x) = 6x 2 :		x 3 + 2x — 1 6x 2

Найдя общую степень функции, мы можем узнать, является ли предел функции 0, бесконечностью, -Бесконечностью или легко вычисляется из коэффициентов.

Подробнее читайте в разделе «Пределы бесконечности».

5. Правило L’Hôpital

Правило L’Hôpital может помочь нам оценить пределы, которые сначала кажутся «неопределенными», например 0 0 и ∞ ∞ .

Подробнее читайте на сайте L’Hôpital’s Rule.

6. Формальный метод

Формальный метод приступает к доказательству того, что мы можем получить настолько близко, насколько мы хотим, к ответу, сделав «x» близким к «a».

Подробнее читайте в разделе «Пределы» (формальное определение)

Исчисление I — Бесконечные пределы, часть I

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-7: Пределы на бесконечности, Часть I

В предыдущем разделе мы видели пределы, которые были бесконечностью, и теперь пора взглянуть на пределы в бесконечности.Под предельными значениями на бесконечности мы понимаем один из следующих двух пределов.

\ [\ mathop {\ lim} \ limits_ {x \ to \ infty} f \ left (x \ right) \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim} \ limit_ {x \ to — \ infty} f \ left (x \ right) \]

Другими словами, мы собираемся посмотреть, что произойдет с функцией, если мы позволим \ (x \) стать очень большим в положительном или отрицательном смысле. Кроме того, как мы скоро увидим, эти пределы могут иметь бесконечность в качестве значения.

Во-первых, отметим, что набор фактов из раздела «Бесконечный предел» также сохраняется, если мы заменим \ (\ mathop {\ lim} \ limits_ {x \ to \, c} \) на \ (\ mathop {\ lim} \ limits_ {x \ to \ infty} \) или \ (\ mathop {\ lim} \ limits_ {x \ to — \ infty} \). r}}} = 0 \]

Если задуматься, первая часть этого факта должна иметь смысл.{r} \) определяется для отрицательного \ (x \). Это условие здесь, чтобы избежать таких случаев, как \ (r = \ frac {1} {2} \). Если бы это \ (r \) было разрешено, мы бы извлекали квадратный корень из отрицательных чисел, которые были бы комплексными, и мы хотим избежать этого на этом уровне.

Также обратите внимание, что знак \ (c \) не повлияет на ответ. Независимо от знака \ (c \) у нас все равно будет постоянная, деленная на очень большое число, что приведет к очень маленькому числу, и чем больше \ (x \), тем меньше становится дробь.Знак \ (c \) будет влиять на то, в каком направлении дробь приближается к нулю (, т.е. с положительной или отрицательной стороны), но она все равно приближается к нулю.

Если задуматься, это действительно частный случай последнего факта из фактов в предыдущем разделе. Однако, чтобы увидеть прямое доказательство этого факта, см. Раздел Доказательство различных предельных свойств в главе «Дополнительные возможности».

Давайте начнем с примеров, которые приведут нас к хорошей идее, которую мы будем использовать на регулярной основе, относительно пределов на бесконечности для многочленов.2} — 8x} \ right) \) Показать решение

Наша первая мысль здесь, вероятно, состоит в том, чтобы просто «вставить» бесконечность в полином и «оценить» каждый член, чтобы определить значение предела. Довольно просто увидеть, что будет делать каждый член в пределе, и поэтому это кажется очевидным шагом, особенно с учетом того, что мы делали это для других ограничений в предыдущих разделах.

Итак, давайте посмотрим, что мы получим, если это сделаем. Когда \ (x \) приближается к бесконечности, тогда \ (x \) в степени может только увеличиваться, а коэффициент при каждом члене (первом и третьем) только сделает член еще больше.2} — 8x} \ right) = \ infty — \ infty — \ infty \]

Теперь у нас есть небольшая, но легко решаемая проблема. У нас, вероятно, есть искушение сказать, что ответ равен нулю (потому что у нас есть бесконечность минус бесконечность) или, возможно, \ (- \ infty \) (потому что мы вычитаем две бесконечности из одной бесконечности). Однако в обоих случаях мы ошибаемся. Это одна из тех неопределенных форм , которые мы впервые начали видеть в предыдущем разделе.

Бесконечности просто не всегда ведут себя так, как действительные числа, когда дело доходит до арифметики.5} \) в этом случае.

Теперь все, что нам нужно сделать, это взять предел в два члена. В первом случае не забывайте, что, поскольку мы идем в сторону \ (- \ infty \) и повышаем \ (t \) до степени 5 ^th , предел будет отрицательным (отрицательное число возведено в нечетная мощность по-прежнему отрицательна). Во втором члене мы снова будем активно использовать вышеизложенный факт, чтобы увидеть, что это конечное число.

Следовательно, используя модификацию Фактов из предыдущего раздела, значение лимита равно

. 2}) + 8} \ right) = — \ infty \]

Хорошо, теперь, когда мы увидели, как работает пара многочленов, мы можем привести простой факт о многочленах в целом.n} \]

Этот факт на самом деле говорит о том, что когда мы берем предел на бесконечность для многочлена, все, что нам действительно нужно сделать, это посмотреть на член с наибольшей степенью и спросить, что этот член делает в пределе, поскольку многочлен будет иметь такое же поведение.

Вы можете увидеть доказательство в разделе «Доказательство различных предельных свойств» в главе «Дополнительно».

Давайте теперь перейдем к более сложным ограничениям.

Пример 2 Оцените оба следующих предела.4} + 7}} \] Показать решение

Во-первых, единственное различие между этими двумя состоит в том, что один стремится к положительной бесконечности, а другой — к отрицательной бесконечности. Иногда эта небольшая разница влияет на значение лимита, а иногда — нет.

Давайте начнем с первого предела, и, как и в случае с нашим первым набором примеров, может возникнуть соблазн просто «подключить» бесконечность. Поскольку числитель и знаменатель являются многочленами, мы можем использовать вышеуказанный факт для определения поведения каждого из них.4} + 7}} = \ frac {\ infty} {{- \ infty}} \]

Это еще одна неопределенная форма . В этом случае у нас может возникнуть соблазн сказать, что предел равен бесконечности (из-за бесконечности в числителе), нулю (из-за бесконечности в знаменателе) или -1 (потому что что-то, что делится само на себя, равно единице). Здесь работают три отдельных арифметических «правила», и без работы невозможно узнать, какое «правило» будет правильным, и, что еще хуже, возможно, что ни одно из них не может сработать, и мы можем получить совершенно другой ответ, скажем, \ (- \ frac {2} {5} \), чтобы выбрать число наугад.4}}}}} \\ & = \ frac {{2 + 0 + 0}} {{- 5 + 0}} \\ & = — \ frac {2} {5} \ end {align *} \]

В этом случае неопределенная форма не была ни одним из «очевидных» вариантов выбора бесконечности, нуля или -1, поэтому будьте осторожны с такими предположениями с такими неопределенными формами. 2}}}}}} {{\ frac {5} {x} — 2}} = \ frac {{\ sqrt {3 + 0}}} {{0 — 2}} = — \ frac { {\ sqrt 3}} {2} \ end {align *} \]

Давайте теперь посмотрим на второй предел (с отрицательной бесконечностью).2}}}}}} {{\ frac {5} {x} — 2}} \\ & = \ frac {{\ sqrt 3}} {2} \ end {align *} \]

Итак, как мы видели в последних двух примерах, иногда бесконечность в пределе влияет на ответ, а иногда — нет. Также обратите внимание, что он не всегда просто меняет знак числа. Иногда это может полностью изменить значение. Мы увидим один или два примера в следующем разделе.

Прежде чем перейти к еще парочкам примеров, давайте вернемся к идее асимптот, которую мы впервые увидели в предыдущем разделе.Точно так же, как мы можем иметь вертикальные асимптоты, определенные в терминах пределов, мы можем также иметь горизонтальные асимптоты, определенные в терминах пределов.

Определение

Функция \ (f (x) \) будет иметь горизонтальную асимптоту в точке \ (y = L \), если выполняется одно из следующих условий.

\ [\ mathop {\ lim} \ limits_ {x \ to \ infty} f \ left (x \ right) = L \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim } \ limits_ {x \ to — \ infty} f \ left (x \ right) = L \]

Мы не собираемся здесь много делать с асимптотами, но это несложный факт, и мы можем использовать предыдущий пример, чтобы проиллюстрировать все идеи асимптот, которые мы видели как в этом, так и в предыдущем разделах.4}}}}} {{2 + \ frac {3} {t}}} \\ & = \ frac {0} {2} \\ & = 0 \ end {align *} \]

В этом случае, используя Факт 1, мы можем видеть, что числитель равен нулю, и, поскольку знаменатель также не равен нулю, дробь и, следовательно, предел будут равны нулю.

В этом разделе мы сосредоточились на пределах на бесконечности с функциями, которые включают только многочлены и / или рациональные выражения, содержащие многочлены. Есть еще много типов функций, которые мы могли бы использовать здесь.Это тема следующего раздела.

Чтобы увидеть точное и математическое определение этого вида предела, см. Раздел «Определение предела» в конце этой главы.

Как рассчитать пределы для различных функций

Аналогично, если x приближается к -∞, функция f в этом случае также становится произвольно близкой к нулю.

Но нам не нужно ограничивать пределы крайними значениями независимой переменной.А как насчет других интересных особенностей этой функции? Давайте рассмотрим, как работать с ограничениями, когда мы приближаемся к x = 0. Во-первых, обратите внимание, что предел зависит от направления, с которого приближается значение x .

В этом случае, если мы начнем с левой стороны и приблизимся к x = 0, функция f будет становиться все меньше и меньше (в смысле большей величины, но с отрицательным знаком) без ограничений. Чтобы представить эту ситуацию символически, мы называем предел -∞, но это просто означает, что функция не имеет минимального действительного значения. Мы используем небольшой надстрочный индекс «-«, чтобы указать подход слева:

Когда мы приближаемся к x = 0 справа (обозначено надстрочным индексом «+»), f становится произвольно большим, поэтому мы говорим, что предел равен ∞.

Мы также можем посмотреть предел любой произвольной точки, а не только «особых» точек. Рассмотрим x = 1.

Итак, давайте еще раз посмотрим на общее выражение для ограничения данной функции f ( x ), поскольку x приближается к некоторой константе c.

Рассматривая все приведенные выше примеры, мы можем теперь сказать, что если функция f становится произвольно близкой (но не обязательно достигает) некоторого значения L , поскольку x приближается к c с любой стороны, тогда L будет предел этой функции для x приближается к c. В этом случае мы говорим, что предел существует. Односторонние ограничения — это когда функция приближается к определенному значению только с одной стороны (как в функции ниже). В этом случае предел не существует; однако мы можем найти односторонние ограничения, как мы это делали выше.

Часто мы можем определить предел, просто вычислив f ( c ), но очевидно, что это не всегда работает (особенно если c не находится в области f ).Кроме того, нам может потребоваться рассмотреть направление, с которого мы приближаемся к c (для односторонних ограничений). Однако обычно вы можете легко вычислить предел, если вы также посмотрите на график или таблицу значений около x = c.

Практическая задача: Рассчитайте следующие пределы.

а. г. г. г.

Решение: Это помогает сначала построить график функции, чтобы увидеть эти пределы.

а. Для этого предела рассмотрим значение ln x , поскольку x становится все ближе и ближе к 0. Функция приближается к -∞, поэтому предел равен

.

г.В этом случае мы можем просто подключить c к функции. Обратите внимание, что предел равен 0 независимо от направления подхода.

г. Здесь, поскольку x становится произвольно большим, то же самое происходит и с ln x (т.е. функция не имеет реального максимального значения). Таким образом,

г.Опять же, в этом случае направление подхода не имеет значения. Мы можем просто подключить и к функции.

Правила лимитов

Некоторые ограничения могут включать сложные выражения. В этих и других случаях часто бывает полезно использовать правила, упрощающие вычисления. Ниже приведены основные свойства пределов для произвольных функций f ( x ) и g ( x ) и произвольной постоянной k.

Эти правила для пределов позволяют нам разбивать сложные выражения на более простые с целью нахождения предела.

Практическая задача: Опишите словами, почему для многочлена p ( x ) всегда верно следующее.

Решение: Напомним, что многочлен p ( x ) имеет следующий вид, где значения c _i (где i = 0, 1, 2, 3 ,. , n ) — константы:

Когда x приближается к k, , многочлен (независимо от его формы) приближается к p ( k ), потому что область полинома — это все действительные числа. Таким образом, когда мы имеем дело с пределами для многочленов, мы можем просто подставить предельное значение для x непосредственно в функцию.Математическое доказательство этого факта не слишком сложно, но результат довольно интуитивно понятен.

Практическая задача: Рассчитайте следующие пределы.

а. г. г.

Решение: В каждом случае можно использовать несколько подходов.Один из них — построить график функции и посмотреть на поведение функции вблизи предельного значения x (это часто полезно независимо от того, какой подход вы используете). В качестве альтернативы вы можете использовать правила ограничений и, при необходимости, просто заменить их.

а. Здесь замена возможна без проблем. Вы также можете использовать правила лимитов.

г.В данном случае функция является многочленом степени 2. Мы можем просто подставить.

г. Для этой функции вы не можете напрямую применять правила ограничений и подстановки. Обратите особое внимание на примечание к графику: значение x приближается справа.

Применение ограничений: непрерывность

Давайте рассмотрим более простое применение ограничений: непрерывность функции.Посмотрите еще раз на функцию .

Интуитивно мы можем сказать, что функция непрерывна (т. Е. В ней нет «разрывов») слева от x = 0 и справа от x = 0, но не на x = 0. А как насчет более математического определения? Мы можем использовать ограничения. Функция непрерывна в определенной точке x = c , если выполняются все следующие условия:

c находится в домене f

существует

Обратите внимание, что функция является непрерывной на открытом интервале ( a, b ), если она непрерывна во всех точках этого интервала.

Практическая задача: Определите, является ли функция непрерывной в данной точке.

а. при x = 1 б. при x = 0 гр. ln x при x = e

Решение: Для проблемы a обратите внимание, что функция равна строке x + 2, за исключением того, что в ней отсутствует точка (1, 3).Интересно, что лимит здесь есть:

Однако функция не определена при x = 1. Следовательно, мы не можем использовать подстановку, чтобы найти предел. Поскольку функция нарушает одно (фактически нарушает два) из условий непрерывности, она не является непрерывной при x = 1.

Для части b обратите внимание, что ни одно из условий непрерывности не выполняется.Предел не существует (это ∞), и функция не определена при x = 0. Следовательно, функция не является непрерывной при x = 0.

Для части c обратите внимание, что функция определена как x = e:

ln e = 1

Кроме того, предел определен и может быть рассчитан путем замены:

Таким образом, ln x является непрерывным при x = e.

2.3 Предельные законы — Расчет, том 1

Цели обучения

• Признать основные предельные законы.
• Используйте законы пределов, чтобы оценить предел функции.
• Вычислите предел функции путем факторизации.
• Используйте предельные законы, чтобы оценить предел полиномиальной или рациональной функции.
• Оцените предел функции путем факторизации или использования конъюгатов.
• Вычислите предел функции, используя теорему сжатия.

В предыдущем разделе мы оценили пределы, глядя на графики или создавая таблицу значений. В этом разделе мы устанавливаем законы для расчета пределов и узнаем, как применять эти законы. В Студенческом проекте в конце этого раздела у вас есть возможность применить эти предельные законы, чтобы вывести формулу для площади круга, адаптировав метод, разработанный греческим математиком Архимедом. Начнем с повторения двух полезных результатов о пределе из предыдущего раздела.Эти два результата вместе с предельными законами служат основой для расчета многих пределов.

Первые два предельных закона были указаны на (Рисунок), и мы повторяем их здесь. Эти основные результаты вместе с другими предельными законами позволяют нам оценить пределы многих алгебраических функций.

Результаты базового предела

Для любого действительного числа и любой константы

Оценка базового предела

Оцените каждый из следующих пределов, используя (Рисунок).

Теперь посмотрим на законы пределов, индивидуальные свойства пределов. Доказательства справедливости этих законов здесь не приводятся.

Сейчас мы практикуем применение этих законов о лимитах для оценки лимита.

Оценка лимита с помощью законов о лимитах

Используйте законы пределов для оценки.

Решение

Давайте применим законы предельных значений пошагово, чтобы убедиться, что мы понимаем, как они работают. Нам необходимо иметь в виду требование, согласно которому при каждом применении предельного закона должны существовать новые пределы для применения предельного закона.

Многократное использование предельных законов

Используйте законы пределов для оценки.

Решение

Чтобы найти этот предел, нам нужно применить законы пределов несколько раз. Опять же, нам нужно иметь в виду, что, когда мы переписываем предел с точки зрения других ограничений, каждый новый предел должен существовать для применения закона предела.

Используйте законы пределов для оценки. На каждом этапе указывайте применяемый предельный закон.

Решение

К настоящему времени вы, вероятно, заметили, что в каждом из предыдущих примеров именно так было.Это не всегда верно, но это верно для всех многочленов при любом выборе и для всех рациональных функций при всех значениях, для которых рациональная функция определена.

Чтобы убедиться, что эта теорема верна, рассмотрим многочлен. Применяя законы суммы, постоянного кратного и степенного, мы получаем

Теперь из частного закона следует, что если и — многочлены, для которых, то

.

(рисунок) применяет этот результат.

Оценка предела рациональной функции

Оцените.

Решение

Поскольку 3 находится в области определения рациональной функции, мы можем вычислить предел, подставив 3 вместо в функцию. Таким образом,

.

Оценить.

Как мы видели, мы можем легко вычислить пределы многочленов и пределы некоторых (но не всех) рациональных функций с помощью прямой подстановки. Однако, как мы видели во вводном разделе, посвященном ограничениям, определенно возможно существование, когда не определено. Следующее наблюдение позволяет нам оценить многие ограничения этого типа:

Если на всем протяжении некоторого открытого интервала, содержащего, то.

Чтобы лучше понять эту идею, рассмотрим предел.

Функция

и функция идентичны для всех значений. Графики этих двух функций показаны на (Рисунок).

Рисунок 1. Графики и идентичны для всех. Их пределы на 1 равны.

Мы видим, что

Предел имеет вид, где и. (В этом случае мы говорим, что имеет неопределенную форму 0/0.) Следующая стратегия решения проблем предоставляет общий план для оценки пределов этого типа.

Следующие примеры демонстрируют использование этой стратегии решения проблем. (Рисунок) иллюстрирует метод множителя и отмены; (Рисунок) показывает умножение на конъюгат. На (Рисунок) мы рассмотрим упрощение сложной дроби.

Оценка лимита путем факторинга и отмены

Оценить.

Оценить.

Решение

Вычисление предела умножением на конъюгат

Оценить.

Оценить.

Решение

Оценка предела путем упрощения сложной дроби

Оценить.

Оценить.

(рисунок) не соответствует ни одному из шаблонов, установленных в предыдущих примерах. Однако, проявив немного творчества, мы все же можем использовать те же самые техники.

Оценка лимита, когда законы о лимитах не применяются

Оценить.

Решение

Давайте вернемся к односторонним ограничениям.Простые модификации предельных законов позволяют применять их к односторонним пределам. Например, чтобы применить предельные законы к пределу формы, мы требуем, чтобы функция была определена на открытом интервале формы; для предела формы мы требуем, чтобы функция была определена на открытом интервале формы. (Рисунок) иллюстрирует этот момент.

Оценка одностороннего лимита с использованием предельных законов

По возможности оцените каждый из следующих пределов.

На (Рисунок) мы смотрим на односторонние пределы кусочно определенной функции и используем эти пределы, чтобы сделать вывод о двустороннем пределе той же функции.

Оценка двустороннего лимита с использованием предельных законов

Для оценки каждого из следующих пределов:

Постройте график и оцените.

Решение

-1, который пересекал ось x и ось y в начале координат ».>

Теперь мы обратим наше внимание на оценку предела формы, где, где и. То есть имеет вид при.

Оценка предела формы с использованием предельных законов

Оценить.

Оценить.

Решение

Техника, которую мы разработали до сих пор, очень хорошо работает для алгебраических функций, но мы все еще не можем оценить пределы самых основных тригонометрических функций. Следующая теорема, получившая название теорема сжатия , оказывается очень полезной для установления основных тригонометрических пределов. Эта теорема позволяет нам вычислять пределы, «сжимая» функцию с пределом в неизвестной точке между двумя функциями, имеющими общий известный предел в.(Рисунок) иллюстрирует эту идею.

Рисунок 4. Теорема сжатия применима, когда и.

Применение теоремы о сжатии

Примените теорему сжатия для оценки.

Используйте теорему сжатия для оценки.

Теперь мы используем теорему сжатия, чтобы найти несколько очень важных ограничений. Хотя это обсуждение довольно продолжительное, эти ограничения оказываются неоценимыми для развития материала как в следующем разделе, так и в следующей главе. Первый из этих ограничений -.Рассмотрим единичный круг, показанный на (Рисунок). На рисунке мы видим, что это координата на единичной окружности, которая соответствует отрезку линии, показанному синим цветом. Радианная мера угла θ — это длина дуги, которую он проходит на единичной окружности. Следовательно, мы видим, что для.

Рис. 6. Синусоидальная функция показана в виде линии на единичном круге.

Поскольку и, используя теорему сжатия, мы заключаем, что

.

Чтобы увидеть это, обратите внимание на это для и, следовательно, для.Следовательно, Отсюда следует, что. Применение теоремы сжатия дает желаемый предел. Таким образом, поскольку и,

.

Далее, используя идентификатор для, мы видим, что

.

Теперь мы рассмотрим предел, который играет важную роль в следующих главах, а именно,. Чтобы оценить этот предел, мы используем единичный круг на (Рисунок). Обратите внимание, что этот рисунок добавляет еще один треугольник к (Рисунок). Мы видим, что длина стороны противоположного угла в этом новом треугольнике равна. Таким образом, мы видим, что для.

Рис. 7. Функции синуса и тангенса показаны линиями на единичной окружности.

Разделив на все части неравенства, получим

.

Эквивалентно

.

Так как, заключаем, что. Применяя манипуляции, подобные тем, которые использовались при демонстрации этого, мы можем это показать. Таким образом,

.

В (Рисунок) мы используем этот предел для установления. Этот предел также окажется полезным в следующих главах.

Оценка важного тригонометрического предела

Оценить.

Решение

На первом этапе мы умножаем на сопряжение, чтобы мы могли использовать тригонометрическую идентичность для преобразования косинуса в числителе в синус:

Следовательно,

.

Оценить.

Ключевые понятия

• Предельные законы позволяют нам оценивать пределы функций без необходимости каждый раз проходить пошаговые процессы.
• Для многочленов и рациональных функций.
• Вы можете оценить предел функции, разложив на множители и отменив, умножив на конъюгат или упростив сложную дробь.
• Теорема сжатия позволяет вам найти предел функции, если функция всегда больше одной функции и меньше другой функции с известными пределами.

В следующих упражнениях используйте законы пределов для оценки каждого предела. Обоснуйте каждый шаг, указав соответствующий предельный закон (законы).

1.

Решение

Использовать постоянный множественный закон и разностный закон:

2.

3.

Решение

Использовать корневой закон:

4.

В следующих упражнениях используйте прямую замену для оценки каждого предела.

5.

6.

7.

8.

9.

Решение

10.

В следующих упражнениях используйте прямую замену, чтобы показать, что каждый предел приводит к неопределенной форме 0/0.Затем оцените предел.

12.

14.

16. , где — действительная константа

18.

20.

В следующих упражнениях используйте прямую подстановку, чтобы получить неопределенное выражение. Затем используйте метод (рисунок), чтобы упростить функцию и определить предел.

21.

Решение

22.

23.

Решение

24.

В следующих упражнениях предположим, что, и. Используйте эти три факта и законы пределов для оценки каждого предела.

25.

Решение

26.

27.

Решение

28.

29.

Решение

30.

31.

Решение

.

32.

В следующих упражнениях используйте калькулятор, чтобы построить график каждой кусочно определенной функции, и изучите график, чтобы оценить заданные пределы.

Решение

3. В точках (3, 7) есть открытый кружок, а наклон равен 1. ”>
a. 9; б. 7

Решение

= 2.Он имеет наклон -1 и точку пересечения по оси x в точке (3,0) ».>
a. 1; б. 1

В следующих упражнениях используйте следующие графики и законы пределов для оценки каждого предела.

-3. Другие ключевые точки: (0, 1), (-5,2), (1,2), (-7, 4) и (-9,6). Нижняя кусочная функция имеет линейный и криволинейный сегменты. Линейный сегмент существует для x <-3 и имеет убывающий наклон. Он переходит в (-3, -2) при x = -3. Изогнутый сегмент кажется правой половиной открывающейся вниз параболы.Он переходит в точку вершины (-3,2) при x = -3. Он пересекает ось y немного ниже y = -2. Другие ключевые точки: (0, -7/3), (-5,0), (1, -5), (-7, 2) и (-9, 4). ">

36.

37.

Решение

38.

39.

Решение

40.

41.

[detect-answer q = ”957757 ″] Показать решение [/ show-answer]
[hidden-answer a = ”957757 ″]

42.

43.

Решение

Для следующих задач оцените предел с помощью теоремы сжатия. По возможности используйте калькулятор для построения графиков функций.

44. [T] Верно или нет? Если, то.

45. [Т]

Решение

Предел равен нулю.

46. , где

Решение

а.

г. . Величина электрического поля по мере приближения к частице становится бесконечной. Оценивать отрицательное расстояние не имеет физического смысла.

48. [T] Плотность объекта определяется делением его массы на его объем:.

1. Воспользуйтесь калькулятором, чтобы построить график зависимости объема от плотности, предполагая, что вы исследуете объект массой 8 кг ().
2. Оцените и объясните физический смысл.

Пределы — Пределы Бесконечности

Пределы Бесконечности

Что самое большое, что вы когда-либо видели? Самый большой в мире мяч из резиновой ленты? Может, океан? На самом деле, солнце довольно большое (мягко говоря), и мы видим это каждый день. Но тогда мы могли бы сказать, что небо покрывает почти всю вселенную.

Кажется, это сложно превзойти. Однако даже это ничтожно по сравнению с некоторыми пределами, потому что они могут доходить до бесконечности. Мы говорим о x , поскольку он становится действительно очень большим или действительно очень маленьким. Эта идея известна как конечное поведение функции, и это то, что эти ограничения на бесконечности помогут нам описать.

По большей части эти ограничения делятся на три категории. Вместо того, чтобы тратить зря ваше и наше время, мы просто покажем вам каждую задачу в виде образца.После этого мы расскажем о нескольких сложностях и о том, как их исправить, чтобы вы могли по-настоящему удивить своих друзей на вечеринках.

Пример задачи

Оценить.

И снова здравствуйте. Давно не виделись. Но посмотрите на этот предел; x не приближается к какой-то цифре, это будет продолжаться и продолжаться бесконечно. Есть несколько способов взглянуть на это. Давайте еще раз посмотрим на его график:

Обратите внимание, что происходит, когда x становится все больше и больше.Значения y все ближе и ближе к нулю. Это означает:

Другой способ подумать об этом — подумать о том, что происходит, когда мы подставляем действительно большие значения вместо x . Что, если бы мы использовали, например, 1000? В итоге мы получаем долю. Это действительно мало, то есть близкое к нулю. И оттуда он станет только меньше. Следовательно:

Наши ответы совпадают. Ура. Мы ненавидим, когда наши ответы противоречат друг другу.

Есть третий способ найти пределы на бесконечности, и он даже более полезен.Всякий раз, когда нас просят оценить предел дроби, мы должны смотреть и сравнивать степень числителя и знаменателя. Как и судьи на соревнованиях по помпадурам, мы хотим знать, кто из них больше.

Для, больший член стоит в знаменателе. Это означает, что чем больше и больше чисел вводятся для x , знаменатель растет быстрее, чем числитель. Хорошо, это плохой пример, потому что числитель постоянный, но идею вы поняли. Функция имеет тяжелое дно, что заставляет ее опускаться до нуля на бесконечности.

Пример задачи

Оценить.

На этот раз мы сразу перейдем к проверке степени (хотя ввод чисел тоже всегда будет работать). Если числитель больше (например, x , ^3, в данном случае больше, чем x ), функция перейдет в бесконечность по мере увеличения размера x . Это означает, что:

Функция будет перемещаться вверх и вправо, всегда достигая звезд. Вы идете, маленькая функция.Большая мечта.

Этот результат имеет смысл, потому что числитель станет совершенно огромным, в то время как знаменатель станет немного большим, но не до смешного. Мы знаем, что очень точно.

Пример задачи

Оценить.

Теперь этот предел немного отличается от того, что мы видели в предыдущих разделах. У вас может возникнуть соблазн упростить, разделить и делать подобные сумасшедшие вещи. Боритесь с искушением, не поддавайтесь. Подумайте о другом, например, о животных, играющих музыку.Вместо этого мы будем умножать вещи, но лишь немного.

Да, вы правильно прочитали; «Кого волнует» и «не имеет значения» теперь стало официальным лингвистическим языком Шмоопа. Все, что нам нужно, чтобы оценить этот предел, — это члены с наибольшим показателем.

На этот раз степень та же, 2. Теперь у нас есть гонка шеи и шеи. Это будет фото финиш — ну, финиш — и все сводится к ведущему коэффициенту.

У нас есть 2 в числителе (от 2 x ² ) и 1 внизу (от x ² ).Переменные по существу компенсируют друг друга. Не буквально, а только с точки зрения приближения функции к бесконечности. Итак, наш лимит будет:

Не верите? Посмотрите график здесь. Прямо при y = 2 есть горизонтальная асимптота, которая идеально согласуется с тем, что мы только что нашли.

Пример задачи

Оценить.

Степень числителя больше, чем степень знаменателя. Ответ: ∞, да? Проблема: сделано, правда? Не так быстро.

У нас есть предел: x на этот раз приближается к минус бесконечности. Мы не можем просто бросить эту сумасшедшую восьмерку и двинуться дальше. Вместо этого мы вынуждены учитывать знак нашего окончательного ответа.

Квадрат чего угодно будет положительным, даже сверхотрицательным, как -∞, поэтому числитель будет положительным. Однако знаменатель будет отрицательным, если вы введете отрицательные числа для x .

Надо следить за знаками наших ответов.Один знак минус может повернуть наш ответ от отрицательной бесконечности к положительной бесконечности. Это должен быть самый отвратительный случай хлыстовой травмы.

Пример задачи

Оценить.

Беглый взгляд может предположить, что эта функция имеет x по сравнению с x ² , и поэтому предел будет равен нулю. Извините, но проблема еще более странная, потому что с нашим самым большим сроком творится странные вещи. Здесь самый большой член в знаменателе имеет квадратный корень.Это означает, что наибольший порядок больше нельзя рассматривать как 2, это на самом деле:

( x ² ) ^1/2 = x ^2/2 = x

Внезапно числитель и знаменатель имеют тот же порядок, что заставляет нас смотреть на коэффициенты. Только будьте осторожны с квадратным корнем. Края острые.

Да, нам тоже нужно извлечь квадратный корень из 9. Это дает нам предел 1, поскольку x приближается к бесконечной пустоте в правой части графика.

Пример задачи

Оценить.

Хорошо, последний раз проблема, а это проблема триггера. Мы не можем смотреть на степень функции, поэтому наш предыдущий метод не сработает. Вместо этого попробуйте изобразить синусоидальный график.

Может быть, вы спрашиваете себя: «Как будет работать этот предел? Когда x уходит в бесконечность, синус делает это (вы двигаете рукой волнообразным движением перед собой) навсегда и во веки веков».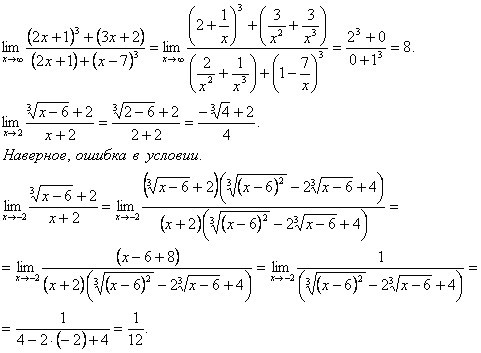

Это движение руки описывает поведение синуса, поскольку x становится бесконечно большим.Он возвращается и четвертый между 1 и -1 снова, и снова, и снова. Так что на самом деле это не имеет значения.

Иногда просто нет предела. Функция не приближается к единственному значению, но и не становится без конца ни больше, ни меньше. Почему ты просто не можешь принять решение, синус?

Сводка

• Если верхний градус дроби меньше нижнего градуса, он приближается к нулю.
• Если же градус больше наверху, функция стремится к бесконечности.
• Когда степени равны, мы сравниваем ведущие коэффициенты. Их отношение — это горизонтальная асимптота, к которой приближается функция.

• Обратите внимание на знак своего ответа, особенно когда задействовано -∞.
• Превратите любые радикалы в дробные показатели, упростите и только потом сравнивайте степени.
• Некоторые функции, например триггерные, не приближаются ни к чему на бесконечности.

предел | Определение, пример и факты

предел , математическая концепция, основанная на идее близости, используется в основном для присвоения значений определенным функциям в точках, где значения не определены, таким образом, чтобы они согласовывались с соседними значениями.Например, функция ( x ² — 1) / ( x — 1) не определена, когда x равно 1, поскольку деление на ноль не является допустимой математической операцией. Для любого другого значения x числитель можно разложить на множители и разделить на ( x — 1), получив x + 1. Таким образом, это частное равно x + 1 для всех значений . x , кроме 1, которая не имеет значения. Однако 2 может быть присвоено функции ( x ² — 1) / ( x — 1) не как ее значение, когда x равно 1, а как ее предел, когда x приближается к 1. См. Анализ : Непрерывность функций.

Один из способов определения предела функции f ( x ) в точке x ₀ , записанный как есть следующим образом: если существует непрерывная (непрерывная) функция g ( x ) таким образом, что g ( x ) = f ( x ) в некотором интервале около x ₀ , за исключением, возможно, x ₀ , затем

Британская викторина

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы говорите на языке математики в этой викторине.

Следующее более базовое определение предела, независимо от концепции непрерывности, также может быть дано: если для любой желаемой степени близости ε можно найти интервал около x ₀ , так что все значения f ( x ), вычисленное здесь, отличается от L на величину меньше ε (то есть, если | x — x ₀ | <δ, то | f ( x ) — L | <ε). Это последнее определение можно использовать, чтобы определить, действительно ли данное число является пределом. Расчет пределов, особенно частных, обычно включает в себя манипуляции с функцией, чтобы ее можно было записать в форме, в которой предел более очевиден, как в приведенном выше примере ( x ² — 1) / ( х — 1).

Пределы — это метод, с помощью которого вычисляется производная или скорость изменения функции, и они используются на протяжении всего анализа как способ приближения к точным величинам, например, когда площадь внутри изогнутой области определяется как предел приближений прямоугольниками.

The Editors of Encyclopaedia Britannica Эта статья была недавно отредактирована и обновлена ​​Эриком Грегерсеном.

Неопределенные формы

Неопределенные формы \ (\ frac {0} {0} \)

Пусть \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) — две функции такие, что

\ [\ lim \ limits_ {x \ to a} f \ left (x \ right) = 0 \; \; \; \ text {and} \; \; \ lim \ limits_ {x \ to a} g \ left (x \ right) = 0. \]

Тогда функция \ (\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}}}) имеет неопределенный вид \ (\ frac {0} {0} \) при \ (х = а.\) Чтобы найти предел в \ (x = a \), когда функция \ (\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} \) имеет неопределенное form \ (\ frac {0} {0} \) на этом этапе мы должны разложить числитель и знаменатель на множители, а затем уменьшить члены, приближающиеся к нулю.

Примечание. В этом разделе мы не применяем правило L’Hopital.

Неопределенные формы \ (\ frac {\ infty} {\ infty} \)

Пусть \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) — две функции такие, что

\ [\ lim \ limits_ {x \ to a} f \ left (x \ right) = \ pm \ infty \; \; \; \ text {and} \; \; \ lim \ limits_ {x \ to a} g \ left (x \ right) = \ pm \ infty.2} — y — 6}} = \ left [{\ frac {0} {0}} \ right] = \ lim \ limits_ {y \ to — 2} \ frac {{y \ left ({y + 1} \ right) \ cancel {\ left ({y + 2} \ right)}}} {{\ left ({y — 3} \ right) \ cancel {\ left ({y + 2} \ right)}}} = \ lim \ limits_ {y \ to — 2} \ frac {{y \ left ({y + 1} \ right)}} {{y — 3}} = \ frac {{\ lim \ limits_ {y \ to — 2} y \ cdot \ lim \ limits_ {y \ to — 2} \ left ({y + 1} \ right)}} {{\ lim \ limits_ {y \ to — 2} \ left ({y — 3 } \ right)}} = \ frac {{- 2 \ cdot \ left ({- 1} \ right)}} {{- 5}} = — \ frac {2} {5}.