Модуль в модуле
Среди примеров на модули часто встречаются уравнения где нужно найти корни модуля в модуле, то есть уравнение вида
||a*x-b|-c|=k*x+m.
Если k=0, то есть правая сторона равна постоянной (m) то проще искать решение уравнения с модулями графически. Ниже приведена методика раскрытия двойных модулей на распространенных для практики примерах. Хорошо разберите алгоритм вычисления уравнений с модулями, чтобы не иметь проблем на контрольных, тестах, и просто, чтобы знать.
Пример 1. Решить уравнение модуль в модуле |3|x|-5|=-2x-2.
Решение: Всегда начинают раскрывать уравнения с внутреннего модуля
|x|=0 <-> x=0.
В точке x=0 уравнения с модулем разделяется на 2.
При x < 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
При x>0 или равно, раскрывая модуль получим
|3x-5|=-2x-2.
Решим уравнение для отрицательных переменных (x < 0). Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе — раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная — меняем знак правой или левой части (зависит от методики преподавания).
Из первого уравнения получим что решение не должно превышать (-1), т.е.
Это ограничение полностью принадлежит области в которой решаем. Перенесем переменные и постоянные по разные стороны равенства в первой и второй системе
и найдем решение
Оба значения принадлежат промежутку что рассматривается, то есть являются корнями.
Рассмотрим уравнение с модулями при положительных переменных
|3x-5|=-2x-2.
Раскрывая модуль получим две системы уравнений
Из первого уравнения, которое является общим для двух сиcтем, получим знакомое условие
которое в пересечении с множеством, на котором ищем решение дает пустое множество (нет точек пересечения). Итак единственными корнями модуля с модулем являются значения
x=-3; x=-1,4.
Пример 2. Решить уравнение с модулем ||x-1|-2|=3x-4.
Решение: Начнем с раскрытия внутреннего модуля
|x-1|=0 <=> x=1.
Подмодульная функция меняет знак в единице. При меньших значениях она отрицательная, при больших — положительная. В соответствии с этим при раскрытии внутреннего модуля получим два уравнения с модулем
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Обязательно проверяем правую сторону уравнения с модулем, она должна быть больше нуля.
3x-4>=0 -> x>=4/3.
Это означает, что первое из уравнений нет необхидноcти решать, поcкольку оно выпиcано для x< 1,что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4 или x-3=4-3x;
4-3=3x-x или x+3x=4+3;
2x=1 или 4x=7;
x=1/2 или x=7/4.
Получили два значения, первое из которых отвергаем, поскольку не принадлежит нужному интервалу. Окончательно уравнение имеет одно решение x=7/4.
Пример 3. Решить уравнение с модулем ||2x-5|-1|=x+3.
Решение: Раскроем внутренний модуль
|2x-5|=0 <=> x=5/2=2,5.
Точка x=2,5 разбивает числовую ось на два интервала. Соответственно, подмодульная функция меняет знак при переходе через 2,5. Выпишем условие на решение с правой стороны уравнения с модулем.
x+3>=0 -> x>=-3.
Итак решением могут быть значения, не меньше (-3). Раскроем модуль для отрицательного значения внутреннего модуля
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Этот модуль также при раскрытии даст 2 уравнения
-2x+4=x+3 или 2x-4=x+3;
2x+x=4-3 или 2x-x=3+4;
3x=1; x=1/3 или x=7.
Значение x=7 отвергаем, поскольку мы искали решение на промежутке [-3;2,5]. Теперь раскрываем внутренний модуль для x>2,5. Получим уравнение с одним модулем
|2x-5-1|=x+3;
|2x-6|=x+3.
При раскрытии модуля получим следующие линейные уравнения
-2x+6=x+3 или 2x-6=x+3;
2x+x=6-3 или 2x-x=3+6;
3x=3; x=1 или x=9.
Первое значение x=1 не удовлетворяет условие x>2,5. Так что на этом интервале имеем один корень уравнения с модулем x=9, а всего их два (x=1/3).Подстановкой можно проверять правильность выполненных вычислений
Ответ: x=1/3; x=9.
Пример 4. Найти решения двойного модуля ||3x-1|-5|=2x-3.
Решение: Раскроем внутренний модуль уравнения
|3x-1|=0 <=> x=1/3.
Точка x=2,5 делит числовую ось на два интервала, а заданное уравнение на два случая. Записываем условие на решение, исходя из вида уравнения с правой стороны
2x-3>=0 -> x>=3/2=1,5.
Отсюда следует, что нас интересуют значения >=1,5. Таким образом модульное уравнения рассматриваем на двух интервалах
[1,5; 2,5], [2,5; +бесконечность).
Раскроем модуль при отрицательных значениях внутреннего модуля [1,5; 2,5]
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Полученный модуль при раскрытии делится на 2 уравнения
-3x-4=2x-3 или 3x+4=2x-3;
2x+3x=-4+3 или 3x-2x=-3-4;
5x=-1; x=-1/5 или x=-7.
Оба значения не попадают в промежуток [1,5; 2,5], то есть не являются решениями уравнения с модулями. Далее раскроем модуль для x>2,5. Получим следующее уравнение
|3x-1-5|=2x-3;
|3x-6|=2x-3.
yukhym.com
19. Уравнения с модулем | Решение задач по математике и другим предмета
Модулем (Абсолютной величиной) Числа называется неотрицательное число:
(3.9)
Геометрическая интерпретация модуля: – это расстояние от точки А до точки Х на координатной оси, в частности, – это расстояние от точки 0 до точки Х.
Свойства модуля:
1) 2) 3)
4) 5) 6)
7) 8) 9)
Пусть – некоторое алгебраическое выражение. Тогда, используя определение модуля (3.9) при соответствующих предположениях, можно раскрыть знак абсолютной величины данного выражения:
Уравнение, содержащее выражение с неизвестной Х под знаком модуля, называется Уравнением с модулем. Рассмотрим основные типы уравнений с модулем и методы их решения.
I тип: уравнение вида
(3.10)
Где А – число, – некоторое выражение с неизвестной Х.
1. Если уравнение (3.10) решений не имеет.
2. Если уравнение (3.10) равносильно уравнению
3. Если уравнение (3.10) равносильно совокупности уравнений:
II тип: Уравнение вида
Где – некоторые выражения с неизвестной Х.
Решать это уравнение можно несколькими способами.
1-й способ – используя определения модуля:
2-й способ – используя подход к решению, как к уравнениям I типа с дополнительным условием на знак выражения
З а м е ч а н и е. 1-й или 2-й способ решения таких уравнений выбирают в зависимости от того, какое из неравенств или решается легче.
3-й способ – метод интервалов. Необходимо:
1) найти те значения Х, для которых
2) нанести полученные значения Х на числовую ось;
3) определить знаки для каждого из полученных интервалов;
4) нарисовать кривую знаков;
5) решить уравнение на каждом промежутке в отдельности, раскрывая модуль согласно рисунку;
6) для каждого конкретного промежутка проверить, принадлежат ли полученные корни этому промежутку;
7) в ответе указать совокупность всех полученных корней.
III тип: Уравнения, содержащие несколько модулей. Если их два, то это уравнение вида
(3.11)
Где – некоторые выражения с неизвестной Х.
1-й способ – можно использовать определение модуля и рассматривать 4 случая возможных знаков Этот способ, как правило, не является рациональным.
2-й способ – Метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей в уравнении. Для уравнения (3.11) рисуют две оси, располагая их одна под другой (одна ось для вторая – для ). Для каждого выражения и следует изобразить кривую знаков на соответствующей оси. Затем раскрывают модули, используя рисунок, и решают уравнение отдельно на каждом промежутке. Подходят только те корни, которые принадлежат рассматриваемому промежутку. В ответе необходимо указать совокупность полученных корней.
IV тип: Уравнение вида
(3.12)
Где – некоторые выражения с неизвестной Х;
1-й способ – решение уравнения (3.12) сводится к решению совокупности уравнений:
2-й способ – метод интервалов (не рационально).
3-й способ – после возведения уравнения в квадрат и использования свойства модуля уравнение сводится к равносильному:
Полученное уравнение решается в зависимости от его типа.
V тип: Уравнения, решаемые заменой переменной, например:
Где – некоторые выражения с неизвестной Х;
По свойству модуля оно записывается в виде
Вводят замену и решают полученное квадратное уравнение относительно неизвестной У. Затем необходимо вернуться к старой переменной. В случае 2-х различных корней квадратного уравнения это будет совокупность уравнений I типа:
Если корень единственный, то остается решить уравнение
Необходимо помнить, что в случае отрицательного значения уравнение с модулем не имеет решений.
Пример 1. Решить уравнение
Решение. Это уравнение I типа. Его ОДЗ:
Уравнение записывается в виде
На ОДЗ можно сократить и получаем
откуда т. е.
Получаем корни которые подходят по ОДЗ.
Пример 2. Решить уравнение
Решение. Это уравнение II типа. Его ОДЗ: Оно имеет решение, если т. е. при Таким образом, для получаем:
(3.13)
Решим отдельно полученные дробно-рациональные уравнения. Первое уравнение сводится к виду
откуда
Это квадратное уравнение решений не имеет, так как
Из второго уравнения совокупности (3.13) получаем
т. е.
Квадратное уравнение имеет корни:
Т. е. первый корень не принадлежит множеству на котором решали уравнение, следовательно, ответом является только
Пример 3. Решить уравнение
Решение. Имеем уравнение II типа, которое решим по определению модуля:
(3.14)
Решаем первую систему совокупности (3.14):
Значение не подходит по условию Следовательно, корнем является
Решаем вторую систему совокупности (3.14):
Получили ответ
Пример 4. Решить уравнение
Решение. Поскольку то уравнение записывается в виде
Это уравнение относится к III типу уравнений.
Его ОДЗ: Решим методом интервалов.
Нулями выражений, стоящих под модулем, являются и Эти значения разбивают числовую ось на три промежутка (рис. 3.1).
Рис. 3.1
Раскрыв модули на каждом из полученных промежутков, с учетом их знаков, получим совокупность систем:
Решим отдельно системы:
III.
Решением данного уравнения являются значения и
Пример 5. Решить уравнение
Решение. Запишем уравнение в виде
Оно относится к IV типу. Возведем обе его части в квадрат:
После упрощения имеем:
т. е.
Получаем – корень.
Пример 6. Решить уравнение
Решение. ОДЗ: т. е.
Преобразуем данное уравнение к виду
Заменяем
Уравнение приобретает вид
Решаем его как дробно-рациональное и получаем:
Последнее квадратное уравнение имеет корни:
Возвращаясь к переменной Х, получаем:
Второе уравнение совокупности решений не имеет, так как слева положительное выражение, а справа – отрицательное.
Первое уравнение совокупности сводится к I типу уравнений с модулем и равносильно совокупности при условии
Приходим к совокупности
т. е.
Решение имеет только второе уравнение совокупности, его корни:
Оба они подходят по ОДЗ.
Пришли к ответу:
Пример 7. Решить уравнение
Решение. ОДЗ:
С учетом ОДЗ данное уравнение равносильно уравнению:
Используя свойства модуля (имеем сумму двух неотрицательных величин), получаем:
Т. е. – решение полученной системы, оно подходит по ОДЗ.
Получили ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Занятие элективного курса «Методы решения уравнений. содержащих модуль»
Цели и задачи:
- познакомить с методами решения уравнений, содержащих под знаком модуля выражение с переменной;
- формирование умения решать данные уравнения, научить выбирать наиболее рациональный метод решения уравнений;
- развитие логического мышления, речи;
- создание условий, способствующих воспитанию у учащихся внимательности и аккуратности в решении уравнения.
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: самопроверка самостоятельно решенных задач.
Оборудование: компьютер, мультимедийный проектор, экран, папка с файлами (практикум), презентация урока (слайды).
Ход занятия
Фронтальный опрос.
Сформулируйте определение модуля числа.
Сформулируйте геометрическое истолкование модуля.
Может ли быть отрицательным значение суммы 2+?
Может ли равняться нулю значение разности 2-?
Как сравниваются два отрицательных числа?
Устная работа. Раскрыть модуль:
Проверка домашнего задания (класс разбит на 6 групп, каждая группа готовила презентацию по заранее выбранному методу, которая и будет представлять, и защищать ее).
Изучение нового материала.
1. Метод интервалов
Для того, чтобы решить уравнение, содержащее неизвестную под знаком модуля, необходимо освободиться от знака модуля, используя его определение. Для этого следует:
1) Найти критические точки, т.е. значение неизвестной, при которых выражение, стоящее под знаком модуля, обращается в нуль;
2) Разбить область допустимых значений уравнения на промежутки, на каждом из которых, выражения, стоящие под знаком модуля сохраняют знак;
3) На каждом из этих промежутков уравнение записать без знака модуля, а затем решить его.
Объединение решений, найденных на всех промежутках, и составляет решение исходного уравнения.
Пример 1. Решите уравнение: |x+4|=2x -10.
Ответ: 14.
Пример 2. Решите уравнение: х 2-5|x|+6=0
Ответ: 2; 3.
Пример 3. Решите уравнение: |5-2x|+|x+3|=2-3x
5-2x=0 x+3=0
х=2,5 х=-3
| (- ;-3) | [-3;+2,5) | [-2,5;+ ) | |
| 5-2х | + | + | |
| х+3 | — | + | + |
| (- ;-3) | [-3;+2,5) | [-2,5;+ ) |
| 5-2х-х-3-2+3х=0 0х=0 х-любое число (- ;-3) |
5-2x+x+3-2+3x=0 2х=-6 х=-3 [-3;2,5) |
2х-5+х+3-2+3х=0 6х=4 x=2/3 [2,5;+ ) |
(- ;-3) {-3}=(- ;-3]
Ответ: (- ;-3].
2. Возведение обеих частей уравнения в квадрат.
Для того, чтобы решить уравнение содержащее модуль, необходимо освободиться от знака модуля. Для этого следует: возвести в квадрат обе части уравнения, решить его. Но не забывать, что при возведении в квадрат появляются лишние корни, поэтому, надо найти ОДЗ и выявить принадлежат ли корни данному условию.
Пример 4. Решите уравнение: |x+4|=2x-10.
Возведем в квадрат обе части уравнения
X2 +8x+16=4x2 -40x+100
3x2 -48x+84=0 /3
X2 -16x+28=0
X1=14, X2=2
Найдём ОДЗ:
2x-100;
2×10 ;
x5.
x1=14 [5;+ ), х2=2 [5;+ )
Ответ:14
Пример 5. Решите уравнение: |x+3|=2x-3
Возведем в квадрат обе части уравнения
х2 +6x+9=4x2 -12x+9; 3x2 -18x=0 /:3
х2 -6x=0; x(x-6)=0
x=0, x=6.
Найдём ОДЗ: 2х-30, 2×3, x1,5
x=0 [1,5;+)
x=6 [1,5;+ )
Ответ: 6.
3. Метод введения новой переменной
Иногда уравнение, содержащее переменную под знаком модуля, можно решить довольно просто, используя метод введения новой переменной.
Продемонстрируем данный метод на конкретных примерах:
Пример 6. Решите уравнение: х2 -5|x|+6=0.
Пусть |x |=t,тогда
|x|2 =x2 =t2 ,тогда уравнение примет вид:
t2 -5t+6=0
t1=2, |x |=2, x1,2= 2,
t2=3, |x |=3, x3,4= 3.
Ответ: 2, 3.
Пример 7. Решите уравнение: (x-2)2 — 8|x-2|+15=0.
Пусть |x-2|=t ,|x-2|2 =(x-2)2 =t2 ,
тогда уравнение примет вид: t2 -8t+15=0, D=16-15=1.
t1=3, t2=5.
t1=3, |x-2|=3, x1=5, x2=-1.
t2=5, |x-2|=5, x3=7, x4=3.
Ответ: -1; 3; 5; 7.
4. Метод замены уравнения совокупностью систем.
Рассмотрим ещё один метод решения подобных уравнений — метод замены уравнения совокупностью систем. Методом замены уравнения совокупностью систем можно решать уравнения вида
(2)
Причём данное уравнение можно заменять совокупностью систем двумя способами.
I способ:
II способ:
Если в уравнении функция имеет более простой вид, нежели функция , то имеет смысл исходное уравнение заменять первой совокупностью систем, а если более простой вид имеет функция , тогда исходное уравнение следует заменять второй совокупностью систем.
В частности, используя определение модуля, уравнение: ,
при С 0 равносильно совокупности уравнений и , т.е.
при С=0
при С0 уравнение решений не имеет.
Воспользуемся данным методом при решении следующих уравнений.
Пример 8. Решите уравнение: 2|х2+2х-5|=х-1.
Данное уравнение равносильно совокупности систем:
Ответ: .
Пример 9. Решите уравнение: |2|x-1|-3|=5.
Используя определение модуля уравнение <=> совокупности двух уравнений:
Первое уравнение совокупности равносильно совокупности двух уравнений:
Второе уравнение совокупности решений не имеет, т.к.
Ответ: -3; 5.
5. Графический метод
Существует ещё один метод решения уравнений с модулем. Он основан на геометрической интерпретации понятия абсолютной величины числа, а именно модуль х равен расстоянию от точки с координатой х до точки с координатой 0 на числовой прямой Ох. Используя геометрическую интерпретацию, легко решаются уравнения вида:
(4)
(5)
(6) где а,в,с — числа.
Решить уравнение (4) — это значит найти все точки на числовой оси Ох, которые отстоят от точки с координатой а на расстояние с.
При уравнение решений не имеет;
при уравнение имеет один корень;
при уравнение имеет два корня
Решить уравнение (5) — это значит найти все точки на числовой оси Ох, для каждой из которых сумма расстояний от неё до точки с координатами а и в равна с.
Аналогично интерпретируется решение уравнения вида (6).
Пример 12. Решите уравнение: |x-1|-|x-3|=2
Для того, чтобы решить данное уравнение, нужно на числовой оси Ох найти все такие точки, для каждой из которых разность расстояния от нее до точки с координатой 1 и расстояния от неё до точки с координатой 3 равна 2. Так как длина отрезка [1;3] равна 2,то ясно, что любая точка с координатой х3 удовлетворяет данному уравнению, а любая точка с координатой х<3 не удовлетворяет ему. Таким образом, решением исходного уравнения является множество чисел промежутка [3;+ ).
Ответ: [3;+ ).
Рассмотренный метод можно отнести к графическим методам решения уравнения. Все необходимые построения здесь производились на числовой оси. Рассмотрим теперь метод решения уравнения, в котором будем использовать построения на координатной плоскости. Этим методом, теоретически, можно решать уравнения с модулем любого вида, однако практическая реализация метода иногда бывает довольно сложной.
Суть метода состоит в следующем. Решить уравнение f(х)=q(x) это значит найти все значения х, для которых значение функций y=f(x) и y=q(x) равны, т.е. найти абсциссы всех точек пересечения графиков этих функций. Если же графики не имеют общих точек, то уравнение не имеет корней. Следует, однако, иметь в виду, что точное построение графиков функций практически невозможно, поэтому решение, найденное графическим способом требует проверки подстановкой.
Воспользуемся этим методом для решения уравнения вида (3).
Пример 13. Решите уравнение: |- 1| = 3.
Решение. Построим графики двух функций y=|-1| и y=3
Из чертежа видно, что графики имеют 2 общие точки. Координаты одной точки: (8; 3) , другой: (-4; 3).
Следовательно, исходное уравнение имеет два решения: х1=8, x2= -4. Как уже говорилось, при каждом методе значения корней уравнения определяются приблизительно, и только проверка позволит доказать, что найденные значения действительно являются корнями исходного уравнения. При подстановке х1=8, x2= -4 в уравнение получаем, соответственно два верных числовых равенства: |-3|=3 и |3|=3.
Ответ: -4; 8.
Так как при графическом методе решения зачастую не удается найти точное значение корня, но применение данного метода бывает обосновано, если требуется найти не сами корни, а всего лишь определить их количество.
6. Решение уравнений, содержащих модуль под знаком модуля.
При решении уравнения, в котором под знаком модуля находится выражение, также содержащее модуль, можно сначала освобождаться от внутренних модулей, а затем в полученных уравнениях раскрывать оставшиеся модули.
Пример 10. Решите уравнение: |x-|4-х||- 2x = 4
Уравнение |x-|4-х||-2x=4 совокупности двух систем:
urok.1sept.ru
Методическое пособие по теме «Уравнения с модулем» (10 класс)
Комсомольская ОШ №5 І – ІІІ ступеней
РЕШЕНИЯ УРАВНЕНИЙ, СОДЕРЖАЩИХ ЗНАК МОДУЛЯ
2017 год
АННОТАЦИЯ
Решение уравнений с модулем вызывает у учащихся затруднения.
Анализируя задания вступительных экзаменов, необходимо отметить, что очень часто предлагаются задания с модулями. Чтобы помочь учащимся научиться решать уравнения с модулями предлагается данный материал.
Уравнения с модулем разделены на группы по способу их решения. К каждой группе дается теоретический материал, необходимый для решения уравнений данной группы.
Даны решения уравнений каждой группы, а к отдельным уравнениям алгоритм их решения, что позволяет учащимся самообучаться.
Этот материал можно применять на уроках при работе по группам и индивидуально как в классе, так и для домашней работы.
Предназначается учащимся стерших классов.
РЕШЕНИЕ УРАВНЕНИЙ
СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ
Определение модуля
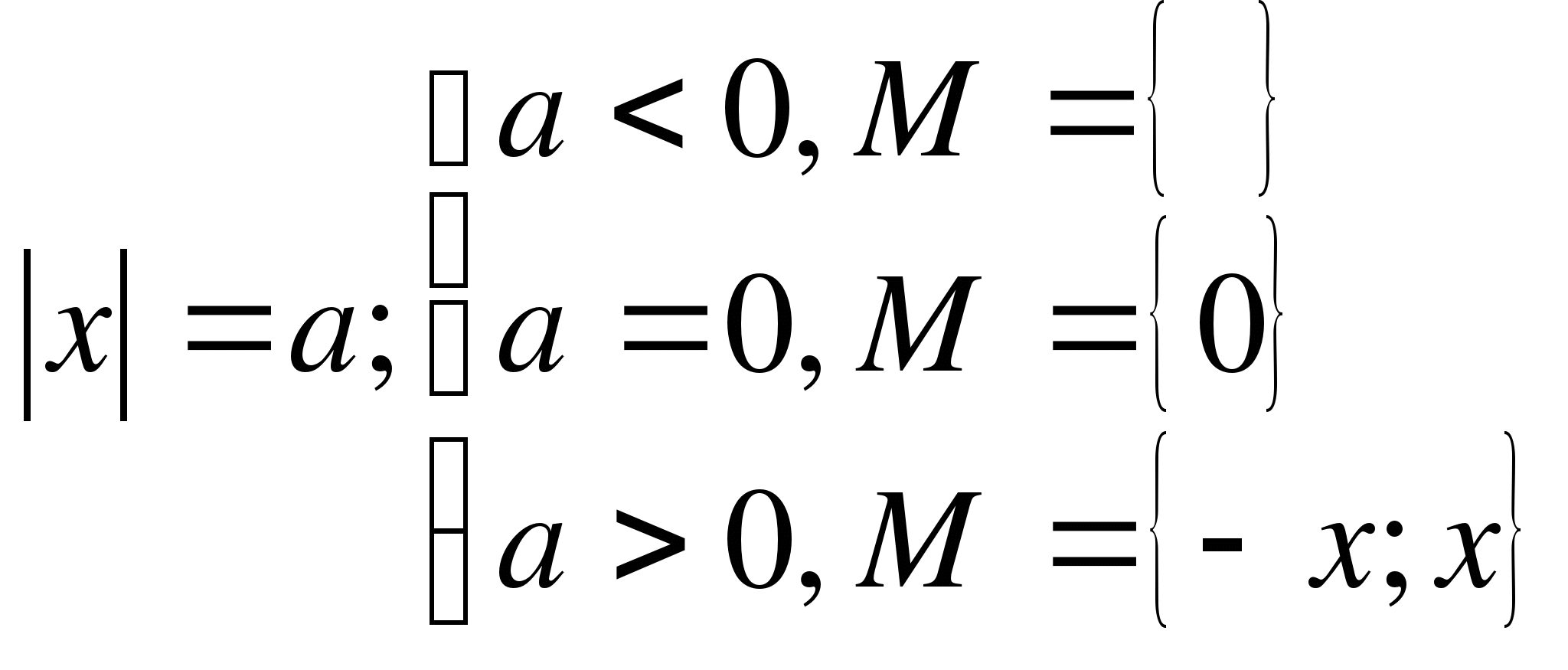
Простейшими уравнениями с модулем являются уравнения вида
 , (1)
, (1)
где 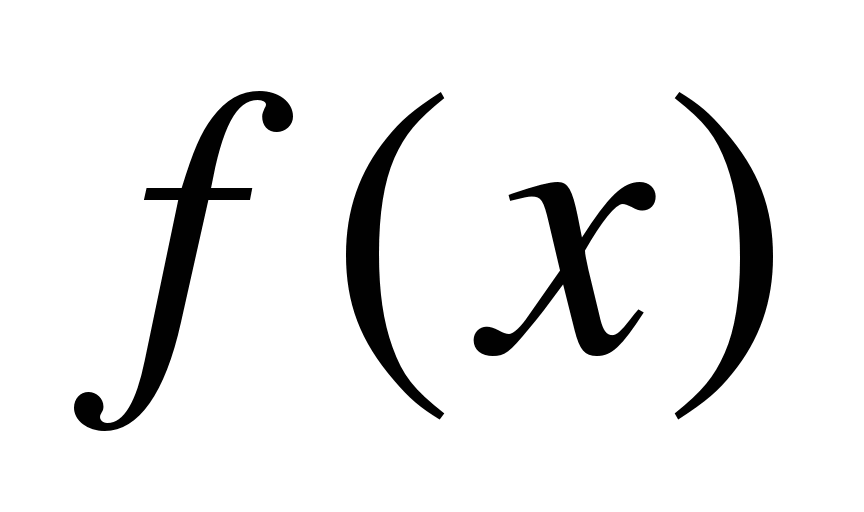 и
и 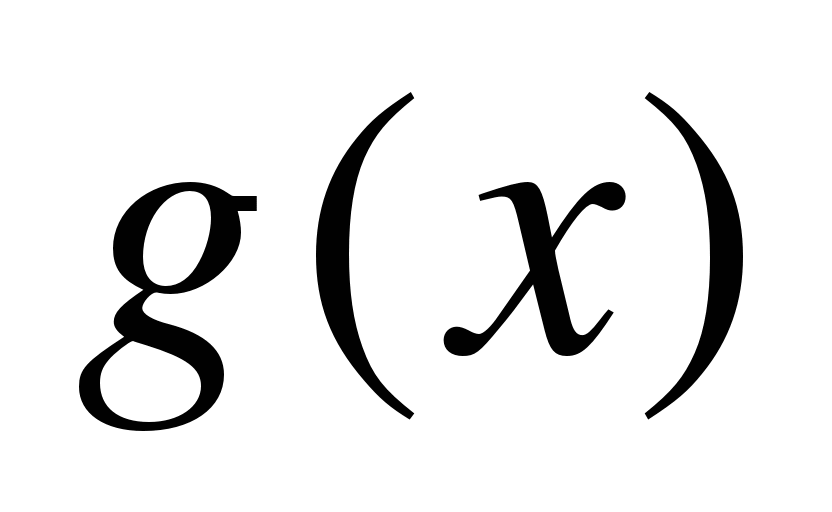 — некоторые функции.
— некоторые функции.
Для того чтобы решить данное уравнение, нужно найти сначала все решения уравнения 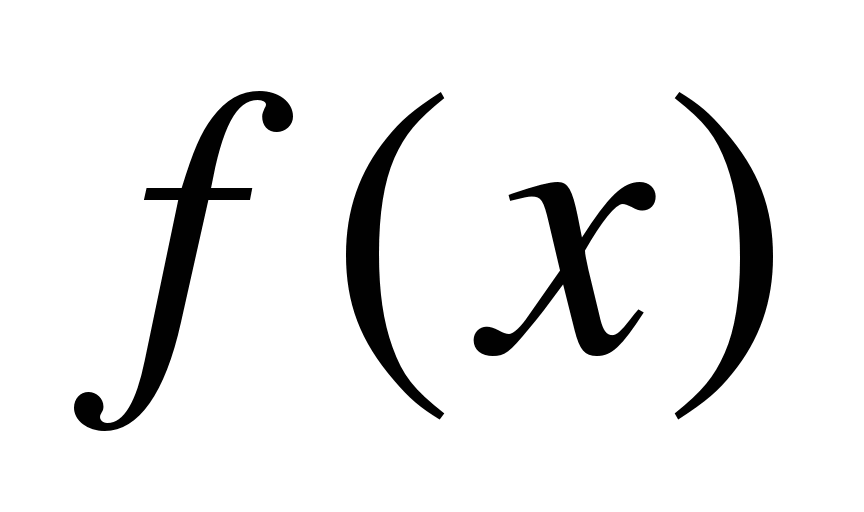 =
=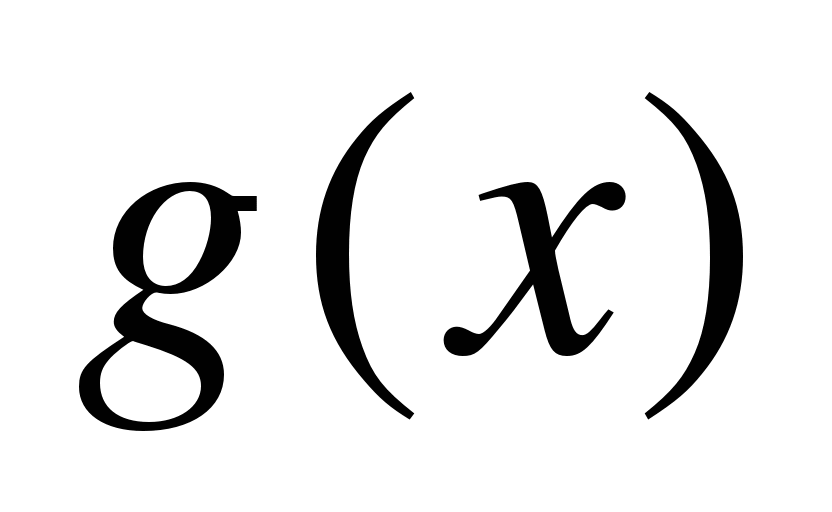 , принадлежащие множеству
, принадлежащие множеству 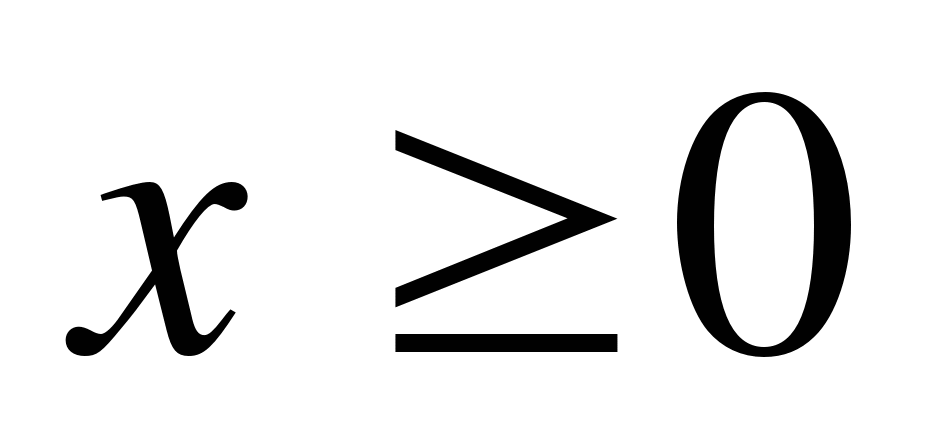 , затем решить уравнение
, затем решить уравнение 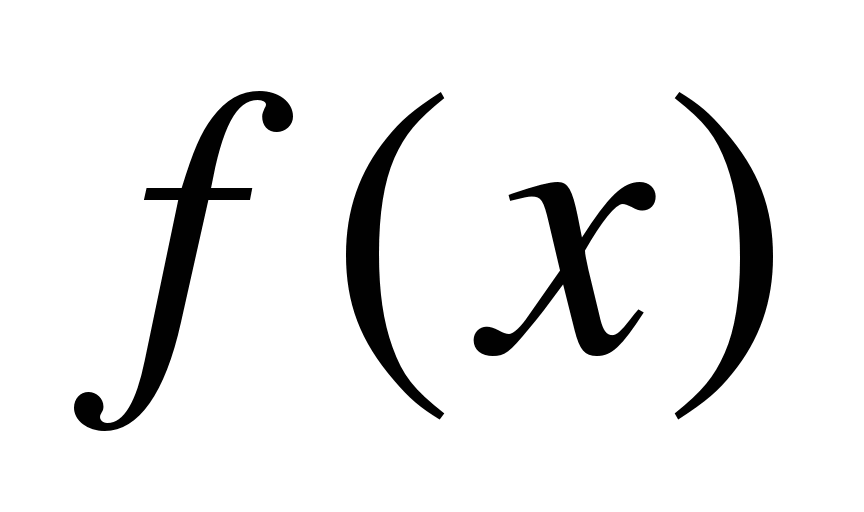 =
=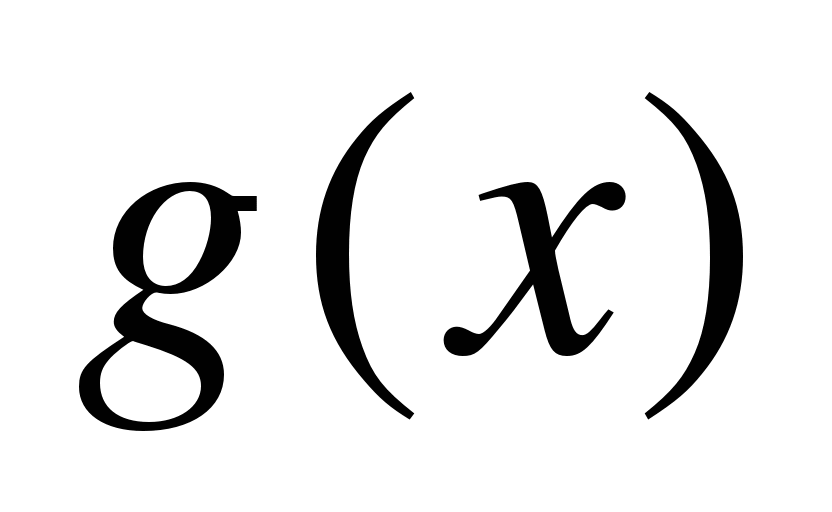 на множестве
на множестве 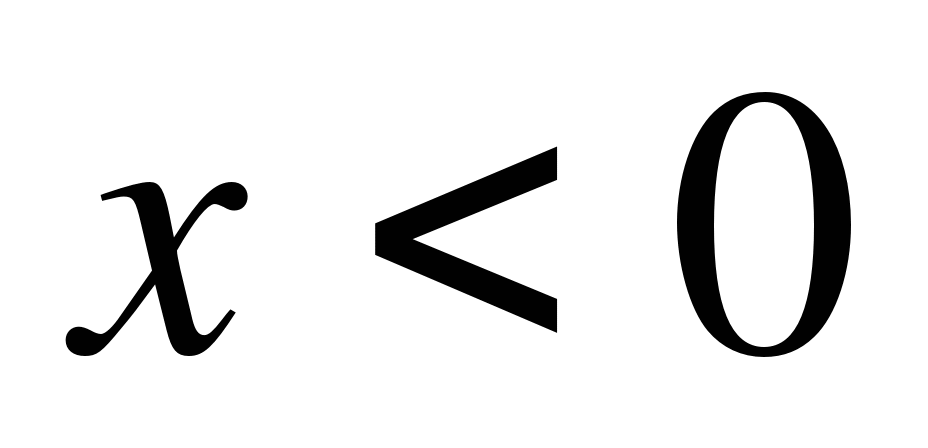 ; объединение множеств найденных решений составляет множество всех решений уравнения (1). Другими словами, уравнение (1) равносильно совокупности систем
; объединение множеств найденных решений составляет множество всех решений уравнения (1). Другими словами, уравнение (1) равносильно совокупности систем
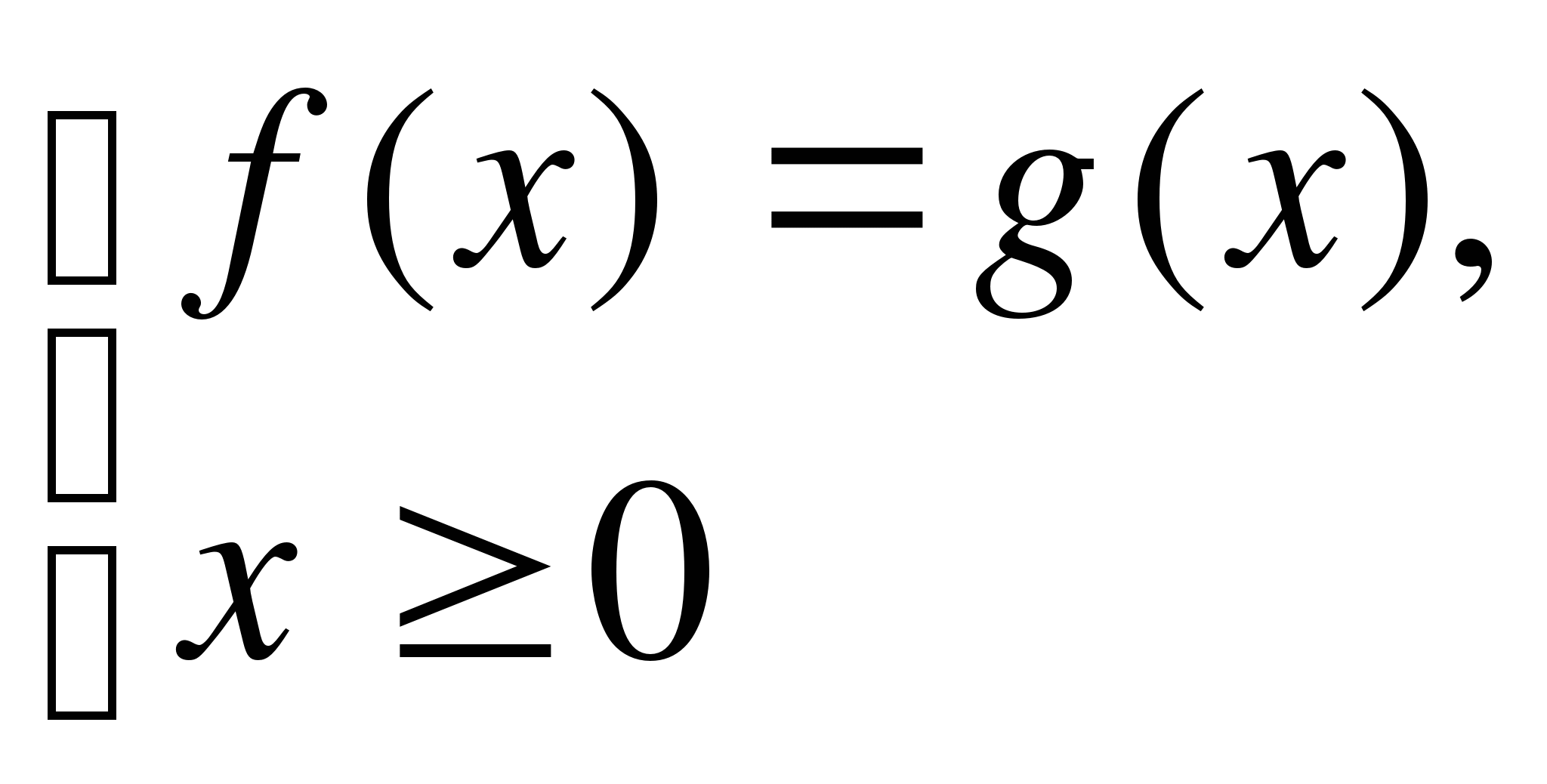 или
или 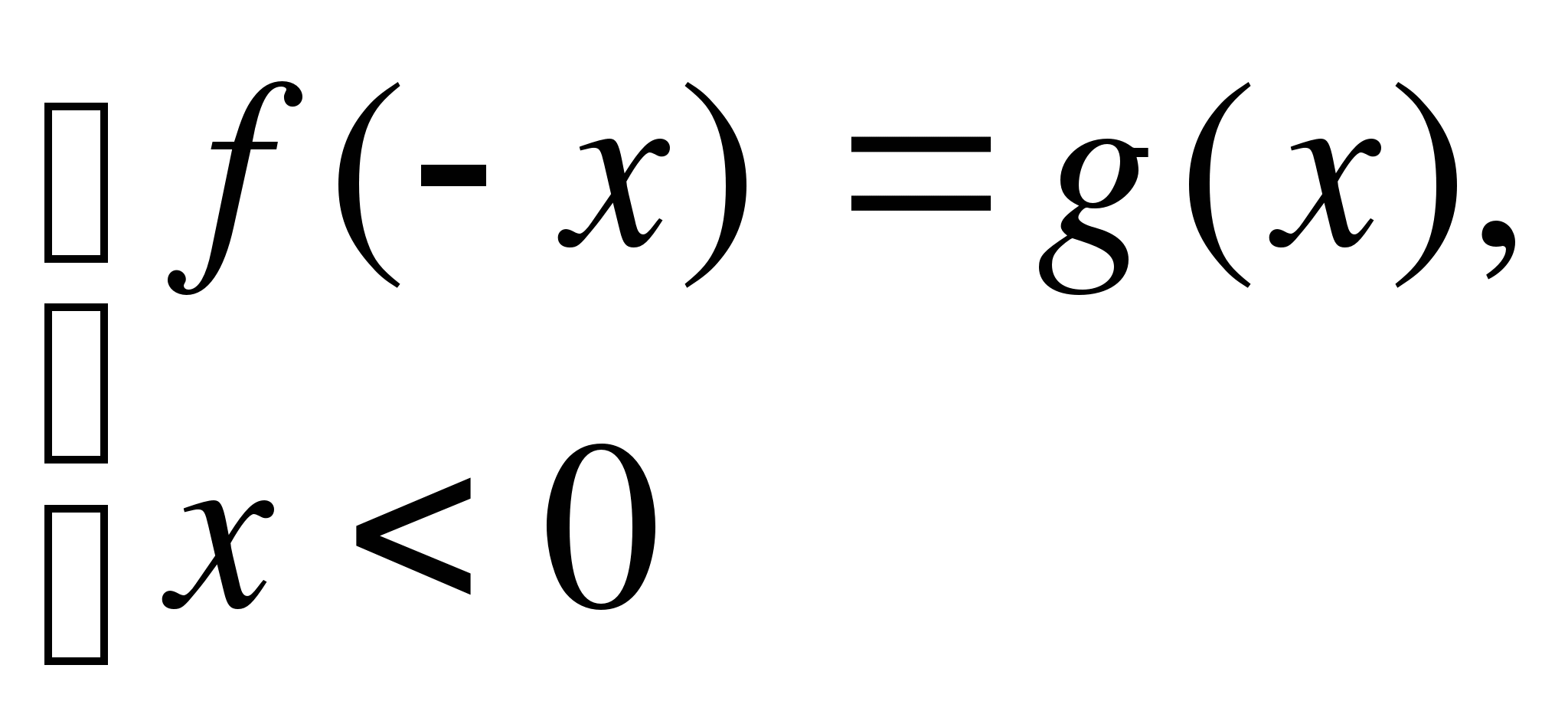
Пример 1.
Решите уравнение 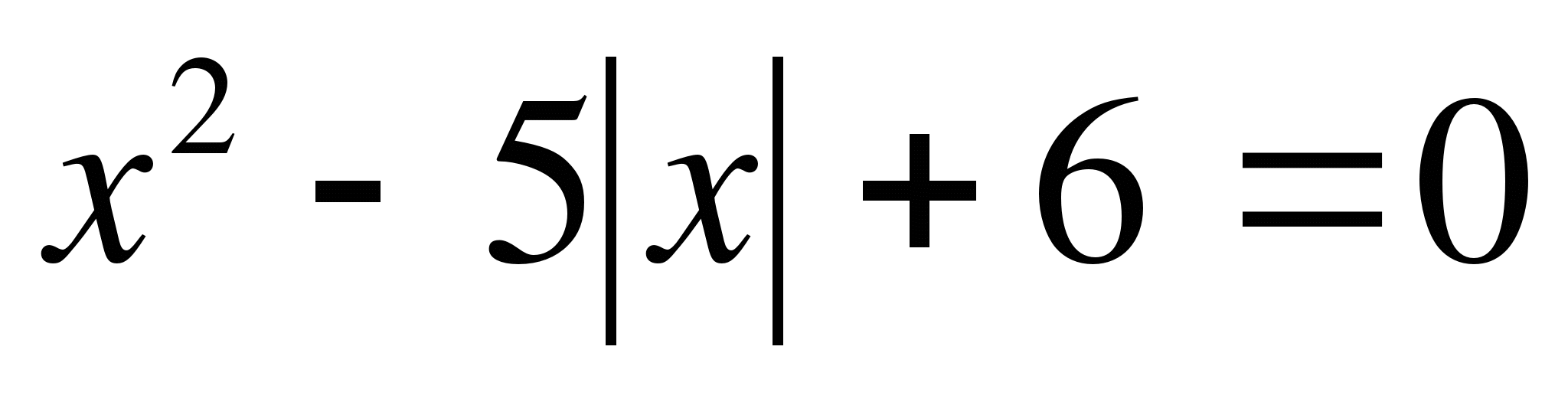 .
.
Решение.
Исходное уравнение равносильно совокупности систем:
 или
или 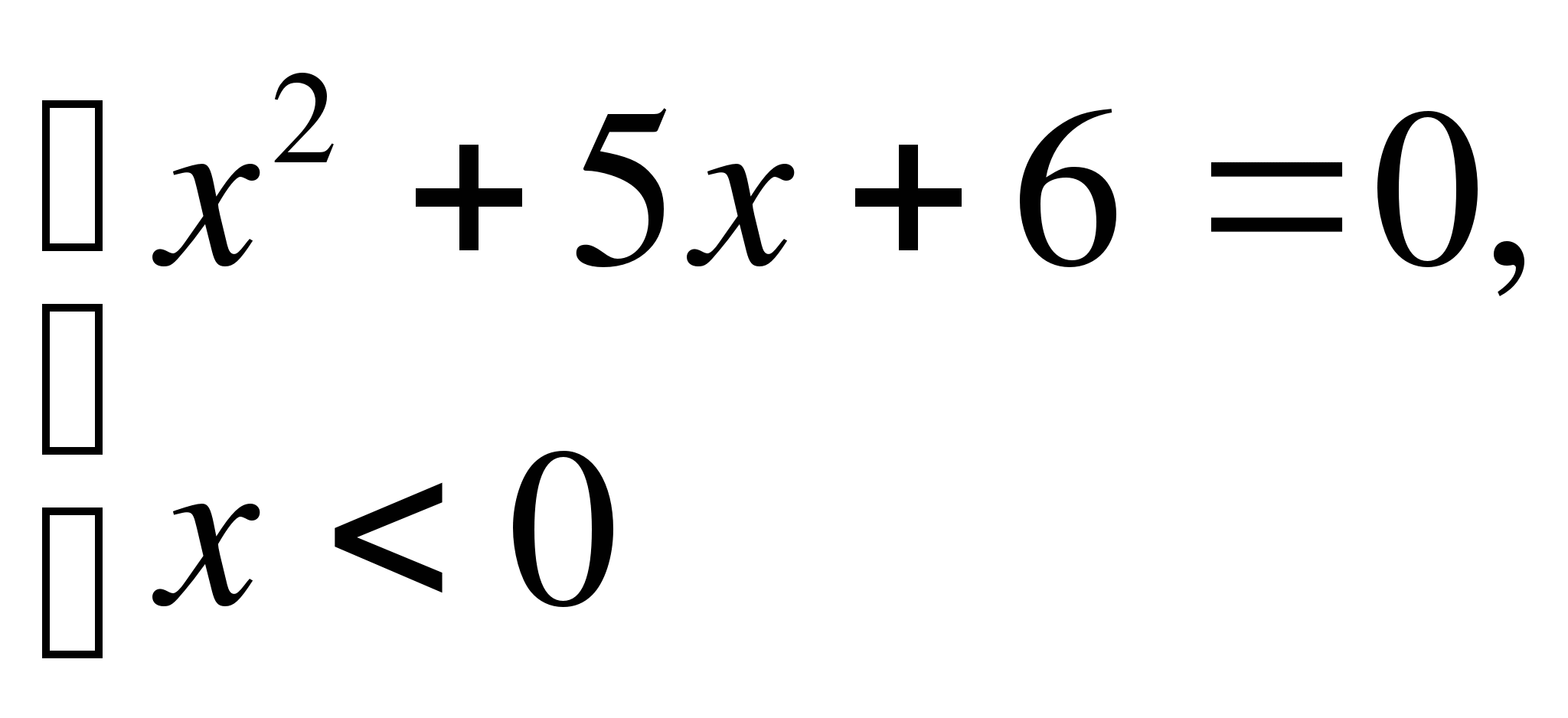
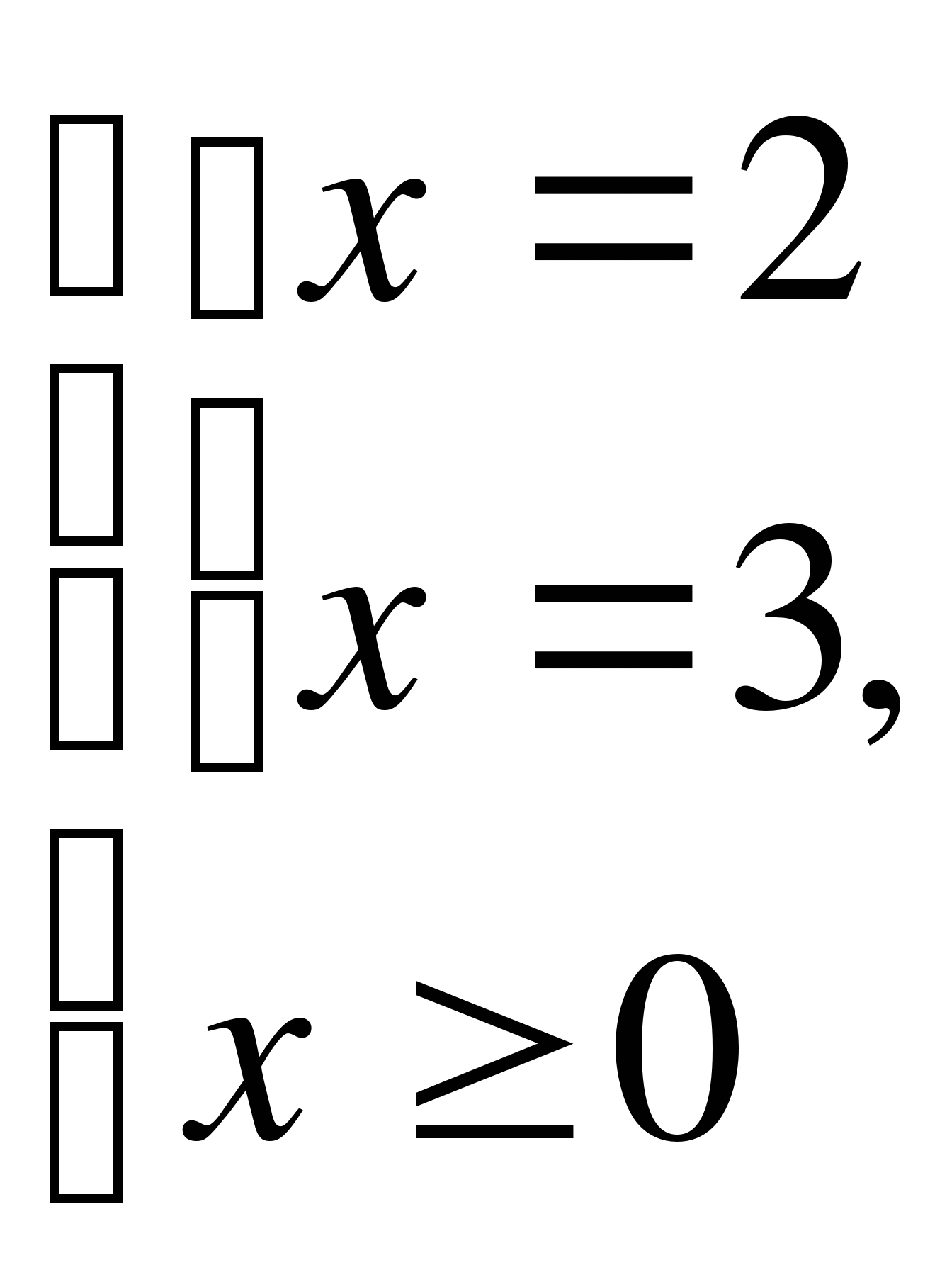 или
или 
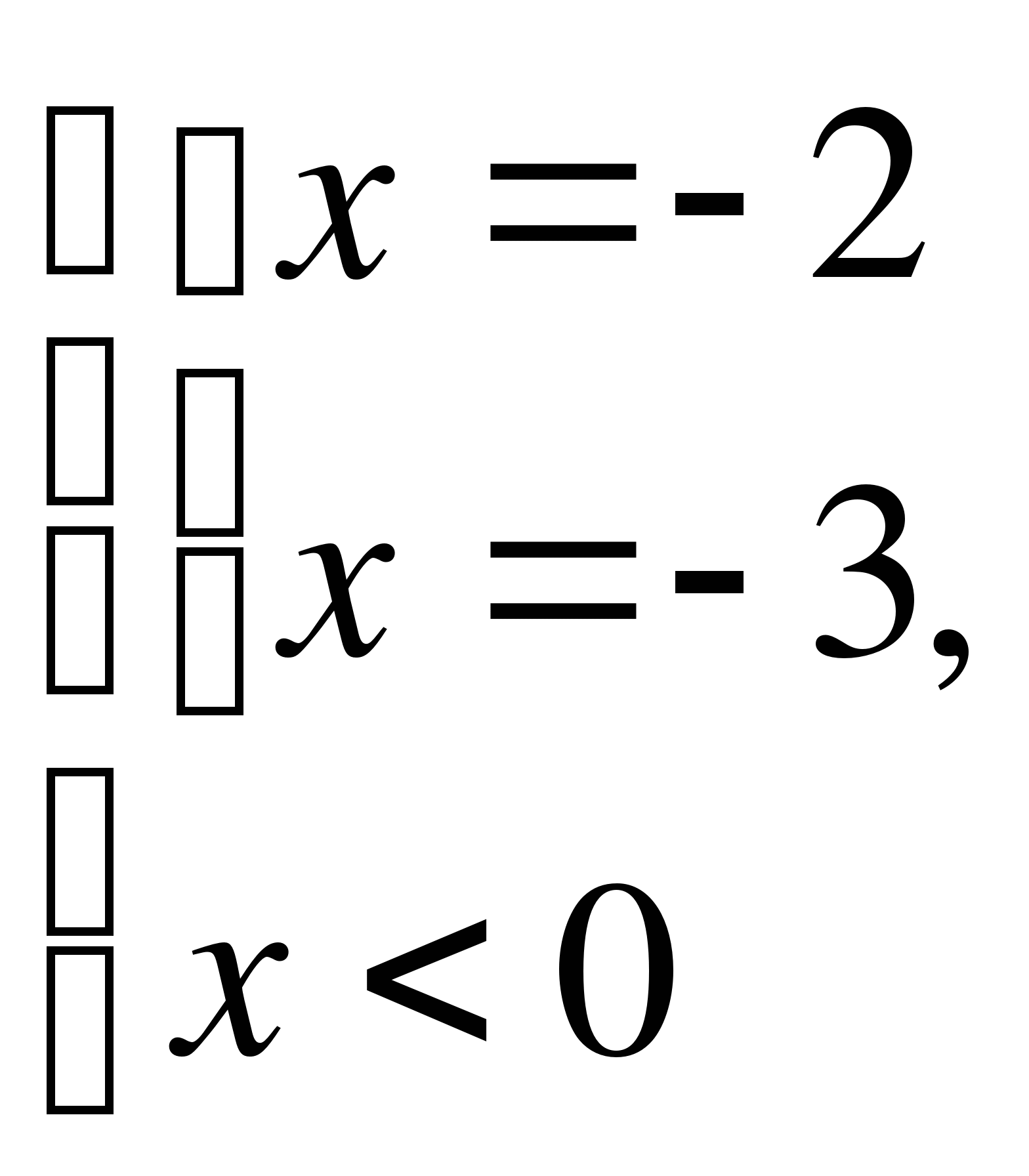
Ответ:  — 3; — 2; 2; 3.
— 3; — 2; 2; 3.
Уравнение вида
 равносильно совокупности систем (можно решить двумя способами)
равносильно совокупности систем (можно решить двумя способами)
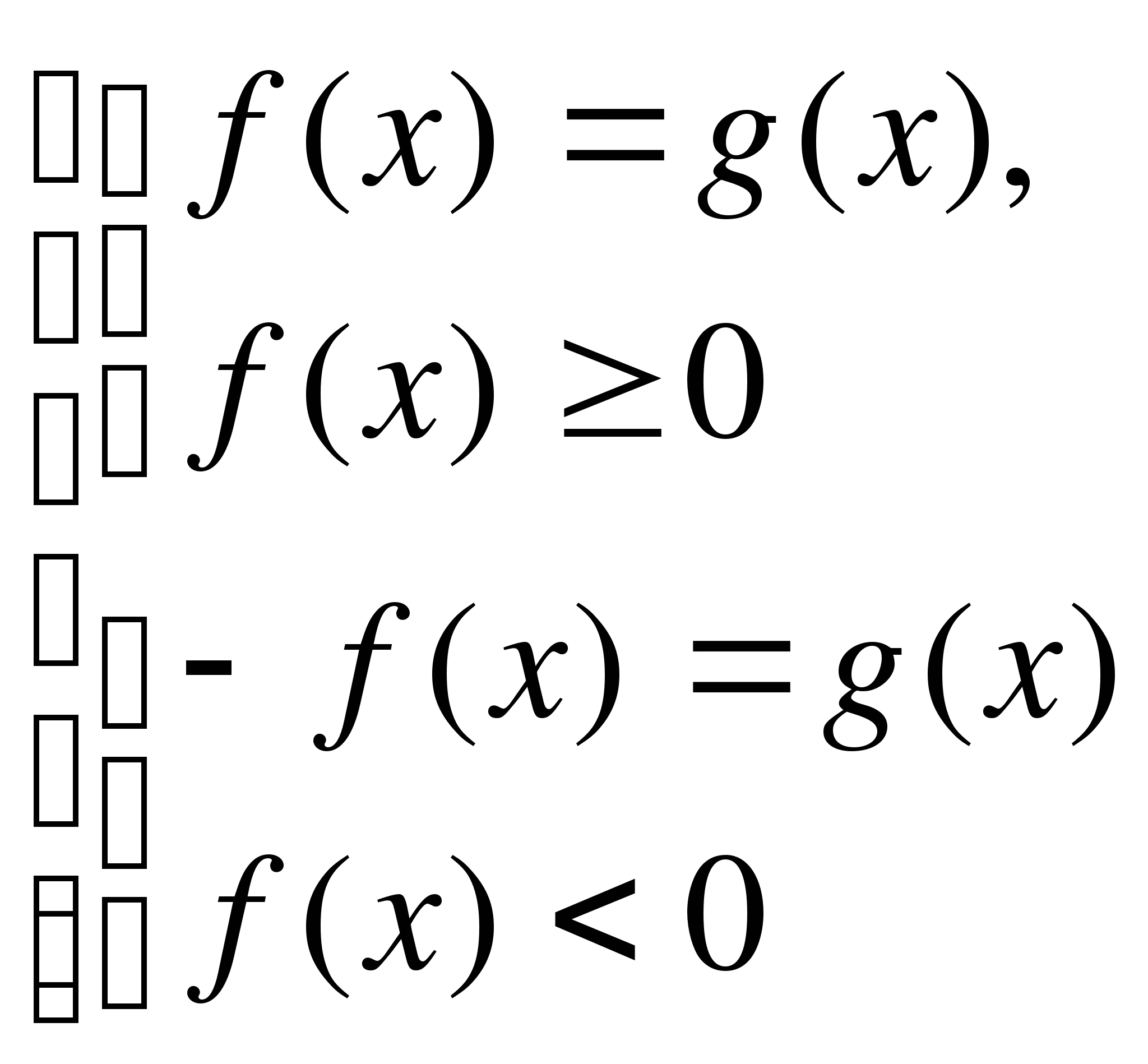 или
или 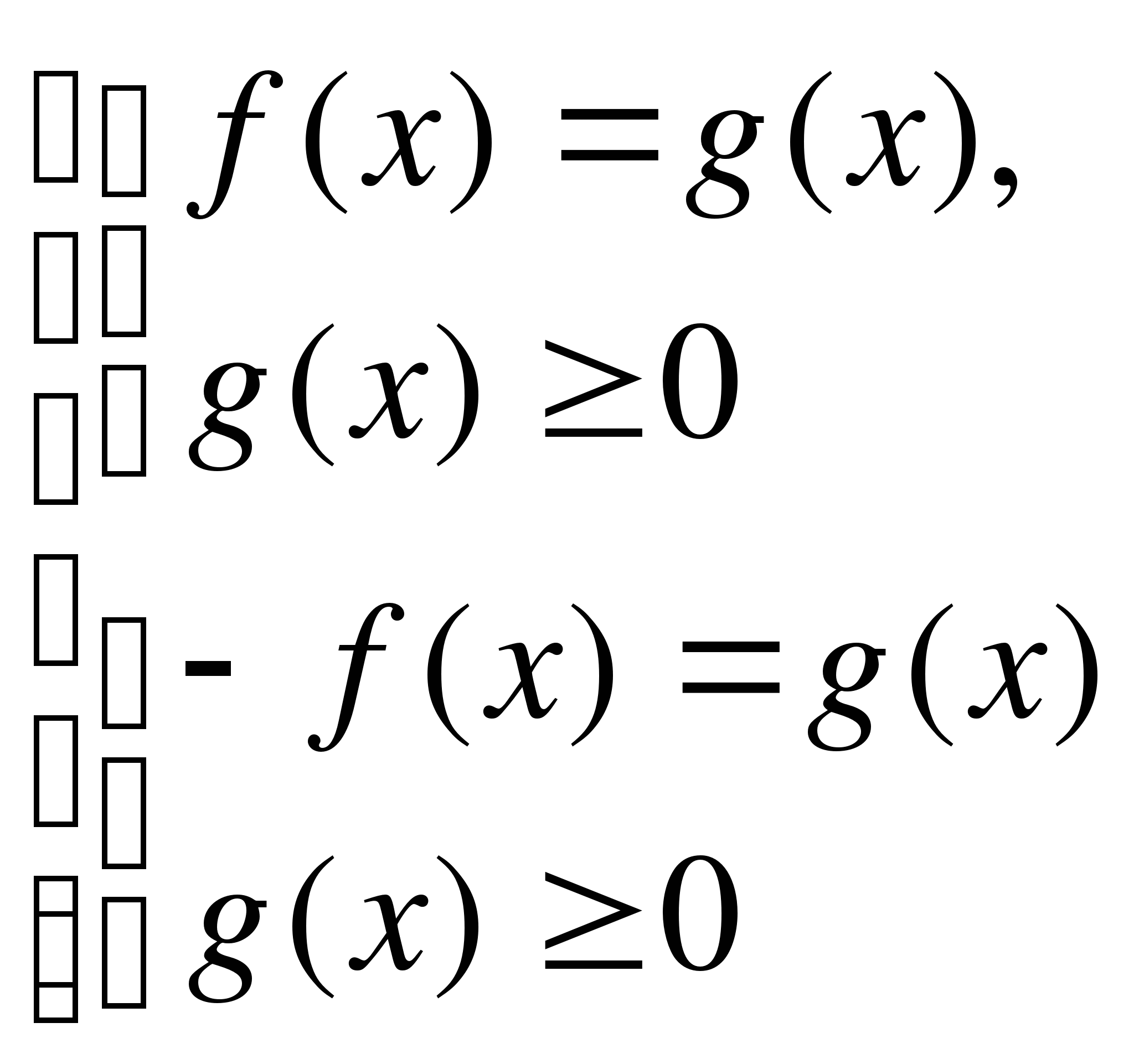
Пример 2.
Решите уравнение 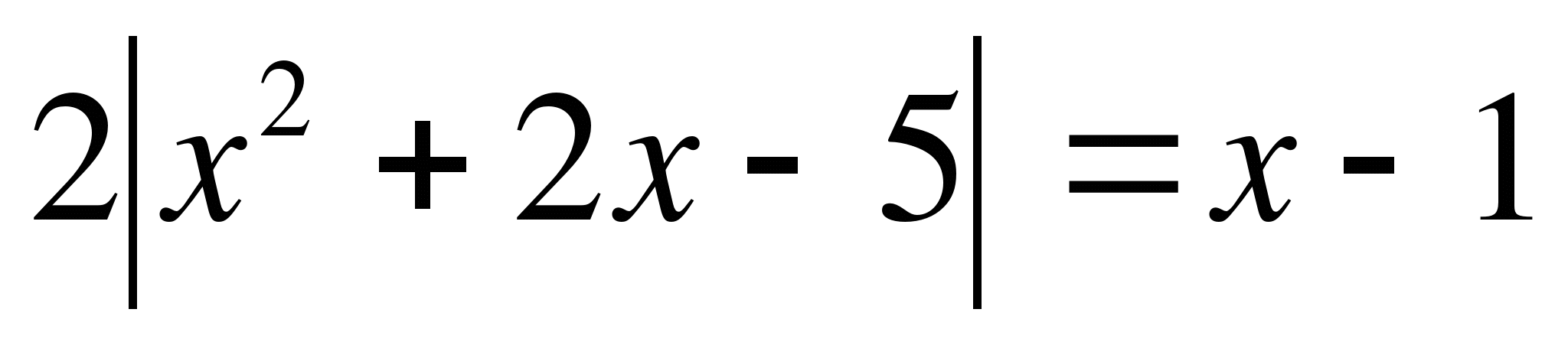
Решение.
Данное уравнение равносильно совокупности систем:
1) 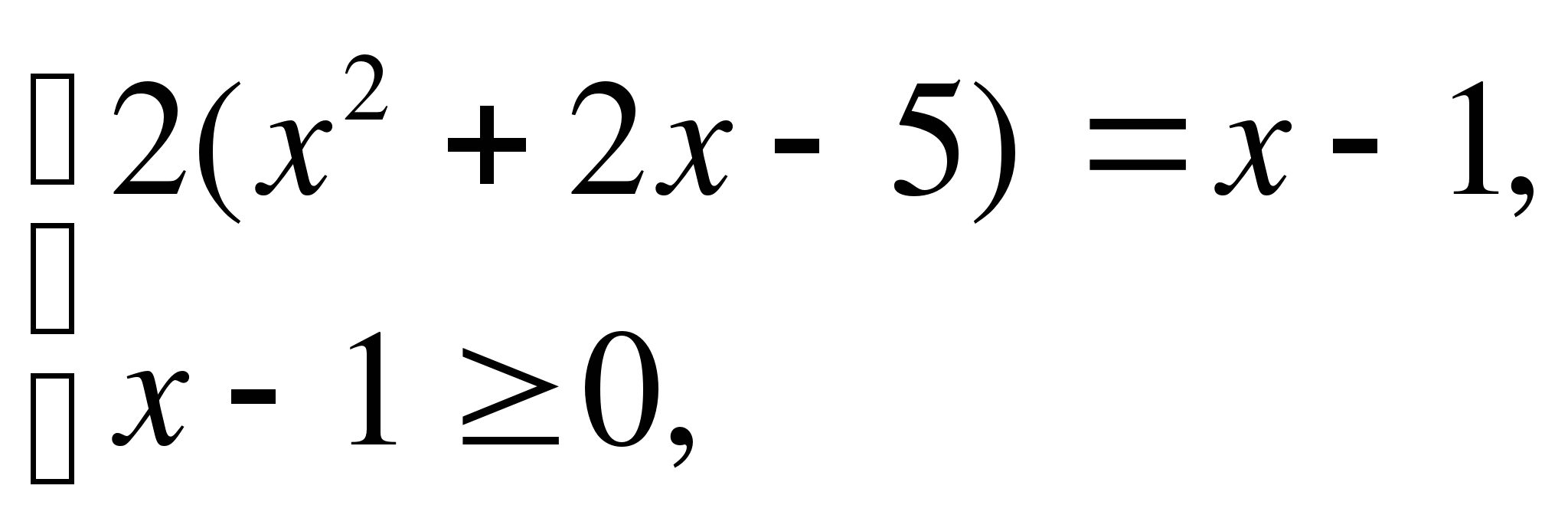
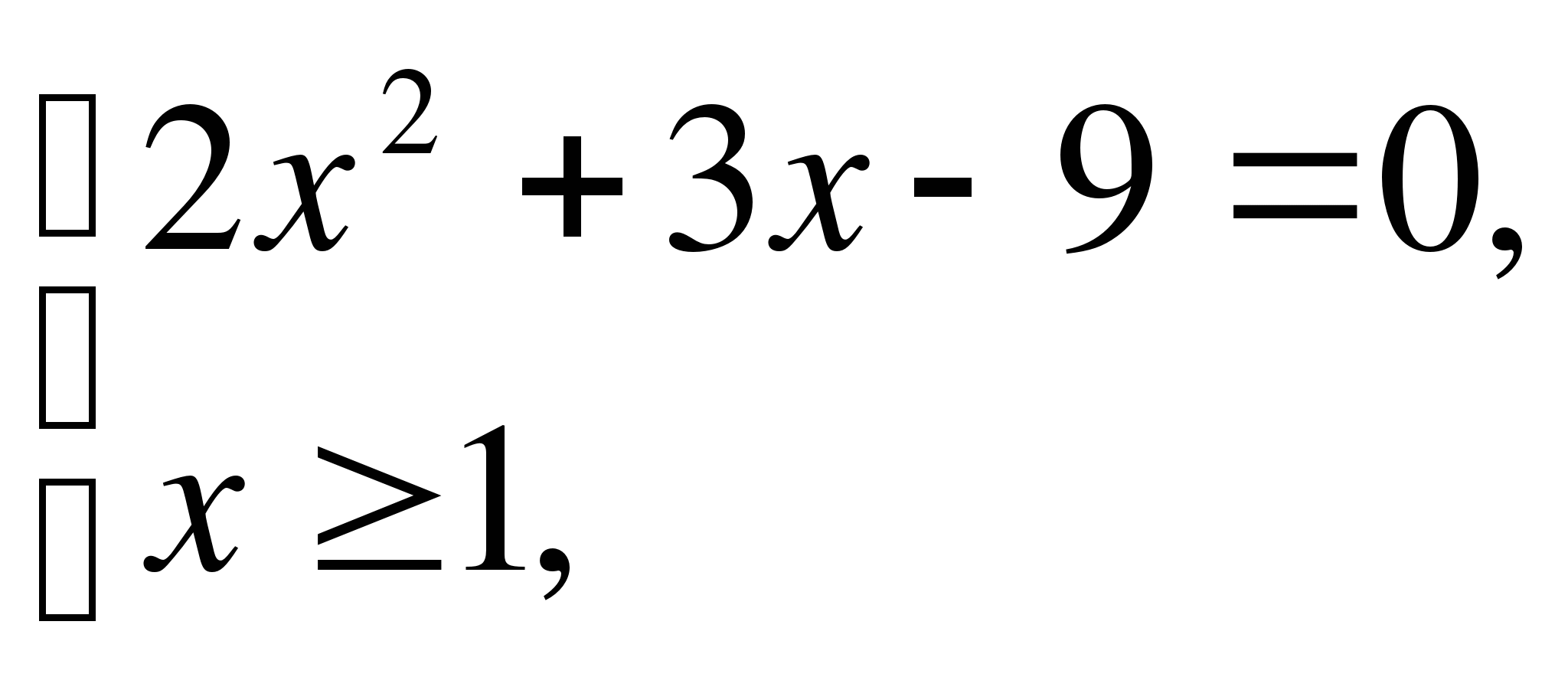
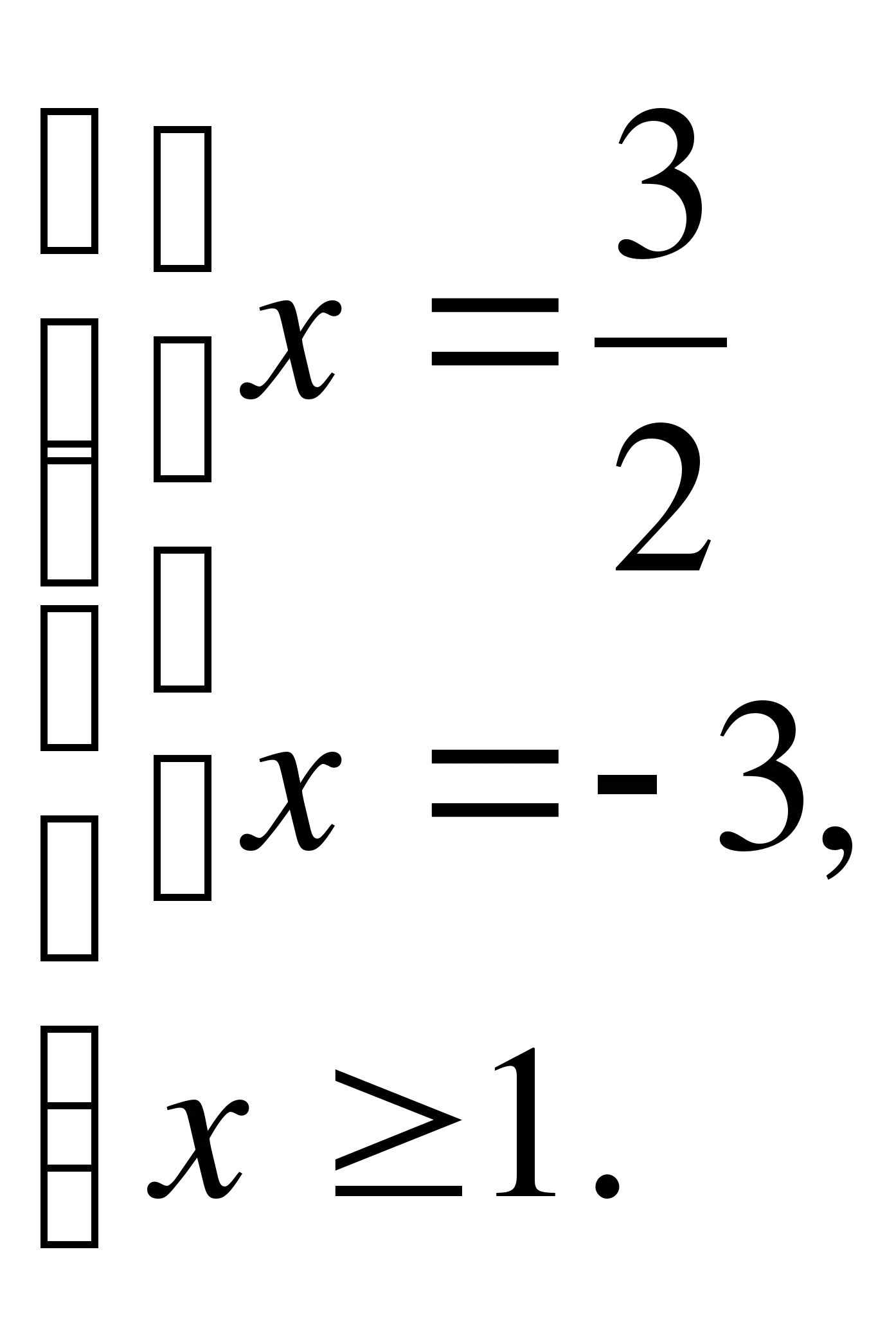
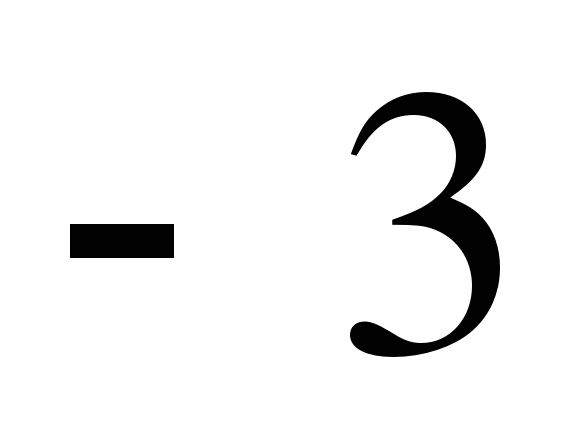 не удовлетворяет условию
не удовлетворяет условию 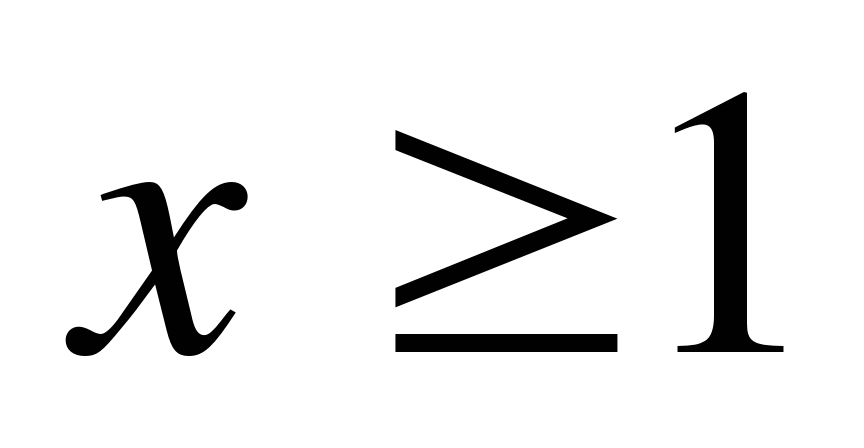 , следовательно, система имеет решение
, следовательно, система имеет решение 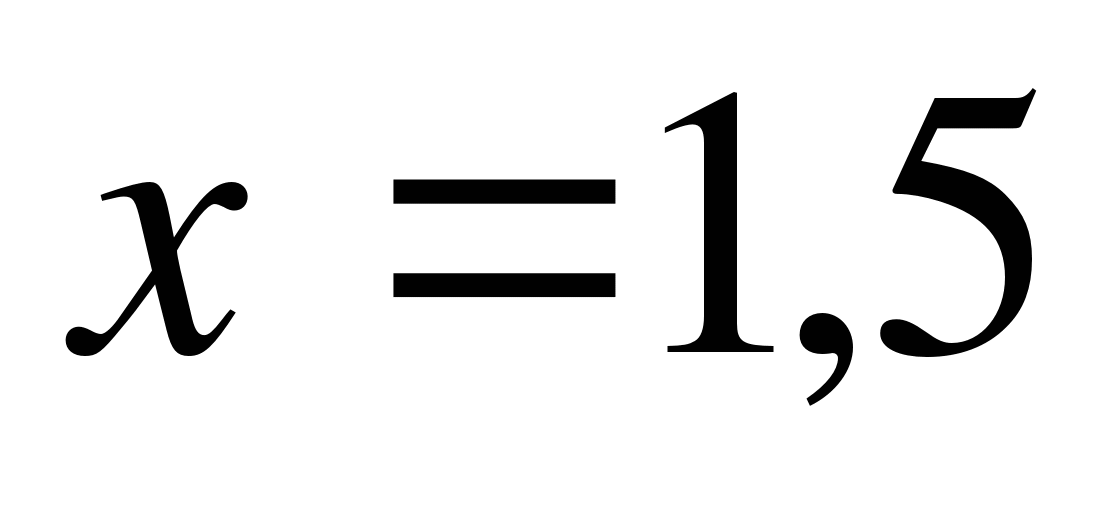 .
.
2)
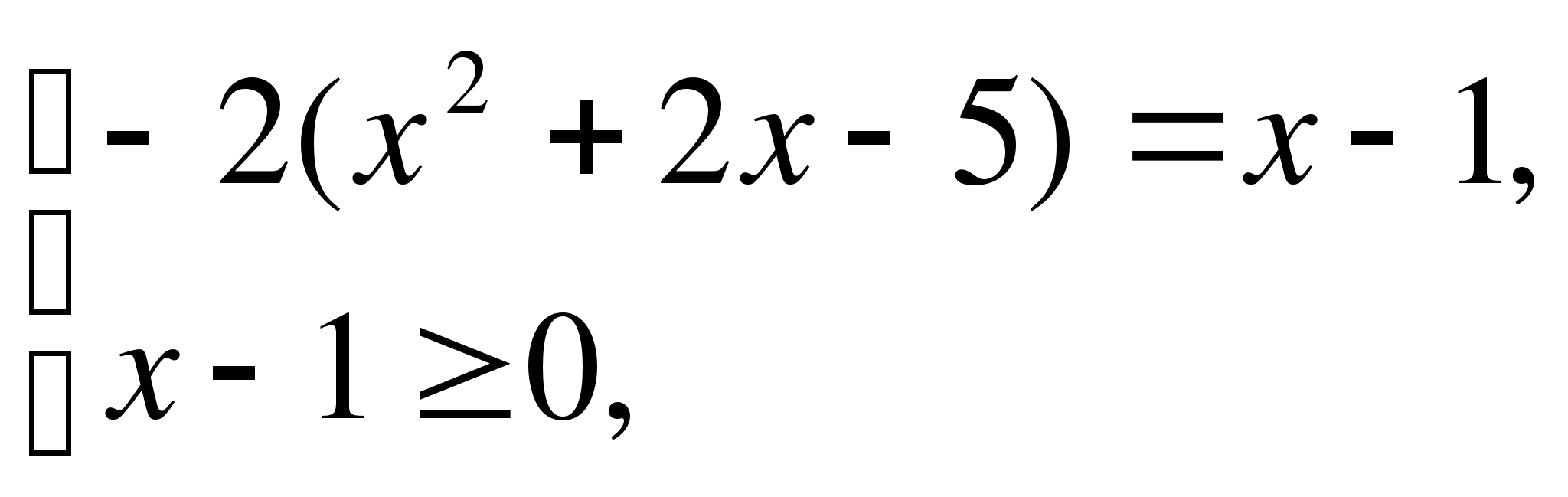
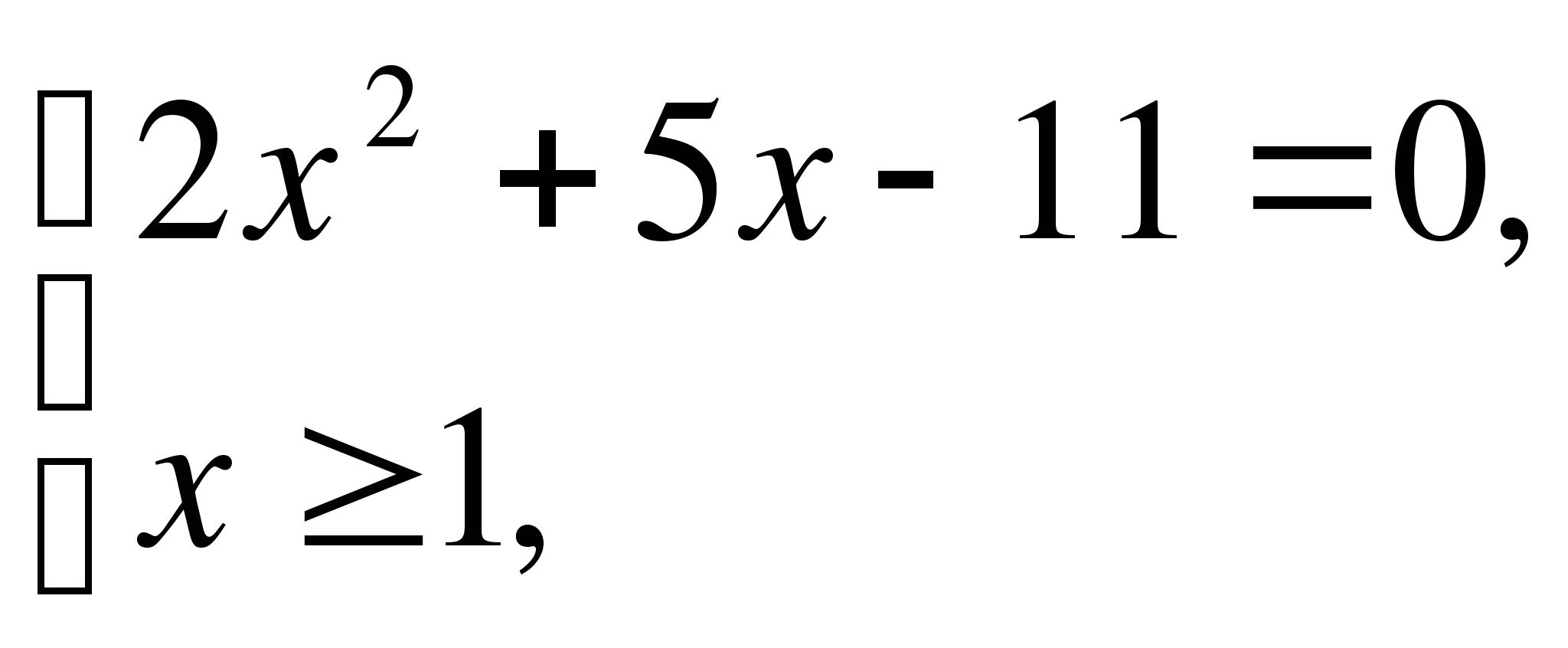
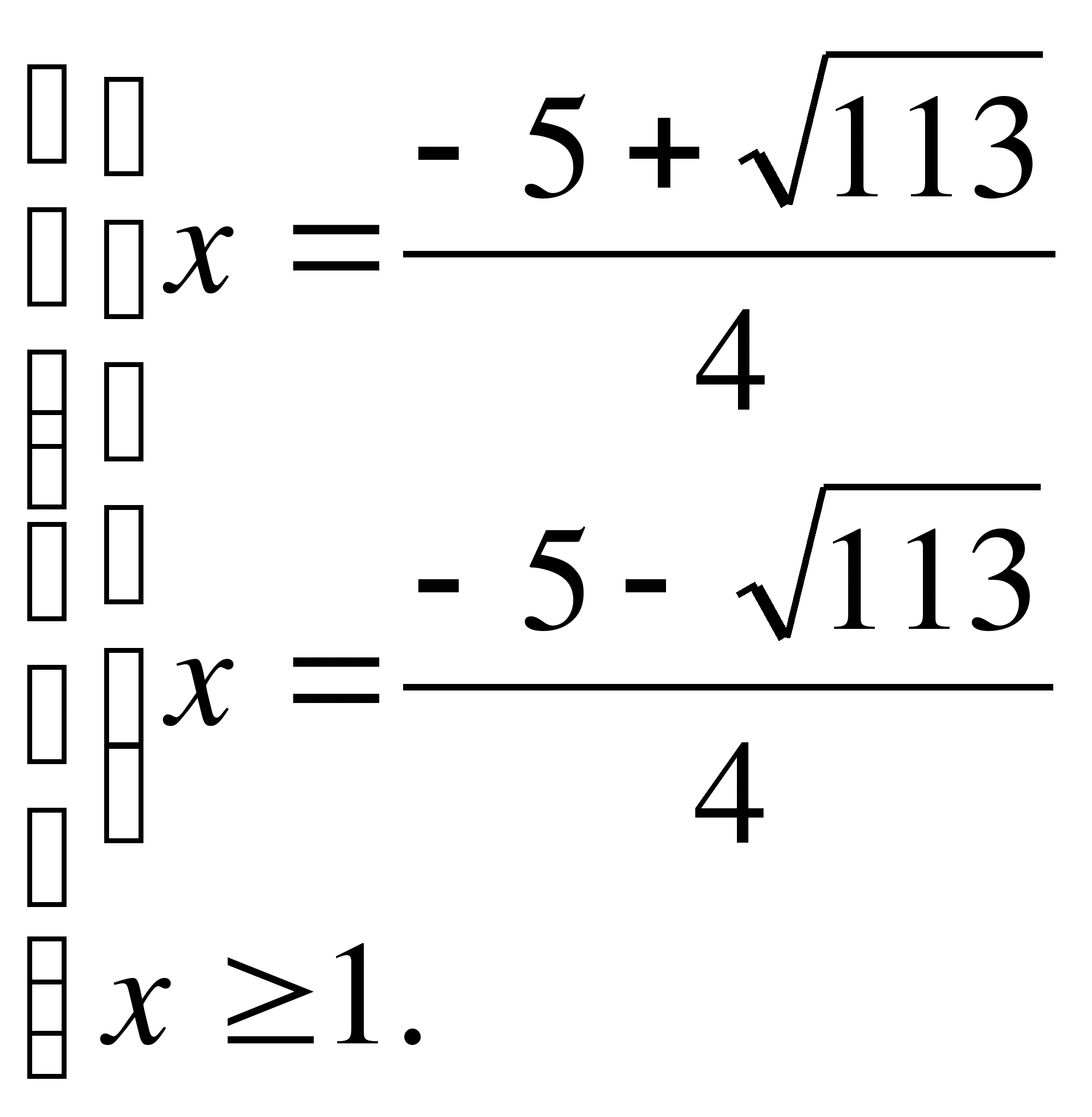
 не удовлетворяет условию
не удовлетворяет условию 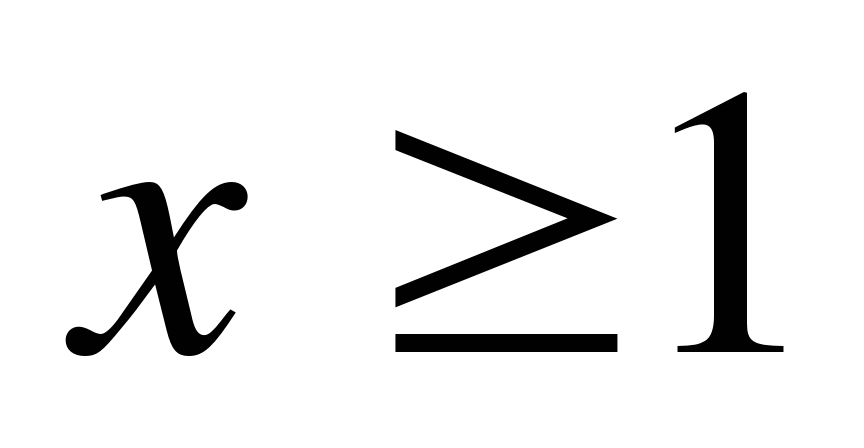 , следовательно, вторая система имеет решение
, следовательно, вторая система имеет решение 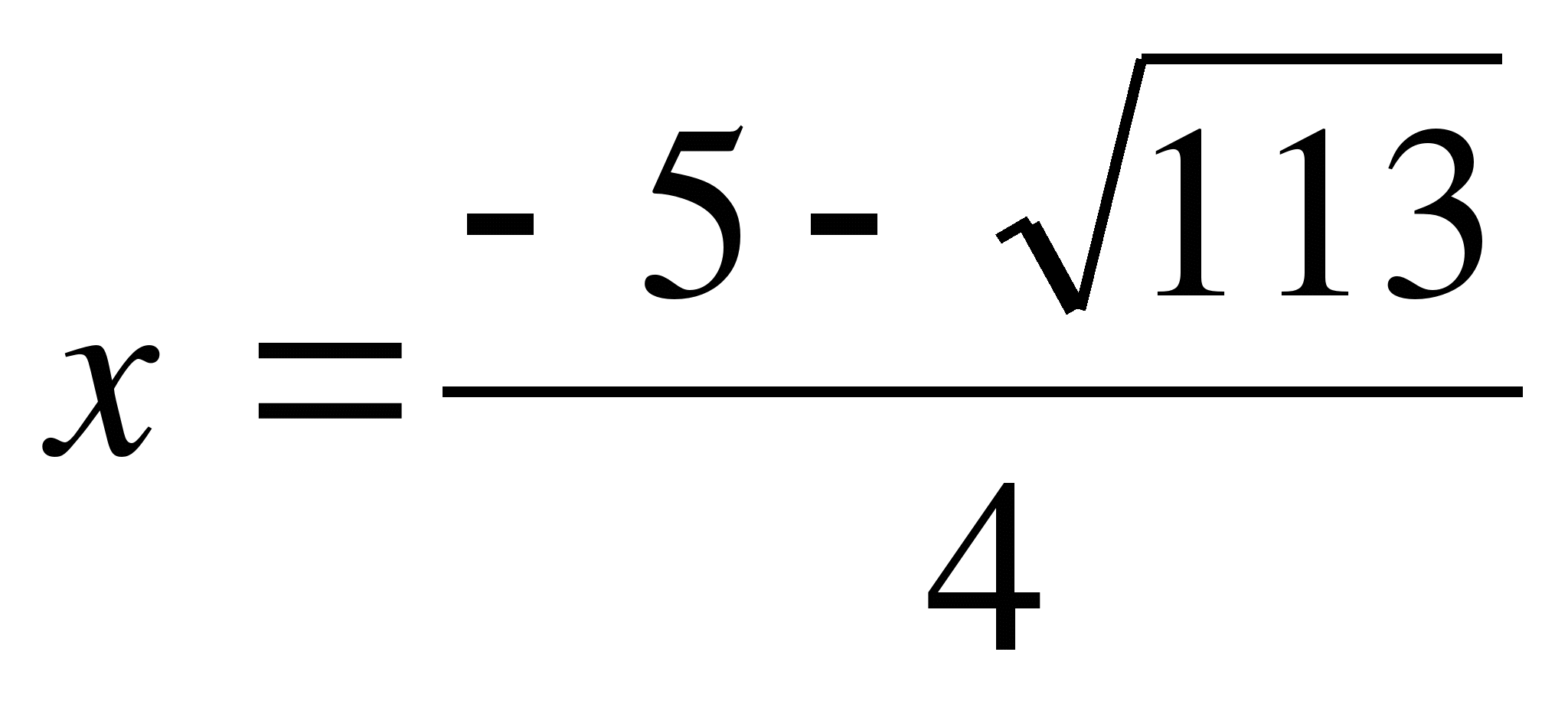 .
.
Ответ: 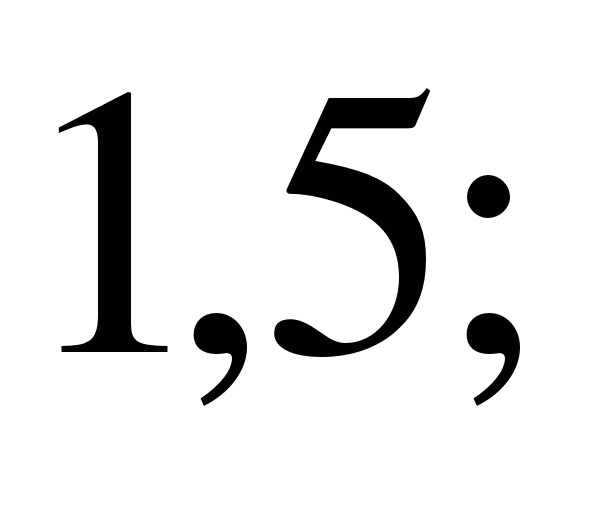
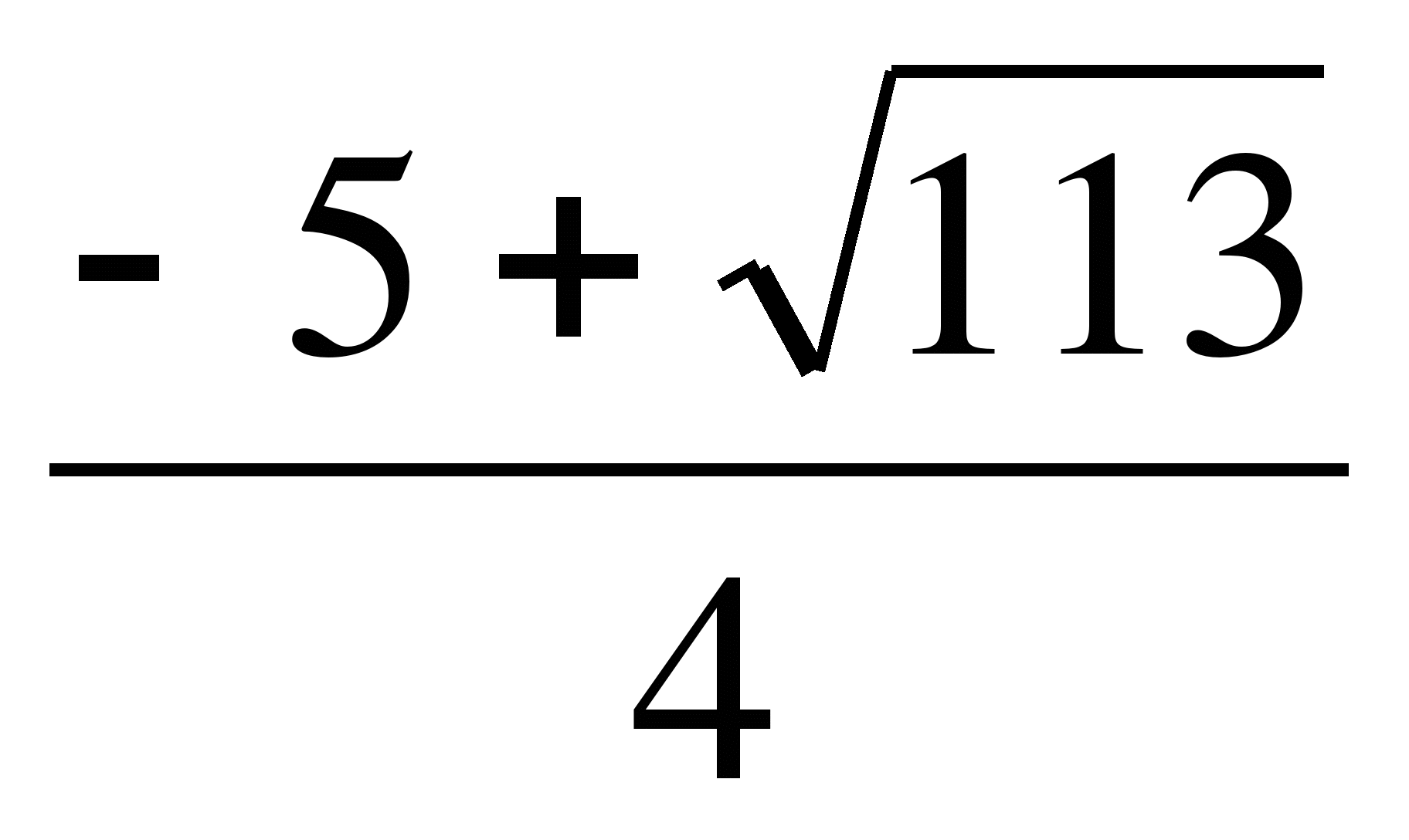 .
.
Уравнение вида
 , где
, где  — некоторые функции, равносильно совокупности систем
— некоторые функции, равносильно совокупности систем
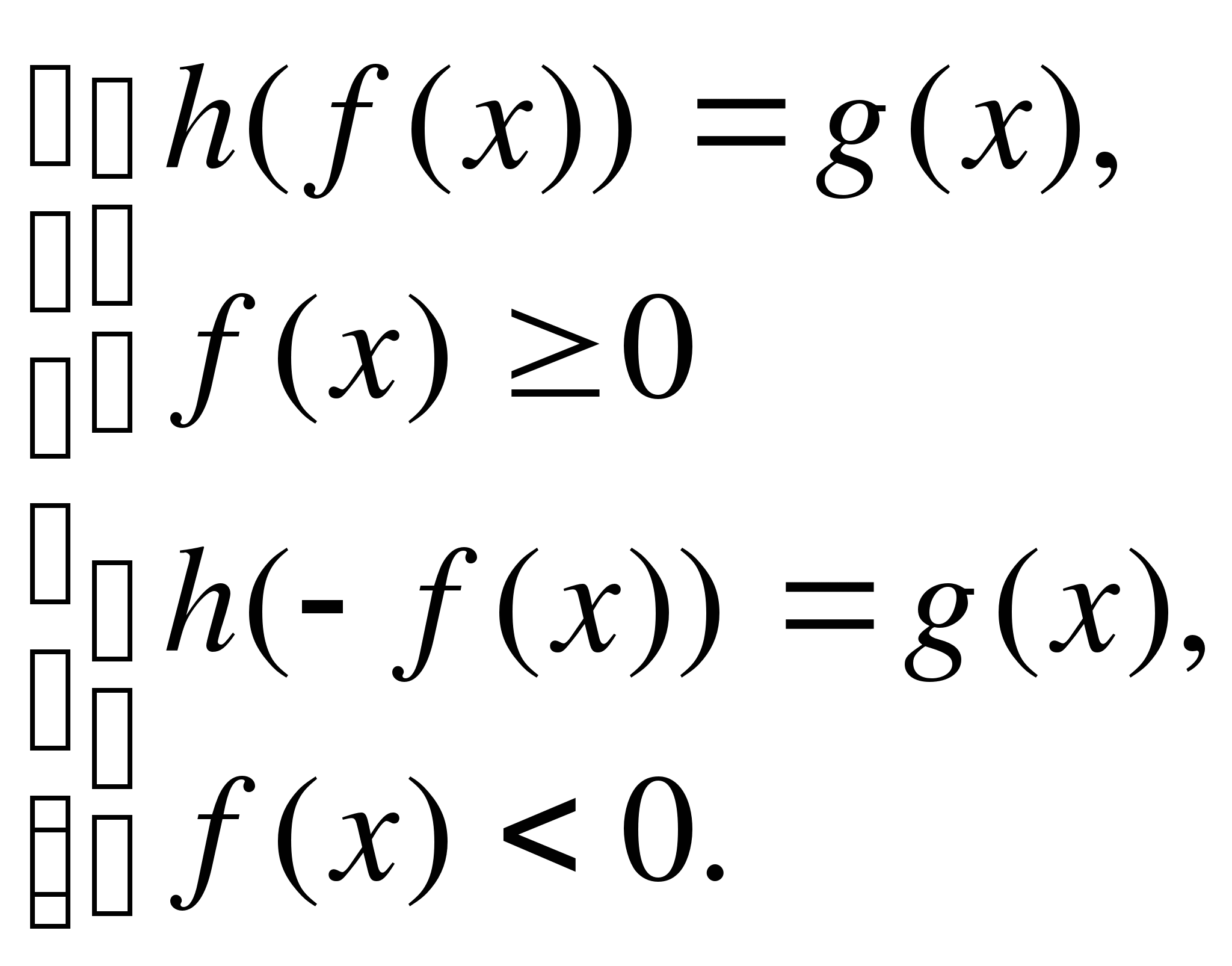
Пример 3.
Решите уравнение 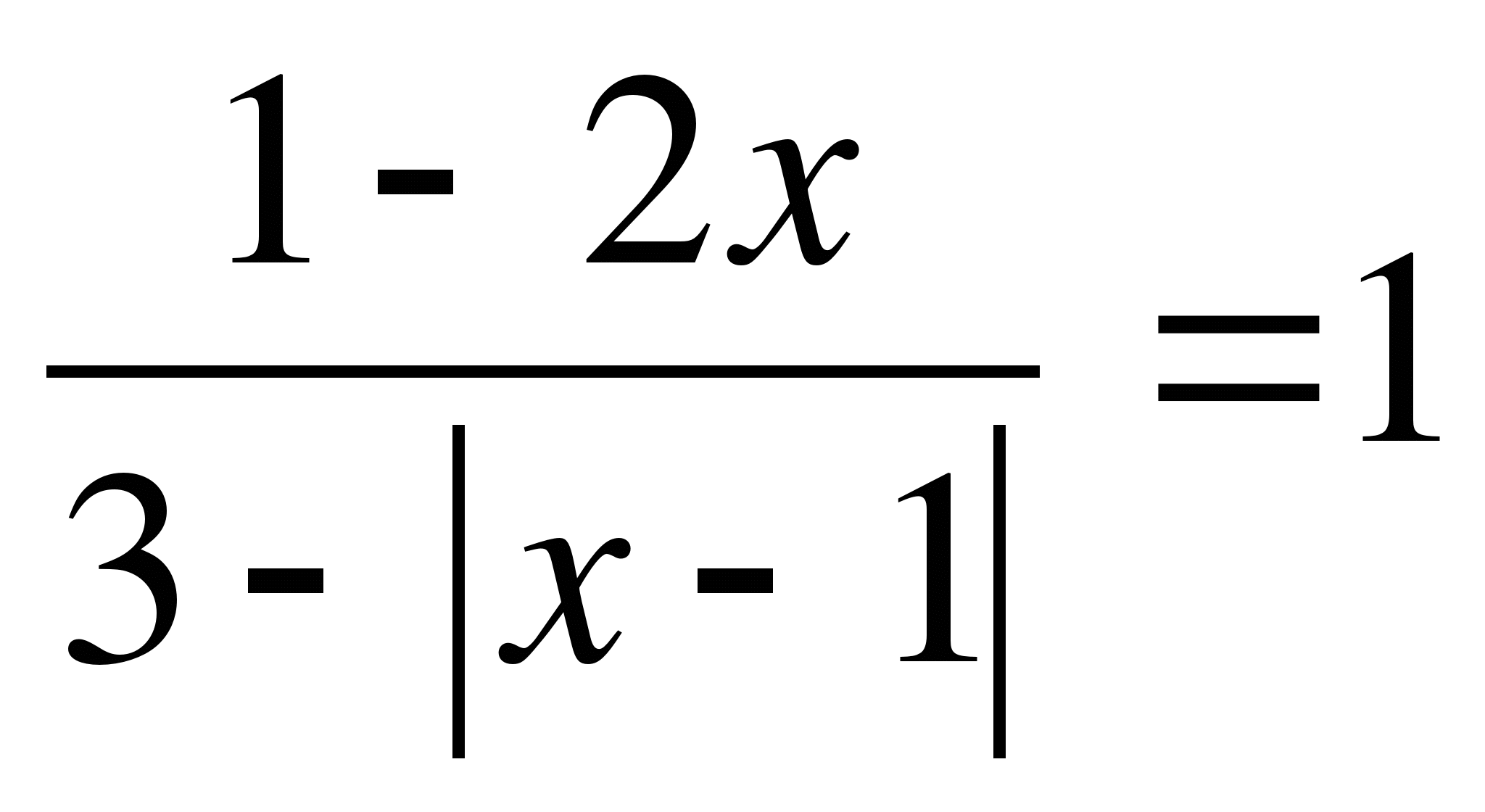
Решение.
Данное уравнение равносильно совокупности двух систем:
1) 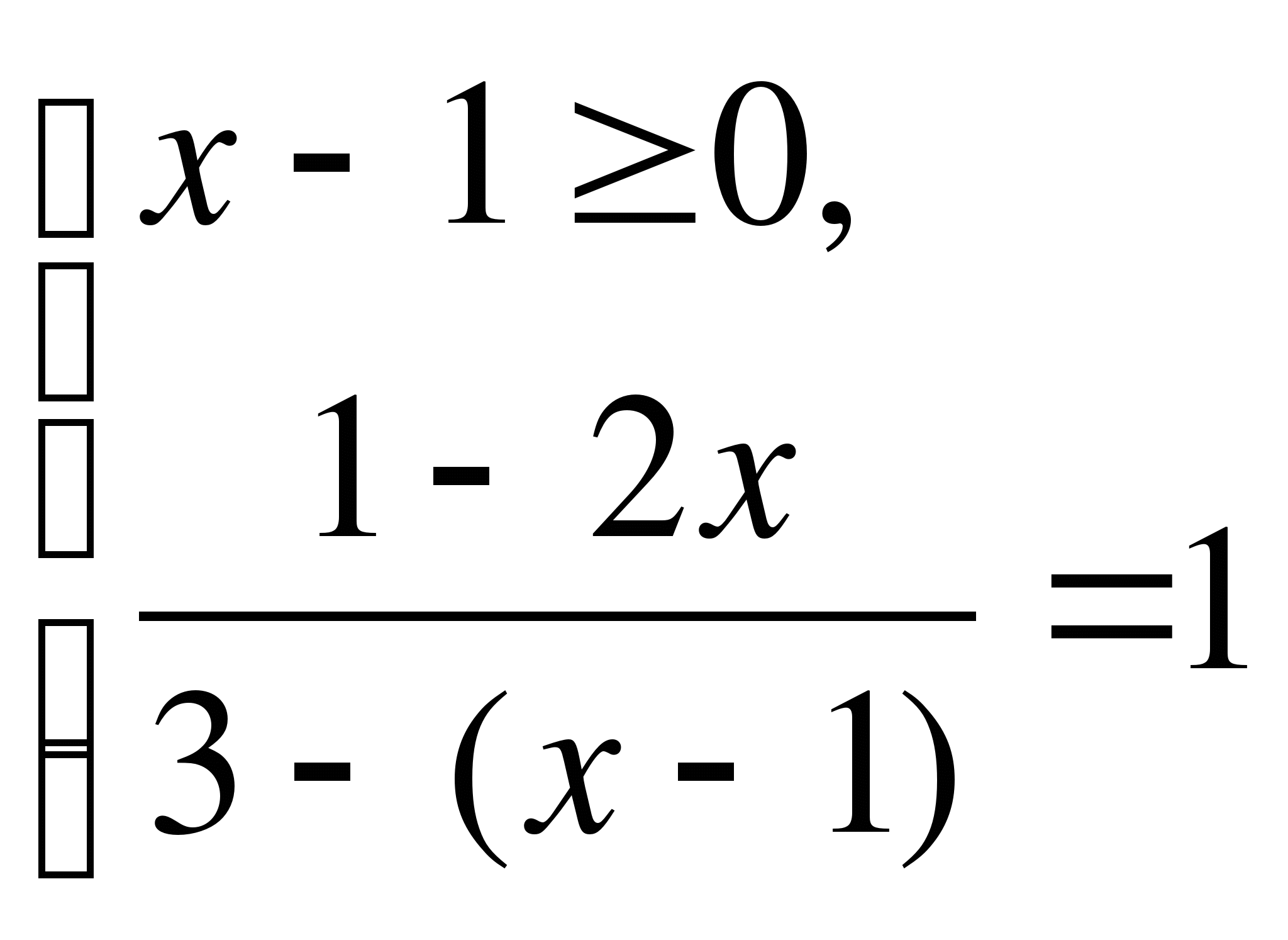
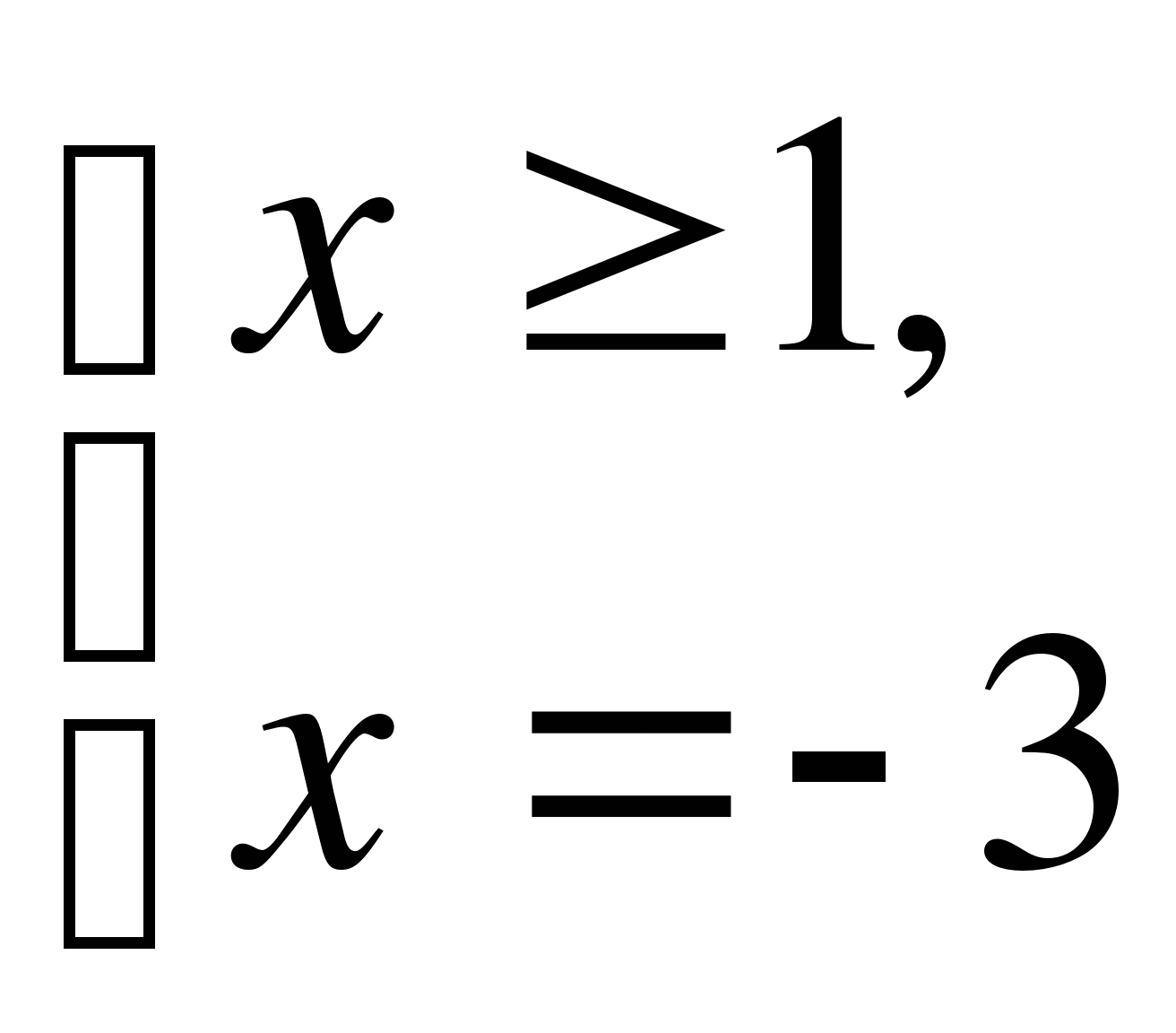 , система не имеет решений.
, система не имеет решений.
2) 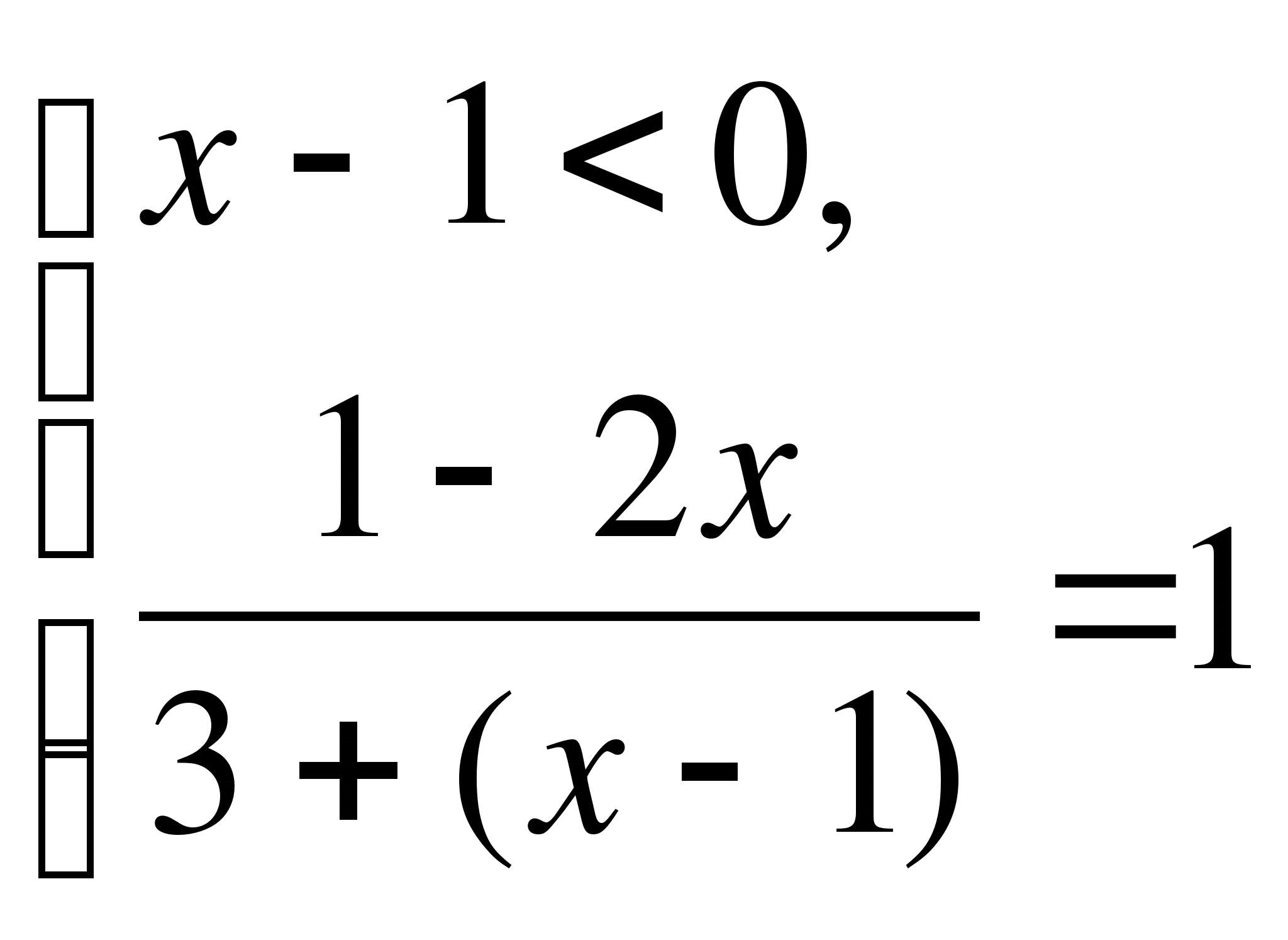
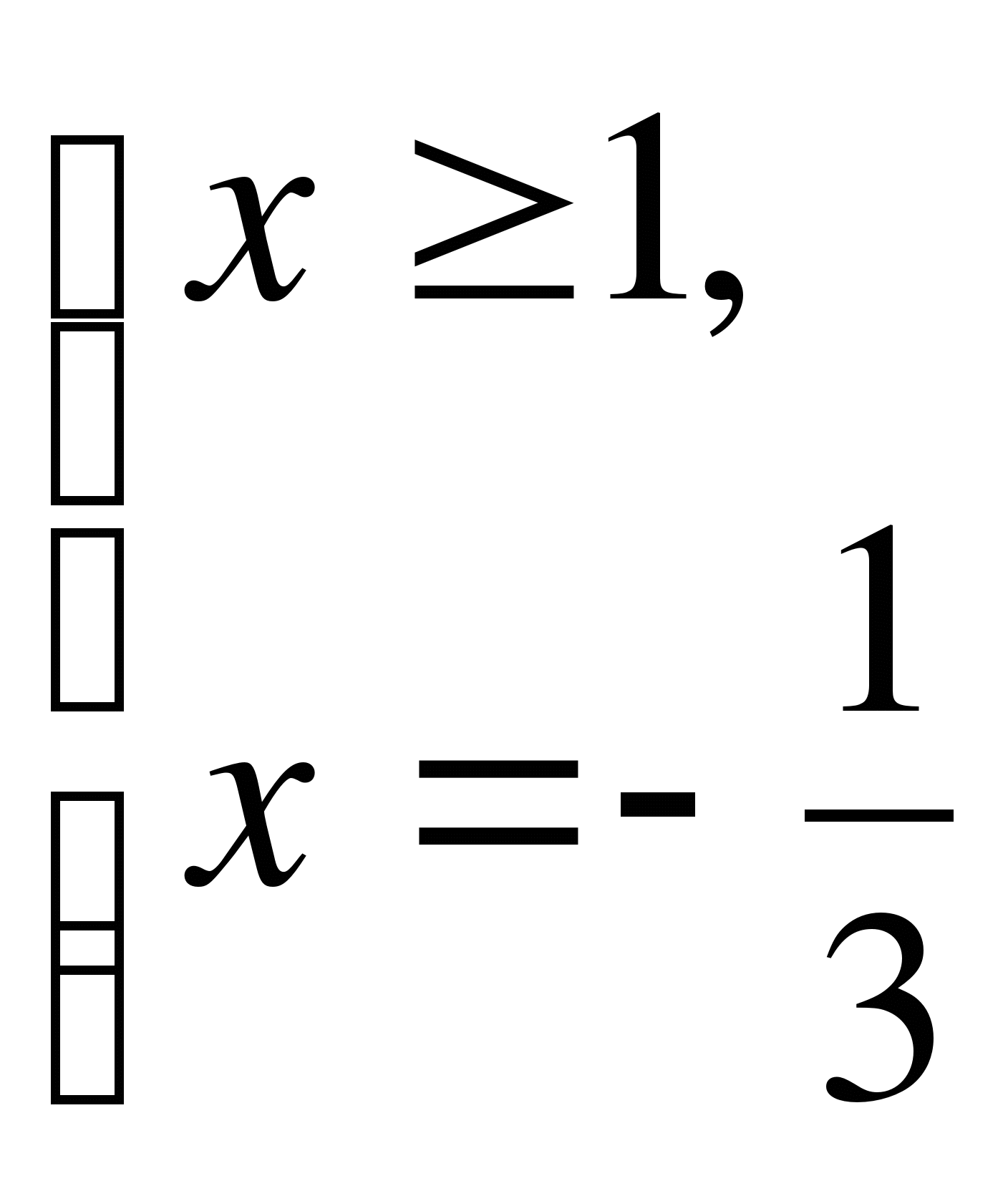 ,
,  .
.
Ответ: 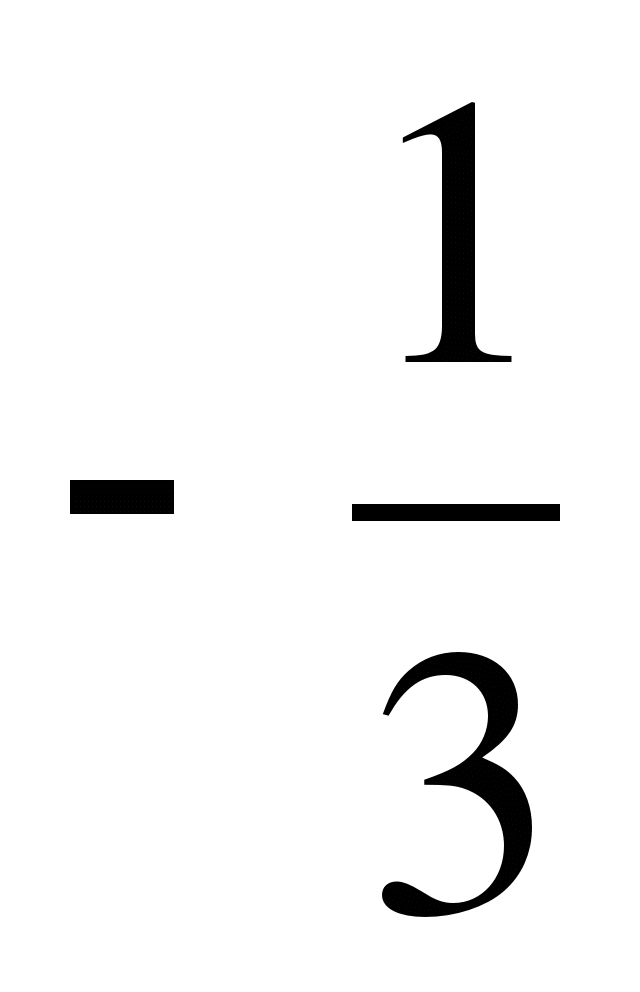
При решении уравнения, в котором под знаком модуля находится выражение, содержащее модуль, следует сначала освободиться от внутренних модулей, а затем в полученных уравнениях раскрыть оставшиеся модули.
Пример 4.
Решите уравнение 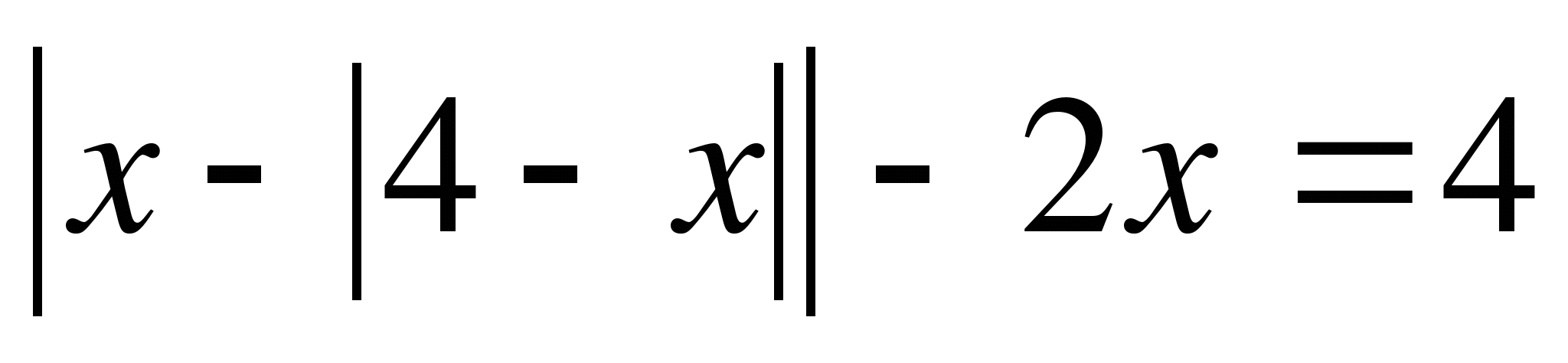 .
.
Решение.
Данное уравнение равносильно совокупности двух систем
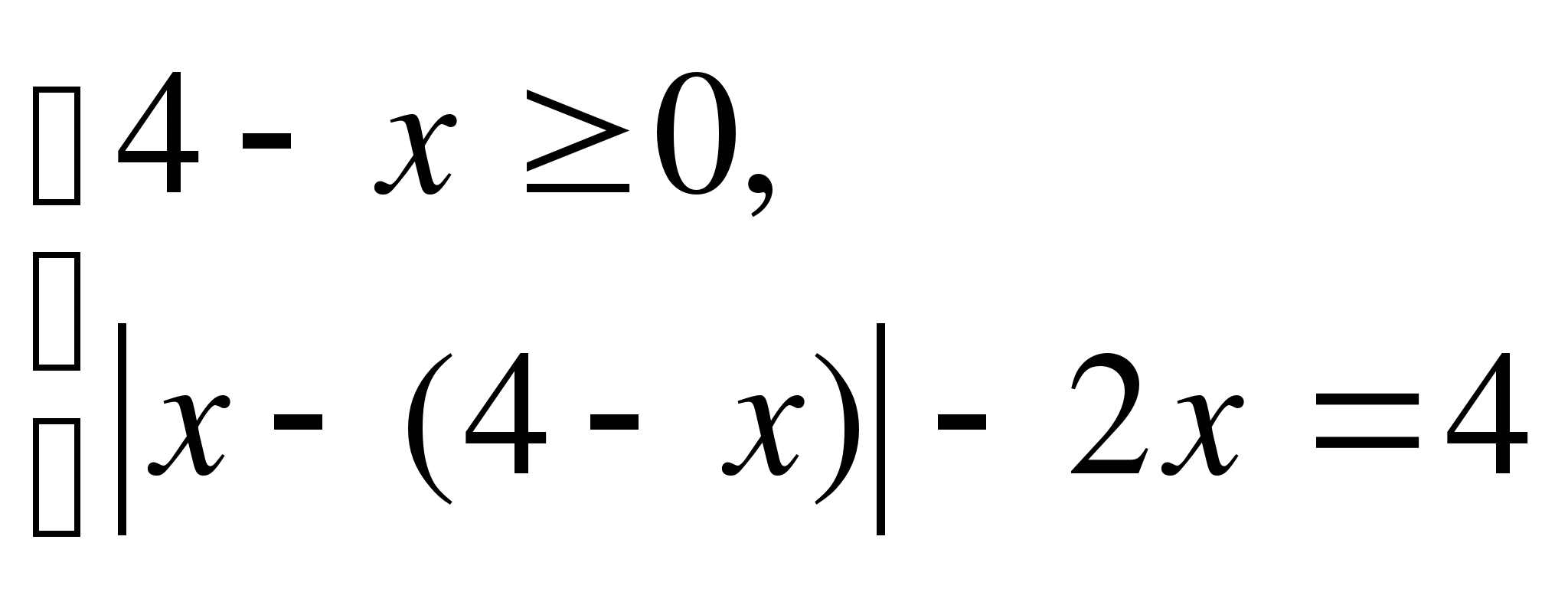 или
или 
то есть совокупности систем
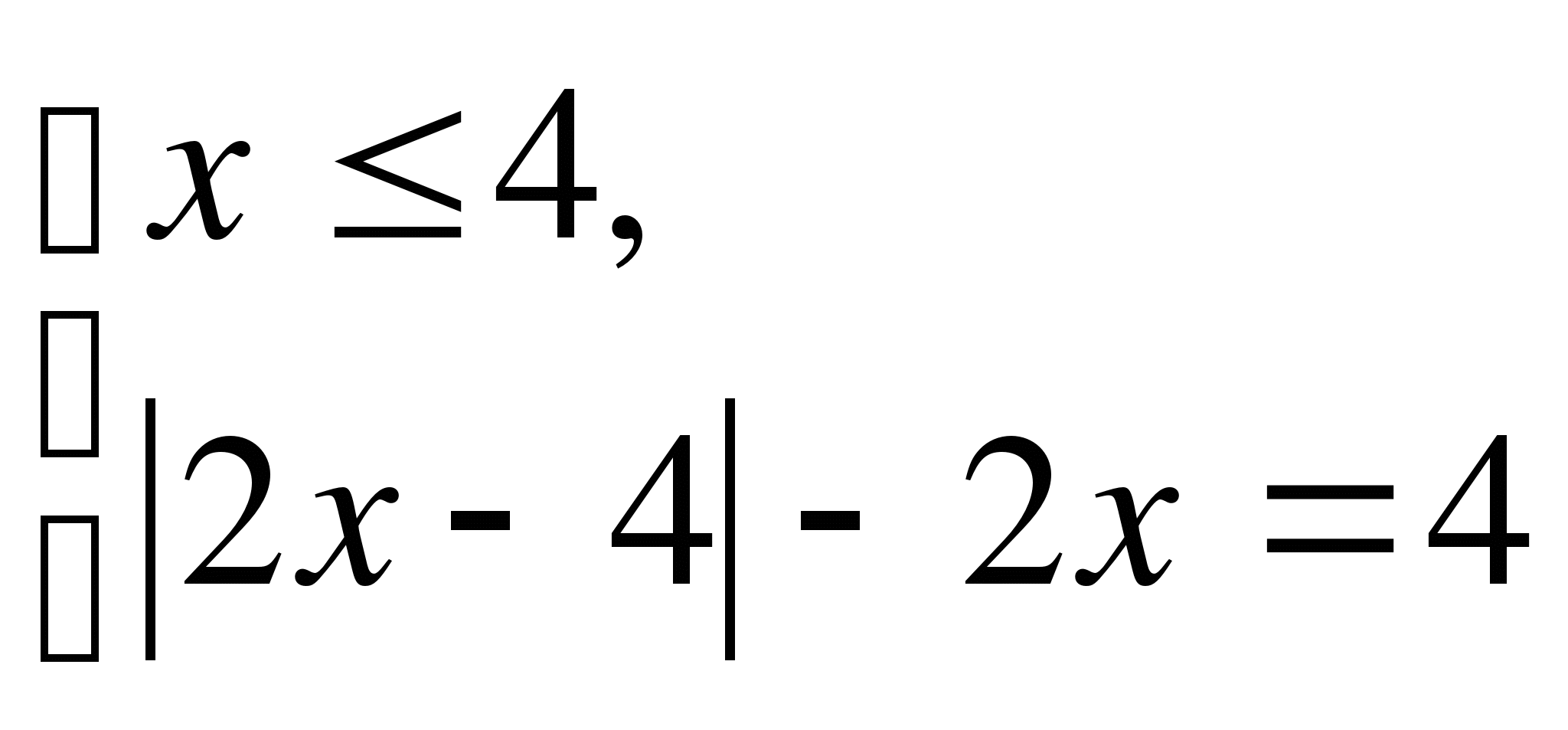 или
или 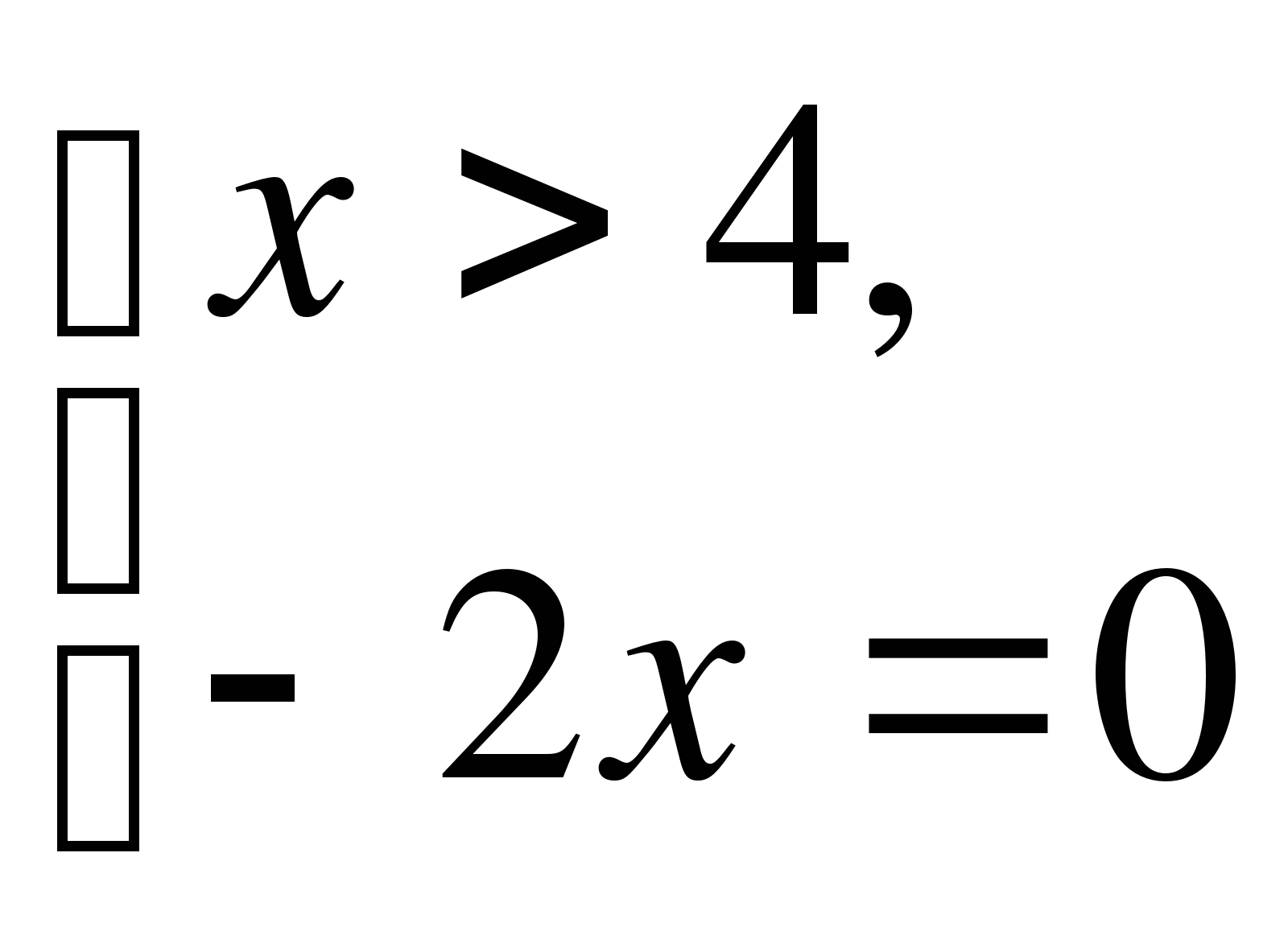
Вторая система решений не имеет. Первая система равносильна двум следующим системам:
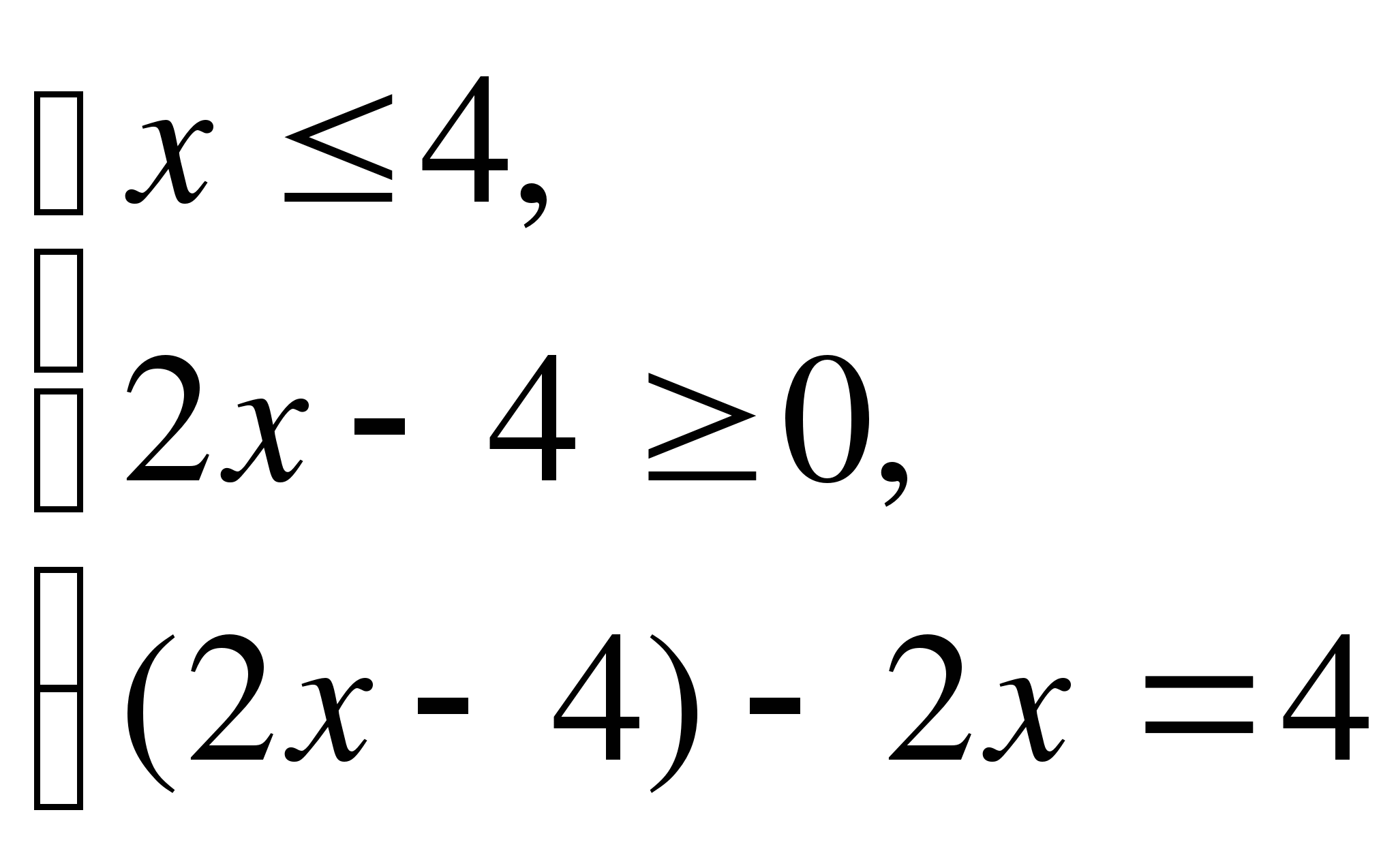 или
или 
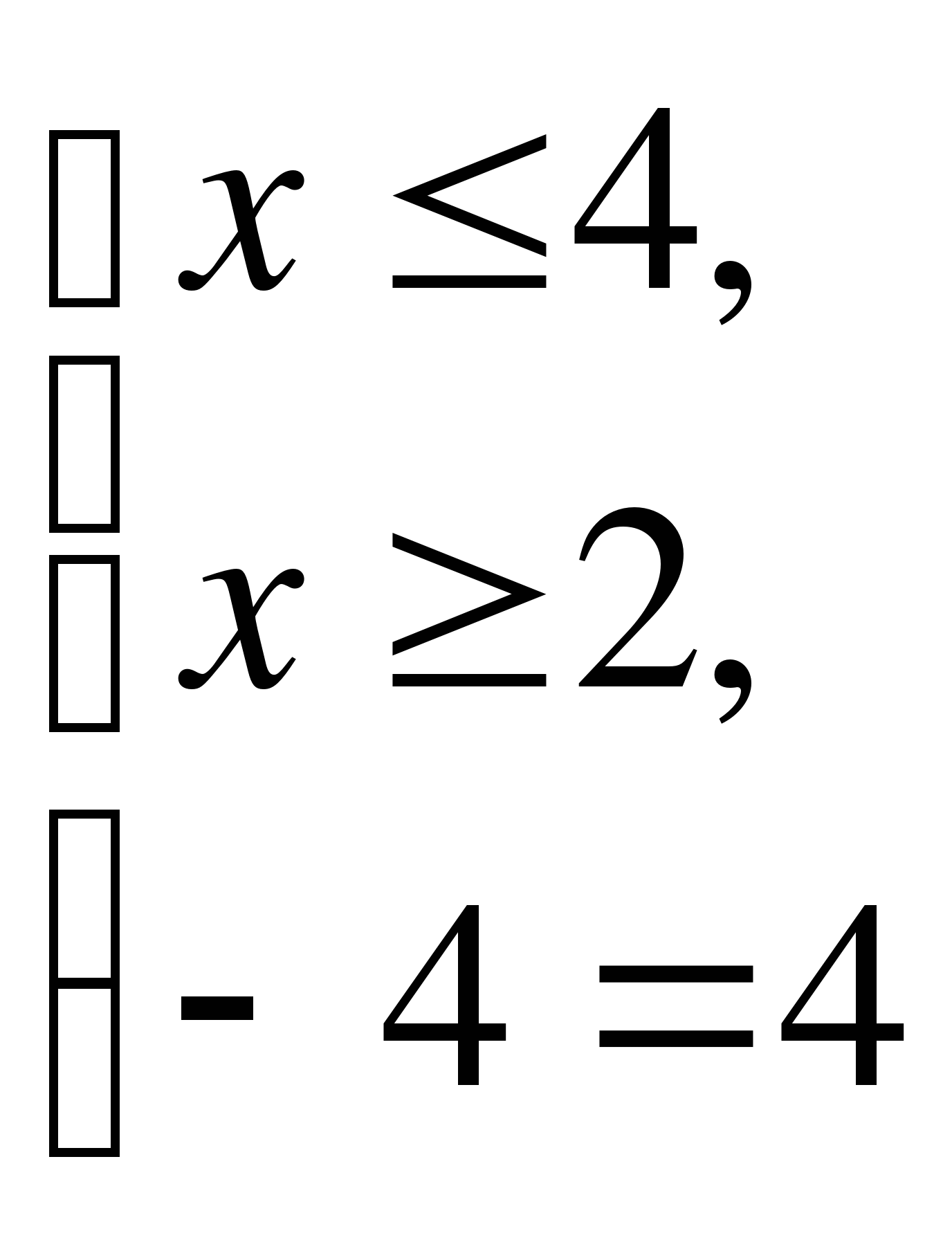 или
или 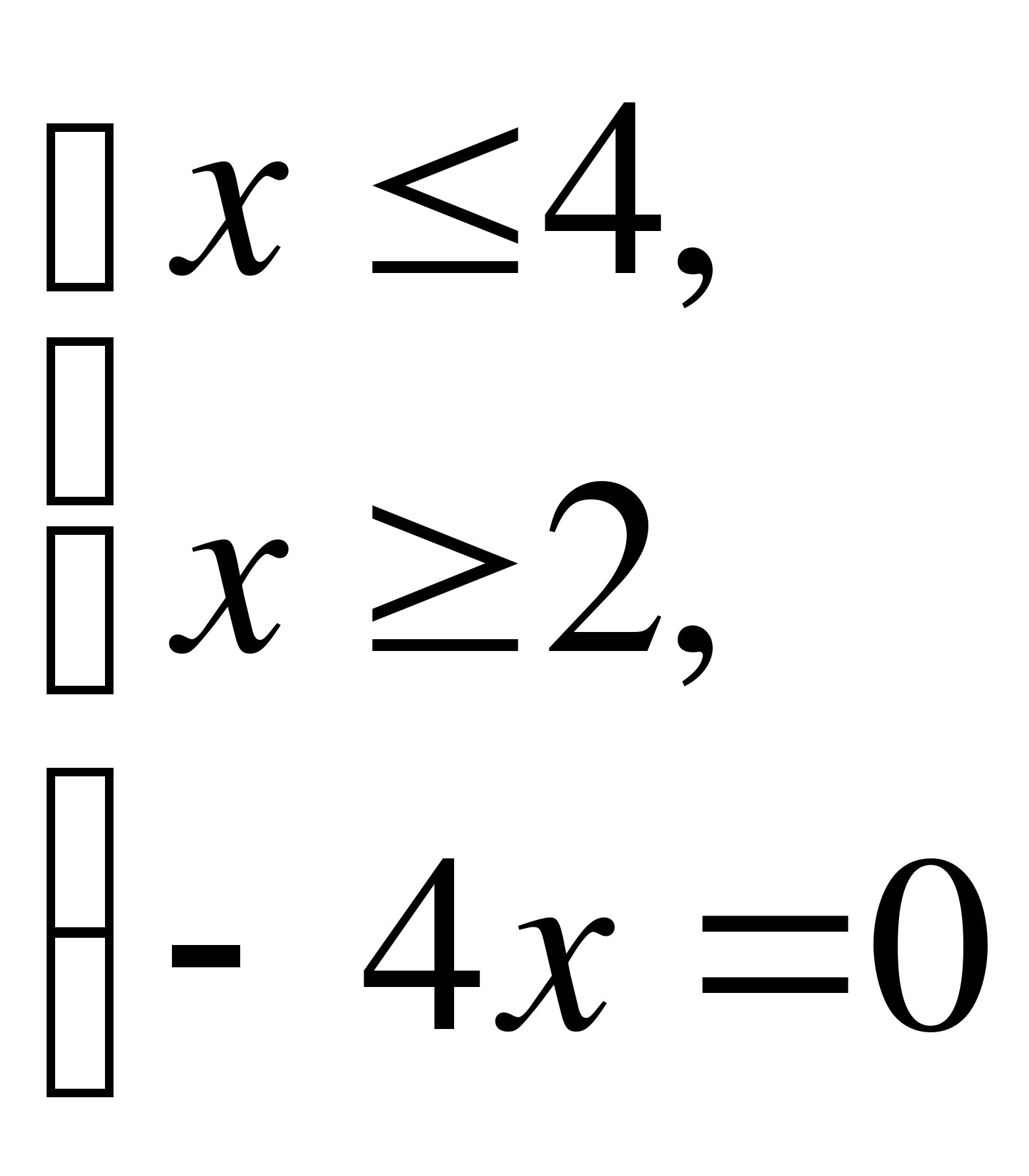
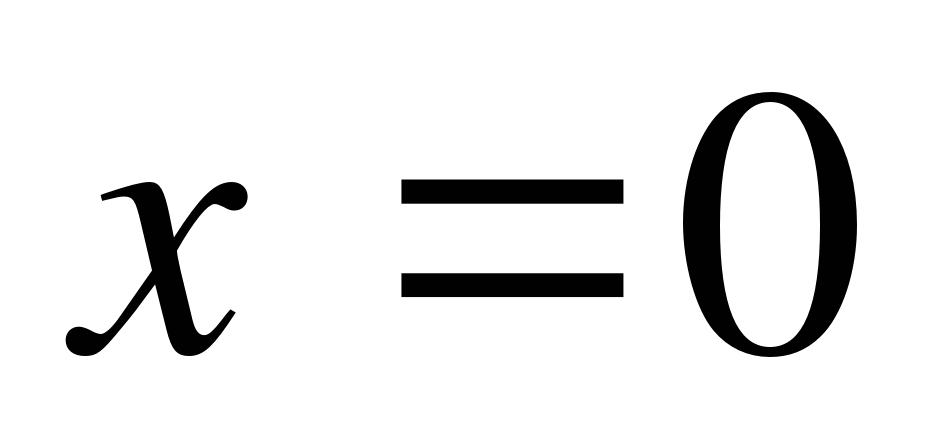
Ответ: 0.
5.Метод разбиения на промежутки. Уравнение вида 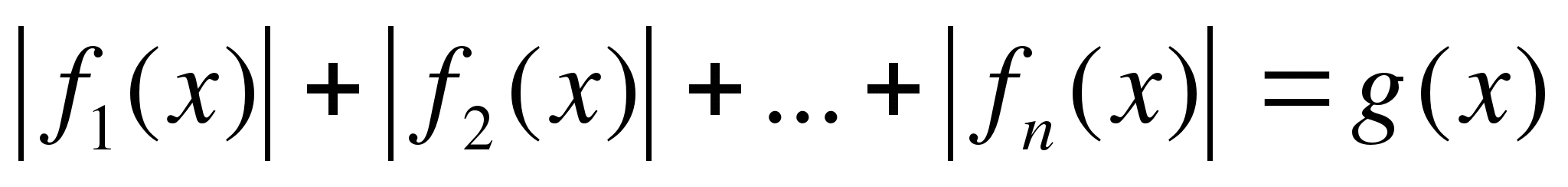 (2)
(2)
Решается методом интервалов (или методом разбиения на промежутки). Для этого находят сначала все точки, в которых
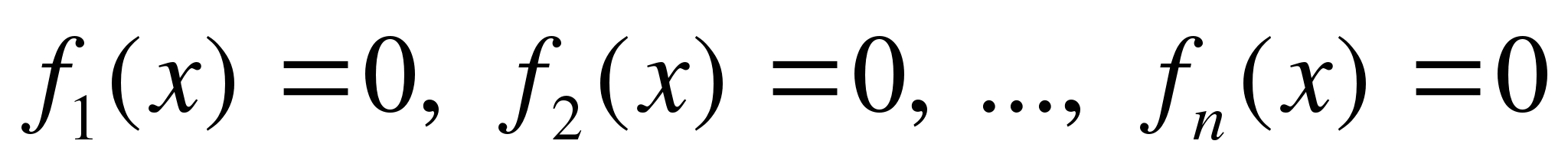
Эти точки делят область допустимых значений уравнения (2) на промежутки, на каждом из которых все функции 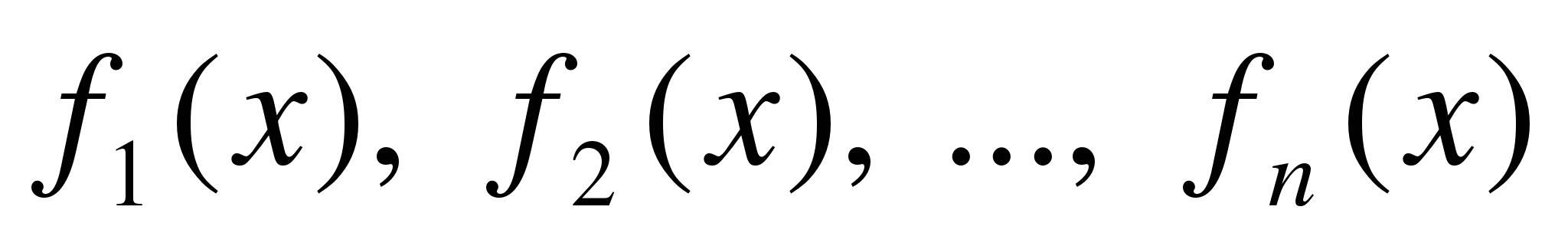 сохраняют знак (считаем знак каждого модуля на указанном промежутке). Затем переходят от уравнения (2) и совокупности систем, не содержащих знаков модуля.
сохраняют знак (считаем знак каждого модуля на указанном промежутке). Затем переходят от уравнения (2) и совокупности систем, не содержащих знаков модуля.
Пример 5.
Решите уравнение 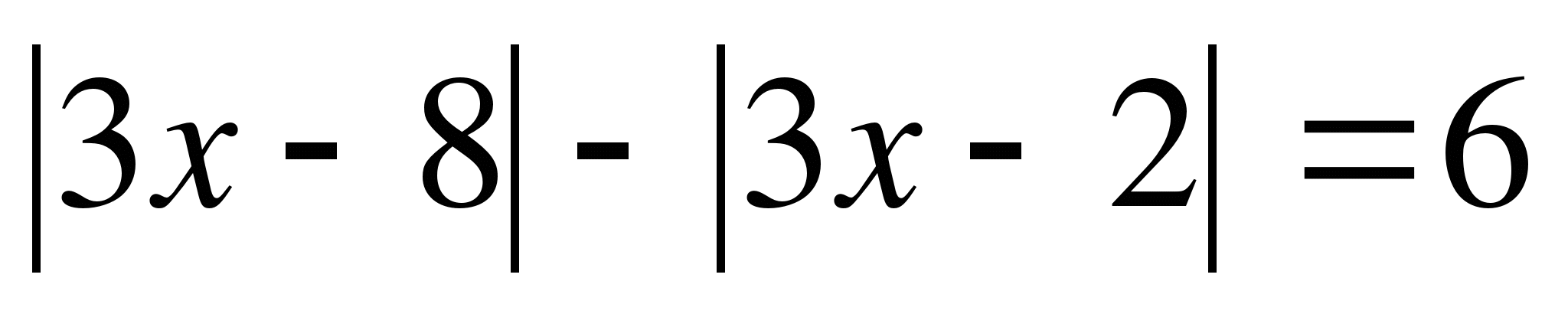 .
.
Решение.
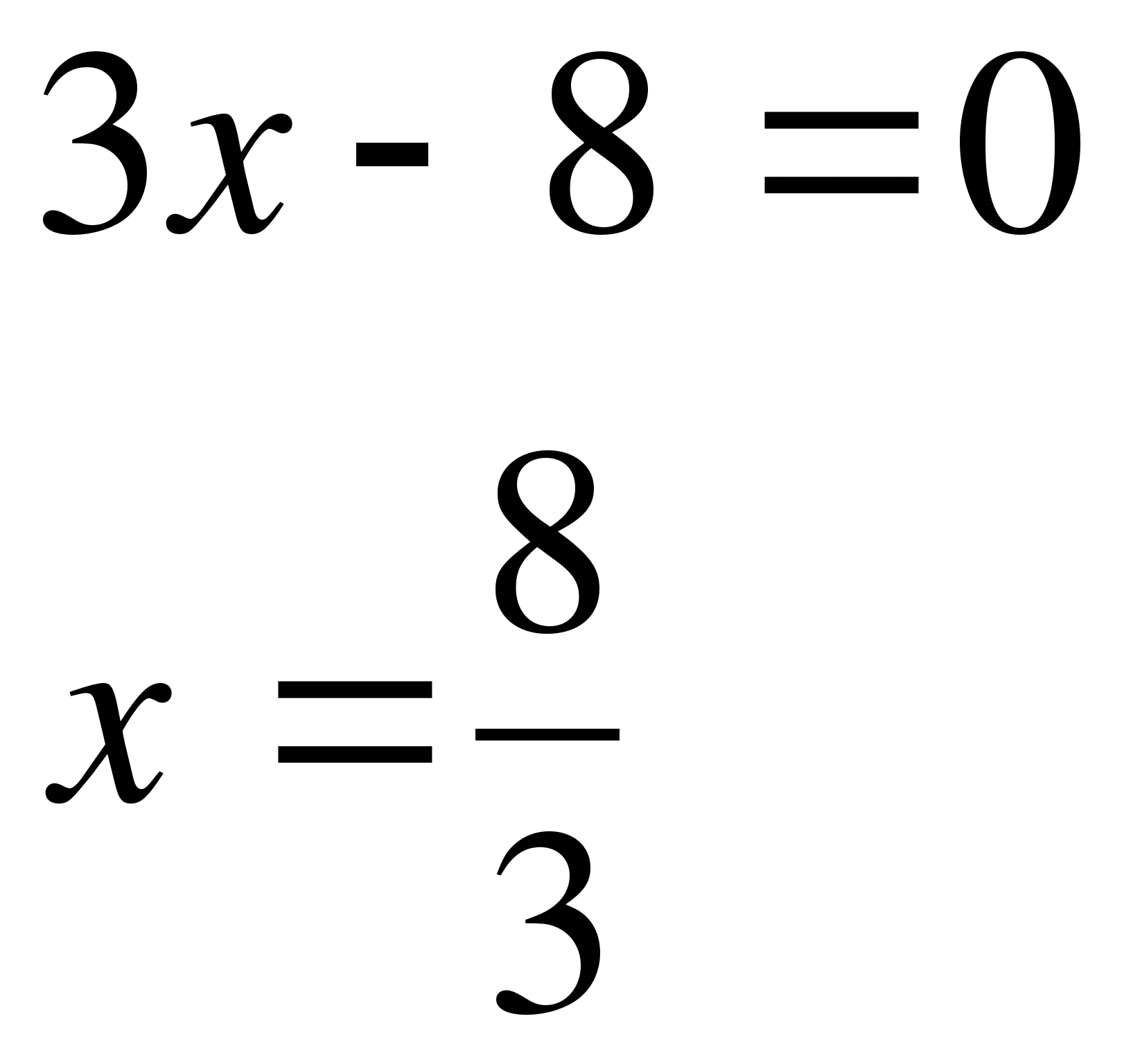
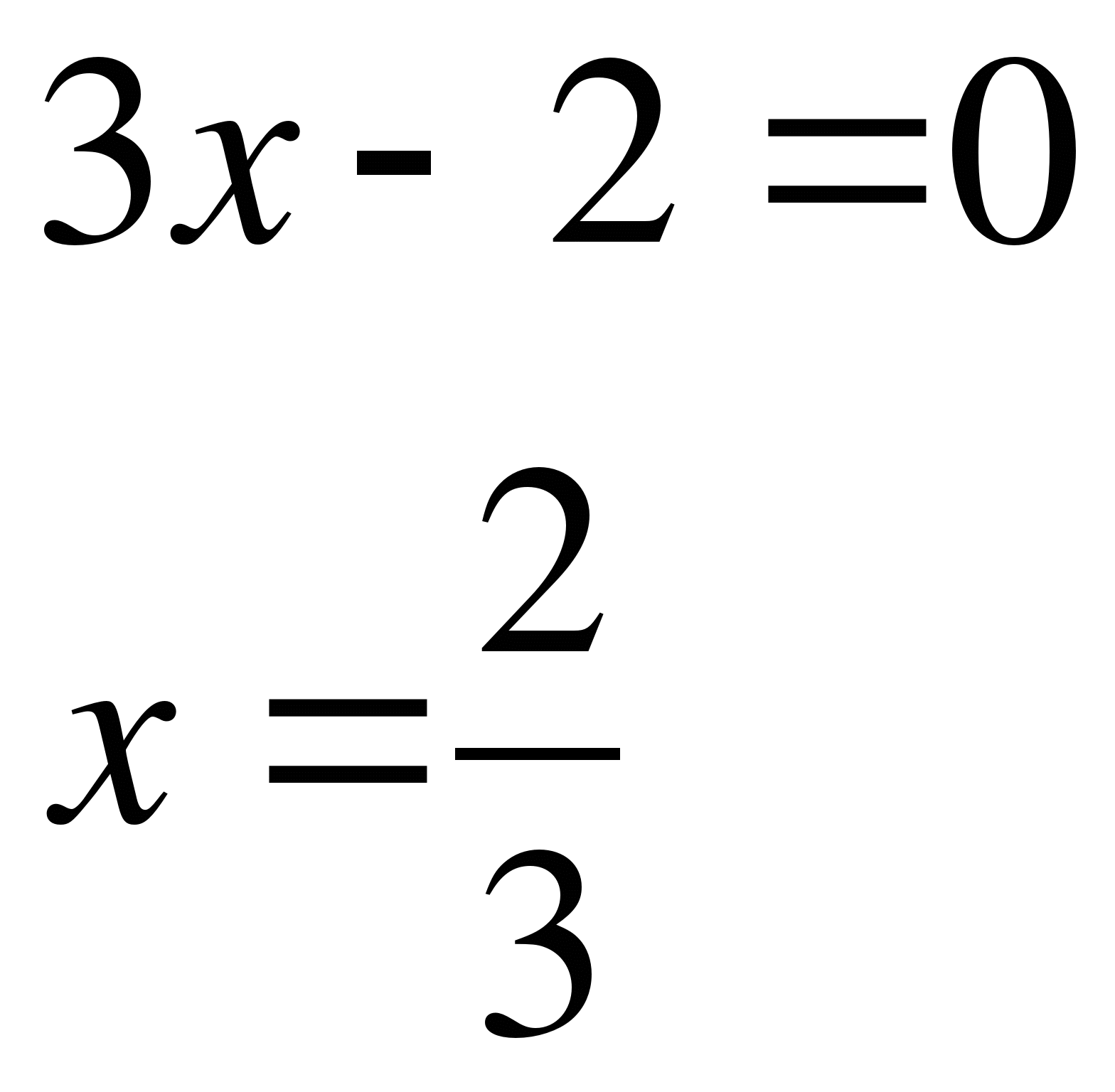


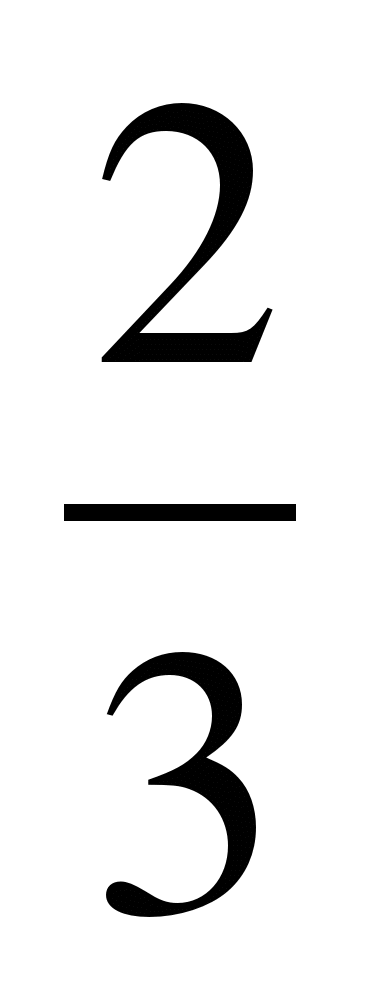
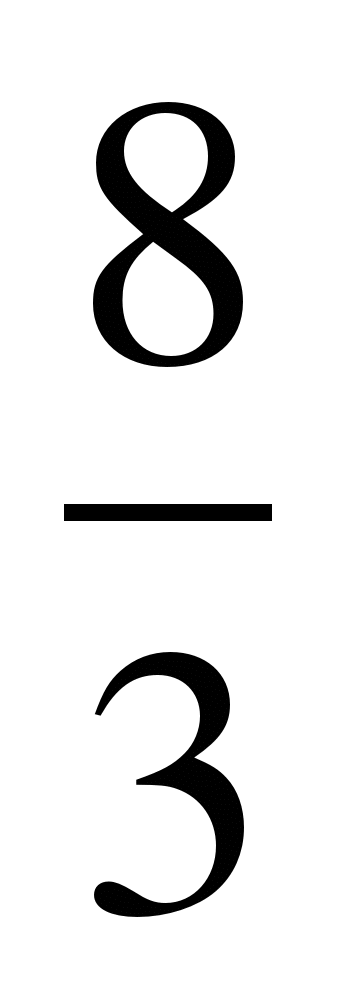
1) 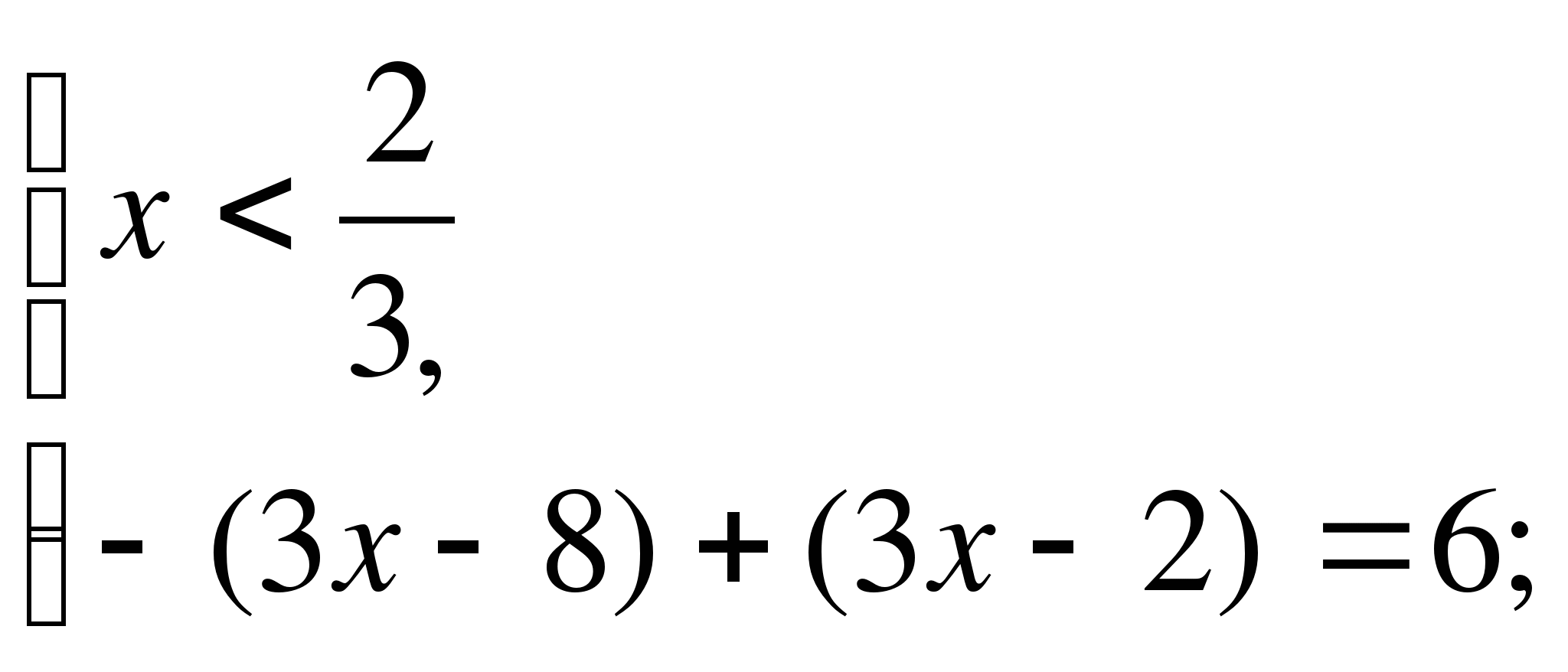
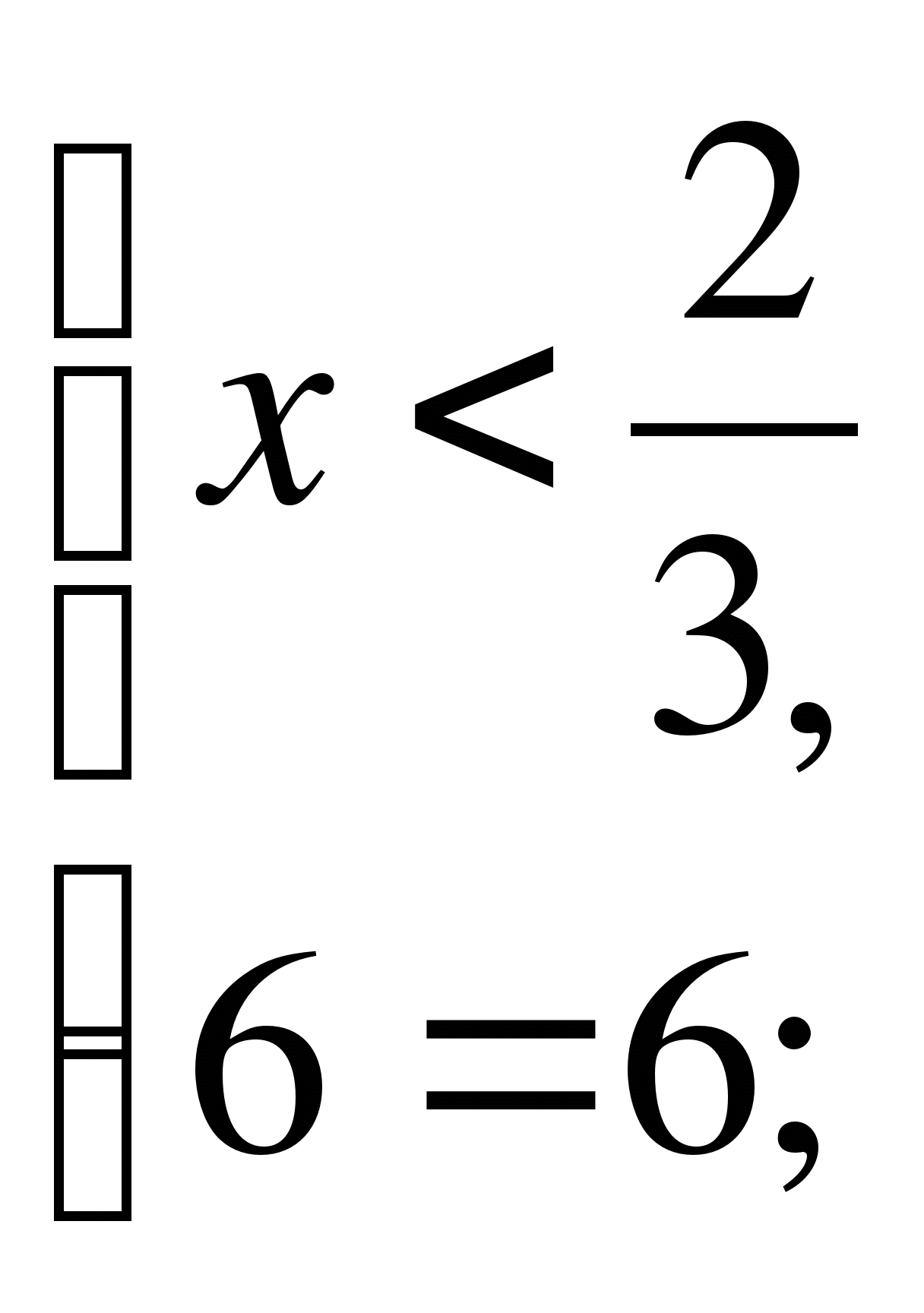
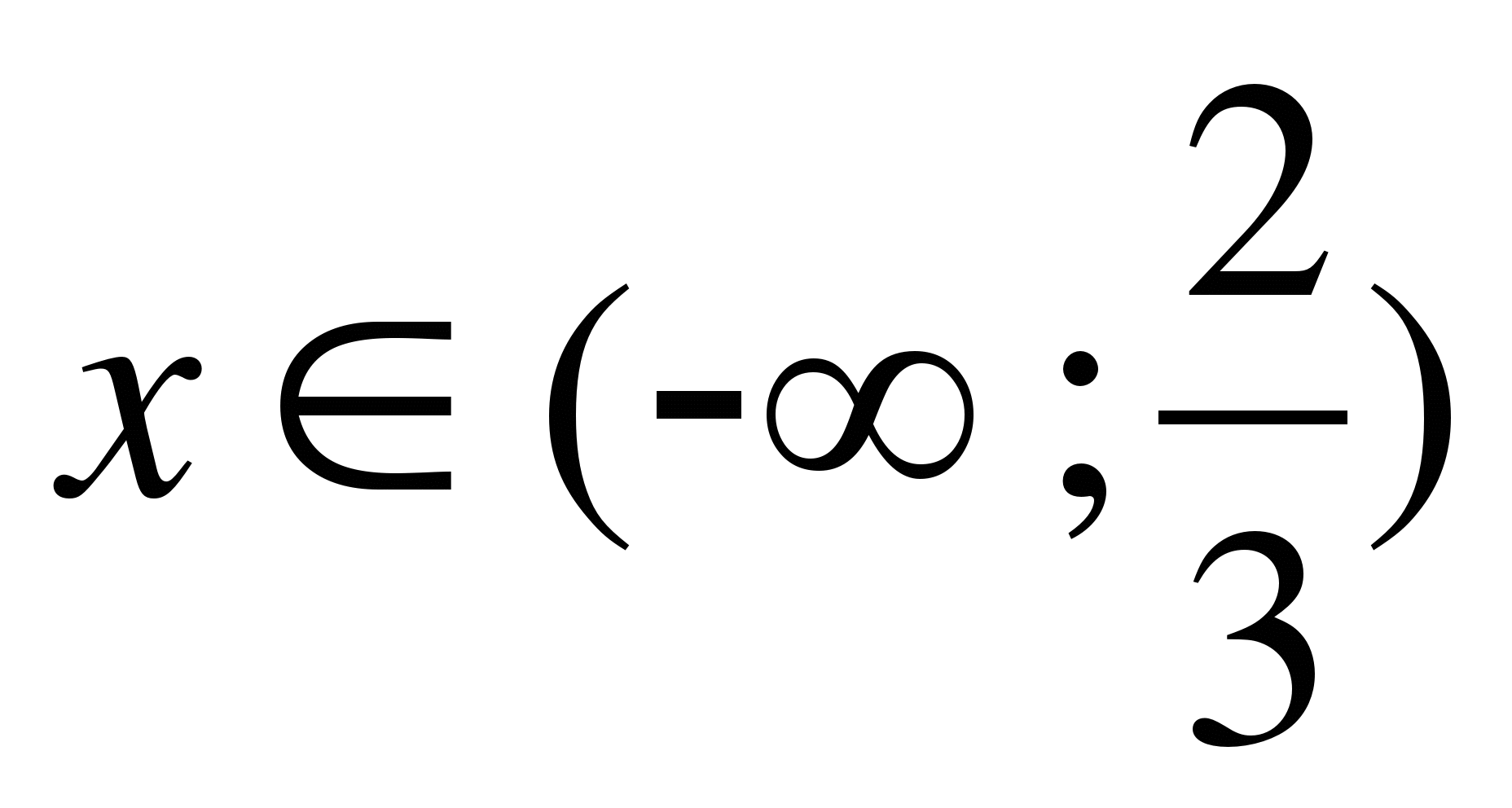
2) 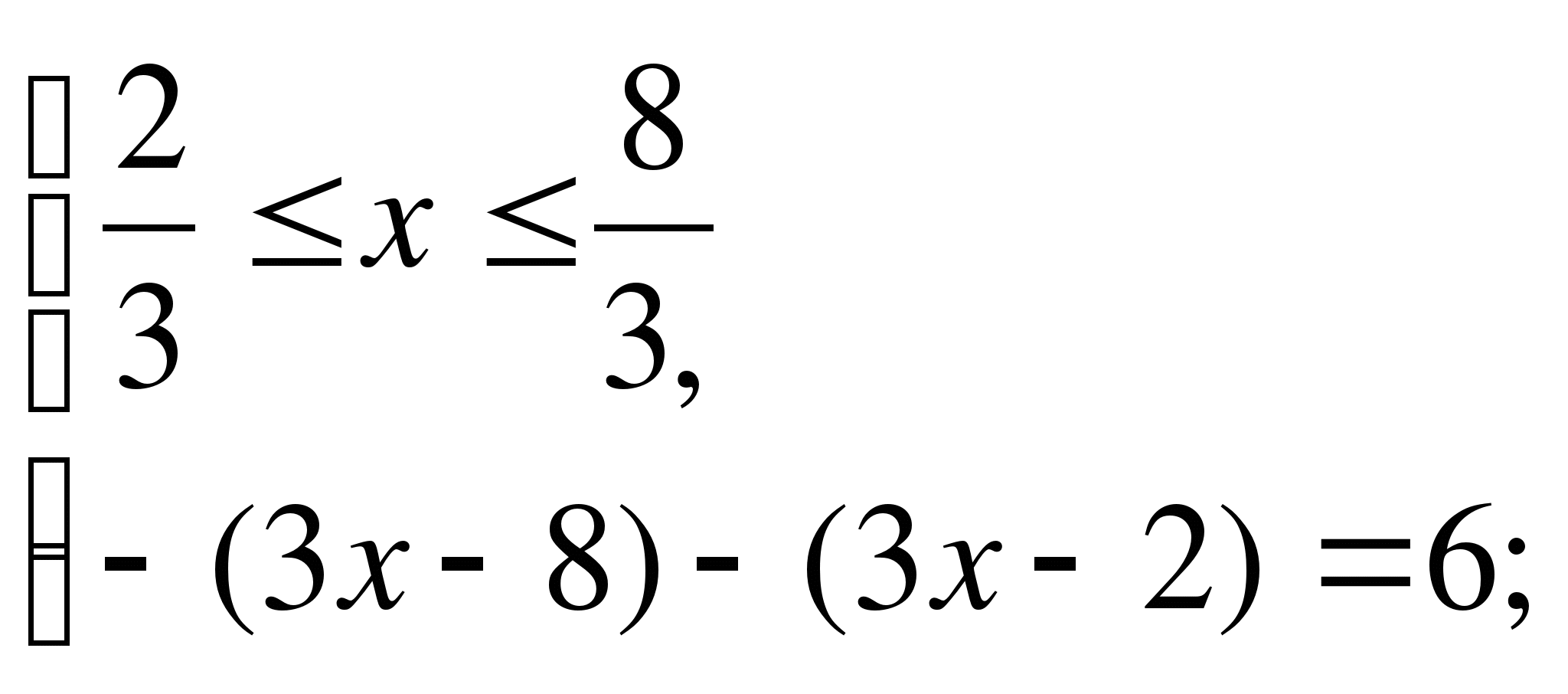
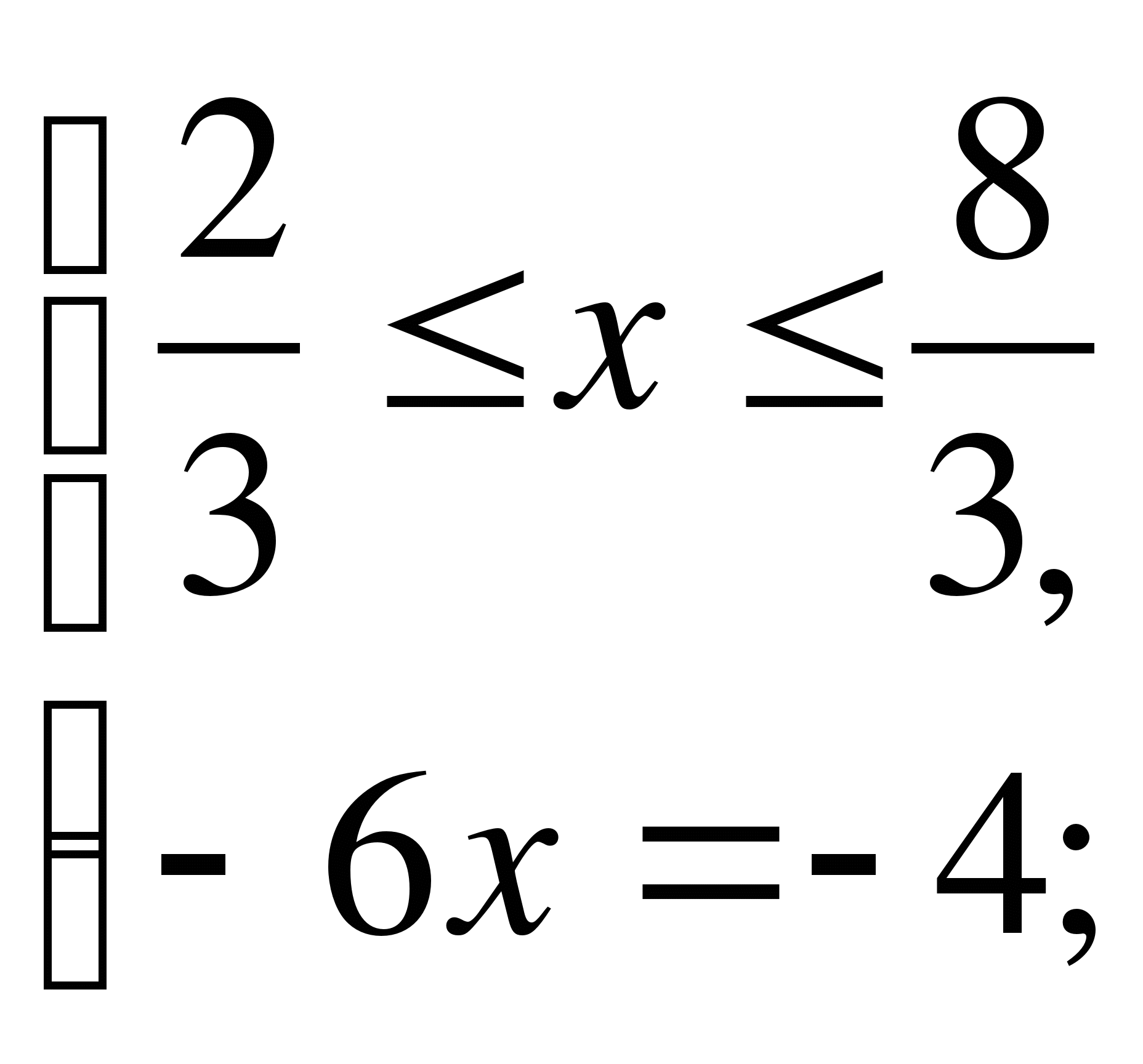
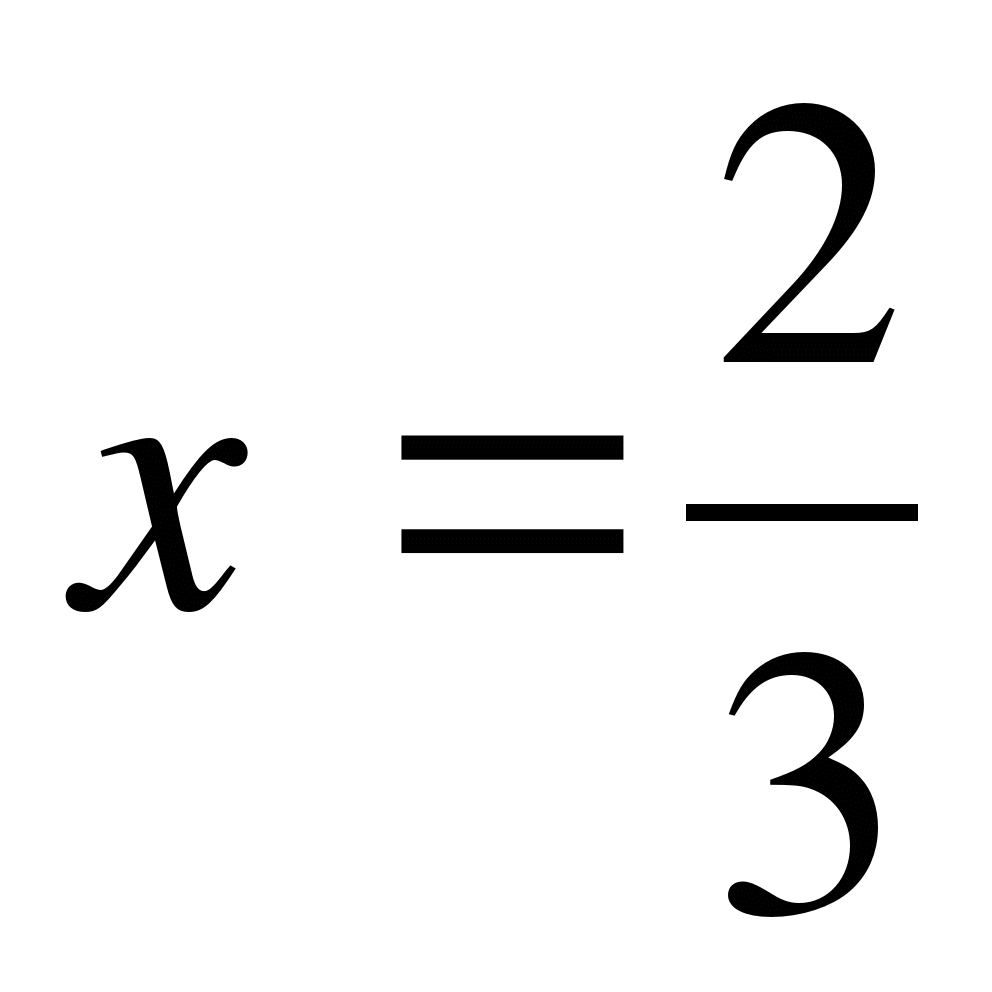
3) 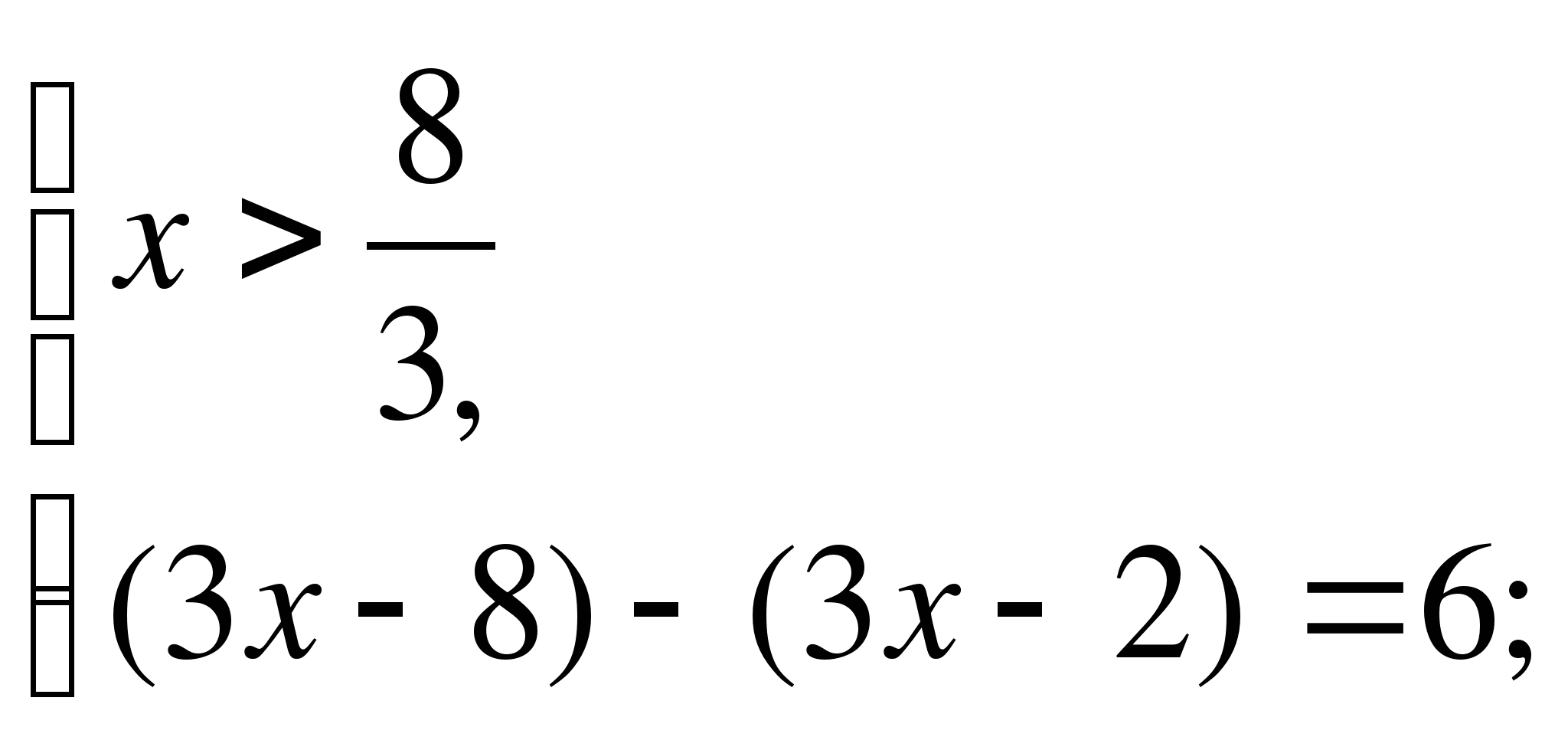
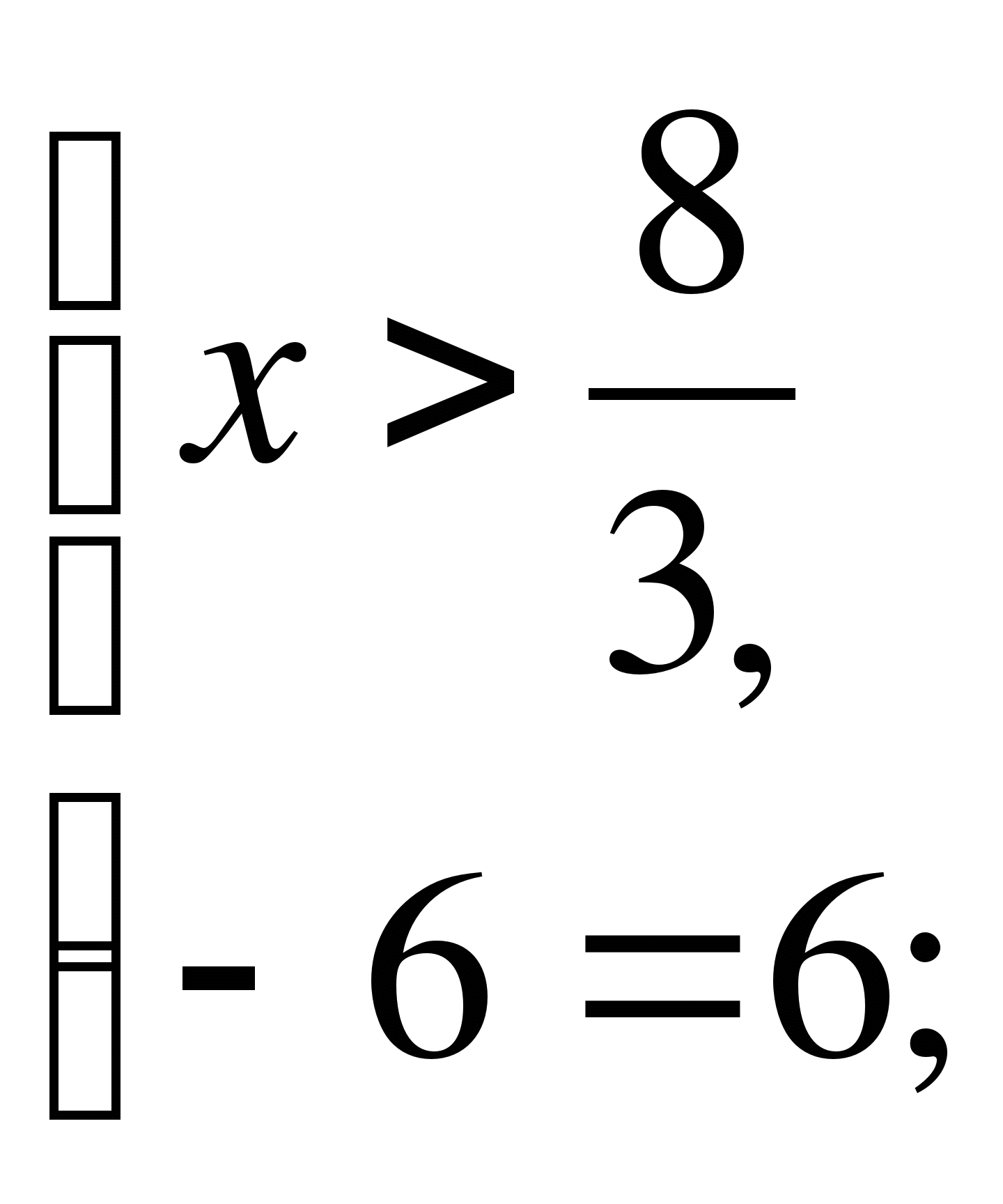
Ответ: 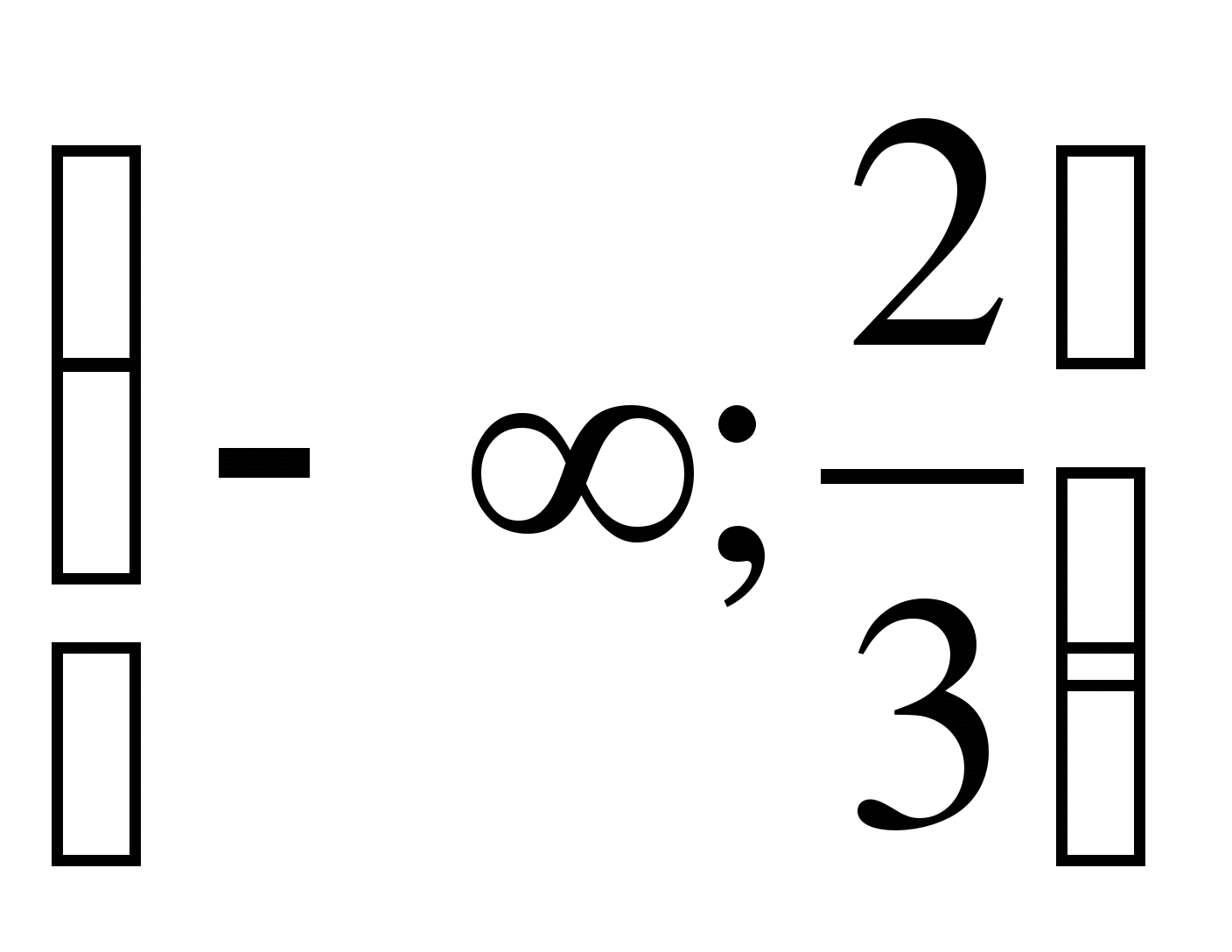
Пример 6.
Решите уравнение 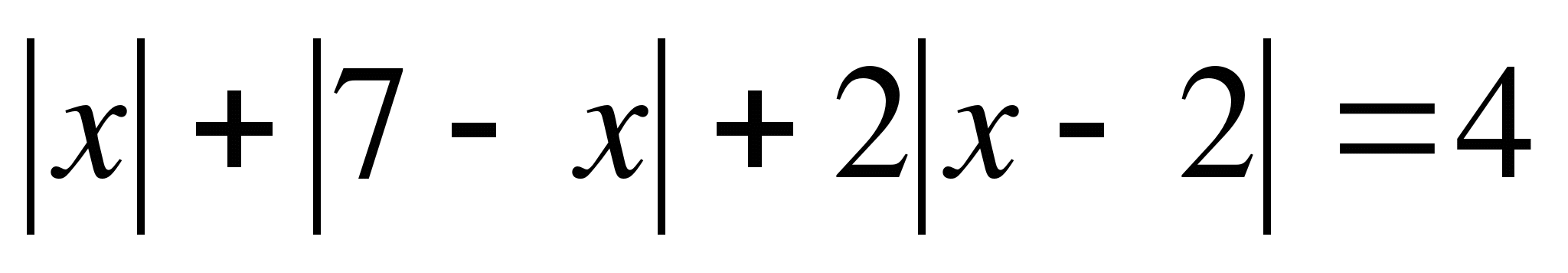 .
.
Решение.
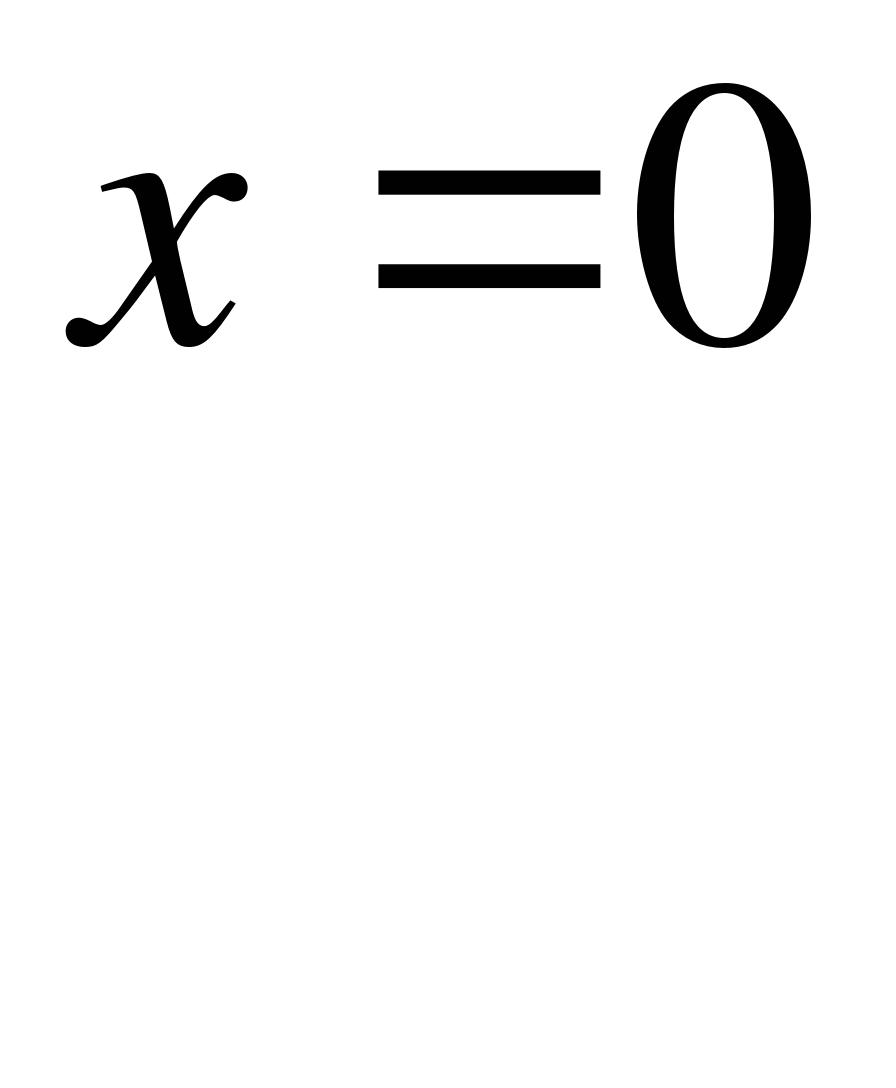
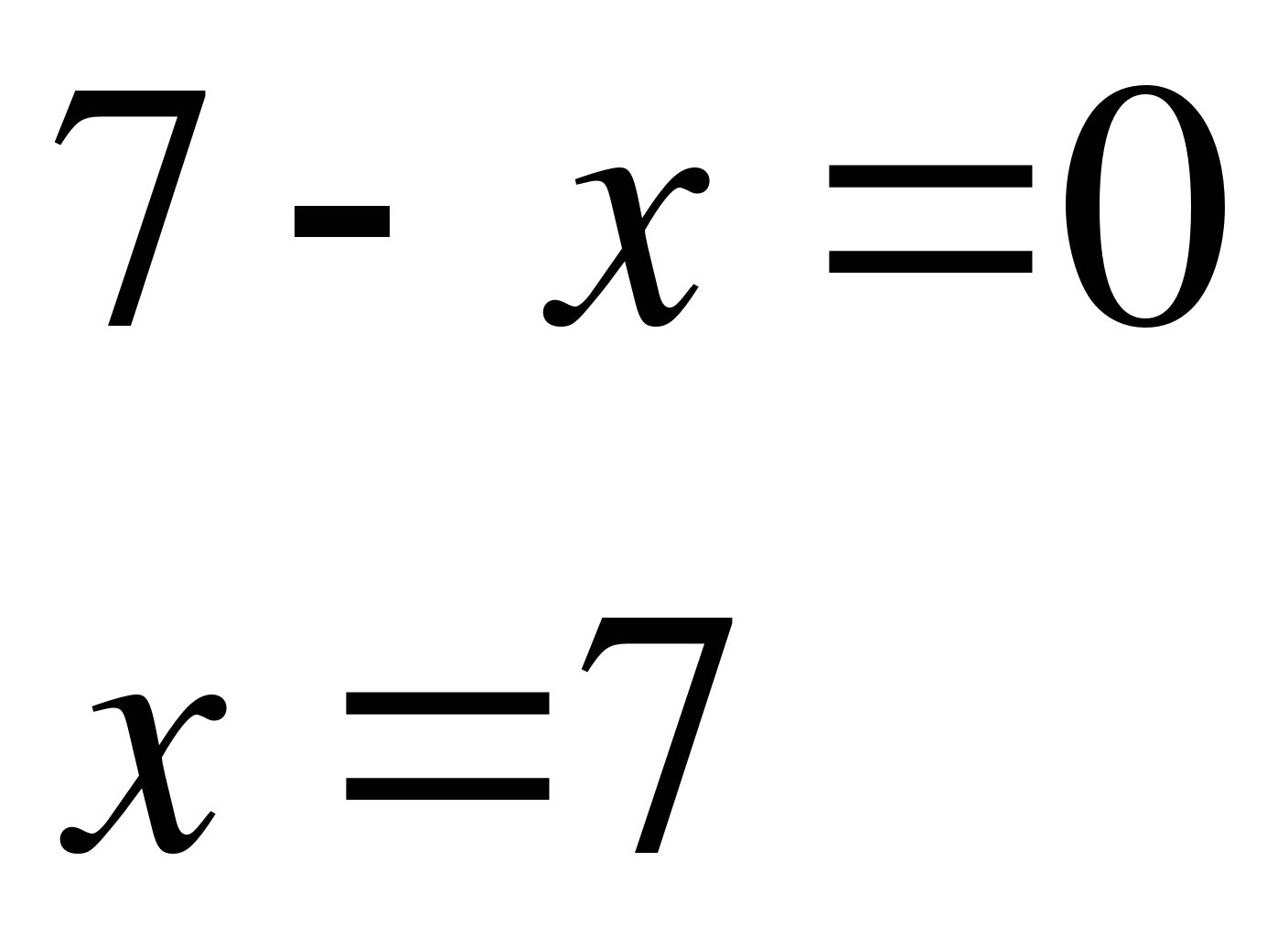
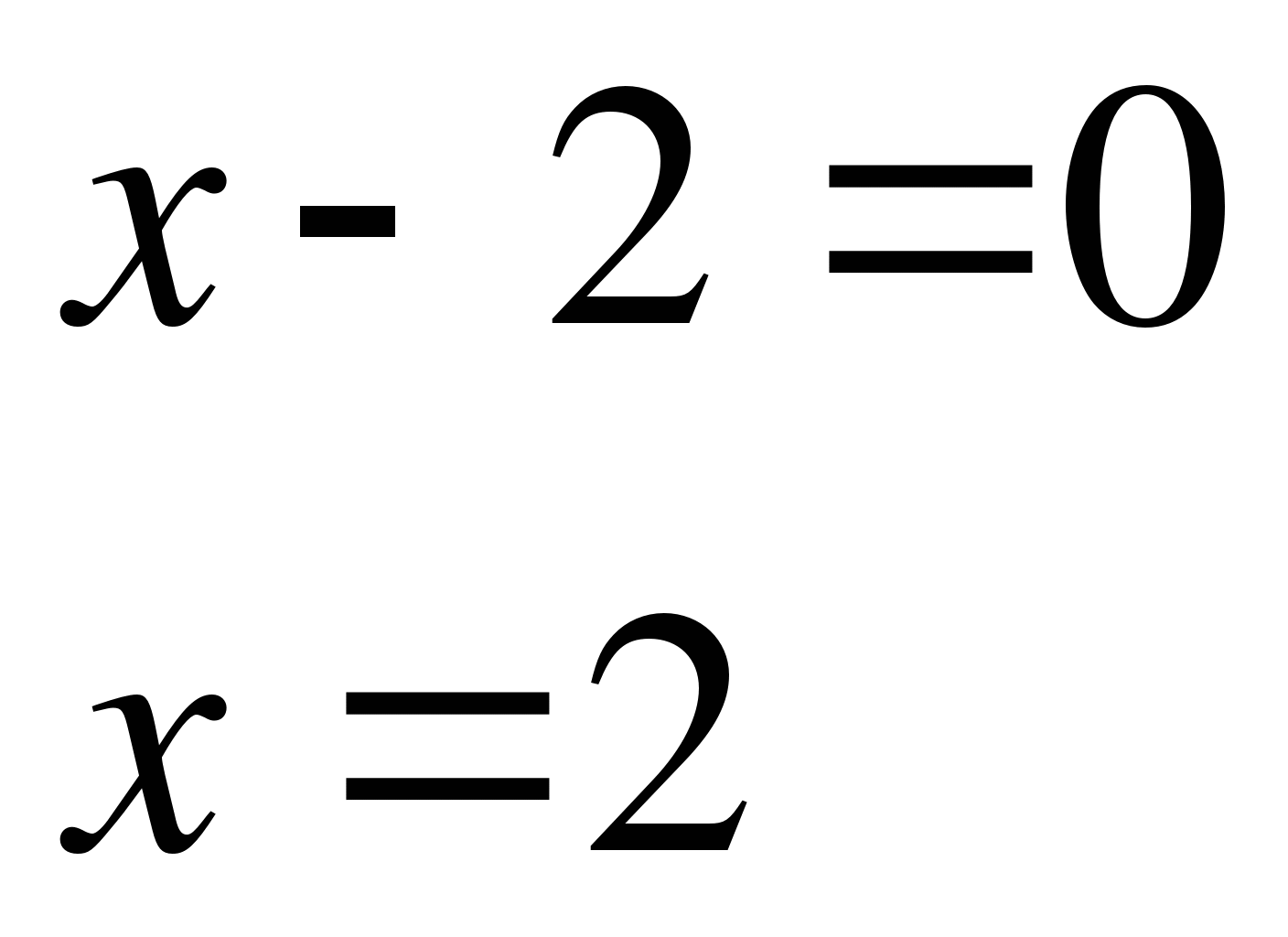

0 2 7
1) 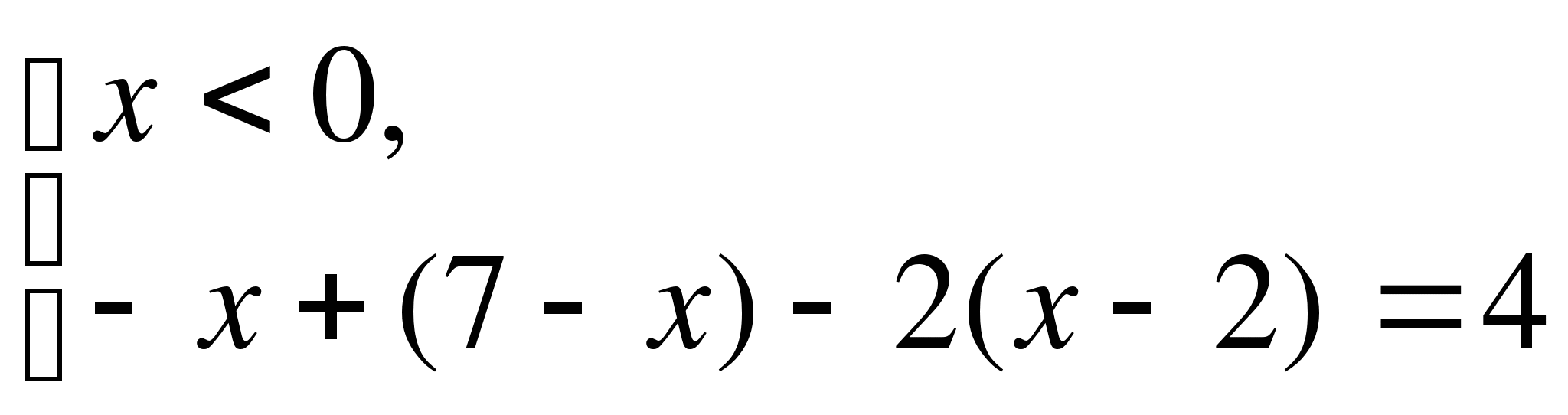

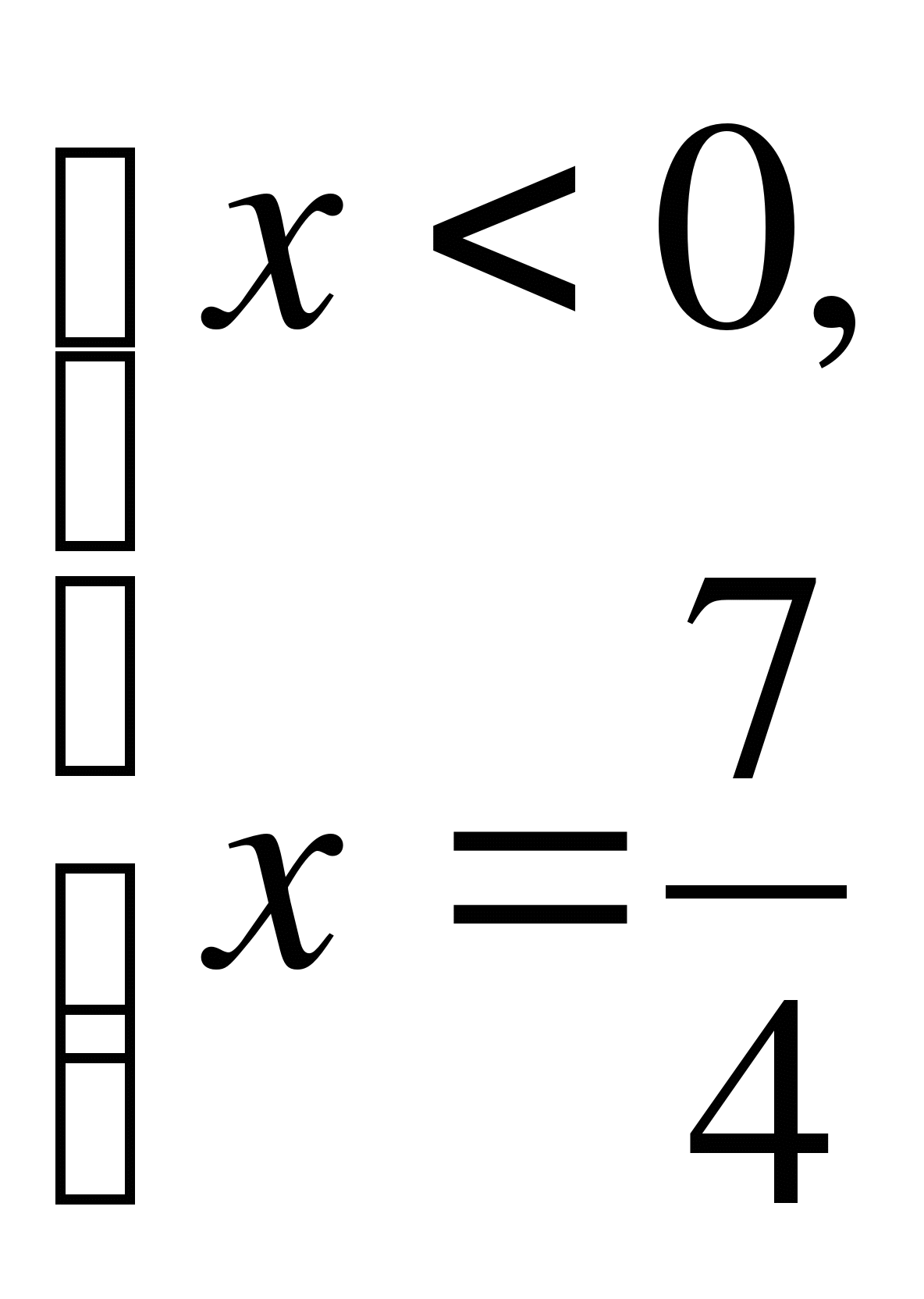 нет решений.
нет решений.
2) 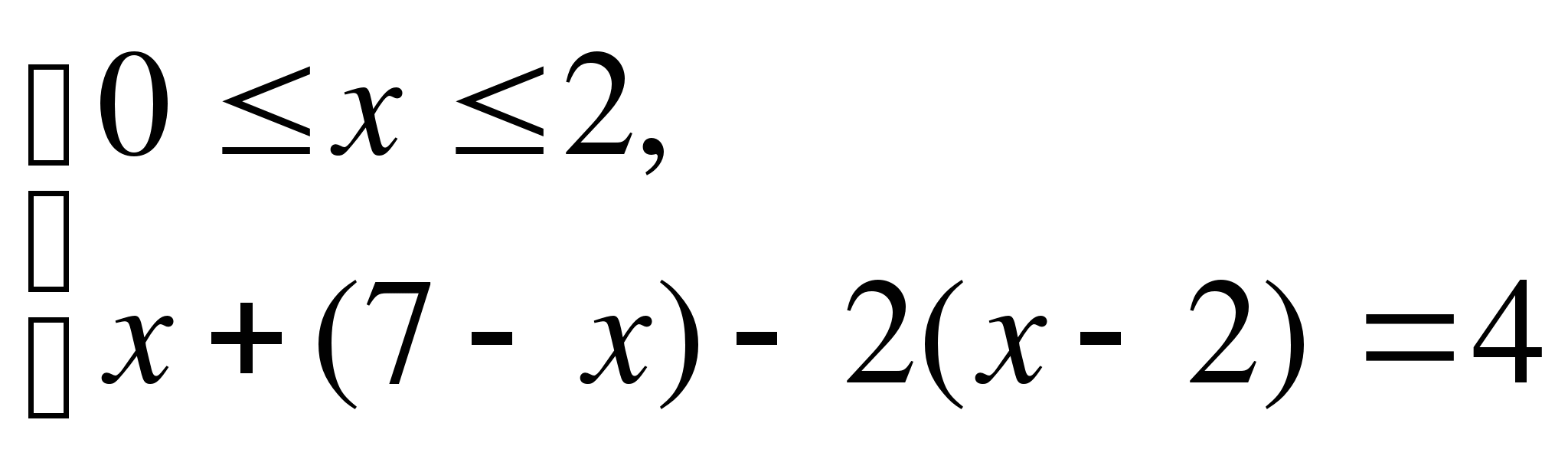

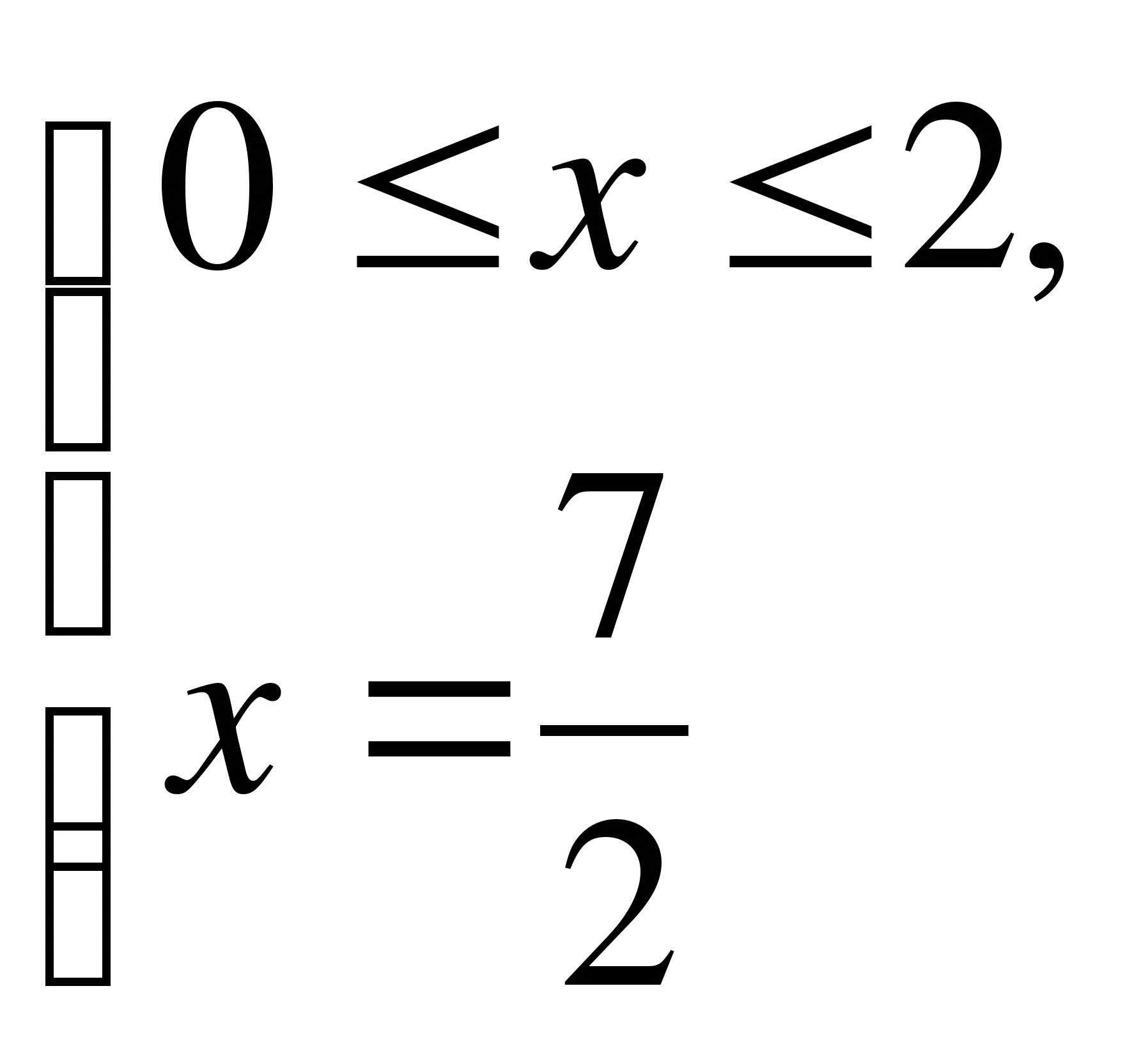 нет решений.
нет решений.
3) 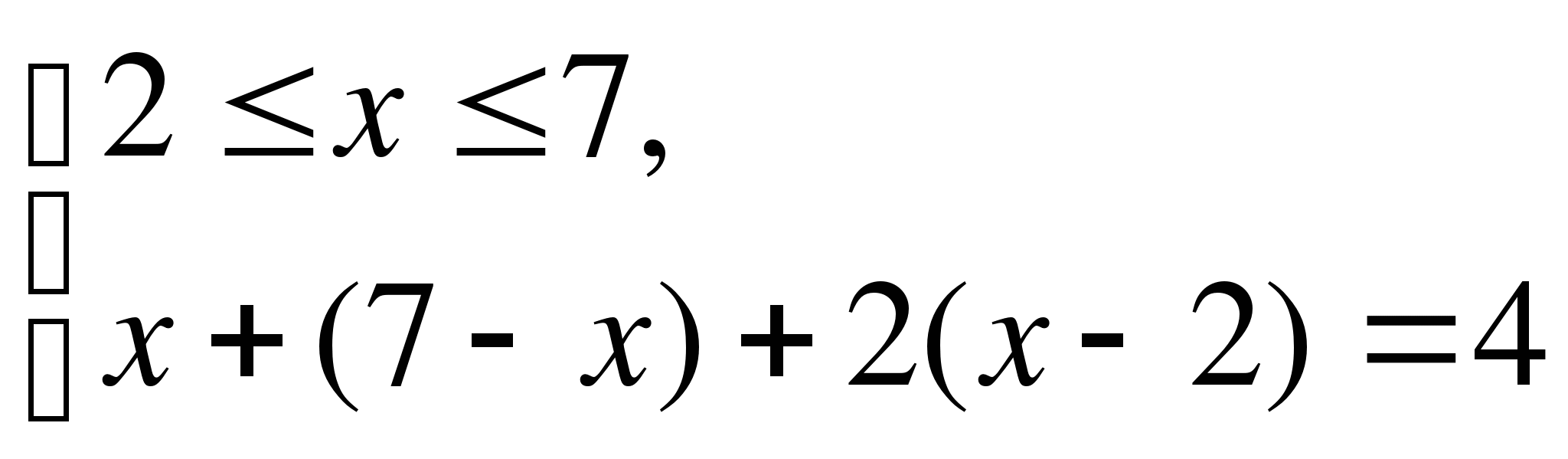

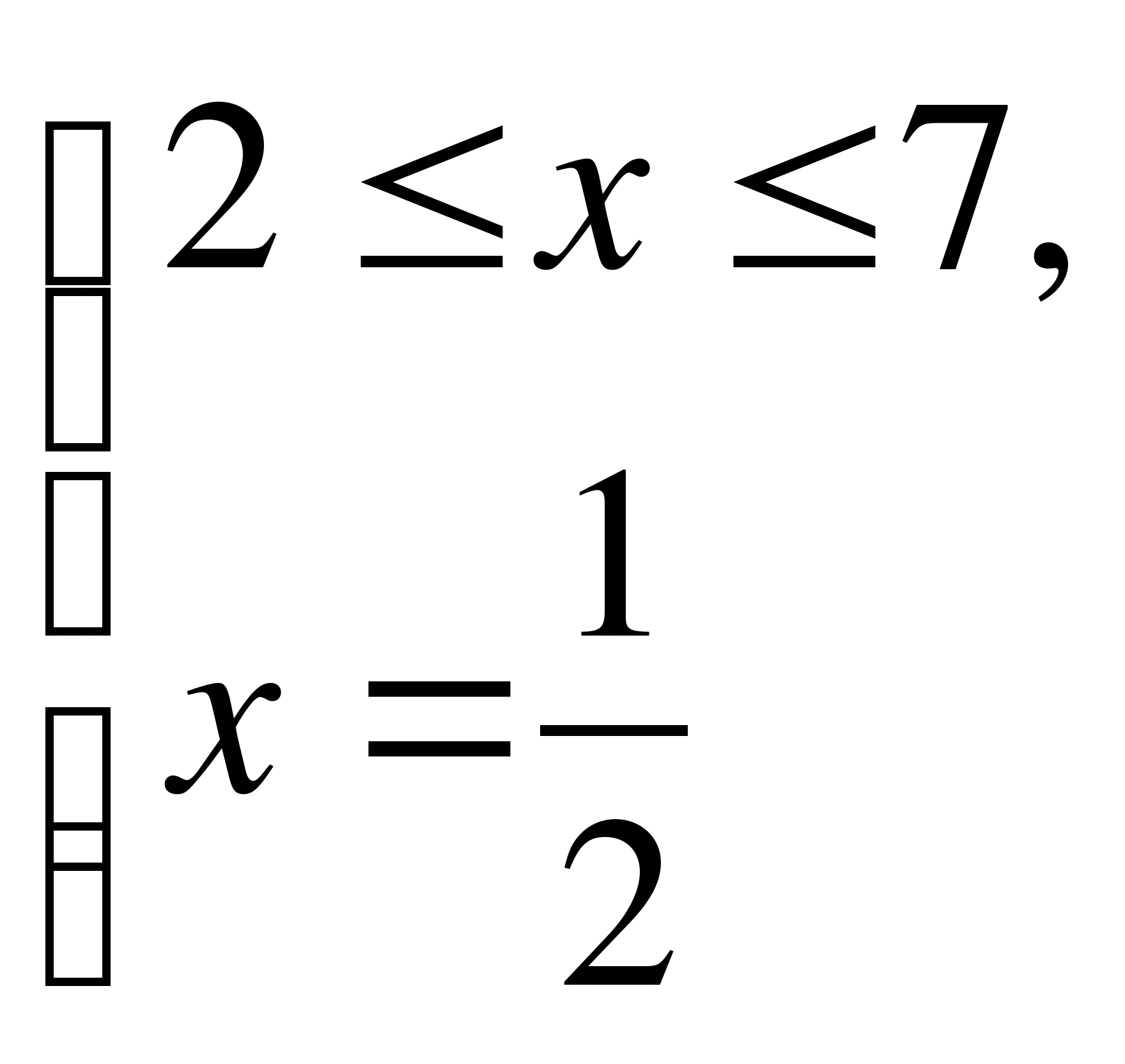 нет решений.
нет решений.
4) 

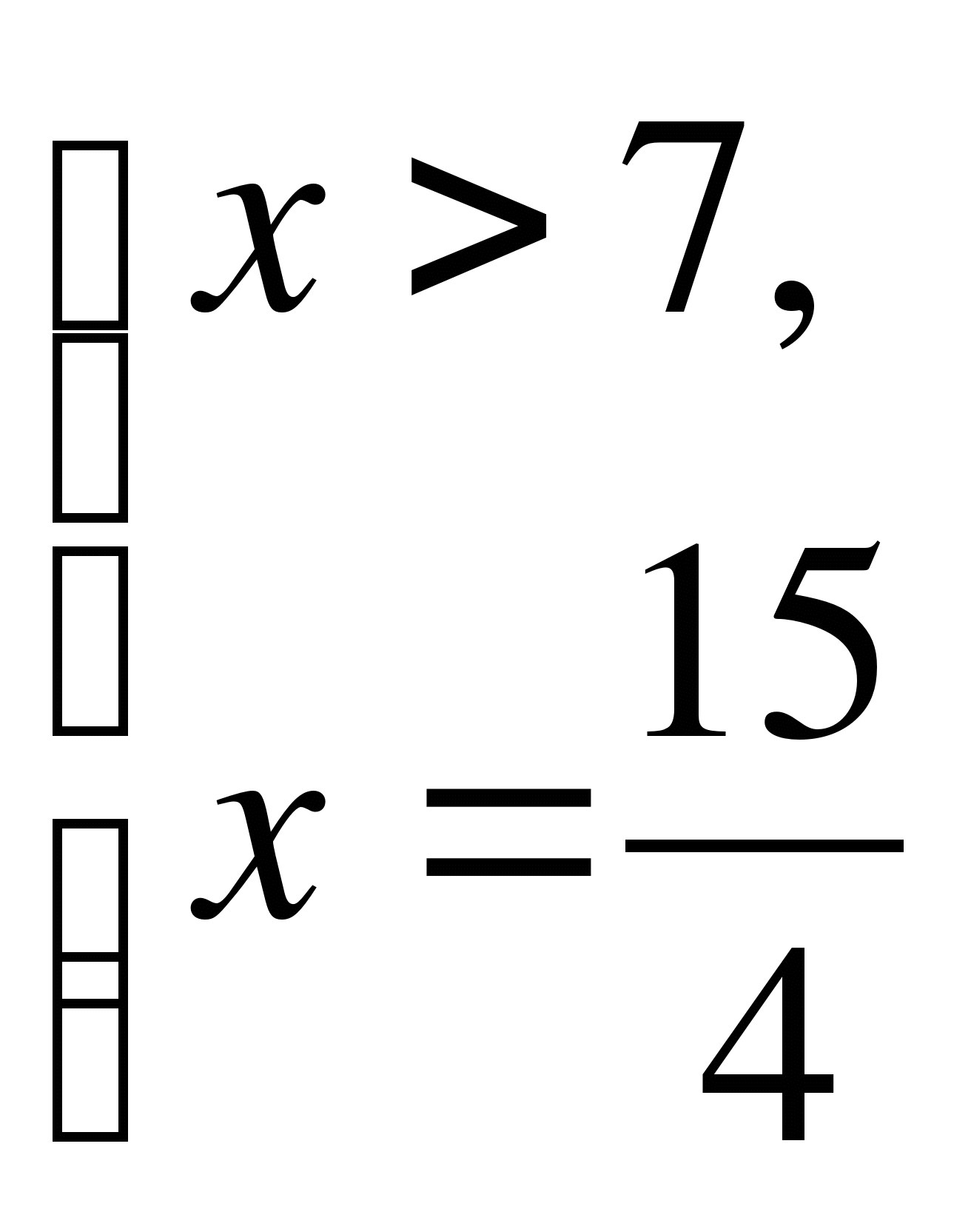 нет решений.
нет решений.
Ответ: корней нет.
РЕШЕНИЕ УРАВНЕНИЙ 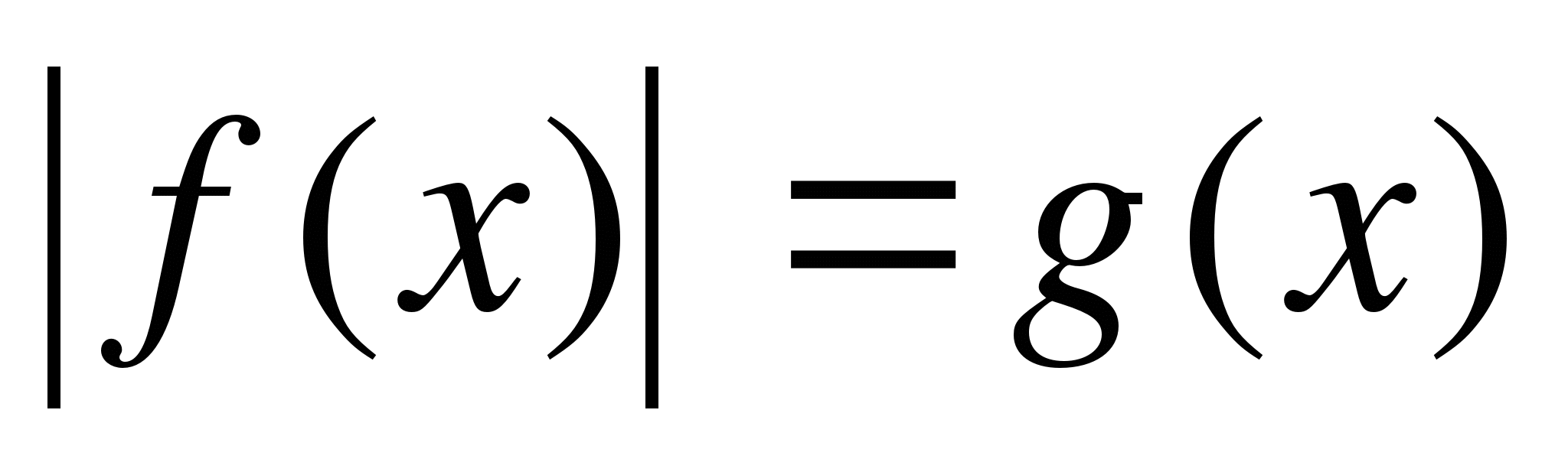
І способ
Раскрыть модуль по определению

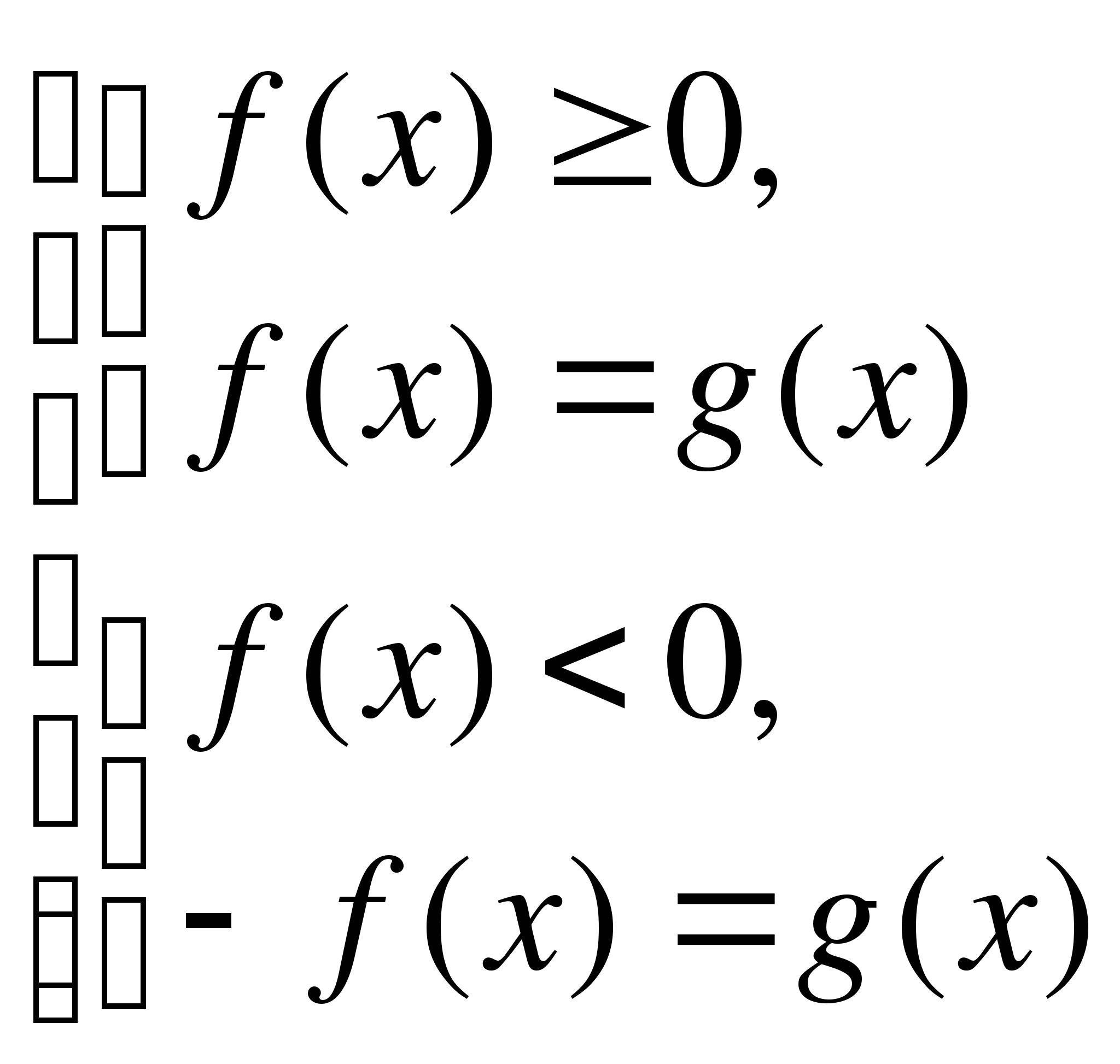
ІІ способ
Возведение обеих частей в квадрат
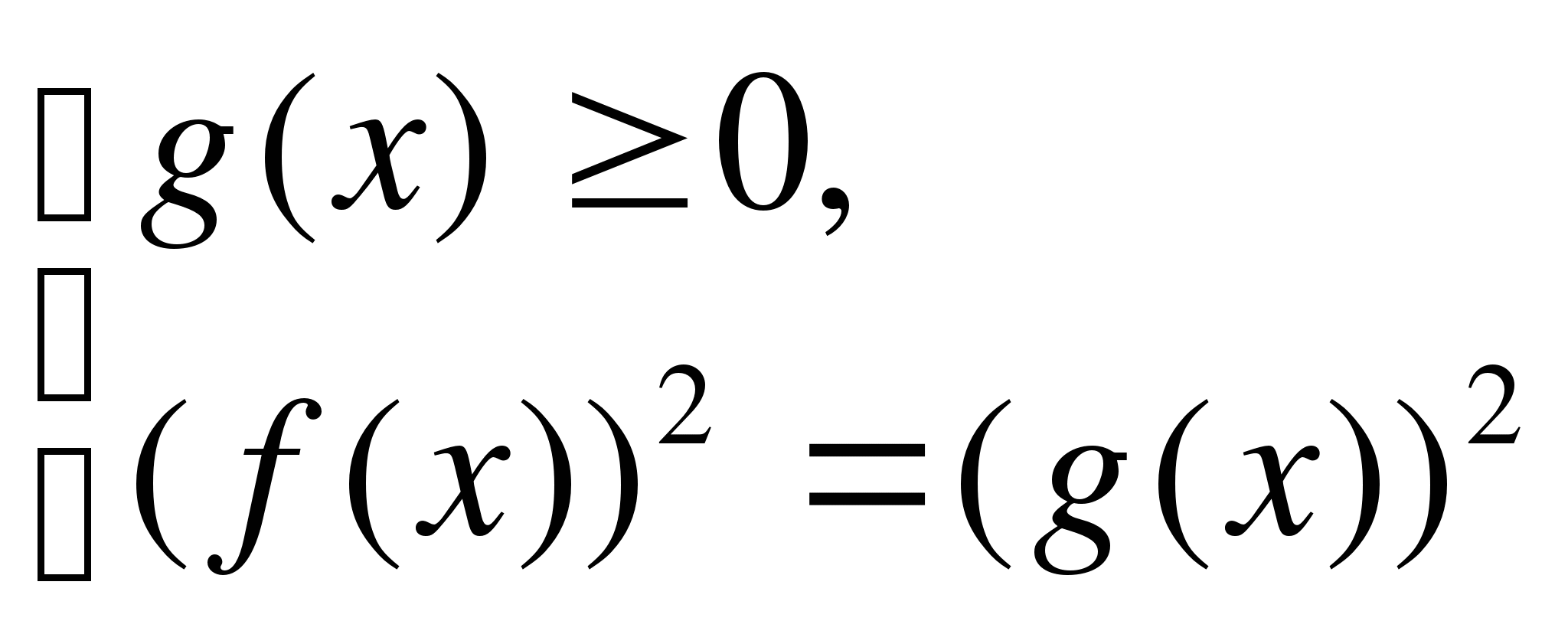
ІІІ способ
Метод разбиения на промежутки
ПРИМЕРЫ
Пример №1
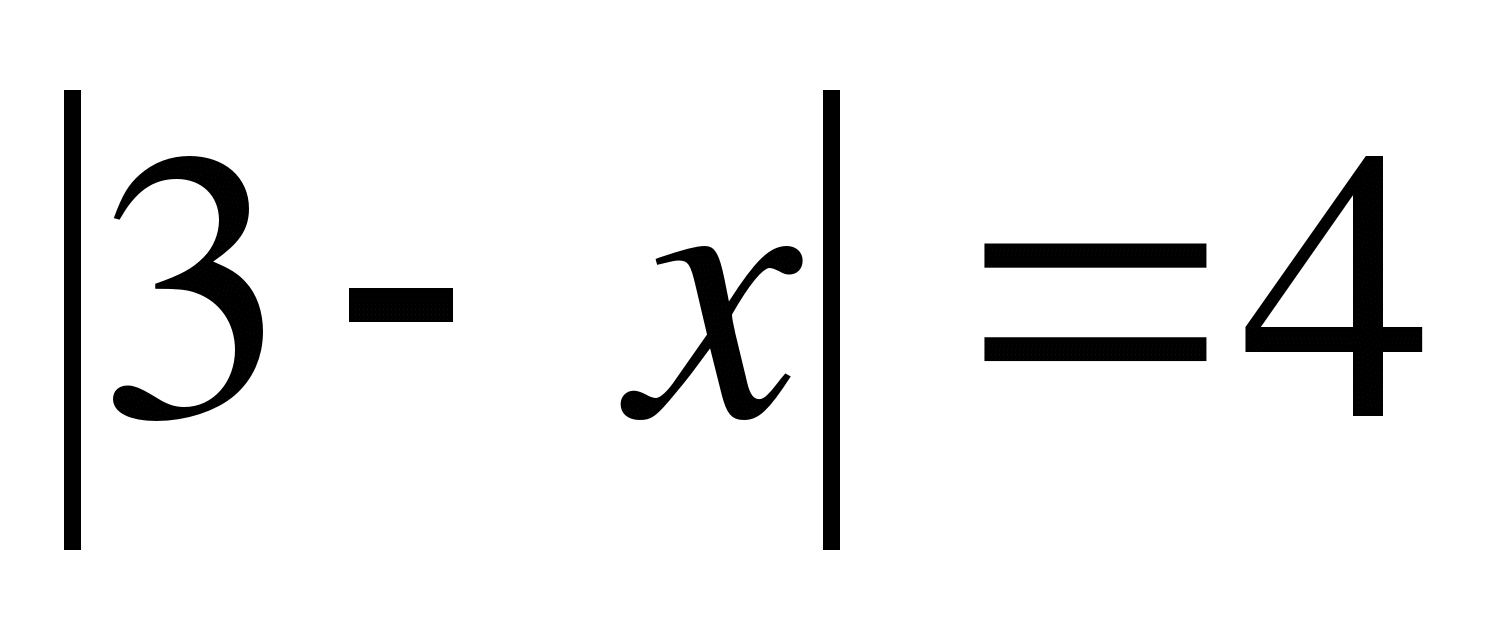
Решение
І способ (по определению)
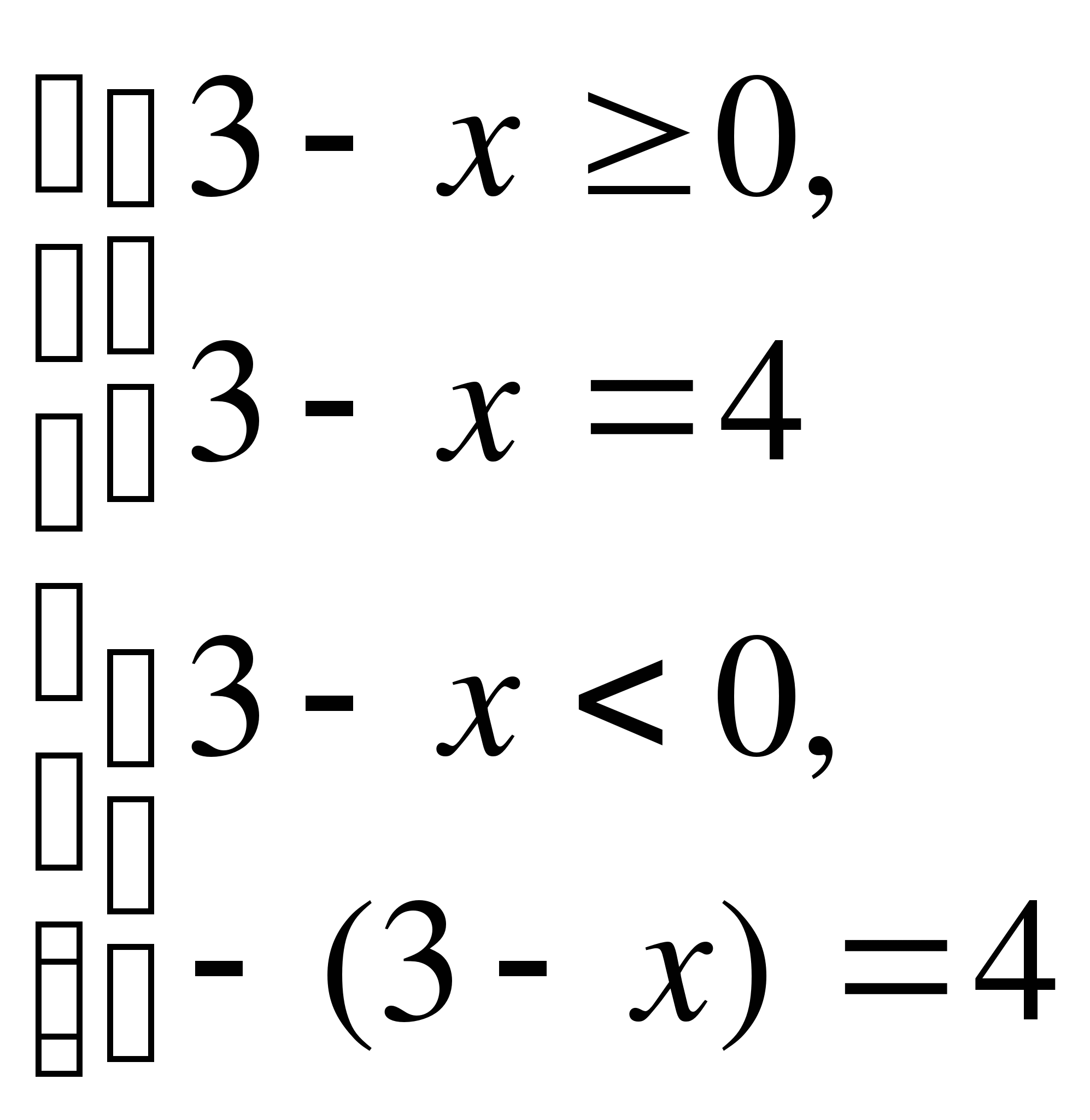
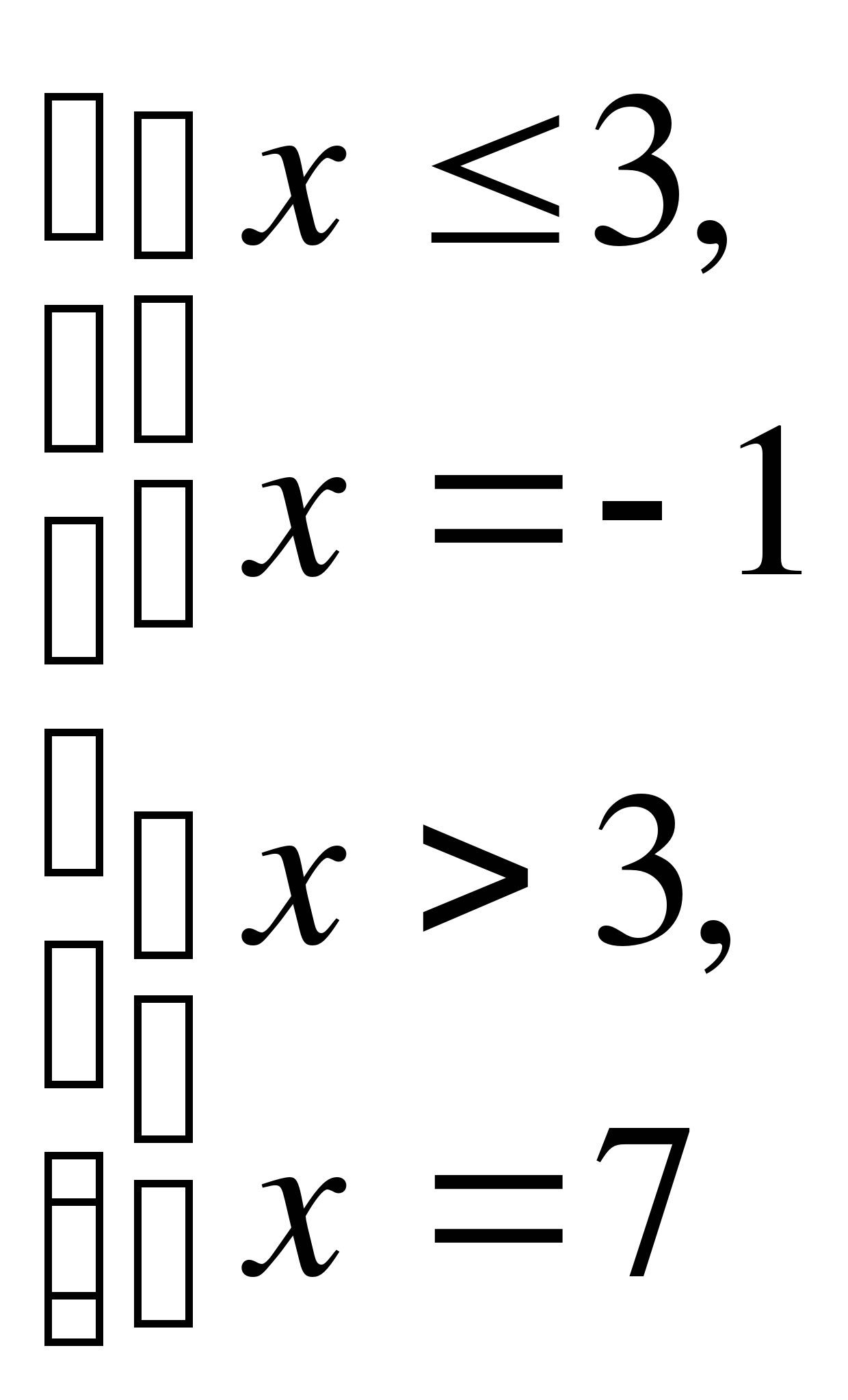
Ответ: -1; 7.
ІІ способ (возведение обеих частей в квадрат)
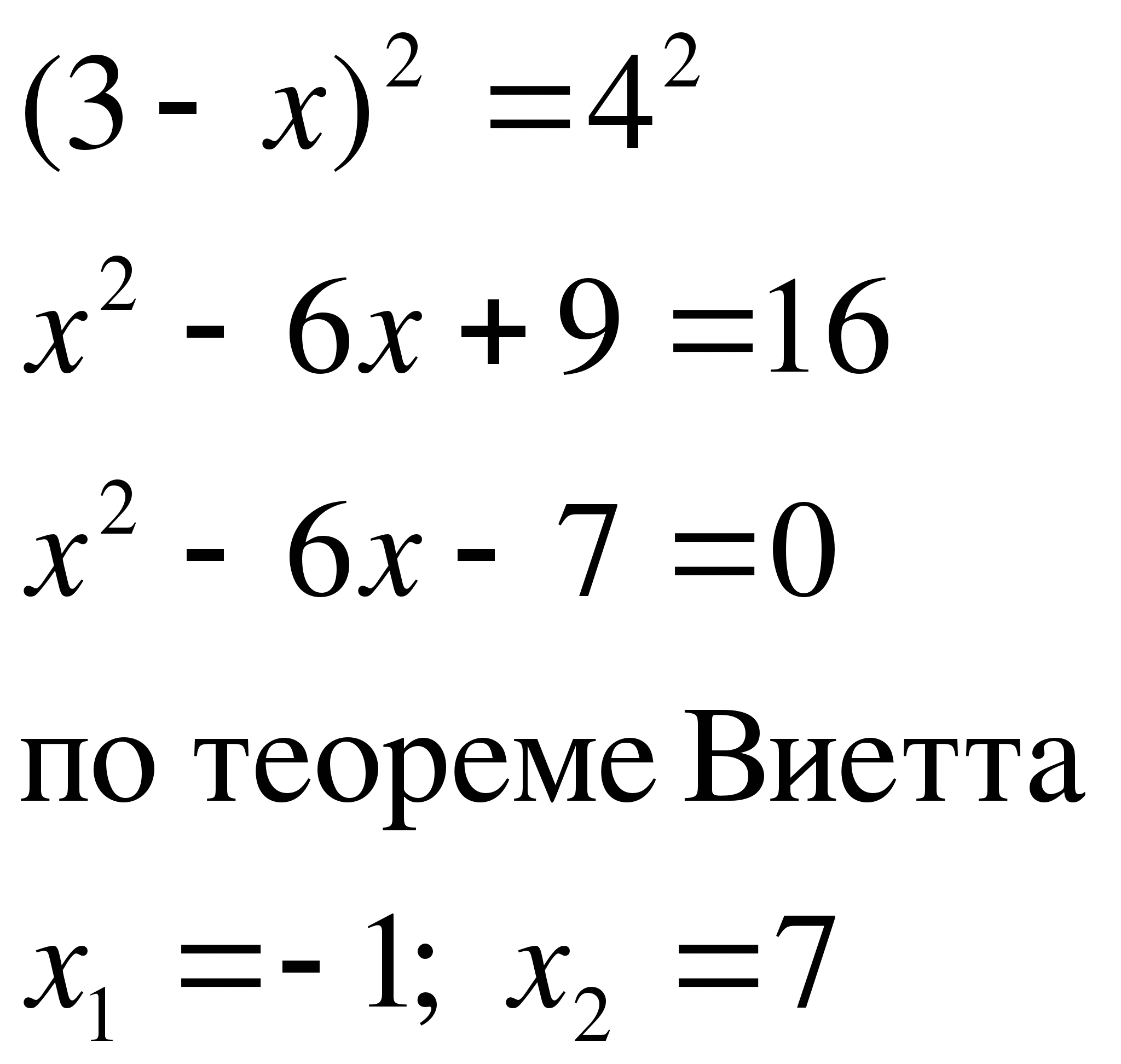
Ответ: -1; 7.
Пример №2
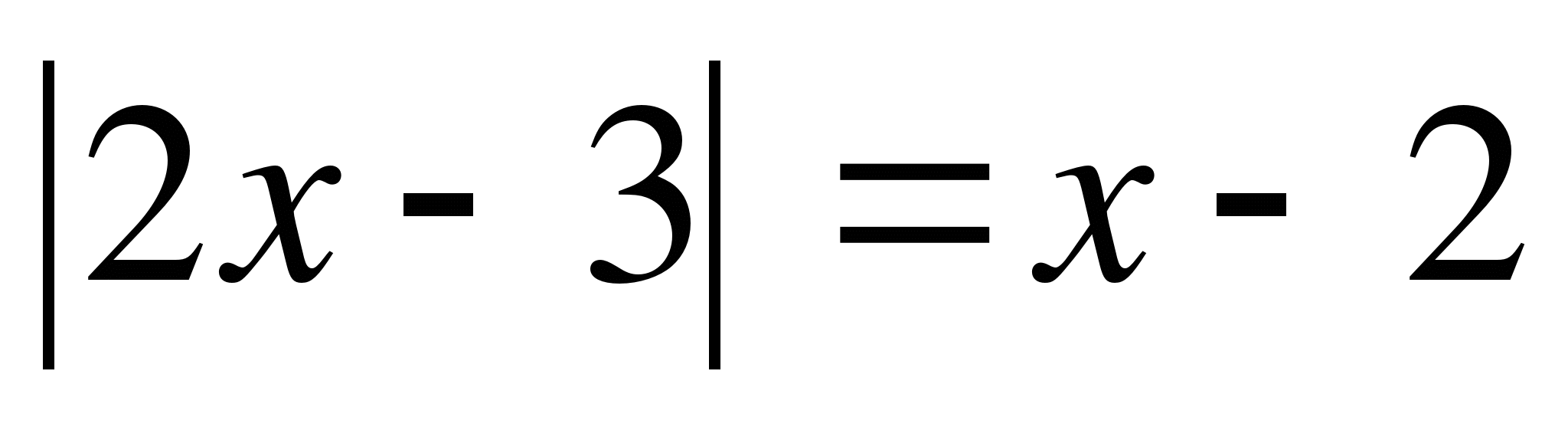
Решение
І способ (по определению)
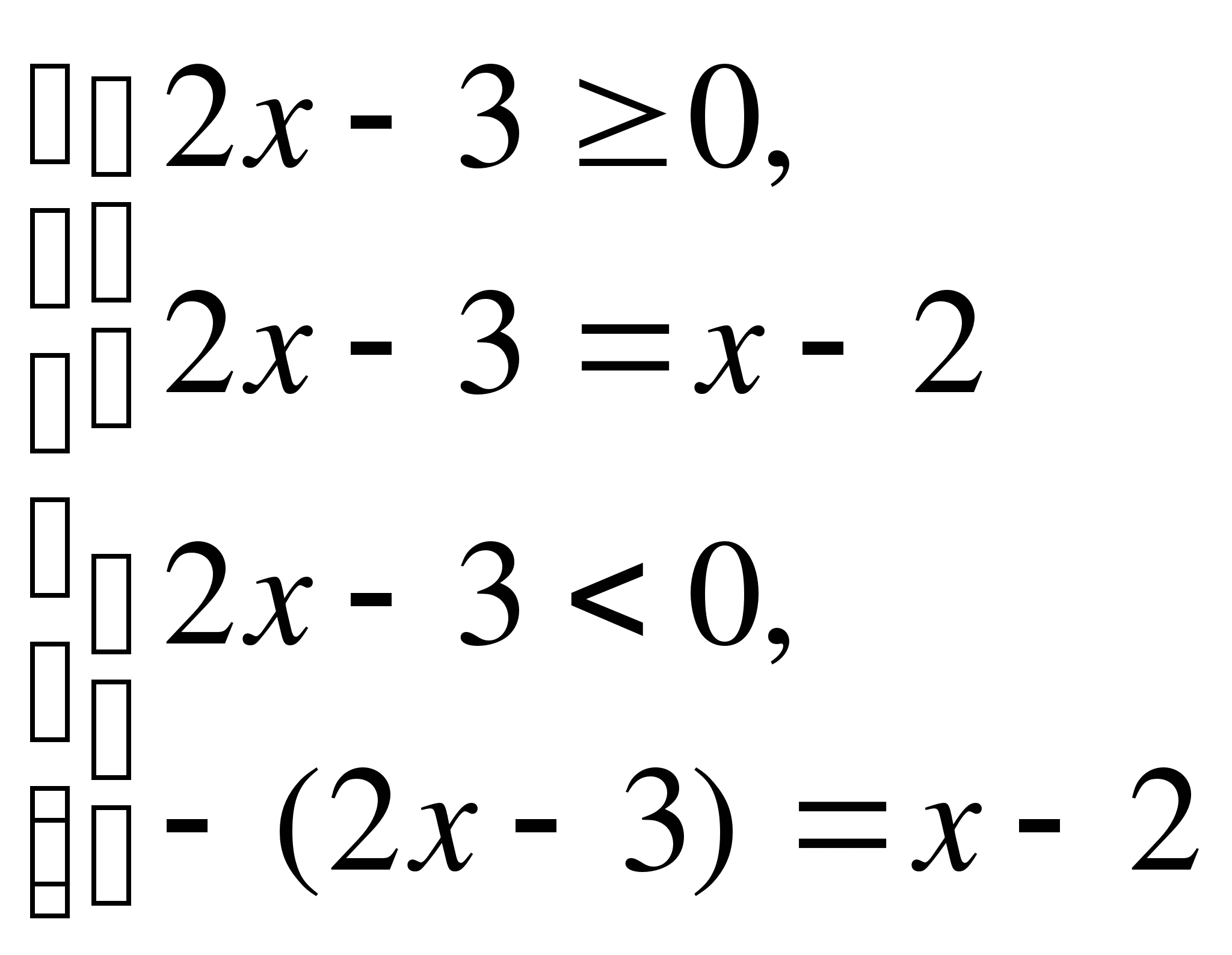
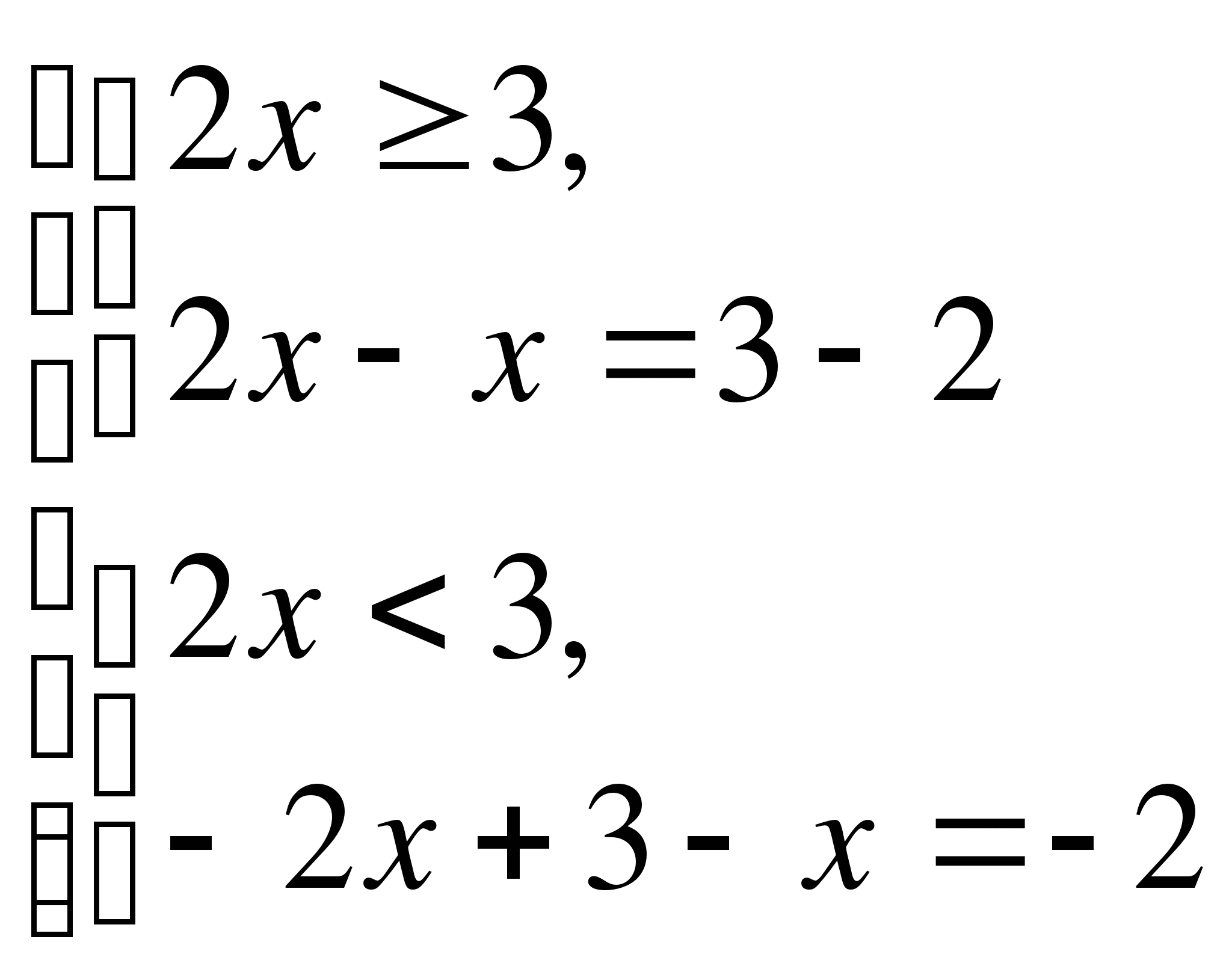
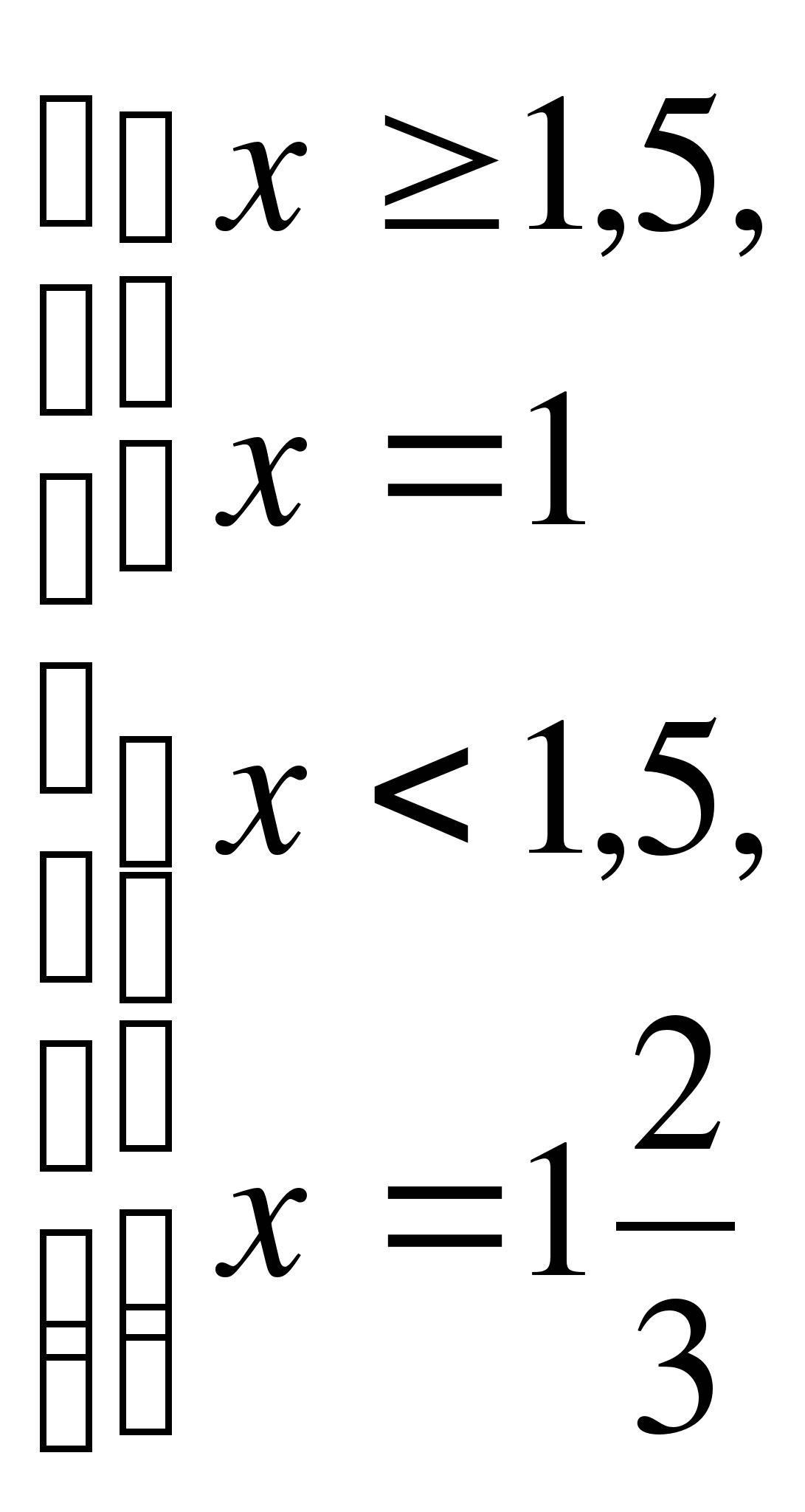
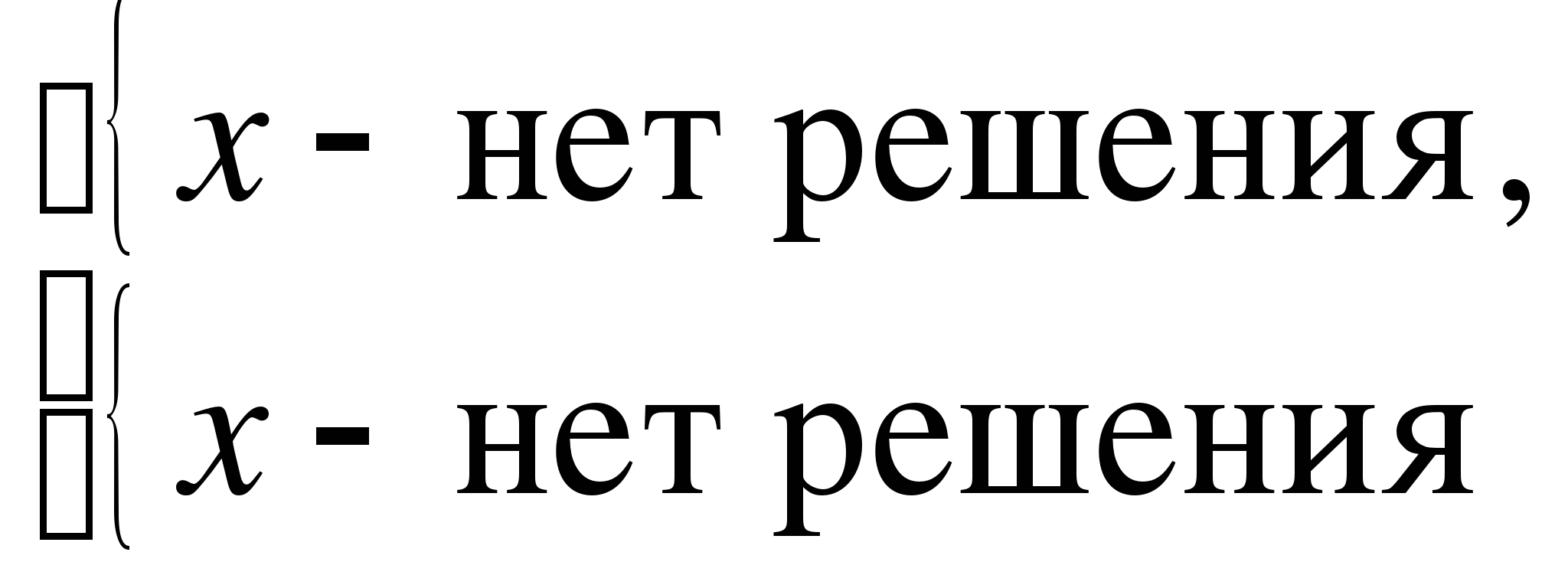
Ответ: нет решения
ІІ способ (возведение обеих частей в квадрат)
Так как правая часть функция, то
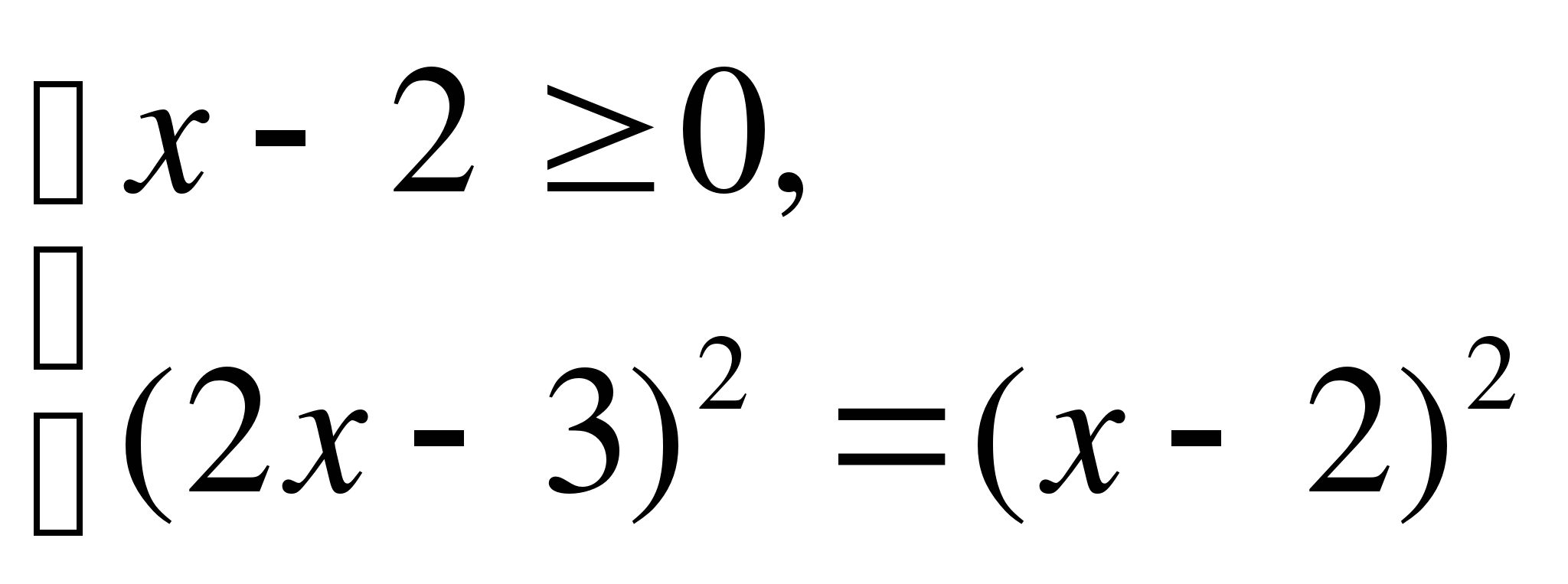
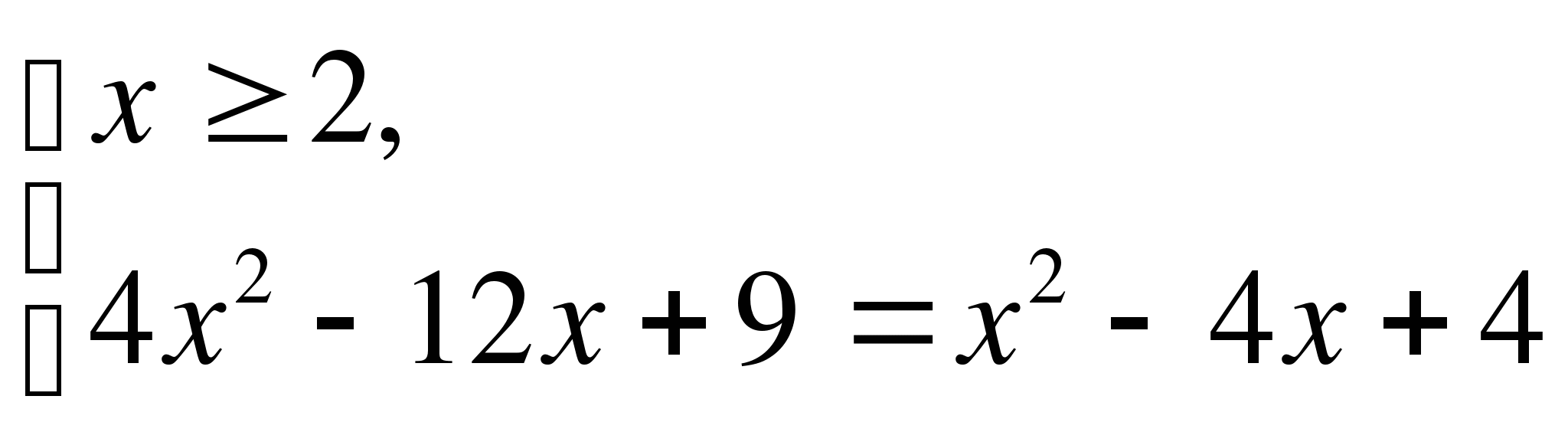
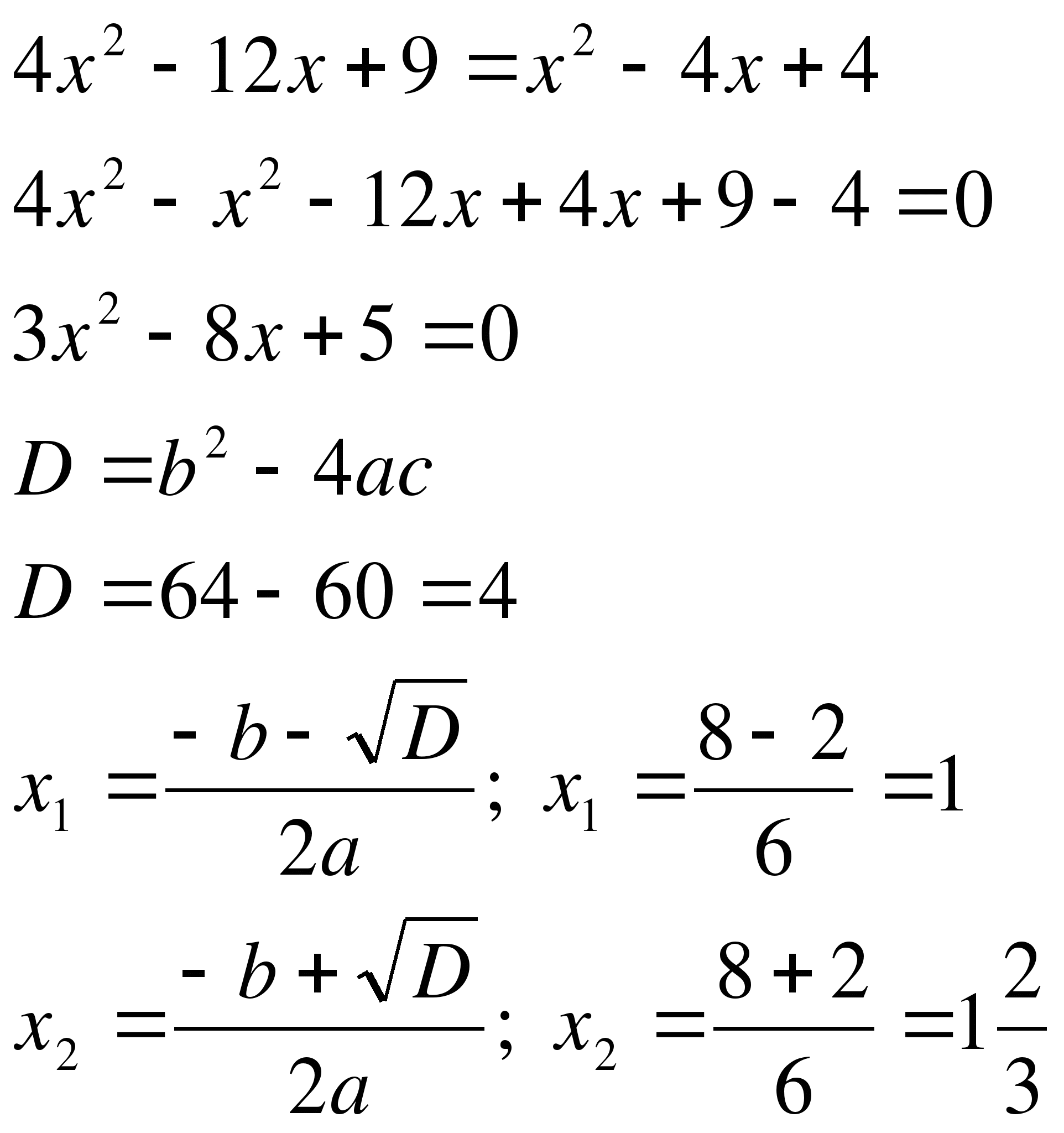
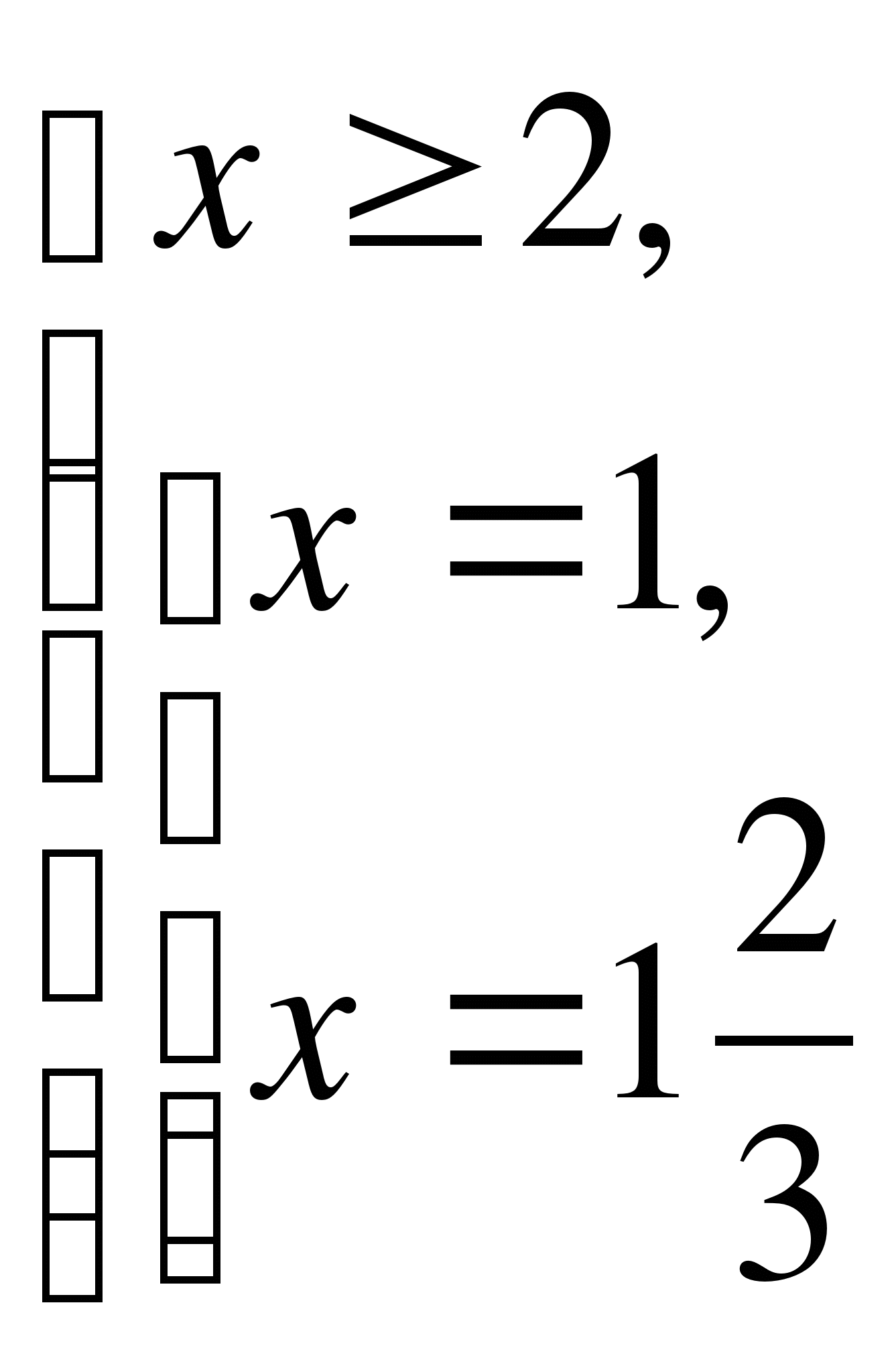 Ответ: нет решения.
Ответ: нет решения.
Пример №3
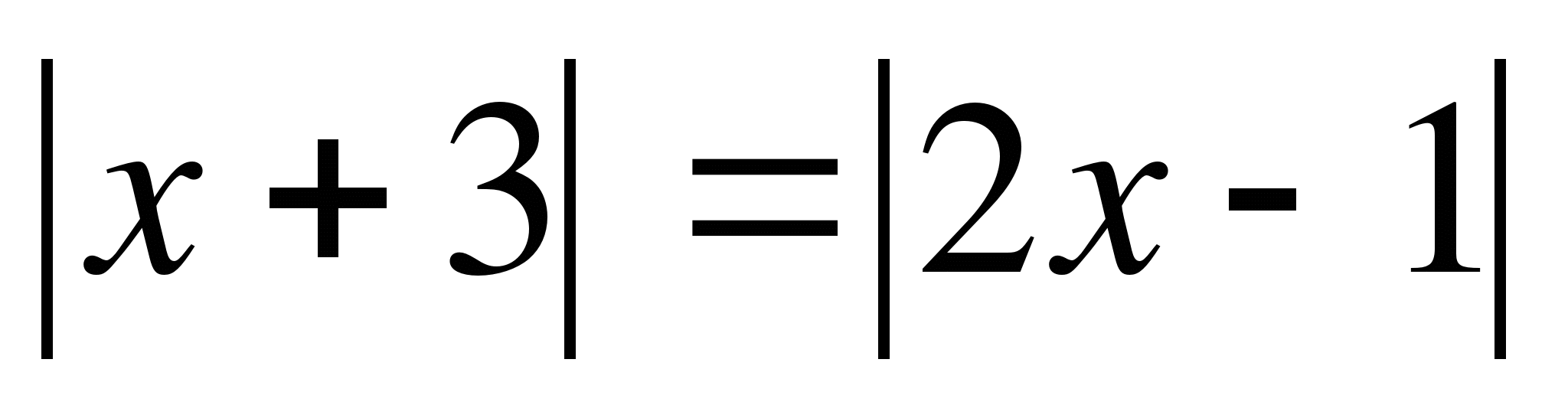
Решение
Воспользуемся методом возведения в квадрат обеих частей.
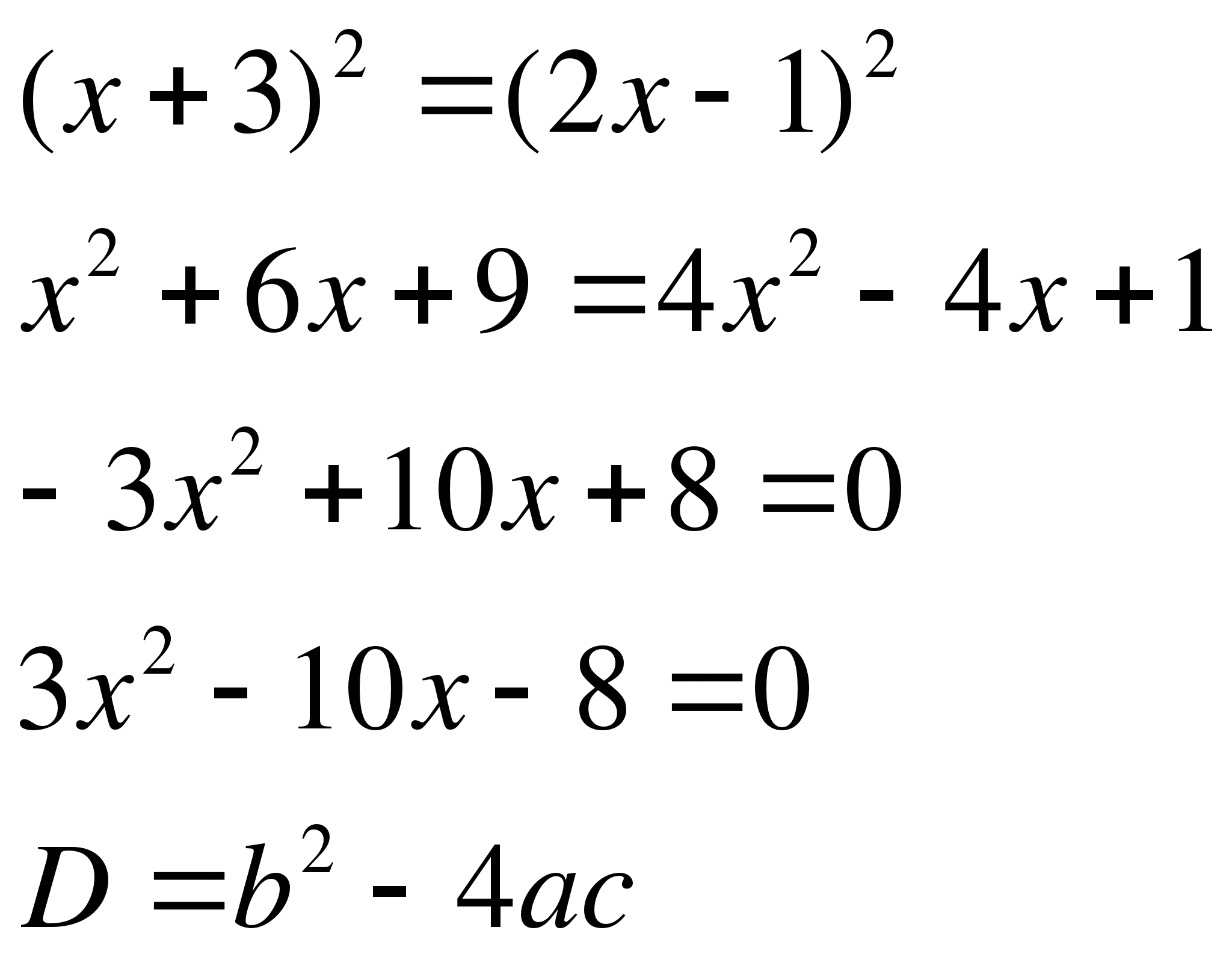
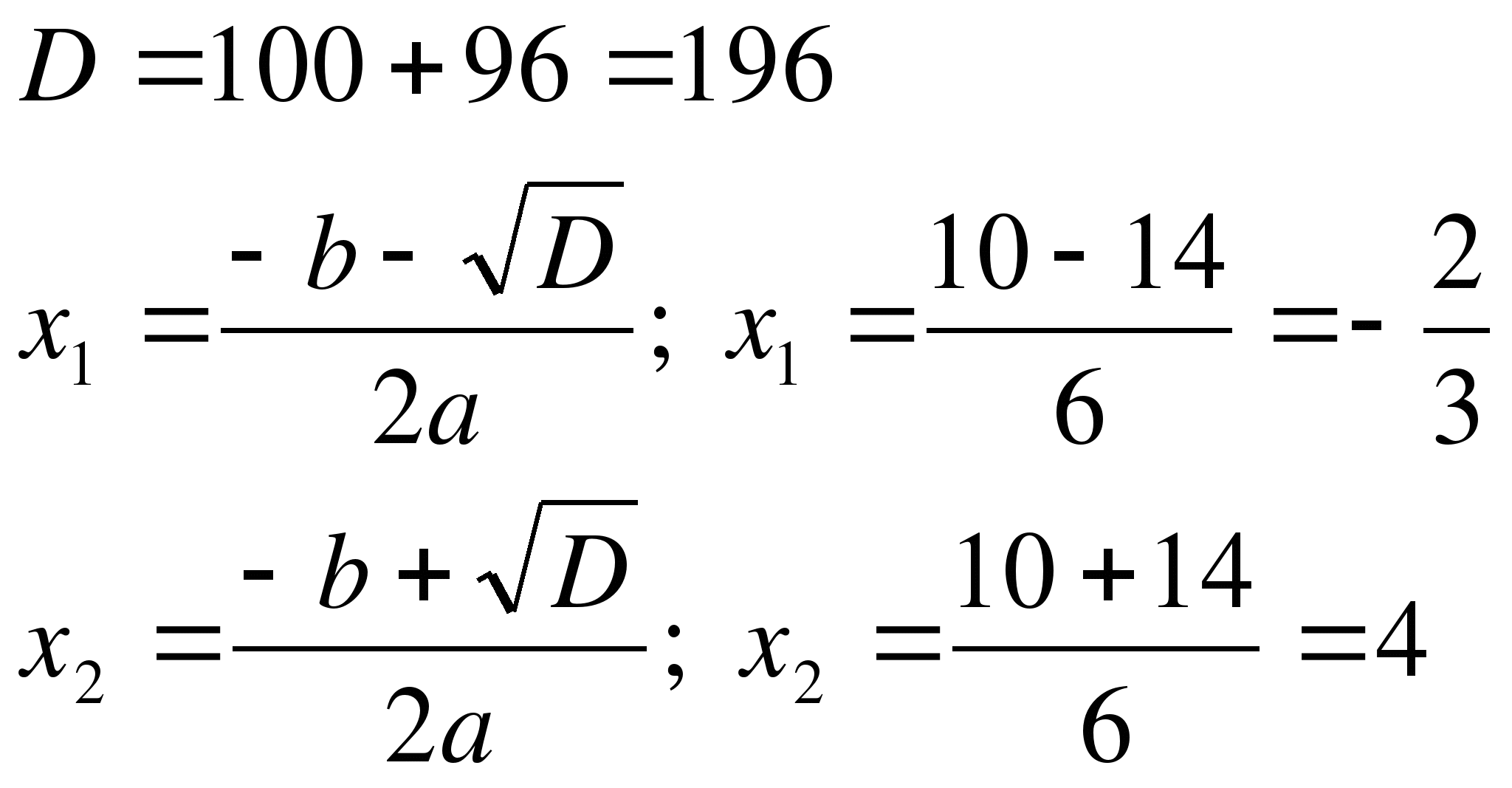
Ответ: 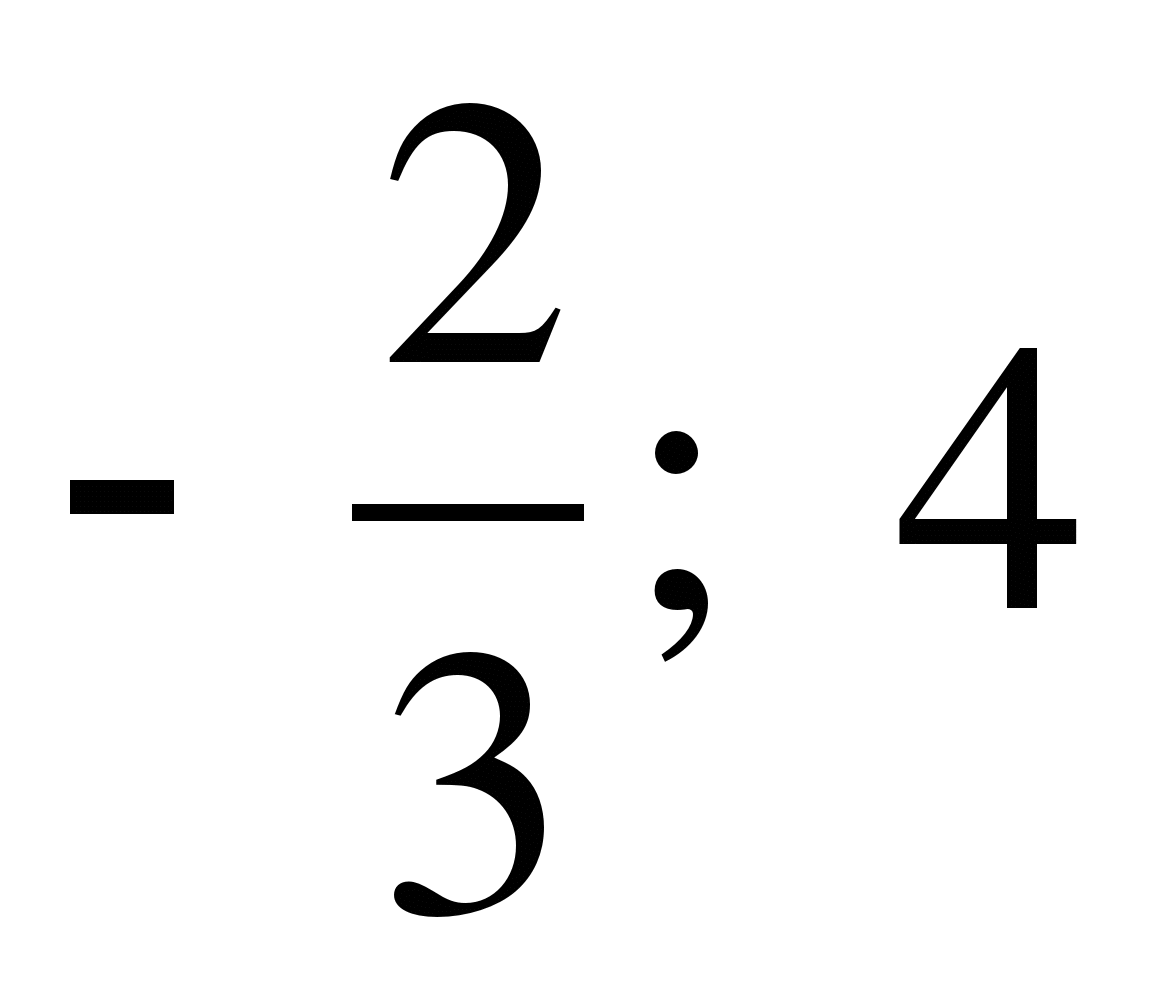
Пример №4
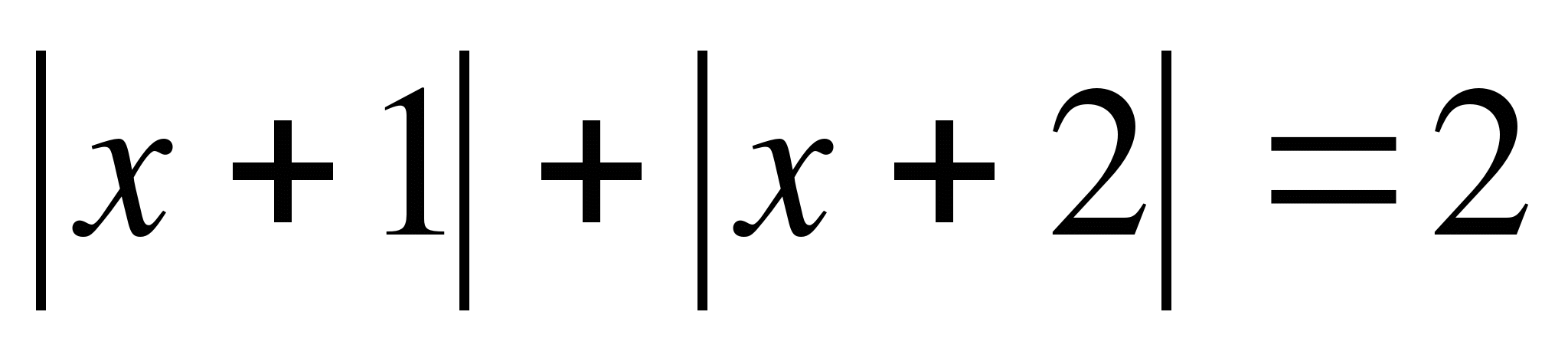
Решение
Используем метод разбиения на промежутки.

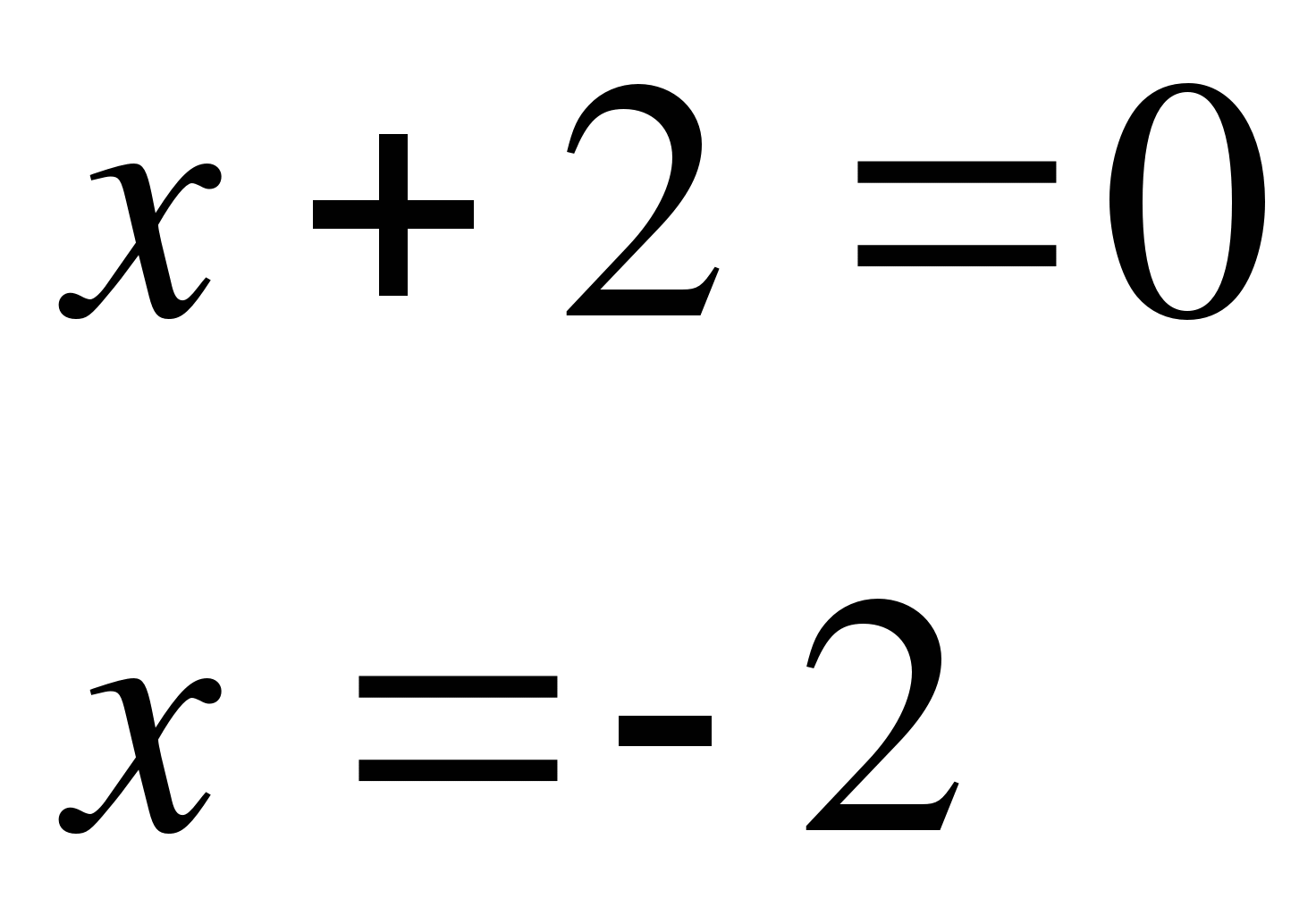


-2 -1
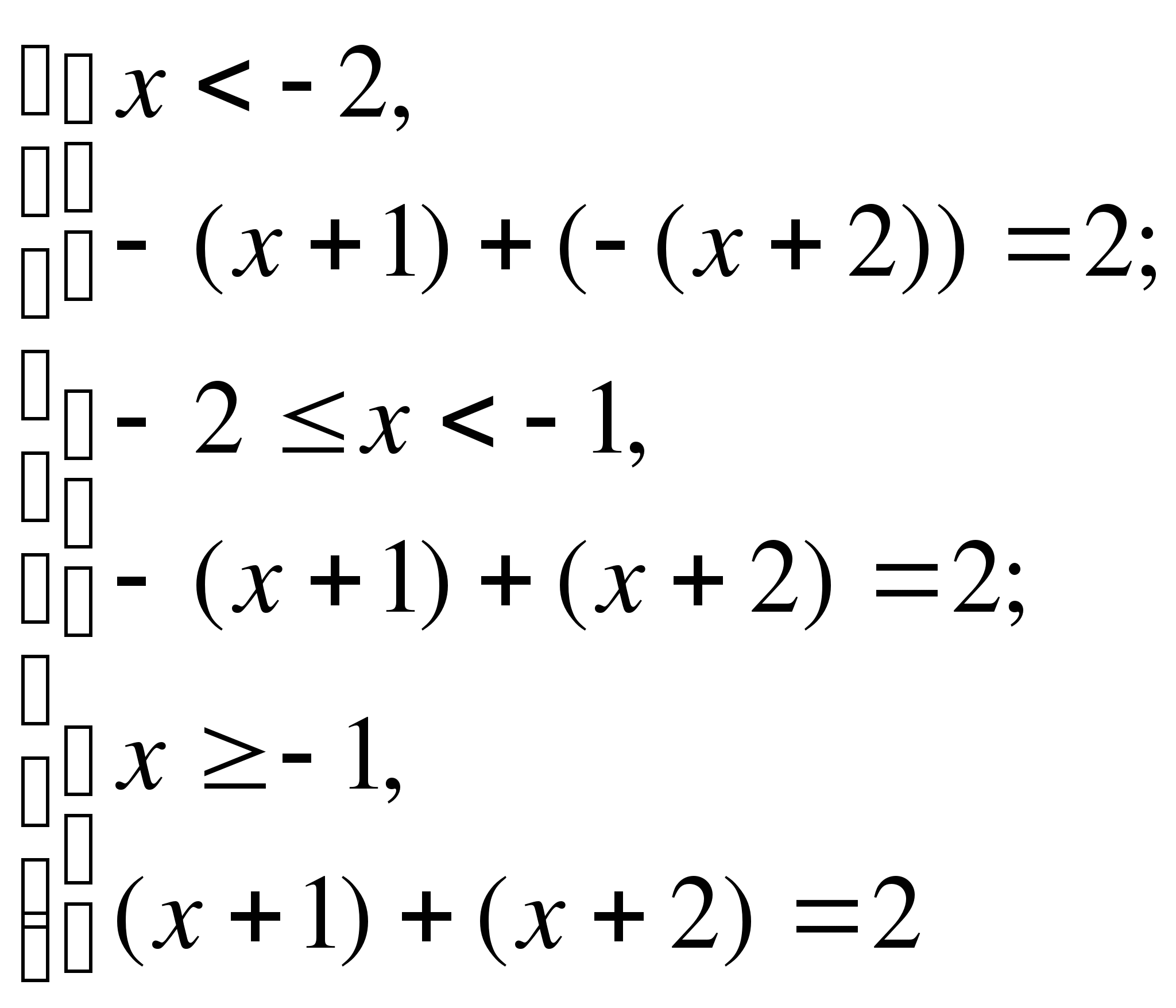
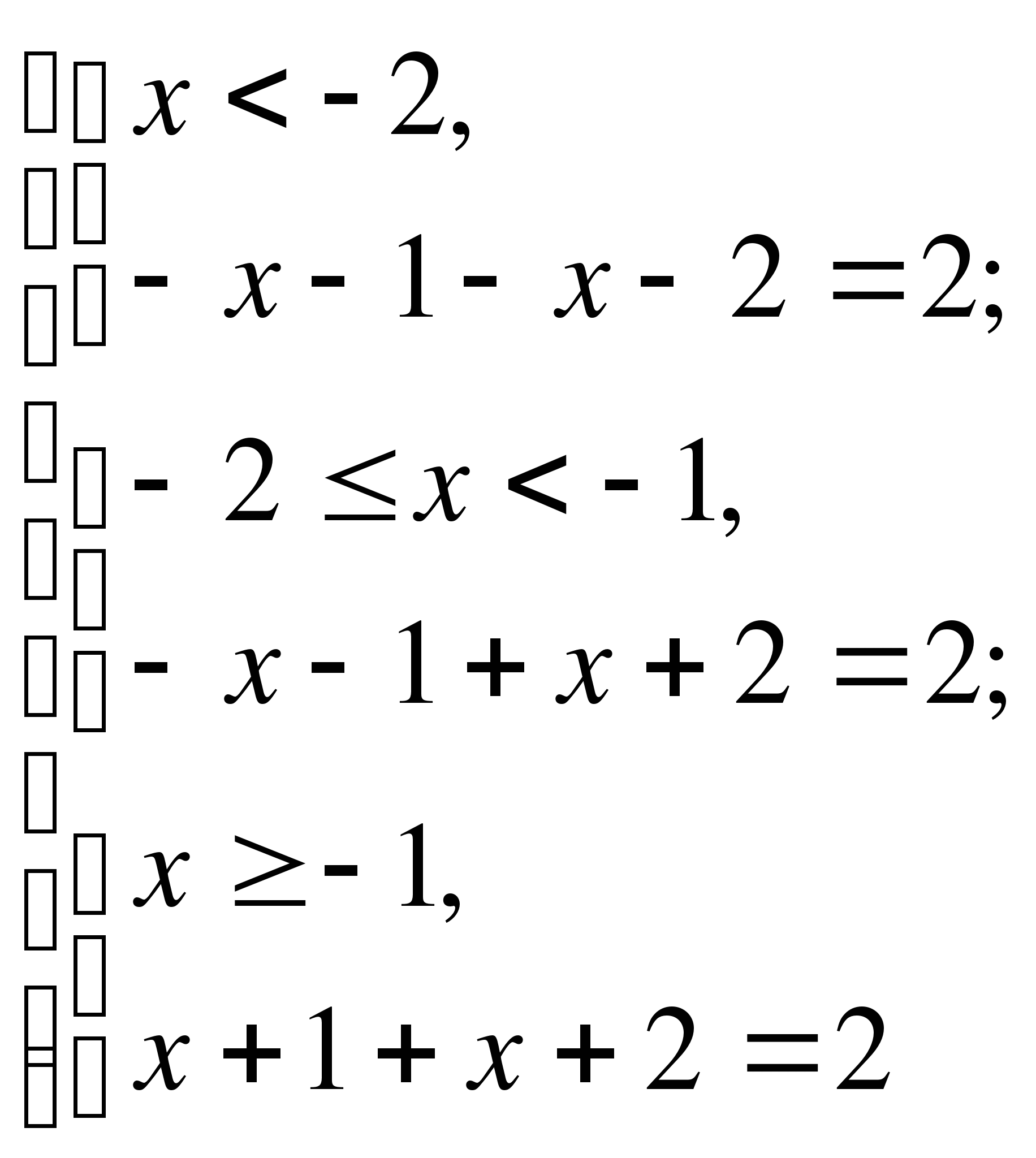
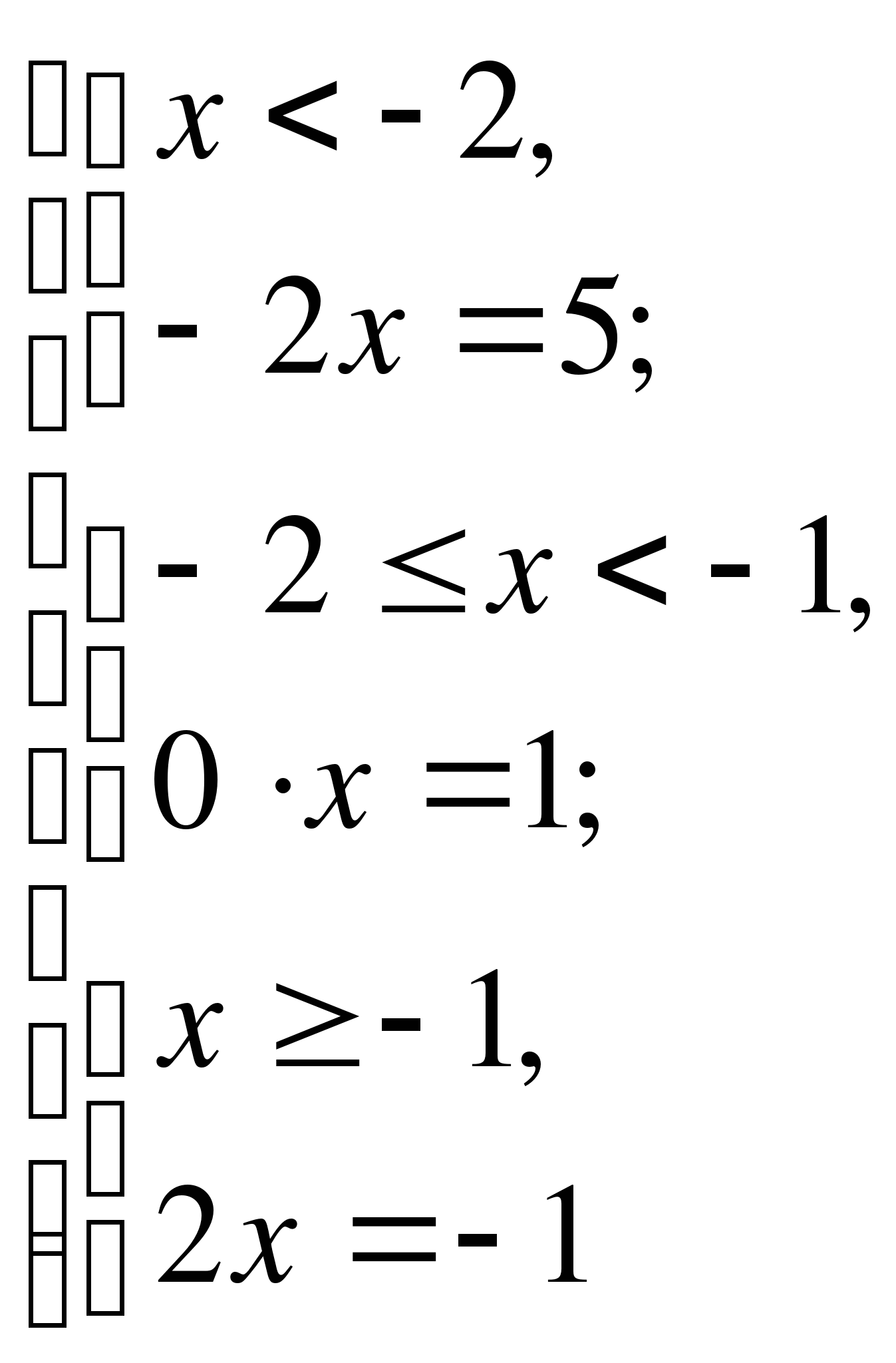
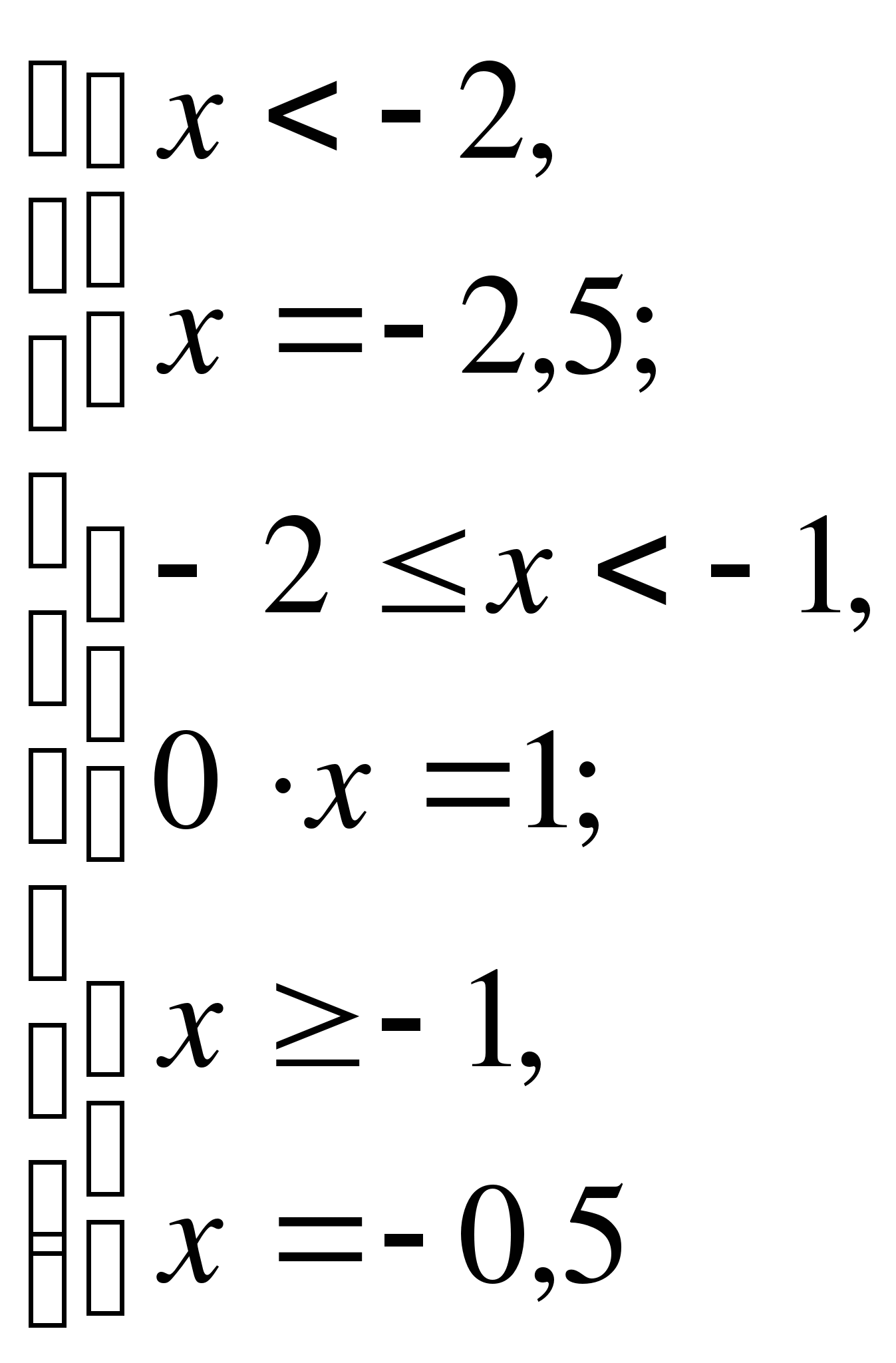
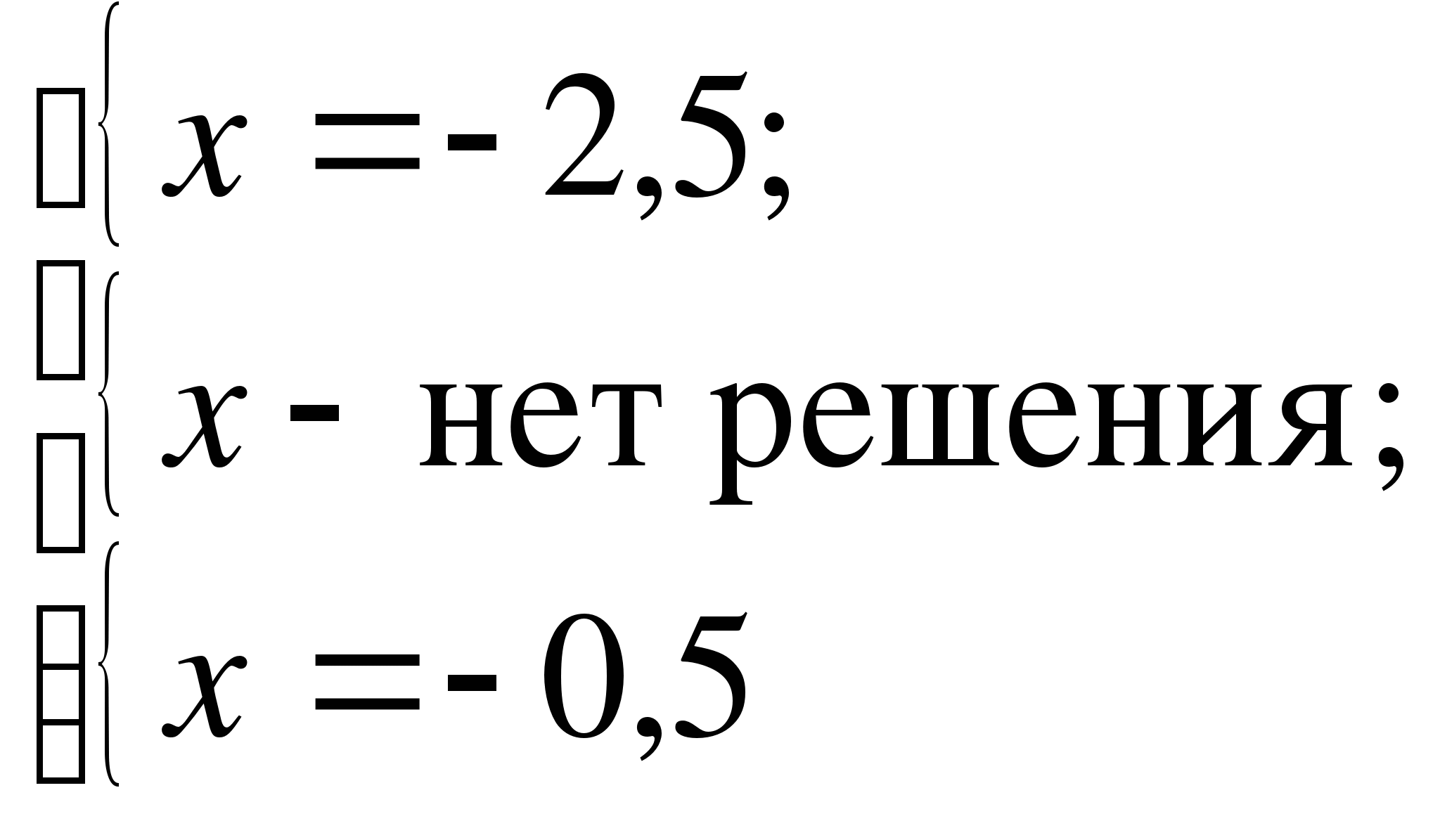
Ответ: -2,5; -0,5.
Пример №5
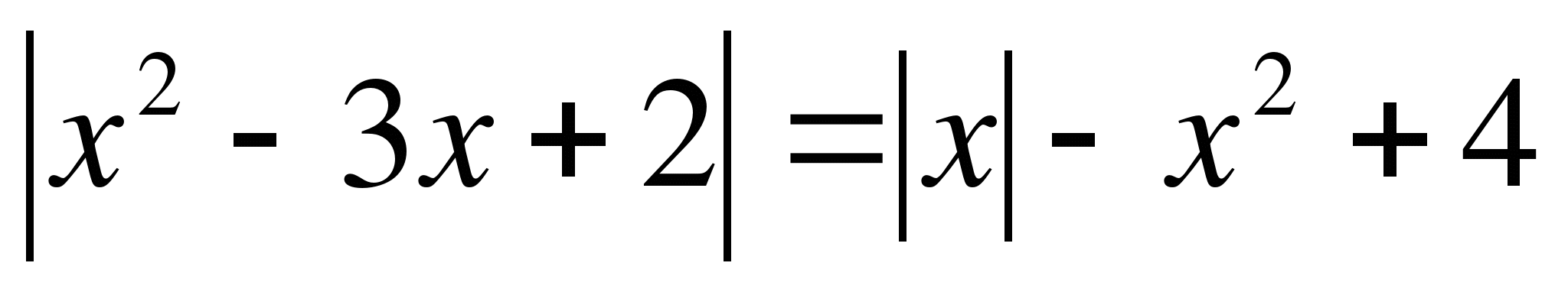
Решение.
Разложим 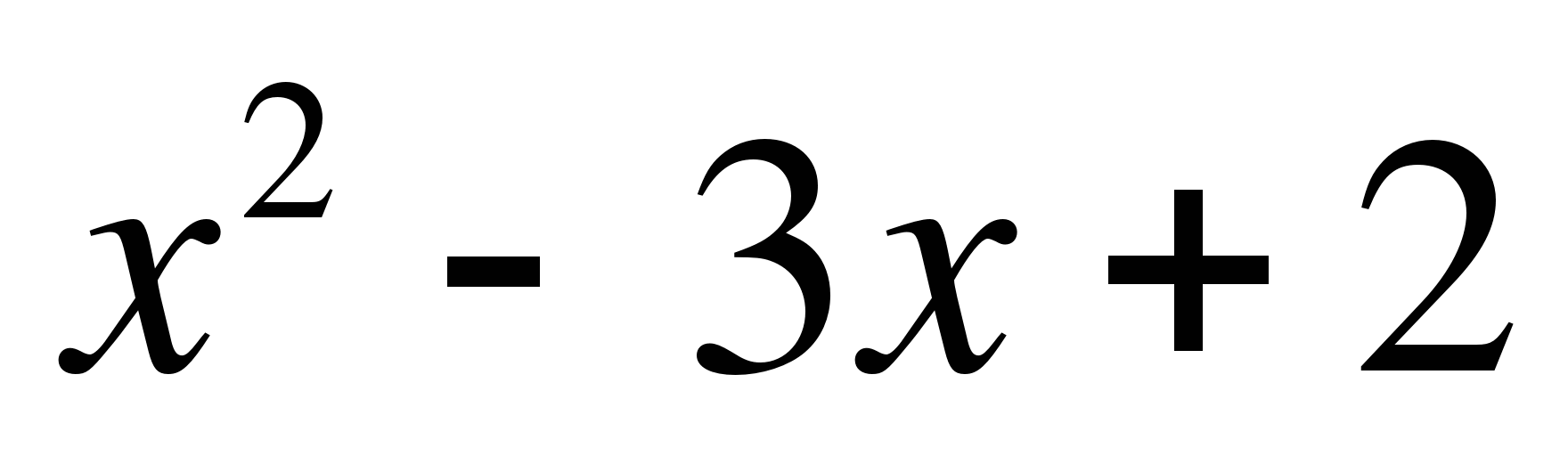 на линейные множители.
на линейные множители.
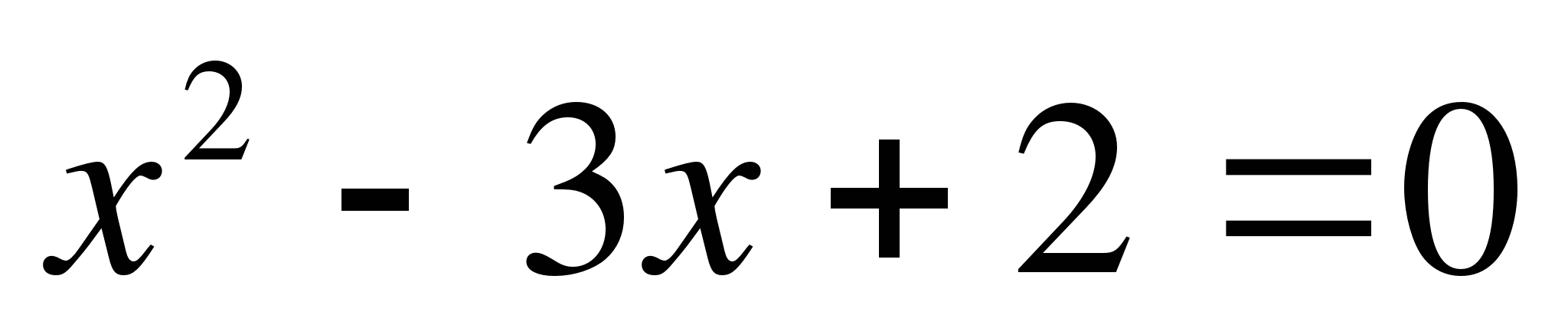
По теореме Виета 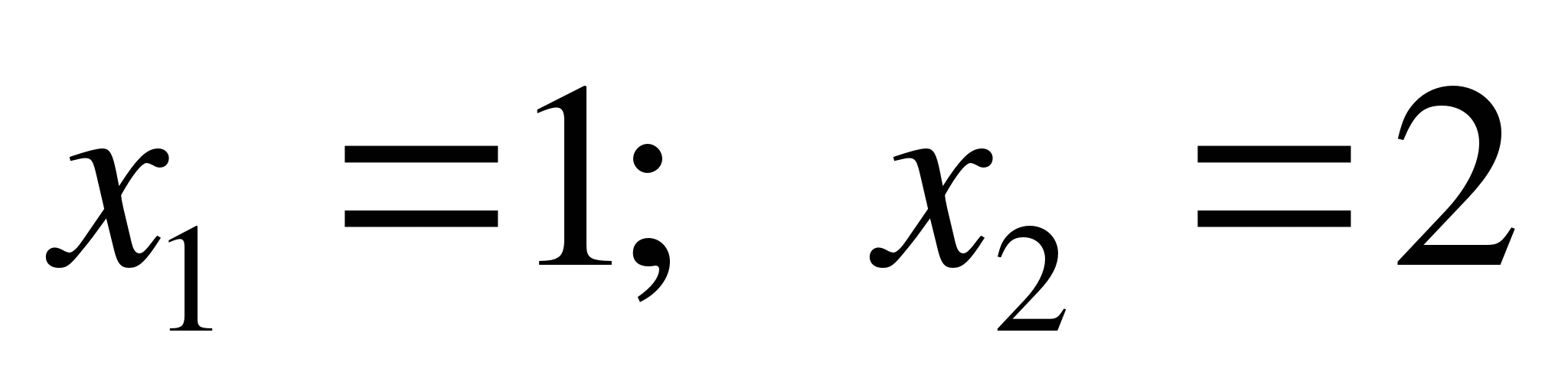
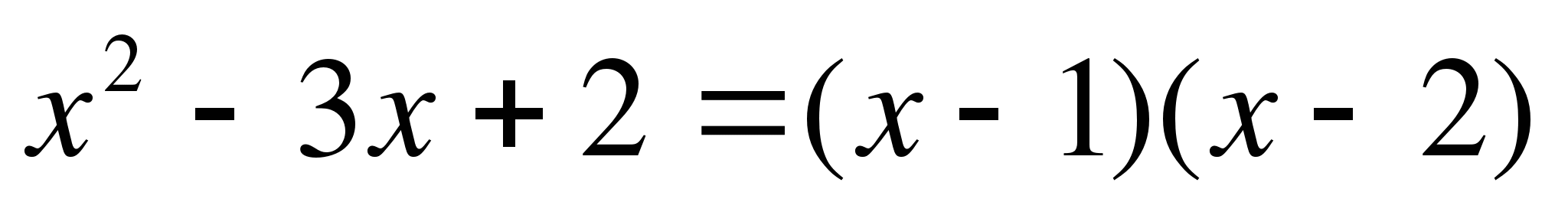
Получили 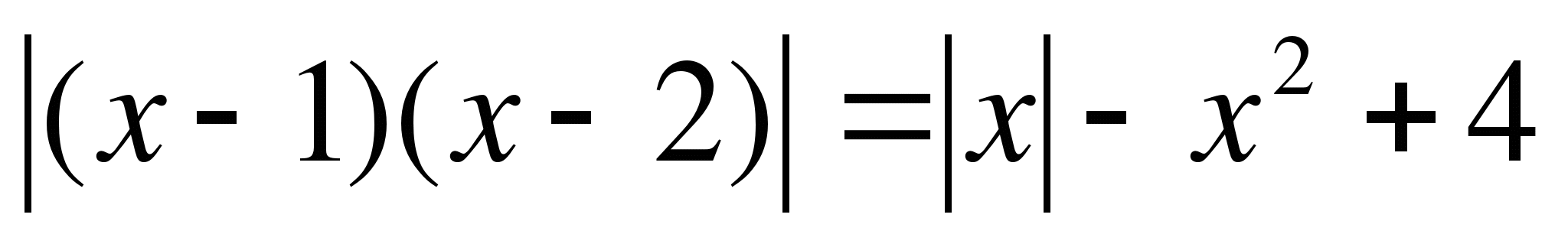
Решим методом разбиения на интервалы



0 1 2
Если  , тогда
, тогда
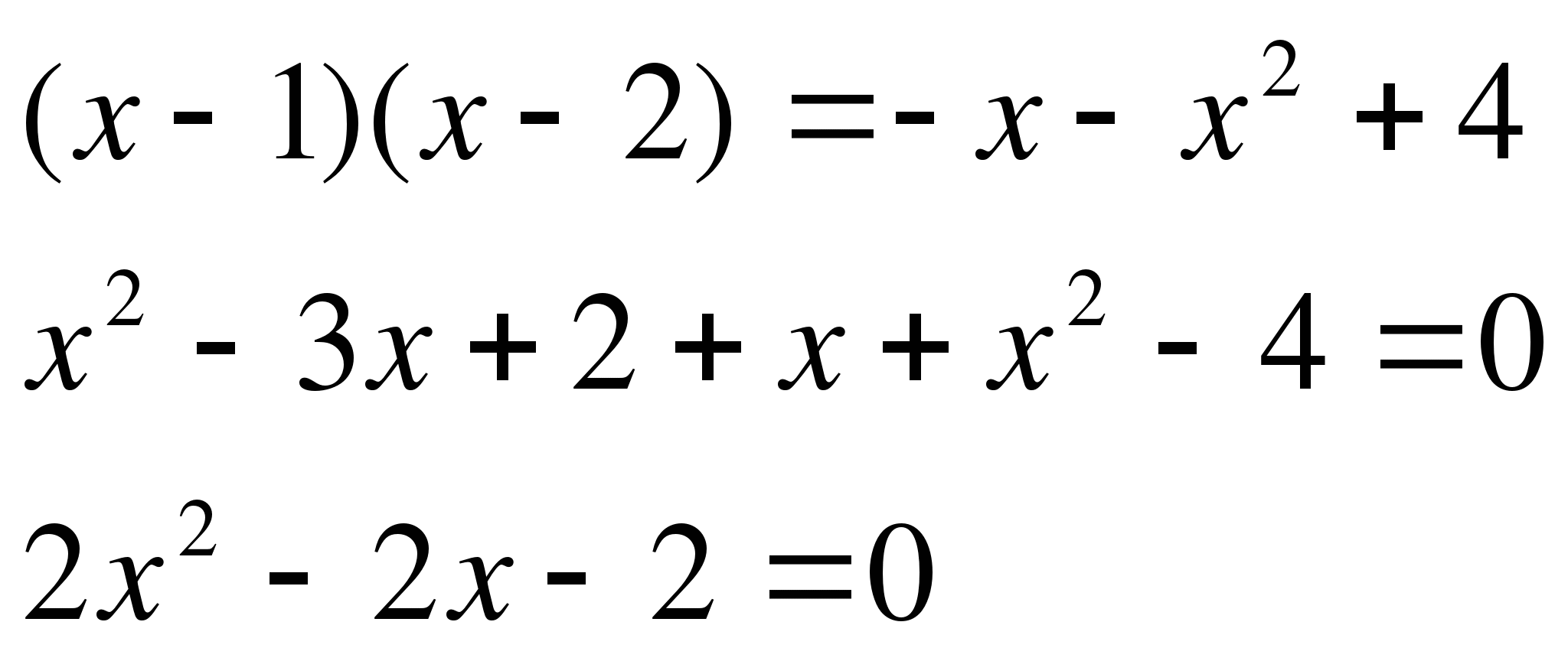
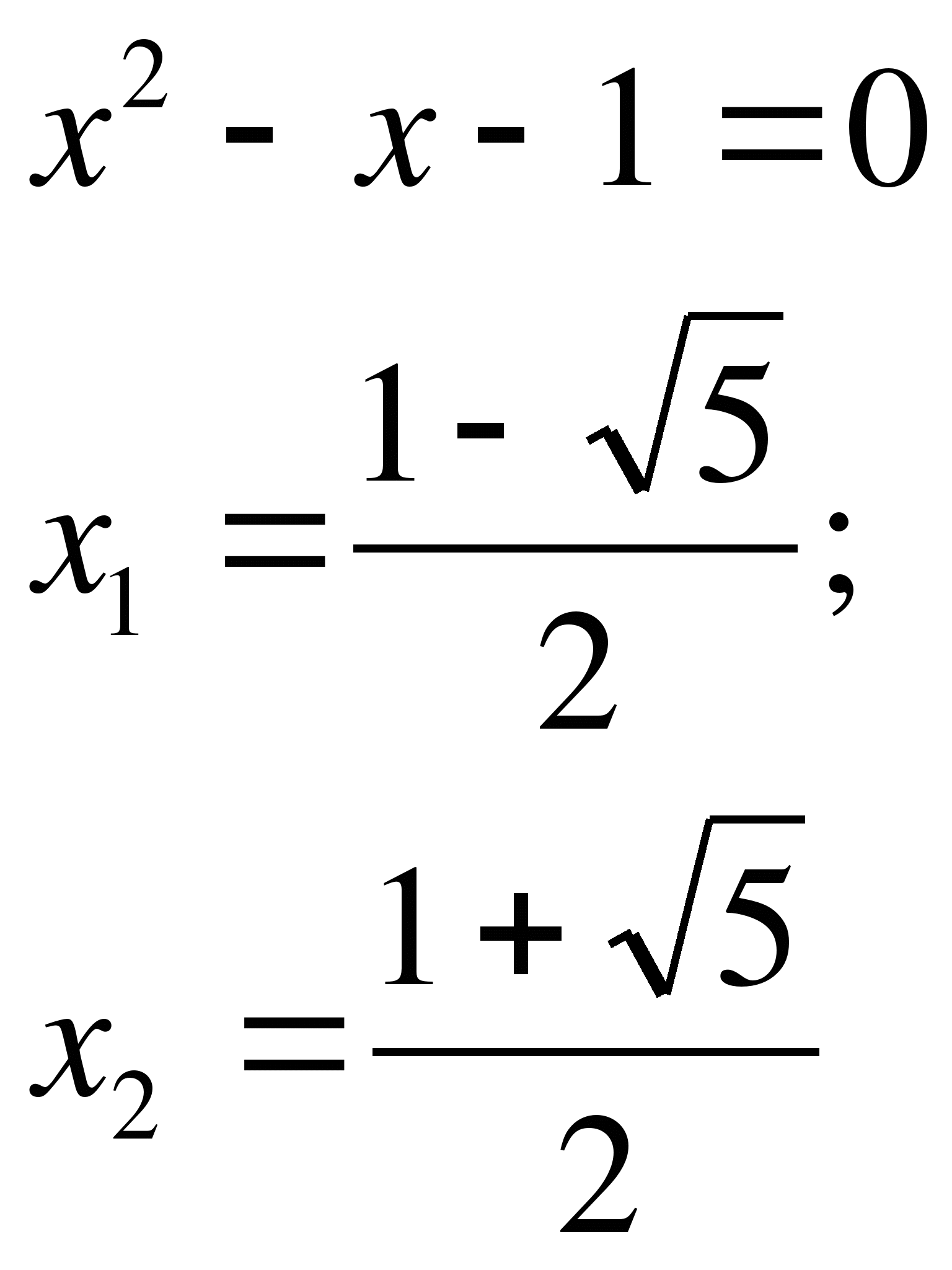
Так как 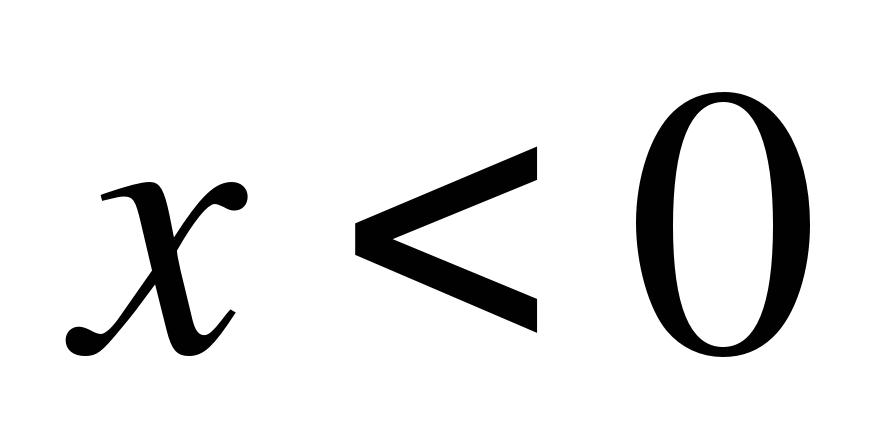 , то на данном промежутке решением является
, то на данном промежутке решением является 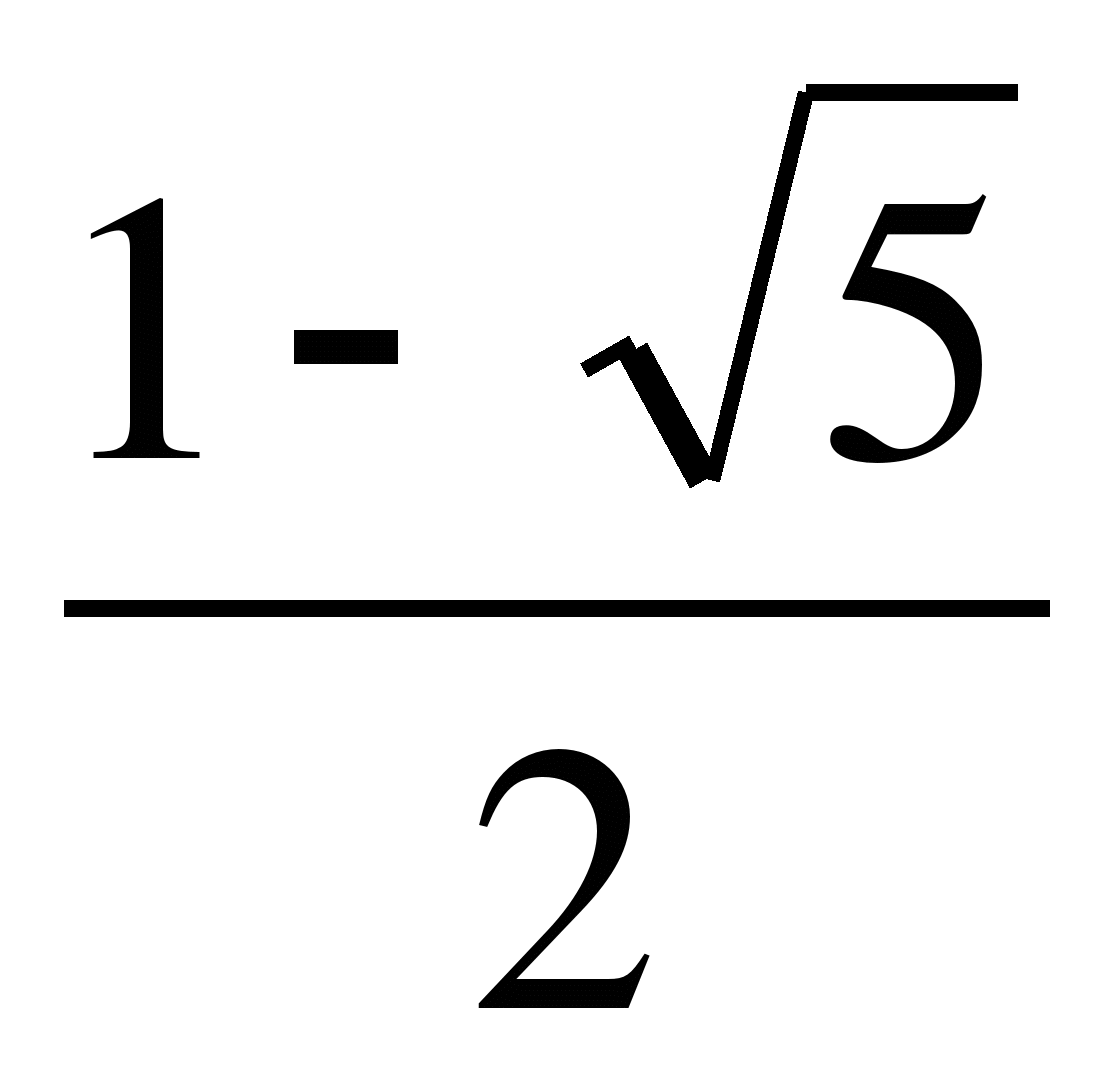 .
.
Если 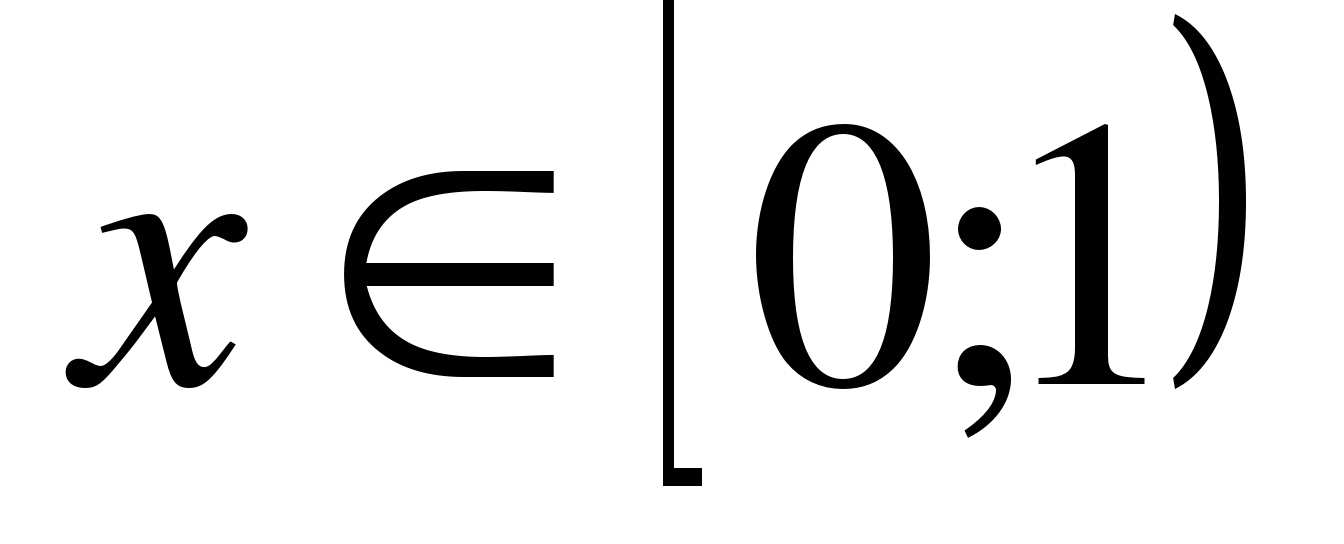 , тогда
, тогда
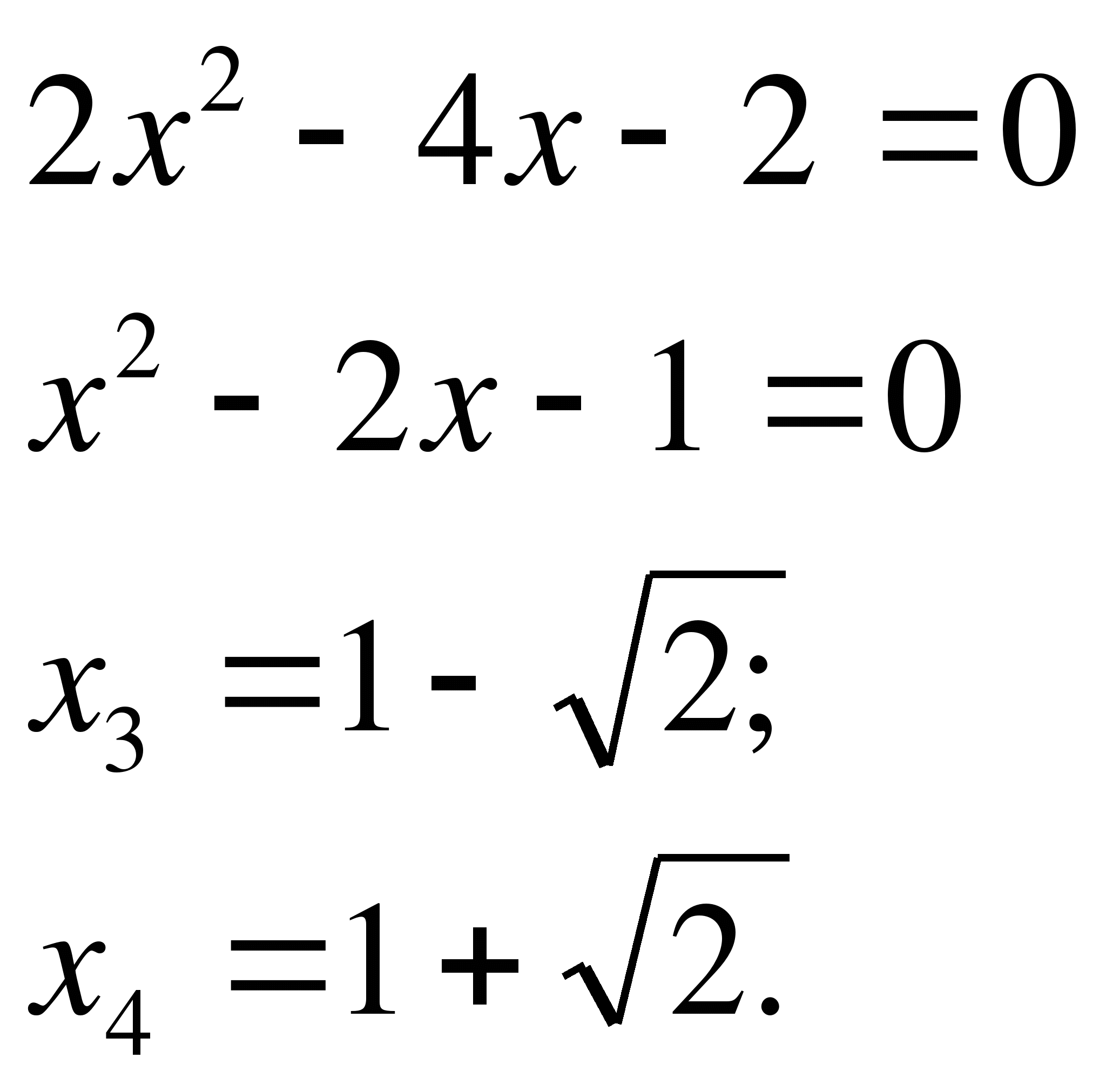
Так как 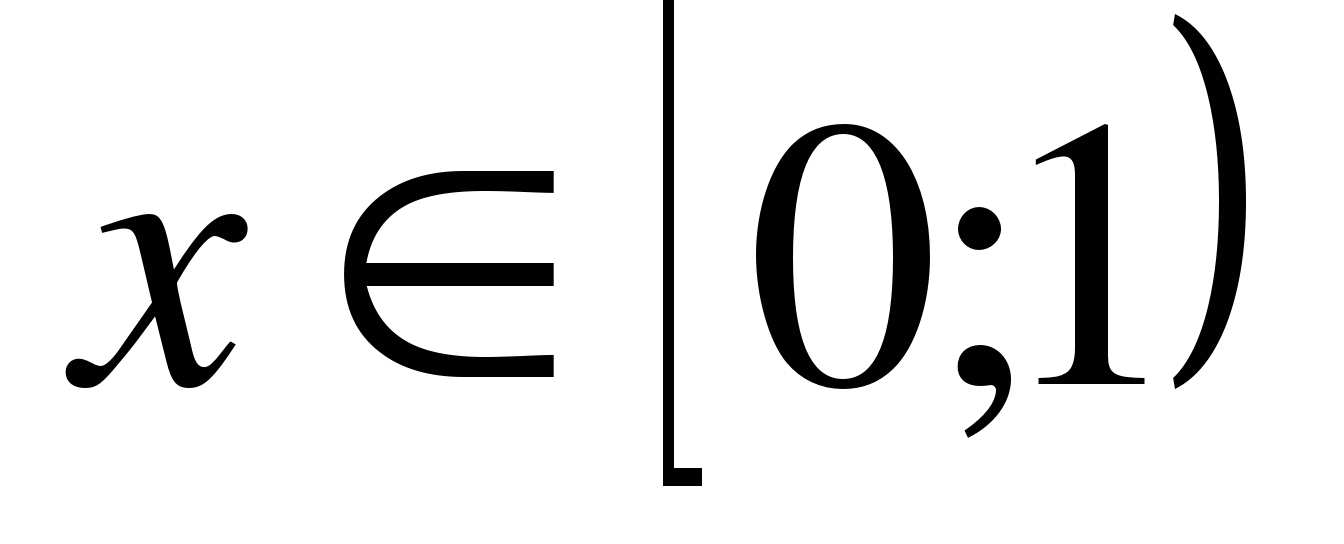 , то на данном промежутке нет решения.
, то на данном промежутке нет решения.
Если 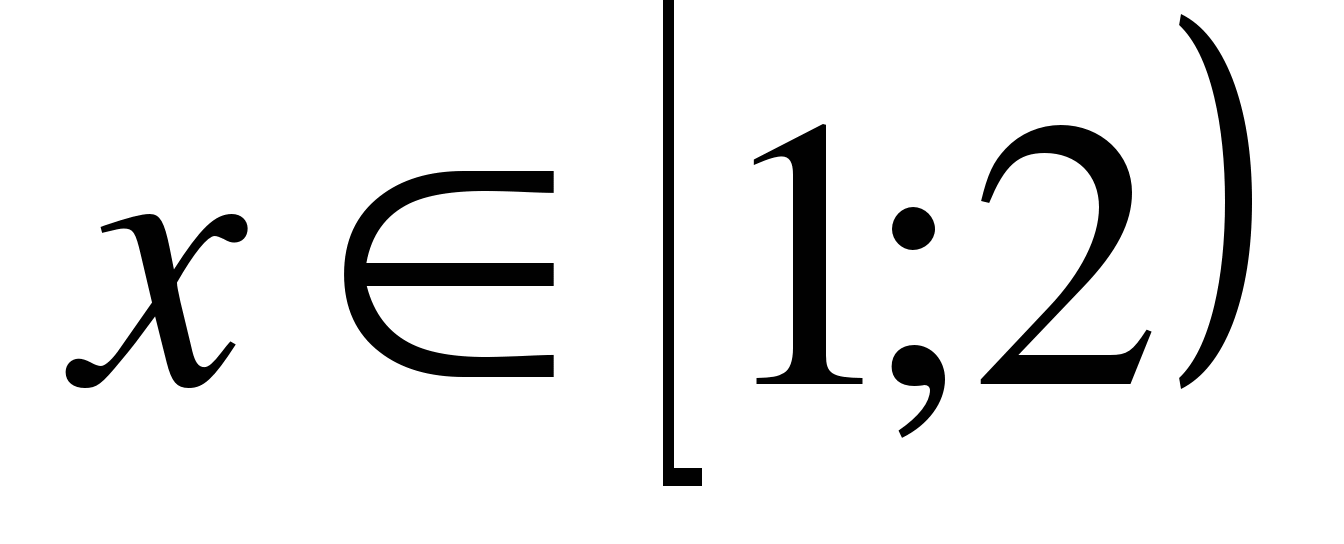 , тогда
, тогда
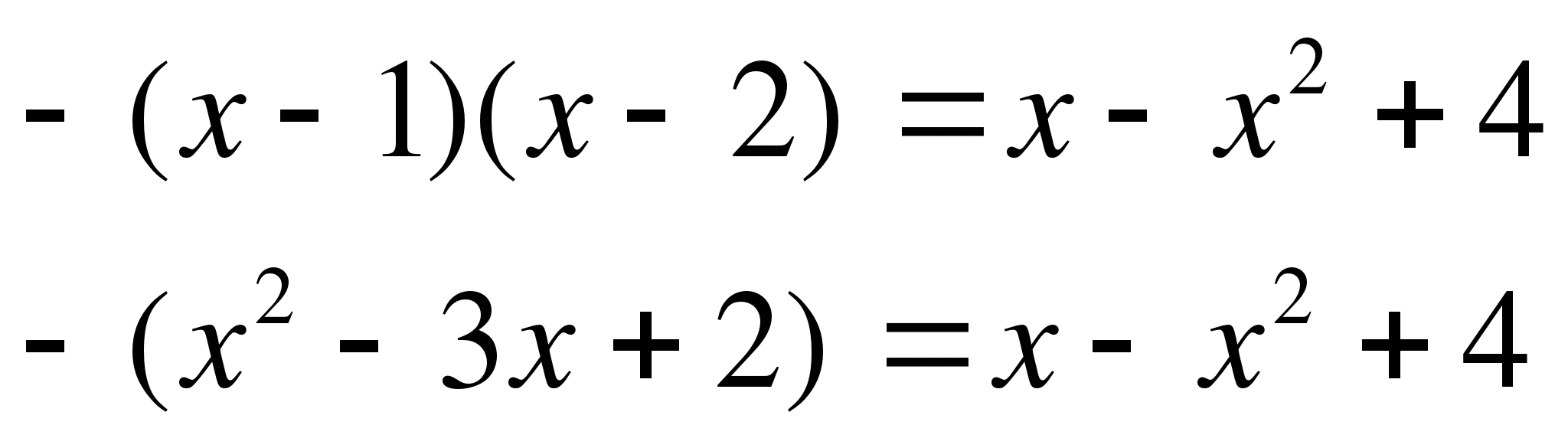
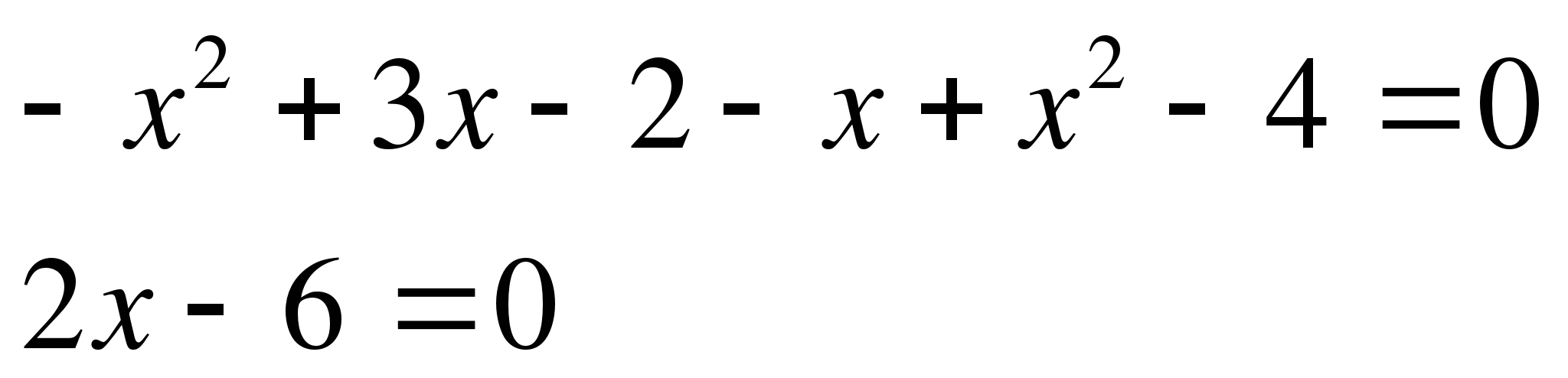

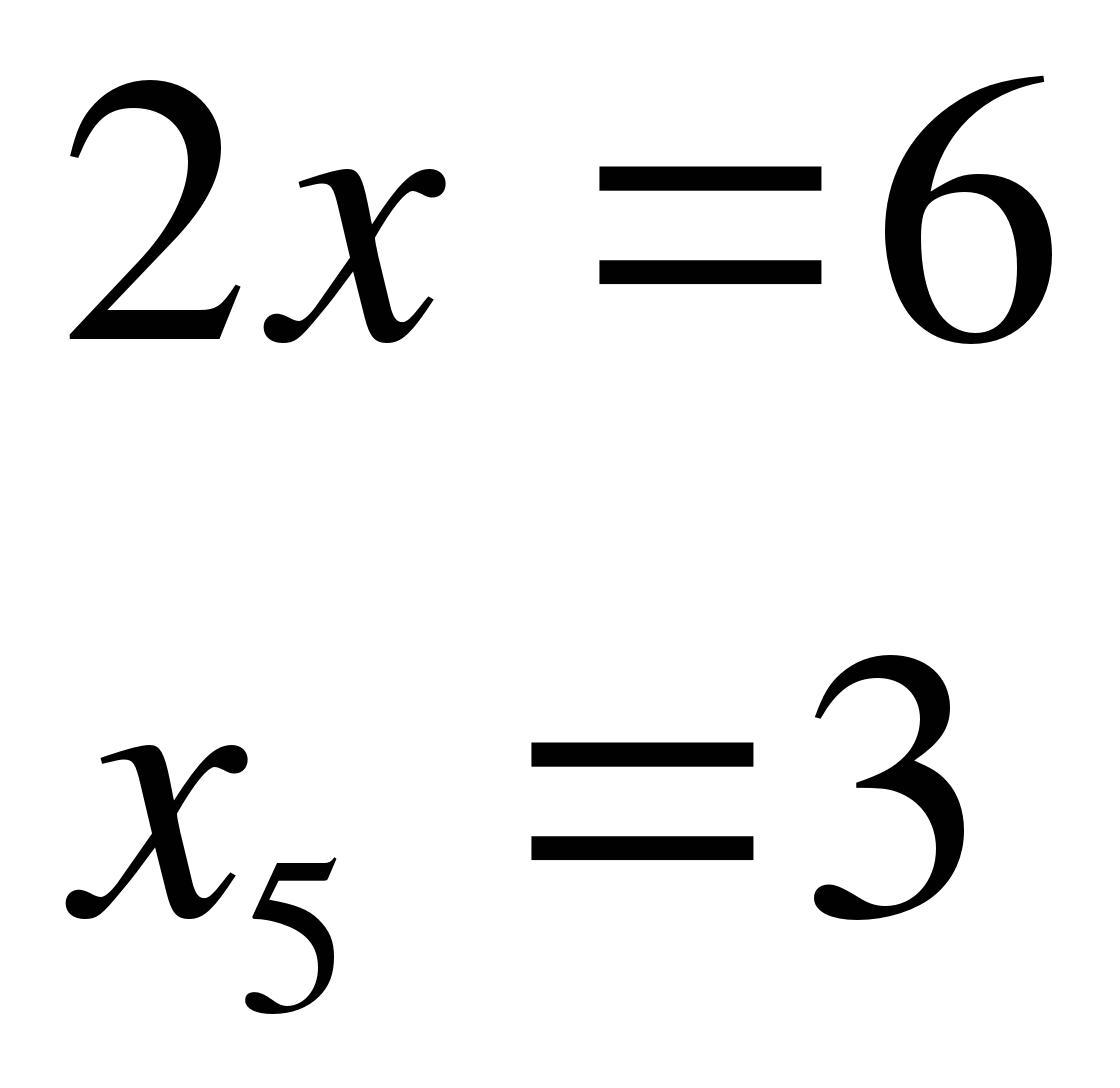
Так как 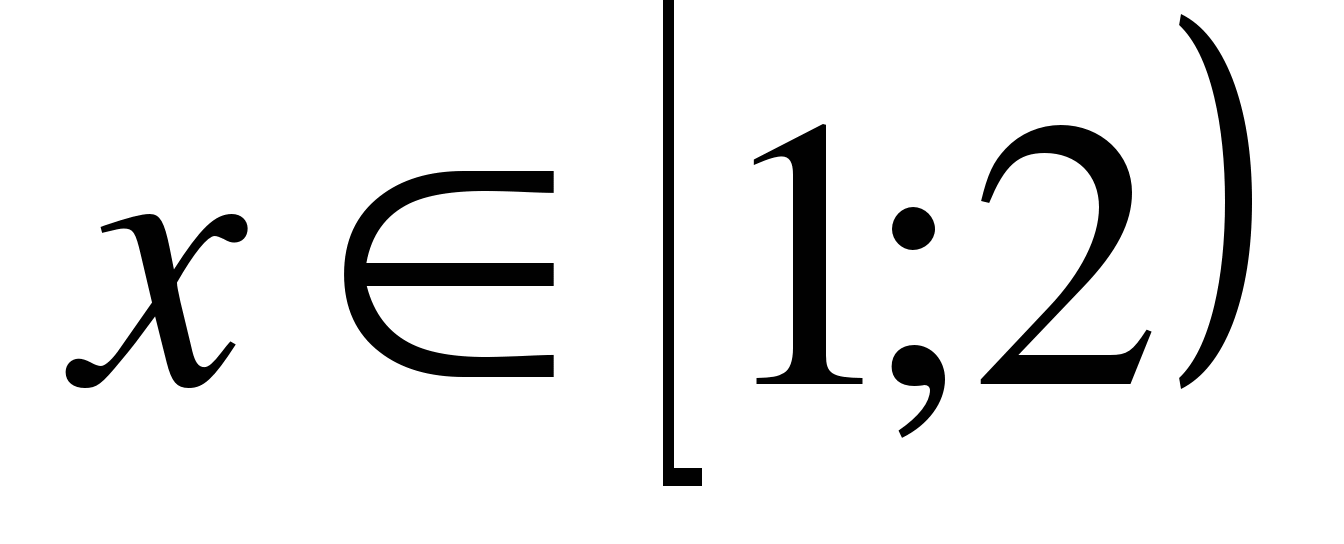 , то на данном промежутке нет решения.
, то на данном промежутке нет решения.
Если  , тогда
, тогда
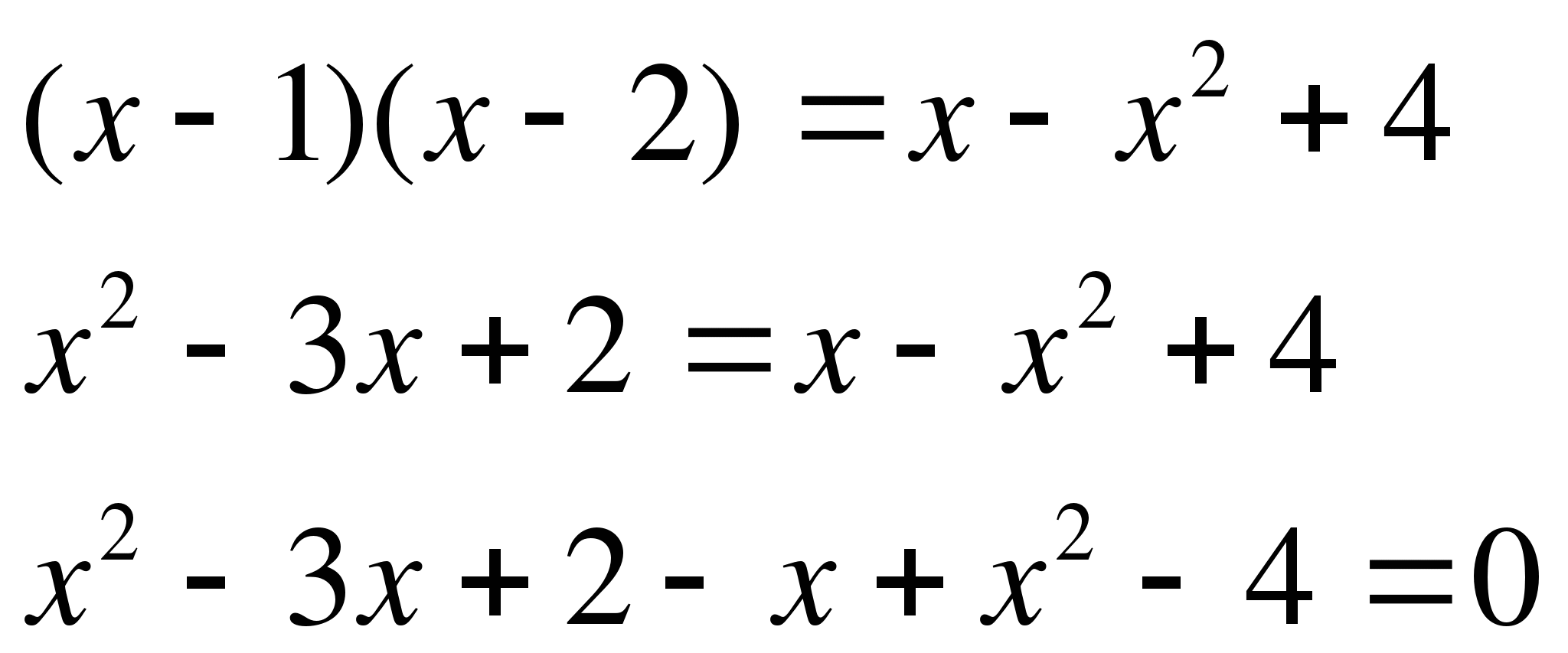
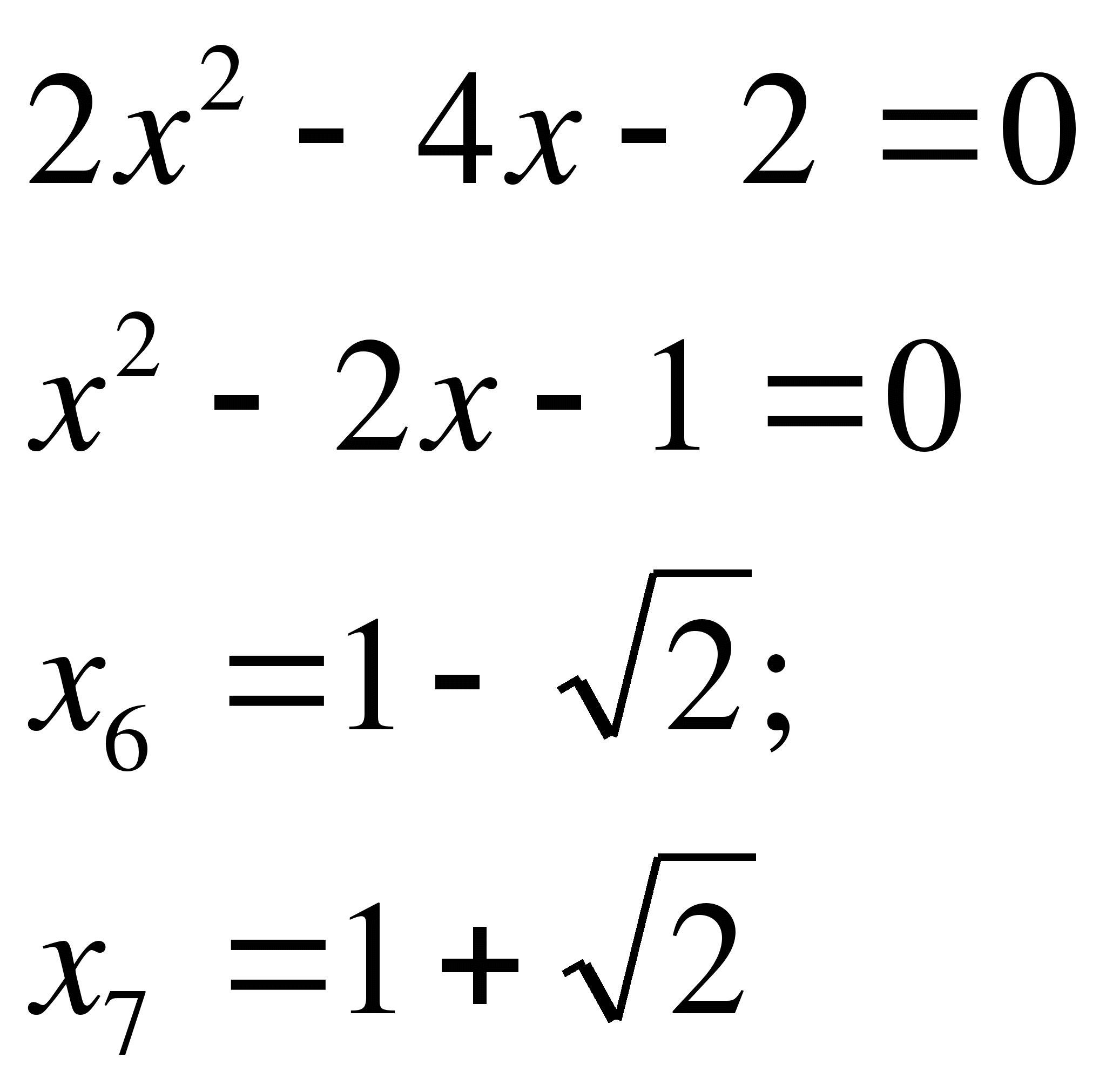
Так как  , то на данном промежутке решением является
, то на данном промежутке решением является 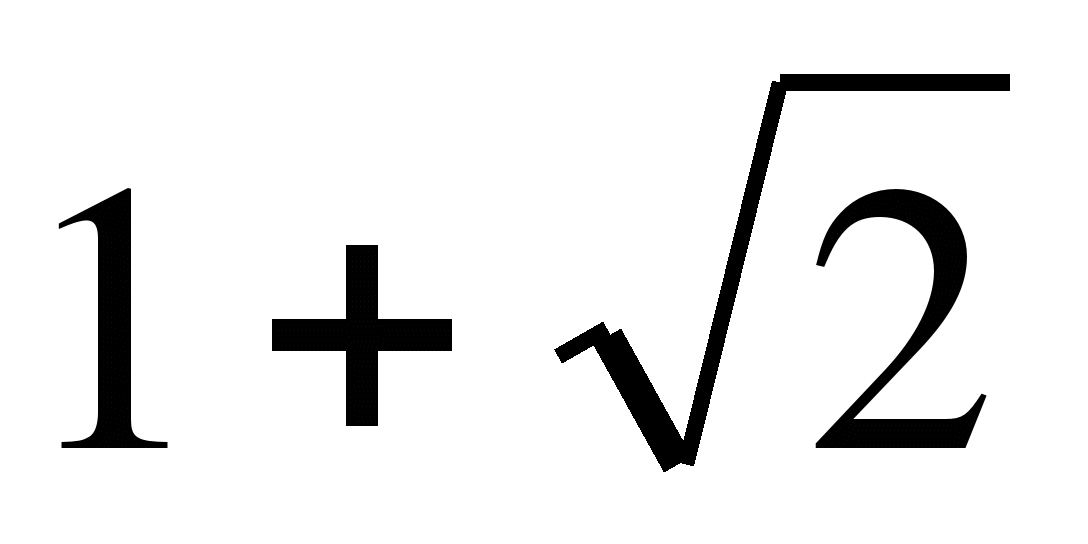 .
.
Ответ: 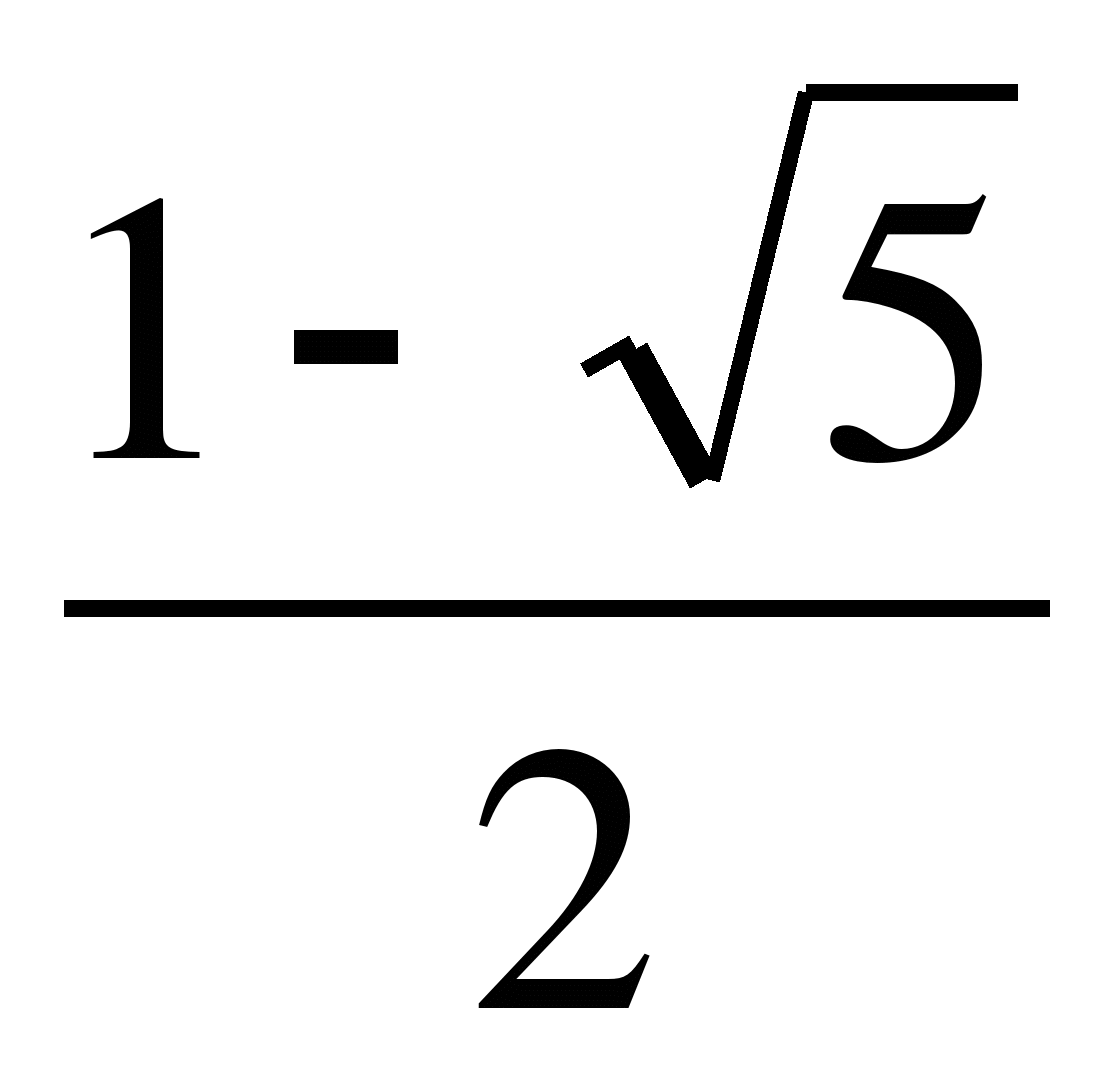 ;
; 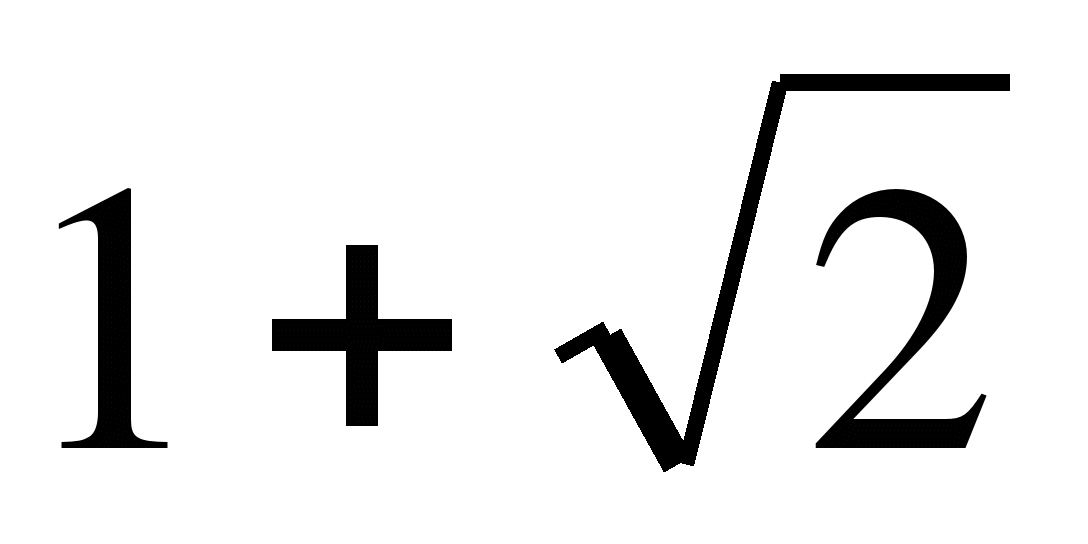 .
.
РЕШИ САМОСТОЯТЕЛЬНО.
1. 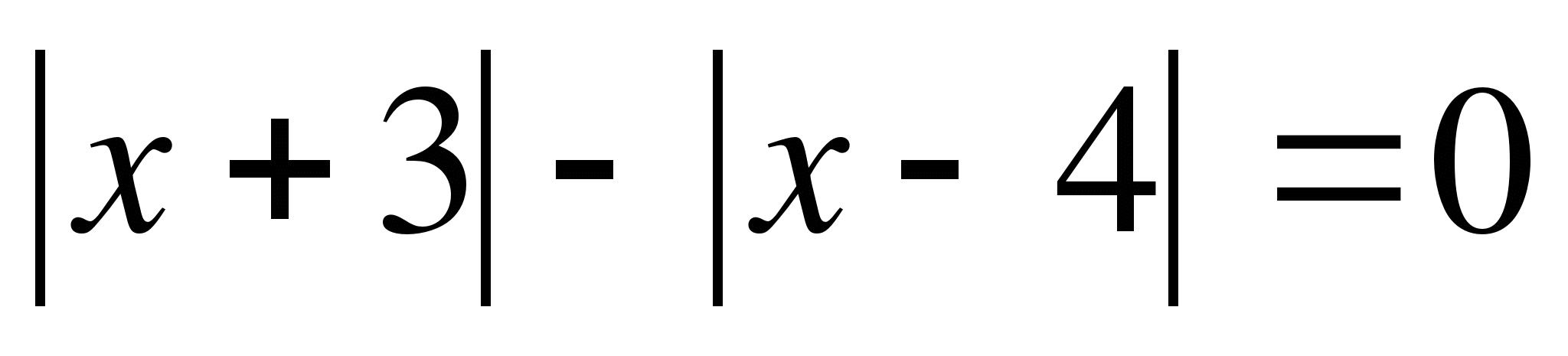
2. 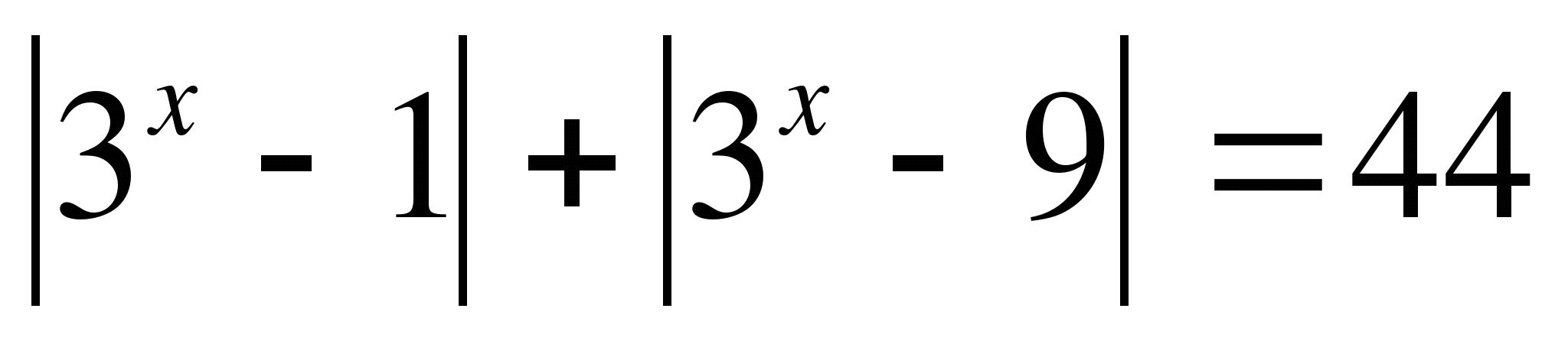
3. 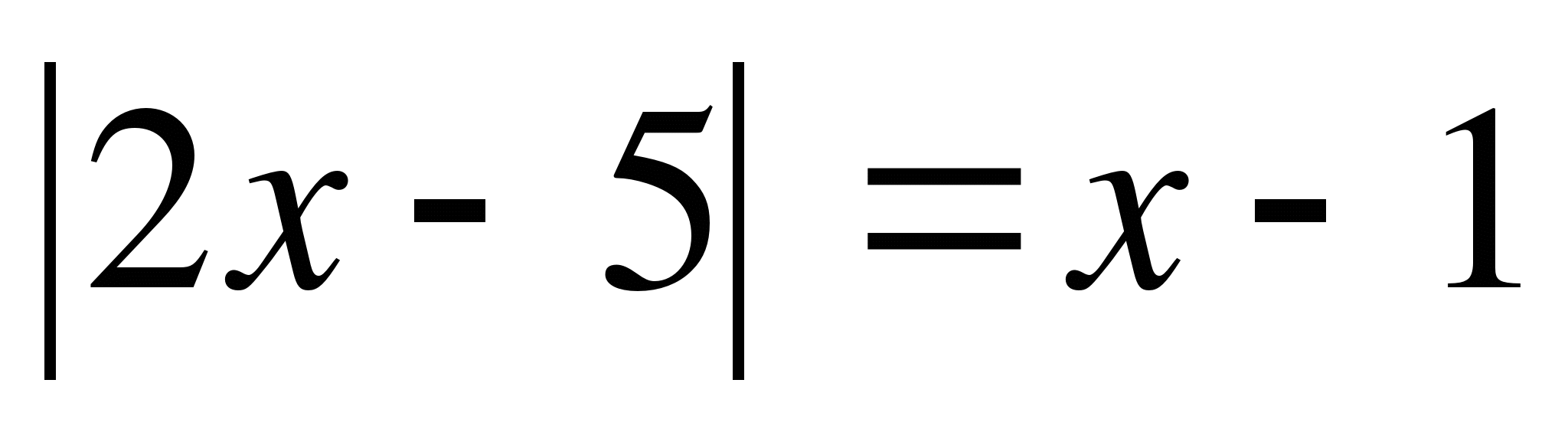
4. 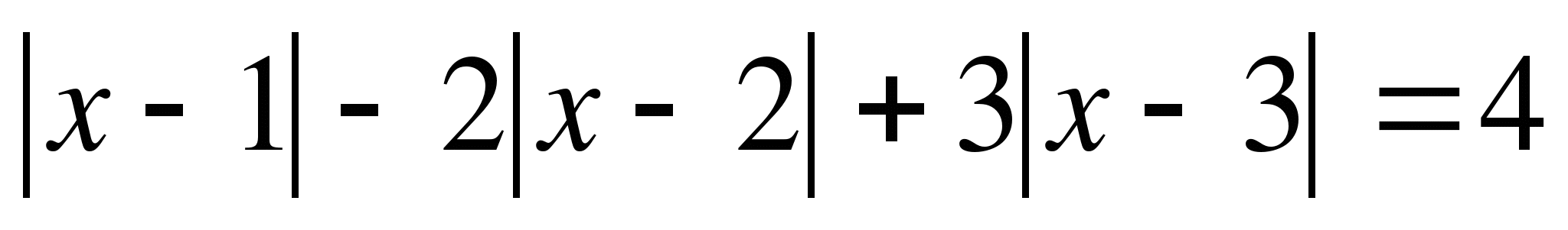
5. 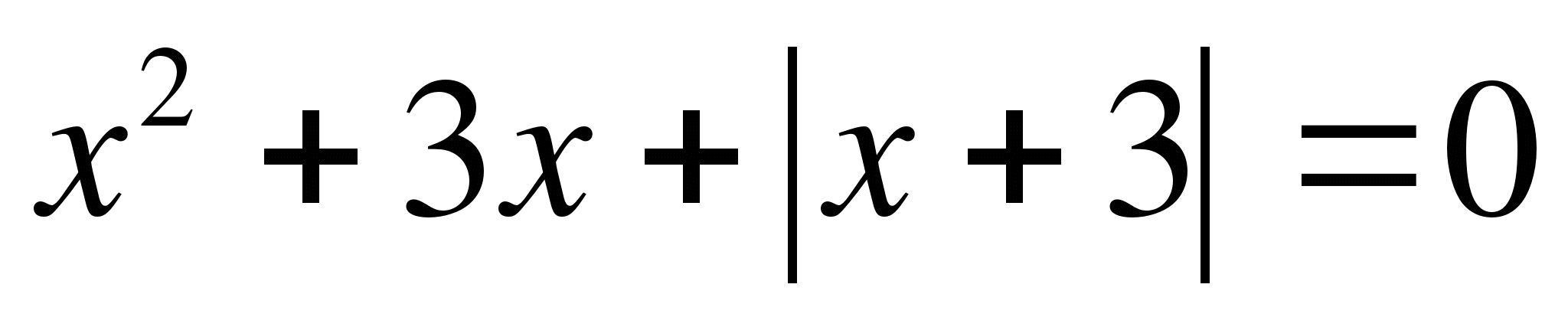
6. 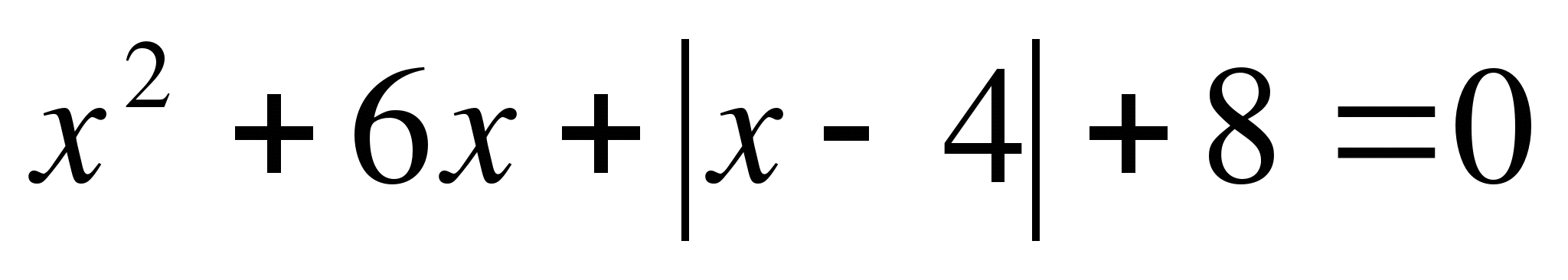
7. 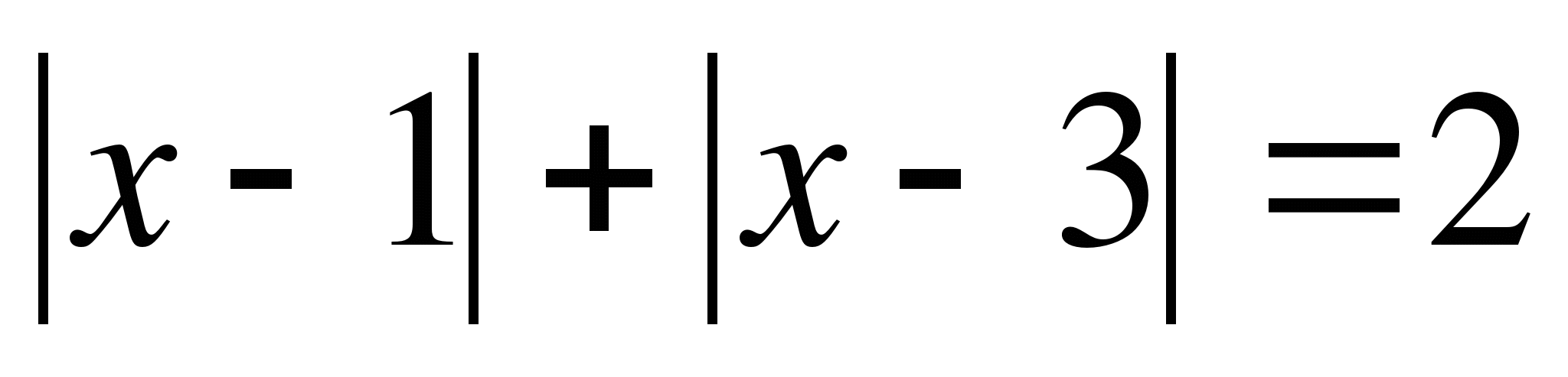
8. 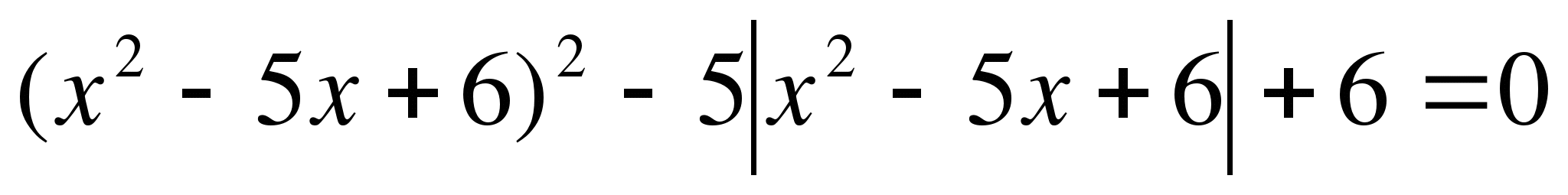
9. 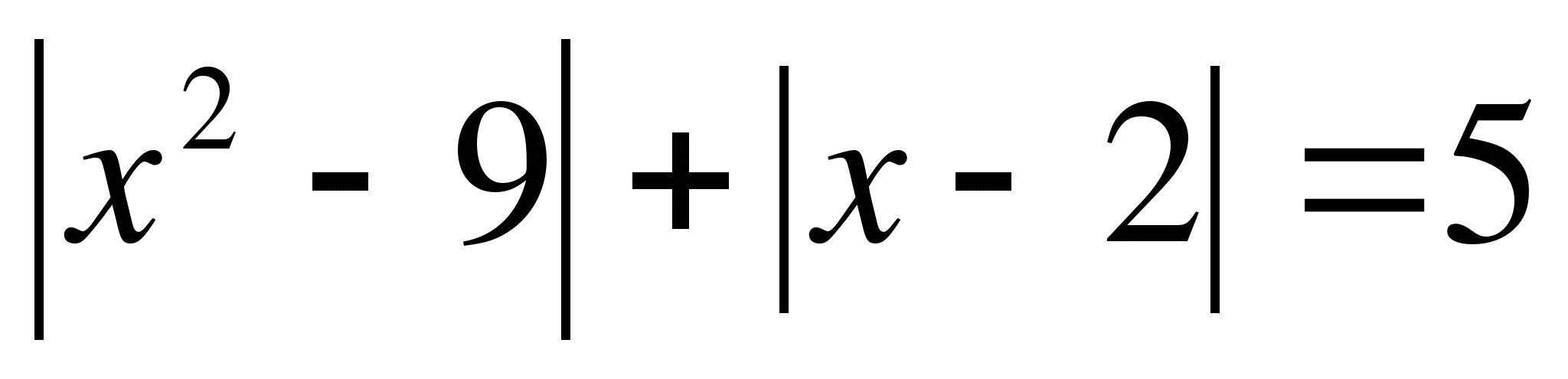
10. 
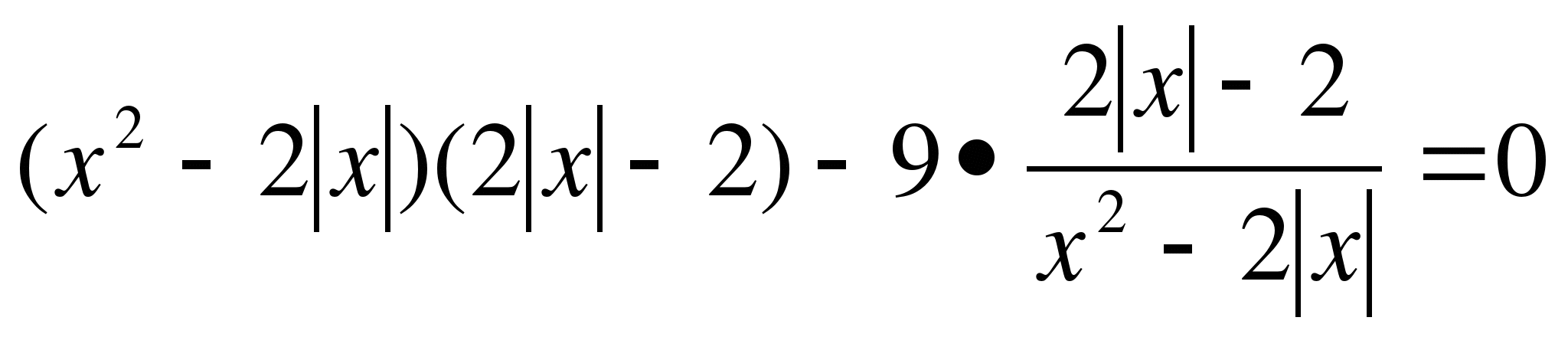
11. 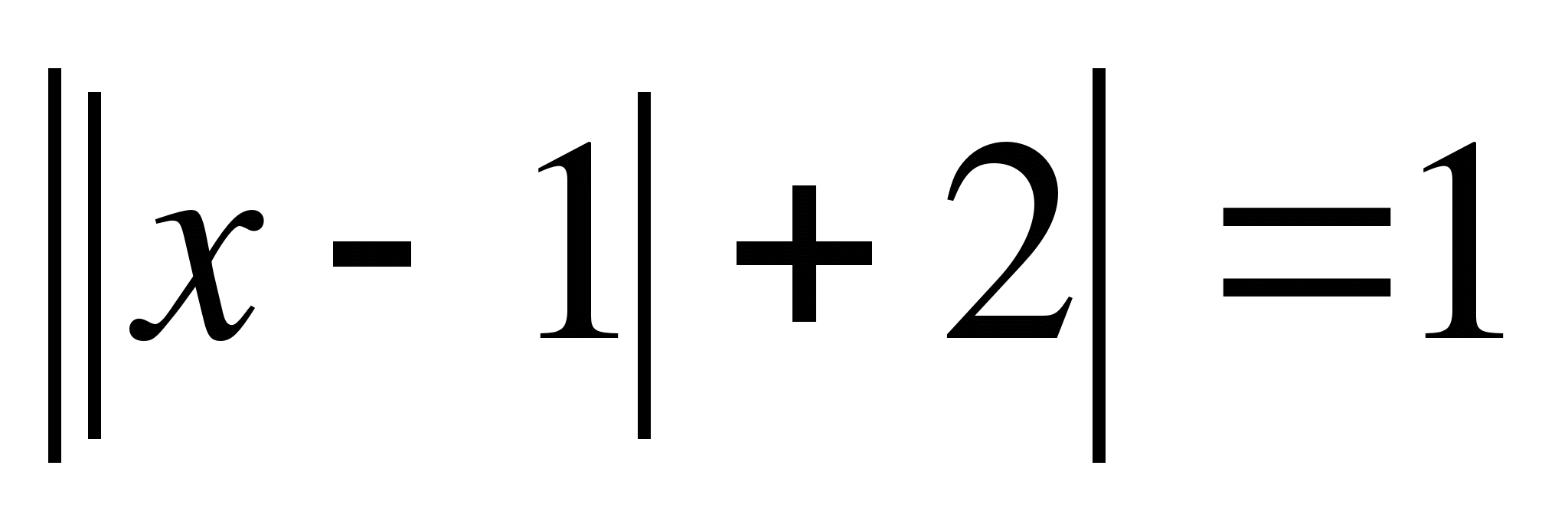
12. 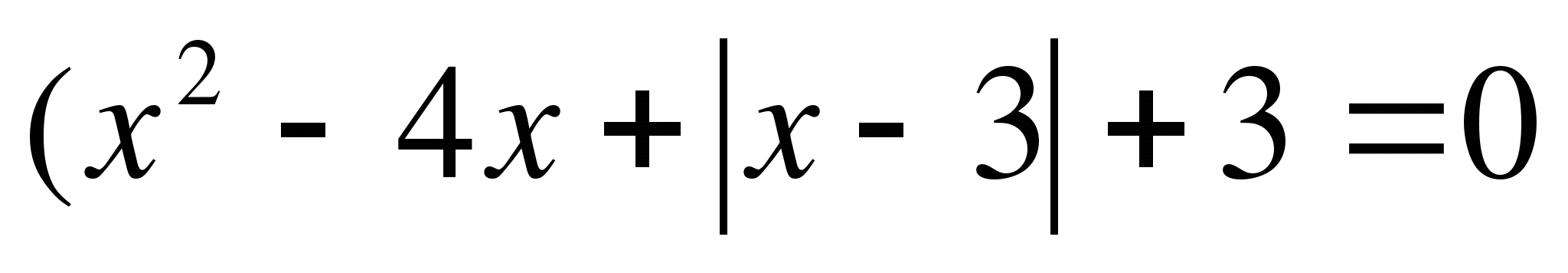
13. 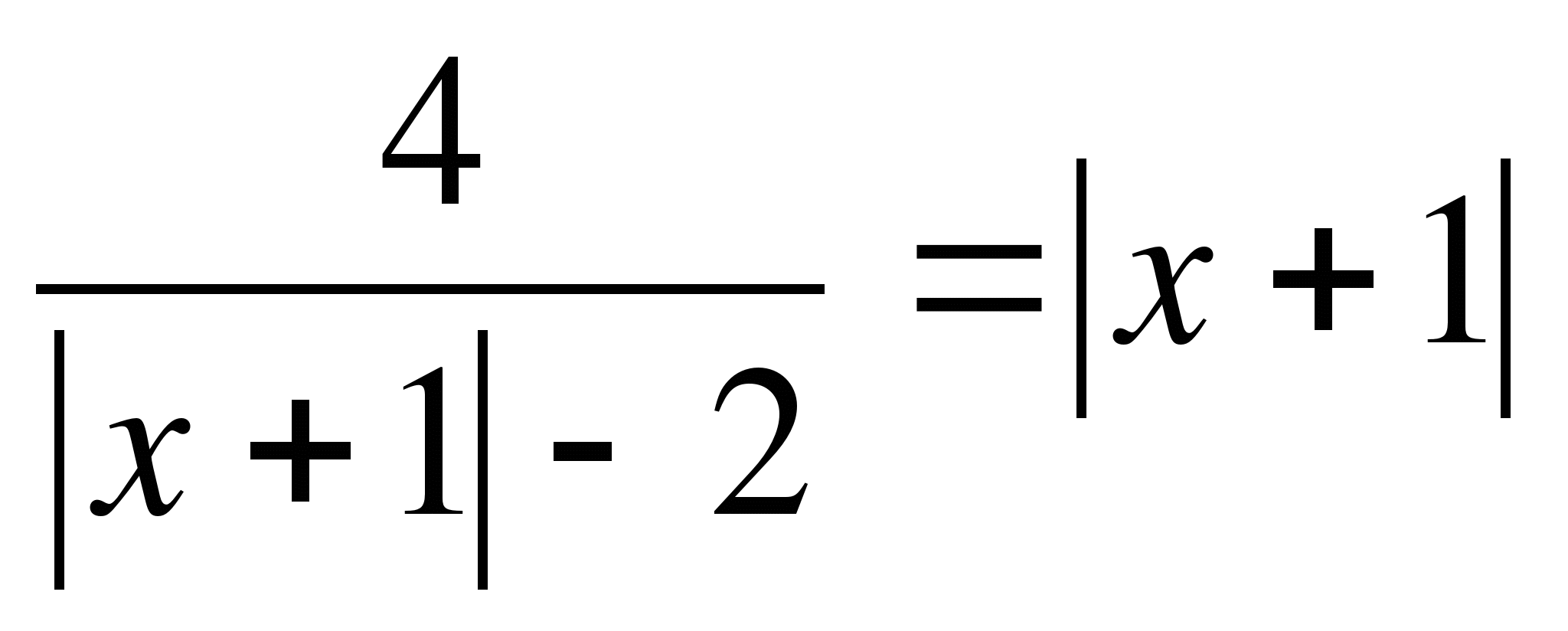
14. 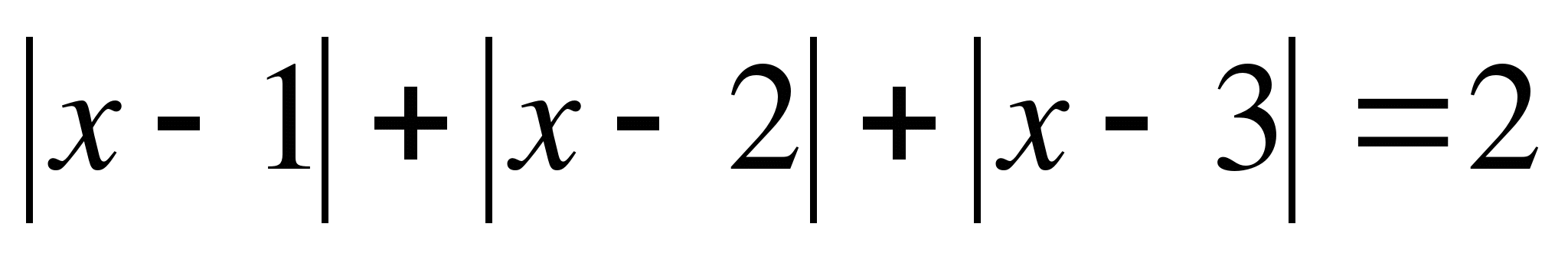
15. 
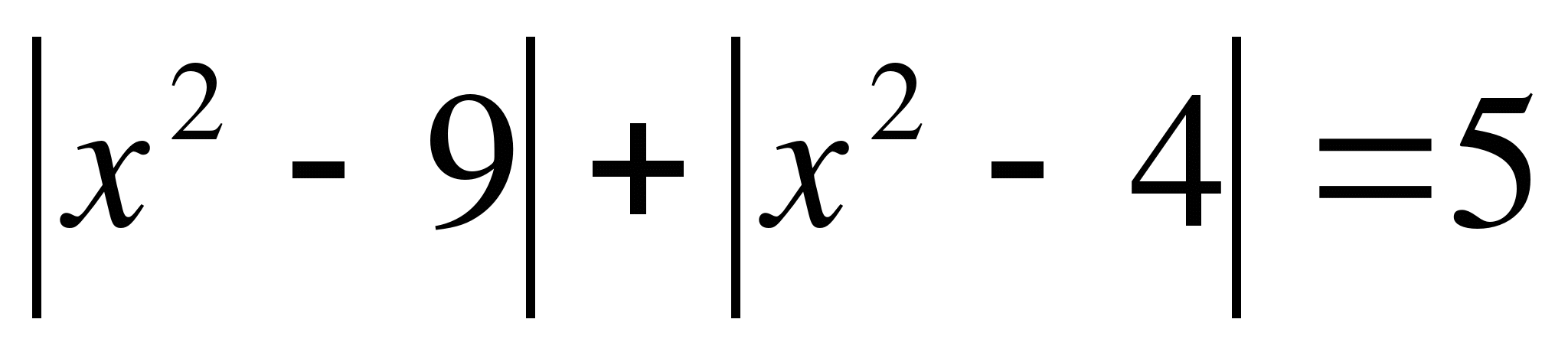
16. 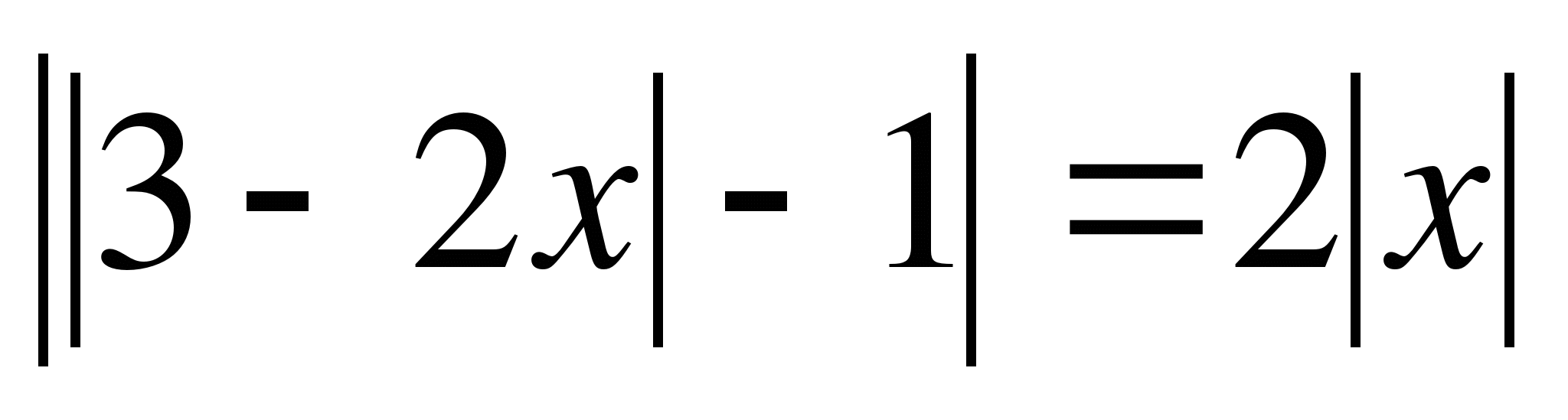
17. Найдите наименьшее целое значение 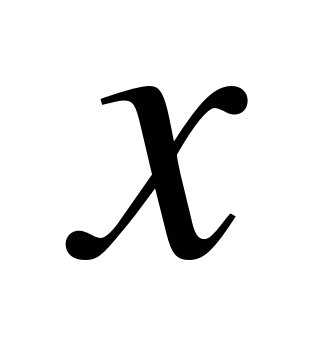 , удовлетворяющее уравнению
, удовлетворяющее уравнению 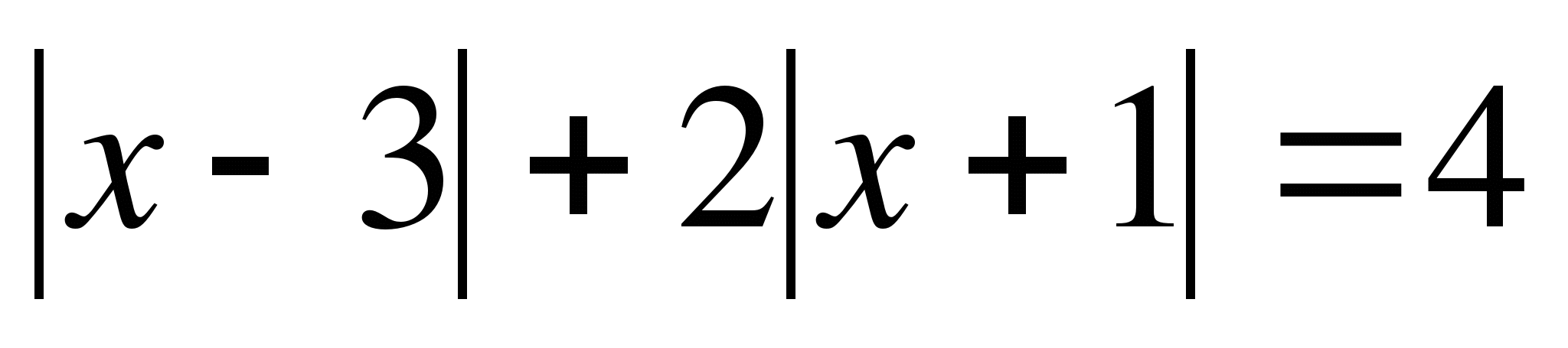 .
.
18. Найдите все корни уравнения 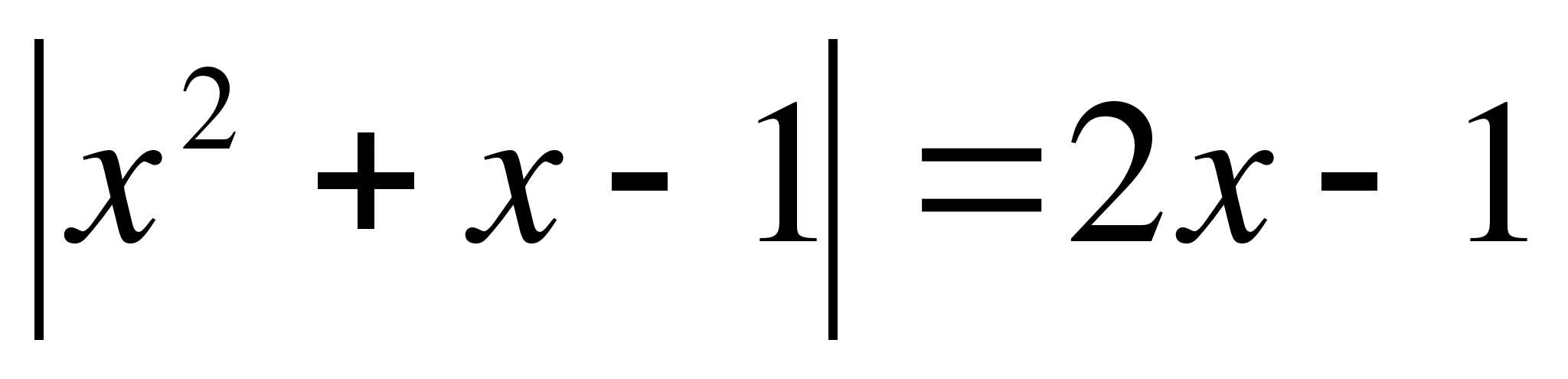 , удовлетворяющие неравенству
, удовлетворяющие неравенству 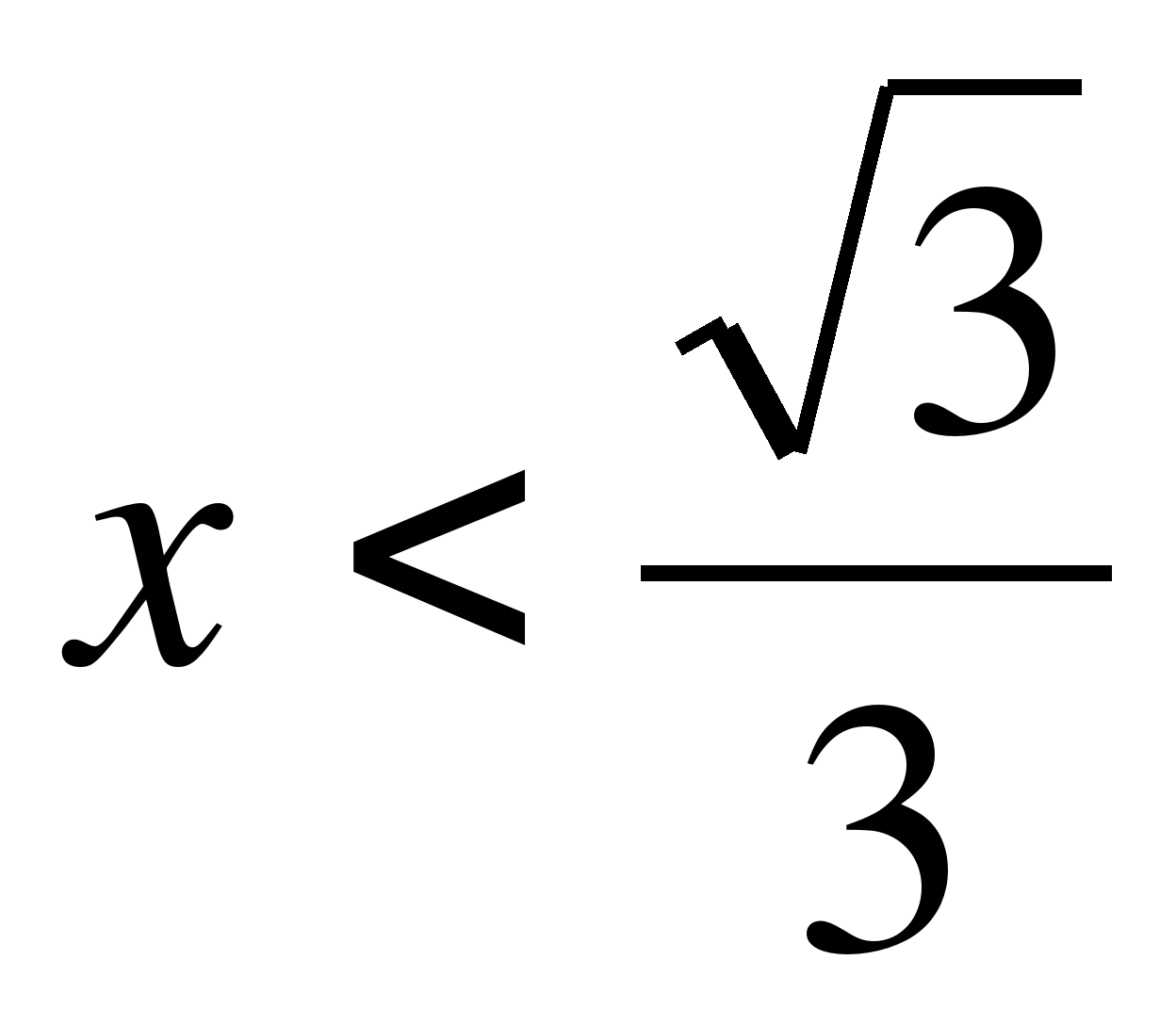 .
.
ОТВЕТЫ И РЕШЕНИЯ.
1. 
2. Воспользуйтесь методом разбиения на промежутки.
16.  . 17.
. 17. 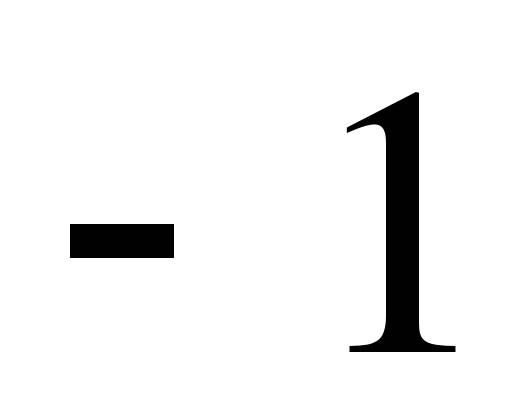 . 18.
. 18. 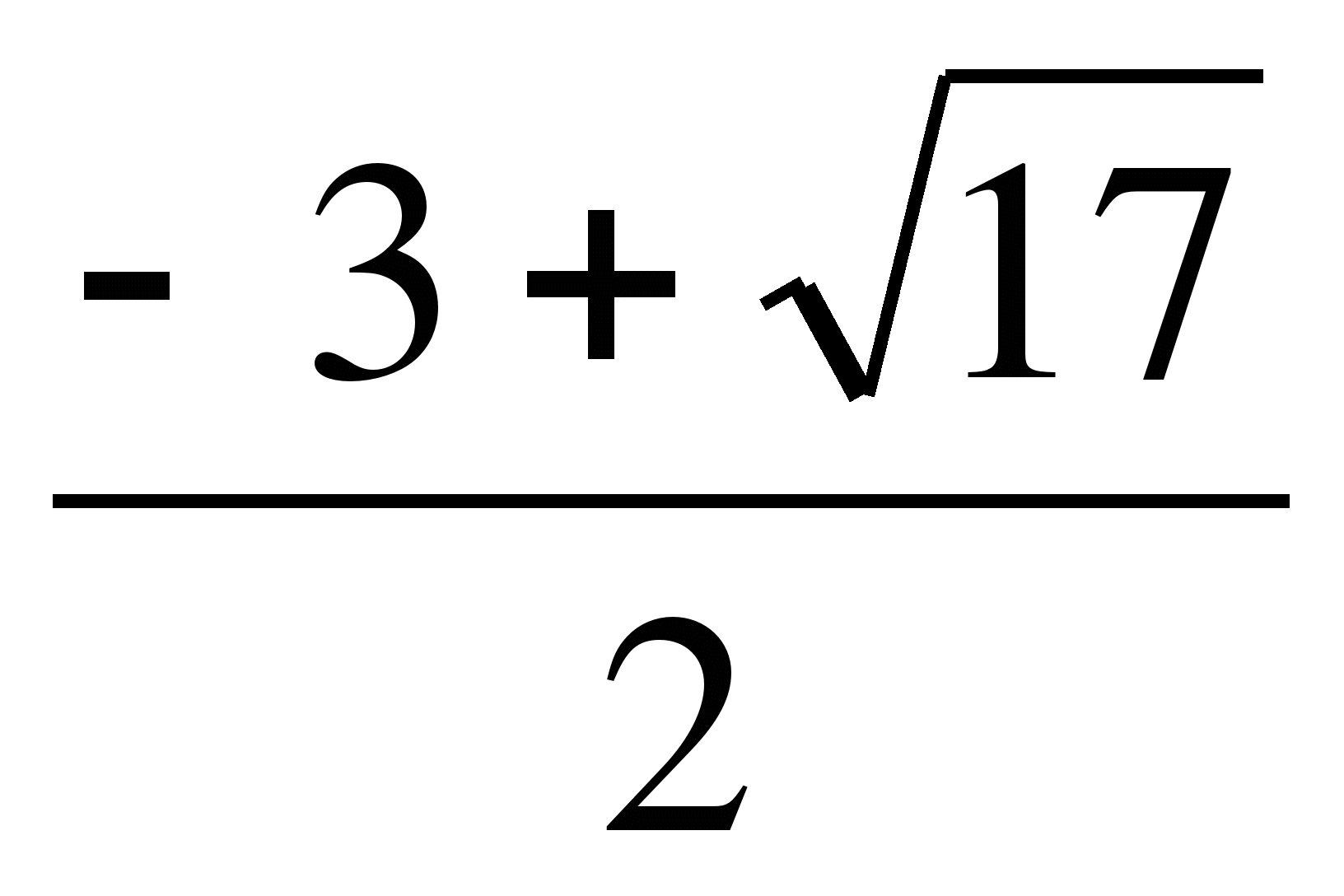
РЕШЕНИЕ УРАВНЕНИЙ
С МОДУЛЕМ, СОДЕРЖАЩИЕ ПАРАМЕТР.
1. Для каждого значения параметра 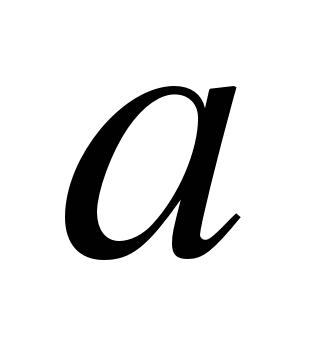 найдите число корней уравнения
найдите число корней уравнения 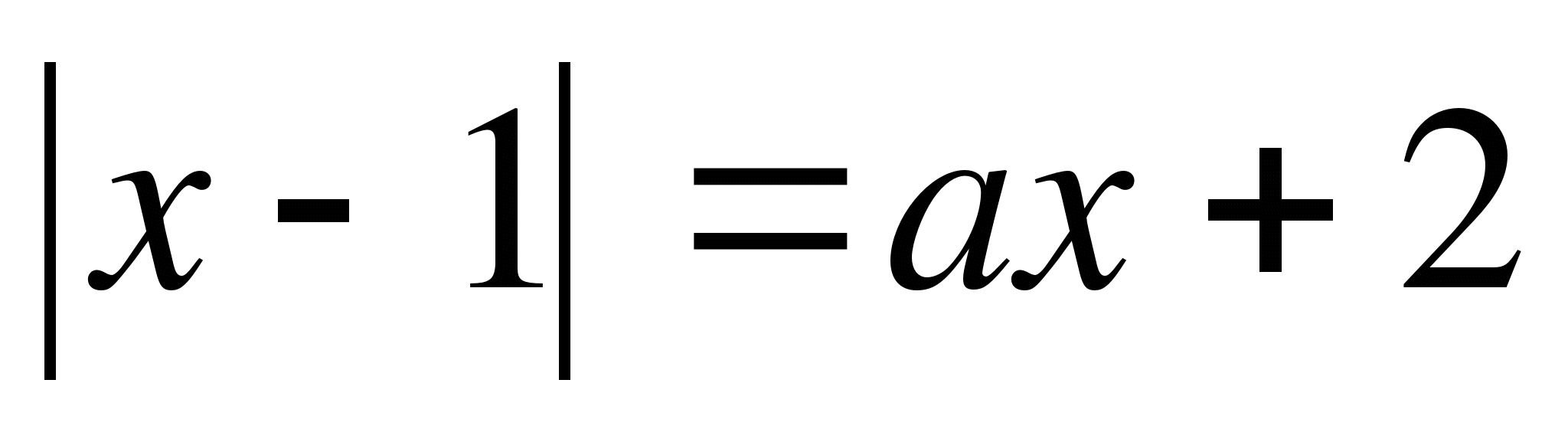 .
.
Решение. Запишем уравнение в виде 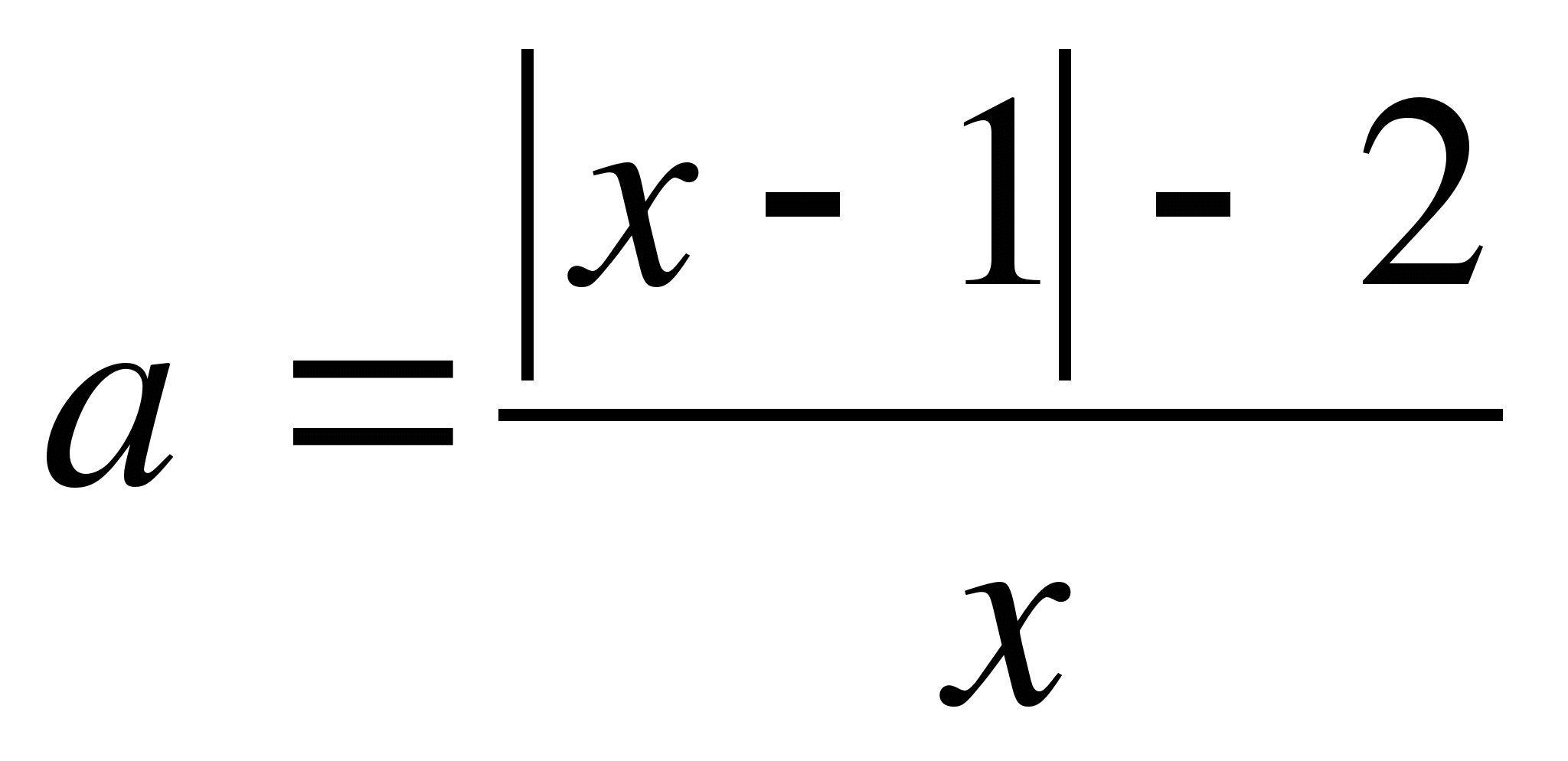 , так как
, так как 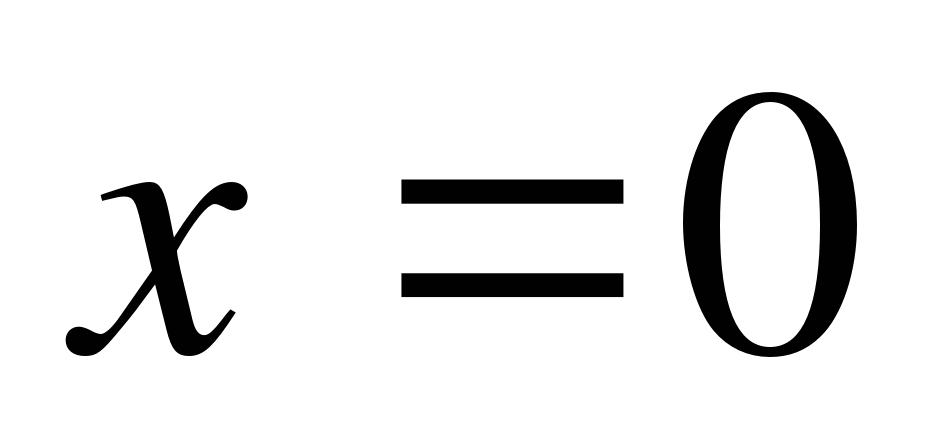 не является корнем уравнения. Количество корней данного уравнения будет соответствовать количеству точек пересечения графика функции
не является корнем уравнения. Количество корней данного уравнения будет соответствовать количеству точек пересечения графика функции 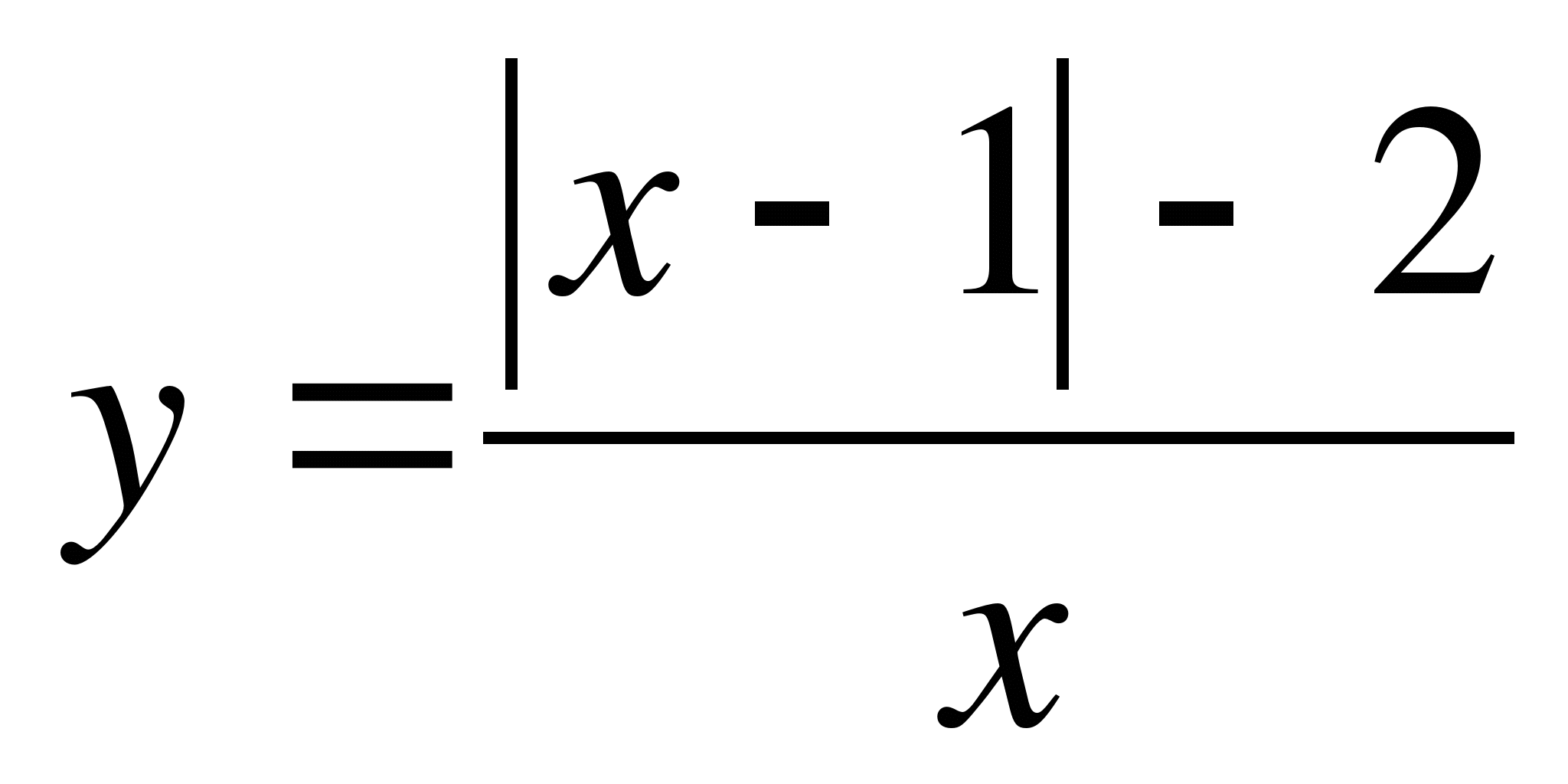 с прямой
с прямой 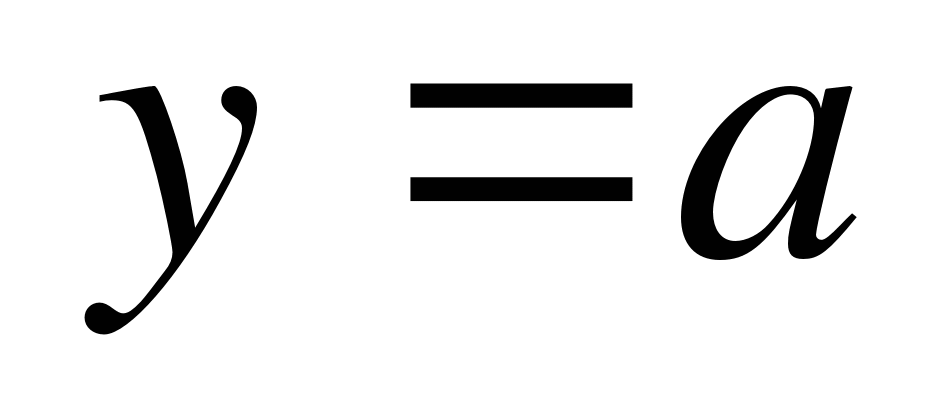 . Построим график функции
. Построим график функции 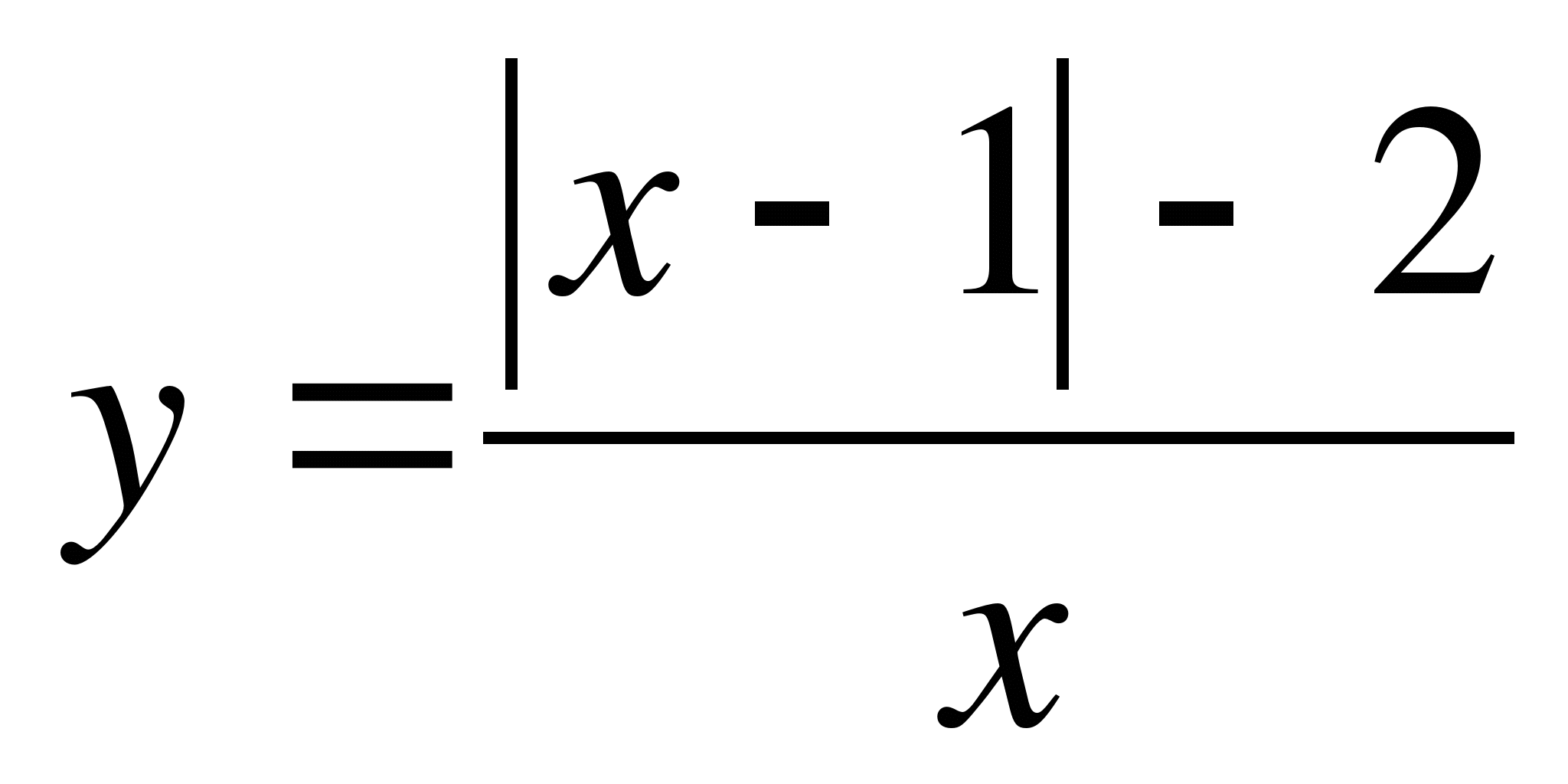 , который состоит из двух частей:
, который состоит из двух частей:
при 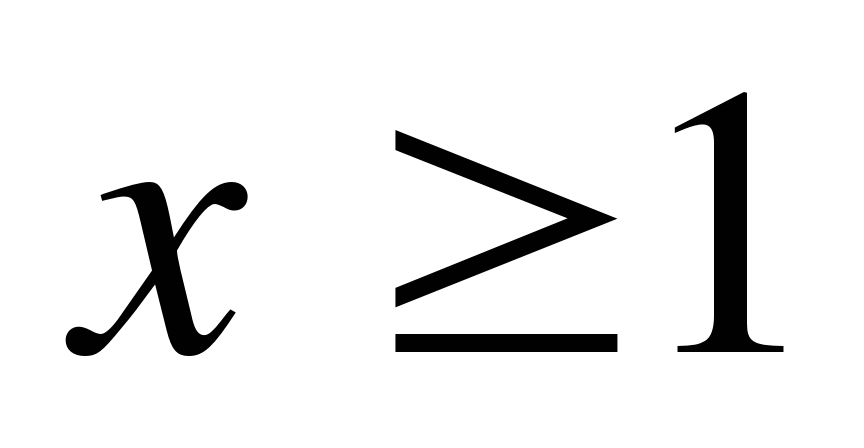
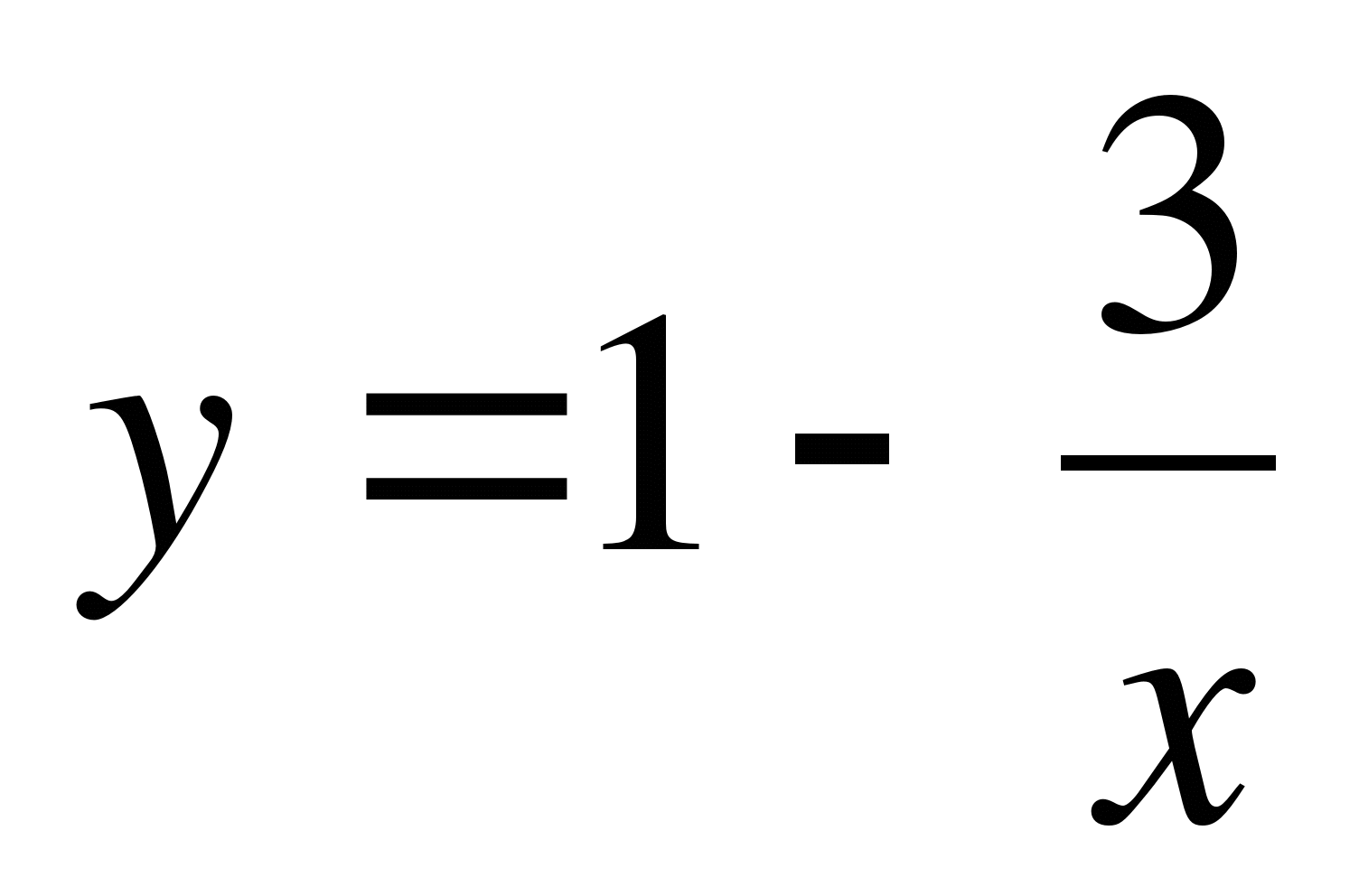 ;
;
при 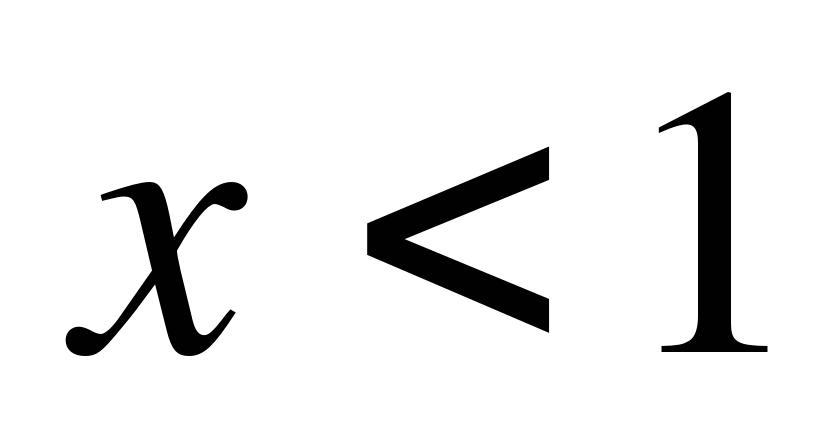
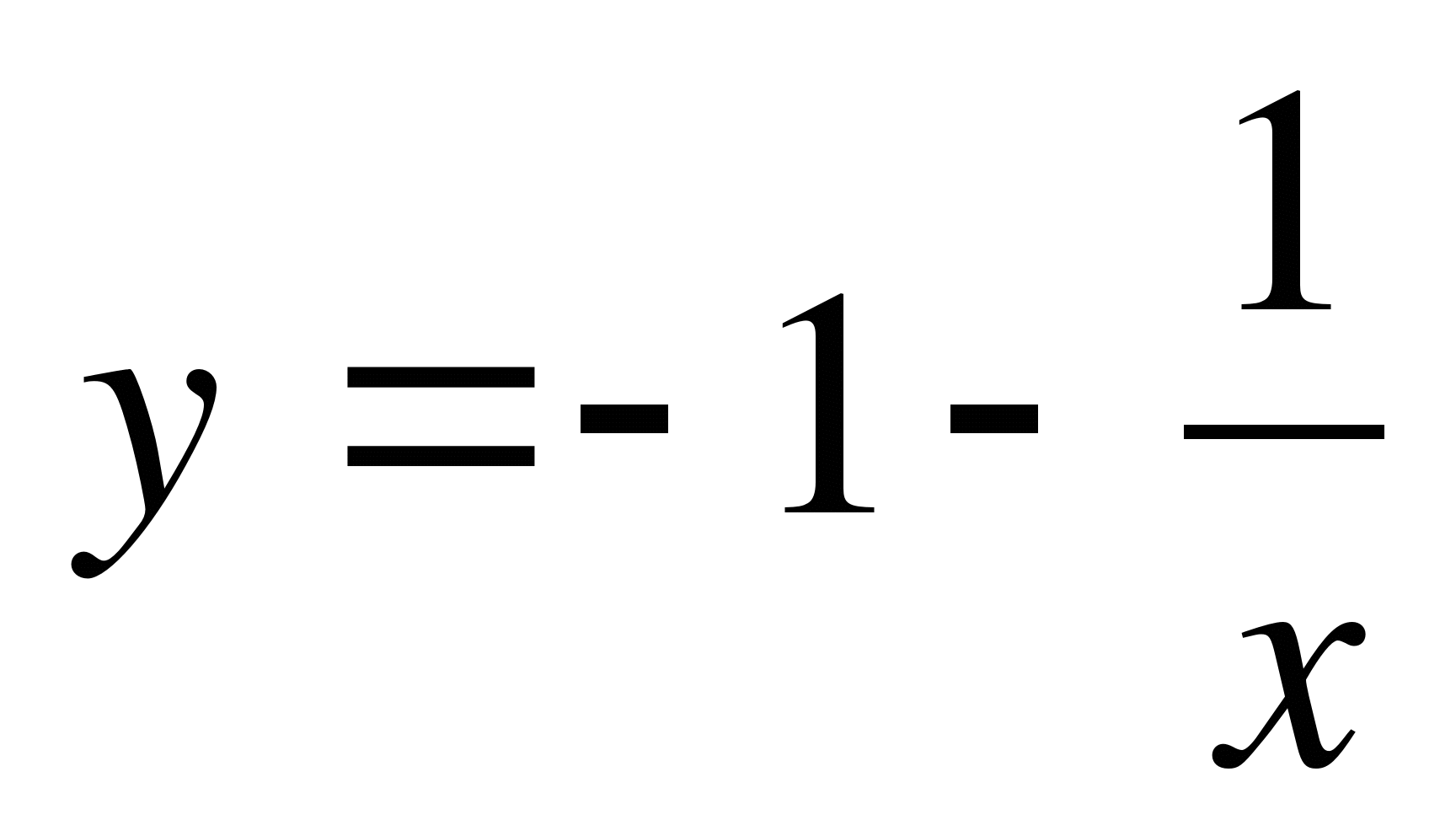 .
.
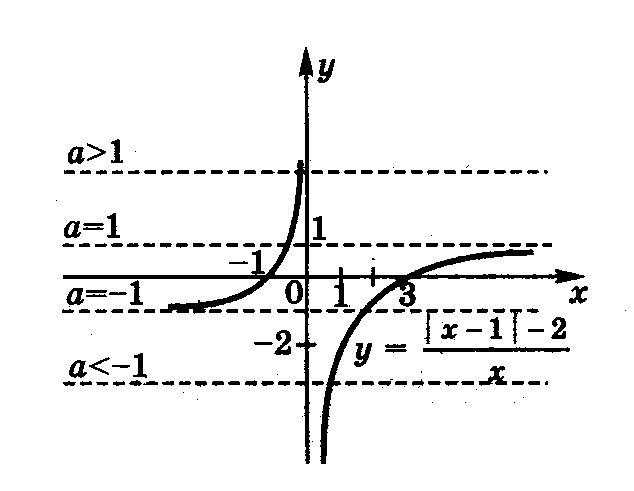
Из рисун
infourok.ru
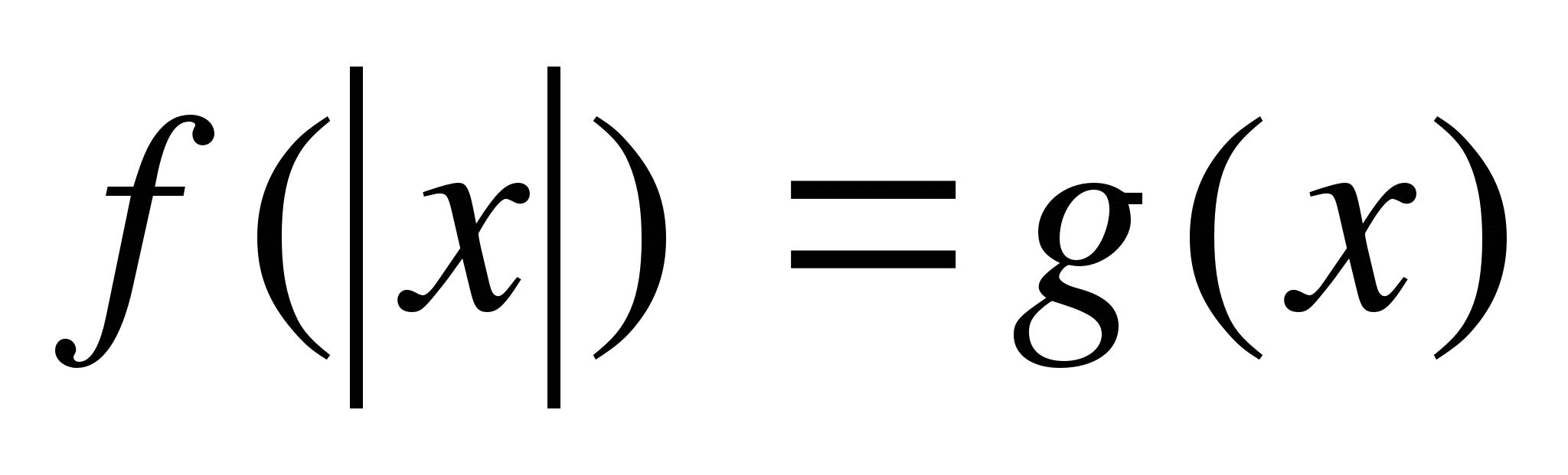 , (1)
, (1)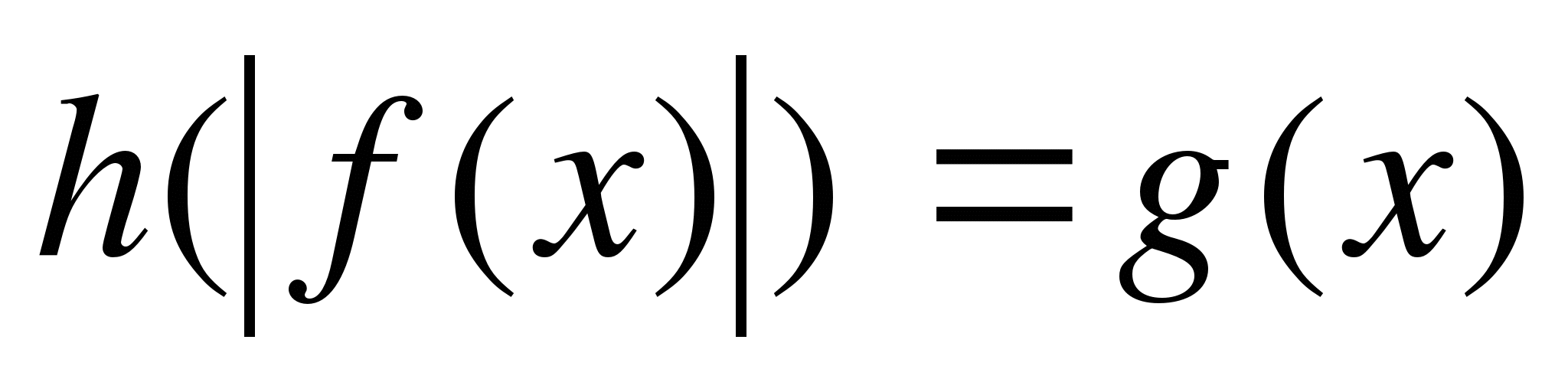 , где
, где  — некоторые функции, равносильно совокупности систем
— некоторые функции, равносильно совокупности систем