Рациональные уравнения и системы — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Формулы сокращенного умножения

К оглавлению…

При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения. Квадрат суммы:

Квадрат разности:

Предыдущие две формулы также иногда записывают в несколько другом виде, который даёт нам какое-то выражение для суммы квадратов:

Также нужно понимать, что будет получаться если в скобках в квадрате знаки будут расставлены «нестандартным» способом:

Теперь идём далее.

Формула сокращенного умножения разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

 

Квадратное уравнение и квадратный трехчлен

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то

разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т. е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (

a > 0), значение квадратного трехчлена:

 

Основные свойства степеней

К оглавлению…

У математических степеней есть несколько важных свойств, перечислим их. При умножении степеней с одинаковыми основаниями показатели степеней складываются:

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель степени делителя:

При возведении степени в степень показатели степеней перемножаются:

Если перемножаются числа с одинаковой степенью, но разным основанием, то можно сначала перемножить числа, а затем произведение возвести в эту степень. Обратная процедура также возможна, если имеется произведение в степени, то можно каждое из умножаемых возвести в эту степень по отдельности а результаты перемножить:

Также, если делятся числа с одинаковой степенью, но разным основанием, то можно сначала поделить числа, а затем частное возвести в эту степень (обратная процедура также возможна):

Несколько простых свойств степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

 

Основные свойства математических корней

К оглавлению…

Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:

Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:

Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при неотрицательном a. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):

Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:

 

Некоторые дополнительные сведения из алгебры

К оглавлению…

Если x₀ – корень многочлена n-ой степени P_n(x), то выполняется следующее равенство (здесь Q_n-1(x) – некоторый многочлен (n – 1)-ой степени):

Процедура в рамках которой квадратный трехчлен представляется как скобка в квадрате и еще некоторое слагаемое называется

выделением полного квадрата. И хотя операцию выделения полного квадрата проще выполнять каждый раз «с ноля» в конкретных цифрах, тем не менее имеется и общая формула, с помощью которой можно записывать сразу результат выделения полного квадрата:

Существует операция, обратная операции сложения дробей с одинаковыми знаменателями, и которая называется почленным делением. Она заключается в том, чтобы наоборот каждое слагаемое из суммы в числителе некоторой дроби, записать отдельно над знаменателем этой дроби. Для операции почленного деления также можно записать общую формулу:

Существует также формула для разложения суммы квадратов на множители:

 

Решение рациональных уравнений

К оглавлению…

Решить уравнение – значит найти все его корни. Основной метод решения – путем алгебраических преобразований или замены переменных свести уравнение к равносильному, которое решается просто (например, к квадратному). Если свести уравнение к равносильному не получается, то могут возникать побочные корни. Сомневаетесь – проверяйте корни подстановкой.

Для многих уравнений важно понятие области допустимых значений для корней, далее – ОДЗ. На данном этапе (в рациональных уравнениях, т.е. тех, которые не содержат арифметических корней, тригонометрических функций, логарифмов и т.д.), основное условие которому должны отвечать корни уравнения, это чтобы при их подстановке в изначальный вид уравнения знаменатели дробей не обращались в ноль, т. к. на ноль делить нельзя. Таким образом, ОДЗ включает все возможные значения кроме тех которые обращают в ноль знаменатели дробей.

При решении уравнений (а в дальнейшем и неравенств) нельзя сокращать множители с переменной в левой и правой части уравнения (неравенства), в этом случае Вы потеряете корни. Нужно переносить все выражения налево от знака равно и выносить «сокращающийся» множитель за скобки, в дальнейшем нужно учесть корни, которые он дает.

Для того чтобы произведение двух или более скобок было равно нулю, достаточно чтобы любая из них по отдельности была равна нулю, а остальные существовали. Поэтому в таких случаях нужно по очереди приравнивать все скобки к нулю. В итоговый ответ нужно записать корни всех этих «веток» решения (если конечно эти корни входят в ОДЗ).

Иногда некоторые из дробей в рациональном уравнении можно сократить. Это нужно обязательно попытаться сделать и не упустить ни одной такой возможности. Но при сокращении дроби Вы можете потерять ОДЗ, поэтому дроби нужно сокращать только после записи ОДЗ, или же в конце решения полученные корни подставлять в первоначальное уравнение для проверки существования знаменателей.

Итак, для решения рационального уравнения необходимо:

1. Разложить все знаменатели всех дробей на множители.
2. Перенести все слагаемые влево, чтобы справа получился ноль.
3. Записать ОДЗ.
4. Сократить дроби, если это возможно.
5. Привести к общему знаменателю.
6. Упростить выражение в числителе.
7. Приравнять числитель к нулю и решать полученное уравнение.
8. Не забыть проверить корни на соответствие ОДЗ.

Одним из самых распространённых методов решения уравнений является метод замены переменных. Зачастую замена переменных выбирается индивидуально для каждого конкретного примера. При этом важно помнить о двух основных критериях введения замены в уравнения. Итак после введения замены в некоторое уравнение это уравнение должно:

• во-первых, стать проще;
• во-вторых, больше не содержать первоначальной переменной.

Кроме того, важно не забывать выполнять обратную замену, т. е. после нахождения значений для новой переменной (для замены), записывать вместо замены то, чему она равна через первоначальную переменную, приравнивать это выражение к найденным значениям для замены и опять решать уравнения.

Отдельно остановимся на алгоритме решения очень распространённых однородных уравнений. Однородные уравнения имеют вид:

Здесь А, В и С – числа, не равные нулю, а f(x) и g(x) – некоторые функции с переменной х. Однородные уравнения решают так: разделим все уравнение на g²(x) и получим:

Производим замену переменных:

И решаем квадратное уравнение:

Получив корни этого уравнения не забываем выполнить обратную замену, а также проверить корни на соответствие ОДЗ.

Также при решении некоторых рациональных уравнений хорошо бы помнить про следующие полезные преобразования:

 

Решение систем рациональных уравнений

К оглавлению. ..

Решить систему уравнений – значит найти не просто решение, а комплекты решений, то есть такие значения всех переменных которые, будучи одновременно подставленными в систему, обращают каждое ее уравнение в тождество. При решении систем уравнений можно применять следующие методы (про ОДЗ при этом не забываем):

• Метод подстановки. Метод состоит в том, чтобы выразив одну из переменных из одного из уравнений, подставить это выражение вместо данной неизвестной в остальные уравнения, уменьшив таким образом количество неизвестных в оставшихся уравнениях. Данная процедура повторяется пока не останется одно уравнение с одной переменной, которое затем и решается. Остальные неизвестные последовательно находятся по уже известным значениям найденных переменных.
• Метод расщепления системы. Этот метод состоит в том, чтобы разложить одно из уравнений системы на множители. При этом необходимо чтобы справа в этом уравнении был ноль. Тогда приравнивая по очереди каждый множитель этого уравнения к нолю и дописывая остальные уравнения первоначальной системы, получим несколько систем, но каждая из них будет проще первоначальной.
• Метод сложения и вычитания. Данный метод состоит в том, чтобы складывая либо вычитая два уравнения системы (их предварительно можно и часто нужно умножать на некоторый коэффициент) получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.
• Метод деления и умножения. Данный метод состоит в том, чтобы разделив либо умножив соответственно левые и правые части двух уравнений системы получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура опять таки имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.

Существуют и другие методы решения систем рациональных уравнений. В числе которых — замена переменных. Зачастую замена переменных подбирается индивидуально под каждый конкретный пример. Но есть два случая, где всегда нужно вводить совершенно определённую замену. Первый из этих случаев, это случай когда оба уравнения системы с двумя неизвестными являются однородными многочленами приравненными к некоторому числу. В этом случае нужно использовать замену: 

После применения этой замены, к слову, нужно будет для продолжения решения таких систем использовать метод деления. Второй случай, это симметричные системы с двумя переменными, т.е. такие системы, которые не изменяются при замене x на y, а y на x. В таких системах необходимо применять следующую двойную замену переменных:

При этом, для того чтобы ввести такую замену в симметричную систему, первоначальные уравнения скорее всего придется сильно преобразовывать. Про ОДЗ и обязательность выполнения обратной замены в обоих этих методах, конечно нельзя забывать.

Методы решения уравнений: замены, подстановки, примеры, тесты

Тестирование онлайн

Потерянные и посторонние корни

К потере корней может привести сокращение обеих частей уравнения на общий множитель.

Посторонние корни могут появится при умножении обеих частей уравнения на множитель, содержащий неизвестное.

При возведении обеих частей уравнения в квадрат (или любую четную степень) могут появляться посторонние корни.

Посторонние корни могут появляться при решении иррационального уравнения, поэтому лучше выполнять проверку.

Метод замены переменной

В ряде случаев решение уравнения можно упростить введением новой переменной (нового неизвестного).

Например, уравнение вида

где a, b, c — числа, называется биквадратным. Решается введением замены x²=t

Метод замены используют не только при решении биквадратных уравнений.

Сложные замены переменной

Основная трудность решения задач методом подстановки заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.

Очень сложные замены переменной

Графический способ решения уравнений

Графический способ решения уравнений f(x)=g(x) заключается в следующем: строят в одной системе координат графики двух функций y=f(x) и y=g(x) и находят абсциссы точек пересечения графиков. Абсциссы точек пересечения графиков и являются корнями уравнения.

Преобразуем выражение a⁴+b⁴=(a+b)⁴:

При решении уравнения f(x)=g(x) можно исследовать функции y=f(x) и y=g(x) на монотонность. Если одна из этих функций на промежутке монотонно убывает, а другая функция монотонно возрастает, то уравнение или имеет один корень, или вообще не имеет корней. Корень уравнения можно найти методом подбора или графическим методом.

Если функция y=f(x) возрастает, а y=g(x) убывает на промежутке , и при этом f(a)>g(a), то корней нет.

Примеры уравнений вида f(f(x))=x, где f(x) — некоторая функция:

1. Любой корень уравнения f(x)=x является корнем уравнения f(f(x))=x;
2. Если функция f(x) возрастает на некотором множестве и значения x и значения функции f(x) принадлежат этому множеству, то уравнения f(x)=x и f(f(x))=x равносильны на этом множестве.

Для убывающей функции f(x) правило 2 применить нельзя.

Суть метода состоит в замене переменной х тригонометрической функцией, например . Решение исходного уравнения сводится к решению тригонометрического уравнения. Но тригонометрическое уравнение обычно имеет бесконечное множество решений, а исходное — конечное.

Неравенство Коши.

Неравенство Бернулли.

Равенство достигается при x=0 или n=1.

Неравенство Коши-Буняковского.

Равенство достигается в том и только в том случае, когда существует положительная константа a такая, что x₁=ay₁, x₂=ay₂,…,x_n=ay_n.

Как репетитор по математике оформляет объединение систем

Системы уравнений и неравенств входили в состав выпускных и вступительных экзаменов по математике во все времена. Даже если в экзаменационном варианте нет прямого задания на решение системы, то существует достаточно высокая вероятность ее появления процессе решения других задач. Репетитор по математике обязан это учитывать. Привести к системам могут задачи на модули, на логарифмы, на графики и даже на синусы с косинусы. Несмотря на то, что подготовка к ЕГЭ по математике нередко сводится к натаскиванию на решение однотипных номеров части «В», не стоит полностью отказываться от тренировки навыков поиска пересечения (объединения) ответов разных объектов. Хотя бы на элементарном уровне. Какими приемами репетитор по математике обеспечивает оптимальную работу ученика с системами? Какая техника оформления систем была бы самой удобной и продуктивной?

К сожалению, школьные учителя и даже некоторые профессиональные репетиторы требуют от детей (уже в 8 классе) оформление систем по принципу «все в одном», упаковывая содержащиеся в них неравенства в единый объект согласно строгим правилам проведения равносильных преобразований. Широко применяются квадратные и фигурные скобки, причем часто в весьма сложном сочетании. Мой опыт репетиторской работы свидетельствует о том, что дети с огромнейшим трудом воспринимают, казалось бы, несложные для математиков логические конструкции с конъюнкциями и дизъюнкциями. Примерно 60-70% всех школьников с трудом припоминают (или не знают вообще) чем отличается квадратная скобка от линейной. А среди тех, кто приходит к репетитору по математике, этот процент повышается в среднем до 90-95%.

Но, тем не менее, для обозначения объединения, некоторые школьные преподаватели все равно используют квадратные скобки. Видимо по привычке. При таком раскладе репетитор по математике оказывается в крайне сложном положении, ибо уровень ученика часто не позволяет осознать сложные логические сочетания. Я не сторонник любой ценой следовать школьным стандартам и часто полностью отказываюсь от постановки квадратных скобок. Без них проще. Особенно когда на носу подготовка к ЕГЭ. Если все же репетитор математики вынужден принимать школьные правила, он мог бы это сделать следующим образом:

Когда репетитор по математике вводит квадратную скобку?

К пониманию разницы между скобками лучше всего подводить ученика постепенно, начиная с 8 класса, когда изучается тема «неравенства». В решении самих неравенств восьмиклассники используют понятие «пересечение ответов» . Почему бы репетитору по математике не показать что такое «объединение ответов»? Задачи на объединение присутствуют в учебнике Макарычева, но они ограничиваются операцияями с уже сформированными промежутками. Это не совсем то, что нужно. Вот пример, на котором репетитор по математике мог бы объяснить назначение квадратной скобки:

Как видите, используется самое простое сочетание. Скобку лучше всего ввести после того, как ученик поймет суть задания. А она заключается в том, чтобы подобрать числа, обеспечивающие выполнение хотя бы одного неравенства (я употребляю общий термин: «условие»). Фразу «хотя бы одного» репетитор по математике сразу же меняет на фразу «или одно или другое». Процент учеников, правильно нашедших репетитору ответ, оказывается не таким и уж низким. Половина детей схватывают суть задания сразу же. Другим нужно показывать, как проверяется наугад взятое число (главное не объяснять только словами).

Данный номер рассматривается репетитором сразу после примера на совокупность, то есть на поиск числа, обеспечивающего выполнение каждого условия:

К сожалению, родители редко приглашают репетитора по математике в 8 классе и подготовкой к ЕГЭ занимаются только с 10 или с 11 класса. В этом случае репетитору приходится объяснять оформление объединения по формальному признаку фигурной скобки: если для проверки произвольно взятого числа достаточно проверить верность одного из нескольких условий (неравенств, уравнений или их систем), то проверяемые объекты можно заключить в квадратную скобку. Корректируя общую формулировку, репетитор по математике вставляет в нее союз «или». Например, для того, чтобы число x было корнем уравнения необходимо чтобы или первый множитель равнялся нулю, или второй. Преподаватель отдельно акцентирует внимание ученика на участии «или» и в случае его уместного употребления разрешает заключить объекты в квадратную скобку.

Если репетитор математики примет строгое оформление, он усложнит ученику одновременно и понимание и практическую работу. Школьные учителя берут за образец оформление систем в задачниках, в которых решения излагаются кратко. Из-за пропусков некоторых его частей удается компактно расписать все равносильные переходы, сохраняя целостность объекта. Репетитору по математике данная методика не подходит категорически. Почему? Ученики начинают вырывать по отдельности неравенства из огромной системы через весьма приличные промежутки времени. Переключение внимания на частные операции сбивает школьников с главного направления. Они забывают что именно им надо пересекать, а что объединять. Путаница возникает страшная. Хорошо, если репетитор по математике рядом и сможет подсказать. А что делать на ЕГЭ? Вряд ли стоит рисковать. Техника действий должна быть максимально прозрачной и удобной в практическом смысле.

Принимая квадратную скобку, репетитор по математике усложняет еще и сортировку решенного. Приходится оформлять отдельные неравенства в колонку (одно под другим) и запоминать какое именно решено, а какое еще нет. Если сами решения длинные, то ученику может не хватить страницы и придется ее переворачивать. Рассеивание внимания при этом гарантировано.

Может ли репетитор по математике обойтись без квадратной скобки

?

Да, вполне. Для этого применяются стрелочный эквивалент. Например:

Чаще всего в объединение попадают две системы (если больше — лучше использовать иные методы изначально). В нашем случае одна из систем решается в левой части тетрадного листа, а другая в правой. Репетитор по математике разделяет квадратную скобку на две совокупности отдельных систем. На мой взгляд, это самая удобная форма для практической работы ученика. Почему? Те ответы, которые нужно пересечь, распределены по колонкам, при этом операции в левой и в правой колонке проводятся локально и не перемешиваются. Слева — свое пересечение, справа — свое. Очень удобно. Под каждой системой – решение. Системы не нужно вырывать из «квадратной скобки», не нужно переписывать. Финальные ответы, которые репетитор по математике и ученик получают слева и справа «сваливаются в общий ответ» без какой-либо коррекции и пересечения.

Исключение составляют случаи, когда промежутки имеют общую часть. Однако практика показывает, что даже если репетитор по математике забудет напомнить о «склеивании частей», то большинство учеников догадаются до него сами.

Преимущество стрелок для запоминания:
Когда ученик разделяет тетрадный лист на две части, то находясь на любом этапе решения по левой колонке, он помнит о том, что предстоит еще заполнить и правую часть. Это очень важно. Если вы репетитр, то наверняка знаете, что школьники часто забывают разобрать какой-нибуь случай или решить какое-нибдуь неравенство из системы.

Сложность работы с объединением и пересечением носит часто чисто технический характер и связана с проблемой механики решений, то есть запоминанием и сортировкой обрабатываемой информации. При подготовке к ЕГЭ по математике важно получить навык автоматического выполнения операций. Поэтому репетитору по математике крайне необходимо использовать в работе простые и удобные методы, каким является прием стрелочного разделения. Если потребуется объединить три или более системы, репетитор по математике может взять лист формата А4, развернуть его в длину и аккуратно решить задание распределяя системы по нескольким колонкам. Такой подход к оформлению позволит ученику четко разделить и запомнить логическую структуру объекта.

Репетитор по математике, Колпаков А.Н. Москва.

Урок разноуровневого обобщающего повторения по теме «решение систем линейных уравнений»

Лавринова Т.В. МОУ СОШ № 16

Урок разноуровневого обобщающего повторения по теме:

«Решение систем линейных уравнений»

Перед началом урока учащиеся рассаживаются в соответствии с тремя уровнями подготовки на определенные ряды. При этом учащиеся знают, что по мере усвоения материала они могу переходить в следующую по уровню подготовки группу.

Оборудование: на столах лежат конверты с карточками для организации самостоятельной работы, которые учащиеся используют на различных этапах урока. Задания для каждой группы учащихся напечатаны на карточках различных цветов; для 1-й группы зеленые, для 2-й группы – желтые, для 3-й группы – красные.

Урок рассчитан на 40 минут.

I этап урока – организационный (2 минуты)

Учитель сообщает учащимся тему урока, и для каждой группы определяет основную цель.

Для 1-й группы: развивать умения решать системы линейных уравнений.

Для 2-й группы : закрепить и развить умение решать системы линейных уравнений базового и повышенного уровня сложности.

Для 3-й группы закрепить умения решать системы линейных уравнений повышенного уровня сложности.

Учитель поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится на партах.

II этап урока (3 минуты)

Повторение теоретического материала по теме

«Линейное уравнение с двумя переменными»

Учитель. Какие уравнения называются линейными с двумя переменными?

Ученик. Линейным уравнением с двумя переменными называется уравнение вида aх+ву=с, где х и у – переменные, a, в,с – некоторые числа.

Учитель. Что является решением линейного уравнения с двумя переменными?

Ученик. Решением уравнения с двумя переменными называется пара значений переменных, обращающих уравнение в верное равенство.

Учитель. Какие уравнения с двумя переменными называют равносильными.

Ученик. Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными , не имеющие решений, также считают равносильными.

III этап урока (3 минуты)

Устная работа по решению простейших задач на тему «Линейное уравнение с двумя переменными»

Учащимся раздаются листы с заданиями. Ученики устно отвечают на сформулированные вопросы, комментируя свой ответ ссылкой на соответствующий теоретический факт.

1.Является ли уравнение с двумя переменными линейным ?

а)3х-у=17 ; б) х²-2у=5; в)13х+6у=0; г) ху+2х=9

2.Выразив из уравнения х-6у=4 переменную х через у, найдите два каких- либо решения этого уравнения.

3.Какая из пар (3;1), (0;10), (2,4) и (3,2,5) являются решениями уравнения 3х+у=10.

IV этап урока (5 минут)

Повторение теоретического материала по теме

«Системы линейных уравнений с двумя переменными».

Учитель. Что называется решением системы уравнений с двумя переменными?

Ученик. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Учитель. Объясните в чем заключается способ подстановки.

Ученик.При решении системы двух уравнений с двумя переменными способом подстановки поступают следующим образом:

1)выражают из какого-нибудь уравнения системы одну переменную через другую;

2)подставляют в другое уравнение системы вместо этой переменной полученное выражение;

3)решают получившееся уравнение с одной переменной;

4)находят соответствующее значение второй переменной.

Учитель. Объясните в чем заключается способ решения систем уравнений – способ сложения.

Ученик. При решении системы двух уравнений с двумя переменными способом сложения поступают следующим образом

1)умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) складывают почленно левые и правые части уравнений системы;

3)решают получившееся уравнение с одной переменной;

4) находят соответствующее значение второй переменной.

V этап урока (10 минут)

Работа в разноуровневых группах

Со всеми учащимися класса рассматривается решение систем уравнений.

Учитель приглашает к доске одного человека решать систему уравнений.

3х+у=7,

-5х+2у=3.

Решение.

Выразим из первого уравнения у через х:

у=7-3х.

Подставив во второе уравнение вместо у выражение 7-3х, получим систему:

3х+у=7

-5х+2(7-3х)=3.

Решим второе уравнение:

-5х+14-6х=3

-11х=-11

х=1.

Подставив в равенство у=7-3х вместо х число 1, найдем соответствующее значение у:

у=7-3·1,

у=4

Пара (1;4) – решение системы.

Ответ: (1;4)

Учащийся, выполнявший задание у доски, комментирует свое решение, ссылаясь на соответствующий теоретический материал, а остальные вносят при необходимости корректировки.

Далее первая группа учащихся самостоятельно выполняет задание.

Зеленая карточка

Вариант 1. Вариант 2

Решите систему уравнений: Решите систему уравнений:

у=х-1 х=2-у

5х+2у=16 3х-2у-11=0

В это время учитель с учащимися 2-й и 3-й группы рассматривает задания повышенного уровня сложности.

Учитель приглашает к доске одного человека решать систему уравнений.

7х+6у=6,

3х+4у=9.

Решение.

Выразим из второго уравнения х через у:

3х=9-4у,

9-4у

х= 3

Подставив в первое уравнение вместо х выражение 9-4у

3

получим:

9-4у

7· +6 у=6

3

7(9-4у)+3·6у=3·6,

63-28у+18у=18,

-10у=-45,

у=4,5.

Подставив в уравнение 9-4у

х= 3 вместо у число 4,5:

получим х=3

Ответ: х=-3, у=4,5

Учащиеся второй группы приступают к самостоятельному выполнению заданий.

Желтая карточка.

Вариант 1. Вариант2

Решите систему: Решите систему

3х+4у=0 7х+2у=0

2х+3у=1 4у+х=10

С учащимися третьей группы учитель рассматривает следующую систему уравнений.

х у

3 2 4

х у

2 4 -2

Решение.

Умножим первое уравнение системы на 6, а второе на 4. Получим:

2х-3у=-4

2х+у=-8

Выразим из второго уравнения у, получим у =-8-2х.

Подставим в первое уравнение вместо у выражение , получим:

2х-3(-8-2х)=-24,

2х+24+6х=-24

8х=-48,

х=-6

Найдем значение у.

у=-8-2(-6)=-8+12=4

Далее учащиеся третьей группы выполняют задание самостоятельно

Красная карточка

Вариант1 Вариант2

Решите систему уравнений Решите систему уравнений

5у+8(х-3у)=7х-12, -2(а-в)+16=3(в+7)

9х+3(х-9у)=11у+46 6а-(а-5)=-8-(в+1)

Учитель проверяет правильность выполнения у учащихся первой и второй группы, если появляется необходимость корректирует решения.

По завершении проверки все учащиеся класса пишут разноуровневую самостоятельную работу.

VI. этап урока

Разноуровневая самостоятельная работа. (15 минут)

Учитель выдает задания для самостоятельной работы, сообщая учащимся, что на ее выполнение отводится 15 минут.

Для учащихся 3-й группы учителем составлены зеленые карточки в 3-х вариантах. Учащиеся 3-й группы — это, как правило, учащиеся со слабой математической подготовкой.Работа для них содержит простейшие задания аналогичные тем, которые разбирались на уроке (2 задания) и два задания на темы, по которым они уже демонстрировали успешное выполнение заданий. Все задания в варианте базового уровня сложности. Вместе с заданиями учащиеся получают бланки для выполнения заданий.

I уровень сложности.(зеленые карточки)

Работа содержит простейшие задания. Все задания в работе базового уровня сложности.

Вариант 1.

1.Вычислите 0,5·√3,2·√20

2.Решите неравенство 3(х+1)≤2х3

3.Решите систему уравнений

4х+у=1,

-2х+2у=-3

4.Решите систему уравнений

2х+3у=-4

2х+у=2

Вариант 2.

1.Вычислите 2√3+√121-√12.

2.Решите уравнение7х²-14=0.В ответе укажите наибольший корень.

3.Решите систему уравнений

2х-у=0,

-2х+4у=3.

4.Решите систему уравнений

4х-2у=11

-х+2у=-5

II уровень сложности.

Желтые карточки.

Вариант 1

1.Решите систему

4u+3v=14,

5u-3v=25.

2.Решите систему:

3(х-5)-1=6-2х,

3(х-у)-7у=-4

Найдите х + у

Вариант 2

1.Решите систему

10p+7q=-2,

2p-22=5q

2.Решите систему:

(6х+у)-у=-1

7(у+4)-(у+2)=0

Найдите х –у

III уровень сложности. Задачи повышенного уровня сложности.

В своих работах учащиеся должны представить краткий ответ на первую задачу и развернутое решение второй задачи.

Вариант 1.

1.Решите систему: 40х+3у=10

20х-7у=5

2.Решите задачу:За 4 ч езды на автомашине и 7ч езды на поезде туристы проехали 640км. Какова скорость поезда, если она на 5км/ч больше скорости автошины?

Вариант 2

1. Решите систему: 4в+7а=90,

5а-6в=20.

2.Решите задачу: Основание равнобедренного треугольника на 7см больше его боковой стороны Найдите боковую сторону треугольника, если его периметр равен 43 см.

По истечении времени учащиеся сдают работы.

Во время выполнения работы учитель, при необходимости, помогает слабым учащимся выполнять задания наводящими вопросами .По истечении времени учащиеся сдают работы.

VII этап урока (2 минуты)

Подведение итогов урока, комментарии по домашнему заданию

Учитель еще раз обращает внимание, на способы решения систем уравнений и те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет отметки.

В качестве домашнего задания учащиеся получают по варианту из предыдущей краевой контрольной работы и по циклу обмениваются вариантами самостоятельной работы, в своей группе

Решите систему квадратных уравнений

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

 

Системы решения и построения графиков квадратных уравнений

Решение с помощью графика

Существует несколько различных способов решения системы квадратных уравнений. Во-первых, давайте посмотрим на решение с помощью графика. К счастью, этот процесс является одним из самых простых! Важным примечанием при решении с помощью графика является то, что для этого процесса абсолютно необходим графический калькулятор, который может находить точки пересечения.

Чтобы решить систему квадратных уравнений с помощью графика, мы выполняем следующие шаги;

1. Начертите оба уравнения на одной координатной плоскости.
2. Найдите точки пересечения двух графиков. Точки пересечения — это ваши решения.

Это имеет смысл, потому что точки пересечения графиков уравнений — это точки, которые находятся на обоих графиках и, следовательно, удовлетворяют обоим уравнениям, что и является определением решения квадратичной системы уравнений.

Хорошо! Вернуться к работе! Давайте рассмотрим нашу систему квадратных уравнений по шагам, чтобы найти решение проблемы.

Первый шаг — изобразить два уравнения на одном графике.

График системы

Второй шаг — найти точки пересечения графиков.

Точка пересечения

Теперь, наверное, ясно, почему нам нужно использовать графический калькулятор, который делает это за нас. Не знаю, как вы, но я точно не могу определить точное значение точки пересечения, просто взглянув на нее! Слава богу, что в таких случаях есть калькуляторы! Нажимаем несколько кнопок и ва-ля! У нас есть точка пересечения!

Мы видим, что точка пересечения, имеющая смысл для задачи, находится в точке (211.69631, 386019.09) Отлично! Округление этих значений говорит нам о том, что если оба предприятия взимают 211,70 долларов за свой продукт, то они получат одинаковую прибыль в размере 386 019,09 долларов.

Алгебраическое решение

Конечно, если у вас нет под рукой утилиты для построения графиков, вы можете решить систему алгебраически. Чтобы решить эту систему алгебраически, мы выполним следующие шаги;

1. Решите оба уравнения для y или, в данном случае, P . В нашем примере этот шаг сделан за нас.

2. Приравняйте два выражения, которые вы нашли для y на шаге 1, и решите для x . В нашем примере у нас есть следующее;

-15 x 2 + 8400 x — 720000 = -12 x 2 + 4600 x — 50000

Решение этого уравнения для x и округление дает x = 211,69631 или x = 1054,970355.

3.Последний шаг — подставить значение x обратно в любое из исходных уравнений системы и найти y .

Видим, что получаем решения (211.69631, 386019.09) и (1054.97, -8552685.77). На второе решение можно не обращать внимания, так как оно дает отрицательную прибыль, а этого мы точно не хотим! Мы видим, что первое решение — это то, что мы получили, когда начертили его. Здорово!

Резюме урока

Квадратная система уравнений представляет собой набор квадратных уравнений с одинаковыми переменными.

Решение квадратичной системы уравнений состоит из значений переменных, которые делают все уравнения системы верными. Одним из способов решения квадратной системы уравнений является построение графика. Чтобы решить систему квадратных уравнений с помощью графика, мы выполняем следующие шаги;

1. Начертите оба уравнения на одной координатной плоскости.
2. Найдите точки пересечения двух графиков.Точки пересечения — это ваши решения.

При решении системы квадратных уравнений с помощью графика крайне важно использовать графическое устройство, способное находить точки пересечения графиков, чтобы исключить возможность ошибки. Если у вас нет графической утилиты, которая делает это, вы можете решить алгебраически, используя эти шаги.

1. Решите оба уравнения для y .
2. Приравняйте два выражения, которые вы нашли для y на шаге 1, и решите x .
3. Последний шаг — подставить значение x обратно в любое из исходных уравнений системы и найти y .

Компания, в которой вы работаете, будет очень рада, что вы разобрались с их проблемой! Вы должны просить повышения!

Объяснение урока: линейно-квадратичные системы уравнений

Пример 3. Решение систем линейных и квадратных уравнений для нахождения множества точек пересечения двух графиков

Найдите множество точек пересечения графиков 𝑥+5𝑦= 0 и 𝑦=−𝑥.

Ответ

Чтобы точка была на обоих графиках, ее координаты должны удовлетворять обоим уравнениям. Следовательно, для определения множества точек пересечения данных уравнений необходимо решить совместные уравнения 𝑥+5𝑦=0,𝑦=−𝑥.

Поскольку одно из данных уравнений линейное, попробуем решить эти уравнения подстановкой. Начнем с перестановки линейного уравнения, чтобы сделать 𝑥 предметом следующим образом: 𝑥+5𝑦=0𝑥=−5𝑦.

Затем мы подставляем это выражение для 𝑥 в другое уравнение и упрощаем следующим образом: 𝑦=−𝑥𝑦=−(−5𝑦)𝑦=5𝑦.

Затем мы можем решить это уравнение, переставив и разложив на множители следующим образом: 𝑦−5𝑦=0𝑦(𝑦−5)=0.

Чтобы произведение было равно нулю, один из множителей должен быть равен нулю; следовательно, у нас есть 𝑦=0𝑦=5.или

Чтобы найти 𝑥-координаты точек пересечения, мы можем подставить 𝑦-координату в уравнение для любой кривой. Поскольку 𝑥+5𝑦=0 является линейным уравнением, его будет проще использовать.

Сначала мы подставляем 𝑦=0 в уравнение, что дает нам 𝑥+5(0)=0𝑥=0.

Затем мы подставляем 𝑦=5 в уравнение, что дает нам 𝑥+5(5)=0𝑥+25=0𝑥=−25.

Это дает нам две точки пересечения: (0,0) и (−25,5).

Наконец, мы можем проверить правильность этих решений, подставив их в одновременные уравнения. Например, у нас есть 𝑥=−25 и 𝑦=5, которые мы подставляем в следующие уравнения соответственно: 𝑦=−𝑥5=−(−25)25=25,𝑥+5𝑦=0−25+5(5)=0. 

Поскольку оба уравнения верны для этих значений 𝑥 и 𝑦, мы подтвердили это является решением одновременных уравнений.Точно так же мы можем проверить решение 𝑥=0 и 𝑦=0.

Так как вопросы задают набор точек пересечения, мы запишем их в наборе как {(0,0),(−25,5)}.

Решение системы квадратных уравнений —

Если предположить, что каждое из значений с плавающей запятой, таких как 12,28, следует считать точным (например, если бы оно было записано как 1228/100), то эти уравнения несовместимы. Вы можете решить для трех переменных, а четвертая выпадет, оставив ненулевое значение на месте, которое должно быть 0, чтобы уравнения были непротиворечивыми.Другими словами, дело не в том, что четыре переменные можно переписать как три согласованные переменные: уравнение нельзя заставить работать в показанной форме.

Каждый раз, когда в уравнениях появляются значения с плавающей запятой, вам нужно остановиться и задаться вопросом, почему вы используетеsolve(). solve() предназначен для поиска точных алгебраических решений (если они существуют), но числа с плавающей запятой по своей сути неточны. Предназначен ли 12.28 для 1228/100 или он предназначен для представления некоторого значения в диапазоне 1228/100 +/- 5/1000? И теперь, имея это сомнение о том, что 12.28 на самом деле означает, действительно ли «2» в «2*r1» означает точно 2 или означает какое-то число рядом с 2? Для квадратичных уравнений решения обычно не так уж чувствительны к небольшим флуктуациям, но к тому времени, когда вы доберетесь до квартик, решения будут очень чувствительны к небольшим флуктуациям входных данных. И если у вас есть два квадратичных числа вместе, вы в значительной степени должны предположить, что у вас такая же чувствительность, как если бы вы имели дело с квартиком.

Я просмотрел ваши уравнения, изменяя член за членом, предполагая, что член не был задан точно, например, предположим, что 12.28 может быть (1228/100 + дельта) для какой-то неизвестной дельты, или 0*x*rr может быть (0+дельта)*x*rr для какой-то неизвестной дельты. Я бы изменил термин и решил выяснить, каким должен быть «шум» в термине, чтобы сделать уравнения согласованными. Например, мы могли бы предположить, что, возможно, 12,28 может привести к несогласованности, но, возможно, 12,28003582 может позволить уравнениям быть непротиворечивыми. Я проделал это для каждой возможности в термине, выясняя, насколько неправильным должен быть указанный термин, чтобы существовало решение уравнений.2 или -6994,94 должно быть около -15000, чтобы было решение. Большинство возможностей так и остались несовместимыми по своей сути. Некоторые возможности привели к последовательной серии уравнений, решения которых зависели от величины шума (которые я называл «дельта», когда решал), но в каждом из этих случаев согласованные решения включали выражения, разделенные на дельту, поэтому решения «взорвались», когда предполагаемый шум был уменьшен, что противоречит предположению о том, что в системе был лишь небольшой шум.2-25,82*x+r1*x+0*rr*x+271,28*r1+0*rr+B*bd-135,64*B-6994,94

если бы вместо 135,64 было 135,21, то уравнения можно было бы согласовать . Но это изменение на 135,64 применимо только к этой одной строке: если вы сделаете такое же изменение для 135,64 в функциях g и h, тогда уравнения снова разорвутся. А также, когда я говорю «согласованные», я имею в виду, что их можно записать в виде трех уравнений с тремя переменными без четвертого вычисления, приравнивающего два разных ненулевых значения. Во всех случаях, когда вы настраиваете коэффициент, чтобы создать непротиворечивую серию из 4 уравнений с 4 неизвестными, решения взрываются, когда предполагаемый шум сводится к нулю.

Это, кстати, изменения в 135,64 по различным строкам, которые вы, скорее всего, сможете составить последовательный ряд уравнений.

Локальная выпуклость решения систем квадратных уравнений

1

Алексеев Б., Бандейра А.С., Фикус М., Миксон Д.Г.: Восстановление фазы с поляризацией. SIAM J. Imaging Sci. 7 (1), 35–66 (2014)

Статья МАТЕМАТИКА Google Scholar

2

Балан Р.: Реконструкция сигналов по величинам избыточных представлений (2012 г.). Препринт arXiv arXiv: 1207.1134

3

Балан Р. , Бодманн Б.Г., Казацца П.Г., Эдидин Д.: Безболезненная реконструкция по величинам кадровых коэффициентов. Ж. Анал Фурье. заявл. 15 (4), 488–501 (2009)

MathSciNet Статья МАТЕМАТИКА Google Scholar

4

Балан Р., Казацца П., Эдидин Д.: При восстановлении сигнала без фазы. заявл. вычисл. Гармоничный анал. 20 (3), 345–356 (2006)

MathSciNet Статья МАТЕМАТИКА Google Scholar

5

Бенткус В.: Неравенство для хвостовых вероятностей мартингалов с разностями, ограниченными с одной стороны. Дж. Теор. Вероятно. 16 (1), 161–173 (2003)

MathSciNet Статья МАТЕМАТИКА Google Scholar

6

Чен Ю., Candes, E.: Решение случайных квадратичных систем уравнений почти так же просто, как решение линейных систем. Препринт Arxiv (2015)

7

Чен Ю., Чи Ю. , Голдсмит А.: Точная и стабильная ковариационная оценка на основе квадратичной выборки с помощью выпуклого программирования (2013). Препринт arXiv arXiv: 1310.0807

8

Candes E.J., Eldar Y.C., Strohmer T., Voroninski V.: Восстановление фазы с помощью заполнения матрицы. SIAM Rev. 57 (2), 225–251 (2015)

MathSciNet Статья МАТЕМАТИКА Google Scholar

9

Кандес Э.J., Li X.: Решение квадратных уравнений с помощью фазового подъема, когда уравнений примерно столько же, сколько неизвестных. Нашел. вычисл. Мат. 14 (5), 1017–1026 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

10

Кандес, Э., Ли, X., Солтанолкотаби, М.: Восстановление фазы с помощью потока Виртингера: теория и алгоритмы (2014). Препринт arXiv arXiv: 1407.1065

11

Чай А., Москосо М. , Папаниколау Г.: Визуализация массива с использованием измерений только интенсивности. обратная задача 27 (1), 015005 (2011)

Артикул МАТЕМАТИКА Google Scholar

12

Candes E.J., Strohmer T., Voroninski V.: Phaselift: точное и стабильное восстановление сигнала из измерений амплитуды с помощью выпуклого программирования. коммун. Чистое приложение Мат. 66 (8), 1241–1274 (2013)

MathSciNet Статья МАТЕМАТИКА Google Scholar

13

Кандес Э.Дж., Тао Т.: Почти оптимальное восстановление сигнала из случайных проекций: универсальные стратегии кодирования? IEEE транс. Сообщить. Теория 52 (12), 5406–5425 (2006)

MathSciNet Статья МАТЕМАТИКА Google Scholar

14

Демане Л., Хэнд П.: Стабильное восстановление без оптимизации из бесфазных линейных измерений. Ж. Анал Фурье. заявл. 20 (1), 199–221 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

15

Донохо Д.Л.: Сжатое зондирование. IEEE транс. Сообщить. Теория 52 (4), 1289–1306 (2006)

MathSciNet Статья МАТЕМАТИКА Google Scholar

16

Дофин, Ю.Н., Паскану, Р., Гулчере, К., Чо, К., Гангули, С., Бенжио, Ю.: Выявление и решение проблемы седловой точки в многомерной невыпуклой оптимизации. В: Достижения в системах обработки нейронной информации, стр. 2933–2941 (2014)

17

Дасарати, Г., Шах, П., Бхаскар, Б.Н., Новак, Р.: Зарисовка ковариации. В: 50-я ежегодная Аллертонская конференция по коммуникациям, управлению и вычислениям, 2012 г. (Аллертон), стр. 1026–1033. IEEE (2012)

18

Де Са, К., Олукотун, К., Ре, К.: Глобальная сходимость стохастического градиентного спуска для некоторых невыпуклых матричных задач (2014). Препринт arXiv arXiv: 1411.1134

19

Эльдар Ю., Мендельсон С.: Восстановление фаз: гарантии стабильности и восстановления. заявл.вычисл. Гармоничный анал. 36 , 473–494 (2014)

MathSciNet Статья МАТЕМАТИКА Google Scholar

20

Файнап Дж. Р.: Алгоритмы поиска фаз: сравнение. заявл. Опц. 21 , 2758–2769 (1982)

Артикул Google Scholar

21

Фикус, М., Миксон, Д.: Поиск проекций: Теория и алгоритмы. проц. SampTA, (2015)

22

Герчберг, Р.В.: Практический алгоритм определения фазы по изображениям и изображениям плоскости дифракции. Optik 35 , 237 (1972)

23

Krahmer, F., Liu, Y.-K.: Фазовый поиск без предположений вероятности смоллбола: стабильность и уникальность. SampTA (2015)

24

Куенг, Р., Раухут, Х., Терстиге, У.: Восстановление матрицы низкого ранга из измерений первого ранга (2014). Препринт arXiv arXiv: 1410.6913

25

Нетрапалли, П., Джайн, П., Сангхави, С.: Поиск фазы с использованием попеременной минимизации. В: Достижения в системах обработки нейронной информации, стр. 2796–2804 (2013)

26

Реймер М., Бек М., Макалистер Д.: Комплексная реконструкция волнового поля с использованием фазово-пространственной томографии. физ. Преподобный Летт. 72 (8), 1137 (1994)

MathSciNet Статья МАТЕМАТИКА Google Scholar

27

Рехт Б., Фазель М., Паррило П.А.: Гарантированные решения линейных матричных уравнений минимального ранга посредством минимизации ядерной нормы.SIAM Rev. 52 (3), 471–501 (2010)

MathSciNet Статья МАТЕМАТИКА Google Scholar

28

Schönemann P.H.: Обобщенное решение проблемы ортогонального прокруста. Психометрика 31 (1), 1–10 (1966)

MathSciNet Статья МАТЕМАТИКА Google Scholar

29

Солтанолкотаби, М. : Алгоритмы и теория кластеризации и невыпуклого квадратичного программирования.Кандидатская диссертация, Стэнфордский университет (2014 г.)

30

Сан, Дж., Ку, К., Райт, Дж.: Полное восстановление словаря по сфере (2015). Препринт arXiv arXiv: 1504.06785

31

Тянь Л., Ли Дж., О С.Б., Барбастатис Г.: Экспериментальная компрессионная томография фазового пространства. Опц. Экспресс 20 (8), 8296–8308 (2012)

Артикул Google Scholar

32

Tropp J.A.: Удобные хвостовые границы для сумм случайных матриц.Нашел. вычисл. Мат. 12 (4), 389–434 (2012)

MathSciNet Статья МАТЕМАТИКА Google Scholar

33

Вальдспургер И., д’Апремон А., Маллат С.: Восстановление фаз, максимальное и сложное полуопределенное программирование. Мат. Программа. 149 (1–2), 47–81 (2015)

MathSciNet Статья МАТЕМАТИКА Google Scholar

34

Ю Ю. , Ван Т., Сэмворт Р.Дж.: Полезный вариант теоремы Дэвиса-Кахана для статистиков. Биометрика 102 (2), 315–323 (2015)

MathSciNet Статья МАТЕМАТИКА Google Scholar

35

Чжан Д., Бальзано Л.: Глобальная сходимость алгоритма грассманова градиентного спуска для оценки подпространства (2015). Препринт arXiv arXiv: 1506.07405

Алгебра. Квадратные уравнения. Часть I

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-5: Квадратные уравнения — Часть I

Прежде чем перейти к этому разделу, следует отметить, что тема решения квадратных уравнений будет рассмотрена в двух разделах.2}\) в уравнении. Мы гарантируем, что этот член будет присутствовать в уравнении, требуя \(a \ne 0\). Обратите внимание, однако, что это нормально, если \(b\) и/или \(c\) равны нулю.

Существует множество способов решения квадратных уравнений. В следующих двух разделах мы рассмотрим четыре из них. Первые два метода не всегда будут работать, но, вероятно, их немного проще использовать, когда они работают. В этом разделе будут рассмотрены эти два метода. Последние два метода всегда будут работать, но часто требуют немного больше работы или внимания, чтобы получить правильный результат.Мы рассмотрим эти методы в следующем разделе.

Итак, приступим.

Решение факторингом

Как следует из заголовка, здесь мы будем решать квадратные уравнения, разлагая их на множители. Для этого нам понадобится следующий факт.

\[{\mbox{Если}}ab = 0{\mbox{тогда либо}}a = 0{\mbox{и/или}}b = 0\]

Этот факт называется свойством нулевого фактора или принципом нулевого фактора .Все дело в том, что если произведение двух слагаемых равно нулю, то по крайней мере один из слагаемых должен был быть равен нулю с самого начала.

Обратите внимание, что этот факт будет работать, ТОЛЬКО если произведение равно нулю. Рассмотрим следующий продукт.

\[аб = 6\]

В этом случае нет оснований полагать, что либо \(a\), либо \(b\) будет равно 6. Например, мы могли бы иметь \(a = 2\) и \(b = 3\). Так что не злоупотребляйте этим фактом!

Чтобы решить квадратное уравнение с помощью факторизации, мы сначала должны переместить все члены в одну часть уравнения.Это служит двум целям. Во-первых, он приводит квадратичные уравнения в форму, которую можно разложить на множители. Во-вторых, и, возможно, более важно, чтобы использовать свойство нулевого фактора, мы ДОЛЖНЫ иметь ноль на одной стороне уравнения. Если у нас нет нуля на одной стороне уравнения, мы не сможем использовать свойство нулевого фактора.

Давайте рассмотрим пару примеров. Обратите внимание, что предполагается, что вы можете провести факторинг на этом этапе, поэтому мы не будем давать никаких подробностей о факторинге.2} — x — 12 & = 0\\ \left( {x — 4} \right)\left( {x + 3} \right) & = 0\end{align*}\]

Теперь у нас есть произведение двух слагаемых, равное нулю. Это означает, что хотя бы одно из следующего должно быть истинным.

\[\begin{align*}x — 4 & = 0 & \hspace{0,25 дюйма}{\mbox{OR}}\hspace{0,25 дюйма} & & x + 3 & = 0\\ x & = 4&\hspace {0,25 дюйма}{\mbox{ИЛИ}}\hspace{0,25 дюйма} & & x & = — 3\end{align*}\]

Обратите внимание, что каждое из этих уравнений представляет собой линейное уравнение, которое достаточно легко решить.2} + 40 + 14x & = 0\\ \left( {x + 4} \right)\left( {x + 10} \right) & = 0\end{align*}\]

Теперь у нас снова есть произведение двух членов, равное нулю, поэтому мы знаем, что одно или оба из них должны быть равны нулю. Итак, технически нам нужно установить каждую из них равной нулю и решить. Однако обычно это достаточно легко сделать в уме, поэтому с этого момента мы будем решать это в уме.

Решения этого уравнения:

\[х = — 4\hspace{0.2} & = 0\\ \left( {y + 6} \right)\left( {y + 6} \right) & = 0\end{align*}\]

В этом случае у нас есть идеальный квадрат. Мы разбили квадрат, чтобы обозначить, что у нас действительно есть применение свойства нулевого фактора. Однако обычно мы этого не делаем. Обычно мы сразу переходим к ответу из возведенной в квадрат части.

Решение уравнения в этом случае

\[у = — 6\]

Здесь у нас есть только одно значение, в отличие от двух решений, которые мы получили до этого момента.2} — 1 & = 0\\ \left( {2m — 1} \right)\left( {2m + 1} \right) & = 0\end{align*}\]

Теперь примените свойство нулевого коэффициента. Свойство нулевого фактора говорит нам, что

\[\begin{align*}2 м — 1 & = 0 & \hspace{0,25 дюйма}{\mbox{ИЛИ}}\hspace{0,25 дюйма} & & 2 м + 1 & = 0\\ 2 м & = 1 & \ hspace{0,25 дюйма}{\mbox{ИЛИ}}\hspace{0,25 дюйма} & & m & = — 1\\ m & = \frac{1}{2} & \hspace{0,25 дюйма}{\mbox{ИЛИ }}\hspace{0,25 дюйма} & & m & = — \frac{1}{2}\end{align*}\]

Опять же, мы, как правило, решаем их в уме, но нам нужно было сделать хотя бы одно в деталях. 2} — 2х = 0\]

Теперь заметьте, что все, что мы можем сделать для разложения на множители, это разложить на множители \(x\) всего. Выполнение этого дает,

\[х\влево( {5x — 2} \вправо) = 0\]

Из первого множителя получаем, что \(x = 0\), а из второго получаем, что \(x = \frac{2}{5}\). Это два решения этого уравнения. Обратите внимание: если бы мы отменили \(x\) на первом шаге, мы НЕ получили бы \(x = 0\) в качестве ответа!

Давайте поработаем над другим типом задач.Мы видели некоторые из них еще в разделе «Решение линейных уравнений», и, поскольку они также могут встречаться с квадратными уравнениями, мы должны продолжить и поработать над тем, чтобы убедиться, что мы можем делать их и здесь.

Пример 2. Решите каждое из следующих уравнений.

1. \(\displaystyle \frac{1}{{x + 1}} = 1 — \frac{5}{{2x — 4}}\)
2. \(\displaystyle x + 3 + \frac{3}{{x — 1}} = \frac{{4 — x}}{{x — 1}}\)

Показать все решения Скрыть все решения Показать обсуждение

Итак, как и в случае с линейными уравнениями, первое, что нам нужно сделать, это очистить знаменатели, умножив их на ЖКИ. Напомним, что нам также нужно будет отметить значения \(x\), которые дадут деление на ноль, чтобы мы могли убедиться, что они не включены в решение.

a \(\displaystyle \frac{1}{{x + 1}} = 1 — \frac{5}{{2x — 4}}\) Показать решение

ЖКИ для этой проблемы: \(\left( {x + 1} \right)\left( {2x — 4} \right)\), и нам нужно избегать \(x = — 1\) и \( x = 2\), чтобы убедиться, что мы не получили деление на ноль. Вот работа для этого уравнения.2} — 9x — 5\\ 0 & = \left( {2x + 1} \right)\left( {x — 5} \right)\end{align*}\]

Итак, похоже, два решения этого уравнения таковы:

\[x = — \frac{1}{2}\,\,\,\,\,\,\,{\mbox{and}}x = 5\]

Заметьте также, что ни одно из этих значений не является тем значением \(x\), которого нам нужно было избежать, и поэтому оба являются решениями.

b \(\displaystyle x + 3 + \frac{3}{{x — 1}} = \frac{{4 — x}}{{x — 1}}\) Показать решение

В этом случае LCD равно \(x — 1\), и нам нужно будет избегать \(x = 1\), чтобы не получить деление на ноль. 2} + 3x — 4 & = 0\\ \left( {x — 1} \right)\left( {x + 4} \right) & = 0\end{align*}\]

Итак, квадратное уравнение, которое мы разложили на множители и решили, имеет два решения: \(x = 1\) и \(x = — 4\). Однако, когда мы нашли LCD, мы также увидели, что нам нужно избегать \(x = 1\), чтобы мы не получили деление на ноль. Следовательно, это уравнение имеет единственное решение,

\[х = — 4\]

Перед тем, как перейти к следующей теме, следует обратить внимание на то, что идея разложения на множители может быть использована и для решения уравнений со степенью больше двух.2} — x — 2} \right) & = 0\\ 5x\left( {x — 2} \right)\left( {x + 1} \right) & = 0\end{align*}\]

Теперь свойство нулевого множителя останется в силе. В этом случае у нас есть произведение трех слагаемых, равное нулю. Единственный способ, которым этот продукт может быть равен нулю, — это если один из членов равен нулю. Это означает, что

\[\begin{align*}5x & = 0\hspace{0. 2} = d{\mbox{тогда}}p = \pm \sqrt d \]

Здесь есть (потенциально) новый символ, который мы должны сначала определить, если вы его еще не видели.Символ «\( \pm \)» читается как: «плюс или минус» и именно это он нам и говорит. Этот символ является сокращением, которое говорит нам, что у нас действительно есть два числа. Один из них \(p = \sqrt d \), а другой — \(p = — \sqrt d \). Привыкайте к этому обозначению, так как оно будет часто использоваться в следующих парах разделов, когда мы будем обсуждать оставшиеся методы решения. Он также возникнет в других разделах этой главы и даже в других главах.

Это довольно простое свойство, однако его можно использовать только в небольшой части уравнений, с которыми мы когда-либо столкнемся.2} & = \frac{3}{{25}}\hspace{0,25 дюйма} \Rightarrow \hspace{0,25in}y = \pm \sqrt {\frac{3}{{25}}} = \pm \ frac{{\sqrt 3}}{5}\end{align*}\]

В этом случае решения немного запутаны, но многие из них подойдут, так что не беспокойтесь об этом. 2} = 5\) Показать решение

Внешне отличается от предыдущих частей, но работает точно так же.Свойство квадратного корня можно использовать в любое время, когда у нас есть , где в квадрате равно числу. Это то, что мы имеем здесь. Основное отличие, конечно, в том, что нечто, что возводится в квадрат, — это не одна переменная, а что-то другое. Итак, вот применение свойства квадратного корня для этого уравнения.

\[2t — 9 = \pm \sqrt 5 \]

Теперь нам просто нужно найти \(t\), и, несмотря на «плюс-минус» в уравнении, оно работает так же, как мы решаем любое линейное уравнение.Мы добавим 9 к обеим сторонам, а затем разделим на 2.

\[\begin{align*}2t & = 9 \pm \sqrt 5 \\ t & = \frac{1}{2}\left( {9 \pm \sqrt 5 } \right) = \frac{9} {2} \pm \frac{{\sqrt 5}}{2}\end{align*}\]

Обратите внимание, что мы умножили дробь через скобки для окончательного ответа. Обычно мы будем делать это в этих задачах. Кроме того, НЕ конвертируйте их в десятичные числа, если вас об этом не попросят. Это стандартная форма для этих ответов.2} & = — 81\\ 3x + 10 & = \pm \,9\,i\\ 3x & = — 10 \pm \,9\,i\\ x & = — \frac{{10}}{ 3} \pm 3\,i\end{выравнивание*}\]

Итак, мы снова получили два сложных решения, и обратите внимание, что в обеих предыдущих частях мы поставили часть «плюс или минус» последней. Обычно так пишут.

Как упоминалось в начале этого раздела, мы разобьем эту тему на две части для удобства тех, кто просматривает ее в Интернете.Следующие два метода решения квадратных уравнений, завершающие формулу квадрата и квадрата, приведены в следующем разделе.

Решатель квадратных одновременных уравнений

Бесплатный онлайн-решатель квадратных уравнений, который решает любую систему уравнений, показывает все действия шаг за шагом. Прежде чем мы углубимся в то, как работает онлайн-решатель, давайте немного познакомимся с тем, что квалифицируется как квадратное уравнение. В частности, мы будем рассматривать систему квадратного и линейного уравнений

Линейное уравнение — это уравнение вида y=ax+b, где степень переменной x равна единице.2)=1,у=2х-5

Бесплатная программа для решения квадратных уравнений с шагами

При решении системы линейных и квадратных уравнений с помощью онлайн-решателя вам нужно больше, чем просто ответы. Наш онлайн-калькулятор дает вам пошаговое решение вашей системы уравнений. Калькулятор можно использовать для решения любых систем уравнений, линейных, квадратных или их комбинации. Кроме того, калькулятор системы уравнений помогает быстро и точно найти решение линейной или квадратичной системы уравнений.Кроме того, калькулятор позволяет использовать любое количество переменных и до 5 уравнений.

Лучшим способом представить решение системы уравнений является использование графиков. Решатель EquationCalc для одновременных уравнений также имеет графический инструмент для графического представления решения для одновременных уравнений.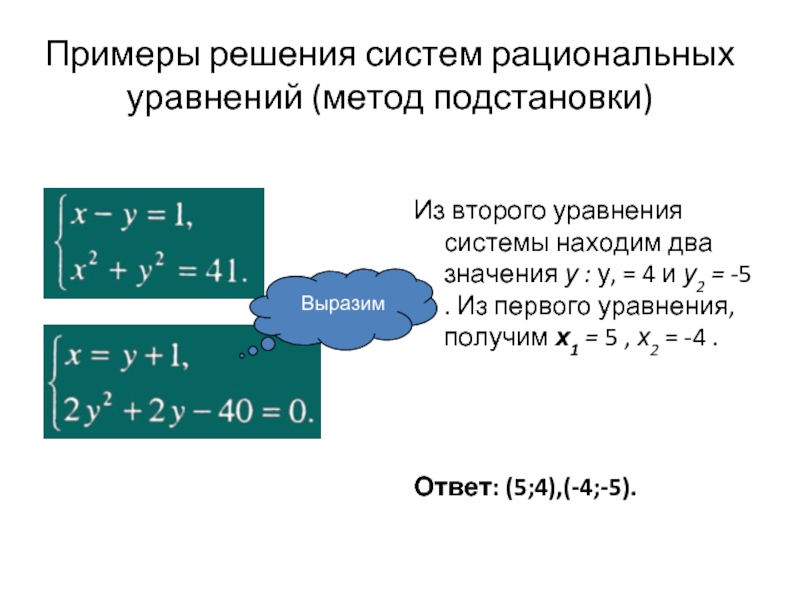

При решении системы линейных и квадратных уравнений обычно дается 2 пары ответов. В основном, квадратика представляет кривые конического сечения, такие как круг, парабола, эллипс и гипербола.С другой стороны, линейное уравнение представляет собой линию на плоскости. Следовательно, решением системы будут точки пересечения графиков двух уравнений. Решатель квадратных уравнений с шагами

Решение одновременных уравнений онлайн с помощью онлайн-калькулятора алгебры EquationCalc выполняется быстро и точно. Кроме того, калькулятор показывает вам все действия и пояснения о том, как получить решения. Калькулятор метода подстановки одновременных уравнений

Решение системы уравнений, состоящей из линейного и квадратного уравнений, методом подстановки.2+х-2х-2=0

х(х+1)-2(х+1)=0

(х-2)(х+1)=0

\Стрелка вправо x-2=0 Или x+1=0 \Стрелка вправо1 x=2, Или x=-1

Используя приведенные выше пары решений, вы можете найти значение или y, подставив значение x в уравнение 1. 2+x-2x-2=0

Посмотреть больше Перейти к решаемым примерам алгебры с шагами

Вы также можете использовать наш решатель систем линейных уравнений: Решатель систем уравнений

Работающий решатель одновременных линейных уравнений

Бесплатная онлайн-система решения уравнений, работает с линейными нелинейными уравнениями до 5 переменных.Этот онлайн-калькулятор алгебры поможет вам найти решение любой системы уравнений. Это работает для любых систем уравнений. Калькулятор бесплатный и поставляется с премиальным пакетом для тех, кому нужно больше, чем просто решение. Премиум-пакет дает вам доступ к пошаговому решению, включая объяснение того, как был получен ответ. Решите для x и y одновременно онлайн, используя онлайн-калькуляторы EquationCalc.

Калькулятор одновременных линейных уравнений с двумя переменными

Чтобы решить систему линейных уравнений с 2 ​​переменными, вам потребуется как минимум 2 уравнения.Точно так же, чтобы решить систему с тремя переменными, необходимо иметь как минимум 3 уравнения. Таким образом, вы не можете решить систему уравнений, если количество переменных больше, чем количество уравнений. Такие системы не имеют решений. Кроме того, система уравнений также может не иметь решения, если графики полученных уравнений не пересекаются ни в одной заданной точке

Одновременный решатель уравнений с рабочим

Калькулятор алгебры EquationCalc для системы уравнений не похож ни на один другой онлайн-калькулятор.Калькулятор показывает вам всю работу через пошаговую стратегию решения. Это онлайн-решатель систем уравнений. Он показывает все работы, включая пошаговое решение.

Как использовать онлайн-решатель одновременных уравнений EquationsCalc

Как это работает

Вот рабочий пример, иллюстрирующий, как работает одновременный калькулятор:

Пользоваться калькулятором очень легко и просто.

Следующие шаги иллюстрируют, как найти решения для квадратных уравнений онлайн.

Шаг 1: Введите пары или уравнения, разделенные запятой (,) или точкой с запятой (;). (Обратите внимание, если вы не введете разделитель, калькулятор выдаст ошибку.

Шаг 2: Убедившись, что введенные данные верны, нажмите кнопку «Рассчитать сейчас», чтобы получить мгновенное решение.

Шаг 3: Используйте решение: Получив решение, вы можете применить его по своему усмотрению для решения своих заданий или любых математических задач.Вы можете скопировать или распечатать решение для дальнейшего использования.

Узнайте, как алгебраически решать квадратные уравнения для одновременных уравнений, используя примеры

.

Возможно, будет лучше, если вы будете изучать математику на примерах. Ознакомьтесь с нашими примерами алгебры, каждый из которых содержит пошаговое решение. Примеры также помогут вам использовать этот калькулятор уравнений для решения ваших задач по алгебре.

Перейти к примерам решенных квадратных уравнений с шагами

Допустимые математические символы и их использование Если вы решите написать свои математические выражения, вот список допустимых математических символов и операторов. Используется для экспоненты или для возведения в степень

sqrtКвадратный корень

Pi : Представляет математическую константу pi или \pi

Что еще или каковы ограничения онлайн калькулятора алгебры

Нам приятно слышать ваши отзывы. Если у вас возникнут проблемы при использовании этого калькулятора, сообщите нам об этом: Хотите увидеть больше возможностей? Присылайте нам свои рекомендации и идеи приложений. Мы всегда прилагаем все усилия, чтобы сделать алгебру легкой и увлекательной.

.