Решение задач и уравнений (продолжение). Видеоурок. Алгебра 10 Класс

На уроке рассматривается методика решения однородных тригонометрических  уравнений второй и первой степени, решаются уравнения с применением данной методики.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»

Тема: Преобразование тригонометрических выражений

Урок: Решение задач и уравнений (продолжение)

На уроке рассматривается методика решения однородных тригонометрических  уравнений второй и первой степени, решаются задачи и уравнения с применением данной методики.

Определение: уравнение вида

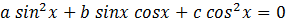
называется однородным тригонометрическим уравнением второй степени относительно функций синус и косинус.

Пример: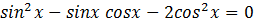      

,

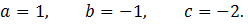
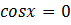· Разделить обе части уравнения на старшую степень одной из функций, например, , рассмотрев оба случая, т.е. когда  и когда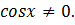

· Решить полученное квадратное уравнение относительно тригонометрической функции.

Решить уравнение:

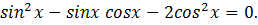
Решение:

1-й случай.

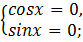
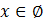, т.к.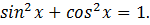

2-й случай.

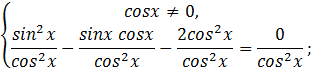
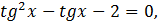
Ответ: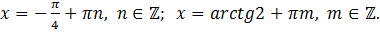

Решить уравнение:

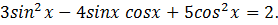
Решение: данное уравнение равносильно

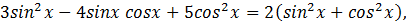
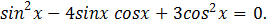
Применяя методику решения для полученного однородного уравнения, имеем:

Первая система не имеет решений, вторая дает совокупность двух уравнений

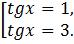
Ответ: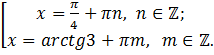

Определение: уравнение вида

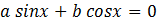
называется однородным тригонометрическим уравнением первой          степени относительно функций синус и косинус.

Пример: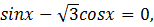    

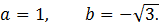
Решение примера однородного тригонометрического уравнения первой степени выполняется по аналогичной методике.

1)    

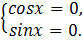
Решение системы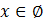   

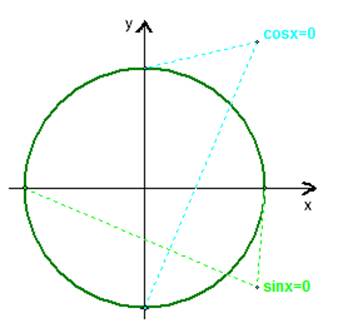
  проиллюстрировано на рисунке 1.

Рис. 1.

2)    

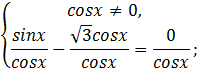
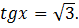
Ответ:

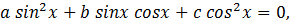
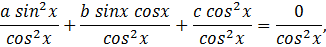
1) Решить уравнение:

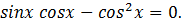
Решение: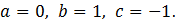

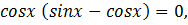
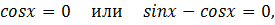
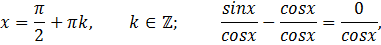
Ответ: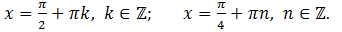

2) Решить уравнение:

Решение: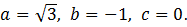

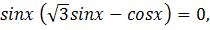
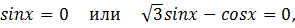
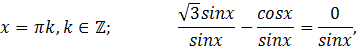
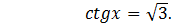
Ответ: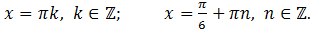

3) Решить уравнение:

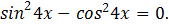
Решение:

1-й способ.

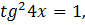
Объединяя решения (см. рис. 2), получим:

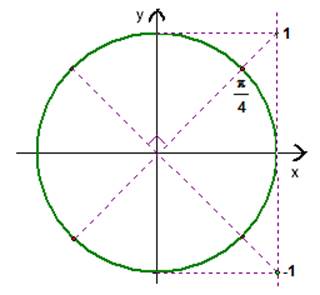
Рис. 2.

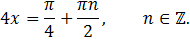
Ответ: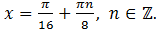

2-й способ.

Используя формулы понижения степени, получаем:

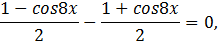
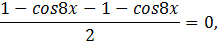
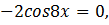
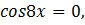
Ответ: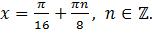

На уроке рассматривались решения однородных уравнений.

На следующем уроке продолжается решение задач и уравнений.

 

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Звавич Л.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

 

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник). 

2. Портал Естественных Наук (Источник). 

3. Интернет-портал exponenta.ru (Источник).  

 

Сделай дома

№№ 23.14(а, б), 23.15(a), 23.17(a) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)

interneturok.ru

Методы решения тригонометрических уравнений. Алгебра, 10 класс: уроки, тесты, задания.

1.	Тригонометрическое уравнение вида sinx = a Сложность: лёгкое	2
2.	Тригонометрическое уравнение вида cosx = a Сложность: лёгкое	2
3.	Тригонометрическое уравнение вида tgx = a Сложность: лёгкое	2
4.	Тригонометрическое уравнение вида sin5x = a Сложность: среднее	3
5.	Уравнение (разложение на множители, sin, cos) Сложность: среднее	3
6.	Уравнение (использование формулы двойного угла) Сложность: среднее	4
7.	Уравнение (разложение на множители, sin, tg) Сложность: сложное	3
8.	Уравнение (введение новой переменной, sin) Сложность: сложное	2
9.	Уравнение (введение новой переменной, tg) Сложность: среднее	2
10.	Уравнение (равенство произведения нулю) Сложность: сложное	2

www.yaklass.ru

«Решение рациональных уравнений». 10-й класс

Основные методы решения уравнений высших степеней — замена переменной и разложение на множители, а также нетрадиционные методы, которые являются наиболее сложными для учащихся.

Определения:

Уравнения вида где называются биквадратными.

Уравнения вида называются возвратными, если его коэффициенты, одинаково удалённые от начала и конца равны между собой.

Уравнения вида где называются симметричными уравнениями третьей степени.

Уравнения вида где называются симметричными уравнениями четвёртой степени.

Уравнение вида называются однородным уравнением степени k относительно u и v, если — однородный многочлен степени k, то есть степень каждого его члена равна одному и тому же числу k.

Однородные уравнения относительно u и v обладают тем свойством, что если разделить всё уравнение на наивысшую степень одной из переменных, например, u (если u=0 не является корнем уравнения), то оно становится уравнением с одной переменной

Теорема. Если целое рациональное уравнение с целыми коэффициентами имеет целые корни, то оно являются делителями свободного члена уравнения.

Теорема. Если уравнение с целыми коэффициентами имеет рациональный корень где - несократимая дробь, то p – делитель свободного члена, а q – делитель старшего члена.

1. Разложение на множители.

Решение уравнений тесно связано с разложением левой части на множители. Полезно вспомнить различные приёмы разложения многочленов на множители:

Вынесение общего множителя за скобки.

Применение формул сокращённого умножения.

Способ группировки.

Применение теоремы Безу.

Из “Сборника задач 8-9” М. Л Галицкого можно предложить задания № 9. 1-9. 3.

2. Замена переменной.

Метод введения новой переменной заключается в том, что для решения уравнения вводят новую переменную (подстановку) и выражают через y, получая новое уравнение

После этого получают совокупность уравнений, из которых находят корни исходного уравнения.

Решим уравнение:

Пусть , тогда

Ответ: -6; -2; -4

3. Биквадратные уравнения.

Для решения уравнение вида где надо сделать подстановку найти корни и квадратного уравнения и решить уравнения и

Решим уравнение:

Пусть тогда

Ответ: -1; 1.

4. Возвратные уравнения.

Уравнения вида можно решить, введя новую переменную

Решим уравнение:

Так как x=0 не является корнем уравнения, то разделим обе части уравнения на x². Получим:

Пусть тогда

Ответ:

Из “Сборника задач 8-9” М. Л Галицкого можно предложить задания № 9. 25.

5. Симметричные уравнения

В уравнении вида где разделим обе части уравнения на x², так как^{x=0 не является корнем уравнения, и сделаем замену}

Решим уравнение:

Это уравнение является симметричным уравнением четвёртой степени. Так как x=0 не является корнем уравнения, то разделив обе части на x² получим:

Пусть тогда:

Ответ: 1;

Из “Сборника задач 8-9” М. Л Галицкого можно предложить задания № 9. 24.

6. Однородные уравнения.

Однородные уравнения обладают тем свойством, что если разделить все члены уравнения на наивысшую степень одной из переменных, то оно превращается в уравнение с одной переменной.

Решим уравнение:

Пусть тогда получим:

Затем,

Ответ: 1.

Из “Сборника задач 8-9” М. Л Галицкого можно предложить задания № 9. 26; № 9. 27.

7. Метод неопределённых коэффициентов.

Довольно часто трудно увидеть требуемую группировку или формулу. Тогда можно сделать попытку реализовать метод разложения — метод неопределённых коэффициентов.

Рассмотрим уравнение четвёртой степени. Многочлен четвёртой степени можно разложить на множители так:

Решим уравнение

Учитывая сделанные выше рассуждения составим систему:

Так как произведение двух целых чисел равно 5, то b=1, d=-5 или b=-1, d= -5. Решением системы является a=-1, b=-1, c=2, d=-5. Тогда данное уравнение можно записать так:

Ответ:

Для успешного изучения материала можно включить следующие уравнения:

Материал этой статьи поможет при подготовке к урокам по данной теме в математических классах или работы математического кружка.

urok.1sept.ru

Тригонометрические уравнения. Алгебра, 10 класс: уроки, тесты, задания.

Вход Вход Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Новости Переменка Отправить отзыв

• Предметы
• Алгебра
• 10 класс

1. Арккосинус и решение уравнения cos х = a

2. Арксинус и решение уравнения sin x = a

3. Арктангенс и арккотангенс. Решение уравнения tg x = a, ctg x = a

4. Методы решения тригонометрических уравнений

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2019 ООО ЯКласс Контакты Пользовательское соглашение

www.yaklass.ru