Решение задач с применением процентов, 8 класс
эЗадачи для 1 ряда
Задача 1. Шоколад — вкусный и изысканный десерт, любимый многими. Самый полезный тёмный шоколад. Его польза основана на положительных свойствах какао-бобов. Употребление какао стимулирует мозговое кровообращение; активизирует выработку гормона радости; укрепляет стенки сосудов; уменьшает риск инсульта. Но большое количество кофеина в горьком шоколаде приводит к возбуждению нервной системы, нарушению сна, появлению изжоги. Кроме того, не все любят тёмный шоколад из-за характерной горечи. Кондитерская фабрика производит два вида шоколада с содержанием какао: 25% (молочный) и 70% (горький). В каком отношении надо смешать молочный и горький шоколад, чтобы получился шоколад, содержащий 45% какао?
Задача 2. Молоко и мороженное содержат по 15 г. жира, при их смешивании получилось 600г молочного коктейля. Определите массу молока и мороженного, если известно, что процентное содержание жира в мороженном на 12% больше, чем в молоке.
Задача 3. Какую массу воды надо добавить к водному раствору соды массой 90кг, содержащему 5% соды, чтобы получить раствор, содержащий 3% соды
__________________________________________________________________________
Задачи для 2 ряда
Задача 1. Ни один Новый год не обходится без цветной палитры фейерверков. Но из-за лёгкой воспламеняемости этих веществ, ни в коем случае нельзя хранить их в домах в больших количествах. Для тушения пожаров часто применяют воздушно-механические пены. В среднем, воздушно-механическая пена – смесь воздуха (90%), заключенного в пузырьки пенообразователя (10%). Высокократная воздушно — механическая пена содержит 98% воздуха, и 2% пенообразователя. Сколько грамм пенообразователя надо добавить к 400 г 10% пены, чтобы она стала высокократной?
Задача 2. Молоко и мороженное содержат по 15 г. жира, при их смешивании получилось 600г молочного коктейля. Определите массу молока и мороженного, если известно, что процентное содержание жира в мороженном на 12% больше, чем в молоке.
Задача 3. Свежий виноград содержит 80% воды, а сухой – 15% воды. Сколько получится сухого изюма из 25 кг винограда?
Задачи для 3 ряда
Задача 1. Для приготовления новогоднего печенья очень часто используется молоко. Хозяйки всегда сталкиваются с затруднениями, когда им приходится решать подобные задачи: Сколько литров молока жирностью 2,5% надо смешать со сливками жирностью 6%, чтобы получилось 5 литров молока жирностью 4,6%.
Задача 2. Молоко и мороженное содержат по 15 г. жира, при их смешивании получилось 600г молочного коктейля. Определите массу молока и мороженного, если известно, что процентное содержание жира в мороженном на 12% больше, чем в молоке.
Задача 3. Сколько грамм воды надо добавить к 200 г 40% раствора уксусной кислоты, чтобы раствор стал 10%?
__________________________________________________________________________
Лист оценивания учащегося
ФИ учащегося______________________________________
Оценка за урок
8-9 баллов — пятёрка
6 -7 баллов – четвёрка
4-5 баллов – тройка
Менее 3 баллов — двойка
__________________________________________________________________________
Лист оценивания учащегося
ФИ учащегося______________________________________
Оценка за урок
8-9 баллов — пятёрка
6 -7 баллов – четвёрка
4-5 баллов – тройка
Менее 3 баллов — двойка
Лист оценивания учащегося
ФИ учащегося______________________________________
Оценка за урок
8-9 баллов — пятёрка
6 -7 баллов – четвёрка
4-5 баллов – тройка
Менее 3 баллов — двойка
__________________________________________________________________________
Лист оценивания учащегося
ФИ учащегося______________________________________
Оценка за урок
8-9 баллов — пятёрка
6 -7 баллов – четвёрка
4-5 баллов – тройка
Менее 3 баллов — двойка
__________________________________________________________________________
Лист оценивания учащегося
ФИ учащегося______________________________________
Оценка за урок
8-9 баллов — пятёрка4-5 баллов – тройка
6 -7 баллов – четвёркаМенее 3 баллов — двойка
Домашнее задание:
Решить уравнения: 2х2-50х=0; (х-1)2- 1 =0; (х+2)2- 4 =0; х2+ 20х + 91 =0.
Решить задачу: Два раствора, из которых первый содержит 800г спирта, а второй 600г соединили и получили 10 кг спирта. Определить массу первого и второго растворов, если известно, что процент содержания спирта в первом растворе на 10% больше, чем процентное содержание спирта во втором растворе.
Решить уравнения: х2-5\х\ = 0; 3х2 + 4\х\ = 0; 4х2 – 3\х\+х= 0.
Найти все значения а, при которых уравнение 3х2+ (а- 1)х + 1-а2=0.
infourok.ru
Текстовые задачи на проценты. Решение задач 1-3
Решение текстовых задач на проценты
Задачи 1 — 3
Весь список текстовых задач на проценты здесь.
- Условие задачи: Учитель зарабатывает на 25% меньше, чем профессор. На сколько процентов больше, чем учитель, зарабатывает профессор?
Решение: Пусть — зарплата профессора, тогда — зарплата учителя, так как по условию он зарабатывает на 25% меньше профессора, то есть зарплата профессора составляет 100%. Далее за 100% берем зарплату учителя. Тогда зарплата профессора составляет % зарплаты учителя, что на % больше.
Ответ: 100/3 % - Условие задачи: Найти число, если известно, что 25% его равны 45% от 640 000.
Решение: 45% от 640 000 равны . И это 25% от неизвестного числа. Тогда само число есть 100%, то есть в 4 раза больше (). Поэтому ответом является число .
Ответ: 1152000 - Условие задачи: После двух последовательных повышений зарплата возросла в раза. На сколько процентов повысилась зарплата в первый раз, если второе повышение было в процентном отношении вдвое больше первого?
Решение: Пусть первоначально зарплата составляла р. Значит, после двукратного повышения она стала равной р. Если в первый раз зарплата повысилась на p %, то во второй раз она повысилась на 2p%. Применим формулу сложных процентов. Тогда . Сократим на и введем замену , получим уравнение , то есть . Откуда или . Второе значение не удовлетворяет условию задачи.
Метки решение, текстовые задачи. Смотреть запись.
www.itmathrepetitor.ru
Урок «Решение задач на проценты»
Урок «Задачи на проценты».
Цель урока: сформировать умение решать задачи на проценты: находить процент от величины, величину по проценту, выработать общий алгоритм решения.
Задачи урока:
обучающая – научить различать типы задач на проценты и решать задачи по алгоритму арифметическим способом;
развивающая – вырабатывание навыков применять полученные знания в различных ситуациях, развитие мышления;
-
воспитательная – формирование способности к самообразованию.
Тип урока: урок объяснения нового материала.
Форма работы на уроке: фронтальная, коллективная, самостоятельная.
Методы обучения: наглядные, словесные, практические.
Оборудование: компоненты УМК «Сферы. Математика. 5-6», (Е.А.Бунимович и др.), интерактивная доска, проектор, ноутбук, презентация.
План урока:
Организационный этап (1 минута)
Этап актуализации знаний (7 минут)
Объяснение нового материала (15 минут)
Физкультминутка (2 минуты)
Закрепление полученных знаний (13 минут)
Домашнее задание (1 минута)
Рефлексия (1 минута)
Формируемые универсальные учебные действия:
Познавательные УУД: сформировать умения производить процентные вычисления, необходимые для применения в практической деятельности.
Коммуникативные и личностные УУД: умение слушать и вступать в диалог, участие в коллективном обсуждении проблем, воспитание активности и аккуратности.
Регулятивные УУД: выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Таблица 2.1. Технологическая карта урока.
Включает на МД презентацию. Предлагает упражнения устного счета для перевода десятичной дроби в процент, и процента в десятичную дробь.Вызывает одного учащегося для заполнения таблицы на интерактивной доске.
Поочередно отвечают на поставленные вопросы. Переводят десятичную дробь в процент и процент в десятичную дробь. Исправляют неправильно полученные ответы.
Перечерчивают таблицу в тетрадь и заполняют её.
Объяснение нового материала (15 минут)

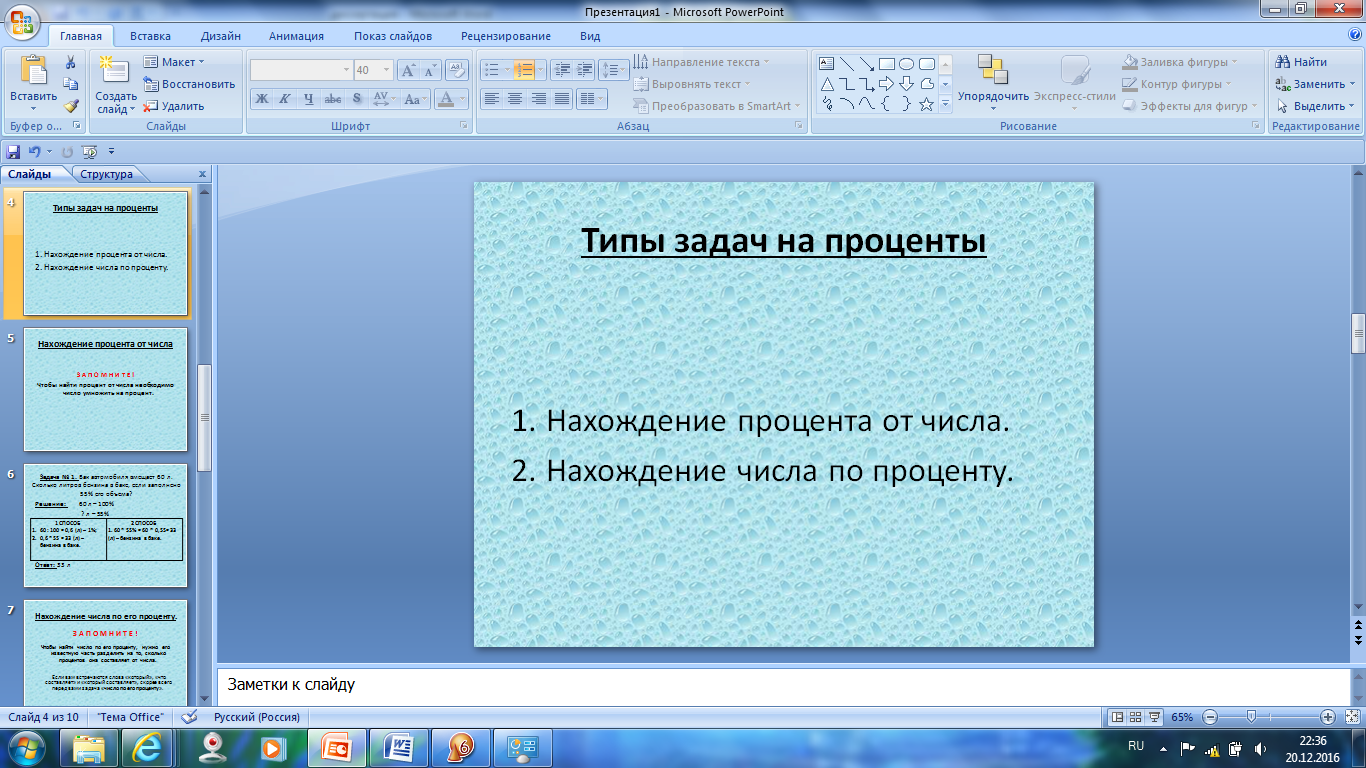

Рассказывает о типах задач на проценты, алгоритмы их решения, демонстрирует с помощью презентации примеры решения задач.
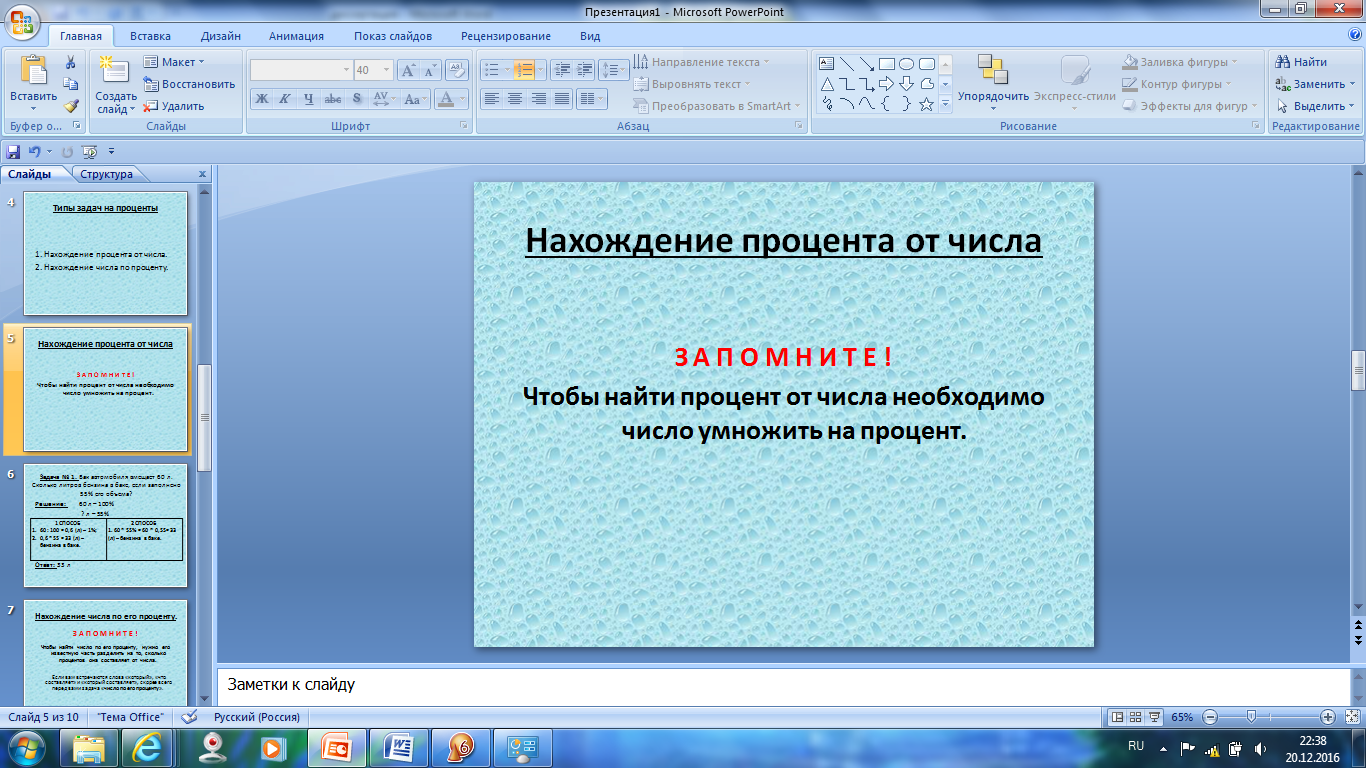
Объясняет алгоритм решения задачи по нахождению процента от числа.
Показывает решение элементарной задачи несколькими способами.
Объясняет алгоритм решения задачи по нахождению числа по его проценту.
Смотрят презентацию, записывают в тетрадь алгоритмы решения задач на проценты, задают вопросы.
Записывают способы решения задачи по нахождению процента от числа.
Принимают участие в обсуждении задачи, задают вопросы.
Записывают алгоритм решения задачи по нахождению числа по его проценту.
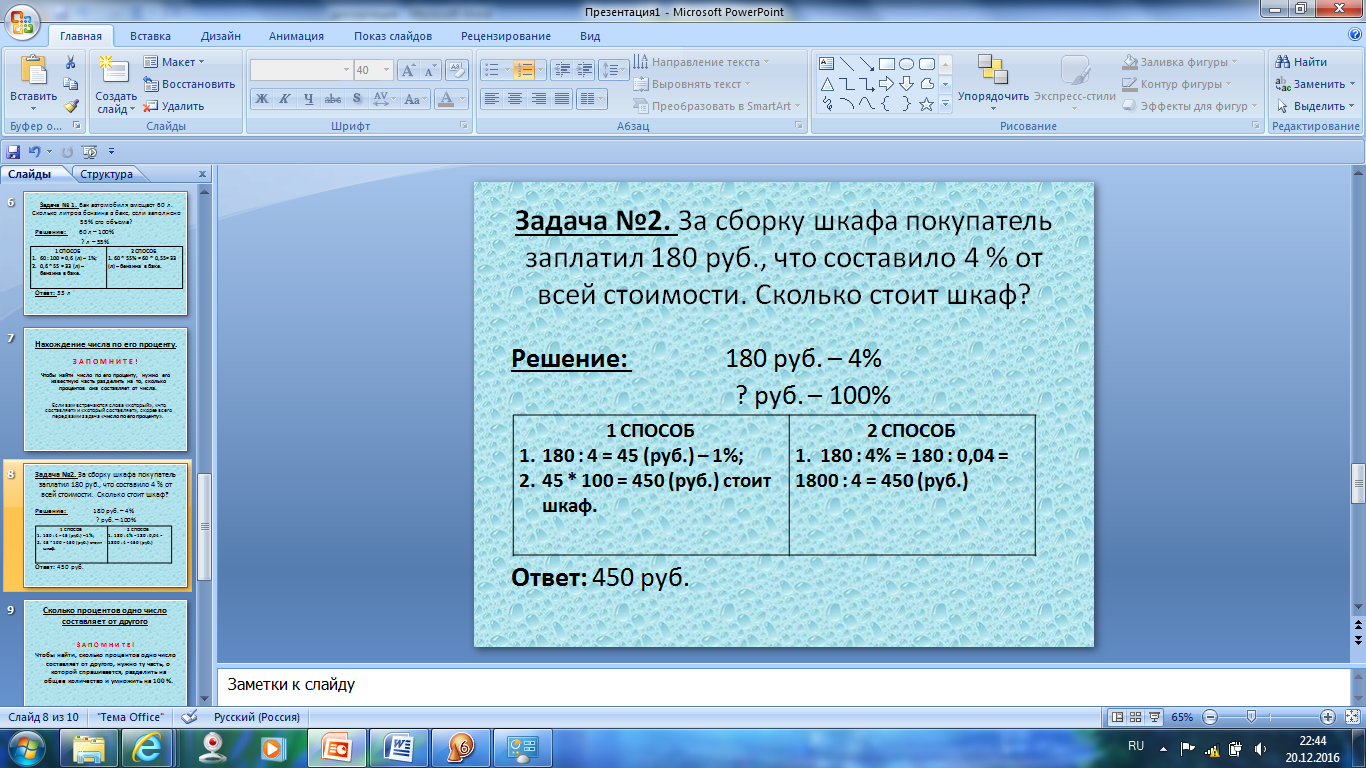
Объясняет решение простейшей задачи несколькими способами.
Принимают участие в обсуждении, задают вопросы.
Физкультминутка (2 минуты)
Вызывает к доске одного учащегося для демонстрации физических упражнений для профилактики переутомления.
Повторяют за одноклассниками комплекс физических упражнений.
Закрепление полученных знаний (13 минут)
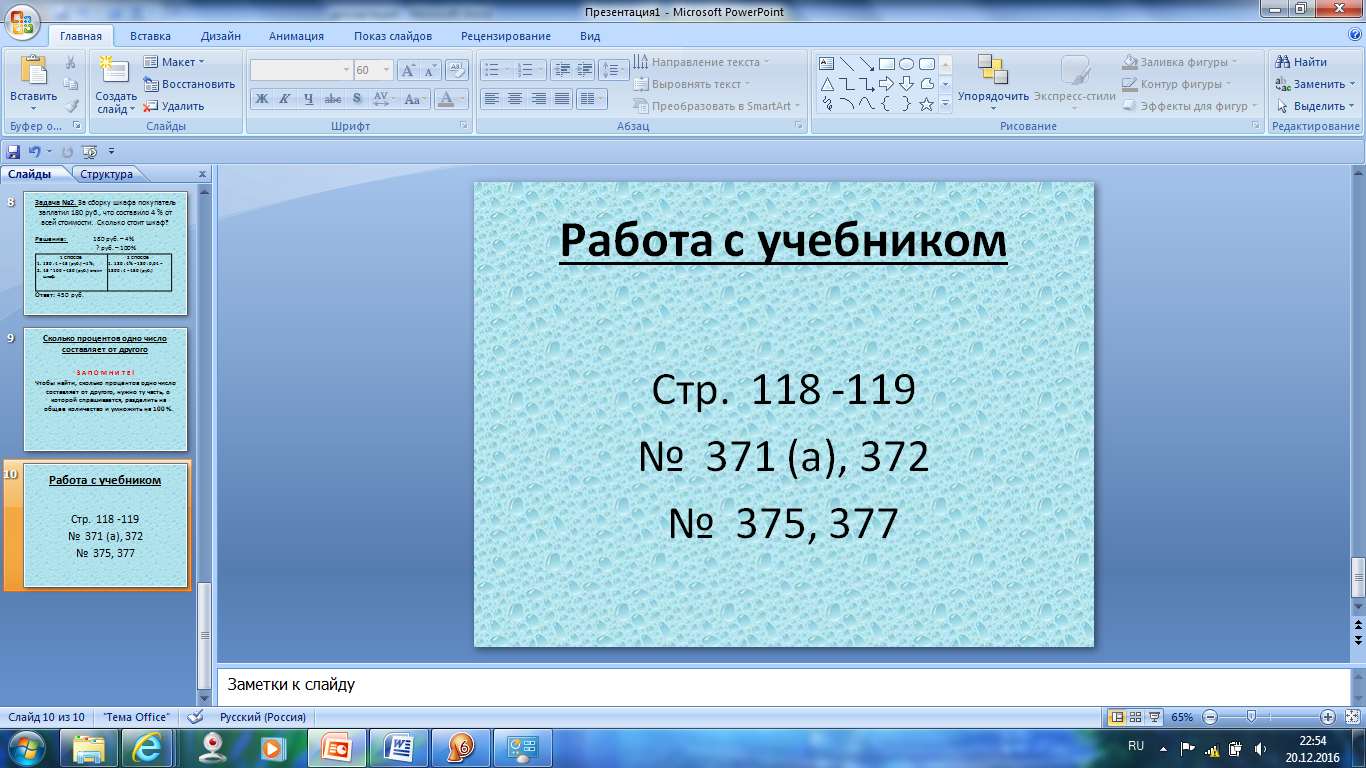
Вызывает учащихся к доске для решения типовых задач на проценты (нахождения числа по проценту и процента от числа)
Выходят к доске, решают задачи, задают интересующие вопросы.
Домашнее задание (1 минута)
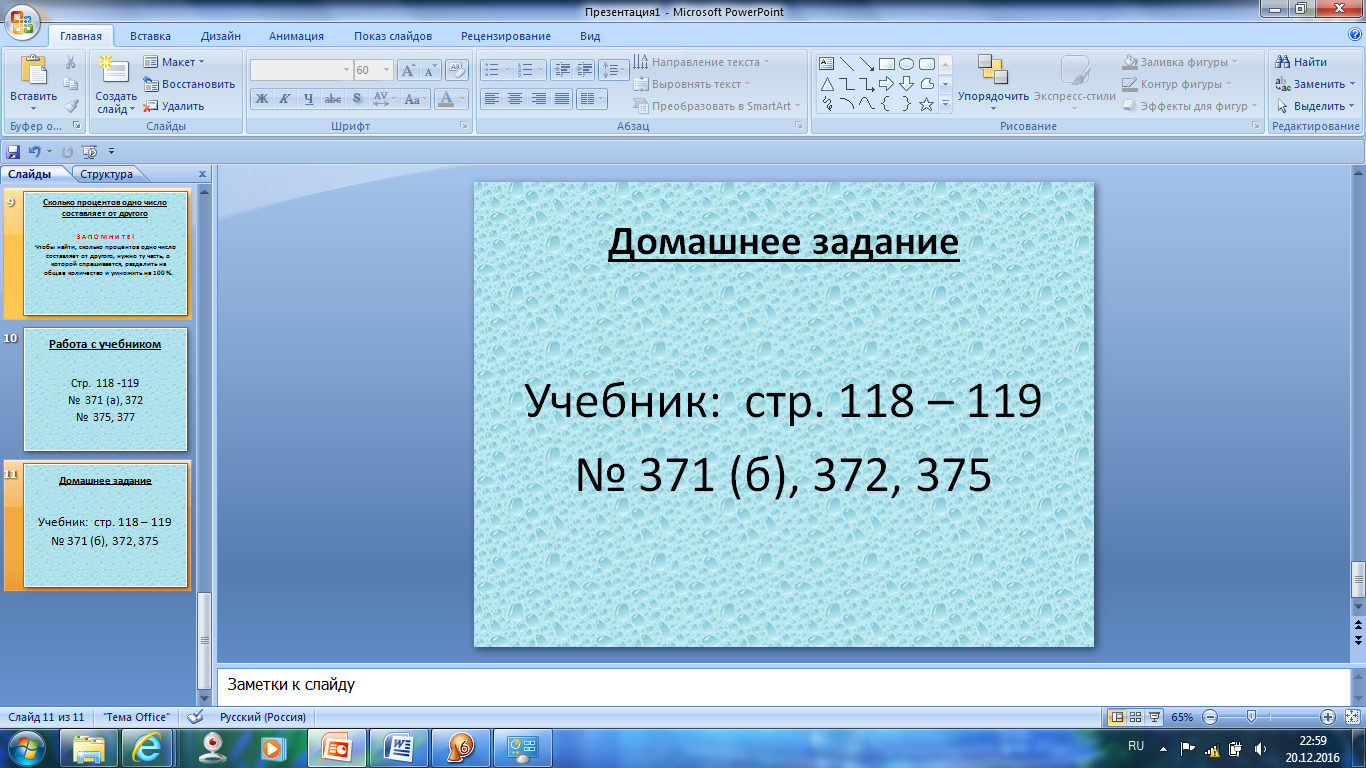
Учитель информирует о домашнем задании, комментирует методику его выполнения. Выставляет оценки в журнал.
Записывают домашнее задание в дневники
Рефлексия (1 минута)
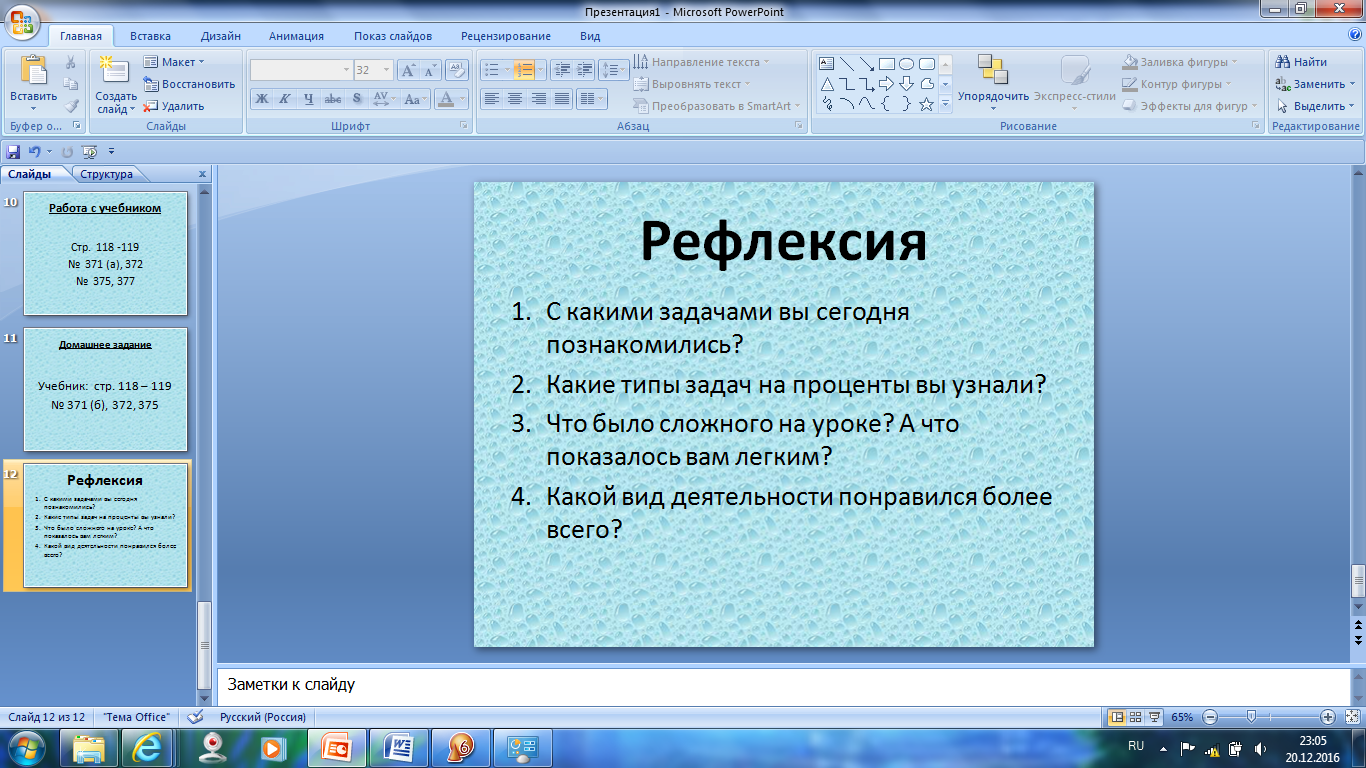
Организует рефлексию.
Участвуют в рефлексии.
infourok.ru