Задачи на сплавы и смеси: подробный разбор

Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.

Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!

Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.

1. Как решить задачу на смеси и сплавы: 3 действия
2. Примеры решения задач на смеси: от простого к сложному
3. Примеры решения задач на сплавы: от простого к сложному

Как решить задачу на смеси и сплавы: 3 действия

 Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:

1. Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
2. Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
3. После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.

 Примеры решения задач на смеси: от простого к сложному

 А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.

Задача 1

Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.

Решение:

Для решения задачи выполняем три действия, о которых мы говорили выше:

1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.

Из условий задачи имеем три раствора:

Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6

Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2

Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:Первое действие выполнено, переходим ко второму.

2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:

3 + 5 = х

0,6 + 2 = у

Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.

Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.

3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.

Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.

Таким образом, концентрация кислоты в растворе 3 равна:

2,6 / 8 = 0,325

Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:

0,325 * 100 = 32,5%

Ответ: 32,5%

Задача 2

Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.

Решение:

1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:2. Составляем уравнение. Известно, что третий газ имеет содержание кислорода 14,6%, соответственно мы можем приравнять массу чистого вещества газа 3 к 0,146 * (х + (х +300)). Получим уравнение:

(х +300)  * 0,21 + х * 0,05 = 0,146 (х + (х +300))

0,21х + 63 + 0,05х = 0,292х + 43,8

0,26х + 63 = 0,292х + 43,8

0,032х = 19,2

х = 600

3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:

600 + 600 + 300 = 1500 г

Ответ: масса третьего газа равна 1500 г.

Задача 3

Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?

Решение:

1. Составляем таблицу. По условиям задачи мы имеем пять растворов:

Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х

Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х

Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0

Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4

Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0

Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.

Сводим полученные результаты в таблицу:2. Составляем уравнение.

По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:

 (х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4

Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:

(х + у + 3) * 0,2 = 0,4х + 0,15у

Объединяем полученные уравнения в систему:Решаем систему и получаем х = 3,4, у = 1,6

3. Возвращаемся к условиям задачи.

По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.

Примеры решения задач на сплавы: от простого к сложному

Задача 1

Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг

Решение:

1. Составим таблицу. Обозначим массу второго куска – х.2. Составим уравнение. По условию задачи сплав 3 содержит 1/11 часть олова, тогда масса чистого вещества равна  1/11 * (84 + х). Таким образом, можно составить следующее уравнение:

1/12 * 84 + 1/10 * х = 1/11 * (84 + х)

7 + х/10 = 84/11 + х/11

х/10 – х/11 = 7/11

х/110 = 7/11

х/10 = 7

х = 70

3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.

Ответ: 70 кг.

Задача 2

Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Решение.

1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:2. По условиям задачи масса третьего сплава равна 200 г, значит:

х + у = 200

Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:

0,15х + 0,65у = 0,3(х + у)

Получившиеся уравнения сводим в систему и решаем ее:х = 200 – у

0,15(200 – у) + 0,65у = 0,3 * 200

30 – 0,15у + 0,65у = 60

0,5у = 30

у = 60

х = 140

3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.

Ответ: 140 г и 60 г.

Задача 3

В первом сплаве  содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?

Решение:

1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:2. По условиям задачи содержание меди в третьем сплаве равно 50%. Таким образом, масса чистого вещества равна 0,5 (х + у). Приравняем полученное уравнение к массе чистого вещества в составе третьего сплава из таблицы, получим:

0,7х + 0,4у = 0,5 (х + у)

0,7х + 0,4у = 0,5х + 0,5у

0,2х = 0,1у

х/у = ½

3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.

Ответ: ½

Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или в нашей группе Вконтакте.

 

Задачи на смеси и сплавы .

Задачи на смеси, сплавы и растворы.

1. Подход к решению задач на смеси.

Человеку часто приходится смешивать различные жидкости, порошки, или твердые вещества, или разбавлять что-либо водой.

Задачи на смеси имеют практическую направленность. Например, мы пьём чай и кладем в чашку столько сахара, чтобы не пересластить (создаём нужную нам концентрацию), а если пересластили, то добавляем воды.

Летом мы ходим за грибами, затем их сушим. И мы понимаем, что чем дольше их сушить, тем меньше в них остается воды, при этом масса сухого вещества не меняется.

Врач выписывает рецепт, и мы покупаем мази, микстуры с определенной концентрацией лекарственных веществ. Решая задачи данного типа, нам нужно будет выделить компоненты, которые изменяются, и те, что остаются неизменными.

Говоря о смесях, растворах и сплавах будем употреблять термин «смесь» независимо от её вида (твердая, жидкая, сыпучая, газообразная). Смесь состоит из основного вещества и примеси. Что такое основное вещество, в каждой задаче определяется отдельно.

Текстовые задачи на смеси, сплавы и растворы входят в различные сборники заданий по математике и химии ОГЭ и ЕГЭ.

При решении любых задач, прежде всего, нужно грамотно прочитать условие, последовательно остановиться на каждой строчке, и попытаться выразить условие в качестве какого-то уравнения.

. Что же отличает задачи на смеси? Уравнение трудно составить, если не знать основную формулу для всех задач на смеси.

В «Занимательной алгебре» Я.И. Перельмана есть любопытная задача под названием: «В парикмахерской»:

Задача: Может ли алгебра понадобиться в парикмахерской? Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:

-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?

— Уж сколько раствора испортили из-за этого!- добавил другой

— В чем задача?

— У нас имеется два раствора перекиси водорода: 30%- ыйи 3 % -ый. Нужно их смешать так, чтобы составился 12% -ый раствор. Не можем подыскать правильной пропорции.

Мне дали бумажку, и требуемая пропорция была найдена.

Она оказалась очень простой. Какой именно?

Решение: Пусть для составления 12%-ной смеси требуется взять x граммов 3%-ного раствора и y граммов 30% -ного раствора. Тогда в первой пропорции содержится 0,03x граммов чистой перекиси водорода, во второй 0,3y, а всего 0,03x + 0,3y

В результате получается (x + y) граммов раствора, в котором чистой перекиси должно быть 0,12 (x + y)

Имеем уравнение: 0,03x + 0,3y=0,12 (x + y)

Из этого уравнения находим x =2y, т.е. 3%-ного раствора надо взять вдвое больше.

Задача, описанная Перельманом, встречается не только в парикмахерских.

Например, для зарядки аккумуляторов бывает необходимо приготовить электролит, который должен содержать 24% серной кислоты из двух растворов с содержанием 92% и 10% серной кислоты.

2. Теоретические основы решения задач на смеси и сплавы.

Задачи на смеси, растворы и сплавы называют еще задачами на процентное содержание или концентрацию. Данный тип задач охватывает большой круг ситуаций – смешение товаров разной цены, жидкостей с различным содержанием соли, кислот различной концентрации, сплавление металлов с различным содержанием некоторого металла и пр. При решении задач данного типа используются следующие допущения:

1. Все получающиеся смеси и сплавы однородны;

2.Всегда выполняется «Закон сохранения объема или массы»:

если два раствора (сплава) соединяют в «новый» раствор (сплав), то выполняются равенства:

V = V₁+V₂ –сохраняется объем;

m = m₁ + m₂ – сохраняется масса.

3 Данный закон выполняется и для отдельных составляющих частей (компонентов)сплава (раствора).

Определение. Процентным содержанием (концентрацией или массовой долей) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.

3.Задачи на смешение растворов разных концентраций.

Решим типовую задачу в общем виде и выведем формулу.

Задача:Имеются два куска сплава меди с цинком. Процентное содержание меди в них

p₁% иp₂ % соответственно. В каком отношении нужно взять массы этих сплавов, чтобы, переплавив взятые куски вместе, получить сплав, содержащий p%меди?

Решение.Понаблюдаем за содержанием меди.

Исследуем уравнение (*) при условии, что будем брать ненулевые массы сплавов.

I случай. Если p₁ ,p₂ и p попарно не равны, то получим формулу

m₁ (p₁ — p) =m₂(p –

p₂) (*)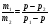

II случай. Возьмём два сплава с одинаковым процентным содержанием меди, т.е. p₁=p₂ . Решая уравнение (*), получим, что p₁=p₂=p, т. к. ни большей, ни меньшей концентрации сплав просто не получится, если исходные материалы имеют одинаковую процентную концентрацию меди, каковы бы ни были массы исходных сплавов.

III случай. Если p₂ =p, или p₁= p ,то вывод тот же.

Если взять два сплава, массы которых одинаковы, т.е. m₁ = m₂ , то

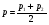
то есть процентное содержание нового сплава станет равно среднему арифметическому процентных концентраций исходных сплавов. А теперь рассмотрим однотипные задачи, решение которых очень удобно по этой формуле:

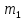
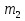
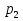
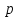
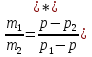
Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 19%-го раствора этого же вещества. Найдите концентрацию раствора.

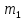
11%

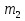
19%

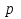
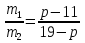
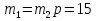
Или т. к. массы исходных растворов равны, то

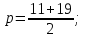
Сколько килограммов 20%-го раствора соли нужно добавить к 1 кг 10%-го раствора, чтобы получить 12%-ый раствор соли?

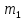
20%

1кг

10%

12%

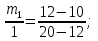
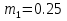
В сосуд, содержащий 13л 18%-го водного раствора некоторого вещества, добавили 5л воды. Найти концентрацию получившегося раствора.

13л

18%

5л

0%

%

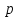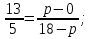
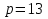
Старинный способ решения задач на смешивание двух веществ.

Предположим, что смешиваются два вещества – первое стоимостью а гривен за фунт и второе стоимостью b гривен за фунт. Желательно получить вещество стоимостью с гривен за фунт. Будем считать, что а<b( если с>

b или c<a , то задача неразрешима, ибо, смешивая дешевые вещества, дорогое не получишь). Поэтому можно считать, что a<c<b. Смешиваем один фунт первого вещества и q фунт второго. В результате получится 1+q фунтов вещества стоимостью a+bq гривен. Один фунт смеси должен стоить с гривен. Значит должно выполняться равенство

a+bq=c*(1+q). Отсюда находим q=(c-a)/(b-c) или (b-c):(c-a).

Это соотношение дает старинный способ.

«Правило креста»

При решении задач на смешивание растворов разных концентраций используется «правило креста». В точке пересечения двух прямых обозначают концентрацию смеси. У концов этих прямых слева от точки пересечения указывают концентрации составных частей смеси, а справа – разности концентраций смеси и ее составных частей:

Для приготовления 30 г 80%-го раствора кислоты требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты.

Задача:У некоторого человека были на продажу масла двух сортов: одно ценою 10 гривен за ведро, другое же 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла ценою 7 гривен?

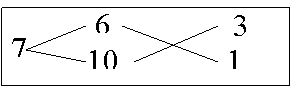
Из схемы делаем заключение, что дешевого масла нужно взять втрое больше, чем дорогого, т.е. для получения одного ведра ценою 7 гривен нужно взять дорогого масла 1/4 ведра, а дешевого масла 3/4.

Способ Л.Ф.Магницкого для трех веществ

Указанный Л. Ф. Магницким способ состоит в следующем. Надо дважды применить способ записи исходных данных и необходимых количеств веществ, причем в первый раз взять вещества с большей и меньшей стоимостью, а во второй раз с наименьшей и средней стоимостью. Повторив действие вычитания и соответствующей записи разности, получим доли, в которых нужно смешивать вещества наибольшей и средней стоимости (на соответствующих строках). Сложив доли дешевого вещества, найденные в первый и во второй раз, получим долю дешевого вещества в общей смеси.

Задача: Некто имеет чай трех сортов – цейлонский по 5 гривен за фунт, индийский по 8 гривен за фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти сорта, чтобы получить чай стоимостью 6 гривен за фунт?

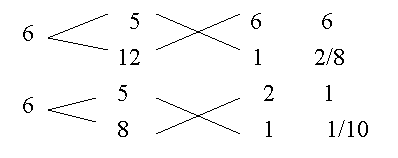
Взять 6+2=8 частей чая ценой по 5 гривен и по одной части ценой 8 гривен и 12 гривен за один фунт.

Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и по1/10 фунта чая ценой 8 и 12 гривен за фунт, то получим 1 фунт чая ценой 8/10*5 + 1/10*8 + 1/10*12 = 6 гривен

Ответ: 100 т и 40 т.

4. Задачи на многократные переливания.

Рассмотрим задачи, при решении которых можно выявить общую закономерность изменения концентрации раствора в результате многократно повторяющейся операции.

Решим в общем виде такую задачу:

В сосуде, объём которого равен V₀ литров, содержится раствор соли концентрации С₀. Из сосуда выливается a литров смеси и доливается a литров воды, после чего раствор тщательно перемешивается. Эта процедура повторяется n раз. Какова станет концентрация соли в растворе после n таких процедур?

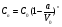Если в задаче n раз отливают некоторое количество раствора и затем столько же раз приливают такое же количество воды или другого однородного вещества, то для решения задачи пригодится формула:

Где n– количество шагов, V₀— начальный объём, который сохраняют неизменным при каждом шаге С_n— конечная концентрация,C₀— начальная концентрация,

a – объём отливаемой каждый раз смеси

Докажем эту формулу:

Последовательность С₀, С₁, С₂, С_n-1, С_n представляет собой убывающую

геометрическую прогрессию концентраций раствора.

Выражение С_n* V₀соответствует количеству соли после проведения n-ой процедуры.

Но эта же соль присутствовала в (V₀ – a) л предыдущего раствора

в количестве С_n-1 (V₀ –a)л Составим уравнение: С_n* V₀ = С_n-1 (V₀ –a) и разделим обе части на V₀ 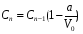, откуда получаем .

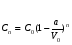Однотипные задачи, которые уже легко решить с помощью данной формулы.

С₀

V₀

a

n

C_n

В сосуде имелось 1250 л 80%-го р-ра к-ты. Из него три раза отливали некоторое кол-во р-ра, добавляя такое же кол-во воды. В результате в сос. осталось 125л чистой к-ты. Какое кол-во р-ра брали изсосуда каждый раз?

Ответ:625 л.

С₃=С₀(1-a/1250)³

0,1=0,8(1-a/1250)³

0,125=(1-a/1250)³

0,5=1-a/1250

a/1250=0,5

a=625

Сколько литров чистого спирта останется в сосуде, если из 50л 80%-ного раствора 20 раз отливать по 1л раствора, каждый раз добавляя по 1 л воды?

Ответ:26,7 л.

С₂₀=0,8(1-1/50)²⁰

С₂₀=0,534

0,534*50=26,7(л)

Существуют задачи, внешне похожие на применение формулы Сn, но при внимательном чтении оказывается, что цикл переливаний не закончен. В таких случаях надо быть очень внимательным.

Задача:Из сосуда, наполненного кислотой, вылили несколько литров и долили водой; потом опять вылили столько же литров смеси; тогда в сосуде осталось 24 л чистой кислоты. Ёмкость сосуда 54 л. Сколько кислоты вылили в первый раз и второй раз?

Решение: Будем иметь в виду, что на втором шаге воду не доливали.

По условию задачи объём сосуда, наполненного кислотой, 54 л. Её концентрация 100%. Пусть вылили х литров смеси, тогда в сосуде осталось (54-х) литров 100%-ной кислоты. В сосуд доливают хл воды. По определению концентрации надо массу кислоты разделить на массу раствора: (54-х)/54.

Опять выливают х литров смеси, в сосуде остаётся (54-х) л смеси с массовой долей кислоты (54-х)/54.

Чтобы найти массу кислоты в этой оставшейся смеси, надо массу раствора умножить на концентрацию кислоты в этом растворе. По условию масса чистой кислоты в этом растворе стала 24л.

Составим и решим уравнение:

(54-х)* ((54-х)/54) = 24,

(54-х)²= 1296,

зная, что х<54, получим единственное решение: х = 18.

В первый раз вылили 18 литров чистой кислоты. Но во второй раз выливали 18 литров смеси, в ней чистой кислоты было

18* (54-18)/5 =12 (л)

Ответ: 18 л; 12л

Задача: Имеются сплавы золота и серебра. В одном эти металлы находятся в отношении 2: 3, а в другом в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11?

По этой схеме уравнение х + у =1 показывает массу нового сплава.

Определяем массу золота в каждом сплаве и получаем уравнение

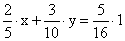
Аналогично определяем массу серебра и получаем уравнение

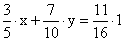
Записываем одну из систем:

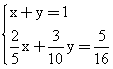
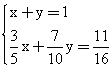
Решая ее, получаем х = 0,125 и у = 0,875

Ответ: 125 г и 875 г.

Есть очень легкий, быстрый и «хитрый» способ решения подобных задач, предложенный американским физиком ( русского происхождения) Алексеем Султановым:

= ==

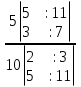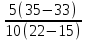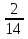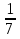
Использованная литература.

1. Алгебра-7:учебник автор: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков,

С.Б. Суворова, Просвещение, 2010

2. Прокопенко Н. И.Задачи на смеси и сплавы. – М.: Чистые пруды, 2010.

3. Под редакцией М.И. Сканави. Сборник задач по математике. Москва, 2002г.

4. И.Н. Сергеев ,С. Н. Олехник. Примени математику. Москва «Наука»,1990 г.

5. Сборник задач по математике. Под редакцией А. И. Прилепко.

Москва «Высшая школа», 1998 г.

2. О. А.Городнова Статья «Учимся решать задачи на«смеси и сплавы»,

г-та«Математика»№36 за 2004 г.

2. А.В. Шевкин Школьные математические олимпиады,

изд-во «Русское слово», 2002г.

8.« Занимательной алгебры» авт. Я.И. Перельман.

Научно-исследовательская работа по математике ученика 9 класса Адмакина Кирилла «Задачи на смеси,сплавы и расстворы».

˅ΙΙΙ районная научно-практическая конференция школьников

Яшкинского муниципального района «Открытия юных исследователей»

Секция: математика

«Различные способы решения задач на смеси, сплавы, растворы.»

Авторы: Адмакин Кирилл

ученик 8 класса МБОУ « СОШ №2 »

дата рождения 12.10.2002г.

Адрес: 652010 , пгт. Яшкино, ул.Весенняя 4 -1

Научный руководитель:

Оленева Лариса Павловна

учитель математики МБОУ «СОШ №2»

адрес: 652010, пгт.Яшкино, пер. Заводской,

дом 15.

Яшкино 2017.

Содержание:

1.Введение ………………………………………………………………….. 3

2.Анализ ситуации………………………………… 4

3.Классификация задач. Способы решения задач ….. ….5

4.Задачи на растворы и смеси……………… 6

5. задачи на процентное содержание влаги…………………. 7

6.Вывод ……………….. 11

7.Повторный опрос … 12

8.Заключение……………. . 13

9. Список литературы ……………………………………….. 14

10.Приложение 1 15

Введение

Просматривая КИМы ОГЭ, я обратил внимание, что в 30% работ в каче-

стве текстовой задачи предлагается задача на смеси, сплавы или растворы. . Что не удивительно,так как в современном мире множество отраслей, связанных с химией, например такие, как пищевая, фармацевтическая, тяжёлая промышленность, медицина, фармакология и т.д.

Эти задачи при первом знакомстве с ними вызывают у учащихся общеобра-

зовательных классов затруднения. Самостоятельно справиться с ними могут

немногие. Задачи данного типа, ранее встречающиеся практически только на

вступительных экзаменах в ВУЗы и олимпиадах, сейчас включены в КИМы

для подготовки и проведения экзамена по математике за курс основной шко-

лы. Эти задачи, имеющие практическое значение, являются также хорошим

средством развития мышления. Поэтому я считаю, что на сегодняшний день

тема решений таких задач является актуальной.

Цель работы: изучить способы решения различных типов «химиче-

ских» задач, подготовиться к сдаче выпускного экзамена.

Для достижения поставленной цели требуется выполнить ряд следую-

щих задач:

• Систематизировать задачи на растворы, смеси и сплавы;

• Найти единый алгоритм решения этих задач;

• Научиться решать задачи по заданной теме.

Чтобы решить любую задачу, надо создать математическую модель. В

каждом типе задач я использую удобные для меня схемы. В начале своей ра-

боты я покажу способы, которыми обычно решаю данного вида задачи, а за-

тем перейду к способам, которые нашёл в дополнительной литературе и ин-

тернете.

Анализ ситуации

В ходе проектной деятельности я проводил опрос «Можете ли вы решать задачи на растворы?».
Вот результаты первого:

Конечно! — 6%

Скорее всего — 10%

Затруднились ответить — 5%

Нет-3%

Чтобы лучше понимать условия задач, необходимо знать следующие понятия:

• Все получающиеся сплавы или смеси однородны.

• При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.

• Процент — одна сотая любого вещества.  

• Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.  

• Это отношение может быть выражено либо в дробях, либо в процентах.

• Сумма концентраций всех компонент, составляющих смесь, равна единице

Классификация задач:

В открытом банке заданий рассматриваются 4 основных видов таких за-

дач.

• На понижение и повышение концентрации

• На «высушивание» (Задачи на процентное содержание влаги.)

• На смешивание растворов разных концентраций

• На вычисление массы смеси (сплава).

Существуют следующие способы решения задач:

• с помощью таблиц;

• с помощью схемы;

• старинным арифметическим способом;

• алгебраическим способом;

• с помощью графика;

с помощью формулы.

Рассмотрим решение таких задач различными спообами и выясним какой из этих способов окажется легче для восприятия учащихся нашего класса.

1. Задач на растворы, смеси и сплавы.

Задача 1. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение: 1 способ – с помощью таблицы:

Наименование веществ, смесей

Наименование веществ, смесей

Масса

раствора (г)

Масса вещества (г)

Исходный раствор

70 % = 0,7

200

0,7·200

Воды долили

—

x

—

Новый раствор

8 % = 0,08

200 + x

0,08(200 + x)

Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение :

0,08(200 + х) = 0,7·200

16 + 0,08х = 140

0,08х = 124

х = 1550

Ответ :1,55 кг воды.

2 способ — с помощью схемы:

Пусть в сосуд долили х литров воды. Получаем схему:

Уксусная Уксусная кислота кислота

200 г. (200 + х) г.

0,08(200 + х) = 0,7·200

16 + 0,08х = 140

0,08х = 124

х = 1550

Ответ :1,55 кг воды.

3способ — Правило креста:

70 8

8

0 62

Значит, 200г – 8 частей тогда, чтобы получить 8% р-р нужно добавить 62 части воды

200:8·62=1550г.

Ответ: 1550г

2. Задачи на процентное содержание влаги.

Задача №2:

Пчелы перерабатывают цветочный нектар в мёд, освобождая его от воды. Нектар содержит 84% воды, а полученный мёд — 20%. Сколько кг нектара нужно переработать пчелам для получения 1 кг мёда?

При решении таких задач надо разделять вещество на воду и «сухой остаток», масса которого не меняется в условиях задачи

1. Арифметический

1) 100-20=80% — составляет основное вещество от полученного мёда.

2) 1*0,8=0,8 кг – масса основное вещество в 1 кг.

3) 100-84 = 16% — составляет основное вещество от собранного нектара.

4) 0,8:0,16 = 5 кг нектара.

Ответ: 5 кг нектара нужно переработать пчелам для получения 1 кг мёда.

2. Правило «креста»

84 80

100

20 16

Значит, 1 кг составляет 16 частей, тогда 80 частей:

1 : 16 * 80 = 5 кг.

Ответ: 5 кг

3. Решим эту задачу с помощью схемы

Нектар вода мед

вода сух.вещ. вода сух.вещ

х кг (1-х) кг 1 кг

Составим уравнение 0,16 х = 0,8* 1 ,

х = 0,8:0,16 ,

х = 5

Ответ : 5 кг

Задачи, которые решаются с помощью систем линейных уравнений.

Задача №3

Имеется 2 раствора поваренной соли разной концентрации. Если слить вместе 100г первого раствора и 200г второго раствора, то получится 50%-ный раствор. Если же слить вместе 300г первого раствора и 200 г второго, то получится 42%-ный раствор.
Найти концентрацию второго раствора.

Решим задачу с помощью схем

р.соли р.соли р.соли

100 г 200 г 100+200=300г

р.соли р.соли р.соли

300 г 200 г 300+200=500г

100*0,01х + 200*0,01у = 300*0,5

300*0,01х + 200*0,01у = 500*0,42

Упростив эти уравнения и решив систему, получим х=30 и у=60.

Следовательно, концентрация второго раствора равна 60%

Ответ. 60%

Решение задач на смеси методом прямоугольников.

Одним из универсальных методов является метод прямоугольников. Дан-

ный способ удобен, так как зрительное восприятие данных, расположенных

в определенном задуманном порядке, позволяет компактно представить про-

цессы соединения растворов, упростить составление уравнения, а также об-

легчить процесс как решения, так и проверки задачи. Наиболее распростра-

нены задачи, в которых из двух смесей (растворов или сплавов) получается

новая смесь (раствор или сплав).

Задача 4.

Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получи-

ли 600 г 15%-го раствора На сколько граммов масса первого раствора меньше массы второго?

Решение: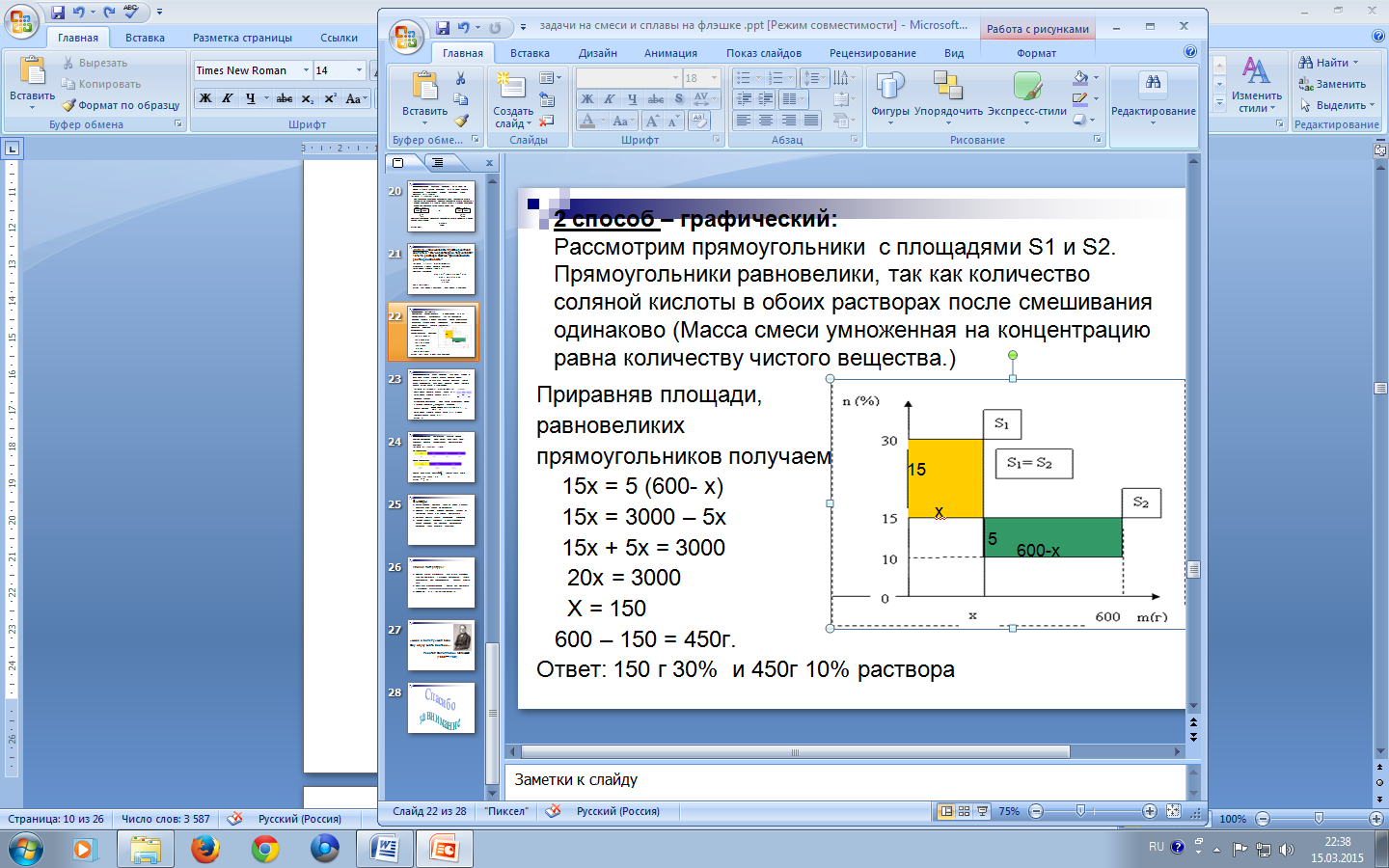

Обозначим x массу первого раствора, тогда масса второго (600 — x).

Приравняв площади, равновеликих прямоугольников получаем

15x = 5 (600- x)

15х = 3000 – 5х

15х + 5х = 3000

20х = 3000

Х = 150

600 – 150 = 450г.

450-150 = 300 (г.)

Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора

В классе мы решили несколько задач на смеси, сплавы и высушивание. Обсудили все способы решения таких задач и пришли к выводу:

Вывод: Задачи на смеси, растворы и сплавы входят в обязательный курс школьной математики и встречаются на ОГЭ, но умеют решать их, увы, не многие. Перебрав несколько способов решения задач, мы нашли для себя наиболее легкий для восприятия учащихся нашего класса ( способ решения с помощью схем) . Наша гипотеза подтвердилась

Повторный опрос
«Можете ли вы решать задачи на растворы?»

Да! — 14%

Скорее всего — 9%

Затруднились ответить— 1 %

Заключение:

В современном мире множество отраслей, связанных с химией, например такие, как пищевая, фармацевтическая, тяжёлая промышленность, медицина, фармакология и т.д. Однако все они связаны не только с химией, но и с математикой, так как приходится решать задачи на процентное содержание в продукте питания, металле, лекарстве, косметике и т.д. тех или иных веществ.

В ходе рассмотрения способов решения задач на смеси, сплавы, растворы мы увидели красоту, сложность и притягательность данных способов. Выбор способа решения зависит от конкретной задачи и от умения решающего.

Таким образом, данная научная работа имеет практическое значение, так как может служить пособием при подготовке к сдаче экзаменов.

Список литературы:

• М.В. Лурье и др. Задачи на составление уравнений, изд-во «Наука», М., 1976 г.

• Н.А. Терёшин Прикладная направленность школьного курса математики, «Просвещение», М., 1990 г.

• А.В. Шевкин Школьные математические олимпиады, изд-во «Русское слово», 2002г.

• О. Городнова Статья «Учимся решать задачи на «смеси и сплавы», г-та «Математика» №36 за 2004 г.

Интернет-ресурсы:

1. Открытый банк заданий ЕГЭ по математике

http://www.mathege.ru

2. Шабон оформления презентации

http://www.pedsovet.su

ПРИЛОЖЕНИЕ 1

Задачи для самостоятельного решения.

1. В лаборатории изготовили 1кг 16% солевого раствора. Через неделю из

этого раствора испарилось 200г воды. Какова стала концентрация соли в

растворе?

Ответ:20%.

2. При выплавке стали из чугуна, выжигается углерод. Содержание угле-

рода в чугуне 4%. Сколько тонн углерода нужно выжечь из 245т чугуна,

чтобы получилась сталь с содержанием углерода 2%?

Ответ:5т.

3. Слиток сплава меди и цинка массой 36 кг содержит 45% меди. Какую

массу меди надо добавить к этому куску, чтобы полученный сплав со-

держал 60% меди?

Ответ:13,5кг.

4. После смешивания двух растворов, один из которых содержал 48 г, а

другой — 20 г безводного йодистого калия, получилось 200 г нового

раствора. Найдите концентрацию каждого из первоначальных раство-

ров, если концентрация первого на 15% больше концентрации второго.

Ответ:40% и 25%.

5. Имелось два слитка меди. Процент содержания меди в первом слитке на

40% меньше, чем во втором. После того как оба слитка сплавили, полу-

чился слиток, содержащий 36% меди. Найдите процентное содержание

меди в каждом слитке, если в первом было 6 кг меди, а во втором — 12

кг.

Ответ:20% и 60%

6. Смешали 30%-ный раствор соляной кислоты с ее 10%-ным раствором и

получили 600 г 15%-ного раствора. Сколько граммов 30 % -ного рас-

твора было взято?

Ответ:150г.

Решение задач на смеси, сплавы и концентрации

Селенгинское районное управление образования

Муниципальное бюджетное общеобразовательное учреждение

Иройская СОШ

Районная научно исследовательская конференция школьников «Шаг в будущее»

Секция «Математика»

Решение задач на концентрации, смеси и сплавы

Исполнитель Балданова С, ученица 10 класса

Руководитель Чултумова И.Н., учитель математики

первой категории

2015г

Оглавление

1. Введение.. ………………………………………………………………………….3

2. Задачи на смеси и сплавы

2.1. Задача из « Занимательной алгебры» Я.И. Перельмана 4

2.2 Старинный способ решения задач 5

2.3 Квадрат Пирсона 7

З. Заключение ………………………………………………..………………….…… 9

4. Список литературы .……………………………………………….………….… 10

5. Приложения ……………………………………………………………………….. 11

1. Введение.

В вариантах ЕГЭ по математике 11 класса встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в 5-6  классах, причем недолго, закрепляется в 7-9 классах при решениях задач, а в старших классах к этой теме, совсем не возвращаются.

Поэтому, изучение  наиболее часто встречающихся типов задач на проценты, в частности, задач на концентрацию, смеси и сплавы считаю актуальным.

Объектом  исследования является изучение различных типов задач по теме «Проценты».

Предмет исследования: решение задач  на концентрацию, смеси и сплавы с использованием квадрата Пирсона и способа Леонтия Филлиповича Магницкого.

Гипотеза: Задача, решенная способами Пирсона и Магницкого приводят к одному и тому же результату, что и задача решенная алгебраическим методом.

Цель работы. Использование квадрата Пирсона и старинного метода для решения задач на концентрацию, смеси и сплавы.

Задачи исследования: Изучить исторический и теоретический материалы по интересующему вопросу; выявить практическое применение таких задач.

Практическая значимость работы.  Данный способ решения задач на концентрацию, смеси и сплавы будет интересен выпускникам 9 и 11 класса, которым нужно сдать ЕГЭ и ОГЭ.

2. Задачи на смеси и сплавы

.1. В «Занимательной алгебре» Яков Исидорович. Перельмана есть любопытная задача под названием « В парикмахерской». В этой задаче автор рассказывает, что, однажды заглянув в парикмахерскую, он увидел , как мастера пытались безуспешно пытались приготовить 12-процентный раствор перекиси водорода из двух имевшихся в наличии растворов –трех и тридцатипроцентного…

Может ли алгебра понадобиться в парикмахерской? Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:

-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?

— Уж сколько раствора испортили из-за этого!- добавил другой

— В чем задача?

— У нас имеется два раствора перекиси водорода: 30%- ный и 3 % -ный. Нужно их смешать так, чтобы составился 12% -ный раствор. Не можем подыскать правильной пропорции…

Мне дали бумажку, и требуемая пропорция была найдена.

Она оказалась очень простой. Какой именно?

Мы учащиеся в первую очередь такие текстовые задачи решаем алгебраическим способом с помощью уравнений или систем уравнений.

Вот два способа, какими можно решить задачу. 1 способ (алгебраический). Обозначим искомую часть 30% раствора – х, а 3% -раствора — y. Соответственно, надо получить 0,12 (х+у).

Запишем уравнение:

0,03у+0,3х=0.12(x+y)

0,3х-0,12х=0,12у-0,03у

0,18х=0,09у

х=2у

Ответ: для получения 12%-го раствора нужно взять одну часть 30% раствора и две части 3%-го раствора перекиси. А ещё как можно решить?

2.2 2 способ — старинный способ решения задач

В центре пишем концентрацию первого раствора – 30 %. Под ним, отступив вниз, пишем концентрацию второго раствора- 3% или 0, 03. Слева, примерно посередине между верхней и нижней цифрами пишем концентрацию желаемого раствора – 12% или 0,12. Соединяем три цифры отрезками прямых. Из первой концентрации, поскольку она больше желаемой, вычтем 0,12, подпишем справа от 0,03 результат 0, 18, который оказался по диагонали от 0,3. Из 0, 12 вычитаем 0, 03 и подписываем справа от 0,3 результат – 0,09, который тоже оказывается по диагонали от значения 0, 03. Соединяем все отрезками и получаем «рыбку» (рис. 3).

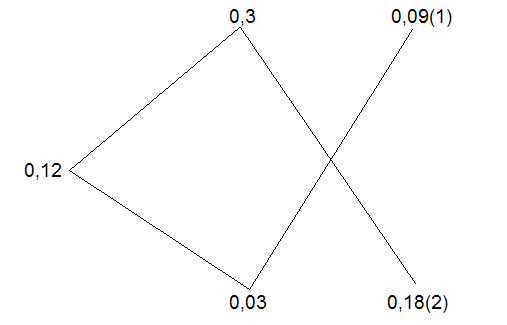
Соотношение полученных величин – 0, 09 и 0,18 – составляет 1 к 2, т. е. первого раствора концентрацией 30 % надо взять в 2 раза меньше, чем 3%-го раствора. Ответы, полученные двумя методами одинаковы.

Давайте вернемся к задаче из тренировочного варианта: «Имеется два сплава с разным содержанием золота. В первом сплаве – 35% золота, а во втором 60% , в каком отношении надо взять первый и второй сплав, чтобы получить из них новый, содержащий 40% золота». Решим задачу двумя способами:

1 способ. Пусть часть первого сплава – х, а второго – у

Тогда количество золота в первом сплаве составляет 0, 35х, а во втором 0,6у. Масса нового сплава равна х+у, а кол-во золота составляет 0,4( х+у). Составим уравнение

0, 35х+0,6у=0,4(х+у)

35х+60у=40х+40у

20у=5х

х/у=4/1

Ответ: для получения сплава, содержащего 40% золота из двух сплавов с содержанием 35% и 60%, нужно взять в 4 раза больше 35%-го сплава.

2 способ – метод Магницкого (метод рыбки).

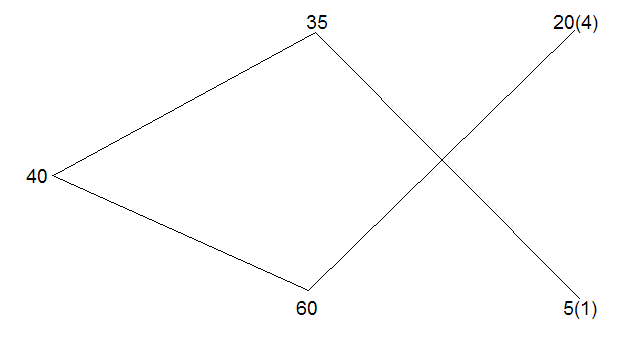Результат: соотношение полученных величин составляет 1 к 4, значит 35%-го сплава надо взять в 4 раза больше, чем 60%-го.

Старинный способ решения задач на смеси, сплавы и растворы (метод «рыбка»).

Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого, нашего земляка. Ввиду большой простоты предложенный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо, как в предыдущей задаче, рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ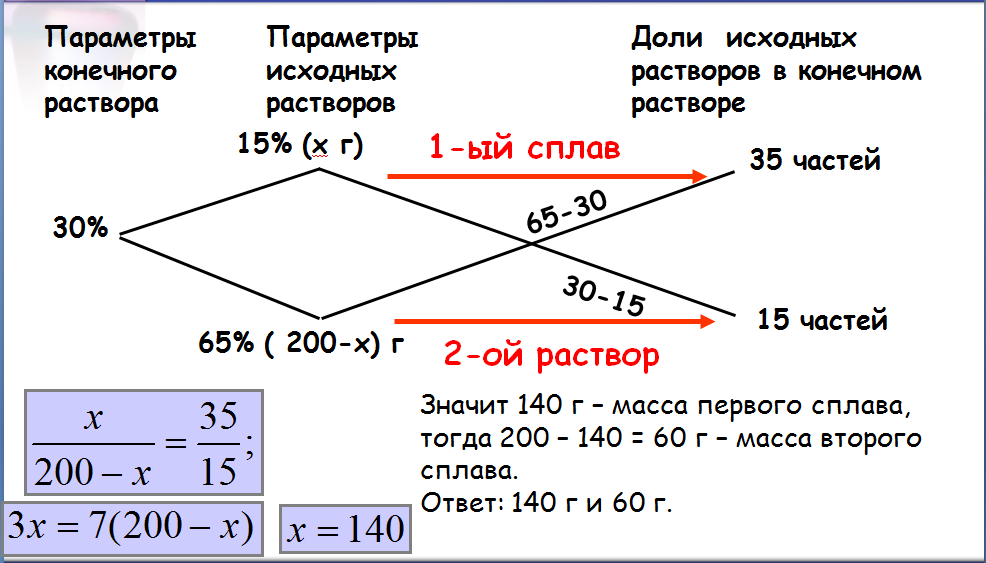

На представленных выше примерах я показала как используется графический метод решения задач на смешение веществ Магницкого Л. Ф. (метод рыбки).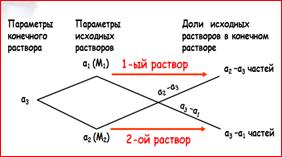

Теория метода:

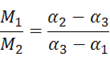
Немного об авторе:

Замечательный русский математик и педагог Леонтий Филиппович Магницкий (1669—1739) фамилию свою получил (1700) от Петра I за умение притягивать к наукам молодых людей. Понимая необходимость улучшения системы образования в России, Петр I издал ряд указов об организации новых учебных заведений. В начале 1701 г. была создана Школа математических и навигацких наук в Москве. Распоряжением царя Магницкий был назначен туда преподавателем математики. В этой школе он и работал до конца жизни. В 1703 г. Магницкий издал свою «Арифметику», представляющую собой для России того времени энциклопедию математических знаний. Она состояла из двух книг, содержащих в общей сложности 662 страницы. Многие задачи и их решения приведены в виде стихотворных поучений. Сборник получился настолько удачным, что более ста лет являлся основным учебным пособием по математике в России. Недаром великий русский ученый Михаил Васильевич Ломоносов назвал «Арифметику» «вратами своей учености».

2.3. Правило креста или квадрат Пирсона

При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения. При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

ω₁, ω₂ – массовые части первого и второго растворов соответственно.

Для решения подобных задач удобно пользоваться « квадратом Пирсона». Вот как это делается. Рисуют квадрат и проводят две диагонали. ( рис. 1) В левом верхнем углу проставляют больший показатель крепости исходных веществ А (бпк), а в нижнем углу-В(впк) а на пересечении диагоналей записывают требуемый показатель С(тпк).

Затем производят вычитание по первой диагонали (а — с) и находят количество второй части (у). Из центра производят вычитание по второй диагонали (c — b) и находят количество первой части смеси (x) . Значения x и y записывают по одной линии с показателями. На x частей первого вещества надо взять y частей второго вещества, тогда получится смесь с показателем с.

a x 36 12

b y 6 18

Рис .1 Рис.2

Для пояснения этого правила сначала решим простейшую задачу. 

Задача 3. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?

Ответ: 7 килограммов.

Данный метод может использоваться и при решения задач на смеси и сплавы. Отлили часть раствора, отрезали кусок сплава. При этой операции остается неизменной концентрация веществ.

А теперь немного о Пирсоне…Карл Пирсон родился 27 марта в 1857 году в Лондоне. Он был разносторонним человеком, активно изучал историю, математику, статистику   и германистику. Большую часть 80-х годов XIX века он провел в Берлине, Гейдельберге, Вене и Брикслеге. Интересовали его религия и поэзия – с одинаковым интересом он изучал Гёте и Священное Писание. Занимали Пирсона и вопросы пола – он даже основал Клуб Мужчин и Женщин. В 1898 году получил медаль Дарвина. Карл Пирсон Погиб в Англии в городе Суррее 27 апреля 1936 года. Прожил он 79 лет.    

Как и все методы решений, квадрат Пирсона имеет свои преимущества и недостатки. Одним из преимуществ этого способа является то, что он доступен ученикам, которые не умеют решать уравнения. Также квадрат Пирсона очень полезен для домохозяек, чтобы   получать нужную концентрацию уксуса или сиропа.

Недостатком этого метода является то, что его можно применять только при смешивании двух растворов. То есть если нужно смешать три или более веществ, квадрат Пирсона здесь не поможет.

Заключение

Итак, гипотеза о том, что задача, решенные способами Пирсона и Магницкого приводят к одному и тому же результату, что и задача решенная алгебраическим методом подтвердилась. При внешнем различии сюжета задачи на сплавы, смеси, концентрации, на соединение либо на разделение различных веществ, решаются по общей схеме. (См. примеры решения задач в Презентации). Таким образом, дополнительная работа по развитию и совершенствованию навыка решения задач на проценты имеет значимость не только для будущих абитуриентов, которые возможно встретятся с такими заданиями на ЕГЭ, но и для всех учащихся, так как современная жизнь неминуемо заставит в своей повседневности решать задачи на проценты.

Литература

1. ГИА-2014: экзамен в новой форме : алгебра : 9-й кл. : тренировочные варианты экзаменационных работ для проведения государственной итоговой аттестации в новой форме / авт.-сост. Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др. – М.: АСТ: Астрель, 2014 – (ФИПИ)

2. Перельман Я.И.Занимательная алгебра. Издательство «Наука», Москва 1967г

3. Азия А., Вольпер И. Квадрат Пирсона. — М., Квант, № 3/73. С. 61.

Приложение

Интегрированный урок математика — химия по теме: » Задачи на смеси и сплавы»

Данные об учителе: Бруяка Оксана Дмитриевна

Предмет

Алгебра (УМК линия Мордкович А.Г.)

Класс

8

Тема урока

Решение задач на растворы и смеси .

Планируемые образовательные результаты:

Применять понятия и определения математики в решении задач по химии на растворы и смеси из реальной жизни.

Предметные

Метапредметные

Личностные

Научится: Оперировать понятиями раствор, растворитель, концентрация, процент, массовая доля, нахождение процента от числа, нахождение числа по его части, строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи.

Доказывать и опровергать с помощью контр примеров утверждения

Ученик получит возможность повторить и откорректировать знания по теме: «Решение задач на растворы и смеси»:

Углубить и развить представления о решении задач на растворы и смеси.

Исследовать новые простейшие, необычные представления о числовых закономерностях в решении задач.

Познавательные:

— Выдвижение гипотез и их обоснование;

— Умение составлять схемы и уравнения к текстовым задачам.

— Поиск и выделение необходимой информации;

Регулятивные: Коррекция; Целеполагание

Коммуникативные: Эффективно сотрудничать и способствовать продуктивной кооперации

— Развитие логического мышления, внимания;

-Развитие математической и химической речи;

-Развитие интереса к предметам;

— Умение контролировать процесс и результат учебной математической деятельности;

Решаемые учебные проблемы

Осмысленное решение химических задач на уроке математики. Поиск более простого решения задач. Применение знаний в реальной жизни.

Основные понятия, изучаемые на уроке

раствор, растворитель, концентрация, процент, массовая доля, нахождение процента от числа, нахождение числа по его части, построение логической цепочки рассуждений, сопоставление полученного результата с условием задачи.

Вид, используемых на уроке средств ИКТ

Презентация

Методическое назначение средств ИКТ

Активизация познавательного процесса на уроке

Аппаратное и программное обеспечение

Мультимедийный проектор, компьютер, раздаточный материал

Образовательные Интернет-ресурсы

Дли-тель

ность этапа

Основной вид учебной деятельности, направленной на формирование данного образовательного результата

Методы обучения

Средства ИКТ для реализации данного вида учебной деятельно-сти

Форма организации деятельности учащихся

Функции (роль учителя на данном этапе)

Основные виды деятельности учителя

Личностные: Нравственно-этическое оценивание исходя из социальных и личностных ценностей

2 мин.

Эмоциональный настрой и познавательный интерес к теме. Быстрое включение учащихся в деловой режим.

Работа с высказыванием:

Н.И. Лобачевский «Математика – это язык, на котором говорят все точные науки».

М.В. Ломоносов «Далеко простирает химия руки свои в дела человеческие»

Презентация,

Просмотр слайда и диалог с учителем.

проблемного характера: эмоционально настроить учащихся на интегрированный урок.

Проводит диалог с учащимися

учитель по высказыванию Н.И. Лобачевского;

М.В. Ломоносова

ЭТАП 2. Вхождение в тему урока и создание условий для осознанного восприятия нового материала

П- Поиск и выделение необходимой информации

К- оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли

5 мин.

Установить правильность, осознанность усвоения учащимися типов текстовых задач

Диалог

Отвечают на вопрос учителя: 1. Какие типы текстовых задач решаем в школьном курсе математики?

2.Какой тип задач более связан с химией?

3.Какие слова навели вас на правильный ответ?

Организовать самопроверку

Учитель: Использование небольшой психологической паузы и вопроса: Какой тип задач более связан с химией?

побуждающего внимание учащихся к теме урока.

ЭТАП 3. Актуализация знаний. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

П- самостоятельное выделение и формулирование познавательной цели

Р- Целеполагание

5 мин.

1.Осмысленное восприятие информации

2.Формулировка темы и целей урока.

Практическая «разминка»

вопросы для «разминки».

1.Отвечают на вопросы. Выполняют задания, сообщают о результатах.

2.Делятся мнениями на поставленную проблему.

3.Выдвигают гипотезу.

4.Формулируют тему урока и цель урока.

Подвести ответы детей к проблеме: Решали или нет такого типа задачи на уроках химии и математики? И что же предстоит сделать на этом уроке? Актуальность этих задач?

Помогает сформулировать тему урока

1. Учитель даёт задания устного счёта на проценты.

ЭТАП 4. Применение знаний решения задач на растворы в реальной жизни.

П- самостоятельное выделение и формулирование познавательной цели

Л- Развитие математической и химической речи;

Р- Целеполагание

К- оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли

10

мин

Текстовая постановка проблемных задач из реальной жизни.

Работа с химическими понятиями.

.1.Делятся мнениями на поставленную проблему.

2.Работают с химическими определениями и понятиями.

Настроить детей на применение методов решения задач

Учитель : Организация работы у доски по карточкам-заданиям.

ЭТАП 5. Организация и самоорганизация учащихся в ходе дальнейшего обобщения и систематизации знаний материала. Практикум.

П-Выбор эффективных способов решения задач

П-Извлечение необходимой информации из прослушанных, прочитанных текстов различных задач

К- оценка действий партнёра умение с достаточной полнотой и точностью выражать свои мысли

10 мин

1.Выполнение задачи №1 (на растворы ) по карточкам в тетрадях и у доски.

2, Защита приёмов решения задачи.

Работа с текстом ,

представление основного материала одновременно в словесной, знаково-символической форме и в виде таблицы

1.Выполняют задание №1 письменно.

2.Делятся мнениями на поставленную проблему.

3.Работают с определением молярной массы и концентрации.

4.Делают выводы в выборе метода решения, в выборе схемы решения, учитывая знание формул по химии и химических обозначений.

Создание условий для освоения учащимися знаний преимущественно в форме деятельности

Учитель:

1.Руководит последователь

ностью защиты методов решения задачи.

2. Предлагает сделать

выводы.

3.Организует обсуждение результатов.

.

ЭТАП 6. Новое, давно забытое старое. Или арифметический способ решения задач на растворы.

П-Выбор эффективных способов решения задач

Умение составлять схемы и уравнения к текстовым задачам.

Р— Коррекция; Целеполагание

Л — Развитие интереса к предметам;

5мин

1.Выполнение задач арифметическим методом.

Работа со схемой и самостоятельное составление схемы и решение задачи.

1.Работают в парах.

2.Делают выводы в выборе решения.

Создание условий для освоения учащимися знаний преимущественно в форме деятельности.

Предлагает сделать

выводы.

Организует обсуждение результатов.

Руководит работой на местах.

ЭТАП 7. Первичная проверка полученных результатов. Коррекция.

Длительность этапа

Виды учебной деятельности для проверки полученных образовательных результатов

Средства ИКТ для реализации данного вида учебной деятельности

Методы контроля

Способы коррекции

Форма организации деятельности учащихся

Функции(роль учителя на данном этапе)

Основные виды деятельности учителя

3-5мин.

Выполнение по карточкам: 1 вариант: задача №3;

2 вариант: задача №4.

Слайд с текстом

проверка выполнения в тетради

Комментарии

учеников и учителя к решению на слайде

Работа с карточками-заданиями

Настраивает детей на быстрое выполнение задания

Помогает комментировать

задания после проверки тетрадей.

ЭТАП 8. Информация о домашнем задании, инструктаж по его выполнению.

Образовательные задачи этапа учебного занятия

Содержание этапа учебного занятия

Показатели выполнения образовательных задач этапа

Условия выполнения образовательных задач этапа

Возможный метод и приём обучения

Обеспечить понимание учащихся цели содержания и способов выполнения домашнего задания.

1.информация о домашнем задании

2.инструктаж по выполнению д/з.

находить необходимую для выполнения работы информацию в материалах учебника

Соответствие содержания д/з уровню обученности учащихся.

Запись домашнего задания в дневник

Задание:

1 уровень: на карточках две задачи

2уровень: на карточках две задачи

ЭТАП 9. Рефлексия (Подведение итогов занятия)

Образовательные задачи этапа учебного занятия

Содержание этапа учебного занятия

Показатели выполнения образовательных задач этапа

Условия выполнения образовательных задач этапа

Возможный метод и приём обучения

1.Дать качественную оценку работы класса

2.Инициировать рефлексию учащихся по поводу своего эмоционального состояния, мотивации своей деятельности и взаимодействия с учителями и одноклассниками

1.Подведение итогов урока

2.Мобилизация учащихся на рефлексию своего поведения

1.Чёткость и краткость

2.Открытость учащихся в осмыслении своих действий и самооценке

Умение учителя давать качественную характеристику работы класса

Развитие способностей учащихся к рефлексии

Приём «Смайлики»:

Суть- зафиксировать свои достижения на уроке:

Я разобрался в теме…

Я пропускаю ход…

Сокращения в технологической карте: П- познавательные УУД; К- коммуникативные; Р- регулятивные; Л-личностные

Ход урока:

Этапы урока

Деятельность

учителя

ученика

ЭТАП 1.

Организационный этап

Здравствуйте, дети.

Я рада вас видеть.

Кто сегодня дежурный? Назовите отсутствующих. Сегодняшнее число? (учитель записывает число на доске). Совершенно верно.

Итак, начинаем наш урок.

Сегодня у нас не совсем обычный урок, у нас интегрированный урок по решению задач на растворы. Просим вас по ходу урока активно работать.

Эпиграфом к уроку мы взяли слова:

Н.И. Лобачевского «Математика – это язык, на котором говорят все точные науки» Ну а М.В. Ломоносов — «Далеко простирает химия руки свои в дела человеческие» (говорит учитель математики)

1.Приветствуют учителя. Готовятся к уроку:

в тетрадях записывают число и классная

работа.

2.Смотрят

на слайд презентации.

3.Отвечают

на вопрос учителя.

ЭТАП 2.

Вхождение в тему урока и создание условий для осознанного восприятия нового материала

Учитель: В курсе школьной математики изучают различные практические, текстовые задачи. Давайте вспомним их и кто мне подскажет типы этих задач? (ведётся диалог).

Задачи на числа

Задачи на движение

Задачи на работу

Задачи на растворы, смеси и сплавы

Скажите: какой тип задач более связан с химией? (Высказывания детей)

Да! Ближе всех к химии задачи на растворы, смеси и сплавы. Какие слова навели вас на правильный ответ? (ответы детей).

Когда мы решаем такие задачи на уроке математики, то нам не хватает химического обоснования этих задач.

1.Ученики отвечают на вопросы учителя:

1. Какие типы текстовых задач решаем в школьном курсе математики?

2.Какой тип задач более связан с химией?

3.Какие слова навели вас на правильный ответ?

ЭТАП 3. Актуализация знаний. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Учитель : Давайте мы с вами подумаем и сформулируем цель урока: чем же сегодня будем заниматься на уроке математики? (Учитель подводит ответы детей к проблеме: Решали или нет такого типа задачи на уроках химии и математики? И что же предстоит сделать на этом уроке? Актуальны ли эти задачи? Учитель помогает сформулировать тему и цель урока).

Итак, мы пришли к цели урока:

— Вспомним, обобщим, свяжем решение задач на растворы, сплавы и смеси с химическими понятиями и, конечно же, будем искать более простое и оригинальное решение.

А нужно ли нам это? Актуальны ли эти задачи? Для чего же нужно уметь решать такие задачи? (Учитель подводит диалог с учащимися к ответам:

— Для успешной сдачи ОГЭ и по химии и по математике.

— Для дальнейшей нашей жизни и деятельности.).

Запишем тему урока: Систематизация и обобщение знаний по решению задач на растворы и смеси (учитель записывает тему на доске).

А для старта нам необходима небольшая «разминка» (проводится устный счёт по теме «Проценты»):

Посмотрите на слайд, и проведём небольшой устный счёт.

(Понятие «процент». Предоставлены примеры на темы: Перевод процентов в десятичную дробь и десятичной дроби в проценты. Как найти процент от числа? Как найти число по его части?).

1.Отвечают на вопросы учителя

. 2.Делятся мнениями на поставленную проблему.

3.Выдвигают гипотезу.

4.Формулируют с помощью учителя тему урока и цель урока.

ЭТАП 4. Применение знаний решения задач на растворы в реальной жизни.

Учитель : Размялись, а теперь за задачи на растворы:

К доске пойдут Грищенко Катя ,Потовский Владислав , Семененко Катя .(Всем троим предстоит решить одну и ту же задачу, но только применяя указанный на листочке метод. Эта задача №1 из раздаточного материала к уроку, которая есть у каждого ученика на его столе. Учитель контролирует решение и оформление решения на доске).А также обращается к ученикам со следующими вопросами:

У нас дома есть скутер и машина. И мне часто приходится слышать об аккумуляторах и электролите. Что это такое? В чём могут быть проблемы? Как их решить? И нужно ли мне это знать?

Ответ: (в виде диалога учителя с учениками). Конечно, всё готовое в наше время можно купить в специализированных магазинах, но знать, с чем имеешь дело, должен каждый. Бывают моменты, когда магазина рядом нет, а проблема есть и необходимо её решить.

— Кто знает: Что такое электролит?

— Электролит — это раствор солей, щелочей и кислот.

— Что такое кислотный электролит?

— Раствор концентрированной серной кислоты h3SO4 в дистиллированной воде H 2O.

— Для чего он используется?

— Электролит в аккумуляторе является средой, в которой происходят химические реакции, позволяющие накапливать электрическую энергию и отдавать её.

Саша, ты понял, что такое электролит? А как приготовить электролит, ты узнаешь подробнее на уроке химии . А в следующей задаче указана одна из проблем, которая может возникнуть с аккумулятором. Эта проблема представлена в задаче.

Задача: Приготовить 980 граммов кислотного электролита для аккумулятора, имея 98% раствор серной кислоты h3SO4 . Сколько нужно взять воды h3O и серной кислоты h3SO4, чтобы получить 37%-ный раствор электролита?

Теперь послушаем Катю.

Катя: А меня интересует, как решить вот такую задачу:

Как из 78%-ной уксусной эссенции в домашних условиях приготовить 9%-ный уксус. И для чего в заготовках на зиму используют уксус?

Ответ: (в виде диалога: учитель и ученики)

Учитель математики: Задачи-проблемы Саши и Кати мы увидели. Как видите это задачи из нашей повседневной жизни. Но решать мы их сейчас не будем. В конце урока вы сами сможете помочь им решить их задачи, применяя выбранный вами способ решения.

1.Делятся мнениями на поставленную проблему.

2.Работают с химическими определениями и понятиями.

3.Отвечают у доски по заданиям.

ЭТАП 5. Организация и самоорганизация учащихся в ходе дальнейшего обобщения и систематизации знаний материала. Практикум.

Учитель: А сейчас рассмотрим алгоритмы решения задач, в которых фигурируют растворы.

Ученики-консультанты по химии и математике подготовили нам решение задачи №1, которая есть на каждом столе. Вначале мы с вами ознакомимся с текстом. (Читает вслух один из учеников)

Задача №1: Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором и получили 600г 15%-ного раствора. Сколько граммов каждого раствора было взято?

Решение задачи №1:

Алгебраический способ (слово предоставлено ученикам у доски):

(Учитель руководит последовательностью защиты метода решения задачи №1с помощью системы уравнений с двумя переменными).

р-ра

Масса р-ра в граммах

«Сухое вещество» в %

«Сухое вещество» в граммах

1

х

30% = 0,3

0,3х

2

у

10% = 0,1

0,1 * у

3

600

15% = 0,15

0,15 * 600 = 90

Составляем систему уравнений:

х + у = 600,

0,3х + 0,1у = 90; выразив из первого уравнения У через Х и подставив во второе уравнение полученный результат получим уравнение:

0,3х + 0,1 (600 — х) = 90

0,3х + 60 — 0,1х = 90

0,2х = 30

x = 30 / 0,2

x = 300 / 2

x = 150 (г) – масса 1 р-ра

Тогда y = 600 – x = 600 – 150 = 450 – масса 2 р-ра

Ответ: 150г.; 450г.

Учитель руководит последовательностью защиты метода решения задачи №1 математическим с помощью уравнения :

р-ра

Масса р-ра в граммах

«Сухое вещество» в %

«Сухое вещество» в граммах

1

х

30% = 0,3

0,3х

2

600 — х

10% = 0,1

0,1 (600 — х)

3

600

15% = 0,15

0,15 * 600 = 90

0,3х + 0,1 (600 — х) = 90

0,3х + 60 — 0,1х = 90

0,2х = 30

x = 30 : 0,2

x =300 : 2

x = 150 (г) – масса 1 р-ра

600 – 150 = 450 – масса 2 р-ра Ответ: 150г.; 450г.

Сравним решение задачи всеми способами. Кто может сделать вывод? (Учитель предлагает сделать

выводы. Организует обсуждение результатов.)

ВЫВОД: Разница в решении в том, что в математике — схема, а в химии – описание и формула расчёта, а уравнение для расчёта одно и то же. Может быть стоит совместить решения? А это будет выглядеть так:

р-ра

m(р-ра)в граммах*(массовая доля)=m (сух. в-ва)

1

х

30% = 0,3

0,3х

2

600 — х

10% = 0,1

0,1 * (600 – х)

3

600

15% = 0,15

0,15 * 600 = 90

В тетрадях пишем № задачи и перепишем обобщённую таблицу. Запишем уравнение:

0,3х + 0,1 (600 — х) = 90

и ответ: 150г.; 450г.

1.Выполняют задание №1 письменно, применяя последнюю обобщённую схему.

2.Делятся мнениями на поставленную проблему.

3.Работают с определением молярной массы и концентрации.

4.Делают выводы в выборе метода решения, в выборе схемы решения, учитывая знание формул по химии и химических обозначений.

ЭТАП 6. Новое, давно забытое старое. Или арифметический способ решения задач на растворы.

Существует ещё один способ решения задач такого типа – это арифметический способ. Этот способ более приближён к реальной жизни и его иногда называют «решение крестом».

Решим арифметическим методом задачу №1. Текст у вас есть. (Учитель, составляя схему решения данной задачи, читает каждую строчку. Комментирует каждую запись. Попутно отвечая на возникшие вопросы.)

Задача №1

Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов каждого раствора было взято?

Решение:

Итак, читаем условие задачи №1 и составляем в тетради схему по условию задачи:

Числа 5 и 15 – это части! первого и второго растворов

Отношение 5 : 15 или, упрощая получим 1 : 3. Т.е. взяв 1 часть 1 р-ра и 3 части 2-го р-ра получим третий раствор нужной концентрации. Значит в третьем растворе массой 600 граммов 1 +3 = 4 части. Отсюда следует:

(600 : 4) * 1 = 150(г) – масса 1 раствора,

(600 : 4) * 3 = 450(г) – масса 2 раствора,

Ответ: 150г, 450г

Теперь читаем задачу №2 и, вместе со мной учимся записывать решение « крестом» этой задачи.

Итак, читаем условие задачи №2 (учитель просит ученика прочитать задачу) и составляем в тетради схему по условию задачи самостоятельно. А теперь проверим себя (учитель составляет схему пошагово для этой задачи):

1р-р 30 50 – 45 = 5(частей)

3 р-р 45

2 р-р 50 45 – 30 = 15(частей)

Числа 5 и 15 – это части! первого и второго р-ров

берём отношение 5 : 15 или 1 : 3.

Ответ: 1 : 3

1.Выполняют задание №1и №2 письменно, применяя предложенную схему арифметического решения.

2.Делятся мнениями. 3.Работают в парах.

4.Делают выводы в выборе решения для данного типа задач.

ЭТАП 7. Первичная проверка полученных результатов. Коррекция.

Наконец пришло время помочь Саше и Кате справиться с их проблемой. Их задачи – это №3, №4 на карточках.

Попробуем поработать в парах: по вариантам.

(учителя проверяют правильность решения тех, кто быстрее справился с заданием, и оценивают их)

А теперь обменяемся тетрадями, сверим решение и найдём ошибки:

Задача: Как из 78%-ной уксусной эссенции в домашних условиях приготовить 9%-ный уксус?

Решение:

1 р-р: 78%(эссенция) 9 – 0 = 9(частей)

3 р-р 9%

2 (р-р) вода 0% 78 – 9 = 69 (частей)

Итак 9 : 69 или 3 : 23. Ответ: 3 : 23.

Задача: Приготовить 980 граммов кислотного электролита для аккумулятора, имея 98% раствор серной кислоты h3SO4 . Сколько нужно взять воды h3O и серной кислоты h3SO4, чтобы получить 37%-ный раствор электролита?

Решение:

. h3SO4 98% 37 – 0 = 37(частей)

Электролит(980г) 37%

h3O 0% 98 – 37 = 61(частей)

980 : (37+61) * 37 = 980 : 98 * 37 = 370(г) — кислоты,

980 : 98 * 61 = 610(г) – воды

Ответ: 370г (h3SO4) , 610г (h3O).

Всё выполнено? Обратите внимание на последний пункт: поиск более простого решения задач. Да, мы познакомились с необычной схемой решения для одного из видов химических задач на растворы и смеси, схема «креста». Для других видов задач, может быть, вы придумаете или найдёте схемы сами? Всё в ваших руках.

Работа с карточками-заданиями: задачи №3 и №4.

ЭТАП 8. Информация о домашнем задании, инструктаж по его выполнению.

А теперь запишем домашнее задание: у каждого на столе лежат карточки с домашним заданием, положите в дневник. На обратной стороне листка написаны дополнительные

задания «для тех, кто хочет знать больше».

Задание:

1 уровень: на карточках две задачи — это для всех.

2 уровень: на карточках две задачи для более сильных.

ЭТАП 9. Рефлексия (Подведение итогов занятия)

Учитель: Мне хочется сказать вам дети, что вы все сегодня на уроке работали замечательно.

Сегодня кого нам хочется похвалить?… Я с вами согласна. В тетради некоторым из вас поставлены оценки за решение задач в самостоятельной работе. Я их выставила в журнал. Можете подать дневники. А кто хочет тоже себя похвалить пусть за самое маленькое, но открытие для себя, вам наши аплодисменты.

А кому сегодня не повезло, то повезёт потом, нужно только постараться.

А сейчас, ребята, я бы хотела узнать мнение об уроке. Для этого заполните, пожалуйста, листочки со смайликами и на переменке мне их на стол.

До свидания.

Приём «Смайлики»:

Суть — зафиксировать свои достижения на уроке:

Я понял…

Я пропускаю ход

Приложение:

Задания на карточке к уроку (на каждый стол):

1. Смешали 30%-ный раствор соляной кислоты с 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов каждого раствора было взято?

2. Смешали 30%-ный и 50%-ный растворы азотной кислоты и получили 45%-ный раствор. Найдите отношение массы 30%-ного раствора к массе 50%-ного раствора, взятых первоначально.

3. Задача: Приготовить 980 граммов кислотного электролита для аккумулятора, имея 98% раствор серной кислоты h3SO4 . Сколько нужно взять воды h3O и серной кислоты h3SO4, чтобы получить 37%-ный раствор электролита?

4. Задача: Как из 78%-ной уксусной эссенции в домашних условиях приготовить 9%-ный уксус?

Карточки с домашним заданиеь (на каждый стол):

1. Смешали 20%-ный раствор соляной кислоты с 40%-ным раствором и получили 800 г 25%-ного раствора. Сколько граммов каждого раствора было взято?

2. Смешали 75%-ный и 25%-ный растворы азотной кислоты и получили 40%-ный раствор. Найдите отношение массы 75%-ного раствора к массе 25%-ного раствора, взятых первоначально.

3. Задача: Приготовить 490 граммов кислотного электролита для аккумулятора, имея 49% раствор серной кислоты h3SO4 . Сколько нужно взять воды h3O и серной кислоты h3SO4, чтобы получить 20%-ный раствор электролита?

4. Задача: Как из 72%-ной уксусной эссенции в домашних условиях приготовить 8%-ный уксус?

Доклад на тему «Обучение учащихся решению текстовых задач на сплавы и смеси»

Доклад на тему «Обучение учащихся решению текстовых задач на сплавы и смеси»

Клокова Г.А.

1. Теоретические основы решения задач на сплавы и смеси

Задачи на смеси, сплавы и проценты всегда вызывали сложности у учащихся. Статистические данные по анализу результатов ЕГЭ по математике показывают, что решаемость задания, содержащего текстовую задачу, приблизительно равна 30%.

Данные задачи имеют практическое значение, являются хорошим средством развития мышления учащихся. Они расширяют базовый курс математики и позволяют учащимся осознать практическую ценность математики. Задачи на растворы, смеси и сплавы обладают диагностической и прогностической ценностью, то есть с их помощью можно проверить знания основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности, то есть лишний раз проверить и оценить свои способности к математике. При решении задач на растворы, смеси и сплавы очевидны межпредметные связи с химией, физикой и экономикой, знание этого повышает учебную мотивацию учащихся по всем предметам.

Трудности при решении этих задач могут возникнуть на различных этапах:

• составления математической модели ( уравнения, системы уравнений, неравенства)

• решения полученной модели;

• анализа математической модели ( по причине кажущейся ее неполноты: не хватает уравнений в системе или слишком много неизвестных и пр.)

Решение задач на смеси, сплавы, растворы требует определенной теоретической базы.

Это различные определения, такие как концентрация, процентное содержание и др., а также и всевозможные допущения, например:

1) всё, что мы рассматриваем, считается однородным;

2) все процессы происходят мгновенно;

3) полученное вещество состоит из смешиваемых веществ и равно сумме их объемов;

4) величины, получаемые в результате вычислений, не могут быть со знаком минус.

Существует несколько способов решения задач на слияние растворов. Например, можно воспользоваться расчетной формулой, как это делают на уроках химии. Из области математики можно пользоваться графическим или же алгебраическим методами. Более простым в применении является метод, в котором указанные задачи решают по «правилу креста».

Задачи на смеси и сплавы бывают двух видов:

1. Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.

2. В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.

В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.

Концентрация вещества — это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.

Масса раствора равна сумме масс всех составляющих.

Алгоритм решения задач на смеси и сплавы:

1. Определить, какое вещество влияет на концентрацию раствора (главное вещество).

2. Следить за весом главного вещества при добавлении других веществ в раствор.

3. Исходя из данных об изменениях состояния главного вещества — сделать выводы.

Как правило, концентрация выражается в процентах.

Процент – это сотая доля числа. Она может выражаться либо в виде десятичной дроби (0,11), либо в виде процента (11%).

Мысль 1

Если мы смешаем 3 литра апельсинового сока и 77 литров воды, то получим 10

10 литров апельсинового нектара (сделаем предположение, что смешивание происходит в автоматическом режиме, а не вручную).

Мысль 2

Если мы смешаем 6 литров яблочного сока и 66 литров персикового сока – то получится 12 литров яблочно-персикового сока.

И еще одна очевидность (последняя).

Мысль 3

Если мы смешаем 3 литра яблочного сока с 10% мякоти (0,3 л), и 55 литров яблочного сока с 5% мякоти (0,25 л), то получим 88 литров сока с 0,55 л мякоти

(0,3+0,25).

Перейдем к задачам.

2. Простейшие задачи на смеси и сплавы

Задачи на смеси и сплавы бывают двух основных видов:

1. Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.

2. В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.

Строго говоря, подход к решению от этого не меняется. Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.

Пример 1.

В 5% раствор кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала равна концентрация раствора (в процентах)?

Решение:

1. Для начала вычислим, сколько кислоты содержится в 5% растворе. Из 3,8 кг 5% — это кислота, а значит в растворе 0,05 * 3,8=0,19 кг кислоты

2. Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т.е. 3,8 кг + 1,2 кг = 5 кг.

3. Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – 0,19 кг. Таким образом, концентрация кислоты стала равна 0,19:5=0,038

4. Теперь выразим концентрацию в процентах — 0,038⋅100%=3,8%

Ответ: 3,8

Теперь давай попробуем решить задачу посложнее.

Пример 2.

Смешали 3 кг 5%-го водного раствора щелочи и 7 кг 15%-го. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.

Решение:

Давай попробуем визуализировать ситуацию. 3 кг 5% водного раствора. Значит воды в этом растворе 95%.

Нарисуем:

А теперь второй раствор:

После смешивания, вновь получившийся раствор будет весить 3кг + 7 кг = 10 кг. Обозначим количество щелочи в новом растворе за x, а количество воды – (10−x):

Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе –0,05⋅3=0,15 кг щелочи

и 3−0,15=2,85 кг воды,

во втором — 0,15⋅7=1,05 кг щелочи

и 7−1,05=5,95 кг воды:

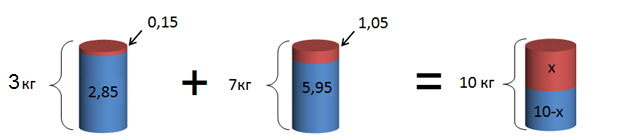
Из картинки видно, что количество щелочи в новом растворе равно сумме весов кислоты в старых растворах: x=0,15+1,05=1,2 кг кислоты.

Теперь, зная количество щелочи в новом растворе и зная его массу, мы можем легко определить концентрацию:

1,2:10=0,12

​Поскольку ответ просят дать в процентах – умножим на 100%

0,12⋅100%=12%.

Ответ: 12.

Эту визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.

3. Старинный метод решения задач или «метод креста»

Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого. Ввиду большой простоты предложенный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо, как в предыдущей задаче, рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.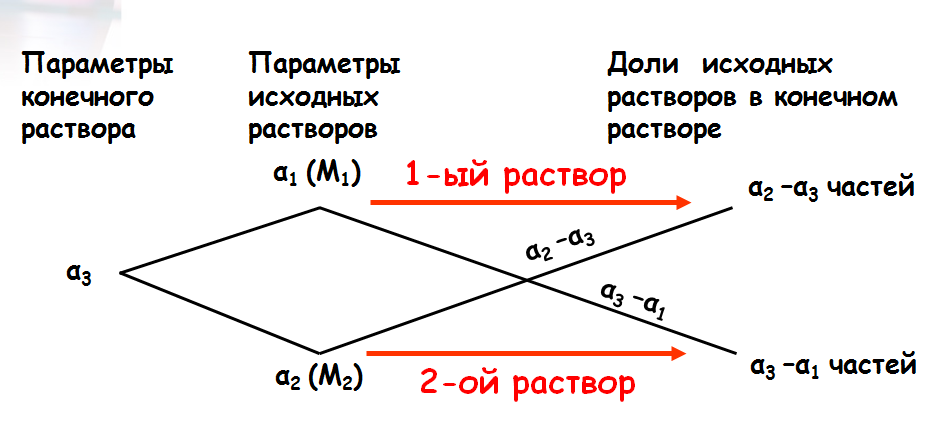

«Правилом креста» называют диагональную схему правила смешения для случаев с двумя растворами. Слева на концах отрезков записывают исходные массовые доли растворов (обычно слева вверху – большая), на пересечении отрезков – заданная, а справа на их концах записываются разности между исходными и заданной массовыми долями. Получаемые массовые части показывают, в каком отношении надо слить исходные растворы.

Пример 3. (смешивание двух веществ, предлагалась на экзамене в 2006 году). Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?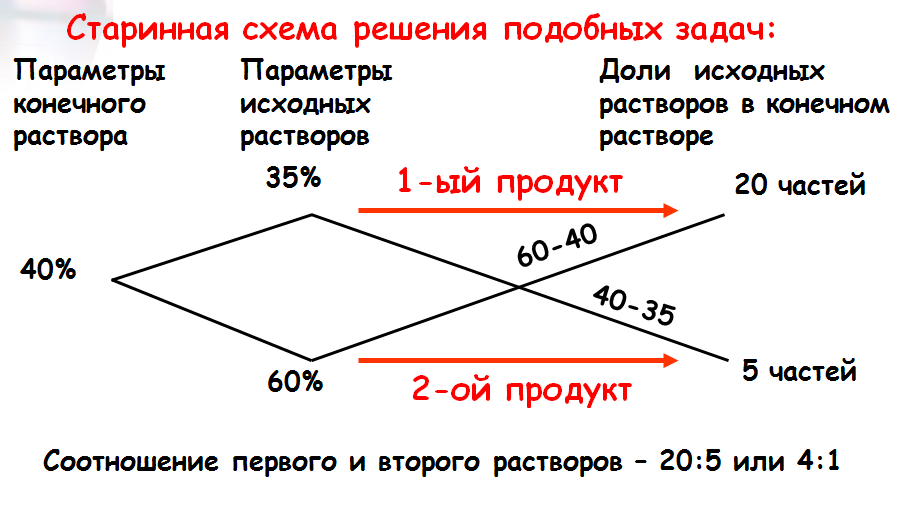

4. Алгебраический метод

Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или систем неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.

Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений. Главное внимание при обучении учащихся способу решения текстовых задач методом составления уравнений должно быть обращено на сознательную отработку этапности решения.

В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.

1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.

2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.

3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.

4. Изучение полученного решения, критический анализ результата.

Обратим внимание на семь критериев полноценности решения задачи,

сформулированных В. М. Брадисом: безошибочность, обоснованность, исчерпывающий характер, простота, ясность пути, приведшего к решению задачи, рациональность записи, завершающее обобщение решения.

При решении задач удобно составлять следующую таблицу, которая помогает зрительно воспринимать задачу.

Пример 4. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?

Решение.

Сначала составим таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа в рудеапишем массу руды, массу железа, концентрацию () руде?

нем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20) до и после удаления примесей.

Пусть х кг – масса железа в руде. Так как масса всей руды равна 500 кг, то концентрация железа в ней равна .

Так как масса железа в 200 кг примесей равна 0,125200=25 (кг), то его масса в руде после удаления примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300 кг следует, что концентрация железа в ней равна .

По условию, содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:

Найдём, что 212,5 кг – масса железа в руде. Найдём остаток железа в руде после удаления примесей: 212,5-25=187,5 (кг).

Ответ: 187,5 кг.

Пример 5. Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

1 способ решения

Сумма масс меди в двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном сплаве (третья строка таблицы):

Решив это уравнение, получаем х=140. При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять140г, а второго 60г.

Ответ:140г. 60г.

2 способ решения

Рассмотрим решение этой же задачи с помощью следующей модели. Изобразим каждый из растворов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Для того, чтобы показать, что происходит смешивание веществ поставим знак «+» между первым и вторым прямоугольниками, а знак «=» между вторым и третьим прямоугольниками показывает, что третий раствор получен в результате смешивания первых двух. Полученная схема имеет следующий вид:

Решение.

Пусть хг – масса первого сплава. Тогда, (200-х)г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:

Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

Решив это уравнение, получаем х=140. При этом значении х выражение 200-х=60. Это означает, что первого сплава надо взять140г, а второго-60г.

Ответ: 140 г меди и 60 г свинца.

Пример 6. (Типовые тестовые задания ЕГЭ 2012 п/р А.Л.Семенова, И.В.Ященко). Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%го раствора той же кислоты, то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора использовали для получения смеси?

Решение.

Задача содержит два неизвестных, поэтому необходимо решить систему двух уравнений с двумя неизвестными. Составим эти уравнения. Обозначим через х кг – массу первого раствора, через у кг- массу второго раствора. Рассмотрим первую ситуацию:

Составим первое уравнение: + + = . После упрощения уравнение примет вид: 2х +у = 10.

Рассмотрим вторую ситуацию:

Составим второе уравнение: + + = . После упрощения уравнение примет вид: у = 4. Тогда х = 3

Ответ: 3 кг использовали 70%-й кислоты

Пример 7. Первый раствор содержит 40% кислоты, а второй — 60% кислоты. Смешав эти растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо воды добавили 5 л 80 % раствора, то получился бы 70 % раствор. Сколько литров 60 % раствора кислоты было первоначально?

Пусть х л было 40 %,

а у л – 60 %. Тогда нового, 20 % раствора – (х + у + 5) л.

0,4х (л) – кислоты в первом растворе;

0,6у (л) – кислоты во втором растворе;

0,2·(х + у + 5) (л) – кислоты в новом растворе.

Получим уравнение

кислоты в 80 процентном растворе;

кислоты в новом, 70 процентном растворе.

Получим второе уравнение

Получим систему уравнений:

2 л 60 процентного раствора было первоначально.

Ответ: 2 л.

Подведем итоги

Если ты заметил, во всех задачах мы сначала определяли, какое вещество влияет на концентрацию, назовем его «главным». А дальше следили за абсолютной величиной этого главного вещества (в килограммах, литрах). Если в раствор (сплав) что-то доливали, добавляли, то, в зависимости от состава «добавки», вес «главного» вещества либо изменялся, либо нет. Важно определить, что произошло с «главным» веществом, а дальше решение становится совсем простым.

Список использованной литературы.

1. Кузнецова Л.В. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе. — М.: Просвещение, 2010.

2. Прокопенко Н.И. Задачи на смеси и сплавы.- М. :Чистые пруды, 2010 (Библиотечка «Первого сентября». Выпуск 31 )

3. Лурье М.В., Александров Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.

4. Малахова Н. А., Орлов В. В. и др. Методика работы с сюжетными задачами: Учебно-методич. пособие. СПб.: Изд-во РГПУ, 1992. 46 с.

5.  Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов сред.школы. – 3-е изд., доработанное. М.: Просвещение, 1989

6.  www.mathege.ru

7. www.fipi.ru

8. www. festival.1september.ru

9. http://www.shevkin.ru/

10. http://mat-ege.ru

«Решение задач на смеси, растворы и сплавы»

Инфоурок › Математика ›Презентации›Проект по математике на тему: «Решение задач на смеси, растворы и сплавы»

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Проект по математике на тему: «Решение задач на смеси и сплавы» Выполнила: студентка ПНК-22 Баранова А.С.

2 слайд Описание слайда:

Введение Если хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Великий математик Дьердь Пойа

3 слайд Описание слайда:

Теоретические основы решения задач  Все получающиеся сплавы или смеси однородны. При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов. Процент — одна сотая любого вещества.   Процентным содержанием ( концентрацией)  вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.   Это отношение может быть выражено либо в дробях, либо в процентах.  Сумма концентраций всех компонент, составляющих смесь, равна единице.

4 слайд Описание слайда:

Способы решения задач на смеси и сплавы: Задачи на процентное содержание влаги. С помощью таблицы. Способ «стаканчиков». Решение задач на растворы, смеси и сплавы с помощью модели. Старинный алгебраический метод или правило квадрата. Способ креста(квадрат Пирсона)

5 слайд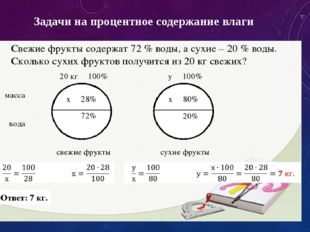 Описание слайда:

Задачи на процентное содержание влаги

6 слайд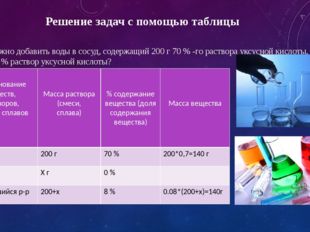 Описание слайда:

Решение задач с помощью таблицы Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты? Наименование веществ, растворов, смесей, сплавов Масса раствора (смеси, сплава) % содержание вещества (доля содержания вещества) Масса вещества 1 200 г 70 % 200*0,7=140 г 2 Х г 0 % Получившийся р-р 200+х 8 % 0.08*(200+х)=140г

7 слайд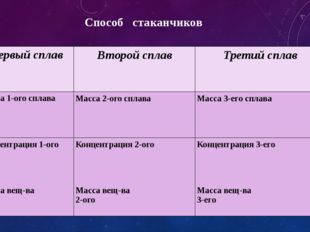 Описание слайда:

Способ стаканчиков Первый сплав Второй сплав Третий сплав Масса 1-ого сплава Масса 2-ого сплава Масса 3-его сплава Концентрация 1-ого Концентрация 2-ого Концентрация 3-его Массавещ-ва 1-ого Масса вещ-ва 2-ого Масса вещ-ва 3-его

8 слайд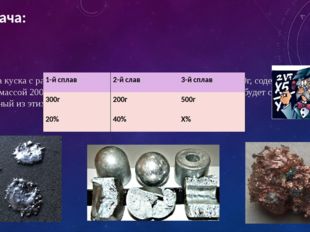 Описание слайда:

Задача: Даны два куска с различным содержанием олова. Первый, массой 300г, содержит 20% олова. Второй, массой 200г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков? 1-й сплав 2-й слав 3-й сплав 300г 200г 500г 20% 40% Х%

9 слайд Описание слайда:

Решение с помощью модели В сосуд, содержащий 6 литров 20-процентного водного раствора некоторого вещества, добавили 6 литров воды. Сколько процентов составляет концентрация получившегося раствора? Решение с помощью модели: 12 л х% 6л 20 % 6 л 0 %

10 слайд Описание слайда:

Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 т стали с содержанием 30% никеля? Решение задач с помощью старинного алгебраического метода 5 10 30 40 25

11 слайд Описание слайда:

Решение задач способом креста (квадрат Пирсона) В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

12 слайд Описание слайда:

ВЫвод В ходе рассмотрения способов решения задач на смеси, сплавы, растворы мы увидели красоту, сложность и притягательность данных способов. Выбор способа решения зависит от конкретной задачи и от умения решающего.

13 слайд Описание слайда:

Спасибо за внимание

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Проверен экспертом

Общая информация

Номер материала: ДБ-896815

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий