Решение задач на применение аксиом и их следствий (разные задачи)
Тема: Аксиомы стереометрии и их следствия
Урок: Решение задач на применение аксиом и их следствий (разные задачи)
Аксиомы стереометрии и следствия из них устанавливают взаимоотношения между основными фигурами стереометрии: точкой, прямой и плоскостью.
Точка может лежать на прямой, может не лежать на прямой.
Прямая может принадлежать плоскости, может не принадлежать плоскости.
Плоскость может проходить через прямую, не проходить через нее, содержать точку, не содержать точку.
Подобные задачи мы решали для пирамиды и для параллелепипеда. Теперь мы будем решать задачи в общем виде.
Вспомним для этого сначала аксиомы и теоремы-следствия.
Аксиома 1 (А1)
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Иллюстрация аксиомы А1.
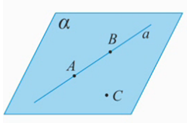
Рис. 1.
Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: (Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость
(Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость  , и притом только одна. Плоскость
, и притом только одна. Плоскость  можно также обозначить через три точки АВС.
можно также обозначить через три точки АВС.
Аксиома 2 (А2)
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Иллюстрация аксиомы А2. (Рис. 2.)
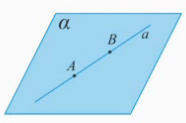
Рис. 2.

Аксиома 3 (А3).
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой).
Иллюстрация аксиомы А3. (Рис. 3.)

Рис. 3.
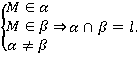
Повторение теорем, которые следуют из аксиом стереометрии.
Теорема 1
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Иллюстрация теоремы 1. (Рис. 4.)
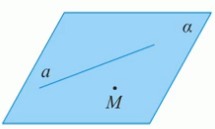
Рис. 4.
 единственная
единственная
Теорема 2
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Иллюстрация теоремы 2. (Рис. 5.)
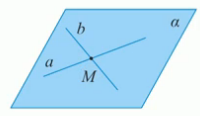
Рис. 5.
Задача 1.
Даны две прямые, которые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости (Рис. 6.).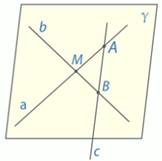
Рис. 6.
Решение:
Нам даны две прямые а и b, которые пересекаются в некоторой точке М. Возьмем произвольную прямую с, которая не проходит через точку М, но пересекает исходные прямые а и b в точках А, В, соответственно.
Через две пересекающиеся прямые проходит плоскость, и притом только одна, согласно 2 теореме. Значит через пересекающиеся прямые а и b проходит единственная плоскость, обозначим ее  .
.
Две разные точки  . А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.
. А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.
Таким образом, мы доказали, что все прямые, пересекающие А и В, но не проходящие через М, лежат в одной плоскости.
Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
Решение:
Пусть нам даны три точки: А, В, и С. Нужно доказать, что отрезки АВ, ВС, СА лежат в одной плоскости (Рис. 7.).

Рис. 7.
Если точка С лежит на прямой АВ, то ответ очевиден. Предположим, что точка С не принадлежит прямой АВ. Тогда через три точки A, B, C, не лежащие на одной прямой, проходит плоскость, и притом только одна, в силу аксиомы 1. Обозначим эту плоскость 
Прямая АВ целиком лежит в плоскости  , потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости
, потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости  .
.
Аналогично и с другими отрезками. Прямая ВС лежит в плоскости 
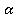 , значит, и отрезок ВС лежит в плоскости
, значит, и отрезок ВС лежит в плоскости  .
.И аналогично, отрезок АС лежит в плоскости  . Что и требовалось доказать.
. Что и требовалось доказать.
Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости  . Лежат ли 2 другие вершины параллелограмма в плоскости
. Лежат ли 2 другие вершины параллелограмма в плоскости 
Решение:
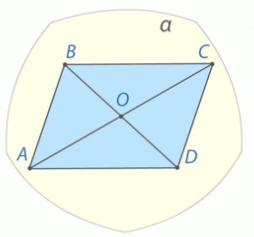
Рис. 8.
Пусть дан параллелограмм АВСD. Известно: точка А, точка В, точка О – точка пересечения диагоналей, лежат в плоскости  . Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.
. Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.
Через три точки А, В и О проходит плоскость, и притом только одна. Это плоскость  . Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка
. Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка  .
.
Аналогично, прямая ВО целиком лежит в плоскости  , значит, точка D этой прямой тоже лежит в плоскости
, значит, точка D этой прямой тоже лежит в плоскости  .
.
Ответ: Да, вершины С и D лежат в плоскости  .
.
Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
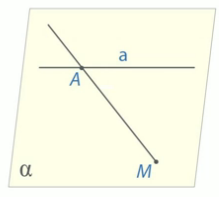
Рис. 9.
Решение:
Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а лежат в некоторой единственной плоскости.
Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит единственная плоскость, обозначим через  . Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости
. Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости  , потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости
, потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости 
Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи, и доказали, что она лежит в плоскости  . Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости
. Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости  , что и требовалось доказать.
, что и требовалось доказать.
Верно ли утверждение:
а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости;
б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
Рис. 10.
Решение:
а) Пусть дана окружность и точки А, В, С. В случае если только две точки В и С принадлежат некоторой плоскости, то совсем необязательно, что и любая другая точка окружности лежит в этой плоскости. Поэтому, данное утверждение неверно.
Ответ: нет.
б) Даны три точки окружности А, В, и С. В силу аксиомы 1, через эти три различные точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Назовем эту плоскость  .
.
Теперь докажем, что любая точка М окружности лежит в плоскости  . Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости
. Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости  , потому что две ее точки А и D лежат в плоскости
, потому что две ее точки А и D лежат в плоскости  . Значит, и точка М окружности лежит в плоскости
. Значит, и точка М окружности лежит в плоскости
Примеры решения стереометрических задач
Стереометрия – это один из самых сложных предметов в школьной математике. На вступительных экзаменах во многие вузы, а так же на ЕГЭ задачи по стереометрии предлагаются в обязательном порядке. Они дают возможность отобрать самых подготовленных по математике учащихся.
Разберем несколько стереометрических задач.
Задача 1.
Найдите объем многогранника, вершинами которого являются середины ребер тетраэдра, если объем тетраэдра равен V.
Решение.
Новый многогранник, объем которого необходимо найти в задаче, получен отсечением от тетраэдра четырех маленьких пирамид.
Объем каждой из отсеченных пирамид равен 1/3 · 1/4S · 1/2H, где S и H – площадь основания и высота исходного тетраэдра.
Таким образом, каждая маленькая пирамида имеет объем 1/4 · 1/2 · (1/3 · SH) = 1/3V.
Объем полученного многогранника равен V – 4 · 1/2V = V – 1/2V = 1/2V.
Ответ: 1/2V.
Задача 2.
Шар касается всех ребер куба. Найдите площадь поверхности шара, лежащей внутри куба, если ребро куба равно 1.
Решение.
Чтобы шар, касающийся всех ребер призмы, существовал, необходимо и достаточно, чтобы призма была правильной и все ее ребра были равными между собой. В задаче речь идет о кубе.
Центр шара является и центром куба. Пусть R – радиус шара.
R = √((1/2)2 + (1/2)2) = √2/2.
Наружу куба выходят 6 сегментов шара. Пусть h – высота одного сегмента, тогда h = R – 1/2 = (√2 – 1)/2.
Sсегм = 2πRh, а площадь поверхности шара, лежащей внутри куба можно найти по формуле S = 4πR2 – 6Sсегм.
Таким образом, S = 4π · 1/2 – 6 ·2π · √2/2 · (√2 – 1)/2 = π(3√2 – 4).
Ответ: π(3√2 – 4).
Задача 3.
В треугольную пирамиду, высота которой равна 4, вписан конус. В основании пирамиды лежит прямоугольный треугольник с гипотенузой, равной 15. Вершина конуса совпадает с вершиной пирамиды, а его основанием является вписанная в треугольник окружность с радиусом, равным 3. Найдите отношение площади полной поверхности конуса к площади полной поверхности пирамиды.
Решение.
Рассмотрим пирамиду SАВС (рис. 1).
Боковые грани пирамиды SABC наклонены к плоскости основания под одинаковым углом, вершина S проектируется в центр вписанной в треугольник ABC окружности, точку O.
Составим систему уравнений. По теореме Пифагора для треугольника АВС имеем: АС2 + ВС2 = 152.
Кроме того, по формуле площади треугольника S = r · p, можно записать
1/2 · АС · ВС = 1/2 · (АС + ВС + 15) · 3
или
АС · ВС = (АС + ВС + 15) · 3.
Решая полученную систему, найдем, что AC = 9 и BC = 12.
Пусть теперь точка D – точка касания с BC вписанной в треугольник ABC окружности. Образующая конуса SD перпендикулярна к OD по теореме о трех перпендикулярах и является высотой грани SBC. Таким образом, получается, что высоты (обозначим их через h) всех боковых граней к ребрам основания пирамиды равны между собой. По теореме Пифагора h = √(32 + 42) = 5.
Sбок = 5/2 · (9 + 12 + 15) = 90, Sпир = 90 + 54 = 144, Sкон = 9π + 15π = 24π.
Отношение площади полной поверхности конуса к площади полной поверхности пирамиды будет равно
24π/144 = π/6.
Ответ: π/6.
Задача 4.
Основанием пирамиды является прямоугольник, площадь которого равна Q. Две боковые грани пирамиды перпендикулярны плоскости основания, а две другие образуют с ней углы α и β. Найдите объем пирамиды.
Решение.
 Пусть в пирамиде SABCD грани SAB и SBC перпендикулярны основанию ABCD (рис. 2). Исходя из этого, можно утверждать, что, боковое ребро SB перпендикулярно плоскости основания ABCD, а значит по теореме о трех перпендикулярах прямая SА перпендикулярна прямой AD и именно угол SAB и равен α. Аналогично показывается, что угол SCB равен β.
Пусть в пирамиде SABCD грани SAB и SBC перпендикулярны основанию ABCD (рис. 2). Исходя из этого, можно утверждать, что, боковое ребро SB перпендикулярно плоскости основания ABCD, а значит по теореме о трех перпендикулярах прямая SА перпендикулярна прямой AD и именно угол SAB и равен α. Аналогично показывается, что угол SCB равен β.
SB = AB · tg α = BC · tg β. По условию задачи площадь основания равна Q, то есть AB · BC = Q, следовательно, АВ = √(Q · tg β/tg α).
V = 1/3Q · SB = 1/3Q · √(Q · tg β/tg α) · tg α. После упрощения получим V = 1/3Q · √(Q · tg α · tg β).
Ответ: 1/3Q · √(Q · tg α · tg β).
Задача 5.
Найдите радиус шара, описанного около пирамиды, все боковые ребра которой равны 5, а высота равна 4.
Решение.
Центр шара – точка O лежит на высоте SD заданной пирамиды. Точка E – середина ребра AS. Треугольник АОS – равнобедренный, поэтому EO перпендикулярно AS.
В прямоугольном треугольнике ADS сторона SD равна 4, а AS = 5. Треугольники EOS и ASD подобны по двум углам, поэтому имеет место отношение сторон SO : AS = ES : SD.
Таким образом, SO : 5 = 2,5 : 4, а значит SO = R = 25/8.
Ответ: 3,125.
Задача 6.
Через вершину прямого кругового конуса проведено сечение наибольшей площади. Площадь этого сечения в два раза больше площади осевого сечения конуса. Найдите угол при вершине осевого сечения конуса.
Решение.
Пусть l – образующая конуса.
Угол при вершине конуса больше 90°, иначе осевое сечение имело бы наибольшую площадь.
В ситуации задачи наибольшую площадь имеет сечение, являющееся прямоугольным треугольником.
Sнаиб = 1/2 · l2.
Sос.сеч = 1/2 · l2 · sin α, следовательно, sin α = 1/2, значит α = 150°.
Ответ: 150°.
Задача 7.
Две взаимно перпендикулярные образующие конуса делят окружность его основания на две дуги в 120° и в 240°. Найдите объем конуса, если его высота равна H.
Решение.
 Пусть R – радиус основания конуса, l – его образующая, а d – хорда основания, стягивающая дугу в 120° (рис. 3).
Пусть R – радиус основания конуса, l – его образующая, а d – хорда основания, стягивающая дугу в 120° (рис. 3).
Имеем: d = I · √2, d = R√3, l = R√(3/2),
следовательно, R2 = l2 – H2 = 3/2 · R2 – H2,
следовательно, 1/2R2 = H2.
Объем V = 1/3π · R2 · H = 1/3π · 2H2 · H = 2/3 · π · H3.
Ответ: 2/3 · π · H3.
Задача 8.
Основанием пирамиды SABC является равнобедренный треугольник ABC (AC = BC = a) с углом С равным α. Боковая грань SAB перпендикулярна к основанию пирамиды, а две другие наклонены к основанию под углом 60°. Найдите объем пирамиды.
Решение.
Ребро SD пирамиды SABCD перпендикулярно ребру основания AB, следовательно, SD перпендикулярно плоскости (АВС), т.к. плоскость (SAB) перпендикулярна плоскости (АВС).
С другой стороны, точка S проектируется на биссектрису угла ACB (теорема о трехгранном угле с двумя равными плоскими углами), следовательно, СD перпендикулярно АВ (CD – биссектриса угла ACB равнобедренного треугольника ACB) и D – середина AB.
Если SE перпендикулярно АС, то DE перпендикулярно АС. Пусть BP – высота треугольника ACB, тогда DE легко находится как средняя линия треугольника ABP. ВР = а · sin α, следовательно, DE = (а · sin α)/2.
Из треугольника SDE: SD = DE · tg 60° = 1/2a · √3 sin α.
Объем V = 1/12 · а3√3 · sin2 α.
Ответ: 1/12 · а3√3 · sin2 α.
Для успешного решения стереометрических задач требуется хорошее пространственное воображение, которое необходимо постоянно развивать. Кроме того, хорошее пространственное воображение может понадобиться в дальнейшем, например, для работы архитектором, хирургом, конструктором и т.д.
Остались вопросы? Не знаете, как решать задачи по стереометрии?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности
Стереометрия на ЕГЭ. Вычисление объемов и площадей поверхности
 Стереометрия на ЕГЭ по математике — это целых три задачи. Для начала надо выучить формулы. Все они есть в наших таблицах:
Стереометрия на ЕГЭ по математике — это целых три задачи. Для начала надо выучить формулы. Все они есть в наших таблицах:
Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.
Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Если в задаче по стереометрии речь идет о многограннике, вам встретятся термины «вершины» «грани» и «ребра». Вот они, на картинке.
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма, правильная призма, правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Ты нашел то, что искал? Поделись с друзьями!
Перейдем к практике.

. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем:
А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей». В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 🙂
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна . А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна .

А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна ! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Ответ: .
Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:
 . Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной — на верхней и нижней гранях.
. Из площади поверхности «целого кирпича» вычитаем площади двух квадратиков со стороной — на верхней и нижней гранях.
 А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Правильный ответ: .
Следующий тип задач — когда одно объемное тело вписано в другое.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна , высота равна , объем равен .
 . В основании прямой призмы лежит прямоугольный треугольник с катетами и . Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите .
. В основании прямой призмы лежит прямоугольный треугольник с катетами и . Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите .
Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна . Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: .

. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: .
Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.
 . В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.
. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.
Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в раза уменьшится высота.
Ответ: .
. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.
Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен .
Считаем объем второй кружки. Он равен . Получается, что он в два раза больше, чем объем первой.
 . Следующая задача тоже решается сразу и без формул.
. Следующая задача тоже решается сразу и без формул.
Через среднюю линию основания треугольной призмы, объем которой равен , проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Высота меньшей призмы высота такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен .
И еще одна классическая задача. Никаких формул!
. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?
Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в раз, поскольку .
Ответ: .
 Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды. Они тоже решаются элементарно.
Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды. Они тоже решаются элементарно.
. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите .
Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом градусов, а — это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на , записываем ответ: .
Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!
Профильный ЕГЭ по математике. Задание №8. Стереометрия
Задание 8 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.
Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.
Как решать задания по стереометрии из первой части Профильного ЕГЭ?
Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)
Проверим себя – умеем ли мы рисовать чертежи?
Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.
Запоминаем один из главных лайфхаков решения задач по стереометрии:
Отношение объемов подобных тел равно кубу коэффициента подобия.
Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в раз, а объем в раз.

И решаем задачи. У нас все получится!
1. Во сколько раз увеличатся площадь поверхности и объем куба, если его ребро увеличить в два раза?
Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.
2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.
3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.

Меньшая пирамида подобна большой, коэффициент подобия Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен
4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.

Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен
5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна Найти объем пирамиды SABCD .

Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника SAE получаем, что Соответственно, сторона основания пирамиды равна Если обозначить центр основания за H, то высоту пирамиды найдем по теореме Пифагора для треугольника SHE – она равна 2.
Применяя формулу для объема пирамиды , получаем ответ: 16.
Многие задания №8 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.
Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.
6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.

Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.
Радиус описанной окружности найдем по формуле
Площадь найдем по формуле Герона:
, где – полупериметр.
Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.
7. В правильной треугольной призме , все ребра которой равны 3, найдите угол между прямыми и Ответ дайте в градусах.

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку и параллельны, найдем угол между и . Он равен 45 градусов, так как грань – квадрат.
Ответ: 45.