Решение показательных уравнений. Основы. | Александр Будников
Что такое показательное уравнение? Примеры.
Итак, показательное уравнение… Новый уникальный экспонат на нашей общей выставке самых разнообразных уравнений!) Как это почти всегда бывает, ключевым словом любого нового математического термина является соответствующее прилагательное, которое его характеризует. Так и тут. Ключевым словом в термине «показательное уравнение» является слово «показательное». Что оно означает? Это слово означает, что неизвестное (икс) находится в показателях каких-либо степеней. И только там! Это крайне важно.
Например, такие простые уравнения:
3x+1 = 81
5x + 5x+2 = 130
4·22x-17·2x+4 = 0
Или даже такие монстры:
2sinx = 0,5
И так далее, и тому подобное…
Прошу сразу обратить внимание на одну важную вещь: в основаниях степеней (снизу) – только числа. А вот в показателях степеней (сверху) – самые разнообразные выражения с иксом. Совершенно любые.) Всё от конкретного уравнения зависит. Если, вдруг, в уравнении вылезет икс где-нибудь ещё, помимо показателя (скажем, 3x = 18+x2), то такое уравнение будет уже уравнением смешанного типа. Такие уравнения не имеют чётких правил решения. Поэтому в данном уроке мы их рассматривать не будем. На радость ученикам.) Здесь мы будем рассматривать только показательные уравнения в «чистом» виде.
Вообще говоря, даже чистые показательные уравнения чётко решаются далеко не все и не всегда. Но среди всего богатого многообразия показательных уравнений есть определённые типы, которые решать можно и нужно. Вот именно эти типы уравнений мы с вами и рассмотрим. И примеры обязательно порешаем.) Так что устраиваемся поудобнее и – в путь! Как и в компьютерных «стрелялках», наше путешествие будет проходить по уровням.) От элементарного к простому, от простого – к среднему и от среднего — к сложному. По пути вас также будет ждать секретный уровень – приёмы и методы решения нестандартных примеров. Те, о которых вы не прочитаете в большинстве школьных учебников… Ну, а в конце вас, разумеется, ждёт финальный босс в виде домашки.)
Уровень 0. Что такое простейшее показательное уравнение? Решение простейших показательных уравнений.
Для начала рассмотрим какую-нибудь откровенную элементарщину. С чего-то же надо начинать, верно? Например, такое уравнение:
2х = 22
Даже безо всяких теорий, по простой логике и здравому смыслу ясно, что х = 2. Иначе же никак, верно? Никакое другое значение икса не годится… А теперь обратим наш взор на
2х = 22
х = 2
Что же у нас произошло? А произошло следующее. Мы, фактически, взяли и… просто выкинули одинаковые основания (двойки)! Совсем выкинули. И, что радует, попали в яблочко!
Да, действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, то эти числа можно отбросить и просто приравнять показатели степеней. Математика разрешает.) И дальше можно работать уже отдельно с показателями и решать куда более простое уравнение. Здорово, правда?
Вот и ключевая идея решения любого (да-да, именно любого!) показательного уравнения: с помощью тождественных преобразований необходимо добиться того, чтобы слева и справа в уравнении стояли
одинаковые числа-основания в различных степенях. А дальше можно смело убрать одинаковые основания и приравнять показатели степеней. И работать с более простым уравнением.А теперь запоминаем железное правило: убирать одинаковые основания можно тогда и только тогда, когда в уравнении слева и справа числа-основания стоят в гордом одиночестве.
Что значит, в гордом одиночестве? Это значит, безо всяких соседей и коэффициентов. Поясняю.
Например, в уравнении
3·3x-5 = 32x+1
тройки убирать нельзя! Почему? Потому что слева у нас стоит не просто одинокая тройка в степени, а произведение 3·3x-5. Лишняя тройка мешает: коэффициент, понимаешь.)
То же самое можно сказать и про уравнение
53x = 52x+5x
Здесь тоже все основания одинаковые – пятёрка. Но справа у нас не одинокая степень пятёрки: там – сумма степеней!
Короче говоря, убирать одинаковые основания мы имеем право лишь тогда, когда наше показательное уравнение выглядит так и только так:
af(x) = ag(x)
Такой вид показательного уравнения называют простейшим. Или, по-научному, каноническим. И какое бы накрученное уравнение перед нами ни было, мы его, так или иначе, будем сводить именно к такому простейшему (каноническому) виду. Или, в некоторых случаях, к совокупности уравнений такого вида. Тогда наше простейшее уравнение можно в общем виде переписать вот так:
f(x) = g(x)И всё. Это будет эквивалентным преобразованием. При этом в качестве f(x) и g(x) могут стоять совершенно любые выражения с иксом. Какие угодно.
Возможно, особо любознательный ученик поинтересуется: а с какой такой стати мы вот так легко и просто отбрасываем одинаковые основания слева и справа и приравниваем показатели степеней? Интуиция интуицией, но вдруг, в каком-то уравнении и для какого-то основания данный подход окажется неверным? Всегда ли законно выкидывать одинаковые основания? К сожалению, для строгого математического ответа на этот интересный вопрос нужно довольно глубоко и серьёзно погружаться в общую теорию устройства и поведения функций. А чуть конкретнее – в явление строгой монотонности. В частности, строгой монотонности показательной функции y=ax. Поскольку именно показательная функция и её свойства лежат в основе решения показательных уравнений, да.) Развёрнутый ответ на этот вопрос будет дан в отдельном спецуроке, посвящённом решению сложных нестандартных уравнений с использованием монотонности разных функций.)
Объяснять подробно этот момент сейчас – это лишь выносить мозг среднестатистическому школьнику и отпугивать его раньше времени сухой и грузной теорией. Я этого делать не буду.) Ибо наша основная на данный момент задача – научиться решать показательные уравнения! Самые-самые простые! Посему – пока не паримся и смело выкидываем одинаковые основания. Это можно, поверьте мне на слово!) А дальше уже решаем эквивалентное уравнение f(x) = g(x). Как правило, более простое, чем исходное показательное.
Предполагается, конечно же, что решать хотя бы линейные, квадратные и дробные уравнения, уже без иксов в показателях, народ на данный момент уже умеет.) Кто до сих пор не умеет – смело закрывайте эту страницу, гуляйте по соответствующим ссылочкам и восполняйте старые пробелы. Иначе несладко вам придётся, да…
Я уж молчу про иррациональные, тригонометрические и прочие зверские уравнения, которые также могут всплыть в процессе ликвидации оснований. Но не пугайтесь, откровенную жесть в показателях степеней мы с вами пока рассматривать не будем: рано ещё. Будем тренироваться лишь на самых простых уравнениях.)
Теперь рассмотрим уравнения, которые требуют некоторых дополнительных усилий для сведения их к простейшим. Для отличия назовём их простыми показательными уравнениями. Итак, двигаемся на следующий уровень!
Уровень 1. Простые показательные уравнения. Распознаём степени! Натуральные показатели.
Ключевыми правилами в решении любых показательных уравнений являются правила действий со степенями. Без этих знаний и умений ничего не получится. Увы. Так что, если со степенями проблемы, то для начала милости прошу
Но одних только действий со степенями и тождественных преобразований мало. Необходима ещё личная наблюдательность и смекалка. Нам ведь требуются одинаковые основания, не так ли? Вот и осматриваем пример и ищем их в явном или замаскированном виде!
Например, такое уравнение:
32x – 27x+2 = 0
Первый взгляд на основания. Они… разные! Тройка и двадцать семь. Но паниковать и впадать в отчаяние рано. Самое время вспомнить, что
27 = 33
Числа 3 и 27 – родственнички по степени! Причём близкие.) Стало быть, имеем полное право записать:
27x+2 = (33)x+2
А вот теперь подключаем наши знания о действиях со степенями (а я предупреждал!). Есть там такая очень полезная формулка:
(am)n = amn
Если теперь запустить её в ход, то вообще отлично получается:
27x+2 = (33)x+2 = 33(x+2)
Исходный пример теперь выглядит вот так:
32x – 33(x+2) = 0
Отлично, основания степеней выровнялись. Чего мы и добивались. Полдела сделано.) А вот теперь запускаем в ход базовое тождественное преобразование – переносим 33(x+2) вправо. Элементарных действий математики никто не отменял, да.) Получаем:
32x = 33(
Что нам даёт такой вид уравнения? А то, что теперь наше уравнение сведено к каноническому виду: слева и справа стоят одинаковые числа (тройки) в степенях. Причём обе тройки — в гордом одиночестве. Смело убираем тройки и получаем:
2х = 3(х+2)
Решаем это линейное уравнение и получаем:
x = -6
Вот и все дела. Это правильный ответ.)
А теперь осмысливаем ход решения. Что нас спасло в этом примере? Нас спасло знание степеней тройки. Как именно? Мы опознали в числе 27 зашифрованную тройку! Этот приёмчик (шифровка одного и того же основания под разными числами) – один из самых популярных в показательных уравнениях! Если только не самый популярный. Да и в логарифмах тоже, кстати. Именно поэтому в показательных уравнениях так важна наблюдательность и умение распознавать в числах степени других чисел!
Практический совет:
Степени популярных чисел надо знать. В лицо!
Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но в показательных уравнениях гораздо чаще надо не возводить в степень, а наоборот — узнавать, какое число и в какой степени скрывается за числом, скажем, 128 или 243. А это уже посложнее, чем простое возведение, согласитесь. Почувствуйте разницу, что называется!
Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:
Определить, какими степенями и каких чисел являются числа:
4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.
Ответы (вразброс, естественно):
272; 210; 36; 72; 26; 92; 34; 43; 102; 25; 35; 73; 162; 27; 53; 28; 62; 33; 29; 24; 22; 45; 252; 44; 63; 82; 93.
Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 28, 44 и 162 – это всё 256.
А теперь движемся дальше.)
Уровень 2. Простые показательные уравнения. Распознаём степени! Отрицательные и дробные показатели.
На этом уровне мы уже используем наши знания о степенях на полную катушку. А именно – вовлекаем в сей увлекательный процесс отрицательные и дробные показатели! Да-да! Нам же надо наращивать мощь, верно?
Например, такое страшное уравнение:
Опять первый взгляд – на основания. Основания – разные! Причём на этот раз даже отдалённо не похожие друг на друга! 5 и 0,04… А для ликвидации оснований нужны одинаковые… Что же делать?
Ничего страшного! На самом деле всё то же самое, просто связь между пятёркой и 0,04 визуально просматривается плохо. Как выкрутимся? А перейдём-ка в числе 0,04 к обычной дроби! А там, глядишь, всё и образуется.)
0,04 = 4/100 = 1/25
Ух ты! Оказывается, 0,04 – это 1/25! Ну кто бы мог подумать!)
Ну как? Теперь связь между числами 5 и 1/25 легче углядеть? Вот то-то и оно…
А теперь уже по правилам действий со степенями с отрицательным показателем можно твёрдой рукой записать:
Вот и отлично. Вот мы и добрались до одинакового основания – пятёрки. Заменяем теперь в уравнении неудобное нам число 0,04 на 5-2 и получаем:
Опять же, по правилам действий со степенями, теперь можно записать:
(5-2)x-1 = 5-2(x-1)
На всякий случай, напоминаю (вдруг, кто не в курсе), что базовые правила действий со степенями справедливы для любых показателей! В том числе и для отрицательных.) Так что смело берём и перемножаем показатели (-2) и (х-1) по соответствующему правилу. Наше уравнение становится всё лучше и лучше:
Всё! Кроме одиноких пятёрок в степенях слева и справа больше ничего нет. Уравнение сведено к каноническому виду. А дальше – по накатанной колее. Убираем пятёрки и приравниваем показатели:
x2–6x+5=-2(x-1)
Пример практически решён. Осталась элементарная математика средних классов – раскрываем (правильно!) скобки и собираем всё слева:
x2–6x+5 = -2x+2
x2–4x+3 = 0
Решаем это квадратное уравнение и получаем два корня:
x1 = 1; x2 = 3
Вот и всё.)
А теперь снова поразмышляем. В данном примере нам вновь пришлось распознать одно и то же число в разной степени! А именно — увидеть в числе 0,04 зашифрованную пятёрку. Причём на этот раз – в отрицательной степени! Как же нам это удалось? С ходу – никак. А вот после перехода от десятичной дроби 0,04 к обыкновенной дроби 1/25 всё и высветилось! И дальше всё решение пошло как по маслу.)
Поэтому очередной зелёный практический совет.
Если в показательном уравнении присутствуют десятичные дроби, то переходим от десятичных дробей к обыкновенным. В обыкновенных дробях гораздо проще распознать степени многих популярных чисел! После распознавания переходим от дробей к степеням с отрицательными показателями.
Имейте в виду, что такой финт в показательных уравнениях встречается очень и очень часто! А человек не в теме. Смотрит он, например, на числа 32 и 0,125 и огорчается. Неведомо ему, что это одна и та же двойка, только в разных степенях… Но вы-то ведь уже в теме!)
Дальше – больше! Развлекаться, так развлекаться.)
Решить уравнение:
Во! На вид – тихий ужас… Однако внешность обманчива. Это простейшее показательное уравнение, несмотря на его устрашающий внешний вид. И сейчас я вам это покажу.)
Конечно, возиться да считать побольше придётся, но ведь и наш с вами уровень тоже растёт, не правда ли? Итак, ничего не боимся и приступаем.)
Во-первых, разбираемся со всеми чиселками, сидящими в основаниях и в коэффициентах. Они, ясное дело, разные, да. Но мы всё же рискнём и попробуем сделать их одинаковыми! Попробуем добраться до одного и того же числа в разных степенях. Причём, желательно, числа самого возможно малого. Итак, начинаем расшифровку!
Ну, с четвёркой сразу всё ясно – это 22. Так, уже кое-что.)
С дробью 0,25 – пока непонятно. Проверять надо. Используем практический совет – переходим от десятичной дроби к обыкновенной:
0,25 = 25/100 = 1/4
Уже гораздо лучше. Ибо теперь уже отчётливо видно, что 1/4 – это 2-2. Отлично, и число 0,25 тоже сроднили с двойкой.)
Пока всё идёт хорошо. Но осталось самое нехорошее число из всех – корень квадратный из двух! А с этим перцем что делать? Можно ли его тоже представить как степень двойки? А кто ж его знает…
Что ж, снова лезем в нашу сокровищницу знаний о степенях! На этот раз дополнительно подключаем наши знания о корнях. Из курса 9-го класса мы с вами должны были вынести, что любой корень, при желании, всегда можно превратить в степень с дробным показателем.
Вот так:
В нашем случае:
Во как! Оказывается, корень квадратный из двух – это 21/2. Вот оно что!
Вот и прекрасно! Все наши неудобные числа на самом деле оказались зашифрованной двойкой.) Не спорю, где-то весьма изощрённо зашифрованной. Но и мы ведь тоже повышаем свой профессионализм в разгадке подобных шифров! А дальше уже всё очевидно. Заменяем в нашем уравнении числа 4, 0,25 и корень из двух на степени двойки:
Всё! Основания всех степеней в примере стали одинаковыми – двойка. А теперь в ход идут стандартные действия со степенями:
am·an = am+n
am:an = am-n
(am)n = amn
Для левой части получится:
2-2·(22)5x-16 = 2-2+2(5x-16)
Для правой части будет:
И теперь наше злое уравнение стало выглядеть вот так:
Кто не врубился, как именно получилось это уравнение, то тут вопрос не к показательным уравнениям. Вопрос – к действиям со степенями. Я же просил срочно повторить тем, у кого проблемы!
Вот и финишная прямая! Получен канонический вид показательного уравнения! Ну как? Убедил я вас, что не всё так страшно? 😉 Убираем двойки и приравниваем показатели:
Осталось всего лишь решить это линейное уравнение. Как? С помощью тождественных преобразований, вестимо.) Дорешайте, чего уж там! Умножайте обе части на двойку (чтобы убрать дробь 3/2), переносите слагаемые с иксами влево, без иксов вправо, приводите подобные, считайте – и будет вам счастье!
Должно всё получиться красиво:
x = 4
А теперь снова осмысливаем ход решения. В данном примере нас выручил переход от квадратного корня к степени с показателем 1/2. Причём только такое хитрое преобразование нам помогло везде выйти на одинаковое основание (двойку), которое и спасло положение! И, если бы не оно, то мы бы имели все шансы навсегда зависнуть и так и не справиться с этим примером, да…
Поэтому не пренебрегаем очередным практическим советом:
Если в показательном уравнении присутствуют корни, то переходим от корней к степеням с дробными показателями. Очень часто только такое преобразование и проясняет дальнейшую ситуацию.
Конечно же, отрицательные да дробные степени уже гораздо сложнее натуральных степеней. Хотя бы с точки зрения визуального восприятия и, особенно, распознавания справа налево!
Понятно, что напрямую возвести, например, двойку в степень -3 или же четвёрку в степень -3/2 не такая уж и большая проблема. Для знающих.)
А вот поди, например, с ходу сообрази, что
0,125 = 2-3
или
Тут только практика и богатый опыт рулят, да. И, конечно же, чёткое представление, что такое отрицательная и дробная степень. А также – практические советы! Да-да, те самые зелёные.) Надеюсь, что они всё-таки помогут вам лучше ориентироваться во всём разношёрстном многообразии степеней и значительно увеличат ваши шансы на успех! Так что не пренебрегаем ими. Я не зря зелёным цветом пишу иногда.)
Зато, если вы станете на «ты» даже с такими экзотическими степенями, как отрицательные и дробные, то ваши возможности в решении показательных уравнений колоссально расширятся, и вам уже будет по плечу практически любой тип показательных уравнений. Ну, если не любой, то процентов 80 всех показательных уравнений – уж точно! Да-да, я не шучу!
Итак, наша первая часть знакомства с показательными уравнениями подошла к своему логическому завершению. И, в качестве промежуточной тренировки, я традиционно предлагаю немного порешать самостоятельно.)
Задание 1.
Чтобы мои слова о расшифровке отрицательных и дробных степеней не пропали даром, предлагаю сыграть в небольшую игру!
Представьте в виде степени двойки числа:
Ответы (в беспорядке):
Получилось? Отлично! Тогда делаем боевое задание – решаем простейшие и простые показательные уравнения!
Задание 2.
Решить уравнения (все ответы – в беспорядке!):
52x-8 = 25
25x-4 – 16x+3 = 0
Ответы:
x = 16
x1 = -1; x2 = 2
x = 5
Получилось? Действительно, уж куда проще-то!
Тогда решаем следующую партию:
(2x+4)x-3 = 0,5x·4x-4
351-x = 0,2—x·7x
Ответы:
x1 = -2; x2 = 2
x = 0,5
x1 = 3; x2 = 5
И эти примеры одной левой? Отлично! Вы растёте! Тогда вот вам на закуску ещё примерчики:
Ответы:
x = 6
x = 13/31
x = -0,75
x1 = 1; x2 = 8/3
И это решено? Что ж, респект! Снимаю шляпу.) Значит, урок прошёл не напрасно, и начальный уровень решения показательных уравнений можно считать успешно освоенным. Впереди – следующие уровни и более сложные уравнения! И новые приёмы и подходы. И нестандартные примеры. И новые сюрпризы.) Всё это – в следующем уроке!
Что-то не получилось? Значит, скорее всего, проблемы в действиях со степенями. Или в тождественных преобразованиях. Или в том и другом сразу. Тут уж я бессилен. Могу в очередной раз предложить лишь одно – не лениться и прогуляться по ссылочкам.)
Продолжение следует.)
abudnikov.ru
Задача C1: показательные уравнения с ограничением
В большинстве учебников при подготовке к ЕГЭ по математике рассматриваются задачи C1, состоящие из тригонометрических уравнений. Учителя рассказывают о многочисленных приемах работы с тригонометрией, но совершенно упускают из виду, что существует множество задач C1 совсем другого типа. Например, вместо «классического» тригонометрического уравнения может стоять показательное и логарифмическое. На первый взгляд, такие уравнения решаются даже легче, однако основные проблемы начинаются дальше — в процессе отборе корней.
Сегодня мы разберем еще одну задачу С1, но в отличии от предыдущих, она будет не тригонометрическим уравнением, а показательным. Но даже это показательное уравнение, будет отнюдь не самым простым.
Правила работы со степенями
Прежде чем решать любое показательное уравнение, хотел бы обратить ваше внимание на правило работы со степенными показателями. Таких правил, основных, самых важных, всего три, и все их вы уже, наверняка, знаете:
- ax⋅ay=ax+y{{a}^{x}}\cdot {{a}^{y}}={{a}^{x+y}}. Другими словами, при умножении степеней с одинаковыми основаниями, их показатели складываются.
- axay=ax−y\frac{{{a}^{x}}}{{{a}^{y}}}={{a}^{x-y}}. При делении степеней с одинаковыми основаниями, их показатели вычитаются.
- (ax)y=ax⋅y{{({{a}^{x}})}^{y}}={{a}^{x\cdot y}}. Правило возведения степени в степень. Другими словами, при возведении степени в степень, их показатели перемножаются.
Вот и все основные правила, которые нам нужно знать для решения сегодняшнего примера.
Решаем задачу
Итак, задача:
Решите показательное уравнение. Найдите все корни этого уравнения, принадлежащие промежутку:
25x−32−12⋅5x−2+7=0,x∈(2;83)
{{25}^{x-\frac{3}{2}}}-12\cdot {{5}^{x-2}}+7=0,x\in \left( 2;\frac{8}{3} \right)
Давайте внимательно посмотрим на наше показательное уравнение: у нас есть 5 в каком-то степенном значении и 25, кроме того, 25=5225={{5}^{2}}. Теперь мы можем переписать наше исходное уравнение следующим образом:
(52)x−32−12⋅5x−2+7=0
{{\left( {{5}^{2}} \right)}^{x-\frac{3}{2}}}-12\cdot {{5}^{x-2}}+7=0
Вот здесь мы вспоминаем формулу возведения степени в степень:
52⋅(x−32)−12⋅5x−2+7=0
{{5}^{2\cdot \left( x-\frac{3}{2} \right)}}-12\cdot {{5}^{x-2}}+7=0
52x−3−12⋅5x−2+7=0
{{5}^{2x-3}}-12\cdot {{5}^{x-2}}+7=0
52x−4+1−12⋅5x−2+7=0
{{5}^{2x-4+1}}-12\cdot {{5}^{x-2}}+7=0
52x−4⋅51−12⋅5x−2+7=0
{{5}^{2x-4}}\cdot {{5}^{1}}-12\cdot {{5}^{x-2}}+7=0
52(x−2)⋅5−12⋅5x−2+7=0
{{5}^{2\left( x-2 \right)}}\cdot 5-12\cdot {{5}^{x-2}}+7=0
Обратите внимание: на каждом шаге преобразовании мы работали исключительно с первым элементом, который изначально звучал как 25x−32{{25}^{x-\frac{3}{2}}}. В итоге мы получил конструкцию вида 52(x−2)⋅5{{5}^{2(x-2)}}\cdot 5. Возникает сразу два вопроса: в первую очередь, зачем нам нужно было это делать?
Потому что теперь мы можем сделать следующую замену:
5x−2=t−12⋅5x−2+7=0
\begin{align}& {{5}^{x-2}}=t \\& -12\cdot {{5}^{x-2}}+7=0 \\\end{align}
Теперь у нас получится красивое квадратное показательное уравнение:
5t2⋅5−12t+7=0
5{{t}^{2}}\cdot 5-12t+7=0
Но есть одна проблема: как добавить 1 и вычесть ее на одном из шагов? Все очень просто. У нас уже есть готовая конструкция 5x−2{{5}^{x-2}}. Следовательно, при возведении ее в квадрат, мы должны перемножить степенные показатели:
5x−2=5(x−2)2=52x−4
{{5}^{x-2}}={{5}^{(x-2)2}}={{5}^{2x-4}}
Именно в этом состоит тактика решения показательных уравнений, основания степеней в которых неодинаковые, в нашем случае это 5 и 25.
Еще раз: чтобы там не стояло в показателе старшего элемента, мы должны преобразовать его таким образом, чтобы получился удвоенный показатель младшего элемента. И тогда, как мы уже убедились, получится красивое квадратное показательное уравнение, которое легко решается. Давайте его решим.
Очевидно, поскольку перед t2{{t}^{2}} стоит 5, это уравнение не является приведенным, поэтому решать мы его будем через дискриминант. Итак, дискриминант равен:
D=144−4⋅5⋅7=4
D=144-4\cdot 5\cdot 7=4
Корень равен 2. Находим tt:
\[\begin{array}{·{35}{l}}
{{t}_{1}}\text{=}\frac{12+2}{10}=\frac{7}{5} \\{{t}_{2}}=\frac{12-2}{10}=\text{ }1 \\\end{array}\]
Итак, мы получили корни квадратного уравнения: 75\frac{7}{5} и 1. Теперь возвращаемся к нашему исходному выражению и вспоминаем, что t=5x−2t={{5}^{x-2}}:
5x−2=15x−2=50x−2=0x=2
\begin{align}& {{5}^{x-2}}=1 \\& {{5}^{x-2}}={{5}^{0}} \\& x-2=0 \\& x=2 \\\end{align}
Подставляем второй корень:
5x−2=75
{{5}^{x-2}}=\frac{7}{5}
Вспомним формулу:
a=blogba
a={{b}^{{{\log }_{b}}a}}
Другими словами, мы можем переписать наше показательное уравнение следующим образом:
5x−2=5log575
{{5}^{x-2}}={{5}^{{{\log }_{5}}\frac{7}{5}}}
Почему мы выбрали основание именно 5? Потому что у нас слева стоит 5x−2{{5}^{x-2}}, т. е. основание у нас задается самим уравнением. Теперь мы можем избавиться от 5:
\[\begin{array}{·{35}{l}}
x-2={{\log }_{5}}\frac{7}{5} \\x={{\log }_{5}}\frac{7}{5}+2={{\log }_{5}}\frac{7}{5}+{{\log }_{5}}25 \\x={{\log }_{5}}35 \\\end{array}\]
Вот наши два ответа: 2 и log535.
{{\log }_{5}}35
Мы решили первую часть задачи и нашли корни. Теперь из этих корней нам нужно отобрать те, которые принадлежат интервалу \[\left( 2;\frac{8}{3} \right)\].
Для этого давайте для начала перепишем значения, входящие в сам интервал. Дело в том, что 83\frac{8}{3} — это дробь, поэтому из нее нужно выделить целую часть. Интервал будет выглядеть следующим образом:
x∈(2;223)
x˜\in \left( 2;2\frac{2}{3} \right)
Из двух корней, 2 и log535, нам нужно выбрать такие числа, которые принадлежат нашему интервалу. В первую очередь, давайте сразу заметим, что x=2x=2 не принадлежит нашему интервалу:
x∉(2;223)
x\notin \left( 2;2\frac{2}{3} \right)
Потому что, с одной стороны, 2 является концом интервала, но, с другой стороны, поскольку скобки круглые, сама 2 не принадлежит этому интервалу.
Остается лишь один корень log535. Разумеется, поскольку это один единственный ответ нашего показательного выражения, то у нас есть все основания полагать, что он лежит на данном интервале, однако если мы не обоснуем это утверждение, то проверяющие снимут из нас 1 балл. Другими словами, нам нужно доказать, что число log535 лежит на нашем интервале. Но проблема в том, что мы не знаем, чему равен log535. И как поступать в таком случае? Сейчас внимание! Я расскажу вам четкий пошаговый алгоритм, который часто требуется применять в задачах С1, С3 и С5 из ЕГЭ по математике, т. е. всех алгебраических задачах части С.
Пошаговый алгоритм решения задач
Итак, нам нужно узнать, чему хотя бы примерно равен log535. Прежде всего, давайте рассмотрим значения вида
log551
{{\log }_{5}}{{5}^{1}}
log552
{{\log }_{5}}{{5}^{2}}
log553
{{\log }_{5}}{{5}^{3}}
Мы просто перебираем 5 натурального степенного значения. Получим:
log551=log55
{{\log }_{5}}{{5}^{1}}={{\log }_{5}}5
log552=log525
{{\log }_{5}}{{5}^{2}}={{\log }_{5}}25
log553=log5125
{{\log }_{5}}{{5}^{3}}={{\log }_{5}}125
Разумеется, можно было бы выписать больше, но нам важно понять, между какими числами видами 5, 25 и 125, лежит наше исходное 35. Очевидно, оно лежит между 25 и 125. Следовательно, log535 будет лежать между
log525
{{\log }_{5}}25 и
log5125
{{\log }_{5}}125. Также мы можем посчитать показательное выражение:
log552=2
{{\log }_{5}}{{5}^{2}}=2
log553=3
{{\log }_{5}}{{5}^{3}}=3
Отсюда заключаем, что
˜2<log535<3
˜2<{{\log }_{5}}35<3.
Но легче нам не стало, потому что, с одной стороны логарифм от 2 до 3, а, с другой стороны, нужно, чтобы он лежал на промежутке (2;223)\left( 2;2\frac{2}{3} \right), т. е. то, что логарифм лежит на промежутке от 2 до 3, нам не помогает. Поэтому переходим к следующему шагу и начинаем рассматривать половинки, значения вида 1,5; 2,5; 3,5. Давайте посмотрим: возьмем среднее арифметическое чисел 2 и 3 и возводим 5 в степень этого среднего арифметического:
log552+32=log552,5=log552 ⋅ 512=log5255√
{{\log }_{5}}{{5}^{\frac{2+3}{2}}}={{\log }_{5}}{{5}^{2,5}}={{\log }_{5}}{{5}^{2}}\text{ }\!\!\cdot\!\!\text{ }{{\text{5}}^{\frac{\text{1}}{\text{2}}}}={{\log }_{5}}25\sqrt{5}
А теперь нам нужно понять, что больше
255√
25\sqrt{5} или 35. Давайте сравним их:
35⋃255√|:5
35\bigcup 25\sqrt{5}|:5
7⋃55√↑2
7\bigcup 5\sqrt{5}\uparrow 2
49⋃25⋅5
49\bigcup 25\cdot 5
49<125
49<125
Здесь уже очевидно, что 49 меньше, чем 125. Следовательно,
log535<log5255√
{{\log }_{5}}35<{{\log }_{5}}25\sqrt{5}
Что мы получаем? Новое вычисление, новое ограничение:
˜2<log535<2510
˜2<{{\log }_{5}}35<2\frac{5}{10}
Тут уже все замечательно, потому что
2<log535<2510<223
2<{{\log }_{5}}35<{{2}^{5}}10<2\frac{2}{3}
Это обоснованное решение. Мы доказали, что
=log535
={{\log }_{5}}35 после отбора с учетом ограничений.
Еще раз, это очень важный шаг. Когда у нас есть логарифм по какому-то нормальному основанию, но от числа, которое не считается, т. е. не является точным показателем основания, мы сначала рассматриваем целые значения и находим, между степенями каких чисел лежит наше число. В нашем случае получилось, что
log535
{{\log }_{5}}35 будет лежать между
log525
{{\log }_{5}}25 и
log5125
{{\log }_{5}}125, и мы получили такое неравенство
2<log535<3
2<{{\log }_{5}}35<3
Однако зачастую показательные задачи составлены так, что этого ограничения недостаточно. В этом случае мы начинаем рассматривать не натуральные числа, а дроби, стоящие посередине, между этими натуральными значениями, т. е. числа вида 1,5; 2,5; 3,5…В этом случае при возведении основания, т. е. 51,5{{5}^{1,5}} или 52,5{{5}^{2,5}}, у нас, естественно, получаются корни, которые потом придется сравнивать при помощи галочки неизвестности. Однако не стоит переживать, это сравнение не вызывает каких-либо сложностей, и после небольшой тренировки сравнивать корни таким образом сможет даже неподготовленный ученик. В результате мы получили уточненное ограничение, которое уже точно даст нам понять, принадлежит ли наш корень данному интервалу или не принадлежит.
Обратите внимание, более глубокого разделения, т. е. уже на четверти, а не на половинки в реальной части С ЕГЭ по математике я не видел ни разу, т. е. шага выписывания половинок уже будет достаточно. Более сложное задание на настоящем ЕГЭ по математике вам точно не попадется. Вот и все, получив уточненное ограничение, вы уже сможете обоснованно утверждать, что данный корень принадлежит указанному интервалу. И, следовательно, является ответом ко второй части задачи. Вы получите два балла из двух возможных на ЕГЭ по математике. Так что обязательно изучите этот прием. Он будет очень полезен не только в задачах С1 в ЕГЭ по математике, но также и в задачах С3 и С5.
Ключевые моменты
На примере этой задачи C1из ЕГЭ по математике хочу прояснить сразу два принципиально важных моментов:
Если вы видите, что уравнение сводится к квадратному, то старайтесь обозначать новой переменной степенное выражение с наименьшим показателем. Это избавит вас от возникновения дробей в дальнейших вычислениях и значительно упростит итоговое решение;
Если при решении показательного уравнения возник «некрасивый логарифм» (в нашем случае это
log535
{{\log }_{5}}35), для получения его примерного значения сначала считайте натуральные степенные показатели:
log551
{{\log }_{5}}51;
log552
{{\log }_{5}}52; log553{{\log }_{5}}{{5}^{3}} … Если же этих ограничений окажется недостаточно, начинайте перебирать числа, стоящие посередине между соседними натуральными:
log551,5
{{\log }_{5}}{{5}^{1,5}};
log552,5
{{\log }_{5}}{{5}^{2,5}};
log553,5
{{\log }_{5}}{{5}^{3,5}}.
www.berdov.com
УРОК «ТИПЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ»
ТИПЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ
Разработала: Троицкая И.В.
I. Простейшие показательные уравнения
Рассмотрите решение уравнения
а) 5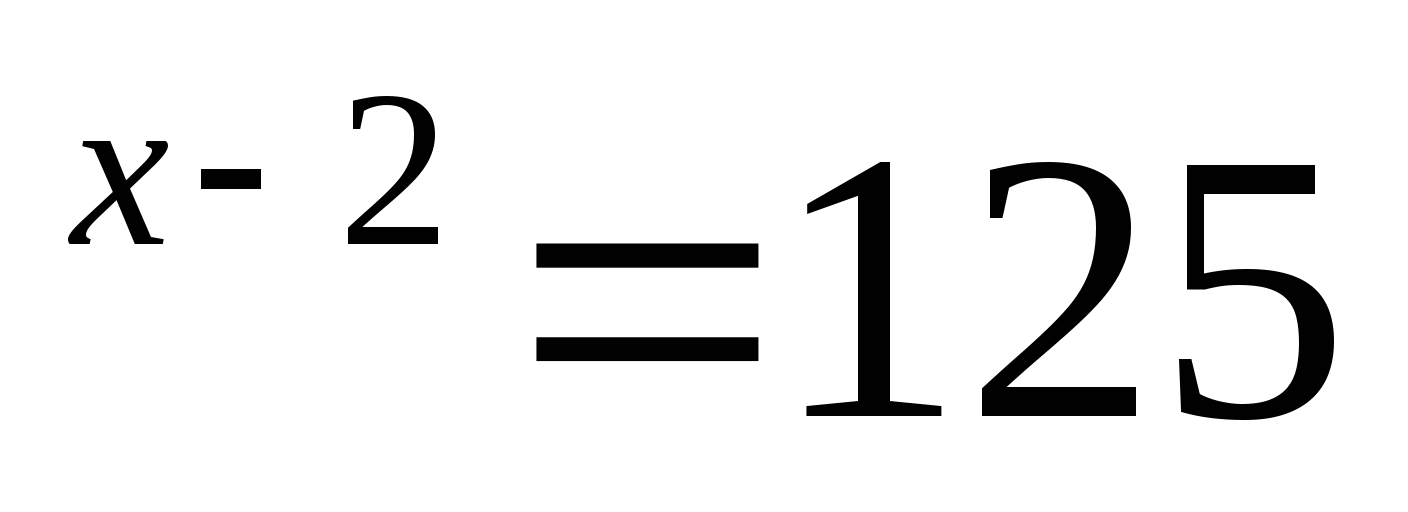
 Решение 5
Решение 5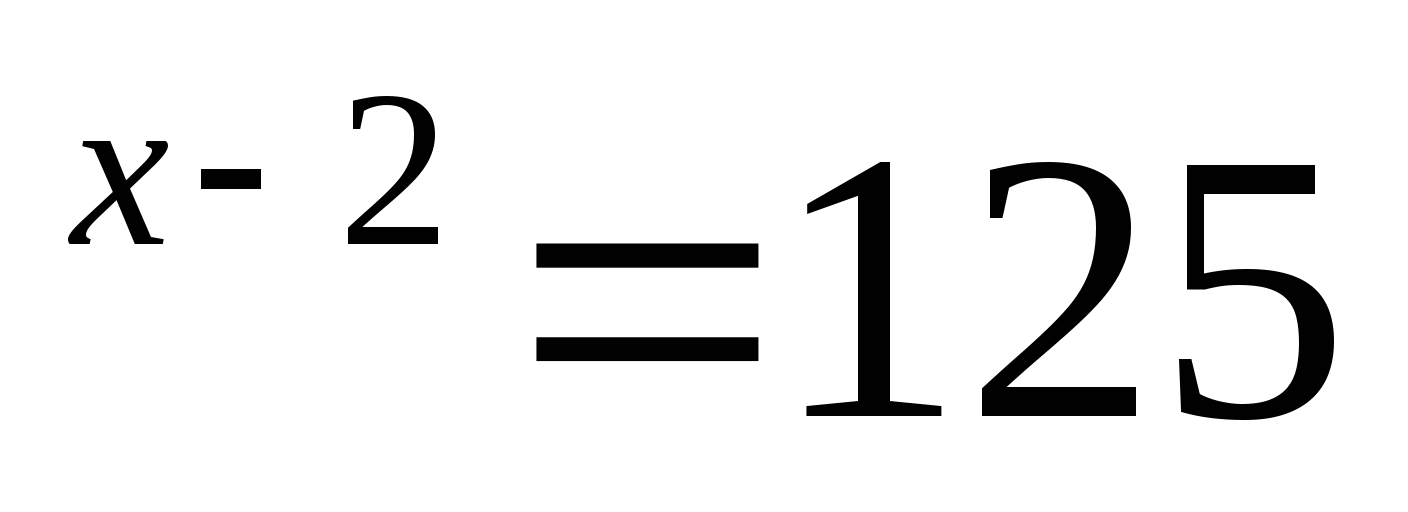 (приводим к одинаковому основанию)
(приводим к одинаковому основанию) 5
5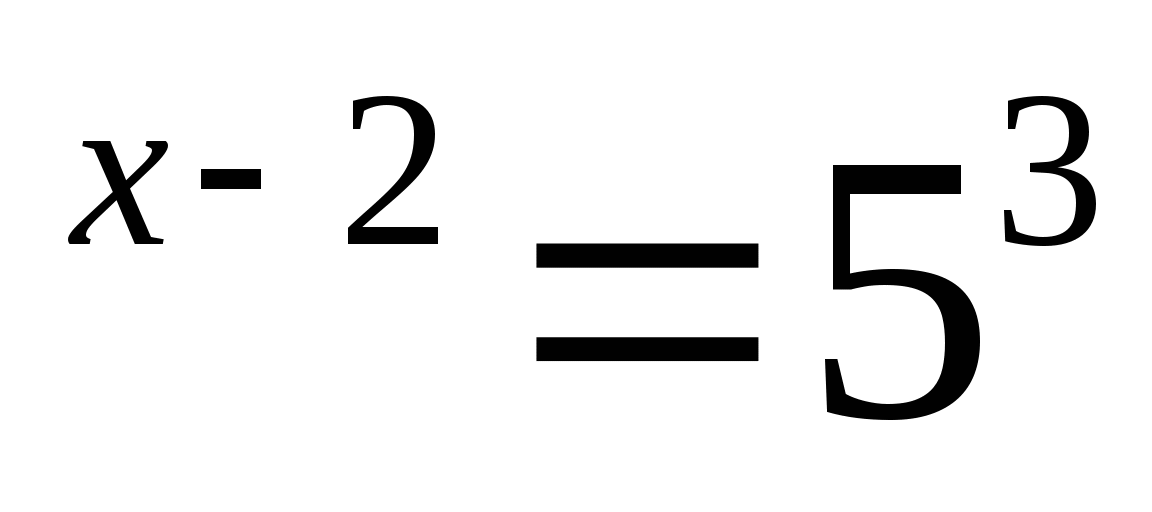
 х-2 = 3
х-2 = 3 х = 5.
х = 5.
Ответ: 5.
б) 
 2х = 4
2х = 4 х = 2.
х = 2.
Ответ: 2.
в) 4 * 2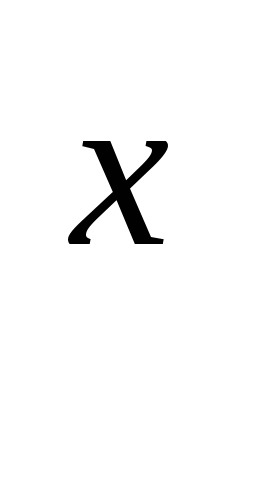 = 1
= 1 2
2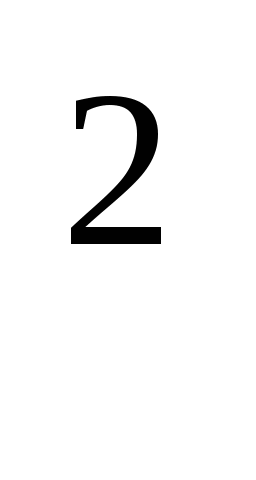 2
2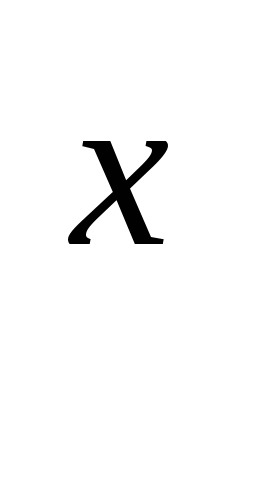 = 2
= 2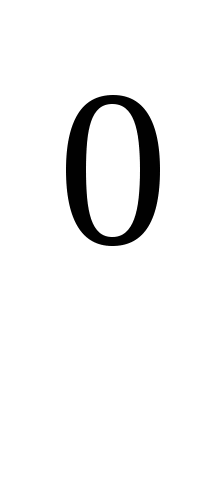
 2
2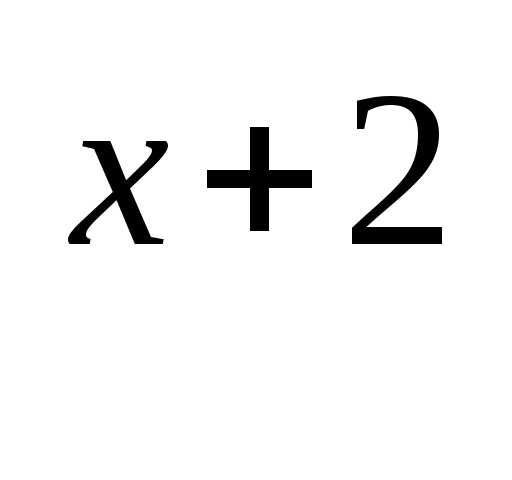 = 20
= 20 х+2 = 0
х+2 = 0  х = -2.
х = -2.
Ответ: -2.
II. Второй стандартный вид показательных уравнений
a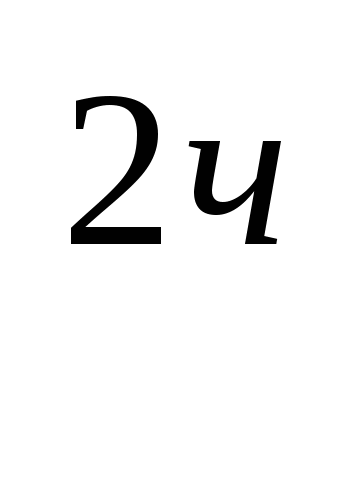 + pa
+ pa + q = 0 (сводимое к квадратному). Решать его следует введением новой переменной.
+ q = 0 (сводимое к квадратному). Решать его следует введением новой переменной.
Рассмотрим решение примера
a) 9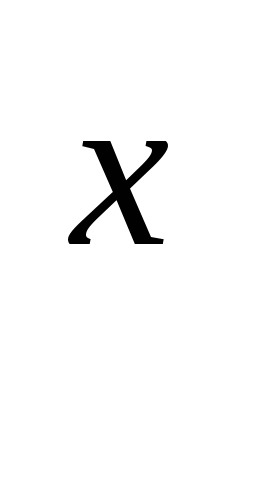 — 4 3
— 4 3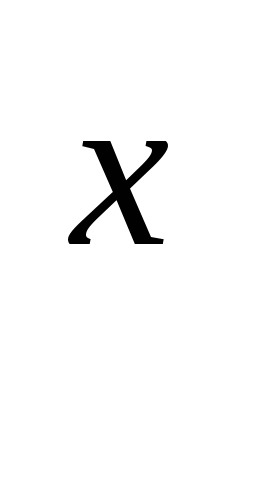 — 45 = 0. 3
— 45 = 0. 3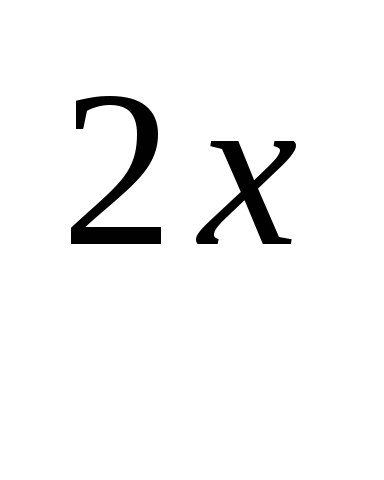 — 4 3
— 4 3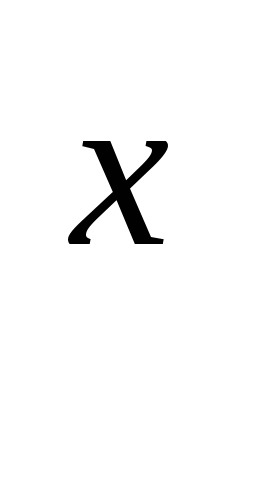 — 45 = 0
— 45 = 0
Пусть 3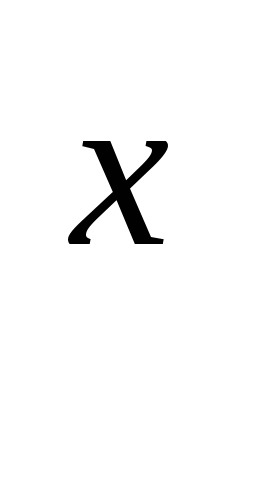 = t (t
= t (t  0), тогда получим t
0), тогда получим t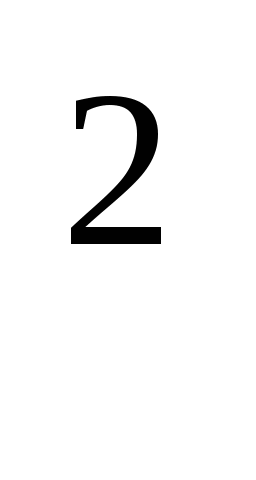 — 4t -45 =0;
— 4t -45 =0;
D = 16 – 4(-45) = 196;
t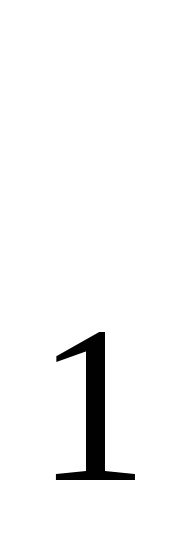 =
= 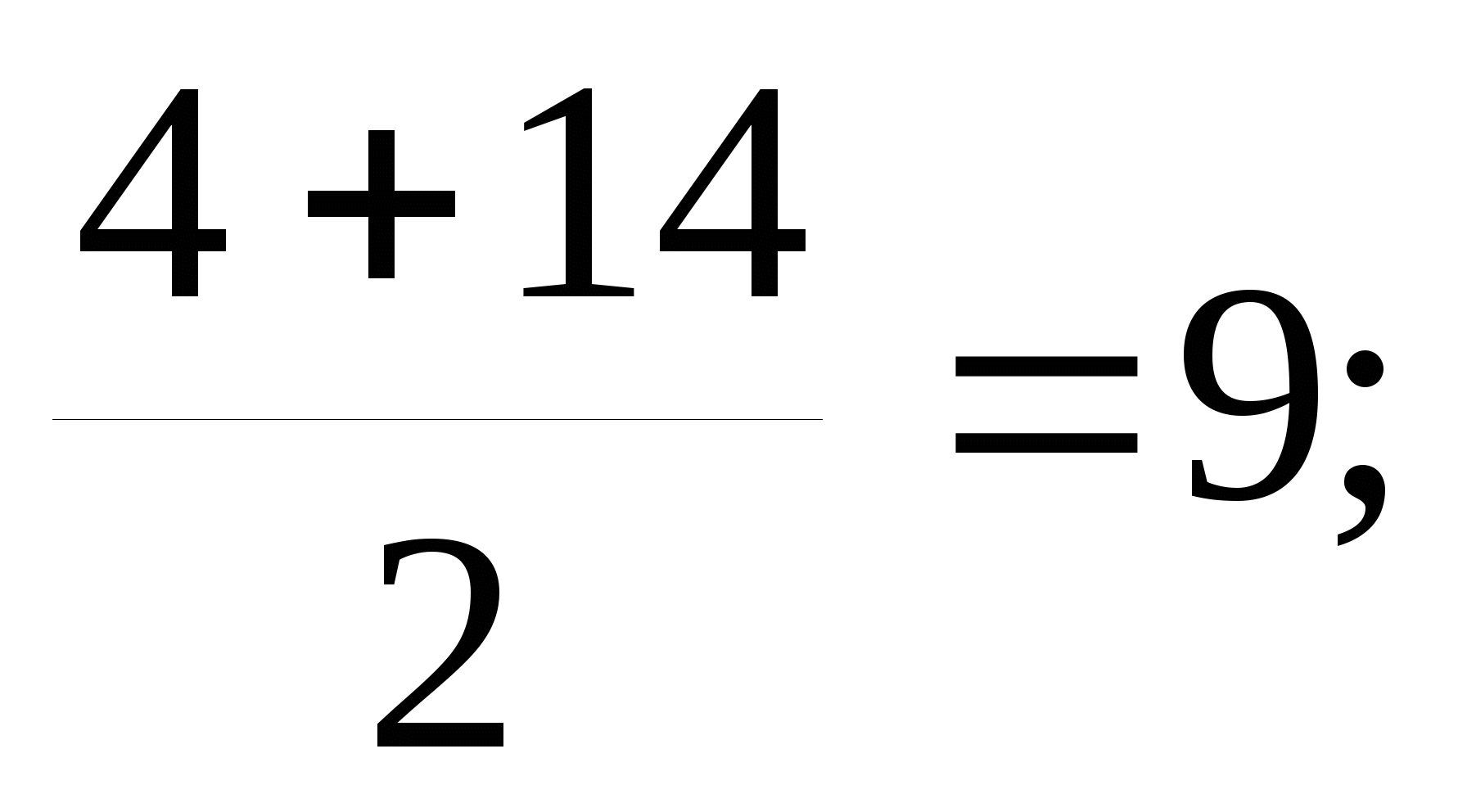 t
t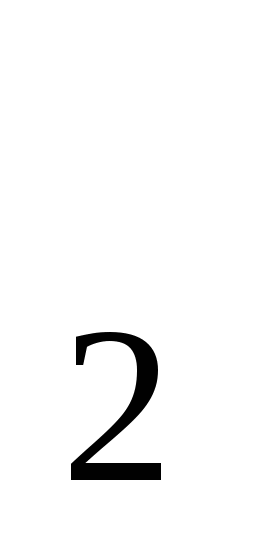 =
=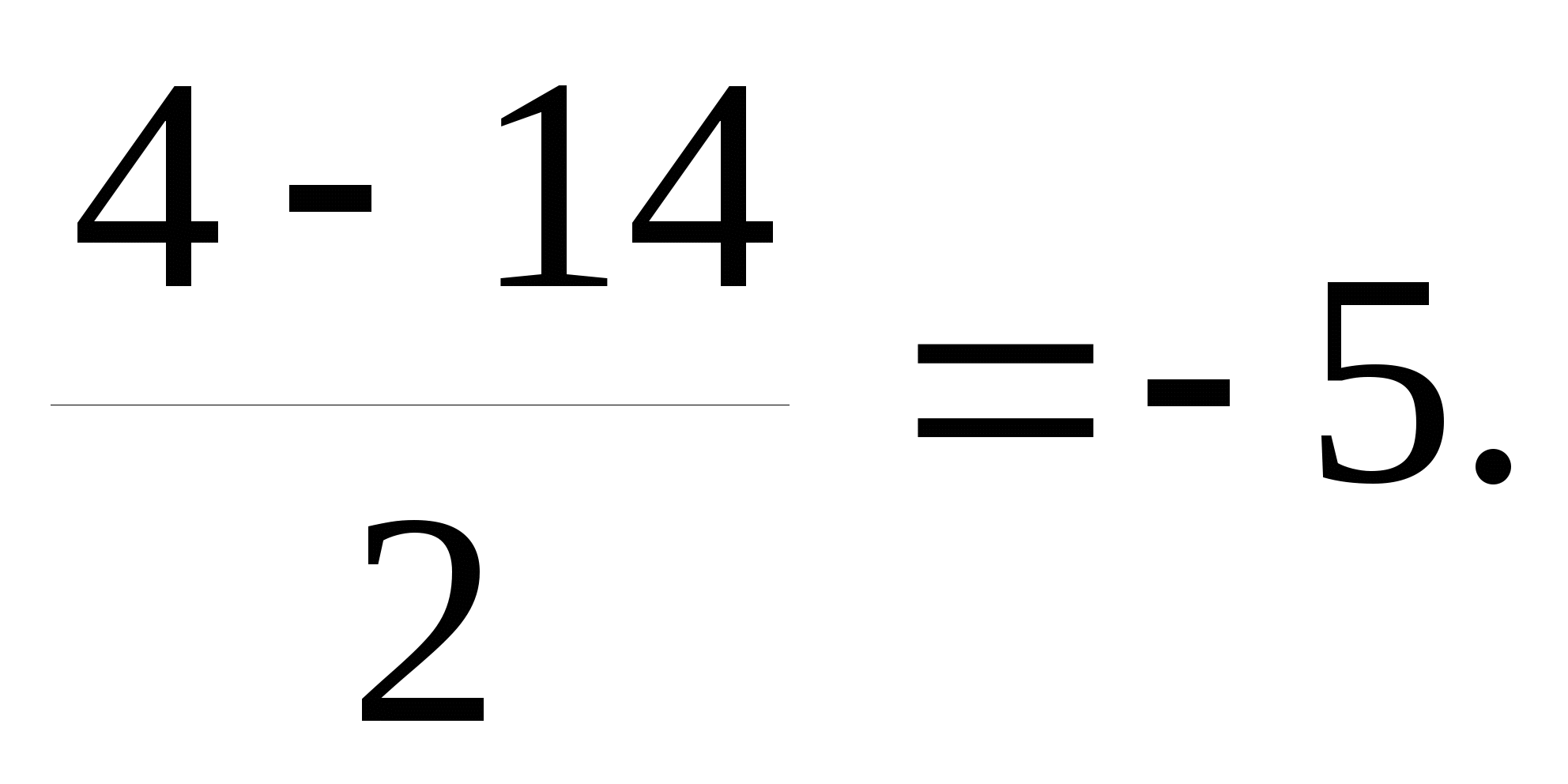
Обратная замена. (Используем алгоритм решения простейшего уравнения)
3
 = 9
= 9 3
3 = 3
= 3
 х = 2;
х = 2;3
 = -5 – нет решений.(-5 не удовлетворяет условию замены)
= -5 – нет решений.(-5 не удовлетворяет условию замены)
Ответ: 2.
III . Метод вынесения общего множителя
Рассмотрите решение примера
а) 3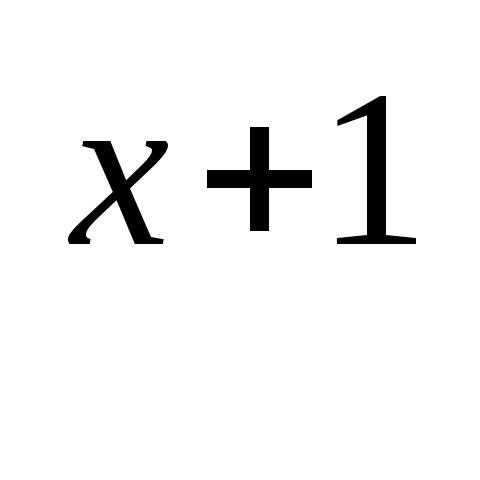 — 2 3
— 2 3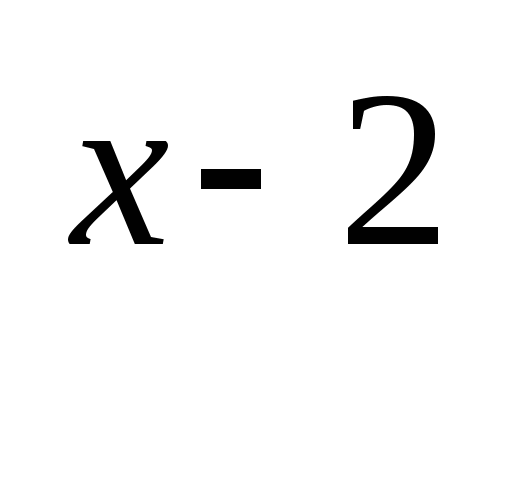 =75.
=75.
3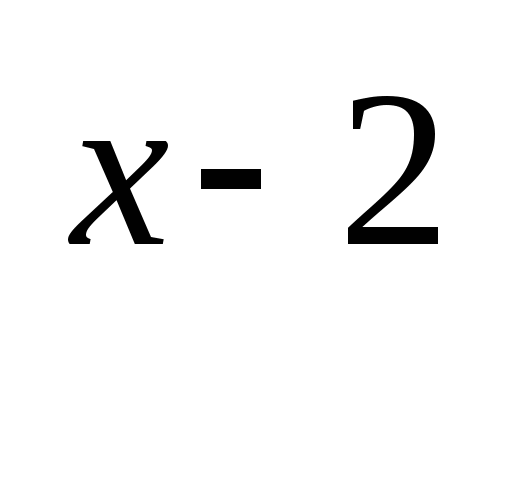 (3
(3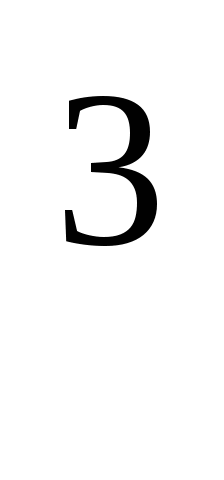 — 2)=75
— 2)=75  3
3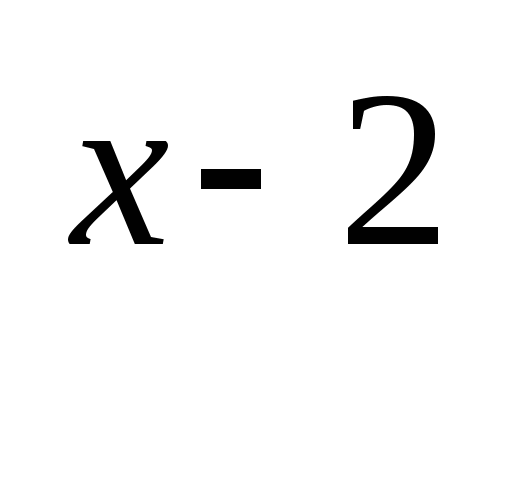 (27 — 2)=75
(27 — 2)=75  3
3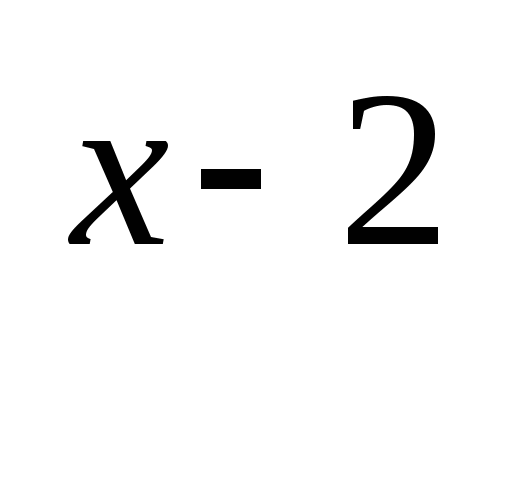
 25 =75 /: 25
25 =75 /: 25
 3
3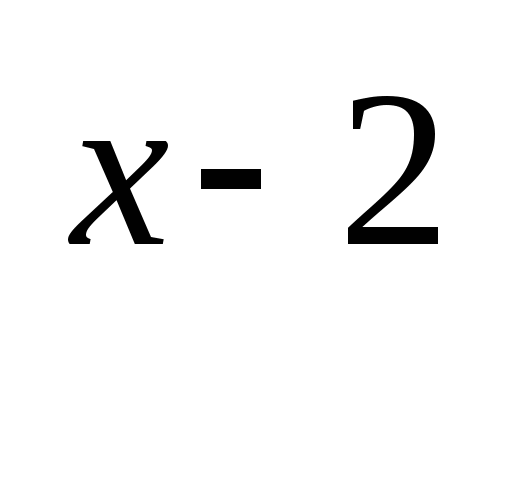 = 3 (простейшее уравнение)
= 3 (простейшее уравнение)
х-2 =1 х = 3.
х = 3.
Ответ: 3.
IV. Применение свойств степени.
Рассмотрите решение примера
a) 3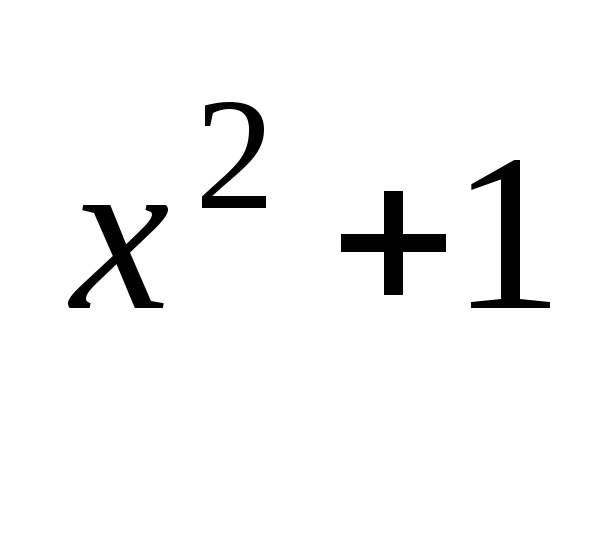 + 3
+ 3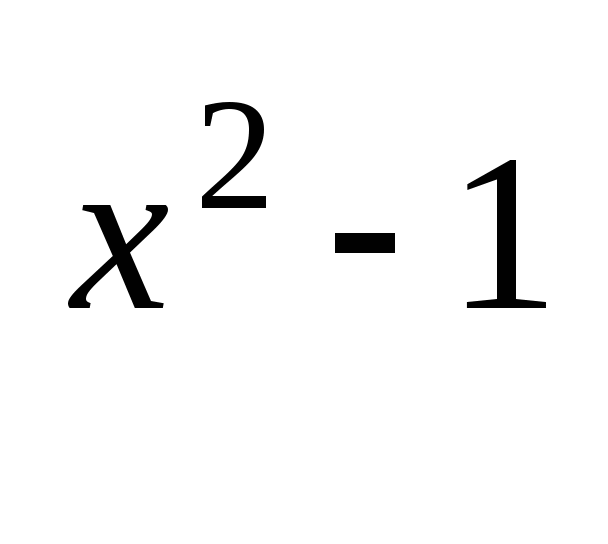 = 270.
= 270.
Представим данное уравнение в виде 3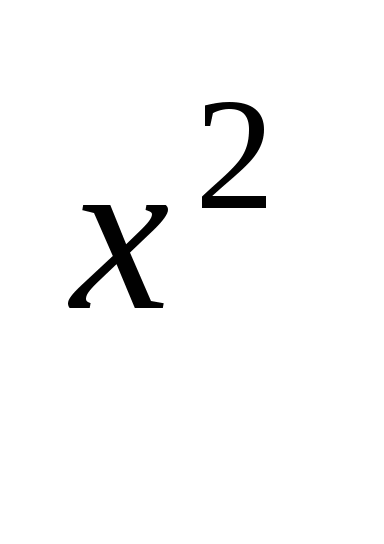 3 + 3
3 + 3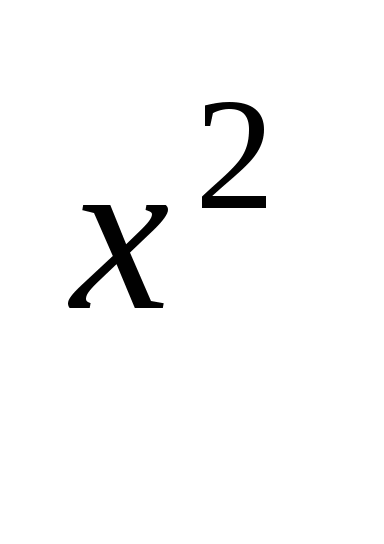
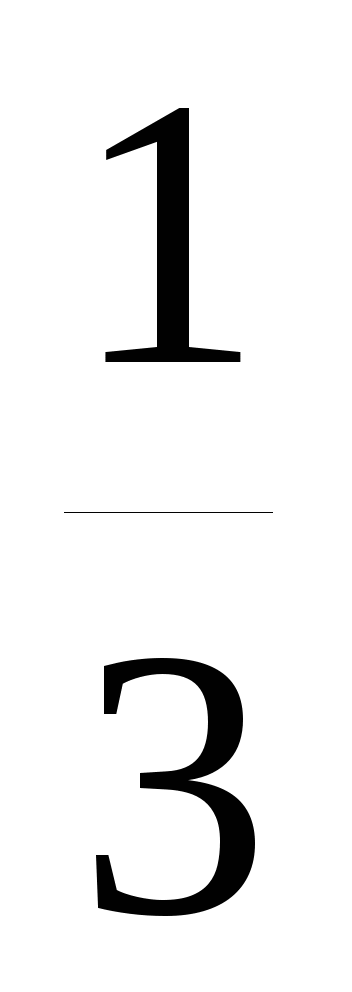 =270.
=270.
Если показатели степеней складывали, то переходим к произведению. Если вычитали – к делению.
Обозначим 3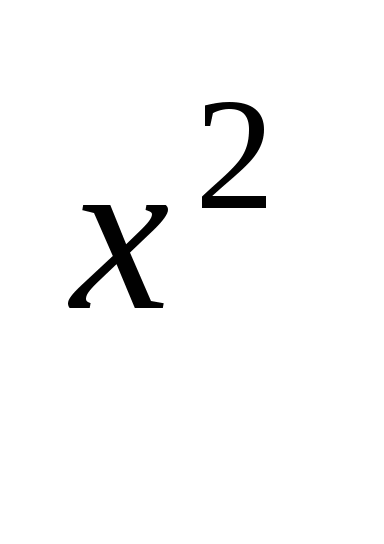 = t, тогда 3t +
= t, тогда 3t + 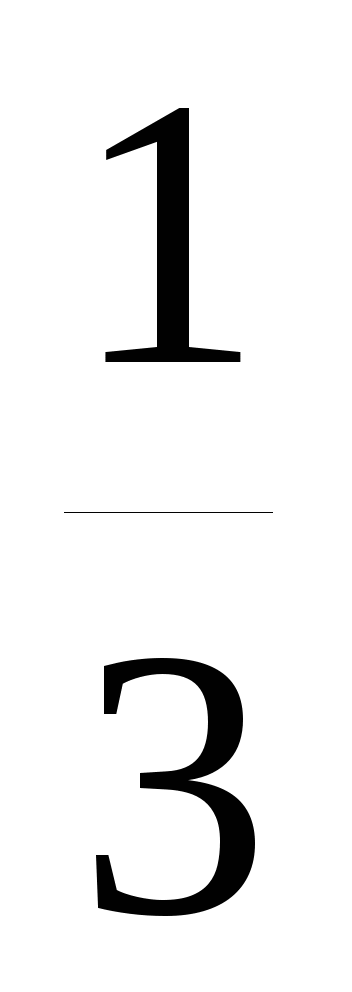 t = 270, приводим подобные
t = 270, приводим подобные
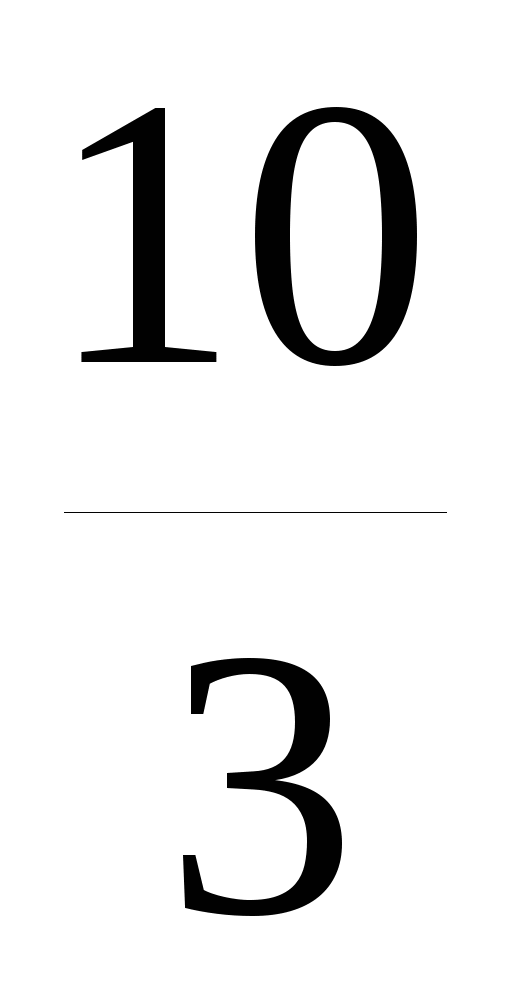 t = 270, t = 81.
t = 270, t = 81.
Обратная замена 3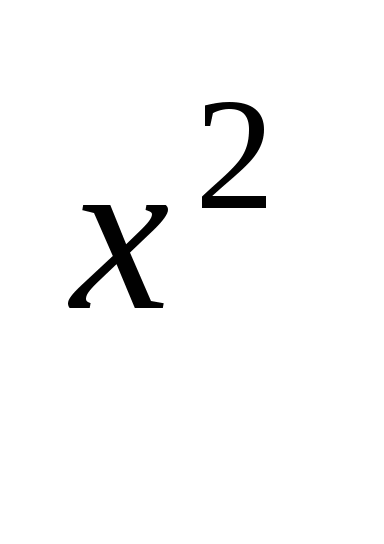 = 81 (простейшее уравнение), 3
= 81 (простейшее уравнение), 3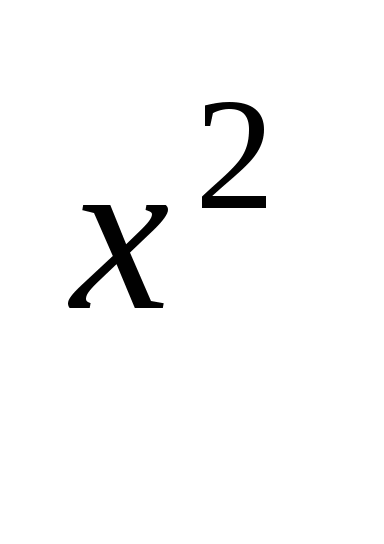 = 3
= 3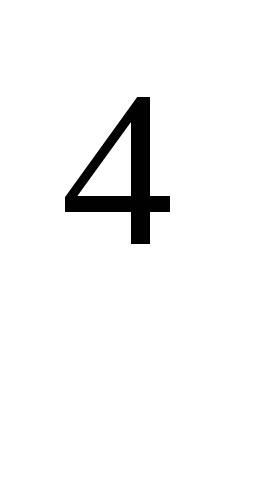 , х
, х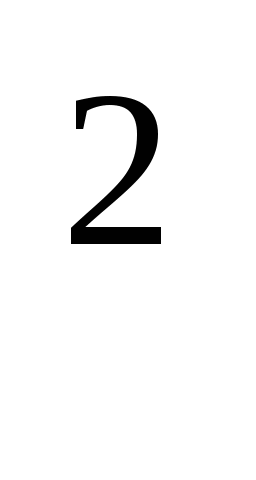 = 4, х
= 4, х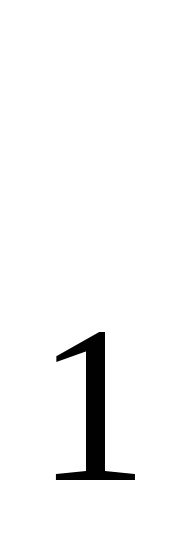 = -2, х
= -2, х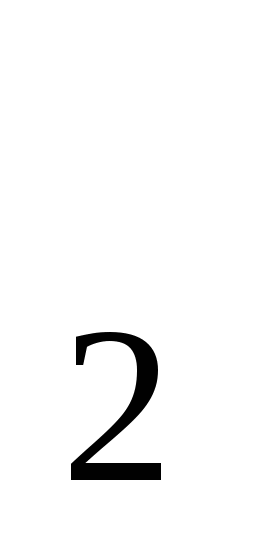 = 2.
= 2.
Ответ: -2; 2
Алгоритм работы в паре:
обучающиеся работают с карточками – консультантами, рассматривая определённый метод решения показательного уравнения. Записывают решение в тетрадь.
представитель пары на доске объясняет решение своего типа уравнения, обучающиеся слушают, записывают в тетрадь решение.
Действия обучающегося у доски:
предлагает записать название типа уравнения;
записывает и объясняет (неторопясь) решение уравнения. Одноклассники записывают решение в свои тетради.
Алгоритм работы в паре:
обучающиеся работают с карточками – консультантами, рассматривая определённый метод решения показательного уравнения. Записывают решение в тетрадь.
представитель пары на доске объясняет решение своего типа уравнения, учащиеся слушают, записывают в тетрадь решение.
Действия обучающегося у доски:
1. предлагает записать название типа уравнения;
записывает и объясняет (неторопясь) решение уравнения. Одноклассники записывают решение в свои тетради.
Вопросник по теме «решение показательных уравнений и неравенств».
Дайте определение показательного уравнения.
Запишите стандартный вид показательного уравнения.
Когда показательное уравнение имеет корни? Не имеет корней?
Алгоритм решения простейшего показательного уравнения.
Типы показательных уравнений и методы их решения.
Вопросник по теме «Решение показательных уравнений и неравенств».
1 .Дайте определение показательного уравнения.
2. Запишите стандартный вид показательного уравнения.
3 .Когда показательное уравнение имеет корни? Не имеет корней?
4. Алгоритм решения простейшего показательного уравнения.
5. Типы показательных уравнений и методы их решения.
Вопросник по теме «Решение показательных уравнений и неравенств».
1. Дайте определение показательного уравнения.
2. Запишите стандартный вид показательного уравнения.
3. Когда показательное уравнение имеет корни? Не имеет корней?
4. Алгоритм решения простейшего показательного уравнения.
5. Типы показательных уравнений и методы их решения.
ДОМАШНЯЯ САМОСТОЯТЕЛЬНАЯ РАБОТА

ДОМАШНЯЯ САМОСТОЯТЕЛЬНАЯ РАБОТА

infourok.ru