Графическое решение уравнений, неравенств. Видеоурок. Алгебра 9 Класс
В ходе урока вы сможете самостоятельно изучить тему «Графическое решение уравнений, неравенств». Преподаватель на занятии разберет графические методы решения уравнений и неравенств. Научит строить графики, анализировать их и получать решения уравнений и неравенств. На уроке также будут разобраны конкретные примеры по этой теме.
Тема: Числовые функции
Урок: Графическое решение уравнений, неравенств
Мы рассмотрели графики элементарных функций, в том числе графики степенных функций c разными показателями. Также мы рассмотрели правила сдвига и преобразований графиков функций. Все эти навыки необходимо применить, когда требуется графическоерешение уравнений или графическое решениенеравенств.
Пример 1. Графически решить уравнение: 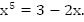
Решение:
Построим графики функций 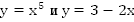 (Рис. 1).
(Рис. 1).
Графиком функции  является парабола, проходящая через точки
является парабола, проходящая через точки 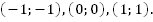
График функции 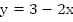 – прямая, построим её по таблице.
– прямая, построим её по таблице.
|
|
0 |
|
|
|
3 |
0 |
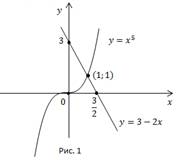
Графики пересекаются в точке 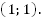 Других точек пересечения нет, т.к. функция
Других точек пересечения нет, т.к. функция 
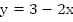 монотонно убывает, а, значит, их точка пересечения является единственной.
монотонно убывает, а, значит, их точка пересечения является единственной.Ответ: 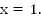
Пример 2. Решить неравенство
a. 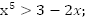
b. 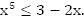
Решение:
a. Чтобы выполнялось неравенство, график функции  должен располагаться над прямой
должен располагаться над прямой 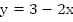
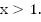
b. В этом случае, наоборот, парабола  должна находиться под прямой. Это выполняется при
должна находиться под прямой. Это выполняется при 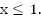
Ответ:
a. 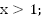
b. 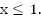
Пример 3. Решить неравенство 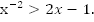
Решение:
Построим графики функций 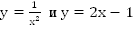 (Рис. 2).
(Рис. 2).
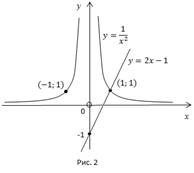
Найдем корень уравнения 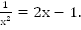 При
При 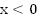 нет решений. При
нет решений. При 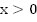 существует одно решение
существует одно решение 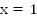 .
.
Чтобы выполнялось неравенство 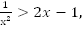
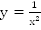 должна располагаться над прямой
должна располагаться над прямой 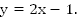 Это выполняется при
Это выполняется при 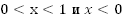 .
.Ответ: 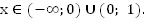
Пример 4. Решить графически неравенство:
a. 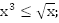
b. 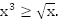
Решение.
Область определения: 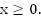
Построим графики функций 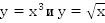 для
для 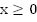 (Рис. 3).
(Рис. 3).
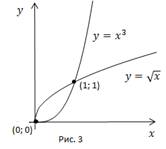
a. График функции 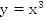 должен располагаться под графиком
должен располагаться под графиком 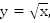
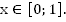
b. График функции 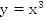 расположен над графиком
расположен над графиком 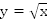 при
при 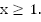 Но т.к. в условии имеем нестрогий знак, важно не потерять изолированный корень
Но т.к. в условии имеем нестрогий знак, важно не потерять изолированный корень 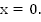
Ответ:
a. 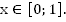
b. 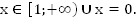
Мы рассмотрели графический метод решения уравнений и неравенств; рассмотрели конкретные примеры, при решении которых использовали такие свойства функций, как монотонность и четность.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 355, 356, 364.
Урок по математике для 9 класса «Графический способ решения систем уравнений»
Графический способ решения систем уравнений
(9-й класс)
Учебник: Алгебра, 9 класс, под редакцией Теляковского С.А.
Тип урока: урок комплексного применения знаний, умений, навыков.
Цели урока:
Образовательные: Выработать умение самостоятельно применять знания в комплексе, переносить их в новые условия, в том числе работать с компьютерной программой для построения графиков функции и нахождения количества корней в заданных уравнениях.
Развивающие: Формировать у учащихся умение выделять основные признаки, устанавливать сходства и различия. Обогащать словарный запас. Развивать речь, усложняя её смысловую функцию. Развивать логическое мышление, познавательный интерес, культуру графического построения, память, любознательность.
Воспитательные: Воспитывать чувство ответственности за результат своего труда. Учить сопереживать успехам и неудачам одноклассников.
Средства обучения: компьютер, мультимедийный проектор, раздаточный материал.
План урока:
Организационный момент. Домашнее задание – 2 мин.
Актуализация, повторение, коррекция знаний — 8 мин.
Изучение нового материала – 10 мин.
Практическая работа – 20 мин.
Подведение итогов – 4 мин.
Рефлексия – 1 мин.
ХОД УРОКА
Организационный момент – 2 мин.
Здравствуйте, ребята! Сегодня урок по важной теме: «Решение систем уравнений».
Нет таких областей знаний в точных науках, где бы ни применялась данная тема. Эпиграфом к нашему уроку являются следующие слова: «Ум заключается не только в знании, но и в умении прилагать знания на деле». (Аристотель)
Постановка темы, целей и задач урока.
Учитель сообщает классу о том, что на уроке будет изучаться и ставит задачу научиться решать системы уравнений с двумя переменными графическим способом.
Задание на дом (П.18 № 416, 418, 419 а).
Повторение теоретического материала – 8 мин.

А) Учитель математики: По готовым чертежам ответить на вопросы и обосновать свой ответ.
1). Найти график квадратичной функции D=0 (Учащиеся отвечают на вопрос и называют график 3в).
2). Найти график обратно — пропорциональной функции при k>0 (Учащиеся отвечают на вопрос, называют график 3a).
3). Найти график окружности с центром O(-1; -5). (Учащиеся отвечают на вопрос, называют график 1б).
4). Найти график функции y=3x-2. (Учащиеся отвечают на вопрос и называют график 3б).
5). Найти график квадратичной функции D>0, a>0. (Учащиеся отвечают на вопрос и называют график 1a).
Учитель математики: – Для того, что бы успешно решать системы уравнений, давайте вспомним:
1). Что называется системой уравнений? (Системой уравнений называется несколько уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям).
2). Что значит решить систему уравнений? (Решить систему уравнений, значит найти все решения или доказать, что решений нет).
3). Что называется решением системы уравнений? (Решением системы уравнений называют пару чисел (x; у), при которой все уравнения системы обращаются в верные равенства).
4) Выясните, является ли решением системы уравнений  пара чисел: а) х = 1, у = 2; (–) б) х = 2, у = 4; (+) в) х = – 2, у = – 4? (+)
пара чисел: а) х = 1, у = 2; (–) б) х = 2, у = 4; (+) в) х = – 2, у = – 4? (+)
III Новый материал – 10 мин.
П.18 учебника излагается методом беседы.
Учитель математики: В курсе алгебры 7 класса мы рассматривали системы уравнений первой степени. Теперь займёмся решением систем, составленных из уравнений первой и второй степени.
1.Что называется системой уравнений?
2.Что значит решить систему уравнений?
Мы знаем, что алгебраический способ позволяет находить точные решения системы, а графический способ позволяет наглядно увидеть, сколько корней имеет система и найти их приблизительно. Поэтому учиться решать системы уравнений второй степени мы продолжим на следующих уроках, а сегодня основной целью урока будет практическое применение компьютерной программы для построения графиков функции и нахождения количества корней систем уравнений.
IV. Практическая работа – 20 мин. Решение систем уравнений графическим способом. Определение корней уравнений. (Построение графика на компьютере.)
Задания выполняются учащимися на компьютерах. Решения проверяются во время работы.
Уравнения для 1-й группы учащихся:
Уравнения для 2-й группы учащихся:
Уравнения для 3-й группы учащихся:
 y = 2x2 + 5x+3
y = 2x2 + 5x+3
y = 4
 y= -2x2 +5х+3
y= -2x2 +5х+3
y = -3x + 4

y= -2x2 -5х-3
y = -4+2x

y = 4x2 + 5x+3
y = 2

y= -4x2 +5х+3
y = -3x + 2
 y= -4x2 -5х-3
y= -4x2 -5х-3
y = -2+2x

y = 4x2 + 5x+5
y = 3

y= -4x2 +5х+5
y = -x + 3

y= -4x2 -5х-5
y = -2+3x
Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и её решение.












– Какие из перечисленных систем можно решать с помощью данного рисунка?


– Были даны 4 системы, их нужно было соотнести с графиками. Сейчас задание обратное: есть графики, их нужно соотнести с системой.

Подведение итогов урока. Выставление оценок– 4 мин.
* Решение систем уравнений. (Задания со звёздочкой*.)
Уравнения для 1-й группы учащихся:
Уравнения для 2-й группы учащихся:
Уравнения для 3-й группы учащихся:

x y = 6
x2 + y = 4

x2 + y = 3
x — y + 1= 0

x2 — y = 3
y = 6
Уравнения для 4-й группы учащихся:
Уравнения для 5-й группы учащихся:
Уравнения для 6-й группы учащихся:

y = -8/x
2x + y = -1

y = — 3/x
y + x = — 2

y x = 4
2x — y = 2
VI . Рефлексия – 1 мин.
ОЦЕНИТЕ ВАШУ РАБОТУ НА УРОКЕ
1
2
3
4
5
6
7
8
9
10
ВЫБЕРИТЕ ЭМОЦИОНАЛЬНУЮ СОСТАВЛЯЮЩУЮ УРОКА







НАСКОЛЬКО ВЫ ОЦЕНИВАЕТЕ УСВОЕНИЕ ВАМИ ДАННОЙ ИНФОРМАЦИИ
1
2
3
4
5
6
7
8
9
10
ОЦЕНОЧНАЯ ШКАЛА:
1 ВОПРОС: 123-НЕЗНАЧИТЕЛЬНО, 456- В БОЛЬШЕЙ СТЕПЕНИ, 789- ПОЛНОЕ ВКЛЮЧЕНИЕ, 10- АБСОЛЮТНОЕ ВКЛЮЧЕНИЕ.
2 ВОПРОС: 123- НИЗКИЙ, 456- СРЕДНИЙ, 789- ДОСТИГ MAX- ЗНАНИЙ, ВЫСОЧАЙШИЙ.
infourok.ru
Урок алгебры по теме «Графический способ решения систем уравнений». 9-й класс
Основная дидактическая цель: введение графического способа решения систем уравнений, построение алгоритма.
Задачи урока:
Образовательные:
- показать один из способов решения систем уравнений – графический;
- в ходе урока разработать алгоритм решения.
Воспитательные:
- прививать внимательность, аккуратность, культуру графических построений;
- стимулировать интерес к изучаемому предмету;
Развивающие:
- развивать логическое и критическое мышление, умение анализировать, делать выводы.
Ход урока
Эпиграф.
В математике есть своя красота,
как в живописи и поэзии.
Н.Е. Жуковский.
I. Оргпсихологический момент.
Презентация: тема урока, эпиграф урока. Приложение 1 (Слайд 1–3)
Перед вами лежит листок бумаги. Обведите на нем свою руку. Продолжите предложения, характеризующие ваше эмоциональное состояние в данный момент:
Мизинец – Мне сейчас …
Безымянный – Я хочу …
Средний – Я буду…
Указательный – Чего я жду от урока…
Большой – Мне интересно …
II. Актуализация знаний
Повторение: Что называется графиком уравнения с двумя переменными?
На листочках записать уравнение, которое соответствует данному графику.
Тест по теме: “Графики функций”.
Приложение 2.
Взаимопроверка: обменяться листочками и проверить.
III. Изучение нового материала.
Учитель: В 7 классе мы рассматривали системы уравнений первой степени с двумя переменными. Теперь займемся решением систем, составленных из двух уравнений второй степени или из одного уравнения первой степени, а другого второй степени.
Вспомним, что решением системы двух уравнений с двумя переменными является пара чисел, обращающая каждое уравнение системы в верное равенство. Решить систему – значит найти все ее решения или доказать, что решений нет
Приложение 3.
Задание. При просмотре презентации постарайтесь составить алгоритм решения систем уравнений графическим способом и записать в тетрадь.
Алгоритм решения систем уравнений графическим способом:
- Построить в одной системе координат графики уравнений, входящих в систему.
- Найти координаты точек пересечения графиков.
- Записать ответ.
Учащиеся читают записанный алгоритм в тетрадь. При необходимости вносятся поправки.
IV. Закрепление.
Приложение 4.
1. Устно с помощью презентации ответить на вопрос:
Сколько решений имеет система? Найти решение системы.
2. Письменно в тетрадях № 416, 417. (на доске и в тетрадях).
V. Итог урока. Домашнее задание.
Мы сегодня рассмотрели один из способов решения систем уравнений, заглянули в прекрасный мир графиков, надеюсь, увидели и оценили красоту в математике.
Оценки за урок.
Выполнить дома: № 418, № 421 (а, б).
VI. Рефлексия.
Написать небольшое сочинение – синквейн.
Возьмите листочки и на обратной стороне напишите небольшое сочинение – синквейн, отражающее ваше эмоциональное состояние после нашего урока.
Кстати, а вы знаете что такое синквейн? Слово синквейн – японского происхождения. Это пятистрочный стих, неимеющий рифмы. Японская поэзия тоже не имеет рифмы. Когда первый раз слышишь слово “синквейн”, то кажется, что это что-то непонятное и экзотическое. На самом же деле здесь нет абсолютно ничего сложного. Французы придумали стихотворение, которое назвал “синквейн”. “Cing” во французском языке значит “пять”. Так вот “синквейн” в вольном переводе означает “пять вдохновений” или “пять удач”. Не правда ли занятно получается? Развлекаться таким сочинительством легко, весело и полезно. Речь развивается, сложные понятия усваиваются, отношение к чему-либо осознается.
1-я строка – существительное, которое нужно осмыслить;
2-я строка – два прилагательных, определяющих это существительное и описывающих ваше представление о нем;
3-я строка – три глагола; действия, которые производит существительное;
4-я строка – фраза из четырех слов, передающая ваше отношение к существительному;
5-я строка – одно слово с “!” на конце.
Пример синквейна. Приложение 1 (Слайд 4, 5)
Всем спасибо. Урок окончен.
Отзывы об уроке. Приложение 5.
urok.1sept.ru
Методическая разработка по алгебре (9 класс) по теме: Урок алгебры в 9 классе по теме «Графический способ решения систем уравнений»
Урок алгебры в 9 классе по теме:
«Графический способ решения систем уравнений»
Цель изучения:
- Продолжить работу по формированию навыков решения систем уравнений графическим способом.
- Развивать познавательный интерес и творческую активность обучающихся.
- Формировать навыки самостоятельной деятельности.
Прогнозируемый результат: Закрепить построение графиков, работать с рисунком.
План урока:
- Организационный момент.
- Актуализация знаний обучающихся.
III.Решение задач.
IV. Самостоятельная работа.
V. Подведение итога урока.
VI. Домашнее задание.
Эпиграф:
Китайская мудрость: « Я слышу – я забываю, я вижу – запоминаю,
я делаю – я усваиваю»
ХОД УРОКА
I.Организационный момент. Рефлексия.
Учащимся сообщается тема урока, формируются цель и задачи урока, виды деятельности учащихся для достижения цели.
II.Актуализация знаний обучающихся.
Прежде чем перейти к закреплению давайте вспомним некоторые знания по данной теме, которые помогут нам.
- Слайды 5-11
- Повторим теорию:
— Что значит решить графически систему уравнений с двумя переменными?
— Что называется решением системы уравнений с двумя переменными, которая решается графически?
— Сформулируйте алгоритм графического решения системы уравнений. Слайд12
- Работа устно:
— Установи соответствие между графиками функций и формулами. Слайд 13-14
III.Решение задач.
- Работа у доски и на месте:
— Решить графически систему уравнений:
1) У = х2 — 4х + 3,
У = — 2х + 3, слайд 15-17
У = — 2/х;
— Перед вами графики двух уравнений. Запишите систему, определяемую этими уравнениями и её решение.
1) у = 2х, 2) х2 + у2 = 9, 3) у = х2 + 2, 4) х – у = 1,
у = 2/х; у = — /х/ +3; у = — х2 + 4; 3х +2у = 1.
Слайды 18-21
IV.Самостоятельная работа.
Решить графически систему уравнений:
у = х3, слайд 22
ух = — 12
V.Подведение итога урока. Рефлексия.
Комментируются и выставляются оценки за урок ученикам, работавшим у доски, а также наиболее отличившимся на уроке.
— Наш урок подошел к концу. Благодарю всех за работу и желаю успехов при выполнении домашнего задания. Урок окончен. До свидания.
VI. Домашнее задание.
— В библейской легенде голубка приносит Ною весть о том, что Бог сменил гнев на милость и что потоп кончился. Выражение «Голубь мира» приобрело особую популярность после того, как голубь, несущий в клюве оливковую ветвь, был использован художником при создании эмблемы для Всемирного конгресса сторонников мира (1949 год).
Решите графически систему уравнений. Используя найденные ответы, узнайте фамилию художника, создавшего эту эмблему.
{х2 + у2 = 16, слайд 23-24
{х + у + 2 = 0.
Сальвадор Дали | Александр Дейнека | Пабло Пикассо |
(-2,25;2,25), (0,25;-0,25) | (2,25; -0,25), (-0,25;2,25) | (-2,25;0,25), (0,25;-2,25) |
Вывод: Пабло Пикассо.
Учитель: Пикассо-и-Руис, Пабло испанец. Годы жизни: 1881 — 1973. Великий художник 20-го века, живописец, рисовальщик, скульптор, график, керамист. Жил и работал в Париже и разных окрестностях Франции. В Эрмитаже — 35 картин, богатое собрание графики, а также произведения керамики.
Урок алгебры в 9 классе по теме:
«Графический способ решения систем уравнений»
« Я слышу – я забываю,
я вижу – запоминаю,
я делаю – я усваиваю»
Китайская мудрость
3.Решение задач.
— Решить графически систему уравнений:
У = х2 — 4х + 3,
У = — 2х + 3,
У = — 2/х;
4.Самостоятельная работа.
Решить графически систему уравнений:
у = х3,
ух = — 12
Домашнее задание.
— В библейской легенде голубка приносит Ною весть о том, что Бог сменил гнев на милость и что потоп кончился. Выражение «Голубь мира» приобрело особую популярность после того, как голубь, несущий в клюве оливковую ветвь, был использован художником при создании эмблемы для Всемирного конгресса сторонников мира (1949 год).
Решите графически систему уравнений. Используя найденные ответы, узнайте фамилию художника, создавшего эту эмблему.
{х2 + у2 = 16,
{х + у + 2 = 0.
Сальвадор Дали | Александр Дейнека | Пабло Пикассо |
(-2,25;2,25), (0,25;-0,25) | (2,25; -0,25), (-0,25;2,25) | (-2,25;0,25), (0,25;-2,25) |
nsportal.ru
Название раздела: | Графический метод решения уравнений |
Тема урока: | Решение систем уравнений с двумя переменными графическим способом. |
Цели обучения | МР9.2 Решают системы уравнений с двумя неизвестными графическим методом; |
Изученный материал | ММ9.1 Геометрически интерпретируют уравнение с двумя неизвестными; ММ9.2 Изображают множество точек, заданных уравнением с двумя неизвестными; ММ9.3 Используют ПО для графического построения уравнений с двумя неизвестными; МН9.6 Формулируют правила построения и строят графики функций |
Фронтальный опрос теоретического материала | Цель обучения: ММ9.1 Геометрически интерпретируют уравнение с двумя неизвестными.
xy – 2 = 2x – y, x2+2x-3=0, 2x+5=y, xy=-12, 6x-8=0, у2+у =81.
(Каждая пара значений переменных, удовлетворяющих уравнению с двумя переменными, называется решением уравнения.)
1.Что является графиком уравнения ху=9 ? (Гипербола) 2. Что является графиком уравнения х+у=9 ? (Прямая) 3. Что является графиком уравнения х2+у2=25? (Окружность радиусом равное 5, центром которого является точка (0; 0)) 4. Что является графиком уравнения х2+у =9 ? (Парабола) 5. Что является графиком уравнения х2+16у2=64? (Эллипс) 6. Что является графиком уравнения (х+4)2+(у-1)2=49? (Окружность радиусом равное 7, центром которого является точка (-4; 1)) ММ9.1 Геометрически интерпретируют уравнение с двумя неизвестными. Установите соответствие между графиком функции и формулой
|
Индивидуальная работа по построению | Цели обучения: ММ9.1 Геометрически интерпретируют уравнение с двумя неизвестными; ММ9.2 Изображают множество точек, заданных уравнением с двумя неизвестными. МН9.6 Формулируют правила построения и строят графики функций . Учащимся предлагаются карточки, на которых написано уравнение с двумя неизвестными. Работая на прозрачных листах (кальке) с готовой координатной плоскостью, каждый из учащихся выполняет построение графика выбранного им уравнение. Задание. Опиши график уравнения и построй его. Карточка №1. Карточка №2. xy=8 Карточка №3. y=x2+3 Карточка №4. y=x2 Карточка №6. y=2x+3 Карточка №7. y= Карточка №8. y=x2+2x+1 Карточка №9. Карточка №12. x – y = 5 Для проверки верности построения см. приложение 2 |
Вызов | Условие 1. В классе 12 учеников. х – мальчиков и у – девочек. Составьте уравнение с двумя переменными. х+у=12 Что является решением уравнения с двумя неизвестными? (Множество пар значений переменных, удовлетворяющих уравнению с двумя переменными) Какие пары являются решениями вышеуказанного уравнения? ((6;6), (4;8), (8;4), (5;7), (7;5), (3;9), (9;3), (2;10), (10;2), (1;11), (11;1)) Условие 2. Мальчиков на два больше, чем девочек. х=у+2 Как, используя математическую символику показать, что мне нужно пара чисел, удовлетворяющее двум поставленным условиям? Какая пара будет решением этой системы? (Решением системы будет пара (7; 5)). Что значить решить систему уравнений? (Решить систему уравнений – это значит найти все её решения, или установить, что решений нет). |
Групповая работа по составлению и решению систем уравнений графическим методом. | Цель обучения: МР9.2 Решают системы уравнений с двумя неизвестными графическим методом Учащиеся работают в группах по 4 ученика. Задание 1. Учащимся предлагается составить систему уравнений, объединяя свое уравнение с уравнением каждого в группе. Таким образом каждый ученик составляет по 3 системы. Задание 2. Решение полученных систем графическим методом. Найдите решения построенных вами систем уравнений. Что значит решить систему графическим методом? Почему он так называется? (В одной и той же системе координат строим графики обоих уравнений и находим координаты точек их пересечения.) Как вы думаете для чего на прозрачных бумагах каждый из вас построил график уравнения с двумя неизвестными? (При наложении прозрачных листов с графиками можно найти и указать точки пересечения. Или доказать, что графики уравнений некоторых систем не пересекаются, следовательно не имеют решений.) Когда система является правильно решенной графическим методом? Критерий успеха: Верно интерпретирует график первого уравнения; Верно выполняет построение графика первого уравнения; Верно определяет вид графика второго уравнения; Верно выполняет построение графика второго уравнения; Верно определяет точки пересечения; Верно определяет координаты точек пересечения; Верно интерпретирует ответ. |
Индивидуальная работа по решению систем уравнений графическим методом. | Цель обучения: МР9.2 Решают системы уравнений с двумя неизвестными графическим методом. Учащимся предлагаются практические задания из учебного ресурса (приложение 3). I вариант Решите систему графическим методом II вариант Решите систему графическим методом |
Оценивание | Цель обучения: ММ9.3 Используют ПО для графического построения уравнений с двумя неизвестными. Учащиеся, объединившись в пары, обмениваются выполненными работами. Индивидуально каждый из них с помощью программы «GEOGEBRA» проверяет и оценивает работу другого варианта. (Выполнившие I вариант, проверяют в паре работу II-го варианта. Выполнившие II вариант, проверяют в паре работу I-го варианта.) Затем заполняют следующую таблицу (приложение 4) |
Подведение итогов. Рефлексия | Вопросы рефлексии (приложение 5)
|
Список использованной литературы |
|
infourok.ru
«Графический способ решения системы уравнений с двумя переменными.»
Министерство образования, науки и молодежи Республики Крым
Государственное бюджетное общеобразовательное учреждение Республики Крым «Лозовская специальная школа-интернат»
План-конспект урока
по алгебре в 9 классе на тему:
«Графический способ решения системы уравнений с двумя переменными.»
Подготовила
учитель математики
Мамутова Г. С.
с. Ферсманово.
алгебраТема: «Графический способ решения системы уравнений с двумя переменными.»
Класс: 8
Тип урока: урок изучения нового материала
Урок № :
Дата:
Цель урока: формирование умений и навыков решения систем уравнений графическим способом.
Образовательная: создать условия для решения систем линейных уравнений с двумя переменными графическим способом.
Развивающая : развитие исследовательских способностей учащихся, умение делать выводы, самоконтроля, речи, логическое мышление.
Воспитательная : воспитывать интерес к предмету, аккуратность, самостоятельность.
Коррекционная: коррекция и развитие связной устной речи;
Планируемые результаты:
Познавательные УУД:
Регулятивные УУД:
Коммуникативные УУД:
Личностные УУД:
— способствовать строить речевые высказывания, упражнять обучающихся в выполнении мыслительных операций: анализ, обобщение.
— формировать умение планировать свою работу с учетом конечного результата.
— формировать умение работать в группах, умение принимать участие в коллективном обсуждении проблем.
— создать условия для формирования интереса к познавательной деятельности.
Оборудование:
Учебник, мел, доска, карточки, презентация, мультимедийное устройство.
Методы обучения:
Словесные;
Наглядные;
Практические;
Проблемно – поисковые.
Организационные формы обучения:
— индивидуальные;
— коллективные;
— работа в парах.
Ход урока:
Организационный момент.
Деятельность учителя
Деятельность учащихся
Учитель проверяет готовность к уроку настраивает их на работу.
Проверка домашнего задания.
Мотивационная беседа с последующей постановкой цели учащимися.
Эмоционально настраиваются на работу
Актуализация опорных знаний и умений
Устные упражнения:
задание показаны на слайдах.
1) Является ли пара чисел (2;0) решением уравнения;
а) б) ху+3=0 в) у(х+2)=0
2) Выберите схематически график функции
1) у = 5х 2) у = 3) у= 4) у=
а) б)
б)  в)
в)  г)
г)
Слушают учителя, отвечают на вопросы, воспринимают информацию зрительно и на слух, выполняют задание.
Усвоение новых знаний
Объяснение учителя:
Если ставится задача найти все общие решения двух (и более) уравнения с двумя переменными, то говорят, что нужно решить систему уравнений с двумя переменными.
Решением системы уравнений с двумя переменными х и у называется такая пара значений переменных (х;у) , которая является решением каждого из уравнений системы.
Например: пара (2 ; 3) является решением системы уравнений
Так как х=2 и у=3 является решением каждого из уравнений системы.
Решить систему уравнений с двумя переменными значит найти все ее решения или доказать, что их нет.
Если система не имеет решений, ее называют несовместимой.
Алгоритм решения систем уравнений с двумя переменными х и у графическим способом.
Строим график каждой из уравнений системы в одной прямоугольной системе координат.
Находим все точки пересечения построенных графиков и определяем их координаты. Эти координаты и являются решением данной системы уравнений.
Пример:
Координаты любой точки окружности является решением уравнения а координаты любой точки параболы — решением уравнения Значит, координаты любой точки пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму. Используя рисунок, находим приближённые значения координатной точки пересечения графиков: А(-2,2; 4,5), В(0;5), С(2,2; 4,5), Д(4;-3).
Следовательно, система имеет четыре решения. Подставив найденные значения в уравнения системы, можно убедиться, что В(0;5), Д(4;-3) являются точками, А(-2,2; 4,5) и С(2,2; 4,5) — приближенными.
Слушают учителя, выполняют задание
Физминутка
Закрепление новых знаний.
является ли решением системы:
пара чисел: а) (-2;1), (1; -2)
Решите графически систему уравнений:
3) Работа в парах:
с помощью графика решите систему уравнений:
Слушают учителя, выполняют задание.
Итог урока. Рефлексия.
-Что называется решением системы уравнений с двумя переменными?
-С каким способом решение систем уравнений с двумя переменными вы познакомились?
-Дает ли данный способ точные результаты?
-В каком случае система уравнений не будет иметь решений?
Отвечают на вопросы, анализируют свою работу на уроке.
Домашнее задание.
Решить: № 416,417
infourok.ru
Графический способ решения систем уравнений. 9-й класс
Тип урока: урок изучения нового материала.
Цели урока:
дидактические:
- открыть совместно с учащимися новый способ решения систем уравнений;
- вывести алгоритм решения систем уравнений графическим способом;
- уметь определять сколько решений имеет система уравнений;
- учить находить решения системы уравнений графическим способом;
- повторить построение графиков элементарных функций;
- создать условия для контроля (самоконтроля) учащихся:
воспитательные:
- воспитание ответственного отношения к труду,
- аккуратности ведения записей.
Ход урока.
I. Организационный момент.
II. Повторение. Подготовка к изучению нового материала. (Приложение 1)
- Что такое функция? (слайд 3-11)
- Что называется графиком функции?
- Какие виды функций вы знаете?
- Какой формулой задается линейная функция? Что является графиком линейной функции?
- Какой формулой задается прямая пропорциональность? Что является ее графиком?
- Какой формулой задается обратная пропорциональность? Что является ее графиком?
- Какой формулой задается квадратичная функция? Что является ее графиком?
- Каким уравнением задается уравнение окружности?
- Что называют уравнением с двумя переменными; (слайд 12)
- Выразите переменную у через переменную х:
а) у – х² = 0
б) х + у + 2 = 0
в) 2х – у + 3 = 0
г) ху = -12 - Является ли пара чисел (1; 0) решением уравнения
а) х² +у = 1;
б) ху + 3 = х;
в) у(х +2) = 0. - Что является решением системы уравнений с двумя переменными?
- Какая из пар чисел является решением системы уравнений
а) (6; 3)
б) (- 3; — 6)
в) (2; — 1)
г) (3; 0) - Из каких уравнений можно составить систему уравнений, решением которой будет пара чисел (2; 1)
а) 2х – у = 3
б) 3х – 2у = 5
в) х² + у² = 4
г) ху = 2
III. Изучение нового материала. (слайд 16, 17)
Сегодня мы разберем один из способов решения систем уравнений. Изучение нового материала осуществляется с помощью наглядного восприятия (на слайде представлено графическое решение системы уравнений):
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство. Графики уравнений с двумя неизвестными весьма разнообразны.
Вопросы по данному слайду:
- Что является графиком уравнения x² + y²=25?
- Что является графиком уравнения y = — x² +2x +5?
Координаты любой точки окружности будут удовлетворять уравнению x² + y²=25, координаты любой точки параболы будут удовлетворять уравнению y = — x² +2x +5.
- Координаты каких точек будут удовлетворять и первому и второму уравнениям?
- Сколько точек пересечения у данных графиков?
- Сколько решений имеет данная система?
- Назвать эти решения?
- Что нужно сделать, чтобы графически решить систему уравнений с двумя переменными?
Предлагается слайд, на котором приведен алгоритм графического способа решения систем уравнений с двумя неизвестными.
Графический способ применим к решению любой системы, но с помощью графиков уравнений можно приближенно находить решения системы. Лишь некоторые найденные решения системы могут оказаться точными. В этом можно убедиться, подставив их координаты в уравнения системы.
IV. Первичное осмысление и применение изученного способа решения систем уравнений.
1. Решить графически систему уравнений (слайд 18)
Постановка наводящих вопросов:
- Что является графиком уравнения ху = 3?
- Что является графиком уравнения 3х – у =0?
- Сколько точек пересечения имеют данные графики?
- Сколько решений имеет данная система уравнений?
- Назвать решения данной системы уравнений?
2. Запишите систему, определяемую этими уравнениями и ее решение. (слайд 19)
Постановка наводящих вопросов:
- Запишите систему, определяемую данными уравнениями?
- Сколько точек пересечения имеют данные графики?
- Сколько решений имеет данная система уравнений?
- Назвать решения данной системы уравнений?
3. Выполнение задание из ГИА (слайд 20).
4. Решить графически систему уравнений (слайд 21)
а) б)
Задание выполняется учащимися в тетрадях. Решение проверяется.
5. Тест. (Приложение 2)
V. Итоги урока.
- Что называется решением системы уравнений с двумя переменными?
- С каким способом решения систем уравнений с двумя переменными вы познакомились?
- В чём его суть?
- Дает ли данный способ точные результаты?
- В каком случае система уравнений не будет иметь решений?
VI . Домашнее задание.
П. 12, №№ 236(а), 237
urok.1sept.ru