Решение системы линейных уравнений методом сложения: алгоритм, примеры
Алгоритм решения системы линейных уравнений методом сложения
- Умножить обе части одного или обоих уравнений так, чтобы коэффициенты при одной из переменных стали противоположными (или равными) числами.
- Сложить (или отнять) уравнения, чтобы избавиться от одной из переменных.
- Решить второе уравнение относительно выраженной переменной.
- Решить полученное уравнение с одной переменной.
- Найти вторую переменную.
- Записать ответ в виде упорядоченной пары найденных значений переменных.
Например: $ {\left\{ \begin{array}{c} 3x+y = 5 \\ x+2y = 5 \end{array} \right.}$
Шаг 1
Умножаем первое уравнение на 2
${\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right.}$
Шаг 2
Отнимаем от первого уравнения второе:
5x = 5
Шаг 3
Находим x:
x = 1
Шаг 4
Находим y из первого уравнения:
y = 5-3x = 2
Шаг 5
Ответ: (1;2)
$$ {\left\{ \begin{array}{c} 3x+y = 5 | \times 2 \\ x+2y = 5 \end{array} \right. } \Rightarrow (-) {\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x = 5 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 5-3x = 2 \end{array} \right.} $$
} \Rightarrow (-) {\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x = 5 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 5-3x = 2 \end{array} \right.} $$
Ответ: (1;2)
Примеры
Пример 1. Решите систему уравнений методом сложения:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 | \times 2 \\ 2x-3y = 4 | \times 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 10x-8y = 6 \\ 10x-15y = 20 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7y = -14 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = \frac{3y+4}{2} = -1 \\ y=-2 \end{array} \right.} $
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 | \times 3 \\ 3x-4y = 0 | \times 4 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 12x-9y = 21 \\ 12x-16y = 0 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7y = 21 \\ x = \frac{4}{3} y \end{array} \right.
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 | \times 2 \\ 2a+3b = -1 | \times 5 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 10a-8b = 18 \\ 10a+15b = -5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} -23b = 23 \\ a = \frac{-3b-1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $
Ответ: (1;-1)
$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 | \times (-2) \end{array} \right.} \Rightarrow (+) {\left\{ \begin{array}{c} 7a+4b = 5 \\ -6a-4b = -2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = \frac{1-3a}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -4 \end{array} \right.}$
Ответ: (3;-4)
Пример 2. Найдите решение системы уравнений:
$$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right. } \Rightarrow (+) {\left\{ \begin{array}{c} \frac{x}{4} -y = 7 \\ 6x+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 6 \frac{1}{4} x = 25 \\ y = 18-6x\end{array} \right.} \Rightarrow $$
} \Rightarrow (+) {\left\{ \begin{array}{c} \frac{x}{4} -y = 7 \\ 6x+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 6 \frac{1}{4} x = 25 \\ y = 18-6x\end{array} \right.} \Rightarrow $$
$$\Rightarrow {\left\{ \begin{array}{c} x = 25: \frac{25}{4} = 25 \cdot \frac{4}{25} = 4 \\ y = 18-6 \cdot 4 = -6 \end{array} \right.} $$
Ответ: (4;-6)
$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 2 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 3 \end{array} \right.}\Rightarrow (-) {\left\{ \begin{array}{c} x+ \frac{2}{3} y = \frac{1}{3} \\ x+ \frac{3}{2} y = — \frac{1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} \left( \frac{2}{3}- \frac{3}{2}\right) y = \frac{1}{3}+ \frac{1}{2} \\ x = \frac{1}{3}- \frac{2}{3} y\end{array} \right.} \Rightarrow$
$$ \Rightarrow {\left\{ \begin{array}{c} y = \frac{5}{6}:\left(-\frac{5}{6}\right) = -1 \\ x = \frac{1}{3}+ \frac{2}{3} = 1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right. } $$
} $$
Ответ: (1;-1)
$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $
$$ \Rightarrow (+) {\left\{ \begin{array}{c} 10x-8y = -14 \\ x+8y = 25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 11x = 11 \\ y = \frac{25-x}{8} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.}$$
Ответ: (1;3)
$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 | \times 7 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 7x+22y = 57 \\ 7x-21y = 14 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$
} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$
Ответ: (5;1)
Пример 3*. Найдите решение системы уравнений:
$ {\left\{ \begin{array}{c} \frac{2}{x} + \frac{3}{y} = 1 \\ \frac{3}{x} — \frac{5}{y} = 11 \end{array} \right.} $
Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{x} \\ b = \frac{1}{y} \end{array} \right.} $
Перепишем систему и найдём решение для новых переменных:
$$ {\left\{ \begin{array}{c}2a+3b = 1| \times 3 \\ 3a-5b = 11 | \times 2 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 6a+9b = 3 \\ 6a-10b = 22 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 19b = -19 \\ a = \frac{1-3b}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 2 \\ b = -1 \end{array} \right.} $$
Исходные переменные:
$$ {\left\{ \begin{array}{c} x = \frac{1}{a} = \frac{1}{2} \\ y = \frac{1}{b} = -1 \end{array} \right. } $$
} $$
Ответ:$ \left(\frac{1}{2} ;-1 \right)$
Способ решения системы уравнений методом сложения. Решение сложных систем уравнений
Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
Пример №1:
Решим методом подстановки
Решение системы уравнений методом подстановки 2x+5y=1 (1 уравнение)x-10y=3 (2 уравнение)
1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y
2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1
3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2
Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1
Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)
Пример №2:
Решим методом почленного сложения (вычитания).
Решение системы уравнений методом сложения3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)
1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
5y=32 | :5
y=6,4
3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6
Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно .
Метод алгебраического сложения
Решить систему уравнений с двумя неизвестными можно различными способами — графическим методом или методом замены переменной.
В этом уроке познакомимся с ещё одним способом решения систем, который Вам наверняка понравится — это способ алгебраического сложения.
А откуда вообще взялась идея — что-то складывать в системах? При решении систем главной проблемой является наличие двух переменных, ведь решать уравнения с двумя переменными мы не умеем. Значит, надо каким-либо законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.
Одно из таких свойств звучит так: сумма противоположных чисел равна нулю. Значит, если при одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и нам удастся исключить эту переменную из уравнения. Понятно, что складывать только слагаемые с нужной нам переменной мы не имеем право. Складывать надо уравнения целиком, т.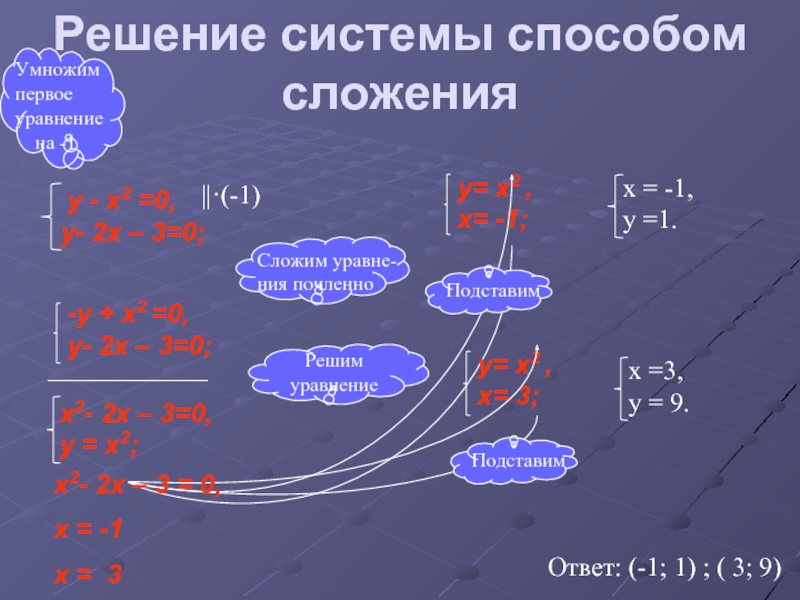
Мы видим, что в первом уравнении есть переменная у, а во втором противоположное число -у. Значит, это уравнение можно решить методом сложения.
Одно из уравнений оставляют в том виде, каком оно есть. Любое, какое Вам больше нравится.
А вот второе уравнение будет получено сложением этих двух уравнений почленно. Т.е. 3х сложим с 2х, у сложим с -у, 8 сложим с 7.
Получим систему уравнений
Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = -1.
Ответ: (3; — 1).
Образец оформления:
Решить методом алгебраического сложения систему уравнений
В данной системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.
Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.
Тогда первое уравнение примет вид:
Теперь видим, что при переменной х есть противоположные коэффициенты. Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.
Теперь у нас система уравнений:
Легко находим из второго уравнения у = 1, а затем из первого уравнения х = 4.
Образец оформления:
Давайте подведём итоги:
Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, нам теперь известны три основных метода решения таких систем: графический, метод замены переменной и метод сложения. Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.
Список использованной литературы:
- Мордкович А.
 Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007. - Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
- Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.
Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.
Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.
Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным.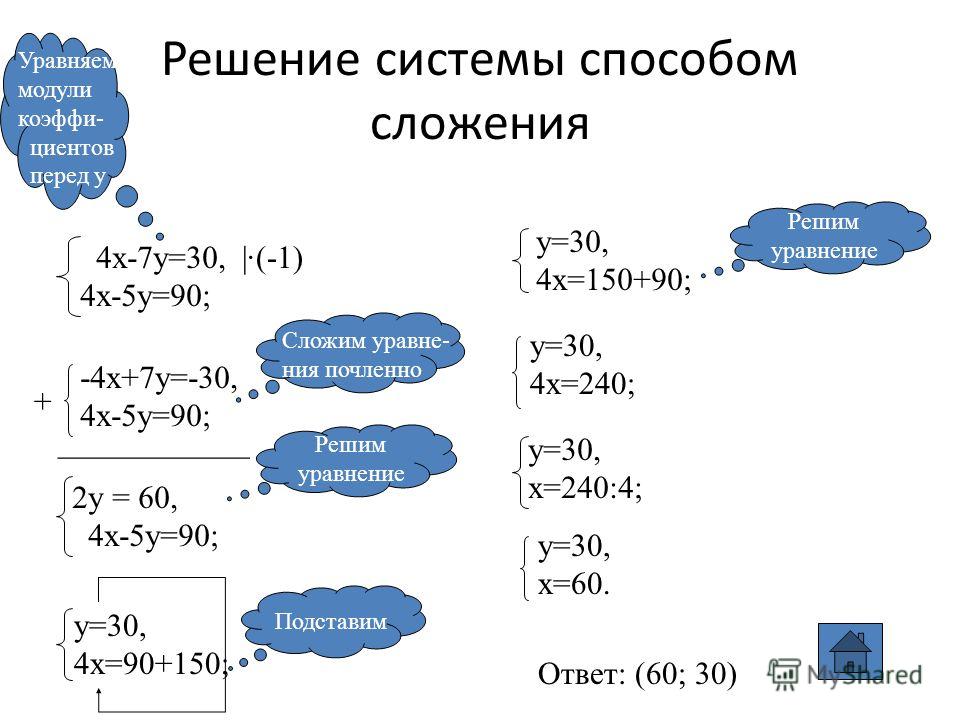 Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.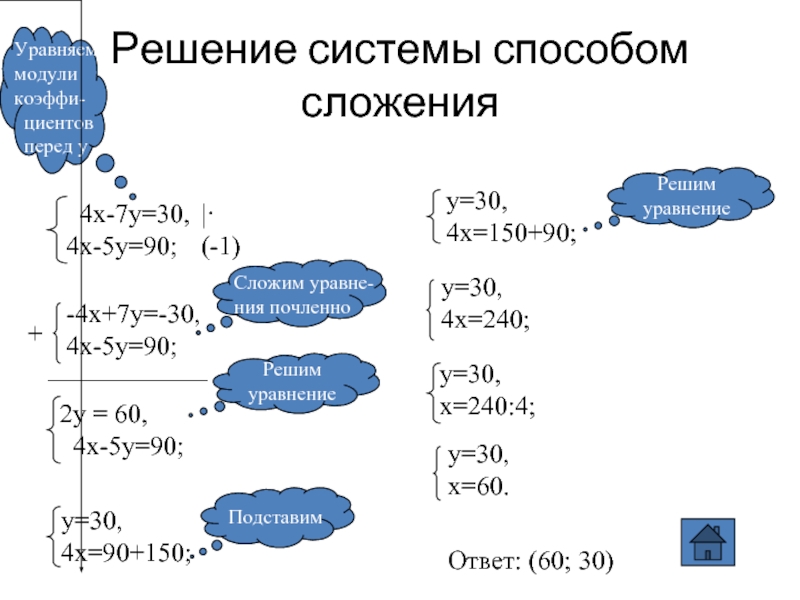
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y — (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны. Эта пара чисел и есть решение системы уравнений. Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны, то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х, на втором у.
Ответ: (4; 3)
Пример 2 . Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
4х + 3(-2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Ответ: (1/2; — 2)
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение систем линейных уравнений способом сложения
Вопросы занятия:
· показать еще один способ решения систем линейных уравнений – способ сложения.
Материал урока
Мы
с вами уже познакомились с двумя способами решения систем линейных уравнений с
двумя переменными, а именно, с графическим способом и способом подстановки.
На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.
Рассмотрим следующую систему
Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений
Приведём подобные слагаемые в обеих частях получившегося уравнения
Видим, что получили уравнение с одной переменной.
Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.
Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.
Пример.
Пример.
Пример.
Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:
1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) сложить почленно левые и правые части уравнений системы;
3) решить получившееся уравнение с одной переменной;
4)
найти
соответствующее значение второй переменной.
При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.
Решение систем линейных уравнений методом подстановки онлайн
Самым простым методом решения системы линейных алгебраических уравнений (СЛУ) является метод подстановкиили метод исключения. Рассмотрим его более подробно, предположим, нам дана СЛУ вида:
a11x1a12x2b1a21x1a22x2b2
Требуется её решить, т.е. найти такие значения переменных x1, x2, чтобы при подстановке их в исходную СЛУ, последняя обращалась в верное тождество. Метод подстановки заключается в следующем:
1. Решим первое уравнение относительно переменной x1:
x11a11b1a12x2a21x1a22x2b2
2. Подставим полученное для переменной
x1
выражение во второе уравнение системы:
Подставим полученное для переменной
x1
выражение во второе уравнение системы:
x11a11b1a12x2a211a11b1a12x2a22x2b2
3. Упростим второе уравнение системы:
x11a11b1a12x2a22a12a21a11x2b2a21b1a11
4. Решим второе уравнение системы относительно x2:
x11a11b1a12x2x2b2a11b1a21a11a22a12a21
5. Подставим полученное для переменной x2 выражение в первое уравнение системы:
x11a11b1a12b2a11b1a21a11a22a12a21x2b2a11b1a21a11a22a12a21
6. Упростим первое уравнение системы:
x1b1a22b2a12a11a22a12a21x2b2a11b1a21a11a22a12a21
Данный онлайн калькулятор
решает СЛУ методом методом подстановки
с описанием пошагового хода решения на русском языке. Коэффициенты СЛУ могут быть не только числами или дробями, но также и параметрами. Для работы калькулятора необходимо ввести уравнения и выбрать переменные СЛУ, которые необходимо найти.
Коэффициенты СЛУ могут быть не только числами или дробями, но также и параметрами. Для работы калькулятора необходимо ввести уравнения и выбрать переменные СЛУ, которые необходимо найти.
Решения систем линейных уравнений. Метод подстановки и метод сложения. 7 класс
Решения системлинейных уравнений.
Метод подстановки и
метод сложения
7 класс.
Основными методами решения
систем уравнений считают:
Метод подстановки
Метод алгебраического сложения
Графический метод решения систем
уравнений
Повторим решение систем уравнений
методом подстановки.
Этапы решения
Пример
1. С помощью какого-либо
из уравнений выразить
одно неизвестное через
другое.
2. Подставить найденное
выражение в другое
уравнение системы: решить
получившееся уравнение с
одним неизвестным.
2 x y 4,
x 3 y 9;
Из первого уравнения
y = 2x − 4
x + 3(2x − 4) = 9;
x + 6x −12 = 9;
7x = 21;
x = 3.

Далее :
Этапы решения
3. Подставить найденное
значение одного
неизвестного в выражение
для другого неизвестного.
4. Записать ответ.
Пример
x = 3, тогда
y = 2x − 4 = 2∙3−4 = 2.
Ответ: (3; 2)
Решить систему уравнений способом подстановки
3x 2 y 27,
x 5 y 35.
Решение. 1) Из второго уравнения x = 35 − 5y
подставим в первое уравнение;
2) Решим его ,при этом второе уравнение пока
переписываем.
3) Теперь у подставим во второе уравнение .
Ответ: (5; 6)
Решить систему способом подстановки
Если же нужно решить систему у которой
Коэффициенты, например при х одинаковые.
2 x 3 y 10,
2 x 5 y 6;
1) Из первого уравнения
2) 2x = 10 + 3y подставим во второе уравнение:
10 + 3y + 5y = −6;
8y = −16; y = −2.
3) y = −2, 2x = 10 + 3∙(−2) =
= 4;
x = 2.
Ответ: (2; −2) Такие системы можно решить
другим способом –способом сложения.
Метод алгебраического сложения
Пример №1
Решить систему уравнений
7 x 2 y 27,
5 x 2 y 33.

Предположим, что x и y − это такие числа, при которых
оба равенства этой системы верны, т. е. (x ; y) − решение
данной системы.
Сложим эти равенства. Тогда снова получим верное
равенство, так как к равным числам прибавляются
равные числа:
7 x 2 y 27,
5 x 2 y 33.
12х = 60,
откуда х = 5.
Подставим х = 5 в одно из уравнений данной
системы, например в первое:
7∙5− 2y = 27,
35 − 2y = 27,
− 2y = − 8, y= 4.
Итак, если данная система имеет решение, то
этим решением может быть только пара чисел:
x = 5, y = 4.
Ответ: (5; 4)
5 x 3 y 29,
Решить систему уравнений
5 x 4 y 8.
Пример №2
Видим что коэффициенты при х одинаковые . Можно умножить
одно из них на (-1) , а можно вычесть из первого уравнения второе:
5 x 3 y 29,
5 x 4 y 8.
7 y 21,
откуда y = 3.
Подставим y = 3 в первое уравнение системы:
5x + 3∙3 = 29, 5х +9 = 29,
Ответ: (4; 3)
5х = 20, х = 4.

Рассмотренный способ решения систем
уравнений называется способом
алгебраического сложения.
Для исключения одного из неизвестных
нужно выполнить сложение или вычитание
левых и правых частей уравнений системы.
Способ алгебраического сложения оказывается
удобным для решения системы в том случае,
когда у обоих линейных уравнений
коэффициенты при каком-нибудь неизвестном
одинаковы или отличаются только знаком.
Метод алгебраического сложения
Этапы решения
1. Сложить почленно уравнения
системы, предварительно
умножив каждое из них на
подходящее число так, чтобы
после этого получилось одно
уравнение с одним неизвестным.
Пример
4 x 5 y 19 4
5
7
x
4
y
5
16 x 20 y 76
35x 20 y 25
51x = 51
2. Найти корень этого уравнения,
то есть найти значение одного из
неизвестных системы.
x=1
Метод алгебраического сложения
Этапы решения
3.
 Подставить найденное
Подставить найденноезначение одного из неизвестных
в любое из уравнений системы:
в результате снова получится
уравнение с одним неизвестным.
4. Решить это уравнение,
то есть найти значение второго
неизвестного.
5. Записать ответ
Пример
4 x 5 y 19
7 x 4 y 5
Подстановка в
первое уравнение даёт:
4∙1 + 5y = 19
5y = 15, y = 3
Ответ: ( 1; 3)
13. Пример №3. Если коэффициенты разные ,то можно их уравнять умножением всего уравнения на число .Первое умножаем на 3 ,второе на
(-2) ,чтобы получить противоположные коэффициенты .14. Задание на дом.
«Решение систем линейных уравнений способом сложения»
Цель:
1. Научить решать системы уравнений способом сложения;
2. Отработать алгоритм решения систем уравнений методом подстановки и сложения;
3. Воспитание внимания, точности, логики рассуждения.
Оборудование : учебник Ю. Н. Макарычев, Н.Г.
Миндюк, Алгебра-7 класс, проверочный материал.
Н. Макарычев, Н.Г.
Миндюк, Алгебра-7 класс, проверочный материал.
Ход урока
I. Организационный момент:
Сегодня на уроке мы должны научиться решать системы уравнений способом сложения.
II. Устный счет:
- Дано уравнение 4x-3y=-2. Укажите какое-либо решение (пару чисел (x;y)) этого уравнения.
- Выразите переменную y через x , если 3x-0.5y=1.
- Решите систему уравнений
- Является ли пара чисел (-2; -1) решением системы уравнений
- Четыре медвежонка тяжелее медведицы на 30 кг, а два таких медвежонка легче медведицы на 80 кг. Найдите массу медведицы.
III. Объяснение нового материала.
Составим систему уравнений для задачи с медвежатами. Пусть масса медведицы х кг, а одного медвежонка у кг.
Решим данную систему способом подстановки, при этом ответим на вопросы:
Метод подстановки
- Правильно ли выразили одно неизвестное через другое в одном из уравнений?
- Правильно ли вы подставили полученное выражение в другое уравнение?
- Правильно ли вы решили уравнение с одной неизвестной?
- Правильно ли вы подставили найденное значение для вычисления значения другой неизвестной?
В результате получаем: х=190, у=55.
А теперь подумаем, как решить эту систему методом сложения?
Умножить одно из уравнений системы или каждое из них на какое-либо число, чтобы коэффициенты при одной из переменных стали противоположными.
2у=110
у=55, а х=80+2*55 , х=190.
Какие можно поставить вопросы к методу сложения?
Метод сложения
- Каковы коэффициенты при х и y?
- При какой неизвестной вы делали коэффициенты противоположными?
- Для какого уравнения требуется дополнительный множитель, и какой именно?
- Все ли члены выбранного уравнения вы умножили на этот множитель?
- Правильно ли вы выполнили сложение левых и правых частей уравнений в полученной системе?
- Правильно ли вы решили уравнение с одной неизвестной?
- В какое уравнение вы подставили полученное значение неизвестной?
- Правильно ли вычислено значение другой неизвестной?
Подумайте, а можно ли решить данную систему графически?
Если да, то дома оформить решение графически.
IV. Закрепление изученного материала.
Решите систему уравнений методом сложения.
а)3
19у=76
у=4, 4х+3*4=6
4х=6-12
х=-1,5 Ответ: (-1,5; 4)
Закончите решение системы:
Ответ: (2;-3)
б)
Ответ: (13;-6).
Работа с учебником. Глава VI,§ 16 п 43 стр 203, алгоритм стр205- прочитать.
Выполнить у доски (парами) № 1147 (а;б)
а)Ответ:(2;1)
б) Ответ: (-8;-4).
Самостоятельная работа по учебнику: № 1147 (в;г)
в)
г)
Ответ: в) (60;30), г) (2; -1/4).
V. Домашняя работа:
выполнить графически систему уравнений, если сможете, рассмотреть примеры 1-3 учебника, решить №1148 (а), повторить №1162.
VI. Познакомимся с контрольным листом и домашней недельной проверочной работой.
Лист контроля
- Какое уравнение называется линейным уравнением с двумя неизвестными?
- Что значит решить линейное уравнение с двумя неизвестными?
- Что называется решением линейного уравнения с двумя неизвестными? Как записывается это решение?
- Что является графиком линейного уравнения с двумя неизвестными?
- Что называется системой двух линейных уравнений с двумя неизвестными?
- Что называется решение системы двух линейных уравнений с двумя неизвестными?
- Что значит решить систему двух линейных уравнений с двумя неизвестными?
- Какими методами можно решить систему двух линейных уравнений с двумя неизвестными? Каков алгоритм решения каждым методом?
- Как решается одно линейное уравнение с двумя неизвестными?
- Сколько решений имеет линейное уравнение с двумя неизвестными?
Как записывается общее решение линейного уравнения с двумя неизвестными?
Практикум
Решить системы уравнений способом сложения онлайн.
 Способ сложения в решении систем уравнений
Способ сложения в решении систем уравнений Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
Пример №1:
Решим методом подстановки
Решение системы уравнений методом подстановки2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)
1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y
2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1
3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2
Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1
Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)
Пример №2:
Решим методом почленного сложения (вычитания).
 Решение системы уравнений методом сложения
Решение системы уравнений методом сложения3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)
1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
5y=32 | :5
y=6,4
3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6
Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.
Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y — (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны. Эта пара чисел и есть решение системы уравнений. Каждая пара значений неизвестных, которая одновременно удовлетворяет обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны, то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х, на втором у.
Ответ: (4; 3)
Пример 2 . Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
4х + 3(-2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Ответ: (1/2; — 2)
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612. blogspot.ru/2011/06/blog-post_25.html
blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
На этом уроке мы продолжим изучение метод решения систем уравнений, а именно: метода алгебраического сложения. Вначале рассмотрим применение этого метода на примере линейных уравнений и его суть. Также вспомним, как уравнивать коэффициенты в уравнениях. И решим ряд задач на применение этого метода.
Тема: Системы уравнений
Урок: Метод алгебраического сложения
1. Метод алгебраического сложения на примере линейных системРассмотрим метод алгебраического сложения на примере линейных систем.
Пример 1. Решить систему
Если мы сложим эти два уравнения, то y взаимно уничтожатся, и останется уравнение относительно x.
Если же вычтем из первого уравнения второе, взаимно уничтожатся x, и мы получим уравнение относительно y. В этом и заключается смысл метода алгебраического сложения.
Мы решили систему и вспомнили метод алгебраического сложения. Повторим его суть: мы можем складывать и вычитать уравнения, но при этом необходимо обеспечить, чтобы получилось уравнение только с одним неизвестным.
2. Метод алгебраического сложения с предварительным уравниванием коэффициентовПример 2. Решить систему
Член присутствует в обоих уравнениях, поэтому удобен метод алгебраического сложения. Вычтем из первого уравнения второе.
Ответ: (2; -1).
Таким образом, проанализировав систему уравнений, можно увидеть, что она удобна для метода алгебраического сложения, и применить его.
Рассмотрим еще одну линейную систему.
3. Решение нелинейных системПример 3. Решить систему
Мы хотим избавиться от y, но в двух уравнениях коэффициенты при y разные. Уравняем их, для этого умножим первое уравнение на 3, второе — на 4.
Уравняем их, для этого умножим первое уравнение на 3, второе — на 4.
Пример 4. Решить систему
Уравняем коэффициенты при x
Можно сделать иначе — уравнять коэффициенты при y.
Мы решили систему, дважды применив метод алгебраического сложения.
Метод алгебраического сложения применим и при решении нелинейных систем.
Пример 5. Решить систему
Сложим эти уравнения, и мы избавимся от y.
Эту же систему можно решить, дважды применив метод алгебраического сложения. Сложим и вычтем из одного уравнения другое.
Пример 6. Решить систему
Ответ:
Пример 7. Решить систему
Методом алгебраического сложения избавимся от члена xy. Умножим первое уравнение на .
Первое уравнение остается без изменений, вместо второго записываем алгебраическую сумму.
Ответ:
Пример 8. Решить систему
Умножим второе уравнение на 2, чтобы выделить полный квадрат.
Наша задача свелась к решению четырех простейших систем.
Мы рассмотрели метод алгебраического сложения на примере решения линейных и нелинейных систем. На следующем уроке рассмотрим метод введения новых переменных.
1. Мордкович А. Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А. Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с. : ил.
: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Раздел College. ru по математике.
2. Интернет-проект «Задачи» .
3. Образовательный портал «РЕШУ ЕГЭ» .
1. Мордкович А. Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 125 — 127.
Нужно скачать поурочный план по теме » Метод алгебраического сложения ?
Решение путем сложения / исключения
Системы
линейных уравнений:
Решение сложением /
Ликвидация (стр.
5 из 7)
Разделы: Определения, Решение с помощью построения графиков, Подстановка,
Исключение / добавление, исключение по Гауссу.
Метод сложения решения систем уравнений также называют методом исключения.Этот метод похож на метод, который вы, вероятно, изучили для решения простых уравнений.
Если бы у вас было уравнение « x + 6 = 11», вы бы написали «–6» под каждой стороной уравнения, а затем «сложили», чтобы получить « x = 5» в качестве решение.
Вы проделаете нечто подобное с методом сложения.
- Решите следующую систему, используя сложение.
Обратите внимание, что если я добавлю, и аннулируется.Я нарисую полоску «равно» под системой, и складываем:
Теперь я могу разделить решить для x = 5, а затем решить, используя любое из исходных уравнений, чтобы найти значение y . Первое уравнение имеет меньшие числа, поэтому я верну его обратно:
2 (5) + y = 9
10 + и = 9
y = –1
Тогда решение
равно ( x , y ) = (5, –1) .
Неважно, какое уравнение вы используете для обратной обработки; в любом случае вы получите один и тот же ответ. Если Я бы воспользовался вторым уравнением и получил бы:
… это тот же результат как прежде.
- Решите следующие проблемы система с использованием сложения.
Обратите внимание, что термины x отменили бы, если бы только у них были противоположные знаки.Я могу создать это отмены путем умножения любого из уравнений на –1, а затем добавляю как обычно. Неважно, какое уравнение я выберу, при условии, что я буду осторожен, чтобы умножить –1 на все уравнение. (Это означает, что обе стороны «равно» знак!)
умножу второй уравнение.
«–1 R 2 »
Обозначение над стрелкой означает, что я умножил строку 2 на –1. Теперь я могу решить уравнение «–5 y = –25», чтобы получить y = 5. Обратное решение в
первое уравнение, я получаю:
Теперь я могу решить уравнение «–5 y = –25», чтобы получить y = 5. Обратное решение в
первое уравнение, я получаю:
x —
2 (5) = –9
x — 10 = –9
x = 1
Тогда решение равно ( x , y ) = (1, 5) .
Очень распространенное искушение — записать решение в виде «(первое число, которое я нашел, второе номер, который я нашел) «. Однако иногда, как в этом случае, вы найдете значение y сначала, а затем значение x во-вторых, и, конечно же, в пунктах значение x на первом месте. Так что просто будьте осторожны и пишите координаты для ваших решений. правильно.авторское право © Элизабет Стапель 2003-2011 Все права защищены
- Решите следующие проблемы
система с использованием сложения.

Здесь ничего не отменяется, но Я могу умножить, чтобы создать отмену. Я могу умножить первое уравнение на 4, и это создаст условия и . отменить.
Решив это, я получу, что x = 2. Я воспользуюсь первым уравнение для обратного решения, потому что коэффициенты меньше.
2 (2) — y = 9
4 — y = 9
— y = 5
y = –5
Решение: ( x , y ) = (2, –5) .
- Решите следующие проблемы. система с использованием сложения.
Хм … ничего не отменяет.
Но я могу умножить, чтобы создать отмену. В этом случае ни одна из переменных
это очевидный выбор для отмены. Я могу умножить, чтобы преобразовать x -термов
до 12 x ‘s
или условия y к 24 y ‘s. Так как я ленив и 12 меньше 24,
Я произведу умножение, чтобы отменить условия x .
(Я бы получил тот же ответ в конце, если бы установил y -terms
отменить. Дело не в том, что я делаю это «правильно»;
это был только мой выбор. Вы могли бы сделать другой выбор, и это
быть столь же правильным.)
Так как я ленив и 12 меньше 24,
Я произведу умножение, чтобы отменить условия x .
(Я бы получил тот же ответ в конце, если бы установил y -terms
отменить. Дело не в том, что я делаю это «правильно»;
это был только мой выбор. Вы могли бы сделать другой выбор, и это
быть столь же правильным.)
умножу первый ряд по 3 и второй ряд по 4; тогда я добавлю и решу.
Решая, я получаю, что y = 5. Ни одно из уравнений выглядит особенно лучше, чем другой для обратного решения, поэтому я переверну монету и используйте первое уравнение.
Не забудьте поставить координату x . сначала в решении я получаю:
Обычно при решении
«по сложению», вам нужно будет создать отмену. Предупреждение:
Самая распространенная ошибка — забыть умножить на всем протяжении
уравнение, умноженное на обе стороны знака «равно». Быть
осторожно с этим.
Предупреждение:
Самая распространенная ошибка — забыть умножить на всем протяжении
уравнение, умноженное на обе стороны знака «равно». Быть
осторожно с этим.
- Решите следующие проблемы с помощью сложения.
Думаю умножу второе уравнение на 2; это, по крайней мере, избавит от десятичного знака.
Ой! Этот результат не истинный! Итак, это противоречивая система (две параллельные линии) без каких-либо решение (без точки пересечения).
- Решите следующие проблемы. с помощью сложения.
думаю будет проще всего отменить условия и , поэтому я умножу вторую строку на –3.
Ну да, но …? я уже знал, что ноль равен нулю. Итак, это зависимая система, и, решая для « y =» решение это:
(Ваш текст может отформатировать
ответьте как «( s ,
4 с — 2) «,
или что-то вроде того. )
)
Запомните разницу: глупый ответ (например, «0 = –2 «в предыдущем проблема) означает противоречивую систему без решения; бесполезный ответ (например, «0 = 0 «выше) означает зависимая система, в которой вся линия является решением.
В некоторых книгах используется только « x »
и « y »
для своих переменных, но многие используют дополнительные переменные.Когда ты пишешь
решение для точки x , y ,
вы знаете, что координата x идет первым, а координата y идет вторым. Когда вы имеете дело с другими переменными, предполагайте (если только
явно указано иное), что эти переменные записываются в алфавитном порядке
приказ. Например, если переменные в данной системе равны a и b ,
точка решения будет ( a , b ); это не будет
быть ( b , a ). Если иначе
указано, переменные записываются в алфавитном порядке.
Если иначе
указано, переменные записываются в алфавитном порядке.
<< Предыдущий Наверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета.«Системы линейных уравнений: решение сложением / исключением». Пурпурная математика . Доступна с |
Решение уравнений с помощью метода сложения
Существует два способа решения уравнения: метод сложения и метод подстановки. Здесь мы рассмотрим метод сложения. Метод сложения решения уравнений — это простой и легкий метод, используемый в алгебре. Его также называют методом исключения .
Метод сложения решения уравнений — это простой и легкий метод, используемый в алгебре. Его также называют методом исключения .
Понимание частей уравнения
Прежде чем мы научимся использовать метод сложения, давайте разберем части уравнения.
Это наш пример:
3x + 4y = 10
Числа 3 и 4 — это коэффициенты, которые умножаются на переменные.
x и y — это переменные, которые могут иметь разные значения в зависимости от результата.
Решение с использованием метода сложения
Как бы вы решили это уравнение? В идеале вы могли бы объединить это уравнение с другим, скажем, 4x + 2y = 20 , и решить его. Но поскольку оба уравнения имеют две разные переменные, невозможно определить значения переменных. Вам нужно будет утомительно угадать значение x и y , нанести его на график и найти точку пересечения двух линий, которая затем даст вам координаты x и y . Даже в этом случае, если вы проведете линию или нанесете точки неправильно, вы не получите правильных значений x и y .
Даже в этом случае, если вы проведете линию или нанесете точки неправильно, вы не получите правильных значений x и y .
Чтобы избавить нас от хлопот, связанных с этим процессом, мы используем метод сложения для решения уравнений с одной или двумя переменными.
Метод сложения состоит из ряда шагов, которые необходимо выполнить, чтобы правильно решить уравнение.
Шаг 1Поместите два заданных уравнения друг на друга и пометьте их.
Сначала вам нужно определить, что это за два уравнения. После этого нам нужно положить их друг на друга, как в стандартной задаче сложения. Мы будем использовать эти два уравнения в качестве примера:
2 x + 4 y = 10 уравнение (1)
4 x — 2 y = 15 уравнение (2)
Шаг 2Выберите переменную, которую нужно удалить.
Теперь нам нужно выбрать переменную, которую нужно удалить из уравнения. Выберем переменную y .
Выберем переменную y .
Выберите уравнение для преобразования коэффициента переменной.
Теперь нам нужно выбрать уравнение, в котором мы будем изменять коэффициент выбранной переменной. В зависимости от данного уравнения вы можете выбрать одно или оба. Перейдем к уравнению (2).
Шаг 4Измените коэффициент уравнения.
После выбора уравнения удалите переменную, чтобы изменить коэффициент на противоположный.Мы выбрали уравнение (2). Поскольку коэффициент на уже отрицательный, нам не нужно преобразовывать знак. Мы просто умножим обе части уравнения на 2. В итоге мы получим новое уравнение (3).
(4 x -2 y ) x 2 = 15 x 2
8 x — 4 y = 30 Уравнение (3)
Шаг 5Сложите два уравнения и подставьте результат в исходное уравнение.
После того, как новые уравнения сформированы, нам нужно добавить два уравнения и удалить выбранную переменную. Это показано ниже:
Это показано ниже:
2 x + 4 y = 10 Уравнение (1)
8 x — 4 y = 30 Уравнение (3)
Складываем уравнение (1) и (3)
10 х = 40
Разделите на 10 с обеих сторон, чтобы выделить и решить для x .
х = 4
Теперь, когда мы нашли значение x , нам нужно подставить его в исходное уравнение (1)
2 (4) + 4 y = 10
8 + 4 y = 10
Вычтем 8 с обеих сторон
4 y = 2
Разделим обе стороны на 4
y = 0.5
Теперь у нас есть значения двух переменных x = 4 и y = 0,5. Мы закончили решение этого уравнения.
Заключение Вот и все! Простой и эффективный способ изучить метод сложения или исключения для решения уравнений. Не волнуйтесь, неважно, какие два уравнения вы получите. Выполните указанные выше действия, и у вас не будет проблем с решением любого вопроса с уравнением с двумя переменными, который вам предложат.
Оставьте первый комментарий ниже.
Решение одновременных уравнений: метод подстановки и метод сложения | Справочник по алгебре
Что такое одновременные уравнения и системы уравнений?
Термины одновременных уравнений и системы уравнений относятся к условиям, при которых две или более неизвестных переменных связаны друг с другом посредством равного числа уравнений.
Пример:
Для этой системы уравнений существует только одна комбинация значений для x и y, которая удовлетворяет обоим.
Любое уравнение, рассматриваемое по отдельности, имеет бесконечное количество допустимых (x, y) решений, но вместе существует только одно. На графике это условие становится очевидным:
Каждая линия на самом деле представляет собой континуум точек, представляющих возможные пары решений x и y для каждого уравнения.
Каждое уравнение в отдельности имеет бесконечное количество упорядоченных парных (x, y) решений. Есть только одна точка, где две линейные функции x + y = 24 и 2x — y = -6 пересекаются (где одно из многих их независимых решений работает для обоих уравнений), и это где x равно значению 6 и y равно значению 18.
Есть только одна точка, где две линейные функции x + y = 24 и 2x — y = -6 пересекаются (где одно из многих их независимых решений работает для обоих уравнений), и это где x равно значению 6 и y равно значению 18.
Однако обычно построение графиков не является очень эффективным способом определения набора одновременных решений для двух или более уравнений. Это особенно непрактично для систем из трех и более переменных.
В системе с тремя переменными, например, решение будет найдено по точкам пересечения трех плоскостей в трехмерном координатном пространстве — сценарий непростой для визуализации.
Решение одновременных уравнений методом подстановки
Существует несколько алгебраических методов решения одновременных уравнений.
Возможно, самый простой для понимания — это метод замены на .
Возьмем, к примеру, нашу задачу с двумя переменными:
В методе подстановки мы манипулируем одним из уравнений таким образом, что одна переменная определяется в терминах другой:
Затем мы берем это новое определение одной переменной и заменяем его на ту же переменную в другом уравнении.
В этом случае мы берем определение y, равное 24 — x, и подставляем его вместо члена y, найденного в другом уравнении:
Теперь, когда у нас есть уравнение с одной переменной (x), мы можем решить его, используя «нормальные» алгебраические методы:
Теперь, когда x известен, мы можем подставить это значение в любое из исходных уравнений и получить значение для y.
Или, чтобы сэкономить нам немного времени, мы можем вставить это значение (6) в уравнение, которое мы только что сгенерировали, чтобы определить y через x, поскольку оно уже находится в форме для решения для y:
Применение метода подстановки к системам из трех или более переменных включает аналогичный шаблон, только с дополнительными усилиями.
Это обычно верно для любого метода решения: количество шагов, необходимых для получения решения, быстро увеличивается с каждой дополнительной переменной в системе.
Чтобы решить для трех неизвестных переменных, нам нужно как минимум три уравнения. Рассмотрим этот пример:
Поскольку первое уравнение имеет простейшие коэффициенты (1, -1 и 1 для x, y и z соответственно), кажется логичным использовать его для разработки определения одной переменной в терминах двух других.
Решите относительно x через y и z:
Теперь мы можем заменить это определение x, где x фигурирует в двух других уравнениях:
Приведение этих двух уравнений к их простейшей форме:
До сих пор наши усилия привели к сокращению системы с трех переменных в трех уравнениях до двух переменных в двух уравнениях.
Теперь мы можем снова применить технику подстановки к двум уравнениям 4y — z = 4 и -3y + 4z = 36, чтобы решить для y или z.Во-первых, я манипулирую первым уравнением, чтобы определить z через y:
Затем мы заменим это определение z на y, где мы видим z в другом уравнении:
Теперь, когда y — известное значение, мы можем подставить его в уравнение, определяющее z через y, и получить число для z:
Теперь, когда значения y и z известны, мы можем вставить их в уравнение, в котором мы определили x через y и z, чтобы получить значение x:
В заключение, мы нашли для x, y и z значения 2, 4 и 12 соответственно, которые удовлетворяют всем трем уравнениям.
Решение одновременных уравнений с использованием метода сложения
Хотя метод подстановки может быть самым простым для понимания на концептуальном уровне, нам доступны и другие методы решения.
Одним из таких методов является так называемый метод сложения , при котором уравнения складываются друг с другом с целью сокращения переменных членов.
Давайте возьмем нашу систему с двумя переменными, использованную для демонстрации метода подстановки:
Одно из наиболее часто используемых правил алгебры состоит в том, что вы можете выполнять любые арифметические операции с уравнением, если вы делаете это одинаково для обеих сторон .
Что касается сложения, это означает, что мы можем добавить любую величину, какую захотим, к обеим сторонам уравнения — при условии, что это то же самое количество — без изменения истинности уравнения.
У нас есть возможность сложить соответствующие части уравнений вместе, чтобы сформировать новое уравнение.
Поскольку каждое уравнение является выражением равенства (одна и та же величина по обе стороны от знака =), добавление левой части одного уравнения к левой части другого уравнения действительно до тех пор, пока мы добавляем два правые части уравнений вместе.
В нашем примере набора уравнений, например, мы можем добавить x + y к 2x — y, а также сложить 24 и -6 вместе, чтобы сформировать новое уравнение.
Какую пользу это дает нам? Изучите, что произойдет, когда мы сделаем это с нашим примером набора уравнений:
Поскольку верхнее уравнение содержало положительный член y, а нижнее уравнение содержало отрицательный член y, эти два члена компенсировали друг друга в процессе сложения, не оставляя члена y в сумме.
У нас осталось новое уравнение, но с единственной неизвестной переменной x! Это позволяет нам легко найти значение x:
Если у нас есть известное значение x, конечно, определение значения y — это простой вопрос подстановки (замены x числом 6) в одно из исходных уравнений.
В этом примере метод сложения уравнений хорошо сработал для создания уравнения с единственной неизвестной переменной.
Как насчет примера, когда все не так просто? Рассмотрим следующий набор уравнений:
Мы могли бы сложить эти два уравнения вместе — это вполне допустимая алгебраическая операция — но это не принесет нам пользы для получения значений для x и y:
Полученное уравнение по-прежнему содержит две неизвестные переменные, как и исходные уравнения, поэтому мы не продвинемся дальше в поиске решения.
Однако что, если бы мы могли манипулировать одним из уравнений так, чтобы получить отрицательный член, который при добавлении отменял бы соответствующий член в другом уравнении?
Тогда система сведется к одному уравнению с единственной неизвестной переменной, как в последнем (случайном) примере.
Если бы мы могли только превратить член y в нижнем уравнении в член — 2y, чтобы при сложении двух уравнений оба члена y в уравнениях сократились бы, оставив нам только член x, это принесло бы нам ближе к решению.
К счастью, сделать это несложно. Если мы умножим каждый член нижнего уравнения на -2, получится результат, который мы ищем:
Теперь мы можем добавить это новое уравнение к исходному, верхнему уравнению:
Решая относительно x, получаем значение 3:
Подставляя это новое найденное значение для x в одно из исходных уравнений, значение y легко определяется:
Использование этого метода решения в системе с тремя переменными немного сложнее.
Как и в случае подстановки, вы должны использовать этот метод, чтобы уменьшить систему из трех уравнений с тремя переменными до двух уравнений с двумя переменными, а затем применить его снова, чтобы получить одно уравнение с одной неизвестной переменной.
Для демонстрации я воспользуюсь системой уравнений с тремя переменными из раздела о заменах:
Поскольку верхнее уравнение имеет значения коэффициента, равные 1 для каждой переменной, это уравнение будет простым для обработки и использования в качестве инструмента отмены.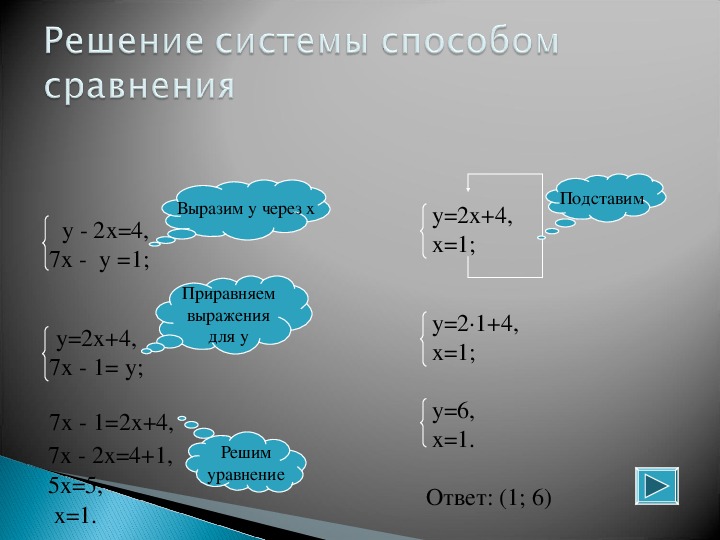
Например, если мы хотим отменить 3-кратный член из среднего уравнения, все, что нам нужно сделать, это взять верхнее уравнение, умножить каждый из его членов на -3, а затем добавить его в среднее уравнение следующим образом:
Таким же образом мы можем избавить нижнее уравнение от члена -5x: возьмите исходное верхнее уравнение, умножьте каждый из его членов на 5, затем добавьте это модифицированное уравнение к нижнему уравнению, оставив новое уравнение только с y и z сроки:
На данный момент у нас есть два уравнения с теми же двумя неизвестными переменными, y и z:
При осмотре должно быть очевидно, что член -z верхнего уравнения может быть использован для отмены члена 4z в нижнем уравнении, если только мы умножим каждый член верхнего уравнения на 4 и сложим два уравнения вместе:
Взяв новое уравнение 13y = 52 и решив относительно y (разделив обе части на 13), мы получим значение 4 для y.
Подстановка этого значения 4 вместо y в любое из уравнений с двумя переменными позволяет нам решить относительно z.
Подстановка обоих значений y и z в любое из исходных уравнений с тремя переменными позволяет нам решить относительно x.
Окончательный результат (я избавлю вас от алгебраических шагов, поскольку вы уже должны быть с ними знакомы!) Состоит в том, что x = 2, y = 4 и z = 12.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Метод исключения — бесплатная помощь по математике
Решение системы линейных уравнений: (урок 2 из 5)
Метод исключения
Метод исключения решения систем уравнений также называют методом сложения.Чтобы решить систему уравнений методом исключения, мы преобразуем систему так, чтобы одна переменная «сокращалась».
Пример 1: Решить систему уравнений методом исключения
$$ \ begin {выровнено} 3х — у & = 5 \\ х + у & = 3 \ end {выровнен} $$Решение:
В этом примере мы «отменим» член y. Для этого мы можем сложить уравнения.
Для этого мы можем сложить уравнения.
Теперь мы можем найти: $ x = 2 $
Чтобы найти y, возьмите значение x и подставьте его обратно в любое из исходных уравнения.
$$ \ begin {выровнено} \ color {красный} {x} + y & = 3 \\ \ color {красный} {2} + y & = 3 \\ у & = 1 \ end {выровнен} $$Решение: $ (x, y) = (2, 1) $.
Пример 2: Решите систему с помощью исключения
$$ \ begin {выровнено} х + 3у & = -5 \\ 4x — y & = 6 \ end {выровнен} $$Решение:
Посмотрите на коэффициенты x. Умножьте первое уравнение на -4, чтобы задать коэффициенты x для отмены.
$$ \ begin {выровнено} & х + 3у = -5 \ color {red} {\, \, \, \, \ text {умножить на -4}} \\ & \ underline {4x — y = 6} \ конец {выровнено} \\ \ begin {выровнено} & \ underline {\ left. \ begin {выровнено}
\ color {red} {- 4x} — 12y = 20 \\
\ color {красный} {4} x — y = 6
\ end {выровнен}
\правильно\}}
\ text {Добавить уравнения} \\
& -13x = 26
\ end {выровнен}
$$
\ begin {выровнено}
\ color {red} {- 4x} — 12y = 20 \\
\ color {красный} {4} x — y = 6
\ end {выровнен}
\правильно\}}
\ text {Добавить уравнения} \\
& -13x = 26
\ end {выровнен}
$$Теперь мы можем найти: $ y = -2 $
Возьмите значение и и подставьте его обратно в любое из исходных уравнений.
$$ \ begin {выровнено} х + 3у & = -5 \\ x + 3 \ cdot (\ color {red} {- 2}) & = -5 \\ х — 6 & = -5 \\ х & = 1 \ end {выровнен} $$Решение: $ (x, y) = (1, -2) $.
Пример 3: Решите систему, используя метод исключения
$$ \ begin {выровнено} 2х — 5л & = 11 \\ 3x + 2y & = 7 \ end {выровнен} $$Решение:
В этом примере мы умножим первую строку на -3 , а вторую строку на 2 ; тогда мы будем прибавлять, как и раньше.
$$ \ begin {выровнено} & 2x — 5y = 11 \ color {red} {\, \, \, \, \ text {умножить на -3}} \\ & \ underline {3x + 2y = 7 \ color {red} {\, \, \, \, \ text {умножить на 2}}} \ конец {выровнено} \\ \ begin {выровнено} & \ underline {\ left. \ begin {выровнено}
\ color {red} {- 6} + 15y = -33 \\
\ color {red} {6} x + 4y = 14
\ end {выровнен}
\правильно\}}
\ text {Добавить уравнения} \\
& 19лет = -19
\ end {выровнен}
$$
\ begin {выровнено}
\ color {red} {- 6} + 15y = -33 \\
\ color {red} {6} x + 4y = 14
\ end {выровнен}
\правильно\}}
\ text {Добавить уравнения} \\
& 19лет = -19
\ end {выровнен}
$$Теперь мы можем найти: y = -1
Подставим y = -1 обратно в первое уравнение:
$$ \ begin {выровнено} 2x — 5 \ color {синий} {y} & = 11 \\ 2x — 5 \ cdot \ color {blue} {(- 1)} & = 11 \\ 2х + 5 & = 11 \\ \ color {blue} {x} & \ color {blue} {=} \ color {blue} {3} \ end {выровнен} $$Решение: $ (x, y) = (3, -1) $.
Упражнение: Решите следующие системы, используя метод исключения
.Системы уравнений — Решения линейных уравнений — Метод, исключение, значение и переменные
Поскольку предыдущая проблема возраста представляет собой систему с двумя уравнениями и двумя неизвестными, она называется системой двух переменных. Обычно используются три метода для определения решений для системы с двумя переменными, включая графический, замену и исключение.
Построив графики линий, образованных каждым из линейных уравнений в системе, можно было бы получить решение возрастной проблемы. Координаты любой точки , в которой графики пересекаются или встречаются, представляют решение системы, потому что они должны удовлетворять обоим уравнениям. Из графика этих уравнений очевидно, что существует только одно решение системы. В общем, прямые в системе координат связаны только тремя способами. Во-первых, это могут быть параллельные линии, которые никогда не пересекаются и, таким образом, представляют собой противоречивую систему без решения.Во-вторых, они могут пересекаться в одной точке, как в предыдущем примере, представляя согласованную систему с одним решением. И в-третьих, они могут совпадать или пересекаться во всех точках, что указывает на зависимую систему, имеющую бесконечное количество решений. Хотя он может предоставить некоторую полезную информацию, графический метод часто бывает трудным в использовании, потому что он обычно дает нам только приблизительные значения для решения системы уравнений.
Методы замены и исключения сложением дают результаты с хорошей степенью точности .Метод подстановки включает использование одного из уравнений системы для решения одной переменной через другую. Затем это значение подставляется в первое уравнение и получается решение. Применяя этот метод к системе уравнений в задаче о возрасте, мы сначала переформулируем уравнение 1 в терминах x так, чтобы оно стало x = 2y. Затем это значение x можно было бы подставить в уравнение 2, которое превратилось бы в 2y — 3y = -4 или просто y = 4. Затем значение x получается путем подстановки y = 4 в любое уравнение.
Вероятно, наиболее важным методом решения системы уравнений является метод исключения, поскольку его можно использовать для систем более высокого порядка. Метод исключения сложением предполагает замену систем уравнений более простыми уравнениями, называемыми эквивалентными системами. Рассмотрим систему со следующими уравнениями: уравнение 1: x — y = 1; и уравнение 2: x + y = 5. Метод исключения одна из переменных исключается путем сложения обоих уравнений и получения более простой формы.Таким образом, уравнение 1 + уравнение 2 приводит к более простому уравнению 2x = 6 или x = 3. Затем это значение возвращается в первое уравнение, чтобы получить y = 2.
Метод исключения одна из переменных исключается путем сложения обоих уравнений и получения более простой формы.Таким образом, уравнение 1 + уравнение 2 приводит к более простому уравнению 2x = 6 или x = 3. Затем это значение возвращается в первое уравнение, чтобы получить y = 2.
Часто необходимо умножать уравнения на другие переменные или числа, чтобы использовать метод исключения. Это можно проиллюстрировать системой, представленной следующими уравнениями:
В этом случае сложение уравнений не приведет к единому уравнению с единственной переменной. Однако, умножая обе части уравнения 2 на -2, оно преобразуется в -2x — 4y = -20.Теперь это эквивалентное уравнение можно добавить к первому уравнению, чтобы получить простое уравнение, -3y = — 18 или y = 6.
Система линейных уравнений (одновременные уравнения)
Когда у нас будет больше переменных для работы, нам просто нужно не забывать придерживаться определенного метода и продолжать сокращать количество уравнений или переменных.
x + 3y − z = 62x − y + 2z = 13x + 2y − z = 2. \ begin {выровнено} х + 3у — z & = 6 \\ 2х — у + 2z & = 1 \\ 3х + 2у — z & = 2. \ end {align} x + 3y − z2x − y + 2z3x + 2y − z = 6 = 1 = 2.
Решите следующую систему уравнений:
x + 2y − 3z = −32x − 5y + 4z = 135x + 4y − z = 5. \ begin {выровнено} х + 2у — 3z & = -3 \\ 2х — 5у + 4z & = 13 \\ 5х + 4у — z & = 5. \\ \ end {align} x + 2y − 3z2x − 5y + 4z5x + 4y − z = −3 = 13 = 5.
Начнем с последнего уравнения. Решая для zzz, получаем
z = 5x + 4y − 5.z = 5x + 4y — 5.z = 5x + 4y − 5.
Подставляя это во второе уравнение, получаем
2x − 5y + 4 (5x + 4y − 5) = 1322x + 11y − 33 = 02x + y − 3 = 0. \ begin {выровнено} 2х — 5у + 4 (5х + 4у — 5) & = 13 \\ 22x + 11y — 33 & = 0 \\ 2х + у — 3 & = 0.\ end {align} 2x − 5y + 4 (5x + 4y − 5) 22x + 11y − 332x + y − 3 = 13 = 0 = 0.
Подставляя это в первое уравнение, получаем
x + 2y − 3 (5x + 4y − 5) = — 3x + 2y − 15x − 12y + 15 + 3 = 0−14x − 10y + 18 = 0−7x − 5y + 9 = 0. \ begin {выровнено}
х + 2у — 3 (5х + 4у — 5) & = -3 \\
х + 2у — 15х -12у + 15 + 3 & = 0 \\
-14x — 10y + 18 & = 0 \\
-7x — 5y + 9 & = 0.
\ end {align} x + 2y − 3 (5x + 4y − 5) x + 2y − 15x − 12y + 15 + 3−14x − 10y + 18−7x − 5y + 9 = −3 = 0 = 0 = 0
\ begin {выровнено}
х + 2у — 3 (5х + 4у — 5) & = -3 \\
х + 2у — 15х -12у + 15 + 3 & = 0 \\
-14x — 10y + 18 & = 0 \\
-7x — 5y + 9 & = 0.
\ end {align} x + 2y − 3 (5x + 4y − 5) x + 2y − 15x − 12y + 15 + 3−14x − 10y + 18−7x − 5y + 9 = −3 = 0 = 0 = 0
Таким образом, мы свели нашу систему к паре уравнений с двумя переменными:
2x + y − 3 = 0−7x − 5y + 9 = 0.\ begin {выровнено} 2х + у — 3 & = 0 \\ -7x — 5y + 9 & = 0. \ end {align} 2x + y − 3−7x − 5y + 9 = 0 = 0.
Решая yyy в первом уравнении, получаем
y = 3−2x. у = 3 — 2х. у = 3−2x.
Подставляя это во второе уравнение, получаем
−7x − 5 (3−2x) + 9 = 0−7x − 15 + 10x + 9 = 03x − 6 = 0x = 2. \ begin {выровнено} -7x — 5 (3-2x) + 9 & = 0 \\ -7x-15 + 10x + 9 & = 0 \\ 3х — 6 & = 0 \\ х & = 2. \ end {align} −7x − 5 (3−2x) + 9−7x − 15 + 10x + 93x − 6x = 0 = 0 = 0 = 2.
Следовательно,
y = 3−2⋅2 = −1, z = 5⋅2 + 4⋅ (−1) −5 = 1.y = 3-2 \ cdot2 = -1, z = 5 \ cdot2 + 4 \ cdot (-1) -5 = 1. y = 3−2⋅2 = −1, z = 5⋅2 + 4⋅ (- 1) −5 = 1.
y = 3−2⋅2 = −1, z = 5⋅2 + 4⋅ (- 1) −5 = 1.
Таким образом, значения x, y, x, y, x, y и zzz, которые удовлетворяют данной системе уравнений, равны (2, −1,1). □ (2, -1,1). \ _ \ квадрат (2, -1,1). □
Численность, математика и статистика — Набор академических навыков
Решение одновременных линейных уравнений (экономика)
Решение одновременных линейных уравнений
Два или более линейных уравнения, которые содержат одни и те же неизвестные переменные, называются системой одновременных линейных уравнений .Решение такой системы означает нахождение значений неизвестных переменных, которые одновременно удовлетворяют всем уравнениям.
См. Ниже примеры использования одновременных уравнений в экономике.
Существует два распространенных метода решения одновременных линейных уравнений: замена и исключение . В некоторых вопросах один метод является более очевидным выбором, часто потому, что он упрощает процесс решения уравнений; в других случаях выбор метода зависит от личных предпочтений. В любом случае оба метода в конечном итоге приведут к одному и тому же решению.
В любом случае оба метода в конечном итоге приведут к одному и тому же решению.
Примечание : Чтобы иметь возможность решать любую систему линейных уравнений, мы должны иметь как минимум столько же уравнений, сколько переменных.
Здесь мы сосредоточимся на системах с двумя уравнениями и двумя переменными.
Сколько решений?
Система одновременных линейных уравнений может иметь: одно уникальное решение , бесконечно много решений или отсутствие решений .
Мы знаем, что график линейного уравнения представляет собой прямую линию, поэтому система двух линейных уравнений имеет две прямые. Если эти строки:
1) Пересечение есть одно уникальное решение системы уравнений. Это имеет смысл, поскольку может быть только пара значений (по одному для каждой переменной), которые одновременно удовлетворяют обоим уравнениям. Эта пара значений будет соответствовать точке пересечения.
2) одна и та же строка там, как говорят, бесконечно много решений системы уравнений: все пары значений переменных в одной строке удовлетворяют уравнению другой строки, так как они являются той же строкой .
3) параллельны нет решений : нет пар значений $ x $ и $ y $, которые лежат на обеих линиях (поскольку линии никогда не могут пересекаться!), И поэтому не может быть пар значений значения переменных, которые удовлетворяют обоим уравнениям.
Один из способов определить, может ли система двух линейных уравнений быть решена и сколько решений она имеет, состоит в том, чтобы преобразовать оба уравнения в форму: \ [y = ax + b \], где $ a $ — наклон прямой и $ b $ — точка пересечения оси $ y $.Теперь должно быть ясно, соответствуют ли два уравнения:
1) Различные и непараллельные линии (разные наклоны), поэтому есть одно уникальное решение.
2) Та же линия (тот же угол наклона и точка пересечения), значит, решений бесконечно много.
3) Параллельные прямые (у них одинаковый наклон, но разная точка пересечения), поэтому решений нет.
Метод замещения
Метод замены включает замену одного уравнения в другое, чтобы исключить одну из переменных.Затем мы можем найти другую переменную. Следующий шаг — подставить значение этой переменной в одно из уравнений, чтобы определить значение другой переменной. Обратите внимание, что это может потребовать перестройки одного из уравнений таким образом, чтобы оно было в форме, которую можно легко подставить в другое уравнение.
Рабочий пример
Решите эту пару одновременных линейных уравнений
\ begin {align} y \, — \, 2x & = 1 \\ 2y-3x & = 5 \ end {align}
Решение
Хорошая идея — пометить уравнения, чтобы на них было легче ссылаться.\ begin {align} y \, — \, 2x & = 1 & \ textbf {(1)} \\ 2y-3x & = 5 & \ textbf {(2)} \ end {align}
Затем первым шагом является преобразование уравнений $ (1) $ и $ (2) $ в форму $ y = ax + b $. Это дает: \ begin {align} y & = 2x + 1 & \ textbf {(3)} \\ y & = \ frac {3} {2} x + \ frac {5} {2} & \ textbf {(4)} \ end {align}
Это дает: \ begin {align} y & = 2x + 1 & \ textbf {(3)} \\ y & = \ frac {3} {2} x + \ frac {5} {2} & \ textbf {(4)} \ end {align}
, где уравнение $ \ textbf {(3)} $ соответствует уравнению $ \ textbf {(1)} $, а уравнение $ \ textbf {(4)} $ соответствует уравнению $ \ textbf {(2)} $.Теперь мы можем видеть, что два уравнения соответствуют различным и непараллельным линиям (поскольку они имеют разные наклоны), и поэтому существует одно уникальное решение этой системы уравнений. Теперь мы решим эту систему, используя метод подстановки.
Подстановка уравнения $ \ textbf {(3)} $ в уравнение $ \ textbf {(2)} $ дает:
\ [2 (1 + 2x) -3x = 5 \] Примечание : мы можем подставить уравнение $ \ textbf {(3)} $ в уравнение $ \ textbf {(2)} $, потому что уравнение $ \ textbf {( 3)} $ — это просто измененная версия уравнения $ \ textbf {(1)} $.Мы также могли бы заменить уравнение $ \ textbf {(4)} $ в уравнение $ \ textbf {(1)} $. Однако мы не могли заменить уравнение $ \ textbf {(3)} $ в уравнение $ \ textbf {(1)} $ (или $ \ textbf {(4)} $ в $ \ textbf {(2)} $), потому что это то же уравнение .
Теперь у нас есть уравнение только для одной переменной, которое можно преобразовать и решить, чтобы найти $ x $.
\ begin {align} 2 (1 + 2x) -3x & = 5 \\ 2 + 4x-3x & = 5 \\ 2 + x & = 5 \\ x & = 3 \ end {align}
Теперь у нас есть значение для $ x $, которое можно подставить в любое из исходных уравнений, чтобы найти $ y $.Проще всего использовать преобразованное уравнение $ \ textbf {(1)} $ (уравнение $ \ textbf {(3)} $):
\ [y = 2 \ times 3 + 1 = 7. \]
Решение $ x = 3 $ и $ y = 7 $ удовлетворяет обоим уравнениям. Рекомендуется проверить свое решение, подставив эти значения $ x $ и $ y $ в исходные уравнения.
\ begin {align} y — 2x & = 1 & \ textbf {(1)} \\ 7 — 2 \ times 3 & = 7 — 6 = 1. \\ \\ 2y — 3x & = 5 & \ textbf { (2)} \\ 2 \ times 7 — 3 \ times 3 & = 14 — 9 = 5. \ end {align}
| центр
На этом графике показаны линии $ y-2x = 1 $ и $ 2y-3x = 5 $.Решением этих одновременных уравнений является точка пересечения двух линий. Мы видим, что это точка $ (3,7) $, которая согласуется с нашим решением.
Мы видим, что это точка $ (3,7) $, которая согласуется с нашим решением.
Рабочий пример
Решите эту систему двух одновременных линейных уравнений.
\ begin {align} 5y-2x = 45 \\ 6x = 15y-135 \ end {align}
Решение
Преобразование двух уравнений в форму $ y = ax + b $ дает: \ begin {align} y = & \ dfrac {2x} {5} +9 \\ y & = \ dfrac {2x} {5} +9 \ конец
Строки одинаковые, значит решений бесконечно много.
Видео пример
Профессор Робин Джонсон использует метод подстановки для решения одновременных уравнений $ 3x-2y = 7 $ и $ y + 4x = 5 $.
Ликвидация
Определение
Когда даны два одновременных линейных уравнения с двумя неизвестными, мы также можем применить метод исключения . Метод исключения включает выбор переменной, которую необходимо исключить.
Начните с умножения обоих уравнений на соответствующие константы, чтобы в каждом уравнении выбранная переменная имела один и тот же коэффициент (независимо от ее знака: положительный он или отрицательный).
Затем, в зависимости от знака коэффициента этой же переменной, либо прибавляет , либо вычитает одно уравнение из другого, так что члены, включающие исключаемую переменную, уравняются.
Остающееся уравнение состоит из одной переменной и может быть решено обычным способом; значение этой переменной затем подставляется в одно из исходных уравнений, чтобы найти значение исключенной переменной.
Рабочие примеры
Рабочий пример
Решите одновременные линейные уравнения
\ begin {align} 2x + y & = 7 \\ 3x-y & = 8 \ end {align}
Решение
Преобразование двух уравнений в форму $ y = ax + b $ дает: \ begin {align} y = & — 2x + 7 \\ y & = 3x-8 \ end {align}
Линии имеют разный уклон, поэтому есть одно уникальное решение. Теперь мы найдем его, используя метод исключения.
Теперь мы найдем его, используя метод исключения.
Сначала обозначим уравнения: \ begin {align} 2x + y & = 7 & \ textbf {(1)} \\ 3x-y & = 8 & \ textbf {(2)} \ end {align}
Обратите внимание, что коэффициент при $ y $ одинаков до момента входа в оба уравнения. Поскольку одно положительное, а второе отрицательное, если мы сложим два уравнения вместе, $ y $ сократится.
\ begin {align} & 2x + y = 7 \\ & 3x-y = 8 \\ & \ overline {5x \ quad \; \; \, = 15} \ end {align}
Итак, $ x = 3 $.
Теперь замените это значение на $ x $ обратно в уравнение $ \ textbf {(1)} $.
\ begin {align} 2x + y & = 7 \\ 2 \ times 3 + y & = 7 \\ 6 + y & = 7 \\ y & = 1 \ end {align}
Значения $ x = 3 $, $ y = 1 $ удовлетворяют обоим полученным нами уравнениям.
| центр
На этом графике показаны линии $ 2x + y = 7 $ и $ 3x-y = 8 $. Решением этих одновременных уравнений является точка пересечения двух линий. Мы видим, что это точка (3,1), которая согласуется с нашим решением.
Рабочий пример
Решите эту систему двух одновременных линейных уравнений.
\ begin {align} 2x + 3y & = 4 \\ x — 2y & = -5 \ end {align}
Решение
Преобразование двух уравнений в форму $ y = ax + b $ дает: \ begin {align} y = & — \ dfrac {2x} {3} + \ frac {4} {3} \\ y & = \ dfrac { x} {2} + \ frac {5} {2} \ end {align}
Линии имеют разный уклон, поэтому есть одно уникальное решение. Теперь мы найдем его, используя метод исключения.Сначала пометьте уравнения 1 и 2 соответственно.
\ begin {align} 2x + 3y & = 4 & \ textbf {(1)} \\ x — 2y & = -5 & \ textbf {(2)} \ end {align}
Мы хотим сделать коэффициенты $ x $ одинаковыми в обоих уравнениях. Для этого умножьте уравнение (2) на $ 2 $.
\ [2x-4y = -10 \]
Поскольку коэффициенты при $ x $ в обоих уравнениях положительны, мы вычитаем уравнение 2 из уравнения 1 .
\ begin {align} & 2x + 3y = 4 \\ & 2x-4y = -10 \\ & \ overline {\ qquad \; 7y = 14} \ end {align}
Итак, $ y = 2 $.
Подстановка этого значения на $ y $ обратно в одно из исходных уравнений даст $ x $.
\ begin {align} x — 2y & = -5 & \ textbf {(2)} \\ x-2 \ times 2 & = — 5 \\ x-4 & = — 5 \\ x & = — 1 \ end {align }
Значения $ x = -1 $ и $ y = 2 $ удовлетворяют обоим полученным нами уравнениям.
| центр
На этом графике показаны линии $ 2x + 3y = 4 $ и $ x-2y = -5 $. Решением этих одновременных уравнений является точка пересечения двух линий.
Рабочий пример
Решите эту систему двух одновременных линейных уравнений.
\ begin {align} 3y-4x = 15 \\ -12x = 18-9y \ end {align}
Решение
Преобразование двух уравнений в форму $ y = ax + b $ дает: \ begin {align} y = & — \ dfrac {4x} {3} +5 \\ y & = \ dfrac {4x} {3} +2 \ end {align}
Прямые имеют одинаковый наклон, но разные точки пересечения $ y $ (они параллельны), поэтому решений нет, поскольку они никогда не пересекаются.
Приложения одновременных линейных уравнений в экономике
Спрос и предложение
Вышеупомянутые методы решения пар одновременных линейных уравнений можно использовать для нахождения рыночного равновесия, когда у нас есть линейные функции рыночного предложения и рыночного спроса.S $ равно $ q $. Функции спроса и предложения становятся: \ begin {align} & q = 5p-25 & \ textbf {(1)} \\ & q = -2p + 24 & \ textbf {(2)} \ end {align} Чтобы найти равновесия, мы можем использовать любой из вышеупомянутых методов, чтобы найти значения переменных $ q $ и $ p $, которые удовлетворяют обеим этим функциям. Здесь мы воспользуемся методом подстановки.
Подстановка уравнения $ \ textbf {(1)} $ в уравнение $ \ textbf {(2)} $ дает: \ begin {align} 5p-25 & = — 2p + 24 \\ \ Rightarrow 7p & = 49 \\ \ Rightarrow p & = 7 \ end {align}
Подстановка этого значения $ p $ в уравнение $ \ textbf {(1)} $ дает: \ begin {align} q & = 5 \ times 7-25 \\ \ Rightarrow q & = 10 \ end {align}
Итак, решение этой системы уравнений: $ q = 10 $ и $ p = 7 $. Это решение показано графически ниже, где мы построили обратную функцию спроса (синим цветом) и обратную функцию предложения (красным цветом) на одном графике. Мы видим, что равновесие соответствует пересечению этих двух функций. То есть точка, где $ q = 10 $ и $ p = 7 $.
Это решение показано графически ниже, где мы построили обратную функцию спроса (синим цветом) и обратную функцию предложения (красным цветом) на одном графике. Мы видим, что равновесие соответствует пересечению этих двух функций. То есть точка, где $ q = 10 $ и $ p = 7 $.
Обратные уравнения спроса и предложения
Преобразование функций спроса и предложения таким образом, чтобы сделать $ p $ предметом обсуждения, дает нам то, что известно как обратные функции спроса и предложения .S $. Затем две функции становятся: \ begin {align} & p = \ dfrac {q} {5} +5 \\ & p = — \ dfrac {q} {2} +12 \ end {align} Теперь у нас есть два уравнения и два неизвестные и поэтому могут решить эту систему уравнений. Попробуйте это сами (подсказка: вы должны получить те же значения для $ p $ и $ q $, что и выше).
Сравнительная статика
Примером сравнительной статики является влияние налога. Здесь мы рассмотрим два вида налога: налог на единицу продукции и адвалорный налог.
Налог на единицу продукции
за единицу или специальный налог — это фиксированная сумма, которая взимается за каждую проданную единицу товара или услуги.S $, поэтому, чтобы найти рыночное равновесие, мы можем записать функции спроса и (с поправкой на налоги) предложения как: \ begin {align} & p = \ dfrac {q} {5} +5.7 & \ textbf {(1)} \ \ & p = — \ dfrac {q} {2} +12 & \ textbf {(2)} \\ \ end {align} Поскольку оба уравнения имеют разные наклоны, система разрешима. Теперь мы решим эту систему уравнений, используя метод подстановки. Преобразуя уравнение $ \ textbf {(1)} $ в $ q $, объект дает: \ begin {align} \ dfrac {q} {5} & = p-5.7 \\ \ Rightarrow q & = 5p-28.5 & \ textbf {(3)} \\ \ end {align} Теперь мы можем заменить уравнение $ \ textbf {(3)} $ в уравнение $ \ textbf {(2)} $ следующим образом: \ begin {align} & p = — \ dfrac {5п-28.5} {2} +12 \\ \ Rightarrow & 2p = -5p + 28,5 + 24 \\ \ Rightarrow & 7p = 52,5 \\ \ Rightarrow & p = 7,5 \\ \ end {align}
Подстановка этого значения $ p $ в уравнение $ \ textbf {(3)} $ дает: \ begin {align} q & = 5 \ times 7. 5-28.5 \\ & = 9 \ end {align}
5-28.5 \\ & = 9 \ end {align}
Таким образом, с учетом налога, взимаемого с производителей, равновесное количество упало с 10 долларов до 9 долларов за килограмм, а равновесная цена выросла с 7 до 7,05 доллара за килограмм.
На приведенном выше графике мы видим, что эффект налога сдвигает кривую предложения влево. Следовательно, точка равновесия (точка пересечения функции предложения с измененными налогами и функции спроса) также сместилась влево.
Чтобы определить доход, полученный от этого налога, мы умножаем сумму налога на единицу на количество, произведенное в равновесии: \ [\ text {tax} = £ (0,70 \ times 9) = 6,30 £ \] Это равно площадь заштрихованного розового прямоугольника, показанного на приведенном выше графике.
Ad Valorem Tax
Адвалорный налог взимается как процент от количества облагаемых налогом товара или услуги.S $, поэтому, чтобы найти рыночное равновесие, мы можем записать функции спроса и (с поправкой на налоги) предложения как: \ begin {align} & p = 0. 21q + 5.25 & \ textbf {(1)} \\ & p = — \ dfrac {q} {2} +12 & \ textbf {(2)} \\ \ end {align} Поскольку оба уравнения имеют разные наклоны, система разрешима. Теперь мы решим эту систему уравнений, используя метод подстановки. Преобразуя уравнение $ (2) $ в объект $ q $, получаем: \ [q = -2p + 24 \; \; \; \ textbf {(3)} \] Подстановка уравнения $ (3) $ в уравнение $ (1) $ дает: \ begin {align} p & = 0.21 (-2p + 24) +5.25 \\ & = — 0.42p + 10.29 \\ & \ Rightarrow 1.42p = 10.29 \\ & \ Rightarrow p = 7.246 … \ end {align}
21q + 5.25 & \ textbf {(1)} \\ & p = — \ dfrac {q} {2} +12 & \ textbf {(2)} \\ \ end {align} Поскольку оба уравнения имеют разные наклоны, система разрешима. Теперь мы решим эту систему уравнений, используя метод подстановки. Преобразуя уравнение $ (2) $ в объект $ q $, получаем: \ [q = -2p + 24 \; \; \; \ textbf {(3)} \] Подстановка уравнения $ (3) $ в уравнение $ (1) $ дает: \ begin {align} p & = 0.21 (-2p + 24) +5.25 \\ & = — 0.42p + 10.29 \\ & \ Rightarrow 1.42p = 10.29 \\ & \ Rightarrow p = 7.246 … \ end {align}
Подстановка этого значения $ p $ в уравнение $ (3) $ дает: \ begin {align} q & = — 2 \ times 7.246 … + 24 \\ & = 9.507 … \ end {align}
Таким образом, новая равновесная цена и количество бананов (до 2 долл. США в сутки) равны p = 7,25 долл. США и q = 9,51 долл. США. Другими словами, равновесная цена бананов (в долларах США) составляет 7,25 доллара США, а равновесное количество — 9,51 доллара США за килограмм. Чтобы рассчитать доход, полученный от адвалорного налога, мы должны найти произведение равновесного количества и суммы налога:
$ 0. 05 \ times 9,507 … = 0,48 $ (до 2 $ d.p.)
05 \ times 9,507 … = 0,48 $ (до 2 $ d.p.)
Таким образом, налоговые поступления составляют 0,48 доллара США.
Анализ ввода-вывода
Анализ затрат и выпуска используется, чтобы показать, как отрасли в одной экономике взаимосвязаны. В частности, он показывает, как продукция одной отрасли часто используется в качестве исходных данных для другой отрасли и что продукция отрасли может использоваться в качестве исходных данных для той же отрасли. Для простоты мы предположим, что в экономике может быть только 2 доллара промышленности.
Например, рассмотрим экономику, которая производит уголь $ \ left (X \ right) $ и сталь $ \ left (Y \ right) $. Уголь необходим для производства стали, а сталь используется для изготовления инструментов, необходимых для добычи угля: отрасли взаимосвязаны между собой .
Предположим, что для производства одной единицы (1 доллар США кг) угля требуется 0,18 доллара США за кг угля и 0,03 доллара США за кг стали, в то время как для производства одной единицы (1 доллар США кг) стали требуется 0,21 доллара США за кг угля и 0,04 доллара США за кг угля.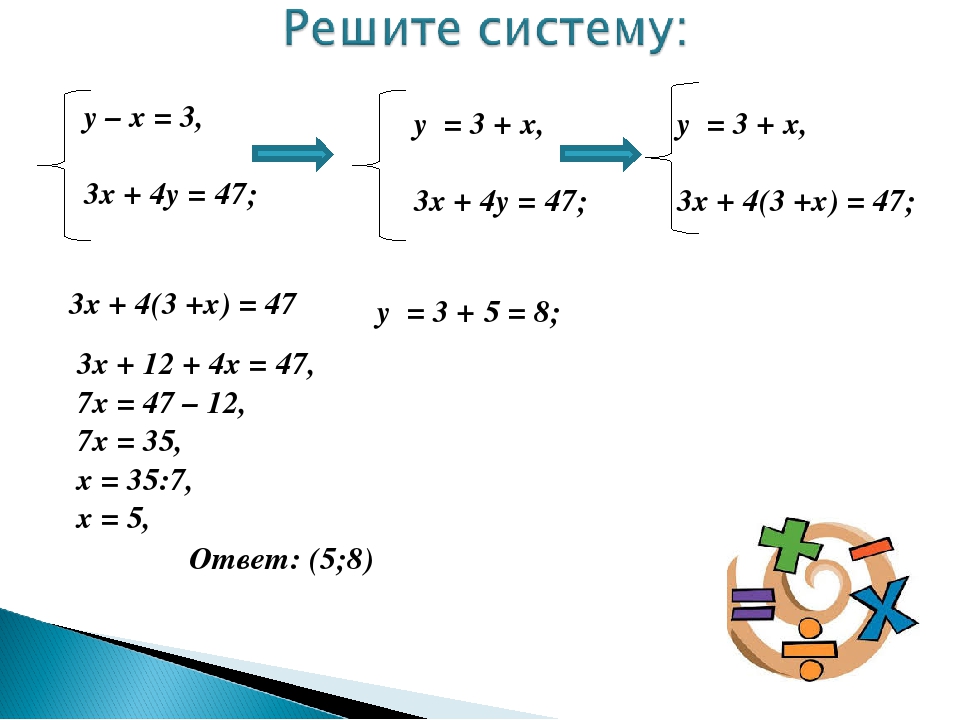 стали. Мы можем выразить эту информацию в виде таблицы:
стали. Мы можем выразить эту информацию в виде таблицы:
$ X $ | 0 руб.* $ — нетто произведено (в кг) стали и угля. Теперь предположим, что для удовлетворения потребительских потребностей этой экономики необходимо произвести 36,06 доллара за кг стали и 26,53 доллара за кг угля. Это чистый объем производства стали и угля соответственно, поэтому мы можем переписать (и обозначить) приведенные выше уравнения как: \ begin {align} 26.53 & = 0.82x-0.03y & \ textbf {(1)} \\ 36.06 & = 0.96y-0.21x & \ textbf {(2)} \\ \ end {align} Теперь у нас есть система одновременных линейных уравнений, которую мы можем решить, используя любой из вышеперечисленных методов.Как обычно, первым делом нужно переписать уравнения в виде $ y = mx + c $. Это дает: \ begin {align} y & = \ dfrac {82x} {3} — \ dfrac {26.53} {0.03} & \ textbf {(3)} \\ y & = \ dfrac {7x} {32} + \ frac {36.06} {0.96} & \ textbf {(4)} \\ \ end {align} Поскольку линии имеют разный наклон, существует единственное решение этой системы уравнений. Общее количество угля и стали, которое необходимо произвести для удовлетворения потребительских потребностей этой экономики, составляет 34 доллара за кг угля и 45 долларов за кг стали. Макроэкономическое равновесие Здесь мы рассмотрим, как методы решения систем одновременных уравнений могут быть использованы для определения равновесного уровня дохода для всей экономики.Для этого мы должны сначала рассмотреть ключевые взаимосвязи в нашей модели экономики. Если мы сделаем упрощающее предположение, что домохозяйства зарабатывают свой доход исключительно на том, сколько продукции они производят, то совокупный доход домохозяйства в долларах Y $ должен быть равен объему производства в $ Q $. Мы можем записать это как тождество \ [Y \ Equiv Q \]. Если мы также предположим, что весь выпуск приобретен кем-то, у нас есть этот выпуск $ Q $ равен спросу или совокупным расходам $ E $, поэтому: \ [Q \ Equiv E \] Объединение приведенных выше уравнений дает: \ [Y \ Equiv E \; \; \; \ textbf {(1)} \] Теперь, поскольку совокупные расходы состоят из потребительских расходов домохозяйств $ C $ и инвестиционных расходов фирмами $ I $ имеем другое тождество: \ [E \ Equiv C + I \; \; \; \ textbf {(2)} \] Функция потребления утверждает, что плановое потребление домохозяйства $ \ hat {C} $ является функцией дохода домохозяйства.Если предположить, что это соотношение является линейным, то мы можем записать: \ [\ hat {C} = aY + b \; \; \; \ textbf {(3)} \], где $ a $ и $ b $ — оба положительные константы и $ a \ lt 1 $. Примечание : $ a $ — наклон функции потребления, который также называется предельной склонностью к потреблению (ПДК). Значение $ a $ говорит нам о доле совокупного увеличения дохода, которая будет потрачена на потребление товаров и услуг. $ b $ — член перехвата. В равновесии плановое потребление домохозяйства должно быть равно фактическому потреблению домохозяйства: \ [C = \ hat {C} \; \; \; \ textbf {(4)} \] Теперь, если мы предположим, что инвестиционные расходы равны некоторому фиксированному значению $ \ hat {I} $, мы можем написать: \ [I = \ hat {I} \; \; \; \ textbf {(5)} \ ] и поэтому уравнение $ \ textbf {(2)} $ можно записать как: \ [E \ Equiv C + \ hat {I} \; \; \; \ textbf {(2)} \] Уравнения от $ \ textbf {(1)} $ до $ \ textbf {(5)} $ составляют нашу макроэкономическую модель.Однако мы можем упростить эту модель, объединив уравнения, чтобы уменьшить их количество. Объединение уравнения $ \ textbf {(1)} $ с уравнением $ \ textbf {(2)} $ дает: \ [Y \ Equiv C + \ hat {I} \; \; \; \ textbf {(1. Рабочий примерУчитывая следующую макроэкономическую модель: \ begin {align} Y & \ Equiv E \\ E & \ Equiv C + I \\ \ hat {C} & = 0,25Y + 50 \\ I & = 250 \\ C & = \ hat {C } \ end {align} a) Найдите равновесные уровни дохода и потребления и изобразите их схематически. b) Если инвестиции вырастут до 550 долларов, найдите новые уровни равновесия доходов и потребления. Решение a) Что касается общей модели, мы можем упростить эту модель экономики, объединив уравнения для уменьшения их количества. Объединение второго уравнения с первым дает: \ [Y \ Equiv C + 250 \; \; \; \ textbf {(1)} \], где $ 250 $ заменено на $ I $. Объединение третьего уравнения с пятым дает: \ [C = 0.25Y + 50 \; \; \; \ textbf {(2)} \] Теперь у нас есть $ 2 $ уравнений и $ 2 $ неизвестных, поэтому мы можем решить систему уравнений .Подстановка уравнения $ \ textbf {(2)} $ в уравнение $ \ textbf {(1)} $ дает: \ begin {align} Y & = (0,25Y + 50) +250 \\ & = 0,25Y + 300 \\ \ Rightarrow 0.75Y & = 300 \\ \ Rightarrow Y & = 400 \ end {align} и замена этого значения $ Y $ в уравнение $ \ textbf {(2)} $ дает: \ begin {align} C & = 0.25 \ times 400+ 50 \\ & = 150 \ end {align}, поэтому равновесный уровень дохода равен Y = 400 $, а равновесный уровень потребления равен C = 150 $. b) Если инвестиции увеличиваются до 400 долларов США, уравнение $ \ textbf {(1)} $ из части a) принимает следующий вид: \ [Y \ Equiv C + 550 \; \; \; \ textbf {(1.1)} \] и уравнение $ \ textbf {(2)} $ остается без изменений, поскольку оно не содержит члена $ I $: \ [C = 0.25Y + 50 \; \; \; \ textbf {(2.1)} \] Теперь мы воспользуемся методом подстановки для решения этих уравнений. Подстановка уравнения $ \ textbf {(2)} $ в уравнение $ \ textbf {(1)} $ дает: \ begin {align} Y & = (0,25Y + 50) +550 \\ & = 0,25Y + 600 \\ \ Rightarrow 0.75Y & = 600 \\ \ Rightarrow Y & = 450 \ end {align} и замена этого значения $ Y $ в уравнение $ \ textbf {(2.1)} $ дает: \ begin {align} C & = 0.25 \ times 450+ 50 \\ & = 162.50 \ end {align}, поэтому, когда инвестиции увеличиваются до 550 долларов, равновесный уровень дохода повышается до Y = 450 долларов, а равновесный уровень потребления повышается до C = 162,50 долларов. Это имеет смысл, поскольку инвестиции являются частью совокупного спроса, поэтому, когда инвестиции увеличивают объем производства, и, следовательно, совокупный доход также должен расти. Видео примерПроф. Робин Джонсон решает системы уравнений $ 2x-3y = 5 $ и $ 7x + 2y = 1 $, используя метод исключения.
Рабочая тетрадьЭта рабочая тетрадь, созданная HELM, является хорошим помощником при проверке, содержит ключевые моменты для проверки и множество рабочих примеров. Проверьте себяПроверьте себя: Numbas-тест по системным уравнениям Внешние ресурсы. |
 Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
 Здесь мы воспользуемся методом подстановки. Подстановка уравнения $ \ textbf {(4)} $ в уравнение $ \ textbf {(1)} $ дает: \ begin {align} 26,53 & = 0,82x-0,03 \ left (\ dfrac {7x} {32} + \ frac {36.06} {0.96} \ right) \\ \ Rightarrow x & = 34 \ end {align} Теперь мы можем заменить это значение $ x $ can либо в уравнение $ \ textbf {(3)} $, либо в $ \ textbf {(4 )} $, чтобы найти значение $ y $. Подстановка $ x = 34 $ в уравнение $ \ textbf {(3)} $ дает: \ begin {align} y & = \ dfrac {82 \ times 34} {3} — \ dfrac {26.53} {0.03} \\ & = 45 \ end {align}
Здесь мы воспользуемся методом подстановки. Подстановка уравнения $ \ textbf {(4)} $ в уравнение $ \ textbf {(1)} $ дает: \ begin {align} 26,53 & = 0,82x-0,03 \ left (\ dfrac {7x} {32} + \ frac {36.06} {0.96} \ right) \\ \ Rightarrow x & = 34 \ end {align} Теперь мы можем заменить это значение $ x $ can либо в уравнение $ \ textbf {(3)} $, либо в $ \ textbf {(4 )} $, чтобы найти значение $ y $. Подстановка $ x = 34 $ в уравнение $ \ textbf {(3)} $ дает: \ begin {align} y & = \ dfrac {82 \ times 34} {3} — \ dfrac {26.53} {0.03} \\ & = 45 \ end {align}

 1}) \] Затем мы можем объединить уравнения $ \ textbf {(3)} $ и $ \ textbf {(4)} $, чтобы получить: \ [C = aY + b \; \; \; \ textbf {(1.2}) \] Мы теперь есть $ 2 $ уравнения (уравнение $ \ textbf {(1.1)} $ и уравнение $ \ textbf {(1.2)} $) и $ 2 $ неизвестных ($ C $ и $ Y $), поэтому мы можем использовать вышеуказанные методы для решения эта система уравнений. Здесь мы воспользуемся методом подстановки.Подстановка уравнения $ \ textbf {(1.1}) $ в уравнение $ \ textbf {(1.2}) $ дает: \ begin {align} Y & = (aY + b) + \ hat {I} \\ \ Rightarrow (1 & -a ) Y = b + \ hat {I} \\ \ Rightarrow Y & = \ dfrac {b + \ hat {I}} {1-a} \ end {align} Это говорит нам, что равновесный уровень дохода равен сумме член пересечения $ млрд и инвестиции, деленные на $ 1 минус ПДК.
1}) \] Затем мы можем объединить уравнения $ \ textbf {(3)} $ и $ \ textbf {(4)} $, чтобы получить: \ [C = aY + b \; \; \; \ textbf {(1.2}) \] Мы теперь есть $ 2 $ уравнения (уравнение $ \ textbf {(1.1)} $ и уравнение $ \ textbf {(1.2)} $) и $ 2 $ неизвестных ($ C $ и $ Y $), поэтому мы можем использовать вышеуказанные методы для решения эта система уравнений. Здесь мы воспользуемся методом подстановки.Подстановка уравнения $ \ textbf {(1.1}) $ в уравнение $ \ textbf {(1.2}) $ дает: \ begin {align} Y & = (aY + b) + \ hat {I} \\ \ Rightarrow (1 & -a ) Y = b + \ hat {I} \\ \ Rightarrow Y & = \ dfrac {b + \ hat {I}} {1-a} \ end {align} Это говорит нам, что равновесный уровень дохода равен сумме член пересечения $ млрд и инвестиции, деленные на $ 1 минус ПДК.

