Тригонометрические уравнения в 10 классе, примеры и решения
Дата публикации: .
Урок и презентация на тему: «Решение простейших тригонометрических уравнений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Тригонометрические уравнения (PPTX)
Что будем изучать:
1. Что такое тригонометрические уравнения?
2. Простейшие тригонометрические уравнения.
3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.
Что такое тригонометрические уравнения?
Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.
Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции.
Ещё примеры тригонометрических уравнений.
Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3
Решение:
а) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:
x/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk
Ответ: x=5πk, где k – целое число.
б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Ответ: x=2π/9 + πk/3, где k – целое число.
Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке [0; π].
Решение:
Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
x= ± π/16+ πk/2;
Теперь давайте посмотрим какие корни попадут на наш отрезок. При k
При k=0, x= π/16, мы попали в заданный отрезок [0; π].
При к=1, x= π/16+ π/2=9π/16, опять попали.
При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.
Ответ: x= π/16, x= 9π/16
Два основных метода решения.
Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.
Решим уравнение:
Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).
В результате замены получим: t2 + 2t -1 = 0
Найдем корни квадратного уравнения: t=-1 и t=1/3
Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.
x=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Ответ: x= -π/4+πk; x=arctg(1/3) + πk.
Пример решения уравнения
Решить уравнений: 2sin2(x) + 3 cos(x) = 0
Решение:
Воспользуемся тождеством: sin2(x) + cos2(x)=1
Наше уравнение примет вид:2-2cos2(x) + 3 cos (x) = 0
2 cos2(x) — 3 cos(x) -2 = 0
введем замену t=cos(x): 2t2 -3t — 2 = 0
Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2
Тогда cos(x)=2 и cos(x)=-1/2.
Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.
Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Ответ: x= ±2π/3 + 2πk
Однородные тригонометрические уравнения.
Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.
Уравнения вида
однородными тригонометрическими уравнениями второй степени.
Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.
Решить уравнение:
Пример: cos2(x) + sin(x) cos(x) = 0
Решение:
Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0
Тогда нам надо решить два уравнения:
cos(x)=0 и cos(x)+sin(x)=0
cos(x)=0 при x= π/2 + πk;
Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Ответ: x= π/2 + πk и x= -π/4+πk
Однородные тригонометрические уравнения второй степени
Как решать однородные тригонометрические уравнения второй степени?Ребята, придерживайтесь этих правил всегда!
1.
Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:
Делаем замену переменной t=tg(x) получаем уравнение:
Решить пример №:3
Решить уравнение:
Решение:
Разделим обе части уравнения на косинус квадрат:
Делаем замену переменной t=tg(x): t2 + 2 t — 3 = 0
Найдем корни квадратного уравнения: t=-3 и t=1
Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
tg(x)=1 => x= π/4+ πk
Ответ: x=-arctg(3) + πk и x= π/4+ πk
Решить пример №:4
Решить уравнение:
Решение:
Преобразуем наше выражение:
Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk
Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk
Решить пример №:5
Решить уравнение:
Решение:
Преобразуем наше выражение:
Введем замену tg(2x)=t:22 — 5t + 2 = 0
Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2
Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2
2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2
Задачи для самостоятельного решения.
1) Решить уравнение
а) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7
2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].
3) Решить уравнение: ctg2(x) + 2ctg(x) + 1 =0
4) Решить уравнение: 3 sin 2(x) + √3sin (x) cos(x) = 0
5) Решить уравнение:3sin2(3x) + 10 sin(3x)cos(3x) + 3 cos2(3x) =0
6)Решить уравнение:cos2(2x) -1 — cos(x) =√3/2 -sin2(2x)
Простейшие тригонометрические уравнения и их решение
К простейшим тригонометрическим уравнениям относятся уравнения вида
Решение простейших тригонометрических уравнений
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . Так как для любого x, то при и уравнение не имеет корней. При , корни этого уравнения находятся по формуле
Особые случаи
Примеры решения задач
Уравнение вида .
Так как для любого x, то при и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
ПРИМЕР 4| Задание | Решить уравнение — |
| Решение | Косинус – функция ограниченная и лежит в пределах , поэтому данное равенство не имеет смысла. |
| Ответ | Решений нет. |
Простейшие тригонометрические уравнения с тангенсами и котангенсами
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 5
| Задание | Решить уравнение |
| Решение | Выразим из этого равенства тангенс
В последнем равенстве положив , получим простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 2, тогда окончательно получим
|
| Ответ |
Уравнение вида .
Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 6
| Задание | Решить уравнение
|
| Решение | Ведем замену , тогда исходное уравнение преобразуется в простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 5, тогда окончательно получим
|
| Ответ |
Приведение тригонометрических уравнений к простейшим
Примеры тригонометрических уравнений, которые приводятся к простейшим тригонометрическим уравнениям с помощью элементарных преобразований или тригонометрических формул.
| Задание | Решить уравнение |
| Решение | Применим к правой части заданного уравнения формулу суммы синусов:
или
Последнее равенство равносильно совокупности простейших уравнений
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
Урок 46. однородные тригонометрические уравнения — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №46.
Однородные тригонометрические уравнения.
Перечень вопросов, рассматриваемых в теме:
1) Однородные тригонометрические уравнения первой и второй степени.
2) Рассмотреть решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки.
3) Рассмотреть решение более сложных тригонометрических уравнений.
Глоссарий по теме
- Арккосинусом числа называется такое число α, что: . Арккосинус числа m обозначают: .
- Арксинусом числа называется такое число α, что: и . Арксинус числа m обозначают: .
- Арктангенсом числа m называется такое число α, что: и . Арктангенс числа m обозначают: .
- Арккотангенсом числа n называется такое число α, что: и . Арккотангенс числа n обозначают:
- Уравнение вида:
называется однородным.
Здесь f и g произвольные функции, коэффициенты.
6. Универсальная тригонометрическая подстановка — это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:
Основная литература:
Колягин Ю.
М., Ткачева М. В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Шахмейстер А.Х. Тригонометрия. М. 2014, 712 с.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Мы уже знаем, как решаются простейшие тригонометрические уравнения, а также тригонометрические уравнения, которые могут быть сведены к квадратным, дробно-рациональным или алгебраическим степени выше второй с помощью замены переменной. Но это лишь маленькое количество тригонометрических уравнений. Как, например, быть в том случае, когда тригонометрическое уравнение выглядит, например, так:
.
Для этого нам нужно рассмотреть некоторые вспомогательные приемы решения уравнений, а также формулы преобразования тригонометрических выражений.
Задание:
Как Вы думаете, какие факты и формулы мы будем использовать при решении этого уравнения?
Ответ: определение тангенса, формулу синуса двойного аргумента.
1. Итак, рассмотрим однородное тригонометрическое уравнение.
Напомним определение однородного уравнения
Определение
Уравнение вида:
называется однородным.
Здесь f и g произвольные функции, коэффициенты.
В зависимости от значения показателя n, мы можем получить однородное уравнение первой, второй или более высокой степени.
Например, уравнение является однородным, а уравнение однородным не является.
2. Теперь перейдем к рассмотрению однородных тригонометрических уравнений.
Если функции f и g это синус и косинус одного и того же аргумента, то мы получим тригонометрическое однородное уравнение.
Рассмотрим сначала однородное тригонометрическое уравнение первой степени.
Запишем его в общем виде: (1).
Разделим это уравнение на (или на ) и получим: .
Решать такие уравнения мы умеем: , .
Заметим, что, решая это уравнение, мы выполняли деление уравнения на выражение с переменной. Так как это действие не является равносильным, проверим, не потеряли ли мы корни.
Если , то . То есть при подстановке в уравнение (1) таких значений х, при которых , оно не обратиться в верное числовое равенство, а значит такие х корнями исходного уравнения не являются, и значит наше действие не приведет к потере корней.
Рассмотрим конкретный пример.
Пример 1.
Решить уравнение:
Решение:
.
Ответ:
Решим теперь однородное тригонометрическое уравнение второй степени
Общий вид такого уравнения:
(2)
Так же, как и уравнение (1), разделим его на наибольшую степень косинуса х.
Так же, как и при решении уравнения (1), мы должны убедиться в том, что при делении уравнения на выражение с переменной мы не потеряли корней. Это не произойдет в том случае, если .
После деления мы получили квадратное уравнение относительно тангенса х, которое и решаем известными способами.
.
При решении этого уравнения мы можем вводить новую переменную , но можем этого и не делать.
.
В зависимости от значения дискриминанта этого квадратного уравнения оно может иметь от 0 до 2 корней. И, соответственно, исходное уравнение может иметь две серии решений, одну или ни одной.
Рассмотрим пример.
Пример 2.
Решить уравнение:
Решение:
.
.
Ответ: .
Даже если исходное тригонометрическое уравнение второй степени не является однородным, можно его преобразовать к такому виду.
Рассмотрим это сначала на примере уравнения второй степени.
Пример 3.
Решить уравнение:
Решение:
Сначала умножим 3 на тригонометрическую единицу, то есть на выражение
(. Мы получим:
Теперь преобразуем полученное уравнение к однородному виду:
Теперь решим полученное однородное уравнение:
.
.
Ответ:.
3. Теперь рассмотрим, как можно привести к однородному уравнение вида
, то есть левая часть которого является однородной первой степени, а в правой стоит число.
Рассмотрим это на примере.
Пример 4.
Решение:
Используем формулы двойного аргумента:
Подставим их в исходное уравнение и домножим на тригонометрическую единицу 2, стоящую в правой части.
.
.
Ответ:.
Заметим, что подобные уравнения можно решить и по-другому, а именно, применив формулу вспомогательного аргумента:
Рассмотрим решение примера 4 этим способом.
Пример 4-а.
Решение:
Преобразуем левую часть:
Ответ:
Мы видим, что результат, полученный при решении разными способами, кажется разным. Но на самом деле в тригонометрии одно и то же число может быть записано разными способами.
Можно сказать, что первый способ в этом случае приводит к более короткому и красивому результату.
Решите уравнение
Решение:
В такой записи уравнение не является однородным.
Используем формулу синуса двойного аргумента.
Теперь уравнение однородное.
Решим его.
, .
Ответ: .
Решить уравнение
1) с помощью формулы вспомогательного аргумента
Решение
Ответ:
2) с помощью формул синуса и косинуса двойного аргумента
Решение
Ответ:
3) Решите уравнение:
Решение
Ответ:
4. Рассмотрим теперь решение тригонометрических уравнений с использованием универсальной тригонометрической подстановки.
Она называется универсальной, так как позволяет любое уравнение вида
(*), где рациональная функция, свести к рациональному алгебраическому уравнению.
Универсальная тригонометрическая подстановка – это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:
То есть если сразу обозначить , то уравнение (*) примет вид: .
А так как сама функция F является рациональной, то и получающееся уравнение будет рациональным алгебраическим.
Рассмотрим пример 5.
Решить уравнение .
Решение:
Область определения исходного уравнения:
Преобразуем исходное уравнение:
или
Используем универсальную тригонометрическую подстановку.
Если , то получим уравнение:
Решим его.
, .
Ответ: .
Заметим, что когда мы используем универсальную тригонометрическую подстановку, у нас появляется тангенс половинного угла, который не всегда определен. Поэтому мы можем потерять корни. Нужно проверить.
определен для всех .
Так как эти числа, не принадлежат области исходного уравнения, то мы не потеряем корней.
Решите уравнение
Рассмотрим решение уравнения
(**)
Решение:
Найдем область допустимых значений:
Теперь используем универсальную тригонометрическую подстановку и формулу тангенса суммы аргументов.
Область допустимых значений полученного уравнения уже, чем исходного:
.
Решим полученное уравнение:
.
Но необходимо проверить те числа, которые выпали из области определения после использования универсальной тригонометрической подготовки.
Это числа вида .
Подставим π в (**): верное равенство. Это означает, что числа вида тоже являются решениями исходного уравнения.
Таким образом, получается ответ.
.
Ответ: .
Примеры и разбор решения заданий тренировочного модуля
№ 1.
Даны уравнения.
Запишите номера однородных уравнений
Ответ: однородными являются 1), 5) , 7) и 8) уравнения.
№ 2.
Даны уравнения.
Распределите их по группам в зависимости от того, являются они однородными или не являются.
Однородные уравнения | Неоднородные уравнения |
№ 3.
Даны уравнения.
Выделите цветом уравнения, которые могут быть приведены к однородному
Ответ:
№ 4.
Автоматически заполняемый кроссворд.
Решите уравнения. Укажите значение k, при котором его корень становится больше .
1)
k=1
Слово МИНУС
2)
k=1
Слово КОРЕНЬ
3)
k= 2
Слово РАВЕНСТВО
№ 5.
Выберите простейшие тригонометрические уравнения, которые получаются при решении данного уравнения
Ответ: 16
№ 6.
Подчеркните простейшее тригонометрическое уравнение вида , которое получается при решении данного уравнения
1)
2)
3)
4)
5)
Ответ: 3
№ 7.
Выберите из списка простейшие тригонометрические уравнения вида , которые получаются при решении данного уравнения.
1)
2)
3)
4)
5)
6)
Ответ: 25
№ 8.
Решите уравнение
Перетащите в ответ составляющие
1)
2)
3)
4)
5)
6)
Ответ:
№ 9*.
Автоматически заполняемый кроссворд
Решите уравнения. Определите, сколько корней имеет каждое из этих уравнений на интервале (-π; π).
Ответ: 4
Слово ПРОМЕЖУТОК
Ответ: 20
Слово ОТРЕЗОК
Ответ: 8
Слово ИНТЕРВАЛ
№ 10.*
Заполните пропуски в решении.
Растащите элементы по пропускам
Домножим второе и третье слагаемые на ____________
____+_____
Разделим уравнение на ___________
___+____-1=0
После решения вспомогательного уравнения получим:
Получим ответ:
Элементы для перетаскивания
тригонометрическую единицу
Ответ:
Домножим второе и третье слагаемые на тригонометрическую единицу
Разделим уравнение на
Получим ответ:
№ 11.
*АЗК
Решите уравнение. Впишите в формулу ответа правильные коэффициенты.
Ответ:
№ 12.**
Решите уравнение.
Выберите серии, из которых состоит решение
1)
2)
3)
4)
5)
6)
7)
Ответ: 3, 5, 6
№ 13.**
Автоматически заполняемый кроссворд
Выберите номер наименьшего положительного корня
1) 1
2)
3)
4)
5)
6)
7)
Ответ: 2
Слово РЕШЕНИЕ
Выберите номер наименьшего положительного корня
1) 1
2)
3)
4)
5)
6)
7)
Решение:
Умножим второе и третье слагаемые на тригонометрическую единицу:
Разделим уравнение на
Вспомогательное уравнение:
Оно имеет единственный корень t=1
Ответ: 5
Слово ТРИГОНОМЕТРИЯ
Выберите номер правильного ответа
1) 1
2)
3)
4)
5)
6)
7)
Ответ: 4
Слово АЛГЕБРА
№ 14.
**АЗК
Решите уравнение. Впишите в формулу ответа правильные коэффициенты.
Решение:
Разделим обе части уравнения на
Введем новую переменную: .
Вспомогательное уравнение:
Так как t неотрицательное, то t=1.
Поэтому
1)
2)
3)
Ответ:
Проверочная работа:
№ 1.
А)Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ:
1) a=1 слово ТРИГОНОМЕТРИЯ
2) b=12 слово КОСИНУС
3) c=1 слово МИНУС
4) d=2 слово КВАДРАТ
Ответ:
Б)Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ:
1) a=1 слово УРАВНЕНИЕ
2) b=6 слово СИНУС
3) c=1 слово СТЕПЕНЬ
4) d=2 слово ТОЖДЕСТВО
Ответ:
№ 2.
А)Решите уравнение. Выберите наибольший отрицательный корень.
Б) Решите уравнение.
Выберите наименьший положительный корень
Ответ:
№ 3.
А)Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ: а = 30 слово ДЕЛИМОЕ, b = 2 слово ДЕЛИТЕЛЬ, c = 5 слово ЧАСТНОЕ
Б)Автоматически заполняемый кроссворд
Решите уравнение. Введите значения коэффициентов
Ответ: а = 18 слово МНОЖИТЕЛЬ, b = 2 слово ПРОИЗВЕДЕНИЕ, c = 3 слово УМНОЖЕНИЕ
Методы, используемые для решения тригонометрических уравнений. Алгебра, 10 класс: уроки, тесты, задания.
| 1. |
Тригонометрическое уравнение вида sinx = a
Сложность: лёгкое |
2 |
2.
|
Тригонометрическое уравнение вида cosx = a
Сложность: лёгкое |
2 |
| 3. |
Тригонометрическое уравнение вида tgx = a
Сложность: лёгкое |
2 |
4.
|
Тригонометрическое уравнение вида sin5x = a
Сложность: среднее |
3 |
| 5. |
Уравнение (разложение на множители, sin, cos)
Сложность: среднее |
3 |
6.
|
Уравнение (использование формулы двойного угла)
Сложность: среднее |
4 |
| 7. |
Уравнение (разложение на множители, sin, tg)
Сложность: сложное |
3 |
8.
|
Уравнение (введение новой переменной, sin)
Сложность: сложное |
2 |
| 9. |
Уравнение (введение новой переменной, tg)
Сложность: среднее |
2 |
10.
|
Уравнение (равенство произведения нулю)
Сложность: сложное |
2 |
Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений»
III. Объяснение нового.1.
В предыдущих параграфах были выведены формулы корней простейших тригонометрических уравнений: sin x=a, cos x=a, tg x=a
К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства из них требуется применение формул преобразований тригонометрических выражений.
Сегодня на уроке мы рассмотрим уравнение, сводящиеся к квадратным.
2.
а) 3х-8=х+6 (линейное уравнение)
б) х2+2х-15=0 (квадратное уравнение)
в) х4-5х2+4=0 (квадратное уравнение относительно х2).
г) 2 cos2x-cosx-1=0 (квадратное уравнение относительно cosx)
ax2+bx+c=0
,
Корни квадратного уравнения, приведенного, т.е. х2+рх+q=0 можно находить по теореме Виета:
Х1+х2=-р; х1х2=q
х4-5х2+4=0 – квадратное уравнение относительно х2. Это уравнение назвали биквадратным. Общий вид ах4+вх2+с=0, где а± 0.
Его легко решить методом введения новой переменной, т.е. х2=а и уравнение принимает вид: а2-5а+4=0
3.
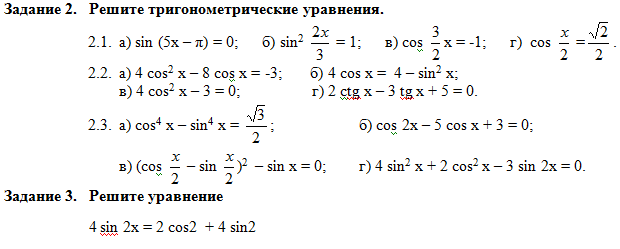Последнее уравнение тоже квадратное, относительно cosx. Для его решения введем новую переменную. Пусть y=cosx, тогда уравнение можно записать виде: 2у2-у-1=0. Получили квадратное уравнение.
Д=1+8=9;
Следовательно:
а) cosx=1 б) cosx=
х=2p n, n z , n z
, n n
Ответ: 2 n, n z; , n z
4. Решим уравнение:
Надо привести уравнение к одной функции. Для этого заменим cos2 x на 1-sin2x. Получим относительно xinx квадратное уравнение:
Пусть xinx=у, тогда 2у2+5у-3=0
Получили квадратное уравнение
Д=25+24=49
;
Следовательно:
а) б) xinx=-3 – решение не имеет
, к z
, к z
Ответ: , к z
5.
tgx-2ctgx=-1. Функции разные. Используя тождество tgx? ctgx=1, выразим , заменим ctgxчерез tgx.
пусть tgx=у, то у2+у-2=0 (дальше, как в предыдущем случае).
6. Для закрепления
4 xin2x- cosx-1=0
Заменим xin2x на 1- cos2x. Получим
4(1- cos2x)- cosx-1=0
4-4 cos2x- cosx-1=0
-4 cos2x- cosx+3=0
4 cos2x+ cosx-3=0
пусть cosx=у, то
4у2+у-3=0
Д=1-48=49 ;
Следовательно,
а) cosx=-1 б)
х= +2 n, n z , n z
Ответ: +2 n; , n z
7. №164 (в) — cамостоятельно
2 xin2x- xinx-1=0
пусть xinx=у, то
2у2-у-1=0
Д=1+8=9;
Следовательно,
а) xinx=1 б)
, n z , n z
,к z.
Ответ: , n z
, к z
№ 165(б)
2 xin2x+3 cosx=0
Заменим xin2x на 1- cos2x получим
2(1- cos2x)+3 cosx=0
2-2 cos2x+3 cosx=0
-2 cos2x+3 cosx+2=0, т.
е.
2 cos2x-3 cosx-2=0
пусть cosx=у, то
2у2-3у=0
Д=9+16=25
;
Следовательно,
а) cosx=2 б)
решение не имеет , n z
, n z
, n z
Ответ: , n z
8.
Итог урока
Алгоритм решения тригонометрических уравнений.
Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества.
Ввести новую переменную.
Записать данное уравнение, используя эту переменную.
Найти корни полученного квадратного уравнения.
Перейти от новой переменной к первоначальной.
Решить простейшие тригонометрические уравнения.
Записать ответ.
Решение простейших тригонометрических неравенств | Подготовка к ЕГЭ по математике
Часть 1.(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков , .
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие – левее точки на оси косинусов.
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до .
Обратите внимание, многие, назвав первую точку вместо второй точки указывают точку , что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные – правее точки , включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что .
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси синусов
Все значения , большие или равные – выше точки , включая саму точку.
«Транслируем» выделенные точки на тригонометрический круг:
Пример 4.
Решить неравенство:
Решение:
Кратко:
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению , так как область значений функции –
Пример 6.
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
Если не очень понятно, загляните сюда –>+ показать
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен
А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.
Поэтому
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3.
Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
План-конспект урока по математике на тему «Примеры решения тригонометрических уравнений»
Министерство образования и молодежной политики Чувашской Республики
Автономное учреждение Чувашской Республики
среднего профессионального образования
«Чебоксарский техникум транспортных и строительных технологий»
План-конспект урока
по дисциплине: Математика: алгебра и начала математического анализа; геометрия
по теме: «Примеры решения тригонометрических уравнений»
Разработала:
преподаватель математики
Андреева Н.
А.
Чебоксары 2012г.
План урока
Дисциплина | Математика |
Тема программы | Примеры решения тригонометрических уравнений |
Тема урока | Примеры решения тригонометрических уравнений |
Тип урока | Урок усвоения навыков и умений |
Оборудование урока | 1) компьютер 2) раздаточный материал 3) таблица |
Цель урока: | Формирование
навыков решения тригонометрических уравнений, сводящих к квадратным
уравнениям. |
Задачи: |
|
Обучающие: | Повторить основные тригонометрические формулы, формулы корней простейших тригонометрических уравнений, решение квадратных уравнений, решение простейших тригонометрических уравнений. |
Развивающие: | Способствовать развитию практических навыков решения тригонометрических уравнений, умений выделять главное, логически излагать свои мысли, умение работать по заданному алгоритму. |
Воспитательные: | Воспитывать интерес к предмету, самостоятельность, умения оценивать свои знания, учиться работать на доверии. |
Методы обучения | Словесный Наглядно-демонстративный Практический |
Форма обучения | Фронтальная Индивидуальная |
Ход урока
1.
Организационный момент (1мин.)
2. Постановка цели (3мин.)
3. Актуализация опорных знаний (10мин.)
3.1 Проверка знаний основных формул.
3.2 Устная работа.
3.3 Тест на умения.
3.4 Проверка домашнего задания.
4. Закрепление знаний и умений (25мин.)
4.1 Тренировочные упражнения.
4.2 Самостоятельная работа.
5. Домашнее задание(1мин.).
6. Подведение итогов (5мин.)
План-конспект урока
1.Организационный момент
Преподаватель: Здравствуйте, ребята. Здравствуйте наши гости. Садитесь.
Пусть эпиграфом сегодняшнего урока будет «Уравнения – золотой ключ, открывающий все математические сезамы» (С. Коваль).
Открывайте тетради, запишите число и тему сегодняшнего урока «Примеры решения тригонометрических уравнений».
2.Постановка цели
Преподаватель: Давайте поставим цель урока.
Что мы
изучали на прошлом уроке?
Обучающийся: решали тригонометрические уравнения, приводящие к квадратным уравнениям.
Преподаватель: Что мы должны знать для того, чтобы решить уравнения.
Обучающийся: 1) решение квадратных уравнений (формула дискриминанта, свойства дискриминанта, формулы корней)
2) таблицу обратных тригонометрических функций
3) решение простейших тригонометрических уравнений (формулы корней)
Значит, на уроке мы должны использовать наши знания и умения и закрепить решение тригонометрических уравнений, приводящие к квадратным уравнениям. На партах оценочные листы. В течения урока вы должны оценить каждый вид задания, согласно критериям. И в конце урока выполним самостоятельную работу, чтобы оценить ваши знания.
3.Актуализация опорных знаний
В математике всегда приходиться опираться на предыдущие знания, ее нельзя изучать отрывками, необходима систематическая работа.
Давайте
проверим, что мы знаем (показ слайдов).
1) Решение квадратных уравнений вида
2) Основные тригонометрические формулы
3) Формулы корней простейших тригонометрических уравнений
Преподаватель: Проверим, что мы умеем?
1) Устная работа
Какие из уравнений имеют решения?
| Вычислите:
|
Оцените устную работу, согласно критериям. Поставьте, пожалуйста, отметку в оценочный лист.
2) тестовая работа (показ слайда)
С помощью теста проверим решение простейших тригонометрических уравнений.
Решите уравнения:
Ответы: 1) а; 2) в; 3) б; 4) а; 5) (а)
Поставьте, пожалуйста, отметку за тест в оценочный лист.
3) проверка домашнего задания (правильное решение на слайде)
№164(г)
№165(а)
№165(б)
Преподаватель:
Расскажите алгоритм решения этого
примера.
Обучающийся: перечисляет и описывает шаги решения.
Поставьте, пожалуйста, отметку за домашнее задание в оценочный лист.
4. Закрепление знаний и умений (тренировочные упражнения)
Используем эти знания и умения при решении тригонометрических уравнений, приводящих к квадратным уравнениям.
А теперь решаем по учебнику № 165(в), 166(б) на доске.
Для тех, кто закончит раньше дополнительные примеры № 165 (г).
Выполним самостоятельную работу (карточки-задания)
1 уровень
Вариант 1
Решите уравнения:
Вариант 2
Решите уравнения:
2 уровень
Вариант 1
Решите уравнения:
Вариант 2
Решите уравнения:
5. Домашнее задание
№ 166(в), 167(а).
6. Подведение итогов
Все
ваши оценки суммируются и средняя оценка ставится в журнал.
Посмотрите на дерево и подумайте, на какой высоте Вы находились, или ощущали себя, во время этого урока.
Преподаватель: я думаю, что все оказались на дереве, и никто не сорвался. Еще будем рассматривать другие способы решения тригонометрических уравнений, и все окажемся на вершине.
Преподаватель: «Уравнения – золотой ключ, открывающий все математические сезамы» (С. Коваль).
Мне хотелось бы Вам пожелать, чтобы каждый из Вас нашел в жизни свой золотой ключ, с помощью которого перед Вами открывались бы любые двери.
Урок окончен. Спасибо за работу. Будьте здоровы.
Оценочный лист
Фамилия, имя _______________________________________
№ п/п | Виды работ | Оценка | Критерии оценивания |
1) | Устный счет |
| Самооценка |
2) | Тестовая работа |
| «5»-5 правильных ответов «4»-4 правильных ответов «3»-3 правильных ответов |
3) | Домашняя работа |
| «5»-3 правильных примеров «4»-2 правильных примеров «3»-1 правильный пример |
4) | Самостоятельная работа |
| Оценка преподавателя |
5.
Тригонометрические уравненияМ. Борна
Тригонометрические уравнения могут быть решены с помощью алгебраические методы и тригонометрические тождества и ценности обсуждалось в предыдущих разделах. Возможно, вы захотите вернуться и взглянуть на тригонометрические функции любого угла, где мы видим предысторию следующих решений.
Безболезненный способ решить эти проблемы — использовать график. Там, где график пересекает ось x , вы найдете свои решения (значения x , которые «работают»).Графики также помогают понять, почему иногда есть один ответ, а иногда — много ответов. Я использую Scientific Notebook или аналогичную математическую программу для построения графиков функций.
Вы можете использовать этот онлайн-калькулятор для построения графиков, чтобы решить следующие уравнения (или проверить свои решения).
Пример 1
Решите уравнение 2 cos θ — 1 = 0 для 0 ≤ θ <2 π .
Ответ
Преобразуя приведенное выше уравнение, получаем:
`cos theta = 1 / 2`
Нам известно следующее:
С
`cos (pi / 3) = 1 / 2`
и `cos θ` положителен в первом и четвертом квадрантах, мы имеем:
`тета = пи / 3`
или
`theta = 2pi-pi / 3 = (5pi) / 3`
Итак, `theta = pi / 3` или` theta = (5pi) / 3`
Пример 2
Решите графически уравнение
2 cos 2 x — sin x — 1 = 0
такой, что 0 ≤ θ <2 π .
Ответ
Используя программное обеспечение для построения графиков, мы рисуем кривую y = 2 cos 2 x — sin x — 1 в области 0 ≤ θ <2π. Везде, где кривая пересекает ось x , будет решением нашего уравнения.
Мы видим из графика, что решения примерно:
x = 0,5
x = 2,6
x = 4,7
Для получения более точных решений мы просто увеличим масштаб графика.
На следующем графике я увеличил масштаб до второго корня (около x = 2,6). Мы видим, что этот корень равен x = 2,618 с точностью до 3 знаков после запятой.
Мы можем продолжать увеличивать изображение настолько близко, насколько захотим, чтобы получить требуемую точность.
Решение уравнений, кратных
θПример 3
Решите уравнение sin 2 θ = 0,8 для 0 ≤ θ <2π.
Ответ
Если проблема касается только θ , мы ожидаем 2 решения; один
в первом квадранте и один во втором квадранте.
Но здесь наша задача включает в себя `2θ`, поэтому мы должны удвоить область ( θ значений) для учета всех возможные решения.
Действуем следующим образом:
Решаем
`sin 2θ = 0,8` для 0 ≤ 2 θ <4 π .
Базовый угол
`α = arcsin 0,8 = 0,9273`
Значения для 2 θ будут в квадрантах I, II, V, VI.
2 θ = 0.9273, или π — 0,9273, или 2 π + 0,9273, или 3 π — 0,9273
То есть
`2θ = 0,9273, 2,2143, 7,2105, 8,4975`
Но нам нужны значения для θ , а не 2 θ , поэтому разделим на 2:
`θ = 0,4637, 1,1072, 3,6053, 4,2488`
Наши ответы верны? В виде обычно, мы проверим, построив график исходного выражения:
Из графика видно, что
наши 4 значения разумны, так как это единственные 4 значения
которые удовлетворяют `sin 2θ = 0.
2theta = 1/16`
для 0 ≤ θ <2π.
Ответ
Решение относительно cos θ дает:
`cos theta = + — 1 / 4`
Если cos alpha = 1/4, то ссылка угол α = 1,3181.
Таким образом, для cos theta = 1/4 мы имеем θ в первом и четвертом квадрантах. Итак
`θ = 1,3181 или 4,9651`
Для cos theta = -1 / 4, мы имеем θ во 2-м и 3-м квадрантах.2θ — грех θ — 1 = 0`
`(2 sin θ — 1) (3 sin θ + 1) = 0`
Так либо
`2 sin θ — 1 = 0`
`грех θ = 1 / 2`
θ будет в 1-м и 2-м квадрантах.
`θ = 0,52360, 2,6180` (то есть` pi / 6` или `(5pi) / 6`)
ИЛИ
`3 грех θ + 1 = 0`
`sin θ = — 1 / 3`
θ будет в 3-м и 4-м квадрантах.
`θ = 3. 4814, 5. 9433`
Проверяем наше решение на график:
Так что `θ =
0.
2 \ х + 3 \ соз х + 1 = 0`
`(2 \ co \ s x + 1) (cos x + 1) = 0`
Решая, получаем
`cos x = — 0,5` или` cos x = — 1`
Теперь `cos x = -1 / 2` дает` x = (2pi) / 3, (4pi) / 3`.
Однако при проверке исходного уравнения , отметим, что
`» LHS «= cos ((4pi) / 3xx1 / 2)` `= cos ((2pi) / 3)` = -1 / 2`
но
«» RHS «= 1 + cos (4pi) / 3 = + 1 / 2`
Итак, единственное решение для этой части — `x = (2pi) / 3.`
Кроме того, cos x = -1 дает x = pi.
Итак, решение уравнения: `x = (2pi) / 3or pi.`
Проверка графика y = cos x / 2-1-cos x подтверждает эти результаты:
(2π / 3 ≈ 2,0944 и π ≈ 3,14).
Пример 7
Решите уравнение
загар 2 θ — детская кроватка 2 θ = 0
для 0 ≤ θ <2π.
Ответ
`cot 2theta = 1 / (tan 2 theta)`, поэтому имеем:
`tan 2 theta-1 / (tan 2 theta) = 0`
`тангенс ^ 2 2θ = 1`
`tan 2θ = ± 1`
Поскольку `0 ≤ θ <2π`, нам нужно учитывать такие значения` 2theta`, что `0 ≤ 2θ <4π`.
Следовательно, решая
в приведенном выше уравнении имеем:
`2 theta = pi / 4, (3pi) / 4, (5pi) / 4 (7pi) / 4,` `(9pi) / 4, (11pi) / 4,` (13pi) / 4, (15pi) ) / 4`
Разделение на 2 дает нам полный набор решений в требуемой области, `0 <= theta <2pi`:
`theta = pi / 8, (3pi) / 8,` `(5pi) / 8, (7pi) / 8, » (9pi) / 8, (11pi) / 8,` `(13pi) / 8, (15pi) / 8`
Упражнения
Примечание 1: «Аналитически» означает использование методов и формул из предыдущих разделов.Это означает, что для ее решения нельзя просто использовать график.
Примечание 2: Однако я всегда использую график для проверки своей аналитической работы. Я сразу вижу, произошла ли какая-то ошибка. Я призываю вас поступить так же!
1. Решите тригонометрическое уравнение аналитически
4 загар x — сек 2 x = 0 (для 0 ≤ x <2 π )
Ответ
`4 \ tan x− sec ^ 2x = 0`
Записывая это только в терминах `sin x` и` cos x`:
`4 (sin x) / (cos x) -1 / (cos ^ 2x) = 0`
Умножение на `cos x`:
`4 \ sin x \ cos x = 1`
Делим обе стороны на 2:
`2 \ sin x \ cos x = 1 / 2`
Распознавание LHS — это `sin 2x`, от до:
`sin 2x, = 0.
5`При 0 ≤ x <2π нам нужно найти значения 2 x такие, что 0 ≤ 2 x <4π. (В два раза больше исходного домена.)
Значит, 2x:
.`2x = pi / 6, (5pi) / 6, (13pi) / 6, (17pi) / 6`
Если разделить на 2, то получим требуемые значения для `x`:
`x = pi / 12, (5pi) / 12, (13pi) / 12, (17pi) / 12`
или в десятичной форме:
`х = 0,2618, 1,309, 3.403, 4.451`
2. Решите тригонометрическое уравнение. аналитически для 0 ≤ x <2 π :
sin 2 x cos x — cos 2 x sin x = 0
Ответ
Мы узнаем, что левая сторона находится в форма:
`sin (a — b) =` sin a cos b — cos a sin b, `
, где `a = 2x` и` b = x`.
Так
`sin 2x \ cos x — cos 2x \ sin x`
`= sin (2x — x)`
`= грех x`
Теперь мы знаем решения `sin x = 0` быть:
`x = 0, π`.
[Почему?]
3. Решите данное тригонометрическое уравнение. аналитически и графическим методом (для 0 ≤ x <2 π ):
sin 4 x — cos 2 x = 0
Ответ
sin 4 x — cos 2 x = 0
2sin 2 x cos 2 x — cos 2 x = 0
Факторинг дает:
cos 2 x (2 sin 2 x — 1) = 0
ЛИБО
`cos 2x = 0`
`2x = pi / 2, (3pi) / 2, (5pi) / 2, (7pi) / 2`
`x = pi / 4, (3pi) / 4, (5pi) / 4, (7pi) / 4`
ИЛИ
`грех 2x = 1 / 2`
`2x = pi / 6, (5pi) / 6, (13pi) / 6, (17pi) / 6`
`x = pi / 12, (5pi) / 12, (13pi) / 12, (17pi) / 12`
Или в десятичной форме:
`х = 0.26, 0,79, «1,31, 2,36,« 3,40, 3,93, «4.45, 5.50.»
График y = sin 4x− cos 2x выглядит следующим образом.
Мы можем видеть, откуда график пересекает ось x , что наши ответы разумны.
Решение тригонометрических уравнений — тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Тригонометрические уравнения
Тригонометрические тождества верны для всех значений замены для переменных, для которых определены обе части уравнения.
Условные тригонометрические уравнения верны только для некоторых значений замены.Решения в определенном интервале, например 0 ≤ x ≤ 2π, обычно называются первичными решениями . Общее решение — это формула, в которой перечислены все возможные решения.
Процесс решения общих тригонометрических уравнений не является однозначным. Не существует правил, которые всегда приводят к решению. Процедура обычно включает использование тождеств, алгебраические манипуляции, проб и ошибок. Следующие рекомендации могут помочь найти решение.
Если уравнение содержит более одной тригонометрической функции, используйте тождества и алгебраические манипуляции (например, разложение на множители), чтобы переписать уравнение в терминах только одной тригонометрической функции. Найдите выражения в квадратичной форме и решите их с помощью разложения на множители. Не все уравнения имеют решения, но те, которые имеют, обычно могут быть решены с использованием соответствующих тождеств и алгебраических манипуляций.
Ищите шаблоны. Нет замены опыту.
Пример 1: Найдите точное решение:
Сначала преобразуйте уравнение, используя тождество sin 2 α + cos2α = 1.
Следовательно,
Таким образом,
Пример 2: Решите cos 2 x = 3 (sin x — 1) для всех действительных значений x .
Первый ответ, −2,351, не является решением, так как функция синуса должна находиться в диапазоне от -1 до 1. Второй ответ, 0,8508, является допустимым значением. Таким образом, если k — целое число,
В радианах,
По форме,
Пример 3 : Найдите точное решение:
Сначала преобразуйте уравнение, используя тождество двойного угла cos 2θ = 2 cos 2 θ — 1.\ circ \)
6.4 Тригонометрические уравнения | Тригонометрия
\ (\ sin \ theta = \ text {0,6} \)
\ begin {align *} \ sin \ theta & = \ text {0,6} \\ \ text {ref} \ angle & = \ sin ^ {- 1} \ text {0,6} \\ & = \ текст {36,9} \ текст {°} \\ \ поэтому \ theta & = \ text {36,9} \ text {°} \ end {выровнять *}Во втором квадранте:
\ begin {align *} \ theta & = \ text {180} \ text {°} — \ text {36,9} \ text {°} \\ & = \ текст {143,1} \ текст {°} \ end {выровнять *}Отрицательные углы:
\ begin {align *} \ theta & = \ text {36,9} \ text {°} — \ text {360} \ text {°} \\ & = — \ text {323,1} \ text {°} \\ \ text {And} \ theta & = \ text {143,1} \ text {°} — \ текст {360} \ текст {°} \\ & = — \ текст {216,9} \ текст {°} \ end {выровнять *}\ (\ theta = — \ text {323,1} \ text {°}; — \ text {216,9} \ text {°}; \ текст {36,9} \ текст {°}; \ text {143,1} \ text {°} \)
\ (\ cos \ theta + \ frac {3} {4} = 0 \)
\ begin {align *} \ cos \ theta + \ frac {3} {4} & = 0 \\ \ cos \ theta & = — \ frac {3} {4} \\ \ text {ref} \ angle & = \ cos ^ {- 1} \ left (\ frac {3} {4} \ right) \\ & = \ текст {41,4} \ текст {°} \ end {выровнять *}Во втором квадранте:
\ begin {align *} \ theta & = \ text {180} \ text {°} — \ text {41,4} \ text {°} \\ & = \ текст {138,6} \ текст {°} \ end {выровнять *}В третьем квадранте:
\ begin {align *} \ theta & = \ text {180} \ text {°} + \ text {41,4} \ text {°} \\ & = \ текст {221,4} \ текст {°} \ end {выровнять *}Отрицательные углы:
\ begin {align *} \ theta & = \ text {138,6} \ text {°} — \ текст {360} \ текст {°} \\ & = — \ text {221,4} \ text {°} \\ \ text {And} \ theta & = \ text {221,4} \ text {°} — \ текст {360} \ текст {°} \\ & = — \ текст {138,6} \ текст {°} \ end {выровнять *}\ (\ theta = — \ text {221,4} \ text {°}; — \ text {138,6} \ text {°}; \ текст {138,6} \ текст {°}; \ text {221,4} \ text {°} \)
\ begin {align *} 3 \ tan \ theta & = 20 \\ \ tan \ theta & = \ frac {20} {3} \\ \ text {ref} \ angle & = \ tan ^ {- 1} \ left (\ frac {20} {3} \ right) \\ & = \ текст {81,5} \ текст {°} \\ \ theta & = \ text {81,5} \ text {°} \ end {выровнять *}В третьем квадранте:
\ begin {align *} \ theta & = \ text {180} \ text {°} + \ text {81,5} \ text {°} \\ & = \ текст {261,5} \ текст {°} \ end {выровнять *}Отрицательные углы:
\ begin {align *} \ theta & = \ text {81,5} \ text {°} — \ text {360} \ text {°} \\ & = — \ text {278,5} \ text {°} \\ \ text {And} \ theta & = \ text {261,5} \ text {°} — \ текст {360} \ текст {°} \\ & = — \ текст {98,5} \ текст {°} \ end {выровнять *}\ (\ theta = — \ text {278,5} \ text {°}; — \ text {98,5} \ text {°}; \ текст {81,5} \ текст {°}; \ text {261,5} \ text {°} \)
\ (\ sin \ theta = \ cos \ text {180} \ text {°} \)
\ begin {align *} \ sin \ theta & = \ cos \ text {180} \ text {°} \\ \ sin \ theta & = -1 \\ \ text {ref} \ angle & = \ sin ^ {- 1} \ left (1 \ right) \\ & = \ текст {90} \ текст {°} \ end {выровнять *}В третьем квадранте:
\ begin {align *} \ theta & = \ text {180} \ text {°} + \ text {90} \ text {°} \\ & = \ текст {270} \ текст {°} \ end {выровнять *}Отрицательные углы:
\ begin {align *} \ theta & = \ text {270} \ text {°} — \ text {360} \ text {°} \\ & = — \ текст {90} \ текст {°} \ end {выровнять *}\ (\ theta = — \ text {90} \ text {°}; \ text {270} \ text {°} \)
\ (2 \ cos \ theta = \ frac {4} {5} \)
\ begin {align *} 2 \ cos \ theta & = \ frac {4} {5} \\ \ cos \ theta & = \ frac {2} {5} \\ \ text {ref} \ angle & = \ cos ^ {- 1} \ left (\ frac {2} {5} \ right) \\ & = \ текст {66,4} \ текст {°} \\ \ theta & = \ text {66,4} \ text {°} \ end {выровнять *}В четвертом квадранте:
\ begin {align *} \ theta & = \ text {360} \ text {°} — \ text {66,4} \ text {°} \\ & = \ текст {293,6} \ текст {°} \ end {выровнять *}Отрицательные углы:
\ begin {align *} \ theta & = \ text {66,4} \ text {°} — \ text {360} \ text {°} \\ & = — \ text {293,6} \ text {°} \\ \ text {And} \ theta & = \ text {293,6} \ text {°} — \ текст {360} \ текст {°} \\ & = — \ текст {66,4} \ текст {°} \ end {выровнять *}\ (\ theta = — \ text {293,6} \ text {°}; — \ text {66,4} \ text {°}; \ текст {66,4} \ текст {°}; \ text {293,6} \ text {°} \)
Как решить тригонометрические уравнения второй степени
Тригонометрические уравнения
Проще говоря, тригонометрические уравнения — это просто уравнения, которые содержат тригонометрические отношения, такие как синус и косинус переменной «x».
2y-4 \ cos y +3 = 0cos2y − 4cosy + 3 = 0
Обратите внимание, что в приведенных выше уравнениях используется наш знакомый полиномиальный формат, но с добавлением тригонометрических соотношений синуса и косинуса. Теперь, когда у нас есть представление о том, как выглядят триггерные уравнения, давайте посмотрим, как решать триггерные уравнения!
Решение тригонометрических уравнений
Чтобы решить тригонометрические задачи, которые мы рассмотрим в этой статье, сначала важно убедиться, что вы хорошо знакомы с основными, нетригонометрическими функциями и отношениями, а также с факторизацией многочленов.Чтобы освежить память, вам помогут видеоролики о функциях умножения и факторизации трехчленов!
Имея в виду эти концепции, давайте приступим к решению тригонометрических уравнений. Существует множество различных методов решения триггерных проблем, поэтому в зависимости от того, куда вы посмотрите, вы можете получить много разных ответов! В этой статье дается подробный обзор двух основных методов, которые мы можем использовать для решения триггеров.
2 x + 3 \ sin x = 06sin2x + 3sinx = 0
Этот вопрос просит нас найти решения для x в диапазоне от 0 до 2pi.2 + 3w = 06w2 + 3w = 0
3w (2w + 1) = 03w (2w + 1) = 03w (2w + 1) = 0
Шаг 3: Решите относительно x
Надеюсь, вы помните, как решать разложенные на множители многочлены. В этом случае w = 0 и w = -1/2
Шаг 4. Замените w на sinx и измените решения
Теперь, когда мы решили уравнение для w, мы должны не забыть заменить w обратно на sin x и скорректировать наши решения, чтобы учесть это.
Следовательно: sin x = 0 и sin x = -1/2
Используя наш калькулятор или наши знания о неизменно важном единичном круге, мы приходим к следующим решениям: x = 0 и x = -pi / 6
Чтобы попрактиковаться в решении таких вычислений, ознакомьтесь с уроком по поиску тригонометрических значений.
Шаг 5: Найдите решения во всем заданном диапазоне
Хотя мы нашли решения для нашего уравнения, помните, что нас попросили найти всех решений в диапазоне 0≤x≤2π0 \ leq x \ leq 2 \ pi0≤x≤2π! Из-за повторяющегося характера функций синуса и косинуса у нас, вероятно, будет несколько значений x, которые могут решить это уравнение.
Кроме того, -pi / 6 не решает это уравнение, так как оно выходит за пределы допустимого диапазона.
Опять же, как и в большинстве случаев в математике, есть несколько способов найти другие значения x.Самый простой способ — быстро набросать синусоидальный график от 0 до 2pi и посмотреть, когда pi равно 0 и -1/2.
Взглянув на наше изображение выше, легко заметить, где sinx = 0, дает нам значения x 0, pi и 2pi . Теперь ищем sinx = -1/2, мы знаем из нашего начального решения –pi / 6, что sinx = -1/2 для некоторых кратных pi / 6. Глядя на наш график, становится ясно, что sinx = -1/2 для двух значений между пи и 2 пи, эти значения — пи + пи / 6 и 2 пи — пи / 6. Следовательно, дает нам значения x 7pi / 6 и 11pi / 6 .2 x + 3 \ cos x + 1 = 02cos2x + 3 cosx + 1 = 0
Для этого второго и последнего примера мы будем использовать Method 2 , который был описан ранее. Это означает, что мы не будем делать никакой замены и будем решать тригонометрическое уравнение как есть.
Шаг 1. Разложите на множители и упростите уравнение
(2cosx + 1) (cosx + 1) = 0 (2 \ cos x + 1) (\ cos x +1) = 0 (2cosx + 1) (cosx + 1) = 0
Шаг 2: Решить
Теперь, когда мы разложили на множители наше уравнение, легко решить и определить, что:
cosx = -1/2 и cosx = -1
Решение относительно x дает нам решения: x = 2pi / 3 и pi
Шаг 3. Найдите решения во всем заданном диапазоне
В этом примере, в отличие от первого, не указан указанный диапазон.Следовательно, мы должны давать решения, учитывающие постоянно повторяющийся характер функции косинуса. Кроме того, мы должны учитывать, что могут быть другие значения для x, которые наши калькуляторы не выплюнули. Опять же, лучший способ понять все это — взглянуть на график cosx.
Еще раз взглянув на график выше, легко заметить, когда cosx = -1. Cosx будет равен -1 в пи, повторяя каждый «n-й» (где n = целое) полный цикл (2pi) волны, таким образом, x = pi + n2pi .
Для cosx = -1 / 2 решение аналогично тому, как мы нашли наши решения в примере 1 . Кроме того, нам нужно помнить о повторяющейся природе, как мы это делали для решений для cosx = -1 для каждого полного цикла (2pi). Таким образом, функция будет равна -1/2 , когда x = 2pi / 3 = n2pi и когда x = 4pi / 3 + n2pi .
Таким образом, наш окончательный ответ: , таким образом, x = pi + n2pi, x = 2pi / 3 = n2pi и x = 4pi / 3 + n2pi
Вот и все! Чтобы узнать больше о тригонометрических уравнениях и о том, как они связаны с производными, ознакомьтесь с этим уроком о производных тригонометрических функций.
7.6 Решение квадратичных тригонометрических уравнений
|
73 или a ≐-0,23
Это приводит к квадратному тригонометрическому уравнению, которое можно решить алгебраически.
или графически.