Презентация к уроку (алгебра, 7 класс) по теме: Решение систем линейных уравнений способом сложения. 7 класс.

Слайд 1

Метод решения хорош, если с самого начала мы можем предвидеть – и далее подтвердить это, — что, следуя этому методу, мы достигнем цели. Г. Лейбниц

Слайд 2

Устный счет . Назовите решения уравнения: а) y = 2x + 5 б) x – y = 1 2 . Разложите на множители: а) 2a 2 +16a 5 б) 64х 2 — 9 3. В какой точке пересекаются прямые? x – y = 11 и y = 3 ?

Слайд 3

Тема урока «Решение систем линейных уравнений способом сложения».

Слайд 4

Цель урока : Научиться решать системы двух линейных уравнений с двумя переменными методом алгебраического сложения.

Слайд 5

Повторение. Что называется решением системы уравнений с двумя переменными? Какие способы решения систем двух линейных уравнений мы уже изучили?

Слайд 6

Восстановите алгоритм решения системы способом подстановки. Выразить из любого уравнения системы одну переменную через другую. Подставить полученное выражение вместо этой переменной в другое уравнение системы. Решить полученное уравнение с одной переменной. Найти соответствующее значение второй переменной.

Слайд 7

Самостоятельная работа .

Слайд 11

для чего мы выражали одну переменную через другую и подставляли полученный результат в первое уравнение? чтобы исключить одну переменную. Но её можно исключить и значительно проще – достаточно сложить оба уравнения системы.

Слайд 12

Разберем решение системы уравнений методом сложения

Слайд 17

Что необходимо, чтобы исключить одну из переменных? Для чего мы исключаем ее? Что мы делаем после решения уравнения с одной переменной? Попробуйте сформулировать алгоритм метода сложения.

Слайд 18

Алгоритм метода сложения. Привести уравнения системы к одинаковым по модулю коэффициентам при переменных x или y . Если коэффициенты одинаковы, то из одного уравнения вычесть другое. Если коэффициенты противоположны, уравнения складываются. Решить полученное уравнение с одной переменной Подставить полученное значение переменной в одно из уравнений и найти значение второй.

Слайд 20

Домашнее задание. Алгоритм № 1082 ( а,в ) № 1097( а,б ) № 1098 (а)

Разработка урока по алгебре на тему «Решение систем уравнений методом алгебраического сложения» (7 класс)

Тема урока: «Решение систем линейных уравнений методом алгебраического сложения»

Цели урока: познакомить обучающихся с методом решения систем уравнений методом алгебраического сложения;

Развивающая:

Развивать память, речь, наблюдательность, подмечать закономерность, обобщать, проводить логическое мышление, суждения по аналогии, умение работать с учебником.

Воспитательная:

Воспитание дисциплины, аккуратности, настойчивости, ответственного отношения к учёбе, умение контролировать свою деятельность.

Оборудование: ноутбук, проектор, доска.

ХОД УРОКА

1. Организационный момент.

Слайд 1.

Здравствуйте, ребята! Сегодня у нас на уроке будут присутствовать гости. Поприветствуйте их. Садитесь.

Учитель: Любой человек, который начинает какое-то новое дело, обычно задумывается над тем, что он хочет получить в результате, чего достичь. Давайте и мы подумаем, чего мы сегодня должны достичь на уроке?

Ученик: Познакомиться с новым методом решения систем. Научиться решать системы линейных уравнений методом алгебраического сложения.

Слайд 2. Девизом нашего урока будут слова «Математику нельзя изучать,
наблюдая как это делает сосед». А.Нивен.

Слайд 3. Учитель: Ничего нового не бывает без старого. Давайте ответим на вопросы.

Слайд 4

2. Ответить на вопросы

1. Что называют решением системы уравнений? (пару значений (х;у), которая является решением и первого и второго уравнений системы)

2. Сколько решений может иметь система двух линейных уравнений с двумя неизвестными? ( 1 решение, бесконечно много решений или не иметь решения)

3. Как называется система, если она не имеет решений? (система несовместна – прямые параллельны)

4. Как называется система, если она имеет бесконечно много решений (неопределенна – прямые совпадают)

5. Какие методы решения систем уравнений вам известны?

6. Сформулируйте алгоритм решения систем уравнений методом подстановки. — Слайд 5

Слайд 6

Решить систему методом подстановки

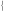у-х=30,

х-2у=80

1 ученик выполняет на интерактивной доске.

Решим систему способом подстановки, при этом ответим на вопросы:

1. Что нужно сделать? Выразить одну переменную через другую, например, х=80+2у.

2. Подставить полученное выражение в первое уравнение:

у- ( 80+2у)= 30

3. Решим полученное уравнение: 4у-80-2у=30, 2у=110, у=55.

4. Подставим найденное значение переменной в выражение, полученное в 1 и найдем х. х=80+ 2*55, х=190.

Ответ: (190, 55)

Изучение нового материала

Учитель: А теперь проанализируем, для чего мы выражали одну переменную через другую и подставляли полученный результат в первое уравнение?

Ученик: Чтобы получить уравнение с одной переменной.

Учитель: Правильно, чтобы исключить одну переменную. Но её можно исключить и значительно проще – достаточно сложить оба уравнения системы.

4у-х=30,

х-2у=80

4у-х+х-2у=30+80

2у=110

у= 110:2

у=55

Затем найденное значение переменной подставить в любое уравнение системы и найти значение другой переменной.

4*55 – х = 30

220- х = 30

-х = 30 -220

-х = -190

х= 190

Ответ: (190; 55)      

Рассмотрим еще один пример.

  Рассмотрим систему, где сложение уравнений на первом этапе  
        не позволяет исключить ни одной переменной.  

  

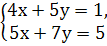
обратите внимание, коэффициент перед   х (1 уравнение)   =4, 
коэффициент перед   х (2 уравнение),     =5, найдем для этих двух чисел наименьшее общее кратное число — это 20 значит,  
умножим левую и правую часть 1-го уравнения на   5, а второго уравнения на 4:    

 

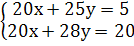
теперь мы можем вычесть второе уравнение из первого,  
   вычтем левую часть 2-го уравнения из левой части 1-го уравнения,  
     приравняв результат разности соответствующих правых частей,         

               3у=15

у=5

подставим полученное значение   y = 5 в любое уравнение системы,  
            например в 1-ое,  

 4х+5*5=1,

4х=-24,

х=-6

Ответ: (-6; 5)

Учитель: Теперь я думаю, что вы сможете сформулировать алгоритм метода алгебраического сложения (учащиеся формулируют, учитель корректирует)

Первичное закрепление в устной речи

Работа со слайдом: учащиеся читают алгоритм.

ФИЗМИНУТКА

Этап первичной проверки знаний

1. Решить систему методом алгебраического сложения

а) 2х-у=5,

х+у=7

б) 2х+у=-3,

3х+у=1

в) 2х+у =1

3х-у=4

г) 3х+4у=14,

5х+2у=14

д) е) ж)

                

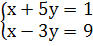
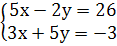
• 2. Работа с учебником

• Решить у доски

•  № 13.2, 13.5, 13.9 (а,б)

Этап проверки усвоения нового материала

Выполнение самостоятельной работы по карточкам с последующей самопроверкой

Самостоятельная работа

Вариант 1

Способом сложения решите систему линейных уравнений:

Самостоятельная работа (для слабых обучающихся)

Вариант 2

Способом сложения решите систему линейных уравнений:

х + у = 49,

-х + у =17

 Этап подведения итогов.

Д/з: № 13.2, 13.5, 13.9 (б)

Самостоятельная работа

Вариант 1

Способом сложения решите систему линейных уравнений:

 

Самостоятельная работа

Вариант 2

Способом сложения решите систему линейных уравнений:

х + у = 49,

-х + у =17.

Самостоятельная работа

Вариант 1

Способом сложения решите систему линейных уравнений:

 

Самостоятельная работа

Вариант 2

Способом сложения решите систему линейных уравнений:

х + у = 49,

-х + у =17.

Конспект урока по математике «Решение систем линейных уравнений способом сложения» (7 класс)

Муниципальное казенное общеобразовательное учреждение «Вечерняя (сменная) общеобразовательная школа №2 при ИК»

с. Чугуевка Чугуевского района Приморского края

План-конспект урока математики в 7 классе

по теме: «Решение систем линейных уравнений способом сложения».

Разработал:

учитель математики Черняк О.А.

План-конспект урока математики в 7 классе

Тема: Решение систем линейных уравнений способом сложения.

Методические цели:

Образовательные: вызвать объективную необходимость будущей деятельности; способствовать овладению знаниями по теме «Решение систем линейных уравнений»

Развивающие: содействовать развитию речи, мышления, познавательных и общетрудовых умений; содействовать овладению методами научного исследовании: анализа и синтеза.

Воспитательные: формировать добросовестное отношение к учебному труду, положительной мотивации к учению, коммуникативных умений; способствовать воспитанию гуманности, дисциплинированности, эстетического восприятия мира.

Тип урока: Урок изучения нового материала.

Форма работы учащихся: фронтальная, парная, индивидуальная.

План занятия:

I.Организационный этап. 1 мин.

II. Этап актуализации опорных знаний 3 мин.

III. Этап постановки целей и задач урока 5 мин.

IV. Этап первичного усвоения новых знаний 10 мин.

V. Физкультминутка 2 мин

VI. Этап закрепления изученного материала. Первичное закрепление. 16 мин

VII. Рефлексия. 2 мин.

VIII. Домашнее задание 1 мин.

Ход урока:

I. Организационный этап.

Слайд 1.

Учитель:

Здравствуйте ребята. Садитесь. Меня зовут Оксана Александровна и этот урок я проведу вместе с вами.

Слайд 2.

Посмотрите, как светит солнце

В кабинете у нас сейчас,

Потому что счастливые лица

От улыбок стали у вас.

Друг на друга скорей посмотрите,

Повернитесь к соседу назад

И улыбку свою подарите

Всем, чей встретите добрый вы взгляд.

И вот с таким хорошим настроением мы и начнем урок математики.

II. Этап актуализации опорных знаний 3 мин.

Учитель: Перед вами лежат листочки №1. Напишите на них свою фамилию и имя. Для рассмотрения вам будет предложено 6 утверждений. Одни из них несут правильную информацию (правильный ответ), а другие не верную. Если вы согласны с ответом, то напротив номера вопроса поставьте 1, если не согласны, то 0.

(выполняется математический диктант) (Слайд 3-9)

Учитель: Обменяйтесь листочками с соседом по парте. Проверьте правильность выполнения задания и поставьте оценку исходя из критериев оценивания: Слайд 10

0 ошибок – 5

1 ошибка – 4

2 ошибки – 3

Обменяйтесь листочками обратно.

Поднимите руки те, кто получил оценку 5? Спасибо.

Поднимите руки те, кто получил оценку 4? Спасибо.

Я вижу, что материал предыдущих уроков вами усвоен хорошо. Молодцы!

III. Этап постановки целей и задач урока 5 мин.

(Проблемная ситуация)

Учитель: Ребята, какую тему вы изучали на предыдущих уроках?

Ученик: Решение систем линейных уравнений с двумя переменными.

Учитель: Что значит «решить систему уравнений»?

Ученик: Найти все ее решения или доказать, что решений нет.

Слайд 11

Учитель: Перед вами на проектной доске система линейных уравнений с двумя переменными (слайд № ). Какими способами можно ее решить?

Ученик: Графическим способом и способом подстановки.

(рассматриваем решение графическим способом и способом подстановки).

Слайд 12

Чтобы решить данную систему уравнений графическим способом, надо …?

Выразить в каждом уравнении переменную у через х. Затем подставить в полученные формулы значения х и вычислить значения у в этих точках. Построить в одной координатной плоскости графики этих функций. Точка пересечения этих графиков и будет решением этой системы.

Слайд 13

Чтобы решить данную систему уравнений способом подстановки, надо…?

Выразить из какого-нибудь уравнения системы одну переменную через другую. Затем подставить в другое уравнение системы вместо этой переменной полученное выражение. Решить полученное уравнение с одной переменной и найти соответствующее значение второй переменной.

Учитель: Как вы видете, решение данной системы линейных уравнений с двумя переменными этими способами очень объемное и трудоемкое.

Слайд 14

Но может есть способ, который позволит данную систему уравнений решить менее объемно?

Что можно сказать про коэффициенты переменных х и у?

Ученик: Коэффициенты при х равны, но с противоположным знаком, а при у разные.

Учитель: С помощью какого математического действия противоположные числа станут равны 0?

Ученик: Сложения.

Учитель: Значит, что можно сделать с этими уравнениями, чтобы переменная х исчезла?

Ученик: Сложить.

Учитель: Тогда какой способ решения системы линейных уравнений мы с вами изучим на уроке?

Ученик: Способ сложения.

Учитель: Молодцы! Это и будет темой нашего урока. Открыли тетради, записали число и тему урока: Решение систем линейных уравнений способом сложения. Слайд 15

Учитель: Как вы думаете, какова цель нашего урока?

Ученик: Рассмотреть способ сложения и научиться решать системы линейных уравнений с двумя переменными способом сложения.

IV. Этап первичного усвоения новых знаний 10 мин.

Слайд 16

Учитель: Вернемся к нашей системе уравнений. Запишите систему в тетради. Обратим внимание, что коэффициенты при переменной х в уравнениях системы противоположны. Давайте сложим почленно уравнения системы.

-2у=8

у=8:(-2)

у=-4

Подставляем в одно из уравнений системы у=-4, находим х:

8х-17*(-4)=4

8х+68=4

8х=4-68

8х=-64

х=-64:8

х=-8

Получили, что пара чисел (-8; -4) является решением нашей системы.

Слайд 17

Решим еще одну систему уравнений способом сложения.

_{Есть желающие решить эту систему уравнений у доски?}

_{(Решает ученик, комментирует, учитель помогает)}

_4х=4

_{х= 4:4}

_х=1

_1+2у=-4

_2у=-4-1

_у=-5:2

_{у=-2,5 Ответ: (1;-2,5)}

V. Физкультминутка 2 мин Слайд 18

VI. Этап закрепления изученного материала. Первичное закрепление. 16 мин

Учитель: Очень хорошо решаются системы уравнений способом сложения, когда коэффициенты при одной из переменных противоположны. А если это не так?

Слайд 19

Перед вами на проектной доске представлена система линейных уравнений с двумя переменными.

Что можно сказать про коэффициенты при х и у?

Ученик: Они разные.

Учитель: Каким способом можно сделать коэффициенты при х противоположными числами?

Ученик: Умножить второе уравнение на (-2).

Учитель: Молодцы! Действительно, если все части уравнения умножить или разделить на одно и тоже число, отличное от 0, то полученное уравнение будет равносильно данному. Слайд 19

Первое уравнение системы осталось без изменения. Теперь к новой, равносильной предыдущей системе уравнений, можно применить способ сложения.

Слайд 20

Возьмите листочки №2, напишите фамилию, имя и используя свойство равносильности уравнений решите следующую систему линейных уравнений способом сложения. (самостоятельная работа учащихся)

Слайд 21

Решением системы уравнений будет пара чисел (4; 2)

Ребята, кто справился с заданием? Поднимите руки.

Слайд 22

На слайде представлено одно из возможных решений способом сложения данной системы.

*(-3)

-8у=-16

у=-16:(-8)

у=2

х+2=6

х=4 Ответ (4; 2)

Почему одно из возможных?

Ученик: Можно было умножить на 5 первое уравнение и сложить со вторым.

Учитель: Ребята, а кто привел системы к равносильности с помощью другого множителя? Молодцы!

Учитель: Сформулируем и устно закрепим алгоритм решения системы линейных уравнений с двумя переменными способом сложения.

Слайд 23

(ученики говорят, учитель корректирует и выводит на экран алгоритм)

Слайд 24

Учитель: Откройте учебник на стр. 217 и опираясь на алгоритм решения систем линейных уравнений с двумя переменными решите №1084 (а, б)

Кто желает пойти к доске?

(Решают системы уравнений)

VII. Рефлексия. 2 мин.

Учитель: Как звучит тема нашего урока?

Ученик: Решение систем линейных уравнений способом сложения.

Учитель: Какую цель вы ставили?

Ученик: Научиться решать системы линейных уравнений с двумя переменными способом сложения.

Учитель: Вы достигли поставленной цели?

Ученик: Да.

Учитель: Оцените свою работу на уроке.

Перед вами, на листочке №3, лежат три стикера разных цветов. Слайд 25

Желтый цвет означает, что «я все понял, но у меня еще есть вопросы», зеленый означает «я все понял, могу работать по алгоритму», розовый – «я все понял, могу объяснить другим». Наклейте соответствующий стикер на доску.

. Слайд 26

Каждый из вас на уроке получил хотя бы одну оценку. Я оставляю за собой право подкорректировать выставленные оценки, потому что я так же смотрела за работой каждого из вас на уроке.

VIII. Домашнее задание 1 мин.

Слайд 27

_{Стр. 125 пар. 44 (выучить алгоритм), №1083 (в), №1084 (в)}

_{Учитель: При выполнении домашней работы, я бы хотела, чтобы вы помнили слова одного замечательного стихотворения, послушайте: Слайд 28}

_{«Хоть выйди ты не в белый свет,}

_{А в поле за околицей, —}

_{Пока идешь за кем-то вслед,}

_{Дорога не запомнится,}

_{Зато, куда б ты ни попал}

_{И по какой распутице,}

_{Дорога та, что сам искал,}

_{Вовек не позабудется»}

_{Н. Рыленков}

_{Если вы самостоятельно найдете решение для каждого домашнего номера, значит, на последующих уроках вы не забудете, как они решаются.}

_{Спасибо большое за урок. Мне очень приятно было с вами работать.}

План-конспект урока по алгебре (7 класс) на тему: Решение систем уравнений методом алгебраического сложения

Открытый урок по алгебре в 7б классе. «Где есть желание, найдется путь».

Тема: Решение систем линейных уравнений методом  алгебраического сложения.

Слайд 1

Цели урока:

1. Образовательные:

• Систематизировать знания о различных способах решения системы двух линейных уравнений.
•  Совершенствовать навык решения системы двух линейных уравнений с двумя переменными методом алгебраического сложения;

2. Развивающие:

• развитие математической речи учащихся;
• умения анализировать, сравнивать, сопоставлять;
• развитие внимания, наблюдательности, памяти;
• развитие познавательного интереса учащихся через введение исторического материала;

3. Воспитательные:

• формирование таких качеств личности, как организованность, ответственность, аккуратность;
• выработать умение анализировать проделанную работу и адекватно её оценивать.

1.Организационная часть

Здраствуйте, все участники образовательного процесса! Я хочу всем пожелать с пользой провести  предстоящий урок алгебры. Ребята, на прошлом занятии мы начали изучение темы « Решение систем линейных уравнений методом алгебраического сложения». А на этом уроке мы продолжим эту тему. Попробуйте формулировать цель сегодняшнего урока.

             Ученики формулируют цель урока. Слайд 2.

Давайте настроимся на урок и проведём небольшую разминку.

2.   Устная работа (3 мин.)

1. Упростите выражения

а)  5а+а;   б) -7х+7х;  в) 4у-8у;  г) -3в+3в;   д) 2с+9

     2. Согласны ли вы с решением  следующего уравнения

3х — 5 = 7х — 3,

3х- 7х = -3- 5,

     -4х = -8,

        х =2.        Ответ: х =2. ?                       (-0,5)

3 На листе было записано решение линейных уравнений, но со временем оно исчезло. Восстановите её.

а) 3х =                     б) 5х =                       в)   х =                г) 5х =  

   х = -11.                     х = 0.                         х = 14.                х = -9.

3.Проверка домашнего задания (8 мин)

2 ученика у доски показывают решения

№ 13.6 а)

 х+ у=4        *5     5х + 5у=20

 4х- 5у=7              4х- 5у =7

                              9х=27

                              х=3

Подставим  х=3 в уравнение(1)

3+у=4

у=1

Ответ (3;1)

№13.8 а)

3х+7у=46     *3           9х+21у=138

4х-3у=12       *7          28х-21у=84

                                         37х=222

                                         х=6

Подставим  х=6 в уравнение (2)

4*6-3у=12

-3у=12-24

-3у=-12

у=4

Ответ (6;4)

Пока ученики готовят решения  мы с вами повторим прошлый материал

Фронтальный опрос (6мин.)

1. Какие методы решения систем уравнений вы знаете?

2. Суть графического метода

3. Сколько решений может иметь система уравнений?

Слайд

а)  б)  в)

4.Алгоритм метода подстановки.

слайд

5.Алгоритм метода сложения.

слайд

6.Зависит ли ответ системы уравнений от выбора метода?

Проверка решения на доске.

4.Тест (10мин)

1. вариант

А1. Выразить х через у х+3у=6
а)х=6-3у
б)х=-6-3у
в) х=6+3у

А2.  Если графики прямых параллельны, то система имеет решение:
   а) единственное
  б) много решений
 в) не имеет решений

А3. Для решения системы уравнений  3х+5у=3

                                                                      2х+5у=7

методом алгебраического сложения лучше

а) сложить уравнения
б) вычитать из одного уравнения другое

В1. Решением системы уравнений    х — 2у =1

                                                         у — х= 1    является пара 
а) (3;-2)
б) (-3; -2),
в) (-2; -3)

В2. Результат сложения уравнений х+5у =7, 3х-2у=4 равен
а) 4х-3у =11
б) 4х+7у 11
в) 4х+3у =11

С. Запишите для системы уравнений   х+4у=6

                                                                              3х-2у=4

равносильную систему, у которой противоположные коэффициенты при переменной Х

2 вариант

А1. Выразить х через у х-2у= 8
а)  х=8-2у,
б ) х=-8-2у,
в)  х=8+2у

А2. Если графики прямых совпадают, то система имеет решение:
   а) единственное
  б) много решений
 в) не имеет решений

А3. Для решения системы уравнений  3х + 5у = 3

                                                                      2х — 5у = 7

методом алгебраического сложения лучше

а) сложить уравнения
б) вычитать из одного уравнения другое

В1. Решением системы уравнений    х + 4у = 6

                                                        3х – 2у = 4    является пара 
а) (-2;1)
б) (2; 1),
в) (1; 2)

В2. Результат сложения уравнений 3х + 7у = 2, х — 2у = 1 равен
а) 4х+5у =3
б) 4х+9у=3
в) 4х-5у =3

С. Запишите для системы уравнений   5х+7у=4

                                                                               х-2у=3

равносильную систему, у которой противоположные коэффициенты при переменной Х

Ответы записать в бланке ответов

Бланк ответов

№ задания	Ответ	Правильность (+или -)	Балл
А1      (2 балла)
А2    (2балла)
А3    (2балла)
В1    (3 балла)
В2    (3 балла)
С   (4балла)
Система уравнений (1-5 баллов)
ИТОГ

Взаимопроверка. Учащиеся меняются бланками ответов. Проверяющие заполняют 3и4 колонки.( Слайд с правильными ответами)

4. Физкультминутка (1мин)

1)Игра «Великаны и карлики».

Если согласны с утверждением, то встаем и два раза хлопаем, если нет, то сидя мотаем головой  и топаем ногами.(упражнение для мышц шеи)

1.Уравнение 8ху+2у=12 является линейным уравнением с двумя переменными

2.График функции у =-2х проходит через начало координат.

3. Функция  у= 2х-5 является возрастающей.

Решением  системы уравнений являются х=6 и у=4. Значит система уравнений имеет два решения.

2) А теперь все встаём и показываем возрастаюшую прямую иповторяем 4 раза.

3)Показываем убывающую прямую и повторяем ещё 4 раза.

4) Пересекающиеся прямые и повторяем ещё 4 раза.

Вдох, выдох. Садимся на свои места и с продуктивно продолжим работу.

5.Работа у доски.(5мин)

№13.9 г)

4х-3у=12   *3

3х-4у=30    *(-4)

                     12х-9у=36

                -12х+16у=-120

12х-12х-9у+16у=36-120

7у=-84

у=-12

Подставим у=-12 в ур-е (1) 4х-3*(-12)=12

                                                4х=12-36

                                                  х=-24/4

                                                   х=-6

Ответ (-6;-12)

5. Работа в группах. (6 мин)

Учащиеся группируются группы по 4 человека.

I группа -№13.9 а)            II группа -№13.9 б)                  III группа -№13.9 в)

4х+5у=1            *5 5х+7у=5            *-4	3х-5у=25            *4 4х-3у=37             *-3	7х+5у=-5            *-5 5х+3у=1              *7
20х+25у=5 -20х-28у=-20 25у-28у=5-20 -3у=-15 у=5 4х+5*5=1 4х=1-25 х=-24/4 х=-6 Ответ (-6;5)	12х-20у=100 -12х+9у=-111 -20у+9у=100-111 -11у=-11   у=1 3х-5*1=25 3х=25+5 х=30/3 х=10 Ответ (10;1)	-35х-25у=25 35х+21у=7 -25у+21у=25+7 -4у=32 у=-8 5х+3*(-8)=1 5х=1+24 х=25/5 х=5 Ответ (5;-8)

Узнать кто автор известных оперетт. Вовремя работы в группах звучит музыка.

Слайд.

6.Решить у доски №13.10а),б,)в). 3 ученика у доски.1вариант а), 2вариант-б) 3вариант-в)

Ответы: а) (-3;-2)     б) (35;-46),  в)  (5;1)

7.Рефлексия

Учитель монотонным голосом предлагает отдохнуть учащимся.

Закройте глаза.

 Расслабьтесь. Поводите глазами вверх, вниз, влево, вправо.

Откройте глаза.

Потянитесь как маленькие котята.

Улыбнитесь друг другу.

И с хорошим настроением продолжим работу.

8.Самостоятельная работа (5мин)  решить на бланке ответов

1 вариант 4х+7у=90 -6х+5у=20	2 вариант 9х+8у=-2 4х+5у=-11	3 вариант -3х+10у=0,1 4х-15у=2,7
Ответ (5;10)	Ответ(6;-7)	Ответ(-5,7; -1,7)

Проверяют ответы. Решение проверяет учитель(собирает работы)

9.Домашнее задание №13.7(а,б), по желанию  либо №13.10(г), либо №13.11(а)-

10. Итог урока.

Вы активно поработали на уроке, приятно было с вами работать. Что сегодня на уроке вам понравилось? Мы достигли цели урока?

За работу у доски отметки:

За групповую работу отметки

За тест и самостоятельную работу отметки узнаем на следующем уроке.

Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу.

У первого спросил: «Что ты делал целый день?» И тот ответил с ухмылкой, что целый день возил эти проклятые камни.  

У второго мудрец спросил: «А что ты делал  целый день?», и тот ответил: «А я добросовестно выполнял свою работу».

А  третий улыбнулся, лицо его  просияло: «А я принимал участие в строительстве Храма!»

Ребята, каждый для себя оцените свою работу.

Спасибо всем за работу!

Обощающий урок в 7 классе по теме » Решение систем уравнений способом сложения»

«Образование — клад, Труд — ключ к нему»

П. Буаст

  Французский лексикограф и философ

“ Чтобы переварить знания надо поглощать их с аппетитом”

Анатоль Франс

французский писатель

23.12.14. Классная работа.

Обобщающий урок по теме «Решение систем линейных уравнений

с двумя переменными».

Цели урока:

• Повторить способы решения систем двух линейных уравнений с двумя переменными;
• Обобщить и систематизировать знания по данной теме.

Повторение теоретических знаний.

Линейным уравнением с двумя переменными называется…

прямая.

уравнение вида ах+by =c

Решением уравнения с двумя переменными называют…

пару чисел (х;y),обращающую это уравнение в верное равенство.

Графиком уравнения ах+by=c является…

Какое уравнение лишнее?

х + 4у = 7

2х +3у = 5

3х – 4 = 8

5х – 6у = 10

Пользуясь рисунком, укажите систему уравнений,

Решением которой является пара ( 4;0 )

Г.

Такой системы нет

Повторение

теоретических знаний.

• Решением системы уравнений

с двумя переменными

называется пара

значений переменных,

обращающая каждое уравнение системы в верное равенство.

• Системой уравнений

называется некоторое

количество уравнений, объединенных фигурной скобкой.

• Решить систему уравнений

Фигурная скобка означает,

— значит найти все её решения или установить, что их нет.

что все уравнения должны

выполняться одновременно.

Способы решения систем линейных уравнений с двумя переменными:

Графический способ

Способ подстановки

Способ сложения

Решить системы уравнений графическим способом

у — х=2 ,

у+х=10 ;

Способом подстановки

Способом сложения

у — 2х=4 ,

7х — у =1 ;

7х+2у=1,

17х+6у=-9;

Решение системы графическим способом

Выразим у

через х

у — х=2,

у+х=10;

y

y=x+2

10

у=х+2,

у=10-х;

Построим график

первого уравнения

6

у=х+2

y=10 — x

х

0

-2

у

2

2

0

1

Построим график

второго уравнения

-2

4

1

0

10

x

у=10 — х

х

0

10

Ответ: (4; 6)

у

10

0

Решение системы способом подстановки

Выразим у через х

у=2х+4,

7х — (2х+4)=1;

у=2х+4,

7х — у=1;

у — 2х=4,

7х — у =1;

Решим

уравнение

Подставим

7х — 2х — 4 = 1;

у=2х+4,

у=6,

х=1;

х=1.

5х = 5;

х=1 ;

Ответ: х=1; у=6.

Подставим

12

Решение системы способом сложения

Уравняем

модули

коэффи-

циентов

перед у

Решим

уравнение

х=3,

7·3+2у=1;

||·(-3)

7х+2у=1,

17х+6у=-9;

Сложим уравне-

х=3,

ния почленно

21+2у=1;

-21х-6у=-3,

17х+6у=-9;

+

____________

Решим

х=3,

2у=-20;

уравнение

— 4х = — 12,

7х+2у=1;

х=3,

у=-10.

Подставим

х=3,

7х+2у=1;

Ответ: (3; — 10)

8=6?

Рассмотрим систему уравнений

Подставим у из второго уравнения системы в первое, получим

Где ошибка?

 

 

Тогда

Как определить сколько решений имеет система уравнений

без построения графиков?

у = 3х + 1

у = 3х + 1

K 1 ≠ K 2 , значит прямые пересекаются.

Система имеет одно решение!

K 1 = K 2, значит прямые параллельны.

Система не имеет решения!

прямые совпадают.

Система имеет бесконечно много решений!

y

y

y

x

x

x

Зарядка для глаз

Следите за движениями «веселого» робота

БЕРЕГИТЕ ЗРЕНИЕ!!!

Способы решения систем уравнений

Способ сравнения (алгоритм)

• Выразить у через х (или х через у) в каждом уравнении
• Приравнять выражения, полученные для одноимённых переменных
• Решить полученное уравнение и найти значение одной переменной
• Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение
• Записать ответ: х=…; у=… .

-5

Взаимопроверка

Ответ: (2;3)

№ 13.9(а) , 13. 11(а,)

Подведем итоги!

Графический способ

Способ подстановки

Наглядный, трудоемкий, не точный

Способ сложения

Точный,

трудоемкий

Точный, быстрый, но

не всегда легко подобрать коэффициенты.

Задание на дом: разноуровневые задания Решить систему уравнений удобным для вас способом (карточки)

Рефлексия

урок был интересен и полезен для меня,

я хорошо работал,

всё понимал,

мне было достаточно комфортно.

урок был интересен и в определенной степени полезен для меня

я принимал участие,

но понимал не все задания,

с домашним заданием, думаю, справлюсь.

пользы от урока я получил мало,

я не очень понимаю, о чем идет речь,

мне это не понятно, не нужно, не интересно,

домашнее задание я не смогу сделать.

Конспект урока алгебры в 7 классе на тему «Решение систем линейных уравнений способом сложения»

Муниципальное общеобразовательное учреждение

Хлевищенская средняя общеобразовательная школа

Выполнила: Головченко И.В.,

учитель математики

МОУ Хлевищенская СОШ

с.Хлевище

Тема урока: Решение систем уравнений способом сложения.

Цели: 1) организовать деятельность учащихся по отработке навыка

решения систем линейных уравнений различными способами;

2) содействовать развитию у детей умений осуществлять само-

контроль, самооценку учебной деятельности;

3) содействовать у детей умению общаться;

4) помочь учащимся осознать ценность совместной деятельности.

Ход урока

1. Организационный момент.

Девиз урока «Математику нельзя изучать, наблюдая, как это делает сосед !»

2. Устная работа.

1.Имеет ли решения система и сколько:

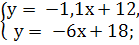
1. решение) ( нет решений) ( много решений)

2.Поставить в соответствие каждой системе уравнений пару чисел

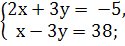
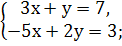
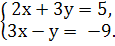
( -2; 3) ( 11; -9 ) ( 1; 4)

3.Математический диктант. Закончите предложения:

1) Линейным уравнением с двумя переменными называется уравнение вида ах +ву =с, где х и у- переменные, а,в и с – некоторые числа.

2) Решением линейного уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

3) Решением системы двух линейных уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

4) Решить систему линейных уравнений с двумя переменными – значит найти все её решения или доказать, что решений нет.

5) Существуют следующие способы решения систем линейных уравнений с двумя переменными: графический способ, способ подстановки, способ сложения.

4.Индивидуальная работа по карточкам.

5. Работа по теме урока.

Вспомнить алгоритмы решения систем линейных уравнений с двумя переменными графическим способом, способом подстановки и способом сложения.

6. Работа в группах.

Решить систему уравнений тремя способами.

1 группа – графическим способом, 2 группа – способом подстановки, 3 группа – способом сложения.

7. Тест.

1.Решением какой системы уравнений является пара чисел ( -1; 2)

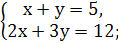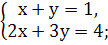а) б) в)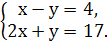

2. Дана система 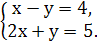Какая из пар чисел является решением?

а) ( 4; 0) б) ( 3; 0) в) ( 3; -1 )

3. Сколько решений имеет система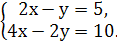

а) одно б) бесконечно много в) не имеет решений

4. В уравнении 2х + у = 8 выразить х через у:

а) х=4 + у б) х = 8 – 2у в) х = 4 — у

8.Самостоятельная работа.

Работа предусматривает три уровня сложности.

«3»

«4» Решить систему уравнений способом сложения: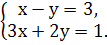

«5» Решить систему уравнений способом сложения:

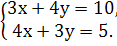
9. Повторение.

Выполните умножение дробей 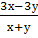* , если х – у = 0.

10. Домашнее задание.

№ 1158(б), №1161,

Выполните деление дробей 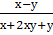: 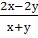, если х – у = 0.

Решить систему уравнений способом сложения

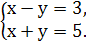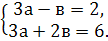«3» «4» «5»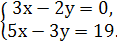

11. Рефлексия.

Выбрать «мордашку», соответствующую вашему настроению во время урока.

План-конспект урока по алгебре (7 класс): УРОК АЛГЕБРЫ В 7 КЛАССЕ ПО ТЕМЕ «РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ»

По теме: методические разработки, презентации и конспекты

Методическая разработка урока алгебры в 7 классе «Различные способы решения систем линейных уравнений» способы решения систем уравнений

Урок алгебры в 7 классе направлен на обобщение и систематизацию различных способов решения систем уравнений: метода сравнения, сложения, подстановки, графического метода, метода Крамера, выбора рацион…

Урок по алгебре «Решение систем линейных уравнений способом сложения» + презентация

Материал содержит конспект урока по алгебре 7 класса и презентации к данному уроку. А также интерактивный материал из «Коллекции учебных материалов»….

Решение систем линейных уравнений способом подстановки (урок применения знаний и умений)

Урок-игра «Фабрика звезд» . 7 классРешение систем линейныхуравнений способом подстановки (урок применения знаний и умений)…

Решение систем линейных уравнений способом сложения. 7 класс.

Презентация….

Конспект урока алгебры в 7 классе на тему «Решение систем линейных уравнений способом подстановки»

Урок изучения нового материала с применением новых обучающих структур….

Решение систем линейных уравнений способом подстановки и алгебраического сложения

Методическая разработка коррекционно-развивающего урока алгебры в 7 классе по теме «Решение систем  уравнений способом подстановки и алгебраического сложения». Тип урока: закрепление знаний и уме…

Тема урока «Способ сложения при решении систем линейных уравнений»

Упражнять учащихся в решении систем уравнений способом сложения; вырабатывать умения и навыки решения систем уравнений способом сложения. …