Системы двух линейных уравнений с двумя переменными. Видеоурок. Алгебра 7 Класс

На данном уроке мы вспомним понятие системы двух линейных уравнений с двумя неизвестными, ее общий вид, варианты и способы решения. Мы вспомним некоторую терминологию и решим несколько примеров.

Напомним, что из себя представляет система двух линейных уравнений с двумя переменными. Это система вида:

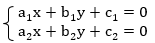
Из первого уравнения 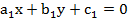 можно получить линейную функцию, в случае если 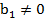: . График данного уравнения – прямая линия.

Bторое линейное уравнение:

, из него также можно получить линейную функцию, при условии, что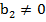

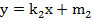: . График данного уравнения – также прямая линия.

Запишем систему в другом виде:

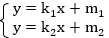
Мы знаем, что множеством решений первого уравнения является множество точек, лежащих на соответствующей ему прямой, аналогично и для второго уравнения множество решений – это множество точек на другой прямой. Две прямые могут пересекаться – и тогда у системы будет единственное решение, единственная пара чисел х и у будет удовлетворять одновременно обоим уравнениям. Это происходит, если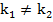

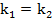. Две прямые также при некоторых значениях численных параметров могут быть параллельны, в таком случае они никогда не пересекутся и не будут иметь ни одной общей точки, значит в этом случае система не будет иметь решений. Для этого должны выполняться условия:  и 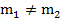. Кроме того, две прямые могут совпадать, и тогда каждая точка будет решением обоих уравнений, а значит система будет иметь бесчисленное множество решений. Для этого должны выполняться условия:  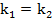и .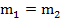

Пример 1:

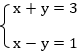
На данном уравнении можно продемонстрировать сразу несколько способов решения систем уравнений.

1 способ – способ подстановки: выразим во втором уравнении х и подставим полученное выражение в первое уравнение:

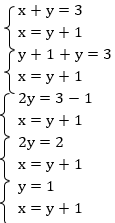
Подставим найденное значение у во второе уравнение и найдем значение х:

2 способ – способ алгебраического сложения: выполним сложение уравнений:

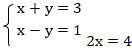
Из полученного уравнения найдем х:

Теперь вычтем из первого уравнения системы второе:

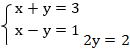
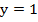
Таким образом, мы получили решение системы двумя способами, и это решение – точка с координатами (2; 1).

Пример 2:

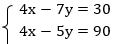
В данном случае удобнее применить способ алгебраического сложения, вычтем из второго уравнения первое. Получаем:

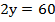
Найдем значение у:

Подставим значение у во второе уравнение и найдем х:

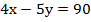
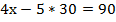
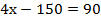
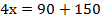
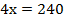
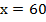
Ответ: (60; 30).

Пример 3:

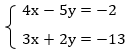
В данной системе нет переменных с одинаковыми коэффициентами, но мы можем их уравнять самостоятельно, для этого выполним преобразования:

Выполним сложение уравнений:

23y = -46, y = -2

Подставим полученное значение у в первое уравнение и определим значение х:

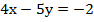
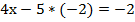
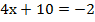
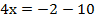
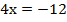
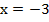
Ответ: (-3; -2).

Пример 4:

Разделим второе уравнение на два:

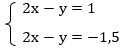
Вычтем из первого уравнения второе:

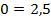
Очевидно, что полученное выражение не зависит от значений переменных системы и не является верным числовым равенством, значит, система не имеет решений. В данном случае рекомендуется графически доказать, что система не имеет решений, для этого из уравнений записать линейные функции, построить их и показать, что прямые параллельны.

Пример 5:

Очевидно, что, если разделить второе уравнение на два, получим первое уравнение:

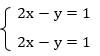
Мы получили два одинаковых уравнения, значит, чтобы довести решение системы до конца, можем оставить одно: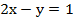

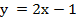; это линейное уравнение с двумя переменными, график его – прямая линия, и оно имеет бесчисленное множество решений, а значит и система имеет бесчисленное множество решений. Чтобы записать решения, выразим у: , таким образом, дадим ответ: х – любое число,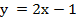

Графическая иллюстрация (рис. 1):

Рис. 1

Вывод: мы рассмотрели системы двух линейных уравнений с двумя переменными, варианты и способы их решения. Мы вспомнили некоторые термины, понятия и свойства и решили примеры для закрепления техники.

 

Список литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. – 6 изд. – М.: Просвещение, 2010.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Nado5.ru (Источник).
2. Интернет-портал Nado5.ru (Источник).
3. ЕГЭ по математике (Источник).
4. Школьный помощник (Источник).
5. Интернет-портал Nado5.ru (Источник).
6. Интернет-портал Nado5.ru (Источник).

 

Домашнее задание

1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, №1072, ст. 200;
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, №1084, ст. 204;
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, №1086, ст. 204.

interneturok.ru

Решение систем двух уравнений с двумя переменными способом сложения

Рассмотрим систему:

{2х + 3у = 7,
{2х + 3у = 7,

При графическом решении системы уравнений увидим, что прямые, являющиеся графиками уравнений системы, пересекаются в точке с координатами (5; -1).

Если мы сложим соответственно левые и правые части данных уравнений 2х + 3у + х – у = 7 + 6, получим новое уравнение: 3х + 2у = 13.

Пройдёт ли прямая, являющаяся графиком уравнения 3х + 2у = 13 через точку с координатами (5; -1)?

Получается, пара чисел х = 5; у = -1 удовлетворяет не только каждому из уравнений системы 

{2х + 3у = 7,
{х – у = 6,

но и уравнению 3х + 2у = 13. Следовательно, прямая, являющаяся графиком уравнения 3х + 2у = 13 пройдёт через точку с координатами (5; -1). Так как данная прямая не совпадает с прямыми графиками системы, то системы уравнений

{2х + 3у = 7,
{х – у = 6

и

{2х + 3у = 7,
{3х + 2у = 13,

и

{3х + 2у = 13,
{х – у = 6

имеют одно  и то же решение: х = 5; у = -1 (координаты точки пересечения прямых).

Рассмотренный пример показывает важное свойство, которое используется при решении систем линейных уравнений:

Если одно из уравнений системы линейных уравнений заменить уравнением. Полученным почленным сложением данных уравнений, то новая система будет иметь то же множество решений, что и первоначальная.

Рассмотрим примеры решения систем линейных уравнений с помощью использования этого свойства.

Пример 1. 

Решить систему уравнений:

{2х + у = 9,
{х – у = 24.

Решение.

Заменим одно из уравнений системы новым уравнением, левая часть которого равна сумме левых частей данных уравнений. А правая часть – сумме правых частей:

{3х = 33
{х – у = 24.

Из первого уравнений полученной системы находим: х = 11. Подставив найденное значение х во второе уравнение, узнаем, что у = -13.

Ответ:  х = 11, у = -13.

Пример 2.

Решить систему уравнений:

{5х + 11у = 8,
{10х – 7у = 74.

Решение.

Если почленно сложить уравнения системы, то это не приведёт к упрощениям, так так ни одна из переменных при этом не исключится. Однако если предварительно умножить все члены первого уравнения на -2 (а второе оставить без изменений), то коэффициенты при х в обоих уравнениях будут противоположными числами:

{-10х – 22у = -16,
{10х – 7у = 74.

Теперь почленное сложение приведёт к уравнению -29у = 58, в котором коэффициент при х равен нулю.

Заменим первое уравнение системы уравнением -29у = 58, получим новую систему:

{-29у = 58,
{10х – 7у = 74.

Из уравнения -29у = 58 находим: у = -2. Из второго уравнения, подставив в него у = -2, найдём значение х.

Ответ: х = 6; у = -2.

Пример 3.

Решить систему уравнений:

{9х + 7у = 7,
{2х – 3у = -85.

Решение.

Умножим каждый член первого уравнения на 3, а второго на 7:

{27х + 21у = 21,
{14х – 21у = -595.

Выполнив почленное сложение имеем:

{41х = -574,
{2х – 3у = -85.

Отсюда

{х = -14,
{2х – 3у = -85.

Подставив значение х во второе уравнение и найдем у.

Ответ: х = -14; у = 19.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Как решать системы уравнений с двумя переменными графическим способом?

Сделай плиз, лучшем за труд 0 баллов (( Как решать систему уравнений с двумя неизвестными Уравнение – это тождество, где среди известных членов скрывается одно число, которое необходимо поставить вместо латинской буквы, для того чтобы с левой и правой стороны получилось одинаковое числовое выражение. Чтобы его найти, нужно перенести в одну сторону все известные члены, в другую — все неизвестные члены уравнения. А как решать систему из двух таких уравнений? По отдельности – нельзя, следует связать искомые величины из системы друг с другом. Сделать это можно тремя способами: методом подстановки, методом сложения и методом построения графиков. Инструкция ➊. Способ сложения: Нужно записать два уравнения строго друг под другом: 2 –5у=61 -9х+5у=-40. Далее, сложить каждое слагаемое уравнений соответственно, учитывая их знаки: 2х+(-9х) =-7х, -5у+5у=0, 61+(-40)=21. Как правило, одна из сумм, содержащая неизвестную величину, будет равна нулю. Составить уравнение из полученных членов: -7х+0=21. Найти неизвестное: -7х=21, ч=21:(-7)=-3. Подставить уже найденное значение в любое из исходных уравнений и получить второе неизвестное, решив линейное уравнение: 2х–5у=61, 2(-3)–5у=61, -6-5у=61, -5у=61+6, -5у=67, у=-13,4. Ответ системы уравнений: х=-3, у=-13,4. ➋. Способ подстановки: Из одного уравнения следует выразить любое из искомых членов: х–5у=61 -9х+4у=-7. х=61+5у, х=61+5у. Подставить получившееся уравнение во второе вместо числа «икс» (в данном случае) : -9(61+5у) +4у=-7. Далее решив линейное уравнение, найти число «игрек» : -549+45у+4у=-7, 45у+4у=549-7, 49у=542, у=542:49, у≈11. В произвольно выбранное (из системы) уравнение вставить вместо уже найденного «игрека» число 11 и вычислить второе неизвестное: Х=61+5*11, х=61+55, х=116. Ответ данной системы уравнений: х=116, у=11. ➌. Графический способ: Заключается в практическом нахождении координаты точки, в которой пересекаются прямые, математически записанные в системе уравнений. Следует начертить графики обоих прямых по отдельности в одной системе координат. Общий вид уравнения прямой: – у=kх+b. Чтобы построить прямую, достаточно найти координаты двух точек, причем, х выбирается произвольно. Пусть дана система: 2х – у=4 у=-3х+1. Строится прямая по первому уравнению, для удобства его нужно записать: у=2х-4. Придумать (полегче) значения для икс, подставляя его в уравнение, решив его, найти игрек. Получаются две точки, по которым строится прямая. (см рис. ) х 0 1 у -4 -2 Строится прямая по второму уравнению: у=-3х+1. Так же построить прямую. (см рис. ) х 0 2 у 1 -5 Найти координаты точки пересечения двух построенных прямых на графике (если прямые не пересекаются, то система уравнений не имеет решения – так бывает). <img src=»//otvet.imgsmail.ru/download/227597002_d11b0f6f7c44b2d5921e2ab770fe35ee_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/227597002_d11b0f6f7c44b2d5921e2ab770fe35ee_120x120.jpg» data-big=»1″>

Здравствуй, Аня, есть чуваки крутые, они решают такое за копейки: <a rel=»nofollow» href=»https://vk.com/away.php?to=http://reshimdz.ru» target=»_blank»>reshimdz.ru</a>

Вы знаете — попробуйте еще спросить на сайте: <a rel=»nofollow» href=»https://vk.cc/5WD2GN» target=»_blank» >Помощь в решении заданий</a> Итам получите решение. Уже помогли 5521 студентам Или на крайний случай — напишите мне на почту: anka-241@mail.ru

Проще говоря, если надо решить систему двух уравнений с двумя переменными графически, надо построить графики, а координаты (х; у) точки или точек пересечения и есть решение системы уравнений. Суть в том, что если графики пересекаются в точках, например А и В, с координатами x(A), y(A) и x(B). y(B), то при подстановке этих значений в уравнения системы каждое их уравнений должно сойтись (как в и в случае решение обыкновенной системы уравнений).

touch.otvet.mail.ru

Число решений системы двух линейных уравнений с двумя переменными

Предположим, требуется найти все пары значений переменных х и у, которые удовлетворяют уравнение
ху – 6 = 0 и уравнение у – х – 1 = 0, то есть необходимо найти пересечение множеств решений этих уравнений. В таких случаях говорят, что надо решить систему уравнений ху – 6 = 0 и у – х – 1 = 0.

Систему уравнений принято записывать с помощью фигурной скобки. Например, рассматриваемую систему уравнений можно записать так:

{ху – 6 = 0,
{у – х – 1 = 0.

Пара значений переменных, обращающая в истинное равенство каждое уравнение системы, называется решением системы уравнений с двумя переменными.

Решить систему уравнений – значит найти множество её решений.

Рассмотрим системы двух линейных уравнений с двумя переменными, в которых в каждом уравнении хотя бы один из коэффициентов отличен от нуля.

Графическое решение систем такого вида сводится к отысканию координат общих точек двух прямых.

Как известно, две прямые на плоскости могут быть пересекающимися или параллельными. В случае параллельности прямые либо не имеют общих точек, либо совпадают.

Рассмотрим каждый из этих случаев.

Пример 1.

Решим систему уравнений:

{2х + у = -11,
{х – 2у = 8.

Решение.

Выразив из каждого уравнения у через х, получим систему:

{у = -3х – 11,
{у  = 0,5х – 4.

Угловые коэффициенты прямых – графиков уравнений системы различны (-3 и 0,5), значит, прямые пересекаются.

Координаты точки их пересечения являются решением этой системы, единственным решением.

Пример 2.

Решим систему уравнений:

{3х – 2у = 12,
{6х – 4у = 11.

Решение.

Выразив из каждого уравнения у через х, получим систему:

{у = 1,5х – 6,
{у = 1,5х – 2,75.

Прямые  у = 1,5х – 6 и у = 1,5х – 2,75 имеют равные угловые коэффициенты, значит эти прямые параллельны, причём прямая  у = 1,5х – 6 пересекает ось у в точке (0; -6), а прямая у = 1,5х – 2,75 – в точке (0; -2,75), следовательно, прямые не имеют общих точек. Поэтому система уравнений не имеет решений.

В том, что данная система не имеет решений можно убедиться рассуждая следующим образом. Умножив все члены первого уравнения на 2, получим уравнение 6х – 4у = 24.

Сравнивая это уравнение со втором уравнением системы, видим, что левые части уравнений одинаковы, поэтому при тех же значениях х и у они не могут принимать различных значений (24 и 11). Следовательно, система

{6х – 4у = 24,
{6х – 4у = 11.

не имеет решений, значит, не имеет решений и система

{3х – 2у = 12,
{6х – 4у = 11.

Пример 3.

Решим систему уравнений:

{5х – 7у = 16,
{20х – 28у = 64.

Решение.

Разделив каждый член второго уравнения на 4, получим систему:

{5х – 7у = 16,
{5х – 7у = 16,

состоящую из двух одинаковых уравнений. Графики этих уравнений совпадают, поэтому координаты любой точки графика будут удовлетворять каждому из уравнений системы, то есть являться решением системы. Значит, данная система имеет бесконечное множество решений.

Если в каждом уравнении системы двух линейных уравнений с двумя переменными хотя бы один из коэффициентов при переменной не равен нулю, то система либо имеет единственное решение, либо имеет бесконечно много решений.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

7 класс. Алгебра. Системы двух уравнений с двумя переменными. — Способы решения систем уравнений с двумя неизвестными.

Комментарии преподавателя

Метод подстановки.

Су­ще­ству­ет несколь­ко ме­то­дов ре­ше­ния си­стем. Один из них метод под­ста­нов­ки. Рас­смот­рим при­мер.

При­мер 1:

Суть ме­то­да под­ста­нов­ки за­клю­ча­ет­ся в том, что в одном из урав­не­ний нужно вы­ра­зить одну пе­ре­мен­ную через вто­рую и под­ста­вить по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние.

В дан­ном слу­чае удоб­но вы­ра­зить х во вто­ром урав­не­нии:

Под­ста­вим по­лу­чен­ное вы­ра­же­ние в пер­вое урав­не­ние:

Пре­об­ра­зу­ем пер­вое урав­не­ние:

,

 ,

 ,

 

Под­ста­вим по­лу­чен­ное зна­че­ние во вто­рое урав­не­ние:

, ,

 

По­лу­ча­ем сле­ду­ю­щее ре­ше­ние си­сте­мы:

При­мер 2:

В дан­ном слу­чае неко­то­рая слож­ность за­клю­ча­ет­ся в том, что ис­ход­ную си­сте­му нужно пре­об­ра­зо­вать, чтобы была воз­мож­ность удоб­но и без оши­бок при­ме­нить метод под­ста­нов­ки. Для этого умно­жим оба урав­не­ния на шесть:

Вы­ра­зим у из пер­во­го урав­не­ния:

Под­ста­вим по­лу­чен­ное вы­ра­же­ние во вто­рое урав­не­ние и вы­пол­ним пре­об­ра­зо­ва­ния:

, ,

 ,

 

 

Под­ста­вим по­лу­чен­ное зна­че­ние в пер­вое урав­не­ние:

По­лу­ча­ем един­ствен­ное ре­ше­ние си­сте­мы, пара чисел:

Вывод:

на дан­ном уроке мы озна­ко­ми­лись с по­ня­ти­ем си­сте­мы двух ли­ней­ных урав­не­ний с двумя неиз­вест­ны­ми и одним из ме­то­дов ее ре­ше­ния – спо­со­бом под­ста­нов­ки. Мы ре­ши­ли при­ме­ры для по­ни­ма­ния и за­креп­ле­ния дан­ной тех­ни­ки.

Источник ко

www.kursoteka.ru

Системы уравнений с двумя переменными

Определение и формулы систем уравнений с двумя переменными

Например.

Например.

Решение систем линейных уравнений методом подстановки

Суть метода заключается в следующем: в системе уравнений выбираете наиболее простое уравнение, в котором одна из переменных выражаете через другую.

Результат (выражение) подставляете в другое уравнение системы, в результате чего приходим к уравнению от одной переменной. Решая его, находим значение этой переменной. Полученное значение подставляем в первое уравнение и получаем значение второй переменной.

Решение систем линейных уравнений методом сложения

Для того, чтобы применить указанный метод, необходимо, чтобы коэффициенты при какой-либо неизвестной были равными или противоположными по знаку числами. В таком случае в результате сложения (или вычитания) уравнений системы одно из неизвестных пропадает. В результате система преобразуется к линейному уравнению от одной переменной.

Решение систем уравнений с двумя неизвестными методом введения новой переменной

Суть метода продемонстрируем на примере.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Системы уравнений второй степени с двумя переменными

Вопросы занятия:

·  вспомнить, что такое системы уравнений второй степени с двумя переменными;

·  рассмотреть несколько способов решения таких систем уравнений.

Материал урока

Определение.

Системой уравнений второй степени с двумя переменными называются такие системы уравнений с двумя переменными, что хотя бы одно из этих уравнений – уравнение второй степени, а второе – не выше второй степени.

Сначала давайте рассмотрим системы, которые состоят из одного уравнения второй степени и одного уравнения первой степени.

Это системы вида

Пример.

Ещё одним способом решения систем уравнения, в которых одно уравнение – уравнение второй степени, а второе – линейное уравнение, является метод алгебраического сложения.

Пример.

Теперь давайте рассмотрим пример системы, оба уравнения которой являются уравнениями второй степени.

Это системы вида

Рассмотрим один из методов решения таких систем на примере.

Пример.

Пример.

Пример.

Пример.

Пример.

Итоги урока

Сегодня на уроке мы вспомнили, какие системы называются системами уравнений второй степени с двумя неизвестными. Рассмотрели несколько способов решения систем уравнений второй степени с двумя переменными.

videouroki.net