Как найти площадь равнобедренной трапеции
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
1
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
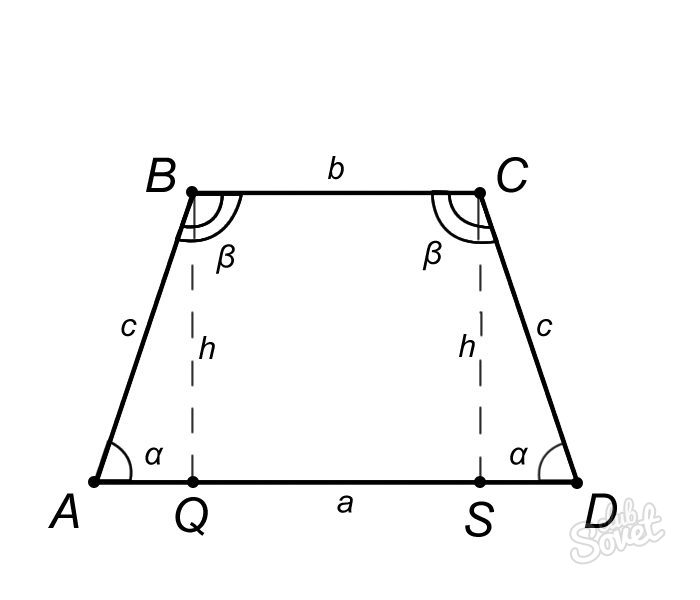
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
- Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.

2
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а – нижнее основание, b – верхнее основание, а h – это высота.
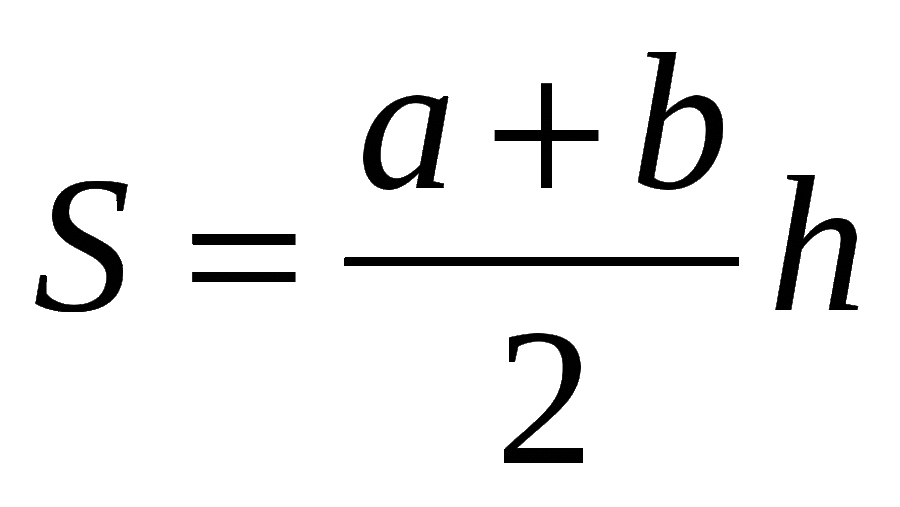
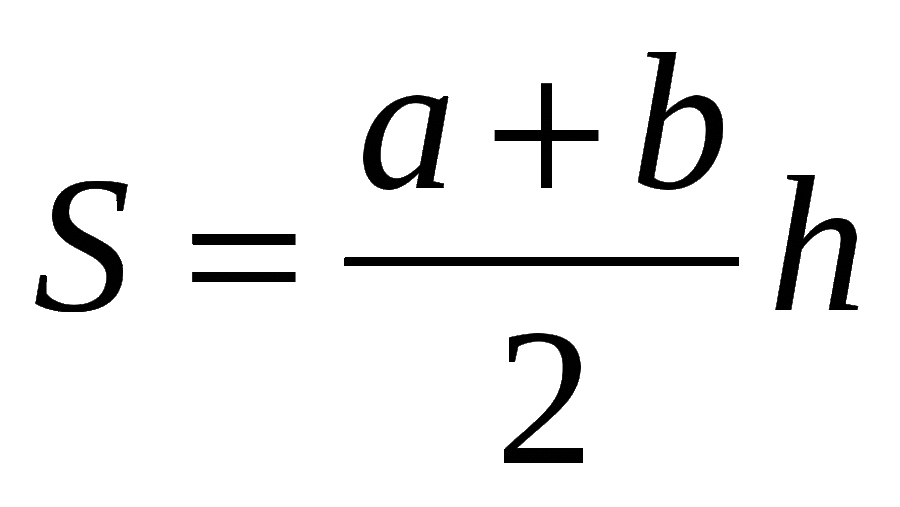
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
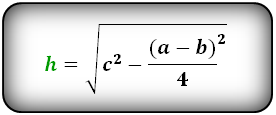
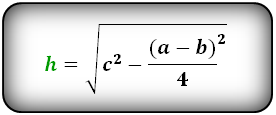
- Итоговая формула имеет такой вид:
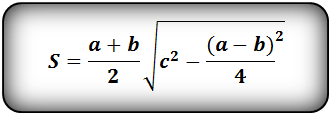
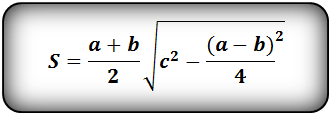
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту. Формула такова: S = mh.
Рассмотрим условие, когда в трапецию будет вписана окружность.


В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
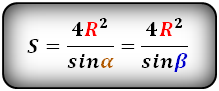
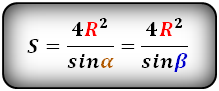
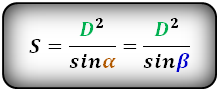
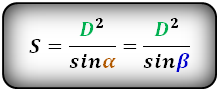
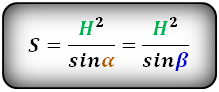
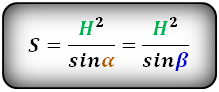
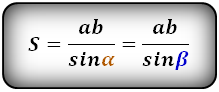
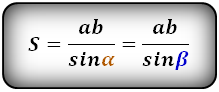
- Теперь попробуем найти площадь через диагонали и углы между ними.
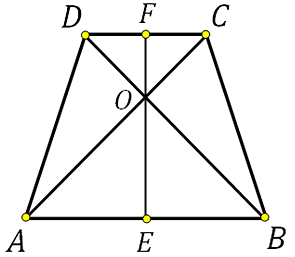

На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S) такова:
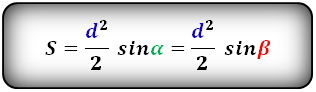
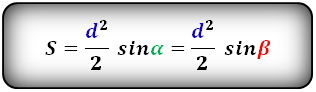
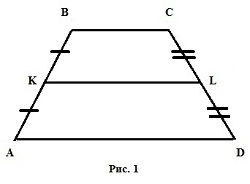
- Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, где:
AB, CD – c – боковая сторона;
KL – m – средняя линия трапеции;
α (BAD, CDA) β (ABC, CDA) – углы при основании.

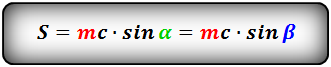
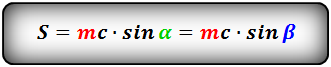
Теперь вы с легкость сможете решить любую задачу, которая раньше казалась вам невыполнимой. Самое главное – определиться с нужной формулой и ее элементами, а теперь это и вовсе просто – наша “статья-шпаргалка” открыла вам все секреты: формулы, свойства, подсказки, нужные элементы и их нахождение. Удачи в решении!
sovetclub.ru
Как найти площадь равнобедренной трапеции
Инструкция
Четырехугольник, у которого пара противолежащих сторон параллельна, называют трапецией. В трапеции определяют основания, стороны, диагонали, высоту, среднюю линию. Зная различные элементы трапеции, можно найти ее площадь. Иногда специальными случаями равнобедренных трапеций считаются прямоугольники и квадраты, но во многих источниках они к трапециям не относятся. Еще одним специальным случаем равнобедренной трапеции считается такая геометрическая фигура с 3 равными сторона. Ее называют трехсторонней трапецией, или триравнобедренной трапецией, или, реже, symtra. Такую трапецию можно рассматривать как отсечение 4 последовательных вершин от правильного многоугольника, имеющего 5 или более сторон. Трапеция состоит из оснований (параллельные противоположные стороны), боковых сторон (две другие стороны), средней линии (отрезок, соединяющий середины боковых сторон). Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.Чтобы трапеция считалась равнобедренной, должно выполняться как минимум одно из следующих условий. Первое: углы при основе трапеции должны быть равны: ∠ABC = ∠BCD и ∠BAD = ∠ADC. Второе: диагонали трапеции должны быть равны: AC = BD. Третье: если углы между диагоналями и основаниями одинаковы, трапеция считается равнобедренной: ∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC. Четвертое: сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°. Пятое: если вокруг трапеции можно описать окружность, она считается равнобедренной.
Равнобедренная трапеция, как и любая другая геометрическая фигура, обладает рядом неизменных свойств. Первое из них: сумма углов, прилегающих к боковой стороне равнобедренной трапеции равна 180°: ∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°. Второе: если в равнобедренную трапецию можно вписать окружность, то ее боковая сторона равна средней линии трапеции: AB = CD = m. Третье: вокруг равнобедренной трапеции всегда можно описать окружность. Четвертое: если диагонали взаимно перпендикулярны, то высота трапеции равна полусумме оснований (средней линии): h=m. Пятое: если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты: SABCD = h3 . Шестое: если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции: h3 = BC • AD. Седьмое: сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции: AC2 + BD2 = AB2 + CD2 + 2BC • AD. Восьмое: прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции: HF ┴ BC ┴ AD. Девятое: высота ((CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) — равен полуразности оснований: AP=BC+AD/2, PD=AD-BC/2.
Самая распространенная формула для вычисления площади трапеции — S = (a+b)h/2. Для случая равнобедренной трапеции она явным образом не поменяется. Можно лишь отметить, что у равнобедренной трапеции углы при любом из оснований будут равны (DAB = CDA = x). Так как ее боковые стороны тоже равны (AB = CD = с), то и высоту h можно посчитать по формуле h = с*sin(x).Аналогично, площадь трапеции можно записать через среднюю сторону трапеции: S = mh.
Рассмотрим частный случай равнобедренной трапеции, когда ее диагонали перпендикулярны. В этом случае, по свойству трапеции, ее высота равна полусумме оснований.Тогда площадь трапеции можно вычислить по формуле: S = (a+b)^2/4.
Рассмотрим также еще одну формулу для определения площади трапеции: S = ((a+b)/2)*sqrt(c^2 — ((b-a)^2+c^2-d^2)/2(b-a))^2), где c и d — боковые стороны трапеции. Тогда в случае равнобедренной трапеции, когда c = d, формула принимает вид: S = ((a+b)/2)*sqrt(c^2-((b-a)^2/2(b-a))^2).
Найдите площадь трапеции по формуле S=0,5×(a+b)×h, если известны a и b — длины оснований трапеции, то есть параллельные стороны четырехугольника, и h — высота трапеции (наименьшее расстояние между основаниями). Например, пусть дана трапеция с основаниями a=3 см, b=4 см и высотой h=7 см. Тогда ее площадь будет равна S=0,5×(3+4)×7=24,5 см².
Воспользуйтесь следующей формулой для вычисления площади трапеции: S=0,5×AC×BD×sin(β), где AC и BD — диагонали трапеции, а β — угол между этими диагоналями. Например, задана трапеция с диагоналями AC=4 см и BD=6 см и углом β=52°, тогда sin(52°)≈0,79. Подставьте значения в формулу S=0,5×4×6×0,79≈9,5 см².
Посчитайте площадь трапеции, когда известны ее m — средняя линия (отрезок, соединяющий середины сторон трапеции) и h — высота. В этом случае площадь будет равна S=m×h. К примеру, пусть у трапеции средняя линия m=10 см, а высота h=4 см. В этом случае получается, что площадь заданной трапеции равна S=10×4=40 см².
Вычислите площадь трапеции, в случае когда даны длины ее боковых сторон и оснований по формуле: S=0,5×(a+b)×√(c²−(((b−a)²+c²−d²)÷(2×(b−a)))²), где a и b — основания трапеции, а c и d — ее боковые стороны. Например, пусть дана трапеция с основаниями 40 см и 14 см и боковыми сторонами 17 см и 25 см. По вышеуказанной формуле S=0,5×(40+14)×√(17²−(((14−40)²+17²−25²)÷(2×(14−40)))²)≈423,7 см².
Рассчитайте площадь равнобедренной (равнобокой) трапеции, то есть трапеции у которой боковые стороны равны, если в нее вписана окружность по формуле: S=(4×r²)÷sin(α), где r — радиус вписанной окружности, α — угол при основании трапеции. В равнобедренной трапеции углы при основании равны. Например, пусть в трапецию вписана окружность радиусом r=3 см, а угол при основании α=30°, тогда sin(30°)=0,5. Подставьте значения в формулу: S=(4×3²)÷0,5=72 см².
www.kakprosto.ru
Все формулы средней линии равнобедренной трапеции
1. Формула средней линии равнобедренной трапеции через основания

a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):

2. Формулы средней линии через основание, высоту и углы при нижнем основании

a — нижнее основание
b — верхнее основание
c — боковая сторона
α — угол при нижнем осровании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):




3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

d — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции
h — высота трапеции
α — угол при нижнем осровании
m — средняя линия
Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Площадь равнобедренной трапеции по основаниям и диагонали
Как найти площадь равнобедренной трапеции по основаниям и диагонали?
Площадь трапеции равна произведению полусуммы оснований на высоту. Поскольку основания уже известны, остаётся найти высоту трапеции.
Дано: ABCD — трапеция,
AD∥BC,AB=CD,
AD=a, BC=b, AC=d
Найти:
Решение:
Проведем высоту трапеции
По свойству равнобедренной трапеции,
Рассмотрим прямоугольный треугольник BDF.
По теореме Пифагора
По формуле
находим площадь трапеции ABCD
Запоминать эту формулу не нужно. При решении конкретной задачи достаточно провести аналогичные рассуждения, найти высоту трапеции и подставить её в стандартную формулу для нахождения площади трапеции.
Задача.
Основания равнобедренной трапеции равны 38 см и 22 см. Найти площадь трапеции, если её диагональ равна 50 см.
Решение:
Ответ: 1200 см².
Площадь трапеции, Трапецияwww.treugolniki.ru
Как найти площадь равнобедренной трапеции, если все стороны известны, а высота нет?
Пусть АВСД-равнобедренная трапеция. АВ=СД, АД-большее основание, Вс-меньшее основание .Провести 2 высоты ВК и СМ к основанию АД КМ=ВС, АД=МД= (АД-ВС): 2 ВK^2=AB^2 — AK^2-по т. Пифагора из прямоуг. треуг. АВК. так и найдёшь высоту ВК
из большего основания вычитаешь меньшее и делишь разность на 2. Полученное число берешь за катет, бедро трапеции — за гипотенузу. по теореме пифагора вычисляешь второй катет-это и будет высота. сумму оснований делишь на 2 и умножаешь на высоту-это и будет площадь трапеции
если у тебя a,b — основания трапеции c — боковая сторона трапеции то высота будет <img data-big=»1″ data-lsrc=»http://content-1.foto.my.mail.ru/mail/jashur/_answers/p-1411.jpg» src=»//otvet.imgsmail.ru/download/3b4b502fadba267368d86631a516c9df_h-1411.jpg»>
<img src=»//otvet.imgsmail.ru/download/ac6d61e7275a901729d2a9c0db491f0f_p-5.jpg» data-hsrc=»http://content-29.foto.my.mail.ru/bk/tolm92/_answers/h-5.jpg»><img src=»//otvet.imgsmail.ru/download/4cc25ca48eb27bd1eecc014962b34744_p-6.jpg» data-hsrc=»http://content-15.foto.my.mail.ru/bk/tolm92/_answers/h-6.jpg»>
touch.otvet.mail.ru
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
то
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
откуда
www.uznateshe.ru