Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
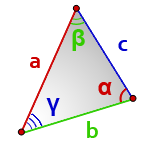
a, b, c — стороны произвольного треугольника
α, β, γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
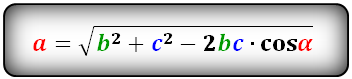
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
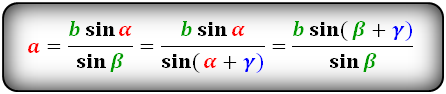
- Подробности
- Автор: Administrator

www-formula.ru
Две стороны и угол треугольника
Зная две стороны в треугольнике и угол между ними, можно с помощью теоремы косинусов вычислить третью сторону треугольника. Для этого нужно извлечь квадратный корень из суммы квадратов известных сторон и разности с их удвоенным произведением на косинус угла между ними. (рис.76) a^2=b^2+c^2-2bc cosα a=√(b^2+c^2-2bc cosα )
Угол β или γ можно рассчитать через ту же теорему косинусов, зная две, образующие их стороны, при этом один из них – последний, проще найти, отняв два известных от 180 градусов. cosβ=(a^2+c^2-b^2)/2ac=(b^2+c^2-2bc cosα+c^2-b^2)/(2c√(b^2+c^2-2bc cosα ))=(2c^2-2bc cosα)/(2c√(b^2+c^2-2bc cosα ))=(c-b cosα)/√(b^2+c^2-2bc cosα ) cosγ=(a^2+b^2-c^2)/2ab=(b^2+c^2-2bc cosα+b^2-c^2)/(2b√(b^2+c^2-2bc cosα ))=(b-c cosα)/√(b^2+c^2-2bc cosα )
Медиана треугольника рассчитывается по вполне однозначной формуле, тогда как если нужно найти медианы через две стороны и угол между ними, то требуются преобразования. m_a=√(2b^2+2c^2-a^2 )/2=√(2b^2+2c^2-b^2-c^2+2bc cosα )/2=√(b^2+c^2+2bc cosα )/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2b^2+2c^2-4bc cosα+2c^2-b^2 )/2=√(b^2+4c^2-4bc cosα )/2 m_c=√(2a^2+2b^2-c^2 )/2=√(2b^2+2c^2-4bc cosα+2b^2-c^2 )/2=√(4b^2+c^2-4bc cosα )/2
Для расчета биссектрис в произвольном треугольнике также существуют стандартные формулы, из которых только одна может быть преобразована и упрощена для двух сторон и угла между ними. l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)=√(bc((b-c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-b^2-c^2+2bc cosα ) )/(b+c)=(bc√(2(1+cosα ) ))/(b+c)
Чтобы найти высоту, нужно знать все три стороны в треугольнике. Подставив их в формулу так, чтобы сторона, на которую опущена искомая высота была в знаменателе, рассчитываются их величины. h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c
Вычислить среднюю линию треугольника можно, зная лишь ту сторону, которой она параллельна, так как сторона будет в два раза больше. В случае с неизвестной стороной, можно подставить в формулу радикал,выведенный по теореме косинусов. M_a=a/2=√(b^2+c^2-2bc cosα )/2 M_b=b/2 M_c=c/2
На пересечении биссектрис в треугольнике расположен центр окружности, которую можно в него вписать. Радиус такой окружности рассчитывается по следующей формуле(рис.75.5) r=√(((p-a)(p-b)(p-c))/p)
Центр описанной вокруг треугольника окружности в свою очередь расположен в точке пересечения медиатрисс, и его формула значительно видоизменена в сравнении с радиусом вписанной окружности. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))
geleot.ru
Два угла и сторона треугольника C
Для того чтобы рассчитать в треугольнике все возможные показатели, необходимо, как минимум, иметь данные о его сторонах. Зная два угла и сторону а, можно найти остальные две стороны и угол, построив высоту в таком треугольнике. (рис. 76.1) Высота разделит произвольный треугольник на два прямоугольных, в которых катетами будет высота и часть известной стороны x или y, а гипотенузами – неизвестные стороны a и b. Кроме того, что мы задаем известную сторону a, как сумму двух катетов x и y, тригонометрия полученных треугольников, определяет высоту с одной стороны как произведение y на тангенс β, а с другой стороны как произведение x на тангенс γ. Приравнивая эти выражения друг к другу, можно составить систему уравнений, из которых могут быть найдены части x и y, а затем неизвестные стороны первоначального треугольника a и b. {█(x+y=a@y tanβ=x tanγ )┤{█(x=a-y@y(tanβ+tanγ )=a tanγ )┤{█(x=a-y@y=(a tanγ)/(tanβ+tanγ ))┤ b=x/cosγ , c=y/cosβ h_a=y tanβ
Можно также найти сразу две другие высоты треугольника, опущенные на стороны b и c соответственно. (рис. 76.2) h_b=a sinβ h_c=a sinγ
Третий угол можно найти, зная, что сумма всех углов в треугольнике равна 180 градусам. α=180°-β-γ
Теперь, зная все стороны, углы и высоты, можно найти все остальные параметры треугольника. Вычислить периметр можно, сложив все три стороны, а площадь – умножив половину любой стороны на опущенную на нее высоту. P=a+b+c S=(ah_a)/2
Если провести в треугольнике медианы, то каждая из них разделит сторону, на которую она опущена, на две равные части. Для того, чтобы вычислить медиану в треугольнике, необходимо знать все три стороны. Формула медианы заключается в том, чтобы сложить удвоенные квадраты двух нетронутых сторон, отнять квадрат стороны, на которую опущена медиана, извлечь из этого выражения квадратный корень и разделить его на два. (рис. 75.1) m_c=√(2a^2+2b^2-c^2 )/2 m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2
Чтобы найти биссектрисы треугольника, которые делят пополам его углы, также необходимо знать все три стороны треугольника. Формула биссектрисы выглядит немного сложнее, чем формула медианы, но достаточно проста в расчетах. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)
Средняя линия треугольника – это прямая, проведенная параллельно одной из его сторон. Ее особенность заключается в том, что она делит стороны на которые опирается на две равные части, и сама равна половине стороны, ей параллельной. (рис.75.7) M_a=a/2 M_b=b/2 M_c=c/2
Также в произвольном треугольнике через стороны можно найти радиус окружности, которую можно вписать в треугольник или описать около него. Радиус вписанной окружности будет начинаться в точке пересечения биссектрис треугольника и опускаться на любую из сторон под прямым углом. Радиус описанной окружности начинается в точке пересечения медиатрисс треугольника и заканчивается в любой из его вершин. (рис. 75.5, 75.6) r=√(((p-a)(p-b)(p-c))/p) R=abc/(4√(p(p-a)(p-b)(p-c)))
geleot.ru
