Формула периметра трапеции
Трапе́ция (от др. -греч. τράπέζιου — «столик» ; τράπεζα — «стол, еда» ) — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого произвольная пара противолежащих сторон параллельна, в этом случае параллелограмм является частным случаем трапеции
Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a, BC=b, CD=c, AD=d, имеет вид:
\[ \LARGE P_{ABCD} = a + b + c + d \]
где:
P — периметр трапеции
a, b, c, d — стороны трапеции
Периметр равнобокой трапеции
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
Периметр произвольной трапеции, в которой AB=CD=a, BC=b, AD=c, имеет вид:
\[ \LARGE P_{ABCD} = 2 \cdot a + b + c \]
где:
P — периметр трапеции
a, b, c, d — стороны трапеции
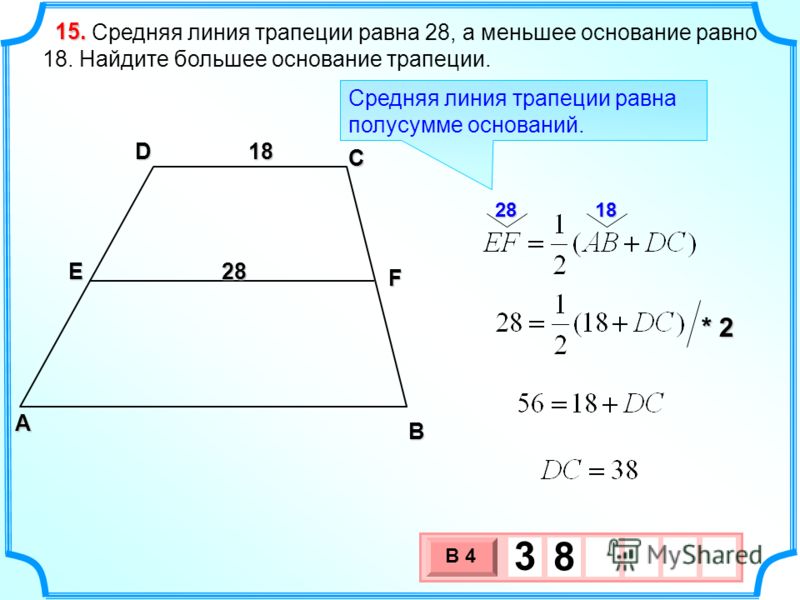
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны: AC = BD
3. Одинаковые углы между диагоналями и основаниями: ∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°: ∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Также можно найти периметр трапеции, не зная длин оснований, но имея среднюю линию m. Средняя линия по определению представляет собой полусумму оснований трапеции, поэтому умножив ее на два, можно подставить ее вместо оснований в формулу периметра: \( P = 2 \cdot m + c + d \).
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Площадь трапеции через синус угла и основания. Площадь трапеции
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях.
 Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен. Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
—
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон.
 Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований) - Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Прежде чем найти площадь трапеции, необходимо определится с известными элементами трапеции. Трапеция – это геометрический объект, а именно: четырёхугольник, который имеет две параллельные стороны (два основания). Другие две стороны – боковые. Если же параллельны будут и эти две стороны четырёхугольника, то это уже будет не трапеция, а параллелограмм. Если хотя бы один угол трапеции равен 90 градусов, то такая трапеция называется прямоугольной. Как найти площадь прямоугольной трапеции, рассмотрим позже. d2) – это синус угла, между диагоналями трапеции.
d2) – это синус угла, между диагоналями трапеции.
Существуют также различные формулы, выведенные из основных, а также формула для расчёта площади трапеции, когда известны все её стороны. Однако эта формула достаточно громоздкая и используется редко, ведь, зная все стороны трапеции можно просто определить высоту или её среднюю линию. Также в равнобедренную трапецию можно вписать окружность. В этом случае площадь трапеции будет высчитываться по формуле: 8*радиус окружности в квадрате.
Как найти площадь прямоугольной трапеции
Как и говорилось ранее, прямоугольной называется та трапеция, у которой хотя бы один угол прямой. Найти площадь такой трапеции очень просто. В основном, для поиска площади прямоугольной трапеции используются те же формулы, что и для обычной трапеции. Однако стоит помнить, что одна из боковых сторон такой трапеции и будет являться высотой. Также часто решение задач поиска площади прямоугольной трапеции сводится к поиску площади прямоугольника и треугольника, образованных опущенной высотой.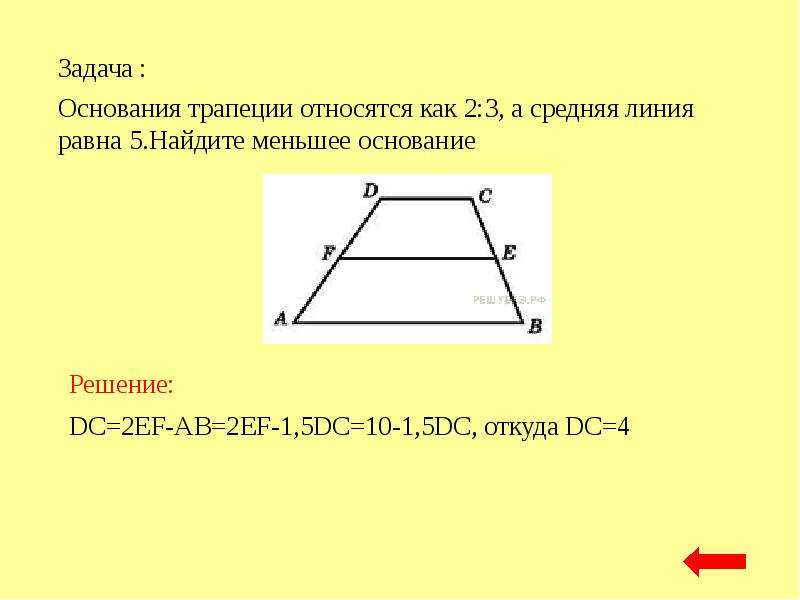
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению .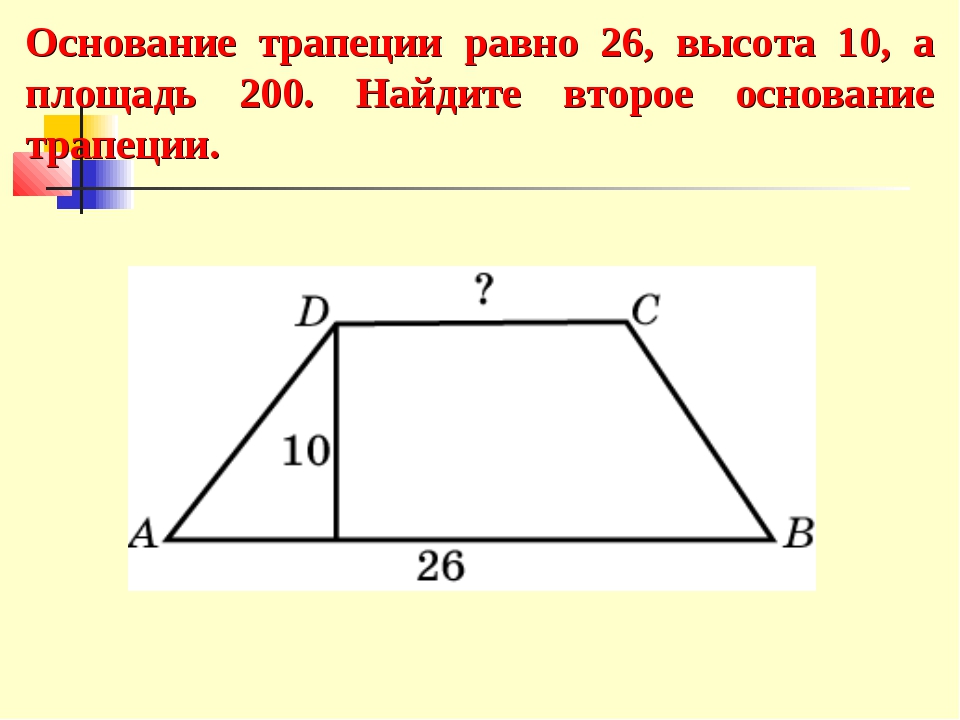
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции.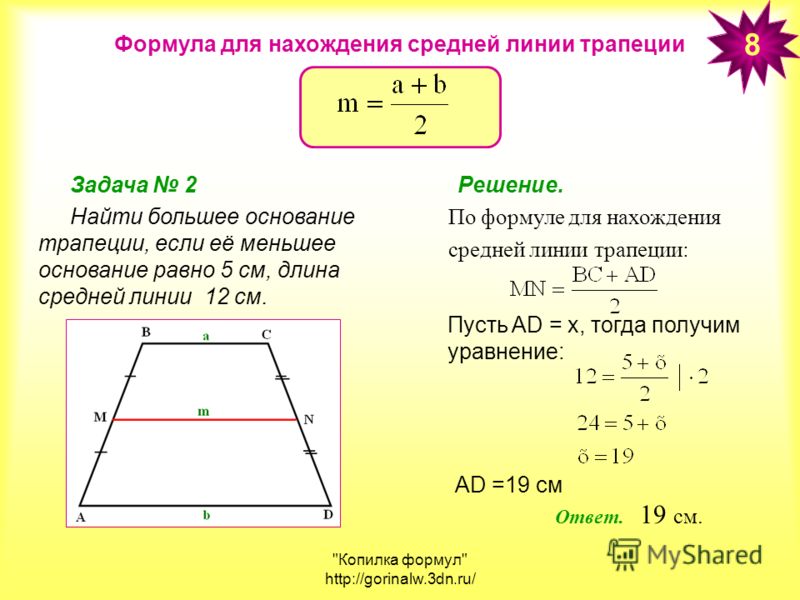 С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол .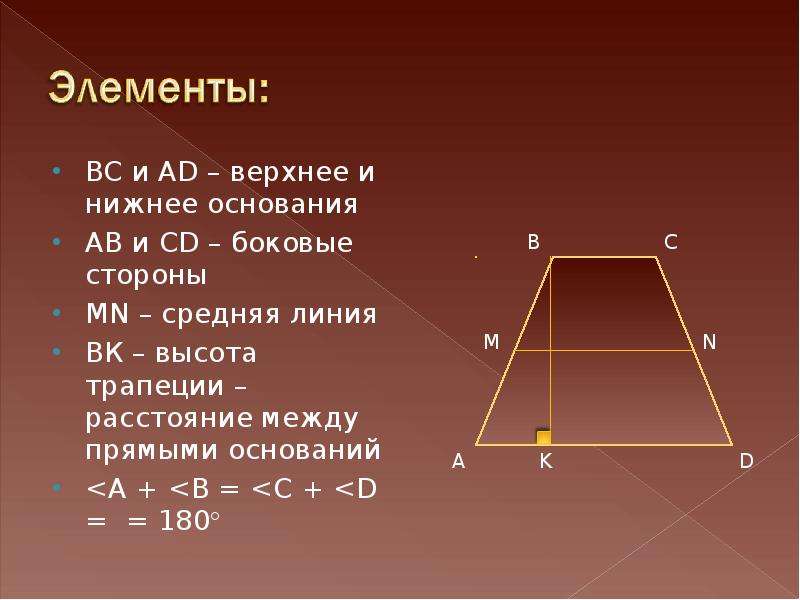 Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .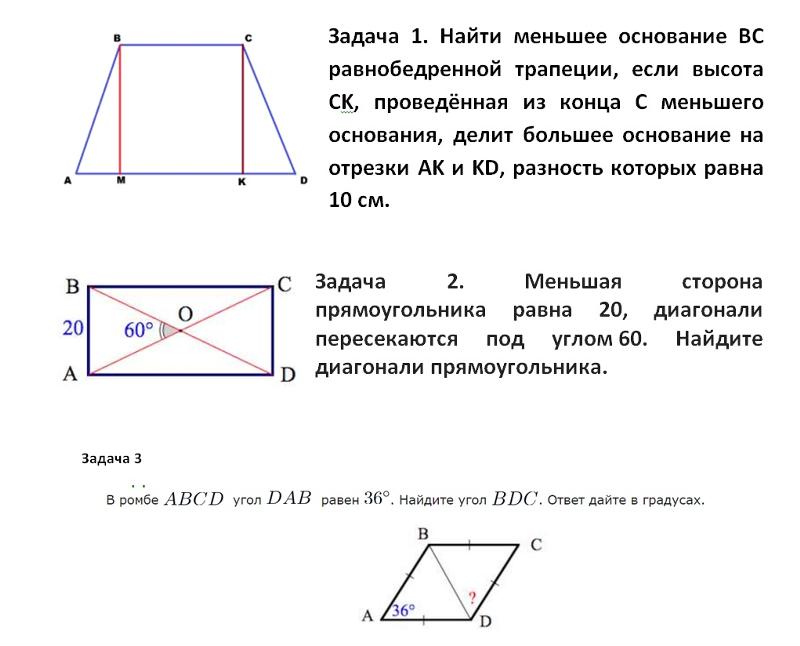
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.

- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Высота трапеции через основания 8 и 28 | Геометрия
Высота трапеции через основания 8 и 28 | Геометрия — просто!Задача. Дана трапеция с основаниями 8 и 28 и боковыми сторонами 12 и 16.
Найти высоту трапеции.
Решение: Опустим из вершин В и С высоты
ВК и СМ на основание АД.
Получим два прямоугольных треугольника АВК и ДСМ
и прямоугольник ВСМК.
КМ в прямоугольнике равна 8, примем АК за Х,
тогда МД будет равно 28 — 8 — Х = 20 — Х.
Поскольку катеты ВК=СМ, то, решая эти треугольники по теореме Пифагора,
составим следующее уравнение:
12² — Х² = 16² — (20 — Х)²
144 — Х² = 256 -(400 — 40Х + Х²)
144 — Х² = 256 — 400 + 40Х — Х²
144 — 256 + 400 = 40Х
40Х = 288
Х = 7,2
Из треугольника АВК находим ВК.

ВК² = 12² — 7,2²
ВК² = 92,16
ВК = 9,6
Ответ: высота трапеции 9,6
Задача. Боковая сторона и меньшее основание
равнобедренной трапеции равны радиусу
описанной окружности. Найти высоту трапеции, если
её средняя линия равна 6√3.
Решение: Из условия задачи следует, что треугольники
ABO, BCO, OCD — равносторонние.
Из этого получается, что сумма углов AOB, BOC и COD равна 180º.
А раз это так, то AOD — развернутый угол,
и AD диаметр описанной окружности.
Отсюда имеем: (2R + R)/2 = 6√3.
3R/2 = 6√3
3R = 12√3
R = 4√3.
Из равностороннего треугольника ВСО, зная сторону,
которая равна 4√3, находим высоту.
По теореме Пифагора:
Квадрат высоты = R² -(R/2)² = 16*3 — 4*3 = 48 — 12 = 36.
Отсюда, высота трапеции равна √36 = 6.
Ответ: высота трапеции равна 6.
Вам так же будет интересно:
Оставить комментарий
Видео-вопрос: нахождение длины основания трапеции по длине, высоте и площади другого основания
Стенограмма видео
Трапеция площадью 132 и основанием 20
имеет высоту 11. Какова длина другого
база?
Какова длина другого
база?
Было бы разумно начать с этого вопрос, нарисовав диаграмму для моделирования информации. В этом вопросе нам говорят, что мы есть трапеция.Мы помним, что трапеция четырехугольник, это четырехсторонняя фигура с парой параллельных сторон. Высота 11 единиц. Нам сказали, что одна из баз 20, и нам нужно найти длину другого основания. Когда мы говорим о базах в трапеции, то есть длины параллельных сторон. Мы не знаем, какое основание равно 20, но напишем это как нижнее основание.
Для определения длины
другая база, нам нужно будет использовать информацию о районе.В некоторых странах слово
трапеция используется для обозначения формы с одной парой параллельных сторон. Здесь нам говорят, что область
132 кв. И мы можем использовать формулу для
площадь трапеции или трапеции, что говорит нам о том, что площадь равна половине
ℎ раз 𝑏 меньше одного плюс 𝑏 меньше двух. ℎ представляет собой высоту
трапеция, а 𝑏 sub one и 𝑏 sub two — два основания. Итак, взяв эту формулу, мы
можно заполнить тем, что площадь 132, высота 11.И мы не знаем ни одной из баз,
поэтому давайте сохраним это как 𝑏 подпункт. А затем мы добавляем основание 20.
ℎ представляет собой высоту
трапеция, а 𝑏 sub one и 𝑏 sub two — два основания. Итак, взяв эту формулу, мы
можно заполнить тем, что площадь 132, высота 11.И мы не знаем ни одной из баз,
поэтому давайте сохраним это как 𝑏 подпункт. А затем мы добавляем основание 20.
Мы можем преобразовать это уравнение в
найти 𝑏 sub один несколькими способами. Но давайте начнем с удаления этого
половину, умножив обе части уравнения на два. 132 умножить на два дает нам
264. А с правой стороны мы
все еще есть 11 раз 𝑏 меньше одного плюс 20. Затем мы можем разделить обе части
уравнение на 11.264, деленное на 11, дает нам 24. И тогда справа,
у нас будет 𝑏 меньше единицы плюс 20. Затем мы можем найти 𝑏 меньше единицы,
вычитание 20 из обеих частей уравнения. Итак, наш ответ заключается в том, что
другая база должна была иметь длину четыре единицы.
Линия, параллельная основанию трапеции
Есть ряд интересных особенностей линий, проведенных параллельно основаниям трапеции. Одну из них мы видели в этой задаче — линию, параллельную основаниям и соединяющую середины катетов.
Если основания трапеции равны a и b, то длина этой линии равна ½(a+b). Позже мы займемся еще одной такой интересной линией — линией, параллельной основаниям трапеции, которая разбивает ее на две подобные трапеции.
Но здесь мы рассмотрим следующую линию, проведенную параллельно основаниям трапеции и разделяющую трапецию на 2 равные части. Эту линию иногда называют биссектрисой площади.
Задача
ABCD — трапеция, AB||CD.Ef параллелен основаниям (EF||AB, EF||AB) и делит ABCD на две равные области. Найдите формулу длины EF, используя AB и CD.
Стратегия
Назовем верхнюю базу «а», нижнюю базу «b» и среднюю линию «с».
Линия c создает две трапеции внутри исходной трапеции. Площади двух маленьких трапеций равны, поэтому назовем эту площадь «S», а площадь большой трапеции равна 2S.
Площади двух маленьких трапеций равны, поэтому назовем эту площадь «S», а площадь большой трапеции равна 2S.
Мы запишем формулы площадей двух маленьких трапеций, используя основания a, b и c, а затем воспользуемся элементарной алгеброй для вычисления c, используя тот факт, что площади равны, и что сумма высот меньших трапеций равна высоте большой: h 1 +h 2 =h
Решение
Для верхней малой трапеции:
(1) S=(a+ в) · h 1 / 2 → h 1 = 2S/(a+c)
Для нижней малой трапеции:
(2) S=(b+c) · h 2 / 2 → h 2 = 2S/(b+c)
Для большой трапеции h= h 1 +h 2 и площадь равна 2S, поэтому
(3) 2S = (a+b)·h/ 2 = (а+b)·[2S/(а+с)+2S/(b+с)]/2
(4) 1 = (а+b)/[1/(а+с) +1/ (b+c)]/2 //делим обе части на 2S
(5) 2 = (a+b)/(a+c) +(a+b)/(b+c) // переставляем
(6 ) 2·(a+c)·(b+c) = (a+b)(b+c)+(a+b)(a+c) //общий знаменатель и перекрестное умножение
(7) 2ab+2ac +2cb+2c 2 =ab +ac+b 2 +bc+a 2 +ac+ba+bc
(8) 2c 2 =b 2 +a 2
(9) c=√[(b 2) +a 2 )/2]
Итак, c — среднеквадратичное (или среднеквадратичное значение — RMS) двух оснований трапеции.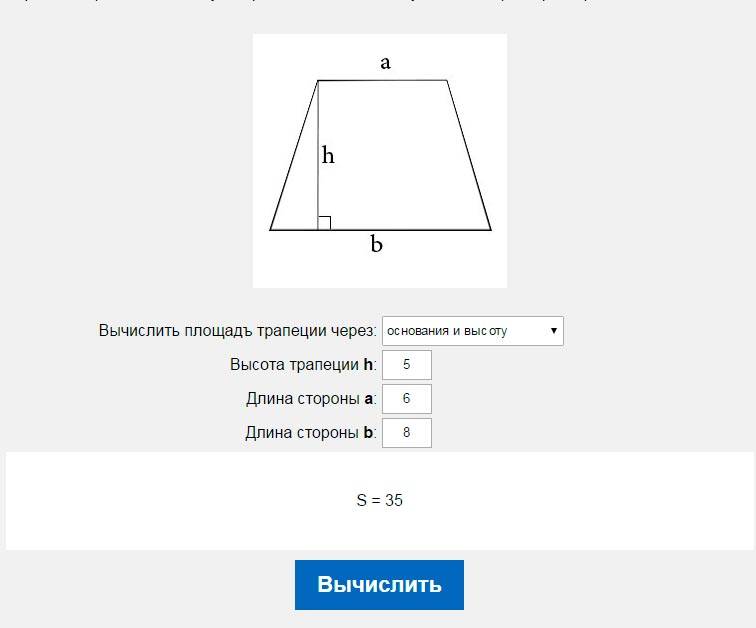
Как найти высоту трапеции — видео и расшифровка урока
Геометрический пример
Давайте посмотрим, как мы можем рассчитать высоту трапеции на примере:
Шаг 1:
Мы начнем с рисования линии от вершины наверху трапеции к основанию, чтобы создать прямоугольный треугольник или треугольник с углом 90 градусов.
Шаг 2:
Далее мы вычислим основание только что нарисованного треугольника.Этот пример представляет собой равнобедренный треугольник , потому что у него две равные стороны. В этом примере основание трапеции (14 дюймов) равно вершине трапеции (6 дюймов) плюс два основания прямоугольных треугольников ( x ).
В алгебраических терминах 14 = 6 + 2 x .
Шаг 3:
Теперь воспользуемся теоремой Пифагора для вычисления высоты или одного катета прямоугольного треугольника.
Шаг 4:
Наконец, мы отформатируем наш ответ в соответствии с исходной задачей. Высота этой трапеции равна 3 дюймам.
Совет
Важно помнить, что вы можете найти высоту трапеции только в том случае, если сможете точно вычислить основание прямоугольного треугольника, один из катетов которого является гипотенузой. Это возможно в равнобедренных трапециях и в трапециях с прямым углом.Неправильные трапеции необходимо внимательно рассмотреть, чтобы определить, можно ли вычислить основание образуемого прямоугольного треугольника.
Пример из реальной жизни
Прачечная Мэри имеет форму трапеции, показанной на этом рисунке.
Она решила повесить бельевую веревку вдоль угловой стены комнаты, но не знает длину стены. Давайте поможем ей, найдя длину наклонной стены.
Шаг 1:
Мы начнем с рисования прямой линии от правого угла верхней стены, чтобы создать прямоугольный треугольник с угловой стеной.
 Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)