§1.3 Графические информационные модели
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (учебник ФГОС Л.Л. Босова, А.Ю. Босова) | §1.3 Графические информационные модели
Ключевые слова:
• схема
• карта
• чертёж
• график
• диаграмма
• граф
• сеть
• дерево
1.3.1. Многообразие графических информационных моделей
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.
Рис. 1.5. Примеры схем, используемых на уроках физики, биологии, истории
Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.
Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.
График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
1.3.2. Графы
Если некоторые объекты изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д. Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром. Линия направленная (со стрелкой) называется дугой; при этом вершина, из которой дуга исходит, называется начальной, а вершина, куда дуга входит, — конечной.
Граф называется неориентированным, если его вершины соединены рёбрами (рис. 1.6, а). Вершины ориентированного графа соединены дугами (рис. 1.6, б). Путь — это последовательность рёбер (дуг), по которым можно перейти из одной вершины в другую.
Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер. На рис. 1.6, в с помощью взвешенного неориентированного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Рис. 1.6. Графы
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс1* высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
Ресурс «Живая Родословная» (145555) — инструмент для формирования и анализа генеалогических деревьев, содержащий примеры родословных. С его помощью вы можете изучить генеалогические деревья многих известных семей и построить генеалогическое дерево своей семьи (http://sc.edu.ru/).
Класс — множество объектов, обладающих общими признаками.
1.3.3. Использование графов при решении задач
Графы удобно использовать при решении некоторых классов задач.
Пример 1. На рисунке 1.7 изображена схема дорог, связывающих торговые точки А, В, С, D, Е. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки Е?
Рис. 1.7. Схема дорог, представленная ориентированным графом
В вершину Е можно попасть только из вершин С и D. Если мы будем знать число путей из вершины А в вершину С и из вершины А в вершину D, то, сложив их, получим искомое число путей из А в Е. Действительно, для того чтобы попасть из вершины А в вершину Е, мы просто все пути из вершины А в вершину С дополним дугой СЕ, а пути из вершины А в вершину D дополним дугой DE. Число путей при этом не изменится. Итак, число путей из вершины А в вершину Е равно сумме путей из А в С и из А в П.
Можно сказать, что наша задача распалась на две более простые задачи. Решим каждую из них в отдельности.
В вершину С можно попасть непосредственно из вершины А и из вершины В. В свою очередь, существует единственный путь из вершины А в вершину В. Таким образом, из вершины А в вершину С можно попасть двумя путями: 1 (напрямую из А) + 1 (через В) = 2.
Попробуйте доказать, что путь из вершины А в вершину В — единственный.
Что касается вершины D, она является конечной вершиной для трёх дуг: BD, AD и CD. Следовательно, в неё можно попасть из вершин А, В и С:
1 (напрямую из А) + 1 (через В) + 2 (через С) = 4.
Итак, существуют четыре пути из вершины А в вершину D.
Теперь выполним подсчёт путей из А в Е:
2 (через С) + 4 (через D) = 6.
Решение задачи будет гораздо проще, если двигаться от вершины А (начало маршрута) к вершине Е и проставлять веса вершин — число путей из А в текущую вершину (рис. 1.8). При этом вес вершины А можно принять за 1. Действительно, существует единственный способ попасть из А в А — оставаться на месте.
Рис. 1.8. Схема дорог, представленная взвешенным ориентированным графом
Пример 2. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.9.
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.
Рис. 1.9. Дерево для решения задачи о записи трёхзначных чисел
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить. (Вспомните правило умножения из комбинаторики!)
Пример 3. Рассмотрим несколько видоизменённую классическую задачу о переправе.
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусём без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?
Для решения этой задачи составим граф, вершинами которого будут исходное и результирующее размещение персонажей на берегах реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.10).
Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.
На графе видно, что существуют два решения этой задачи. Приведём соответствующий одному из них план переправы:
2) крестьянин возвращается;
3) крестьянин перевозит собаку;
4) крестьянин возвращается с лисой;
5) крестьянин перевозит гуся;
6) крестьянин возвращается;
7) крестьянин перевозит лису.
Пример 4. Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).
Если игрок I оставил 4 спички, игрок II может своим ходом оставить 3 или 2 спички. Если же после хода первого игро- . ка останутся 3 спички, второй игрок может выиграть, взяв две спички и оставив одну.
Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.
На рис. 1.11 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Рис. 1.11. Дерево игры
САМОЕ ГЛАВНОЕ
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы, графы.
Граф состоит из вершин, связанных линиями — рёбрами или дугами. Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весами вершин (рёбер, дуг).
Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Какие информационные модели относят к графическим?
3. Приведите примеры графических информационных моделей, с которыми вы имеете дело:
а) при изучении других предметов;
б) в повседневной жизни.
4. Что такое граф? Что является вершинами и рёбрами графа на рис. 1.6, в? Приведите примеры цепей и циклов, имеющихся в этом графе. Определите, какие два пункта наиболее удалены друг от друга (два пункта считаются самыми удалёнными, если длина кратчайшего пути между ними больше, чем длина кратчайшего пути между любыми другими двумя пунктами). Укажите длину кратчайшего пути между этими пунктами.
5. Приведите пример системы, модель которой можно представить в форме графа. Изобразите соответствующий граф.
6. Грунтовая дорога проходит последовательно через населённые пункты А, В, С и D. При этом длина грунтовой дороги между А и В равна 40 км, между В и С — 25 км, и между С и D — 10 км. Между А и D дороги нет. Между А и С построили новое асфальтовое шоссе длиной 30 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 30 км/ч.
7. На рисунке изображена схема дорог, связывающих торговые точки А, Б, В, Г, Д, Б, К. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки К?
8. Работая в группе, составьте семантическую сеть по одной из русских народных сказок: «Колобок», «Курочка Ряба», «Репка».
9. Что такое дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы.
10. Сколько трёхзначных чисел можно записать с помощью цифр 2, 4, 6 и 8 при условии, что в записи числа не должно быть одинаковых цифр?
11. Сколько существует трёхзначных чисел, все цифры которых различны?
12. Для составления цепочек используются бусины, помеченные буквами А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква гласная, и любая согласная, если первая согласная. На третьем месте — одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?
13. Два игрока играют в следующую игру. Перед ними лежит куча из 6 камней. Игроки берут камни по очереди. За один ход можно взять 1, 2 или 3 камня. Проигрывает тот, кто забирает последний камень. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Электронное приложение к уроку
 |
 |
 |
||
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
Графический способ записи алгоритмов — Мегаобучалка
Система качества
Методические указания и задания на выполнение типового расчета
«Алгоритмы и блок-схемы»
«1 семестр
< Б.2 Информатика >
| Направление подготовки | <270800 Строительство > |
| Профиль подготовки | < Городское и строительство и хозяйство > |
| Квалификация (степень) выпускника | <бакалавр > |
| Форма обучения | <очная> |
Волжский, 2012
ПОНЯТИЕ АЛГОРИТМА
Алгоритм — это одно из основных понятий математики и информатики. Более 1000 лет назад в Багдаде, крупном научном центре Востока, жил абд Джафар Мужамед ибн Муса аль-Хорезми. Ему принадлежит книга по математике, которая в течение нескольких столетий пользовалась широкой популярностью. В ней Аль-Хорезми сформулировал правила выполнения четырёх арифметических действий над многозначными числами.
При переводе на латынь имя автора переделали в Algorithmi (Алгоритми). В книге аль-Хорезми приводились методы решения разных задач. Ссылаясь на них, европейцы упоминали: «Так говорил Алгоритми…». Со временем методы решения задач стали называться алгоритмами. В дальнейшем алгоритмом стали называть описание любой последовательности действий, которую следует выполнить для решения поставленной задачи.
Алгоритм — строго упорядоченная последовательность действий, направленная на выполнение поставленной задачи.
Алгоритмы, предназначенные для выполнения компьютерами, обычно называются компьютерными программами, или просто программами. Программа содержит команды на языке, понятном компьютеру. Она сообщает компьютеру, где брать и как надо обрабатывать данные для получения желаемого результата. Все функции компьютера, любое его действие задается программой.
Программа — это алгоритм, представленный на языке, понятном компьютеру.
Свойства алгоритма
Алгоритм должен удовлетворять следующим требованиям:
1. «Понятность» для исполнителя – исполнитель алгоритма должен знать, как его выполнить.
2. «Дискретность» (прерывность, раздельность)- алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определённых ) шагов (этапов).
3. «Определённость»— каждое правило алгоритма должно быть чётким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
4. «Результативность» (или конечность) состоит в том, что алгоритм должен приводить к решению задачи за конечное число шагов.
5. «Массовость» — означает, что алгоритм решения задачи разрабатывается в общем, виде, т. е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторого множества, которое называется областью применимости алгоритма. Данное свойство алгоритмов является наиболее важным.
Алгоритм считается правильным, если его выполнение всегда дает правильный результат. Соответственно алгоритм содержит ошибки, если можно указать такие допустимые исходные данные или условия, при которых выполнение алгоритма либо не завершится вообще, либо не будет получено никаких результатов, либо полученные результаты окажутся неправильными.
Способы описания алгоритма
На практике наиболее распространены следующие формы представления алгоритмов:
· Словесный способ
· Графический способ
· Псевдокоды
· Программный способ
Словесный способ записи алгоритмов
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
ПРИМЕР 1: Задача о сортировке шариков
Имеются три урны (белая, черная и полосатая). В полосатой урне находятся белые и черные шарики. Надо из этой урны все черные шарики переложить в черную урну, а белые — в белую. Сортировка производится так: по очереди вынимаются шарики из полосатой урны и в зависимости от цвета кладутся или в черную или в белую урну.
Алгоритм:
1. взять шарик из полосатой урны;
2. если он белый, то опустить в белую урну и перейти к действию 4;
3. если он черный, то опустить в черную урну и перейти к действию 4;
4. если полосатая урна не пуста, то перейти к действию 1;
конец.
Словесный способ не имеет широкого распространения, так как такие описания:
· строго не формализуемы;
· страдают многословностью записей;
· допускают неоднозначность толкования отдельных предписаний.
Графический способ записи алгоритмов
Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т. п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.
Псевдокоды
Псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и другое).
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
В псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они, как правило, выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. Примером псевдокода является «школьный алгоритмический язык».
Общий вид алгоритма:
Решение 1.3 Графические информационные модели по информатике 9 класс
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Какими слайдами вы могли бы дополнить презентацию?
Презентация: Перейти2. Какие информационные модели относят к графическим?
К графическим информационным моделям являются простейшим видом моделей, которые передают внешние признаки объекты — размеры, форму, цвет.3. Приведите примеры графических информационных моделей, с которыми вы имеете дело:
а) при изучении других предметов;
б) в повседневной жизни.
а) Электрические схемы по физике, схема Куликовской битвы по истории, политическая карта мира, чертежи по черчению.б) График погоды на неделю, карта.
4. Что такое граф? Что является вершинами и рёбрами графа на рис. 1.6? Приведите примеры цепей и циклов, имеющихся в этом графе. Определите, какие два пункта наиболее удалены друг от друга (два пункта считаются самыми удалёнными, если длина кратчайшего пути между ними больше, чем длина кратчайшего пути между любыми другими двумя пунктами). Укажите длину кратчайшего пути между этими пунктами.
Граф — это объект изображенный с помощью вершин, а связи между ними — линиями (ребрами).
На данном рисунке вершины — города A, B, C, D, E; рёбра — дороги(линии) между ними.
Города B и D — наиболее удалены друг от друга. Длина кратчайшего пути между ними составляет 170.
5. Приведите пример системы, модель которой можно представить в форме графа. Изобразите соответствующий граф.
Пример графа: Персональный компьютер
6. Грунтовая дорога проходит последовательно через населённые пункты А, В, С и D. При этом длина грунтовой дороги между А и В равна 40 км, между В и С — 25 км, и между С и D — 10 км. Между А и D дороги нет. Между A и С построили новое асфальтовое шоссе длиной 30 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 30 км/ч.
На графе черная линия — асфальтированное шоссе, а серая линия — грунтовая дорога.
По условию скорость велосипедиста по грунтовой — 20 км/ч, по шоссе — 30 км/ч.
От A до B можно добраться двумя способами: 1) 40 км по грунтовой дороге; 2) 30 по шоссе и 25 км по грунту.
Найдем время, которое может затратить велосипедист этими двумя способами(Расстояние делим на скорость).
1) 40:20 = 2 часа.
2) 25:20 = 1,25 часа по грунту, 30:30 = 1 час по шоссе, 2,25 часа займёт весь путь.
Ответ: 2 часа по грунтовой дороге в 40 км.
7. Составьте семантическую сеть по русской народной сказке «Колобок».
8. Что такое дерево? Моделями каких систем могут служить деревья? Приведите пример такой системы.
Дерево — это граф, в котором нет циклов. Все иерархические системы можно представить в виде дерева.Пример: генеалогическое дерево.
9. Сколько трёхзначных чисел можно записать с помощью цифр 2, 4, 6 и 8 при условии, что в записи числа не должно быть одинаковых цифр?
246; 248; 264; 284; 268; 286426; 428; 462; 468; 482; 486
624; 628; 642; 648; 682; 684
824; 826; 842; 846; 862; 864
Всего 24 числа.
10. Сколько существует трёхзначных чисел, все цифры которых различны?
Всего цифр 10: 0,1,2,3,4,5,6,7,8,9В трёхзначном числе три места
На первое можно поставить любую из девяти цифр( 0 нельзя)- 9 способов
На второе место останется 8 цифр + 0 = 9 цифр — 9 способов
На третье место 8 цифр, — 8 способов
Всего 9·9·8=648 чисел
11. Для составления цепочек используются бусины, помеченные буквами А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква гласная, и любая согласная, если первая согласная. На третьем месте — одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?
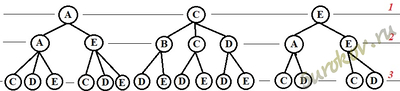
Составляем дерево вариантов и мы получаем:
Ветки начинающиеся с A: AAC AAD AAE; AEC AED AEE.
Ветки начинающиеся с C: CBD CBE; CCD CCE; CDD CDE.
Ветки начинающиеся с E: EAC EAD; EEC EED.
Ответ: 16 вариантов
12. Два игрока играют в следующую игру. Перед ними лежит куча из 6 камней. Игроки берут камни по очереди. За один ход можно взять 1, 2 или 3 камня. Проигрывает тот, кто забирает последний камень. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
При безошибочной игре выигрывает первый игрок. Своим первых ходом он должен взять один камень. В куче остается пять камней. Какой бы ход ни сделал второй игрок, в куче останется 4, 3 или 2 камня. Это позволяет первому игроку своим вторым ходом оставить в куче ровно один камень, его и должен будет забрать своим вторым ходом второй игрок.
Графический учебный исполнитель
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год | Графический учебный исполнитель
Содержание урока
Назначение и возможности графического исполнителя (ГРИС)
Линейные программы для ГРИС
Компьютерный практикум ЦОР. Графический учебный исполнитель
Назначение и возможности графического исполнителя (ГРИС)
Назначение и возможности графического исполнителя (ГРИС)
Учебные исполнители используются для обучения составлению управляющих алгоритмов.
Есть много учебных исполнителей, придуманных для занятий по информатике. У них разные, часто забавные названия: Черепашка, Робот, Чертежник, Кенгуренок, Пылесосик, Муравей, Кукарача и другие. Одни исполнители создают рисунки на экране компьютера, другие складывают слова из кубиков с буквами, третьи перетаскивают предметы из одного места в другое. Все эти исполнители управляются программным путем. Любому из них свойственна определенная среда деятельности, система команд управления, режимы работы.
В этой главе мы не будем детально описывать работу с каким-то реальным учебным исполнителем из вышеперечисленных (в компьютерных классах разных школ может быть разное программное обеспечение). Мы опишем условного исполнителя, который очень похож на некоторых из существующих в главном: системой команд, языком и приемами программирования.
Многие из учебных исполнителей занимаются рисованием на экране компьютера. Из названных выше это Черепашка, Кенгуренок, Чертежник. Эту группу можно назвать графическими исполнителями. Пусть наш гипотетический (придуманный) исполнитель тоже будет из этой «компании». Назовем его ГРИС, что значит «ГРафический ИСполнитель».
Что умеет делать ГРИС? Он может перемещаться по полю и своим хвостом рисовать на этом поле (предположим, что у него есть хвост, к которому привязан кусочек мела).
Обстановка, в которой действует исполнитель, называется средой исполнителя. Среда графического исполнителя показана на рисунке ниже. Это лист (страница экрана) для рисования. ГРИС может перемещаться в горизонтальном и вертикальном направлениях с постоянным шагом. На рисунке пунктиром показана сетка с шагом, равным шагу исполнителя. Исполнитель может двигаться только по линиям этой сетки. ГРИС не может выходить за границы поля.
Состояние исполнителя на поле определяется, во-первых, его местоположением (в какой точке поля он находится), во-вторых, направлением (куда он смотрит). Направление будем определять, как на географической карте: вверх — на север, вниз — на юг, влево — на запад, вправо – на восток. ГРИС может шагать или прыгать по линиям сетки, а также поворачиваться. Поворачиваться он умеет только против часовой стрелки.
Графический исполнитель — это объект управления. А управлять им будем мы с вами. Целью управления является получение определенного рисунка. Понятно, что этот рисунок может состоять только из горизонтальных и вертикальных отрезков, в других направлениях ГРИС двигаться не умеет.
Задача обычно ставится так: исполнитель находится в данной точке поля, смотрит в данном направлении. Требуется получить определенный рисунок. Например: ГРИС находится в середине поля и смотрит на восток. Надо нарисовать букву «Т» с длиной каждой линии, равной четырем шагам.
Первоначально исполнителю придается исходное состояние. Это делается в специальном режиме установки.
Теперь перейдем к управлению графическим исполнителем. Здесь возможны два режима: режим прямого управления и режим программного управления.
Простые команды ГРИС
Работа в режиме прямого управления происходит так: человек отдает команду, ГРИС ее выполняет; затем отдается следующая команда и т. д. (как в примере с хозяином и собакой).
В режиме прямого управления система команд исполнителя следующая:
- шаг — перемещение ГРИС на один шаг вперед с рисованием линии;
- поворот — поворот на 90° против часовой стрелки;
- прыжок — перемещение на один шаг вперед без рисования линии.
Эти команды будем называть простыми командами.
Например, пусть требуется нарисовать квадрат со стороной, равной одному шагу. Исходное положение ГРИС – в левом нижнем углу квадрата, направление — на восток. Будем отмечать состояние исполнителя маленькой стрелкой. Тогда последовательность команд и результаты их выполнения будут следующими:
Работа в программном режиме
Работа в программном режиме имитирует автоматическое управление исполнителем. Управляющая система (компьютер) обладает памятью, в которую заносится программа. Человек составляет программу и вводит ее в память. Затем ГРИС переводится в режим установки и человек вручную (с помощью определенных клавиш) устанавливает исходное состояние исполнителя. После этого производится переход в режим исполнения и ГРИС начинает работать по программе. Если возникает ситуация, при которой он не может выполнить очередную команду (выход за границу поля), то выполнение программы завершается аварийно. Если аварии не происходит, то работа исполнителя заканчивается на последней команде.
Таким образом, программное управление графическим исполнителем проходит этап подготовки (программирование и установка исходного состояния) и этап исполнения программы.
В режиме программного управления по-прежнему используются команды шаг, поворот, прыжок. Однако в этом режиме есть еще и другие команды. С ними вы познакомитесь позже.
Язык программирования для графического исполнителя — это учебный Алгоритмический язык (АЯ). Поэтому алгоритмы управления ГРИСом, записанные на АЯ, являются для него одновременно и программами.
Статистические графики Правила построения графиков Лекции
Содержание курса лекций «Статистика»
Графический метод в статистике
В результате сводки и дальнейшей обработки данных отчетности, различного рода обследований, переписей, наблюдений и т.п. экономист получает большое количество различных статистических показателей, которые он располагает в виде таблиц. Применение табличного метода значительно облегчает ориентацию в материале. Однако из этого не следует, что можно ограничиться одними таблицами. Для того чтобы сделать дальнейший шаг в понимании материала, надо от табличного метода перейти, к графическому.
График в статистике — условное изображение статистических данных в виде различных геометрических образов: точек, линий, фигур и т.п. Главное достоинство графиков ‑ наглядность.
Для чего используются в статистике графики?
Во-первых, в целях широкой популяризации данных и для облегчения их восприятия неспециалистами. Поэтому в различного рода докладах, речах и сообщениях представление статистических данных часто осуществляется при помощи графиков. Графики облегчают ознакомление масс со статистическими данными, оживляют таблицу, делают ее более доступной.
Во-вторых, графики широко используются для обобщения и анализа статистических данных. Они находят большое применение в исследовательской работе. Именно при помощи графиков легче уяснить закономерности развития, распределения и размещения явлений. При помощи графиков в ряде случаев можно сделать выводы, которые на базе табличного метода были бы затруднительными.
В-третьих, надо еще указать и на контрольное значение графиков. Под этим следует понимать тот факт, что во многих случаях различного рода ошибки и неточности выявляются при применении графиков, т.е. они иногда являются контролером точности расчётов и вычислений.
В настоящее время графики прочно вошли в практику экономического анализа в связи с внедрением в статистическую работу новых математических методов и современной вычислительной техники и информационных технологий, с использованием пакетов прикладных программ компьютерной графики.
Наиболее распространёнными пакетами прикладных программ являются: «Excel», «Stat Graff», «Super call», «Hazard graphics» и др. Эти программы облегчают задачу исследователя в практическом применении графиков, так как с помощью дисплеев можно демонстрировать графики на световом экране, при необходимости оперативно изменяя в них одни данные, вводя другие и т. д. Такого рода графики в принципе могут заменить громоздкие таблицы компактными изображениями.
Графики различаются по своему виду, и задача состоит в том, чтобы найти наиболее подходящий график. Нужно научиться правильно пользоваться орудием графического метода при изображении статистических данных. Кроме этого, график надо уметь строить, понимать принцип его построения. В противном случае можно выбрать правильный график, но сделать его таким, что он исказит действительную картину.
Общие правила построения графиков, классификация
При построении графика важно найти такие способы изображения, которые наилучшим образом отвечают содержанию и логической природе изображаемых показателей.
В графике, кроме заголовка, обязательно даются словесные пояснения условных знаков и смысла отдельных элементов графического образа. Сюда относятся названия и цифры масштабов, названия ломаных линий, цифры, характеризующие величины отдельных частей графика, ссылки на источники и т.д.
Классификация статистических графиков
по : характеру графического образа, способу построения и назначению (содержанию)
По способу построения графики можно разделить на диаграммы и статистические карты представлены на (рис. 7.1).
Различные виды диаграмм применяются для сравнения одноименных статистических данных, характеризующих разные территории или объекты. Наиболее распространённым видом таких диаграмм являются столбиковые диаграммы.
Столбиковые диаграммы представляют собой график, в котором различные величины представлены расположенными в высоту прямоугольниками. Столбиковые диаграммы применяются для сравнения некоторых объектов во времени. Масштабная шкала должна начинаться с нуля, быть непрерывной и на ней записываются лишь круглые или округленные значения. Столбики должны быть даны на некотором, одинаковом для всех расстоянии или вплотную друг к другу. Ширина столбиков берется произвольно. На шкале должна быть указана единица измерения. При выборе масштаба надо рассчитать так, чтобы максимальное число было представлено на графике.
Примеры построения графиков и диаграмм
Пример 1 . Требуется изобразить с помощью столбиковой диаграммы данные о трудоустройстве граждан органами государственной службы занятости региона (цифры условные): в 2007 г. трудоустроено 2822 чел.; в 2006 г. – 2398 чел.; в 2005 г. – 2406 чел.; в 2004 г. – 2218 чел. Примем масштаб: 500 чел. Наглядность данной диаграммы достигается сравнением высоты столбиков (рис. 7.2).
Если прямоугольники, изображающие показатели, расположить не по вертикали, а по горизонтали, то диаграмма получит название ленточной. В качестве примера приведем полосовую диаграмму сравнения, характеризующую данные о количестве сотрудников на предприятии N за 2009 г. (рис. 7.3, табл. 7.1,)
Таблица 7.1 ‑ Данные о количестве сотрудников на предприятии N за 2018 г. (цифры условные)
Квартал | 1 | 2 | 3 | 4 |
| Количество работников , чел | 2040 | 2000 | 950 | 960 |
Вторую большую группу показательных графиков составляют структурные диаграммы.
Структурные диаграммы — диаграммы, в которых отдельные статистические совокупности сопоставляются по их структуре, характеризующейся соотношением разных параметров совокупности или ее отдельных частей.
Пример. Рассмотрим построение секторной диаграммы по данным табл. 5.4 .
Таблица 7.2 ‑ Структура иностранных инвестиций в РФ в 2018 г
Тип инвестиций | прямые | портфельные | прочие |
| Доля инвестиций, в % | 20 | 2 | 78 |
Секторные диаграммы выглядят убедительно при существенных различиях сравниваемых структур, а при небольших различиях они могут быть не достаточно выразительны.
Для изображения и внесения суждений о развитии явления во времени строится диаграммы динамики. В рядах динамики используются для наглядного изображения явлений многие диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и другие. Выбор вида диаграмм зависит в основном от особенностей исходных данных, от цели исследования. Например, если имеется ряд динамики с неравноотстоящими уровнями во времени (1913, 1940, 1950, 1980, 2000, 2005, 2015, 2018 гг), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки, и если число уровней в ряду динамики велико, то целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии.
Для построения линейных диаграмм используют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяца и т.д.), а по оси ординат наносят масштабы для отображения явлений или процессов. Особое внимание следует обратить на масштаб осей координат, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в диаграмме, так как нарушение равновесия дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебание в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Если в ряду динамики данные за некоторые года отсутствуют, это должно быть учтено при построении графика. Равным периодом времени и размером уровня должны соответствовать равные отрезки масштабной шкалы.
Пример. Рассмотрим построение линейной диаграммы на основании следующих данных:
Таблица 7.3 ‑ Динамика валового сбора кормовых в регионе за 1995-2004 гг.
| Год | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| Валовой сбор, млн. тонн | 237 | 179 | 189 | 158 | 186 | 192 | 172 | 190 | 210 | 211 |
Изображение динамики валового сбора кормовых культур на координатной сетке с неразрывной шкалой значений, начинающихся с нуля, вряд ли целесообразно, так как 2/3 поля диаграммы остается неиспользованным и ничего не дает для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, то есть шкала значений разрывается недалеко от нулевой линии и на диаграмму попадает лишь часть возможного поля графика. Это не приводит к искажениям в изображении динамики явления и процесс его изменения рисуется диаграммой более четко (Рис. 7.5).
Контрольные задания
По данным статистических сборников о численности населения, динамики производства отдельных видов продукции, экспорта, импорта товаров и др. показателям за последние 5-10 лет постройте диаграммы и графики.
Содержание курса лекций «Статистика»