Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения
Сначала создайте уравнение с помощью рукописного ввода или текста.
На вкладке «Рисовать» напишите или введите уравнение. Используйте инструмент «Лассо», чтобы нарисовать круг вокруг формулы. Затем выберите пункт Математическое выражение. Откроется панель помощника по преобразованию в математические выражения.
В меню Выберите действие в области Математические вычисления выберите пункт Graph двухгодной или Graph двухуголей.
Чтобы изменить граф, созданный помощником по преобразованию в математические выражения, выполните одно из указанных ниже действий (по возможности).
-

-
Если нужно изменить значения параметров в уравнении, щелкните или коснитесь кнопок увеличительного стекла + и –, чтобы увеличить или уменьшить масштаб.
Примечание: Если вы используете OneNote на сенсорном устройстве, вы также можете настроить граф с помощью пальцев. Используйте один палец, чтобы переместить граф, или два пальца, чтобы изменить масштаб увеличения. В OneNote для Интернета положение графа можно изменить с помощью стрелок, расположенных по сторонам графа.
-
Чтобы восстановить исходное состояние графа, щелкните или коснитесь значка Сброс в форме двойной стрелки.
-
Когда граф приобретет нужный вид, щелкните или коснитесь пункта Вставить на страницу, чтобы поместить его в виде снимка экрана на текущей странице.

Примечание: Чтобы изменить способ измерения графа (градусы, радиан, градианы), щелкните или коснитесь пункта Параметры, когда открыта область «Математическое выражение».
Расширенные функции графики
Другие возможности доступны в зависимости от типа графа.
Чтение значений x-y: Чтобы увидеть значения x и y в OneNote для Windows 10, наведите указатель мыши на точку на линии графа. Чтобы увидеть значения в OneNote для Интернета, щелкните линию графа.
-
Управление параметрами Если у вас есть формула с такими параметрами, как ax+b, используйте знаки «плюс» и «минус» под графом, чтобы изменить значения a и b.

-
Основные функции графиков: Помощник по преобразованию в математические выражения рассчитывает интересные сведения о графе (нули, перехваты, минимум, максимум и т. д.). Установите флажки для тех возможностей, которые вы хотите отобразить на графе.
Создание математических формул с помощью рукописного ввода или текста с использованием помощника по преобразованию в математические выражения в OneNote
Решение математических уравнений с использованием помощника по преобразованию в математические выражения в OneNote
Типы задач, поддерживаемые помощником по преобразованию в математические выражения
Создание математического теста для практики
Типы задач, которые можно из графики в двухсмятьных диаграммах
При использовании помощникапо OneNote в формуле вы заметите, что в зависимости от выбранного уравнения изменяется в dropdown Select an action (Выбрать действие) под формулой. С помощью помощника по математическим вычислениям можно построить двухуголовые графики для следующих типов задач.
С помощью помощника по математическим вычислениям можно построить двухуголовые графики для следующих типов задач.
|
Выражения (с переменной) |
|
|
Полиномиальные массивы |
|
|
Формулы |
При работе с уравнениями Graph двухугодными или двухуголными Graph двухугодными. Выберите Graph 2D, чтобы увидеть решение для уравнения.
Выберите Graph обеих сторонах двумеда, чтобы просмотреть график двух функций на противоположной стороне знака равно.
|
|
Системы уравнений |
|
|
Координаты координат |
Для графизации функции в координатах координаты r должны быть выражены как функцияta. |
|
Неравенства |
При работе с Graph двухугодными или двухуголными Graph можно использовать двухуголевую разную сторону. Выберите Graph 2D, чтобы увидеть решение проблемы.
Выберите Graph двухуголовые диаграммы, чтобы просмотреть график двух функций на обеих сторонах знака сравнения.
|
|
Система о-ва |
|
Подробнее
Создание математического теста в Microsoft Forms
Решение математических уравнений с помощью помощника по преобразованию в математические выражения в OneNote
Интегрированыый открытый урок в 9-м классе (математика + информатика) на тему «Построение графиков с модулями»
Тема: Построение графиков с модулем.
Цели:
- Закрепить понятие «График функции; научить строить графики с модулем; научить построению графиков с модулем в табличном процессоре Excel;
- Развивать аналитическое мышление путем сравнения способов построения графиков функции с модулем в математике и информатике;
- Воспитывать культуру общения учащихся друг с другом при работе в группах.
ХОД УРОКА
1. Повторение пройденного материала
Ответить на вопросы:
а) Что такое область определения функции?
Определение. Областью определения функции называется множество значений переменной, при которых данная функция имеет смысл.
б) Что такое график функции?
Определение. Графиком функции
называется множество всех точек координатной
плоскости, абсциссы которых равны значениям
независимой переменной из области определения
этой функции, а координаты – соответствующим
значениям функции.
2. Объяснение нового материала
Выступление учащегося.
а) Графиком функции у = |х| есть прямой угол с
вершиной в т.(0,0), т.к. функция определена на
множестве всех действительных чисел,
б) Графиком функции у = – |х| является прямой угол с вершиной в т. (0,0), но стороны угла направлены вниз.
Учитель математики: Построить графики функций у = |х – 2| + |х + 3| и у = |х – 2| – |х + 3|
Как вы думаете, как построить первый график? (Взять значения и сложить ординаты графиков функций у = |х – 2| и у = |х + 3| соответствующих одним и тем же абсциссам)
При х = – 3, у = 5 и при х = 2, у = 5. Возьмем еще
значения х = – 4, у = 7 и х = 3, у = 7. Поэтому, для
построения такого графика достаточно взять
значения х = – 3, 2, – 4, 3. То есть значения, при
которых каждый из модулей равен 0 и по одному
значению больше их или меньше.
Поэтому, для
построения такого графика достаточно взять
значения х = – 3, 2, – 4, 3. То есть значения, при
которых каждый из модулей равен 0 и по одному
значению больше их или меньше.
Вообще, для построения графика функции у = |х – а| + |х – в|, достаточно взять значение данной функции в точках а и в и в точках, меньших или больших а иb.
Такой график называется «Корыто»
Таким же способом строится график функции у = |х – а| – |х – в|.
Такой график называется «ступенька».
Построим график функции у = |х + 1| – |х – 2|
Такие функции называются полезными. Есть еще полезные функции, для которых можно построить графики, которые имеют свои названия. Например, график функции: («Волна»)
График функции («W»)
График функции а > 0 («Канава»)
График функции а < b («Горка»)
3.
Учитель информатики: Ребята, давайте теперь вспомним, как можно построить графики функций в табличном процессоре Excel.
Выступление учащегося.
Электронные таблицы позволяют обрабатывать большие массивы числовых данных. В отличие от таблиц на бумаге электронные таблицы обеспечивают проведение динамических вычислений, то есть пересчет по формулам при введении новых чисел. В математике с помощью электронных таблиц можно представить функцию в числовой форме и построить ее график.
Для того чтобы построить график функции необходимо выполнить следующие действия:
1. Сначала нужно ввести в ячейки таблицы Excel
значения аргумента функции, при этом используя
операцию Автозаполнение. Сначала в первую
ячейку строки аргументов вводится наименьшее
значение аргумента, а во вторую ячейку следующее
за ним значение. Далее выделяются эти две ячейки
и все остальные ячейки заполняются
автоматически до конечного значения аргумента.
2. Затем нужно вычислить значения функции в указанных точках при помощи клавиатуры или при помощи Мастера функций. Заполнение таблицы можно существенно ускорить, если использовать операцию Заполнить. Сначала в первую ячейку строки значений функции вводится формула вычисления функции, которая начинается со знака «равно», далее эта формула вводится во все остальные ячейки таблицы с использованием операции Заполнить вправо.
3. После этого производится построение диаграммы-графика с помощью мастера диаграмм, который позволяет создать диаграмму по шагам с помощью серии диалоговых панелей:
- На первом шаге необходимо выделить в полученной таблице диапазон исходных данных и выбрать тип диаграммы.
- На втором шаге необходимо определить, в строках
или в столбцах хранятся названия категорий и ряд
данных, а также уточнить, в какой строке или каком
столбце содержатся категории.

- На третьем шаге необходимо настроить внешний вид диаграммы: ввести заголовок диаграммы и название осей, уточнить параметры шкал осей категорий и значений, определить наличие и внешний вид сетки и легенды и т.д.
- На четвертом шаге необходимо выбрать вариант размещения диаграммы: на отдельном листе или на листе с данными (внедренная диаграмма)
В результате будет построен нужный график функции.
Учитель информатики: Ну что,
вспомнили, как строится диаграмма в табличном
процессоре Excel? А теперь давайте выясним, на что
именно нужно обратить внимание при построении
графиков функций с модулем.
Во-первых, правильно выбрать диапазон значений
аргумента (то есть взять нужные точки для того,
чтобы график отобразился полностью).
Во-вторых, правильно ввести формулу в первую
ячейку. Для этого в электронных таблицах имеется
несколько сотен встроенных функций, среди
которых есть и категория Математические. Так как
мы сегодня строим графики с модулем, то будем
использовать функцию ABS – абсолютное значение
аргумента (то есть модуль). Запишите эту функцию.
Так как
мы сегодня строим графики с модулем, то будем
использовать функцию ABS – абсолютное значение
аргумента (то есть модуль). Запишите эту функцию.
Далее для полученного набора данных нужно
построить график с помощью Мастера диаграмм, при
этом правильно подобрав тип диаграммы. В нашем
случае мы должны выбрать точечную диаграмму со
значениями, соединенными отрезкам, так как
графики строятся по точкам.
После того, как график построен, нужно обратить
внимание на шкалу и задать цену основных делений
– 1, а промежуточных – 0,5, для того, чтобы
построить график в привычном для нас восприятии.
4. Самостоятельная работа
Задание по группам: (3 группы): Построить графики данных функций в тетрадях и в табличном процессоре Excel.
I группа |
II группа |
III группа |
|
|
|
Ответы:
I группа
II группа
| y = |x – 2| + 5 | y = |x + 2| + |x – 5| | y = |x + 2| – |x – 5| |
III группа
| y = |x + 3| – 4 | y = |x – 3| + |x + 4| | y = |x – 3| – |x + 4| |
5. Итог урока. Оценки
Итог урока. Оценки
Проверка правильности построения графиков в тетрадях и на компьютере.
Учитель математики: Ребята, скажите пожалуйста, сколько нужно взять точек, чтобы построить такие графики?
Предполагаемый ответ: Достаточно взять четыре точки (значения a и b и по одному значению больше и меньше a и b)
Учитель информатики: А теперь скажите, какие точки нужно взять, чтобы построить такие графики в табличном процессоре Excel.
Предполагаемый ответ: Нужно пройти все значения с шагом в единицу от меньшего, чем a или b до большего a или b в зависимости от того b < a или b > a
Общий вывод: Без знания построения графиков с модулем в математике (то есть выбор значений аргумента функции) невозможно правильно построить график функции с модулем в табличном процессоре Excel.
Домашнее задание: § 12 № 163 (1, 5, 6)
| у = |x + 3| + 2 | у = |x| + |x – 2| | y = |x + 1| – |x| |
Придумайте и постройте в тетради и на
компьютере подобные графики.
Приложение
Открытая Математика. Функции и Графики. Алгебраические операции над функциями
Построение графика суммы (произведения) двух функций производится сложением (умножением) ординат точек графиков с одинаковыми абсциссами. Приведем для примера графики функций y = x + sin x и y = x sin x, являющихся соответственно суммой и произведением графиков y = x и y = sin x.
Правило построения графика функции 1f(x), если график функции f(x) уже построен.
Если x = a – вертикальная асимптота графика функции f(x), то есть limx→a+0f(x)=∞ или limx→a-0f(x)=∞, то limx→a+01f(x)=0 или соответственно limx→a-01f(x)=0.
Таким образорм, в случае, когда x = a – двусторонняя вертикальная асимптота графика функции f(x), x = a будет нулем функции 1f(x).
Если у графика функции f(x) есть горизонтальная асимптота y = 0 при x→∞, то limx→∞1f(x)=∞.
Если у графика функции f(x) есть горизонтальная асимптота y = b при x→∞, то график функции 1f(x) будет иметь горизонтальную асимптоту y=1b.
Если график функции f(x) пересекает ось абсцисс в точке (x0; 0), то есть x0 – нуль функции f(x): f(x0)=0, то x=x0 – вертикальная асимптота графика функции y=1f(x).
Если точка (x0; y0) – точка максимума (минимума) функции f(x) и y0≠0, то (x0; 1y0) – точка минимума (максимума) функции 1f(x).
Промежуткам возрастания (убывания) графика функции f(x) соответствуют промежутки убывания (возрастания) графика функции 1f(x).
Пусть известен график y = f (x) и нужно построить график функции y = |f (x)|. По определению, |fx|={fxпри fx≥0,-fxпри fx<0. Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.
Пусть известен график y = f (x) и нужно построить график функции y = f (|x|). Заметим, что при x ≥ 0 f (|x|) = f (x), а функция y = f (|x|) четная. Поэтому, чтобы построить график функции y = f (|x|), нужно часть графика функции y = f (x), лежащую в левой координатной полуплоскости, отбросить, а часть графика, лежащую в правой координатной полуплоскости, отобразить симметрично относительно оси OY.
 2 или y=1/x. А как строить графики со знаком модуля?
2 или y=1/x. А как строить графики со знаком модуля?Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y=|x| — чётная, так как |-a|=|a|. Значит, график функции y=|x| симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|. Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
Пусть -1< = x < = 4. 2 — |x| — 3|
2 — |x| — 3|
Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
График функции — Энциклопедия по экономике
График функции Th = f(x) в рассматриваемых пределах изменения величины х представлен на рис. 21. [c.133]Так, если мы хотим проанализировать чувствительность (иу.э.с)опт к изменению стойкости элементов ленточного тормоза в условиях нашего примера, необходимо на основании выражений (ПО), (111), (121) и (123) построить графики функций [c.149]
Рис. 4 дает возможность графически представить некоторые особенности производственной функции с двумя ресурсами производства. На двумерном рисунке нельзя изобразить сам график функции У = F (K, L), так что приходится ограничиваться лишь анализом изоквант. Построение графика производственной функции было бы, однако, весьма желательным, поэтому прибегают к следующему приему, основанному на свойстве (2.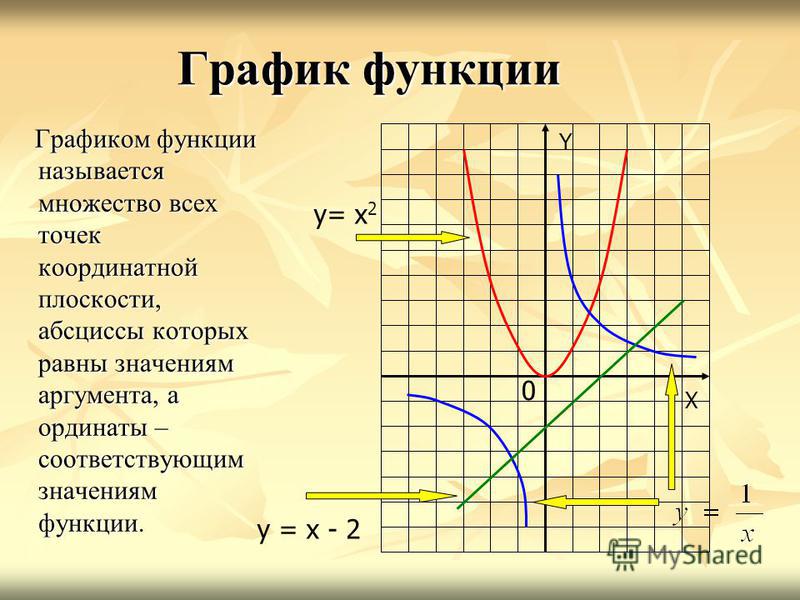 5) производственной функции. Поскольку мы рассматриваем значения L > 0, то на основе (2.5) можно сделать преобразование соотношения У = = F (К, L), представив его в виде У = LF (K/L, 1) или Y/L = F (K/L, 1). Введем следующие обозначения у = = Y/L, k = K/L, f (k) = F (k, 1). Здесь у имеет смысл национального дохода на одного трудящегося, k — количество основных фондов на одного трудящегося (фондовооруженность), функция / (k) связывает эти два показателя и является одной из форм представления производственной функции. Зная функцию F (К, L), можно построить f (k),
[c.58]
5) производственной функции. Поскольку мы рассматриваем значения L > 0, то на основе (2.5) можно сделать преобразование соотношения У = = F (К, L), представив его в виде У = LF (K/L, 1) или Y/L = F (K/L, 1). Введем следующие обозначения у = = Y/L, k = K/L, f (k) = F (k, 1). Здесь у имеет смысл национального дохода на одного трудящегося, k — количество основных фондов на одного трудящегося (фондовооруженность), функция / (k) связывает эти два показателя и является одной из форм представления производственной функции. Зная функцию F (К, L), можно построить f (k),
[c.58]
Сначала проведем графический анализ задачи. Для этого построим графики функций у = sf (k) и у = t]k. [c.74]
На рис. 3.3 изображены графики функций фактора фонда накопления для обычного и авансового аннуитетов. [c.315]
Графики функций А(у), АГ( ), h»(y), g(y) и h (y)/g(y) для функции затрат (2.7) при а = 0,5 приведены на рис. 2.12. [c.97]
График функции у(Г) для т г = 4 приведен на рис.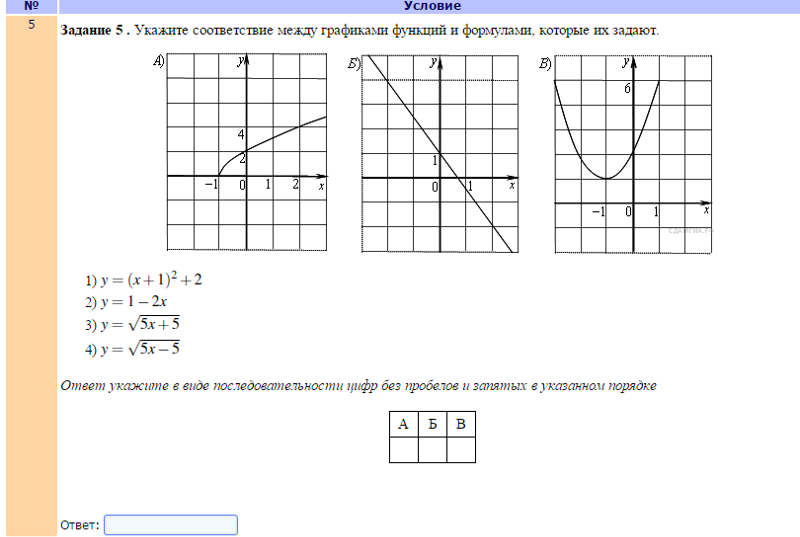 2.15. Изломы на графике соответствуют переходам к новым, до этого не использовавшимся, менее эффективным производственным способам.
[c.103]
2.15. Изломы на графике соответствуют переходам к новым, до этого не использовавшимся, менее эффективным производственным способам.
[c.103]
Проведем сначала графический анализ задачи. Построим графики функций у = stf(k) и y = ( i + t])k (см. рис. 4.1). Из рисунка следует, что имеются два решения (3.13). Это / = 0 и k = k. Точка f = 0 является решением уравнения (3.13) при любых значениях параметров л и т) и параметров производственной функции в силу того, что ф(0)=0. Ненулевая точка пересечения графиков у = s p(k) и у = (ц + т))А , вообще говоря, может существовать не всегда или быть не единственной. При сформулированных в предыдущем параграфе свойствах производственных функций и некоторых других естественных предположениях о народном хозяйстве точка k существует и единственна (доказательство см., например, в гл. 2 книги [34]). [c.245]
В связи с этим график функции имеет начальную ординату 77,08 дол. Начальная ордината — это постоянный элемент формулы, который обеспечивает наилучшую линейную аппроксимацию поведения затрат внутри релевантной области. [c.234]
[c.234]
Для построения кривой спроса отложим на оси абсцисс точки, характеризующие количество товара, на которое предъявлен спрос, а на оси ординат — соответствующую им цену. Данная кривая есть график функции спроса от цены. [c.15]
Кофе, полученный смешиванием разных сортов, нельзя сравнить с аналогичными продуктами в других киосках. Наш кофе самый лучший, мы предлагаем вам не просто кофе, а допинг для переговоров на выставке . График функции спроса для кофе, продаваемого на выставке, мог бы иметь вид S-образной кривой, как на рис. 10. На ней есть ограниченная область крутого, не эластичного по отношению к цене спроса. В этой области возможно проведение индивидуальной политики цен. [c.61]
То обстоятельство, что точки заданного набора занумерованы в порядке возрастания их абсцисс, позволяет искать кривую в классе графиков функции. Мы сможем описать основные проблемы сглаживания этого дискретного набора, ограничившись многочленами. [c.125]
[c.125]Сбор > i и ставка процента По мнению Дж. М. Кейнса, реальная процентная ставка не является основным детерминантом уровня сбережения и потребления населения. Вместо этого он утверждал, что уровень сбережения и потребления главным образом зависит от реального дохода. Экономисты-классики принимали реальный доход за постоянную величину. При полной занятости, как в классической модели, можно принять доход за постоянную величину и утверждать, что потребление в основном зависит от размера процентной ставки. Но поскольку может ли экономика достичь уровня полной занятости — это еще вопрос, то не следует доход принимать за постоянную величину. Предполагать неизменность национального дохода в силу допущения о полной занятости, как считают Дж. М. Кейнс и его последователи, не совсем верно. Таким образом, каждый раз, когда совокупный реальный доход изменяется, график функции сбережения (и потребления) в классической модели смещается. Короче говоря, Дж. М. Кейнс утверждал, что функция сбережения в классической модели характеризуется изменчивостью (подверженностью колебаниям), поскольку основной детерминант уровня сбережения — реальный доход — не является постоянной величиной.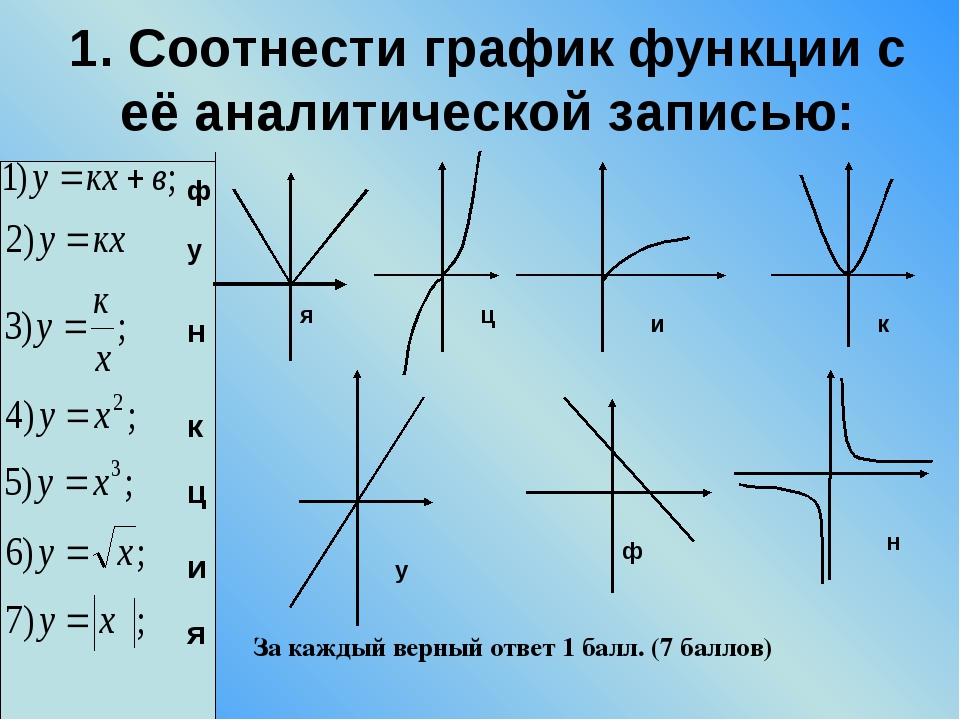 В дальнейшем, когда мы перейдем к рассмотрению кейнсианской модели в этой главе, станет очевидно, что уровни реального сбережения и реальное потребление являются функцией реального располагаемого дохода, а не реальной процентной ставки.
[c.494]
В дальнейшем, когда мы перейдем к рассмотрению кейнсианской модели в этой главе, станет очевидно, что уровни реального сбережения и реальное потребление являются функцией реального располагаемого дохода, а не реальной процентной ставки.
[c.494]
На рис. 19-3 приведен пример линейной функции сбережения. Угловой коэффициент функции сбережения (1 — Ь) является MPS, или 1 — МРС. Отметим, что b + + (1 — К) = 1, так что графики функций потребления и сбережения предполагают равенство МРС + MPS = 1. [c.501]
График совокупных расходов в закрытой экономике представляет собой сумму графиков ожидаемого потребления, инвестиций и государственных расходов. Отрезок, отсекаемый графиком на вертикальной оси, равен величине чистых совокупных автономных расходов потребителей, фирм и государства. Когда инвестиции, государственные расходы и чистые налоги являются автономными, угловой коэффициент графика совокупных расходов равен угловому коэффициенту графика функции потребления, или предельной склонности к потреблению, которая является дробным числом. [c.518]
[c.518]
Функцию потребления в кейнсианской модели экономики можно представить в виде с = с0 + ЬУ . Дайте определение и краткое объяснение каждого из двух компонентов ожидаемого потребления, заданных уравнением. Постройте график функции потребления. Чему равен его угловой коэффициент Какое экономическое толкование можно дать этому коэффициенту [c.521]
При этом Р(х [c.118]
Показанный в предыдущем параграфе график функции предельной полезности (рис. 1.1, б) представляет собой линию с отрицательным наклоном, построенную в координатах MU, Q. Подобным же образом изображается обычно и линия индивидуального спроса, основное назначение которой состоит в том, чтобы выражать зависимость объема спроса конкретного индивидуума на определенное благо (QD) от уровня его цены (Р). [c.18]
| Рис. 6.2. Графики функций принадлежности. |
 4.2.2. Как можно заметить из рис. 4.2.2, в графике функции sn(n) присутствует некоторая точка перегиба га, определяющая номер периода, начиная с которого скорость расхождения границ доверительного интервала качественно возрастает. Последний факт может быть использован для определения того количества периодов, на которое мы в рамках мультипликативной модели можем получить относительно осмысленную оценку границ отклонений фактических значений от прогнозных.
[c.158]
4.2.2. Как можно заметить из рис. 4.2.2, в графике функции sn(n) присутствует некоторая точка перегиба га, определяющая номер периода, начиная с которого скорость расхождения границ доверительного интервала качественно возрастает. Последний факт может быть использован для определения того количества периодов, на которое мы в рамках мультипликативной модели можем получить относительно осмысленную оценку границ отклонений фактических значений от прогнозных.
[c.158]График функции приведен на рис. 5,6. [c.73]
Если для каждого свойства каждого вида продукции строить свой график функции, то сложность и большой объем работы сделают крайне затруднительным практическое применение метода. Следовательно, не должно быть чрезмерно большого множества кривых. [c.78]
Рассмотрим график функции Д у (Pj) (рис. 12). [c.117]
| Рисунок 9 — График функций желательности и ее приращения |
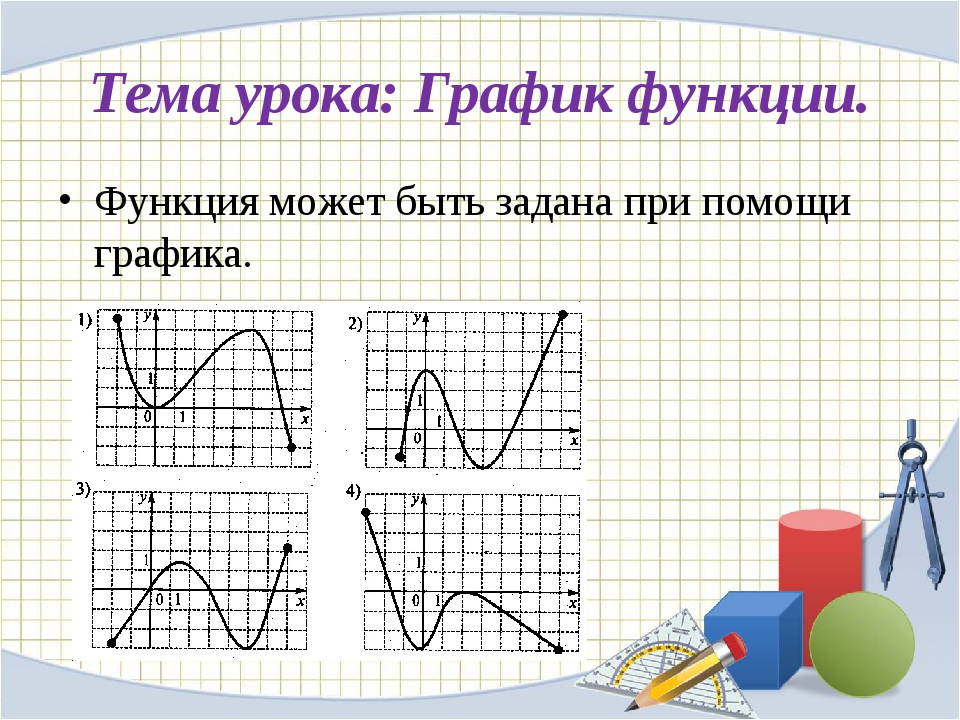 Подобные графики позволяют оценивать и результаты деятельности территориальных геологических управлений, определяя фактически достигнутую надежность плана. Любое решение в геологоразведочной отрасли связано с некоторым уровнем риска, определяющим величину показателя надежности. Эту величину можно планировать заранее, т. е. задавать допустимый уровень надежности или стратегию риска. Планирование
[c.215]
Подобные графики позволяют оценивать и результаты деятельности территориальных геологических управлений, определяя фактически достигнутую надежность плана. Любое решение в геологоразведочной отрасли связано с некоторым уровнем риска, определяющим величину показателя надежности. Эту величину можно планировать заранее, т. е. задавать допустимый уровень надежности или стратегию риска. Планирование
[c.215]Итак, в обоих потоках орел выпал четыре раза из десяти (аналогично, решка выпала в обоих потоках четыре раза из десяти), что дает вероятность 0,4. Обратите внимание, что если функция линейна, то есть изображается на графике прямой линией, то эта прямая проходит через точку, соответствующую коэффициенту корреляции 0,6 и вероятности 0,4. Если бы график функции отличался от прямой, то коэффициенту корреляции 0,6 соответствовало бы все, что угодно, кроме 0,4 (см. рис. 3.3). [c.146]
Зная, что многие поставщики данных не имеют в своих программах построения графиков функции постоянного масштаба, нами так разработано программное обеспечение, чтобы пользователи могли выбирать или полноэкранное масштабирование самых последних загруженных данных или постоянный масштаб от самого высокого максимума до самого низкого минимума всего ряда данных для инвесторов, испытывающих неудобство из-за необходимости конвертировать данные своих рядов данных.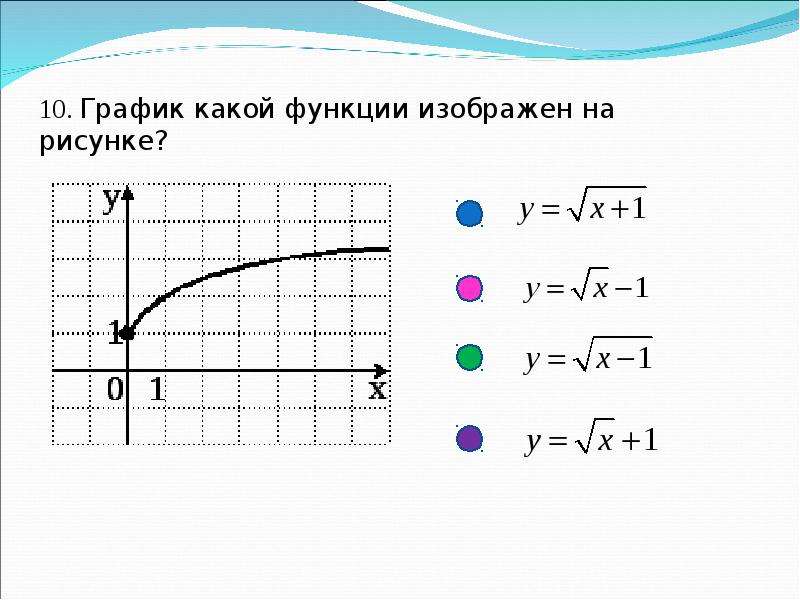 [c.34]
[c.34]
| Рис. 5. График функции 1(а) в примере 1. |
 е. b = MF .
[c.504]
е. b = MF .
[c.504]График совокупных расходов в закрытой экономике без государственного сектора. В экономике без государственного сектора совокупные ожидаемые реальные расходы равны сумме потребительских расходов домашних хозяйств и ожидаемых реальных инвестиционных расходов фирм. Следовательно, если мы сложим график автономных инвестиций с графиком функции потребления по вертикали, то получим график, отражающий уровни совокупных ожидаемых реальных расходов для любого данного уровня реального дохода. Это и есть график совокупных расюдов (с + / ). [c.505]
Совок ипь лвтономные расходы и смещение графика совокупных расходов Что является причиной смещения графика совокупных расходов Чтобы ответить на этот вопрос, полезно рассмотреть уравнение, которым задан график совокупных расходов. Предположим, что величина автономных инвестиций равна /0. К тому же нужно помнить, что поскольку упрощенная модель экономики предполагает отсутствие государственного сектора (yd = у), то располагаемый доход равен доходу без налоговых вычетов. Поскольку график совокупных расходов строится путем сложения графиков функции потребления и автономных инвестиций, то уровень совокупных расходов будет равен
[c.510]
Поскольку график совокупных расходов строится путем сложения графиков функции потребления и автономных инвестиций, то уровень совокупных расходов будет равен
[c.510]
Предельная склонность к потреблению (marginal propensity to onsume, MP ) — дополнительное потребление вследствие роста дохода после уплаты налогов прирост потребительских расходов, деленный на соответствующий прирост располагаемого дохода угловой коэффициент графика функции потребления, когда по оси ординат откладываются значения располагаемого дохода. [c.519]
Предельная склонность к сбережению (marginal propensity to save, MPS) — дополнительно сберегаемые средства при увеличении располагаемого дохода отношение прироста сбережений к соответствующему приросту располагаемого дохода. Представляет собой угловой коэффициент графика функции сбережения, когда по оси ординат откладываются значения располагаемого дохода. [c.519]
Майклом Брэдли (Bradley) из университета Джорджа Вашингтона в 1989 г. Если ФРС нужно задать величину номинального национального дохода, то она будет изменять параметры инструментов своей политики, чтобы постоянно поддерживать номинальный доход на заданном уровне У. Это означает, что она будет проводить политику с учетом обеспечения равенства Р X у = Y. Предположим, что целью ФРС является сохранение номинального национального дохода на заданном уровне Y = 4000 млрд. долл. тогда множество комбинаций уровень цен—национальный доход будет соответствовать этой цели. Примерами могут служить РО = 4, у0 = 1000, /, = 5, у = 800 и Р2 = 8, у2 = 500. Все эти и другие возможные комбинации уровня цен и реального дохода будут представлены на графике функции Рх у = Y (рис. 24-12). Этот график, как и график совокупного спроса в классической модели, описанный в главе 18, является гиперболой.
[c.664]
Это означает, что она будет проводить политику с учетом обеспечения равенства Р X у = Y. Предположим, что целью ФРС является сохранение номинального национального дохода на заданном уровне Y = 4000 млрд. долл. тогда множество комбинаций уровень цен—национальный доход будет соответствовать этой цели. Примерами могут служить РО = 4, у0 = 1000, /, = 5, у = 800 и Р2 = 8, у2 = 500. Все эти и другие возможные комбинации уровня цен и реального дохода будут представлены на графике функции Рх у = Y (рис. 24-12). Этот график, как и график совокупного спроса в классической модели, описанный в главе 18, является гиперболой.
[c.664]
Теперь рассмотрим рис. 24-13, на котором представлена точка А — точка равновесия графиков совокупного спроса и совокупного предложения, в которой уровень цен РО = 4, а реальный уровень производства у( = 1000. К тому же естественный уровень производства (рис. 24-13) равен у = lOOO, что означает, что равновесный реальный объем производства при естественном уровне производства, описываемый графиком долгосрочного совокупного предложения (у к), достигается и точке А. К тому же точка равновесия А принадлежит графику функции Р X у = Y (рис. 24-12). Следовательно, равновесный номинальный доход в точке А есть YQ = Рп х у( — 4 X X 1000, что равно номинальному доходу Y, выступающему в качестве промежуточной цели ФРС.
[c.665]
К тому же точка равновесия А принадлежит графику функции Р X у = Y (рис. 24-12). Следовательно, равновесный номинальный доход в точке А есть YQ = Рп х у( — 4 X X 1000, что равно номинальному доходу Y, выступающему в качестве промежуточной цели ФРС.
[c.665]
Протабулируем данную функцию на отрезке [-4,0 10,0] (расширять границы не имеет смысла, так как значения / (-4,0) и /(10,0) близки к предельным) с шагом 0,2. Кроме того, найдем приращение функции желательности на каждом шаге. По полученным значениям построим графики функции желательности и ее приращения (рисунок 9). [c.49]
Линейное программирование (планирование) — математический метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изоб- [c.58]
Функциии тест вертикальной линии
Ученик: Я не могу решить, являются ли некоторые из более сложных графов правильными.
функции или нет.
Наставник: Есть много способов определить, является ли это функцией.
Ученик: Можно ли что-то сделать, просто взглянув на график?
Ментор: На самом деле есть. Это называется тестом вертикальной линии.
Ученик: Какое отношение вертикальная линия имеет к функциям?
Наставник: Посмотрите на один из графиков, о котором у вас есть вопрос.Затем возьмите вертикальную линию и поместите ее на графике. Если график является функцией, то в какое бы место на графике вы ни поместили вертикальная линия, график должен пересекать вертикальную линию только один раз.
Ученик: Правда? Это работает постоянно?
Наставник: Да, постоянно. Давайте попробуем один.
Можете ли вы сказать мне, является ли это функцией в этом графике?
Студент: Да, это так.Я не могу поставить вертикальную линию на этом графике так, чтобы она касалась
функционировать более одного раза. Это прекрасно работает, особенно если я вижу сетку.
Это прекрасно работает, особенно если я вижу сетку.
Наставник: А как насчет обычных форм, таких как круги и квадраты?
Ученик: Это не функции.
Воспитатель: Можете ли вы сказать мне, почему?
Ученик: Они не прошли бы тест вертикальной линии.
Наставник: Почему они не проходят?
Ученик: Обе эти фигуры пересекают вертикальную линию дважды во многих местах! Смотри, вот только один пример:
Наставник: Да! Помните, что попадание в вертикальную линию более одного раза означает, что их больше.
чем одно значение y для определенных значений x.Это работает для формул, когда вы не уверены,
они функции. Каждый раз, когда вы получаете более одного значения y при вводе значения x, это
означает, что формула не является функцией. Наличие не более одного значения y для каждого значения x означает
что существует четко определенная связь или, другими словами, функция.
Ученик: Это означает, что графики типа x = 2 не являются функциями, а графики типа y = 2 — функциями.
Наставник: Вы правы.Теперь попробуем посложнее.
Ученик: Что происходит в точке x=7? Похоже, график прыгает вниз?
Наставник: Это верно. Он находится вверху на плоской части при x = 7, но для x больше 7 он находится на изогнутой части. часть. Закрашенная точка говорит нам, что в точке 7 мы должны использовать y-значение 9, точку без затенение говорит нам, что криволинейная часть графика — это то, что можно использовать для чего-то большего, чем x = 7, но не для самой 7.Мы называем это кусочным графом, и когда у нас есть такая ситуация, мы нужно сказать, где находятся открытые и закрытые (заполненные или нет) кружки.
Ученик: Если вы так это читаете, то это функция. Нигде на этом графике я не могу сделать
вертикальная линия касается функции более чем в одном месте. Это значительно упрощает задачу и
имеет смысл.
Это значительно упрощает задачу и
имеет смысл.
Наставник: Можете ли вы нарисовать мне график, который не является функцией?
Студент: Конечно! Вот один:
Как это называется?
Наставник: Каждый график, описывающий отношение между x и y, называется отношение .Также графики, построенные на декартовой плоскости, называются плоские кривые , 2-мерные кривые , или просто кривых . Итак, функции — это все эти вещи, но, чтобы ответить на ваш вопрос, графики, которые не являются функции могут быть вызваны любым из этих имен.
В этом разделе мы рассмотрим графики многочленов. мы уже обсуждали
предельное поведение полиномов четной и нечетной степени с положительными
и отрицательные ведущие коэффициенты.Также напомним, что полином n th степени может иметь при
большинство n действительных корней (включая кратности) и n −1 точек поворота. Кубические функции могут иметь не более 3 действительных корней (включая кратности) и 2 точки поворота. мы будем смотреть на графиках кубических функций с различными сочетаниями корней и поворотов точки, как показано на рисунке ниже. Кратность корня влияет на форму графика многочлена. В частности,
Как множественность
корня увеличивается, график уплощается все больше и больше вблизи корня. В
на красном графике выше есть один отдельный действительный корень, x = 0, имеющий кратность
3. На самом деле мы можем посмотреть, как увеличение множественности влияет на форму
граф около корня. ***** Теперь попробуйте решить несколько задач, которые проверят ваши знания полиномиальных функций. Проблемы |
Функции — линейные функции и уравнения
Наклон линейного уравнения — это число, которое показывает, насколько круто поднимается или опускается линия на нашем графике. Если мы притворимся, что линия представляет собой гору, мы как будто говорим о склоне горы.Если вам это поможет, нарисуйте вверху снежную шапку. Некоторые альпинисты. Подъемник. Впрочем, ничего слишком сложного.
Подъемник. Впрочем, ничего слишком сложного.
Двигаемся слева направо по оси x , так же, как мы читаем. Если линия становится выше, когда мы движемся вправо, то мы поднимаемся на гору, поэтому линия имеет положительный наклон
Если линия становится ниже, когда мы движемся вправо, то мы спускаемся с горы, поэтому линия имеет наклон отрицательный наклон.
Если мы остаемся на той же высоте, то наклон равен нулю, потому что мы не поднимаемся и не спускаемся.Довольно скучная гора, если вы спросите нас.
Теперь давайте найдем реальные числа для уклонов. Говоря о горах, наклон — это соотношение, которое описывает, насколько быстро меняется наша высота, когда мы движемся вправо. Не наш реальный физический рост, заметьте. Мы не станем ниже или выше на протяжении этих примеров, даже если к концу вы почувствуете, что выросли.
Джули взбирается на гору. На каждые 10 футов, которые проходит Джулия (измеряется по земле), она поднимается на 20 футов выше. Каков наклон горы?
Каков наклон горы?
Склон горы .
На каждый фут, пройденный Джули (измеряется по земле), она поднимается на 2 фута над землей. Она была бы еще выше над землей, если бы носила каблуки, но мы полагаем, что это был бы странный выбор для альпинизма.
Проверьте это. Посмотрите на график линии y = x :
Наклон линии y = x равен 1. Если мы переместимся вправо на 1 по оси x , мы также переместитесь на единицу вверх по оси y :
Найдите наклон линии, изображенной ниже.Если мы не получим от вас вестей в течение трех часов, мы пошлем за вами смотрителя парка.
Давайте посмотрим, что происходит между парой точек графика:
На этой линии или горе мы поднимаемся на 2 на каждые 3, которые мы преодолеваем. За исключением одного раза, когда мы поднялись на 2, столкнулись с горным львом и побежали обратно на 7.
Наш склон .
Один из способов представить уклон .
Чтобы использовать эту формулу для определения наклона линии, мы сначала фиксируем две точки на графике, координаты которых мы можем легко вычислить.
Рост — это сумма y изменений между этими двумя точками, и это число может быть положительным или отрицательным. Помните, вы можете подняться по или по спуститься с горы. Прогон — это сумма x изменений между этими двумя точками. Обычно мы думаем о движении от точки слева к точке справа, имея в виду, что x увеличивается, а «бег» всегда положителен. Вы можете подниматься или опускаться, но вы никогда не будете бежать назад, правильно Мы имеем в виду, кроме того случая, когда вы пятились от горного льва.
Тогда наклон этой линии равен:
Будьте осторожны: Это все очень хорошо и полезно запомнить формулу, но чтобы правильно ею пользоваться, нужно знать, что такое «подъем» и «бег». » на самом деле означает. Это не относится к вашему нижнему белью, задирающемуся на вас, или к вашим чулкам, которые в них сползают, хотя и то, и другое было бы чудесно запоминающимся изображением. В дополнение к формуле может быть полезно иметь в голове картинку, подобную приведенной ниже:
Это не относится к вашему нижнему белью, задирающемуся на вас, или к вашим чулкам, которые в них сползают, хотя и то, и другое было бы чудесно запоминающимся изображением. В дополнение к формуле может быть полезно иметь в голове картинку, подобную приведенной ниже:
Пример задачи
Найдите наклон линии, показанной ниже.
Давайте найдем пару точек, с координатами которых удобно и легко работать, и посмотрим, какой подъем и разбег между этими двумя точками. Используйте изображение нижнего белья, если хотите. Это не поможет вам с этой проблемой, но вас никто не останавливает.
Наклон:
Пример задачи
Найдите наклон линии, показанной ниже.
Если мы попытаемся применить формулу к вертикальной линии, у нас будут проблемы.Поскольку «пробег» между любыми двумя точками на вертикальной линии равен 0, и мы не можем делить на 0, наклон вертикальной линии не определен. Таким образом, наклон линии x = 1 не определен.
Разумно, так как для того, чтобы бежать прямо на отвесную гору, потребуются мощные бедра. Если вы попытаетесь это сделать, вы также скоро потеряете определение.
Пример задачи
Найдите наклон проходящей линии через точки (1, 3) и (2, 7)
Мы можем найти наклон прямой, если даны любые две точки на прямой.Мы знаем, что часть линии будет выглядеть так:
Чтобы попасть из точки (1, 3) в точку (2, 7), нам нужно двигаться вправо 1 и вверх 4:
Значит наклон линии . Йоделай-хи-ху!
Пример задачи
Найдите наклон прямой, проходящей через (-3, 1) и (2, -2).
Часть линии выглядит так:
Расстояние, которое мы проходим, чтобы добраться от одного значения x до другого, равно 3 + 2 = 5, так как сначала мы должны пройти от x = -3 до х = 0, а затем от х = 0 до х = 2.У нас есть остановка на оси и , где мы можем перекусить фаст-фудом по завышенной цене, пока ждем нашей соединительной линии.
Чтобы перейти от одного значения y к другому, сначала мы переходим от y = 1 к y = 0, а затем от y = 0 к y = -2, для общий подъем -3. Еще раз, мы не могли получить прямой рейс. Ах хорошо. Это даст нам больше времени, чтобы прочитать книгу, над которой мы работали.
Таким образом, наклон этой линии равен .
Будьте осторожны: Часто делаются ошибки при расчете подъема и разбега, когда используются отрицательные координаты. Чтобы не ошибиться, рекомендуем нарисовать рисунок, который поможет в расчетах. Если искусство вам не по душе, найдите гору или забронируйте билет на самолет, чтобы воплотить в жизнь один из наших предыдущих примеров. Донести мысль таким образом будет дороже и отнять много времени, но это, безусловно, донесет идею до дома.
Итак, теперь мы можем считать наклон линии по графику или по любым двум точкам на линии.Мы хорошо себя чувствуем. Как насчет построения графика линии, если задана одна точка и наклон?
Пример задачи
Изобразите линию, проходящую через (0, 0) и имеющую наклон 2.
Начнем с рисования заданной точки:
Нам сказали, что линия имеет наклон из 2, что означает, что по мере того, как x перемещается по 1, y увеличивается на 2:
Теперь у нас есть две точки, которых достаточно, чтобы провести линию:
Отношения и определение того, является ли отношение Функция — Задача 3
Используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.Если вертикальная линия перемещается по графику и в каждый момент времени касается графика только в одной точке, то график является функцией. Если вертикальная линия касается графика более чем в одной точке, то график не является функцией.
Одна из замечательных особенностей функций заключается в том, что мы знаем, что что-то является функцией, если каждый x имеет ровно один y, но иногда вам не дают баллы, вам не дают числа, все, что вам дают, это забавный график. Итак, о чем я хочу поговорить здесь, так это о том, как вы можете сказать, что что-то является функцией, просто основываясь на графике, и вы увидите, что это на самом деле довольно просто. Он использует так называемый тест вертикальной линии.
Итак, о чем я хочу поговорить здесь, так это о том, как вы можете сказать, что что-то является функцией, просто основываясь на графике, и вы увидите, что это на самом деле довольно просто. Он использует так называемый тест вертикальной линии.
Итак, что я собираюсь сделать, так это пройтись по этим графикам и нарисовать вертикальные линии, и если они совпадают, если моя вертикальная линия пересекается с графиком более одного раза в каждой строке, тогда это не функция, потому что это представляет место, где значение x имеет два значения y.
Давайте проверим. Думайте об этом как о своем карандаше, это большой карандаш.Что бы вы сделали с графиком на бумаге, так это возьмите свой карандаш, положите его туда, а затем проведите им по графику, посмотрите, не попали ли вы в какие-либо места на этом графике, где ваш карандаш пересекает волнистую линию более чем в одном месте. И вы увидите на этом графике множество мест, посмотрите.
Я просто наткнулся на свой график, например, раз, два, три, четыре, например, 10 раз, что бы это ни было, не имеет значения, я наткнулся на него более одного раза, так что это не функция. Это значение x прямо здесь, что бы оно ни было, имеет множество значений y, есть значение y, есть еще одно, нет никого, это не функция.Каждый x получает только одно значение y.
Это значение x прямо здесь, что бы оно ни было, имеет множество значений y, есть значение y, есть еще одно, нет никого, это не функция.Каждый x получает только одно значение y.
Давайте попробуем нарисовать следующий график, используя карандаш, и убедитесь, что он вертикальный, а не горизонтальный. Вертикаль о-о! Вы можете видеть, как карандаш попадает в те места, где вертикальная линия пересекает график более чем в одном месте. Это снова означает, что x имеет два значения y, а не функцию.
Вот пара, которые немного отличаются, когда вы используете тест вертикальной линии здесь. Проверьте это, куда бы я ни двигал пером, оно пересекает график правильно только один раз, я никогда не попадаю на эту линию графика более одного раза.Итак, в этом случае да, это функция, потому что это значение x имеет только одно значение y.
Здесь очень похоже, когда я использую перо и перемещаю его вертикально по графику, я нигде не нажимаю на фигуру дважды, я нажимаю только один раз, поэтому d, да, это тоже функция.
Если вы больше ничего не помните из этого видео, надеюсь, вы помните тест на вертикальную линию. Если график проходит тест вертикальной линии, то это функция. Я имею в виду, что если вы двигаете ручкой, и она нажимает только один раз, то да, это функция, если она нажимает более одного раза, нет, это не функция.
Лично мне нравятся эти задачи. Я думаю, что они не слишком сложны, и в них не используются числа, так что это круто.
Графики и геометрия функций
Мы дадим ряд способов, которыми свойства функции $f$ можно связать с особенностями ее графика.
1 Мы можем определить, когда множество на плоскости является графиком функции. Функции имеют
свойство, состоящее в том, что для данного значения в домене назначено ровно одно целевое значение.Следует
что ни одна вертикальная линия $\displaystyle{ x=h }$ не может пересекать график функции более одного раза.
Это полностью идентифицирует графики функций. 2 -5\, }$ мы имеем $D=\mathbb{R}\;$ .В самом деле, для любого
многочлен $P(x)\,$ , областью определения $P$ является $D(P)=\mathbb{R}\; $ . Это потому что,
как обсуждалось при описании нашей стратегии изучения многочлена,
полином не имеет плохих значений – для любых $h\in\mathbb{R}\,$ оценка $P(h)$
имеет смысл.
2 -5\, }$ мы имеем $D=\mathbb{R}\;$ .В самом деле, для любого
многочлен $P(x)\,$ , областью определения $P$ является $D(P)=\mathbb{R}\; $ . Это потому что,
как обсуждалось при описании нашей стратегии изучения многочлена,
полином не имеет плохих значений – для любых $h\in\mathbb{R}\,$ оценка $P(h)$
имеет смысл.
В наших примерах рациональных функций мы видим, что вертикальные асимптоты
линии $x=h$, которые никогда не пересекаются с графиками. Пропущенные точки возникают, когда точки на вертикальных линиях, которые
в противном случае встречаются кривые удаляются.2}\, }$ , упомянутых выше, имеем $D(f)=[-1,1] \; $ .
3 Диапазон $R(f)$ представляет собой набор значений $k$ , для которых
горизонтальная линия $y=k$ пересекает график. Если линия $y=k$ попадает на график
$f$ в точке $(h,k)\,$ , то в силу того, что $(h,k)$ находится на графике, мы должны иметь
$k=f(h)\,$ , и функция принимает значение $k$ хотя бы для одного $x\in D(f)\; $ . 2 +4\,x}\, }$ , имеем $R(f)=(-\infty, 1) \, \cup \, (16,\infty)\; $ .
Обратите внимание, что это всего лишь предположения из графиков. Чтобы получить реальную ярость этих функций, нам нужно было бы сделать
некоторый серьезный анализ самих функций.
2 +4\,x}\, }$ , имеем $R(f)=(-\infty, 1) \, \cup \, (16,\infty)\; $ .
Обратите внимание, что это всего лишь предположения из графиков. Чтобы получить реальную ярость этих функций, нам нужно было бы сделать
некоторый серьезный анализ самих функций.
4 Мы можем сказать, где функция принимает значение $0$ , найдя, где линия $y=0$ пересекает график функции. Эти точки пересечения будут иметь вид $(a,0)\,$ , а $a$ встречающиеся значения являются решениями $f\,(x)=0\;$ .2 +4\,x}\, }$ , по-видимому, принимает значение $20$ ровно для двух $x$ значения. На графике видно, что это примерно $x=-1$ и $x=-3\;$ .
5 Мы можем сказать, где данная функция является положительной (отрицательной), наблюдая, для каких значений $x$ график находится выше (ниже) горизонтальной оси. Когда дело обстоит именно так, это то, что устанавливается на шаге 3 метода непрерывности.
Пример определения положительности функции
В примере, открывающем этот раздел, мы видим, что $\displaystyle{ x^2 -5 \gt 0 }$ для
$(-\infty, -\sqrt{5}) \, \cup \, (\sqrt{5},\infty) \; $ .
6 Мы говорим, что функция возрастает на интервале $[a,b]$ в точности, если для любого $\displaystyle{ x_1 \, }$ , $\displaystyle{ \, x_2\in [a,b] }$ с $\displaystyle{ x_1 \lt x_2\, }$ , имеем $\displaystyle{ f\,\left(x_1\right) \lt f\,\left(x_2\right)\; }$ . Оно убывает по $[a,b]$ именно в том случае, если для любого $\displaystyle{ x_1\, }$ , $\displaystyle{ \, x_2\in [a,b] }$ с $\displaystyle{ x_1 \lt x_2\, }$ , имеем $\displaystyle{ f\,\left(x_1\right) \gt f\,\left(x_2\right)\; }$ .Чтобы проверить, является ли функция возрастающей или убывающей на $[a,b]\,$ , необходимо либо существенно проверить каждую пару точек между $a$ и $b\,$ (обычно бесконечно много пар) или еще придумать какую-нибудь хитрость. Недостаточно просто проверить один пару пунктов, не давая какого-либо обоснования/объяснения используемого трюка .
Эти понятия сопровождаются красивыми картинками, которые помогают сделать их осмысленными. Возрастающие функции имеют свои графики
идущие из нижнего левого угла в верхний правый, в то время как убывающие функции имеют свои графики, идущие из верхнего левого угла в нижний правый.
Возрастающие функции имеют свои графики
идущие из нижнего левого угла в верхний правый, в то время как убывающие функции имеют свои графики, идущие из верхнего левого угла в нижний правый.
| графики возрастающих функций идут снизу слева направо вверх | |
| графики убывающих функций идут сверху слева направо снизу | |
Одна из причин, по которой может быть важно возрастание или убывание функции, заключается в том, что такая функция равна $1-1\;$ .2 -5 }$ предполагает, что эта функция убывает на $(-\infty,0)$ и возрастает по $(0,\infty)\;$ .
Функции
Функции — это очень специфические типы отношений. Перед определением функции важно определить отношение.
Отношения
Любой набор упорядоченных пар называется отношением . На рис. 1 показан набор упорядоченных пар.
А = {(–1, 1), (1, 3), (2, 2), (3, 4)}
Рисунок 1.График множества упорядоченных пар (–1, 1), (1, 3), (2, 2), (3, 4).
Домен и диапазон
Набор всех x называется доменом отношения. Набор всех y называется диапазоном отношения. Домен набора A на рисунке 1 — {–1, 1, 2, 3}, а диапазон набора A — {1, 2, 3, 4}.
Пример 1
Найдите домен и диапазон набора точек на рисунке 2.
Домен представляет собой набор {–2, –1, 1, 3}.Диапазон представляет собой набор {–1, 2, 3}.
Рис. 2. Нанесенные точки.
Определение функции
Отношение в примере
имеет пары координат с уникальными первыми членами. Когда значение x каждой пары координат отличается, отношение называется функцией . Функция — это отношение, в котором каждый элемент домена связан ровно с одним элементом диапазона. Все функции являются отношениями, но не все отношения являются функциями. Хороший пример функционального отношения можно увидеть в линейном уравнении y = x + 1, изображенном на рис. потому что для любого значения x существует уникальное значение y.
Все функции являются отношениями, но не все отношения являются функциями. Хороший пример функционального отношения можно увидеть в линейном уравнении y = x + 1, изображенном на рис. потому что для любого значения x существует уникальное значение y.
Рисунок 3. График линейного уравнения y = x + 1.
Графики функций
В каждом случае на рис. 4 (a), (b) и (c) для любого значения x существует только одно значение y .Сравните это с графиками на рисунке 5.
Рисунок 4. Графики функций.
Графики отношений, не являющиеся функциями
В каждом из соотношений на рис. 5 (a), (b) и (c) одно значение x связано с двумя или более значениями y . Эти отношения не являются функциями.
Рисунок 5. Графики отношений, не являющихся функциями.
Определение домена, диапазона и того, является ли отношение функцией
Пример 2
Обратите внимание, что примеры 2(e) и (f) являются иллюстрациями обратных отношений : отношений, в которых домен и диапазон поменялись местами. Обратите внимание, что хотя отношение в (e) является функцией, обратное отношение в (f) ею не является.
Обратите внимание, что хотя отношение в (e) является функцией, обратное отношение в (f) ею не является.
Нахождение значений функций
Значение функции на самом деле является значением диапазона отношения. Учитывая функцию
f = {(1, –3), (2, 4), (–1, 5), (3, –2)}
значение функции в 1 равно –3, в 2 равно 4 и так далее. Это записывается как f (1) = –3 и f (2) = 4 и обычно читается как « f of 1 = –3 и f of 2 = 4».Строчная буква f использовалась здесь для обозначения понятия функции, но могла использоваться любая строчная буква.
Пример 3
Пусть ч = {(3, 1), (2, 2), (1, –2), (–2, 3)} Найдите каждое из следующих.
Пример 4
Если г ( x ) = 2 x + 1, найдите каждое из следующих чисел.
Пример 5
Если f ( x ) = 3 x 2 + x –1, найдите диапазон f для домена {–2, –1, 1}.
Обзор типов графиков — Физика 132 Лабораторное руководство
В этом разделе рассматриваются различные типы графиков в целом. Мы предполагаем, что большинство из вас, вероятно, знакомы с этой информацией, поэтому не стесняйтесь ее пропустить.Тем не менее, на случай, если вам понадобится освежить в памяти материал, приведенный ниже, предоставлен из
.E. Hoib, Электронная книга помощи по алгебре . Раздел 5.2 Справочник – Графики восьми основных типов функций. Copyright 2018. Используется с разрешения.
Не стесняйтесь следовать любой из ссылок для получения дополнительной информации о каждом типе графика.
Цель этого справочного раздела состоит в том, чтобы показать вам графики различных типов функций , чтобы вы могли ознакомиться с этими типами.Вы обнаружите, что у каждого типа есть свой отличительный график. Показывая несколько графиков на одном графике, вы сможете увидеть их общие черты. В этой галерее показаны примеры следующих типов функций:
В каждом случае аргумент (вход) функции называется x , а значение (выход) функции называется y .
Это функции вида:
y = m x + b ,
, где м и b — константы.Типичное использование линейных функций — преобразование одной величины или набора единиц в другую. Графики этих функций представляют собой прямых линий . м — уклон, b — точка пересечения y . Если м положительно, то линия поднимается вправо, а если м отрицательно, то прямая падает вправо. Линейные функции подробно описаны здесь.
Это функции вида:
у = а х 2 + б х + с ,
, где a , b и c — константы.Их графики называются параболами . Это следующий простейший тип функции после линейной функции. Падающие предметы движутся по параболическим траекториям. Если a — положительное число, то парабола открывается вверх, а если a — отрицательное число, то парабола открывается вниз. Квадратичные функции подробно описаны здесь.
Квадратичные функции подробно описаны здесь.
Это функции вида:
y = a x b ,
, где a и b — константы.Они получили свое название из-за того, что переменная x возведена в некоторую степень. Многие физические законы (например, гравитационная сила как функция расстояния между двумя объектами или изгиб балки как функция нагрузки на нее) имеют форму степенных функций. Предположим, что a = 1, и рассмотрим несколько случаев для b ниже. Функция мощности подробно обсуждается здесь.
Степень
b является положительным целым числом.См. график ниже.Когда x = 0, все эти функции равны нулю. Когда x большое и положительное, они все большие и положительные. Когда x большое и отрицательное, то числа с четными степенями большие и положительные, а числа с нечетными степенями большие и отрицательные.
Степень
b является отрицательным целым числом.
См. график справа. Когда x = 0, эти функции подвергаются делению на ноль и, следовательно, все бесконечны. Когда x большое и положительное, они маленькие и положительное.Когда x большое и отрицательное, то числа с четными степенями маленькие и положительные, а числа с нечетными степенями маленькие и отрицательные.
Степень
b представляет собой дробь от 0 до 1.См. график ниже. Когда x = 0, все эти функции равны нулю. Кривые вертикальны в начале координат, и по мере увеличения x они увеличиваются, но изгибаются к оси x .
Это функции вида:
Y = N N · N + + N -1 N -1 N -1
4 N
-1 + … + A 2 · x 2 + a 1 · x + a 0 ,
Где N , , , N -1 , . .., A 2 , A 1 , A 0 — это константы.Допускаются только целые степени x . Наивысшая степень x , которая встречается, называется степенью многочлена. На графике показаны примеры полиномов степени 4 и степени 5. Степень дает максимальное количество « подъемов и спадов», которые может иметь полином, а также максимальное количество пересечений оси x , которые он может иметь.
.., A 2 , A 1 , A 0 — это константы.Допускаются только целые степени x . Наивысшая степень x , которая встречается, называется степенью многочлена. На графике показаны примеры полиномов степени 4 и степени 5. Степень дает максимальное количество « подъемов и спадов», которые может иметь полином, а также максимальное количество пересечений оси x , которые он может иметь.
Полиномы полезны для создания гладких кривых в приложениях компьютерной графики и для аппроксимации других типов функций.Полиномы подробно описаны здесь.
Это функции вида:
y = a b x ,
, где x находится в степени (а не в основании, как в случае со степенными функциями), а a и b являются константами. (Обратите внимание, что только b возводится в степень x , а не a . ) Если основание b больше 1, то результатом будет экспоненциальный рост.Многие физические величины растут экспоненциально (например, популяция животных и наличные деньги на процентном счете).
) Если основание b больше 1, то результатом будет экспоненциальный рост.Многие физические величины растут экспоненциально (например, популяция животных и наличные деньги на процентном счете).
Если основание b меньше 1, результатом будет экспоненциальное затухание. Многие величины затухают экспоненциально (например, количество солнечного света, достигающего заданной глубины океана, и скорость объекта, замедляющегося из-за трения).
Экспоненциальные функции подробно описаны здесь.
Существует множество эквивалентных способов определения логарифмических функций.Мы определим их в виде:
y = a ln ( x ) + b ,
или
y = a log ( x ) + b ,
, где x — натуральный логарифм, а a и b — константы. Они определены только для положительных x . Для маленьких x они отрицательны, а для больших x они положительны, но остаются маленькими.Логарифмические функции точно описывают реакцию человеческого уха на звуки различной громкости и реакцию человеческого глаза на свет различной яркости. Логарифмические функции подробно описаны здесь.
Для маленьких x они отрицательны, а для больших x они положительны, но остаются маленькими.Логарифмические функции точно описывают реакцию человеческого уха на звуки различной громкости и реакцию человеческого глаза на свет различной яркости. Логарифмические функции подробно описаны здесь.
Это функции вида:
y = a sin ( b x + c ),
или
y = a cos ( b x + c ),
, где a , b и c — константы.Синусоидальные функции полезны для описания всего, что имеет форму волны относительно положения или времени. Примерами являются волны на воде, высота прилива в течение дня и переменный ток в электричестве. Параметр a (называемый амплитудой) влияет на высоту волны, b (угловая скорость) влияет на ширину волны, а c (фазовый угол) сдвигает волну влево или вправо.



 Мы рассмотрим эти идеи, посмотрев
на графиках различных многочленов.
Мы рассмотрим эти идеи, посмотрев
на графиках различных многочленов. Поскольку кратность нечетная, график пересекает ось x в корне, но
график выравнивается около этого корня, потому что корень не простой. В зелени
На приведенном выше графике есть два различных действительных корня: x 1 = -1 и x 2 = 2.Заметь
график не пересекает ось x в корне x 2 = 2 (он просто касается оси x ). Это означает, что x 2 = 2 является корнем четной кратности (на самом деле
кратность равна 2, потому что кубика имеет только степень 3). Таким образом, куб, изображенный на
зеленый имеет один простой корень, x = -1, и один двойной корень, x = 2 (в сумме,
включая кратность 3).
Поскольку кратность нечетная, график пересекает ось x в корне, но
график выравнивается около этого корня, потому что корень не простой. В зелени
На приведенном выше графике есть два различных действительных корня: x 1 = -1 и x 2 = 2.Заметь
график не пересекает ось x в корне x 2 = 2 (он просто касается оси x ). Это означает, что x 2 = 2 является корнем четной кратности (на самом деле
кратность равна 2, потому что кубика имеет только степень 3). Таким образом, куб, изображенный на
зеленый имеет один простой корень, x = -1, и один двойной корень, x = 2 (в сумме,
включая кратность 3). На рисунке ниже показаны полиномы с одним различным
реальный корень, x = 0. Как видите, график касается корня без пересечения
ось x, когда кратность четная, и пересекает ось x через корень
когда кратность нечетная. Кроме того, график становится все более и более плоским.
вблизи корня по мере увеличения кратности.
На рисунке ниже показаны полиномы с одним различным
реальный корень, x = 0. Как видите, график касается корня без пересечения
ось x, когда кратность четная, и пересекает ось x через корень
когда кратность нечетная. Кроме того, график становится все более и более плоским.
вблизи корня по мере увеличения кратности.