Для чего нужен масштаб? Какие виды масштабов существуют?
Зачем нужен масштаб?
Ни один географический объект, например реку, мост, поселок, невозможно изобразить на топографическом плане в натуральную величину. В древности люди рисовали уменьшенные изображения местности, на которых разные участки уменьшались произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т. д. Чтобы план местности был более точным, необходимо все расстояния уменьшать в одинаковое число раз с сохранением всех пропорций, делать изображение в масштабе.
Масштаб показывает, во сколько раз расстояния на плане уменьшены по отношению к реальным расстояниям.
Длина школы на плане школьного двора в 1000 раз меньше, чем в действительности. Это означает, что на данном плане все расстояния уменьшены в 1000 раз.
Численный и именованный масштабы
Масштаб пишут по-разному. В виде числа масштаб изображается так: 1:100 (это означает, что 1 см плана заменяет 100 см на местности). Это численный масштаб. 100 см — это 1 м, поэтому можно просто написать: в 1 см — 1м. Масштаб, записанный в таком виде, — именованный масштаб.
В виде числа масштаб изображается так: 1:100 (это означает, что 1 см плана заменяет 100 см на местности). Это численный масштаб. 100 см — это 1 м, поэтому можно просто написать: в 1 см — 1м. Масштаб, записанный в таком виде, — именованный масштаб.
Линейный масштаб
Обычно на планах, кроме численного и именованного масштабов, помещают линейный масштаб. Он представляет собой линию, разделенную на равные отрезки. Отрезки справа от 0 показывают, какому расстоянию на местности соответствуют расстояния на плане в 1 см, 2 см и т. д. Отрезок слева от 0 разделен на равные мелкие части. Зная расстояние на местности, которому соответствует большой отрезок, и количество мелких отрезков, можно вычислить, какому расстоянию на местности соответствует каждый мелкий отрезок. Например, длина большого отрезка слева от 0 на рисунке равна 10м. Этот отрезок разделен на 5 мелких частей, значит, длина одной такой части составляет 10м:5=2 м.
Линейный масштаб позволяет измерять расстояния на плане при помощи циркуля-измерителя или полоски бумаги.
При помощи линейного масштаба можно определять длину кривых линий, например реки, дороги. Для этого надо отметить на полоске бумаги небольшое расстояние или установить небольшой раствор между иглами циркуля-измерителя и переставлять бумагу с отметкой или циркуль вдоль измеряемой линии, считая число перестановок. Определив при помощи линейного масштаба длину одного «шага» в метрах и умножив ее на число перестановок, мы получим длину кривой линии.
Выбор масштаба
Масштаб выбирают в зависимости от величины расстояний. Например, надо изобразить расстояние в 6 км. Тогда масштаб в 1 см — 10 м не годится, потому что это расстояние изображается линией в 600 см, то есть в 6 м; но линию в 6 м нельзя поместить на обычном листе бумаги. Удобнее взять масштаб: в 1 см — 1 км. При таком масштабе расстояние в 6 км будет соответствовать линии в 6 см.
Какие бывают масштабы топографических планов
Автор Илья Чернышев На чтение 6 мин Просмотров 13. 8к. Обновлено
8к. Обновлено
Назначение у такого распространённого и широко востребованного комплекса работ, как топографическая съёмка, может быть довольно разным. Поэтому и итоговые топографические планы могут довольно значительно различаться. Так как топосъёмка — неизбежная спутница практически всех геодезических изысканий, ориентироваться в основных её параметрах и областях применения таковых наверняка будет полезно каждому. В этой статье вкратце описано применение разных масштабов топографических планов для строительства и проектирования.
Что такое масштаб топоплана?
Так что же такое масштаб? Пришло это слово из немецкого языка и переводится как «мерная палка». Масштаб топографического плана — это соотношение линейных объектов на местности и их изображению на плане. То есть во сколько раз размер на плане меньше натурального. Чем больше цифра указана во второй части масштаба- тем мельче план и тем бОльшую площадь он охватывает. Например, карта Масштаба 1:200000 может охватить целую страну, а масштаба 1:200 только один участок в 6 соток.
Например, карта Масштаба 1:200000 может охватить целую страну, а масштаба 1:200 только один участок в 6 соток.
Масштаб топографической съёмки с точки зрения заказчика — самая важная характеристика. Обычно проектировщики, ландшафтные дизайнеры и другие подобные специалисты сразу оговаривают, какого масштаба топографический план им понадобится для работы, а также какие должны быть дополнительные условия съёмки. Специалисты ООО «Землемер» с удовольствием дадут совет касательно той или иной ситуации, если у Вас возникли вопросы по составлению технического задания. В общем же выбор масштаба топографической съёмки диктуется областью использования его результатов.
Точность планов различных масштабовКогда говорят о точности топографического плана- имеют ввиду среднюю погрешность определения местоположения объекта на плане относительно ближайших пунктов ГГС (государственная геодезическая сеть). Иными словами- это точность, с которой по бумажному плану можно узнать координаты объекта. Для разных масштабов она, соответственно, разная. Принято для равнинного рельефа -0.5 мм в масштабе плана. Считается, что человеческий глаз четко различает именно эту величину, и по плану расстояние можно измерить с точностью в полмиллиметра. Это значит, что для масштаба 1:1000, например, погрешность составит 0.5 метра. Чем мельче масштаб- тем значительнее погрешность. Даже если топосъемка была выполнена с бОльшей точностью- это не повлияет на точность определения координат по бумажному чертежу.
Для разных масштабов она, соответственно, разная. Принято для равнинного рельефа -0.5 мм в масштабе плана. Считается, что человеческий глаз четко различает именно эту величину, и по плану расстояние можно измерить с точностью в полмиллиметра. Это значит, что для масштаба 1:1000, например, погрешность составит 0.5 метра. Чем мельче масштаб- тем значительнее погрешность. Даже если топосъемка была выполнена с бОльшей точностью- это не повлияет на точность определения координат по бумажному чертежу.
Что касается цифровых моделей местности- там точность обусловлена не разрешающей способностью глаза, а нормативными актами для топосъемок разных масштабов.
Какие бывают виды масштаба?Говоря о топографических планах, масштабы могут быть 1:10000 и крупнее. Все более мелкие масштабы относятся уже к картам. Это обусловлено тем, что планы изображаются на плоскости (без учета кривизны земли). И максимальный участок местности, который можно изобразить на плоскости помещается на план масштаба 1:10000. Участки большей площади уже проектируют на плоскость с искажениями, поправками или в виде «лепестков» на карте.
Участки большей площади уже проектируют на плоскость с искажениями, поправками или в виде «лепестков» на карте.
К видам масштаба можно отнести и обозначение их на картах и планах. Различают линейный, численный и именованный. Линейный и именованный используются в основном на картах мелких масштабов и не так распространены. Численный масштаб присутствует практически на всех чертежах и планах. Он более лаконичный и емкий.
Масштаб топоплана можно установить любой крупнее 1:10000. Это можно указать в техническом задании на проведение топографо-геодезических работ. Но существуют общепринятые масштабы, которые в большинстве своем и используются. К ним относятся 1:10000, 1:5000, 1:2000, 1:1000, 1:500, 1:200, 1:100. Далее рассмотрим подробнее.
Масштаб
1:5000Он применяется для самых разнообразных целей. В их числе может быть проектирование строительства первой очереди для городов от средних до крупных размеров, проектирование инженерных сооружений, автотрасс, железных дорог, планировка промышленных районов, техническое проектирование предприятий, составление планов разведки месторождений полезных ископаемых и проектов их разработки, ведение Государственного кадастра недвижимости и т.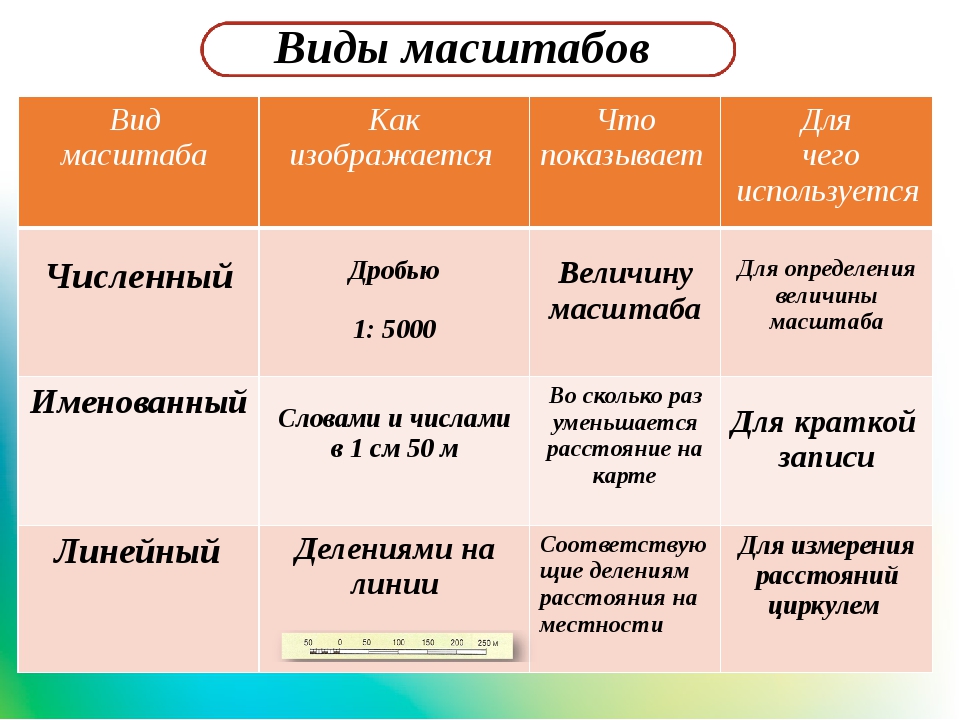 д.
д.
Соответственно такой масштаб используется скорее как ситуационный план для проведения первичного проектирования крупных, или обладающих большой протяженностью объектов.
Масштаб
1:2000Его применяют для технического проектирования железнодорожных и автомобильных путей в горных районах и для их же рабочего проектирования — в районах равнинных и холмистых, для детальной разведки месторождений полезных ископаемых и для исполнительного планирования предприятий горной промышленности, для технического проектирования гидротехнических сооружений и тепловых электростанций, для прокладки в горной местности трасс напорных трубопроводов и каналов, для использования под каналы участков речных русел, для создания рабочих чертежей строительства водохранилищ, насосных, компрессорных и трубопроводных станций, для разработки генеральных схем сложного линейного строительства.
Этот масштаб уже крупнее, но все же не подразумевает нанесение на планы всей разветвленной сети подземных коммуникаций, что также приближает его к разряду ситуационных.
Масштаб 1:1000
Его выбирают для съёмки, результаты которой нужны для непростых инженерных изысканий, для технического проектирования автомобильных и железных дорог, для технического и рабочего проектирования застройки территорий пустых либо с одноэтажной застройкой, для рабочего проектирования гидроэлектростанций и плотин, железнодорожных узлов и станций, гидротехнических сооружений и напорных трубопроводов, предприятий горнодобывающих, а также обогатительных, для детальной разведки с подсчётом запасов месторождений полезных ископаемых, строение которых очень сложное, а рудные жилы — невыраженные.
По сути это самый мелкий масштаб, используемый для проектирования и строительства на незастроенной территории.
Масштаб 1:500
Предназначен для съёмки, результаты которой будут использоваться для создания рабочих чертежей басейнов и плотин, для проектирования порталов туннелей, зданий гидроэлектростанций, напорных трубопроводов и уравнительных шахт, для составления генеральных планов участков строительства, а также рабочих чертежей промышленных предприятий и многоэтажных объектов капитальной застройки с густыми сетями подземных коммуникаций и решений вертикальной планировки.
Основной используемый масштаб для проектирования практически любого строительства на застроенной территории.Масштабы 1:200 и 1:100
Используют для так называемой крупномасштабной топографической съёмки. Она выполняется на небольших отдельных участках и нужна при строительстве объектов очень сложных (например, резервуаров или шахт), для ландшафтного проектирования, а также для строительства в непростых условиях: при наличии очень густой сети разнообразных наземных и подземных сооружений или сложных природных процессов. Высота сечения рельефа определяется проводящими топографическую съёмку специалистами в зависимости от выбранного масштаба и типа рельефа конкретной местности.
Нет. Написано очень общо
25%
Пусть специалисты с этим разбираются!
5%
Показать результатыПроголосовало: 20
В заключениеХочется отметить, что Вам необязательно вникать во все тонкости использования различных масштабов. В 90% случаев для строительства используют масштаб 1:500. Если существуют предпосылки для использования иных масштабов- наши специалисты проведут грамотную консультацию и все подробно объяснят.
В 90% случаев для строительства используют масштаб 1:500. Если существуют предпосылки для использования иных масштабов- наши специалисты проведут грамотную консультацию и все подробно объяснят.
Можно просто написать
ООО «Землемер» Для Вас!
Какие бывают виды масштабов. Что такое масштаб карты в географии
Масштаб можно написать цифрами или словами, или изобразить графически.
- Численный.
- Именованный.
- Графический.
- Линейный.
- Поперечный.
Численный масштаб
Численный масштаб подписывают цифрами внизу плана или карты. Например, масштаб «1: 1000» означает, что на плане все расстояния уменьшены в 1000 раз. 1 см на плане соответствует 1000 см на местности, или, по-скольку 1000 см =10 м, 1 см на плане соответствует 10 м на мест-ности.
Именованный масштаб
Именованный масштаб плана или карты обозначают словами. Например может быть написано «в 1 см — 10 м».
Например может быть написано «в 1 см — 10 м».
Линейный масштаб
Удобнее всего пользоваться масштабом, изображённым в виде отрезка прямой линии, разделённой на равные части, обычно сантиметры (рис. 15). Такой масштаб называется линейным , он также показывается внизу карты или плана. Обратите внимание , что при вычерчивании линейного масштаба нуль ставят, отступая на 1 см от левого конца отрезка, а первый сантиметр делят на пять частей (по 2 мм).
Возле каждого сантимет-ра подписано, какому расстоянию это соответствует на плане. Один сантиметр разделен на части, возле которых написано, како-му расстоянию на карте они соответствуют. Циркулем-измерите-лем или линейкой измеряют длину какого-либо отрезка на плане и, прикладывая этот отрезок к линейному масштабу, определяют его длину на местности.
Зная масштаб, можно определять расстояния между географи-ческими объектами, измерять сами объекты.
Если расстояние от дороги до реки на плане с масштабом 1: 1000 («в 1 см — 10 м») равно 3 см, значит, на местности оно равно 30 м. Материал с сайта
Материал с сайта
Предположим, от одного объекта до другого 780 м. По-казать в натуральную величину это расстояние на бумаге невоз-можно, поэтому придётся вычертить его в масштабе. Например, если все расстояния будут изображены в 10 000 раз меньшими, чем в дей-ствительности, т. е. 1 см на бумаге будет соответствовать 10 тыс. см (или 100 м) на местности. Тогда в масштабе расстоя-ние в нашем примере от одного объекта до другого будет равно 7 см и 8 мм.
Картинки (фото, рисунки)
На этой странице материал по темам:
Масштаб — это отношение 2-х линейных размеров, которое используется при создании чертежей и моделей и позволяет показывать крупные объекты в уменьшенном виде, а мелкие в укрупненном. Иными словами, это отношение длины отрезка на карте к истинной длине на местности. Разные практические ситуации могут потребовать от вас знания о том, как найти масштаб.
Когда появляется необходимость в определении масштаба? В основном это происходит в следующих ситуациях:
- при использовании карты;
- при выполнении чертежа;
- при изготовлении моделей различных объектов.

Виды масштаба
Под численным масштабом следует понимать масштаб, выраженный дробью. Ее числитель — единица, а знаменателем является число, показывающее, во сколько раз изображение меньше реального объекта.
Линейный масштаб — это мерная линейка, которую вы можете увидеть на картах. Этот отрезок поделен на равные части, подписанные значениями соразмерных им расстояний на реальной местности. Удобен линейный масштаб тем, что обеспечивает возможность измерять и строить расстояния на планах и картах.
Именованный масштаб представляет собой словесное описание того, какое расстояние в реальности соответствует одному сантиметру на карте. К примеру, в одном километре 100000 сантиметров. При этом численный масштаб выглядел бы следующим образом: 1:100000.
Как найти масштаб карты?
Возьмите, к примеру, школьный атлас и взгляните на любую его страницу. В нижней части вы можете увидеть линейку, на которой указано, какое расстояние на реальной местности соответствует одному сантиметру на вашей карте.
Масштаб в атласах обычно указывается в сантиметрах, которые нужно будет перевести в километры. К примеру, увидев надпись 1:9 500 000, вы поймете, что 95 километрам реальной местности соответствует всего-навсего 1 см карты.
Если, вы к примеру знаете, что расстояние между вашим городом и соседним — 40 км, то можно просто измерить линейкой промежуток между ними на карте и определить соотношение. Итак, если путем измерения вы получили расстояние 2 см, то получите масштаб 2:40=2:4000000=1:2000000. Как видите, находить масштаб совсем несложно.
Другие случаи использования масштаба
При изготовлении моделей самолетов, танков, кораблей, автомобилей и других объектов используются определенные стандарты масштабирования. К примеру, это может быть масштаб 1:24, 1:48, 1:144. При этом изготовленные модели должны быть меньше своих прототипов именно в указанное число раз.
Масштабирование может понадобиться, к примеру, при увеличении какого-либо рисунка. При этом изображение разделяется на клетки определенного размера, к примеру, 0. 5 см. Лист бумаги надо будет тоже расчертить на клетки, но уже увеличенные в необходимое число раз (примеру, длины их сторон могут составлять полтора сантиметра, если рисунок нужно увеличить в 3 раза). Нанеся контуры исходного рисунка на расчерченный лист, можно будет получить изображение, очень близкое к оригиналу.
5 см. Лист бумаги надо будет тоже расчертить на клетки, но уже увеличенные в необходимое число раз (примеру, длины их сторон могут составлять полтора сантиметра, если рисунок нужно увеличить в 3 раза). Нанеся контуры исходного рисунка на расчерченный лист, можно будет получить изображение, очень близкое к оригиналу.
Конечным результатом топографо-геодезических работ являются чертежи земной поверхности, числовые данные для составления цифровых моделей местности и др. материал, представленный в упорядоченном виде. Чертежи могут быть составлены на бумажной основе, представлены в электронной форме или в виде компьютерной базы данных. Традиционными формами чертежей являются: карта, план, профиль .
При изображении на бумаге, т.е. на плоскости всей земной поверхности или значительных её участков невозможно избежать искажений изображения вследствие кривизны изображаемой поверхности, поскольку при любом способе проектирования на плоскость возникают искажения в длинах линий и углах между ними.
Уменьшенное искаженное за счёт влияния кривизны Земли, плоское изображение всей земной поверхности или значительной её части, построенное по определённым математическим законам, называется картой .
В зависимости от назначения карты при её создании выбирается определённая картографическая проекция, т.е. математический закон проектирования местности на плоскость.
Ортогональную проекцию небольших участков местности (до 20×20 км) на уровенную поверхность можно считать плоской, пренебрегая кривизной Земли. Уменьшенное изображение такой проекции на бумаге будет без искажений, вызванных кривизной Земли, и подобным участку местности.
Таким образом, уменьшенное, подобное изображение на плоскости горизонтального проложения сравнительно небольшого участка земной поверхности называется планом .
Наглядным изображением неровностей земной поверхности является профиль , т.е. уменьшенное изображение её вертикального разреза по выбранной линии .
На планах и картах могут изображаться ситуация и рельеф, либо только ситуация (от франц. Situation — местоположение).
Совокупность изображений на плане местных предметов естественного и искуственного происхождения (река, лес, кустарник, земельный участок, здание, улица и др.), называетсяситуацией местности .
Совокупность неровностей земной поверхности естественного происхождения называется рельефом местности.
Если на плане изображены только границы объектов ме стности, его называют контурным (рис. 3.1, а ). Если, кроме контуров, на план нанесен и рельеф, такой план называюттопографическим (рис. 3.1,б ).
Рис.3.1. Контурный (а) и топографический (б) планы.
Картой называют чертёж, на котором может быть изображена поверхность всей Земли или любой её части в обобщенном и уменьшенном виде.
Карты могут иметь различное назначение: сельскохозяйственные, кадастровые, экономические, политические и т.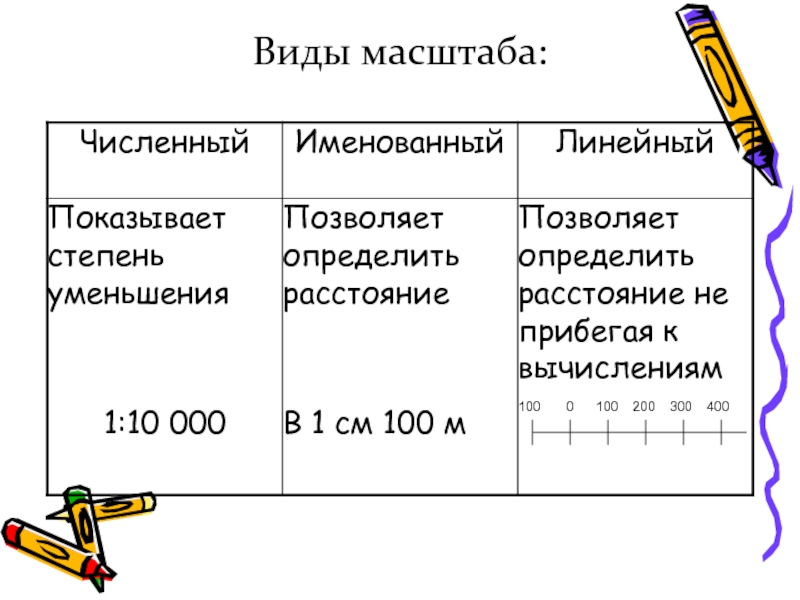 д. — это так называемые тематические или специальные карты, на них показывают контуры ситуации и специальную нагрузку. Карты на которых, кроме контуров ситуации, изображен рельеф земной поверхности, называют общегеографическими. Общегеографическая основа карты является каркасом для построения тематических карт.
д. — это так называемые тематические или специальные карты, на них показывают контуры ситуации и специальную нагрузку. Карты на которых, кроме контуров ситуации, изображен рельеф земной поверхности, называют общегеографическими. Общегеографическая основа карты является каркасом для построения тематических карт.
При любых измерениях по планам и картам следует помнить, что масштаб плана во всех его точках одинаковый, а масштаб во всех точках карты, как правило, различен.
Понятие о топографических планах и картах. Масштабы. Точность масштаба. Понятие о масштабах плана и карты.При составлении планов, карт, профилей результаты измерения линий на местности уменьшают в несколько сотен или тысяч раз.
Степень уменьшения горизонтальных проложений линий местности при изображении их на плане называется масштабом.
Под масштабом карты в общем случае понимается отношение длины линии на карте к её длине на поверхности относимости. В зависимости от картографической проекции изображения на карте в разных местах имеют различные по величине искажения, поэтому масштаб карты неодинаков. Для карт, составленных в мелком масштабе, обычно подписывается средний масштаб.
В зависимости от картографической проекции изображения на карте в разных местах имеют различные по величине искажения, поэтому масштаб карты неодинаков. Для карт, составленных в мелком масштабе, обычно подписывается средний масштаб.
Масштаб, выраженный числом в виде простой дроби называется численным . У него числитель равен единице, а знаменатель круглое число, например, 1/500, 1/1000 или 1:500, 1:1000. Масштаб 1:500 показывает, что горизонтальное проложение линии местности уменьшено на плане в 500 раз и одной единице длины на плане, карте или профиле соответствует на местности 500 таких единиц, т.е. одному сантиметру на плане, карте или профиле соответствует 500 см или 5 м на местности.
Численный масштаб подписывают на планах, картах или профилях в их нижней части, сопровождая пояснительной надписью, например, «в 1 сантиметре 5 м», так как длины линий местности удобно выражать в метрах. Чтобы определить количество метров на местности в одном сантиметре плана (карты), надо у знаменателя численного масштаба отбросить два последних нуля, например, 1 см плана масштаба 1:2000 соответствует 20м на местности.
Чтобы на плане (карте) показать больше подробностей, их надо составлять в более крупном масштабе. Чем меньше знаменатель численного масштаба, тем масштаб крупнее, а масштаб с большим знаменателем считается мелким. К крупным масштабам относят: 1: 500, 1: 1000, 1: 2000, 1: 5000; к средним — 1:10 000, 1:25 000, 1:50 000; к мелким — 1: 100 000, 1: 200 000, 1: 500 000, 1: 1 000 000 и мельче.
Планы и карты в России создаются в принятых масштабах, образующих строго определенную систему, называемую масштабным рядом . Масштабный ряд установлен с таким расчетом, чтобы он удовлетворял всем условиям потребителей и имелась возможность легко переходить от одного масштаба к другому.
Зная численный масштаб, легко длины линий местности переводить в длины линий на плане (карте) и наоборот. Такой перевод сопряжен с вычислениями, поэтому, чтобы не производить таких вычислений, пользуются шкалой (номограммой) графически построенной. Такая шкала называется линейным масштабом (рис. 3.2).
3.2).
Рис. 3.2. Численный и линейный масштабы.
Линейный масштаб представляет собой график в виде отрезка прямой горизонтальной линии, на которой последовательно отложены равные отрезки, называемые основанием масштаба. Основание масштаба соответствует целому числу десятков или сотен метров на местности. Для повышения точности измерений крайнее левое основание делится на более мелкие отрезки.
Началом счета является нуль (0) — общая точка первого и второго основания масштаба. Остальные отрезки подписывают в соответствии с величиной численного масштаба. Если основание масштаба равно 2 см, то такой линейный масштаб называется нормальным . На рис. 3.1 нормальный линейный масштаб построен для численного 1: 10000 (в 1 см — 100 м, а в 2 см — 200 м).
Измерения по линейному масштабу обычно производят циркулем-измерителем (рис.3.3), который перед работой должен быть хорошо отрегулирован. При измерении циркуль следует держать одной рукой, наклоняя его несколько от себя так, чтобы хорошо были видны одновременно оба острия иголок.
Рис. 3.3. Определение расстояний по линейному масштабу.
При измерении расстояний раствор циркуля устанавливают по точкам А и В на плане, а затем прикладывают циркуль к линейному масштабу так, чтобы его левая ножка пришлась слева от нуля, а правая стояла точно на одном из делений вправо от нуля. Определяемое расстояние будет равно сумме отсчетов по обоим концам иголок циркуля, т.е. 100 + 86 = 186м. При этом десятые доли мелких делений определяются «на глаз» .
При выполнении картометрических работ на планах (картах) основными элементами графического построения являются точки-наколы иглы циркуля и линии. Накол представляет собой кружок очень малого диаметра. Физиологическое свойство человеческого глаза таково, что при рассматривании с расстояния 25-30 см двух рядом расположенных точек (наколов) они сливаются в одну, если расстояние между ними меньше 0,1 мм (по исследованиям кафедры геодезии ГУЗа — 0,08 мм). Это связано с критическим углом зрения человека, равным 1¢. Величина 0,1 мм принята за предельную графическую точность измерения по карте, т.е. является такой минимальной величиной, которую можно видеть невооруженным глазом и ощущать при измерениях циркулем.
Величина 0,1 мм принята за предельную графическую точность измерения по карте, т.е. является такой минимальной величиной, которую можно видеть невооруженным глазом и ощущать при измерениях циркулем.
При выполнении съемочных работ мерой точности работы наряду с величиной 0,1 мм является соответствующее этой величине расстояние на местности, называемое предельной точностью масштаба. Это та максимальная точность, с которой может быть определено расстояние по данному плану (карте). При этом следует учитывать, что вследствие накопления неизбежных погрешностей в технологическом процессе изготовления плана (карты) практическая точность результата измерения расстояний по планам (картам) значительно грубее предельной графической точности и может достигать 1мм.
Предельную точность масштаба легко рассчитать, разделив знаменатель численного масштаба на 10 000. Например, точность масштаба 1:5 000 равна 0,5м. Знать величину точности масштаба необходимо при выборе масштаба съемки и при определении, какие объекты местности не следует снимать, так как они не изобразятся в данном масштабе.
Например, земельный участок размером 10×10 м на картах масштабов 1: 50 000, 1: 100 000 и 1: 200 000 изобразятся в виде точки, а при масштабах плана (карты) 1: 5000, 1: 10 000, 1: 25 000, будет иметь размеры соответственно 2,0×2,0 мм, 1,0×1,0мм, 0,4×0,4мм, т.е. чем больше знаменатель численного масштаба, тем детальность плана меньше и, наоборот, чем меньше знаменатель численного масштаба, тем детальность больше.
Построение поперечного масштаба, его точность. Измерение длин линий на плане.Для повышения точности измерения расстояний на плане (карте), чтобы не измерять величину отрезка «на глаз», используют шкалу поперечного масштаба, которую можно построить следующим образом.
Рис. 3.4. Нормальный поперечный масштаб.
На горизонтальной прямой КL (рис. 3.4) откладывают несколько раз основание масштаба, равное 2 см. Через полученные точки проводят линии, перпендикулярные к КL . Первое основание КС делят на десять равных частей. Крайние перпендикуляры КМ и LN делят на десять равных частей и через деления на перпендикулярах проводят линии, параллельные основаниюКL. Отрезок МВ также делят на 10 равных частей. При этом C соединяют с точкой А , а остальные наклонные линии, называемые трансверсалями , проводятся параллельно. В результате графических построений получают, так называемый, поперечный масштаб . Отрезок а 1 b 1 называется наименьшим делением поперечного масштаба.
Крайние перпендикуляры КМ и LN делят на десять равных частей и через деления на перпендикулярах проводят линии, параллельные основаниюКL. Отрезок МВ также делят на 10 равных частей. При этом C соединяют с точкой А , а остальные наклонные линии, называемые трансверсалями , проводятся параллельно. В результате графических построений получают, так называемый, поперечный масштаб . Отрезок а 1 b 1 называется наименьшим делением поперечного масштаба.
Если число делений основания масштаба n , число делений на перпендикуляре m, то наименьшее деление поперечного масштаба а 1 b 1 будет равно:
а 1 b 1 = КС /nm . (3.1)
Пример . Если КС = 2 см, n = 10, m = 10, то а 1 b 1 = 2 см/10х10 = 0.02см,
что при масштабе 1:10 000 соответствует 2 м, а 2 b 2 — 4 м и т.д., АB — 20 м.
Так как основание поперечного масштаба выбирают равным 2 см, то практически значение всех его делений в метрах можно рассчитать для любого численного масштаба.
Поперечный масштаб обычно гравируется на специальных металлических линейках, называемых масштабными, а также на геодезическом транспортире.
На таких масштабных линейках обычно указываются порядковые номера малых и больших делений, поэтому для каждого конкретного масштаба плана необходимо предварительно определить какому значению в метрах соответствует наименьшее деление масштаба и другие деления.
Поперечным масштабом пользуются следующим образом. Пусть требуется отложить на плане (карте) масштаба 1:10000 линию длиной 246 м (рис. 3.3). При основании масштаба, равном 2 см, одно деление справа от нуля будет соответствовать 200 м, слева — 20 м. Наименьшее деление согласно формуле (3.1) — 2 м. Ставят правую ножку измерителя на деление с отметкой 200 (порядковый номер 1), а вторую ножку — влево от нуля на второе деление (т.к. одно деление соответствует 20 м), что будет соответствовать 240 м.
Затем переставив измеритель вверх так, чтобы левая ножка измерителя шла по наклонной линии (трансверсали), а правая — по вертикальной до третьей горизонтальной линии, на которой имеется отрезок а 3 в 3 соответствующий 6м и получают общую длину линии 246 м. Полученным раствором измерителя откладывают расстояние на плане (карте).
Полученным раствором измерителя откладывают расстояние на плане (карте).
Для определения длины линии на плане, берут соответствующий раствор измерителя и прикладывают к поперечному масштабу так, чтобы правая его ножка совпала с делением справа от нуля, а вторая — находилась в пределах левого от нуля основания. Затем подсчитывают число метров. Если левая ножка измерителя не совпадает с делением на основании, то раствор измерителя передвигают вверх до совпадения её с трансверсалью, при этом обе ножки должны лежать на одной горизонтальной линии. После этого отсчитывают длину горизонтального проложения линии местности. Если длина линии превышает длину шкалы поперечного масштаба, то её измеряют или откладывают по частям.
С помощью нормального поперечного масштаба можно откладывать и измерять расстояния с точностью до 0,2 мм, что соответствует одной сотой основания. Если же положение ножек циркуля между горизонтальными линиями шкалы оценивать на глаз, то можно отсчитывать расстояния с точностью до 0,1мм.
Отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например, дом, в натуральную величину, поэтому, при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Масштаб в геодезии, картографии и проектировании
Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби , в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы , построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0.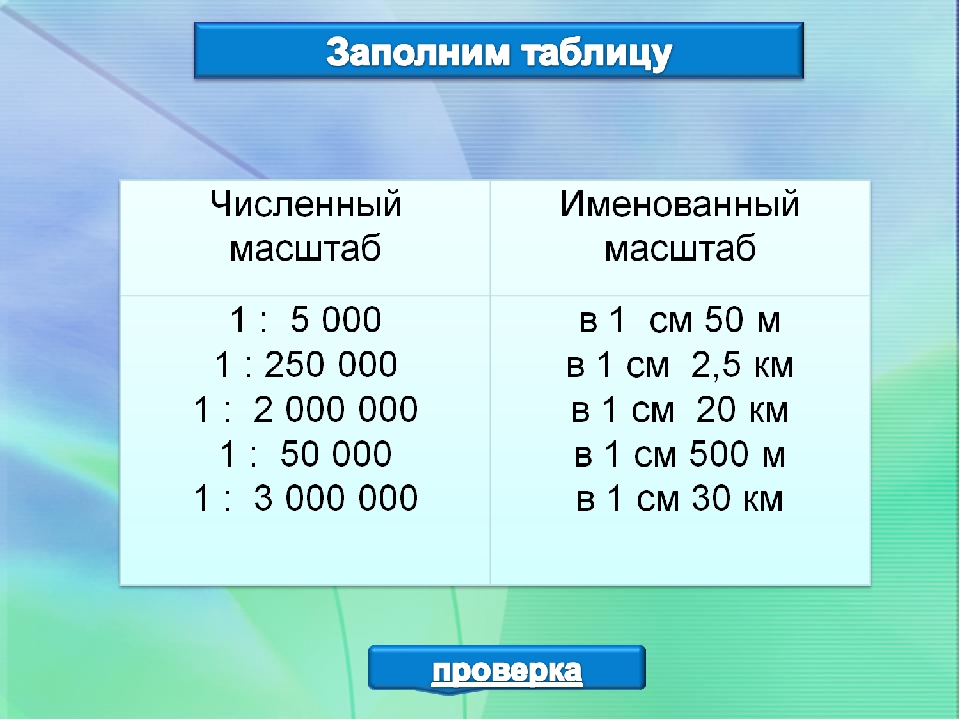 Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.
Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда:
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштаб в фотографии
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчете глубины резко изображаемого пространства . Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Масштаб-число,показывающее, во сколько раз уменьшены или увеличены настоящие размеры на чертеже.
Примечания
Wikimedia Foundation . 2010 .
Синонимы :Смотреть что такое «Масштаб» в других словарях:
— (нем. Masstaq, от нем. Mass мера). 1) мерило, мера линейная, принятая при чертежах в уменьшенном виде. 2) в артиллерии: медная линейка с обозначением на ней калибра орудий, снарядов и употребительнейших мер в артиллерии. Словарь иностранных слов … Словарь иностранных слов русского языка
2) в артиллерии: медная линейка с обозначением на ней калибра орудий, снарядов и употребительнейших мер в артиллерии. Словарь иностранных слов … Словарь иностранных слов русского языка
Масштаб — – отношение длины данной линии, изображенной на чертеже, плане или карте, к длине ее в натуре. [Словарь основных терминов, необходимых при проектировании, строительстве и эксплуатации автомобильных дорог.] Масштаб – это отношение… … Энциклопедия терминов, определений и пояснений строительных материалов
См … Словарь синонимов
Отношение линейных размеров изображенного на карте, аэрофотоснимке и т. д предмета к его размерам в натуре. Различают масштаб уменьшения и увеличения, может быть выражен численным отношением (численный масштаб) или изображен графически… … Морской словарь
— [аш] (или маштаб), масштаба, муж. (нем. Masstab). 1. Отношение уменьшенных расстояний и размеров на карте и чертеже к действительным. Географическая карта крупного масштаба. Масштаб 10 верст в дюйме. В десятиверстном масштабе. 2. Мера. В большом … Толковый словарь Ушакова
В десятиверстном масштабе. 2. Мера. В большом … Толковый словарь Ушакова
масштаб 1:1 — полный масштаб — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы полный масштаб EN full scale … Справочник технического переводчика
— (нем. Ma?stab) отношение длины линии на чертеже, плане или карте к длине соответствующей линии в натуре. Обозначается в виде дроби, числитель которой равен единице, а знаменатель числу, показывающему степень уменьшения длин линий (напр., 1: 100… … Большой Энциклопедический словарь
— (нем. Maβstab; от Maβ мера и Stab палка * a. scale; н. Maβstab, Skala; ф. echelle; и. escala) отношение длины линии на чертеже, плане, карте, предметной модели к длине соответствующей линии в натуре. Ha геогр. картах различают главный M.… … Геологическая энциклопедия
— (от нем. Ma?stab) англ. scale; нем. Ma?stab. 1. Отношение линейных размеров объекта, изображенного на чертеже, плане, карте к его размерам в натуре. 2. Размеры, относительная величина ч. л. (напр., масштаб цен). Antinazi. Энциклопедия социологии … Энциклопедия социологии
2. Размеры, относительная величина ч. л. (напр., масштаб цен). Antinazi. Энциклопедия социологии … Энциклопедия социологии
Инструкция
Внимательно рассмотрите карту и найдите километровую сетку, которая должна быть на ней проставлена. Стороны квадратов сетки соответствуют определенному количеству , узнать это количество вы можете по подписям на выходах линии стеки у края рамки карты. К примеру, расстояние между двумя соседними линиями сетки равно 1 км. Измерьте это расстояние линейкой. Допустим, вы получили 2 см. Таким образом, масштаб карты: в 1 см 500 м или 1:50000.
Второй способ определения масштаб а – по номенклатуре карты. Внимательно рассмотрите реквизиты карты. Номенклатура представляет собой буквенно-числовое листа карты. Любой масштаб ный ряд имеет свое конкретное , по которому специалист легко определит масштаб карты. Например, номенклатурное обозначение М-35 масштаб 1:1000000; М-35-XI обозначает масштаб 1:200000; М-35-18-А-6-1 – масштаб 1:10000 и т. д. Разумеется, для определения масштаб а таким способом необходимо иметь представление о номенклатурных обозначениях и определенный опыт обращения с топографическими картами.
д. Разумеется, для определения масштаб а таким способом необходимо иметь представление о номенклатурных обозначениях и определенный опыт обращения с топографическими картами.
Третий способ определения масштаб а карты – по известным расстояниям. Найдите изображения километровых столбов на шоссейных дорогах. Измерьте по расстояние от одного столба до другого. Вы сразу узнаете масштаб карты (число сантиметров карты будет соответствовать одному километру местности).
На картах масштаб а 1:200000 на дорогах обозначены расстояния между населенными пунктами в . В таком случае измерьте по карте при помощи линейки расстояние в сантиметрах от одного населенного пункта до другого, а подписанное количество километров разделите на расстояние, выраженное в сантиметрах. Таким образом, вы получили величину масштаб а карты, то есть число километров в .
Если вы находитесь на местности, которая изображена на карте, определите ее масштаб по измеренным расстояниям. Для этого измерьте расстояние между нанесенными на карту объектами.
Для этого измерьте расстояние между нанесенными на карту объектами.
Используйте также знание длины дуги меридиана. Одна минута по равна примерно 2 км, а более точно – 1,85 км. На боковой стороне рамки карты даны подписи градусов и минут, каждая минута шашечкой. Если, допустим, длина одной минуты равна 3,7 см, то масштаб карты будет 1:50000 (один сантиметр на карте равен 0,5 км на местности).
Источники:
- Как определить масштаб
- Точность масштаба Длины линий на местности, соответствующие
Изображение крупных обьектов можно получить на бумажном или любом другом носителе только в уменьшенном виде. Это, в первую очередь, касается различных карт местности. Масштабом карты называется отношение длины линии, нанесенной между двумя точками на плане или карте к тому же расстоянию на местности. Знать масштаб необходимо для того, чтобы измерять расстояния по карте.
Инструкция
Обычно, любой карты или указан в ее легенде – сопровождающем пояснительном тексте. Масштаб может быть изображен в виде шкалы или текста, в котором указывается, сколько метров или километров на местности равен 1 см расстояния, отложенного по данной . Масштаб 1: 50000 , что 1 см, отложенный на данной карте, равен 500 метрам или 0,5 км в натуре. Чем крупнее масштаб, тем меньшее число указывается в его числителе. Топографические карты масштаба 1:10000 и крупнее относятся к сведениям, гриф «секретно».
Масштаб может быть изображен в виде шкалы или текста, в котором указывается, сколько метров или километров на местности равен 1 см расстояния, отложенного по данной . Масштаб 1: 50000 , что 1 см, отложенный на данной карте, равен 500 метрам или 0,5 км в натуре. Чем крупнее масштаб, тем меньшее число указывается в его числителе. Топографические карты масштаба 1:10000 и крупнее относятся к сведениям, гриф «секретно».
Если по какой-то причине масштаб карты не указан, отсутствует зарамочное или легенда, то определить его можно с помощью геоинформационных картографических серверов GoogleEarth или YandexMap, включив их в режиме «Гибрид», который позволяет одновременно со спутниковой фотографической основой видеть оцифрованное изображение местности – , границы городов, отдельно стоящие здания.
Определите географическое положение изображенной на ней местности. Выберите на ней две характерные точки, которые можно будет легко идентифицировать по спутниковому снимку данной местности. Обычно, удобно использовать для этого перекрестки магистралей или усовершенствованных шоссе, автодорог.
Обычно, удобно использовать для этого перекрестки магистралей или усовершенствованных шоссе, автодорог.
Найдите эти две точки по спутниковому снимку местности. Инструментом «Линейка» измерьте расстояние между ними. При активации инструмента появляется табличка, где автоматически будет высвечиваться расстояние между двумя указанными вами точками на космическом спутниковом снимке. Задайте удобные для вас единицы измерения – метры, километры.
Разделите полученное по спутниковым снимкам расстояние на количество сантиметров, измеренных по карте. Вы получите значение масштаба данной карты .
Видео по теме
Масштаб показывает, во сколько раз карта уменьшает реальную местность, которая на ней изображена. Только зная эту величину, можно откладывать на карте или схеме местности реальные расстояния. Узнать масштаб можно по маркировке на карте. Если таковой не имеется, рассчитайте его по линиям параллелей.
Вам понадобится
- — различные карты;
- — линейка;
- — калькулятор.

Инструкция
Если на плане или нанесена номенклатура листа, то по специальной таблице определите масштаб карты. Например, если на листе карты есть М-35-А, то ее масштаб составляет 1:500000. Это значит, что 1 см , на местности составляет 500000 см или 5 км.
Если маркировки нет, обратите внимание на километровую сетку, которая наносится на любую топографическую карту. Сторона квадрата такой сетки соответствует фиксированному количеству . Измерьте линейкой сторону этого квадрата в см и найдите отношение расстояния на карте к реальному. Это и будет масштаб. Например, если стека на карте 4 км, а расстояние между линиями составляет 2 см, то масштаб будет равен 2:4 км=2:400000 см=1:200000 см.
Если более крупного с параллелями, то определите его с помощью этой сетки. Для этого измерьте расстояние между двумя нанесенными рядом параллелями в сантиметрах. На этих рядом стоящих параллелях от большего числового значения вычтите меньшее. Поскольку один параллели соответствует 111 км, непосредственно на местности, умножьте полученную разницу на это число, а также число 100000 для того, чтобы это расстояние в сантиметры.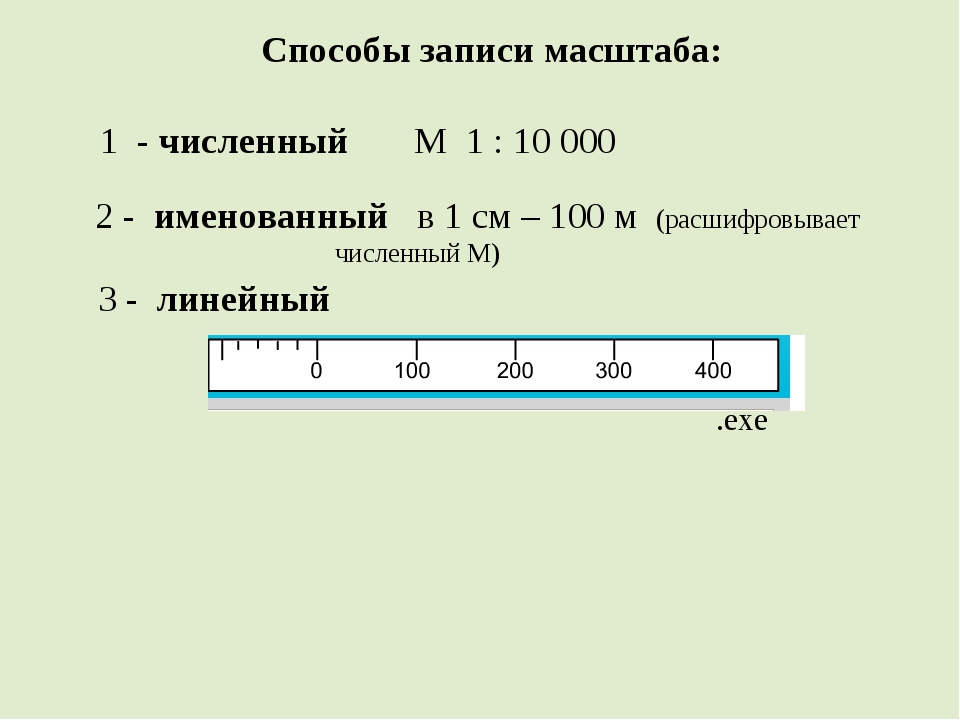
Найдите отношение измеренного линейкой расстояния к результату вычислений. Получите масштаб карты. Например, если параллели идут 0?, 10?, 20? и т.д. найдите разницу двух близлежащих линий. Она составит 10. Затем, умножьте это число на 111 и 100000. Получите 10 111 100000=111000000. Если расстояние измеренное линейкой равно 4,5 см, получите масштаб 4,5:111000000 см?1:25000000 см. Это значит, что одном карты умещается 250 км местности.
Измеряйте масштаб по реальным расстояниям. Для этого известное расстояние отложите на карте, и соотнесите с реальным. Например, если расстояние между двумя составляет 400 км, а на карте оно равно 8 см, найдите соотношение 8:400 км=8:40000000=1:5000000. Это и есть масштаб карты.
Топографические планы и карты, составленные на их основе, являются точными изображениями земной поверхности, спроектированными на плоскость. Масштаб – отношение размера любого топографического объекта на карте к его реальному размеру на местности, позволяет производить по ней линейные и площадные измерения.
География — 7
Деятельность
Учитывая масштаб, определите по картам протяженность Каспийского моря с севера на юг.
1: 22000000 1: 10 000000 1: 6000000Обсудим: Почему на картах Каспий имеет разные размеры?
Вспомните. Масштаб — это дробь, которая показывает, во сколько раз уменьшены реальные размеры при изображении их на планах, картах и глобусе.
Некоторые географические объекты занимают большие территории. Поэтому при изображении их на планах и картах приходится уменьшать реальное расстояние между ними. Для этого используют масштаб. Масштаб бывает трех видов: численный, именованный и линейный.
| Численный масштаб | Именованный масштаб | Линейный масштаб |
| 1:100 | 1 см = 1м | |
| 1:1000 | 1см = 10м | |
| 1:100000 | 1см = 1000м или 1см=1км |
|
| 1:1000000 | 1см = 10 км |
Численный масштаб – это дробь, числитель которой единица, а знаменатель
показывает, во сколько раз уменьшены размеры объекта.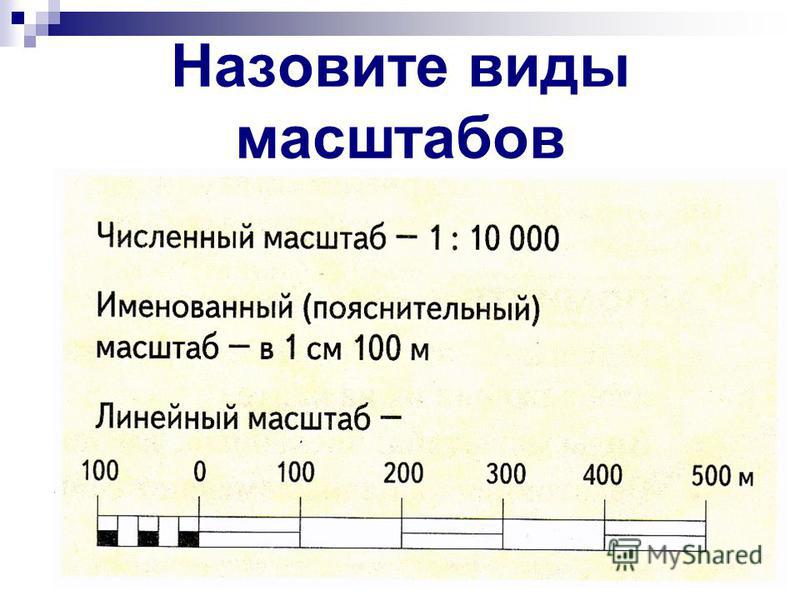 Например,
в численных масштабах 1:500, 1: 5000 размеры уменьшены в 500 и
5000 раз. Чем больше знаменатель масштаба, тем больше уменьшается
реальный размер, т.е. масштаб становится мельче.
Например,
в численных масштабах 1:500, 1: 5000 размеры уменьшены в 500 и
5000 раз. Чем больше знаменатель масштаба, тем больше уменьшается
реальный размер, т.е. масштаб становится мельче.
Численный масштаб можно показать и в виде именованного масштаба. При этом числитель дроби (единица) показывают в сантиметрах, а знаменатель — в метрах или километрах. Например, численный масштаб 1:500 можно записать как в 1 см — 5м; численный масштаб 1:100000 как в 1 см -1 км.
Условные знаки и масштаб карты
1. Условные знаки
УСЛОВНЫЕ ЗНАКИ – ЭТОСВОЕГО РОДА
АЗБУКА КАРТЫ ,БЕЗ КОТОРОЙ НЕЛЬЗЯ ПРОЧИТАТЬ
И ПОНЯТЬ ИЗОБРАЖЕНИЕ МЕСТНОСТИ, КАК БЕЗ
БУКВ НЕЛЬЗЯ ПРОЧИТАТЬ КНИГУ
УСЛОВНЫЕ ЗНАКИ
РИСОВАННЫЕ
ГРАФИЧЕСКИЕ
Шк .
Оз .
Ветрянные мельницы
река
река Енисей
Смешанный лес
Колодец
К.
карьер
Домик лесника
Лесн.

Карточки усл.зн.
Начертите в тетради
класс в натуральную
величину:
ширина класса- 6м
длина класса-8м
Что нужно сделать,
чтобы выполнить
задание?
Нужно уменьшить размер
класса так, чтобы поместить
его на листе бумаги.
Какую тему нужно изучить,
чтобы ответить на этот
вопрос?
15. Масштаб
16. Что вы знаете о масштабе?
17. нам предстоит узнать на уроке о масштабе:
1. Что такое масштаб?2. Выяснить что показывает масштаб?
3. Узнать какие виды записи масштаба
бывают на карте
4. Познакомиться с правилами перевода
численного в именованный масштаб
5. Научимся измерять расстояния с
помощью масштаба.
18. Работа с учебником
Чтотакое масштаб?
Стр. 33 (или 37- если учебник издания
2020)
Что
показывает масштаб?
Определение в рамке: стр. 33
(или 37- если учебник издания
2020)
Масштаб
показывает во сколько раз длина
линии на карте уменьшена в
сравнении с ее
длиной на местности
Существуют три вида
масштаба
Численный
именованный
1: 20 000 000
В 1 см 300 км
линейный
Дайте определение каждому
виду масштаба
Что показывает численный масштаб?
22.
 Численный масштаб вспомним математику: В 1 м- 100 см в 1 км – 1000 м • 1: 500000
Численный масштаб вспомним математику: В 1 м- 100 см в 1 км – 1000 м • 1: 500000• В численном масштабе 1 – это
1 сантиметр
• 500000- это тоже сантиметры
• Сантиметры мы можем переводить в метры и
километры
• 500000см-это 5000 м т.к., а 5000 м-можем перевести
в км- получаем 5 км
• Это значит 500000см- это 5 км
• ПОЛУЧАЕТСЯ 1: 500000 мы можем записать иначе
в 1 см- 5000м или в 1 см- 5 км
Именованный масштаб показывает
соответствие 1 см на карте расстоянию
на местности
• 1: 500000 мы перевели в численный
масштаб
в 1 см- 5000м
в 1 см- 5 км
•К каждой цифре подписали
имя- см., м., км., поэтому
назвали именованный
24. 1: 10000000
Перевод численного масштаба вименованный
1: 10000000
м
в 1 см — 100 000 м
25. 1: 10000000
Перевод численного масштаба вименованный
1: 10000000
км
в 1 см – 100 км
Перевод численного масштаба в
именованный
При переводе численного
масштаба в именованный
в метры — убираем два нуля,
в километры — пять нулей
27.
 Перевести численный масштаб в именованный 1: 3 000 000
Перевести численный масштаб в именованный 1: 3 000 000• в 1 см – 30 км
1: 40 000
• в 1 см – 400 м
1: 2 000
• в 1 см – 20 м
Проверка
Переведите именованный
масштаб в численный
в 1 см – 5м
в 1см — 600м
в 1см -250км
1: 500
1: 60 000
1:25 000 000
Линейный масштаб
10 м
0
10
В 1 см – 10 м
1 : 1000
20
30
40
50
Именованный масштаб
Численный масштаб
60 м
30. Какой масштаб более крупный? Почему?
А) 1: 10 000Б) 1: 3 000
31. Помни
1.Чем крупнее масштаб,тем подробнее
изображена местность
2. Чем больше делитель в
численном масштабе,
тем меньше изображение
32. Пример решения задания
• Если нам надо изобразить в тетрадирасстояние от дома до школы в
900метров, в масштабе
в 1 см-100м, то мы нарисуем дом,
а через 9 см нарисуем школу, т. к.
900 метров на листе бумаги это 9 см.
33.
 Выполним перевод масштабов •1:1500
Выполним перевод масштабов •1:1500•1:10 000
•1:250 000
•В 1см 15 м
•В 1см 100м
•В 1см 2500м
В 1см 4 км или
1:400 000
34. Практическая работа
1) Переведите численный масштаб вименованный
А)1:10 000
Б)1:250 000
В)1:1000 000
2 ) Переведите именованный
масштаб в численный
А) в 1 см -2 м
Б) в 1 см -400 м
В) в 1 см – 2 км
35. 3) Расположите масштабы от более крупных к более мелким. А) В 1 см 30 км Б) 1: 80 000 В) 1: 25 000
3) Расположите масштабыот более крупных к более
мелким.
А) В 1 см 30 км
Б) 1: 80 000
В) 1: 25 000
36. 4) Изобразите в тетради хвойное дерево к западу от родника не расстоянии 600 метров в масштабе в 1 см 100 метров А лиственное
дерево на расстоянии 400метров от родника в направлении на юг
37. Домашнее задание:
1) Прочитать §9, только страница 33У кого учебник новый, 2020 года, у
тех §10, только страница 37
Выполнить в тетради практическую
работу из этой презентации 1, 2, 3 ,4
задания
Сфотографируйте работу и отправьте учителю до 16
декабря на проверку
Географическая карта и ее масштаб.
 6-й класс
6-й класс
Цель:
- Дать определения понятиям: «Карта», «Масштаб», «Чертёж».
- Назвать виды масштаба и виды географических карт по масштабу.
- Определить расстояние между предметами по плану карты.
- Перевести численный масштаб в именованный и наоборот
Оборудование. Географические атласы, настенные географические карты, чертёжные принадлежности, раздаточный материал (карточки-задания).
Форма урока: комбинированный.
Ход урока
Организационный момент.
Здравствуйте, ребята!
Попробуйте отгадать загадку: «Земля есть - копать нельзя! Дороги есть — ехать нельзя! Реки есть — плыть нельзя!». Как Вы думаете, о чём пойдёт речь? (о географической карте). Правильно.
Сегодня мы узнаем как работать с картами, зачем
нужен масштаб и какова его роль при составлении
карты. Но, сначала, давайте вспомним, что мы
изучали на предыдущем уроке и двинемся дальше в
неизведанный мир географических карт.
Но, сначала, давайте вспомним, что мы
изучали на предыдущем уроке и двинемся дальше в
неизведанный мир географических карт.
Проверка раннее изученного материала.
Перед Вами карточки, каждая с тремя заданиями. Вы выполняете задания, затем меняетесь карточками. С моей помощью мы проверим выполненные задания, посчитаем количество правильных и неправильных ответов, оценим их. Каждый из Вас увидит свои ошибки.
Карточки-задания:
1-я. Установите соответствие между датой и положением Солнца:
1.21 марта
2. 22 июня
3. 23 сентября
4. 22 декабря
А. Солнце в зените над Северным тропиком
Б. Солнце в зените над Южным тропиком
В. Солнце в зените над Экватором
Ответ: ____________________________
2-я. Установите соответствие между условными линиями на карте и значениями географической широты:
Северный тропик
Северный полярный круг
Южный тропик
Южный полярный круг
А. 66,5 ю.ш.
66,5 ю.ш.
Б. 23,5 с.ш.
В. 23,5 ю.ш.
Г. 66,5 с.ш.
Ответ:____________________________
3-я. О каком поясе освещённости говорится в описании: Данный пояс освещённости в течении всего года получает большее количество солнечного тепла и света. На параллелях, ограничивающих пояс, Солнце бывает в зените по одному разу в год, а между данными параллелями - по два.
Ответ: ____________________________
Работа парами: проверка задания, выставление оценок.
Изучение нового материала.
Подготовка к основному этапу.
Ребята, сейчас я попрошу три человека подойти к
доске и нарисовать маршрут от школы до станции. А
один человек расскажет как найти дорогу от школы
до станции (рисунки выполняются, одновременно,
звучит рассказ о заданном маршруте). Что же
проще, идти по нарисованному маршруту или по
рассказанному? Почему? (ответы учащихся). Посмотрите внимательно на доску, что Вы видите? (рисунки
у всех разные). Правильно, у всех получились
рисунки разными. Первые карты тоже были похожи на
рисунки. Ваши рисунки будут понятны только тем,
кому Вы их будете рисовать, одновременно,
рассказывая дорогу. Так?
Посмотрите внимательно на доску, что Вы видите? (рисунки
у всех разные). Правильно, у всех получились
рисунки разными. Первые карты тоже были похожи на
рисунки. Ваши рисунки будут понятны только тем,
кому Вы их будете рисовать, одновременно,
рассказывая дорогу. Так?
Работа с рис. 18.
Значит, карта — это не рисунок. Географическая
карта — это чертёж местности. А чем чертёж
отличается от рисунка? (варианты ответов
учащихся). Тем, что он выполняется с
соблюдением определённых, причём, очень строгих,
правил. Если три человека нарисуют одну и ту же
местность, то у каждого получиться свой рисунок,
непохожий на другие. Так? Если же они делают
чертёж одной и той же местности с соблюдением
всех правил, то он у всех получиться одинаковым.
А, значит, он одинаково понятен всем кто на него
смотрит. Однако, есть сложность. Для того, что бы
понять, что изображено на чертеже, нужно уметь
его читать, т. е. знать правила по которым он
выполнен.
е. знать правила по которым он
выполнен.
Давайте запомним: итак, географическая карта — это чертёж местности, выполненный в системе географических координат с помощью масштаба и условных знаков. Про географические координаты мы уже говорили, займёмся теперь масштабом.
Посмотрите на наши рисунки, кто может сказать, каково расстояние от школы до станции? (попытки учащихся дать правильный ответ). Правильно, никто. Чего-то не хватает? Может быть, масштаба, с помощью которого мы смогли бы сделать чертёж.
Усвоение новых знаний и способов действий.
Слово «масштаб» немецкое и означает нечто странное — «мерная палочка». Что же такое «мерная палочка», и какова её роль при составлении карты?
Постановка проблемы:
Давайте подумаем! Зачем потребовалось вводить масштаб?
Карта — это не просто чертёж, это уменьшенный
чертёж. Поэтому, при вычерчивании карты,
расстояния уменьшаются. Но уменьшаются не «на
глазок», а в определённое количество раз.
Поэтому, при вычерчивании карты,
расстояния уменьшаются. Но уменьшаются не «на
глазок», а в определённое количество раз.
Давайте запомним: масштаб показывает, во сколько раз длина линии на карте уменьшена относительно длины линии на местности.
Демонстрация настенных карт и атласов.
На карте, где-нибудь, в уголке обязательно указан масштаб. Без него мы не разберёмся с расстояниями на карте. Причём, существуют несколько способов записи масштаба. На данных картах Вы видите большие цифры:
1: 25000000
1: 10000000
1: 10000
1: 20000
Это численный масштаб.
Он указывает во сколько раз изображение уменьшено.
Решение задач. Например, если на карте
обозначен масштаб 1: 10000, это означает, что
изображение уменьшено в 10000 раз. Значит длина
линии на карте в 1 см. соответствует длине линии
на местности в 10000 см. А что такое 10000 см.?
Правильно, это 100 метров. А значит в нашей карте 1
см. соответствует 100 м. на местности. Или мы
говорим в 1 см. — 100 метров. Это второй способ
записи масштаба, называется он именованным.
Он расшифровывает численный масштаб, переводя
сантиметры в метры или километры.
А что такое 10000 см.?
Правильно, это 100 метров. А значит в нашей карте 1
см. соответствует 100 м. на местности. Или мы
говорим в 1 см. — 100 метров. Это второй способ
записи масштаба, называется он именованным.
Он расшифровывает численный масштаб, переводя
сантиметры в метры или километры.
Практическая работа.
Давайте переведём численные масштабы других карт в именованные:
1: 25000000 — это 1 см.: 250 км.
1: 10000000 — это 1 см.: 100 км.
1: 20000 — это 1 см.: 200 м.
Работа с учебником.
Третий вид масштаба — линейный. На карте (рис. 19)
изображена короткая линейка с сантиметровыми
делениями, где указывается, какому расстоянию на
местности соответствует один сантиметр в
масштабе этой карты. Линейный масштаб позволяет
производить определений расстояний на карте без
вычислений. Мы, просто, прикладываем иголки
измерителя к интересующему нас отрезку на карте,
а потом к линейке масштаба. И всё, мы сразу узнаём
расстояние.
И всё, мы сразу узнаём
расстояние.
Практическая работа.
Давайте попробуем: с помощью топографического плана местности, на форзаце в начале учебника, определим расстояние между колодцем и отметкой высоты 151,8. Прикладываем измеритель на карту, а, затем, переносим его на линеечку линейного масштаба, получаем 250 метров.
Давайте запомним.
Итак, существует три способа записи масштаба: численный, именованный и линейный. Хотя бы один из них, обязательно, указывается на карте.
Первичная проверка понимания.
Мы с Вами выяснили, масштаб карты может быть
разным. Мы можем уменьшить реальные размеры
территории, в какое угодно число раз. Чем сильнее
мы уменьшим расстояние на местности, тем мельче
изображение на карте, тем меньше масштаб. Какой
масштаб мельче: 1: 1000 или 1: 1000000? Мельче -
миллионный. Почему? (ответы учащихся).
Правильно, ведь масштаб показывает во сколько
раз уменьшено изображение. Понятно, что
изображение, уменьшенное в 1000000 раз мельче, чем
уменьшенное в 1000 раз. Выбор масштаба зависит от
размеров участка земли, который мы хотим
изобразить на карте. Чем больше территория,
изображаемая на карте, тем мельче должен быть
масштаб. А то, может, получиться неловко.
Почему? (ответы учащихся).
Правильно, ведь масштаб показывает во сколько
раз уменьшено изображение. Понятно, что
изображение, уменьшенное в 1000000 раз мельче, чем
уменьшенное в 1000 раз. Выбор масштаба зависит от
размеров участка земли, который мы хотим
изобразить на карте. Чем больше территория,
изображаемая на карте, тем мельче должен быть
масштаб. А то, может, получиться неловко.
Практическая работа.
Давайте попробуем подобрать масштаб. Расстояние между точками на местности составляет 6 км, а мы выбрали тысячный масштаб — 1: 1000 (в 1 см — 10 м). И что получиться? Сможем мы нарисовать этот отрезок в тетради? Нет, ведь, получается 6 м! Лучше выбрать масштаб помельче. Какой? (1: 100000 (1 см : 1км)) Правильно! Тогда 6 км на местности будет соответствовать 6 см на карте.
Итак, ребята, давайте ответим на наш главный
вопрос: «Зачем потребовалось вводить
масштаб?» (ответы учащихся, как правило,
верные).
Рефлексия. Подведение итогов занятия. Проблема на следующий урок.
На следующем уроке мы подберём масштаб к нашему чертежу, с которого мы начали наш урок, начертим маршрут от школы до станции.
Давайте подведём итог:
В зависимости от местности различают карты:
Крупномасштабные — от 1: 10000 до 1: 200000
Среднемасштабные — от 1: 200000 до 1: 1000000
Мелкомасштабные — мельче 1: 1000000
Самый мелкий масштаб используется для карты мира.
По пространственному масштабу выделяют: карты мира, карты материков и океанов, отдельных стран и их частей.
Проверка знания.
Что означает слово «чертёж»? Чем чертёж отличается от рисунка?
Что такое «масштаб»? Какие существуют формы записи масштаба?
Что такое географическая карта? Чем отличается мелкомасштабная карта от крупномасштабной?
А теперь посложнее:
Какой масштаб мельче: 1: 10000 или в 1 см — 1 км?
Какую длину имеет экватор на карте масштаба 1: 100000000?
Давайте сделаем.
Масштаб карты 1: 30000000. Переведите этот численный масштаб в именованный.
Определите масштаб карты, если длина линии на местности составляет 5 км, а длина линии на карте 0,5 см?
Информация о домашнем задании.
Домашнее задание: параграф № 5.
Откройте рабочие тетради стр. 15 задание № 2. Перед вами карта, на ней точка и 7 направлений в разные стороны на географические объекты. Определить расстояние от данной точки до географических объектов, но прежде чем это сделать, нужно перевести численный масштаб в именованный.
Урок окончен. До свидания.
Масштаб и его применение | Обучонок
В представленной исследовательской работе по математике на тему «Масштаб и его применение» я постараюсь выяснить при каком масштабе будет удобно располагать объекты на листе А4. Работа над исследовательским проектом о масштабе поможет закрепить мне полученные знания по математике.
В моем исследовательском проекте по математике «Масштаб и его применение» мне необходимо будет уточнить и сопоставить математические расчёты с полученными данными.
В ходе исследовательской работы по математике о масштабе и его применении я надеюсь, что масштабы которые я задам, позволят расположить мне объекты на альбомном листе А4.
Также, в практической части своей работы я рассмотрю и математически решу интересные задачи на расстояние и масштаб.
Оглавление
Введение
Основная часть
1. Определение масштаба.
2. Решение интересных задач на масштаб.
Выводы
Приложения.
Введение
На уроках математики в 6 классе мы проходили эту интересную тему, из которой узнали, как, используя масштаб, можно найти расстояние на местности, зная длину отрезка на карте, соответствующего этому расстоянию на местности, и наоборот.
Рисуя на бумаге изображение предметов, мы чаще всего вынуждены изменять их настоящие размеры: большие предметы приходится изображать в уменьшенном виде, а маленькие – увеличивать.

Участки земной поверхности изображают на бумаге в уменьшенном виде. Примером такого изображения служит любая карта, план. А маленькие детали изображают на чертежах в увеличенном виде.
Но чертеж, карта или план должны давать представление о настоящих размерах предметов. Поэтому на чертежах и картах делают специальную запись, показывающую отношение длины отрезка на карте или чертеже к его настоящей длине.
Тема моего исследовательского проекта по математике «Масштаб и его применение».
Цель проекта: выяснить при каком масштабе будет удобно располагать объекты на листе А4.
Задачи проекта:
- закрепить школьные знания по математике;
- уточнить, сопоставимы ли математические расчёты с полученными данными.
Гипотеза: выкройки наиболее эффективно чертить 1:10, планировку квартиры 1:100; паспорт дома 1:1000; карту города 1:10000; карту района 1:100000.
Ожидаемый результат: заданные мною масштабы, позволят расположить объекты на альбомном листе.
Оборудование:
При математических расчётах: линейка, карандаш, циркуль, калькулятор, карта.
На практике: лист А 4, линейка, карандаш.
Определение масштаба
Масштаб – это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на местности.
Например: 1:1000 (одна тысячная) значит, все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Масштаб бывает:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м – это величина масштаба;
- линейный, зная величину масштаба, мы можем определить расстояния.

Посмотрим на карту. Вверху указан масштаб (1 : 500 000). Говорят, что карта сделана в масштабе одна пятисоттысячная. Это значит, что 1 см на карте соответствует 500 000 см на местности. Значит, отрезок на карте в 1 см соответствует отрезку на местности в 5 км.
А если я возьму на карте отрезок длиной в 3 см, то на местности это будет отрезок длиной в 15 км.
Я скачал с интернета карту Кабардино-Балкарской Республики. Карта республики с масштабом 1:10000, то есть в 1 см 100 метров, а масштаб окрестностей 1:100000 в 1 см 1 километр. Я сразу нашёл по ней мое родное село.
Итак, масштаб (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем, отношение двух линейных размеров.
Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
Понятие масштаба наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения.
Человек не в состоянии изобразить большие объекты, например дом, в натуральную величину, и поэтому при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее раз. Число показывающее, во сколько раз уменьшен изображенный объект, есть масштаб.
Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз.
Число, показывающее во сколько раз, произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе.
Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Выводы
Сравнил свои предположения, выдвинутые в моей гипотезе с надписями на выкройках, картах и технических планах дома и квартиры. Оказалось, что кое-где я ошибся в 10 и даже в 100 раз.
Оказалось, что кое-где я ошибся в 10 и даже в 100 раз.
Итак, я предположил, что:
- выкройки наиболее эффективно чертить 1:10;
- планировку квартиры 1:100;
- паспорт дома 1:1000;
- карту города 1:10000;
- карту района 1:100000.
На самом деле, план квартиры обычно берут в масштабе 1:200; масштабы карт оказались точно такими же, как и в оригинале, но располагаются они аж на 6 альбомных листах!
Так что в который раз, я убеждаюсь, что прежде чем предполагать, нужно несколько раз пересчитать.
Таким образом, мы сформировали понятие масштаба, карты, чертежа, отрабатывали решение задач на вычисление длины отрезка на местности и на карте.
Решение задач на масштаб
Задача 1. Расстояние между двумя городами равно 400 км. Найдите длину отрезка, соединяющего эти города на карте, выполненной в масштабе 1:5000000.
Решение:
400км = 400000м = 40000000см
40000000 : 5000000 = 40 : 5 = 8 (см)
Задача 2. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км от центра до центра. По автотрассе протяженность маршрута 700 км.
Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км от центра до центра. По автотрассе протяженность маршрута 700 км.
Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить на слайде в виде отрезка длиной в 14 см?
Решение:
700км = 700000м = 70000000см
70000000см : 14см = 5000000(раз)
Задача 3. По физической карте России определите реальное расстояние между Москвой и Санкт-Петербургом.
М1 : 20000000, если на карте расстояние равно 3 см.
Решение:
| на карте | на местности |
|---|---|
| 1см | 20000000см = 200км |
| 3см | Х км |
Х = 3 ∙ 200 = 600 (км)
Задача 4. На карте с масштабом 1/50000 расстояние равно 5 см. Найдите расстояние на местности.
Решение:
5 см ∙ 50000 = 250000 см = 2500 м = 2,5 км
Алгоритм нахождения расстояния на местности
Если масштаб задан дробью с числителем 1, то: |
Задача 5. На карте с масштабом 1 : 150000 расстояние между деревней и станцией равно 2,8 см. Найти расстояние между ними на местности.
Решение:
2,8 см ∙ 150000 = 420000 см = 4200 м = 4,2 км.
Выводы
Цель моей исследовательской работы по математике «Масштаб и его применение» достигнута, так как в ходе проекта я выяснил масштаб, в котором будет удобно располагать объекты на листе А4.
Также, в процессе исследовательского проекта по математике о применении масштаба я закрепил знания, полученные на уроках математики, а также подтвердил свою гипотезу. Все-таки выкройки наиболее эффективно чертить в масштабе 1:10, планировку квартиры 1:100; паспорт дома 1:1000; карту города 1:10000, а карту района в масштабе 1:100000.
В итоге работы я получил, что заданные мною масштабы позволяют расположить объекты на альбомном листе.
Если страница Вам понравилась, поделитесь в социальных сетях:
2.
 1 Что такое масштаб? | GEOG 160: Отображение нашего меняющегося мира
1 Что такое масштаб? | GEOG 160: Отображение нашего меняющегося мираСлово « в масштабе » часто встречается, когда вы работаете с людьми, которые производят или используют географическую информацию. Если вы внимательно прислушаетесь, то заметите, что этот термин имеет несколько разных значений в зависимости от контекста, в котором он используется. Вы услышите разговоры о масштабах географических явлений и о масштабах, в которых явления представлены на картах. Вы даже можете слышать это слово как глагол, например, «масштабирование карты» или «уменьшение масштаба».»Цель этого раздела — научить вас различать эти разные значения и научиться использовать концепции масштаба, чтобы помочь разобраться в географических данных.
2.1.1 Объем или объем
Часто «масштаб» используется как синоним «объема» или «размаха». Например, в названии статьи «Подрядчики обвиняются в крупномасштабном хищении продовольственной помощи в Сомали» используется термин «крупномасштабный» для описания широко распространенной кражи продовольственной помощи. Это обычное использование среди публики. Термин «масштаб» может иметь и другие значения.
Это обычное использование среди публики. Термин «масштаб» может иметь и другие значения.
2.1.2 Измерение
Слово «шкала» также может использоваться как синоним линейки — измерительной шкалы. Поскольку данные состоят из символов, которые представляют измерения явлений, важно прежде всего понимать системы отсчета, используемые для проведения измерений. В этом разделе мы рассмотрим шкалу измерений, известную как географическая система координат , которая используется для определения положений на приблизительно сферической поверхности Земли. В других разделах мы встретимся с двумерными (плоскими) системами координат, а также со шкалами измерений, используемыми для задания данных атрибутов.
2.1.3 Масштаб карты
Масштаб карты — это пропорция между расстоянием на карте и соответствующим расстоянием на земле (Dm / Dg). По соглашению пропорция выражается как репрезентативная дробь , в которой расстояние на карте (Dm) всегда уменьшается до 1. Репрезентативная дробь 1: 100 000, например, означает, что участок дороги длиной 1 единицу на карта обозначает участок дороги длиной 100 000 единиц. Репрезентативная дробь — без единиц , она имеет то же значение, если мы измеряем на карте дюймы, сантиметры или любые другие единицы (в этом примере часть мира, представленная на карте, в 100000 раз больше как представление карты).Если бы мы изменили масштаб карты так, чтобы длина участка дороги на карте была уменьшена, скажем, до 0,1 единицы длины, мы бы создали карту меньшего масштаба с репрезентативной долей 0,1: 100 000 или 1: 1 000 000.
Репрезентативная дробь 1: 100 000, например, означает, что участок дороги длиной 1 единицу на карта обозначает участок дороги длиной 100 000 единиц. Репрезентативная дробь — без единиц , она имеет то же значение, если мы измеряем на карте дюймы, сантиметры или любые другие единицы (в этом примере часть мира, представленная на карте, в 100000 раз больше как представление карты).Если бы мы изменили масштаб карты так, чтобы длина участка дороги на карте была уменьшена, скажем, до 0,1 единицы длины, мы бы создали карту меньшего масштаба с репрезентативной долей 0,1: 100 000 или 1: 1 000 000.
2.1.4 Графические шкалы
Рисунок 2.1. Барная шкала и переменная шкала.
Другой способ выразить масштаб карты — использовать графический (или «полосатый») масштаб (рисунок 2.1). В отличие от репрезентативных дробей, графических масштабов остается верным, когда карты уменьшаются или увеличиваются, поэтому они особенно полезны на веб-картах, где невозможно предсказать размер, в котором пользователи будут их просматривать.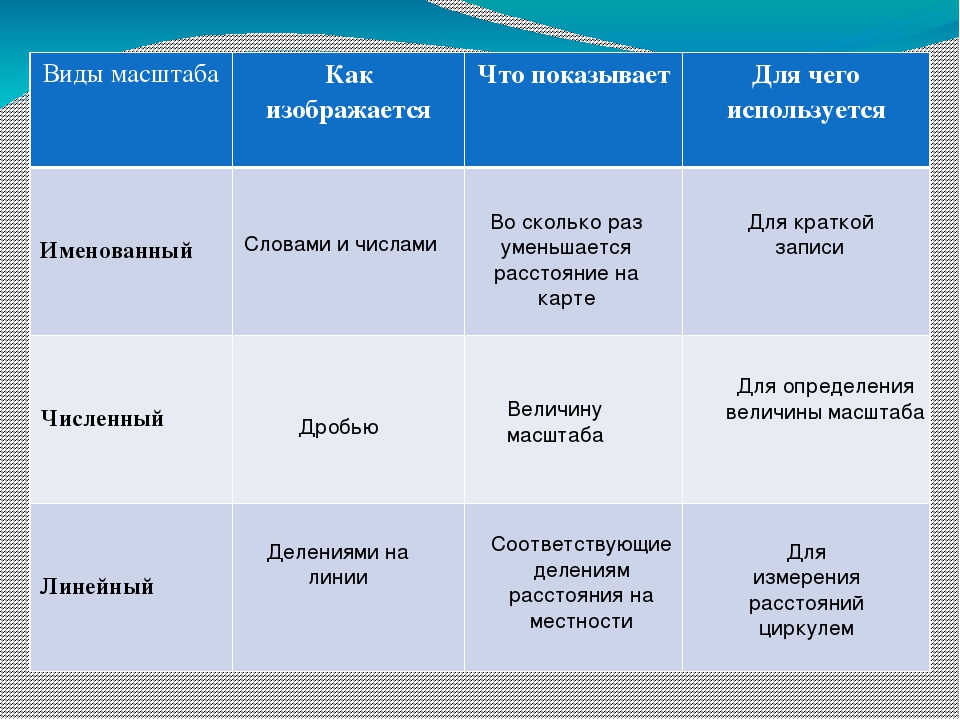 Большинство карт имеют линейную шкалу, подобную показанной выше слева. Некоторые также выражают масштаб карты как репрезентативную дробь. В любом случае подразумевается, что масштаб на всей карте одинаков. Однако, за исключением карт, которые показывают только очень маленькие области, масштаб варьируется на каждой карте. Это следует из того факта, что позиции на Земле, близкой к сферической, должны быть преобразованы в позиции на двумерных листах бумаги. Систематические преобразования мира (или его частей) на плоские карты называются картографическими проекциями .Как мы обсудим более подробно позже в этой главе, все картографические проекции сопровождаются деформацией объектов в некоторых или всех областях карты. Эта деформация приводит к изменению масштаба карты по всей карте. Поэтому типичные фракции обычно указывают масштаб карты вдоль линии, на которой деформация минимальна (номинальный масштаб ). Мы обсудим номинальный масштаб более подробно позже.
Большинство карт имеют линейную шкалу, подобную показанной выше слева. Некоторые также выражают масштаб карты как репрезентативную дробь. В любом случае подразумевается, что масштаб на всей карте одинаков. Однако, за исключением карт, которые показывают только очень маленькие области, масштаб варьируется на каждой карте. Это следует из того факта, что позиции на Земле, близкой к сферической, должны быть преобразованы в позиции на двумерных листах бумаги. Систематические преобразования мира (или его частей) на плоские карты называются картографическими проекциями .Как мы обсудим более подробно позже в этой главе, все картографические проекции сопровождаются деформацией объектов в некоторых или всех областях карты. Эта деформация приводит к изменению масштаба карты по всей карте. Поэтому типичные фракции обычно указывают масштаб карты вдоль линии, на которой деформация минимальна (номинальный масштаб ). Мы обсудим номинальный масштаб более подробно позже. Барные шкалы также обычно обозначают только номинальный или средний масштаб карты. Альтернативой простой линейчатой шкале, учитывающей искажение карты, является переменный масштаб .Переменные масштабы, подобные показанному выше справа, показывают, как масштаб изменяется, в данном случае по широте, из-за деформации, вызванной проекцией карты.
Барные шкалы также обычно обозначают только номинальный или средний масштаб карты. Альтернативой простой линейчатой шкале, учитывающей искажение карты, является переменный масштаб .Переменные масштабы, подобные показанному выше справа, показывают, как масштаб изменяется, в данном случае по широте, из-за деформации, вызванной проекцией карты.
2.1.5 Изменение размера карты
Как отмечалось выше, еще один способ использования термина «масштаб» — глагол. «Масштабировать карту в масштабе » означает воспроизвести ее в другом размере. Например, если вы фотографически уменьшите карту в масштабе 1: 100 000 до 50 процентов от ее исходной ширины и высоты, результатом будет четверть площади оригинала.Очевидно, что масштаб карты уменьшения тоже будет меньше: 1/2 x 1/100 000 = 1/200 000 (или характерный масштаб дробной части 1: 200 000). Из-за неточностей, присущих всем географическим данным, скрупулезные специалисты по географической информации избегают увеличения исходных карт. Поступать так — значит преувеличивать обобщения и ошибки.
Поступать так — значит преувеличивать обобщения и ошибки.
В следующих разделах вы узнаете больше о процессе преобразования трехмерной Земли в двухмерное визуальное представление, карту.По мере продвижения по главе помните о различных значениях термина «масштаб» и думайте о том, как он связан с процессом создания карты.
Практика викторины
Зарегистрированные студенты штата Пенсильвания должны вернуться, чтобы пройти тест для самооценки по карте масштаба .
Вы можете проходить практические викторины сколько угодно раз. Они не оцениваются и никак не влияют на вашу оценку.
Что такое коэффициент масштабирования? — Определение, формула и примеры — Видео и стенограмма урока
Использование масштабного коэффициента
Если две фигуры похожи, вы можете связать разные характеристики фигуры с помощью масштабного коэффициента.В качестве примера представьте себе два одинаковых квадрата. У одного длина стороны 2 дюйма, а у другого — 4 дюйма. Это дает масштабный коэффициент 1: 2 от маленького квадрата к большому квадрату.
Это дает масштабный коэффициент 1: 2 от маленького квадрата к большому квадрату.
Чтобы получить длину стороны одного квадрата с учетом длины стороны другого, вы можете умножить или разделить на коэффициент масштабирования.Давайте посмотрим на квадраты, показанные выше.
Предположим, вам сказали, что меньший квадрат имеет длину стороны 2 дюйма, а масштабный коэффициент от меньшего к большему составляет 1: 2. Помните, это означает, что 1 дюйм на меньшем квадрате равен 2 дюймам на большем квадрате. . Если мы умножим на коэффициент масштабирования 1/2, мы получим меньшее число. Поэтому мы должны «разделить» на коэффициент масштабирования, чтобы получить большее число.
Мы видим, что этот результат соответствует картинке.
Чтобы получить периметр одного квадрата по периметру другого, вы можете умножить или разделить его на масштабный коэффициент. Меньший квадрат имеет периметр 8 дюймов. Мы хотим найти периметр большего квадрата. Нам снова нужно будет разделить на коэффициент масштабирования 1: 2.
У большего квадрата будет периметр 16 дюймов. Имеет ли это смысл? Спросите себя: «Я перехожу от меньшей фигуры к большей или от большей к меньшей?» В этом случае мы перешли от меньшего числа к большему, поэтому мы ожидаем, что наш ответ будет больше, чем исходный периметр.Следовательно, наш ответ имеет смысл!
Чтобы получить площадь одного квадрата по площади другого, вы можете умножить или разделить на квадрат масштабного коэффициента. В нашем примере меньший квадрат имеет площадь 4 квадратных дюйма. Так же, как мы разделили на коэффициент масштабирования, чтобы определить периметр большего квадрата, мы теперь разделим на квадрат коэффициента масштабирования.
Чтобы получить объем одного куба с учетом объема другого, вы можете умножить или разделить на куб масштабный коэффициент.Чтобы решить, следует ли вам умножать или делить, вы должны учитывать значение коэффициента масштабирования и переходить от большего к меньшему значению или от меньшего к большему.
Представьте, что вместо квадратов у нас есть два куба, похожие на большие игральные кости. У меньшего куба длина стороны 2 дюйма, а у другого — 6 дюймов. Объем первого куба составляет 8 кубических дюймов, а масштабный коэффициент от большего куба к меньшему равен 3: 1. Чтобы найти объем большего куба, мы можем умножить на куб масштабный коэффициент (обратите внимание, как наш масштабный коэффициент больше единицы; мы знаем, что хотим получить больший ответ, поэтому мы умножаем, а не делим).
Таким образом, объем второго куба составляет 216 кубических дюймов. Проверяя нашу работу, мы видим, что:
Проверяя нашу работу, мы видим, что:
Мы можем использовать эти примеры определения длины стороны, периметра, площади и объема для любой пары похожих фигур. Это делает знание масштабного коэффициента невероятно полезным.
Пример задач из математического класса
Вы можете показать, что две фигуры похожи, найдя масштабный коэффициент для каждой пары соответствующих сторон.На картинке красная и черная фигуры слева похожи, а цифры справа — нет.
Мы можем записать отношения соответствующих сторон — обратите внимание, что цифры обращены в противоположные стороны, поэтому мы должны быть осторожны, чтобы сопоставить самую короткую сторону с самой короткой стороной, самую длинную сторону с самой длинной стороной и так далее.Начиная с диагональной стороны каждой фигуры, получаем:
| BD: JK | AB: IK | AC: HI | CD: HJ |
|---|---|---|---|
| 2,82: 1,41 | 4: 2 | 2: 1 | 2: 1 |
Все эти отношения равны, поэтому цифры аналогичны.
Во второй паре цифр мы получаем следующие соотношения, переходя от красного к черному:
| BD: JK | AB: IK | AC: HI | CD: HJ |
|---|---|---|---|
| 2.82: 4.47 | 4: 4 | 2: 4 | 2: 2 |
Легко видеть, что эти соотношения не равны. Поэтому цифры не похожи.
Если вам сказали, что две цифры похожи, вы можете использовать масштабный коэффициент, чтобы найти недостающую длину стороны. Например, треугольники на этой картинке похожи. Нам говорят, что масштабный коэффициент от зеленого треугольника к черному равен 1: 2, а длина сторон зеленого треугольника составляет 3, 4 и 5 единиц.Какова длина сторон черного треугольника?
Поскольку коэффициент масштабирования от зеленого к черному равен 1: 2, это означает, что на каждую единицу длины зеленого треугольника приходится 2 единицы длины черного треугольника.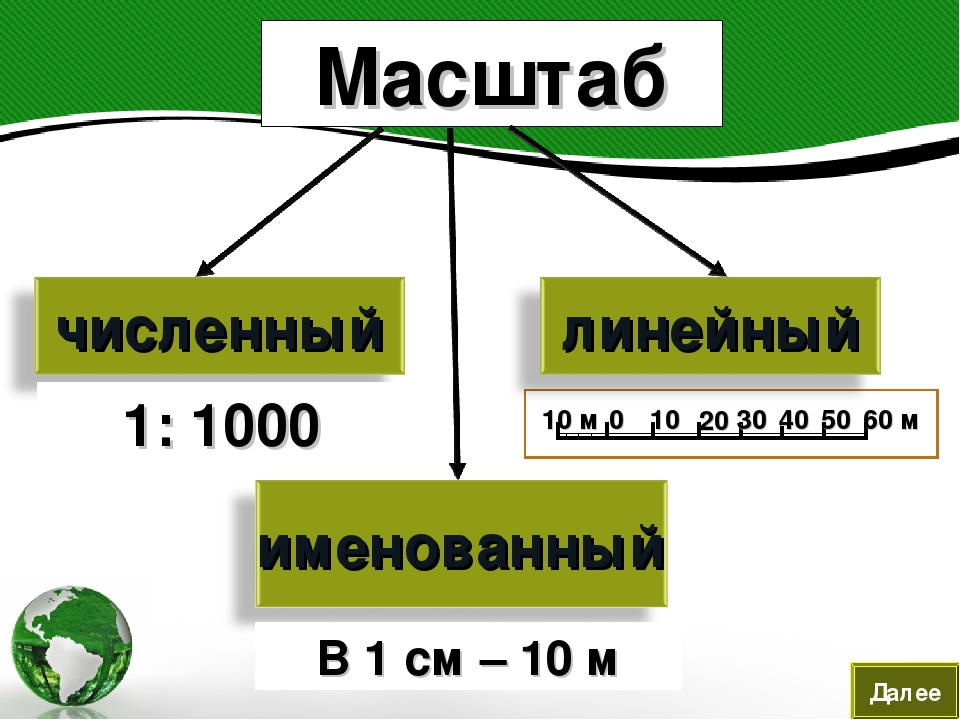 Итак, длины сторон черного треугольника вдвое больше, чем соответствующие стороны зеленого треугольника. Следовательно, черный треугольник имеет длину стороны 6, 8 и 10 единиц.
Итак, длины сторон черного треугольника вдвое больше, чем соответствующие стороны зеленого треугольника. Следовательно, черный треугольник имеет длину стороны 6, 8 и 10 единиц.
Чтение чертежей
Масштабный коэффициент критически важен для чертежей. Если здание или его часть должны быть построены должным образом, необходимо точно следовать плану. Некоторые распространенные масштабы чертежей — 1:20, или 1:50, и 1: 4, или 1: 8. Если чертеж имеет масштаб 1: 4, это означает, что один дюйм на чертеже равен 4 дюймам на готовом. часть. Окно шириной 28 дюймов в готовом здании, следовательно, будет 7 дюймов на чертеже в масштабе 1: 4.
Фигурки моделей
Конструирование моделей — популярное хобби.Модели автомобилей, поездов и фигурок созданы в масштабе, чтобы выглядеть более реалистично. Некоторые общие модели автомобилей масштабируются 1:18, 1:24 и 1:25. Это означает, что размер модели составляет 1/18, 1/24 или 1/25 от фактического размера автомобиля. Когда второе число в масштабном коэффициенте становится больше, размер модели становится меньше по сравнению с реальным объектом. На изображении, представленном здесь, модель автомобиля выполнена в масштабе 1:36. Один дюйм на модели равен 36 дюймам на реальной машине.
На изображении, представленном здесь, модель автомобиля выполнена в масштабе 1:36. Один дюйм на модели равен 36 дюймам на реальной машине.
Краткое содержание урока
Масштабный коэффициент используется во многих приложениях, в которых используются аналогичные фигуры, включая чертежи и модели.Масштабный коэффициент представляет собой сравнение размера одной геометрической фигуры и размера аналогичной геометрической фигуры. Чтобы найти коэффициент масштабирования между двумя похожими фигурами, найдите две соответствующие стороны и запишите соотношение этих двух сторон.
Если вы начнете с меньшего числа, ваш масштабный коэффициент будет меньше единицы. Если вы начнете с большей цифры, ваш масштабный коэффициент будет больше единицы. Отношение площади одной фигуры к площади другой аналогичной фигуры равно квадрату масштабного коэффициента между двумя фигурами. Отношение объема одной фигуры к объему другой подобной фигуры равно кубу масштабного коэффициента между двумя фигурами.
Отношение объема одной фигуры к объему другой подобной фигуры равно кубу масштабного коэффициента между двумя фигурами.
Результаты обучения
Когда вы закончите, вы сможете:
- Объяснить, что такое коэффициент масштабирования
- Найдите коэффициент масштабирования между двумя похожими фигурами
- Перечислите некоторые варианты использования масштабных коэффициентов в реальной жизни
| Определение, формула и как найти
Определение масштабного коэффициента
Масштабный коэффициент в математике — это соотношение между соответствующими измерениями объекта и представлением этого объекта.Если масштабный коэффициент — целое число, копия будет больше. Если коэффициент масштабирования дробный, копия будет меньше.
Коэффициент масштабного коэффициента может быть выражен дробью 12 или двоеточием 1: 2.
Коэффициент измеряет взаимосвязь между двумя вещами. Вы можете создать соотношение студентов-левшей ко всем студентам, но это соотношение будет , а не масштабный коэффициент.
Вы можете создать соотношение студентов-левшей ко всем студентам, но это соотношение будет , а не масштабный коэффициент.
Как найти коэффициент масштабирования
Чтобы найти масштабный коэффициент, вы сначала решаете, в каком направлении вы масштабируете:
| Направление шкалы | Формула |
|---|---|
| Масштаб Вверх (от меньшего к большему) | = размер большей фигуры меньший размер фигуры |
| Масштаб Вниз (от большего к меньшему) | = измерение меньшего числа Объём большего размера |
Коэффициент масштабирования для масштабирования равен коэффициенту , большему 1 .Масштабный коэффициент для при уменьшении составляет коэффициент меньше 1 .
Как только вы узнаете, в каком направлении вы масштабируете, вы сравниваете соответствующие стороны, используя правильное базовое уравнение. Сравните длину стороны реального объекта с длиной соответствующей стороны изображения.
Нахождение масштабного коэффициента аналогичных цифр
Вот два похожих треугольника. Какой масштабный коэффициент используется для создания второй, большей фигуры?
Поскольку мы увеличиваем до , мы делим большее число на меньшее:
3612 = 31 = 3
Масштабный коэффициент равен 3 .Чтобы перейти от ножек 12 см к ножкам 36 см, нам потребовалось умножить 12 см на 3.
А теперь попробуем уменьшить масштаб. Вот два похожих пятиугольника. Какой масштабный коэффициент используется для создания второй, меньшей фигуры?
Поскольку мы уменьшаем масштаб, мы делим соответствующие длины сторон (меньшее число на большее число):
321 = 17
Масштабный коэффициент равен 17 . Чтобы получить вторую, меньшую фигуру, умножаем 21 × 17; на рисунке справа используется масштабный коэффициент 1: 7, 17 или одна седьмая.
Чтобы получить вторую, меньшую фигуру, умножаем 21 × 17; на рисунке справа используется масштабный коэффициент 1: 7, 17 или одна седьмая.
Давайте рассмотрим еще один пример и увеличим и уменьшим масштаб. Рассмотрим эти два похожих прямоугольных треугольника с помеченными сторонами.
Если у нас есть маленький прямоугольный треугольник наверху и мы хотим масштабировать его до большего треугольника, мы напишем это:
, 18537 = 51; масштабный коэффициент равен 5: 1
Таким образом, любая другая линейная мера умножается на 5.
Если у нас есть большой прямоугольный треугольник и мы хотим уменьшить его, чтобы сделать меньший, мы запишем это:
37185 = 15; масштабный коэффициент 1: 5
Итак, любая другая линейная мера умножается на 15; или делится на 5
Масштабный коэффициент по геометрии
Масштаб используется в геометрии для точного воспроизведения фигур; они разных размеров, но не пропорции. Цифры похожи, но в масштабе.
Цифры похожи, но в масштабе.
Масштабный коэффициент используется на аналогичных геометрических фигурах. Вы можете найти масштабный коэффициент соответствующих углов, сторон и даже диагоналей.
Как уменьшить форму с помощью коэффициента масштабирования?
Предположим, вам дали цифру и сказали уменьшить ее на 25% . Думайте поэтапно:
- Вы делаете большую или меньшую дилатацию?
- Вы уменьшаете оригинал, поэтому коэффициент масштабирования будет меньше целого числа.
- Затем измерьте (или прочтите) любую сторону фигуры и произведите вычисления.
Предположим, у нас есть прямоугольник шириной 16 дюймов, и нам нужно уменьшить его на 25%, или на одну четверть (14).
Это означает, что это будет 75% оригинала (100% — 25% = 75%). В качестве масштабного коэффициента мы будем использовать или 3: 4.
Умножьте 16 × масштабный коэффициент (34):
161 × 34 = 484
Теперь мы упрощаем наш ответ:
484 = 121 = 12 дюймов
Ширина нашей новой меньшей формы должна быть 12 дюймов. . Мы повторяем эти шаги с другим размером, 6 дюймов:
. Мы повторяем эти шаги с другим размером, 6 дюймов:
61 × 34 = 184
Упрощать:184 × 4,51 = 4,5 дюйма
Высота нашего меньшего прямоугольника должна быть 4,5 дюйма.
Как сделать масштабную модель
Модель в масштабе — это модель с точностью до коэффициента масштабирования. Если копия реального объекта не масштабирована, она будет выглядеть нереально, как маленькая детская игрушка.
Один объект тоже может иметь разный масштаб. Чем больше разница между двумя числами отношения, тем меньше будет модель.Модель 1:87, как правило, будет намного меньше модели с соотношением 1:12.
Для изготовления масштабных моделей вам нужны точные планы исходного предмета, такие как масштабный чертеж . Чертеж в масштабе — это точный план реального объекта, нарисованный с использованием масштабного коэффициента, чтобы сделать чертеж достаточно маленьким, чтобы его можно было обрабатывать.
Вы умножаете каждый напечатанный размер на масштабном чертеже на масштабный коэффициент, чтобы получить правильные размеры для деталей модели. Если, например, вы хотите построить простой сарай для своей модели железной дороги, вы должны использовать коэффициент 187, чтобы получился сарай длиной 32 фута 4.4 дюйма в длину!
Если, например, вы хотите построить простой сарай для своей модели железной дороги, вы должны использовать коэффициент 187, чтобы получился сарай длиной 32 фута 4.4 дюйма в длину!
Примеры масштабного коэффициента
Попробуйте свои силы в этих вопросах, чтобы увидеть, понимаете ли вы концепцию масштабного коэффициента в математике. Не уклоняйся от этого! Сделайте невероятное усилие!
- Что такое масштабный коэффициент?
- Как найти масштабный коэффициент подобных фигур?
- Какую информацию дает масштабный коэффициент?
- Определите чертеж в масштабе.
Пожалуйста, не заглядывайте вперед, пока не постараетесь найти ответы изо всех сил.
- Масштабный коэффициент определяется как число, умноженное на заданное количество, чтобы получить меньшую или большую версию исходного числа. Это отношение рисунка, карты, модели или чертежа к фактическому объекту или расстоянию.
- Вы вычисляете масштабный коэффициент аналогичных фигур, беря соотношение соответствующих частей двух фигур.
 При увеличении формы большее значение является числителем, а меньшее — знаменателем.При сжатии формы меньшее значение является числителем, а большее значение — знаменателем.
При увеличении формы большее значение является числителем, а меньшее — знаменателем.При сжатии формы меньшее значение является числителем, а большее значение — знаменателем. - Масштабный коэффициент дает отношение изображения к реальному объекту.
- Чертеж в масштабе — это точный рисунок объекта, выполненный с использованием масштабного коэффициента для уменьшения исходных размеров объекта.
Как использовать масштабный коэффициент
Масштабирование объекта помогает визуализировать большие объекты реального мира в небольших помещениях или увеличивать небольшие объекты для лучшего обзора.Коэффициент масштабирования — это то, как мы гарантируем, что представление объекта отличается только по размеру от исходного объекта.
Мы используем масштаб до:
- Нарисуйте аналогичные геометрические фигуры
- Изготовить масштабные модели
- Нарисовать масштабные чертежи архитектуры и машин
В реальной жизни масштабный коэффициент часто используется для того, чтобы представить обширные площади земли на небольших листах бумаги, как на карте.
используется, чтобы позволить дизайнерам, архитекторам и машинистам обрабатывать модели объектов, которые были бы слишком большими, чтобы сохранить их, если бы они имели реальный размер.
Теория гамм в музыке
Что такое шкала? Самый простой способ объяснить гаммы — это набор нот, которые по музыкальной причине были сгруппированы вместе. Преимущество знания гамм в музыке состоит в том, что вы умеете ориентироваться среди нот. Это, среди прочего, даст вам основу для импровизации (ноты в определенной гамме всегда хорошо звучат, сыгранные вместе) и для сочинения музыки.
Вам не обязательно читать ноты, чтобы уметь учить гаммы (но всегда полезно знать, как читать ноты).Вам также не нужно знать много аккордов, но если вы уже знаете некоторые аккорды, вам будет намного легче сопоставить гаммы и впоследствии запомнить. А зная гаммы, вы сможете легче разучивать аккорды — аккорды происходят от гамм.
Основы
Шкала часто состоит из семи нот — это случай мажорной и минорной гамм. Шкалы также повторяются на октаву, что означает, что паттерн нот будет одинаковым независимо от того, играете ли вы гамму слева, в середине или справа от клавиатуры.
Шкалы также повторяются на октаву, что означает, что паттерн нот будет одинаковым независимо от того, играете ли вы гамму слева, в середине или справа от клавиатуры.
На полномасштабном фортепиано всего 88 клавиш, но есть только двенадцать различных тонов, которые повторяются от низких до высоких, от базового до высоких .
На иллюстрации выше вы можете увидеть двенадцать тонов, составляющих одну октаву, и эти ноты также образуют хроматическую шкалу. C # иногда пишется Db, D # иногда Eb и так далее. Они называются энгармоническими нотами , и то, как они записываются, зависит от ключа, к которому они принадлежат.Символы после буквы ( случайный знак ) известны как острый предмет и плоский . C # пишется «до-диез», а Db пишется «ре-бемоль». Это, конечно, только теория и не влияет на звук, но, тем не менее, о ней полезно знать.
В качестве первого примера мы можем использовать гамму соль мажор:
Ноты: G — A — B — C — D — E — F # — G.
А теперь посмотрите на мажорную шкалу F:
Ноты: F — G — A — Bb — C — D — E — Ф.
Вы видели две разные шкалы, в которых используются диезы (#) и плоские (b). Правило, определяющее, является ли нота поднятой или опущенной , зависит от интервалов между нотами в гамме. В приведенных выше примерах F # — это повышенная F, а Bb — пониженная B.
В некоторых случаях вы можете наблюдать две диезы или бемоль в сочетании с описанной нотой в партитуре для фортепиано. Они называются дугой и дуплекс и требуют теоретического объяснения.Если взять для примера ключ D #. Этот ключ включает как D #, так и D, но для того, чтобы он работал в партитуре с подписью ключа, он должен быть D # и C ##; в противном случае вас соблазнят сыграть D # вместо D.
Это влияет на то, как записываются ноты в гаммах. Например, основная шкала C # правильно написана: C #, D #, E #, F #, G #, A #, B #. Обратите внимание, что B # пишется вместо C. B # на самом деле не существует, и нота воспроизводится как C. (Есть много новичков, использующих сайт, и упоминания, такие как B #, явно сбивают с толку некоторых, поэтому C иногда пишется вместо B # чтобы избежать путаницы, тогда как формально правильные примечания представлены ниже в обзорах шкал.)
B # на самом деле не существует, и нота воспроизводится как C. (Есть много новичков, использующих сайт, и упоминания, такие как B #, явно сбивают с толку некоторых, поэтому C иногда пишется вместо B # чтобы избежать путаницы, тогда как формально правильные примечания представлены ниже в обзорах шкал.)
См. Все двойные и двойные лезвия, перечисленные в Приложении A.
Замена ключей
Музыкальные произведения написаны в определенной тональности, как, например, «Бранденбургский концерт № 1 фа мажор» И.С. Бах. Было бы возможно перенастроить этот концерт на другую тональность, например, ре мажор. В музыкальном плане он по большей части остался бы таким же, но тембр был бы другим. См. Также «Разница между весами и ключами».
Относительные и параллельные ключи
Определенные мажорные и минорные гаммы связаны одними и теми же нотами.Например, до мажор и ля минор наследуют одни и те же ноты (различаются тем, что начинаются с разных нот и, следовательно, также различаются интервалами). Это отношение называется , относительные ключи , что не то же самое, что параллельные ключи. До мажор и до минор — примеры последнего.
Это отношение называется , относительные ключи , что не то же самое, что параллельные ключи. До мажор и до минор — примеры последнего.
Тональность
Большинство песен начинаются и заканчиваются одним и тем же тоном, который, как правило, является первой нотой, тоникой в гамме. Затем вы играете ноты гаммы, вы можете услышать, что музыка тяготеет к первой ноте, это как будто некоторое напряжение остается, пока вы не вернетесь к первой ноте.Это явление называется тональностью .
Градусы шкалы
Существует также что-то, называемое шкалой градус , которое относится к отношениям каждой конкретной ноты в шкале на общей основе. Например, основная шкала может быть записана как 1, 2, 3, 4, 5, 6, 7, а натуральная минорная может быть записана как 1, 2, b3, 4, 5, b6, b7, относясь к градусам.
Степени шкалы имеют римские цифры, как вы можете видеть ниже:
Тоника (I): первая нота шкалы, на которой основана шкала, иногда называемая корнем.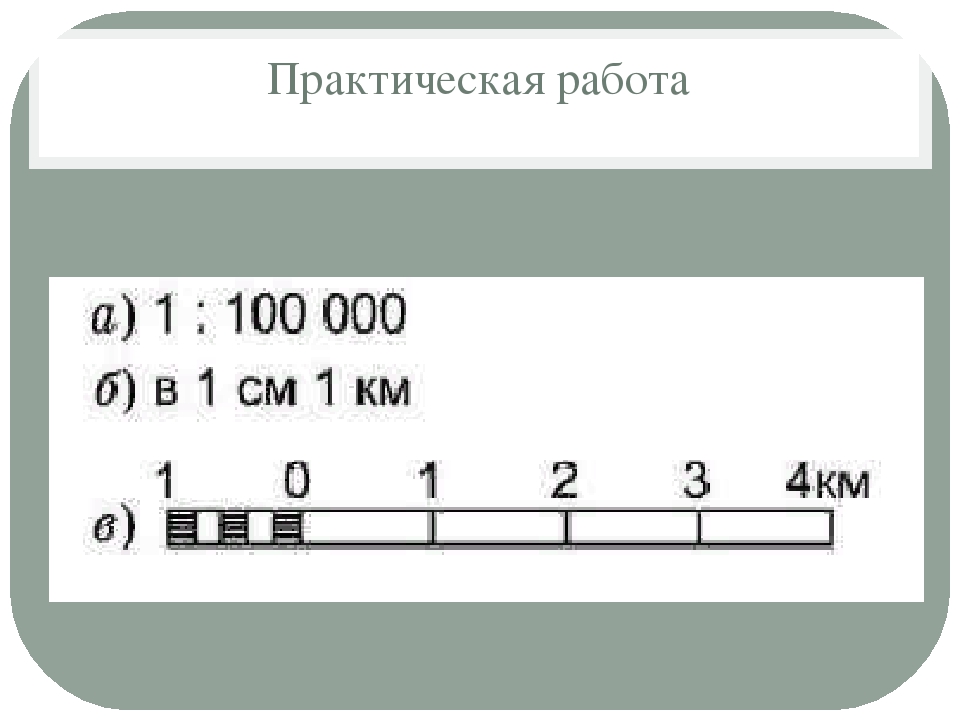
Супертоник (II): вторая ступень шкалы, на одну ступень выше тоника.
Медиант (III): третья ступень шкалы с положением посередине между тоникой и доминантой.
Субдоминанта (IV): четвертая ступень шкалы, пятая ниже тоники и рядом с доминантой.
Доминанта (V): пятая ступень шкалы.
Субмедиант (VI): шестая степень по шкале, иногда называемый супермедиантом .
Subtonic (VII): седьмая ступень шкалы, которая также упоминается как ведущий тон , потому что музыкально «ведет» обратно к тонике.
В то время как семизначные шкалы включают в себя все эти ступени, пяти нотные шкалы не имеют двух из них, что влияет на характер звука.
Зачем вам изучать эти термины? В их знании замечательно то, что вы можете лучше понимать гаммы и аккорды абстрактно. По одной из многих причин это поможет вам транспонировать музыку в другую тональность и даст вам подсказки при сочинении музыки.
Приведу конкретный пример: в блюзе вы часто используете тонику (I), субдоминанту (IV) и доминанту (V) в отношении последовательностей аккордов. Зная это теоретическое соотношение, вы сможете лучше понять, как играть блюз в разных тональностях.
Зная это теоретическое соотношение, вы сможете лучше понять, как играть блюз в разных тональностях.
Интервалы
Интервалы в музыке описывают расстояние между двумя нотами. Наиболее распространенные интервалы: простое (унисон), второе, третье, четвертое, пятое, шестое, седьмое и октавное. См. Эти интервалы, проиллюстрированные ниже:
Интервалы можно разделить на второстепенные, большие, уменьшенные и увеличенные. Их можно использовать для описания структуры масштабной категории.Например, мажорная гамма построена по секундным интервалам: две минорные и пять мажорных секунд.
Вот самые важные интервалы:
См. Также примеры интервалов нот, перечисленные в Приложении B.
Тренировка слуха: слушайте интервалы.
ступеней
Можно описать структуру гаммы с помощью шагов , которые относятся к расстоянию между нотами. Чаще всего используются термины полушаг и полушаг . Между C и C # есть один полушаг, а между C и D — один полный шаг.
В обзорах шкал на этом сайте вы также увидите «полутона» (эквивалент полушага) и «формулы», используемые для описания шкал. В основном это то же самое, только описанное иначе. Для мажорной шкалы это будет выглядеть так: 2 — 2 — 1 — 2 — 2 — 2 — 1 (полутоновые ноты) и Целое, Целое, Половинное, Целое, Целое, Целое, Половинное (формула).
См. Все шаги, перечисленные в Приложении C.
Заказать
Когда представлена гамма, тоны располагаются в порядке от основной ноты, за которой следуют тоны, которые идут по порядку.Это не означает, что гаммы следует играть в определенном порядке. Во время практики — да, во время импровизации — нет.
Так как тоны в гаммах не воспроизводятся одновременно, нет необходимости в инверсии гамм фортепьяно, как это иногда бывает с аккордами.
Продолжить и узнать больше об основных терминах для фортепиано
Приложение A
Все диезы и дупли и ноты, которые они представляют.
C ##: то же, что и D natural.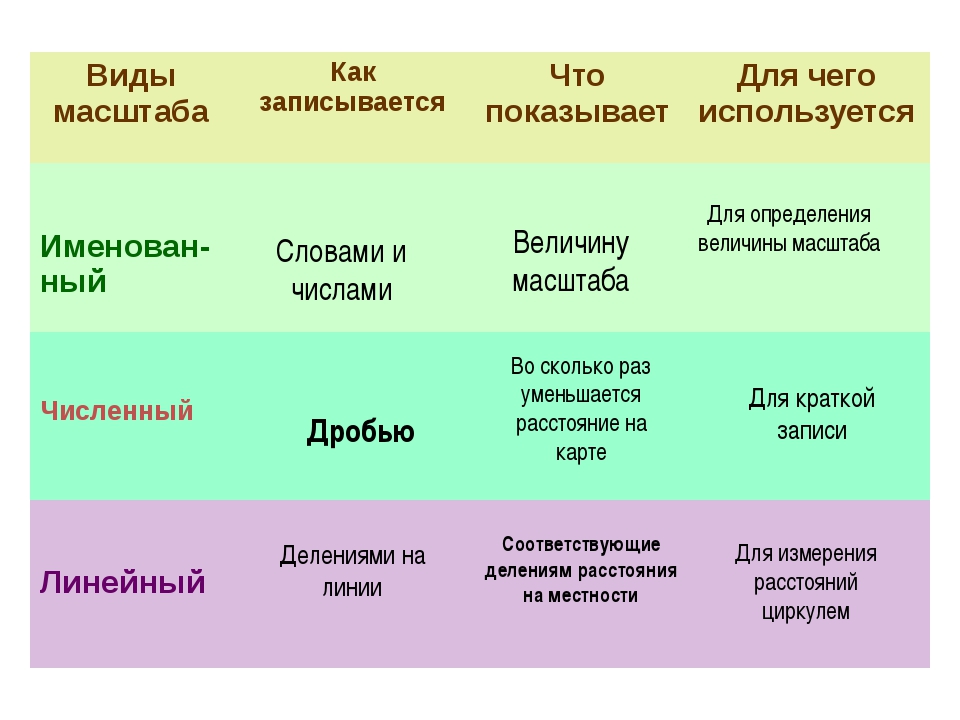
D ##: то же, что и E.
E #: то же, что F.
F ##: то же, что G.
G ##: то же, что A.
A ##: то же, что B.
B #: то же, что C.
Cb: то же, что B .
Dbb: то же, что C.
Ebb: то же, что D.
Fb: то же, что E.
Gbb: то же, что F.
Abb: то же, что G.
Bbb: то же, что A.
Приложение B
Примеры интервалов.
Основная секунда: CD, GA
Дополнительная третья: C-Eb, G-Bb
Основная третья: CE, GB
Идеальная четвертая: CF, GC
Идеальная пятая: CG, GD
Основная шестая: CA, GE
Второстепенная седьмая: C-Bb, GF
Мажорный седьмой: CB, GF #
Приложение C
Все шаги и расстояния в полушагах (полутонах), к которым они относятся.
Половина: один шаг.
Целое: два шага.
Целых полтора: три шага.
Quadra-step: четыре шага.
Что означает масштаб?
Скаленон
блюдо весов; следовательно, сам баланс; прибор или машина для взвешивания; как, чтобы повернуть шкалу; — в основном используется во множественном числе, когда применяется ко всему прибору или устройству для взвешивания. Также используется в переносном смысле
Также используется в переносном смысле
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scalenoun
знак или созвездие Весов
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scaleverb
для взвешивания или измерения по шкале; измерять; также, оценивать или варьировать в соответствии со шкалой или системой
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scalenoun
один из небольших, тонких, перепончатых, костных или роговых кусочков, которые образуют покров многих рыб, рептилий и некоторых млекопитающих, принадлежащих к кожной части скелета или дерматоскелету. См. Циклоид, ктеноид и ганоид
Этимология: [L. scalae, pl. , лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
, лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
следовательно, любой слой или лист металла или другого материала, по размеру и толщине напоминающий чешую рыбы; as, железная, костная и т. д.
Этимология: [L.scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
одна из небольших чешуевидных структур, покрывающих части некоторых беспозвоночных, например, на крыльях чешуекрылых и на теле Thysanura; надкрылья некоторых кольчатых червей. См. Lepidoptera
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Скаленун
щитовка.(См. Ниже.)
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
небольшой отросток, похожий на рудиментарный лист, напоминающий чешую рыбы по форме, а часто и по расположению; как, чешуя бутона, сосновая шишка и тому подобное. Название дано также плевелам на стеблях папоротников
Название дано также плевелам на стеблях папоротников
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scalenoun
тонкая металлическая боковая пластина ручки карманного ножа. См. Иллюстрацию. of Pocketknife
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
налет на внутренней стороне сосуда, в котором вода нагревается, как паровой котел
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scalenoun
тонкий оксид, образующийся на поверхности железных поковок. Он состоит в основном из магнитного оксида Fe3O4. Также аналогичное покрытие на других металлах
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
См. Сканирование; ср. Escalade.]
Scaleverb
, чтобы удалить или очистить от накипи или чешуек; как, чтобы очистить рыбу; для масштабирования внутренней части котла
Этимология: [L.scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scaleverb
для снятия тонкими слоями или чешуей, как зубной камень с зубов; отрезать, как поверхность
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scaleverb
to scatter; распространить
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scaleverb
для очистки внутренней части пушки путем взрыва небольшого количества пороха
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
См. Сканирование; ср. Escalade.]
Scaleverb
для отделения и отделения тонкими слоями или пластинками; as, некоторые чешуйки песчаника по экспозиции
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scaleverb
отделить; to scatter
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
лестница; серия шагов; средство восхождения
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
, следовательно, все градуированные, особенно если они используются в качестве меры или правила или отмечены линиями через равные промежутки времени
Этимология: [L.scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
См. Сканирование; ср. Escalade.]
Scalenoun
математический инструмент, состоящий из заготовки из дерева, слоновой кости или металла, с одним или несколькими наборами градуированных и пронумерованных пространств на его поверхности для измерения или уменьшения расстояний и т. Д., как рисование, черчение и тому подобное. См. Шкалу Гюнтера
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср.Escalade.]
Scalenoun
ряд пространств, отмеченных линиями и представляющих пропорционально большие расстояния; as, масштаб в милях, ярдах, футах и т. д. для карты или плана
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
основа системы счисления; as — десятичная шкала; двоичная шкала и т. д.
Этимология: [L.scalae, pl.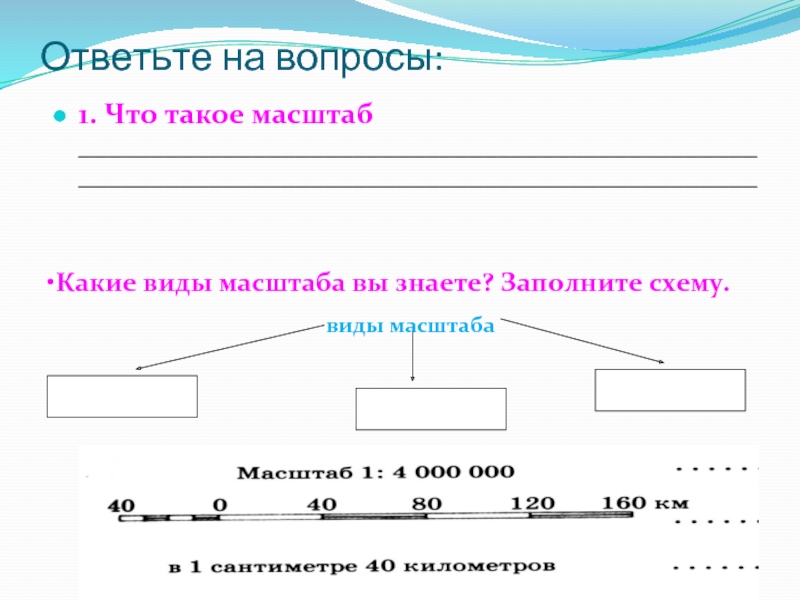 , лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
, лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
ступенчатая последовательность всех тонов, восходящих или нисходящих, от основного тона до его октавы; — называется также гаммой. Его можно повторять через любое количество октав. См. Хроматическая шкала, Диатоническая шкала, Большая шкала и Минорная шкала в разделе Хроматическая, Диатоническая, Мажорная и Минорная
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scalenoun
градации; чередование ступеней и ступеней подъема и спуска; прогрессивная серия; схема сравнительного ранга или порядка; as, масштаб
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scalenoun
относительные размеры, без различия в пропорциях частей; размер или степень частей или компонентов в любой сложной вещи по сравнению с другими подобными вещами; особенно относительная пропорция линейных размеров частей чертежа, карты, модели и т. д., к размерам соответствующих частей изображаемого объекта; as, карта в масштабе от дюйма до мили
д., к размерам соответствующих частей изображаемого объекта; as, карта в масштабе от дюйма до мили
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Scaleverb
, чтобы подняться по лестнице или как по лестнице; подниматься по ступенькам или лазанием; карабкаться вверх; as, масштабировать стену форта
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить.См. Сканирование; ср. Escalade.]
Scaleverb
для перехода вверх по ступеням; to ascend
Этимология: [L. scalae, pl., лестница scala, лестница; сродни скандере лазить. См. Сканирование; ср. Escalade.]
Какой масштабный коэффициент у шкалы 1/4 дюйма = 2 фута?
Кэролайн Т.
задано • 17.01.18попробуйте объяснить, как вы получили свой ответ
Более
(1/4) f = 2
f = 2 / (1/4) = 2 (4) = 8
Масштабный коэффициент равен 8.
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊ Шкала интервалов
и шкала соотношения: в чем разница?
Шкала интервалов и шкала соотношений представляют собой шкалы переменных измерений. Они предлагают количественное определение переменных атрибутов.
Они предлагают количественное определение переменных атрибутов.
Разница между шкалами интервалов и соотношений связана с их способностью опускаться ниже нуля. Шкалы интервалов не содержат истинного нуля и могут представлять значения ниже нуля. Например, вы можете измерить температуру ниже 0 градусов Цельсия, например -10 градусов.
С другой стороны, переменные отношенияникогда не опускаются ниже нуля. Рост и вес измеряются от 0 и выше, но никогда не опускаются ниже него.
Интервальная шкала позволяет измерять все количественные атрибуты.Любое измерение шкалы интервалов может быть ранжировано, подсчитано, вычтено или добавлено, и равные интервалы отделяют каждое число на шкале. Однако эти измерения не дают никакого представления о соотношении между собой.
Шкала отношений имеет те же свойства, что и шкалы интервалов. Вы можете использовать его для сложения, вычитания или подсчета измерений. Шкалы отношения различаются наличием символа происхождения, который является начальной или нулевой точкой шкалы.
Соотношение интервалов Сравнение шкал
Измерение температуры — отличный пример интервальных шкал.Температура в помещении с кондиционером составляет 16 градусов по Цельсию, а температура за пределами помещения — 32 градуса по Цельсию. Можно сделать вывод, что температура на улице на 16 градусов выше, чем внутри помещения.
Но если бы вы сказали: «На улице в два раза жарче, чем внутри», вы ошиблись бы. Заявив, что температура снаружи вдвое выше, чем внутри, вы используете 0 градусов в качестве точки отсчета для сравнения двух температур. Поскольку можно измерить температуру ниже 0 градусов, вы не можете использовать ее в качестве ориентира для сравнения.Вместо этого вы должны использовать фактическое число (например, 16 градусов).
Интервальные переменные обычно называются масштабируемыми переменными. Они часто выражаются в виде единиц, например, градусов. В статистике среднее значение, режим и медиана также могут определять интервальные переменные.
Шкала соотношений отображает порядок и количество объектов между значениями шкалы. Ноль — это вариант. Эта шкала позволяет исследователю применять статистические методы, такие как среднее геометрическое и гармоническое.
Если вы не можете подразумевать, что температура на улице вдвое теплее, потому что это интервальная шкала, вы можете сказать, что вы вдвое старше другого, потому что это переменная отношения.
Возраст, деньги и вес являются общими переменными шкалы отношения. Например, если вам 50 лет, а вашему ребенку 25 лет, вы можете точно заявить, что вы вдвое старше его.
Интервал измерений шкалы
Понимание различных шкал измерения позволяет вам видеть различные типы данных, которые вы можете собирать. Эти различия помогут вам определить тип статистического анализа, необходимый для вашего исследования.
Вот краткое описание разницы в интервале и соотношении уровней измерения:
Интервальный уровень измерения классифицирует и упорядочивает измерение. Он определяет расстояние между каждым интервалом эквивалентной шкалы, от нижнего интервала до верхнего интервала. Например, разница между 90 градусами по Фаренгейту и 100 градусами по Фаренгейту такая же, как 110 градусов по Фаренгейту и 120 градусов по Фаренгейту.
Он определяет расстояние между каждым интервалом эквивалентной шкалы, от нижнего интервала до верхнего интервала. Например, разница между 90 градусами по Фаренгейту и 100 градусами по Фаренгейту такая же, как 110 градусов по Фаренгейту и 120 градусов по Фаренгейту.
В дополнение к тому же качеству, что и уровни интервалов, уровни отношения могут иметь нулевое значение. Разница в стоимости между двумя парами обуви, которые составляют 10 и 20 долларов соответственно, такая же, как и между двумя парами, которые составляют 20 и 30 долларов.Однако вы не найдете туфли дешевле 0 долларов.
Шкала интервалов по шкале соотношений: точки различия
| Характеристики | Интервальная шкала | Масштаб передаточного отношения |
| Переменное свойство | Все переменные, измеренные в интервальной шкале, можно складывать, вычитать и умножать. Вы не можете рассчитать соотношение между ними. | Шкала отношенийобладает всеми характеристиками интервальной шкалы, кроме того, она позволяет вычислять коэффициенты. То есть вы можете использовать числа на шкале против 0. |
| Абсолютная нулевая точка | Нулевая точка на интервальной шкале произвольна. Например, температура может быть ниже 0 градусов по Цельсию и может быть отрицательной. | Шкала отношения имеет абсолютный ноль или знак начала отсчета. Рост и вес не могут быть нулевыми или ниже нуля. |
| Расчет | Статистически в интервальной шкале вычисляется среднее арифметическое. | Статистически в шкале соотношений вычисляется геометрическое или гармоническое среднее значение. |
| Измерение | Интервальная шкала может измерять размер и величину как несколько факторов определенной единицы. | Шкала отношения может измерять размер и величину как коэффициент одной определенной единицы по отношению к другой. |




 При увеличении формы большее значение является числителем, а меньшее — знаменателем.При сжатии формы меньшее значение является числителем, а большее значение — знаменателем.
При увеличении формы большее значение является числителем, а меньшее — знаменателем.При сжатии формы меньшее значение является числителем, а большее значение — знаменателем.