Степень с натуральным показателем
Предварительные навыкиЧто такое степень?
Степенью называют произведение из нескольких одинаковых множителей. Например:
2 × 2 × 2
Значение данного выражения равно 8
2 × 2 × 2 = 8
Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:
23 = 8
Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».
Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.
Например, если дано выражение 53, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.
Число, которое повторяется называют основанием степени. В выражении 53 основанием степени является число 5.
А число, которое надписано над числом 5 называют показателем степени. В выражении 53 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза
Саму операцию перемножения одинаковых множителей называют возведением в степень.
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:
Видим, что число 2 в четвёртой степени есть число 16.
Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля.
Вообще, определение степени с натуральным показателем выглядит следующим образом:
Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен a
Примеры:
Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.
Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25
Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2
Получилась ошибка, поскольку число 5 во второй степени не равно 10.
Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:
Например, число 5 в первой степени есть само число 5
Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1
А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:
А выражение 00 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 00 может иметь смысл.
Для тренировки решим несколько примеров на возведение чисел в степени.
Пример 1. Возвести число 3 во вторую степень.
Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3
32 = 3 × 3 = 9
Пример 2. Возвести число 2 в четвертую степень.
Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2
24 =2 × 2 × 2 × 2 = 16
Пример 3. Возвести число 2 в третью степень.
Возвести число 2 в третью степень.
Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2
23 =2 × 2 × 2 = 8
Возведение в степень числа 10
Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.
Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2
102
Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени
102 = 100
Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10
102 = 10 × 10 = 100
Пример 2. Возведём число 10 в третью степень.
В данном случае после единицы будут стоять три нуля:
103 = 1000
Пример 3. Возведем число 10 в четвёртую степень.
Возведем число 10 в четвёртую степень.
В данном случае после единицы будут стоять четыре нуля:
104 = 10000
Пример 4. Возведем число 10 в первую степень.
В данном случае после единицы будет стоять один нуль:
101 = 10
Представление чисел 10, 100, 1000 в виде степени с основанием 10
Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.
Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 101
10 = 101
Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 102
100 = 102
Пример 3. Представим число 1 000 в виде степени с основанием 10.
Представим число 1 000 в виде степени с основанием 10.
1 000 = 103
Пример 4. Представим число 10 000 в виде степени с основанием 10.
10 000 = 104
Возведение в степень отрицательного числа
При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)
(−2)2 = (−2) × (−2) = 4
Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −22, которое не равно 4. Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.
Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.
Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.
В случае с выражением −22 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.
Поэтому выражение −22 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2
Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4
−22 = −4
Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2.
Пример 2. Возвести число −2 в третью степень.
Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)
(−2)3 = (−2) × (−2) × (−2) = −8
Пример 3. Возвести число −2 в четвёртую степень.
Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)
(−2)4 = (−2) × (−2) × (−2) × (−2) = 16
Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.
Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3
В первом и в третьем случае показатель был нечётным
числом, поэтому ответ стал отрицательным.
Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.
Пример 7. Возвести число −5 в третью степень.
Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:
(−5)3 = (−5) × (−5) × (−5) = −125
Пример 8. Возвести число −4 в четвёртую степень.
Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:
(−4)4 = (−4) × (−4) × (−4) × (−4) = 256
Нахождение значений выражений

Пример 1. Найти значение выражения 2 + 52
Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2
2 + 52 = 2 + 25 = 27
Пример 10. Найти значение выражения −62 × (−12)
Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:
−62 × (−12) = −36 × (−12)
Завершаем пример, умножив −36 на (−12)
−62 × (−12) = −36 × (−12) = 432
Пример 11. Найти значение выражения −3 × 22
Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3
−3 × 22 = −3 × 4 = −12
Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.
Пример 12. Найти значение выражения (32 + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:
(32 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2
Пример 13. Найти значение выражения 2 × 53 + 5 × 23
Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:
2 × 53 + 5 × 23 = 2 × 125 + 5 × 8 = 250 + 40 = 290
Тождественные преобразования степеней
Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.
Допустим, потребовалось вычислить выражение (23)2. В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.
(23)2это произведение двух степеней, каждая из которых равна 23
При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2
Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (23)2 или равно 64
Этот пример можно значительно упростить. Для этого показатели выражения (23)2 можно перемножить и записать это произведение над основанием 2
Получили 26. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64
Данное свойство работает по причине того, что 23 это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз.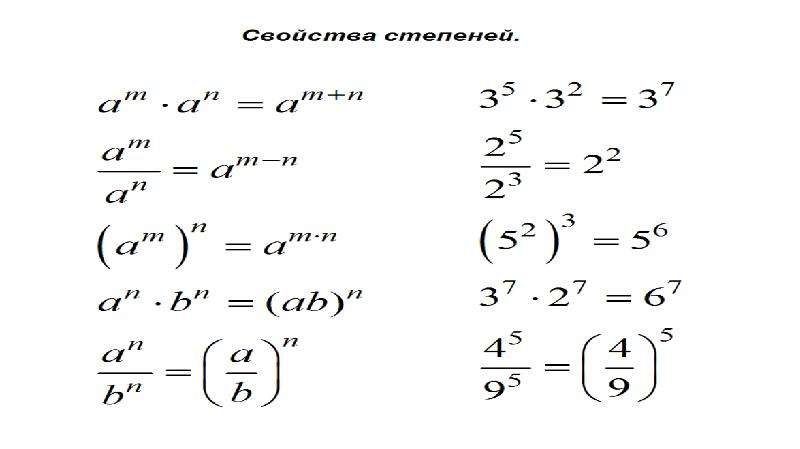 Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 26
Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:
(an)m = an × m
Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».
После перемножения показателей, получится другая степень, значение которой можно найти.
Пример 2. Найти значение выражения (32)2
В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:
Получили 34. А число 3 в четвёртой степени есть 81
Рассмотрим остальные преобразования.
Умножение степеней
Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.
Например, умножим 22 на 33.
22 это число 4, а 33 это число 27. Перемножаем числа 4 и 27, получаем 108
22 × 33 = 4 × 27 = 108
В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.
Например, умножим 22 на 23
В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 22 и 23. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:
Получили 25. Число 2 в пятой степени есть 32
Данное свойство работает по причине того, что 22 это произведение 2 × 2, а 23 это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2. Это произведение представимо в виде 25
Это произведение представимо в виде 25
Вообще, для любого a и показателей m и n выполняется следующее равенство:
Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».
Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.
Например, найдем значение выражения 21 × 22 × 23. Основание 2 оставим без изменений, а показатели сложим:
В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.
Пример 1. Представить в виде степени выражение 58 × 25
В данной задаче нужно сделать так, чтобы вместо выражения 58 × 25 получилась одна степень.
Число 25 можно представить в виде 52. Тогда получим следующее выражение:
В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:
Задачу можно считать решённой, поскольку мы представили выражение 58 × 25 в виде одной степени, а именно в виде степени 510.
Запишем решение покороче:
Пример 2. Представить в виде степени выражение 29 × 32
Число 32 можно представить в виде 25. Тогда получим выражение 29 × 25. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:
Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.
Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?
Как это сделать?
Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 31 и 31
31 × 31
Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:
31 × 31 = 32
Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9
31 × 31 = 32 = 9
Пример 4. Вычислите произведение 2 × 2 × 32 × 33, используя основное свойство степени.
Произведение 2 × 2 заменим на 21 × 21, затем на 21 + 1, а затем на 22. Произведение 32 × 33 заменим на 32 + 3, а затем на 35
Далее вычисляем значение каждой степени и находим произведение:
Пример 5. Выполнить умножение x × x
Выполнить умножение x × x
Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:
Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.
Решение данного примера желательно записать так:
Пример 6. Выполнить умножение x2 × x
Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 7. Выполнить умножение y3y2y
Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 8. Выполнить умножение aa3a2a5
Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:
Пример 9. Представить степень 38 в виде произведения степеней с одинаковыми основаниями.
В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 38 в виде произведения степеней 35 и 33
В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 35 × 33 можно записать как 35 + 3, откуда 38.
Конечно можно было представить степень 38 в виде произведения других степеней. Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Например, в виде 37 × 31, поскольку это произведение тоже равно 38
Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.
Пример 10. Представить степень x12 в виде различных произведений степеней с основаниями x.
Воспользуемся основным свойство степени. Представим x12 в виде произведений с основаниями x, и сумма показателей которых равна 12
Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:
Возведение в степень произведения
Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.
Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2
Возьмём в скобки данное произведение и в качестве показателя укажем 2
Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:
Принцип работы данного правила основан на определении степени, которое было дано в самом начале.
Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:
2 × 3 × 2 × 3
От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:
2 × 2 × 3 × 3
Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 22, а произведение 3 × 3 можно заменить на 32. Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 22 × 32.
Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n
Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:
Следующие выражения также справедливы:
Пример 2. Найти значение выражения (2 × 3 × 4)2
В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:
Пример 3. Возвести в третью степень произведение a × b × c
Заключим в скобки данное произведение, и в качестве показателя укажем число 3
Далее возводим в третью степень каждый множитель данного произведения:
Пример 4. Возвести в третью степень произведение 3xyz
Заключим в скобки данное произведение, и в качестве показателя укажем 3
(3xyz)3
Возведём в третью степень каждый множитель данного произведения:
(3xyz)3 = 33x3y3z3
Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:
Остальное оставим без изменений:
(3xyz)3 = 33x3y3z3 = 27x3y3z3
В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.
Например, вычислим значение выражения 52 × 32. Возведем каждое число во вторую степень и перемножим полученные результаты:
52 × 32 = 25 × 9 = 225
Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)2. Далее вычислить значение в скобках и возвести полученный результат во вторую степень:
52 × 32 = (5 × 3)2 = (15)2 = 225
В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)n = an × bn, то an × bn = (a × b)n. То есть левая и правая часть равенства поменялись местами.
То есть левая и правая часть равенства поменялись местами.
Возведение степени в степень
Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.
При возведении степени в степень основание оставляют без изменений, а показатели перемножают:
(an)m = an × m
К примеру, выражение (23)2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:
(23)2 = 23 × 2 = 26
Далее вычислить степень 26, которая равна 64
(23)2 = 23 × 2 = 26 = 64
Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.
Вернёмся к выражению (23)2. Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
Выражение в скобках 23 представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (23)2 степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.
(2 × 2 × 2)2
А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:
(2 × 2 × 2)2 = 22 × 22 × 22
Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26
Как и раньше получили 26. Значение этой степени равно 64
(2 × 2 × 2)2 = 22 × 22 × 22 = 22 + 2 + 2 = 26 = 64
В степень также может возводиться произведение, сомножители которого тоже являются степенями.
Например, найдём значение выражения (22 × 32)3. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:
(22 × 32)3 = 22×3 × 32×3 = 26 × 36 = 64 × 729 = 46656
Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.
Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:
Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 21 × 41. А это есть возведение степени в степень.
Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:
У нас должен получиться тот же результат:
Пример 2. Найти значение выражения (33)2
Основание оставляем без изменений, а показатели перемножаем:
Получили 36. Число 3 в шестой степени есть число 729
Пример 3. Выполнить возведение в степень в выражении (xy)³
Возведём в третью степень каждый множитель произведения:
Пример 4. Выполнить возведение в степень в выражении (abc)⁵
Возведём в пятую степень каждый множитель произведения:
Пример 5. Выполнить возведение в степень в выражении (−2ax)3
Возведём в третью степень каждый множитель произведения:
Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.
Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)3 — получится −8. Буквенная часть останется без изменений:
Буквенная часть останется без изменений:
Пример 6. Выполнить возведение в степень в выражении (10xy)2
Пример 7. Выполнить возведение в степень в выражении (−5x)3
Пример 8. Выполнить возведение в степень в выражении (−3y)4
Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴
Пример 10. Упростите выражение x5 × (x2)3
Степень x5 пока оставим без изменений, а в выражении (x2)3 выполним возведение степени в степени:
x5 × (x2)3 = x5 × x2 × 3 = x5 × x6
Теперь выполним умножение x5× x6. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:
x5 × (x2)3 = x5 × x2× 3 = x5 × x6 = x5 + 6 = x11
Пример 9. Найти значение выражения 43 × 22, используя основное свойство степени.
Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.
Посмотрим внимательно на степень 43. Основание у этой степени есть число 4, которое можно представить в виде 22. Тогда исходное выражение примет вид (22)3 × 22. Выполнив возведение степени в степень в выражении (22)3, мы получим 26. Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Тогда исходное выражение примет вид 26 × 22, вычислить которое можно, используя основное свойство степени.
Запишем решение данного примера:
Деление степеней
Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.
Например, разделим 43 на 22.
Вычислим 43, получим 64. Вычислим 22, получим 4. Теперь разделим 64 на 4, получим 16
Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.
Например, найдем значение выражения 23 : 22
Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Значит, значение выражения 23 : 22 равно 2.
Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.
Вернемся к предыдущему примеру 23 : 22. Здесь делимое это 23, а делитель 22.
Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.
В нашем случае, разделить 23 на 22 означает найти такую степень, которая при умножении на делитель 22 даст в результате 23. А какую степень можно умножить на 22, чтобы получить 23 ? Очевидно, что только степень 21. Из основного свойства степени имеем:
Убедиться, что значение выражения 23 : 22 равно 21 можно непосредственно вычислив само выражение 23 : 22. Для этого сначала найдём значение степени 23, получим 8. Затем найдём значение степени 22, получим 4. Разделим 8 на 4, получим 2 или 21, поскольку 2 = 21.
23 : 22 = 8 : 4 = 2
Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:
Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.
В этом случае в ответе получится единица.
Например, найдём значение выражения 22 : 22. Вычислим значение каждой степени и выполним деление получившихся чисел:
При решении примера 22 : 22 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 22 и 22 равна нулю:
В математике принято считать, что любое число в нулевой степени есть единица:
Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 22 : 22 обычным методом, не используя правило деления степеней, получится единица.
Пример 2. Найти значение выражения 412 : 410
Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
412 : 410 = 412 − 10 = 42 = 16
Пример 3. Представить частное x3 : x в виде степени с основанием x
Представить частное x3 : x в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:
Пример 4. Представить частное x3 : x2 в виде степени с основанием x
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:
Числитель и знаменатель дроби разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x3 можно записать как x × x × x, а степень x2 как x × x. Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Тогда конструкцию x3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x
Или ещё короче:
Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь можно сократить на x2. Чтобы сократить дробь на x2 нужно числитель и знаменатель дроби разделить на x2
Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:
Или ещё короче:
Пример 5. Выполнить деление x12 : x3
Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Запишем решение при помощи сокращения дроби. Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Деление степеней x12 : x3 запишем в виде . Далее сократим данную дробь на x3.
Пример 6. Найти значение выражения
В числителе выполним умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:
Завершаем пример, вычислив степень 72
Пример 7. Найти значение выражения
Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (23)4
Теперь выполним в числителе умножение степеней с одинаковыми основаниями:
Теперь применяем правило деления степеней с одинаковыми основаниями:
Значит, значение выражения равно 16
В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.
Это позволяет упростить выражение и само вычисление в целом.
Например, найдём значение выражения . Степень 43 запишем в виде возведения степени в степень (22)3. Тогда получим следующее выражение:
В числителе выполним возведение степени в степень. Сделать это нужно с выражением (22)3
В числителе и в знаменателе получившегося выражения содержится степень 26, которую можно сократить на 26
Видим, что в результате осталась единственная степень 32, значение которой равно 9.
Пример 8. Найти значение выражения
В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 75 × 45 можно представить в виде степени с одним показателем (7 × 4)5. Далее перемножим выражение в скобках, получим 285. В результате исходное выражение примет следующий вид:
Теперь можно применить правило деления степеней:
Значит, значение выражения равно 28. Запишем решение полностью:
Запишем решение полностью:
Возведение в степень обыкновенных дробей
Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.
Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2
Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .
Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:
Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности
Значит обыкновенная дробь во второй степени равна дроби .
Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна
Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:
А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 22 и 32 соответственно:
Откуда и получится ответ .
Вообще, для любого a и b ≠ 0 выполняется следующее равенство:
Это тождественное преобразование называют возведением в степень обыкновенной дроби.
Пример 2. Возвести дробь в третью степень
Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:
Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.
Например, возведём дробь во вторую степень:
Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:
Ответ положителен по причине того, что выражение представляет собой произведение двух сомножителей, каждый из которых равен дроби
А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:
Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:
Здесь ответ отрицателем по причине того, что выражение представляет собой произведение трёх множителей, каждый из которых равен дроби
Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ
Пример 3. Найти значение выражения
Выполним возведение в степень обыкновенной дроби:
Далее вычислим значение получившегося выражения:
Возведение в степень десятичных дробей
При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5
Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
Пример 2. Найти значение степени (−1,5)3
Показатель степени является нечётным числом. Значит ответ будет отрицательным
Значит ответ будет отрицательным
Пример 3. Найти значение степени (−2,4)2
Показатель степени является чётным числом. Значит ответ будет положительным:
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Представьте в виде степени произведение:
Решение:
Задание 8. Представьте в виде степени произведение:
Решение:
Задание 9. Представьте в виде степени произведение:
Решение:
Задание 10. Представьте в виде степени произведение:
Решение:
Задание 11. Представьте в виде степени произведение:
Представьте в виде степени произведение:
Решение:
Задание 12. Представьте в виде степени произведение:
Решение:
Задание 13. Представьте в виде степени частное:
Решение:
Задание 14. Представьте в виде степени частное:
Решение:
Задание 15. Представьте в виде степени частное:
Решение:
Задание 16. Представьте в виде степени частное:
Решение:
Задание 17. Представьте в виде степени частное:
Решение:
Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2Решение:
Задание 19. Представьте в виде степени частное:
Решение:
Задание 20. Сократите дробь на c¹Решение:
Задание 21. Представьте в виде степени следующее произведение:
Решение:
Задание 22. Представьте в виде степени следующее произведение:
Решение:
Задание 23. Представьте в виде степени следующее произведение:
Представьте в виде степени следующее произведение:
Решение:
Задание 24. Представьте в виде степени следующее произведение:
Решение:
Задание 25. Представьте в виде степени следующее произведение:
Решение:
Задание 26. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 27. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 28. Представьте следующую степень в виде произведения степеней:
Решение:
Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:
Решение:
Задание 32. Представьте в виде степени следующее выражение:
Решение:
Задание 33. Представьте в виде степени следующее выражение:
Представьте в виде степени следующее выражение:
Решение:
Задание 34. Представьте в виде степени следующее выражение:
Решение:
Задание 35. Представьте в виде степени следующее выражение:
Решение:
Задание 36. Представьте в виде степени следующее выражение:
Решение:
Задание 37. Представьте в виде степени следующее выражение:
Решение:
Задание 38. Найдите значение следующего выражения:
Решение:
Задание 39. Найдите значение следующего выражения:
Решение:
Задание 40. Найдите значение следующего выражения:
Решение:
Задание 41. Найдите значение следующего выражения:
Решение:
Задание 42. Найдите значение следующего выражения:
Решение:
Задание 43. Найдите значение следующего выражения:
Решение:
Задание 44. Найдите значение следующего выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Степень с целым показателем (8 класс)
. 1=2\)
1=2\)
Готов ответ.
Таблица степеней 2 (двойки)
Приведенная таблица кроме степени двойки показывает максимальные числа, которые может хранить компьютер для заданного числа бит. Причем как для целых так и чисел со знаком.
Исторически сложилось, что компьютеры используют двоичную систему счисления, а, соответственно, и хранения данных. Таким образом, любое число можно представить как последовательность нулей и единиц (бит информации). Существует несколько способов представления чисел в виде двоичной последовательности.
Рассмотрим наиболее простой из них — это целое положительное число. Тогда чем больше число нам нужно записать, тем более длинная последовательность бит нам необходима.
Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.
Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.
Как пользоваться
таблицей степеней числа два?Первый столбец — это степень двойки, который одновременно, обозначает число бит, которое представляет число.
Второй столбец — значение двойки в соответствующей степени (n).
Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) — это 128
Третий столбец — максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце).
Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое количество чисел, можно представить с помощью семи бит. Но, поскольку первое число — это ноль, то максимальное число, которое можно представить с помощью семи бит 128 — 1 = 127 . Это и есть значение третьего столбца.
Но, поскольку первое число — это ноль, то максимальное число, которое можно представить с помощью семи бит 128 — 1 = 127 . Это и есть значение третьего столбца.
| Степень двойки (n) |
Значение степени двойки 2n |
Максимальное число без знака, записанное с помощью n бит |
Максимальное число со знаком, записанное с помощью n бит |
| 0 | 1 | - | - |
| 1 | 2 | 1 | - |
| 2 | 4 | 3 | 1 |
| 3 | 8 | 7 | 3 |
| 4 | 16 | 15 | 7 |
| 5 | 32 | 31 | 15 |
| 6 | 64 | 63 | 31 |
| 7 | 128 | 127 | 63 |
| 8 | 256 | 255 | 127 |
| 9 | 512 | 511 | 255 |
| 10 | 1 024 | 1 023 | 511 |
| 11 | 2 048 | 2 047 | 1023 |
| 12 | 40 96 | 4 095 | 2047 |
| 13 | 8 192 | 8 191 | 4095 |
| 14 | 16 384 | 16 383 | 8191 |
| 15 | 32 768 | 32 767 | 16383 |
| 16 | 65 536 | 65 535 | 32767 |
| 17 | 131 072 | 131 071 | 65 535 |
| 18 | 262 144 | 262 143 | 131 071 |
| 19 | 524 288 | 524 287 | 262 143 |
| 20 | 1 048 576 | 1 048 575 | 524 287 |
| 21 | 2 097 152 | 2 097 151 | 1 048 575 |
| 22 | 4 194 304 | 4 194 303 | 2 097 151 |
| 23 | 8 388 608 | 8 388 607 | 4 194 303 |
| 24 | 16 777 216 | 16 777 215 | 8 388 607 |
| 25 | 33 554 432 | 33 554 431 | 16 777 215 |
| 26 | 67 108 864 | 67 108 863 | 33 554 431 |
| 27 | 134 217 728 | 134 217 727 | 67 108 863 |
| 28 | 268 435 456 | 268 435 455 | 134 217 727 |
| 29 | 536 870 912 | 536 870 911 | 268 435 455 |
| 30 | 1 073 741 824 | 1 073 741 823 | 536 870 911 |
| 31 | 2 147 483 648 | 2 147 483 647 | 1 073 741 823 |
| 32 | 4 294 967 296 | 4 294 967 295 | 2 147 483 647 |
Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Существуют и другие способы представления данных. Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.
Для этого же самого примера ( 27 ) семью битами можно записать максимум число +63, поскольку один бит занят знаком «плюс». Но мы можем хранить и число «-63», что было бы невозможно, если бы все биты были бы зарезервированы под хранение числа.
Примеры использования таблицы степеней числа два
Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.
Аналогично, 2 в 11 степени равно 2048. {200} $
{200} $
Калькулятор степеней онлайн: формула, примеры с решением
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
am × an = a(m+n).
Если разделить 134 на 132, то нам потребуется вычислить дробь вида:
(13 × 13 × 13 × 13) / (13 × 13).
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:
Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:
am / an = a(m – n).
Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:
(am)n = a(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь:
154 / 154.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150. Следовательно:
Но согласно правилу действий со степенными числами это будет эквивалентно 150. Следовательно:
154 / 154 = 150 = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:
a0 = 1.
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.
(8 × 8) / (8 × 8 × 8 × 8).
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
a-m = 1 / am
При этом для значения -1 правило трансформируется в элегантную формулу:
a-1 = 1 / a.
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:
Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:
a(m/n) есть корень n-ной степени из am.
Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:
Рост = a × e(kt),
где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.
Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
Заключение
Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.
Функция СТЕПЕНЬ
Предположим, что вам нужно вычислить очень маленький допуск для детали механизма или огромное расстояние между двумя галактиками. Для возведения числа в степень используйте функцию СТЕПЕНЬ.
Описание
Возвращает результат возведения числа в степень.
Синтаксис
СТЕПЕНЬ(число;степень)
Аргументы функции СТЕПЕНЬ описаны ниже. 2.
2.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=СТЕПЕНЬ(5;2) |
Число 5 в квадрате. |
25 |
|
=СТЕПЕНЬ(98,6;3,2) |
Число 98,6, возведенное в степень 3,2. |
2401077,222 |
|
=СТЕПЕНЬ(4;5/4) |
Число 4, возведенное в степень 5/4. |
5,656854249 |
Обобщение понятия степени и решение примеров со степенями
Здравствуйте. Многие ученики испытывают сложности при решении заданий, в которых встречаются выражения с корнями. В данной статье я попытаюсь обобщить материал по темам «Радикал» и «Степень». Покажу как решать некоторые задания. Если у Вас во время прочтения статьи появятся вопросы, Вы можете записаться ко мне на занятие, я с радостью помогу Вам во всем разобраться, помогу с решением именно Ваших задач!
В данной статье я попытаюсь обобщить материал по темам «Радикал» и «Степень». Покажу как решать некоторые задания. Если у Вас во время прочтения статьи появятся вопросы, Вы можете записаться ко мне на занятие, я с радостью помогу Вам во всем разобраться, помогу с решением именно Ваших задач!
1. Свойства степеней и корней
Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равняется а.
Степень числа а с показателем n обозначают an, например:
В общем случае при n > 1 имеем
Число a называется основой степени, число n — показателем степени.
Приведем основные свойства действий со степенями.
Приведенные свойства обобщаются для любых показателей степени
Часто в вычислениях используются степени с рациональным показателем. При этом удобным оказалось такое обозначение:
Корнем n— ой степени из числа а называется число b, n— я степень которого равняется a:
Корень также называется радикалом.
Корень нечетной степени n всегда существует. Корень четной степени 2n из отрицательного числа не существует. Существуют два противоположных числа, которые являются корнями четной степени из положительного числа а > 0. Положительный корень n— ой степени из положительного числа называют арифметическим корнем.
Из формул (3), (4) вытекают такие свойства радикалов
Если степень корня n = 2, то показатель корня обычно не пишется.
Пример 1.1. Найти значение выражения
Подкоренное выражение разложим на простые множители:
Пример 1.2. Упростить выражение
Имеем:
Пример 1.3. Извлечь корень
Имеем:
Пример 1.4. Упростить выражение
Поскольку при
2. Действия с радикалами
1) Преобразование корня по формуле называется внесением множителя под знак радикала.
Пример 2.1. Внести множитель под знак корня 5√2.
Исходя из формулы (7) получим
Пример 2.2. Внести множитель под знак радикала x√y при x< 0.
Имеем равенство
2) Преобразование корня исходя из формулы называется вынесением множителя из-под знака радикала.
Пример 2.3. Вынести множитель из-под знака корня в выражении
Получим:
Пример 2.4. Вынести множитель из-под знака корня
Имеем:
Пример 2.5. Вынести множитель из-под знака корня:
Радикалы вида , где a, b — рациональные числа, называются подобными. Их можно прибавлять и отнимать:
Пример 2.6. Упростить:
Пример 2.7. Сложить радикалы:
Пример 2.8. Выполнить действие:
Заметим, что равенство не выполняется. В этом можно убедиться на таком примере:
Приведем примеры умножения радикалов.
Пример 2.9.
Аналогично освобождаются от кубических иррациональностей в знаменателе:
Рассмотрим более сложные примеры рационализации знаменателей:
Чтобы перемножить радикалы с разными степенями, их сначала превращают в радикалы с одинаковыми степенями.
Пример 2.10. Перемножим радикалы:
Во время умножения радикалов можно использовать формулы сокращенного умножения. Например:
Если радикалы находятся в знаменателе дроби, то, используя свойства радикалов, можно избавиться от иррациональности.
Пример 2.11. Рационализируем знаменатели дробей
Выражения называются сопряженными. Произведение сопряженных выражений не содержит радикалов:
Это свойство используется для рационализации знаменателей.
Пример 2.12. Избавиться от иррациональности в знаменателе:
Избавимся от иррациональности в знаменателе дроби:
3. Вычисление иррациональных выражений
С помощью свойств корней можно упрощать и вычислять иррациональные выражения.
Пример 3.1. Вычислить
Выполним последовательно действия:
Пример 3. 2. Вычислить:
2. Вычислить:
Выполним действия.
Часто используется формула двойного радикала:
Пример 3.3. Исходя из формулы (8) находим:
Пример 3.4. Вычислить
Исходя из формулы (8) находим:
Окончательно получаем:
Аналогично вычисляются кубические корни. Имеем:
Возводим обе части равенства в куб:
Сравнивая выражения при √с, получаем однородную систему уравнений:
Поделив уравнение почленно, приходим к уравнению для z = y/x:
Пример 3.5. Вычислить значение радикала
После возведения в куб уравнения приходим к системе уравнений:
Поделив почленно первое уравнение на второе, получим уравнение для z= y/x:
По схеме Горнера находим корень z = — ½
Из системы уравнений и уравнения y/x = — ½ находим x = 2, y = -1. Итак,
Итак,
Пример 3.6. Вычислить .
Возьмем .
Возведя обе части уравнения в куб, получаем откуда вытекает система уравнений
Система уравнений имеет очевидное решение x= 1, y= 1.
Поэтому .
Вычисляем радикал
Окончательно имеем a = — 1.
Пример 3.7. Вычислить
Поскольку
Дальше имеем:
Итак, a = — 2.
Пример 3.8. Вычислить
Возведем уравнение в куб, воспользовавшись равенством .
Получили для x кубическое уравнение
или x3 – 3x – 18 = 0,
имеет корни
Во множестве действительных чисел имеем корень x = 3.
4. Оценки для радикалов
Если
Это неравенство можно использовать для доведения неровностей, которые содержат радикалы.
Пример 4.1. Доказать, что .
Возведя неравенство в шестую степень, получим очевидное неравенство
Можно приводить радикалы к одной и то й же самой степени :
Пример 4.2. Оценим .
Поскольку
При преобразовании неравенств можно использовать символ V, понимая под ним знаки « > », « < », или « ».
Пример 4.3. Какое число больше
.
Поскольку
На этом все. Напоминаю, что Вы можете записываться ко мне на занятия в расписании, я с радостью помогу Вам с любыми вопросами по математике или высшей математике.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Слово «степень» в примерах предложений
2892311 Том имеет закон степень .СК 1 2280194 Это шесть градуса ниже нуля. _undertoad 1 315365 Имеет степень по биологии. СК 1 73477 У меня температура 102 градуса . СК 1 2892807 Где вы получили степень ? СК 1 241851 Сейчас десять градуса ниже нуля. СК 1 3024108 Сегодня в Бостоне было 36 градуса градуса. СК 1 2641664 У Тома нет диплома .СК 1 2331901 У меня было два года, чтобы получить степень . СК 1 1025499 Том имеет степень по музыкальному образованию. СК 1 680652 Том получит лучшую работу с высшим образованием , степень . Source_VOA 1 1893798 Нам не удалось выяснить, где Том получил степень . СК 1 1545343 Том работает уборщиком, несмотря на то, что имеет высшее образование , степень . Спамстер 1 2655081 Прошлой ночью температура опустилась до десяти градуса ниже нуля. СК 1 2655082 Прошлой ночью температура упала до минус десяти градуса градуса по Цельсию.СК 1 2543997 Том имеет четырехлетнюю степень .
СК 270781 Вода закипает при 100 градусах . СК 20595 Согласен с вами в степени . СК 430025 У меня температура 38,9 градуса . Витброк 633583 Я получил высшее образование , степень . СМ 251396 Моя температура 38 градуса . СК 680358 Это тридцать градусов ниже нуля. Source_VOA 303656 Имеет степень магистра по праву . СК 249258 В какой степени мы можем ему доверять? СК 278236 Прямой угол составляет девяносто градуса .Неро 680650 Мэри получит степень в июне. Source_VOA 310345 Ей можно доверять до какой-то степени . СК 1422370 Сегодняшний минимум составил 3 градуса Цельсия. СК 270789 Вода закипает при 100 градусах Цельсия. СК 3070805 Я вас понимаю до определенной степени . Patgfisher 20351 Температура упала на несколько градусов . СК 2959115 Температура упала на десять градуса . острозубый 2662350 Температура поднялась до 30 градусов .острозубый 270776 Вода замерзает при 0 градусах Цельсия.
СК 681014 Вода замерзает при нуле градуса Цельсия. Source_VOA 299850 Имеет степень доктора психологии . СК 270784 Вода замерзает при 32 градусах Фаренгейта. СК 2268588 Температура упала на три градуса . _undertoad 680653 В каждой работе степени стресса. Source_VOA 248928 Мы знаем, что вода закипает при 100 градусах . СМ 310174 Три года назад получила степень магистра .СК 1482467 Я получаю степень магистра по специальности . Weihaiping 242172 Сегодня утром было десять градуса ниже нуля. СК 59135 Эта работа требует высокого мастерства степени . СМ 2318383 Три года назад получила степень магистра . СК 681825 Цель Тома в колледже - получить степень . Source_VOA 3039950 Тому предъявлено обвинение в убийстве первой степени . СК 72301 Угол в 90 градуса называется прямым углом.СМ 486480 Наш учитель сказал: «Вода закипает при 100 градусах ». СК 271593 Точная температура составляет 22,68 градуса Цельсия.
СК
Степень сравнения | Что такое грамматическая степень?
Наша историяКаковы степени сравнения? (с примерами)
В грамматике степени сравнения относятся к прилагательным и наречиям. Каждое прилагательное и наречие можно записать в одной из трех степеней:- Положительная степень .Это не предлагает никакого сравнения. Это просто говорит нам о существовании качества. Например:
- прилагательные: медленный, красивый, счастливый
- наречия: медленно, красиво, счастливо
- Сравнительная степень . При этом сравниваются две вещи, чтобы показать, какая из них имеет меньшую или большую степень качества. Например:
- прилагательные: медленнее, красивее, счастливее
- наречия: медленнее, красивее, счастливее
- Высшая степень .При этом сравнивается более двух вещей, чтобы показать, какая из них имеет наименьшую или наибольшую степень качества, например:
- прилагательные: самый медленный, самый красивый, самый счастливый
- наречия: самый медленный, самый красивый, самый счастливый

Простые примеры степеней сравнения
Вот прилагательное «голодный» во всех трех степенях сравнения:- Ли голоден.(положительная степень)
- Ли голоднее Марка. (сравнительная степень)
- Ли самый голодный из всех. (превосходная степень)
- Сегодня опасно сыграл Ли. (положительная степень)
- Ли играл опаснее Марка. (сравнительная степень)
- Опаснее всего сыграл Ли. (превосходная степень)
Реальные примеры степеней сравнения
Вот прилагательное «уродливый» во всех трех степенях сравнения.- Я могу быть пьян, мисс, но утром я буду трезв, а вы все равно будете уродливы. (Уинстон Черчилль) ( Ugly находится в положительной степени. Он не предлагает сравнения.)
- В 18 лет дети попадают в реальный мир и показывают его уродливую сторону, но не раньше. (Австралийский писатель Марго Ланаган) ( Уродливее относится к сравнительной степени, описывая взрослую жизнь как имеющую черту уродливой в большей степени, чем детство.
- На прошлой неделе я заявил, что эта женщина была самой уродливой женщиной, которую я когда-либо видел. С тех пор меня посетила ее сестра, и теперь я хочу отказаться от этого заявления. (Сценарист Марк Твен) ( Уродливее находится в превосходной степени, описывая женщину как имеющую черту уродливую в высшей степени.)
 )
)- Зарабатывать деньги — это хобби, которое прекрасно дополнит любые другие ваши увлечения.(Бизнесмен Скотт Александр)
- Это будет наш ответ насилию: делать музыку интенсивнее, красивее и преданнее, чем когда-либо прежде. (Композитор Леонард Бернштейн) ( Более красиво (сравнительная степень) говорит нам, как будет создаваться музыка по сравнению с прошлым; то есть это сравнение двух вещей.)
- Палермо — самый красиво расположенный город в мире. Он мечтает о своей жизни в Конка-до-Оро, изысканной долине, расположенной между двумя морями.
 (Драматург Оскар Уайльд) ( Самое красивое, что (превосходная степень) говорит нам, что Палермо превосходит все остальные города по своему местоположению; то есть это сравнение больше, чем двух вещей.)
(Драматург Оскар Уайльд) ( Самое красивое, что (превосходная степень) говорит нам, что Палермо превосходит все остальные города по своему местоположению; то есть это сравнение больше, чем двух вещей.)
Формирование сравнительной и превосходной степеней
Вот правила образования сравнительной и превосходной степеней прилагательных:| Тип прилагательного | Пример положительной степени | Как сформировать сравнительную степень | Как сформировать превосходную степень | |
|---|---|---|---|---|
| односложный | | прибавить est | ||
| односложный конечный гласный согласный | | двойной согласный | ||
| более одного слога | | добавить меньше или больше больше | самый известный более известный наименее известный ||
| более чем односложное окончание | | удалить y добавить ier для менее23 9016 silly | iest минимум за наименее глупый | |
| неправильный | | без правил | без правил |
| Тип наречия | Пример в положительной степени | Как сформировать сравнительную | Как сформировать превосходную степень | |
|---|---|---|---|---|
| на один слог | | | 9016 | добавить est |
| более одного слога | | добавить меньше или больше 0909 больше04 или минимум | ||
| нерегулярный | | нет правил | 12 | |
Почему я должен заботиться о Степень?
Если вы планируете изучать иностранный язык, то знание терминов сравнительная и превосходная является полезной отправной точкой для изучения их правил их формирования. Помимо этого, вот пять заслуживающих внимания вопросов, связанных со степенью.
Помимо этого, вот пять заслуживающих внимания вопросов, связанных со степенью.(Выпуск 1) Двойные сравнительные и двойные превосходные степени являются серьезными грамматическими ошибками.
Не применяйте два правила для получения сравнительной или превосходной степени.- С наступлением ночи ты становишься глупее.
- Она быстрее всех бегает.
(Выпуск 2) Используйте сравнительную, а не превосходную степень при сравнении двух вещей.
Распространенная ошибка - использовать превосходную степень при сравнении двух вещей. (Вот когда вам следует использовать сравнительную степень.)- Из двух она самый подходящий кандидат. (Более подходящий кандидат будет правильным.
- Белый я называю самым сильным нецветным; он чистый, оптимистичный и мощный. (Художник Джейсон Ву) (Когда я нашел эту цитату, я хотел, чтобы нецветные были просто черно-белыми, что означало, что более мощный был бы правильным. Оказывается, нецветные включают также все серые цвета. Итак, цитата Ву верна. Выпотрошен.)
 )
)- Она самый подходящий кандидат. (Читая это, мы могли бы предположить, что было более двух кандидатов. Если бы было только два, это должно было бы сказать «более подходящий».)
(Выпуск 3) «Мертвый» означает мертвый. Ты не можешь быть более мертвым, не так ли?
Возможно, существуют прилагательные, которые не должны иметь сравнительных или превосходных форм, потому что их значения уже выражают качества в максимально возможной степени. Вот четыре прилагательных, которые могли бы вызвать критику, если бы вы использовали их в сравнительной или превосходной степени. (Они упорядочены по их способности раздражать.)
(Они упорядочены по их способности раздражать.)- Мертвый (Что может быть мертвее или мертвее?)
- Сингл (может быть что-то большее или самое простое?)
- Уникальный (Может ли что-то быть более или более уникальным?)
- Мгновенно (может быть что-то более или более мгновенное?)
(выпуск 4) Вы можете использовать наречие «быстрее» или «быстрее».
«Быстрее» и «быстрее» - приемлемые формы сравнения наречия «быстро».Распространено заблуждение, что слово «быстрее» только недавно перешло в английский язык как наречие из-за обычного употребления и игнорирования разницы между наречиями и прилагательными. На протяжении большей части XIX и XX веков «быстрее» было гораздо более распространенным, чем «быстрее». Только с 1970-х «шустрее» догнал «шустрее». Другой причудливый сравнительный вариант - «глупее», что является приемлемой альтернативой «глупее».- Подумайте, какой глупый средний человек, половина из нас глупее этого.
 (Комик Джордж Карлин)
(Комик Джордж Карлин)
(Выпуск 5) «Выше меня» и «Выше меня» допустимы.
При использовании сравнительной степени многие авторы не уверены, использовать ли конструкцию типа «выше меня» или «выше меня». Быстрый ответ - оба правильны, но не все согласны с тем, что оба правильны, и в этом проблема. Вот корень дискуссии: слово than может быть союзом или предлогом. Когда чем используется как союз (помните, что союз объединяется как термины), это выглядит так:- Джон выше меня или
- Джон выше меня.(Это просто более емкая версия.)
 Однако для других версия «чем я» звучит претенциозно. Итак, есть что взвесить без каких-либо окончательных рекомендаций.
Однако для других версия «чем я» звучит претенциозно. Итак, есть что взвесить без каких-либо окончательных рекомендаций.К сожалению, это не так просто, как делать все, что вы хотите, и заявлять, если это оспаривается, что мировые грамматики спорят на протяжении сотен лет по этому поводу. Иногда нужно учитывать еще одну проблему: версия «чем я» вносит двусмысленность. Взгляните на этот пример:
- Джон любит Питер больше, чем я.
- Джон любит Питер больше, чем мне. или
- Джон предпочитает Питера мне.
- Джон любит Питер больше, чем я. или
- Джон любит Питер больше, чем я.
Читаю больше о нем.
Ключевые моменты
- Не применяйте два правила для создания сравнительной таблицы (например,g.
 , красивее ) или в превосходной степени (например, лучше всего ). Это серьезная ошибка.
, красивее ) или в превосходной степени (например, лучше всего ). Это серьезная ошибка. - Используйте сравнительную степень (а не превосходную степень) при сравнении только двух вещей.
См. Также
Сравнительная и превосходная степень прилагательных Сравнительная и превосходная степень наречий Словарь грамматических терминовПростые примеры дипломов по грамматике английского языка »Easy Learning
простые примеры степенейОбычно мы используем прилагательные для описания различных уровней качеств, природы и характеристик существительных, будь то положительные или отрицательные, чтобы сделать их более значимыми.Чтобы это работало соответственно, необходимо принять правильные формы степеней прилагательных, будь то регулярные или неправильные, чтобы обеспечить естественное значение. Давайте посмотрим на использование и простые примеры степеней.
Правила положительной степени
Давайте посмотрим на несколько простых правил положительной степени.
- Это основная форма степени.
- Также называется несравнительный
- Прилагательные или наречия используются для описания положительных, а также отрицательных качеств существительных.
- Это не требует изменения формы прилагательных для формулировки положительной степени.
- Когда мы меняем сравнительную или превосходную степень на положительную, тогда это требует сравнения.
- Предложение с положительной степенью может быть начато с «Нет другого» или «Очень мало»
- Как… .подобная форма сравнения .
Несколько простых примеров положительной степени
Сначала рассмотрим простые примеры положительных степеней прилагательных, а затем последовательно основные формы примеров.
- Мудрый, большой, легкий, богатый
- Маленький, Слабый, сильный, Богатый
- Great, Clean, Big– (обычные прилагательные)
- Хорошо • Плохо • Многие и т.
 Д. (Неправильные прилагательные)
Д. (Неправильные прилагательные)
Использование в предложениях без сравнения
Это некоторые основные формы примеров положительной степени без сравнения.
- Джонатан - мудрый человек.
- Гималаи - большая гора.
- Бег - легкое упражнение.
- Коралловые полипы - маленькие организмы.
- Уоррен Баффет - богатый человек.
- Биоудобрение подходит для зерновых культур.
Примеры со сравнением положительной степени
Очень мало, никто другой -
- Никакой другой ресурс на земле не имеет такого значения, как почва.
- Очень мало ресурсов на Земле, как важные как почвы.
- Никакой другой лес не как густой как экваториальный лес.
- Очень немногие леса как густые как экваториальные леса.

- Никакое другое животное из в пустыне не равно , так как полезно как верблюд.
- Очень немногие животных в пустыне так же полезны как верблюды.
- Ни один другой фрукт в мире не вкуснее манго.
- Очень немногие фрукты в мире настолько вкусны, как манго.
- Ни одно другое животное не более беззаботно, чем тигр.
- Очень немногие животные столь же беззаботны, как тигры.
Вот еще несколько примеров сравнительных и превосходных степеней для общего обзора.
Сравнительная степень Правила и примеры
Некоторые правила сравнительной формы ..
- Это второй уровень сравнительной формы между двумя существительными.
- Обращение предмета происходит, когда мы переводим положительную степень в сравнительную форму.

- Наречие помещается в конец предложения.
Примеры конкурсной формы:
- Почва важнее любых других ресурсов на Земле.
- Почва важнее большинства других ресурсов на Земле.
- Экваториальный лес гуще любого другого леса.
- Экваториальный лес гуще, чем большинство других лесов.
- Верблюд более полезен, чем любые другие животные в пустыне.
- Верблюд более полезен, чем большинство других животных в пустыне.
- Манго вкуснее любых других фруктов в мире.
- Манго вкуснее большинства других фруктов в мире.
- Тигр беззаботнее других животных.
- Тигр беззаботнее большинства других животных
Правила и примеры высшей степени
Правила образования превосходной степени.
- Это высший уровень сравнительных форм.
- Используется для сравнения между более чем двумя существительными.

- Изменение формы прилагательного необходимо для соответствующего сравнения.
- Правила орфографии применяются для изменения формы прилагательных.
- "Определитель" - это , помещенное перед превосходной степенью прилагательных и наречий.
Некоторые полезные примеры превосходной степени ..
- Почва - самый важный ресурс на Земле.
- Почва - один из важнейших ресурсов на Земле.
- Экваториальный лес - самый густой лес.
- Экваториальный лес - один из самых густых лесов.
- Верблюд - самое полезное животное в пустыне.
- Верблюд - одно из самых подходящих животных в пустыне.
- Манго - самый вкусный фрукт в мире.
- Манго - один из самых вкусных фруктов в мире.
- Тигр - самое беззаботное животное.
- Тигр - одно из самых беззаботных животных.
Это несколько простых примеров положительных, сравнительных и превосходных степеней. Надеюсь, эта тема обогатит ваши знания и понимание.
Надеюсь, эта тема обогатит ваши знания и понимание.
А также совокупное соединение
Функции предлога
https://www.youtube.com/channel/UCTkyAZY15L6UOEUl3y85XYw
высшее образование в предложении
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
Образовательный уровень отцов был схожим: 33% получили колледж степень и 18% получили послевузовское образование.
Что касается жен с ученой степенью, 80 процентов их супругов имеют как минимум колледж степень .
Таким образом, она закончила колледж со степенью по психологии.
Однако сотрудники с высшим образованием со степенью сообщают о значительно более высокой оценке своих планов, что, вероятно, отражает их большее понимание.
В архитектуре начальная зарплата в 1996 году составляла в среднем 22 125 долларов по стране, для тех, кто имел профессиональное образование колледж степень .
Студенты, которые могут найти работу и пройти курс обучения на судне, завершают программу и получают колледж степень .
Подобные голоса говорят о том, что идеал этих женщин состоит в том, что колледж степень позволит им не быть финансовым бременем для своих будущих мужей.
Один предназначен для неполной средней школы, а другой - для колледжа степени (или более).
Примерно каждый третий работник имеет как минимум высшее образование степень , что одинаково для мужчин и женщин.
College степень - это хорошо знакомая конструкция, которая, тем не менее, записывается в виде двух слов.
Уровень образования кодировался 1 = ниже аттестата средней школы, 2 = окончил среднюю школу, 3 = ниже колледж степень , 4 = колледж степень или выше.
Что меня беспокоит, так это проблема желающих поступить в вуз и техникум колледж диплом курсов.
Отборщики менеджеров, когда они назначают руководителей угольных шахт, теперь склонны брать людей со старой школой, которые имеют колледж степень .
Курсы засчитываются в счет требований к окончанию средней школы и для получения колледжа степени .
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Он открыт для всех людей с высшим образованием со степенью , включая недавних выпускников и соискателей среднего возраста.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.К сожалению, он должен иметь колледж степень , чтобы получить приз.
ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
Положительная степень 20 Примеры на английском языке
Положительная степень 20 Примеры на английском языке
Положительная степень 20 Примеры
В этом уроке мы внимательно рассмотрим предмет под названием «Примеры положительной степени 20». Для описания, количественной оценки, изменения или определения существительных / местоимений используются или повторно используются прилагательные. У прилагательных есть степени, называемые степенями прилагательных или степенями сравнения, которые сравнивают одну вещь / человека с другой.
Прилагательные имеют 3 степени сравнения- Положительная степень прилагательных
- Сравнительная степень прилагательных
- Превосходная степень прилагательных
- Положительная степень - Кот быстро бегает.

- Сравнительная степень - кошка бегает быстрее собак.
- Превосходная степень - кошка бегает быстрее всех животных.
Правила степени сравнения
1.После сравнения двух предметов / людей в сравнительной степени используется слово «эр» по отношению к прилагательному слову в ассоциации со словом «чем». В некоторых случаях используется «больше».
Пример сравнительной степени
- Она умнее своей сестры.
- Она веселее своей сестры.
Точно так же, когда сравниваются две вещи / люди, используется превосходная степень, добавляя «эст» к прилагательному слову, или в некоторых случаях употребляется «большинство».
Превосходная степень сравнения примеров
- Сильнейший борец.
- Он самый красивый актер.
- «Больше» используется, когда вы сравниваете качества одной вещи / человека. даже если первичное прилагательное могло быть односложным словом.

Степень сравнения примеров
- Неправильно - Она умнее умницы.
- Правильно - Она разумнее, чем умен.
- Не используйте двойные сравнительные прилагательные или превосходные прилагательные.
Степень сравнения примеров
- Неправильно - Эти яблоки вкуснее этих.
- Правильно - эти яблоки вкуснее тех.
- Есть некоторые прилагательные, которые относятся к «к», вроде, ниже, предпочтительнее, предпочитаю, старший. не используйте "чем" с этими прилагательными.
Степень примеров прилагательных
- Неправильно: я старше ее.
- Правильно: я старше ее.
- Неправильно - эта автомобильная марка превосходит эту.
- Правильно - эта автомобильная марка превосходит эту.
- При сравнении двух вещей должно быть сходство, то есть похожие вещи следует сравнивать.
Примеры степени сравнения
- Неправильно - этот цвет стены более красивый, чем предыдущий.
 (цвет стены сравнивается со стеной)
(цвет стены сравнивается со стеной) - Правильно - этот цвет стены красивее, чем предыдущий. (сравните цвет стены с цветом стены)
- Когда сравнительная степень используется в превосходном смысле степени
Используйте слово «любой другой» при сравнении объекта / человека из той же группы.
Пример степени сравнения
- Неправильно: Рина умнее любого ученика в своей категории.
- Верно: Рина умнее любого другого ученика в своей категории.
Используйте «любое», если сравнение вещей / человека не входит в группу.
- Неправильно: Дели чище, чем другие города Бангладеша.
- Правильно: любой другой город чище, чем любой город в Бангладеш.
- Чтобы указать, является ли различие между сравниваемым предметом / человеком маленьким или огромным, мы склонны использовать квантификаторы для сравнительной степени прилагательного, например (Немного, немного, много, далеко, много, отличная сделка).
 , значительно и т. д.).
, значительно и т. д.).
Пример:
- Мой хостел лишь ненамного больше вашего.
- Она могла быть немного более стандартной, чем ее сестра в их колледже.
- Австралия немного меньше континента.
Мы не используем количественные показатели с превосходной степенью прилагательных, однако есть определенные фразы, которые обычно используются с превосходной степенью сравнения.
Степень сравнения Пример
- В развитых городах метро - самый дешевый вид транспорта.
- Этот язык - один из старейших в мире.
- Этот шедевр является вторым по богатству храмом азиатской страны.
- Принимая во внимание динамическую степень сравнения неправильных прилагательных, слово полностью изменяется, а не добавляет «эр» или «эст».
Примеры:
- У нее в банке мало молока.
- У нее меньше молока, чем у него.
Наречий степени | EF
Наречия степени говорят нам об интенсивности чего-то. Наречия степени обычно помещаются перед прилагательным, наречием или глаголом, которые они модифицируют, хотя есть некоторые исключения. Слова «слишком», «достаточно», «очень» и «чрезвычайно» являются примерами наречий степени.
Наречия степени обычно помещаются перед прилагательным, наречием или глаголом, которые они модифицируют, хотя есть некоторые исключения. Слова «слишком», «достаточно», «очень» и «чрезвычайно» являются примерами наречий степени.
Проверьте свои знания
| Наречие степени | Изменение | Пример |
|---|---|---|
| очень | прилагательное | Вода была очень холодной. |
| довольно | прилагательное | Ролик довольно интересный. |
| всего | глагол | Он как раз уходил. |
| почти | глагол | Она почти закончила. |
| очень | наречие | Она очень быстро бежит. |
| тоже | наречие | Вы идете слишком медленно. |
| достаточно | наречие | Вы бежите достаточно быстро. |
Использование «достаточно»
Достаточно может использоваться как наречие и как определяющее.
Достаточно наречие
Достаточно того, что наречие, означающее «в необходимой степени», идет после прилагательного или наречия, которое оно модифицирует, а не перед ним, как это делают другие наречия. Его можно использовать как в положительных, так и в отрицательных предложениях.
Примеры
- Ваш кофе достаточно горячий ?
- Эта коробка не достаточно большая .
- Он работал недостаточно .
- Я попал сюда достаточно рано .
Достаточно часто следует за «до» + инфинитив.
Примеры
- Он недостаточно много работал , чтобы сдать экзамен .
- Ваш кофе достаточно горячий , чтобы пить ?
- Ей недостаточно , чтобы выйти замуж .

- Я приехал достаточно рано , чтобы подписаться на .
Достаточно может также сопровождаться словами «для кого-то» или «для чего-то».
Примеры
- Платье было достаточно большим для меня .
- У нее недостаточно опыта для этой работы .
- Кофе достаточно горячий для вас ?
- Он недостаточно много работал для повышения по службе .
Достаточно как определитель
Достаточно определителя, означающего «столько / сколько необходимо», перед существительным, которое оно модифицирует. Он используется с исчисляемыми существительными во множественном числе и с бесчисленными существительными.
Примеры
- Хлеба у нас хватит .
- У вас ребенка достаточно .
- У них не хватает еды .
- У меня не хватает яблок .

Использование "тоже"
«Слишком» - всегда наречие, но оно имеет два разных значения, каждое со своими особенностями использования.
Слишком много значит "также"
Слишком уж наречие, означающее «также», стоит в конце изменяемой фразы.
Примеры
- Я тоже хочу искупаться , если позволите.
- Могу я тоже пойти в зоопарк ?
- Мне этот подарок тоже ?
- Я не собираюсь убирать и твою комнату тоже !
Слишком много значит "чрезмерно"
Слишком уж наречие, означающее «чрезмерно», предшествует прилагательному или наречию, которое оно модифицирует. Его можно использовать как в утвердительных, так и в отрицательных предложениях.
Примеры
- Этот кофе слишком горячий .
- Он работает слишком много .
- Разве она не слишком молода ?
- Я не короче !
Слишком часто следует за «to» + инфинитив.
Примеры
- Кофе был слишком горячим для питья .
- Ты слишком молод , чтобы иметь внуков !
- Я не слишком устал , чтобы выйти сегодня вечером .
- Разве вы не слишком много работаете , чтобы у вас было свободное время ?
Также может сопровождаться словами «для кого-то» или «для чего-то».
Примеры
- Кофе был слишком горячим для меня .
- Платье было слишком маленьким для нее .
- Он не слишком стар для этой работы .
- Салли не слишком медленная для нашей команды .
Использование слова «очень»
Очень предшествует наречию или прилагательному, чтобы усилить его.
Примеры
- Девушка была очень красивой.
- Дом очень дорогой.
- Работал очень шустро.
- Она очень быстро бегает.

Если мы хотим образовать отрицательную форму прилагательного или наречия, мы можем добавить «не» к глаголу, мы можем использовать прилагательное или наречие противоположного значения, или мы можем использовать «не очень» с исходным прилагательным или наречием. . Значения фраз не идентичны. Обычно фраза, в которой используется слово «не очень», менее прямолинейна и, следовательно, более вежлива, чем другие фразы.
Примеры
| Исходная фраза | Противоположное значение с "не" | Значение, противоположное слову «не очень» | Противоположное значение с противоположным словом |
|---|---|---|---|
| Девушка была красивой. | Девушка не была красивой. | Девушка была не очень красивой. | Девушка была уродливой. |
| Работал быстро. | Он не работал быстро. | Работал не очень быстро. | Работал медленно. |
Разница в значении между "очень" и "слишком"
Значения «слишком» и «очень» сильно различаются. «Очень» выражает факт, а «слишком» предполагает наличие проблемы.
«Очень» выражает факт, а «слишком» предполагает наличие проблемы.
Примеры
- Он говорит очень быстро .
- Он говорит слишком быстро , чтобы я мог понять.
- Это очень жарко на улице.
- Слишком жарко на улице гулять.
Другое употребление наречий, например, "очень"
Некоторые общеупотребительные наречия используются так же, как «очень», чтобы усилить степень прилагательных и наречий.
| Выражение очень сильных чувств | Выражение сильных чувств | Выражение несколько сомнительных чувств |
|---|---|---|
| чрезвычайно, ужасно, удивительно, чудесно, безумно | особенно, особенно, необычно, необычно, замечательно, совсем | красиво, скорее, честно, не особо, не особо |
| Ролик получился потрясающе интересным. | Фильм получился особенно интересным. | Ролик получился довольно интересным. |
| Прекрасно пела. | Она необычайно хорошо спела. | Она неплохо спела. |
| Лекция была ужасно скучной. | Лекция была довольно скучной. | Лекция была довольно скучной. |
Обращение с отрицательными наречиями
Обычно подлежащее ставится перед глаголом, однако некоторые отрицательные наречия могут вызывать инверсию, если помещены в начало предложения.Порядок обратный, глагол ставится перед подлежащим. Эта инверсия используется только в письменной форме, а не в устной речи.
| Наречие | Нормальный порядок слов | инверсия |
|---|---|---|
| Никогда | Я никогда не видел такой смелости. | Никогда я не видел такого мужества. |
| Редко | Она редко выходила из дома. | Редко она выходила из дома . |
| Не только | Она не только готовила, но и убирала. | Она не только готовила, но и убирала. |
| Вряд ли | Едва я закрыл дверь, как он заговорил. | Едва я закрыл дверь, как он заговорил. |
| Редко | Мы редко переходим реку после захода солнца. | Редко мы пересекаем закат реки. |
Проверьте свои знания
| A.A.C.C. | Ассистент гуманитарных наук по основной учебной программе или А.А. в основной учебной программе (XYZ Pathway) Путь XYZ (A.A.) | UNG предлагает младшего специалиста по гуманитарным наукам по основной учебной программе с подготовительными курсами, связанными с политологией. Путь политологии... |
| A.A.S.P.S. | Ассоциированный специалист по прикладным наукам в области параюридических исследований | UNG предлагает A. Программа параюридических исследований ... |
| A.S.C.C. | Научный сотрудник по основной учебной программе Научный сотрудник по основной учебной программе (XYZ Pathway) Путь XYZ (A.S.) | UNG предлагает степень младшего научного сотрудника по основной учебной программе (курс политологии). Биологический путь ... |
| B.A. | Art Major с концентрацией цифрового искусства (BA) Бакалавр искусств со специализацией в искусстве и со специализацией в области цифровых искусств Бакалавр искусств со специализацией в искусстве (концентрация цифровых искусств) Art Major с концентрацией цифрового искусства (BA) Бакалавр искусств со специализацией в искусстве и со специализацией в графическом дизайне Бакалавр искусств со специализацией в искусстве (концентрация на графическом дизайне) | UNG предлагает степень бакалавра искусств со специализацией в искусстве в кампусе Далонега. UNG предлагает степень бакалавра искусств. со специализацией в искусстве и концентрацией в цифровых искусствах. Концентрация в области цифрового искусства подготавливает специалистов в области искусства к созданию инновационных дизайнов с использованием передовых инструментов. |
| B.A. | Специальность по коммуникации с концентрацией мультимедийной журналистики (бакалавр) Бакалавр гуманитарных наук со специализацией в области коммуникации и мультимедийной журналистикой Бакалавр искусств со специализацией в области коммуникации (концентрация организационного лидерства) | UNG предлагает степень бакалавра искусств со специализацией в области коммуникации и мультимедийной журналистикой в кампусе Гейнсвилля. Концентрация в мультимедийной журналистике ... Специалисты в области коммуникаций, которые сосредоточены на лидерстве в организации ... |
B. A. A. | Исследования Восточной Азии (бакалавриат) Бакалавр искусств со специализацией в восточноазиатских исследованиях | UNG предлагает степень бакалавра искусств со специализацией в восточноазиатских исследованиях. |
| B.A. | Английский язык со специализацией в литературе (Б.А.) Бакалавр искусств со специализацией на английском языке и литературой Бакалавр искусств со специализацией по английскому языку (письменная и издательская деятельность) Английский язык (бакалавриат) с сертификатом учителя | UNG предлагает степень бакалавра искусств со специализацией на английском языке. UNG предлагает степень бакалавра искусств. со специализацией по английскому языку и литературой. UNG предлагает степень бакалавра искусств. со специализацией по английскому языку и писательской и издательской специализацией. |
B. A. A. | История (BA) Бакалавр искусств по специальности история История (бакалавр) с сертификатом учителя Бакалавр искусств со специализацией в истории и аттестат учителя | UNG предлагает степень бакалавра искусств со специализацией в истории. |
| B.A. | Международные отношения (BA) Бакалавр гуманитарных наук по специальности "Международные отношения" | UNG предлагает степень бакалавра искусств со специализацией в международных делах. Бакалавриат по международным отношениям ... |
| B.A. | Специальность по современным языкам с концентрацией арабского языка и литературы (бакалавр) Бакалавр искусств со специализацией в современных языках и со специализацией в арабском языке и литературе Специалист по современным языкам с концентрацией китайского языка и литературы (бакалавр) Бакалавр искусств со специализацией в современных языках и со специализацией в китайском языке и литературе Бакалавр гуманитарных наук со специализацией в современных языках и концентрацией на китайском языке для специалистов со всего мира Современные языки с концентрацией французского языка и литературы (B. Бакалавр искусств со специализацией в современных языках и со знанием французского языка и литературы Специальность по современным языкам с французским и деловым акцентом (бакалавр) Бакалавр гуманитарных наук со специализацией в современных языках с концентрацией на французском языке и упором на бизнес Бакалавр искусств по специальности «Современные языки» и со специализацией «Русский язык и литература» Бакалавр искусств со специализацией в современных языках и со специализацией в испанском языке и литературе Бакалавр искусств со специализацией в современных языках с концентрацией на испанском языке и упором на бизнес | UNG предлагает степень бакалавра искусств со специализацией в современных языках. |
| B.A. | Музыка (бакалавр) Бакалавр искусств по специальности музыка | UNG предлагает степень бакалавра искусств со специализацией в музыке. |
| B.A. | Исследования в области стратегии и безопасности (бакалавриат) Бакалавр гуманитарных наук со специализацией в области стратегии и безопасности | UNG предлагает степень бакалавра искусств со специализацией в области стратегии и безопасности. B.A. со специализацией в программе стратегических исследований и исследований в области безопасности ... Студенты, изучающие стратегии и безопасность ... |
| B.A.S. | Параюридические исследования (бакалавриат) Бакалавр прикладных наук со специализацией в параюридических исследованиях | UNG предлагает степень бакалавра прикладных наук со специализацией в области параюридических исследований. |
| B.A.S. | Управление технологиями (Б.А.С.) Бакалавр прикладных наук по специальности «Менеджмент технологий» | UNG предлагает степень бакалавра прикладных наук со специализацией в области управления технологиями. Специальности в области управления технологиями ... |
| B.B.A. | Информационные системы (B.B.A.) Бакалавр делового администрирования по специальности "Информационные системы" | UNG предлагает степень бакалавра делового администрирования со специализацией в информационных системах. |
| B.B.A. | Бухгалтерский учет (B.B.A.) Бакалавр делового администрирования со специализацией в области бухгалтерского учета | UNG предлагает степень бакалавра делового администрирования со специализацией в области бухгалтерского учета. |
| B.B.A. | Финансы (B.B.A.) Бакалавр делового администрирования со специализацией в области финансов | UNG предлагает степень бакалавра делового администрирования со специализацией в области финансов. |
| B.B.A. | Менеджмент (B. Бакалавр делового администрирования по специальности менеджмент | UNG предлагает степень бакалавра делового администрирования со специализацией в менеджменте. |
| B.B.A. | Маркетинг (B.B.A) Бакалавр делового администрирования со специализацией в маркетинге | UNG предлагает степень бакалавра делового администрирования со специализацией в маркетинге. |
| B.F.A.D.T.T. | Дизайн и технологии для театра (B.F.A.) Бакалавр изящных искусств в области дизайна и технологий театра | UNG предлагает степень бакалавра изящных искусств в области дизайна и технологий для театра. |
| B.F.A. | Изобразительное искусство (B.F.A.) Бакалавр изящных искусств со специализацией «Визуальные искусства» | UNG предлагает степень бакалавра изящных искусств со специализацией в изобразительном искусстве. Диплом по изобразительному искусству ... Изобразительное искусство B.F.A. градус ... |
| B.S. | Художественное образование (бакалавриат) Бакалавр наук по специальности «Художественное образование» | UNG предлагает степень бакалавра наук со специализацией в области художественного образования. |
| B.S. | Арт-маркетинг (бакалавриат) Бакалавр наук по специальности арт-маркетинг | UNG предлагает степень бакалавра наук по специальности арт-маркетинг. |
| B.S. | Биология (бакалавриат) Бакалавр наук по специальности биология | UNG предлагает степень бакалавра наук со специализацией в биологии. |
| B.S. | Программа двойного диплома в области химического машиностроения (бакалавриат) Бакалавр наук по программе двойного диплома по химической инженерии | UNG предлагает программу двойной степени бакалавра наук со специализацией в области химического машиностроения. |
| B.S. | Химия (бакалавриат) Бакалавр наук по специальности химия Специальность по химии с концентрацией биохимии (B.S) Бакалавр наук со специализацией в области химии и концентрацией в области биохимии Специальность по химии с концентрацией химической физики (B.S.) Бакалавр наук по специальности «химия» и со специализацией «химическая физика» | UNG предлагает степень бакалавра наук по специальности химия. |
| B.S. | Компьютерные науки (бакалавриат) Бакалавр наук по специальности «Компьютерные науки» | UNG предлагает степень бакалавра наук со специализацией в области компьютерных наук. |
| B.S. | Уголовное правосудие (B.S.) Бакалавр наук со специализацией в области уголовного правосудия Майор уголовного правосудия с концентрацией криминалистики (Б.С.) Бакалавр наук со специализацией в области уголовного правосудия и специализацией в области судебной медицины | UNG предлагает степень бакалавра наук со специализацией в области уголовного правосудия. |
| B.S. | Начальное и специальное образование (бакалавриат) Бакалавр наук по специальности «Начальное и специальное образование» | UNG предлагает степень бакалавра наук со специализацией в области начального и специального образования. |
| B.S. | Экологический пространственный анализ (B.S.) Бакалавр наук со специализацией в области пространственного анализа окружающей среды | UNG предлагает степень бакалавра наук со специализацией в области пространственного анализа окружающей среды. |
| B.S. | Общие исследования (бакалавриат) Бакалавр наук по специальности "Общие исследования" | UNG предлагает степень бакалавра наук со специализацией в области общих исследований. |
| B.S. | Управление здравоохранения и информатики (B.S.) Бакалавр наук по специальности «Управление здравоохранением и информатикой» | UNG предлагает основные услуги в области здравоохранения и администрирования информатики. |
| B.S. | Предоставление социальных услуг и администрирование (B.S) Бакалавр наук со специализацией в сфере предоставления социальных услуг и администрирования | UNG предлагает степень бакалавра наук со специализацией в области предоставления и администрирования социальных услуг. |
| B.S. | Кинезиология (бакалавриат) Бакалавр наук по специальности кинезиология Специальность по кинезиологии с концентрацией на науке о физических упражнениях (B.S.) Бакалавр наук со специализацией в кинезиологии со специализацией в науке о физических упражнениях Специальность по кинезиологии с концентрацией здоровья и фитнеса (B.S.) Бакалавр наук со специализацией в области кинезиологии со специализацией в области здоровья и фитнеса Специальность по кинезиологии со спортивной медициной (B.С.) Бакалавр наук со специализацией в кинезиологии со специализацией в спортивной медицине Кинезиология (бакалавриат) с сертификатом учителя Бакалавр наук по специальности кинезиология (с аттестацией учителя) | UNG предлагает степень бакалавра наук по специальности кинезиология. |
| B.S. | Математика (бакалавриат) Бакалавр наук по специальности математика Математика (B.S.) с сертификатом учителя Бакалавр наук по специальности математика (с аттестацией учителя) | UNG предлагает степень бакалавра наук со специализацией в математике. |
| B.S. | Программа двойного диплома по математике и инженерии (бакалавриат) Бакалавр наук со специализацией в области математики и инженерии Программа двойного диплома | UNG предлагает программу двойной степени бакалавра наук по математике и инженерии. |
| B.S. | Среднее образование (бакалавриат) Бакалавр наук со специализацией в средних классах | UNG предлагает степень бакалавра наук со специализацией в средних классах образования. |
| B.S. | Музыкальное образование (бакалавриат) Бакалавр наук по специальности «Музыкальное образование» Музыкальное образование с хоровым треком (Б. Бакалавр наук по специальности «Музыкальное образование» (хоровой трек) Специальность по музыкальному образованию с инструментальной музыкой (B.S.) Бакалавр наук по специальности «Музыкальное образование» (Инструментальная композиция) | UNG предлагает степень бакалавра наук со специализацией в области музыкального образования. UNG предлагает степень бакалавра наук со специализацией в области музыкального образования (хоровой трек). |
| Б.С. | Физика (бакалавриат) Бакалавр наук по специальности физика | UNG предлагает степень бакалавра наук по специальности физика. |
| B.S. | Программа двойного диплома по физике и инженерии (бакалавриат) Бакалавр наук со специализацией в области физики и инженерии Программа двойного диплома | UNG предлагает программу двойной степени бакалавра наук по специальностям физика и инженерия. |
| B.S. | Политология (бакалавр наук) Бакалавр наук по специальности «Политология» Политология с концентрацией на американской политике (B.S.) Бакалавр наук со специализацией в области политологии со специализацией в американской политике Политология с предзаконной концентрацией (B.S.) Бакалавр наук со специализацией в области политологии с концентрацией на предварительном праве | UNG предлагает степень бакалавра наук со специализацией в области политологии. |
| B.S. | Психология (бакалавр наук) Бакалавр наук по специальности психология | UNG предлагает степень бакалавра наук со специализацией в области психологии. |
| B.S. | Социология (бакалавриат) Бакалавр наук по специальности социология | UNG предлагает степень бакалавра наук со специальностью социология. |
| Б.С. | Среднее образование (бакалавриат) Бакалавр наук со средним образованием | UNG предлагает степень бакалавра наук со специализацией в среднем образовании. |
| B.S.F.D.M. | Кино и цифровые медиа (B.S.) Бакалавр наук в области кино и цифровых медиа Специальность «Кино и цифровые медиа», специализирующаяся на изучении медиа (B.С.) Бакалавр наук в области кино и цифровых медиа со специализацией в медиа исследованиях Крупнейшая компания в сфере кино и цифровых медиа с производственной концентрацией (B.S.) Бакалавр наук в области кино и цифровых медиа с концентрацией в производстве | UNG предлагает степень бакалавра наук в области кино и цифровых медиа. UNG предлагает степень бакалавра наук в области кино и цифровых медиа с концентрацией в производстве. |
| BSN | Бакалавр сестринского дела | UNG предлагает степень бакалавра наук по сестринскому делу. |

 СК 1
2280194 Это шесть градуса ниже нуля. _undertoad 1
315365 Имеет степень по биологии. СК 1
73477 У меня температура 102 градуса . СК 1
2892807 Где вы получили степень ? СК 1
241851 Сейчас десять градуса ниже нуля. СК 1
3024108 Сегодня в Бостоне было 36 градуса градуса. СК 1
2641664 У Тома нет диплома .СК 1
2331901 У меня было два года, чтобы получить степень . СК 1
1025499 Том имеет степень по музыкальному образованию. СК 1
680652 Том получит лучшую работу с высшим образованием , степень . Source_VOA 1
1893798 Нам не удалось выяснить, где Том получил степень . СК 1
1545343 Том работает уборщиком, несмотря на то, что имеет высшее образование , степень . Спамстер 1
2655081 Прошлой ночью температура опустилась до десяти градуса ниже нуля. СК 1
2655082 Прошлой ночью температура упала до минус десяти градуса градуса по Цельсию.СК 1
2543997 Том имеет четырехлетнюю степень .
СК 1
2280194 Это шесть градуса ниже нуля. _undertoad 1
315365 Имеет степень по биологии. СК 1
73477 У меня температура 102 градуса . СК 1
2892807 Где вы получили степень ? СК 1
241851 Сейчас десять градуса ниже нуля. СК 1
3024108 Сегодня в Бостоне было 36 градуса градуса. СК 1
2641664 У Тома нет диплома .СК 1
2331901 У меня было два года, чтобы получить степень . СК 1
1025499 Том имеет степень по музыкальному образованию. СК 1
680652 Том получит лучшую работу с высшим образованием , степень . Source_VOA 1
1893798 Нам не удалось выяснить, где Том получил степень . СК 1
1545343 Том работает уборщиком, несмотря на то, что имеет высшее образование , степень . Спамстер 1
2655081 Прошлой ночью температура опустилась до десяти градуса ниже нуля. СК 1
2655082 Прошлой ночью температура упала до минус десяти градуса градуса по Цельсию.СК 1
2543997 Том имеет четырехлетнюю степень . СК
270781 Вода закипает при 100 градусах . СК
20595 Согласен с вами в степени . СК
430025 У меня температура 38,9 градуса . Витброк
633583 Я получил высшее образование , степень . СМ
251396 Моя температура 38 градуса . СК
680358 Это тридцать градусов ниже нуля. Source_VOA
303656 Имеет степень магистра по праву . СК
249258 В какой степени мы можем ему доверять? СК
278236 Прямой угол составляет девяносто градуса .Неро
680650 Мэри получит степень в июне. Source_VOA
310345 Ей можно доверять до какой-то степени . СК
1422370 Сегодняшний минимум составил 3 градуса Цельсия. СК
270789 Вода закипает при 100 градусах Цельсия. СК
3070805 Я вас понимаю до определенной степени . Patgfisher
20351 Температура упала на несколько градусов . СК
2959115 Температура упала на десять градуса . острозубый
2662350 Температура поднялась до 30 градусов .острозубый
270776 Вода замерзает при 0 градусах Цельсия.
СК
270781 Вода закипает при 100 градусах . СК
20595 Согласен с вами в степени . СК
430025 У меня температура 38,9 градуса . Витброк
633583 Я получил высшее образование , степень . СМ
251396 Моя температура 38 градуса . СК
680358 Это тридцать градусов ниже нуля. Source_VOA
303656 Имеет степень магистра по праву . СК
249258 В какой степени мы можем ему доверять? СК
278236 Прямой угол составляет девяносто градуса .Неро
680650 Мэри получит степень в июне. Source_VOA
310345 Ей можно доверять до какой-то степени . СК
1422370 Сегодняшний минимум составил 3 градуса Цельсия. СК
270789 Вода закипает при 100 градусах Цельсия. СК
3070805 Я вас понимаю до определенной степени . Patgfisher
20351 Температура упала на несколько градусов . СК
2959115 Температура упала на десять градуса . острозубый
2662350 Температура поднялась до 30 градусов .острозубый
270776 Вода замерзает при 0 градусах Цельсия. СК
681014 Вода замерзает при нуле градуса Цельсия. Source_VOA
299850 Имеет степень доктора психологии . СК
270784 Вода замерзает при 32 градусах Фаренгейта. СК
2268588 Температура упала на три градуса . _undertoad
680653 В каждой работе степени стресса. Source_VOA
248928 Мы знаем, что вода закипает при 100 градусах . СМ
310174 Три года назад получила степень магистра .СК
1482467 Я получаю степень магистра по специальности . Weihaiping
242172 Сегодня утром было десять градуса ниже нуля. СК
59135 Эта работа требует высокого мастерства степени . СМ
2318383 Три года назад получила степень магистра . СК
681825 Цель Тома в колледже - получить степень . Source_VOA
3039950 Тому предъявлено обвинение в убийстве первой степени . СК
72301 Угол в 90 градуса называется прямым углом.СМ
486480 Наш учитель сказал: «Вода закипает при 100 градусах ». СК
271593 Точная температура составляет 22,68 градуса Цельсия.
СК
681014 Вода замерзает при нуле градуса Цельсия. Source_VOA
299850 Имеет степень доктора психологии . СК
270784 Вода замерзает при 32 градусах Фаренгейта. СК
2268588 Температура упала на три градуса . _undertoad
680653 В каждой работе степени стресса. Source_VOA
248928 Мы знаем, что вода закипает при 100 градусах . СМ
310174 Три года назад получила степень магистра .СК
1482467 Я получаю степень магистра по специальности . Weihaiping
242172 Сегодня утром было десять градуса ниже нуля. СК
59135 Эта работа требует высокого мастерства степени . СМ
2318383 Три года назад получила степень магистра . СК
681825 Цель Тома в колледже - получить степень . Source_VOA
3039950 Тому предъявлено обвинение в убийстве первой степени . СК
72301 Угол в 90 градуса называется прямым углом.СМ
486480 Наш учитель сказал: «Вода закипает при 100 градусах ». СК
271593 Точная температура составляет 22,68 градуса Цельсия. СК
СК
 (Драматург Оскар Уайльд)
(Драматург Оскар Уайльд) (Комик Джордж Карлин)
(Комик Джордж Карлин) , красивее ) или в превосходной степени (например, лучше всего ). Это серьезная ошибка.
, красивее ) или в превосходной степени (например, лучше всего ). Это серьезная ошибка. Д. (Неправильные прилагательные)
Д. (Неправильные прилагательные)




 (цвет стены сравнивается со стеной)
(цвет стены сравнивается со стеной) , значительно и т. д.).
, значительно и т. д.).


 A.S. в Параюридических исследованиях.
A.S. в Параюридических исследованиях.
 А.)
А.)
 B.A.)
B.A.)
 С.)
С.)