11. Кинетическая энергия частицы и системы частиц. Связь кинетической энергии системы с работой действующих на нее сил.

Кинетическая энергия механической системы — это энергия механического движения этой системы.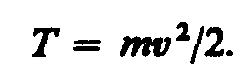

(12.1)

Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.

Кинетической энергией системы называется скалярная величина Т, равная арифметиче­ской сумме кинетических энергий всех точек системы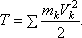

Кинетическая энергия является характеристикой и поступатель­ного и вращательного движения системы.

Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел: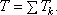

Кинетическая энергия – скалярная и всегда положительная величина.

1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости дви­жения центра масс. То есть, для любой точки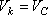

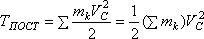
2. Кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. 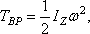От направления вращения значениеТ не зависит.

Если — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как: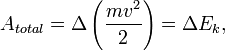

где 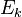называется кинетической энергией. Т.е. работа равна изменению кинетической энергии.

12. Кинетическая энергия и работа при вращении твердого тела.

Кинетическая энергия вращения твердого тела

Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси 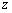, проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами

, находящиеся на расстоянииот оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы ма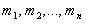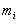ссамиопишут окружности различных радиусов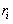и имеют различные линейные скорости. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова: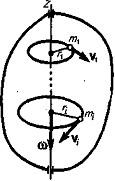

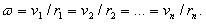                                       (1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов: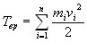

.

Используя выражение (1), получаем: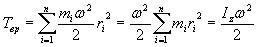

где 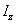– момент инерции тела относительно оси. При вращательном движении роль массы играет момент инерции, а роль линейной скорости – угловая скорость.

13.Консервативные и неконсервативные силы. Потенциальная энергия частицы и ее связь с силой поля.

Все силы, встречающиеся в механике , принято разделять на консервативные и неконсервативные.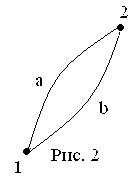

Сила, действующая на материальную точку, называется консервативной (потенциальной), если работа этой силы зависит только от начального и конечного положений точки. Работа консервативной силы не зависит ни от вида траектории, ни от закона движения материальной точки по траектории (см. рис. 2):

.

Изменение направления движения точки вдоль малого участка на противоположное вызывает изменение знака элементарной работы 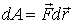, следовательно,. Поэтому работа консервативной силы вдоль замкнутой траектории 1a2b1 равна нулю: .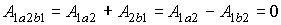

Точки 1и 2, а также участки замкнутой траектории 1a2 и 2b1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю: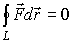

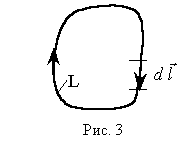
или

В этой формуле кружок на знаке интеграла показывает, что интегрирование производится по замкнутой траектории. Часто замкнутую траекторию L называют замкнутым контуром L (рис. 3). Обычно задаются направлением обхода контура L по ходу часовой стрелки. Направление элементарного вектора перемещения 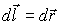совпадает с направлением обхода контураL. В этом случае формула (5) утверждает: циркуляция вектора по замкнутому контуру L равна нулю

.

Следует отметить, что силы тяготения и упругости являются консервативными, а силы трения неконсервативными. В самом деле, поскольку сила трения направлена в сторону, противоположную перемещению или скорости, то работа сил трения по замкнутому пути всегда отрицательна и, следовательно, не равна нулю.

studfile.net

Кинетическая энергия и энергия покоя частицы

В этой статье будем разгонять электроны в трубках, сообщая им кинетическую энергию, и определять их скорости, зная, какую долю от полной энергии составляет энергия покоя.

Задача 1. Кинетическая энергия электрона МэВ. Во сколько раз его релятивистская масса больше массы покоя? Сделать такой же подсчет для протона.

Переведем энергию в джоули:

   

Отношение масс для электрона равно:

   

Заметим, что . Тогда

   

Для протона:

   

Ответ: для электрона , для протона .

Задача 2. Найти скорость частицы, если ее кинетическая энергия составляет половину энергии покоя.

Полная энергия , так как по условию , то

   

   

   

   

Возводим в квадрат:

   

   

   

   

Ответ: м/с.

Задача 3. Найти скорость космической частицы, если ее полная энергия в 5 раз больше энергии покоя.

Задача решается полностью аналогично, решите ее сами. Ответ: м/с.

Задача 4. До какой кинетической энергии можно ускорить частицы в циклотроне, если относительное увеличение массы частицы не должно превышать % ? Задачу решить для электронов и протонов.

   

Откуда

   

Для электрона:

   

В эВ это

Для протона:

   

В эВ это , или 47 МэВ.

Ответ: для электрона  эВ, для протона 47 МэВ.
Задача 5. Максимальная скорость движения электронов в катодной трубке . Найти разность потенциалов между электродами.

Кинетическая энергия электрона равна разности его полной энергии и энергии покоя, а с другой стороны, сообщает эту энергию электрону поле, совершая работу, поэтому  :

   

   

   

   

   

На самом деле, проще было сразу приравнять:

   

   

   

Ответ: 410 В.

Задача 6. Электрон, ускоренный электрическим полем, приобрел скорость, при которой его полная энергия стала равна удвоенной энергии покоя. Чему равна ускоряющая разность потенциалов? Отношение заряда электрона к его массе Кл/кг.

Если , то кинетическая энергия равна энергии покоя:

   

Откуда

   

Задача 7. Какую ускоряющую разность потенциалов должен пройти протон, чтобы его продольные размеры стали меньше в раза?

По условию  релятивистское изменение длины:

   

Поэтому

   

   

   

   

Тогда

   

   

Ответ: В

 

easy-physic.ru

7.6. Кинетическая энергия релятивистской частицы

Определим эту величину таким же путём, как и в ньютоновской механике. Было доказано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:

.

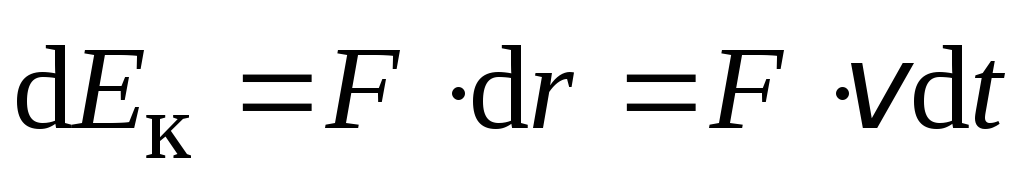Согласно основному закону релятивистской динамики

,

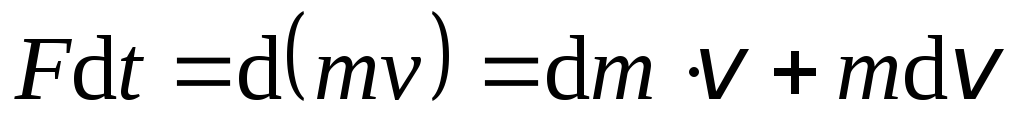где m – релятивистская масса. Поэтому

, (7.52)

где учтено, что 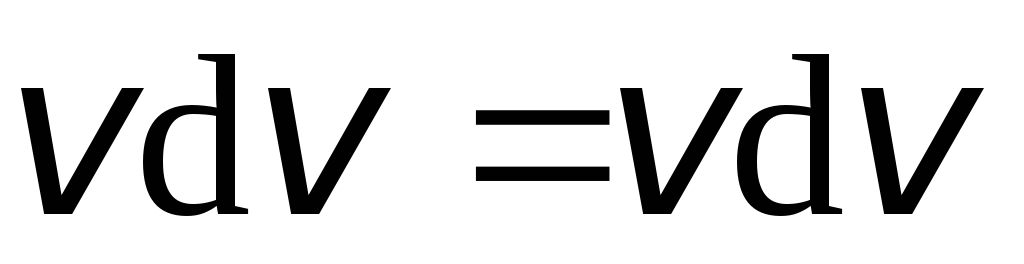и. Эту формулу можно упростить. Для этого формулу зависимости массы от скорости возведём в квадрат и риведём её к виду:m²c² = m^{2 2} + m₀²c².

Найдём дифференциал этого выражения, имея в виду, что m₀ и с – постоянные величины.

2 mc²dm = 2m²dm + 2 m²d.

Если теперь разделить это равенство на 2m, то его правая часть совпадёт с выражением для (7.52). Отсюда следует

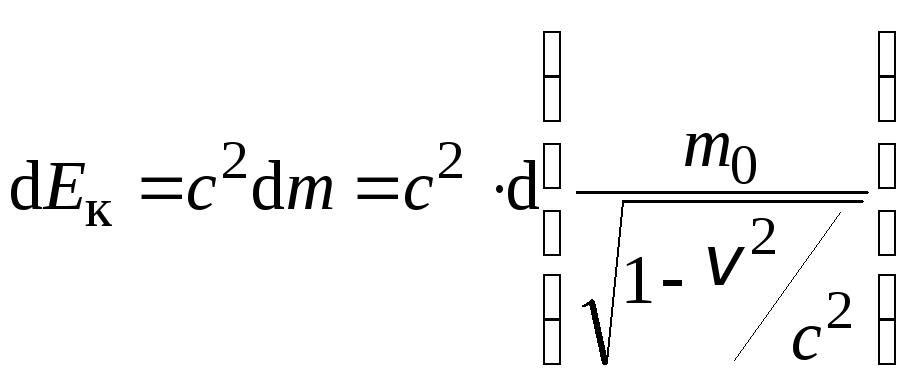. (7.53)

Таким образом, приращение кинетической энергии частицы пропорционально приращению её релятивистской массы.

Кинетическая энергия покоящейся частицы равна нулю, а её масса равна массе покоя m₀. Поэтому, проинтегрировав выражение (7.53), получаем

, (7.54)

или

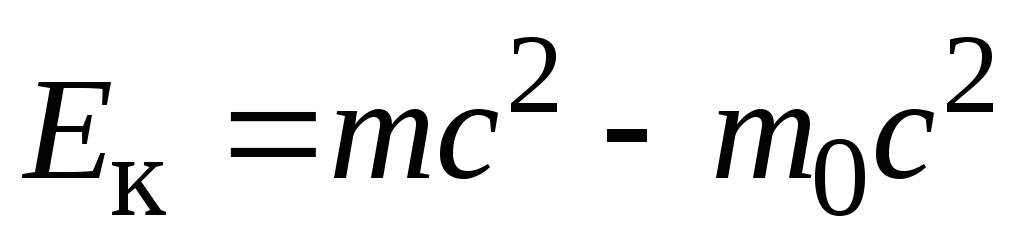; . (7.55)

Это и есть выражение для релятивистской кинетической энергии частицы. Как видно, оно сильно отличается от ньютоновского m₀²/2. Легко убедиться (пользуясь формулой бинома Ньютона), что при малых скоростях <<c, выражение (7.55) переходит в ньютоновское.

7.7. Закон взаимосвязи массы и энергии релятивистской частицы

Из формулы (7.53) следует, что приращение кинетической энергии частицы сопровождается пропорциональным приращением её релятивистской массы:

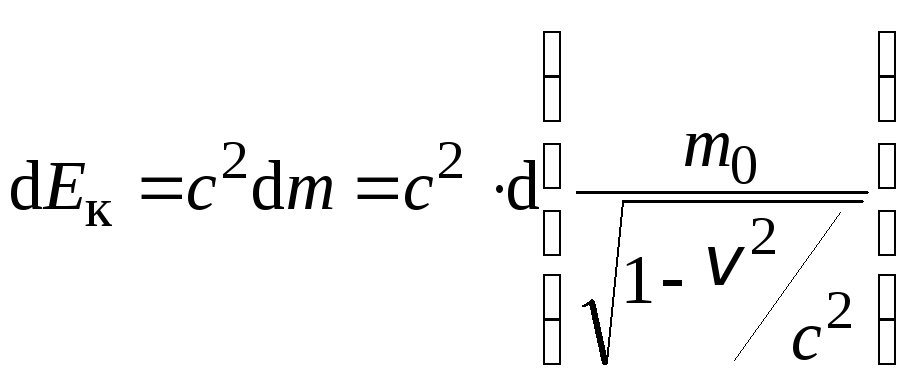, или ,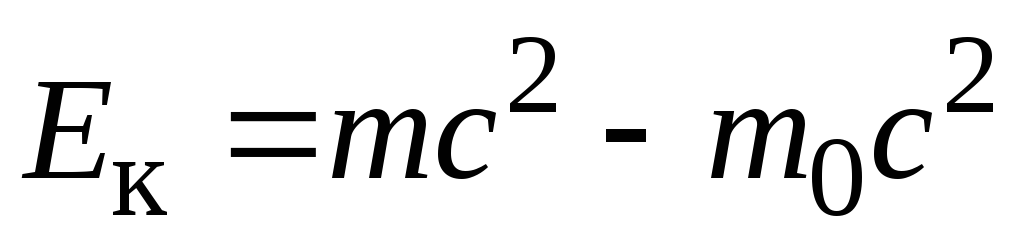

где 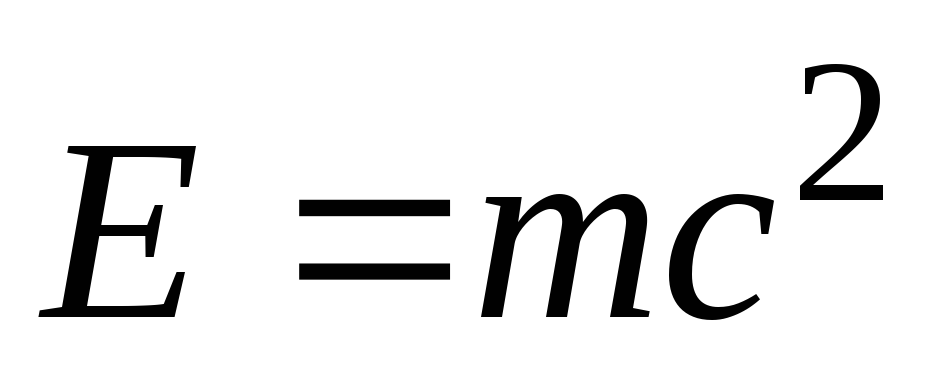– называют полной энергией тела, а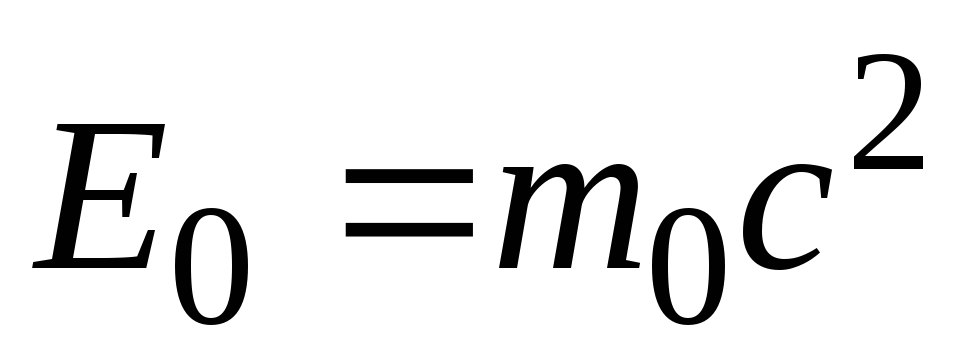– энергией покоя.

Эйнштейн пришёл к выводу, что масса тела будет вырастать не только при сообщении ему кинетической энергии, но и при увеличении общего запаса энергии (кинетической, электрической, тепловой, химической и т.д.). Полная энергия тела E связана с массой этого тела m соотношением

E = mc². (7.56)

Эта формула выражает один из наиболее фундаментальных законов природы – закон взаимосвязи (пропорциональности) массы и полной энергии тела.

Соотношение (7.56) можно записать и в другой форме:

E = m₀c² + 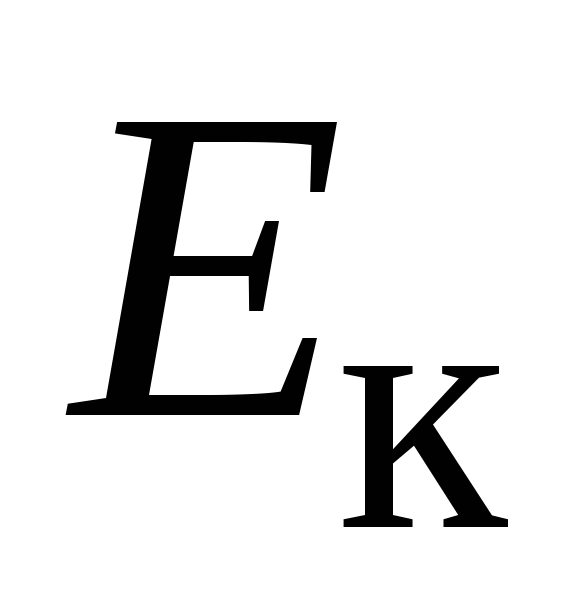, (7.57)

где m₀ – масса покоя тела; – его кинетическая энергия. Отсюда непосредственно следует, что покоящееся тело (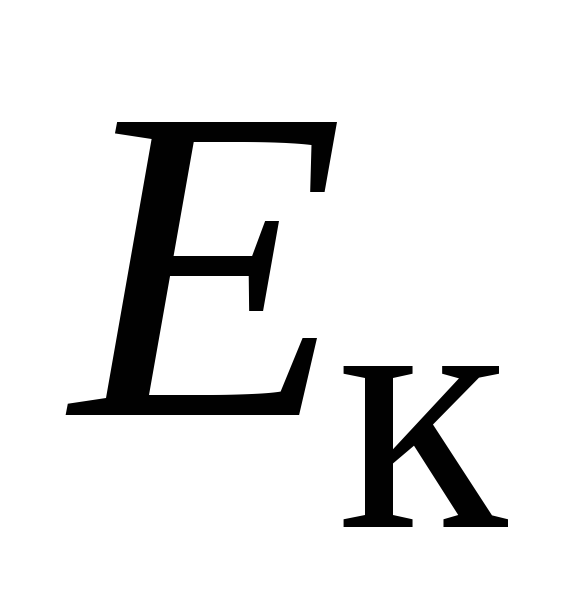= 0) также обладает энергией:

E₀= m₀c². (7.58)

Эту энергию называют энергией покоя.

Мы видим, что масса тела, которая в классической механике выступала как мера инертности (во втором законе Ньютона) теперь выступает в новой функции – как мера энергосодержания тела. Даже покоящееся тело, согласно теории относительности, обладает запасом энергии – энергией покоя.

Изменение полной энергии тела сопровождается эквивалентным изменением его массы 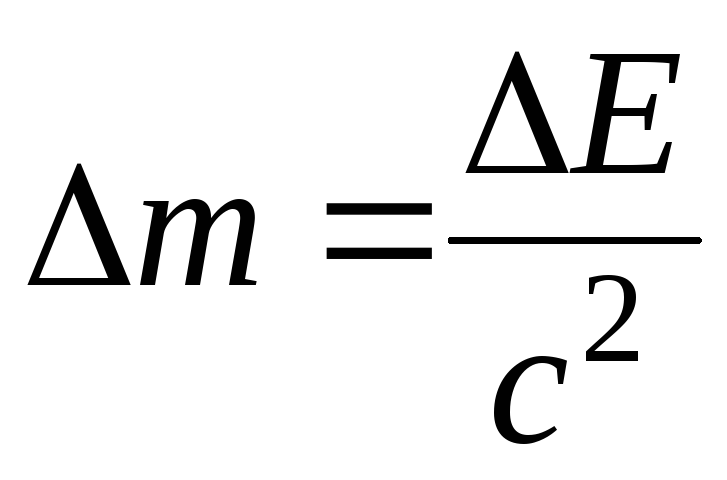и наоборот. При обычных макроскопических процессах изменение массы тела оказывается чрезвычайно малым, недоступным для измерений. Справедливость закона взаимосвязи массы и энергии экспериментально проверена в ядерной физике. Это обусловлено тем, что ядерные процессы и процессы превращения элементарных частиц сопровождаются весьма большими изменениями энергии, сравнимыми с энергией покоя самих частиц.

7.8. Связь полной энергии и импульса

Связь кинетической энергии и импульса в классической механике Ньютона выражается формулой 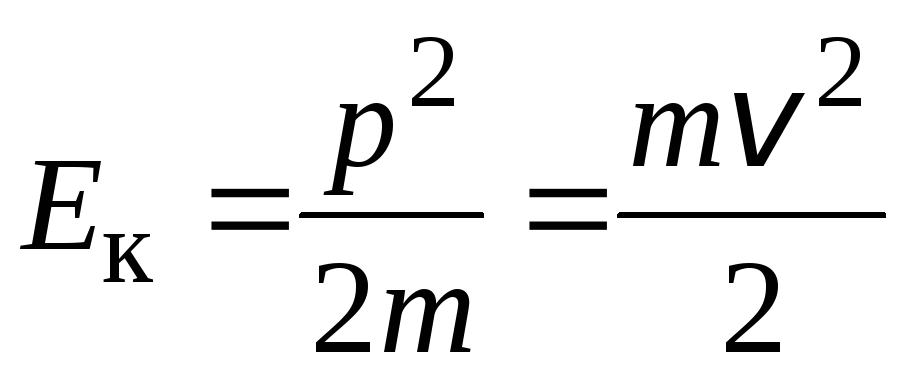, при этомm=m₀ =const. Если потенциальную энергию не учитываем, то полная энергия частицы равна её кинетической энергии, в этом случае .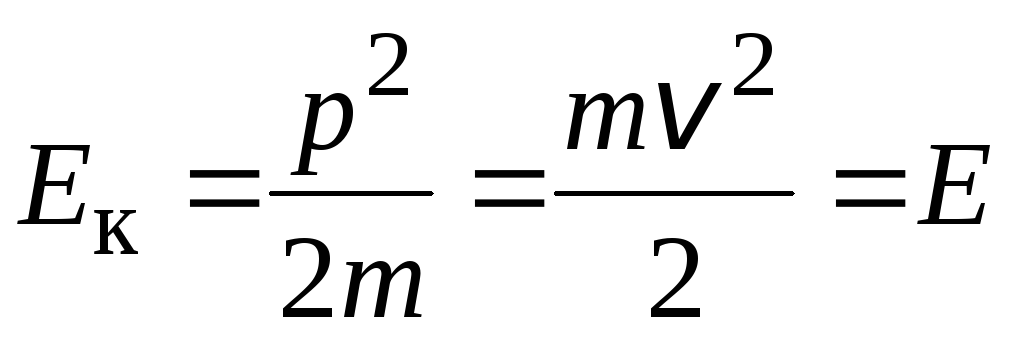

Найдем связь полной энергии и импульса для тела, движущегося со скоростью, близкой к скорости света:

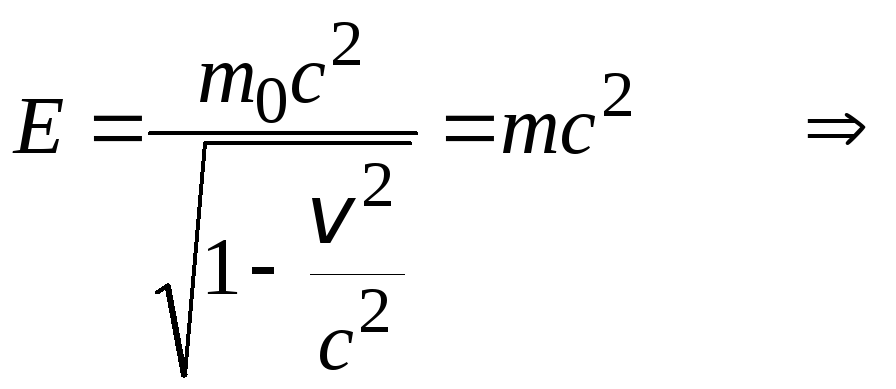
Преобразуем выражение (избавимся от квадратного корня):

.

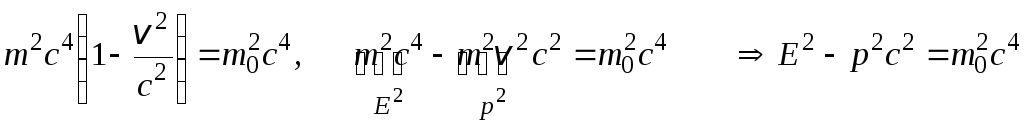Отсюда

(7.59)

studfile.net

3.7. Кинетическая энергия частицы в силовом поле.

П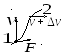

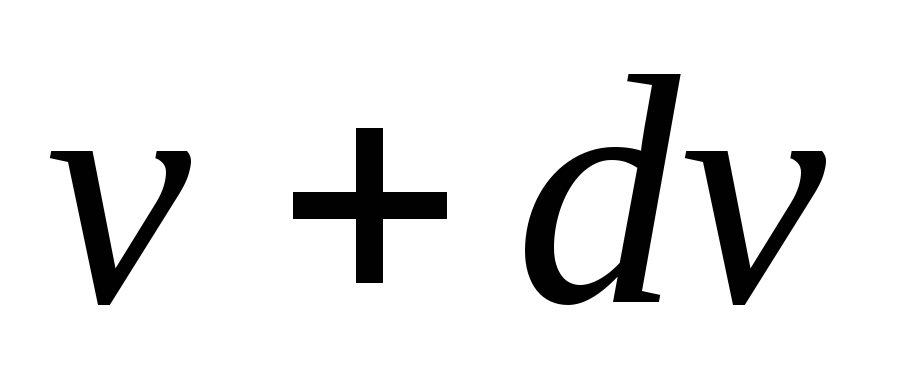
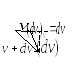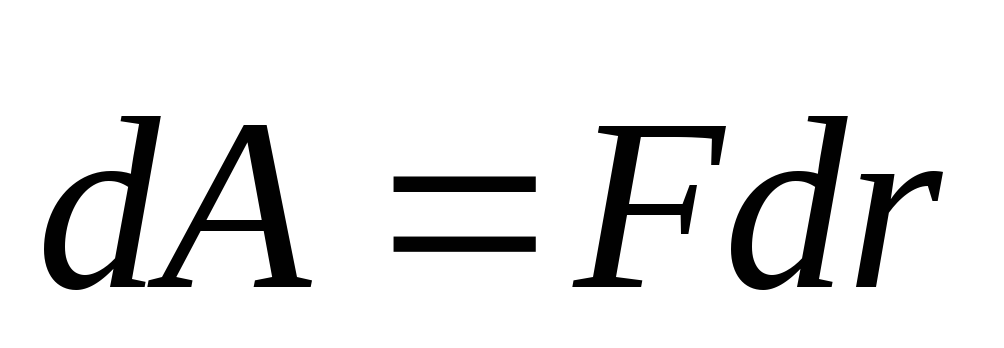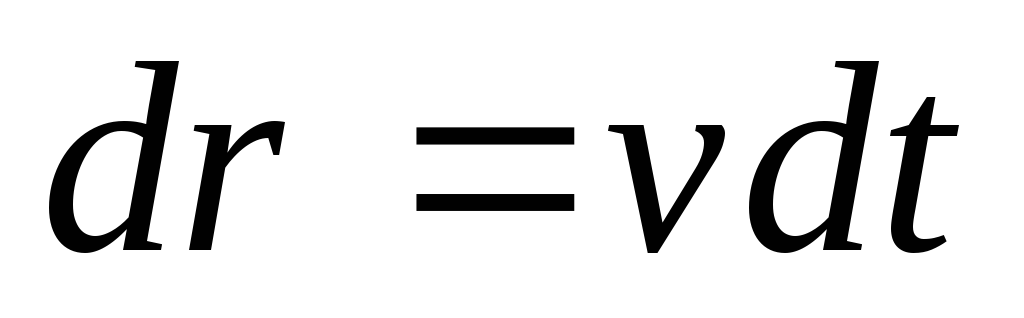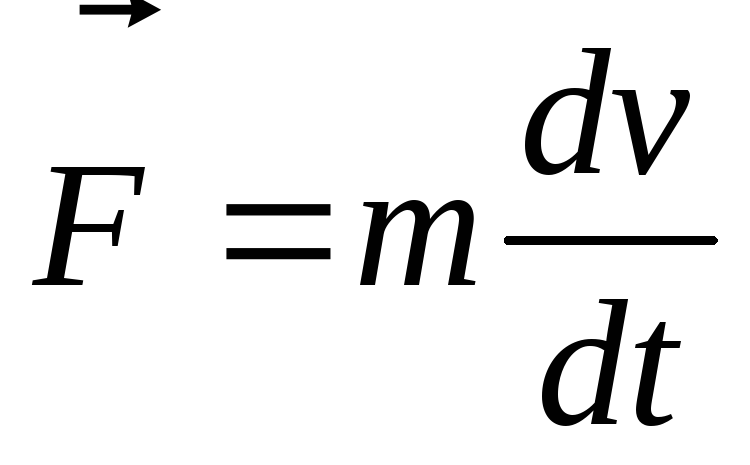
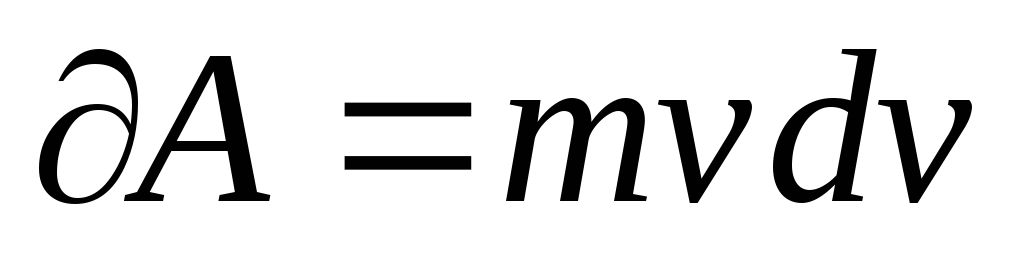
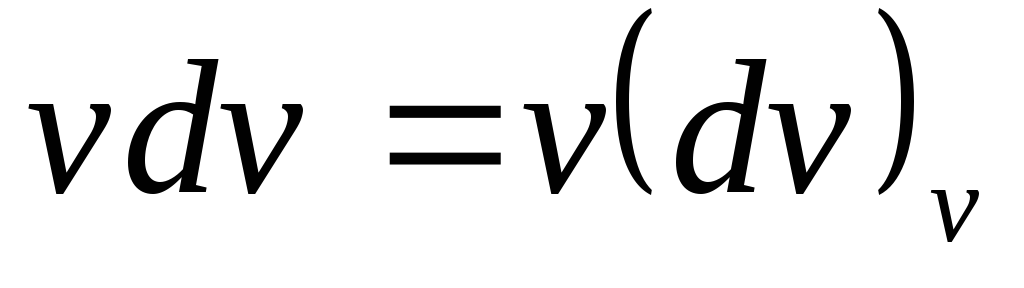усть частица массойдвижется пол действием силы. Элементарная работа этой силы:; () . Скалярное произведение;— проекция вектора приращения скоростина направление вектора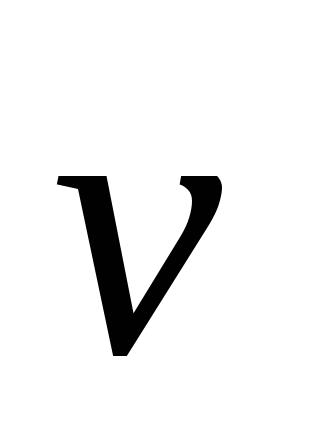. Она равна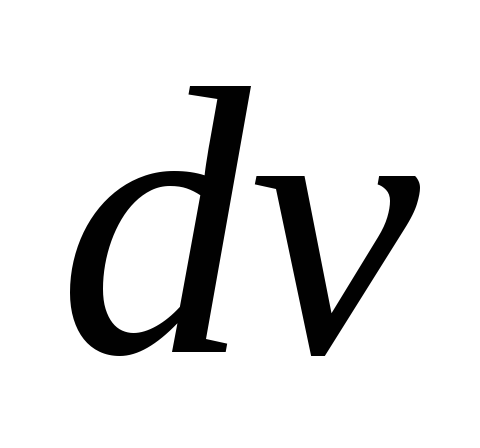— приращениюмодуля вектора скорости, тогда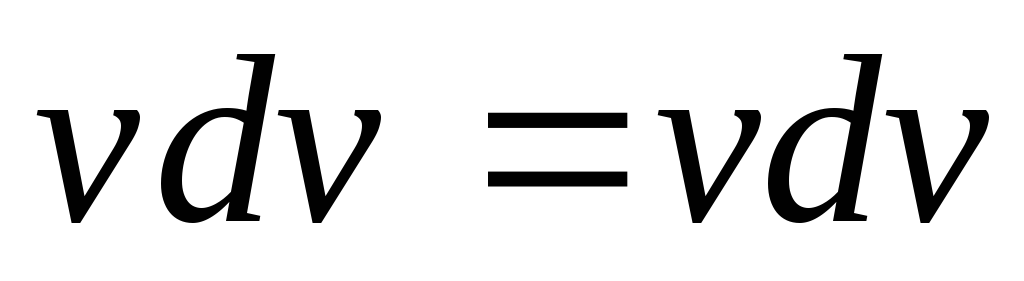и работа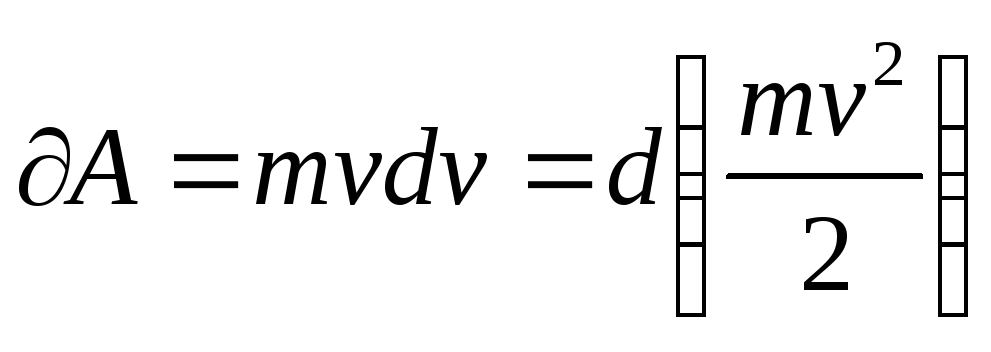. Отсюда видно, что работа результирующей силы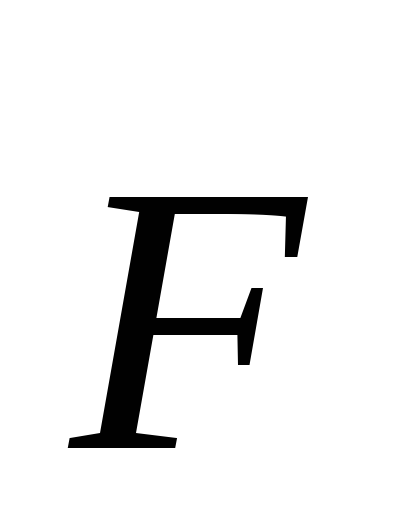идет на приращение некоторой физической величины , которую называют кинетической энергией и которая является мерой энергии движения материальной точки.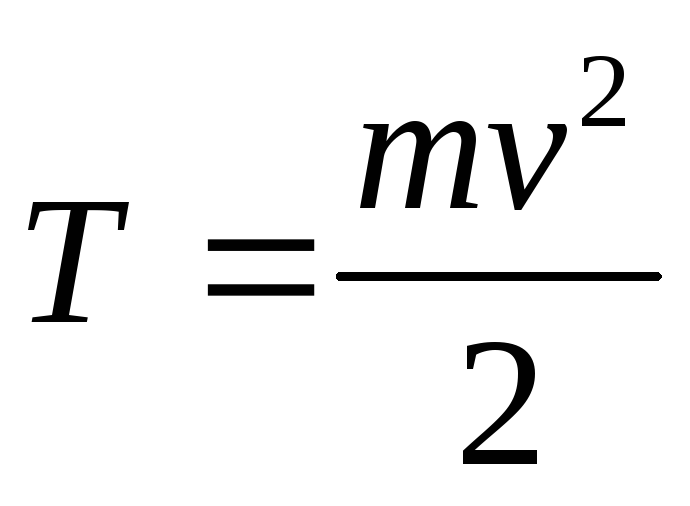

, т.о.(*)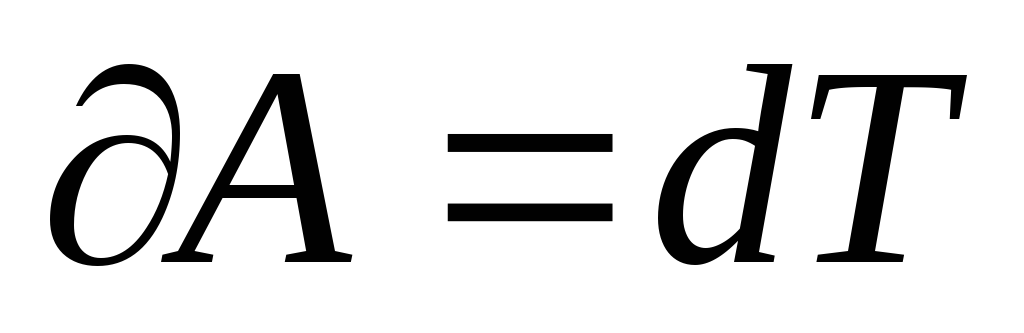

При конечном перемещении из т.1 в т.2

;(**)

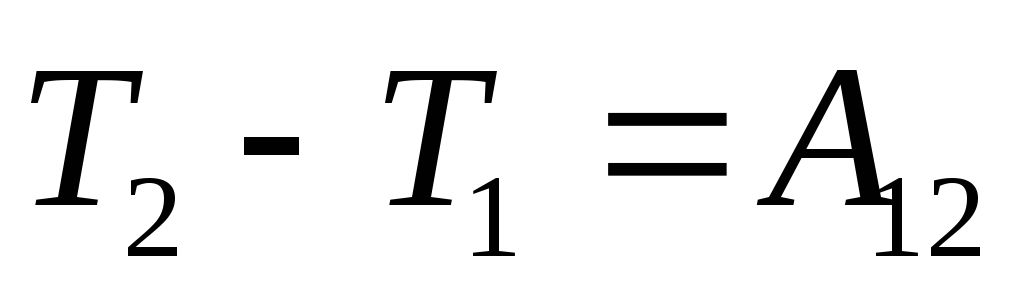Т.е. приращении кинетической энергии частицы при перемещении из т.1 в т.2 равно алгебраической сумме работ всех сил, действующих на частицу на этом перемещении. Если 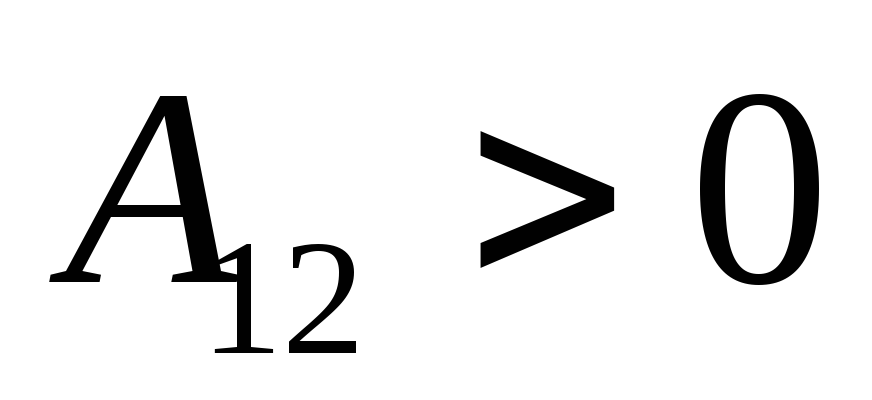то

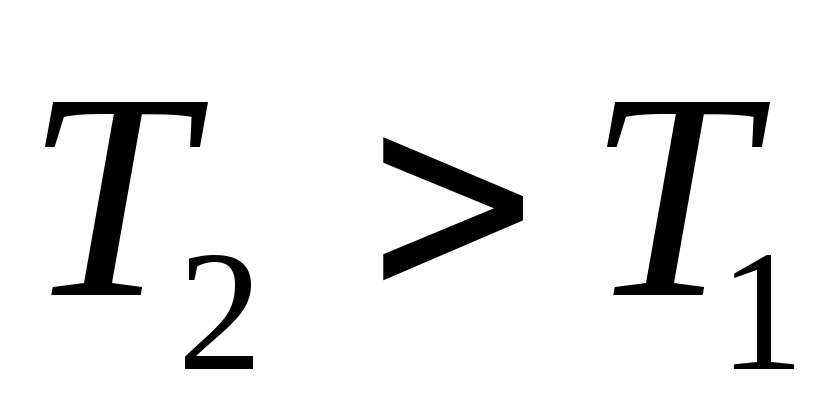
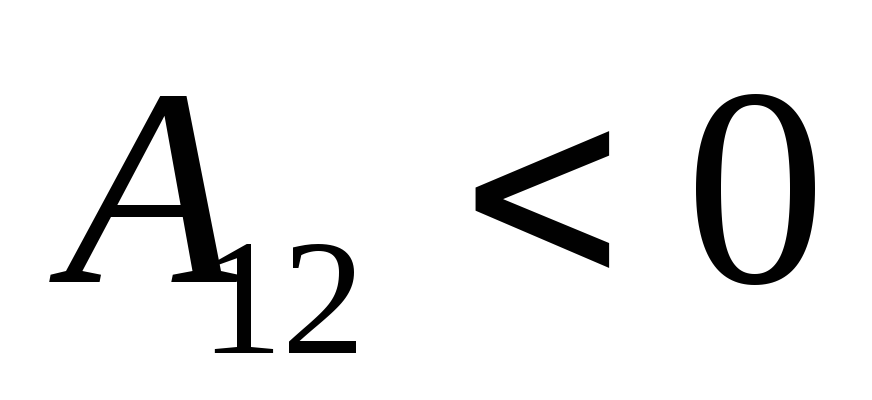— кинетическая энергия растет. Если— уменьшается (силы трения). Уравнения (*, **) справедливы в инерциальных и неинерциальных системах отсчета. А в последних, необходимо в работу всех сил учитывать работ сил инерции.

3.8. Полная механическая энергия частицы.

Т.о. приращение кинетической энергии частицы равно элементарной работевсех сил, действующих на частицу. Если частица находится в стационарном поле консервативных сил, то на нее действует консервативная сила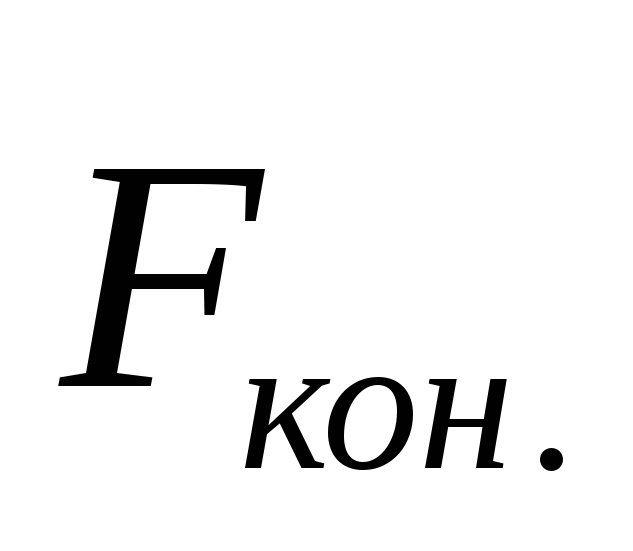со стороны поля. кроме этого на неё могут действовать и другие силы; т.е. результирующая сила.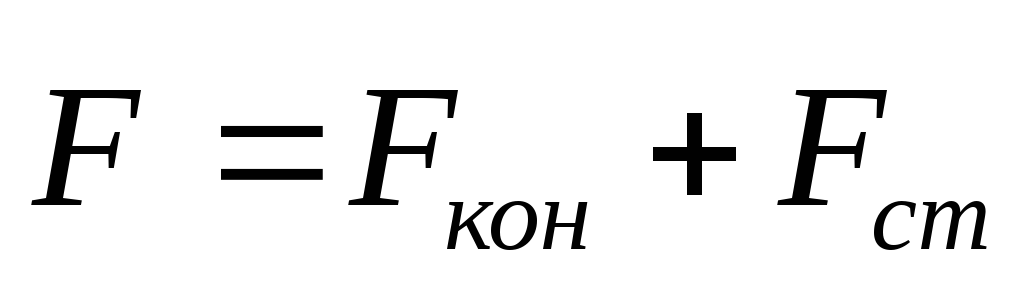

Работа всех этих сил идет на изменение приращения кинетической энергии частицы

Известно также, что работа консервативных сил поля равна убыли потенциальной энергии частицы.

, значитили

Т.о. работа сторонних сил идёт на приращение величины . Эту величину называютполной механической энергиейчастицы в поле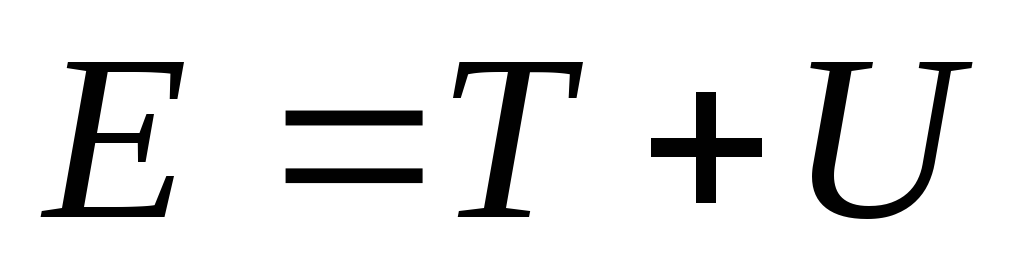. Отсюда видно, чтоопределяется с точностью до постоянной, так как с точность доопределяется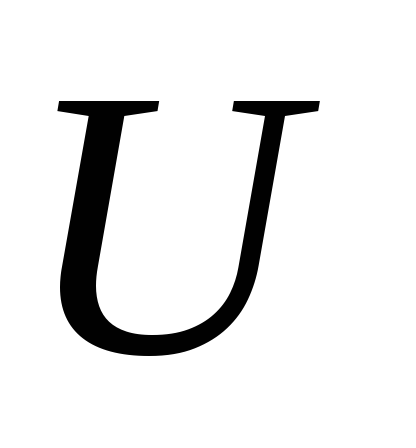. Теперь можно записать

(***)

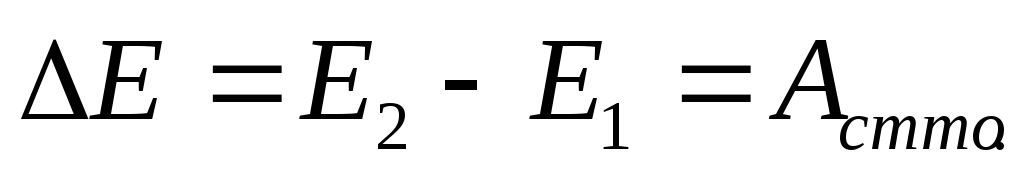т.е. приращение полной механической энергии частицы на некотором пути равно работе сторонних сил, действующих на частицу на этом пути; Если , то полная механическая энергия частицы растёт при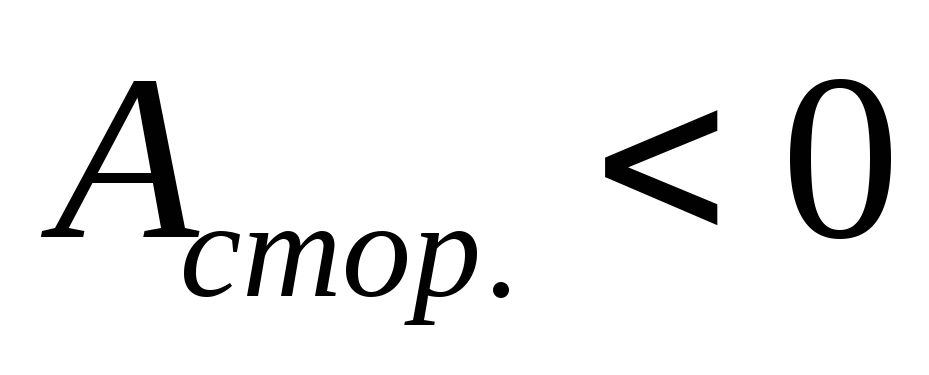, — уменьшается.

Пример: Тело, падающее с обрыва

.

3.9. Закон сохранения механической энергии частицы.

Из выражения 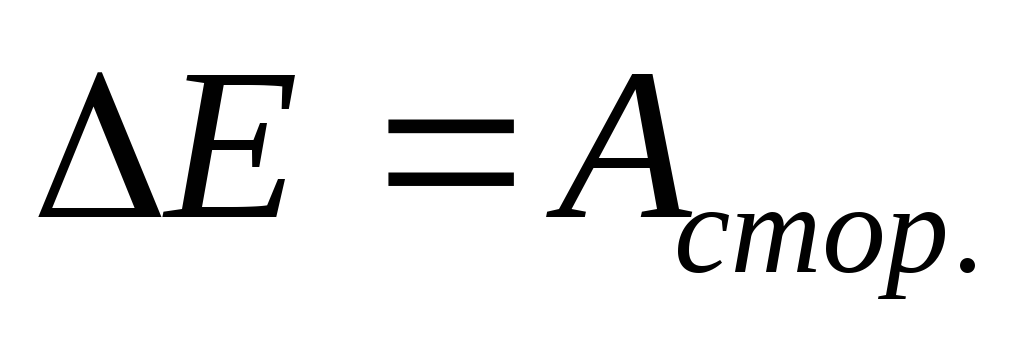следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться под действием только сторонних сил, отсюда вытекает закон сохранения механической энергии частицы.

Если сторонние силы отсутствуют, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной.

;

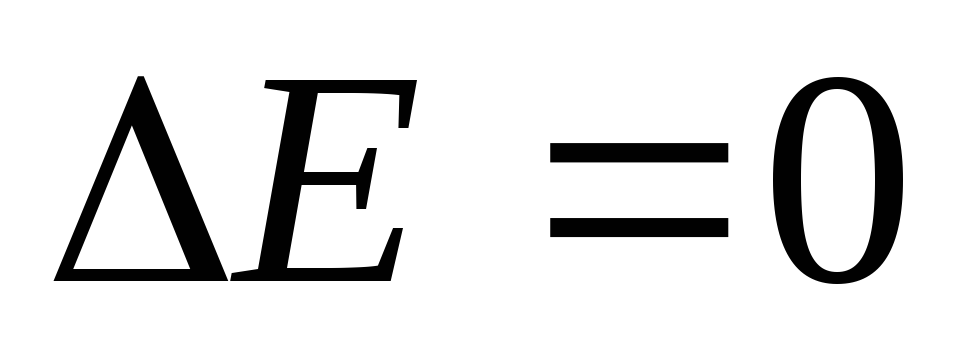Закон сохранения позволяет решать многие вопросы, не привлекая уравнения движения, которые часто приводят к ??? расчетам.

4. Кинематика и динамика вращательного движения.

1. Кинематика.

Поворот тела на некоторый уголможно задать в виде отрезка длина которого, а направление совпадает с осью вращения и определяется правилом правого винта: Направление должно быть таким, чтобы глядя вдоль него, мы видели поворот совершающийся по часовой стрелке.

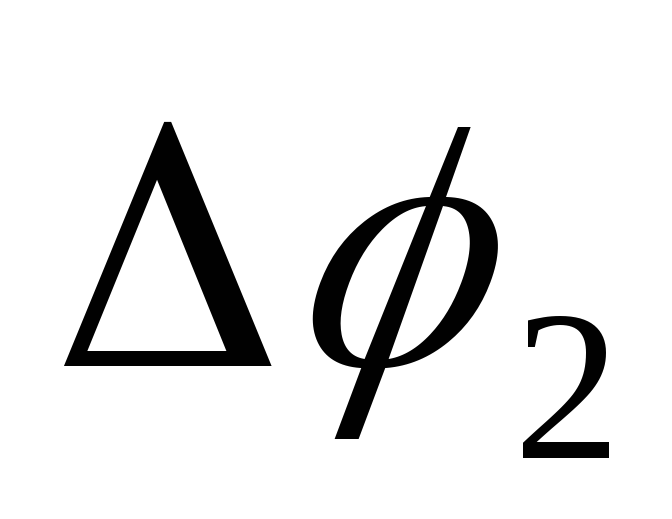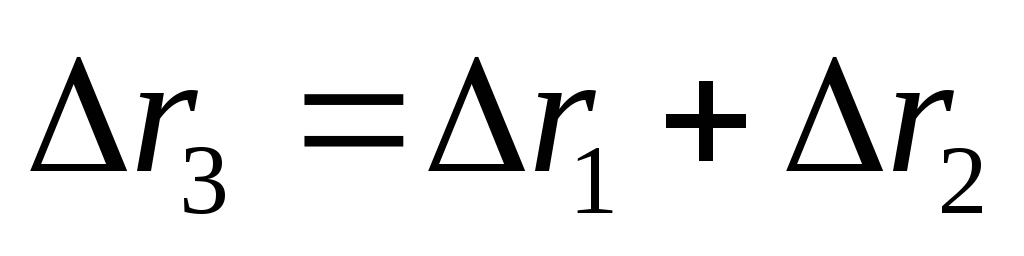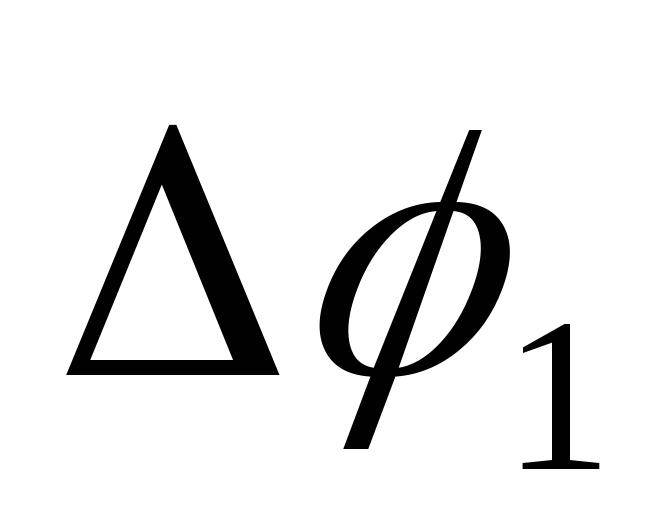При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворотаи(вокруг разных осей, осив данном случае) обуславливают как видно из рис., такое же перемещение,любой точки тела, как и поворотполучаемый изи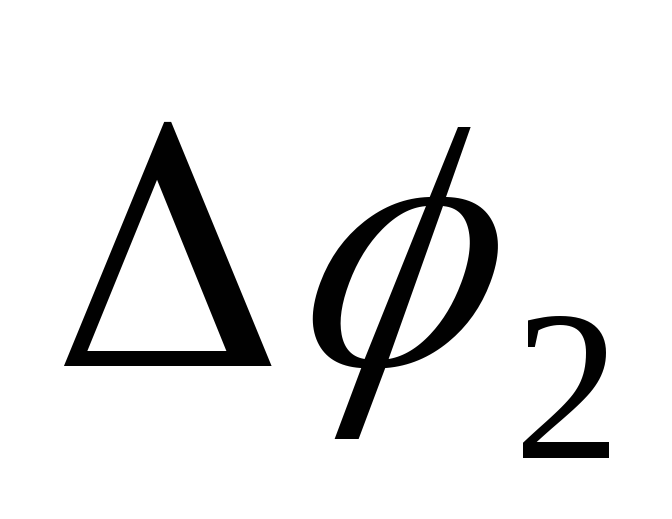сложением о правилу параллелограмма. Значит очень малые повороты можно рассматривать как векторы. Направление вектора поворота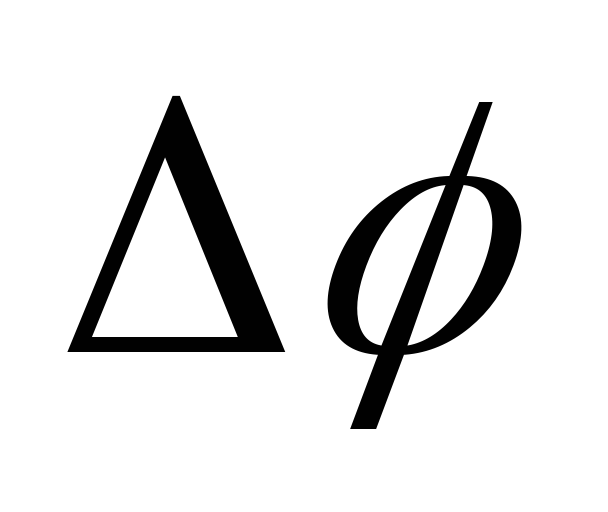, связывается с направлением вращения тела, следовательно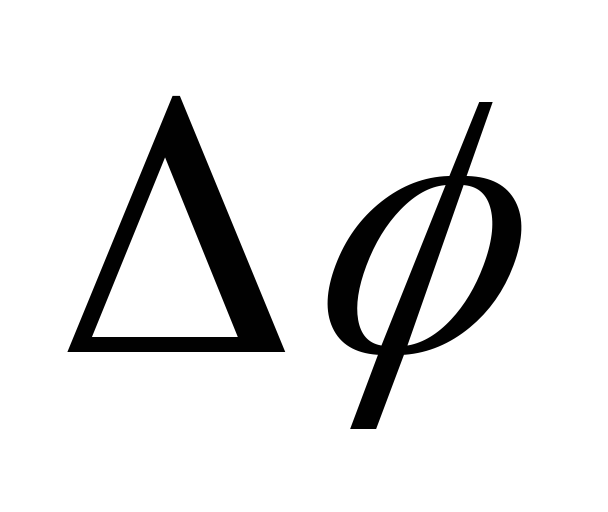не является истинным вектором, а является псевдовектором.

В

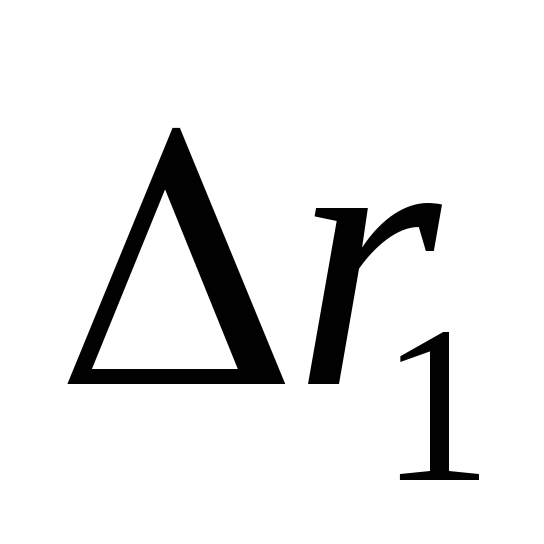
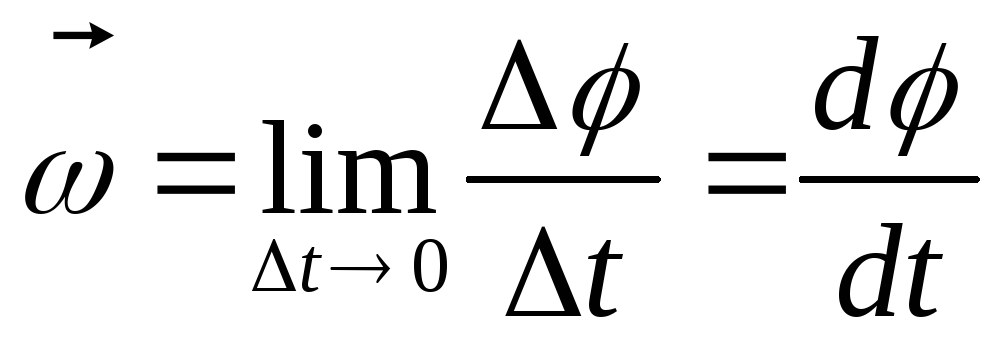екторная величинаназывается угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль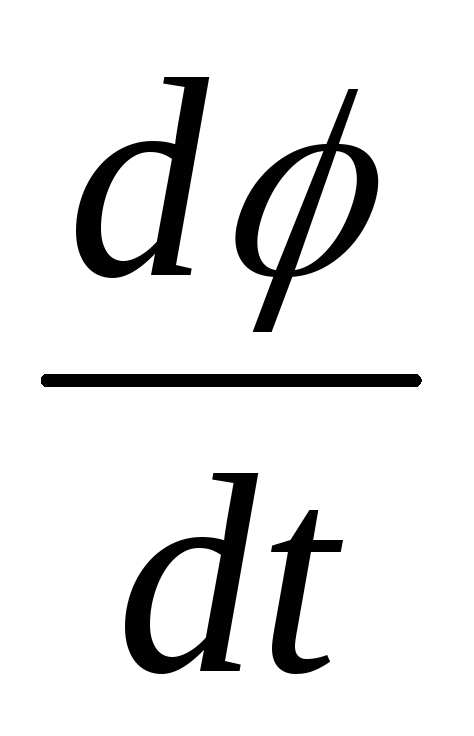, если— равномерное вращение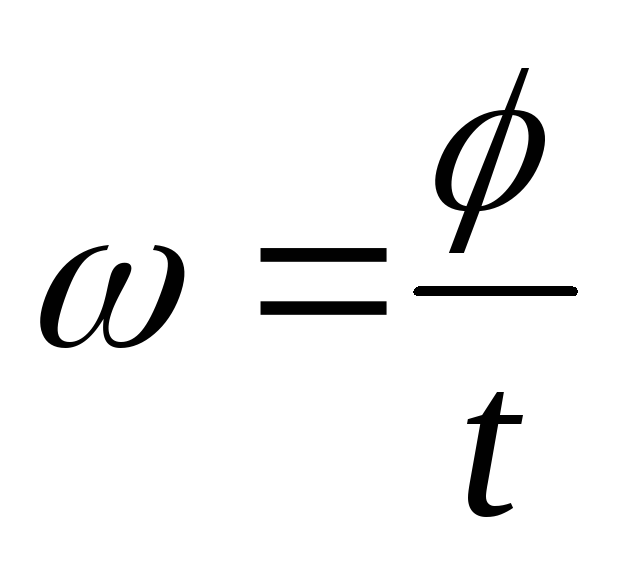, для равномерного движения-угол поворота в единицу времени.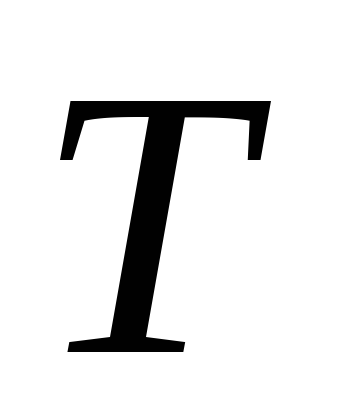период вращениячисло оборотов, а.

Понятияиможно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.

Вектор может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если заполучает приращението изменение угловой скорости со временем характеризуется угловым ускорением

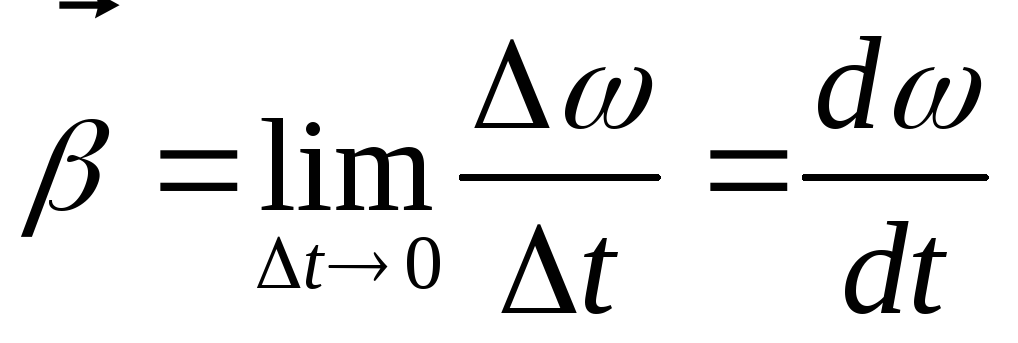
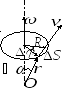— тоже псевдовектор.

Точки вращающегося тела имеют разные линейные скорости, которые определяют и. Если затело повернулось на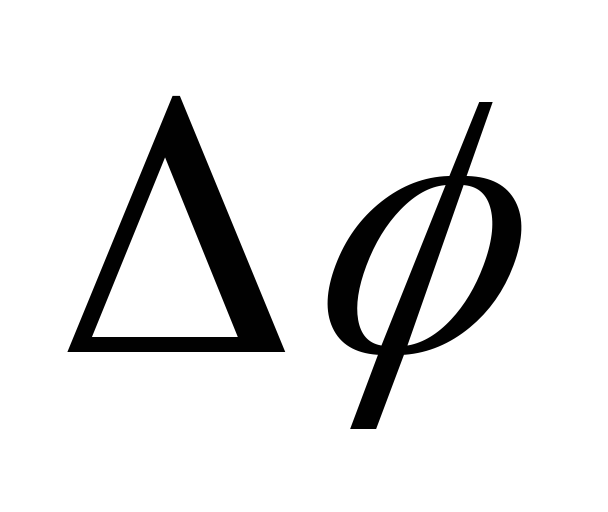, то. Линейная скорость точки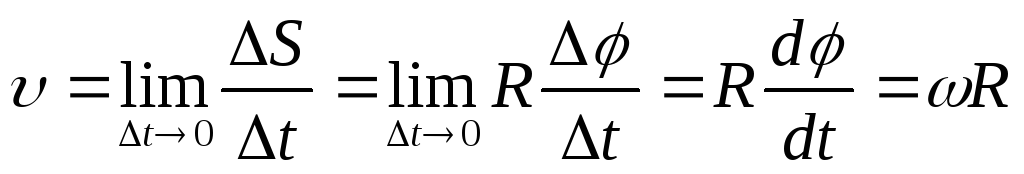; т.е..

Найдем связь между векторами и. Положение для модулей точки определяет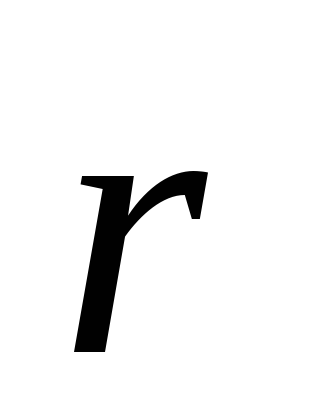. Из рис. видно, чтосовпадает спо направлению, модуль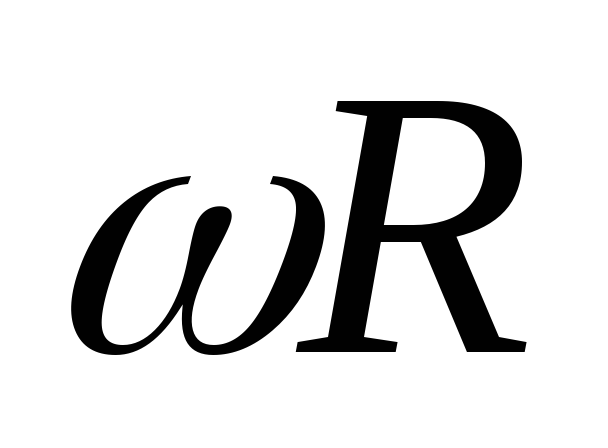равен.

Модуль нормального ускорения точек 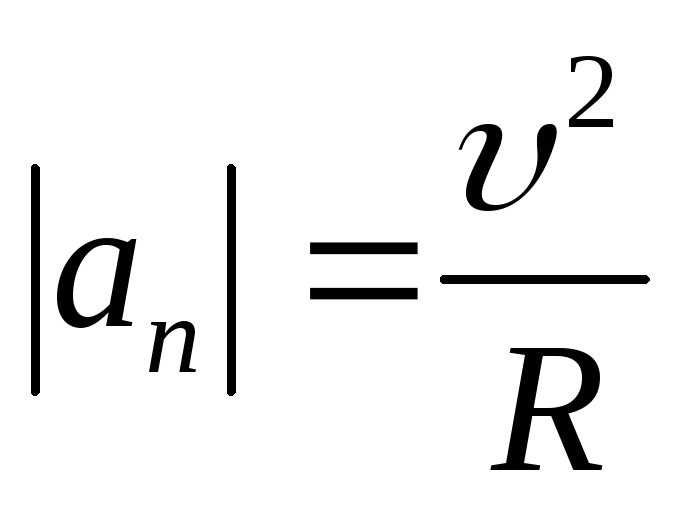или через.

Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:

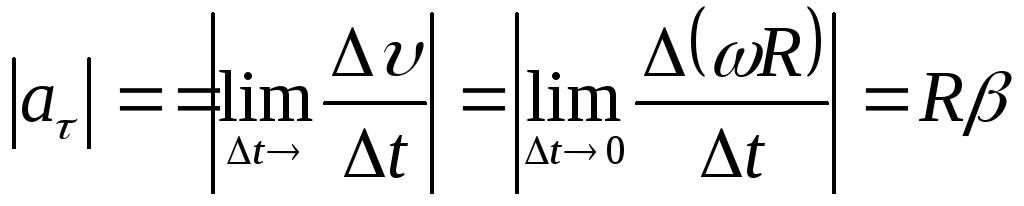;-модуль угловой скорости, т.е.

Т.о. нормальное и тангенциальное ускорение растут пропорционально .

studfile.net

Импульс и энергия релятивистской частицы

Мы уже ввели релятивистскую частицу и эффекты, связанные с релятивистским движением. Напомним, что прилагательное «релятивистское» обозначает движение тел с близкими к световой скоростями. Большинство соотношений в данной теме вывести достаточно сложно, поэтому просто верим.

Итак, введённый нами импульс (

) при условии релятивистской массы () может быть записан как:

(1)

Немного о 

— массе неподвижного в данной системе тела, называемой массой покоя.

Великим Эйнштейном было получено уникальное соотношение, характеризующее полную энергию движущейся частицы:

(2)

Логично предположить, что наименьшей энергией обладает тело, которое покоится в данной системе, назовём эту энергию энергией покоя:

(3)

Тогда кинетическая энергия движущегося тела может быть найдена как разность между полной энергией и энергией покоя:

(4)

Или:

(5)

При условии 

(скорость тела очень мала по сравнению со скоростью света) получим  (отношение скорости тела к скорости света стремиться к нулю), и соотношение (5) принимает вид  — т.е. вид кинетической энергии в классической механике.

Вывод: в случае релятивистской механики (скорость частицы велика) достаточно помнить, что энергетические характеристики тела выражаются через более сложные соотношения (1) — (5). С точки зрения энергии, главное понять по задаче, какую энергию нам необходимо найти — покоя, полную или кинетическую.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

www.abitur.by

Энергия кинетическая частиц — Справочник химика 21

    При данной температуре кинетическая энергия отдельных частиц может несколько раз меняться, но средняя кинетическая энергия молекул постоянна и зависит только от абсолютной температуры. [c.392]

    Температура есть основная величина, характеризующая тепловое состояние тела она является мерой тепловой энергии тела и в случае газов определяет собой кинетическую энергию их частиц (атомов, молекул). В технике температура всегда измеряется в градусах стоградусной шкалы (/°С). Однако в очень многие расчетные формулы входит а б с о, 1 ю т и а я те м п ера-тура Т (температура шкалы Кельвина, °К), которая представляет собой температуру, приведенную к так называемому абсолютному нулю , т. е. к —273° С (точнее —273,16° С)  [c.22]

    Энергия (кинетическая) частиц или фотонов, эв [c.385]

    О влиянии кинетической энергии частиц на условия их агрегации говорится в [76] Кинетическая энергия взаимодействующих частиц способствует преодолению энергетического барьера и тем самым облегчает агрегацию . Так, например, вибрация бетонных смесей, которой придается особое значение в технологии бетонов, имеет двоякое значение. В начале процесса она разрушает коагуляционную структуру и тем самым придает бетонной смеси необходимую подвижность, после укладки в формы вибрация не только обеспечивает плотную ее упаковку, но и содействует преодолению энергетического барьера, приводит к образованию агрегатов. Все сказанное выше имеет отношение к агрегации частиц с линейными размерами больше или равными 5 мк, т. е. для которых имеют смысл уравнения движения (1.58), Наши выводы ни в коей мере не [c.86]

    Здесь опущен индекс с, напоминающий о том, что рассматриваются компоненты скорости вдоль линии центров в момент столкновения. Произведя замену в соответствии с уравнением (VII.ЗА.3), получим величину относительной кинетической энергии, передаваемой частицей типа 1 .  [c.149]

    Например, при пористости 40% скорость псевдоожижения составляет только 7,6% от скорости свободного падения. Возможное объяснение такого поведения заключается в следующем. Подвергающиеся псевдоожижению слои всегда содержат некоторое количество более мелких частиц, которые имеют скорости падения, значительно меньшие, чем общая скорость газового потока при псевдоожижении. Эти мелкие частицы могут быть подняты газом и могут упасть, передав свою кинетическую энергию большим частицам, затем опять могут быть подняты и т. д., пока в конце концов вся масса не придет в движение. [c.254]

    Стабильная молекула может образоваться в результате столкновения двух атомов или радикалов только в том случае, если некоторое количество энергии, не меньшее, чем суммарная кинетическая энергия сталкивающихся частиц, теряется в результате излучения или при столкновении с третьей частицей (роль которой может играть и поверхность твердого тела). Если потери энергии не будет, то молекула, возникшая в результате столкновения, после одного колебания разрушится, так как выделяющаяся при образовании связи энергия останется в возникшей молекуле, а ее достаточно, чтобы разорвать возникшую связь. Кроме того, возникающая молекула будет обладать и кинетической энергией сталкивающихся частиц, которая после разрыва связи вновь перейдет в кинетическую энергию поступательного движения образовавшихся осколков (атомов или радикалов). [c.85]

    Соударения молекул газа упруги. Это значит, что, хотя отдельные частицы могут менять свою кинетическую энергию, суммарная энергия сталкивающихся частиц постоянна. [c.392]

    Кинетическая энергия твердых частиц (масса частицы т , средняя скорость в псевдоожиженном слое возрастает с увеличением скорости ожижающего агента 7, так что, по аналогии с выражением (XI,2), можно записать [c.476]

    Температура Средняя кинетическая энергия всех частиц [c.63]

    Первое слагаемое в правой части уравнения (1.79) означает приток (отток) тепла в г-фазу за счет фазового превращения, теплообмена с поверхностью раздела фаз, агрегации частиц (где ягь у = [1 г—р)—удельный поток тепла, приносимый у-фазой при объединении частиц). Первое слагаемое (во второй квадратной скобке) характеризует изменение внутренней энергии за счет работы внутренних сил второе слагаемое отражает переход части кинетической энергии силового взаимодействия несущей и г-фаз во внутреннюю энергию третье и четвертое слагаемые представляют переход во внутреннюю энергию кинетической энергии из-за неравновесного обмена импульсом при фазовых превращениях и при столкновении частиц, происходящих при неравных скоростях. Легко показать, что избыток кинетической энергии, возникающий за счет столкновения, переходит только во внутреннюю энергию г-фазы. Доказательство аналогично проведенному относительно соотношения (1.70). [c.36]

    Кинетическая теория газов показывает, что такие понятия, как температура и давление, играющие основную роль в термодинамике, обладают по существу статистической природой, т. е. являются выражением некоторых свойств вещества, обусловленных совместным действием очень большого числа частиц. Температура определяется средней кинетической энергией поступательного движения, хотя кинетическая энергия отдельных частиц может значительно отличаться от этой величины. Точно так же давление газа выражает суммарный эффект ударов молекул о стенку сосуда и является величиной, средней для большого числа молекул, которые обладают в момент удара самыми различными количествами движения и ударяются о стенку под самыми различными углами. Статистической природой обладают и такие величины, как плотность. [c.210]

    Каждое колебательное движение можно разложить по трем координатам. Средняя кинетическая энергия движения частицы по одной координате равна 8а=1/2 -Т, а по трем координатам 8 » = 3/2 кТ. [c.32]

    Для гармонического колебания кинетическая энергия равна потенциальной, то есть еп»=3/2 7 . Для моля частиц общий запас энергии колеблющихся частиц в твердом теле будет равен  [c.32]

    Следует, однако, указать, что при изменении энергии реагирующих частиц возможно превращение реакции одного типа в другой. Известны примеры [378], когда ио мере повышения кинетической анергии сталкивающихся молекул механизм реакции, протекающей через долгоживущий комплекс, изменяется и становится прямым. [c.137]

    Механическая энергия газовой частицы в относительном движении, определяемая суммой энергии давления и кинетической энергии, равна [c.30]

    Энергия активации является статистической величиной и в случае почти р>авновесных реакций может быть определена из кинетического эксперимента с помощью общеизвестной логарифмической анаморфозы. Энергией активации называется разность

www.chem21.info

Кинетическая энергия — Википедия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

T=∑mivi22{\displaystyle T=\sum {{m_{i}v_{i}^{2}} \over 2}},

где индекс  i{\displaystyle \ i} нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[2]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[3]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T{\displaystyle T}, Ekin{\displaystyle E_{kin}}, K{\displaystyle K} и другие. В системе СИ она измеряется в джоулях (Дж).

История понятия

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвящённых понятию «живой силы»^[4].

Кинетическая энергия в классической механике

Случай одной материальной точки

По определению, кинетической энергией материальной точки массой m{\displaystyle m} называется величина

T=mv22{\displaystyle T={{mv^{2}} \over 2}},

при этом предполагается, что скорость точки v{\displaystyle v} всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}) данное выражение примет вид  T=p2/2m{\displaystyle \ T=p^{2}/2m}.

Если F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}. Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} и учитывая, что a→=dv→/dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}, причём d(v2)/dt=d(v→⋅v→)/dt=2v→⋅dv→/dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}, получим  F→ds→=d(mv2/2)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина  T{\displaystyle \ T} остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}

Здесь  M{\displaystyle \ M} — масса тела,  v{\displaystyle \ v} — скорость центра масс, ω→{\displaystyle {\vec {\omega }}} и I{\displaystyle I} — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[5].

Кинетическая энергия в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dM/dV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}}, то есть плотность кинетической энергии wT=dT/dV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V} (Дж/м³), запишется:

wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}

где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[6]. Если, в согласии с методом Рейнольдса, представить  ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}

где Es=ρ¯vα¯vα¯/2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯/2+ρ′vα′vα′¯/2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[6], часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (p^=−jℏ∇{\displaystyle {\hat {p}}=-j\hbar \nabla },  j{\displaystyle \ j} — мнимая единица):

T^=p^22m=−ℏ22mΔ{\displaystyle {\hat {T}}={\frac {{\hat {p}}^{2}}{2m}}=-{\frac {\hbar ^{2}}{2m}}\Delta }

где ℏ{\displaystyle \hbar } — редуцированная постоянная Планка, ∇{\displaystyle \nabla } — оператор набла, Δ{\displaystyle \Delta } — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[7].

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как

T=mc21−v2/c2−mc2,{\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}

где  m{\displaystyle \ m} — масса,  v{\displaystyle \ v} — скорость движения в выбранной инерциальной системе отсчёта,  c{\displaystyle \ c} — скорость света в вакууме (mc2{\displaystyle mc^{2}} — энергия покоя). Как и в классическом случае, имеет место соотношение  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}, получаемое посредством умножения на ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} выражения второго закона Ньютона (в виде  F→=m⋅d(v→/1−v2/c2)/dt{\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}).

Выражение для  T{\displaystyle \ T} можно переписать в форме T=mv2/(1−v2/c2+1−v2/c2).{\displaystyle T=mv^{2}/(1-v^{2}/c^{2}+{\sqrt {1-v^{2}/c^{2}}}).} При малых скоростях (v≪c{\displaystyle v\ll c}) оно переходит в классическую формулу  T=1/2⋅mv2{\displaystyle \ T=1/2\cdot mv^{2}}.

Свойства кинетической энергии

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[8][9].

Физический смысл кинетической энергии

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[10]:

 A12=T2−T1.{\displaystyle \ A_{12}=T_{2}-T_{1}.}

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T} между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также

Примечания

1. ↑ ^{1 2 3 4} Айзерман, 1980, с. 49.
2. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
3. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
4. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
5. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245.
6. ↑ ^{1 2} Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
7. ↑ Блохинцев Д. И. Основы квантовой механики, 5-е изд. Наука, 1976. — 664 с., см. § 26.
8. ↑ Айзерман, 1980, с. 54.
9. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325—362, (1956)
10. ↑ Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.

Литература

wikipedia.green