Сопротивление качению и промышленные колёса
Трение и сопротивление качению
Процесс трения (фрикционное взаимодействие) играет важную роль в промышленном мире и повседневной жизни. Сила трения оказывает сопротивление скольжению, вращению, качению, полёту объекта из-за его контакта с другим объектом. Она может быть полезной (к примеру, когда нужно задействовать тормоза, чтобы остановить автомобиль), или вредной (при попытке ехать с ногой на педали тормоза). Эта статья расскажет о важном аспекте промышленных колёс – о сопротивлении качению.
Сопротивление качению – притормаживающее действие, которое оказывает поверхность пола на шинку (контактный слой) катящегося колеса. Оно является мерой энергии, потерянной на определённом расстоянии.
Рассмотрим катящееся по плоской поверхности колесо. Его шинка деформируется, что вызывает некоторое сопротивление движению качения. Плоская поверхность также может деформироваться, особенно если она мягкая.
Факторы, влияющие на рассеивание энергии катящегося промышленного колеса:
- трение контактирующих поверхностей;
- упругие свойства материалов;
- грубость поверхностей.
Трение качения и трение скольжения
Коэффициент трения качения не следует путать с коэффициентом трения скольжения. Коэффициент трения скольжения выражает отношение силы трения между телами и силы, прижимающей тела друг к другу. Данный коэффициент зависит от типа используемых материалов. К примеру, сталь на льду имеет низкий коэффициент трения, а резина на асфальте имеет высокий коэффициент трения.
Рисунок 2 поясняет понятие трения скольжения. Представьте силу, которую нужно применить, чтобы протянуть тяжёлый ящик по полу.
Причина, по которой мы используем колёса для перемещения материалов в том, что они позволяют тратить значительно меньше силы. Представьте, что приходится волочь холодильник или пианино! Более того, подумайте, насколько легче было бы передвинуть вышеупомянутый ящик, если бы применялись колёса.
Сила, требуемая для передвижения оборудования на колёсах, велика только при старте. Ее часто называют «первоначальной или «стартовой» силой. Как только получено нужное ускорение, для продолжения движения необходима гораздо меньшая сила, которую называют «перманентной» или «катящей». Как правило «стартовая» сила превышает ее в 2-2.
Расчёт силы трения качения
Помочь узнать сопротивление качению промышленных колёс помогает коэффициент трения качения. Его значение для различных материалов получено эмпирическим путем и может варьироваться в зависимости от скорости вращения колеса, нагрузки на колесо, материала опорной поверхности.
В таблице ниже приведены коэффициенты трения качения наиболее распространенных материалов, из которых изготавливают промышленные колеса. Неудивительно, что самый мягкий, легко деформирующийся материал (резина) обладает самым высоким коэффициентом трения качения, а самый твёрдый материал (кованая сталь) – самым низким.
Материал шинки (контактного слоя колеса) | Материал пола | Коэффициент трения качения (масса груза – 600 кг, скорость – 5 км/ч) |
Кованая сталь | сталь | 0.019 |
Чугун | сталь | 0. |
Твёрдая резина | сталь | 0.303 |
Полиуретан | сталь | 0.03–0.057 |
Литой нейлон | сталь | 0.027 |
Фенол | сталь | 0.026 |
Формула для расчётов
F = f х F/R
F = сила трения качения
f = коэффициент трения качения
W = сила давления на опору (вес)
R = радиус колеса
Из формулы видно, что сила трения качения F пропорциональна силе давления на опору W и обратно пропорциональна радиусу R колеса. Таким образом, диаметр колес играет важную роль при транспортировке тяжёлых грузов.
Узнав силу трения качения каждого и умножив ее на число, можно узнать примерную силу сопротивления движению. Однако вышеприведенная формула неточна, потому что не учитывает другие факторы, влияющие на лёгкость качения (к примеру, силу адгезии).
Как выбрать промышленные колёса для лёгкого передвижения?
Чтобы снизить сопротивление качению, необходимо выбирать колёса большого диаметра и из материалов с низким коэффициентом трения.
Выбор подшипников не столь критичен для лёгкости хода тележки, как диаметр и материал шинки. Понятно, что подшипники качения предпочтительнее подшипников скольжения. Также стоит учитывать, что шариковые и роликовые подшипники лучше выдерживают нагрузки, меньше изнашиваются и дольше служат.
Главные факторы, влияющие на сопротивление качению:
- масса;
- диаметр колес;
- материал и мягкость шинки;
- материал и качество поверхности пола;
- условия на полу (грубость поверхности, чистота, наклон и т.д.).
Факторы, которые обычно игнорируют:
- тип подшипников;
- рисунок протектора;
- эффект скольжения или адгезии;
- температура окружающей среды;
- уклоны поверхности.

Общие рекомендации:
- Покупайте колесо промышленное, основываясь на грузоподъёмности и состоянии полов.
- Дополнительно принимайте во внимание: диапазон температур, ударопрочность, устойчивость к влаге, стойкость к свету и химикатам, возможность восстановления.
- Выбирайте максимально большой из возможных диаметров.
- Остановите выбор на шинке с минимальным сопротивлением качению.
- Подсчитайте силу сопротивления качению, принимая во внимание величину «стартовой» силы.
- Учитывайте фактор безопасности.
- Помните про уклоны поверхности. Сопротивление качению возрастает на подъёмах и снижается на спусках. F = Fx/cosa.
- Для буксировки самоходным транспортом лучше выбирать промышленные колёса с шариковыми подшипниками в оси. Только они обеспечат большой пробег, выдержат высокие скорости и нагрузки.
Легкой вам работы!
Коэффициент трения (скольжения) — Словарь терминов | ПластЭксперт
Коэффициент трения (скольжения)
Понятие и общие сведения о процессе
Трением называется известный всем процесс механического взаимодействия предметов, находящихся в контакте друг с другом, он бывает внешним и внутренним. Внешний процесс происходит при относительном перемещении тел в плоскости касания. То есть, если взять один предмет и начать скользить им по поверхности другого. Внутренняя (вязкая) разновидность процесса появляется при смещении друг относительно друга параллельных слоёв жидкости, газообразного или твёрдого тела, подвергнутого деформации. Таким образом, слои любого материала, находящегося в газовой или жидкостной фазе, также трутся между собой.
Внешний процесс происходит при относительном перемещении тел в плоскости касания. То есть, если взять один предмет и начать скользить им по поверхности другого. Внутренняя (вязкая) разновидность процесса появляется при смещении друг относительно друга параллельных слоёв жидкости, газообразного или твёрдого тела, подвергнутого деформации. Таким образом, слои любого материала, находящегося в газовой или жидкостной фазе, также трутся между собой.
Рассматриваемый коэффициент относится к понятию внешнего трения. Это взаимодействие и возникающие при нем силы изучаются в разделе физики под сложным названием механика фрикционного взаимодействия или трибология.
Разновидности сил
Силовые векторы, возникающие в случае соприкосновения тел в твердом, жидком или газообразном агрегатных состояниях работают в соответствии с законами Ньютона. Сила трения по этим законам направлена в противоположную движению сторону. Так же ее вектор противоположен направлению сил, стремящимся привести предмет в движение.
Рис.1. Векторы сил при трении
Таким образом, можно утверждать, что в случае движения касающихся тел, одного относительно другого, происходит взаимодействие, известное как трение скольжения. Этот процесс сопровождается возникновением определенного усилия – силы трения скольжения. Соответственно при ее численном описании применяется коэффициент трения скольжения.
Упрощенно значение описанных выше сил при скольжении рассчитывается по формуле:
Fтр = k * N, в которой
k — описанный выше коэфф-т,
N — сила нормальной реакции опоры.
Другая разновидность рассматриваемого процесса – трение качения. Сила такого взаимодействия тел находится по следующей формуле:
Fтр= Ктр *(Fn/r), где Ктр — коэфф-т трения, Fn — прижимающая сила, r — радиус катящегося предмета.
Для примера значения коэффициента при качении пневматической шины по асфальту варьируется от 0,006 до 0,02.
Коэффициент трения скольжения
Величина, применяемая к паре материалов и характеризующая поверхности при их скольжении друг относительно друга, называется коэффициентом трения скольжения. Эта постоянная для каждых двух материалов обозначается буквой μ и определяется опытным путём.
Коэффициент трения этого типа зависит от свойств материалов, качества поверхности, наличия смазок и т.д. Массы тел на его значение не влияют. Примечательно, что значение коэффициента находится в незначительной зависимости и от скорости перемещения тел. Несмотря на это, обычно до простоты расчетов его значение считают постоянной величиной.
Численные значения данного коэффициента трения для некоторых пар материалов.
— Каучук по металлу – от 0,55 до 0,8.
— Фторопласт по нержавеющей стали – от 0,064 до 0,080.
— Фторопласт-4 по фторопласту – от 0,052 до 0,086.
Таким образом можно вывести, что из представленных материалов именно фторопласты «трутся» друг о друга с наименьшими потерями, то есть скользят, особенно друг по другу, лучше всего. Прочие полимеры и особенно резины, как видно из представленных данных, скользят даже по металлу гораздо хуже. Коэффициенты таких пар материалов близок к единице.
Прочие полимеры и особенно резины, как видно из представленных данных, скользят даже по металлу гораздо хуже. Коэффициенты таких пар материалов близок к единице.
Сила трения скольжения — урок. Физика, 9 класс.
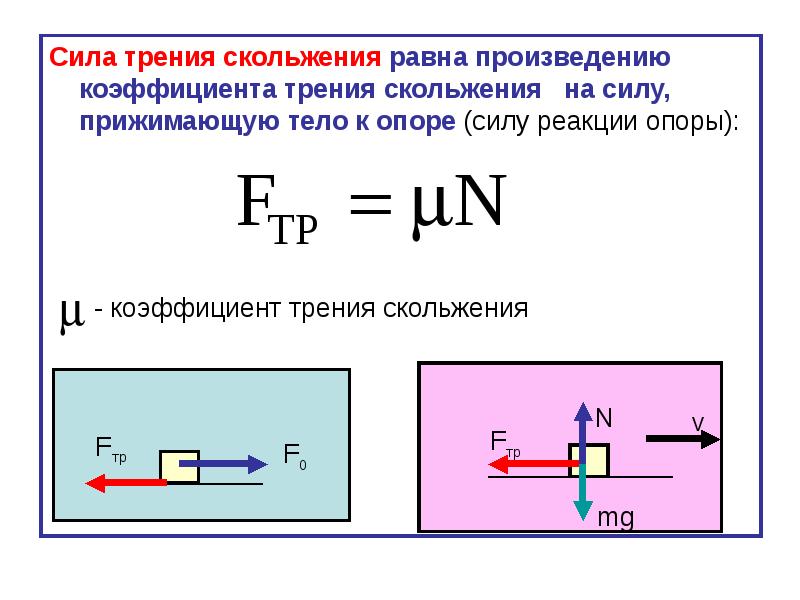
Сила трения скольжения возникает, если одно тело скользит по поверхности другого тела. Трение скольжения характеризуется силой трения, которая тормозит движение скольжения.
Сила трения скольжения прямо пропорциональна силе реакции опоры и коэффициенту трения скольжения.
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры и вычисляется по формуле: Fтр=μ⋅Fр.При увеличении веса тела и коэффициента трения увеличивается сила трения. Сила трения скольжения действует в тех случаях, когда тело движется или его пытаются сдвинуть с места.
Сила реакции опоры — сила, при помощи которой опора действует на тело. Сила реакции опоры — сила, при помощи которой опора давит на тело, которое находится на ней. Из третьего закона Ньютона следует, что сила реакции опоры всегда равна силе, при помощи которой тело воздействует на опору. На неподвижной горизонтальной поверхности сила реакции опоры всегда равна весу тела или силе тяжести: Fр=Fт. На наклонной плоскости сила тяжести и сила, при помощи которой тело воздействует на опору, различаются.
На неподвижной горизонтальной поверхности сила реакции опоры всегда равна весу тела или силе тяжести: Fр=Fт. На наклонной плоскости сила тяжести и сила, при помощи которой тело воздействует на опору, различаются.
Обрати внимание!
Сила реакции опоры всегда направлена перпендикулярно поверхности опоры.
Коэффициент трения скольжения — отношение силы трения к силе реакции опоры. Коэффициент трения между двумя любыми материалами легко определить, если возможно измерить силу трения, которая равна силе тяги, при которой тело перемещается равномерно, и силу тяжести, которая на горизонтальной поверхности равна силе реакции опоры. В таблице представлены различные коэффициенты трения скольжения.
| Пары материалов | Коэффициент трения скольжения |
| Сталь — лёд (коньки) | \(0,015\) |
| Древесина — древесина | \(0,2\)–\(0,5\) |
| Покрышка — мокрый асфальт | \(0,35\)–\(0,45\) |
| Покрышка — сухой асфальт | \(0,50\)–\(0,75\) |
Обрати внимание!
Коэффициент трения скольжения не имеет размерности.
Если сравнивать коэффициенты трения покрышки на сухом и мокром асфальте, то на мокром асфальте у одной и той же машины коэффициент трения, а также сила трения почти в \(2\) раза меньше, чем на сухом асфальте. В результате также увеличивается замедление торможения почти в \(2\) раза, поэтому тормозной путь может увеличиться почти в \(4\) раза.
У силы трения имеются как положительные, так и отрицательные свойства. Если бы не было силы трения, то мы не могли бы оттолкнуться при ходьбе от земли, а машина не могла бы «оттолкнуться» от поверхности дороги. Но в технике трение между различными вращающимися и скользящими поверхностями весьма нежелательно, поэтому такое оборудование смазывают, чтобы снизить влияние силы трения.Коэффициент трения скольжения, формула и примеры
Определение и формула коэффициента трения скольжения
Силой трения () называют силу, возникающую при относительном движении тел. Эмпирически установлено, что сила трения скольжения зависит от силы взаимного давления тел (реакции опоры) (N), материалов поверхностей трущихся тел, скоростей относительного движения.
В общем случае коэффициент трения зависит от скорости движения тел относительно друг друга. Надо отметить, что зависимость обычно не принимается во внимание и коэффициент трения скольжения считают постоянным. В большинстве случаев силу трения
Коэффициент трения скольжения величина безразмерная. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Коэффициент трения, который соответствует максимальной силе трения покоя в большинстве случаев больше, чем коэффициент трения скольжения.
Для большего числа пар материалов величина коэффициента трения не больше единицы и лежит в пределах
На значение коэффициента трения любой пары тел, между которыми рассматривается сила трения, оказывает влияние давление, степень загрязненности, площади поверхности тел и другое, что обычно не учитывается. Поэтому те значения коэффициентов сил трения, которые указаны в справочных таблицах, полностью совпадают с действительностью лишь при условиях, в которых они были получены. Следовательно, значения коэффициентов сил трения нельзя считать неизменной для одной и той де пары трущихся тел. Так, различают коэффициенты терния для сухих поверхностей и поверхностей со смазкой. Например, коэффициент терния скольжения для тела из бронзы и тела из чугуна, если поверхности материалов сухие равен Для этой же пары материалов коэффициент терния скольжения при наличии смазки
Поэтому те значения коэффициентов сил трения, которые указаны в справочных таблицах, полностью совпадают с действительностью лишь при условиях, в которых они были получены. Следовательно, значения коэффициентов сил трения нельзя считать неизменной для одной и той де пары трущихся тел. Так, различают коэффициенты терния для сухих поверхностей и поверхностей со смазкой. Например, коэффициент терния скольжения для тела из бронзы и тела из чугуна, если поверхности материалов сухие равен Для этой же пары материалов коэффициент терния скольжения при наличии смазки
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Что такое сила трения, виды силы трения; силы трения покоя и скольжения, законы и модуль силы трения
Определение силы трения
Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.
Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.
Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.
Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел.Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.
Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга.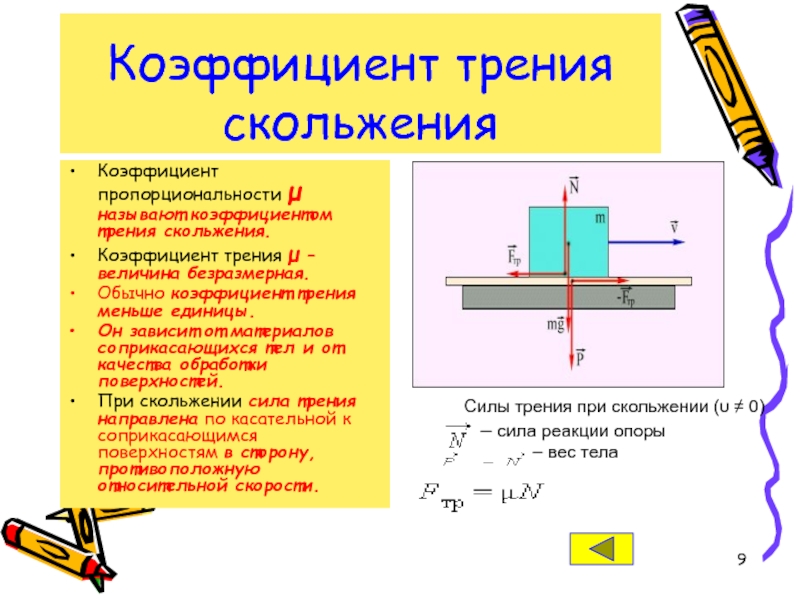 Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.
Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.
Откуда берётся трение
Трение возникает по двум причинам:
- Все тела имеют шероховатости. Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
- Между атомами и молекулами поверхностей тел действуют электромагнитные силы притяжения и отталкивания. Таким образом, сила трения имеет электромагнитную природу.
Виды силы трения
В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.
В свою очередь, оба подразделяются на другие виды силы трения.
- Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
- трение скольжения,
- трение покоя,
- трение качения.
- Вязкое трение возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения сильно увеличиваются.

Сила трения покоя
Рассмотрим силу трения покоя подробнее.
Обычная ситуация: на кухне имеется холодильник, его нужно переставить на другое место.
Когда никто не пытается двигать холодильник, стоящий на горизонтальном полу, трения между ним и полом нет. Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.
Пока силы равны, холодильник остаётся на месте:
Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя
Сила трения скольжения
Что же делать с холодильником и можно ли победить силу трения покоя? Не будет же она расти до бесконечности?
Зовём на помощь друга, и вдвоём уже удаётся передвинуть холодильник. Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Теперь на движущийся холодильник действует сила трения скольжения. Она возникает при относительном движении контактирующих твёрдых тел.
Итак, сила трения покоя может меняться от нуля до некоторого максимального значения — Fтр. пок. макс И если приложенная сила больше, чем Fтр. пок. макс, то у холодильника появляется шанс сдвинуться с места.
Теперь, после начала движения, можно прекратить наращивать усилие и ещё одного друга можно не звать. Чтобы холодильник продолжал двигаться равномерно, достаточно прикладывать силу, равную силе трения скольжения:
Как рассчитать и измерить силу трения
Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?
Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче!
Пустой холодильник сдвинуть с места гораздо легче!
Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.
Сила реакции опоры обозначается N. Можно сделать вывод
Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.
<<Форма демодоступа>>
Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.
Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.
Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.
Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.
Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.
Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:
где μ — коэффициент трения, N — сила нормальной реакции опоры.
Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:
Сила трения качения
Ещё древние строители заметили, что если тяжёлый предмет водрузить на колёсики, то сдвинуть с места и затем катить его будет гораздо легче, чем тянуть волоком. Вот бы пригодилась эта древняя мудрость, когда мы тянули холодильник! Однако всё равно нужно толкать или тянуть тело, чтобы оно не остановилось. Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Причина трения качения — деформация катка и опорной поверхности. Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.
Направление силы трения
Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел. Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения.
Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.
Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое.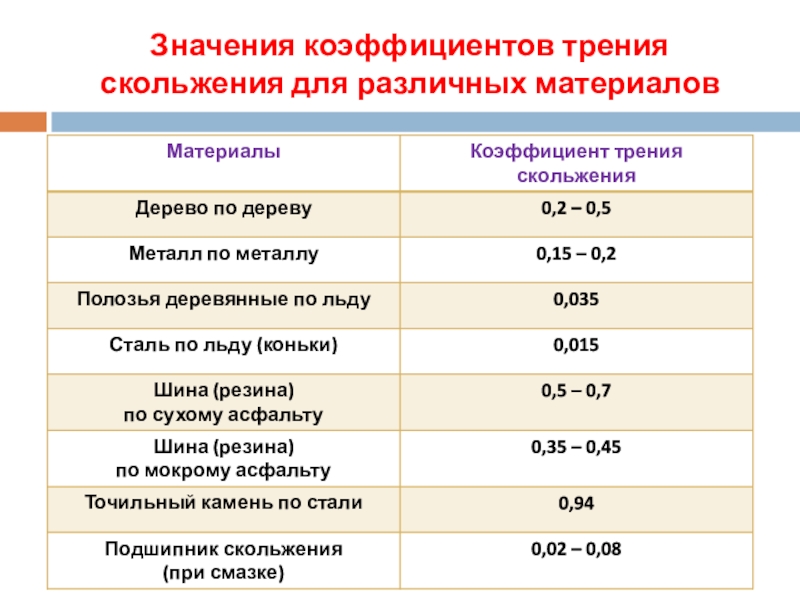 На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.
На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.
Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.
Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля сила трения покоя и вовсе направлена к центру окружности.
Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.
Подведём итоги
- Сила трения покоя меняется от нуля до максимального значения 0 < Fтр.покоя < Fтр.пок.макс в зависимости от внешнего воздействия.

- Максимальная сила трения покоя почти равна силе трения скольжения, лишь немного её превышая. Можно приближенно считать, что Fтр. = Fтр.пок.макс
- Силу трения скольжения можно рассчитать по формуле Fтр. = μ ⋅ N, где μ — коэффициент трения, N — сила нормальной реакции опоры.
- При равномерном прямолинейном скольжении по горизонтальной поверхности сила тяги равна силе трения скольжения Fтр. = Fтяги.
- Коэффициент трения μ зависит от рода и степени обработки поверхностей 0 < μ < 1 .
- При одинаковых силе нормального давления и коэффициенте трения сила трения качения всегда меньше силы трения скольжения.
Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду PHYSICS72021 вы получите
бесплатный доступ к курсу физики 7 класса, в котором изучается закон силы трения.Задачи на силу трения
Проверьте, насколько хорошо вы разобрались в теме «Сила трения», — решите несколько задач. Решение — приведено ниже. Но чур не смотреть, пока не попробуете разобраться сами.
Решение — приведено ниже. Но чур не смотреть, пока не попробуете разобраться сами.
- Однажды в день открытия железной дороги произошёл конфуз: угодливый чиновник, желая выслужиться перед Николаем I, приказал выкрасить рельсы белой масляной краской. Какая возникла проблема и как её удалось решить с помощью сажи?
- В один зимний день бабушка Нюра катала внука Алексея по заснеженной горизонтальной дороге. Чему равен коэффициент трения полозьев о снег, если сила трения, действующая на санки, равна 250 Н, а их масса вместе с Алексеем составляет 50 кг?
- На брусок массой m = 5 кг, находящийся на горизонтальной шероховатой поверхности μ = 0,7, начинает действовать сила F = 25 Н, направленная вдоль плоскости. Чему при этом равна сила трения, действующая на брусок?
Решения
- Масляная краска снизила коэффициент трения между колёсами и рельсами, что привело к пробуксовке, поезд не смог двигаться вперёд. Посыпав рельсы сажей, удалось решить проблему, так как коэффициент трения увеличился, и колёса перестали буксовать.

- Санки находятся в движении, следовательно, на них будет действовать сила трения скольжения, численно равная Fтр. = μ ⋅ N, где N — сила реакции опоры, которая, при условии горизонтальной поверхности, равняется весу санок с мальчиком: N = m ⋅ g. Получаем формулу Fтр. = μ ⋅ m ⋅ g , откуда выразим искомую величину
Ответ задачи зависит от того, сдвинется ли брусок под действием внешнего воздействия. Поэтому вначале узнаем значение силы, которую нужно приложить к бруску для скольжения. Это будет максимально возможная сила трения покоя, определяющаяся по формуле Fтр. = μ ⋅ N , где N = m ⋅ g (при условии горизонтальной поверхности). Подставляя значения, получаем, что Fтр. = 35 Н. Данное значение больше прикладываемой силы, следовательно брусок не сдвинется с места. Тогда сила трения покоя будет равна внешней силе: Fтр. = F = 25 H .
| Трущиеся материалы | Коэффициент трения | |||
| покоя | скольжения | |||
| без смазки | со смазкой | без смазки | со смазкой | |
| Сталь — сталь | 0,15 | 0,1-0,12 | 0,15 | 0,05-0,1 |
| Сталь—мягкая сталь | — | — | 0,2 | 0,1-0,2 |
| Сталь — чугун | 0,3 | — | 0,18 | 0,05-0,15 |
| Сталь — бронза | 0,12 | 0,08-0,12 | 0,10 | 0,07-0,10 |
| Сталь — текстолит | — | — | — | 0,02-0,06 |
| Чугун — бронза | — | — | 0,15-0,2 | 0,07-0,15 |
| Бронза—бронза | — | 0,1 | 0,2 | 0,07-0,1 |
| Резина — чугун | — | — | 0,8 | 0,5 |
| Металл — дерево | 0,5—0,6 | 0,1 — 0,2 | 0,3-0,6 | 0,1-0,2 |
| Кожа — металл | 0,3-0,5 | 0,15 | 0,6 | 0,15 |
| Материал подшипника | Коэффициент трения | Материал подшипника | Коэффициент трения | |
| Серый чугун | 0,15-0,20 | Полиамиды, капрон | 0,15-0,20 | |
| Антифрикционный чугун | 0,12-0,15 | Нейлон | 0,10-0,20 | |
| Бронза | 0,10-0,15 | Пластик древесный слоистый | 0,15-0,25 | |
| Баббитовая заливка | 0,07-0,12 | Фторопласт без смазки | 0,04-0,06 | |
| Текстолит | 0,15-0,25 | Резина при смазке водой | 0,02-0,06 | |
Урок 10.
 силы трения — Физика — 10 класс
силы трения — Физика — 10 классФизика, 10 класс
Урок 10. Силы трения
Перечень вопросов, рассматриваемых на уроке:
- Сухое и жидкое (вязкое) трение.
- Максимальная сила трения покоя.
- Формула для вычисления силы трения скольжения.
- Особенности сил сопротивления при движении твердых тел в жидкостях и газах.
- Формулы вычисления сил сопротивления при движении твердых тел в жидкостях и газах.
Глоссарий по теме:
Сухое трение — трение, возникающее при соприкосновении двух твёрдых тел при отсутствии между ними жидкой или газообразной прослойки.
Сила трения покоя — сила трения, действующая между двумя телами, неподвижными относительно друг друга.
Максимальная сила трения покоя — наибольшее значение силы трения, при котором скольжение еще не наступает.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Трение качения — сопротивление движению, возникающее при перекатывании тел друг по другу т.е. сопротивление качению одного тела (катка) по поверхности другого
Основная и дополнительная литература по теме урока:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 113 – 122.
- Парфентьева Н. А. Сборник задач по физике. 10-11 классы. Базовый уровень.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1978/05/kuda_napravlena_sila_treniya.htm
http://kvant.mccme.ru/1985/10/trenie_vrednoe_poleznoe_intere.htm
Теоретический материал для самостоятельного изучения
Трение – физическое явление, сопровождающее всякое движение на Земле. При любом механическом движении тела соприкасаются либо друг с другом, либо с окружающей их сплошной жидкой или газообразной средой. В результате соприкосновения возникает сила трения, которая препятствует движению. Трение может быть полезно, и тогда мы стремимся его увеличить. В случаях, когда трение вредно, принимаются меры для его уменьшения.
Трение может быть полезно, и тогда мы стремимся его увеличить. В случаях, когда трение вредно, принимаются меры для его уменьшения.
История открытия. Свой вклад в попытки объяснить природу трения внесли многие ученые, начиная с Аристотеля, Леонардо да Винчи, Амонтона, Леонарда Эйлера, Кулона. Дальнейший вклад в теорию трения сделали Майер, Джоуль, Гельмгольц, Кузнецов, Дерягин, Томлинсон, Рейнольдс, Штрибек, Боуден и другие.
Различают следующие виды трения:
- сухое;
- жидкое (вязкое).
Сухое трение бывает трех видов:
- трение покоя;
- трение скольжения;
- трение качения.
Причины возникновения силы трения:
- шероховатость поверхностей соприкасающихся тел.
- взаимное притяжение молекул соприкасающихся тел.
Сухое трение − трение, возникающее при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Силы сухого трения всегда направлены по касательной к соприкасающимся поверхностям.
Сухое трение, возникающее при относительном покое тел, называют трением покоя.
Сухое трение, возникающее при относительном движении тел, называют трением скольжения.
Трение качения возникает, когда одно тело катится по поверхности другого тела.
Закон, выражающий зависимость максимального значения модуля силы трения покоя от модуля силы нормальной реакции опоры впервые экспериментально установил французский военный инженер и учёный-физик Шарль Огюстен де Кулон. Согласно этому закону, максимальное значение модуля силы трения покоя прямо пропорционально модулю силы нормальной реакции опоры
Fтр.макс = µN,
где Fтр.макс — модуль максимальной силы трения покоя, µ- коэффициент пропорциональности, называемый коэффициентом трения покоя.
Коэффициент трения µ характеризует обе трущиеся поверхности и зависит не только от материала этих поверхностей, но и от качества их обработки. Коэффициент трения определяется экспериментально.
Трение скольжения. Сила трения скольжения также направлена вдоль поверхности соприкосновения тел, но в отличие от силы трения покоя, которая противоположна внешней силе, стремящейся сдвинуть тело, сила трения скольжения всегда направлена противоположно относительной скорости. Модуль силы трения скольжения, как и максимальной силы трения покоя, тоже пропорционален прижимающей силе, а значит, нормальной силе реакции опоры:
При не слишком больших относительных скоростях движения сила трения скольжения мало отличается от максимальной силы трения покоя. Поэтому приближенно можно считать ее постоянной и равной максимальной силе трения покоя:
Fтр ≈ Fтр.макс = µN.
Важно! Сила трения зависит от относительной скорости движения тел. В этом ее главное отличие от сил тяготения и упругости, зависящих только от расстояний.
При движении твердого тела в жидкости или газе возникает силa жидкого (вязкого) трения. Сила жидкого трения значительно меньше силы сухого трения. Эта сила направлена против скорости тела относительно среды и тормозит движение.
Сила жидкого трения значительно меньше силы сухого трения. Эта сила направлена против скорости тела относительно среды и тормозит движение.
Главная особенность силы сопротивления состоит в том, что она появляется только при наличии относительного движения тела и окружающей среды. Сила трения покоя в жидкостях и газах полностью отсутствует. Поэтому усилием рук можно сдвинуть тяжелую баржу в воде, а сдвинуть поезд усилием рук невозможно.
Модуль силы сопротивления Fc зависит от размеров, формы и состояния поверхности тела, свойств среды (жидкости или газа), в которой тело движется, и, наконец, от относительной скорости движения тела и среды.
Примерный характер зависимости модуля силы сопротивления от модуля относительной скорости тела показан на рисунке
При относительной скорости, равной нулю, сила сопротивления не действует на тело (Fc=0). С увеличением относительной скорости сила сопротивления сначала растет медленно, а затем все быстрее и быстрее.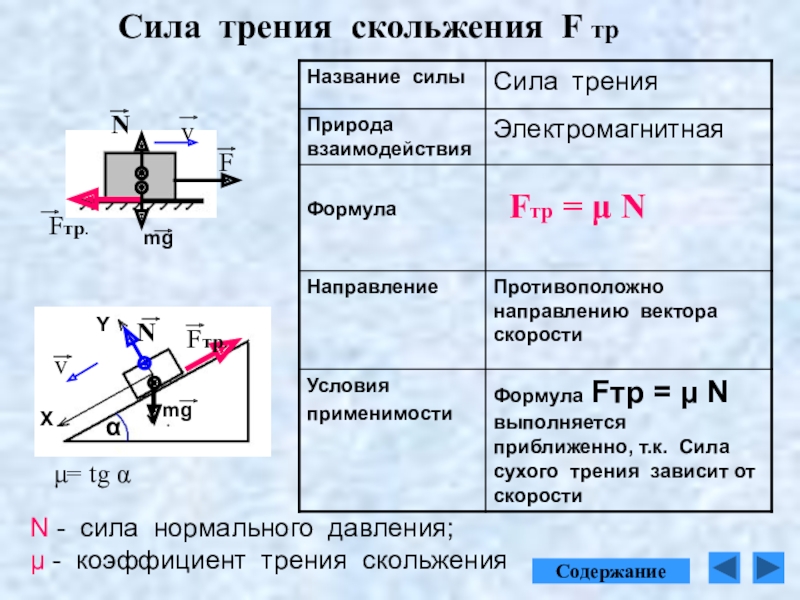 При малых скоростях движения силу сопротивления можно считать прямо пропорциональной скорости движения тела относительно среды:
При малых скоростях движения силу сопротивления можно считать прямо пропорциональной скорости движения тела относительно среды:
Fc = k1v, (1)
где k1— коэффициент сопротивления, зависящий от формы, размеров, состояния поверхности тела и свойств среды — ее вязкости.
Вычислить коэффициент k1 теоретически для тел сколько-нибудь сложной формы не представляется возможным, его определяют опытным путем.
При больших скоростях относительного движения сила сопротивления пропорциональна квадрату скорости:
Fc = k2v2, (2)
где k2 — коэффициент сопротивления, отличный от k1.
Только опытным путём можно определить, какая из формул — (1) или (2) — подходит для использования в конкретной практической задаче.
Итак, основными особенностями силы сопротивления, действующей на тело, являются:
1) отсутствие силы трения покоя; 2) зависимость от относительной скорости движения.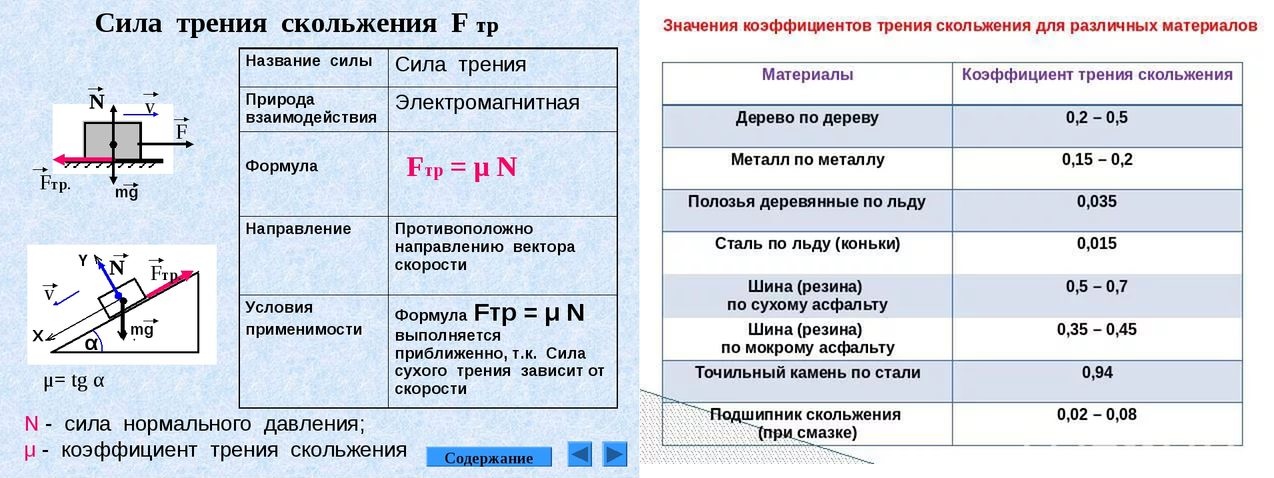
Примеры и разбор решения заданий
1. Какая сила не позволяет человеку сдвинуть с места дом?
- Силы трения скольжения;
- сила трения покоя;
- сила тяжести.
Ответ: 2) Сила трения покоя.
2. Деревянный ящик равномерно движется по поверхности длинного стола. Сила давления ящика на поверхность равна 30 Н, сила трения 6 Н. Найдите коэффициент трения скольжения.
Решение.
Воспользуемся формулой, которая связывает силу давления на плоскость, силу трения и коэффициент трения Fтр = µP. Из этой формулы легко получить формулу для расчёта коэффициента трения µ = Fтр / P. Подставляя в неё численные значения, получаем:
µ = Fтр / P = 6Н/30Н = 0,2.
Ответ: 0,2.
3. Кубик из детского конструктора покоится на наклонной плоскости, образующей угол α = 40° с горизонтом. Сила трения покоя равна 0,32 Н. Определите значение силы тяжести, которая действует на кубик.
Решение.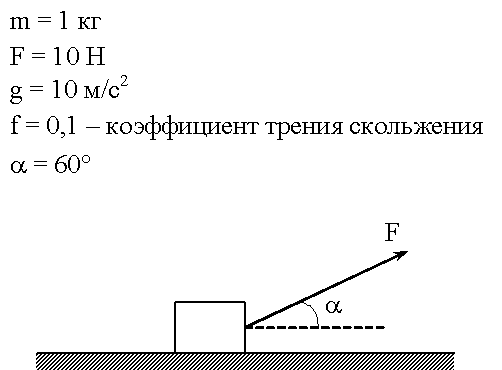
По условию задачи кубик покоится. Следовательно, сумма всех действующих на него сил равна нулю. В проекции на ось, идущей вдоль склона плоскости, получаем соотношение: mg sin α – Fтр = 0. Из него выражаем формулу для расчета силы тяжести, действующей на кубик
Ответ: 0,5 Н.
Коэффициент трения скольжения Рона Куртуса
SfC Главная > Физика > Сила > Трение >
Рона Куртуса
Коэффициент трения скольжения — это число, указывающее, насколько велико трение скольжения между двумя объектами при заданной нормальной силе, толкающей их вместе.
Существует два коэффициента трения скольжения, в зависимости от того, являются ли объекты статичными или стационарными, кинетическими они или движущимися относительно друг друга.Для данного набора материалов статический коэффициент трения скольжения обычно больше, чем кинетический коэффициент трения.
На коэффициент трения может влиять ряд факторов, в том числе состояние поверхности. Значения коэффициента трения скольжения могут быть хорошим ориентиром для конкретных комбинаций материалов.
Значения коэффициента трения скольжения могут быть хорошим ориентиром для конкретных комбинаций материалов.
Возможные вопросы:
- Какой коэффициент отношения?
- Какие факторы влияют на коэффициент трения скольжения?
- Какие значения коэффициентов?
Этот урок ответит на эти вопросы.Полезный инструмент: Преобразование единиц измерения
Соотношение коэффициентов
Когда к объекту прикладывается сила, сила сопротивления трения скольжения действует в противоположном направлении, параллельно поверхностям.
Статический коэффициент
Когда объекты неподвижны по отношению друг к другу и на один из них действует внешняя сила, сила сопротивления трения равна:
F нержавеющая сталь = μ нержавеющая сталь N
, а статический коэффициент трения скольжения:
.μ нержавеющая сталь = F нержавеющая сталь /N
где:
- μ сс — статический коэффициент трения скольжения для двух поверхностей (греческая буква «мю»)
- F ss статическая сила трения скольжения
- Н — нормальная или перпендикулярная сила, сталкивающая два объекта вместе
Кинетический коэффициент
Когда один объект скользит по другому, кинетический коэффициент трения скольжения составляет:
μ кс = F кс /N
где:
- μ ks — кинетический коэффициент трения скольжения для двух поверхностей (греческая буква «мю»)
- F ks – кинетическая сила сопротивления трения скольжения
Связь коэффициентов
Статический коэффициент больше кинетического:
мк сс > мк кс
и, следовательно,
F нерж.
сталь > F кс
Факторы, влияющие на коэффициент
существует несколько факторов, влияющих на коэффициент трения скольжения.
Независимо от скорости
В большинстве случаев скорость скользящего объекта не влияет на коэффициент трения. Однако при более высоких скоростях μ кс могут измениться. Было проведено не так много экспериментов по измерению изменения μ кс в зависимости от скорости скольжения.
Независимо от региона
Хотя это может показаться нелогичным, коэффициент трения скольжения не зависит от площади соприкасающихся поверхностей при условии, что нормальная сила постоянна.Это справедливо только тогда, когда поверхности твердые и не смазанные.
Например, трение скольжения книги по краю такое же, как когда она лежит на столе.
Обоснование этого правила заключается в том, что большая часть коэффициента трения возникает из-за шероховатости поверхности. Когда объект с небольшой площадью основания прижимается к поверхности с заданной силой, возникающее давление равно силе, деленной на площадь.
Когда объект с небольшой площадью основания прижимается к поверхности с заданной силой, возникающее давление равно силе, деленной на площадь.
Состояние поверхности
Другие эффекты, такие как окисление металлической поверхности, грязь, вода или жир, могут резко изменить коэффициент трения для данных материалов.
Эффект окисления
Например, чистая сухая сталь, скользящая по стали, имеет коэффициент трения μ = 0,78, но если поверхность окислена, коэффициент изменяется до μ = 0,27.
Точно так же чистая сухая медь скольжения по меди имеет коэффициент μ = 1,21, а окисленная медь имеет значение μ = 0,76.
Необходимо знать состояние поверхности
Самая большая проблема при использовании значений, установленных другими в таких таблицах, заключается в том, что вы не знаете фактического состояния поверхности используемых материалов или того, как были определены значения.
Таблица значений
Коэффициент трения может принимать значения от 0 (ноль) до ∞ (бесконечность).
При приближении к нулю
Когда μ = 0, трения нет. Если μ близко к 0, трения мало. Например, обувь на кожаной подошве на скользком льду имеет очень маленький коэффициент трения, близкий к нулю. Вот почему вы можете легко поскользнуться на льду или даже упасть. Даже обувь на резиновой подошве на льду имеет очень маленький коэффициент трения.
Когда близко к бесконечности
Многие студенты и учителя ошибочно думают, что μ должно быть меньше 1. Это неверно, поскольку F r может быть во много раз больше нормальной силы.
Крайний пример: вы приклеили один объект к другому. Сопротивление движению объектов было бы очень большим, и коэффициент трения также был бы очень большим. Если бы клей был настолько прочным, что их нельзя было бы скользить друг по другу, то μ равнялось бы бесконечности.
Причина, по которой люди думают, что μ должно быть меньше 1, вероятно, заключается в том, что большинство списков коэффициентов трения имеют значения меньше 1. Это связано с тем, что большинство интересующих материалов обычно относительно легко скользят друг по другу.
Это связано с тем, что большинство интересующих материалов обычно относительно легко скользят друг по другу.
Диаграмма
В следующей таблице перечислены статические и кинетические коэффициенты трения скольжения для некоторых типичных материалов. Предполагается, что поверхности чистые, твердые и без смазки.
Однако, поскольку качество поверхностей не упоминается, вы должны использовать эти показания только в качестве ориентира.Лучше всего измерить коэффициенты для ваших конкретных материалов и условий использования, чтобы получить точные значения.
Коэффициент трения скольжения | |||
Материал 1 | Материал 2 | Статическая | Кинетический |
| Алюминий | Мягкая сталь | 0,61 | 0,47 |
| Чугун | Чугун | 1. 1 1 | 0,15 |
| Медь | Чугун | 1,05 | 0,29 |
| Медь | Мягкая сталь | 0,53 | 0,36 |
| Стекло | Стекло | 0,9 — 1,0 | 0,4 |
| Стекло | Никель | 0,78 | 0.56 |
| Кожа | Дуб (параллельные волокна) | 0,61 | 0,52 |
| Никель | Никель | 0,7 — 1,1 | 0,53 |
| Дуб | Дуб (параллельные волокна) | 0,62 | 0,48 |
| Дуб | Дуб (поперечная структура) | 0,54 | 0.32 |
| Сталь (мягкая) | Латунь | 0,51 | 0,44 |
| Сталь (мягкая) | Свинец | 0,95 | 0,95 |
| Сталь (мягкая) | Сталь (мягкая) | 0,74 | 0,57 |
| Сталь (твердая) | Сталь (твердая) | 0,78 | 0. 42 42 |
| Сталь | Цинк (покрытие на стали) | 0,5 | 0,45 |
| Цинк | Чугун | 0,85 | 0,21 |
Резюме
Коэффициент трения для ряда материалов сведен в таблицу. Эти значения применимы только к твердым, чистым поверхностям, скользящим друг относительно друга. Поскольку различные экспериментальные параметры не перечислены, следует учитывать эти табличные значения, поскольку они могут не иметь прямого отношения к вашему приложению.
Гордись тем, что ты делаешь
Ресурсы и ссылки
Полномочия Рона Куртуса
веб-сайтов
Ресурсы трения — Расширенный список
Коэффициент трения — Статические значения трения (чистые и смазанные) из Engineering Toolbox
Инженерная библиотека — Коэффициент трения
Engineer’s Edge COF — Расширенные столы
Приблизительные коэффициенты трения — Википедия
РойМех (Великобритания) — Факторы трения — Различные списки
Книги
(Примечание: Школа чемпионов может получать комиссионные за покупку книг)
Лучшие книги по науке о трении
Лучшие книги по экспериментам с трением
Наука и технология трения (Серия машиностроения) Питера Дж. синий; Марсель Деккер Паб. (1995) 89,95 $
синий; Марсель Деккер Паб. (1995) 89,95 $
Физика трения скольжения (NATO Science Series E 🙂 Б.Н. Перссон, Э. Тосатти; Паб Спрингер. (1996) $358,00
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
коэффициент трения_скольжения.хтм
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа Чемпионов
Темы трения
Коэффициент трения скольжения
Трение скольжения – обзор
3.4.2 Классическая модель трения скольжения
Классическая модель трения металлов скольжения основана на важной работе Боудена и Табора, выполненной в основном в Кембридже между 1930-ми и 1970-ми годами. Модель Боудена и Табора для трения скольжения в ее простейшей форме предполагает, что сила трения возникает из двух источников: силы сцепления , возникающей в областях реального контакта между поверхностями (стыки неровностей), и силы деформации необходимо было прорезать неровности более твердой поверхности через более мягкую. Хотя в более позднем развитии теории стало ясно, что эти два вклада нельзя рассматривать как строго независимые, удобно и поучительно рассматривать их по отдельности; результирующая сила трения F затем принимается как сумма двух составляющих: F adh из-за сцепления и F def из-за деформации.
Модель Боудена и Табора для трения скольжения в ее простейшей форме предполагает, что сила трения возникает из двух источников: силы сцепления , возникающей в областях реального контакта между поверхностями (стыки неровностей), и силы деформации необходимо было прорезать неровности более твердой поверхности через более мягкую. Хотя в более позднем развитии теории стало ясно, что эти два вклада нельзя рассматривать как строго независимые, удобно и поучительно рассматривать их по отдельности; результирующая сила трения F затем принимается как сумма двух составляющих: F adh из-за сцепления и F def из-за деформации.
Термин адгезии возникает из-за сил притяжения, которые, как предполагается, действуют на контактах неровностей. На первый взгляд это предположение может показаться неправдоподобным; в конце концов, общеизвестно, что когда две металлические поверхности прижимаются друг к другу, они обычно не сцепляются. Однако если поверхности действительно чистые, свободные от оксидных и других поверхностных пленок и адсорбированных газов, то между металлами наблюдается значительная адгезия; такие условия могут быть достигнуты в условиях сверхвысокого вакуума (СВВ) (обычно при давлении газа <10 90 531 - 8 Па).Сильная адгезия, при которой силы сцепления иногда превышают нагрузку, используемую для прижатия поверхностей друг к другу, наблюдается при сверхвысоком вакууме для пластичных металлов, таких как медь и золото. В менее пластичных материалах, например в металлах с гексагональной кристаллической структурой и небольшим количеством действующих систем скольжения, или в керамике, адгезия оказывается слабее.
Однако если поверхности действительно чистые, свободные от оксидных и других поверхностных пленок и адсорбированных газов, то между металлами наблюдается значительная адгезия; такие условия могут быть достигнуты в условиях сверхвысокого вакуума (СВВ) (обычно при давлении газа <10 90 531 - 8 Па).Сильная адгезия, при которой силы сцепления иногда превышают нагрузку, используемую для прижатия поверхностей друг к другу, наблюдается при сверхвысоком вакууме для пластичных металлов, таких как медь и золото. В менее пластичных материалах, например в металлах с гексагональной кристаллической структурой и небольшим количеством действующих систем скольжения, или в керамике, адгезия оказывается слабее.
В очень мягких и пластичных металлах, таких как свинец и индий, адгезия может быть легко продемонстрирована в обычных лабораторных условиях (рис. 3.5). Если закругленный конец латунного или стального стержня обезжирить и отшлифовать, чтобы удалить часть поверхностных загрязнений, а затем прижать к свежезачищенной поверхности бруска индия, произойдет сильное сцепление.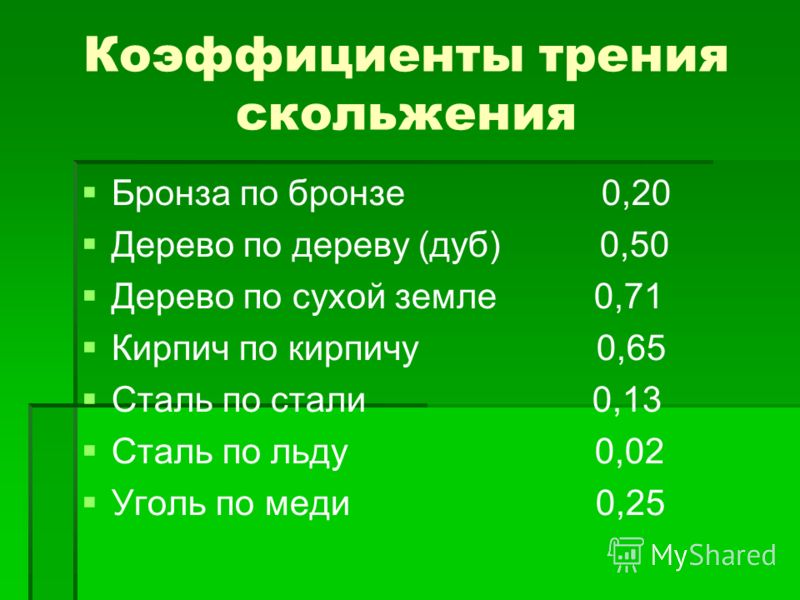 Кроме того, когда стержень отсоединен, фрагменты индия прилипают к стержню, показывая, что силы сцепления в местах соединения больше, чем когезионная прочность самого индия. Подобные эффекты наблюдаются в экспериментах с сверхвысоким вакуумом: если чистую железную поверхность слегка прижать к медной поверхности, а затем удалить, то при осмотре железной поверхности выявляются следы меди.
Кроме того, когда стержень отсоединен, фрагменты индия прилипают к стержню, показывая, что силы сцепления в местах соединения больше, чем когезионная прочность самого индия. Подобные эффекты наблюдаются в экспериментах с сверхвысоким вакуумом: если чистую железную поверхность слегка прижать к медной поверхности, а затем удалить, то при осмотре железной поверхности выявляются следы меди.
Рис. 3.5. Эксперимент, иллюстрирующий адгезию между металлами. Чистый стальной или латунный стержень легким вращательным движением прижимают к свежезачищенной поверхности индиевого блока.Чтобы отделить стержень от блока, требуется значительное усилие, и фрагменты индия прилипают к поверхности стали
Моделирование взаимодействия между контактирующими разнородными чистыми металлами с использованием моделей молекулярной динамики (МД) для соответствующих межатомных сил также демонстрирует значительные адгезия и перенос материала. На рис. 3.6 показан результат молекулярно-динамического моделирования контакта между никелевым индентором и изначально плоской поверхностью золота. Когда индентор приближается к поверхности, силы сцепления достаточно, чтобы вызвать деформацию золота, так что плотный контакт происходит, когда никелевый наконечник все еще находится на некотором расстоянии от исходного уровня поверхности.Последовательность изображений начинается, когда индентор находится в точке максимального вдавливания в золото. Когда индентор поднимают с поверхности, соединение внутри золота разрывается, и значительное количество атомов золота переносится на никелевый наконечник.
Когда индентор приближается к поверхности, силы сцепления достаточно, чтобы вызвать деформацию золота, так что плотный контакт происходит, когда никелевый наконечник все еще находится на некотором расстоянии от исходного уровня поверхности.Последовательность изображений начинается, когда индентор находится в точке максимального вдавливания в золото. Когда индентор поднимают с поверхности, соединение внутри золота разрывается, и значительное количество атомов золота переносится на никелевый наконечник.
Рис. 3.6. Атомные конфигурации, предсказанные теоретическим моделированием контакта между никелевым индентором (верхняя часть тела) и изначально плоской золотой поверхностью. В модели не учитываются адсорбированные или прореагировавшие атомы кислорода, поэтому моделируемая система соответствует контакту атомарно чистых металлов в идеальном вакууме.Изображения сверху слева вниз справа показывают прилипание атомов золота к индентору и постепенное формирование «шейки» атомов золота, вытягивающейся по мере того, как индентор поднимается с поверхности
от Landman, U.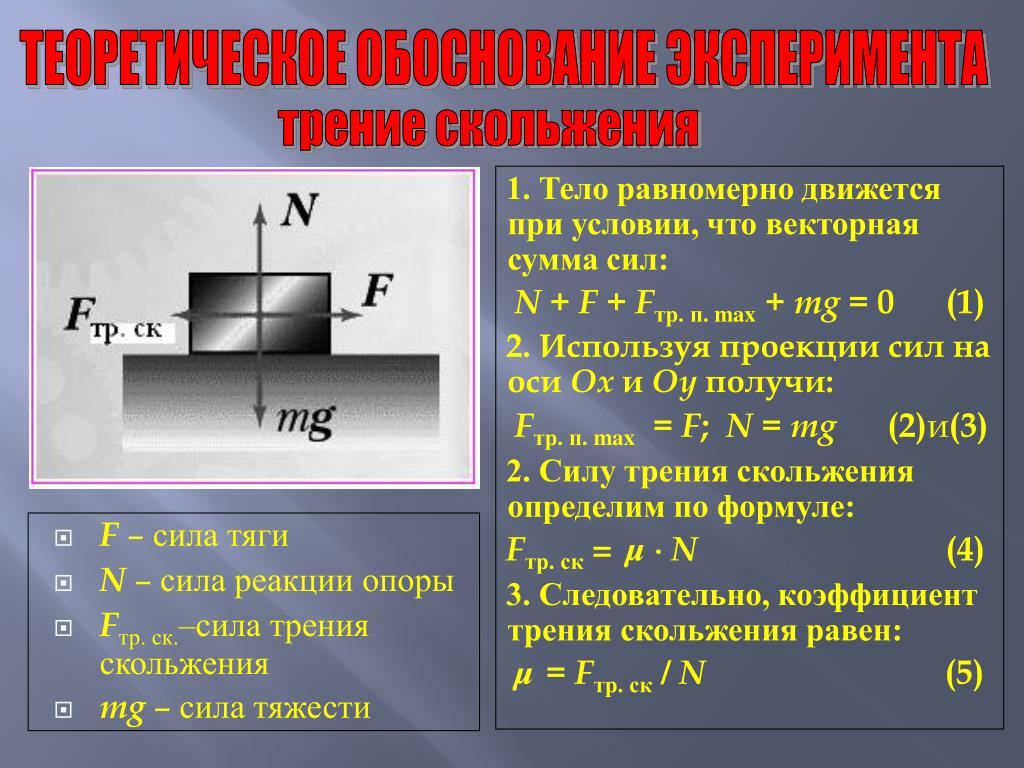 , Luedtke, WD, Ringer. , EM, 1992. Wear 153, 3–30
, Luedtke, WD, Ringer. , EM, 1992. Wear 153, 3–30Все эти данные указывают на установление прочных межфазных связей через стыки неровностей, по крайней мере, для чистых поверхностей пластичных металлов. Причины, по которым не наблюдается значительной адгезии при соединении двух металлических поверхностей в обычных условиях, двояки: во-первых, поверхности покрыты оксидными и адсорбированными пленками, которые ослабляют адгезию, и, во-вторых, упругие деформации вокруг неровностей при воздействии нагрузка создает достаточное напряжение, чтобы сломать стыки неровностей в процессе разгрузки, если только металл не является особенно пластичным.Таким образом, только в мягких пластичных металлах и в тех случаях, когда оксидные пленки хотя бы частично удалены, в обычных условиях может быть продемонстрирована заметная адгезия.
Данные экспериментов по адгезии и теоретического моделирования также предполагают, что, когда два разнородных металла скользят друг относительно друга, образующиеся стыки шероховатостей будут на самом деле прочнее, чем более слабый из двух металлов, что приведет к выдергиванию и перемещению фрагментов более мягкий металл к более твердому. Это действительно наблюдается и приводит к сильному износу более мягкого металла (см. главу 5).
Это действительно наблюдается и приводит к сильному износу более мягкого металла (см. главу 5).
Если мы обозначим истинную площадь контакта, сумму площадей поперечных сечений всех узлов неровностей, через A и предположим, что все соединения имеют одинаковую прочность на сдвиг с , то сила трения из-за адгезия будет равна
(3.3)Fadh=As
В разделе 2.5.6 мы видели, что в первом приближении, независимо от того, является ли контакт между неровностями преимущественно упругим или преимущественно пластическим, реальная площадь контакта почти линейно пропорциональна приложенная нормальная нагрузка.Для контакта между металлическими поверхностями, обработанными большинством обычных инженерных процессов, начальные контакты неровностей будут эффективно пластичными (см. раздел 2.5.6), и мы можем написать
(3.4)W≈AH
, поскольку нормальное напряжение, которому подвергаются неровности способность поддерживать, если они пластически деформируются, будет близка к твердости на вдавливание 90 515 H 90 516 более мягкого материала (см.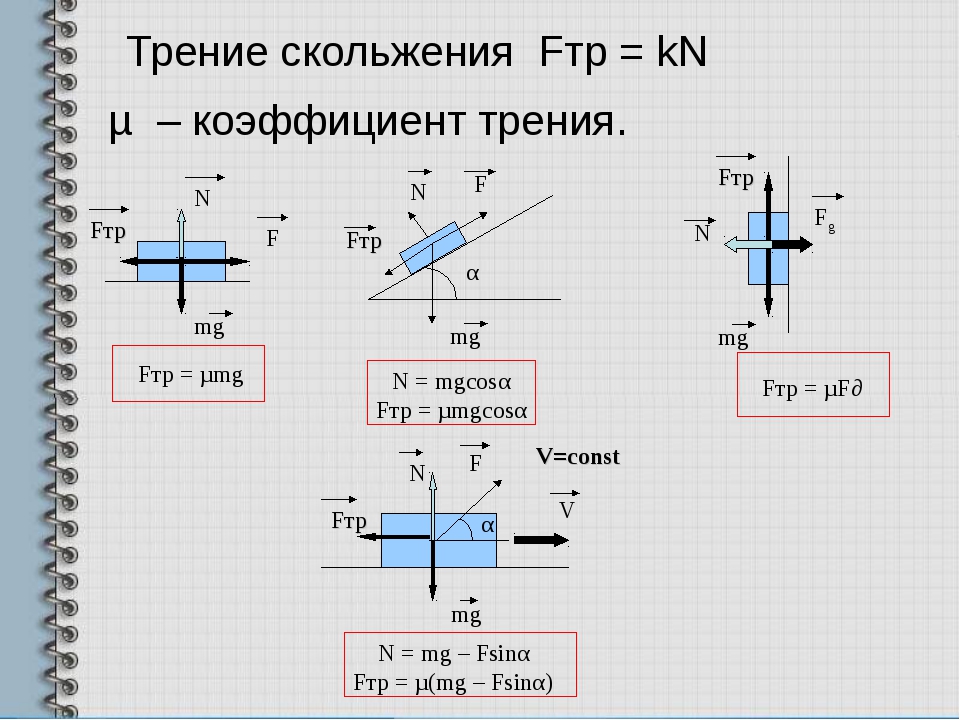 раздел 2.5.2 и приложение A).
раздел 2.5.2 и приложение A).
Таким образом, вклад сил сцепления в коэффициент трения составляет
(3.5)µadh=Fadh/W≈s/H
Поскольку стыки шероховатостей разрушаются из-за разрыва внутри более слабого из двух материалов, мы можем принять с в первом приближении за прочность на сдвиг этого материала; H — твердость на вдавливание того же материала. Для металлов твердость при вдавливании примерно в три раза превышает одноосный предел текучести, как описано в Приложении A:
(3,6)H≈3Y
Предел текучести Y будет примерно в 1,7 или 2 раза выше предела текучести при чистом сдвиге , s , точный коэффициент, зависящий от выбранного критерия доходности.Поэтому мы ожидаем, что
(3,7)H≈5s
и, следовательно, что
(3,8)µadh≈s/H≈0,2
деформация срок, можно оценить, рассматривая простую неровность идеализированной формы.
Если жесткая коническая неровность полуугла α (см. рис. 3.7) скользит по плоской поверхности, то касательная сила, необходимая для ее смещения, будет давлением потока, которое можно принять за твердость при вдавливании H материала поверхности, умноженное на площадь поперечного сечения канавки:
рис. 3.7) скользит по плоской поверхности, то касательная сила, необходимая для ее смещения, будет давлением потока, которое можно принять за твердость при вдавливании H материала поверхности, умноженное на площадь поперечного сечения канавки:
Рис.3.7. Модель деформационной составляющей трения, при которой конический выступ полуугла α вдавливается и скользит по поверхности пластически деформируемого материала
(3.9)Fdef=Hax=Hx2tanα
Нормальная нагрузка, воспринимаемая выступом определяется как
(3.10)W=Hπa2/2=Hπx2tan2α
Таким образом, коэффициент трения из-за вспашки будет
(3.11)µdef=Fdef/W=2/πcotα
Модель плоской деформации, где неровность принята за клин полуугла α , ведет аналогично
(3.12)µdef=cotα
Эти отношения подтверждаются данными экспериментов, в которых неровности макроскопической модели перемещались по более мягким металлическим поверхностям.
Наклоны реальных поверхностей почти всегда меньше 10° (т. е. α > 80°), поэтому из уравнений 3.11 и 3.12 можно ожидать, что μ def будет меньше примерно 0,1.
е. α > 80°), поэтому из уравнений 3.11 и 3.12 можно ожидать, что μ def будет меньше примерно 0,1.
Таким образом, из нашей простой модели мы заключаем, что даже для твердого металла, скользящего по более мягкому, общий коэффициент трения, представляющий вклад как вспашки, так и сцепления, не должен превышать 0.3 или около того. Для металла, скользящего по поверхности из того же материала, где вклад от вспашки должен быть пренебрежимо мал, μ должно быть несколько меньше, порядка 0,2.
Если мы посмотрим на экспериментальные измерения μ для скольжения металлов без смазки, перечисленные ниже в Таблице 3.1, мы обнаружим, что измеренные значения фактически в несколько раз превышают эти оценки. Расхождение настолько велико, что другие эффекты должны играть роль. Доминируют два эффекта: упрочнение и рост соединения .
Таблица 3.1. Типичные значения коэффициента трения покоя, μ s , для комбинаций металлов на воздухе и без смазки. Следует понимать, что значение μ s зависит от точных условий испытания, и эти значения следует рассматривать только как репрезентативные. Там, где цитируются два значения, они относятся к условиям, при которых оксидные пленки натуральные, а в которых они проникают
Следует понимать, что значение μ s зависит от точных условий испытания, и эти значения следует рассматривать только как репрезентативные. Там, где цитируются два значения, они относятся к условиям, при которых оксидные пленки натуральные, а в которых они проникают
| μ S S | ||
|---|---|---|
| ( A ) сопряженные металлы в воздухе | ||
| Золото | 2 | |
| Серебро | 0.8-1 | |
| Олово 1 | ||
| Алюминий 0,8-1,2 | ||
| Медь 0,7-1,4 | ||
| индий 2 | ||
| магния 0,5 | ||
| LEAD | 1.5 | 1,5 |
0. 5 5 | ||
| Chromium | 0,4 | |
| ( B ) Чистые металлы и сплавы скольжения на сталь ( 0.13% С ) в воздухе | ||
| Серебро | 0,5 | |
| Алюминиевый | 0,5 | |
| Кадмий | 0,4 | |
| Медь | 0,8 | |
| Хром | 0,5 | |
| INDIUM | 2 | |
| LEAD | 1.2 | |
| 902 | ||
| 0,2 | ||
| Whitemetal (SN на основе SN) | 0.8 | |
| Whitemetal (PB на основе PB) | 0.5 | 0.5 |
| α-латунь (Cu-30% Zn) | 0. 5 5 | |
| Проведенная α / β латунь (Cu-40% Zn) | 0.2 | |
| Серый чугун | 0,4 | 0,4 |
| Мягкая сталь (0,13% в) | 0,8 |
Данные из Боудена, FP, Tabor, D., 1964. Трикционные и смазки твердых веществ, часть II . Кларендон Пресс, Оксфорд; Табор, Д., 1973. В: Нил, М.J. (Ed.), Справочник по трибологии. Butterworths
В разработанной выше простой модели предполагается, что материал имеет постоянное напряжение течения. Однако почти все металлы в той или иной степени упрочняются, и хотя нормальная нагрузка поддерживается пластическим течением на некотором расстоянии от непосредственной близости от стыков неровностей, сами стыки будут значительно упрочняться, что приведет к увеличению относительного значения s по сравнению с H . Следовательно, упрочнение будет иметь тенденцию к увеличению μ adh , хотя это явление трудно поддается количественной оценке.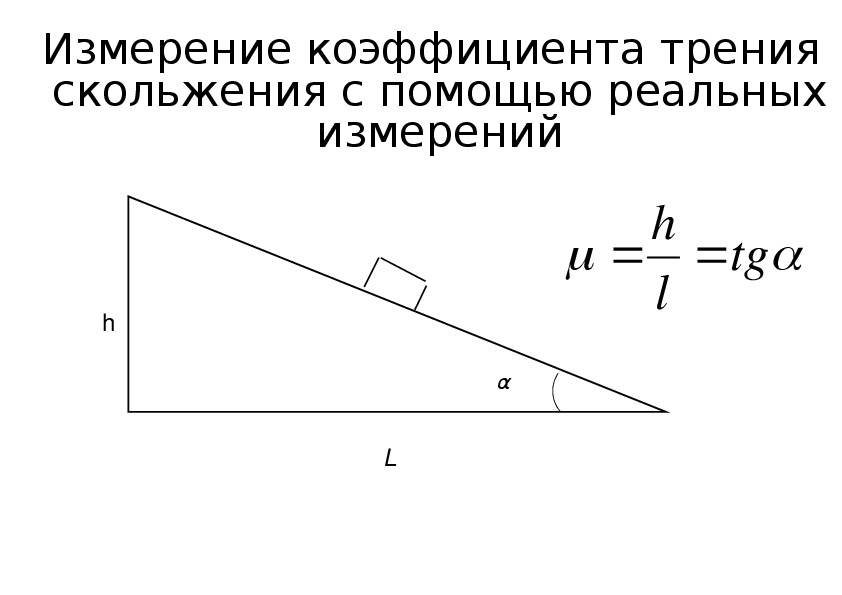 Вероятно, более важным является эффект роста перехода, который будет рассмотрен в следующем разделе.
Вероятно, более важным является эффект роста перехода, который будет рассмотрен в следующем разделе.
Трение скольжения: определение, формула и примеры — видео и расшифровка урока
Формула трения скольжения
Уравнение трения скольжения на плоской поверхности довольно простое — это коэффициент трения скольжения, умноженный на нормальную силу.
Нормальная сила смущает Ганса, пока он не понимает, что «нормальный» — это научный термин, означающий перпендикулярно поверхности или под прямым углом.Большинство книг дают уравнение на наклонной плоскости. Однако Ганс игнорирует их, поскольку все сражения происходят на плоской поверхности.
Увеличение трения скольжения
Ганс думает обо всех фактах, которые он узнал о трении скольжения, и о том, что они означают для его сражений роботов. Поскольку существует всего несколько способов увеличить трение скольжения, Ганс может улучшить своего робота только несколькими способами: утяжелить его или изменить материалы.
Добавление дополнительных колес к его роботу для увеличения тяги, что он собирался сделать, не поможет.Он также не может увеличить вес своего робота, даже если это увеличит трение скольжения. Добавление большего веса также переместит его в следующую весовую категорию, чего Ганс не хочет делать прямо сейчас.
Единственное, что он может сделать, это изменить тип шин, которые он использует. Он проведет небольшое исследование и выяснит, есть ли шины с лучшим коэффициентом трения скольжения, чем у него сейчас.
Примеры задач
Робот, которого Ганс использует в битвах, весит 25 кг, а коэффициент трения скольжения между его текущими шинами и бетоном, на котором он сражается, равен 0.6. Какая сила требуется, чтобы поддерживать движение его робота, если он уже скользил из-за маневра со стороны Хана? Используйте ускорение свободного падения как г = 9,8 м/с/с, чтобы понять это.
(9,8)(25)(0,6) = 147 ньютонов
На сколько процентов увеличилась бы эта сила, если бы он смог найти шину с коэффициентом трения скольжения 0,8 в том же сценарии? Чтобы узнать это, сначала вычислите новую силу:
(9,8)(25)(0,8) = 196 ньютонов.
Затем получите увеличение в %:
(196 — 147) / 147 = 33%
С помощью этой новой информации Ганс решает, что использовать шины с коэффициентом трения скольжения, равным 0.8 поможет его роботу не так легко помыкать, и, возможно, даже поможет его роботу выиграть больше сражений, будучи тем, кто толкает других роботов.
Резюме урока
Трение скольжения , кинетическое трение или движущееся трение — это сила, необходимая для удержания двух поверхностей в движении относительно друг друга. Величина этой силы зависит только от двух факторов для немикроскопических ситуаций: коэффициента трения скольжения между двумя материалами и нормальной силы.Нормальная сила — это просто сила, перпендикулярная рассматриваемым поверхностям.
Коэффициент кинетического трения: определение, формула и примеры — видео и расшифровка урока
Трение о наклонную плоскость
Для трения о наклонные поверхности нормальная сила такова:
На диаграмме, которую вы видите на экране, объект находится в состоянии покоя, на него не действуют никакие внешние силы. В зависимости от других сил нормальная сила может изменяться по величине или сила трения может действовать в противоположном направлении.
В зависимости от других сил нормальная сила может изменяться по величине или сила трения может действовать в противоположном направлении.
Н = нормальная сила (это сила, действующая вверх и вправо от поверхности, и сила, действующая вниз и влево от объекта)
м(г) = сила тяжести
Пример 1 — плоская поверхность
Мэгги только что завершила эксперимент по физическому трению со следующими данными:
Материал объекта: резина
Материал поверхности: деревянная доска
Масса перетаскиваемого объекта = 2.11 кг
Сила, необходимая для удержания объекта в движении (среднее значение 10 показаний) = 12,6 ньютонов
Объект тянули по ровной поверхности.
Принятое ускорение свободного падения в этом месте составляет 9,82 м/с/с
Каков коэффициент кинетического трения? Используя формулу кинетического трения, мы можем рассчитать следующее:
Коэффициент кинетического трения = (12,6 Н) / (2,11 кг)(9,82 м/с/с) = 0,608
Пример 2: Вниз по наклонной плоскости
Мэгги ставит свой эксперимент под углом 30 градусов к горизонтали, а затем измеряет силу, необходимую для того, чтобы объект двигался по деревянной доске. Ожидаете ли вы, что оно будет больше или меньше 12,6 ньютонов в первом эксперименте? Чтобы рассчитать это, нам нужно подумать обо всех силах, действующих на этот объект, как перпендикулярных поверхностям, так и параллельных поверхностям.
Ожидаете ли вы, что оно будет больше или меньше 12,6 ньютонов в первом эксперименте? Чтобы рассчитать это, нам нужно подумать обо всех силах, действующих на этот объект, как перпендикулярных поверхностям, так и параллельных поверхностям.
Перпендикулярно: единственная сила, действующая перпендикулярно поверхности, — это нормальная сила.
Нормальная сила = мг cos(30) = (2,11 кг)(9,82 м/с/с)(0,866) = 17,9 Н резиновый блок и сила кинетического трения, действующая вверх по склону.
Сила тяжести, действующая вниз по склону = mg sin(30) = (2,11 кг)(9,82 м/с/с)(0,5) = 10,4 Н
Сила кинетического трения, действующая против направления движения = (нормальная сила )(коэффициент кинетического трения) = (17,9 Н)(0,608) = 10,9 Н. Следовательно, сила, которую применяет Мэгги, должна быть разницей между кинетическим трением, действующим вверх по склону, и силой тяжести, действующей вниз по склону.
= 10,9 Н — 10,4 Н = 0,5 Н
Экспериментальный результат Мэгги относительно близок к теоретическому, рассчитанному нами.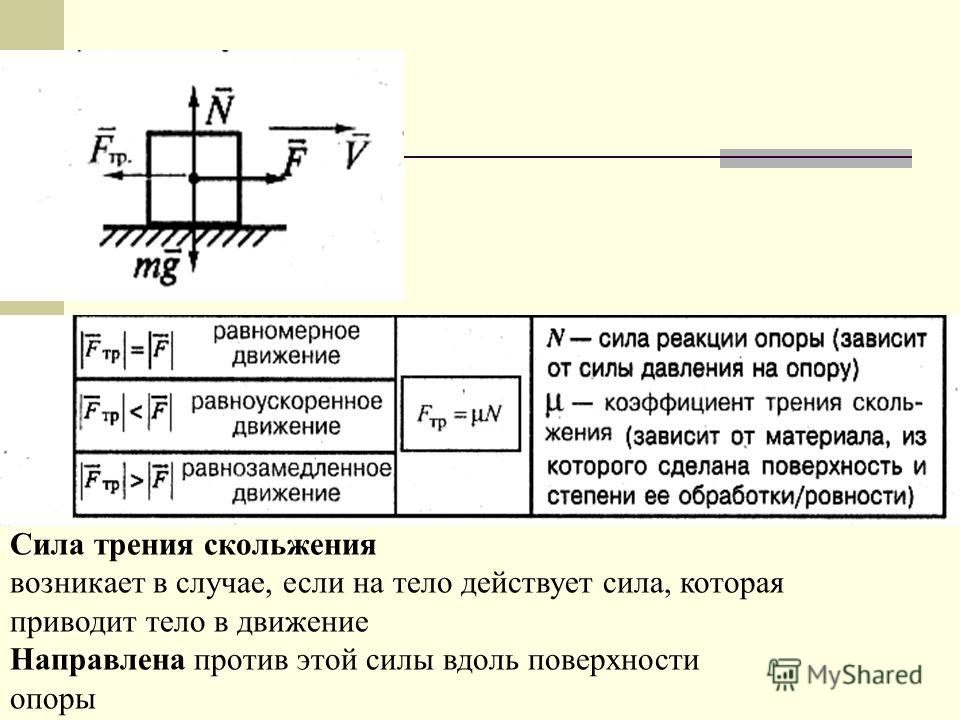
Пример 2.5. Вверх по наклонной плоскости
В этом случае мы можем использовать те же рассуждения и расчеты, что и в примере спуска. Основные отличия заключаются в том, что теперь гравитация и трение действуют вниз по склону, а сила, приложенная Мэгги, действует вверх. Таким образом, новая рассчитанная сила Мэгги будет суммой этих двух: 10,9 Н + 10,4 Н = 21.3 N
Таким образом, этот блок более чем в два раза труднее тянуть вверх по склону, чем на ровной поверхности!
Резюме урока
Во-первых, мы должны помнить, что кинетическое трение , также известное как трение скольжения или движущееся трение, представляет собой величину тормозящей силы между двумя объектами, которые движутся друг относительно друга. Тогда мы можем понять коэффициент кинетического трения , который рассчитывается путем деления силы кинетического трения на нормальную силу, удерживающую две поверхности вместе.Уравнение, которое поможет вам найти коэффициент кинетического трения, выглядит следующим образом:
Нормальная сила — это сила, перпендикулярная к соприкасающимся поверхностям, или сила, удерживающая объекты вместе. А сила кинетического трения — это сила, необходимая для того, чтобы два объекта двигались относительно друг друга.
А сила кинетического трения — это сила, необходимая для того, чтобы два объекта двигались относительно друг друга.
Ожидается, что этот коэффициент кинетического трения будет больше нуля для большинства макроскопических ситуаций и может быть намного больше единицы, если поверхности особенно шероховатые.Задачи на плоской поверхности довольно просты, а задачи на наклонное трение более сложны. Последние требуют, чтобы вы думали о силах, действующих на объект, которые параллельны и перпендикулярны поверхностям. Наконец, помните, что коэффициент трения скольжения, необходимый для того, чтобы только гравитация удерживала объект, скользящий по поверхности, равен 1,
.Статическое сопротивление трению будет соответствовать приложенной силе до порога движения.Тогда кинетическое сопротивление трению остается примерно постоянным. Этот график иллюстрирует стандартную модель трения. Приведенный выше график, хотя и представляет упрощенное представление о трении, довольно хорошо согласуется с результатами простых экспериментов с деревянными блоками на деревянных наклонных поверхностях. Проведя этот эксперимент с большим количеством студентов, я могу сообщить, что полученный коэффициент статического трения почти всегда больше, чем коэффициент кинетического трения.Типичные результаты для древесины, которую я использовал, составляют 0,4 для статического коэффициента и 0,3 для кинетического коэффициента. Когда для измерения коэффициентов трения используются тщательно стандартизированные поверхности, разница между статическими и кинетическими коэффициентами имеет тенденцию исчезать, что указывает на то, что разница может быть связана с неровными поверхностями, загрязнениями или другими факторами, которые могут быть досадно невоспроизводимыми. Чтобы процитировать счетчик просмотров приведенной выше модели трения: | Индекс Концепции трения Ссылка |
Границы | Переходное и устойчивое трение эластомеров при скольжении: влияние вертикального подъема
Введение
Хорошо известно, что скользящий контакт эластомеров связан с различными типами динамики из-за трения.Физические явления, такие как распространение волн (Schallamach, 1971; Barquins, 1985; Rubinstein et al., 2004; Maegawa and Nakano, 2010), образование моделей износа (Schallamach, 1957; Fukahori and Yamazaki, 1994) и нелинейные вибрации (Nakano и Maegawa, 2009; Yamaguchi et al., 2011; Nakano et al. , 2019) привлекли внимание многих научных и инженерных исследователей. Среди различных эластомеров каучуку уделяется наибольшее внимание в различных практических приложениях (например,г., шины, уплотнения и колодки). После исследования, проведенного Грошем (1963 г.), показывающего основную кривую коэффициента трения в соответствии с теорией Вильямса-Ландела-Ферри (WLF) (Вильямс и др., 1955 г.), была признана важность вязкоупругости, и зависимость коэффициента трения был исследован коэффициент температуры и скорости [например, Popov et al. (2018)]. Совсем недавно было обнаружено несколько набухших полимеров, демонстрирующих высокую эластичность и сверхнизкое трение (например, гидрогели и полимерные щетки) (Gong et al., 2001; Nomura et al., 2011), некоторые из которых разрабатываются для практического применения (Belin et al., 2018; Tadokoro et al., 2020), и их трибологические свойства также обсуждались в связи с их вязкоупругими свойствами (Mizukami et al. др., 2019).
, 2019) привлекли внимание многих научных и инженерных исследователей. Среди различных эластомеров каучуку уделяется наибольшее внимание в различных практических приложениях (например,г., шины, уплотнения и колодки). После исследования, проведенного Грошем (1963 г.), показывающего основную кривую коэффициента трения в соответствии с теорией Вильямса-Ландела-Ферри (WLF) (Вильямс и др., 1955 г.), была признана важность вязкоупругости, и зависимость коэффициента трения был исследован коэффициент температуры и скорости [например, Popov et al. (2018)]. Совсем недавно было обнаружено несколько набухших полимеров, демонстрирующих высокую эластичность и сверхнизкое трение (например, гидрогели и полимерные щетки) (Gong et al., 2001; Nomura et al., 2011), некоторые из которых разрабатываются для практического применения (Belin et al., 2018; Tadokoro et al., 2020), и их трибологические свойства также обсуждались в связи с их вязкоупругими свойствами (Mizukami et al. др., 2019).
Чтобы понять трение скольжения эластомеров, были предложены различные типы методов моделирования. Известно, что среди них те, у которых есть «вязкоупругие основания», обладают сильными преимуществами не только в том, что они позволяют избежать трудностей теории упругого контактного напряжения, но и дают интуитивное представление о том, как происходит диссипация энергии внутри контакта.Первым было расширение упругого основания (т. е. основания Винклера) от стационарных контактных задач тонких пленок до стационарных контактных задач скольжения эластомеров (May et al., 1959; Johnson, 1985). Затем, недавно, в новой структуре «Метода уменьшения размерности», изобретенного Поповым и его коллегами, метод моделирования получил развитие, позволив нам анализировать настоящий трехмерный контакт с высокой точностью (Попов, 2010; Попов и Хесс, 2015; Куще, 2017). Например, Ли и др.(2015) численно и теоретически исследовали кинетику коэффициента трения для скользящего контакта между плоским эластомером (моделируется фундаментом Кельвина-Фойгта) и шероховатым жестким индентором (моделируется самоаффинным фракталом) при резком изменении скорости привода.
Известно, что среди них те, у которых есть «вязкоупругие основания», обладают сильными преимуществами не только в том, что они позволяют избежать трудностей теории упругого контактного напряжения, но и дают интуитивное представление о том, как происходит диссипация энергии внутри контакта.Первым было расширение упругого основания (т. е. основания Винклера) от стационарных контактных задач тонких пленок до стационарных контактных задач скольжения эластомеров (May et al., 1959; Johnson, 1985). Затем, недавно, в новой структуре «Метода уменьшения размерности», изобретенного Поповым и его коллегами, метод моделирования получил развитие, позволив нам анализировать настоящий трехмерный контакт с высокой точностью (Попов, 2010; Попов и Хесс, 2015; Куще, 2017). Например, Ли и др.(2015) численно и теоретически исследовали кинетику коэффициента трения для скользящего контакта между плоским эластомером (моделируется фундаментом Кельвина-Фойгта) и шероховатым жестким индентором (моделируется самоаффинным фракталом) при резком изменении скорости привода. . В результате были обнаружены интересные временные изменения (т.е. скачки и релаксации) коэффициента трения в зависимости от скорости привода и показателя Херста самоаффинного фрактала при рассмотрении квазистатических процессов.
. В результате были обнаружены интересные временные изменения (т.е. скачки и релаксации) коэффициента трения в зависимости от скорости привода и показателя Херста самоаффинного фрактала при рассмотрении квазистатических процессов.
Исходя из вышеизложенного, целью данного исследования было найти ответ на следующий вопрос: каковы минимальные требования для моделирования с использованием вязкоупругих оснований для описания нестационарного трения, возникающего в начале скольжения между эластомером и индентором? В этой статье, чтобы дать возможный ответ в минимальной ситуации, мы рассматриваем простой линейный контакт между плоским эластомером и цилиндрическим жестким индентором, ориентируясь на граничное условие жесткого индентора в вертикальном направлении, при условии, что эластомер моделируется обычным фондом Кельвина-Фойгта.Два типа моделей с разными граничными условиями показывают, что вертикальная динамика жесткого индентора сильно влияет не только на возникновение переходного трения скольжения, но и на характеристики установившегося трения скольжения.
Заметим, что приведенное выше представление о граничном условии в вертикальном направлении исходит из типичной структуры систем скольжения при жидкостно-пленочной смазке, поскольку при теоретическом рассмотрении жидкостно-пленочной смазки естественно предположить, что «ползун» (соответствующий к «индентору» в этом исследовании) смещается по вертикали, чтобы найти положение для баланса с приложенной нормальной нагрузкой.Также обратите внимание, что в целом было известно, что трение эластомеров возникает по двум различным механизмам. Одним из них является «адгезия», диссипация энергии которой происходит на контактной поверхности между эластомером и индентором [т. е. адгезионное трение (например, Moore and Geyer (1972))], а другим — «вязкоупругость», т.е. диссипация энергии которого происходит внутри эластомеров [т.е. гистерезисное трение (например, Moore and Geyer (1974)]). Хотя оба механизма важны и должны быть взаимосвязаны, в данном исследовании игнорируется первый и основное внимание уделяется второму.
Модели
Конструкции
На рис. 1 показаны два типа моделей трения скольжения эластомеров, рассматриваемых в данном исследовании. Левая часть называется «моделью с фиксированным индентором (FI)», а правая — «моделью с подвижным индентором (MI)». Это модели, описывающие двумерный скользящий контакт между жестким индентором и вязкоупругим основанием в плоскости xz , где оси x и z взяты в горизонтальном и вертикальном направлениях соответственно.
Рисунок 1 . Два типа моделей скользящего контакта между цилиндрическим жестким индентором и плоским эластомером (моделируется вязкоупругим основанием). (слева) Модель с фиксированным индентором (FI). (справа) Модель с подвижным индентором (MI).
Жесткий индентор (масса на единицу ширины: M ) имеет цилиндрическую форму (радиус кривизны: R ), нижняя поверхность которого контактирует с вязкоупругим основанием. В модели FI жесткий индентор крепится к жестким стенкам, чтобы не иметь возможности двигаться в любом направлении.С другой стороны, в модели MI жесткий индентор опирается на линейный подшипник без трения, что позволяет ему двигаться только в вертикальном направлении. Обратите внимание, что граничное условие жесткого индентора является единственной разницей между ними.
В модели FI жесткий индентор крепится к жестким стенкам, чтобы не иметь возможности двигаться в любом направлении.С другой стороны, в модели MI жесткий индентор опирается на линейный подшипник без трения, что позволяет ему двигаться только в вертикальном направлении. Обратите внимание, что граничное условие жесткого индентора является единственной разницей между ними.
Вязкоупругий фундамент состоит из бесконечного числа вязкоупругих элементов, установленных на жестком основании через равные промежутки в горизонтальном направлении. Каждый вязкоупругий элемент представляет собой элемент Кельвина-Фойгта с одной степенью свободы, состоящий из вертикальной пружины (жесткость на единицу ширины: k ) и вертикального демпфера (коэффициент демпфирования на единицу ширины: c ) с одинаковыми естественными длина; в результате его невозмущенной поверхностью является горизонтальная плоскость z = 0.Обратите внимание, что при использовании жесткости на единицу площади ( K ) и коэффициента демпфирования на единицу площади ( C ) вязкоупругого основания, k и c определяются как k = K / N. и c = C / N соответственно, где N — количество вязкоупругих элементов на единицу длины. Также обратите внимание, что здесь мы предполагаем, что верхний конец каждого вязкоупругого элемента контактирует с жесткой поверхностью индентора без сцепления и без трения.
и c = C / N соответственно, где N — количество вязкоупругих элементов на единицу длины. Также обратите внимание, что здесь мы предполагаем, что верхний конец каждого вязкоупругого элемента контактирует с жесткой поверхностью индентора без сцепления и без трения.
Благодаря вышеупомянутым структурам нормальная нагрузка на единицу ширины ( Вт ) модели ИЛ определяется глубиной вдавливания δ [т.е. Вт = Вт (δ), где δ является постоянной], а модель MI определяется гравитацией [т.е. Вт = Mg , где г — гравитационная постоянная]. Кроме того, в обеих моделях жесткое основание движется горизонтально со скоростью привода V . Следовательно, мы можем сказать, что модель FI представляет собой «систему скольжения с постоянным зазором», а модель MI представляет собой «систему скольжения с собственным весом».Или мы можем также сказать, что модели FI и MI представляют собой два предельных случая, соответствующих «очень жесткому аппарату» и «очень мягкому аппарату» соответственно.
Основные уравнения
При проникновении жесткого индентора в вязкоупругое основание на δ > 0 поверхности индентора в моделях FI и MI задаются как
z=h (x)-δ (модель FI) (1) z=h (x)-δ (t) (модель MI) (2)соответственно, где t — время, а ч ( x ) — функция формы индентора:
Предположим, что i -й вязкоупругий элемент при x = x i ( t ) контактирует с поверхностью индентора (см. рис. 2).Сжатие и степень сжатия и -го вязкоупругого элемента в модели FI задаются как
ui (t)=-h (xi)+δ (модель FI) (4) u.i (t)=-h′(xi) V (модель FI) (5)соответственно, а в модели MI
ui (t)=-h (xi)+δ (t) (модель MI) (6) u.i(t)=-h′(xi)V+δ. (t) (модель MI) (7) соответственно, где ( · ) и (′) — производные по t и x соответственно. Тогда, как показано в левой части рис. 2, на подэлемент PQR действуют четыре вида местных сил: нормальная сила f Ni в точке P (от жесткого индентора), восстанавливающая сила ку i при Q (от пружины), демпфирующая сила куб. i at R (от демпфера) и горизонтальной силы f Ci (от пружины и демпфера). Учитывая, что подэлемент PQR безмассовый, получаем следующие уравнения баланса сил в вертикальном и горизонтальном направлениях:
i at R (от демпфера) и горизонтальной силы f Ci (от пружины и демпфера). Учитывая, что подэлемент PQR безмассовый, получаем следующие уравнения баланса сил в вертикальном и горизонтальном направлениях:
соответственно, где
тангенс θi=-h′(xi) (10)при –π/2 < θ i < π/2 и из уравнения (8)
fNi=kui+cu.icos θi (11)Теперь, как показано в правой части рисунка 2, на жесткий индентор в точке P действует нормальная сила со стороны i -го вязкоупругого элемента, которая является силой реакции нормальной силы f Ni слева от Фигура 2.Следовательно, вертикальная и горизонтальная составляющие нормальной силы равны
fzi=fNi cos θi=kui+cu.i (12) fxi=fNi sin θi=-h′(xi)fzi (13) соответственно. Обратите внимание, что из уравнений (9) и (13) горизонтальная ограничивающая сила определяется как f Ci = f xi . Следовательно, полная вертикальная сила F z и полная горизонтальная сила F x , действующие на жесткий индентор со стороны вязкоупругого основания, равны
Следовательно, полная вертикальная сила F z и полная горизонтальная сила F x , действующие на жесткий индентор со стороны вязкоупругого основания, равны
соответственно.Наконец, вертикальное положение дна индентора А в модели FI определяется как
. zA=-δ (модель FI) (16), а в модели МИ определяется уравнением движения:
Mz¨A=Fz-Mg (модель MI) (17), который определяет δ и δ. в уравнениях (6) и (7) следующим образом:
δ (t)=-zA (t) (модель MI) (18) дельта (t)=-z.A (t) (модель MI) (19)Примечание. = 0.Тогда степень сжатия бесконтактного элемента равна
u.i=-uiτ(бесконтактный) (20), где τ — время замедления вязкоупругого элемента, определяемое как
.или, используя макроскопические свойства вязкоупругой основы,
Следовательно, при нарушении контактным элементом следующего условия:
ui≥h′ (xi) Vτ (модель FI) (23) ui≥h′ (xi) Vτ+z˙Aτ (модель MI) (24) отделяется от жесткой поверхности индентора.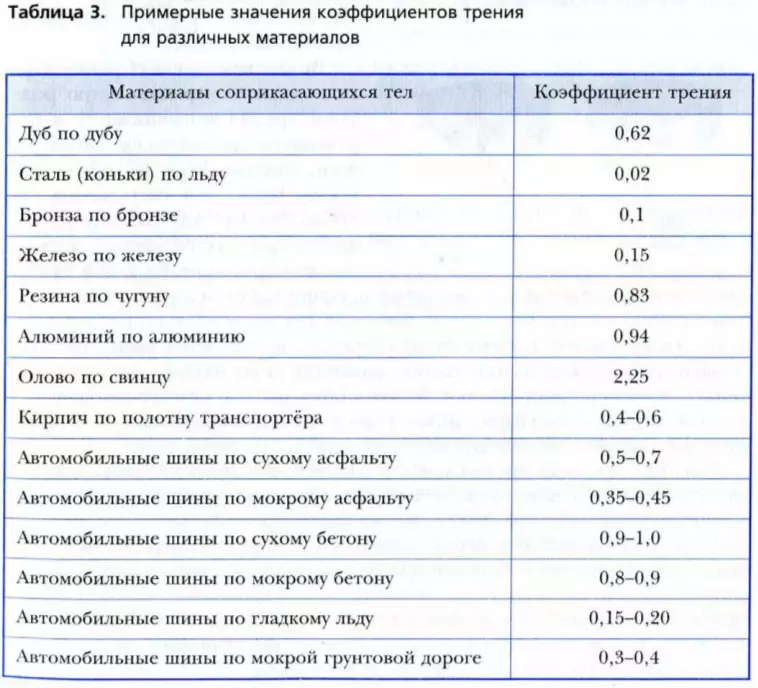 Отметим, что дифференциальное уравнение первого порядка (20) для неконтактного элемента имеет следующее решение:
Отметим, что дифференциальное уравнение первого порядка (20) для неконтактного элемента имеет следующее решение:
, где t 0 — константа.
Рисунок 2 . Локальные силы на и -м вязкоупругом (Кельвина–Фойгта) элементе. (слева) Локальные силы, действующие на подэлемент PQR в вязкоупругом элементе и . (справа) Локальная сила, действующая на жесткий индентор из вязкоупругого элемента и .
Методы
Наборы основных уравнений в предыдущем разделе были решены численно для моделей FI и MI. Для решения обыкновенного дифференциального уравнения второго порядка (17) для модели ИМ использовался метод Рунге-Кутты, где дискретность по времени определялась по формуле .
Стандартные значения параметров для численного моделирования перечислены в таблице 1. Обратите внимание, что обе модели включают шесть независимых параметров ( R, K , τ, N , δ и V в модели FI; R, M , K , τ, N и V в модели MI).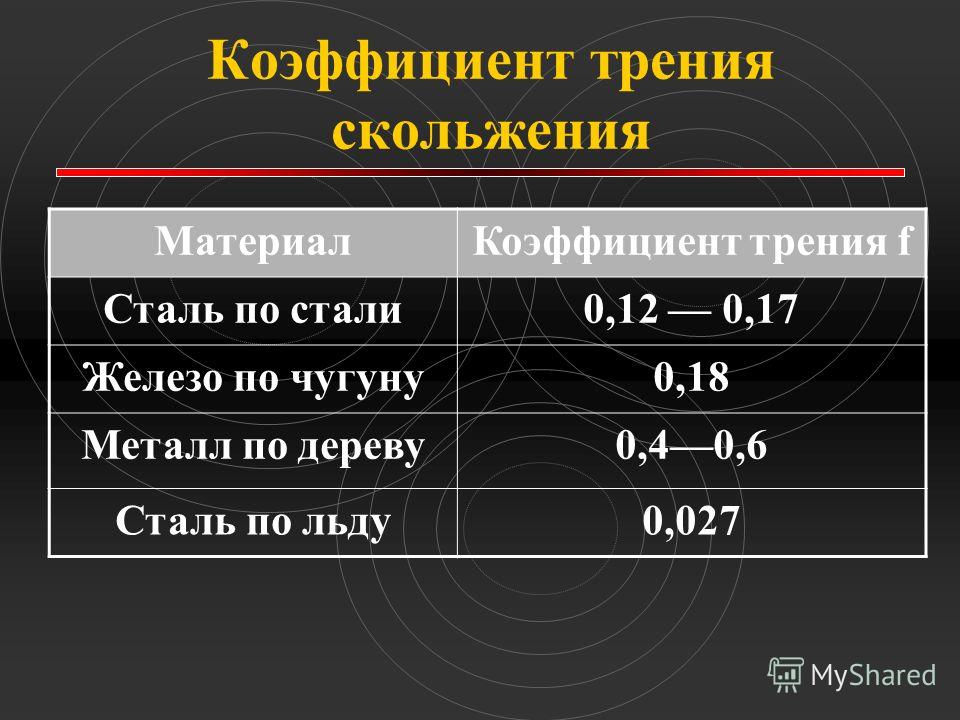 Однако, поскольку N (= 1/ Δ x ) является параметром пространственной дискретизации, количество основных параметров равно пяти для каждой модели. Также отметим, что если представить в качестве вязкоупругого основания «тонкий» упругий лист толщиной h = 1 мм, то можно сказать, что жесткость на единицу площади К = 10 Гн/м 3 соответствует эффективный модуль упругости E ~ Kh = 10 МПа, хотя сильно зависит от граничного условия крепления эластомера на жестком основании [т.е.г., Попов (2010)].
Однако, поскольку N (= 1/ Δ x ) является параметром пространственной дискретизации, количество основных параметров равно пяти для каждой модели. Также отметим, что если представить в качестве вязкоупругого основания «тонкий» упругий лист толщиной h = 1 мм, то можно сказать, что жесткость на единицу площади К = 10 Гн/м 3 соответствует эффективный модуль упругости E ~ Kh = 10 МПа, хотя сильно зависит от граничного условия крепления эластомера на жестком основании [т.е.г., Попов (2010)].
Таблица 1 . Стандартные значения параметров для численного моделирования.
Результаты
На рис. 3 показаны численные результаты временных изменений репрезентативных переменных для модели FI (левый столбец) и модели MI (правый столбец) при стандартных условиях (таблица 1). Обратите внимание, что, как показано синими линиями в верхнем ряду, скорость привода резко увеличилась с В = 0 до 100 мм/с при t = 0,
.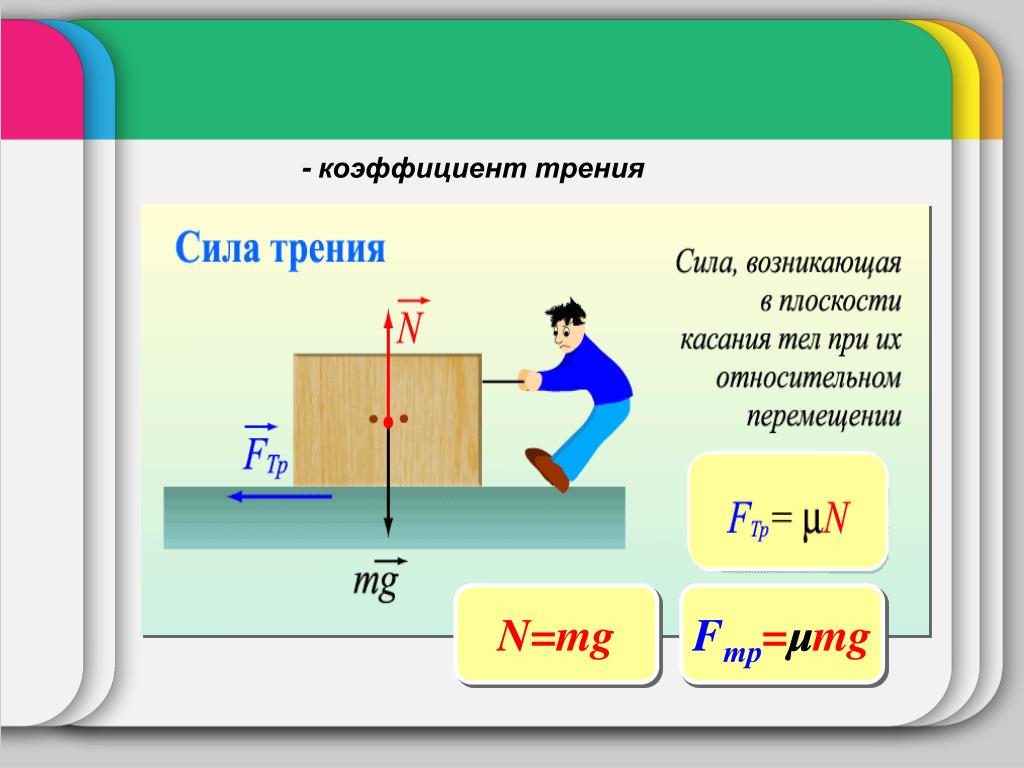
Рисунок 3 .Численные результаты для модели неподвижного индентора (слева) и модели подвижного индентора (справа) : временные изменения скорости привода V (верхний ряд), положение индентора z A (второй ряд), общая вертикальная сила F z (третий ряд) и суммарная горизонтальная сила F x (нижний ряд) при стандартных условиях (значения параметров см. в таблице 1).
Во-первых, из результатов для модели FI мы находим, что положение индентора обеспечивало начальное условие ( z A = −0.3 мм, F z ~ 10 Н/мм и F x = 0). Затем, F Z и F x были немедленно увеличены при т = 0 и поддерживали повышенные значения ( Z A = -0,3 мм, F z ~ 35 Н/мм и F x ~ 5 Н/мм).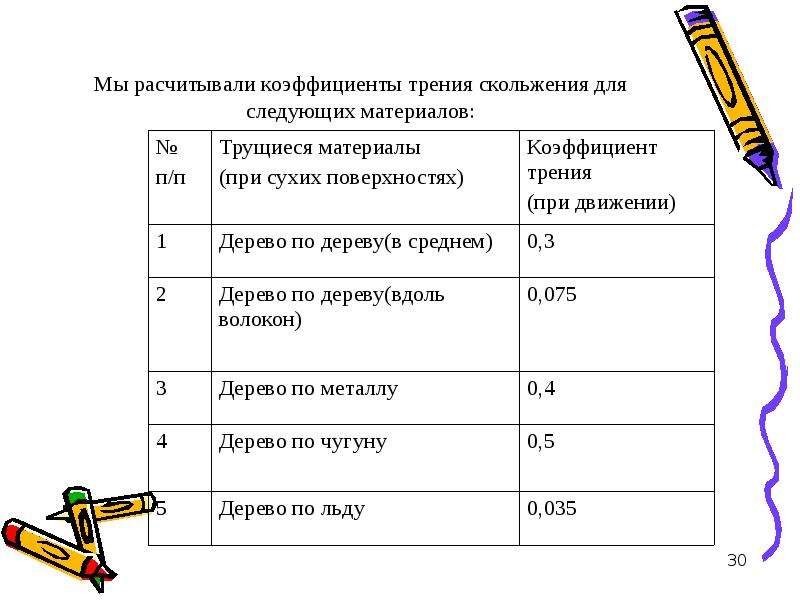
Затем, исходя из результатов для модели MI, мы находим, что сила тяжести обеспечивала те же начальные условия, что и в предыдущей модели.Однако ответы были совершенно разными, демонстрируя отчетливое «временное скольжение» к «устойчивому скольжению». Жесткий индентор начинал двигаться «вверх» при t = 0, а затем постепенно приближался к z A ~ −0,1 мм с постоянной времени порядка «10 мс» (второй ряд). Ответ F Z был Spiky: он сразу увеличился до F Z Z ~ 30 N / мм при T = 0, затем быстро снизился до F Z ~ 9 Н/мм с постоянной времени порядка «1 мс» и постепенно возвращалась к F z ~ 10 Н/мм (третий ряд).Ответ F x Был также Spiky: он сразу увеличился до F x ~ 5 N / мм при T = 0, затем быстро снизился до F x ~ 2 Н/мм с постоянной времени «1 мс» и постепенно приблизились к F x ~ 1 Н/мм с постоянной времени «10 мс» (нижний ряд). Следует отметить, что отклик F x напоминает типичный переход от статического трения к кинетическому трению, хотя статическое трение не рассматривалось.Это переходное поведение будет обсуждаться в следующем разделе.
Следует отметить, что отклик F x напоминает типичный переход от статического трения к кинетическому трению, хотя статическое трение не рассматривалось.Это переходное поведение будет обсуждаться в следующем разделе.
На рис. 4 представлены численные результаты пространственно-временных изменений контактного давления p ( x,t ) = Nf N ( x,t ) при тех же условиях, что и на предыдущем рисунке, где абсцисса — это положение по горизонтали x , ордината — это время t , а величина p представлена оттенком красного цвета. Синие линии показывают временные изменения горизонтального положения передней и задней кромок контактной площадки, обозначенные как x LE ( t ) и x TE ( t ) соответственно.
Рисунок 4 . Численные результаты для фиксированного индентора модели (слева) и подвижного индентора модели (справа) : пространственно-временные изменения контактного давления p ( x,t ) при стандартных условиях (значения параметров см.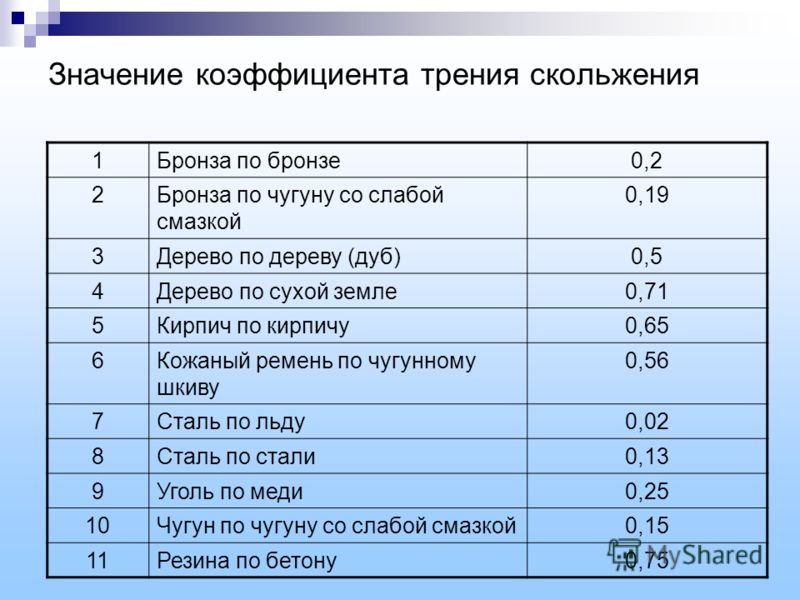 в таблице 1). LE — передняя кромка контакта; TE, задний фронт контакта.
в таблице 1). LE — передняя кромка контакта; TE, задний фронт контакта.
Во-первых, из результатов для модели FI мы снова находим, что отклик не сопровождался какими-либо переходными процессами. Что касается краев, то они располагались на x LE = −2.4 мм и x TE = 2,4 мм в исходном состоянии. После t = 0 передняя кромка сохраняла положение, а задняя кромка сразу смещалась влево на x TE = 0,3 мм при t = 0 и сохраняла положение t > 0 ( что наблюдается в виде отслоения контактной площадки на выходной стороне). Что касается контактного давления, то оно было симметричным для t < 0, демонстрируя максимум p max ~ 3 МПа в центре контакта и минимум p min = 0 на обоих краях.После t = 0 он показал максимум p max > 20 МПа на передней кромке и минимум p min = 0 на задней кромке.
Затем из результатов для модели ИМ мы снова обнаруживаем, что реакция сопровождалась отчетливыми переходными процессами. Что касается граней, то они располагались на тех же позициях, что и у предыдущей модели. Однако после t = 0 перемещалась не только задняя, но и передняя кромка (что проявляется одновременным отслаиванием контактной площадки с обеих сторон).Передний фронт начал двигаться вправо при t = 0, а затем постепенно приблизился к x LE = −1,3 мм с постоянной времени «10 мс». При этом задняя кромка сразу переместилась влево на x TE ~ 0 при t = 0, затем продолжила движение влево на x TE ~ −1 мм с постоянной времени «1». мс», а затем постепенно приблизились к предельному значению х TE = 0,1 мм с постоянной времени «10 мс.Что касается контактного давления, начиная с того же начального состояния, что и у предыдущей модели, после t = 0 оно показало максимум на передней кромке и минимум на задней кромке. Например, при устойчивом скольжении p max ~ 14 МПа на передней кромке и p min = 0 на задней кромке.
Что касается граней, то они располагались на тех же позициях, что и у предыдущей модели. Однако после t = 0 перемещалась не только задняя, но и передняя кромка (что проявляется одновременным отслаиванием контактной площадки с обеих сторон).Передний фронт начал двигаться вправо при t = 0, а затем постепенно приблизился к x LE = −1,3 мм с постоянной времени «10 мс». При этом задняя кромка сразу переместилась влево на x TE ~ 0 при t = 0, затем продолжила движение влево на x TE ~ −1 мм с постоянной времени «1». мс», а затем постепенно приблизились к предельному значению х TE = 0,1 мм с постоянной времени «10 мс.Что касается контактного давления, начиная с того же начального состояния, что и у предыдущей модели, после t = 0 оно показало максимум на передней кромке и минимум на задней кромке. Например, при устойчивом скольжении p max ~ 14 МПа на передней кромке и p min = 0 на задней кромке.
Обсуждение
Переходное трение скольжения
Путем прямого сравнения численных результатов для двух типов моделей (рис. 1) мы обнаружили, что граничное условие жесткого индентора является критическим для возникновения переходного скольжения.Вертикальное перемещение жесткого индентора вызывает его движение вверх (называемое «вертикальным подъемом» жесткого индентора) при приложении скорости привода (рис. 3), что приводит к резкому пространственно-временному изменению площади и давления контакта (рис. 4).
Во-первых, в модели FI горизонтальное положение передней и задней кромки определяется как
. xLE=-a (модель FI) (26) xTE=a2+lr2-lr (модель FI) (27)соответственно, где a — половина длины неподвижного контакта, а l r — длина замедления, определяемая как
соответственно.Обратите внимание, что x LE является константой, а x TE является функцией l r . Из уравнений (26) и (27) мы находим, что есть два предельных случая:
Из уравнений (26) и (27) мы находим, что есть два предельных случая:
, где первое означает «не отслаивание» всей контактной площадки, а второе означает «полное отслоение» контактной площадки на выходной стороне. Поэтому, например, по мере увеличения скорости привода площадь контакта изменяется с «симметричной» [уравнение (30)] на «асимметричную» [уравнение (31)].Обратите внимание, что x TE , заданное уравнением (27), сразу определяется при приложении скорости привода, поэтому отклик модели FI не сопровождается какими-либо переходными процессами.
Тогда в модели MI горизонтальное положение передней и задней кромки определяется как
xLE=-a (модель MI) (32) xTE=a2(1+τδ.δ)+lr2-lr (модель MI) (33) соответственно, где δ = δ( t ) и, следовательно, a = a (δ) = a ( t ), что является причиной того, что модель ИМ создает переходные процессы. В уравнениях (32) и (33) мы находим два источника, создающих временные изменения. Один из них — a ~ δ 1/2 , что симметрично уменьшает площадь контакта за счет вертикального подъема жесткого индентора. Из временного изменения x LE в правой части рисунка 4 мы можем сказать, что при стандартных условиях постоянная времени «10 мс» была вызвана этим эффектом. (Кроме того, временное изменение z A справа на рисунке 3 подтверждает этот вывод.) Другой — δ./δ, расположенный под знаком квадратного корня в уравнении (33), работает только для задней кромки, которая асимметрично деформирует контактную площадку. Из временного изменения x TE справа на рис. 4 можно сказать, что при стандартных условиях постоянная времени «1 мс» была вызвана этим эффектом.
В уравнениях (32) и (33) мы находим два источника, создающих временные изменения. Один из них — a ~ δ 1/2 , что симметрично уменьшает площадь контакта за счет вертикального подъема жесткого индентора. Из временного изменения x LE в правой части рисунка 4 мы можем сказать, что при стандартных условиях постоянная времени «10 мс» была вызвана этим эффектом. (Кроме того, временное изменение z A справа на рисунке 3 подтверждает этот вывод.) Другой — δ./δ, расположенный под знаком квадратного корня в уравнении (33), работает только для задней кромки, которая асимметрично деформирует контактную площадку. Из временного изменения x TE справа на рис. 4 можно сказать, что при стандартных условиях постоянная времени «1 мс» была вызвана этим эффектом.
Основываясь на вышеизложенном, рассмотрим пиковый ответ F x справа на рис. 3. Как мы видели в предыдущем разделе, временное изменение Модель MI очень похожа на типичный переход от статического трения к кинетическому трению, несмотря на то, что статическое трение не учитывается при моделировании. Если мы видели этот тип реакции в экспериментах, мы, вероятно, полагали, что это вызвано типичным адгезионным трением, состоящим из двух видов трения. Фактически остроконечный ответ состоит из следующих трех частей. Во-первых, это немедленное увеличение в ответ на резкое увеличение скорости привода при t = 0. Это, очевидно, вызвано затуханием C фундамента Кельвина–Фойгта, которое практически идентично отклику, наблюдаемому в FI модель на т = 0.Второй – быстрое убывание с постоянной времени «1 мс». Учитывая обсуждение в предыдущем абзаце, мы можем сделать вывод, что быстрое уменьшение вызвано быстрым движением задней кромки для уменьшения площади контакта. Третий – постепенное уменьшение с постоянной времени «10 мс». Учитывая обсуждение в предыдущем абзаце, естественно сказать, что постепенное уменьшение F x вызвано постепенным движением обоих ребер. Однако, учитывая также, что контактное давление принимает максимум p max на передней кромке и минимум p min = 0 на задней кромке (рис.
Если мы видели этот тип реакции в экспериментах, мы, вероятно, полагали, что это вызвано типичным адгезионным трением, состоящим из двух видов трения. Фактически остроконечный ответ состоит из следующих трех частей. Во-первых, это немедленное увеличение в ответ на резкое увеличение скорости привода при t = 0. Это, очевидно, вызвано затуханием C фундамента Кельвина–Фойгта, которое практически идентично отклику, наблюдаемому в FI модель на т = 0.Второй – быстрое убывание с постоянной времени «1 мс». Учитывая обсуждение в предыдущем абзаце, мы можем сделать вывод, что быстрое уменьшение вызвано быстрым движением задней кромки для уменьшения площади контакта. Третий – постепенное уменьшение с постоянной времени «10 мс». Учитывая обсуждение в предыдущем абзаце, естественно сказать, что постепенное уменьшение F x вызвано постепенным движением обоих ребер. Однако, учитывая также, что контактное давление принимает максимум p max на передней кромке и минимум p min = 0 на задней кромке (рис.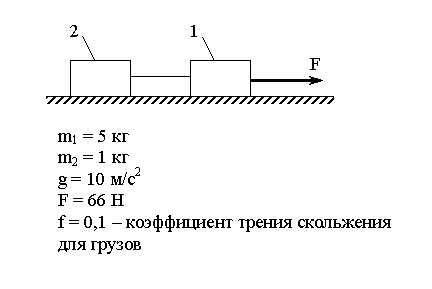 4), можно сделать вывод, что постепенное уменьшение F x в основном вызвано постепенным движением передней кромки.Снова обратите внимание, что вторая и третья части F x в модели MI никогда не появляются в модели FI, что говорит нам о том, что вертикальный подъем жесткого индентора необходим для остроконечной реакции.
4), можно сделать вывод, что постепенное уменьшение F x в основном вызвано постепенным движением передней кромки.Снова обратите внимание, что вторая и третья части F x в модели MI никогда не появляются в модели FI, что говорит нам о том, что вертикальный подъем жесткого индентора необходим для остроконечной реакции.
Устойчивое трение скольжения
Путем численного моделирования реакции на скачкообразное увеличение скорости привода мы обнаружили, что реакция модели FI не сопровождается какими-либо переходными процессами (это означает, что установившееся трение скольжения возникает сразу), в то время как реакция модели ИМ сопровождается ярко выраженными переходными процессами, за которыми следует стационарное трение скольжения.В этом разделе мы сосредоточимся на стационарном трении скольжения.
Ситуация устойчивого скольжения задается
δ.=0 (устойчивое скольжение) (34), в результате чего основные уравнения для модели MI сводятся к уравнениям для модели FI. Например,
Например,
Однако, как видно из численных результатов для t > 100 мс на рисунке 3, нормальная нагрузка Вт (= F z при установившемся скольжении) и сила трения F (= F) x при устойчивом скольжении) для модели МИ существенно отличаются от таковых для модели FI (т.например, W ~ 35 Н/мм и F ~ 5 Н/мм для модели FI, тогда как W ~ 10 Н/мм и F ~ 1 Н/мм для модели MI). Обратите внимание, что разница вызвана граничным условием жесткого индентора: модель FI представляет собой «систему скольжения с постоянным зазором», в которой контролируется глубина вдавливания δ, а модель MI представляет собой «систему скольжения с собственным весом» в которой регулируется нормальная нагрузка Вт (= Мг ). Поэтому при попытке измерить трение скольжения эластомеров необходимо уделять большое внимание граничному условию контрповерхности: в противном случае измеренные значения могут потерять смысл.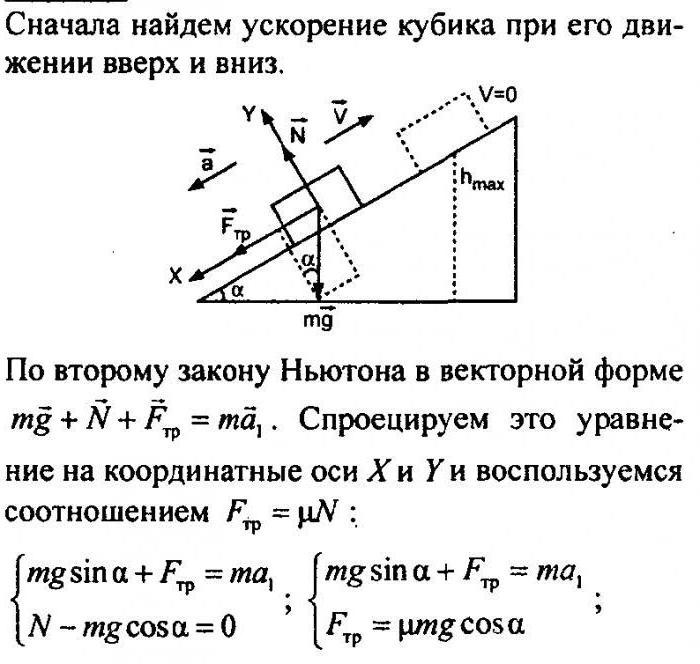
Предыдущее обсуждение подтверждается рис. 5, который показывает численные результаты в устойчивом скольжении для модели FI (левый столбец) и модели MI (правый столбец). Суммированы зависимости δ (верхний ряд), Вт (второй ряд), F (третий ряд) и μ (нижний ряд) от В в установившемся скольжении, где μ — коэффициент трения в установившемся режиме. скользящий, определенный как
μ=FW(устойчивое скольжение) (37) Значения τ составляют 10 −2 с (черный), 10 −1 с (синий) и 10 0 с (красный), а значения других параметров такие же, как и для стандартных условий. (Таблица 1).Из-за различия граничных условий скоростные зависимости µ для моделей FI и MI отличаются друг от друга: в условиях высоких V модель FI показывает предельное значение µ ~ 0,2, а модель MI показывает отрицательная зависимость μ от В с наклоном −0,5. Кроме того, три кривые на каждом графике на рис. 5 расположены через равные интервалы, а это означает, что произведение V и τ (т.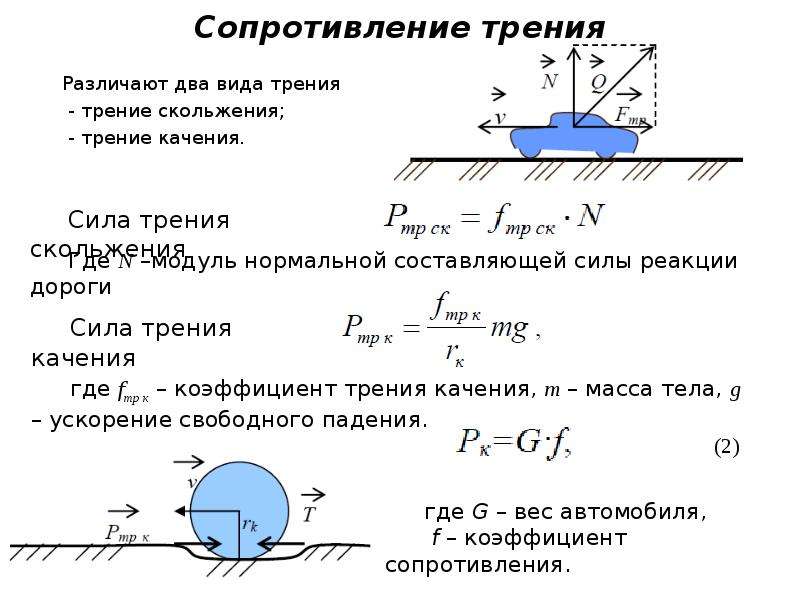 е. l r = Vτ ) является важным параметром. для обеих моделей.
е. l r = Vτ ) является важным параметром. для обеих моделей.
Рисунок 5 . Численные результаты в устойчивом скольжении для модели неподвижного индентора (слева) и модели подвижного индентора (справа) : влияние времени замедления τ на зависимости глубины вдавливания δ от скорости (вверху) , нормальная нагрузка Вт (вторая строка ), сила трения F (третий ряд) и коэффициент трения μ (нижний ряд). Черные линии, τ = 10 −2 с; синие линии, τ = 10 −1 с; красные линии, τ = 10 0 с (другие значения параметров см. в табл. 1).
В ходе серии численных симуляций при различных наборах параметров были получены эталонные кривые зависимости μ при устойчивом скольжении для двух типов моделей (см. рис. 6). Красная кривая на левом графике — эталонная кривая для модели FI, ордината и абсцисса которой равны /2 соответственно, а красная кривая на правом графике — эталонная кривая для модели ИМ, ордината и абсцисса которой равны V τ( K / RW ) 1/3 соответственно. Следует подчеркнуть, что каждая величина, отнесенная к осям на рисунке 6, является безразмерной.
Следует подчеркнуть, что каждая величина, отнесенная к осям на рисунке 6, является безразмерной.
Рисунок 6 . Основные кривые коэффициента трения μ при устойчивом скольжении для неподвижного индентора модели (слева) и подвижного индентора модели (справа) . Красные сплошные линии: эталонные кривые, полученные численно, черные пунктирные линии: асимптоты, полученные теоретически.
Чтобы исследовать асимптоты мастер-кривых, мы снова рассмотрим два предельных случая:
(xLE,xTE)=(-a,a) для lr≪a (устойчивое скольжение) (38) (xLE,xTE)=(-a,0) для lr≫a (устойчивое скольжение) (39), где снова первое означает «не отслаивание» всей контактной площадки, а второе означает «полное отслоение» контактной площадки на стороне выхода.Во-первых, когда l r ≪ a , W и F можно оценить как
W~∫-aaKu (x) dx=2αR1/2Kδ3/2 (40) F~∫-aa-h′ (x) Cu. (x) dx=2αR-1/2CVδ3/2 (41) соответственно, где α=22/3. Следовательно, µ для первого предельного случая [уравнение (38)] равно
Следовательно, µ для первого предельного случая [уравнение (38)] равно
Тогда, когда l r ≫ a , W и F можно оценить как
W~∫-a0Cu.(x) dx=CVδ (43) F~∫-a0-h′ (x) Cu. (x) dx=αR-1/2CVδ3/2 (44)соответственно. Следовательно, μ для второго предельного случая [уравнение (39)] определяется как
μ=αδR(асимптота L2-FI) (45)или, используя уравнение (43),
μ=αWRCV(асимптота L2-MI) (46)Черные пунктирные линии на рис. 6 — приведенные выше асимптоты. Теперь мы находим прекрасное совпадение асимптот с эталонными кривыми. Обратите внимание, что уравнения (42) и (46) такие же, как те, что показаны Поповым (2010).
Зависимости коэффициента трения от скорости
В этом разделе на основе рисунка 6 рассмотрим зависимости коэффициента трения от скорости.На рисунке 6 скорость привода V включена только по оси абсцисс. Поэтому из пересечения двух асимптот введем критическую скорость V * , определяемую как
V*~KRδC(модель FI) (47) V*~RK2W3C(модель MI) (48) При использовании В * формулы для оценки коэффициента трения приведены в таблице 2.
Таблица 2 . Скоростные зависимости коэффициента трения при установившемся скольжении (α=22/3).
Сначала рассмотрим случай В ≪ В * . Из третьей строки табл. 2 находим, что формулы для обеих моделей одинаковы, а это означает, что при В ≪ В * эффект вертикального подъема пренебрежимо мал, хотя жесткий индентор мог двигаться вертикально в модель МИ. Кроме того, учитывая допущение, данное уравнением (38), мы находим, что при В ≪ В * отслоение контактной площадки на выходной стороне также незначительно в обеих моделях.Зависимость μ от скорости μ ~ В 1 , что означает, что она вызвана затуханием фундамента Кельвина–Фойгта.
Затем мы рассматриваем случай В ≫ В * . Из нижней строки таблицы 2 видно, что формулы для двух типов моделей различаются, а это означает, что при В ≫ В * эффект вертикального подъема сильно проявляется в модели МИ.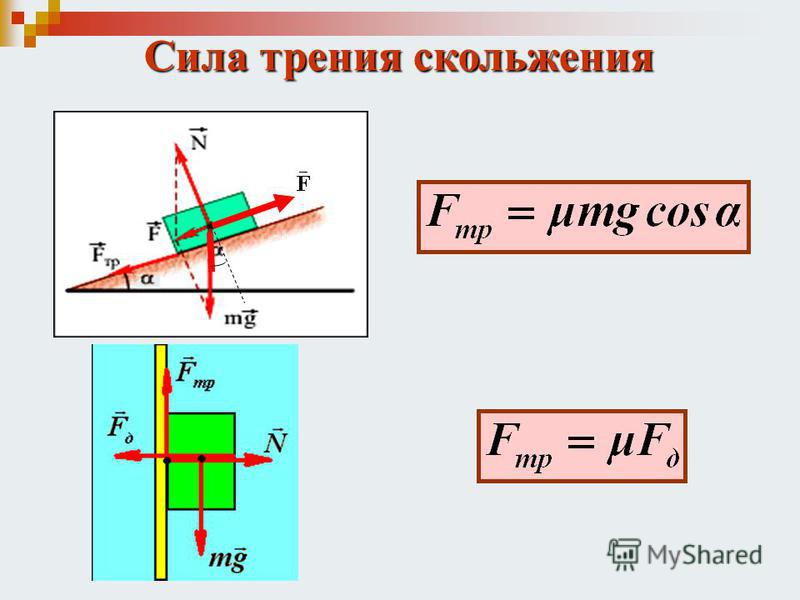 Из уравнения (43) мы находим, что эффект вертикального подъема возникает в соответствии с
Из уравнения (43) мы находим, что эффект вертикального подъема возникает в соответствии с
, что подтверждается численными результатами, показанными на верхнем правом графике рисунка 5, где уменьшение δ означает увеличение z A (= –δ): то есть вертикального подъема жесткого индентора.Кроме того, учитывая допущение, данное уравнением (39), находим, что при В ≫ В * полное отслоение контактной площадки на выходной стороне происходит в обеих моделях. Что касается зависимости μ от скорости в модели FI, то она составляет μ ~ В 0 (т. е. μ постоянна). Это связано с тем, что при В ≫ В * демпфирование становится преобладающим, и поэтому восстановление становится незначительным, что приводит к тому, что оба Вт и F пропорциональны В , т.к. показано в уравнениях (43) и (44).Что касается скоростной зависимости μ в модели ИМ, то она показывает отрицательную зависимость μ ~ V −1/2 , что обусловлено вертикальным подъемом жесткого индентора.
В результате получаем, что в модели ИМ функция µ = µ( В ) имеет локальный максимум при В ~ В * . Отметим, что в течение многих десятилетий этот тип зависимости скорости наблюдался и обсуждался рядом исследователей для трения скольжения эластомеров, что, по-видимому, в основном понимается как зависимость вязкоупругости от частоты (Persson, 2001; Momozono et al., 2010; Карбоне и Путиньяно, 2013 г.). Однако модель ИМ дает качественно аналогичную зависимость, хотя частотная зависимость основы Кельвина–Фойгта не имеет локального максимума, где она обусловлена вертикальным подъемом жесткого индентора.
Также отметим, что отрицательная зависимость μ ~ В −1/2 означает
μ→0 для VV*→∞ (модель MI) (50), что дает нам представление о сверхнизком трении. Если мы попытаемся воплотить ситуацию уравнения (50) в реальных системах, то перспективным будет не только увеличение V , но и уменьшение V * , способ которого показан уравнением (48).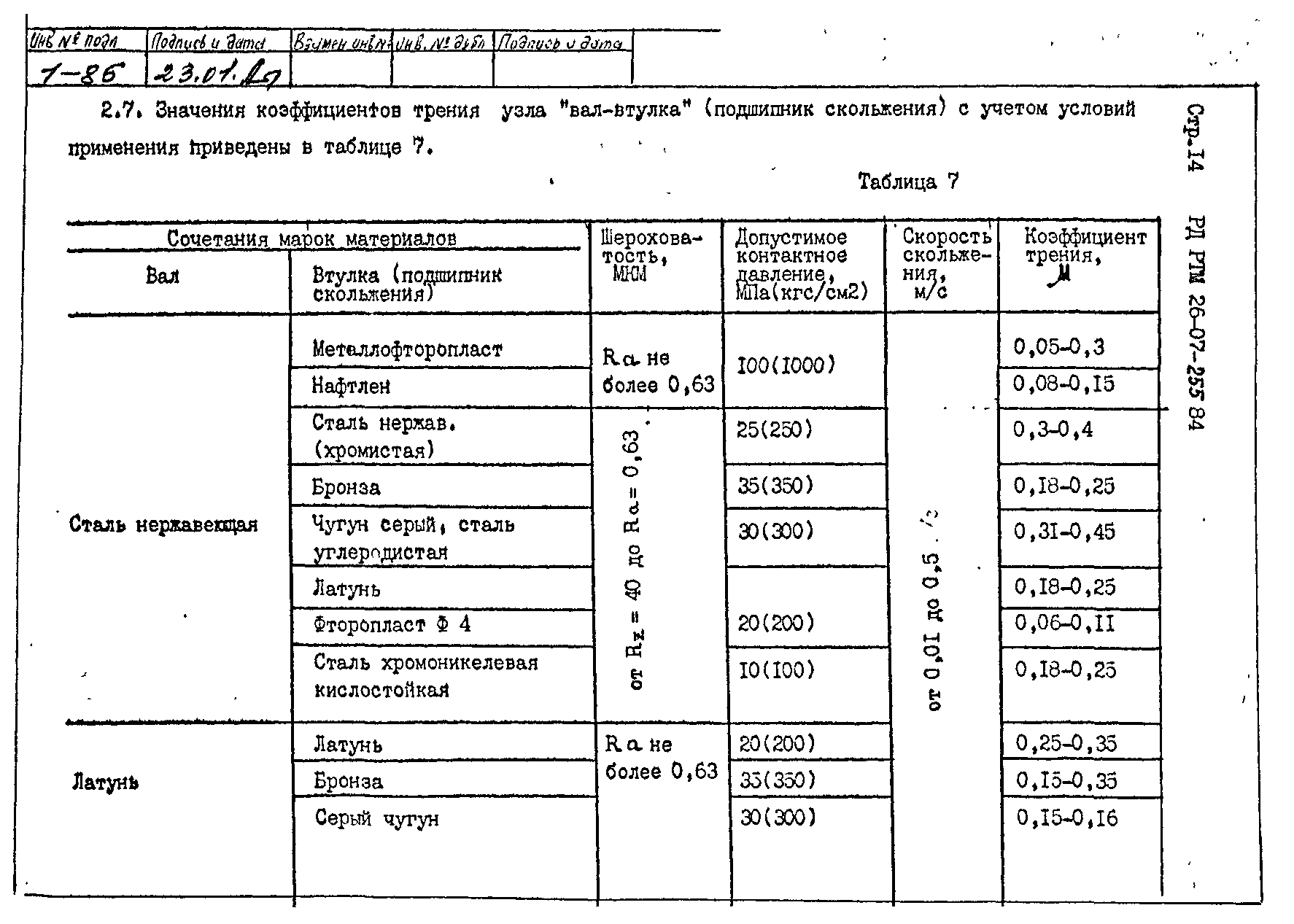 Вероятно, наиболее эффективным параметром является затухание C (или время запаздывания τ = C / K ). Согласно уравнению, увеличение C приводит к уменьшению V * , что приводит к приближению к ситуации уравнения (50). Следует отметить, что эта концепция никогда не может быть воплощена в модели FI, поскольку увеличение C при постоянном значении δ просто линейно увеличивает F , как показано в уравнении (44). Таким образом, ключевым является эффект вертикальной подъемной силы, возникающий при подвижном граничном условии жесткого индентора.
Вероятно, наиболее эффективным параметром является затухание C (или время запаздывания τ = C / K ). Согласно уравнению, увеличение C приводит к уменьшению V * , что приводит к приближению к ситуации уравнения (50). Следует отметить, что эта концепция никогда не может быть воплощена в модели FI, поскольку увеличение C при постоянном значении δ просто линейно увеличивает F , как показано в уравнении (44). Таким образом, ключевым является эффект вертикальной подъемной силы, возникающий при подвижном граничном условии жесткого индентора.
В последнее время внимание привлекли несколько набухающих полимеров со сверхнизким трением (например, гидрогели и полимерные щетки), вдохновленных природными трибосистемами в организме человека (например, глазами и суставами) (Klein et al., 1994; Lee and Spencer, 2008). Важным аспектом, очевидно, являются низкоадгезионные свойства поверхностей, обусловленные их «микроскопической» структурой.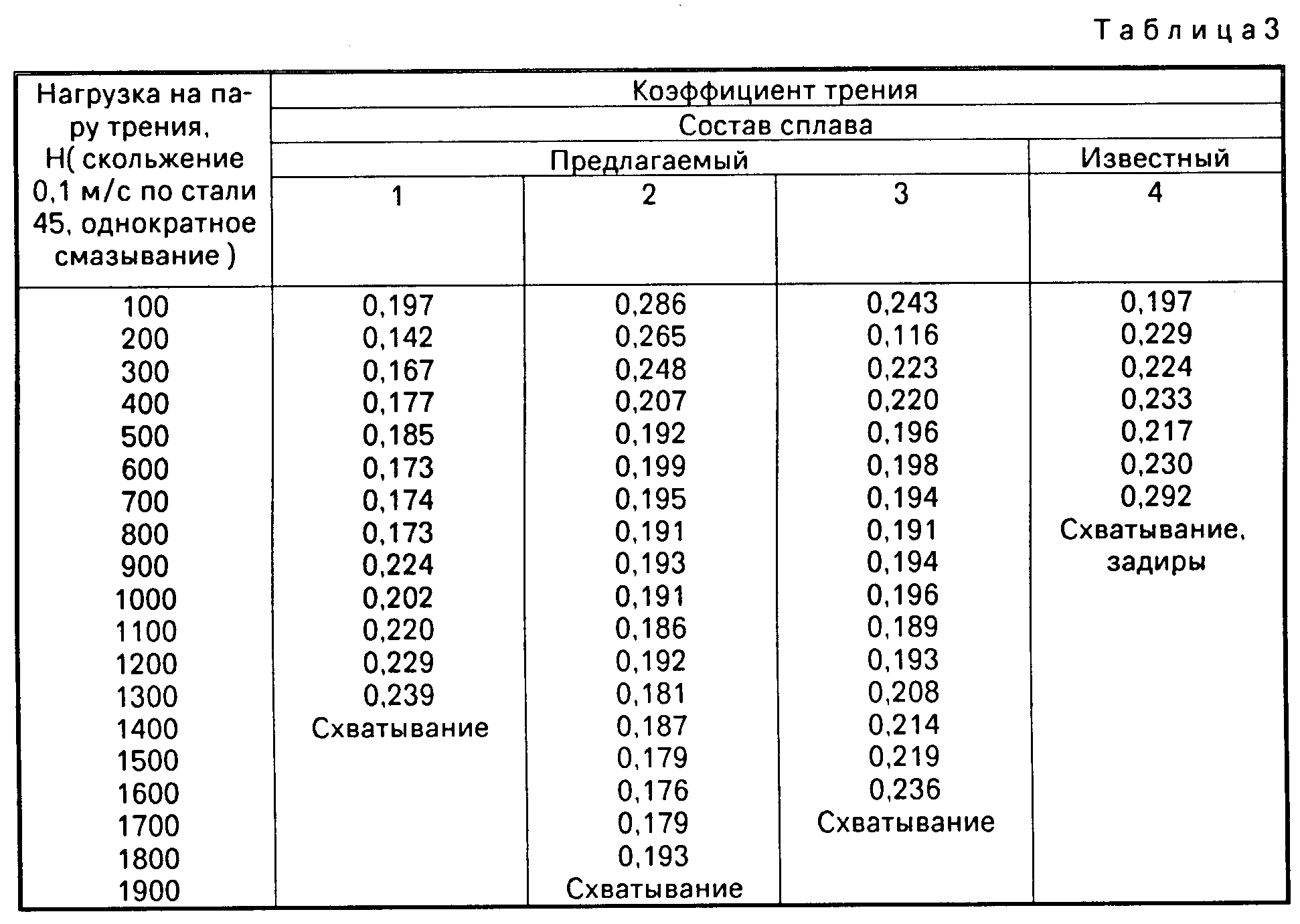 Однако, в качестве еще одного важного аспекта, также необходимы надлежащие «макроскопические» структуры для их правильного использования в различных условиях.По крайней мере, вспоминая результаты по переходному скольжению (рис. 3), мы можем сказать, что при скольжении эластомеров со смазкой макроскопические структуры, использующие эффект вертикального подъема за счет вязкоупругости, по-видимому, имеют сильные преимущества для плавного перехода к режиму жидкостно-пленочной смазки. особенно в начале скольжения.
Однако, в качестве еще одного важного аспекта, также необходимы надлежащие «макроскопические» структуры для их правильного использования в различных условиях.По крайней мере, вспоминая результаты по переходному скольжению (рис. 3), мы можем сказать, что при скольжении эластомеров со смазкой макроскопические структуры, использующие эффект вертикального подъема за счет вязкоупругости, по-видимому, имеют сильные преимущества для плавного перехода к режиму жидкостно-пленочной смазки. особенно в начале скольжения.
Выводы
В этом исследовании трение скольжения эластомеров исследовано численно и теоретически для линейного контакта между цилиндрическим жестким индентором и «без трения» основанием Кельвина-Фойгта.Начало скольжения при резком увеличении скорости привода моделировалось с различными граничными условиями жесткого индентора. Основные выводы следующие:
1. Когда жесткому индентору не дают двигаться ни в какую сторону, возникает просто скачкообразное изменение силы трения, не сопровождающееся какими-либо переходными процессами. Однако, когда жесткий индентор может двигаться в вертикальном направлении, появляется переходное трение скольжения, включающее три разные постоянные времени, напоминающее типичный переход от статического трения к кинетическому трению, несмотря на то, что статическое трение не учитывается при моделировании.Вышеупомянутая резкая разница вызвана «вертикальным подъемом» жесткого индентора, вызванным демпфированием основания Кельвина-Фойгта.
Однако, когда жесткий индентор может двигаться в вертикальном направлении, появляется переходное трение скольжения, включающее три разные постоянные времени, напоминающее типичный переход от статического трения к кинетическому трению, несмотря на то, что статическое трение не учитывается при моделировании.Вышеупомянутая резкая разница вызвана «вертикальным подъемом» жесткого индентора, вызванным демпфированием основания Кельвина-Фойгта.
2. Когда скорость привода достаточно низкая, эффект вертикальной подъемной силы пренебрежимо мал, а восстановление преобладает над демпфированием, что приводит к небольшому отслаиванию всей площади контакта и коэффициенту трения, пропорциональному скорости привода. С другой стороны, когда скорость привода достаточно высока, эффект вертикального подъема становится сильным, когда демпфирование преобладает над восстановлением, что приводит к полному отслаиванию контактной площадки на выходной стороне.Вертикальный подъем жесткого индентора сильно влияет на характеристики установившегося трения скольжения, что хорошо объясняется использованием критической скорости, определяемой по асимптотам на эталонной кривой коэффициента трения.
В заключение еще раз отметим, что приведенные выше выводы получены для основания Кельвина–Фойгта против цилиндрического жесткого индентора. В целом, поскольку на поведение сильно влияет реология вязкоупругого основания или форма жесткого индентора (Popov and Heß, 2015), необходимы дальнейшие исследования.
Заявление о доступности данных
Все наборы данных, созданные для этого исследования, включены в статью/дополнительный материал.
Вклад авторов
KN разработал исследование и написал рукопись. МК провел моделирование. KN и MK проанализировали результаты. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Это исследование было частично поддержано ACCEL (Инициатива по ускоренным инновационным исследованиям, превращающая передовую науку и идеи в высокоэффективные ценности) в рамках гранта No.JPMJAC1503 спонсируется Японским агентством по науке и технологиям.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Авторы благодарят профессора Валентина Л. Попова и профессора Хироши Ватанабэ за плодотворные и стимулирующие дискуссии.
Ссылки
Баркинс, М.(1985). Трение скольжения резины и волны Шалламаха: обзор. Матер. науч. англ. 73, 45–63. дои: 10.1016/0025-5416(85)-2
Полнотекстовая перекрестная ссылка | Академия Google
Белин, М., Арафун, Х., Камиджо, Т., Перре-Лиоде, Дж., Моринага, Т., Хонма, С., и др. (2018). Низкое трение, смазывающая способность и долговечность полимерных щеточных покрытий, охарактеризованных методом релаксационного трибометра. Смазочные материалы 6:52. doi: 10.3390/lubricants6020052
Полнотекстовая перекрестная ссылка | Академия Google
Карбоне, Г.и Путиньяно, К. (2013). Новая методология прогнозирования трения скольжения и качения вязкоупругих материалов: теория и эксперименты. Дж. Мех. физ. Твердые вещества 61, 1822–1834 гг. doi: 10.1016/j.jmps. 2013.03.005
2013.03.005
Полнотекстовая перекрестная ссылка | Академия Google
Фукахори Ю. и Ямадзаки Х. (1994). Механизм истирания резины: часть I: формирование картины истирания в вулканизате натурального каучука. Одежда 171, 195–202. дои: 10.1016/0043-1648(94)
Полнотекстовая перекрестная ссылка | Академия Google
Гонг, Дж.П., Курокава Т., Нарита Т., Кагата Г., Осада Ю., Нисимура Г. и др. (2001). Синтез гидрогелей с чрезвычайно низким поверхностным трением. Дж. Ам. хим. соц. 123, 5582–5583. дои: 10.1021/ja003794q
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Грош, К.А. (1963). Связь между трением и вязкоупругими свойствами резины. Проц. Рой. соц. сер. А 274, 21–39. doi: 10.1098/rspa.1963.0112
Полнотекстовая перекрестная ссылка | Академия Google
Кляйн, Дж., Кумачева Э., Махалу Д., Перахиа Д. и Феттерс Л.Дж. (1994). Снижение сил трения между твердыми поверхностями с полимерными щетками.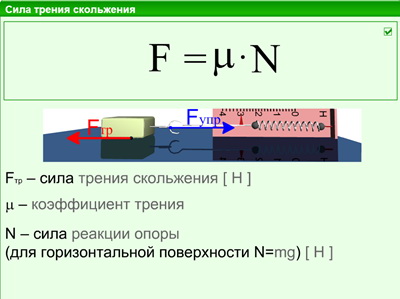 Природа 370, 634–636. дои: 10.1038/370634a0
Природа 370, 634–636. дои: 10.1038/370634a0
Полнотекстовая перекрестная ссылка | Академия Google
Куще, К. (2017). Сила трения между осесимметричным индентором и вязкоупругим полупространством. З. Ангью. Мат. мех. 97, 226–239. doi: 10.1002/zamm.201500169
Полнотекстовая перекрестная ссылка | Академия Google
Маэгава, С.и Накано, К. (2010). Механизм прерывистого скольжения, связанный с волнами Шалламаха. Одежда 268, 924–930. doi: 10.1016/j.wear.2009.12.018
Полнотекстовая перекрестная ссылка | Академия Google
May, W.D., Morris, E.L., and Atack, D. (1959). Трение качения твердого цилиндра по вязкоупругому материалу. J. Appl. Физ . 30, 1713–1724 гг. дои: 10.1063/1.1735042
Полнотекстовая перекрестная ссылка | Академия Google
Мизуками М., Ген М., Хсу С. Ю., Цудзи Ю.и Курихара, К. (2019). Динамика смазывающих, концентрированных щеточных слоев из ПММА, изученная с помощью поверхностных сил и измерений резонансного сдвига. Мягкая материя . 15, 7765–7776. дои: 10.1039/C9SM01133A
Мягкая материя . 15, 7765–7776. дои: 10.1039/C9SM01133A
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Момозоно, С., Накаяма, К., и Киогоку, К. (2010). Теоретическая модель адгезионного трения между эластомерами и шероховатыми твердыми поверхностями. J. Chem. физ. 132:114105. дои: 10.1063/1.3356220
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Мур, Д.Ф. и Гейер, В. А. (1972). Обзор теорий адгезии эластомеров. Одежда 22, 113–141. дои: 10.1016/0043-1648(72)
Полнотекстовая перекрестная ссылка | Академия Google
Мур Д.Ф. и Гейер В.А. (1974). Обзор теорий гистерезиса для эластомеров. Одежда 30, 1–34. дои: 10.1016/0043-1648(74)-6
Полнотекстовая перекрестная ссылка | Академия Google
Накано К., Кавагути К., Такэсима К., Шираиси Ю., Форсбах Ф., Бенад Дж., и другие. (2019). Исследование динамической реакции резины при фрикционном контакте. Фронт. мех. англ. 5:9. doi: 10.3389/fmech.2019.00009
Фронт. мех. англ. 5:9. doi: 10.3389/fmech.2019.00009
Полнотекстовая перекрестная ссылка | Академия Google
Накано, К., и Маэгава, С. (2009). Прерывистое скольжение в скользящих системах с тангенциальным контактным податливостью. Трибол. Междунар. 42, 1771–1780. doi: 10.1016/j.triboint.2009.04.039
Полнотекстовая перекрестная ссылка | Академия Google
Номура А., Окаясу К., Оно К., Фукуда Т.и Цудзи, Ю. (2011). Механизм смазывания концентрированных полимерных щеток в растворителях: влияние качества растворителя и, следовательно, степени набухания. Макромолекулы 44, 5013–5019. дои: 10.1021/ma200340d
Полнотекстовая перекрестная ссылка | Академия Google
Перссон, Б.Н.Дж. (2001). Теория трения резины и контактная механика. J. Chem. физ. 115, 3840–3861. дои: 10.1063/1.1388626
Полнотекстовая перекрестная ссылка | Академия Google
Попов В.Л.(2010). Контактная механика и трение: физические принципы и приложения . Берлин: Спрингер. дои: 10.1007/978-3-642-10803-7
Берлин: Спрингер. дои: 10.1007/978-3-642-10803-7
Полнотекстовая перекрестная ссылка | Академия Google
Попов В.Л. и Хесс М. (2015). Метод уменьшения размерности в контактной механике и трении. Берлин: Springer. дои: 10.1007/978-3-642-53876-6
Полнотекстовая перекрестная ссылка | Академия Google
Попов В.Л., Фолл Л., Куще С., Ли К. и Рожкова С.В. (2018). Процедура обобщенной основной кривой для трения эластомеров с учетом зависимости от скорости, температуры и нормальной силы. Трибол. Междунар. 120, 376–380. doi: 10.1016/j.triboint.2017.12.047
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Тадокоро Т., Сато К., Нагамин Т., Накано К., Сасаки С., Сато Т. и др. (2020). Концентрированная полимерная щетка в качестве материала возвратно-поступательного уплотнения для низкой утечки и низкого трения. Трибол.Транс. 63, 20–27. дои: 10.1080/10402004.2019.1650213
Полнотекстовая перекрестная ссылка | Академия Google
Уильямс М. Л., Ландел Р.Ф. и Ферри Д.Д. (1955). Температурная зависимость механизмов релаксации в аморфных полимерах и других стеклообразующих жидкостях. Дж. Ам. хим. соц. 77, 3701–3707. дои: 10.1021/ja01619a008
Л., Ландел Р.Ф. и Ферри Д.Д. (1955). Температурная зависимость механизмов релаксации в аморфных полимерах и других стеклообразующих жидкостях. Дж. Ам. хим. соц. 77, 3701–3707. дои: 10.1021/ja01619a008
Полнотекстовая перекрестная ссылка | Академия Google
Ямагути Т., Моришита М., Дои М., Хори Т., Сакагути Х. и Ампуэро Дж.П. (2011). Закон Гутенберга-Рихтера при трении скольжения гелей. Ж. Геофиз. Рез. 116, B12306. дои: 10.1029/2011JB008415
Полнотекстовая перекрестная ссылка | Академия Google
Уравнение коэффициента трения и табличная диаграмма
Уравнение коэффициента трения и табличная диаграмма
Дизайнерские ресурсы | Расчетные данные трения
Сила трения для статического трения может быть выражена как:
F макс. = мкФ n
где
F макс. = сила трения (Н, фунт)
μ = статический (мкс) или кинетический (мкк) коэффициент трения
F n = приложенная нормальная сила (Н, фунт)
Сила трения для Dynamic Friction может быть выражена как:
Для объекта, который тянут или толкают горизонтально, нормальная сила — Н — это просто вес:
Н = мг г
Где:
м = Масса (кг, снаряды)
г = Сила тяжести (9.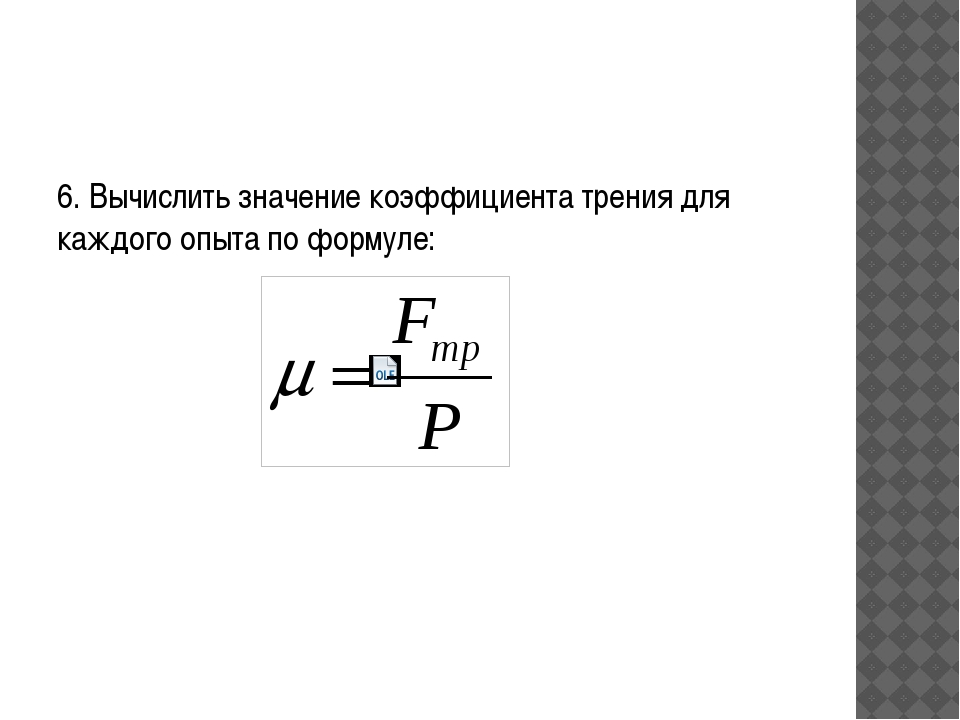 81 м/с 2 , 32 фут/с 2 )
81 м/с 2 , 32 фут/с 2 )
| Материал | против Материал | Статическая Коэффициент трения | |
| Сухой Контактный | Смазанный Контактный | ||
Алюминий | Алюминий | 1,10 -1,35 | .30 |
| Алюминиево-бронзовый сплав | Сталь | . 46 46 | — |
| Алюминий | Сталь | .61 | — |
| Тормоз (композитный) | Чугун | .40 | .21 (мокрый) |
| Латунь | Сталь | .50 | .19 |
| Латунь | Чугун | . 28 28 | |
| Кирпич | Дерево | .60 | — |
| Бронза | Чугун | .21 | — |
| Бронза Спеченная | Сталь | — | .12 |
| Бронза | Сталь | . 16 16 | |
| Кадмий | Кадмий | .50 | .05 |
| Кадмий | Хром (хром) | .40 | .35 |
| Кадмий | Сталь мягкая | .46 | |
| Углерод | Углерод | . 15 15 | .12 — .14 |
| Углерод | Сталь | .14 | .12 — .14 |
| Чугун | Чугун | 1.1 | .08 |
| Чугун | Медь | 1,05 | — |
| Чугун | Дубовая древесина | . 485 485 | .08 |
| Чугун | Сталь | .40 | .21 |
| Чугун | Цинк | .85 | — |
| Хром (хром) | Хром (хром) | .41 | .34 |
| Кольбальт (70°C) | Кобальт | . 3 3 | — |
| Бетон | Резина | 1.0 | .30 (мокрый) |
| Бетон | Дерево | .62 | — |
| Медь | Чугун | 1,05 | — |
| Медь | Медь | 1,00 | .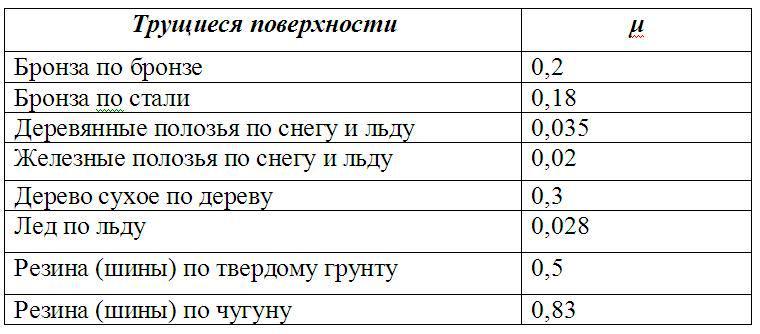 08 08 |
| Медь | Стекло | .94 | — |
| Медь | Сталь | .53 | — |
| Медно-свинцовый сплав | Сталь | .22 | — |
| Пробка | Железо | . 35 35 | — |
| Алмаз | Алмаз | .10 | .05 — .10 |
| Алмаз | Металл | .10 — .15 | .10 |
| Стекло | Стекло | .90 — 1,0 | .10 — .60 |
| Стекло | Металл | . 50 — .70 50 — .70 | .20 — .30 |
| Стекло | Никель | .78 | .57 |
| Графит | Графит | .10 | .10 |
| Графит | Сталь | .1 | .1 |
| Подкова | Бетон | . 67 67 | — |
| Подкова | Резина | .28 | — |
| Лед | Дерево | .05 | — |
| Лед | Сталь | .04 | — |
| Железо | Железо | 1,0 | .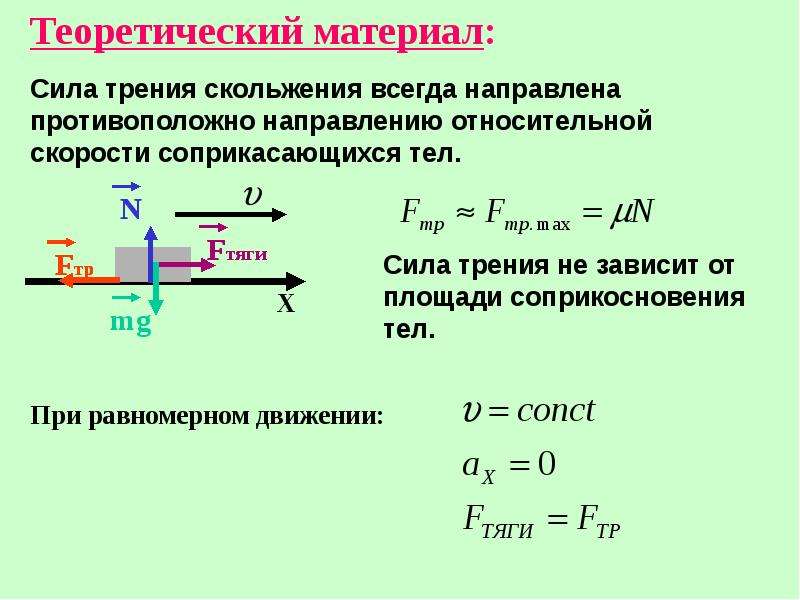 15 -. .20 15 -. .20 |
| Свинец | Чугун | .41 | — |
| Кожа | Железо | .3 | |
| Кожа | Дерево | .30 — .40 | — |
| Кожа | Металл | .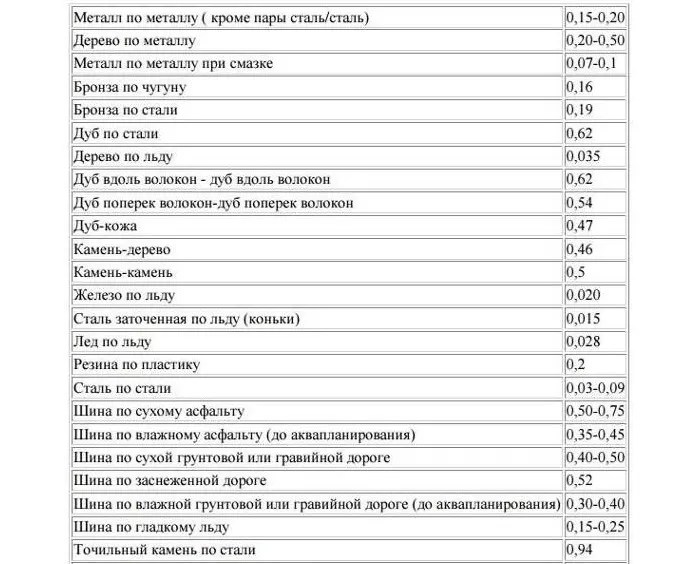 60 60 | — |
| Кожа (жирная) | Железо | .2 — .25 | |
| Магний | Магний | .60 | .079 |
| Каменная кладка | Кирпич | .65 | — |
| Никель | Никель | .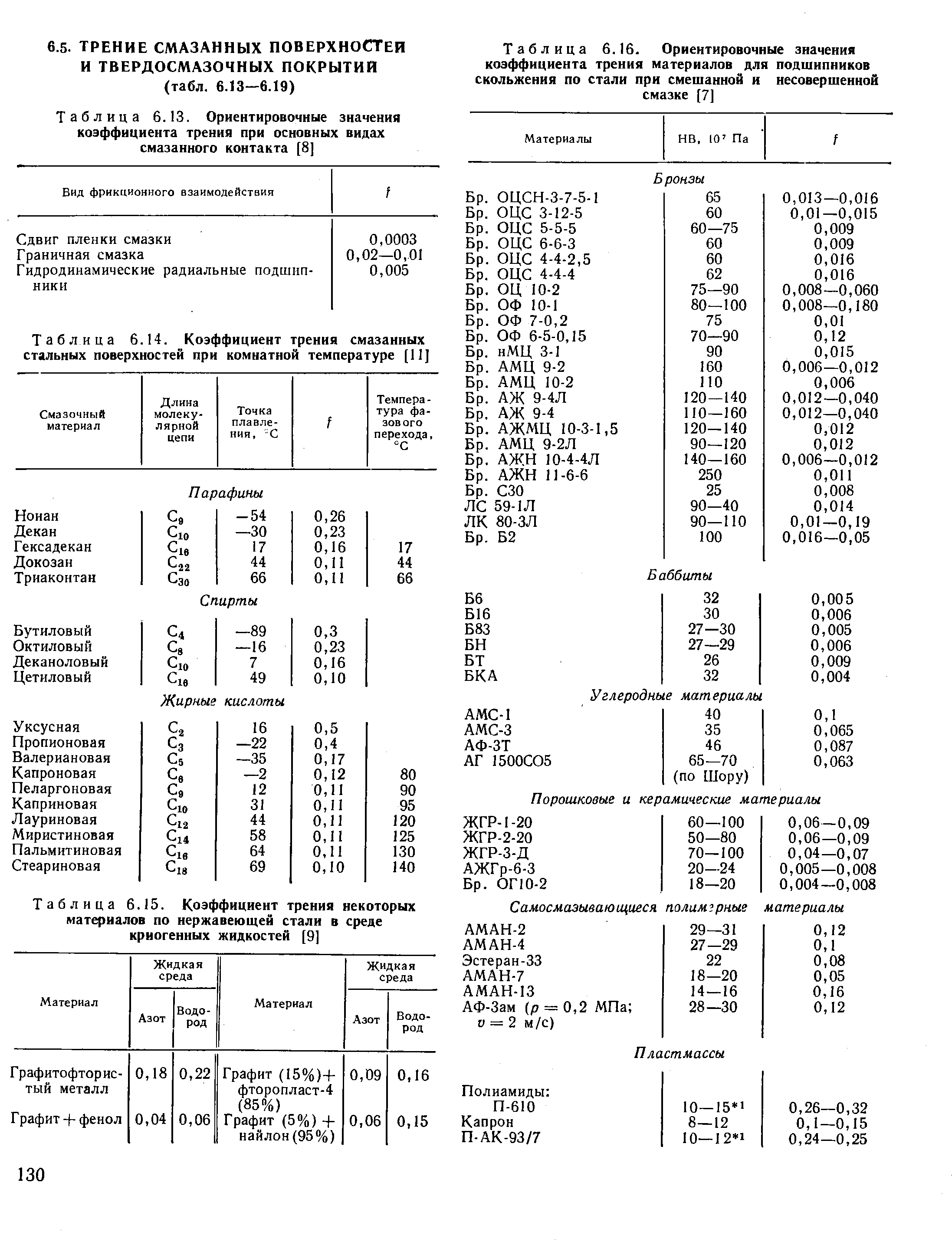 70 70 | .28 |
| Нейлон | Нейлон | .15 — .25 | — |
| Дуб | Дуб | .61 | — |
| Бумага | Чугун | .19 | — |
| Фосфористая бронза | Сталь | .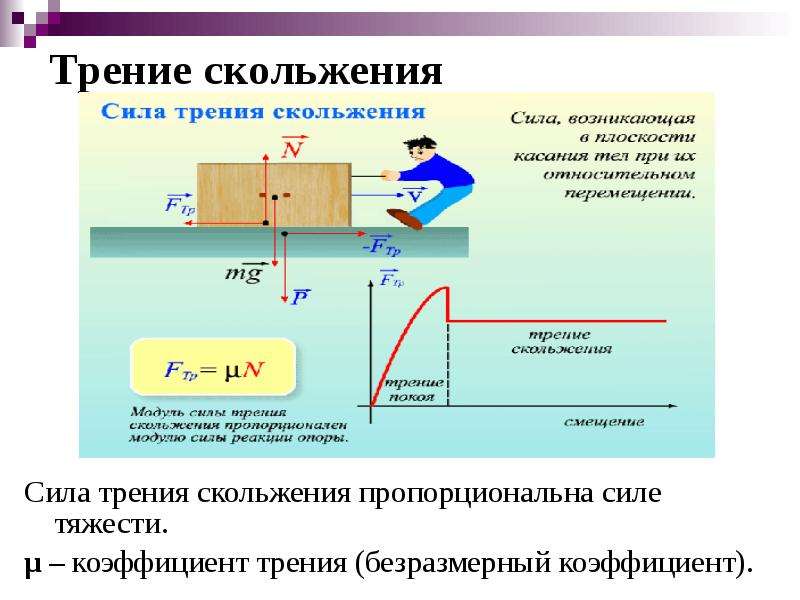 35 35 | — |
| Платина | Платина | 1,20 | .25 |
| Оргстекло | Оргстекло | .80 | .80 |
| Оргстекло | Сталь | .40 — .50 | .40 — .50 |
| Полиэтилен | Сталь | . 2 2 | .2 |
| Полистирол | Полистирол | .50 | .50 |
| Полистирол | Сталь | .30 — .35 | .30 — .35 |
| Резина | Резина | 1,15 | — |
| Резина | Асфальт | . 9 9 | — |
| Резина | Бетон | .6 | — |
| Резина (ремень 60 А) | Нержавеющая сталь 316 | .64 | — |
| Резина (ремень 60 А) | Резина (ремень 40 А) | .62 | — |
| Резина (ремень 60 А) | Резина (ремень 60 А) | . 73 73 | — |
| Резина (ремень 60 А) | Инструментальная сталь | .86 | — |
| Резина (ремень 60 А) | Карбид вольфрама | .62 | — |
| Резина (ремень 60 А) | СВМ | .56 | — |
| Резина (ремень 60 А) | Уретан 50 | .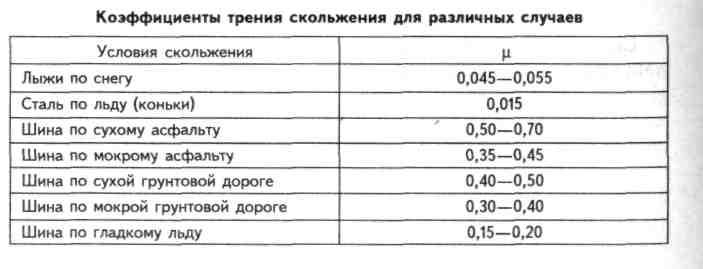 60 60 | — |
| Резина (ремень 60 А) | Уретан 80A | .70 | — |
| Резина (ремень 60 А) | Уретан | .67 | — |
| Серебро | Серебро | 1.40 | .52 |
| Кожа человека | Металлы (63 Ra) | . 9 9 | — |
| Сталь | Сталь | .80 | .16 |
| Тефлон | Сталь | .04 | .04 |
| Тефлон | Тефлон | .05 — .20 | .04 |
| Олово | Чугун | . 31 31 | — |
| Шина, резина | Асфальт | .71 | — |
| Шина, резина | Трава | .36 | — |
| Карбид вольфрама | Сталь | .40 — .60 | .10 — .20 |
| Карбид вольфрама | Карбид вольфрама | . 20 — .25 20 — .25 | .12 |
| Дерево | Дерево | .25 — .50 | .20 |
| Дерево | Металлы | .20 — .60 | .20 (мокрый) |
| Цинк | Цинк | .60 | .04 |
Статическое трение — это трение между двумя или более твердыми телами, которые не движутся друг относительно друга.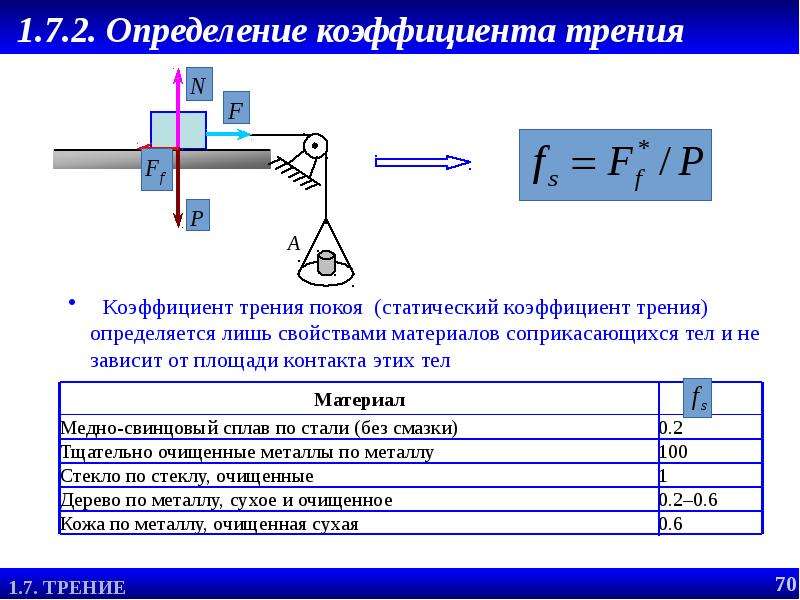 Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как μ с , обычно выше, чем коэффициент кинетического трения.
Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как μ с , обычно выше, чем коэффициент кинетического трения.
Материал | Раздвижной | |
Сухой | Смазанный | |
Алюминий на алюминии | — | — |
Брезентовый ремень на резиновом футляре | — | — |
Брезентовый ремень, прошитый, на стали | 0. | 0,10 |
Брезентовый ремень, тканый, на стали | 0,22 | 0,10 |
Чугун на асбесте, тканевый тормозной материал | 0,35-0,40 | — |
Чугун на латуни | 0,30 | — |
Чугун на бронзе | 0.22 | 0,07-0,08 |
Чугун на чугуне | 0,15 | 0,06-0,10 |
Чугун на меди | 0,29 | — |
Чугун на свинце | 0,43 | 0,13-0,36 |
Чугун на коже | — | 0. |
Чугун на дубе (параллельный) | 0,30-0,50 | — |
Чугун на магнии | 0,25 | 0,133 |
Чугун на стали, мягкая | 0,23 | — |
Чугун на жести | 0.32 | — |
Чугун на цинке | 0,21 | — |
Земля на земле | — | — |
Стекло на стекле | 0,40 | — |
Пеньковая веревка на дереве | 0. | — |
Никель на никеле | 0,53 | 0,12 |
Дуб на коже (параллельно) | 0,30-0,50 | — |
Дуб на дубе (параллельно) | 0,48 | 0,16 |
Дуб на дубе (перпендикулярно) | 0.32 | 0,07 |
Резиновая шина для дорожного покрытия | 0,75-0,85 | 0,5-0,7* |
Сталь на льду | 0,01 | — |
Сталь твердая на баббите | 0,33-0,35 | 0,05-0,16 |
Сталь, твердая, на стали, твердая | 0. | 0,03-0,12 |
Сталь мягкая на алюминии | 0,47 | — |
Сталь мягкая, на латуни | 0,44 | — |
Сталь мягкая на бронзе | 0,34 | 0,17 |
Сталь мягкая на меди | 0.36 | 0,18 |
Сталь мягкая, на стали мягкой | 0,57 | 0,09-0,19 |
Каменная кладка на бетоне | — | — |
Каменная кладка на грунте | — | — |
Кованое железо в бронзе | 0. | |
 021
021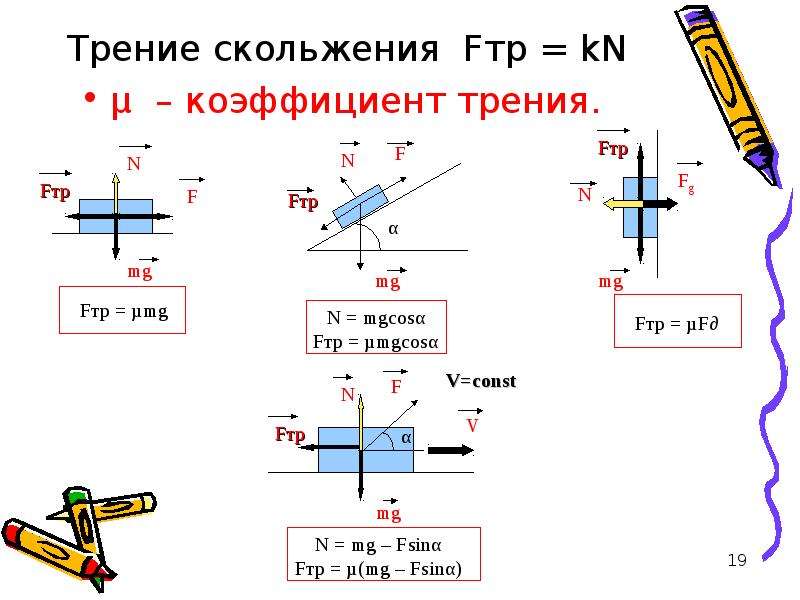



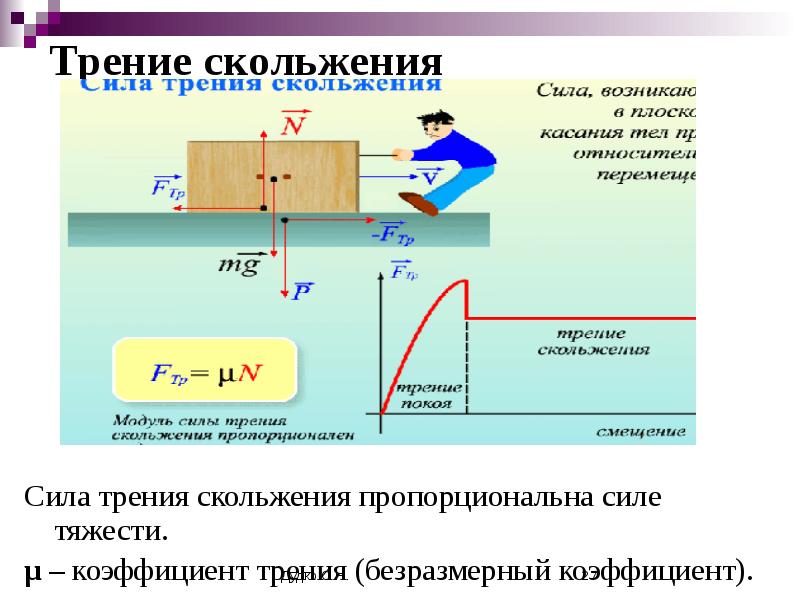 сталь > F кс
сталь > F кс  Экспериментальная процедура, описанная ниже, приравнивает векторную составляющую веса вниз по склону к коэффициенту трения, умноженному на нормальную силу, создаваемую весом на склоне.
Экспериментальная процедура, описанная ниже, приравнивает векторную составляющую веса вниз по склону к коэффициенту трения, умноженному на нормальную силу, создаваемую весом на склоне. Это мнение, вероятно, возникло из опыта, когда присутствуют небольшие кусочки масла или смазки или когда блоки, например, поддерживаются пружинами или другими гибкими опорами, так что кажется, что они связаны». RP Feynman, RP Leighton и M. Sands, Лекции Фейнмана по физике, т. I, стр. 12-5, Addison-Wesley, 1964.
Это мнение, вероятно, возникло из опыта, когда присутствуют небольшие кусочки масла или смазки или когда блоки, например, поддерживаются пружинами или другими гибкими опорами, так что кажется, что они связаны». RP Feynman, RP Leighton и M. Sands, Лекции Фейнмана по физике, т. I, стр. 12-5, Addison-Wesley, 1964.  20
20 07-0.20
07-0.20 40-0,70
40-0,70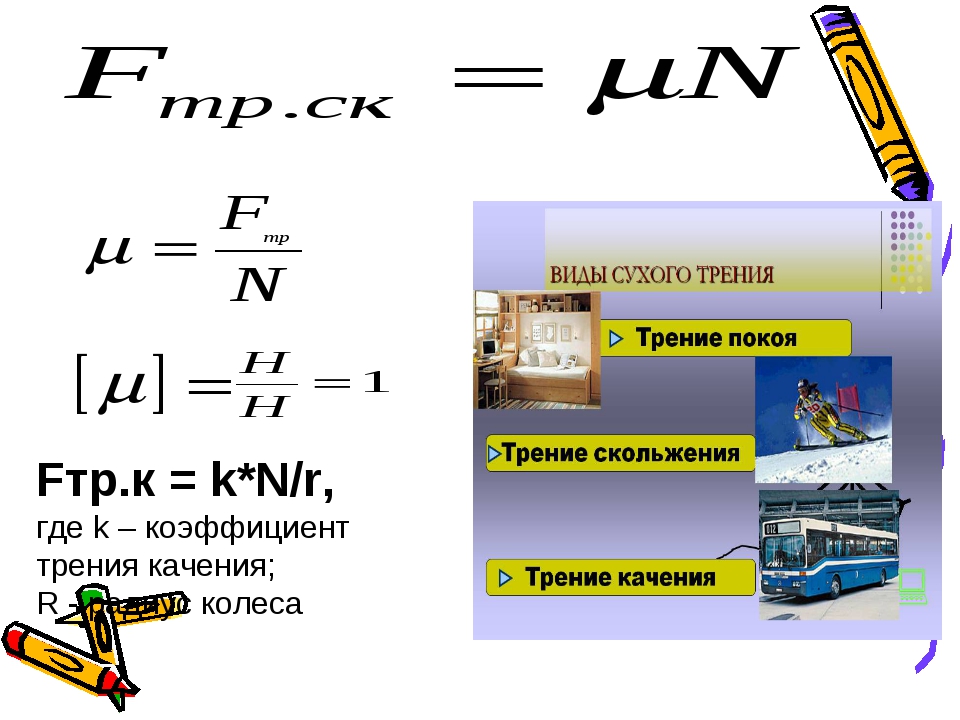 42
42