Закон Ампера

      В 1820 г. А.М. Ампер экспериментально установил, что два проводника с током взаимодействуют друг с другом с силой:

,

(2.1.1)

       где b – расстояние между проводниками, а k – коэффициент пропорциональности, зависящий от системы единиц.

Ампер Андре Мари (1775–1836) – французский физик, математик и химик. Основные физические работы посвящены электродинамике. Сформулировал правило для определения действия магнитного поля тока на магнитную стрелку. Обнаружил влияние магнитного поля Земли на движущиеся проводники с током. В первоначальное выражение закона Ампера не входила никакая величина, характеризующая магнитное поле. Однако, взаимодействие токов осуществляется через магнитное поле, и следовательно в закон должна входить характеристика магнитного поля.

      В современной записи в СИ, закон Ампера выражается формулой

,

(2.1.2)

где  – сила, с которой магнитное поле действует на бесконечно малый проводник  с током I.

      Модуль силы, действующей на проводник,

,

(2.1.3)

      Если магнитное поле однородно и проводник перпендикулярен силовым линиям магнитного поля, то

,

(2.1.4)

где  – ток через проводник сечением S.

          

Рис. 2.1

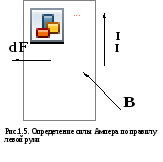
      Направление силы  определяется, как показано на рис. 2.1, направлением векторного произведения или правилом левой руки:

ориентируем пальцы по направлению первого вектора, второй вектор должен входить в ладонь и большой палец показывает направление векторного произведения.

      Закон Ампера – это первое открытие фундаментальных сил, зависящих от скоростей.

      Из закона Ампера хорошо виден физический смысл магнитной индукции.  В – величина, численно равная силе, с которой магнитное поле действует на проводник единичной длины, по которому течет единичный ток:

      Размерность индукции

---

формулировка и применение 🚩 Естественные науки

В самом деле, XIX век во многом перевернул представления ученых о строении мира и подтолкнул к множеству удивительных открытий и изобретений. Именно на этой волне и возник повышенный интерес к электричеству.

Открытия следовали одно за другим. Электрической силе и магнетизму приписывались самые фантастические свойства. Исследования ученых обрастали самыми невероятными слухами, но тем не менее все это в целом подхлестнуло небывалый интерес к научной деятельности и науке в частности.

Наука привлекала как никогда много различных людей, так произошло и с Андре-Мари Ампером. Он родился в Лионе в семье обычного торговца. Получил всего лишь домашнее образование, но поскольку Андре-Мари имел доступ к семейной библиотеке, то благодаря усердию и стремлению к знаниям, он самостоятельно выучил латынь с единственной целью — прочесть работы великих математиков.

Андре-Мари Ампер кроме занятий научной деятельностью сделал ощутимую карьеру в системе образования. При Наполеоне Бонапарте он был назначен на пост генерального инспектора университетов Франции.

В 1827 году увидела свет его фундаментальная работа «Теория электродинамических явлений, выведенная исключительно из опыта», где автор объединил свои исследования и дал им математические определения.

В своем труде Ампер описал принципы взаимодействия постоянных токов. Они были исследованы Андре-Мари Ампером еще в 1820 году. В результате экспериментов и расчетов Андре-Мари Ампер пришел к некоторым выводам. Ученый заметил, что направление тока, текущего в параллельных проводниках, оказывает влияние на их притяжение. Если Ампер пускал ток в двух проводниках в одном направлении, то они притягивались. Когда ток пускался в одном и проводников в обратном направлении, он отталкивался от другого проводника. Полученная информация легла в основу всем известного закона Ампера.

Суть эксперимента заключалась в выявлении силы притяжения или отталкивания, зависящей от направления движения электрического тока в двух проводниках.

Кроме того, ученый заметил, что если пропускать достаточно сильный электрический ток по проводникам, то их смещение хорошо видно невооруженным глазом. Будучи математиком, Ампер измерил и установил, что механическое взаимодействие имеет силу, пропорциональную силе тока и зависящую от расстояния между проводниками. Чем это расстояние больше, тем сила механического взаимодействия меньше. Так эксперимент навел Ампера на мысль о существовании магнитных полей, порождаемых электрическим током. В этом и состоит закон Ампера.

1.2. Закон Ампера.@

В 1820 г. А.Ампер установил, что сила, с которой магнитное поле действует на элементарный проводник с токомI и длиной

:

.

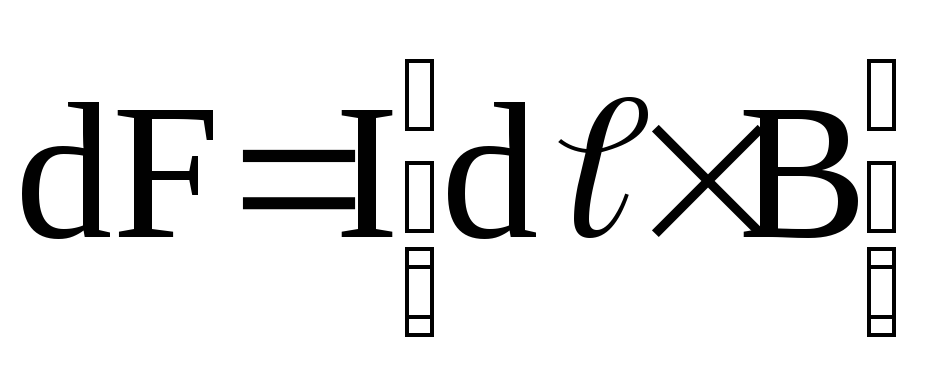Вектор 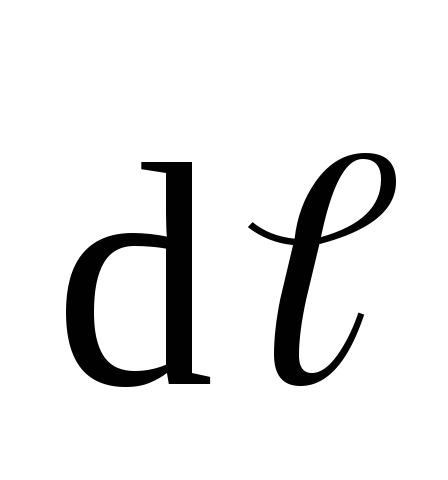совпадает по направлению с током.Данная формула выражает закон Ампера: сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника и магнитной индукции поля.

Если поместить проводник с током между полюсов постоянного магнита, то сила Ампера будет действовать на него в направлении, показанном на рис. 1.4. Направление может быть найдено по правилу левой руки: если ладонь левой руки расположить так, чтобы вектор

был направлен в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отставленный под прямым углом большой палец укажет направление силы, действующей на элемент проводника с током (рис.4.5).

Модуль силы Ампера вычисляется по формуле

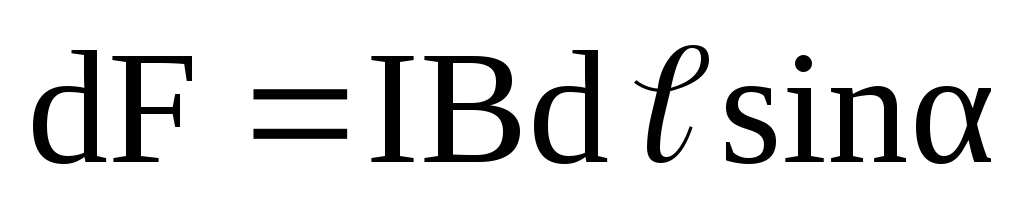, где α –угол между векторами и. Чтобы найти силу, действующую на проводник конечной длины 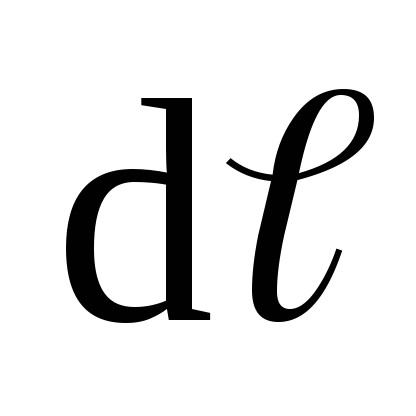в магнитном поле, необходимо определить геометрическую сумму сил, действующих на все малые элементы данного проводника, т.е.

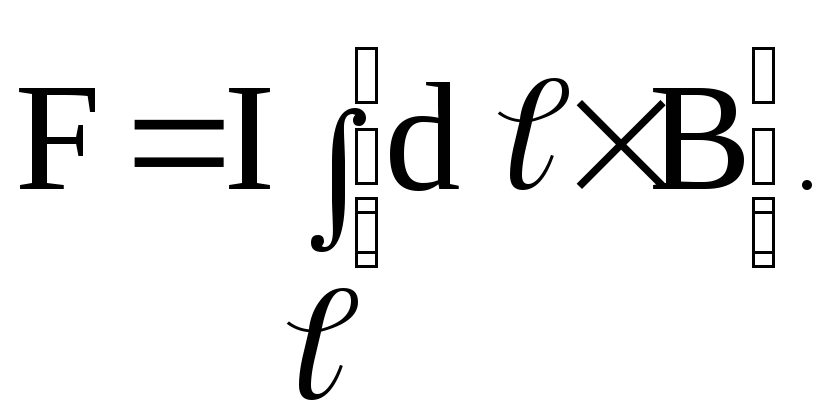
Пусть элемент проводника с током перпендикулярен направлению магнитного поля. Тогда sinα=1 и dF=IВ. Отсюда получаем

П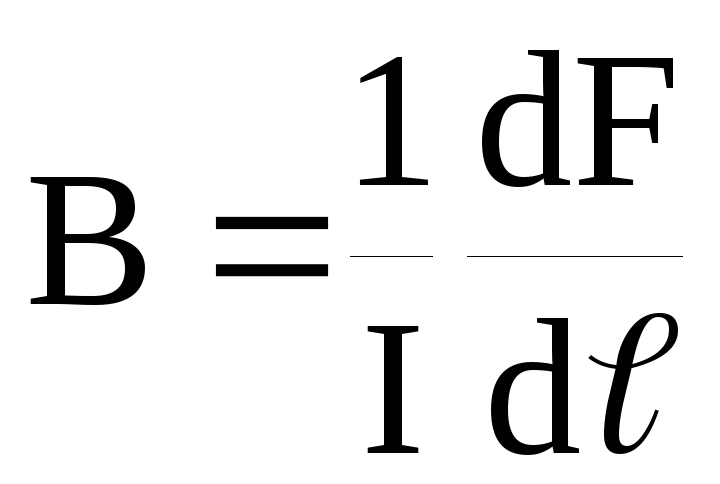оследнее выражение помогает определить физический смысл величины В:магнитная индукция численно равна силе, действующей со стороны магнитного поля на 1 м проводника, по которому течет ток в 1 А и который расположен перпендикулярно направлению магнитного поля. Таким образом, магнитная индукция является силовой характеристикой магнитного поля.

Из закона Ампера следует, что магнитные силы нецентральные, так как они направлены перпендикулярно силовым линиям магнитного поля. Напомним, что электростатические силы – центральные.

1.3. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля.@

Французские физики Ф. Савар и Ж.Б. Био изучали магнитное поле, создаваемое проводниками с постоянным током различной формы. На основании многочисленных опытов они пришли к выводу, что магнитная индукция поля проводника с током пропорциональна силе тока I, зависит от формы и размеров проводника, а также от расположения рассматриваемой точки по отношению к проводнику. Био и Савар пытались получить самый общий закон – для проводника любой формы и любой точки поля. Однако сделать это им не удалось. По их просьбе этой проблемой занялся французский математик П.С.Лаплас. Он высказал важную гипотезу о том, что при наложении магнитных полей справедлив принцип суперпозиции, т.е. принцип независимости действия полей. Если имеется несколько проводников с током, каждый из которых создает в исследуемой точке магнитное поле с индукциями 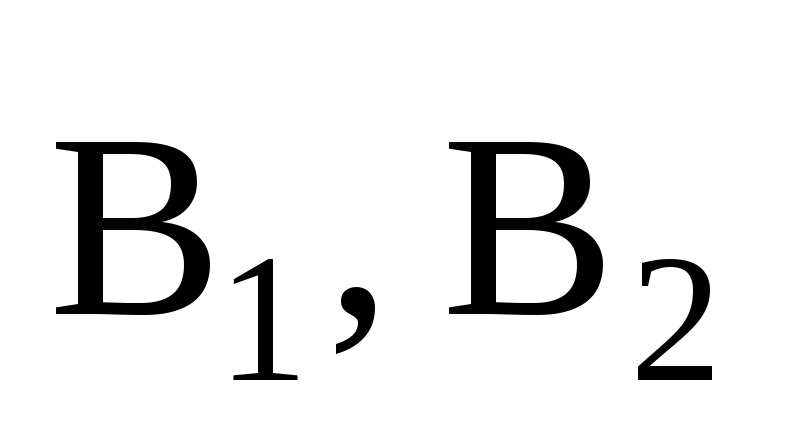…, то результирующая магнитная индукция будет равна векторной сумме всех

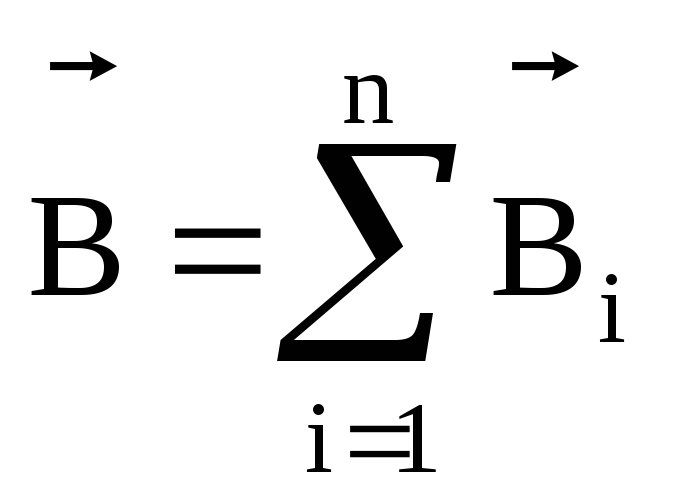:. Если перейти к малым отрезкам провода с током, то суммирование надо заменить интегрированием и тогда индукция, создаваемая всем проводником с токомI, будет равна: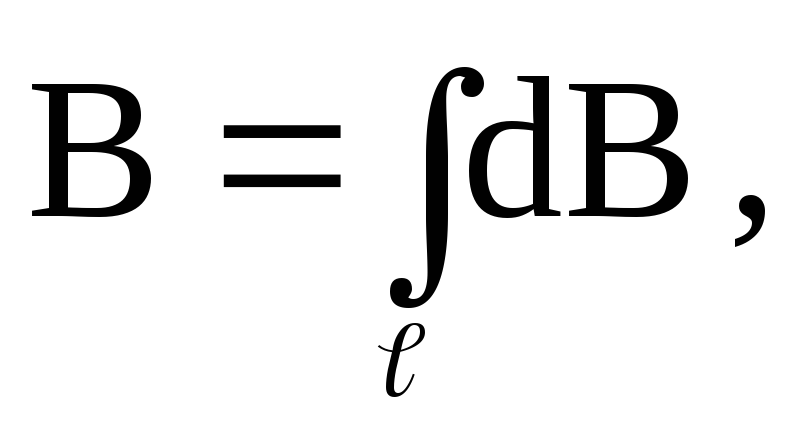где– индукция, создаваемая элементом длины проводникаdℓ, интегрирование проводится по всей длине проводника. 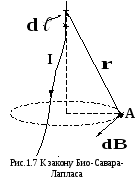Лаплас обобщил экспериментальные результаты Био и Савара в виде дифференциального закона, называемого законом Био – Савара – Лапласа, по которому магнитная индукция , создаваемая в некоторой точке А элементом проводникаdℓ с током I, определяется формулой

В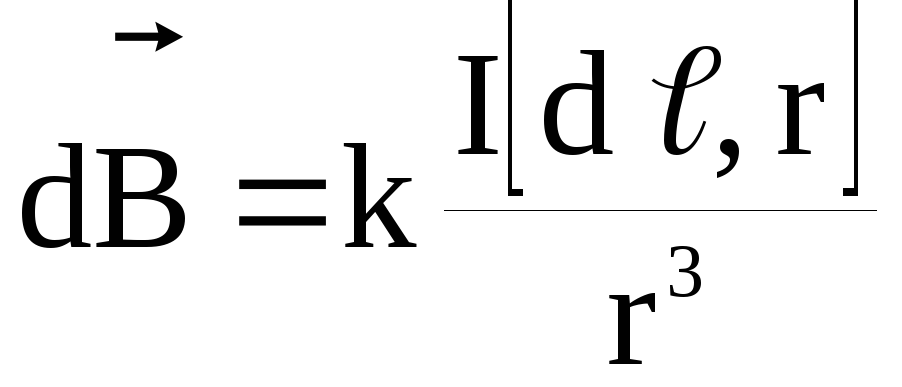ыберем произвольную точку А вблизи проводника. Векторнаправлен в точке А перпендикулярно плоскости, построенной на векторахи 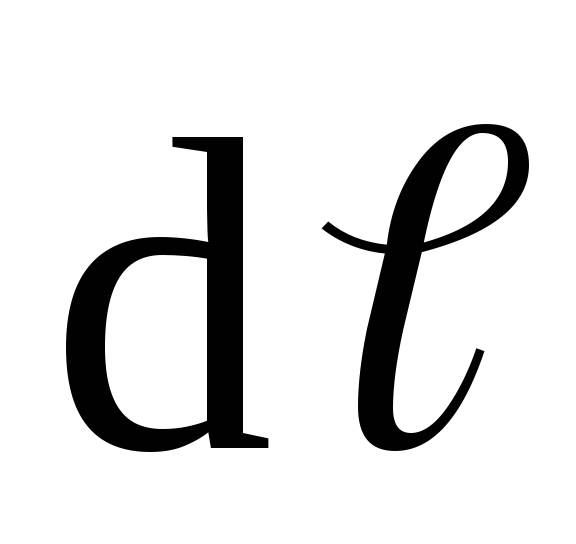по правилу правого винта (буравчика), и совпадает с направлением касательной к линии индукции в точке А (пунктирный круг) (рис.1.7). Коэффициент пропорциональности k зависит от выбора системы единиц. В СИ это размерная величина, равная μ₀/4π, где μ₀ — магнитная постоянная, равная 4π∙10

-7Гн/м. Все выше изложенное относится к вакууму.

Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле

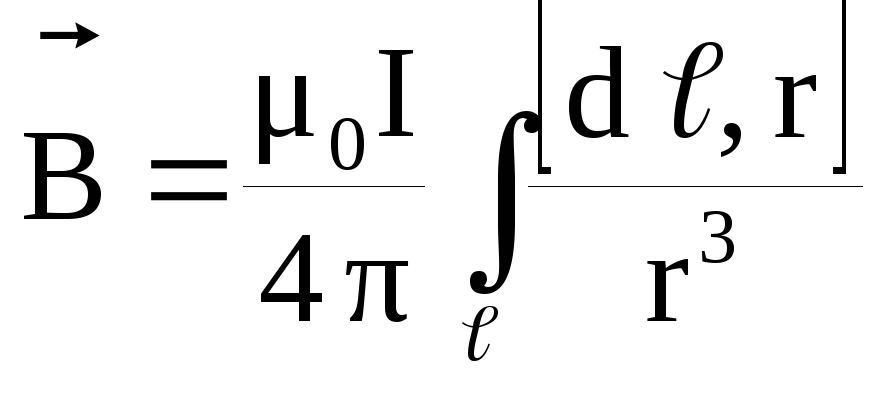
Магнитное поле в центре кругового проводника с током. Рассмотрим круговой проводник с током, изображенный на рис.1.8. Все элементы данного проводника dℓ создают в его центре (точке А) магнитные поля одинакового направления – вдоль нормали к площади витка. Поэтому, как и в предыдущем случае, сложение векторов можно заменить сложением их модулей. Элементыdℓ перпендикулярны R и sinα=1. Используя закон Био-Савара-Лапласа, получим:

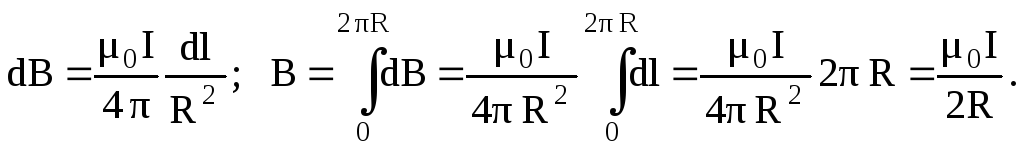
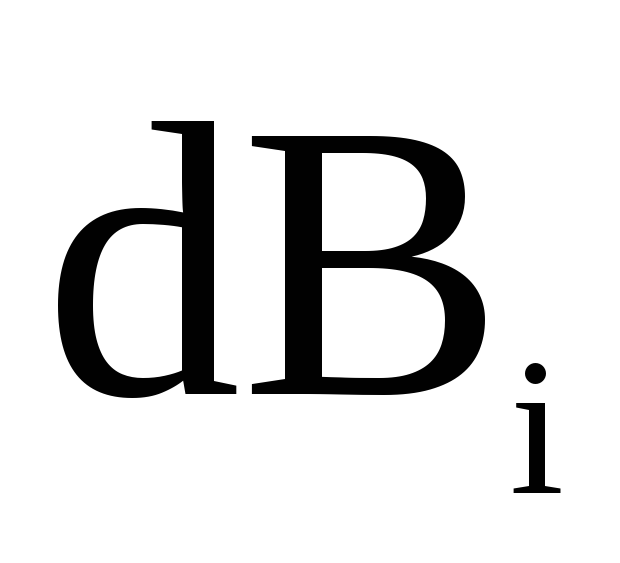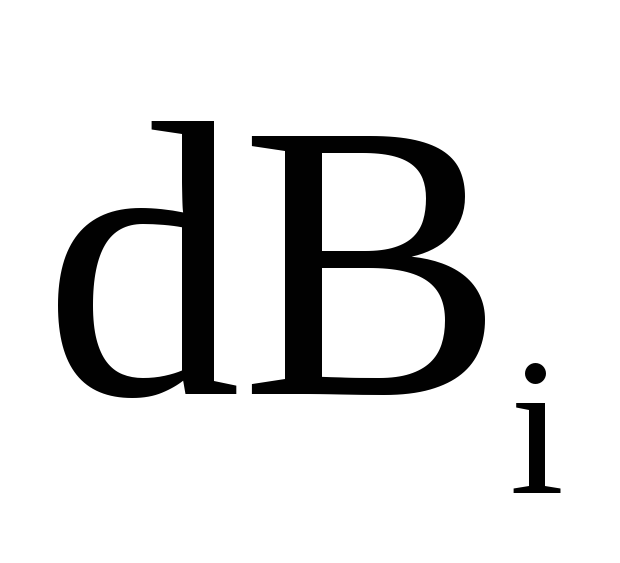Магнитное поле прямолинейного проводника с током. Представим себе ток, текущий по тонкому прямому проводу бесконечной длины (рис. 1.9). Возьмем произвольную точку А на расстоянии R от проводника. Согласно правилу правого винта (буравчика), векторы от каждого элемента токаdℓ_i имеют одинаковое направление, перпендикулярное плоскости чертежа (на нас). Поэтому сложение векторов можно заменить сложением их модулей. При суммировании всех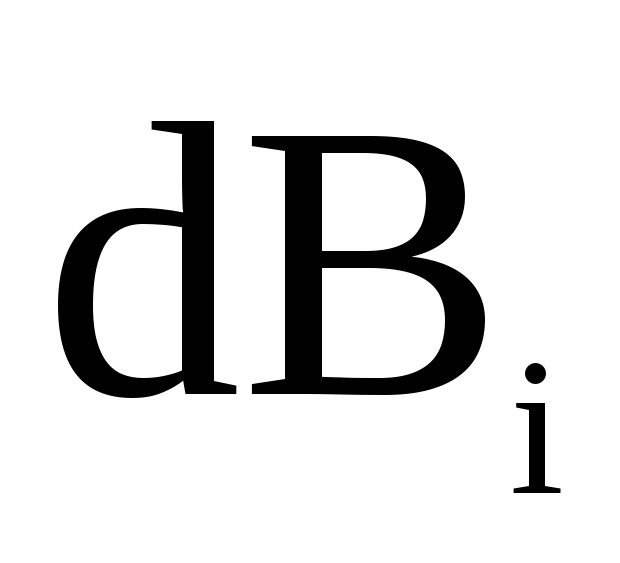будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ.

Итак, из треугольника АСЕ выразим r через известное нам расстояние R и переменную α:

П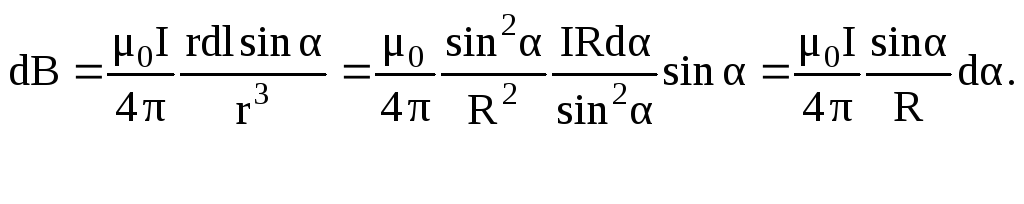о закону Био-Савара-Лапласа получим:

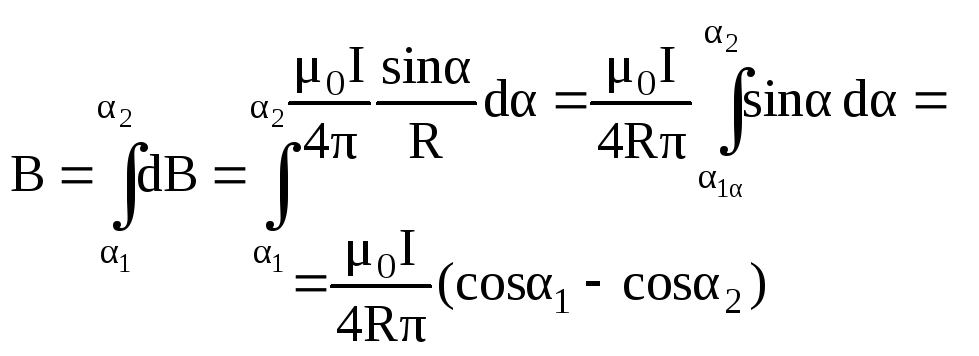
В данном выражении α₁ и α₂ — значения угла α для крайних точек проводника. Если прямолинейный проводник бесконечно длинный, то α₁ = 0, α₂ = π. Магнитная индукция в любой точке поля такого проводника с током:

Н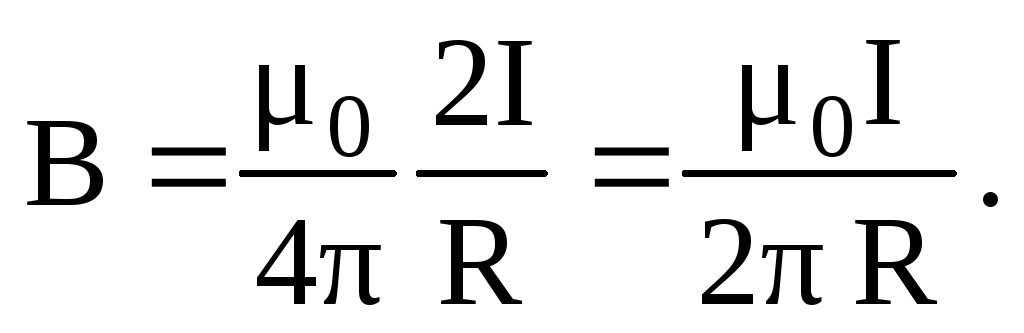апомним, что линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.

Магнитное поле соленоида. Если витки соленоида расположены вплотную друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью. Обозначим через L длину соленоида, а через n — число витков, приходящихся на единицу длины соленоида. Магнитная индукция поля соленоида В равна геометрической сумме магнитных индукций В_i полей всех его витков. Если L>>R (радиуса витков), тогда В в точке А, лежащей на оси вдали от концов такого соленоида, вычисляется по формуле (без вывода): В = μ₀nI.

Разработка урока «Закон Ампера и его применение»

Закон Ампера и его применение

Цель: сформулировать закон Ампера и показать его практическую применимость.

Ход урока

I. Организационный момент

П. Актуализация знаний

— Опишите опыт Эрстеда.

— Каким является магнитное поле?

— Что можно сказать об основных линиях магнитного поля?

— Что такое соленоид?

— Сформулируйте правила для определения направлений силовых линий магнитного поля?

— Что можно сказать о магнитных монополях?

III. Выполнение лабораторной работы

Лабораторная работа по теме «Изучение свойств постоянных магнитов»

Цели: получить картины силовых линий магнитного поля вокруг постоянных магнитов.

Оборудование: магнит полюсовой (2 шт.), магнит подковообразный, магнитная стрелка, скрепки, медный провод, ластик, железные опилки.

Ход работы

1. Найдите северный полюс стрелки, установите полюса полюсо-вого магнита и подковообразного. Обозначьте северный и южный полюса магнитов.

2. Положите лист картона на полюсовой магнит и равномерно посыпьте его железными опилками. Не двигая магнит и картонку, осторожно постучите по картонке, чтобы опилки могли перемещаться. Обратите внимание, как выстроились опилки на листе. Сделайте рисунок в тетради.

3. Получите картину магнитного поля двух пол юсовых магнитов, расположенных параллельно друг другу, и подковообразного магнита.

4. Что можно сказать о линиях магнитной индукции?

IV. Изучение нового материала

1. Проведение эксперимента.

По двум параллельным проводникам пропускаем электрический ток. В том случае, если ток направлен в одну сторону, наблюдается притяжение проводников, если в разные стороны, то отталкивание-Притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока называют магнитным взаимодействием токов.

На проводник с током в магнитном поле действует сила, которая получила название силы Ампера. Направление этой силы можно найти при помощи правила левой руки. Математическая запись имеет следующий вид:

Fa = IBls‘ma,

где /- сила тока в проводнике; В — магнитная индукция; / — длина проводника; а — угол между направлением проводника и направлением вектора магнитной индукции. Где /- сила тока в проводнике; В — магнитная индукция; / — длина проводника; а — угол между направлением проводника и направлением вектора магнитной индукции.

2. Работа с учебником.

Учащиеся открывают с. 900 учебника, читают § 64 и отвечают на следующие вопросы:

— Как устроен измерительный прибор магнитоэлектрической

Системы^?

— Каково устройство электродвигателя постоянного тока?

— От чего зависит вращающийся магнит электродвигателя постоянного тока?

— Как можно изменить направление вращения якоря электродвигателя?

— Как можно изменить скорость вращения якоря электродвигателя?

V. Решение задач

1. Какая сила действует на каждый метр длины воздушных проводов троллейбусной линии, расположенных на расстоянии 52 м друг от друга, если сила тока в проводах — 2000 А? (Ответ: 1,5 Н.)

2. Вычислите индукцию магнитного поля на расстоянии 10 м от длинного прямого проводника при силе тока в проводнике 20 А. [Ответ: 4\0′⁵ Тл.)

3. Вычислите индукцию магнитного поля внутри цилиндрической катушки длиной 10 м, содержащей 200 витков провода, при силе тока в катушке 5 А. (Ответ: 1,310~² Тл.)

Задачи повышенной сложности:

1. В вертикально однородном магнитном поле на двух тонких лентах горизонтально подвешен проводник длиной 20 см и массой 20,4 г. Индукция магнитного поля равна 0,5 Тл. На какой угол от вертикали отклонятся ленты, если сила тока в проводнике равна 2 А. (Ответ: 45°.)

2. Прямолинейный проводник массой 2 кг и длиной 50 см помещен в однородное магнитное поле перпендикулярно линиям индукции. Индукция поля равна 15 Тл. Какой силы ток должен проходить по нему, чтобы он висел не падая? {Ответ: 2,7Тл.)

3. Проводящий стержень лежит на горизонтальной поверхности перпендикулярно однородному горизонтальному магнитному полю с индукцией 0,2 Тл. Какую силу в горизонтальном направлении нужно приложить перпендикулярному проводнику для его равномерного поступательного движения? Сила тока в проводнике — 10 А, масса — 100 г, длина — 25 см, коэффициент трения — 0,1. (Ответ: 0,548 Н или 0,402 Н.)

13.2. Закон Ампера

Одним из главных проявлений магнитного поля является его силовое действие на движущиеся электрические заряды и токи.В результате обобщения многочисленных опытных данных А. М. Ампером был установлен закон, определяющий это силовое воздействие.

Приведем его в дифференциальной форме, что позволит вычис­лять силу, действующую на различные контуры с током, располо­женные в магнитном поле.

В проводнике, находящемся в магнитном поле, выделим достаточно малый участок , который можно рассматривать как вектор, направленный по току (рис. 13.5). Произведение называют элементом тока. Сила, действующая со стороны магнитного поля на элемент тока,

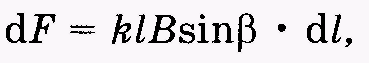(13.9)

где k — коэффициент пропорциональности; в СИk = 1, поэтому

(13.10)

или в векторной форме

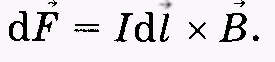(13.11)

Для плоского контура с током находим силу, действующую на участок l проводника со стороны магнитного поля, интегрированием скалярного выражения (13.10):

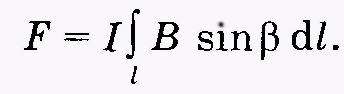(13.12)

Соотношения (13.9)—(13.12) выражают закон Ампера.

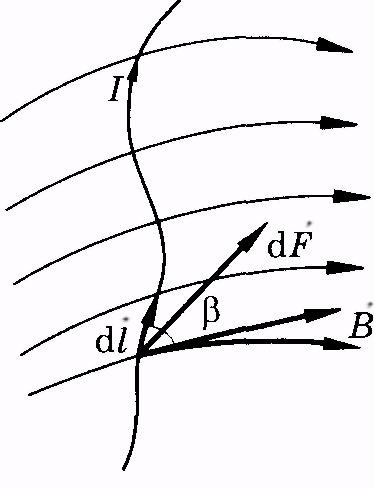
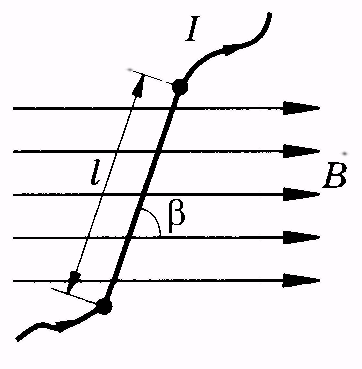
Рис. 13.5 Рис. 13.6

Рассмотрим некоторые примеры на применение формулы (13.11).

1. Прямолинейный участок проводника с током I длиной l, расположенный в однородном магнитном поле под угломк магнитной индукции 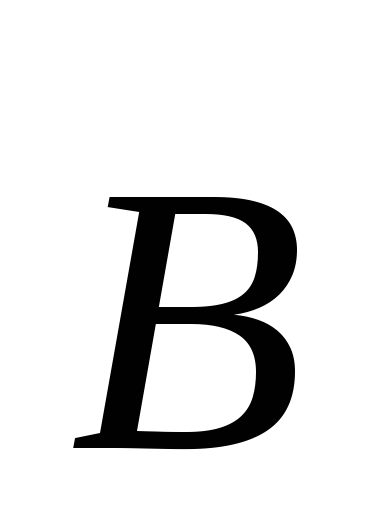(рис. 13.6). Для нахождения силы, действую­щей на эту часть проводника со стороны магнитного поля, интег-оиоуем (13.12) и получаем

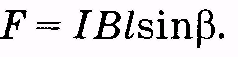(13.13)

2. Прямоугольная рамка KLMN с током I, помещенная в одн­родное магнитное поле индукции (рис. 13.7, а). Пронумеруем стороны рамки и обозначим силы, действующие на них со стороны магнитного поля,F₁, F₂, F₃, F₄.

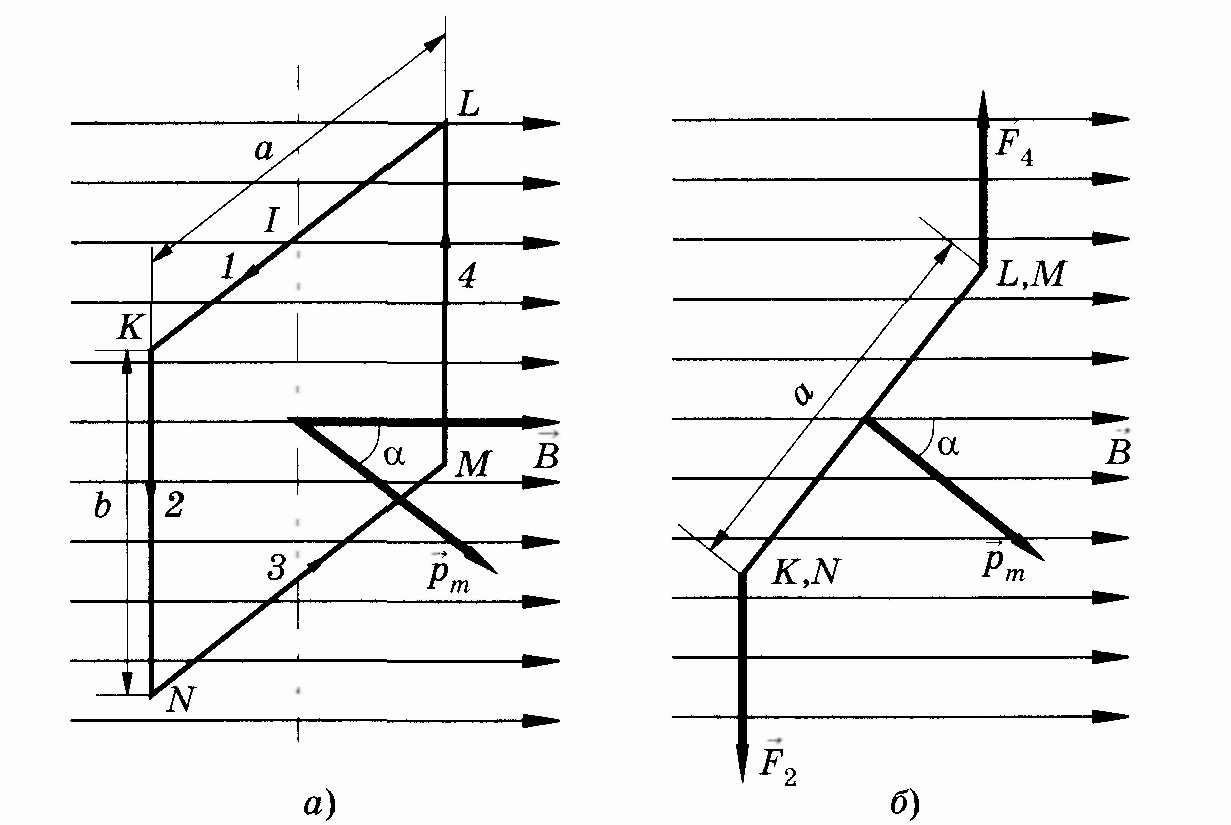
Силы F₁ и F₃, приложенные к серединам соответствующих сторон, направлены противоположно вдоль оси и по формуле (13.13) равны. Силы же F₂ = F₄ = IBb создают пару сил, момент которой (рис. 13.7, б)

М = IBb (a/2) sin + IBb(a/2) sin = IBbasin. (13.14)

Так как Iba = IS = p_m, то из (13.14) имеем

M=p_mBsin, (13.15)

или в векторной форме

(13.16)

Фактически на основе этой зависимости в § 13.1 было введено понятие вектора магнитной индукции.

13.3. Действие магнитного поля на движущийся электрический заряд. Сила Лоренца

Сила, действующая, согласно закону Ампера, на проводник с током в магнитном поле, есть результат его воздействия на движущиеся электрические заряды, создающие этот ток.

Р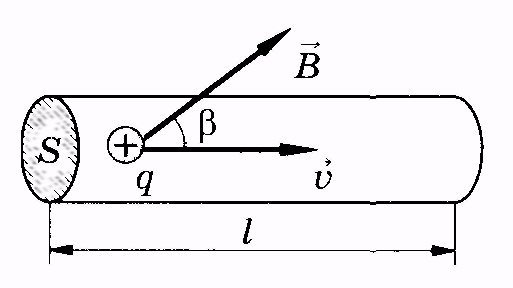ассмотрим цилиндрический проводник длинойl с токомI,расположенный в магнитном поле индукции (рис. 13.8). Скорость направленного движения некоторого положительного заряда q равна . Сила, действующая на отдельный движущийся заряд, определяется отношением силы F, приложенной к проводнику с током, к общему числу .N этих зарядов в нем:

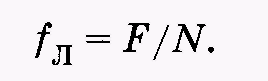(13.17)

Рис. 13.8

Раскроем выражение для силы, используя (13.13) и полагая, что сила тока равна

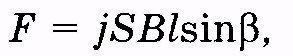
где j — плотность тока. Учитывая (12.50), получаем

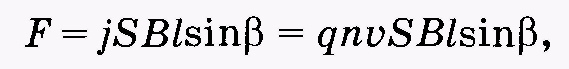(13.18)

где п = N/(Sl) — концентрация частиц. Подставляя (13.18) в (13.17), получаемвыражение для силы, действующей со стороны магнитного поля на отдельный движущийся электрический заряд и называемой силой Лоренца:

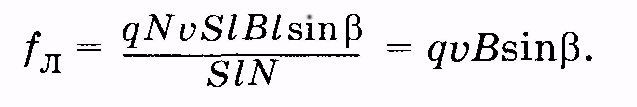
Направление силы Лоренца можно определить из векторной записи уравнения (13.19) с учетом знака заряда q:

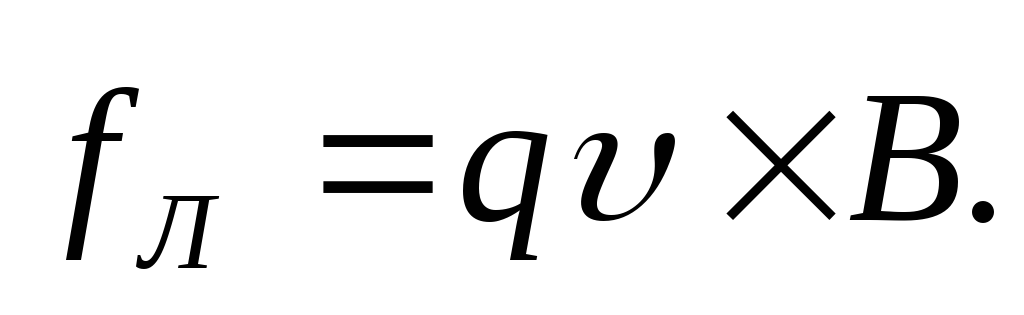(13.20)

Как видно из (13.20), эта сила всегда перпендикулярна плоскос­ти, в которой лежат векторы и 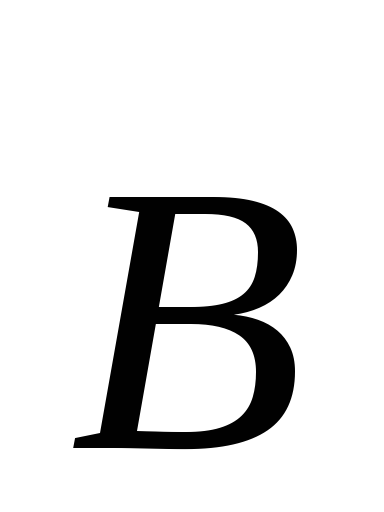. Из механики известно, что если сила перпендикулярна скорости, то она изменяет лишь ее направление, но не значение. Следовательно, сила Лоренца не изменяет кинетической энергии движущегося заряда и не совершает работы.

Если заряд неподвижен относительно магнитного поля или его скорость параллельна (антипараллельна) вектору магнитной индукции, то сила Лоренца равна нулю.

П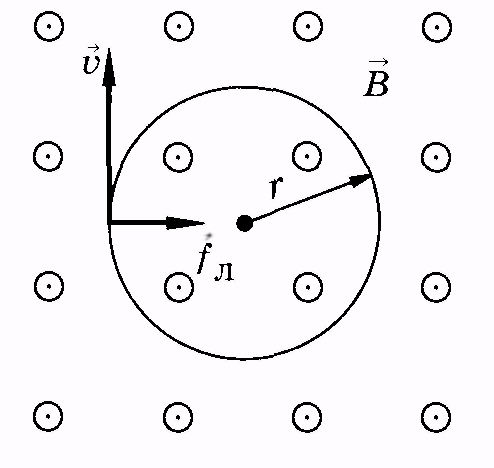усть в однородное магнитное поле перпендикулярно векторуиндукции 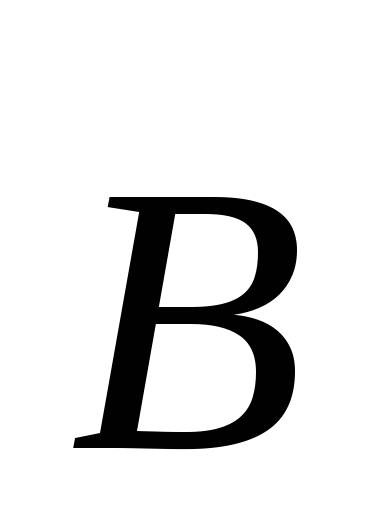влетает со скоростью v положительно заряженная частица (рис. 13.9). На нее действует сила Лоренца f_Л, которая вызовет центростремительное ускорение, и, по второму закону Ньютона,

m²/r=qB, (13.21)

где q и т — заряд и масса частицы, r — радиус траектории, по которой она будет двигаться. Из (13.21) получаем

Рис. 13.9 r = m/(qB). (13.22)

Отсюда следует, что радиус траектории остается постоянным, а сама траектория есть окружность.

Используя (13.22) и считая, что значение скорости частицы не изменяется, найдем период вращения ее по окружности:

(13.23)

Отношение q/m называют удельным зарядом частицы. Период вращения ее в магнитном поле [см. (13.23)] не зависит от радиуса окружности и скорости, а определяется только магнитной индукцией и удельным зарядом. Эту особенность используют в ускорителе заряженных частиц — циклотроне.

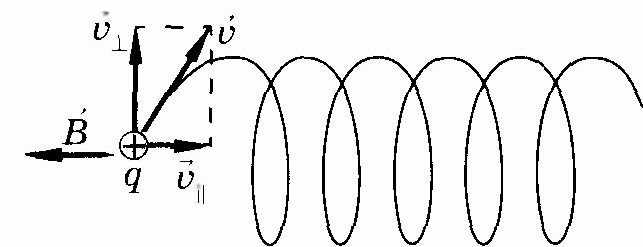
Чтобы описать форму траектории заряженной частицы, влетающей со скоростью в однородное магнитное поле под произвольным углом к (рис. 13.10), разложим вектор и на две составляющие и _|| и _, направленные соответственно вдоль вектора магнитной индукции магнитного поля и перпендикулярно ему. Составляющая _|| при движении частицы в магнитном поле остается постоянной; сила Лоренца, действующая на частицу, изменит направление составляющей скорости _. Под действием этой силы частица вращается по окружности. Таким образом, траекторией движения будет винтовая линия — вращение по окружности со скоростью _ совместно с перемещением вдоль вектора магнитной индукции со скоростью _||.

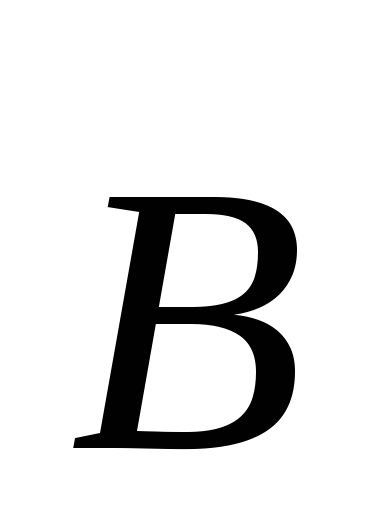Если на движущуюся заряженную частицу q действуют электрическое поле с напряженностью и магнитное поле с магнитнойиндукцией (рис. 13.11), то результирующая сила равна

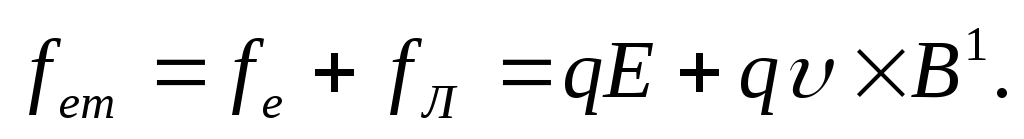(13.24)

Во многих системах (осциллограф, телевизор, электронный микроскоп) осуществляют управление электронами или другими заряженными частицами, воздействуя на них электрическими и магнитными полями, в этом случае основной расчетной формулой является (13.24).