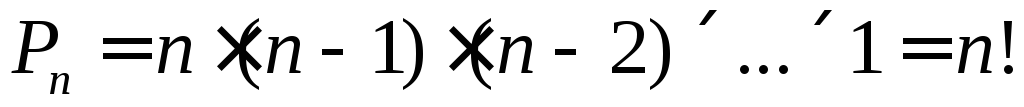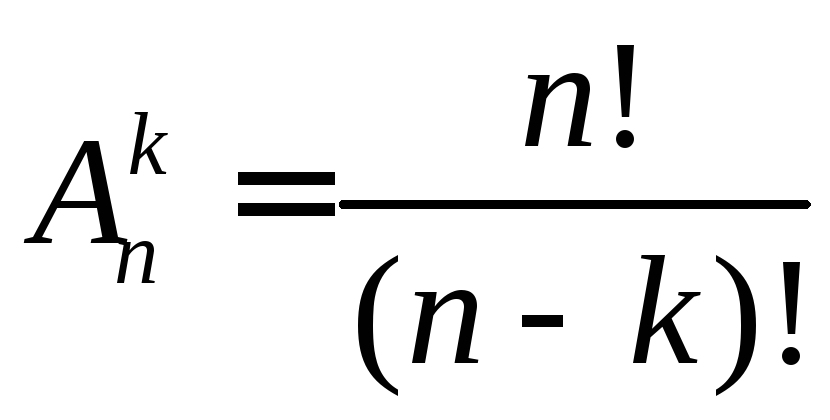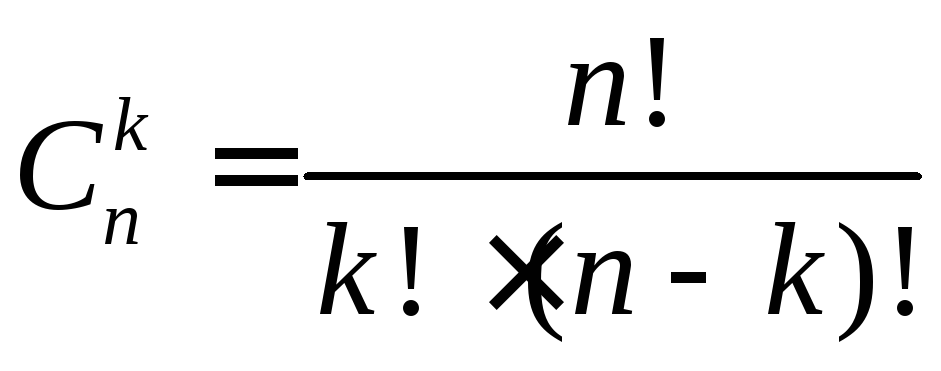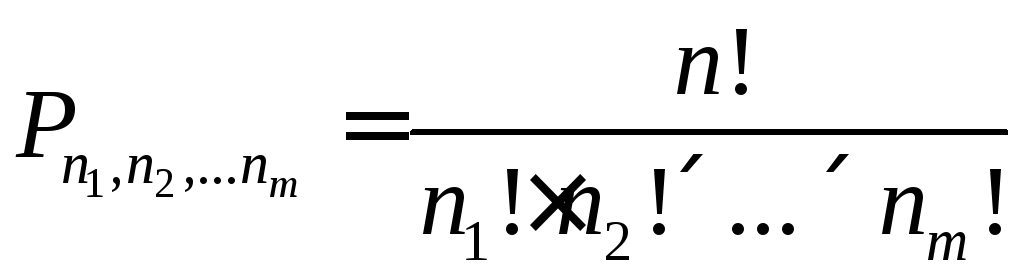Комбинаторика — Википедия
Комбинато́рика (комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана с другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Примеры комбинаторных конфигураций и задач[править | править код]
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
- Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого
- Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
- Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
- Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
- Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.
Примеры комбинаторных задач:
- Сколькими способами можно разместить n предметов по m ящикам, чтобы выполнялись заданные ограничения?
- Сколько существует функций F{\displaystyle F} из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?
- Сколько существует различных перестановок из 52 игральных карт?
- Ответ: 52! (52 факториал), то есть, 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000 или примерно 8,0658 ⋅ 1067.
- При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати?
- Решение: Каждый возможный исход соответствует функции F:{1,2}→{1,2,3,4,5,6}{\displaystyle F:\{1,2\}\to \{1,2,3,4,5,6\}} (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6 + 6 даёт нам нужный результат 12. Таким образом, существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.
Перечислительная комбинаторика[править | править код]
Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.
Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.
Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.
Структурная комбинаторика[править | править код]
К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.
Экстремальная комбинаторика[править | править код]
Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.
Теория Рамсея[править | править код]
Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:- в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.
В терминах структурной комбинаторики это же утверждение формулируется так:
- в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.
Вероятностная комбинаторика[править | править код]
Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.
Топологическая комбинаторика[править | править код]
Топологическая комбинаторика применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.
Инфинитарная комбинаторика[править | править код]
Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.
Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).
Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока Шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.
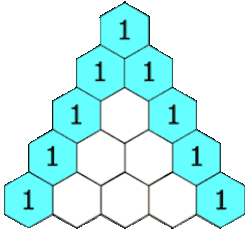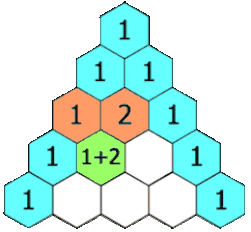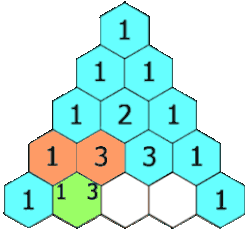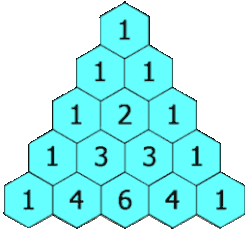
Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику[2]. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.
В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation
После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.[3]
Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:
Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.
Комбинаторика (языкознание) — это свойство единиц языка и соответствующих им единиц речи вступать в синтагматические отношения, то есть в отношения сочетаемости.
- Андерсон, Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — 960 с. — ISBN 0-13-086998-8.
- Виленкин Н. Я. . Популярная комбинаторика. — М.: Наука, 1975.
- Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.
- Липский В. . Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.
- Райгородский А. М. . Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.
- Райзер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.
- Рейнгольд Э., Нивергельт Ю., Део Н. . Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.
- Риордан Дж . Введение в комбинаторный анализ. — пер. с англ. — М., 1963.
- Стенли Р . Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — 440 с. — ISBN 5-03-001348-2.
- Стенли Р . Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — 767 с. — ISBN 978-5-03-003476-8.
Основы комбинаторики
Комбинаторика – это раздел математики, касающийся свойств комбинаций элементов. Комбинации элементов, сформированные по определенным правилам, возникают при решении многих вероятностных задач и потому заслуживают особого внимания.
Перестановки. Пусть из элементов некоторого множества,
включающего  значений, формируются комбинации,
содержащиевсе
значений, формируются комбинации,
содержащиевсе 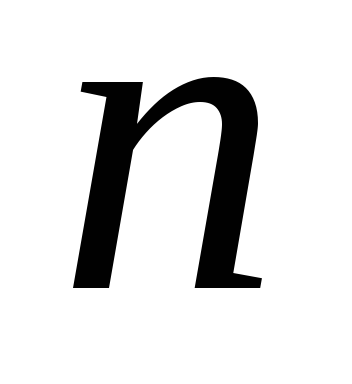
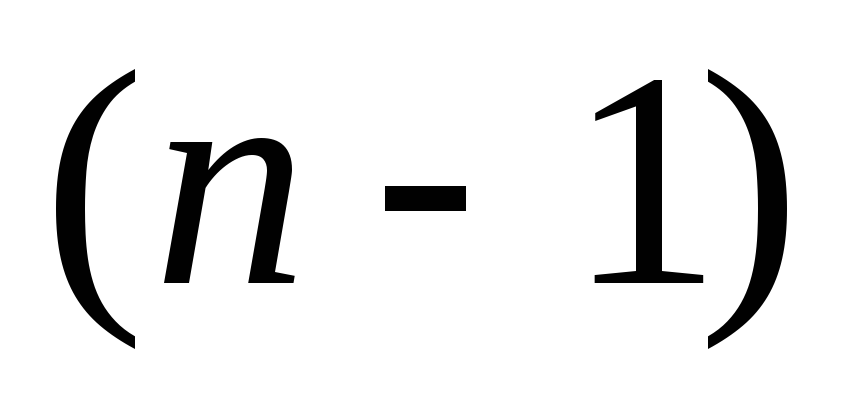 элемент. При
каждой конкретной паре начальных
элементов на третью позицию
можно поставить любой из оставшихся
элемент. При
каждой конкретной паре начальных
элементов на третью позицию
можно поставить любой из оставшихся 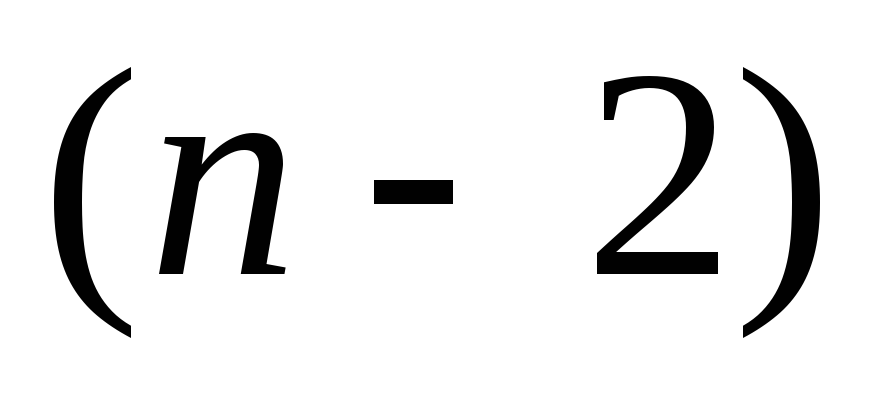 элементов и
т.д. Тогда, согласно правилу
произведения (см. с. 16), число способов
заполнения элементами позиций в
комбинации равно
элементов и
т.д. Тогда, согласно правилу
произведения (см. с. 16), число способов
заполнения элементами позиций в
комбинации равно | (1.0) |
Пример 1: Если набор пронумерованных шариков , , переупорядочивать различными способами, то можно получить комбинации
, ,;,,;,,;,,;,,;,,.
С позиций
комбинаторики речь идет о множестве из 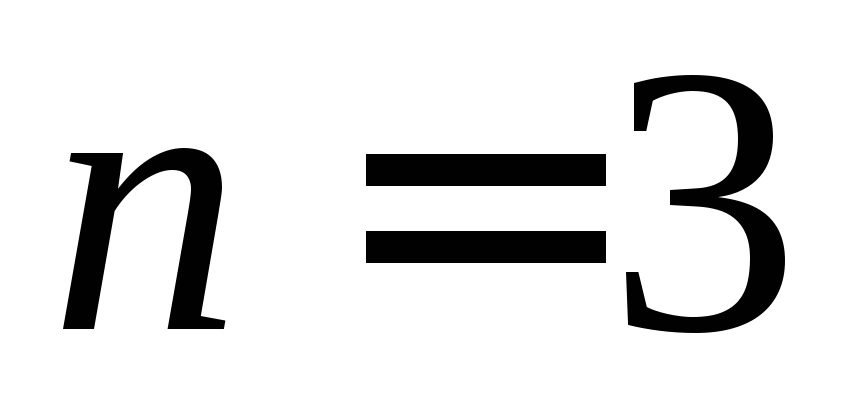 разнотипных
элементов. Для формирования комбинации
каждый раз
берут все
разнотипных
элементов. Для формирования комбинации
каждый раз
берут все 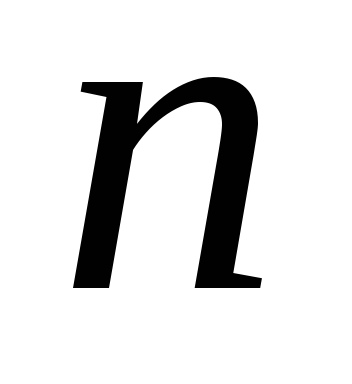 шариков, а отличаются
друг от друга комбинации порядком
расположения элементов. Таким образом,
речь идет о различных перестановках набора из n = 3 элементов. Соответствующее
число комбинаций согласно ( 1 .0) равно
шариков, а отличаются
друг от друга комбинации порядком
расположения элементов. Таким образом,
речь идет о различных перестановках набора из n = 3 элементов. Соответствующее
число комбинаций согласно ( 1 .0) равно 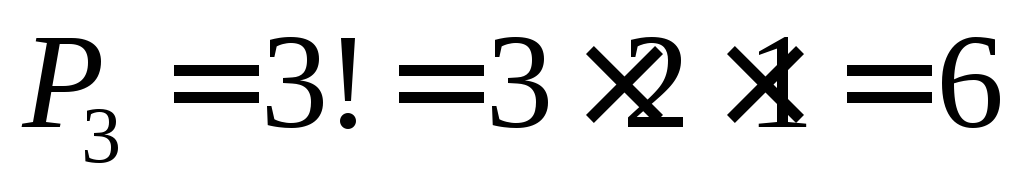 .
.
Размещения.Пусть из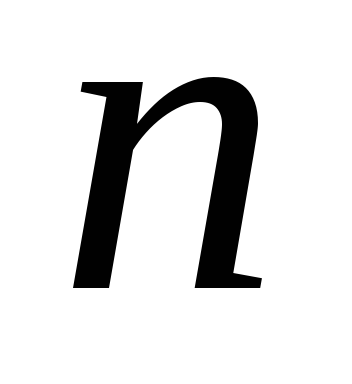 различных элементов для формирования
комбинации выбираются какие-либо
различных элементов для формирования
комбинации выбираются какие-либо 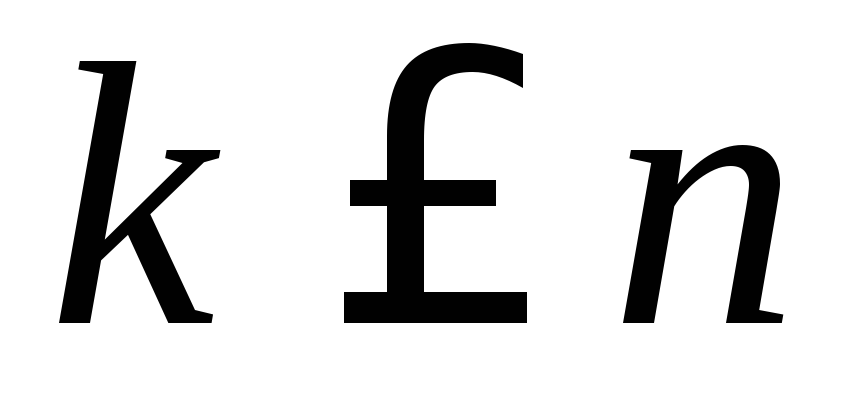 элементов, и
пусть различными считаются комбинации
отличающиеся друг
от друга или составом, или порядком
взаимного расположения элементов. Такие
комбинации называютразмещениями.
Дляопределения
числа различимых размещений предположим
сначала, что для формирования
комбинации используются все элементы
множества (т.е.
создаются перестановки), а затем внесем
поправку на тот факт, что на самом деле
значимыми являются лишь первые
элементов, и
пусть различными считаются комбинации
отличающиеся друг
от друга или составом, или порядком
взаимного расположения элементов. Такие
комбинации называютразмещениями.
Дляопределения
числа различимых размещений предположим
сначала, что для формирования
комбинации используются все элементы
множества (т.е.
создаются перестановки), а затем внесем
поправку на тот факт, что на самом деле
значимыми являются лишь первые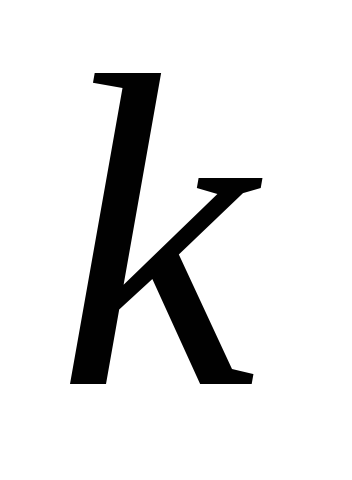 элементов комбинации. При “фиксации”
элементов комбинации. При “фиксации”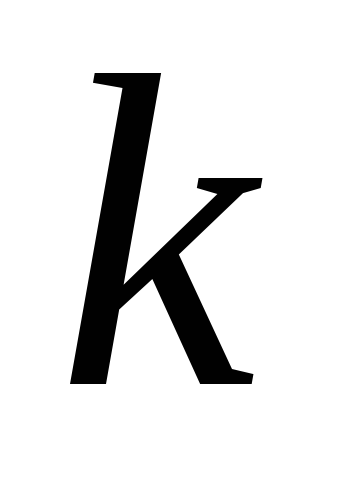 начальных элементов сформированные
первоначально
перестановки могут
отличаться лишь порядком размещения
последних
начальных элементов сформированные
первоначально
перестановки могут
отличаться лишь порядком размещения
последних  элементов (см. Рис. 1), упорядочить
которые можно
элементов (см. Рис. 1), упорядочить
которые можно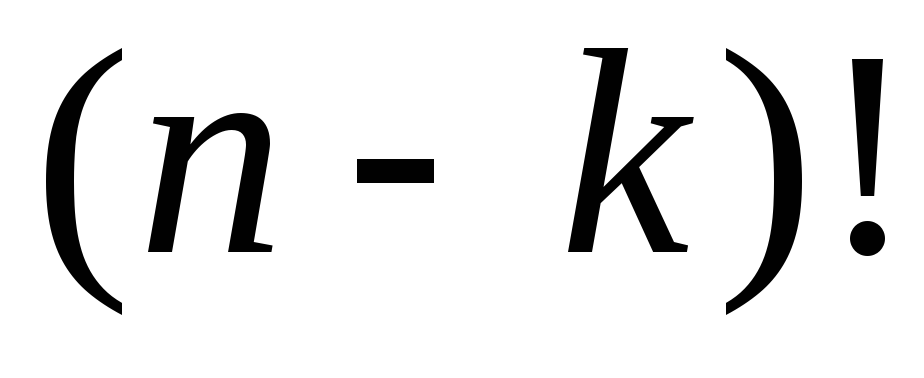 способами. Итак, каждые
способами. Итак, каждые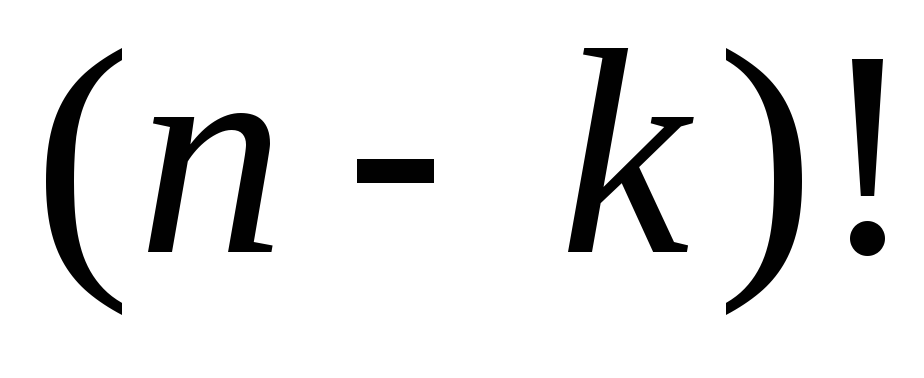 ранее различимых перестановок приводят
к одному и тому же размещению элементов,
а потому правило расчета числа возможных
размещений имеет вид
ранее различимых перестановок приводят
к одному и тому же размещению элементов,
а потому правило расчета числа возможных
размещений имеет вид
| (1.0) |
Приведенное в ( 1 .0)
обозначение 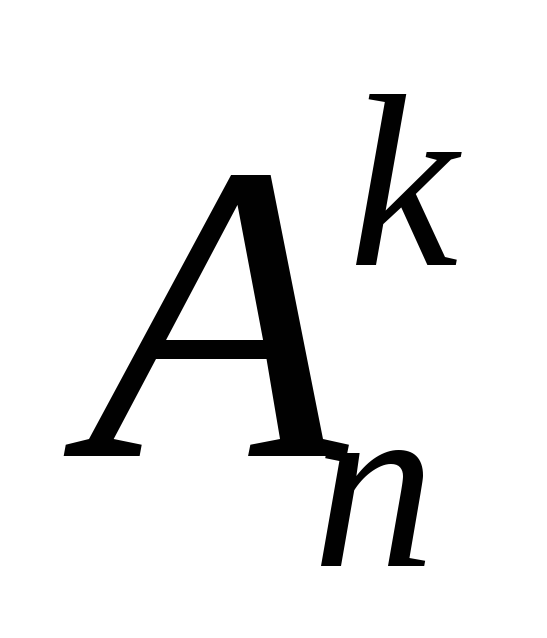 для числа размещений читается как “Aизnпоkэлементов”.
для числа размещений читается как “Aизnпоkэлементов”.
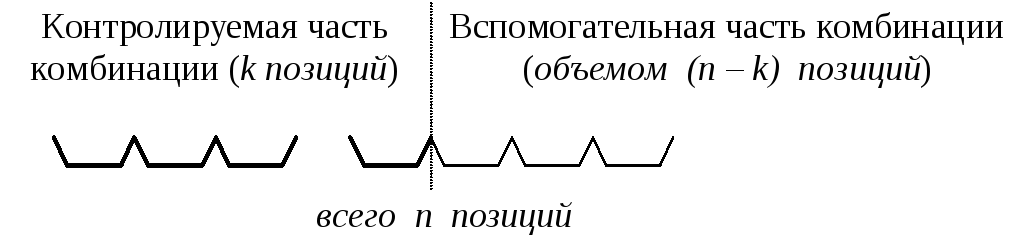
Рис. 1. Иллюстрация к определению числа размещений элементов
Пример 2: Если из набора пронумерованных шариков , , выбирать для образования комбинаций по 2 шарика, то комбинации, отличающиеся составом или порядком выбора элементов, будут иметь вид
, ;,;,;,;,;,.
С позиций
комбинаторики число различных
размещений из n
= 3 по k = 2 элементов будет определяться
соотношением 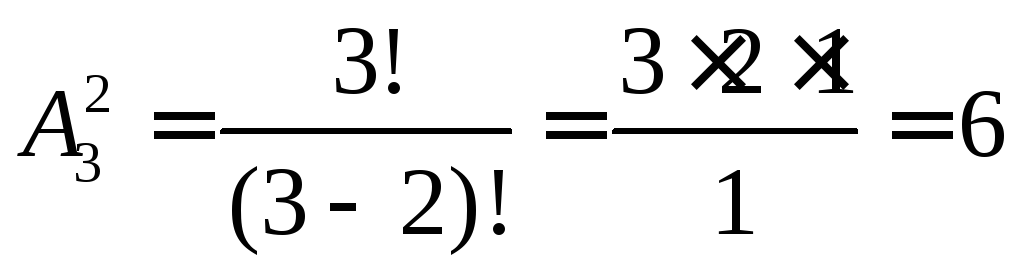 .
.
Сочетания.Если при выборе из 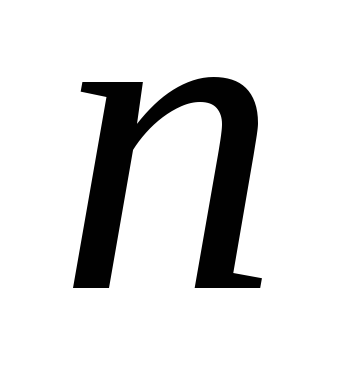 различных элементов множества
каких-либо
различных элементов множества
каких-либо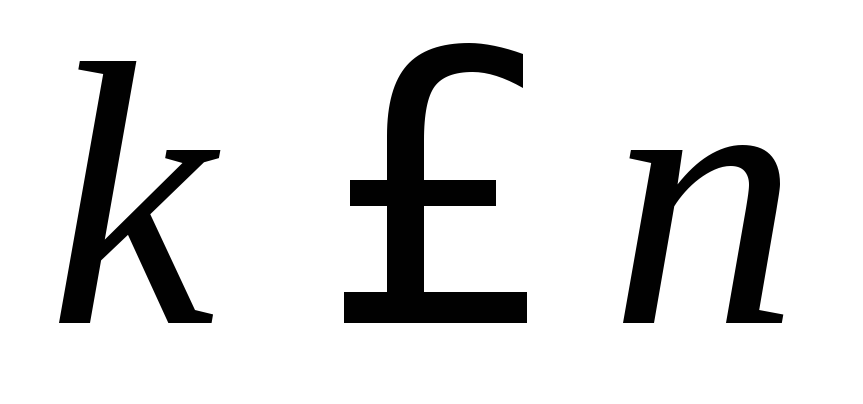 элементов порядок
их следованияне
является существенным, и различными
считаются лишь комбинации отличающиеся
входящими в них элементами, то такие
комбинации называютсясочетаниями.
элементов порядок
их следованияне
является существенным, и различными
считаются лишь комбинации отличающиеся
входящими в них элементами, то такие
комбинации называютсясочетаниями.
Для определения
числа различимых сочетаний элементов
учтем, что в рассмотренных ранее
размещениях при “фиксации”
совокупности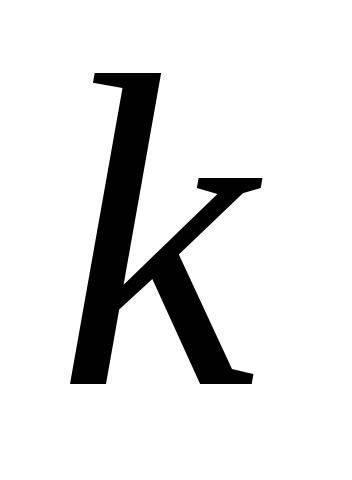 элементов,
входящих в начало комбинации, можно
было получать по
элементов,
входящих в начало комбинации, можно
было получать по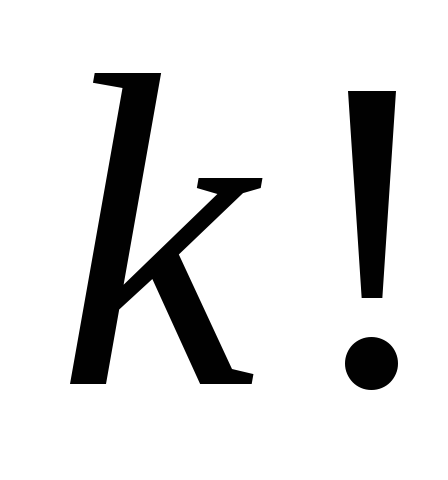 различных расстановок, переупорядочивая
начальные элементы относительно друг
друга. Теперь эти расстановки преобразуются
в единственное сочетание элементов, а
потому число сочетаний, получаемых из
расстановок, оказывается в
различных расстановок, переупорядочивая
начальные элементы относительно друг
друга. Теперь эти расстановки преобразуются
в единственное сочетание элементов, а
потому число сочетаний, получаемых из
расстановок, оказывается в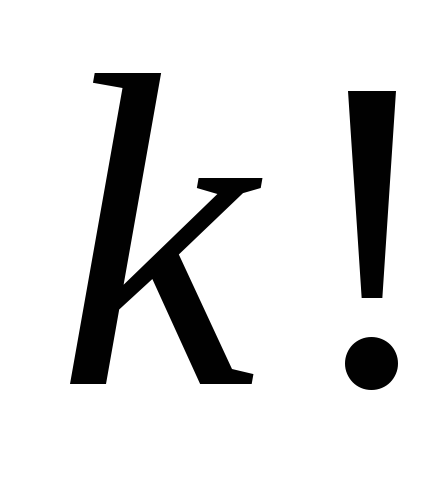 раз меньше. Итак, число различимых
сочетаний элементов определяется
правилом
раз меньше. Итак, число различимых
сочетаний элементов определяется
правилом
| (1.0) |
Приведенное в ( 1 .0)
обозначение 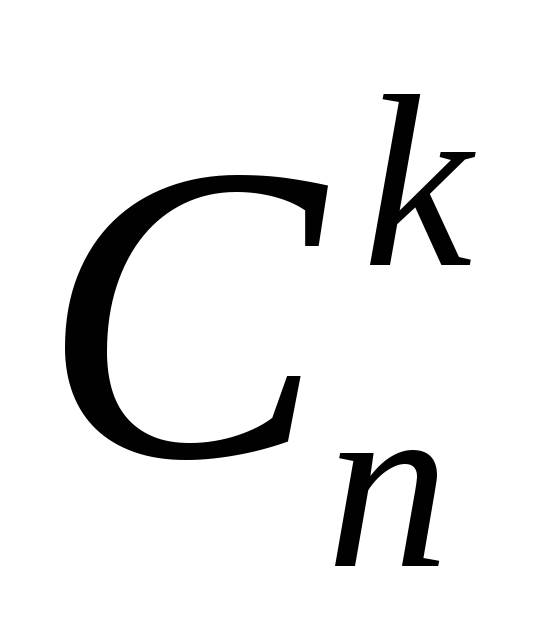 для числа сочетаний читается как “Cиз
для числа сочетаний читается как “Cиз 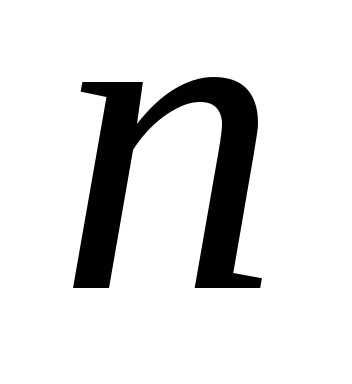 по
по  элементов”.
элементов”.
Пример 3: Если в предыдущем примере комбинации, отличающиеся лишь порядком следования элементов, считать неразличимыми, то остается лишь три варианта выбора
+ , + и + .
Тот же результат можно получить по формуле ( 1 .0) как
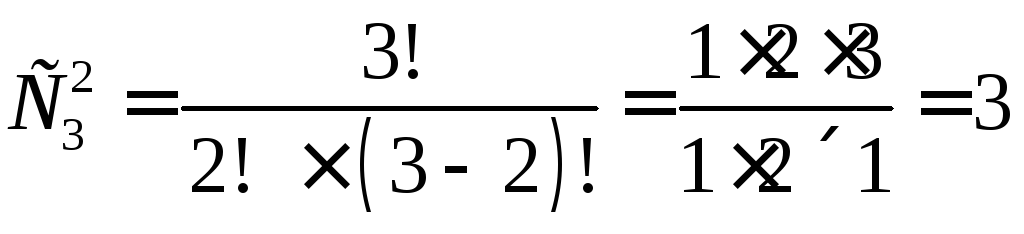
Пример
4: Определить
число способов, которыми можно разложить
в 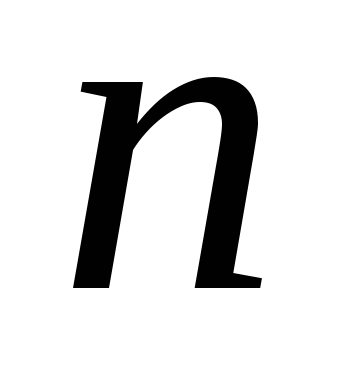 различных ящиков
различных ящиков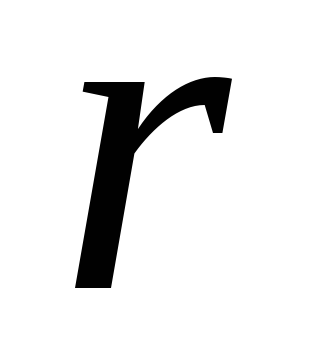 белых и
белых и чёрных шариков, если в каждом ящике
может находиться любое количество
шариков (некоторые
ящики могут оставаться пустыми)?
чёрных шариков, если в каждом ящике
может находиться любое количество
шариков (некоторые
ящики могут оставаться пустыми)?
Решение:Сперва подсчитаем отдельно количество
способов
распределения по ящикам белых шариков.
Все возможные варианты
распределения белых шариков по ящикам
можно представить как некоторую
последовательность чередования
разложенных шариков («0») и границ между
ящиками («|»). Например, применительно
к  =
4,
=
4,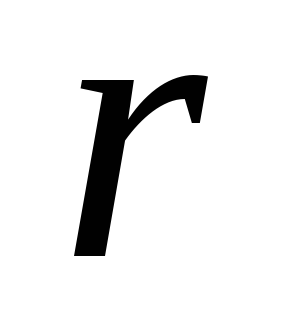 =
10 размещению шариков по схеме
«3+2+0+5» (см. Рис. 2а) соответствует
чередование элементов « 000 | 00 | | 00000
», а схеме размещения «1+3+3+3» (см. Рис. 2б)
соответствует чередование элементов
« 0 | 000 | 000 | 000 ».
=
10 размещению шариков по схеме
«3+2+0+5» (см. Рис. 2а) соответствует
чередование элементов « 000 | 00 | | 00000
», а схеме размещения «1+3+3+3» (см. Рис. 2б)
соответствует чередование элементов
« 0 | 000 | 000 | 000 ».
а) 
б) 
Рис. 2. Возможные варианты размещения шариков
Итак,
число различных вариантов размещения
белых шаров по ящикам совпадает
с числом способов упорядочивания
последовательностей
из  шариков и
шариков и  границ. Количество способов, которыми
в совокупности из
границ. Количество способов, которыми
в совокупности из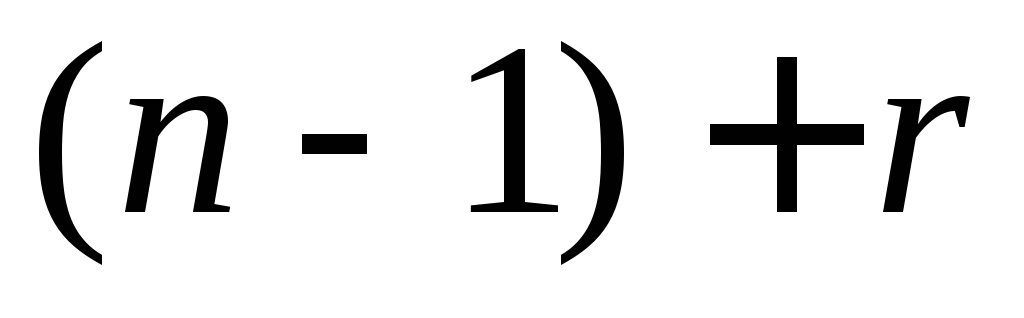 элементов можно выбрать
элементов можно выбрать 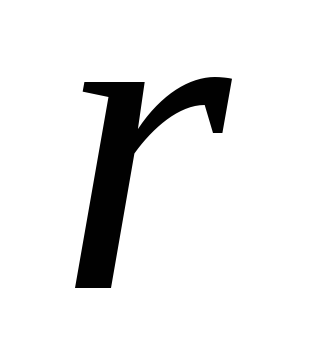 мест для размещения шариков составляет
мест для размещения шариков составляет 
Аналогично
для расчета числа различных распределений
черных шариков получаем расчетное
выражение 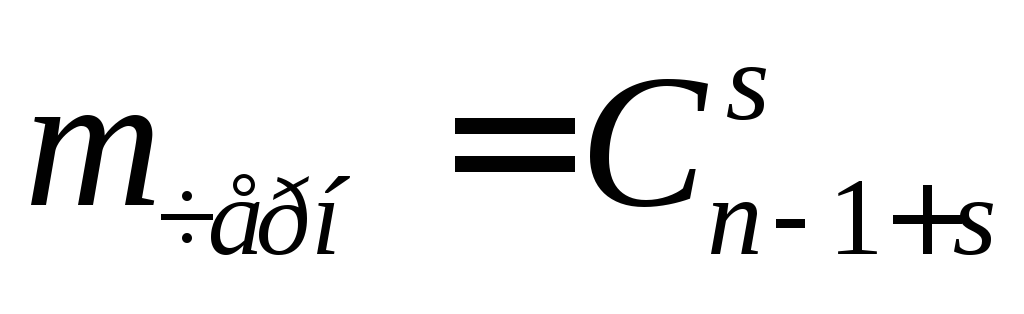 и, используя правило произведения(см.
с. 16), для общего
числа способов распределения черных и
белых шариков имеем
и, используя правило произведения(см.
с. 16), для общего
числа способов распределения черных и
белых шариков имеем 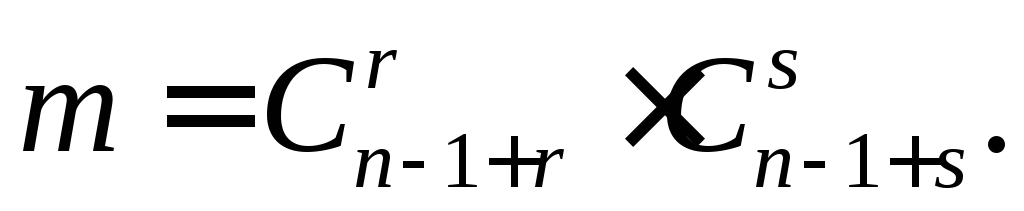
.
Перестановки
с повторениями.Пусть теперь
набориз 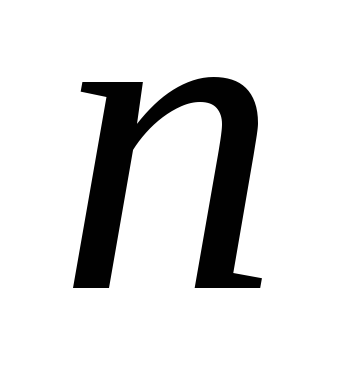 элементов множества включает
элементов множества включает элемент первого типа,
элемент первого типа, элементов второго типа и т.д., завершая
элементов второго типа и т.д., завершая элементами
элементами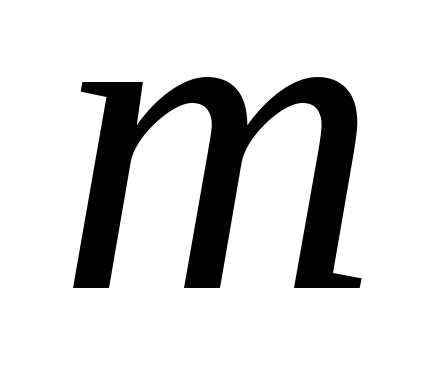 -го
типа. Если из этих элементов формировать
комбинации, включающие все
-го
типа. Если из этих элементов формировать
комбинации, включающие все  элементов, и считать различимыми
лишь комбинации элементов, отличающиеся
взаимным расположением элементов разных
типов, то такие комбинации называютсяперестановками с повторениями.
Число различимых перестановок определяется
при этом правилом
элементов, и считать различимыми
лишь комбинации элементов, отличающиеся
взаимным расположением элементов разных
типов, то такие комбинации называютсяперестановками с повторениями.
Число различимых перестановок определяется
при этом правилом
| (1.0) |
Пример
5: В название
города “БОБРОВ”, входят 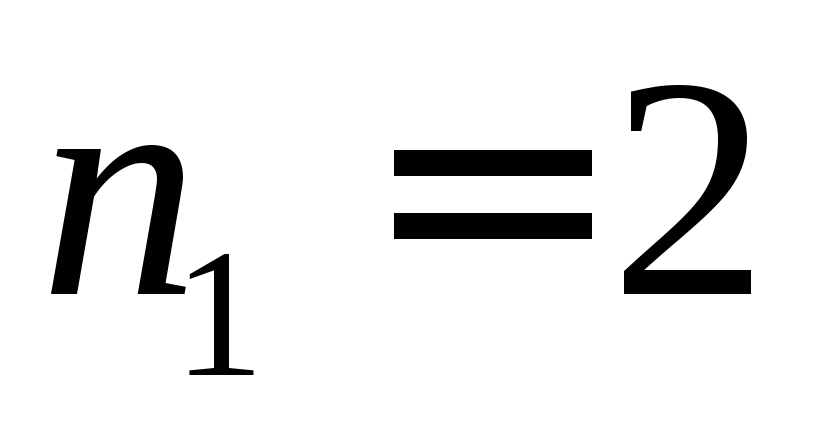 буквы ‘Б’,
буквы ‘Б’, буквы ‘О’ и по одной букве ‘Р’ и ‘В’.
Таким образом, переставляя буквы названия
в разном порядке можно сформировать
буквы ‘О’ и по одной букве ‘Р’ и ‘В’.
Таким образом, переставляя буквы названия
в разном порядке можно сформировать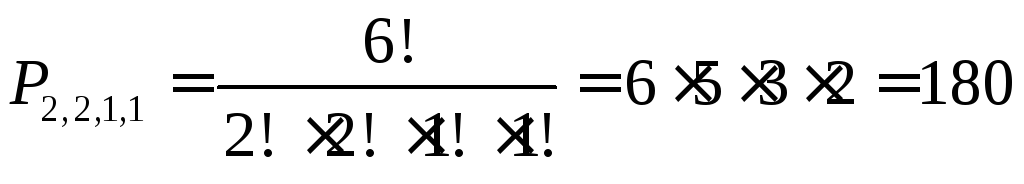 различимых буквенных комбинаций.
различимых буквенных комбинаций.
Рассмотрим два примера применения алгебраического метода расчета вероятности.
Пример 6: Подбрасывается 12 игральных кубиков. Какова вероятность того, что каждая грань выпадет ровно 2 раза?
Решение:При подсчете общего числа исходов, соответствующих
проводимому эксперименту, учтем, что
на каждом кубике независимо
от прочих может оказаться вверху любая
грань из 6 имеющихся, поэтому 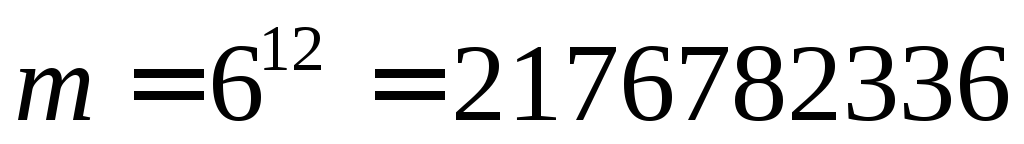 .
.
Для реализации
же события A на каких-то двух кубиках
должна выпасть «1», на двух других – «2»
и т.д. Выбрать из 12 кубиков ту пару,
которая будет давать «1» можно  способами. Среди оставшихся 10 кубиков
выбрать те, на которых будет «2» можно
способами. Среди оставшихся 10 кубиков
выбрать те, на которых будет «2» можно способами. Выбор пары кубиков с «3»
осуществляется
способами. Выбор пары кубиков с «3»
осуществляется способами и т.д. Согласно правилу
произведения (см. с. 16), общее число
вариантов падения кубиков, соответствующих
событиюA, равно
способами и т.д. Согласно правилу
произведения (см. с. 16), общее число
вариантов падения кубиков, соответствующих
событиюA, равно
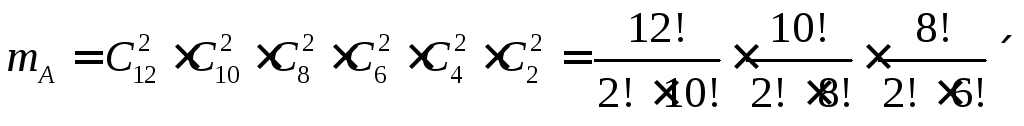
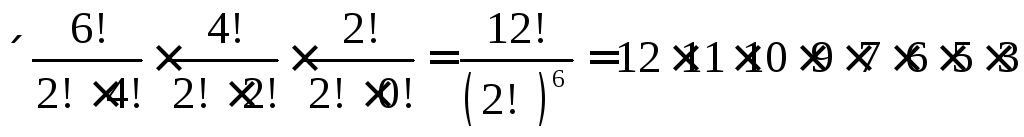 .
.
В итоге для вероятности появления каждой грани ровно 2 раза получаем
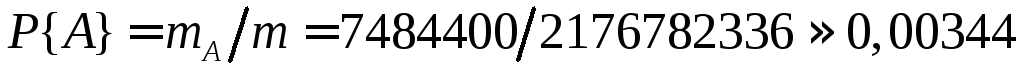 .
.
Примечание 1. В этом расчете используются именно числа сочетаний, поскольку уникальность варианта выбора определяется номерами выбранных для появления конкретной грани кубиков, а внутри каждой пары кубики неразличимы и пытаться учитывать порядок их взаимного расположения, применяя в расчетах число размещений, — бессмысленно.
Примечание 2.
Соответствующие анализируемому событию
варианты выпадения кубиков каждый раз
содержат 2 кубика с верхней гранью «1», ещё 2 кубика с верхней
гранью «2» и т.п., а различаются
лишь порядком взаимного расположения
этих кубиков. Таким
образом, при подсчете числа благоприятных
для наступления события A вариантов можно было бы (вместо учета
набора сочетаний) определять число
различимых перестановок с повторениями,
что также дало бы 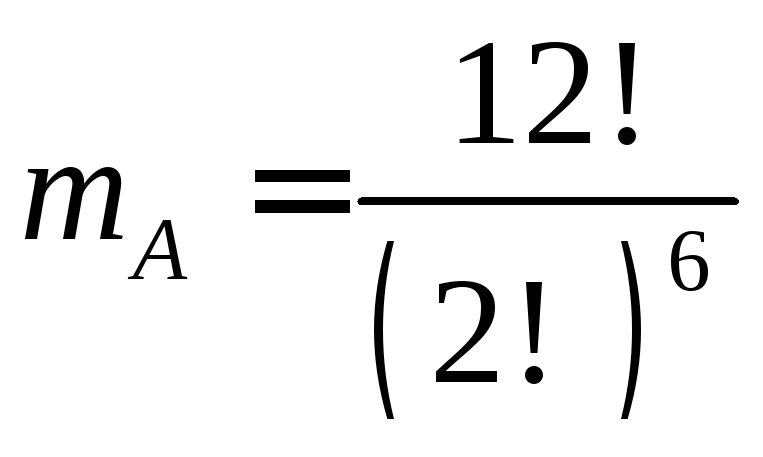 .
.
Пример 7: В лифт 9-этажного дома вошли 4 человека. Если считать, что каждый из вошедших равновероятно и независимо от других может выйти из лифта на любом этаже, то какова вероятность того, что по меньшей мере трое из них выйдут на каком-то этаже вместе?
Решение:В этой задаче, как и в парадоксе де Мере (см. с. 17) для обеспечения равной вероятности рассматриваемых исходов необходимо учитывать не только то, на каких этажах выходят пассажиры, но и то, кто – где вышел.
Каждый из вошедших в лифт может равновероятно выйти на любом из 8 этажей (со второго по девятый), т.е. каждому варианту выхода первого из пассажиров, соответствует 8 подвариантов выхода второго из пассажиров. При любом исходе, соответствующей этой паре, существует ещё 8 подвариантов, определяемых действиями третьего пассажира и т.д. Таким образом, общее число исходов, отличающихся друг от друга тем, кто именно на каком этаже вышел из лифта, равно .
При подсчете числа благоприятных вариантов учтём, что формулировка «по меньшей мере трое…» подразумевает, что условиям задачи удовлетворяют как случаи, когда на каком-то из этажей выйдут ровно 3 пассажиров, так и случаи, когда все 4 пассажира выходят из лифта вместе.
Разных вариантов
выхода из лифта всех 4 пассажиров
существует, очевидно, 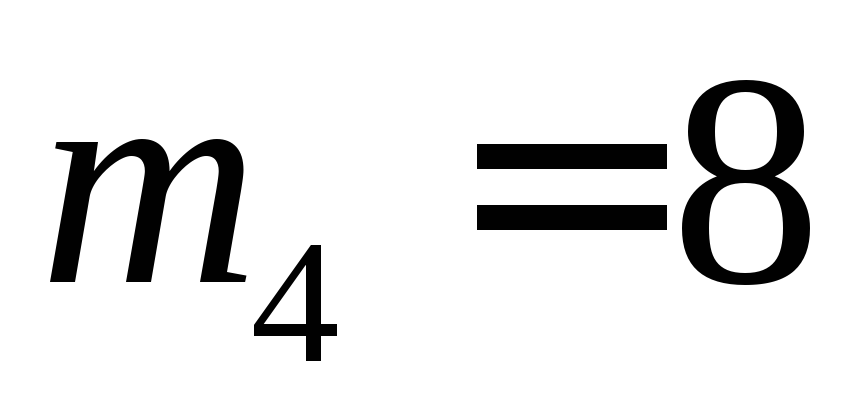 .
Реализации же альтернативного
сценария будут отличаться друг от друга
тем,
.
Реализации же альтернативного
сценария будут отличаться друг от друга
тем,
1) кто из пассажиров войдет в тройку, а кто выйдет отдельно от других;
2) на каком из 8 этажей (со второго по девятый) выйдет трое людей, а на котором – одинокий пассажир.
Так как люди,
входящие в тройку, всё равно выходят
вместе, то контролировать их «взаимное
расположение» не имеет смысла, поэтому
при расчете числа вариантов выбора
тройки следует использовать сочетания,
что дает 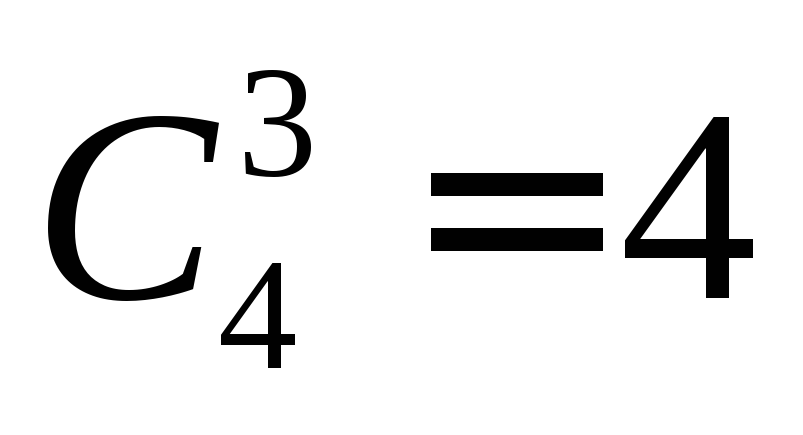 .
Впрочем, так как выбрать одиночного
пассажира из четырех можно, очевидно,
лишь 4 способами, то в этой части расчета
можно было бы обойтись и без комбинаторных
формул.
.
Впрочем, так как выбрать одиночного
пассажира из четырех можно, очевидно,
лишь 4 способами, то в этой части расчета
можно было бы обойтись и без комбинаторных
формул.
Что
же касается той пары этажей, на которых
выйдет тройка и одиночный пассажир, то
выбирать пару этажей из 8 возможных
следует, контролируя порядок выбора,
т.е. различая случаи, скажем, когда тройка
выходит на втором, а один – на третьем,
и когда один пассажир выходит на втором
этаже, а остальные
– на третьем. Таким образом, различных
пар этажей,
используемых для выхода, существует 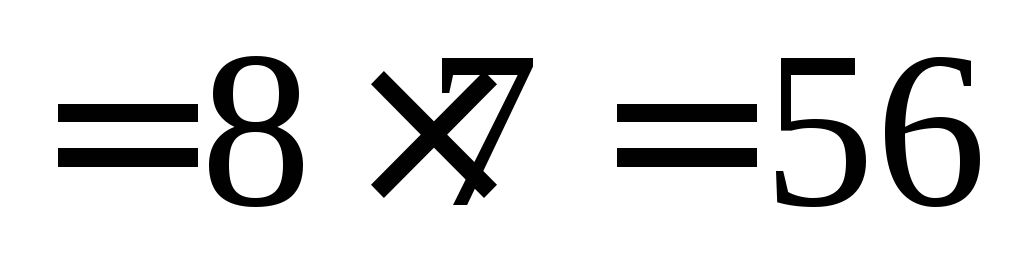 ,
а общее число вариантов выхода на одном
этаже ровно 3 пассажиров составляет
,
а общее число вариантов выхода на одном
этаже ровно 3 пассажиров составляет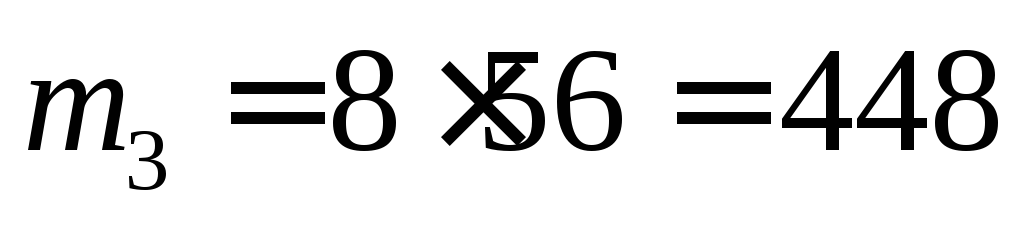 .
.
Учитывая, что
способы совместного выхода ровно трех и всех четырех пассажиров не
совмещаются, а дополняют друг друга, по
правилу сложения получаем, что общее
число благоприятных исходов
составляет  .
В итоге, вероятность того, что по
меньшей мере трое из пассажиров выйдут
из лифта вместе, составит
.
В итоге, вероятность того, что по
меньшей мере трое из пассажиров выйдут
из лифта вместе, составит
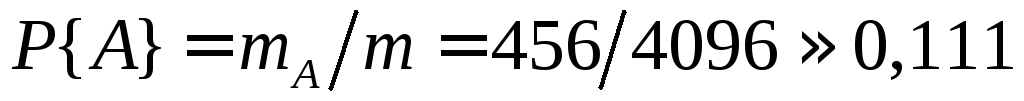 .
.
Элементы комбинаторики
Правило сложения
Правило сложения используется в том случае, если у нас есть два или более множеств, которые попарно не пересекаются, то есть не имеют общих элементов. И нам нужно найти сколько элементов содержится в объединении этих множеств. В этом случае мы складываем число элементов в каждом множестве. Простейший пример: если у нас есть две корзинки с фруктами: в одной 5 яблок, а в другой 7 груш. Если мы эти фрукты пересыпаем в одну корзинку (объединяем множества), тогда в новой корзинке окажется 5+7=12 фруктов.
Правило умножения
Правило умножения используется в том случае, если у нас есть два множества, и мы составляем всевозможные пары из элементов этих множеств. Например, если взять множество, состоящее из 5-ти яблок и множество, состоящее из 7-ми груш и составить всевозможные пары из этих фруктов, то мы получим  всевозможных пар.
всевозможных пар.
Действительно. Возьмем первое яблоко. Мы можем положить к нему любую из семи груш, то есть получаем 7 пар. Возьмем второе яблоко, и к нему мы также можем положить любую из 7-ми груш, получаем ещё 7 пар. И так далее. Всего получается  пар.
пар.
Правило умножения легко понять, если попытаться ответить, например, на такой вопрос: «сколько существует двузначных чисел?«
Пусть двузначное чиcло имеет вид  , где
, где  — число десятков,
— число десятков,  — число единиц. При этом цифра
— число единиц. При этом цифра  может принимать значения от 1 до 9 ( цифра 0 не может стоять на первом месте, так как в этом случаем мы получим однозначное число), цифра
может принимать значения от 1 до 9 ( цифра 0 не может стоять на первом месте, так как в этом случаем мы получим однозначное число), цифра  может принимать значения от 0 до 9.
может принимать значения от 0 до 9.
Пусть  , и у нас есть 10 вариантов цифр, которые могут стоять на втором месте. Тогда мы имеем 10 двузначных чисел, содержащих 1 десяток.
, и у нас есть 10 вариантов цифр, которые могут стоять на втором месте. Тогда мы имеем 10 двузначных чисел, содержащих 1 десяток.
Затем мы берем  и так же получаем 10 двузначных чисел, у которых теперь уже 2 десятка.
и так же получаем 10 двузначных чисел, у которых теперь уже 2 десятка.
И так далее.
Так как цифра  может принимать 9 различных значений, то получаем
может принимать 9 различных значений, то получаем  двузначных чисел.
двузначных чисел.
Зная, что на первом месте может стоять 9 различных цифр, а на втором — 10, мы получаем  комбинаций этих цифр, то есть все возможные двузначные числа. Здесь важно понимать, что любая цифра, стоящая на первом месте, может сочетаться с любой цифрой, стоящей на втором месте.
комбинаций этих цифр, то есть все возможные двузначные числа. Здесь важно понимать, что любая цифра, стоящая на первом месте, может сочетаться с любой цифрой, стоящей на втором месте.
В общем случае правило умножения звучит так:
Если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Это правило распространяется на любое число независимо выбираемых элементов.
Если мы хотим ответить на вопрос, сколько существует трехзначных чисел, мы заметим, что в трехзначном числе  первая цифра
первая цифра  может принимать 9 значений, вторая
может принимать 9 значений, вторая  — 10, и третья
— 10, и третья  — 10 значений. И мы получаем
— 10 значений. И мы получаем  трехзначных чисел.
трехзначных чисел.
Формула включений-исключений
используется в том случае, если нам нужно найти число элементов в объединении двух множеств, в том случае, если эти множества пересекаются.
Пусть множество А содержит n элементов, множество В содержит m элементов, и пересечение этих множеств  содержит k элементов. То есть k элементов содержатся и в множестве А, и в множестве В. Тогда объединение множеств
содержит k элементов. То есть k элементов содержатся и в множестве А, и в множестве В. Тогда объединение множеств  содержит m+n-k элементов.
содержит m+n-k элементов.
Действительно, при объединении двух множеств мы k элементов посчитали два раза, и теперь один раз мы должны их вычесть.
Число элементов в множестве обозначается общепринятым значком #. Тогда формула для подсчета числа элементов в объединении трех множеств имеет вид:
# #
# #
# #
# #
# #
# #
# #
#
Рассмотрим примеры задач.
1. Сколько трехзначных чисел содержит хотя бы одну цифру 3?
Решение.
показать
2. Сколько четырехзначных чисел, кратных 5.
Решение.
показать
Перестановки
Воспользуемся правилом умножения чтобы ответить на вопрос, «сколькими способами можно построить 7 человек в шеренгу?».
Человека, стоящего первым в шеренге можно выбрать семью способами, второго можно выбрать из оставшихся шести человек, то есть шестью способами. Третьего, соответственно, пятью. И так далее. Последнего можно выбрать единственным способом. Всего получаем  способов построить 7 человек в шеренгу.
способов построить 7 человек в шеренгу.
В общем случае, если мы имеем  объектов, которые хотим расположить в определенном порядке (пронумеровать их), то мы получим
объектов, которые хотим расположить в определенном порядке (пронумеровать их), то мы получим

способов расположения этих объектов.
Факториалом натурального числа  называется произведение всех натуральных чисел от 1 до
называется произведение всех натуральных чисел от 1 до  :
: 
По определению 0!=1; 1!=1.
Перестановкой из  предметов называется любой способ нумерации этих предметов (способ расположения их в ряд).
предметов называется любой способ нумерации этих предметов (способ расположения их в ряд).
Число перестановок  предметов равно
предметов равно  .
.
3. Имеется 10 компьютерных дисков и 10 коробок от них. Найдите вероятность того, что случайным образом уложив диски в коробки, мы обнаружим, что
1. Каждый диск лежит в своей коробке.
2. Хотя бы один диск лежит не в своей коробке.
3. Два определенных диска перепутаны местами, а остальные в своих коробках.
4. Ровно один лежит не в своей коробке, а остальные — в своих коробках.
Решение.
показать
1. Пронумеруем диски и коробки. Расположим коробки в определенной последовательности. Нам нужно, чтобы при случайном расположении дисков в ряд, их номера тоже оказались расположены в той же последовательности.
Расположить 10 чисел в определенной последовательности можно единственным способом, то есть мы имеем 1 благоприятный исход.
Расположить 10 чисел в произвольном порядке можно 10! способами.
Следовательно, вероятность того, что каждый диск окажется в своей коробке равна

2. Событие «хотя бы один диск лежит не в свой коробке» противоположно событию «каждый диск лежит в своей коробке«, и его вероятность равна

3. Событие «два определенных диска перепутаны местами, а остальные в своих коробках», также как событие «каждый диск лежит в своей коробке«, имеет единственный благоприятный исход, поэтому вероятность этого события равна

4. Событие «ровно один лежит не в своей коробке, а остальные — в своих коробках» невозможно, так как если один диск лежит не своей коробке, то обязательно должен найтись ещё один, который так же лежит не в своей коробке. Поэтому вероятность этого события равна нулю.
4. Слово «МАТЕМАТИКА» написали на полоске картона и разрезали полоску на буквы. Найдите вероятность того, что составив все эти буквы случайным образом в ряд, мы снова получим слово «МАТЕМАТИКА».
Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?
Решение.
показать
1 способ.
Вероятность того, что на первом месте будет стоять буква М равна 2/10 — у нас две буквы М, и всего 10 букв.
Вероятность того, что на втором месте будет стоять буква А равна 3/9 — у нас осталось 9 букв, из которых 3 буквы А.
Вероятность того, что на втором месте будет стоять буква Т равна 2/8 — у нас осталось 8 букв, из которых 2 буквы Т.
И так далее. В итоге получаем:

2 способ.
Пронумеруем все буквы в слове «МАТЕМАТИКА». Найдем, сколькими способами мы можем их расположить в определенном порядке. В слове 10 букв, и мы можем их расположить 10!=3628800 различными способами.
Поскольку в слове есть одинаковые буквы, то при перестановке этих букв мы получим то же слово:
в слове «МАТЕМАТИКА» 2 буквы «М»; 3 буквы «А»; 2 буквы «Т», следовательно по правилу произведения это дает нам  способов перестановки этих букв с сохранением слова «МАТЕМАТИКА».
способов перестановки этих букв с сохранением слова «МАТЕМАТИКА».
Таким образом, вероятность снова получить слово «МАТЕМАТИКА» равна:

Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?
Из 10 букв слова «МАТЕМАТИКА» можно составить 10! буквосочетаний. Но некоторые из них будут одинаковыми, так как при перестановке одинаковых букв, мы будем получать те же буквосочетания. То есть в итоге мы получим

буквосочетаний.
Размещения
В задачах по теории вероятностей часто возникает необходимость определить, сколькими способами можно выбрать определенное число предметов и расположить их в определенном порядке.
5. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
Воспользуемся правилом умножения.
В первую страну мы выбираем из 9 специалистов, то есть у нас 9 вариантов выбора. После того, как специалист для поездки в первую страну выбран, у нас осталось 8 специалистов, и для поездки во вторую страну у нас 8 вариантов выбора. И так далее… в четвертую страну мы можем выбрать кандидата из 6 специалистов.
Таким образом, мы получаем  вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны.
вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны.
Обобщим эту задачу на случай выбора k кандидатур из n специалистов для поездки в k различных стран.
Рассуждая аналогичным образом, мы получаем

вариантов.
Если умножить и разделить это выражение на  , то получим следующую формулу:
, то получим следующую формулу:

В этой задаче из множества, состоящего из  элементов мы выбрали упорядоченные подмножества (для нас был важен порядок расположения элементов в подмножестве), состоящие из
элементов мы выбрали упорядоченные подмножества (для нас был важен порядок расположения элементов в подмножестве), состоящие из  элементов. Задача сводилась к нахождению числа таких подмножеств.
элементов. Задача сводилась к нахождению числа таких подмножеств.
Такие упорядоченные подмножества называются размещениями из n элементов по k.
Пусть у нас есть множество  , состоящее из
, состоящее из  элементов. Размещением (из n по k) называется упорядоченное подмножество из
элементов. Размещением (из n по k) называется упорядоченное подмножество из  различных элементов из некоторого множества
различных элементов из некоторого множества  , состоящего из различных
, состоящего из различных  элементов.
элементов.
Число размещений из  элементов по
элементов по  обозначается
обозначается  и находится по формуле:
и находится по формуле:

Размещения с повторениями
6. Игральную кость бросают трижды. Сколько различных комбинаций выпавших очков при этом получится?
При бросании кости первый раз мы получим 6 различных вариантов: 1 очко, 2, 3… или 6. Аналогично при бросании кости во второй и в третий раз мы получим также по 6 различных вариантов. По правилу умножения получим число различных комбинаций трех чисел, принимающих значения от 1 до 6: 
В общем случае:
Пусть у нас есть множество  , состоящее из
, состоящее из  элементов.
элементов.
Любой упорядоченный набор  элементов множества, состоящего из
элементов множества, состоящего из  элементов называется размещением с повторением из
элементов называется размещением с повторением из  элементов по
элементов по  . Число различных размещений с повторениями равно
. Число различных размещений с повторениями равно

.
Действительно. Представим ящик с  пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так
пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так  раз. Сколько комбинаций из
раз. Сколько комбинаций из  номеров мы можем получить?
номеров мы можем получить?
Поскольку шары каждый раз возвращаются, каждый раз, вынимая шар из коробки, в которой  шаров, мы можем получить
шаров, мы можем получить  различных чисел. По правилу умножения имеем
различных чисел. По правилу умножения имеем

Сочетания
Рассмотрим задачу, аналогичную задаче 5, но с существенным отличием.
7. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов?
В этой задаче нам нужно выбрать 4 кандидатуры, но при этом не важно, в каком порядке мы их выбираем, нас интересует только состав выбранных элементов, но не порядок их расположения.
Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:

4 различных элемента можно расположить в определенном порядке 4! различными способами. Поскольку нас не интересует порядок расположения элементов, число способов, которыми мы можем выбрать 4 элемента, не располагая их в определенном порядке, уменьшается в 4! раза по сравнению с предыдущей задачей (так как для данной задачи различное расположение данных элементов считается одним способом), и мы получаем

способов.
В этой задаче появляется понятие сочетания.
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества  (множества, состоящего из n элементов).
(множества, состоящего из n элементов).
Внимание! Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).
Число сочетаний из n элементов по k элементов обозначается

и находится по формуле:

Число сочетаний из n по k показывает, сколькими способами мы можем выбрать k элементов из n элементов, или сколькими способами мы можем расположить k объектов по n местам.
Легко заметить, что


8. В коробке лежат 8 красных карандашей и 4 синих. Из коробки наугад вынимают 4 карандаша. Какова вероятность того, что среди них окажется 2 красных и 2 синих?
Решение.
показать
Всего в коробке 12 карандашей. Найдем, сколькими способами способами можно извлечь из коробки 4 карандаша. Так как нас не интересует порядок, в котором карандаши извлекаются из коробки, а только состав карандашей, это число равно числу сочетаний из 12 по 4:

Из 8 красных карандашей можно извлечь два карандаша  способами.
способами.
Из 4 синих карандашей можно извлечь два карандаша  способами.
способами.
По правилу произведения получаем, что извлечь 2 синих и 2 красных карандаша можно  способами.
способами.
Таким образом, искомая вероятность равна:

Метод шаров и перегородок
9. Сколькими способами можно разложить 10 шаров в 4 коробки? Предполагается, что некоторые коробки могут оказаться пустыми.
Решение.
Рассмотрим 10 шаров:

Будем «раскладывать шары по коробкам», ставя перегородки.
Например, так:

В этом примере в первой коробке 3 шара, во второй — 2, в третьей — 4, и в четвертой — 2. Переставляя шары и перегородки, мы получаем различные комбинации шаров в коробках. Например, переставив последний шар в первой коробке и первую внутреннюю перегородку, мы получим такую комбинацию:

Таким образом, мы получаем различное число шаров в коробках, комбинируя позиции 10-ти шаров и 3-х внутренних перегородок. Чтобы определить, сколько различных комбинаций мы можем получить, нам нужно найти число сочетаний из 13 по 3. (Или, что то же самое, что число сочетаний из 13 по 10.) Столько способов выбрать 3 места для перегородок из 13 возможных позиций. Или, что то же самое, 10 мест для шаров.

10. Сколько решений имеет уравнение  в целых неотрицательных числах?
в целых неотрицательных числах?
Решение.
Так как переменные  могут принимать только целые неотрицательные значения, следовательно, у нас есть 10 переменных, и они могут принимать значения 0, 1, 2, 3 и 4. Представим, что у нас есть 10 коробок (это переменные), и мы должны разложить по этим коробкам 4 шара. Сколько шаров попадет в коробку, таково значение соответствующей переменной. Если у нас 10 коробок, следовательно, 10-1=9 внутренних перегородки. И 4 шара. Всего 13 мест. Нам надо расположить на этих 13 местах 4 шара. Число таких возможностей:
могут принимать только целые неотрицательные значения, следовательно, у нас есть 10 переменных, и они могут принимать значения 0, 1, 2, 3 и 4. Представим, что у нас есть 10 коробок (это переменные), и мы должны разложить по этим коробкам 4 шара. Сколько шаров попадет в коробку, таково значение соответствующей переменной. Если у нас 10 коробок, следовательно, 10-1=9 внутренних перегородки. И 4 шара. Всего 13 мест. Нам надо расположить на этих 13 местах 4 шара. Число таких возможностей:

В общем случае, если нам нужно разложить  шаров в
шаров в  коробок, мы получаем комбинации из
коробок, мы получаем комбинации из  шаров и
шаров и  внутренней перегородки. И число таких комбинаций равно числу сочетаний из
внутренней перегородки. И число таких комбинаций равно числу сочетаний из  по
по  .
.

В этой задаче мы имели дело с сочетаниями с повторениями.
Сочетания с повторениями
Сочетаниями из  элементов по
элементов по  элементов с повторениями называются группы, содержащие
элементов с повторениями называются группы, содержащие  элементов, причем каждый элемент принадлежит к одному из
элементов, причем каждый элемент принадлежит к одному из  типов.
типов.
Что такое сочетания из  элементов по
элементов по  элементов с повторениями можно понять с помощью такого мысленного эксперимента. Представим ящик с
элементов с повторениями можно понять с помощью такого мысленного эксперимента. Представим ящик с  пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так
пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так  раз. В отличие от размещений с повторениями нас не интересует порядок записанных чисел, а только их состав. Например, группы чисел {1,1,2,1,3,1,2} и {1,1,1,1,2,2,3} считаются одинаковыми. Сколько таких групп из
раз. В отличие от размещений с повторениями нас не интересует порядок записанных чисел, а только их состав. Например, группы чисел {1,1,2,1,3,1,2} и {1,1,1,1,2,2,3} считаются одинаковыми. Сколько таких групп из  номеров мы можем получить?
номеров мы можем получить?
В конечном итоге нас интересует сколько элементов каждого типа (всего n типов элементов) содержится в каждой группе (из k элементов), и сколько таких различных вариантов может быть. То есть мы находим, сколько в целых неотрицательных решений имеет уравнение уравнение  — задача аналогична задаче по раскладыванию n шаров в k коробок.
— задача аналогична задаче по раскладыванию n шаров в k коробок.
Число сочетаний с повторениями находится по такой формуле:

Таким образом, число сочетаний с повторениями — это количество способов представить число k в виде суммы n слагаемых.
И.В. Фельдман, репетитор по математике.