Линейные уравнения с модулем
Просмотр содержимого документа
«Линейные уравнения с модулем»
Уравнения с модулем
Определение модуля числа: 
Модуль числа есть всегда неотрицательное число. Модуль положительного числа есть само число, а отрицательного – противоположное. Модуль нуля – ноль.
Рассмотрим простейшие уравнения с модулем
1.Решить уравнение |x|= 3. Из определения модуля корнем уравнения может быть либо само число 3 или противоположное ему -3. Вот и все.
Ответ: x1= 3, x2= 3.
1.Решить уравнение |x|= -3. Уравнение решения не имеет, модуль любого числа неотрицателен, а правая часть уравнения отрицательна.
3. Решить уравнение |x – 5|= 3. Снова решаем на основании определения, может быть снова два варианта 1) x – 5 = 3, 2) x – 5 = — 3. Получаем x1 = 8, x2 = 2.
Ответ: x1= 8, x2= 2. Числа 8 и 2 находятся на расстоянии 3 от числа 5 на координатной прямой.
Метод интервалов при решении уравнений с модулем
4. Решить уравнение |x – 5|+|x – 1|= 10.
Рассмотрим промежутки на числовой оси между точками, где модули равны нулю.
Первый промежуток 
. На этом числовом промежутке |x – 5|=-(x – 5) = -x + 5;
|x – 1|= -(x – 1) = — x + 1. Упростим уравнение -x + 5 — x + 1 = 10 -2x + 6 = 10 x = — 2. 
. Значит – 2 корень этого уравнения. Второй промежуток 
по аналогии x – 5 + x – 1 = 10 2x= 16 x = 8. 
Ответ: x1 = -2; x2 = 8.
5. Решить уравнение|x+1| — |x -2| + |x -3| = 6.
Аналогично решаем уравнение методом интервалов, здесь интервалов уже 4.
1) x x – 1 + x — 2 – x + 3 = 6 x = — 6, корень уравнения -6
2) -1 ≤ x x + 1 + x – 2 – x + 3 = 6 x = 4, решения нет — 1 ≤ 4
3) 2 ≤ x x + 1 –x + 2 – x + 3 = 6 x = 0, решения нет 2 ≤ 0
4) x ≥ 3, x + 1 – x + 2 + x – 3 = 6 x = 6, корень уравнения 6 ≥ 3 верное,
Ответ: x1 = — 6, x2 = 6.
При решении методом интервалов важно, чтобы полученное значение на решение было из своего интервала.
6. Решить уравнение |x – 5|=|x – 1|. Из определения модуля следует 
Ответ: x = 3.
Можно решить и другим способом:
Примеры для самостоятельного решения уравнений с модулем.
|x + 1|+ |x+5| = 6;
|x — 2|+|x — 3| = 8;
|x — 4|- |x — 3| = 7;
multiurok.ru
Уравнение с модулем. наглядное пособие по алгебре ( 7 класс)
Уравнение, содержащие переменную под знаком модуля.
Модулем неотрицательного действительного числа a называют само это число:
|а| = а
Модулем отрицательного
действительного числа х называют противоположное число: |
а| = — а
Короче это записывают так: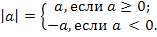
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули:
|-а| = |а|
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:
|0| = 0
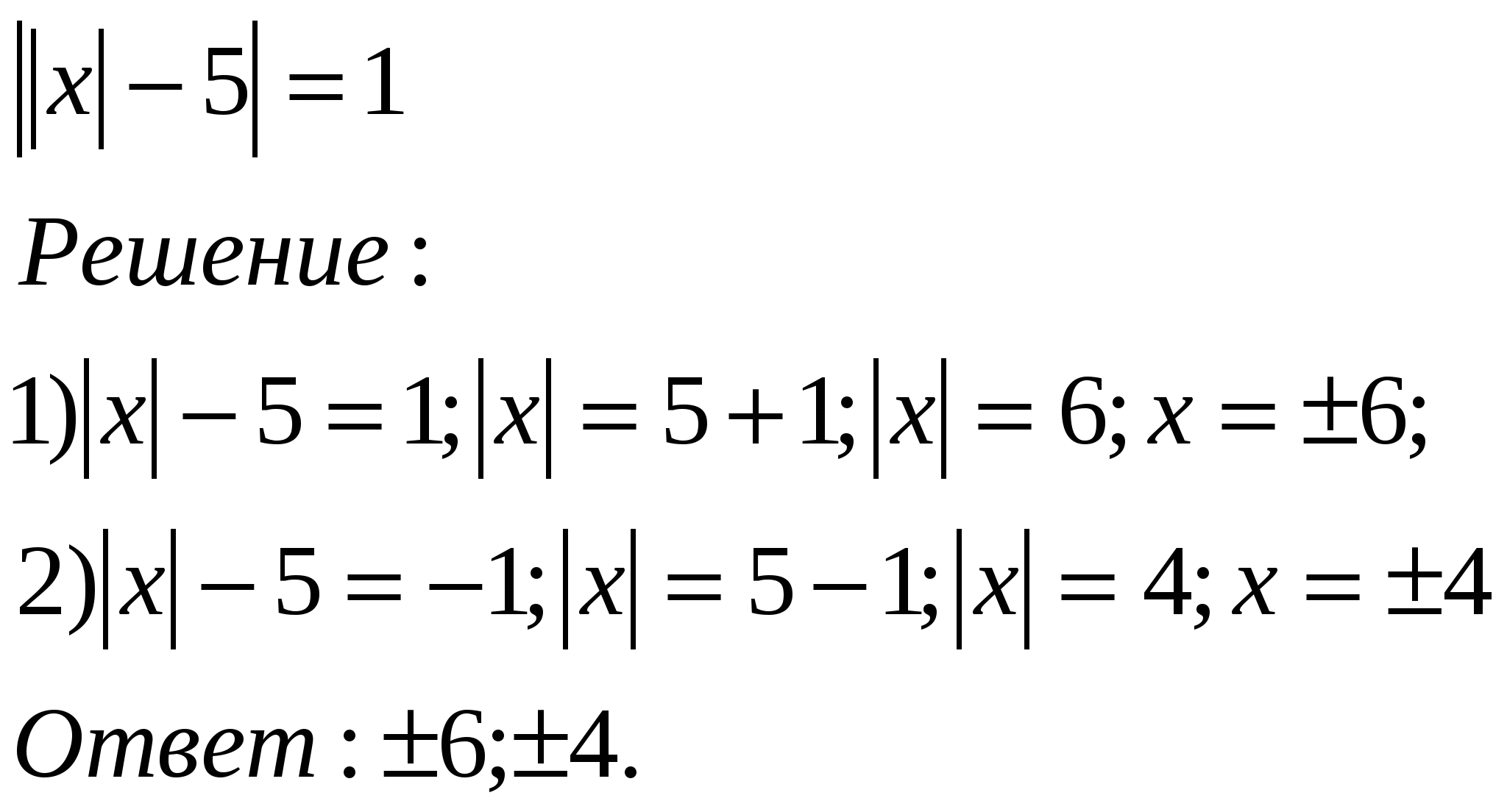
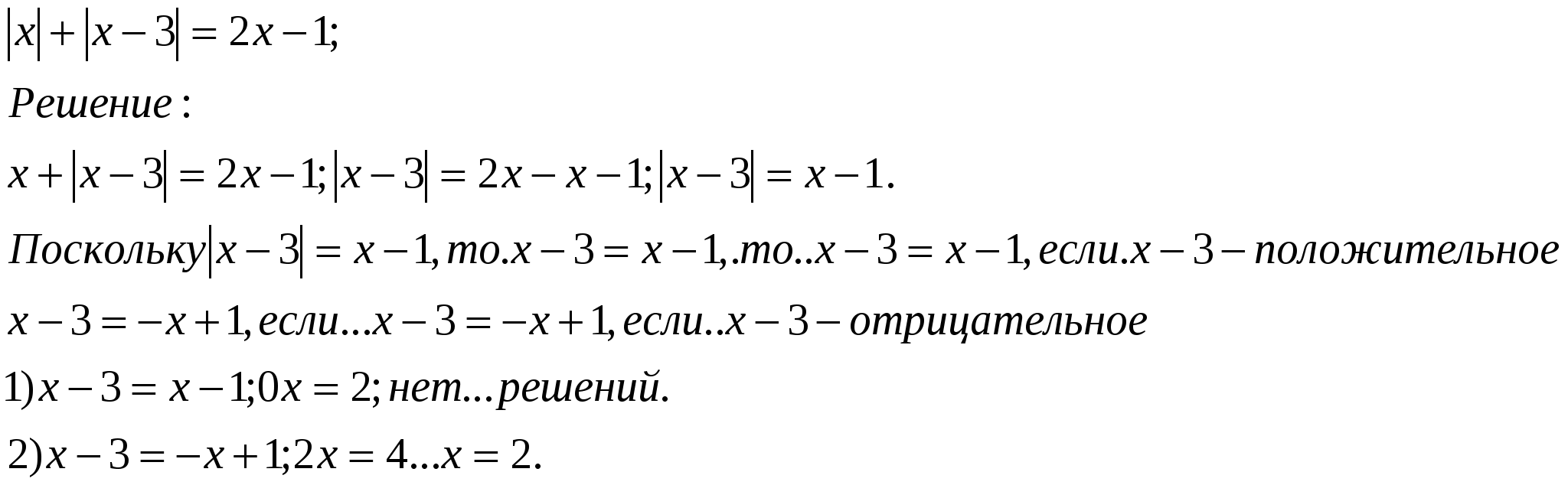
На доске записали решение линейного уравнения, но часть уравнения вытерли. Восстановите их.
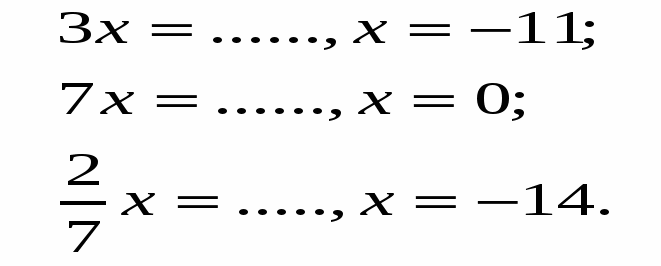
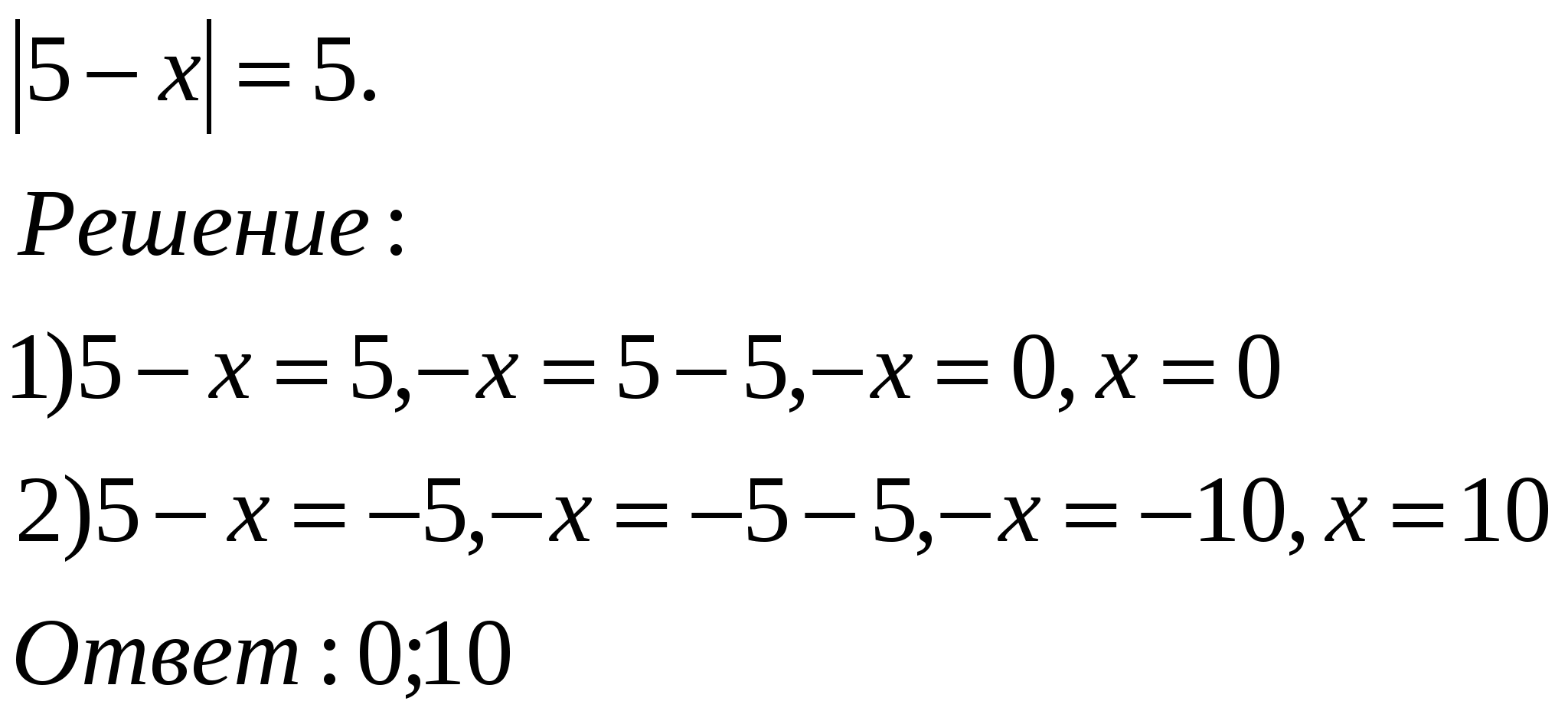
infourok.ru
Решение линейных уравнений с модулем
Уравнение — это равенство, содержащее букву, значение которой надо найти.Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
Рассмотрим уравнение вида |kx + b| = c, где x — неизвестная величина, k ≠ 0.Если c<0, то уравнение не имеет решений, так как модуль числа не может принимать отрицательные значения.
Если c = 0, то уравнение принимает вид kx + b = 0. Оно имеет единственный корень x = −b/k.
Если же c>0, то выражение под знаком модуля может принимать значения c и −c. Значит, возможны два случая:kx + b = c, то есть x = (c−b) / k.
kx + b = −c, то есть x=( −c−b) / k
Рассмотрим теперь уравнение вида |ax+b| = |cx+d|, где a, b, c, d – некоторые числа.
Решите уравнение: |2x−5| = |3x+6|.
РЕШЕНИЕ
Согласно определению модуля, указанное равенство возможно в следующих случаях:
2x−5 = 3x+6, то есть x=−11;
2x−5 = −(3x+6), то есть x=−0,2.
Ответ. {−11;−0,2}.
Алгоритм решения уравнений с модулями:1. Найти в уравнении все выражения, содержащиеся под знаком модуля.
2. Найти, при каких значениях переменной они обращаются в нуль.
3. Разбить найденными значениями числовую прямую на непересекающиеся промежутки.
4. Определить для каждого числового промежутка, чему равно значение каждого модуля: самому выражению, содержащемуся под знаком модуля, или противоположному ему.
5. Для каждого числового промежутка записать и решить исходное уравнение без знаков модуля.
6. Оставить только те решения, которые соответствуют числовому промежутку, и записать их в ответе.
ПРИМЕР 2
Решите уравнение: |x−3| − |2x+4| = 5.
Точки −2 и 3 разбивают ось на три непересекающихся промежутка: (−∞;−2) (−∞;−2), [−2;3) [−2;3), [3;∞)[3;∞). Решим уравнение на каждом из них:
Решение уравнения
−(x−3) + (2x+4) = 5
x+7=5
x =−2
Учет промежутка
x∈∅
Второй Промежуток x∈[−2;3)Решение уравнения
−(x−3) − (2x+4) = 5
−3x−1 = 5
x = −2
Учет промежутка
x = −2
Третий Промежуток x∈[3;∞)
Решение уравнения
(x−3) − (2x+4) = 5
−x−7 = 5
x = −12
Учет промежутка
x∈∅
Ответ: x = −2
ПРИМЕР 3
Решите уравнение |x−1| = 3.Решение задачи
Если |x−1| = 3, то x−1 = ±3. То есть либо x = 3+1 = 4, либо x = −3+1 = −2.
ПРИМЕР 4
Найдите количество целых решений уравнения 5x+|5x| = 0 на отрезке [−2015;2015].Решение задачи
Заметим, то так как модуль — величина неотрицательная, а из уравнения получаем, что 5x ≤ 0 или x ≤ 0. Поэтому |5x| =−5x и уравнение примет вид 5x−5x = 0. Следовательно, x≤0 — это множество решений уравнения. Тогда количество целых решений на отрезке [−2015;2015] равно 2016.
ПРИМЕР 5
Решите уравнение |||x|−2|−2|=2. В ответе укажите произведение всех решений.Решение задачи
Будем последовательно раскрывать каждый из модулей и разбирать каждый случай отдельно.
По условию |||x|−2|−2|=2, поэтому ||x|−2|−2=−2 или ||x|−2|−2=2.
Случай 1:
||x|−2|−2=−2.
Из первого равенства: ||x|−2|=0, тогда |x|−2=0 или |x|=2. Следовательно, x=−2 или x=2.
Случай 2:
||x|−2|−2=2.
Из второго равенства: ||x|−2|=4. Значит, случай разбивается на два: |x|−2=4 или |x|−2=−4.
Случай 2(а):
|x|−2=4.
Из первого равенства: |x|=6. Следовательно, x=−6 или x=6.
Случай 2(б):
|x|−2=−4.
Из второго равенства: |x|=−2. Но модуль есть величина неотрицательная, поэтому в этом случае решений нет.
В итоге мы получили 4 различных решения — −2,2,−6,6. Их произведение равно 144.
spishy-u-antoshki.ru
Решение линейных уравнений с модулем.
Тест, вариант 1
«Решение линейных уравнений с модулем»
Решите уравнения:
|x| = 5
a) x=5; b) x= -5; c) решений нет;
d) х – любое число; е) х=
5|x-2| = 1
a) x=3; b) x=1; c) x=3 и x=1
d) х – любое число; е) решений нет
|x+4| = — 3
a) x= -7; b) x=1; c) x=-7 и x=1
d) х – любое число; е) решений нет
|у| + 4 = 14
a) у=10; b) у = -10; c) у =18 и у =-18
d) у=10 и у =18; е) у=10 и у =-10
7 + |у| = 7
a) у=14; b) у =14 и у =-14
c) решений нет; d) у=0; е) у- любое число
|x-5|·5 = 35
a) x=12; b) x= -2; c) x=7; d) х =12 и x=-2
е) х =12 и x=7
- 15|x| + 3 = 8|x| — 39
a) x=6; b) x= — 6; c) x=6 и x=-6
d) х – любое число; е) решений нет
5|x| -13 = — 2|x| + 1
a) x=7; b) x=2; c) x– любое число
d) х =7 и x=-7; е) x=2 и x=-2
-5,4|x| — 3,6 = — 1,2 — 6|x|
Ответ: ______________
4,5|2x-13| — 35,7 = — 13,2
Ответ: ______________
Ответ: ______________
|7x+3| = 24
Ответ: ______________
Тест, вариант 2
«Решение линейных уравнений с модулем»
Решите уравнения:
|x| = 13
a) x=13; b) x= -13; c) решений нет;
d) х – любое число; е) х=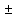
|x-5| = 3
a) x=8; b) x=2; c) x=8 и x=2
d) х – любое число; е) решений нет
|x+4| = — 4
a) x= — 8; b) x=0; c) x=-8 и x=0
d) х – любое число; е) решений нет
|у| + 4 = 14
a) у=10; b) у = -10; c) у =18 и у =-18
d) у=10 и у =18; е) у=10 и у =-10
2 + |у| = 2
a) у= 4; b) у = 4 и у = — 4
c) решений нет; d) у=0; е) у- любое число
|x-6|·3 = 30
a) x=16; b) x= — 4; c) x=10;
d) х =16 и x= — 4; е) х =10 и x = 4
- 15|x | — 3 = 9|x| — 39
a) x=6; b) x= — 6; c) x=6 и x=-6
d) х – любое число; е) решений нет
5|x| -13 = — 5|x| + 7
a) x=2; b) x=20; c) x– любое число
d) х =2 и x= — 2; е) x=0 и x= -2
— 2,2|x| – 10,3 = — 3,7|x|+ 12.2
Ответ: ______________
4,5|2x-13| — 35,7 = — 13,2
Ответ: ______________
Ответ: ______________
|4x+3| = 3
Ответ: ______________
infourok.ru