Определение координат вектора заданного координатами его начальной и конечной точки.
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A .. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
.. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + A
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
ABz = Bz — Az => Az = Bz — ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).Решение:
AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}. Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).Решение:
AB1 = B1 — A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8AB2 = B2 — A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 — A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 — A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Ответ: B(8; -3; 5; 3).
AB2 = B2 — A2 => A2 = B2 — AB2 => A2 = -4 — 1 = -5
AB3 = B3 — A3 => A3 = B3 — AB3 => A3 = 1 — 4 = -3
AB4 = B4 — A4 => A4 = B4 — AB4 => A4 = 8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Формулы векторов
1. Координаты вектора
Если вектор задан координатами своих начала и конца: , то его координаты равны разности соответствующих координат конца и начала:
2. Длина или модуль вектора
Если вектор , то его длина равна корню квадратному из суммы квадратов координат:
3.
 Сумма векторов
Сумма векторовЕсли векторы и заданы своими координатами, то суммой этих векторов есть вектор, координаты которого равны сумме соответствующих координат векторов-слагаемых:
4. Умножение вектора на число
Чтобы найти произведение вектора на некоторое число , нужно каждую координату заданного вектора умножить на это число:
5. Скалярное произведение векторов
Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
6. Векторное произведение векторов
Если векторы и заданы своими координатами в некотором ортонормированном базисе , то их векторное произведение находится по формуле:
7. Смешанное произведение векторов
Если заданы три вектора и , то их смешанное произведение равно определителю, по строкам которого записаны координаты этих векторов:
Замечание. Обычно такой определитель вычисляется методом треугольников.
Обычно такой определитель вычисляется методом треугольников.
8. Угол между векторами
Косинус угла между двумя векторами и , заданными своими координатами, равен частному скалярного произведения этих векторов и произведению их модулей:
9. Проекция вектора на вектор
Проекция вектора на направление вектора равна отношение скалярного произведения этих векторов к модулю вектора :
| Понравился сайт? Расскажи друзьям! | |||
Скалярное произведение векторов. Формулы и определение
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Значок угла ∠ можно опустить и писать просто: (→a;→b).
Пусть даны два вектора →a, →b.
Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).
Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:
1. Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.
Также векторы могут образовывать тупой угол. Это выглядит так:
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
- Алгебраическая интерпретация.
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
- Если угол между векторами прямой, то скалярное произведение равно 0 так как , то есть cosα = 0.
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
- Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
- Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
Так как:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
откуда
- Вспомнив формулу вычисления длины вектора по координатам, получаем
- Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.

- Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В плоской задаче скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти по формуле:
a * b = ax * bx + ay * by
Формула скалярного произведения векторов для пространственных задач
В пространственной задаче скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти по формуле:
a * b = ax * bx + ay * by + az * bz
Формула скалярного произведения n-мерных векторов
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + . .. + an * bn
.. + an * bn
Свойства скалярного произведения
Свойства скалярного произведения векторов:
- Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.
→а * →а > 0
→0 * →0 = 0
- Скалярное произведение вектора самого на себя равно квадрату его модуля:
→a * →a = →∣∣a∣∣2
- Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
→a * →b = →b * →a
- Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
(→a + →b) * →c = →a * →c + →b * →c
- Сочетательный закон для скалярного произведения:
(k * →a) * →b = k * (→a * →b)
- Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
a ≠ 0, b ≠ 0, a * b = 0 <=> a ┴ b
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)
По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,
и,
откуда следует:
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.
Ответ: (→a,→b) = 21/2 = 10,5.
Пример 2.
Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.
Как решаем:
Используем формулу →a * →b = →|a| * →|b| * cosα.
В данном случае:
→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3
Ответ: →a * →b = 5√3.
Пример 3.
Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Как решаем:
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ: (→a,→b) = 411.
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
Как решаем:
- Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
- Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
- Найдем координаты векторов →AB1 и →BC1:
- Найдем длины векторов →AB1 и →BC1:
- Найдем скалярное произведение векторов →AB1 и →BC1:
- Найдем косинус угла между прямыми AB1 и BC1:
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Определение координат вектора заданного координатами его начальной и конечной точки.
Навигация по странице:
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; . .. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
.. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).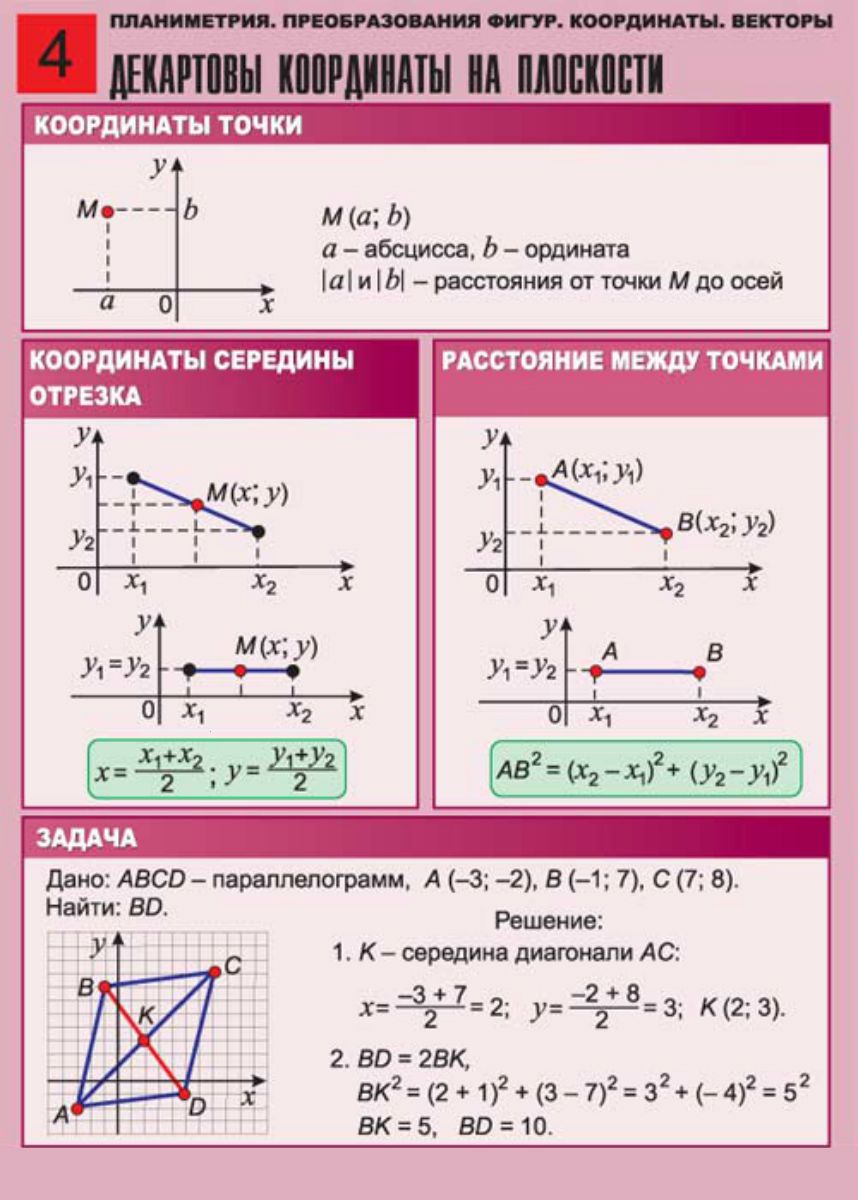
Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
ABz = Bz — Az => Az = Bz — ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).Решение:
AB1 = B1 — A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8AB2 = B2 — A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 — A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 — A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Решение:
AB1 = B1 — A1 => A1 = B1 — AB1 => A1 = 3 — 5 = -2AB2 = B2 — A2 => A2 = B2 — AB2 => A2 = -4 — 1 = -5
AB3 = B3 — A3 => A3 = B3 — AB3 => A3 = 1 — 4 = -3
AB4 = B4 — A4 => A4 = B4 — AB4 => A4 = 8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Координаты вектора. Сложение векторов. Скалярное произведение
Координаты вектора
Пусть вектор имеет началом точку , а концом – точку . Координатами вектора называются числа . Обозначают так:
Координатами вектора называются числа . Обозначают так:
Координаты нулевого вектора равны нулю.
Длина вектора (или абсолютная величина вектора) выражается формулой
Равные векторы имеют равные соответствующие координаты.
И наоборот. Если у векторов соответствующие координаты равны, то векторы равны.
Сложение векторов
Суммой векторов и называется вектор с координатами
Умножение вектора на число
Произведением вектора на число называется вектор , то есть
Коллинеарные вектора
Пусть и – отличные от нуля коллинеарные векторы. Тогда существует число такое, что
Угол между векторами
Углом между любыми двумя ненулевыми векторами и называется угол между равными им векторами с общим началом (наименьший угол).
Угол между двумя векторами находится в промежутке .
Угол между одинаково направленными векторами равен нулю.
Скалярное произведение векторов
I. Скалярным произведением векторов и называется число , то есть
II. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними, то есть
Следовательно, если векторы перпендикулярны, то их скалярное произведение равно нулю. Верно и обратное.
Из формул I и II скалярного произведения вытекает, что угол между векторами можно найти, используя формулу:
Также, следствием, например, формулы II скалярного произведения есть следующий важный момент:
Как определяются координаты вектора в пространстве. Координаты вектора. Направляющие косинусы. Свойства скалярного произведения векторов
Нахождение координат вектора довольно часто встречаемое условие многих задач в математике. Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.
Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.
Нахождение координат вектора в плоскости
Что такое плоскость? Плоскостью считается двухмерное пространство, пространство с двумя измерениями (измерение x и измерение y). К примеру, бумага – плоскость. Поверхность стола – плоскость. Какая-нибудь необъемная фигура (квадрат, треугольник, трапеция) тоже является плоскостью. Таким образом, если в условии задачи нужно найти координаты вектора, который лежит на плоскости, сразу вспоминаем про x и y. Найти координаты такого вектора можно следующим образом: Координаты AB вектора = (xB – xA; yB – xA). Из формулы видно, что от координат конечной точки нужно отнять координаты начальной точки.
Пример:
- Вектор CD имеет начальные (5; 6) и конечные (7; 8) координаты.
- Найти координаты самого вектора.
- Используя вышеупомянутую формулу, получим следующее выражение: CD = (7-5; 8-6) = (2; 2).

- Таким образом, координаты CD вектора = (2; 2).
- Соответственно, x координата равна двум, y координата – тоже двум.
Нахождение координат вектора в пространстве
Что такое пространство? Пространство это уже трехмерное измерение, где даны 3 координаты: x, y, z. В случае, если нужно найти вектор, который лежит в пространстве, формула практически не меняется. Добавляется только одна координата. Для нахождения вектора нужно от координат конца отнять координаты начала. AB = (xB – xA; yB – yA; zB – zA)
Пример:
- Вектор DF имеет начальные (2; 3; 1) и конечные (1; 5; 2).
- Применяя вышеупомянутую формулу, получим: Координаты вектора DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
- Помните, значение координат может быть и отрицательным, в этом нет никакой проблемы.
Как найти координаты вектора онлайн?
Если по каким-то причинам вам не хочется находить координаты самостоятельно, можно воспользоваться онлайн калькулятором . Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 – что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.
Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 – что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.
Нажав на кнопку, страница автоматически прокрутится вниз и выдаст вам правильный ответ вместе с этапами решения.
Рекомендовано хорошо изучить данную тему, потому что понятие вектора встречается не только в математике, но и в физике. Студенты факультета Информационных Технологий тоже изучают тему векторов, но на более сложном уровне.
Необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Координаты вектора
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$
и произвольный вектор $\overline{a}$, начало которого совпадает
с началом системы координат (рис. 1).
1).
Определение
Координатами вектора $\overline{a}$ называются проекции $a_{x}$ и $a_{y}$ данного вектора на оси $O x$ и $O y$ соответственно:
Величина $a_{x}$ называется абсциссой вектора $\overline{a}$, а число $a_{y}$ — его ординатой . То, что вектор $\overline{a}$ имеет координаты $a_{x}$ и $a_{y}$, записывается следующим образом: $\overline{a}=\left(a_{x} ; a_{y}\right)$.
Пример
Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$ имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Сумма двух векторов, заданных координатами
Пусть заданы $\overline{a}=\left(a_{x} ; a_{y}\right)$ и $\overline{b}=\left(b_{x} ; b_{y}\right)$, тогда вектор $\overline{c}=\overline{a}+\overline{b}$ имеет координаты $\left(a_{x}+b_{x} ; a_{y}+b_{y}\right)$ (рис. 2).
Определение
Чтобы найти сумму двух векторов , заданных своими координатами, надо сложить их соответствующие координаты.
Пример
Задание. Заданы $\overline{a}=(-3 ; 5)$ и $\overline{b}=(0 ;-1)$. Найти координаты вектора $\overline{c}=\overline{a}+\overline{b}$
Решение. $\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Умножение вектора на число
Если задан $\overline{a}=\left(a_{x} ; a_{y}\right)$, то тогда вектор $m \overline{a}$ имеет координаты $m \overline{a}=\left(m a_{x} ; m a_{y}\right)$, здесь $m$ — некоторое число (рис. 3).
Пример
Задание. Вектор $\overline{a}=(3 ;-2)$. Найти координаты вектора 2$\overline{a}$
Решение. $2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4)$
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две
точки $A\left(a_{x} ; a_{y}\right)$ и $B\left(b_{x} ; b_{y}\right)$.
Тогда координаты вектора $\overline{A B}=\left(x_{1} ; y_{1}\right)$ находятся по формулам (рис. {2}}}$
{2}}}$
Здесь $\alpha$, $\beta$ и $\gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.
Определение 1
Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.
С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.
Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач
Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y).
Пример 1
Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i → и j → являются координатными векторами.
То есть в данном случае i → и j → являются координатными векторами.
Координатные векторы
Определение 2Векторы i → и j → называются координатными векторами для заданной системы координат.
Пример 2
Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.
Разложение вектора
Определение 3Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .
Определение 4
Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.
Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = (2 ; — 3) означает, что вектор a → имеет координаты (2 ; — 3) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .
Замечание
Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты (1 ; 0) и (0 ; 1) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .
Также имеет место быть нулевой вектор 0 → с координатами (0 ; 0) и разложением 0 → = 0 · i → + 0 · j → .
Равные и противоположные векторы
Определение 5Векторы a → и b → равны тогда, когда их соответствующие координаты равны.
Определение 6
Противоположным вектором называется вектор противоположный данному.
Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = (- a x ; — a y) .
Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения (a x ; a y ; a z) называются координатами вектора в данной (трехмерной) системе координат.
Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = (1 ; 0 ; 0) , j → = (0 ; 1 ; 0) , k → = (0 ; 0 ; 1) , координаты нулевого вектора также равны нулю 0 → = (0 ; 0 ; 0) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = (- a x ; — a y ; — a z) .
Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.
Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M (x M ; y M) .
Определение 7
Вектор O M → называется радиус-вектором точки M .
Определим, какие координаты в данной системе координат имеет радиус-вектор точки
Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты (x M ; y M) в данной системе координат.
Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.
Аналогично в трехмерном пространстве радиус-вектор точки M (x M ; y M ; z M) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = (x M ; y M ; z M) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
До сих пор считалось, что векторы
рассматриваются в пространстве. Начиная
с этого момента будим считать, что все
векторы рассматриваются на плоскости.
Будем также полагать, что на плоскости
задана Декартова система координат
(даже если об этом не говорится),
представляющая две взаимно перпендикулярные
числовые оси – горизонтальная ось
и
вертикальная ось.
Тогда каждой точке
на
плоскости ставится в соответствие пара
чисел
,
которые являются ее координатами.
Обратно, каждой паре чисел
соответствует точка плоскости такая,
что пара чисел
являются ее координатами.
Из элементарной геометрии известно,
что если на плоскости имеются две точки
и
,
то расстояние
между
этими точками выражается через их
координаты по формуле
Пусть на плоскости задана Декартова
система координат. Орт оси
будем обозначать символом,
а орт осисимволом.
Проекцию произвольноговекторана осьбудем обозначать символом
Орт оси
будем обозначать символом,
а орт осисимволом.
Проекцию произвольноговекторана осьбудем обозначать символом
,
а проекцию на осьсимволом
.
Пусть — произвольный вектор на плоскости. Имеет место следующая теорема.
Теорема 22.
Для любого вектора
на плоскости существует пара чисел
.
При этом
,
.
Доказательство.
Пусть дан вектор. Отложим векторот начала координат. Обозначим черезвектор-проекцию векторана ось, а черезвектор-проекцию векторана ось. Тогда, как видно из рисунка 21, имеет место равенство
.
Согласно теореме 9,
,
.
Обозначим
,
.
Тогда получаем
.
Итак, доказано, что для любого вектора
существует пара чисел
таких, что справедливо равенство
,
,
.
При другом расположении вектора относительно осей доказательство аналогично.
Определение.
Пара чисел
итаких, что
,
называются координатами вектора. Числоназывается иксовой координатой, а числоигрековой координатой.
Числоназывается иксовой координатой, а числоигрековой координатой.
Определение.
Пара ортов осей координат
называется ортонормированным базисом
на плоскости. Представление любого
векторав виде
называется разложением векторапо базису
.
Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.
Теорема.
Равные векторы имеют равные координаты.
Доказательство.
,
и
.
Докажем, что
,
.
Из равенства векторов следует, что
.
Допустим, что
,
а
.
Тогда
и значит
,
что не верно. Аналогично, если
,
но
,
то
.
Отсюда
,
что не верно. Наконец, если допустить,
что
и
,
то получаем, что
.
Это означает, что векторы
иколлинеареы. Но это не верно, так как
они перпендикулярны. Следовательно,
остается, что
,
,
что и требовалось доказать.
Таким образом, координаты вектора
полностью определяют сам вектор. Зная
координаты
ивектораможно построить сам вектор, построив векторы
и
и сложив их. Поэтому часто сам векторобозначают в виде пары его координат и
пишут
.
Такая запись означает, что
.
Непосредственно из определения координат вектора следует следующая теорема.
Теорема.
При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде
.
Доказательство.
,
Теорема.
Пусть
,
причем начало вектора точкаимеет координаты
,
а конец вектора есть точка
.
Тогда координаты вектора связаны с
координатами его концов следующими
соотношениями
,
.
Доказательство.
Пусть
и пусть вектор-проекция векторана осьсонаправлен с осью(см. рис. 22). Тогда
так
как длина отрезка на числовой осиравна координате правого конца минус
координата левого конца.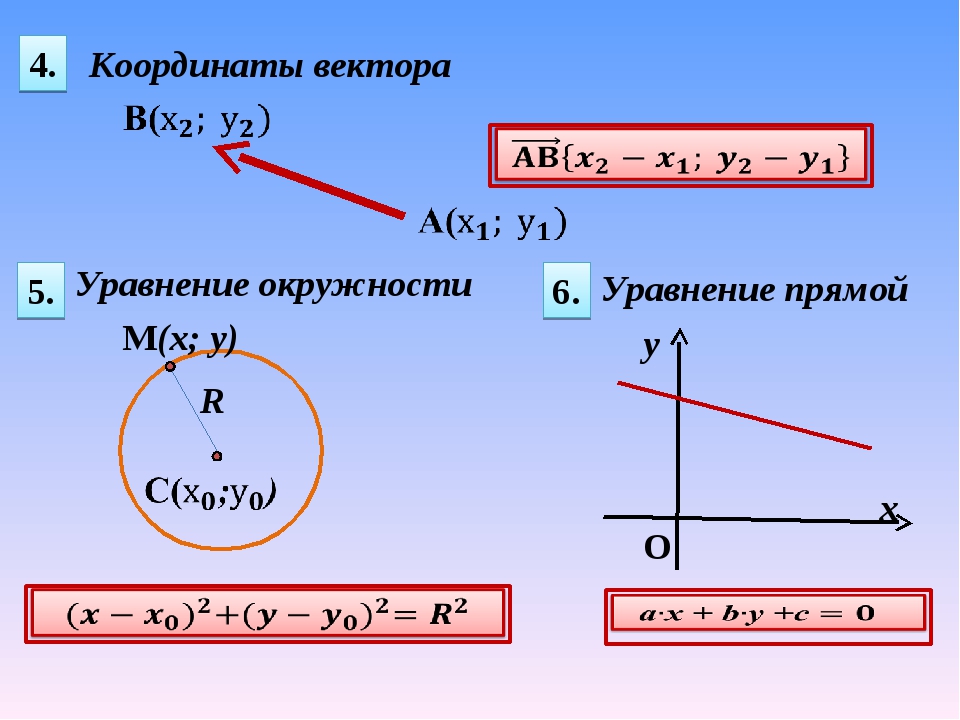 Если вектор
Если вектор
противонаправлен оси(как на Рис. 23), то
Рис. 23.
Если
,
то в этом случае
и тогда получаем
.
Таким образом, при любом расположении
вектора
относительно
осей координат его координатаравна
.
Аналогично доказывается, что
.
Пример.
Даны координаты концов вектора
:
.
Найти координаты вектора
.
Решение.
В следующей теореме приводится выражение длины вектора через его координаты.
Теорема 15.
Пусть
.Тогда
.
Доказательство.
Пусть и- вектор-проекции векторана осии, соответственно. Тогда, как показано при доказательстве теоремы 9, имеет место равенство
.
При этом, векторы ивзаимно перпендикулярны. При сложении этих векторов по правилу треугольника получаем прямоугольный треугольник (см. Рис. 24).
По теореме Пифагора имеем
.
,
.
Следовательно
,
.
.
.
Пример.
.Найти.
Введем понятие направляющих косинусов вектора.
Определение.
Пусть вектор
составляет с осьюугол,
а с осьюугол(см. Рис. 25).
,
.
Следовательно,
Так как для любого вектора имеет место равенство
,
Где — орт вектора, то есть вектор единичной длины, сонаправленный с вектором, то
Вектор
определяет направление вектора.
Его координаты
и
называются направляющими косинусами
вектора.
Направляющие косинусы вектора можно
выразить через его координаты по формулам
,
.
Имеет место соотношение
.
До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.
Будем считать, что в пространстве задана Декартова система координат с осями ,и.
Орты осей ,ибудем обозначать символами,и, соответственно (Рис. 26).
Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для
Рис. 26.
26.
векторов в пространстве. Тройка векторов
называется ортонормированным базисом
в пространстве.
Пусть ,и- вектор-проекции векторана оси,и, соответственно. Тогда
.
В свою очередь
,
,
.
Если обозначить
,
,
,
То получаем равенство
.
Коэффициенты перед базисными векторами ,иназываются координатами вектора. Таким образом, для любого векторав пространстве существует тройка чисел,,, называемых координатами векторатаких, что для этого вектора справедливо представление
.
Вектор
в этом случае также обозначают в виде
.
При этом, координаты вектора равны
проекциям этого вектора на координатные
оси
,
,
,
где — угол между вектороми осью,- угол между вектороми осью,- угол между вектороми осью.
Длина вектора выражается через его координаты по формуле
.
Справедливы утверждения о том, что
равные векторы имеют равные координаты,
при сложении векторов их координаты
складываются, а при умножении вектора
на число его координаты умножаются на
это число.
,
и
называются
направляющими косинусами вектора.
Они связаны с координатами вектора
формулами
,
,
.
Отсюда следует соотношение
Если концы вектора
имеют
координаты
,
,
то координаты вектора
связаны с координатами концов вектора
соотношениями
,
,
.
Пример.
Даны точки
и
.
Найти координаты вектора
.
Нахождение длины вектора через координаты начала и. Вектор. Координаты вектора
На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:
= (x 2 — x 1 ; y 2 — y 1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:
= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты .
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат .
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.
Вектор — это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Здесь точка А — начало вектора, а точка В — его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора
— это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается
Длина вектора обозначается
Два вектора называются равными , если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными , если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:
Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:
Вектора, лежащие на параллельных прямых называются коллинеарными : вектора , и — коллинеарны.
Произведением вектора на число называется вектор, сонаправленный вектору , если title=»k>0″>, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :
Чтобы сложить два вектора и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :
Это правило сложения векторов называется правилом треугольника
.
Чтобы сложить два вектора по правилу параллелограмма , нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:
Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :
Отсюда вытекает правило нахождения разности двух векторов : чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора (то есть конец вычитаемого с концом уменьшаемого):
Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Предлагаю вам решить задачи из Открытого банка заданий для , а затем сверить све решение с ВИДЕОУРОКАМИ:
1
. Задание 4 (№ 27709)
Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .
2 . Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
3 . Задание 4 (№ 27711)
Две стороны прямоугольника ABCD O . Найдите длину суммы векторов и .
4 . Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O . Найдите длину разности векторов и . (чертеж из предыдущей задачи).
5 . Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
6 . Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
7 .Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
8 .Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .
Найдите длину вектора — .
9 . Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
10 . Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
11 .Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
12 . Задание 4 (№ 27720)
ABC равны Найдите длину вектора +.
13 . Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).
14 . Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox
Oxy
О А ОА .
, откуда ОА .
Таким образом, .
Рассмотрим пример.
Пример.
Решение.
:
Ответ:
Oxyz в пространстве.
А ОА будет диагональю.
В этом случае (так как ОА ОА .
Таким образом, длина вектора .
Пример.
Вычислите длину вектора
Решение.
, следовательно,
Ответ:
Прямая на плоскости
Общее уравнение
Ax + By + C ( > 0).
Вектор = (А; В) — нормальный вектор прямой.
В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 — прямая параллельна оси Ox ;
2) Ax + C = 0 — прямая параллельна оси Oy ;
3) Ax + By = 0 — прямая проходит через начало координат;
4) y = 0 — ось Ox ;
5) x = 0 — ось Oy .
Уравнение прямой в отрезках
где a, b — величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .
Нахождение длины вектора по координатам.
Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.
Начнем с нахождения длины вектора на плоскости по координатам.
Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .
Отложим от начала координат (от точки О ) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .
В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .
Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .
Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.
Рассмотрим пример.
Пример.
Найдите длину вектора , заданного в декартовой системе координат.
Решение.
Сразу применяем формулу для нахождения длины вектора по координатам :
Ответ:
Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.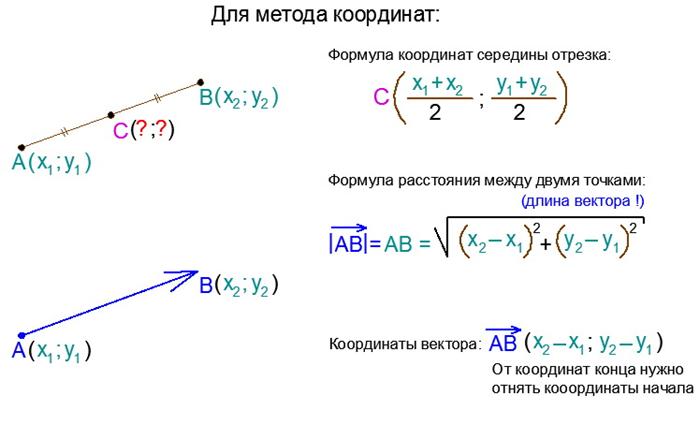
Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.
В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .
Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .
Пример.
Вычислите длину вектора , где — орты прямоугольной системы координат.
Решение.
Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .
Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем теперь, непосредственно, понятие длин вектора.
Определение 3
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.
Определение 4
Два вектора будем называть равными, если они удовлетворяют двух условиям:
1. Они сонаправлены;
1. Их длины равны (рис. 2).
Они сонаправлены;
1. Их длины равны (рис. 2).
Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.
Определение 5
Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:
$\overline{c}={m,n}$
Как найти длину вектора?
Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:
Пример 1
Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.
Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. 2}$.
2}$.
Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.
Пример задач
Пример 2
Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.
Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что
Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.
Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:
Понятие вектора
Вектор — это направленный отрезок.
Все векторы, имеющие одинаковое направление и равные по длине являются равными.
*Все представленные выше четыре вектора равны!
То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.
Обозначение векторов
Вектор может быть обозначен латинскими заглавными буквами, например:
При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.
Ещё вектор обозначается одной буквой латинского алфавита (прописной):
Возможно также обозначение без стрелок:
Суммой двух векторов АВ и ВС будет являться вектор АС .
Записывается как АВ +ВС =АС .
Это правило называется – правилом треугольника .
То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).
Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:
Перенесём вектор b , или по-другому – построим равный ему:
Как находится сумма нескольких векторов? По тому же принципу:
* * *
Правило параллелограмма
Это правило является следствием изложенного выше.
Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a , и мы можем построить вектор, который будет являться их суммой:
Ещё немного важной информации, необходимой для решения задач.
Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:
Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.
Пусть даны два вектора, найдём их разность:
Мы построили вектор противоположный вектору b, и нашли разность.
Координаты вектора
Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:
То есть, координаты вектора представляют собой пару чисел.
Если
И координаты векторов имеют вид:
То c 1 = a 1 + b 1 c 2 = a 2 + b 2
Если
То c 1 = a 1 – b 1 c 2 = a 2 – b 2
Модуль вектора
Модулем вектора называется его длина, определяется по формуле:
Формула для определения длины вектора, если известны координаты его начала и конца:
Рассмотрим задачи:
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО
.
Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО
.
Найдём вектор, который будет являться результатом АО –ВО:
АО –ВО =АО +(–ВО )=АВ
То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ +AD .
Найдём вектор, который будет являться суммой векторов AD и AB BC равен вектору AD . Значит AB +AD =AB +BC =AC
AC это длина диагонали ромба АС , она равна 16.Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО +ВО .
Найдём вектор, который будет являться суммой векторов АО и ВО ВО равен вектору OD, з начит
AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:По теореме Пифагора:
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО
–ВО
.
Найдём вектор, который будет являться результатом АО –ВО :
АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:По теореме Пифагора:
Стороны правильного треугольника ABC равны 3.
Найдите длину вектора АВ –АС .
Найдём результат разности векторов:
СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.27663. Найдите длину вектора а (6;8).
27664. Найдите квадрат длины вектора АВ .
Величина и направление векторов
Величина вектора
Величина вектора
п
Вопрос
→
это расстояние между начальной точкой
п
и конечная точка
Вопрос
. В символах величина
п
Вопрос
→
записывается как
|
п
Вопрос
→
|
.
Если заданы координаты начальной и конечной точек вектора, то Формула расстояния можно использовать для нахождения его величины.
| п Вопрос → | знак равно ( Икс 2 − Икс 1 ) 2 + ( у 2 − у 1 ) 2
Пример 1:
Найдите величину вектора
п
Вопрос
→
чья начальная точка
п
я сидела
(
1
,
1
)
и конечная точка находится в
Вопрос
я сидела
(
5
,
3
)
.
Решение:
Используйте формулу расстояния.
Подставьте значения Икс 1 , у 1 , Икс 2 , и у 2 .
|
п
Вопрос
→
|
знак равно
(
5
−
1
)
2
+
(
3
−
1
)
2
знак равно
4
2
+
2
2
знак равно
16
+
4
знак равно
20
≈
4. 5
5
Величина п Вопрос → около 4,5 .
Направление вектора
Направление вектора — это мера угла, который он образует с горизонтальная линия .
Для нахождения направления вектора можно использовать одну из следующих формул:
загар θ знак равно у Икс , где Икс горизонтальное изменение и у вертикальное изменение
или
загар
θ
знак равно
у
2
−
у
1
Икс
2
−
Икс
1
, где
(
Икс
1
,
у
1
)
является начальной точкой и
(
Икс
2
,
у
2
)
является конечной точкой.
Пример 2:
Найдите направление вектора п Вопрос → чья начальная точка п я сидела ( 2 , 3 ) и конечная точка находится в Вопрос я сидела ( 5 , 8 ) .
Заданы координаты начальной и конечной точки.Подставляем их в формулу загар θ знак равно у 2 − у 1 Икс 2 − Икс 1 .
загар θ знак равно 8 − 3 5 − 2 знак равно 5 3
Найдите обратный загар, затем воспользуйтесь калькулятором.
θ знак равно загар − 1 ( 5 3 ) ≈ 59 °
Вектор п Вопрос → имеет направление около 59 ° .
Найти вектор направления по двум точкам
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Вектор положения — определение, формула, примеры, часто задаваемые вопросы
Вектор положения используется, чтобы помочь нам найти положение одного объекта относительно другого объекта. Векторы положения обычно начинаются в начале координат, а затем заканчиваются в любой другой произвольной точке. Таким образом, эти векторы используются для определения положения конкретной точки относительно ее начала.
Векторы положения обычно начинаются в начале координат, а затем заканчиваются в любой другой произвольной точке. Таким образом, эти векторы используются для определения положения конкретной точки относительно ее начала.
В этой статье давайте узнаем о позиционных векторах, их определении, формулах с решенными примерами.
Что такое вектор положения?
Вектор положения представляет собой прямую линию, один конец которой прикреплен к телу, а другой конец прикреплен к движущейся точке, и используется для описания положения точки относительно тела.По мере перемещения точки вектор положения будет изменяться по длине или по направлению, или по длине и по направлению одновременно.
Определение вектора положения
Вектор положения определяется как вектор, указывающий либо положение, либо положение любой заданной точки относительно любой произвольной контрольной точки, такой как начало координат. Направление вектора положения всегда указывает от начала этого вектора к заданной точке.
- В декартовой системе координат, если O является началом координат, а P(x 1 , y 1 ) является другой точкой, то вектор положения, направленный из точки O в точку P, может быть представлен как ОП.
- В трехмерном пространстве, если начало координат O = (0,0,0) и P = (x 1 , y 1 , z 1 ), то вектор положения v точки P может быть представлено как: v = x 1 i + y 1 j + z 1 k
Рассмотрим два вектора P и Q с векторами положения p = (2,4) и q = (3, 5) соответственно. Координаты векторов P и Q можно записать в виде: P = (2,4), Q = (3, 5). Давайте рассмотрим начало координат O, как показано на изображении ниже.Мы будем рассматривать частицу, которая движется из точки P в точку Q. Вектор положения частицы можно определить как вектор, который начинается от начала координат до точки, в которой находится частица.
На приведенной выше диаграмме вектор положения частицы, когда она находится в точке P, является вектором OP, а когда она находится в точке Q, это вектор OQ.
Как найти вектор положения?
Очень важно сначала определить координаты точки, прежде чем найти вектор положения этой точки.Рассмотрим две точки, A и B, где A = (x 1 , y 1 ) и B = (x 2 , y 2 ).
- Далее найдем вектор положения из точки А в точку В, вектор АВ.
- Чтобы определить этот вектор положения, нам нужно вычесть соответствующие компоненты A из B: AB = (x 2 — x 1 , y 2 — y 1 ) = (x 2 — x 1 ) я + (у 2 — у 1 ) у
Формула вектора положения
Если мы знаем положение любой точки в плоскости xy, то мы можем использовать формулу для определения вектора положения между этими двумя точками.Например, рассмотрим точку A с координатами (x k , y k ) в плоскости xy и другую точку B с координатами (x k+1 , y k+ 1 ).
- Формула для определения вектора положения от A до B: AB = (x k+1 — x k , y k+1 — y k ).
- Вектор положения AB относится к вектору, который начинается в точке A и заканчивается в точке B.
- Точно так же, если мы хотим найти вектор положения из точки B в точку A, то мы можем использовать: BA = (x k — x k+1 , y k — y k+1 )
Похожие статьи о позиционном векторе
Ознакомьтесь со следующими страницами, связанными с вектором положения
Важные замечания по вектору положения
Вот список нескольких моментов, которые следует помнить при изучении вектора положения
- Вектор положения определяется как вектор, указывающий либо позицию, либо положение любой заданной точки относительно любой произвольной контрольной точки, такой как начало координат.

- Направление вектора положения всегда указывает от начала этого вектора к заданной точке.
Часто задаваемые вопросы о векторе положения
Что такое
позиционный вектор в математике?Вектор положения представляет собой прямую линию, один конец которой прикреплен к телу, а другой конец прикреплен к движущейся точке, и используется для описания положения точки относительно тела. Направление вектора положения всегда указывает от начала этого вектора к заданной точке.
Как найти вектор положения?
Очень важно сначала определить координаты точки, прежде чем найти вектор положения этой точки. Рассмотрим две точки, A и B, где A = (x 1 , y 1 ) и B = (x 2 , y 2 ).
- Далее найдем вектор положения из точки А в точку В, вектор АВ.
- Чтобы определить этот вектор положения, нам нужно вычесть соответствующие компоненты A из B: AB = (x 2 — x 1 , y 2 — y 1 )
В чем разница между вектором положения и вектором смещения?
Вектор положения определяется как вектор, указывающий либо положение, либо положение любой заданной точки относительно любой произвольной контрольной точки, такой как начало координат. Принимая во внимание, что вектор смещения помогает нам найти изменение вектора положения данного объекта.
Принимая во внимание, что вектор смещения помогает нам найти изменение вектора положения данного объекта.
Где всегда начинается вектор положения?
Вектор положения начинается в начале координат и заканчивается в любой другой произвольной точке. Они используются для определения положения точки относительно начала координат.
В чем разница между вектором положения и единичным вектором?
Вектор считается единичным, если он используется для указания только направления и имеет модуль, равный 1.Для направления не требуется величина , поэтому величина единичного вектора всегда равна 1. Вектор положения определяется как вектор, который указывает либо положение, либо местоположение любой заданной точки по отношению к любой произвольной опорной точке, такой как источник.
Какая формула для вектора положения?
Если мы знаем положение любой точки в плоскости xy, то мы можем использовать формулу для определения вектора положения между этими двумя точками. Например, рассмотрим точку A с координатами (x k , y k ) в плоскости xy и другую точку B с координатами (x k+1 , y k+ 1 ).Формула для определения вектора положения от A до B: AB = (x k+1 — x k , y k+1 — y k ).
Например, рассмотрим точку A с координатами (x k , y k ) в плоскости xy и другую точку B с координатами (x k+1 , y k+ 1 ).Формула для определения вектора положения от A до B: AB = (x k+1 — x k , y k+1 — y k ).
Является ли смещение вектором положения?
Нет, смещение не является вектором положения. Вектор положения используется, чтобы помочь нам найти местоположение одного объекта относительно другого объекта. Важно знать положение тела, когда мы описываем его движение. Но тогда вектор смещения можно определить как изменение или вариацию заданного вектора положения.
8.8: Векторы — Математика LibreTexts
Пример \(\PageIndex{2B}\): демонстрация равенства двух векторов
Показать, что вектор \(\vec{v}\) с начальной точкой в \((5,−3)\) и конечной точкой в \((−1,2)\) равен вектору \(\vec{ u}\) с начальной точкой в \((−1,−3)\) и конечной точкой в \((−7,2)\). Нарисуйте вектор положения на той же сетке, что и \(\vec{v}\) и \(\vec{u}\). Затем найдите величину и направление каждого вектора.
Нарисуйте вектор положения на той же сетке, что и \(\vec{v}\) и \(\vec{u}\). Затем найдите величину и направление каждого вектора.
Раствор
Как показано на рисунке \(\PageIndex{8}\), нарисуйте вектор \(\vec{v}\), начиная с начальной \((5,−3)\) и конечной точки \((−1,2 )\).Нарисуйте вектор \(\vec{u}\) с начальной точкой \((−1,−3)\) и конечной точкой \((−7,2)\). Найдите стандартное положение для каждого.
Затем найдите и зарисуйте вектор положения для \(\vec{v}\) и \(\vec{u}\). У нас есть
\[\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7− (−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}\]
Поскольку векторы положения одинаковы, \(\vec{v}\) и \(\vec{u}\) совпадают.
Альтернативный способ проверки равенства векторов — показать, что величина и направление одинаковы для обоих векторов.{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39,8° \end{align*}\]
Однако мы видим, что вектор положения заканчивается во втором квадранте, поэтому мы добавляем \(180°\). Таким образом, направление равно \(−39,8°+180°=140,2°\).
Таким образом, направление равно \(−39,8°+180°=140,2°\).
Рисунок \(\PageIndex{8}\)
Нахождение координат точек с помощью векторов? (см. рисунок)
Чтобы найти координаты ABC , нам нужно найти пересечение векторных линий.Это можно сделать, приравняв каждую пару векторных прямых.
Чтобы найти точку A , мы будем использовать векторные линии AB и AC . См. схему.
#АВ=АС#
#((0),(2))+r((2),(1))=((0),(5))+t((1),(-1))#
#цвет(белый)(->)2r=t#
#2+r=5-t#
Решение для #r# и #t#:
#р=3-т#
#2(3-t)=t=>t=2#
#2r=2=>r=1#
Использование их в #AB =AC#
#((0),(2))+1((2),(1))=((0),(5))+2((1),(-1))#
#((2),(3))=((2),(3))#
Координата A : #color(white)(8)( 2 color(white)(1), 3)#
Чтобы найти точку B , мы будем использовать векторные линии AB и BC .
#АВ = БК#
#((0),(2))+r((2),(1))=((8),(6))+s((-1),(-2))#
#цвет(белый)(888)2r=8-s#
#2+r=6-2s#
#г=4-2с#
#2(4-2s)=8-s=>s=0#
#2+r=6-2(0)=>r=4#
Использование их в #AB =BC#
#((0),(2))+4((2),(1))=((8),(6))+0((-1),(-2))#
#((8),(6))=((8),(6))#
Координата B : #color(white)(8)( 8 color(white)(1), 6 )#
Чтобы найти точку C , мы будем использовать векторные линии AC и BC .
#АС=БК#
#((0),(5))+t((1),(-1))=((8),(6))+s((-1),(-2))#
#color(white)(8888)t=8-s#
#5-t=6-2s#
#5-(8-s)=6-2s=>s=3#
#t=8-3=>t=5#
Использование их в #AC =BC#
#((0),(5))+5((1),(-1))=((8),(6))+3((-1),(-2))#
#((5),(0))=((5),(0))#
Координата C : #color(white)(8)( 5 color(white)(1), 0 )#
Чтобы вычислить длины сторон, мы могли бы либо использовать формулу расстояния, либо найти векторы #vec(AB), vec(AC) и vec(CB)# и найти их величину. 2))=кв.(45)=3кв.(5)#
2))=кв.(45)=3кв.(5)#
Стороны AB и BC имеют одинаковую длину.
Координаты:
#A=(2, 3)#
#B=(8, 6)#
#C=(5,0)#
Длина сторон:
#AB=3sqrt(5)#
#BC=3sqrt(5)#
#AC=3sqrt(2)#
Видео-вопрос: Использование операций над векторами для нахождения координат неизвестной точки
Стенограмма видео
На решетке, где вектор 𝐀𝐂 есть равно трем, трем; вектор 𝐁𝐂 равен 13, минус семь; и два 𝐂 плюс два 𝐀𝐁 равно минус четыре, минус четыре, найти координаты точки 𝐶.
Если мы начнем с рассмотрения
три точки 𝐴, 𝐵 и 𝐶, показанные на диаграмме, мы знаем, что вектор 𝐀𝐂 равен
до трех, до трех. Это означает, что мы двигаемся на три единицы
в положительном 𝑥-направлении и три единицы в положительном 𝑦-направлении. Вектор 𝐁𝐂 равен 13,
минус семь. Чтобы добраться из точки 𝐵 в точку
𝐶, мы перемещаемся на 13 единиц в положительном 𝑥-направлении и на семь единиц в отрицательном
𝑦-направление.
Чтобы добраться из точки 𝐵 в точку
𝐶, мы перемещаемся на 13 единиц в положительном 𝑥-направлении и на семь единиц в отрицательном
𝑦-направление.
Мы можем использовать эту информацию, чтобы найти вектор 𝐀𝐁. Один из способов добраться из точки 𝐴 к точке 𝐵 будет через точку 𝐶. Чтобы сделать это, мы бы путешествовать по векторам 𝐀𝐂 и 𝐂𝐁. Мы знаем, что вектор 𝐀𝐂 равен трем, три. Вектор 𝐂𝐁 будет иметь то же самое величина как вектор 𝐁𝐂, но действует в противоположном направлении. Это означает, что вектор 𝐂𝐁 равно отрицательному 13, семь. Таким образом, вектор 𝐀𝐁 равен три, три плюс минус 13, семь.
Мы знаем, что можем сложить два вектора
путем добавления соответствующих им компонентов. Три плюс минус 13 равно
минус 10, а три плюс семь равно 10. Следовательно, вектор 𝐀𝐁 равен
минус 10, 10. Если мы позволим точке 𝐶 иметь
координаты 𝑥, 𝑦, то вектор положения точки 𝐶, также обозначаемый 𝐎𝐂, равен
равно вектору 𝑥, 𝑦. Подставив это вместе с
вектор 𝐀𝐁 в данное уравнение, мы имеем два, умноженные на 𝑥, 𝑦 плюс два
умножить на минус 10, 10 равно минус четыре, минус четыре.
Если мы позволим точке 𝐶 иметь
координаты 𝑥, 𝑦, то вектор положения точки 𝐶, также обозначаемый 𝐎𝐂, равен
равно вектору 𝑥, 𝑦. Подставив это вместе с
вектор 𝐀𝐁 в данное уравнение, мы имеем два, умноженные на 𝑥, 𝑦 плюс два
умножить на минус 10, 10 равно минус четыре, минус четыре.
Вспомним, что мы можем умножать
вектор на скаляр путем умножения каждого из компонентов на этот скаляр. Наше уравнение упрощается до двух 𝑥,
два 𝑦 плюс минус 20, 20 равно минус четыре, минус четыре. Мы можем сложить два вектора на
левая часть такая, что два 𝑥 минус 20, два 𝑦 плюс 20 равно минус четырем,
минус четыре. И, наконец, для расчета
значения 𝑥 и 𝑦, мы можем приравнять соответствующие компоненты.У нас есть два уравнения: два 𝑥 минус
20 равно минус четырем, а два 𝑦 плюс 20 равно минус четырем. Решение первого уравнения дает нам
𝑥 равно восьми. И решая второе уравнение, мы
есть 𝑦 равно отрицательному 12. Таким образом, мы можем заключить, что
координаты точки 𝐶 восемь, минус 12.
И решая второе уравнение, мы
есть 𝑦 равно отрицательному 12. Таким образом, мы можем заключить, что
координаты точки 𝐶 восемь, минус 12.
Vector Equations and Spans
Уравнение, включающее векторы с n координатами, аналогично n уравнениям, включающим только числа.Например, уравнение
хC126D+yC-1-2-1D=C8163D
упрощается до
Cx2x6xD+C-y-2y-yD=C8163DorCx-y2x-2y6x-yD=C8163D.
Чтобы два вектора были равны, все их координаты должны быть равны, так что это просто система линейных уравнений
Ex-y=82x-2y=166x-y=3.
Определение
Векторное уравнение — это уравнение, включающее линейную комбинацию векторов с возможными неизвестными коэффициентами.
Спрашивать, имеет ли векторное уравнение решение, это то же самое, что спрашивать, является ли данный вектор линейной комбинацией некоторых других заданных векторов.
Например, приведенное выше векторное уравнение спрашивает, является ли вектор (8,16,3) линейной комбинацией векторов (1,2,6) и (−1,2,−1).
На самом деле нас волнует решение систем линейных уравнений, а не решение векторных уравнений. Весь смысл векторных уравнений в том, что они дают нам другой, более геометрический способ рассмотрения систем линейных уравнений.
Figure4A изображение приведенного выше векторного уравнения. Попробуйте решить уравнение геометрически, перемещая ползунки.Чтобы действительно решить векторное уравнение
хC126D+yC-1-2-1D=C8163D,
надо решить систему линейных уравнений
Ex-y=82x-2y=166x-y=3.
Это означает формирование расширенной матрицы
и уменьшение ряда. Обратите внимание, что столбцы расширенной матрицы являются векторами из исходного векторного уравнения , поэтому на самом деле нет необходимости записывать систему уравнений: можно напрямую перейти от векторного уравнения к расширенной матрице, «сложив векторы вместе». ».В следующем примере мы выполняем сокращение строки и находим решение.
Рецепт: Решение векторного уравнения
В общем, векторное уравнение
x1v1+x2v2+···+xkvk=b
, где v1,v2,. ..,vk,b — векторы в Rn, а x1,x2,…,xk — неизвестные скаляры, имеет тот же набор решений, что и линейная система с расширенной матрицей
..,vk,b — векторы в Rn, а x1,x2,…,xk — неизвестные скаляры, имеет тот же набор решений, что и линейная система с расширенной матрицей
, столбцами которого являются vi и b.
Теперь у нас есть три эквивалентных способа представить себе линейную систему:
- В виде системы уравнений:
ч3х1+3х2-2х3=7х1-х2-3х3=5
- В качестве расширенной матрицы:
- В виде векторного уравнения (x1v1+x2v2+···+xnvn=b):
x1F21G+x2F3-1G+x3F-2-3G=F75G
Третий по своей природе геометрический: он поддается рисованию картинок.
Будет важно знать, что такое всех линейных комбинаций набора векторов v1,v2,…,vk в Rn. Другими словами, мы хотели бы понимать множество всех векторов b в Rn таких, что векторное уравнение (относительно неизвестных x1,x2,…,xk)
x1v1+x2v2+···+xkvk=b
имеет решение (т.е. непротиворечиво).
Определение
Пусть v1,v2,…,vk — векторы в Rn. Диапазон v1,v2,.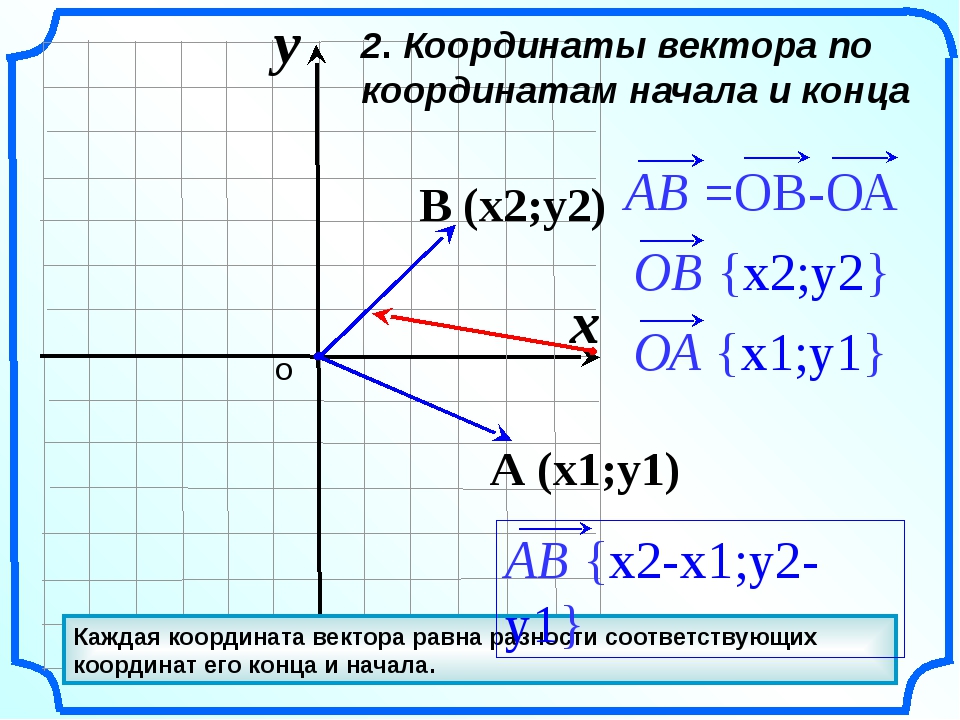 ..,vk представляет собой набор всех линейных комбинаций v1,v2,…,vk и обозначается Span{v1,v2,…,vk}. В символах:
..,vk представляет собой набор всех линейных комбинаций v1,v2,…,vk и обозначается Span{v1,v2,…,vk}. В символах:
Span{v1,v2,…,vk}=Ax1v1+x2v2+···+xkvk|x1,x2,…,xkinRB
Мы также говорим, что Span{v1,v2,…,vk} — это подмножество , натянутое на или , порожденное векторами v1,v2,…,vk.
Приведенное выше определение является первым из нескольких основных определений , которые мы встретим в этом учебнике. Они важны в том смысле, что составляют сущность предмета линейной алгебры: изучение линейной алгебры означает (частично) изучение этих определений.Все определения важны, но очень важно, чтобы вы выучили и поняли определения, помеченные как таковые.
Эквивалент означает, что для любого заданного списка векторов v1,v2,…,vk,b либо все три утверждения верны, либо все три утверждения ложны.
Рисунок 10. Это изображение несовместной линейной системы : вектор w в правой части уравнения x1v1+x2v2=w не лежит в промежутке v1,v2.



