№ п/п |
Этап урока |
Задачи |
Время урока |
Деятельность |
Показатели выполнения задач |
|
учителя |
ученика |
|||||
1. |
Организационный момент |
Сообщение темы и целей урока |
2 мин. |
Приветствует учащихся, сообщает тему и цели урока |
Записывают в тетради тему урока. |
|
2. |
Актуализация прежних знаний учащихся |
Повторить определение квадратного корня и нахождение квадратного корня из числа a |
8 мин. |
1. Найдите квадратные корни из чисел: , 64, 0, , 49. ( числа записаны заранее на доске) Учитель выслушивает разные варианты ответов и мнений учащихся |
Называют числа, которые являются квадратными корнями из указанных чисел. Для одного и того же числа квадратные корни называют несколько учащихся |
|
2. Дайте определение квадратного корня из числа |
Несколько учеников формулируют определение |
|||||
3. От чего зависит наличие квадратных корней из числа a? |
Рассматривают случаи a>0, a<0, a=0. |
|||||
Повторить определение арифметического квадратного корня и его нахождение; сравнить с определением квадратного корня из числа |
1. Учитель, к числам, данным в 1-м задании, дописывает значки квадратного корня. Задает вопрос ученикам: Что нужно найти сейчас для этих чисел? |
Так как значок корня обозначает арифметический квадратный корень, то найдем арифметические квадратные корни из указанных чисел. |
||||
2. А чем отличается квадратный корень из числа a от арифметического квадратного корня из этого же числа? |
Дают определение арифметического квадратного корня. Вычисляют арифметические квадратные корни из указанных чисел и объясняют. |
|||||
акцентировать внимание учащихся на тех значениях a и b, при которых равенство имеет смысл. |
При каких значениях a выполняется равенство ? Что значит извлечь квадратный корень из числа a? |
Если
Найти такое неотрицательное число, квадрат которого равен a. |
В результате появляется запись на доске: . Если 1) 2) |
|||
3. |
Изучение нового материала |
Повторить порядок действий при вычислении значения выражения, содержащего квадратные корни |
Доска приготовлена заранее в виде <Приложения 1>, причем подкоренные выражения во втором и третьем столбце сразу не записаны. 1. Разбейте тетрадный лист на три вертикальные части. В первый столбец запишите квадратные корни и вычислите их. |
Выполняют вычисления в первом столбце. Затем эти вычисления проверяются и исправляются всем классом. |
В результате на доске и в тетрадях учащихся получаются записи в виде <Приложения 2> |
|
2. Во второй столбец запишите квадратные корни и вычислите их. Какой порядок действий при вычислениях? |
Сначала надо найти произведение, а потом извлечь квадратный корень. Выполняют вычисления во втором столбце и проверяют. |
|||||
3. В третий столбец запишите выражения и найдите их значения. Какой порядок действий при вычислениях? |
Сначала нужно извлечь квадратные корни, а затем найти произведение. Выполняют вычисления в третьем столбце и проверяют. |
|||||
Учить учащихся проводить анализ полученных результатов и делать выводы |
1. Посмотрите внимательно на решения во всех трех столбцах. Какой вывод можно сделать? 2. В каких столбцах вычисления для вас были легкими? 3. Объясните, почему. Чем вы пользовались при вычислениях? 4. Почему во втором столбце вычисления были затруднены? 5. Сравните подкоренные выражения во всех трех столбиках. Какой вывод можно сделать? (Учитель выслушивает различные варианты ответов учащихся и подводит под правило) 6. Кто сформулирует правило вычисления квадратного корня из произведения? 7. Это правило справедливо для любых множителей? 8. Запишите правило в общем виде, с помощью букв. 9. Учитель просит нескольких учеников записать правило у доски. |
Во всех столбцах получились одинаковые результаты. В первом и третьем столбце. В первом для вычислений пользовались таблицей квадратов. А в третьем столбце вычисления практически устные. В некоторых примерах потребовалось вычислять произведение чисел в столбик. Подкоренное выражение во втором столбике состоит из множителей, произведение которых равно подкоренному выражению из первого столбика. А в третьем столбике дано произведение квадратных корней из множителей второго столбика. Свои утверждения формулируют несколько учащихся. Нет, только когда множители неотрицательные. Записывают в тетрадях свои варианты. |
||||
4. |
Работа с учебником |
Учить работать с литературой, и проводить сравнение |
3 мин. |
На стр. 80 учебника прочитайте текст, найдите правило и сравните с тем, которое вы сформулировали. |
Работают с учебником. |
В тетрадях появляется запись: |
5. |
Закрепление изученного |
Учить применять изученное правило при решении задач |
12 мин. |
1. № 357 (а, в) Учащиеся комментируют, а учитель у доски показывает оформление. а) в) 2. № 357 (б, г, е) 3. № 360 (а, б, в) Учитель проверяет решение в тетрадях, дает консультации. 4. № 370 (а, в, д, ж) а) Учитель осуществляет индивидуальную помощь. |
Комментируют решение соответственно правилу.
Учащиеся комментируют и записывают самостоятельно. Делают вывод, что свойство применяется не только для двух множителей. Выполняют самостоятельно Выполняют самостоятельно, используя таблицу квадратов. |
В тетрадях учащиеся записывают выполненные задания |
6. |
Организация рефлексии и обратной связи |
скорректировать полученные результаты |
3 мин |
1. Заранее на доске приготовлено задание: а) б) в) Верно ли, что значения указанных квадратных корней можно найти по свойству квадратного корня из произведения? 2. Ученик вычислил значение и получил два варианта ответа 1 и 5. Какой из них верный. Объясните. |
Учащиеся объясняют какие выражения можно вычислить по указанному свойству, а какие нет. Возможны ответы с ошибкой. Выслушать нужно разные варианты ответа. Если ответ ошибочный, то попросить ученика, чтобы объяснил, как он рассуждал |
Повторяется свойство квадратного корня из произведения. |
7. |
Итог урока |
Подвести итог изученного свойства |
2 мин. |
Выставить отметки за урок, объяснить домашнее задание. |
Записывают задание в дневник |
|
urok.1sept.ru
Обобщающий урок по алгебре в 8-м классе. Тема: «Арифметический квадратный корень»
Цель урока: систематизировать полученные знания, использовать их для решения нестандартных примеров.
Чтобы знания стали действительно нашей силой и опорой в различных жизненных ситуациях, нужно в любом изучаемом материале увидеть и осмыслить самое главное. В теме «Арифметический квадратный корень» прежде всего надо помнить, что под знаком корня стоит неотрицательное число, и само значение корня есть также неотрицательная величина. При решении заданий, содержащих квадратный корень, мы использовали два важных равенства. Учащиеся называют их:
Первое равенство верно, если a – неотрицательное число, второе верно при любых значениях a. Для выполнения действий с корнями мы использовали свойства. Учащиеся приводят формулировки свойств.
, где a и b – неотрицательные числа
, где a – неотрицательное, b – положительное число
Повторить и обобщить знания по изученной теме нам поможет игра, именно с ее помощью мы справимся с премудростями корня квадратного. Наша игра будет состоять из четырех туров. Для отражения результатов игры выберем ассистента, который будет вести необходимые записи. Приглашаю за игровые столы первых участников (по два человека за каждый стол). Название первого тура «Если бы я был учителем» и задание этого тура следующее: представить себя в роли учителя и оценить самостоятельную работу, выполненную неким учеником. При оценивании использовать критерии: за одну ошибку ставится «4», за 2-3 ошибки – «3», более трех ошибок – «2». Итак, у вас три минуты на поиск ошибок и оценивание работы (на каждом столе карточка с заданием). Для остальных учащихся задание отражено на слайде, им предлагается выписать в тетрадь примеры, в решении которых допущены ошибки, и найти правильные ответы. В карточках участников и на слайде приведены следующие примеры:
Ассистент следит за временем. Через 3 минуты учитель проверяет карточки участников, объявляет количество ошибок, которое нашли игроки, спрашивает нескольких болельщиков, затем оглашает, сколько баллов заработала каждая пара участников, выставляет им оценки. Ассистент фиксирует результаты тура.
Переходим ко второму туру. Назовем его «Сражение с уравнениями». Приглашаю на поединок с уравнениями следующие две пары игроков. На столах карточки с уравнениями, остальные могут видеть их на слайде. Время на выполнение задания – 5 минут. Предлагается решить следующие уравнения:
Через пять минут учитель проверяет карточки игроков, оглашает полученные правильные ответы. Если участники тура решили не все уравнения, либо получили неверные ответы, учитель спрашивает других учеников. Решение последнего уравнения записывается на доске. Подводятся итоги тура, выставляются оценки игрокам.
Следующий тур называется «В поисках смысла». Для участия в этом туре приглашаются два ученика, которые уверены в своих знаниях по данной теме. Ответы на вопросы нужно будет давать сразу. Отвечать по очереди. Если один из игроков затрудняется ответить, право ответа переходит к сопернику. Ассистент фиксирует количество правильных ответов у каждого игрока. Остальные учащиеся видят задание на слайде и следят за ходом игры. Игрокам предлагаются следующие вопросы:
При каких значениях переменной выражение имеет смысл:
При каких значениях переменной верно равенство:
При каком значении переменной дробь принимает наибольшее значение:
Следующий тур называется так: «Есть идея!». Участникам тура нужно будет выдвинуть идею решения того или иного примера. За игровые столы приглашаются две пары участников, претендующих на высокий балл (на столах карточки с примерами). Игроки той пары, от которой быстрее поступит идея решения, получают балл. Первые три примера на вычисление:
(идея: применить формулы в числителе и знаменателе)
(идея: вынести общий множитель, применить формулы)
(идея: применить способ группировки, формулы)
Следующее задание на упрощение выражения:
(идея: выделить под корнем квадрат суммы)
(идея: выделить под корнем квадрат суммы)
(идея: умножить и разделить подкоренное выражение на 2, выделить квадрат)
Предложить идею построения графика функции:
(идея: под корнем выделить квадрат, получить выражение, содержащее модуль, рассмотреть два случая при раскрытии знака модуля)
Один из участников выполняет построение графика на доске. Все остальные учащиеся строят этот график в тетрадях. Учитель подводит итоги 4 тура, сообщает оценки за работу участникам.
Затем учитель предлагает учащимся поделиться впечатлениями о проведенной игре. Подводит общий итог урока. В качестве домашнего задания предлагает следующие примеры:
Упростить выражение:
Построить график функции:
Приложение
urok.1sept.ru
Урок алгебры в коррекционной школе VII вида «Арифметический квадратный корень. Свойства корня». 8-й класс
Цели урока:
- закрепление определения арифметического квадратного корня, свойств корня;
- формирование навыков применения свойств арифметического квадратного корня при решении задач;
- развитие у учащихся навыков самоконтроля, формирование грамотной математической речи.
Оборудование к уроку:
Раздаточный материал на столах у учащихся:
- карточки для решения примеров на уроке;
- карточки – шаблоны для самостоятельного решения примеров;
- таблица квадратов натуральных чисел от 0 до 99.
Ход урока
На доске заранее приготовлены плакаты:
На столе лежат предметы — морковь, свекла, любое растение с корнями.
Учитель: Назовите слово, объединяющее все эти предметы и понятия. (Желательно, чтобы учащиеся сами догадались, что это слово — «корень»). В курсе алгебры 8 класса мы изучили арифметический квадратный корень и его свойства. Сегодняшний урок мы посвятим обобщению изученного на предыдущих уроках.
1 этап урока
Проводится в виде игры « Я и класс». На доске заранее записаны примеры, их довольно много. Учитель спрашивает учеников с места, любого по своему усмотрению. Тот ученик, на которого указал учитель, называет ответ. При этом если назван верный ответ, то класс получает 1 балл, если дан неверный ответ, то 1 балл получает учитель. Затем баллы суммируются и по их количеству определяется победитель — или учитель, или класс.
2 этап урока
Учащиеся решают примеры на заранее заготовленных листках:
При этом на доске прикреплены с помощью магнитов или на скотч таблички с различными числами и буквами, их где-то 15 штук:
По одному ученики выходят к доске и те же примеры решают на доске, подробно объясняя, на какую теорему необходимо опираться при решении примера. Получив ответ, ученик находит его на табличке и приклеивает эту табличку в заранее приготовленное место. В ходе выполнения этой работы класс повторяет свойства корня и их применение при решении элементарных заданий. Из табличек с правильными ответами получается имя и фамилия:
Учитель: Рене Декарт — французский философ и мыслитель, интересовавшийся математикой. Он ввел современное обозначение корня в 1637 году в своей книге «Геометрия».
| Р | Е | Н | Е | Д | Е | К | А | Р | Т |
Для учащихся коррекционных классов 7 вида полезно будет теоремы, на которые приходится опираться в ходе урока, заготовить в виде плаката на стенде «Сегодня на уроке»:
3 этап урока
Учащиеся решают примеры в тетрадях, ответ называют вслух, ход решения может обсуждаться с учителем.
4 этап урока
Самостоятельная работа, проводится на заготовленных заранее шаблонах. Шаблон состоит из 3 листов, которые скреплены между собой канцелярскими скрепками. Первый лист- это лист с заданиями для самостоятельной работы, на котором ученик решает примеры. Решив пример, ученик обводит получившийся ответ в правом столбце листа.
Следующий лист — копировальная бумага, по размеру соответствующая листу с заданиями для самостоятельной работы. Третий лист — это лист, точно копирующий первый, только правильные ответы на нем заранее обводятся учителем красной ручкой. В ходе выполнения работы ученик решает пример, обводит ответ из трех предложенных, который считает верным. Самостоятельная работа рассчитана на 10 минут урока, затем верхний листок сдается, а нижний остается у ученика для работы над ошибками, при этом верный ли ответ получился — ученик может видеть сразу.
5 этап урока
Учитель: приближенные значения корней умели находить еще жители древнего Вавилона около 4 тысяч лет назад. Не имея вычислительных машин, люди применяли формулу, автор которой неизвестен:
Пример:
Проверим эти вычисления с помощью микрокалькулятора.
Оценки в конце урока выставляются каждому ученику с учетом ответов у доски и результатов самостоятельной работы.
Задание на дом: «Проверь себя» стр. 105, № 379, вычислить по формуле
Литература: Алимов Ш.А., Колягин Ю.М. и др. « Алгебра 8 класс».
Приложение: Таблица квадратов натуральных чисел от 0 до 99.
x2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|---|---|---|---|---|---|---|---|---|---|---|
0 |
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
1 |
100 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
2 |
400 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
3 |
900 |
961 |
1024 |
1089 |
1156 |
1225 |
1296 |
1369 |
1444 |
1521 |
4 |
1600 |
1681 |
1764 |
1849 |
1936 |
2025 |
2116 |
2209 |
2304 |
2401 |
5 |
2500 |
2601 |
2704 |
2809 |
2916 |
3025 |
3136 |
3249 |
3364 |
3481 |
6 |
3600 |
3721 |
3844 |
3969 |
4096 |
4225 |
4356 |
4489 |
4624 |
4761 |
7 |
4900 |
5041 |
5184 |
5329 |
5476 |
5625 |
5776 |
5929 |
6084 |
6241 |
8 |
6400 |
6561 |
6724 |
6889 |
7056 |
7225 |
7396 |
7569 |
7744 |
7921 |
9 |
8100 |
8281 |
8464 |
8649 |
8836 |
9025 |
9216 |
9409 |
9604 |
9801 |
urok.1sept.ru
Урок по алгебре на тему «Квадратный корень из произведения» в 8 классе
Тип урока: изучение новой темы
Цели урока:
— создать условия для вывода обучающимися утверждения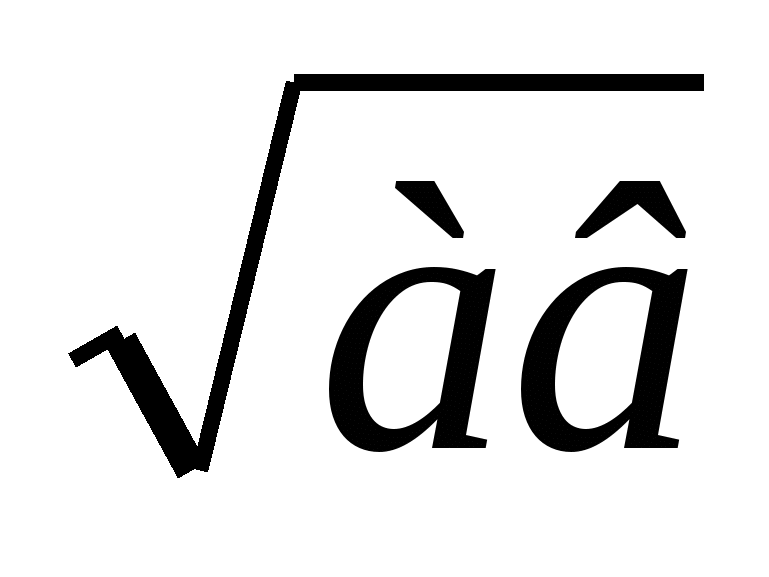 
= 
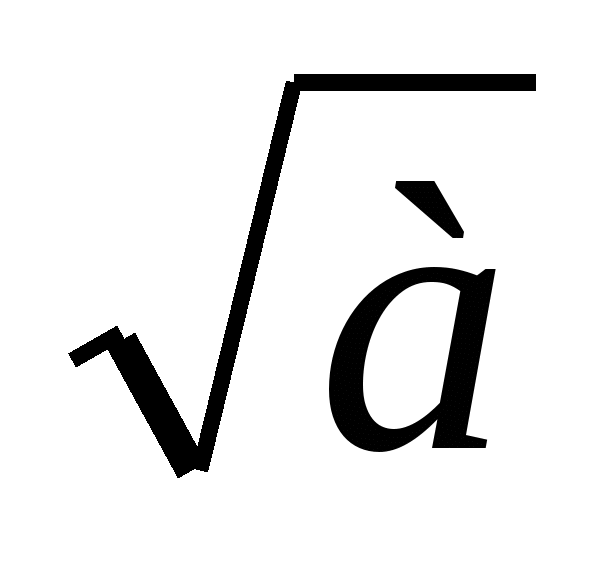
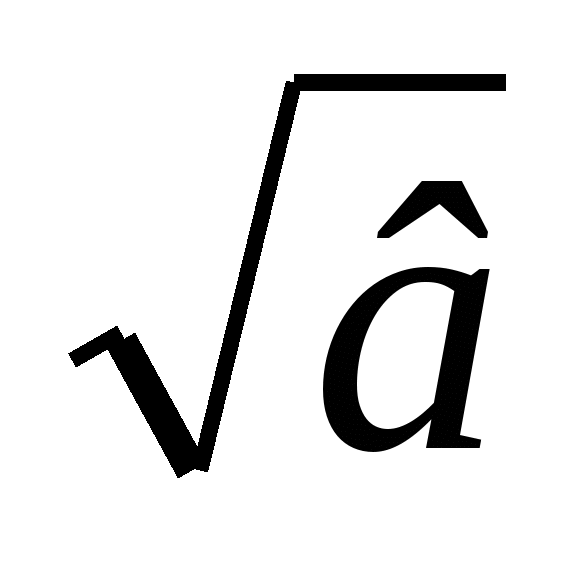и применения его для вычисления квадратных корней;
— способствовать развитию логики, умения проводить анализ и делать выводы;
— продолжать воспитание устойчивого интереса к математике.
ХОД УРОКА:
I. Организационный момент
II. Мотивация
Сегодняшний урок я хотела бы начать со слов Фридриха Адольфа Вильгельма Дистервега — немецкого педагога, политика «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь». (слайд 2)
Миниатюра, которую разыгрывают ученики.
За столом сидит ученик, он в роли учителя математики. К столу прикреплен плакат «Экзамен по математике».
Вбегает ученик.
— Извлекать корни умеешь? – спрашивает экзаменатор.
Ученик:
— Да. Конечно. Нужно потянуть за стебель растения посильнее, и корень его извлечется из почвы.
— Нет, я имела в виду другой корень, например, из девяти.
— Это будет «девя», так как в слове «девять» суффиксом является «ть».
— Ты меня не совсем понял, я имела в виду корень квадратный.
— Квадратных корней не бывает. Они бывают мочковатые и стержневые.
— Арифметический квадратный корень из девяти?
— А, тогда три, так как три в квадрате равно девяти.
При этом ученик берет со стола плакат с записью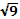 
=3 и показывает его аудитории.
Сегодня на уроке мы продолжим изучение квадратных корней, мы будем учиться извлекать квадратный корень из произведения. (слайд 3)
Знания, полученные по этой теме, помогут вам в дальнейшем изучении математики, а именно при изучении темы « Преобразования выражений, содержащих квадратные корни». А также при сдаче государственного экзамена в 9 классе за курс основной школы.
Я вас попрошу поставить на полях своих тетрадей ту оценку, которую вы хотели бы получить за урок.
Цели урока: (слайд 4)
Повторить определение арифметического квадратного корня.
Вывести правило вычисления квадратного корня из произведения.
Научиться находить квадратный корень из произведения.
Проверить знания и умения с помощью самостоятельной работы.
План урока: (слайд 5)
Теоретический опрос
Устная работа.
Мини лабораторная работа.
Практическая работа.
Самостоятельная работа.
Подведение итогов.
Задание на дом.
III. Актуализация опорных знаний.
Теоретический опрос.
(слайд 6)
Как читается выражение
?При каком значении а выражение
имеет смысл?Что называется арифметическим квадратным корнем из числа а?
Когда равенство
=b является верным?При каком значении а выполняется равенство
?
?
?Устная работа: (слайд 7)
1. Вычислите:
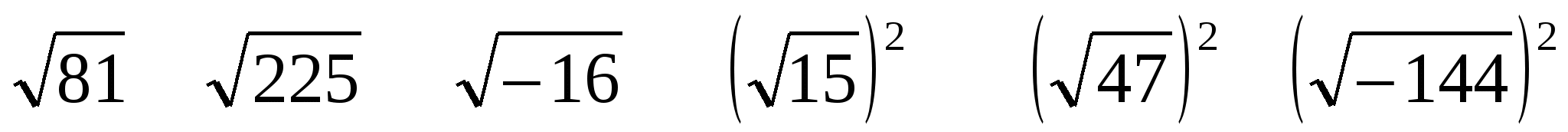
2. Сравните:
IV. Изучение нового материала. (слайды 8, 9)
Мини лабораторная работа.
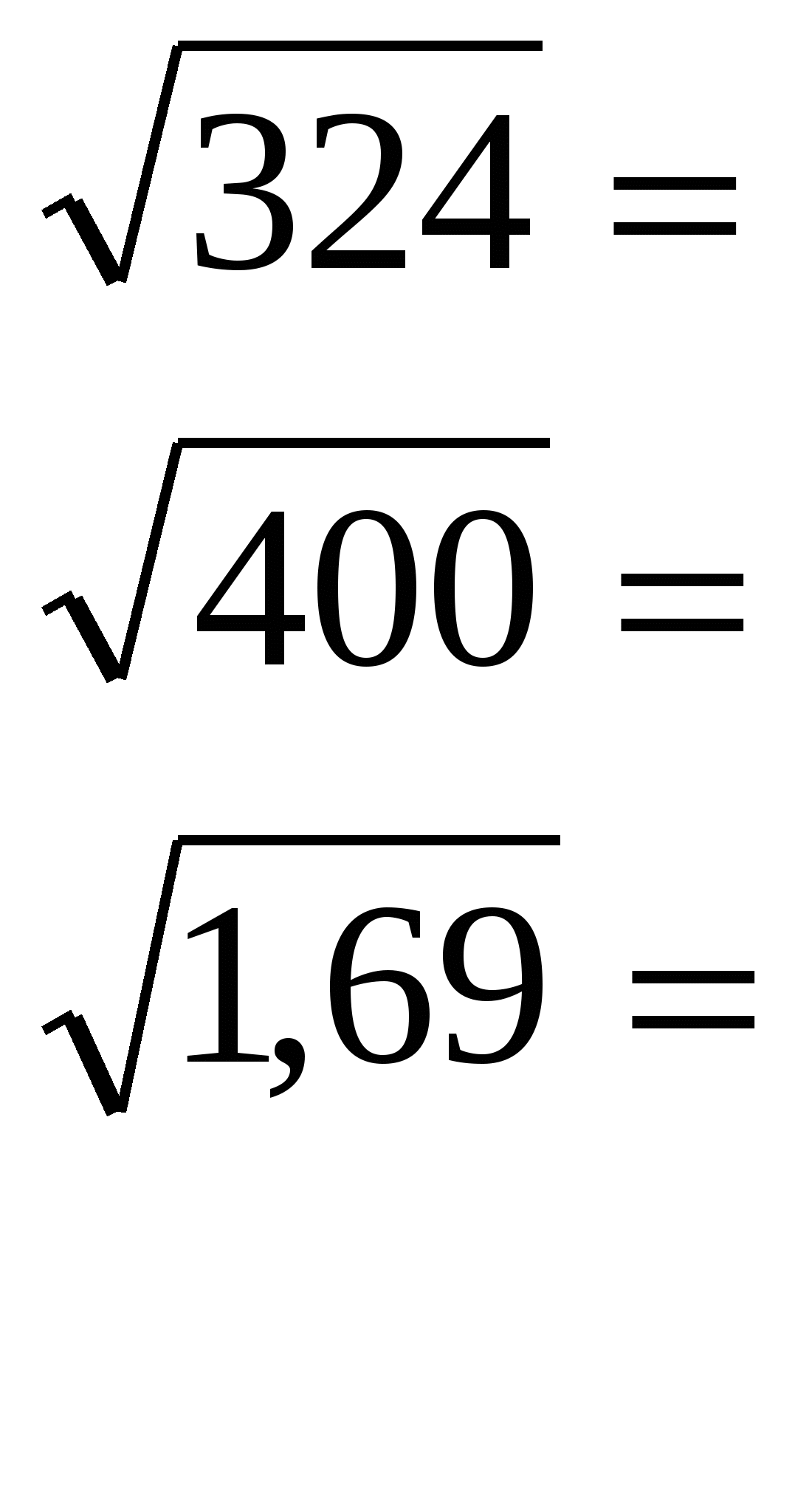
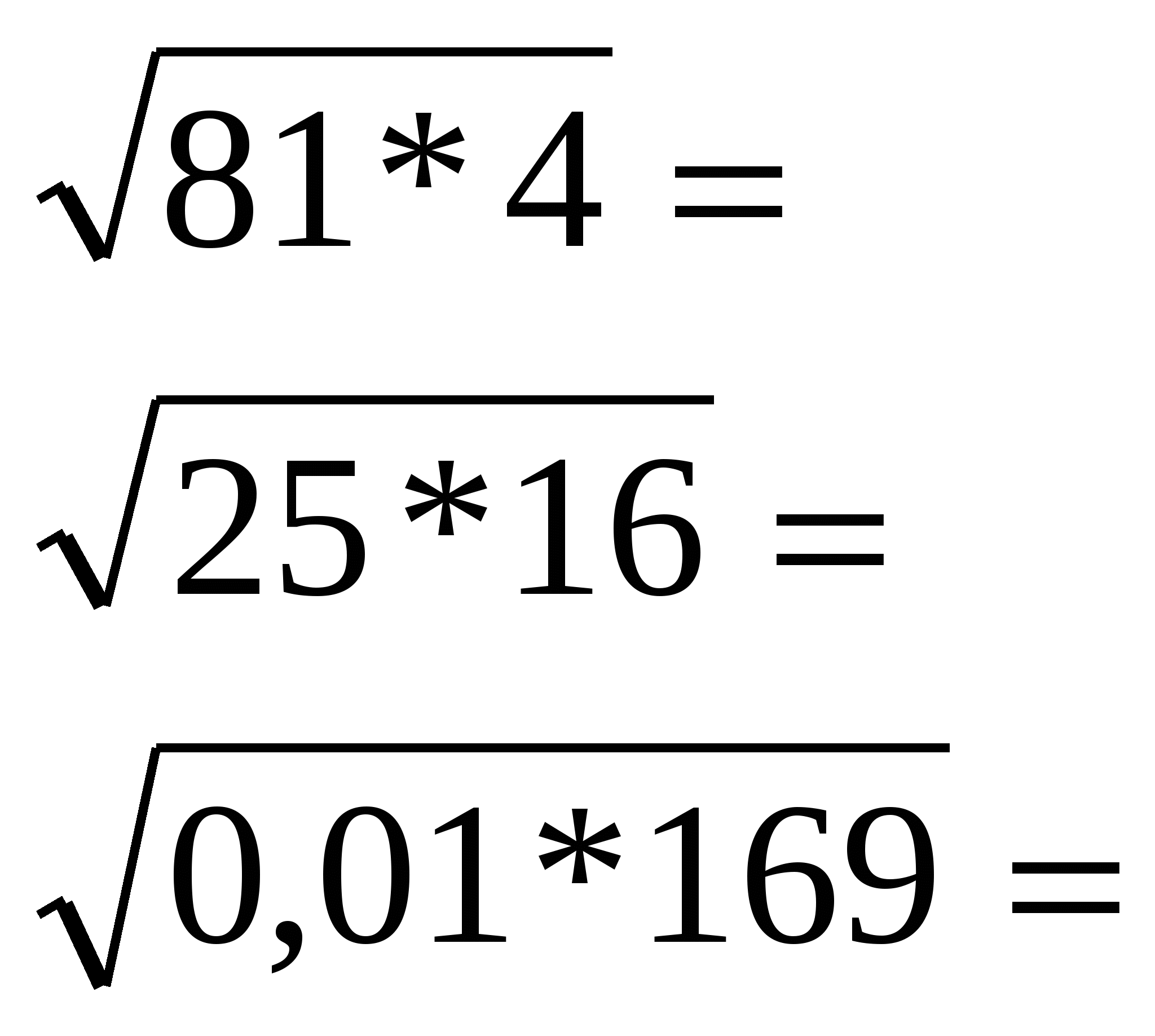
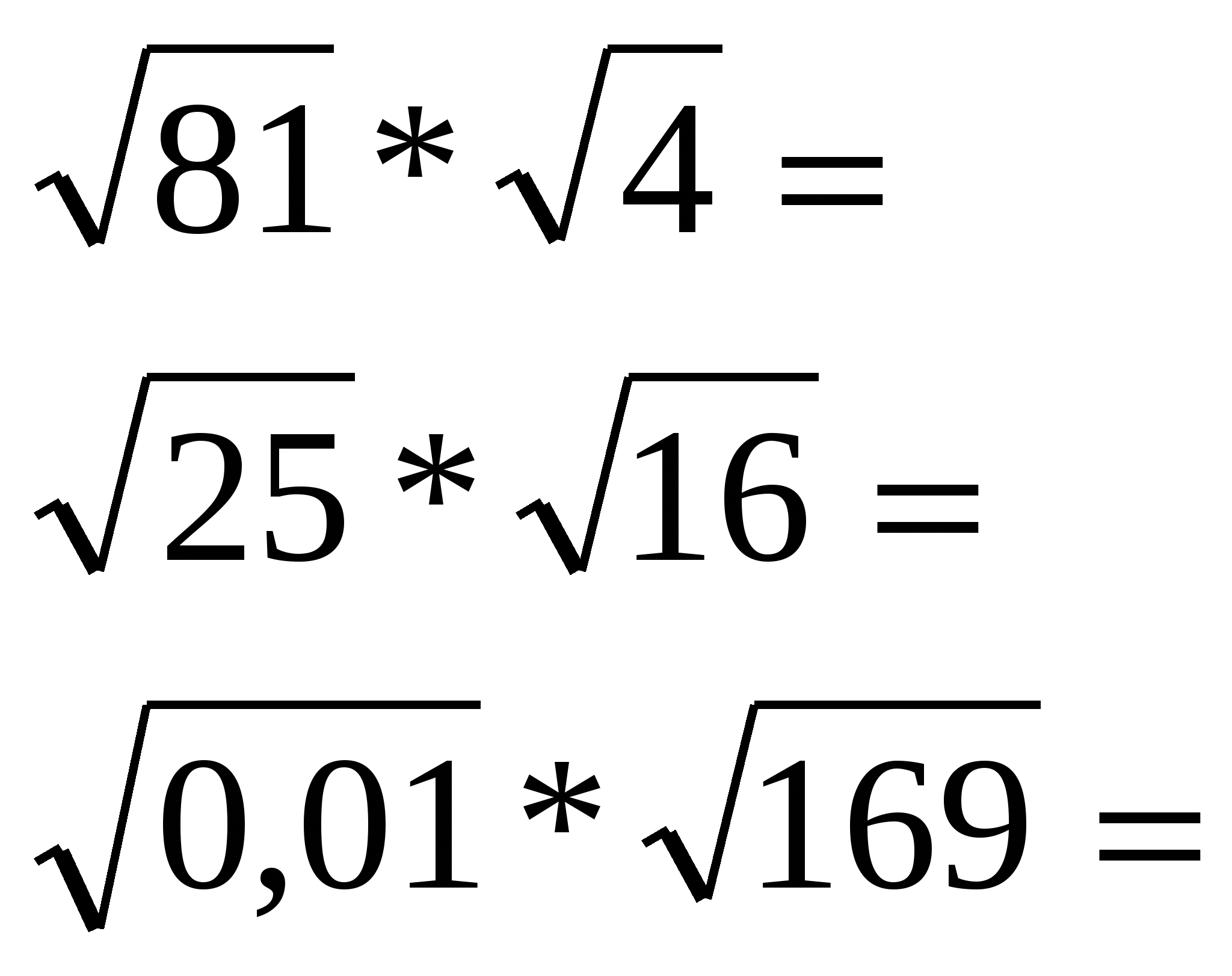
Разбейте тетрадный лист на три вертикальные части. В первый столбец запишите квадратные корни и вычислите их.
Во второй столбец запишите квадратные корни и вычислите их. (корень из произведения) Какой порядок действий при вычислениях?
В третий столбец запишите выражения и найдите их значения. Какой порядок действий при вычислениях? (произведение корней)
Посмотрите внимательно на решения во всех трех столбцах. Какой вывод можно сделать?
— В каких столбцах вычисления для вас были легкими?
— Объясните, почему? Чем вы пользовались при вычислениях?
— Почему во втором столбце вычисления было сделать труднее?
— Сравните подкоренные выражения во всех трех столбиках. Какой вывод можно сделать?
(Учитель выслушивает различные варианты ответов учащихся и подводит под правило)
(слайд 10)
— Кто может сформулировать правило вычисления квадратного корня из произведения?
— Это правило справедливо для любых множителей?
— Запишите правило в общем виде, с помощью букв.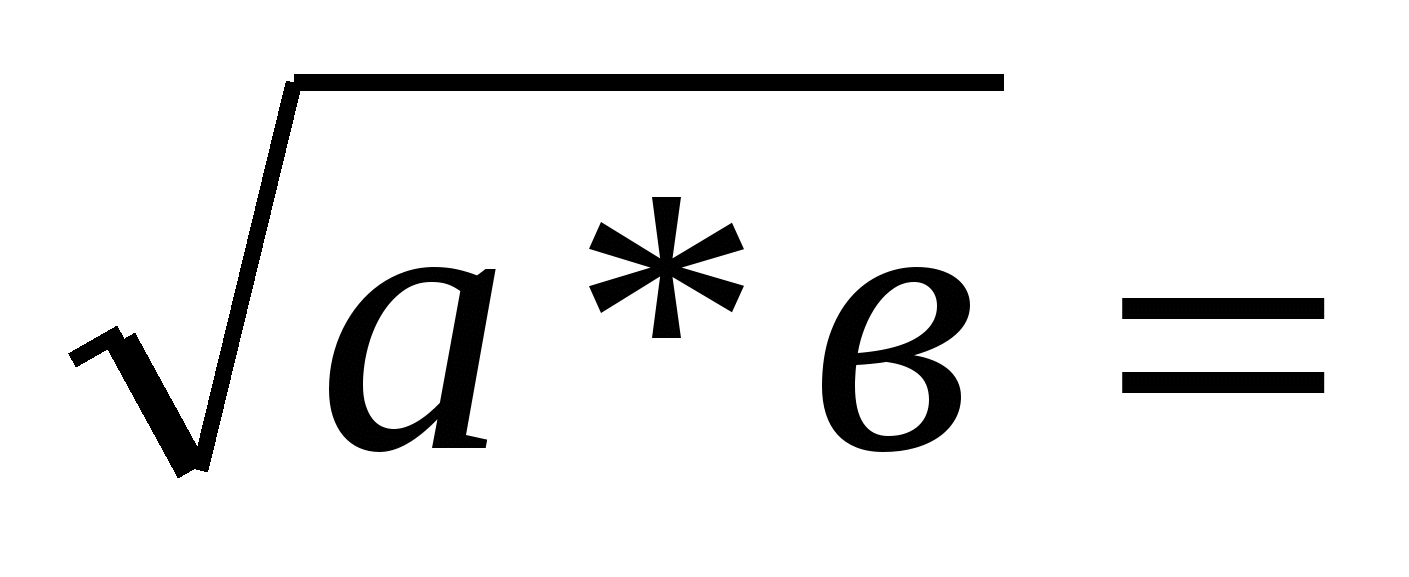 
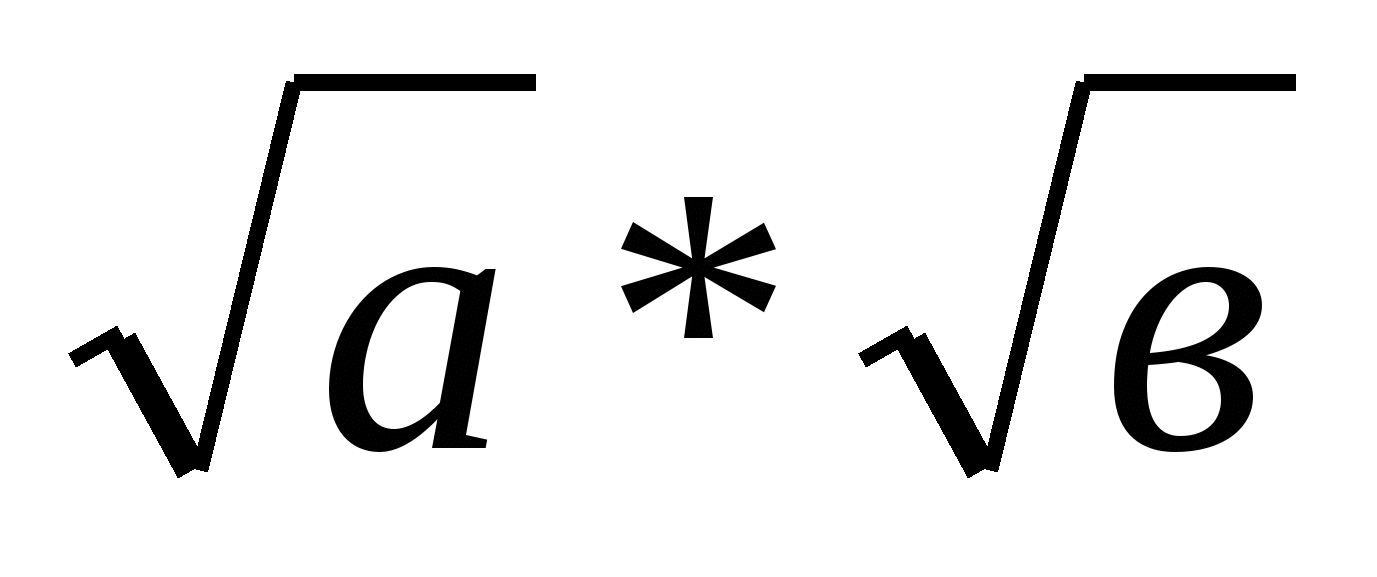
Работа с учебником.
На стр. 84-85 учебника прочитайте текст, найдите правило и сравните с тем, которое вы сформулировали. Рассмотрим пример 1
Учитель:
— Можно ли применить правило для трех и более множителей? (слайд 11)
Закрепление изученного.
Практическая работа.
Вычислите значение квадратного корня, используя теорему о корне из произведения. (слайды 12, 13)
Учащиеся комментируют, а учитель у доски показывает оформление.
Эту формулу можно использовать и для быстрых вычислений. (слайд 14)
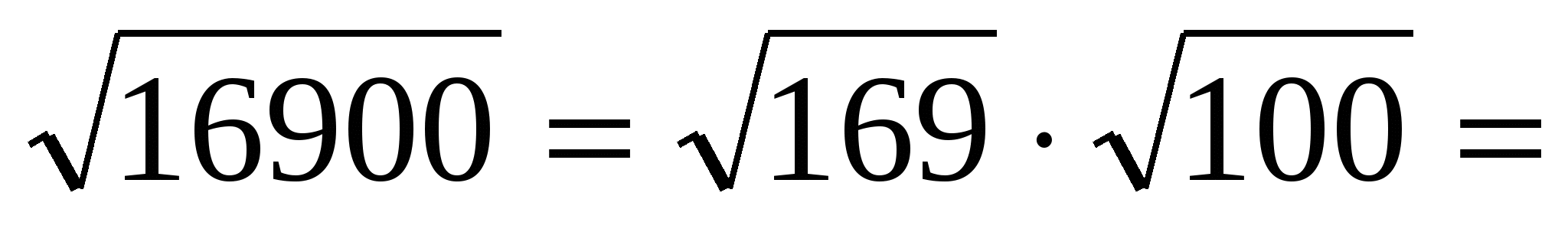
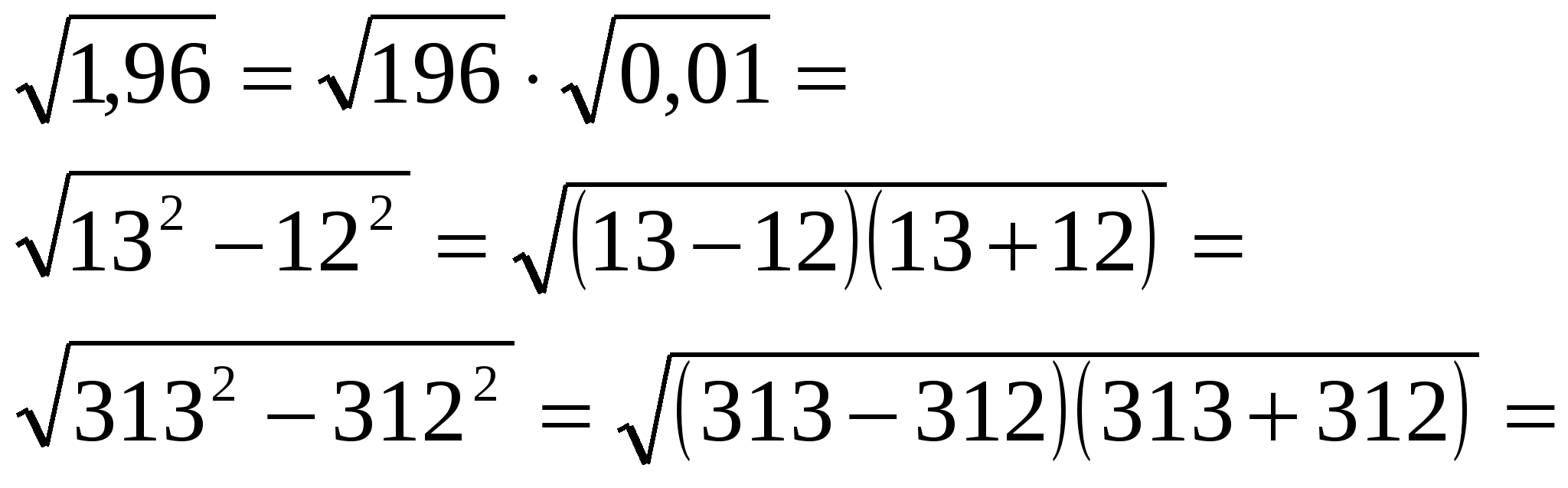
Как бы вы стали вычислять значение следующего выражения?
– ?
Учащиеся предлагают два способа:
Iспособ: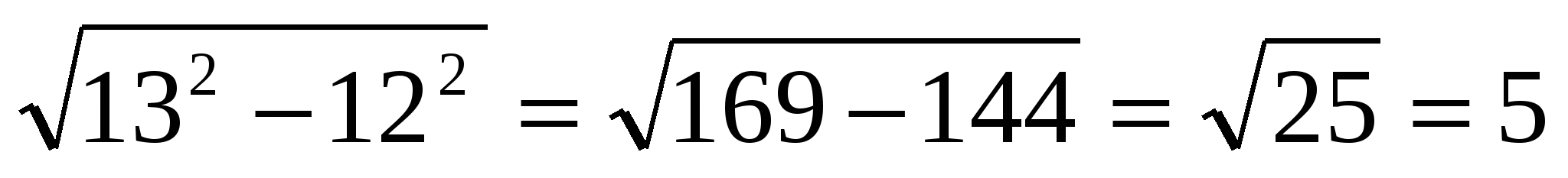 
II способ: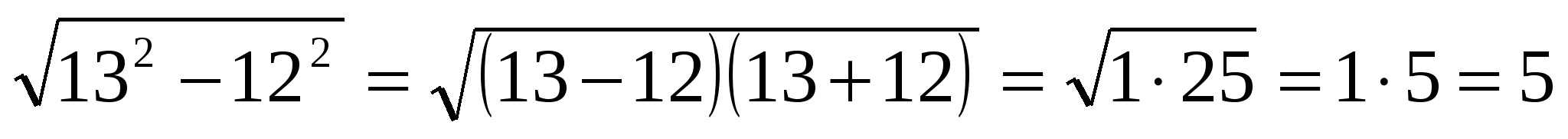 
Второй способ более изящный, мы применили формулу разности квадратов: а2-в2=(а-в)(а+в) и воспользовались свойством квадратных корней.
Гимнастика для глаз (слайды 15,16)
Сейчас я покажу вам решение некоторых примеров.
(слайд 17)
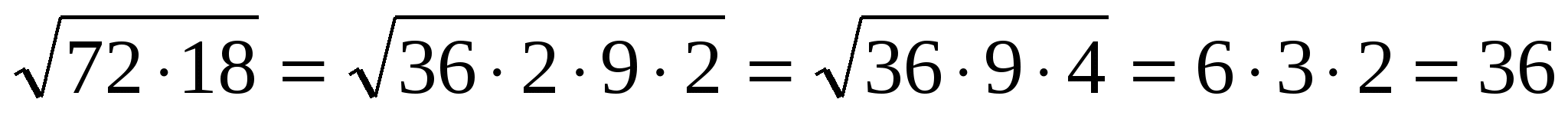
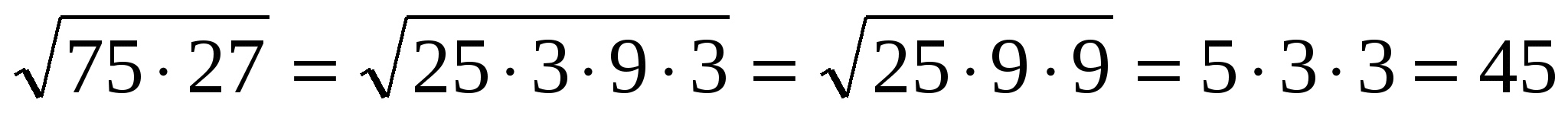
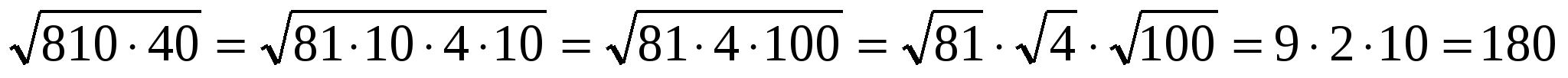
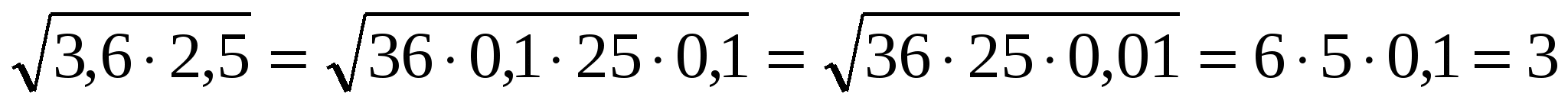
4. Самостоятельная работа. (слайд 18 )
1 вариант
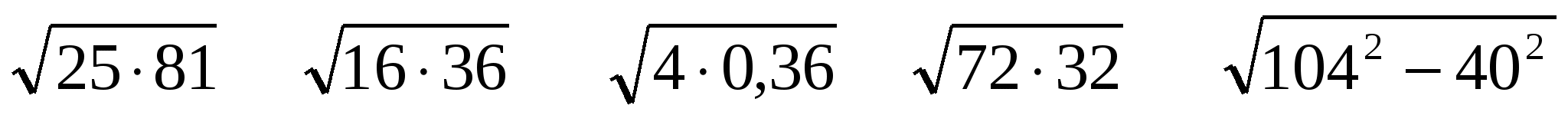
2 вариант
Критерии оценивания – слайд 19
5. Применение изученных свойств квадратных корней в других областях. (слайды20, 21)
Мы находимся на первой ступени преобразования квадратных корней.
Квадратные корни применяются при многих расчетах.
Так, например, в физике при определении первой космической скорости
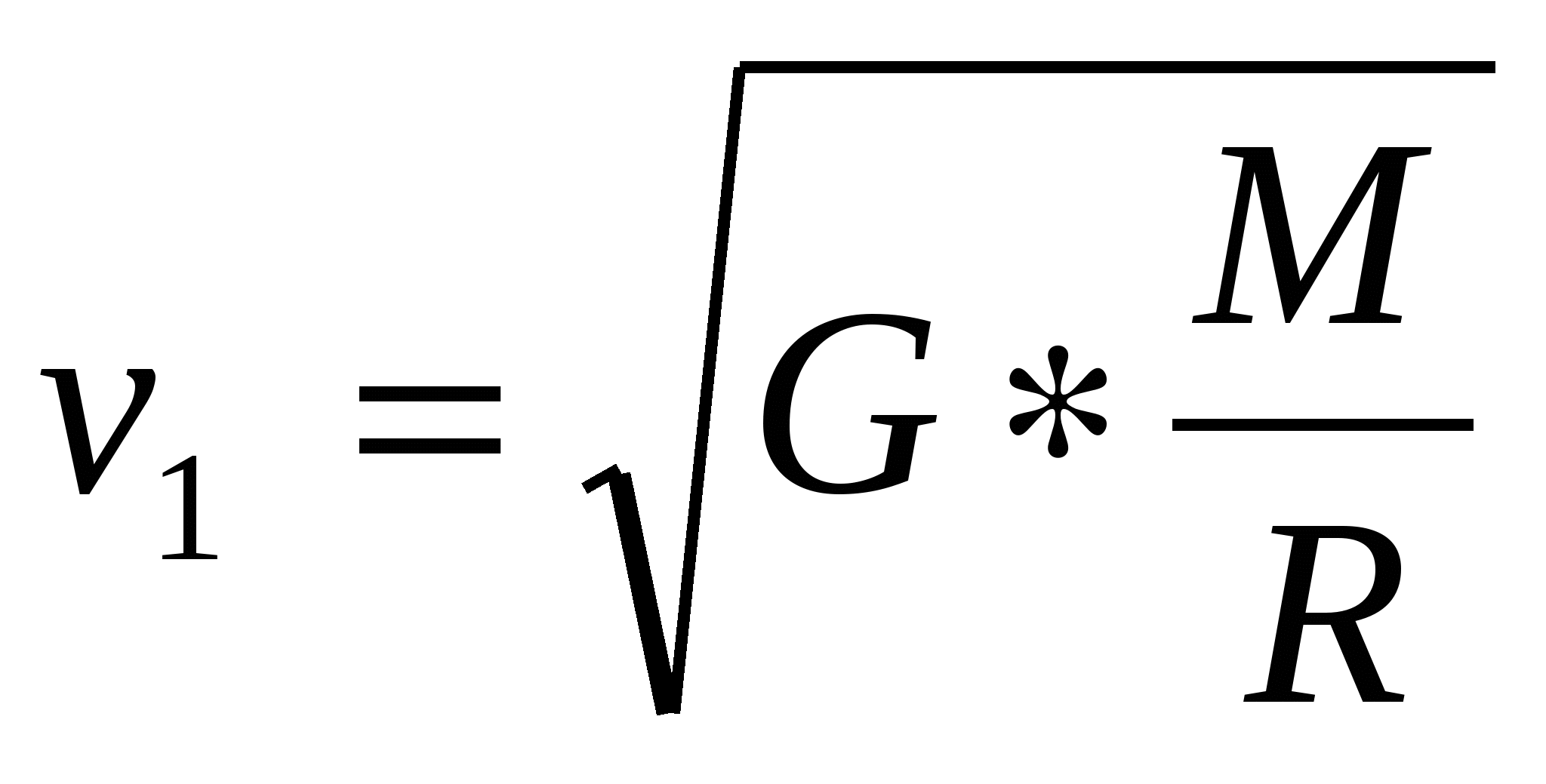
G-гравитационная постоянная:
M-масса Земли;
R-радиус Земли.
Расчетами первой космической скорости вы будете заниматься в 10 классе.
П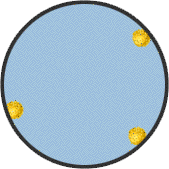
ри броуновском движении средняя квадратичная скорость молекул газа находится по формуле.
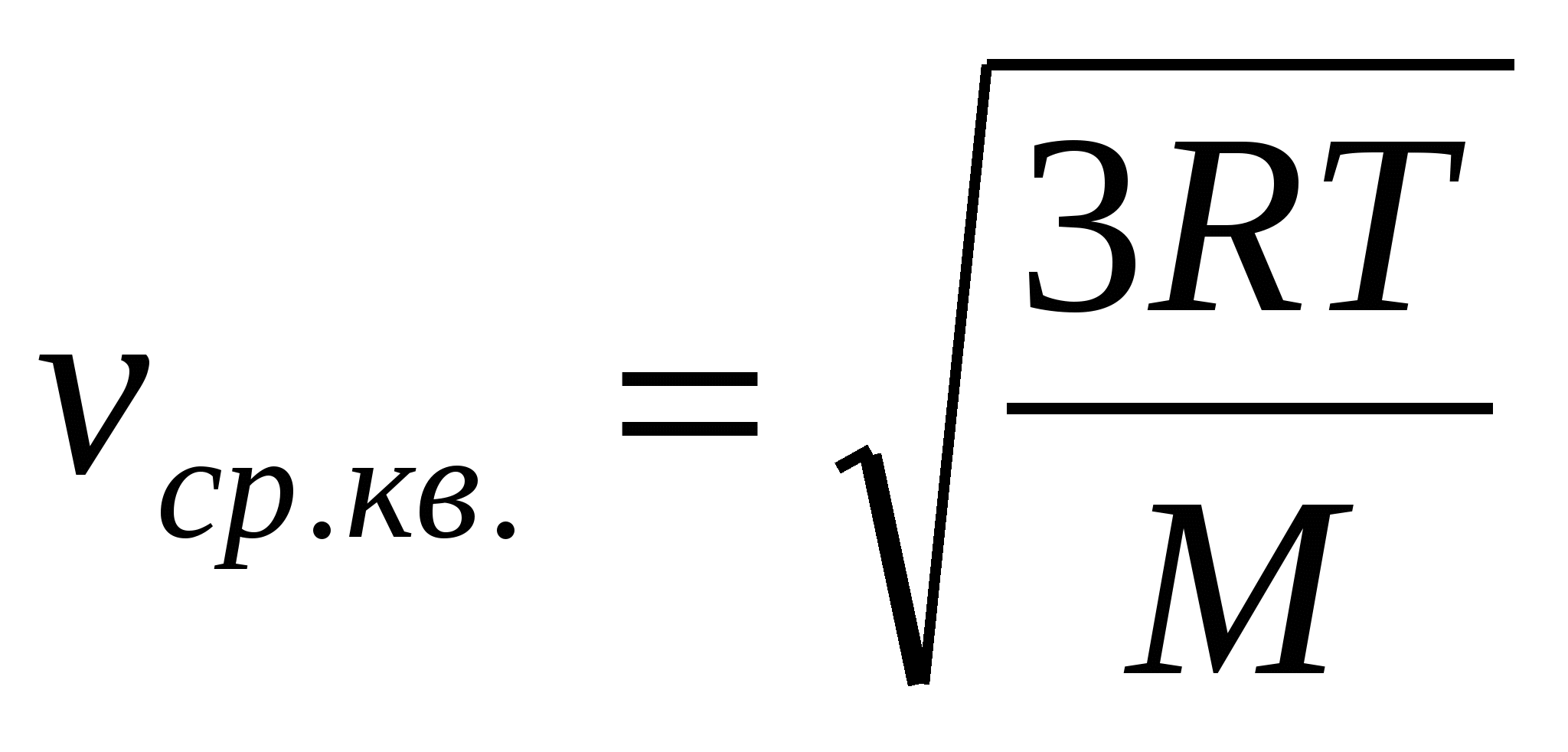
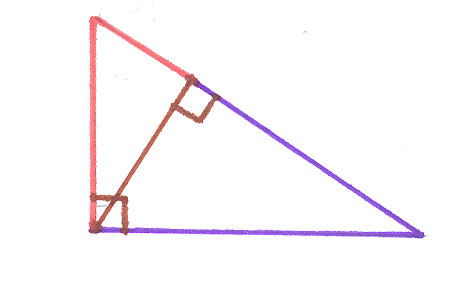
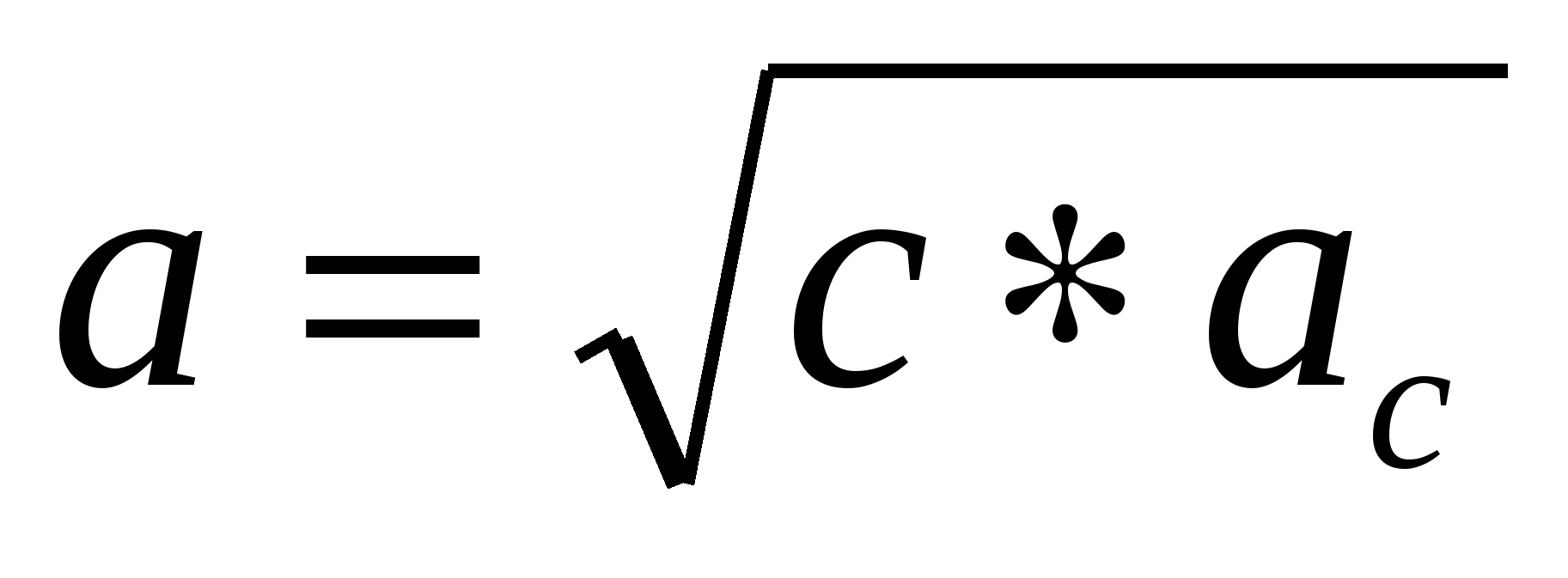
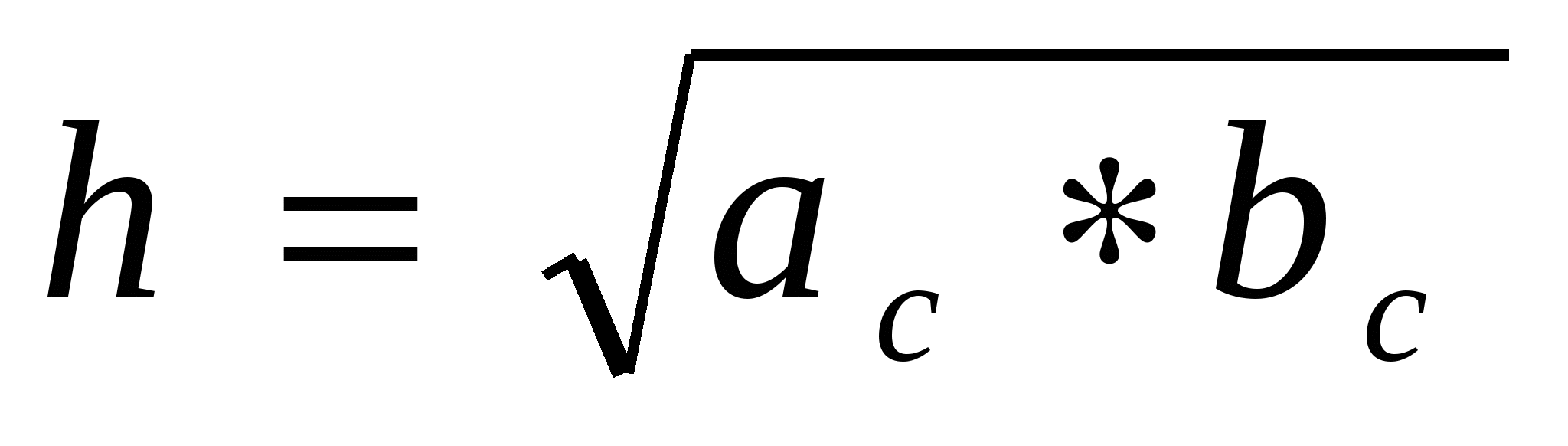
В геометрии часто встречаются средние значения, например катет прямоугольного треугольника равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу. А высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое проекций катета на гипотенузу.
Также площадь треугольника можно вычислить по формуле Герона: 
Итог урока. (слайд 22)
1. Сформулируйте теорему о квадратном корне из произведения.
2. Верно ли, что значения указанных квадратных корней можно найти по свойству квадратного корня из произведения?
а)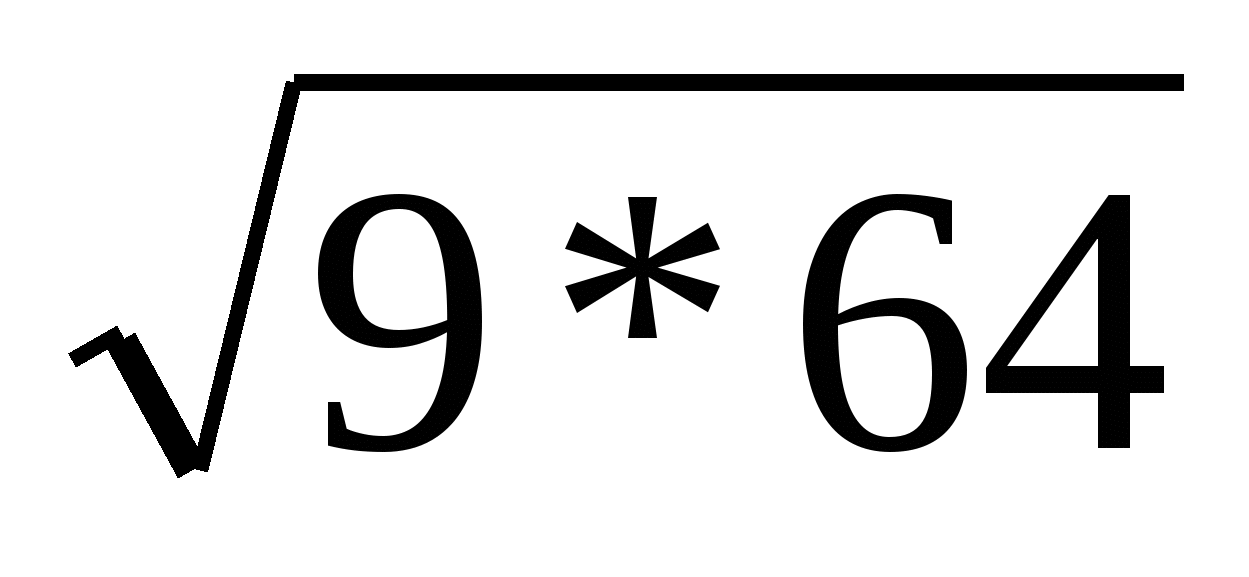 
б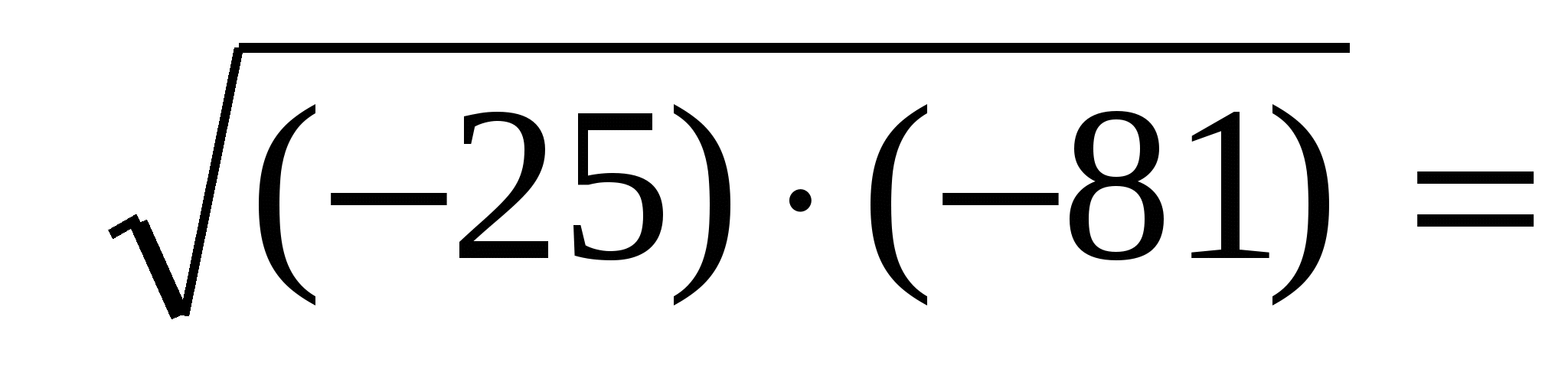
) 
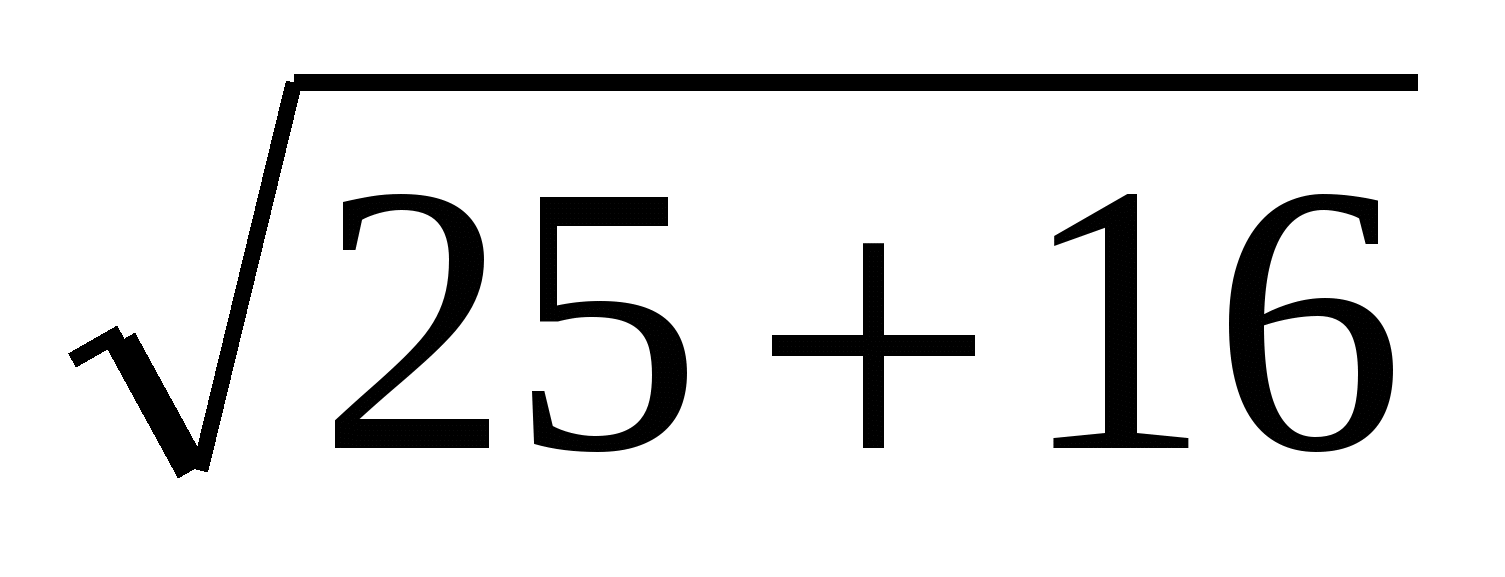
в)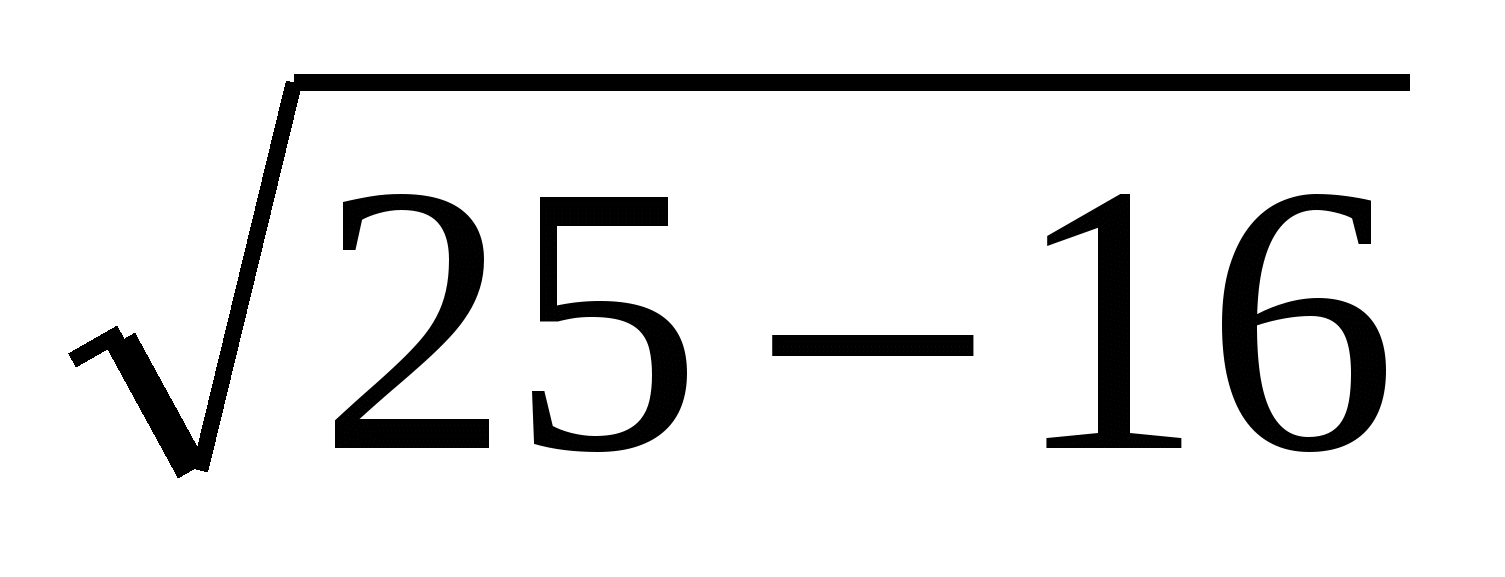 
Ученик вычислил значение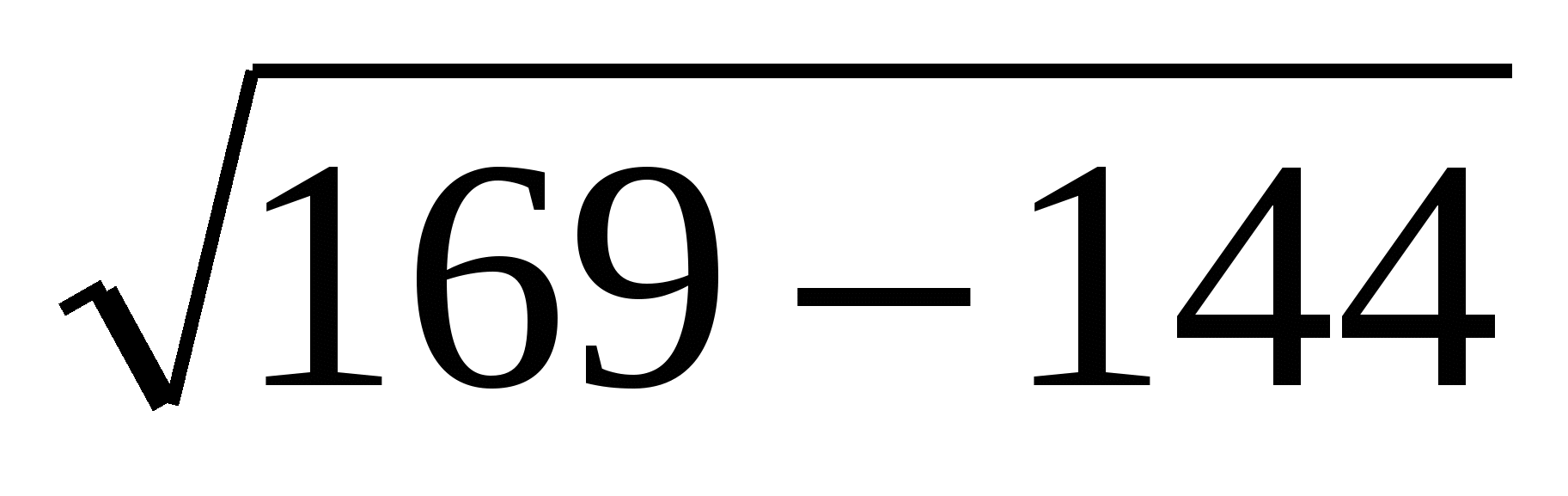 
и получил два варианта ответа 1 и 5. Какой из них верный? Объясните.
Согласно словам Дистервега: «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь», проведите самоанализ, ответив на вопросы на бланке.
Как я знаю и применяю материал по теме: «Квадратный корень из произведения»:
а)на отлично;
б) хорошо;
в) удовлетворительно;
г) совсем не знаю и не могу применять.
Поднимите, пожалуйста, руки те, кто достиг своих поставленных целей.
Поднимите руки те, кто получил оценку выше той, которую поставил себе на полях в начале урока.
А теперь поднимите руки те, кто не достиг тех результатов, которые намечал в начале урока.
Что еще нужно подучить, над чем нужно поработать?
Домашнее задание П.16, №№369(б,г,е), 374(б,г,е,з), 376(б,г,е) (слайд 23)
Слайд 24 На этом уроке вы, ребята, познакомились с теоремой об извлечении квадратного корня из произведения, а также рассмотрели её применение. Вам были предложены упражнения для решения и вы могли проверить себя. Я только хочу вам напомнить, что при решении задач, примеров надо искать рациональные подходы и применять разнообразные способы.
МОБУ СОШ с. Железнодорожный
Открытый урок алгебры в 8 классе
по теме:
«Квадратный корень из произведения»
Провела: учитель математики Гольман Л.М.
2014-2015 учебный год
infourok.ru
Свойства квадратных корней. Видеоурок. Алгебра 8 Класс
На данном уроке мы познакомимся со свойствами квадратных корней. Эти свойства позволяют решать многие примеры, связанные с квадратными корнями. На этом уроке мы не только сформулируем свойства квадратных корней, но и докажем их, а также решим несколько примеров.
Тема: Функция 
. Свойства квадратного корня
Урок: Свойства квадратных корней
На этом уроке мы повторим теорию, изученную ранее, а также сформулируем и докажем свойства квадратных корней и решим несколько примеров.
Напомним определение квадратного корня:
квадратным корнем из неотрицательного числа
называется такое неотрицательное число 
, квадрат которого равен : 
.
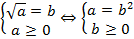К примеру: 
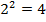, т. к. 
; 
, т. к. 
; 
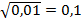, т. к. 
.
Вспомним, как выглядит график функции 
. Он тесно связан с графиком функции 
.
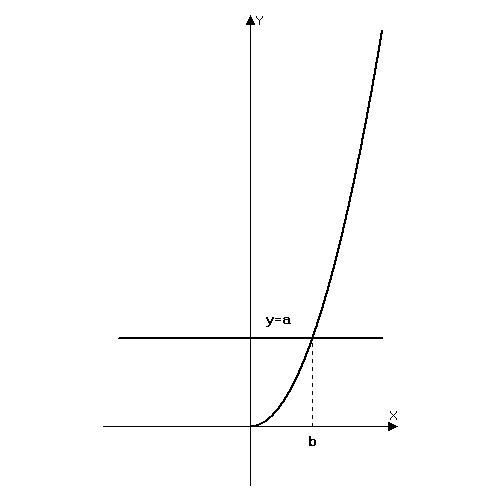
Рис. 1.
График функцией :
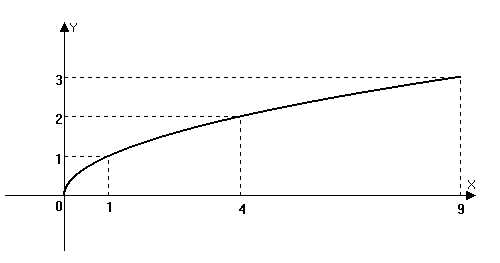
Рис. 2.
Итак, мы вспомнили, что такое корень квадратный из неотрицательного числа (арифметический корень) и как выглядит его график.
Квадратный корень (арифметический корень) обладает целым рядом свойств:
1. 
(
). Если и – неотрицательные числа, то корень из их произведения равен произведению корней.
Доказательство:
Воспользуемся определением квадратного корня: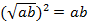
, а с другой стороны: 
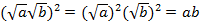. Получаем, что: 
. Но мы знаем, что функция принимает свои значения ровно один раз. Значит, из равенства квадратов, получаем: . Доказано.
Примеры:
1. 
.
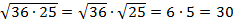2. 
.
Рассмотрим обобщение первого свойства:
.
Примеры:
1. 
.
2. 
.
3. 
(
interneturok.ru
Конспект урока алгебры в 8-м классе по теме «Квадратный корень из степени»
Цели:
- закрепить ранее приобретенные знания, умения и навыки учащихся по изучаемой теме;
- научить обучающихся выполнять действия извлечения квадратного корня из степени;
- способствовать формированию ключевых компетенций: уметь извлекать пользу из опыта, решать проблемы, получать информацию из различных источников;
- способствовать формированию умения учащихся успешно действовать в ситуации выбора.
Оформление и оборудование:
- кодоскоп и кодопленка;
- карточки-задания на три уровня сложности;
- портрет Рене Декарта;
- “Декартов лист”;
- опорные конспекты;
- М/к.
Ход урока
Вводное слово учителя: Мы продолжаем изучение большой и важной темы “Арифметический квадратный корень”. Сегодня нам предстоит научиться выполнять действие извлечения корня квадратного из степени.
І. Актуализация первичного субъектного опыта учащихся.
| Учитель: Начнем с повторения теоретического материала. Вспомните и назовите понятия и термины, изученные вами при прохождении данной темы. | Учащиеся отвечают: Об арифметическом rвадратном корне я знаю, что: |
| Запишите данные определения кратко (с
помощью букв, в общем виде). У доски двое: |
– это неотрицательное число – Действие нахождения , называется извлечением квадратного корня. Способы извлечения квадратного корня: – – иррациональные числа |
Задание 1. Используя определение арифметического квадратного корня и различные способы извлечения квадратных корней выполнить задание:
“Найди ошибку” (5 мин.)
Выпишите номера верных равенств. Назовите их (по 3 чел. с варианта, по желанию).
Через кодоскоп:
I в. : 3, 4, 6*
II в.: 4, 5
Указать типичные ошибки: (через кодоскоп)
ІІ. Мотивирование необходимости выполнения преобразований квадратных корней.
Учитель: Мы говорили с Вами, что действие извлечения квадратных корней из числа возникло в практике людей в связи с необходимостью находить сторону квадрата заданной площади. В дальнейшем упрощение выражений, содержащих квадратные корни, потребуется для решения квадратных, иррациональных уравнений и неравенств, при решении целого ряда геометрических задач.
Проблема: 1. Так как же извлечь корень квадратный из степени, в частности .
Обратите внимание; подчеркните в задании I.
Учитель: Кто готов доказать свою точку зрения?
Запишем строгое доказательство теоремы 1.
Данное равенство выполняется при любых значениях входящих в них букв, говорят, что это равенство выполняется тождественно.
| Определение: Равенства,
справедливые при любых значениях входящих в них
букв, называются тождествами: Например: |
На обратной стороне доски |
| Учитель: Рассмотрим
применение тождества для упрощения
алгебраических выражений, содержащих квадратные
корни из степени. Обратимся к учебнику. Учитель: Кому трудно? Обратитесь к учителю! Кто готов поделиться? |
Работа с учебником § 22 стр 94. Задача 1. Записать решение в тетрадь |
| III. Первичное закрепление. | |
| № 330, № 329 (4-6) Дополнительно: № 331(1)* |
У доски по желанию работают уч-ся. Комментировано № 331(1)* на обратной стороне доски |
IV. Историческая страничка.
Учитель. Всегда интересно знать имя ученого-математика, который ввел новое понятие, либо доказал теорему, либо придумал новый математический символ. Выясним, кто первым ввел знак корня (1637 г.)
Слово предоставляется поисковой группе 1 ряда + (СМС сообщения – 2 ряда).
Рене Декарт (1596-1650) французский дворянин, в 1629 г. переселился в Голландию. Воин, математик, филосов, физиолог, мыслитель. Что мы знаем о Рене Декарте – математике:
Заложил основы аналитической геометрии.
Ввел буквенные обозначения в алгебру x2, y3, a + b и т.д.
Декартовы координаты, определяющие функцию переменной величины.
Дал понятие импульса силы.
Ввел понятие рефлекса (дуга Декарта).
Высказал закон сохранения количества движения.
Учитель: Построил кривую 3 порядка на координатной плоскости.
x2 + y3 – 3axy=0
Вопрос. Как бы вы её назвали. Какие ассоциации? “Декартов лист”.
Физкультпауза. Гимнастика для глаз.
V. Самостоятельная работа по карточкам с самопроверкой и самооценкой.
Учащимся предлагается в течение пяти минут выполнить задания по карточкам.
Они могут избрать один из вариантов выполнения работы:
- 1 вариант – полностью самостоятельно;
- II вариант – по аналогии с решениями упражнений, записанных в тетради и на доске;
- III вариант – с использованием учебника.
Задания по карточкам:
Самопроверка через кодоскоп. Самооценка.
Перед проверкой педагог объявляет нормы оценок.
По желанию учащихся оценки могут быть выставлены в журнал, после проверки работы учителем.
VI. Подведение итогов.
Ученики еще раз на основе выполненных упражнений сформулируют правило извлечения квадратного корня из степени.
VII. Домашнее задание.
Всем учащимся предлагается выполнять задания из учебника № 328, № 321.
Кому будет посильно: вместо № 331 – № 336 (1,2).
Указание: Ообратиться к учебнику § 22.
urok.1sept.ru
Квадратный корень из произведения (8-й класс)
Цели урока:
- Повторить определение и изученные свойства арифметического квадратного корня.
- Закрепить умения применять их для преобразования выражений, содержащих квадратные корни, вычислять значения квадратных корней.
- Формировать у учащихся элементы “само” (самоконтроля, самоанализа, самооценки).
- Проверить знания и умения с помощью тестирования
Тип урока: урок повторения и контроля знаний, умений и навыков.
Формы и методы работы:
Фронтальная.
Индивидуальная работа с дифференциацией (карточки, дидактические материалы).
Групповая.
Оборудование урока:
Оценочный лист на каждого ученика.
Карточки.
Дидактические материалы.
Тесты.
Компьютеры, проектор.
Ход урока
1. Организационный момент.
Сообщение темы и плана урока.
2. План урока: (слайд 2. Презентация)
Повторение — мать учения.
От слов к делу.
Задания с расшифровкой.
Тестирование.
Подведем черту.
Организую деятельность учащихся по целеполаганию урока.
У каждого ученика есть оценочный лист (слайд 3).
Оценочный лист:
Фамилия, имя: ___________________
| Этапы урока | I | II | III | IV | Всего | 0ценка | ||||||||||||||
| Ответы | ||||||||||||||||||||
| Количество баллов | ||||||||||||||||||||
Критерии оценки:
“5” — 17-18 баллов,
“4” — 14-16 баллов,
“3” — 9-13 баллов.
Предлагаю подписать его и в него записывать ответы предложенных заданий на каждом этапе урока. После проверки, под ответом, правильный ответ отметить “+”, а неправильный “ — ”. Каждый правильный ответ оценивается в “1” балл, а неправильный в “0” баллов. По мере выполнения заданий вы будете подсчитать количество правильных ответов и записать их сумму в строку “ количество баллов”. В конце урока вы подсчитаете сумму набранных баллов и поставите себе оценку.
II. Повторение — мать учения.
На этом этапе урока повторяем определение и изученные свойства арифметического квадратного корня. На слайде(4, 5) вы видите вопрос и к нему 3 варианта ответов. Внимательно прочитайте вопрос и выберите тот ответ, который вы считаете правильным. Букву правильного ответа занесите в оценочный лист. Проверьте себя и отметьте правильность своего ответа.
Как называется выражение
а) квадратным корнем;
б) арифметическим квадратным корнем из числа а;
в) корнем из числа а.
2. Что называется арифметическим квадратным корнем из числа
а) число, квадрат которого равен а;
б) положительное число, квадрат которого равен а;
в) неотрицательное число, квадрат которого равен а.
3) При каком значении а выражение имеет смысл
а) при положительном а;
б) при отрицательном а;
в) при неотрицательном а.
4) Чему равно значение выражения
а) Х;
б) – Х;
в)
5. Если , то
а)
б)
в)
Сформулируйте теорему о квадратном корне из произведения и теорему, ей обратную (проверить правильность формулировки по слайду 6, обратить внимание на запись этой теоремы с помощью математических символов).
III. От слов к делу.
На этом этапе урока ученики объясняют (устно) решение заданий и проверяют свое решение по слайду 7.
1) Вычислите значение квадратного корня, используя теорему о корне из произведения:
2) Внесите множитель под знак корня:
3) Вынесите множитель из-под знака корня:
Задания 4, 5 ученики выполняют самостоятельно, ответы записывают в оценочный лист, затем проверяют свое решение по слайду 8, 9.
4) Найдите значение выражения
5) .Определите неизвестный множитель:
5) Определите неизвестный множитель:
IV. Задания с расшифровкой.
Каждому ученику выдается карточка с заданиями (приложение 1), ответы к которым зашифрованы и занесены в таблицу (слайд 10).
Выполнив задания, напротив номера задания ученики записывают букву, соответствующую полученному ответу.
В результате проверки (слайд 11) из букв составляем высказывание французского математика Б. Паскаля (слайд 12).
V. Тестирование.
Учащиеся подсчитывают набранное количество баллов. Предлагаю выполнить или компьютерное тестирование, или самостоятельную работу различного уровня сложности (по выбору учащихся) (приложение 2) (ответы записывают в оценочный лист). Проверив свои ответы (слайд 13), предлагаю учащимся оценить свою работу на уроке. Приложения 1–3
VI. Домашнее задание:
1 группа. № 350-353 (2, 4)
2 группа. № 354-357 (четные).
VII. Подведем итоги: (слайд 14), (слайд 15).
Литература
1. Алгебра: Учебник для 8 класса общеобразовательных учреждений/ Ш.А.Алимов и др. -11 изд. — М.:Просвещение, 2007.
2. Дидактические материалы по алгебре для 8 класса/ В.И Жохов и др. — М.: Просвещение, 2006.
3. “Энциклопедический словарь юного математика, для среднего и старшего школьного возраста” Редакционная коллегия: Гнеденко Б.В. (главный редактор), Савин А.П. (составитель).
urok.1sept.ru
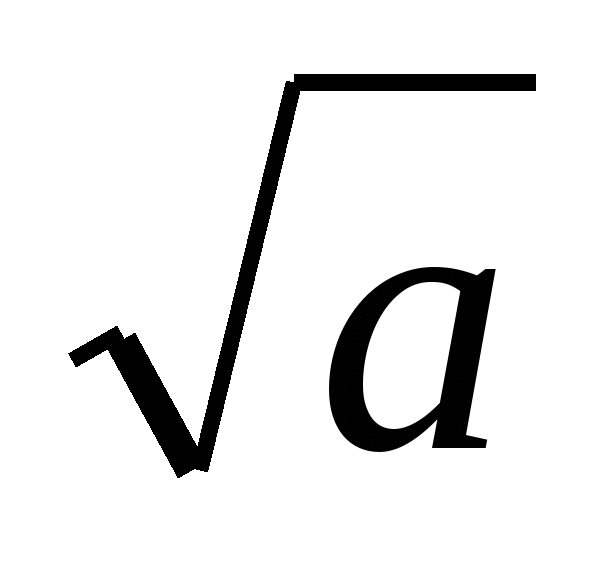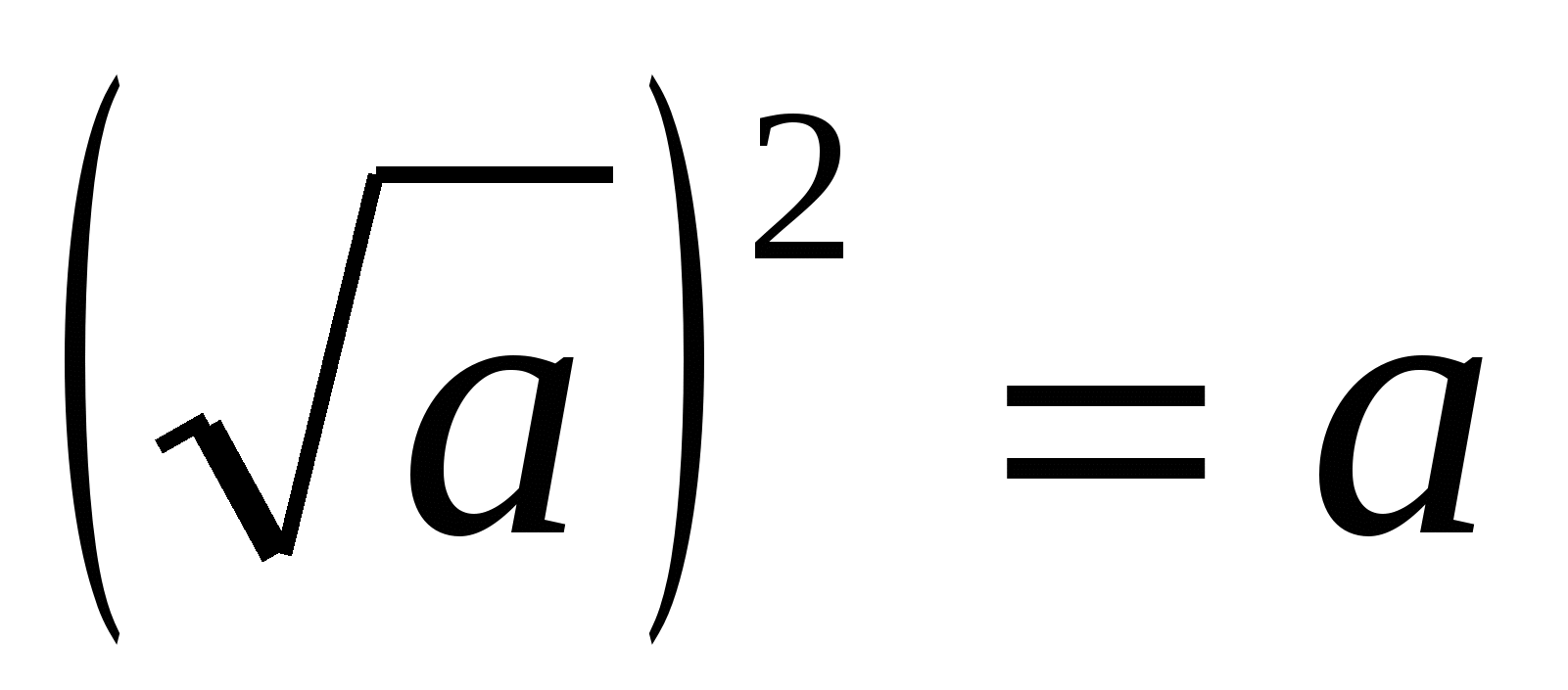