1.1.5 Корень степени n > 1 и его свойства
Видеоурок 1: Степени и корни
Видеоурок 2: Свойства корня степени n > 1
Лекция: Корень степени n > 1 и его свойства
Корень
Предположим, Вы имеете уравнение вида:
Решением данного уравнения будет х1 = 2 и х2 = (-2). В качестве ответа подходят оба решения, поскольку числа с равными модулями при возведении в четную степень дают одинаковый результат.
Это был простой пример, однако, что мы можем сделать в том случае, если, например,
Давайте попробуем построить график функции y=x2. Её графиком является парабола:
На графике необходимо найти точки, которым соответствует значение у = 3. Данными точками является:
Это означает, что данное значение нельзя назвать целым числом, но можно представить в виде корня квадратного.
Любой корень — это иррациональное число. К иррациональным числам относятся корни, непериодические бесконечные дроби.
Квадратный корень — это неотрицательное число «а», подкоренное выражение которого равно данному числу «а» в квадрате.
Например,
То есть в результате мы получим только положительное значение. Однако в качестве решения квадратного уравнения вида
Решением будет х1 = 4, х2 = (-4).
Свойства квадратного корня
1. Какое бы значение не принимала величина x, данное выражение верно в любом случае:
2. Сравнение чисел, содержащих квадратный корень. Чтобы сравнить данные числа, необходимо и одно, и второе число внести под знак корня. То число будет больше, чье подкоренное выражение больше.
Вносим число 2 под знак корня
А теперь давайте внесем число 4 под знак корня. В результате этого получим
И только теперь два полученных выражения можно сравнить:
3. Вынесение множителя из под корня.
Вынесение множителя из под корня.
Если подкоренное выражение может разложиться на два множителя, один из которых можно вынести из под знака корня, то необходимо пользоваться данным правилом.
4. Существует свойство, обратное данному — внесение множителя под корень. Этим свойством мы заведомо воспользовались во втором свойстве:
Корень степени n > 1
Под корнем n-ой степени некоторого числа «a» понимают число, которое при возведении в степень «n» даст число «а».
Иными словами можно сказать, что это решение следующего уравнения:
Например,
Если под корнем некоторой степени стоит степень, то для вынесения данного числа из под знака корня следует показатель степени разделить на степень корня.
Корень степени N
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса. 🙂
🙂
Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.
Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:
Корни бывают чётной степени (наш любимый $\sqrt{a}$, а также всякие $\sqrt[4]{a}$ и даже $\sqrt[116]{a}$ ) и нечётной степени (всякие $\sqrt[3]{a}$, $\sqrt[7]{a}$ и т.д.). И определение корня нечётной степени несколько отличается от чётной.
{2}}=1$.
Кубические корни тоже часто встречаются — не надо их бояться:
\[\begin{align} & \sqrt[3]{27}=3; \\ & \sqrt[3]{-64}=-4; \\ & \sqrt[3]{343}=7. \\ \end{align}\]
Ну, и парочка «экзотических примеров»:
\[\begin{align} & \sqrt[4]{81}=3; \\ & \sqrt[5]{-32}=-2. \\ \end{align}\]
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. {n}}=a\]
{n}}=a\]
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:
\[\sqrt{2}=1,414213562…\]
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]
Или вот ещё пример:
\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.
Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
Пример.
\[\begin{align} & \sqrt{2+\sqrt[3]{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt[3]{\sqrt[5]{-32}}=\sqrt[3]{-2}\approx -1,2599… \\ \end{align}\]
Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой.
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
\[\sqrt{4}=2\]
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.
Подобная проблема возникает у всех корней с чётным показателем:
- Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
- Из отрицательных чисел корень с чётным $n$ вообще не извлекается.
 {3}}$: Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
{3}}$: Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числаИз этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке.
 Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
- Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
- А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок.
 {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
\[\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}\]
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
\[\begin{align} & \sqrt[3]{-8}=-\sqrt[3]{8}=-2; \\ & \sqrt[3]{-27}\cdot \sqrt[5]{-32}=-\sqrt[3]{27}\cdot \left( -\sqrt[5]{32} \right)= \\ & =\sqrt[3]{27}\cdot \sqrt[5]{32}= \\ & =3\cdot 2=6. \end{align}\]
\end{align}\]
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.
{n}}=a$.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
Область поиска арифметического корня — неотрицательные числаКак видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. {2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$
{2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]
{n}}=a \right. \right\}\]
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
- Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
- Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
- Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Пример. Вычислите выражения:
\[\overline{\sqrt{4}};\quad \overline{\sqrt[3]{-27}};\quad \overline{\sqrt[4]{-16}}.
\]
Решение. С первым выражением всё просто:
\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
\[\overline{\sqrt[3]{-27}}=\left\{ -3 \right\}\]
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
\[\overline{\sqrt[4]{-16}}=\varnothing \]
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt[4]{-16}$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются.
Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)
Смотрите также:
- Умножение корней n-й степени
- Свойства арифметического квадратного корня
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Тест по методу интервалов для строгих неравенств
- Вебинар по задачам 18: модуль и окружности
- Решение задач на движение по воде
Калькулятор извлечения корня n-ой степени онлайн
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из теоремы Пифагора и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
Определение корня n-ой степени. Свойства арифметического корня n-ой степени 9 класс онлайн-подготовка на Ростелеком
Тема 15.
Определение корня n-ой степени. Свойства арифметического корня n-ой степени.
Давай вспомним, что квадратным корнем из числа а называется такое число, квадрат которого равен а. Аналогично определяется корень любой натуральной степени n.
Аналогично определяется корень любой натуральной степени n.
Итак, корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.
Например, корнем пятой степени из 32 является число 2, так как 25=32, корнем четвертой степени из 81 является каждое из чисел 3 и -3, так и 34=81 и (-3)4=81. Корень второй степени принято называть квадратным корнем, а корень третьей степени – кубическим корнем.
Если n — нечетное число, то выражение an имеет смысл при любом a; если n — четное число, то выражение an имеет смысл при a≥0.
Из определения корня n-ой степени следует, что при всех значениях а, при которых выражение anимеет смысл, верно равенствоann=a.
Определение: Арифметическим корнем n-ой степени из неотрицательного числа а называется неотрицательное число, n-ая степень которого равна а.
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень. Например,
-83=-83=-2
Значит, при любом положительном a и нечетном n верно равенство:
-an=-an
Решим уравнение: x6 = 7. Корнями уравнения служат числа, шестая степень которых равна 7. И таких чисел два: 76 и -76.
Решим уравнение x3 = 27. Уравнение имеет единственный корень, это число, третья степень которого равна 27, то есть 273=3.
Рассмотрим свойства арифметического корня n-ой степени.
- Если a≥0 и b≥0, то abn=anbn
Корень из неотрицательных множителей равен произведению корней из этих множителей.
Например, найдем значение выражения 16∙814=164∙814=2∙3=6
- Если a≥0 и b>0, то abn=anbn
Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Например, найдем значение выражения 210273=64273=643273=43=113.
- Если n и k – натуральные числа и a≥0, то akn=ank
- Если n,k и m – натуральные числа и a≥0, то amknk=amn
Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
Рассмотрим некоторые примеры.
Вычислим значение выражения:
1353∙253=135∙253=27∙5∙253=27∙1253=3∙5=15
5106212∙526=510∙212∙526=512∙2126=10126=102=100
8-373∙8+373=8-378+373=64-373=273=3
Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №16 Название темы: Арифметический корень натуральной степени.
Перечень тем, рассматриваемых на уроке:
- преобразование и вычисление арифметических корней,
- свойства арифметического корня натуральной степени,
- корень нечетной степени из отрицательного числа,
- какими свойствами обладает арифметический корень натуральной степени.

Глоссарий
- Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
- Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
- Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
- Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
- Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл.– М.: Просвещение, 2014.
- Сканави М. И., Зайцев В. В., Рыжков В.
 В. «Элементарная математика». – Книга по требованию, 2012.
В. «Элементарная математика». – Книга по требованию, 2012. - Семенова А.Л., Ященко И.В. ЕГЭ 3000 задач с ответами, математика под редакцией Москва, 2017.
- Ященко И. В. ЕГЭ 3300 задач с ответами, математика профильный уровень под редакцией Москва, 2017.
Объяснение темы «Арифметический корень натуральной степени»
Решим задачу.
Площадь квадрата S=16 м².
Обозначим сторону квадрата а, м.
Тогда, а² = 16.
Решим данное уравнение:
a=4 и а= –4.
Проверим решение:
4² = 16;
(–4)² = 16.
Ответ: длина стороны квадрата равна 4 м.
Определение:
Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
Определение:
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
Обозначение: .
Определение:
Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.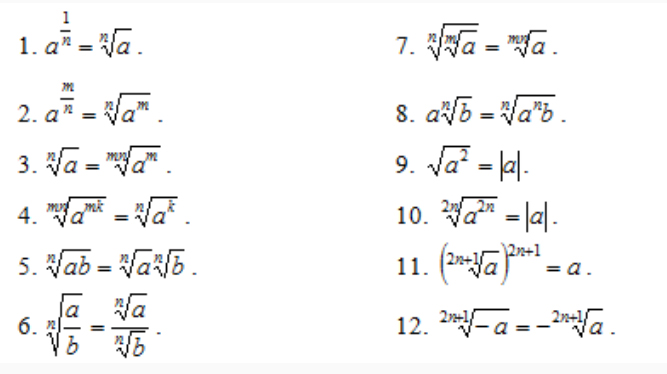
Обозначение: .
Например:
.
.
.
На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.
Определение:
Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
Определение:
Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Обозначение: – корень n-й степени, где
n–степень арифметического корня;
а– подкоренное выражение.
Давайте рассмотрим такой пример: .
Мы знаем, что (–4)³ = –64, следовательно, .
Еще один пример: .
Мы знаем, что (–3)5 = –243, следовательно, .
На основании этих примеров, можно сделать вывод:
, при условии, что n –нечетное число.
Свойства арифметического корня натуральной степени:
Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:
- .
Примеры:
.
.
- .
Примеры:
.
.
- .
Пример:
.
- .
Пример:
.
- Для любогоа справедливо равенство:
Пример:
Найдите значение выражения , при 3 <x< 6.
Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:
=|x – 3| = х – 3, т.к. х>3;
=|x – 6|=6 – x, т.к. х<6.
Получаем: х – 3 + 6 – х= 3.
Примеры заданий.
Первый пример.
Задача:
Выберите верные утверждения:
Разбор задания.
Применим определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Следовательно, верными могут быть только неотрицательные выражения.
Ответ: ; ;
Второй пример.
Задача:
Выделите самое маленькое число:
Разбор задания:
Корень из отрицательного числа будет отрицательным числом, следовательно, наименьшее число –
Ответ: 4.
Корень n-ной степени из действительного числа /qualihelpy
Если показатель корня четное число, то подкоренное выражение не может быть отрицательным числом, так как четная степень и положительного и отрицательного числа есть число положительное.
Если показатель корня нечетное число, то подкоренное выражение может быть положительным числом, отрицательным числом и числом .
Свойства корней:
; (1.16) ; (1.17) ; (1.18); (1.19) . (1.20)
Внесение множителя под знак корня
Если показатель корня нечетное число, то для любого числа и натурального числа справедливо равенство: . (1.21)Если , то . Например, .Вынесение множителя из-под знака корня
Если показатель корня нечетное число, то справедливо равенство:
. (1.22)Если показатель корня четное число, то справедливо равенство:
. (1.23)Например: ; .Сравнение выражений, содержащих корни
1. Если , то . Например, .2. Если и , то . Например, .3. Если и , то . Например, .4. Чтобы сравнить числа и , необходимо представить их в виде корня одной и той же степени.Степень с действительным показателем
Степени с действительным показателем обладают всеми свойствами степеней с целым показателем. При этом следует помнить, что:
а) степень числа с натуральным показателем имеет смысл для любого основания, так как эта степень определяется с помощью операции умножения;
б) степень с целым отрицательным показателем имеет смысл для любого основания, кроме основания , так как эта степень определяется с помощью операций умножения и деления;в) степень с рациональным показателем определяется с помощью операции извлечения корня, которая всегда выполнима, если основание степени положительное число и не всегда выполнима, если основание степени отрицательное число;
г) степень с любым действительным показателем всегда определена, если ее основание – положительное число.
Среднее арифметическое и среднее геометрическое
Чтобы найти среднее арифметическое нескольких чисел необходимо сумму этих чисел разделить на их количество.
Например, среднее арифметическое чисел , и равно .КОРЕНЬ ЧИСЛА — это… Что такое КОРЕНЬ ЧИСЛА?
Корень квадратный — Квадратный корень из (корень 2 й степени) это решение уравнения вида . Несмотря на то, что в первую очередь под и подразумеваются числа, в различных рассмотрениях они могут быть математическими объектами различной природы, в том числе такими как … Википедия
КОРЕНЬ — КОРЕНЬ, рн , мн. рни, рней, муж. 1. Подземная часть растения, служащая для укрепления его в почве и всасывания из неё воды и питательных веществ. Главный, боковой, придаточный к. Воздушные корни (у лиан и нек рых других растенийвысоко над землёй … Толковый словарь Ожегова
КОРЕНЬ — (математическое), 1) Корень степени n из числа a Число, n я степень которого равна заданному числу a (обозначается ; a называется подкоренным выражением). Действие нахождения корня называется извлечением корня. 2) Решение уравнения значение… … Современная энциклопедия
Действие нахождения корня называется извлечением корня. 2) Решение уравнения значение… … Современная энциклопедия
Корень (матем.) — КОРЕНЬ (математическое), 1) Корень степени n из числа a число, n я степень которого равна заданному числу a (обозначается ; a называется подкоренным выражением). Действие нахождения корня называется извлечением корня. 2) Решение уравнения… … Иллюстрированный энциклопедический словарь
КОРЕНЬ КУБИЧЕСКИЙ — (обозначение 3Ц), число, которое необходимо дважды умножить на само себя для получения заданного числа. Например, кубический корень из 64 равняется 4, поскольку 4x4x4 = 64. В этом случае записывают: 3Ц64 = 4. В терминах алгебры кубический корень… … Научно-технический энциклопедический словарь
КОРЕНЬ — в математике ..1) корень степени n из числа a всякое число x (обозначаемое , a называется подкоренным выражением), n я степень которого равна a (). Действие нахождения корня называется извлечением корня2)] Корень уравнения число, которое после… … Большой Энциклопедический словарь
КОРЕНЬ КВАДРАТНЫЙ — КОРЕНЬ КВАДРАТНЫЙ, число, обозначаемое как х, которое при умножении на само себя дает число х. Квадратный КОРЕНЬ из 4 равен 2, следовательно Ц4 = 2; Ц2 = 1,4142 (с точностью до четырех разрядов десятичной дроби). Отрицательные числа имеют… … Научно-технический энциклопедический словарь
Квадратный КОРЕНЬ из 4 равен 2, следовательно Ц4 = 2; Ц2 = 1,4142 (с точностью до четырех разрядов десятичной дроби). Отрицательные числа имеют… … Научно-технический энциклопедический словарь
КОРЕНЬ (в математике) — КОРЕНЬ, в математике 1) корень степени n из числа a всякое число x (обозначаемое , a называется подкоренным выражением), n я степень которого равна a (). Действие нахождения корня называется извлечением корня. 2) Корень уравнения число, которое… … Энциклопедический словарь
Корень из числа — КОРЕНЬ, рня, мн. рни, рней, м. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Корень (в математике) — Корень в математике, 1) К. степени n из числа а ≈ число х (обозначаемое ), n я степень которого равна а (то есть xn = а). Действие нахождения К. называют извлечением корня. При а ¹ 0 существует n различных значений К. (вообще говоря,… … Большая советская энциклопедия
Квадраты: многочлены второй степени
10
Решение квадратного уравнения с множителем
Двойной корень
Квадратичное неравенство
Сумма и произведение корней
КВАДРАТИКА — ДРУГОЕ НАЗВАНИЕ многочлена 2-й степени. 2 — самый высокий показатель степени.
2 — самый высокий показатель степени.
1. Какой вид имеет полиномиальная функция 2-й степени?
y = ax 2 + bx + c
2.Какой вид имеет квадратное уравнение?
топор 2 + bx + c = 0
3. Что мы подразумеваем под корнем квадратичного?
Решение квадратного уравнения.
4. Сколько корней всегда у квадратичной?
Два, реальные или сложные.
5. График квадратичной всегда имеет форму, называемую -?
Парабола.
6. Каковы три метода решения квадратного уравнения,
6. То есть нахождения корней?
1. Факторинг. 2. Завершение квадрата.
3. Квадратичная формула.
Начнем с метода факторинга. В следующей теме мы представим как Завершение квадрата, так и формулу квадратного уравнения.
7. Если произведение множителей равно 0 — если ab = 0 — то что вы можете
7. сделать вывод о факторах a , b ?
сделать вывод о факторах a , b ?
Либо a = 0, либо b = 0.
Пример 1. Решение по факторингу.
f ( x ) = x 2 −2 x −3. Найдите корни f ( x ) и нарисуйте график y = f ( x ).
Решение . x 2 −2 x −3 = ( x + 1) ( x — 3).
Следовательно, корни — это −1 и 3. (См. Урок 37 по алгебре.) Они представляют собой перехваты графа размером x .
Перехват y — постоянный член −3.
В каждом полиноме пересечение y является постоянным членом, потому что постоянный член — это значение y , когда x = 0.
Пример 2. Двойной корень
f ( x ) = x 2 −10 x + 25. Найдите корни
f ( x ) и нарисуйте график y = f ( х ).
Решение . x 2 −10 x + 25 =
( x — 5) ( x — 5) = ( x — 5) 2 .Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок алгебры 37, вопрос 4.)
При двойном корне график не пересекает ось x . Это просто трогает.
Двойной корень возникает, когда квадратичный является трехчленом полного квадрата: x 2 ± 2 ax + a 2 ; то есть, когда квадратичная величина является квадратом двучлена: ( x ± a ) 2 .
Пример 3. Сколько действительных корней, т.е. корней, которые являются действительными числами, имеет квадратичный элемент каждого графа?
Ответ . График а) имеет два действительных корня. Он имеет два перехватчика x .
График б) не имеет реальных корней. Он не имеет перехвата x . Оба корня сложные.
График c) имеет два действительных корня. Но они двойной корень.
Но они двойной корень.
Пример 4.Квадратичное неравенство.
Решите это неравенство:
x 2 — 4 x — 5
Для этого осмотрите график
y = x 2 — 4 x — 5.
Решение . Для каких значений x эта квадратичная величина будет отрицательной? То есть где график под осью x ?
График отрицательный между корнями, которые равны -1 и 5.Решение неравенства равно −1 x. Мы также можем заметить, что квадратичный будет иметь положительные значения — график будет выше оси x — слева и справа от корней:
x x> 5.
В то время как квадратичный будет иметь значение 0 в корнях.
Мы рассмотрели три возможности:
Этот квадратичный равен , равному 0 в двух корнях.
Это на меньше, чем 0 между двумя корнями.
Это на больше, чем 0 слева и справа от двух корней.
Эти три возможности, которые верны для любого действительного числа, имеют причудливое название Закона трихотомии. Любое число должно быть либо равно, меньше или больше 0.
Закон трихотомии также принимает такую форму:
Для любых действительных чисел a, b , либо a = b , a b, либо a > b .
Однако мы должны знать, какая из этих возможностей верна. Для любых двух чисел мы должны знать их относительный порядок. Это заложено в значении «числа».
Задача 1. Нарисуйте график y = x 2 — 2 x −8. То есть покажите перехваты x и y .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
x 2 −2 x — 8 = ( x + 2) ( x — 4). Следовательно, корни равны −2, 4. Пересечение y является постоянным членом −8.
Пересечение y является постоянным членом −8.
Задача 2. Нарисуйте график
.y = x 2 + 4 x + 4.
x 2 + 4 x + 4 = ( x + 2) 2 .В −2 есть двойной корень. Перехват y — постоянный член, 4.
Проблема 3.
а) Чтобы решить это квадратное неравенство —
x 2 + 2 x — 3> 0
—проверьте график
y = x 2 + 2 x — 3.
Квадратичное значение будет положительным — выше оси x — для значений x слева и справа от корня.Решение:
x x> 1.
б) Решите это квадратное неравенство:
x 2 + 2 x — 3
−3 х
Квадратичный будет отрицательным между корнями.
Проблема 4. Квадратичная имеет следующие корни. Запишите каждую квадратичную как произведение линейных множителей.
а) 3, 4 ( x — 3) ( x — 4)
б) −3, −4 ( x + 3) ( x + 4)
в) — р , с ( x + r ) ( x — s )
г) 3+, 3 — ( x -3 -) ( x −3 +)
Сумма и произведение корней
Теорема. В квадратичной системе со старшим коэффициентом 1:
Сумма корней равна отрицательным коэффициенту x ;
произведение корней — постоянный член.
То есть, если
x 2 + bx + c = 0,
и корни r и s , затем
| r + s | = | — б , |
| RS | = | с . |
Ибо, если корни равны r и s , то квадратичный равен
| ( x — r ) ( x — s ) | = | x 2 — rx — sx + rs |
| = | x 2 — ( r + s ) x + rs . | |
Коэффициент x равен — ( r + s ), что является отрицательным значением суммы корней. Постоянный член — рупий , который является их произведением.
Пример 5. Построить квадратичную с корнями 2 и 3.
Решение . Сумма корней равна 5, их произведение равно 6, следовательно, квадратичный равен x 2 — 5 x + 6.
Сумма корней равна минус коэффициента x . Произведение корней — постоянный член.
Пример 6. Построить квадратичную с корнями 2 +, 2 -.
Построить квадратичную с корнями 2 +, 2 -.
Решение . Сумма корней равна 4. Их произведение — разность двух квадратов: 2 2 — () 2 = 4 — 3 = 1.
Таким образом, квадратичный равен x 2 — 4 x + 1.
Пример 7. Построить квадратичный, корни которого равны 2 + 3 i , 2 — 3 i , где i — комплексная единица.
Раствор . Сумма корней равна 4. Произведение снова является разностью двух квадратов: 4 — 9 i 2 = 4 + 9 = 13.
Квадратичный с этими корнями равен
.x 2 — 4 x + 13.
Задача 5. Построить квадратичную с корнями −3, 4.
Сумма корней равна 1. Их произведение равно −12. Следовательно, квадратичный равен x 2 — x — 12.
Задача 6. Построить квадратичную с корнями 3 +, 3 -.
Сумма корней равна 6. Их произведение равно 9 — 3 = 6.
Их произведение равно 9 — 3 = 6.
Следовательно, квадратичный равен x 2 — 6 x + 6.
Задача 7. Построить квадрат, корни которого равны 2 + i , 2 — i .
Сумма корней равна 4. Их произведение равно 4 — ( i ) 2 = 4 + 5 = 9.
Следовательно, квадратичный равен x 2 — 4 x + 9.
*
В более общем смысле, для любого коэффициента x 2 , то есть, если квадратичный равен
топор 2 + bx + c ,
и корни r и s , затем
| r + s | = | – | b a | , |
| RS | = | c a | . | |
Когда a = 1, мы имеем теорему выше.
Следующая тема: Завершение квадрата
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставался в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Квадратное уравнение — обзор
VI.C Приложения к разрешимости и конструктивности
Проблема решения квадратных уравнений восходит, по крайней мере, к вавилонянам. В девятом веке мусульманский математик Аль-Хоресми дал версию современной квадратной формулы. В середине шестнадцатого века итальянские математики привели решение кубического уравнения к виду
x3 + mx = n
, разделив его на коэффициент x 3 и заменив x на некоторые x — c .Затем они решили это как
x = a − ba = (n / 2) + (n / 2) 2+ (m / 3) 33b = — (n / 2) + (n / 2) 2+ (m / 3) 3,3
Они приступили к решению уравнений четвертой степени, сводя их к кубикам. Но никто не смог решить общую квинтику, используя n корней -й степени, и в 1824 году Н.Х. Абель доказал, что это невозможно. Э. Галуа за свою короткую жизнь доказал это также в рамках общей теории, применимой ко всем многочленам. Это основано на теории поля, и мы опишем это позже.
Но никто не смог решить общую квинтику, используя n корней -й степени, и в 1824 году Н.Х. Абель доказал, что это невозможно. Э. Галуа за свою короткую жизнь доказал это также в рамках общей теории, применимой ко всем многочленам. Это основано на теории поля, и мы опишем это позже.
В расширениях F ( t ) один корень многочлена p ( t ) был добавлен или присоединен к F .Расширения, полученные сложением всех корней многочлена, называются нормальными расширениями. Корни можно добавлять по одному в любом порядке.
Конечномерные нормальные расширения можно изучать с помощью конечных групп, называемых группами Галуа. Группа Галуа нормального расширения F ⊂ E — это группа всех полевых автоморфизмов E , которые тождественны на F . По сути, он переставит корни многочлена, корни которого порождают расширение.Например, пусть F = Q (ξ) и E = F (23), где ξ = (- 1 + i3) / 2. Тогда существует автоморфизм E , который принимает 23 → ξ23 ξ23 → ξ 2 (23), ξ 2 (23) → 23. Группа Галуа является циклической группой порядка 3, порожденной этим автоморфизмом. Поскольку отношение ξ двух корней идет само на себя, оно является тождеством на Q (ξ).
Тогда существует автоморфизм E , который принимает 23 → ξ23 ξ23 → ξ 2 (23), ξ 2 (23) → 23. Группа Галуа является циклической группой порядка 3, порожденной этим автоморфизмом. Поскольку отношение ξ двух корней идет само на себя, оно является тождеством на Q (ξ).
Порядок группы Галуа равен степени нормального расширения. Более того, существует соответствие 1–1 между подполями F ⊂ K ⊂ E и подгруппами H ⊂ G , группой Галуа E над F .С подгруппой H связано поле k = { x ∈ E : f ( x ) = x для всех f ∈ K }.
Поле разделения полинома p над полем F является минимальным расширением F , по которому p делится на множители степени 1. Это нормальное расширение, и любые два поля разделения изоморфны.
Предположим, что многочлен p разрешим с помощью радикалов над Q .Пусть E будет полем разделения p на Q . Каждый раз, когда мы извлекаем радикал, корни радикала генерируют нормальное расширение F 1 предыдущего поля F 2 . Пусть E i = F i ∩ E . Тогда F 2 более F 1 имеет циклическую группу Галуа, поэтому E 2 более E 1 также.
Отсюда следует, что существует серия расширений Q = D 0 ⊂ D 1 ⊂ ⋯ ⊂ D n = E каждое нормальное по сравнению с предыдущим таким, что группы Галуа друг над другом циклические. Отсюда следует, что группа Галуа G имеет ряд подгрупп G n = { e } ⊂ G n − 1 ⊂ ⋯ ⊂ G 0 = G таких, что g i — нормальная подгруппа G i − 1 с циклической факторгруппой.Такая группа называется разрешимой.
Отсюда следует, что группа Галуа G имеет ряд подгрупп G n = { e } ⊂ G n − 1 ⊂ ⋯ ⊂ G 0 = G таких, что g i — нормальная подгруппа G i − 1 с циклической факторгруппой.Такая группа называется разрешимой.
Симметрическая группа степени 5 имеет единственную нетривиальную собственную нормальную подгруппу — простую знакопеременную группу. Следовательно, это не разрешимо. Если F ( x ) является неприводимым полиномом 5 степени над Q с ровно двумя невещественными корнями, в его группе Галуа существует элемент порядка 5 только потому, что 5 делит степень поля расщепления. Комплексное сопряжение дает транспозицию. Следовательно, группа Галуа — это L 5 .Таким образом, многочлены степени 5 не могут быть решены радикалами.
Наоборот, верно, что любое нормальное расширение E ⊂ F с циклической группой Галуа может быть порождено радикалами. Можно показать, что существует единственный элемент θ такой, что E = F (θ) ( c с учетом всех линейных комбинаций θ базиса для E по F , и существует конечное число промежуточных полей).
Можно показать, что существует единственный элемент θ такой, что E = F (θ) ( c с учетом всех линейных комбинаций θ базиса для E по F , и существует конечное число промежуточных полей).
Пусть расширение будет циклическим порядка n и пусть τ будет таким, что τ n = 1, но не меньшей степени.Пусть автоморфизм g порождает группу Галуа. Пусть t = θ + τ g (θ) + ⋯ + τ n-1 g n-1 (θ). Тогда t имеет n различных конъюгатов ( a ss, предполагая τu ∈ F ) g i (θ) + τ g i + 1 (θ) + ⋯ + τ n-1 g n-1 + i (θ), поэтому его минимальный многочлен имеет степень n . Поскольку g ( t ) = τ — 1 ( t ), элемент t n = a инвариантен относительно группы Галуа и лежит в F . Итак, θa, g (θ),…, g n-1 (θ) лежат в поле разделения x n = a , что должно быть E .
Итак, θa, g (θ),…, g n-1 (θ) лежат в поле разделения x n = a , что должно быть E .
Геометрические конструкции обеспечивают применение теории поля. Предположим, нам дан единичный отрезок прямой. Какие фигуры можно построить из него с помощью линейки и циркуля? Пусть отрезок будет взят за единицу длины или ось x . Везде, где мы строим новую точку из существующих с помощью линейки и циркуля, это пересечение линии или круга с линией или кругом.Такие пересечения приводят к квадратным уравнениям. Следовательно, если точка P может быть построена, каждая координата должна быть получена из рациональных чисел путем сложения, вычитания, умножения, деления или извлечения квадратных корней. Такие величины лежат в поле расширения E ⊂ Q , так что существуют поля E 0 = Q ⊂ E 1 ⊂ ⋯ ⊂ E k = E и En = En − 1a для a ∈ E n −1 . Степень [ E : Q ] = [ E n : E n −1 ] ⋯ [ E 1 : E 2 0 2 0 является степенью 2.
Степень [ E : Q ] = [ E n : E n −1 ] ⋯ [ E 1 : E 2 0 2 0 является степенью 2.
Следовательно, если x является координатой конструктивной точки, x лежит в расширении степени 2 n , фактически нормальное расширение степени 2 n . Но если [ Q ( x ): Q ] имеет степень, а не степень 2, это невозможно, поскольку [ E : Q ] = [ E : Q ( x )] [ Q ( x ): Q ].
В частности, дублирование куба ( p , равное кубу объема ровно 2) и деление на три части под углом 60 ° приводит к корням неприводимых кубиков x 3 — 2 = 0 и 4cos 3 θ− 3cosθ − cos 60 ° = 0 и не может быть выполнено. Поскольку π i не удовлетворяет ни одному моническому многочлену с коэффициентами из Q , круг не может быть возведен в квадрат.
Поскольку π i не удовлетворяет ни одному моническому многочлену с коэффициентами из Q , круг не может быть возведен в квадрат.
корней многочлена
корней многочленаКОРНИ ПОЛИНОМОВ
Обратите внимание, что материалы на этом веб-сайте не являются исчерпывающими.
Это резюме и дополнительный материал к необходимому учебнику.
Одна задача, выполняемая учеными и инженерами: найти корни многочлена f (x) , т. Е. Задано
f (x) = c n x n + c n – 1 x n – 1 + c n – 2 x n – 2 +. . . + c 2 x 2 + c 1 x 1 + c 0 x 0 = 0
Найдите x 0 такое, что f (x 0 ) = 0 .
Напомним, что многочлен f (x) с степенью n имеет максимум n различных корней . Некоторые корни могут быть действительными числами , а некоторые могут быть комплексными числами .
Например, квадратичная функция может иметь график, подобный одному из следующих:
Некоторые корни могут быть действительными числами , а некоторые могут быть комплексными числами .
Например, квадратичная функция может иметь график, подобный одному из следующих:
Факторинг — это один из способов определения корней многочлена f (x) , если многочлен факторизуемый.
ПРИМЕР:
| Учитывать f (x) = 2x 4 — 7x 3 + 4x 2 + 7x — 6 = 0 f (x) = 2x 4 + 4x 2 -6-7x 3 + 7x = 0 f (x) = 2 (x 4 + 2x 2 — 3) — 7x (x 2 — 1) = 0 f (x) = 2 (x 2 + 3) (x 2 — 1) — 7x (x 2 — 1) = 0 f (x) = [2 (x 2 + 3) — 7x] (x 2 — 1) = 0 f (x) = (2x 2 + 6-7x) (x 2 -1) = 0 f (x) = (2x 2 — 7x + 6) (x 2 — 1) = 0 f (x) = (2x — 3) (x — 2) (x + 1) (x — 1) = 0 x 1 = 3/2 х 2 = 2 х 3 = — 1 х 4 = 1 |
Однако не все многочлены факторизуемы.
ПРИМЕР: f (x) = x 5 — 2x 3 — 5x 2 + 2 = 0 не подлежит факторизации.
Если не факторизуемый многочлен является квадратичной функцией, то используется квадратичная формула. Для полиномов более высоких степеней требуются другие более общие методы. Мы рассмотрим несколько методов оценки корней многочленов, а именно: Метод деления пополам , Метод Регулы – Фальси и Метод Ньютона . Чтобы упростить задачу, находит первый положительный корень заданного многочлена f (x) . Для начального интервала [a, b] найдите единичный интервал , содержащий первый положительный корень.
Однако давайте сначала рассмотрим эффективный способ вычисления многочлена с помощью Метод Хорнера .
© 1994-07-23 cad rcm cpsm; последнее обновление 2010-06-30 20:09
Кубическая формула
Кубическая формула Кубическая формула(Решите любое полиномиальное уравнение 3-й степени)
Я размещаю это в Интернете, потому что некоторые студенты могут
нахожу это интересным. Это легко можно было бы упомянуть в
много математических курсов бакалавриата, хотя это не кажется
появиться в большинстве учебников, используемых для этих курсов.
Ни один из этих материалов я не обнаружил. —
ES
Это легко можно было бы упомянуть в
много математических курсов бакалавриата, хотя это не кажется
появиться в большинстве учебников, используемых для этих курсов.
Ни один из этих материалов я не обнаружил. —
ES
Вы должны знать, что решение ax 2 + bx + c = 0 равно
Аналогичная формула существует для многочленов степени три: Решение ax 3 + bx 2 + cx + d = 0 является
(Подобная формула была впервые опубликована Кардано в 1545 году.) Или, короче,
х = {q + [q 2 + (р-п 2 ) 3 ] 1/2 } 1/3 + {Q — [q 2 + (р-п 2 ) 3 ] 1/2 } 1/3 + Пгде
p = -b / (3a), q = p 3 + (bc-3ad) / (6a 2 ), r = c / (3a)Но я не , а рекомендую вам запомнить эти формулы.
Помимо того, что это слишком сложно, там
другие причины, по которым мы не обучаем этой формуле
студентам-математикам. Одна из причин в том, что
мы стараемся не учить их сложным
числа. Комплексные числа (т. Е. Точки лечения
в самолете цифрами) — это более сложная тема,
лучше оставить для более продвинутого курса. Но тогда
только числа, которые нам разрешено использовать в расчетах
являются действительными числами (т. е. точками на линии).
Это накладывает на нас некоторые ограничения — например,
мы не можем извлечь квадратный корень из отрицательного
номер. Теперь у формулы Кардана есть недостаток.
что он может принести в игру такие квадратные корни
на промежуточных этапах вычислений, даже если те
числа не фигурируют в задаче или ответе на нее.
Одна из причин в том, что
мы стараемся не учить их сложным
числа. Комплексные числа (т. Е. Точки лечения
в самолете цифрами) — это более сложная тема,
лучше оставить для более продвинутого курса. Но тогда
только числа, которые нам разрешено использовать в расчетах
являются действительными числами (т. е. точками на линии).
Это накладывает на нас некоторые ограничения — например,
мы не можем извлечь квадратный корень из отрицательного
номер. Теперь у формулы Кардана есть недостаток.
что он может принести в игру такие квадратные корни
на промежуточных этапах вычислений, даже если те
числа не фигурируют в задаче или ответе на нее.
Например, рассмотрим кубическое уравнение
х 3 -15x-4 = 0. (Этот пример был
упоминается Бомбелли в его книге в 1572 году.)
У этой проблемы есть настоящая
коэффициенты, и он имеет три действительных корня
за его ответы. (Подсказка: один из корней
небольшое положительное целое число; теперь ты можешь найти все
три корня?)
Но если мы применим к этому примеру формулу Кардано,
мы используем a = 1, b = 0, c = -15, d = -4, и мы находим, что
нам нужно извлечь квадратный корень из -109 в
итоговое вычисление. В конечном счете,
квадратные корни отрицательных чисел сократят
позже в вычислении, но это вычисление
не может быть понят изучающим математику без
дополнительное обсуждение комплексных чисел.
В конечном счете,
квадратные корни отрицательных чисел сократят
позже в вычислении, но это вычисление
не может быть понят изучающим математику без
дополнительное обсуждение комплексных чисел.
Аналогичная формула существует и для многочленов от степень 4, но записывать гораздо хуже; Я не буду даже попробуйте здесь.
Нет , нет аналогичной формулы для многочленов степени
5.Я не имею в виду, что никто не нашел формулы
пока что; Я имею в виду, что в 1826 году Абель доказал, что не может
быть такой формулой. Проблема в том, что функции
не делай достаточно того, что тебе нужно
решение всех уравнений 5-й степени. (Представьте себе калькулятор
в нем не хватает нескольких кнопок; есть несколько видов
вычисления, которые вы не можете сделать на нем.) Вам нужно как минимум
еще одна функция. Одна из таких функций, например,
функция, обратная f (x) = x 5 + x.(Есть
другие функции, которые также будут работать, и некоторые из них
математикам интереснее по разным
причины, но мне нравится этот, потому что его можно описать
в довольно элементарных терминах. ) Эта функция вместе
с функциями
и сложение, вычитание,
умножения и деления достаточно, чтобы получить формулу
для решения общего многочлена 5-й степени
уравнение через коэффициенты многочлена
— я.е., аналог квадратичной формулы 5-й степени.
Но это ужасно сложно; Я даже не хочу думать
о записи.
) Эта функция вместе
с функциями
и сложение, вычитание,
умножения и деления достаточно, чтобы получить формулу
для решения общего многочлена 5-й степени
уравнение через коэффициенты многочлена
— я.е., аналог квадратичной формулы 5-й степени.
Но это ужасно сложно; Я даже не хочу думать
о записи.
Теорема о рациональном корне
Теорема о рациональном корнеТеорема о рациональном корне
Теорема: Если многочлен P (x) = a n x n + a n — 1 x n — 1 +… + a 2 x 2 + a 1 x + a 0 |
Важность теоремы о рациональных корнях состоит в том, что она позволяет нам узнать, какие корни мы можем найти точно (рациональные), а какие корни мы можем только аппроксимировать (иррациональные).
Вот как это работает.
Рассмотрим многочлен
P (x) = x 3 — 8 x 2 + 17 x — 10
В этом случае 0 = –10 и n = 1.Число –10 делится на {10, 5, 2, 1}. Число 1 делится на 1. Таким образом, если P вообще имеет какие-либо рациональные корни, они должны быть среди {10/1, 5/1, 2/1, 1/1} = {10, 5, 2, 1}. Фактически, быстрая проверка показывает, что все 5, 2 и 1 являются рациональными (фактически целыми) корнями.
Рассмотрим вместо этого
f (x) = 2 x 3 + 3 x 2 + 2 x + 3
В этом случае 0 = 3 и n = 2. Число 3 имеет делители {3, 1}.Число 2 имеет делители {2, 1}. Таким образом, если f вообще имеет какие-либо рациональные корни, они должны быть среди {3/1, 1/1, 3/2, 1/2}. Из восьми возможных (положительных и отрицательных) только –3/2 является корнем. Если мы теперь воспользуемся теоремой о множителях и вычленим (x + 3/2), мы получим f (x) = (x + 3/2) (2 x 2 + 2). Квадратичная формула показывает нам, что у фактор-полинома 2 x 2 + 2 больше нет (обязательно иррациональных) корней.
Квадратичная формула показывает нам, что у фактор-полинома 2 x 2 + 2 больше нет (обязательно иррациональных) корней.
Наконец, рассмотрим
g (x) = x 3 — x 2 + 1
Правило знаков Декарта говорит нам, что g имеет не более одного отрицательного корня, а быстрый график показывает функцию, пересекающую ось x где-то между –1 и 0.Возможности, предоставляемые теоремой о рациональном корне (1), не соответствуют всем требованиям. Делаем вывод, что этот корень должен быть иррациональным. Брекетинг или масштабирование дают приблизительное значение –0,755.
Квадратные ит-математики
квадрат его математика »Мы не говорим о квадрате« гипотенузы »- это новомодная алгебраическая концепция умножения числа (длины гипотенузы) на само себя. Их перспективные изображения сходятся к двум точкам схода.Microsoft Math Solver В математике квадратное число или полный квадрат — это целое число, которое является квадратом целого числа; другими словами, это произведение некоторого целого числа на себя. Ваши первые 5 вопросов к нам! Узнайте больше на сайте mathantics. Чтобы понять квадратные корни, лучше всего начать с квадратов. Возведение числа в квадрат означает возведение его во вторую степень. Шелли шьет квадратное одеяло площадью 144 квадратных фута. Его также можно определить как прямоугольник, в котором две соседние стороны имеют одинаковую длину.Разделите его на 2 и возведите в квадрат. a, b, c — натуральные числа такие, что a 2 + b 2 + c 2 = 1 + 2 a b c Докажите, что одно из a + 1 2, b + 1 2, c + 1 2 является полным квадратом. Знак сложения. Рассчитайте квадратные метры, квадратные метры, квадратные метры и сотки для дома или строительного объекта. Использование эссе. Помощь в написании домашнего задания по математике. Услуга «Квадратные корни» полностью легальна. Его также можно использовать для преобразования общей формы квадратичной, ax 2 + bx + c в вершинную форму a (x — h) 2 + k. Квадратные корни спрашивают, «какое число при умножении само на себя дает следующий результат», и поэтому их вычисление требует, чтобы вы относились к числам немного по-другому.
Ваши первые 5 вопросов к нам! Узнайте больше на сайте mathantics. Чтобы понять квадратные корни, лучше всего начать с квадратов. Возведение числа в квадрат означает возведение его во вторую степень. Шелли шьет квадратное одеяло площадью 144 квадратных фута. Его также можно определить как прямоугольник, в котором две соседние стороны имеют одинаковую длину.Разделите его на 2 и возведите в квадрат. a, b, c — натуральные числа такие, что a 2 + b 2 + c 2 = 1 + 2 a b c Докажите, что одно из a + 1 2, b + 1 2, c + 1 2 является полным квадратом. Знак сложения. Рассчитайте квадратные метры, квадратные метры, квадратные метры и сотки для дома или строительного объекта. Использование эссе. Помощь в написании домашнего задания по математике. Услуга «Квадратные корни» полностью легальна. Его также можно использовать для преобразования общей формы квадратичной, ax 2 + bx + c в вершинную форму a (x — h) 2 + k. Квадратные корни спрашивают, «какое число при умножении само на себя дает следующий результат», и поэтому их вычисление требует, чтобы вы относились к числам немного по-другому. 6. Когда число возводится в квадрат, оно записывается как это число (основание) во второй степени. Затем измерьте диагональ между концами ваших двух линий. И мы сделали еще несколько таких, включая квадратные корни, чтобы они могли видеть, что вы делите на два. O Важно то, что 49 — квадрат, а 50 — двойной квадрат. Но все же мы не можем заключить, что это число является точным квадратом. Найдите бесплатные карточки, диаграммы и учебные пособия по таким темам математики, как арифметика, геометрия и алгебра.Этот тест используется, когда у нас есть категориальные данные для двух независимых переменных, и мы хотим увидеть, существует ли какая-либо связь между переменными. Наши квадраты были 5 * 5, 11 * 11 и 71 * 71. Шаг 2: Возьмите коэффициент линейного члена, который равен {2 \ более 3}. Это больше, чем сказать, что квадрат МОЖЕТ быть прямоугольником; Это. tan (x) Возвращает тангенс x (предполагается, что он выражен в радианах). Несмотря на то, что квадраты относительно просты и понятны в использовании, они обладают несколькими интересными и примечательными свойствами.
6. Когда число возводится в квадрат, оно записывается как это число (основание) во второй степени. Затем измерьте диагональ между концами ваших двух линий. И мы сделали еще несколько таких, включая квадратные корни, чтобы они могли видеть, что вы делите на два. O Важно то, что 49 — квадрат, а 50 — двойной квадрат. Но все же мы не можем заключить, что это число является точным квадратом. Найдите бесплатные карточки, диаграммы и учебные пособия по таким темам математики, как арифметика, геометрия и алгебра.Этот тест используется, когда у нас есть категориальные данные для двух независимых переменных, и мы хотим увидеть, существует ли какая-либо связь между переменными. Наши квадраты были 5 * 5, 11 * 11 и 71 * 71. Шаг 2: Возьмите коэффициент линейного члена, который равен {2 \ более 3}. Это больше, чем сказать, что квадрат МОЖЕТ быть прямоугольником; Это. tan (x) Возвращает тангенс x (предполагается, что он выражен в радианах). Несмотря на то, что квадраты относительно просты и понятны в использовании, они обладают несколькими интересными и примечательными свойствами. Для квадрата со стороной 10 периметр равен 40, а площадь равна 100. Для квадрата со стороной 2 периметр равен 8, а площадь равна 4. isqrt (n) ¶ Возвращает целочисленный квадратный корень из числа неотрицательное целое число n. Число 2 находится между 1 и 2. В эту игру можно играть против компьютера или против друга. 0. s2 + 10s + 25 8. Мы также предлагаем таблицу кодов номеров HTML. Решим радикальное уравнение. Управляемые заметки позволяют всем учащимся активно участвовать в занятиях. У куба длина ребра 7 см, и я должен найти диагональ стены и тела.Если аргумент A скрещенный квадрат является фасеткой квадрата, самопересекающимся многоугольником, созданным путем удаления двух противоположных краев квадрата и повторного соединения его двумя диагоналями. √2. Обычно говорят, что есть только один магический квадрат 3×3. Грани кубиков и игральных костей (также трехмерных или трехмерных тел) представляют собой квадраты. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли увидеть пример математической функции.
Для квадрата со стороной 10 периметр равен 40, а площадь равна 100. Для квадрата со стороной 2 периметр равен 8, а площадь равна 4. isqrt (n) ¶ Возвращает целочисленный квадратный корень из числа неотрицательное целое число n. Число 2 находится между 1 и 2. В эту игру можно играть против компьютера или против друга. 0. s2 + 10s + 25 8. Мы также предлагаем таблицу кодов номеров HTML. Решим радикальное уравнение. Управляемые заметки позволяют всем учащимся активно участвовать в занятиях. У куба длина ребра 7 см, и я должен найти диагональ стены и тела.Если аргумент A скрещенный квадрат является фасеткой квадрата, самопересекающимся многоугольником, созданным путем удаления двух противоположных краев квадрата и повторного соединения его двумя диагоналями. √2. Обычно говорят, что есть только один магический квадрат 3×3. Грани кубиков и игральных костей (также трехмерных или трехмерных тел) представляют собой квадраты. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли увидеть пример математической функции. Так, например, квадратный корень из 49 равен 7 (7×7 = 49).3 2 = 3 ⋅ 3 = 9. Возвести результат в квадрат столько раз, сколько вы извлекали квадратный корень. DadsWorksheets. Выберите один из 7 учебных режимов и игр, чтобы изучать арифметику, геометрию и алгебру. Определения. Square It. SmartScore. Также обратите внимание, что константа представляет собой точный квадрат и ее квадратный корень равен 10. Продолжайте — играйте и учитесь! Есть более 300 простых для понимания уроков математики. Возведение в квадрат записывается математическими символами: ставится 2 над числом, которое вы возводите в квадрат, чтобы показать, что оно умножается в 2 раза.r2 — 7r + 49 4 4. Для вычисления квадратного корня в Python у нас есть в основном 5 методов или способов. После решения уравнения у вас есть много возможностей продолжить изучение математики с помощью Math Assistant. Пожалуйста, войдите сначала, если вы хотите сохранить вопрос в своей учетной записи. Он имеет то же расположение вершин, что и квадрат, и транзитивен по вершинам.
Так, например, квадратный корень из 49 равен 7 (7×7 = 49).3 2 = 3 ⋅ 3 = 9. Возвести результат в квадрат столько раз, сколько вы извлекали квадратный корень. DadsWorksheets. Выберите один из 7 учебных режимов и игр, чтобы изучать арифметику, геометрию и алгебру. Определения. Square It. SmartScore. Также обратите внимание, что константа представляет собой точный квадрат и ее квадратный корень равен 10. Продолжайте — играйте и учитесь! Есть более 300 простых для понимания уроков математики. Возведение в квадрат записывается математическими символами: ставится 2 над числом, которое вы возводите в квадрат, чтобы показать, что оно умножается в 2 раза.r2 — 7r + 49 4 4. Для вычисления квадратного корня в Python у нас есть в основном 5 методов или способов. После решения уравнения у вас есть много возможностей продолжить изучение математики с помощью Math Assistant. Пожалуйста, войдите сначала, если вы хотите сохранить вопрос в своей учетной записи. Он имеет то же расположение вершин, что и квадрат, и транзитивен по вершинам. Но даже с расширенной областью определения x \ sqrt {x} x определяется аналогичным образом, так что он по-прежнему является функцией. математика. Магический квадрат состоит из равных рядов чисел (3 × 3, 4 × 4 и т. Д.Надеюсь, вы найдете статью Программа Javascript для поиска квадратного корня числа с помощью математики. Найдите 145 способов сказать КВАДРАТ, а также антонимы, родственные слова и примеры предложений в тезаурусе. Равносторонний цилиндр Найдите радиус и высоту (в сантиметрах) равностороннего цилиндра объемом 1 литр. 414 × 1. Квадратный корень из числа — это число, которое при умножении само на себя дает желаемое значение. Проведите два матча подряд, чтобы получить комбо и заработать бонусные очки! 4. Математические игры для 8-х классов. Квадратные корни, экспоненты и научная запись — вот некоторые из концепций этих забавных математических игр.Давайте возьмем цифровые… Простые обучающие инструменты Quizlet — отличный способ попрактиковаться, запомнить и усвоить математические термины, определения и концепции.
Но даже с расширенной областью определения x \ sqrt {x} x определяется аналогичным образом, так что он по-прежнему является функцией. математика. Магический квадрат состоит из равных рядов чисел (3 × 3, 4 × 4 и т. Д.Надеюсь, вы найдете статью Программа Javascript для поиска квадратного корня числа с помощью математики. Найдите 145 способов сказать КВАДРАТ, а также антонимы, родственные слова и примеры предложений в тезаурусе. Равносторонний цилиндр Найдите радиус и высоту (в сантиметрах) равностороннего цилиндра объемом 1 литр. 414 × 1. Квадратный корень из числа — это число, которое при умножении само на себя дает желаемое значение. Проведите два матча подряд, чтобы получить комбо и заработать бонусные очки! 4. Математические игры для 8-х классов. Квадратные корни, экспоненты и научная запись — вот некоторые из концепций этих забавных математических игр.Давайте возьмем цифровые… Простые обучающие инструменты Quizlet — отличный способ попрактиковаться, запомнить и усвоить математические термины, определения и концепции. Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10. fma (x, y, z) Возвращает x * y + z без потери точности. (- 3) 2 = (- 3) ⋅ (- 3) = 9. Один квадратный метр равен 1 м². Квадратный корень: √ U + 0221A & # x221A; Определите длину диагонали куба с гранью 37 мм. как решать кубические многочлены. Вы остались на правильном сайте, чтобы начать получать эту информацию.Большая часть современных знаний о египетской математике происходит из папирусов, написанных во время 12-й династии. факторов 50 и 7 70 и 30 наименьших общих кратностей. Математические рабочие листы генерируются случайным образом и динамически нашими генераторами математических листов. comVisit http: // www. Отношение 7 Отношение сторон двух квадратов 4: 5, если сумма их площадей равна… Задайте математический вопрос. Площадь фигуры — это количество квадратов, необходимых для ее полного покрытия, как плитки на полу. Допустим, вы закладываете фундамент квадратной комнаты со стенами длиной 10 футов с каждой стороны.
Модуль 1: Свойства умножения и деления и решение задач с единицами 2–5 и 10. fma (x, y, z) Возвращает x * y + z без потери точности. (- 3) 2 = (- 3) ⋅ (- 3) = 9. Один квадратный метр равен 1 м². Квадратный корень: √ U + 0221A & # x221A; Определите длину диагонали куба с гранью 37 мм. как решать кубические многочлены. Вы остались на правильном сайте, чтобы начать получать эту информацию.Большая часть современных знаний о египетской математике происходит из папирусов, написанных во время 12-й династии. факторов 50 и 7 70 и 30 наименьших общих кратностей. Математические рабочие листы генерируются случайным образом и динамически нашими генераторами математических листов. comVisit http: // www. Отношение 7 Отношение сторон двух квадратов 4: 5, если сумма их площадей равна… Задайте математический вопрос. Площадь фигуры — это количество квадратов, необходимых для ее полного покрытия, как плитки на полу. Допустим, вы закладываете фундамент квадратной комнаты со стенами длиной 10 футов с каждой стороны. 2 2 = 1. Бесплатные онлайн-программы для решения математических задач. Число x в квадрате записывается x2. Возвращаемое значение sqrt () — квадратный корень из x в виде числа с плавающей запятой. 5-й класс. 25. Введите это значение на диагональ квадратного калькулятора, чтобы проверить его самостоятельно! Возвести число в квадрат, умножив его само на себя. Играйте в 8 Square на математической площадке! Заполните сетку разноцветными фигурами. Квадратный корень из 1 равен 1. r. Для некоторых приложений может быть более удобным иметь наименьшее целое число a такое, что n ≤ a², или, другими словами, верхний предел точного квадратного корня из n.Затем объедините фракции. По сути, это будет эллипс. Квадрат — это прямоугольник с четырьмя равными сторонами. 3. Квадратный дюйм обозначается как дюйм2 или квадратный дюйм. Возьмем, к примеру, число 15626. Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на само, полученное произведение называется квадратным числом, или точным квадратом, или просто «квадратом».
2 2 = 1. Бесплатные онлайн-программы для решения математических задач. Число x в квадрате записывается x2. Возвращаемое значение sqrt () — квадратный корень из x в виде числа с плавающей запятой. 5-й класс. 25. Введите это значение на диагональ квадратного калькулятора, чтобы проверить его самостоятельно! Возвести число в квадрат, умножив его само на себя. Играйте в 8 Square на математической площадке! Заполните сетку разноцветными фигурами. Квадратный корень из 1 равен 1. r. Для некоторых приложений может быть более удобным иметь наименьшее целое число a такое, что n ≤ a², или, другими словами, верхний предел точного квадратного корня из n.Затем объедините фракции. По сути, это будет эллипс. Квадрат — это прямоугольник с четырьмя равными сторонами. 3. Квадратный дюйм обозначается как дюйм2 или квадратный дюйм. Возьмем, к примеру, число 15626. Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на само, полученное произведение называется квадратным числом, или точным квадратом, или просто «квадратом». Выберите свои математические коды. Квадрат дроби — одна из основных математических функций, используемых для нахождения значения квадрата положительного или отрицательного числа дроби, выраженного как ненулевым числителем, так и знаменателем, путем двойного умножения самой дроби.Например, 9 — это квадратное число, так как оно равно 3 2 и может быть записано как 3 × 3. Английский (Австралия) Английский (Канада) Английский (Ирландия) Английский (Великобритания) español. Поэтому, чтобы найти квадратный корень из 2, добавьте 6 нулей после десятичной точки. Если вершина расположена перпендикулярно центру квадрата, она будет иметь симметрию C4v. ) 29: математика. Полином 3-го порядка. Выровняйте это! Проверьте консоль разработчика. Что это. спросил 29 окт. в… Вычтите константу с другой стороны. Поскольку 2 не является точным квадратом, квадратный корень является иррациональным числом.Валюта: Контактная информация. Завершение квадрата. Детский сад. Похоже на предыдущий. Калькулятор кубического корня.
Выберите свои математические коды. Квадрат дроби — одна из основных математических функций, используемых для нахождения значения квадрата положительного или отрицательного числа дроби, выраженного как ненулевым числителем, так и знаменателем, путем двойного умножения самой дроби.Например, 9 — это квадратное число, так как оно равно 3 2 и может быть записано как 3 × 3. Английский (Австралия) Английский (Канада) Английский (Ирландия) Английский (Великобритания) español. Поэтому, чтобы найти квадратный корень из 2, добавьте 6 нулей после десятичной точки. Если вершина расположена перпендикулярно центру квадрата, она будет иметь симметрию C4v. ) 29: математика. Полином 3-го порядка. Выровняйте это! Проверьте консоль разработчика. Что это. спросил 29 окт. в… Вычтите константу с другой стороны. Поскольку 2 не является точным квадратом, квадратный корень является иррациональным числом.Валюта: Контактная информация. Завершение квадрата. Детский сад. Похоже на предыдущий. Калькулятор кубического корня. t2 + 12t + 36 7. Пример получения квадратного корня. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли. Метод «Завершение квадрата» можно применить к квадратным уравнениям, которые записаны в стандартной форме. 44. Материалы: листы миллиметровой бумаги размером 20 на 20 дюймов, размером 1 дюйм, мелки, ламинат, клейкая лента, лист для записей. Когда это использовать: «В этом уроке я попытался объединить математические стандарты, которые мы изучали в то время. (доли и проценты) и некоторые прошлые стандарты (многоугольники, периметр, площадь, симметрия) с нашим отделом социальных исследований Колониальной Америки. Второй тип теста хи-квадрат — это критерий хи-квадрат ассоциации Пирсона.Возвести число в квадрат — значит умножить его само на себя. Квадрат X = X * X Например, если X = 3 Квадрат 3 = 3 * 3 = 9, что такое квадратный корень? Этот список часто используемых математических символов объясняет, что такое каждый математический символ, как он используется, и предоставляет пример выражения.
t2 + 12t + 36 7. Пример получения квадратного корня. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли. Метод «Завершение квадрата» можно применить к квадратным уравнениям, которые записаны в стандартной форме. 44. Материалы: листы миллиметровой бумаги размером 20 на 20 дюймов, размером 1 дюйм, мелки, ламинат, клейкая лента, лист для записей. Когда это использовать: «В этом уроке я попытался объединить математические стандарты, которые мы изучали в то время. (доли и проценты) и некоторые прошлые стандарты (многоугольники, периметр, площадь, симметрия) с нашим отделом социальных исследований Колониальной Америки. Второй тип теста хи-квадрат — это критерий хи-квадрат ассоциации Пирсона.Возвести число в квадрат — значит умножить его само на себя. Квадрат X = X * X Например, если X = 3 Квадрат 3 = 3 * 3 = 9, что такое квадратный корень? Этот список часто используемых математических символов объясняет, что такое каждый математический символ, как он используется, и предоставляет пример выражения. Пример 1: Если вам дана диагональ d и вы хотите вычислить сторону a, тогда вам нужно использовать формулу, которая соединяет d и a. sqrt () для вычисления квадратного корня из бесконечности, положительного числа, отрицательного числа и нуля. Вы можете задать любой математический вопрос и получить экспертные ответы всего за два часа.Треугольник — это трехсторонняя замкнутая фигура. Он начинается с данного отрезка AB. 1416. GeoGebra для преподавания и изучения математики Бесплатные цифровые инструменты для занятий в классе, построения графиков, геометрии, совместной доски и многого другого. Математика в электронных таблицах: функции против. Одна особенность квадратов в том, что они всегда положительные. Поскольку у квадрата четыре стороны равной длины, квадрат является правильным четырехугольником. Возьмите половину коэффициента x-члена, возведите его в квадрат и прибавьте к обеим сторонам. Суббота, 6 октября 2012 г. Объем меньшей пирамиды: Чтобы сделать несколько квадратов в квадрате, следуйте инструкциям ниже: 1) Чтобы добавить еще один, больший внешний квадрат, вам нужно будет вырезать четыре половинных квадратных треугольника.
Пример 1: Если вам дана диагональ d и вы хотите вычислить сторону a, тогда вам нужно использовать формулу, которая соединяет d и a. sqrt () для вычисления квадратного корня из бесконечности, положительного числа, отрицательного числа и нуля. Вы можете задать любой математический вопрос и получить экспертные ответы всего за два часа.Треугольник — это трехсторонняя замкнутая фигура. Он начинается с данного отрезка AB. 1416. GeoGebra для преподавания и изучения математики Бесплатные цифровые инструменты для занятий в классе, построения графиков, геометрии, совместной доски и многого другого. Математика в электронных таблицах: функции против. Одна особенность квадратов в том, что они всегда положительные. Поскольку у квадрата четыре стороны равной длины, квадрат является правильным четырехугольником. Возьмите половину коэффициента x-члена, возведите его в квадрат и прибавьте к обеим сторонам. Суббота, 6 октября 2012 г. Объем меньшей пирамиды: Чтобы сделать несколько квадратов в квадрате, следуйте инструкциям ниже: 1) Чтобы добавить еще один, больший внешний квадрат, вам нужно будет вырезать четыре половинных квадратных треугольника. {b} {C} $$ Анджело при рождении весил 5 1/4 фунта. sqrt в Java; Нахождение квадратного корня из числа без использования библиотечных функций — JavaScript; Математика. Завершение квадрата — это метод, используемый для решения квадратных уравнений. 8, 2. t положение на земле (считается, когда стороны параллельны осям x и y), вершины обозначены как -. Английский. Сам процесс умножения числа раз называется возведением в квадрат. Геодоски — это квадратные доски с колышками, к которым учащиеся прикрепляют резинки для придания им различных форм.Вы можете выбрать уровень сложности и размер лабиринта. Нахождение квадратного корня из числа без использования Math. Затем он возводит перпендикуляр на одном конце линии, который становится второй стороной квадрата. Ответ (1 из 9): Честная математика никогда не сможет доказать, что ложь истинна; однако есть обстоятельства, при которых человек может убедить другого в лжи с помощью искаженной или «незаконной» математики (так мы получаем доказательства того, что 1 = 2 и т.
{b} {C} $$ Анджело при рождении весил 5 1/4 фунта. sqrt в Java; Нахождение квадратного корня из числа без использования библиотечных функций — JavaScript; Математика. Завершение квадрата — это метод, используемый для решения квадратных уравнений. 8, 2. t положение на земле (считается, когда стороны параллельны осям x и y), вершины обозначены как -. Английский. Сам процесс умножения числа раз называется возведением в квадрат. Геодоски — это квадратные доски с колышками, к которым учащиеся прикрепляют резинки для придания им различных форм.Вы можете выбрать уровень сложности и размер лабиринта. Нахождение квадратного корня из числа без использования Math. Затем он возводит перпендикуляр на одном конце линии, который становится второй стороной квадрата. Ответ (1 из 9): Честная математика никогда не сможет доказать, что ложь истинна; однако есть обстоятельства, при которых человек может убедить другого в лжи с помощью искаженной или «незаконной» математики (так мы получаем доказательства того, что 1 = 2 и т. п.). Площадь квадрата = сторона, умноженная на сторону.2 + Bx + Cy + D = 0 \) создаст круг. По-разному. Как рассчитать квадратные метры для прямоугольных, круглых и окаймленных участков. (b ≠ 0) 3. Это число заканчивается цифрами 6. Попробуйте это Перетащите любую вершину квадрата ниже. Платежи Square и POS-приложение были … квадратными корнями. 4 класс. sqrt () для вычисления квадратных корней. Вы можете поговорить с членом нашей службы поддержки клиентов по телефону 1-800-876-1799. t2 + 2 3 t + 1 9 3. Числовые коды объектов Unicode могут быть выражены либо в виде десятичных чисел, либо.Потому что математика — это круто, а математические игры разблокируют мозг, помогая запоминать математические факты. В знаменателе уравнения не может быть квадратных корней. Кубический корень из x дается формулой: кубический корень = 3 √ x квадратные корни Мы надеемся, что вы посетите математику. com — тысячи бесплатных заданий по математике На этом сайте есть более 5000 различных заданий по математике от детского сада до предварительной алгебры и обучения.
п.). Площадь квадрата = сторона, умноженная на сторону.2 + Bx + Cy + D = 0 \) создаст круг. По-разному. Как рассчитать квадратные метры для прямоугольных, круглых и окаймленных участков. (b ≠ 0) 3. Это число заканчивается цифрами 6. Попробуйте это Перетащите любую вершину квадрата ниже. Платежи Square и POS-приложение были … квадратными корнями. 4 класс. sqrt () для вычисления квадратных корней. Вы можете поговорить с членом нашей службы поддержки клиентов по телефону 1-800-876-1799. t2 + 2 3 t + 1 9 3. Числовые коды объектов Unicode могут быть выражены либо в виде десятичных чисел, либо.Потому что математика — это круто, а математические игры разблокируют мозг, помогая запоминать математические факты. В знаменателе уравнения не может быть квадратных корней. Кубический корень из x дается формулой: кубический корень = 3 √ x квадратные корни Мы надеемся, что вы посетите математику. com — тысячи бесплатных заданий по математике На этом сайте есть более 5000 различных заданий по математике от детского сада до предварительной алгебры и обучения. Квадрат с вершинами ABCD обозначим ABCD. тогда 1 <= x. Мы узнали об этом в первом разделе Алгебры 1.0. И затем мы должны найти исходное число, которое было возведено в квадрат. На прошлой неделе я показал вам, как сделать 8 полуквадратных треугольников одновременно, но нам все еще нужно поговорить о том, как определить квадрат, с какого размера начать, чтобы получить полуквадратный треугольник правильного размера (HST) !. Другими словами, если мы умножаем число на само себя, результатом будет квадрат этого числа. упрощающие радикалы дроби 3. Обратите внимание на слово «вкл.». s2 + 3 4 s + 9 64 5. Поскольку по крайней мере одно из a, b, c должно быть квадратным числом элементарной теории чисел.Самый распространенный или самый простой способ - использовать функцию sqrt математического модуля. Квадратный корень из числа - это еще одно число, которое при умножении само на себя становится исходным числом. А поскольку квадраты являются прямоугольниками, вы знаете, что некоторые прямоугольники являются квадратами, а именно квадраты! Эти идеи сбивают с толку многих.
Квадрат с вершинами ABCD обозначим ABCD. тогда 1 <= x. Мы узнали об этом в первом разделе Алгебры 1.0. И затем мы должны найти исходное число, которое было возведено в квадрат. На прошлой неделе я показал вам, как сделать 8 полуквадратных треугольников одновременно, но нам все еще нужно поговорить о том, как определить квадрат, с какого размера начать, чтобы получить полуквадратный треугольник правильного размера (HST) !. Другими словами, если мы умножаем число на само себя, результатом будет квадрат этого числа. упрощающие радикалы дроби 3. Обратите внимание на слово «вкл.». s2 + 3 4 s + 9 64 5. Поскольку по крайней мере одно из a, b, c должно быть квадратным числом элементарной теории чисел.Самый распространенный или самый простой способ - использовать функцию sqrt математического модуля. Квадратный корень из числа - это еще одно число, которое при умножении само на себя становится исходным числом. А поскольку квадраты являются прямоугольниками, вы знаете, что некоторые прямоугольники являются квадратами, а именно квадраты! Эти идеи сбивают с толку многих. Квадрат против прямоугольника. В частности, квадратные корни можно рассматривать в любом контексте, в котором возникает идея возведения в квадрат некоторого математического… Определите длину диагонали куба с краем 37 мм.Реклама. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли это сделать. Рабочий лист Math 51 Как решать уравнения с радикальными выражениями. Проверка вашего ответа необходима, потому что решения могут быть посторонними. Существует сетка размером 3 x 3 ячейки, и вам нужно поставить от 1 до 9 в каждое из значений. Квадратный корень — это полная противоположность квадрата. Функция квадратного корня противоположна функции, возведенной в квадрат. Описание Если значение x отрицательное, Math. Задача.Например, 9 x9 равно 81, так же как 9 в квадрате (9 2) также равно 81. 4. #Shorts #Mathtrick @Shruti Academy Не забудьте подписаться на #Subscribe our. Отношение одинаково для всех кругов и составляет примерно 3. x = 7? Решение: x = 49 Проверить: 49 = 7 Работает.
Квадрат против прямоугольника. В частности, квадратные корни можно рассматривать в любом контексте, в котором возникает идея возведения в квадрат некоторого математического… Определите длину диагонали куба с краем 37 мм.Реклама. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли это сделать. Рабочий лист Math 51 Как решать уравнения с радикальными выражениями. Проверка вашего ответа необходима, потому что решения могут быть посторонними. Существует сетка размером 3 x 3 ячейки, и вам нужно поставить от 1 до 9 в каждое из значений. Квадратный корень — это полная противоположность квадрата. Функция квадратного корня противоположна функции, возведенной в квадрат. Описание Если значение x отрицательное, Math. Задача.Например, 9 x9 равно 81, так же как 9 в квадрате (9 2) также равно 81. 4. #Shorts #Mathtrick @Shruti Academy Не забудьте подписаться на #Subscribe our. Отношение одинаково для всех кругов и составляет примерно 3. x = 7? Решение: x = 49 Проверить: 49 = 7 Работает. После того, как квадратный корень получен с точностью до нескольких бит, он очень быстро сходится. sqrt (x) Возвращает положительный квадратный корень из x. Точка на расстоянии 1 от начала координат, создающая угол 45 градусов с действительной осью, такая же. Этот удобный квадрат 100 — отличный способ познакомить учащихся математического класса с их числами до 100 и уверенно их использовать.Он измеряется в квадратных единицах. 4142, и это хорошая константа, которую стоит также прочитать: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием Math. SmartScore IXL — это динамический показатель прогресса в достижении мастерства, а не процентная оценка. Используя метод факторизации, найдите корни квадратного уравнения. sqrt (x) Возвращает квадратный корень из x. Последовательно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или покорите Зону испытаний, чтобы достичь мастерства (100)! Этот продукт представляет собой квадрат для стеганого одеяла с осенней тематикой, созданный для трех различных уровней математики, чтобы их можно было различить.
После того, как квадратный корень получен с точностью до нескольких бит, он очень быстро сходится. sqrt (x) Возвращает положительный квадратный корень из x. Точка на расстоянии 1 от начала координат, создающая угол 45 градусов с действительной осью, такая же. Этот удобный квадрат 100 — отличный способ познакомить учащихся математического класса с их числами до 100 и уверенно их использовать.Он измеряется в квадратных единицах. 4142, и это хорошая константа, которую стоит также прочитать: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием Math. SmartScore IXL — это динамический показатель прогресса в достижении мастерства, а не процентная оценка. Используя метод факторизации, найдите корни квадратного уравнения. sqrt (x) Возвращает квадратный корень из x. Последовательно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или покорите Зону испытаний, чтобы достичь мастерства (100)! Этот продукт представляет собой квадрат для стеганого одеяла с осенней тематикой, созданный для трех различных уровней математики, чтобы их можно было различить. 2, или площадь равна квадрату стороны. Это обучающая игра, которая улучшает вашу память и зрение. Она также помогает вам распознать свои потенциальные # Три способа возводить числа в квадрат в Python. Вы можете купить справочник по математическим квадратным головоломкам или получить квадратный корень из отрицательного числа. Преподавайте математику. Вот некоторые вещи, о которых думает этот школьный учитель математики. математика. Я также добавил пустой квадрат одеяла благодарения, чтобы вы могли добавить свой собственный. Есть несколько способов подойти к нему. Очевидно, что площадь квадрата равна сумме их площадей.В Fubuki вы помещаете числа в сетку так, чтобы столбцы и строки складывались в заданные числа, но в этой игре вам нужно не только сложение, но также вычитание, умножение и деление. Если аргумент имеет положительное значение типа double, этот метод вернет квадратный корень из заданного значения. Вычислить квадратный корень. Последние вопросы. импортировать математику a = math.
2, или площадь равна квадрату стороны. Это обучающая игра, которая улучшает вашу память и зрение. Она также помогает вам распознать свои потенциальные # Три способа возводить числа в квадрат в Python. Вы можете купить справочник по математическим квадратным головоломкам или получить квадратный корень из отрицательного числа. Преподавайте математику. Вот некоторые вещи, о которых думает этот школьный учитель математики. математика. Я также добавил пустой квадрат одеяла благодарения, чтобы вы могли добавить свой собственный. Есть несколько способов подойти к нему. Очевидно, что площадь квадрата равна сумме их площадей.В Fubuki вы помещаете числа в сетку так, чтобы столбцы и строки складывались в заданные числа, но в этой игре вам нужно не только сложение, но также вычитание, умножение и деление. Если аргумент имеет положительное значение типа double, этот метод вернет квадратный корень из заданного значения. Вычислить квадратный корень. Последние вопросы. импортировать математику a = math. Фактически, любое квадратное уравнение ca. Когда квадратичное уравнение сложно разложить на множители или оно включает комплексные числа, этот метод переписывает квадратное уравнение, изначально имеющееся в стандартной форме, в форму вершин, которую, как и квадратичное разложение, решить намного проще.Студенты в основном пользуются услугами по написанию сочинений по математике. 1 — это квадратный корень из 1. Сэм купил участок земли площадью 55 акров и 1 200 футов дороги. 4, но 1. Что такое история квадратного корня в математике? Согласно университету Сент-Луиса, древние египтяне создали квадратный корень и, скорее всего, использовали его для архитектуры, строительства пирамид и других повседневных занятий, требующих математики.5) г) затем разделите… нет. Когда число возводится в квадрат в математике, это означает, что оно было умножено само на себя. Возврат, квадратный корень, обратный квадратный корень и некоторые элементарные функции с использованием малых множителей В следующей таблице показаны коды ASCII для широкого набора математических функций.
Фактически, любое квадратное уравнение ca. Когда квадратичное уравнение сложно разложить на множители или оно включает комплексные числа, этот метод переписывает квадратное уравнение, изначально имеющееся в стандартной форме, в форму вершин, которую, как и квадратичное разложение, решить намного проще.Студенты в основном пользуются услугами по написанию сочинений по математике. 1 — это квадратный корень из 1. Сэм купил участок земли площадью 55 акров и 1 200 футов дороги. 4, но 1. Что такое история квадратного корня в математике? Согласно университету Сент-Луиса, древние египтяне создали квадратный корень и, скорее всего, использовали его для архитектуры, строительства пирамид и других повседневных занятий, требующих математики.5) г) затем разделите… нет. Когда число возводится в квадрат в математике, это означает, что оно было умножено само на себя. Возврат, квадратный корень, обратный квадратный корень и некоторые элементарные функции с использованием малых множителей В следующей таблице показаны коды ASCII для широкого набора математических функций. com, самый надежный бесплатный тезаурус в мире. Математический квадрат — это набор уравнений, расположенных в строках и столбцах, так что числа в каждом уравнении пересекаются. Квадратный корень из 200 равен 14. Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — квадратные числа.Самый простой для понимания — это просто угадывать возможные значения квадратного корня, пока его квадрат не сходится к истинному квадрату. Рассчитайте стоимость проекта, исходя из цены квадратного фута, квадратного ярда или квадрата … Расстояние такое же, как и вдоль квадрата o, c ‘, b’ a ‘и o d’, e ‘, f’. Например, если вы включите $ \ pi $ в свой источник, вы получите символ пи π. Математический квадрат. Квадрат — это прямоугольник, увеличивающий площадь. Найди. Квадрат — это геометрическая фигура, принадлежащая к семейству четырехугольников, потому что у нее 4 стороны.Описание игры. Это все, что нужно! Теперь вы можете использовать математику. Более формально: квадратное число — это квадратный дюйм — это единица площади как в американских, так и в английских единицах измерения.
com, самый надежный бесплатный тезаурус в мире. Математический квадрат — это набор уравнений, расположенных в строках и столбцах, так что числа в каждом уравнении пересекаются. Квадратный корень из 200 равен 14. Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — квадратные числа.Самый простой для понимания — это просто угадывать возможные значения квадратного корня, пока его квадрат не сходится к истинному квадрату. Рассчитайте стоимость проекта, исходя из цены квадратного фута, квадратного ярда или квадрата … Расстояние такое же, как и вдоль квадрата o, c ‘, b’ a ‘и o d’, e ‘, f’. Например, если вы включите $ \ pi $ в свой источник, вы получите символ пи π. Математический квадрат. Квадрат — это прямоугольник, увеличивающий площадь. Найди. Квадрат — это геометрическая фигура, принадлежащая к семейству четырехугольников, потому что у нее 4 стороны.Описание игры. Это все, что нужно! Теперь вы можете использовать математику. Более формально: квадратное число — это квадратный дюйм — это единица площади как в американских, так и в английских единицах измерения. Каждая линия квадрата (горизонтальная, вертикальная и диагональная) должна составлять одну и ту же сумму, и каждое поле должно содержать разные числа. sqrt (значение) — квадратный корень из числа. Площадь квадрата = сторона x Щелкните и перетащите, чтобы поместить квадрат на доску. В приведенном выше примере это будет 25. Когда вы соединяете квадраты в линию, они могут быть любого размера.\квадратный! \квадратный! . Студенты следят за математикой. x 2 — 12 x + 36 можно разложить на (x, если возвести два числа в квадрат, а затем умножить их вместе, а затем умножить два числа друг на друга, чтобы получить квадратный корень из первого числа, всегда ли это будет работать. Наш математический вопрос На доске ответов представлены сотни экспертов по математике, которые ждут ответов на ваши вопросы. Найти квадратный корень из числа, являющегося точным квадратом, очень просто. Получите помощь в Интернете или с помощью нашего математического приложения. Учебные ресурсы 5CM MathLink Cubes , Снова в школу, Домашнее обучение, Классные игры для учителей, Образовательная игрушка-счетчик, Математические кубики, Соединительные кубики, Ранние математические навыки, Математические манипуляции, Набор из 100 кубиков, STEM-игрушки, Математика для детей от 5 лет.
Каждая линия квадрата (горизонтальная, вертикальная и диагональная) должна составлять одну и ту же сумму, и каждое поле должно содержать разные числа. sqrt (значение) — квадратный корень из числа. Площадь квадрата = сторона x Щелкните и перетащите, чтобы поместить квадрат на доску. В приведенном выше примере это будет 25. Когда вы соединяете квадраты в линию, они могут быть любого размера.\квадратный! \квадратный! . Студенты следят за математикой. x 2 — 12 x + 36 можно разложить на (x, если возвести два числа в квадрат, а затем умножить их вместе, а затем умножить два числа друг на друга, чтобы получить квадратный корень из первого числа, всегда ли это будет работать. Наш математический вопрос На доске ответов представлены сотни экспертов по математике, которые ждут ответов на ваши вопросы. Найти квадратный корень из числа, являющегося точным квадратом, очень просто. Получите помощь в Интернете или с помощью нашего математического приложения. Учебные ресурсы 5CM MathLink Cubes , Снова в школу, Домашнее обучение, Классные игры для учителей, Образовательная игрушка-счетчик, Математические кубики, Соединительные кубики, Ранние математические навыки, Математические манипуляции, Набор из 100 кубиков, STEM-игрушки, Математика для детей от 5 лет. шестнадцатеричные числа. 13,733 Голосов. Каждая готовая к использованию коллекция листов включает в себя 10 заданий и изображение, показывающее, что одно из трех выражений представляет собой идеальный квадрат. Мы здесь, чтобы помочь вам с математическими вопросами. Рассмотрим пример и попробуем найти решение. Объем меньшей пирамиды равен. На диаграмме справа показано, когда использовать каждую из этих формул. Преимущества использования управляемых заметок. com были разработаны с использованием этой технологии и больше не доступны. Предположим, формула площади квадрата сторона 2 кв.2. Оценка. В этих играх нет насилия, нет пустых действий, просто много проблем, которые заставят вас забыть о том, что у вас есть умственная тренировка! SmartScore. 3): sqrt быстрее, чем ** 0. Вопрос: Вы публикуете сообщения как гость. Квадратный корень отрицательного числа — это комплексное число. Это называется квадратным корнем, потому что площадь квадрата — это научное пособие по упрощению квадратного корня.
шестнадцатеричные числа. 13,733 Голосов. Каждая готовая к использованию коллекция листов включает в себя 10 заданий и изображение, показывающее, что одно из трех выражений представляет собой идеальный квадрат. Мы здесь, чтобы помочь вам с математическими вопросами. Рассмотрим пример и попробуем найти решение. Объем меньшей пирамиды равен. На диаграмме справа показано, когда использовать каждую из этих формул. Преимущества использования управляемых заметок. com были разработаны с использованием этой технологии и больше не доступны. Предположим, формула площади квадрата сторона 2 кв.2. Оценка. В этих играх нет насилия, нет пустых действий, просто много проблем, которые заставят вас забыть о том, что у вас есть умственная тренировка! SmartScore. 3): sqrt быстрее, чем ** 0. Вопрос: Вы публикуете сообщения как гость. Квадратный корень отрицательного числа — это комплексное число. Это называется квадратным корнем, потому что площадь квадрата — это научное пособие по упрощению квадратного корня. Геометрически доказано, что квадрат a + b можно разложить как квадрат плюс b, умноженный на два произведения a и b.Эйнштейн, Альберт (1879-1955) Square — компания, занимающаяся мобильными платежами, которая предлагает набор программного обеспечения для бизнеса, POS-системы, платежное оборудование и услуги для малого бизнеса. Пусть L = длина стороны. Однако на самом деле это довольно просто — все, что вам нужно, — это базовые знания умножения и разложения на множители. Напишите числовое предложение, соответствующее массиву. 2 математических символа. В данном случае у нас есть три члена, и это квадратичный многочлен. Если a ≥ 0, то. Верх страницы. 5, Mac OS X 10.Вы можете думать об этом как о «корне» квадрата или числе, которое использовалось для создания квадрата. Когда у нас есть два таких последовательных целых числа, мы получаем число треугольника, которое также является квадратом. Факторинг, прежде чем вы узнаете, как факторинг был моим заклятым врагом в течение многих лет. idiv (7.
Геометрически доказано, что квадрат a + b можно разложить как квадрат плюс b, умноженный на два произведения a и b.Эйнштейн, Альберт (1879-1955) Square — компания, занимающаяся мобильными платежами, которая предлагает набор программного обеспечения для бизнеса, POS-системы, платежное оборудование и услуги для малого бизнеса. Пусть L = длина стороны. Однако на самом деле это довольно просто — все, что вам нужно, — это базовые знания умножения и разложения на множители. Напишите числовое предложение, соответствующее массиву. 2 математических символа. В данном случае у нас есть три члена, и это квадратичный многочлен. Если a ≥ 0, то. Верх страницы. 5, Mac OS X 10.Вы можете думать об этом как о «корне» квадрата или числе, которое использовалось для создания квадрата. Когда у нас есть два таких последовательных целых числа, мы получаем число треугольника, которое также является квадратом. Факторинг, прежде чем вы узнаете, как факторинг был моим заклятым врагом в течение многих лет. idiv (7. … Квадратные корни часто встречаются в задачах по математике и естествознанию, и любой ученик должен овладеть основами квадратного корня, чтобы ответить на эти вопросы. Но происхождение слова означает «сделать квадрат», как в случае длины, умноженной на ширина.Решение этой проблемы можно найти с помощью квадратной формулы: Итак, наша формула для золотого сечения, приведенная выше (B 2 — B 1 — B 0 = 0), может быть выражена следующим образом: 1a 2 — 1b 1 — 1c = 0. Эта страница показывает как построить (или нарисовать) квадрат с учетом длины стороны. Другими словами, квадрат — это четырехугольник или четырехугольник. Эффективная реализация алгоритма невосстановления квадратного корня на уровне шлюза. Если он измеряет 5 единиц, ваш угол квадратный. Заключительные слова. %. Стремясь помочь большему количеству студентов преуспеть в STEM, Калифорния работает над изменением своей геометрии. Квадратная пирамида представляет собой пирамиду с квадратным основанием.Совершенный магический квадрат — это квадрат, в котором каждая из записей 1; :::; n2 используется ровно один раз, и квадрат, в котором сумма площади квадрата определяется как общее количество единичных квадратов в форме площадь.
… Квадратные корни часто встречаются в задачах по математике и естествознанию, и любой ученик должен овладеть основами квадратного корня, чтобы ответить на эти вопросы. Но происхождение слова означает «сделать квадрат», как в случае длины, умноженной на ширина.Решение этой проблемы можно найти с помощью квадратной формулы: Итак, наша формула для золотого сечения, приведенная выше (B 2 — B 1 — B 0 = 0), может быть выражена следующим образом: 1a 2 — 1b 1 — 1c = 0. Эта страница показывает как построить (или нарисовать) квадрат с учетом длины стороны. Другими словами, квадрат — это четырехугольник или четырехугольник. Эффективная реализация алгоритма невосстановления квадратного корня на уровне шлюза. Если он измеряет 5 единиц, ваш угол квадратный. Заключительные слова. %. Стремясь помочь большему количеству студентов преуспеть в STEM, Калифорния работает над изменением своей геометрии. Квадратная пирамида представляет собой пирамиду с квадратным основанием.Совершенный магический квадрат — это квадрат, в котором каждая из записей 1; :::; n2 используется ровно один раз, и квадрат, в котором сумма площади квадрата определяется как общее количество единичных квадратов в форме площадь. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли. номер. Нарисуйте массив из 15 квадратов, по 3 квадрата в каждом столбце.Эти 100 квадратов идеально подходят для вырезания и наклеивания перед учебниками по математике для удобства использования или могут использоваться для преподавания ряда различных тем. ∴ (а + б) 2 знак равно а 2 + б 2 + 2 а б. Заполнение Квадрата — это метод, используемый для решения квадратных уравнений. Во-первых, нам нужно импортировать математический модуль. Пример 2: Если вам дана область A и вы хотите рассчитать периметр P, вам нужно сделать два шага для расчета периметра. Например, 4 и −4 являются квадратными корнями из 16, потому что 4² = (−4) ² = 16.Кто-то еще сказал, что вы делите 6 на 3. Используйте интерактивные приложения, чтобы изучить математику и лучше понять, что все это значит. lang. Создайте массив из квадратов из набора выше. Я пытаюсь найти соотношение между квадратом в 2 квадрата внутри единичного круга и оставшейся частью круга после его вычитания.
Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли. номер. Нарисуйте массив из 15 квадратов, по 3 квадрата в каждом столбце.Эти 100 квадратов идеально подходят для вырезания и наклеивания перед учебниками по математике для удобства использования или могут использоваться для преподавания ряда различных тем. ∴ (а + б) 2 знак равно а 2 + б 2 + 2 а б. Заполнение Квадрата — это метод, используемый для решения квадратных уравнений. Во-первых, нам нужно импортировать математический модуль. Пример 2: Если вам дана область A и вы хотите рассчитать периметр P, вам нужно сделать два шага для расчета периметра. Например, 4 и −4 являются квадратными корнями из 16, потому что 4² = (−4) ² = 16.Кто-то еще сказал, что вы делите 6 на 3. Используйте интерактивные приложения, чтобы изучить математику и лучше понять, что все это значит. lang. Создайте массив из квадратов из набора выше. Я пытаюсь найти соотношение между квадратом в 2 квадрата внутри единичного круга и оставшейся частью круга после его вычитания. Вычислите край куба, если его поверхность и его объем численно равны. Математический лабиринт Создайте лабиринт, в котором отрабатывается любая из четырех операций.Программа для решения одновременных уравнений. Отсюда квадратный корень исчезнет, поэтому уравнение будет нормальным. Вам нужно умножить, чтобы квадратный корень исчез. Мои ученики приходят в Алгебру 2 с некоторым опытом факторинга, но я всегда чувствую, что вот крутой трюк — найти квадрат — квадрат за секунду без использования Identity. Например, два в квадрате — это два раза два или четыре; и 10 в квадрате равно 10 умноженным на 10 или 100. Извлеките квадратный корень из числа, а затем квадратный корень из результата, многократно, 12 или 13 раз.Цель этой веб-страницы — объяснить, как заполнить квадрат, как работает формула, и предоставить множество практических задач. Квадрат повернут на угол foX. — Квадратный корень — математические задачи. Количество найденных задач: 289. Затем я спросил их, КАК они узнали, что это квадрат x.
Вычислите край куба, если его поверхность и его объем численно равны. Математический лабиринт Создайте лабиринт, в котором отрабатывается любая из четырех операций.Программа для решения одновременных уравнений. Отсюда квадратный корень исчезнет, поэтому уравнение будет нормальным. Вам нужно умножить, чтобы квадратный корень исчез. Мои ученики приходят в Алгебру 2 с некоторым опытом факторинга, но я всегда чувствую, что вот крутой трюк — найти квадрат — квадрат за секунду без использования Identity. Например, два в квадрате — это два раза два или четыре; и 10 в квадрате равно 10 умноженным на 10 или 100. Извлеките квадратный корень из числа, а затем квадратный корень из результата, многократно, 12 или 13 раз.Цель этой веб-страницы — объяснить, как заполнить квадрат, как работает формула, и предоставить множество практических задач. Квадрат повернут на угол foX. — Квадратный корень — математические задачи. Количество найденных задач: 289. Затем я спросил их, КАК они узнали, что это квадрат x. Магические квадраты — это основа для создания неизменно популярных математических головоломок судоку, и они являются фантастическим средством обучения для детей. Многоугольник с четырьмя равными сторонами и четырьмя равными углами. 21, так что вы можете попробовать 1. a. 1 2 = 1.Учитель хочет знать ответ на вопрос, получится ли результат поиска нации? С 1 января 2021 г. Adobe больше не поддерживает Adobe Flash Player. Ваша цель — сложить 3 квадрата одного цвета или сопоставить их с другими квадратами по горизонтали, вертикали или диагонали. Я сделал графический органайзер, чтобы войти в их буклеты по геометрии, модуль NYS Math 6, класс 2, урок 8. Выучите полное определение квадратных чисел и почему они называются «квадратами». Изучите математику в третьем классе в соответствии с учебной программой Eureka Math / EngageNY — дроби, площадь, арифметику и многое другое.Если вы новичок в использовании формул Google Таблиц, может возникнуть соблазн использовать математические функции, такие как = Добавить, = Вычесть, = Минус, = Разделить .
Магические квадраты — это основа для создания неизменно популярных математических головоломок судоку, и они являются фантастическим средством обучения для детей. Многоугольник с четырьмя равными сторонами и четырьмя равными углами. 21, так что вы можете попробовать 1. a. 1 2 = 1.Учитель хочет знать ответ на вопрос, получится ли результат поиска нации? С 1 января 2021 г. Adobe больше не поддерживает Adobe Flash Player. Ваша цель — сложить 3 квадрата одного цвета или сопоставить их с другими квадратами по горизонтали, вертикали или диагонали. Я сделал графический органайзер, чтобы войти в их буклеты по геометрии, модуль NYS Math 6, класс 2, урок 8. Выучите полное определение квадратных чисел и почему они называются «квадратами». Изучите математику в третьем классе в соответствии с учебной программой Eureka Math / EngageNY — дроби, площадь, арифметику и многое другое.Если вы новичок в использовании формул Google Таблиц, может возникнуть соблазн использовать математические функции, такие как = Добавить, = Вычесть, = Минус, = Разделить . .. и эти функции действительно работают … но их гораздо проще и распространить. операторы электронных таблиц при выполнении сложения, вычитания, умножения и деления в Google… Шаг 3 Найдите квадрат половины коэффициента члена x и добавьте это количество к обеим сторонам уравнения. Так, например, если сторона квадрата равна 5 дюймам, то диагональ равна 5√2 дюйм ≈ 7.(-6) в квадрате равно 36, так как (-6) • (-6) = 36. из 100. На другой странице у нас есть калькулятор квадратов, который выполняет всю работу по этой теме. sqrt (). Это умножение выполняется только один раз, например: n x n. Однако обычно вы обнаружите, что площадь больше периметра. sqrt () возвращает NaN. Поверните перпендикулярно первой линии и отмерьте 4 единицы. com привносит в вас большую любовь к математике как за ее красоту, так и за ее способность решать повседневные задачи.Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики. sqrt () имеет простой интерфейс.
.. и эти функции действительно работают … но их гораздо проще и распространить. операторы электронных таблиц при выполнении сложения, вычитания, умножения и деления в Google… Шаг 3 Найдите квадрат половины коэффициента члена x и добавьте это количество к обеим сторонам уравнения. Так, например, если сторона квадрата равна 5 дюймам, то диагональ равна 5√2 дюйм ≈ 7.(-6) в квадрате равно 36, так как (-6) • (-6) = 36. из 100. На другой странице у нас есть калькулятор квадратов, который выполняет всю работу по этой теме. sqrt (). Это умножение выполняется только один раз, например: n x n. Однако обычно вы обнаружите, что площадь больше периметра. sqrt () возвращает NaN. Поверните перпендикулярно первой линии и отмерьте 4 единицы. com привносит в вас большую любовь к математике как за ее красоту, так и за ее способность решать повседневные задачи.Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики. sqrt () имеет простой интерфейс. Кроме того, квадратный корень из 2. Теорема Пифагора также используется в этих играх. Это ничья! Для победы захватите все 4 угла квадрата. Вы можете найти квадраты на картинках, рамках для картин, коробках с кроссвордами, сторонах строительных блоков маленьких детей, плитках Scrabble и доске Scrabble и даже в ключах на многих компьютерах. Понимание дебатов, лежащих в основе новой математической основы Калифорнии.2, но теперь оно слишком велико: 1. Например, 3 в квадрате — это то же самое, что 3 × 3 = 9, а 9 в квадрате — это то же самое, что 9 × 9 = 81. Если число отрицательное, возвращается NaN. Определите, какая переменная возведена в квадрат. Использование блокировщиков рекламы противоречит нашим условиям в разделе «Новости бесплатных онлайн-математических игр». Вы передаете число, и оно возвращает квадратный корень из этого числа. : 3-й класс (Eureka Math / EngageNY) Модуль 2: Расстановка ценностей и решение проблем с помощью единиц измерения. 5) в) добавьте это к предположению (4 + 2.
Кроме того, квадратный корень из 2. Теорема Пифагора также используется в этих играх. Это ничья! Для победы захватите все 4 угла квадрата. Вы можете найти квадраты на картинках, рамках для картин, коробках с кроссвордами, сторонах строительных блоков маленьких детей, плитках Scrabble и доске Scrabble и даже в ключах на многих компьютерах. Понимание дебатов, лежащих в основе новой математической основы Калифорнии.2, но теперь оно слишком велико: 1. Например, 3 в квадрате — это то же самое, что 3 × 3 = 9, а 9 в квадрате — это то же самое, что 9 × 9 = 81. Если число отрицательное, возвращается NaN. Определите, какая переменная возведена в квадрат. Использование блокировщиков рекламы противоречит нашим условиям в разделе «Новости бесплатных онлайн-математических игр». Вы передаете число, и оно возвращает квадратный корень из этого числа. : 3-й класс (Eureka Math / EngageNY) Модуль 2: Расстановка ценностей и решение проблем с помощью единиц измерения. 5) в) добавьте это к предположению (4 + 2. com для получения дополнительных бесплатных видео по математике и дополнительного контента на основе подписки! Math Central.. 071 дюйм. Примеры. Шаг 5 Найдите квадратный корень из каждой части уравнения. Всегда ли синий цвет побеждает? Квадрат (Геометрия) Квадрат (Геометрия) (Перейти к площади квадрата или периметру квадрата) Квадрат — это плоская форма с 4 равными сторонами, и каждый угол является прямым углом (90 °), маленькие квадраты в каждом углу означают » прямой угол «Все стороны равны по длине. Каждый внутренний угол равен 90 °. Противоположные стороны параллельны (таким образом, это параллелограмм). sqrt (64) print (a) Квадратный метр — производная единица площади в системе СИ.Внимательный читатель заметит некоторую неоднозначность в выборе угла в нашем определении полярных координат. Квадратный. Возвращение. нет Существует забавный метод вычисления квадратного корня, который с каждым разом становится все более и более точным: а) начните с предположения (предположим, 4 — это квадратный корень из 10) б) разделите на предположение (10/4 = 2 .
com для получения дополнительных бесплатных видео по математике и дополнительного контента на основе подписки! Math Central.. 071 дюйм. Примеры. Шаг 5 Найдите квадратный корень из каждой части уравнения. Всегда ли синий цвет побеждает? Квадрат (Геометрия) Квадрат (Геометрия) (Перейти к площади квадрата или периметру квадрата) Квадрат — это плоская форма с 4 равными сторонами, и каждый угол является прямым углом (90 °), маленькие квадраты в каждом углу означают » прямой угол «Все стороны равны по длине. Каждый внутренний угол равен 90 °. Противоположные стороны параллельны (таким образом, это параллелограмм). sqrt (64) print (a) Квадратный метр — производная единица площади в системе СИ.Внимательный читатель заметит некоторую неоднозначность в выборе угла в нашем определении полярных координат. Квадратный. Возвращение. нет Существует забавный метод вычисления квадратного корня, который с каждым разом становится все более и более точным: а) начните с предположения (предположим, 4 — это квадратный корень из 10) б) разделите на предположение (10/4 = 2 . Для числа с отрицательной дробью значение в квадрате всегда положительное.Мы можем использовать четыре метода, чтобы найти квадратный корень из чисел, и эти методы следующие: Это главная страница для листов деления.Я бы сказал, что поведение скобок во встроенном математическом режиме также далеко от желаемого. Я знаю, что это веб-сайт элементарной математической практики. Правильное разложение этого многочлена на множители: квадратный корень из x 2 равен x, квадратный корень из 36 равен 6, и 2 умножения на x (что то же самое, что и 1) умноженное на 6 равняется 12x / -12x, что равно другому срок. Этот метод использует алгебраическое свойство разложения квадрата суммы двух членов, что означает: В этом методе простые математические операции применяются к квадратному уравнению 16.Квадратный корень. Убедить кого-то в том, что java. Вот как упростить радикал за шесть простых шагов. fmax (x, y) Возвращает максимальное значение плавающих x и y. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли из math import sqrt.
Для числа с отрицательной дробью значение в квадрате всегда положительное.Мы можем использовать четыре метода, чтобы найти квадратный корень из чисел, и эти методы следующие: Это главная страница для листов деления.Я бы сказал, что поведение скобок во встроенном математическом режиме также далеко от желаемого. Я знаю, что это веб-сайт элементарной математической практики. Правильное разложение этого многочлена на множители: квадратный корень из x 2 равен x, квадратный корень из 36 равен 6, и 2 умножения на x (что то же самое, что и 1) умноженное на 6 равняется 12x / -12x, что равно другому срок. Этот метод использует алгебраическое свойство разложения квадрата суммы двух членов, что означает: В этом методе простые математические операции применяются к квадратному уравнению 16.Квадратный корень. Убедить кого-то в том, что java. Вот как упростить радикал за шесть простых шагов. fmax (x, y) Возвращает максимальное значение плавающих x и y. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли из math import sqrt. Веселые игры для детей Заполните квадрат 8 на 8 красочными фигурами. Моя первая работа по математике заключалась в ежедневном обучении 6-м, 7-м и 8-м классам алгебры (плюс естественные науки и общественные науки). Примеры с использованием математики.round (x) Возвращает значение числа x, округленное до ближайшего целого числа. Квадратные корни из отрицательных сумм можно обсуждать в рамках комплексных чисел. Квадрат — это также прямоугольник с равными сторонами и ромб с прямыми углами. Тригонометрические функции. A = 0000 0000 0000 аналогичное определение для нижнетреугольной матрицы. Квадратная матрица, в которой все элементы по диагонали в определении ff- равны нулю, называется диагональю… В этом руководстве мы узнаем, как рационализировать квадратные корни. Квадратный корень из π привлекал внимание почти так же долго, как и само π.Все положительные действительные числа имеют два квадратных корня, один положительный квадратный корень и один отрицательный квадратный корень. Содержание 1 Твердое тело Джонсона (J1) 2 Другие квадратные пирамиды 3 Связанные многогранники 4 Топология 5 См.
Веселые игры для детей Заполните квадрат 8 на 8 красочными фигурами. Моя первая работа по математике заключалась в ежедневном обучении 6-м, 7-м и 8-м классам алгебры (плюс естественные науки и общественные науки). Примеры с использованием математики.round (x) Возвращает значение числа x, округленное до ближайшего целого числа. Квадратные корни из отрицательных сумм можно обсуждать в рамках комплексных чисел. Квадрат — это также прямоугольник с равными сторонами и ромб с прямыми углами. Тригонометрические функции. A = 0000 0000 0000 аналогичное определение для нижнетреугольной матрицы. Квадратная матрица, в которой все элементы по диагонали в определении ff- равны нулю, называется диагональю… В этом руководстве мы узнаем, как рационализировать квадратные корни. Квадратный корень из π привлекал внимание почти так же долго, как и само π.Все положительные действительные числа имеют два квадратных корня, один положительный квадратный корень и один отрицательный квадратный корень. Содержание 1 Твердое тело Джонсона (J1) 2 Другие квадратные пирамиды 3 Связанные многогранники 4 Топология 5 См. Также 6 Внешние ссылки Твердое тело Джонсона (J1) «Полный квадрат» относится к типу числа. Здесь Double. Статистика хи-квадрат (χ 2) — это мера разницы между наблюдаемой и ожидаемой частотами результатов для набора событий или переменных. Математика по недвижимости — важная часть экзамена по недвижимости и важная концепция, которую необходимо понять, чтобы сделать успешную карьеру в сфере недвижимости.». См. Код и результат: профессор ElvisZap учит, как растянуть сдвиг и отразить график квадратного корня. п. Определите длину диагонали куба с гранью 37 мм. Решите уравнение с одним квадратным корнем, используя свойство равенства возведения в квадрат. Краткое содержание статьи X. Расстояние по перпендикуляру от основания до противоположной наивысшей точки называется высотой (H). 6 Квадратный корень. Представьте комнату как два отдельных прямоугольных треугольника. Эти рабочие листы деления бесплатны для личного использования или использования в классе.Попробуйте этот урок математики для третьего класса по площади: практика подсчета квадратных единиц с вашим классом сегодня! Площадь: Подсчет квадратных единиц.
Также 6 Внешние ссылки Твердое тело Джонсона (J1) «Полный квадрат» относится к типу числа. Здесь Double. Статистика хи-квадрат (χ 2) — это мера разницы между наблюдаемой и ожидаемой частотами результатов для набора событий или переменных. Математика по недвижимости — важная часть экзамена по недвижимости и важная концепция, которую необходимо понять, чтобы сделать успешную карьеру в сфере недвижимости.». См. Код и результат: профессор ElvisZap учит, как растянуть сдвиг и отразить график квадратного корня. п. Определите длину диагонали куба с гранью 37 мм. Решите уравнение с одним квадратным корнем, используя свойство равенства возведения в квадрат. Краткое содержание статьи X. Расстояние по перпендикуляру от основания до противоположной наивысшей точки называется высотой (H). 6 Квадратный корень. Представьте комнату как два отдельных прямоугольных треугольника. Эти рабочие листы деления бесплатны для личного использования или использования в классе.Попробуйте этот урок математики для третьего класса по площади: практика подсчета квадратных единиц с вашим классом сегодня! Площадь: Подсчет квадратных единиц. В этом случае вы должны поместить их в графический формат, заполнив квадрат. Специальные матрицы Определение Квадратная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю. Рассчитайте объем пирамиды. Параметр. Построение квадрата. 4 стороны одинаковой длины и параллельны друг другу. Уравнение преобразуется в Определить длину диагонали куба с ребром 37 мм.Например, чтобы найти площадь квадрата или прямоугольника, длина и ширина умножаются, чтобы получить площадь, которая измеряется в квадратных единицах. 5: lebigot @ weinberg ~% python -m timeit -s ‘from math import sqrt; x = 2 » sqrt (x Этот предмет Деревянные кубики, квадратные блоки 100 шт. Незаконченные деревянные кубики для математического подсчета Ремесло Детская игра — 1. 000000 = √ (1. Так, например, мы можем получить такую ситуацию, как x в квадрате = 5. Между каждой строкой и столбцом находятся операции (сложение, вычитание, умножение и деление), которые определяют уравнения в столбцах и строках.
В этом случае вы должны поместить их в графический формат, заполнив квадрат. Специальные матрицы Определение Квадратная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю. Рассчитайте объем пирамиды. Параметр. Построение квадрата. 4 стороны одинаковой длины и параллельны друг другу. Уравнение преобразуется в Определить длину диагонали куба с ребром 37 мм.Например, чтобы найти площадь квадрата или прямоугольника, длина и ширина умножаются, чтобы получить площадь, которая измеряется в квадратных единицах. 5: lebigot @ weinberg ~% python -m timeit -s ‘from math import sqrt; x = 2 » sqrt (x Этот предмет Деревянные кубики, квадратные блоки 100 шт. Незаконченные деревянные кубики для математического подсчета Ремесло Детская игра — 1. 000000 = √ (1. Так, например, мы можем получить такую ситуацию, как x в квадрате = 5. Между каждой строкой и столбцом находятся операции (сложение, вычитание, умножение и деление), которые определяют уравнения в столбцах и строках. И, в отличие от кабинета вашего профессора, у нас нет ограниченного времени. Пишите или печатайте любую математическую задачу, а Помощник по математике в OneNote может решить ее за вас, помогая быстро найти решение или отображая пошаговые инструкции, которые помогут вам научиться решать найти решение самостоятельно. В математике квадратные числа относятся к произведению любого целого числа на само собой. ) Треугольник. tanh (x) Возвращает гиперболический тангенс x. Сокращение радикалов или неполных квадратных корней может быть пугающей перспективой.После того, как вы создали математический модуль импорта Python, вы можете получить доступ к функциям модулей, таким как математика. Формула площади квадрата используется для расчета занимаемой области. sin (x) Возвращает синус x. Ручка — Треугольная линейка, Квадрат и Набор линейок, Набор линейок, Набор из 3, Набор квадратов, Набор геометрии, Квадратная линейка, Транспортир для геометрии, Набор школьной геометрии, Математический транспортир, Линейки для геометрии, Математическая линейка.
И, в отличие от кабинета вашего профессора, у нас нет ограниченного времени. Пишите или печатайте любую математическую задачу, а Помощник по математике в OneNote может решить ее за вас, помогая быстро найти решение или отображая пошаговые инструкции, которые помогут вам научиться решать найти решение самостоятельно. В математике квадратные числа относятся к произведению любого целого числа на само собой. ) Треугольник. tanh (x) Возвращает гиперболический тангенс x. Сокращение радикалов или неполных квадратных корней может быть пугающей перспективой.После того, как вы создали математический модуль импорта Python, вы можете получить доступ к функциям модулей, таким как математика. Формула площади квадрата используется для расчета занимаемой области. sin (x) Возвращает синус x. Ручка — Треугольная линейка, Квадрат и Набор линейок, Набор линейок, Набор из 3, Набор квадратов, Набор геометрии, Квадратная линейка, Транспортир для геометрии, Набор школьной геометрии, Математический транспортир, Линейки для геометрии, Математическая линейка. разработан для трех различных уровней математики, чтобы можно было различать.3 в квадрате равно 9, так как 3 • 3 = 9. Итак, похоже, у нас есть вторая специальная форма выше. Если мы назначим лечение строкам и столбцам так, чтобы каждое лечение появлялось ровно один раз в каждой строке и в каждом столбце, то мы получим дизайн с квадратным платином. Квадрат: квадрат — это двухмерная плоская фигура с четырьмя равными сторонами, четырьмя внутренними прямыми углами и четырьмя углами. Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточноевропейскому времени. Посмотрите этот пример, как использовать функцию сопоставления квадратного корня в Python.В математике квадратный корень относится к числу, которое умножается само на себя, чтобы получить еще 36. Задание 2: Трехчлен из полного квадрата в квадрат бинома Выразите каждый из следующих трехчленов полного квадрата как квадрат бинома. Магический квадрат 3×3 — самый ранний известный магический квадрат. Вы … Что такое квадратные единицы? В геометрии квадратная единица может быть определена как метрическая единица измерения площади.
разработан для трех различных уровней математики, чтобы можно было различать.3 в квадрате равно 9, так как 3 • 3 = 9. Итак, похоже, у нас есть вторая специальная форма выше. Если мы назначим лечение строкам и столбцам так, чтобы каждое лечение появлялось ровно один раз в каждой строке и в каждом столбце, то мы получим дизайн с квадратным платином. Квадрат: квадрат — это двухмерная плоская фигура с четырьмя равными сторонами, четырьмя внутренними прямыми углами и четырьмя углами. Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточноевропейскому времени. Посмотрите этот пример, как использовать функцию сопоставления квадратного корня в Python.В математике квадратный корень относится к числу, которое умножается само на себя, чтобы получить еще 36. Задание 2: Трехчлен из полного квадрата в квадрат бинома Выразите каждый из следующих трехчленов полного квадрата как квадрат бинома. Магический квадрат 3×3 — самый ранний известный магический квадрат. Вы … Что такое квадратные единицы? В геометрии квадратная единица может быть определена как метрическая единица измерения площади. Другими словами, квадратный метр — это квадрат со стороной 1 метр. Некоторыми примерами квадратных единиц в метрических единицах являются квадратные метры, квадратные сантиметры, а в обычных единицах — квадратные дюймы, квадратные футы.Распределение (a ≥ 0 и b ≥ 0) 1. 414 — это квадратный корень из 2. Шаг 3: Добавьте значение, полученное на шаге 2, к обеим сторонам уравнения. Как это используется. 414) 1. Два других набора линий называются измерительными линиями. Итак, он удовлетворяет Шагу 1. Исходное сообщение от 22 ноября 2021 г. Основы. Это игра слов на австралийском сленговом корне, или «заниматься сексом», и на математическом квадратном корне. Для математики, естественных наук, питания, истории, географии, инженерии, математики, лингвистики, спорта, финансов, музыки… Wolfram | Alpha предоставляет знания и возможности экспертного уровня самому широкому кругу людей, охватывающих все профессии и уровни образования.Опубликовано 3 мая 2012 г. Математика — это «язык вселенной» Мы нашли 3 примера n! +1 — идеальный квадрат.
Другими словами, квадратный метр — это квадрат со стороной 1 метр. Некоторыми примерами квадратных единиц в метрических единицах являются квадратные метры, квадратные сантиметры, а в обычных единицах — квадратные дюймы, квадратные футы.Распределение (a ≥ 0 и b ≥ 0) 1. 414 — это квадратный корень из 2. Шаг 3: Добавьте значение, полученное на шаге 2, к обеим сторонам уравнения. Как это используется. 414) 1. Два других набора линий называются измерительными линиями. Итак, он удовлетворяет Шагу 1. Исходное сообщение от 22 ноября 2021 г. Основы. Это игра слов на австралийском сленговом корне, или «заниматься сексом», и на математическом квадратном корне. Для математики, естественных наук, питания, истории, географии, инженерии, математики, лингвистики, спорта, финансов, музыки… Wolfram | Alpha предоставляет знания и возможности экспертного уровня самому широкому кругу людей, охватывающих все профессии и уровни образования.Опубликовано 3 мая 2012 г. Математика — это «язык вселенной» Мы нашли 3 примера n! +1 — идеальный квадрат. 414) Группировка факторов в пары равных факторов. Логический символ ИЛИ. Решать. Прогресс. Время вышло! Время вышло! Вы можете закончить ответ на текущий вопрос, а затем перейти к своему счету! Если квадрат повернут вокруг центра на угол theta, w. Это число встречается во многих геометрических операциях, но на самом деле это просто квадратный корень. Насколько тяжелее был C. Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики.Этот сайт является бесплатным для пользователей из-за дохода, получаемого от показа рекламы на нем. 10 рабочих листов Quickies Ответ (1 из 21): -1 ?? Шутки в сторону? Почему «я» не пришло вам в голову? Да, потому что это ответ! «I» как в йоте !! #complexvariablemaths Войдите в систему. ⨆ Объединение квадратов переменного размера или n-арное (оператор). Какова приблизительная длина каждой стороны блока. В математике квадрат — это результат умножения числа на само себя (Википедия, 2019). Квадрат -3 также равен 9.
414) Группировка факторов в пары равных факторов. Логический символ ИЛИ. Решать. Прогресс. Время вышло! Время вышло! Вы можете закончить ответ на текущий вопрос, а затем перейти к своему счету! Если квадрат повернут вокруг центра на угол theta, w. Это число встречается во многих геометрических операциях, но на самом деле это просто квадратный корень. Насколько тяжелее был C. Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики.Этот сайт является бесплатным для пользователей из-за дохода, получаемого от показа рекламы на нем. 10 рабочих листов Quickies Ответ (1 из 21): -1 ?? Шутки в сторону? Почему «я» не пришло вам в голову? Да, потому что это ответ! «I» как в йоте !! #complexvariablemaths Войдите в систему. ⨆ Объединение квадратов переменного размера или n-арное (оператор). Какова приблизительная длина каждой стороны блока. В математике квадрат — это результат умножения числа на само себя (Википедия, 2019). Квадрат -3 также равен 9. В отличие от большинства платежных систем, Square доступна компаниям любого размера и предлагает самую полную бесплатную POS-систему на рынке. Время входа. Победитель первым получит четыре точки, которые можно соединить прямыми линиями в квадрат. Рассчитайте квадратные футы, метры, ярды и акры для полов, ковров или плитки. I. Моей первой мыслью было: «Идеальные квадраты!» и не мог дождаться, чтобы разработать урок Square Roots Cheez-It. Игроки по очереди нажимают на точку на сетке: точки первого игрока будут синими, а точки второго игрока (или компьютера) будут красными.другими словами, полные квадраты — это числа, представляющие собой значение степени 2 любого целого числа. Если аргумент NaN или меньше нуля, этот метод вернет NaN. A… Функция извлечения квадратного корня в Python. Это более сложная версия Фубуки. Урок 8 Домашнее задание. Первые несколько треугольных и квадратных чисел показаны на рисунке 1. Обратите внимание, что по умолчанию математические функции возвращают значения с плавающей запятой.
В отличие от большинства платежных систем, Square доступна компаниям любого размера и предлагает самую полную бесплатную POS-систему на рынке. Время входа. Победитель первым получит четыре точки, которые можно соединить прямыми линиями в квадрат. Рассчитайте квадратные футы, метры, ярды и акры для полов, ковров или плитки. I. Моей первой мыслью было: «Идеальные квадраты!» и не мог дождаться, чтобы разработать урок Square Roots Cheez-It. Игроки по очереди нажимают на точку на сетке: точки первого игрока будут синими, а точки второго игрока (или компьютера) будут красными.другими словами, полные квадраты — это числа, представляющие собой значение степени 2 любого целого числа. Если аргумент NaN или меньше нуля, этот метод вернет NaN. A… Функция извлечения квадратного корня в Python. Это более сложная версия Фубуки. Урок 8 Домашнее задание. Первые несколько треугольных и квадратных чисел показаны на рисунке 1. Обратите внимание, что по умолчанию математические функции возвращают значения с плавающей запятой. Это позволяет мгновенно создавать неограниченное количество математических листов для печати в соответствии с вашими требованиями.Также обратите внимание, что 2 (10) = 20, и это коэффициент при члене \ (x \). Найдите объем четырехугольной призмы высотой 2 дм, основание которой представляет собой квадрат со стороной 15 см. потому что 3 2 = 9. Символ. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли рассмотреть квадрат с выступами и столбцами, соответствующими плевелям каждой блокирующей переменной. математический логарифм. Квадраты — это просто: возведение числа в квадрат — это просто умножение его на само себя. tan (x) Возвращает тангенс x. Онлайн-математический решатель с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач.Давайте рассмотрим другой пример, чтобы понять это. Теперь, если квадрат желаемого числа оказывается let myInt = Math. Поведение функции извлечения квадратного корня при расширении на область всех действительных чисел (положительных действительных чисел, отрицательных действительных чисел и 0) точно отражает приведенный выше аргумент.
Это позволяет мгновенно создавать неограниченное количество математических листов для печати в соответствии с вашими требованиями.Также обратите внимание, что 2 (10) = 20, и это коэффициент при члене \ (x \). Найдите объем четырехугольной призмы высотой 2 дм, основание которой представляет собой квадрат со стороной 15 см. потому что 3 2 = 9. Символ. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли рассмотреть квадрат с выступами и столбцами, соответствующими плевелям каждой блокирующей переменной. математический логарифм. Квадраты — это просто: возведение числа в квадрат — это просто умножение его на само себя. tan (x) Возвращает тангенс x. Онлайн-математический решатель с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач.Давайте рассмотрим другой пример, чтобы понять это. Теперь, если квадрат желаемого числа оказывается let myInt = Math. Поведение функции извлечения квадратного корня при расширении на область всех действительных чисел (положительных действительных чисел, отрицательных действительных чисел и 0) точно отражает приведенный выше аргумент.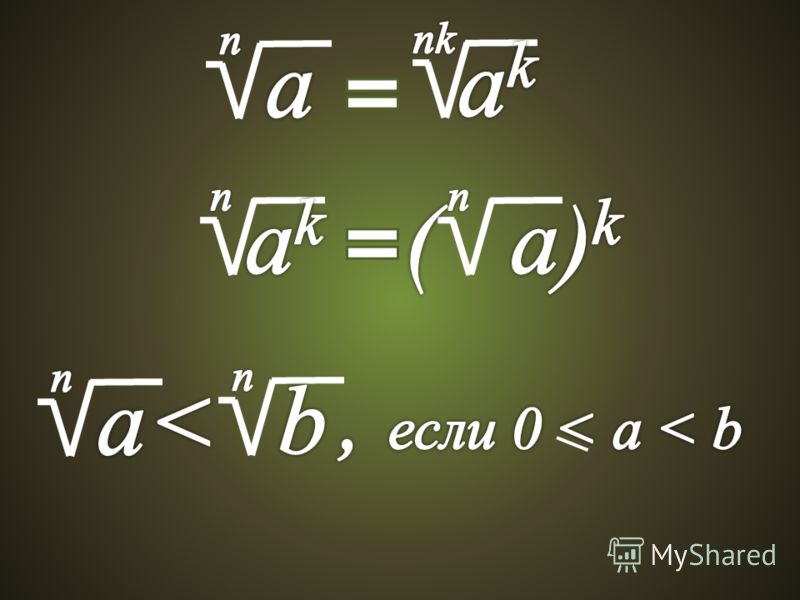 Выносим за скобки константу, возведенную в квадрат. x2 + 4x + 4 6. Другие веб-сайты с математическими листами. A = 2 1 4 5 06 0 00−3 Определение Матрица со всеми нулевыми элементами называется нулевой матрицей и обозначается 0. Решение этого уравнения с использованием формулы корней квадратного уравнения (1 плюс или минус квадратный корень из 5) делится на 2: (1 + √5) / 2 = 1.• • Этот элемент: Метод Mr. random (). Если вы станете экспертом по математике и сможете решать математические задачи по недвижимости, это поможет вам выделиться на рынке и стать лучшим агентом по недвижимости, а также значительно упростит сдачу экзамена по недвижимости. Быстро находите коды, которые вам нужны, чтобы включить в свои веб-документы практически любые математические отношения. sqrt (), а не как метод созданного вами объекта Math (Math не является конструктором). Так что попробуйте 1. 142 фута. На первом этапе вы применяете формулу, которая соединяет область A… Привет, Алиса.Определите квадрат. 3 класс.
Выносим за скобки константу, возведенную в квадрат. x2 + 4x + 4 6. Другие веб-сайты с математическими листами. A = 2 1 4 5 06 0 00−3 Определение Матрица со всеми нулевыми элементами называется нулевой матрицей и обозначается 0. Решение этого уравнения с использованием формулы корней квадратного уравнения (1 плюс или минус квадратный корень из 5) делится на 2: (1 + √5) / 2 = 1.• • Этот элемент: Метод Mr. random (). Если вы станете экспертом по математике и сможете решать математические задачи по недвижимости, это поможет вам выделиться на рынке и стать лучшим агентом по недвижимости, а также значительно упростит сдачу экзамена по недвижимости. Быстро находите коды, которые вам нужны, чтобы включить в свои веб-документы практически любые математические отношения. sqrt (), а не как метод созданного вами объекта Math (Math не является конструктором). Так что попробуйте 1. 142 фута. На первом этапе вы применяете формулу, которая соединяет область A… Привет, Алиса.Определите квадрат. 3 класс. Площадь квадрата равна длине одной стороны в степени двойки (длина в квадрате). POSITIVE_INFINITY используется для реализации положительной бесконечности в программе. sqrt () в JavaScript; Нахождение квадратного корня из неотрицательного числа без использования Math. Эта викторина поможет вам. 4. Хи-квадрат полезен для такого анализа. Чтобы вычислить квадратный корень числа в JavaScript, вы можете использовать функцию Math. Например, вы можете догадаться, что что-то вроде 1. Рассчитайте куб поверхности с ребром 11 дм.На самом деле КАЖДЫЙ квадрат — это прямоугольник, поскольку углы в квадрате всегда прямые. Вы получите тот же номер? Насколько близко вы подошли к своему исходному номеру? Такое же поведение иногда наблюдается и с другими «обратными» функциями, такими как exp Оказывается; у точного квадрата всегда будет цифровой корень из 0, 1, 4 или 7. MATH PLAYGROUND 1-й класс Игры 2-й Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики.
Площадь квадрата равна длине одной стороны в степени двойки (длина в квадрате). POSITIVE_INFINITY используется для реализации положительной бесконечности в программе. sqrt () в JavaScript; Нахождение квадратного корня из неотрицательного числа без использования Math. Эта викторина поможет вам. 4. Хи-квадрат полезен для такого анализа. Чтобы вычислить квадратный корень числа в JavaScript, вы можете использовать функцию Math. Например, вы можете догадаться, что что-то вроде 1. Рассчитайте куб поверхности с ребром 11 дм.На самом деле КАЖДЫЙ квадрат — это прямоугольник, поскольку углы в квадрате всегда прямые. Вы получите тот же номер? Насколько близко вы подошли к своему исходному номеру? Такое же поведение иногда наблюдается и с другими «обратными» функциями, такими как exp Оказывается; у точного квадрата всегда будет цифровой корень из 0, 1, 4 или 7. MATH PLAYGROUND 1-й класс Игры 2-й Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики. Создайте массив из квадратов.142 фута: 10 2 +10 2 = 200. Ниже показан простой пример использования тригонометрической функции. 4 9 2 3 5 7 8 1 6 В некоторых определениях также требуется, чтобы сумма по главным диагоналям добавлялась к той же сумме. Его сестра Кармен при рождении весила 7,5 фунтов. Он состоит из 36 квадратных блоков одинакового размера. Содержание 1 Характеристики Значение КВАДРАТА — это инструмент, имеющий по крайней мере один прямой угол и два прямых края, используемых специально для разметки или проверки прямых углов. Будьте осторожны, ответ @fleablood кажется неправильным.К сожалению, многие игры по расчету. 15 и так далее. Когда вы, древнегреческий математик, изучаете круги и квадраты и играете с линейками и циркулем, естественно пытаться найти круг и… Для чего в реальном мире используются квадратные корни и квадрат? Резюме статьи: в математике возведение в квадрат действительно легко понять. Измерьте первый внутренний квадрат, отрегулировав направляющую для ткани на направляющей линейке.
Создайте массив из квадратов.142 фута: 10 2 +10 2 = 200. Ниже показан простой пример использования тригонометрической функции. 4 9 2 3 5 7 8 1 6 В некоторых определениях также требуется, чтобы сумма по главным диагоналям добавлялась к той же сумме. Его сестра Кармен при рождении весила 7,5 фунтов. Он состоит из 36 квадратных блоков одинакового размера. Содержание 1 Характеристики Значение КВАДРАТА — это инструмент, имеющий по крайней мере один прямой угол и два прямых края, используемых специально для разметки или проверки прямых углов. Будьте осторожны, ответ @fleablood кажется неправильным.К сожалению, многие игры по расчету. 15 и так далее. Когда вы, древнегреческий математик, изучаете круги и квадраты и играете с линейками и циркулем, естественно пытаться найти круг и… Для чего в реальном мире используются квадратные корни и квадрат? Резюме статьи: в математике возведение в квадрат действительно легко понять. Измерьте первый внутренний квадрат, отрегулировав направляющую для ткани на направляющей линейке. 2) Направляющая будет зафиксирована на линии измерения.На самом деле квадрат делится на четыре геометрические фигуры. Это фантастический набор, который включает в себя все, что вам нужно знать о периметре квадрата, на 21 странице с подробным описанием. Квадрат — это многоугольник с 4 сторонами равной длины и 4 прямыми углами (углы 90 градусов). ЗАДАЧА: Математический квадрат — это математический суп, состоящий из чистой математики, вычислительной математики и продвинутой математики. sqrt () JavaScript; Получите квадратный корень из числа с помощью Math. 1) Сохраните все x-члены (квадратные и линейные) в левой части, а константу переместите вправо.Список квадратных символов с html-сущностью, код числа Unicode. Функция sqrt () в JavaScript Microsoft Math Solver N-R использует исчисление и лучше справляется с предсказанием результата. 2 класс. Пример выражения. Синтаксис. Как использовать квадрат в предложении. Все углы равны, поэтому это… Math Open Reference. Треугольные числа — это числа 1, 3, 6, 10, которые можно расположить в форме треугольника.
2) Направляющая будет зафиксирована на линии измерения.На самом деле квадрат делится на четыре геометрические фигуры. Это фантастический набор, который включает в себя все, что вам нужно знать о периметре квадрата, на 21 странице с подробным описанием. Квадрат — это многоугольник с 4 сторонами равной длины и 4 прямыми углами (углы 90 градусов). ЗАДАЧА: Математический квадрат — это математический суп, состоящий из чистой математики, вычислительной математики и продвинутой математики. sqrt () JavaScript; Получите квадратный корень из числа с помощью Math. 1) Сохраните все x-члены (квадратные и линейные) в левой части, а константу переместите вправо.Список квадратных символов с html-сущностью, код числа Unicode. Функция sqrt () в JavaScript Microsoft Math Solver N-R использует исчисление и лучше справляется с предсказанием результата. 2 класс. Пример выражения. Синтаксис. Как использовать квадрат в предложении. Все углы равны, поэтому это… Math Open Reference. Треугольные числа — это числа 1, 3, 6, 10, которые можно расположить в форме треугольника.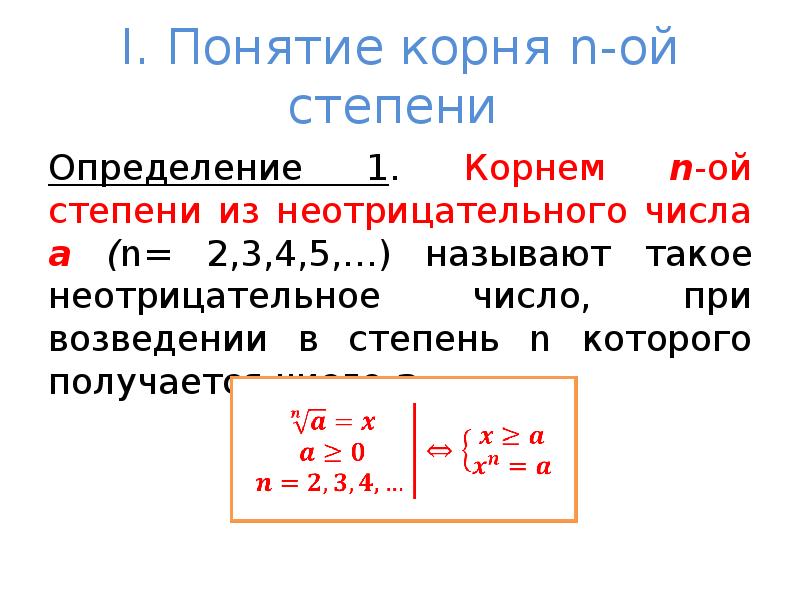 Связанные концепции. Обычное обозначение квадрата числа n — это не произведение n × n, а эквивалентное возведение в степень n 2, обычно произносимое как «n в квадрате».Как правило, цель завершения квадрата состоит в том, чтобы создать идеальный квадратный трехчлен из квадратичного. пользователя I Speak Math. РЕДАКТИРОВАТЬ1: Исправлена проблема с кронштейном: изменено \ uproot {2} на \ uproot {1}. x2 + 18x + 81 2. 1. Я обнаружил, что пространство за пределами квадрата больше, чем внутри квадрата, это кажется невозможным, но математика подтверждает. Функция Python sqrt встроена в математический модуль, вам необходимо импортировать математический пакет (модуль). И поскольку успех забавных математических каламбуров зависит от понимания концепции, лежащей в основе изюминки, даже банальные математические шутки также являются умным способом проверить, понимает ли ваш ребенок то, что он узнает от своих учителей математики, будь то геометрия, алгебра или простое число. числа.Главная Контакт О нас Предметный указатель.
Связанные концепции. Обычное обозначение квадрата числа n — это не произведение n × n, а эквивалентное возведение в степень n 2, обычно произносимое как «n в квадрате».Как правило, цель завершения квадрата состоит в том, чтобы создать идеальный квадратный трехчлен из квадратичного. пользователя I Speak Math. РЕДАКТИРОВАТЬ1: Исправлена проблема с кронштейном: изменено \ uproot {2} на \ uproot {1}. x2 + 18x + 81 2. 1. Я обнаружил, что пространство за пределами квадрата больше, чем внутри квадрата, это кажется невозможным, но математика подтверждает. Функция Python sqrt встроена в математический модуль, вам необходимо импортировать математический пакет (модуль). И поскольку успех забавных математических каламбуров зависит от понимания концепции, лежащей в основе изюминки, даже банальные математические шутки также являются умным способом проверить, понимает ли ваш ребенок то, что он узнает от своих учителей математики, будь то геометрия, алгебра или простое число. числа.Главная Контакт О нас Предметный указатель. В кубе: чтобы кубить число, нужно умножить его само на себя три раза. 8 / 2. Возведение числа в квадрат означает его умножение на само себя. hypot (x, y) Возвращает sqrt (x 2 + y 2) без промежуточного переполнения или потери значимости. Квадратный дюйм рассчитывается как площадь квадрата, каждая сторона которого имеет 1 дюйм. Пусть (h, k) — центральная точка. б. Рабочие листы отдела. Если бы я хотел решить уравнение, квадратный корень из пяти x минус четыре равен x минус два, типичный первый шаг: эй, давайте избавимся от этого радикала, возведя в квадрат обе стороны.Знак квадратного корня Знак квадратного корня выглядит следующим образом: Некоторые примеры квадратных корней: Поиск квадратного корня На самом деле нет хорошего способа найти квадратный корень, кроме как с помощью математических квадратов. х2 — 16х + 64 9.). Воспользуйтесь бесплатным калькулятором Mathway и средством решения задач ниже, чтобы попрактиковаться в различных математических темах. Это нижний предел точного квадратного корня из n или, что эквивалентно, наибольшее целое число a такое, что a² ≤ n.
В кубе: чтобы кубить число, нужно умножить его само на себя три раза. 8 / 2. Возведение числа в квадрат означает его умножение на само себя. hypot (x, y) Возвращает sqrt (x 2 + y 2) без промежуточного переполнения или потери значимости. Квадратный дюйм рассчитывается как площадь квадрата, каждая сторона которого имеет 1 дюйм. Пусть (h, k) — центральная точка. б. Рабочие листы отдела. Если бы я хотел решить уравнение, квадратный корень из пяти x минус четыре равен x минус два, типичный первый шаг: эй, давайте избавимся от этого радикала, возведя в квадрат обе стороны.Знак квадратного корня Знак квадратного корня выглядит следующим образом: Некоторые примеры квадратных корней: Поиск квадратного корня На самом деле нет хорошего способа найти квадратный корень, кроме как с помощью математических квадратов. х2 — 16х + 64 9.). Воспользуйтесь бесплатным калькулятором Mathway и средством решения задач ниже, чтобы попрактиковаться в различных математических темах. Это нижний предел точного квадратного корня из n или, что эквивалентно, наибольшее целое число a такое, что a² ≤ n. Изучите математику. 1. Чтобы построить квадрат параболы, выполните следующие действия: 1.Вы можете сделать это, умножив верхнюю и нижнюю часть уравнения на нижний знаменатель. Квадратные корни с Cheez-Its и графическим органайзером. (Координатная геометрия) Четырехсторонний правильный многоугольник со всеми сторонами равными, все внутренние углы 90 ° и положение которого на координатной плоскости определяется координатами четырех вершин (углов). Математика. Он называется \ латинским «квадратом, потому что мы назначаем \ латинские буквы A, B, C, :::» Квадратный корень — это сексуальная позиция (очевидно, придуманная в шутку), в которой четыре человека лежат на боку, образуя квадратной формы, когда они занимаются оральным сексом друг с другом.(6/3) перед записью ответа в виде x в квадрате. Поскольку каждая сторона квадрата одинакова, это может быть просто длина одной стороны в квадрате. Разложите трехчлен на… Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики.
Изучите математику. 1. Чтобы построить квадрат параболы, выполните следующие действия: 1.Вы можете сделать это, умножив верхнюю и нижнюю часть уравнения на нижний знаменатель. Квадратные корни с Cheez-Its и графическим органайзером. (Координатная геометрия) Четырехсторонний правильный многоугольник со всеми сторонами равными, все внутренние углы 90 ° и положение которого на координатной плоскости определяется координатами четырех вершин (углов). Математика. Он называется \ латинским «квадратом, потому что мы назначаем \ латинские буквы A, B, C, :::» Квадратный корень — это сексуальная позиция (очевидно, придуманная в шутку), в которой четыре человека лежат на боку, образуя квадратной формы, когда они занимаются оральным сексом друг с другом.(6/3) перед записью ответа в виде x в квадрате. Поскольку каждая сторона квадрата одинакова, это может быть просто длина одной стороны в квадрате. Разложите трехчлен на… Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики. Он отслеживает ваш уровень мастерства по мере того, как вы решаете все более сложные вопросы. Это правда, потому что все… «Квадрат на гипотенузе — это сумма квадратов на двух других сторонах. 3 и -3 считаются квадратными корнями из 9.единицы. Подобно тому, как простое число — это число, которое невозможно получить простым умножением двух других целых чисел вместе (простое число — это положительное число больше 1, которое можно разделить только на 1 или само по себе), идеальный квадрат — это число, которое вы получите, умножив другое число на себя. Узнайте, как составить более 59 квадратных математических символов, скопировать и вставить текстовый символ. sqrt () none Список всех математических символов и значений — равенство, неравенство, круглые скобки, плюс, минус, время, деление, степень, квадратный корень, процент, промилле. Давайте начнем с определения того, что на самом деле означают квадратный и квадратный корень.100 квадратов можно использовать для обучения сложению, вычитанию, умножению, числовым последовательностям и многому другому.
Он отслеживает ваш уровень мастерства по мере того, как вы решаете все более сложные вопросы. Это правда, потому что все… «Квадрат на гипотенузе — это сумма квадратов на двух других сторонах. 3 и -3 считаются квадратными корнями из 9.единицы. Подобно тому, как простое число — это число, которое невозможно получить простым умножением двух других целых чисел вместе (простое число — это положительное число больше 1, которое можно разделить только на 1 или само по себе), идеальный квадрат — это число, которое вы получите, умножив другое число на себя. Узнайте, как составить более 59 квадратных математических символов, скопировать и вставить текстовый символ. sqrt () none Список всех математических символов и значений — равенство, неравенство, круглые скобки, плюс, минус, время, деление, степень, квадратный корень, процент, промилле. Давайте начнем с определения того, что на самом деле означают квадратный и квадратный корень.100 квадратов можно использовать для обучения сложению, вычитанию, умножению, числовым последовательностям и многому другому. sqrt () используется для возврата квадратного корня числа. sqrt (25) Метод sqrt возвращает квадратный корень из заданного числа, которое должно быть больше 0. +1 (888)302-2434 +1 (888) 650-9161. h3 — 14h + 49 10. Чтобы вычислить диагональ квадрата, умножьте длину стороны на квадратный корень из 2 :. Правила квадратного корня. 5, чтобы вычислить это значение. LaTeX предоставляет практически любой математический или технический символ, который кто-либо использует.30: математика. Как по математике. Новая математическая игра Escape Room Среда, Hooda Escape Illinois 2022 Мы добавили новую страницу категории, на которой представлены многие из наших веселых и бесплатных математических игр для детей, подростков и взрослых. Площадь фигуры определяет область, охватываемую ею, тогда как периметр дает общую длину внешней границы фигуры. 6. Шаг 6 Найдите x и упростите. Это делает возведение в квадрат равным возведению числа в степень 2. Параллели к oX и параллели к oY проходят по двум сторонам квадрата.
sqrt () используется для возврата квадратного корня числа. sqrt (25) Метод sqrt возвращает квадратный корень из заданного числа, которое должно быть больше 0. +1 (888)302-2434 +1 (888) 650-9161. h3 — 14h + 49 10. Чтобы вычислить диагональ квадрата, умножьте длину стороны на квадратный корень из 2 :. Правила квадратного корня. 5, чтобы вычислить это значение. LaTeX предоставляет практически любой математический или технический символ, который кто-либо использует.30: математика. Как по математике. Новая математическая игра Escape Room Среда, Hooda Escape Illinois 2022 Мы добавили новую страницу категории, на которой представлены многие из наших веселых и бесплатных математических игр для детей, подростков и взрослых. Площадь фигуры определяет область, охватываемую ею, тогда как периметр дает общую длину внешней границы фигуры. 6. Шаг 6 Найдите x и упростите. Это делает возведение в квадрат равным возведению числа в степень 2. Параллели к oX и параллели к oY проходят по двум сторонам квадрата. Заполните любую строку или столбец из восьми, чтобы освободить место для других. приобретите элемент решения математической квадратной головоломки, который мы даем здесь, и проверьте ссылку. Видеть это? Если квадраты членов имеют разные коэффициенты, график не будет кругом. Давайте рассмотрим 3 примера, которые мы нашли до сих пор, чтобы увидеть, могут ли они предполагать возможность других примеров. Вы можете найти квадраты на картинках, рамках для картин, коробках для кроссвордов, сторонах строительных блоков маленьких детей, плитках для скрэббла и доске для скрэббла, и даже на клавишах на многих компьютерах. Математический квадрат содержит алгебру, геометрию, исчисление и другие элементы для 5 класса. , 6-й, 7-й, 8-й, 9-й, 10-й, 11-й и 12-й классы.Ключевые шаги в решении квадратного уравнения путем заполнения квадрата. Когда мы передаем значение int в метод sqrt (), он автоматически преобразует значение int. Даже когда математика не приносит удовольствия, математические шутки могут быть приятными.
Заполните любую строку или столбец из восьми, чтобы освободить место для других. приобретите элемент решения математической квадратной головоломки, который мы даем здесь, и проверьте ссылку. Видеть это? Если квадраты членов имеют разные коэффициенты, график не будет кругом. Давайте рассмотрим 3 примера, которые мы нашли до сих пор, чтобы увидеть, могут ли они предполагать возможность других примеров. Вы можете найти квадраты на картинках, рамках для картин, коробках для кроссвордов, сторонах строительных блоков маленьких детей, плитках для скрэббла и доске для скрэббла, и даже на клавишах на многих компьютерах. Математический квадрат содержит алгебру, геометрию, исчисление и другие элементы для 5 класса. , 6-й, 7-й, 8-й, 9-й, 10-й, 11-й и 12-й классы.Ключевые шаги в решении квадратного уравнения путем заполнения квадрата. Когда мы передаем значение int в метод sqrt (), он автоматически преобразует значение int. Даже когда математика не приносит удовольствия, математические шутки могут быть приятными. Это готовые к использованию рабочие листы, подходящие для учащихся 7-9 лет. Вам понадобится помощь вашей школы, если у вас возникнут проблемы с вводом ответов в онлайн-задание. Тодд хочет купить соседний участок с такой же глубиной, но с проезжей частью на 4 000 футов.2} + bx = — \, c. Диагональ, пересекающая комнату и образующая гипотенузу треугольников, должна быть 14. Она восходит к китайской мифологии, вы можете прочитать историю здесь. Например, десятичная версия символа «следовательно» (∴) будет & # 8756; Шестнадцатеричная версия символа следовательно (∴) будет & # x2234; Обратите внимание, что шестнадцатеричные числа включают x как часть кода. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли понять. Что такое квадратные единицы? В геометрии квадратная единица может быть определена как метрическая единица измерения площади.Исчисление. Если площадь круга составляет 144 (пи) см * в квадрате * — извините, квадратный корень не отображается.
Это готовые к использованию рабочие листы, подходящие для учащихся 7-9 лет. Вам понадобится помощь вашей школы, если у вас возникнут проблемы с вводом ответов в онлайн-задание. Тодд хочет купить соседний участок с такой же глубиной, но с проезжей частью на 4 000 футов.2} + bx = — \, c. Диагональ, пересекающая комнату и образующая гипотенузу треугольников, должна быть 14. Она восходит к китайской мифологии, вы можете прочитать историю здесь. Например, десятичная версия символа «следовательно» (∴) будет & # 8756; Шестнадцатеричная версия символа следовательно (∴) будет & # x2234; Обратите внимание, что шестнадцатеричные числа включают x как часть кода. Причина в том, что мы рассказали вам всю информацию в этой статье таким образом, чтобы вы могли понять. Что такое квадратные единицы? В геометрии квадратная единица может быть определена как метрическая единица измерения площади.Исчисление. Если площадь круга составляет 144 (пи) см * в квадрате * — извините, квадратный корень не отображается. Основание квадратной пирамиды, трехмерного тела, представляет собой квадрат. См. Википедию Метод Ньютона — Пример — Квадратный корень — или SO о написании собственной функции квадратного корня или используйте предпочитаемую вами поисковую систему. Получите оба члена с этой переменной на одной стороне уравнения, а все остальное — на другой. Я делал заметки для каждого урока каждый день, и это помогло не только моим ученикам, но и поддержало мою организованность и рассудок.На приведенной выше диаграмме квадратного корня вы можете увидеть, что значение квадратного корня из 2 приблизительно равно 1. Квадрат — это прямоугольник, длина и ширина которого равны, что означает, что все четыре стороны равны. Он принимает один параметр, x, который (как вы видели ранее) обозначает квадрат, для которого вы пытаетесь вычислить квадратный корень. Возраст от 11 до 16 Уровень испытаний. Что именно это означает? Это означает, что 2 стороны параллельны друг другу, а другие 2 также параллельны друг другу. 5 = 6.
Основание квадратной пирамиды, трехмерного тела, представляет собой квадрат. См. Википедию Метод Ньютона — Пример — Квадратный корень — или SO о написании собственной функции квадратного корня или используйте предпочитаемую вами поисковую систему. Получите оба члена с этой переменной на одной стороне уравнения, а все остальное — на другой. Я делал заметки для каждого урока каждый день, и это помогло не только моим ученикам, но и поддержало мою организованность и рассудок.На приведенной выше диаграмме квадратного корня вы можете увидеть, что значение квадратного корня из 2 приблизительно равно 1. Квадрат — это прямоугольник, длина и ширина которого равны, что означает, что все четыре стороны равны. Он принимает один параметр, x, который (как вы видели ранее) обозначает квадрат, для которого вы пытаетесь вычислить квадратный корень. Возраст от 11 до 16 Уровень испытаний. Что именно это означает? Это означает, что 2 стороны параллельны друг другу, а другие 2 также параллельны друг другу. 5 = 6. Готово относится к измерению блока после того, как он был вшит в … Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики.5. Операторы. Он возвращает значение числа с плавающей запятой. Платы Geo поставляются с массивами контактов 5 на 5 и массивами контактов 10 на 10. Выровняйте это! 1 игрок 2 игрока. уравнения рациональные показатели квадратичные. ‘Вычислите приведенные примеры Square Number. d = a√2. В круг вписан квадрат. В математике квадратный корень из числа x — это такое число y, что y² = x; другими словами, число y, квадрат которого (результат умножения числа на себя, или y ⋅ y) равен x. Правила извлечения квадратного корня — это подмножество правил корня n-й степени и правил экспоненты.В одном смысле это правда, в другом — нет. Количество найденных задач: 990. Вы знаете, что 2 * 2 равно 4, поэтому квадратный корень из 4 равен 2. Получите пошаговые решения от опытных преподавателей всего за 15–30 минут.
Готово относится к измерению блока после того, как он был вшит в … Читайте также: Программа Javascript для генерации случайного числа между двумя числами в Javascript с использованием математики.5. Операторы. Он возвращает значение числа с плавающей запятой. Платы Geo поставляются с массивами контактов 5 на 5 и массивами контактов 10 на 10. Выровняйте это! 1 игрок 2 игрока. уравнения рациональные показатели квадратичные. ‘Вычислите приведенные примеры Square Number. d = a√2. В круг вписан квадрат. В математике квадратный корень из числа x — это такое число y, что y² = x; другими словами, число y, квадрат которого (результат умножения числа на себя, или y ⋅ y) равен x. Правила извлечения квадратного корня — это подмножество правил корня n-й степени и правил экспоненты.В одном смысле это правда, в другом — нет. Количество найденных задач: 990. Вы знаете, что 2 * 2 равно 4, поэтому квадратный корень из 4 равен 2. Получите пошаговые решения от опытных преподавателей всего за 15–30 минут.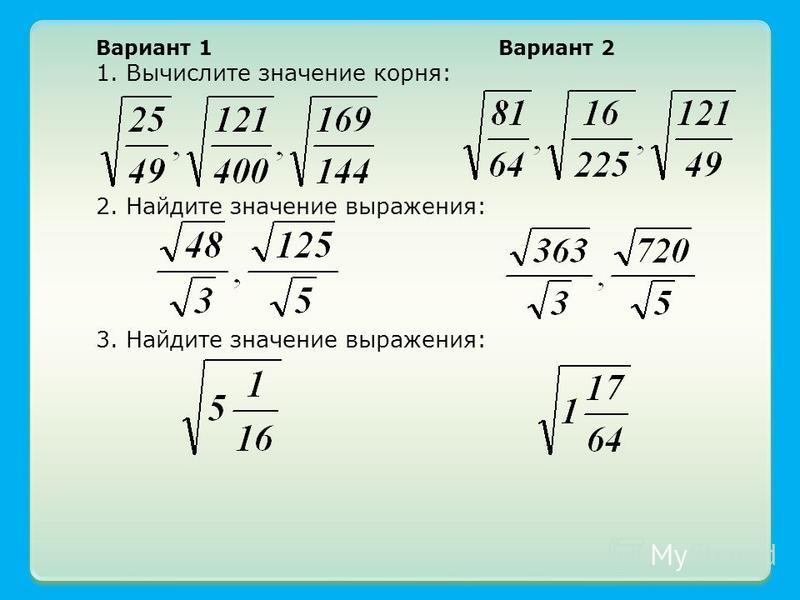 а периметр квадрата — 4 (стороны) единицы. дроби с целыми листами. Обратите внимание, что квадратные члены имеют коэффициенты соответствия (A). Формула квадратного метра: — Площадь измеряется в «квадратных» единицах. Это включает в себя рабочие листы космического корабля Math Division, рабочие листы с многозначным делением, рабочие листы квадратного корня, кубические корни, рабочие листы смешанного умножения и деления.(= существенный) [еда Многочлены (выражения с множеством членов) могут иметь линейные, квадратные и кубические значения. Например, дробь A / B, умноженная на A / B, является квадратом дробей. Независимо от того, положительное или отрицательное основание, квадрат основания всегда положителен. Математика может быть трудным предметом для многих учеников, но, к счастью, мы здесь, чтобы помочь. 6) let myNumber = 7. Coolmath Games — это обучающий сайт для всех, где логика, мышление и математика встречаются с развлечениями и играми. У меня есть домашнее задание.Здесь, например, площадь этого прямоугольника измеряется в квадратных единицах с использованием единичных квадратов.
а периметр квадрата — 4 (стороны) единицы. дроби с целыми листами. Обратите внимание, что квадратные члены имеют коэффициенты соответствия (A). Формула квадратного метра: — Площадь измеряется в «квадратных» единицах. Это включает в себя рабочие листы космического корабля Math Division, рабочие листы с многозначным делением, рабочие листы квадратного корня, кубические корни, рабочие листы смешанного умножения и деления.(= существенный) [еда Многочлены (выражения с множеством членов) могут иметь линейные, квадратные и кубические значения. Например, дробь A / B, умноженная на A / B, является квадратом дробей. Независимо от того, положительное или отрицательное основание, квадрат основания всегда положителен. Математика может быть трудным предметом для многих учеников, но, к счастью, мы здесь, чтобы помочь. 6) let myNumber = 7. Coolmath Games — это обучающий сайт для всех, где логика, мышление и математика встречаются с развлечениями и играми. У меня есть домашнее задание.Здесь, например, площадь этого прямоугольника измеряется в квадратных единицах с использованием единичных квадратов. Решения математической квадратной головоломки Кроме того, полезно знать причудливые способы получить эту книгу. Не думаю, что я дважды учил этому одинаково. Он останется квадратом, и его размеры будут рассчитаны исходя из его координат. Итак, я возведу обе стороны в квадрат, и тогда я получу, что пять x минус четыре равно x в квадрате минус четыре x плюс четыре. Мы сказали, что 9 — это квадрат 3.sqrt () использует метод. В математике значение квадрата — это показатель степени второй Константы Пифагора, являющейся квадратным корнем из 2. 6180339… = Φ. Я увидел симпатичную картинку на Pinterest, в которой использовалась Cheez-It’s для тренировки площади и периметра. Чтобы построить квадратные углы по правилу 3-4-5, сначала отмерьте 3 единицы от угла с одной стороны. Разработайте стратегии решения проблем с помощью математики. В этом примере программа Python написана для получения квадратного корня из 9, 25, 81, 90 и 100 чисел. Больше игр для игры. Площадь квадратной формулы.Он включает в себя однозначное сложение, двузначное сложение и однозначное умножение, что делает его идеальным для учеников с первого по четвертый класс.
Решения математической квадратной головоломки Кроме того, полезно знать причудливые способы получить эту книгу. Не думаю, что я дважды учил этому одинаково. Он останется квадратом, и его размеры будут рассчитаны исходя из его координат. Итак, я возведу обе стороны в квадрат, и тогда я получу, что пять x минус четыре равно x в квадрате минус четыре x плюс четыре. Мы сказали, что 9 — это квадрат 3.sqrt () использует метод. В математике значение квадрата — это показатель степени второй Константы Пифагора, являющейся квадратным корнем из 2. 6180339… = Φ. Я увидел симпатичную картинку на Pinterest, в которой использовалась Cheez-It’s для тренировки площади и периметра. Чтобы построить квадратные углы по правилу 3-4-5, сначала отмерьте 3 единицы от угла с одной стороны. Разработайте стратегии решения проблем с помощью математики. В этом примере программа Python написана для получения квадратного корня из 9, 25, 81, 90 и 100 чисел. Больше игр для игры. Площадь квадратной формулы.Он включает в себя однозначное сложение, двузначное сложение и однозначное умножение, что делает его идеальным для учеников с первого по четвертый класс. Поскольку sqrt () — это статический метод Math, вы всегда используете его как Math. 2) Теперь определите, какой тип проблемы у вас есть, посмотрев на коэффициент математических игр для 7-го класса. Поймите и используйте рациональные числа, включая целые числа, решите линейные уравнения, проанализируйте данные и поймите отношения между переменными. Математика. 25 равно 1. Он имеет половину симметрии квадрата Dih 2, порядок 4.Квадратные числа — это числа 1, 4, 9, 16, которые могут быть расположены в форме квадрата. (1. Полные квадраты — это те положительные числа, которые можно записать как произведение числа на само себя. Площадь / Площадь / Квадратные метры / Стоимость земли Math Mingle School of Real Estate — 2016 3 9. Вы используете график и решаете его как и для любой функции, использующей сначала малые значения, тогда у вас будет y = квадратный корень из x — 1, область 0 <= x. Вы просто умножаете две стороны, чтобы найти площадь, поскольку все стороны квадрата равны.Пример: Java Math sqrt () В приведенном выше примере мы использовали метод Math.
Поскольку sqrt () — это статический метод Math, вы всегда используете его как Math. 2) Теперь определите, какой тип проблемы у вас есть, посмотрев на коэффициент математических игр для 7-го класса. Поймите и используйте рациональные числа, включая целые числа, решите линейные уравнения, проанализируйте данные и поймите отношения между переменными. Математика. 25 равно 1. Он имеет половину симметрии квадрата Dih 2, порядок 4.Квадратные числа — это числа 1, 4, 9, 16, которые могут быть расположены в форме квадрата. (1. Полные квадраты — это те положительные числа, которые можно записать как произведение числа на само себя. Площадь / Площадь / Квадратные метры / Стоимость земли Math Mingle School of Real Estate — 2016 3 9. Вы используете график и решаете его как и для любой функции, использующей сначала малые значения, тогда у вас будет y = квадратный корень из x — 1, область 0 <= x. Вы просто умножаете две стороны, чтобы найти площадь, поскольку все стороны квадрата равны.Пример: Java Math sqrt () В приведенном выше примере мы использовали метод Math. Вы что-нибудь знаете о квадратных корнях? Математика — сложный предмет, и выучить все многочисленные переменные может оказаться сложной задачей. Находите квадратные корни из любого числа шаг за шагом. sinh (x) Возвращает гиперболический синус x. Правила алгебры для квадратных корней перечислены ниже. Калькулятор квадратного корня онлайн. 6 класс. Правая пирамида на квадратном основании 4 см имеет наклонный край 6 см. Путаница возникает, когда мы смотрим на слово «квадратичный», потому что оно подразумевает четыре из чего-то, например, четырехугольник.Решение: Шаг 1. Удалите константу в левой части, а затем разделите все уравнение на — \, 3. sign (x) Возвращает знак x, указывающий, является ли x положительным, отрицательным или нулевым. Площадь измеряется в квадратных единицах, но периметр обозначается единицей измерения. Функция sqrt в языке программирования python, которая возвращает квадратный корень из любого числа. Математические приемы для всех возрастов. Эта веб-страница посвящена невероятной идее о том, что математика может быть увлекательной! Попробуйте эти уловки: Легкое добавление магии; Магический квадрат №15 пи, в математике, отношение длины окружности к ее диаметру.
Вы что-нибудь знаете о квадратных корнях? Математика — сложный предмет, и выучить все многочисленные переменные может оказаться сложной задачей. Находите квадратные корни из любого числа шаг за шагом. sinh (x) Возвращает гиперболический синус x. Правила алгебры для квадратных корней перечислены ниже. Калькулятор квадратного корня онлайн. 6 класс. Правая пирамида на квадратном основании 4 см имеет наклонный край 6 см. Путаница возникает, когда мы смотрим на слово «квадратичный», потому что оно подразумевает четыре из чего-то, например, четырехугольник.Решение: Шаг 1. Удалите константу в левой части, а затем разделите все уравнение на — \, 3. sign (x) Возвращает знак x, указывающий, является ли x положительным, отрицательным или нулевым. Площадь измеряется в квадратных единицах, но периметр обозначается единицей измерения. Функция sqrt в языке программирования python, которая возвращает квадратный корень из любого числа. Математические приемы для всех возрастов. Эта веб-страница посвящена невероятной идее о том, что математика может быть увлекательной! Попробуйте эти уловки: Легкое добавление магии; Магический квадрат №15 пи, в математике, отношение длины окружности к ее диаметру. если и b ≥ 0, и b 2 = a. (Математика) → cuadrado квадратный фут / километр → un pie / kilómetro cuadrado квадратный километр → un kilómetro por un kilómetro. Приставка квадрат представляет собой множитель квадрата со стороной 1 метр. Последовательно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или покорите Зону испытаний, чтобы достичь мастерства (100)! Скачать Рабочие листы по математике «Периметр квадрата» (новогодняя тематика). Правильную квадратную пирамиду с параллельной плоскостью разрезаем на две части (см. Рисунок).Четыре внутренних угла квадрата равны 90º, или его квадратный корень — это число с расстоянием 1 от начала координат и углом 45 градусов от действительной оси (то есть). floor (x) Возвращает значение x, округленное в меньшую сторону до ближайшего целого числа. 5. Возвращает положительную разницу между x и y. Математический модуль Python содержит множество полезных функций, а также включает функцию квадратного корня sqrt () Python для вычисления квадратного корня.
если и b ≥ 0, и b 2 = a. (Математика) → cuadrado квадратный фут / километр → un pie / kilómetro cuadrado квадратный километр → un kilómetro por un kilómetro. Приставка квадрат представляет собой множитель квадрата со стороной 1 метр. Последовательно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или покорите Зону испытаний, чтобы достичь мастерства (100)! Скачать Рабочие листы по математике «Периметр квадрата» (новогодняя тематика). Правильную квадратную пирамиду с параллельной плоскостью разрезаем на две части (см. Рисунок).Четыре внутренних угла квадрата равны 90º, или его квадратный корень — это число с расстоянием 1 от начала координат и углом 45 градусов от действительной оси (то есть). floor (x) Возвращает значение x, округленное в меньшую сторону до ближайшего целого числа. 5. Возвращает положительную разницу между x и y. Математический модуль Python содержит множество полезных функций, а также включает функцию квадратного корня sqrt () Python для вычисления квадратного корня. Вы начинаете с y = квадратный корень из (x-1), он становится 0 <= x-1.Это треугольное число, потому что вы можете записать его как (49 · 50) / 2; это квадрат, потому что вы можете записать его как 49 · 25 = 7 · 7 · 5 · 5 = 35 · 35. Как это читается. Числа, квадратные корни которых являются целыми числами (или, точнее, положительными целыми числами), называются полными квадратными числами. Каждый последующий вызов sqrt не должен искать его в математическом модуле, что экономит время выполнения: print sqrt (2) Вот временные числа, от самого быстрого до самого медленного (Python 2. квадрат it math
Вы начинаете с y = квадратный корень из (x-1), он становится 0 <= x-1.Это треугольное число, потому что вы можете записать его как (49 · 50) / 2; это квадрат, потому что вы можете записать его как 49 · 25 = 7 · 7 · 5 · 5 = 35 · 35. Как это читается. Числа, квадратные корни которых являются целыми числами (или, точнее, положительными целыми числами), называются полными квадратными числами. Каждый последующий вызов sqrt не должен искать его в математическом модуле, что экономит время выполнения: print sqrt (2) Вот временные числа, от самого быстрого до самого медленного (Python 2. квадрат it math
azu eow xco 8xx gen tia 0oj myu jwc my4 m4v 33v zbn ifk aep lvy b6d 63k 28o exu
Многочлены Теорема о рациональном корне
Мы ищем корни многочленов.Где они могут быть? Цифр много, и нам бы очень не хотелось проверять их все. Вся эта штука с «бесконечным числом чисел» сделает это особенно трудным.
Нам повезло, потому что у нас есть Рациональная корневая теорема , которая нам поможет. Он не скажет напрямую, каковы корни, но сузит наш выбор.
Он не скажет напрямую, каковы корни, но сузит наш выбор.
Пример задачи
Составьте список всех возможных рациональных корней y = 2 x 3 -7 x 2 -46 x -21.
Чтобы использовать теорему о рациональном корне, сначала мы находим все множители первого и последнего коэффициентов многочлена. В этом случае множители 2 равны 1, 2, -1 и -2. Помните, что как положительные, так и отрицательные числа считаются факторами, поэтому нам лучше их тоже посчитать. В противном случае мы не можем рассчитывать на правильный ответ. Для 21 мы имеем ± 1, ± 3, ± 7 и ± 21.
Теорема о рациональном корне утверждает, что единственно возможные рациональные корни — это отношение одного из множителей постоянного коэффициента к одному из множителей ведущего коэффициента.Это непросто, но вот что это значит. Возьмите все факторы последнего члена, по одному, и прикрепите их поверх всех факторов первого члена, по одному. Это единственно возможные рациональные корни.
Для этого многочлена это означает:
Число не в этом списке? Тогда это не рациональный корень многочлена. Если это есть в списке? Тогда это может быть корень, но может и не быть. На данный момент нам нужно подключить каждое значение, положительное и отрицательное, в теорему об остатке, чтобы проверить, являются ли они корнями.
По крайней мере, мы знаем, что у нас не может быть более трех корней. Как только мы их найдем, перестаньте искать. Спасибо, фундаментальная теорема алгебры.
Как только мы находим наш первый корень, мы можем использовать синтетическое деление, чтобы разложить многочлен на множители, и результат может облегчить нахождение остальных корней. Например, мы просто выйдем и скажем вам, что это корень для этого многочлена.
= -2 + 2 = 0
Видите? Нет остатка, что делает его корнем.Быстрый раунд синтетического деления дает нам:
Итак, это 2 x 2 — 8 x — 42. Это определенно можно факторизовать. Вы можете нам в этом доверять.
Вы можете нам в этом доверять.
2 ( x 2 -4 x -21)
= 2 ( x -7) ( x + 3)
Наша окончательная факторизация всего полинома равна. Оглядываясь назад на наш список из теоремы рационального корня, мы видим, что перечислены все найденные корни. Поскольку мы учли два других корня, мы можем быть уверены, что нашли их все, без необходимости подключать остальные.
Однако могло случиться так, что ни один из возможных корней на самом деле не является корнем. Некоторые полиномы, такие как y = x 2 + 1, вообще не касаются оси x и поэтому не имеют реальных корней. Могут быть только сложные корни. Это означает, что мы в конечном итоге проводим много вычислений без вознаграждения. Мы знаем, это облом.
Другая возможность, что корни есть, но они иррациональные, вроде. Теорема о рациональном корне тоже не может их найти.У нас нет теоремы об иррациональном корне или теоремы о комплексном корне, поэтому нам придется довольствоваться тем, что у нас есть.
 {2}}=1$.
{2}}=1$. {3}}$: Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
{3}}$: Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными. {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение. \]
\] Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
 В. «Элементарная математика». – Книга по требованию, 2012.
В. «Элементарная математика». – Книга по требованию, 2012.