Самостоятельная работа 7 класс ФГОС тема «Поисковые запросы»

Вариант 1

1. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке убывания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	(Зе­ле­ный | Крас­ный) & Жел­тый
Б	Зе­ле­ный | Жел­тый | Крас­ный
В	Зе­ле­ный & Жел­тый & Крас­ный
Г	Крас­ный | Зе­ле­ный

2. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	Солн­це | Воз­дух | Вода
Б	Солн­це & Воз­дух & Вода
В	(Солн­це | Воз­дух) & Вода
Г	Солн­це | Воз­дух

3. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	Ле­бедь | Рак
Б	Ле­бедь | Рак | Щука
В	Ле­бедь & Рак
Г	Ле­бедь | Рак | Щука | Озеро

4. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	Квар­ти­ра & Кот­тедж & Та­ун­ха­ус
Б	Квар­ти­ра | Кот­тедж | Та­ун­ха­ус
В	(Квар­ти­ра |Кот­тедж) & Та­ун­ха­ус
Г	(Квар­ти­ра & Кот­тедж) |Та­ун­ха­ус

5. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке убывания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	ХИМИЯ & ФИ­ЗИ­КА
Б	ИС­ТО­РИЯ | ФИ­ЗИ­КА
В	ИС­ТО­РИЯ & ХИМИЯ & ФИ­ЗИ­КА
Г	ИС­ТО­РИЯ | ФИ­ЗИ­КА | ХИМИЯ

6. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	Рыжий | Чест­ный | Влюблённый
Б	(Рыжий & Чест­ный)|Влюблённый
В	Рыжий & Чест­ный
Г	Рыжий & Чест­ный & Влюблённый

7. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	Солн­це & Воз­дух
Б	Солн­це | Воз­дух | Вода
В	Солн­це | Воз­дух | Вода | Огонь
Г	Солн­це | Воз­дух

8. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	мопсы
Б	(мопсы & пас­порт) & (ро­до­слов­ная | пу­де­ли)
В	мопсы & пас­порт
Г	мопсы | пу­де­ли

9. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Книга | Жур­нал | Бук­лет
Б	(Книга & Жур­нал) |Бук­лет
В	Книга & Жур­нал & Бук­лет
Г	(Книга |Жур­нал) & Бук­лет

10. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу.

Код	За­прос
А	(Умно­же­ние | Сло­же­ние) & Вы­чи­та­ние
Б	Умно­же­ние & Сло­же­ние & Вы­чи­та­ние
В	(Умно­же­ние & Сло­же­ние) | Вы­чи­та­ние
Г	Умно­же­ние | Сло­же­ние | Вы­чи­та­ние

 11.  В языке за­про­сов по­ис­ко­во­го сер­ве­ра для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — сим­вол «&». В таб­ли­це при­ве­де­ны за­про­сы и ко­ли­че­ство най­ден­ных по ним стра­ниц не­ко­то­ро­го сег­мен­та сети Ин­тер­нет.

За­прос	Най­де­но стра­ниц (в ты­ся­чах)
Пуш­кин	3500
Лер­мон­тов	2000
Пуш­кин |Лер­мон­тов	4500

 Какое ко­ли­че­ство стра­ниц (в ты­ся­чах) будет най­де­но по за­про­су Пуш­кин & Лер­мон­тов? Счи­та­ет­ся, что все за­про­сы вы­пол­ня­лись прак­ти­че­ски од­но­вре­мен­но, так что набор стра­ниц, со­дер­жа­щих все ис­ко­мые слова, не из­ме­нял­ся за время вы­пол­не­ния за­про­сов.

12.   В таб­ли­це при­ве­де­ны за­про­сы и ко­ли­че­ство стра­ниц, ко­то­рые нашел по­ис­ко­вый сер­вер по этим за­про­сам в не­ко­то­ром сег­мен­те Ин­тер­не­та:

За­прос	Ко­ли­че­ство стра­ниц (тыс.)
шах­ма­ты | тен­нис	7770
тен­нис	5500
шах­ма­ты & тен­нис	1000

 Сколь­ко стра­ниц (в ты­ся­чах) будет най­де­но по за­про­су шах­ма­ты

Вариант 2

1. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке убывания количества документов, которые найдёт поисковая система по каждому запросу. 

   Код	За­прос
   А	Солн­це | Воз­дух | Вода
   Б	Солн­це & Воз­дух
   В	Солн­це & Воз­дух & Вода
   Г	Солн­це | Воз­дух

2. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

   Код	За­прос
   А	мопсы
   Б	(мопсы & пас­порт) & (ро­до­слов­ная | пу­де­ли)
   В	мопсы & пас­порт
   Г	мопсы | пу­де­ли

3. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	АЛ­ГЕБ­РА & ФИ­ЗИ­КА
Б	АЛ­ГЕБ­РА | ФИ­ЗИ­КА | БИО­ЛО­ГИЯ
В	АЛ­ГЕБ­РА & ФИ­ЗИ­КА & БИО­ЛО­ГИЯ
Г	ФИ­ЗИ­КА | БИО­ЛО­ГИЯ

 4. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Рыжий & Чест­ный
Б	Рыжий | Чест­ный | Влюблённый
В	Рыжий & Чест­ный & Влюблённый
Г	Рыжий | Чест­ный

5. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Солн­це & Воз­дух
Б	Солн­це | Воз­дух | Вода
В	Солн­це | Воз­дух | Вода | Огонь
Г	Солн­це | Воз­дух

6. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	(Умно­же­ние & Вы­чи­та­ние) | Сло­же­ние
Б	(Умно­же­ние | Вы­чи­та­ние) & Сло­же­ние
В	Умно­же­ние | Вы­чи­та­ние | Сло­же­ние
Г	Умно­же­ние & Вы­чи­та­ние & Сло­же­ние

7. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Эльфы | Гномы | Орки
Б	Эльфы & Гномы & Орки
В	Эльфы & Гномы
Г	Эльфы | Гномы

8. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Солн­це & Воз­дух
Б	Солн­це | Воз­дух | Вода
В	Солн­це | Воз­дух | Вода | Огонь
Г	Солн­це | Воз­дух

9. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке убывания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Рыжий | Чест­ный | Влюблённый | Лис
Б	Рыжий | Чест­ный | Влюблённый
В	Рыжий & Чест­ный
Г	Рыжий | Чест­ный

10. В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу. 

Код	За­прос
А	Эльфы | Гномы | Орки | Хоб­би­ты
Б	Эльфы | Гномы | Орки
В	Эльфы & Гномы
Г	Эльфы | Гномы

1. В языке за­про­сов по­ис­ко­во­го сер­ве­ра для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — сим­вол

За­прос	Ко­ли­че­ство стра­ниц (тыс.)
Сер­бия & Хор­ва­тия	500
Сер­бия|Хор­ва­тия	3000
Сер­бия	2000

 Какое ко­ли­че­ство стра­ниц (в ты­ся­чах) будет най­де­но по за­про­су Хор­ва­тия? Счи­та­ет­ся, что все за­про­сы вы­пол­ня­лись прак­ти­че­ски од­но­вре­мен­но, так что набор стра­ниц, со­дер­жа­щих все ис­ко­мые слова, не из­ме­нял­ся за время вы­пол­не­ния за­про­сов.

1.  В языке за­про­сов по­ис­ко­во­го сер­ве­ра для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» – сим­вол «&».

В таб­ли­це при­ве­де­ны за­про­сы и ко­ли­че­ство най­ден­ных по ним стра­ниц не­ко­то­ро­го сег­мен­та сети Ин­тер­нет.

За­прос	Най­де­но стра­ниц (в ты­ся­чах)
Фре­гат | Эс­ми­нец	3400
Фре­гат & Эс­ми­нец	900
Фре­гат	2100

 Какое ко­ли­че­ство стра­ниц (в ты­ся­чах) будет най­де­но по за­про­су Эс­ми­нец?

Счи­та­ет­ся, что все за­про­сы вы­пол­ня­лись прак­ти­че­ски од­но­вре­мен­но, так что набор стра­ниц, со­дер­жа­щих все ис­ко­мые слова, не из­ме­нял­ся за время вы­пол­не­ния за­про­сов.

Для подготовки

 B 12 № 559. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке убы­ва­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	Бас­кет­бол
Б	Фут­бол & Бас­кет­бол & Во­лей­бол
В	Во­лей­бол | Бас­кет­бол
Г	Фут­бол | Бас­кет­бол | Во­лей­бол

2. B 12 № 459. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Рас­по­ло­жи­те обо­зна­че­ния за­про­сов в по­ряд­ке воз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые найдёт по­ис­ко­вый сер­вер по каж­до­му за­про­су. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	пас­порт | ро­до­слов­ная
Б	(мопсы | пу­де­ли) & (пас­порт | ро­до­слов­ная)
В	мопсы & пу­де­ли & пас­порт & ро­до­слов­ная
Г	мопсы | пу­де­ли | пас­порт | ро­до­слов­ная

3. B 12 № 399. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Рас­по­ло­жи­те коды за­про­сов в по­ряд­ке воз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	рас­ска­зы & Тол­стой & Чехов & по­ве­сти
Б	(рас­ска­зы | Тол­стой) & (Чехов | по­ве­сти)
В	(рас­ска­зы | Тол­стой) & Чехов
Г	Тол­стой | рас­ска­зы | по­ве­сти

4. B 12 № 359. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке воз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	(Тол­стой | рас­ска­зы) & по­ве­сти
Б	Тол­стой & по­ве­сти
В	Чехов & по­ве­сти & Тол­стой & рас­ска­зы
Г	Тол­стой | рас­ска­зы | по­ве­сти

5. B 12 № 699. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке убы­ва­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	Волк | Коза
Б	( Волк | Коза ) & Ка­пу­ста
В	Волк & Коза & Ка­пу­ста
Г	Волк & Ка­пу­ста

6. B 12 № 856. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке воз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц.

Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&».

 

Код	За­прос
А	АЛ­ГЕБ­РА & ФИ­ЗИ­КА
Б	АЛ­ГЕБ­РА | ФИ­ЗИ­КА | БИО­ЛО­ГИЯ
В	АЛ­ГЕБ­РА & ФИ­ЗИ­КА & БИО­ЛО­ГИЯ
Г	ФИ­ЗИ­КА | БИО­ЛО­ГИЯ

 

7. B 12 № 18. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке воз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	Ле­бедь | Рак | Щука
Б	Ле­бедь & Рак
В	Ле­бедь & Рак & Щука
Г	Ле­бедь | Рак

8. B 12 № 814. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­кевоз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые найдёт по­ис­ко­вый сер­вер по каж­до­му за­про­су. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» – «&».

 

Код	За­прос
А	(Умно­же­ние & Вы­чи­та­ние) | Сло­же­ние
Б	(Умно­же­ние | Вы­чи­та­ние) & Сло­же­ние
В	Умно­же­ние | Вы­чи­та­ние | Сло­же­ние
Г	Умно­же­ние & Вы­чи­та­ние & Сло­же­ние

9. B 12 № 238. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке воз­рас­та­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	Эльфы | Гномы | Орки
Б	Эльфы & Гномы & Орки
В	Эльфы & Гномы
Г	Эльфы | Гномы

10. B 12 № 138. В таб­ли­це при­ве­де­ны за­про­сы к по­ис­ко­во­му сер­ве­ру. Для каж­до­го за­про­са ука­зан его код — со­от­вет­ству­ю­щая буква от А до Г. Рас­по­ло­жи­те коды за­про­сов слева на­пра­во в по­ряд­ке убы­ва­ния ко­ли­че­ства стра­ниц, ко­то­рые нашёл по­ис­ко­вый сер­вер по каж­до­му за­про­су. По всем за­про­сам было най­де­но раз­ное ко­ли­че­ство стра­ниц. Для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» в за­про­се ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — «&»:

 

Код	За­прос
А	Рыжий | Чест­ный | Влюблённый | Лис
Б	Рыжий | Чест­ный | Влюблённый
В	Рыжий & Чест­ный
Г	Рыжий | Чест­ный

12 № 6964. В языке за­про­сов по­ис­ко­во­го сер­ве­ра для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» — сим­вол «&». В таб­ли­це при­ве­де­ны за­про­сы и ко­ли­че­ство най­ден­ных по ним стра­ниц не­ко­то­ро­го сег­мен­та сети Ин­тер­нет:

 

За­прос	Най­де­но стра­ниц (в ты­ся­чах)
Нью-Йорк & Бо­стон	348
Нью-Йорк & Чи­ка­го	260
Нью-Йорк & (Бо­стон | Чи­ка­го)	427

 

Какое ко­ли­че­ство стра­ниц (в тыс.) будет най­де­но по за­про­су:

 

Нью-Йорк & Бо­стон & Чи­ка­го?

 

Счи­та­ет­ся, что все за­про­сы вы­пол­ня­лись прак­ти­че­ски од­но­вре­мен­но, так что набор стра­ниц, со­дер­жа­щих все ис­ко­мые слова, не из­ме­нял­ся за время вы­пол­не­ния за­про­сов.

2. B 12 № 3434. В таб­ли­це при­ве­де­ны за­про­сы и ко­ли­че­ство стра­ниц, ко­то­рые нашел по­ис­ко­вый сер­вер по этим за­про­сам в не­ко­то­ром сег­мен­те Ин­тер­не­та:

За­прос	Ко­ли­че­ство стра­ниц (тыс.)
фре­гат | эс­ми­нец	3000
фре­гат	2000
эс­ми­нец	2500

 

Сколь­ко стра­ниц будет най­де­но по за­про­су фре­гат & эс­ми­нец

3. B 12 № 4954. В языке за­про­сов по­ис­ко­во­го сер­ве­ра для обо­зна­че­ния ло­ги­че­ской опе­ра­ции «ИЛИ» ис­поль­зу­ет­ся сим­вол «|», а для ло­ги­че­ской опе­ра­ции «И» – сим­вол «&».

В таб­ли­це при­ве­де­ны за­про­сы и ко­ли­че­ство най­ден­ных по ним стра­ниц не­ко­то­ро­го сег­мен­та сети Ин­тер­нет.

 

За­прос	Най­де­но стра­ниц (в ты­ся­чах)
Пекин & (Москва | Токио)	338
Пекин & Москва	204
Пекин & Москва & Токио	50

 

Какое ко­ли­че­ство стра­ниц (в ты­ся­чах) будет най­де­но по за­про­су Пекин & Токио?

Счи­та­ет­ся, что все за­про­сы вы­пол­ня­лись прак­ти­че­ски од­но­вре­мен­но, так что набор стра­ниц, со­дер­жа­щих все ис­ко­мые слова, не из­ме­нял­ся за время вы­пол­не­ния за­про­сов.

Проверочная работа по информатике «Логика» (7 класс)

Вариант 1

Задача № 1

В хоккейной и лыжной секциях занималось 95 учеников: 57 посещали хоккейную секцию, 11 – тренировки по хоккею и лыжам. Сколько учеников занимались в лыжной секции?

Задача № 2

В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу:

A: Англия & Франция

Б: Англия | Франция

B: Англия & Франция & Германия

Г: Англия | Франция | Германия

Задача № 3

В локальной компьютерной сети несколько документов, в которых встречаются слова «принтер», «сканер» и «монитор». Одно слово «принтер» встречается в 99 документах, слово «сканер» — в 105 документах и слово «монитор» — в 112 документах. Пару слов «принтер» и «сканер» можно найти в 14 документах, слова «сканер» и «монитор» — в 17 и «монитор» и «принтер» — в 11 документах. Все три слова находятся в 10 документах. Сколько документов в сети?

Задача № 4

В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу:

а) ученики | (информатика & математика)

б) ученики & Лицей

г) ученики & информатика & математика & Лицей

в) ученики | математика | информатика

Вариант 2

Задача № 1

В хоккейной и лыжной секциях занималось 87 учеников: 39 посещали хоккейную секцию, 23 – тренировки по хоккею и лыжам. Сколько учеников занимались в лыжной секции?

Задача № 2

В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу:

A: Сыр & Ворона & Лисица

Б: Ворона | Сыр | Лисица

B: Ворона | Сыр

Г: Ворона & Лисица

Задача № 3

В локальной компьютерной сети несколько документов, в которых встречаются слова «принтер», «сканер» и «монитор». Одно слово «принтер» встречается в 109 документах, слово «сканер» — в 103 документах и слово «монитор» — в 115 документах. Пару слов «принтер» и «сканер» можно найти в 17 документах, слова «сканер» и «монитор» — в 11 и «монитор» и «принтер» — в 10 документах. Все три слова находятся в 15 документах. Сколько документов в сети?

Задача № 4

В таблице приведены запросы к поисковой системе. Представьте результаты выполнения этих запросов графически с помощью кругов Эйлера. Укажите обозначения запросов в порядке возрастания количества документов, которые найдёт поисковая система по каждому запросу:

а) студенты & НГУ & ФИТ & программирование

б) студенты | программирование | ФИТ

в) студенты | (ФИТ & программирование)

г) студенты & НГУ

Проект Круги Эйлера в задачах

МБОУ «Новошимкусская СОШ Яльчикского района Чувашской Республики»

Проект по математике

«Круги Эйлера в задачах»

Выполнил:
ученик 6 класса

Руководитель:

Николаева Т.В.,

учитель математики высшей квалификационной категории

с.Новые Шимкусы — 2018

ОГЛАВЛЕНИЕ

Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Глава 1.

Круги Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4

1.1. Леонард Эйлер. Биография. . . . . . . . . . . . . . . . . . . . . . . . . . . . ..4

1.2. Круги Эйлера. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7

Глава 2.

Круги Эйлера в задачах. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

ВВЕДЕНИЕ

На уроках математики учитель непременно знакомит нас, учеников, с историей развития математических понятий, символов, идей, методов. Но из-за нехватки учебного времени ему не всегда удается рассказать о жизни великих творцов математики – интенсивной, целенаправленной, поучительной, хотя подчас и драматичной; раскрыть все стороны древнейшей и, в то же время, современной науки.

В этой работе мне захотелось показать вам решение задач с помощью кругов Эйлера. Задачи решаются значительно быстрее, решение понятно.

Я надеюсь, что вы также поймете, как решаются такого рода задачи и решите те, которые я Вам предложу.

«…Нет ученого, имя которого упоминалось бы в учебной литературе по математике столь же часто, как имя Эйлера. В Энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера…».

Леонард Эйлер жил в 18 веке, но его метод решения целого ряда задач актуален и сегодня, в 21-ом веке.

Один из величайших математиков, петербургский академик Леонард Эйлер за свою долгую жизнь написал более 850 научных работ.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера». Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления». Этот метод даёт наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Задачи таким способом решаются значительно быстрее, решение понятно.

Цель моей работы: научиться решать задачи с помощью кругов Эйлера и научить других.

Для этого я:

Изучил теоретический материал: биографию Леонарда Эйлера, «круги Эйлера».

Научился применять круги в решении задач.

Собрал задачи для учащихся «Круги Эйлера в задачах».

ГЛАВА 1. КРУГИ ЭЙЛЕРА

Леонард Эйлер. Биография

Леонард Эйлер родился 15 апреля 1707 года в семье пастора, жившей в швейцарском городке Базеле. Рано обнаружил математические способности. Отец Леонарда пастор Пауль Эйлер был хорошо образован и увлекался математикой. Именно под руководством отца Эйлер получил начальное обучение. Отец хотел дать Леонарду духовное образование и занимался с ним математикой только для развлечения и для развития логического мышления. 20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета, где преподавались и математика и астрономия. Занятия по этим предметам вел прославленный математик Иоганн Бернулли. Проявив интерес к математике, Эйлер привлек к себе внимание Иоганна Бернулли. Профессор стал лично руководить самостоятельными занятиями юноши и вскоре публично признал, что от проницательности и остроты ума юного Эйлера он ожидает самых больших успехов.

Не забывал Эйлер и другие университетские курсы, поэтому и был широко образован. 8 июня 1724 года 17-летний Леонард Эйлер произнёс на латыни речь о сравнении философских воззрений Декарта и Ньютона и был удостоен учёной степени магистра. В последующие два года юный Эйлер написал несколько научных работ. Одна из них, «Диссертация по физике о звуке», получившая благоприятный отзыв, была представлена на конкурс для замещения неожиданно освободившейся в Базельском университете должности профессора физики (1725). Но, несмотря на положительный отзыв, 19-летнего Эйлера сочли слишком юным, чтобы включить в число кандидатов на профессорскую кафедру. Число научных вакансий в Швейцарии было совсем невелико. Поэтому братья Даниил и Николай Бернулли, сыновья Иоганна Бернулли, уехали в далёкую Россию, где как раз шла организация Академии наук. Своих ученых в России тогда не было совсем. Пришлось привлекать иностранных. В числе первых были приглашены братья Бернулли. По их рекомендации через три года после открытия Петербургской академии наук получил приглашение и двадцатилетний Эйлер на должность адъюнкта по физиологии.

5 апреля 1727 года Эйлер навсегда покинул родную Швейцарию. Одной из важнейших задач Академии стала подготовка отечественных кадров. Позднее при Академии были созданы университет и гимназия. В силу острой нехватки учебников на русском языке Академия обратилась к своим членам с просьбой составить такие руководства. Эйлер, хотя и числился физиологом, составил на немецком языке очень добротное «Руководство к арифметике», которое тут же было переведено на русский и служило не один год в качестве начального учебника. Перевод первой части выполнил первый русский, ученик Эйлера Василий Адодуров. Это было первое систематическое изложение арифметики на русском языке. К всеобщему удивлению, Эйлер уже в следующем по приезде году стал бегло говорить по-русски. Эйлер отличался феноменальной работоспособностью. По отзывам современников, для него жить означало заниматься математикой. А работы у молодого профессора было много: картография, всевозможные экспертизы, консультации для кораблестроителей и артиллеристов, составление учебных руководств, проектирование пожарных насосов и т. д. За первый период пребывания в России (14лет), он написал более 90 крупных научных работ по математике, гидравлике, архитектуре, навигации, картографии и механике. Значительная часть академических «Записок» заполнена трудами Эйлера. Он делал доклады на научных семинарах, читал публичные лекции, участвовал в выполнении различных технических заказов правительственных ведомств. Петербургская академия по достоинству оценила молодого ученого, в двадцать три года он уже профессор физики, а еще через три года Леонард Эйлер получает кафедру высшей математики.

В 1735 году Академия получила задание выполнить срочное и очень громоздкое астрономическое (по другим данным, картографическое) вычисление. Группа академиков просила на эту работу три месяца, а Эйлер взялся выполнить работу за 3 дня — и справился самостоятельно. Однако перенапряжение не прошло бесследно: он заболел и потерял зрение на правый глаз. Однако учёный отнёсся к несчастью с величайшим спокойствием: «Теперь я меньше буду отвлекаться от занятий математикой», — философски заметил он.

В 1730-е годы Эйлер становится известен и в Европе. Двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении», изданное в 1736 году, принесло ему мировую славу. Начиная с этого момента, теоретическая механика становится прикладной частью математики. Осенью 1740 внутренняя обстановка в России осложнилась. Это побудило Эйлера принять приглашение прусского короля, и летом 1741 он переехал в Берлин, где вскоре возглавил математический класс в Берлинской Академии наук и словесности. Годы, проведенные Эйлером в Берлине, были наиболее плодотворными в его научной деятельности. Переезд в Берлин не прервал, однако, тесных связей Эйлера с Петербургской Академией наук. Он по-прежнему регулярно посылал в Россию свои сочинения, участвовал в экспертизах различного рода, обучал посланных к нему из России учеников, подбирал ученых на замещение вакантных должностей в Академии и выполнял много других поручений.

В 1762 году на русский престол вступила Екатерина II, которая хорошо понимая значение науки, как для прогресса государства, так и для собственного престижа, провела ряд важных, благоприятных для науки, преобразований в системе народного просвещения и культуры. Императрица предложила Эйлеру управление математическим классом (отделением), звание конференц-секретаря Академии.

После двадцати пяти лет проживания в Берлине, 60-летний Эйлер снова возвращается в Россию, в Петербург. Эйлер полон энергии и душевных сил, желания работать на благо России. К несчастью, после возвращения в Петербург у Эйлера образовалась катаракта второго, левого глаза — он перестал видеть. Вероятно, по этой причине обещанный пост вице-президента Академии он так и не получил. Однако слепота не отразилась на его работоспособности. Эйлер диктовал свои труды мальчику — портному, который всё записывал по-немецки. Число опубликованных им работ даже возросло; за полтора десятка лет второго пребывания в России он продиктовал более 400 статей и 10 книг.

В 1773 году по рекомендации Даниила Бернулли в Петербург приехал из Базеля ученик Бернулли, Никлаус Фусс. Это было большой удачей для Эйлера. Фусс обладал редким сочетанием математического таланта и умения вести практические дела, что и дало ему возможность сразу же после приезда взять на себя заботы о математических трудах Эйлера. В последующие десять лет — до самой своей смерти — Эйлер преимущественно ему диктовал свои труды, хотя иногда пользовался «глазами старшего сына» и других своих учеников. Эйлер активно трудился до последних дней. В сентябре 1783 года 76-летний учёный стал ощущать головные боли и слабость.

7 сентября после обеда, Эйлер почувствовал себя плохо, успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг.

Великий ученый Леонард Эйлер занимает одно из первых мест в истории мировой науки. Полное собрание его трудов составляет 72 тома, более 850 научных работ. Этот тихий и скромный человек, полностью ослепший, много работал, совершив великое множество научных открытий.

Круги Эйлера

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Используется в математике, логике, менеджменте и других прикладных направлениях. А впервые Эйлер их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».

При решении задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера».

Строгого определения понятия множества не существует.

Множество — совокупность элементов, обладающих некоторым общим свойством, т. е. как единое целое (множество натуральных чисел, множество треугольников на плоскости).

Множества, состоящие из конечного числа элементов, называют конечными, а остальные множества – бесконечными. Например, множество китов в океане конечно, а множество рациональных чисел бесконечно. Конечное множество может быть задано перечислением его элементов (множество учеников в данном классе задается их списком в классном журнале).

Понятие подмножества в определении кругов Эйлера – это, например, во

множестве учеников класса можно выделить множество ударников, которые входят во множество всех учеников (ударники – подмножество).

Множество всех действительных чисел Эйлер изобразил с помощью этих

кругов: N — множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество всех действительных чисел.

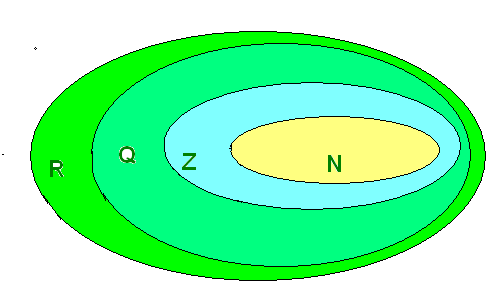
Метод Эйлера является незаменимым при решении целого ряда задач, а также упрощает рассуждения.

ГЛАВА 2. КРУГИ ЭЙЛЕРА В ЗАДАЧАХ

«Разберись и научись»

Алгоритм решения задач

1. Внимательно изучи условия задач.

2. Построй пересечения множеств.

3. Расставь исходные данные.

4. Найдите недостающие данные.

5. Проверь решение.

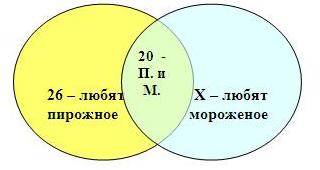
1. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?

Решение:

Так как 26 половина детей любит пирожные, а 20 — и пирожные, и  мороженое, то исключительно пирожное любят ровно 6 человек. Всего ребят 52, из них 6 —  любители только пирожных, значит,  52 – 6 = 46  человек, которые любят мороженое.

2. Часть жителей района, умеет говорить только по-русски, часть – только по-чувашски и часть умеет говорить на обоих языках. По-чувашски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение: Составим схему –

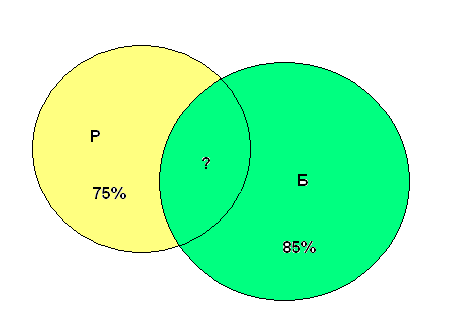
В кружке под буквой «Б» обозначим жителей, говорящих по-чувашски, под буквой

«Р» — по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

3. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?

Решение: Обратимся к кругам Эйлера: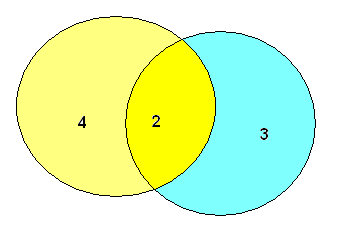

Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

4. В магазине побывало 65 человек. Известно, что они купили 35

холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и

холодильник и микроволновку, 19 — и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?

Решение:

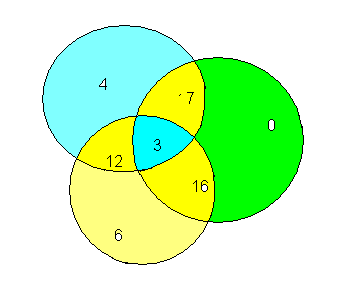
Купили только холодильники: 35-(20-3)-(15-3)-3=4.

Купили только микроволновки: 36-(20-3)-(19-3)-3=0.

Купили только телевизоры: 37-(15-3)-(19-3)-3=6.

Тогда всего покупателей было: 4+17+3+16+12+6=58.

65-58=7 посетителей магазина не купили ничего.

5. На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?
Учитывая условия задачи, чертеж будет таков:

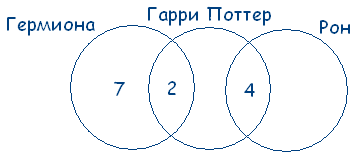
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал толькоРон. А всего Рон прочитал 12 книг.
Ответ: 12 книг прочитал Рон.

6. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу – 8 человек, спортивную школу – 12 человек, музыкальную и художественную школу– 3, художественную и спортивную школу– 2, музыкальную и спортивную школу– 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

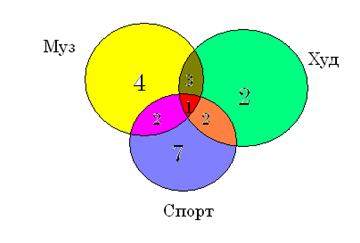
Только музыкальную школу посещают 10-3-2-1=4 учащихся. Только художественную школу посещают 8-3-2-1=2 учащихся. Только спортивную школу посещают 12-2-2-1=7 учащихся.

Только одну школу посещают 4+2+7=13 учеников.

Ни в чем себя не развивают 24-(4+2+7+3+2+2+1)=3 учащихся.

Ответ: 13 учеников посещают только одну школу, 3 учащихся себя не развивают.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

«Реши сам и проверь себя»

7. Миша, Коля, Лева вместе прочитали 3 книги. Миша и Коля вместе прочитали 5  книг; Миша и Лева вместе – 4 книги; Коля и Лева вместе – 3 книги. Миша прочитал 8 книг; Коля – 6 книг; Лева – 5 книг. Сколько книг прочитали дети?

8. Из 110 студентов английский язык изучают 44 человека, немецкий – 50 человек, французский – 49 человек, английский и немецкий – 13, английский и французский – 14, немецкий и французский – 12, все три языка изучают 5 человек. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?

9. К Лене на день рождения пришли гости с подарками. Получилось

так, что дарили только букеты цветов и воздушные шарики.

Шесть гостей подарили букеты цветов, четыре – воздушные

шарики. Сколько было гостей?

ЗАКЛЮЧЕНИЕ

На уроках математики учитель знакомит нас, учеников, с историей развития математических понятий, символов, идей, методов. Но из-за нехватки учебного времени ему не всегда удается рассказать о жизни великих творцов математики – интенсивной, целенаправленной, поучительной хотя подчас и драматичной; раскрыть все стороны древнейшей и, в то же время, современной науки.

Одно из первых мест в истории мировой науки занимает Леонард Эйлер.

Полное собрание его трудов составляет 72 тома, более 850 научных работ.

Леонард Эйлер жил в 18 веке, но его метод решения целого ряда задач актуален и сегодня, в 21-ом веке. Эйлер использовал идею изображения множеств с помощью кругов. Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах. Задачи таким способом решаются значительно быстрее, решение понятно.

Поэтому была поставлены задачи: изучить биографию Леонарда Эйлера и научиться решать задачи, применяя правила и круги Эйлера.

Для этого был разобран весь теоретический материал, решены задачи, используя круги Эйлера.
Применение кругов Эйлера позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
Цель работы считаю достигнутой.

СПИСОК ЛИТЕРАТУРЫ

Академия математики «Леонард Эйлер» научно-практический журнал Математика для школьников №3 2007г., с.41-48

Интернет ресурсы http://logika.vobrazovanie.ru/index.php?link=kr_e.html – Учимся решать логические задачи

Интернет – ресурсы http://olymp.ifmo.ru/archive/problems/inf/ – архив  задач по информатике.

Босова Л.Л. Информатика: Учебник для 6 класса / Л. Л. Босова. –5-е изд–М.: БИНОМ. Лаборатория знаний, 2007. – 208 с.: ил.

Босова Л.Л. Информатика: Рабочая тетрадь для 6 класса /Л. Л. Босова,  – 2-е изд., испр. – М.: БИНОМ. Лаборатория знаний, 2005. –

Угринович Н.Д. Информатика и ИКТ: Учебник для 10 класс. БИНОМ. Лаборатория знаний, 2010. – 371 с.: ил.

Глейзер Г. И. История математики. М., Наука, 1982 г.

Круги Эйлера — информатика, презентации

Презентация может применяться как на уроках, так и на внеурочных занятиях при объяснении нового (в 6 кл), при повторении (в 7, 8, 9кл) для дальнейшего перехода к решению задач о логических операциях с множествами в поисковых системах. Первые слайды посвящены определениям -«тождество», «подчинение», «исключение», «пересечение» понятий, а затем решаются задачи с последующей проверкой. 

Просмотр содержимого документа
«Круги Эйлера »

Круги Эйлера

О графическом способе решения задач

на отношение понятий (множеств)

Отношения между понятиями по объему:

Отношения между понятиями по объему:

1. Тождество или совпадение объемов.

А= В

B

А

A – столица России

B – город Москва

Отношения между понятиями по объему:

2. Подчинение или включение объемов.

B

А

A – заяц

B – живое существо

Отношения между понятиями по объему:

3. Исключение объемов.

B

А

B – человек

A – стол

Отношения между понятиями по объему:

4. Пересечение или частичное совпадение объемов.

B

А

A – школьник

B – первоклассник

Определите отношения между понятиями и изобразите эти отношения с помощью кругов Эйлера: сказка, книга, фантастика, «Репка», стихи

Решение

книга

книга

фантастика

с

сказка

с

«Репка»

стихи

Задачи

1. В классе 30 учащихся. Из них 18 человек занимаются в секции легкой атлетики, 10 – плаванием, 3 – и тем, и другим. Сколько человек не занимается ничем?

2. Ребята посещают три кружка: биологии, физики и истории. Решено было организовать кружок юных экологов и пригласить тех ребят, которые не занимаются ни в одном из трех перечисленных. Сколько таких ребят, если всего в классе 36 человек, биологией занимаются 18, физикой – 14, историей – 10. Двое посещают все три кружка, 8 – биологию и физику, 5 – биологию и историю, 3 – историю и физику.

Решить задачи с помощью кругов Эйлера .

Решение

Решение

Домашнее задание:

№ 1

В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией? 

№ 2

Большая группа туристов выехала в заграничное турне. Из них владеет английским языком 28 человек, французским — 13, немецким — 10, английским и французским — 8, французским и немецким — 5, английским и немецким — 6, всеми тремя языками — двое, а 41 человек не владеет ни одним из трёх языков. Сколько всего туристов?

Решение задачи №1

30 — ( 7 + 3 + 15 ) = 5

30

7

3

15

легкая атлетика

плавание и

легкая атлетика

плавание

Решение задачи №2

7 + 3 + 4 + 1 + 5 + 6 + 2 = 28

36 – 28 = 8

36

биология

28 учащихся посещают хотя бы 1 кружок, следовательно, 8 – не посещают ни один кружок.

7

6

3

2

4

5

1

физика

история