Неевклидова геометрия — Википедия

Материал из Википедии — свободной энциклопедии

(1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского

Неевклидова геометрия — в буквальном понимании — любая геометрическая система, которая отличается от геометрии Евклида; однако традиционно термин «неевклидова геометрия» применяется в более узком смысле и относится только к традиционным неевклидовым геометрическим системам: геометрии Лобачевского и сферической геометрии (или схожей с ней геометрии Римана).

Как и евклидова, эти геометрии относятся к метрическим геометриям пространства постоянной кривизны. Нулевая кривизна соответствует евклидовой геометрии, положительная — совпадающим по локальным свойствам сферической или геометрии Римана, отрицательная — геометрии Лобачевского.

Вид метрики для однородных планиметрий зависит от выбранной системы (криволинейных) координат; далее приводятся формулы для случая полугеодезических координат:

• Александров А. Д., Нецветаев Н. Ю. Геометрия. — Наука, Москва, 1990. ISBN 978-5-9775-0419-5.
• Александров П. С. Что такое неэвклидова геометрия. — УРСС, Москва, 2007. ISBN 978-5-484-00871-1.
• Алексеевский Д. В., Винберг Э. Б., Солодовников А. С. Геометрия пространств постоянной кривизны. — Итоги науки и техники. Серия: Современные проблемы математики. Фундаментальные направления. 1988, том 29, стр. 5–146.
• Берже М. Геометрия. Пер. с франц., в двух томах. М., «Мир», 1984. 928 с. Том II, часть V: Внутренняя геометрия сферы, гиперболическая геометрия.
• История математики с древнейших времён до начала XIX столетия (под ред. А. П. Юшкевича), тома I—III, М., Наука, 1972.
• Делоне Б. Н. Элементарное доказательство непротиворечивости планиметрии Лобачевского, — Гостехиздат, Москва, 1956.
• Клейн Ф. Неевклидова геометрия. М.: изд. НКТП СССР, 1936, 355 с.
• Лаптев Б. Л. Н. И. Лобачевский и его геометрия. М.: Просвещение, 1976.
• Мищенко А. С., Фоменко А. Т. Курс дифференциальной геометрии и топологии, — Факториал, Москва, 2000.
• Прасолов В. В. Геометрия Лобачевского. Изд. 3-е, МЦНМО, 2004. ISBN 5-94057-166-2.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.

Геометрия Римана — Википедия

Материал из Википедии — свободной энциклопедии

Геометрия Римана (называемая также эллиптическая геометрия) — одна из неевклидовых геометрий постоянной кривизны (другие — это геометрия Лобачевского и сферическая геометрия). Если геометрия Евклида реализуется в пространстве с нулевой гауссовой кривизной, Лобачевского — с отрицательной, то геометрия Римана реализуется в пространстве с постоянной положительной кривизной (в двумерном случае — на проективной плоскости и локально на сфере).

В геометрии Римана прямая определяется двумя точками, плоскость — тремя, две плоскости пересекаются по прямой и т. д., но в геометрии Римана нет параллельных прямых. В геометрии Римана, как и в сферической геометрии, справедливо утверждение: сумма углов треугольника больше двух прямых, имеет место формула Σ=π+S/R2,{\displaystyle \Sigma =\pi +{S}/{R^{2}},} где Σ{\displaystyle \Sigma } — сумма углов треугольника, R{\displaystyle R} — радиус сферы, на которой реализована геометрия.

Отождествление противоположных точек сферы в геометрии Римана

Двумерная геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. При отождествлении противоположных точек сферы получается проективная плоскость, геометрия которой удовлетворяет аксиомам геометрии Римана.

Именно, рассмотрим сферу S{\displaystyle S} с центром в точке O{\displaystyle O} в трёхмерном пространстве E{\displaystyle E}. Каждая точка A∈S{\displaystyle A\in S} вместе с центром сферы O{\displaystyle O} определяет некоторую прямую l⊂E{\displaystyle l\subset E}, т. е. некоторую точку A∗{\displaystyle A_{*}} проективной плоскости Π{\displaystyle \Pi }. Сопоставление A→A∗{\displaystyle A\to A_{*}} определяет отображение S→Π{\displaystyle S\to \Pi }, большие круги на S{\displaystyle S} (прямые в сферической геометрии) переходят в прямые на проективной плоскости Π{\displaystyle \Pi }, при этом в одну точку A∗∈Π{\displaystyle A_{*}\in \Pi } переходят ровно две точки сферы: вместе с точкой A∈S{\displaystyle A\in S} и диаметрально противоположная ей точка A′∈S{\displaystyle A’\in S} (см. рисунок). Евклидовы движения пространства E{\displaystyle E}, переводящие сферу S{\displaystyle S} в себя, задают некоторые определенные преобразования проективной плоскости Π{\displaystyle \Pi }, которые являются движениями геометрии Римана. В геометрии Римана любые прямые пересекаются, поскольку это верно для проективной плоскости, и таким образом, в ней нет параллельных прямых.

Одно из отличий геометрии Римана от евклидовой геометрии и геометрии Лобачевского состоит в том, что в ней нет естественного понятия «точка C лежит между точками A и B» (в сферической геометрии это понятие также отсутствует). Действительно, на прямую проективной плоскости Π{\displaystyle \Pi } отображается большой круг на сфере S{\displaystyle S}, причём две диаметрально противоположные точки сферы A{\displaystyle A} и A′{\displaystyle A’} переходят в одну точку A∗∈Π{\displaystyle A_{*}\in \Pi }. Аналогично, точки B,B′{\displaystyle B,B’} переходят в одну точку B∗∈Π{\displaystyle B_{*}\in \Pi } и точки C,C′{\displaystyle C,C’} переходят в одну точку C∗∈Π{\displaystyle C_{*}\in \Pi }. Таким образом, с равным основанием можно считать, что точка C∗{\displaystyle C_{*}} лежит между A∗{\displaystyle A_{*}} и B∗{\displaystyle B_{*}} и что она не лежит между ними (см. рисунок).

• Александров А. Д., Нецветаев Н. Ю. Геометрия. — М.: Наука, 1990.
• Александров П. С. Что такое неэвклидова геометрия. — М.: УРСС, 2007.
• Алексеевский Д. В., Винберг Э. Б., Солодовников А. С. Геометрия пространств постоянной кривизны. В кн.: Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. — М.: ВИНИТИ, 1988. — Т. 29. — С. 1—146.
• Берже М. Геометрия. / Пер. с франц. — М.: Мир, 1984. — Том II, часть V: Внутренняя геометрия сферы, гиперболическая геометрия, пространство сфер.
• Ефимов Н. В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2003. — 584 с. — ISBN 5-9221-0267-2.
• Клейн Ф. Неевклидова геометрия. — Любое издание.
• Степанов Н. Н. Сферическая тригонометрия. — Л.—М., 1948.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009.

Основы геометрии. Видеоурок. Идеи и смыслы

Математика работает с идеальными объектами. Но зачем это нужно? Возьмем два треугольника (см. рис. 1). На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая – выпуклая, а у другого наоборот (см. рис. 2).

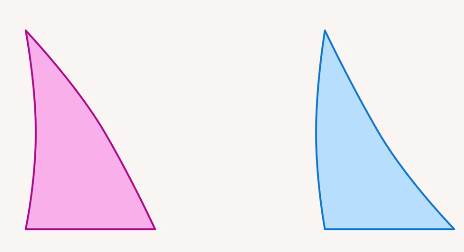
Рис. 1. Два похожих треугольника

 

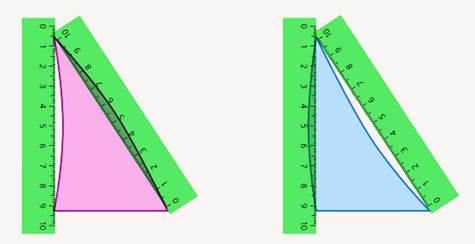
Рис. 2. Вогнутые и выпуклые стороны треугольников

Эти треугольники похожи, и, наверное, о них можно сделать близкое заключение, которое будет описывать свойства обоих. В то же время эти треугольники отличаются, что делать?

Математика занимается идеальными объектами, идеальными треугольниками (см. рис. 3) и делает о них некие заключения, которые называются теоремами (см. рис. 4). Тогда эти заключения помогут описать и первый, и второй треугольник, но с некоторыми приближениями. Чтобы вывести эти теоремы, нужно сказать, что есть идеальный объект – идеальный треугольник. Хотя, если изучать его очень подробно, он тоже будет иметь свои шероховатости (см. рис. 5). Однако мы принимаем, что есть идеальный объект – треугольник, который составлен из трех отрезков прямых (см. рис. 6).

Рис. 3. Идеальные треугольники

Рис. 4. Пример теоремы. Признак равенства треугольников

Рис. 5. Шероховатости треугольника

Рис. 6. Треугольник – фигура, образованная тремя отрезками прямых

Базовые геометрические фигуры – это точки, отрезки, лучи, прямые, плоскости.

Точка – это идеальный математический объект, который не имеет ни длины, ни ширины. Понятно, что если точку нарисовать, то получится далеко не точка (см. рис. 7), в лучшем случае мы можем считать, что это круг. Хотя, на самом деле, если увеличить изображение точки, оно будет иметь кривые края и т. д. (см. рис. 8). Т. е. это непонятная клякса, если подходить к этому совсем строго.

Рис. 7. Точка

Рис. 8. Увеличенное изображение точки

Для решения различных задач мы используем модели: принимаем, что есть такой объект, как точка, который не имеет ни длины, ни ширины (его размерами мы пренебрегаем). Это удобная для нас модель объекта, размеры которого не важны для решения данной задачи. Важным является ее расположение. Например, точка может обозначать начало некоторого пути.

В обычной жизни мы также пренебрегаем размерами некоторых объектов. Например, пешеход вышел из деревни. Если подробно рассматривать задачу, то возникнет вопрос: из какого места деревни он вышел? Если из дома, то какого дома? Если это неважно (пройденный путь гораздо больше, чем размеры самой деревни), мы говорим, что просто из этой деревни, то есть считаем ее точкой. Когда спортсмены соревнуются в беге на соревнованиях, то там уже важно, с какого именно места они стартуют, где у них расположены ноги и т. д. В этом примере мы не можем сказать: «Стартовал из точки». А, например, город мы можем обозначить за точку, если машина выехала из этого города и удаляется от него на большое расстояние. Точка – один из примеров таких идеальных объектов, причем важно подчеркнуть, что у него нет определения, как и у других базовых понятий.

Следующий базовый объект – это отрезок или прямая, так как отрезок – это часть прямой. Прямая – это «не кривая». Более точное определение вряд ли можно сформулировать. Луч – это, условно говоря, половина прямой, часть прямой. Отрезок – часть прямой, ограниченная с двух сторон, то есть имеющая начало и конец (см. рис. 9).

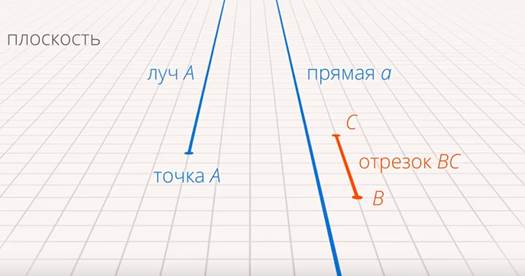
Рис. 9. Плоскость, точка, прямая, отрезок, луч

Говорят, что кратчайшее расстояние между двумя точками на плоскости – это длина отрезка прямой. Но здесь содержится тавтология, так как мы определяем прямую через кратчайшее расстояние, а кратчайшее расстояние – через прямую. Что-то из этого нужно считать определением, а что-то – интуитивно понятным. Важно, что базовые объекты определяются интуитивно (аналогично множествам в алгебре).

Следующие конструкции – это комбинации простейших объектов. Например, две прямые. Они или пересекаются на плоскости (см. рис. 11), или не пересекаются, т. е. параллельны (см. рис. 12). В жизни много примеров параллельных прямых. Например, железнодорожные рельсы (см. рис. 13).

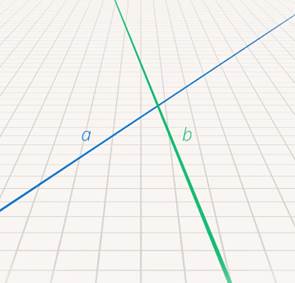
Рис. 11. Пересекающиеся прямые

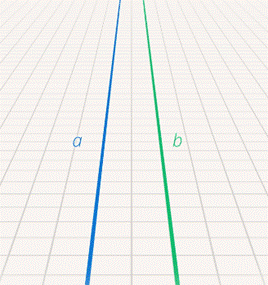
Рис. 12. Параллельные прямые

Рис. 13. Иллюстрация параллельности прямых на примере рельс

Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Т. е. мы сначала вводим объекты, а после – отношения между этими объектами.

Аналогично мы поступали с числами: ввели натуральные числа – количество предметов в множестве. А после этого изучали отношения между этими числами: дроби и т. д. (см. рис. 14).

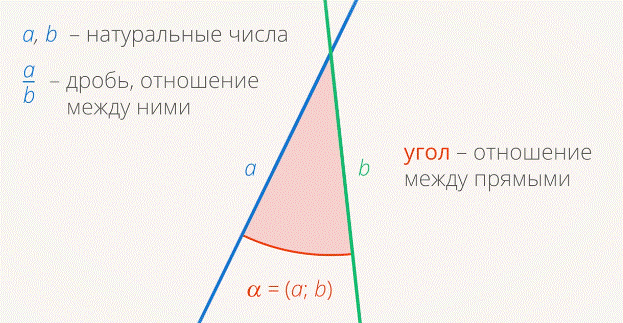
Рис. 14. Угол – отношение между прямыми

Точно так же мы изучали множества, а затем – отношения между множествами, функции.

Две прямые образуют углы (см. рис. 14). Если один из них нулевой, то прямые параллельны; если нет – прямые пересекаются. Т. е. угол – это отношение между прямыми.

Существенное отличие угла от таких отношений, как дроби и т. д., в том, что угол ограничен в своем измерении. Максимальный угол – это полный оборот (см. рис. 15). Мы его считаем равным . Это, конечно, условно. Мы могли бы считать полный оборот равным 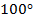 или измерять в радианах – 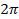. Но есть некая единица измерения угла, и она как бы ограничена. Угла большего, чем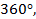

 на практике мы представить не можем.

Рис. 15. Максимальный угол

Можно ввести, как мы делали с отрицательными числами, новые объекты. Повернулись на один полный оборот, потом еще раз повернулись и т. д (см. рис. 16).

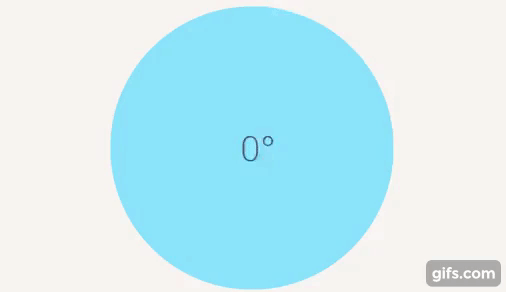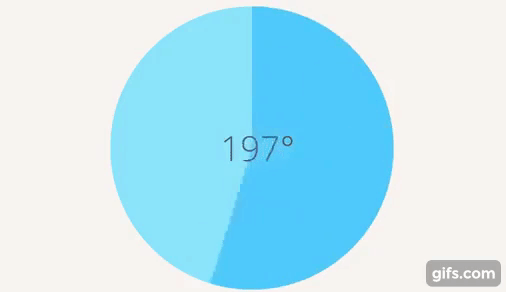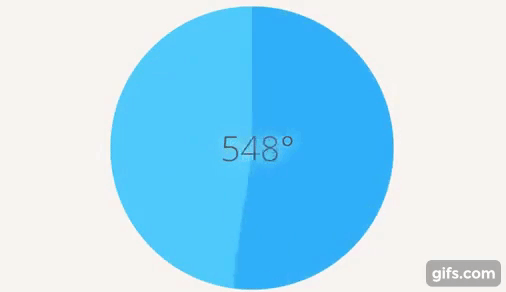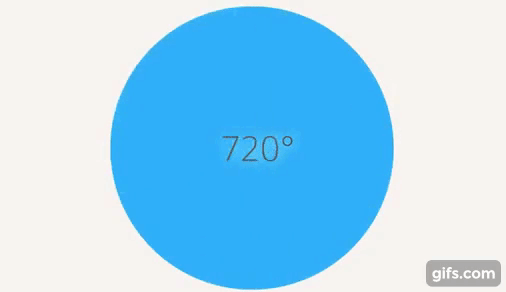
Рис. 16. Несколько полных оборотов

Мы говорили об этом в тригонометрии, когда обсуждали периодические функции. Там тоже возникает эта задача, когда мы делаем несколько оборотов и не знаем, какой именно угол, то ли 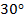, то ли 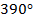,  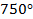и т. д (см. рис. 17).

Рис. 17. Многозначность угла

Важно то, что углы можно измерять. Углов бесконечно много, так как от 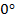 до  угол может принимать бесконечное множество значений. Из всего множества углов можно выделить наиболее часто встречающиеся.

Развернутый угол – угол, который образует прямая, половина от полного оборота (см. рис. 18).

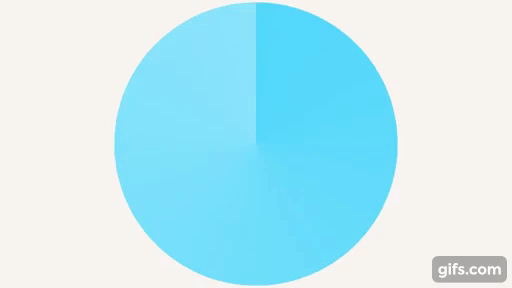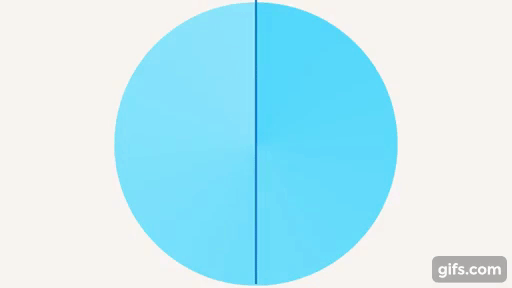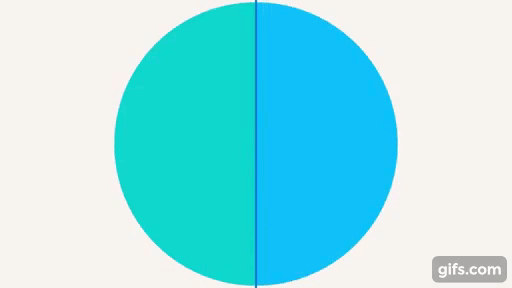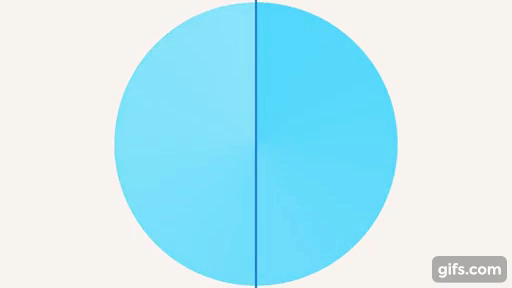
Рис. 18. Развернутый угол

При пересечении прямых может образоваться еще один особый угол – прямой (см. рис. 19).

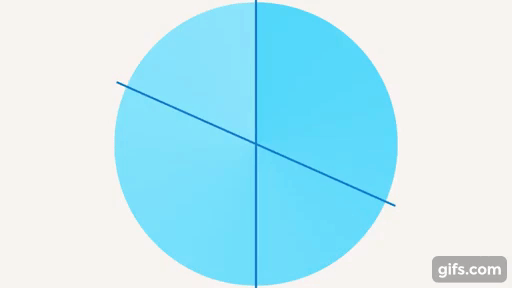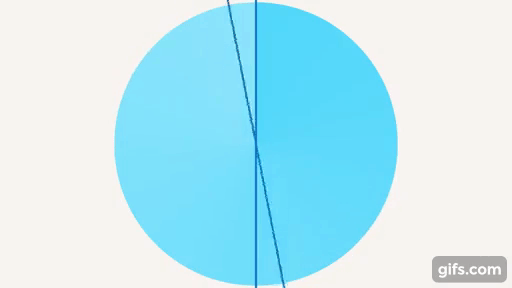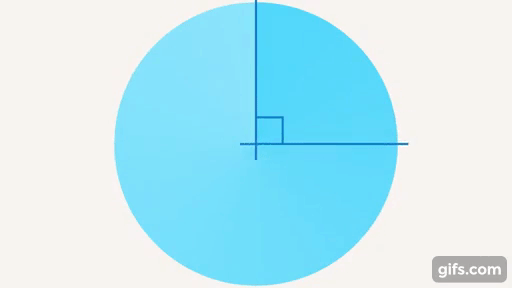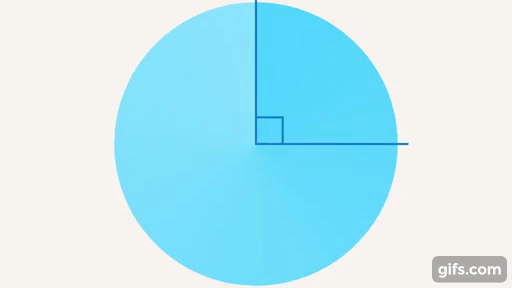
Рис. 19. Прямой угол

Замечателен он тем, что прямые, которые его образуют, расположены таким образом, что одна из них не падает ни вправо, ни влево относительно второй. Поэтому мы говорим, что стена дома должна быть расположена перпендикулярно дому, чтобы он не упал и т. д (см. рис. 20).

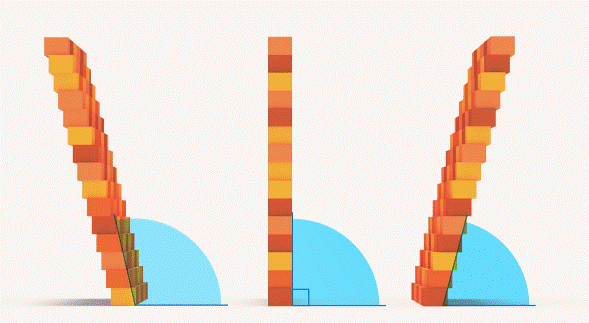
Рис. 20. Расположение стены дома, чтобы он не падал

Немного вернемся и скажем, почему мы вводим полный угол, зачем он нам и почему полный оборот равен . Углы можно сравнивать. Есть две прямые, то, как они связаны, – это значение угла между ними. Этот угол может быть больше, может быть меньше (см. рис. 21).

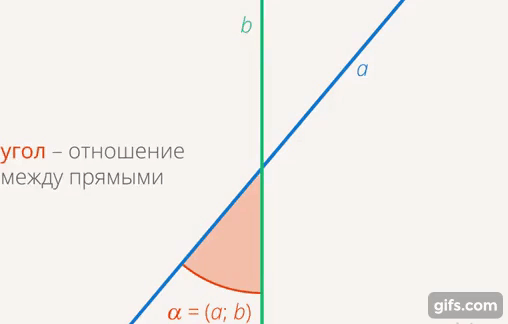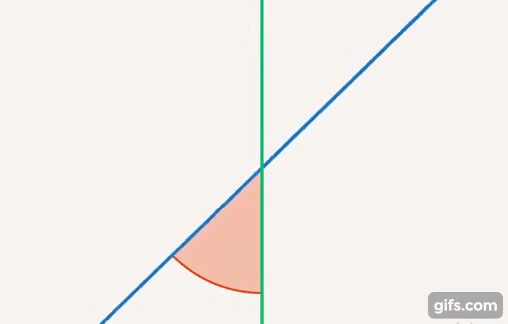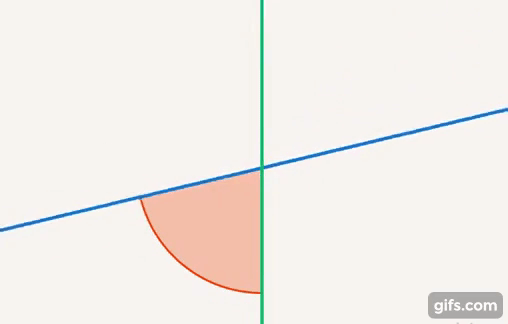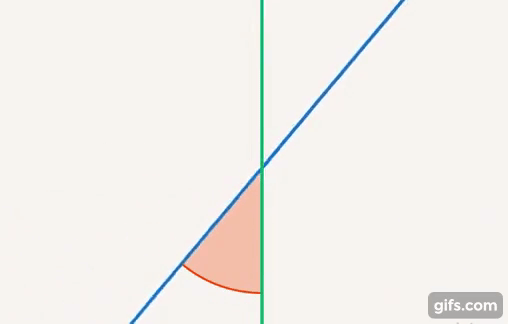
Рис. 21. Угол – отношение между прямыми

Чтобы сравнить величины, мы используем измерения. Как измерить угол? Можно взять полный круг, его за что-то обозначить и дальше выяснить, какую часть этого круга составляет этот угол (см. рис. 22).

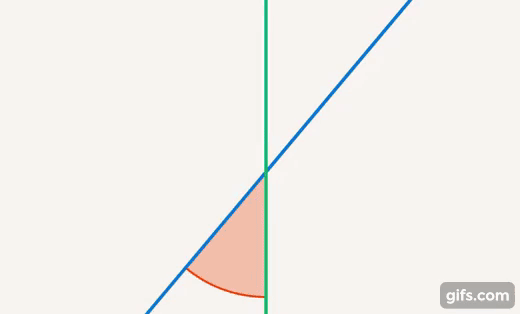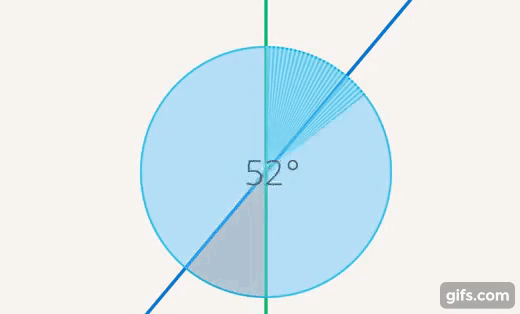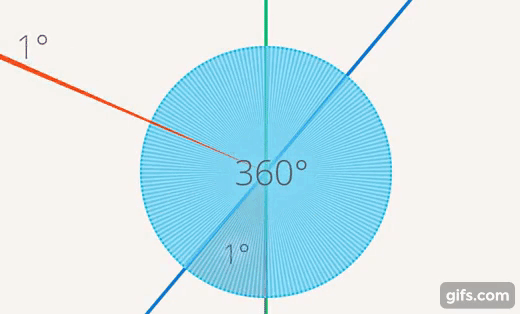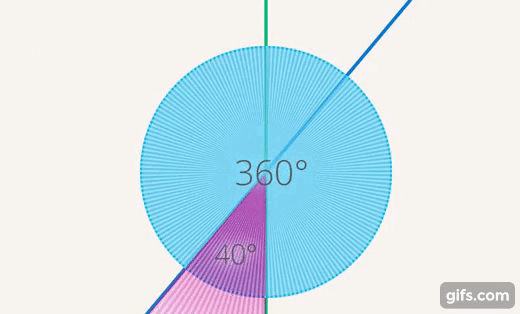
Рис. 22. Сравнение углов

Угол, который меньше прямого, – острый угол. Больше прямого – тупой (см. рис. 23).

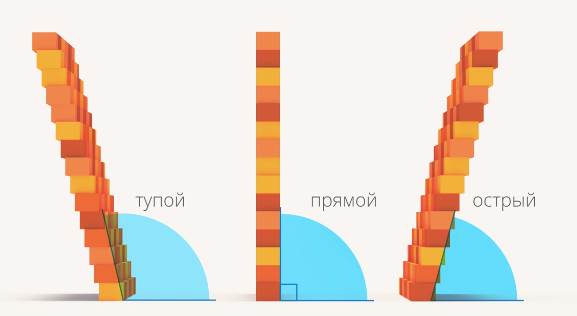
Рис. 23. Тупой, прямой и острый углы

Дальше мы будем использовать угол, то есть отношение между прямыми, в других фигурах, таких как треугольники и т. д. Сейчас мы знаем, что, если у нас есть две прямые, мы можем ввести отношение, которое называется углом, и, соответственно, сделать некую классификацию. Выделены два угла: один нулевой – его образуют параллельные прямые; прямой угол – образуют перпендикулярные прямые (когда все 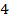 угла, образующихся при пересечении двух прямых, равны (см. рис. 24)).

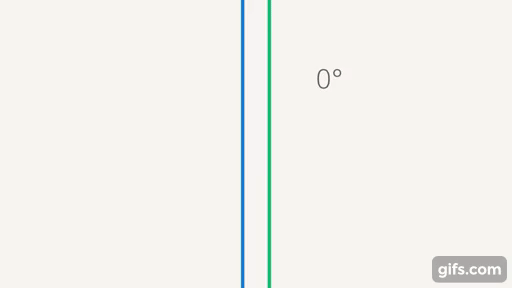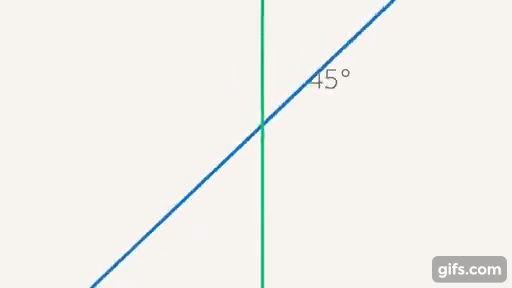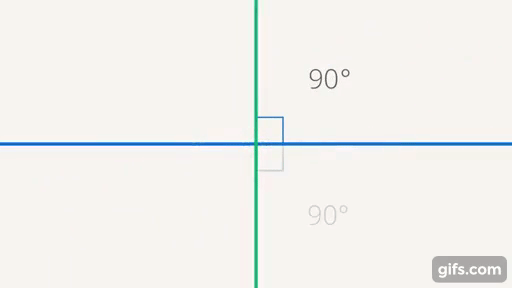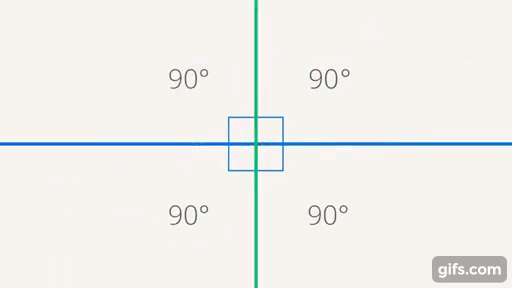
Рис. 24. Параллельные и перпендикулярные прямые

1-й случай: все три прямые параллельны (см. рис. 25).

Рис. 25. Параллельные прямые

2-й случай: две прямые параллельны, а третья их пересекает (см. рис. 26).

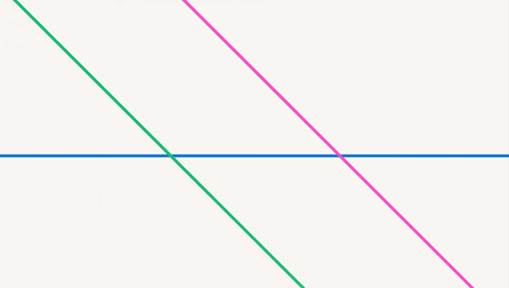
Рис. 26. Две прямые параллельны, а третья их пересекает

Рассмотрим такой пример: один человек с закрытыми глазами проводит прямую карандашом, а другой после этого произвольно поворачивает лист – в результате после трех таких операций получится треугольник. Или, например, если с закрытыми глазами бросить три спички на бумагу и продолжить их, то также получится треугольник (см. рис. 27).

Рис. 27. Получение треугольника

Вывод: три прямые, проведенные на плоскости случайным образом, с вероятностью 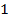 образуют треугольник (все остальные предельные случаи – три прямые параллельны, пересекаются в одной точке, две прямые параллельны, а третья их пересекает – вероятны так же, как и выпадение монеты на ребро). Поэтому эту фигуру мы так подробно и изучаем в школе.

С одной стороны, треугольник образуют три прямые. Посмотрим на треугольник с другой стороны, т. е. как на фигуру, состоящую из отрезков. Про два отрезка ничего нельзя сказать, они не могут замкнуться, так как всегда есть начало, есть конец, и они не совпадают (см. рис. 28).

Рис. 28. Два отрезка

Если добавить третий отрезок, то получим наименьшую возможную замкнутую ломаную – треугольник (см. рис. 29).

Рис. 29. Наименьшая замкнутая ломаная – треугольник

Исходя из этих свойств и особенностей, из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников, и т. д. (см. рис. 30).

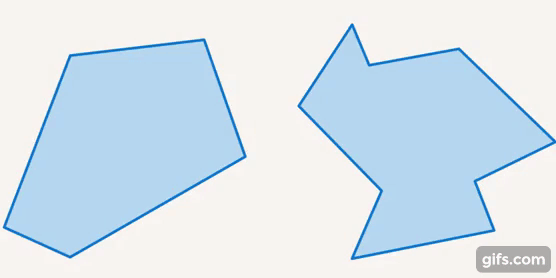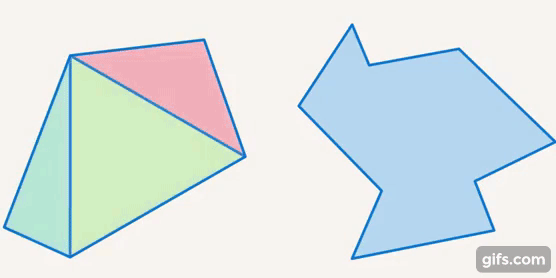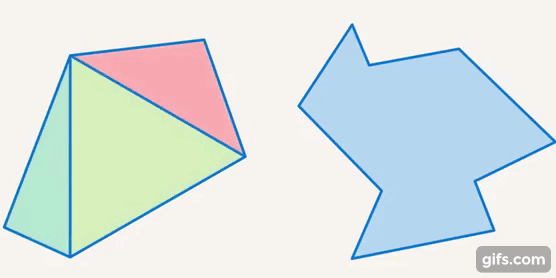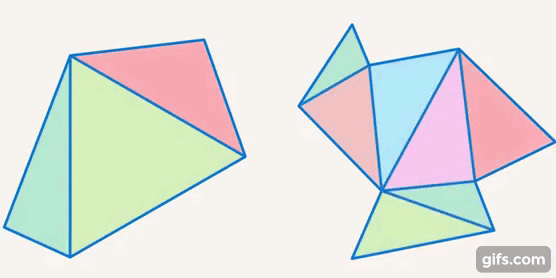
Рис. 30. Многоугольники состоят из треугольников

Треугольники изучаются потому, что на практике имеют большое значение. Для того чтобы построить устойчивую фигуру, нужно использовать треугольники. Например, вантовый мост (см. рис. 31). Несущие конструкции состоят как раз из треугольников.

Рис. 31. Вантовый мост

Треугольник также используется для измерения расстояний (см. рис. 32), а также изучаются его взаимоотношения с о

Геометрия Галуа — Википедия

Материал из Википедии — свободной энциклопедии

Геометрия Галуа (названа именем французского математика 19-го века Эвариста Галуа) — это раздел конечной геометрии, рассматривающий алгебраическую и аналитическую геометрию над конечными полями (или полями Галуа)^[1]. В более узком смысле геометрию Галуа можно определить как проективное пространство над конечным полем^[2].

Объектами изучения служат векторные пространства, аффинные и проективные пространства над конечными полями и различные структуры, содержащихся в них. В частности, дуги^[en], овалы, гиперовалы, униталы^[en], блокирующие множества^[en], овалы, многообразия и другие конечные аналоги структур, имеющихся в бесконечных геометриях.

Джордж Конуэлл продемонстрировал геометрию Галуа в 1910, когда описывал решение задачи Киркмана о школьницах как разбиение множества скрещивающихся прямых в PG(3,2), трёхмерной проективной геометрии над полем Галуа GF(2)^[en][3]. Подобно методам геометрии прямых в пространстве над полем с характеристикой 0, Конуэлл использовал плюккеровы координаты в PG(5,2) и отождествил точки, представляющие прямые в PG(3,2) с точками, лежащими на квадрике Кляйна^[en].

В 1955 году Беньямино Сегре описал овалы для нечётных q. Теорема Сегре^[en] утверждает, что в геометрии Галуа нечётного порядка (проективная алоскость, определённая над конечным полем с нечётной характеристикой) любой овал является коническим сечением. На Международном конгрессе математиков 1958 года Сегре представил обзор имеющихся на то время результатов в геометрии Галуа^[4].

Риманова геометрия — Википедия

Материал из Википедии — свободной энциклопедии

Ри́манова геоме́трия — это раздел дифференциальной геометрии, главным объектом изучения которого являются римановы многообразия, то есть гладкие многообразия с дополнительной структурой, римановой метрикой, иначе говоря — с выбором евклидовой метрики на каждом касательном пространстве, причём эта метрика гладко меняется от точки к точке. Иногда, особенно часто в математической физике, под римановой геометрией подразумевают также и псевдориманову геометрию многообразий с псевдоримановой метрикой, например, геометрию пространства-времени специальной и общей теории относительности.

Основным подразделом римановой геометрии в математике является геометрия в целом — раздел, который выявляет связь глобальных свойств риманова многообразия, таких как: топология, диаметр, объём — и его локальных свойств, к примеру, ограничений на кривизну.

Родоначальником римановой геометрии является немецкий математик Бернхард Риман, который изложил её основные понятия в 1854 году.

После опубликования работ Римана его идеи привлекли внимание ряда математиков, которые развивали дальше аналитический аппарат римановой геометрии и устанавливали в ней новые геометрические теоремы. Важным вкладом в развитие римановой геометрии было создание итальянскими геометрами Риччи-Курбастро и его учеником Леви-Чивита на рубеже XX века тензорного исчисления, которое оказалось наиболее подходящим аналитическим аппаратом. Решающее значение имело применение римановой геометрии в создании общей теории относительности. Это привело к бурному развитию римановой геометрии и её разнообразных обобщений. В настоящее время риманова геометрия вместе с её обобщениями представляет собой обширную область геометрии, которая продолжает успешно развиваться.

Теорема Гаусса-Бонне утверждает, что интеграл от гауссовой кривизны на компактном 2-мерном римановом многообразии равен 2πχ(М), где χ(M) обозначает эйлерову характеристику многообразия. Эта теорема допускает также обобщение на компактное риманово многообразие четной размерности.

• Бураго Ю. Д., Залгаллер В. А. Введение в риманову геометрию, — СПб: Наука, 1994. 318 с.
• Рашевский П. К. Риманова геометрия и тензорный анализ — М.:Наука, 1967.
• Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия. Методы и приложения — М.: Наука, 1979.
• Постников М. М. Риманова геометрия (Лекции по геометрии. семестр V) — М.: Факториал Пресс, 1998. 496 с.
• Громол Д., Клингенберг В., Мейер В. Риманова геометрия в целом — М.: Мир, 1971

Геометрическая теория групп — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 апреля 2016; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 апреля 2016; проверки требуют 2 правки.

Геометрическая теория групп — область математики, изучающая конечно-порождённые группы с помощью связей между их алгебраическими свойствами и топологическими и геометрическими свойствами пространств, на которых такие группы действуют, либо самих групп, рассматриваемых как геометрические объекты (что обычно делается рассмотрением графа Кэли и соответствующей словарной метрики).

Геометрическая теория групп, как отдельная ветвь математики, появилась сравнительно недавно, и стала чётко выделяться в конце 1980-х-начале 1990-х. Геометрическая теория групп взаимодействует с маломерной топологией, гиперболической геометрией, алгебраической топологией, вычислительной теорией групп. Также она связана с теорией сложности, математической логикой, исследованием групп Ли и их дискретных подгрупп, динамическими системами, теорией вероятности, K-теорией, и другими областями математики.

Первым результатом в геометрической теории групп следует считать теорему Громова о группах полиномиального роста. В доказательстве впервые используется так называемая сходимость по Громову — Хаусдорфу.

Тем не менее основной шаг в формировании геометрической теории групп был сделан в статье Громова о гиперболических группах.^[1] Приведённое в этой статье определение гиперболической группы дало наглядную геометрическую интерпретацию теории групп с малыми сокращениями (англ.).

1. ↑ Громов М. Гиперболические группы. — Ижевск: Институт компьютерных исследований, 2002. — 160 с. — ISBN 5-93972-103-6.

Абсолютная геометрия — Википедия

Материал из Википедии — свободной энциклопедии

Абсолютная геометрия (или нейтральная геометрия) — часть классической геометрии, независимая от пятого постулата евклидовой аксиоматики (то есть в абсолютной геометрии пятый постулат может выполняться, а может и не выполняться). Абсолютная геометрия содержит предложения, общие для евклидовой геометрии и для геометрии Лобачевского^[1][2].

Термин был предложен Яношем Бойяи в 1832 году^[3]. Правда, сам Бойяи вкладывал в него несколько иной смысл: он называл абсолютной геометрией специально разработанную им символику, которая позволяла объединять одной формулой теоремы как евклидовой геометрии, так и геометрии Лобачевского^[4].

Примеры теорем абсолютной геометрии[править | править код]

Первые 28 теорем «Начал» Евклида относятся к абсолютной геометрии. Приведём ещё несколько примеров таких теорем^[5]:

• У равнобедренного треугольника углы при основании равны.
• Внешний угол треугольника больше каждого внутреннего, не смежного с ним.
• Во всяком треугольнике по крайней мере два угла острые.
• При пересечении двух прямых вертикальные углы равны.
• Большей из двух сторон треугольника противостоит и больший угол, и наоборот, большему углу противостоит бо́льшая сторона.
• Перпендикуляр (из точки на прямую) короче наклонной.
• Каждая сторона треугольника меньше суммы и больше разности двух других его сторон.
• Сумма углов треугольника не превосходит 180°.

Теоремы, не входящие в абсолютную геометрию[править | править код]

Современная аксиоматика евклидовой геометрии (например, аксиоматика Гильберта) полна, то есть любое корректное утверждение в этой теории может быть доказано или опровергнуто. Абсолютная геометрия неполна: поскольку пятый постулат определяет метрические свойства однородного пространства, отсутствие его в абсолютной геометрии означает, что метрика пространства не определена, и большинство теорем, связанных с измерениями (например, теорема Пифагора или теорема о сумме углов треугольника) не могут быть доказаны в абсолютной геометрии^[6].

Другие примеры теорем, не входящих в абсолютную геометрию:

В абсолютной геометрии параллельные прямые всегда существуют (см. теоремы 27 и 28 «Начал» Евклида, доказанные без опоры на пятый постулат), поэтому сферическая геометрия, в которой нет параллельных, несовместима с абсолютной геометрией. Однако можно построить аксиоматику, объединяющую все три типа неевклидовых геометрий (евклидову, сферическую и геометрию Лобачевского)^[8], и тогда абсолютную геометрию можно определить как их общую часть. Это новое определение более узкое, чем прежнее — например, теорема «сумма углов треугольника не превосходит 180°» перестаёт быть верной.

1. ↑ Абсолютная геометрия // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 34.
2. ↑ Высшая геометрия, 1971, с. 88—89.
3. ↑ Больаи Я. Аппендикс // Об основаниях геометрии (сб. статей), М., ГИТТЛ, 1956. Серия «Классики естествознания».
4. ↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций / Под ред. Колмогорова А. Н., Юшкевича А. П.. — М.: Наука, 1981. — С. 64—65. — 270 с.
5. ↑ Высшая геометрия, 1971, с. 14, 67 и далее, 89.
6. ↑ ^{1 2} school-collection.edu.ru.
7. ↑ См, например: Gunter Ewald. Geometry: an introduction. Wadsworth Publishing. 1st. 1971, 399 pages. ISBN 0534000347.
8. ↑ Peil, Timothy. Hilbert’s Axioms Modified for Plane Elliptic Geometry (англ.). // Survey of Geometry. Дата обращения 18 октября 2016.

• Гильберт Д. Основания геометрии. — М.—Л.: ГИТТЛ, 1948. — 492 с. — (Классики естествознания. Математика, механика, физика, астрономия).
• Ефимов Н. В. Высшая геометрия. — 7-е изд. — М.: Физматлит, 1971.
  • Переиздание: 2004, издательство «Физматлит», ISBN 5-9221-0267-2.