Степени и корни. Действия с ними
Напомним, что степенью с натуральным показателем называется произведение

где
 –
основание степени (
–
основание степени ( ),
),
 –
показатель степени (
–
показатель степени ( ).
).
Возвести

 -ю
степень – это значит найти значение выражения
-ю
степень – это значит найти значение выражения  .
.При
 имеем
имеем
 .
.
Степень
с нулевым показателем:  ,
если
,
если  ,
то есть любое число (кроме
,
то есть любое число (кроме 
 .
.Выражение
 не
имеет смысла.
не
имеет смысла.
Степенью
с отрицательным целым показателем называется число  ,
где
,
где  ,
,
 и
и

При возведении отрицательного числа в нечётную степень получится отрицательное число, а при возведении отрицательного числа в чётную степень получится положительное число.
Для
любых действительных чисел  и
и
 ,
отличных от
,
отличных от  ,
и для любых целых показателей
,
и для любых целых показателей  и
и

1.
 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
Используя
степени с целыми показателями, любое положительное число у можно записать в
виде произведения 
 и
и
 –
целое число. Такая запись называется стандартным видом числа
–
целое число. Такая запись называется стандартным видом числа  ,
а число
,
а число  –
порядком числа
–
порядком числа  .
.Также
напомним, что корнем 
 )
из действительного числа
)
из действительного числа  называют
такое действительное число
называют
такое действительное число  ,
,
 -я
степень которого равна
-я
степень которого равна  ,
то есть
,
то есть  .
.Арифметическим корнем
 -й
степени (
-й
степени ( )
из числа
)
из числа  называется
неотрицательное число,
называется
неотрицательное число,  -я
степень которого равна
-я
степень которого равна  .
Обозначают арифметический корень с помощью знака радикала:
.
Обозначают арифметический корень с помощью знака радикала:  .
.Под
выражением 
1.
единственное значение корня в случае нечётного  ;
;
2.
арифметический корень в случае чётного  ;
;
3.
 ,
если
,
если  ,
при любом
,
при любом  .
.
Заметим,
что 
 ,
но
,
но  при
чётном
при
чётном  .
.Так,
например,  ,
, .
.
То
есть  ,
где
,
где 
Действие,
посредством которого отыскивается корень  -й
й степени, называется извлечением корня
-й
й степени, называется извлечением корня  -й
степени. Это действие является обратным действию возведения в
-й
степени. Это действие является обратным действию возведения в
 -ю
степень.
-ю
степень.
А
теперь давайте вспомним свойства арифметического корня  -й
степени. Итак, при условии, что
-й
степени. Итак, при условии, что 
 ,
а
,
а  ,
,
 и
и
 –
натуральные числа, причём
–
натуральные числа, причём  ,
,
 ,
справедливы равенства:
,
справедливы равенства:1.
 .
(число
.
(число  может
также быть равным
может
также быть равным  )
)
2.
 .
.
3.
 .
(число
.
(число  может
быть любым целым, если
может
быть любым целым, если  )
)
4.
 .
.
5.
 .
.
Также следует вспомнить формулу сложного радикала:
 .
.
И
ещё напомним, что степенью с рациональным показателем называется число  ,
где
,
где  ,
,
 ,
,
 ,
,
 ,
,
 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите значения выражений:
а)
 при
при
 ;
;
б)
 при
при
 .
.
Решение.

Задание
второе. Вычислите  .
.
Решение.

Задание
третье. Упростите выражение  .
.
Решение.




Урок-игра по математике на тему: «Корень n-степени» (9 класс)
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №4» г. Сосногорска
Учитель Панюкова Наталья Васильевна
9 класс
Тема: Корень n -й степени.
Форма проведения урока:
учебная игра.
Цель урока:
систематизировать знания и умения по теме: «Корень n — степени» и закрепить с помощью тестов.
Задачи урока:
задачи обучения:
актуализация знаний учащихся по теме,
обобщить изученный материал;
задачи развития:
совершенствование умения учащихся работать с тестами, делать выводы;
развитие интереса к предмету и процессу познания
задачи воспитания:
воспитание умения оценивать свои знания и возможности в достижении положительных результатов;
воспитание умения работать в коллективе (в паре, как целое).
Подготовка к уроку:
Заранее создаётся презентация с учащимися 10 – 11 классов с заданиями для урока. Заготавливаются эмблемы «отличник», «участник игры», «лучший математик»
В её основе которой лежит модель теле — игры «Кто хочет стать миллионером?». Игра состоит из нескольких туров, каждому из которых предшествует отборочный тур. Содержание учебного материала повторяется несколько раз, только в разных аспектах, что позволяет более глубоко закрепить знания.
Число туров может быть различным: в сильном классе: 4 – 5, а в слабом от 2 — 3. от тура к туру задания усложняются, что позволяет осуществить разноуровневый подход к обучению.
Участвовать в игре может как один человек, так и пара учащихся (примерно имеющих одинаковый уровень знаний).
Задания игровых туров составлены в форме тестов. Все задания проецируются на экране, в заранее подготовленной презентации.
Условия игры:
Участником игрового тура становится тот, кто проходит отборочный тур.
Игроки могут использовать следующие подсказки:
Звонок другу – обращение к любому игроку класса;
Помощь зала – правильный ответ определяется голосованием зрителей.
Звание отличника получает тот, кто пройдёт до конца все туры игры.
Ход урока:
Первый оборочный тур:
Дайте определение корня n – й степени
(Ответ: Корнем n – й степени из числа a называется такое число, n – я степень которого равна а.)
Первый игровой тур:
Вычислите

1) 0,03 2) 0,3 3) 0,09 4) 0,0003
(Ответ: 2) 0,3)
Найдите значение выражения

1) 2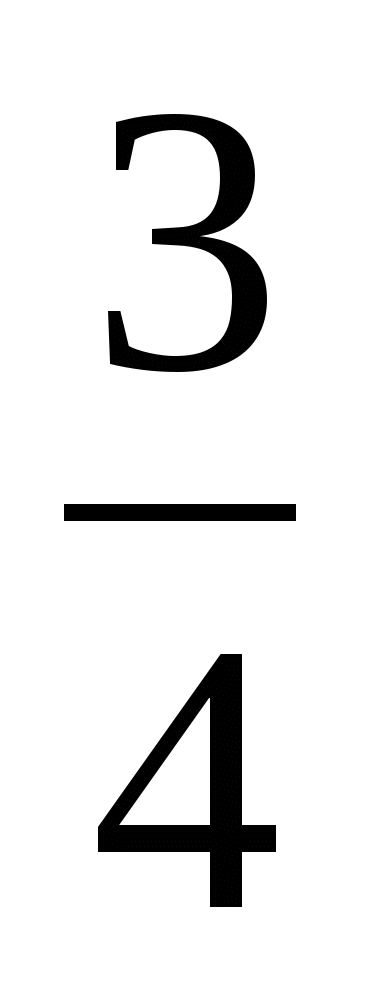 2) -8
2) -8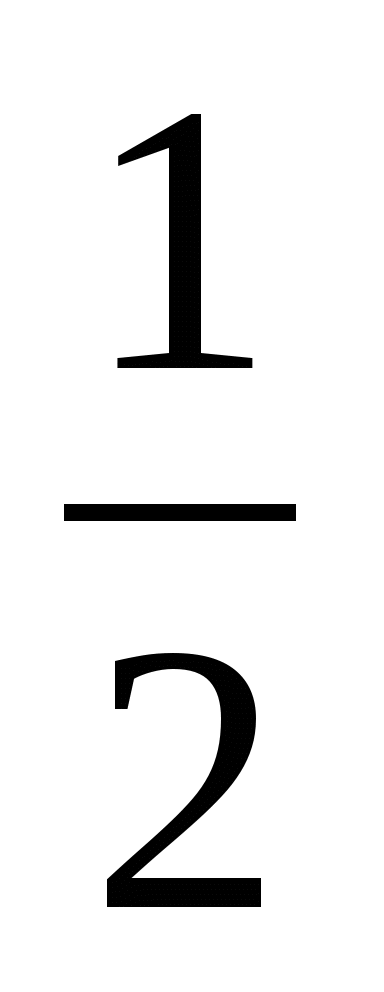 3)-2
3)-2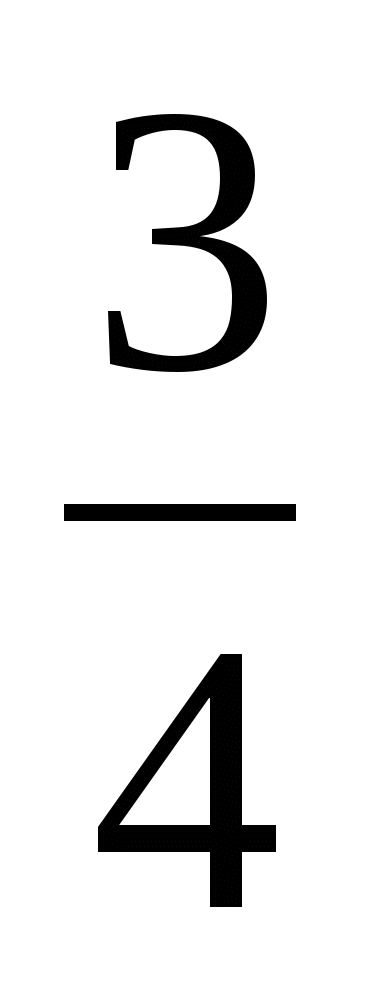 4) -3
4) -3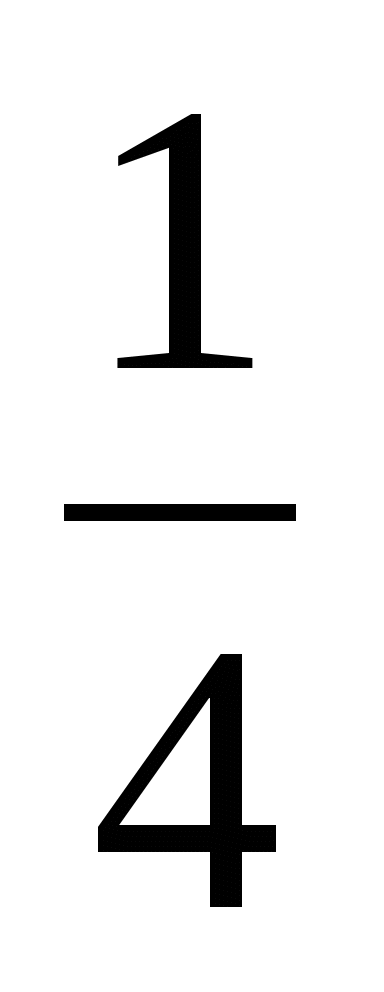
(Ответ: 3) -2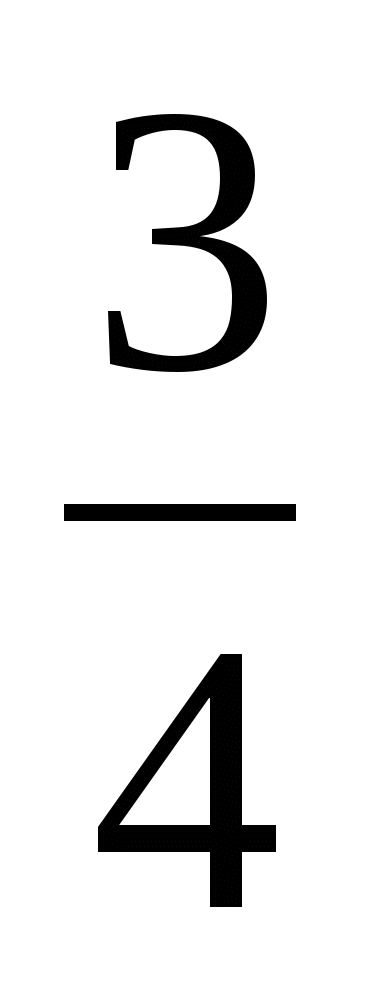 )
)
Решите уравнение 2+ х3= 0
1) — 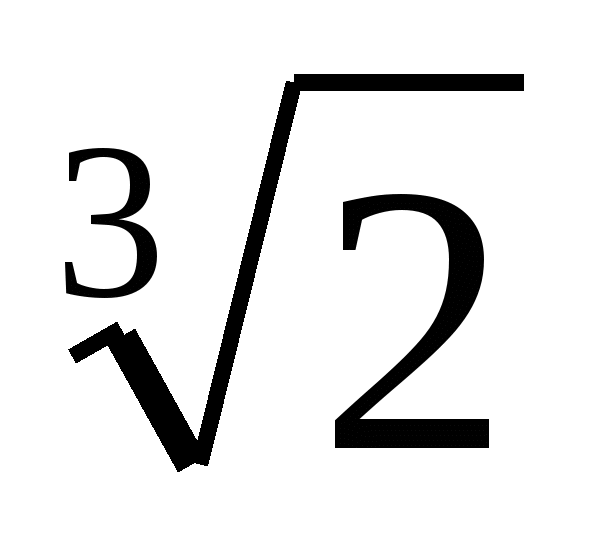 ;
; 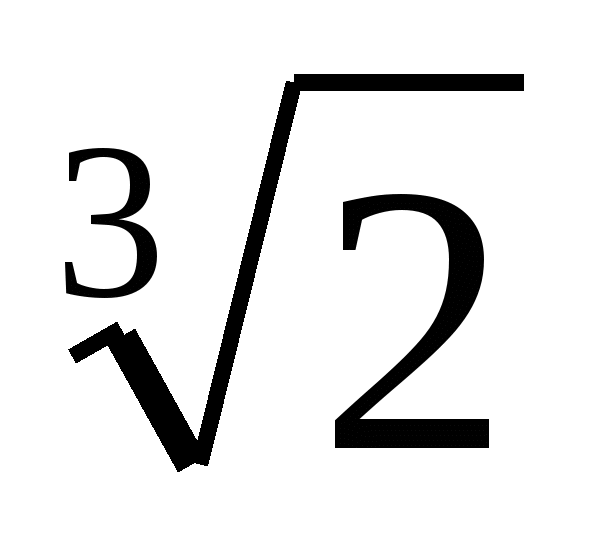 2) — 8 3) —
2) — 8 3) — 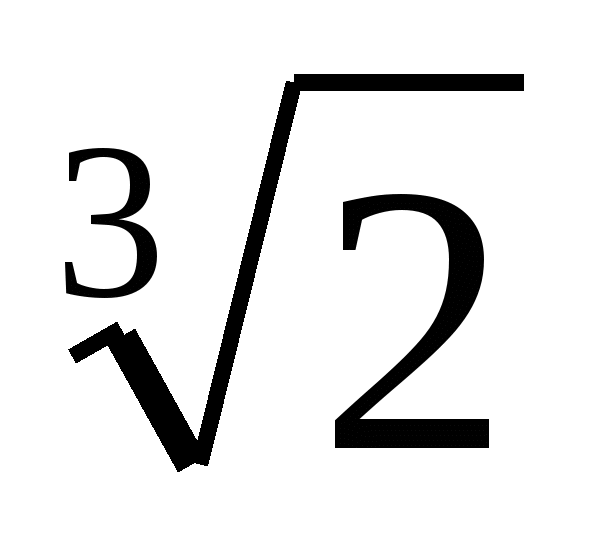 4) 8
4) 8
(Ответ: 3) — 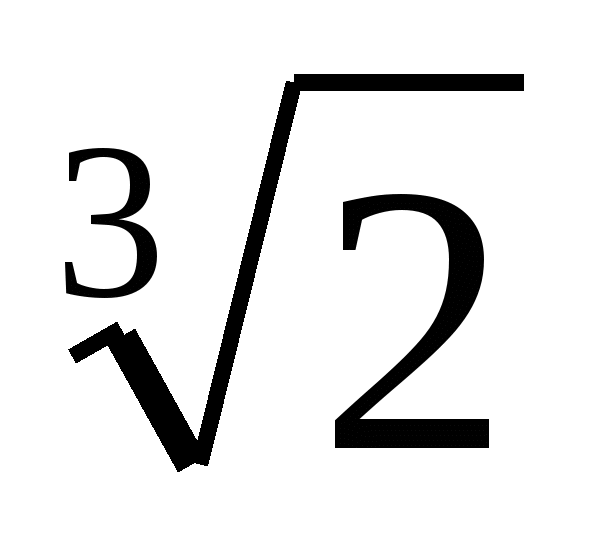 )
)
Вынесите множитель из — под знака корня

 .
.
1) 2ху2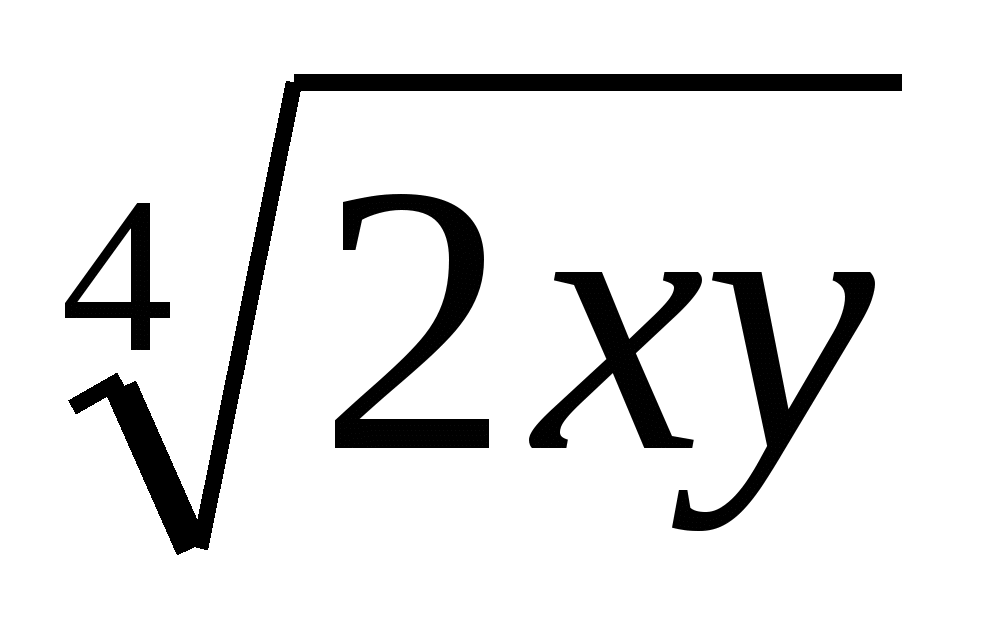 2) 4ху2
2) 4ху2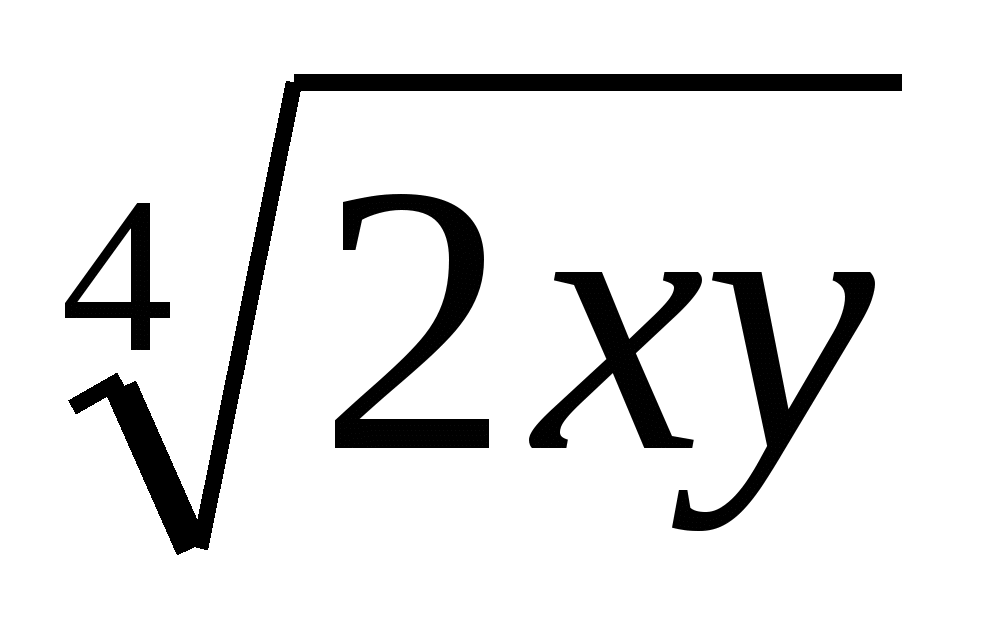 3) 2ху
3) 2ху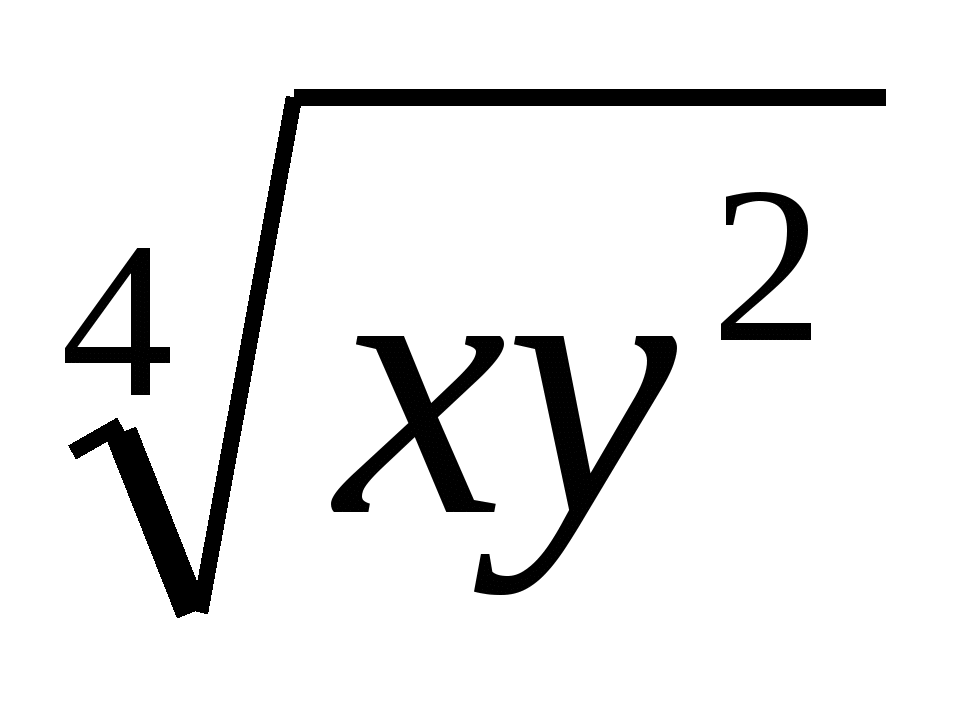 4) 8ху4
4) 8ху4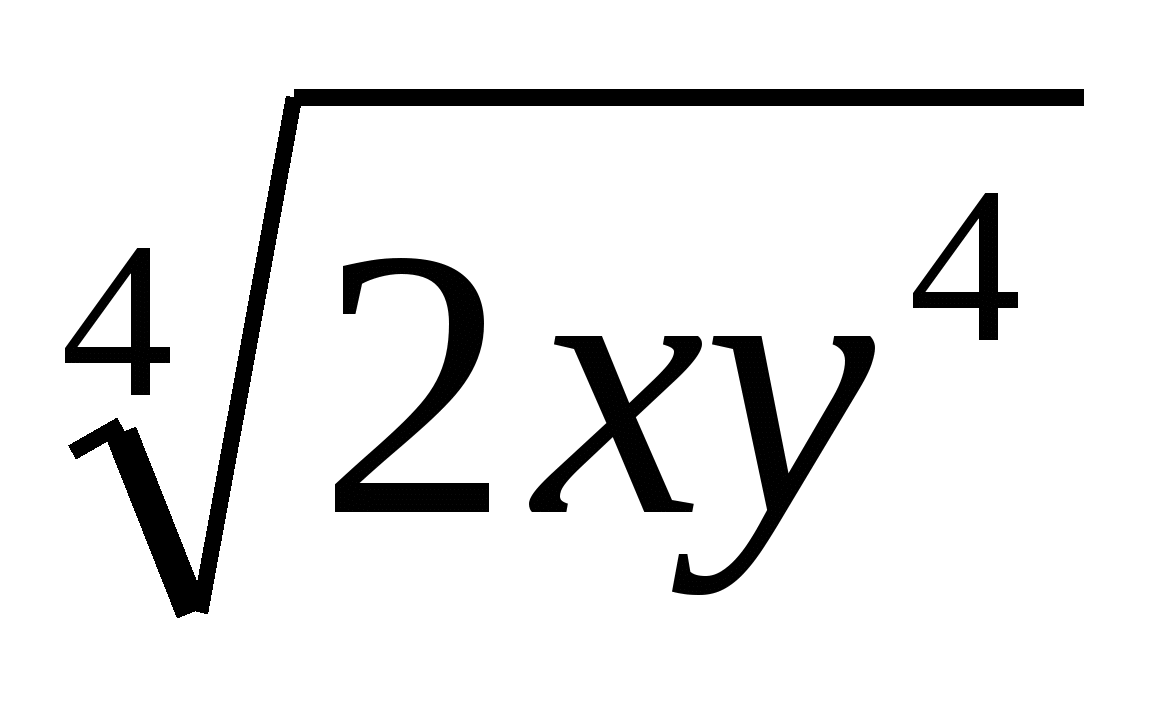
(Ответ: 1) 2ху2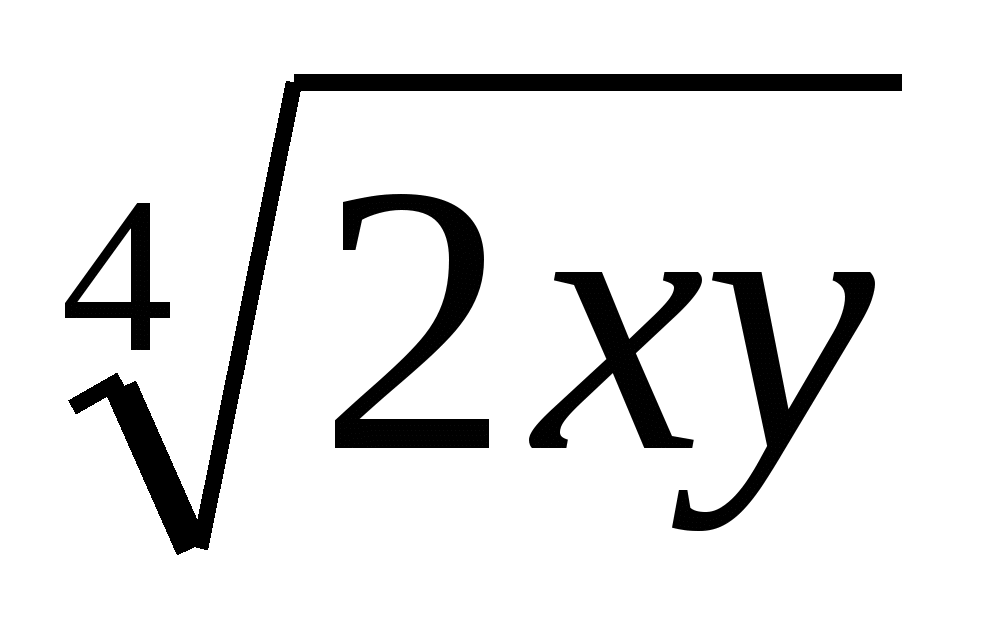 )
)
Внесите множитель под знак корня 2a3b2
 , если а>0, b>0.
, если а>0, b>0.
1)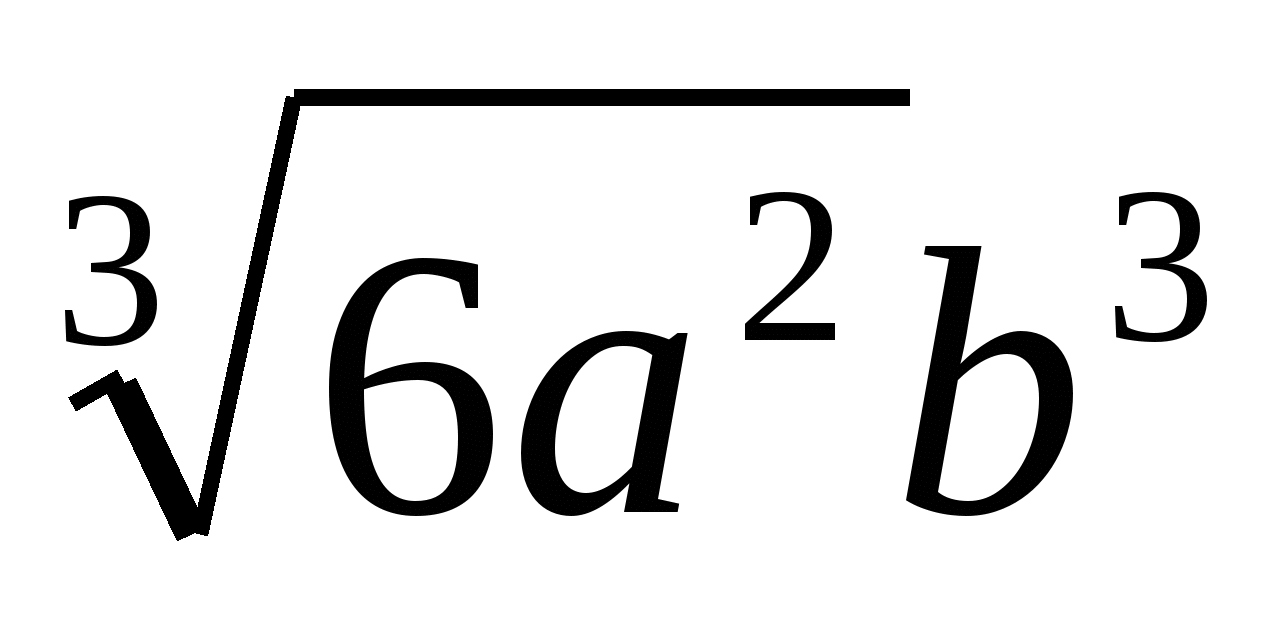 2)
2)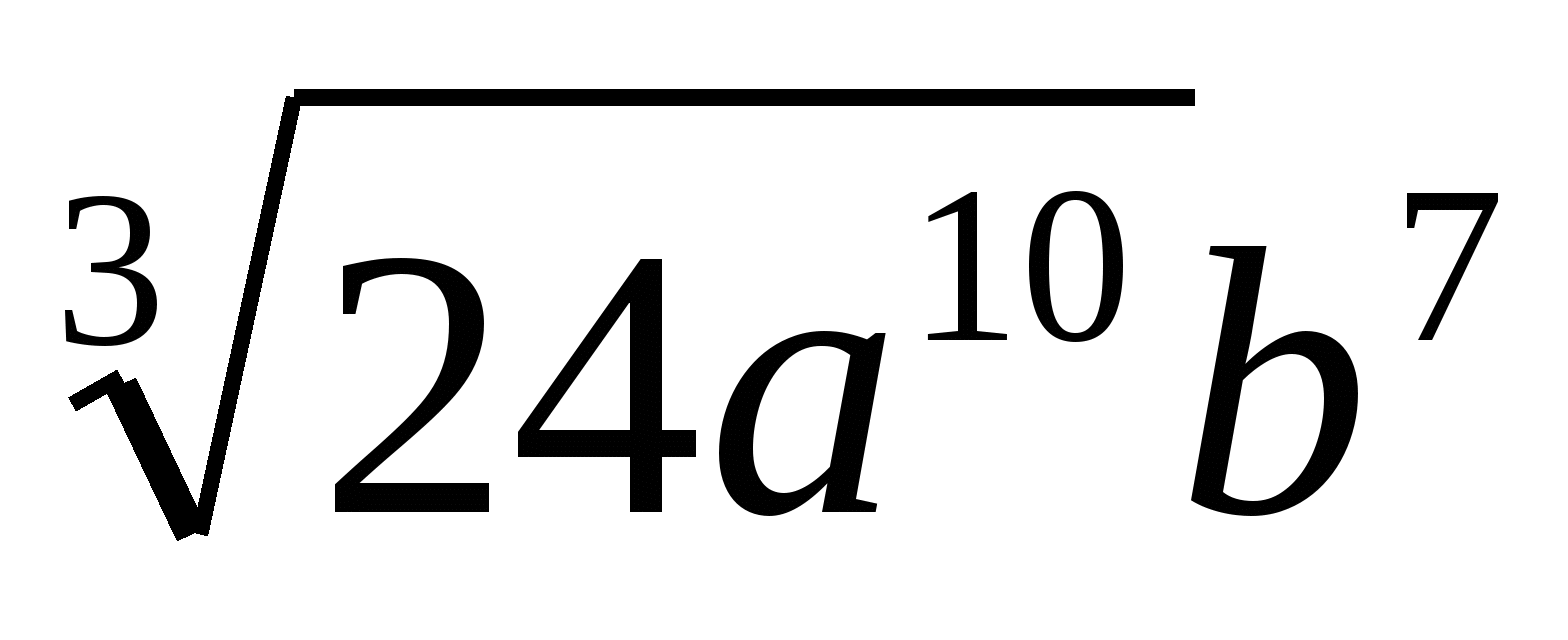 3)
3)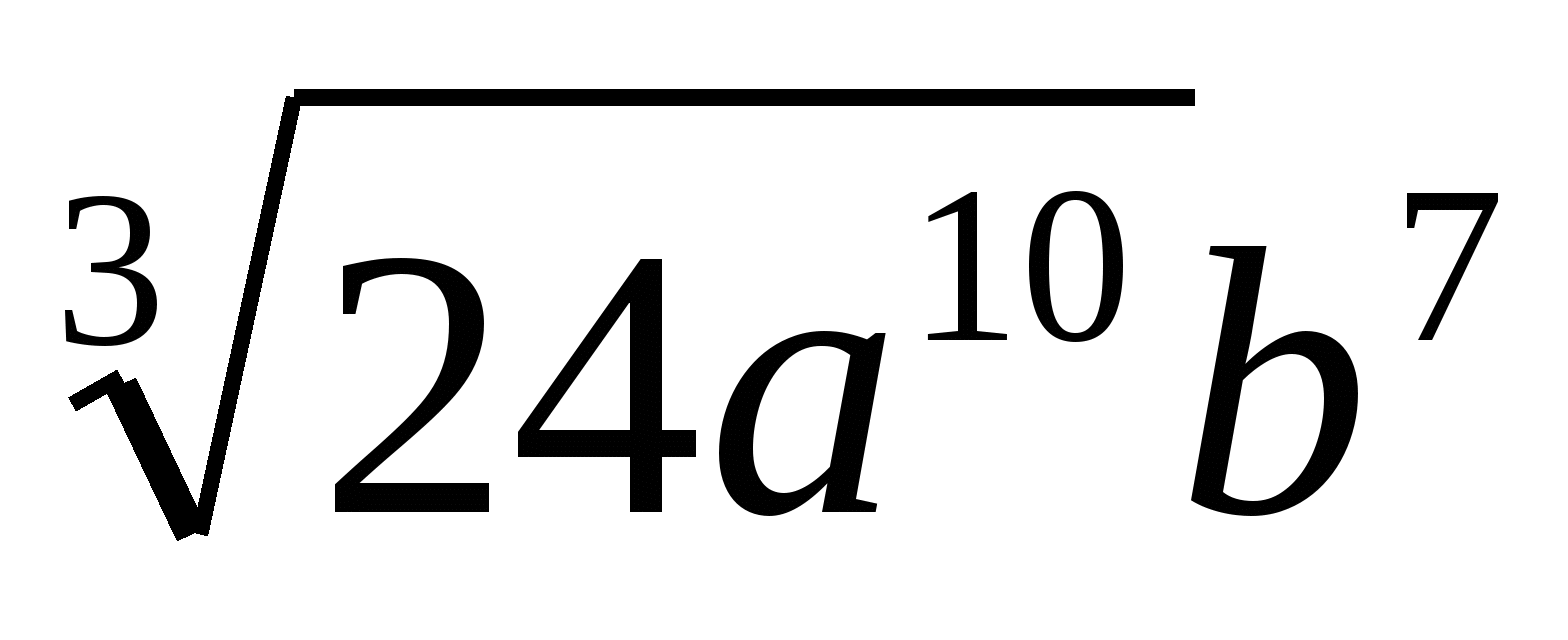 4)
4)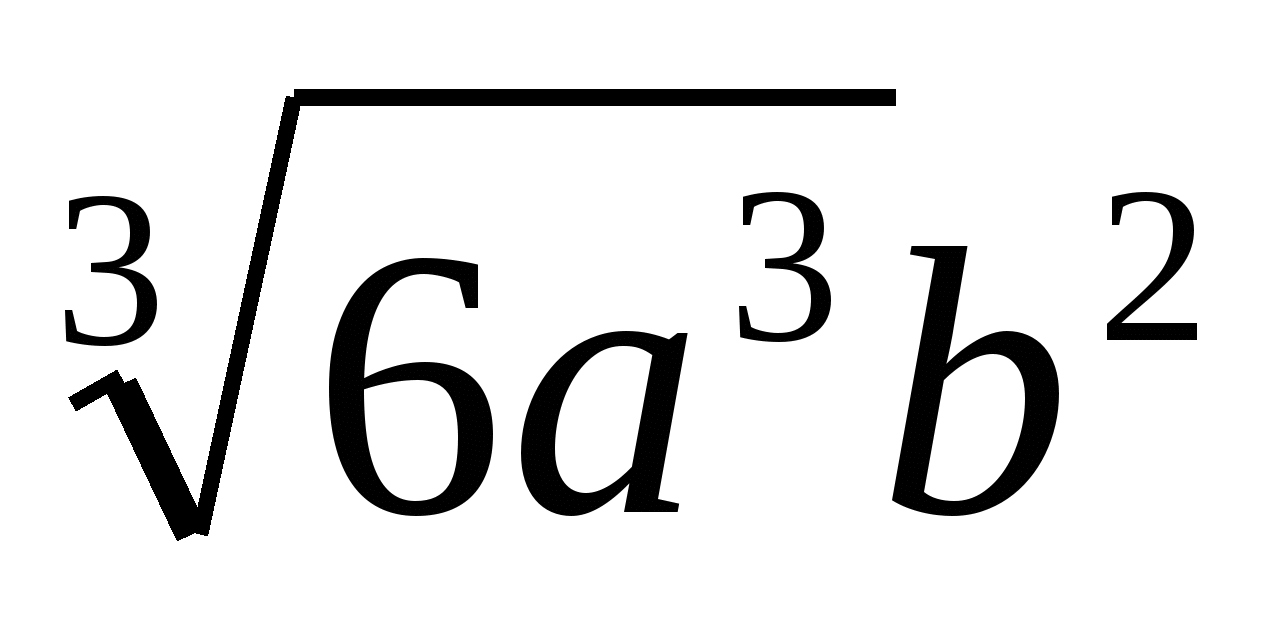
(Ответ: 2) 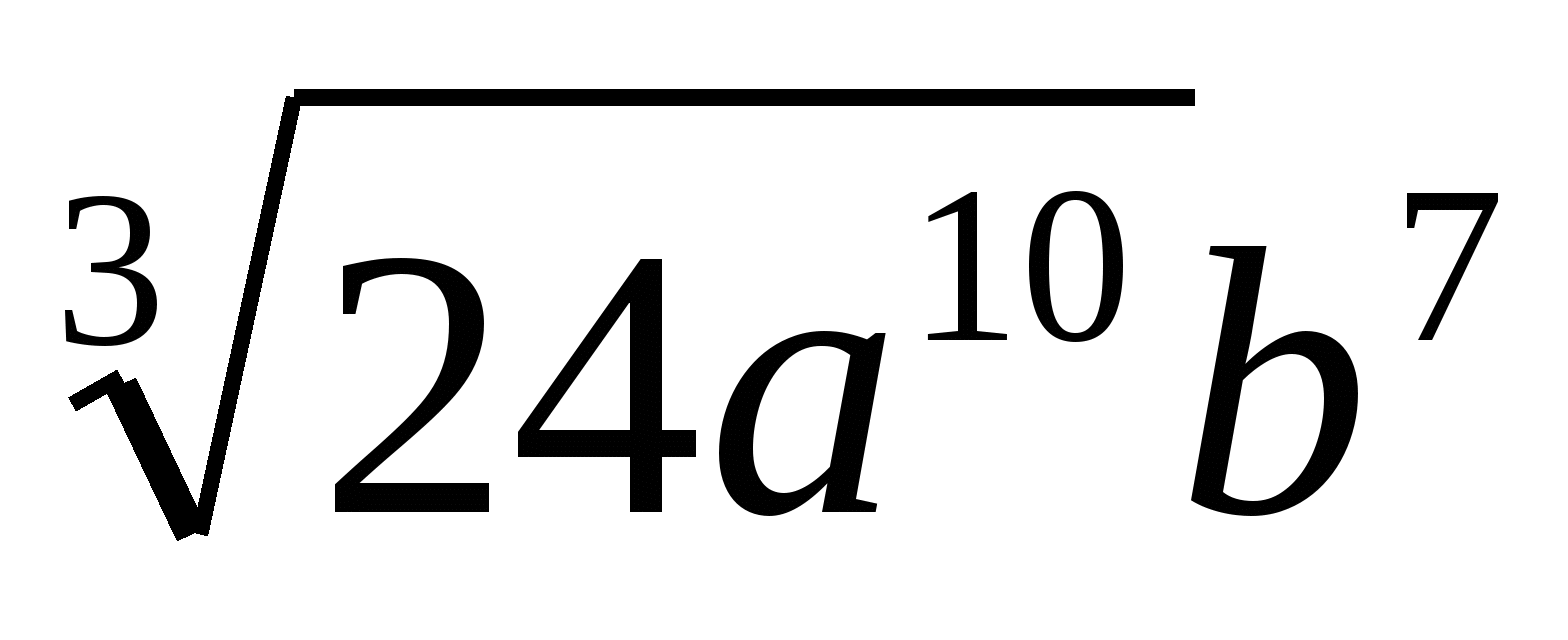 )
)
Упростите выражение
 .
.
1)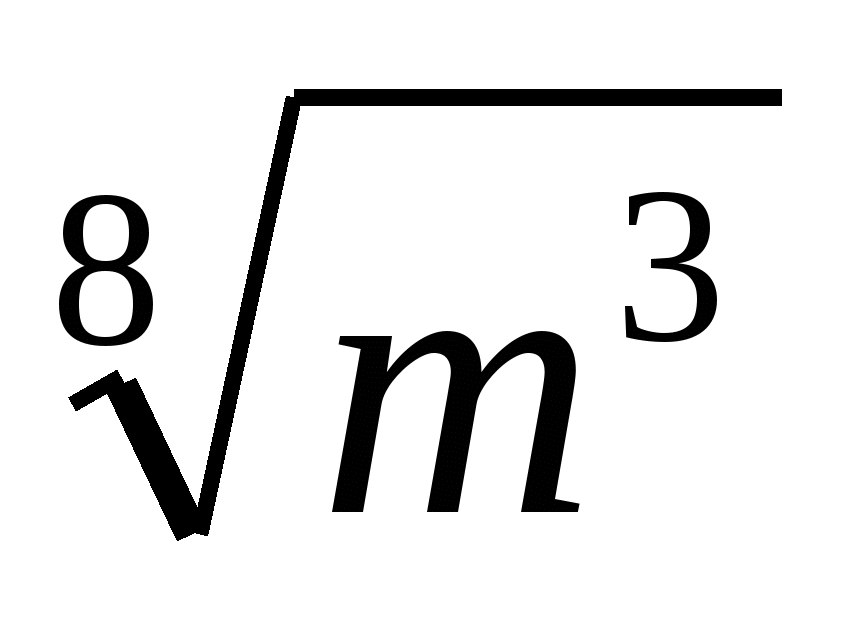 2)
2)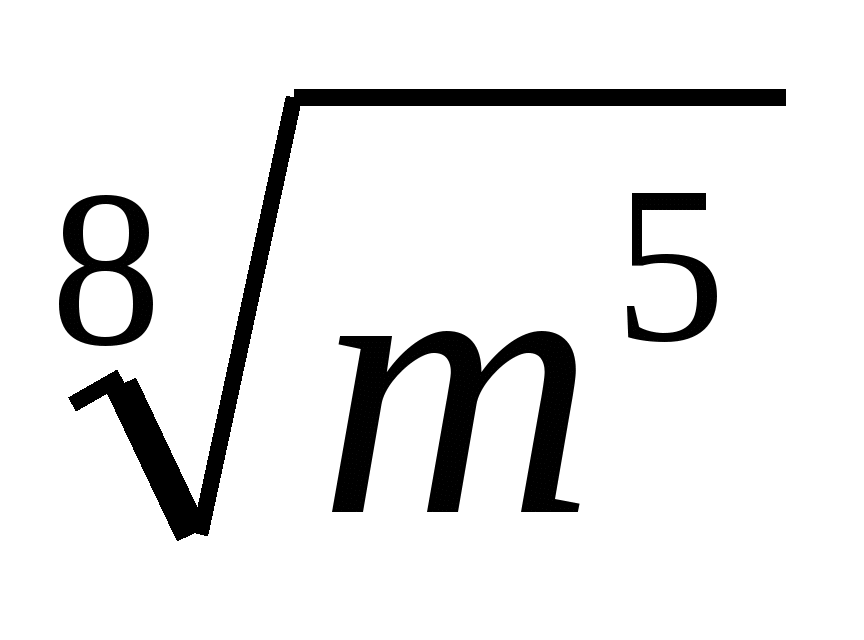 3)
3)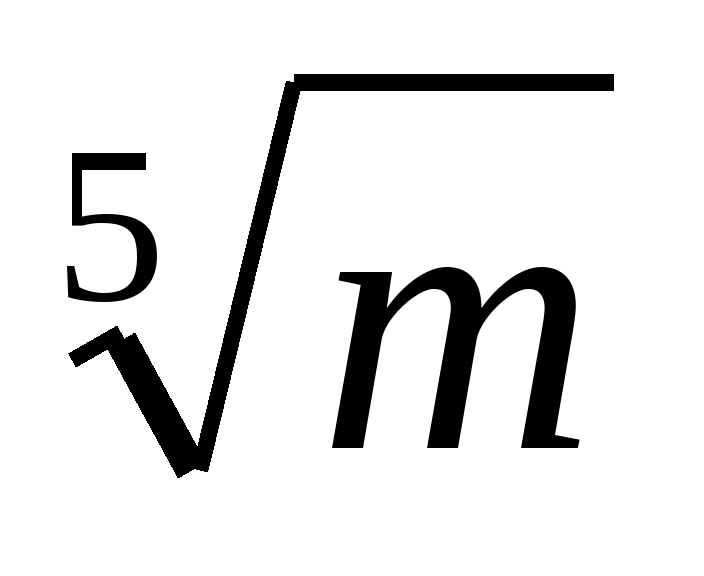 4)
4)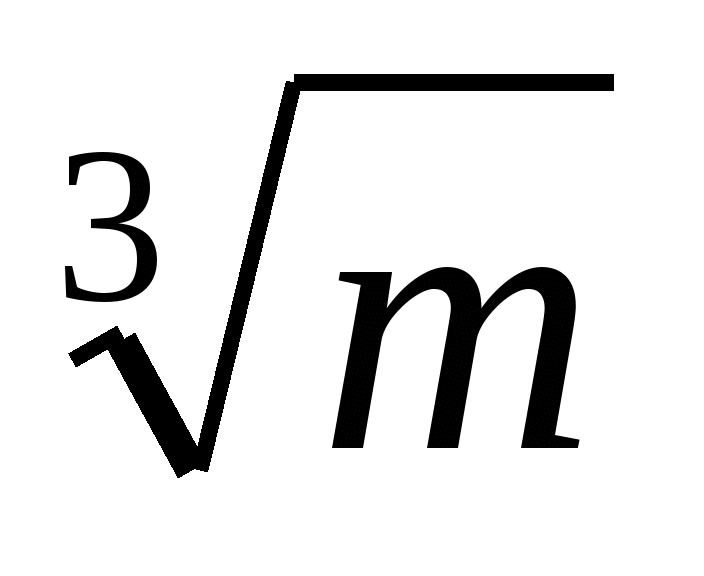
(Ответ: 2) 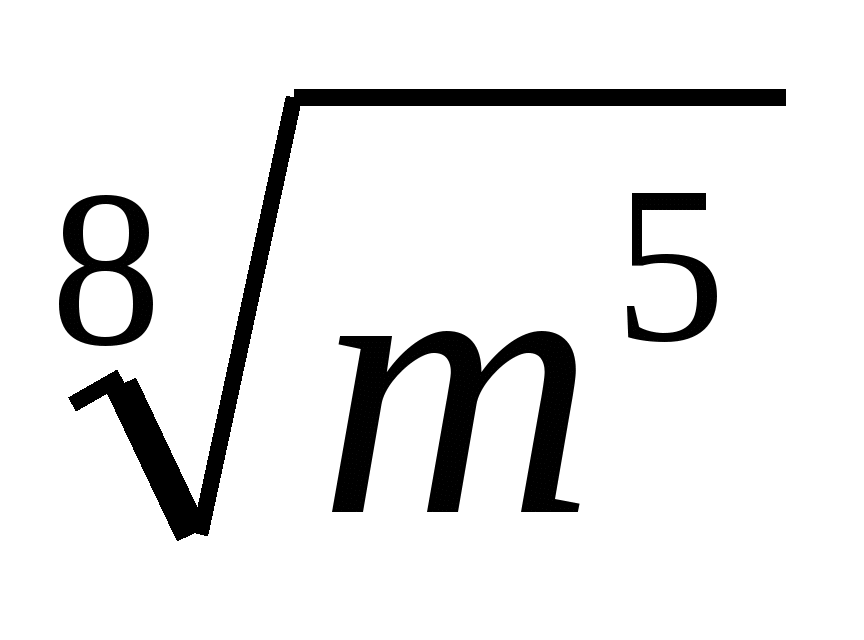 )
)
Сократите дробь

1) 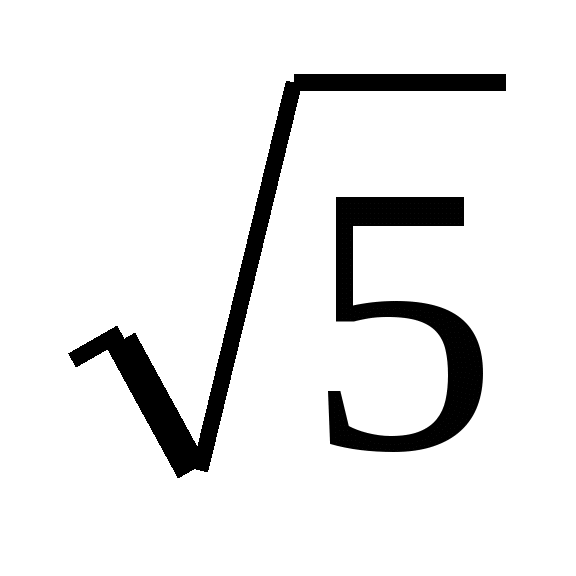 2)
2) 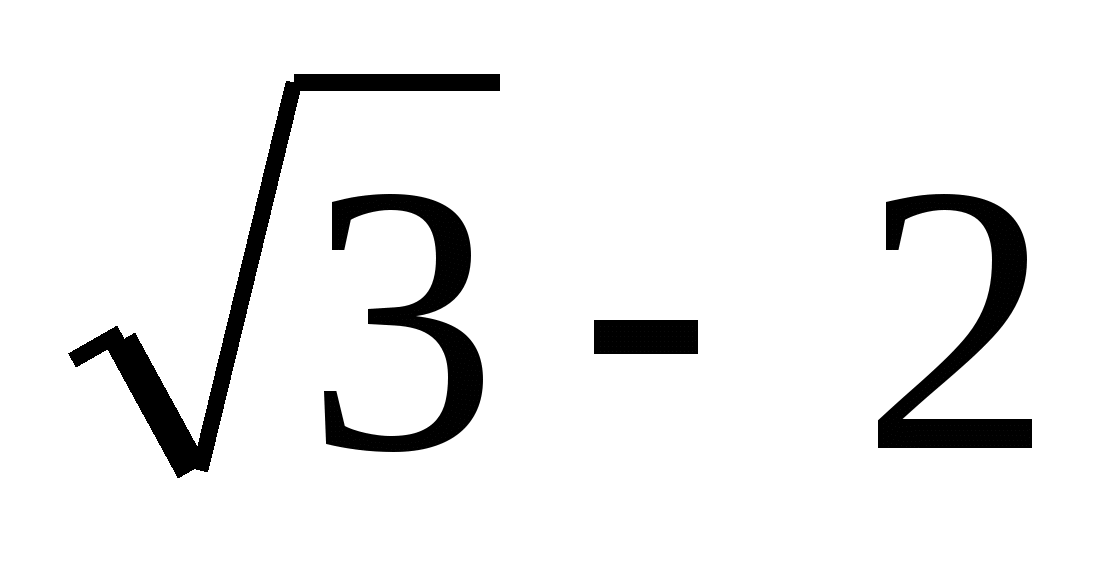 3) 1 4)
3) 1 4) 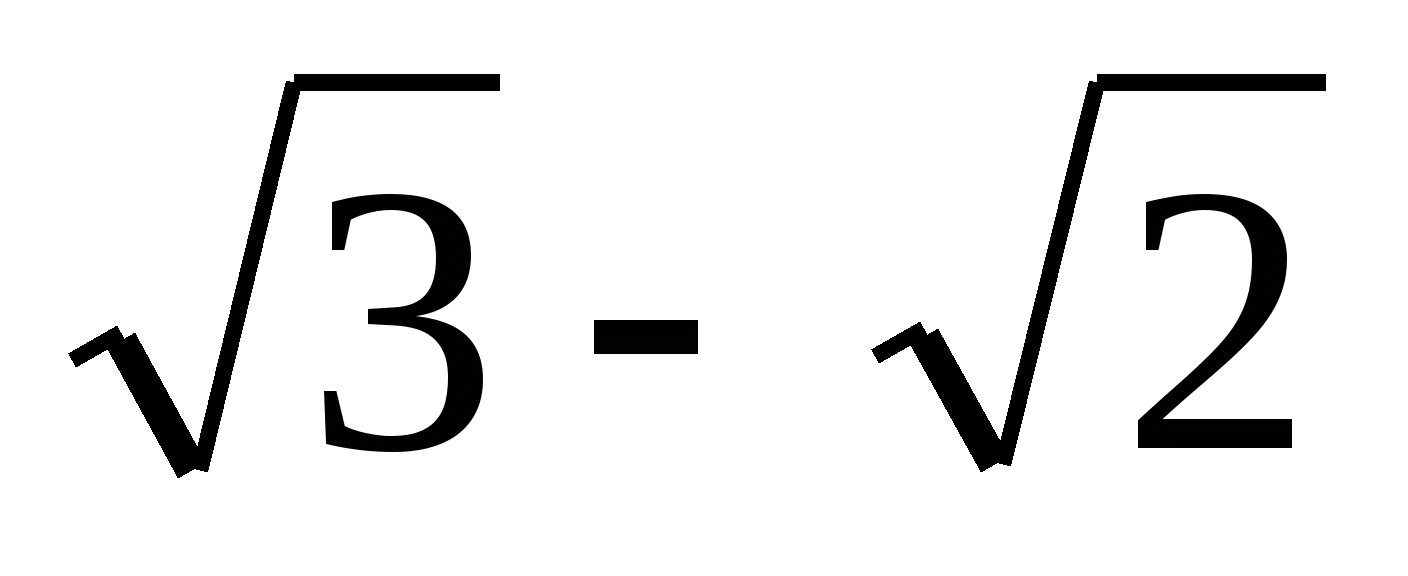
(Ответ: 4) 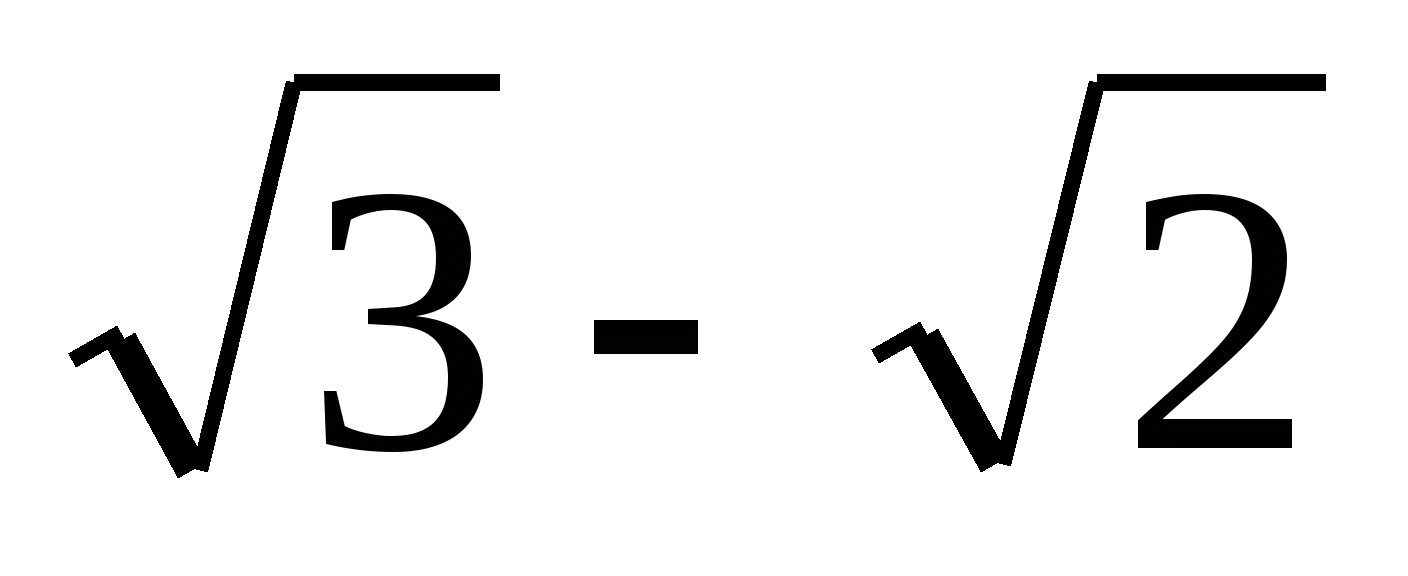 )
)
Второй отборочный тур:
Дайте определение арифметического корня n – й степени
(Ответ: Арифметическим корнем n – й степени из неотрицательного числа а называется неотрицательное число, n – й степень которого равна а.)
Второй игровой тур:
Вычислите

1) 0,04 2) 0,4 3) 0,08 4) 0,004
(Ответ: 2) 0,4 )
Найдите значение выражения

1) -5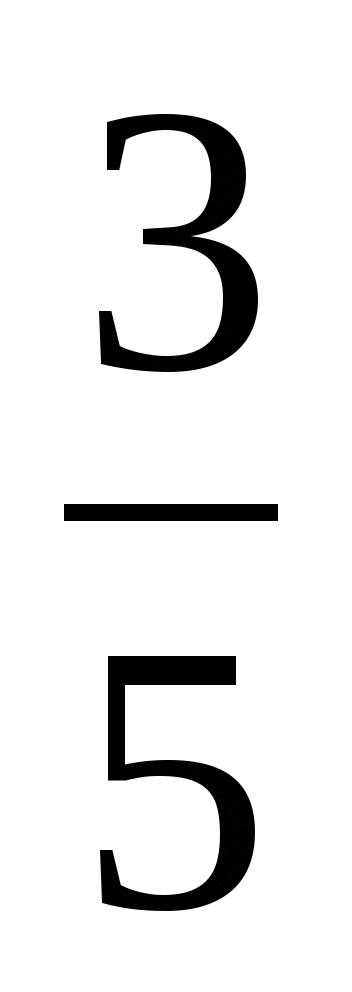 2) -5
2) -5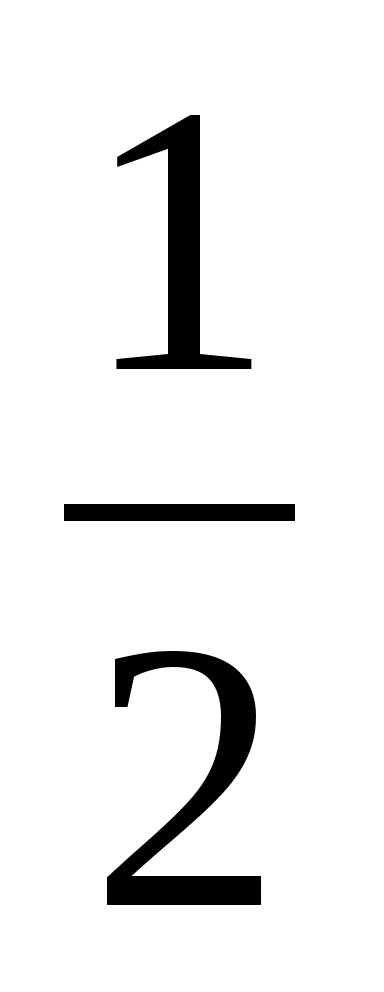 3)-2
3)-2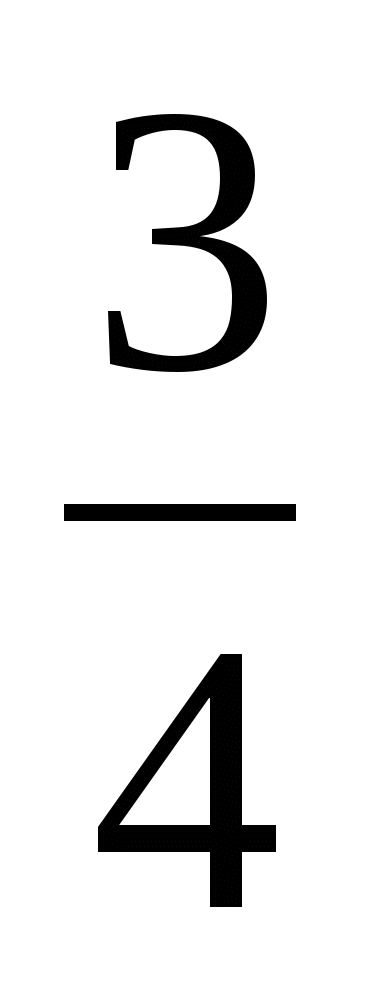 4) -5
4) -5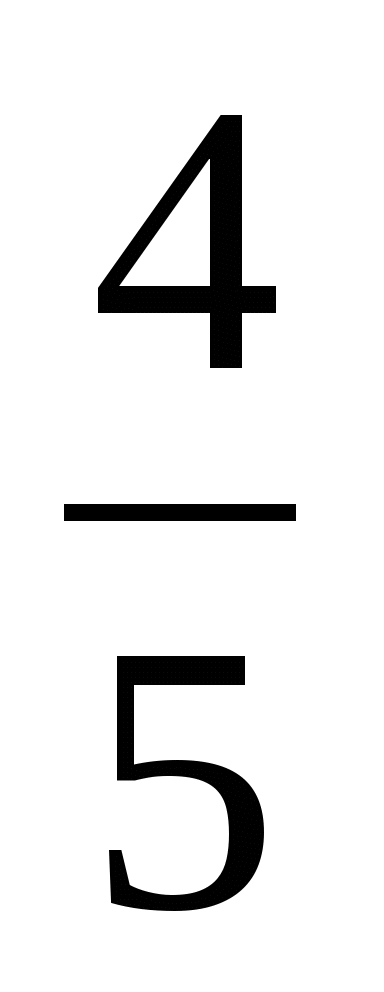
(Ответ: 4) -5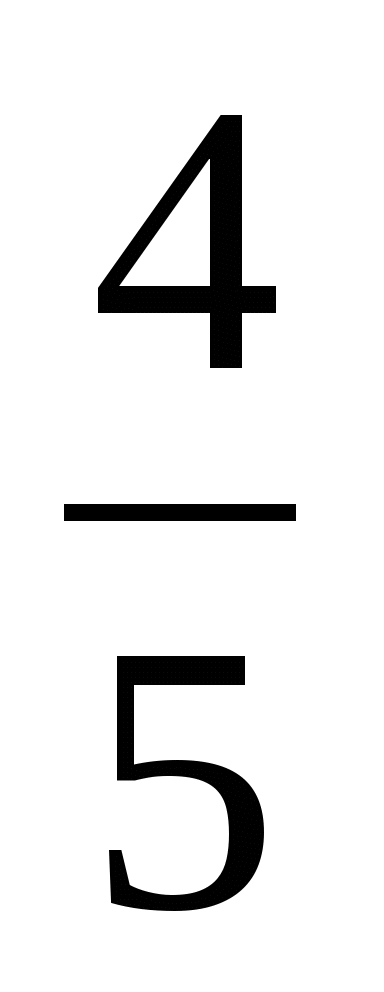 )
)
Решите уравнение 16 + х4= 0
1) -2; 2 2) 4; — 4 3) нет корней 4) много корней
(Ответ: 3) нет корней)
Вынесите множитель из — под знака корня

 .
.
1)3ху2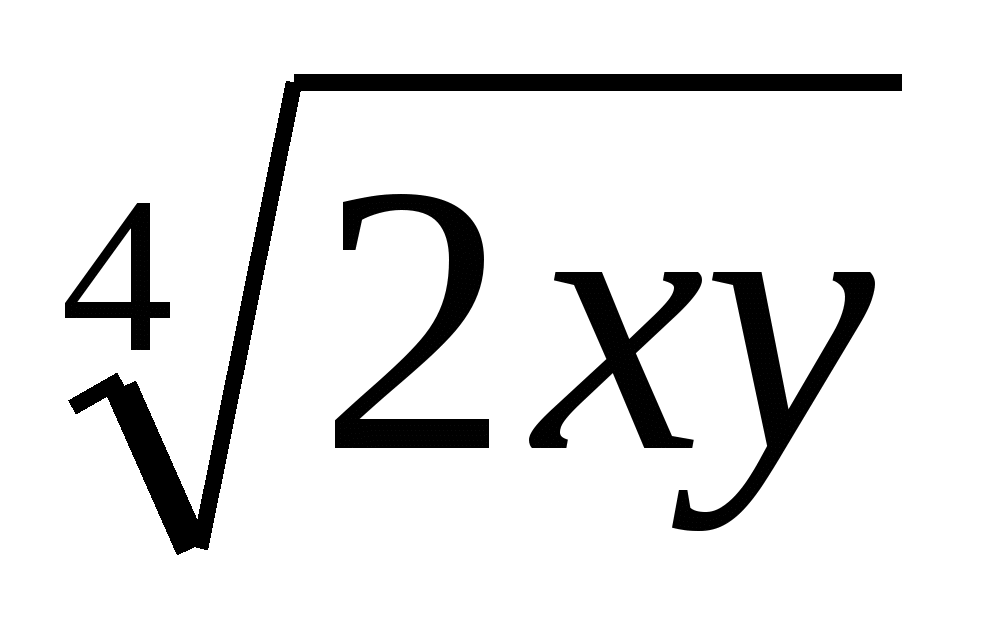 2)9
2)9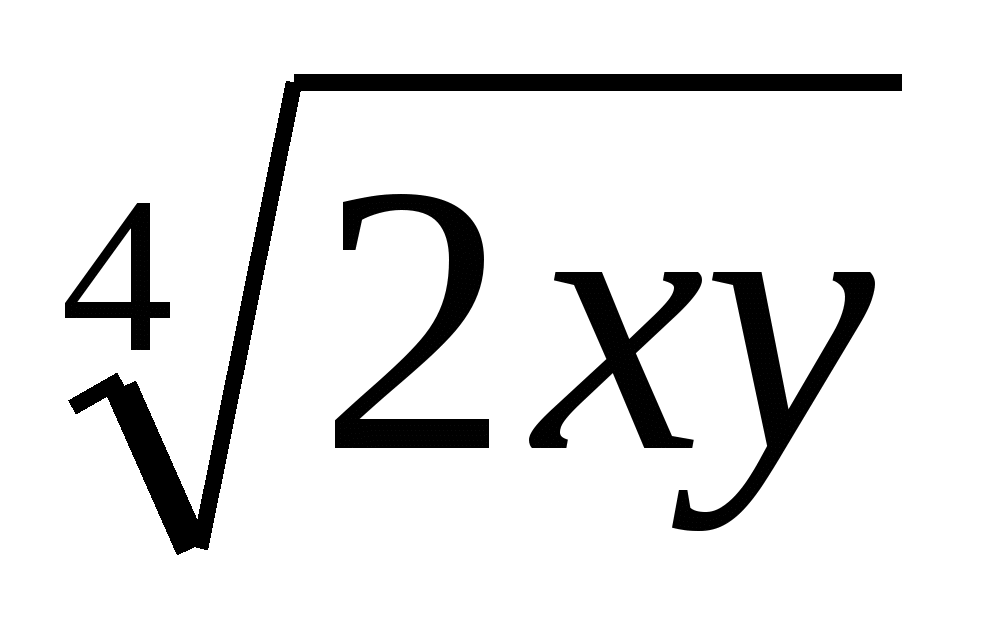 3) 3ху
3) 3ху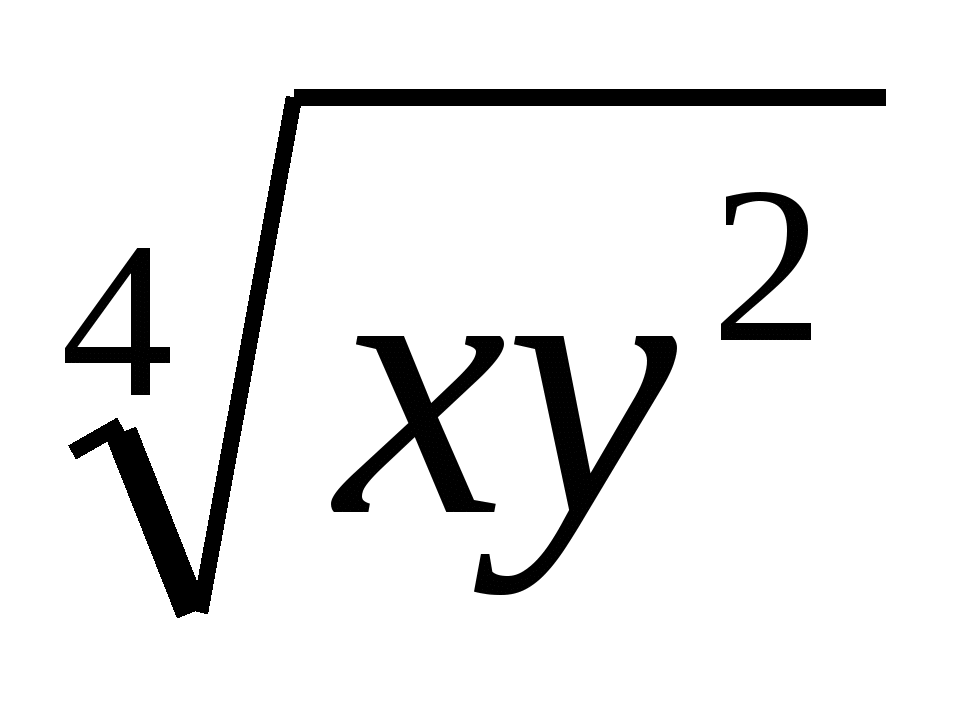 4) 2ху4
4) 2ху4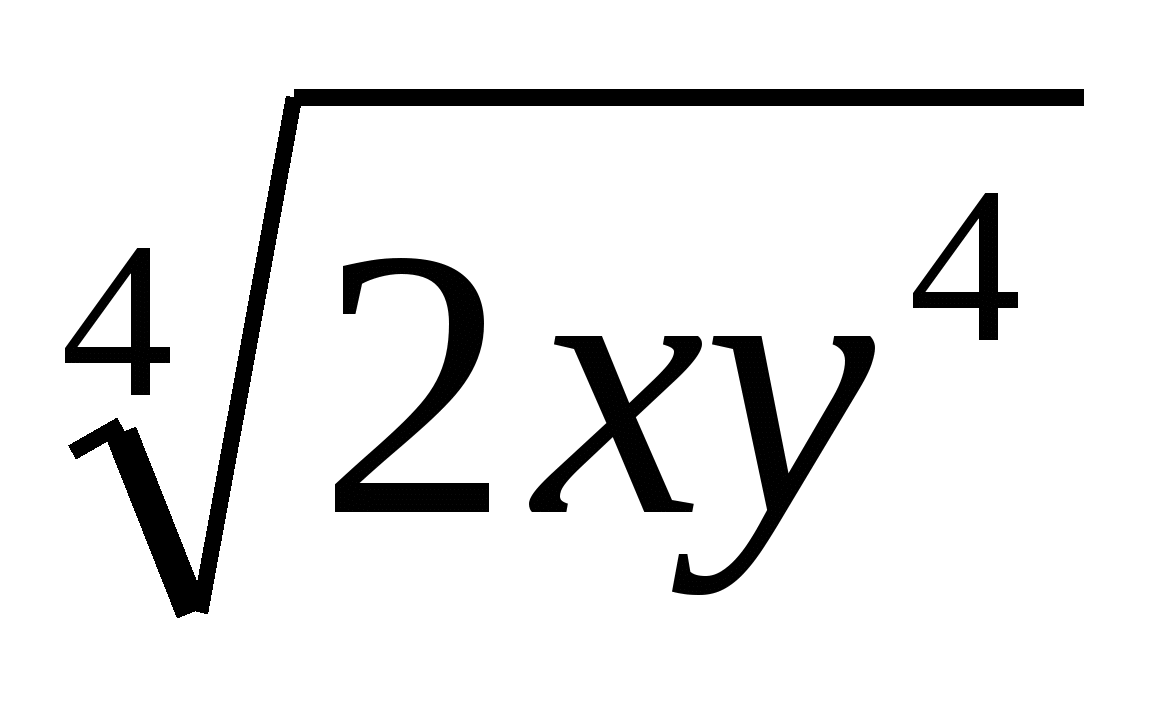
(Ответ: 3) 3ху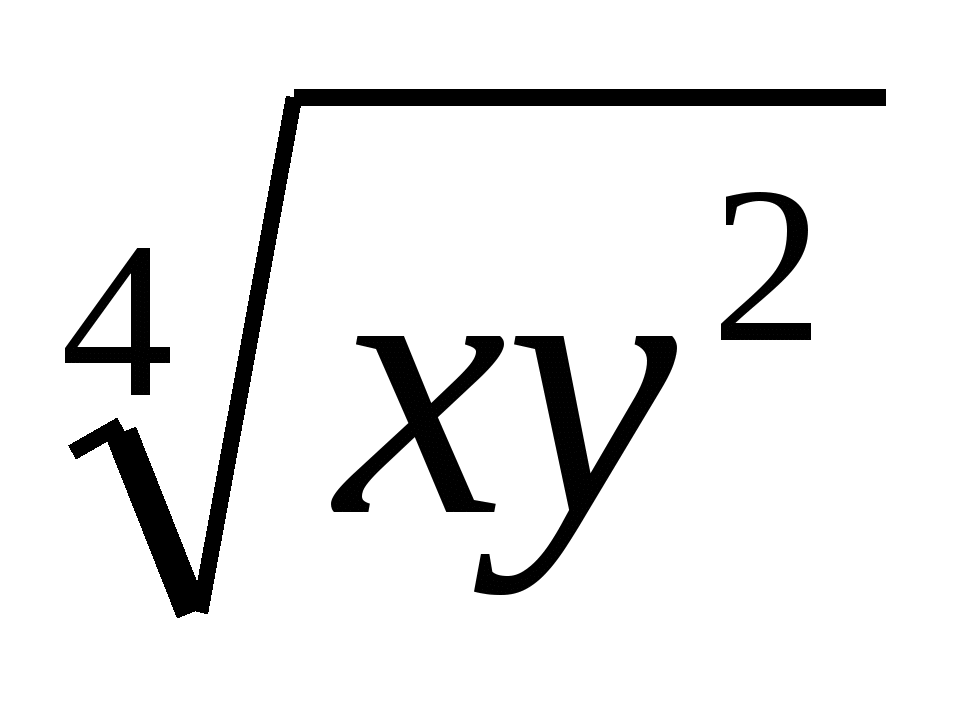 )
)
Внесите множитель под знак корня 3a2b4
 , если а>0,b>0.
, если а>0,b>0.
1)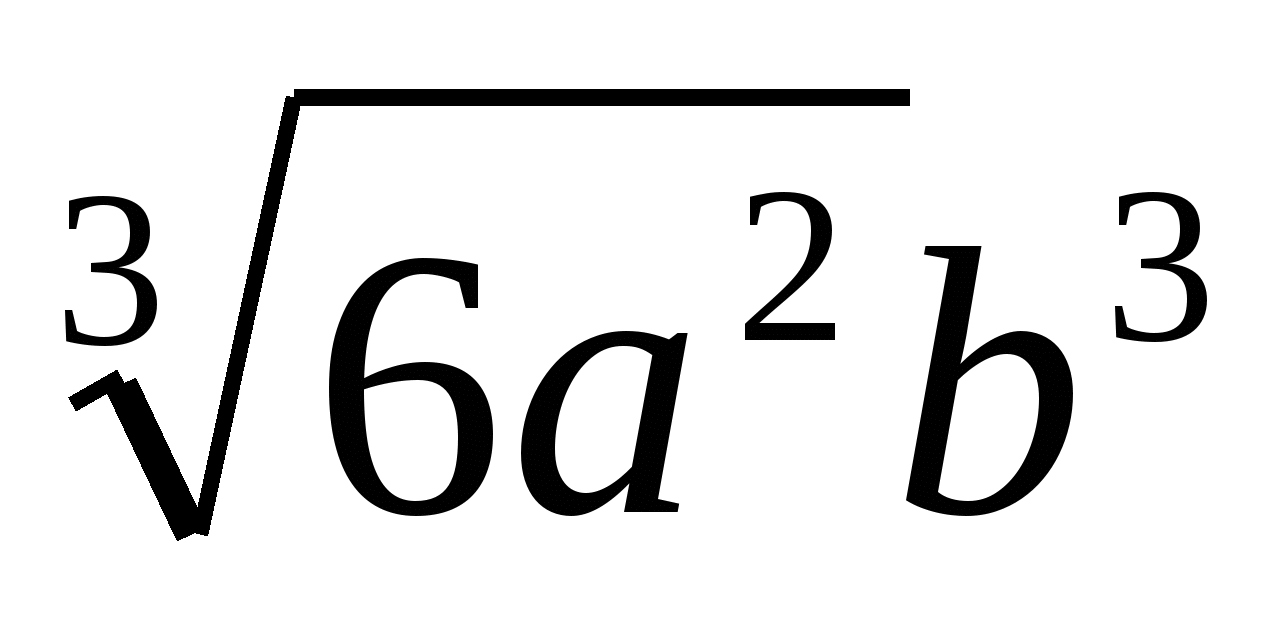 3)
3)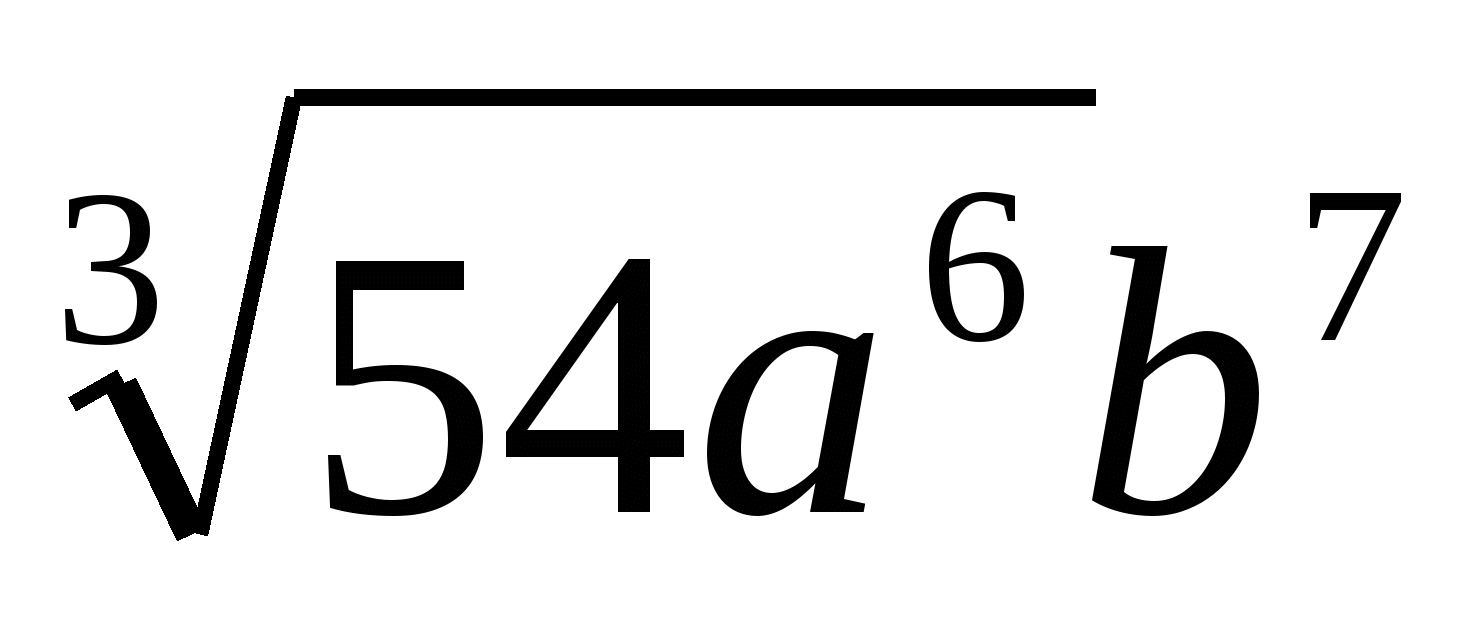 4)
4)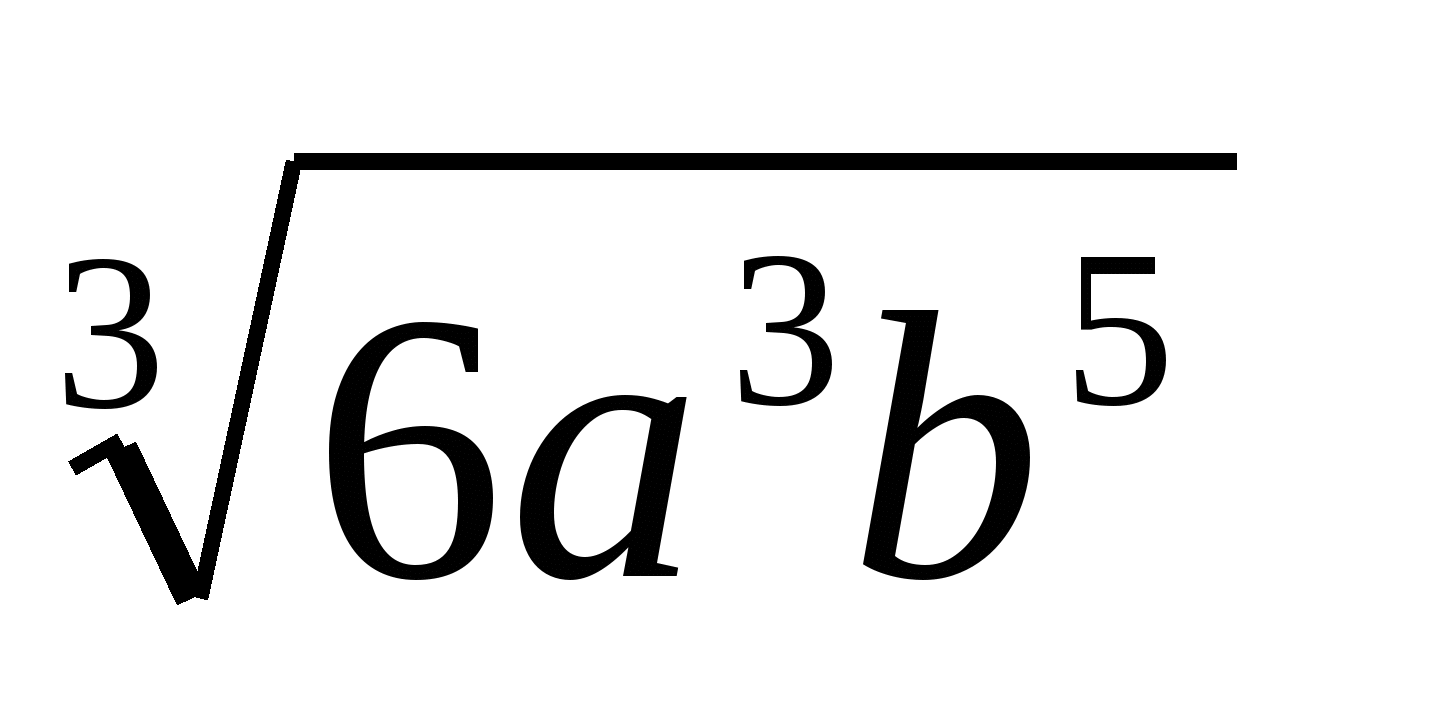
(Ответ: 2) 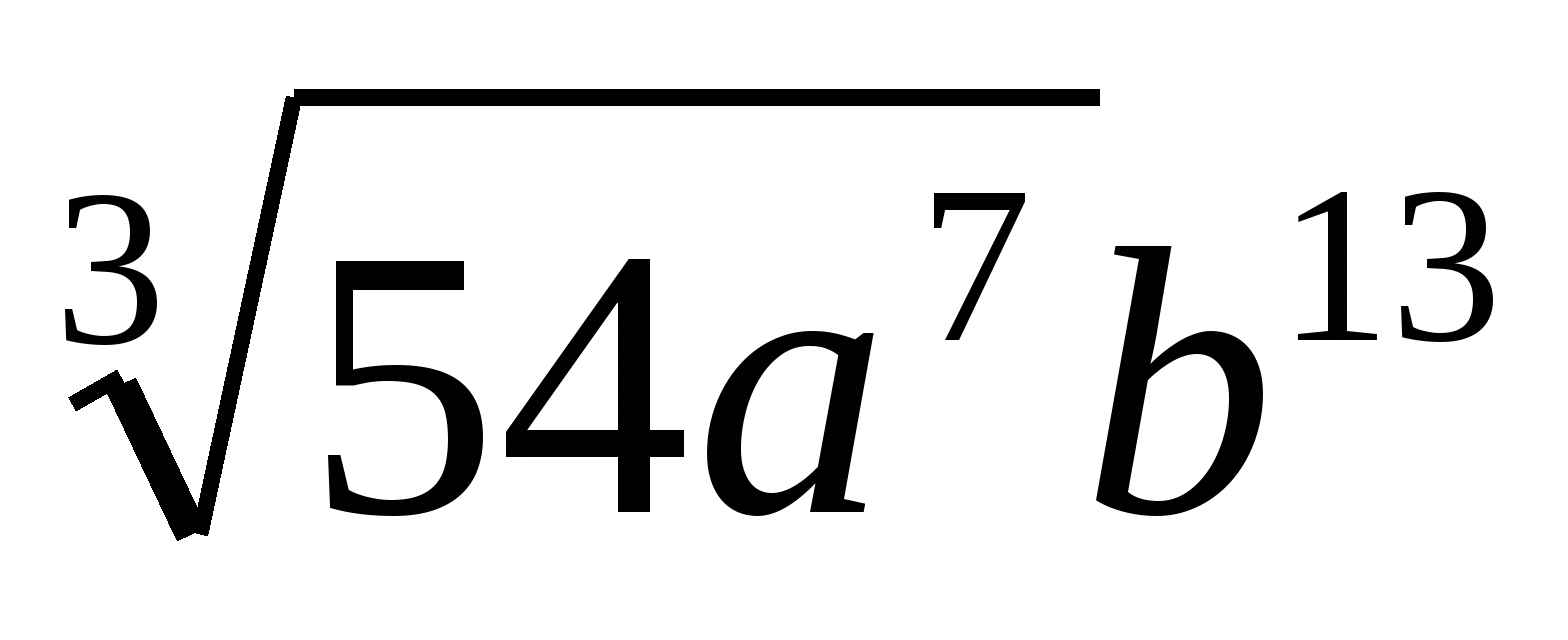 )
)
О
Д
С
В
А
дна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?
. Какая это точка?








5 6 7
1) А 2) В 3) С 4) Д
(Ответ: 1) А)
Упростите выражение
 .
.
1)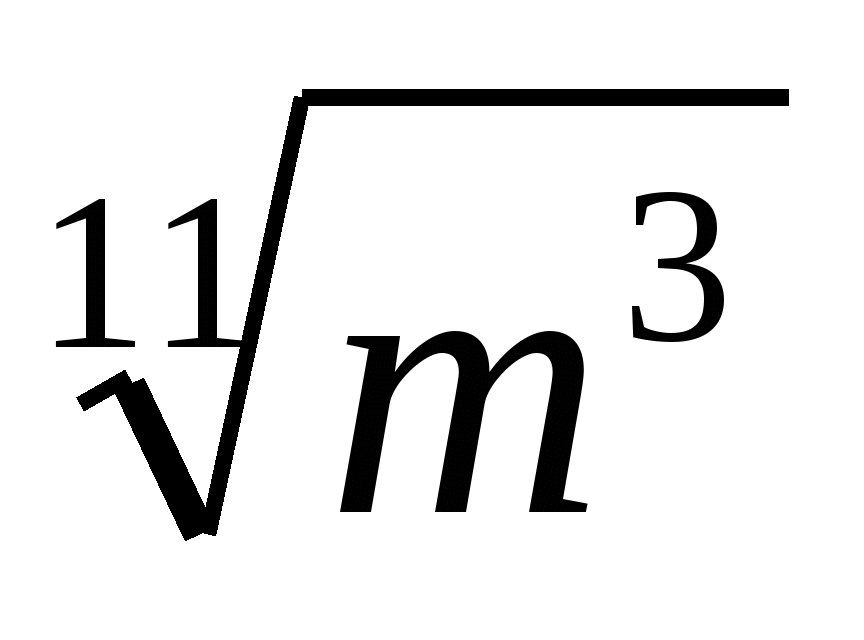 2)
2)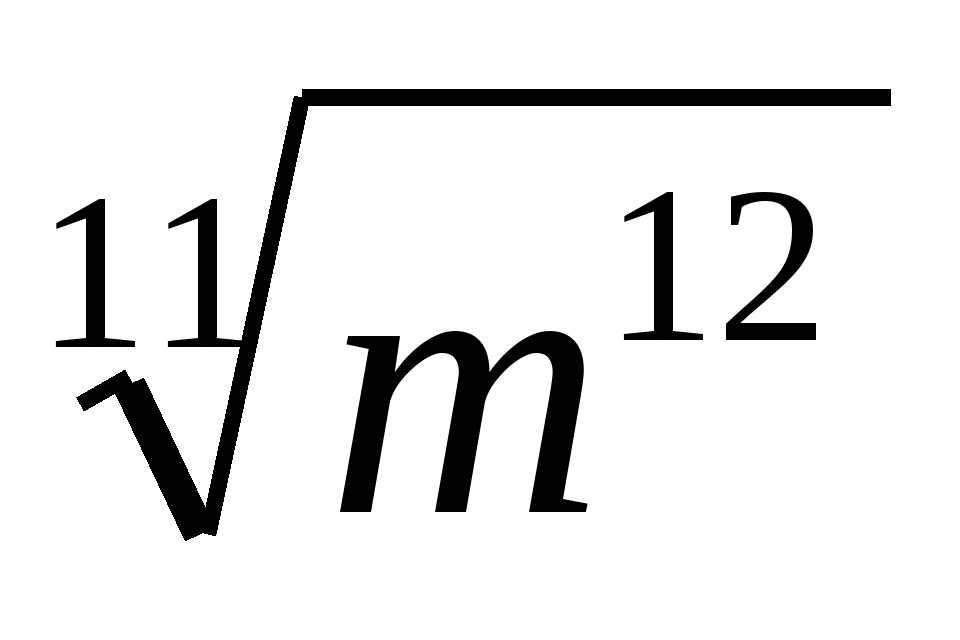 3)
3)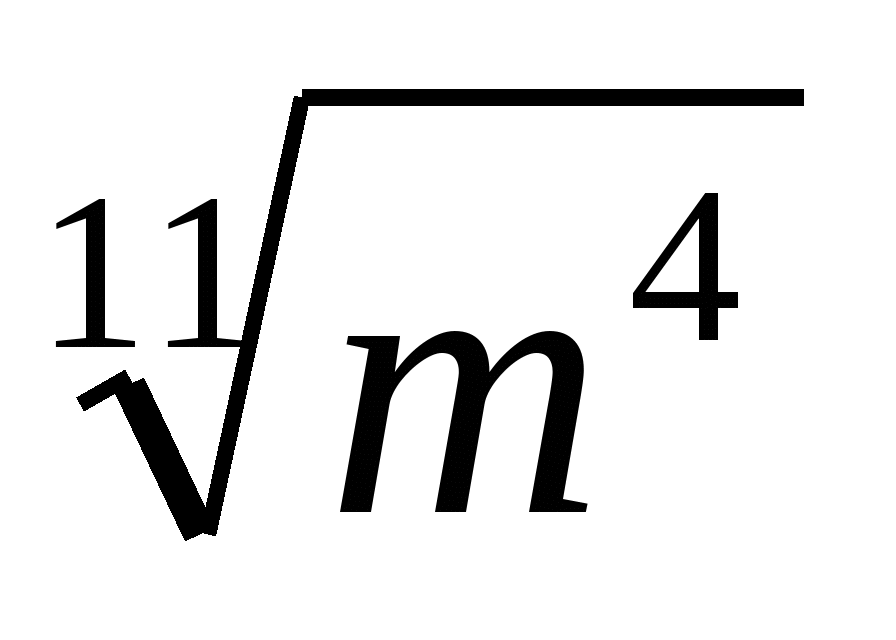 4)
4)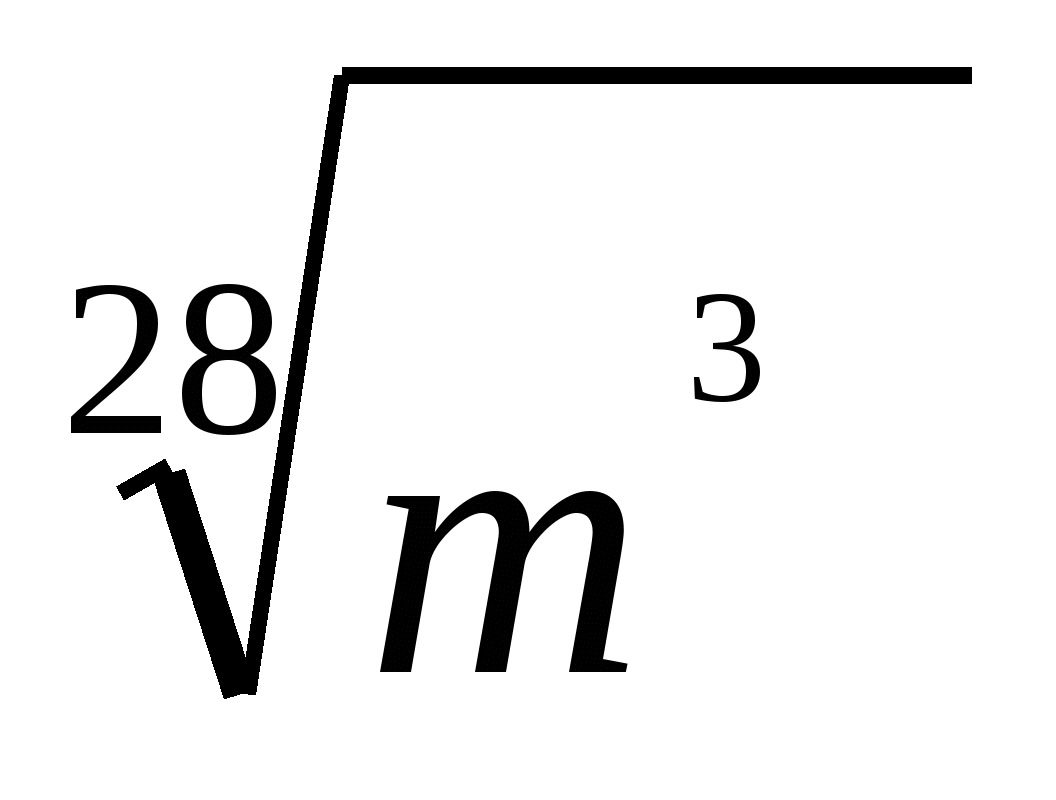
(Ответ: 3)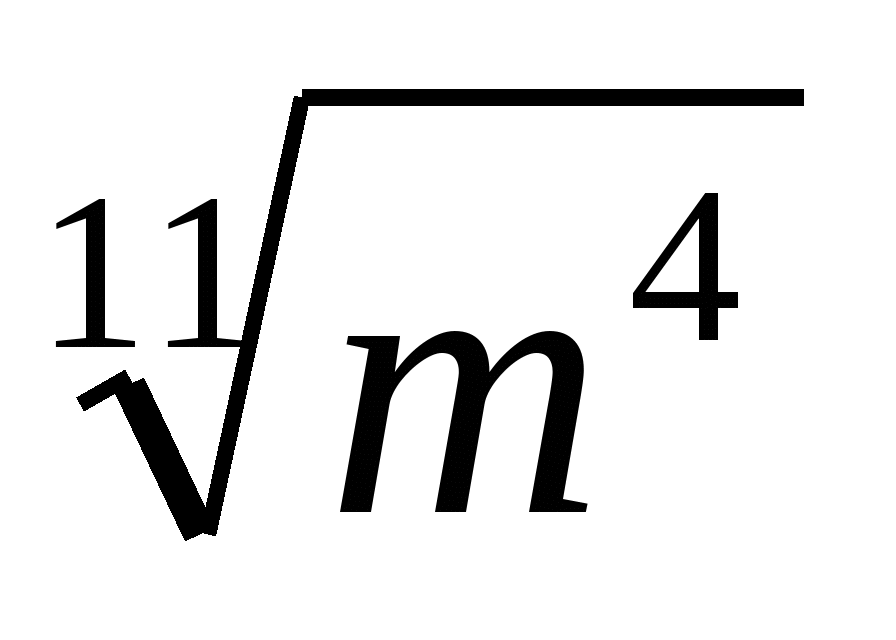 )
)
Третий отборочный тур:
Перечислите основные свойства корня n – й степени
(Ответ: 1. Если а 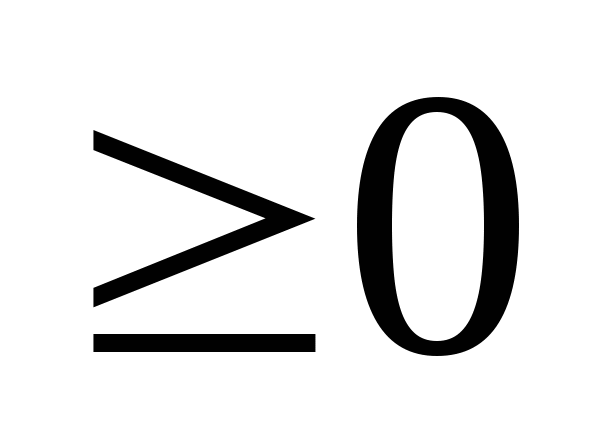 b
b 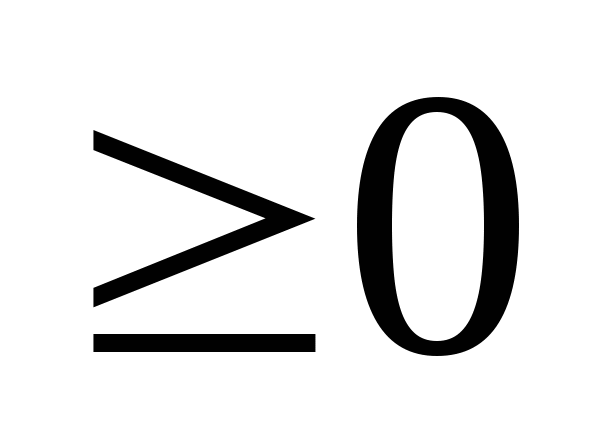 , то
, то 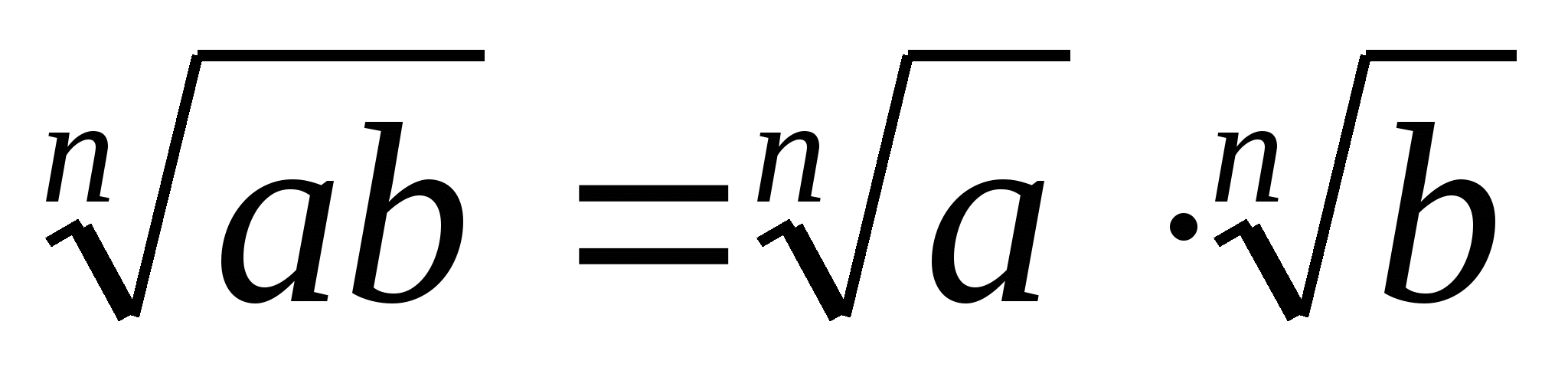
2. Если а 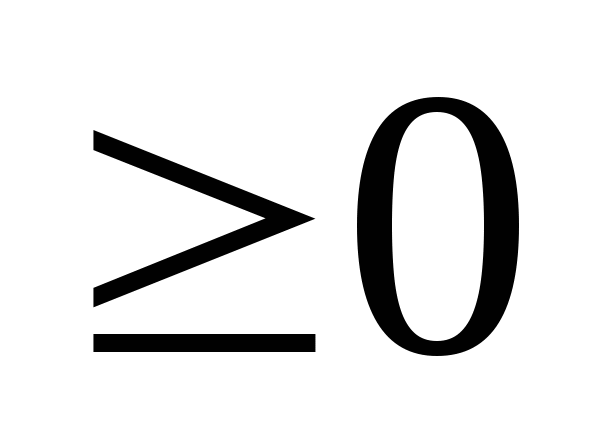 b
b  0 , то
0 , то 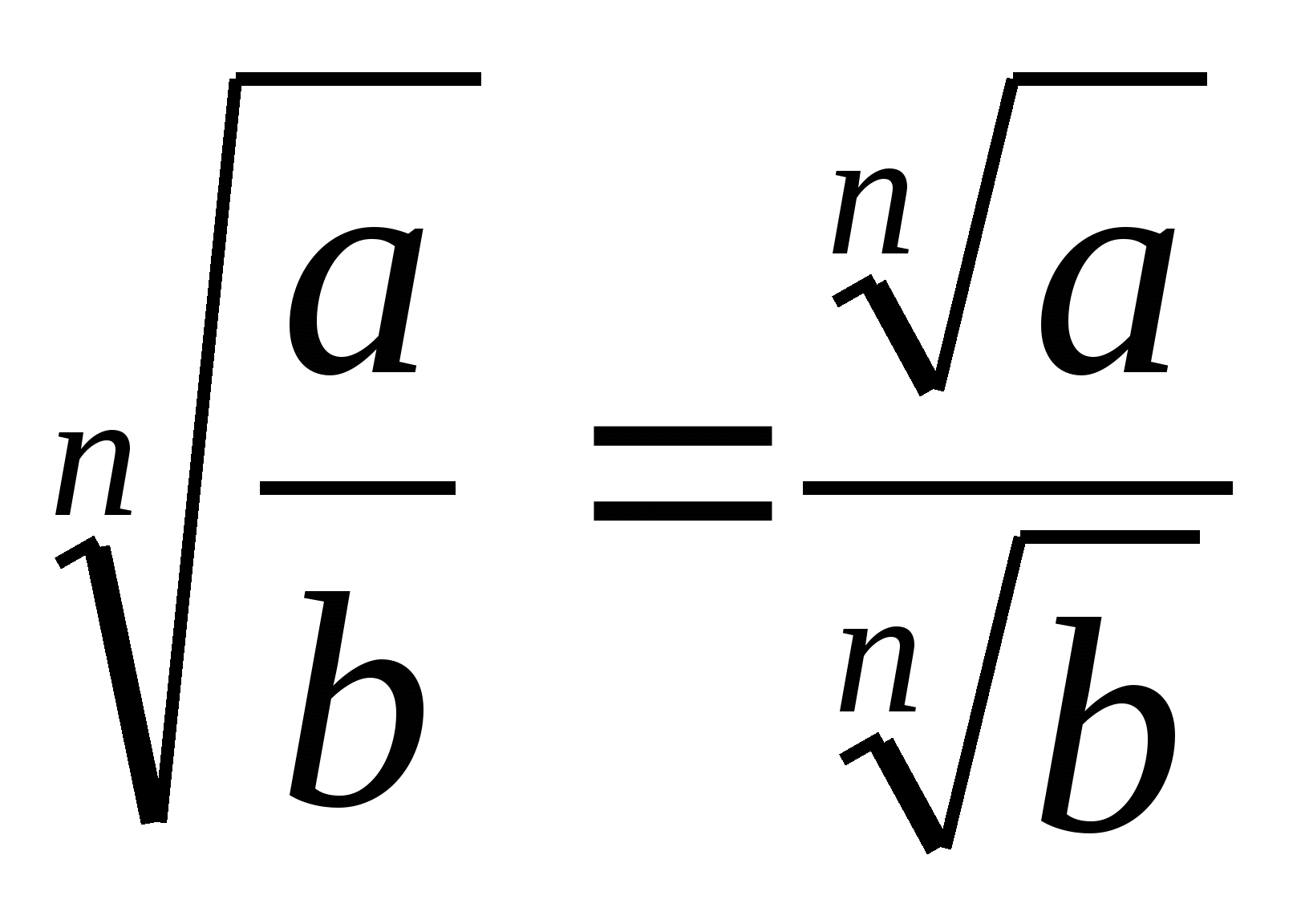
3. Если n и k – натуральные числа и а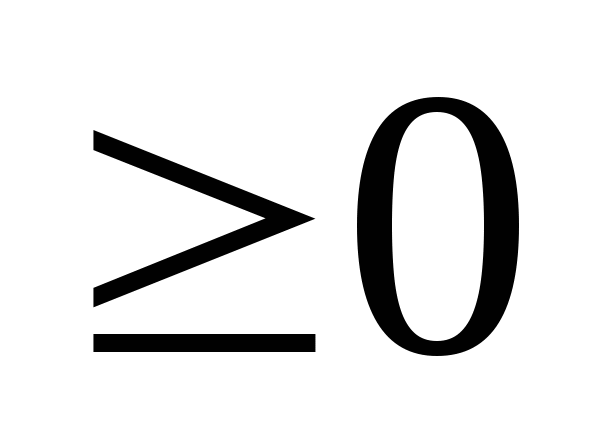 , то
, то 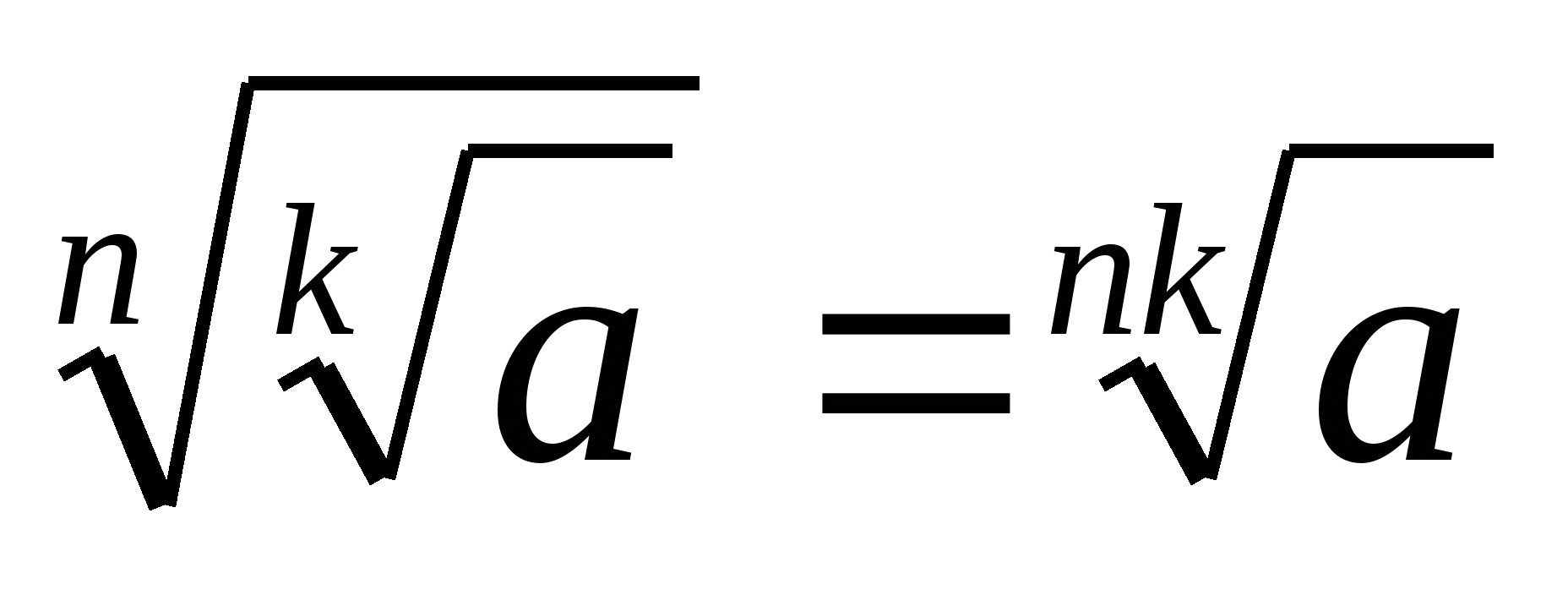
4. Если n , m и k – натуральные числа и а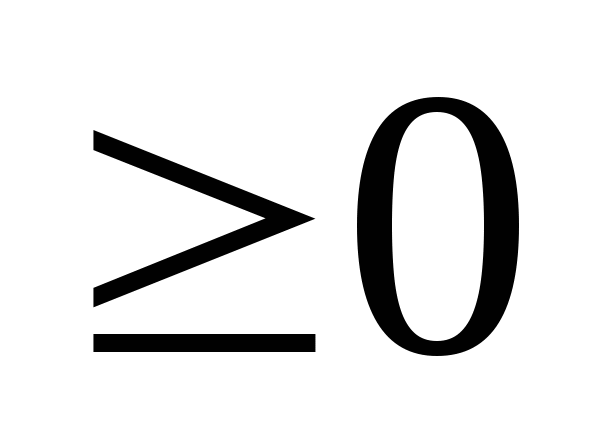 , то
, то 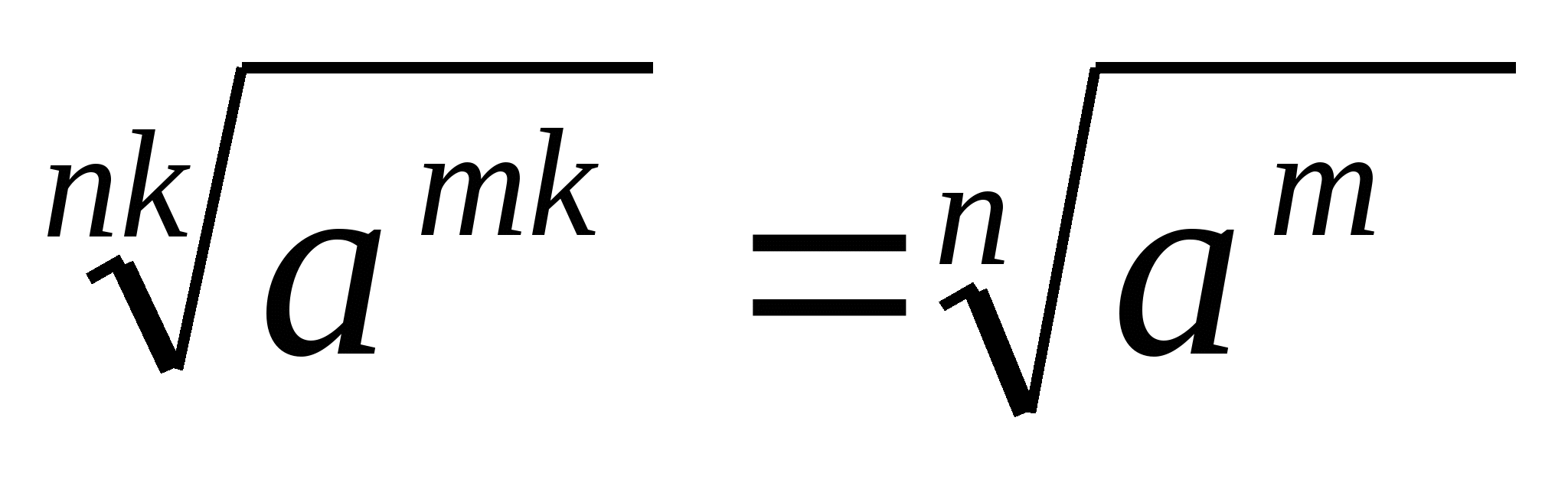 )
)
Третий игровой тур:
Вычислите

1) 0,04 2) 0,16 3) 0,4 4) 0,0004
(Ответ: 3) 0,4 )
Вынесите множитель из- под знака корня

 .
.
1) 2ху2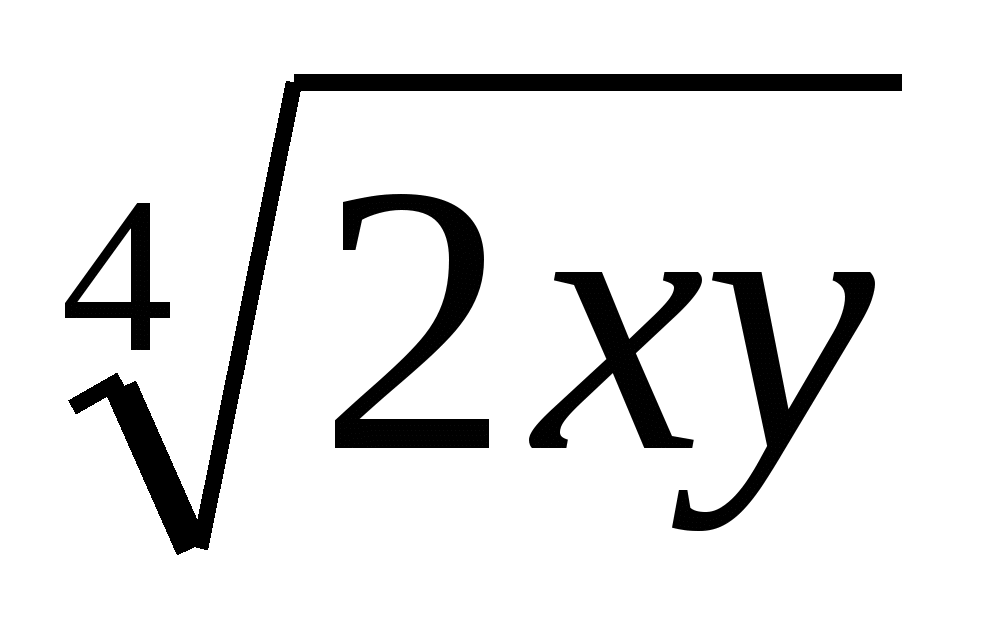 2) 2ху
2) 2ху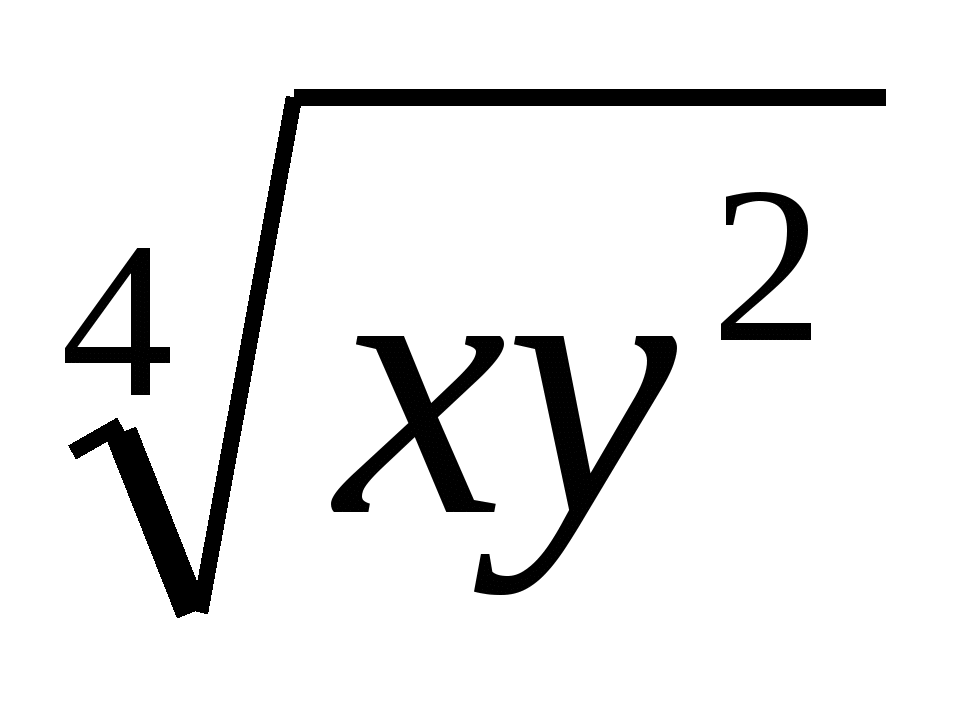 2) 4ху2
2) 4ху2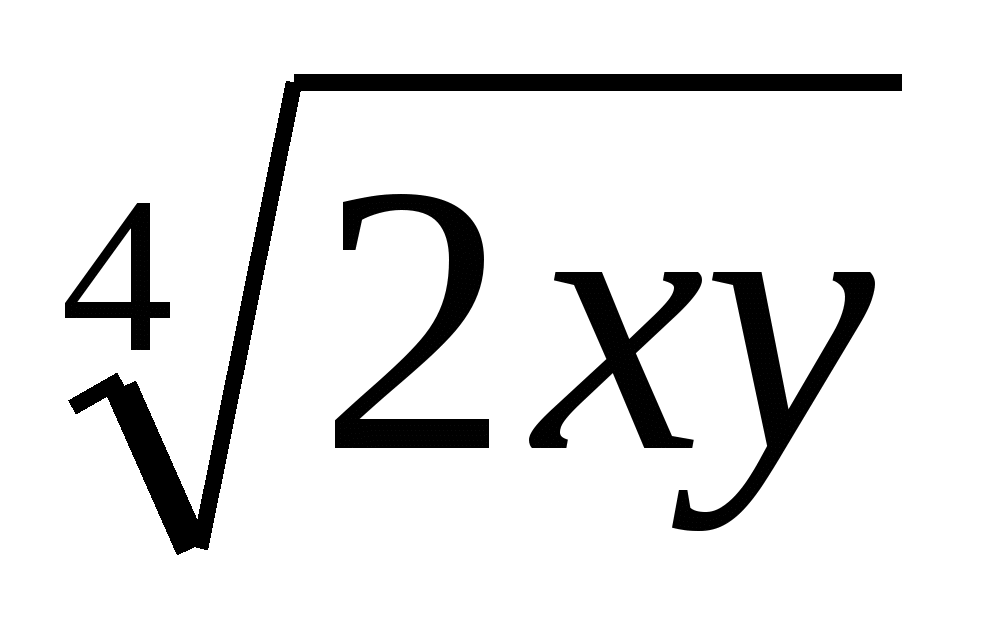 4) 8ху4
4) 8ху4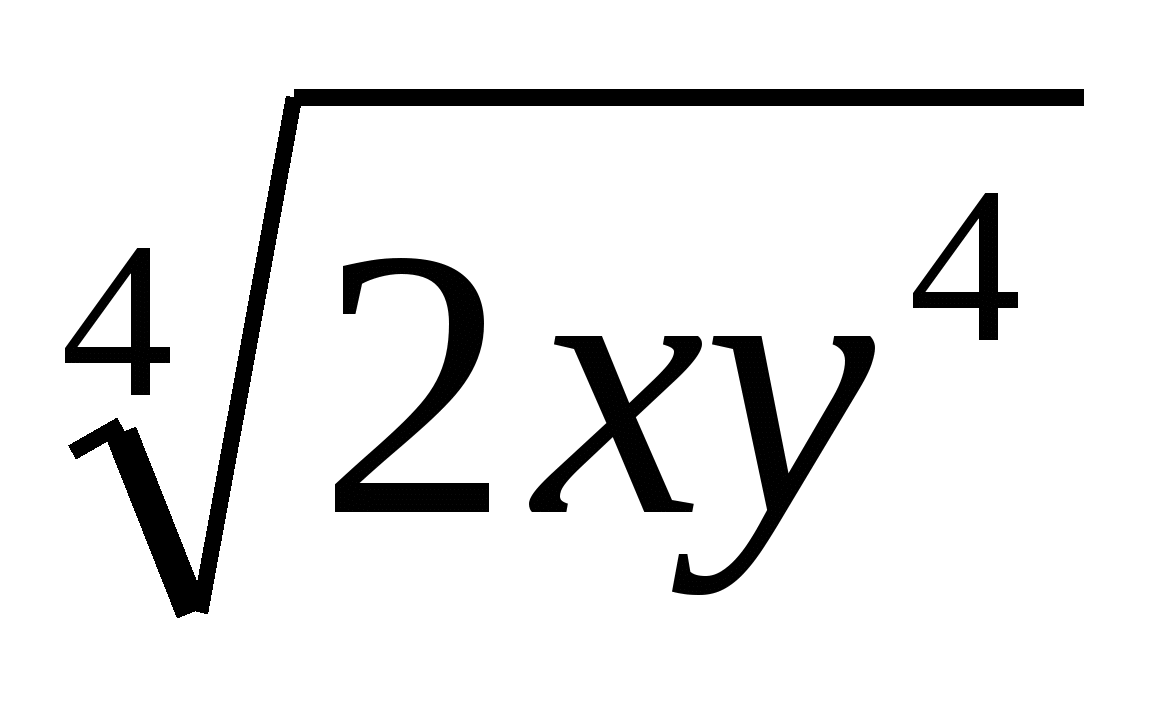
(Ответ: 2) 2ху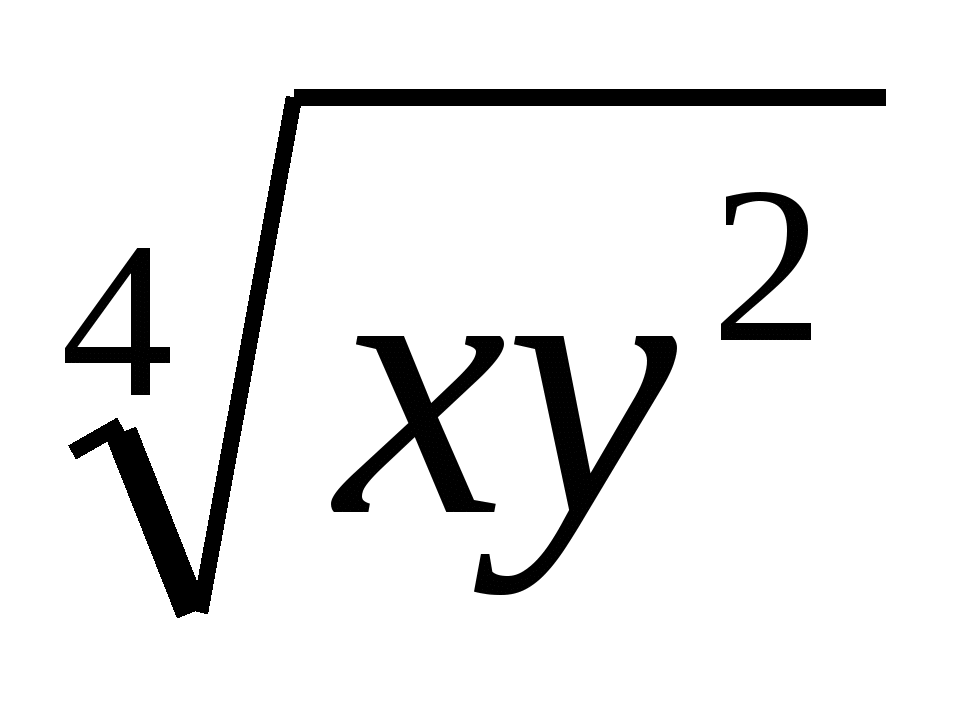 )
)
Найдите значение выражения

1) 16 2) 8 3) -8 4) -16
(Ответ: 2) 8)
Решите уравнение
 х5+ 4= 0
х5+ 4= 0
1) 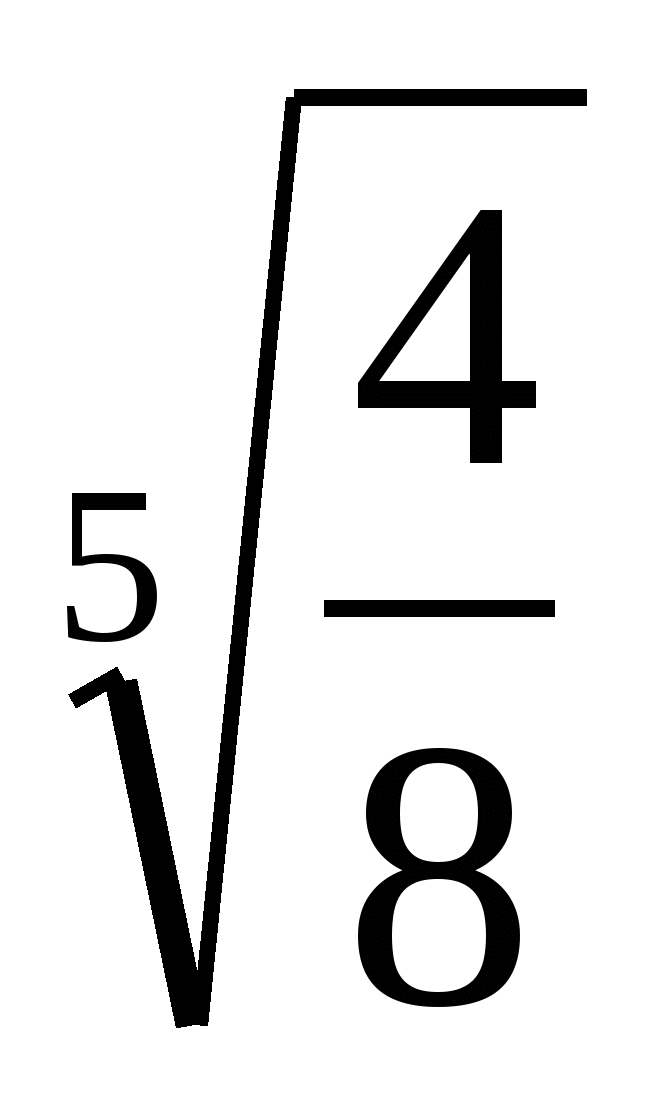 2) 2 3) —
2) 2 3) — 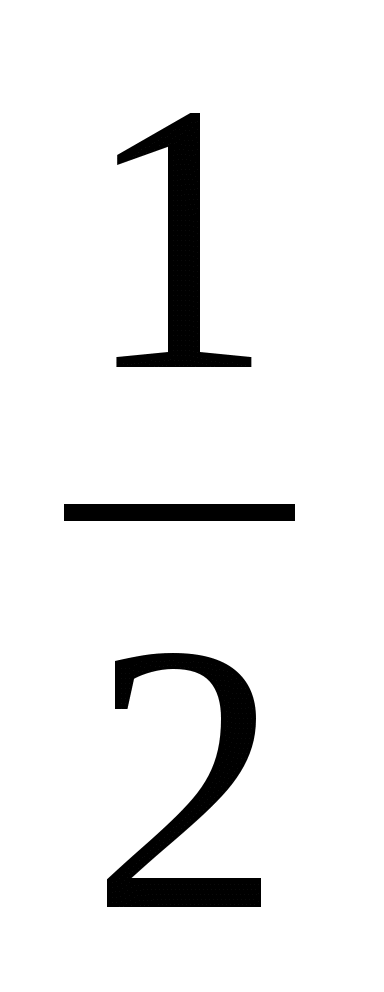 4) — 2
4) — 2
(Ответ: 4) — 2)
Сократите дробь

1) 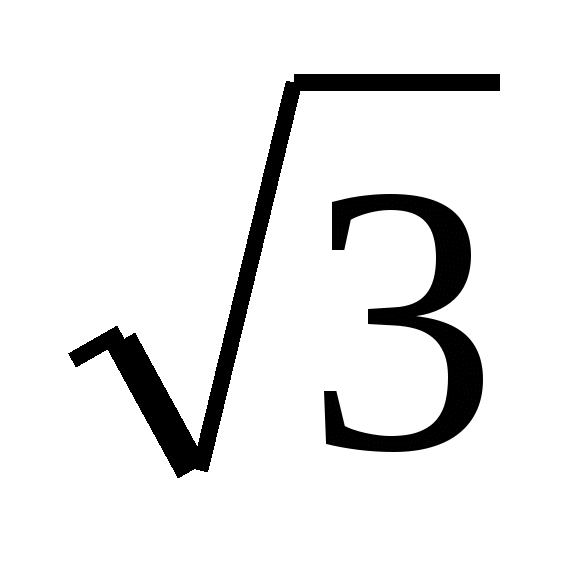 2)
2) 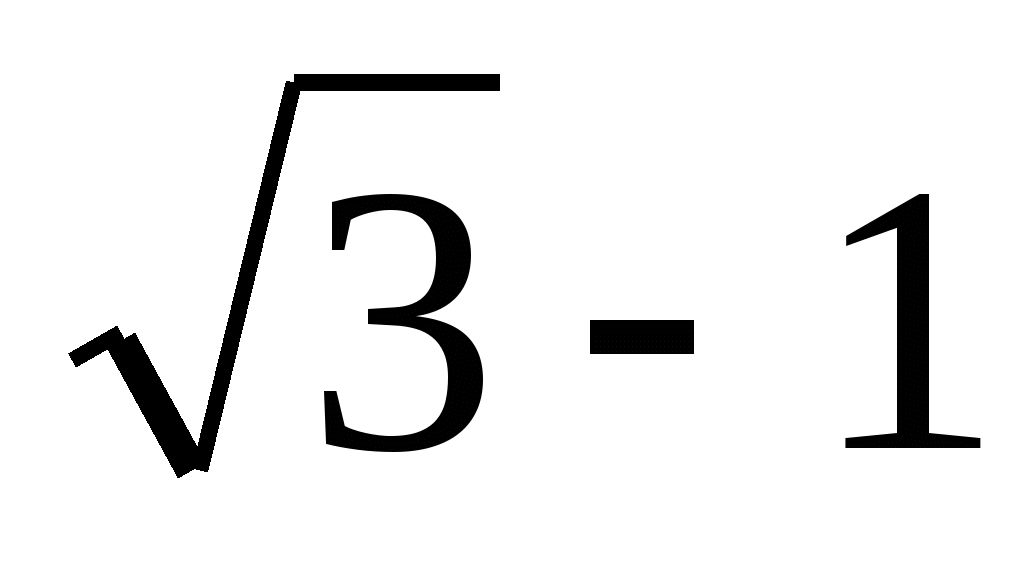 3) 1 4) — 3
3) 1 4) — 3
(Ответ: 2) 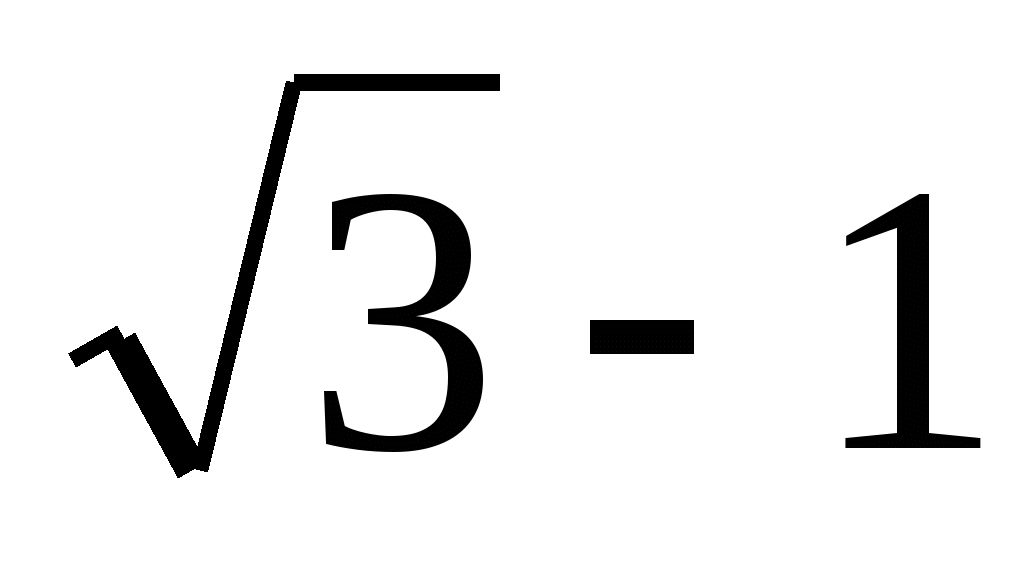 )
)
Упростите выражение
 .
.
1)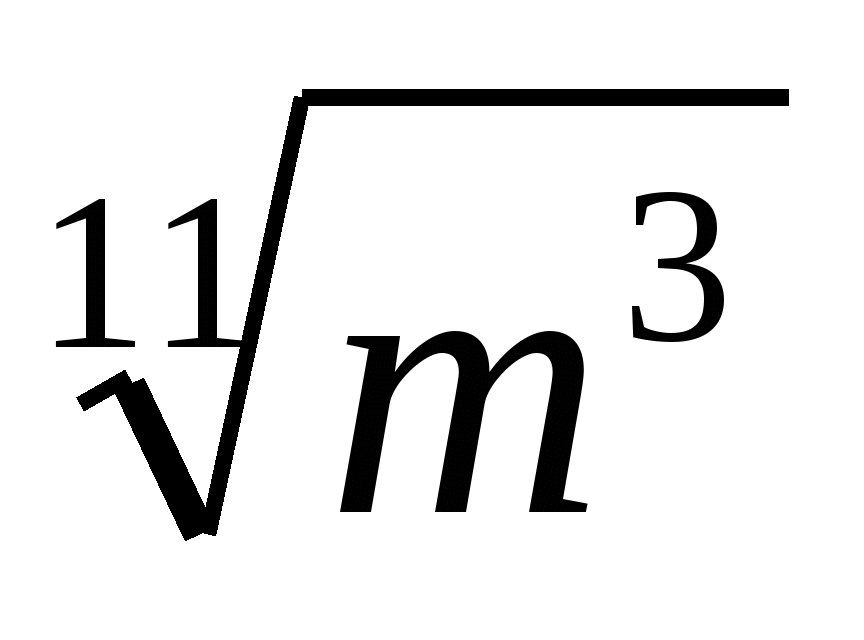 2)
2) 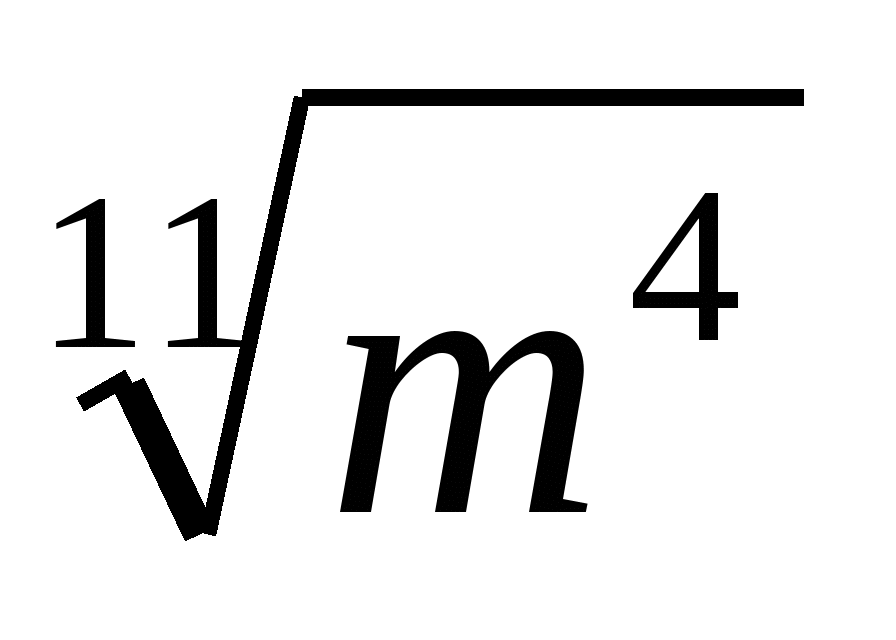 3)
3) 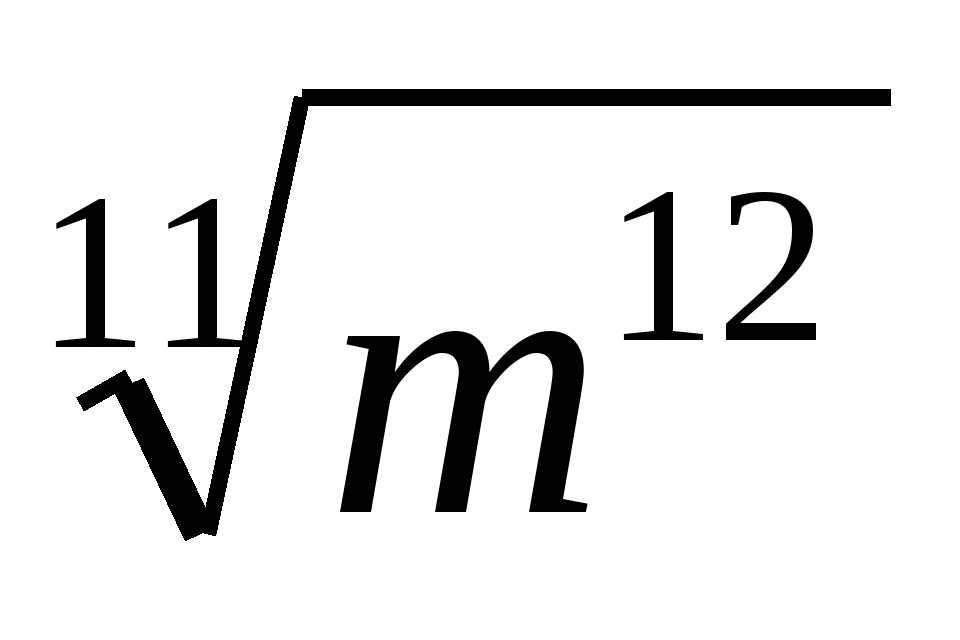 4)
4)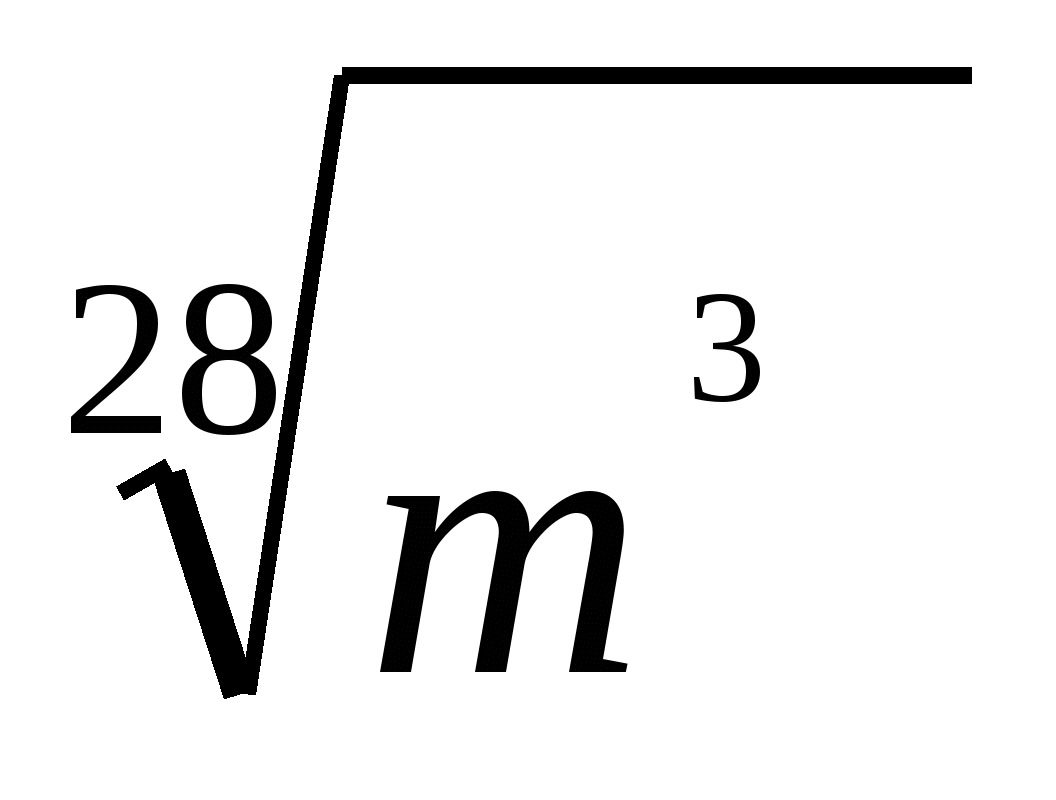
(Ответ: 2)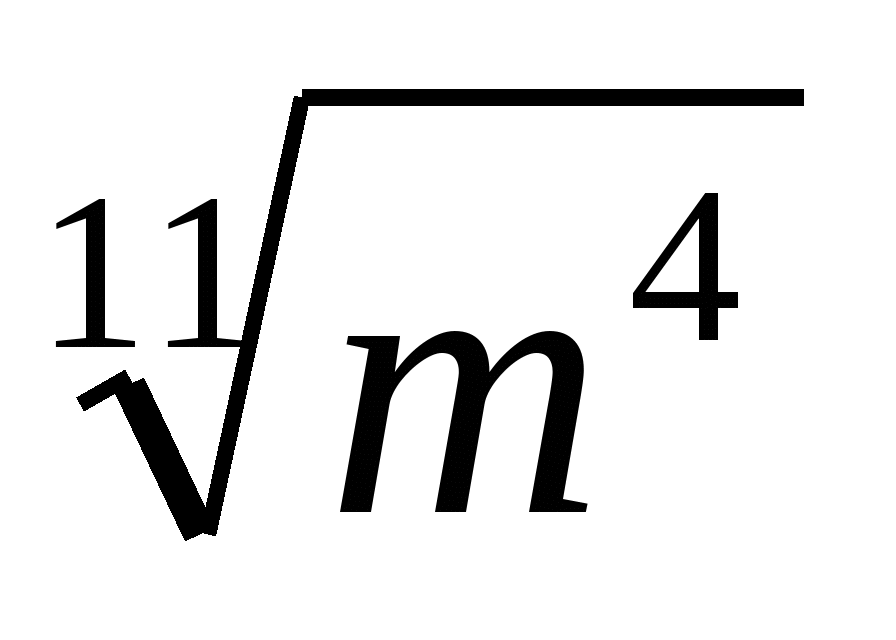 )
)
Итоги игры:
Подводим итоги игры. Игроки, которые правильно ответили на все вопросы получают звание «отличник» и отметки «5» в журнал; не дошедшие до конца тура (использовав все подсказки) – звание «участник игры» и отметку «4». Отметки «5» можно поставить и получившим звание «лучший математик», т. Е. ученикам, которые дали правильно подсказку.
Об окончании игры возвещает гонг – ранее заведённый будильник. Сигнал должен прозвучать за 2 – 3 минуты до окончания урока. Этого времени достаточно для подведения итогов урока и задания на дом.
Урок в 11 классе «Корни и степени»
Открытый урок
по алгебре и началам анализа
«Степени и корни» (Микс из витаминов для ЕГЭ)
Степени и корни. ( Микс из витаминов для ЕГЭ)
Тип урока: урок повторения и обобщения материала.
Цель:
Успешная сдача итоговой аттестации в форме ЕГЭ
Задачи:
Образовательные:
Организовать деятельность учащихся по изучению и осмыслению понятия степени.
Способствовать формированию у учащихся новых способов деятельности по одновременному применению свойств корня и степени в преобразованиях и вычислениях выражений.
Организовать работу учащихся с материалами ЕГЭ.
Воспитательные:
Способствовать привитию у учащихся организованности, внимательности, настойчивости.
Развивающие:
Создать условия для развития у учащихся умений формулировать проблемы, сравнивать познавательные объекты и выделять основную мысль.
Приучать учащихся контролировать свою деятельность с целью оправданного использования рабочего времени при сдаче ЕГЭ.
План урока.
1 Организационный этап.
Добрый день, дорогие друзья! Сегодня у нас необычный урок. К нам пришли гости, уважаемые мною коллеги . Но всё же я попрошу вас принять царственную осанку — спина прямая, мышцы головы без напряжения, выражение лица значительное, ведь вы –выпускники школы, и вы знаете такое количество формул, которое не под силу даже царственным особам.
А пока вы входите в образ, послушайте притчу.
Притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному замку. «Кто первым откроет, тот и будет первым помощником». Никто даже не притронулся к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, а надеешься на собственные силы и не боишься сделать попытку». И мы сегодня будем пытаться, пробовать, чтобы прийти к правильному решению.
Итак, вы успокоились. сосредоточились? Готовы работать?( Ссылка про витамины!) (Ученики смотрят фильм о значении витаминов в жизни людей). -Как вы думаете, почему наш урок начался с этого видеофрагмента?
Ученики отвечают.
Учитель: Действительно, мы заговорили о витаминах потому, что их названия точно такие же, как названия заданий на экзамене по математике в форме ЕГЭ
Сегодня вы будете проводить исследования, направленные на укрепление не только знаний по алгебре, но и здоровья.
Для этого ответьте на вопрос: Как при таком объёме информации сохранить здоровье во время урока, накануне и во время экзамена?
(Правильная осанка, хорошее освещение, сбалансированное питание с витаминами и минералами, не волноваться, избегать стрессов. )
А чтобы на экзаменах у вас не было стресса, вы должны уже сейчас свободно выполнять задания из материалов ЕГЭ, уметь жёстко работать по времени, контролировать свою деятельность, уметь методом прикидки и минимальной подстановки выполнять проверку и тогда вы будете уверенными в себе.
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Итак! Посмотрите внимательно несколько секунд на рисунок, запомните. 
Ответьте на мои вопросы:
Перечислите все корни, которые вы видели (
 ;
; ;
; )
)В какой геометрической фигуре расположен
 ? (в окружности)
? (в окружности)Какого цвета эта окружность? (синяя)
Квадратный корень из какого числа находится в квадрате? (из 5)
Какого цвета этот квадрат? (зелёного)
В какой геометрической фигуре расположен корень кубический? (в треугольнике)
Какого цвета этот треугольник? (красного)
Молодцы! Вы хорошо справились с первым испытанием! Внимательность очень нужна на экзаменах.
1. С каким математическим понятием связаны слова:
Основание, Показатель (Степень)
Какими словом можно заменить радикал?( извлечение арифметического корня)
Попробуйте сформулировать тему урока. (Степени и корни)
2. Какая наша стратегическая цель? (ЕГЭ)
Какова цель нашего урока?
– Продолжить работу над степенями и корнями.
Задачи:
– повторить свойства степеней и корней
– рассмотреть применение свойств степени при вычислениях и упрощениях выражений
– отработка вычислительных навыков.
3. Воспроизведение и коррекция опорных знаний учащихся. Актуализация знаний.
1. Какие действия (математические операции) можно выполнять со степенями?
Установите соответствие:
ОТВЕТ 3 5 1 6 4 2Поменяться тетрадями и оценить работу соседа.(взаимопроверка)
Пока все выполняют задание на соответсвие, два учащихся у доски: пишут свойства степеней и свойства корней с натуральным показателем.
Знание теории и формул не достаточно для успешной сдачи ЕГЭ. Но вы справились и со вторым испытанием: знание необходимого материала на ЕГЭ по теме.Аристотель сказал: «Ум заключается не только в знании, но и в умении прилагать знание на деле.» Так вот и мы с вами перейдём от слов к делу.
4. Отработка знаний умений и навыков.
Сейчас, мы проведём эксперимент — сколько баллов можно набрать за 5 минут
Внимание!На работу отводится только 5мин. За это время вы можете выполнить 2-3 задания по выбору. Оценка соответствует количеству набранных баллов.
Сосредоточься!
1. Начинай с просмотра всего теста, оцени объективные и субъективные трудности заданий, сделай разумный выбор.
2. При выполнении заданий разделов А и В расписывать решения нет необходимости.
3. Методом прикидки и минимальной подстановки выполни проверку задания сразу после решения.
Помни о жестком регламенте времени.
Торопись не спеша!
А2 Вычислить 
Вот вы справились и с третьим испытанием- работа по времени и контроль своей деятельности.
Динамическая пауза-музыка и Минута релаксации на основе закрепления полученных знаний
Упражнение на релаксацию
Принять удобное положение. Расслабиться. Закрыть глаза и представить большой белый экран. Мысленно раскрасить этот экран любимым цветом. Получается ровно, красиво, радует глаз, залюбуешься.
Раз, два, три – открыли глаза. Каким цветом был ваш экран?
2.А теперь попрошу вас сесть на краешек стула, обхватить себя руками, выгнуть спину. Проверим вашу внимательность и немного разомнёмся.
Я буду называть выражение, если оно не имеет смысл вам — вытянуть руки перед грудью, потянуться, вернуть руки к груди.
Если выражение имеет смысл — поднять руки, потянуться, напрячь мышцы, вернуть руки к груди.



Обхватите себя руками, выгните спину, примите царственную осанку и
прочтите историческую справку.
До XVв. на нахождение степени корня смотрели как на два совершенно независимых действия, но в XVIв. фламандский учёный Симон Стевин предложил понимать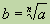 как степень с дробным показателем а 1/п . Ещё раньше узбекский учёный Гияс Эддинал Каши в своих трудах ввёл понятие нулевого, отрицательного, дробного показателя степени.
как степень с дробным показателем а 1/п . Ещё раньше узбекский учёный Гияс Эддинал Каши в своих трудах ввёл понятие нулевого, отрицательного, дробного показателя степени.
2. a0 = 1; если a€R, a 0.
3. a – n =1/ a n; если a€R , a 0, n€N.
4. a1/q =q√a
Работа в парах.
Заполните пропуски. Знание формул сокращённого умножения.
а) х – 2√х= … * (√х – …)
б) √6 – 2… = √2* (… –√2 )
в) а – b = (√а + √b) * (… – …)
г) а + b = (… + …) *(3√а2— 3√а 3√ b 2 + 3√ b 2)
Ответы
а) х – 2√х= √х * (√х – 2)
б) √6 – 2… = √2* (√3 –√2 )
в) а – b = (√а + √b) * (√а – √b )
г) а + b = (3√а + 3√ b) *(3√а2— 3√а 3√ b + 3√ b 2)
2 задания- «3»
3задания- «4»
4задания- «5»
Взаимопроверка.
Какие витамины и минералы необходимы человеку, чтобы быть здоровым?
Давайте вычислим суточную потребность организма в витаминах В1, В2 , Fe, в миллиграммах.
Дефицит витамина В1 может привести к нарушению обмена углеводов. Витамин В2 отвечает за состояние зрения, он необходим для построения защитного слоя сетчатки.
Дефицит железа сказывается на росте и устойчивости к инфекциям. От железа зависит построение гемоглобина – переносчика кислорода ко всем органам.
5. Этап закрепления и осмысления изученного материала.
. «Математическое домино»- в парах
Парам выдается набор карточек. Среди них участники находят начальную. Решают, ответы прикладывают к самому заданию. Получается цепь из примеров и ответов. Максимальное количество баллов – 9 (слайд 2).
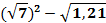
88
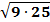
15
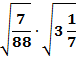
5,9
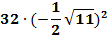
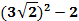
5
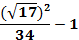
17
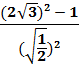
16
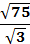
0,5
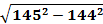
22
Проверка (слайд 3).
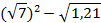
5,9
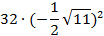
88
17
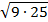
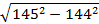
15
22
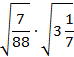
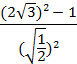
16

5
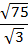
0,5
6.Самостоятельная работа
А теперь самое время потренироваться. Перед вами примеры из вариантов ЕГЭ №9. Вы их видите как на доске, так и на листочках. Ваша задача – быстро решать и заполнять таблицы с ответами. Соответствие букв и ответов перед вами. Правильно вычислив или упростив выражения в таблице, вы прочтете то, что необходимо вам при сдаче ЕГЭ.
Коллективно ! Можно исправлять неправильный ответ товарища.
1 вариант-удача, знания
2 вариант-уверенность
6.Этап информирования и инструктажа домашнего задания
Вернемся к целям урока, которые себе поставили. Давайте отметим то, что у нас получилось из намеченного. Что нового сегодня вы узнали?
Молодцы, вы активно работали на разных этапах занятия.
Ответы достаточно аргументированы, оперировали понятиями, сочетая теоретические знания с практическими, активно вносили поправки.
_____________работали особенно старательно.
Дома:
1.В учебнике повторить свойства степеней
2. Работать по карточкам (внимательно читать рекомендации, завтра подготовка к контрольной работе и к/р).
Корзина с витаминами (по уровням-задания: яблоко-1, апельсин-2, груша-3)
7.Этап подведения итогов занятия и рефлексии
Ребята, перед вашими глазами часть высказывания английского математика Джеймса Джозефа Сильвестра (1814-1897) о математике.
«Математика-это музыка разума» Не правда ли, как романтично?
А как вы думаете, как определил он музыку?
«Музыка- это математика чувств ». К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ, и как следствие, поступление в вуз. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность! А это- наши знания и навыки. Сегодня на уроке мы внесли очередной вклад в вашу подготовку к ЕГЭ, повторяя понятие степени и преобразуя выражения с радикалами.
Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей» – Так сказал американский математик Морис Клайн.
– Спасибо за урок!
Из этих пейзажей выберите, пожалуйста, тот, который лучше всего отражает ваше внутреннее состояние и с помощью которой вы могли бы рассказать нам о своем настроении, о своем самочувствии и о степени своей удовлетворенности».
Урок закончен. Спасибо за урок!
Оценочный лист (Ф.И.)
Кол-во баллов соответствуют оценке
3
Заполните пропуски.
(Знание формул сокращённого умножения.)
«5»- 4 задания
«4»- 3 задания
«3»- 2 задания
4
Вычисление суточной потребности организма в витаминах В1, В2 , Fe, в миллиграммах. «5»-выполнил задание
5.
Домино ( в парах)
«5»- 9 примеров
«4»- 8-7 примеров
«3»- 5-6 примеров
6.
Работа с карточками 5 мин по вариантам
(оценивает учитель)
Оценка
за урок
Методическая разработка по алгебре (11 класс) на тему: Конспекты уроков 11 класс «Степени и корни. Степенные функции»
По теме: методические разработки, презентации и конспекты
 Разработка урока по теме «Производная степенной функции. Применение производной в решении задач физики» 11 класс
Разработка урока по теме «Производная степенной функции. Применение производной в решении задач физики» 11 классУрок соответствует технологии модульного обучения….
 Нестандартный урок: «Ссора в царстве степенных функций»
Нестандартный урок: «Ссора в царстве степенных функций»Методическая разработка нестандартного урока в 9 классе с применением театрализованной и игровой формы работы….
 План-конспект урока в 6 классе «Степени сравнения имен прилагательных. Прилагательные в сравнительной степени»
План-конспект урока в 6 классе «Степени сравнения имен прилагательных. Прилагательные в сравнительной степени»Основная цель урока — дать понятие о сравнительной степени имён прилагательных; актуализировать знания о морфологических признаках имен прилагательных. Урок проводится с применением презентации и карт…
 Урок-игра по теме: «Степенная функция. Корень n-й степени»
Урок-игра по теме: «Степенная функция. Корень n-й степени»Материал на тему: «Степенная функция. Корень n-й степени»…
 Зачет по теме Степени и корни. Степеная функция.
Зачет по теме Степени и корни. Степеная функция.Данный зачет расчитан на учащихся 11 класса. По учебнику Мордкович….
План-конспект урока алгебры в 9 классе «Функция. Область определения и область значений функции»План-конспект урока алгебры в 9 классе «Функция. Область определения и область значений функции"…
Методическая разработка урока по теме: «Корни, степени, логарифмы».Цель урока: создать условия для систематизации изученного материала, выявления уровня овладения системой знаний и умений.Задачи:— обучающие: закрепить умение работы с корнями, степеням…
урок по теме корень п-й степени
27.11.2014 г.Тема урока: «Корень п-й степени и его свойства»
(урок проводится с применением элементов блочно – модульной технологии обучения и уровневой дифференциации)
Цель:
Способствовать выработке навыков применения к действиям над корнями знания определений, навыков сравнения чисел, используя свойства корней;
Развивать логическое мышление, интуицию, умение устанавливать причинно – следственные связи;
Воспитывать умение проводить оценку и самооценку знаний и умений, высокую работоспособность и организованность.
Три пути ведут к знанию: Путь размышления – это путь
Самый благородный,
Путь подражания – это путь
Самый легкий
и Путь опыта – это путь
Самый горький.
Конфуций
Организационный момент
Посмотрите внимательно несколько секунд на запись, запомните и ответьте на вопросы
1,71….. ; 2 , √3 , π.
В каком порядке были записаны числа?
Какое число лишнее?
Что в записи было не правильно?
Молодцы! Итак, тема нашего разговора –корень п-й степени. Мы будем работать с выражениями, содержащими корни, вы сами научитесь упрощать выражения и сравнивать. Вы расширите свои знания о корне.
А к знанию ведут три пути (прочитать эпиграф к уроку). Мы пройдем по трем дорогам. Итак, в добрый путь!
1.Фронтальная беседа по материалу 8 класса Путь размышления – это путь
Самый благородный,
Вспомните определение квадратного корня , арифметического квадратного корня;
Вспомните основные свойства арифметического квадратного корня;
* Как называется знак корня?
По размышляйте и по аналогии дайте определение корня п-й степени и арифметического корня п-й степени.
Стр 207 учебника, прочитайте определение.
Стр 209 учебника, спишите свойства.
Запишите на доске свойства какие запомнили.( 1 ученик)
Корни.
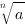
 :
:
Арифметическим корнем n-ой степени из неотрицательного числа  называется неотрицательное число, n-я степень которого равна
называется неотрицательное число, n-я степень которого равна  :
:
Внимание! Степень корня – это натуральное число, большее 1.
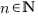 ,
, 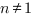
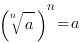 ,
, 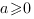 Свойства корня n-ой степени:
Свойства корня n-ой степени:
1. 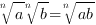
2. 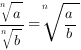
3. 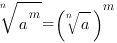
4. 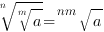
5.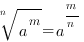
Частные случаи:
1. Если показатель корня целое нечетное число (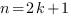 ), то подкоренное выражение может быть отрицательным.
), то подкоренное выражение может быть отрицательным.
В случае нечетного показателя уравнение 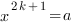
 при любом действительном значении
при любом действительном значении  и целом
и целом 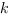 ВСЕГДА имеет единственный корень:
ВСЕГДА имеет единственный корень:
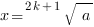 ,
,
Для корня нечетной степени справедливо тождество:
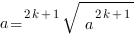 ,
,
2. Если показатель корня целое четное число (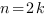 ), то подкоренное выражение не может быть отрицательным.
), то подкоренное выражение не может быть отрицательным.
В случае четного показателя уравнение 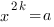 имеет
имеет
при 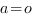 единственный корень
единственный корень 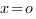
и, если 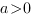 , два корня:
, два корня:
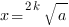
 и
и 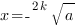
Для корня четной степени справедливо тождество:
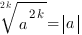
Внимание! Для корня четной степени справедливы равенства:
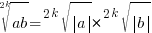
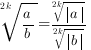
Путь подражания – это путь
Самый легкий
Работа по цепочке у доски
(№389-393по одному заданию а )
Самостоятельная работа с взаимопроверкой карточки по вариантам
или
№389-393 по одному заданию б- 1вариант
№389-393 по одному заданию в 2-вариант
Пауза
Упражнение на релаксацию
Принять удобное положение. Расслабиться. Закрыть глаза и представить большой белый экран. Мысленно раскрасить этот экран любимым цветом. Получается ровно, красиво, радует глаз, залюбуешься.
Раз, два, три – открыли глаза. Каким цветом был ваш экран?
Упражнение на сосредоточения внимания – «пальчики»
Одновременно под счёт пальчиками левой и правой руки касаться большого пальца.
Путь опыта – это путь
Самый горький.
4.Учебный элемент
Целью дальнейшей вашей работы является применение своих знаний в подготовке к ЕГЭ. У доски: По карточкам
№394б,в задание по типу №1 базового уровня.-(Леонова Анжела)
№415а,б заданиепо типу № 10 профильного уровня (Коробкова Диана)
Остальные выбирают уровень с кем решают.
Итог урока
Какие знания вы получили, чему учились и чему научились?
По всем ли дорогам мы прошли к знаниям? Прав ли был Конфуций?
Получили:
«5»-
«4»-
«3»-
Домашнее задание №389—.394 остальные.
Всем спасибо за урок!
Методическая разработка по алгебре (8 класс) на тему: Открытый урок по теме «Корень из степени»
Слайд 1
Уроки алгебры в 8 классе Васютина Елена Геннадьевна Санкт-Петербург, Лицей 126 2018 годСлайд 2
Квадратные корни Алгебра. 8 класс 28 ноября 2018 г. « Величие человека в его способности мыслить » Блез Паскаль
Слайд 3
Определите к какому множеству относятся следующие числа: Повторяем Проверим: Натуральные Целые Рациональные Иррациональные Действительные 12 1,2 5 13 − 80
Слайд 4
Найдите значение выражения: Повторяем Проверим: 2 24 93 36 1,8
Слайд 5
Повторяем Проверим : Известно, что a = − 16 . Найдите соответствие между столбцами и строками в таблице.
Слайд 6
Выполните задания 1 − 6 и вычеркните в таблице буквы, соответствующие ответам: М К Ж В А Ю Д Г Р Н А О Т 0,5 3 − 2 6 − 5 0 8 0,6 0,3 2 0,9 8 3 Повторяем
Слайд 7
Выполните задания 1 − 6 и вычеркните в таблице буквы, соответствующие ответам: М К Ж В А Ю Д Г Р Н А О Т 0,5 3 − 2 6 − 5 0 8 0,6 0,3 2 0,9 8 3 КВАДРАТ Повторяем
Слайд 8
Квадратный корень из степени Замените выражение тождественно равным: Повторяем
Слайд 9
Квадратный корень из степени Упростите выражения : Повторяем
Слайд 10
Найдите значение выражения: Квадратный корень из степени Двигаемся дальше
Слайд 11
Найдите значение выражения: Квадратный корень из степени Двигаемся дальше НО!
Слайд 12
Квадратный корень из степени Самостоятельно Вычислите:
Слайд 13
Верно ли, что 1) Квадратный корень можно извлечь из любого числа Немного отдохнем Нет
Слайд 14
Верно ли, что 2) Каждое целое число является рациональным Да Немного отдохнем
Слайд 15
Верно ли, что 3) Каждое число, оканчивающееся двумя нулями является полным квадратом Нет Немного отдохнем
Слайд 16
Верно ли, что 4) 0 − целое число Да Немного отдохнем
Слайд 17
Верно ли, что 5) Иррациональный − неразумный (в переводе с латыни). Да Немного отдохнем
Слайд 18
Верно ли, что 6 ) Из натурального числа , оканчивающегося тремя нулями, корень не извлекается Да Немного отдохнем
Слайд 19
Верно ли, что 8) Радикал – сторонник крайних, решительных действий, мероприятий, взглядов Да В химии: Радикал — это стойкая группа атомов в молекуле, которая в химических реакциях без изменений переходит из одного соединения в другое Немного отдохнем
Слайд 20
Верно ли, что 7) Впервые использовал знак радикала для обозначения арифметических корней Рене Декарт уже в 1637 году Да Немного отдохнем
Слайд 21
извлекается, если Квадратный корень из степени Двигаемся дальше под корнем четная степень Замените выражение тождественно равным:
Слайд 22
извлекается, если Квадратный корень из степени Двигаемся дальше под корнем четная степень Упростите выражение:
Слайд 23
извлекается, если Квадратный корень из степени Двигаемся дальше под корнем четная степень Упростите выражение:
Слайд 24
Квадратный корень из степени Самостоятельно Упростите выражение:
Слайд 25
Квадратный корень из степени Для самых-самых! Упростите выражение:
Слайд 26
В течении урока вы честно подсчитывали количество правильно выполненных (самостоятельно) заданий Подведем итоги! Подсчитайте количество набранных баллов и оцените свою работу на уроке, заполнив таблицу Я доволен своей работой на уроке На уроке я работал неплохо На уроке мне иногда было трудновато Я даже смогу объяснить своему однокласснику те задания, которые решил сам Что получалось хорошо? Что нужно еще разобрать?
Слайд 27
Домашнее задание Стр. 136 № 329, 330, 345, 399(1) Урок закончен ! Спасибо за внимание!
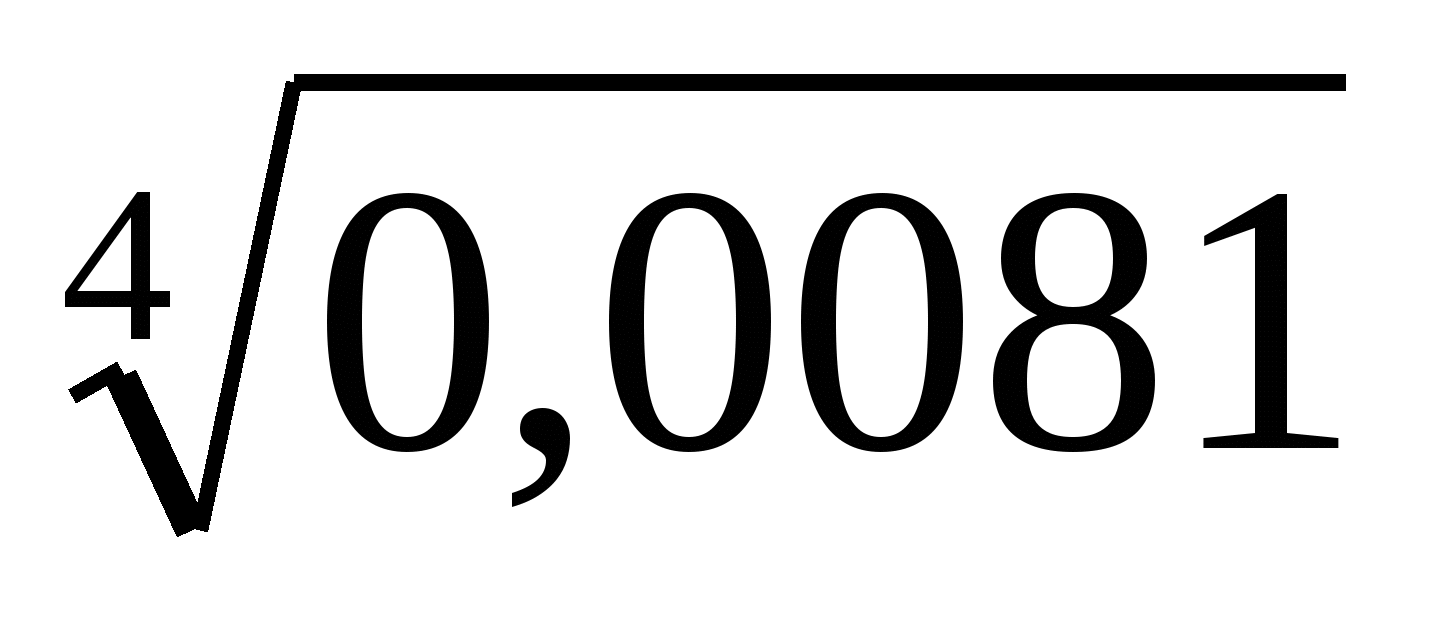
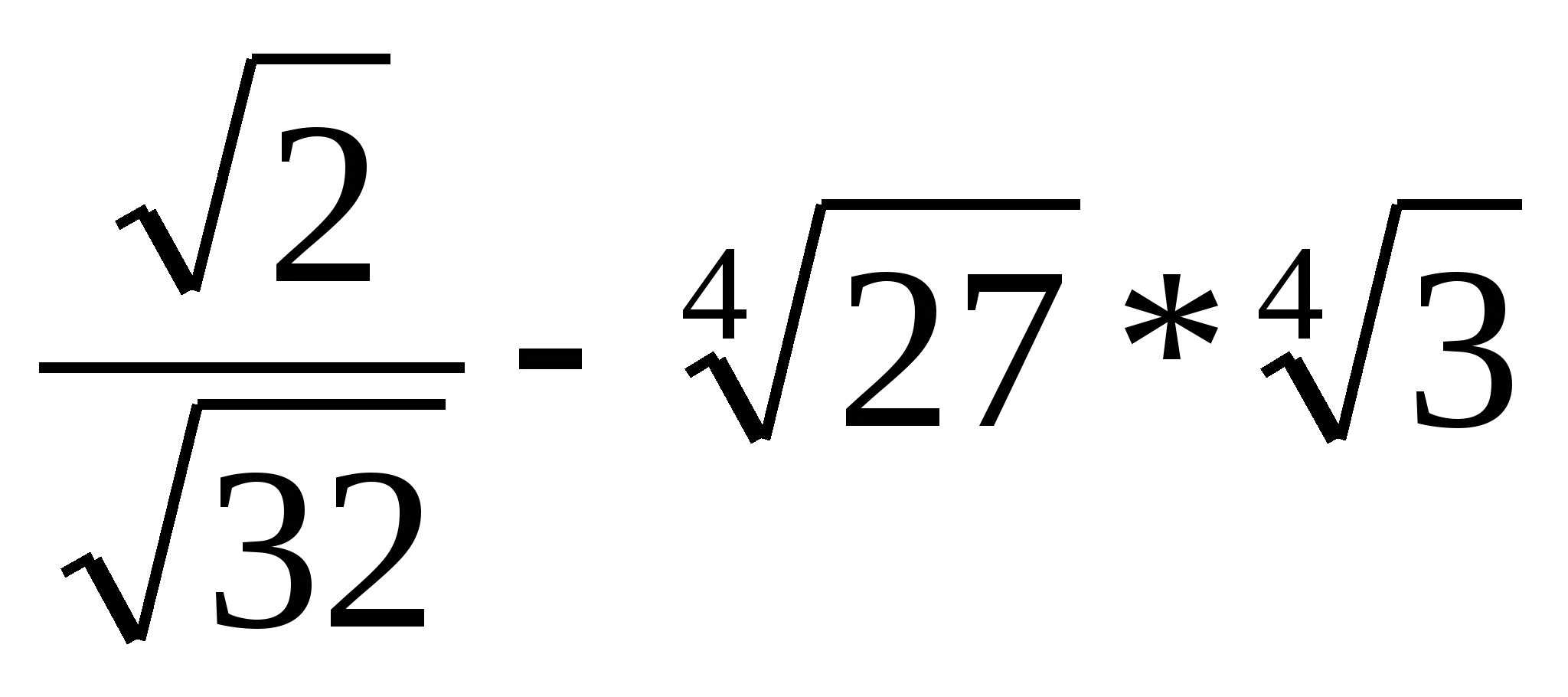

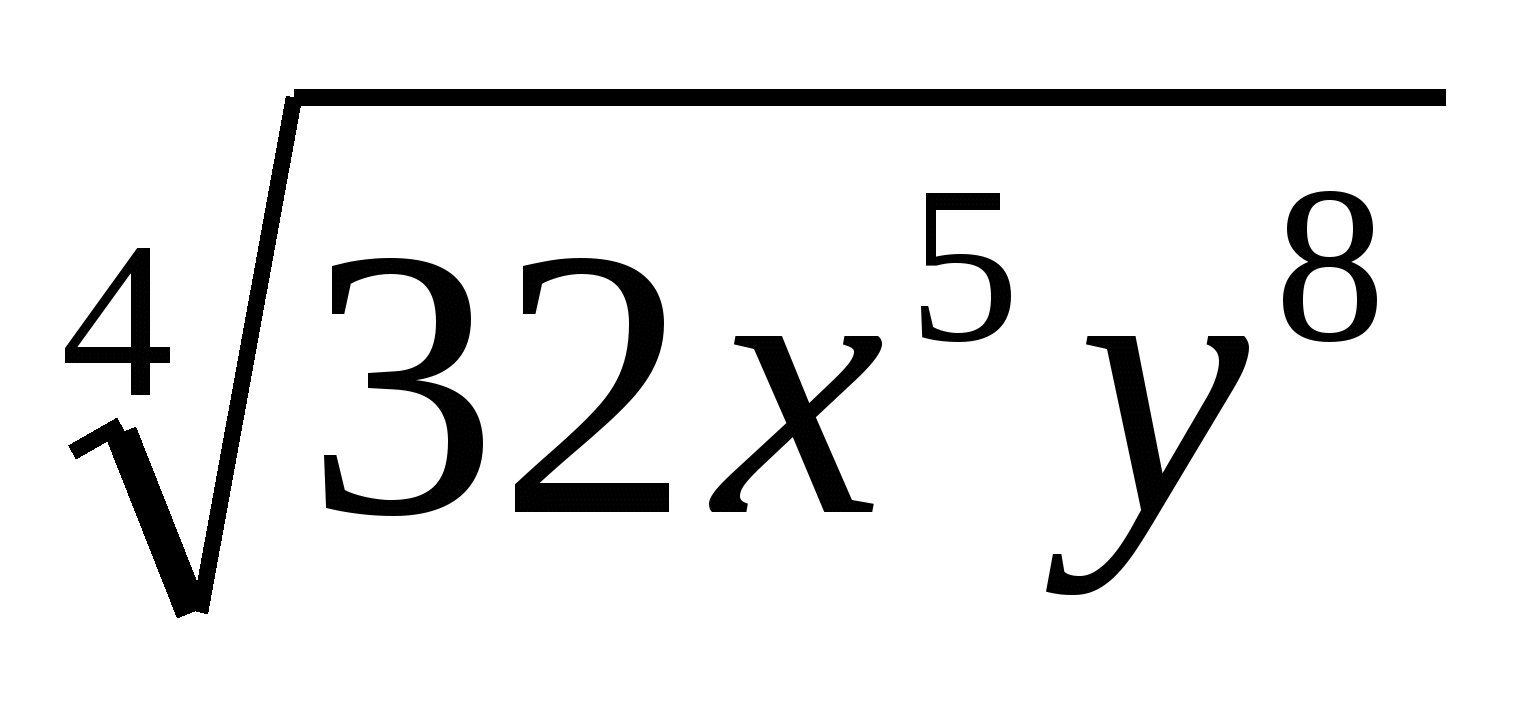 .
.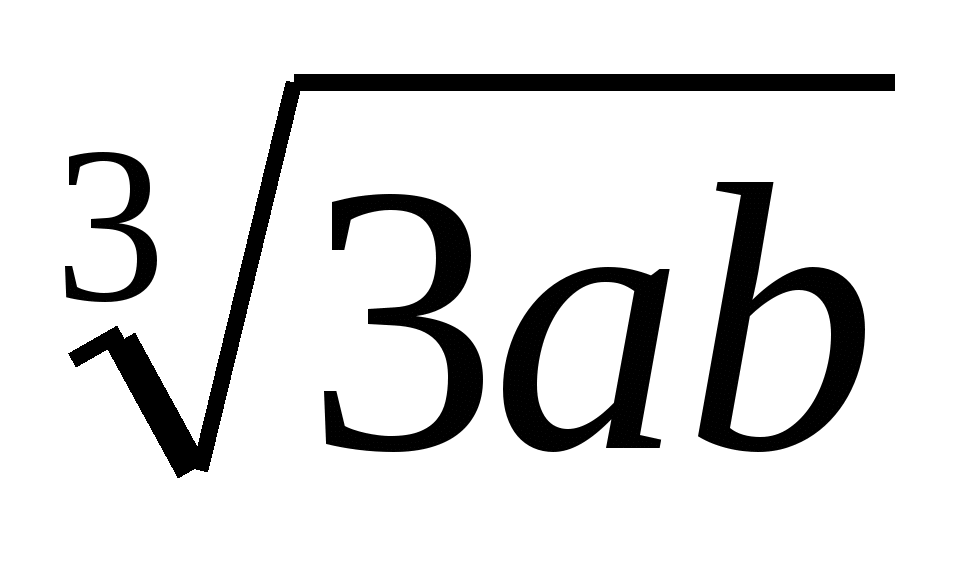 , если а>0, b>0.
, если а>0, b>0.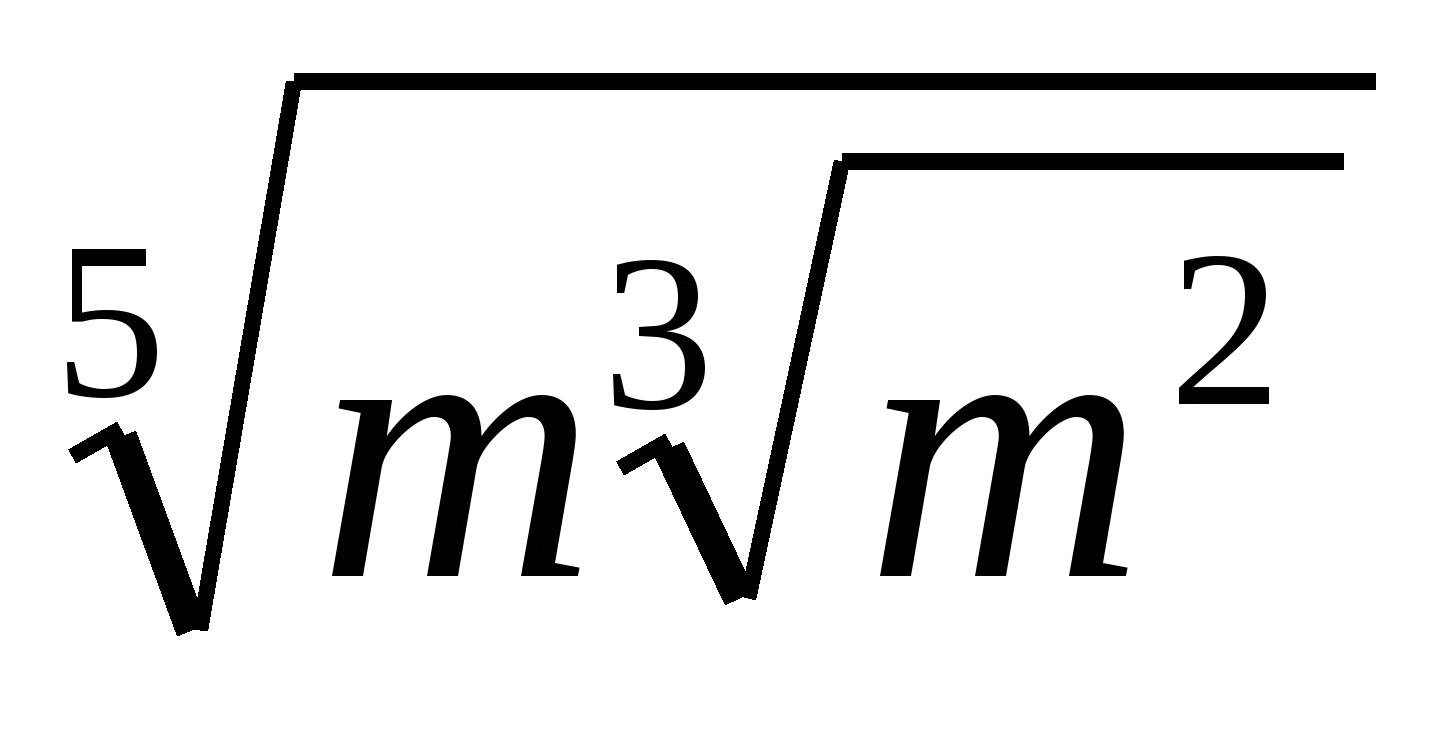 .
.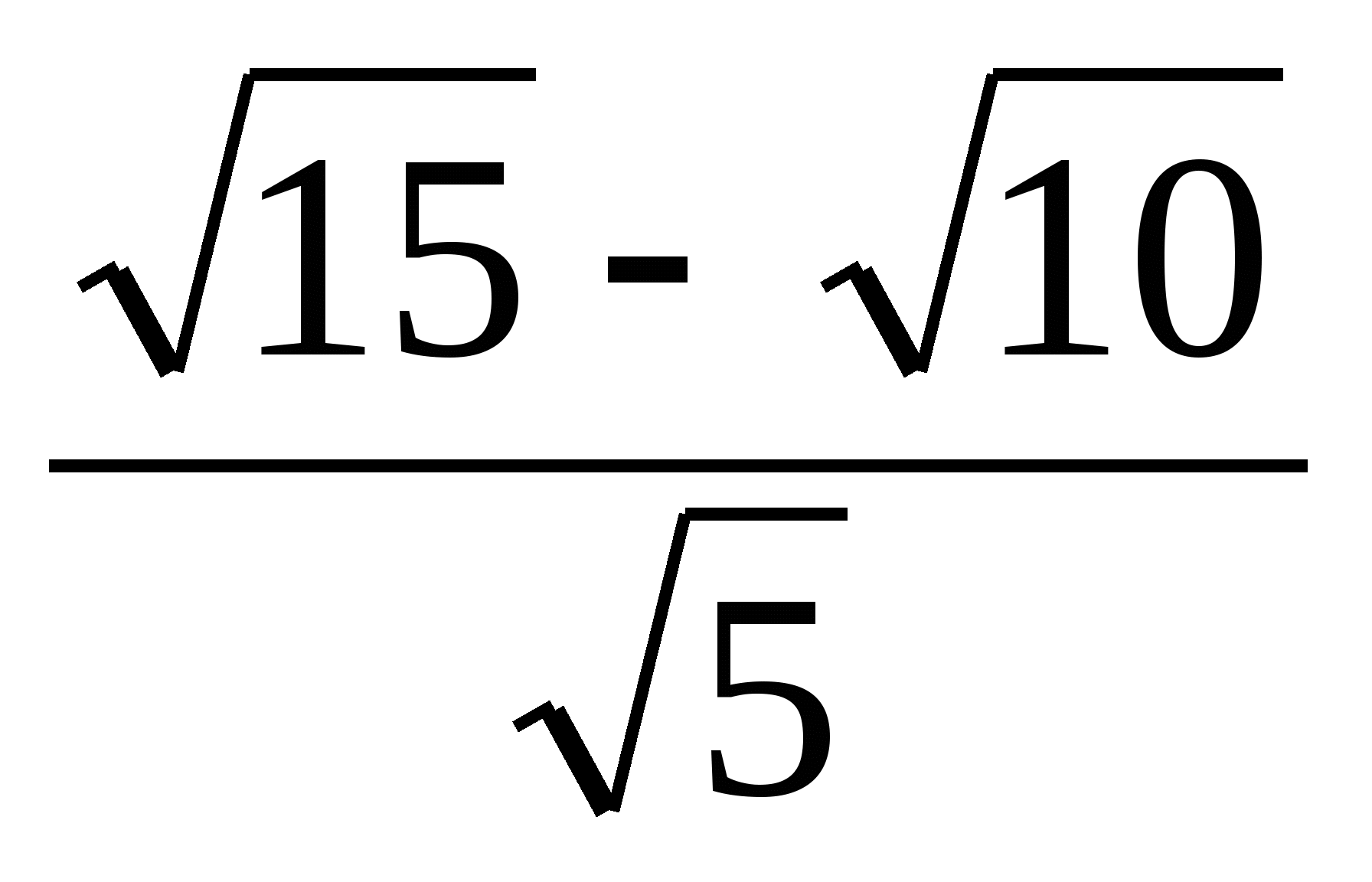
 .
.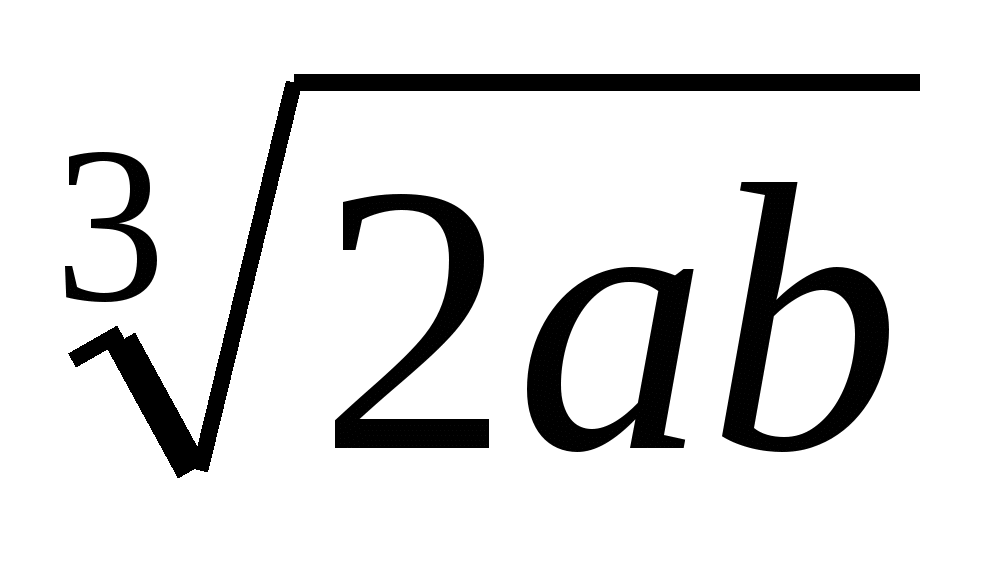 , если а>0,b>0.
, если а>0,b>0.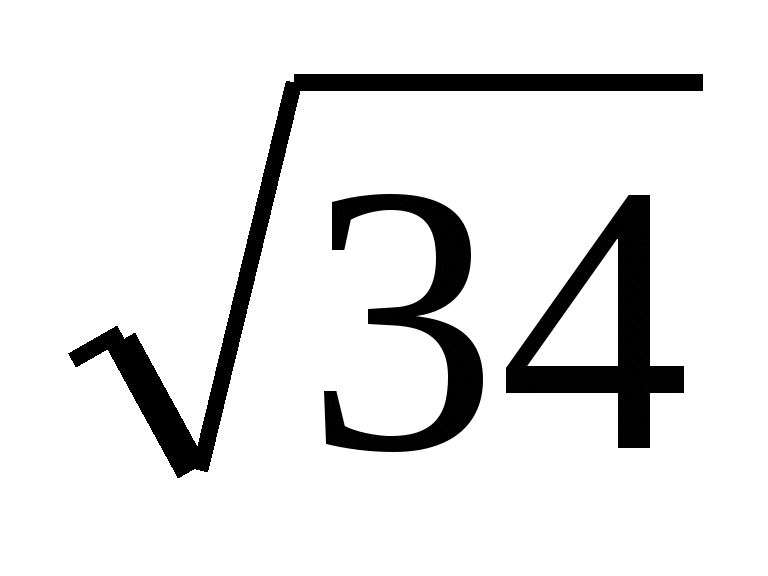 . Какая это точка?
. Какая это точка?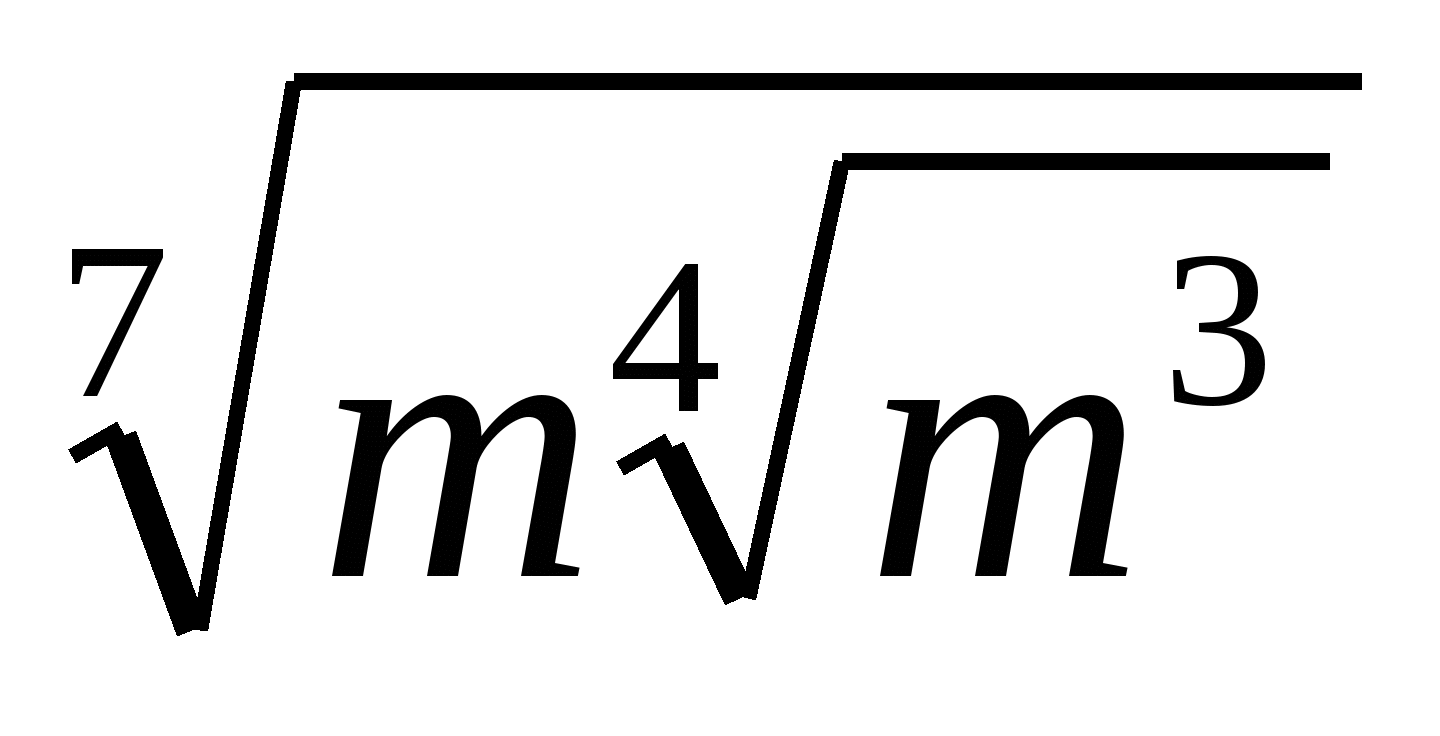 .
.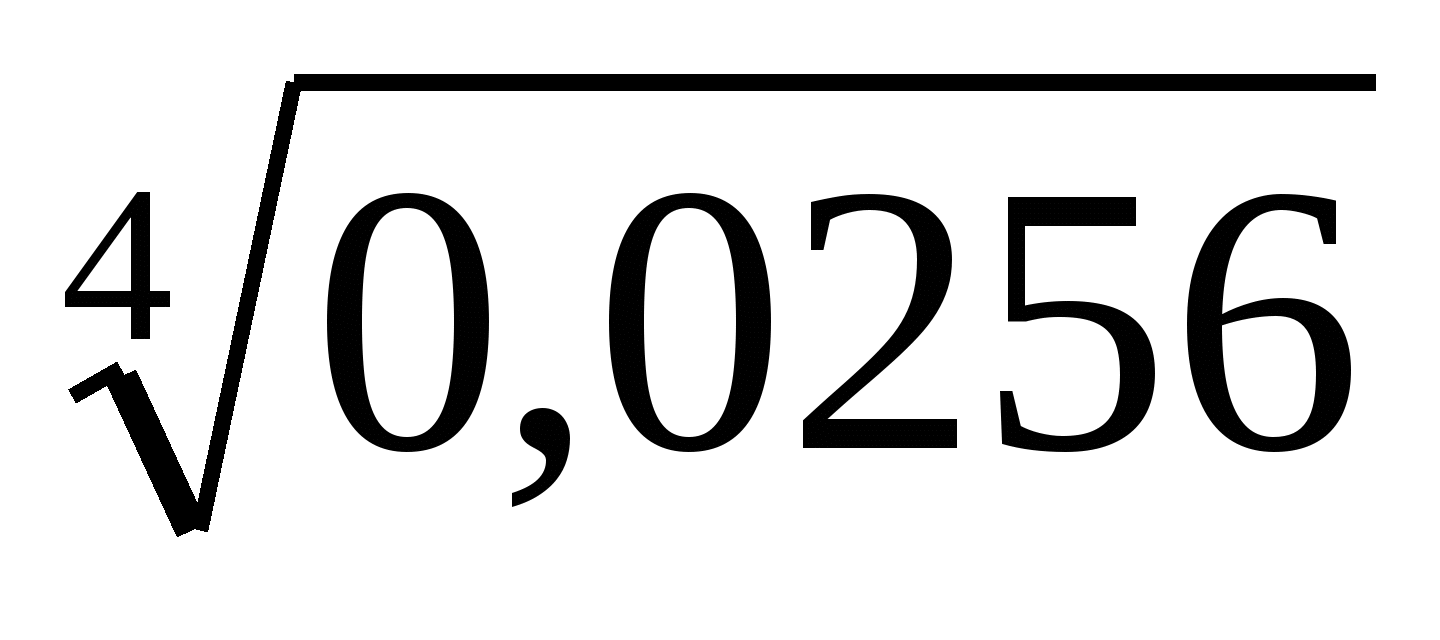
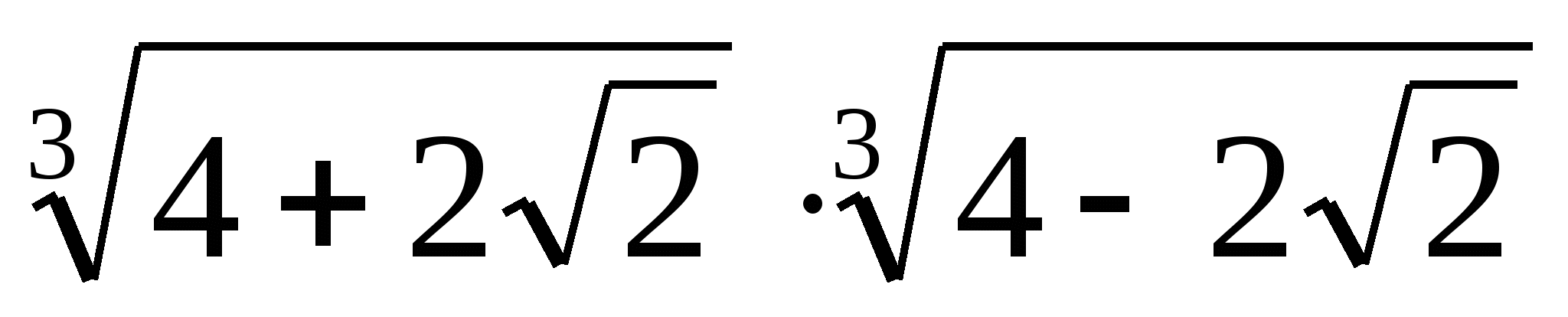
 х5+ 4= 0
х5+ 4= 0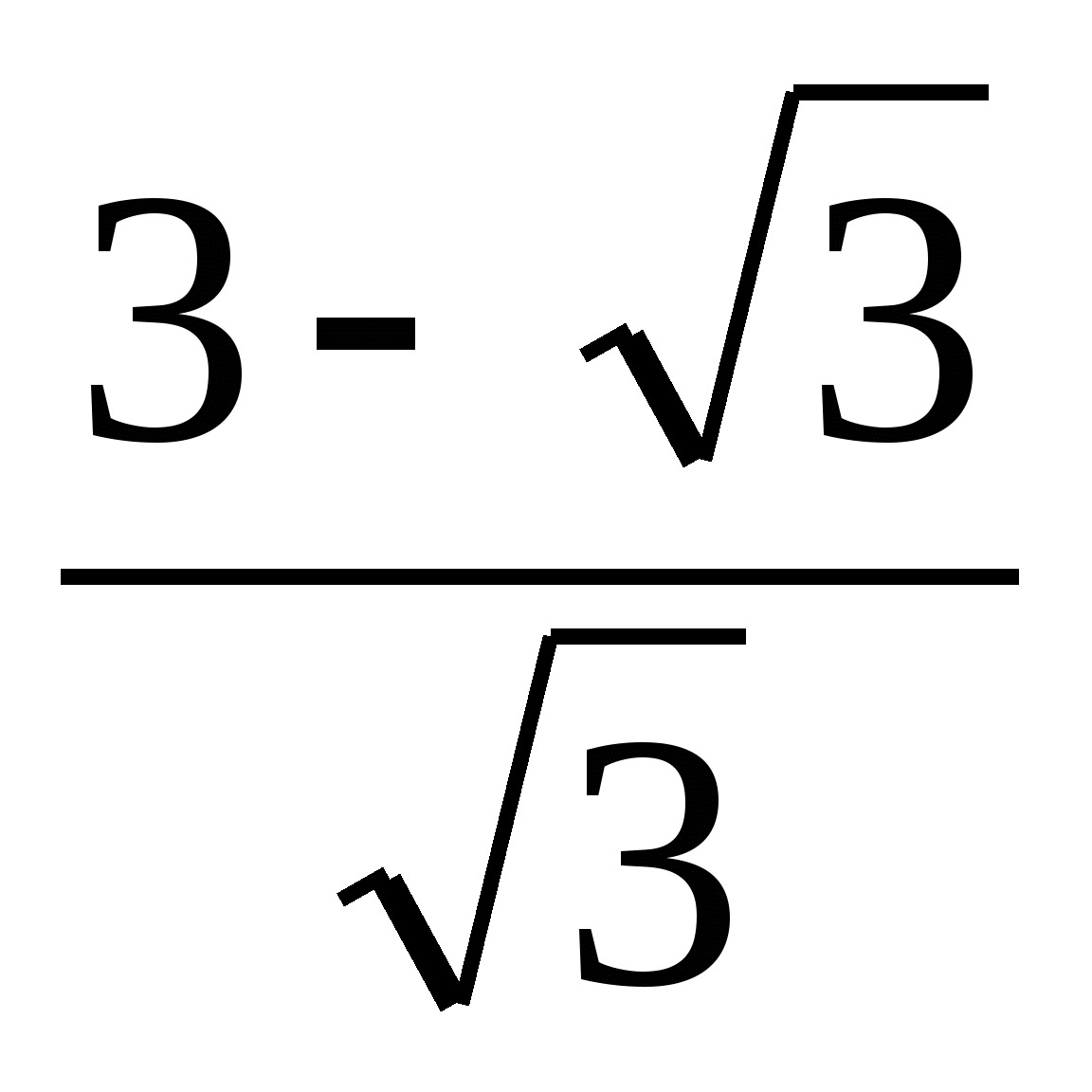
 ;
;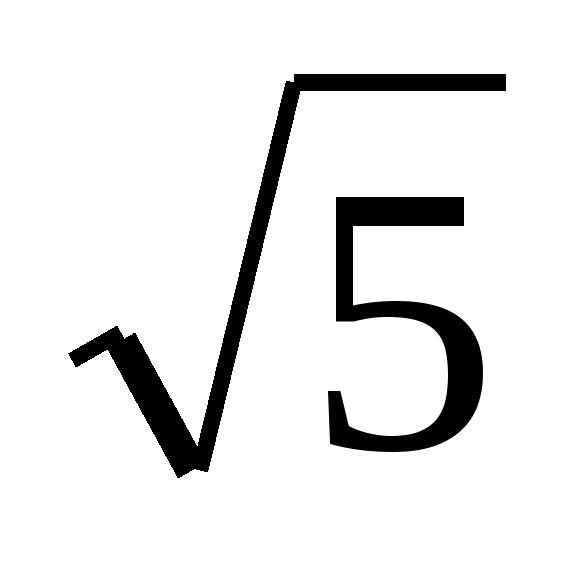 ;
;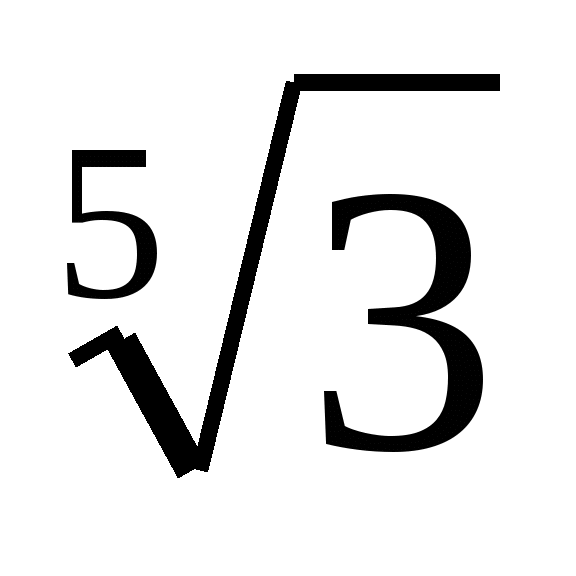 )
)