На кого можно поступить сдавая обществознание. Куда поступить с базовой математикой
ЕГЭ по математике разделён на 2 уровня: базовый и профильный, которые абитуриенты уже по-свойски оркрестили «базой» и «профилем».
ЕГЭ по математике на профильном уровне придется сдавать тем, кто планирует поступать в вузы на специальности, где математика является, соответственно профильной — главной, основной. На те специальности, где математика входит в перечень вступительных испытаний, поступить можно будет только с результатами профильного ЕГЭ по этому предмету. Это в основном, направления подготовки, связанные с техникой, технологиями и естественными науками. Хотя для поступления на некоторые гуманитарные специальности тоже требуется ЕГЭ по математике (профильной). Это, например, и другие.
Базовый ЕГЭ по математике придуман, в общем-то, для тех, кто с математикой не дружит и не планирует дружить в дальнейшей жизни. То есть даже самых положительных результатов ЕГЭ по математике на базовом уровне хватит только для того, чтобы получить аттестат.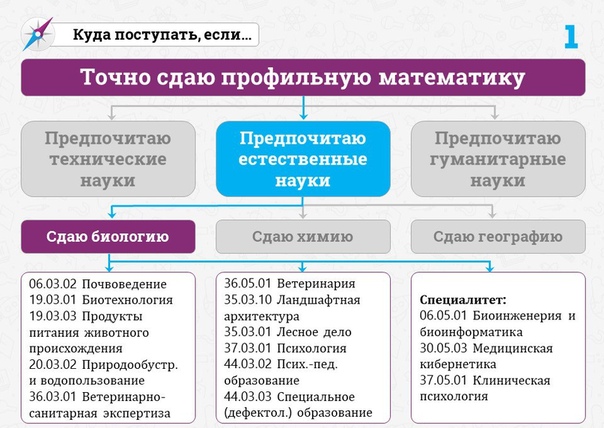
В вузах есть такие специальности, для поступления на которые математика не требуется. Это в основном гуманитарные и медицинские направления подготовки. Например,
ЕГЭ по математике на профильном уровне придется сдавать тем, кто планирует поступать в вузы на специальности, где математика является, соответственно профильной — главной, основной. На те специальности, где математика входит в перечень вступительных испытаний, поступить можно будет только с результатами профильного ЕГЭ по этому предмету.
Из четырех вступительных испытаний на все специальности обязательно нужно будет сдавать русский язык. Один предмет из четырех будет обозначен как профильный. До 1 февраля все вузы объявят, по каким специальностям они будут набирать студентов и какие предметы предстоит сдавать.
— Скажем, набранный балл по какому-либо предмету ниже границы, установленной Рособрнадзором, или по профильному предмету ниже установленной вузом границы. Причем нижняя граница для поступления в вуз должна быть объявлена приемной комиссией заранее — до 20 июня.
Если по тем предметам, которые нужно сдавать для этой специальности, выпускник на ЕГЭ набрал меньше баллов, чем установленная Рособрнадзором нижняя граница, он не имеет права участвовать в конкурсе в вуз.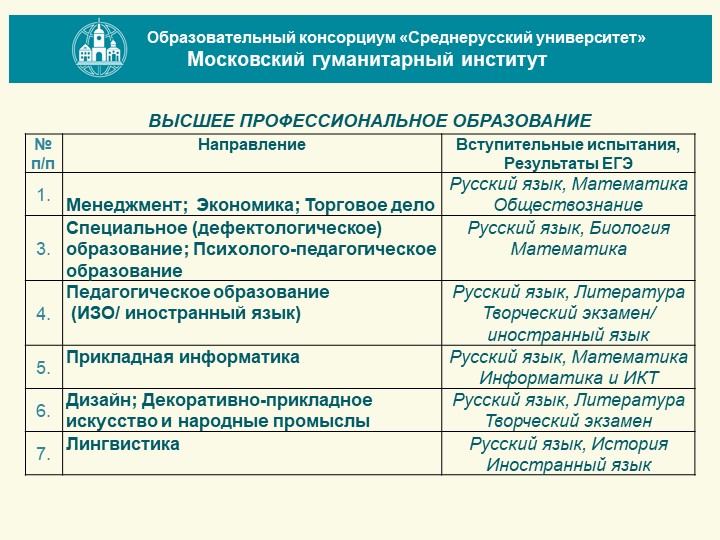 Вузы могут по профильному предмету устанавливать свою границу. Но не ниже нашей.
Вузы могут по профильному предмету устанавливать свою границу. Но не ниже нашей.
Еще совсем недавно продолжительность обучения в любом вузе составляла 4-5 лет, после чего выпускникам присваивалась квалификация специалиста. Те, кто хотел продолжить свою научную деятельность, оставались доучиваться в аспирантуре. Однако с изменениями в системе российского образования в институтах и университетах появились такие понятия, как бакалавриат и магистратура. Для присвоения степени бакалавра необходимо обучаться 4 года. Если у студентов появляется желание закончить более углубленную программу, они поступают в магистратуру, которая предполагает еще два года обучения.
Куда лучше поступать после 11 класса — в вуз или колледж? Большинство, конечно, склоняется к первому варианту, ведь, по мнению многих, высшее образование – залог светлого будущего. Однако это клише постепенно разрушается, так как современные колледжи ничуть не уступают уровнем преподавания и выпускают достойных квалифицированных специалистов. При выборе специальности и вида образования важно руководствоваться своими интересами, талантами и умениями. Если вас привлекает профессия, которая преподается только в колледже, не нужно от нее отказываться из-за того, что кто-то считает ее непрестижной.
При выборе специальности и вида образования важно руководствоваться своими интересами, талантами и умениями. Если вас привлекает профессия, которая преподается только в колледже, не нужно от нее отказываться из-за того, что кто-то считает ее непрестижной.
Кстати, поступить можно даже в Московский государственный педагогический университет, где имеется подобная специальность. Сейчас филиалы Московского педагогического университета есть во многих городах России, в частности, в Самаре. Вот только проблема заключается в том, что обучение в лишь на коммерческой основе. В филиал Московского педагогического университета в Самаре можно поступить практически на все специальности только с результатами по русскому и математике. При этом, в университете дают отличный запас знаний и умений по тем или иным дисциплинам. Диплом выдают Московского образца, поэтому он отлично котируется на территории всей Российской федерации. Кстати, обучение в Самарском ВУЗе стоит совсем недорого, особенно если сравнивать с ценам в среднем показателе по России.
Базовый ЕГЭ по математике придуман, в общем-то, для тех, кто с математикой не дружит и не планирует дружить в дальнейшей жизни. То есть даже самых положительных результатов ЕГЭ по математике на базовом уровне хватит только для того, чтобы получить аттестат. Результаты «базы» не переводят в стобалльную систему. Их переводят в традиционную пятибалльную, чтобы просто вписать эту оценку в аттестат. А аттестата достаточно только для поступления в колледж или техникум. Но! Если дополнительно сдать еще и несколько ЕГЭ по другим предметам (русский язык не считается) и набрать достаточное количество баллов или хотя бы преодолеть минимальный порог, то шанс поступить в вуз появится. Однако для поступления на бюджет сумма баллов по всем необходимым ЕГЭ должна быть около 200.
Однако для поступления на бюджет сумма баллов по всем необходимым ЕГЭ должна быть около 200.
Зависит от того, на какие предметы Вы делаете упор. Если брать связку «русский язык-математика-обществознание», то можно поступать на направления экономики, менеджмента, маркетинга или связей с общественностью. С русским, математикой и литературой можно попробовать поступать на журналиста.
Если вы до сих пор думаете, куда можно поступить после 11 класса, и у вас на примете есть много вариантов, то рекомендуем подать заявку одновременно на несколько специальностей в разные колледжи. К настоящему времени какие-либо ограничения на количество подаваемых заявлений отсутствуют. Так вы обеспечите себе гарантированное зачисление на одно из направлений.
Куда можно поступить с Обществом, Русским и Математикой после 11 класса. Последние новости.
Сейчас в формате курсов можно найти программы абсолютно по всем специальностям, которым обучают в вузах и колледжах. Но такой вид обучения не может расцениваться как основной и чаще всего становится лишь как дополненый.
В оценка по пятибалльной шкале. Если нет двоек — ученик допущен к государственной итоговой аттестации. А вот сама аттестация проходит в виде Единого госэкзамена.
Куда можно поступить с Обществом, Русским и Математикой после 11 класса. Последние события.
— На федеральном уровне это не определено. Если региональный орган управления образованием решит организовать единые для всех своих школ правила допуска — это его дело. Если же региональные чиновники не сочтут нужным вмешиваться, школа сама вправе решить, оценки в аттестат. Итоговые зачетные работы должны быть проведены. Это традиционно. Но в какой форме? Думаю, учителям виднее.
На днях выпускники российских школ сдали последние в основном периоде ЕГЭ экзамены. По некоторым предметам уже известны результаты, и кто-то рад высоким баллам, а кто-то огорчен тем, что не смог преодолеть минимальный порог. Так, 14,3% участников ЕГЭ по
математике профильного уровня не справились с решеним заданий, и теперь задаются вопросом: «Куда можно поступить с базовой математикой?». Ответ на данный вопрос мы дадим в нашей статье.
— А где они берут темы для сочинений в течение учебного года? Не волнуйтесь, у учителя все необходимые материалы есть.
— Нет. На сегодняшний день в правилах приема учет этих особенностей не оговорен. Есть олимпиады, есть дополнительные испытания, есть те, кто принимается в традиционной форме, и те, кто поступает по результатам ЕГЭ. Медаль в этом году никаких льгот не дает!
Набор экзаменов «Русский язык Литература Обществознание» не дает широкого выбора программ обучения. Тут 43 программы от 20 вузов с проходными баллами. Данные актуальные. Если захотите проверить шансы поступить, то вот в этом Калькуляторе ЕГЭ введите ваши баллы
Куда можно поступить с Обществом, Русским и Математикой после 11 класса. Сводка на сегодня.
Обществознание выбирают многие с намерениями поступить в ВУЗы на специальности связанную с этим предметом. Другие же выбирают в качестве спасательного круга, который может помочь набрать большие баллы.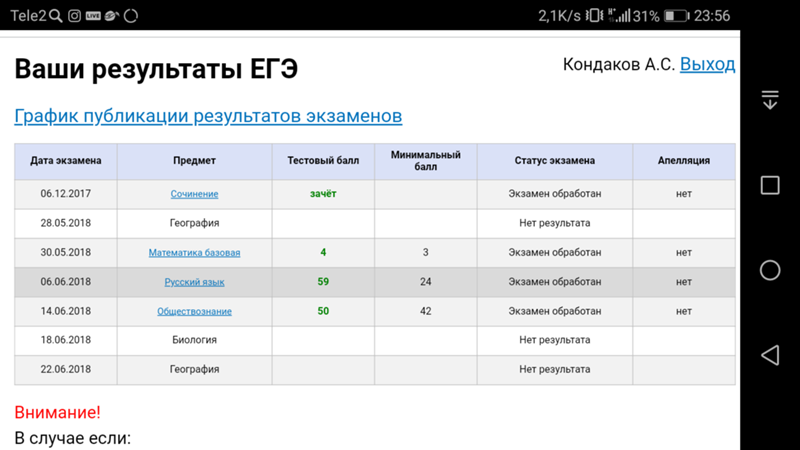 В нем нет этих страшных формул и других математических примочек. Не все любят математику. И вот приходит время, отталкиваясь от полученных результатов ЕГЭ и делать выбор.
В нем нет этих страшных формул и других математических примочек. Не все любят математику. И вот приходит время, отталкиваясь от полученных результатов ЕГЭ и делать выбор.
Какие возможности даёт набор математика-русский язык-обществознание?
Среди специальностей, доступных с этим набором экзаменов доминируют специальности экономического профиля, при этом профиль достаточно широк: на факультете экономики и менеджмента поступающие могут выбрать из специальностей «Экономика», «Управление персоналом», «Бизнес-информатика»; также предлагается специальность «Менеджмент» сразу с четырьмя профилями – абитуриенту на выбор предлагаются логистика, маркетинг, финансовый и производственный менеджмент. С учетом темпов роста экономики нашей страны, экономические специальности будут более востребованы чем сейчас. Соответственно каждый год выпускается огромное множество экономистов. Но успех имею те, кто действительно предан своей работе и знает о ней все.
Еще одна очень популярная специальность «Социология», однако нельзя сказать, что она популярна среди работодателей — даже поверхностное изучение ситуации на рынке труда позволяет понять, что социологи сегодня не востребованы.
Из-за того что способностями к математике обладает не каждый, это ограничивает выбор поступающего. Но есть возможность расширить круг доступных специальностей. В этом случае абитуриент может сдать ещё один экзамен по выбору, например, иностранный язык.
Таможенное дело. В последние годы у поступающих, эта специальность становится популярной. И соответственно на каждое место имеется огромный конкурс. Это связанно с тем, что у них имеется определенные представление об этой сфере деятельности. Их мотивируют высокие заработки, которые, как они думают, им обеспечены. Однако специалисты поясняют, что, несмотря на достаточную востребованность, таможенное дело — это обычная госслужба, о заоблачных доходах здесь и речи не может быть.
При сдаче набора ЕГЭ русский язык-обществознание-иностранный язык доступна специальность «Реклама и связи с общественностью». Эта специальность интересна тем, что находится на своеобразной границе между экономикой и творчеством, так что она рекомендуется выпускникам с оригинальным мышлением, также здесь приветствуется коммуникабельность.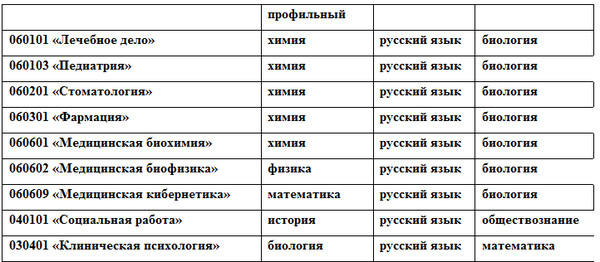 Специалисты в области рекламы сегодня высоко ценятся, ведь, как известно «реклама – двигатель торговли», и после окончания ВУЗа выпускники легко находят работу.
Специалисты в области рекламы сегодня высоко ценятся, ведь, как известно «реклама – двигатель торговли», и после окончания ВУЗа выпускники легко находят работу.
Обществознание считается одним из самых популярных предметов, которые выпускники сдают на ЕГЭ. Ввиду высокого рейтинга дисциплины Рособрнадзор даже принял решение выделить на сдачу этого предмета отдельный день. Такой ажиотаж вокруг обществознания вызван тем, что, во-первых, это относительно несложная гуманитарная дисциплина; во-вторых, с результатами по ней можно поступить на ряд специальностей. Если и вы в списке тех выпускников, кто выбрал данный предмет в качестве профильного, тогда вам стоит просмотреть список вузов и факультетов, куда можно подать заявление.
Направления подготовки
Гостиничное дело
Это направление воспитывает таких специалистов, как администратор, туроператор, менеджер по работе с клиентами и метрдотель. Данное отделение, куда можно поступить с хорошими знаниями по математике, русскому, истории и обществознанию, выпускает экспертов, способных планировать производственную деятельность гостиниц, прогнозировать результаты их работы, оценивать рынки сбыта и составлять маркетинговую политику отелей.
Многие выпускники, владеющие английским языком на высоком уровне, находят себе должности и за рубежом, что говорит о высокой перспективности такой специализации.
Отделение правоохранительной деятельности
Профессии этого профиля связаны с административной деятельностью и обеспечением безопасности граждан. Кандидатам предоставляется на выбор множество специальностей, среди которых наиболее популярны:
- адвокат,
- прокурор,
- следователь,
- нотариус,
- полицейский,
- правовед.
Большинство выпускников по окончании вуза поступают на службу в государственные правоохранительные органы: организации юридической защиты, таможенные службы, ГИБДД, прокуратуру т. д. Некоторые находят высокооплачиваемые должности в частных охранных агентствах и сыскных бюро. Для поступления наряду с профильным обществознанием потребуется предъявить результаты ЕГЭ по истории.
Издательское дело
Если вы любите работать с документацией и у вас есть талант к написанию и редактированию текстов, то данная область полностью соответствует вашим потребностям. Поступив на это направление, вы сможете выучиться на художественного редактора, журналиста, верстальщика, корректора и трафик-менеджера. Для поступления на издательское отделение вам понадобятся высокие баллы по обществознанию и английскому языку.
Часто специалисты этой сферы работают с иностранными текстами, чем и обуславливается необходимость знаний английского языка. В дальнейшем выпускники факультета осуществляют свою деятельность в различных книжных издательствах, газетах, журналах, типографиях и библиотеках.
Поступив на это направление, вы сможете выучиться на художественного редактора, журналиста, верстальщика, корректора и трафик-менеджера. Для поступления на издательское отделение вам понадобятся высокие баллы по обществознанию и английскому языку.
Часто специалисты этой сферы работают с иностранными текстами, чем и обуславливается необходимость знаний английского языка. В дальнейшем выпускники факультета осуществляют свою деятельность в различных книжных издательствах, газетах, журналах, типографиях и библиотеках.
Психолого-педагогический факультет
С обществознанием можно и педагога. Для освоения этих профессий вам также необходимо предъявить результаты ЕГЭ по биологии . Специальность прежде всего связана с осуществлением психологических обследований, разработкой оздоровительных программ и созданием благоприятных условий для обучения детей. Здесь выпускники могут учиться на таких экспертов:
- воспитатель детского сада,
- школьный психолог,
- социальный педагог,
- специалист психокоррекции.

Зачастую представители психолого-педагогического отделения работают с детьми с нарушениями зрения, слуха, речи и интеллекта и разрабатывают для них программы реабилитации.
Медиакоммуникации
Здесь воспитываются разноплановые специалисты, осуществляющие свою деятельность в области радио- и телекоммуникаций, в печатных изданиях, рекламных и PR-агентствах. Для того чтобы поступить на данное направление, абитуриенты должны предъявить сертификат с результатами ЕГЭ по обществознанию, русскому языку и литературе. По окончании университета выпускники имеют возможность получить такие квалификации, как маркетолог, звукорежиссер, редактор, продюсер, PR-менеджер и корреспондент.
Старшие классы в школе — прекраснейшее время в жизни человека. Наверное, у каждого в том возрасте во взгляде виделись надежда на светлое будущее, ожидание того, что все сложится и получится. В глазах молодых людей можно увидеть тот самый огонек о мечтах и целях, которые юная душа намерена покорить.
Тяжелый выбор специальности
Наступает время для ЕГЭ, и ученики выбирают предметы, которые будут сдавать при поступлении в учебные заведения. При выборе экзамена главное — не допустить ошибок, о которых потом многие жалеют всю жизнь.
Хотя это и очень трудно, выбрать жизненный путь в таком возрасте, когда ещё так мало знаний о жизни. Но все же это первый значительный шаг уже взрослого человека. Шаг, который юному абитуриенту задаст дальнейший вектор развития его как профессионала, как личности и как человека.
Как бы хитро не складывались перипетии судьбы, в конечном итоге каждый, кто найдет себя, найдет и место под солнцем, и свой путь. Кто-то пойдет по стопам великих врачей, произнесет клятву Гиппократа и посвятит свою жизнь служению людскому здоровью. Другой станет великим инженером, по чьим проектам будет построено множество самолетов и мостов. А кто-то будет служить людям на гуманитарном поприще.
Дисциплины
Все без исключения должны сдавать русский язык. Потому что это — государственный язык, без которого не обходится ни одна сфера жизни, будь то делопроизводство или частная беседа.
Потому что это — государственный язык, без которого не обходится ни одна сфера жизни, будь то делопроизводство или частная беседа.
И все же, те, кто решился пойти гуманитарным путём, должны будут сдавать на ЕГЭ обществознание и английский. Куда поступать, сдав эти учебные дисциплины на экзамене? Специальностей масса. А если, помимо русского языка, обществоведения и английского языка, сдать еще и историю, то перед абитуриентом откроется ещё больше дверей. Они приведут к интереснейшим жизненным деятельностям.
Культурология
Куда поступать с обществознанием и английским? Вопрос, конечно же, интересный и требует детального разбора вследствие своей обширности. Начать описание стоит с такой специальности, как культурология. Что же это такое? Сказать, что это — наука о культуре будет верным определением. Однако не даст объективного освещения этой деятельности.
Можно сказать, что культура — это продукты деятельности за все время существования человечества в его привычном понимании. Говоря продукты деятельности, имеются ввиду и разные стороны человека. То есть материальная, интеллектуальная, духовная. Как можно увидеть, одна только культурологическая составляющая является невспаханным полем для трудовой интеллектуальной деятельности и новых невероятных открытий и умозаключений. Профессия культуролога будет являться замечательным вариантом того, куда можно поступить, сдавая английский и обществознание.
Говоря продукты деятельности, имеются ввиду и разные стороны человека. То есть материальная, интеллектуальная, духовная. Как можно увидеть, одна только культурологическая составляющая является невспаханным полем для трудовой интеллектуальной деятельности и новых невероятных открытий и умозаключений. Профессия культуролога будет являться замечательным вариантом того, куда можно поступить, сдавая английский и обществознание.
Философия
Особого внимания заслуживает и такая наука, как философия. Что это такое? Философия является таким бескрайним океаном мысли, конца которому до сих пор никто не нашел.
Пожалуй, одним из наилучших вариантов, куда поступать с обществознанием и английским, является именно философский факультет. Один раз погрузившись в этот океан мудрости, человек уже не может противиться течениям, что затягивают его все глубже и все дальше. Перед получившим диплом философа выпускником открывается обширнейшая деятельность, в которой он сможет реализоваться как творческая и независимая личность: преподавание в школах и вузах, научная деятельность, журналистика. А уж сколько философов доносят свои мысли через художественную литературу, становясь культовыми писателями. Не следует забывать также и о духовной деятельности.
А уж сколько философов доносят свои мысли через художественную литературу, становясь культовыми писателями. Не следует забывать также и о духовной деятельности.
Ведь отучившись на философа, многие люди с головой уходят в религию, становясь активными деятелями христианства, ислама, буддизма и других мировых религий. Так что факультет философии — отличный вариант, куда можно поступить с обществознанием и английским.
Филологические специальности
Есть народная мудрость: «Великому человеку дай небо, пусть распускает крылья. Маленькому человеку дай землю, пусть пускает корень». Если юному абитуриенту не по нраву копаться в дебрях философских размышлений о высоких материях, а тянет к более приземленной деятельности, то и на этот случай найдется особое занятие. Оно с годами набирает свою актуальность. Если ещё нет конкретных решений по поводу того, куда поступить с обществознанием, английским, русским, то здесь на помощь приходит бесчисленное множество филологических специальностей. Множество их потому, что, сколько в мире существует языков, столько и направлений можно выбрать для себя. И даже больше.
Множество их потому, что, сколько в мире существует языков, столько и направлений можно выбрать для себя. И даже больше.
Но что же такое филология? На этот вопрос так же нет однозначного ответа. С общепринятой распространенной точки зрения филология — это наука о языках. А если говорить более научно, филология — это наука, изучающая культуру, которая выражается в устной и письменной речи. Также филология изучает и многие другие языковые аспекты, такие как нелитературная речь, в которую входят жаргон, сленги, местные афоризмы, мемы и прочие достояния различных микрокультур.
Особое место в данной науке занимает изучение языков, которые не используются в обыденной современной жизни, таких как, например, мертвые, вроде латинского, древнеегипетского или слогов коренных народов Америки. Не забудем вспомнить и про множество искусственных языков. Они создавались и создаются с целью глобализации человечества. Или же используются в фантастической литературе, как, например, эльфийский язык с его наречиями, изобретенный английским писателем Джоном Толкином. Так что посвящение своей жизни изучению филологии — это ещё одна перспектива, если вы раздумываете, куда можно поступать с обществознанием и английским. Если вам по душе языки, то обязательно обратите внимание на данную специальность.
Так что посвящение своей жизни изучению филологии — это ещё одна перспектива, если вы раздумываете, куда можно поступать с обществознанием и английским. Если вам по душе языки, то обязательно обратите внимание на данную специальность.
Туризм — достаточно популярная деятельность
Итак, выпускник на ЕГЭ сдал обществознание и английский. Куда поступать после 11 класса, чтобы потом не было сомнений в выбранной профессии? Ответом может быть изучение земного шара. Но не всего, а только тех мест, в которых можно отдыхать, расслабляться и веселиться. Речь идет о профессии турагента. В последние несколько десятилетий эта сфера деятельности набирает немалые обороты. В ней можно реализовать себя, обеспечить безбедное существование и ознакомиться с красотами мира, в котором мы живем.
Правоведение
Если в жизни человека интересует не только творческая самореализация, но и материальное благополучие, то куда поступать с обществознанием и английским? Факультет правоведения — это подходящий вариант. Получившему юридическое образование выпускнику предлагается множество мест, где он мог бы работать. В судебной системе, например, адвокатура, прокуратура или судебная практика. Во многие престижные фирмы требуются грамотные юристы со знанием своего дела. Ну и, конечно, с таким образованием открыта дорога к большинству государственных должностей.
Получившему юридическое образование выпускнику предлагается множество мест, где он мог бы работать. В судебной системе, например, адвокатура, прокуратура или судебная практика. Во многие престижные фирмы требуются грамотные юристы со знанием своего дела. Ну и, конечно, с таким образованием открыта дорога к большинству государственных должностей.
Менеджер
Некоторые разносторонне развитые абитуриенты задаются вопросом: «Сдаю английский и обществознание, куда поступать, если к списку экзаменов прибавляется ещё и математика?».
При таком раскладе имеются все возможности выучиться на менеджера. Получив данную профессию, юные одаренные специалисты смогут занимать управленческие места во многих компаниях, предприятиях, государственных и частных проектах. Менеджер — это новая специальность, которая возникла в связи с радикальным изменением рыночной структуры нашей страны. К плюсам данной управленческой профессии можно отнести не только престижность и высокую оплату, но и навыки, с помощью которых менеджер умеет подстраиваться под любую жизненную ситуацию и находить выходы из неприятных положений.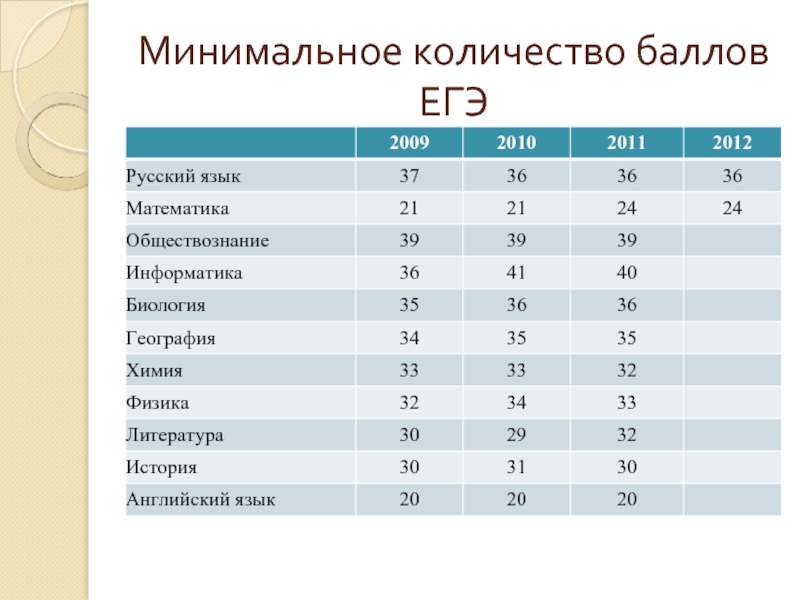
Небольшое заключение
«Все профессии нужны, все профессии важны». Так говорилось раньше. Не потеряла эта фраза актуальности и сегодня. При выборе специальности важно помнить, что не следует идти на ту профессию, к которой не лежит душа. Неважно, насколько актуальна выбранная. Если человек любит то, что делает, то его деятельность будет востребована.
| Наименование специальности | Перечень вступительных испытаний в форме ЕГЭ |
| Самарский государственный университет (СамГУ) | |
| Математика | Математика, физика, русский язык |
| Прикладная математика и информатика | Математика, физика, русский язык |
| Физика | Физика, математика, русский язык |
| Механика | Математика, физика, русский язык |
| Химия | Химия, математика, русский язык |
| Биология | Биология, математика, русский язык |
| Социология | Обществознание, русский язык, иностранный язык |
| Психология | Обществознание, русский язык, биология |
| Культурология | Обществознание, русский язык, иностранный язык |
| История | История Россия, русский язык, обществознание или иностранный язык (по выбору абитуриента) |
| Юриспруденция | Обществознание, русский язык, история России |
| Филология русский язык и литература | Русский язык, литература, история России |
| Английская филология | Английский язык, русский язык, история России |
| Немецкая филология | Немецкий язык, русский язык, обществознание |
| Социальная педагогика | Обществознание, русский язык, биология |
| Государственное и муниципальное управление | Обществознание, русский язык, математика |
| Менеджмент организации | Математика, русский язык, обществознание |
| Математические методы в экономике | Математика, русский язык, обществознание |
| Компьютерная безопасность | Математика, физика, русский язык |
| Организация и технология защиты информации | Математика, физика, русский язык |
| Социальная работа | Обществознание, русский язык, биология |
| Документоведение и документационное обеспечение управления | История России, русский язык, обществознание или иностранный язык (по выбору абитуриента) |
| Международные отношения | История России, русский язык, иностранный язык |
| Журналистика | Обществознание, русский язык, иностранный язык |
| Математическое обеспечение и администрирование информационных систем | Математика, физика, русский язык |
| Самарский государственный аэрокосмический университет (СГАУ) | |
| Ракетостроение | Математика, физика, русский язык |
| Космические летательные аппараты и разгонные блоки | Математика, физика, русский язык |
| Динамика и прочность машин | Математика, физика, русский язык |
| Управление качеством | Математика, физика, русский язык |
| Моделироваание и исследование операций в организационно-технических системах | Математика, физика, русский язык |
| Автоматизированное управление жизненным циклом продукции | Математика, физика, русский язык |
| Ракетные двигатели | Математика, физика, русский язык |
| Лазерные системы в ракетной технике и космонавтике | Математика, физика, русский язык |
| Гидравлические машины, гидроприводы и гидропневмоавтоматика | Математика, физика, русский язык |
| Техническая эксплуатация авиационных электросистем и пилотажно-навигационных комплексов | Математика, физика, русский язык |
| Машины и технология обработки металлов давлением | Математика, физика, русский язык |
| Бытовая радиоэлектронная аппаратура | Математика, физика, русский язык |
| Биотехнические и медицинские аппараты и системы | Математика, физика, русский язык |
| Экономика и управление на предприятии (по отраслям) | Математика, физика, русский язык |
| Математические методы в экономике | Математика, физика, русский язык |
| Самолето- и вертолетостроение | Математика, физика, русский язык |
| Стандартизация и сертификация (по отраслям) | Математика, физика, русский язык |
| Механика | Математика, физика, русский язык |
| Авиационные двигатели и энергетические установки | Математика, физика, русский язык |
| Двигатели внутреннего сгорания | Математика, физика, русский язык |
| Техническая эксплуатация летательных аппаратов и двигателей | Математика, физика, русский язык |
| Нанотехнология в электронике | Математика, физика, русский язык |
| Обработка металлов давлением | Математика, физика, русский язык |
| Радиотехника | Математика, физика, русский язык |
| Проектирование и технология радиоэлектронных средств | Математика, физика, русский язык |
| Автоматизированные системы обработки информации и управления | Математика, физика, русский язык |
| Компьютерные системы управления качеством для автоматизированных производств | Математика, физика, русский язык |
| Прикладная математика и информатика | Математика, физика, русский язык |
| Прикладные математика и физика | Математика, физика, русский язык |
| Организация перевозок и управление на транспорте (по видам) | Математика, физика, русский язык |
| Менеджмент организации | Математика, иностранный язык, русский язык |
| Самарский государственный технический университет (СамГТУ) | |
| Прикладная математика и информатика | Математика, физика, русский язык |
| Профессиональное обучение (по отраслям) | Математика, физика, русский язык |
| Национальная экономика | Математика, обществознание, русский язык |
| Экономика и управление на предприятии (в машиностроении и ТЭК) | Математика, обществознание, русский язык |
| Государственное и муниципальное управление | Математика, обществознание, русский язык |
| Управление персоналом | Математика, обществознание, русский язык |
| Комплексная защита объектов информации | Математика, физика, русский язык |
| Прикладная информатика (в экономике) | Математика, физика, русский язык |
| Разработка и эксплуатация нефтяных и газовых месторождений | Математика, физика, русский язык |
| Проектирование, сооружение и эксплуатация нефтегазопроводов и нефтегазохранилищ | Математика, физика, русский язык |
| Бурение нефтяных и газовых скважин | Математика, физика, русский язык |
| Тепловые электрические станции | Математика, физика, русский язык |
| Промышленная теплоэнергетика | Математика, физика, русский язык |
| Энергетика теплотехнологий | Математика, физика, русский язык |
| Электрические станции | Математика, физика, русский язык |
| Электроэнергетические системы и сети | Математика, физика, русский язык |
| Электроснабжение (по отраслям) | Математика, физика, русский язык |
| Металловедение и термическая обработка металлов | Математика, физика, русский язык |
| Порошковая металлургия, композиционные материалы, покрытия | Математика, физика, русский язык |
| Машины и технология литейного производства | Математика, физика, русский язык |
| Оборудование и технология повышения износостойкости и восстановления деталей машин и аппаратов | Математика, физика, русский язык |
| Машины и технология высокоэффективных процессов обработки материалов | Математика, физика, русский язык |
| Управление и информатика в технических системах | Математика, физика, русский язык |
| Автономные информационные и управляющие системы | Математика, физика, русский язык |
| Автомобили и автомобильное хозяйство | Математика, физика, русский язык |
| Сервис транспортных и технологических машин и оборудования | Математика, физика, русский язык |
| Организация и безопасность движения | Математика, физика, русский язык |
| Информационно-измерительная техника и технологии | Математика, физика, русский язык |
| Стандартизация и сертификация | Математика, физика, русский язык |
| Метрология и метрологическое обеспечение | Математика, физика, русский язык |
| Бытовая радиоэлектронная аппаратура | Математика, физика, русский язык |
| Электромеханика | Математика, физика, русский язык |
| Электропривод и автоматика промышленных установок и технологических комплексов | Математика, физика, русский язык |
| Электротехнологические установки и системы | Математика, физика, русский язык |
| Вычислительные машины, комплексы, системы и сети | Математика, физика, русский язык |
| Автоматизированные системы обработки информации и управления | Математика, физика, русский язык |
| Химическая технология органических веществ | Математика, физика или химия (по выбору абитуриента), русский язык |
| Химическая технология природных энергоносителей и углеродных материалов | Математика, физика или химия (по выбору абитуриента), русский язык |
| Технология переработки пластических масс и эластомеров | Математика, физика или химия (по выбору абитуриента), русский язык |
| Химическая технология высокомолекулярных соединений | Математика, физика или химия (по выбору абитуриента), русский язык |
| Химическая технология полимерных композиций, порохов и твердых ракетных топлив | Математика, физика или химия (по выбору абитуриента), русский язык |
| Технология твердых энергонасыщенных материалов и изделий | Математика, физика или химия (по выбору абитуриента), русский язык |
| Технология бродильных производств и виноделие | Математика, физика или химия (по выбору абитуриента), русский язык |
| Технология хлеба, кондитерских и макаронных изделий | Математика, физика или химия (по выбору абитуриента), русский язык |
| Технология жиров, эфирных масел и парфюмерно-косметических продуктов | Математика, физика или химия (по выбору абитуриента), русский язык |
| Защита в чрезвычайных ситуациях | Математика, физика, русский язык |
| Охрана окружающей среды и рациональное использование природных ресурсов | Математика, физика или химия (по выбору абитуриента), русский язык |
| Машины и оборудование нефтяных и газовых промыслов | Математика, физика, русский язык |
| Оборудование нефтегазопереработки | Математика, физика, русский язык |
| Технология машиностроения | Математика, физика, русский язык |
| Металлообрабатывающие станки и комплексы | Математика, физика, русский язык |
| Автоматизация технологических процессов и производств | Математика, физика, русский язык |
| Электроснабжение предприятий | Математика, физика, русский язык |
| Релейная защита и автоматизация электроэнергетических систем | Математика, физика, русский язык |
| Товароведение и экспертиза товаров (по областям применения) | Математика, физика, русский язык |
| Литейное производство черных и цветных металлов | Математика, физика, русский язык |
| Инструментальные системы машиностроительных производств | Математика, физика, русский язык |
| Биотехнология | Математика, физика или химия (по выбору абитуриента), русский язык |
| Химия | Математика, химия, русский язык |
| Физические процессы горного или нефтегазового производства | Математика, физика, русский язык |
| Связи с общественностью | Математика, обществознание, русский язык |
| Самарский государственный экономический университет (СГЭУ) | |
| Юриспруденция | Обществознание, история России, русский язык |
| Экономическая теория | Математика, обществознание, русский язык |
| Экономика труда | Математика, обществознание, русский язык |
| Финансы и кредит | Математика, обществознание, русский язык |
| Статистика | Математика, обществознание, русский язык |
| Бухгалтерский учет, анализ и аудит | Математика, обществознание, русский язык |
| Мировая экономика | Математика, обществознание, русский язык |
| Национальная экономика | Математика, обществознание, русский язык |
| Экономика и управление на предприятии: -в машиностроении; -АПК; -пищевая промышленность | Математика, обществознание, русский язык |
| Менеджмент организации | Математика, обществознание, русский язык |
| Сервис | Математика, обществознание, русский язык |
| Маркетинг | Математика, обществознание, русский язык |
| Управление персоналом | Математика, обществознание, русский язык |
| Коммерция (торговое дело) | Математика, обществознание, русский язык |
| Прикладная информатика | Математика, обществознание, русский язык |
| Социально-экономическое образование (бакалавриат) | Математика, обществознание, русский язык |
| Экономика (бакалавриат) | Математика, обществознание, русский язык |
| Реклама | Математика, обществознание, русский язык |
| Самарская государственная сельскохозяйственная академия (СГСХА) | |
| Механизация сельского хозяйства | Математика, физика, русский язык |
| Бухгалтерский учет, анализ и аудит | Математика, биология, русский язык |
| Экономика и управление на предприятии | Математика, биология, русский язык |
| Технология производства и переработки сельскохозяйственной продукции | Биология, математика, русский язык |
| Профессиональное обучение | Математика, физика, русский язык |
| Технология обслуживания и ремонта машин в АПК | Математика, физика, русский язык |
| Товароведение и экспертиза товаров (в сфере обращения сельскохозяйственного сырья и продовольственных товаров) | Математика, биология, русский язык |
| Товароведение и экспертиза товаров (в области таможенной деятельности) | Математика, физика, русский язык |
| Самарская государственная академия путей собщения (СамГАПС) | |
| Бухгалтерский учет, анализ и аудит | Математика, обществознание, русский язык |
| Экономика и управление на предприятии (железнодорожный транспорт) | Математика, обществознание, русский язык |
| Управление персоналом | Математика, обществознание, русский язык |
| Информационные системы и технологии | Математика, физика, русский язык |
| Поволжская государственная академия телекоммуникаций и информатики (ПГАТИ) | |
| Информационные системы и технологии | Математика, физика, русский язык |
| Защищенные системы связи | Математика, физика, русский язык |
| Информационная безопасность телекоммуникационных систем | Математика, физика, русский язык |
| Радиосвязь, радиовещание и телевидение | Математика, физика, русский язык |
| Радиотехника | Математика, физика, русский язык |
| Самарский государственный медицинский университет Федерального агентства по здравоохранению и социальному развитию (СамГМУ) | |
| Медико-профилактическое дело | Биология, химия, русский язык |
| Специальная психология | Биология, математика, русский язык |
| Экономика и управление здравоохранением | Биология, математика, русский язык |
| Клиническая психология | Биология, математика, русский язык |
| Самарский государственный архитектурно-строительный университет (СамГАСу) | |
| Дизайн | Русский язык |
| Архитектура | Русский язык |
| Промышленное и гражданское строительство | Математика, физика, русский язык |
| Гидротехническое строительство | Математика, физика, русский язык |
| Городское строительство и хозяйство | Математика, физика, русский язык |
| Производство строительных материалов, изделий и конструкций | Математика, физика, русский язык |
| Теплогазоснабжение и вентиляция | Математика, физика, русский язык |
| Водоснабжение и водоотведение | Математика, физика, русский язык |
| Автомобильные дороги и аэродромы | Математика, физика, русский язык |
| Механизация и автоматизация строительства | Математика, физика, русский язык |
| Инженерная защита окружающей среды | Математика, физика, русский язык |
| Экономика и управление на предприятии: -в городском хозяйстве; -операции с недвижимым имуществом; -строительстве | Математика, физика, русский язык |
| Менеджмент организации | Математика, физика, русский язык |
| Управление качеством | Математика, физика, русский язык |
| Экспертиза и управление недвижимостью | Математика, физика, русский язык |
| Менеджмент (бакалавриат) | Математика, физика, русский язык |
| Архитектура (бакалавриат) | Математика, физика, русский язык |
| Искусство (бакалавриат) | Русский язык, иностранный язык |
| Защита окружающей среды (бакалавриат) | Математика, физика, русский язык |
| Строительство (бакалавриат) | Математика, физика, русский язык |
| Информационные системы и технологии | Математика, физика, русский язык |
| Пожарная безопасность | Математика, физика, русский язык |
| Самарский государственный педагогический университет (СамГПУ) | |
| Журналистика | Русский язык, обществознание или история России (по выбору абитуриента) |
| Информатика | Математика, физика, русский язык |
| Музыкальное образование | Русский язык |
| Педагогика и психология | Математика, биология или обществознание (по выбору абитуриента), русский язык |
| Педагогика и методика начального образования | Русский язык, математика, биология или обществознание (по выбору абитуриента) |
| Специальная психология | Русский язык, биология, литература или история России, или обществознание, или математика (по выбору абитуриента) |
| Математика | Математика, физика, русский язык |
| Физика | Физика, математика, русский язык |
| Химия | Химия, биология или математика (по выбору абитуриента), русский язык |
| Биология | Биология, химия или математика (по выбору абитуриента), русский язык |
| Русский язык и литература | Русский язык, литература, обществознание или история России (по выбору абитуриента) |
| Педагогика балета | Русский язык |
| Менеджмент организации | Математика, обществознание, русский язык |
| Психология | Биология, математика или обществознание (по выбору абитуриента), русский язык |
| Физическая культура и спорт | Биология, русский язык |
| Изобразительное искусство | Русский язык |
| Педагогика и методика дошкольного образования | Русский язык, математика, биология или обществознание (по выбору абитуриента) |
| Социальная педагогика | Обществознание, русский язык, биология или обществознание (по выбору абитуриента) |
| Олигофренопедагогика | Русский язык, биология, литература или история России, или обществознание, или математика (по выбору абитуриента) |
| Логопедия | Русский язык, биология, литература или история России, или обществознание, или математика (по выбору абитуриента) |
| География | География, биология или математика (по выбору абитуриента), русский язык |
| История | История России, обществознание, русский язык |
| Культурология | История России, литература или обществознание (по выбору абитуриента), русский язык |
| Иностранный язык | Иностранный язык, русский язык, обществознание или история России или литература |
| Экономическая теория | Обществознание, математика, русский язык |
| Тифлопедагогика | Русский язык, биология, литература или история России, или обществознание, или математика (по выбору абитуриента) |
| Сурдопедагогика | Русский язык, биология, литература или история России, или обществознание, или математика (по выбору абитуриента) |
| Физическая культура | Биология, русский язык |
| Самарская государственная академия культуры и искусств (СГАКИ) | |
| Культурология | Русский язык, история России, иностранный язык или обществознание (по выбору абитуриента) |
| Библиотечно-информационная деятельность | Русский язык, история России, иностранный язык или обществознание (по выбору абитуриента) |
| Социальная работа | Русский язык, история России, иностранный язык или обществознание (по выбору абитуриента) |
| Тольяттинский государственный университет (ТГУ) | |
| Двигатели внутреннего сгорания | Физика, математика, русский язык |
| Автомобиле- и тракторостроение | Физика, математика, русский язык |
| Автомобили и автомобильное хозяйство | Физика, математика, русский язык |
| Безопасность технологических процессов и производств | Физика, математика, русский язык |
| Технология машиностроения | Физика, математика, русский язык |
| Инженерная защита окружающей среды | Физика, математика, русский язык |
| Металлообрабатывающие станки и комплексы | Физика, математика, русский язык |
| Машины и технология обработки металлов давлением | Физика, математика, русский язык |
| Оборудование и технология сварочного производства | Физика, математика, русский язык |
| Физика | Физика, математика, русский язык |
| Математическое обеспечение и администри- рование информационных систем | Математика, физика, русский язык |
| Физика металлов | Физика, математика, русский язык |
| Роботы и робототехнические системы | Физика, математика, русский язык |
| Изобразительное искусство | Русский язык |
| Дизайн | Русский язык |
| Декоративно-прикладное искусство | Русский язык |
| Технология и предпринимательство | Математика, русский язык |
| Дошкольная педагогика и психология | Русский язык, биология |
| Социология | Русский язык, история России или обществознание (по выбору абитуриента) |
| Физическая культура и спорт | Биология, русский язык |
| Физическая культура для лиц с отклонениями в состоянии здоровья | Биология, русский язык |
| Промышленное и гражданское строительство | Физика, математика, русский язык |
| Городское строительство и хозяйство | Физика, математика, русский язык |
| Теплогазоснабжение и вентиляция | Физика, математика, русский язык |
| Водоснабжение и водоотведение | Физика, математика, русский язык |
| Химия | Химия, математика, русский язык |
| Машины и аппараты химических производств | Химия или физика, математика, русский язык |
| Химическая технология органических веществ | Химия, математика, русский язык |
| Технология продуктов общественного питания | Химия, математика, русский язык |
| Товароведение и экспертиза товаров | Химия, математика, русский язык |
| Финансы и кредит | Математика, русский язык |
| Бухгалтерский учет, анализ и аудит | Математика, русский язык |
| Экономика и управление на предприятии машиностроения | Математика, русский язык |
| Экономика труда | Математика, русский язык |
| Управление персоналом | Математика, русский язык |
| Управление качеством | Математика, русский язык |
| Электроснабжение | Физика, математика, русский язык |
| Электрооборудование и электрохозяйства предприятий, организаций и учреждений | Физика, математика, русский язык |
| Электрооборудование автомобилей и тракторов | Физика, математика, русский язык |
| Промышленная электроника | Физика, математика, русский язык |
| Автоматизация технологических процессов и производств | Физика, математика, русский язык |
| Математика с дополнительной специальностью информатика | Математика, русский язык |
| Прикладная информатика (в социальной сфере) | Математика, русский язык |
| История | История России, русский язык |
| Перевод и переводоведение | Иностранный язык, русский язык |
| Теория и методика преподавания иностранного языка и культуры | Иностранный язык, русский язык |
| Педагогика и психология | Русский язык, биология |
| Психология | Биология, русский язык |
| Русский язык и литература | Русский язык, литература |
| Прикладная математика и информатика | Математика, русский язык |
| Журналистика | Русский язык, литература |
| Тольяттинский государственный университет сервиса (ТГУС) | |
| Финансы и кредит | Математика, история России, русский язык |
| Бухгалтерский учет, анализ и аудит | Математика, история России, русский язык |
| Экономика и управление на предприятии | Математика, история России, русский язык |
| Маркетинг | Математика, русский язык |
| Управление качеством | Математика, русский язык |
| Декоративно-прикладное искусство и народные промыслы | Русский язык |
| Дизайн | Русский язык |
| Искусство интерьера | Русский язык |
| Художественное проектирование костюма | Русский язык |
| Домоведение | Русский язык, история России |
| Социальная работа | Русский язык, история России |
| Социальная работа | Русский язык, история России |
| Туризм | Иностранный язык, русский язык, история России |
| Туризм | Иностранный язык, русский язык, история России |
| Социально-культурный сервис и туризм | Иностранный язык, русский язык, история России |
| Сервис | Математика, русский язык |
| Товароведение и экспертиза товаров (в сфере производства и обращения непродовольственных товаров и сырья) | Математика, русский язык |
| Коммерция (торговое дело) | Математика, русский язык |
| Прикладная информатика (в экономике) | Математика, история России, русский язык |
| Бытовая радиоэлектронная аппаратура | Математика, русский язык |
| Бытовые машины и приборы | Математика, русский язык |
| Конструирование швейных изделий | Математика, русский язык |
| Экономика | Математика, история России, русский язык |
| Менеджмент | Математика, история России, русский язык |
| Коммерция (торговое дело) | Математика, история России, русский язык |
| Информатика и вычислительная техника | Математика, история России, русский язык |
| Электроника и микроэлектроника | Математика, русский язык |
| Тольяттинский институт искусств | |
| Инструментальное исполнительство (по видам инструментов) | Русский язык |
| Вокальное искусство (по видам вокального искусства) | Русский язык |
| Самарский филиал НОУ ВПО Высшая школа приватизации и предпринимательства-институт | |
| Менеджмент организации | Математика, русский язык |
| Финансы и кредит | Математика, русский язык |
Филиал НОУ ВПО Самарской гуманитарной академии в г. Тольятти Тольятти | |
| Юриспруденция | Обществознание, русский язык |
| Бухгалтерский учет, анализ и аудит | Математика, русский язык |
| Налоги и налогообложение | Математика, русский язык |
| Филология | Иностранный язык, русский язык |
| Психология | Русский язык |
| НОУ ВПО Тольяттинская академия управления* | |
| Финансы и кредит | Русский язык, английский язык, математика |
| Менеджмент организации | Русский язык, английский язык, математика |
| Прикладная информатика | Русский язык, английский язык, математика |
| Связи с общественностью | Русский язык, английский язык, математика |
| Дизайн | Русский язык, английский язык, математика |
| *Бюджетных форм обучения в Тольяттинской академии управления не существует. Обучение производится на платной основе | |
| Самарский филиал ГОУ ВПО Саратовский юридический институт Министерства внутренних дел Российской Федерации | |
| Юриспруденция | История России, обществознание, русский язык |
| Правоохранительная деятельность | История России, обществознание, русский язык |
| Правоохранительная деятельность | История России, русский язык |
| Самарский муниципальный университет Наяновой | |
| Прикладная математика и информатика | Математика, русский язык |
| Философия | Русский язык |
| Биология | Русский язык, математика |
| Бухгалтерский учет, анализ и аудит | Математика, русский язык |
| Юриспруденция | Русский язык |
| Связи с общественностью | Русский язык |
| Управление качеством | Математика, русский язык |
Три причины сдавать ЕГЭ по профильной математике — Российская газета
1 февраля заканчивается срок подачи заявлений на ЕГЭ. Никаких изменений по датам на этот счет пока не объявлено, так что просчитываем варианты поступления в вузы и обращаем самое пристальное внимание на… ЕГЭ по профильной математике.
Никаких изменений по датам на этот счет пока не объявлено, так что просчитываем варианты поступления в вузы и обращаем самое пристальное внимание на… ЕГЭ по профильной математике.
Три причины выбрать ЕГЭ по математике
Первая. ЕГЭ по профильной математике на очень большом количестве вузовских специальностей и направлений — в числе однозначно обязательных для всех вузов, как и ЕГЭ по русскому языку (а вот с третьим экзаменом ситуация другая. О ней расскажем ниже). Каких больших групп направлений подготовки это касается? «Математика, информационные науки и технологии», «машиностроение, автоматизация и робототехника», «энергетика и электротехника», а также касается специальностей, связанных с транспортом, строительством, экономикой. К слову, именно на эти направления выделено самое большое количество бюджетных мест.
Вторая. Представьте себе, на таких вроде бы нематематических направлениях, как «промышленное рыболовство», «ландшафтная архитектура», «управление персоналом», «реконструкция и реставрация архитектурного наследия» и даже «сервис» (!) от абитуриента в вузах потребуют ЕГЭ по математике.
Третья. Есть специальности, где ЕГЭ по математике не является обязательным абсолютно для всех вузов, НО (!) учебное заведение теперь имеет право добавить математику в качестве третьего экзамена из списка предложенных. Например, вы собираетесь поступать на «психологию» — популярное, перспективное направление, которое есть во многих вузах. Два ЕГЭ обязательны на «психологии» абсолютно для всех вузов. Это ЕГЭ по русскому языку и биологии, а вот третьим экзаменом может быть обществознание, иностранный язык или… математика. В Санкт-Петербургском госуниверситете, например, на «психологии» от вас попросят именно ЕГЭ по математике (плюс русский и биология). А вот в Южно-Уральском государственном гуманитарно-педагогическом университете абитуриентам вместо математики нужно будет принести ЕГЭ по обществознанию.
Хотите быть режиссером или продюсером? Готовьтесь, что будут вузы, которые потребуют не только ЕГЭ по русскому и литературе, но, возможно, и по профильной математике. Неожиданно? Но дела обстоят именно так. Как узнать, какие ЕГЭ нужны вузам на ваших специальностях? Самый надежный способ — зайти самому на сайт выбранного вуза и изучить список экзаменов. Советуем поторопиться, до 1 февраля не так уж далеко.
Неожиданно? Но дела обстоят именно так. Как узнать, какие ЕГЭ нужны вузам на ваших специальностях? Самый надежный способ — зайти самому на сайт выбранного вуза и изучить список экзаменов. Советуем поторопиться, до 1 февраля не так уж далеко.
PS. Если уж совсем дела с математикой обстоят туго, сдавайте ЕГЭ по информатике. Информатику в качестве третьего предмета тоже наверняка будут спрашивать на многих специальностях.
Куда меня приведет математика?
Направление математики бакалавриата предлагает основу для студентов, заинтересованных в понимании того, как подходить к задачам с математическими решениями. Специальность «Математическая экономика» предлагает студентам программу, сочетающую математику, статистику и экономику.
Куда может привести меня математика?
Куда может привести меня математическая экономика?
Карьера в цифрах? Вы делаете математику
Математика сложная, полезная и веселая. Это и логично, и креативно. Студенты, изучающие математику, имеют множество возможностей. Специальность по математике готовит студентов к традиционным занятиям, таким как аспирантура, преподавание и работа актуарием. Учащиеся, любящие математику, находят, что специализацию по математике можно сочетать с предпрофессиональной учебной программой или специализацией в области естественных или инженерных наук, чтобы обеспечить прочную основу для учебы в аспирантуре или работы в области, связанной с математикой.
Это и логично, и креативно. Студенты, изучающие математику, имеют множество возможностей. Специальность по математике готовит студентов к традиционным занятиям, таким как аспирантура, преподавание и работа актуарием. Учащиеся, любящие математику, находят, что специализацию по математике можно сочетать с предпрофессиональной учебной программой или специализацией в области естественных или инженерных наук, чтобы обеспечить прочную основу для учебы в аспирантуре или работы в области, связанной с математикой.
Специальность «Математическая экономика» дает возможность студентам, интересующимся математикой и бизнесом или экономикой, объединить эти интересы.Департамент математики предлагает как степень бакалавра наук, так и степень бакалавра гуманитарных наук. Каждая степень может быть получена с помощью варианта A: математика или варианта B: математические науки. Вариант математики выбирают большинство учащихся. Вариант математических наук сочетает в себе изучение математики, статистики и информатики и готовит студентов к карьере, связанной с приложениями математики. Несовершеннолетний по математике доступен для студентов, которые хотели бы продолжить изучение математики, специализируясь в другой области.В дополнение к степеням бакалавра математический факультет предлагает программы, ведущие к получению степени магистра гуманитарных наук (MA), магистра наук (MS) и доктора философии (Ph.D).
Несовершеннолетний по математике доступен для студентов, которые хотели бы продолжить изучение математики, специализируясь в другой области.В дополнение к степеням бакалавра математический факультет предлагает программы, ведущие к получению степени магистра гуманитарных наук (MA), магистра наук (MS) и доктора философии (Ph.D).
Какие навыки развивает изучение математики?
- критическое мышление
- решение проблем
- аналитическое мышление
- количественные рассуждения
- способность манипулировать точными и сложными идеями
- создавать логические аргументы и выявлять нелогичные аргументы
- связь
- управление временем
- работа в команде
- независимость
Карьерные возможности
Карьерные возможности не ограничены для математических специальностей.Они могут получить последипломное образование, сделать карьеру в бизнесе, науке или технических областях или дисциплинах, таких как социальные услуги, образование и правительство. Некоторые из профессий, которыми занимаются математики, включают:
Некоторые из профессий, которыми занимаются математики, включают:
- бухгалтер
- актуарий
- программист
- доктор
- инженер
- инвестиционный менеджер
- адвокат
- государственные исследования и лаборатории
- математик-теоретик
- математик
- численный аналитик
- статистик
- учитель
- исследователь рынка
- системный аналитик
- банковское дело
- правительство
- космическая/авиационная промышленность
Для получения дополнительной информации о карьере перейдите по следующему адресу:
Для получения дополнительной информации о возможностях карьерного роста свяжитесь с консультантом по вопросам карьеры Джейми Джонсон по адресу [email protected] или (859) 257-4023.
Сборник компетенций: степень математической экономики
Специальность «Математическая экономика» предлагает студентам программу на получение степени, сочетающую математику, статистику и экономику. Во многих отношениях программа математической экономики параллельна инженерной философии. Он сочетает количественные методы математики с прикладными науками для решения реальных задач. В связи с постоянно растущим значением сектора услуг в нашей экономике степень математической экономики окажется ценным активом.Программа даст студенту возможность изучить увлекательную коллекцию идей, а также предоставит студенту очень востребованные на рынке навыки.
Во многих отношениях программа математической экономики параллельна инженерной философии. Он сочетает количественные методы математики с прикладными науками для решения реальных задач. В связи с постоянно растущим значением сектора услуг в нашей экономике степень математической экономики окажется ценным активом.Программа даст студенту возможность изучить увлекательную коллекцию идей, а также предоставит студенту очень востребованные на рынке навыки.
Какие навыки развивает изучение математической экономики?
- способность к математике и статистике
- способность решать проблемы
- умение общаться с публичными выступлениями и письменными заданиями
- способность сотрудничать с другими
Карьерные возможности
В сегодняшнем все более усложняющемся мире международного бизнеса для успеха необходима сильная подготовка в области основ экономики и математики.Эта программа на получение степени предназначена для подготовки студента к непосредственному погружению в мир бизнеса с навыками, которые пользуются большим спросом, или к продолжению обучения в аспирантуре по экономике или финансам. Степень в области математической экономики подготовит студента к началу карьеры в области исследования операций или актуарной науки. Другие профессии включают, но не ограничиваются следующим:
Степень в области математической экономики подготовит студента к началу карьеры в области исследования операций или актуарной науки. Другие профессии включают, но не ограничиваются следующим:
- экономист
- бухгалтер по управленческому учету
- актуарий
- банковский ревизор
- аналитик по маркетинговым исследованиям
- финансовый аналитик
- менеджер по маркетингу/продажам
- финансовый план
- эксперт по претензиям
- инвестиционный менеджер
- специалист по международной торговле
- инвестор в недвижимость
- статистик
- учитель
- профессор
Для получения дополнительной информации о карьере перейдите по следующему адресу:
Для получения дополнительной информации о карьерных возможностях обращайтесь в UK Career Center.
Какое математическое образование может подготовить учащихся к жизни в обществе будущего?
Несмотря на то, что в (публичных) дискуссиях об образовании будущего доминируют навыки 21-го века, мы считаем содержание, которое необходимо преподавать, не менее важным, особенно в случае математики. На наш взгляд, математическое образование должно готовить учащихся к применению математики во всех видах рабочих и повседневных ситуаций. Далее мы в первую очередь рассмотрим использование математики с точки зрения возможности трудоустройства, поскольку именно здесь мы видим наибольшее влияние цифровизации нашего общества.Чтобы понять, каковы на самом деле требования математики, мы рассмотрим три различных точки зрения. (1) Поскольку математика на рабочем месте существенно отличается от школьной математики, мы попытаемся составить схему характеристик математики на рабочем месте , чтобы получить представление о том, к какой математической деятельности должны быть готовы учащиеся. (2) Чтобы предвидеть потребности 21-го века, мы возьмем за отправную точку перспективу того, что все будут работать в компьютеризированной среде.Здесь мы будем использовать более аналитический подход при попытке определить математические компетенции , которые дополняют работу компьютеров . (3) Наконец, мы будем размышлять о том, как растущее использование информационных технологий повлияет на математические темы, которые приобретают значение под влиянием использования информационных технологий, чтобы определить, какое математическое содержание придется изучать.
На наш взгляд, математическое образование должно готовить учащихся к применению математики во всех видах рабочих и повседневных ситуаций. Далее мы в первую очередь рассмотрим использование математики с точки зрения возможности трудоустройства, поскольку именно здесь мы видим наибольшее влияние цифровизации нашего общества.Чтобы понять, каковы на самом деле требования математики, мы рассмотрим три различных точки зрения. (1) Поскольку математика на рабочем месте существенно отличается от школьной математики, мы попытаемся составить схему характеристик математики на рабочем месте , чтобы получить представление о том, к какой математической деятельности должны быть готовы учащиеся. (2) Чтобы предвидеть потребности 21-го века, мы возьмем за отправную точку перспективу того, что все будут работать в компьютеризированной среде.Здесь мы будем использовать более аналитический подход при попытке определить математические компетенции , которые дополняют работу компьютеров . (3) Наконец, мы будем размышлять о том, как растущее использование информационных технологий повлияет на математические темы, которые приобретают значение под влиянием использования информационных технологий, чтобы определить, какое математическое содержание придется изучать.
Характеристики математики на рабочем месте
Многие исследователи математики на рабочем месте обнаружили, что математика, которой люди занимаются вне школы, значительно отличается от характера школьной математики (Lave, 1988; Nunes, Schliemann & Carraher, 1993; Saxe , 1988).Хотя требования на рабочем месте изменились после этих исследований, текущие исследования продолжают выявлять разрыв между математикой на рабочем месте и школьной математикой (FitzSimons, 2013; Wedege, 2002). Поэтому мы считаем целесообразным изучить характер рабочего места, чтобы расширить границы того, как должна выглядеть математика для достижения успеха в будущем.
Неформальный характер математики на рабочем месте.
За последние несколько десятилетий большое количество работ было сосредоточено на математике взрослых и рабочих в различных культурах.Примеры этого типа анализа включают математику плотников (Millroy, 1991), строителей бассейнов (Zevenbergen, 1997), каменщиков (Moreira & Pardal, 2012), строителей (Bessot, 1996), медсестер (Hoyles, Noss & Pozzi, 2001). ) и инженеры-строители (Gainsburg, 2007), и это лишь некоторые из них. Главный вывод этих исследований заключается в том, что математика, преподаваемая в школе, обычно отличается от той математики, которую люди используют для достижения успеха на работе (Marr & Hagston, 2007; Mills, 2012; Wedege, 2002).Например, медсестры не используют традиционные стратегии пропорционального мышления, которым обучают в школе (например, перекрестное умножение), чтобы определить подходящие соотношения для выдачи лекарств пациентам. Скорее, они используют более эффективные, неформальные стратегии, типичные для их ситуации. На самом деле, одно исследование показало, что, хотя большинство медсестер не справляются со школьными тестами на пропорции, они на 100% точны при назначении лекарств в правильных пропорциях с использованием лично разработанных стратегий (Hoyles, Noss, Kent & Bakker, 2013; Perlstein, Callison). , Уайт, Барнс и Эдвардс, 1979).
) и инженеры-строители (Gainsburg, 2007), и это лишь некоторые из них. Главный вывод этих исследований заключается в том, что математика, преподаваемая в школе, обычно отличается от той математики, которую люди используют для достижения успеха на работе (Marr & Hagston, 2007; Mills, 2012; Wedege, 2002).Например, медсестры не используют традиционные стратегии пропорционального мышления, которым обучают в школе (например, перекрестное умножение), чтобы определить подходящие соотношения для выдачи лекарств пациентам. Скорее, они используют более эффективные, неформальные стратегии, типичные для их ситуации. На самом деле, одно исследование показало, что, хотя большинство медсестер не справляются со школьными тестами на пропорции, они на 100% точны при назначении лекарств в правильных пропорциях с использованием лично разработанных стратегий (Hoyles, Noss, Kent & Bakker, 2013; Perlstein, Callison). , Уайт, Барнс и Эдвардс, 1979).
Значение контекста на рабочем месте.

Несмотря на призывы многих отчетных, исследовательских и математических организаций сделать математику контекстуализированной, многие школы продолжают представлять математику как абстрактные, вырванные из контекста задачи. Напротив, исследования математики на рабочем месте показывают, что математика обычно не выполняется вне контекста, состоящего из целей и задач. Например, на рабочем месте редко можно встретить отдельные случаи десятичных операций.Скорее, большинство расчетов выполняется в областях математики, таких как алгебра, числа и геометрия, и выполняются как часть контекстуализированной задачи (Wake & Williams, 2001). На этом фоне преподаватели STEM рекомендуют изучать математику, представляя задачи в реалистичных контекстах, таких как биология, физика, инженерия и т. д. (например, Cox, Reynolds, Schunn & Schuchardt, 2016). Здесь необходимы два слова предостережения. Инглиш (2016) отмечает, что исследования STEM, как правило, отодвигают математику на задний план, отводя ее поддержке контекстов STEM, а не важности самой по себе. Во-вторых, контексты, которые используются в обучении математике, имеют тенденцию отражать надуманные ситуации, а не те, которые действительно реалистичны и являются богатыми местами для математизации. Одним отмеченным исключением является работа, проделанная исследователями из Института Фрейденталя (Freudenthal, 1991; Gravemeijer, 2008).
Во-вторых, контексты, которые используются в обучении математике, имеют тенденцию отражать надуманные ситуации, а не те, которые действительно реалистичны и являются богатыми местами для математизации. Одним отмеченным исключением является работа, проделанная исследователями из Института Фрейденталя (Freudenthal, 1991; Gravemeijer, 2008).
Мало того, что работники используют ситуативные, неформальные математические стратегии, они также обычно не считают себя «занимающимися математикой» в своей работе, хотя посторонний может найти математику в изобилии их деятельности (Mills, 2012; Nicol, 2002). .Уэйк и Уильямс (2001) используют теорию деятельности, чтобы объяснить, что математика на рабочем месте и в школе/колледже — это разные жанры, которые пересекаются и имеют определенные границы. С одной стороны, школьная математика находится под влиянием формальной, профессиональной практики математиков и учителей, изучавших математику в этой системе. С другой стороны, в математике на рабочем месте преобладают практические задачи с культурно специфическими инструментами, практиками и дискурсом (Wake & Williams, 2001). Это наблюдение ведет непосредственно к следующей характеристике математики на рабочем месте — значению контекста в обоих жанрах.
Это наблюдение ведет непосредственно к следующей характеристике математики на рабочем месте — значению контекста в обоих жанрах.
Инструменты, практика и дискурс на рабочем месте.
Математические инструменты, методы и дискурс можно рассматривать как сформированные целями и проблемами, возникающими на рабочем месте (Magajna & Monaghan, 2003). Например, Williams, Wake and Boreham (2001) представляют анализ математики работников промышленно развитой химической лаборатории, в которой сотрудники эффективно используют неканонические графы, которые значительно отличаются от обычных графов, изученных в колледже.Хойлс и Носс (Hoyles, Noss, Kent & Bakker, 2010) ввели термин «технико-математическая грамотность» (TML). TML определяются как идиосинкразические формы математики, которые формируются с помощью методов, задач и инструментов на рабочем месте. TML состоят из комбинации математических знаний и контекстуальных знаний.
В уникальном использовании рабочих инструментов доминирует цель, для которой они их используют. Школьные математические практики рассматривают артефакты как концептуальные инструменты, а не как практические инструменты на рабочем месте (Jurdak & Shahin, 2001).Уэйк и Уильямс (2001) предполагают, что целью использования инструментов в школьных условиях является сдача экзамена. Рабочие, напротив, заинтересованы в использовании определенных инструментов для достижения очень четких целей для клиентов. Например, школьники интерпретируют и рассуждают с декартовыми графиками очень формальными способами, в то время как работники химической лаборатории строят их для собственной эффективности (например, имея наименьшее значение переменной справа на оси X).
Школьные математические практики рассматривают артефакты как концептуальные инструменты, а не как практические инструменты на рабочем месте (Jurdak & Shahin, 2001).Уэйк и Уильямс (2001) предполагают, что целью использования инструментов в школьных условиях является сдача экзамена. Рабочие, напротив, заинтересованы в использовании определенных инструментов для достижения очень четких целей для клиентов. Например, школьники интерпретируют и рассуждают с декартовыми графиками очень формальными способами, в то время как работники химической лаборатории строят их для собственной эффективности (например, имея наименьшее значение переменной справа на оси X).
Различаются не только типы инструментов и действий с ними в зависимости от рабочего и школьного жанров, но и практики.Практика решения проблем в обоих жанрах также существенно различается. Мы уже упоминали, что работники используют инструменты не так, как студенты, из-за их общей цели — удовлетворить босса или клиента. Кроме того, рабочие часто сталкиваются со сложными, запутанными проблемами, которые могут иметь несколько правильных решений. Цель для них состоит в том, чтобы найти эти решения и работать в рамках ограничений ситуации, чтобы выбрать наиболее жизнеспособный путь (Brady, Eames & Lesh, 2015). Например, наиболее эффективное решение проблемы архитектурного дизайна может быть не самым дешевым, и фирма может проиграть предложение, если представит его заказчику.Поэтому при выборе пути решения необходимо учитывать определенные компромиссы. Это отличается от школьной математики, в которой учителя представляют аккуратные задачи с одним правильным решением. Цель студентов — найти это решение, чтобы сдать экзамен. Кроме того, проблемы представляются учителем, тогда как на рабочем месте проблемы часто создаются работником. Чтобы подчеркнуть этот момент, инженеры в исследовании Тосмур-Баязита и Убуза предложили изменить методы обучения таким образом, чтобы обучение должно было быть направлено не только на правильное решение уравнений, но и на то, как представлять ключевые особенности реального явления (Тосмур-Баязит).
Кроме того, рабочие часто сталкиваются со сложными, запутанными проблемами, которые могут иметь несколько правильных решений. Цель для них состоит в том, чтобы найти эти решения и работать в рамках ограничений ситуации, чтобы выбрать наиболее жизнеспособный путь (Brady, Eames & Lesh, 2015). Например, наиболее эффективное решение проблемы архитектурного дизайна может быть не самым дешевым, и фирма может проиграть предложение, если представит его заказчику.Поэтому при выборе пути решения необходимо учитывать определенные компромиссы. Это отличается от школьной математики, в которой учителя представляют аккуратные задачи с одним правильным решением. Цель студентов — найти это решение, чтобы сдать экзамен. Кроме того, проблемы представляются учителем, тогда как на рабочем месте проблемы часто создаются работником. Чтобы подчеркнуть этот момент, инженеры в исследовании Тосмур-Баязита и Убуза предложили изменить методы обучения таким образом, чтобы обучение должно было быть направлено не только на правильное решение уравнений, но и на то, как представлять ключевые особенности реального явления (Тосмур-Баязит). и Убуз, 2013).
и Убуз, 2013).
Дискуссия на рабочем месте также радикально отличается от школьной. Значения определенных математических символов и слов оговариваются в условиях деятельности, частью которой являются рабочие или студенты (Wake & Williams, 2001). Это означает, что математический язык и символы, которые используют рабочие, могут не иметь формального значения, используемого в школьных условиях (вспомните идиосинкразическое использование декартовой плоскости лабораторными химиками).
Изменения со временем.
Технический прогресс быстро меняет роль квалифицированных и неквалифицированных рабочих на рабочем месте. Функции планирования в организации когда-то были прерогативой работников управленческого звена; однако технология взяла на себя работу многих неквалифицированных рабочих, которым для достижения успеха на рабочем месте требуется другой набор навыков (Wedege, 2002). Эволюция технологических устройств существенно уменьшила потребность в вычислениях на рабочем месте, и часто работники не осознают необходимость и присутствие математики в своей работе. Технологии также превратили математику в «черный ящик», сделав ее невидимой для рабочего (Williams & Wake, 2007a). Глобализация рабочего места теперь позволяет предприятиям изготавливать продукты на заказ для клиентов по всему миру. Таким образом, глобализация привела к тому, что методы работы на рабочем месте сместились от создания прототипов продуктов (один размер подходит всем) к использованию математических рассуждений и критического мышления для настройки продуктов. Со сложной математикой, скрытой в технологических черных ящиках, крайне важно, чтобы работник понимал математические расчеты в достаточной степени, чтобы создавать входные данные и интерпретировать выходные данные технологии (Kent, Noss, Guile, Hoyles & Bakker, 2007; Gainsburg, 2007).Сотрудники также должны иметь возможность донести математику черного ящика до своих коллег и начальников (Williams & Wake, 2007b). Учитывая необходимость передачи математики, скрытой в технологических черных ящиках, неудивительно, что работодатели считают общение и критическое мышление одними из самых важных навыков, которые они ищут в выпускниках колледжей (Hoyles, Wolf, Kent & Molyneux-Hodgson, 2002).
Технологии также превратили математику в «черный ящик», сделав ее невидимой для рабочего (Williams & Wake, 2007a). Глобализация рабочего места теперь позволяет предприятиям изготавливать продукты на заказ для клиентов по всему миру. Таким образом, глобализация привела к тому, что методы работы на рабочем месте сместились от создания прототипов продуктов (один размер подходит всем) к использованию математических рассуждений и критического мышления для настройки продуктов. Со сложной математикой, скрытой в технологических черных ящиках, крайне важно, чтобы работник понимал математические расчеты в достаточной степени, чтобы создавать входные данные и интерпретировать выходные данные технологии (Kent, Noss, Guile, Hoyles & Bakker, 2007; Gainsburg, 2007).Сотрудники также должны иметь возможность донести математику черного ящика до своих коллег и начальников (Williams & Wake, 2007b). Учитывая необходимость передачи математики, скрытой в технологических черных ящиках, неудивительно, что работодатели считают общение и критическое мышление одними из самых важных навыков, которые они ищут в выпускниках колледжей (Hoyles, Wolf, Kent & Molyneux-Hodgson, 2002).
Этот очерк характеристик математики на рабочем месте предлагает основу для обсуждения целей математического образования.Однако, чтобы определить цели на будущее, мы должны быть более конкретными из-за возросших требований цифрового общества. Теперь мы обратимся к обсуждению математических компетенций, на которые повлияла компьютерная эпоха.
Математические компетенции, дополняющие работу на компьютере
Если будет признано, что одной из целей математического образования является подготовка учащихся к жизни и работе, то при математическом образовании необходимо будет учитывать вышеупомянутые характеристики рабочего места.Эта идея не нова; это выражается в призывах к моделированию и аппликации, к использованию аутентичных проблемных ситуаций в обучении. В настоящее время последний является одним из главных инициаторов движения STEM. Оборотная сторона медали, однако, привлекает меньше внимания, а именно характер преподаваемой математики также должен быть адаптирован. Математика, изучаемая в школе, должна позволять гибкое использование и адаптацию. В связи с этим мы можем вернуться к Фрейденталю (1968), который еще в 1960-х годах говорил о том, что преподавание математики может быть полезным.Он утверждал, что формальная математика обычно применима в теории, но только для экспертов с высоким уровнем знаний, а не для среднего студента. Мы вернемся к этому моменту позже.
Математика, изучаемая в школе, должна позволять гибкое использование и адаптацию. В связи с этим мы можем вернуться к Фрейденталю (1968), который еще в 1960-х годах говорил о том, что преподавание математики может быть полезным.Он утверждал, что формальная математика обычно применима в теории, но только для экспертов с высоким уровнем знаний, а не для среднего студента. Мы вернемся к этому моменту позже.
Во-первых, мы хотим подчеркнуть, что когда мы рассматриваем математическое образование в будущем, это больше, чем предвидение характеристик рабочего места. Мы движемся к будущему, в котором все математические расчеты будут выполнять машины. Таким образом, возникает вопрос: «Какую математику мы учим, когда всю математику делают компьютеры?» (Вольфрам, 2010).Вольфрам (2010) пытается ответить на этот вопрос, анализируя, что связано с математикой в реальном мире. Он утверждает, что это включает в себя следующие шаги:
Понимание того, где применима математика
Перевод практических задач в математические задачи
Решение математической задачи
Интерпретация и оценка результатов
Он отмечает, что, как правило, в математическом образовании систематически рассматривается только третий шаг, и что именно этот шаг все чаще выполняется с помощью компьютеров! В математическом образовании внимание должно быть смещено к остальным трем шагам. Более того, как ясно выяснилось в исследованиях на рабочем месте, когда компьютеры выполняют математические расчеты, нужно понимать математику, лежащую в основе этих расчетов.
Более того, как ясно выяснилось в исследованиях на рабочем месте, когда компьютеры выполняют математические расчеты, нужно понимать математику, лежащую в основе этих расчетов.
Мы можем объединить первый, второй и последний этапы под заголовком «моделирование и применение», отделив при этом «проверку расчетов» от интерпретации и оценки результатов. Как мы покажем позже, приоритетность проверки вычислений над выполнением стандартных процедур имеет серьезные последствия для содержания и структуры учебного плана.Это предлагает нам три категории для обсуждения того, какие математические компетенции требуются для цифрового общества: применение/моделирование , понимание и проверка .
Применение/Моделирование.
Моделирование и приложения уже давно находятся в повестке дня Международного сообщества преподавателей математического моделирования и приложений (ICTMA). Однако модельному бизнесу по-прежнему уделяется мало внимания в повседневной школьной практике. Исследования по моделированию в математическом образовании, как правило, больше сосредоточены на роли моделирования в обучении и реализации определенных математических концепций (Gravemeijer, Lehrer, van Oers & Verschaffel, 2002). Однако мотивацией для создания и интерпретации моделей на рабочем месте является математизация реалистичной ситуации с целью ответа на практический вопрос, а не изучение математической идеи. Заметным исключением в сфере образования является работа в группе «Модели и перспектива моделирования» (Hamilton, Lesh, Lester & Brilleslyper, 2008), которая разработала один из наиболее проработанных учебных подходов, направленных на развитие навыков моделирования у учащихся, обозначенный как деятельность по выявлению моделей. (МЕА).Деятельность по выявлению модели задумана как подлинная проблема в реальной ситуации, которая требует от учащихся создания модели для интерпретации, объяснения и прогнозирования этой ситуации для решения проблемы. Эти MEA также рассматриваются как катализатор образования STEM; в связи с этим Hamilton et al.
Исследования по моделированию в математическом образовании, как правило, больше сосредоточены на роли моделирования в обучении и реализации определенных математических концепций (Gravemeijer, Lehrer, van Oers & Verschaffel, 2002). Однако мотивацией для создания и интерпретации моделей на рабочем месте является математизация реалистичной ситуации с целью ответа на практический вопрос, а не изучение математической идеи. Заметным исключением в сфере образования является работа в группе «Модели и перспектива моделирования» (Hamilton, Lesh, Lester & Brilleslyper, 2008), которая разработала один из наиболее проработанных учебных подходов, направленных на развитие навыков моделирования у учащихся, обозначенный как деятельность по выявлению моделей. (МЕА).Деятельность по выявлению модели задумана как подлинная проблема в реальной ситуации, которая требует от учащихся создания модели для интерпретации, объяснения и прогнозирования этой ситуации для решения проблемы. Эти MEA также рассматриваются как катализатор образования STEM; в связи с этим Hamilton et al. (2008) особенно указывают на возможности соединения математики и техники.
(2008) особенно указывают на возможности соединения математики и техники.
Мы можем расширить это обсуждение различий между реальным решением задач в цифровом обществе и школьной математикой на основе Brady et al.(2015). Они делают следующие наблюдения, в которых повторяется большая часть выводов, изложенных в разделе о рабочем месте. Люди часто работают в группах, чтобы воспользоваться разнообразием опыта, который они могут предложить. При решении проблем в реальности потребности реального клиента определяют критерии, которым должно соответствовать решение. В то же время, однако, качества, которые клиент считает важными, возможно, придется уточнить или операционализировать. Работа для конкретного клиента часто также определяет, какие измерения доступны, в то время как источники данных, возможно, придется сначала интерпретировать или создать.Для реальных проблем также характерно, что решения должны учитывать неопределенные или меняющиеся условия и компромиссы.
Чтобы определить компетенции, необходимые для моделирования реальных проблем, мы можем обратиться к математической структуре PISA 2015 (OECD, 2016). Эта структура содержит те же шаги, которые Вольфрам (2010) использует для описания процесса моделирования реальных проблем и которые можно найти в большинстве моделей решения реальных проблем (Verschaffel, Greer & De Corte, 2000; Vorhölter, Kaiser & Ferri, 2014).Наряду с математическими знаниями, концепциями и навыками, структура ссылается на различные математические возможности, которые особенно важны для моделирования. Эти компетенции отражают два основных вида деятельности, которые мы поместили в категорию «применение и моделирование», переход от реальности к математике и обратный переход от математики к реальности. В связи с переходом от реальности к математике в структуре упоминаются такие возможности, как декодирование и интерпретация информации, структурирование и осмысление проблемной ситуации, создание выводов и предположений и формулирование модели. Для обратной деятельности они упоминают способности, такие как обобщение и представление результатов, предоставление объяснения или обоснования, а также интерпретация или оценка математического результата. Кроме того, они также относятся к использованию графиков, таблиц, диаграмм, рисунков, уравнений и формул. Обратите внимание, что, как мы отмечали выше, моделирование предполагает использование математических понятий и процедур, которые разработчики моделей должны связывать с приложениями, что часто является проблемой для школьной математики. Таким образом, принятие моделирования и применения в качестве целей влияет на характер преподаваемой математики.Мы подробнее остановимся на этом вопросе при обсуждении категории «понимание».
Для обратной деятельности они упоминают способности, такие как обобщение и представление результатов, предоставление объяснения или обоснования, а также интерпретация или оценка математического результата. Кроме того, они также относятся к использованию графиков, таблиц, диаграмм, рисунков, уравнений и формул. Обратите внимание, что, как мы отмечали выше, моделирование предполагает использование математических понятий и процедур, которые разработчики моделей должны связывать с приложениями, что часто является проблемой для школьной математики. Таким образом, принятие моделирования и применения в качестве целей влияет на характер преподаваемой математики.Мы подробнее остановимся на этом вопросе при обсуждении категории «понимание».
Есть, однако, еще один момент, который мы хотим поднять: не все рабочие будут активными моделистами. Во многих случаях они будут использовать модели, изобретенные другими. В этом отношении мы утверждаем, что понятие технико-математической грамотности обычно указывает на необходимость понимания скрытой, идиосинкразической математики, которая формируется инструментами и практиками, разработанными другими. Кроме того, может быть более распространенным явлением, когда работникам приходится использовать или адаптировать результаты деятельности других людей по моделированию. Олденбург (2011), например, отмечает, что на рабочем месте люди довольно часто сталкиваются с проблемой и выбирают из множества уже созданных моделей, хотя может случиться так, что предварительно структурированная модель нуждается в изменении и, таким образом, может развиваться по мере необходимости. он используется в ряде различных ситуаций. С точки зрения Ольденбурга (2011), стрела от реального мира к моделям также должна указывать назад.Таким образом, необходимо рассмотреть оба типа моделирования. Мы можем также добавить, что наряду с моделированием или использованием моделей многие люди будут использовать результаты работы по моделированию, выполненной другими. Это также повлияет на необходимые навыки моделирования.
Кроме того, может быть более распространенным явлением, когда работникам приходится использовать или адаптировать результаты деятельности других людей по моделированию. Олденбург (2011), например, отмечает, что на рабочем месте люди довольно часто сталкиваются с проблемой и выбирают из множества уже созданных моделей, хотя может случиться так, что предварительно структурированная модель нуждается в изменении и, таким образом, может развиваться по мере необходимости. он используется в ряде различных ситуаций. С точки зрения Ольденбурга (2011), стрела от реального мира к моделям также должна указывать назад.Таким образом, необходимо рассмотреть оба типа моделирования. Мы можем также добавить, что наряду с моделированием или использованием моделей многие люди будут использовать результаты работы по моделированию, выполненной другими. Это также повлияет на необходимые навыки моделирования.
Мы можем закрыть этот раздел кратким обсуждением препятствий, которые могут возникнуть при обучении. Часто учителя рассматривают контексты реального мира только как инструменты мотивации и не уделяют этому контексту должного внимания.Многие учителя быстро превращают контекстуальную задачу в математическую, выдвигая на первый план расчеты, которые необходимо выполнить. В связи с этим Томпсон, Филипп, Томпсон и Бойд (1994) говорят о расчетливой ориентации, которую они противопоставляют концептуальной ориентации. Учителя с вычислительной ориентацией, как правило, игнорируют как контекст, так и способ, которым вычисления возникают из понимания контекста. Они в основном говорят с помощью чисел и операций, сосредоточены на определении и выполнении процедур и нацелены на получение численных решений.Учителя с концептуальной ориентацией, напротив, стремятся к концептуальной согласованности и сосредотачиваются на том, чтобы помочь учащимся понять роль и значение числовых значений в ситуации и то, как это проявляется в числовых операциях. Следствием этой работы является то, что концептуальная ориентация на математику более способствует пониманию математического моделирования.
Часто учителя рассматривают контексты реального мира только как инструменты мотивации и не уделяют этому контексту должного внимания.Многие учителя быстро превращают контекстуальную задачу в математическую, выдвигая на первый план расчеты, которые необходимо выполнить. В связи с этим Томпсон, Филипп, Томпсон и Бойд (1994) говорят о расчетливой ориентации, которую они противопоставляют концептуальной ориентации. Учителя с вычислительной ориентацией, как правило, игнорируют как контекст, так и способ, которым вычисления возникают из понимания контекста. Они в основном говорят с помощью чисел и операций, сосредоточены на определении и выполнении процедур и нацелены на получение численных решений.Учителя с концептуальной ориентацией, напротив, стремятся к концептуальной согласованности и сосредотачиваются на том, чтобы помочь учащимся понять роль и значение числовых значений в ситуации и то, как это проявляется в числовых операциях. Следствием этой работы является то, что концептуальная ориентация на математику более способствует пониманию математического моделирования.
Понимание.
Рабочие места не только становятся все более автоматизированными, но и компании стараются гибко реагировать на потребности клиентов.Следствием этого является то, что сотрудники на многих уровнях должны понимать, что происходит, чтобы иметь возможность общаться как с коллегами, так и с клиентами. Тезис о том, что людям необходимо понимать математику, связанную с работой машин, подтверждается наблюдениями за технологически насыщенными рабочими местами (Kent et al., 2007; Gainsburg, 2007).
Мы видели, что знания на рабочем месте обычно уникальны и привязаны к конкретным контекстам и инструментам. В связи с этим мы уже ссылались на понятие TML (Hoyles & Noss, 2003).Эти TML состоят из комбинации математических знаний и контекстуальных знаний. В связи с этим возникает вопрос: какая форма математических знаний могла бы лучше всего подготовить учащихся к усвоению TML? Кажется само собой разумеющимся, что понимание лежащих в основе концепций будет более полезным, чем овладение жесткими процедурами. Обратите внимание, что это не меняет того факта, что потребуется определенный уровень процедурного мастерства, хотя бы для разработки этих концепций. Однако мы можем возразить, что с ростом доступности технологий эта потребность в овладении рутинными навыками уменьшается.Это создает пространство для работы над концептуальным математическим пониманием, которое необходимо для понимания математики, скрытой в цифровых инструментах, которыми изобилует наше технологическое общество. Говоря о концептуальном понимании, мы можем сослаться на хорошо известное различие, которое Скемп (Skemp, 1978) проводит между инструментальным и относительным пониманием. Мы можем прояснить разницу, взяв в качестве примера среднее арифметическое. Понимание среднего инструментально относится к пониманию процедуры и рецепта: сложите отдельные меры и разделите на количество мер.Реляционное понимание касается концептуального значения. Среднее значение относится к значению, которое представляет меры в наборе данных допустимым образом.
Обратите внимание, что это не меняет того факта, что потребуется определенный уровень процедурного мастерства, хотя бы для разработки этих концепций. Однако мы можем возразить, что с ростом доступности технологий эта потребность в овладении рутинными навыками уменьшается.Это создает пространство для работы над концептуальным математическим пониманием, которое необходимо для понимания математики, скрытой в цифровых инструментах, которыми изобилует наше технологическое общество. Говоря о концептуальном понимании, мы можем сослаться на хорошо известное различие, которое Скемп (Skemp, 1978) проводит между инструментальным и относительным пониманием. Мы можем прояснить разницу, взяв в качестве примера среднее арифметическое. Понимание среднего инструментально относится к пониманию процедуры и рецепта: сложите отдельные меры и разделите на количество мер.Реляционное понимание касается концептуального значения. Среднее значение относится к значению, которое представляет меры в наборе данных допустимым образом. В качестве метафоры мы можем думать о «среднем человеке». В основе лежит концепция индивидуальных расстояний между средним значением и другими значениями данных, сумма которых равна нулю. Концептуальное понимание среднего также включает понимание чувствительности среднего к асимметричному распределению или экстремальным значениям.
В качестве метафоры мы можем думать о «среднем человеке». В основе лежит концепция индивидуальных расстояний между средним значением и другими значениями данных, сумма которых равна нулю. Концептуальное понимание среднего также включает понимание чувствительности среднего к асимметричному распределению или экстремальным значениям.
Помимо относительного понимания, к которому нужно стремиться, мы должны рассмотреть, какой уровень понимания необходим и для кого.Мы можем предположить, что во многих случаях будет достаточно какого-то глобального, общего понимания. В связи с этим можно сослаться на работы Капута (1994, 1997), который в 1990-е годы обратил внимание на то, что рост компьютеризации создал потребность в обучении исчислению гораздо большей части населения. Он утверждал, что только 10% студентов получили доступ к исчислению, хотя гораздо большей части населения необходимо было знать идеи и методы исчисления.В связи с этим он призвал к «демократизации доступа к математике изменений и вариаций» (Vahey, Lara-Meloy & Knudsen, 2009, стр. 417). Чтобы угодить остальным 90% студентов, нам пришлось бы сосредоточиться на «ключевых основополагающих идеях скорости изменения, накопления, связи между переменными темпами и накоплением и приближении» (Капут, 1997, стр. 733). По его мнению, этого можно достичь путем развертывания динамических представлений, которые допускают компьютеры, из которых работа над SimCalc (Roschelle et.al., 2010) является примером. В заключение мы можем утверждать, что тезис Капута (1997) применим ко многим другим темам в наши дни; в цифровом обществе люди должны понимать ключевые идеи, лежащие в основе математики, используемой машинами. Это находит отклик в работе Hoyles и Noss cum suis (Hoyles, Noss, Kent & Bakker, 2010), которые также выступают за концептуальное понимание задействованной математики и разрабатывают артефакты, такие как компьютерные инструменты, для поддержки работников в развитии этого понимания.
417). Чтобы угодить остальным 90% студентов, нам пришлось бы сосредоточиться на «ключевых основополагающих идеях скорости изменения, накопления, связи между переменными темпами и накоплением и приближении» (Капут, 1997, стр. 733). По его мнению, этого можно достичь путем развертывания динамических представлений, которые допускают компьютеры, из которых работа над SimCalc (Roschelle et.al., 2010) является примером. В заключение мы можем утверждать, что тезис Капута (1997) применим ко многим другим темам в наши дни; в цифровом обществе люди должны понимать ключевые идеи, лежащие в основе математики, используемой машинами. Это находит отклик в работе Hoyles и Noss cum suis (Hoyles, Noss, Kent & Bakker, 2010), которые также выступают за концептуальное понимание задействованной математики и разрабатывают артефакты, такие как компьютерные инструменты, для поддержки работников в развитии этого понимания.
Это подводит нас к роли компьютерных инструментов, специально разработанных для поддержки разработки ключевых идей в конкретных областях. Наряду с компьютерными инструментами, разработанными группой Hoyles cum suis (например, Bakker, Kent, Noss & Hoyles, 2009), и программным обеспечением Simcalc, разработанным Капутом и его коллегами, мы можем сослаться на компьютерные инструменты, разработанные некоторыми из нас в экспериментах по проектированию. принимали участие, например, в анализе данных (Cobb, McClain, & Gravemeijer, 2003), исчислении (de Beer, Gravemeijer & van Eijck, 2015; Doorman & Gravemeijer, 2009) и функциях (Doorman, Drijvers, Gravemeijer, Boon и Рид, 2012).На наш взгляд, при рассмотрении вопроса о том, какой предмет может быть подходящим для большинства учащихся, необходимо учитывать цель овладения ключевыми идеями и потенциал специализированных образовательных компьютерных инструментов для достижения этой цели.
Наряду с компьютерными инструментами, разработанными группой Hoyles cum suis (например, Bakker, Kent, Noss & Hoyles, 2009), и программным обеспечением Simcalc, разработанным Капутом и его коллегами, мы можем сослаться на компьютерные инструменты, разработанные некоторыми из нас в экспериментах по проектированию. принимали участие, например, в анализе данных (Cobb, McClain, & Gravemeijer, 2003), исчислении (de Beer, Gravemeijer & van Eijck, 2015; Doorman & Gravemeijer, 2009) и функциях (Doorman, Drijvers, Gravemeijer, Boon и Рид, 2012).На наш взгляд, при рассмотрении вопроса о том, какой предмет может быть подходящим для большинства учащихся, необходимо учитывать цель овладения ключевыми идеями и потенциал специализированных образовательных компьютерных инструментов для достижения этой цели.
Проверка.
Важный аспект оценки результатов сгенерированного компьютером ответа на некоторую проблему касается вопроса о том, насколько результаты соответствуют контексту проблемы и возможно ли решение в этом контексте. Другой аспект касается математической корректности вычисляемого результата. Мы можем начать с того, что отметим, что идея состоит не в том, чтобы пользователи компьютеризированной аппаратуры повторяли расчеты вручную. Вместо этого мы хотим, чтобы они могли проверить, кажется ли результат правдоподобным. На наш взгляд, это имеет большое значение для школьной программы по математике. Мы можем проиллюстрировать это, проверив ответ на арифметическое вычисление. Здесь можно выполнить некоторую «глобальную арифметику», изменив числа для упрощения вычислений и используя эти модифицированные вычисления, чтобы оценить, является ли ответ разумным.Разрабатывая этот пример, мы хотим пояснить, что для этого требуется другой вид арифметики, чем преподают в настоящее время.
Другой аспект касается математической корректности вычисляемого результата. Мы можем начать с того, что отметим, что идея состоит не в том, чтобы пользователи компьютеризированной аппаратуры повторяли расчеты вручную. Вместо этого мы хотим, чтобы они могли проверить, кажется ли результат правдоподобным. На наш взгляд, это имеет большое значение для школьной программы по математике. Мы можем проиллюстрировать это, проверив ответ на арифметическое вычисление. Здесь можно выполнить некоторую «глобальную арифметику», изменив числа для упрощения вычислений и используя эти модифицированные вычисления, чтобы оценить, является ли ответ разумным.Разрабатывая этот пример, мы хотим пояснить, что для этого требуется другой вид арифметики, чем преподают в настоящее время.
В основе глобальной арифметики лежат гибкие рассуждения с числовыми отношениями, работа с нулями и арифметическими свойствами (Gravemeijer, 2015). Возьмем для примера 78 × 1261. Это можно приблизительно представить как 75 × 1200, используя 12 = 4 × 3, таким образом, 1200 = 4 x 300, а 75 × 4 = 300 и 300 × 300 равно 90 000, или 80 × 1250, и используя 8 × 125 =≀1. 1000 × 100 = 100 000.Gravemeijer (2015) утверждает, что ключевое значение здесь имеет использование числовых отношений; когда решатель использует числовые отношения, которые ему знакомы и всегда под рукой, он или она может быть уверен, что аппроксимация верна. Следуя этой линии рассуждений, мы можем заключить, что мы должны поддерживать учащихся в разработке числовых отношений, которые можно использовать в различных расчетных ситуациях (например, числа, кратные 25, 75, 125 и т. д., и связи этих чисел с десятичные дроби, дроби и проценты). В идеале учащиеся должны разработать сети числовых отношений, которые они могут гибко подключать, что, в свою очередь, может укрепить их уверенность в знакомых им числовых отношениях.Мы можем добавить, что гибкое использование числовых отношений также подразумевает использование арифметических свойств, таких как свойство коммутативности, ассоциативности и дистрибутивности, подготавливающих студентов к алгебре.
1000 × 100 = 100 000.Gravemeijer (2015) утверждает, что ключевое значение здесь имеет использование числовых отношений; когда решатель использует числовые отношения, которые ему знакомы и всегда под рукой, он или она может быть уверен, что аппроксимация верна. Следуя этой линии рассуждений, мы можем заключить, что мы должны поддерживать учащихся в разработке числовых отношений, которые можно использовать в различных расчетных ситуациях (например, числа, кратные 25, 75, 125 и т. д., и связи этих чисел с десятичные дроби, дроби и проценты). В идеале учащиеся должны разработать сети числовых отношений, которые они могут гибко подключать, что, в свою очередь, может укрепить их уверенность в знакомых им числовых отношениях.Мы можем добавить, что гибкое использование числовых отношений также подразумевает использование арифметических свойств, таких как свойство коммутативности, ассоциативности и дистрибутивности, подготавливающих студентов к алгебре.
Далее мы можем отметить, что проверка математической правильности включает в себя больше, чем глобальный пересчет. Математическая правильность может также касаться адекватности математических процедур, приближений или обобщений. В связи с этим мы можем указать на Левитина (2016), который исследовал, как посторонние могут судить о достоверности и достоверности результатов статистических процедур, выполненных другими.
Математическая правильность может также касаться адекватности математических процедур, приближений или обобщений. В связи с этим мы можем указать на Левитина (2016), который исследовал, как посторонние могут судить о достоверности и достоверности результатов статистических процедур, выполненных другими.
Приведенный выше арифметический пример показывает, что учебная программа, направленная на развитие арифметических навыков, связанных с проверкой результатов работы компьютера, будет значительно отличаться от обычной учебной программы, направленной на быстрое получение точных ответов. То же самое относится и к статистике, особенно потому, что усилия, направленные на то, чтобы помочь студентам получить опыт работы со статистикой, часто касаются упрощенных экспериментов, которые просто не соответствуют требованиям, к которым «потребители статистики» должны относиться критически (Левитин, 2016).
Математики преувеличивают идею о том, что «математика повсюду»
Большинство людей никогда не становятся математиками, но все заинтересованы в математике. Почти с самого начала человеческой цивилизации общество наделяло экспертов-математиков особым авторитетом. Вопрос о том, как и почему общественность должна поддерживать элитарную математику, остается как никогда актуальным, и за последние пять столетий (особенно за последние два) к нему присоединился связанный с этим вопрос о том, какую математику должно знать большинство представителей общественности.
Почти с самого начала человеческой цивилизации общество наделяло экспертов-математиков особым авторитетом. Вопрос о том, как и почему общественность должна поддерживать элитарную математику, остается как никогда актуальным, и за последние пять столетий (особенно за последние два) к нему присоединился связанный с этим вопрос о том, какую математику должно знать большинство представителей общественности.
Почему математика важна для общества в целом? Послушайте математиков, политиков и педагогов, и ответ кажется единодушным: математика повсюду, поэтому все должны заботиться о ней. Книги и статьи изобилуют примерами математики, которая, как утверждают их авторы, скрыта во всех аспектах повседневной жизни или открывает мощные истины и технологии, формирующие судьбы людей и народов. Возьмем, к примеру, профессора математики Джордана Элленберга, автора бестселлера « Как не ошибаться, », который утверждает, что «математику можно найти везде, куда бы вы ни посмотрели.
Безусловно, числа и измерения регулярно присутствуют в жизни большинства людей, но это может привести к тому, что базовые математические знания будут смешаны с той математикой, которая больше всего влияет на вашу жизнь. Когда мы говорим о математике в государственной политике, особенно об инвестициях общества в математическое обучение и исследования, мы не говорим о простых суммах и мерах. На протяжении большей части своей истории математика, имеющая наибольшее значение для общества, была прерогативой избранных. Общество ценит и культивирует математику не потому, что она везде и для всех, а потому, что она сложна и эксклюзивна.Признание того, что математика имеет элитарность, встроенную в ее историческое ядро, вместо того, чтобы притворяться, что она скрыта повсюду вокруг нас, дает более реалистичное понимание того, как математика вписывается в общество, и может помочь обществу потребовать более ответственной и инклюзивной дисциплины.
Когда мы говорим о математике в государственной политике, особенно об инвестициях общества в математическое обучение и исследования, мы не говорим о простых суммах и мерах. На протяжении большей части своей истории математика, имеющая наибольшее значение для общества, была прерогативой избранных. Общество ценит и культивирует математику не потому, что она везде и для всех, а потому, что она сложна и эксклюзивна.Признание того, что математика имеет элитарность, встроенную в ее историческое ядро, вместо того, чтобы притворяться, что она скрыта повсюду вокруг нас, дает более реалистичное понимание того, как математика вписывается в общество, и может помочь обществу потребовать более ответственной и инклюзивной дисциплины.
В первых земледельческих обществах в колыбели цивилизации математика соединяла небо и землю. Жрецы использовали астрономические расчеты для обозначения времен года и интерпретации божественной воли, а их особое знание математики давало им власть и привилегии в их обществах. По мере того как ранняя экономика росла и становилась все более сложной, купцы и ремесленники включали в свою работу все больше и больше элементарной математики, но для них математика была скорее торговой уловкой, чем общественным благом. На протяжении тысячелетий передовая математика оставалась заботой состоятельных людей либо как философское времяпрепровождение, либо как средство утверждения особого авторитета.
По мере того как ранняя экономика росла и становилась все более сложной, купцы и ремесленники включали в свою работу все больше и больше элементарной математики, но для них математика была скорее торговой уловкой, чем общественным благом. На протяжении тысячелетий передовая математика оставалась заботой состоятельных людей либо как философское времяпрепровождение, либо как средство утверждения особого авторитета.
Первые относительно широко распространенные предположения о том, что все, что выходит за рамки простой практической математики, должно иметь более широкое распространение, относятся к тому, что историки называют ранним современным периодом, начавшимся около пяти столетий назад, когда начали формироваться многие из наших современных социальных структур и институтов.Точно так же, как Мартин Лютер и другие ранние протестанты начали настаивать на том, чтобы Священное Писание было доступно массам на их родных языках, такие научные писатели, как валлийский эрудит Роберт Рекорд, использовали относительно новую технологию печатного станка для популяризации математики среди людей. Учебник по английской арифметике Рекорда 1543 года начинался с аргумента, что «ни один человек не может ничего делать в одиночку, тем более говорить или торговаться с другим, но ему все равно придется иметь дело с числами» и что числа используются «бесчисленно» (каламбур). ).
Учебник по английской арифметике Рекорда 1543 года начинался с аргумента, что «ни один человек не может ничего делать в одиночку, тем более говорить или торговаться с другим, но ему все равно придется иметь дело с числами» и что числа используются «бесчисленно» (каламбур). ).
Гораздо более влиятельным и представительным представителем этого периода, однако, был Джон Ди, современник Рекорда, который использовал свою репутацию в области математики, чтобы получить влиятельное положение, консультируя королеву Елизавету I. Ди так близко относился к идее математики как тайного и привилегированного вида знаний. что недоброжелатели обвиняли его в колдовстве и других оккультных практиках. Во время научной революции семнадцатого века новые пропагандисты экспериментальной науки, которая была (по крайней мере, в принципе) открыта для любого наблюдателя, с подозрением относились к математическим аргументам как к недоступным, стремясь закрыть различные точки зрения с ложным чувством уверенности. Напротив, в эпоху Просвещения восемнадцатого века ученые Французской академии наук использовали свое мастерство в сложной математике, чтобы занять особое место в общественной жизни, одинаково взвешивая как философские дебаты, так и гражданские дела, закрывая свои ряды для женщин. меньшинства и низшие социальные классы.
Напротив, в эпоху Просвещения восемнадцатого века ученые Французской академии наук использовали свое мастерство в сложной математике, чтобы занять особое место в общественной жизни, одинаково взвешивая как философские дебаты, так и гражданские дела, закрывая свои ряды для женщин. меньшинства и низшие социальные классы.
Общества по всему миру преобразовывались в девятнадцатом веке волна за волной политических и экономических революций, но французская модель привилегированного математического знания на службе государства сохранилась.Разница заключалась в том, кто стал частью этой математической элиты. Рождение в правильной семье по-прежнему помогало, но после Французской революции сменявшие друг друга правительства также проявляли больший интерес к начальному и среднему образованию, и хорошие результаты на экзаменах могли помочь некоторым учащимся подняться, несмотря на их более низкое происхождение. Политические и военные лидеры получили единообразное образование в области высшей математики в нескольких выдающихся академиях, которые готовили их к решению специализированных проблем современных государств, и эта французская модель государственного участия в массовом образовании в сочетании со специальной математической подготовкой для самых лучших подражателей во всем мире Европе и даже через Атлантику.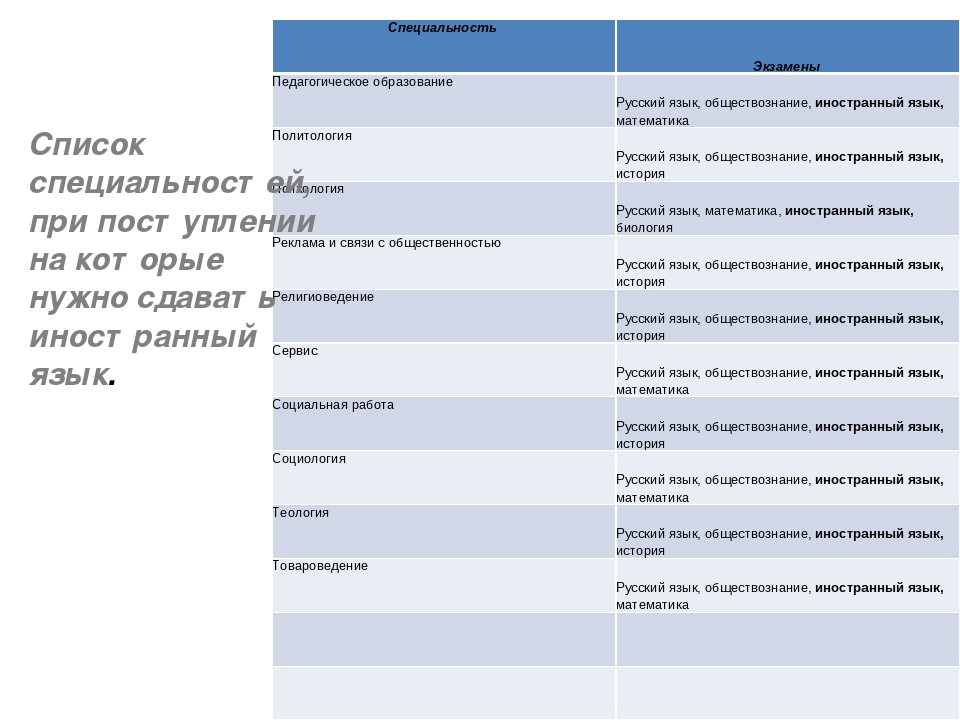 Несмотря на то, что базовая математика достигала все большего числа людей посредством массового образования, математика оставалась чем-то особенным, что отличало элиту. Больше людей потенциально могли бы стать элитой, но математика определенно была не для всех.
Несмотря на то, что базовая математика достигала все большего числа людей посредством массового образования, математика оставалась чем-то особенным, что отличало элиту. Больше людей потенциально могли бы стать элитой, но математика определенно была не для всех.
Вступив в двадцатый век, система направления студентов через элитное обучение продолжала приобретать все большее значение в западном мире, но сама математика стала менее важной в этом обучении. Отчасти это отражало изменение приоритетов правительства, но отчасти это было связано с тем, что высшая математика оставила проблемы правительства позади.Там, где когда-то математики эпохи Просвещения рассматривали практические и технологические вопросы наряду со своими более философскими исследованиями, более поздние современные математики все чаще обращались к неприступно абстрактным теориям, не претендуя на непосредственное рассмотрение мирских вопросов.
Следующим поворотным моментом, который во многом продолжает определять отношения между математикой и обществом сегодня, стала Вторая мировая война. Ведя войну такого масштаба, основные участники боевых действий столкнулись с новыми проблемами в логистике, разработке и использовании оружия и в других областях, которые математики оказались особенно способны решать.Дело было не в том, что самая продвинутая математика вдруг стала более практичной, а в том, что государства нашли новое применение для тех, у кого была продвинутая математическая подготовка, а математики нашли новые способы обратиться к государствам за поддержкой. После войны математики получили существенную поддержку со стороны Соединенных Штатов и других правительств на том основании, что независимо от того, были ли полезны их исследования в мирное время, теперь у них были доказательства того, что в следующей войне потребуются высококвалифицированные математики.
Ведя войну такого масштаба, основные участники боевых действий столкнулись с новыми проблемами в логистике, разработке и использовании оружия и в других областях, которые математики оказались особенно способны решать.Дело было не в том, что самая продвинутая математика вдруг стала более практичной, а в том, что государства нашли новое применение для тех, у кого была продвинутая математическая подготовка, а математики нашли новые способы обратиться к государствам за поддержкой. После войны математики получили существенную поддержку со стороны Соединенных Штатов и других правительств на том основании, что независимо от того, были ли полезны их исследования в мирное время, теперь у них были доказательства того, что в следующей войне потребуются высококвалифицированные математики.
Некоторые из этих видов деятельности военного времени по-прежнему занимают профессионалов-математиков как в штате, так и за его пределами — от специалистов по безопасности и взломщиков кодов в технологических компаниях и АНБ до исследователей операций, оптимизирующих заводы и цепочки поставок в рамках глобальной экономики.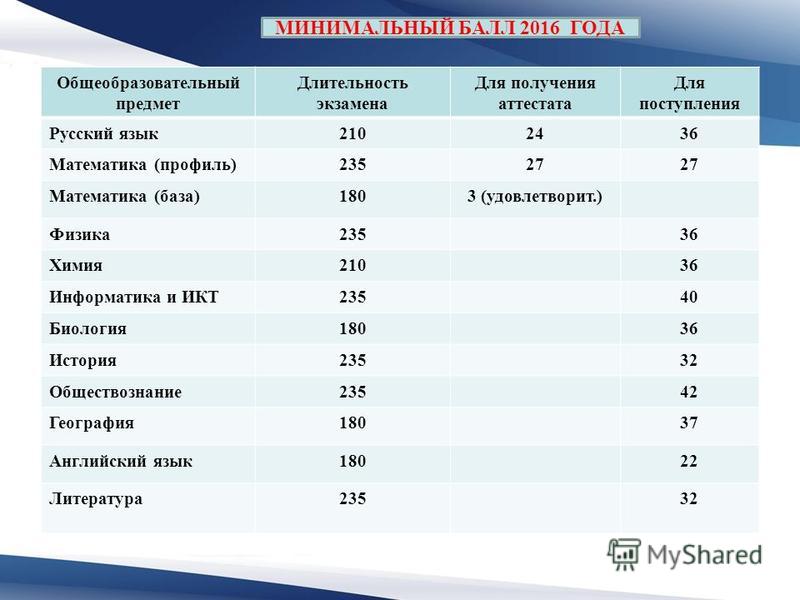 Послевоенные электронные вычисления стали еще одной областью, в которой математики стали необходимы. Во всех этих областях именно особые математические успехи немногих элит являются мотивом для государственных инвестиций, которые математики продолжают получать и сегодня. Было бы здорово, если бы все были уверены в числах, могли написать компьютерную программу и оценить статистические данные, а все это важные цели начального и среднего образования. Но мы не должны путать их с основными целями и причинами общественной поддержки математики, которые всегда касались математики наверху, а не математики для всех.
Послевоенные электронные вычисления стали еще одной областью, в которой математики стали необходимы. Во всех этих областях именно особые математические успехи немногих элит являются мотивом для государственных инвестиций, которые математики продолжают получать и сегодня. Было бы здорово, если бы все были уверены в числах, могли написать компьютерную программу и оценить статистические данные, а все это важные цели начального и среднего образования. Но мы не должны путать их с основными целями и причинами общественной поддержки математики, которые всегда касались математики наверху, а не математики для всех.
Воображая, что математика повсюду, слишком легко игнорировать очень реальную политику того, кто станет частью математической элиты, которая действительно имеет значение — для технологий, безопасности и экономики, для прошлой войны и следующей. Вместо этого, если мы увидим, что этот вид математики исторически создавался очень немногими и для очень немногих, мы призваны спросить, кто может быть частью этих немногих и какова ответственность, связанная с их опытом. Мы должны признать, что элитарная математика сегодня, хотя и гораздо более инклюзивная, чем она была один, пять или пятьдесят веков назад, остается дисциплиной, которая наделяет особым авторитетом тех, кто в силу пола, расы и класса часто уже входит в нашу группу. самое могущественное общество.Если бы математика действительно была повсюду, она уже принадлежала бы всем в равной степени. Но когда дело доходит до доступа к математике и ее поддержки, предстоит проделать большую работу. Математика есть не везде.
Мы должны признать, что элитарная математика сегодня, хотя и гораздо более инклюзивная, чем она была один, пять или пятьдесят веков назад, остается дисциплиной, которая наделяет особым авторитетом тех, кто в силу пола, расы и класса часто уже входит в нашу группу. самое могущественное общество.Если бы математика действительно была повсюду, она уже принадлежала бы всем в равной степени. Но когда дело доходит до доступа к математике и ее поддержки, предстоит проделать большую работу. Математика есть не везде.
Часть первая: Связь математики с работой и жизнью | Математика средней школы на работе: эссе и примеры для обучения всех учащихся
большая часть необходимых нам данных по Японии просто недоступна, потому что японский рынок менее развит, чем в США.S. Данные о водительских правах, данные о доходах, данные об образе жизни — все это обычное здесь и недоступное там. Американские ритейлеры до этого мало проникли в обе страны, поэтому у нас нет опыта, на который мы могли бы опереться. Мы все слышали, как трудно будет открыть торговые операции в Японии, но последние тенденции продаж среди продавцов компьютеров и продаж автозапчастей намекают на ослабление трудностей.
Мы все слышали, как трудно будет открыть торговые операции в Японии, но последние тенденции продаж среди продавцов компьютеров и продаж автозапчастей намекают на ослабление трудностей.
«План состоит в том, чтобы открывать три магазина в год, по 5000 квадратных футов каждый. Мы рассчитываем получать 700 долларов за квадратный фут, что более чем вдвое превышает опыт американских ритейлеров в США.с., но на 45% меньше, чем в наших магазинах. Кроме того, цены будут на 20% выше, чтобы компенсировать стоимость земли и зданий. Стоимость активов примерно в два раза выше, чем в США, но стоимость рабочей силы немного меньше. Пособия более тщательно покрываются государством. Конечно, есть большая неопределенность в объемах продаж, которые мы планируем. Ценообразование частично покроет неопределенность, но все же меньше, чем у товаров сопоставимого качества, уже предлагаемых в Японии.
«Позвольте мне перейти к соревнованиям и рассказать вам, что мы узнали.Мы установили долгосрочные отношения с 500 до 1000 семей в каждой стране. Это сопоставимо с нашей практикой в США. Эти семьи не знают, что они работают именно с нашей компанией, так как это могло бы исказить их отчетность. Они держат нас в курсе своего каталога и опыта покупок, независимо от компании, в которой они покупают. Размер выборки достаточно велик, чтобы быть значимым, но, конечно, вы должны быть осторожны с небольшими различиями.
Это сопоставимо с нашей практикой в США. Эти семьи не знают, что они работают именно с нашей компанией, так как это могло бы исказить их отчетность. Они держат нас в курсе своего каталога и опыта покупок, независимо от компании, в которой они покупают. Размер выборки достаточно велик, чтобы быть значимым, но, конечно, вы должны быть осторожны с небольшими различиями.
«Все семьи получают наш каталог и каталоги от нескольких наших конкурентов.Они соответствуют демографическому профилю образа жизни, дохода и образования людей, которых мы хотим видеть в качестве клиентов. Они являются опытными покупателями по каталогам, и это будет искажать их отзывы по сравнению с новыми покупателями по каталогам.
«Один из конкурентов присылает один 100-страничный каталог в квартал. Ассортимент довольно узкий — 200 товаров из 3000 отечественных. Они выбрали товары, которые вряд ли создадут проблемы с посадкой: в основном верхняя одежда и трикотажные рубашки, не много штанов, в основном мужские товары, не женские. Копия их каталога написана на кандзи, но, как нам сказали, стиль немного неестественный, вероятно, потому, что она была написана на английском и переведена, но нам нужно проверить эту гипотезу. Напротив, мы просто отправили им по почте тот же каталог, которым пользуемся в США, даже написанный на английском языке.
Копия их каталога написана на кандзи, но, как нам сказали, стиль немного неестественный, вероятно, потому, что она была написана на английском и переведена, но нам нужно проверить эту гипотезу. Напротив, мы просто отправили им по почте тот же каталог, которым пользуемся в США, даже написанный на английском языке.
«Отзывы клиентов были достаточно однозначными. Они предпочитают наш более широкий ассортимент в соотношении 3:1, хотя и не покупают большую часть продукции. Как рассчитали конкуренты, продажи сосредоточены на верхней одежде и трикотаже, увеличение продаж, видимо, потому, что им нравится смотреть каталог и проводить с ним больше времени.Опять же, нам нужны дополнительные испытания. Другая гипотеза заключается в том, что наша торговая марка просто более известна.
«Интересно, что они предпочитают нашу англоязычную версию, потому что им больше нравится читать каталог на другом языке. Вероятно, это
Социально-политический поворот в математическом образовании на JSTOR
Абстрактный За последнее десятилетие исследовательское сообщество в области математического образования включило больше социокультурных аспектов в свои способы понимания и изучения преподавания и обучения. Однако исследователи, которые имеют долгую историю решения проблем борьбы с расизмом и социальной справедливости в математике, вышли за рамки этой социокультурной точки зрения и стали поддерживать социально-политические концепции и теории, подчеркивая идентичность и силу в игре. В этой статье освещаются некоторые многообещающие концептуальные инструменты критической теории и постструктурализма и приводятся аргументы в пользу того, почему социально-политический поворот важен как для исследователей, так и для практиков.
Однако исследователи, которые имеют долгую историю решения проблем борьбы с расизмом и социальной справедливости в математике, вышли за рамки этой социокультурной точки зрения и стали поддерживать социально-политические концепции и теории, подчеркивая идентичность и силу в игре. В этой статье освещаются некоторые многообещающие концептуальные инструменты критической теории и постструктурализма и приводятся аргументы в пользу того, почему социально-политический поворот важен как для исследователей, так и для практиков.
Официальный журнал Национального совета учителей математики (NCTM), JRME является ведущим научно-исследовательским журналом в области математического образования и посвящен интересам учителей и исследователей на всех уровнях — от дошкольного до колледжа.
Информация об издателе Национальный совет учителей математики является общественным голосом математического образования, обеспечивающим видение, лидерство и профессиональное развитие для поддержки учителей в обеспечении обучения математике самого высокого качества для всех учащихся. NCTM, насчитывающая почти 90 000 членов и 250 филиалов, является крупнейшей в мире организацией, занимающейся улучшением математического образования в классах от дошкольного до 12 класса.«Принципы и стандарты школьной математики» Совета представляют собой руководство по совершенствованию математического образования и призывают всех учащихся заниматься более сложной математикой. NCTM стремится к постоянному диалогу и конструктивному обсуждению со всеми заинтересованными сторонами того, что лучше всего подходит для учащихся нашей страны.
NCTM, насчитывающая почти 90 000 членов и 250 филиалов, является крупнейшей в мире организацией, занимающейся улучшением математического образования в классах от дошкольного до 12 класса.«Принципы и стандарты школьной математики» Совета представляют собой руководство по совершенствованию математического образования и призывают всех учащихся заниматься более сложной математикой. NCTM стремится к постоянному диалогу и конструктивному обсуждению со всеми заинтересованными сторонами того, что лучше всего подходит для учащихся нашей страны.
Этот предмет является частью коллекции JSTOR.
Условия использования см. в наших Условиях использования
Copyright 2013 Национальный совет учителей математики, Inc.
Запросить разрешения
| Math 1A | Calculus | 5 | |||
| Math 1AH | CALTUS 1AH | 5 | |||
| MATH 1B | CALLUS | 5 | |||
| Math 1BH | Calculus — Почести | 5 | |||
| Math 1C | Calculus | 5 | 9033|||
| Math 1CH | CALLUS | 9 | |||
| Math | |||||
| Math | 5 | ||||
| Math 1DH | Исчисление — ПОЧЕТЫ | 5 | |||
| МАТЕМАТИКА 2A | Дифференциальные уравнения | 5 | |||
| МАТЕМАТИКА 2AH | Дифференциальные уравнения | 5 | 5 | ||
| Math 2B | Линейная алгебра | 9 | |||
| Math 2BH | Linear Algebra 9031 | 5 | 0|||
| Math 10 | вступительная статистика | 5 | |||
| Math 10H | Вступительная статистика — почетные | 5 | |||
| математика 11 | 5 | 5 | 0|||
| Естествознание | 5 | ||||
| МАТЕМАТИКА 17 | Интегрированная статистика 2 | 5 | |||
| МАТЕМАТИКА 22 | Дискретная математика | 0 5||||
| Math 22H | Дискретная математика — отличия | 5 | |||
| Mathing 23 | Инженерная статистика | 5 | |||
| Math 31 | Precalculus I | 5 | |||
| Math 31A | Предварительный расчет I (Часть 1) | 2. 5 5 | |||
| Math 31b | Precalculus I (часть 2) | 2.5 | |||
| 9036 | |||||
| Math 31h | Precalculus I — отличия | 5 | |||
| Math 32 | Precalculus II | 5 | |||
| MATH 32H | Precalculus II — награды | 5 | |||
| Math 41 | Precalculus I: Теория функций | 5 | |||
| Math 41H | Precalculus I: Теория функций — отличия | 5 | |||
| Math 42 | Precalculus II: тригонометрические функции | 5 | |||
| Math 42H | Math 42H | Precalculus II: тригонометрические функции — отличия | 5 | ||
| Math 43 | Precalculus II Я: Усовершенствованные темы | 5 | |||
| Math 43H | Precalculus III: Усовершенствованные темы — Почести | 5 | |||
| Математика 44 | Математика в искусстве, культуре и общество: Либеральное искусство Математический класс | 5 | |||
| Математика 46 | Математика для начального образования | 5 | |||
| Math 76 | Специальные проекты по вероятности и статистике | 1 | |||
| Math 76x | Специальные проекты по вероятности и статистике | 2 | |||
| Math 76y | Специальные проекты в вероятности и статистике | 3 | |||
| Math 77 | Специальные проекты в математике | 1 | |||
| Math 77x | Специальные проекты в математике | 2 | |||
| Math 77y | |||||
| Специальные проекты в математике | 3 | ||||
| Math 78 | Специальные проекты в чистой математике | 1 | |||
| Math 78x | Специальные проекты в Чистая математика | 2 | 2 | ||
| Math 78y | Специальные проекты в чистом математике | 3 | 9036|||
| Math 79 | 9 | Специальные проекты в прикладной математике | 1 | ||
| Math 79x | Специальные проекты в прикладной математике | 2 | |||
| МАТЕМАТИКА 79Y | Специальные проекты по прикладной математике | 3 | |||
| МАТЕМАТИКА 109 | Средний уровень Tixtixtix | 5 | 5 | ||
| Math 114 | Math 114 | Колледж Математика Подготовка 9033: Промежуточная алгебра | 5 | ||
| Mathbra 130 | Промежуточная алгебра для Precalculus | 5 | |||
| Math 210 | Уровень подготовки к математике 1: Предварительная алгебра | 5 | |||
| МАТЕМАТИКА 210X | Поддержка статистики | 2. 5 5 | |||
| Math 211x | ALGEBRA Поддержка для конечных математики | 2.5 | |||
| Math 212 | Math 212 | College Math | Algebra | 5 | |
| Math 217 | |||||
| MATH 231 | Algebra Support for Precalculus I | 2.5 | |||
| MATH 231A | Algebra Support for Precalculus I (Part 11)5 | ||||
| Math 231B | ALGEBRA Поддержка ALGEBRA для Precalculus I (часть 2) | 2.5 | |||
| Mathbra 232 | Algebra поддержка ALGEBRA для PrecalCulus II | 29 | |||
| Math 241 | Академическое превосходное превосходство в Precalculus | 1 | 9 | ||
| Mathem 242 | |||||
| Академическое превосходство в Precalculus II | 1 | ||||
| Math 243 | академическое превосходство в Precalculus III | 1 | |||
| Mathbra 309 | Промежуточная алгебра для статистики | 0 | |||
| МАТЕМАТИКА 314 | Подготовка к колледжу по математике, уровень 3: средний уровень алгебры | 0 | |||
| МАТЕМАТИКА 330 | Средний уровень алгебры для предварительного исчисления 0331 | ||||
| Math 410 | College Math Complement Уровень подготовки 1: Pre-Algebra | 0 | Math 410x | Поддержка статистики | 0 |
| Math 412 | Колледж Математическая подготовка уровня 2: Начальная алгебра | 0 | |||
| Mathbra 431 | |||||
| Algebra поддержки для Precalculus I | 0 | ||||
| Mathbra поддержка ALGEBRA для Precalculus I (Часть 1) | 0 | ||||
| Mathbra 431B | Алгебра поддержка алгебры для Precalculus I (Часть 2) | 0 | |||
| MATH 432 | Алгебра Поддержка Precalculus II | 0 |
Society for Industrial and Applied Mathematics
Математический факультет Портлендского университета является членом Общества промышленной и прикладной математики (SIAM). SIAM способствует развитию прикладных математических и вычислительных методологий, необходимых в различных областях применения. Прикладная математика в партнерстве с вычислительной наукой необходима для решения многих реальных проблем. Через публикации, исследования и сообщество миссия SIAM состоит в том, чтобы наладить сотрудничество между математикой и миром науки и техники.
SIAM способствует развитию прикладных математических и вычислительных методологий, необходимых в различных областях применения. Прикладная математика в партнерстве с вычислительной наукой необходима для решения многих реальных проблем. Через публикации, исследования и сообщество миссия SIAM состоит в том, чтобы наладить сотрудничество между математикой и миром науки и техники.
SIAM — это международное сообщество, насчитывающее более 14 500 отдельных членов. Почти 500 академических, производственных, научно-исследовательских, сервисных и консалтинговых организаций, правительственных и военных организаций по всему миру являются институциональными членами.SIAM была зарегистрирована в 1952 году как некоммерческая организация для передачи полезных математических знаний другим специалистам, которые могли применять математическую теорию для практического, промышленного или научного использования. С тех пор цели SIAM остались прежними:
- Способствовать применению математики и вычислительной техники в технике, промышленности, науке и обществе.

- Содействовать исследованиям, которые приведут к созданию новых эффективных математических и вычислительных методов и технологий для науки, техники, промышленности и общества.
- Для обмена информацией и идеями между математиками, инженерами и учеными.
Узнайте больше о миссии и областях деятельности SIAM.
UP Студенческие пособия
Наше членство на факультете включает доступ к журналу SIAM Review, а также неограниченное количество студенческих членств. Если вы студент, заинтересованный в присоединении к SIAM, пожалуйста, свяжитесь с доктором Якобом Котасом, [email protected], для получения дополнительной информации.
СтудентовUP также может заинтересовать страница SIAM «Студенты и образование», которая содержит множество ресурсов и информации для старшеклассников и студентов бакалавриата, изучающих математику, в том числе:
- Студенческие гранты на поездки для участия в конференциях
- Список студенческих отделений SIAM
- Различные программы и инициативы
- Советы по карьере в области прикладной математики
- Преимущества студенческого членства
- Студенческие призы
- Онлайн-журнал студенческих исследований SIAM (SIURO)
- Информация о поступлении в аспирантуру и программах
- Информация о математических встречах
- Консультации по публикации и представлению вашего исследования
- Консультации по поиску стажировок, стипендий и работы
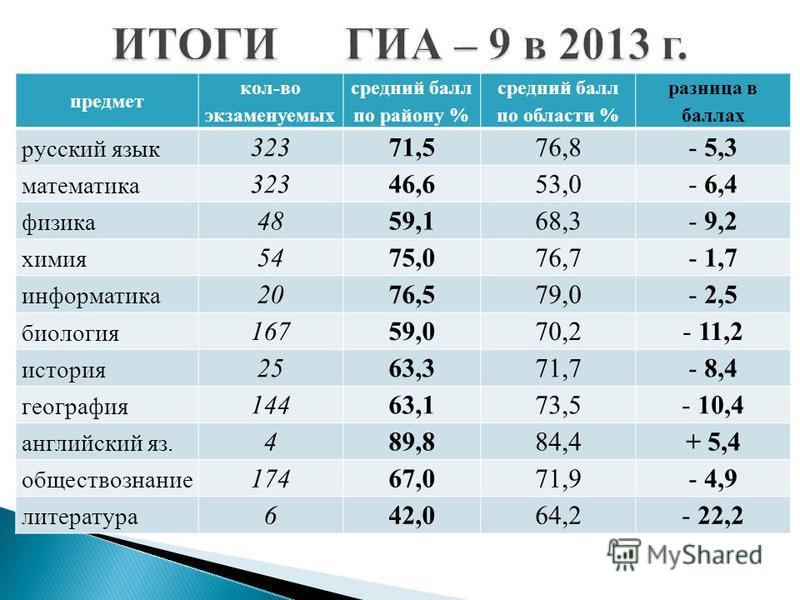
 Ответ на данный вопрос мы дадим в нашей статье.
Ответ на данный вопрос мы дадим в нашей статье.
