Правила квадратного корня — Квадратный Корень
Применение операции корня к числам
Квадратный корень из числа — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной .[1][2] Часто под этим понятием подразумевают более узкое — т. н. арифметический квадратный корень — неотрицательное число.
Рациональные числа
Корень из рационального числа является рациональным числом, только если и (после сокращения общих множителей) являются квадратами натуральных чисел.
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: , где зависит от [3][4]. Верно и обратное: любая периодическая цепная дробь является квадратичной иррациональностью.
Действительные числа
При натуральных уравнение не всегда
Корень квадратный — это… Что такое Корень квадратный?
Квадра́тный ко́рень из 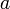 (корень 2-й степени) — это решение
(корень 2-й степени) — это решение 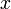 уравнения вида
уравнения вида 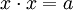 . Несмотря на то, что в первую очередь под
. Несмотря на то, что в первую очередь под 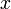 и
и 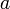 подразумеваются числа, в различных рассмотрениях они могут быть математическими объектами различной природы, в том числе такими как матрицы и операторы. При использовании термина следует уточнять его значение в конкретном разделе математики.
подразумеваются числа, в различных рассмотрениях они могут быть математическими объектами различной природы, в том числе такими как матрицы и операторы. При использовании термина следует уточнять его значение в конкретном разделе математики.
Применение операции корня к числам
Квадратный корень из числа 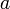 — это такое число, квадрат которого (результат умножения на себя) равен
— это такое число, квадрат которого (результат умножения на себя) равен 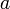 , то есть решение уравнения
, то есть решение уравнения 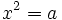 относительно переменной
относительно переменной 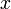 .[1][2]
.[1][2]
Рациональные числа
Корень из рационального числа 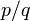 является рациональным числом, только если
является рациональным числом, только если 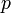 и
и 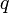 (после сокращения общих множителей) являются квадратами натуральных чисел.
(после сокращения общих множителей) являются квадратами натуральных чисел.
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: 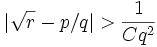 , где
, где 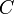 зависит от
зависит от  [3][4].
[3][4].
Действительные числа
При натуральных 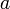 уравнение
уравнение 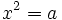 не всегда разрешимо в рациональных числах, что и привело к появлению новых числовых полей. Древнейшее из таких расширений — поле вещественных (действительных) чисел.
не всегда разрешимо в рациональных числах, что и привело к появлению новых числовых полей. Древнейшее из таких расширений — поле вещественных (действительных) чисел.
Теорема. Для любого положительного числа a существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку. [5]
Неотрицательный квадратный корень из положительного числа 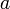 называется арифметическим квадратным корнем и обозначается с использованием знака радикала
называется арифметическим квадратным корнем и обозначается с использованием знака радикала 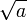 .[6]
.[6]
Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа 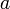 часто обозначают как
часто обозначают как 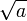 , однако использовать это обозначение нужно осторожно. Распространенная ошибка:
, однако использовать это обозначение нужно осторожно. Распространенная ошибка:
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
 ,
,
то (см. Формула Муавра)
 ,
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.
Квадратный корень как элементарная функция
Вещественный анализ
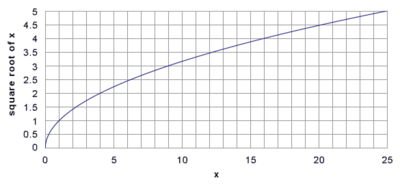 График функции
График функции 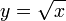
Квадратным корнем называют также функцию 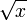 вещественной переменной
вещественной переменной 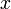 , которая каждому
, которая каждому 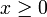 ставит в соответствие арифметическое значение корня.[7] Эта функция является частным случаем степенной функции
ставит в соответствие арифметическое значение корня.[7] Эта функция является частным случаем степенной функции 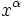 с
с 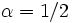 . Эта функция является гладкой при
. Эта функция является гладкой при 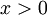 , в нуле же она непрерывна справа, но не дифференцируема.
, в нуле же она непрерывна справа, но не дифференцируема.
Комплексный анализ
Обобщения
Квадратные корни вводятся как решения уравнений вида 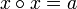 и для других объектов: матриц [8], функций [9], операторов[10] и т. п. В качестве операции
и для других объектов: матриц [8], функций [9], операторов[10] и т. п. В качестве операции  при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.
при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.
В алгебре применяется следующее формальное определение: Пусть 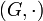 — группоид и
— группоид и 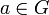 . Элемент
. Элемент 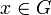 называется квадратным корнем из
называется квадратным корнем из 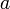 если
если 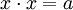 .
.
Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырех действий арифметики, квадратные корни и ничего сверх того. [11]
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа sqrt, от англ. square root «квадратный корень».
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
- 1 = 12
- 1 + 3 = 22
- 1 + 3 + 5 = 32
и так далее.
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и сочтя количество выполненных действий. Например, так:
- 9 − 1 = 8
- 8 − 3 = 5
- 5 − 5 = 0
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
Геометрическое извлечение квадратного корня
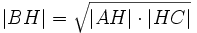
В частности, если 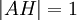 , а
, а 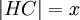 , то
, то 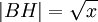 [12]
[12]
Столбиком
Этот способ позволяет найти приближённоё значение корня из любого действительного числа с любой наперёд заданной точностью.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Пусть извлекается корень из целого числа A. В отличие от деления снос производится группами по 2 цифры, причём группы следует отмечать, начиная с десятичной запятой (в обе стороны), дописывая необходимым количеством нулей.
- Найти an, квадрат которого наиболее близко подходит к группе старших разрядов числа A, оставаясь меньше последнего.
- Провести вычитание из старших разрядов A квадрата числа an.
- Удвоить an.
- Сдвинуть остаток от вычитания на 2 разряда влево, а величину 2an — на один разряд влево. Под сдвигом в данном алгоритме понимается умножение/деление на степени 10, что соответственно является сдвигом влево и вправо.
- Приписать справа от остатка вычитания два следующих старших разряда числа A.
- Сравнить полученное число с нулём.
- Если полученное число не равно 0, то найти такое 2an − 1, которое, будучи умноженным на

- Если в п.5 получено равенство, то перейти к п.4, предварительно приписв справа от an нуль.
- После получения количества цифр, равного
 , прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
, прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
Примечания
- ↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
- ↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число (
 )… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
)… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания. - ↑ Теорема Лиувилля о приближении алгебраических чисел
- ↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
- ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
- ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
- ↑ Фихтенгольц, гл. 2, § 1
- ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148
См. также
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru
Квадратный корень | Математика | Fandom
Квадратные корни из натуральных чисел до 25 включительно. В квадрат со стороною √2 вписана окружность.
Квадра́тный ко́рень из $ \! a $ (корень 2-й степени, $ \sqrt{a} $) — это решение уравнения: $ x^2 = a $. Иначе говоря, квадратный корень из $ \! a $ — число, дающее $ \! a $ при возведении в квадрат. Операция вычисления значения $ \sqrt{a} $ называется «извлечением квадратного корня» из числа $ a $. Наиболее часто под $ \! x $ и $ \! a $ подразумеваются числа, но в некоторых приложениях они могут быть и другими математическими объектами, например матрицами и операторами.
Пример для вещественных чисел: $ \sqrt{9}=\pm 3, $ потому что $ {(\pm 3)}^2=9. $ У квадратного корня существуют противоположные, т.е. отличающиеся знаком значения (в данном примере, положительное и отрицательное числа), и это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого при $ \! a \geqslant 0 $ всегда неотрицательно (а на положительных $ \! a $ — положительно; в примере это число 3
Квадратный корень из числа $ \! a $ — это такое число, квадрат которого (результат умножения на себя) равен $ \! a $, то есть решение уравнения $ \! x^2=a $ относительно переменной $ \! x $.[1][2]
- $ -1=(\sqrt{-1})^2=\sqrt{(-1)^2}=\sqrt{1}=1 $
- $ \! a=|a|e^{i\phi} $,
- $ \sqrt{a}=\sqrt{|a|}e^{i(\phi+2\pi k)/2} $,
- Квадратный корень из произведения равен произведению квадратных корней, при условии, что подкоренные выражения больше либо равны 0.
- При возведении корня квадратного в степень достаточно возвести в эту степень подкоренное выражение, при условии, что оно больше нуля.
- Квадратный корень из дроби равен корню из числителя, разделенному на корень из знаменателя, при условии, что подкоренное выражение числителя больше либо равно 0, а подкоренное выражение знаменателя строго больше 0.
- Подкоренное выражение, если оно больше нуля, можно разбить на несколько частей, из которых, в свою очередь, допустимо извлечь корень. Например: √75=√25*3=5√3.
- Под знак корня можно вводить любое число, при этом возведя его в квадрат. Например: 5√8=√25*√8=√200.

Рациональные числа
При натуральных $ \! a $ уравнение $ \! x^2=a $ не всегда разрешимо в рациональных числах. Более того, такое уравнение, даже при положительном $ \! a $, разрешимо в рациональных числах тогда и только тогда когда и числитель и знаменатель числа $ \! a $, представленного в виде несократимой дроби, являются квадратными числами.
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к наничивает точность приближения: $ |\sqrt{r}-p/q|>\frac{1}{Cq^2} $, где $ \! C $ зависит от [3][4]. Верно и $ \! r $то, что любая периодическая цепная дробь является квадратичной иррациональностью.
Действительные (вещественные) числа
Теорема. Для любого положительного числа $ a $ существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку.[5]
Неотрицательный квадратный корень из неотрицательного числа $ \! a $ называется арифметическим квадратным корнем и обозначается с использованием знака радикала $ \sqrt a $[6].
Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля).Дичь из комплексного числа $ \! a $ часто обозначают как $ \sqrt{a} $, однако использовать это обозначение нужно осторожно. Распространённая ошибка:
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
то (см. Формула Муавра)
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом в итоге в ответе получаются два различных результата.Ты втираешь мне какую то дичь!
График функции $ y=\sqrt x $
Квадратный корень является элементарной функцией и частным случаем степенной функции $ \! x^\alpha $ с $ \! \alpha=1/2 $. Арифметический квадратный корень является гладким при $ \! x>0 $, в нуле же он непрерывен справа, но не дифференцируем.[7]
Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в нуле.
Обобщения
Квадратные корни вводятся как решения уравнений вида $ x \circ x = a $ и для других объектов: матриц[8],
math.wikia.org
формулы вычисления. Формула нахождения корней квадратного уравнения
Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает «корень» на латыни).

Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y2 = x.
Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x < 0), то его результатом уже будет комплексное число, включающее мнимую единицу i.
Приведем два простых примера:
√9 = 3, поскольку 32 = 9; √(-9) = 3i, поскольку i2 = -1.
Итерационная формула Герона для нахождения значений корней квадратных
Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).
Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
an+1 = 1/2(an+x/an), где limn->∞(an) => x.
Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a0 (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a0)2 было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a1, которое уже будет ближе к искомому значению. После этого необходимо уже a1 подставить в выражение и получить a2. Эту процедуру следует повторять до получения необходимой точности.
Пример применения итерационной формулы Герона
Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a0).
Приведем простой пример: необходимо вычислить √11. Выберем a0 = 3, так как 32 = 9, что ближе к 11, чем 42 = 16. Подставляя в формулу, получим:
a1 = 1/2(3 + 11/3) = 3,333333;
a2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Дальше нет смысла продолжать вычисления, поскольку мы получили, что a2 и a3 начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.
В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.
Уравнения второго порядка
Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.
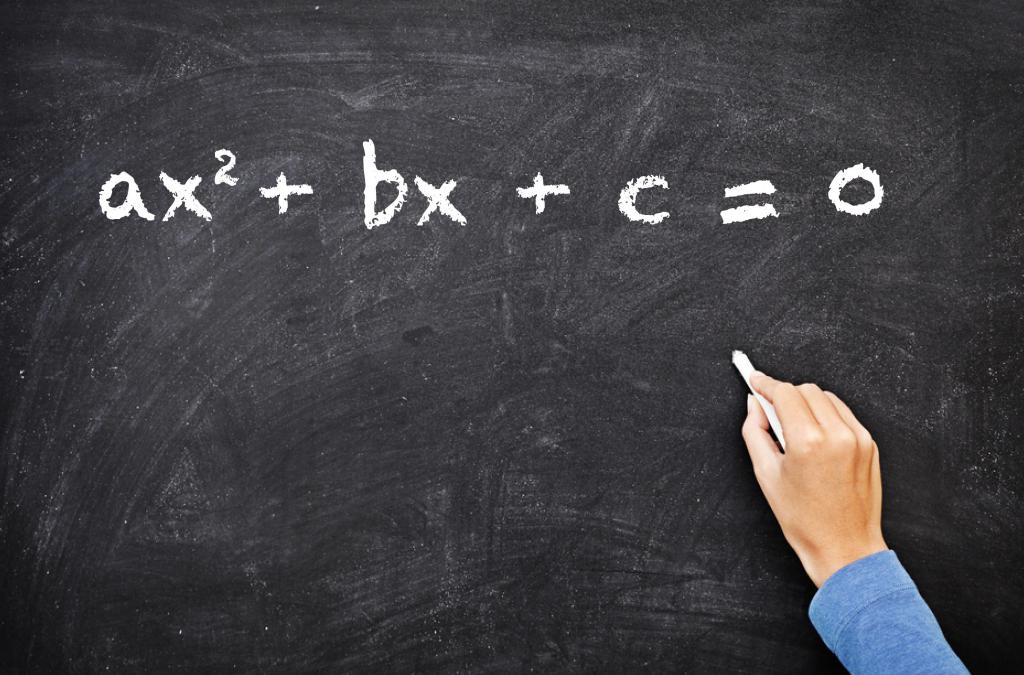
Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.
Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Нахождения корней квадратного уравнения (формула)
Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:
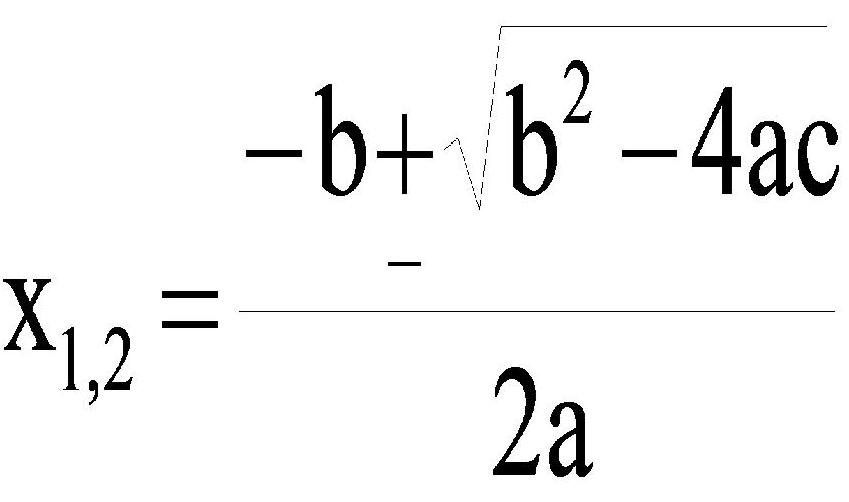
Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x1 отличается от расчета x2 только знаком перед корнем квадратным. Подкоренное выражение, которое равно b2 — 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x1 и x2.
Теорема Виета или некоторые свойства корней уравнений второго порядка
В конце XVI века один из основоположников современной алгебры француз Франсуа Виет, изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:
x1 + x2 = -b / a и x1 * x2 = c / a.
Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.

Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.
Задача на закрепление полученных знаний
Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.

Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:
x1 + x2 = -b / a = 4;
x1 * x2 = c / a = -13.
Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x2 — 4x — 13 = 0.
Воспользуемся формулой с дискриминантом, получим следующие корни:
x1,2 = (4 ± √D)/2, D = 16 — 4 * 1 * (-13) = 68.
То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a0 = 4, тогда:
a1 = 1/2(4 + 17/4) = 4,125;
a2 = 1/2(4,125 + 17/4,125) = 4,1231.
В вычислении a3 нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x1,2, получим:
x1 = (4 + 8,246)/2 = 6,123 и x2 = (4 — 8,246)/2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.
fb.ru
Выделение полного квадрата под корнем
Часто в процессе преобразований или решения уравнений встречаются выражения, содержащие корень под знаком квадратного корня. В большинстве случаев эти выражения можно упростить, выделив полный квадрат под корнем.
Посмотрим, как это делается.
Найти значение выражения:

Упростим первое слагаемое. Предположим, мы можем представить выражение  в виде полного квадрата.
в виде полного квадрата.
 (1)
(1)
Если слагаемое  или
или  содержит корень, то при возведении в квадрат этот корень останется в удвоенном произведении. Поэтом приравняв правую и левую части равенства (1), мы получим систему:
содержит корень, то при возведении в квадрат этот корень останется в удвоенном произведении. Поэтом приравняв правую и левую части равенства (1), мы получим систему:

Разделим второе уравнение на 2:

То есть произведение чисел  и
и  равно
равно 
Выражение  можно представить в виде произведения двух множителей двумя способами:
можно представить в виде произведения двух множителей двумя способами:
 и
и 
или
 и
и 
Проверим, в каком случае 
 — эта пара нам подходит.
— эта пара нам подходит.
Следовательно, 

Внимание! Помним, что квадратный корень из квадрата выражения равен модулю этого выражения.
 Чтобы раскрыть модуль, выясняем знак подмодульного выражения. Если подмодульное выражение больше нуля, то раскрываем модуль с тем же знаком, а если меньше нуля, то с противоположным.
Чтобы раскрыть модуль, выясняем знак подмодульного выражения. Если подмодульное выражение больше нуля, то раскрываем модуль с тем же знаком, а если меньше нуля, то с противоположным.
Упростим второе слагаемое.

Представим подкоренное выражение в виде квадрата разности.

Получим систему:

Разделим второе уравнение на 2:

То есть произведение чисел  и
и  равно
равно 
Выражение  можно представить в виде произведения двух множителей двумя способами:
можно представить в виде произведения двух множителей двумя способами:
 и
и 
или
 и
и 
Проверим, в каком случае 

 — эта пара нам не подходит.
— эта пара нам не подходит.
 — эта пара нам подходит.
— эта пара нам подходит.
Следовательно, 
 — подмодульное выражение
— подмодульное выражение  меньше нуля, поэтому мы раскрыли модуль с противоположным знаком.
меньше нуля, поэтому мы раскрыли модуль с противоположным знаком.
Итак, после упрощения корней мы получили равенство:

Ответ: 3
ege-ok.ru
Как найти квадратный корень? Свойства, примеры извлечения корня :: SYL.ru
Математика зародилась тогда, когда человек осознал себя и стал позиционироваться как автономная единица мира. Желание измерить, сравнить, посчитать то, что тебя окружает, — вот что лежало в основе одной из фундаментальных наук наших дней. Сначала это были частички элементарной математики, что позволили связать числа с их физическими выражениями, позже выводы стали излагаться лишь теоретически (в силу своей абстрактности), ну а через некоторое время, как выразился один ученый, «математика достигла потолка сложности, когда из нее исчезли все числа». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
С чего все начиналось
Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике. Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.

Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.
Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.
Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению. На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R2a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.
Наши дни
С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z2=y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.
В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным. Таким образом, в силу того, что z2=y и (-z)2=y, имеем: √y=±z или √y=|z|.
Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.
Свойства квадратного корня на поле R
Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.
Как найти корень числа?
Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:
1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю. Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
25-1=24
24-3=21
21-5=17
17-7=10
10-9=1
Следующее нечетное число — это 11, остаток у нас следующий: 1<11. Количество ходов — 5, так что корень из 25 равен 5. Вроде все легко и просто, но представьте, что придется вычислять из 18769?
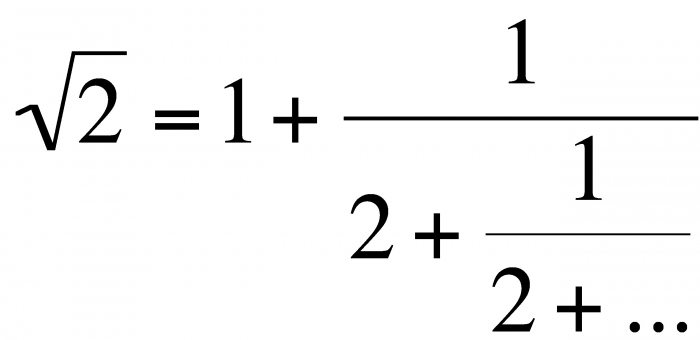 Для таких случаев существует разложение в ряд Тейлора:
Для таких случаев существует разложение в ряд Тейлора:√(1+y)=∑((-1)n(2n)!/(1-2n)(n!)2(4n))yn, где n принимает значения от 0 до
+∞, а |y|≤1.
Графическое изображение функции z=√y
Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:
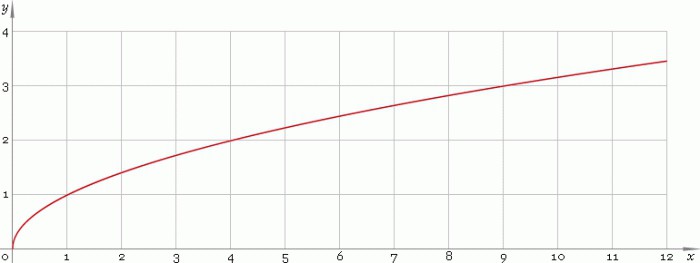
Кривая растет из начала координат и обязательно пересекает точку (1; 1).
Свойства функции z=√y на поле действительных чисел R
1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).
2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).
3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.
4. Функция z=√y ни четная, ни нечетная.
5. Функция z=√y не является периодической.
6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).
7. Точка пересечения графика функции z=√y также является и нулем этой функции.
8. Функция z=√y непрерывно растет.
9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.
Варианты изображения функции z=√y
В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y1/2. Такой вариант удобен, например, в возведении функции в степень: (√y)4=(y1/2)4=y2. Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.
А в программировании заменой символа √ является комбинация букв sqrt.
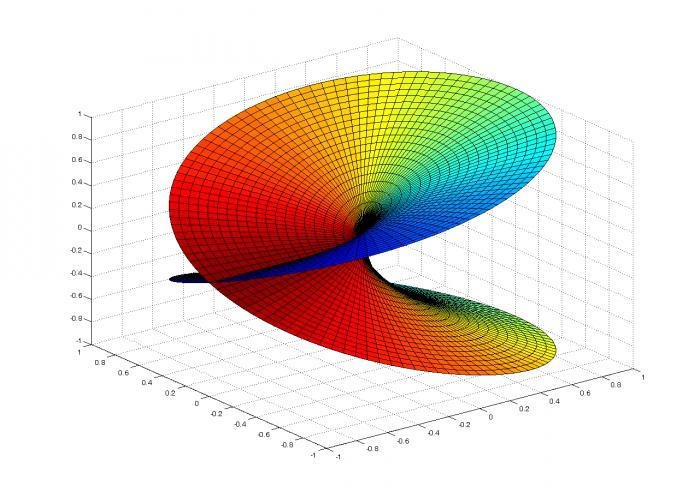 Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).Корень квадратный в комплексном поле С
По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.
www.syl.ru
Таблица квадратных корней
В таблице приведены квадратные корни натуральных чисел от 1 до 100.
|
√1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 |
√121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20 |
√441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √784 = 28 √841 = 29 √900 = 30 |
√961 = 31 √1024 = 32 √1089 = 33 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40 |
√1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50 |
|
√2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60 |
√3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70 |
√5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80 |
√6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7396 = 86 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90 |
√8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √9801 = 99 √10000 = 100 |
naobumium.info
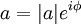 ,
,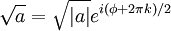 ,
,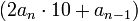
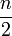 , прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
, прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.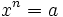 )… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
)… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.