Квадратичная функция: ее график и свойства 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 4.
Всем привет! Сегодня мы поговорим об одной из самых важных функций, о квадратичной функции.
Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.
Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.
Построим в одной системе координат
y = x2; y = 2x2; y = 3x2.
y = x2
|
x |
-3 |
|
-1 |
0 |
1 |
2 |
3 |
|
y |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
y = 2x2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
18 |
8 |
2 |
0 |
2 |
8 |
18 |
При любом x ≠ 0 значение функции y = x2 в 2 раза больше соответствующих значений функции  То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
Аналогично, график функции y = 3x2 можно получить из графика функции y = x2 растяжением от оси x в 3 раза.
Построим теперь в одной системе координат графики функции y = x2, y=12×2, y=13×2.
y=12×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
4,5 |
2 |
0,5 |
0 |
0,5 |
2 |
4,5 |
Заметим, что при любом x ≠ 0 значения функции y=12×2меньше соответствующих значений функции y = x2 в 2 раза.
Таким образом, график функции y=12×2 можно получить из параболы
y=13×2
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
3 |
43 |
13 |
0 |
13 |
43 |
3 |
Аналогично график функции y=13×2 можно получить из графика функции = x2 сжатием к оси x в 3 раза.
Давай сделаем вывод:
График функции y = ax2 можно получить из параболы y = x2 растяжением от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0 a
Рассмотрим теперь случай, когда a y=-13×2. Составим таблицу значений:
|
x |
-3 |
-2 |
|
0 |
1 |
2 |
3 |
|
y |
-3 |
-43 |
-13 |
0 |
-13 |
-43 |
-3 |
Сравним графики функций y=13×2 и y=-13×2.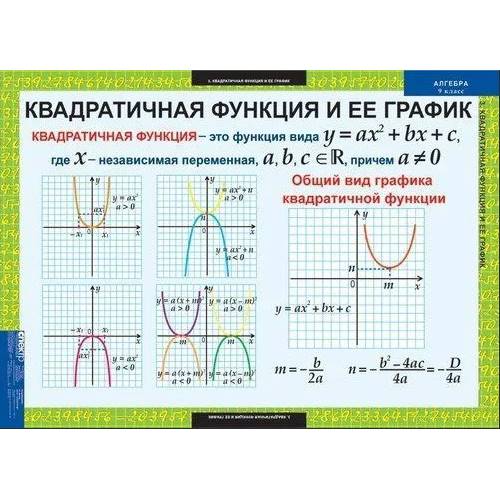 При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
То есть графики функций y = ax2 и y = —ax2 при a ≠ 0 симметричны относительно оси x. Графиком функции y = ax2, как и графиком функции y = x2 является парабола
Сформулируем свойства функции y = ax2 при a > 0.
- Область определения -∞;+∞;
- Область значений функций 0;+∞
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
-
График функции симметричен относительно оси y.

- Функция убывает в промежутке -∞;0 и возрастает в промежутке 0;+∞.
- При x = 0 функция принимает наименьшее значение, равное 0. Наибольшего значения функции нет.
Сформулируем свойства функции y = ax2 при a
- Область определения -∞;+∞;
- Область значений функций -∞;0
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y
- График функции симметричен относительно оси y.
- Функция убывает в промежутке 0;+∞ и возрастает в промежутке -∞;0.
- При x = 0 функция принимает наибольшее значение, равное 0. Наименьшего значения функции нет.
От коэффициента a зависит направление ветвей параболы. Если a > 0, то ветви параболы направлены вверх, если a
Если a > 0, то ветви параболы направлены вверх, если a
Построение графика, симметричного данному относительно оси x, или сжатие к оси x – различные виды преобразований графиков функций. Преобразования графиков функции, рассмотренные нами сегодня для функций y = ax2, применимы к любой функции.
График функции y=-fx можно получить из графика функции y=fx с помощью симметрии относительно оси абсцисс.
График функции y=afx можно получить из графика функции y=fx с помощью растяжения от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0
Квадратичная функция, ее график и свойства
1. Квадратичная функция. Её свойства и график.
Определение квадратичнойфункции
Квадратичной функцией называется
функция , которую можно задать формулой
y=
2
ax +bx
+c
где: a, b, c –
числа
Х – независимая переменная
а 0
График квадратичной функции – парабола.

3. Алгоритм построения параболы у = ах2 + bх + с :
1. Найти координаты вершины параболы, построитьна координатной плоскости соответствующую точку,
провести ось симметрии.
2.
Определить направление ветвей параболы.
3. Найти координаты еще нескольких точек,
принадлежащих искомому графику ( в частности,
координаты точки пересечения параболы с осью у и
нули функции, если они существуют).
4. Отметить на координатной плоскости
найденные точки и соединить их плавной линией.
—
.
Графиком квадратичной функции
у = ах2 + bх + с является парабола, которая получается из
параболы
у = ах2 параллельным переносом.
Вершина параболы — ( х0; уо) ,
b
где : хо = 2a
у0 =
4ac b 2
4a
Осью параболы будет прямая
b
х=2a
5. Свойства квадратичной функции
Функция непрерывнаМножество значений при a>0 —
Множество значений при a
8
6
4
2
0
-3
-2
-1
0
-2
1
2
3
4
5
Многие свойства
квадратичной функции
зависят от значения
дискриминанта.

Дискриминантом квадратного уравнения
ах2 + bх + с = 0 называется выражение
D =b2 – 4ac
Возможны три случая:
D 0
D 0
D 0
если дискриминант больше нуля, то парабола
пересекает ось абсцисс в двух точках,
если дискриминант равен нулю, то парабола
касается оси абсцисс,
если дискриминант меньше нуля, то парабола не
пересекает ось абсцисс,
абсцисса вершины параболы равна
—
ветви параболы
направлены вверх,
При
у
b
2a
При
ветви параболы
направлены
вниз
у
f(x0)
х
х
b
2a
9. Область значений функции – Е (f) = [ -1 ; + )
Функция возрастает впромежутке [ +3; +
)
Функция убывает в
промежутке ( ;+3]
Наименьшее значение
функции равно -1
Наибольшего значения
функции не существует
f(x) > 0 при х
х>4
f(x)
Ось симметрии
Область значений функции –
10. Постройте график функции у=2х²+4х-6, опишите его свойства
Проверь себя:1.
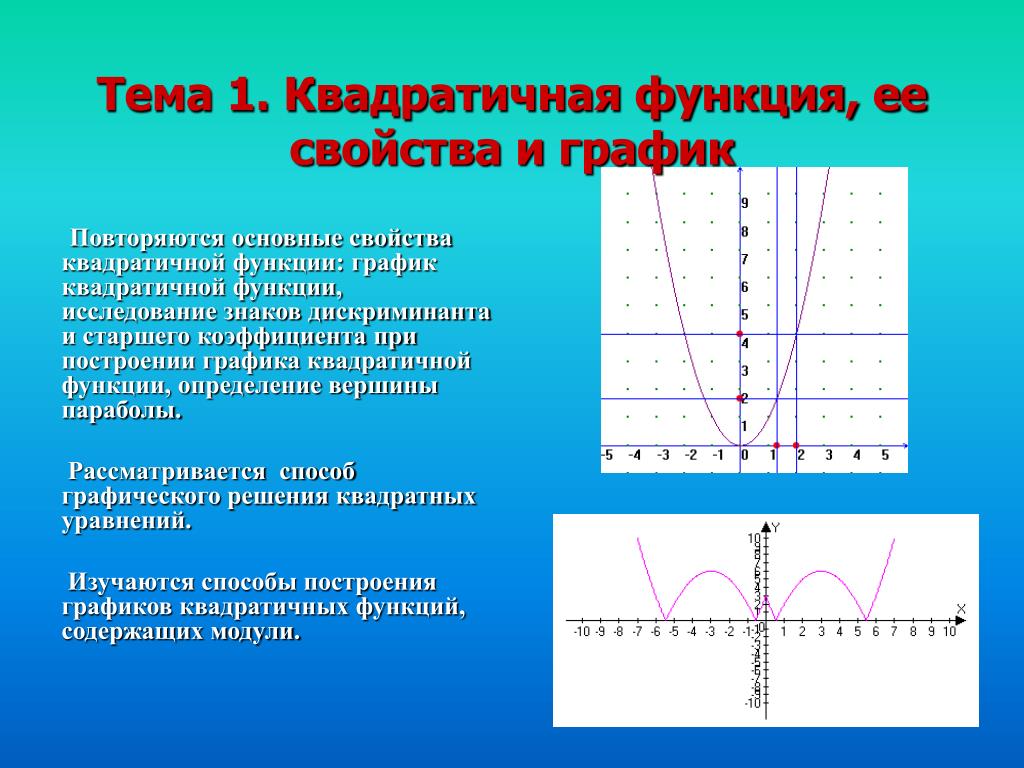 D(y)=
D(y)=;
У
2. у=0, при х=1; -3
3. у>0, при х ; 3 1;
у
4. у↓, если х ; 1
у↑, если х 1;
5. унаим= -8, если х= -1
унаиб – не существует.
6. Е(y): 8 ;
1
-1
-2
1 2 3
Х
Задание
1. Построить график функции и
описать ее свойства у=2х²+4х-1
2. Построить график функции и
описать ее свойства у= -7х²-х+3
Квадратичная Функция Y=ax2 Bx C
Квадратичная Функция Y=ax2 Bx CA-Z Keywords
Keyword Suggestions
Images for Квадратичная Функция Y=ax2 Bx C
КВАДРАТИЧНАЯ ФУНКЦИЯ y=ax2+bx+c свойства и график …
ytimg.com
Квадратичная функция y = ax2 +bx+c — Презентация 208263-6
900igr.net
3. Квадратичная функция общего вида y = ax2 + bx + c также …
900igr.net
Презентация к уроку алгебры в 9 классе на тему «Функции и .
 ..
..metod-kopilka.ru
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
Построить график функции y=ax2+bx+c (квадратичная функция …
fxyz.ru
Пожалуйста помогите решить Дана квадратичная функция y=ax2 …
z-dn.net
Построение графика y=ax2+bx+c — Презентация 240014-14
900igr.net
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
y= ax2 +bx + c — Презентация 134593-3
900igr.net
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
y = ax2 — Презентация 158601-21
900igr.net
Функция y=ax2+bx+c, её свойства и график — презентация по .
 ..
..ppt4web.ru
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Презентация по математике «Квадратичная функция, её …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
Презентация на тему: «Квадратичная функция Урок алгебры в …
myshared.ru
Презентация 9 класс «Урок «Функция и его свойства»
infourok.ru
Зачетная работа по теме: Квадратичная функция y=ax2 +bx+c .
 ..
..infourok.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Презентация по математике «Исследование зависимости вида y …
ppt4web.ru
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
Презентация на тему «Функция y=ax2+bx+c» по математике
digitaloceanspaces.com
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.
 ru
ru Математика 13+| Функция вида y=ax²+bx+c и её график |Урок …
ytimg.com
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Функция y=ax2,ее график — Презентация 8408-2
900igr.net
Квадратичная функция и её график — презентация по Геометрии
ppt4web.ru
Презентация по математике «Квадратичная функция, её …
ppt4web.ru
Презентация по математике «Функция y=ax2+bx+c» — скачать …
ppt4web.ru
Презентация по математике «Свойства и графики элементарных …
ppt4web.ru
Функция y=ax2+bx+c, её свойства и график — презентация по …
ppt4web.ru
Презентация по математике «Функция y=ax2+bx+c» — скачать …
ppt4web.ru Tags: КВАДРАТИЧНАЯ ФУНКЦИЯ yax2bxc свойства и график, Квадратичная функция y ax2 bxc Презентация 2082636, 3 Квадратичная функция общего вида y ax2 bx c также, Квадратичная функция yax2bxc схема таблица, Презентация к уроку алгебры в 9 классе на тему quotФункции и, Презентация на тему quotФункция yax2bxcquot по математике, Построить график функции yax2bxc квадратичная функция, Пожалуйста помогите решить Дана квадратичная функция yax2, Построение графика yax2bxc Презентация 24001414, Презентация на тему quotФункция yax2bxcquot по математике, y ax2 bx c Презентация 1345933,
Keyword examples:
Внеклассный урок — Квадратичная функция.
 Функция y = ax2, ее график и свойстваКвадратичная функция. Функция y = ax2, ее график и свойства
Функция y = ax2, ее график и свойстваКвадратичная функция. Функция y = ax2, ее график и свойства
Квадратичная функция – это функция, которую можно задать формулой вида
y = ax2 + bx + c,
где x – независимая переменная, a, b и c – некоторые числа, причем а ≠ 0.
Областью определения квадратичной функции является множество всех чисел. (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)
Функция y = ax2.
Функция y = ax2 – это частный случай квадратичной функции.
Графиком функции y = ax2 является парабола.
Свойства функции y = ax2 при a > 0:
1. Если x = 0, то y = 0. График функции проходит через начало координат.
2. Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. Пояснение: допустим, x = –2, y = 8. При x = 2 значение y не меняется и составляет 8.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) — возрастает.
5. Наименьшее значение функции равно нулю. Это значение она принимает при x = 0 (см. Наибольшего значения функция не имеет. Т.е. областью значений функции является промежуток [0; +∞). |
Свойства функции y = ax2 при a < 0:
1. Если x = 0, то y = 0. График функции проходит через начало координат.
2. Если x ≠ 0, то y < 0. График функции расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции представляет собой симметричную фигуру относительно оси y. Пояснение: допустим, x = –4, y = –8. При x = 4 значение y не меняется и составляет –8.
4. В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) — убывает.
5. Наибольшее значение функции равно нулю. Это значение она принимает при x = 0 (см.пункт 1). Наименьшего значения функция не имеет. Т.е. областью значений функции является промежуток (–∞; 0]. |
3.3.3 Квадратичная функция, её график
Видеоурок 1: Квадратичная функция. Часть 1
Видеоурок 2: Квадратичная функция. Часть 2
Видеоурок 3: Построение графика квадратичной функции
Лекция: Квадратичная функция, её график
Квадратичная функцияЕсли перед Вами появилась функция вида у = ах2 + bx + c, то такая функция будет иметь название квадратичной.
Обратите внимание, функция будет квадратичной только в том случае, если коэффициент а ≠ 0.
Итак, в данной функции а, b и с — это коэффициенты:
а — коэффициент при старшем члене,
b — второй коэффициент,
с — свободных член.
Любая квадратичная функция на координатной плоскости изображается в виде параболы, однако функция у = х2 имеет вид:
При с = 0 график всегда начинается в начале координат, а остальные 4 точки определяются самостоятельно:
Если коэффициент а < 0, то данный график будет иметь немного другой вид — ветки параболы будут направлены вниз:
Характеристика функции у = х21. Область значения функции — существует для всех действительных чисел.
2. Область значения функции — функция не может принимать отрицательные значения.
3. Парная функция, симметрична относительно оси ОУ.
4. Монотонно убывает на промежутке от минус бесконечности до нуля, монотонно возрастает на промежутке от нуля до бесконечности.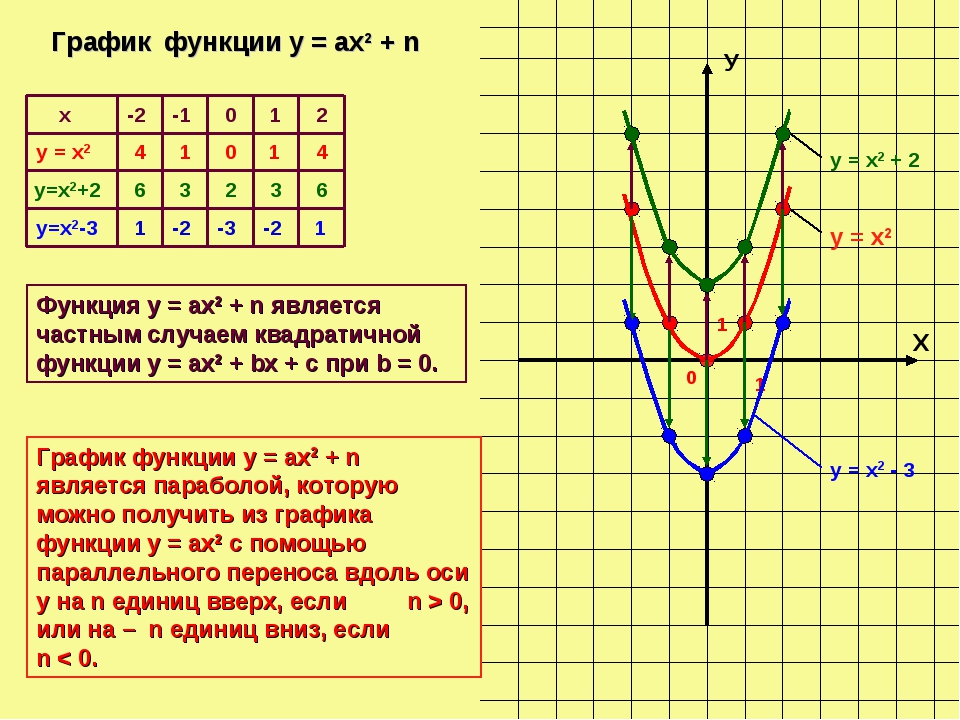
5. Минимум функции на все рассматриваемом промежутке в точке [0; 0].
Решение квадратного уравненияКак мы знаем, при решении квадратного уравнения может существовать несколько случаев, которые влияют на количество корней. Напомним Вам, что найти решение уравнения — значит найти точку, в которой график пересекает ось ОХ. Именно поэтому функция приравнивается к нулю: у = 0.
1. Если мы имеем уравнение вида у = ах2 + bx + c, то решая его по дискриминанту, можем получить D < 0. С точки зрения графика квадратичной функции это значит, что вершина параболы находится над осью ОХ, а её ветки направлены вверх. Именно из-за того, что не существует пересечения с осью ОХ, решений данное уравнение не имеет.
2. Если дискриминант равен нулю D = 0, то это означает, что уравнение имеет один корень. Следовательно, на графике это можно показать в качестве вершины, которая лежит на оси ОХ.
3. Если дискриминант больше нуля D > 0, это значит, что уравнение имеет два корня.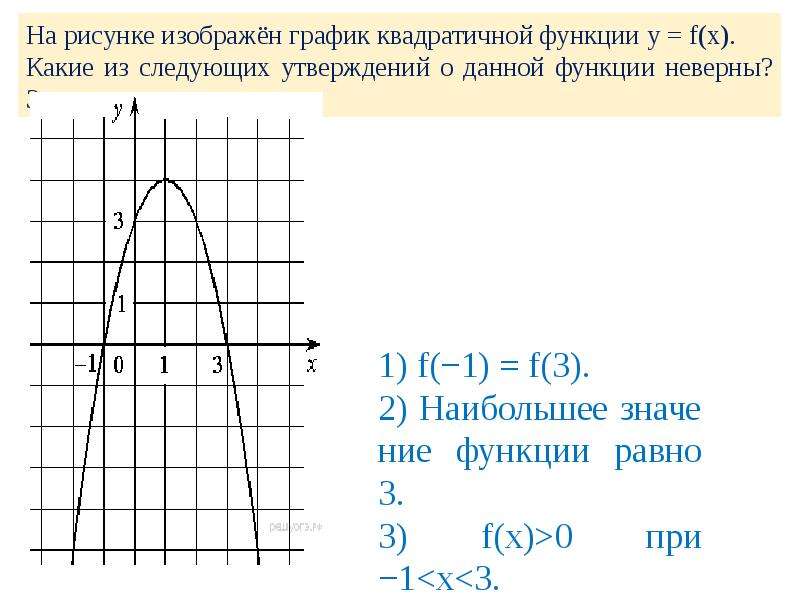 На графике это можно показать, как пересечение оси ОХ ветвями параболы.
На графике это можно показать, как пересечение оси ОХ ветвями параболы.
Давайте рассмотри алгоритм построение параболы по квадратичной функции на примере следующей функции: у = 2х2 + 3х — 5.
1. Первым делом следует определиться с направлением ветвей параболы. Для этого необходимо обратить внимание на коэффициент, который стоит перед старшим членом. Если коэффициент положительный, то ветви параболы направлены вверх. Следовательно, 2 > 0, а значит, в нашей функции ветви параболы направлены вверх.
2. Дальше следует приравнять функцию к нулю для нахождения дискриминанта. В данном получившемся уравнении дискриминант больше нуля, а это значит, что мы будем иметь два решения, а значит, два пересечение графика с осью ОХ.
3. Теперь давайте определим, в каких точках график будет пересекать ось ОХ. Для этого необходимо решить получившееся уравнение.
В данном случае мы получили корни:
х1 = 1, х2 = -2,5.
4. Находим координату вершины параболы. Для этого необходимо воспользоваться формулой:
5. Еще дополнительные две симметричные точки находятся через подстановку вместо «х» нуля. В нашем уравнении мы получили, что при х = 0, у = -5.
6. А теперь нанесем вершину, точки пересечения с осью ОХ и ОУ на график. В результате этого получим:
Квадратичная функция и ее график
На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x2. Давайте расширим знания по квадратичной функции.
Задание 1.
Построить график функции y = x2. Масштаб: 1 = 2 см. Отметьте на оси Oy точку F(0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1). Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?
Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1). Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?
Результат: какую бы точку на параболе y = x2 вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.
Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4. Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x2, а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.
Интересные свойства параболы:
1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
2. Если вращать параболу вокруг оси симметрии (например, параболу y = x2 вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.
Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).
4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис. 3).
5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.
6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.
7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.
Построение графика квадратичной функции
На уроках математики вы изучали получение из графика функции y = x2 графиков функций вида:
1) y = ax2 – растяжение графика y = x2 вдоль оси Oy в |a| раз (при |a| < 0 – это сжатие в 1/|a| раз, рис. 4).
2) y = x2 + n – сдвиг графика на n единиц вдоль оси Oy, причем, если n > 0, то сдвиг вверх, а если n < 0, то вниз, (или же можно переносить ось абсцисс).
3) y = (x + m)2 – сдвиг графика на m единиц вдоль оси Ox: если m < 0, то вправо, а если m > 0, то влево, (рис. 5).
5).
4) y = -x2 – симметричное отображение относительно оси Ox графика y = x2.
Подробнее остановимся на построении графика функции y = a(x – m)2 + n.
Квадратичную функцию вида y = ax2 + bx + c всегда можно привести к виду
y = a(x – m)2 + n, где m = -b/(2a), n = -(b2 – 4ac)/(4a).
Докажем это.
Действительно,
y = ax2 + bx + c = a(x2 + (b/a) x + c/a) =
= a(x2 + 2x · (b/a) + b2/(4a2) – b2/(4a2) + c/a) =
= a((x + b/2a) 2 – (b2 – 4ac)/(4a2)) = a(x + b/2a) 2 – (b2 – 4ac)/(4a).
Введем новые обозначения.
Пусть m = -b/(2a), а n = -(b2 – 4ac)/(4a),
тогда получим y = a(x – m)2 + n или y – n = a(x – m)2.
Сделаем еще замены: пусть y – n = Y, x – m = X (*).
Тогда получим функцию Y = aX2, графиком которой является парабола.
Вершина параболы находится в начале координат. X = 0; Y = 0.
Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m)2 + n: x = m, y = n.
Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде
y = a(x – m)2 + n
путем преобразований, можно действовать следующим образом:
a) построить график функции y = x2;
б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис. 6).
Запись преобразований:
y = x2 → y = (x – m)2 → y = a(x – m)2 → y = a(x – m)2 + n.
Пример.
С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3)2– 2.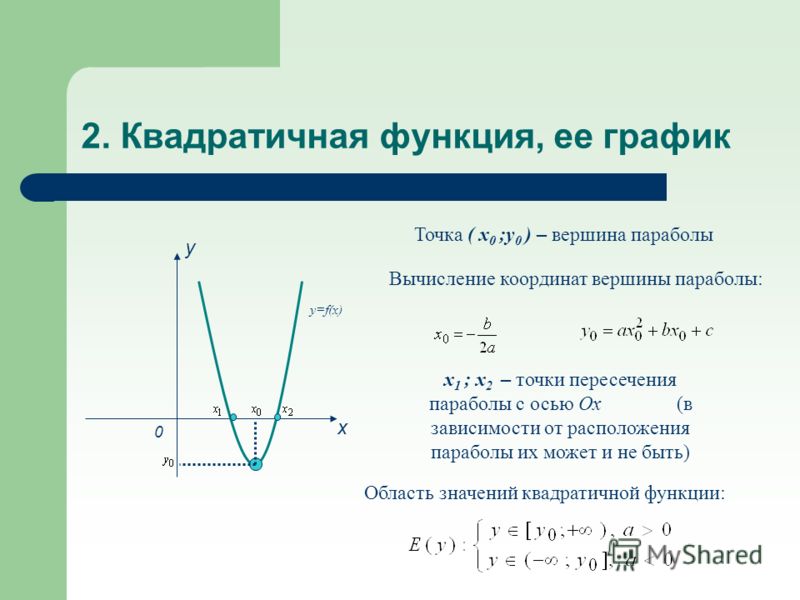
Решение.
Цепочка преобразований:
y = x2(1) → y = (x – 3)2(2) → y = 2(x – 3)2(3) → y = 2(x – 3)2 – 2 (4).
Построение графика изображено на рис. 7.
Вы можете практиковаться в построении графиков квадратичной функции самостоятельно. Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3)2 + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации. Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.
Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog. tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Построение графика квадратичной функции | Алгебра
Построение графика квадратичной функции продолжим рассмотрением способа, базирующегося на преобразованиях координатной плоскости.
II способ.
1) Находим координаты вершины параболы y=ax²+bx+c — точку (xo; yo)
2) Осуществляем параллельный перенос начала отсчёта — точки O (0; 0) — в точку (xo; yo). При таком преобразовании новыми осями координат x’ и y’ становятся прямые y=yo и x=xo.
2) Строим параболу y=x² (если a>o)либо y= -x² (если a<0) с вершиной в новом начале отсчёта (достаточно отметить базовые точки).
3) От вершины строим график функции y=ax². При |a|>1 график может быть получен растяжением от оси y=y0 в |a| раз, при |a|<1 — сжатием в |a| раз.
(Вариант — график функции y=ax² можно построить с началом отсчёта в точке O (0; 0), а затем осуществить его параллельный перенос).
Примеры.
1) Построить график функции y=3x²-24x+43.
Решение:
y=3x²-24x+43 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=3>0). Координаты вершины параболы
Точка (4; -5) — новое начало отсчёта. Построим параболу y=x² с вершиной в этой точке (достаточно отметить базовые точки — 1 единица вправо, 1 — вверх, 2 вправо. 4 — вверх, 1 — влево, 1 — вверх, 2 — влево, 4 — вверх.
График функции y=3x² может быть получен из графика y=x² растяжением от оси x’ (x= -5) в 3 раза:
Построение графика квадратичной функции y=3x²-24x+43
2) Построить график функции y= -0,5x²-2x+1
Решение:
y= -0,5x²-2x+1 — квадратичная функция. График — парабола ветвями вниз (так как a= -0,5<0).
Координаты вершины параболы
Точка (-2; 3) — новое начало отсчёта.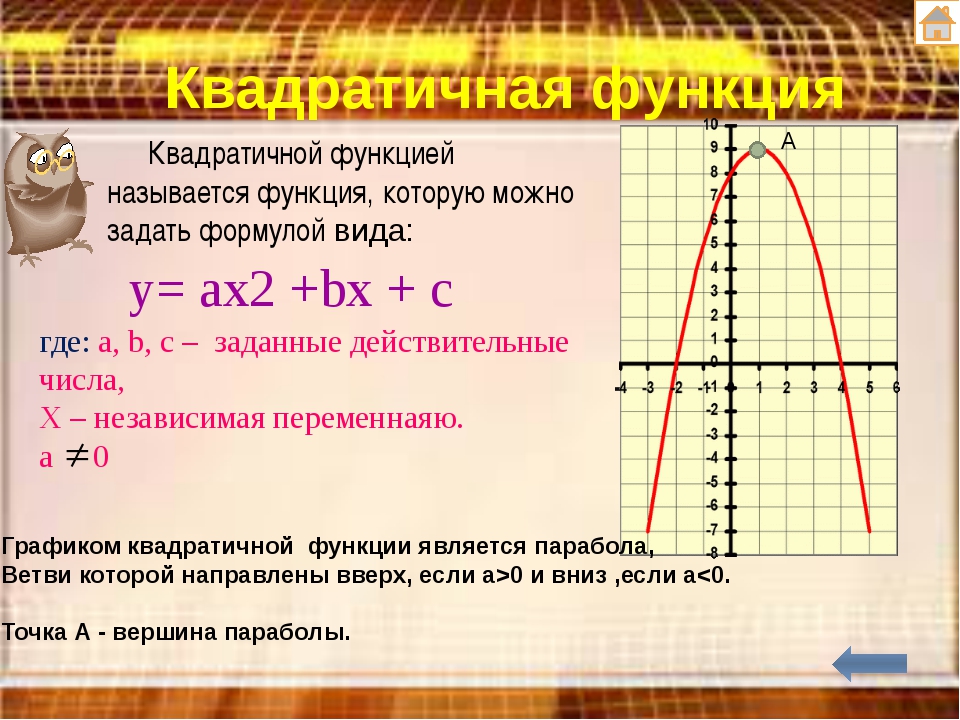 Построим параболу y= -x² с вершиной в этой точке. График функции
Построим параболу y= -x² с вершиной в этой точке. График функции
может быть получен из графика y= -x² сжатием к оси x’ (y=3) в 2 раза.
Построение графика функции y= -0,5x²-2x+1
Для построения графика квадратичной функции этим способом нужно хорошее владение навыками геометрических преобразований графиков.
Если координаты вершины параболы не являются целыми числами, этот способ менее удобен, чем построение по точкам.
Какой бы способ вы для себя ни выбрали, важно вовремя качественно усвоить данную тему, поскольку с построением графиков функций в алгебре придётся иметь дело ещё не раз.
Квадратичная функция
Общий вид квадратичной функции: ж ( Икс ) знак равно а Икс 2 + б Икс + c . График квадратичной функции — это парабола , тип 2 -мерная кривая.
«Основная» парабола, у знак равно Икс 2 , выглядит так:
Функция коэффициента а в общем уравнении — сделать параболу «шире» или «тоньше» или перевернуть ее вверх ногами (если отрицательно):
Если коэффициент
Икс
2
положительный, парабола раскрывается; в противном случае он откроется.
Вершина
В вершина параболы — это точка внизу » U «форма» (или вершина, если парабола открывается вниз).
Уравнение для параболы также можно записать в «вершинной форме»:
у знак равно а ( Икс — час ) 2 + k
В этом уравнении вершиной параболы является точка ( час , k ) .
Вы можете увидеть, как это соотносится со стандартным уравнением, умножив его:
у знак равно а ( Икс — час ) ( Икс — час ) + k
у знак равно а Икс 2 — 2 а час Икс + а час 2 + k
Коэффициент
Икс
вот
—
2
а
час
. Это означает, что в стандартной форме
у
знак равно
а
Икс
2
+
б
Икс
+
c
, выражение
Это означает, что в стандартной форме
у
знак равно
а
Икс
2
+
б
Икс
+
c
, выражение
— б 2 а
дает Икс -координата вершины.
Пример:
Найдите вершину параболы.
у знак равно 3 Икс 2 + 12 Икс — 12
Здесь, а знак равно 3 и б знак равно 12 .Так что Икс -координата вершины:
— 12 2 ( 3 ) знак равно — 2
Подставляя в исходное уравнение, чтобы получить у -координат, получаем:
у знак равно 3 ( — 2 ) 2 + 12 ( — 2 ) — 12
знак равно — 24
Итак, вершина параболы находится в точке
(
—
2
,
—
24
)
.
Ось симметрии
Ось симметрии параболы — это вертикальная линия, проходящая через вершину. Для параболы стандартной формы у знак равно а Икс 2 + б Икс + c , ось симметрии имеет уравнение
Икс знак равно — б 2 а
Обратите внимание, что — б 2 а также Икс -координата вершины параболы.
Пример:
Найдите ось симметрии.
у знак равно 2 Икс 2 + Икс — 1
Здесь, а знак равно 2 и б знак равно 1 . Итак, ось симметрии — это вертикальная линия
Икс знак равно — 1 4
Перехваты
Вы можете найти
у
-перехват параболы простым вводом
0
за
Икс
. Если уравнение имеет стандартную форму, то можно просто взять
c
как
у
-перехват. Например, в приведенном выше примере:
Если уравнение имеет стандартную форму, то можно просто взять
c
как
у
-перехват. Например, в приведенном выше примере:
у знак равно 2 ( 0 ) 2 + ( 0 ) — 1 знак равно — 1
Так что у -перехват — 1 .
В Икс -перехват немного сложнее. Ты можешь использовать факторинг , или завершение квадрата , или квадратичная формула найти их (если они есть!).
Домен и диапазон
Как и в случае с любой другой функцией, домен квадратичной функции
ж
(
Икс
)
это набор
Икс
-значения, для которых определена функция, и диапазон — это набор всех выходных значений (значения
ж
).
Квадратичные функции обычно имеют целую вещественную линию в качестве области определения: любой Икс это законный ввод.Диапазон ограничен теми точками, которые больше или равны у -координата вершины (или меньше или равна, в зависимости от того, открывается парабола вверх или вниз).
Обратная квадратичная функция — ChiliMath
Здесь мы хотим найти обратную функцию , которая подразумевает, что обратная функция ДОЛЖНА быть самой функцией. В противном случае мы получили инверсию, не являющуюся функцией.
Не всем функциям, естественно, «везет» иметь обратные функции.{- 1}} \ left (x \ right), если ни одна горизонтальная линия не пересекает его график более одного раза.
- Пример графика с обратным
- Пример графика без обратного
Ниже приведены основные стратегии алгебраического решения обратной функции.
Ключевые шаги в поиске функции, обратной квадратичной функции
- Заменить f (x) на y.
- Поменяйте роли \ color {red} x и \ color {blue} y.2} + 2, если он существует. Укажите его домен и диапазон.
Первое, что я понимаю, это то, что у этой квадратичной функции нет ограничений на ее область определения. Я уверен, что при построении графика я смогу нарисовать горизонтальную линию, которая будет пересекать ее более одного раза. Следовательно, обратное — не функция. Я даже не буду утруждать себя приведенными выше ключевыми шагами, чтобы найти обратное.
На диаграмме показано, что он не проходит проверку горизонтальной линии, поэтому обратная функция не является функцией. Я остановлюсь здесь.2} + 2, \, \, x \ ge 0, если он существует. Укажите его домен и диапазон.
Та же самая квадратичная функция, как показано в примере 1, имеет ограничение на ее область определения x \ ge 0. После построения функции по оси xy я вижу, что график представляет собой разрезанную пополам параболу для всех значений x.
 равно или больше нуля. Он должен пройти тест горизонтальной линии, который говорит мне, что я действительно могу найти его обратную функцию, выполнив предложенные шаги.
равно или больше нуля. Он должен пройти тест горизонтальной линии, который говорит мне, что я действительно могу найти его обратную функцию, выполнив предложенные шаги.На приведенном ниже графике я четко определил домен и диапазон, потому что мне понадобится эта информация, чтобы в конечном итоге определить правильную обратную функцию.
Помните, что домен и диапазон обратной функции берутся из диапазона и домена исходной функции, соответственно. Это называется заменой домена на диапазон .
Даже не решая пока обратную функцию, я могу легко определить ее область и диапазон, используя информацию из графика исходной функции: область — это x ≥ 2 , а диапазон — y ≥ 0 .
Вы видите, как я меняю местами домен и диапазон исходной функции, чтобы получить домен и диапазон ее обратной функции?
Теперь давайте продолжим и решим алгебраически обратное.2} — 1, \, \, x \ le 0, если он существует.
 Укажите его домен и диапазон.
Укажите его домен и диапазон.Эта проблема очень похожа на Пример 2. Диапазон начинается с \ color {red} y = -1, и он может опускаться как можно ниже.
Теперь, это шаги, как найти обратное.
Применение операции извлечения квадратного корня приводит к получению двух уравнений из-за положительного и отрицательного случаев. Чтобы выбрать правильную обратную функцию из двух, я предлагаю вам найти область и диапазон каждого возможного ответа.Теперь правильная обратная функция должна иметь домен, происходящий из диапазона исходной функции; и диапазон, происходящий из домена той же функции.
Ниже приведены графики исходной функции и обратной функции на одной и той же координатной оси.
Пример 4: Найдите обратную функцию для функции ниже, если она существует. Укажите его домен и диапазон.
Сначала я бы построил график этой функции и четко определил бы домен и диапазон.2} — 4ac}} \ over {2a}}}}
где a, b и c могут содержать переменные.

Это ожидаемо, поскольку мы ищем функцию, а не точные значения.
Ключевой шаг здесь — выбрать подходящую обратную функцию в конце, потому что у нас будут случаи плюса (+) и минуса (-). Мы можем сделать это, найдя домен и диапазон каждого из них и сравнив их с доменом и диапазоном исходной функции. Помните, что мы меняем местами домен и диапазон исходной функции, чтобы получить домен и диапазон ее инверсии.
- Метод заполнения квадратов позволяет нам изолировать переменную в квадратичном трехчлене. Как вы увидите в шагах, квадратный трехчлен преобразуется в линейный бином в степени 2. Очевидно, что мы можем применить операцию извлечения квадратного корня, чтобы избавиться от экспоненты 2, что оставляет нам простое уравнение для решения.
Если вы заметили, графики функции и ее обратной симметричны по линии y = x (см. Пунктирную линию).Они как зеркальные отражения друг друга.
Я надеюсь, что вы получите некоторое представление о том, как найти обратную квадратичную функцию .
 Хотя это может быть немного утомительно, как видите, в целом это не так уж и плохо. Я рекомендую вам ознакомиться с соответствующими уроками о том, как находить инверсии других видов функций.
Хотя это может быть немного утомительно, как видите, в целом это не так уж и плохо. Я рекомендую вам ознакомиться с соответствующими уроками о том, как находить инверсии других видов функций.
Практика с рабочими листамиВозможно, вас заинтересует:
Инверсия матрицы 2 × 2
Функция, обратная абсолютному значению
Функция, обратная постоянной
Функция, обратная экспоненциальной
Функция, обратная линейной
Обратная логарифмическая функция
Обратная рациональная функция
Функция, обратная квадратному корню
математических изображений | Полиномиальные функции и производная (2): Квадратичные функции
Квадратичная функция — это полиномиальная функция степени 2.
Многочлены степени 2 — это квадратичные функции. Их графики — параболы. Чтобы найти точки пересечения по оси x, мы должны решить квадратное уравнение.
 Вершина параболы — это максимум минимума функции.
Вершина параболы — это максимум минимума функции.Мы заинтересованы в изучении производных простых функций с помощью интуитивно понятного и наглядного подхода. Чтобы изучить производную квадратичной функции, мы будем следовать тому же подходу, который мы использовали в случай линейной функции.
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ
Производная функции в точке может быть определена как мгновенная скорость изменения или как наклон касательной линии к график функции в этой точке.Можно сказать, что этот наклон касательной функции в точке — это наклон функция.
Наклон функции, как правило, зависит от x. Тогда, начиная с функции, мы можем получить новую функцию, производную функцию исходной функции.
Процесс нахождения производной функции называется дифференцированием.
Значение производной функции для любого значения x — это наклон исходной функции в точке x.
Затем мы начинаем рисовать касательную к параболе в точке.

Но как провести касательную? Мы можем использовать увеличительное стекло !. Если мы посмотрим очень близко к точке параболы, мы увидим, как парабола похожа на касательную. Эта касательная линия является наилучшим линейным приближением параболы в этой точке:
Затем мы проводим параллельную линию касательной, проходящую через значение x-1, и получаем прямоугольный треугольник. Длина вертикальной стороны — наклон касательной.
Производная функция квадратичной функции является линейной функцией.
Производная квадратичной функции:
Как уже знал Ферма, в локальном максимуме или минимуме касательная горизонтальна, производная равна 0. Мы можем видеть что в вершине параболы касательная горизонтальна и что производная функции пересекает ось x в точке это значение.
Когда a — отрицательное число, парабола открывается вниз, а ее производная является линейной функцией с отрицательным наклоном.
В этом случае вершина максимальна и касательная, как и раньше, горизонтальна в этой точке.

Одна простая и интересная идея заключается в том, что когда мы переводим график функции вверх и вниз (мы добавляем или вычитаем число из исходной функции) производная не меняется. Причина очень интуитивно понятна, и мы можем поиграть с интерактивным приложением, чтобы увидеть это свойство. Когда ты переместите фиолетовую точку, которую вы переводите вверх и вниз по графику функции, но производная останется той же:
Важно отметить, что производная многочлена степени 1 является постоянной функцией (многочленом степени 0).А производная многочлена степени 2 есть многочлен степени 1.
Когда мы получить такую полиномиальную функцию, результатом будет многочлен, степень которого на 1 меньше, чем у исходной функции.
Когда мы изучаем интеграл от многочлена степени 2, мы видим, что в этом случае новая функция является многочлен степени 3. На одну степень больше чем исходная функция.
Эти результаты связаны с основной теоремой исчисления.

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
Майкл Спивак, Calculus, Third Edition, Publish-or-Perish, Inc.
Том М. Апостол, Calculus, Second Edition, John Willey and Sons, Inc.
Гельфанд И. Глаголева, Э.Е.Шноль, « Функции и графы », Dover Publications, Mineola, N.Y.
СЛЕДУЮЩИЙ
Производная кубической функции — это квадратичная функция, парабола.
ПРЕДЫДУЩИЙ
Производная линейной функции — постоянная функция.
БОЛЬШЕ ССЫЛКИ
Многочлены Лагранжа — это многочлены, проходящие через n заданных точек.Мы используем полиномы Лагранжа, чтобы исследовать общую полиномиальную функцию и ее производную.
Если производная от F (x) равна f (x), то мы говорим, что неопределенный интеграл от f (x) относительно x равен F (x). Мы также говорим, что F — первообразная или примитивная функция от f.
Две точки определяют прямую линию. Как функцию мы называем это линейной функцией.
 Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки. Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.
Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки. Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.Степень с натуральными показателями — простые и важные функции. Их обратные функции — это степени с рациональными показателями (радикал или корень n-й степени)
Многочлены степени 2 — это квадратичные функции. Их графики — параболы. Чтобы найти точки пересечения по оси x, мы должны решить квадратное уравнение. Вершина параболы — это максимум минимума функции.
Многочлены степени 3 — это кубические функции. Реальная кубическая функция всегда пересекает ось x хотя бы один раз.
Мы можем рассматривать полиномиальную функцию, проходящую через серию точек плоскости. Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
В качестве введения в кусочно-линейные функции мы изучаем линейные функции, ограниченные открытым интервалом: их графики подобны отрезкам.

Кусочная функция — это функция, которая определяется несколькими подфункциями. Если каждый кусок является постоянной функцией, то кусочная функция называется кусочно-постоянной функцией или ступенчатой функцией.
Непрерывная кусочно-линейная функция определяется несколькими отрезками или лучами, соединенными без скачков между ними.
Целостное понятие ассоциируется с понятием площади. Мы начали рассматривать область, ограниченную графиком функции и осью абсцисс между двумя вертикальными линиями.
Монотонные функции на отрезке интегрируемы. В этих случаях мы можем ограничить ошибку, которую делаем при приближении интеграла с помощью прямоугольников.
Если мы рассматриваем нижний предел интегрирования a как фиксированный и если мы можем вычислить интеграл для различных значений верхнего предела интегрирования b, то мы можем определить новую функцию: неопределенный интеграл от f.
Подсчитать площадь под прямой несложно.
 Это первый пример интеграции, который позволяет нам понять идею и ввести несколько основных понятий: интегральное как область, пределы интеграции, положительные и отрицательные области.
Это первый пример интеграции, который позволяет нам понять идею и ввести несколько основных понятий: интегральное как область, пределы интеграции, положительные и отрицательные области.Вычислить площадь по параболе сложнее, чем вычислить площадь по линейной функции. Мы покажем, как аппроксимировать эту область с помощью прямоугольников и что интегральная функция многочлена степени 2 является многочленом степени 3.
Мы можем увидеть некоторые основные концепции интегрирования, применяемые к общей полиномиальной функции. Интегральные функции от полиномиальных функций — это полиномиальные функции с одной степенью выше, чем исходная функция.
Фундаментальная теорема исчисления говорит нам, что каждая непрерывная функция имеет первообразную, и показывает, как построить ее с помощью интеграла.
Вторая основная теорема исчисления — мощный инструмент для вычисления определенного интеграла (если мы знаем первообразную функции).
Увеличивая степень, полином Тейлора все больше и больше приближает экспоненциальную функцию.

Увеличивая степень, полином Тейлора все больше и больше приближает функцию синуса.
Функция не определена для значений меньше -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Эта функция имеет две действительные особенности в точках -1 и 1. Многочлены Тейлора аппроксимируют функцию в интервале с центром в центре ряда. Его радиус — это расстояние до ближайшей особенности.
Это непрерывная функция, не имеющая реальных особенностей. Однако ряд Тейлора приближает функцию только в интервале.Чтобы понять это поведение, мы должны рассмотреть сложную функцию.
Многочлен степени 2 имеет два нуля или корня. На этом изображении вы видите овалы Кассини и лемнискату.

Комплексный полином степени 3 имеет три корня или ноль.
Графические квадратичные функции: Введение
Графики Квадратичные функции (стр. 1 из 4)
Разделы: Введение, Значение ведущего коэффициента / Вершина, Примеры
Общая методика для графическая квадратичная диаграмма такая же, как и для графической линейные уравнения.Однако, поскольку квадратичный график представляет собой кривые линии (называемые «параболами»), вместо прямых линий, порожденных линейными уравнениями, есть некоторые дополнительные соображения.
Самый простой квадратичный равно y = x 2 . Когда вы строили прямые линии, вам нужно было всего две точки, чтобы построить график.
 линии, хотя вы обычно наносили три или более точек, чтобы
безопасная сторона.Тем не менее, трех точек почти наверняка будет , а не , которых будет достаточно для построения квадратичного графика, по крайней мере, до тех пор, пока вы не станете очень опытным. Например, предположим, что ученик вычисляет эти три точки:
линии, хотя вы обычно наносили три или более точек, чтобы
безопасная сторона.Тем не менее, трех точек почти наверняка будет , а не , которых будет достаточно для построения квадратичного графика, по крайней мере, до тех пор, пока вы не станете очень опытным. Например, предположим, что ученик вычисляет эти три точки:Тогда, исходя только из на своем опыте работы с линейными графиками он пытается поставить прямую линия через точки.
неверный график
Он ошибся в графике.
 Вы же более осторожны.
Вы же более осторожны.Вы найдете много точек:
Эта последняя точка имеет довольно большой y -значение, поэтому вы решаете, что не будете утруждать себя рисованием достаточно большого графика, чтобы построить это.
Но вы все замышляете остальные точки:
Даже если вы забыли этот график квадратиков в виде кривых парабол, эти точки будут напоминать вам этого факта.
Вы красиво рисуете плавная изгибающаяся линия, аккуратно проходящая через нанесенные точки:
авторское право © Элизабет Стапель 2002-2011 Все права защищены.

правильный график y = x 2
В отличие от нерадивого школьника, вы только что получили правильный график.
Некоторые студенты будут Постройте точки правильно, но затем соедините точки с отрезки прямых линий, например:
неверный «сегментный» график Это неверно.
 Ты
по-прежнему нужна линейка для построения графиков, но только для рисования
оси, а не для рисования парабол. График парабол как плавно изогнутый
линии, а не как соединенные сегменты.
Ты
по-прежнему нужна линейка для построения графиков, но только для рисования
оси, а не для рисования парабол. График парабол как плавно изогнутый
линии, а не как соединенные сегменты.Вверх | 1 | 2 | 3 | 4 | Возвращение к указателю Вперед >>
Цитируйте эту статью как:
Стапель, Елизавета.«Графические квадратичные функции: Введение». Purplemath . Доступна с
https://www.purplemath.com/modules/grphquad.htm . Дата обращения [Дата] [Месяц] 2016 г.Объяснитель урока: построение графиков квадратичных функций
В этом объяснителе мы узнаем, как построить график любой квадратичной функции, представленной в его стандартная, вершинная или факторизованная форма с использованием ключевых особенностей графика функции.

Напомним, что квадратичная функция — это полиномиальная функция, у которой наивысшая порядок одной из переменных равен 2. Он также принимает форму в определении нижеприведенный.
Определение: квадратичная функция
Квадратичная функция — это функция, которую можно описать как 𝑓 (𝑥) = 𝑎𝑥 + 𝑏𝑥 + 𝑐, где 𝑎, 𝑏 и 𝑐∈ℝ и 𝑎 ≠ 0.
Мы называем график квадратичной функции параболой , так как это форму, которую он принимает.
В зависимости от того, в 𝑓 (𝑥) = 𝑎𝑥 + 𝑏𝑥 + 𝑐 положительно или при отрицательном значении парабола открывается вверх или вниз, как показано на рисунках ниже.
Существуют разные подходы к построению графиков квадратичных функций. Первый использует таблица значений. Это означает, что при выборе или при задании значений для 𝑥, затем мы генерируем значения для 𝑦, подставляя их в квадратичную функцию мы пытаемся построить график. Как только мы это сделаем, мы можем использовать упорядоченные пары для нанесите координаты на набор осей, а затем нарисуйте график квадратичная функция, использующая эти координаты и наши знания о форме квадратичной функции.

Мы исследуем, как нарисовать график квадратичной функции в нашем первом пример.
Пример 1: Нахождение графика квадратичной функции с помощью Таблица значений
Какой из следующих графиков представляет уравнение 𝑦 = 𝑥 + 3?
Ответ
Найти график, представляющий функцию 𝑦 = 𝑥 + 3 мы можем использовать таблицу значений. Для этого нам нужно выбрать некоторые значения для 𝑥 которые мы собираемся заменить, чтобы найти их соответствующие 𝑦-значения, которые затем образуют координаты, которые мы можно использовать для наброска графика.
Поскольку квадратичная функция является параболой, полезно использовать не менее 5 координаты для начала, чтобы нарисовать график, а затем больше, если это непонятно, какова его форма. Неважно, какие 𝑥-значения вы обычно выбрать, но значения, близкие к нулю, вычислить легче. Поэтому мы выберем −2, −1, 0, 1 и 2 в качестве наших 𝑥-значений для начала с, как показано в таблице значений ниже.

Чтобы вычислить 𝑦-значения, подставляем каждое -значение выше в функцию 𝑦 = 𝑥 + 3.Так мы получим следующее.
Когда 𝑥 = −2, 𝑦 = (- 2) + 3𝑦 = 7.
Когда 𝑥 = −1, 𝑦 = (- 1) + 3𝑦 = 4.
Когда 𝑥 = 0, 𝑦 = (0) + 3𝑦 = 3.
Когда 𝑥 = 1, 𝑦 = 1 + 3𝑦 = 4.
Когда 𝑥 = 2, 𝑦 = 2 + 3𝑦 = 7.
Вычислив значения 𝑦, теперь мы можем поместить их в наша таблица ценностей.
Это означает, что наша функция проходит через точки (−2,7), (-1,4), (0,3), (1,4), и (2,7). Если мы нанесем их на набор осей, мы получим следующее.
Глядя на график, мы видим, что он принимает форму обращенного вверх парабола, которую можно было бы ожидать как коэффициент 𝑥-член положительный. Также кажется, что поворотный момент квадратичная функция находится в точке (0,3). Если мы нарисуем график функции, проходящей через точки, получаем следующее.

Если мы сравним этот график с приведенными вариантами, то увидим, что только Вариант E имеет ту же точку поворота, что и наш график.Мы также можем видеть, что график в варианте E проходит через те же точки, что и наш график; следовательно, ответ должен быть вариантом E.
Из предыдущего примера видно, что использование таблицы значений является одним из методов. нахождения графика квадратичной функции. Однако мы также можем найти ключевые особенности графика и использовать их для наброска графика функций.
В первом примере функция была задана в стандартной форме . Это когда квадратичная функция записывается в виде 𝑦 = 𝑎𝑥 + 𝑏𝑥 + 𝑐, 𝑎 ≠ 0.
Когда функция записана в такой форме, мы можем легко найти 𝑦-отрезок от функции. Мы также можем найти поворотный точка, называемая вершиной , и 𝑥-пересечения для построения графика функция.
Сначала мы обсудим, как найти 𝑦-координату квадратичная функция в стандартной форме.
 Теперь, чтобы найти 𝑦-перехват
любой функции используем тот факт, что 𝑥-координата равна нулю, и подставляем
𝑥 = 0 в функцию.Это делается с помощью квадратичной функции в стандартной форме
дает нам
𝑦 = 𝑎 (0) + 𝑏 (0) + 𝑐𝑦 = 𝑐.
Теперь, чтобы найти 𝑦-перехват
любой функции используем тот факт, что 𝑥-координата равна нулю, и подставляем
𝑥 = 0 в функцию.Это делается с помощью квадратичной функции в стандартной форме
дает нам
𝑦 = 𝑎 (0) + 𝑏 (0) + 𝑐𝑦 = 𝑐.Следовательно,-пересечение (0,) квадратичной функции в стандартная форма — 𝑐, постоянный член.
Во-вторых, мы обсудим, как найти-пересечения квадратичной функции. в стандартной форме. Как и раньше, чтобы найти 𝑥-точку пересечения любой функции, используем тот факт, что 𝑦-координата равна нулю, и подставляем 𝑦 = 0 в функцию. Делая это с квадратичной функцией в стандартная форма дает нам 0 = 𝑎𝑥 + 𝑏𝑥 + 𝑐.
Напомним, что для решения квадратного уравнения, равного нулю, у нас есть три ключевых алгебраические методы: факторизация, завершение квадрата и квадратичная формула. Поскольку некоторые квадраты не факторизуемы, мы можем использовать либо завершение квадрат или квадратная формула.
 Обычно мы будем использовать формулу корней квадратного уравнения
в случаях, когда функция имеет стандартный вид. Напомним квадратичный
формула.
Обычно мы будем использовать формулу корней квадратного уравнения
в случаях, когда функция имеет стандартный вид. Напомним квадратичный
формула.Определение: квадратная формула
Чтобы решить квадратное уравнение в форме 𝑎𝑥 + 𝑏𝑥 + 𝑐 = 0, 𝑎 ≠ 0, с переменной 𝑥 и константы 𝑎, 𝑏 и 𝑐, мы можем использовать формулу корней квадратного уравнения, чтобы найти 𝑥, когда 𝑏 − 4𝑎𝑐 больше или равно нулю.𝑥 = −𝑏 ± √𝑏 − 4𝑎𝑐2𝑎.
Следовательно, используя приведенную выше формулу, если они существуют, 𝑥-пересечения квадратичной функции в стандартной форме − 𝑏 − √𝑏 − 4𝑎𝑐2𝑎, 0 и − 𝑏 + √𝑏 − 4𝑎𝑐2𝑎, 0.
В-третьих, мы обсудим, как найти вершину квадратичной функции в стандартная форма. Поскольку квадратичные функции симметричны относительно вершины, тогда линия симметрии проходит через вершину вертикально. Это также означает, что линия симметрии проходит через середину 𝑥-перехватывает.
 Используя этот факт, мы можем вывести формулу для нахождения
𝑥-координата вершины.
Используя этот факт, мы можем вывести формулу для нахождения
𝑥-координата вершины.Поскольку 𝑥-координата вершины является серединой 𝑥-пересечения, то из середины получаем следующее формула: 𝑥 = 𝑥 + 𝑥2 = + 2.√√
Теперь, поскольку −√𝑏 − 4𝑎𝑐 и + √𝑏 − 4𝑎𝑐 сокращаются, получаем 𝑥 = + 2 = −𝑏2𝑎.
Следовательно, чтобы найти 𝑥-координату вершины квадратичной функции в стандартной форме воспользуемся формулой 𝑥 = −𝑏2𝑎.
Чтобы найти 𝑦-координату вершины, подставим 𝑥-координата обратно в квадратичную функцию. Мы можем использовать ту же формулу для вершины, даже если мы нет двух 𝑥-перехватчиков.
Как только мы нашли 𝑦-координату, 𝑥-координаты и вершину, мы можем использовать эти функции для эскиза график квадратичной функции. Мы также можем проверить, является ли коэффициент -члена положительна или отрицательна, чтобы определить, является ли парабола открывается вверх или вниз соответственно, чтобы помочь нам нарисовать график.
 Подведем итог в приведенном ниже руководстве.
Подведем итог в приведенном ниже руководстве.Практическое руководство. Поиск основных характеристик графика квадратичной функции в Стандартная форма
Для квадратичной функции в стандартной форме 𝑦 = 𝑎𝑥 + 𝑏𝑥 + 𝑐, 𝑎 ≠ 0, мы можем нарисовать его график, найдя его ключ особенности и направление, в котором он открывается с помощью следующих шагов.
Шаг 1. Поиск точки пересечения 𝒚
Перехват 𝑦 — (0,).
Шаг 2: Поиск 𝒙 -перехватывания
Когда они существуют, 𝑥-перехваты − 𝑏 − √𝑏 − 4𝑎𝑐2𝑎, 0 и − 𝑏 + √𝑏 − 4𝑎𝑐2𝑎, 0, которые находятся по формуле корней квадратного уравнения (или иным образом).
Шаг 3: Нахождение вершины
-координата вершины 𝑥 = −𝑏2𝑎, а 𝑦-координата находится заменой 𝑥-координату в функцию.
Шаг 4. Определение того, открывается ли график вверх или вниз
График открывается вверх, если 𝑎> 0, и вниз если 𝑎0.

Далее мы найдем график квадратичной функции в стандартной форме, используя шаги, которые мы обсуждали выше.
Пример 2: Нахождение графика квадратичной функции в Стандартная форма
Какой из следующих графиков представляет уравнение 𝑦 = −5𝑥 − 10𝑥 + 6?
Ответ
Чтобы найти график функции 𝑦 = −5𝑥 − 10𝑥 + 6, мы можем сначала найти его ключевые особенности, а затем использовать их для построения графика.
Мы видим, что квадратичная функция имеет стандартную форму или форму 𝑦 = 𝑎𝑥 + 𝑏𝑥 + 𝑐, 𝑎 ≠ 0.
Когда квадратичная функция находится в этой форме, мы используем определенные методы, чтобы найти-точку пересечения, 𝑥-точку пересечения и вершину график.
Мы знаем, что-точка пересечения — это когда 𝑥-координата равна нулю. Таким образом, мы получаем 𝑦-координата точки, которая в случае 𝑦 = −5𝑥 − 10𝑥 + 6 равно 6. Итак, 𝑦-точка пересечения равна (0,6).

Точно так же мы знаем, что-точка пересечения — это когда 𝑦-координата равна нулю. Это дает нам 0 = −5𝑥 − 10𝑥 + 6, которое является квадратным уравнением. Напомним, что для решения квадратного уравнения мы можем использовать факторизация, завершение квадрата или квадратная формула.Поскольку это не появляется быть легко факторизуемым, и поскольку заполнить квадрат не так просто без дробей воспользуемся формулой корней квадратного уравнения.
Квадратичная формула утверждает, что для решения уравнения в виде 0 = 𝑎𝑥 + 𝑏𝑥 + 𝑐, 𝑎 ≠ 0, то имеем 𝑥 = −𝑏 ± √𝑏 − 4𝑎𝑐2𝑎.
Для уравнения 𝑦 = −5𝑥 − 10𝑥 + 6, где 𝑎 = −5, 𝑏 = −10 и 𝑐 = 6, это дает нам 𝑥 = — (- 10) ± (−10) −4 (−5) (6) 2 (−5) = 10 ± √220−10 = 5 ± √55−5𝑥 = −2.48… 𝑥 = 0,48… .или
Следовательно,-точки пересечения (−2,48,0) и (0,48,0) с точностью до 2 десятичных знаков.
Чтобы найти 𝑥-координату вершины в стандартном виде, мы может найти середину 𝑥-пересечений, что дает нас 𝑥 = −2,48 + 0,482 = −1.

Чтобы найти 𝑦-координату вершины, подставим 𝑥-координату −1 в функцию 𝑦 = −5 (−1) −10 (−1) + 6 = −5 + 10 + 6 = 11.
Следовательно, координаты вершины равны (-1,11).
Теперь, когда мы нашли точки пересечения и вершину, мы можем нарисовать график функция. Нанося эту информацию на набор осей, мы получаем следующее.
Используя эту информацию, мы можем нарисовать график. Кроме того, мы также можем использовать коэффициент при-члене, который для 𝑦 = −5𝑥 − 10𝑥 + 6 отрицательно, чтобы сказать нам, что функция открывается вниз. Набросок графика дает нам следующее.
Сравнивая это с различными вариантами, мы видим, что открываются только варианты D и E вниз, значит, это должен быть один из этих вариантов.Мы видим из вершины этот вариант D имеет ту же вершину, что и наш граф. Следовательно, ответ должна быть опцией D.
После того, как мы рассмотрели, как нарисовать график, где функция представлена в стандартной форме, мы теперь обсудим, как нарисовать график, где функция находится в форма вершины .

Под формой вершины мы понимаем форму, которая позволяет нам легко читать координаты вершины из функции. Здесь функция находится в форме 𝑦 = 𝑎 (𝑥 − ℎ) + 𝑘, 𝑎 ≠ 0.
Когда функция находится в этой форме, координаты вершины равны (ℎ, 𝑘).
Чтобы нарисовать граф в виде вершин, полезно найти ключевые особенности график, 𝑥-пересечения, 𝑦-перехват, и вершина (как и для стандартной формы).
Как и раньше, для определения координат-точки пересечения положим 𝑥 = 0 и решаем относительно 𝑦. Аналогично, чтобы найти координаты -пересечения, полагаем = 0 и решаем относительно 𝑥.Поскольку форма вершины аналогична той, которую мы получаем при завершении квадрата, то обычно это лучший метод решения квадратного уравнения.
Чтобы определить, открывается ли график вверх или вниз, мы используем 𝑎, как и прежде, независимо от того, является ли он положительным или отрицательным, чтобы определить, открывается ли график соответственно вверх или вниз.

Обнаружив все ключевые особенности, мы можем затем использовать их для построения графика квадратичного функция в вершинной форме. Это кратко изложено в приведенном ниже руководстве.
Практическое руководство. Поиск основных характеристик графика квадратичной функции в Вершинная форма
Для квадратичной функции в вершинной форме 𝑦 = 𝑎 (𝑥 − ℎ) + 𝑘, 𝑎 ≠ 0, мы можем нарисовать его график, найдя его ключевые особенности и направление, в котором он открывается, используя следующие шаги.
Шаг 1. Нахождение вершины
Вершиной является (ℎ, 𝑘).
Шаг 2: Нахождение точки пересечения 𝒚
-точка пересечения — это когда 𝑥 = 0.Чтобы найти это, подставляем 𝑥 = 0 в функцию и решаем относительно 𝑦.
Шаг 3: Поиск 𝒙 -перехватывания
Когда они существуют,-точки пересечения имеют место, когда 𝑦 = 0. Чтобы найти их, подставляем 𝑦 = 0 в функцию и решаем относительно 𝑥, заполнив квадрат, или иным образом.

Шаг 4. Определение того, открывается ли график вверх или вниз
График открывается вверх, если 𝑎> 0, и вниз если 𝑎0.
В следующем примере мы исследуем, как найти график квадратичной функция в форме вершины, найдя особенности графика.
Пример 3: Нахождение графика квадратичной функции в Vertex Form
Какой из следующих графиков представляет уравнение? 𝑦 = 2 (𝑥 + 3) −2?
Ответ
Нам предлагается найти график функции 𝑦 = 2 (𝑥 + 3) −2. Мы видим, что квадратичная функция находится в форме вершины, которая обычно 𝑦 = 𝑎 (𝑥 − ℎ) + 𝑘, 𝑎 ≠ 0.
Чтобы набросать функцию в форме вершины, мы можем использовать особенности графика чтобы помочь нам.
Первая особенность, которую мы можем найти, как следует из названия, — это вершина. Обычно это (ℎ, 𝑘) для 𝑦 = 𝑎 (𝑥 − ℎ) + 𝑘. Следовательно, для функции 𝑦 = 2 (𝑥 + 3) −2, вершина находится в (−3, −2).
 Обратите внимание, что на данный момент только два из наших вариантов имеют одинаковые
вершина, и мы можем определить, какой это вариант, посмотрев, есть ли
𝑎 положительный или отрицательный, но мы рассмотрим, как
изобразите функцию так, как будто мы не можем ее расшифровать.
Обратите внимание, что на данный момент только два из наших вариантов имеют одинаковые
вершина, и мы можем определить, какой это вариант, посмотрев, есть ли
𝑎 положительный или отрицательный, но мы рассмотрим, как
изобразите функцию так, как будто мы не можем ее расшифровать.Во-вторых, мы можем найти-точку пересечения.Для всех функций -перехват — это когда 𝑥 = 0, поэтому мы можем найти значение 𝑦, подставив 𝑥 = 0 в 𝑦 = 2 (𝑥 + 3) −2. Это дает нам 𝑦 = 2 (0 + 3) −2 = 2 (9) −2 = 16.
Следовательно,-пересечение (0,16).
В-третьих, мы можем найти-перехватчики. Как и раньше, мы знаем, что для всех функций-точки пересечения — это когда 𝑦 = 0, поэтому мы можем найти-пересечения с помощью подставив 𝑦 = 0 в функцию и решив для 𝑥.Это дает нам 0 = 2 (𝑥 + 3) −2.
Поскольку это квадратное уравнение, нам нужно использовать либо факторизацию, завершая квадрат или квадратная формула для решения этого.
 Поскольку это уже частично
решается методом
завершая квадрат, мы склонны использовать этот метод для решения уравнений в
форма вершины. Это дает нам
0 = 2 (𝑥 + 3) −22 (𝑥 + 3) = 2 (𝑥 + 3) = 1𝑥 + 3 = ± √1𝑥 = −3 ± 1𝑥 = −4𝑥 = −2.или
Поскольку это уже частично
решается методом
завершая квадрат, мы склонны использовать этот метод для решения уравнений в
форма вершины. Это дает нам
0 = 2 (𝑥 + 3) −22 (𝑥 + 3) = 2 (𝑥 + 3) = 1𝑥 + 3 = ± √1𝑥 = −3 ± 1𝑥 = −4𝑥 = −2.илиСледовательно, 𝑥-точки пересечения (−4,0) и (−2,0).
Найдя вершину, 𝑦-точку пересечения и 𝑥-пересечения, теперь мы можем нанести их на некоторые оси чтобы помочь построить график функции, как показано ниже.
Используя эту информацию, мы можем нарисовать график. Далее мы можем использовать является ли 𝑎 положительным или отрицательным, чтобы определить, открывается ли график вверх или вниз. Поскольку = 2, что положительно, то граф open вверх. Набросок графика дает нам следующее.
Из представленных вариантов мы видим, что варианты B, C и D открываются вверх, так что наш график должен быть одним из них.Мы видим, что вариант D имеет то же 𝑥-пересечения и вершины; следовательно, ответ должен быть вариант D.

После того, как мы рассмотрели, как построить график из функции в стандарте и вершине формы, теперь мы обсудим, как нарисовать график функции в факторизованной форме. форма . Факторная форма — это когда квадратичная функция записывается как произведение его факторы, или 𝑦 = 𝑎 (𝑥 − 𝑝) (𝑥 − 𝑞), 𝑎 ≠ 0.
Как и в случае с другими формами, мы можем найти ключевые особенности графика, которые помогут нам график функции.
В таком виде легко расшифровать 𝑥-перехваты функция. Мы можем определить 𝑥-пересечения, полагая 𝑦 = 0 и решение относительно. Это дает нам 0 = 𝑎 (𝑥 − 𝑝) (𝑥 − 𝑞), и поскольку один из множителей должен быть равен нулю, имеем 𝑥 = 𝑝𝑥 = 𝑞.or
Итак,-точки пересечения (, 0) и (𝑞, 0).
Чтобы найти-точки пересечения, мы просто подставляем 𝑥 = 0 в функцию и решаем относительно 𝑦.
Чтобы найти координаты вершины, мы используем симметрию графа относительно вершина; мы знаем, что вершина — это середина -пересекает, что означает, что 𝑥-координата вершина находится посередине между-пересечениями.
 С помощью
Формула средней точки дает нам
𝑥 = 𝑥 + 𝑥2𝑥 = 𝑝 + 𝑞2.
С помощью
Формула средней точки дает нам
𝑥 = 𝑥 + 𝑥2𝑥 = 𝑝 + 𝑞2.Следовательно, 𝑥-координата вершины равна 𝑥 = 𝑝 + 𝑞2. Чтобы найти-координату, мы подставляем ее обратно в функцию и решите относительно 𝑦.
Чтобы определить, открывается ли график вверх или вниз, мы используем 𝑎, как и прежде, и положительный он или отрицательный, чтобы определить если график открывается вверх или вниз соответственно.
Давайте суммируем эти моменты в приведенном ниже руководстве.
Практическое руководство. Нахождение характеристик графика квадратичной функции в факторизованной форме
Для квадратичной функции в факторизованной форме 𝑦 = 𝑎 (𝑥 − 𝑝) (𝑥 − 𝑞), 𝑎 ≠ 0, мы можем нарисовать его график, найдя его ключевые особенности и направление, в котором он открывается, используя следующие шаги.
Шаг 1: Поиск точек пересечения 𝒙
-точки пересечения: (𝑝, 0) и (𝑞, 0).
Шаг 2: Нахождение точки пересечения 𝒚
-точка пересечения — это когда 𝑥 = 0.
 Чтобы найти это, подставьте
𝑥 = 0 в функцию и решаем относительно 𝑦.
Чтобы найти это, подставьте
𝑥 = 0 в функцию и решаем относительно 𝑦.Шаг 3: Нахождение вершины
-координата вершины 𝑥 = 𝑝 + 𝑞2. Чтобы найти-координату, подставьте ее в функцию и решите относительно 𝑦.
Шаг 4. Определение того, открывается ли график вверх или вниз
График открывается вверх, если 𝑎> 0, и вниз, если 𝑎0.
В следующем примере мы исследуем, как найти график квадратичной функция в факторизованной форме путем нахождения особенностей графика.
Пример 4: Нахождение графика квадратичной функции в Factored Form
Какой из следующих графиков представляет уравнение 𝑦 = (𝑥 + 4) (𝑥 − 2)?
Ответ
Чтобы найти график квадратичной функции 𝑦 = (𝑥 + 4) (𝑥 − 2), мы можем найти особенности графика и использовать их, чтобы нарисовать график.Мы найдем точки пересечения и вершина для построения графика функции.

Поскольку функция является факторизованной, как в 𝑦 = 𝑎 (𝑥 − 𝑝) (𝑥 − 𝑞), 𝑎 ≠ 0, то легко сначала найти его 𝑥-пересечения, так как это (𝑝, 0) и (𝑞, 0).
Итак, для квадратичной функции 𝑦 = (𝑥 + 4) (𝑥 − 2), 𝑥-точки пересечения (−4,0) и (2,0). Обратите внимание, что на этом этапе мы можем сделать вывод, какой из вариантов правильно, но для полноты картины мы рассмотрим, как построить график функции с помощью все особенности.
Далее мы можем найти координаты 𝑦-точки пересечения с помощью подставив 𝑥 = 0. Это дает нам 𝑦 = (0 + 4) (0−2) 𝑦 = −8.
Следовательно, координаты 𝑦-точки пересечения равны (0, -8).
Чтобы найти координаты вершины, мы можем использовать симметрию граф о вершине. Поскольку 𝑥-координата вершина находится на полпути между 𝑥-пересечениями, то обычно для функции в факторизованном виде-координата вершина 𝑥 = 𝑝 + 𝑞2.

Для нашей функции = −4 и 𝑞 = 2, поэтому 𝑥-координата вершины 𝑥 = −4 + 22𝑥 = −1.
Затем берем 𝑥-координату вершины и подставляем ее обратно в функцию, чтобы найти 𝑦-координату. Это дает нам 𝑦 = (- 1 + 4) (- 1−2) 𝑦 = −9.
Следовательно, координаты вершины равны (−1, −9).
Теперь мы нашли 𝑥-перехваты, 𝑦-пересечение и вершину, мы можем построить эти координаты на набор осей, чтобы помочь нам построить график функции.Это дает нам следующий.
Используя эту информацию, мы можем нарисовать график. Далее мы можем использовать является ли 𝑎 положительным или отрицательным, чтобы определить, открывается ли график вверх или вниз. Поскольку = 1, что положительно, граф открывается вверх. Набросок графика дает нам следующее.
Из представленных вариантов мы видим, что только вариант E имеет то же 𝑥-перехват, 𝑦-перехват и вершина; следовательно, ответ должен быть вариантом E.

До сих пор мы рассмотрели, как найти график функции с учетом ее уравнение. Далее мы обсудим, как найти уравнение функции учитывая его график. В общем, мы рассматриваем, какие особенности графа даны и в какой форме мы хотим, чтобы наше уравнение было, чтобы помочь нам определить подход.
В последнем примере мы обсудим, как найти уравнение функции в форма вершины с учетом ее графа.
Пример 5: Нахождение уравнения функции в вершинной форме учитывая его график
Что из следующего является уравнением функции, нарисованной на графике?
- 𝑦 = 14 (𝑥 + 2) −5
- 𝑦 = −14 (𝑥 + 2) + 5
- 𝑦 = 14 (𝑥 + 2) + 5
- 𝑦 = −14 (𝑥− 2) + 5
- 𝑦 = −14 (𝑥 + 2) −5
Ответ
Чтобы определить, какая функция соответствует приведенному графику, полезно использовать ключевые особенности графика.Поскольку все указанные функции имеют вершинную форму, который 𝑦 = 𝑎 (𝑥 − ℎ) + 𝑘, 𝑎 ≠ 0, то мы знаем, что для функции в таком виде координаты вершины (ℎ, 𝑘).

Из графика видно, что координаты вершины равны (−2,5), как указано точкой на графике ниже.
Это означает, что ℎ = −2 и 𝑘 = 5, что дает нам уравнение 𝑦 = 𝑎 (𝑥 — (- 2)) + 5𝑦 = 𝑎 (𝑥 + 2) + 5.
Чтобы найти 𝑎, нам нужно подставить точку на графике в уравнение.Обычно для этого проще всего использовать один из перехватчиков.
Из графика видно, что непонятно, какие точные значения 𝑥-пересечения есть, но мы можем определить точное значение 𝑦-перехват. Поэтому воспользуемся этой точкой.
Глядя на график, мы видим, что-точка пересечения (0,4), что показано точкой на графике ниже.
Это означает, что когда 𝑥 = 0, то 𝑦 = 4. Подставляя это в 𝑦 = 𝑎 (𝑥 + 2) + 5 и решая относительно 𝑎, получаем 4 = 𝑎 (0 + 2) + 54 = 4𝑎 + 5−1 = 4𝑎𝑎 = −14.
Мы видим, что если график открывается вниз, то 𝑎 должно быть отрицательным, что и имеет место здесь.

Подставляя 𝑎 в 𝑦 = 𝑎 (𝑥 + 2) + 5, мы можем затем определите функцию графика, которая 𝑦 = −14 (𝑥 + 2) + 5.
Это означает, что ответ — вариант B.
В этом объяснении мы узнали, как построить график квадратичных функций, используя разные подходы, когда они находятся в разных формах. Мы также научились найти уравнение функции по ее графику.Подведем итоги ключевых моментов.
Ключевые точки
- Один из методов построения графика квадратичной функции — использовать таблицу значений. Мы делаем это, выбирая не менее 5 точек вместо 𝑥 и подставляя их в функция, чтобы найти 𝑦. Затем мы можем использовать точки для построения графика.
- Для квадратичной функции в стандартной форме 𝑦 = 𝑎𝑥 + 𝑏𝑥 + 𝑐,
𝑎 ≠ 0, мы используем следующие функции, чтобы построить график
функция:
- -точка пересечения (0, 𝑐),
- -точка пересечения путем подстановки = 0 и используя формулу корней квадратного уравнения, или, иначе, чтобы найти 𝑥-координаты, или если они существуют,
- вершина по формуле 𝑥 = −𝑏2𝑎 для 𝑥-координату, а затем подставив, чтобы найти -координата,
- , является ли положительным или отрицательным, чтобы определить,
открывается вверх или вниз.

- Для квадратичной функции в форме вершины
𝑦 = 𝑎 (𝑥 − ℎ) + 𝑘, 𝑎 ≠ 0, используем
следующие функции, которые помогут построить график функции:
- вершина (ℎ, 𝑘),
- -точка пересечения путем подстановки 𝑥 = 0 и решения для,
- -пересечения путем замены = 0 и используя завершение квадрата, или, иначе, чтобы найти -координаты, или если они существуют,
- , является ли 𝑎 положительным или отрицательным, чтобы определить, есть ли график открывается вверх или вниз.
- Для квадратичной функции в факторизованной форме 𝑦 = 𝑎 (𝑥 − 𝑝) (𝑥 − 𝑞),
𝑎 ≠ 0, мы используем следующие функции, чтобы построить график функции:
- -точки пересечения (𝑝, 0) и (𝑞, 0),
- -точку пересечения путем подстановки 𝑥 = 0 и решения для 𝑦,
- вершина по формуле 𝑥 = 𝑝 + 𝑞2 для 𝑥-координаты, а затем подставив, чтобы найти-координату,
- независимо от того, положительно или отрицательно 𝑎, чтобы определить, является ли график
открывается вверх или вниз.

- Чтобы найти уравнение квадратичной функции по ее графику, мы идентифицируем ее ключевые особенности и используйте их, чтобы найти уравнение в требуемой форме.
Квадратичная функция — формулы, определение, значение, примеры
Квадратичные функции используются в различных областях техники и науки для получения значений различных параметров. Графически они представлены параболой. В зависимости от коэффициента наивысшей степени определяется направление кривой.Слово «квадратичный» происходит от слова «четырехугольник», что означает квадрат. Другими словами, квадратичная функция — это «полиномиальная функция степени 2». Есть много сценариев, в которых используются квадратичные функции. Знаете ли вы, что при запуске ракеты ее путь описывается решением квадратичной функции?
В этой статье мы исследуем мир квадратичных функций в математике. Вы узнаете о графиках квадратичных функций, формулах квадратичных функций и других интересных фактах по теме.

Что такое квадратичная функция?
Квадратичная функция — это полиномиальная функция с одной или несколькими переменными, у которой наивысший показатель степени переменной равен двум. Поскольку член наивысшей степени в квадратичной функции имеет вторую степень, его также называют полиномом степени 2. Квадратичная функция имеет минимум один член второй степени. Это алгебраическая функция.
Стандартная форма квадратичной функции
Стандартная форма квадратичной функции имеет вид f (x) = ax 2 + bx + c, где a, b и c — действительные числа с a 0.
Примеры квадратичных функций
Уравнение квадратичной функции: f (x) = ax 2 + bx + c, где a ≠ 0. Давайте посмотрим на несколько примеров квадратичных функций:
- f (x) = 2x 2 + 4x — 5; Здесь a = 2, b = 4, c = -5
- f (x) = 3x 2 — 9; Здесь a = 3, b = 0, c = -9
- f (x) = x 2 — x; Здесь a = 1, b = -1, c = 0
Теперь рассмотрим f (x) = 4x-11; Здесь a = 0, поэтому f (x) не является квадратичной функцией.

Вершина квадратичной функции
Вершина квадратичной функции (имеющая U-образную форму) — это место, где функция имеет максимальное или минимальное значение. Ось симметрии квадратичной функции пересекает функцию (параболу) в вершине.
Различные формы квадратичной функции
Квадратичная функция может быть в разных формах: стандартной форме, форме вершины и форме пересечения. Вот общие формы каждого из них:
- Стандартная форма: f (x) = ax 2 + bx + c, где a ≠ 0.
- Форма вершины: f (x) = a (x — h) 2 + k, где a ≠ 0 и (h, k) — вершина параболы, представляющей квадратичную функцию.
- Форма пересечения: f (x) = a (x — p) (x — q), где a ≠ 0, а (p, 0) и (q, 0) — точки пересечения по оси x параболы, представляющей квадратичную функцию.
Парабола открывается вверх или вниз в зависимости от значения ‘a’:
- Если a> 0, то парабола открывается вверх.

- Если a <0, то парабола открывается вниз.
Мы всегда можем преобразовать одну форму в другую. Мы можем легко преобразовать форму вершины или форму перехвата в стандартную форму, просто упростив алгебраические выражения. Давайте посмотрим, как преобразовать стандартную форму в форму вершины и форму перехвата.
Преобразование стандартной формы квадратичной функции в форму вершины
Квадратичная функция f (x) = ax 2 + bx + c может быть легко преобразована в форму вершин f (x) = a (x — h) 2 + k, используя значения h = -b / 2a и k = f (-b / 2a).Вот пример.
Пример: Преобразуйте квадратичную функцию f (x) = 2x 2 — 8x + 3 в форму вершины.
- Шаг — 1: Сравнивая заданную функцию с f (x) = ax 2 + bx + c, мы получаем a = 2, b = -8 и c = 3.
- Шаг — 2: Найдите ‘h’ по формуле: h = -b / 2a = — (- 8) / 2 (2) = 2.

- Шаг — 3: Найдите ‘k’ по формуле: k = f (-b / 2a) = f (2) = 2 (2) 2 — 8 (2) + 3 = 8-16 + 3 = -5.
- Шаг — 4: Подставьте значения в форму вершины: f (x) = 2 (x — 2) 2 — 5.
Преобразование стандартной формы квадратичной функции в форму пересечения
Квадратичная функция f (x) = ax 2 + bx + c может быть легко преобразована в форму вершин f (x) = a (x — p) (x — q), используя значения p и q ( x-точки пересечения) путем решения квадратного уравнения ax 2 + bx + c = 0.
Пример: Преобразуйте квадратичную функцию f (x) = x 2 — 5x + 6 в форму пересечения.
- Шаг — 1: Сравнивая заданную функцию с f (x) = ax 2 + bx + c, получаем a = 1.
- Шаг — 2: Решите квадратное уравнение: x 2 — 5x + 6 = 0
Разложив левую часть на множители, получим
(х — 3) (х — 2) = 0
х = 3, х = 2 - Шаг — 3: Подставьте значения в форму пересечения: f (x) = 1 (x — 3) (x — 2).

Область и диапазон квадратичной функции
Область квадратичной функции — это набор всех значений x, которые определяют функцию, а диапазон квадратичной функции — это набор всех значений y, получаемых функцией путем подстановки различных значений x.
Область квадратичной функции
Квадратичная функция — это полиномиальная функция, которая определена для всех действительных значений x. Итак, область определения квадратичной функции — это набор действительных чисел, то есть R. В интервальной записи область определения любой квадратичной функции равна (-∞, ∞).
Диапазон квадратичной функции
Диапазон квадратичной функции зависит от открытой стороны и вершины графика. Итак, ищите самое нижнее и самое верхнее значения f (x) на графике функции, чтобы определить диапазон квадратичной функции. Диапазон любой квадратичной функции с вершиной (h, k) и уравнением f (x) = a (x — h) 2 + k равен:
- y ≥ k (или) [k, ∞) при a> 0 (поскольку парабола открывается при a> 0).

- y ≤ k (или) (-∞, k], когда a <0 (поскольку парабола открывается вниз, когда a <0).
Графики квадратичной функции
Теперь, с точки зрения построения графиков квадратичных функций, мы поймем пошаговую процедуру построения графика любой квадратичной функции.Шаги объясняются на примере, где мы собираемся построить график квадратичной функции f (x) = 2x 2 — 8x + 3. Сравнивая это с f (x) = ax 2 + bx + c, мы получаем a = 2, b = -8 и c = 3.
- Шаг — 1: Найдите вершину.
x-c координата вершины = -b / 2a = 8/4 = 2
y-координата вершины = f (-b / 2a) = 2 (2) 2 -8 (2) + 3 = 8-16 + 3 = -5.
Следовательно, vertex = (2, -5). - Шаг — 2: Вычислите таблицу квадратичных функций с двумя столбцами x и y с 5 строками (мы также можем взять больше строк) с вершиной, которая будет одной из следующих точек:
x л 2 -5 - Шаг — 3: Возьмите любые два случайных числа для x в левой части x-координаты вершины и два случайных числа в правой части x-координаты вершины следующим образом:
x л 0 1 2 -5 3 4 - Шаг — 4: Найдите соответствующие значения y, подставив каждое значение x в заданную квадратичную функцию.
 Например, когда x = 0, y = 2 (0) 2 -8 (0) + 3 = 3.
Например, когда x = 0, y = 2 (0) 2 -8 (0) + 3 = 3.x л 0 3 1 -3 2 -5 3 -3 4 3 - Step — 5: Теперь у нас есть две точки по обе стороны от вершины, так что, построив их и соединив кривой, мы можем получить идеальную форму.Также растяните график с обеих сторон. Вот график квадратичной функции.
Примечание: Мы можем построить пересечение по оси x и точку пересечения по оси y квадратичной функции, чтобы получить более аккуратную форму графика.
График квадратичных функций можно также получить с помощью калькулятора квадратичных функций.
Максимумы и минимумы квадратичной функции
Максимумы или минимумы квадратичных функций находятся в его вершине.
 Его также можно найти с помощью дифференцирования. Чтобы лучше понять концепцию, давайте рассмотрим пример и решим его. Возьмем пример квадратичной функции f (x) = 3x 2 + 4x + 7.
Его также можно найти с помощью дифференцирования. Чтобы лучше понять концепцию, давайте рассмотрим пример и решим его. Возьмем пример квадратичной функции f (x) = 3x 2 + 4x + 7.Дифференцирующая функция,
⇒f ‘(x) = 6x + 4
Приравнивая к нулю,
⇒ 6x + 4 = 0
⇒ х = -2/3
Двойное дифференцирование функции,
⇒f » (x) = 6> 0
Поскольку двойная производная функции больше нуля, у нас будут минимумы при x = -2/3 (по проверке второй производной), а парабола направлена вверх.
Аналогично, если двойная производная в стационарной точке меньше нуля, тогда функция будет иметь максимумы. Следовательно, с помощью дифференцирования мы можем найти минимум или максимум квадратичной функции.
Формула квадратичных функций
Квадратичную функцию всегда можно факторизовать, но процесс факторизации может быть затруднен, если нули выражения являются нецелыми действительными числами или не действительными числами.
 В таких случаях мы можем использовать формулу корней квадратного уравнения для определения нулей выражения.2-4ac}} {2a} \ end {align} \).
В таких случаях мы можем использовать формулу корней квадратного уравнения для определения нулей выражения.2-4ac}} {2a} \ end {align} \). - Дискриминант квадратного уравнения ax 2 + bx + c = 0 определяется выражением b 2 -4ac. Это используется для определения природы решений квадратичной функции.
Часто задаваемые вопросы о квадратичной функции
Что такое определение квадратичной функции?
Значение «четырехугольник» означает «квадрат». Следовательно, многочлен степени 2 называется квадратичной функцией.
Что такое уравнение квадратной функции?
Квадратичная функция — это многочлен степени 2, поэтому уравнение квадратичной функции имеет вид f (x) = ax 2 + bx + c, где ‘a’ — ненулевое число; а, b и c — действительные числа.
Что такое вершина квадратичной функции?
Вершиной квадратичной функции называется точка, в которой парабола меняет направление и пересекает ось симметрии.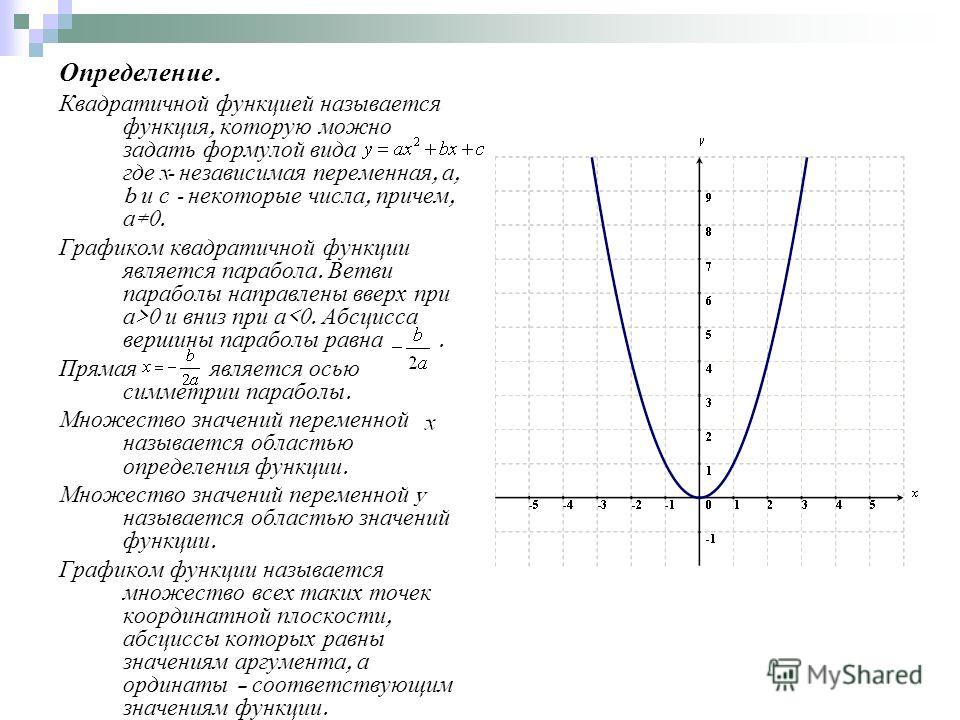 Это точка, в которой парабола изменяется от увеличения к уменьшению или от уменьшения к увеличению. В этот момент производная квадратичной функции равна 0.
Это точка, в которой парабола изменяется от увеличения к уменьшению или от уменьшения к увеличению. В этот момент производная квадратичной функции равна 0.
Что такое нули квадратичной функции?
Нули квадратичной функции — это точки, в которых график функции пересекает ось X.В нулях функции координата y равна 0, а координата x представляет нули квадратичной функции. Нули квадратичной функции также называют корнями функции.
Что такое таблица квадратичных функций?
Таблица квадратичных функций — это таблица, в которой мы определяем значения координат y, соответствующие каждой координате x, и наоборот. Таблица состоит из координат графика квадратичных функций. Обычно мы записываем вершину квадратичных функций в таблицу квадратичных функций.
Как построить график квадратичных функций?
График квадратичной функции — парабола. Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y и, следовательно, получаем координаты графика.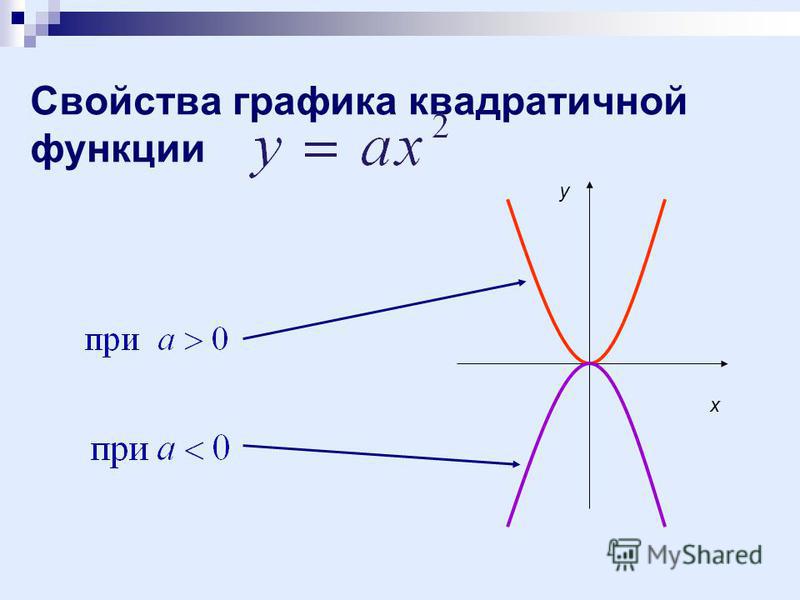 После нанесения координат на график, мы соединяем точки, используя свободную руку, чтобы получить график квадратичных функций.
После нанесения координат на график, мы соединяем точки, используя свободную руку, чтобы получить график квадратичных функций.
Как найти точку пересечения с координатой x квадратичной функции?
Пересечение X квадратичной функции можно найти, рассматривая квадратичную функцию f (x) = 0 и затем определяя значение x.Другими словами, точка пересечения по оси x есть не что иное, как ноль квадратного уравнения.
Является ли парабола квадратичной функцией?
Парабола — это график квадратичной функции. Квадратичная функция имеет вид ax 2 + bx + c, где a не равно 0. Парабола — это U-образный или перевернутый U-образный график квадратичной функции.
Как найти обратную квадратичную функцию?
Обратный к квадратичной функции f (x) можно найти, заменив f (x) на y.Затем мы меняем роли x и y, то есть заменяем x на y и y на x. После этого мы решаем y относительно x, а затем заменяем y на f -1 (x), чтобы получить обратную квадратичную функцию f (x).
Квадратичная функция
Квадратичный функция имеет вид:
где a, b и c — числовые константы, а c не равно нулю.
Примечание что если бы c было равно нулю, функция была бы линейной.
Преимущество Это обозначение состоит в том, что его можно легко обобщить, добавив больше терминов. Мы могли бы, например, написать уравнения, такие как
Во многих книги квадратные уравнения записываются как
В этом случае квадратная формула дается
Примечание что знаменатель тогда будет 2a вместо 2c.
Некоторые общие примеры квадратичной функции
Уведомление
что график квадратичной функции — парабола.Это значит
кривая с единственным выступом. График симметричен относительно линии, называемой
ось симметрии. Точка пересечения оси симметрии
парабола называется вершиной.
Графики квадратичная функция
Постройте таблицу со значениями x и f (x).
Постройте точки данных.
Соедините точки данных плавной линией.
Это легко сделать с помощью Excel.
Пример 1 f (x) = 12 — 8x + x 2
Пример 2 f (x) = -4 + 5x -x 2
квадратная формула, пример.
В целом
предложение товара увеличивается с ростом цены, а спрос уменьшается.
Рынок товара находится в равновесии, когда предложение равно спросу.
В этом Например, мы рассматриваем две функции одной и той же независимой переменной, цена. Мы хотим найти равновесную цену и соответствующий спрос.
Поставка функция — квадратное уравнение, задаваемое формулой S (п) = 2п + 4п 2
Спрос функция — это линейная функция, заданная формулой D (p) = 231 — 18p
Найти пересечение двух кривых устанавливает предложение равное спросу и решает для п.
S (p) = 2p + 4p 2 = 231 — 18p = D (p)
После Собирая члены, получаем квадратное уравнение
231 — 20p -4p 2 = 0
Примечание что это имеет форму квадратного уравнения
у = а + bx + сх 2
0 = 231 -20p -4p 2
Решить
уравнение с помощью квадратной формулы где a = 231, b = -20,
и c = -4.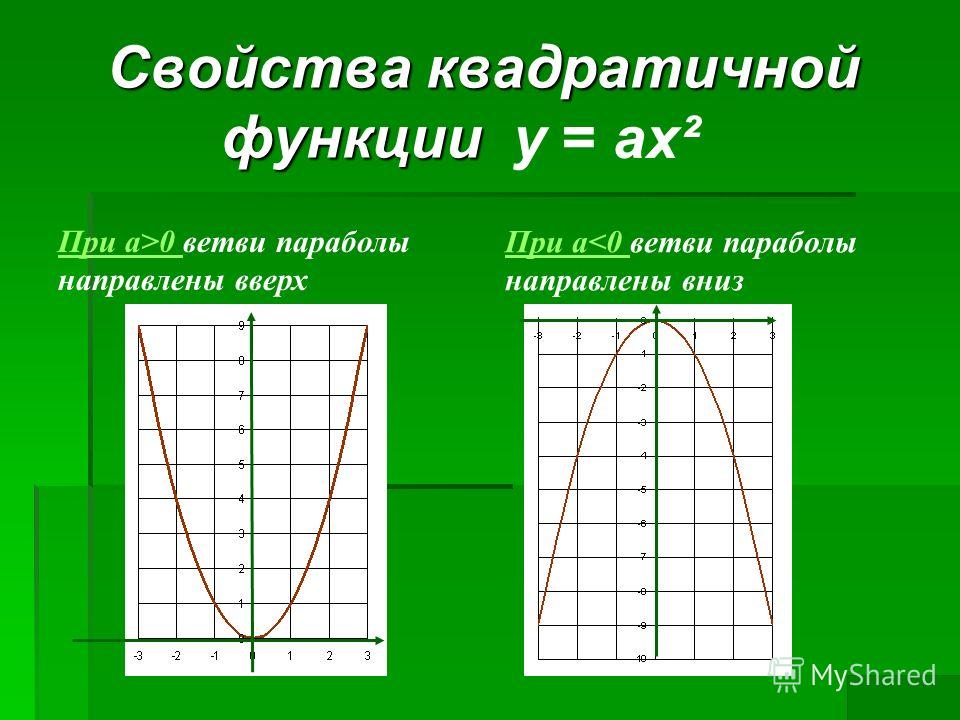

 пункт 1).
пункт 1).
 равно или больше нуля. Он должен пройти тест горизонтальной линии, который говорит мне, что я действительно могу найти его обратную функцию, выполнив предложенные шаги.
равно или больше нуля. Он должен пройти тест горизонтальной линии, который говорит мне, что я действительно могу найти его обратную функцию, выполнив предложенные шаги.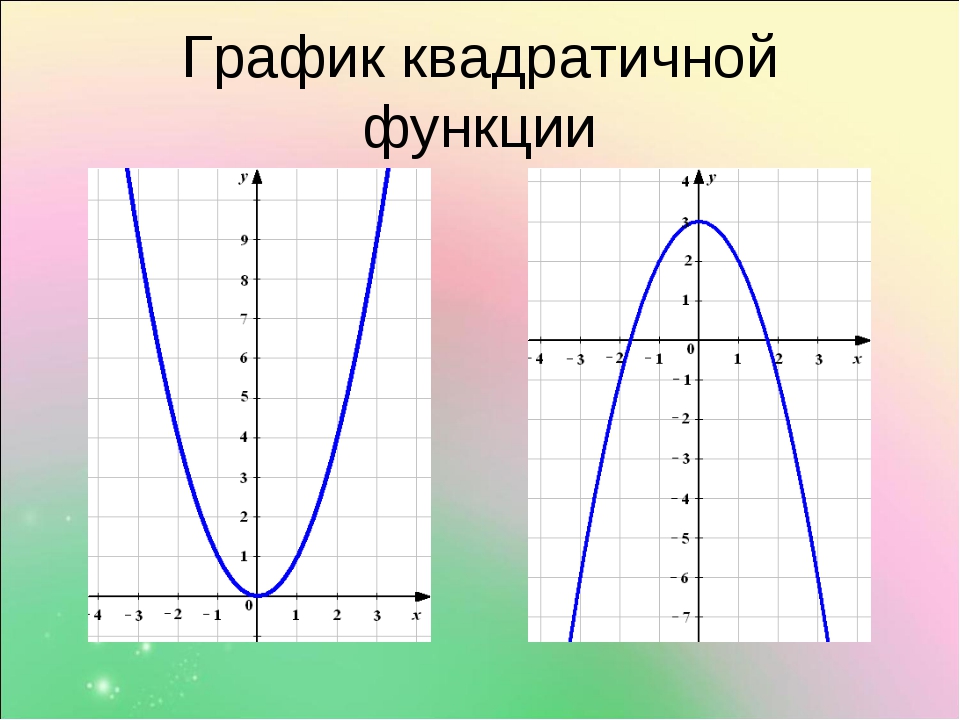 Укажите его домен и диапазон.
Укажите его домен и диапазон.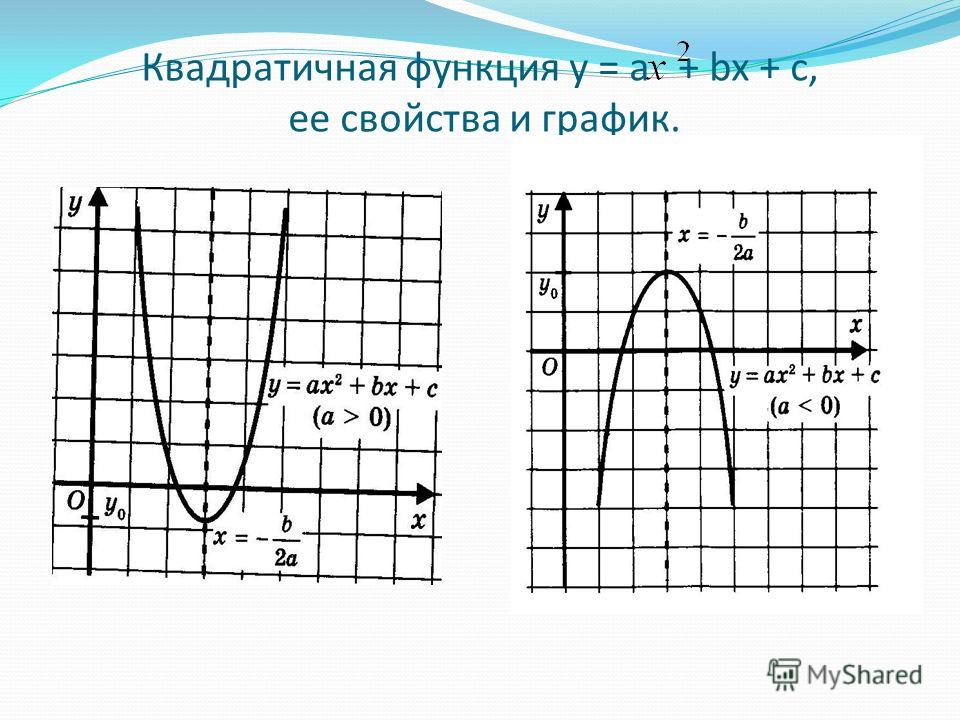
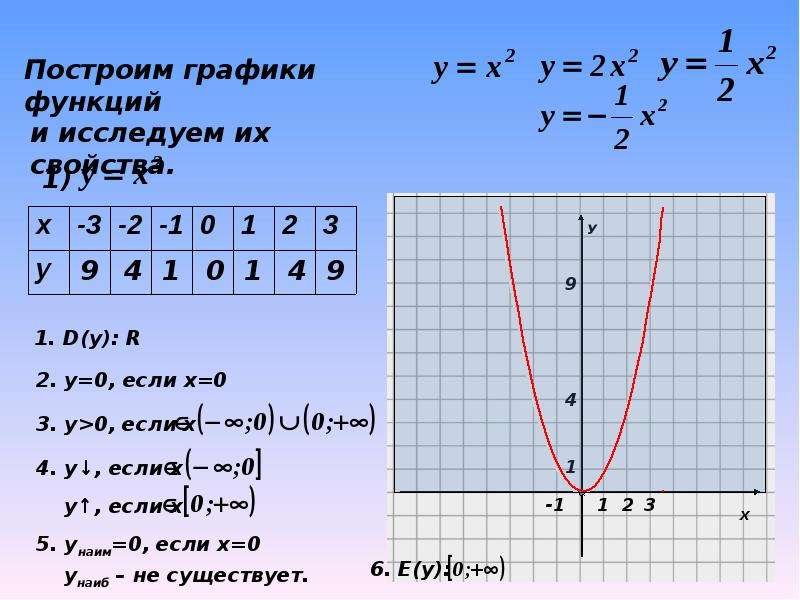 Хотя это может быть немного утомительно, как видите, в целом это не так уж и плохо. Я рекомендую вам ознакомиться с соответствующими уроками о том, как находить инверсии других видов функций.
Хотя это может быть немного утомительно, как видите, в целом это не так уж и плохо. Я рекомендую вам ознакомиться с соответствующими уроками о том, как находить инверсии других видов функций. Вершина параболы — это максимум минимума функции.
Вершина параболы — это максимум минимума функции.


 Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки. Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.
Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки. Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.
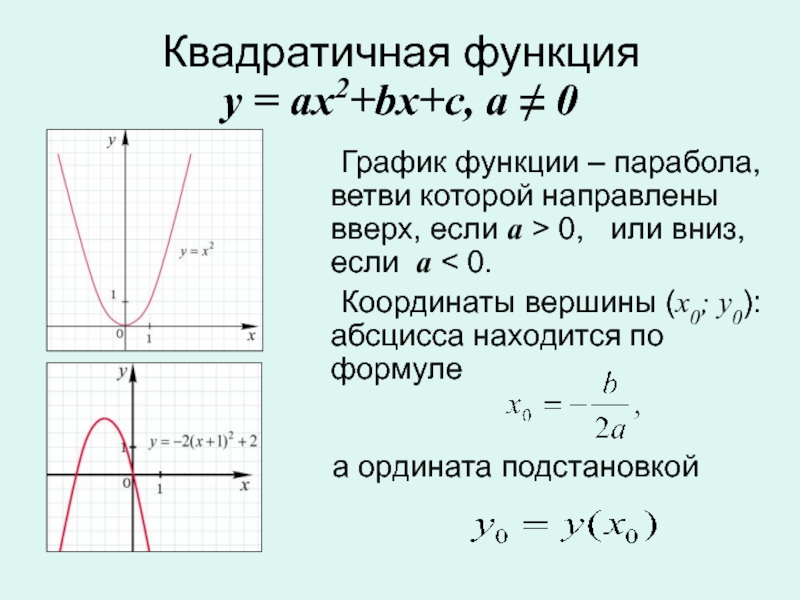 Это первый пример интеграции, который позволяет нам понять идею и ввести несколько основных понятий: интегральное как область, пределы интеграции, положительные и отрицательные области.
Это первый пример интеграции, который позволяет нам понять идею и ввести несколько основных понятий: интегральное как область, пределы интеграции, положительные и отрицательные области.

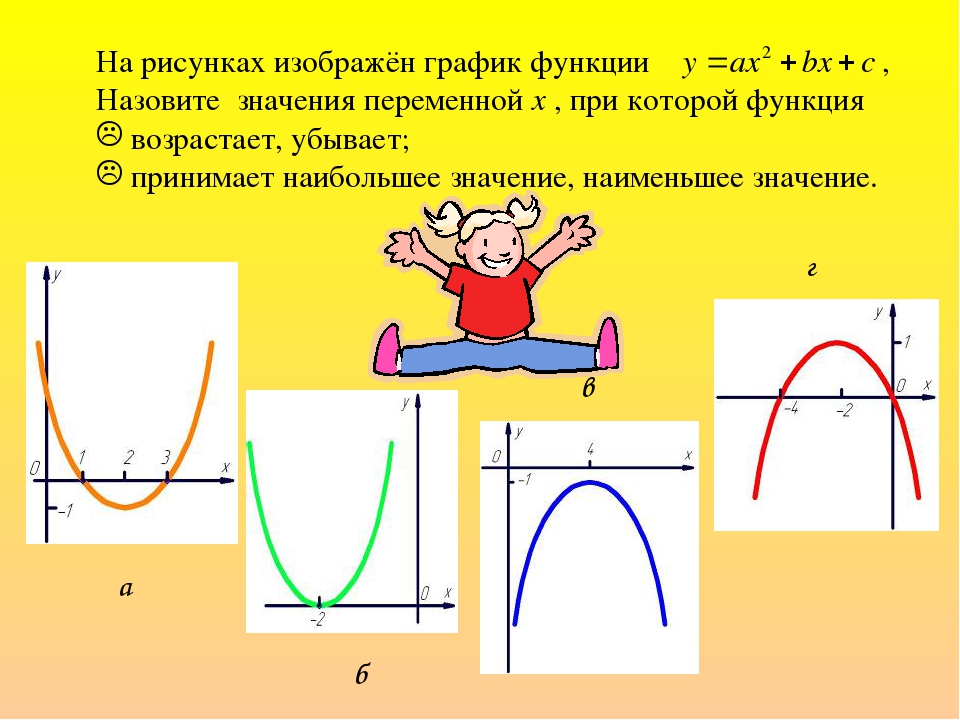 линии, хотя вы обычно наносили три или более точек, чтобы
безопасная сторона.Тем не менее, трех точек почти наверняка будет , а не , которых будет достаточно для построения квадратичного графика, по крайней мере, до тех пор, пока вы не станете очень опытным. Например, предположим, что ученик вычисляет эти три точки:
линии, хотя вы обычно наносили три или более точек, чтобы
безопасная сторона.Тем не менее, трех точек почти наверняка будет , а не , которых будет достаточно для построения квадратичного графика, по крайней мере, до тех пор, пока вы не станете очень опытным. Например, предположим, что ученик вычисляет эти три точки: Вы же более осторожны.
Вы же более осторожны.
 Ты
по-прежнему нужна линейка для построения графиков, но только для рисования
оси, а не для рисования парабол. График парабол как плавно изогнутый
линии, а не как соединенные сегменты.
Ты
по-прежнему нужна линейка для построения графиков, но только для рисования
оси, а не для рисования парабол. График парабол как плавно изогнутый
линии, а не как соединенные сегменты.

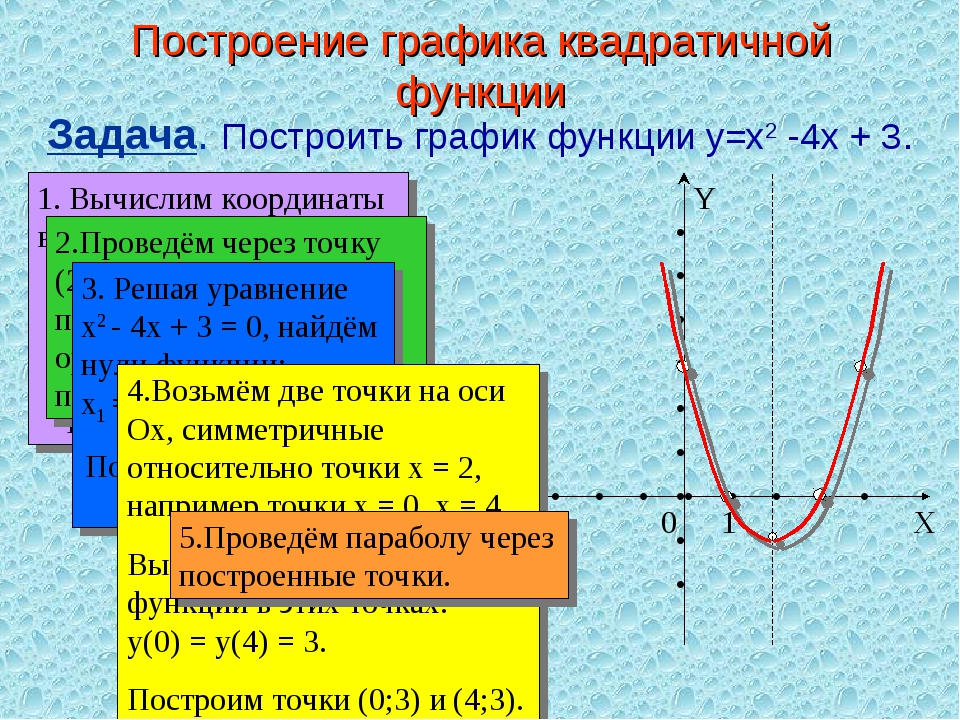

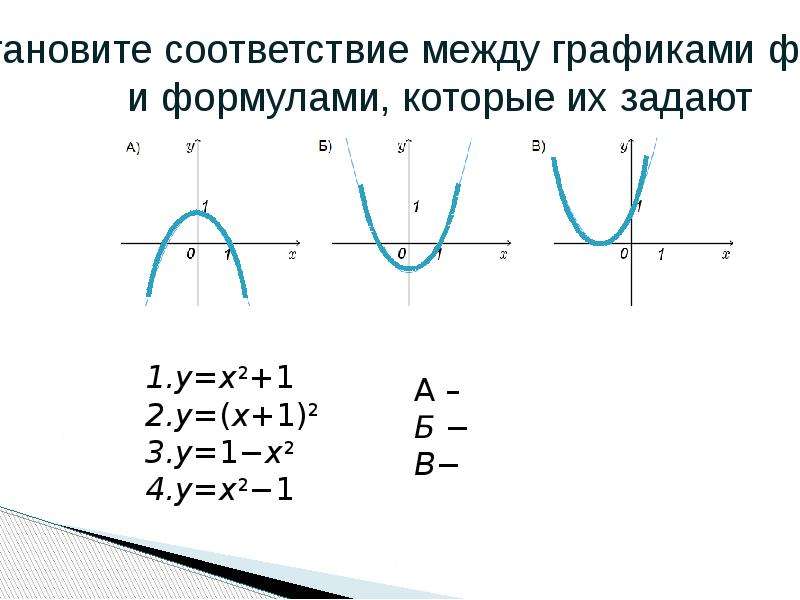 Теперь, чтобы найти 𝑦-перехват
любой функции используем тот факт, что 𝑥-координата равна нулю, и подставляем
𝑥 = 0 в функцию.Это делается с помощью квадратичной функции в стандартной форме
дает нам
𝑦 = 𝑎 (0) + 𝑏 (0) + 𝑐𝑦 = 𝑐.
Теперь, чтобы найти 𝑦-перехват
любой функции используем тот факт, что 𝑥-координата равна нулю, и подставляем
𝑥 = 0 в функцию.Это делается с помощью квадратичной функции в стандартной форме
дает нам
𝑦 = 𝑎 (0) + 𝑏 (0) + 𝑐𝑦 = 𝑐.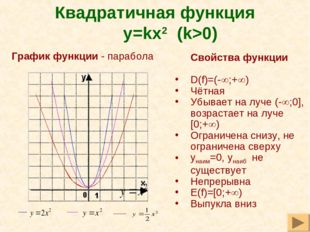 Обычно мы будем использовать формулу корней квадратного уравнения
в случаях, когда функция имеет стандартный вид. Напомним квадратичный
формула.
Обычно мы будем использовать формулу корней квадратного уравнения
в случаях, когда функция имеет стандартный вид. Напомним квадратичный
формула. Используя этот факт, мы можем вывести формулу для нахождения
𝑥-координата вершины.
Используя этот факт, мы можем вывести формулу для нахождения
𝑥-координата вершины.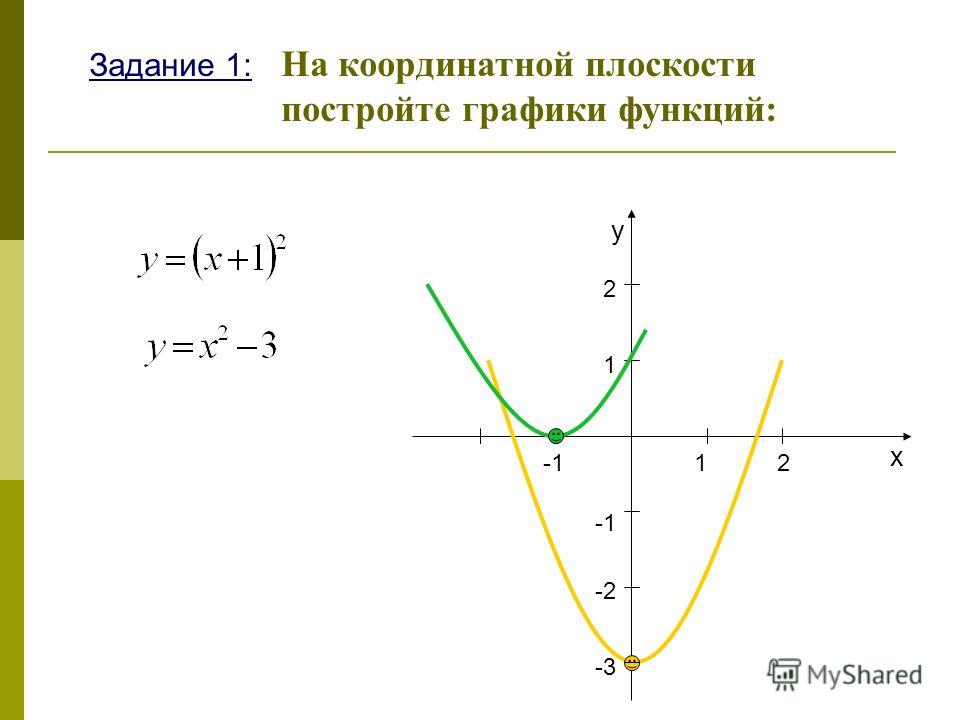 Подведем итог в приведенном ниже руководстве.
Подведем итог в приведенном ниже руководстве.





 Обратите внимание, что на данный момент только два из наших вариантов имеют одинаковые
вершина, и мы можем определить, какой это вариант, посмотрев, есть ли
𝑎 положительный или отрицательный, но мы рассмотрим, как
изобразите функцию так, как будто мы не можем ее расшифровать.
Обратите внимание, что на данный момент только два из наших вариантов имеют одинаковые
вершина, и мы можем определить, какой это вариант, посмотрев, есть ли
𝑎 положительный или отрицательный, но мы рассмотрим, как
изобразите функцию так, как будто мы не можем ее расшифровать.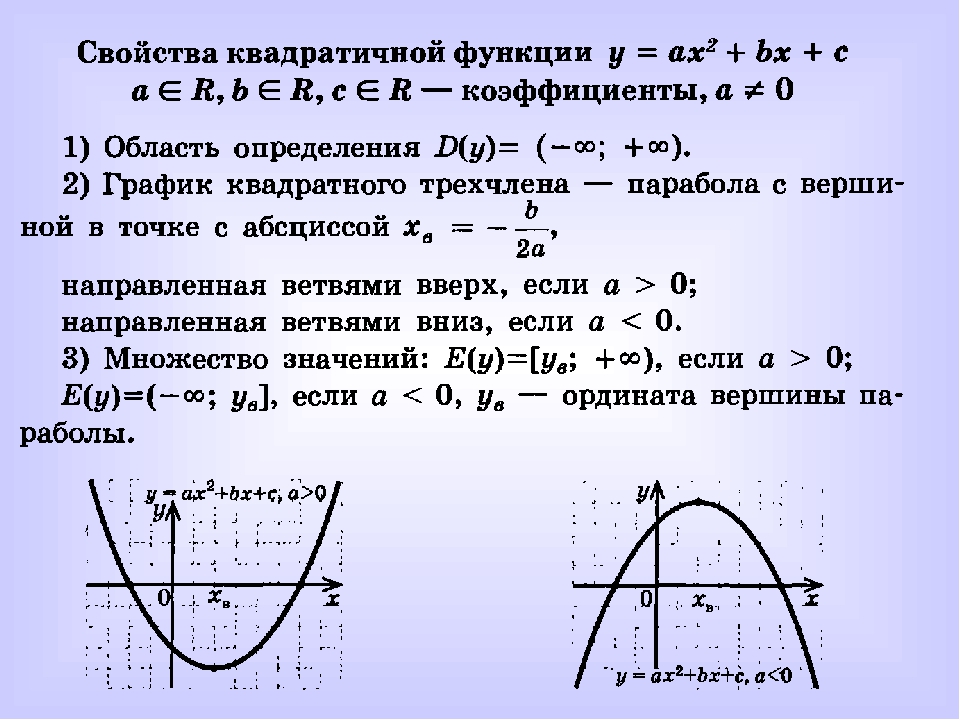 Поскольку это уже частично
решается методом
завершая квадрат, мы склонны использовать этот метод для решения уравнений в
форма вершины. Это дает нам
0 = 2 (𝑥 + 3) −22 (𝑥 + 3) = 2 (𝑥 + 3) = 1𝑥 + 3 = ± √1𝑥 = −3 ± 1𝑥 = −4𝑥 = −2.или
Поскольку это уже частично
решается методом
завершая квадрат, мы склонны использовать этот метод для решения уравнений в
форма вершины. Это дает нам
0 = 2 (𝑥 + 3) −22 (𝑥 + 3) = 2 (𝑥 + 3) = 1𝑥 + 3 = ± √1𝑥 = −3 ± 1𝑥 = −4𝑥 = −2.или
 С помощью
Формула средней точки дает нам
𝑥 = 𝑥 + 𝑥2𝑥 = 𝑝 + 𝑞2.
С помощью
Формула средней точки дает нам
𝑥 = 𝑥 + 𝑥2𝑥 = 𝑝 + 𝑞2.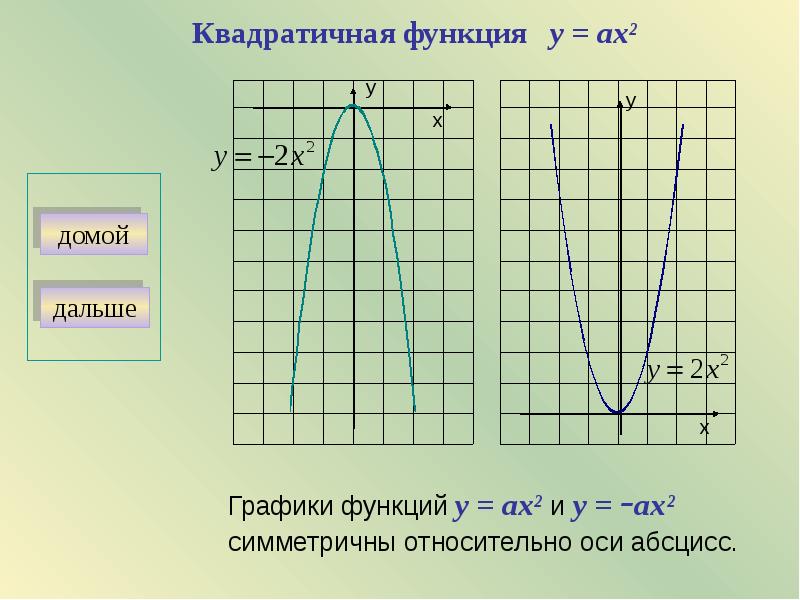 Чтобы найти это, подставьте
𝑥 = 0 в функцию и решаем относительно 𝑦.
Чтобы найти это, подставьте
𝑥 = 0 в функцию и решаем относительно 𝑦.










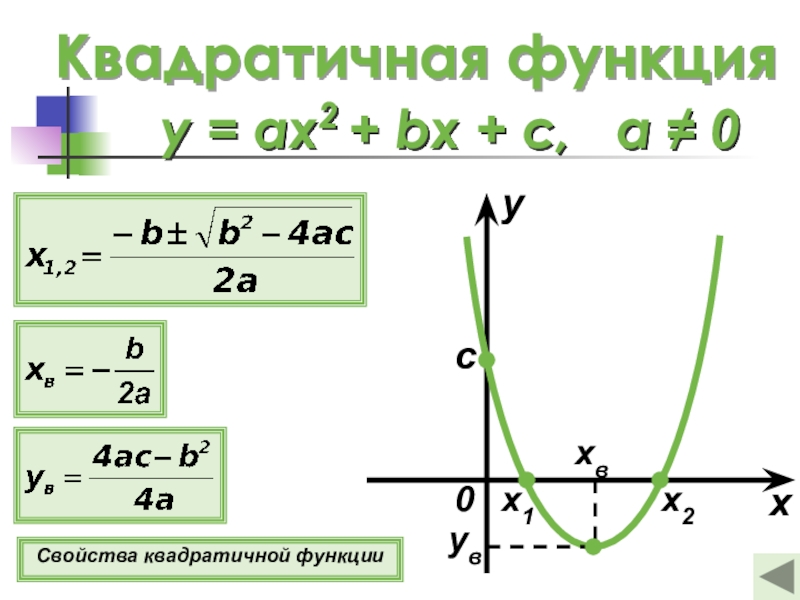

 Например, когда x = 0, y = 2 (0) 2 -8 (0) + 3 = 3.
Например, когда x = 0, y = 2 (0) 2 -8 (0) + 3 = 3.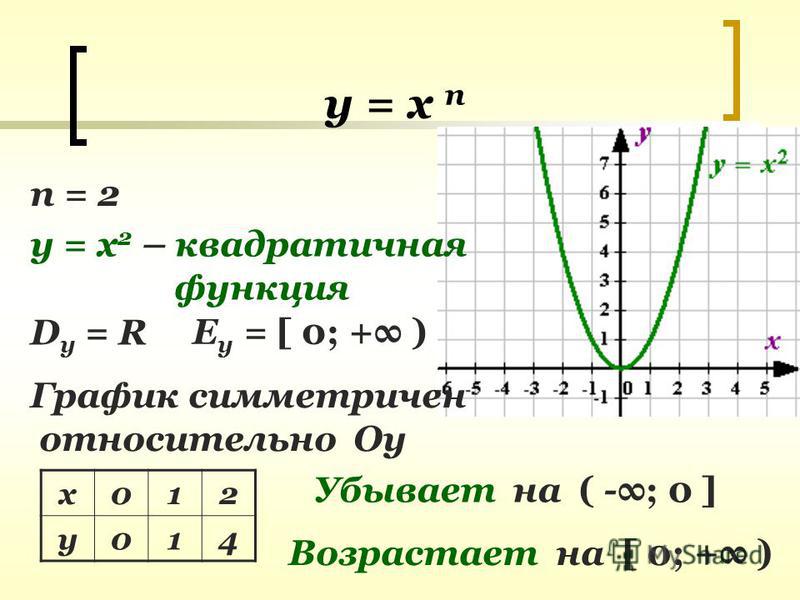 Его также можно найти с помощью дифференцирования. Чтобы лучше понять концепцию, давайте рассмотрим пример и решим его. Возьмем пример квадратичной функции f (x) = 3x 2 + 4x + 7.
Его также можно найти с помощью дифференцирования. Чтобы лучше понять концепцию, давайте рассмотрим пример и решим его. Возьмем пример квадратичной функции f (x) = 3x 2 + 4x + 7. В таких случаях мы можем использовать формулу корней квадратного уравнения для определения нулей выражения.2-4ac}} {2a} \ end {align} \).
В таких случаях мы можем использовать формулу корней квадратного уравнения для определения нулей выражения.2-4ac}} {2a} \ end {align} \).