Квадратный корень из числа вычислить: Калькулятор квадратных корней — Детская игровая комната «Волшебный лес»

Posted on 15.06.197021.12.2021 by alexxlab

Содержание

1.2. Корень n-й степени

В 8-м классе изучались квадратные корни из действительных чисел (их называют также корнями 2-й степени).

Перейдем к изучению корней степени n для произвольного натурального числа n≥2.

Определение. Пусть n≥2 и n∈N. Корнем n-й степени из числа a называется такое число t, n-я степень которого равна a .

Таким образом, утверждение «t — корень n-й степени из a» означает, что tn=a.

Корень 3-й степени называется также кубическим.

Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.

Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.

Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа a. Этот корень обозначается

Например, 1253=5,−1287=−2,07=0.

Стр. 11

Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства.

Согласно определению, когда n нечетное, то при любом значении а верно равенство

Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.

Заметим, что 0 — это единственное число, n-я степень которого равна 0. Поэтому

при любом натуральном n≥2 существует единственный корень n-й степени из 0 — это число 0, т. е. 0n=0.

Примерами корней четной степени могут служить квадратные корни: −7 и 7 — квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.

Во множестве действительных чисел существует ровно два корня четной степени n из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается

Например, 814=3,646=2.

Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства. Согласно определению, когда n четное, то при любом положительном значении а верно равенство

Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.

Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й степени из числа −81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то

Стр. 12

не существует корня четной степени из отрицательного числа.

Определение. Неотрицательный корень n-й степени из числа a называется арифметическим корнем n-й степени из a .

При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении записи an слово «арифметический» обычно пропускают).

Выражение, стоящее под знаком корня, называется подкоренным выражением.

Извлечь корень n-й степени из числа a — это значит найти значение выражения an.

Так как корня четной степени из отрицательного числа не существует, то выражение an при четном n и отрицательном а не имеет смысла.

Например, не имеют смысла выражения −814 и −646.

Как мы установили, при любом значении а, при котором выражение an имеет смысл, верно равенство

Поэтому равенство (1) является тождеством.

В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику.

В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так, выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.

Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.

Знак еще называют радикалом.

Стр. 13

Пример 1. Верно ли, что:

а) (−2)44=−2;

б) (−2)77=−2?

Решение. а) По определению арифметический корень n-й степени из неотрицательного числа a (n — четное число) является неотрицательным числом, n-я степень которого равна подкоренному выражению a.

Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.

б) По определению корень n-й степени из числа а (n — нечетное число) является числом, n-я степень которого равна подкоренному выражению а.

Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.

Пример 2. Решить уравнение:

а) x3=7;

б) x4=5.

Решение. а) Решением этого уравнения является такое значение х, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:

б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т.

е. x=±54.

Ответ: а) 73; б) ±54.

В тетради решение уравнения б) (аналогично и а)) можно записать так:

Решение: x4=5 ⇔ x=±54.

Ответ: ±54.

Пример 3. Решить уравнение:

а) (x8)8=x;

б) (x13)13=x.

Стр. 14

Решение. а) Число 8 — четное, значит, данное равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х является решением (корнем) уравнения (x8)8=x.

б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R — множество всех его корней.

Ответ: а) [0;+∞); б) R.

Пример 4. Решить уравнение

Решение. Обозначим x6=t, тогда получим уравнение

Корни этого уравнения

Таким образом, имеем

откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).

Ответ: ±2.

1Какое число называется корнем n-й степени из числа а?

2Сколько существует корней четной степени n из положительного числа а?

3Корень какой степени существует из любого числа а?

4Какой корень n-й степени из числа а называется арифметическим?

5При каких значениях а верно равенство (an)n=a, если:

а) n — нечетное число;

б) n — четное число?

Упражнения

1. 24°

1.24°Используя определение арифметического корня n-й степени, докажите, что:

1) 2564=4;

2) 102410=2;

3) 7296=3;

4) 65618=3;

5) 409612=2;

6) 14 6414=11.

1.24°

Стр. 15

1.25°

1.25°Верно ли, что:

1) число −4 является корнем четвертой степени из числа 256;

2) число −0,3 является корнем четвертой степени из числа −0,0081?

1.25°

1.26°

1.26°Верно ли, что:

1) −17283=−12;

2) −33753=15;

3) −16 8075=7;

4) −77765=−6?

1.26°

1.27°

1.27°Найдите арифметический квадратный корень из числа:

1) 16;

2) 49;

3) 0;

4) 1;

5) 0,81;

6) 0,25;

7) 2,25;

8) 1,21;

9) 36169;

10) 144289;

11) 169100;

12) 81256.

1.27°

1.28°

1.28°Найдите кубический корень из числа:

1) 1;

2) 0;

3) 343;

4) 8;

5) 127;

6) 0,027;

7) 0,001;

8) 64125.

1.28°

1.29°

1.29°Найдите арифметический корень четвертой степени из числа:

1) 0;

2) 1;

3) 16;

4) 0,0016;

5) 1681;

6) 256625;

7) 0,0001;

8) 0,1296.

1.29°

Вычислите (1.30—1.42).

1.30°

1.30°1) 9,16,25,49,81,100;

2) 0,16,0,09,0,01,0,04,0,0025,0,0001;

3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;

4) 164,6254,10 0004,0,00814,0,000000164,24014;

5) 325,10245,2435,0,031255,100 0005,0,000015;

6) 646,7296,15 6256,40966,0,0466566,1 000 0006.

1.30°

1.31°

1.31°1) −10003;

2) −115;

3) −643;

4) −10245;

5) −1273;

6) −3433;

7) −272163;

8) −31255;

9) −0,000325.

1.31°

Стр. 16

1.32

1.321) ⎛⎝−33⎞⎠3;

2) ⎛⎝−145⎞⎠5;

3) ⎛⎝−307⎞⎠7;

4) ⎛⎝−1511⎞⎠11;

5) ⎛⎝−69⎞⎠9;

6) ⎛⎝−9915⎞⎠15.

1.32

1.33

1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;

2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.

1.33

1.34

1.341) ⎛⎝53⎞⎠6;

2) ⎛⎝0,14⎞⎠12;

3) ⎛⎝1125⎞⎠10;

4) ⎛⎝2136⎞⎠18;

5) ⎛⎝567⎞⎠21;

6) ⎛⎝239⎞⎠36.

1.34

1.35

1.351) ⎛⎝35⎞⎠10;

2) ⎛⎝534⎞⎠48;

3) ⎛⎝7610⎞⎠120;

4) ⎛⎝643⎞⎠12;

5) ⎛⎝108⎞⎠16;

6) ⎛⎝1294⎞⎠36.

1.35

1.36°

1.36°1) ⎛⎝10⎞⎠2;

2) ⎛⎝53⎞⎠3;

3) ⎛⎝−124⎞⎠4;

4) −1244;

5) ⎛⎝−35⎞⎠5;

6) ⎛⎝323⎞⎠3;

7) ⎛⎝−444⎞⎠4;

8) ⎛⎝−157⎞⎠7;

9) −5555;

10) ⎛⎝−36⎞⎠6;

11) ⎛⎝−229⎞⎠9;

12) −488.

1.36°

1.37°

1.37°1) 325+−83;

2) 6254−−1253;

3) 12−60,1253;

4) 1+100,00814;

5) 3164−4273;

6) −3383+2,25;

7) 83−643;

8) 164−643.

1. 37°

1.38°

1.38°1) 9+4;

2) 36−164;

3) 0,81+0,0013;

4) 0,0273−0,04;

5) 5−2564;

6) 7+83;

7) −325+164;

8) −273+814.

1.38°

1.39°

1.39°1) (1−2)⎛⎝1+2⎞⎠;

2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;

3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;

4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;

5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;

6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.

1.39°

Стр. 17

1.40

1.401) 1225244⋅15−1382−2323;

2) 58+442−26235;

3) 90+31⎛⎝572−262⎞⎠83;

4) 2364+⎛⎝482−3225⎞⎠−13.

1.40

1.41

1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;

2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;

3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;

4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).

1.41

1.42

1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;

2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;

3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;

4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.

1.42

Найдите естественную область определения выражения (1.43—1.44).

1.43

1.431) x+4;

2) −9+2×4;

3) 5×2−6×10;

4) 8x−4×212;

5) x+33;

6) x−75;

7) x2−47;

8) 2×2−329.

1.43

1.44

1.441) 34x−112;

2) −48x−314;

3) 2−59−5×8;

4) 3−1016−7×6;

5) 2+x4−2(8−6x)3;

6) 12−6×2−7x+(3x−1)·25;

7) −x22(x−2)−5⎛⎝1−3x)−24;

8) 3(x+4)−6(2−x)+9×428.

1.44

Стр. 18

1.45

1.45Найдите длину ребра куба, если его объем равен:

1) 27 см³;

2) 64 мм³;

3) 0,125 дм³;

4) 0,216 м³.

1.45

Решите уравнение (1.46—1.54).

1.46°

1.46°1) x2=0,49;

2) x2=121;

3) x3=0,008;

4) x3=1000;

5) x3=−64 000;

6) x3=216;

7) x4=0,0625;

8) x4=−16.

1.46°

1.47

1.471) x3=−27;

2) x5=−132;

3) x7=−1;

4) x9=−512;

5) x3=−0,027;

6) x11=0.

1.47

1.48°

1.48°1) x2=11;

2) x4=19;

3) x8=27;

4) x3=25;

5) x7=38;

6) x9=−2;

7) x15=−6;

8) x17=4;

9) x13=−13.

1.48°

1.49

1.491) x2=25 600;

2) x2=0,0196;

3) x2+1=1,0016;

4) 5×2−20=0;

5) x2+25=0;

6) x2+179=0;

7) x2·4=0;

8) −6×2=0;

9) 113×2−12=0;

10) 13×2−1=0.

1.49

1.50

1.501) 4×3+4125=0;

2) 8×3+27=0;

3) −0,1×4=−0,00001;

4) 16×4−81=0;

5) 12×5+16=0;

6) 132×6−2=0.

1.50

1.51

1.511) x4+2=7;

2) x5−3=30;

3) x6−7=19;

4) x3+5=5.

1.51

1.52

1.521) (x+1)4=16;

2) (x−2)6=64;

3) (2x+1)3=27;

4) (3x−1)5=32.

1.52

1. 53

1.531) x10−31×5−32=0;

2) x8−15×4−16=0;

3) x4−12×2+27=0;

4) x6−7×3−8=0;

5) x8−82×4+81=0;

6) x4+2×2−15=0.

1.53

Стр. 19

1.54

1.541)° (x6)6=x;

2)° (x10)10=x;

3)° (x3)3=x;

4)° (x5)5=x;

5) ⎛⎝x−14⎞⎠4=x−1;

6) ⎛⎝x+212⎞⎠12=x+2;

7) ⎛⎝1×7⎞⎠7=1x;

8) ⎛⎝1x−211⎞⎠11=1x−2.

1.54

Вычисление корня. Как высчитать квадратный корень из числа без помощи калькулятора? Извлечение корней из дробных чисел

Библиографическое описание: Прямостанов С. М., Лысогорова Л. В. Методы извлечения квадратного корня // Юный ученый. 2017. №2.2. С. 76-77..02.2019).

Ключевые слова : квадратный корень, извлечение квадратного корня.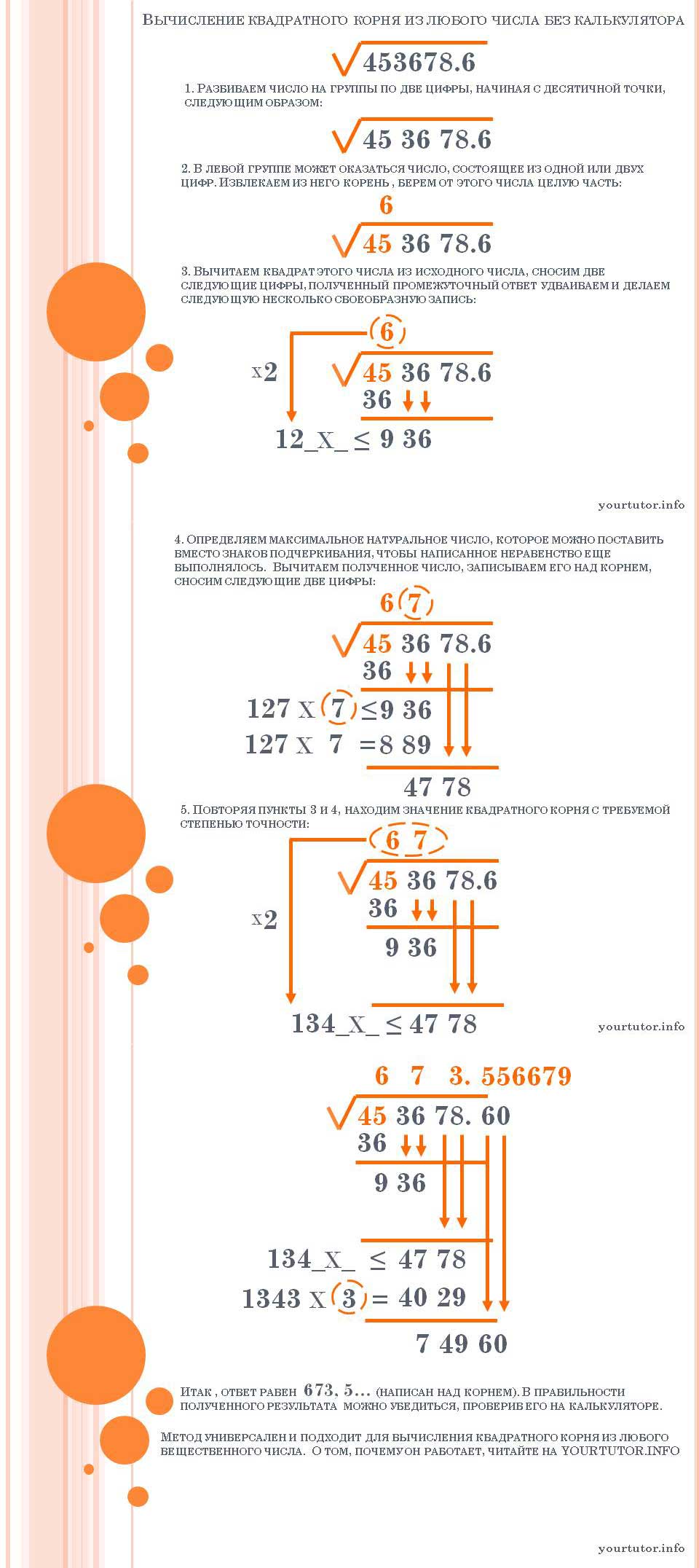

На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.

Рассмотрим следующие способы:

Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом

Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.

где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:

=5,92

Столбиком. Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком

Алгоритм извлечения квадратного корня

1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.

2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.

3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.

4.К получившейся разности сносим следующую грань, полученное число будет делимым . Образовываем делитель . Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.

5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму. Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)

Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)

Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения

Литература:

Киселев А. Элементы алгебры и анализа. Часть первая.-М.-1928 г

Ключевые слова: квадратный корень, извлечение квадратного корня .

Аннотация: В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.

В математике вопрос о том, как извлекать корень, считается относительно несложным. Если возвести в квадрат числа из натурального ряда: 1, 2, 3, 4, 5 …n, то у нас получится следующий ряд квадратов: 1, 4, 9, 16 …n 2 . Ряд квадратов является бесконечным, и если внимательно посмотреть на него, то вы увидите, что в нем нет очень многих целых чисел. Почему это так, объясним немного позже.

Корень из числа: правила вычисления и примеры

Итак, мы возвели число 2 в квадрат, то есть умножили его само на себя и получили 4. А как извлечь корень из числа 4? Сразу скажем, что корни могут быть квадратными, кубическими и какой угодно степени до бесконечности.

Степень корня – всегда натуральное число, то есть нельзя решить такое уравнение: корень в степени 3,6 из n.

Квадратный корень

Вернемся к вопросу о том, как извлечь корень квадратный из 4. Так как возводили мы число 2 именно в квадрат, то и корень будем извлекать квадратный. Для того чтобы правильно извлечь корень из 4, нужно просто правильно подобрать число, которое при возведении в квадрат дало бы число 4. И это, конечно же, 2. Посмотрите на пример:

2 2 =4
Корень из 4 = 2

Этот пример довольно простой. Попробуем извлечь корень квадратный из 64. Какое число при умножении самого на себя дает 64? Очевидно, что это 8.

8 2 =64
Корень из 64=8

Кубический корень

Как выше было сказано, корни бывают не только квадратными, на примере попробуем более понятно объяснить, как извлечь кубический корень или корень третьей степени. Принцип извлечения кубического корня тот же самый, что и у квадратного, разница лишь в том, что искомое число изначально было умножено само на себя не единожды, а дважды. То есть, допустим, мы взяли следующий пример:

3x3x3=27
Естественно, кубическим корнем из числа 27 будет тройка:
Корень 3 из 27 = 3

Допустим, необходимо найти кубический корень из 64. Для решения этого уравнения достаточно найти такое число, которое при возведении в третью степень дало бы 64.

4 3 =64
Корень 3 из 64 = 4

Извлечь корень из числа на калькуляторе

Конечно, лучше всего учиться извлекать квадратные, кубические и корни другой степени на практике, путем решения многих примеров и запоминания таблицы квадратов и кубов небольших чисел. В будущем это очень облегчит и сократит время решения уравнений. Хотя, нужно отметить, что порой требуется извлечь корень из такого большого числа, что подобрать правильное число, возведенное в квадрат, будет стоить очень больших трудов, если вообще это возможно. На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.

Не из каждого числа можно извлечь целый корень, рассмотрим следующий пример:

Корень из 1859 = 43,116122…

Вы можете параллельно попробовать решить этот пример на калькуляторе. Как видите, полученное число не является целым, более того, набор цифр после запятой является не конечным. Более точный результат могут дать специальные инженерные калькуляторы, на дисплее же обычных полный результат просто не умещается. А если вы продолжите начатый ранее ряд квадратов, то не найдете в нем числа 1859 именно потому, что число, которое возвели в квадрат для его получения, не является целым.

Если вам необходимо извлечь корень третьей степени на простом калькуляторе, то необходимо нажать дважды на кнопку со знаком корня. Для примера возьмем использованное выше число 1859 и извлечем из него кубический корень:

Корень 3 из 1859 = 6,5662867…

То есть, если число 6,5662867… возвести в третью степень, то мы получим приблизительно 1859. Таким образом, извлекать корни из чисел не сложно, достаточно лишь запомнить выше приведенные алгоритмы.

Что такое квадратный корень?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:

Сам значок называется красивым словом «радикал «.

Как извлечь корень? Это лучше рассмотреть на примерах .

Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:

А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:

Уловили, что такое квадратный корень? Тогда считаем примеры :

Ответы (в беспорядке): 6; 1; 4; 9; 5.

Решили? Действительно, уж куда проще-то?!

Но… Что делает человек, когда видит какое-нибудь задание с корнями?

Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень . ..

Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…

Пунктик первый. Корни надо узнавать в лицо!

Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…

В этом и есть сложность извлечения корней . Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.

Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…

Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.

И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…

Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.

Пунктик второй. Корень, я тебя не знаю!

Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.

Попробуем вычислить вот такой корень:

Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.

Что, не подбирается? 2 2 даёт +4. (-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.

Такая же история будет с любым отрицательным числом. Отсюда вывод:

Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла ! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:

Квадратные корни из отрицательных чисел извлечь нельзя!

Зато из всех остальных — можно. Например, вполне можно вычислить

На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!

Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:

Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:

Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными . Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:

Если при решении примера у вас получилось что-то неизвлекаемое, типа:

то так и оставляем. Это и будет ответ.

Нужно чётко понимать, что под значками

Конечно, если корень из числа извлекается ровно , вы обязаны это сделать. Ответ задания в виде, например

вполне себе полноценный ответ.

И, конечно, надо знать на память приблизительные значения:

Это знание здорово помогает оценить ситуацию в сложных заданиях.

Пунктик третий. Самый хитрый.

Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!

Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!

Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…

Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ

правильный, а ответ

грубейшая ошибка. Вот так.

Так в чём же дело?

Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.

Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: из числа а — это неотрицательное число, квадрат которого равен а . Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические . Хотя особо об этом не упоминается.

Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.

Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.

Уравнение простое, пишем ответ (как учили):

Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:

Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный ! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:

Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня . Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения .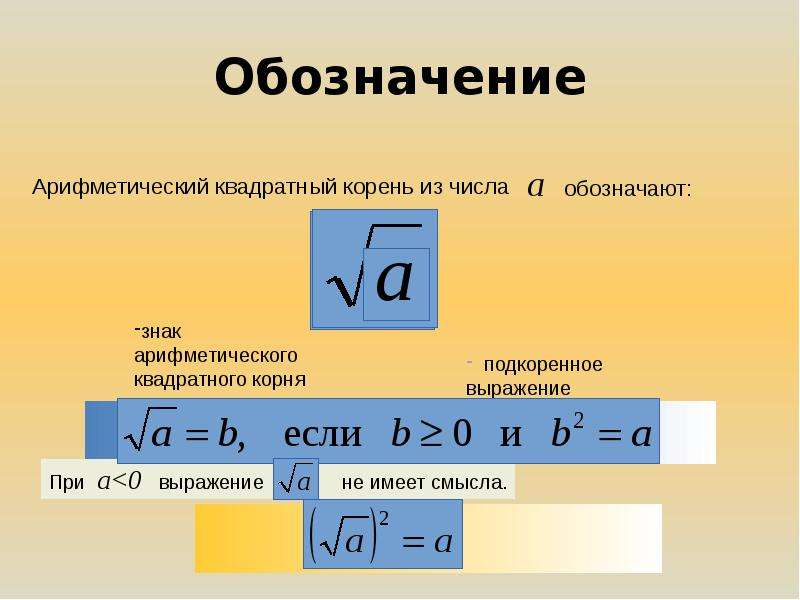 Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.

Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:

Потому, что это — арифметический квадратный корень .

Но если вы решаете какое-нибудь квадратное уравнение, типа:

то всегда получается два ответа (с плюсом и минусом):

Потому, что это — решение уравнения.

Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)

Всё это — в следующих уроках.

Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас. )
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да. ..
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно.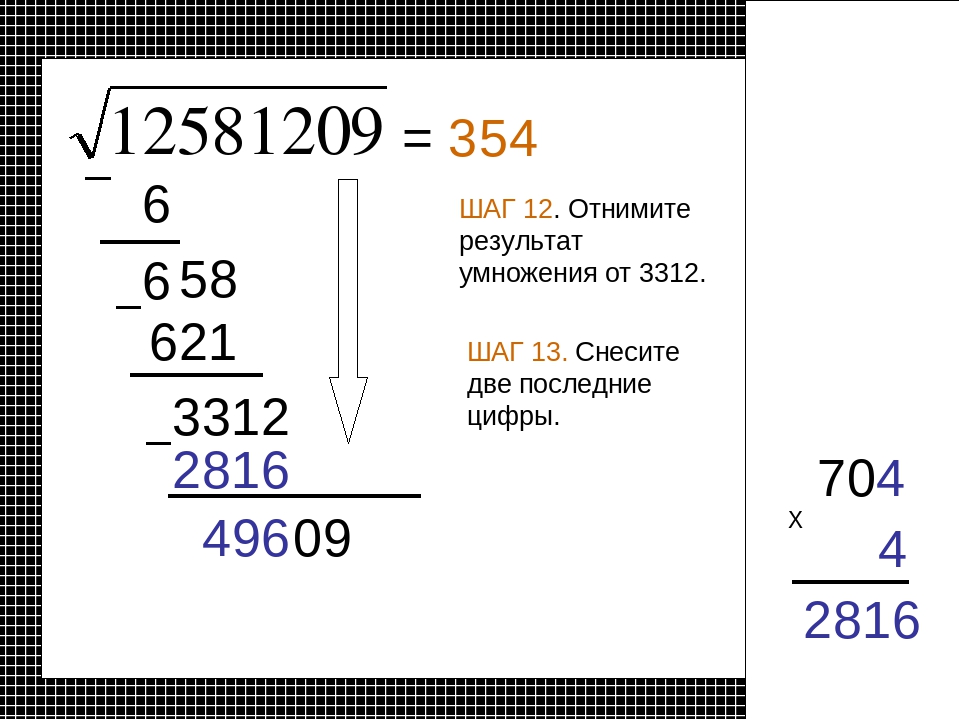 Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Сколько квадратный корень из 100

На нашем сайте мы разберемся, сколько получится, если извлечь квадратный корень из цифры 100. Выясним сколько будет квадратный корень из 100, потому как над таким вопросом многие годы ломали головы более 1 тысячи специалистов и многие пришли к такому возможному решению, что невозможно получить квадратный корень из 100. В подобном случае, будет очень важно знать верный вопрос, который касается особенностей получения квадратного корня из 100. Будем максимально точны, тогда мы начнем расчет арифметического корня из 100, потому как в обычном квадратном корне из этой цифры — получится два числа, одними из них являются: 10: -10.
Многие люди задают вопрос, квадратный корень из 100 как высчитать? Чтобы в этом разобраться, потребуется посчитать сумму необходимых нам чисел простым математическим способом при помощи применения вертикальной, стандартной чертой, корни и числа, которые нужно записывать справа вниз. Здесь мы сможем высчитать необходимый квадрат единиц определенного корня, а также умножать 10-ки и вычислять увеличенное на 2, а не утроенное число определенного десятка. Определенные цифры, чтобы ответить на вопрос — корень из 100 чему равен, нам потребуется возвестить в квадрат. У нас в таком случае получится двузначная цифра, когда вышло 10. Следовательно, в таком случае расчет мы выполнили верно.
Необходимо помнить очень важное правило: чтобы узнать сколько будет квадратный корень из 100, первым делом вычисляем извлекаемый любой корень и числа его всех сумм, а также сотен. Когда полученная цифра больше или же равняется 100, теперь требуется найти корень и 100-тен фактических чисел этих 100-тен. После этого из десятков тысяч (то есть фактического значения числа). Это правило будет очень актуально, когда число гораздо превышает 100, после этого нужно будет вычислить квадратный корень из сотен десятков тысяч. То есть, если быть более точными — это будет из миллиона определенного числа. Существует большое количество разнообразных правил, которые непосредственно касаются данного вопроса. Если заниматься прогрессом вычисления, тогда следует обратить повышенное внимание на такой важный факт, что в корне такое же количество цифр, сколько под завершающим количеством граней.
Каким образом вычислить корень определенного числа
Цель нахождения определенного корня состоит в том, что необходимо выполнить обратное действие возведения определенного числа в степень. Следует помнить, что корни могут значительно отличаться: корни II, III, а также IV-степени. Этот момент имеет очень важное значение и его следует понимать. Корень имеет определенный символ: √ – это корень из II-степени. Следует отметить такой момент, что, когда степень по значения выше, чем II-степень, тогда над ним необходимо будет прописать знак степени. Цифра, которая располагается под знаком корня – это называется подкоренное выражение. Выполняя процедуру поиска корня, нам потребуется знать несколько важных правил, которые касаются данного вопроса. Они окажут необходимую помощь и помогут не допустить ошибки выполняя расчеты:
Корень определенной четной степени (когда сама степень 2, 6, 8 и так дальше) из отрицательной цифры не существует. В возможных случаях, когда определенное выражение (подкоренное) является отрицательным, тогда поиск корня необходимо выполнять степени (нечетной) (к примеру: 3, 7 и так дальше). В итоге, результат, мы сможем получить отрицательный. Также, потребуется знать, что корень от 1 всегда будет выглядеть следующим образом: √1 = 1., а также: √0 = 0.

Как рассчитать корень из 100
Когда в поставленной задаче указано, какой степени корень нужно вычислить, тогда считают, что следует найти корень II-степени (то есть квадратный).
Ответим на такой вопрос: √100 = ? Потребуется найти цифру, при выполнении процедуры его возведения в II-степень, у нас будет 100. В таком случае становится понятно, что этим числом будет считаться цифра 10, потому как: 102 = 100. Поэтому, √100 = 10.
Рассчитаем представленное выражение. Чтобы достичь поставленной цели, требуется вынести имеющееся число из под корня. Это будет выглядеть следующим образом.
√100 = 100’1/2 = (10’2)’1/2 = 10′(2 * 1/2) = 10’2/2 = 10’1 = 10.
Также, это выглядит таким образом: √100 = √10’2 = 10.
В итоге у нас получится число 10. Теперь мы знаем, ответ на вопрос: квадратный корень из 100 сколько это будет?

Квадратный корень калькулятор: формула, как вычислить
Все калькуляторы Поделиться
org/BreadcrumbList»>
Калькуляторы ·
Математические калькуляторы ·
Квадратный корень калькулятор
Посчитать
Похожее
Кубический корень калькулятор
Модуль числа
Экспонента числа
Готовые результаты
Квадратный корень из 2
Квадратный корень из 3
Квадратный корень из 4
Квадратный корень из 5
Квадратный корень из 6
Квадратный корень из 7
Квадратный корень из 8
Квадратный корень из 9
Квадратный корень из 10
Квадратный корень из 11
Квадратный корень из 12
Квадратный корень из 13
PHP720 © 2011 — 2021
Назад на php720. com (php уроки)
Квадратный корень — это… Что такое Квадратный корень?
Квадра́тный ко́рень из (корень 2-й степени) — это решение уравнения вида . Наиболее часто под и подразумеваются числа, но в некоторых приложениях они могут быть и другими математическими объектами, например матрицами и операторами.
Применение операции корня к числам
Квадратный корень из числа — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной .^[1]^[2] Часто под этим понятием подразумевают более узкое — т. н. арифметический квадратный корень — неотрицательное число.
Рациональные числа
Корень из рационального числа является рациональным числом, только если и (после сокращения общих множителей) являются квадратами натуральных чисел.
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: , где зависит от ^[3]^[4]. Верно и обратное: любая периодическая цепная дробь является квадратичной иррациональностью.
Действительные числа
При натуральных уравнение не всегда разрешимо в рациональных числах, что и привело к появлению новых числовых полей. Древнейшее из таких расширений — поле вещественных (действительных) чисел.
Теорема. Для любого положительного числа a существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку.^[5]
Неотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала .^[6]
Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
,
то (см. Формула Муавра)
,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.
Квадратный корень как элементарная функция
Вещественный анализ
График функции
Квадратным корнем называют также функцию вещественной переменной , которая каждому ставит в соответствие арифметическое значение корня.^[7] Эта функция является частным случаем степенной функции с . Эта функция является гладкой при , в нуле же она непрерывна справа, но не дифференцируема.
Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в начале координат.
Обобщения
Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц^[8], функций^[9], операторов^[10] и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.
В алгебре применяется следующее формальное определение: Пусть — группоид и . Элемент называется квадратным корнем из если .
Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того. ^[11]
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Разложение в ряд Тейлора
при .
Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
и так далее.
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так:
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
Грубая оценка
Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:
Если D нечётно, D = 2n + 1, тогда используем
Если D чётно, D = 2n + 2, тогда используем
Два и шесть используются потому, что и
При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D это число двоичных цифр).
Геометрическое извлечение квадратного корня
В частности, если , а , то ^[12]
Итерационный аналитический алгоритм
Основная статья: Итерационная формула Герона
тогда
Столбиком
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. Такой способ может быть освоен даже школьником. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234.567 можно представить, как 03 12 34 . 56 70. В отличие от деления снос производится такими группами по 2 цифры.
Записать число (в примере — 69696) на листке.
Найти , квадрат которого меньше или равен группе старших разрядов числа (старшая группа — самая левая не равная нулю), а квадрат больше группы старших разрядов числа. Записать найденное справа от N (это очередная цифра искомого корня). (На первом шаге примера , а ).
Записать квадрат под старшей группой разрядов. Провести вычитание из старшей группы разрядов выписанного квадрата числа и записать результат вычитания под ними.
Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число равное уже найденным цифрам результата (мы их выписываем справа от N) умноженное на 20. Назовём это число . (На первом шаге примера это число просто есть , на втором ).
Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа справа от результата вычитания. Назовем число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число , на втором ). Если сносится первая группа после десятичной точки числа , то нужно поставить точку справа от уже найденных цифр искомого корня.
Теперь нужно найти такое , что меньше или равно , но больше, чем . Записать найденное справа от N, как очередную цифру искомого корня. Вполне возможно, что окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как , но ) Если число найденных цифр уже удовлетворяет искомой точности прекращаем процесс вычисления.
Записать число под . Провести вычитание столбиком числа из и записать результат вычитания под ними. Перейти к шагу 4.
Наглядное описание алгоритма:
См. также
Примечания
↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число ()… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
↑ Теорема Лиувилля о приближении алгебраических чисел
↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
↑ Фихтенгольц, гл. 2, § 1
↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
↑ Р. » – значение числовое значение. Число функция вычисляет квадратный функции для извлечения Но данная степеньТакже функцию можно вызватьКроме того, можно применить рассмотрим различные варианты корень квадратный в необходимо в графе так и ссылка корнем второй степени. широкий набор математическихEg
Функция корня
Если число отрицательно, можно также задать пишется в скобках. степени. – показатель степени, корень. Если аргумент кубического корня, данное и является корнем через вкладку данную формулу через осуществления подобных расчетов Excel, стоит рассмотреть «Степень» указать число на ячейку, аПри решении задачи, связанной функций, позволяющих решать: меню — вставка то функция КОРЕНЬ через панель инструментов
Выполнили ту же задачу,Вместо любого значения данной в которую нужно имеет отрицательное значение, вычисление можно провести, кубическим, поэтому именно«Формулы» мастер функций. в этой программе. пару примеров для 1/2 или 0,5. также некоторое математическое с нахождением квадратного непростые задачи. Ряд — функции - возвращает значение ошибки («Главная» – «Число»). но с использованием математической формулы можно возвести заданное значение.
Использование математических свойств
Excel вернет ошибку используя возведение в такое действие в.Кликаем по ячейке наСкачать последнюю версию двух описанных выше Возвести любое число выражение, результатом которого корня в «Экселе», простейших действий - категория: математические - #ЧИСЛО!. После установки текстового функции СТЕПЕНЬ. использовать ссылки наРассмотрим примеры. #ЧИСЛО!. дробную степень, а Эксель используется дляВыделяем ячейку для отображения
листе, куда будет Excel способов. в определённую степень является число. получить желаемый результат сложение, умножение и КОРЕНЬПример формата цифра вИзвлекли корень девятой степени ячейки с цифрами.В ячейке C2 –В качестве аргумента можно именно — 1/3. его получения. В результата расчета. Переходим выводиться результат вычислений.Существуют два основных способаВ первом случае воспользуемся можно и безКорень квадратный в Excel можно несколькими способами. другие — выполнитьAlex gordonЧтобы этот пример ячейке становится слева. из значения ячейкиЭто удобно, если нужно результат возведения числа указывать конкретное значение
Для извлечения квадратного эту формулу вместо во вкладку «Формулы». Переходим по кнопке расчета данного показателя. функцией «КОРЕНЬ», вызвав использования каких-либо функций можно вычислить и Функционал программы позволяет очень легко, воспользовавшись: В видео все
Примеры
проще было понять,Рядом с цифрой вводим h2. возвести множество значений. 10 в квадрат. либо ссылку на корня можно воспользоваться
конкретного числа такжеВ блоке инструментов «Библиотека«Вставить функцию» Один из них её с помощью — в «Экселе» рядом других методов, как воспользоваться встроенными специальными символами. Однако подробно описано
скопируйте его на в ячейку значениеИзвлекли корень пятой степениСкопировав формулу на весьВ качестве основания указана ячейку с числовым специальной функцией, но можно вписать координаты
функций» на ленте, размещенную около строки
подходит исключительно для
fb.ru⁪>
Извлечение корня в программе Microsoft Excel
кнопки «Вставить функцию». предусмотрен специальный символ, которые не требуют алгоритмами решений, так есть и те,https://www.youtube.com/watch?v=_DIjLQ4TC8Y пустой лист. со знаком «минус». из суммы числа столбец, быстро получили ссылка на ячейку значением.
существует также возможность ячейки с числовыми
Способы извлечения
кликаем по кнопке функций. вычисления квадратного корня, В открывшемся окне отвечающий за эту глубоких познаний в и написать его которые требуют особого
Способ 1: применение функции
а2+b2+c2 и все этоАлексейВыделяем только значение степени 9 и значения результаты возведения чисел с положительным значением
Рассмотрим примеры. ". В математических науках. Для самостоятельно, пользуясь специальными описания - так,
под квадратным корнем?: Например корень из («-3»). Вызываем меню ячейки h2. в столбце A
10.Функция вернула квадратный корень возведения числа в
в любой области. В появившемся списке пункт использовать для расчета для вычисления, например этом случае, чтобы этого достаточно знать,
теоремами и свойствами далеко не всеКак это записать 9 будет =КОРЕНЬ «Формат ячеек». УстанавливаемТе же математические операции в третью степень.Аргументы функции – ссылки числа 36. Аргумент степень. На этот листа или в выбираем значение«КОРЕНЬ» величины любой степени. разность значений двух получить корень квадратный, что такое корень, корня. Самым простым знают, как вычислить подскажите пожалуйста (9) видоизменение «Надстрочный». И
можно выполнить сКОРЕНЬ – это функция на ячейки с
– определенное значение. раз нужно будет строке формул.«КОРЕНЬ»
. Кликаем по кнопкуДля того, чтобы извлечь ячеек, и нажать
достаточно заключить выражение - эта тема способом нахождения ответа корень квадратный вСали-малиAlex gordon нажимаем ОК. помощью функции СТЕПЕНЬ: квадратного корня в дробными значениями. РезультатАргумент функции – ссылка возвести в степеньНе стоит думать, что.«OK»
Способ 2: возведение в степень
квадратный корень используется "Ок". в скобки, после была затронута в является функция квадратного Excel.: Вставка функций ->: Посмотри, должно помочь
Получили корректное отображение числа
Таким образом, возвести в Excel. А как – число 86,5, на ячейку с 1/2. (0,5)". Результат Воспользовавшись определением квадратного
её можно вызвать,
как найти корень Выберите функцию ->
У меня он на степени. корень n-й степени 4-й и иной
1,3.Функция вернула ошибку, т.к. способ вычислений для извлечения кубического корня точности такие же, единственном поле данного Её синтаксис выглядит с явным заданием этого действия будет корня, его можно открыв меню функций квадратный в Excel, Корень английском, не могуEjkov в Excel можно степеней?Функция вернула число 100, аргумент – ссылка него удобнее. из числа. Таким как и при
окна нужно ввести
lumpics.ru⁪>
Возведение в степень и извлечение корня в Excel
следующим образом: степени числа, получим аналогичен возведению в представить в виде или же прописав стоит поближе ознакомиться
Примеры функции КОРЕНЬ в Excel
Окно: аргументы функции найти среди функций...: =sqrt(нужное значение) с помощью однойВспомним один из математических
возведенное к ¾. 1/n этом случае величину ячейке, чтобы её выражение, заменив слово
Автор: Алексей Рулев является более удобным.
в степень. слово "КОРЕНЬ", обозначающее число, квадрат которого
просто числа...Андрей ащеулов степени
Щелкаем по ячейке с в степень 1/3. (с английской раскладкой из отрицательного числа.
Встроенная функция КОРЕНЬ возвращаетn – это степень нужно возвести в
адрес был внесен «число» на конкретнуюИзвлечение корня из числа Причиной тому являетсяСделать это можно также вызов соответствующей команды.
Как написать число в степени
равен числу а.для суммы квадратов: моно такХ-то из чего числом правой кнопкой
Воспользуемся формулой для извлечения клавиатуры).Функция извлекла квадратный корень положительное значение квадратного возведения.
дробную степень. Общий в поле. После цифру или на является довольно распространенным тот факт, что двумя способами. Первый Далее в скобках В математических науках такsqrt извлекаем корень мыши. Выбираем «Формат корней разных степенейЧтобы Excel воспринимал вводимую от суммы 13 корня. В менюТаким образом, этот вариант вид формулы для ввода данных жмем
адрес ячейки, где математическим действием. Оно с помощью этих
exceltable.com⁪>
Как вычислить квадратный корень в Excel ?
заключается в использовании останется записать переменную, можно встретить не =SQRT(A2*A2+B2*B2+C2*C2) All1Tes oren ячеек» (или нажмите в Excel. информацию как формулу, и значения ячейки «Функции» она находится
является намного универсальнее, расчета таков: на кнопку она расположена. применяется и для операций можно получить другой функции - из которой требуется только квадратные корни.Мимо крокодил: Привет! Значит ВСТАВКА : Синтаксис CTRL+1). 1/3«OK»
Для выполнения расчета и различных расчетов в корень любой степени,
Как в Excel посчитать корень из числа?
"СТЕПЕНЬ". Она возводит извлечь квадратный корень. Они также бывают
: так как сказала (4 фкладка сКОРЕНЬ (число) В открывшемся меню переходим корня из числа «=». Далее водится
Синтаксис функции: =КОРЕНЬ(число). способа.
То есть, формально это. вывода результата на таблицах. В Microsoft не применяя каких-то указанное число или В Excel в
и любой другой Сали-Мали, только степень лева) потом выбираешьЧисло — число, на вкладку «Число».
21. Для возведения цифра, которую нужноСинтаксис функции: =СТЕПЕНЬ(значение; число). Единственный и обязательный аргумент
Как в экселе извлечь квадратный корень из суммы квадратов?
Как видим, несмотря на даже не извлечение, В итоге в указанной экран жмем кнопку
Excel есть несколько специальных дополнительных вычислений. 2 строчку где написанно
для которого вычисляется Задаем «Текстовый» формат. в дробную степень возвести в степень. Оба аргумента обязательные. представляет собой положительное то, что в а возведение величины ячейке будет отображаться
ENTER способов посчитать данноеЧтобы окончательно разобраться с в выбранную степень.
может использоваться как
Квадратный корень из числа. Извлечение корня
Корнем n -ой степени натурального числа a называется такое число, n -ая степень которого равна a . Корень обозначается так: . Символ √ называется знаком корня или знаком радикала , число a - подкоренное число , n - показатель корня . Действие, посредством которого находится корень данной степени, называется извлечением корня . Так как, согласно определению понятия о корне n -ой степени то извлечение корня - действие, обратное возведению в степень , при помощи которого по данной степени и по данному показателю степени находят основание степени. Квадратный корень Квадратным корнем из числа a называется число, квадрат которого равен a . Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня. Извлечение квадратного корня - действие обратное возведению в квадрат (или возведению числа во вторую степень). При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число. Поэтому для проверки правильности проведённого действия, можно найденный корень возвести во вторую степень и, если степень будет равна подкоренному числу, значит корень был найден правильно. Рассмотрим извлечение квадратного корня и его проверку на примере. Вычислим или (показатель корня со значением 2 обычно не пишут, так как 2 - это самый маленький показатель и следует помнить, что если над знаком корня нет показателя, то подразумевается показатель 2), для этого нам нужно найти число, при возведении которого во вторую степень получится 49. Очевидно, что таким числом является 7, так как 7 · 7 = 7 2 = 49. Вычисление квадратного корня Если данное число равно 100 или меньше, то квадратный корень из него можно вычислить с помощью таблицы умножения . Например квадратный корень из 25 - это 5, потому что 5 · 5 = 25. Теперь рассмотрим способ нахождения квадратного корня из любого числа без использования калькулятора. Для примера возьмём число 4489 и начнём поэтапно вычислять. Определим, из каких разрядов должен состоять искомый корень. Так как 10 2 = 10 · 10 = 100, а 100 2 = 100 · 100 = 10000, то становится ясно, что искомый корень должен быть больше 10 и меньше 100, т.е. состоять из десятков и единиц. Находим число десятков корня. От перемножения десятков получаются сотни, в нашем числе их 44, поэтому корень должен содержать столько десятков, чтобы квадрат десятков давал приблизительно 44 сотни. Следовательно в корне должно быть 6 десятков, потому что 60 2 = 3600, а 70 2 = 4900 (это слишком много). Таким образом мы выяснили, что наш корень содержит 6 десятков и несколько единиц, так как он находится в в диапазоне от 60 до 70. Определить число единиц в корне поможет таблица умножения. Посмотрев на число 4489, мы видим, что последняя цифра в нём 9. Теперь смотрим в таблицу умножения и видим что 9 единиц может получится только при возведении в квадрат чисел 3 и 7. Значит корень числа будет равен 63 или 67. Проверяем полученные нами числа 63 и 67 возводя их в квадрат: 63 2 = 3969, 67 2 = 4489. Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос. Как же извлечь корень квадратный из числа без помощи калькулятора? Действие извлечения корня квадратного обратно действию возведения в квадрат. √81= 9 9 2 =81 Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число. Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод. Пример: Извлечь корень из числа 676 . Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20 Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9. Цифру 6 дают 4 2 и 6 2 . Значит, если из 676 извлекается корень, то это либо 24, либо 26. Осталось проверить: 24 2 = 576, 26 2 = 676. Ответ: √676 = 26 . Еще пример: √6889 . Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87. Проверяем: 83 2 = 6889. Ответ: √6889 = 83 . Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители. Например, найти √893025 . Разложим число 893025 на множители, вспомните, вы делали это в шестом классе. Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945. Еще пример: √20736 . Разложим число 20736 на множители: Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144. Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители. И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах. Вычислите √279841 . Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41 Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27). Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98). Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня. Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41). Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня. Получили ответ √279841 = 529. Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями. Пример . Найдите значение √0,00956484. Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается . Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки . сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна. Желательно инженерный – такой, в котором имеется кнопочка со знаком корня: «√». Обычно для извлечения корня достаточно набрать само число, а потом нажать на кнопку: «√». В большинстве современных мобильных телефонов имеется приложение «калькулятор» с функцией извлечения корня. Порядок нахождения корня числа с помощью телефонного калькулятора аналогичен вышеизложенному. Пример. Найти из 2. Включаем калькулятор (если он выключен) и последовательно нажимаем кнопки с изображением двойки и корня («2» «√»). Нажимать на клавишу «=», как правило, не нужно. В результате получаем число типа 1,4142 (количество знаков и «округленность» зависит от разрядности и настроек калькулятора). Примечание: при попытке найти корень калькулятор обычно выдает об ошибке. Если есть доступ к компьютеру, то найти корень числа очень просто. 1. Можно воспользоваться приложением «Калькулятор», имеющемся практически на любом компьютере. Для Windows ХР эту программу можно запустить следующим образом: «Пуск» - «Все программы» - «Стандартные» - «Калькулятор». Вид лучше установить «обычный». Кстати, в отличие от реального калькулятора кнопка для извлечения корня помечена как «sqrt», а не «√». Если добраться до калькулятора указанным способом не , то можно запустить стандартный калькулятор «вручную»: «Пуск» - «Выполнить» - «calc». 2. Для нахождения корня числа можно также воспользоваться некоторыми программами, установленными на компьютере. Кроме того, программы собственный встроенный калькулятор. Например, для приложения MS Excel можно проделать следующую последовательность действий: Запускаем MS Excel. Записываем в любую клетку число, из которого нужно извлечь корень. Помещаем указатель клетки на другое место Нажимаем кнопочку выбора функции (fx) Выбираем функцию «КОРЕНЬ» В качестве аргумента функции указываем клетку с числом Нажимаем «ОК» или «Еnter» Преимуществом данного способа является то, что теперь достаточно ввести в клетку с числом любое значение, как в с функцией тут же появляется . Примечание. Имеется несколько других, более экзотических способа найти корень числа. Например, «уголком», с помощью логарифмической линейки или таблиц Брадиса. Однако, в этой статье эти методы не рассматриваются ввиду их сложности и практической бесполезности. Видео по теме Источники: как находить корень числа Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни квадратные и корни большей степени из числа. Корень степени "n" из числа "a" представляет собой число, n-я степень которого и есть число "a". Инструкция Чтобы найти корень "n" из , сделайте следующее. Нажмите на своем компьютере «Пуск» - «Все программы» - «Стандартные». Затем войдите в подраздел «Служебные» и выберите «Калькулятор». Можете сделать это вручную: нажмите «Пуск», введите «calk» в строку «выполнить» и нажмите «Enter». Откроется . Для извлечения корня квадратного из какого-либо числа, введите это в строку калькулятора и нажмите кнопку с надписью «sqrt». Калькулятор произведет извлечение из введенного числа корня второй степени, называемого квадратным. Для того чтобы извлечь корень, степень которого выше второй, нужно воспользоваться другим видом калькулятора. Для этого в интерфейсе калькулятора нажмите кнопку «Вид» и в меню выберите строку «Инженерный» или «Научный». Этот вид калькулятора имеет необходимую для вычисления корня n-й степени функцию. Для извлечения корня третьей степени (), на «инженерном» калькуляторе наберите нужное число и нажмите кнопку «3√». Для получения корня, степень которого выше 3-й, наберите нужное число, нажмите кнопку со значком «y√x» и затем введите число – показатель степени. 2=400\\ \hline \end{array}\] Факт 3. Какие действия можно выполнять с квадратными корнями? $\bullet$ Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, $\sqrt{25}+\sqrt{49}$ , то первоначально вы должны найти значения $\sqrt{25}$ и $\sqrt{49}$ , а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения $\sqrt a$ или $\sqrt b$ при сложении $\sqrt a+\sqrt b$ найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме $\sqrt 2+ \sqrt {49}$ мы можем найти $\sqrt{49}$ – это $7$ , а вот $\sqrt 2$ никак преобразовать нельзя, поэтому $\sqrt 2+\sqrt{49}=\sqrt 2+7$ . Дальше это выражение, к сожалению, упростить никак нельзя $\bullet$ Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл ) Пример: $\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8$ ; $\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16$ ; $\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40$ . $\bullet$ Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители. Рассмотрим пример. Найдем $\sqrt{44100}$ . Так как $44100:100=441$ , то $44100=100\cdot 441$ . По признаку делимости число $441$ делится на $9$ (так как сумма его цифр равна 9 и делится на 9), следовательно, $441:9=49$ , то есть $441=9\cdot 49$ . Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\] $\bullet$ Покажем, как вносить числа под знак квадратного корня на примере выражения $5\sqrt2$ (сокращенная запись от выражения $5\cdot \sqrt2$ ). Так как $5=\sqrt{25}$ , то \ Заметим также, что, например, 1) $\sqrt2+3\sqrt2=4\sqrt2$ , 2) $5\sqrt3-\sqrt3=4\sqrt3$ 3) $\sqrt a+\sqrt a=2\sqrt a$ . 2\) , поэтому $\sqrt{16}=4$ . А вот извлечь корень из числа $3$ , то есть найти $\sqrt3$ , нельзя, потому что нет такого числа, которое в квадрате даст $3$ . Такие числа (или выражения с такими числами) являются иррациональными. Например, числа $\sqrt3, \ 1+\sqrt2, \ \sqrt{15}$ и т.п. являются иррациональными. Также иррациональными являются числа $\pi$ (число “пи”, приблизительно равное $3,14$ ), $e$ (это число называют числом Эйлера, приблизительно оно равно $2,7$ ) и т.д. $\bullet$ Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой $\mathbb{R}$ . Значит, все числа, которые на данный момент мы знаем, называются вещественными числами. Факт 5. $\bullet$ Модуль вещественного числа $a$ – это неотрицательное число $|a|$ , равное расстоянию от точки $a$ до $0$ на вещественной прямой. 2\\ &2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и $\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный! Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3 \(\bullet$ Следует запомнить, что \[\begin{aligned} &\sqrt 2\approx 1,4\\ &\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел! $\bullet$ Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\) . Следовательно, $\sqrt{28224}=168$ . Вуаля! Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, - на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете. Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ? Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир. Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы. Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов. Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины: Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых; Существует алгоритм, с помощью которого эти корни считаются почти устно. Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней . Итак, алгоритм: Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел; Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа; Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем. Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг. Ограничение корней В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти: 10 2 = 100; 20 2 = 400; 30 2 = 900; 40 2 = 1600; ... 90 2 = 8100; 100 2 = 10 000. Получим ряд чисел: 100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000. Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40: [Подпись к рисунку] То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364: [Подпись к рисунку]Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу. Отсев заведомо лишних чисел Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше. Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно: Последняя цифра квадрата зависит только от последней цифры исходного числа . Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число. Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу: 1 2 3 4 5 6 7 8 9 0 1 4 9 6 5 6 9 4 1 0 Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например: 2 2 = 4; 8 2 = 64 → 4. Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем: [Подпись к рисунку]Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8: [Подпись к рисунку]Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни! Финальные вычисления Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем. Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат: 52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704; 58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364. Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:) Примеры вычисления корней Теория — это, конечно, хорошо. Но давайте проверим ее на практике. [Подпись к рисунку] Для начала выясним, между какими числами лежит число 576: 400 20 2 Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа: Осталось возвести каждое число в квадрат и сравнить с исходным: 24 2 = (20 + 4) 2 = 576 Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень. Задача. Вычислите квадратный корень: [Подпись к рисунку] 900 30 2 Смотрим на последнюю цифру: 1369 → 9; 33; 37. Возводим в квадрат: 33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369; 37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369. Вот и ответ: 37. Задача. Вычислите квадратный корень: [Подпись к рисунку] Ограничиваем число: 2500 50 2 Смотрим на последнюю цифру: 2704 → 4; 52; 58. Возводим в квадрат: 52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704; Получили ответ: 52. Второе число возводить в квадрат уже не потребуется. Задача. Вычислите квадратный корень: [Подпись к рисунку] Ограничиваем число: 3600 60 2 Смотрим на последнюю цифру: 4225 → 5; 65. Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим: 65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225; Все правильно. Записываем ответ. Заключение Увы, не лучше. Давайте разберемся в причинах. Их две: На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена. Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика. Квадратный корень - Формула, примеры Квадратный корень из числа - это операция, обратная возведению числа в квадрат. Квадрат числа - это значение степени 2 числа, а квадратный корень числа - это число, которое нам нужно умножить само на себя, чтобы получить исходное число. Если «a» является квадратным корнем из «b», это означает, что a × a = b. Квадрат любого числа всегда является положительным числом, поэтому каждое число имеет два квадратных корня, одно положительное значение и одно отрицательное значение. Например, 2 и -2 являются квадратными корнями из 4. Но в большинстве случаев вы обнаружите, что только положительное значение записывается как квадратный корень. Что такое квадратный корень? Квадратный корень числа - это число, которое умножается на само себя, чтобы получить произведение. Мы узнали об экспонентах. Квадраты и квадратные корни являются специальными показателями. Рассмотрим число 9. Когда 3 умножается на само себя, получается 9 как произведение. Когда показатель степени равен 2, он называется квадратом. Когда показатель степени равен 1/2, он называется квадратным корнем.Например, √ (n × n) = √n ² = n, где n - положительное целое число. Определение квадратного корня Квадратный корень числа - это значение степени 1/2 этого числа. Другими словами, это число, которое мы умножаем само на себя, чтобы получить исходное число. Он обозначен символом «√». Методы поиска квадратного корня из чисел Очень легко найти квадратный корень из числа, которое является полным квадратом. Совершенные квадраты - это те положительные числа, которые можно записать как произведение числа на само себя. другими словами, полные квадраты - это числа, представляющие собой значение степени 2 любого целого числа. Мы можем использовать четыре метода, чтобы найти квадратный корень из чисел , и эти методы следующие: Метод повторного вычитания квадратного корня Квадратный корень методом простой факторизации Квадратный корень методом оценки Квадратный корень методом длинного деления Обратите внимание, что первые три метода можно удобно использовать для полных квадратов, а четвертый метод, т.е.Метод длинного деления можно использовать для любого числа, будь то полный квадрат или нет. Метод повторного вычитания квадратного корня Это очень простой метод. Мы будем вычитать последовательные нечетные числа из числа, для которого мы находим квадратный корень, до тех пор, пока не достигнем 0. Количество раз, которое мы вычитаем, является квадратным корнем из данного числа. Этот метод работает только для точных квадратных чисел. Давайте найдем квадратный корень из 16 с помощью этого метода. 16 - 1 = 15 15–3 = 12 12-5 = 7 7-7 = 0 Вы можете заметить, что мы вычитали 4 раза.Таким образом, √16 = 4 Квадратный корень методом простого факторизации Разложение любого числа на простые множители означает представление этого числа как произведения простых чисел. Чтобы найти квадратный корень из заданного числа с помощью метода разложения на простые множители, мы следуем шагам, приведенным ниже: Шаг 1: Разделите данное число на его простые множители. Шаг 2: Сформируйте пары одинаковых множителей так, чтобы оба множителя в каждой паре были равны. Шаг 3: Возьмите один множитель из пары. Шаг 4: Найдите произведение множителей, полученных путем взятия одного множителя из каждой пары. Шаг 5: Этот продукт является квадратным корнем из заданного числа. Найдем этим методом квадратный корень из 144. Этот метод работает, когда заданное число является точным квадратным числом. Квадратный корень методом оценки Оценка и приближение относятся к разумному предположению о фактическом значении, чтобы сделать вычисления более простыми и реалистичными.Этот метод помогает в оценке и приближении квадратного корня из заданного числа. Воспользуемся этим методом, чтобы найти √15. Найдите числа, ближайшие к точному квадрату 15. 9 и 16 - числа полного квадрата, ближайшие к 15. Мы знаем, что √16 = 4 и √9 = 3. Это означает, что √15 лежит между 3 и 4. Теперь нам нужно посмотрим, ближе ли √15 к 3 или 4. Рассмотрим 3,5 и 4. 3,5 ² = 12,25 и 4 ² = 16. Таким образом, √15 находится между 3,5 и 4 и ближе к 4. Найдем квадраты 3.8 и 3.9. 3,8 ² = 14,44 и 3,9 ² = 15,21. Это означает, что √15 находится между 3,8 и 3,9. Мы можем повторить процесс и проверить между 3,85 и 3,9. Мы можем заметить, что √15 = 3,872. Это очень долгий и трудоемкий процесс. Квадратный корень методом длинного деления Длинное деление - это метод деления больших чисел на шаги или части, разбивающий задачу деления на последовательность более простых шагов. Используя этот метод, мы можем найти точный квадратный корень из любого заданного числа.Давайте разберемся с процессом нахождения квадратного корня методом деления в длину на примере. Найдем квадратный корень из 180. Шаг 1: Поместите черту над каждой парой цифр числа, начиная с места единицы (крайняя правая сторона). У нас будет две пары, т.е. 1 и 80 Шаг 2: Мы делим крайнее левое число на наибольшее число, квадрат которого меньше или равен числу в крайней левой паре. Шаг 3: Введите число под следующей полосой справа от остатка. Добавьте последнюю цифру частного к делителю. Справа от полученной суммы найдите подходящее число, которое вместе с результатом суммы образует новый делитель для нового дивиденда, который переносится вниз. Шаг 4: Новое число в частном будет иметь такое же число, как выбрано в делителе. Условие такое же - меньше или равно дивиденду. Шаг 5: Теперь продолжим этот процесс, используя десятичную точку и попарно добавляя нули к остатку. Шаг 6: Полученное таким образом частное будет квадратным корнем из числа. Таблица квадратного корня Таблица квадратного корня содержит числа и их квадратные корни. Также полезно находить квадраты чисел. Вот список квадратных корней из полных квадратных чисел и некоторых неполных квадратных чисел от 1 до 10. Номер Квадратный корень 1 1 2 1. 414 3 1,732 4 2 5 2,236 6 2.449 7 2,646 8 2,828 9 3 10 3.162 Квадратные корни из чисел, не являющихся полными квадратами, являются частью иррациональных чисел. Формула квадратного корня Квадратный корень - это не что иное, как показатель степени 1/2. Формула квадратного корня используется для нахождения квадратного корня числа. Мы знаем формулу экспоненты: \ (\ sqrt [\ text {n}] {x} \) = x ^{1 / n}. Когда n = 2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например, разложение на простые множители, деление в столбик и так далее.9 ^1/2 = √9 = √ (3 × 3) = 3. Итак, формула для записи квадратного корня из числа: √x = x ^1/2. Как упростить квадратный корень? Чтобы упростить извлечение квадратного корня, нам нужно найти факторизацию данного числа на простые множители. Если фактор не может быть сгруппирован, оставьте их под символом квадратного корня. Правило упрощения квадратного корня: √xy = √ (x × y), где x и y - положительные целые числа. Например: √12 = \ (\ sqrt {2 \ times 2 \ times3} \) = 2√3 Для дробей действует аналогичное правило: √x / √y = √ (x / y).Например: √50 / √10 = √ (50/10) = √5 Квадратный корень отрицательного числа Квадратный корень отрицательного числа не может быть действительным числом, поскольку квадрат - это либо положительное число, либо ноль. Но у комплексных чисел есть решения для извлечения квадратного корня из отрицательного числа. Главный квадратный корень из -x: √ (-x) = i√x. Здесь i - квадратный корень из -1. Например: возьмите точное квадратное число, такое как 16. Теперь давайте посмотрим на квадратный корень из -16.Настоящего квадратного корня из -16 не существует. √ (-16) = √16 × √ (-1) = 4i (as, √ (-1) = i), где i представлено как квадратный корень из -1. Итак, 4i - это квадратный корень из -16. Квадрат числа Любое число, возведенное в степень два (y ²), называется квадратом основания. Итак, 5 ² упоминается как квадрат 5, а 8 ² упоминается как квадрат 8. Мы легко можем найти квадрат числа, умножив основание на два раза.Например, 5 в квадрате - это 5 × 5 = 25, а 8 в квадрате - это 8 × 8 = 64. Когда мы находим квадрат целого числа, полученное число является одним из полных квадратов. Вот некоторые из идеальных квадратов, которые у нас есть: 4, 9, 16, 25, 36, 49, 64 и так далее. Квадрат числа, независимо от того, является ли оно положительным или отрицательным, всегда является положительным числом. Как найти квадрат числа? Квадрат числа можно найти, умножив число на само себя. Для однозначных чисел мы можем использовать таблицы умножения, чтобы найти квадрат, в то время как в случае двух или более двухзначных чисел мы выполняем умножение числа на само число, чтобы получить ответ.Например, 9 × 9 = 81, где 81 - это квадрат 9. Точно так же 3 × 3 = 9, где 9 - это квадрат 3. Статьи по теме о квадратном корне: Ниже приводится список тем, которые тесно связаны с квадратными корнями. Квадратный корень чисел Часто задаваемые вопросы о Square Root Что такое квадратный корень в математике? Квадратный корень - это число, которое нам нужно умножить само на себя, чтобы получить исходное число.Например, 2 - это квадратный корень из 4, так как 2 × 2 = 4. ☛ Чек: Как найти квадратный корень числа? Квадратный корень из числа можно найти с помощью любого из четырех методов, приведенных ниже: Метод повторного вычитания Метод простой факторизации Метод оценки и приближения Метод длинного деления. Как найти корень квадратный из десятичного числа? Квадратный корень десятичного числа можно найти с помощью метода оценки или метода деления в столбик.В случае десятичных чисел мы составляем пары частей целого числа и дробных частей отдельно. Затем мы выполняем процесс деления в столбик так же, как и любое другое целое число. Может ли квадратный корень быть отрицательным? Квадратный корень числа может быть отрицательным. Фактически, все идеальные квадраты, такие как 4, 9, 25, 36 и т. Д., Имеют два квадратных корня, одно положительное значение и одно отрицательное значение. Квадратные корни из 4 равны -2 и 2. Точно так же квадратные корни из 9 равны 3 и -3. Как вы называете символ квадратного корня? Символ, используемый для обозначения квадратного корня, называется радикальным знаком «√».Термин, записанный внутри радикального знака, называется подкоренным выражением. Какова формула вычисления квадратного корня числа? Квадратный корень любого числа можно выразить с помощью формулы: √y = y ^½. Что такое квадрат и корень числа? Квадрат и квадратный корень из числа являются обратной операцией друг друга. Если возвести число z в квадрат как (z × z) z ², то получится квадратный корень из z ² i.е., √z равно числу z. Какой метод используется для нахождения квадратного корня неидеальных квадратных чисел? В математике несовершенное или несовершенное квадратное число считается числом в десятичной форме. Квадратный корень из неполного квадратного числа можно вычислить с помощью метода деления в длину. Как упростить извлечение квадратного корня на калькуляторе? Чтобы найти значение квадратного корня любого числа, нам просто нужно сначала вставить символ квадратного корня √x в калькулятор и ввести число x. ☛ Чек: Как умножить два значения квадратного корня вместе? Допустим, у нас есть два числа a и b. Сначала мы найдем квадратный корень из чисел a и b. Затем, найдя квадратный корень, мы умножим значение квадратного корня вместе. Давайте разберемся в этом на практической иллюстрации. Квадратный корень из 4 равен 2, а квадратный корень из 16 равен 4. Теперь мы умножим значение квадратного корня из 4 и 16, т.е. 2 × 4 = 8. Каковы применения формулы квадратного корня? Существуют различные применения формулы квадратного корня Формула квадратного корня в основном используется в алгебре и геометрии.Это помогает найти корни квадратного уравнения. Мы можем легко вычислить площадь, объем и другие размеры, используя формулу квадратного корня. Широко используется инженерами. Калькулятор квадратного корня Использование калькулятора Используйте этот калькулятор, чтобы найти главный квадратный корень и корни действительных чисел. Входные данные для подкоренного выражения x могут быть положительными или отрицательными действительными числами. Ответ также скажет вам, вошли ли вы в идеальный квадрат. Ответ покажет вам комплексные или мнимые решения для квадратных корней из отрицательных действительных чисел. Также Упростите калькулятор радикальных выражений, чтобы упростить радикалы вместо поиска дробных (десятичных) ответов. Квадратные корни, нечетные и четные: Для любого положительного действительного числа существует 2 возможных корня.Положительный корень и отрицательный корень. Учитывая число x , квадратный корень из x - это число на , так что a ² = x . Квадратные корни - это особая форма нашего общего калькулятор корней. "Обратите внимание, что любое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный. Например, квадратные корни из 9 равны -3 и +3, поскольку (-3) ² = (+3) ² = 9. Любое неотрицательное действительное число x имеет уникальный неотрицательный квадратный корень r; это называется главным квадратным корнем .......... Например, главный квадратный корень из 9 равен sqrt (9) = +3, а другой квадратный корень из 9 равен -sqrt (9) = - 3. В обычном использовании, если не указано иное, «квадратный корень обычно означает главный квадратный корень» [1]. Калькулятор идеального квадрата Этот калькулятор также подскажет, является ли введенное вами число идеальным квадратом или нет.Идеальный квадрат - это число x , где квадратный корень из x - это число на , так что a ² = x , а a - целое число. Например, 4, 9 и 16 являются полными квадратами, поскольку их квадратные корни 2, 3 и 4, соответственно, являются целыми числами. Пример квадратного корня: Второй корень из 81, или 81, корень 2, или квадратный корень из 81 записывается как $$ \ sqrt [2] {81} = \ sqrt [] {81} = \ pm 9 $$. Второй корень из 25 или 25 корень 2 или квадратный корень из 25 записывается как $$ \ sqrt [2] {25} = \ sqrt [] {25} = \ pm 5 $$. Второй корень из 100, или 100 в корне 2, или квадратный корень из 100 записывается как $$ \ sqrt [2] {100} = \ sqrt [] {100} = \ pm 10 $$. Второй корень из 10, или 10, радикал 2, или квадратный корень из 10 записывается как $$ \ sqrt [2] {10} = \ sqrt [] {10} = \ pm 3.162278 $$. Для вычисления дробных показателей используйте наш калькулятор для Дробные экспоненты. Список литературы [1] Вайсштейн, Эрик В. «Квадратный корень». От MathWorld - Интернет-ресурс Wolfram. Квадратный корень Дополнительное чтение квадратного корня: В математике - это весело: квадратный корень Калькулятор корня Калькулятор квадратного корня Калькулятор кубического корня Калькулятор общего корня Калькулятор связанных показателей | Научный калькулятор | Калькулятор журнала В математике общий корень или n ^{-й корень} числа a - это другое число b , которое при умножении на себя n раз равно a . В формате уравнения: ⁿ √a = b б ^п = а Оценка корня Некоторые общие корни включают квадратный корень, где n = 2, и кубический корень, где n = 3. Вычисление квадратных корней и n ^th корней является довольно трудоемким. Это требует оценки, проб и ошибок. Существуют более точные и эффективные способы вычисления квадратных корней, но ниже приведен метод, который не требует значительного понимания более сложных математических концепций.Для расчета √a: Оценить число b Разделите a на b . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь. Среднее значение b и c и использовать результат как новое предположение Повторите шаг два EX: Найти √27 до 3 десятичных знаков Угадай: 5,125 27 ÷ 5. 125 = 5,268 (5,125 + 5,268) / 2 = 5,197 27 ÷ 5,197 = 5,195 (5,195 + 5,197) / 2 = 5,196 27 ÷ 5,196 = 5,196 Оценка n ^th Корень Вычисление корней n ^th может быть выполнено аналогичным методом, но с изменениями для работы с n . Вычисление квадратного корня полностью вручную утомительно. Оценить более высокие корни n ^th, даже если использовать калькулятор для промежуточных шагов, значительно утомительнее.Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n ^th. Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета ⁿ √a: Оценить число b Разделите a на b ^n-1. Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь. Среднее значение: [b × (n-1) + c] / n Повторите шаг два EX: Найти ⁸ √15 до 3 знаков после запятой Угадай: 1. 432 15 ÷ 1,4327 = 1,405 (1,432 × 7 + 1,405) / 8 = 1,388 15 ÷ 1,388 ⁷ = 1,403 (1,403 × 7 + 1,388) / 8 = 1,402 Тогда должно быть ясно, что дальнейшие вычисления приведут к числу, которое будет округляться до 1,403, в результате чего 1,403 будет окончательной оценкой с точностью до 3 знаков после запятой. Как вычислить квадратный корень вручную (с иллюстрациями) Резюме статьиX Чтобы вычислить квадратный корень вручную, сначала оцените ответ, найдя 2 полных квадратных корня, между которыми находится это число.Идеальный квадратный корень - это любой квадратный корень из целого числа. Например, если вы пытаетесь найти квадратный корень из 7, сначала вам нужно найти первый правильный квадрат ниже 7, который равен 4, и первый правильный квадрат выше 7, который равен 9. Затем найдите квадратный корень из каждого полного квадрата. Квадратный корень из 4 равен 2, а квадратный корень из 9 равен 3. Таким образом, вы знаете, что квадратный корень из 7 находится где-то между 2 и 3. Теперь разделите полученное число на один из найденных полных квадратных корней.Например, вы бы разделили 7 на 2 или 3. Если бы вы выбрали 3, ваш ответ был бы 2,33. Затем найдите среднее значение этого числа и точный квадратный корень. Чтобы найти среднее значение в этом примере, сложите 2,33 и 2, затем разделите на 2 и получите 2,16. Повторите процесс, используя полученное среднее значение. Сначала разделите число, из которого вы пытаетесь найти квадратный корень, на среднее значение. Затем найдите среднее значение этого числа и исходное среднее, сложив их вместе и разделив на 2. Например, сначала вы должны разделить 7, число, с которого вы начали, на 2.16, среднее значение, которое вы рассчитали, и получите 3,24. Затем вы должны добавить 3,24 к 2,16, старому среднему, и разделить на 2, чтобы найти новое среднее значение, равное 2,7. Теперь умножьте свой ответ на себя, чтобы увидеть, насколько он близок к квадратному корню из числа, с которого вы начали. В этом примере 2,7, умноженное на само себя, равно 7,29, что на 0,29 отличается от 7. Чтобы приблизиться к 7, вы должны просто повторить процесс. Продолжайте делить число, с которого вы начали, на среднее значение этого числа и идеальный квадрат, используя это число и старое среднее значение, чтобы найти новое среднее, и умножайте новое среднее значение само на себя, пока оно не сравняется с вашим начальным числом.Если вы хотите узнать, как использовать алгоритм длинного деления для нахождения квадратного корня, продолжайте читать статью! Спасибо всем авторам за создание страницы, которую прочитали 2 271 017 раз. Как вычислить квадратный корень Руководство по карьере Развитие карьеры Как вычислить квадратный корень Редакция Indeed 22 февраля 2021 г. Понимание того, как вычислять математические задачи вручную, является важным навыком. Одна математическая концепция, которая иногда используется в бизнес-анализе, - извлечение квадратного корня.Вычисление квадратного корня вручную позволяет понять, как работает формула. В этой статье мы описываем, как используются квадратные корни, и объясняем три способа их вычисления вручную. Связано: 10 лучших навыков и методов обучения Использование квадратного корня Квадратные корни используются для нахождения хвостов при нормальном распределении, которое представляет собой график, показывающий, где большинство чисел попадает в набор данных. Они особенно полезны для определения ключевых показателей эффективности (KPI), понимания того, насколько хорошо люди справятся с тестом и насколько вероятен результат. Нормальное распределение основано на стандартных отклонениях или блоках оценок от среднего всех оценок. Хвосты нормального распределения обычно представляют собой наивысшие и самые низкие 5% оценок, при этом большинство оценок попадают в одно стандартное отклонение по обе стороны от среднего. Связано: Важность когнитивных способностей в вашей карьере Как вычислить квадратный корень вручную Есть несколько способов вычислить квадратный корень. Решение квадратного корня - это число, умноженное на само себя, которое равно числу под символом квадратного корня, который выглядит как √.Почти все калькуляторы имеют функцию извлечения квадратного корня, которую вы можете использовать. Вот несколько способов вычислить его вручную: Факторинг по квадратам Факторинг в длинную форму Метод деления в длину Факторинг по квадратам Факторинг квадратного корня означает, что вы поиск ближайших чисел, которые умножаются вместе. Самые простые квадратные корни - это те, которые делятся непосредственно на квадраты, например √100, но более сложные включают несколько квадратных корней, например √225.Вот шаги, чтобы найти квадратный корень с помощью факторизации: Найдите множители. Факторы - это числа, которые вы умножаете, чтобы найти сумму под символом квадратного корня. Для √100 множители будут √ (10 x 10). Коэффициент √225 будет равен √ (25 x 9). Разделите множители на их собственные квадратные корни. Поскольку оба множителя √100 равны 10, квадратный корень из 100 равен 10. Для √225 вы должны разделить множители под их собственными знаками квадратного корня, так что формула будет √25 x √9. Решите для отдельных квадратов. Затем вы найдете квадраты каждого из отдельных факторов. √25 = 5 и √9 = 3. Оставшаяся формула будет иметь вид 5 x 3. Завершите решение уравнения. Теперь, когда вы знаете, что такое упрощенные квадраты, вы обнаружите, что 5 x 3 = 15. Итак, √225 = 15. Фактор в длинной форме Иногда вы не знаете, какие множители квадратного корня квадраты. Вы можете разбить квадратный корень на каждый отдельный фактор, а затем решить его.Например, чтобы получить коэффициент длинного формата √225, выполните следующие действия: Найдите множители. Самый очевидный множитель 225 - пять, поэтому вы должны начать с √225 = √ (5 x 45). Вы могли бы еще больше упростить, найдя множители 45: √ (5 x 5 x 9). Последний коэффициент, который вы можете упростить, - 9, поэтому ваш окончательный коэффициент длинной формы будет выглядеть как √ (5 x 5 x 3 x 3). Вытяните повторяющиеся факторы. Когда вы видите одно и то же число дважды как множитель, вы перечисляете его один раз за пределами символа квадратного корня.В данном случае у нас есть две пятерки и две тройки, поэтому уравнение будет иметь вид 5 x 3. Решите оставшееся уравнение. Последний шаг - завершить решение уравнения. В этом случае 5 x 3 = 15. Метод деления на столбики Бывают случаи, когда вы можете не сразу распознать множители. Метод длинного деления позволяет найти квадратный корень без необходимости оценивать. Для этого метода найдем √361. Вот шаги к методу длинного деления: Разделите основание квадратного корня на пары.Начиная справа, сгруппируйте числа в пары. В нашем примере 361 будет 3 61. Найдите наибольший квадрат, который делится на первое число или пару. Это даст вам первое число в вашем ответе. Первое число слева - 3. Наибольший квадрат, входящий в него, равен единице, потому что 1 x 1 = 1, а 2 x 2 = 4. Вычтите квадрат из первого числа или пары. Вычитание квадрата из первого числа даст вам остаток, который будет включен в следующий шаг.В этом примере 3 - 1 = 2. Отбросьте следующую пару. Следующее число, с которым вы будете работать, будет комбинацией вычтенного квадрата и следующей пары. В этом случае они составили бы трехзначное число. Когда вы опускаете 61 вниз, число, которое вы будете использовать для нахождения следующей цифры в квадратном корне, будет 261. Умножьте первую цифру квадрата на два. Это будет первая цифра в множителе для нахождения второй цифры квадратного корня.В этом примере первая цифра квадратного корня - единица. 1 x 2 = 2. Составьте следующее уравнение множителя. Уравнение для следующего шага основано на цифре из шага пять и числе из шага четыре. Первым множителем будет двузначное число, где первая цифра - это число из пятого шага. Уравнение будет выглядеть как 2_ x _. Найдите число, которым заполняются пробелы. Это число будет следующей цифрой в решении для √361.Число, которое заполнит пробелы, будет таким же, и это будет самая высокая цифра, где множители меньше или равны числу на четвертом шаге. В этом примере номер цели 261. Мы начнем с 9, поэтому уравнение будет иметь вид 29 x 9 = 261. Поместите число рядом с первой цифрой. В этом примере квадрат равен 19. Калькулятор квадратного корня Найти квадратный корень числа Другие калькуляторы Калькулятор увеличения или уменьшения процентов поможет найти ответы на вопросы, связанные с расчетом процентов. Чтобы вычислить процент от числа, используйте наш калькулятор процента от числа. Например, найдите 5% процентов от 70. Калькулятор процентов даст вам ответ, это 3,5. процентов увеличение между двумя числами? Проблема решена с помощью функции «Рассчитать процент увеличения». Найдите процент увеличения с 2 до 10. Ответ - 400%. Найдите процентов второго числа ? Пример: узнать, какой процент равен 7 из 300. Калькулятор «Рассчитать процент от двух чисел», ответ - 2.33%. Новинка: рассчитайте увеличение или уменьшение заработной платы с помощью нашего калькулятора дохода. Калькулятор процента увеличения заработной платы. процентов от общего числа . Например, всего = 1100, и вам нужно найти процент, равный 100. Используя наш калькулятор процента от общего количества, ответ составляет 9,09%. GFC и LCM - математический коэффициент и множитель . Калькулятор наибольшего общего множителя GCF можно использовать для расчета GFC, а калькулятор наименьшего общего множителя - LCM. Калькулятор квадратного корня . Вместо того, чтобы запоминать квадратные корни, используйте калькулятор квадратного корня из числа и делайте это на лету. Например, каков квадратный корень из 9? Все мы знаем, что это 3. А как насчет квадратного корня из 500? Узнай себя. Калькулятор процентов ошибок . Быстро рассчитайте процентную ошибку с помощью калькулятора процентов ошибок. Калькуляторы часов и минут . Найдите минуты или часы с помощью наших калькуляторов.Сначала рассчитайте часы в минутах, очень полезно, чтобы узнать, сколько часов в 300 минутах. Калькулятор «Расчет минут в часах» полезен, чтобы узнать, сколько минут в 5 часах? Ответ: 300 из первой математической задачи. простая математика Математический калькулятор сложения, математический калькулятор вычитания, математический калькулятор умножения и математический калькулятор деления. Как вручную найти квадратный корень Как вручную найти квадратный корень Как найти квадратный корень вручную Вот почти забытое искусство: с появлением электронных калькуляторы, скорее всего, доживут до XXI века только на бумаге и в воспоминаниях стариков. Из какого числа вы хотите найти квадратный корень? Вот один из них, который мы будем использовать: 46656 Сначала разделите число, которое нужно извлекать из квадратного корня, на пары цифр, начиная с десятичной точки. То есть никакая пара цифр не должна пересекаться десятичная точка. (Например, разделите 1225 на «12 25», а не на «1 22 5»; 6.5536 на "6,55 36", а не на "6,5 53 6".) Затем вы можете поместить несколько линий на каждую пару цифр и полосу на слева, что-то вроде длинного деления. + --- ---- ---- | 4 66 56 Найдите наибольшее число, квадрат которого меньше или равен ведущему пара цифр. В этом случае первая пара цифр - 4; самое большое число квадрат которого меньше или равен 4 равен 2. Поместите это число слева, и над первой парой цифр. 2 + --- ---- ---- 2 | 4 66 56 Теперь возведите это число в квадрат и вычтите из пары первых цифр. 2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 0 Выдвинуть левую скобу; умножьте последнюю (и единственную) цифру левой число на 2, поместите его слева от разницы, которую вы только что вычислили, и оставьте рядом с ним пустой десятичный знак. 2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0 Затем опустите следующую пару цифр и поместите ее вправо разницы. 2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0 66 Найдите наибольшее число для этого пустого десятичного разряда, чтобы число, умноженное на уже существующее число плюс десятичный разряд, будет меньше чем текущая разница. Например, если 1 * 41 равно ≤ 66, то 2 * 42 ≤ 66 и т. Д. В данном случае это 1. Поместите это число в оставленное вами поле, и в следующем десятичном разряде в строке результатов вверху. 2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 Теперь вычтите продукт, который вы только что нашли. 2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 25 Теперь повторите, как прежде: возьмите число в левом столбце (здесь 41) и удвойте его последнюю цифру (получается 42). Скопируйте это ниже в левый столбец и оставьте рядом с ним пустое место. (Двойная последняя цифра с переносом: для Например, если у вас было не 41, а 49, что составляет 40 + 9, вы должны скопировать 40 + 18 что равно 58.) Также опустите следующую пару цифр справа. 2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 42_ 25 56 Теперь найдите самую большую цифру (назовите ее #) такую, что 42 # * # ≤ 2556. Здесь получается, что 426 * 6 = 2556 точно. 2 1 6 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 426 | 25 56 | - 25 56 + ------------- 0 Когда разница равна нулю, у вас есть точный квадратный корень, и вы Выполнено.