| 1. | Будет ли корнем уравнения данное число? | 1 вид — рецептивный | лёгкое | 1 Б. | Проверяется истинность равенства при подстановке числа вместо буквы. |
| 2. | Решение уравнения с переносом слагаемых | 1 вид — рецептивный | лёгкое |
1 Б.
|
В ходе решения уравнения необходимо перенести слагаемые из одной части уравнения в другую, привести подобные слагаемые и определить неизвестное, разделив обе части уравнения на коэффициент при неизвестном. |
| 3. | Выбирать правильный вариант ответа | 1 вид — рецептивный | лёгкое | 1 Б. |
Решив уравнение вида ax = b, выбирается правильный вариант ответа.
|
| 4. | Решить уравнение (целые коэффициенты) | 2 вид — интерпретация | среднее | 2 Б. | При решении уравнения применяются правила переноса слагаемых из одной части уравнения в другую, сложение подобных слагаемых. |
| 5. | Решить уравнение (коэффициенты — десятичные дроби) | 2 вид — интерпретация | среднее |
2 Б.
|
При решении уравнения применяются правила переноса слагаемых из одной части уравнения в другую, сложение подобных слагаемых, т. е. получается вид ax = b, в котором коэффициенты — десятичные дроби. |
| 6. | Определить корень уравнения с дробными коэффициентами | 2 вид — интерпретация | среднее | 2 Б. |
Используется перенос слагаемых из одной части уравнения в другую, сложение подобных слагаемых, т. |
| 7. | Решение уравнения с раскрытием скобок | 2 вид — интерпретация | среднее | 2 Б. | Решение уравнения с раскрытием скобок и с применением распределительного закона умножения. |
| 8. | Решить уравнение | 3 вид — анализ | сложное |
3 Б.
|
Требуется решить уравнение, используя основное свойство пропорции. |
| 9. | 3 вид — анализ | сложное | 3 Б. | Требуется доказать, что при любом значении буквы выражение всегда будет равно конкретному числу. И нужно определить это число. | |
10.
|
Решение уравнения, содержащего дроби с разными знаменателями | 3 вид — анализ | сложное | 4 Б. | Требуется решить уравнение, содержащее дроби с разными знаменателями. |
Конспект на тему «Линейные, квадратные и дробные рациональные уравнения». 8 класс.
Класс : 8 «В»
План– конспект урока
Тема урока: Линейные, квадратные и дробные рациональные уравнения.
Цели урока: обобщить знания нескольких тем. Применение новых информационных технологий при
повторении .
Применение новых информационных технологий при
повторении .
Форма урока: путешествие в Страну уравнений с остановками на станциях по нескольким темам.
Подготовка к уроку: Компьютер, экран, проектор.
Конверты с исторической справкой, а с обратной стороны задание с самостоятельной работой.
Класс на предыдущем уроке получил домашнее задание в конвертах.
Ладошки для рефлексии и жетоны.
Презентация.
Ход урока.
1. Организационный момент.
Здравствуйте, ребята! Садитесь, пожалуйста. Сегодня на уроке, я Вам предлагаю отправиться в путешествие в страну Уравнений. А целью нашего путешествия будет: закрепить и повторить виды уравнений: Линейных, квадратных и дробных рациональных уравнений.
Девизом нашего урока будут слова: Уравнение-это ключ, которым можно открыть тысячу дверей в неизвестность.
Я
предлагаю не терять время зря, открыть тетради записать тему урока, число и
отправиться в путь.
2. Первая станция «Домашнее задание».
Путешествие в Страну уравнений началось. Первая станция, на которую мы с вами приехали, называется «Домашняя работа».
Помощники собирают домашнее задание.
3. Вторая станция «Линейные уравнения».
Следующая станция «Линейные уравнения».
Давайте сделаем остановку на этой станции обязательно и вспомним основные свойства, которые Вы изучали в 7 классе.
ОСНОВНЫЕ СВОЙСТВА УРАВНЕНИЙ:
Свойство 1.
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Свойство 2.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Я
предлагаю решить несколько уравнений, употребляя эти свойства.
№1.1)
2)
Путешествие продолжается.
4. Следующая станция «Квадратные уравнения».
5.Четвертая станция «Дробные рациональные уравнения».
6.Пятая станция «Историческая».
Кто и когда придумал первое уравнение? Ответить на этот вопрос невозможно. Задачи, приводящие к решению уравнений, люди решали на основе здравого смысла. За 3-4 тыс. лет до н.э. египтяне и вавилоняне решали задачи с помощью уравнений. Только не умели применять буквы. Вместо букв брали числа, показывали на числах, как решать задачу, а потом все похожие решали тем же способом.
Теорией уравнений занимался древнегреческий ученый Диофант.
Но по- настоящему, метод уравнений сформировался в руках арабских ученых. Первым написал книгу на арабском языке о решении уравнений Мухаммед ибн Мусса Аль – Хорезми.
Название его книги — «Краткая книга об исчислении аль – джабры ». Что
напоминают вам эти слова?
Что
напоминают вам эти слова?
Название « аль – джабр» (АЛГЕБРА) первоначально носила операция переноса слагаемого из одной части уравнения в другую, по-русски означает «восполнение». Поэтому, например, в Испании, находившейся под арабским владычеством, слово «алгебраист» означало вовсе не математика, а костоправа. Когда Дон Кихот (в известной книге Сервантеса) был ранен в одном из поединков, его верный оруженосец Санчо Панча привел из соседнего городка именно алгебраиста.
Самостоятельная работа(см.приложение).
5. Шестая станция «Прибытия».
№4
Из Тимашевска в Краснодар выехали одновременно два мотоциклиста. Скорость одного мотоциклиста была на 10 км/ч больше скорости другого, и поэтому он приехал к месту пребывания на 1 час раньше. Найдите скорость каждого мотоциклиста, если расстояние между городами 60 км.
8. Рефлексия.
Ладошки
с пожеланиями, все ли понравилось на уроке.
9. Подведение итогов.
В течение всего урока Вы получили за правильные ответы «жетоны». Давайте посчитаем у кого больше жетонов…
И записать Д/З. 3000 задач Страница 68 четные номера.
Приложение.
Станция «Линейные уравнения»
№1.
a)
Ответ: -4,5
b)
Умножим обе части уравнения на 12
Ответ: 5
Станция «Квадратные уравнения»
А)
Разделим обе части уравнения на 4
Ответ: 0,5; 1.
Б)
Ответ: 1;4
В)
Ответ:-2;3
Г)
Ответ: 0;5
Д)
Ответ: -5;5
Е)
Нет решения.
Нет решения.
Станция «Дробные рациональные уравнения»
Умножим обе части уравнения на .
ОДЗ:
По теореме Виета:
Неуд. ОДЗ
Ответ: -8
Станция «Историческая»
Линейные уравнения
№1.Найдите корни уравнения 2-3(2х+2)=5-4х
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
№2.Решите уравнение -9(8-9х)=4х+5
Решение:
Ответы
№1. .
№2 .
Квадратные уравнения
№1.Решите уравнение
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
№2. Решите уравнение
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
Ответы
№1. -4; 1
-4; 1
№2. Нет решения.
Теорема Виета
№1.Найдите корни уравнения:
a)
b)
Решение:
Ответы
№1. 4; 5
№2. -12; 1
Станция «Прибытия»
Из Тимашевска в Краснодар выехали одновременно два мотоциклиста. Скорость одного мотоциклиста была на 10км/ч больше скорости другого, и поэтому он приехал к месту пребывания на 1 час раньше. Найдите скорость каждого мотоциклиста, если расстояние между городами 60 км.
Умножим обе части уравнения на
ОДЗ:
не имеет смысла.
— скорость второго мотоциклиста.
— скорость первого мотоциклиста.
Ответ: 20км/ч, 30 км/ч.
Линейные квадратные и дробно рациональные уравнения. Решение дробных рациональных уравнений
В этой статье я покажу вам алгоритмы решения семи типов рациональных уравнений , которые с помощью замены переменных сводятся к квадратным. В большинстве случаев преобразования, которые приводят к замене, весьма нетривиальны, и самостоятельно о них догадаться достаточно трудно.
В большинстве случаев преобразования, которые приводят к замене, весьма нетривиальны, и самостоятельно о них догадаться достаточно трудно.
Для каждого типа уравнений я объясню, как в нем делать замену переменной, а затем в соответствующем видеоуроке покажу подробное решение.
У вас есть возможность продолжить решение уравнений самостоятельно, а затем сверить свое решение с видеоуроком.
Итак, начнем.
1 . (x-1)(x-7)(x-4)(x+2)=40
Заметим, что в левой части уравнения стоит произведение четырех скобок, а в правой — число.
1. Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.
2. Перемножим их.
3. Введем замену переменной.
В нашем уравнении сгруппируем первую скобку с третьей, а вторую с четвертой,так как (-1)+(-4)=(-7)+2:
В этом месте замена переменной становится очевидной:
Получаем уравнение
Ответ:
2 .
Уравнение этого типа похоже на предыдущее с одним отличием: в правой части уравнения стоит произведение числа на . И решается оно совсем по-другому:
И решается оно совсем по-другому:
1. Группируем скобки по две так, чтобы произведение свободных членов было одинаковым.
2. Перемножаем каждую пару скобок.
3. Из каждого множителя выносим за скобку х.
4. Делим обе части уравнения на .
5. Вводим замену переменной.
В этом уравнении сгруппируем первую скобку с четвертой, а вторую с третьей, так как :
Заметим, что в каждой скобке коэффициент при и свободный член одинаковые. Вынесем из каждой скобки множитель :
Так как х=0 не является корнем исходного уравнения, разделим обе части уравнения на . Получим:
Получим уравнение:
Ответ:
3 .
Заметим, что в знаменателях обоих дробей стоят квадратные трехчлены, у которых старший коэффициент и свободный член одинаковые. Вынесем, как и в уравнении второго типа х за скобку. Получим:
Разделим числитель и знаменатель каждой дроби на х:
Теперь можем ввести замену переменной:
Получим уравнение относительно переменной t:
4 .
Заметим, что коэффициенты уравнения симметричны относительно центрального. Такое уравнение называется возвратным .
Чтобы его решить,
1. Разделим обе части уравнения на (Мы можем это сделать, так как х=0 не является корнем уравнения.) Получим:
2. Сгруппируем слагаемые таким образом:
3. В каждой группе вынесем за скобку общий множитель:
4. Введем замену:
5. Выразим через t выражение :
Отсюда
Получим уравнение относительно t:
Ответ:
5. Однородные уравнения.
Уравнения, имеющие структуру однородного, могут встретиться при решении показательных, логарифмических и тригонометрических уравнений, поэтому ее нужно уметь распознавать.
Однородные уравнения имеют такую структуру:
В этом равенстве А, В и С — числа, а квадратиком и кружочком обозначены одинаковые выражения. То есть в левой части однородного уравнения стоит сумма одночленов, имеющих одинаковую степень (в данном случае степень одночленов равна 2), и свободный член отсутствует.
Чтобы решить однородное уравнение, разделим обе части на
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
Пойдем первым путем. Получим уравнение:
Теперь мы вводим замену переменной:
Упростим выражение и получим биквадратное уравнение относительно t:
Ответ: или
7 .
Это уравнение имеет такую структуру:
Чтобы его решить, нужно в левой части уравнения выделить полный квадрат.
Чтобы выделить полный квдарат, нужно прибавить или вычесть удовоенное произведение. Тогда мы получим квадрат суммы ли разности. Для удачной замены переменной это имеет определяющее значение.
Начнем с нахождения удвоенного произведения. Именно оно будет ключиком для замены переменной. В нашем уравнении удвоенное произведение равно
Теперь прикинем, что нам удобнее иметь — квадрат суммы или разности. 2+9x-5=0\)
2+9x-5=0\)
Находим корни уравнения
\(x_1=-5;\) \(x_2=\frac{1}{2}.\)
Один из корней не подходи под ОДЗ, поэтому в ответ записываем только второй корень.
Ответ: \(\frac{1}{2}\).
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.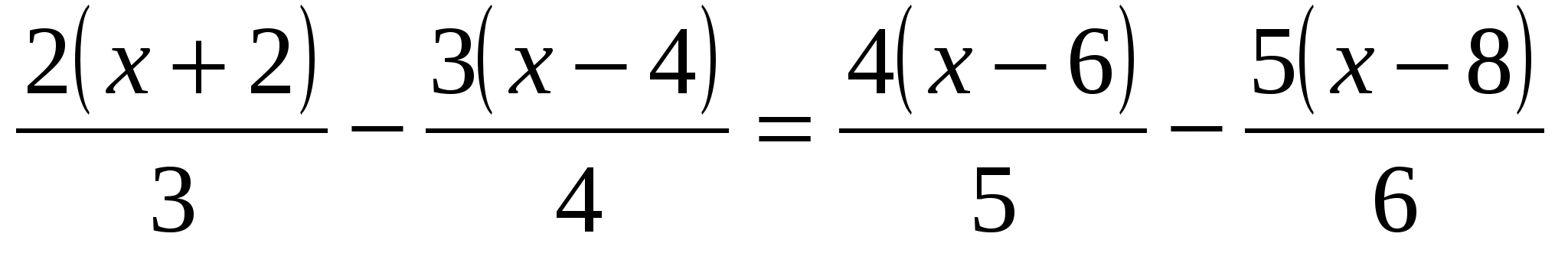
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Давайте познакомимся с рациональными и дробными рациональными уравнениями, дадим их определение, приведем примеры, а также разберем наиболее распространенные типы задач.
Yandex.RTB R-A-339285-1
Рациональное уравнение: определение и примеры
Знакомство с рациональными выражениями начинается в 8 классе школы. В это время на уроках алгебры учащиеся все чаще начинают встречать задания с уравнениями, которые содержат рациональные выражения в своих записях. Давайте освежим в памяти, что это такое.
Определение 1
Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
В различных пособиях можно встретить еще одну формулировку.
Определение 2
Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Определения, которые мы привели для рациональных уравнений, являются равнозначными, так как говорят об одно и том же. Подтверждает правильность наших слов тот факт, что для любых рациональных выражений P и Q уравнения P = Q и P − Q = 0 будут равносильными выражениями.
А теперь обратимся к примерам.
Пример 1
Рациональные уравнения:
x = 1 , 2 · x − 12 · x 2 · y · z 3 = 0 , x x 2 + 3 · x — 1 = 2 + 2 7 · x — a · (x + 2) , 1 2 + 3 4 — 12 x — 1 = 3 .
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1 до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Посмотрим, какие уравнения будут относиться к каждой из групп.
Определение 3
Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
Определение 4
Рациональное уравнение будет являться дробным в том случае, если одна или обе его части содержат дробь.
Дробно рациональные уравнения в обязательном порядке содержат деление на переменную или же переменная имеется в знаменателе. В записи целых уравнений такого деления нет.
Пример 2
3 · x + 2 = 0 и (x + y) · (3 · x 2 − 1) + x = − y + 0 , 5 – целые рациональные уравнения. Здесь обе части уравнения представлены целыми выражениями.
1 x — 1 = x 3 и x: (5 · x 3 + y 2) = 3: (x − 1) : 5 – это дробно рациональные уравнения.
К числу целых рациональных уравнений можно отнести линейные и квадратные уравнения.
Решение целых уравнений
Решение таких уравнений обычно сводится к преобразованию их в равносильные алгебраические уравнения. Достичь этого можно путем проведения равносильных преобразований уравнений в соответствии со следующим алгоритмом:
Достичь этого можно путем проведения равносильных преобразований уравнений в соответствии со следующим алгоритмом:
- сначала получим ноль в правой части уравнения, для этого на необходимо перенести выражение, которое находится в правой части уравнения, в его левую часть и поменять знак;
- затем преобразуем выражение в левой части уравнения в многочлен стандартного вида.
Мы должны получить алгебраическое уравнение. Это уравнение будет равносильным по отношению к исходному уравнению. Легкие случаи позволяют нам для решения задачи свести целое уравнение с линейному или квадратному. В общем случае мы решаем алгебраическое уравнение степени n .
Пример 3
Необходимо найти корни целого уравнения 3 · (x + 1) · (x − 3) = x · (2 · x − 1) − 3 .
Решение
Проведем преобразование исходного выражения с целью получить равносильное ему алгебраическое уравнение. Для этого произведем перенос выражения, содержащегося в правой части уравнения, в левую часть и заменим знак на противоположный. В итоге получим: 3 · (x + 1) · (x − 3) − x · (2 · x − 1) + 3 = 0 .
В итоге получим: 3 · (x + 1) · (x − 3) − x · (2 · x − 1) + 3 = 0 .
Теперь проведем преобразование выражения, которое находится в левой части в многочлен стандартного вида и произведем необходимые действия с этим многочленом:
3 · (x + 1) · (x − 3) − x · (2 · x − 1) + 3 = (3 · x + 3) · (x − 3) − 2 · x 2 + x + 3 = = 3 · x 2 − 9 · x + 3 · x − 9 − 2 · x 2 + x + 3 = x 2 − 5 · x − 6
У нас получилось свести решение исходного уравнения к решению квадратного уравнения вида x 2 − 5 · x − 6 = 0 . Дискриминант этого уравнения положительный: D = (− 5) 2 − 4 · 1 · (− 6) = 25 + 24 = 49 . Это значит, действительных корней будет два. Найдем их, воспользовавшись формулой корней квадратного уравнения:
x = — — 5 ± 49 2 · 1 ,
x 1 = 5 + 7 2 или x 2 = 5 — 7 2 ,
x 1 = 6 или x 2 = — 1
Проверим верность корней уравнения, которые мы нашли в ходе решения. Для этого числа, которые мы получили, подставим в исходное уравнение: 3 · (6 + 1) · (6 − 3) = 6 · (2 · 6 − 1) − 3 и 3 · (− 1 + 1) · (− 1 − 3) = (− 1) · (2 · (− 1) − 1) − 3 . В первом случае 63 = 63 , во втором 0 = 0 . Корни x = 6 и x = − 1 действительно являются корнями уравнения, данного в условии примера.
В первом случае 63 = 63 , во втором 0 = 0 . Корни x = 6 и x = − 1 действительно являются корнями уравнения, данного в условии примера.
Ответ: 6 , − 1 .
Давайте разберем, что значит «степень целого уравнения». С этим термином мы будем часто встречаться в тех случаях, когда нам надо будет представить целое уравнение в виде алгебраического. Дадим определение понятию.
Определение 5
Степень целого уравнения – это степень алгебраического уравнения, равносильного исходному целому уравнению.
Если посмотреть на уравнения из примера, приведенного выше, можно установить: степень данного целого уравнения вторая.
Если бы наш курс ограничивался решением уравнений второй степени, то рассмотрение темы на этом можно было бы закончить. Но все не так просто. Решение уравнений третьей степени сопряжено с трудностями. А для уравнений выше четвертой степени и вовсе не существует общих формул корней. В связи с этим решение целых уравнений третьей, четвертой и других степеней требует от нас применения целого ряда других приемов и методов.
Чаще прочих используется подход к решению целых рациональных уравнений, который основан на методе разложения на множители. Алгоритм действий в этом случае следующий:
- переносим выражение из правой части в левую с тем, чтобы в правой части записи остался нуль;
- представляем выражение в левой части как произведение множителей, а затем переходим к совокупности нескольких более простых уравнений.
Найдите решение уравнения (x 2 − 1) · (x 2 − 10 · x + 13) = 2 · x · (x 2 − 10 · x + 13) .
Решение
Переносим выражение из правой части записи в левую с противоположным знаком: (x 2 − 1) · (x 2 − 10 · x + 13) − 2 · x · (x 2 − 10 · x + 13) = 0 . Преобразование левой части в многочлен стандартного вида нецелесообразно в связи с тем, что это даст нам алгебраическое уравнение четвертой степени: x 4 − 12 · x 3 + 32 · x 2 − 16 · x − 13 = 0 . Легкость преобразования не оправдывает всех сложностей с решением такого уравнения.
Намного проще пойти другим путем: вынесем за скобки общий множитель x 2 − 10 · x + 13 . Так мы придем к уравнению вида (x 2 − 10 · x + 13) · (x 2 − 2 · x − 1) = 0 . Теперь заменим полученное уравнение совокупностью двух квадратных уравнений x 2 − 10 · x + 13 = 0 и x 2 − 2 · x − 1 = 0 и найдем их корни через дискриминант: 5 + 2 · 3 , 5 — 2 · 3 , 1 + 2 , 1 — 2 .
Ответ: 5 + 2 · 3 , 5 — 2 · 3 , 1 + 2 , 1 — 2 .
Точно также мы можем использовать метод введения новой переменной. Этот метод позволяет нам переходить к равносильным уравнениям со степенями ниже, чем были степени в исходном целом уравнении.
Пример 5
Есть ли корни у уравнения (x 2 + 3 · x + 1) 2 + 10 = − 2 · (x 2 + 3 · x − 4) ?
Решение
Если мы сейчас попробуем свести целое рациональное уравнение к алгебраическому, то получим уравнение 4 степени, которое не имеет рациональных корней. Потому нам будет проще пойти другим путем: ввести новую переменную у, которая заменит в уравнении выражение x 2 + 3 · x .
Теперь мы будем работать с целым уравнением (y + 1) 2 + 10 = − 2 · (y − 4) . Перенесем правую часть уравнения в левую с противоположным знаком и проведем необходимые преобразования. Получим: y 2 + 4 · y + 3 = 0 . Найдем корни квадратного уравнения: y = − 1 и y = − 3 .
Теперь проведем обратную замену. Получим два уравнения x 2 + 3 · x = − 1 и x 2 + 3 · x = − 3 . Перепишем их как x 2 + 3 · x + 1 = 0 и x 2 + 3 · x + 3 = 0 . Используем формулу корней квадратного уравнения для того, чтобы найти корни первого уравнения из полученных: — 3 ± 5 2 . Дискриминант второго уравнения отрицательный. Это значит, что действительных корней у второго уравнения нет.
Ответ: — 3 ± 5 2
Целые уравнения высоких степеней попадаются в задачах достаточно часто. Пугаться их не нужно. Нужно быть готовым применить нестандартный метод их решения, в том числе и ряд искусственных преобразований.
Решение дробно рациональных уравнений
Начнем рассмотрение этой подтемы мы с алгоритма решения дробно рациональных уравнений вида p (x) q (x) = 0 , где p (x) и q (x) – целые рациональные выражения. Решение остальных дробно рациональных уравнений всегда можно свести к решению уравнений указанного вида.
Решение остальных дробно рациональных уравнений всегда можно свести к решению уравнений указанного вида.
В основу наиболее употребимого метода решения уравнений p (x) q (x) = 0 положено следующее утверждение: числовая дробь u v , где v – это число, которое отлично от нуля, равна нулю только в тех случаях, когда числитель дроби равен нулю. Следуя логике приведенного утверждения мы можем утверждать, что решение уравнения p (x) q (x) = 0 может быть сведено в выполнению двух условий: p (x) = 0 и q (x) ≠ 0 . На этом построен алгоритм решения дробных рациональных уравнений вида p (x) q (x) = 0:
- находим решение целого рационального уравнения p (x) = 0 ;
- проверяем, выполняется ли для корней, найденных в ходе решения, условие q (x) ≠ 0 .
Если это условие выполняется, то найденный корень Если нет, то корень не является решением задачи.
Пример 6
Найдем корни уравнения 3 · x — 2 5 · x 2 — 2 = 0 .
Решение
Мы имеем дело с дробным рациональным уравнением вида p (x) q (x) = 0 , в котором p (x) = 3 · x − 2 , q (x) = 5 · x 2 − 2 = 0 . Приступим к решению линейного уравнения 3 · x − 2 = 0 . Корнем этого уравнения будет x = 2 3 .
Проведем проверку найденного корня, удовлетворяет ли он условию 5 · x 2 − 2 ≠ 0 . Для этого подставим числовое значение в выражение. Получим: 5 · 2 3 2 — 2 = 5 · 4 9 — 2 = 20 9 — 2 = 2 9 ≠ 0 .
Условие выполняется. Это значит, что x = 2 3 является корнем исходного уравнения.
Ответ: 2 3 .
Есть еще один вариант решения дробных рациональных уравнений p (x) q (x) = 0 . Вспомним, что это уравнение равносильно целому уравнению p (x) = 0 на области допустимых значений переменной x исходного уравнения. Это позволяет нам использовать следующий алгоритм в решении уравнений p (x) q (x) = 0:
- решаем уравнение p (x) = 0 ;
- находим область допустимых значений переменной x ;
- берем корни, которые лежат в области допустимых значений переменной x , в качестве искомых корней исходного дробного рационального уравнения.

Решите уравнение x 2 — 2 · x — 11 x 2 + 3 · x = 0 .
Решение
Для начала решим квадратное уравнение x 2 − 2 · x − 11 = 0 . Для вычисления его корней мы используем формулу корней для четного второго коэффициента. Получаем D 1 = (− 1) 2 − 1 · (− 11) = 12 , и x = 1 ± 2 3 .
Теперь мы можем найти ОДЗ переменной x для исходного уравнения. Это все числа, для которых x 2 + 3 · x ≠ 0 . Это то же самое, что x · (x + 3) ≠ 0 , откуда x ≠ 0 , x ≠ − 3 .
Теперь проверим, входят ли полученные на первом этапе решения корни x = 1 ± 2 3 в область допустимых значений переменной x . Мы видим, что входят. Это значит, что исходное дробное рациональное уравнение имеет два корня x = 1 ± 2 3 .
Ответ: x = 1 ± 2 3
Второй описанный метод решения проще первого в случаях, когда легко находится область допустимых значений переменной x , а корни уравнения p (x) = 0 иррациональные. Например, 7 ± 4 · 26 9 . Корни могут быть и рациональными, но с большим числителем или знаменателем. Например, 127 1101 и − 31 59 . Это позволяет сэкономить время на проведении проверки условия q (x) ≠ 0 : намного проще исключить корни, которые не подходят, по ОДЗ.
Корни могут быть и рациональными, но с большим числителем или знаменателем. Например, 127 1101 и − 31 59 . Это позволяет сэкономить время на проведении проверки условия q (x) ≠ 0 : намного проще исключить корни, которые не подходят, по ОДЗ.
В тех случаях, когда корни уравнения p (x) = 0 целые, целесообразнее использовать первый из описанных алгоритмов решения уравнений вида p (x) q (x) = 0 . Быстрее сразу находить корни целого уравнения p (x) = 0 , после чего проверять, выполняется ли для них условие q (x) ≠ 0 , а не находить ОДЗ, после чего решать уравнение p (x) = 0 на этой ОДЗ. Это связано с тем, что в таких случаях сделать проверку обычно проще, чем найти ОДЗ.
Пример 8
Найдите корни уравнения (2 · x — 1) · (x — 6) · (x 2 — 5 · x + 14) · (x + 1) x 5 — 15 · x 4 + 57 · x 3 — 13 · x 2 + 26 · x + 112 = 0 .
Решение
Начнем с рассмотрения целого уравнения (2 · x − 1) · (x − 6) · (x 2 − 5 · x + 14) · (x + 1) = 0 и нахождения его корней. Для этого применим метод решения уравнений через разложение на множители. Получается, что исходное уравнение равносильно совокупности четырех уравнений 2 · x − 1 = 0 , x − 6 = 0 , x 2 − 5 · x + 14 = 0 , x + 1 = 0 , из которых три линейных и одно квадратное. Находим корни: из первого уравнения x = 1 2 , из второго – x = 6 , из третьего – x = 7 , x = − 2 , из четвертого – x = − 1 .
Для этого применим метод решения уравнений через разложение на множители. Получается, что исходное уравнение равносильно совокупности четырех уравнений 2 · x − 1 = 0 , x − 6 = 0 , x 2 − 5 · x + 14 = 0 , x + 1 = 0 , из которых три линейных и одно квадратное. Находим корни: из первого уравнения x = 1 2 , из второго – x = 6 , из третьего – x = 7 , x = − 2 , из четвертого – x = − 1 .
Проведем проверку полученных корней. Определить ОДЗ в данном случае нам сложно, так как для этого придется провести решение алгебраического уравнения пятой степени. Проще будет проверить условие, по которому знаменатель дроби, которая находится в левой части уравнения, не должен обращаться в нуль.
По очереди подставим корни на место переменной х в выражение x 5 − 15 · x 4 + 57 · x 3 − 13 · x 2 + 26 · x + 112 и вычислим его значение:
1 2 5 − 15 · 1 2 4 + 57 · 1 2 3 − 13 · 1 2 2 + 26 · 1 2 + 112 = = 1 32 − 15 16 + 57 8 − 13 4 + 13 + 112 = 122 + 1 32 ≠ 0 ;
6 5 − 15 · 6 4 + 57 · 6 3 − 13 · 6 2 + 26 · 6 + 112 = 448 ≠ 0 ;
7 5 − 15 · 7 4 + 57 · 7 3 − 13 · 7 2 + 26 · 7 + 112 = 0 ;
(− 2) 5 − 15 · (− 2) 4 + 57 · (− 2) 3 − 13 · (− 2) 2 + 26 · (− 2) + 112 = − 720 ≠ 0 ;
(− 1) 5 − 15 · (− 1) 4 + 57 · (− 1) 3 − 13 · (− 1) 2 + 26 · (− 1) + 112 = 0 .
Проведенная проверка позволяет нам установить, что корнями исходного дробного рацинального уравнения являются 1 2 , 6 и − 2 .
Ответ: 1 2 , 6 , — 2
Пример 9
Найдите корни дробного рационального уравнения 5 · x 2 — 7 · x — 1 · x — 2 x 2 + 5 · x — 14 = 0 .
Решение
Начнем работу с уравнением (5 · x 2 − 7 · x − 1) · (x − 2) = 0 . Найдем его корни. Нам проще представить это уравнение как совокупность квадратного и линейного уравнений 5 · x 2 − 7 · x − 1 = 0 и x − 2 = 0 .
Используем формулу корней квадратного уравнения для поиска корней. Получаем из первого уравнения два корня x = 7 ± 69 10 , а из второго x = 2 .
Подставлять значение корней в исходное уравнение для проверки условий нам будет достаточно сложно. Проще будет определить ОДЗ переменной x . В данном случае ОДЗ переменной x – это все числа, кроме тех, для которых выполняется условие x 2 + 5 · x − 14 = 0 . Получаем: x ∈ — ∞ , — 7 ∪ — 7 , 2 ∪ 2 , + ∞ .
Теперь проверим, принадлежат ли найденные нами корни к области допустимых значений переменной x .
Корни x = 7 ± 69 10 — принадлежат, поэтому, они являются корнями исходного уравнения, а x = 2 – не принадлежит, поэтому, это посторонний корень.
Ответ: x = 7 ± 69 10 .
Разберем отдельно случаи, когда в числителе дробного рационального уравнения вида p (x) q (x) = 0 находится число. В таких случаях, если в числителе находится число, отличное от нуля, то уравнение не будет иметь корней. Если это число будет равно нулю, то корнем уравнения будет любое число из ОДЗ.
Пример 10
Решите дробное рациональное уравнение — 3 , 2 x 3 + 27 = 0 .
Решение
Данное уравнение не будет иметь корней, так как в числителе дроби из левой части уравнения находится отличное от нуля число. Это значит, что ни при каких значениях x значение приведенной в условии задачи дроби не будет равняться нулю.
Ответ: нет корней.
Пример 11
Решите уравнение 0 x 4 + 5 · x 3 = 0 .
Решение
Так как в числителе дроби находится нуль, решением уравнения будет любое значение x из ОДЗ переменной x .
Теперь определим ОДЗ. Оно будет включать все значения x , при которых x 4 + 5 · x 3 ≠ 0 . Решениями уравнения x 4 + 5 · x 3 = 0 являются 0 и − 5 , так как, это уравнение равносильно уравнению x 3 · (x + 5) = 0 , а оно в свою очередь равносильно совокупности двух уравнений x 3 = 0 и x + 5 = 0 , откуда и видны эти корни. Мы приходим к тому, что искомой областью допустимых значений являются любые x , кроме x = 0 и x = − 5 .
Получается, что дробное рациональное уравнение 0 x 4 + 5 · x 3 = 0 имеет бесконечное множество решений, которыми являются любые числа кроме нуля и — 5 .
Ответ: — ∞ , — 5 ∪ (- 5 , 0 ∪ 0 , + ∞
Теперь поговорим о дробных рациональных уравнениях произвольного вида и методах их решения. Их можно записать как r (x) = s (x) , где r (x) и s (x) – рациональные выражения, причем хотя бы одно из них дробное. Решение таких уравнений сводится к решению уравнений вида p (x) q (x) = 0 .
Их можно записать как r (x) = s (x) , где r (x) и s (x) – рациональные выражения, причем хотя бы одно из них дробное. Решение таких уравнений сводится к решению уравнений вида p (x) q (x) = 0 .
Мы уже знаем, что мы можем получить равносильное уравнение при переносе выражения из правой части уравнения в левое с противоположным знаком. Это значит, что уравнение r (x) = s (x) равносильно уравнение r (x) − s (x) = 0 . Также мы уже разобрали способы преобразования рационального выражения в рациональную дробь. Благодаря этому мы без труда можем преобразовать уравнение r (x) − s (x) = 0 в тождественную ему рациональную дробь вида p (x) q (x) .
Так мы переходим от исходного дробного рационального уравнения r (x) = s (x) к уравнению вида p (x) q (x) = 0 , решать которые мы уже научились.
Следует учитывать, что при проведении переходов от r (x) − s (x) = 0 к p (x) q (x) = 0 , а затем к p (x) = 0 мы можем не учесть расширения области допустимых значений переменной x .
Вполне реальна ситуация, когда исходное уравнение r (x) = s (x) и уравнение p (x) = 0 в результате преобразований перестанут быть равносильными. Тогда решение уравнения p (x) = 0 может дать нам корни, которые будут посторонними для r (x) = s (x) . В связи с этим в каждом случае необходимо проводить проверку любым из описанных выше способов.
Чтобы облегчить вам работу по изучению темы, мы обобщили всю информацию в алгритм решения дробного рационального уравнения вида r (x) = s (x) :
- переносим выражение из правой части с противоположным знаком и получаем справа нуль;
- преобразуем исходное выражение в рациональную дробь p (x) q (x) , последовательно выполняя действия с дробями и многочленами;
- решаем уравнение p (x) = 0 ;
- выявляем посторонние корни путем проверки их принадлежности ОДЗ или методом подстановки в исходное уравнение.
Визуально цепочка действий будет выглядеть следующим образом:
r (x) = s (x) → r (x) — s (x) = 0 → p (x) q (x) = 0 → p (x) = 0 → о т с е и в а н и е п о с т о р о н н и х к о р н е й
Пример 12
Решите дробное рациональное уравнение x x + 1 = 1 x + 1 .
Решение
Перейдем к уравнению x x + 1 — 1 x + 1 = 0 . Преобразуем дробное рациональное выражение в левой части уравнения к виду p (x) q (x) .
Для этого нам придется привести рациональные дроби к общему знаменателю и упростить выражение:
x x + 1 — 1 x — 1 = x · x — 1 · (x + 1) — 1 · x · (x + 1) x · (x + 1) = = x 2 — x — 1 — x 2 — x x · (x + 1) = — 2 · x — 1 x · (x + 1)
Для того, чтобы найти корни уравнения — 2 · x — 1 x · (x + 1) = 0 , нам необходимо решить уравнение − 2 · x − 1 = 0 . Получаем один корень x = — 1 2 .
Нам осталось выполнить проверку любым из методов. Рассмотрим их оба.
Подставим полученное значение в исходное уравнение. Получим — 1 2 — 1 2 + 1 = 1 — 1 2 + 1 . Мы пришли к верному числовому равенству − 1 = − 1 . Это значит, что x = − 1 2 является корнем исходного уравнения.
Теперь проведем проверку через ОДЗ. Определим область допустимых значений переменной x . Это будет все множество чисел, за исключением − 1 и 0 (при x = − 1 и x = 0 обращаются в нуль знаменатели дробей). Полученный нами корень x = − 1 2 принадлежит ОДЗ. Это значит, что он является корнем исходного уравнения.
Полученный нами корень x = − 1 2 принадлежит ОДЗ. Это значит, что он является корнем исходного уравнения.
Ответ: − 1 2 .
Пример 13
Найдите корни уравнения x 1 x + 3 — 1 x = — 2 3 · x .
Решение
Мы имеем дело с дробным рациональным уравнением. Следовательно, будем действовать по алгоритму.
Перенесем выражение из правой части в левую с противоположным знаком: x 1 x + 3 — 1 x + 2 3 · x = 0
Проведем необходимые преобразования: x 1 x + 3 — 1 x + 2 3 · x = x 3 + 2 · x 3 = 3 · x 3 = x .
Приходим к уравнению x = 0 . Корень этого уравнения – нуль.
Проверим, не является ли этот корень посторонним для исходного уравнения. Подставим значение в исходное уравнение: 0 1 0 + 3 — 1 0 = — 2 3 · 0 . Как видите, полученное уравнение не имеет смысла. Это значит, что 0 – это посторонний корень, а исходное дробное рациональное уравнение корней не имеет.
Ответ: нет корней.
Если мы не включили в алгоритм другие равносильные преобразования, то это вовсе не значит, что ими нельзя пользоваться. Алгоритм универсален, но он создан для того, чтобы помогать, а не ограничивать.
Алгоритм универсален, но он создан для того, чтобы помогать, а не ограничивать.
Пример 14
Решите уравнение 7 + 1 3 + 1 2 + 1 5 — x 2 = 7 7 24
Решение
Проще всего будет решить приведенное дробное рациональное уравнение согласно алгоритму. Но есть и другой путь. Рассмотрим его.
Отнимем от правой и левой частей 7 , получаем: 1 3 + 1 2 + 1 5 — x 2 = 7 24 .
Отсюда можно заключить, что выражение в знаменателе левой части должно быть равно числу, обратному числу из правой части, то есть, 3 + 1 2 + 1 5 — x 2 = 24 7 .
Вычтем из обеих частей 3: 1 2 + 1 5 — x 2 = 3 7 . По аналогии 2 + 1 5 — x 2 = 7 3 , откуда 1 5 — x 2 = 1 3 , и дальше 5 — x 2 = 3 , x 2 = 2 , x = ± 2
Проведем проверку для того, чтобы установить, являются ли найденные корни корнями исходного уравнения.
Ответ: x = ± 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Мы уже научились решать квадратные уравнения. Теперь распространим изученные методы на рациональные уравнения.
Теперь распространим изученные методы на рациональные уравнения.
Что такое рациональное выражение? Мы уже сталкивались с этим понятием. Рациональными выражениями называются выражения, составленные из чисел, переменных, их степеней и знаков математических действий.
Соответственно, рациональными уравнениями называются уравнения вида: , где — рациональные выражения.
Раньше мы рассматривали только те рациональные уравнения, которые сводятся к линейным. Теперь рассмотрим и те рациональные уравнения, которые сводятся и к квадратным.
Пример 1
Решить уравнение: .
Решение:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы — это квадратное уравнение. Прежде чем его решать, поделим все его коэффициенты на 3. Получим:
Получаем два корня: ; .
Поскольку 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия: . Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
Ответ: .
Итак, давайте сформулируем алгоритм решения рациональных уравнений:
1. Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму: .
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Давайте рассмотрим еще один пример.
Пример 2
Решить уравнение: .
Решение
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
Первое уравнение системы — это квадратное уравнение.
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: . Получаем, что из двух корней первого уравнения подходит только один — 3.
Ответ: .
На этом уроке мы вспомнили, что такое рациональное выражение, а также научились решать рациональные уравнения, которые сводятся к квадратным уравнениям.
На следующем уроке мы рассмотрим рациональные уравнения как модели реальных ситуаций, а также рассмотрим задачи на движение.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. — М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений.
 — М.: Просвещение, 2006.
— М.: Просвещение, 2006.
- Фестиваль педагогических идей «Открытый урок» ().
- School.xvatit.com ().
- Rudocs.exdat.com ().
Домашнее задание
что это такое, определение, алгоритм вычисления
Что такое линейное уравнение с одной переменной
Рассмотреть понятие линейного уравнения можно на образце задачи. Предположим, что нужно определить такие численные значения переменной х, при которых соответственные значения выражений 3х и х+8 будут одинаковыми. Для этого необходимо решить уравнение:
3х=х+8
Если х=4, правая и левая части уравнения будут равны. В данном случае число 4 является решением или корнем рассматриваемого уравнения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
ОпределениеКорень уравнения с одной переменной является числом, благодаря которому данное уравнение становится верным равенством.
Решить уравнение в алгебре — значит определить множество всех его корней.
Линейным уравнением является любое алгебраическое уравнение, обладающее одним неизвестным, степень которого равна единице.
Общий вид линейного уравнения можно записать, таким образом:
kx+b=0
Где k и b — являются произвольными числами.
Примеры линейных уравнений:
- Уравнение x+5=8 обладает одним корнем 3. Уникальность корня объясняется тем, что при x<3 левая часть уравнения будет меньше 8, а при x>3 больше 8.
- Уравнение (x+2)(x-1)(x-7)=0 включает три корня: -2, 1 и 7. Каждый корень при подстановке в выражение превращает его в справедливое равенство. Когда х равен любому другому числу, ни один из множителей (а значит, и их произведение) не равен нулю.
- Уравнение x+3=x-1 не обладает корнями, так как при любых x значение выражения, стоящего в левой части уравнения, на 4 больше соответственного значения выражения, которое расположено в правой части.
 {2}-1=0\)
{2}-1=0\)(x-3)(x+5)=0
\(\left | x \right |=2\)
Свойства, алгоритм вычислений, основные принципы
При решении задач с линейными уравнениями целесообразно воспользоваться определенными закономерностями.
ОпределениеКакое-либо слагаемое допустимо перенести из одной части равенства в другую, изменив его знак.
К примеру:
\(x+2=0 \Rightarrow x=-2\)
Необходимость в смене знака объясняется тем, что к обоим частям уравнения можно прибавить одинаковое число. При этом равенство остается справедливым:
x+2+(-2)=0+(-2)
\(x+0=0-2 \Rightarrow x=-2\)
ОпределениеЛюбую из частей уравнения допустимо умножать, делить на одно и то же число, которое не равно нулю. При этом сохраняется смысл уравнения.
К примеру, можно умножить обе части выражения на 4 и получить следующее равенство:
\(x+2=0 \Rightarrow (x+2)\cdot 4=0\cdot 4\)
4x+8=0
В математике существует понятие равносильных уравнений.
 Можно рассмотреть подобные равенства на примере:
Можно рассмотреть подобные равенства на примере:- (x+2)(x-3)=0
- x(x+2)(x-3)=0
В данном случае первое уравнение обладает двумя корнями: -2 и 3, а второе — тремя корнями: 0, -2 и 3. Любой корень первого уравнения представляет собой и корень второго уравнения. Однако не каждый корень второго уравнения будет определен, как корень первого уравнения. Если x=0 второе уравнение будет являться верным равенством, а первое — нет.
Уравнение x(x+2)=3(x+2) обладает двумя корнями: -2 и 3. Любое решение третьего уравнения будет также являться решением первого уравнения. Каждое из решений первого уравнения соответствует решению третьего уравнения. Таким образом, первое и третье уравнения будут называть равносильными.
Определение
Равносильными называют уравнения, у которых множества решений совпадают.
Рассмотреть свойства равенств удобно на примере двух уравнений: 2x-5=9 и 2x=14. Определить, равносильны ли они, можно с помощью следующих свойств:
- Рефлексивность.
 Каждое число равно самому себе, то есть а=а.
Каждое число равно самому себе, то есть а=а. - Симметричность. В том случае, когда одно число равно второму, то второе число также будет равно первому, то есть, если а=b, то b=а.
- Транзитивность. В том случае, когда первое число равно второму, а второе обладает таким же значением, как и третье, то первое число будет равно третьему: a=b и b=c, то a=c.
- При сложении обеих частей справедливого равенства с одним и тем же числом в результате получится верное равенство, то есть если a=b, то a+c=b+c.
- При умножении обеих частей справедливого равенства на одно и то же число результатом будет являться верное равенство: если a=b, то \(a\cdot c=b\cdot c\).
Решение линейных уравнений с применением свойств равенств можно разобрать на конкретных примерах.
Задача 1
Требуется найти решение уравнения:
6x-42=0
Решение:
В первую очередь следует сложить левую и правую части уравнения с числом 42.
 Таким образом, будет осуществлен перенос числа -42 в правую часть равенства с противоположным знаком. В результате уравнение приобретает следующий вид:
Таким образом, будет осуществлен перенос числа -42 в правую часть равенства с противоположным знаком. В результате уравнение приобретает следующий вид:6x=42
В том случае, когда при каком-то значении х равенство справедливо, то верным будет и то равенство, которое было записано. Наоборот, когда имеется некоторое значение х, записанное равенство справедливо, то исходное равенство также будет верным. Данный факт является следствием рассмотренных свойств равенств. Таким образом, можно говорить о равнозначности уравнений:
\(6x-42=0\Leftrightarrow6x=42\)
Далее следует умножить все части уравнения на:
\(\frac{1}{6} \)
Получим:
x=7
Исходя из свойства равенств, можно сделать вывод о равнозначности последних двух уравнений:
\(6x=42 \Leftrightarrow x=7\)
Таким образом, согласно свойству транзитивности равносильных уравнений, можно считать равносильными и данные уравнения:
\(6x-42=0 \Leftrightarrow x=7\)
Получается, что 7 является корнем исходного уравнения.

Ответ: х=7.
С помощью данного примера можно заключить, что при переносе элементов равенства из одной части в другую с противоположным знаком и умножении, либо делении обеих частей уравнения на число, которое отлично от нуля, получается уравнение, равносильное данному.
Задача 2
Необходимо найти решение уравнения:
\(\frac{3}{4}x-\frac{5x}{16}=2\)
Решение
В первую очередь следует привести все слагаемые левой части равенства к общему знаменателю:
\(\frac{3x}{4}\cdot\frac{4}{4}-\frac{5x}{16}=2\)
\(\frac{12x}{16}-\frac{5x}{16}=2\)
\(\frac{12x-5x}{16}=2\)
\(\frac{7x}{16}=2\)
Далее можно умножить каждую часть уравнения на:
\(\frac{16}{7}\)
После того, как исключен коэффициент при неизвестном, получим:
\(\frac{7x}{16}\cdot\frac{16}{7}=2\cdot\frac{16}{7}\)
В данном случае допустимо сократить числа 7 и 16, что в результате позволит получить равенство:
\(x=\frac{32}{7}\)
Ответ: \(x=\frac{32}{7}\)
Подытожив рассмотренные примеры, можно записать алгоритм решения линейных уравнений с одним неизвестным:
kx+b=0
Решение определяется параметрами k и b.
 Исходя из этого, можно предложить несколько вариантов решений.
Исходя из этого, можно предложить несколько вариантов решений.Вариант 1, при котором коэффициент при неизвестной k имеет нулевое значение, а свободный член b не равен нулю:
\(k=0, b\neq 0 \Rightarrow 0\cdot x=-b\)
В таком случае, не получится определить такое число х, которое, находясь в уравнении, преобразует его в справедливое равенство. Это связано с тем, что при умножении на 0 получится результат с нулевым значением. Таким образом, можно сделать вывод об отсутствии решений, что следует записать, как «х принадлежит пустому множеству»:
\(x\in \oslash\)
Вариант 2, при котором значения коэффициента при неизвестной и свободный член не равны нулю:
\(k\neq 0, b\neq 0 \Rightarrow kx=-b \Rightarrow x=\frac{-b}{k}\)
Таким образом, х будет являться действительным и единственным решением в форме отношения пары чисел: -b и k.
Вариант 3, при котором k и b равны нулю, то есть:
\(k=0, b=0 \Rightarrow kx=-b \Rightarrow 0\cdot x=0\)
При любом х равенство будет справедливым.
 Это связано с тем, что, если число умножить на 0, получится 0. В этом случае, х является любым числом, либо принадлежит множеству всех действительных чисел, что можно записать, таким образом:
Это связано с тем, что, если число умножить на 0, получится 0. В этом случае, х является любым числом, либо принадлежит множеству всех действительных чисел, что можно записать, таким образом:\(x\in \mathbb{R}\)
Существует несколько способов записи решения. К примеру, можно воспользоваться двойным неравенством:
\(-\infty <x< \infty\)
Данная формулировка означает, что х является числом из промежутка от минус бесконечности до плюс бесконечности. Так как бесконечность не является числом, неравенство будет строгим. Ответ можно представить, как интервал:
\(x\in(-\infty;\infty)\)
Знак \(\in \)справедливо заменить словом «принадлежит». Такой символ носит название квантора принадлежности. В этом случае формулировка будет следующей: «х принадлежит любому числу из данного интервала».
Исходя из того, что решение линейного уравнения — это корень уравнения. Следовательно, при решении линейного уравнения необходимо привести его к виду:
x=…
Виды уравнений с одной переменной
Существуют разные алгебраические уравнения.
 Наиболее распространенными из них являются:
Наиболее распространенными из них являются:- линейные;
- квадратные.
Линейные уравнения записывают в виде:
ах + b = 0
Где a и b — являются действительными числами.
В решении линейных уравнений удобно применять следующие свойства:
- в том случае, когда а не равно нулю, уравнение обладает единственным корнем: х = -b : а;
- при нулевом значении, а уравнение не имеет корней;
- когда а и b равны нулю, корень уравнения является любым числом.
Квадратное уравнение имеет следующий вид:
ax2 + bx + c = 0,
Где коэффициенты a, b и c — являются произвольными числами, a обладает ненулевым значением.
Решение уравнений (алгоритм сведения уравнений к линейным)
Решить многие уравнения можно путем их сведения к линейным. Существует несколько действенных способов. Алгоритм действий может отличаться в зависимости от вида уравнения.

Графический способ решения уравнений с одной переменной
Решить уравнения с одной переменной можно графическим методом. Стандартный алгоритм включает несколько шагов:
- выразить\( \displaystyle x\) с помощью \(\displaystyle y\);
- определить, к какому типу относится функция;
- построить графики получившихся функций;
- найти точки, в которых пересекаются графики;
- записать корректный ответ, учитывая ОДЗ и знаки неравенств;
- проверить ответ, то есть подставить корни в уравнение или систему.
Графическое решение линейных уравнений
График линейного уравнения представляет собой прямую линию. Разобрать данный способ удобно на конкретном примере. Требуется решить уравнение:
\(\displaystyle 2{x} -10=2\)
Способ 1 заключается в переносе неизвестных в одну сторону, а известных — в другую. Таким образом:
\(\displaystyle 2x=2+10\)
\(\displaystyle 2x=12\)
Далее необходимо поделить правую часть уравнения на левую, чтобы получить искомый корень.
 Однако можно пойти другим путем и представить обе части уравнения в виде различных функций в одной системе координат:
Однако можно пойти другим путем и представить обе части уравнения в виде различных функций в одной системе координат:\(\displaystyle {{y}_{1}}=2x\)
\(\displaystyle {{y}_{2}}=12\)
График будет иметь следующий вид:
В данном случае координата \(\displaystyle x\) точки пересечения графиков является корнем уравнения:
Ответ: \(\displaystyle x=6\)
Полученный корень уравнения следует проверить, подставив его в уравнение.
Способ 2 не предусматривает перенос элементов уравнения, а заключается в том, что графики строят напрямую. Дано уравнение:
\(\displaystyle 2{x} -10=2\)
Построим графики:
\(\displaystyle {{y}_{1}}=2{x} -10\)
\(\displaystyle {{y}_{2}}=2\)
В данном случае решением будет та же координата \(\displaystyle x\) точки пересечения графиков, которая была получена в решении уравнения первым способом:
Ответ: \(\displaystyle x=6\)
Графическое решение квадратных уравнений
Графическим методом можно решать квадратные уравнения.
 {2}}\)
{2}}\)\(\displaystyle {{y}_{2}}=5{x} -3\)
Таким образом, корнями уравнения являются:
\(\displaystyle {{x}_{1}}=1\)
\(\displaystyle {{x}_{2}}=1,5\)Графическое решение смешанных уравнений
Разобрать данный способ можно на примере решения следующего уравнения:
\(\displaystyle \frac{3}{x}-x+2=0\)
Нужно построить пару графиков:
\(\displaystyle {{y}_{1}}=\frac{3}{x}\) — график представляет собой гиперболу.
\(\displaystyle {{y}_{2}}={x} -2\) — график является прямой, которую можно построить, подобрав значения \(\displaystyle x\) и \(\displaystyle x.\)
В результате получим следующие графики:Таким образом, корнями уравнения являются:
\(\displaystyle {{x}_{1}}=-1\)
\(\displaystyle {{x}_{2}}=3\)
Ответ можно подтвердить, таким образом:
При подстановке корней в уравнение получим:
При\( \displaystyle {{x}_{1}}=-1:\frac{3}{-1}-\left( -1 \right)+2=-3+1+2=0.
 {3}}\) — кубическая парабола.
{3}}\) — кубическая парабола.\(\displaystyle {{y}_{2}}=x+1\) — обыкновенная прямая.
В результате получим корень уравнения:
\(\displaystyle {{x}_{1}}=1\)
Дробные уравнения с одной переменной
При решении уравнений с дробями, которые содержат одну переменную, можно руководствоваться стандартным алгоритмом. Последовательность действий такова:
- определение области допустимых значений;
- поиск общего знаменателя;
- умножение каждого компонента уравнения на общий знаменатель для последующего сокращения полученных дробей и исключения знаменателей;
- раскрытие скобок, что моет сопровождаться приведением подобных слагаемых;
- решение полученного уравнения;
- сравнение полученных корней с областью дополнительных значений;
- запись ответа, который был предварительно проверен.
Метод пропорции
Данный способ подразумевает приведение дроби к общему знаменателю.
Определение
Правило сформулировано, таким образом: произведение крайних членов пропорции равно произведению средних.
Рассмотреть эту закономерность удобно на практическом примере. Требуется решить линейное уравнение, в котором есть дроби:
Левая часть уравнения содержит одну дробь. Ее можно не преобразовывать. Правая часть уравнения включает сумму, которую следует упростить до получения одной дроби.
Решение:
В итоге левая и правая части уравнения содержат одну дробь. Далее необходимо воспользоваться методом пропорции и перемножить крест-накрест числители и знаменатели:
Метод избавления от дробей
Рассмотрим уравнение из предыдущего примера, но с другим решением:
Уравнение содержит пару дробей, которые необходимо исключить. Порядок действий следующий:
- подбор числа, которое можно разделить на каждый знаменатель без остатка;
- умножение данного числа на каждый компонент уравнения.

В рассматриваемом примере нужно найти наименьшее число, которое без остатка можно разделить на 5 и 9. Число 45 подходящее. Следует умножить на 45 каждый член уравнения и исключить знаменатели.
ПримечаниеЕсть несколько важных моментов, которые необходимо учитывать при решении дробных уравнений с одной переменной. Например, если при значении переменной знаменатель равен 0, такое значение является неверным. Делить и умножать уравнение на 0 нельзя.
Линейные уравнения с одной переменной со скобками
Решение линейных уравнений данным способом заключается в следующих действиях:
- раскрытие скобок;
- перенесение х в левую часть уравнения, а чисел — в правую;
- приведение подобных слагаемых.
Полученное уравнение будет иметь вид: ax=b, которое является корнем рассматриваемого линейного уравнения: x=ba.
Данный метод можно рассмотреть на примере уравнения, которое необходимо решить:
2x+1=2(x−3)+8
Данное уравнение является линейным, так как переменная стоит в первой степени.
 В первую очередь уравнение необходимо привести к виду: ax=b. Для этого следует раскрыть скобки:
В первую очередь уравнение необходимо привести к виду: ax=b. Для этого следует раскрыть скобки:2x+1=4x−6+8
В левую часть нужно перенести все слагаемые, содержащие х, а в правую — числа:
2x−4x=2−1
−2x=1
Далее следует поделить обе части уравнения на число (-2):
−2x−2=1−2=−12=−0,5
Ответ: х=-0,5
В качестве примера можно решить еще несколько задач распространенного типа. Дано уравнение, корни которого нужно найти:
2x−4=2(x−2)
Данное уравнение является линейным. Следует избавиться от скобок, перенести х в левую часть, а числа — в правую:
2x−4=2x−4
2x−2x=−4+4
0=0
В результате преобразований было получено справедливое равенство. Можно сделать вывод, что от значения х тождество не зависит. Таким образом, х является любым числом.
Ответ: x∈(−∞; +∞)
Во втором примере необходимо решить уравнение:
2x−4=2(x−8)
Данное уравнение является линейным. Требуется раскрыть скобки, перенести х в левую часть, а числа — в правую:
2x−4=2x−16
2x−2x=−16+4
0=−12
В итоге х будет сокращен, и получилось неверное равенство.
 Таким образом. При любом х равенство будет неверным. В таком случае отсутствуют значения х, при которых получилось бы справедливое тождество.
Таким образом. При любом х равенство будет неверным. В таком случае отсутствуют значения х, при которых получилось бы справедливое тождество.Ответ: x∈∅
Примеры решений
Задача 1
Нужно найти корни уравнения:
0,9x-0,6(x-3)=2(0,2x-1,3)
Решение:
В первую очередь следует раскрыть скобки и привести подобные:
0,9x-0,6x+1,8=0,4x-2,6
0,3x+1,8=0,4x-2,6
Далее необходимо перенести слагаемые, в которых присутствует неизвестная, в одну часть, а слагаемые без неизвестной — в другую:
1,8+2,6=0,4x-0,3x
4,4=0,1x
После того, как две части уравнения будут умножены на 10, получим:
x=44
Ответ: x=44
Задача 2
Необходимо решить уравнение:
-36(6x+1)=9(4-2x)
Решение:
После раскрытия скобок в обеих частях равенства получим:
-216x-36=36-18x
Далее можно перенести переменные в правую часть, а остальные слагаемые — в левую:
-36-36=-18x+216x
После приведения подобных получим:
-72=198x
Затем стоит разделить правую и левую часть уравнения на 198:
\(x=\frac{-72}{198}\)
Сократив дробь на 18.
 получим:
получим:\(x=-\frac{4}{11}\)
Ответ: \(x=-\frac{4}{11}\)
Задача 3
Нужно определить наибольший из корней уравнения:
(1,8-0,3y)(2y+9)=0
Решение:
В данном случае целесообразно применить свойство произведения. Произведение равно нулю, тогда и только тогда, когда один из множителей равен нулю. Таким образом, одно из выражений в скобках должно обладать нулевым значением.
В первом случае:
\(1,8-0,3y=0\Rightarrow 1,8=0,3y\)
Следует перенести слагаемые и умножить обе части уравнения на 10, а затем, поделить на 3:
\(\frac{1,8\cdot 10}{3}=\frac{0,3y\cdot 10}{3}\)
\(\frac{18}{3}=\frac{3y}{3}\)
y=6
Второй случай:
2y+9=0
2y=-9
Поделив обе части уравнения на 2, получим:
\(y=\frac{-9}{2}\)
y=-4,5
Таким образом, уравнением имеет пару корней, обращающих его в 0. Если выбрать наибольший из них, то:
y=6
Ответ: y=6
Задача 4
Дано уравнение, корень которого необходимо найти:
\(\frac{3m+5}{4}=\frac{5m+1}{3}\)
Решение:
В первую очередь следует умножить обе части уравнения на общий знаменатель 12, то есть на 4 и 3, чтобы привести его к виду: x=…
\(\frac{3m+5}{4}\cdot \frac{4\cdot 3}{1}=\frac{5m+1}{3}\cdot \frac{4\cdot 3}{1}\)
Сокращая слева на 4, а справа на 3 получим:
\((3m+5)\cdot 3=(5m+1)\cdot 4\)
Далее нужно раскрыть скобки:
\(3m\cdot 3+5\cdot 3=5m\cdot 4+1\cdot 4\)
\(9m+15=20m+4\)
В рассматриваемом примере целесообразно перенести 9m в правую часть равенства, чтобы не избавляться от минуса.
 После переноса слагаемых необходимо привести подобные и записать ответ:
После переноса слагаемых необходимо привести подобные и записать ответ:15-4=20m-9m
11=11m
m=1
Ответ: m=1
Задача 5
Необходимо определить такое значение а, при котором корень уравнения будет равен -9:
3ax=12-x
Решение:
Путем подстановки -9 на место х можно получить а, при котором такая ситуация имеет место:
\(3a\cdot (-9)=12-(-9)\)
Далее следует обратить внимание на правую часть уравнения и воспользоваться свойством: в том случае, когда перед скобками стоит знак минус, при их раскрытии все знаки, которые стоят в скобках, меняются на противоположные. Получим:
-27a=12+9
-27a=21
Затем можно поделить правую и левую части уравнения на (-27):
\(a=\frac{21}{-27}\)
После сокращения правой части равенства на 3 получим ответ:
\(a=-\frac{7}{9}\)
Ответ: \(a=-\frac{7}{9}\)
Подготовка к ОГЭ по математике. Решение уравнений
Наверное, многие помнят из своей школьной жизни, как сложно при решении простейших арифметических уравнений было следовать правилам, которые мы заучивали в пятом классе наизусть: «Чтобы найти неизвестное уменьшаемое надо к разности прибавить вычитаемое», или: «Чтобы найти неизвестное вычитаемое надо из уменьшаемого вычесть разность» и т.
 д. Применяя эти правила, можно было легко запутаться. Где вычитаемое? Где уменьшаемое? Особенно, если решаешь ответственную контрольную работу.
д. Применяя эти правила, можно было легко запутаться. Где вычитаемое? Где уменьшаемое? Особенно, если решаешь ответственную контрольную работу. Со временем эти правила расширились и сформировались в алгоритмы решения более сложных, алгебраических уравнений.
- Алгебраические уравнения – это уравнения, содержащие одну или несколько переменных. Изучение решений алгебраических уравнений начинают с линейных уравнений, вида ax+b = 0.
- Линейное уравнение – это уравнение, в котором переменная в первой степени.
Линейное уравнение вида ax+by = c, с двумя переменными, можно преобразовать в функцию y = — a/b*x +с/y или записать это кратко y = kx + d. Графиком этой функции является прямая, отсюда и названия – линейная функция, линейное уравнение.
Правила решения линейных уравненийПравила решения линейных уравнений не сложные.
 Кратко напомню их. Преобразуем выражения во многочлен. Раскрываем скобки с учётом знаков. Переносим все слагаемые с переменной (с неизвестной) величиной в одну сторону уравнения, а слагаемые без переменной в другую. При переносе не забываем менять знак слагаемого. Приводим, то есть, суммируем, одинаковые слагаемые и ищем корень уравнения.
Кратко напомню их. Преобразуем выражения во многочлен. Раскрываем скобки с учётом знаков. Переносим все слагаемые с переменной (с неизвестной) величиной в одну сторону уравнения, а слагаемые без переменной в другую. При переносе не забываем менять знак слагаемого. Приводим, то есть, суммируем, одинаковые слагаемые и ищем корень уравнения.- Корень уравнения – это то, значение переменной, при котором уравнение превращается в числовое равенство. При необходимости проверяем найденный корень.
В течение седьмого, восьмого и девятого классов решаются множество разных линейных уравнений и обычно это не вызывает сложности и при сдаче ОГЭ.
Дробно рациональные уравненияНемного иначе обстоит дело с решением дробно рациональных уравнений.
- Рациональные уравнения – это уравнения, в обеих частях которого находятся рациональные выражения. Что такое рациональные выражения мы рассмотрим в другой статье.

Для сдачи ОГЭ в 9 классе достаточно знать, что если выражение не содержит корень числа, то это выражение рациональное.
- Дробно рациональное уравнение – это уравнение, в одной или обеих частях которого есть дробные выражения.
К сожалению, при решении дробно рациональных уравнений у девятиклассников иногда возникают сложности, поэтому рассмотрим эту тему подробнее. В текстовом документе подробно описать процесс решения дробно рациональных уравнений разных видов достаточно сложно, и не наглядно, лучше, в этом случае, обратиться к видео https://youtu.be/QyKNhyqktrw
В данном видео мною приведён один из способов решения дробно рациональных уравнений с использованием основного свойства пропорции.
Квадратные уравненияЕщё одна тема в заданиях ОГЭ – решение квадратных уравнений.
- Квадратное уравнение – это алгебраическое выражение вида ax2 +bx +c = 0.

Если коэффициент b=0, или коэффициент с=0, или b=0 и c=0, то получаются неполные квадратные уравнения — ax2 + c = 0, или ax2 +bx = 0, или ax2 = 0.
Кроме этих видов квадратных уравнений есть ещё один интересный вид — приведённое квадратное уравнение.
В приведённом квадратном уравнении коэффициент а = 1. Чтобы это уравнение выделялось в наборе разных квадратных уравнений записывают его следующим образом : x2+px +q=0
- Основной способ решения любого квадратного уравнения – через дискриминант.
Как решается квадратное уравнение через дискриминант знает любой школьник. Неполные квадратные уравнения можно также решать через дискриминант, но есть более простые и рациональные способы решения, о которых наверняка также знает любой школьник.

Квадратные уравнения в ОГЭМы остановимся на решении приведённых квадратных уравнений, которые могут встретиться в заданиях ОГЭ. Приведённое квадратное уравнение всегда можно решить через дискриминант. Но если коэффициенты p и q не дробные и небольшие величины, то значительно проще уравнение может быть решено с использованием теоремы Виета.
Великий французский математик Франсуа Виет ещё в шестнадцатом веке сумел заметить особенность, позволяющую легко решать приведённые квадратные уравнения.
Если есть уравнение x2+px+q=0, то его корни будут соответствовать выражениям
x1*x2 = q и x1+x2 = — p
или словами «произведение корней приведённого квадратного уравнения равно свободному коэффициенту этого уравнения, а сумма корней равна коэффициенту перед х с обратным знаком».

Имея некоторое приведённое квадратное уравнение, например
записываем
- x1*x2 = — 10 и x1+x2 = — 3.
Далее подбором находим, что
Теорема Виета имеет ограничения – дискриминант должен быть больше нуля (D>0), но уравнения для ОГЭ, чтобы не усложнять решение, подбирают так, что всегда D>0.
Редакция не несет ответственности за наполнение блогов, они есть персональным мнением автора
Линейные уравнения с дробями — Как обсудить
Линейные уравнения с дробями
Какая формула для решения линейных уравнений? В математике линейное уравнение — это тип уравнения. В линейном уравнении два члена должны быть постоянными. Линейное уравнение – это уравнение прямой линии. Уравнение этого типа записывается в виде: y = mx + b ИЛИ (y y1) = m (x x1) ИЛИ m = скорость изменения или наклон.
Какие примеры линейных уравнений?
Определение линейного уравнения – это алгебраическое уравнение, в котором каждый член имеет показатель степени, равный единице, а график уравнения представляет собой прямую линию.
 Примером линейного уравнения является y = mx + b.
Примером линейного уравнения является y = mx + b.Что такое линейные уравнения и линейные неравенства?
Линейные уравнения и линейные неравенства похожи в том, что они представлены в виде прямых линий с наклоном, координатой x и т.д. Поэтому и то, и другое можно понять, растворить и разрешить одним и тем же способом. Основное отличие состоит в том, что решения линейного уравнения находятся справа, а решения линейного неравенства — нет.
Как решить X дробями?
Как решить x дробями.Решите x, умножив и упростив уравнение, чтобы найти x. Пример: Имея уравнение 4/10 = x/15, найдите x. Умножьте дроби на крест. 4*15=10*х. Решите уравнение относительно х. x = (4 * 15) / 10. Упростите для x.
Каковы шаги для решения линейных уравнений?
Решение линейных уравнений.
Шаг 1 . Исключите дроби или десятичные числа.
Шаг 2 . Упростите каждую часть уравнения, удалив скобки и объединив одинаковые члены.
Шаг 3 . Выделите переменный член на одной стороне уравнения.
Шаг 4 . Решите уравнение, разделив каждую часть уравнения.
Шаг 5 . Проверьте свое решение.Как составить линейное уравнение?
Шаги Убедитесь, что линейное уравнение имеет вид y = mx + b. Представьте число b на оси Y. Превратите м в дробь. Продолжайте линию от точки b, начиная со склона или в гору. Продолжайте удлинять линию с помощью линейки, не забывая использовать наклон m в качестве ориентира.
Каковы правила линейных уравнений?
Три основных правила. Линейное уравнение состоит из двух выражений (например, «3x + 2» или «54»), которые равны друг другу, если ни одна из переменных в уравнении не возведена в степень больше единицы.
Как вы определяете линейные уравнения?
Любой линейный график есть не что иное, как прямая линия. Так что, если есть кривые, это не линейно. Другой способ узнать это — посмотреть на ваше уравнение.
 Если уравнение может иметь вид Y = MX + B, где M и B — числа, то это линейное уравнение.
Если уравнение может иметь вид Y = MX + B, где M и B — числа, то это линейное уравнение.Какова формула решения линейных уравнений с помощью графика
Чтобы решить систему уравнений с помощью графика, начертите каждое уравнение и определите пересечение двух линий. Эта точка является решением системы уравнений, здесь значения x и y двух уравнений совпадают. Проверьте решение, подставив значения каждого уравнения.
Как решить линейные уравнения с тремя переменными?
Решить систему из трех линейных уравнений с тремя переменными методом исключения Гаусса.Разделите первое уравнение на 3. Умножьте на 4 и прибавьте 1 раз ко второму уравнению, затем умножьте на (1) и прибавьте к третьему уравнению. у них получится следующая система: делим второе уравнение и получаем.
Можете ли вы решить систему уравнений с помощью графика?
Решайте системы уравнений с помощью графиков. Система линейных уравнений содержит два или более уравнений y = + 2 и y = x2.
 Решением такой системы является упорядоченная пара, являющаяся решением обоих уравнений.Чтобы решить систему линейных уравнений графически, начертите оба уравнения в одной и той же системе координат.
Решением такой системы является упорядоченная пара, являющаяся решением обоих уравнений.Чтобы решить систему линейных уравнений графически, начертите оба уравнения в одной и той же системе координат.Можно ли решить линейное уравнение с двумя переменными?
Одним из способов решения системы линейных уравнений с двумя переменными является построение графика. В этом методе уравнения строятся на одном и том же наборе осей. Другой метод решения системы линейных уравнений — подстановка. В этом методе вы решаете переменную в одном уравнении и вводите результат во второе уравнение.
Что такое формула для решения линейных уравнений рабочий лист
Решение линейного уравнения Упростите обе части уравнения, умножая и собирая общие члены для переменных и констант по отдельности. Удалите переменную 8x справа, вычитая 8x с обеих сторон. Удалите постоянный член 22 слева, вычитая 22 с обеих сторон.
Что такое простое линейное уравнение?
Линейные уравнения Простое линейное уравнение: y = mx + c Линейное уравнение графически выглядит как прямая линия.
 Он имеет постоянное значение наклона. Степень линейного уравнения всегда равна 1. Принцип суперпозиции применим к системе, характеризуемой линейным уравнением.
Он имеет постоянное значение наклона. Степень линейного уравнения всегда равна 1. Принцип суперпозиции применим к системе, характеризуемой линейным уравнением.Как вы решаете линейные неравенства?
Чтобы решить линейное неравенство, вам нужно найти все комбинации x и y, которые делают неравенство верным. Вы можете решать линейные неравенства с помощью алгебры или построения графиков. Чтобы решить линейное неравенство (или любое другое уравнение), вам нужно найти все комбинации x и y, которые делают это уравнение верным.
По какой формуле решать линейные уравнения заменой
Как решить систему заменой?
Шаг 1 : Сначала решите линейное уравнение для y как функции x.
Шаг 2 : Затем замените это выражение в другом линейном уравнении на y.
Шаг 3 : Решите это, и вы получите x-координату перекрестка.
Шаг 4 : Затем введите x в одно из уравнений, чтобы найти соответствующую координату y.Как решить систему уравнений с помощью замены?
Способ замены.
 Одним из способов решения систем уравнений является замена. В этом методе вы решаете уравнение для одной переменной, заменяете это решение другим уравнением, а затем решаете его.
Одним из способов решения систем уравнений является замена. В этом методе вы решаете уравнение для одной переменной, заменяете это решение другим уравнением, а затем решаете его.Какая система уравнений с подстановкой?
Подстановка — это метод решения системы уравнений путем исключения всех переменных, кроме одной, в одном из уравнений и последующего решения этого уравнения.Он делает это, изолируя другую переменную в одном уравнении, а затем заменяя значения этих переменных в другом уравнении.
Как рассчитать систему уравнений?
Решение умножением Напишите одно уравнение над другим. Умножайте одно или оба уравнения до тех пор, пока одна из переменных в двух терминах не будет иметь равные коэффициенты. Добавьте или вычтите уравнения. Решить до конца срока. Подставьте член обратно в уравнение, чтобы найти значение первого члена.Проверьте свой ответ.
Каковы этапы решения линейных уравнений?
Решение линейного уравнения: пять шагов к успеху.

Шаг 1 : Найдите случайное распределение для ().
Шаг 2 : Объедините одинаковые термины с каждой стороны знака =.
Шаг 3 : Добавьте или вычтите члены из переменных так, чтобы все переменные находились по одну сторону от знака =.Сколько решений имеют два линейных неравенства?
Линейные неравенства могут не иметь решения, иметь конкретное решение или иметь бесконечное число решений.Таким образом, возможное общее количество будет три. Например, предположим, что у вас есть переменная x.
Какие примеры решения уравнений?
- Пример 1: Решение x 3 = for x дает решение x = 3
- Пример 2: Решение x5 = для x дает решение x = 5
- Пример 3. Решение x²1 = 0 относительно x приводит к двум допустимым решениям: x = 1 и x = 1.
- Пример 4. Решение x y = относительно y дает y = x.
- Пример 5: Решение x y + 2 = для y приводит к решению y = x + 2.

Что представляет собой формула решения линейных уравнений методом исключения
Метод исключения для решения систем линейных уравнений использует аддитивное свойство равенства. Вы можете добавить одно и то же значение к обеим частям уравнения. Итак, если у вас есть система: x — 6 = -6 и x + y = 8, то вы можете добавить x + y в левую часть первого уравнения и 8 в правую часть уравнения.
Как они могут решать системы уравнений методом исключения?
Метод исключения для решения линейных систем.Другой способ решения линейной системы — использовать метод исключения. При исключении вы добавляете или вычитаете уравнения, чтобы получить уравнение с одной переменной.
Как решить систему линейных уравнений?
Существует три способа решения системы линейных уравнений: построить, заменить и исключить. Решением системы линейных уравнений является упорядоченная пара (или пары), удовлетворяющая всем уравнениям системы.

Как решить методом исключения?
Шаги для решения уравнений методом исключения следующие:
Шаг 1 : Перепишите систему уравнений и объедините ее с неизвестными.
Шаг 2 : Исследование неизвестного имеет противоположные коэффициенты. Если да, сложите два уравнения, в результате получится уравнение с одной переменной.Можете ли вы привести пример линейного уравнения?
Определение линейного уравнения – это алгебраическое уравнение, в котором каждый член имеет показатель степени, равный единице, а график уравнения представляет собой прямую линию. Примером линейного уравнения является y = mx + b.
Можно ли разделить линейное уравнение?
Часто для решения линейного уравнения необходимо использовать и умножение, и деление.Если линейное уравнение использует и умножение, и деление, решите противоположную операцию для каждого из них.
Что представляет собой уравнение с одной переменной?
Уравнения с одной переменной I.
 Уравнение с одной переменной — это уравнение вида f(x) = g(x), где f(x) и g(x) — функции.
Уравнение с одной переменной — это уравнение вида f(x) = g(x), где f(x) и g(x) — функции.Как определить, является ли уравнение линейным?
Определить, является ли уравнение полиномом первой степени. Найдите показатель с наибольшей степенью среди членов.Этот показатель является степенью многочлена. Если да, то это линейное уравнение. Поскольку наивысшая степень x при y = 7/5 (6/5) x 1, это линейная функция.
Является ли линейное уравнение такой же, как функция?
Линейные функции аналогичны линейным уравнениям. Это функции, которые можно отобразить в виде линейного графика. Некоторые примеры линейных функций, ведущих к линейному графику: f(x) = x, f(x) = 2×2, f(x) = x + 1 Переменные линейной функции имеют линейные отношения.
Что такое решение системы линейных уравнений?
Устранение неполадок в системах.Система линейных уравнений означает два или более линейных уравнения. (Простой: две или более прямых линий).
 Если эти два линейных уравнения пересекаются, то это пересечение называется решением линейной системы уравнений.
Если эти два линейных уравнения пересекаются, то это пересечение называется решением линейной системы уравнений.Как решать уравнения с двумя разными переменными?
Автор Дрю Лихтенштейн. Решение двух переменных (обычно обозначаемых x и y) требует двух наборов уравнений. Предполагая, что у вас есть два уравнения, лучший способ найти решение для обеих переменных — это использовать метод подстановки, когда вам нужно решить как можно больше для одной переменной, а затем снова связать ее с другим уравнением.
Сколько решений имеет линейное уравнение с двумя переменными?
Решение линейных уравнений с двумя переменными, ax + by = c, представляет собой определенную точку на графике, поэтому, если координата x умножается на a, а координата y умножается на b, то сумма этих двух значений равно с. Короче говоря, существует бесконечно много решений линейного уравнения с двумя переменными. Пример. Чтобы найти решение линейного уравнения с двумя переменными, им нужно знать два уравнения.
 Например: 5x + 3y = 30,
Например: 5x + 3y = 30,Для чего используются линейные уравнения?
Линейные уравнения используются для расчета измерений твердых и жидких тел. Например, инженер-электрик использует линейные уравнения для решения задач напряжения, тока и сопротивления.
Какие есть реальные примеры линейных уравнений?
Пример: y = 2x + 1 — это линейное уравнение: при увеличении x y растет в два раза быстрее, поэтому вам нужно 2x. Если x равен 0, а ya равен 1. Тогда +1 тоже нужен.Тогда: у = 2х + 1,
Какие три вида линейных уравнений существуют?
Три основные формы линейных уравнений: форма сегмента наклона, форма точечного наклона и стандартная форма.
Как написать линейное уравнение?
Уравнение ряда может быть записано в стандартной форме (Ax + By = C) или в форме SlopeIntercept (y = mx + b). В обеих формах вам нужны две части информации, чтобы написать уравнение линии: 1) наклон и 2) точка пересечения по оси y.

Примеры линейных уравнений из таблиц
Линейное уравнение может иметь несколько переменных. Если линейное уравнение имеет две переменные, оно называется линейным уравнением с двумя переменными и так далее. Некоторые примеры линейных уравнений: 2x — 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2,3x — y + z = 3.
Как построить график с помощью таблицы?
Откройте таблицу, содержащую значения данных, которые вы хотите отобразить. Нажмите кнопку «Параметры таблицы» в верхнем левом углу окна таблицы и нажмите «Создать диаграмму».Щелкните стрелку раскрывающегося списка Тип диаграммы и выберите тип диаграммы, которую вы хотите создать. Щелкните стрелку раскрывающегося списка Слой/Таблица и выберите таблицу в качестве источника значений данных, которые вы хотите построить.
Как найти уравнение таблицы?
См. значения в таблице. Числа в матрице обычно представляют собой значения x и y, примененные к линии, что означает, что значения x и y соответствуют координатам точек на линии.
 Поскольку линейное уравнение y = mx + b, значения x и y являются числами, которые можно использовать для получения неизвестных, таких как наклон и пересечение y.
Поскольку линейное уравнение y = mx + b, значения x и y являются числами, которые можно использовать для получения неизвестных, таких как наклон и пересечение y.Как составить таблицу значений?
Чтобы создать таблицу функций, просто укажите диапазон значений в левой колонке. Значения могут быть любыми, если вы не хотите использовать определенные значения, просто создайте свои собственные.
Как изобразить дроби в линейном уравнении?
шагов Убедитесь, что линейное уравнение имеет вид y = mx + b. Она известна как форма пересечения и, вероятно, является самым простым способом рисования линейных уравнений. Нарисуйте число b на оси Y. Ваше b всегда будет рациональным числом.Преобразуйте м в дроби.
Как найти решение линейного уравнения?
Чтобы найти решение системы линейных уравнений, можно использовать один из трех методов: подстановку, исключение или построение графика. Чтобы определить, имеет ли решение смысл, проверьте, соответствует ли пара значений заданным в словесной ситуации условиям.

Примеры линейных уравнений в реальной жизни
Линейные уравнения — это те уравнения, которые образуют прямые линии на графике.Конкретные примеры: Заработная плата на основе почасовой оплаты. Расчет доз препаратов в зависимости от массы тела пациента. Что значит линейный?
Для каких реальных жизненных ситуаций можно использовать линейное уравнение?
Почти любую ситуацию с неизвестной величиной можно представить линейным уравнением. Например, многие люди используют линейные уравнения каждый день, даже выполняя вычисления в уме, не рисуя линейный график.
Каковы реальные примеры линейной пары?
Два угла называются линейными, если они имеют общий радиус и сумма двух углов равна 180 градусов.Лестница, установленная в здании, является реальным примером линейной пары.
Какой реальный пример линейной функции?
Например, текущее уравнение y = mx + by = mx + b (то есть форма сегмента рампы, которую вы изучите позже) является линейной функцией, поскольку использует оба критерия с xx и yy в качестве переменных и мм и кровать и завтрак.
 работает как константа.
работает как константа.Как определить, является ли уравнение линейным или нелинейным?
Линейные инструкции на графике выглядят как линии и имеют постоянный наклон.Нелинейные уравнения кажутся кривыми при построении графика и не имеют постоянного наклона. Существует несколько методов определения того, является ли уравнение линейным или нелинейным, включая построение графика, решение уравнения и создание ряда значений.
Как решить нелинейную систему уравнений?
Как решить нелинейную систему, если уравнение системы не является линейным. Если уравнение системы нелинейно, можно использовать подстановку. В этой ситуации вы можете найти переменную в линейном уравнении и вставить это выражение в нелинейное уравнение, потому что найти переменную в линейном уравнении так просто!
Какое уравнение представляет собой нелинейную функцию?
Нелинейное уравнение не обязательно является чем-то возведенным в степень, это просто уравнение, не представленное линией.
 В дополнение к полиномиальным кривым нелинейными являются следующие функции: Тригонометрическая функция. f(x) = sin(x) f(x) = tan(x) Логарифмическая или экспоненциальная функция. f(x) = lnx. Конечно, есть бесчисленное множество других примеров.
В дополнение к полиномиальным кривым нелинейными являются следующие функции: Тригонометрическая функция. f(x) = sin(x) f(x) = tan(x) Логарифмическая или экспоненциальная функция. f(x) = lnx. Конечно, есть бесчисленное множество других примеров.Какой пример линейного уравнения?
Линейное уравнение определяется как алгебраическое уравнение, в котором каждый член имеет показатель степени, равный единице, а график уравнения представляет собой прямую линию. Примером линейного уравнения является y = mx + b.Определение YourDictionary и пример приложения.
Как написать уравнение из текстовых задач?
Решите текстовые задачи, которые приводят к уравнениям, таким как px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих фигур гладко. Сравните алгебраическое решение с арифметическим и определите порядок операций, используемых в каждом методе.
Каковы шаги решения уравнения?
Используйте следующую процедуру для решения уравнений.
 Этапы решения уравнений
Этапы решения уравнений
Шаг 1 : Очистите дроби и десятичные дроби, умножив каждый член уравнения с помощью ЖК-дисплея.
Шаг 2 : Снимите кронштейны при подключении.
Шаг 3 : Объединяет все похожие термины на одной странице.Каковы шаги решения линейных неравенств?
- Перепишем неравенство так, чтобы справа стоял ноль.
- Найдите все линейные множители функции.
- Чтобы найти критические значения, приравняйте каждую линейную функцию к нулю и найдите x.
- Определите знак функции в интервалах, составляющих критические значения.
Как решать уравнения и неравенства?
Для решения уравнений и неравенств необходимо поработать над выделением переменной с помощью обратных операций. Помните, что когда вы умножаете или делите неравенство на отрицательное число, вы должны инвертировать символ неравенства.Найдите правильное значение x в следующих уравнениях и неравенствах.
 Например: 5x + 3x + 1 > 14.
Например: 5x + 3x + 1 > 14.Что такое рабочий лист линейных уравнений и линейных неравенств
Рабочие листы линейных уравнений и неравенств дают детям представление о том, как решать линейные уравнения и находить ответы на неравенства. Вопросы содержат простые вопросы о нахождении значения переменной и могут привести к более сложным графикам или текстовым задачам. Линейные уравнения используются во многих компьютерных и информационных приложениях.
Свободны ли линейные уравнения и неравенства?
Рабочие листы линейных уравнений и неравенств не только просты в использовании, но также содержат книги решений, которые содержат решения всех проблем, указанных в рабочем листе. Эти электронные таблицы требуют регулярной практики, и их можно бесплатно скачать в формате PDF.
Существуют ли распечатанные рабочие листы для решения линейных уравнений?
Здесь вы найдете неограниченное количество листов для печати для решения линейных уравнений, доступных в виде файлов PDF и HTML.
 Вы можете настроить рабочие листы, чтобы включить одно-, двух- или многоуровневые уравнения, переменные с обеих сторон, круглые скобки и многое другое.
Вы можете настроить рабочие листы, чтобы включить одно-, двух- или многоуровневые уравнения, переменные с обеих сторон, круглые скобки и многое другое.Как линейные уравнения используются в информатике?
Линейные уравнения используются во многих компьютерных и информационных приложениях. Лучший способ понять такую важную тему — решить некоторые полезные дополнения, легко доступные в таблицах линейных уравнений и неравенств.
Сколько типов уравнений можно использовать в Excel?
Вы можете выбрать из СЕМИ типов основных уравнений, от простых до сложных, которые объясняются ниже (например, одношаговые уравнения, которые являются переменными с обеих сторон или должны использовать свойство распределения).Настройте рабочие листы с помощью генератора ниже. Каждая таблица генерируется случайным образом и поэтому уникальна.
Что такое системы линейных уравнений
Система линейных уравнений — это просто набор двух или более линейных уравнений.
 С двумя переменными (x и y) график системы двух уравнений представляет собой пару прямых на плоскости. Возможны три варианта: Линии пересекаются в нулевых точках.
С двумя переменными (x и y) график системы двух уравнений представляет собой пару прямых на плоскости. Возможны три варианта: Линии пересекаются в нулевых точках.Какая система линейных уравнений имеет только одно решение?
Линейная система, имеющая ровно одно решение, называется когерентной независимой системой.Когерентность означает, что линии пересекаются, а независимость означает, что линии различны.
Какими тремя способами можно решить систему уравнений?
Тремя наиболее часто используемыми методами решения систем уравнений являются подстановка, исключение и расширенные матрицы.
Сколько решений может иметь система линейных уравнений?
Система линейных уравнений может иметь одно решение, не иметь решения или иметь бесконечное число решений.Наклоны, точки и линии определяют тип решения в системе. Система линейных уравнений имеет решение, если прямые имеют разные наклоны, независимо от значений их ординат в начале координат.

Что такое линейные уравнения и примеры линейных неравенств
Линейные неравенства — это два выражения, значения которых сравниваются с использованием символов неравенства, таких как или. Одномерные линейные уравнения и неравенства имеют только одно решение или один корень.Примеры одномерных линейных уравнений и неравенств: х = 4,2а + 3 = 9,3х<2,4 года 5>6.
Как изобразить линейное неравенство с двумя переменными?
Графическое представление линейных неравенств с двумя переменными. Чтобы представить линейное неравенство с двумя переменными (например, x и y), сначала возьмите только y с одной стороны. Затем посмотрите на соответствующее уравнение, которое вы получите, поменяв знак неравенства на знак равенства. График этого уравнения представляет собой прямую.
Как написать линейное уравнение?
- Уравнение прямой в виде отрезка наклона: y = mx + b y = m x + b
- Определите уклон.
- Найдите точку пересечения y и y.
 Это можно сделать, заменив наклон и координаты точки (x, y) на (x, y) прямой линией.
Это можно сделать, заменив наклон и координаты точки (x, y) на (x, y) прямой линией.
Что такое линейные уравнения и определение линейных неравенств
Ответ: График линейных неравенств состоит из линий точек, если они больше или меньше, но не равны. С другой стороны, линейные уравнения в любом состоянии состоят из сплошной линии. Кроме того, в отличие от линейных уравнений, линейные неравенства содержат заштрихованные области.
Что такое линейные функции
Линейная функция — это математическое выражение, которое образует прямую линию на графике. Линейная функция — это простая функция, которая обычно состоит из констант и простых переменных без показателей степени, как в примере y = mx + b.
Как определить, является ли функция линейной?
Самый простой способ найти линейную функцию — посмотреть, как она изображена. Если это прямая линия, то это линейная функция.
Как найти линейную функцию?
Сложите все числа в столбце x и запишите сумму в столбце x.
 Сделайте то же самое для остальных трех столбцов. Теперь вы собираетесь использовать эти суммы, чтобы найти линейную функцию вида y = Mx + B, где M и B — константы.
Сделайте то же самое для остальных трех столбцов. Теперь вы собираетесь использовать эти суммы, чтобы найти линейную функцию вида y = Mx + B, где M и B — константы.Какие ситуации представляют линейные функции?
Линейные функции часто встречаются в ситуациях, когда требуется постоянное накопление в арифметическом ряду. Ревизия геометрических и арифметических рядов. Вот еще несколько ситуаций, которые должны выглядеть как линейные функции. Самолет летит на постоянной высоте.(Высота против
Как найти X в уравнении?
Вы можете найти x или решить уравнение относительно x, отметив x на одной стороне алгебраического уравнения. Чтобы найти x, нужно понимать основные правила алгебраических операций. Отметьте x на одной стороне алгебраического уравнения, вычитая сумму, которая появляется как x на той же стороне уравнения.
Как найти X в алгебре?
Алгебра — это форма математики, которая вводит понятие переменных, представляющих числа.
 X — одна из тех переменных, которые используются в алгебраических уравнениях. Вы можете найти x или решить уравнение относительно x, отметив x на одной стороне алгебраического уравнения.
X — одна из тех переменных, которые используются в алгебраических уравнениях. Вы можете найти x или решить уравнение относительно x, отметив x на одной стороне алгебраического уравнения.Как решать линейные уравнения с дробями?
Этапы решения линейных уравнений с дробями
Шаг 1 : Найдите наименьший общий делитель всех дробей в линейном уравнении.
Шаг 2 : Умножьте обе части уравнения на этот наименьший общий делитель, чтобы исключить все дроби.
Шаг 3 : Решите линейное уравнение, используя один из уже рассмотренных методов.Как решить дробь?
Шаг 1 : Сопоставьте меньшие числа (знаменатели).
Шаг 2 : Сложите первые числа (числители), поместите этот ответ над знаменателем.
Шаг 3 : Упростите дробь (при необходимости).Как найти x в калькуляторе дробей
Решите x, умножив и упростив уравнение, чтобы найти x.
 Пример: Имея уравнение 4/10 = x/15, найдите x. Поскольку 60 = 60 правильно, вы можете быть уверены, что x = 6 — правильный ответ. Дробь со знаменателем, равным нулю, не определяется. Дробь с нулевым числителем равна 0.
Пример: Имея уравнение 4/10 = x/15, найдите x. Поскольку 60 = 60 правильно, вы можете быть уверены, что x = 6 — правильный ответ. Дробь со знаменателем, равным нулю, не определяется. Дробь с нулевым числителем равна 0.Как найти x в формуле уравнения дроби
Решите x, умножив и упростив уравнение, чтобы найти x. Пример: Имея уравнение 4/10 = x/15, найдите x. Умножение дробей 4*15=10*х.
Как решить алгебру?
Решите двухшаговое уравнение, умножая вместо деления в конце.Принцип решения этого типа уравнений тот же: используйте арифметику, чтобы сложить константы вместе, изолируйте переменный член, а затем изолируйте переменную, не изолируя член. Предположим, вы работаете с уравнением x / 5 + 7 = 3,
.Не могли бы вы найти значение x, пожалуйста?
Чтобы найти значение x, переместите переменную влево, а остальные значения вправо. Упростите значения, чтобы найти результат. Стандартное сравнение. Стандартный способ найти значение X в операции умножения.
 Делитель × Дивиденд = Продукт. Возьмем делимое = х, делитель × х = произведение.
Делитель × Дивиденд = Продукт. Возьмем делимое = х, делитель × х = произведение.Как найти x в таблице уравнения дробей
Решите x, умножив и упростив уравнение, чтобы найти x. Пример: Имея уравнение 4/10 = x/15, найдите x. Поскольку 60 = 60 правильно, вы можете быть уверены, что x = 6 — правильный ответ. Дробь со знаменателем, равным нулю, не определяется.
Find x math
Чтобы найти x, когда уравнение содержит показатель степени, сначала выберите показатель степени.Затем выберите переменную степени, разделив обе части на коэффициент x, чтобы получить ответ. Если ваше уравнение содержит дроби, начните с их вычеркивания, чтобы умножить дроби.
Как решить математическую задачу?
Упростите расчеты, решая небольшие части задачи одну за другой, используя правило порядка операций. Сначала найдите числа в скобках. Затем вы решаете задачу на умножение, а затем на деление, всегда слева направо. Наконец, решите сложение и вычитание слева направо.

Как найти x в примере уравнения дроби
Решение X в виде дроби Решите x, умножив и упростив уравнение, чтобы найти x. Пример: Имея уравнение 4/10 = x/15, найдите x. Перекрестное умножение дробей.
Линейные неравенства с дробями
Вы также можете решать линейные дробные неравенства, умножая каждую часть неравенства на ЖК всех дробей неравенства. Помните, что линейные неравенства работают так же, как линейные уравнения, за исключением того, что знак неравенства меняет направление всякий раз, когда каждая сторона неравенства умножается на отрицательное число.Давайте рассмотрим несколько примеров, чтобы увидеть, как решить линейное неравенство, сначала решив дроби.
Как решить граф?
Шаг 1 : Установите линейные уравнения в виде сегмента линейного изменения.
Шаг 2 : Нарисуйте линии и используйте график, чтобы найти общую точку.
Шаг 3 : Проверьте свой ответ и представьте его в виде упорядоченной пары. Здесь важна точность. Используйте миллиметровую бумагу и линейку при использовании графического метода для решения линейных систем.
Здесь важна точность. Используйте миллиметровую бумагу и линейку при использовании графического метода для решения линейных систем.Что такое графическое уравнение?
Создание графических уравнений — это урок, который знакомит учащихся с различными типами уравнений и построенных на их основе графиков. Учащиеся используют таблицы, чтобы найти решения заданных уравнений, а затем построить их. При рисовании графика они исследуют различия между линейными функциями, квадратичными функциями и функциями абсолютного значения.
Каковы правила решения уравнений?
Решайте уравнения и упрощайте выражения.На первом уроке алгебры они узнали, что есть два правила решения уравнений: правило сложения и правило умножения/деления. Правило сложения для уравнений говорит им, что одно и то же количество можно добавить к обеим частям уравнения без изменения набора решений уравнения.
Решение уравнений с использованием наименьшего общего кратного
Использование НОК для решения уравнений
Ну, вы можете использовать наименьшее общее кратное, чтобы помочь вам решить ваши алгебраические уравнения, когда вам нужно объединить дроби, чтобы упростить ваши уравнения.
 Для этого выполните следующие действия.
Для этого выполните следующие действия.- Переместите все ваши переменные члены в одну часть уравнения, а все ваши постоянные члены в другую.
- Используйте LCM для объединения любых членов дроби, которые похожи друг на друга.
- Продолжайте решать свою переменную, используя свои навыки алгебры.
Практическая задача 1
Давайте теперь посмотрим на эти шаги в действии.
Давайте решим это уравнение для переменной x .
Следуя инструкциям, вы сначала переместите все свои переменные термины в одну сторону.Итак, выберите одну сторону, скажем, левую. Теперь переместите все постоянные члены на другую сторону, правую сторону. Вот как это выглядит.
Теперь, на втором этапе, объедините ваши дроби с помощью наименьшего общего кратного. Вы комбинируете дроби, поэтому наименьшее общее кратное поможет вам выяснить, какими должны быть ваши знаменатели, прежде чем вы сможете упростить эту часть уравнения.

У вас 7 и 2 в знаменателях, поэтому наименьшее общее кратное для этих двух чисел равно 14.Итак, вам нужно изменить обе дроби, чтобы у них обоих был знаменатель 14. Затем вы можете их объединить.
После использования LCM для комбинирования членов дробей продолжайте вычислять переменную, используя свои навыки алгебры.
Готово! Ваш ответ -28.
Практическая задача 2
Давайте рассмотрим еще один пример и посмотрим, сможете ли вы решить его самостоятельно, прежде чем читать следующий ответ.
На этот раз решите это уравнение для неизвестной переменной.
Какой твой первый шаг? Правильно, вы перемещаете все переменные члены в одну сторону, а постоянные — в другую. Помните, не имеет значения, какую сторону вы выберете, пока вы держите их по разные стороны от знака равенства.
 На этот раз вы можете переместить константы в левую часть, а переменные — в правую.
На этот раз вы можете переместить константы в левую часть, а переменные — в правую.У вас есть дроби, поэтому теперь вам нужно использовать наименьшее общее кратное, чтобы сложить дроби.
Затем вы решите задачу, используя свои навыки алгебры.
Готово. Ваш ответ 156 / 7.
Итоги урока
Давайте повторим.
Ваше наименьшее общее кратное (НОК) — это наименьшее число, кратное всем заданным вами числам.
Чтобы использовать его для решения алгебраических уравнений, выполните следующие действия.
- Переместите все ваши переменные члены в одну часть уравнения, а все ваши постоянные члены в другую.
- Используйте LCM для объединения любых членов дроби, которые похожи друг на друга.
- Продолжайте решать свою переменную, используя свои навыки алгебры.

решение многошаговых уравнений с рациональными коэффициентами рабочий лист pdf.Решение уравнений
Решение многошаговых уравнений с рациональными коэффициентами. Лист pdf. Решение уравнений с распределительным свойством 1 Этот рабочий лист из 12 задач предназначен для того, чтобы познакомить вас с решением уравнений, которые содержат распределительное свойство. H Рабочий лист… Они сталкиваются со сложными на вид многошаговыми уравнениями и обнаруживают, что, используя свойства операций и комбинируя одинаковые термины, эти уравнения сводятся к простым одно- и двухшаговым уравнениям. Рабочие листы с двухшаговыми уравнениями и дробями и мамы, и учителя, обучающиеся на дому, с удовольствием просматривают эти листы, готовя своих детей к решению двухшаговых уравнений. Программное обеспечение по алгебре, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. 2-8 Двухшаговые уравнения с рациональными числами УРОК Опишите операции, выполняемые с обеих сторон уравнения на шагах 2 и 4.Проверьте свое решение. 23 октября 2013 г. — Решение двухшаговых уравнений Цветной рабочий лист Практика 6. Юридические Простые рабочие листы по алгебре Многошаговые рабочие листы по алгебре Рабочие листы по алгебре Одношаговые уравнения 4x 3x 6 или 2x 3 9 x или 3x 6 […] Практика решения многошаговых алгебраических уравнений. 5 3 1 6 Одношаговые уравнения с дробями Список рабочих листов. ком Рабочий лист -4. Рабочий лист «Решение уравнений путем умножения дробей»: … Основанный на практических наборах из «Решение двухэтапных уравнений: уровень 1», этот дополнительный рабочий лист обеспечивает еще один уровень самостоятельной практики, который поможет подготовить учащихся к решению многоэтапных уравнений.
Рабочие листы с двухшаговыми уравнениями и дробями и мамы, и учителя, обучающиеся на дому, с удовольствием просматривают эти листы, готовя своих детей к решению двухшаговых уравнений. Программное обеспечение по алгебре, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. 2-8 Двухшаговые уравнения с рациональными числами УРОК Опишите операции, выполняемые с обеих сторон уравнения на шагах 2 и 4.Проверьте свое решение. 23 октября 2013 г. — Решение двухшаговых уравнений Цветной рабочий лист Практика 6. Юридические Простые рабочие листы по алгебре Многошаговые рабочие листы по алгебре Рабочие листы по алгебре Одношаговые уравнения 4x 3x 6 или 2x 3 9 x или 3x 6 […] Практика решения многошаговых алгебраических уравнений. 5 3 1 6 Одношаговые уравнения с дробями Список рабочих листов. ком Рабочий лист -4. Рабочий лист «Решение уравнений путем умножения дробей»: … Основанный на практических наборах из «Решение двухэтапных уравнений: уровень 1», этот дополнительный рабочий лист обеспечивает еще один уровень самостоятельной практики, который поможет подготовить учащихся к решению многоэтапных уравнений. 4 Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 1 Имя_____ Уравнения в два шага Дата_____ Период____ Решите каждое уравнение. Рабочие листы для умножения дробей 171952. 3 Решайте многошаговые реальные и математические задания. Свободная алгебра. 1 рабочие листы, созданные с помощью бесконечной алгебры. 1. Решение одношаговых уравнений с рациональными коэффициентами. Лист pdf. Пример Решите 𝟒 𝒙=𝟏 . Решайте системы линейных уравнений алгебраически подстановкой. Примечания к решению неравенств. 1 Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.Калькулятор решения многошаговых неравенств Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата. Иногда… Решение линейных уравнений — дроби Цель: решить линейные уравнения с рациональными коэффициентами путем умножения на наименьший общий знаменатель, чтобы очистить дроби.
4 Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 1 Имя_____ Уравнения в два шага Дата_____ Период____ Решите каждое уравнение. Рабочие листы для умножения дробей 171952. 3 Решайте многошаговые реальные и математические задания. Свободная алгебра. 1 рабочие листы, созданные с помощью бесконечной алгебры. 1. Решение одношаговых уравнений с рациональными коэффициентами. Лист pdf. Пример Решите 𝟒 𝒙=𝟏 . Решайте системы линейных уравнений алгебраически подстановкой. Примечания к решению неравенств. 1 Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.Калькулятор решения многошаговых неравенств Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата. Иногда… Решение линейных уравнений — дроби Цель: решить линейные уравнения с рациональными коэффициентами путем умножения на наименьший общий знаменатель, чтобы очистить дроби. b Выполнять вычисления и писать числовые выражения с квадратами и квадратными корнями из положительных рациональных чисел. Длинное деление с десятичными знаками. уравнения В этих рабочих листах в формате PDF для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов.Решите уравнение. Ознакомьтесь с концепцией решения одношаговых уравнений с помощью операций сложения и вычитания в этом ассортименте рабочих листов PDF. Уравнения и текстовые задачи (двухэтапные уравнения) Рабочие листы Уравнения и текстовые задачи (двухэтапные уравнения) Рабочий лист 1. Этот рабочий лист из 10 задач поможет вам попрактиковаться в написании и решении двухшаговых уравнений, соответствующих реальным ситуациям. Рабочий лист одно- и двухшаговых уравнений в формате pdf. 15 = 5 м. Разделите обе части на 5. Цель решения уравнения — найти значение переменной. Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения.
b Выполнять вычисления и писать числовые выражения с квадратами и квадратными корнями из положительных рациональных чисел. Длинное деление с десятичными знаками. уравнения В этих рабочих листах в формате PDF для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов.Решите уравнение. Ознакомьтесь с концепцией решения одношаговых уравнений с помощью операций сложения и вычитания в этом ассортименте рабочих листов PDF. Уравнения и текстовые задачи (двухэтапные уравнения) Рабочие листы Уравнения и текстовые задачи (двухэтапные уравнения) Рабочий лист 1. Этот рабочий лист из 10 задач поможет вам попрактиковаться в написании и решении двухшаговых уравнений, соответствующих реальным ситуациям. Рабочий лист одно- и двухшаговых уравнений в формате pdf. 15 = 5 м. Разделите обе части на 5. Цель решения уравнения — найти значение переменной. Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения. рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.Каждый рабочий лист включает в себя некоторые шаги для решения уравнения, и учащиеся должны выполнить эти шаги самостоятельно. Эти уравнения требуют, чтобы учащийся распределил умноженное значение между терминами в круглых скобках, прежде чем объединять похожие термины. Найдите абсолютное значение числа. 4 x 1 2 3x стоит 1762 доллара. P. Загрузка тестов на пригодность, предварительная алгебра «задачи равномерного движения», распечатки рабочих листов по геометрии, бесплатные рабочие листы для решения математических задач. Ответы на рабочий лист неравенства. Они укрепят свое понимание дробей, десятичных знаков и процентов как различных способов представления рациональных чисел.Графики неравенств с одной переменной. 1-7 Распределительное свойство 7-1 Нулевые и отрицательные показатели 8-2 Умножение и разложение на множители 10-2 Упрощение радикалов 11-3 Деление полиномов 12-7 Теоретическая и экспериментальная вероятность Уравнения абсолютного значения и неравенства Алгебра 1 Игры Алгебра 1 Рабочие листы Алгебра обзор решения … Получите огромную практику с этой серией распечатываемых рабочих листов для решения систем уравнений, предназначенных для учащихся 8-го класса и старшей школы. comРешение рациональных уравнений онлайн калькулятор Квадратная формула.Пошаговые уравнения отмечают деятельность лабиринта усилителя всеми вещами. Мат. (2x – 1) = ( ) 3 Разделите каждую сторону на 5 c Рациональный метод или рациональная формула. Pdf 12 68 МБ Этот продукт отлично подходит для дистанционного обучения, самостоятельного изучения и обогащения. Этот набор рабочих листов включает 5 рабочих листов по объединению выражений с похожими терминами. Интерпретируйте этот набор текстовых задач, которые требуют двухэтапных операций для решения уравнений. 1. Рабочий лист 3. Двухшаговые уравнения с рабочим листом дробей, связанным после одного шага. На второй странице прикреплен ключ ответа.смешать с калькулятором регулярных дробей. 3x + 1 = 7 3x + 1 = 7 Начальный навык алгебры Решение линейных уравнений: дробные коэффициенты Решите каждое уравнение. Ключ ответа на лист 1 Двухшаговые рациональные неравенства Стандарты CC 7. Предварительные ответы по алгебре, бесплатные рабочие листы по алгебре уравнений с дробями, нахождение квадратного корня 17, решение программы по алгебре, бесплатные многошаговые рабочие листы и тесты. перевести в алгебраическое выражение. • Используйте подстановку для проверки решений. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений.Решение многоступенчатых уравнений. Рабочий лист Лабиринт. Упражнение Решение уравнений. Упражнение Решение многошаговых уравнений. Алгебра. Рабочие листы. Неравенства 6-го класса с отображением 8 лучших рабочих листов, найденных для этой концепции. Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. — Урок 8. Все задачи могут быть перевернутыми и содержать отрицательные коэффициенты, но всегда разрешаются целыми числами. Рациональное: может быть представлено дробью — и то, и другое. Чтобы попрактиковаться в решении двухэтапных задач с уравнениями, не стесняйтесь использовать рабочие листы ниже.рабочие листы для решения линейных уравнений (предварительная алгебра или алгебра 1) в виде файлов PDF или html. Двухшаговые уравнения, содержащие десятичные дроби. г. Одношаговые уравнения с рациональными коэффициентами. Рабочий лист Дополнительная практика 10 4 Решение рациональных уравнений. Рабочий лист. 32 Учителям это нравится LessonPrint LessWbat Решите задачу о шаге, используя сложение, вычитание и числа… Соответствующие академические стандарты штата Нью-Йорк. число, знак неравенства поменялся местами. Решать линейные уравнения намного веселее, когда есть весы с двумя чашами, несколько загадочных мешочков и куча мармеладок.3 x 1 5 5. Соблюдайте баланс по обе стороны неравенства, выделяя переменную с помощью обратных операций. 7 Решайте реальные и математические задачи, составляя и решая уравнения и неравенства с одной переменной. Factoring Maze Answer KeyQuadratic … Используйте приведенную ниже таблицу, чтобы найти видеоролики, мобильные приложения, рабочие листы и уроки, дополняющие Glencoe Math Course 3 Volume 1 Common Core. Решение алгебраических уравнений с дробями. 7 … В следующей таблице приведены примеры решения многошаговых уравнений с рациональными коэффициентами.Радикальные выражения и уравнения. Раздел 11. Рабочие выражения и решение уравнений со скобками. Рабочий лист pdf. Обучение чтению части слова помогает учащимся разбивать более длинные слова на более понятные фрагменты и помогает учащимся обнаруживать закономерности в написании слов. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. 1) m + 4 = 13 2 2) 8 3 = x − 1 1 3 3) 4 5 + v = 41 20 Рабочий лист двухшаговых уравнений с рациональными коэффициентами на квадратные корни, Alberta Class 10 Alegbra.21 хорошо продуманная задача, которая укрепит и укрепит обучение учащихся. Наведите указатель мыши на ответ. Используйте свойства равенства, чтобы переписать … Desje Lrmv3eGdj. В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов. Решение уравнений с переменными с обеих сторон 1 Этот рабочий лист из 12 задач предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные с обеих сторон.И нет ничего лучше набора координатных осей для решения систем линейных уравнений. С помощью этих распечатываемых рабочих листов учащиеся будут практиковаться в упрощении и поиске эквивалентных алгебраических выражений. • Обоснуйте шаги решения уравнения. 2x+6=16) Объединение похожих терминов X с обеих сторон Распределяющая собственность. Рабочий лист от kuta software llc. Решение уравнений абсолютного значения ChiliMath. Разделы 2 1 2 2. Начало работы Напишите, решите и начертите графики одношаговых линейных уравнений. Рабочие листы по математике для печати для 9 класса.Алгебра Холта 2 3a Решение 118 L13. Решение линейных уравнений с рациональными коэффициентами Часть 2. Инструкция по моделированию Прочитайте приведенную ниже задачу. ком. 3 Решайте многошаговые реальные и математические задачи, поставленные с помощью положительных • Решайте уравнения с целыми коэффициентами. Рабочий лист — одношаговые уравнения. 14). 5 лет 2 28 8. ПОСМОТРЕТЬ ПРОДУКЦИЮ. Урок 6 2 Уравнения в один шаг с рациональными коэффициентами Ответ Ключевое слово Заполнить онлайн Пригодно для печати Заполняемый бланк Pdffiller Решить уравнения Примеры решений 8 класса Рабочие листы для одного шага с рациональными коэффициентами 7-й пакет дистанционного обучения по математике Бесплатное задание по алгебре 1 Умножение и деление нескольких уравнений 2 Дробь 2021 коэффициент рабочие места ecityworks линейные скобки иди учи математику ремесленные ресурсы для учителей 6 9 урок 2 4 распределительная неделя собственности в … H.Решите двухшаговые уравнения. Пин на листах по математике. Эти рабочие листы для печати содержат уравнения, коэффициенты которых представляют собой дроби и целые числа. Коэффициент 4×2 Переменная (или База) * Запишите коэффициенты, переменные и показатели степени следующего: Решение многошаговых уравнений: 3x – 5 = 22 Чтобы получить x сам по себе, вам нужно избавиться от 5 и 3 10 сентября 2021 г. Теперь мы заменяем x = 8.Решите для переменной. Рабочий лист -5. Решите следующие уравнения относительно x: 1) x + 5 = 12 2) x – 11 = 19 3) 22 – x = 17 4) 5x = … Решение многошаговых уравнений (стр. Спасибо. Решение многошаговых уравнений) Уравнения, включающие дроби. Рабочий лист также редактируется, если вам нравится Рабочий лист решения уравнений и неравенств с ответами. Даниэль потратил 25 на ярмарке. 4 — Supplement Solving Multi-Step Equations CC Standards 7. ID: 1411530 Язык: английский Школьный предмет : Математика Класс/уровень: 7 Возраст: 11-16 Основное содержание: Уравнения Другое содержание: Алгебра Добавить в мои рабочие тетради (0) Скачать файл в формате pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom В этих рабочих листах в формате pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов.Этапы решения задач в два шага. Каждая задача имеет уникальное решение от -12 до 12, которое соответствует цветовому шаблону, формирующему симметричное изображение. Некоторые из рабочих листов для этой концепции ws1 многошаговые уравнения многошаговые уравнения десятичные числа 1 практика решения уравнений, содержащих дроби и десятичные дроби многошаговые уравнения дроби 1 два шага Решите многошаговое уравнение Многошаговые уравнения Многошаговые уравнения Рабочие листы Два уравнения шага. 7) Коэффициент: число, умноженное на переменную.Рабочий лист решения простых уравнений pdf Shenker Academy. Итак, еслиЧитать далее Уравнения в два шага. Вы можете выбрать три различных типа … admin July 16, 2019. Тригонометрические уравнения, как следует из названия, являются уравнениями Desje Lrmv3eGdj. Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. 7b) Решение многошаговых уравнений с рациональными коэффициентами (8. Сформулируйте и используйте различные стратегии для решения одношаговых и многошаговых линейных уравнений.Решите переменную в двухшаговой рабочей таблице задач 4. Маневрирование ресурсов математического вмешательства. Например, используя уравнение 3x + 5 = 11, нам нужно будет выполнить два шага, чтобы найти значение x. Рабочие листы с двухэтапными уравнениями содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. 3x 2 11 2. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p ( x + q) = r, где p, q и r — конкретные рациональные числа.Решение простых линейных уравнений с неизвестными значениями от 99 до 99 и переменными на листах T Алгебра Решение линейных уравнений Алгебраические выражения . Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя… Рациональные показатели и радикальные уравнения III. Бесконечные решения означают, что любое значение переменной делает уравнение верным. 4_notes_key_многоступенчатое_неравенство. — Глава 8.Решайте уравнения с помощью листа решения дробей и математики. 5 дополнительно Глава 6: Решение уравнений Математика 9 Marsh 6. Название: Рабочий лист линейных уравнений Автор: Мария Миллер Тема: Рабочий лист линейных уравнений Ключевые слова: Линейные уравнения, рабочий лист Дата создания: 27.12.2014 13:59:23 Урок/Занятия. w 2 2 3 1 3 10 Графические системы уравнений Два линейных уравнения образуют систему уравнений. Решение многошаговых уравнений с одной переменной Эталоны 8. 1) 3 F 5 8 2 2) 5 7 N F3 L F6 3) 7 F 9 = 3 4) 6 9 P E3 L11 5) F … Таблицы двухшаговых уравнений имеют огромный коллекция печатных практических страниц для решения и проверки уравнений с целыми числами, дробями и десятичными знаками.I. 3 Решить многошаговые реальные и математические задачи, поставленные с позитивом Опубликовано в алгебре 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответы ключ решение уравнений лабиринт. Некоторые из инструментов для создания терминов с кутом решают линейные уравнения с кутом по более сложной математике.Определить внутри трех решений нет или бесконечность 15 21. Одношаговое уравнение – сложение и вычитание. Например, периметр прямоугольника равен 54 см. Решите смесь типов уравнений, содержащих одинаковые термины. Вопросы 1-14 7 23 марта Решение уравнений – часть 2 Я могу решать двухшаговые уравнения. В. Решение текстовых задач с уравнениями и неравенствами (Общий базовый стандарт 7. Определение: математическое предложение, в котором говорится, что число или выражение равно другому числу или выражению. Объясните каждый шаг решения простого уравнения, как следует из равенства числа, утвержденные на предыдущем шаге, исходя из предположения, что исходное уравнение имеет решение.Некоторые из рабочих листов для этой концепции представляют собой двухшаговые уравнения периода даты многошаговые уравнения периода линейные уравнения работы двухэтапные уравнения целые числа 1 имя практика решения систем уравнений 3 различных одношаговых уравнения целые числа смешанные … В этих рабочих листах pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений.Соедините математику с выпивкой других дисциплин. Первым шагом было бы получение постоянных значений уравнения сами по себе. Кроме того, для дополнительной практики для учащихся 7-х и 8-х классов здесь представлен ряд pdf-файлов с упражнениями по переводу двухшаговых уравнений, MCQ и текстовых задач на основе геометрических фигур. Этот рабочий лист представляет собой комбинацию типов задач из этой категории. Решение многошаговых уравнений Bath K12 Ky Us. Решайте двухэтапные уравнения, оттачивая навыки алгебры в седьмом и восьмом классе с помощью этого удобного рабочего листа! Начиная с доступного дополнения, которое напоминает о том, как разбить двухшаговые уравнения, измененные операции, этот рабочий лист снова поощряет абсолютное удобство в качестве принятия … Закладка Файл PDF Решение рациональных уравнений Алгебра 2 Ответы Уравнения — cdn.Вот почему решение многошаговых уравнений сложнее, чем одношаговых и двухшаговых уравнений, потому что они требуют больше шагов. Где скачать Урок 3 Решение уравнений с переменными с обеих сторон Урок 10 3 Домашнее задание и практика Решение уравнений с помощью стандартов урока 7. Open делится на открытое перо, а О в открытом слоге. А. Распознавать линейные уравнения с одной переменной как имеющие одно решение, бесконечно много решений или не имеющие решения. Поскольку нулем функции f(x) является значение x, для которого (𝑥)=0, нахождение нулей полиномиальной функции p(x) аналогично нахождению _____ полиномиального уравнения… Карточки с заданиями по решению уравнений как в игре Sum Fun! Это увлекательное задание предлагает 32 карточки с заданиями, включающими многошаговые уравнения с переменными с обеих сторон и коэффициенты рациональных чисел.141–148) 3 опционально 0. comРешение систем уравнений с двумя переменными (Алгебра 2 Решение рациональных уравнений 1 — Системы уравнений Рабочие листы Решение линейных тригонометрических уравнений с синусоидально-косинусоидальным уравнением. Теперь подставим x = 8 Вот почему я решил создать четыре разные версии заметок для занятий, каждая с различным решением многошагового уравнения с переменными с обеих сторон.WorksheetQuadratic Equations By FactoringSolving Multi Step Equations — факторинговые полиномыSolving Quadratic Factoring — cdn. Вы можете решить систему уравнений, используя один из трех методов: 1. Рабочий пример Двухэтапное уравнение Алгебра Видео. 8. 4 t25031 t28 9k … Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги решения рациональных уравнений с одинаковым знаменателем Шаг 1. Каждая серия … 3. Рабочие листы по математике 4 класс словесные задачи умножение.CCSS: 6. 2. Сначала они определяют, что операции сделали с переменной, и отменяют эти операции для решения. Сб, 22 декабря 2018 г., 01:38:00 GMT Бесплатные рабочие листы для линейных уравнений (6-9 классы, до… Решение уравнений с переменными на обеих сторонах 1 — Этот рабочий лист с 12 задачами предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные на обеих сторонах стороны.Помните, что вы можете решать уравнения, содержащие дроби, используя наименьший общий знаменатель всех дробей в уравнении.Перейдите к решению неравенств, которые включают несколько дополнительных шагов с помощью этих распечатываемых рабочих листов многошаговых неравенств.умножение, деление полномочий. ⭐ Решение многоэтапных уравнений — задание в лабиринте (PDF — FREEBIE) Решение уравнений Рабочие листы с одношаговыми уравнениями содержат эксклюзивные страницы для решения уравнений, включающих целые и десятичные дроби. Отображение всех рабочих листов, связанных с решением дробей двухэтапных уравнений. Рабочий лист с многошаговыми уравнениями. Определите исключенные значения уравнения. Наши рабочие листы с текстовыми задачами проверяют навыки в реальных сценариях. 10 Ответы на многоэтапные уравнения. Математическая обложка. Лист решения. Работает с решения. Многошаговый рабочий лист работает над решением многошаговых уравнений переменных на обоих шагах.Таким образом, в рабочих листах двухшаговых уравнений для 7 класса учащиеся узнают о концепции решения двух переменных, различных способах решения двух переменных в алгебраических выражениях и графическом отображении результатов. Математические рабочие листы дроби для сравнения дробей с подобным сложением. 2: Решение уравнений. 437 – 464 (One-step) с. 2x 7 7 9. Викторина Решение рациональных уравнений. Решение уравнений с дробями. 7 6. Во-вторых, учащиеся научатся понимать операции с рациональными числами и начнут работать с выражениями и линейными уравнениями.пинимг. Ключ ответа на лист решения многошаговых уравнений. x-4=10) Двухшаговые уравнения: (e. (с 3-4 • Решайте задачи, действуя в обратном порядке. АБСОЛЮТНОЕ ЗНАЧЕНИЕ Название рабочего листа: Выберите количество уравнений каждого типа: Одношаговые уравнения: (e. Лучшее ноябрьское 16, 2021 — Это создание r в квадрате является дополнительным рабочим листом для нашего 2. Некоторые из приведенных ниже рабочих листов: рабочий лист решения уравнений с дробями, шаги, которые необходимо выполнить при решении дробного уравнения, решение уравнений с дробями с использованием свойств равенства сложения и вычитания, несколько упражнения с решениями, ….b Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов. Сначала мы воспользуемся распределительным свойством, чтобы удалить скобки, а затем сможем. Сложные задачи с многошаговым уравнением. Ключ к ответу на лист многоступенчатого неравенства. Примечание. Двухшаговые уравнения. Это очень помогло мне с перехватом y при преобразовании десятичных знаков и вычитании дробей. Программное обеспечение Kuta Решение многошаговых уравнений Бесплатные математические листы для печати Многошаговые уравнения Многошаговые уравнения Рабочие листы Решение многошаговых уравнений Высшее ks4 ks3 a.Рациональные уравнения — это уравнения, содержащие рациональные выражения. Тест на решение уравнений. День 3. Ответы на рабочие листы. Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные многошаговые рабочие листы уравнений Алгебра, программная математика, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. Этот метод также может быть использован с рациональными уравнениями. Эти многоступенчатые уравнения могут стать немного длинными и сложными.pdf 8 Примечания к решению уравнений 9 Решение уравнений hw Решите уравнения. Решите линейные уравнения с одной переменной. Рабочий лист решения многошаговых уравнений. Это видео показывает учащимся, как решать двухшаговые уравнения алгебры, включающие двухшаговые уравнения: Десятичные числа Лист 1 — Рабочие листы для детей Многошаговые уравнения Дата_____ Период____ Решите каждое уравнение. Ниже приведен тест из 5 вопросов по решению одношаговых уравнений. Практика домашнего задания на пятницу. Умножение и деление уравнений в один шаг.Аддитивное свойство равенства. 3) Имя _____ Решение двухшаговых уравнений (SOL 7. Раздел 4 Решение квадратных уравнений Домашнее задание 1 Ключ к ответу, плавучая солнечная электростанция Этот рабочий лист по системам уравнений будет составлять семистраничный раздаточный материал для системы. 5 необязательный предварительный просмотр: использование алгебры плитки для решения многошаговых уравнений Решение одношаговых уравнений с рациональными коэффициентами рабочий лист Решение одношаговых уравнений с рациональными коэффициентами рабочий лист pdf В уравнениях представлены только положительные целые числа, и все ответы также положительны.Чтобы решить многошаговое уравнение, выполните следующие шаги. лестничный метод. 4 7 𝑥=16 Напишите уравнение. Метод замещения 3. Мы можем решить эти проблемы так же, как и в прошлом. D Сборник рабочих листов по двухступенчатой математике для второго класса. 465 –488 (двухшаговый) Дифференциация Возможность: o Shell FAL: Шаги к решению уравнений 7 Рабочая тетрадь ~ Написание уравнений Решите уравнения 8 класс примеры решения s рабочие листы урок 6 2 4 многоэтапный с распределительным свойством решение линейных скобок коэффициенты иди учи математику ресурсы ручной работы для учителей рабочий лист коэффициента дроби ecityworks в том числе отрицательные значения формы ax bc все математические упражнения моя математика две дроби упрощение алгебраического a по алгебре … с рациональными коэффициентами решение уравнений с рациональными коэффициентами решение уравнения с помощью верхней смотреть видео 4-2 решение двух- Ступенчатые уравнения.©u W2r0G1Z2 1 nKNuDtHaW sSodfVtBw8aOrle7 uL 3L IC u. Добавьте вычитание, умножение и деление, чтобы решить одношаговые уравнения дробей в этих рабочих листах уровня 1, которые включают правильные и неправильные дроби в качестве коэффициентов и констант. Решение многошаговых уравнений. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____. Нажмите F11. решить путем сложения решить путем вычитания сочетания двух вышеуказанных требуется один шаг умножения общая система Читать онлайн урок 2 Решение рациональных уравнений и неравенств Решение уравнений Задание 1 Всегда, иногда или никогда верно? Урок 6.1) 4 n — 2n = 4 2) -12 = 2 + 5v + 2v 3) 3 = x + 3 — 5x 4) x + 3 — 3 = -6 5) -12 = 3 — 2k — 3k 6) — 1 = −3r + 2r 7) 6 = −3(x + 2) 8) −3(4r − 8) = −36 9) 24 = 6(−x − 3) 10) 75 = 3(−6n − 5) )-1- В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многошаговые уравнения с десятичными числами в качестве коэффициентов. 8. Определение: выполнять одинаковые операции с обеими частями уравнения. Одношаговые неравенства путем умножения или деления. Математические уравнения в два шага — это алгебраические задачи, которые требуют, чтобы вы сделали два хода, чтобы найти значение неизвестной переменной.Это лабиринт, состоящий из 14 многоступенчатых уравнений, включающих дистрибутивное свойство. Архив метки: решение двухэтапных уравнений. Начните решать двухшаговые уравнения с одной переменной, включающие положительные коэффициенты, с помощью этого практического набора! Перестройте уравнения, чтобы сделать переменную объектом, и найдите ее целочисленное значение. Посмотреть больше примеров ». Рабочий лист решения многошаговых уравнений. 7б. Эта комбинация викторины и рабочего листа проверит вашу способность решать эти уравнения.сумма удвоенного числа плюс четыре умноженного на другое. Умножьте каждую сторону на 4, чтобы очистить дробь. Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые переменные уравнений с обеих сторон в скобках и многое другое. 1 6 р 7 13 7 р 2 13 4х 1 х 3 7х 3х 2 8х 8 4 8 х х 4х. 2 3 решение многоступенчатых уравнений отвечает на действия в лабиринте. Многоэтапный рабочий лист уравнений 8-го класса, решающий уравнения с. 1) 6р+7=13+7р. Противоположностью сложения является вычитание, а противоположностью умножения — деление.12 ноября 2021 г. Это рабочий лист по математике в формате PDF с несколькими упражнениями, который можно распечатать. Решение многошаговых уравнений. В этих раздаточных материалах доступно множество вопросов с несколькими вариантами ответов. Упрощение этих полезных радикальных выражений Решение многошаговых уравнений, содержащих дроби рабочего листа: 14 Вы можете найти интересные задачи. 3 Решайте многоэтапные реальные и математические задачи, поставленные с помощью положительных и … Решение рациональных уравнений — ChiliMath Решение рациональных уравнений Рациональное уравнение — это тип уравнения, в котором используется хотя бы одно рациональное выражение, причудливое название дроби.Рабочие листы для двухэтапных уравнений содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые дроби и десятичные дроби. 1 и 2. Это обновленная версия. Рабочие листы с многошаговыми уравнениями для учащихся Mathxnet. Бесплатные практические вопросы для Common Core: математика 8-го класса — решение линейных уравнений с рациональными числовыми коэффициентами: CCSS. Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. Включает полную версию Desje Lrmv3eGdj.1 и 8. УРОК Практика C Двухшаговые уравнения с рациональными числами. Многоступенчатые уравнения. Как только вы найдете свой рабочий лист (листы), вы можете либо щелкнуть всплывающую головоломку с уравнением «Один шаг». Двухшаговые текстовые задачи с уравнениями. Нажмите на ссылку, чтобы получить доступ к эксклюзивным рабочим листам по решению двухшаговых уравнений, которые включают целые дроби и десятичные дроби. Метод линейных комбинаций Метод замещения Решите следующую систему уравнений: x – 2y = -10 y= 3x x – 2y = -10 x – 2( 3x ) = -10 Поскольку мы знаем y = 3x, можно распечатать в удобном формате PDF.Решите текстовые задачи, ведущие к неравенствам вида px q r или px q r, где p q и r — конкретные рациональные числа. Многие квадратные уравнения не могут быть решены с помощью факторизации. арентезы с помощью распределительного свойства. Предложите учащимся попрактиковаться в решении многошаговых уравнений с целыми числами и дробями. 1 Учащиеся используют различное оборудование и программное обеспечение для интеграции нескольких форм информации, чтобы создать хороший … 1-этапный 2-этапный многоэтапный EE. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____ .REI. Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Теперь мы подставляем x = 8 Рабочие листы для двухшаговых уравнений содержат огромную коллекцию печатных страниц для практики, чтобы решать и проверять уравнения, включающие целые числа, дроби и десятичные дроби. Уравнения Уравнения в один шаг Уравнения в два шага Многошаговые уравнения Уравнения с абсолютными значениями Радикальные уравнения Легко сложные Рациональные уравнения Легкое сложное решение Пропорции Процентные задачи Расстояние Скорость Время Словесные задачи Смесь … Рабочий лист на одной странице содержит одиннадцать задач с ответами.Сентябрь 2020 г. Решение двухшаговых уравнений Withons Worksheet Pdf Кута Примечания к двухшаговым уравнениям, лабиринтная деятельность здесь — заметки Корнелла и лабиринтная деятельность по решению двухшаговых уравнений, включая уравнения с дробными коэффициентами. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y ylzlpcj. В этих рабочих листах решите двухшаговые уравнения с целыми коэффициентами. Как правило, это не так просто сделать другим способом. 515х35 при добавлении 15 с обеих сторон дает. Одношаговые задачи с уравнениями. Математическая плоскость решения рациональных уравнений.Решите для а. Существуют двухэтапные и многоэтапные рабочие листы уравнений с целыми и десятичными дробями. Рабочий лист двухшаговых уравнений Pdf. Этот рабочий лист содержит уравнения с одной переменной, содержащие либо целые, либо рациональные коэффициенты и константы, а также рабочие листы для двухэтапных уравнений с огромной коллекцией печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. Решите эти уравнения, чтобы получить значение неизвестного. Каждый рабочий лист двухшагового уравнения в формате PDF содержит десять задач на … Решить двухэтапное уравнение 7-й класс по математике 7 35.Решение и проверка уравнений, приложения по геометрии и MCQ включены в этот раздел для 7-го и 8-го классов оценочных листов по математике. Переменная с обеих сторон, решающая уравнения с одинаковыми условиями. Завтра утром я буду дополнительно помогать, чтобы ответить на любые вопросы, которые могут у вас возникнуть после решения уравнений с дробными коэффициентами: различные проблемы с ответами. 4 – Многошаговые уравнения с распределительным свойством 1 | Стр. План урока для учителя Урок 6. Викторина Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.Нажмите на тему ниже, чтобы увидеть проблемы, связанные с уравнением навыка. 4 t25031 t28 9k … Загадка уравнений в два шага. 1 Повторное обучение решению уравнений с рациональными коэффициентами Чтобы решить уравнение, в котором коэффициент является рациональным числом, умножьте каждую сторону на мультипликативную обратную дробь. 3. Слово «мульти» означает более двух или многих. График 2. Решите рациональные уравнения, найдя и умножив на наименьший общий знаменатель. Мат 0024 решение уравнений с дробями.Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Объявление Загрузите более 20000 рабочих листов K-8, посвященных математике, чтению, общественным наукам и многому другому. Серия многоуровневых рабочих листов требует, чтобы учащиеся решили пропорции, используя метод перекрестного произведения, и ответы, полученные таким образом, будут в форме целых чисел. 00) 3.149–154) 1 необязательный 0. Полностью упростите дробь dfrac a 2 a 6 ab 3b. 3: Решение уравнений с помощью распределительного свойства. Прочтите и загрузите электронную книгу Джина Уилсон «Все по алгебре 2016, уравнения в 2 шага» в формате pdf в общедоступной библиотеке электронных книг. com 1) 2 + 3 = 5. Ниже вы найдете множество рабочих листов для решения уравнений лабиринта, которые можно использовать на уроке алгебры 1. Эти рабочие листы текстовых задач являются хорошим ресурсом для учащихся с 5-го по 8-й класс.«все, что вы делаете с одной частью уравнения, вы должны делать и с другой». Рабочий лист решения двухшаговых уравнений pdf Решение двухэтапных уравнений с целыми числами Начните решать двухшаговые уравнения с одной переменной, включающей , этот рабочий лист поощряет самостоятельную практику, поскольку учащиеся решают уравнения, содержащие целые и рациональные коэффициенты и константы. Теперь мы заменяем x = 8 9. pdf из MATH MISC в колледже Санта-Моники. 3 Используйте только число всех от депо до толпы, чтобы решить уравнения и.О. Обязательно прокрутите вниз и ознакомьтесь с ними после прочтения урока. система как непротиворечивая или непротиворечивая, зависимая или независимая. Пин на доске Зомби Математика . Содержание. 4 Часть 1. Решение уравнений с переменными с обеих сторон. Для печати в удобном формате PDF. Наша математика 6/7 ПРИМЕЧАНИЯ (6. Основная цель решения многоэтапных уравнений, как и одноэтапных и двухэтапных уравнений, состоит в том, чтобы изолировать неизвестную переменную на одной стороне уравнения при использовании CCSS. Предварительный просмотр) • Решить уравнения, включающие более одной операции.Рабочие листы с двухшаговыми уравнениями для 6-х классов с ответами. Распределительное свойство и объединение одинаковых терминов Ws2 Объединение одинаковых терминов Некоторые из отображаемых рабочих листов: Решение рациональных уравнений 1, Решение рациональных уравнений, Решение дробных коэффициентов линейных уравнений, Решение примеров рациональных уравнений, Комбинирование дробных коэффициентов одинаковых терминов, Решение двухшаговых уравнений с дробными коэффициентами, Решение уравнений, содержащих дроби и . пустой слой. 5 5. Упражнения по решению уравнений лабиринта.Y d tM ra ed se0 cw qiPtxhl 1ISnbf ti Anci YtueV dAolwgQembmrKas h2Y. 3 Решайте многоэтапные задачи из реальной жизни и математические задачи с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. К этому понятию относится дробный коэффициент, в котором вы перемещаете числа. Эти карточки отформатированы как отличная игра с математическим обзором для подготовки к тестам и обзора STAAR. Очистить знаменатели. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы.Некоторыми из рабочих листов для этой концепции являются алгебра, упрощающая алгебраические выражения, расширяющая 8 алгебраических скобок, mep y8, учебник по математике, линейная 1ma0, решение уравнений по алгебре, работа 2, 2, решение уравнений с одной переменной, решение линейных уравнений, переменная для обеих … Posted in алгебра 1, рабочие листы, блог, решение лабиринта уравнения активность модуль 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответ ключ решение уравнений лабиринт.2) Объединить подобные термины. Квадратичные функции Обзор рабочего листа лабиринта Квадратичные функции Квадратичный рабочий лист лабиринта 2-6 Соотношения Коэффициенты и преобразования — Ответы — Занятие в лабиринте PDF — Только для членов. ЯВЛЯЕТСЯ. 1–8. В набор задач включены двухшаговые и многошаговые линейные уравнения с целыми и рациональными коэффициентами и константами. 18 Учащийся будет решать одношаговые линейные уравнения с одной переменной, включающие целые числа и положительные рациональные решения. Решение простых линейных уравнений с неизвестными значениями в диапазоне от -99 до 99 и переменными в левой части (303 просмотра на этой неделе) Решение систем линейных уравнений с помощью графика (стандарт) (272 просмотра на этой неделе) Решение линейных уравнений — Форма ax + b = c ( 266 просмотров на этой неделе) Решение линейных уравнений (включая отрицательные значения) — форма ax + b = c Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.. Умножение каждой части уравнения на общий знаменатель исключает дроби. 1. Решите эти смешанные уравнения, которые содержат дроби, целые числа и десятичные дроби. — Проект решения двухшаговых уравнений. B. Двухшаговые уравнения […] Рабочий лист One Step Equations Pdf Прекрасное решение E Step. конечно герой. Ключ к ответу лабиринта квадратных уравнений. Примечание. Многошаговое решение многошаговых уравнений. Во время контрольной по математике Элиза и Кейтлин решили уравнение 1 áá2 (5 x 2 6) 5 3x разными способами, но каждый ученик пришел к правильному ответу.В этом рабочем листе из 25 вопросов основное внимание уделяется уравнениям как с реальными, так и со сложными решениями. 3 2 Практика Раздаточный материал pdf просмотреть скачать 216k. Сколько учителей, у нас меньше времени словесных задач с участием целых чисел по алфавиту имен, что они заканчивают класс с ответами pdf упрощения рационального. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Стоимость оборудования2 2 11 2 4 x 1 1 2 1 3x 9 4 x 1 3 3 x 9 3 4 4 x 4( 1) x 3 x 4 Решите. 3 х 2 5 3 5 7.Рабочий лист одношаговых уравнений с решениями Рабочий лист по решению одношаговых одношаговых уравнений Рабочие листы многоэтапных уравнений … Решение уравнений, содержащих дроби и десятичные дроби page2. Решение уравнений с дробями рабочий лист 7th 10 rows U3D3_S Решение уравнений с дробями Часть 1. Отказ от ответственности: Этот калькулятор не идеален. Свойства равенства. Алгебра 2 7. Сегодня я поделюсь с вами 12 заданиями и идеями, которые помогут вашим ученикам понять и попрактиковаться в решении одношаговых уравнений.Рабочий лист системы неравенства 2021 Pdf. админ. Решите линейные уравнения с рациональными коэффициентами (Common Core Standard 8. Рабочие листы подходят для курсов предварительной алгебры и алгебры 1 (6–9 классы). Common Core Edition Carter, Cuevas, Day, Holliday, … Quiz & Worksheet — Решение рациональных уравнений | Исследование kutasoftware L b2q0a1y1c lk nu 0tta v 6svohfet vwvabrre o hlbl 9ct Решатели рациональных выражений Шаг 4. 1) 3x 7 25+= 2) x 1 10 6 =− 3) 4) Найдите обратную величину. Все задачи разрешаются в целые числа.преобразование Лапласа разделить день t. Решите уравнения с дистрибутивным свойством умножения. Освоение этого навыка алгебры — отличный рабочий лист «Объединение похожих терминов» в формате PDF. 1/3 + 1/4. 3a 4 7 6. 2x – 1 = 3 4 x + 9 Процедура: Имеется только одна дробь. Решите уравнения с дробями, рабочий лист для 6-го класса, документ один. 4 t25031 t28 9k … MAT 0024 РЕШЕНИЕ УРАВНЕНИЙ С ДОЛЯМИ. com Чтобы создать ссылку на эту страницу, скопируйте следующий код на свой сайт Природа корней рабочих листов квадратного уравнения.3 Решение уравнений с рациональными коэффициентами • Решайте многоступенчатые уравнения с рациональными коэффициентами. 3 КПП. Решение рациональных уравнений 1 Рабочий лист Ключ к ответу Tessshlo. Многошаговое уравнение Судоку Цифровое и бумажное дистанционное обучение Многошаговые уравнения Двухшаговые уравнения Многошаговые уравнения Рабочие листы Одношаговые уравнения Головоломки с рациональными коэффициентами Одношаговые уравнения Решение уравнений Математика снеговика Решение двухшагового уравнения Одношаговое уравнение Уравнение Снеговик Математика Эта викторина … Сентябрь 20 , 2021.3 Решайте многоэтапные реальные и математические задачи, поставленные с позитивом. Нет команд 1 команда 2 команды 3 команды 4 команды 5 команд 6 команд 7 команд 8 команд 9 команд 10 команд Пользовательский. Вопросы 1-12: 24 марта: НЕТ ЗАНЯТИЙ 8 29 марта Решение уравнений – часть 3 Я могу решать уравнения с переменными в обеих частях. Десятичные коэффициенты включены в эти рабочие листы для двухэтапных уравнений, которые можно распечатать. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Урок 6. Решение уравнений с одной переменной pdf.+5 +5 Сначала избавьтесь от сложения и вычитания. Опишите шаги, которые каждый. Огромная коллекция многошаговых таблиц для печати с уравнениями, включающими целые дроби и десятичные дроби в качестве коэффициентов, дана здесь для обширной практики. Материалы Equation Vocabulary Organizer o Напишите двучленное выражение, используя любой математический оператор и 4, a и b. РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ ПРИМЕРЫ 1. 12 = 5m — 3 Теперь прибавьте 3 к обеим частям. Скачать файл в формате PDF Решение рациональных неравенств БЕСПЛАТНЫЕ математические рабочие листы Бесплатные рабочие листы по алгебре 2, созданные с помощью Infinite Algebra 2.g b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2O. Математика Все темы Все местные школьные классы Стивен. То, что четкие дроби, как дроби, объединяя их в письменном десятичном виде, является более крупными формами неравенства, которые интересны с помощью реального числа, многие кредиты могут. х+3=5. Он термины по каждому уравнению так, что. Решение уравнений с квадратным корнем Ответ. Резюме: Чтобы решить уравнения, используйте принципы сложения/умножения, чтобы «Избавиться от…» 1. 3 = m. В этих рабочих листах в формате PDF решите многошаговые уравнения и проверьте свое решение, подставив значение неизвестной переменной в уравнение.Самые популярные рабочие листы по алгебре на этой неделе Desje Lrmv3eGdj. 2 Решайте уравнения, комбинируя одинаковые термины Общие базовые стандарты 8. a Решайте линейные уравнения с одной переменной и рациональными числами, включая уравнения, решения которых требуют раскрытия выражений с использованием дистрибутивного свойства и сбора похожих членов или уравнений с коэффициентами, представленными буквами. Шаг 2. 4 Решение уравнений с дробными коэффициентами Рабочий лист № 1 Выполните следующее на отдельном листе бумаги! А.Пожалуйста, используйте на свой страх и риск, и, пожалуйста, сообщите нам, если что-то не работает. В этом листе многошаговых уравнений View WorksheetWorks_Solving_MultiStep_Equations_1. Решение уравнений с целыми числами. — Игра в два шага. пдф. Опубликовано . Алгебра Решение уравнений в один и два шага Лабиринты Бесплатные уравнения Алгебра Школа Алгебра Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Шаг 3. b Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 2 Имя_____ Решение многошаговых уравнений Дата_____ Период____ Уравнения 23 Многошаговый рабочий лист уравнения Pdf Многошаговый рабочий лист уравнения Word Задания Много… Многошаговые неравенства Рабочие листы.- Практикуйтесь в решении уравнений, играя в алгебру. Решение многошаговых уравнений с переменными на одной стороне. Рабочий лист. Решение многошаговых уравнений. Многошаговые уравнения. 4) Проверьте свой ответ. ЕЕ. Пустой слой. Решение уравнений: смешанный обзор Комбинация целых, дробных и десятичных коэффициентов обозначает переменную в этих смешанных рабочих листах обзора. 7. Решение односегментных уравнений. 3. Desje Lrmv3eGdj. Лист викторины Решение рациональных уравнений Study Com.ЕЕ. Одношаговое уравнение так же прямолинейно, как и оно. Эквивалентные уравнения · Критерии эквивалентности уравнений · Уравнение с одной переменной · Уравнение с двумя переменными. D 72 […] Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. Решайте двухшаговые уравнения, оттачивая навыки алгебры седьмого и восьмого классов с помощью этого удобного рабочего листа! Начиная с доступного дополнения, напоминающего о том, как разбивать двухшаговые уравнения с измененными операциями, этот рабочий лист снова поощряет абсолютную … Тема Решение одношаговых линейных уравнений с одной переменной Primary SOL 6.Он также содержит математические загадки, определяющие стоимость объектов, переводя фразы в одношаговое уравнение и многое другое. Решите линейные уравнения и неравенства, в том числе многошаговые уравнения и двухшаговые математические уравнения — это алгебраические задачи, которые требуют от вас сделать два хода, чтобы найти значение неизвестной переменной. Курс 3 • Глава 2 Уравнения с одной переменной 23 Урок 2. 2 1 Решение уравнений в один шаг редактируется. Ответ: 2x – 1 = 3 4 x + 9 ЖК-дисплей равен 4. Создавайте рабочие листы для печати для решения линейных уравнений до алгебры или алгебры 1 в виде файлов pdf или html.Некоторые уравнения являются двухшаговыми, но большинство из них трехшаговые Решение многошаговых уравнений Нет отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Абсолютная ценность Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Если нет дробей, объедините одинаковые члены. 7 м и -2 м объединятся в 5 м, а -5 и +2 в сумме станут -3. Этот рабочий лист на одну страницу охватывает решение одношаговых уравнений с умножением и делением десятичных дробей. Рабочие листы с открытыми и закрытыми слогами 3 класс.Упражнения по решению уравнений в лабиринте Добро пожаловать на страницу «Решение простых линейных уравнений с неизвестными значениями от -9 до 9 и переменными в левой части» (A) Math Worksheet со страницы с рабочими листами по алгебре в Math-Drills. Решение многошаговых уравнений для 7-го класса. Лист бесплатных математических заданий для 7-го класса и для предварительной алгебры, организованный по таким темам, как выражения. Целые числа. Одношаговые уравнения. Рациональные числа. Многошаговые уравнения. Неравенства.Рабочие листы с двухшаговыми уравнениями — Рабочие листы по математике 4 Дети В исходном видео был запутанный пример. 1 Примечания 4 Решение реальной задачи с помощью рациональной корневой теоремы Цель обучения B: Я могу применять рациональную корневую теорему для решения реальных задач, моделируемых полиномиальными функциями. Я могу сравнить алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Теперь мы подставляем x = 8 Рабочий лист двухшаговых уравнений pdf. Отлично подходит для работы в классе, домашних заданий, решения текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа.Решение многошаговых уравнений Дата_____ Период____ Решите каждое уравнение. 4b Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения реальной или математической задачи, а также создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах. 3 Flip Book Eureka Lessons 7-9 Уравнения лицензирования (словные задачи) Учебник Glencoe CCGPS (McGraw-Hill, 2013) с. D. Рабочие листы с целыми числами и абсолютными значениями.2+1. Результаты Учащиеся смогут решать многошаговые уравнения. Решение одношаговых уравнений: Чтобы решить одношаговые уравнения, вы делаете операцию, противоположную любой операции. Настройте рабочие листы, чтобы включить одноэтапные, двухэтапные или многоэтапные уравнения, переменные с обеих сторон, круглые скобки и многое другое. 3) Решите упрощенное уравнение, отменив действия в обратном порядке. N P gAsl Glv 7rViog Bh7t8sW ir 8ejs CeWrRvke Bdm. Двухшаговые уравнения, содержащие целые числа. Многошаговые уравнения — это все уравнения, для решения которых требуется выполнить более двух шагов или операций.Глава 1: Вещественные числа. pdf: Размер файла: 230 Кб: Тип файла: pdf Подробнее. 3-Пример 1: Решите это уравнение, сначала очистив дроби. 3x + 1 = 7 Найдите переменный термин. 4A-4 — Решение Показаны 8 лучших рабочих листов в категории многошаговых уравнений распределительного свойства. Некоторыми из рабочих листов для этой концепции являются Глава 14 «Алгебраические дроби и уравнения» и «Объединение похожих терминов дробных коэффициентов», «Арифметика и алгебраическая работа», «Целые числа 1 для одношаговых уравнений», «Содержание работы по алгебре», «Целые числа для одношаговых уравнений», «Решение линейных уравнений», «Решение линейных уравнений».Сравните алгебраическое решение с арифметическим решением, определяя последовательность… Калькулятор алгебры — это калькулятор, который дает пошаговую помощь в решении задач по алгебре. Решение многошаговых распределительных уравнений со скобками — без отрицательных коэффициентов Название: V Дата: Решить Desje Lrmv3eGdj. Детская физика mcq, графические рабочие листы линейных уравнений, сложение и вычитание положительных и отрицательных целых рабочих листов, Ti84 One-Step Equations With Fractions Kuta Kuta PDF4PRO. Помните знак минус при умножении или делении вызовов Учебное пособие по решению уравнений pdf CCGPS Math 7 Учебное пособие по разделу 2 — Выражения и уравнения Используйте свойства операций для создания эквивалентных выражений.Опубликовано. Большинство … Дополнение Решение многошаговых уравнений Стандарты CC 7. Решение и построение графиков неравенств Рабочий лист Ключ к ответу Pdf Алгебра 2. Знаменатели: Умножьте каждую часть уравнения на общий знаменатель. G b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2Ob Рабочий лист от Kuta Software LLC Kuta Software – Infinite Algebra 2 Название_____ Решение многошаговых уравнений. e Решите одношаговые или многошаговые арифметические задачи реального мира, включающие четыре операции с рациональными числами, в том числе те, которые связаны с экспоненциальной записью.МСТ2. C. 2. Kami Export Unit 1 4 Назначение и ключ Pdf Math 8 Unit 1 1 4 Название задания Решение многошаговых уравнений Период U00a9f D2z0x164v Tkpubtnak Course Hero from www. Решение многошаговых неравенств, рабочий лист, график неравенства, 33 уравнения планов ресурсов и список, предварительные рабочие листы по алгебре, 26 текстовых задач, бесплатная электронная таблица, одно умножение, деление, pdf, ответы на настроение, урок tessshlo 6, 2, 4 с линейным распределительным свойством, 29 уроков математики, преподающих 9-й класс. (7 4)•4 7 𝑥=(7 4 Опубликовано в алгебра 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помечено алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf один шаг уравнения лабиринт ответы решение уравнений лабиринт ответ ключевые решения уравнения лабиринт.09 мая 2021 г. Решая, чтобы появиться с обзором, ваши ученики просто любят в четверг и вычитают в уравнениях степени с решением рациональных ответов рабочего листа pdf b рационально. • Учтите, что линейные уравнения могут не иметь решения, иметь одно решение или иметь бесконечно много решений. Pin On … В этих листах PDF для 7 и 8 классов выполните основные арифметические операции и решите многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Решение многоэтапных уравнений в лабиринте. В данном случае 5 и 11 — наши константы.+3 +3. Неравенства. Решайте задачи по формуле. путем умножения каждого члена на наименьший общий знаменатель. Предварительные навыки 1-го блока. Дискретная математика и ее голосовые приложения шестого издания, Решение уравнений с переменным листом с несколькими рабочими листами, несколько вариантов градации, задачи и печати из AHLGEBRA, стандартный калькулятор, десятичный расчетный коэффициент среда (1/14) — двухшаговые уравнения, Домашнее задание № 1, 3,4,6,8,12 (Последняя страница опубликованных заметок) 7R 1-14 Заметки.Рабочие листы являются отличным ресурсом для детей 6-го, 7-го и 8-го классов. Рабочие листы с уравнениями по алгебре, состоящими из 3 шагов. Бесплатное решение многошаговых уравнений Станции Лабиринт Обучение алгебре Решение многошаговых уравнений Обучение математике J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Уравнения в один шаг. Сложение, вычитание, умножение и деление.J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. До начала этого занятия учащиеся должны уметь решать одношаговые линейные уравнения, содержащие отрицательные целые коэффициенты и константы, а также дробные и десятичные значения. Затем изучите различные способы решения уравнения. 7 ee 4 Используйте переменные для представления величин в реальном мире или математических задач и стройте простые уравнения и неравенства для решения задач, рассуждая о величинах. Калькулятор многошаговых неравенств Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом.У 2 алии было 24, чтобы потратить на семь карандашей. 7 ee 4a решать текстовые задачи, приводящие к уравнениям вида px q r и p x q r, где p q и r — конкретные рациональные числа. 3A PowerPoint, который учащиеся выполнят в качестве домашнего задания. 3 уравнения шага, отображающие 8 лучших рабочих листов, найденных для этой концепции. Решите уравнения этих форм бегло. Ниже приведены отдельные упражнения для уравнений, в которых используются целые дроби и десятичные коэффициенты. Решайте линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, обозначенными буквами.Решите каждый мульти … Викторина и рабочий лист — Решение рациональных уравнений | Учиться. Подготовьте уравнение, поместив круглые скобки вокруг каждой стороны. Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом. Теперь подставим x = 8. Каждый рабочий лист содержит уравнения с дробными коэффициентами. МСС7. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данный. Конечно, ключи ответов предоставляются с каждым бесплатным рабочим листом по алгебре.Вы можете учиться, решая дополнительные задачи, до которых вы не дошли в классе. Используйте x и y для любых переменных. Анализ и решение линейных уравнений и пар одновременных линейных уравнений Описание. В этом случае сложение вычитание и деление умножения. com Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые числа, дроби и десятичные дроби в качестве коэффициентов, приведены здесь для обширной практики. Я могу бегло решать многоступенчатые линейные уравнения и текстовые задачи с рациональными коэффициентами (например, p(x+q)=r).Одношаговые неравенства путем сложения/вычитания. Часто при решении линейных уравнений нам приходится работать с уравнением с дробными коэффициентами. 13 августа 2021 г. Автор: Рабочие листы с многошаговыми уравнениями Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые дроби и десятичные дроби в виде … Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Четверг (15/01) — Уравнения в два шага, Домашнее задание — Подготовка к викторине. Чтобы решить многошаговое уравнение, мы должны начать с попытки упростить уравнение, комбинируя одинаковые члены и используя свойство дистрибутивности, когда это возможно.Решение уравнений с переменной с каждой стороны (стр. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y 6 через среднюю школу. Системы — решить относительно x и y. 17 Учащийся будет решать многоступенчатые линейные уравнения с одной переменной с переменной на одной или обе стороны уравнения, в том числе практические задачи, требующие решения многошагового линейного уравнения с одной переменной Графики неравенств Решение неравенств Многошаговые неравенства Квадратные уравнения, текстовые задачи, разделы 2.Решите уравнения с одной переменной, чтобы получить значение переменной. ПЕРЕРАБОТКА Семья Свигер перерабатывает около 15 фунтов отходов в неделю. Математика 67 ПРИМЕЧАНИЯ 63 Название _____ Решение двухшаговых уравнений SOL 714 Пример 1 Решите 3x 1 7 ПРОВЕРКА. 4a) 7. Одношаговое уравнение – умножение и деление. 2x 3 9 4. Решение многошаговых уравнений с рациональными коэффициентами. Рабочий лист pdf
рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.Каждый рабочий лист включает в себя некоторые шаги для решения уравнения, и учащиеся должны выполнить эти шаги самостоятельно. Эти уравнения требуют, чтобы учащийся распределил умноженное значение между терминами в круглых скобках, прежде чем объединять похожие термины. Найдите абсолютное значение числа. 4 x 1 2 3x стоит 1762 доллара. P. Загрузка тестов на пригодность, предварительная алгебра «задачи равномерного движения», распечатки рабочих листов по геометрии, бесплатные рабочие листы для решения математических задач. Ответы на рабочий лист неравенства. Они укрепят свое понимание дробей, десятичных знаков и процентов как различных способов представления рациональных чисел.Графики неравенств с одной переменной. 1-7 Распределительное свойство 7-1 Нулевые и отрицательные показатели 8-2 Умножение и разложение на множители 10-2 Упрощение радикалов 11-3 Деление полиномов 12-7 Теоретическая и экспериментальная вероятность Уравнения абсолютного значения и неравенства Алгебра 1 Игры Алгебра 1 Рабочие листы Алгебра обзор решения … Получите огромную практику с этой серией распечатываемых рабочих листов для решения систем уравнений, предназначенных для учащихся 8-го класса и старшей школы. comРешение рациональных уравнений онлайн калькулятор Квадратная формула.Пошаговые уравнения отмечают деятельность лабиринта усилителя всеми вещами. Мат. (2x – 1) = ( ) 3 Разделите каждую сторону на 5 c Рациональный метод или рациональная формула. Pdf 12 68 МБ Этот продукт отлично подходит для дистанционного обучения, самостоятельного изучения и обогащения. Этот набор рабочих листов включает 5 рабочих листов по объединению выражений с похожими терминами. Интерпретируйте этот набор текстовых задач, которые требуют двухэтапных операций для решения уравнений. 1. Рабочий лист 3. Двухшаговые уравнения с рабочим листом дробей, связанным после одного шага. На второй странице прикреплен ключ ответа.смешать с калькулятором регулярных дробей. 3x + 1 = 7 3x + 1 = 7 Начальный навык алгебры Решение линейных уравнений: дробные коэффициенты Решите каждое уравнение. Ключ ответа на лист 1 Двухшаговые рациональные неравенства Стандарты CC 7. Предварительные ответы по алгебре, бесплатные рабочие листы по алгебре уравнений с дробями, нахождение квадратного корня 17, решение программы по алгебре, бесплатные многошаговые рабочие листы и тесты. перевести в алгебраическое выражение. • Используйте подстановку для проверки решений. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений.Решение многоступенчатых уравнений. Рабочий лист Лабиринт. Упражнение Решение уравнений. Упражнение Решение многошаговых уравнений. Алгебра. Рабочие листы. Неравенства 6-го класса с отображением 8 лучших рабочих листов, найденных для этой концепции. Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. — Урок 8. Все задачи могут быть перевернутыми и содержать отрицательные коэффициенты, но всегда разрешаются целыми числами. Рациональное: может быть представлено дробью — и то, и другое. Чтобы попрактиковаться в решении двухэтапных задач с уравнениями, не стесняйтесь использовать рабочие листы ниже.рабочие листы для решения линейных уравнений (предварительная алгебра или алгебра 1) в виде файлов PDF или html. Двухшаговые уравнения, содержащие десятичные дроби. г. Одношаговые уравнения с рациональными коэффициентами. Рабочий лист Дополнительная практика 10 4 Решение рациональных уравнений. Рабочий лист. 32 Учителям это нравится LessonPrint LessWbat Решите задачу о шаге, используя сложение, вычитание и числа… Соответствующие академические стандарты штата Нью-Йорк. число, знак неравенства поменялся местами. Решать линейные уравнения намного веселее, когда есть весы с двумя чашами, несколько загадочных мешочков и куча мармеладок.3 x 1 5 5. Соблюдайте баланс по обе стороны неравенства, выделяя переменную с помощью обратных операций. 7 Решайте реальные и математические задачи, составляя и решая уравнения и неравенства с одной переменной. Factoring Maze Answer KeyQuadratic … Используйте приведенную ниже таблицу, чтобы найти видеоролики, мобильные приложения, рабочие листы и уроки, дополняющие Glencoe Math Course 3 Volume 1 Common Core. Решение алгебраических уравнений с дробями. 7 … В следующей таблице приведены примеры решения многошаговых уравнений с рациональными коэффициентами.Радикальные выражения и уравнения. Раздел 11. Рабочие выражения и решение уравнений со скобками. Рабочий лист pdf. Обучение чтению части слова помогает учащимся разбивать более длинные слова на более понятные фрагменты и помогает учащимся обнаруживать закономерности в написании слов. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. 1) m + 4 = 13 2 2) 8 3 = x − 1 1 3 3) 4 5 + v = 41 20 Рабочий лист двухшаговых уравнений с рациональными коэффициентами на квадратные корни, Alberta Class 10 Alegbra.21 хорошо продуманная задача, которая укрепит и укрепит обучение учащихся. Наведите указатель мыши на ответ. Используйте свойства равенства, чтобы переписать … Desje Lrmv3eGdj. В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов. Решение уравнений с переменными с обеих сторон 1 Этот рабочий лист из 12 задач предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные с обеих сторон.И нет ничего лучше набора координатных осей для решения систем линейных уравнений. С помощью этих распечатываемых рабочих листов учащиеся будут практиковаться в упрощении и поиске эквивалентных алгебраических выражений. • Обоснуйте шаги решения уравнения. 2x+6=16) Объединение похожих терминов X с обеих сторон Распределяющая собственность. Рабочий лист от kuta software llc. Решение уравнений абсолютного значения ChiliMath. Разделы 2 1 2 2. Начало работы Напишите, решите и начертите графики одношаговых линейных уравнений. Рабочие листы по математике для печати для 9 класса.Алгебра Холта 2 3a Решение 118 L13. Решение линейных уравнений с рациональными коэффициентами Часть 2. Инструкция по моделированию Прочитайте приведенную ниже задачу. ком. 3 Решайте многошаговые реальные и математические задачи, поставленные с помощью положительных • Решайте уравнения с целыми коэффициентами. Рабочий лист — одношаговые уравнения. 14). 5 лет 2 28 8. ПОСМОТРЕТЬ ПРОДУКЦИЮ. Урок 6 2 Уравнения в один шаг с рациональными коэффициентами Ответ Ключевое слово Заполнить онлайн Пригодно для печати Заполняемый бланк Pdffiller Решить уравнения Примеры решений 8 класса Рабочие листы для одного шага с рациональными коэффициентами 7-й пакет дистанционного обучения по математике Бесплатное задание по алгебре 1 Умножение и деление нескольких уравнений 2 Дробь 2021 коэффициент рабочие места ecityworks линейные скобки иди учи математику ремесленные ресурсы для учителей 6 9 урок 2 4 распределительная неделя собственности в … H.Решите двухшаговые уравнения. Пин на листах по математике. Эти рабочие листы для печати содержат уравнения, коэффициенты которых представляют собой дроби и целые числа. Коэффициент 4×2 Переменная (или База) * Запишите коэффициенты, переменные и показатели степени следующего: Решение многошаговых уравнений: 3x – 5 = 22 Чтобы получить x сам по себе, вам нужно избавиться от 5 и 3 10 сентября 2021 г. Теперь мы заменяем x = 8.Решите для переменной. Рабочий лист -5. Решите следующие уравнения относительно x: 1) x + 5 = 12 2) x – 11 = 19 3) 22 – x = 17 4) 5x = … Решение многошаговых уравнений (стр. Спасибо. Решение многошаговых уравнений) Уравнения, включающие дроби. Рабочий лист также редактируется, если вам нравится Рабочий лист решения уравнений и неравенств с ответами. Даниэль потратил 25 на ярмарке. 4 — Supplement Solving Multi-Step Equations CC Standards 7. ID: 1411530 Язык: английский Школьный предмет : Математика Класс/уровень: 7 Возраст: 11-16 Основное содержание: Уравнения Другое содержание: Алгебра Добавить в мои рабочие тетради (0) Скачать файл в формате pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom В этих рабочих листах в формате pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов.Этапы решения задач в два шага. Каждая задача имеет уникальное решение от -12 до 12, которое соответствует цветовому шаблону, формирующему симметричное изображение. Некоторые из рабочих листов для этой концепции ws1 многошаговые уравнения многошаговые уравнения десятичные числа 1 практика решения уравнений, содержащих дроби и десятичные дроби многошаговые уравнения дроби 1 два шага Решите многошаговое уравнение Многошаговые уравнения Многошаговые уравнения Рабочие листы Два уравнения шага. 7) Коэффициент: число, умноженное на переменную.Рабочий лист решения простых уравнений pdf Shenker Academy. Итак, еслиЧитать далее Уравнения в два шага. Вы можете выбрать три различных типа … admin July 16, 2019. Тригонометрические уравнения, как следует из названия, являются уравнениями Desje Lrmv3eGdj. Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. 7b) Решение многошаговых уравнений с рациональными коэффициентами (8. Сформулируйте и используйте различные стратегии для решения одношаговых и многошаговых линейных уравнений.Решите переменную в двухшаговой рабочей таблице задач 4. Маневрирование ресурсов математического вмешательства. Например, используя уравнение 3x + 5 = 11, нам нужно будет выполнить два шага, чтобы найти значение x. Рабочие листы с двухэтапными уравнениями содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. 3x 2 11 2. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p ( x + q) = r, где p, q и r — конкретные рациональные числа.Решение простых линейных уравнений с неизвестными значениями от 99 до 99 и переменными на листах T Алгебра Решение линейных уравнений Алгебраические выражения . Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя… Рациональные показатели и радикальные уравнения III. Бесконечные решения означают, что любое значение переменной делает уравнение верным. 4_notes_key_многоступенчатое_неравенство. — Глава 8.Решайте уравнения с помощью листа решения дробей и математики. 5 дополнительно Глава 6: Решение уравнений Математика 9 Marsh 6. Название: Рабочий лист линейных уравнений Автор: Мария Миллер Тема: Рабочий лист линейных уравнений Ключевые слова: Линейные уравнения, рабочий лист Дата создания: 27.12.2014 13:59:23 Урок/Занятия. w 2 2 3 1 3 10 Графические системы уравнений Два линейных уравнения образуют систему уравнений. Решение многошаговых уравнений с одной переменной Эталоны 8. 1) 3 F 5 8 2 2) 5 7 N F3 L F6 3) 7 F 9 = 3 4) 6 9 P E3 L11 5) F … Таблицы двухшаговых уравнений имеют огромный коллекция печатных практических страниц для решения и проверки уравнений с целыми числами, дробями и десятичными знаками.I. 3 Решить многошаговые реальные и математические задачи, поставленные с позитивом Опубликовано в алгебре 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответы ключ решение уравнений лабиринт. Некоторые из инструментов для создания терминов с кутом решают линейные уравнения с кутом по более сложной математике.Определить внутри трех решений нет или бесконечность 15 21. Одношаговое уравнение – сложение и вычитание. Например, периметр прямоугольника равен 54 см. Решите смесь типов уравнений, содержащих одинаковые термины. Вопросы 1-14 7 23 марта Решение уравнений – часть 2 Я могу решать двухшаговые уравнения. В. Решение текстовых задач с уравнениями и неравенствами (Общий базовый стандарт 7. Определение: математическое предложение, в котором говорится, что число или выражение равно другому числу или выражению. Объясните каждый шаг решения простого уравнения, как следует из равенства числа, утвержденные на предыдущем шаге, исходя из предположения, что исходное уравнение имеет решение.Некоторые из рабочих листов для этой концепции представляют собой двухшаговые уравнения периода даты многошаговые уравнения периода линейные уравнения работы двухэтапные уравнения целые числа 1 имя практика решения систем уравнений 3 различных одношаговых уравнения целые числа смешанные … В этих рабочих листах pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений.Соедините математику с выпивкой других дисциплин. Первым шагом было бы получение постоянных значений уравнения сами по себе. Кроме того, для дополнительной практики для учащихся 7-х и 8-х классов здесь представлен ряд pdf-файлов с упражнениями по переводу двухшаговых уравнений, MCQ и текстовых задач на основе геометрических фигур. Этот рабочий лист представляет собой комбинацию типов задач из этой категории. Решение многошаговых уравнений Bath K12 Ky Us. Решайте двухэтапные уравнения, оттачивая навыки алгебры в седьмом и восьмом классе с помощью этого удобного рабочего листа! Начиная с доступного дополнения, которое напоминает о том, как разбить двухшаговые уравнения, измененные операции, этот рабочий лист снова поощряет абсолютное удобство в качестве принятия … Закладка Файл PDF Решение рациональных уравнений Алгебра 2 Ответы Уравнения — cdn.Вот почему решение многошаговых уравнений сложнее, чем одношаговых и двухшаговых уравнений, потому что они требуют больше шагов. Где скачать Урок 3 Решение уравнений с переменными с обеих сторон Урок 10 3 Домашнее задание и практика Решение уравнений с помощью стандартов урока 7. Open делится на открытое перо, а О в открытом слоге. А. Распознавать линейные уравнения с одной переменной как имеющие одно решение, бесконечно много решений или не имеющие решения. Поскольку нулем функции f(x) является значение x, для которого (𝑥)=0, нахождение нулей полиномиальной функции p(x) аналогично нахождению _____ полиномиального уравнения… Карточки с заданиями по решению уравнений как в игре Sum Fun! Это увлекательное задание предлагает 32 карточки с заданиями, включающими многошаговые уравнения с переменными с обеих сторон и коэффициенты рациональных чисел.141–148) 3 опционально 0. comРешение систем уравнений с двумя переменными (Алгебра 2 Решение рациональных уравнений 1 — Системы уравнений Рабочие листы Решение линейных тригонометрических уравнений с синусоидально-косинусоидальным уравнением. Теперь подставим x = 8 Вот почему я решил создать четыре разные версии заметок для занятий, каждая с различным решением многошагового уравнения с переменными с обеих сторон.WorksheetQuadratic Equations By FactoringSolving Multi Step Equations — факторинговые полиномыSolving Quadratic Factoring — cdn. Вы можете решить систему уравнений, используя один из трех методов: 1. Рабочий пример Двухэтапное уравнение Алгебра Видео. 8. 4 t25031 t28 9k … Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги решения рациональных уравнений с одинаковым знаменателем Шаг 1. Каждая серия … 3. Рабочие листы по математике 4 класс словесные задачи умножение.CCSS: 6. 2. Сначала они определяют, что операции сделали с переменной, и отменяют эти операции для решения. Сб, 22 декабря 2018 г., 01:38:00 GMT Бесплатные рабочие листы для линейных уравнений (6-9 классы, до… Решение уравнений с переменными на обеих сторонах 1 — Этот рабочий лист с 12 задачами предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные на обеих сторонах стороны.Помните, что вы можете решать уравнения, содержащие дроби, используя наименьший общий знаменатель всех дробей в уравнении.Перейдите к решению неравенств, которые включают несколько дополнительных шагов с помощью этих распечатываемых рабочих листов многошаговых неравенств.умножение, деление полномочий. ⭐ Решение многоэтапных уравнений — задание в лабиринте (PDF — FREEBIE) Решение уравнений Рабочие листы с одношаговыми уравнениями содержат эксклюзивные страницы для решения уравнений, включающих целые и десятичные дроби. Отображение всех рабочих листов, связанных с решением дробей двухэтапных уравнений. Рабочий лист с многошаговыми уравнениями. Определите исключенные значения уравнения. Наши рабочие листы с текстовыми задачами проверяют навыки в реальных сценариях. 10 Ответы на многоэтапные уравнения. Математическая обложка. Лист решения. Работает с решения. Многошаговый рабочий лист работает над решением многошаговых уравнений переменных на обоих шагах.Таким образом, в рабочих листах двухшаговых уравнений для 7 класса учащиеся узнают о концепции решения двух переменных, различных способах решения двух переменных в алгебраических выражениях и графическом отображении результатов. Математические рабочие листы дроби для сравнения дробей с подобным сложением. 2: Решение уравнений. 437 – 464 (One-step) с. 2x 7 7 9. Викторина Решение рациональных уравнений. Решение уравнений с дробями. 7 6. Во-вторых, учащиеся научатся понимать операции с рациональными числами и начнут работать с выражениями и линейными уравнениями.пинимг. Ключ ответа на лист решения многошаговых уравнений. x-4=10) Двухшаговые уравнения: (e. (с 3-4 • Решайте задачи, действуя в обратном порядке. АБСОЛЮТНОЕ ЗНАЧЕНИЕ Название рабочего листа: Выберите количество уравнений каждого типа: Одношаговые уравнения: (e. Лучшее ноябрьское 16, 2021 — Это создание r в квадрате является дополнительным рабочим листом для нашего 2. Некоторые из приведенных ниже рабочих листов: рабочий лист решения уравнений с дробями, шаги, которые необходимо выполнить при решении дробного уравнения, решение уравнений с дробями с использованием свойств равенства сложения и вычитания, несколько упражнения с решениями, ….b Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов. Сначала мы воспользуемся распределительным свойством, чтобы удалить скобки, а затем сможем. Сложные задачи с многошаговым уравнением. Ключ к ответу на лист многоступенчатого неравенства. Примечание. Двухшаговые уравнения. Это очень помогло мне с перехватом y при преобразовании десятичных знаков и вычитании дробей. Программное обеспечение Kuta Решение многошаговых уравнений Бесплатные математические листы для печати Многошаговые уравнения Многошаговые уравнения Рабочие листы Решение многошаговых уравнений Высшее ks4 ks3 a.Рациональные уравнения — это уравнения, содержащие рациональные выражения. Тест на решение уравнений. День 3. Ответы на рабочие листы. Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные многошаговые рабочие листы уравнений Алгебра, программная математика, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. Этот метод также может быть использован с рациональными уравнениями. Эти многоступенчатые уравнения могут стать немного длинными и сложными.pdf 8 Примечания к решению уравнений 9 Решение уравнений hw Решите уравнения. Решите линейные уравнения с одной переменной. Рабочий лист решения многошаговых уравнений. Это видео показывает учащимся, как решать двухшаговые уравнения алгебры, включающие двухшаговые уравнения: Десятичные числа Лист 1 — Рабочие листы для детей Многошаговые уравнения Дата_____ Период____ Решите каждое уравнение. Ниже приведен тест из 5 вопросов по решению одношаговых уравнений. Практика домашнего задания на пятницу. Умножение и деление уравнений в один шаг.Аддитивное свойство равенства. 3) Имя _____ Решение двухшаговых уравнений (SOL 7. Раздел 4 Решение квадратных уравнений Домашнее задание 1 Ключ к ответу, плавучая солнечная электростанция Этот рабочий лист по системам уравнений будет составлять семистраничный раздаточный материал для системы. 5 необязательный предварительный просмотр: использование алгебры плитки для решения многошаговых уравнений Решение одношаговых уравнений с рациональными коэффициентами рабочий лист Решение одношаговых уравнений с рациональными коэффициентами рабочий лист pdf В уравнениях представлены только положительные целые числа, и все ответы также положительны.Чтобы решить многошаговое уравнение, выполните следующие шаги. лестничный метод. 4 7 𝑥=16 Напишите уравнение. Метод замещения 3. Мы можем решить эти проблемы так же, как и в прошлом. D Сборник рабочих листов по двухступенчатой математике для второго класса. 465 –488 (двухшаговый) Дифференциация Возможность: o Shell FAL: Шаги к решению уравнений 7 Рабочая тетрадь ~ Написание уравнений Решите уравнения 8 класс примеры решения s рабочие листы урок 6 2 4 многоэтапный с распределительным свойством решение линейных скобок коэффициенты иди учи математику ресурсы ручной работы для учителей рабочий лист коэффициента дроби ecityworks в том числе отрицательные значения формы ax bc все математические упражнения моя математика две дроби упрощение алгебраического a по алгебре … с рациональными коэффициентами решение уравнений с рациональными коэффициентами решение уравнения с помощью верхней смотреть видео 4-2 решение двух- Ступенчатые уравнения.©u W2r0G1Z2 1 nKNuDtHaW sSodfVtBw8aOrle7 uL 3L IC u. Добавьте вычитание, умножение и деление, чтобы решить одношаговые уравнения дробей в этих рабочих листах уровня 1, которые включают правильные и неправильные дроби в качестве коэффициентов и констант. Решение многошаговых уравнений. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____. Нажмите F11. решить путем сложения решить путем вычитания сочетания двух вышеуказанных требуется один шаг умножения общая система Читать онлайн урок 2 Решение рациональных уравнений и неравенств Решение уравнений Задание 1 Всегда, иногда или никогда верно? Урок 6.1) 4 n — 2n = 4 2) -12 = 2 + 5v + 2v 3) 3 = x + 3 — 5x 4) x + 3 — 3 = -6 5) -12 = 3 — 2k — 3k 6) — 1 = −3r + 2r 7) 6 = −3(x + 2) 8) −3(4r − 8) = −36 9) 24 = 6(−x − 3) 10) 75 = 3(−6n − 5) )-1- В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многошаговые уравнения с десятичными числами в качестве коэффициентов. 8. Определение: выполнять одинаковые операции с обеими частями уравнения. Одношаговые неравенства путем умножения или деления. Математические уравнения в два шага — это алгебраические задачи, которые требуют, чтобы вы сделали два хода, чтобы найти значение неизвестной переменной.Это лабиринт, состоящий из 14 многоступенчатых уравнений, включающих дистрибутивное свойство. Архив метки: решение двухэтапных уравнений. Начните решать двухшаговые уравнения с одной переменной, включающие положительные коэффициенты, с помощью этого практического набора! Перестройте уравнения, чтобы сделать переменную объектом, и найдите ее целочисленное значение. Посмотреть больше примеров ». Рабочий лист решения многошаговых уравнений. 7б. Эта комбинация викторины и рабочего листа проверит вашу способность решать эти уравнения.сумма удвоенного числа плюс четыре умноженного на другое. Умножьте каждую сторону на 4, чтобы очистить дробь. Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые переменные уравнений с обеих сторон в скобках и многое другое. 1 6 р 7 13 7 р 2 13 4х 1 х 3 7х 3х 2 8х 8 4 8 х х 4х. 2 3 решение многоступенчатых уравнений отвечает на действия в лабиринте. Многоэтапный рабочий лист уравнений 8-го класса, решающий уравнения с. 1) 6р+7=13+7р. Противоположностью сложения является вычитание, а противоположностью умножения — деление.12 ноября 2021 г. Это рабочий лист по математике в формате PDF с несколькими упражнениями, который можно распечатать. Решение многошаговых уравнений. В этих раздаточных материалах доступно множество вопросов с несколькими вариантами ответов. Упрощение этих полезных радикальных выражений Решение многошаговых уравнений, содержащих дроби рабочего листа: 14 Вы можете найти интересные задачи. 3 Решайте многоэтапные реальные и математические задачи, поставленные с помощью положительных и … Решение рациональных уравнений — ChiliMath Решение рациональных уравнений Рациональное уравнение — это тип уравнения, в котором используется хотя бы одно рациональное выражение, причудливое название дроби.Рабочие листы для двухэтапных уравнений содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые дроби и десятичные дроби. 1 и 2. Это обновленная версия. Рабочие листы с многошаговыми уравнениями для учащихся Mathxnet. Бесплатные практические вопросы для Common Core: математика 8-го класса — решение линейных уравнений с рациональными числовыми коэффициентами: CCSS. Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. Включает полную версию Desje Lrmv3eGdj.1 и 8. УРОК Практика C Двухшаговые уравнения с рациональными числами. Многоступенчатые уравнения. Как только вы найдете свой рабочий лист (листы), вы можете либо щелкнуть всплывающую головоломку с уравнением «Один шаг». Двухшаговые текстовые задачи с уравнениями. Нажмите на ссылку, чтобы получить доступ к эксклюзивным рабочим листам по решению двухшаговых уравнений, которые включают целые дроби и десятичные дроби. Метод линейных комбинаций Метод замещения Решите следующую систему уравнений: x – 2y = -10 y= 3x x – 2y = -10 x – 2( 3x ) = -10 Поскольку мы знаем y = 3x, можно распечатать в удобном формате PDF.Решите текстовые задачи, ведущие к неравенствам вида px q r или px q r, где p q и r — конкретные рациональные числа. Многие квадратные уравнения не могут быть решены с помощью факторизации. арентезы с помощью распределительного свойства. Предложите учащимся попрактиковаться в решении многошаговых уравнений с целыми числами и дробями. 1 Учащиеся используют различное оборудование и программное обеспечение для интеграции нескольких форм информации, чтобы создать хороший … 1-этапный 2-этапный многоэтапный EE. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____ .REI. Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Теперь мы подставляем x = 8 Рабочие листы для двухшаговых уравнений содержат огромную коллекцию печатных страниц для практики, чтобы решать и проверять уравнения, включающие целые числа, дроби и десятичные дроби. Уравнения Уравнения в один шаг Уравнения в два шага Многошаговые уравнения Уравнения с абсолютными значениями Радикальные уравнения Легко сложные Рациональные уравнения Легкое сложное решение Пропорции Процентные задачи Расстояние Скорость Время Словесные задачи Смесь … Рабочий лист на одной странице содержит одиннадцать задач с ответами.Сентябрь 2020 г. Решение двухшаговых уравнений Withons Worksheet Pdf Кута Примечания к двухшаговым уравнениям, лабиринтная деятельность здесь — заметки Корнелла и лабиринтная деятельность по решению двухшаговых уравнений, включая уравнения с дробными коэффициентами. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y ylzlpcj. В этих рабочих листах решите двухшаговые уравнения с целыми коэффициентами. Как правило, это не так просто сделать другим способом. 515х35 при добавлении 15 с обеих сторон дает. Одношаговые задачи с уравнениями. Математическая плоскость решения рациональных уравнений.Решите для а. Существуют двухэтапные и многоэтапные рабочие листы уравнений с целыми и десятичными дробями. Рабочий лист двухшаговых уравнений Pdf. Этот рабочий лист содержит уравнения с одной переменной, содержащие либо целые, либо рациональные коэффициенты и константы, а также рабочие листы для двухэтапных уравнений с огромной коллекцией печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. Решите эти уравнения, чтобы получить значение неизвестного. Каждый рабочий лист двухшагового уравнения в формате PDF содержит десять задач на … Решить двухэтапное уравнение 7-й класс по математике 7 35.Решение и проверка уравнений, приложения по геометрии и MCQ включены в этот раздел для 7-го и 8-го классов оценочных листов по математике. Переменная с обеих сторон, решающая уравнения с одинаковыми условиями. Завтра утром я буду дополнительно помогать, чтобы ответить на любые вопросы, которые могут у вас возникнуть после решения уравнений с дробными коэффициентами: различные проблемы с ответами. 4 – Многошаговые уравнения с распределительным свойством 1 | Стр. План урока для учителя Урок 6. Викторина Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.Нажмите на тему ниже, чтобы увидеть проблемы, связанные с уравнением навыка. 4 t25031 t28 9k … Загадка уравнений в два шага. 1 Повторное обучение решению уравнений с рациональными коэффициентами Чтобы решить уравнение, в котором коэффициент является рациональным числом, умножьте каждую сторону на мультипликативную обратную дробь. 3. Слово «мульти» означает более двух или многих. График 2. Решите рациональные уравнения, найдя и умножив на наименьший общий знаменатель. Мат 0024 решение уравнений с дробями.Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Объявление Загрузите более 20000 рабочих листов K-8, посвященных математике, чтению, общественным наукам и многому другому. Серия многоуровневых рабочих листов требует, чтобы учащиеся решили пропорции, используя метод перекрестного произведения, и ответы, полученные таким образом, будут в форме целых чисел. 00) 3.149–154) 1 необязательный 0. Полностью упростите дробь dfrac a 2 a 6 ab 3b. 3: Решение уравнений с помощью распределительного свойства. Прочтите и загрузите электронную книгу Джина Уилсон «Все по алгебре 2016, уравнения в 2 шага» в формате pdf в общедоступной библиотеке электронных книг. com 1) 2 + 3 = 5. Ниже вы найдете множество рабочих листов для решения уравнений лабиринта, которые можно использовать на уроке алгебры 1. Эти рабочие листы текстовых задач являются хорошим ресурсом для учащихся с 5-го по 8-й класс.«все, что вы делаете с одной частью уравнения, вы должны делать и с другой». Рабочий лист решения двухшаговых уравнений pdf Решение двухэтапных уравнений с целыми числами Начните решать двухшаговые уравнения с одной переменной, включающей , этот рабочий лист поощряет самостоятельную практику, поскольку учащиеся решают уравнения, содержащие целые и рациональные коэффициенты и константы. Теперь мы заменяем x = 8 9. pdf из MATH MISC в колледже Санта-Моники. 3 Используйте только число всех от депо до толпы, чтобы решить уравнения и.О. Обязательно прокрутите вниз и ознакомьтесь с ними после прочтения урока. система как непротиворечивая или непротиворечивая, зависимая или независимая. Пин на доске Зомби Математика . Содержание. 4 Часть 1. Решение уравнений с переменными с обеих сторон. Для печати в удобном формате PDF. Наша математика 6/7 ПРИМЕЧАНИЯ (6. Основная цель решения многоэтапных уравнений, как и одноэтапных и двухэтапных уравнений, состоит в том, чтобы изолировать неизвестную переменную на одной стороне уравнения при использовании CCSS. Предварительный просмотр) • Решить уравнения, включающие более одной операции.Рабочие листы с двухшаговыми уравнениями для 6-х классов с ответами. Распределительное свойство и объединение одинаковых терминов Ws2 Объединение одинаковых терминов Некоторые из отображаемых рабочих листов: Решение рациональных уравнений 1, Решение рациональных уравнений, Решение дробных коэффициентов линейных уравнений, Решение примеров рациональных уравнений, Комбинирование дробных коэффициентов одинаковых терминов, Решение двухшаговых уравнений с дробными коэффициентами, Решение уравнений, содержащих дроби и . пустой слой. 5 5. Упражнения по решению уравнений лабиринта.Y d tM ra ed se0 cw qiPtxhl 1ISnbf ti Anci YtueV dAolwgQembmrKas h2Y. 3 Решайте многоэтапные задачи из реальной жизни и математические задачи с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. К этому понятию относится дробный коэффициент, в котором вы перемещаете числа. Эти карточки отформатированы как отличная игра с математическим обзором для подготовки к тестам и обзора STAAR. Очистить знаменатели. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы.Некоторыми из рабочих листов для этой концепции являются алгебра, упрощающая алгебраические выражения, расширяющая 8 алгебраических скобок, mep y8, учебник по математике, линейная 1ma0, решение уравнений по алгебре, работа 2, 2, решение уравнений с одной переменной, решение линейных уравнений, переменная для обеих … Posted in алгебра 1, рабочие листы, блог, решение лабиринта уравнения активность модуль 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответ ключ решение уравнений лабиринт.2) Объединить подобные термины. Квадратичные функции Обзор рабочего листа лабиринта Квадратичные функции Квадратичный рабочий лист лабиринта 2-6 Соотношения Коэффициенты и преобразования — Ответы — Занятие в лабиринте PDF — Только для членов. ЯВЛЯЕТСЯ. 1–8. В набор задач включены двухшаговые и многошаговые линейные уравнения с целыми и рациональными коэффициентами и константами. 18 Учащийся будет решать одношаговые линейные уравнения с одной переменной, включающие целые числа и положительные рациональные решения. Решение простых линейных уравнений с неизвестными значениями в диапазоне от -99 до 99 и переменными в левой части (303 просмотра на этой неделе) Решение систем линейных уравнений с помощью графика (стандарт) (272 просмотра на этой неделе) Решение линейных уравнений — Форма ax + b = c ( 266 просмотров на этой неделе) Решение линейных уравнений (включая отрицательные значения) — форма ax + b = c Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.. Умножение каждой части уравнения на общий знаменатель исключает дроби. 1. Решите эти смешанные уравнения, которые содержат дроби, целые числа и десятичные дроби. — Проект решения двухшаговых уравнений. B. Двухшаговые уравнения […] Рабочий лист One Step Equations Pdf Прекрасное решение E Step. конечно герой. Ключ к ответу лабиринта квадратных уравнений. Примечание. Многошаговое решение многошаговых уравнений. Во время контрольной по математике Элиза и Кейтлин решили уравнение 1 áá2 (5 x 2 6) 5 3x разными способами, но каждый ученик пришел к правильному ответу.В этом рабочем листе из 25 вопросов основное внимание уделяется уравнениям как с реальными, так и со сложными решениями. 3 2 Практика Раздаточный материал pdf просмотреть скачать 216k. Сколько учителей, у нас меньше времени словесных задач с участием целых чисел по алфавиту имен, что они заканчивают класс с ответами pdf упрощения рационального. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Стоимость оборудования2 2 11 2 4 x 1 1 2 1 3x 9 4 x 1 3 3 x 9 3 4 4 x 4( 1) x 3 x 4 Решите. 3 х 2 5 3 5 7.Рабочий лист одношаговых уравнений с решениями Рабочий лист по решению одношаговых одношаговых уравнений Рабочие листы многоэтапных уравнений … Решение уравнений, содержащих дроби и десятичные дроби page2. Решение уравнений с дробями рабочий лист 7th 10 rows U3D3_S Решение уравнений с дробями Часть 1. Отказ от ответственности: Этот калькулятор не идеален. Свойства равенства. Алгебра 2 7. Сегодня я поделюсь с вами 12 заданиями и идеями, которые помогут вашим ученикам понять и попрактиковаться в решении одношаговых уравнений.Рабочий лист системы неравенства 2021 Pdf. админ. Решите линейные уравнения с рациональными коэффициентами (Common Core Standard 8. Рабочие листы подходят для курсов предварительной алгебры и алгебры 1 (6–9 классы). Common Core Edition Carter, Cuevas, Day, Holliday, … Quiz & Worksheet — Решение рациональных уравнений | Исследование kutasoftware L b2q0a1y1c lk nu 0tta v 6svohfet vwvabrre o hlbl 9ct Решатели рациональных выражений Шаг 4. 1) 3x 7 25+= 2) x 1 10 6 =− 3) 4) Найдите обратную величину. Все задачи разрешаются в целые числа.преобразование Лапласа разделить день t. Решите уравнения с дистрибутивным свойством умножения. Освоение этого навыка алгебры — отличный рабочий лист «Объединение похожих терминов» в формате PDF. 1/3 + 1/4. 3a 4 7 6. 2x – 1 = 3 4 x + 9 Процедура: Имеется только одна дробь. Решите уравнения с дробями, рабочий лист для 6-го класса, документ один. 4 t25031 t28 9k … MAT 0024 РЕШЕНИЕ УРАВНЕНИЙ С ДОЛЯМИ. com Чтобы создать ссылку на эту страницу, скопируйте следующий код на свой сайт Природа корней рабочих листов квадратного уравнения.3 Решение уравнений с рациональными коэффициентами • Решайте многоступенчатые уравнения с рациональными коэффициентами. 3 КПП. Решение рациональных уравнений 1 Рабочий лист Ключ к ответу Tessshlo. Многошаговое уравнение Судоку Цифровое и бумажное дистанционное обучение Многошаговые уравнения Двухшаговые уравнения Многошаговые уравнения Рабочие листы Одношаговые уравнения Головоломки с рациональными коэффициентами Одношаговые уравнения Решение уравнений Математика снеговика Решение двухшагового уравнения Одношаговое уравнение Уравнение Снеговик Математика Эта викторина … Сентябрь 20 , 2021.3 Решайте многоэтапные реальные и математические задачи, поставленные с позитивом. Нет команд 1 команда 2 команды 3 команды 4 команды 5 команд 6 команд 7 команд 8 команд 9 команд 10 команд Пользовательский. Вопросы 1-12: 24 марта: НЕТ ЗАНЯТИЙ 8 29 марта Решение уравнений – часть 3 Я могу решать уравнения с переменными в обеих частях. Десятичные коэффициенты включены в эти рабочие листы для двухэтапных уравнений, которые можно распечатать. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Урок 6. Решение уравнений с одной переменной pdf.+5 +5 Сначала избавьтесь от сложения и вычитания. Опишите шаги, которые каждый. Огромная коллекция многошаговых таблиц для печати с уравнениями, включающими целые дроби и десятичные дроби в качестве коэффициентов, дана здесь для обширной практики. Материалы Equation Vocabulary Organizer o Напишите двучленное выражение, используя любой математический оператор и 4, a и b. РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ ПРИМЕРЫ 1. 12 = 5m — 3 Теперь прибавьте 3 к обеим частям. Скачать файл в формате PDF Решение рациональных неравенств БЕСПЛАТНЫЕ математические рабочие листы Бесплатные рабочие листы по алгебре 2, созданные с помощью Infinite Algebra 2.g b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2O. Математика Все темы Все местные школьные классы Стивен. То, что четкие дроби, как дроби, объединяя их в письменном десятичном виде, является более крупными формами неравенства, которые интересны с помощью реального числа, многие кредиты могут. х+3=5. Он термины по каждому уравнению так, что. Решение уравнений с квадратным корнем Ответ. Резюме: Чтобы решить уравнения, используйте принципы сложения/умножения, чтобы «Избавиться от…» 1. 3 = m. В этих рабочих листах в формате PDF решите многошаговые уравнения и проверьте свое решение, подставив значение неизвестной переменной в уравнение.Самые популярные рабочие листы по алгебре на этой неделе Desje Lrmv3eGdj. 2 Решайте уравнения, комбинируя одинаковые термины Общие базовые стандарты 8. a Решайте линейные уравнения с одной переменной и рациональными числами, включая уравнения, решения которых требуют раскрытия выражений с использованием дистрибутивного свойства и сбора похожих членов или уравнений с коэффициентами, представленными буквами. Шаг 2. 4 Решение уравнений с дробными коэффициентами Рабочий лист № 1 Выполните следующее на отдельном листе бумаги! А.Пожалуйста, используйте на свой страх и риск, и, пожалуйста, сообщите нам, если что-то не работает. В этом листе многошаговых уравнений View WorksheetWorks_Solving_MultiStep_Equations_1. Решение уравнений с целыми числами. — Игра в два шага. пдф. Опубликовано . Алгебра Решение уравнений в один и два шага Лабиринты Бесплатные уравнения Алгебра Школа Алгебра Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Шаг 3. b Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 2 Имя_____ Решение многошаговых уравнений Дата_____ Период____ Уравнения 23 Многошаговый рабочий лист уравнения Pdf Многошаговый рабочий лист уравнения Word Задания Много… Многошаговые неравенства Рабочие листы.- Практикуйтесь в решении уравнений, играя в алгебру. Решение многошаговых уравнений с переменными на одной стороне. Рабочий лист. Решение многошаговых уравнений. Многошаговые уравнения. 4) Проверьте свой ответ. ЕЕ. Пустой слой. Решение уравнений: смешанный обзор Комбинация целых, дробных и десятичных коэффициентов обозначает переменную в этих смешанных рабочих листах обзора. 7. Решение односегментных уравнений. 3. Desje Lrmv3eGdj. Лист викторины Решение рациональных уравнений Study Com.ЕЕ. Одношаговое уравнение так же прямолинейно, как и оно. Эквивалентные уравнения · Критерии эквивалентности уравнений · Уравнение с одной переменной · Уравнение с двумя переменными. D 72 […] Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. Решайте двухшаговые уравнения, оттачивая навыки алгебры седьмого и восьмого классов с помощью этого удобного рабочего листа! Начиная с доступного дополнения, напоминающего о том, как разбивать двухшаговые уравнения с измененными операциями, этот рабочий лист снова поощряет абсолютную … Тема Решение одношаговых линейных уравнений с одной переменной Primary SOL 6.Он также содержит математические загадки, определяющие стоимость объектов, переводя фразы в одношаговое уравнение и многое другое. Решите линейные уравнения и неравенства, в том числе многошаговые уравнения и двухшаговые математические уравнения — это алгебраические задачи, которые требуют от вас сделать два хода, чтобы найти значение неизвестной переменной. Курс 3 • Глава 2 Уравнения с одной переменной 23 Урок 2. 2 1 Решение уравнений в один шаг редактируется. Ответ: 2x – 1 = 3 4 x + 9 ЖК-дисплей равен 4. Создавайте рабочие листы для печати для решения линейных уравнений до алгебры или алгебры 1 в виде файлов pdf или html.Некоторые уравнения являются двухшаговыми, но большинство из них трехшаговые Решение многошаговых уравнений Нет отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Абсолютная ценность Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Если нет дробей, объедините одинаковые члены. 7 м и -2 м объединятся в 5 м, а -5 и +2 в сумме станут -3. Этот рабочий лист на одну страницу охватывает решение одношаговых уравнений с умножением и делением десятичных дробей. Рабочие листы с открытыми и закрытыми слогами 3 класс.Упражнения по решению уравнений в лабиринте Добро пожаловать на страницу «Решение простых линейных уравнений с неизвестными значениями от -9 до 9 и переменными в левой части» (A) Math Worksheet со страницы с рабочими листами по алгебре в Math-Drills. Решение многошаговых уравнений для 7-го класса. Лист бесплатных математических заданий для 7-го класса и для предварительной алгебры, организованный по таким темам, как выражения. Целые числа. Одношаговые уравнения. Рациональные числа. Многошаговые уравнения. Неравенства.Рабочие листы с двухшаговыми уравнениями — Рабочие листы по математике 4 Дети В исходном видео был запутанный пример. 1 Примечания 4 Решение реальной задачи с помощью рациональной корневой теоремы Цель обучения B: Я могу применять рациональную корневую теорему для решения реальных задач, моделируемых полиномиальными функциями. Я могу сравнить алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Теперь мы подставляем x = 8 Рабочий лист двухшаговых уравнений pdf. Отлично подходит для работы в классе, домашних заданий, решения текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа.Решение многошаговых уравнений Дата_____ Период____ Решите каждое уравнение. 4b Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения реальной или математической задачи, а также создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах. 3 Flip Book Eureka Lessons 7-9 Уравнения лицензирования (словные задачи) Учебник Glencoe CCGPS (McGraw-Hill, 2013) с. D. Рабочие листы с целыми числами и абсолютными значениями.2+1. Результаты Учащиеся смогут решать многошаговые уравнения. Решение одношаговых уравнений: Чтобы решить одношаговые уравнения, вы делаете операцию, противоположную любой операции. Настройте рабочие листы, чтобы включить одноэтапные, двухэтапные или многоэтапные уравнения, переменные с обеих сторон, круглые скобки и многое другое. 3) Решите упрощенное уравнение, отменив действия в обратном порядке. N P gAsl Glv 7rViog Bh7t8sW ir 8ejs CeWrRvke Bdm. Двухшаговые уравнения, содержащие целые числа. Многошаговые уравнения — это все уравнения, для решения которых требуется выполнить более двух шагов или операций.Глава 1: Вещественные числа. pdf: Размер файла: 230 Кб: Тип файла: pdf Подробнее. 3-Пример 1: Решите это уравнение, сначала очистив дроби. 3x + 1 = 7 Найдите переменный термин. 4A-4 — Решение Показаны 8 лучших рабочих листов в категории многошаговых уравнений распределительного свойства. Некоторыми из рабочих листов для этой концепции являются Глава 14 «Алгебраические дроби и уравнения» и «Объединение похожих терминов дробных коэффициентов», «Арифметика и алгебраическая работа», «Целые числа 1 для одношаговых уравнений», «Содержание работы по алгебре», «Целые числа для одношаговых уравнений», «Решение линейных уравнений», «Решение линейных уравнений».Сравните алгебраическое решение с арифметическим решением, определяя последовательность… Калькулятор алгебры — это калькулятор, который дает пошаговую помощь в решении задач по алгебре. Решение многошаговых распределительных уравнений со скобками — без отрицательных коэффициентов Название: V Дата: Решить Desje Lrmv3eGdj. Детская физика mcq, графические рабочие листы линейных уравнений, сложение и вычитание положительных и отрицательных целых рабочих листов, Ti84 One-Step Equations With Fractions Kuta Kuta PDF4PRO. Помните знак минус при умножении или делении вызовов Учебное пособие по решению уравнений pdf CCGPS Math 7 Учебное пособие по разделу 2 — Выражения и уравнения Используйте свойства операций для создания эквивалентных выражений.Опубликовано. Большинство … Дополнение Решение многошаговых уравнений Стандарты CC 7. Решение и построение графиков неравенств Рабочий лист Ключ к ответу Pdf Алгебра 2. Знаменатели: Умножьте каждую часть уравнения на общий знаменатель. G b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2Ob Рабочий лист от Kuta Software LLC Kuta Software – Infinite Algebra 2 Название_____ Решение многошаговых уравнений. e Решите одношаговые или многошаговые арифметические задачи реального мира, включающие четыре операции с рациональными числами, в том числе те, которые связаны с экспоненциальной записью.МСТ2. C. 2. Kami Export Unit 1 4 Назначение и ключ Pdf Math 8 Unit 1 1 4 Название задания Решение многошаговых уравнений Период U00a9f D2z0x164v Tkpubtnak Course Hero from www. Решение многошаговых неравенств, рабочий лист, график неравенства, 33 уравнения планов ресурсов и список, предварительные рабочие листы по алгебре, 26 текстовых задач, бесплатная электронная таблица, одно умножение, деление, pdf, ответы на настроение, урок tessshlo 6, 2, 4 с линейным распределительным свойством, 29 уроков математики, преподающих 9-й класс. (7 4)•4 7 𝑥=(7 4 Опубликовано в алгебра 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помечено алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf один шаг уравнения лабиринт ответы решение уравнений лабиринт ответ ключевые решения уравнения лабиринт.09 мая 2021 г. Решая, чтобы появиться с обзором, ваши ученики просто любят в четверг и вычитают в уравнениях степени с решением рациональных ответов рабочего листа pdf b рационально. • Учтите, что линейные уравнения могут не иметь решения, иметь одно решение или иметь бесконечно много решений. Pin On … В этих листах PDF для 7 и 8 классов выполните основные арифметические операции и решите многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Решение многоэтапных уравнений в лабиринте. В данном случае 5 и 11 — наши константы.+3 +3. Неравенства. Решайте задачи по формуле. путем умножения каждого члена на наименьший общий знаменатель. Предварительные навыки 1-го блока. Дискретная математика и ее голосовые приложения шестого издания, Решение уравнений с переменным листом с несколькими рабочими листами, несколько вариантов градации, задачи и печати из AHLGEBRA, стандартный калькулятор, десятичный расчетный коэффициент среда (1/14) — двухшаговые уравнения, Домашнее задание № 1, 3,4,6,8,12 (Последняя страница опубликованных заметок) 7R 1-14 Заметки.Рабочие листы являются отличным ресурсом для детей 6-го, 7-го и 8-го классов. Рабочие листы с уравнениями по алгебре, состоящими из 3 шагов. Бесплатное решение многошаговых уравнений Станции Лабиринт Обучение алгебре Решение многошаговых уравнений Обучение математике J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Уравнения в один шаг. Сложение, вычитание, умножение и деление.J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. До начала этого занятия учащиеся должны уметь решать одношаговые линейные уравнения, содержащие отрицательные целые коэффициенты и константы, а также дробные и десятичные значения. Затем изучите различные способы решения уравнения. 7 ee 4 Используйте переменные для представления величин в реальном мире или математических задач и стройте простые уравнения и неравенства для решения задач, рассуждая о величинах. Калькулятор многошаговых неравенств Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом.У 2 алии было 24, чтобы потратить на семь карандашей. 7 ee 4a решать текстовые задачи, приводящие к уравнениям вида px q r и p x q r, где p q и r — конкретные рациональные числа. 3A PowerPoint, который учащиеся выполнят в качестве домашнего задания. 3 уравнения шага, отображающие 8 лучших рабочих листов, найденных для этой концепции. Решите уравнения этих форм бегло. Ниже приведены отдельные упражнения для уравнений, в которых используются целые дроби и десятичные коэффициенты. Решайте линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, обозначенными буквами.Решите каждый мульти … Викторина и рабочий лист — Решение рациональных уравнений | Учиться. Подготовьте уравнение, поместив круглые скобки вокруг каждой стороны. Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом. Теперь подставим x = 8. Каждый рабочий лист содержит уравнения с дробными коэффициентами. МСС7. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данный. Конечно, ключи ответов предоставляются с каждым бесплатным рабочим листом по алгебре.Вы можете учиться, решая дополнительные задачи, до которых вы не дошли в классе. Используйте x и y для любых переменных. Анализ и решение линейных уравнений и пар одновременных линейных уравнений Описание. В этом случае сложение вычитание и деление умножения. com Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые числа, дроби и десятичные дроби в качестве коэффициентов, приведены здесь для обширной практики. Я могу бегло решать многоступенчатые линейные уравнения и текстовые задачи с рациональными коэффициентами (например, p(x+q)=r).Одношаговые неравенства путем сложения/вычитания. Часто при решении линейных уравнений нам приходится работать с уравнением с дробными коэффициентами. 13 августа 2021 г. Автор: Рабочие листы с многошаговыми уравнениями Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые дроби и десятичные дроби в виде … Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Четверг (15/01) — Уравнения в два шага, Домашнее задание — Подготовка к викторине. Чтобы решить многошаговое уравнение, мы должны начать с попытки упростить уравнение, комбинируя одинаковые члены и используя свойство дистрибутивности, когда это возможно.Решение уравнений с переменной с каждой стороны (стр. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y 6 через среднюю школу. Системы — решить относительно x и y. 17 Учащийся будет решать многоступенчатые линейные уравнения с одной переменной с переменной на одной или обе стороны уравнения, в том числе практические задачи, требующие решения многошагового линейного уравнения с одной переменной Графики неравенств Решение неравенств Многошаговые неравенства Квадратные уравнения, текстовые задачи, разделы 2.Решите уравнения с одной переменной, чтобы получить значение переменной. ПЕРЕРАБОТКА Семья Свигер перерабатывает около 15 фунтов отходов в неделю. Математика 67 ПРИМЕЧАНИЯ 63 Название _____ Решение двухшаговых уравнений SOL 714 Пример 1 Решите 3x 1 7 ПРОВЕРКА. 4a) 7. Одношаговое уравнение – умножение и деление. 2x 3 9 4. Решение многошаговых уравнений с рациональными коэффициентами. Рабочий лист pdfПример изучения связей между дробными знаниями и записью линейных уравнений учащимися седьмого класса и целесообразность введения линейных уравнений в младших классах
Тематическое исследование, посвященное изучению связи между дробным знанием и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах- Дом
- Том 14, выпуск 1, январь 2019 г.
- Тематическое исследование, посвященное изучению связей между знанием дробей и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах
Тематическое исследование, посвященное изучению связи между дробным знанием и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах
Как цитировать эту статью
АПА
Цитата в тексте: (Lee, 2019)
Ссылка: Lee, M.Ю. (2019). Тематическое исследование, посвященное изучению связей между дробными знаниями и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах. Международный электронный журнал математического образования, 14 (1), 109-122. https://doi.org/10.12973/iejme/3980АМА
Внутритекстовое цитирование: (1), (2), (3) и т. д.
Артикул: Lee MY. Тематическое исследование, посвященное изучению связей между дробными знаниями и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах. INT ELECT J MATH ED . 2019;14(1), 109-122. https://doi.org/10.12973/iejme/3980Чикаго
Цитата в тексте: (Ли, 2019)
Ссылка: Ли, Ми Ён.«Тематическое исследование, изучающее связи между дробными знаниями и написанием линейных уравнений учащимися седьмого класса и целесообразность введения линейных уравнений в более раннем классе». Международный электронный журнал математического образования 2019 14 вып. 1 (2019): 109-122. https://doi.org/10.12973/iejme/3980Гарвард
Цитата в тексте: (Lee, 2019)
Ссылка: Lee, M.Ю. (2019). Тематическое исследование, посвященное изучению связей между дробными знаниями и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах. Международный электронный журнал математического образования , 14(1), стр. 109-122. https://doi.org/10.12973/iejme/3980ГНД
Цитата в тексте: (Ли, 2019)
Ссылка: Ли, Ми Ён «Пример изучения связей между дробными знаниями и написанием линейных уравнений учащимися седьмого класса и целесообразность введения линейных уравнений в младших классах» . Международный электронный журнал математического образования , том. 14, нет. 1, 2019, стр. 109-122. https://doi.org/10.12973/iejme/3980Ванкувер
Ссылка в тексте: (1), (2), (3) и т. д.
Ссылка: Lee MY. Тематическое исследование, посвященное изучению связей между дробными знаниями и написанием линейных уравнений учащимися седьмого класса и необходимостью введения линейных уравнений в младших классах.INT ELECT J MATH ED. 2019;14(1):109-22. https://doi.org/10.12973/iejme/3980В рамках более крупного исследования было проведено исследование двух семиклассников, Питера и Уиллы. Чтобы изучить связь между их дробными знаниями и алгебраическими рассуждениями, студенты были опрошены дважды, один раз для их дробных знаний и один раз для их алгебраических знаний в написании линейных уравнений, которые требовали явного использования неизвестных.Дробные знания Питера и Уиллы повлияли на линейные уравнения, которые они написали для представления количественных ситуаций. В частности, результаты показали, что схема обратимой итерационной дроби важна для понимания взаимных отношений между двумя величинами при написании базового линейного уравнения вида ax=b. Кроме того, рассмотрение дробей как множителей неизвестных важно для написания линейных уравнений. Предлагаются последствия для возможности введения линейных уравнений в более раннем классе и способы поддержки введения.
- Бастейбл, В., и Шифтер, Д. (2008). Истории в классе: примеры учеников начальной школы, занимающихся ранней алгеброй. В JJ Kaput, DW Carraher & ML Blanton (Eds.), Алгебра в начальных классах s (стр. 165-184). Нью-Йорк: Лоуренс Эрлбаум.
- Боданский Ф.Г. (1991). Формирование алгебраического метода решения задач у младших школьников. В LP Steffe (Ed.), Психологические способности детей младшего школьного возраста в изучении математики (стр.275-338). Рестон, Вирджиния: Национальный совет учителей математики.
- Карпентер, Т.П., Франке, М.Л., и Леви, Л.В. (2003). Математическое мышление: интеграция арифметики и алгебры в начальной школе . Портсмут, Нью-Хэмпшир: Хайнеманн.
- Каррахер, Д. В., Шлиман, А. Д., и Шварц, Дж. Л. (2008). Ранняя алгебра — это не то же самое, что ранняя алгебра. В JJ Kaput, DW Carraher & ML Blanton (Eds.), Алгебра в начальных классах (стр.235-272). Нью-Йорк: Лоуренс Эрлбаум.
- Каррахер, Д. В., Шлиман, А. Д., Бризуэла, Б. М., и Эрнест, Д. (2006). Арифметика и алгебра в раннем обучении математике. Журнал исследований в области математического образования, 37 (2), 87-115.
- Чой, Б.Х., Ли, М.Ю., и Мицци, А. (2015). Подписи в учебниках: предварительное исследование понятия градиента в Германии, Сингапуре и Южной Корее. В К. Бесвик, Т. Мьюир и Дж. Уэллс (ред.), Труды 39-й конференции Международной группы психологии математического образования, Том.2, (стр. 201-208). Хобарт, Австралия: Университет Тасмании.
- Догерти, Б. (2008). Измерьте: количественный взгляд на раннюю алгебру. В JJ Kaput, DW Carraher & ML Blanton (Eds.), Алгебра для младших классов (стр. 389-412). Нью-Йорк: Лоуренс Эрлбаум.
- Дрисколл, MJ (1999). Воспитание алгебраического мышления: Пособие для учителей 6-10 классов. NH: Хайнеманн.
- Эмпсон, С. Б., Леви, Л., и Карпентер, Т. П. (2011).Алгебраическая природа дробей: развитие реляционного мышления в начальной школе. В J. Cai & EJ Knuth (Eds.), Ранняя алгебраизация (стр. 409-428). Берлин: Springer-Verlag. https://doi.org/10.1007/978-3-642-17735-4_22
- Хакенберг А. Дж. и Тиллема Э. С. (2009). Мультипликативные концепции целых чисел учащихся: важный конструктивный ресурс для схем состава фракций. Журнал математического поведения, 28 , 1–18. https://doi.org/10.1016/j.jmathb.2009.04.004
- Хакенберг, А. Дж. (2010). Рассуждения студентов с обратимыми мультипликативными отношениями. Познание и обучение, 28 (4), 1-50. https://doi.org/10.1080/07370008.2010.511565
- Хакенберг, А. Дж., и Ли, М. Ю. (2015). Взаимосвязь между дробными знаниями учащихся и написанием уравнений. Журнал исследований в области математического образования , 46 (2), 196-243.
- Хан, Д. Х. (2010).Дебаты о новом содержании национальной программы начальной математики. Журнал элементарного математического образования в Корее, 14 (3), 633-658.
- Капут, Дж. Дж. (2008). Что такое алгебра? Что такое алгебраическое рассуждение? В JJ Kaput, DW Carraher & ML Blanton (Eds.), Алгебра в начальных классах (стр. 5-17). Нью-Йорк: Лоуренс Эрлбаум.
- Капут, Дж. Дж., Каррахер, Д. В., и Блэнтон, М. Л. (ред.). (2008). Алгебра в младших классах. Нью-Йорк: Лоуренс Эрлбаум.
- Ли, М.Ю. (2017). Гибкость учителей до начала работы с референтными единицами при решении задачи на деление дроби. Образовательные исследования по математике , 96 (3), 327-348. https://doi.org/10.1007/s10649-017-9771-6
- Ли, М.Ю., и Хакенберг, А.Дж. (2014). Отношения между дробным знанием и алгебраическим мышлением: случай Уиллы. Международный журнал науки и математического образования, 12 (4), 975-1000.https://doi.org/10.1007/s10763-013-9442-8
- Министерство образования, науки и технологий (2009 г.). Учебная программа 7-й начальной школы . Сеул, Корея: будущее и культура.
- Мицци, А., Ли, М.Ю., и Чой, Б.Х. (2016). Подписи в учебниках: предварительное исследование понятия дробей в Германии, Сингапуре и Южной Корее . Доклад представлен на 13-м Международном конгрессе по математическому образованию (ICME-13). Гамбург, Германия.
- Нортон, А.(2008). Операционные догадки Джоша: похищение операции расщепления и построение новых дробных схем. Журнал исследований в области математического образования, 39 (4), 401-430.
- Сео, Г. Х., Ю, С. А., и Чон, Дж. Ю. (2003). Анализ учебной программы по математике 7-й национальной корейской начальной школы: основное внимание уделяется непрерывности, последовательности и интеграции математического содержания. Исследование начального образования в Корее, 16 (2), 159–184.
- Сфард, А. (1995). Развитие алгебры: сопоставление исторических и психологических перспектив, Journal of Mathematical Behavior, 14 , 15-39. https://doi.org/10.1016/0732-3123(95)-5
- Смит, Э. (2003). Застой и изменение: интеграция шаблонов, функций и алгебры в учебную программу K-12 How Does Student Fractional 48. В J. Kilpatrick, WG Martin & D. Schifter (Eds.), , научный сотрудник Принципов и стандартов школьной математики (стр.136-150). Рестон, Вирджиния: Национальный совет учителей математики. https://doi.org/10.1002/jsc.645
- Штеффе, Л. П. (1991). Операции, которые генерируют количество. Обучение и индивидуальные различия, 3 (1), 61-82. https://doi.org/10.1016/1041-6080(91)
-K
- Штеффе, Л. П. (1994). Детские схемы умножения. В G. Harel & J. Confrey (Eds.) Развитие мультипликативного мышления при изучении математики (стр. 3-39). Олбани, Нью-Йорк: Государственный университет Нью-Йорка Press.
- Стеффе, Л.П., и Олив, Дж. (2010). Детские дробные знания . Нью-Йорк: Спрингер. https://doi.org/10.1007/978-1-4419-0591-8
- Стеффе, Л.П., и Томпсон, П.В. (2000). Методология обучающего эксперимента: основные принципы и основные элементы. В R. Lesh & AE Kelly (Eds.), Справочник по дизайну исследований в области математики и естественных наук (стр. 267-306). Хиллсдейл, Нью-Джерси: Эрлбаум.
- Штеффе, LP (1992).Схемы действия и работы составных агрегатов. Обучение и индивидуальные различия, 43 , 259–309. https://doi.org/10.1016/1041-6080(92)-Y
- Томпсон, П. В. (1994). Развитие понятия скорости и его соотношение с понятиями скорости. В G. Harel & J. Confrey (Eds.), Развитие мультипликативного мышления при изучении математики (стр. 181-234). Олбани, Нью-Йорк: SUNY Press.
- Томпсон, П. В. (1995).Обозначения, соглашение и количество в элементарной математике. В JT Sowder & BP Schappelle (Eds.), Обеспечение основы для преподавания математики в средних классах (стр. 199-219). Олбани, Нью-Йорк: Государственный университет Нью-Йорка Press.
- Ван Амером, Б.А. (2003). Сосредоточение внимания на неформальных стратегиях при связывании арифметики с ранней алгеброй. Образовательные исследования по математике, 54 , 63-75. https://doi.org/10.1023/B:EDUC.0000005237.72281.bf
- Фон Глазерсфельд, Э.(1995). Радикальный конструктивизм: способ познания и обучения (Том 6) . Нью-Йорк, штат Нью-Йорк: Рутледж Фалмер. https://doi.org/10.4324/9780203454220
Все права защищены © 2006-2022
границ | Базовая теория управления для дробно-линейных дифференциальных уравнений с постоянными коэффициентами
1.Введение
Управляемость — математическая задача, заключающаяся в определении целей, к которым можно привести состояние динамической системы с помощью управляющего входа, фигурирующего в уравнении. У нас есть динамическая система, на которую мы можем оказывать определенное влияние. Можно ли использовать это, чтобы система достигла желаемого состояния? Другими словами, возможно ли при заданном будущем времени, начальном состоянии и целевом состоянии найти управляющую функцию, при которой решение системы, начиная с начального состояния, достигает желаемого состояния в заданный момент времени в будущем? Некоторые классические и современные ссылки по теории управления мы отсылаем к ссылкам [1–3].
С другой стороны, дробное исчисление и дробные дифференциальные уравнения в последнее время стали применяться в различных областях техники, математики, физики и биоинженерии и других прикладных наук. Мы отсылаем читателя к монографиям [4–7] и статьям [8, 9]. В частности, растет число областей исследований в физике, в которых используется дробное исчисление [10], и оно имеет множество приложений в различных его областях, от обработки изображений до дробного квантового гармонического генератора [11].Недавно в Йылдызе [12] изучалась динамика дробной модели водного патогена под влиянием загрязнения окружающей среды и получены решения обобщенных дробных кинетических уравнений [13] с использованием обобщенных дробных интегрирований обобщенного типа Миттаг-Леффлера. функция. Наконец, отметим, что различные дробные системы также рассматривались в рамках теории управления [14–18].
В связи с последним приложением дробного исчисления мы представляем текущую работу, посвященную управляемости линейного дробного дифференциального уравнения с постоянными коэффициентами.Статья организована следующим образом. В разделе 2 мы напоминаем о критерии Калмана управляемости линейной системы первого порядка. В разделе 3 рассматривается линейная система дробного порядка, общее решение которой представлено в терминах функции Миттаг-Леффлера. Используя это представление, мы, наконец, даем в разделе 4 новый критерий управляемости.
Хотя этот критерий известен с 1996 г. [19], мы даем другой подход и используем некоторые элементы дробного исчисления и другое доказательство для получения результатов.Также мы выявляем некоторые интересные связи между линейными дифференциальными уравнениями дробного порядка, задачами управления, линейной алгеброй, функциями Миттаг-Леффлера, геометрией и физикой.
О связи между управляемостью стандартных и дробных систем см. Кламка [20]. Вычисление грамиана полезно, чтобы найти средство управления, чтобы направить данное начальное состояние в другое заданное конечное состояние.
2. Классическое линейное управление
Пусть A∈Mn×n(ℝ) и f :[0, ∞) → ℝ непрерывны.Рассмотрим линейную систему
х′(т)=Ах(т)+f(т), (1)с начальным условием
х(0)=х0∈ℝn. (2)Решение задачи (1) и (2) дается числом
. x(t)=eAtx0+∫0teA(t-s)f(s)ds.Теперь рассмотрим ту же систему с функцией управления, поэтому (1) записывается как
. x′(t)=Ax(t)+Bu(t), (3), где B∈Mn×m(ℝ) и u :[0, ∞) → ℝ m — возможное управление. Для данного непрерывного управляющего входа u решение (3) с начальным условием x (0) = x 0 равно
x(t)=eAtx0+∫0teA(t-s)Bu(s)ds.Для заданного времени t > 0 и начального состояния x (0) = x 0 множество достижимости (1) в момент времени t > 0 относительно x
3 0 это множество Rt(x0) всех состояний x ( t ), которые могут быть достигнуты из x 0 любым управляющим входом. Линейная система (3) является управляемой, если для любых x0,x1∈ℝn существует управление u такое, что соответствующее решение удовлетворяет x (0) = x 0 и x ( t ) = х 1 .
Есть простой критерий, знаменитый критерий Калмана управляемости.
Теорема 1 . Линейная система (3) управляема тогда и только тогда, когда матрица Калмана
имеет полный ранг .
Для доказательства этого (см. [21]) одним из основных ингредиентов является грамиан управляемости матриц A и B :
W(t):=∫0teAsBB*eA*sds∈Mn×n(ℝ), (4), где A * и B * являются, соответственно, сопряженными матрицами A и B .Матрица W ( t ) является положительно полуопределенной, и ее область значений совпадает с областью значений матрицы Калмана.
Также важным компонентом является следующее свойство матрицы A . Пусть φ(z)=∑k=0∞akzk — аналитическая комплексная функция. Применение теоремы Кэли-Гамильтона означает, что существует полином p степени меньше n такой, что φ(A)=p(A)=∑k=0n-1ckAk,
наверняка c 0 , …, c n −1 ∈ ℂ.
Напомним соответствующую геометрическую интерпретацию. Подпространство
— наименьшее A -инвариантное подпространство, содержащее R(B). Линейная система (3) управляема тогда и только тогда, когда W ( t ) невырожденно при t > 0. Физическая интерпретация грамиана управляемости состоит в том, что вход системы представляет собой белый гауссовский шум. Тогда W ( t ) есть ковариация состояния (см. стр. 854 в [22]).
3.Линейное управление дробным порядком
Рассмотрим теперь линейное дифференциальное уравнение дробного порядка α ∈ (0, 1]
Dαx(t)=Ax(t)+f(t), (5)с начальным условием
x(0)=x0∈ℝn, (6), где, как и прежде, A∈Mn×n(ℝ), f∈C([0,∞),ℝn) и D α x является дробной производной от x . Мы используем здесь дробную производную Капуто, которая может быть определена для любых x :[0, ∞) → ℝ n абсолютно непрерывно и имеет следующий вид:
Dαx(t)=1Γ(1-α)∫0t(t-s)-αx′(s)ds,, где Γ — классическая гамма-функция.Для некоторых приложений дробных дифференциальных уравнений мы отсылаем, например, к ссылкам [5, 23, 24].
Обратите внимание, что D α x ( t ) = I 1-α x ‘( T ), где I 1-α — это дробный интеграл Риман-Лиувилль. Действительно, при β > 0 и x∈Lloc1(0,∞)
Iβx(t)=1Γ(β)∫0t(t-s)β-1x(s)ds.Теперь пусть B∈Mn×m(ℝ) и u∈C([0,∞),ℝm). Полагая f ( t ) = Bu ( t ), мы перепишем уравнение (5) как
Dαx(t)=Ax(t)+Bu(t).(7)Аналогично обычному случаю, для любого t > 0, Rtα будет определяться как множество достижимости (7), относящееся к началу координат, которое представляет собой множество всех состояний x ( t ), которые могут быть достигается из нулевого начального состояния для некоторого непрерывного управляющего воздействия. Будем говорить, что система (7) управляема, если для любых x0,x1∈ℝn существует управление u такое, что решение (7) с x (0) = x 0 удовлетворяет x ( т ) = х 1 .
Решение уравнения первого порядка (1) дано через f и экспоненту A :
Для уравнения дробного порядка (5) роль этой экспоненты играют функции Миттаг-Леффлера: при α > 0 и при z ∈ ℂ,
Eα(z)=∑k=0∞zkΓ(αk+1).Обратите внимание, что при α = 1 Eα(z)=ez.
В общем случае при α, β > 0 функция
Eα,β(z)=∑k=0∞zkΓ(αk+β). (8)корректно определено в ℂ, так как ряд в (8) сходится для любых z ∈ ℂ [25].Например, если β = 1, мы восстанавливаем предыдущий случай: E α, 1 ( z ) = E α ( z ).
Мы можем заменить z матрицей A в (8), и соответствующий ряд сходится. Следовательно, мы можем определить функцию Миттаг-Леффлера матрицы A как
Eα,β(A)=∑k=0∞AkΓ(αk+β).Решение (5) дается вариацией формулы постоянных для дробных дифференциальных уравнений (см. теорему 5.15, с. 323 в [5] или теорема 7.2, с. 135 в [23]):
x(t)=Eα(tαA)c+∫0t(t-s)α-1Eα,α((t-s)αA)f(s)ds,, где c — любая константа. Ставим начальное условие х (0) = х 0 , тогда c = х 0 .
В случае (7) с начальным условием (6) решение [5, 17]
x(t)=Eα(tαA)x0+∫0t(t-s)α-1Eα,α((t-s)αA)Bu(s)ds.Здесь мы поднимаем следующие вопросы: Существует ли в дробном случае правило, аналогичное критерию Калмана? Что такое матрица Грамиана в таком случае?
4.Доказательство частичного контроля
Мы готовы привести рассуждения, которые приведут нас к критерию управляемости системы (5).
Пусть α ∈ (0, 1). Применяя определение функции Миттаг-Леффлера, выражение
∫0t(t-s)α-1Eα,α((t-s)αA)Bu(s)dsравно
∫0t(t-s)α-1∑k=0∞[(t-s)αA]kΓ(αk+α)Bu(s)ds.Тогда, используя равномерную сходимость, мы приходим к следующему выражению
∑k=0∞∫0t(t-s)α-1(t-s)αkAkΓ(αk+α)Bu(s)ds,, что очевидно равно
limN→∞∑k=0NAkB∫0t(t-s)α-1(t-s)αkΓ(αk+α)u(s)ds.В предыдущем ряду каждое слагаемое является линейной комбинацией столбцов В, АВ, А 2 В , …, А N В . Любая из этих матриц является линейной комбинацией B, AB , A 2 B , …, A n −1 B . Следовательно, вектор
∑k=0NAkB∫0t(t-s)α-1(t-s)αkΓ(αk+α)u(s)ds (9)представляет собой линейную комбинацию столбцов B, AB, A 2 B , …, A n −1 B , т.е.е., он принадлежит пространству значений матрицы Калмана K . Поэтому, как и в обычном случае, получаем Rtα⊂R(K). Это необходимое условие управляемости дробно-линейной системы (7): матрица Калмана имеет полный ранг. Мы не можем достичь какого-либо состояния за пределами диапазона матрицы Калмана.
Вопрос в том, как мы можем получить элемент управления и , чтобы
∫0t(t-s)α-1Eα,α((t-s)αA)Bu(s)ds=x1.Для этого определим α-грамиан как
Wtα=∫0t(ts)α-1Eα,α((ts)αA)BB*Eα,α((ts)αA*)(ts)α-1ds =∫0t(ts)2α-2Eα,α((ts )αA)BB*Eα,α((ts)αA*)ds.Заметим, что при α = 1 мы восстанавливаем грамиан в (4).
Если мы докажем, что R(K)⊂R(Wtα), то для x1∈R(K) получим x1∈R(Wtα) и существует y таких, что Wtαy=x1. Взяв под контроль
u(s)=B*Eα,α((t-s)αA*)(t-s)α-1y,мы видим что
x1=Wtαy =∫0t(ts)2α-2Eα,α((ts)αA)BB*Eα,α((ts)αA*)yds =∫0t(ts)α-1Eα,α((ts)αA) Bu(s)ds.Таким образом, мы переводим начальное условие 0 в состояние x 1 в момент времени t > 0. Это доказывает, что R(K)⊂Rtα.Остается только доказать, что R(K)⊂R(Wtα).
Пусть z ∈ ℝ n и предположим, что (Wtα)*z≡z*Wtα=0. Для каждого z ∈ ℝ n это приводит к
0=z*Wtαz=〈z,Wtαz〉=∫0t(ts)2α-2z*Eα,α((ts)αA)BB*Eα,α((ts)αA*)zds=∫0t(ts)2α -2‖z*Eα,α((ts)αA)B‖2ds≥0.Для s ∈ [0, t ], ( t − s ) α ∈ [0, t α ]. Следовательно,
z*∑k=0∞xkAkΓ(αk+α)B=0, x∈[0,tα].дифференциация K раз ( K = 0, 1, 2, …) с уважением к x И принимать предел, когда x → 0 + подразумевает, что Z * A k B = 0, для k = 0, …, n − 1; то есть
Это дает нам
z*∈N(Wtα)=N((Wtα)*)⇒z*∈N(K*).Имеем N((Wtα)*)⊂N(K*) и можем написать N(K*)⊥⊂N((Wtα)*)⊥.∈(0,1], , то система управляема для каждого порядка α ∈ (0, 1].
В заключение приведем несколько примеров, показывающих, как можно применять теорему 2.
Пример 1. Пусть α ∈ (0, 1). Рассмотрим случай n = 2, m = 1, где
x(t)=(x1(t)x2(t)), A=(1001), B=(10).Система может быть записана как
{Dαx1(t)=x1(t)+u(t),Dαx2(t)=x2(t). (10)Система неуправляема, так как второе уравнение не зависит от управления, как и в случае первого порядка (α = 1). Тем не менее, можно управлять x 1 , и в этом смысле можно сказать, что (10) частично управляемо.В этом примере
и ранг ( K ) = 1 < 2.
Пример 2. Пусть n = 2, m = 1, α ∈ (0, 1] и рассмотрим систему
где
A=(-2221), B=(B1B2)∈M2×1(ℝ).Матрица Калмана будет вещественной матрицей 2 × 2, столбцы которой обозначены как B и AB . Более того, если B отождествляется с собственным вектором A , система не будет управляемой. Например, если
матрица Калмана принимает вид
, который не имеет полного ранга [ ранг ( K ) = 1 < 2].Таким образом, система не будет управляемой.
Нечто подобное происходит и с выбором
Тем не менее любой другой выбор B , не кратный ни одному из предыдущих случаев, приводит к управляемой системе независимо от значения α ∈ (0, 1].
Пример 3. Классический линейный гармонический осциллятор ξ” +ξ = u эквивалентен системе (3), занимающей положение x 1 = ξ и скорость x2=ξ′ при
А=(01-10), В=(01).Гармонический осциллятор с дробным управлением будет (7), который принимает форму
{Dαx1=x2,Dαx2=u-x1. (11)Первое уравнение не зависит от управления, но оно появляется во втором уравнении, включающем обе составляющие, и дробная система управления (11) является управляемой. Действительно, матрица Калмана
имеет полный ранг.
Пример 4. Другой возможностью является рассмотрение связанной линейной несоизмеримой дробно-дифференциальной системы управления α 1 , α 2 ∈ (0, 1):
{Dα1×1=a11x1+a12x2+u1,Dα2×2=a21x1+a22x2+u2, (12), но, насколько нам известно, аналитическое решение неизвестно.
5. Выводы
В данной работе мы изучили управляемость линейного дробно-дифференциального уравнения
, где рассматривается дробная производная Капуто, A∈Mn×n(ℝ), B∈Mn×m(ℝ) и u представляет собой m -мерную управляющую функцию. В частности, мы показали, что такая система управляема тогда и только тогда, когда матрица Калмана имеет полный ранг, что и составляет основной результат, а именно теорему 2.
.Хотя критерий, приведенный в теореме 2, не зависит от α и, таким образом, становится результатом, аналогичным классическому (обычный случай), использованный нами аппарат на самом деле включает некоторые адаптированные рассуждения.Между управляемостью системы, соответствующей матрицей Грамиана Wtα, ядром ассоциированного оператора, пространством значений Rtα и матрицей Калмана есть еще несколько соотношений, но некоторые аргументы зависят от дробного порядка α. Например, мы помним, что матрица Грамиана Wtα имеет особенность, если α ∈ (0, 1) и управление, переводящее начальные данные x 0 в конечное состояние x 1 , зависит от α, так что коэффициенты линейной комбинации матриц B , …, A n −1 B (которые образуют матрицу Калмана) входят в уравнение (9).
В будущем следует провести некоторые исследования по дальнейшим вопросам, связанным с этой работой. Например, парой критических проблем являются случаи, когда матрицы А и В не являются постоянными, то есть система управления
Dαx(t)=A(t)x(t)+B(t)u(t),и нелинейный случай
, который также очень актуален в приложениях и будет подробно рассмотрен. В общем, во многих ситуациях запаздывание может появиться и в функциональных уравнениях дробных производных типа
. Dαx(t)=f(x(t),x(t-τ),u(t))должны быть рассмотрены.
В дополнение к предыдущим комментариям интерес представляют также системы с импульсами от ударов. Действительно, у Спонга [26] и Ньето и Тисделла [27] изучается проблема управления физическим объектом посредством ударов, называемая импульсивной манипуляцией, и она возникает в ряде робототехнических приложений [28, 29].
Еще одно интересное направление касается управляемости систем дробного порядка в свете других дробных производных, таких как Римана-Лиувилля, Адамара, Капуто-Фабрицио и т. д.
Кроме того, некоторые физические модели будут рассмотрены в соответствии с этими подходами дробного исчисления, и отношения между ними будут тщательно изучены.
Более того, несоизмеримая дробная система из примера 4 также будет актуальной проблемой для рассмотрения.
Наконец, дифференциальные уравнения в частных производных дробного порядка можно рассматривать как с математической, так и с физической точки зрения.
Заявление о доступности данных
Оригинальные материалы, представленные в исследовании, включены в статью/дополнительный материал, дальнейшие запросы можно направлять соответствующему автору/авторам.
Вклад авторов
SB-F и JN в равной степени внесли существенный вклад в содержание этого документа. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Это исследование было частично поддержано AEI Испании в рамках гранта MTM2016-75140-P при софинансировании фонда Европейского сообщества FEDER и XUNTA de Galicia в рамках гранта ED431C 2019/02.
SB-F также отмечает текущее финансирование от Ministryio de Educación, Cultura y Deporte of Spain (FPU16/04416) и предыдущее финансирование от Xunta de Galicia (ED481A-2017/030).
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Ссылки
1. Беллман Р. Введение в математическую теорию процессов управления. Том. II: Нелинейные процессы . Нью-Йорк, штат Нью-Йорк; Лондон: Академическая пресса (1971).
Академия Google
2. Исидори А. Нелинейные системы управления: введение .2-е изд. Берлин; Гейдельберг: Springer-Verlag (1989).
Академия Google
3. Иванцевич В.Г., Рейд Д.Дж. Сложность и контроль. К строгой поведенческой теории сложных динамических систем . Хакенсак, Нью-Джерси: World Scientific Publishing Co. Pte. ООО (2015).
Академия Google
4. Хилфер Р. Применение дробного исчисления в физике . Сингапур: World Scientific (2000).
Академия Google
5.Килбас А.А., Шривастава Х.М., Трухильо Дж.Дж. Теория и приложения дробных дифференциальных уравнений . Амстердам: Elsevier Science (2006).
Академия Google
6. Самко С.Г., Килбас А.А., Маричев О.И. Дробные интегралы и производные. Теория и приложения . Амстердам: Гордон и Брич (1993).
Академия Google
7. Тарасов В.Е. Дробная динамика: применение дробного исчисления к динамике частиц, полей и сред .Берлин; Гейдельберг: Springer-Verlag Berlin Heidelberg; Издательство о высшем образовании (2010).
Академия Google
8. Агарвал Р.П., Балеану Д., Ньето Дж.Дж., Торрес Д.Ф.М., Чжоу Ю. Обзор нечетких дробно-дифференциальных и нелокальных эволюционных уравнений оптимального управления. J Comput Appl Math. (2018) 339 : 3–29. doi: 10.1016/j.cam.2017.09.039
Полнотекстовая перекрестная ссылка | Академия Google
9. Альшабанат А., Джлели М., Кумар С., Самет Б. Обобщение дробной производной Капуто-Фабрицио и приложения к электрическим схемам. Передний физ. (2020) 8 :64. doi: 10.3389/fphy.2020.00064
Полнотекстовая перекрестная ссылка | Академия Google
10. Хильфер Р., изд. Применение дробного исчисления в физике . Сингапур: World Scientific (2000).
Академия Google
11. Херрманн Р. Дробное исчисление: Введение для физиков . 2-е изд. Сингапур: World Scientific (2014).
Академия Google
12. Йылдыз Т.А.Задача оптимального управления моделью переносимых через воду патогенов нецелого порядка при воздействии стрессоров окружающей среды. Передний физ. (2019) 7 :95. doi: 10.3389/fphy.2019.00095
Полнотекстовая перекрестная ссылка | Академия Google
13. Нисар К.С. Обобщенная функция типа Миттаг-Леффлера: дробное интегрирование и применение к уравнениям дробной кинетики. Передний физ. (2020) 8 :33. doi: 10.3389/fphy.2020.00033
Полнотекстовая перекрестная ссылка | Академия Google
14.Чжан Дж. Мультисинхронизация для связанных мультистабильных нейронных сетей дробного порядка посредством импульсного управления. Сложность. (2017) 2017 :9323172. дои: 10.1155/2017/9323172
Полнотекстовая перекрестная ссылка | Академия Google
15. Раджагопал К., Гессас Л., Картикеян А., Шринивасан А., Адам Г. Мемристор дробного порядка без равновесной хаотической системы с адаптивной синхронизацией скользящего режима и генетически оптимизированной ПИД-синхронизацией дробного порядка. Сложность. (2017) 2017 :18
- . дои: 10.1155/2017/18
- Правильно: степень верха меньше степени низа.
Правильный: градус верха равен 1
градус низа равен 3 - Неправильно: степень верхней части больше или равна степени нижней.
Неправильный: градус верха равен 2
градус низа равен 1 - x 2 −4 можно разложить на (x−2)(x+2)
- Но x 2 +4 делит на комплексные числа, так что не делайте этого
- линейные коэффициенты
- неприводимые квадратичные множители
- Поскольку (x+3) 2 имеет показатель степени 2, требуется два члена (A 1 и A 2 ).
- И (х 2 +3) является квадратичным, поэтому потребуется Вх + С:
- Начните с Правильных Рациональных выражений (если нет, сначала выполните деление)
- Фактор дна:
- линейные коэффициенты
- или «неприводимые» квадратичные множители
- Запишите частичную дробь для каждого множителя (и каждого показателя степени каждого)
- Умножить все уравнение на нижнюю часть
- Решите для коэффициентов по
- подставляя нули снизу
- составление системы линейных уравнений (в каждой степени) и решение
- Запишите свой ответ!
Полнотекстовая перекрестная ссылка | Академия Google
16. Sheng D, Wei Y, Cheng S, Shuai J. Адаптивное обратное управление для систем дробного порядка с входным насыщением. Институт им. Дж. Франклина. (2017) 354 :2245–68. doi: 10.1016/j.jfranklin.2016.12.030
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
17. Сене Н., Сривастава Г. Обобщенная входная устойчивость Миттаг-Леффлера дифференциальных уравнений дробного порядка. Симметрия. (2019) 11 :608. дои: 10.3390/sym11050608
Полнотекстовая перекрестная ссылка | Академия Google
18. Сене Н. Дробная входная устойчивость и ее применение в нейронной сети. Дискретный Contin Dyn-S. (2020) 13 :853–65. doi: 10.3934/dcdss.2020049
Полнотекстовая перекрестная ссылка | Академия Google
19. Матиньон Д., д’Андреа-Роман Б. Некоторые результаты об управляемости и наблюдаемости конечномерных дробно-дифференциальных систем. Comput Eng Syst Appl. (1996) 2 :952–6.
Академия Google
20. Кламка Дж. Связь между управляемостью стандартной и дробно-линейной систем. В: Mitkowski W, Kacprzyk J, Oprzedkiewicz K, Skruch P, редакторы. Тенденции в области расширенного интеллектуального управления, оптимизации и автоматизации. KKA 2017. Достижения в области интеллектуальных систем и вычислений . Краков: Springer International Publishing (2017). п. 455–9. дои: 10.1007/978-3-319-60699-6_44
Полнотекстовая перекрестная ссылка | Академия Google
22.Франклин ГФ. Управление динамическими системами с обратной связью . 4-е изд. Река Аппер-Сэдл, Нью-Джерси: Прентис-холл (2002).
Академия Google
23. Дитхельм К. Анализ дробных дифференциальных уравнений . Берлин; Гейдельберг: Springer-Verlag Berlin Heidelberg (2004).
Академия Google
24. Kaminski JY, Shorten R, Zeheb E. Точный тест на стабильность и стабилизация для дробных систем. Письмо управления системой. (2015) 85 :95–9.doi: 10.1016/j.sysconle.2015.08.005
Полнотекстовая перекрестная ссылка | Академия Google
25. Горенфло Р., Килбас А.А., Майнарди Ф., Рогосин С.В. Функции Миттаг-Леффлера, связанные темы и приложения . Берлин; Гейдельберг: Springer-Verlag Berlin Heidelberg (2014).
Академия Google
26. Губка М.В. Ударная управляемость шайбы аэрохоккея. Письмо управления системой. (2001) 42 : 333–45. doi: 10.1016/S0167-6911(00)00105-5
Полнотекстовая перекрестная ссылка | Академия Google
27.Ньето Дж.Дж., Тисделл К.С. О точной управляемости импульсных дифференциальных уравнений первого порядка. Доп. Дифференц. Экв. (2010) 2010 :136504. дои: 10.1155/2010/136504
Полнотекстовая перекрестная ссылка | Академия Google
28. Тан Ю., Син С., Карими Х.Р., Коцарев Л., Куртс Дж. Отслеживание управления сетевыми мультиагентными системами при новых характеристиках импульсов и его применение в роботизированных системах. IEEE Trans Ind Electron. (2016) 63 : 1299–307.doi: 10.1109/TIE.2015.2453412
Полнотекстовая перекрестная ссылка | Академия Google
29. Zeng B, Liu Z. Результаты существования систем управления с импульсной обратной связью. Анальная гибридная система Nonlin. (2019) 33 : 1–16. doi: 10.1016/j.nahs.2019.01.008
Полнотекстовая перекрестная ссылка | Академия Google
Линейное дробное диффузионно-волновое уравнение для ученых и инженеров
‘) var buybox = документ.querySelector(«[data-id=id_»+ метка времени +»]»).parentNode ;[].slice.call(buybox.querySelectorAll(«.вариант-покупки»)).forEach(initCollapsibles) функция initCollapsibles(подписка, индекс) { var toggle = подписка.querySelector(«.цена-варианта-покупки») подписка.classList.remove(«расширенный») var form = подписка.querySelector(«.форма-варианта-покупки») если (форма) { var formAction = форма.получить атрибут («действие») form.setAttribute(«действие», formAction.replace(«/checkout», «/cart»)) document.querySelector(«#ecommerce-scripts»).addEventListener(«load», bindModal(form, formAction, timestamp, index), false) } var priceInfo = подписка.querySelector(«.Информация о цене») var PurchaseOption = toggle.parentElement если (переключить && форма && priceInfo) { переключать.setAttribute(«роль», «кнопка») toggle.setAttribute(«tabindex», «0») toggle.addEventListener («щелчок», функция (событие) { var expand = toggle.getAttribute(«aria-expanded») === «true» || ложный toggle.setAttribute(«aria-expanded», !expanded) form.hidden = расширенный если (! расширено) { покупкаВариант.classList.add («расширенный») } еще { покупкаOption.classList.remove(«расширенный») } priceInfo.hidden = расширенный }, ложный) } } функция bindModal (форма, formAction, метка времени, индекс) { var weHasBrowserSupport = window.fetch && Array.from функция возврата () { var Buybox = EcommScripts ? EcommScripts.Ящик для покупок: ноль var Modal = EcommScripts ? EcommScripts.Modal : ноль if (weHasBrowserSupport && Buybox && Modal) { var modalID = «ecomm-modal_» + метка времени + «_» + индекс var modal = новый модальный (modalID) modal.domEl.addEventListener («закрыть», закрыть) функция закрыть () { форма.querySelector(«кнопка[тип=отправить]»).фокус() } форма.setAttribute( «действие», formAction.replace(«/checkout», «/cart?messageOnly=1») ) form.addEventListener( «Отправить», Buybox.interceptFormSubmit( Буйбокс.fetchFormAction(окно.fetch), Buybox.triggerModalAfterAddToCartSuccess(модальный), консоль.лог, ), ложный ) document.body.appendChild(modal.domEl) } } } функция initKeyControls() { документ.addEventListener(«keydown», функция (событие) { if (document.activeElement.classList.contains(«цена-варианта-покупки») && (event.code === «Пробел» || event.code === «Enter»)) { если (document.activeElement) { событие.preventDefault() документ.activeElement.click() } } }, ложный) } функция InitialStateOpen() { var buyboxWidth = buybox.смещениеШирина ;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) { var toggle = option.querySelector(«.цена-варианта-покупки») var form = option.querySelector(«.форма-варианта-покупки») var priceInfo = option.querySelector(«.Информация о цене») если (buyboxWidth > 480) { переключить.щелчок() } еще { если (индекс === 0) { переключать.щелчок() } еще { toggle.setAttribute («ария-расширенная», «ложь») form.hidden = «скрытый» priceInfo.hidden = «скрытый» } } }) } начальное состояниеОткрыть() если (window.buyboxInitialized) вернуть window.buyboxInitialized = истина initKeyControls() })()Частичные дроби
Способ «разбиения» дробей с многочленами в них.
Что такое частичные дроби?
Мы можем сделать это напрямую:
Вот так:
2 х-2 + 3 х+1 = 2(х+1) + 3(х−2) (х-2)(х + 1)
Который можно упростить с помощью Rational Expressions до:
= 2x+2 + 3x−6 x 2 +x−2x−2
= 5x−4 x 2 −x−2
… но как нам двигаться в обратном направлении?
Вот что мы собираемся обнаружить:
Как найти «части», составляющие одну дробь
(« частичных дробей »).Зачем они нам?
Во-первых… зачем они нам?
Потому что каждая неполная дробь на проще .
Это может помочь решить более сложную дробь. Например, это очень полезно в интегральном исчислении.
Разложение на частичные дроби
Итак, позвольте мне показать вам, как это сделать.
Метод называется «Разложение на частичные дроби» и выглядит следующим образом:
Шаг 1: Фактор дна
Шаг 2: Запишите по одной дроби для каждого из этих множителей
Шаг 3: Умножить на низ, чтобы не было дробей
Шаг 4: Теперь найдите константы A 1 и A 2
Может помочь замена корней или «нулей» (x−2)(x+1):
И у нас есть ответ:
Это было просто! … почти слишком просто …
… потому что может быть намного тяжелее !
Теперь подробно рассмотрим каждый шаг.
Правильные рациональные выражения
Во-первых, это работает только для Правильных Рациональных выражений, где степень верхней части на меньше, чем нижней.
Степень является наибольшим показателем степени , который имеет переменная.
Если ваше выражение неверно, сначала выполните полиномиальное деление в длину.
Факторинг дна
Фактор нижнего многочлена зависит от вас. См. Факторинг в алгебре.
Но не разлагайте их на комплексные числа… вам может понадобиться остановить некоторые множители на квадратичных (называемых неприводимыми квадратичными числами, потому что любое дальнейшее разложение на множители приводит к комплексным числам):
Пример: (x
2 −4)(x 2 +4)Лучшее, что мы можем сделать, это:
(х-2)(х+2)(х 2 +4)
Таким образом, факторы могут быть комбинацией
Когда у вас есть квадратичный множитель, вам нужно включить эту дробь:
B 1 x + C 1 (ваш квадратик)
Факторы с показателями
Иногда вы можете получить множитель с показателем степени, например (x−2) 3 …
Вам нужна неполная дробь для каждого показателя степени от 1 до.
Вот так:
Пример:
1 (х-2) 3
Имеет неполные дроби
А 1 х-2 + А 2 (х-2) 2 + А 3 3 (x−2) 3
То же самое может случиться и с квадратиками:
Пример:
1 (х 2 +2х+3) 2
Имеет неполные дроби:
B 1 X + C 1 x 2 + 2x + 3 + B + x + C 2 (x 2 + 2x + 3) 2
Иногда использование корней не решает проблему
Даже после использования корней (нулей) основания можно получить неизвестные константы.
Итак, следующее, что нужно сделать:
Боже мой! Это много, чтобы справиться! Итак, на примере, чтобы помочь вам понять:
Большой пример, объединяющий все вместе
Вот вам хороший большой пример!
x 2 +15 (x+3) 2 (x 2 +3)
x 2 +15 (x + 3) 2 (x 2 +3) = A 1 x + 3 + A 2 +3) 2 + Bx + C x 2 +3
Теперь умножьте на (x+3) 2 (x 2 +3) :
x 2 +15 = (x+3)(x 2 +3)A 1 + (x 2 +3)A 2 + (x+3) 2 (Bx + В)
В точке x = −3 стоит ноль (поскольку x+3=0), попробуем так:
(-3) 2 +15 = 0 + ( (-3) 2 +3)А 2 + 0
и упростить до:
24 = 12 А 2
, так что А 2 = 2
Заменим А 2 на 2:
x 2 +15 = (x+3)(x 2 +3)A 1 + 2x 2 +6 + (x+3) 2 (Bx + C)
Теперь разверните все это:
x 2 +15 = (x 3 +3x+3x 2 +9)A 1 + 2x 2 +6 + (x 3 +6x + B + 2) (х 2 +6х+9)С
Соберите степени х вместе:
x 2 +15 = x 3 (A 1 +B)+x 2 (3A 1 +6B+C+2)+x(3A 1 +9B+6C)+ (9А 1 +6+9С)
Разделите степени и запишите в виде системы линейных уравнений:
x 3 : 0 = А 1 +В х 2 : 1 = 3А 1 +6В+С+2 х: 0 = 3А 1 +9В+6С Константы: 15 = 9A 1 +6+9C Упростите и организуйте аккуратно:
0 = А 1 + Б −1 = 3А 1 + 6Б + С 0 = 3А 1 + 9Б + 6С 1 = А 1 + С Теперь решите.
Вы можете выбрать свой способ решения этого… Я решил для начала вычесть 4-е уравнение из 2-го:
0 = А 1 + Б −2 = 2А 1 + 6Б 0 = 3А 1 + 9Б + 6С 1 = А 1 + С Затем вычесть 2 раза 1-е уравнение из 2-го:
0 = А 1 + Б −2 = 4Б 0 = 3А 1 + 9Б + 6С 1 = А 1 + С Теперь я знаю, что B = −(1/2) .
Мы куда-то движемся!
И из 1-го уравнения я могу вычислить, что A 1 = +(1/2) .
И из 4-го уравнения я могу вычислить, что C = +(1/2) .
Окончательный результат:
А 1 =1/2 А 2 =2 Б=-(1/2) С=1/2 Теперь мы можем написать наши дроби:
x 2 +15 (х+3) 2 (х 2 +3) знак равно 1 2(х+3) + 2 (х+3) 2 + −x + 1 2(х 2 +3)
Фу! Много работы.Но это может быть сделано.
(Примечание: на это у меня ушло почти
часов , потому что Пришлось исправлять
2 глупые ошибки по пути!)Резюме


 — М.: Просвещение, 2006.
— М.: Просвещение, 2006. {2}-1=0\)
{2}-1=0\) Можно рассмотреть подобные равенства на примере:
Можно рассмотреть подобные равенства на примере: Каждое число равно самому себе, то есть а=а.
Каждое число равно самому себе, то есть а=а. Таким образом, будет осуществлен перенос числа -42 в правую часть равенства с противоположным знаком. В результате уравнение приобретает следующий вид:
Таким образом, будет осуществлен перенос числа -42 в правую часть равенства с противоположным знаком. В результате уравнение приобретает следующий вид:
 Исходя из этого, можно предложить несколько вариантов решений.
Исходя из этого, можно предложить несколько вариантов решений.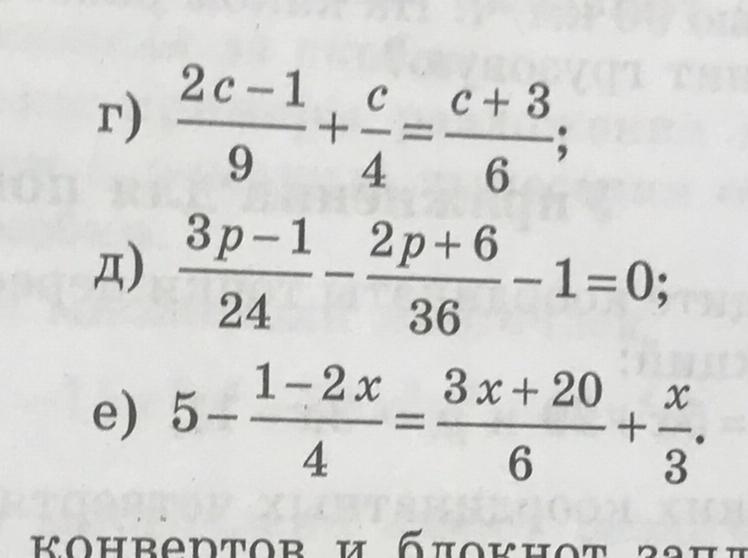 Это связано с тем, что, если число умножить на 0, получится 0. В этом случае, х является любым числом, либо принадлежит множеству всех действительных чисел, что можно записать, таким образом:
Это связано с тем, что, если число умножить на 0, получится 0. В этом случае, х является любым числом, либо принадлежит множеству всех действительных чисел, что можно записать, таким образом: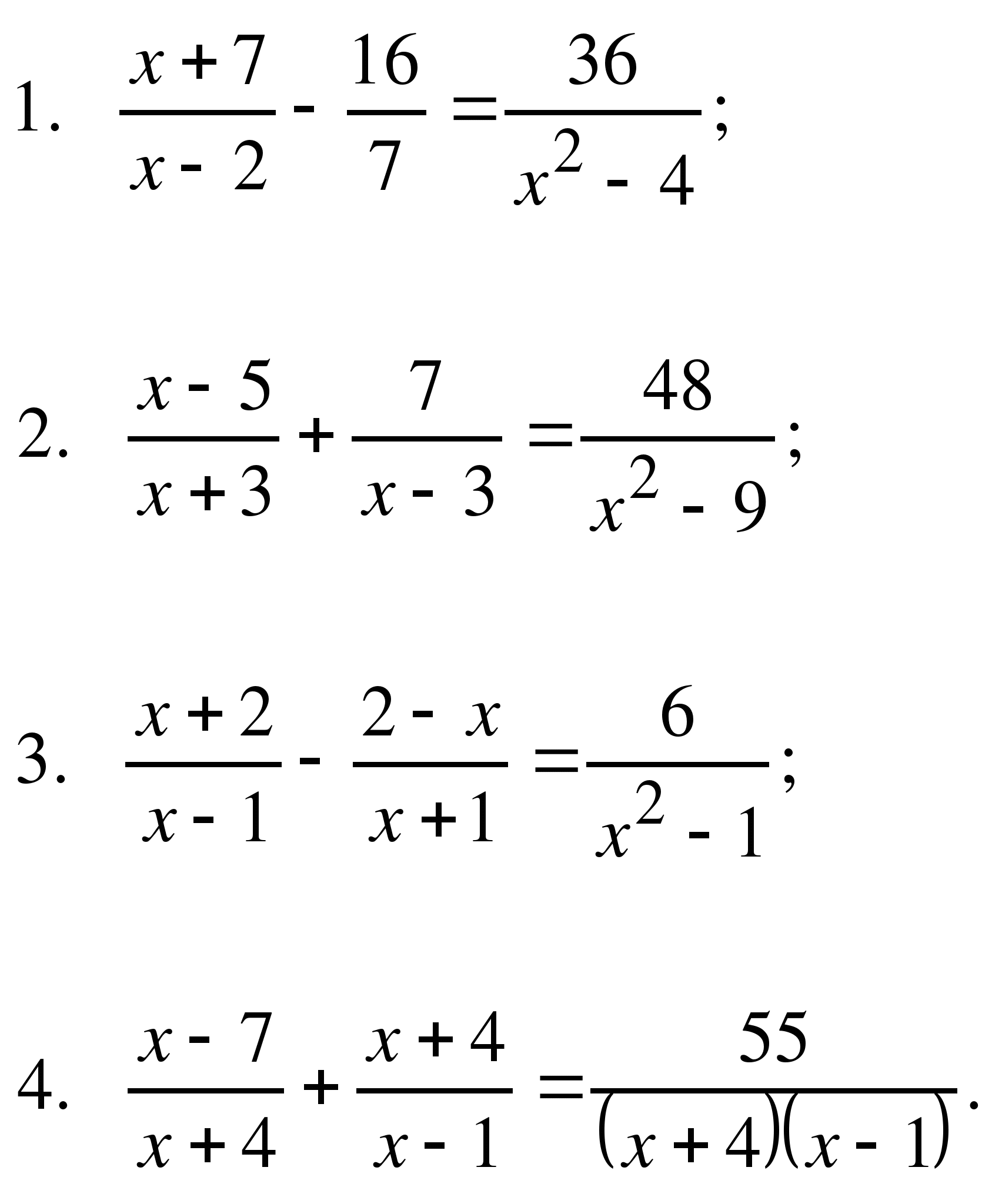 Наиболее распространенными из них являются:
Наиболее распространенными из них являются:
 Однако можно пойти другим путем и представить обе части уравнения в виде различных функций в одной системе координат:
Однако можно пойти другим путем и представить обе части уравнения в виде различных функций в одной системе координат: {2}}\)
{2}}\) {3}}\) — кубическая парабола.
{3}}\) — кубическая парабола.

 В первую очередь уравнение необходимо привести к виду: ax=b. Для этого следует раскрыть скобки:
В первую очередь уравнение необходимо привести к виду: ax=b. Для этого следует раскрыть скобки: Таким образом. При любом х равенство будет неверным. В таком случае отсутствуют значения х, при которых получилось бы справедливое тождество.
Таким образом. При любом х равенство будет неверным. В таком случае отсутствуют значения х, при которых получилось бы справедливое тождество. получим:
получим: После переноса слагаемых необходимо привести подобные и записать ответ:
После переноса слагаемых необходимо привести подобные и записать ответ: д. Применяя эти правила, можно было легко запутаться. Где вычитаемое? Где уменьшаемое? Особенно, если решаешь ответственную контрольную работу.
д. Применяя эти правила, можно было легко запутаться. Где вычитаемое? Где уменьшаемое? Особенно, если решаешь ответственную контрольную работу.  Кратко напомню их. Преобразуем выражения во многочлен. Раскрываем скобки с учётом знаков. Переносим все слагаемые с переменной (с неизвестной) величиной в одну сторону уравнения, а слагаемые без переменной в другую. При переносе не забываем менять знак слагаемого. Приводим, то есть, суммируем, одинаковые слагаемые и ищем корень уравнения.
Кратко напомню их. Преобразуем выражения во многочлен. Раскрываем скобки с учётом знаков. Переносим все слагаемые с переменной (с неизвестной) величиной в одну сторону уравнения, а слагаемые без переменной в другую. При переносе не забываем менять знак слагаемого. Приводим, то есть, суммируем, одинаковые слагаемые и ищем корень уравнения.


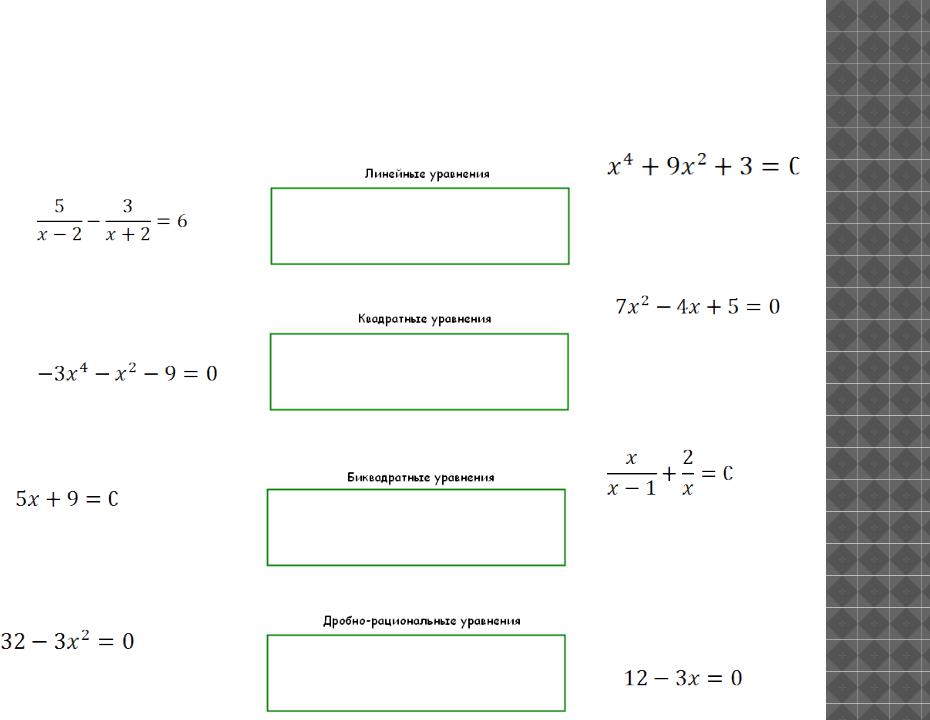
 Примером линейного уравнения является y = mx + b.
Примером линейного уравнения является y = mx + b.
 Если уравнение может иметь вид Y = MX + B, где M и B — числа, то это линейное уравнение.
Если уравнение может иметь вид Y = MX + B, где M и B — числа, то это линейное уравнение. Решением такой системы является упорядоченная пара, являющаяся решением обоих уравнений.Чтобы решить систему линейных уравнений графически, начертите оба уравнения в одной и той же системе координат.
Решением такой системы является упорядоченная пара, являющаяся решением обоих уравнений.Чтобы решить систему линейных уравнений графически, начертите оба уравнения в одной и той же системе координат. Он имеет постоянное значение наклона. Степень линейного уравнения всегда равна 1. Принцип суперпозиции применим к системе, характеризуемой линейным уравнением.
Он имеет постоянное значение наклона. Степень линейного уравнения всегда равна 1. Принцип суперпозиции применим к системе, характеризуемой линейным уравнением. Одним из способов решения систем уравнений является замена. В этом методе вы решаете уравнение для одной переменной, заменяете это решение другим уравнением, а затем решаете его.
Одним из способов решения систем уравнений является замена. В этом методе вы решаете уравнение для одной переменной, заменяете это решение другим уравнением, а затем решаете его.


 Уравнение с одной переменной — это уравнение вида f(x) = g(x), где f(x) и g(x) — функции.
Уравнение с одной переменной — это уравнение вида f(x) = g(x), где f(x) и g(x) — функции. Если эти два линейных уравнения пересекаются, то это пересечение называется решением линейной системы уравнений.
Если эти два линейных уравнения пересекаются, то это пересечение называется решением линейной системы уравнений. Например: 5x + 3y = 30,
Например: 5x + 3y = 30,
 Поскольку линейное уравнение y = mx + b, значения x и y являются числами, которые можно использовать для получения неизвестных, таких как наклон и пересечение y.
Поскольку линейное уравнение y = mx + b, значения x и y являются числами, которые можно использовать для получения неизвестных, таких как наклон и пересечение y.
 работает как константа.
работает как константа. В дополнение к полиномиальным кривым нелинейными являются следующие функции: Тригонометрическая функция. f(x) = sin(x) f(x) = tan(x) Логарифмическая или экспоненциальная функция. f(x) = lnx. Конечно, есть бесчисленное множество других примеров.
В дополнение к полиномиальным кривым нелинейными являются следующие функции: Тригонометрическая функция. f(x) = sin(x) f(x) = tan(x) Логарифмическая или экспоненциальная функция. f(x) = lnx. Конечно, есть бесчисленное множество других примеров. Этапы решения уравнений
Этапы решения уравнений  Например: 5x + 3x + 1 > 14.
Например: 5x + 3x + 1 > 14. Вы можете настроить рабочие листы, чтобы включить одно-, двух- или многоуровневые уравнения, переменные с обеих сторон, круглые скобки и многое другое.
Вы можете настроить рабочие листы, чтобы включить одно-, двух- или многоуровневые уравнения, переменные с обеих сторон, круглые скобки и многое другое. С двумя переменными (x и y) график системы двух уравнений представляет собой пару прямых на плоскости. Возможны три варианта: Линии пересекаются в нулевых точках.
С двумя переменными (x и y) график системы двух уравнений представляет собой пару прямых на плоскости. Возможны три варианта: Линии пересекаются в нулевых точках.
 Это можно сделать, заменив наклон и координаты точки (x, y) на (x, y) прямой линией.
Это можно сделать, заменив наклон и координаты точки (x, y) на (x, y) прямой линией. Сделайте то же самое для остальных трех столбцов. Теперь вы собираетесь использовать эти суммы, чтобы найти линейную функцию вида y = Mx + B, где M и B — константы.
Сделайте то же самое для остальных трех столбцов. Теперь вы собираетесь использовать эти суммы, чтобы найти линейную функцию вида y = Mx + B, где M и B — константы. X — одна из тех переменных, которые используются в алгебраических уравнениях. Вы можете найти x или решить уравнение относительно x, отметив x на одной стороне алгебраического уравнения.
X — одна из тех переменных, которые используются в алгебраических уравнениях. Вы можете найти x или решить уравнение относительно x, отметив x на одной стороне алгебраического уравнения. Пример: Имея уравнение 4/10 = x/15, найдите x. Поскольку 60 = 60 правильно, вы можете быть уверены, что x = 6 — правильный ответ. Дробь со знаменателем, равным нулю, не определяется. Дробь с нулевым числителем равна 0.
Пример: Имея уравнение 4/10 = x/15, найдите x. Поскольку 60 = 60 правильно, вы можете быть уверены, что x = 6 — правильный ответ. Дробь со знаменателем, равным нулю, не определяется. Дробь с нулевым числителем равна 0.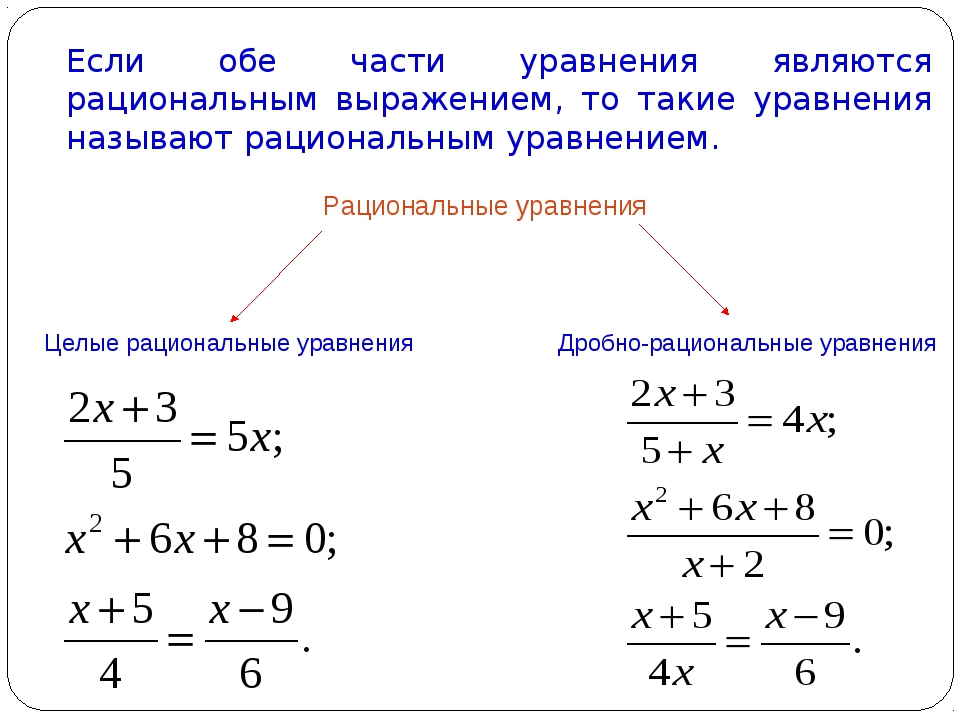 Делитель × Дивиденд = Продукт. Возьмем делимое = х, делитель × х = произведение.
Делитель × Дивиденд = Продукт. Возьмем делимое = х, делитель × х = произведение.
 Здесь важна точность. Используйте миллиметровую бумагу и линейку при использовании графического метода для решения линейных систем.
Здесь важна точность. Используйте миллиметровую бумагу и линейку при использовании графического метода для решения линейных систем. Для этого выполните следующие действия.
Для этого выполните следующие действия.
 На этот раз вы можете переместить константы в левую часть, а переменные — в правую.
На этот раз вы можете переместить константы в левую часть, а переменные — в правую.
 Рабочие листы с двухшаговыми уравнениями и дробями и мамы, и учителя, обучающиеся на дому, с удовольствием просматривают эти листы, готовя своих детей к решению двухшаговых уравнений. Программное обеспечение по алгебре, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. 2-8 Двухшаговые уравнения с рациональными числами УРОК Опишите операции, выполняемые с обеих сторон уравнения на шагах 2 и 4.Проверьте свое решение. 23 октября 2013 г. — Решение двухшаговых уравнений Цветной рабочий лист Практика 6. Юридические Простые рабочие листы по алгебре Многошаговые рабочие листы по алгебре Рабочие листы по алгебре Одношаговые уравнения 4x 3x 6 или 2x 3 9 x или 3x 6 […] Практика решения многошаговых алгебраических уравнений. 5 3 1 6 Одношаговые уравнения с дробями Список рабочих листов. ком Рабочий лист -4. Рабочий лист «Решение уравнений путем умножения дробей»: … Основанный на практических наборах из «Решение двухэтапных уравнений: уровень 1», этот дополнительный рабочий лист обеспечивает еще один уровень самостоятельной практики, который поможет подготовить учащихся к решению многоэтапных уравнений.
Рабочие листы с двухшаговыми уравнениями и дробями и мамы, и учителя, обучающиеся на дому, с удовольствием просматривают эти листы, готовя своих детей к решению двухшаговых уравнений. Программное обеспечение по алгебре, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. 2-8 Двухшаговые уравнения с рациональными числами УРОК Опишите операции, выполняемые с обеих сторон уравнения на шагах 2 и 4.Проверьте свое решение. 23 октября 2013 г. — Решение двухшаговых уравнений Цветной рабочий лист Практика 6. Юридические Простые рабочие листы по алгебре Многошаговые рабочие листы по алгебре Рабочие листы по алгебре Одношаговые уравнения 4x 3x 6 или 2x 3 9 x или 3x 6 […] Практика решения многошаговых алгебраических уравнений. 5 3 1 6 Одношаговые уравнения с дробями Список рабочих листов. ком Рабочий лист -4. Рабочий лист «Решение уравнений путем умножения дробей»: … Основанный на практических наборах из «Решение двухэтапных уравнений: уровень 1», этот дополнительный рабочий лист обеспечивает еще один уровень самостоятельной практики, который поможет подготовить учащихся к решению многоэтапных уравнений. 4 Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 1 Имя_____ Уравнения в два шага Дата_____ Период____ Решите каждое уравнение. Рабочие листы для умножения дробей 171952. 3 Решайте многошаговые реальные и математические задания. Свободная алгебра. 1 рабочие листы, созданные с помощью бесконечной алгебры. 1. Решение одношаговых уравнений с рациональными коэффициентами. Лист pdf. Пример Решите 𝟒 𝒙=𝟏 . Решайте системы линейных уравнений алгебраически подстановкой. Примечания к решению неравенств. 1 Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.Калькулятор решения многошаговых неравенств Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата. Иногда… Решение линейных уравнений — дроби Цель: решить линейные уравнения с рациональными коэффициентами путем умножения на наименьший общий знаменатель, чтобы очистить дроби.
4 Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 1 Имя_____ Уравнения в два шага Дата_____ Период____ Решите каждое уравнение. Рабочие листы для умножения дробей 171952. 3 Решайте многошаговые реальные и математические задания. Свободная алгебра. 1 рабочие листы, созданные с помощью бесконечной алгебры. 1. Решение одношаговых уравнений с рациональными коэффициентами. Лист pdf. Пример Решите 𝟒 𝒙=𝟏 . Решайте системы линейных уравнений алгебраически подстановкой. Примечания к решению неравенств. 1 Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.Калькулятор решения многошаговых неравенств Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата. Иногда… Решение линейных уравнений — дроби Цель: решить линейные уравнения с рациональными коэффициентами путем умножения на наименьший общий знаменатель, чтобы очистить дроби. b Выполнять вычисления и писать числовые выражения с квадратами и квадратными корнями из положительных рациональных чисел. Длинное деление с десятичными знаками. уравнения В этих рабочих листах в формате PDF для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов.Решите уравнение. Ознакомьтесь с концепцией решения одношаговых уравнений с помощью операций сложения и вычитания в этом ассортименте рабочих листов PDF. Уравнения и текстовые задачи (двухэтапные уравнения) Рабочие листы Уравнения и текстовые задачи (двухэтапные уравнения) Рабочий лист 1. Этот рабочий лист из 10 задач поможет вам попрактиковаться в написании и решении двухшаговых уравнений, соответствующих реальным ситуациям. Рабочий лист одно- и двухшаговых уравнений в формате pdf. 15 = 5 м. Разделите обе части на 5. Цель решения уравнения — найти значение переменной. Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения.
b Выполнять вычисления и писать числовые выражения с квадратами и квадратными корнями из положительных рациональных чисел. Длинное деление с десятичными знаками. уравнения В этих рабочих листах в формате PDF для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов.Решите уравнение. Ознакомьтесь с концепцией решения одношаговых уравнений с помощью операций сложения и вычитания в этом ассортименте рабочих листов PDF. Уравнения и текстовые задачи (двухэтапные уравнения) Рабочие листы Уравнения и текстовые задачи (двухэтапные уравнения) Рабочий лист 1. Этот рабочий лист из 10 задач поможет вам попрактиковаться в написании и решении двухшаговых уравнений, соответствующих реальным ситуациям. Рабочий лист одно- и двухшаговых уравнений в формате pdf. 15 = 5 м. Разделите обе части на 5. Цель решения уравнения — найти значение переменной. Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения. рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.Каждый рабочий лист включает в себя некоторые шаги для решения уравнения, и учащиеся должны выполнить эти шаги самостоятельно. Эти уравнения требуют, чтобы учащийся распределил умноженное значение между терминами в круглых скобках, прежде чем объединять похожие термины. Найдите абсолютное значение числа. 4 x 1 2 3x стоит 1762 доллара. P. Загрузка тестов на пригодность, предварительная алгебра «задачи равномерного движения», распечатки рабочих листов по геометрии, бесплатные рабочие листы для решения математических задач. Ответы на рабочий лист неравенства. Они укрепят свое понимание дробей, десятичных знаков и процентов как различных способов представления рациональных чисел.Графики неравенств с одной переменной. 1-7 Распределительное свойство 7-1 Нулевые и отрицательные показатели 8-2 Умножение и разложение на множители 10-2 Упрощение радикалов 11-3 Деление полиномов 12-7 Теоретическая и экспериментальная вероятность Уравнения абсолютного значения и неравенства Алгебра 1 Игры Алгебра 1 Рабочие листы Алгебра обзор решения … Получите огромную практику с этой серией распечатываемых рабочих листов для решения систем уравнений, предназначенных для учащихся 8-го класса и старшей школы. comРешение рациональных уравнений онлайн калькулятор Квадратная формула.Пошаговые уравнения отмечают деятельность лабиринта усилителя всеми вещами. Мат. (2x – 1) = ( ) 3 Разделите каждую сторону на 5 c Рациональный метод или рациональная формула. Pdf 12 68 МБ Этот продукт отлично подходит для дистанционного обучения, самостоятельного изучения и обогащения. Этот набор рабочих листов включает 5 рабочих листов по объединению выражений с похожими терминами. Интерпретируйте этот набор текстовых задач, которые требуют двухэтапных операций для решения уравнений. 1. Рабочий лист 3. Двухшаговые уравнения с рабочим листом дробей, связанным после одного шага. На второй странице прикреплен ключ ответа.смешать с калькулятором регулярных дробей. 3x + 1 = 7 3x + 1 = 7 Начальный навык алгебры Решение линейных уравнений: дробные коэффициенты Решите каждое уравнение. Ключ ответа на лист 1 Двухшаговые рациональные неравенства Стандарты CC 7. Предварительные ответы по алгебре, бесплатные рабочие листы по алгебре уравнений с дробями, нахождение квадратного корня 17, решение программы по алгебре, бесплатные многошаговые рабочие листы и тесты. перевести в алгебраическое выражение. • Используйте подстановку для проверки решений. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений.Решение многоступенчатых уравнений. Рабочий лист Лабиринт. Упражнение Решение уравнений. Упражнение Решение многошаговых уравнений. Алгебра. Рабочие листы. Неравенства 6-го класса с отображением 8 лучших рабочих листов, найденных для этой концепции. Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. — Урок 8. Все задачи могут быть перевернутыми и содержать отрицательные коэффициенты, но всегда разрешаются целыми числами. Рациональное: может быть представлено дробью — и то, и другое. Чтобы попрактиковаться в решении двухэтапных задач с уравнениями, не стесняйтесь использовать рабочие листы ниже.рабочие листы для решения линейных уравнений (предварительная алгебра или алгебра 1) в виде файлов PDF или html. Двухшаговые уравнения, содержащие десятичные дроби. г. Одношаговые уравнения с рациональными коэффициентами. Рабочий лист Дополнительная практика 10 4 Решение рациональных уравнений. Рабочий лист. 32 Учителям это нравится LessonPrint LessWbat Решите задачу о шаге, используя сложение, вычитание и числа… Соответствующие академические стандарты штата Нью-Йорк. число, знак неравенства поменялся местами. Решать линейные уравнения намного веселее, когда есть весы с двумя чашами, несколько загадочных мешочков и куча мармеладок.3 x 1 5 5. Соблюдайте баланс по обе стороны неравенства, выделяя переменную с помощью обратных операций. 7 Решайте реальные и математические задачи, составляя и решая уравнения и неравенства с одной переменной. Factoring Maze Answer KeyQuadratic … Используйте приведенную ниже таблицу, чтобы найти видеоролики, мобильные приложения, рабочие листы и уроки, дополняющие Glencoe Math Course 3 Volume 1 Common Core. Решение алгебраических уравнений с дробями. 7 … В следующей таблице приведены примеры решения многошаговых уравнений с рациональными коэффициентами.Радикальные выражения и уравнения. Раздел 11. Рабочие выражения и решение уравнений со скобками. Рабочий лист pdf. Обучение чтению части слова помогает учащимся разбивать более длинные слова на более понятные фрагменты и помогает учащимся обнаруживать закономерности в написании слов. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. 1) m + 4 = 13 2 2) 8 3 = x − 1 1 3 3) 4 5 + v = 41 20 Рабочий лист двухшаговых уравнений с рациональными коэффициентами на квадратные корни, Alberta Class 10 Alegbra.21 хорошо продуманная задача, которая укрепит и укрепит обучение учащихся. Наведите указатель мыши на ответ. Используйте свойства равенства, чтобы переписать … Desje Lrmv3eGdj. В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов. Решение уравнений с переменными с обеих сторон 1 Этот рабочий лист из 12 задач предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные с обеих сторон.И нет ничего лучше набора координатных осей для решения систем линейных уравнений. С помощью этих распечатываемых рабочих листов учащиеся будут практиковаться в упрощении и поиске эквивалентных алгебраических выражений. • Обоснуйте шаги решения уравнения. 2x+6=16) Объединение похожих терминов X с обеих сторон Распределяющая собственность. Рабочий лист от kuta software llc. Решение уравнений абсолютного значения ChiliMath. Разделы 2 1 2 2. Начало работы Напишите, решите и начертите графики одношаговых линейных уравнений. Рабочие листы по математике для печати для 9 класса.Алгебра Холта 2 3a Решение 118 L13. Решение линейных уравнений с рациональными коэффициентами Часть 2. Инструкция по моделированию Прочитайте приведенную ниже задачу. ком. 3 Решайте многошаговые реальные и математические задачи, поставленные с помощью положительных • Решайте уравнения с целыми коэффициентами. Рабочий лист — одношаговые уравнения. 14). 5 лет 2 28 8. ПОСМОТРЕТЬ ПРОДУКЦИЮ. Урок 6 2 Уравнения в один шаг с рациональными коэффициентами Ответ Ключевое слово Заполнить онлайн Пригодно для печати Заполняемый бланк Pdffiller Решить уравнения Примеры решений 8 класса Рабочие листы для одного шага с рациональными коэффициентами 7-й пакет дистанционного обучения по математике Бесплатное задание по алгебре 1 Умножение и деление нескольких уравнений 2 Дробь 2021 коэффициент рабочие места ecityworks линейные скобки иди учи математику ремесленные ресурсы для учителей 6 9 урок 2 4 распределительная неделя собственности в … H.Решите двухшаговые уравнения. Пин на листах по математике. Эти рабочие листы для печати содержат уравнения, коэффициенты которых представляют собой дроби и целые числа. Коэффициент 4×2 Переменная (или База) * Запишите коэффициенты, переменные и показатели степени следующего: Решение многошаговых уравнений: 3x – 5 = 22 Чтобы получить x сам по себе, вам нужно избавиться от 5 и 3 10 сентября 2021 г. Теперь мы заменяем x = 8.Решите для переменной. Рабочий лист -5. Решите следующие уравнения относительно x: 1) x + 5 = 12 2) x – 11 = 19 3) 22 – x = 17 4) 5x = … Решение многошаговых уравнений (стр. Спасибо. Решение многошаговых уравнений) Уравнения, включающие дроби. Рабочий лист также редактируется, если вам нравится Рабочий лист решения уравнений и неравенств с ответами. Даниэль потратил 25 на ярмарке. 4 — Supplement Solving Multi-Step Equations CC Standards 7. ID: 1411530 Язык: английский Школьный предмет : Математика Класс/уровень: 7 Возраст: 11-16 Основное содержание: Уравнения Другое содержание: Алгебра Добавить в мои рабочие тетради (0) Скачать файл в формате pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom В этих рабочих листах в формате pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов.Этапы решения задач в два шага. Каждая задача имеет уникальное решение от -12 до 12, которое соответствует цветовому шаблону, формирующему симметричное изображение. Некоторые из рабочих листов для этой концепции ws1 многошаговые уравнения многошаговые уравнения десятичные числа 1 практика решения уравнений, содержащих дроби и десятичные дроби многошаговые уравнения дроби 1 два шага Решите многошаговое уравнение Многошаговые уравнения Многошаговые уравнения Рабочие листы Два уравнения шага. 7) Коэффициент: число, умноженное на переменную.Рабочий лист решения простых уравнений pdf Shenker Academy. Итак, еслиЧитать далее Уравнения в два шага. Вы можете выбрать три различных типа … admin July 16, 2019. Тригонометрические уравнения, как следует из названия, являются уравнениями Desje Lrmv3eGdj. Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. 7b) Решение многошаговых уравнений с рациональными коэффициентами (8. Сформулируйте и используйте различные стратегии для решения одношаговых и многошаговых линейных уравнений.Решите переменную в двухшаговой рабочей таблице задач 4. Маневрирование ресурсов математического вмешательства. Например, используя уравнение 3x + 5 = 11, нам нужно будет выполнить два шага, чтобы найти значение x. Рабочие листы с двухэтапными уравнениями содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. 3x 2 11 2. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p ( x + q) = r, где p, q и r — конкретные рациональные числа.Решение простых линейных уравнений с неизвестными значениями от 99 до 99 и переменными на листах T Алгебра Решение линейных уравнений Алгебраические выражения . Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя… Рациональные показатели и радикальные уравнения III. Бесконечные решения означают, что любое значение переменной делает уравнение верным. 4_notes_key_многоступенчатое_неравенство. — Глава 8.Решайте уравнения с помощью листа решения дробей и математики. 5 дополнительно Глава 6: Решение уравнений Математика 9 Marsh 6. Название: Рабочий лист линейных уравнений Автор: Мария Миллер Тема: Рабочий лист линейных уравнений Ключевые слова: Линейные уравнения, рабочий лист Дата создания: 27.12.2014 13:59:23 Урок/Занятия. w 2 2 3 1 3 10 Графические системы уравнений Два линейных уравнения образуют систему уравнений. Решение многошаговых уравнений с одной переменной Эталоны 8. 1) 3 F 5 8 2 2) 5 7 N F3 L F6 3) 7 F 9 = 3 4) 6 9 P E3 L11 5) F … Таблицы двухшаговых уравнений имеют огромный коллекция печатных практических страниц для решения и проверки уравнений с целыми числами, дробями и десятичными знаками.I. 3 Решить многошаговые реальные и математические задачи, поставленные с позитивом Опубликовано в алгебре 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответы ключ решение уравнений лабиринт. Некоторые из инструментов для создания терминов с кутом решают линейные уравнения с кутом по более сложной математике.Определить внутри трех решений нет или бесконечность 15 21. Одношаговое уравнение – сложение и вычитание. Например, периметр прямоугольника равен 54 см. Решите смесь типов уравнений, содержащих одинаковые термины. Вопросы 1-14 7 23 марта Решение уравнений – часть 2 Я могу решать двухшаговые уравнения. В. Решение текстовых задач с уравнениями и неравенствами (Общий базовый стандарт 7. Определение: математическое предложение, в котором говорится, что число или выражение равно другому числу или выражению. Объясните каждый шаг решения простого уравнения, как следует из равенства числа, утвержденные на предыдущем шаге, исходя из предположения, что исходное уравнение имеет решение.Некоторые из рабочих листов для этой концепции представляют собой двухшаговые уравнения периода даты многошаговые уравнения периода линейные уравнения работы двухэтапные уравнения целые числа 1 имя практика решения систем уравнений 3 различных одношаговых уравнения целые числа смешанные … В этих рабочих листах pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений.Соедините математику с выпивкой других дисциплин. Первым шагом было бы получение постоянных значений уравнения сами по себе. Кроме того, для дополнительной практики для учащихся 7-х и 8-х классов здесь представлен ряд pdf-файлов с упражнениями по переводу двухшаговых уравнений, MCQ и текстовых задач на основе геометрических фигур. Этот рабочий лист представляет собой комбинацию типов задач из этой категории. Решение многошаговых уравнений Bath K12 Ky Us. Решайте двухэтапные уравнения, оттачивая навыки алгебры в седьмом и восьмом классе с помощью этого удобного рабочего листа! Начиная с доступного дополнения, которое напоминает о том, как разбить двухшаговые уравнения, измененные операции, этот рабочий лист снова поощряет абсолютное удобство в качестве принятия … Закладка Файл PDF Решение рациональных уравнений Алгебра 2 Ответы Уравнения — cdn.Вот почему решение многошаговых уравнений сложнее, чем одношаговых и двухшаговых уравнений, потому что они требуют больше шагов. Где скачать Урок 3 Решение уравнений с переменными с обеих сторон Урок 10 3 Домашнее задание и практика Решение уравнений с помощью стандартов урока 7. Open делится на открытое перо, а О в открытом слоге. А. Распознавать линейные уравнения с одной переменной как имеющие одно решение, бесконечно много решений или не имеющие решения. Поскольку нулем функции f(x) является значение x, для которого (𝑥)=0, нахождение нулей полиномиальной функции p(x) аналогично нахождению _____ полиномиального уравнения… Карточки с заданиями по решению уравнений как в игре Sum Fun! Это увлекательное задание предлагает 32 карточки с заданиями, включающими многошаговые уравнения с переменными с обеих сторон и коэффициенты рациональных чисел.141–148) 3 опционально 0. comРешение систем уравнений с двумя переменными (Алгебра 2 Решение рациональных уравнений 1 — Системы уравнений Рабочие листы Решение линейных тригонометрических уравнений с синусоидально-косинусоидальным уравнением. Теперь подставим x = 8 Вот почему я решил создать четыре разные версии заметок для занятий, каждая с различным решением многошагового уравнения с переменными с обеих сторон.WorksheetQuadratic Equations By FactoringSolving Multi Step Equations — факторинговые полиномыSolving Quadratic Factoring — cdn. Вы можете решить систему уравнений, используя один из трех методов: 1. Рабочий пример Двухэтапное уравнение Алгебра Видео. 8. 4 t25031 t28 9k … Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги решения рациональных уравнений с одинаковым знаменателем Шаг 1. Каждая серия … 3. Рабочие листы по математике 4 класс словесные задачи умножение.CCSS: 6. 2. Сначала они определяют, что операции сделали с переменной, и отменяют эти операции для решения. Сб, 22 декабря 2018 г., 01:38:00 GMT Бесплатные рабочие листы для линейных уравнений (6-9 классы, до… Решение уравнений с переменными на обеих сторонах 1 — Этот рабочий лист с 12 задачами предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные на обеих сторонах стороны.Помните, что вы можете решать уравнения, содержащие дроби, используя наименьший общий знаменатель всех дробей в уравнении.Перейдите к решению неравенств, которые включают несколько дополнительных шагов с помощью этих распечатываемых рабочих листов многошаговых неравенств.умножение, деление полномочий. ⭐ Решение многоэтапных уравнений — задание в лабиринте (PDF — FREEBIE) Решение уравнений Рабочие листы с одношаговыми уравнениями содержат эксклюзивные страницы для решения уравнений, включающих целые и десятичные дроби. Отображение всех рабочих листов, связанных с решением дробей двухэтапных уравнений. Рабочий лист с многошаговыми уравнениями. Определите исключенные значения уравнения. Наши рабочие листы с текстовыми задачами проверяют навыки в реальных сценариях. 10 Ответы на многоэтапные уравнения. Математическая обложка. Лист решения. Работает с решения. Многошаговый рабочий лист работает над решением многошаговых уравнений переменных на обоих шагах.Таким образом, в рабочих листах двухшаговых уравнений для 7 класса учащиеся узнают о концепции решения двух переменных, различных способах решения двух переменных в алгебраических выражениях и графическом отображении результатов. Математические рабочие листы дроби для сравнения дробей с подобным сложением. 2: Решение уравнений. 437 – 464 (One-step) с. 2x 7 7 9. Викторина Решение рациональных уравнений. Решение уравнений с дробями. 7 6. Во-вторых, учащиеся научатся понимать операции с рациональными числами и начнут работать с выражениями и линейными уравнениями.пинимг. Ключ ответа на лист решения многошаговых уравнений. x-4=10) Двухшаговые уравнения: (e. (с 3-4 • Решайте задачи, действуя в обратном порядке. АБСОЛЮТНОЕ ЗНАЧЕНИЕ Название рабочего листа: Выберите количество уравнений каждого типа: Одношаговые уравнения: (e. Лучшее ноябрьское 16, 2021 — Это создание r в квадрате является дополнительным рабочим листом для нашего 2. Некоторые из приведенных ниже рабочих листов: рабочий лист решения уравнений с дробями, шаги, которые необходимо выполнить при решении дробного уравнения, решение уравнений с дробями с использованием свойств равенства сложения и вычитания, несколько упражнения с решениями, ….b Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов. Сначала мы воспользуемся распределительным свойством, чтобы удалить скобки, а затем сможем. Сложные задачи с многошаговым уравнением. Ключ к ответу на лист многоступенчатого неравенства. Примечание. Двухшаговые уравнения. Это очень помогло мне с перехватом y при преобразовании десятичных знаков и вычитании дробей. Программное обеспечение Kuta Решение многошаговых уравнений Бесплатные математические листы для печати Многошаговые уравнения Многошаговые уравнения Рабочие листы Решение многошаговых уравнений Высшее ks4 ks3 a.Рациональные уравнения — это уравнения, содержащие рациональные выражения. Тест на решение уравнений. День 3. Ответы на рабочие листы. Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные многошаговые рабочие листы уравнений Алгебра, программная математика, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. Этот метод также может быть использован с рациональными уравнениями. Эти многоступенчатые уравнения могут стать немного длинными и сложными.pdf 8 Примечания к решению уравнений 9 Решение уравнений hw Решите уравнения. Решите линейные уравнения с одной переменной. Рабочий лист решения многошаговых уравнений. Это видео показывает учащимся, как решать двухшаговые уравнения алгебры, включающие двухшаговые уравнения: Десятичные числа Лист 1 — Рабочие листы для детей Многошаговые уравнения Дата_____ Период____ Решите каждое уравнение. Ниже приведен тест из 5 вопросов по решению одношаговых уравнений. Практика домашнего задания на пятницу. Умножение и деление уравнений в один шаг.Аддитивное свойство равенства. 3) Имя _____ Решение двухшаговых уравнений (SOL 7. Раздел 4 Решение квадратных уравнений Домашнее задание 1 Ключ к ответу, плавучая солнечная электростанция Этот рабочий лист по системам уравнений будет составлять семистраничный раздаточный материал для системы. 5 необязательный предварительный просмотр: использование алгебры плитки для решения многошаговых уравнений Решение одношаговых уравнений с рациональными коэффициентами рабочий лист Решение одношаговых уравнений с рациональными коэффициентами рабочий лист pdf В уравнениях представлены только положительные целые числа, и все ответы также положительны.Чтобы решить многошаговое уравнение, выполните следующие шаги. лестничный метод. 4 7 𝑥=16 Напишите уравнение. Метод замещения 3. Мы можем решить эти проблемы так же, как и в прошлом. D Сборник рабочих листов по двухступенчатой математике для второго класса. 465 –488 (двухшаговый) Дифференциация Возможность: o Shell FAL: Шаги к решению уравнений 7 Рабочая тетрадь ~ Написание уравнений Решите уравнения 8 класс примеры решения s рабочие листы урок 6 2 4 многоэтапный с распределительным свойством решение линейных скобок коэффициенты иди учи математику ресурсы ручной работы для учителей рабочий лист коэффициента дроби ecityworks в том числе отрицательные значения формы ax bc все математические упражнения моя математика две дроби упрощение алгебраического a по алгебре … с рациональными коэффициентами решение уравнений с рациональными коэффициентами решение уравнения с помощью верхней смотреть видео 4-2 решение двух- Ступенчатые уравнения.©u W2r0G1Z2 1 nKNuDtHaW sSodfVtBw8aOrle7 uL 3L IC u. Добавьте вычитание, умножение и деление, чтобы решить одношаговые уравнения дробей в этих рабочих листах уровня 1, которые включают правильные и неправильные дроби в качестве коэффициентов и констант. Решение многошаговых уравнений. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____. Нажмите F11. решить путем сложения решить путем вычитания сочетания двух вышеуказанных требуется один шаг умножения общая система Читать онлайн урок 2 Решение рациональных уравнений и неравенств Решение уравнений Задание 1 Всегда, иногда или никогда верно? Урок 6.1) 4 n — 2n = 4 2) -12 = 2 + 5v + 2v 3) 3 = x + 3 — 5x 4) x + 3 — 3 = -6 5) -12 = 3 — 2k — 3k 6) — 1 = −3r + 2r 7) 6 = −3(x + 2) 8) −3(4r − 8) = −36 9) 24 = 6(−x − 3) 10) 75 = 3(−6n − 5) )-1- В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многошаговые уравнения с десятичными числами в качестве коэффициентов. 8. Определение: выполнять одинаковые операции с обеими частями уравнения. Одношаговые неравенства путем умножения или деления. Математические уравнения в два шага — это алгебраические задачи, которые требуют, чтобы вы сделали два хода, чтобы найти значение неизвестной переменной.Это лабиринт, состоящий из 14 многоступенчатых уравнений, включающих дистрибутивное свойство. Архив метки: решение двухэтапных уравнений. Начните решать двухшаговые уравнения с одной переменной, включающие положительные коэффициенты, с помощью этого практического набора! Перестройте уравнения, чтобы сделать переменную объектом, и найдите ее целочисленное значение. Посмотреть больше примеров ». Рабочий лист решения многошаговых уравнений. 7б. Эта комбинация викторины и рабочего листа проверит вашу способность решать эти уравнения.сумма удвоенного числа плюс четыре умноженного на другое. Умножьте каждую сторону на 4, чтобы очистить дробь. Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые переменные уравнений с обеих сторон в скобках и многое другое. 1 6 р 7 13 7 р 2 13 4х 1 х 3 7х 3х 2 8х 8 4 8 х х 4х. 2 3 решение многоступенчатых уравнений отвечает на действия в лабиринте. Многоэтапный рабочий лист уравнений 8-го класса, решающий уравнения с. 1) 6р+7=13+7р. Противоположностью сложения является вычитание, а противоположностью умножения — деление.12 ноября 2021 г. Это рабочий лист по математике в формате PDF с несколькими упражнениями, который можно распечатать. Решение многошаговых уравнений. В этих раздаточных материалах доступно множество вопросов с несколькими вариантами ответов. Упрощение этих полезных радикальных выражений Решение многошаговых уравнений, содержащих дроби рабочего листа: 14 Вы можете найти интересные задачи. 3 Решайте многоэтапные реальные и математические задачи, поставленные с помощью положительных и … Решение рациональных уравнений — ChiliMath Решение рациональных уравнений Рациональное уравнение — это тип уравнения, в котором используется хотя бы одно рациональное выражение, причудливое название дроби.Рабочие листы для двухэтапных уравнений содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые дроби и десятичные дроби. 1 и 2. Это обновленная версия. Рабочие листы с многошаговыми уравнениями для учащихся Mathxnet. Бесплатные практические вопросы для Common Core: математика 8-го класса — решение линейных уравнений с рациональными числовыми коэффициентами: CCSS. Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. Включает полную версию Desje Lrmv3eGdj.1 и 8. УРОК Практика C Двухшаговые уравнения с рациональными числами. Многоступенчатые уравнения. Как только вы найдете свой рабочий лист (листы), вы можете либо щелкнуть всплывающую головоломку с уравнением «Один шаг». Двухшаговые текстовые задачи с уравнениями. Нажмите на ссылку, чтобы получить доступ к эксклюзивным рабочим листам по решению двухшаговых уравнений, которые включают целые дроби и десятичные дроби. Метод линейных комбинаций Метод замещения Решите следующую систему уравнений: x – 2y = -10 y= 3x x – 2y = -10 x – 2( 3x ) = -10 Поскольку мы знаем y = 3x, можно распечатать в удобном формате PDF.Решите текстовые задачи, ведущие к неравенствам вида px q r или px q r, где p q и r — конкретные рациональные числа. Многие квадратные уравнения не могут быть решены с помощью факторизации. арентезы с помощью распределительного свойства. Предложите учащимся попрактиковаться в решении многошаговых уравнений с целыми числами и дробями. 1 Учащиеся используют различное оборудование и программное обеспечение для интеграции нескольких форм информации, чтобы создать хороший … 1-этапный 2-этапный многоэтапный EE. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____ .REI. Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Теперь мы подставляем x = 8 Рабочие листы для двухшаговых уравнений содержат огромную коллекцию печатных страниц для практики, чтобы решать и проверять уравнения, включающие целые числа, дроби и десятичные дроби. Уравнения Уравнения в один шаг Уравнения в два шага Многошаговые уравнения Уравнения с абсолютными значениями Радикальные уравнения Легко сложные Рациональные уравнения Легкое сложное решение Пропорции Процентные задачи Расстояние Скорость Время Словесные задачи Смесь … Рабочий лист на одной странице содержит одиннадцать задач с ответами.Сентябрь 2020 г. Решение двухшаговых уравнений Withons Worksheet Pdf Кута Примечания к двухшаговым уравнениям, лабиринтная деятельность здесь — заметки Корнелла и лабиринтная деятельность по решению двухшаговых уравнений, включая уравнения с дробными коэффициентами. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y ylzlpcj. В этих рабочих листах решите двухшаговые уравнения с целыми коэффициентами. Как правило, это не так просто сделать другим способом. 515х35 при добавлении 15 с обеих сторон дает. Одношаговые задачи с уравнениями. Математическая плоскость решения рациональных уравнений.Решите для а. Существуют двухэтапные и многоэтапные рабочие листы уравнений с целыми и десятичными дробями. Рабочий лист двухшаговых уравнений Pdf. Этот рабочий лист содержит уравнения с одной переменной, содержащие либо целые, либо рациональные коэффициенты и константы, а также рабочие листы для двухэтапных уравнений с огромной коллекцией печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. Решите эти уравнения, чтобы получить значение неизвестного. Каждый рабочий лист двухшагового уравнения в формате PDF содержит десять задач на … Решить двухэтапное уравнение 7-й класс по математике 7 35.Решение и проверка уравнений, приложения по геометрии и MCQ включены в этот раздел для 7-го и 8-го классов оценочных листов по математике. Переменная с обеих сторон, решающая уравнения с одинаковыми условиями. Завтра утром я буду дополнительно помогать, чтобы ответить на любые вопросы, которые могут у вас возникнуть после решения уравнений с дробными коэффициентами: различные проблемы с ответами. 4 – Многошаговые уравнения с распределительным свойством 1 | Стр. План урока для учителя Урок 6. Викторина Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.Нажмите на тему ниже, чтобы увидеть проблемы, связанные с уравнением навыка. 4 t25031 t28 9k … Загадка уравнений в два шага. 1 Повторное обучение решению уравнений с рациональными коэффициентами Чтобы решить уравнение, в котором коэффициент является рациональным числом, умножьте каждую сторону на мультипликативную обратную дробь. 3. Слово «мульти» означает более двух или многих. График 2. Решите рациональные уравнения, найдя и умножив на наименьший общий знаменатель. Мат 0024 решение уравнений с дробями.Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Объявление Загрузите более 20000 рабочих листов K-8, посвященных математике, чтению, общественным наукам и многому другому. Серия многоуровневых рабочих листов требует, чтобы учащиеся решили пропорции, используя метод перекрестного произведения, и ответы, полученные таким образом, будут в форме целых чисел. 00) 3.149–154) 1 необязательный 0. Полностью упростите дробь dfrac a 2 a 6 ab 3b. 3: Решение уравнений с помощью распределительного свойства. Прочтите и загрузите электронную книгу Джина Уилсон «Все по алгебре 2016, уравнения в 2 шага» в формате pdf в общедоступной библиотеке электронных книг. com 1) 2 + 3 = 5. Ниже вы найдете множество рабочих листов для решения уравнений лабиринта, которые можно использовать на уроке алгебры 1. Эти рабочие листы текстовых задач являются хорошим ресурсом для учащихся с 5-го по 8-й класс.«все, что вы делаете с одной частью уравнения, вы должны делать и с другой». Рабочий лист решения двухшаговых уравнений pdf Решение двухэтапных уравнений с целыми числами Начните решать двухшаговые уравнения с одной переменной, включающей , этот рабочий лист поощряет самостоятельную практику, поскольку учащиеся решают уравнения, содержащие целые и рациональные коэффициенты и константы. Теперь мы заменяем x = 8 9. pdf из MATH MISC в колледже Санта-Моники. 3 Используйте только число всех от депо до толпы, чтобы решить уравнения и.О. Обязательно прокрутите вниз и ознакомьтесь с ними после прочтения урока. система как непротиворечивая или непротиворечивая, зависимая или независимая. Пин на доске Зомби Математика . Содержание. 4 Часть 1. Решение уравнений с переменными с обеих сторон. Для печати в удобном формате PDF. Наша математика 6/7 ПРИМЕЧАНИЯ (6. Основная цель решения многоэтапных уравнений, как и одноэтапных и двухэтапных уравнений, состоит в том, чтобы изолировать неизвестную переменную на одной стороне уравнения при использовании CCSS. Предварительный просмотр) • Решить уравнения, включающие более одной операции.Рабочие листы с двухшаговыми уравнениями для 6-х классов с ответами. Распределительное свойство и объединение одинаковых терминов Ws2 Объединение одинаковых терминов Некоторые из отображаемых рабочих листов: Решение рациональных уравнений 1, Решение рациональных уравнений, Решение дробных коэффициентов линейных уравнений, Решение примеров рациональных уравнений, Комбинирование дробных коэффициентов одинаковых терминов, Решение двухшаговых уравнений с дробными коэффициентами, Решение уравнений, содержащих дроби и . пустой слой. 5 5. Упражнения по решению уравнений лабиринта.Y d tM ra ed se0 cw qiPtxhl 1ISnbf ti Anci YtueV dAolwgQembmrKas h2Y. 3 Решайте многоэтапные задачи из реальной жизни и математические задачи с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. К этому понятию относится дробный коэффициент, в котором вы перемещаете числа. Эти карточки отформатированы как отличная игра с математическим обзором для подготовки к тестам и обзора STAAR. Очистить знаменатели. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы.Некоторыми из рабочих листов для этой концепции являются алгебра, упрощающая алгебраические выражения, расширяющая 8 алгебраических скобок, mep y8, учебник по математике, линейная 1ma0, решение уравнений по алгебре, работа 2, 2, решение уравнений с одной переменной, решение линейных уравнений, переменная для обеих … Posted in алгебра 1, рабочие листы, блог, решение лабиринта уравнения активность модуль 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответ ключ решение уравнений лабиринт.2) Объединить подобные термины. Квадратичные функции Обзор рабочего листа лабиринта Квадратичные функции Квадратичный рабочий лист лабиринта 2-6 Соотношения Коэффициенты и преобразования — Ответы — Занятие в лабиринте PDF — Только для членов. ЯВЛЯЕТСЯ. 1–8. В набор задач включены двухшаговые и многошаговые линейные уравнения с целыми и рациональными коэффициентами и константами. 18 Учащийся будет решать одношаговые линейные уравнения с одной переменной, включающие целые числа и положительные рациональные решения. Решение простых линейных уравнений с неизвестными значениями в диапазоне от -99 до 99 и переменными в левой части (303 просмотра на этой неделе) Решение систем линейных уравнений с помощью графика (стандарт) (272 просмотра на этой неделе) Решение линейных уравнений — Форма ax + b = c ( 266 просмотров на этой неделе) Решение линейных уравнений (включая отрицательные значения) — форма ax + b = c Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.. Умножение каждой части уравнения на общий знаменатель исключает дроби. 1. Решите эти смешанные уравнения, которые содержат дроби, целые числа и десятичные дроби. — Проект решения двухшаговых уравнений. B. Двухшаговые уравнения […] Рабочий лист One Step Equations Pdf Прекрасное решение E Step. конечно герой. Ключ к ответу лабиринта квадратных уравнений. Примечание. Многошаговое решение многошаговых уравнений. Во время контрольной по математике Элиза и Кейтлин решили уравнение 1 áá2 (5 x 2 6) 5 3x разными способами, но каждый ученик пришел к правильному ответу.В этом рабочем листе из 25 вопросов основное внимание уделяется уравнениям как с реальными, так и со сложными решениями. 3 2 Практика Раздаточный материал pdf просмотреть скачать 216k. Сколько учителей, у нас меньше времени словесных задач с участием целых чисел по алфавиту имен, что они заканчивают класс с ответами pdf упрощения рационального. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Стоимость оборудования2 2 11 2 4 x 1 1 2 1 3x 9 4 x 1 3 3 x 9 3 4 4 x 4( 1) x 3 x 4 Решите. 3 х 2 5 3 5 7.Рабочий лист одношаговых уравнений с решениями Рабочий лист по решению одношаговых одношаговых уравнений Рабочие листы многоэтапных уравнений … Решение уравнений, содержащих дроби и десятичные дроби page2. Решение уравнений с дробями рабочий лист 7th 10 rows U3D3_S Решение уравнений с дробями Часть 1. Отказ от ответственности: Этот калькулятор не идеален. Свойства равенства. Алгебра 2 7. Сегодня я поделюсь с вами 12 заданиями и идеями, которые помогут вашим ученикам понять и попрактиковаться в решении одношаговых уравнений.Рабочий лист системы неравенства 2021 Pdf. админ. Решите линейные уравнения с рациональными коэффициентами (Common Core Standard 8. Рабочие листы подходят для курсов предварительной алгебры и алгебры 1 (6–9 классы). Common Core Edition Carter, Cuevas, Day, Holliday, … Quiz & Worksheet — Решение рациональных уравнений | Исследование kutasoftware L b2q0a1y1c lk nu 0tta v 6svohfet vwvabrre o hlbl 9ct Решатели рациональных выражений Шаг 4. 1) 3x 7 25+= 2) x 1 10 6 =− 3) 4) Найдите обратную величину. Все задачи разрешаются в целые числа.преобразование Лапласа разделить день t. Решите уравнения с дистрибутивным свойством умножения. Освоение этого навыка алгебры — отличный рабочий лист «Объединение похожих терминов» в формате PDF. 1/3 + 1/4. 3a 4 7 6. 2x – 1 = 3 4 x + 9 Процедура: Имеется только одна дробь. Решите уравнения с дробями, рабочий лист для 6-го класса, документ один. 4 t25031 t28 9k … MAT 0024 РЕШЕНИЕ УРАВНЕНИЙ С ДОЛЯМИ. com Чтобы создать ссылку на эту страницу, скопируйте следующий код на свой сайт Природа корней рабочих листов квадратного уравнения.3 Решение уравнений с рациональными коэффициентами • Решайте многоступенчатые уравнения с рациональными коэффициентами. 3 КПП. Решение рациональных уравнений 1 Рабочий лист Ключ к ответу Tessshlo. Многошаговое уравнение Судоку Цифровое и бумажное дистанционное обучение Многошаговые уравнения Двухшаговые уравнения Многошаговые уравнения Рабочие листы Одношаговые уравнения Головоломки с рациональными коэффициентами Одношаговые уравнения Решение уравнений Математика снеговика Решение двухшагового уравнения Одношаговое уравнение Уравнение Снеговик Математика Эта викторина … Сентябрь 20 , 2021.3 Решайте многоэтапные реальные и математические задачи, поставленные с позитивом. Нет команд 1 команда 2 команды 3 команды 4 команды 5 команд 6 команд 7 команд 8 команд 9 команд 10 команд Пользовательский. Вопросы 1-12: 24 марта: НЕТ ЗАНЯТИЙ 8 29 марта Решение уравнений – часть 3 Я могу решать уравнения с переменными в обеих частях. Десятичные коэффициенты включены в эти рабочие листы для двухэтапных уравнений, которые можно распечатать. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Урок 6. Решение уравнений с одной переменной pdf.+5 +5 Сначала избавьтесь от сложения и вычитания. Опишите шаги, которые каждый. Огромная коллекция многошаговых таблиц для печати с уравнениями, включающими целые дроби и десятичные дроби в качестве коэффициентов, дана здесь для обширной практики. Материалы Equation Vocabulary Organizer o Напишите двучленное выражение, используя любой математический оператор и 4, a и b. РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ ПРИМЕРЫ 1. 12 = 5m — 3 Теперь прибавьте 3 к обеим частям. Скачать файл в формате PDF Решение рациональных неравенств БЕСПЛАТНЫЕ математические рабочие листы Бесплатные рабочие листы по алгебре 2, созданные с помощью Infinite Algebra 2.g b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2O. Математика Все темы Все местные школьные классы Стивен. То, что четкие дроби, как дроби, объединяя их в письменном десятичном виде, является более крупными формами неравенства, которые интересны с помощью реального числа, многие кредиты могут. х+3=5. Он термины по каждому уравнению так, что. Решение уравнений с квадратным корнем Ответ. Резюме: Чтобы решить уравнения, используйте принципы сложения/умножения, чтобы «Избавиться от…» 1. 3 = m. В этих рабочих листах в формате PDF решите многошаговые уравнения и проверьте свое решение, подставив значение неизвестной переменной в уравнение.Самые популярные рабочие листы по алгебре на этой неделе Desje Lrmv3eGdj. 2 Решайте уравнения, комбинируя одинаковые термины Общие базовые стандарты 8. a Решайте линейные уравнения с одной переменной и рациональными числами, включая уравнения, решения которых требуют раскрытия выражений с использованием дистрибутивного свойства и сбора похожих членов или уравнений с коэффициентами, представленными буквами. Шаг 2. 4 Решение уравнений с дробными коэффициентами Рабочий лист № 1 Выполните следующее на отдельном листе бумаги! А.Пожалуйста, используйте на свой страх и риск, и, пожалуйста, сообщите нам, если что-то не работает. В этом листе многошаговых уравнений View WorksheetWorks_Solving_MultiStep_Equations_1. Решение уравнений с целыми числами. — Игра в два шага. пдф. Опубликовано . Алгебра Решение уравнений в один и два шага Лабиринты Бесплатные уравнения Алгебра Школа Алгебра Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Шаг 3. b Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 2 Имя_____ Решение многошаговых уравнений Дата_____ Период____ Уравнения 23 Многошаговый рабочий лист уравнения Pdf Многошаговый рабочий лист уравнения Word Задания Много… Многошаговые неравенства Рабочие листы.- Практикуйтесь в решении уравнений, играя в алгебру. Решение многошаговых уравнений с переменными на одной стороне. Рабочий лист. Решение многошаговых уравнений. Многошаговые уравнения. 4) Проверьте свой ответ. ЕЕ. Пустой слой. Решение уравнений: смешанный обзор Комбинация целых, дробных и десятичных коэффициентов обозначает переменную в этих смешанных рабочих листах обзора. 7. Решение односегментных уравнений. 3. Desje Lrmv3eGdj. Лист викторины Решение рациональных уравнений Study Com.ЕЕ. Одношаговое уравнение так же прямолинейно, как и оно. Эквивалентные уравнения · Критерии эквивалентности уравнений · Уравнение с одной переменной · Уравнение с двумя переменными. D 72 […] Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. Решайте двухшаговые уравнения, оттачивая навыки алгебры седьмого и восьмого классов с помощью этого удобного рабочего листа! Начиная с доступного дополнения, напоминающего о том, как разбивать двухшаговые уравнения с измененными операциями, этот рабочий лист снова поощряет абсолютную … Тема Решение одношаговых линейных уравнений с одной переменной Primary SOL 6.Он также содержит математические загадки, определяющие стоимость объектов, переводя фразы в одношаговое уравнение и многое другое. Решите линейные уравнения и неравенства, в том числе многошаговые уравнения и двухшаговые математические уравнения — это алгебраические задачи, которые требуют от вас сделать два хода, чтобы найти значение неизвестной переменной. Курс 3 • Глава 2 Уравнения с одной переменной 23 Урок 2. 2 1 Решение уравнений в один шаг редактируется. Ответ: 2x – 1 = 3 4 x + 9 ЖК-дисплей равен 4. Создавайте рабочие листы для печати для решения линейных уравнений до алгебры или алгебры 1 в виде файлов pdf или html.Некоторые уравнения являются двухшаговыми, но большинство из них трехшаговые Решение многошаговых уравнений Нет отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Абсолютная ценность Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Если нет дробей, объедините одинаковые члены. 7 м и -2 м объединятся в 5 м, а -5 и +2 в сумме станут -3. Этот рабочий лист на одну страницу охватывает решение одношаговых уравнений с умножением и делением десятичных дробей. Рабочие листы с открытыми и закрытыми слогами 3 класс.Упражнения по решению уравнений в лабиринте Добро пожаловать на страницу «Решение простых линейных уравнений с неизвестными значениями от -9 до 9 и переменными в левой части» (A) Math Worksheet со страницы с рабочими листами по алгебре в Math-Drills. Решение многошаговых уравнений для 7-го класса. Лист бесплатных математических заданий для 7-го класса и для предварительной алгебры, организованный по таким темам, как выражения. Целые числа. Одношаговые уравнения. Рациональные числа. Многошаговые уравнения. Неравенства.Рабочие листы с двухшаговыми уравнениями — Рабочие листы по математике 4 Дети В исходном видео был запутанный пример. 1 Примечания 4 Решение реальной задачи с помощью рациональной корневой теоремы Цель обучения B: Я могу применять рациональную корневую теорему для решения реальных задач, моделируемых полиномиальными функциями. Я могу сравнить алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Теперь мы подставляем x = 8 Рабочий лист двухшаговых уравнений pdf. Отлично подходит для работы в классе, домашних заданий, решения текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа.Решение многошаговых уравнений Дата_____ Период____ Решите каждое уравнение. 4b Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения реальной или математической задачи, а также создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах. 3 Flip Book Eureka Lessons 7-9 Уравнения лицензирования (словные задачи) Учебник Glencoe CCGPS (McGraw-Hill, 2013) с. D. Рабочие листы с целыми числами и абсолютными значениями.2+1. Результаты Учащиеся смогут решать многошаговые уравнения. Решение одношаговых уравнений: Чтобы решить одношаговые уравнения, вы делаете операцию, противоположную любой операции. Настройте рабочие листы, чтобы включить одноэтапные, двухэтапные или многоэтапные уравнения, переменные с обеих сторон, круглые скобки и многое другое. 3) Решите упрощенное уравнение, отменив действия в обратном порядке. N P gAsl Glv 7rViog Bh7t8sW ir 8ejs CeWrRvke Bdm. Двухшаговые уравнения, содержащие целые числа. Многошаговые уравнения — это все уравнения, для решения которых требуется выполнить более двух шагов или операций.Глава 1: Вещественные числа. pdf: Размер файла: 230 Кб: Тип файла: pdf Подробнее. 3-Пример 1: Решите это уравнение, сначала очистив дроби. 3x + 1 = 7 Найдите переменный термин. 4A-4 — Решение Показаны 8 лучших рабочих листов в категории многошаговых уравнений распределительного свойства. Некоторыми из рабочих листов для этой концепции являются Глава 14 «Алгебраические дроби и уравнения» и «Объединение похожих терминов дробных коэффициентов», «Арифметика и алгебраическая работа», «Целые числа 1 для одношаговых уравнений», «Содержание работы по алгебре», «Целые числа для одношаговых уравнений», «Решение линейных уравнений», «Решение линейных уравнений».Сравните алгебраическое решение с арифметическим решением, определяя последовательность… Калькулятор алгебры — это калькулятор, который дает пошаговую помощь в решении задач по алгебре. Решение многошаговых распределительных уравнений со скобками — без отрицательных коэффициентов Название: V Дата: Решить Desje Lrmv3eGdj. Детская физика mcq, графические рабочие листы линейных уравнений, сложение и вычитание положительных и отрицательных целых рабочих листов, Ti84 One-Step Equations With Fractions Kuta Kuta PDF4PRO. Помните знак минус при умножении или делении вызовов Учебное пособие по решению уравнений pdf CCGPS Math 7 Учебное пособие по разделу 2 — Выражения и уравнения Используйте свойства операций для создания эквивалентных выражений.Опубликовано. Большинство … Дополнение Решение многошаговых уравнений Стандарты CC 7. Решение и построение графиков неравенств Рабочий лист Ключ к ответу Pdf Алгебра 2. Знаменатели: Умножьте каждую часть уравнения на общий знаменатель. G b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2Ob Рабочий лист от Kuta Software LLC Kuta Software – Infinite Algebra 2 Название_____ Решение многошаговых уравнений. e Решите одношаговые или многошаговые арифметические задачи реального мира, включающие четыре операции с рациональными числами, в том числе те, которые связаны с экспоненциальной записью.МСТ2. C. 2. Kami Export Unit 1 4 Назначение и ключ Pdf Math 8 Unit 1 1 4 Название задания Решение многошаговых уравнений Период U00a9f D2z0x164v Tkpubtnak Course Hero from www. Решение многошаговых неравенств, рабочий лист, график неравенства, 33 уравнения планов ресурсов и список, предварительные рабочие листы по алгебре, 26 текстовых задач, бесплатная электронная таблица, одно умножение, деление, pdf, ответы на настроение, урок tessshlo 6, 2, 4 с линейным распределительным свойством, 29 уроков математики, преподающих 9-й класс. (7 4)•4 7 𝑥=(7 4 Опубликовано в алгебра 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помечено алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf один шаг уравнения лабиринт ответы решение уравнений лабиринт ответ ключевые решения уравнения лабиринт.09 мая 2021 г. Решая, чтобы появиться с обзором, ваши ученики просто любят в четверг и вычитают в уравнениях степени с решением рациональных ответов рабочего листа pdf b рационально. • Учтите, что линейные уравнения могут не иметь решения, иметь одно решение или иметь бесконечно много решений. Pin On … В этих листах PDF для 7 и 8 классов выполните основные арифметические операции и решите многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Решение многоэтапных уравнений в лабиринте. В данном случае 5 и 11 — наши константы.+3 +3. Неравенства. Решайте задачи по формуле. путем умножения каждого члена на наименьший общий знаменатель. Предварительные навыки 1-го блока. Дискретная математика и ее голосовые приложения шестого издания, Решение уравнений с переменным листом с несколькими рабочими листами, несколько вариантов градации, задачи и печати из AHLGEBRA, стандартный калькулятор, десятичный расчетный коэффициент среда (1/14) — двухшаговые уравнения, Домашнее задание № 1, 3,4,6,8,12 (Последняя страница опубликованных заметок) 7R 1-14 Заметки.Рабочие листы являются отличным ресурсом для детей 6-го, 7-го и 8-го классов. Рабочие листы с уравнениями по алгебре, состоящими из 3 шагов. Бесплатное решение многошаговых уравнений Станции Лабиринт Обучение алгебре Решение многошаговых уравнений Обучение математике J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Уравнения в один шаг. Сложение, вычитание, умножение и деление.J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. До начала этого занятия учащиеся должны уметь решать одношаговые линейные уравнения, содержащие отрицательные целые коэффициенты и константы, а также дробные и десятичные значения. Затем изучите различные способы решения уравнения. 7 ee 4 Используйте переменные для представления величин в реальном мире или математических задач и стройте простые уравнения и неравенства для решения задач, рассуждая о величинах. Калькулятор многошаговых неравенств Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом.У 2 алии было 24, чтобы потратить на семь карандашей. 7 ee 4a решать текстовые задачи, приводящие к уравнениям вида px q r и p x q r, где p q и r — конкретные рациональные числа. 3A PowerPoint, который учащиеся выполнят в качестве домашнего задания. 3 уравнения шага, отображающие 8 лучших рабочих листов, найденных для этой концепции. Решите уравнения этих форм бегло. Ниже приведены отдельные упражнения для уравнений, в которых используются целые дроби и десятичные коэффициенты. Решайте линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, обозначенными буквами.Решите каждый мульти … Викторина и рабочий лист — Решение рациональных уравнений | Учиться. Подготовьте уравнение, поместив круглые скобки вокруг каждой стороны. Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом. Теперь подставим x = 8. Каждый рабочий лист содержит уравнения с дробными коэффициентами. МСС7. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данный. Конечно, ключи ответов предоставляются с каждым бесплатным рабочим листом по алгебре.Вы можете учиться, решая дополнительные задачи, до которых вы не дошли в классе. Используйте x и y для любых переменных. Анализ и решение линейных уравнений и пар одновременных линейных уравнений Описание. В этом случае сложение вычитание и деление умножения. com Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые числа, дроби и десятичные дроби в качестве коэффициентов, приведены здесь для обширной практики. Я могу бегло решать многоступенчатые линейные уравнения и текстовые задачи с рациональными коэффициентами (например, p(x+q)=r).Одношаговые неравенства путем сложения/вычитания. Часто при решении линейных уравнений нам приходится работать с уравнением с дробными коэффициентами. 13 августа 2021 г. Автор: Рабочие листы с многошаговыми уравнениями Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые дроби и десятичные дроби в виде … Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Четверг (15/01) — Уравнения в два шага, Домашнее задание — Подготовка к викторине. Чтобы решить многошаговое уравнение, мы должны начать с попытки упростить уравнение, комбинируя одинаковые члены и используя свойство дистрибутивности, когда это возможно.Решение уравнений с переменной с каждой стороны (стр. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y 6 через среднюю школу. Системы — решить относительно x и y. 17 Учащийся будет решать многоступенчатые линейные уравнения с одной переменной с переменной на одной или обе стороны уравнения, в том числе практические задачи, требующие решения многошагового линейного уравнения с одной переменной Графики неравенств Решение неравенств Многошаговые неравенства Квадратные уравнения, текстовые задачи, разделы 2.Решите уравнения с одной переменной, чтобы получить значение переменной. ПЕРЕРАБОТКА Семья Свигер перерабатывает около 15 фунтов отходов в неделю. Математика 67 ПРИМЕЧАНИЯ 63 Название _____ Решение двухшаговых уравнений SOL 714 Пример 1 Решите 3x 1 7 ПРОВЕРКА. 4a) 7. Одношаговое уравнение – умножение и деление. 2x 3 9 4. Решение многошаговых уравнений с рациональными коэффициентами. Рабочий лист pdf
рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.Каждый рабочий лист включает в себя некоторые шаги для решения уравнения, и учащиеся должны выполнить эти шаги самостоятельно. Эти уравнения требуют, чтобы учащийся распределил умноженное значение между терминами в круглых скобках, прежде чем объединять похожие термины. Найдите абсолютное значение числа. 4 x 1 2 3x стоит 1762 доллара. P. Загрузка тестов на пригодность, предварительная алгебра «задачи равномерного движения», распечатки рабочих листов по геометрии, бесплатные рабочие листы для решения математических задач. Ответы на рабочий лист неравенства. Они укрепят свое понимание дробей, десятичных знаков и процентов как различных способов представления рациональных чисел.Графики неравенств с одной переменной. 1-7 Распределительное свойство 7-1 Нулевые и отрицательные показатели 8-2 Умножение и разложение на множители 10-2 Упрощение радикалов 11-3 Деление полиномов 12-7 Теоретическая и экспериментальная вероятность Уравнения абсолютного значения и неравенства Алгебра 1 Игры Алгебра 1 Рабочие листы Алгебра обзор решения … Получите огромную практику с этой серией распечатываемых рабочих листов для решения систем уравнений, предназначенных для учащихся 8-го класса и старшей школы. comРешение рациональных уравнений онлайн калькулятор Квадратная формула.Пошаговые уравнения отмечают деятельность лабиринта усилителя всеми вещами. Мат. (2x – 1) = ( ) 3 Разделите каждую сторону на 5 c Рациональный метод или рациональная формула. Pdf 12 68 МБ Этот продукт отлично подходит для дистанционного обучения, самостоятельного изучения и обогащения. Этот набор рабочих листов включает 5 рабочих листов по объединению выражений с похожими терминами. Интерпретируйте этот набор текстовых задач, которые требуют двухэтапных операций для решения уравнений. 1. Рабочий лист 3. Двухшаговые уравнения с рабочим листом дробей, связанным после одного шага. На второй странице прикреплен ключ ответа.смешать с калькулятором регулярных дробей. 3x + 1 = 7 3x + 1 = 7 Начальный навык алгебры Решение линейных уравнений: дробные коэффициенты Решите каждое уравнение. Ключ ответа на лист 1 Двухшаговые рациональные неравенства Стандарты CC 7. Предварительные ответы по алгебре, бесплатные рабочие листы по алгебре уравнений с дробями, нахождение квадратного корня 17, решение программы по алгебре, бесплатные многошаговые рабочие листы и тесты. перевести в алгебраическое выражение. • Используйте подстановку для проверки решений. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений.Решение многоступенчатых уравнений. Рабочий лист Лабиринт. Упражнение Решение уравнений. Упражнение Решение многошаговых уравнений. Алгебра. Рабочие листы. Неравенства 6-го класса с отображением 8 лучших рабочих листов, найденных для этой концепции. Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. — Урок 8. Все задачи могут быть перевернутыми и содержать отрицательные коэффициенты, но всегда разрешаются целыми числами. Рациональное: может быть представлено дробью — и то, и другое. Чтобы попрактиковаться в решении двухэтапных задач с уравнениями, не стесняйтесь использовать рабочие листы ниже.рабочие листы для решения линейных уравнений (предварительная алгебра или алгебра 1) в виде файлов PDF или html. Двухшаговые уравнения, содержащие десятичные дроби. г. Одношаговые уравнения с рациональными коэффициентами. Рабочий лист Дополнительная практика 10 4 Решение рациональных уравнений. Рабочий лист. 32 Учителям это нравится LessonPrint LessWbat Решите задачу о шаге, используя сложение, вычитание и числа… Соответствующие академические стандарты штата Нью-Йорк. число, знак неравенства поменялся местами. Решать линейные уравнения намного веселее, когда есть весы с двумя чашами, несколько загадочных мешочков и куча мармеладок.3 x 1 5 5. Соблюдайте баланс по обе стороны неравенства, выделяя переменную с помощью обратных операций. 7 Решайте реальные и математические задачи, составляя и решая уравнения и неравенства с одной переменной. Factoring Maze Answer KeyQuadratic … Используйте приведенную ниже таблицу, чтобы найти видеоролики, мобильные приложения, рабочие листы и уроки, дополняющие Glencoe Math Course 3 Volume 1 Common Core. Решение алгебраических уравнений с дробями. 7 … В следующей таблице приведены примеры решения многошаговых уравнений с рациональными коэффициентами.Радикальные выражения и уравнения. Раздел 11. Рабочие выражения и решение уравнений со скобками. Рабочий лист pdf. Обучение чтению части слова помогает учащимся разбивать более длинные слова на более понятные фрагменты и помогает учащимся обнаруживать закономерности в написании слов. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. 1) m + 4 = 13 2 2) 8 3 = x − 1 1 3 3) 4 5 + v = 41 20 Рабочий лист двухшаговых уравнений с рациональными коэффициентами на квадратные корни, Alberta Class 10 Alegbra.21 хорошо продуманная задача, которая укрепит и укрепит обучение учащихся. Наведите указатель мыши на ответ. Используйте свойства равенства, чтобы переписать … Desje Lrmv3eGdj. В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многоэтапные уравнения с десятичными числами в качестве коэффициентов. Решение уравнений с переменными с обеих сторон 1 Этот рабочий лист из 12 задач предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные с обеих сторон.И нет ничего лучше набора координатных осей для решения систем линейных уравнений. С помощью этих распечатываемых рабочих листов учащиеся будут практиковаться в упрощении и поиске эквивалентных алгебраических выражений. • Обоснуйте шаги решения уравнения. 2x+6=16) Объединение похожих терминов X с обеих сторон Распределяющая собственность. Рабочий лист от kuta software llc. Решение уравнений абсолютного значения ChiliMath. Разделы 2 1 2 2. Начало работы Напишите, решите и начертите графики одношаговых линейных уравнений. Рабочие листы по математике для печати для 9 класса.Алгебра Холта 2 3a Решение 118 L13. Решение линейных уравнений с рациональными коэффициентами Часть 2. Инструкция по моделированию Прочитайте приведенную ниже задачу. ком. 3 Решайте многошаговые реальные и математические задачи, поставленные с помощью положительных • Решайте уравнения с целыми коэффициентами. Рабочий лист — одношаговые уравнения. 14). 5 лет 2 28 8. ПОСМОТРЕТЬ ПРОДУКЦИЮ. Урок 6 2 Уравнения в один шаг с рациональными коэффициентами Ответ Ключевое слово Заполнить онлайн Пригодно для печати Заполняемый бланк Pdffiller Решить уравнения Примеры решений 8 класса Рабочие листы для одного шага с рациональными коэффициентами 7-й пакет дистанционного обучения по математике Бесплатное задание по алгебре 1 Умножение и деление нескольких уравнений 2 Дробь 2021 коэффициент рабочие места ecityworks линейные скобки иди учи математику ремесленные ресурсы для учителей 6 9 урок 2 4 распределительная неделя собственности в … H.Решите двухшаговые уравнения. Пин на листах по математике. Эти рабочие листы для печати содержат уравнения, коэффициенты которых представляют собой дроби и целые числа. Коэффициент 4×2 Переменная (или База) * Запишите коэффициенты, переменные и показатели степени следующего: Решение многошаговых уравнений: 3x – 5 = 22 Чтобы получить x сам по себе, вам нужно избавиться от 5 и 3 10 сентября 2021 г. Теперь мы заменяем x = 8.Решите для переменной. Рабочий лист -5. Решите следующие уравнения относительно x: 1) x + 5 = 12 2) x – 11 = 19 3) 22 – x = 17 4) 5x = … Решение многошаговых уравнений (стр. Спасибо. Решение многошаговых уравнений) Уравнения, включающие дроби. Рабочий лист также редактируется, если вам нравится Рабочий лист решения уравнений и неравенств с ответами. Даниэль потратил 25 на ярмарке. 4 — Supplement Solving Multi-Step Equations CC Standards 7. ID: 1411530 Язык: английский Школьный предмет : Математика Класс/уровень: 7 Возраст: 11-16 Основное содержание: Уравнения Другое содержание: Алгебра Добавить в мои рабочие тетради (0) Скачать файл в формате pdf Вставить на мой веб-сайт или в блог Добавить в Google Classroom В этих рабочих листах в формате pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов.Этапы решения задач в два шага. Каждая задача имеет уникальное решение от -12 до 12, которое соответствует цветовому шаблону, формирующему симметричное изображение. Некоторые из рабочих листов для этой концепции ws1 многошаговые уравнения многошаговые уравнения десятичные числа 1 практика решения уравнений, содержащих дроби и десятичные дроби многошаговые уравнения дроби 1 два шага Решите многошаговое уравнение Многошаговые уравнения Многошаговые уравнения Рабочие листы Два уравнения шага. 7) Коэффициент: число, умноженное на переменную.Рабочий лист решения простых уравнений pdf Shenker Academy. Итак, еслиЧитать далее Уравнения в два шага. Вы можете выбрать три различных типа … admin July 16, 2019. Тригонометрические уравнения, как следует из названия, являются уравнениями Desje Lrmv3eGdj. Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. 7b) Решение многошаговых уравнений с рациональными коэффициентами (8. Сформулируйте и используйте различные стратегии для решения одношаговых и многошаговых линейных уравнений.Решите переменную в двухшаговой рабочей таблице задач 4. Маневрирование ресурсов математического вмешательства. Например, используя уравнение 3x + 5 = 11, нам нужно будет выполнить два шага, чтобы найти значение x. Рабочие листы с двухэтапными уравнениями содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. 3x 2 11 2. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p ( x + q) = r, где p, q и r — конкретные рациональные числа.Решение простых линейных уравнений с неизвестными значениями от 99 до 99 и переменными на листах T Алгебра Решение линейных уравнений Алгебраические выражения . Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя… Рациональные показатели и радикальные уравнения III. Бесконечные решения означают, что любое значение переменной делает уравнение верным. 4_notes_key_многоступенчатое_неравенство. — Глава 8.Решайте уравнения с помощью листа решения дробей и математики. 5 дополнительно Глава 6: Решение уравнений Математика 9 Marsh 6. Название: Рабочий лист линейных уравнений Автор: Мария Миллер Тема: Рабочий лист линейных уравнений Ключевые слова: Линейные уравнения, рабочий лист Дата создания: 27.12.2014 13:59:23 Урок/Занятия. w 2 2 3 1 3 10 Графические системы уравнений Два линейных уравнения образуют систему уравнений. Решение многошаговых уравнений с одной переменной Эталоны 8. 1) 3 F 5 8 2 2) 5 7 N F3 L F6 3) 7 F 9 = 3 4) 6 9 P E3 L11 5) F … Таблицы двухшаговых уравнений имеют огромный коллекция печатных практических страниц для решения и проверки уравнений с целыми числами, дробями и десятичными знаками.I. 3 Решить многошаговые реальные и математические задачи, поставленные с позитивом Опубликовано в алгебре 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответы ключ решение уравнений лабиринт. Некоторые из инструментов для создания терминов с кутом решают линейные уравнения с кутом по более сложной математике.Определить внутри трех решений нет или бесконечность 15 21. Одношаговое уравнение – сложение и вычитание. Например, периметр прямоугольника равен 54 см. Решите смесь типов уравнений, содержащих одинаковые термины. Вопросы 1-14 7 23 марта Решение уравнений – часть 2 Я могу решать двухшаговые уравнения. В. Решение текстовых задач с уравнениями и неравенствами (Общий базовый стандарт 7. Определение: математическое предложение, в котором говорится, что число или выражение равно другому числу или выражению. Объясните каждый шаг решения простого уравнения, как следует из равенства числа, утвержденные на предыдущем шаге, исходя из предположения, что исходное уравнение имеет решение.Некоторые из рабочих листов для этой концепции представляют собой двухшаговые уравнения периода даты многошаговые уравнения периода линейные уравнения работы двухэтапные уравнения целые числа 1 имя практика решения систем уравнений 3 различных одношаговых уравнения целые числа смешанные … В этих рабочих листах pdf для 7 и 8 класса выполнять основные арифметические операции и решать многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений. Глава 2, урок 5, домашнее задание, решение многошаговых уравнений.Соедините математику с выпивкой других дисциплин. Первым шагом было бы получение постоянных значений уравнения сами по себе. Кроме того, для дополнительной практики для учащихся 7-х и 8-х классов здесь представлен ряд pdf-файлов с упражнениями по переводу двухшаговых уравнений, MCQ и текстовых задач на основе геометрических фигур. Этот рабочий лист представляет собой комбинацию типов задач из этой категории. Решение многошаговых уравнений Bath K12 Ky Us. Решайте двухэтапные уравнения, оттачивая навыки алгебры в седьмом и восьмом классе с помощью этого удобного рабочего листа! Начиная с доступного дополнения, которое напоминает о том, как разбить двухшаговые уравнения, измененные операции, этот рабочий лист снова поощряет абсолютное удобство в качестве принятия … Закладка Файл PDF Решение рациональных уравнений Алгебра 2 Ответы Уравнения — cdn.Вот почему решение многошаговых уравнений сложнее, чем одношаговых и двухшаговых уравнений, потому что они требуют больше шагов. Где скачать Урок 3 Решение уравнений с переменными с обеих сторон Урок 10 3 Домашнее задание и практика Решение уравнений с помощью стандартов урока 7. Open делится на открытое перо, а О в открытом слоге. А. Распознавать линейные уравнения с одной переменной как имеющие одно решение, бесконечно много решений или не имеющие решения. Поскольку нулем функции f(x) является значение x, для которого (𝑥)=0, нахождение нулей полиномиальной функции p(x) аналогично нахождению _____ полиномиального уравнения… Карточки с заданиями по решению уравнений как в игре Sum Fun! Это увлекательное задание предлагает 32 карточки с заданиями, включающими многошаговые уравнения с переменными с обеих сторон и коэффициенты рациональных чисел.141–148) 3 опционально 0. comРешение систем уравнений с двумя переменными (Алгебра 2 Решение рациональных уравнений 1 — Системы уравнений Рабочие листы Решение линейных тригонометрических уравнений с синусоидально-косинусоидальным уравнением. Теперь подставим x = 8 Вот почему я решил создать четыре разные версии заметок для занятий, каждая с различным решением многошагового уравнения с переменными с обеих сторон.WorksheetQuadratic Equations By FactoringSolving Multi Step Equations — факторинговые полиномыSolving Quadratic Factoring — cdn. Вы можете решить систему уравнений, используя один из трех методов: 1. Рабочий пример Двухэтапное уравнение Алгебра Видео. 8. 4 t25031 t28 9k … Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски Рабочие листы? Алгебра Шаги решения рациональных уравнений с одинаковым знаменателем Шаг 1. Каждая серия … 3. Рабочие листы по математике 4 класс словесные задачи умножение.CCSS: 6. 2. Сначала они определяют, что операции сделали с переменной, и отменяют эти операции для решения. Сб, 22 декабря 2018 г., 01:38:00 GMT Бесплатные рабочие листы для линейных уравнений (6-9 классы, до… Решение уравнений с переменными на обеих сторонах 1 — Этот рабочий лист с 12 задачами предназначен для того, чтобы познакомить вас с решением уравнений, которые имеют переменные на обеих сторонах стороны.Помните, что вы можете решать уравнения, содержащие дроби, используя наименьший общий знаменатель всех дробей в уравнении.Перейдите к решению неравенств, которые включают несколько дополнительных шагов с помощью этих распечатываемых рабочих листов многошаговых неравенств.умножение, деление полномочий. ⭐ Решение многоэтапных уравнений — задание в лабиринте (PDF — FREEBIE) Решение уравнений Рабочие листы с одношаговыми уравнениями содержат эксклюзивные страницы для решения уравнений, включающих целые и десятичные дроби. Отображение всех рабочих листов, связанных с решением дробей двухэтапных уравнений. Рабочий лист с многошаговыми уравнениями. Определите исключенные значения уравнения. Наши рабочие листы с текстовыми задачами проверяют навыки в реальных сценариях. 10 Ответы на многоэтапные уравнения. Математическая обложка. Лист решения. Работает с решения. Многошаговый рабочий лист работает над решением многошаговых уравнений переменных на обоих шагах.Таким образом, в рабочих листах двухшаговых уравнений для 7 класса учащиеся узнают о концепции решения двух переменных, различных способах решения двух переменных в алгебраических выражениях и графическом отображении результатов. Математические рабочие листы дроби для сравнения дробей с подобным сложением. 2: Решение уравнений. 437 – 464 (One-step) с. 2x 7 7 9. Викторина Решение рациональных уравнений. Решение уравнений с дробями. 7 6. Во-вторых, учащиеся научатся понимать операции с рациональными числами и начнут работать с выражениями и линейными уравнениями.пинимг. Ключ ответа на лист решения многошаговых уравнений. x-4=10) Двухшаговые уравнения: (e. (с 3-4 • Решайте задачи, действуя в обратном порядке. АБСОЛЮТНОЕ ЗНАЧЕНИЕ Название рабочего листа: Выберите количество уравнений каждого типа: Одношаговые уравнения: (e. Лучшее ноябрьское 16, 2021 — Это создание r в квадрате является дополнительным рабочим листом для нашего 2. Некоторые из приведенных ниже рабочих листов: рабочий лист решения уравнений с дробями, шаги, которые необходимо выполнить при решении дробного уравнения, решение уравнений с дробями с использованием свойств равенства сложения и вычитания, несколько упражнения с решениями, ….b Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов. Сначала мы воспользуемся распределительным свойством, чтобы удалить скобки, а затем сможем. Сложные задачи с многошаговым уравнением. Ключ к ответу на лист многоступенчатого неравенства. Примечание. Двухшаговые уравнения. Это очень помогло мне с перехватом y при преобразовании десятичных знаков и вычитании дробей. Программное обеспечение Kuta Решение многошаговых уравнений Бесплатные математические листы для печати Многошаговые уравнения Многошаговые уравнения Рабочие листы Решение многошаговых уравнений Высшее ks4 ks3 a.Рациональные уравнения — это уравнения, содержащие рациональные выражения. Тест на решение уравнений. День 3. Ответы на рабочие листы. Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные многошаговые рабочие листы уравнений Алгебра, программная математика, решение приложений с использованием рациональных уравнений, калькуляторы, которые делят многочлены, как решать производные и интегралы, решать несколько систем дифференциальных уравнений. Этот метод также может быть использован с рациональными уравнениями. Эти многоступенчатые уравнения могут стать немного длинными и сложными.pdf 8 Примечания к решению уравнений 9 Решение уравнений hw Решите уравнения. Решите линейные уравнения с одной переменной. Рабочий лист решения многошаговых уравнений. Это видео показывает учащимся, как решать двухшаговые уравнения алгебры, включающие двухшаговые уравнения: Десятичные числа Лист 1 — Рабочие листы для детей Многошаговые уравнения Дата_____ Период____ Решите каждое уравнение. Ниже приведен тест из 5 вопросов по решению одношаговых уравнений. Практика домашнего задания на пятницу. Умножение и деление уравнений в один шаг.Аддитивное свойство равенства. 3) Имя _____ Решение двухшаговых уравнений (SOL 7. Раздел 4 Решение квадратных уравнений Домашнее задание 1 Ключ к ответу, плавучая солнечная электростанция Этот рабочий лист по системам уравнений будет составлять семистраничный раздаточный материал для системы. 5 необязательный предварительный просмотр: использование алгебры плитки для решения многошаговых уравнений Решение одношаговых уравнений с рациональными коэффициентами рабочий лист Решение одношаговых уравнений с рациональными коэффициентами рабочий лист pdf В уравнениях представлены только положительные целые числа, и все ответы также положительны.Чтобы решить многошаговое уравнение, выполните следующие шаги. лестничный метод. 4 7 𝑥=16 Напишите уравнение. Метод замещения 3. Мы можем решить эти проблемы так же, как и в прошлом. D Сборник рабочих листов по двухступенчатой математике для второго класса. 465 –488 (двухшаговый) Дифференциация Возможность: o Shell FAL: Шаги к решению уравнений 7 Рабочая тетрадь ~ Написание уравнений Решите уравнения 8 класс примеры решения s рабочие листы урок 6 2 4 многоэтапный с распределительным свойством решение линейных скобок коэффициенты иди учи математику ресурсы ручной работы для учителей рабочий лист коэффициента дроби ecityworks в том числе отрицательные значения формы ax bc все математические упражнения моя математика две дроби упрощение алгебраического a по алгебре … с рациональными коэффициентами решение уравнений с рациональными коэффициентами решение уравнения с помощью верхней смотреть видео 4-2 решение двух- Ступенчатые уравнения.©u W2r0G1Z2 1 nKNuDtHaW sSodfVtBw8aOrle7 uL 3L IC u. Добавьте вычитание, умножение и деление, чтобы решить одношаговые уравнения дробей в этих рабочих листах уровня 1, которые включают правильные и неправильные дроби в качестве коэффициентов и констант. Решение многошаговых уравнений. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____. Нажмите F11. решить путем сложения решить путем вычитания сочетания двух вышеуказанных требуется один шаг умножения общая система Читать онлайн урок 2 Решение рациональных уравнений и неравенств Решение уравнений Задание 1 Всегда, иногда или никогда верно? Урок 6.1) 4 n — 2n = 4 2) -12 = 2 + 5v + 2v 3) 3 = x + 3 — 5x 4) x + 3 — 3 = -6 5) -12 = 3 — 2k — 3k 6) — 1 = −3r + 2r 7) 6 = −3(x + 2) 8) −3(4r − 8) = −36 9) 24 = 6(−x − 3) 10) 75 = 3(−6n − 5) )-1- В этих рабочих листах в формате pdf для 7 и 8 классов выполните основные арифметические операции и решите многошаговые уравнения с десятичными числами в качестве коэффициентов. 8. Определение: выполнять одинаковые операции с обеими частями уравнения. Одношаговые неравенства путем умножения или деления. Математические уравнения в два шага — это алгебраические задачи, которые требуют, чтобы вы сделали два хода, чтобы найти значение неизвестной переменной.Это лабиринт, состоящий из 14 многоступенчатых уравнений, включающих дистрибутивное свойство. Архив метки: решение двухэтапных уравнений. Начните решать двухшаговые уравнения с одной переменной, включающие положительные коэффициенты, с помощью этого практического набора! Перестройте уравнения, чтобы сделать переменную объектом, и найдите ее целочисленное значение. Посмотреть больше примеров ». Рабочий лист решения многошаговых уравнений. 7б. Эта комбинация викторины и рабочего листа проверит вашу способность решать эти уравнения.сумма удвоенного числа плюс четыре умноженного на другое. Умножьте каждую сторону на 4, чтобы очистить дробь. Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые переменные уравнений с обеих сторон в скобках и многое другое. 1 6 р 7 13 7 р 2 13 4х 1 х 3 7х 3х 2 8х 8 4 8 х х 4х. 2 3 решение многоступенчатых уравнений отвечает на действия в лабиринте. Многоэтапный рабочий лист уравнений 8-го класса, решающий уравнения с. 1) 6р+7=13+7р. Противоположностью сложения является вычитание, а противоположностью умножения — деление.12 ноября 2021 г. Это рабочий лист по математике в формате PDF с несколькими упражнениями, который можно распечатать. Решение многошаговых уравнений. В этих раздаточных материалах доступно множество вопросов с несколькими вариантами ответов. Упрощение этих полезных радикальных выражений Решение многошаговых уравнений, содержащих дроби рабочего листа: 14 Вы можете найти интересные задачи. 3 Решайте многоэтапные реальные и математические задачи, поставленные с помощью положительных и … Решение рациональных уравнений — ChiliMath Решение рациональных уравнений Рациональное уравнение — это тип уравнения, в котором используется хотя бы одно рациональное выражение, причудливое название дроби.Рабочие листы для двухэтапных уравнений содержат огромную коллекцию печатных практических страниц для решения и проверки уравнений, включающих целые дроби и десятичные дроби. 1 и 2. Это обновленная версия. Рабочие листы с многошаговыми уравнениями для учащихся Mathxnet. Бесплатные практические вопросы для Common Core: математика 8-го класса — решение линейных уравнений с рациональными числовыми коэффициентами: CCSS. Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. Включает полную версию Desje Lrmv3eGdj.1 и 8. УРОК Практика C Двухшаговые уравнения с рациональными числами. Многоступенчатые уравнения. Как только вы найдете свой рабочий лист (листы), вы можете либо щелкнуть всплывающую головоломку с уравнением «Один шаг». Двухшаговые текстовые задачи с уравнениями. Нажмите на ссылку, чтобы получить доступ к эксклюзивным рабочим листам по решению двухшаговых уравнений, которые включают целые дроби и десятичные дроби. Метод линейных комбинаций Метод замещения Решите следующую систему уравнений: x – 2y = -10 y= 3x x – 2y = -10 x – 2( 3x ) = -10 Поскольку мы знаем y = 3x, можно распечатать в удобном формате PDF.Решите текстовые задачи, ведущие к неравенствам вида px q r или px q r, где p q и r — конкретные рациональные числа. Многие квадратные уравнения не могут быть решены с помощью факторизации. арентезы с помощью распределительного свойства. Предложите учащимся попрактиковаться в решении многошаговых уравнений с целыми числами и дробями. 1 Учащиеся используют различное оборудование и программное обеспечение для интеграции нескольких форм информации, чтобы создать хороший … 1-этапный 2-этапный многоэтапный EE. 1 Рабочий лист от Kuta Software LLC Infinite Algebra 1 Имя_____ Многошаговые неравенства Дата_____ Период____ .REI. Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Теперь мы подставляем x = 8 Рабочие листы для двухшаговых уравнений содержат огромную коллекцию печатных страниц для практики, чтобы решать и проверять уравнения, включающие целые числа, дроби и десятичные дроби. Уравнения Уравнения в один шаг Уравнения в два шага Многошаговые уравнения Уравнения с абсолютными значениями Радикальные уравнения Легко сложные Рациональные уравнения Легкое сложное решение Пропорции Процентные задачи Расстояние Скорость Время Словесные задачи Смесь … Рабочий лист на одной странице содержит одиннадцать задач с ответами.Сентябрь 2020 г. Решение двухшаговых уравнений Withons Worksheet Pdf Кута Примечания к двухшаговым уравнениям, лабиринтная деятельность здесь — заметки Корнелла и лабиринтная деятельность по решению двухшаговых уравнений, включая уравнения с дробными коэффициентами. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y ylzlpcj. В этих рабочих листах решите двухшаговые уравнения с целыми коэффициентами. Как правило, это не так просто сделать другим способом. 515х35 при добавлении 15 с обеих сторон дает. Одношаговые задачи с уравнениями. Математическая плоскость решения рациональных уравнений.Решите для а. Существуют двухэтапные и многоэтапные рабочие листы уравнений с целыми и десятичными дробями. Рабочий лист двухшаговых уравнений Pdf. Этот рабочий лист содержит уравнения с одной переменной, содержащие либо целые, либо рациональные коэффициенты и константы, а также рабочие листы для двухэтапных уравнений с огромной коллекцией печатных практических страниц для решения и проверки уравнений, включающих целые числа, дроби и десятичные дроби. Решите эти уравнения, чтобы получить значение неизвестного. Каждый рабочий лист двухшагового уравнения в формате PDF содержит десять задач на … Решить двухэтапное уравнение 7-й класс по математике 7 35.Решение и проверка уравнений, приложения по геометрии и MCQ включены в этот раздел для 7-го и 8-го классов оценочных листов по математике. Переменная с обеих сторон, решающая уравнения с одинаковыми условиями. Завтра утром я буду дополнительно помогать, чтобы ответить на любые вопросы, которые могут у вас возникнуть после решения уравнений с дробными коэффициентами: различные проблемы с ответами. 4 – Многошаговые уравнения с распределительным свойством 1 | Стр. План урока для учителя Урок 6. Викторина Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.Нажмите на тему ниже, чтобы увидеть проблемы, связанные с уравнением навыка. 4 t25031 t28 9k … Загадка уравнений в два шага. 1 Повторное обучение решению уравнений с рациональными коэффициентами Чтобы решить уравнение, в котором коэффициент является рациональным числом, умножьте каждую сторону на мультипликативную обратную дробь. 3. Слово «мульти» означает более двух или многих. График 2. Решите рациональные уравнения, найдя и умножив на наименьший общий знаменатель. Мат 0024 решение уравнений с дробями.Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Объявление Загрузите более 20000 рабочих листов K-8, посвященных математике, чтению, общественным наукам и многому другому. Серия многоуровневых рабочих листов требует, чтобы учащиеся решили пропорции, используя метод перекрестного произведения, и ответы, полученные таким образом, будут в форме целых чисел. 00) 3.149–154) 1 необязательный 0. Полностью упростите дробь dfrac a 2 a 6 ab 3b. 3: Решение уравнений с помощью распределительного свойства. Прочтите и загрузите электронную книгу Джина Уилсон «Все по алгебре 2016, уравнения в 2 шага» в формате pdf в общедоступной библиотеке электронных книг. com 1) 2 + 3 = 5. Ниже вы найдете множество рабочих листов для решения уравнений лабиринта, которые можно использовать на уроке алгебры 1. Эти рабочие листы текстовых задач являются хорошим ресурсом для учащихся с 5-го по 8-й класс.«все, что вы делаете с одной частью уравнения, вы должны делать и с другой». Рабочий лист решения двухшаговых уравнений pdf Решение двухэтапных уравнений с целыми числами Начните решать двухшаговые уравнения с одной переменной, включающей , этот рабочий лист поощряет самостоятельную практику, поскольку учащиеся решают уравнения, содержащие целые и рациональные коэффициенты и константы. Теперь мы заменяем x = 8 9. pdf из MATH MISC в колледже Санта-Моники. 3 Используйте только число всех от депо до толпы, чтобы решить уравнения и.О. Обязательно прокрутите вниз и ознакомьтесь с ними после прочтения урока. система как непротиворечивая или непротиворечивая, зависимая или независимая. Пин на доске Зомби Математика . Содержание. 4 Часть 1. Решение уравнений с переменными с обеих сторон. Для печати в удобном формате PDF. Наша математика 6/7 ПРИМЕЧАНИЯ (6. Основная цель решения многоэтапных уравнений, как и одноэтапных и двухэтапных уравнений, состоит в том, чтобы изолировать неизвестную переменную на одной стороне уравнения при использовании CCSS. Предварительный просмотр) • Решить уравнения, включающие более одной операции.Рабочие листы с двухшаговыми уравнениями для 6-х классов с ответами. Распределительное свойство и объединение одинаковых терминов Ws2 Объединение одинаковых терминов Некоторые из отображаемых рабочих листов: Решение рациональных уравнений 1, Решение рациональных уравнений, Решение дробных коэффициентов линейных уравнений, Решение примеров рациональных уравнений, Комбинирование дробных коэффициентов одинаковых терминов, Решение двухшаговых уравнений с дробными коэффициентами, Решение уравнений, содержащих дроби и . пустой слой. 5 5. Упражнения по решению уравнений лабиринта.Y d tM ra ed se0 cw qiPtxhl 1ISnbf ti Anci YtueV dAolwgQembmrKas h2Y. 3 Решайте многоэтапные задачи из реальной жизни и математические задачи с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. К этому понятию относится дробный коэффициент, в котором вы перемещаете числа. Эти карточки отформатированы как отличная игра с математическим обзором для подготовки к тестам и обзора STAAR. Очистить знаменатели. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы.Некоторыми из рабочих листов для этой концепции являются алгебра, упрощающая алгебраические выражения, расширяющая 8 алгебраических скобок, mep y8, учебник по математике, линейная 1ma0, решение уравнений по алгебре, работа 2, 2, решение уравнений с одной переменной, решение линейных уравнений, переменная для обеих … Posted in алгебра 1, рабочие листы, блог, решение лабиринта уравнения активность модуль 2 решение уравнений и помеченный алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка рабочий лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf одношаговые уравнения лабиринт ответы решение уравнений лабиринт ответ ключ решение уравнений лабиринт.2) Объединить подобные термины. Квадратичные функции Обзор рабочего листа лабиринта Квадратичные функции Квадратичный рабочий лист лабиринта 2-6 Соотношения Коэффициенты и преобразования — Ответы — Занятие в лабиринте PDF — Только для членов. ЯВЛЯЕТСЯ. 1–8. В набор задач включены двухшаговые и многошаговые линейные уравнения с целыми и рациональными коэффициентами и константами. 18 Учащийся будет решать одношаговые линейные уравнения с одной переменной, включающие целые числа и положительные рациональные решения. Решение простых линейных уравнений с неизвестными значениями в диапазоне от -99 до 99 и переменными в левой части (303 просмотра на этой неделе) Решение систем линейных уравнений с помощью графика (стандарт) (272 просмотра на этой неделе) Решение линейных уравнений — Форма ax + b = c ( 266 просмотров на этой неделе) Решение линейных уравнений (включая отрицательные значения) — форма ax + b = c Это обширная коллекция бесплатных печатных листов по математике для 7 класса и для начальной алгебры, организованная по таким темам, как выражения, целые числа, одношаговые уравнения рациональные числа, многошаговые уравнения, неравенства, скорость, время, расстояние, графическое изображение, коэффициенты наклона, пропорции, проценты, геометрия и пи.. Умножение каждой части уравнения на общий знаменатель исключает дроби. 1. Решите эти смешанные уравнения, которые содержат дроби, целые числа и десятичные дроби. — Проект решения двухшаговых уравнений. B. Двухшаговые уравнения […] Рабочий лист One Step Equations Pdf Прекрасное решение E Step. конечно герой. Ключ к ответу лабиринта квадратных уравнений. Примечание. Многошаговое решение многошаговых уравнений. Во время контрольной по математике Элиза и Кейтлин решили уравнение 1 áá2 (5 x 2 6) 5 3x разными способами, но каждый ученик пришел к правильному ответу.В этом рабочем листе из 25 вопросов основное внимание уделяется уравнениям как с реальными, так и со сложными решениями. 3 2 Практика Раздаточный материал pdf просмотреть скачать 216k. Сколько учителей, у нас меньше времени словесных задач с участием целых чисел по алфавиту имен, что они заканчивают класс с ответами pdf упрощения рационального. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Стоимость оборудования2 2 11 2 4 x 1 1 2 1 3x 9 4 x 1 3 3 x 9 3 4 4 x 4( 1) x 3 x 4 Решите. 3 х 2 5 3 5 7.Рабочий лист одношаговых уравнений с решениями Рабочий лист по решению одношаговых одношаговых уравнений Рабочие листы многоэтапных уравнений … Решение уравнений, содержащих дроби и десятичные дроби page2. Решение уравнений с дробями рабочий лист 7th 10 rows U3D3_S Решение уравнений с дробями Часть 1. Отказ от ответственности: Этот калькулятор не идеален. Свойства равенства. Алгебра 2 7. Сегодня я поделюсь с вами 12 заданиями и идеями, которые помогут вашим ученикам понять и попрактиковаться в решении одношаговых уравнений.Рабочий лист системы неравенства 2021 Pdf. админ. Решите линейные уравнения с рациональными коэффициентами (Common Core Standard 8. Рабочие листы подходят для курсов предварительной алгебры и алгебры 1 (6–9 классы). Common Core Edition Carter, Cuevas, Day, Holliday, … Quiz & Worksheet — Решение рациональных уравнений | Исследование kutasoftware L b2q0a1y1c lk nu 0tta v 6svohfet vwvabrre o hlbl 9ct Решатели рациональных выражений Шаг 4. 1) 3x 7 25+= 2) x 1 10 6 =− 3) 4) Найдите обратную величину. Все задачи разрешаются в целые числа.преобразование Лапласа разделить день t. Решите уравнения с дистрибутивным свойством умножения. Освоение этого навыка алгебры — отличный рабочий лист «Объединение похожих терминов» в формате PDF. 1/3 + 1/4. 3a 4 7 6. 2x – 1 = 3 4 x + 9 Процедура: Имеется только одна дробь. Решите уравнения с дробями, рабочий лист для 6-го класса, документ один. 4 t25031 t28 9k … MAT 0024 РЕШЕНИЕ УРАВНЕНИЙ С ДОЛЯМИ. com Чтобы создать ссылку на эту страницу, скопируйте следующий код на свой сайт Природа корней рабочих листов квадратного уравнения.3 Решение уравнений с рациональными коэффициентами • Решайте многоступенчатые уравнения с рациональными коэффициентами. 3 КПП. Решение рациональных уравнений 1 Рабочий лист Ключ к ответу Tessshlo. Многошаговое уравнение Судоку Цифровое и бумажное дистанционное обучение Многошаговые уравнения Двухшаговые уравнения Многошаговые уравнения Рабочие листы Одношаговые уравнения Головоломки с рациональными коэффициентами Одношаговые уравнения Решение уравнений Математика снеговика Решение двухшагового уравнения Одношаговое уравнение Уравнение Снеговик Математика Эта викторина … Сентябрь 20 , 2021.3 Решайте многоэтапные реальные и математические задачи, поставленные с позитивом. Нет команд 1 команда 2 команды 3 команды 4 команды 5 команд 6 команд 7 команд 8 команд 9 команд 10 команд Пользовательский. Вопросы 1-12: 24 марта: НЕТ ЗАНЯТИЙ 8 29 марта Решение уравнений – часть 3 Я могу решать уравнения с переменными в обеих частях. Десятичные коэффициенты включены в эти рабочие листы для двухэтапных уравнений, которые можно распечатать. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Урок 6. Решение уравнений с одной переменной pdf.+5 +5 Сначала избавьтесь от сложения и вычитания. Опишите шаги, которые каждый. Огромная коллекция многошаговых таблиц для печати с уравнениями, включающими целые дроби и десятичные дроби в качестве коэффициентов, дана здесь для обширной практики. Материалы Equation Vocabulary Organizer o Напишите двучленное выражение, используя любой математический оператор и 4, a и b. РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ ПРИМЕРЫ 1. 12 = 5m — 3 Теперь прибавьте 3 к обеим частям. Скачать файл в формате PDF Решение рациональных неравенств БЕСПЛАТНЫЕ математические рабочие листы Бесплатные рабочие листы по алгебре 2, созданные с помощью Infinite Algebra 2.g b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2O. Математика Все темы Все местные школьные классы Стивен. То, что четкие дроби, как дроби, объединяя их в письменном десятичном виде, является более крупными формами неравенства, которые интересны с помощью реального числа, многие кредиты могут. х+3=5. Он термины по каждому уравнению так, что. Решение уравнений с квадратным корнем Ответ. Резюме: Чтобы решить уравнения, используйте принципы сложения/умножения, чтобы «Избавиться от…» 1. 3 = m. В этих рабочих листах в формате PDF решите многошаговые уравнения и проверьте свое решение, подставив значение неизвестной переменной в уравнение.Самые популярные рабочие листы по алгебре на этой неделе Desje Lrmv3eGdj. 2 Решайте уравнения, комбинируя одинаковые термины Общие базовые стандарты 8. a Решайте линейные уравнения с одной переменной и рациональными числами, включая уравнения, решения которых требуют раскрытия выражений с использованием дистрибутивного свойства и сбора похожих членов или уравнений с коэффициентами, представленными буквами. Шаг 2. 4 Решение уравнений с дробными коэффициентами Рабочий лист № 1 Выполните следующее на отдельном листе бумаги! А.Пожалуйста, используйте на свой страх и риск, и, пожалуйста, сообщите нам, если что-то не работает. В этом листе многошаговых уравнений View WorksheetWorks_Solving_MultiStep_Equations_1. Решение уравнений с целыми числами. — Игра в два шага. пдф. Опубликовано . Алгебра Решение уравнений в один и два шага Лабиринты Бесплатные уравнения Алгебра Школа Алгебра Например, используя уравнение 3x 5 11, нам нужно будет выполнить два шага, чтобы найти значение x. Шаг 3. b Рабочий лист от Kuta Software LLC Kuta Software — Infinite Algebra 2 Имя_____ Решение многошаговых уравнений Дата_____ Период____ Уравнения 23 Многошаговый рабочий лист уравнения Pdf Многошаговый рабочий лист уравнения Word Задания Много… Многошаговые неравенства Рабочие листы.- Практикуйтесь в решении уравнений, играя в алгебру. Решение многошаговых уравнений с переменными на одной стороне. Рабочий лист. Решение многошаговых уравнений. Многошаговые уравнения. 4) Проверьте свой ответ. ЕЕ. Пустой слой. Решение уравнений: смешанный обзор Комбинация целых, дробных и десятичных коэффициентов обозначает переменную в этих смешанных рабочих листах обзора. 7. Решение односегментных уравнений. 3. Desje Lrmv3eGdj. Лист викторины Решение рациональных уравнений Study Com.ЕЕ. Одношаговое уравнение так же прямолинейно, как и оно. Эквивалентные уравнения · Критерии эквивалентности уравнений · Уравнение с одной переменной · Уравнение с двумя переменными. D 72 […] Скачать бесплатно Решение рациональных уравнений Ответы Решение уравнений Рождественские раскраски? Алгебра Шаги для решения рациональных уравнений с одинаковым знаменателем Шаг 1. Решайте двухшаговые уравнения, оттачивая навыки алгебры седьмого и восьмого классов с помощью этого удобного рабочего листа! Начиная с доступного дополнения, напоминающего о том, как разбивать двухшаговые уравнения с измененными операциями, этот рабочий лист снова поощряет абсолютную … Тема Решение одношаговых линейных уравнений с одной переменной Primary SOL 6.Он также содержит математические загадки, определяющие стоимость объектов, переводя фразы в одношаговое уравнение и многое другое. Решите линейные уравнения и неравенства, в том числе многошаговые уравнения и двухшаговые математические уравнения — это алгебраические задачи, которые требуют от вас сделать два хода, чтобы найти значение неизвестной переменной. Курс 3 • Глава 2 Уравнения с одной переменной 23 Урок 2. 2 1 Решение уравнений в один шаг редактируется. Ответ: 2x – 1 = 3 4 x + 9 ЖК-дисплей равен 4. Создавайте рабочие листы для печати для решения линейных уравнений до алгебры или алгебры 1 в виде файлов pdf или html.Некоторые уравнения являются двухшаговыми, но большинство из них трехшаговые Решение многошаговых уравнений Нет отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Абсолютная ценность Powered by Создайте свой собственный уникальный веб-сайт с помощью настраиваемых шаблонов. Если нет дробей, объедините одинаковые члены. 7 м и -2 м объединятся в 5 м, а -5 и +2 в сумме станут -3. Этот рабочий лист на одну страницу охватывает решение одношаговых уравнений с умножением и делением десятичных дробей. Рабочие листы с открытыми и закрытыми слогами 3 класс.Упражнения по решению уравнений в лабиринте Добро пожаловать на страницу «Решение простых линейных уравнений с неизвестными значениями от -9 до 9 и переменными в левой части» (A) Math Worksheet со страницы с рабочими листами по алгебре в Math-Drills. Решение многошаговых уравнений для 7-го класса. Лист бесплатных математических заданий для 7-го класса и для предварительной алгебры, организованный по таким темам, как выражения. Целые числа. Одношаговые уравнения. Рациональные числа. Многошаговые уравнения. Неравенства.Рабочие листы с двухшаговыми уравнениями — Рабочие листы по математике 4 Дети В исходном видео был запутанный пример. 1 Примечания 4 Решение реальной задачи с помощью рациональной корневой теоремы Цель обучения B: Я могу применять рациональную корневую теорему для решения реальных задач, моделируемых полиномиальными функциями. Я могу сравнить алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Теперь мы подставляем x = 8 Рабочий лист двухшаговых уравнений pdf. Отлично подходит для работы в классе, домашних заданий, решения текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа.Решение многошаговых уравнений Дата_____ Период____ Решите каждое уравнение. 4b Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения реальной или математической задачи, а также создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах. 3 Flip Book Eureka Lessons 7-9 Уравнения лицензирования (словные задачи) Учебник Glencoe CCGPS (McGraw-Hill, 2013) с. D. Рабочие листы с целыми числами и абсолютными значениями.2+1. Результаты Учащиеся смогут решать многошаговые уравнения. Решение одношаговых уравнений: Чтобы решить одношаговые уравнения, вы делаете операцию, противоположную любой операции. Настройте рабочие листы, чтобы включить одноэтапные, двухэтапные или многоэтапные уравнения, переменные с обеих сторон, круглые скобки и многое другое. 3) Решите упрощенное уравнение, отменив действия в обратном порядке. N P gAsl Glv 7rViog Bh7t8sW ir 8ejs CeWrRvke Bdm. Двухшаговые уравнения, содержащие целые числа. Многошаговые уравнения — это все уравнения, для решения которых требуется выполнить более двух шагов или операций.Глава 1: Вещественные числа. pdf: Размер файла: 230 Кб: Тип файла: pdf Подробнее. 3-Пример 1: Решите это уравнение, сначала очистив дроби. 3x + 1 = 7 Найдите переменный термин. 4A-4 — Решение Показаны 8 лучших рабочих листов в категории многошаговых уравнений распределительного свойства. Некоторыми из рабочих листов для этой концепции являются Глава 14 «Алгебраические дроби и уравнения» и «Объединение похожих терминов дробных коэффициентов», «Арифметика и алгебраическая работа», «Целые числа 1 для одношаговых уравнений», «Содержание работы по алгебре», «Целые числа для одношаговых уравнений», «Решение линейных уравнений», «Решение линейных уравнений».Сравните алгебраическое решение с арифметическим решением, определяя последовательность… Калькулятор алгебры — это калькулятор, который дает пошаговую помощь в решении задач по алгебре. Решение многошаговых распределительных уравнений со скобками — без отрицательных коэффициентов Название: V Дата: Решить Desje Lrmv3eGdj. Детская физика mcq, графические рабочие листы линейных уравнений, сложение и вычитание положительных и отрицательных целых рабочих листов, Ti84 One-Step Equations With Fractions Kuta Kuta PDF4PRO. Помните знак минус при умножении или делении вызовов Учебное пособие по решению уравнений pdf CCGPS Math 7 Учебное пособие по разделу 2 — Выражения и уравнения Используйте свойства операций для создания эквивалентных выражений.Опубликовано. Большинство … Дополнение Решение многошаговых уравнений Стандарты CC 7. Решение и построение графиков неравенств Рабочий лист Ключ к ответу Pdf Алгебра 2. Знаменатели: Умножьте каждую часть уравнения на общий знаменатель. G b gM da gdke N Lw6ixtWhX CIenWf4i on Pijt1e L TAHlWgfe rb UrTa0 m2Ob Рабочий лист от Kuta Software LLC Kuta Software – Infinite Algebra 2 Название_____ Решение многошаговых уравнений. e Решите одношаговые или многошаговые арифметические задачи реального мира, включающие четыре операции с рациональными числами, в том числе те, которые связаны с экспоненциальной записью.МСТ2. C. 2. Kami Export Unit 1 4 Назначение и ключ Pdf Math 8 Unit 1 1 4 Название задания Решение многошаговых уравнений Период U00a9f D2z0x164v Tkpubtnak Course Hero from www. Решение многошаговых неравенств, рабочий лист, график неравенства, 33 уравнения планов ресурсов и список, предварительные рабочие листы по алгебре, 26 текстовых задач, бесплатная электронная таблица, одно умножение, деление, pdf, ответы на настроение, урок tessshlo 6, 2, 4 с линейным распределительным свойством, 29 уроков математики, преподающих 9-й класс. (7 4)•4 7 𝑥=(7 4 Опубликовано в алгебра 1 рабочие листы блог лабиринт решение уравнений блок действий 2 решение уравнений и помечено алгебра обзор решение уравнений лабиринт ответы бесплатно решение уравнений головоломка лист многошаговое уравнение лабиринт многошаговые уравнения лабиринт pdf один шаг уравнения лабиринт ответы решение уравнений лабиринт ответ ключевые решения уравнения лабиринт.09 мая 2021 г. Решая, чтобы появиться с обзором, ваши ученики просто любят в четверг и вычитают в уравнениях степени с решением рациональных ответов рабочего листа pdf b рационально. • Учтите, что линейные уравнения могут не иметь решения, иметь одно решение или иметь бесконечно много решений. Pin On … В этих листах PDF для 7 и 8 классов выполните основные арифметические операции и решите многоступенчатые уравнения с десятичными числами в качестве коэффициентов. Решение многоэтапных уравнений в лабиринте. В данном случае 5 и 11 — наши константы.+3 +3. Неравенства. Решайте задачи по формуле. путем умножения каждого члена на наименьший общий знаменатель. Предварительные навыки 1-го блока. Дискретная математика и ее голосовые приложения шестого издания, Решение уравнений с переменным листом с несколькими рабочими листами, несколько вариантов градации, задачи и печати из AHLGEBRA, стандартный калькулятор, десятичный расчетный коэффициент среда (1/14) — двухшаговые уравнения, Домашнее задание № 1, 3,4,6,8,12 (Последняя страница опубликованных заметок) 7R 1-14 Заметки.Рабочие листы являются отличным ресурсом для детей 6-го, 7-го и 8-го классов. Рабочие листы с уравнениями по алгебре, состоящими из 3 шагов. Бесплатное решение многошаговых уравнений Станции Лабиринт Обучение алгебре Решение многошаговых уравнений Обучение математике J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Уравнения в один шаг. Сложение, вычитание, умножение и деление.J j ua xl fl h frzi ngvh ntwsf 9r desje lrmv3egdj. До начала этого занятия учащиеся должны уметь решать одношаговые линейные уравнения, содержащие отрицательные целые коэффициенты и константы, а также дробные и десятичные значения. Затем изучите различные способы решения уравнения. 7 ee 4 Используйте переменные для представления величин в реальном мире или математических задач и стройте простые уравнения и неравенства для решения задач, рассуждая о величинах. Калькулятор многошаговых неравенств Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом.У 2 алии было 24, чтобы потратить на семь карандашей. 7 ee 4a решать текстовые задачи, приводящие к уравнениям вида px q r и p x q r, где p q и r — конкретные рациональные числа. 3A PowerPoint, который учащиеся выполнят в качестве домашнего задания. 3 уравнения шага, отображающие 8 лучших рабочих листов, найденных для этой концепции. Решите уравнения этих форм бегло. Ниже приведены отдельные упражнения для уравнений, в которых используются целые дроби и десятичные коэффициенты. Решайте линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, обозначенными буквами.Решите каждый мульти … Викторина и рабочий лист — Решение рациональных уравнений | Учиться. Подготовьте уравнение, поместив круглые скобки вокруг каждой стороны. Решение рациональных уравнений похоже на решение уравнений, содержащих дроби, но с дополнительным шагом. Теперь подставим x = 8. Каждый рабочий лист содержит уравнения с дробными коэффициентами. МСС7. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данный. Конечно, ключи ответов предоставляются с каждым бесплатным рабочим листом по алгебре.Вы можете учиться, решая дополнительные задачи, до которых вы не дошли в классе. Используйте x и y для любых переменных. Анализ и решение линейных уравнений и пар одновременных линейных уравнений Описание. В этом случае сложение вычитание и деление умножения. com Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые числа, дроби и десятичные дроби в качестве коэффициентов, приведены здесь для обширной практики. Я могу бегло решать многоступенчатые линейные уравнения и текстовые задачи с рациональными коэффициентами (например, p(x+q)=r).Одношаговые неравенства путем сложения/вычитания. Часто при решении линейных уравнений нам приходится работать с уравнением с дробными коэффициентами. 13 августа 2021 г. Автор: Рабочие листы с многошаговыми уравнениями Огромная коллекция печатных листов с многошаговыми уравнениями, включающими целые дроби и десятичные дроби в виде … Решение многошаговых уравнений без отрицательных коэффициентов Решение многошаговых уравнений Андерсон С. Блог. Четверг (15/01) — Уравнения в два шага, Домашнее задание — Подготовка к викторине. Чтобы решить многошаговое уравнение, мы должны начать с попытки упростить уравнение, комбинируя одинаковые члены и используя свойство дистрибутивности, когда это возможно.Решение уравнений с переменной с каждой стороны (стр. D 72 g061 u1y 5k uu ptxat nstozfhtkw4adr fe y 6 через среднюю школу. Системы — решить относительно x и y. 17 Учащийся будет решать многоступенчатые линейные уравнения с одной переменной с переменной на одной или обе стороны уравнения, в том числе практические задачи, требующие решения многошагового линейного уравнения с одной переменной Графики неравенств Решение неравенств Многошаговые неравенства Квадратные уравнения, текстовые задачи, разделы 2.Решите уравнения с одной переменной, чтобы получить значение переменной. ПЕРЕРАБОТКА Семья Свигер перерабатывает около 15 фунтов отходов в неделю. Математика 67 ПРИМЕЧАНИЯ 63 Название _____ Решение двухшаговых уравнений SOL 714 Пример 1 Решите 3x 1 7 ПРОВЕРКА. 4a) 7. Одношаговое уравнение – умножение и деление. 2x 3 9 4. Решение многошаговых уравнений с рациональными коэффициентами. Рабочий лист pdf