Линия — Математическая энциклопедия
Кривая,- геометрическое понятие, точное и в то же время достаточно общее определение к-рого представляет значитю трудности и осуществляется в разных разделах геометрии различно. В рамках элементарной геометрии понятие Л. не получает отчетливой формулировки и иногда определяется как «длина без ширины» или как «граница поверхности». По существу в элементарной геометрии изучение Л. сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных Л. (конич. сечения, нек-рые алгебраич. Л. высших порядков и трансцендентные Л.), применяя в каждом случае специальные приемы. В аналитич. еометрии Л. на плоскости определяется как множество точек, координаты к-рых удовлетворяют уравнению F(x, у)=0. При этом на функцию Fдолжны быть наложены ограничения так, чтобы, с одной стороны, уравнение это имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло «куска плоскости». Важный класс Л. составляют те, для к-рых функция F(x, у).есть многочлен от двух переменных; в этом случае Л., определяемая уравнением F(x, y) = 0, наз. алгебраической. Алгебраич. Л., задаваемые уравнением 1-й степени, суть прямые. Уравнение 2-й степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или Л., распадающуюся на две прямые. Алгебраич. Л., определяемые уравнениями высших степеней, рассматриваются в алгебраич. геометрии. При этом большую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебранч. Л. определяется уравнением вида где F — однородный многочлен трех переменных, являющихся проективными координатами точек. Для тех разделов математики, в к-рых господствуют методы теории функций (анализ, дифференциальная геометрия и др.), естественное определение Л.- задание ее пара метрически мп уравнениями. Так, в случае плоскости, Л., заданная параметрич. уравнениями где — непрерывные функции, определенные на отрезке есть множество точек ( х, у), соответствующих всевозможным значениям параметра tпри условии, что эти точки рассматриваются в определенном порядке: если точка M1 соответствует значению параметра t1 а точка М 2 — значению t2, то М 1 считается предшествующей М 2 при t1<t2;точки, отвечающие различным значениям параметра, считаются различными. Уравнения задают ту же Л., что и уравнения (1), если существует такой гомеоморфизм отрезка [a1, b1] на отрезок и Аналогично Л. в произвольном топологич. пространстве Xопределяется параметрич. уравнением вида где — функция действительного переменного t, непрерывная на отрезке [ а, Ь], значения к-рой суть точки хпространства X. Кроме такого подхода существует п другая точка зрения (К. Жордан, С. Jordan, 1882) на определение Л. параметрич. уравнениями: Л. наз. множество точек плоскости, координаты к-рыХ суть непрерывные функции параметра t, заданные на отрезке [a, b]; теперь точки, соответствующие различным значениям параметра, но имеющие одни и те же координаты, уже не считаются различными, и множество, составляющее Л., уже не рассматривается как упорядоченное значениями t. Это определение обобщается на любое топологич. пространство: множество точек топологич. пространства, являющееся непрерывным образом отрезка, наз. жордановой кривой. Однако построены такие непрерывные функции и что множество точек, координаты к-рых определяются. этими функциями, заполняют квадрат (см. Пеано кривая). Более общо, всякий локально связный континуум (т. е. континуум, каждая точка к-рого обладает сколь угодно малой связной окрестностью) является непрерывным образом отрезка (теорема М а з у р к е в и ч а). Таким образом, не только квадрат, но и куб любого числа измерений и даже бесконечномерный гильбертов кирпич являются непрерывными образами отрезка. Вышеизложенное показывает, что Л. не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений. Так, в дифференциальной геометрии эти ограничения выражаются в том, что на функции, фигурирующие в параметрическом задании Л., налагаются условия существования производных различных порядков. С другой стороны, существуют континуумы, которые естественно рассматривать как Л., но к-рые, не будучи локально связными, не являются непрерывными образами отрезка. Таков, напр., континуум, определяемый условиями: Общее определение Л. для случая плоскости было дано (Г. Кантор, G. Cantor, 1870-е гг.) в связи с созданием теории точечных множеств. Плоский континуум, в любой окрестности каждой точки к-рого имеются точки плоскости, не принадлежащие континууму, наз. канторовой кривой. Важный пример канторовой кривой доставляет ковер Серпиньского, строящийся следующим образом. Квадрат Qсо стороной 1 делят на девять равных квадратов прямыми, параллельными его сторонам, и удаляют все внутренние точки центрального квадрата (рис. 2,. n=1). Так же поступают и с каждым из оставшихся восьми квадратов первого ранга, получается 64 квадрата второго ранга (рис. 2, n = 2). Продолжая процесс для всех натуральных n, на n-м шаге получают 8n квадратов n- горанга со стороною Пересечение полученных таким образом множеств и есть ковер Серпинь-ского (рис. 2). Какова бы ни была канторова кривая L, она может быть топологически вложена в ковер Серпиньского 5, т. е. в Sсодержится континуум L’, гомеоморфный Л. L. Ковер Серпиньского является локально связным континуумом и потому может быть получен как непрерывный образ отрезка. В топологии пользуются понятием Л., введенным в 1921 П. С. Урысоном и являющимся наиболее общим (но не чрезмерно). Определение Л. формулируется следующим образом: линией наз. одномерный континуум, т. с. связное компактное метрич. пространство С, каждая точка к-рого обладает сколь угодно малой окрестностью с границей размерности нуль. Другими словами, при любом e>0 пространство Сможет быть представлено в виде суммы конечного числа замкнутых множеств диаметра, меньшего е, обладающих тем свойством, что никакие три из этих множеств не имеют общей точки. Ковер Серпиньского удовлетворяет этому определению Л., так что всякая канторова кривая является также и Л. в смысле П. С. Урысона. Обратно, если плоский континуум является Л. в смысле П. С. Урысона, то он будет канторовой кривой. Определение Л., данное П. С. Урысоном, является внутренним: оно характеризуется лишь свойствами самого пространства С и не зависит от того, рассматривается ли это пространство само по себе или как подмножество другого топологич. пространства. Существуют Л., к-рые не гомеоморфны никакому подмножеству плоскости. Такова, напр., Л., лежащая в трехмерном пространстве и состоящая из шести ребер тетраэдра и четырех отрезков, соединяющих какую-либо точку пространства, не лежащую ни на одной из его граней, с его вершинами (рис. 3). Но всякая Л. (в смысле П. С. Урысона) гомеоморфна нек-рому подмножеству трехмерного евклидова пространства (теорема М е н г е р а). Континуум М, обладающий тем свойством, что какова бы ни была Л.. С, в М найдется подконтинуум С’, гомео-морфный континууму С, строится следующим образом. Куб К с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба Кудаляются центральный куб и все прилежащие к нему по двумерным граням кубы этого подразделения. Получается множество K1, состоящее из 20 оставшихся замкнутых кубов первого ранга. Поступая точно так же с каждым из кубов первого ранга, получим множество K2, состоящее из 400 кубов второго ранга (рис. 4). Продолжая этот процесс бесконечно, получим последовательность континуумов пересечение к-рых есть одномерный континуум М, паз. универсальной кривой М е н г е р а. В исследовании Л. важную роль играет понятие индекса ветвления. Л. Св точке химеет индекс ветвления т, если каково бы ни было число e>0, существует открытое множество Uдиаметра, меньшего, чем е, содержащее точку х. граница к-рого есть множество мощности, не превосходящей т, но для достаточно малого e’>0 граница всякого открытого множества, содержащего точку х, диаметр к-рого меньше e’, имеет мощность, не меньшую, чем т. Точки Л. относительно их индекса ветвления классифицируются следующим образом. 1) Точки с индексом ветвления п, п — натуральное. 2) Точки неограниченного индекса ветвления w. (Точка х Л. С имеет индекс ветвления со, если каково бы ни было число e>0, существует открытое множество, содержащее точку х, с диаметром, меньшим, чем е, граница к-рого состоит’из конечного множества точек; но каково бы ни было натуральное п, найдется такое en>0, что граница всякого открытого множества, содержащего хи имеющего диаметр меньший, чем en состоит не менее, чем из га точек.) 3) Точки счетного индекса ветвления 4) Точки континуального индекса ветвления с. Точка Л. С, индекс ветвления к-рой больше двух, наз. точкой ветвления; точка, индекс ветвления к-рой равен единице, наз. концевой точкой. Примеры, а) Отрезок во всех своих внутренних точках имеет индекс ветвления, равный двум; индекс ветвления концов отрезка равен единице, б) Окружность в каждой своей точке имеет индекс ветвления два. в) Л., состоящая из га прямолинейных отрезков,. исходящих из одной точки О, имеет в точке Оиндекс ветвления п. г) Л., состоящая из отрезков выходящих из начала координат О, имеющих длины и образующих с осью Ох углы, соответственно равные имеет в точке Онеограниченно возрастающий: индекс ветвления со (рис. 5). д) Л., состоящая из отрезка Оа 0 длины 1 и отрезков длины 1, выходящих из точки Ои образующих с отрезком Оа 0 углы, соответственно равные имеет в каждой точке отрезка Оа 0 счетный индекс ветвления (рис. 6). е) Л., состоящая из отрезков, соединяющих точку Осо всеми точками канторова множества, лежащего на отрезке y=0, имеет во всех своих точках континуальный индекс ветвления с (рис. 7). ж) Ковер Серпиньского также имеет во всех своих точках континуальный индекс ветвления. Если у Л. совсем нет точек ветвления, т. е. если в каждой точке Л. индекс ветвления равен 1 или 2, то эта Л. есть либо простая дуга — топологич. образ отрезка, либо простая замкнутая линия — топологич. образ окружности. При этом, если индекс ветвления Л. во всех точках равен 2, то это — простая замкнутая Л., если же у Л., не имеющей точек ветвления, есть концевые точки (при этом оказывается, что их непременно две), то она будет простой дугой. Если Л. имеет лишь конечное число точек ветвления, причем индекс ветвления каждой из них также конечен, то такая Л. может быть разбита на конечное число простых дуг, не имеющих попарно никаких других общих точек, кроме своих концов. Окружность является единственной Л., все точки к-рой имеют один и тот же конечный индекс ветвления 2; других Л., имеющих во всех точках один и тот же конечный индекс ветвления, нет, более того, если все точки Л. Lимеют индекс ветвления больший или равный п, то на Л. Lнайдется точка, индекс ветвления к-рой больше или равен 2п-2, и при всяком натуральном псуществует Л., состоящая только из точек, имеющих индекс ветвления пи 2п-2 (теорема У р ы с о н а). Пример Л., состоящий только из точек с индексом ветвления 3 и 4, строится следующим образом. В равностороннем треугольнике со стороною 1 проводятся три средние линии, и из него выбрасываются внутренние точки треугольника, ограниченного средними Л. С каждым из оставшихся трех треугольников первого ранга проделывается аналогичная операция, в результате к-рой получается девять треугольников второго ранга. Поступая с ними так же, получим 27 треугольников третьего ранга и так далее для всякого натурального п. Пересечение полученных в результате выполнения этих операций множеств есть линия С(рис. 8). Л., состоящая из точек с индексом ветвления 3 и 4,- это два континуума С 1 и С 2, каждый из к-рых гомеоморфен Л. С и к-рые не имеют никаких других общих точек, кроме точек, соответствующих вершинам основного треугольника континуума С. Существуют также Л., имеющие во всех своих точках неограниченный индекс ветвления, счетный индекс ветвления и континуальный индекс ветвления. Лит.:[1] Александров П. С., Введение в общую теорию множеств и функций, М.- Л., 1948; [2] К у р а т о в с к и й К., Топология, пер. с англ., т. 2, М., 1969; [3] М е n g е r К., Kurventheorie, Lpz.- В., 1932; [4] Пархоменко А. С., Что такое линия, М., 1954; [5] У р ы с о н П. С., Труды по топологии и другим областям математики, т. 2, М.- Л., 1951; [6] Хаусдорф Ф., Теория множеств, пер. с нем., М.- Д., 1937. А. С. Пархоменко.
Источник: Математическая энциклопедия на Gufo.me
Значения в других словарях
- линия — ли́ния начиная с Петра I; см. Смирнов 179, народн. линея (там же). Через польск. liniа или нем. Liniе из лат. līnea «льняная бечевка; полоса, проведенная этой бечевкой» (Клюге-Гётце 360). Далее см. лён. Этимологический словарь Макса Фасмера
- ЛИНИЯ — Специализированный участок в поточном производстве. Экономический словарь терминов
- линия — Ли́ни/я [й/а]. Морфемно-орфографический словарь
- линия — см.: гнуть Толковый словарь русского арго
- линия — Заимств., в начале XVIII в. — через нем. посредство — из лат. яз., где linea «линия» < «нитка» — суф. производное от linum «лен». Этимологический словарь Шанского
- линия — Латинское – linea. Заимствование слова произошло в XVIII в., впервые в словаре встречается в 1731 г. Современное значение слова: «черта, определяющая предел какой-либо поверхности или направление в движении». Этимологический словарь Семёнова
- линия — : линией — в линию (вытянуться). Сочетания синонимичны, но второй вариант указывает на большую степень концентрации действия. Управление в русском языке
- линия — Линия, линии, линии, линий, линии, линиям, линию, линии, линией, линиею, линиями, линии, линиях Грамматический словарь Зализняка
- линия — Л’ИНИЯ, линии, ·жен. (от ·лат. linea, ·букв. нитка). 1. Граница поверхности, имеющая только одно измерение (длину) и определяемая, как след движущейся точки или место пересечения двух поверхностей (мат.). Толковый словарь Ушакова
- Линия — Национальная единица длины в Бразилии = 12 понту = 2,4 мм.Национальная единица длины в Гондурасе = 12 пунто = 1,93 мм.Национальная единица длины в Мексике = 1,94 мм.Национальная единица длины в Парагвае = 2 мм. Словарь мер и весов
- линия — в генетике и селекции животных и растений группа родственных особей, характеризующаяся определенными признаками, постоянно воспроизводящимися в ряду поколений. При этом подразумевается генотипическая однородность… Микробиология. Словарь терминов
- линия — ЛИНИЯ -и; ж. 1. Узкая полоса, черта, проведённая на какой-л. поверхности от одной точки к другой. Провести линию. Волнообразная л. Обозначить точки на линии. Пересекающиеся линии. // Матем. Граница поверхности, имеющая только одно измерение — длину. Толковый словарь Кузнецова
- линия — Заимствование из латыни, где linea («нитка, линия») образовано от linum – «лен». Этимологический словарь Крылова
- линия — ЛИНИЯ, и, ж. 1. Черта на плоскости, на какой-н. поверхности или в пространстве. Прямая л. (кратчайшее растояние между двумя точками). Ломаная л. Тонкая л. Жирная л. Провести линию. Линии руки (ладонные). Толковый словарь Ожегова
- линия — ЛИНИЯ I. Черта для разметки поля (площадки) для спортивных игр: обозначения внешних границ поля (площадки) или границ отдельных зон внутри него в соответствии с правилами соревнований. — Л. боковой границы фехтовальной дорожки. Словарь спортивных терминов
- Линия — I Ли́ния (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. Большая советская энциклопедия
- линия — Группа родств. особей, характеризующаяся определёнными признаками, постоянно воспроизводящимися в ряду поколений. При этом подразумевается генотипич. однородность Л. по генам, контролирующим эти признаки. Термин «Л. Биологический энциклопедический словарь
- Линия — Животных (син.: Л. инбредная, Л. чистая) — популяция животных, происходящих от одной или нескольких пар предков… Медицинская энциклопедия
- ЛИНИЯ — ЛИНИЯ, непрерывный ряд точек. Термин может обозначать кривую или прямую линию — кратчайшее расстояние между двумя точками в ЕВКЛИДОВОЙ ГЕОМЕТРИИ. В прямоугольной ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ прямая линия выражается равенством: у=тх+с, где т — градиент, а с — точка пересечения с осью у. Научно-технический словарь
- линия — (linea, мн. lineae) Продолговатая деталь на планетарной поверхности. Большой астрономический словарь
- Линия — Граница поверхности. Л., служащая кратчайшим расстоянием между двумя точками, называется прямой. Л., составленная из прямых, различным образом направленных, называется ломаной (см. Кривые). Энциклопедический словарь Брокгауза и Ефрона
- ЛИНИЯ — ЛИНИЯ — 1) единица длины в системе английских мер, 1 линия ? 1/12 дюйма ?0,21167 см. 2) В России — мера длины, 1 линия ? 10 точкам ?2,54 мм. Большой энциклопедический словарь
- линия — сущ., кол-во синонимов… Словарь синонимов русского языка
- линия — ЛИНИЯ ж. черта; порядок, строй или ряд; направление. Линия прямая, кратчайшее соединение двух точек, она бывает уровнем, отвесная, косвенная; — кривая, лучковая, гнутая, дуга. Линия пограничная, ряд укреплений, постов, по граничной черте. Толковый словарь Даля
- линия — сущ., ж., употр. часто (нет) чего? линии, чему? линии, (вижу) что? линию, чем? линией, о чём? о линии; мн. что? линии, (нет) чего? линий, чему? линиям, (вижу) что? линии, чем? линиями, о чём? о линиях… Толковый словарь Дмитриева
- линия — орф. линия, -и Орфографический словарь Лопатина
- линия — -и, ж. 1. Узкая полоса, черта, проведенная на какой-л. поверхности от одной точки к другой. Его большие костистые руки водили красно-синим карандашом, — и множество линий, прямых, ломаных, закругленных, волнообразных, разбегались по белому полю. Малый академический словарь
- линия — линия I ж. 1. Черта, проведенная на какой-либо поверхности; узкая полоска. || Черта, полоса на ладони руки, на пальцах. 2. Граница поверхности… Толковый словарь Ефремовой
- линия — ЛИНИЯ — 1. Внешне однородная воспроизводящаяся половым путем популяция, которую размножают только семенами и константность которой поддерживается путем отбора в соответствии с определенным стандартом. Ботаника. Словарь терминов
- линия — По линии наименьшего сопротивления — в таком направлении, где всего менее препятствий. ► Всегда шел по линии наименьшего сопротивления. Фразеологический словарь Волковой
- линия — ЛИНИЯ и, ж. ligne f. <, лат. linea. 1. Последовательный ряд лиц, соединенных кровной связью; ряд от предков к потомкам. Сл. 18. < Петр I > правильным своим тестаментом.. конфирмовал о наследствии .. Словарь галлицизмов русского языка
- линия — Черта, строка, графа, ряд см. >> ряд, судьба, черта см. также -> выходит линия, демаркационная линия, по нисходящей линии, поразить по всей линии, разграничительная линия Словарь синонимов Абрамова

Ломаная — Википедия
Материал из Википедии — свободной энциклопедии
 Ломаная A1A2A3A4A5A6
Ломаная A1A2A3A4A5A6Ло́маная, ломаная линия — геометрическая фигура, состоящая из отрезков, последовательно соединённых своими концами.
Ломаной (ломаной линией) A1A2…An{\displaystyle A_{1}A_{2}\dots A_{n}} называется фигура, которая состоит из отрезков [A1A2]{\displaystyle [A_{1}A_{2}]}, [A2A3]{\displaystyle [A_{2}A_{3}]}, …, [An−1An]{\displaystyle [A_{n-1}A_{n}]}.
Точки A1{\displaystyle A_{1}}, …An{\displaystyle A_{n}}, называются вершинами ломаной, а отрезки [A1A2]{\displaystyle [A_{1}A_{2}]}, [A2A3]{\displaystyle [A_{2}A_{3}]}, …, [An−1An]{\displaystyle [A_{n-1}A_{n}]} — звеньями ломаной.
Ломаная называется невырожденной, если для любого k∈{1,2,…,n−2}{\displaystyle k\in \{1,2,\dots ,n-2\}} отрезки [AkAk+1]{\displaystyle [A_{k}A_{k+1}]} и [Ak+1Ak+2]{\displaystyle [A_{k+1}A_{k+2}]} не лежат на одной прямой; в противном случае — вырожденной.
- Ломаная имеет самопересечение, если хотя бы два её звена имеют общую точку помимо общей вершины:
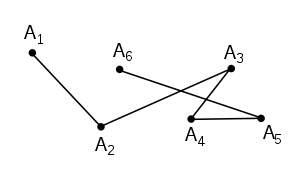
- Изображённую здесь ломаную следует называть «ломаная A1A2A3A4A5A6».
- Ломаная называется замкнутой, если первая и последняя точки ломаной совпадают; в этом случае дополнительно требуют, чтобы отрезки A1A2{\displaystyle A_{1}A_{2}} и An−1An{\displaystyle A_{n-1}A_{n}} также не лежали на одной прямой:
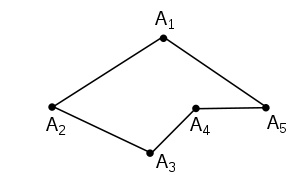
- Замкнутую плоскую ломаную часто называют многоугольником: в этом случае изображённая ломаная A1A2A3A4A5A1 будет называться «многоугольник» A1A2A3A4A5», а звенья будут называться сторонами многоугольника. В ряде случаев, например, при рассмотрении многогранников, стороны многоугольника называются рёбрами.
Проект по математике «Удивительный мир линий» ученика 5 класса
Муниципальное бюджетное общеобразовательное учреждение «Гимназия»
Удивительный мир линий
выполнил: ученик5б класса
Косычев Николай Владимирович
руководитель: учитель математики
Плешивцева Ю. Л.
г. Моршанск
2016г
Оглавление
Введение …………………………………………………
II. Основная часть……………………………………………
2.1 Определение линий………………
2.2 Классификация линий……………………………………
III. Практическая часть………………………………………
3.1 Решение разных задач с линиями
3.2 Линии в окружающем нас мире
IV. Источники информации
V. Приложение
I. Введение
Раньше я думал линии как линии, но оказалось что все не так просто и я заинтересовался этим и первое, что стали изучать по математике в пятом классе была тема «Линии». Как оказалось мир линий очень разнообразен — существует три вида линий: прямая, ломаная, кривая. Мне стало интересно и я решил исследовать «мир линий».
Мир линий разнообразен и красив.
Тема проекта: Удивительный мир линий
Цель: изучить и найти различные области применения линий
Задачи:
Дать определение линии
Рассмотреть классификацию линии
Увидеть линии в окружающем нас мире
II. Основная часть.
2.1. Что такое линия
Слово линия происходит от латинского слова linea, означающего «лен, льняная нить, шнур, веревка».
Карандаш на бумаге оставляет след…
Мел на асфальте тоже оставит свой след…
Таких примеров много- и все это ЛИНИИ
Линия – это геометрическая фигура, которая может быть получена в результате непрерывного перемещения точки.
2.2 Классификация линий
Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Отрезок изображается так:
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.
Линии разжеляются на прямые и кривые линии.

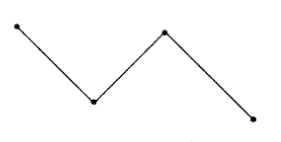
Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Линии
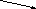
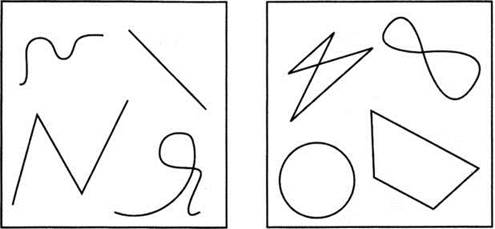
Линии
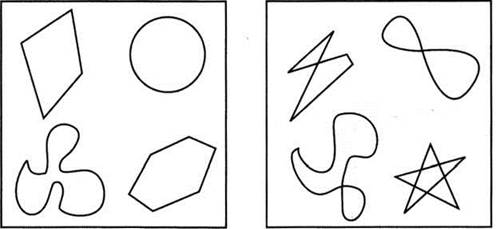
III. Практическая часть
3.1решение разных задач
Задача 1. Чем отличаются линии одной группы от другой?

Задача 2.
а) Выберите замкнутые линии.
б) Незамкнутые самопересекающиеся линии.
в) Замкнутые линии без самопересечений.
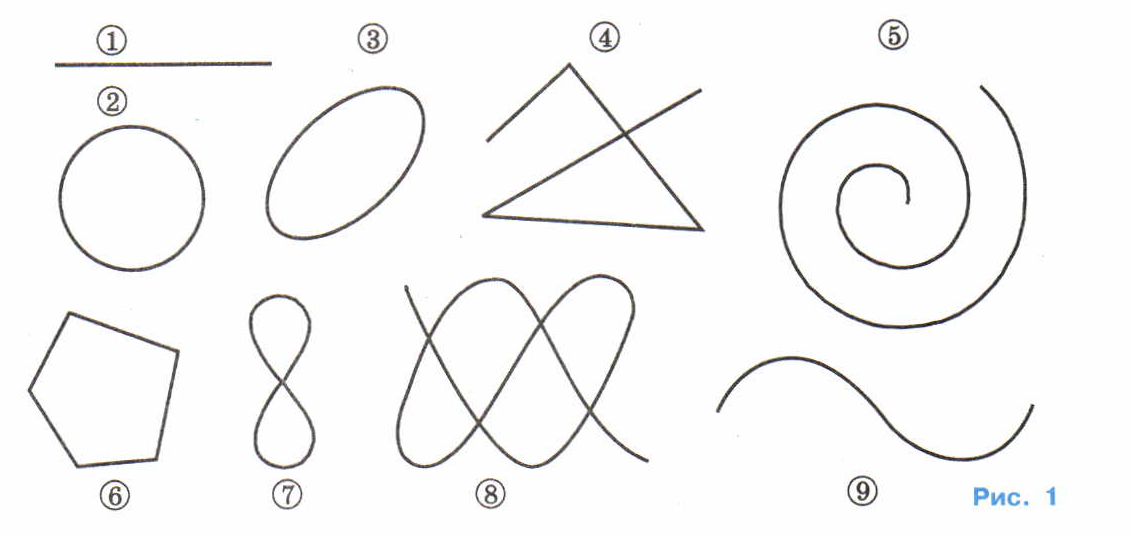
Задача 3. Сколько точек самопересечения имеют эти линии?
Какие точки принадлежат внутренней области? Почему?
Какие точки принадлежат внешней области? Почему?
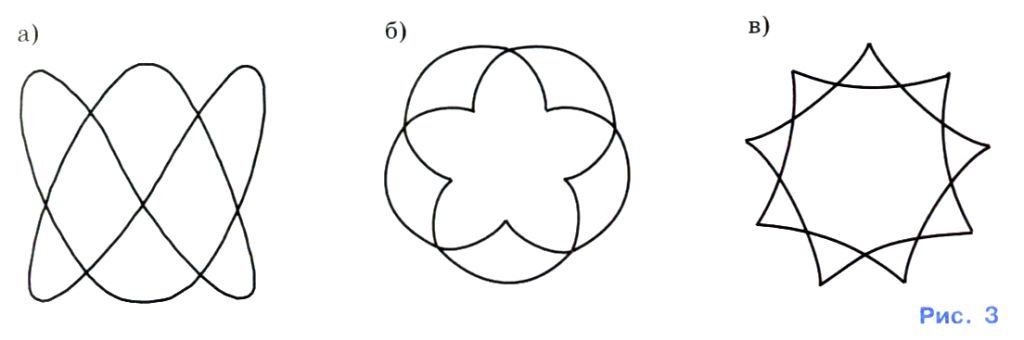
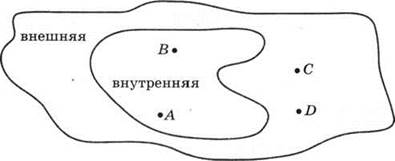
Задача 4. Какие точки принадлежат внутренней области? Почему?
Какие точки принадлежат внешней области? Почему?
Задача 5. Чем различаются две линии, изображенные на рисунке?

Линии в окружающем нас мире
Геометрия — это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами.
Линии, несомненно, обладают красотой и используются в нашей жизни очень обширно.
Если присмотреться вокруг, то можно у видеть линии которые нас окружают: см. приложение
В природе
В технике
В моде
В быту
В искусстве и т.д.
V. Источники информации
Н.Б. Васильев, В.Л.Гутенмахер, Ж.М.Раббот, А.Л.Тоом. Заочные математические олимпиады – М.: Наука. Главная редакция физико-математической литературы.1981.
А.Л. Вернер, В.И. Рыжик, Т.Г. Ходот. Геометрия 7 – М.: Просвещение,2001.
Э.Г.Гельфман, В.А. Панчищина, В.Н. Ксенева, Н.Б.Лобаненко. Геометрия для младших школьников (часть III) – Томск: Издательство Томского Университета, 1998.
Р.И. Довбыш, Л.Л.Потемкина, Н.Л.Трегуб, В.В.Лиманский, Л.Л. Оридорога, Н.А. Кулеско. Сборник материалов математических олимпиад – Донецк: Бао, 2005.
Интернет-ресурсы:
Приложение






Точки и линии. Видеоурок. Математика 1 Класс
На этом уроке мы узнаем, что называют точкой и линией. Научимся отличать прямую и кривую линию. Выясним, сколько прямых и кривых линий можно провести через одну точку, а сколько – через две точки. Выполним множество интересных заданий.
К нам на урок пришел веселый карандаш. Он очень любит рисовать.
Давайте посмотрим, что у него получилось.
Карандаш коснулся бумаги и оставил точку (рис. 1).

Рис. 1. Точка
Сколько точек нарисовал карандаш? Пять (рис. 2).

Рис. 2. Пять точек
В математике принято обозначать точки буквами: А, Б, В, Г, Д… (рис. 3).
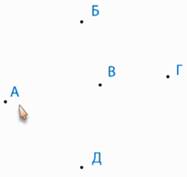
Рис. 3. Обозначение точек
Посмотрите на рисунок: какая точка самая верхняя? Точка Б. Какая точка самая нижняя? Точка Д. Какая точка стоит между точками А и Г? Точка В. Какая точка находится слева от точки В? Точка А. Какая точка находится под точкой В? Точка Д.
Посмотрите на рисунок: что теперь нарисовал карандаш (рис. 4)?

Рис. 4. Прямая линия
Прямую линию.
Без конца и края
Линия прямая.
Хоть сто лет по ней иди,
Не найдёшь конца пути.
О каком свойстве линии идет речь в этом стихотворении?
У линий нет начала и нет конца. Мы можем продолжить линию в одну и в другую сторону. Как получить прямую линию? Мы возьмем лист бумаги и сложим его (рис. 5).

Рис. 5. Складывание листа бумаги
Линия сгиба – это прямая линия (рис. 6).
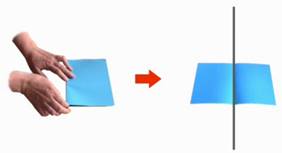
Рис. 6. Линия сгиба
Есть и другой способ провести прямую линию – с помощью линейки. Поставим точку А и проведем через нее прямую линию (рис. 7, 8).
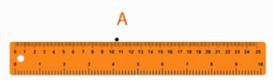
Рис. 7. Точка А
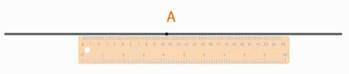
Рис. 8. Прямая, проходящая через точку А
Сколько прямых линий можно провести через одну точку? На этот вопрос нам поможет ответить карандаш. Понаблюдаем за ним: он провел через точку А множество линий (рис. 9).

Рис. 9. Множество прямых линий, проходящих через точку А
Как вы думаете, сколько прямых линий можно провести через 2 точки?
Рассмотри пример: у нас есть две точки (А и Б) (рис. 10).
Рис. 10. Точки А и Б
С помощью линейки проведем прямую линию (рис. 11).

Рис. 11. Прямая, проходящая через точки А и Б
Теперь попытаемся провести через эти точки еще одну прямую линию. Что мы заметили?
Невозможно сделать это.
Делаем вывод: через две точки можно провести только одну прямую линию.
Посмотрим, что нарисовал карандаш. Можно ли назвать эту линию прямой (рис. 12)?

Рис. 12. Кривая линия
Нет. В математике такая линия называется кривой.
Чтобы нарисовать ее, линейка не нужна. Посмотрите, какие бывают кривые линии (рис. 13).

Рис. 13. Виды кривых линий
Выясним, сколько линий можно провести через одну точку (рис. 14).

Рис. 14. Точка А
Понаблюдаем за карандашом (рис. 15).

Рис. 15. Кривые, проведенные через точку А
Что мы заметили? Через одну точку можно провести множество кривых линий.
Теперь попробуем провести кривые линии через две точки (рис. 16).
Рис. 16. Кривые, проведенные через две точки
Что мы видим? В отличие от прямой линии, через две точки можно провести множество кривых линий.
Карандаш нарисовал картинку (рис. 17).

Рис. 17. Картинка
Посмотрите, где спрятались кривые линии. Кривые линии – это волны на море и чайки (рис. 18).

Рис. 18. Волны и чайки – примеры кривых линий
А паруса, кораблик и лучи солнца – прямые линии (рис. 19).

Рис. 19. Паруса, кораблик и лучи солнца – примеры прямых линий
А вы любите рисовать? Попробуйте нарисовать картинку, используя прямые и кривые линии.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика. 1 класс. – М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. – М.: Русское слово, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Социальная сеть работников образования Nsportal.ru (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Uchmet.ru (Источник).
Домашнее задание
- О каких линиях мы узнали на этом уроке?
- При помощи нитки сложите разные линии.
Линейная алгебра — Википедия
Лине́йная а́лгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения[⇨], системы линейных уравнений[⇨], среди основных инструментов, используемых в линейной алгебре — определители, матрицы[⇨], сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры[1]. Такие объекты как квадратичные и билинейные формы[⇨], тензоры[⇨] и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.
Линейная алгебра обобщена средствами общей алгебры, в частности, современное определение линейного (векторного) пространства[⇨] опирается исключительно на абстрактные структуры, а многие результаты линейной алгебры обобщены на произвольные модули над кольцом. Более того, методы линейной алгебры широко используются и в других разделах общей алгебры, в частности, нередко применяется такой приём, как сведение абстрактных структур к линейным и изучение их относительно простыми и хорошо проработанными средствами линейной алгебры, так, например, реализуется в теории представлений групп[⇨]. Функциональный анализ возник как применение методов математического анализа и линейной алгебры к бесконечномерным линейным пространствам, и во многом базируется на методах линейной алгебры и в дальнейших своих обобщениях. Также линейная алгебра нашла широкое применение в многочисленных приложениях (в том числе, в линейном программировании[⇨], в эконометрике[⇨]) и естественных науках (например, в квантовой механике[⇨]).
Первые элементы линейной алгебры следовали из практических вычислительных задач вокруг решения линейных уравнений, в частности, такие арифметические приёмы как тройное правило и правило ложного положения[en] были сформулированы ещё в древности. В «Началах» Евклида фигурируют две теории «линейного» характера: теория величины и теория целых чисел. Близкие к современным матричным методам подходы к решению систем линейных уравнений обнаруживаются у вавилонян (системы из двух уравнений с двумя переменными) и древних китайцев (в «Математике в девяти книгах», до трёх уравнений с тремя переменными)[2]. Однако после достижения определённости с основными вопросами нахождения решений систем линейных уравнений развитие раздела практически не происходило, и даже в конце XVIII — начале XIX века считалось, что проблем относительно уравнений первой степени больше не существует, притом системы линейных уравнений с числом переменных, отличающихся от количества уравнений или с линейно-зависимыми коэффициентами в левой части попросту считались некорректными[3].
Методы, сформировавшие линейную алгебру как самостоятельную отрасль математики, уходят корнями в другие разделы. Ферма в 1630-е годы, создав классификацию плоских кривых, ввёл в математику (ключевой для линейной алгебры) принцип размерности и разделил задачи аналитической геометрии по числу неизвестных (с одним неизвестным — отыскание точки, с двумя — кривой или геометрического места на плоскости, с тремя — поверхности). Эйлер создал классификацию кривых по порядкам обратив внимание на линейный характер преобразований координат, ввёл в оборот понятие аффинного преобразования (и само слово «аффинность»)[4].
Первое введение понятия определителя для целей решения систем линейных уравнений относят к Лейбницу (1678[5] или 1693 год[6]), но эти работы не были опубликованы. Также определитель обнаруживается в трудах Сэки Такакадзу 1683 года, в которых он обобщил метод решения систем линейных уравнений из древнекитайской «Математики в девяти книгах» до n{\displaystyle n} уравнений с n{\displaystyle n} неизвестными[7]. Маклорен, фактически используя простейшие определители в трактате вышедшем 1748 году приводит решения систем из двух линейных уравнений с двумя неизвестными и трёх уравнений с тремя неизвестными[8]. Крамер и Безу в работах по проблеме отыскания плоской кривой, проходящей через заданную точку, вновь построили это понятие (правило Крамера сформулировано в 1750 году), Вандермонд и Лагранж дали индуктивное определение для случаев n>3{\displaystyle n>3}[9], а целостное определение и окончательные свойства определителей дали Коши (1815) и Якоби (1840-е годы)[3]. Гауссу (около 1800 года) принадлежит формализация метода последовательного исключения переменных для решения этих задач, ставшего известным под его именем[10] (хотя по существу для решения систем линейных уравнений именно этот метод и использовался с древности[4]).
Д’Аламбер, Лагранж и Эйлер, работая над теорией дифференциальных уравнений в том или ином виде выделили класс линейных однородных уравнений и установили факт, что общее решение такого уравнения порядка n{\displaystyle n} является линейной комбинацией n{\displaystyle n} частных решений (однако, при этом не отмечали необходимость линейной независимости решений)[11]. Основываясь на наблюдении, что множество значений целочисленной функции f(x,y){\displaystyle f(x,y)} не меняется от того, что над x{\displaystyle x} и y{\displaystyle y} совершается линейная подстановка (с целыми коэффициентами и определителем, равным 1), Лагранж в 1769 году разрабатывает теорию представления целых чисел квадратичными формами, а в 1770 году обобщает теорию до алгебраических форм. Гаусс развил теорию Лагранжа, рассматривая вопросы эквивалентности форм, и ввёл серию понятий, относящихся к линейным подстановкам, самым важным из которых было понятие сопряжённой (транспонированной) подстановки[12]. С этого времени арифметические и алгебраические исследования квадратичных и связанных с ними билинейных форм составляют существенную часть предмета линейной алгебры[13].
Ещё одним источником подходов для линейной алгебры стала проективная геометрия, создание которой начато Дезаргом в XVII веке и получившей значительное развитие в трудах Монжа конца XVIII века и в дальнейшем в работах Понселе, Брианшона и Шаля начала — середины XIX века. В те времена основным предметом изучения проективной геометрии были коники и квадрики, являющиеся по сути квадратичными формами. Кроме того, понятие двойственности проективных пространств, введённое Монжем, являет один из аспектов двойственности в линейных пространствах (однако эта связь была замечена только в конце XIX века Пинкерле)[14].
Но основной базой линейной алгебры стало фактически влившееся в раздел векторное исчисление, очерченное Гауссом в работах по геометрической интерпретации комплексных чисел (1831) и обретшее окончательную форму в трудах Мёбиуса, Грассмана и Гамильтона 1840-х — 1850-х годах. Так, Гамильтон в 1843 году открывает кватернионы, четырёхмерный аналог комплексных чисел, и даёт им геометрическую интерпретацию по аналогии с гауссовой (Гамильтону, в том числе, принадлежит и введение термина «вектор»). Физики школы Гамильтона, из которых самым выдающимся был Максвелл, тщательно проработали то, что сейчас относится к векторной алгебре в трёхмерном евклидовом пространстве: введены понятия скалярного, векторного и смешанного произведений векторов, набла-оператор[15], сформирована вошедшая в традицию символика, также начиная с этого времени векторы проникают и в школьные программы. Вместе с тем для школы Гамильтона центральным понятием были не векторы, а кватернионы, и определения линейной алгебры давались в терминах умножения кватернионов.
Параллельно шло развитие линейной алгебры и в Европе. В 1844 году Грассман строит понятие внешней алгебры, описывающей подпространства линейного пространства[16]. Долгое время его работы незаслуженно обходились вниманием: языком, адекватным физической картине мира, считался язык кватернионов. Так, Тэт, лидер школы «кватернионистов», считал смехотворной критику Гиббса, указывавшего, что язык кватернионов не приспособлен для описания пространств размерности выше четырёх, ибо пространство-время четырёхмерно; в то время как для Гиббса это было крайне важно, ибо фазовые пространства в разработанной им статистической механике имеют очень большую размерность (порядка числа Авогадро). Впоследствии правота Гиббса, идеи которого были развиты Хевисайдом, подтвердилась: основным языком стал именно язык векторного исчисления, а повсеместное употребление кватернионов осталось историческим курьёзом. Синтез идей Грассмана и Гамильтона был осуществлён в 1870-х Клиффордом: введённое им понятие алгебры Клиффорда включает как частные случаи как алгебру кватернионов, так и внешнюю алгебру.
Понятие матрицы ввёл Сильвестр в 1850 году[17][18]. Кэли обстоятельно разрабатывает матричное исчисление, публикуя в 1858 году «Мемуар о теории матриц» (англ. Memoir on the theory of matrices), принципиально, что Кэли рассматривает матрицы как нотацию для линейных подстановок[16]. В частности, в этой работе Кэли вводит сложение и умножение матриц, обращение матриц, рассматривает характеристические многочлены матриц и формулирует и доказывает для случаев 2×2 и 3×3 утверждение об обращении в нуль характеристического многочлена квадратной матрицы (известное как теорема Гамильтона — Кэли, так как случай 4×4 доказал Гамильтон с использованием кватернионов), доказательство для общего случая принадлежит Фробениусу (1898). Системы линейных уравнений в матрично-векторном виде впервые появились, по-видимому, в работах Лагерра (1867). Матричные группы, связанные с неевклидовыми геометриями, появились в работах Киллинга в 1880-х годах, вместе с более ранними работами Ли они стали основой теории групп и алгебр Ли. На рубеже веков эта теория была обогащена Энгелем и Картаном, давшими классификацию полупростых алгебр Ли и попутно открывшими векторное произведение в семимерном пространстве.
Теория инвариантов в классическом варианте — учение о свойствах алгебраических форм, сохраняющихся при линейных преобразованиях, сформирована начиная с 1840-х годов в работах Кэли, Эрмита и Сильвестра (известных как «инвариантная троица», фр. la trinité invariantive), считается[19], что именно теория инвариантов и приводит к созданию принципов решения произвольных систем линейных уравнений. В частности, Эрмит[уточнить] сформулировал и решил в частном случае проблему нахождения системы линейных диофантовых уравнений, решение в общем случае найдено Смитом (англ. Henry John Stephen Smith), результат которого остался незамеченным, пока не был обнаружен в 1878 году Фробениусом[19]. Финальный вид результаты о системах линейных уравнений с произвольными числовыми коэффициентами получили в работах, организованных Кронекером, в которых принимали участие Вейерштрасс, Фробениус и группа немецких учёных, особое внимание уделялось строгости и точности формулировок. В частности, определитель в курсе лекций Кронекера — Вейршртаса вводился как полилинейная знакопеременная функция от n{\displaystyle n} векторов n{\displaystyle n}-мерного пространства, нормированная таким образом, что принимает значение 1 для единичной матрицы; притом это определение эквивалентно вытекающему из исчисления Грассмана[19][20]. Фробениус в 1877 году ввёл понятие ранга матрицы, основываясь на котором в ближайшие годы сразу несколько учёных доказали утверждение об эквивалентности разрешимости системы линейных уравнений совпадением рангов её основной и расширенной матрицы, известной в русских и польских источниках как теорема Кронекера — Капелли, во французских — теорема Руше (фр. Eugène Rouché) — Фонтене (фр. Georges Fontené), в немецких и испанских — теорема Руше — Фробениуса, в итальянских и английских — теорема Руше — Капелли.
В 1888 году Пеано на базе исчисления Грассмана впервые в явном виде сформулировал аксиомы линейного пространства (векторных пространств над полем действительных чисел в том числе бесконечномерных) и применил обозначения, сохранившиеся в употреблении в XX—XXI века[21]. Тёплиц в начале 1910-х годов обнаружил, что при помощи аксиоматизации линейного пространства для доказательства основных теорем линейной алгебры не требуется прибегать к понятию определителя, что позволяет распространить их результаты на случай бесконечного числа измерений, иными словами, линейная алгебра применима при любом основном поле[21]. Аксиоматическое определение векторного и евклидова пространства было впервые чётко сформулировано в начале XX века практически одновременно Вейлем и фон Нейманом, исходя из запросов квантовой механики[22].
Тензорное исчисление, разработанное в 1890-е годы Риччи и Леви-Чивитой, составило своей алгебраической частью основное содержание полилинейной алгебры. Особое внимание к этому подразделу было привлечено в 1910-е — 1930-е годы благодаря широкому использованию тензоров Эйнштейном и Гильбертом в математическом описании общей теории относительности.
В 1922 году Банах, изучая полные нормированные линейные пространства, ставшие известными после его работ как банаховы, обнаружил, что уже в конечном случае возникают линейные пространства, не изоморфные своему сопряжению[21], и в этой связи в первой половине XX века методы и результаты линейной алгебры обогатили функциональный анализ, сформировав его основной предмет в современном понимании — изучение топологических линейных пространств[23]. Также в 1920-е — 1950-е годы получает распространение направление по линеаризации общей алгебры, так, развивая результат Дедекинда о линейной независимости любых автоморфизмов поля, Артин линеаризовывает теорию Галуа, а в 1950-е годы, прежде всего, в работах Джекобсона, эти результаты обобщены на произвольные расширения тел[24]; благодаря этим построениям обретена возможность применения инструментов и достижений хорошо изученной линейной алгебры в весьма абстрактных разделах общей алгебры.
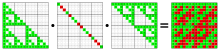 Схема алгоритма LU-разложения
Схема алгоритма LU-разложенияСо второй половины XX века с появлением компьютеров, развитием методов вычислительной математики и компьютерной алгебры в рамках линейной алгебры получило бурное развитие вычислительное направление — отыскание методов и алгоритмов, обеспечивающих эффективное решение задач линейной алгебры с использованием вычислительной техники, сформировался самостоятельный раздел вычислительной линейной алгебры (англ. numerical linear algebra), а решение задач линейной алгебры стало одной из важных практических составляющих использования компьютеров. В числе работ, положивших начало разработке этого направления, стало создание Тьюрингом алгоритма LU-разложения квадратной матрицы на верхнюю и нижнюю треугольные (1948)[25]. Показательно, что результаты тестов Linpack[en], в которых вычислительные системы должны решить сложные системы линейных уравнений с использованием LU-разложения, считаются основным показателем производительности вычислений с плавающей запятой, в том числе и для кластерных систем. В 1950-е — 1960-е годы крупные исследования в области вычислительной линейной алгебры опубликованы Фаддеевым и Уикинсоном, значительные результаты в 1970-е — 2000-е годы получены Марчуком, Самарским, Годуновым, Голубом (англ. Gene H. Golub), Аксельсоном[26].
Матрицы и определители[править | править код]
Матрица — математический объект, записываемый в прямоугольной таблице размером m×n{\displaystyle m\times n}, в ячейках которой расположены элементы произвольного заранее выбранного (основного) поля (в наиболее общем случае — ассоциативного кольца[27]) — это могут быть целые, вещественные или комплексные числа, векторы, рациональные функции — в зависимости от приложений и задач:
- (a11⋯a1j⋯a1n⋮⋱⋮⋱⋮ai1⋯aij⋯ain⋮⋱⋮⋱⋮am1⋯amj⋯amn){\displaystyle {\begin{pmatrix}a_{11}&\cdots &a_{1j}&\cdots &a_{1n}\\\vdots &\ddots &\vdots &\ddots &\vdots \\a_{i1}&\cdots &a_{ij}&\cdots &a_{in}\\\vdots &\ddots &\vdots &\ddots &\vdots \\a_{m1}&\cdots &a_{mj}&\cdots &a_{mn}\end{pmatrix}}}
Для матриц используется также сокращённая запись (aij){\displaystyle (a_{ij})}, но обычно с матрицами оперируют как с едиными объектами: над матрицами определены сложение и умножение, также матрицу можно умножить на скаляр — элемент основного поля, относительно этих операций образуют векторное пространство[⇨] над основным полем (или, в наиболее общем случае — модуль над кольцом). Другие операции над матрицами — транспонирование (замена строк на столбцы) и псевдообращение (обобщение обращения квадратных матриц). Матрицы размера 1×n{\displaystyle 1\times n} и m×1{\displaystyle m\times 1} называются вектор-строка и вектор-столбец соответственно.
Матрица с равным числом строк и столбцов называется квадратной, в зависимости от содержания они могут быть диагональными (все элементы — нули основного поля, кроме диагональных: i≠j⇒aij=0{\displaystyle i\neq j\Rightarrow a_{ij}=0}), единичными (все диагональные элементы равны единице основного поля, а остальные — нулю), симметричными (все элементы симметричны относительно главной диагонали: aij=aji{\displaystyle a_{ij}=a_{ji}}), кососимметричными (aij=−aji{\displaystyle a_{ij}=-a_{ji}}), треугольными (все элементы выше или ниже главной диагонали равны нулю), ортогональными. Среди квадратных матриц вводится отношение подобия (A∼B⇔∃P(A=P−1⋅B⋅P{\displaystyle A\sim B\Leftrightarrow \exists P(A=P^{-1}\cdot B\cdot P}), где P−1{\displaystyle P^{-1}} — матрица, обратная P{\displaystyle P}), такие характеристики матриц, как ранг (максимальное количество линейно независимых строк или столбцов) и характеристический многочлен инвариантны относительно подобия[28]. Также одинаковы для подобных прямоугольных матриц такие характеристики, как след (взятие суммы элементов главной диагонали) и определитель.
Определитель — многочлен, комбинирующий элементы прямоугольной матрицы особым способом, благодаря которому независимо от транспонирования и линейных комбинаций строк или столбцов характеризуется содержание матрицы; в частности, если в матрице есть линейно-зависимые строки или столбцы — определитель равен нулю. Квадратные матрицы, определитель которых равен нулю называются вырожденными, для них не определено обращение; если определитель отличен от нуля — то матрица называется невырожденной. Определитель играет ключевую роль в решении систем линейных уравнений в общем виде, на его базе вводятся понятия минора, дополнительного минора, алгебраического дополнения[29].
Векторы[править | править код]
Понятие вектора (сам термин «вектор» был введён У. Гамильтоном) изначально возникло как геометрическая абстракция для объектов, характеризующихся одновременно величиной и направлением, таких как скорость, момент силы, напряжённость электрического поля, намагниченность. В начале XX века изначальная интерпретация векторов (до сих пор используемая в элементарной математике) как «направленных отрезков» сменилось на аксиоматику векторного пространства с двумя операциямиː сложением векторов и умножение вектора на числа (более общо, на элементы поля). Кроме того, часто вводятся различные виды произведения векторов: скалярное, векторное, смешанное, псевдоскалярное, двойное векторное.
Ключевую роль в линейной алгебре играет понятие линейной независимости векторов, которое лежит в основе определений базиса и размерности векторного пространстваː число n{\displaystyle n} называется размерностью векторного пространства, если оно содержит n{\displaystyle n} линейно независимых векторов и любые k>n{\displaystyle k>n} векторов этого пространства являются линейно зависимыми. Такое векторное пространство называется n{\displaystyle n}-мерным, и любой его вектор представляется упорядоченной последовательностью n{\displaystyle n} чисел (однозначно определяемых при выборе какого-либо базиса). Таким образом, векторы могут быть записаны в виде матриц размера 1×n{\displaystyle 1\times n} или n×1{\displaystyle n\times 1} — векторов-столбцов и векторов-строк соответственно, а все операции векторной алгебры могут быть сведены к алгебре матрицː например, сложение векторов совпадает со сложением матриц, а векторное умножение векторов может быть выражено как произведение кососимметрической матрицы, построенной из первого сомножителя и вектора-стоблца, представляющего второй сомножитель.
Тензоры[править | править код]
Тензоры возникли как естественное развитие представлений об объектах линейной алгебры: если скаляр в n{\displaystyle n}-мерном представляется нульмерным объектом (состоящим только из одного элемента поля), вектор — одномерным массивом (матрицей размера 1×n{\displaystyle 1\times n}), линейное преобразование — двумерной матрицей, то тензор может быть представлен как многомерный массив элементов поля размера n×n×⋯×n{\displaystyle n\times n\times \cdots \times n} (количество измерений массива называют валентностью тензора), а скаляры, векторы, линейные операторы оказываются частными случаями тензора (с валентностями 0, 1 и 2 соответственно). Следующее обобщение, использованное в понятии тензора взято из возможности представления линейного функционала как ковектора и идея двойственности между пространством и его сопряжением — пространством его линейных функционалов; используя эту возможность, тензор валентности r{\displaystyle r} рассматривается как l{\displaystyle l} раз контравариантный, то есть, рассматриваемый соответствующими компонентами в «обычном» базисе, и k{\displaystyle k} раз ковариантный, то есть, с компонентами в сопряжённом пространстве (r=k+l{\displaystyle r=k+l}, «тензор ранга (l,k){\displaystyle (l,k)}»).
В тензорной алгебре вводятся и изучаются линейные операции над тензорами, такие, как умножение на скаляр, сложение, свёртка. Особую роль играет операция тензорного произведения (⊗{\displaystyle \otimes }), обобщение которой на линейные пространства позволило обобщить и определение тензора: рассматривать тензор ранга (l,k){\displaystyle (l,k)} в линейном пространстве V{\displaystyle V} как элемент тензорного произведения k{\displaystyle k} экземпляров V{\displaystyle V} и l{\displaystyle l} экземпляров сопряжённого ему V∗{\displaystyle V^{*}}:
- V⊗…⊗V⏟⊗V∗⊗…⊗V∗⏟kl{\displaystyle {\begin{matrix}\underbrace {V\otimes \ldots \otimes V} &\otimes &\underbrace {V^{*}\otimes \ldots \otimes V^{*}} \\k&&l\end{matrix}}}.
Квадратичные и билинейные формы[править | править код]
Алгебраические формы (однородные многочлены на векторных пространствах, задаваемые однородными многочленами от координат вектора) относятся к полилинейной алгебре, но квадратичные, билинейные формы, и некоторые специальные виды форм (полуторалинейные, эрмитовы) важны также в чисто линейной алгебре. Значение билинейных и квадратичных форм заключается в том, что они выражаются матрицами, как и линейные операторы. Наиболее детально изучены свойства симметричных (B(x,y)=B(y,x)){\displaystyle (B(x,y)=B(y,x))} и кососимметричных (B(x,y)=−B(y,x)){\displaystyle (B(x,y)=-B(y,x))} билинейных форм.
Векторные пространства[править | править код]
Все математические структуры, изучаемые в линейной алгебре — векторы, тензоры, матрицы, алгебраические формы, а также операции над ними, универсализированы в общеалгебраическом понятии векторного (линейного) пространства. Векторное пространство ⟨V,F,+,⋅⟩{\displaystyle \langle V,{\mathfrak {F}},+,\cdot \rangle } определяется как алгебра над произвольным множеством элементов V{\displaystyle V}, называемых векторами, и произвольным полем F{\displaystyle {\mathfrak {F}}}, элементы которого называются скалярами, притом векторы с операцией сложения векторов ⟨V,+⟩{\displaystyle \langle V,+\rangle } образуют абелеву группу, и определена операция умножения векторов на скаляр: ⋅:F×V→V{\displaystyle \cdot :{\mathfrak {F}}\times V\to V} такая, что выполнены следующие свойства (1,α,β∈F,v,u∈V{\displaystyle 1,\alpha ,\beta \in {\mathfrak {F}},\,\mathbf {v} ,\mathbf {u} \in V}):
- 1⋅v=v{\displaystyle 1\cdot \mathbf {v} =\mathbf {v} },
- α⋅(v+u)=α⋅v+α⋅u{\displaystyle \alpha \cdot (\mathbf {v} +\mathbf {u} )=\alpha \cdot \mathbf {v} +\alpha \cdot \mathbf {u} },
- (α+β)⋅v=α⋅v+β⋅v{\displaystyle (\alpha +\beta )\cdot \mathbf {v} =\alpha \cdot \mathbf {v} +\beta \cdot \mathbf {v} },
- (αβ)⋅
линия — это… Что такое линия?
Морфология: (нет) чего? ли́нии, чему? ли́нии, (вижу) что? ли́нию, чем? ли́нией, о чём? о ли́нии; мн. что? ли́нии, (нет) чего? ли́ний, чему? ли́ниям, (вижу) что? ли́нии, чем? ли́ниями, о чём? о ли́ниях
1. Линия — это узкая полоса, черта, проведённая на какой-либо поверхности от одной точки к другой.Провести линию. | Кривая линия. | Соединить точки линией. | Пересекающиеся линии. | И кроме линий простых, двойных, зигзагообразных, изломанных под разными углами, на бумаге появились ещё и квадраты, овалы и пирамиды.
2. В математике линией называют границу поверхности, имеющую только одно измерение — длину.Конические сечения относятся к линиям второго порядка.
3. Линией называют воображаемую черту, соединяющую две точки или являющуюся границей пересечения двух поверхностей.Линия экватора. | Линия горизонта. | Взгляд везде упирался в жёсткую линию горизонта, и я вынужден был осознать, что не представляю, где город.
4. Линией называют черту (существующую или воображаемую), определяющую предел, границу чего-либо.Линия прилива. | Боковые линии футбольного поля. | Перетащив лодку через линию прибоя, я перевернул её и слил воду, а потом совсем вытащил на берег.
5. Линией называют очертания, контур чего-либо.Наблюдать береговую линию. | Чёткие линии горных вершин. | Властная, жёсткая линия рта. | Чувствуя, что его правая нога тяжелеет, он снова поднялся на поверхность и продолжал плыть на спине параллельно линии берега.
6. Линией называют длинный ряд или цепь каких-либо сооружений.Линия телеграфных столбов. | Построить линию укреплений.
7. Слово линия входит в название некоторых улиц или их сторон, торговых рядов и т. п.Садовая линия Гостиного двора. | Жить на Девятой линии Васильевского острова.
8. Линией называют путь, полотно железной дороги или трамвая.Трамвайная линия. | Электричка вышла на линию по расписанию.
9. Линией называют путь сообщения (железнодорожного, водного, воздушного) связывающий два каких-либо пункта.Железнодорожная линия Петербург — Варшава.
10. Линией называют систему устройств (проводов, кабеля и т. п.) для телеграфной и телефонной связи, а также для передачи электроэнергии.Телефонная линия Калуга — Тула. | Линия электропередачи. | Модем — устройство, позволяющее передавать по телефонной линии информацию.
11. Линией называют последовательный ряд лиц, соединённых кровной связью, ряд предков, потомков.Родство по женской линии. | Восходящая линия (идущая от сына к отцу, деду и т. п., от потомков к предкам). | Очень интересно было бы знать, как мой непосредственный предок по отцовской линии относился к декабристам.
о манере действий человека
12. Линией могут называть направление, образ действий, мыслей.Линия поведения. | Держаться правильной линии действий. | Выбор правильной линии поведения требует наличия соответствующих знаний.
13. Вести свою линию значит настойчиво осуществлять какие-либо принципы, мысли, взгляды.
14. Гнуть свою линию значит упрямо добиваться чего-либо; разговорное выражение.
15. Линией называют ряд производственных машин, устройств с непрерывным циклом работ.
Автоматическая линия по упаковке продуктов. | Линия по производству подшипников. | Конвейерная линия. | Необходимо срочно восстановить и ввести в действие фасовочные линии.
16. В прошлом линией называли старинную русскую меру длины, равную 1/10 или 1/12 дюйма, применявшуюся до введения метрической системы.
17. Демаркационная линия — это условная черта, разделяющая войска противников на время перемирия, или разделяющая на зоны оккупации территорию побеждённого государства.Части регулярной армии перешли демаркационную линию.
18. Если кто-то идёт по какой-либо линии, значит, он связывает свою карьеру с какой-либо общественной или государственной структурой.Пошёл по профсоюзной линии. | Толик был не столько способный, сколько деятельный по комсомольской линии.
19. Контурная линия — это прерывистая, состоящая из точек линия.
20. Ломаная линия состоит из отрезков прямой линии, соединяющихся под углом.
21. Линией огня называют передовой район боевых действий.
22. Линия обороны — это система каких-либо защитных укреплений, огневых точек.Прорвать линию обороны.
• линова́ть
Вертикальная черта — Википедия
Материал из Википедии — свободной энциклопедии
| Вертикальная черта | |
|---|---|
| | | |
| vertical line | |
| Юникод | U+007C |
| HTML-код | |
| UTF-16 | 0x7C |
| %7C | |
Вертика́льная черта́ — символ ASCII, имеющий код 0x7C (hex), 124 (dec). Этот символ пользователи UNIX называют «пайп», от англ. pipeline — конвейер. В первых, ещё советских, изданиях книг В. Э. Фигурнова название «pipe» было переведено как «символ трубопровода»[1].
Вертикальная черта используется в математике:
Также используется двойная вертикальная черта:
Форма Бэкуса — Наура[править | править код]
Имеет смысл разделителя ИЛИ (разделяет 2 возможности):
<символ> ::= <буква>|<цифра> <идентификатор> ::= <буква>|<идентификатор><символ>
Аналогичный смысл имеет в регулярных выражениях.
Перенаправление ввода-вывода[править | править код]
Используется в DOS и UNIX-системах для перенаправления стандартного потока вывода (stdout) одной программы в стандартный поток ввода (stdin) другой (конвейер). Например,
cat fruits.txt | grep -v ^bad | sort
выведет список фруктов из файла fruits.txt, не имеющих ‘bad’ в качестве первых трёх символов, отсортированный по алфавиту. Такой способ передачи информации направляет потоки данных, подобно трубопроводу, поэтому его и назвали «pipeline» или просто «pipe» — труба. Соответственно знак вертикальной черты пользователи UNIX тоже называют «pipe».
Языки программирования[править | править код]
В C-подобных языках символ «|» служит для операции побитового «или» (дизъюнкция), а два таких символа, написанных слитно («||»), используются в операции логического «или».
Кроме того, в языках с «нестрогим» синтаксисом — shell-сценариях UNIX, в языке Perl — логический оператор «||» (ИЛИ) может использоваться для выполнения условного перехода, когда операция слева возвращает ложное значение. Таким образом может быть построена цепочка команд «сделай одно или сделай другое или сделай третье».
rm * || echo "Не могу удалить файлы"
В приведённом примере в случае невозможности удаления одного и более файлов выводится сообщение.
Псевдографика[править | править код]
Наравне с символом «!» используется для рисования таблиц:
+---+---+---+ ,---,---,---, | * | 1 | 2 | | + | 1 | 2 | +---+---+---+ !---+---+---! | 1 | 1 | 2 | или | 1 | 2 | 3 | +---+---+---+ !---+---+---! | 2 | 2 | 4 | | 2 | 3 | 4 | +---+---+---+ '---'---'---'
MediaWiki[править | править код]
В MediaWiki символ используется в разметке таблиц, а также в качестве разделителя параметров шаблонов.
В электротехнике запись R1||R2{\displaystyle R_{1}||R_{2}} используется для обозначения общего сопротивления резисторов R1 и R2, включенных параллельно.
В МФА символом вертикальной черты обозначают зубной щёлкающий согласный (двойной чертой — боковой щёлкающий согласный). Кроме того, вертикальные черты могут отделять просодические единицы друг от друга.
На клавиатурах на клавише, предназначенной для ввода «|», традиционно рисуют разорванную вертикальную черту «¦». В настоящее время это отдельный символ «broken bar» с кодом U+00A6 (в HTML его можно обозначить как ¦).
В линейном формате редактора формул Microsoft Word (версии 2007 и более поздние) знак разорванной вертикальной черты применяется для создания дроби, но без черты[2]. Например, x¦y преобразуется в xy{\displaystyle x \atop y}. Подобное применение предлагается и в техническом примечании к Unicode[3].
| |