Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, \( \displaystyle {{\log }_{2}}\left( -4 \right)\) не существует, так как \( 2\) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \( \displaystyle {{\log }_{2}}0\) тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ.
Приведу пример:
Решим уравнение \( \displaystyle {{\log }_{x}}\left( x+2 \right)=2\).
Вспомним определение: логарифм \( \displaystyle {{\log }_{x}}\left( x+2 \right)\) – это степень, в которую надо возвести основание \( x\), чтобы получить аргумент \( \displaystyle \left( x+2 \right)\).
 {2}}-x-2=0\).
{2}}-x-2=0\).Решим его с помощью теоремы Виета: сумма корней равна \( 1\), а произведение \( -2\). Легко подобрать, это числа \( 2\) и \( -1\).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
\( \displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\) – верно.
\( \displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\) – это явно неверно, так как основание не может быть отрицательным, то есть корень \( x=-1\) – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
\( \displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)
Тогда, получив корни \( x=2\) и \( x=-1\), сразу отбросим корень \( -1\), и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\). Если корней несколько, в ответе укажите меньший из них.
Решение:
\( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\).
В первую очередь напишем ОДЗ:
\( \displaystyle \left\{ \begin{array}{l}x+1>0\\x+1\ne 1\\2x+5>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0\\x>-\frac{5}{2}\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0.\end{array} \right.\)
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание \( \displaystyle x+1\), чтобы получить аргумент \( \displaystyle 2x+5\)?
Хотите читать учебник без ограничений? Зарегистрируйтесь:
Во вторую. То есть:
\( \displaystyle {{\left( x+1 \right)}^{2}}=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}+2x+1=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2. \end{array} \right.\)
\end{array} \right.\)
Казалось бы, меньший корень равен \( \displaystyle -2\). Но это не так: согласно ОДЗ корень \( \displaystyle x=-2\) – сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: \( \displaystyle x=2\).
Ответ: \( \displaystyle x=2\).
Десятичный логарифм
Навигация по странице:
Определение. Логарифмом числа b по основанию a, где a > 0, a ≠ 1, b > 0, называется показатель степени, в которую нужно возвести основание a, чтоб получить число b.
Определение. Десятичный логарифм — логарифм по основанию 10.
Другими словами, десятичный логарифм числа b является решением уравнения 10x = b.
Обозначение. Десятичный логарифм обозначается lg x или log x.
Калькулятор десятичных логарифмов
lg 2Свойства десятичного логарифмов
Для любых x > 0 и y > 0 выполняются следующие свойства десятичных логарифмов.

lg x = log10x — так как основание десятичного логарифма равно 10.
10lg b = b.
lg 1 = 0
lg 10 = 1
lg 10n = n
lg(x · y) = lg x + lg y
lg xy = lg x — lg y
lg xn = n lg x
- График функции y = lg x
(lg x)′ = 1x ln 10
∫ lg x dx = x lg x — xln 10 + C
lg 100 = lg 102 = 2
lg 1000 = lg 103 = 3
lg 0.1 = lg 10-1 = -1
lg 0.01 = lg 10-2 = -2
lg 0.001 = lg 10-3 = -3
Пример 2.Доказать равенство: a lg b = b lg a.
Запишем очевидное равенство:
lg b · lg a = lg a · lg ab
Возведем 10 в соответствующие степени
10lg b · lg a = 10lg a · lg b
(10lg b)lg a = (10lg a)lg b
blg a = alg b
Равенство доказано.
Зная, что lg 2 = a, lg 3 = b, lg 5 = c, выразить lg 6; lg 30; lg 16 через a, b, c.
Используем формулы логарифма произведения и степени получим:
lg 6 = lg (2·3)= lg 2 + lg 3 = a + b;
lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c;
lg 16 = lg 24
Вычислить log9 5 · log25 27.
Перейдем к основе 10:
log9 5 · log25 27 = lg 5lg 9 · lg 27lg 25
Используем свойство логарифма степени lg xn = n lg x:
lg 5lg 9 · lg 27lg 25 = lg 5lg 32 · lg 33lg 52 = lg 52 lg 3 · 3 lg 32 lg 5 = 34
Пример 5.Вычислить log30 8, если lg 5 = a, lg 3 = b.
Перейдем к основе 10:
log 30 8 = lg 8lg 30 = lg 23lg (3 · 10) =
Используем свойство логарифма степени, произведения, частного и то что 2= 105:
= 3 lg 2lg 3 + lg 10 = 3 lg 2lg 3 + 1 = 3 lg 105lg 3 + 1 = 3(lg 10 — lg 5)lg 3 + 1 = 3(1 — lg 5)lg 3 + 1 =
Подставим lg 5 = a, lg 3 = b:
= 3(1 — a)b + 1
Ответ:
log30 8 = 3(1 — a)b + 1
Функция LOG — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции LOG в Microsoft Excel.
Описание
Возвращает логарифм числа по заданному основанию.
Синтаксис
LOG(число;[основание])
Аргументы функции LOG описаны ниже.
-
Число Обязательный. Положительное вещественное число, для которого вычисляется логарифм.
-
Основание Необязательный. Основание логарифма. Если аргумент «основание» опущен, предполагается, что он равен 10.

Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=LOG(10) |
Логарифм числа 10. Так как второй аргумент (основание) опущен, предполагается, что он равен 10. |
1 |
|
=LOG(8; 2) |
Логарифм числа 8 по основанию 2. Результат (3) — степень, в которую необходимо возвести основание, чтобы получить число 8. |
3 |
|
=LOG(86; 2,7182818) |
Логарифм числа 86 по основанию e (приблизительно 2,718). Результат (4,454) — степень, в которую необходимо возвести основание, чтобы получить число 86. |
4,4543473 |
Логарифмы. Основание логарифма. Натуральный логарифм. Логарифм 10.
 3.\)
3.\)Область допустимых значений логарифма
- Аргумент и основание не могут быть равны нулю и отрицательными числами.
- Основание не может быть равно единице, поскольку единица в любой степени все равно остается единицей.
- Число b может быть любым.
- ОДЗ логарифма \(log_a x = b ⇒ x > 0, a > 0, a ≠ 1\).
Десятичные логарифмы
Десятичные логарифмы – логарифмы, в основании которых стоит \(10\). Пример \(log_{10}10 =1\),
Log10100 =2. Записывают их в виде \(lg 10 = 1\), \(lg 100 = 2.\)
Натуральный логарифм
Натуральный логарифм – логарифм, в основании которого стоит \(e\). Что означает \(e\)? Это иррациональное число, бесконечное непериодическое десятичное число, математическая константа, которую надо запомнить:
\(e = 2,718281828459…\)
\(ln x = log_e x\)
Краткая история логарифма
Логарифмом имеет много применений в науке и инженерии. Естественный логарифм имеет константу \(e\) в своем основании, его использование широко распространено в дискретной математике, особенно в исчислении. Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке.
Естественный логарифм имеет константу \(e\) в своем основании, его использование широко распространено в дискретной математике, особенно в исчислении. Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Предыдущую статью о показательных уравнениях мы начали с уравнения 2x = 8. Там всё было ясно: x = 3.
Там всё было ясно: x = 3.
А теперь рассмотрим уравнение 2x = 7.
По графику функции y = 2 x мы видим, что это уравнение имеет корень, и притом единственный.
Ясно, что этот корень — не целое число (так как 22 = 4, 23 = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.
Этот корень обозначается log27 (читается: «логарифм семи по основанию два». Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log27 = 2,807354922057604107…
Итак, наше число log27 — это показатель степени, в которую надо возвести 2, чтобы получить 7.
Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).
Определение. Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b.
Иными словами,
Например:
так как
, так как
так как ;
, так как .
Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.
Логарифм с основанием e называется натуральным и обозначается ln.
Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log2(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.
Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.
Основные формулы
По определению, logab — это показатель степени, в которую надо возвести число a, чтобы получить число b:
Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:
logaax=x.
Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.
Логарифм произведения — это сумма логарифмов:
| loga(bc) = logab + logac. | (2) |
Логарифм частного — это разность логарифмов:
| (3) |
Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:
| (4) |
Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:
| (5) |
Формулы (4) и (5) вместе дают:
| (6) |
В частности, если m = n, мы получаем формулу:
| (7) |
Например, .
Наконец, важнейшая формула перехода к новому основанию:
| (8) |
В частности, если c = b, то logbb = 1, и тогда:
| (9) |
Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).
2. (применили основное логарифмическое тождество(1))
3. (применили формулу (4).
4. (применили формулу (9), перейдя к новому основанию 0,8).
5. (применили формулу (3) разности логарифмов)
Немного истории
Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?
Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.
Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?
Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.
В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.
Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.
Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).
А затем по таблице логарифмов найти само произведение чисел b и c.
Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.
Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.
свойства, формулы, основание, виды для школьников и студентов
Формулы и свойства логарифмов
Для любых a>0, a≠1 и b>0, x>0, y>0 выполняются следующие свойства логарифмов.
Именно это свойство логарифмов позволяет вычислять точные значения в отличае от других методов вычисления.
Неточность других методов вычисления основывается на неверной корреляции остаточного члена логарифмического равенства.
Наряду с этим каждое из свойств является индивидуальным, равно как каждый из его членов. Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.
Всё это позволяет сделать вывод, что благодаря формулам, выведенным математиком, вычисления становятся простыми в рамках неравенств.
Основное логарифмическое тождество
Основание a, возведенное в степень логарифма с основанием a, будет равно b.
alogab=b
Логарифм единицы
Логарифмический ноль. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.
Вычисления такого логарифма применяются в балистике при расчете траектории движения объекта, находящегося в непосредственной близости от Земли. Это обусловлено наиболее точным значением ускорением свободного падения, равным 9,81. А при удалении от поверности Земли это значение изменяется, уменьшается пропорционально расстоянию удаления от поверхности.
loga1=0
Логарифм числа, равного основанию
Логарифмическая единица. Если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
logaa=1
Логарифм числа, обратного основанию
Если аргумент логарифма имеет значение обратное основанию, то значение логарифма будет равно -1.
loga1a=-1
Логарифм произведения двух положительных чисел
Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2-х логарифмов, у которых будут одинаковые основания.
logax·y=logax+logay
Логарифм частного
Логарифм частного. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.
logaxy=logax-logay
loga1y=-logay
Логарифм степени положительного числа
Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа.
logaxn=nlogax
Логарифм корня числа
Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.
logaxn=logaxn
Основание логарифма в степени
loganx=logaxn, при n≠0
Формула перехода к новому основанию
logax=logbxlogbalogax=1logxa
Производная логарифма
Производная логарифмической функции по основанию равна единице, деленной на произведение подлогарифмической функции на натуральный логарифм основания.
При расчёте производной логарифма необходимо учитывать ложный коэффициент производной, при котором нарастает его гиперболическая составляющая. Это и есть главное условие корректного нахождения производной логарифма. В то же время, нельзя упускать второстепенные составляющие при расчёте. К ним относятся расчеты с применением общей суммы логарифмов, а также пропорциональная составляющая двух вычисляемых логарифмов. Такой подход можно применить не только для вычисления производной натурального логарифма, но и при расчете производной десятичного логарифма при возведении в степень x по основанию a.
logax′=1xlna
Python. Модуль math. Степенные и логарифмические функции
Содержание
Поиск на других ресурсах:
1. Функция math.exp(x). Экспонента в степени x
Функция math.exp(x) возводит число e в степень x. Функция возвращает результат вещественного типа. Аргумент x может быть целого или вещественного типа. Значение экспоненты: e = 2.718281… служит основой натурального логарифма.
Значение экспоненты: e = 2.718281… служит основой натурального логарифма.
В Python Функция math.exp(x) может быть заменена другими выражениями
- math.e**x – здесь math.e – константа, равная значению экспоненты.
- pow(math.e, x) – здесь pow() – встроенная функция языка Python.
Пример.
# Функция math.exp(x) import math y = math.exp(1) # y = 2.718281828459045 x = 0.0 y = math.exp(x) # y = 1.0 x = 3.85 y = math.exp(x) # y = 46.993063231579285
⇑
2. Функция math.expm1(x). Экспонента от x минус 1
Функция math.expm1(x) вычисляет значение выражения exp(x)-1. При вычислении значения некоторого y, вызов функции
y = math.expm1(x)
можно заменить выражением
y = math.exp(x)-1
Однако, использование функции math.expm1(x) даст более точный результат вычисления. Это и есть основное назначение данной функции.
Пример.
# Функция math.expm1(x) import math x = 1.0 y = math.expm1(x) # y = 1.718281828459045 y = math.expm1(0.0) # y = 0.0
⇑
3. Функция math.log(x). Натуральный логарифм
Функция math.log(x) предназначена для вычисления натурального логарифма числа с заданным основанием.
Общая форма функции следующая
math.log(x [, base])
где
- x – аргумент, для которого вычисляется логарифм;
- base – основание логарифма. Этот параметр функции необязательный. Если параметр base отсутствует, то за основу берется число e = 2.718281…
Если попробовать вызвать функцию log(0.0), то интерпретатор Python выдаст ошибку
ValueError: math domain error
поскольку логарифм нуля не существует.
Пример.
# Функция math.log(x) import math x = 1.0 y = math.log(x) # y = 0.0
⇑
4. Функция math.log1p(x). Логарифм для значений, приближенных к нулю
Функция log1p(x) возвращает натуральный логарифм от 1+x. Основой логарифма есть экспонента e = 2.718281… Функция необходима в случаях, когда значение аргумента x приближается к нулю. Как известно, логарифм нуля не существует. Во избежание исключительной ситуации введена данная функция.
Основой логарифма есть экспонента e = 2.718281… Функция необходима в случаях, когда значение аргумента x приближается к нулю. Как известно, логарифм нуля не существует. Во избежание исключительной ситуации введена данная функция.
Пример.
# Функция math.log1p(x) import math x = 0.0000001 y = math.log1p(x) # y = 9.999999500000032e-08
⇑
5. Функция math.log2(x). Логарифм с основанием 2
Функция math.log2(x) введена начиная с версии Python 3.3 и возвращает логарифм от аргумента x с основанием 2. Функция введена с целью повышения точности вычислений по сравнению с функцией math.log(x, 2). Аргумент x может быть как целого, так и вещественного типа.
Пример.
# Функция math.log2(x) import math x = 2 y = math.log2(x) # y = 1.0 x = 16 y = math.log2(x) # y = 4.0
⇑
6. Функция math.log10(x). Десятичный логарифм
Функция math. log10(x) возвращает логарифм от x с основанием 10 (base = 10). Функция дает более точный результат по сравнению с вызовом функции math.log(x, 10). Аргумент x может быть как целого, так и вещественного типа.
log10(x) возвращает логарифм от x с основанием 10 (base = 10). Функция дает более точный результат по сравнению с вызовом функции math.log(x, 10). Аргумент x может быть как целого, так и вещественного типа.
Пример.
# Функция math.log10(x) import math x = 10 y = math.log10(x) # y = 1.0 x = 100 y = math.log10(x) # y = 2.0 x = 10.00001 y = math.log10(x) # y = 1.0000004342942648
⇑
7. Функция math.pow(x, y). Возведение в степень
Функция math.pow(x, y) выполняет возведение x в степень y. Аргументы x, y могут быть целого и вещественного типа. Операнды комплексного типа не поддерживаются.
Особенности вычисления результата:
- результат pow(1.0, y) всегда будет равен 1.0;
- результат pow(0.0, y) всегда будет равен 1.0.
В отличие от операции ** (возведение в степень), функция math.pow(x, y) целочисленные операнды приводит к вещественному типу float.
Пример.
# Функция math.pow(x, y) import math # для целочисленных операндов x = 3 y = 4 z = math.pow(x, y) # z = 81.0 - вещественный результат # для операндов вещественного типа x = 2.5 y = 1.5 z = math.pow(x, y) # z = 3.952847075210474 # отрицательные числа x = -2 y = -3 z = math.pow(x, y) # z = -0.125 x = -2.0 y = 3.0 z = math.pow(x, y) # z = -8.0 # оператор ** z = (-2) ** 3 # z = -8 - результат целого типа
⇑
8. Функция math.sqrt(x). Корень квадратный
Функция math.sqrt(x) вычисляет квадратный корень от аргумента x. Функция возвращает результат вещественного типа. Значение x может быть положительным или нулевым. Если значение x отрицательное, то интерпретатор выдаст сообщение об ошибке
math domain error
Пример.
# Функция math.sqrt(x) import math # для целых чисел x = 81 y = math.sqrt(x) # y = 9.0 x = -0.0 y = math.sqrt(x) # y = -0.0 x = 2.0 y = math.sqrt(x) # y = 1.4142135623730951
⇑
Связанные темы
⇑
Калькулятор журнала
Укажите любые два значения для вычисления третьего в уравнении логарифма log b x = y . Он может принимать «e» в качестве базового ввода.
Связанный научный калькулятор | Калькулятор экспонентыЧто такое журнал?
Логарифм или журнал — это величина, обратная математической операции возведения в степень. Это означает, что логарифм числа — это число, до которого должно быть увеличено фиксированное основание, чтобы получить число. Обычно лог подразумевает, что используется база 10, хотя технически база может быть чем угодно.Когда основание — e, обычно пишется ln, а не log e . log 2 , двоичный логарифм, является еще одним основанием, которое обычно используется с логарифмами. Если например:
x = b y ; тогда y = log b x; где b — база
Каждая из упомянутых баз обычно используется в разных приложениях. База 10 обычно используется в науке и технике, база E — в математике и физике, а база 2 — в информатике.
База 10 обычно используется в науке и технике, база E — в математике и физике, а база 2 — в информатике.
Основные правила журнала
Когда аргумент логарифма является произведением двух цифр, логарифм можно переписать как сложение логарифма каждой из цифр.
журнал b (x × y) = журнал b x + журнал b y
Пример: журнал (1 × 10) = журнал (1) + журнал (10) = 0 + 1 = 1
Когда аргумент логарифма представляет собой дробь, логарифм можно переписать как вычитание логарифма числителя минус логарифм знаменателя.
журнал b (x / y) = журнал b x — журнал b y
Пример: журнал (10/2) = журнал (10) — журнал (2) = 1 — 0,301 = 0,699
Если в аргументе логарифма есть показатель степени, показатель степени можно вынуть из логарифма и умножить.
журнал b x y = y × журнал b x
Пример: журнал (2 6 ) = 6 × журнал (2) = 1,806
Также можно изменить основание логарифма, используя следующее правило.
Для переключения основания и аргумента используйте следующее правило.
Другие десятичные логарифмы, которые следует учитывать, включают:
журнал b (1) = 0
журнал b (b) = 1
журнал b (0) = не определено
lim x → 0 + журнал b (x) = — ∞
ln (e x ) = x
База логарифма 2 Калькулятор Log2
База логарифма 2 Калькулятор Log2Калькулятор логарифма 2 находит результат функции логарифма по основанию 2.Вычислите логарифм по базе 2 числа.
Калькулятор логарифмической базы 2 журнал 2 Рассчитатьжурнал 2 (x) = y
x: — действительное число, x> 0
журнал 2 (x) = y и x = 2 y
База логарифмов 2 таблицы значений
Список журналов 2 таблиц значений функций, логическая база 2 чисел.
| log 2 (x) | Обозначение | Значение | |||
|---|---|---|---|---|---|
| log 2 (1) | фунт (1) | 0 | |||
| log 2b (2) | 1 | ||||
| log 2 (3) | фунт (3) | 1.584963 | |||
| лог 2 (4) | фунт (4) | 2 | |||
| лог 2 (5) | фунт (5) | 2.321 8 | 9125 912 6) | фунтов (6) | 2,584963 |
| log 2 (7) | фунтов (7) | 2,807355 | |||
| log 2 (8) | 3|||||
| log 2 (9) | фунтов (9) | 3.169925 | |||
| log 2 (10) | фунтов (10) | 3,321928 | |||
| log 2 (11) | фунтов (11) | 3,459432 | 901 12) | фунтов (12) | 3,584963 |
| log 2 (13) | фунтов (13) | 3,70044 | |||
| log 2 (14) | 14 фунтов 3. 807355 807355 | ||||
| log 2 (15) | фунтов (15) | 3. | 1|||
| log 2 (16) | фунт (16) | 4 | |||
| log 2 (17) | фунт (17) | 4.087000 log3 | 32 9012 18) | фунтов (18) | 4,169925 |
| log 2 (19) | фунтов (19) | 4,247928 | |||
| log 2 (20) | 201344,321928 | ||||
| log 2 (21) | фунтов (21) | 4.3 | |||
| log 2 (22) | фунта (22) | 4,459432 | |||
| log 2 (23) | фунта (23) | 4.523562 9137 | фунта (24) | 4.584963 | |
| log 2 (25) | фунта (25) | 4.643856 | |||
| log 2 (26) | 4,70044 | ||||
| log 2 (27) | фунтов (27) | 4. 754888 754888 | |||
| log 2 (28) | фунта (28) | 4.807355 | |||
| log 2 (29) | фунтов (29) | 4.857981 | 4.857981 | 30)фунтов (30) | 4. | 1
| log 2 (31) | фунтов (31) | 4.954196 | |||
| log 2 (32) | 5 | ||||
| log 2 (33) | фунтов (33) | 5.044394 | |||
| log 2 (34) | фунта (34) | 5,087463 | |||
| log 2 (35) | фунтов (35) | 5.129283 | 5.129283 | 36)фунтов (36) | 5.169925 |
| log 2 (37) | фунтов (37) | 5.209453 | |||
| log 2 (38) | 5.247928|||||
| log 2 (39) | фунтов (39) | 5.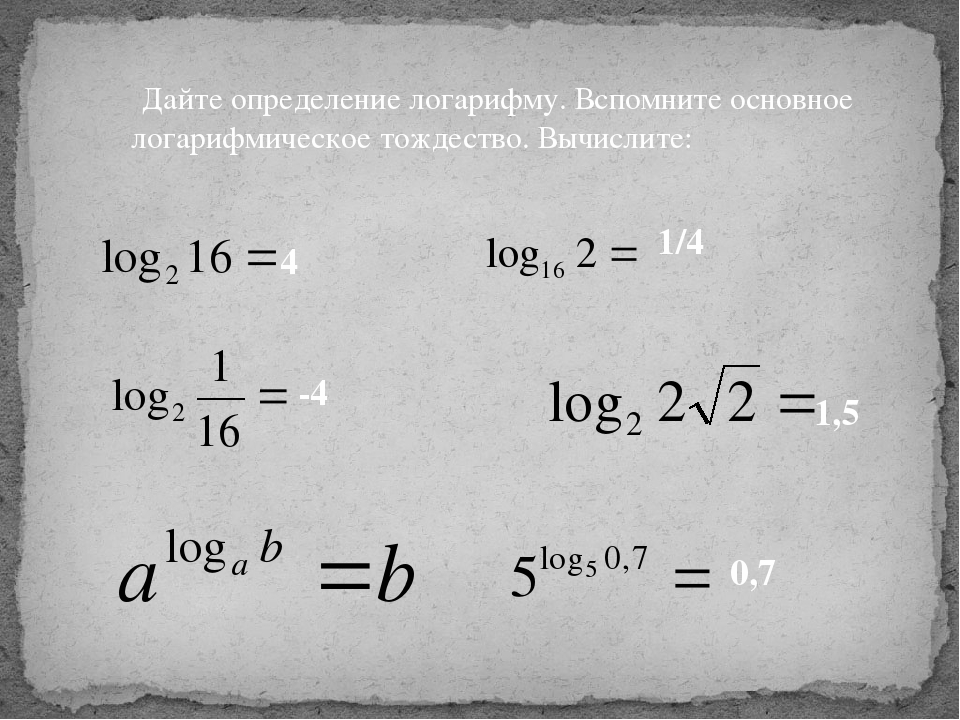 285402 285402 | |||
| log 2 (40) | фунта (40) | 5,321928 | |||
| log 2 (41) | фунтов (41) | 5,357552 9125 | 5,357552 9137 | 42)фунтов (42) | 5,3 |
| log 2 (43) | фунтов (43) | 5,426265 | |||
| log 2 (44) | 445,459432 | ||||
| log 2 (45) | фунтов (45) | 5.4 | |||
| log 2 (46) | фунтов (46) | 5,523562 | |||
| log 2 (47) | фунтов (47) | 5.554589 9325 | 901 48)фунтов (48) | 5,584963 | |
| log 2 (49) | фунтов (49) | 5,61471 | |||
| log 2 (50) | фунтов 5,643856 | ||||
| log 2 (51) | фунтов (51) | 5. 672425 672425 | |||
| log 2 (52) | фунтов (52) | 5.70044 | |||
| log 2 (53) | фунтов (53) | 5.72792 9325 | 901 54)фунтов (54) | 5,754888 | |
| log 2 (55) | фунтов (55) | 5,78136 | |||
| log 2 (56) | 5.807355|||||
| log 2 (57) | фунтов (57) | 5.83289 | |||
| log 2 (58) | фунтов (58) | 5,857981 | |||
| log 2 (59) | фунтов (59) | 5,882643 | 901 60)фунтов (60) | 5. | 1|
| log 2 (61) | фунтов (61) | 5. | 7|||
| log 2 (62) | 90 5.954196|||||
| log 2 (63) | фунтов (63) | 5.97728 | |||
| log 2 (64) | фунтов (64) | 6 | |||
| log 2 (65) | фунтов (65) | 6. 022368 022368 | 9125 912 66) | фунтов (66) | 6.044394 |
| log 2 (67) | фунтов (67) | 6.066089 | |||
| log 2 (68) | 6.087463 | ||||
| log 2 (69) | фунтов (69) | 6.108524 | |||
| лог 2 (70) | фунт (70) | 6,129283 | |||
| лог 2 (71) | фунт (71) | 6,149747 9125 | 6,149747 9137 | 72)фунтов (72) | 6,169925 |
| log 2 (73) | фунтов (73) | 6,189825 | |||
| log 2 (74) | 6.209453 | ||||
| log 2 (75) | фунтов (75) | 6.228819 | |||
| лог 2 (76) | фунт (76) | 6.247928 | |||
| лог 2 (77) | фунт (77) | 6. 2667 2667 | 901 78)фунтов (78) | 6.285402 | |
| log 2 (79) | фунтов (79) | 6.303781 | |||
| log 2 (80) | 801346.321928 | ||||
| log 2 (81) | фунтов (81) | 6.33985 | |||
| log 2 (82) | фунтов (82) | 6.357552 | |||
| log 2 (83) | фунтов (83) | 6,375039 | 901 84) | фунта (84) | 6,3 |
| log 2 (85) | фунта (85) | 6,409391 | |||
| log 2 (86) | 6.426265 | ||||
| log 2 (87) | фунтов (87) | 6.442943 | |||
| лог 2 (88) | фунт (88) | 6.459432 | |||
| лог 2 (89) | фунт (89) | 6.475733 | 901 901 90)фунтов (90) | 6. 4 4 | |
| log 2 (91) | фунтов (91) | 6.507795 | |||
| log 2 (92) | 6.523562 | ||||
| log 2 (93) | фунта (93) | 6.539159 | |||
| log 2 (94) | фунтов (94) | 6.554589 | |||
| log 2 (95) | фунтов (95) | 6.569856 9125 | 6.569856 9137 96) | фунтов (96) | 6.584963 |
| log 2 (97) | фунтов (97) | 6.599913 | |||
| log 2 (98) | 6,61471 | ||||
| журнал 2 (99) | фунтов (99) | 6.629357 | |||
| журнал 2 (100) | фунтов (100) | 6,643856 |
| log 2 (x) | Обозначение | Значение | ||||||
|---|---|---|---|---|---|---|---|---|
| log 2 (101) | фунт (101) | 6,658211 | ||||||
| 9000 102137 9000 102102 (102) | 6,672425 | |||||||
| log 2 (103) | фунта (103) | 6. 686501 686501 | ||||||
| log 2 (104) | фунтов (104) | 70044|||||||
| log 2 (105) | фунтов (105) | 6,714246 | ||||||
| log 2 (106) | фунтов (106) | 6.72792 9325 | 901 107)фунтов (107) | 6,741467 | ||||
| log 2 (108) | фунтов (108) | 6,754888 | ||||||
| log 2 (109) 109137 | 6,768184||||||||
| log 2 (110) | фунтов (110) | 6.78136 | ||||||
| log 2 (111) | фунтов (111) | 6,794416 | ||||||
| log 2 (112) | фунтов (112) | 6.807355 | 6.807355 | 113)фунтов (113) | 6.820179 | |||
| log 2 (114) | фунтов (114) | 6.83289 | ||||||
| log 2 (115) | 90 6,84549||||||||
| лог 2 (116) | фунтов (116) | 6. 857981 857981 | ||||||
| log 2 (117) | фунтов (117) | 6.870365 | ||||||
| log 2 (118) | фунтов (118) | 6.882643 | 6,882643 | 119)фунтов (119) | 6,894818 | |||
| log 2 (120) | фунтов (120) | 6, | 1||||||
| log 2 (121) | 1216. | 3 | ||||||
| log 2 (122) | фунтов (122) | 6. | 7||||||
| log 2 (123) | фунтов (123) | 6.942515 | ||||||
| log 2 (124) | фунтов (124) | 6.954 9134 9134 9134 9134 9134 9134 9134 912 125) | фунтов (125) | 6.965784 | ||||
| log 2 (126) | фунтов (126) | 6.97728 | ||||||
| log 2 (127) | ||||||||
6. 988685 988685 | ||||||||
| log 2 (128) | фунтов (128) | 7 | ||||||
| log 2 (129) | фунтов (129) | 7.011227 | ||||||
| log 2 (130) | фунта (130) | 7.022368 | ||||||
| log 2 (131) | фунта (131) | 7.033423 9125 | 7.033423 9137 | 7.033423 9137 | 132)фунтов (132) | 7.044394 | ||
| log 2 (133) | фунтов (133) | 7.055282 | ||||||
| log 2 (134) | 7.066089||||||||
| log 2 (135) | фунтов (135) | 7.076816 | ||||||
| лог 2 (136) | фунт (136) | 7.087463 | ||||||
| лог 2 (137) | фунт (137) | 7.098032 9125 | 7.098032 9137 | 7.098032 9137 | 138)фунтов (138) | 7. 108524 108524 | ||
| log 2 (139) | фунтов (139) | 7.118941 | ||||||
| log 2 (140) | 1401347.129283 | |||||||
| log 2 (141) | фунтов (141) | 7.139551 | ||||||
| лог 2 (142) | фунта (142) | 7.149747 | ||||||
| лог 2 (143) | фунт (143) | 0 | логн 144) | фунтов (144) | 7.169925 | |||
| log 2 (145) | фунтов (145) | 7.179909 | ||||||
| log 2 (146) | 7.189825||||||||
| log 2 (147) | фунтов (147) | 7.199672 | ||||||
| лог 2 (148) | фунта (148) | 7.209453 | ||||||
| лог 2 (149) | фунт (149) | 9,219169 лог 150) | фунтов (150) | 7. 228819 228819 | ||||
| log 2 (151) | фунтов (151) | 7.238405 | ||||||
| log 234 907 | 7,247928||||||||
| log 2 (153) | фунта (153) | 7.257388 | ||||||
| log 2 (154) | фунта (154) | 7.266787 | ||||||
| log 2 (155) | фунтов (155) | log00037,276124 | 9134 9137 156) | фунтов (156) | 7.285402 | |||
| log 2 (157) | фунтов (157) | 7.294621 | ||||||
log 237| 7.303781 | | |||||||
| log 2 (159) | фунтов (159) | 7.312883 | ||||||
| log 2 (160) | фунтов (160) | 7.321928 | ||||||
| log 2 (161) | фунтов (161) | фунтов 162) | фунтов (162) | 7,33985 | ||||
| log 2 (163) | фунтов (163) | 7,348728 | ||||||
| log 2 (164) | 7,357552 | |||||||
| log 2 (165) | фунтов (165) | 7. 366322 366322 | ||||||
| log 2 (166) | фунта (166) | 7.375039 | ||||||
| log 2 (167) | lb (167) | фунта (167) | 983704 168) | фунтов (168) | 7,3 | |||
| log 2 (169) | фунтов (169) | 7,400879 | ||||||
| log 2 | 17013 | 7,409391|||||||
| log 2 (171) | фунта (171) | 7.417853 | ||||||
| лог 2 (172) | фунта (172) | 7,426265 | ||||||
| лог 2 (173) | фунт (173) | 7,434628 лог. 174) | фунтов (174) | 7,442943 | ||||
| log 2 (175) | фунтов (175) | 7,451211 | ||||||
| log 2 (176134) | 7,459432||||||||
| log 2 (177) | фунтов (177) | 7. 467606 467606 | ||||||
| log 2 (178) | фунтов (178) | 7,475733 | ||||||
| log 2 (179) | фунтов (179) | фунтов (179) | 7,4832 180) | фунтов (180) | 7,4 | |||
| log 2 (181) | фунтов (181) | 7,499846 | ||||||
| log 2 (182) | 7,507795||||||||
| log 2 (183) | фунта (183) | 7.5157 | ||||||
| log 2 (184) | фунтов (184) | 7,523562 | ||||||
| log 2 (185) | фунтов (185) | 7,531332 9125 | 186)фунтов (186) | 7,539159 | ||||
| log 2 (187) | фунтов (187) | 7,546894 | ||||||
| log 2 (184) | 7,554589||||||||
| log 2 (189) | фунтов (189) | 7. 562242 562242 | ||||||
| log 2 (190) | фунтов (190) | 7,569856 | ||||||
| log 2 (191) | фунтов (191) | 7,5134329 | 7,51342 9 | 192)фунтов (192) | 7,584963 | |||
| log 2 (193) | фунтов (193) | 7,5 | ||||||
| log 2 (194) | 7,599913||||||||
| log 2 (195) | фунтов (195) | 7.60733 | ||||||
| log 2 (196) | фунтов (196) | 7,61471 | ||||||
| log 2 (197) | фунтов (197) | 7.622052 | 7,622052 | 198)фунтов (198) | 7,629357 | |||
| log 2 (199) | фунтов (199) | 7,636625 | ||||||
| log 2 (200) | 200 7.643856
| log 2 (x) | Обозначение | Значение | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| log 2 (201) | фунтов (201) | 7. 651052 651052 | ||||||||||
| log 2 (202) | фунта (202) | 7,658211 | ||||||||||
| log 2 (203) | фунта (203) | фунтов 204) | фунтов (204) | 7,672425 | ||||||||
| log 2 (205) | фунтов (205) | 7,67948 | ||||||||||
| log 2 (20134) | 7.686501||||||||||||
| log 2 (207) | фунтов (207) | 7.6 | ||||||||||
| лог 2 (208) | фунта (208) | 7.70044 | ||||||||||
| лог 2 (209) | фунт (209) | 7.70134321 | фунт 210) | фунтов (210) | 7,714246 | |||||||
| log 2 (211) | фунтов (211) | 7,721099 | ||||||||||
| log 237 902 (212) | 902 7,72792||||||||||||
| log 2 (213) | фунтов (213) | 7.73471 | ||||||||||
| log 2 (214) | фунтов (214) | 7,741467 | ||||||||||
| log 2 (215) | фунтов (215) | 9,748191 9,748191 216) | фунтов (216) | 7,754888 | ||||||||
| log 2 (217) | фунтов (217) | 7,761551 | ||||||||||
| log 237 | 7,768184 | |||||||||||
| log 2 (219) | фунтов (219) | 7. 774787 774787 | ||||||||||
| лог 2 (220) | фунт (220) | 7,78136 | ||||||||||
| лог 2 (221) | фунт (221) | 7,7871000 | 9294 9903 222) | фунтов (222) | 7,794416 | |||||||
| log 2 (223) | фунтов (223) | 7.8009 | ||||||||||
| log 237 | 7.807355 | |||||||||||
| log 2 (225) | фунтов (225) | 7.813781 | ||||||||||
| log 2 (226) | фунтов (226) | 7,820179 | ||||||||||
| log 2 (227) | фунтов (227) | 0 | 0 | 0 228) | фунтов (228) | 7,83289 | ||||||
| log 2 (229) | фунтов (229) | 7,839204 | ||||||||||
log 234| 7,84549 | | |||||||||||
| log 2 (231) | фунтов (231) | 7. 851749 851749 | ||||||||||
| лог 2 (232) | фунт (232) | 7,857981 | ||||||||||
| лог 2 (233) | фунт (233) | 7,8134 9186 | 7,8134 9186 234) | фунтов (234) | 7,870365 | |||||||
| log 2 (235) | фунтов (235) | 7,876517 | ||||||||||
| log 237 | 7,882643 | |||||||||||
| log 2 (237) | фунтов (237) | 7.888743 | ||||||||||
| log 2 (238) | фунта (238) | 7,894818 | ||||||||||
| log 2 (239) | фунта (239) | 932 ( | ) | фунта (239) | 7.900 2 240) | фунтов (240) | 7. | 1|||||
| log 2 (241) | фунтов (241) | 7.9 | ||||||||||
| log 2 | 7. | 3 | ||||||||||
| log 2 (243) | фунтов (243) | 7. | 3||||||||||
| log 2 (244) | фунта (244) | 7. | 7||||||||||
| log 2 (245) | фунта (245) | фунта (245) | 7. 246) | фунтов (246) | 7,942515 | |||||||
| log 2 (247) | фунтов (247) | 7.948367 | ||||||||||
| log 237 | 7.954196 | |||||||||||
| log 2 (249) | фунтов (249) | 7.960002 | ||||||||||
| log 2 (250) | фунта (250) | 7.965784 | ||||||||||
| log 2 (251) | фунтов (251) | 7.971532 | 7.971544 | 7.971544 | 252)фунтов (252) | 7,97728 | ||||||
| log 2 (253) | фунтов (253) | 7,982994 | ||||||||||
| log 237 | 904 7.988685||||||||||||
| log 2 (255) | фунтов (255) | 7. 994353 994353 | ||||||||||
| log 2 (256) | фунтов (256) | 8 | ||||||||||
| log 2 (257) | фунтов (257) | 8.005625 9137 901 258) | фунтов (258) | 8,011227 | ||||||||
| log 2 (259) | фунтов (259) | 8,016808 | ||||||||||
| log 2 | (26013) 8,022368||||||||||||
| log 2 (261) | фунтов (261) | 8.027906 | ||||||||||
| log 2 (262) | фунта (262) | 8.033423 | ||||||||||
| log 2 (263) | фунта (263) | фунтов (263) | 8,038919 log000 | 8,038919 264) | фунтов (264) | 8,044394 | ||||||
| log 2 (265) | фунтов (265) | 8,049849 | ||||||||||
| log 237 | 8,055282 | |||||||||||
| log 2 (267) | фунтов (267) | 8.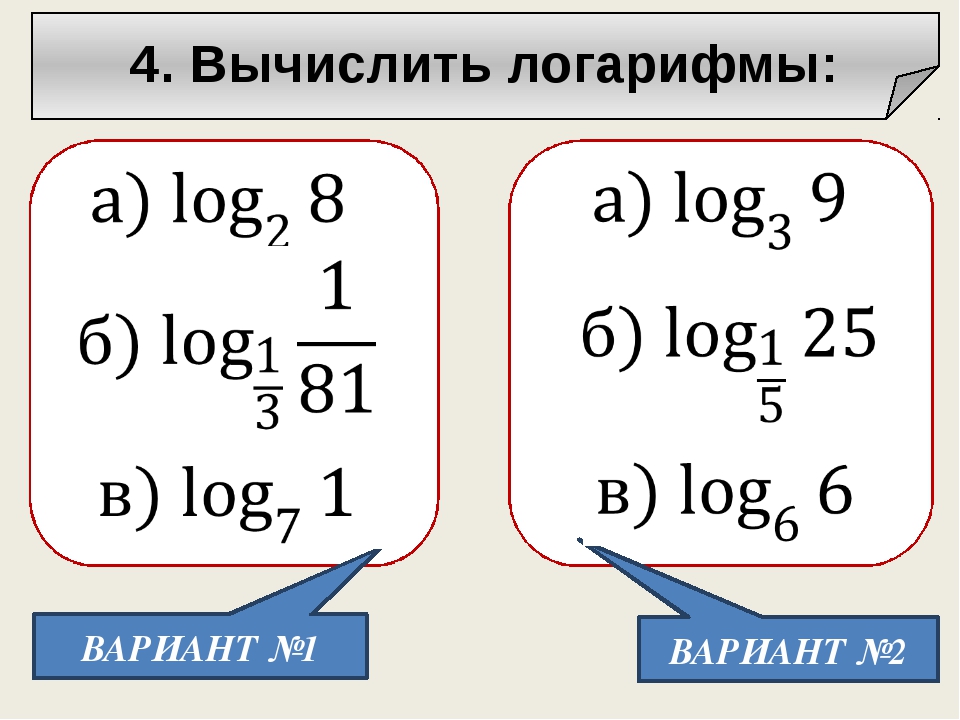 060696 060696 | ||||||||||
| log 2 (268) | фунта (268) | 8.066089 | ||||||||||
| log 2 (269) | фунта (269) | 270) | фунтов (270) | 8.076816 | ||||||||
| log 2 (271) | фунтов (271) | 8.082149 | ||||||||||
| log 2 (272) | 8,087463||||||||||||
| log 2 (273) | фунтов (273) | 8.0 | ||||||||||
| log 2 (274) | фунта (274) | 8.098032 | ||||||||||
| log 2 (275) | фунтов (275) | фунтов (275) | 9.1032882 276) | фунтов (276) | 8,108524 | |||||||
| log 2 (277) | фунтов (277) | 8.113742 | ||||||||||
| log 237 | 8.118941||||||||||||
| log 2 (279) | фунтов (279) | 8. 124121 124121 | ||||||||||
| log 2 (280) | фунтов (280) | 8,129283 | ||||||||||
| log 2 (281) | фунтов (281) | 8,1134 9134 9134 9137 | 9134 9134 9137 282) | фунтов (282) | 8,139551 | |||||||
| log 2 (283) | фунтов (283) | 8,144658 | ||||||||||
| log 237 | 8,149747 | |||||||||||
| журнал 2 (285) | фунтов (285) | 8.154818 | ||||||||||
| log 2 (286) | фунта (286) | 8,159871 | ||||||||||
| log 2 (287) | фунтов (287) | 9102 288) | фунтов (288) | 8,169925 | ||||||||
| log 2 (289) | фунтов (289) | 8,174926 | ||||||||||
log 237| 8,179909 | | |||||||||||
| журнал 2 (291) | фунтов (291) | 8. 184875 184875 | ||||||||||
| лог 2 (292) | фунта (292) | 8,189825 | ||||||||||
| лог 2 (293) | фунт (293) | 9134 фунт 294) | фунтов (294) | 8.199672 | ||||||||
| log 2 (295) | фунтов (295) | 8.204571 | ||||||||||
| log 237 | 8.209453 | |||||||||||
| log 2 (297) | фунтов (297) | 8.214319 | ||||||||||
| log 2 (298) | фунтов (298) | 8,219169 | ||||||||||
| log 2 (299) | фунтов (299) | 8,224002 | 8,224002 | 300)фунтов (300) | 8,228819 |
© 2019-2021 www.logcalculator.net
Формула смены базы | Purplemath
Purplemath
Есть еще одно «правило» журнала, но это больше формула, чем правило.
Возможно, вы заметили, что в вашем калькуляторе есть ключи только для вычисления значений для общего (то есть с основанием 10) журнала и естественного (то есть с основанием e ) журнала. Ключей к другим базам нет. Некоторые студенты пытаются обойти это, «оценивая» что-то вроде «log 3 (6)» следующими нажатиями клавиш:
[ LOG ] [ 3 ] [ (] [ 6 ] [) ]
Конечно, тогда они получают неправильный ответ, потому что вышеупомянутое на самом деле (обычно) вычисляет значение «log 10 (3) × 6».Это не то, что было задумано.
MathHelp.com
Чтобы оценить журнал с нестандартной базой, необходимо использовать формулу изменения базы:
Формула смены базы:
С практической точки зрения это правило говорит о том, что вы можете оценить журнал с нестандартной базой, преобразовав его в долю формы «(стандартный журнал аргумента), разделенный на (журнал с такой же стандартной базой нестандартной базы) ». Я держу это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база имеет нижний индекс), поэтому я оставляю все так, когда разделяю их:
Я держу это прямо, глядя на положение вещей. В исходном журнале аргумент находится «над» базой (поскольку база имеет нижний индекс), поэтому я оставляю все так, когда разделяю их:
Вот простой пример применения этой формулы:
Журнал оценок
3 (6). Округлите ответ до трех десятичных знаков.
Аргумент 6, основание 3.Я подключу их к формуле смены базы, используя натуральный логарифм в качестве журнала новой базы:
Тогда ответ, округленный до трех десятичных знаков, будет:
.Я бы получил тот же окончательный ответ, если бы использовал общий журнал вместо натурального журнала, хотя числитель и знаменатель промежуточной дроби были бы другими, чем то, что я показал выше:
Как видите, не имеет значения, какой стандартный журнал вы используете, если вы используете одну и ту же базу для числителя и знаменателя.
Хотя я показал значения числителя и знаменателя в приведенных выше расчетах, на самом деле лучше всего выполнять вычисления полностью на вашем калькуляторе. Вам не нужно беспокоиться о написании этого промежуточного шага.
На самом деле, чтобы свести к минимуму ошибки округления, лучше попытаться выполнить все шаги деления и вычисления в вашем калькуляторе за один раз. В приведенном выше вычислении вместо того, чтобы записывать первые восемь или около того десятичных знаков в значениях ln (6) и ln (3) и затем делить их, вы просто выполняете «ln (6) ÷ ln (3)» в своем калькулятор.
Вы можете получить несколько простых (но довольно бесполезных) упражнений по этой теме. Не завидуйте им; это простые пункты, пока вы держите в голове формулу смены основы. Например:
Преобразовать журнал
3 (6) в выражение с логарифмами с основанием 5.
Я не могу придумать какую-либо конкретную причину, по которой журнал base-5 может быть полезен, поэтому я думаю, что единственный смысл этих проблем — дать вам возможность попрактиковаться в использовании смены базы.Отлично; Я подключу-н-пыхтю:
Преобразуйте ln (4) в выражение, записанное в виде общего журнала.
Зачем мне это делать («в реальной жизни»), если я уже могу вычислить натуральный логарифм в моем калькуляторе? Я бы не стал; это упражнение предназначено только для практики (и простых моментов).
Я поделюсь с формулой замены базы:
Поскольку получение фактического десятичного значения не является целью в упражнениях подобного рода (главное — преобразование с использованием изменения базы), просто оставьте ответ в виде логарифмической дроби.
Хотя приведенные выше упражнения были довольно бессмысленными, использование формулы изменения базы может быть очень удобно для поиска точек графика при построении графиков нестандартных журналов, особенно когда предполагается, что вы используете графический калькулятор.
Используйте графическую утилиту для построения графика
y = log 2 ( x ).
Если бы я работал вручную, я бы использовал определение журналов, чтобы отметить, что:
- , так как 2 -2 = ¼, то лог 2 (¼) = -2
- , поскольку 2 –1 = ½, тогда журнал 2 (½) = –1
- , так как 2 0 = 1, тогда журнал 2 (1) = 0
- , так как 2 1 = 2, тогда журнал 2 (2) = 1
- , поскольку 2 2 = 4, тогда журнал 2 (4) = 2
- , поскольку 2 3 = 8, тогда журнал 2 (8) = 3
- , поскольку 2 4 = 16, тогда журнал 2 (16) = 4
А потом рисовал бы свой график от руки.
(Почему я выбрал именно эти значения x ? Потому что что-то меньшее было бы слишком крошечным для рисования вручную, а что-то большее привело бы к смехотворно широкому графику. Я выбрал значения, которые соответствуют моим потребностям.)
Но в этом случае я должен строить график с помощью своего графического калькулятора. Как я могу это сделать? (Или что, если бы я просто хотел использовать функцию «ТАБЛИЦА» моего графического калькулятора, чтобы найти несколько хороших аккуратных точек на графике?) У меня нет кнопки «log-base-two».Тем не менее, я могу ввести данную функцию в свой калькулятор, используя формулу изменения базы, чтобы преобразовать исходную функцию в то, что указано в терминах базы, которую мой калькулятор может понять. Подбрасывая монетку, выбираю натуральный логарифм:
(Я мог бы также использовать общий журнал. В этом случае функция была бы « y 1 = log ( x ) / log (2)».)
В моем графическом калькуляторе после настройки окна просмотра для отображения полезных частей плоскости график будет выглядеть примерно так:
Между прочим, вы можете проверить, содержит ли график ожидаемые «аккуратные» точки (то есть точки, которые я бы вычислил вручную, как показано выше), чтобы убедиться, что изображение отображает правильный график:
URL: https: // www.purplemath.com/modules/logrules5.htm
Лог по базе 2 или е или 10?
Когда ваши данные охватывают большой диапазон, графики имеют тенденцию становиться некрасивыми. Значения либо скапливаются внизу, либо расходятся вверху — проблема , плохое разрешение . Скорость изменений трудно отобразить, поскольку у графика обычно очень длинный хвост, или очень жесткая спина, или и то, и другое.
Вот тут-то и пригодится бревенчатая шкала. Например, графики с логической базой 10 могут упростить значения 1, 10, 100, 1000, 10000 до значений 1, 2, 3, 4, 5, помогая вам распознать стабильный рост и решить проблему разрешения.
Рисунок 1 : График с нормальной шкалой (слева) и десятичной логарифмической шкалой (справа) . Значения данных проходят через множество степеней 10, из-за чего левый график страдает плохим разрешением, когда данные переполнены внизу.Разрешение улучшается при использовании десятичной логарифмической шкалы, как показано на правом графике.
Итак, вы решили построить график в логарифмической шкале. Что теперь? Какое основание вы должны взять логарифм: 2, или e , или 10?
Ответ лежит в диапазоне значений ваших данных.
Масштабирование по базе журнала 10, хотя и применяется часто, лучше всего работает для наборов данных, которые претерпевают многократные изменения в степени 10 или большие процентные изменения. Имея такие данные, вы не хотите, чтобы ваш график страдал от плохого разрешения, когда точки данных заполняют нижний конец и распространяются там (см. Рисунок 1).
База 10 логарифма может стать обузой для меньшего диапазона данных, потому что у вас возникнут проблемы с обработкой дробных степеней 10 по осям. Можно легко оценить 0,5 степени 10, но дальнейшие дробные степени 10 требуют больших усилий, что затрудняет анализ данных и понимание графика.
Рисунок 2: Дробные степени 10, встречающиеся в наборах данных небольшого диапазона. Это затрудняет понимание графика аналитиками и зрителями.
Тогда вам следует принять логарифмическую шкалу с основанием 2, так как с ней легче работать с степенями 2. Компьютеры в настоящее время сделали безболезненным вычисление значений. Некоторые дробные степени двойки настолько близки к простым числам, что их легко оценить.
Рисунок 3: Оценка дробных степеней 2База журнала e отлично подходит для иллюстрации процентных изменений от -25% до 25%. Почему? Давайте посмотрим на математику. (Не паникуйте, это очень просто.)
Предположим, что u и v — два значения данных.Изменение v относительно u, , а именно r, рассчитывается следующим образом:
Что означает:
Теперь позвольте d быть разницей v и u в натуральном логарифмическом масштабе,
Если d мало (-0,25 И, следовательно, На словах: если есть небольшая разница между двумя значениями натурального логарифма (d), вы можете легко оценить разницу между двумя исходными точками данных (r), потому что r приблизительно равно d.Таким образом, процентное изменение (100% r) будет близко к 100% d, что позволит вам построить график в натуральном логарифмическом масштабе без потери информации. Но эта оценка не универсальна. Чем больше d (больше 0,25), тем менее точным становится. Вот еще одно предостережение: чтобы вернуться к исходному масштабу, потребуется много работы. Очевидно e³ труднее оценить, чем 2³ или 10³. Возможно, вам потребуется отобразить исходный масштаб на другой оси для облегчения понимания. См. Пример ниже: Рисунок 4: Графические данные с натуральным логарифмом (рисунок повторно опубликован из [1].Авторское право 1985 Уильямом. С. Кливленд) Подводя итог, выбор базы журнала зависит от диапазона значений ваших данных. При правильном применении логарифмы значительно улучшают как анализ, так и передачу данных. Хотя логарифмическая база 10 отлично подходит для больших диапазонов, она может препятствовать изучению небольших наборов данных, которые можно лучше объяснить с помощью логарифмической базы 2 и натурального логарифма. Мы все покрыли? Не стесняйтесь обсудить с нами в поле для комментариев ниже. Команда BioTuring, Артикул: [1] Уильям С. Кливленд, Элементы графических данных, Wadsworth Publ. Ко Бельмонт, Калифорния, США © 1985, ISBN: 0–534–03730–5 Поиск инструмента Логарифм Инструмент для вычисления логарифмов. Функция логарифма обозначается log или ln и определяется основанием (основание e для натурального логарифма). Результаты Логарифм — dCode Тег (и): Функции Поделиться dCode и другие dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день! Определение натурального логарифма . * $. Натуральный логарифм обозначается как log или ln и основан на числе $ e \ приблизительно 2,71828 \ ldots $ (см. Десятичные дроби числа e). Пример: $ \ log (7) = \ ln (7) \ приблизительно 1,94591 $ Некоторые люди и плохие калькуляторы используют $ \ log $ вместо $ \ log_ {10} $, поэтому убедитесь, что вы знаете, какие обозначения используются. Любой логарифм с основанием $ N $ может быть вычислен из натурального логарифма по формуле: $$ \ log_ {N} (x) = \ frac {\ ln (x)} {\ ln (N)} $ $ Неперианский логарифм — другое название натурального логарифма (с основанием е). Десятичный логарифм с записью $ \ log_ {10} $ или log10 является базовым 10 $ логарифмом . Это один из наиболее часто используемых логарифмов в расчетах и логарифмических шкал . $$ \ log_ {10} (x) = \ frac {\ ln (x)} {\ ln (10)} $$ Пример: $ \ log_ {10} (1000) = 3 $ Двоичный логарифм , отмеченный $ \ log_ {2} $ (или иногда $ lb $), является основанием $ 2 логарифма .Этот логарифм используется в основном для компьютерных вычислений. $$ \ log_2 (x) = \ frac {\ ln (x)} {\ ln (2)} $$ Используйте приведенную выше формулу, чтобы вычислить log2 с помощью калькулятора, имеющего только ключ журнала. Любой логарифм имеет как для свойств: — $ \ log_b (x \ cdot y) = \ log_b (x) + \ log_b (y) $ (преобразование произведения в сумму) — $ \ log_b \ left (\ frac {x} {y} \ right) = \ log_b (x) — \ log_b (y) $ (преобразование частного в вычитание) — $ \ log_b (x ^ a) = a \ log_b (x) $ (преобразование степени в умножение) dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Логарифм».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма «Логарифм», апплета или фрагмента (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой функции «Логарифм» (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанные на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.), без загрузки данных, скрипт, копирование -паста или доступ к API для «Логарифма» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн. Пожалуйста, посетите наше сообщество dCode Discord для получения помощи! Сводка Похожие страницы Поддержка Форум / Справка Ключевые слова логарифм, log, log2, log10, ln, непер, непериан, натуральный Ссылки Источник: https: //www.dcode.fr / логарифм В этой статье описаны синтаксис формулы и использование функции LOG в Microsoft Excel. Возвращает логарифм числа по указанному вами основанию. ЖУРНАЛ (номер, [основание]) Аргументы функции LOG следующие: Номер Обязательно.Положительное действительное число, логарифм которого требуется. База Дополнительно. Основание логарифма. Если база не указана, предполагается, что она равна 10. Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные. Формула Описание Результат = ЖУРНАЛ (10) Логарифм 10. Поскольку второй аргумент (основание) опущен, предполагается, что он равен 10.Результат, 1, представляет собой степень, до которой основание должно быть увеличено до 10. 1 = ЖУРНАЛ (8, 2) Логарифм 8 с основанием 2. Результат 3 представляет собой степень, до которой основание должно быть возведено в число 8. 3 = ЖУРНАЛ (86, 2.7182818) Логарифм 86 с основанием е (приблизительно 2,718). Результат 4,454 — это степень, до которой необходимо довести базу до 86. 4,4543473 Я обсуждал большинство правил журнала в отдельном уроке. Однако я намеренно оставил одну, чтобы обсудить это здесь подробно.Правило журнала называется Формула изменения базы . Если вас интересует, почему работает замена формулы, щелкните следующую ссылку, чтобы увидеть доказательство: Доказательства свойств логарифма. Логарифм с основанием 10 известен как десятичный логарифм , а логарифм с основанием e известен как натуральный логарифм . Примечание: Число e — математическая константа, имеющая числовое значение e \ приблизительно 2.71828. Это иррациональное число, потому что оно не может быть выражено как отношение двух целых чисел или дробь. Более того, число e является основанием натурального логарифма. Таким образом, десятичный и натуральный логарифмы используют стандартное основание : 10 и e, соответственно. Прежде чем мы продолжим, я хотел бы указать на некоторые нюансы и тонкости, касающиеся математических выражений десятичного и натурального логарифмов. Большинство графических калькуляторов имеют функции или клавиши, которые непосредственно вычисляют логарифмы чисел по основанию 10 и основанию е. Таким образом, вы увидите только две кнопки: LOG для десятичного логарифма и LN для натурального логарифма. Очевидно, что проблема возникает, когда мы хотим вычислить логарифм числа, используя нестандартные основания, такие как 2, 3, 7, 0,5 и 0,25. В приведенных выше логарифмах используется НЕСТАНДАРТНОЕ основание, потому что они не являются ни \ large {\ color {green} 10}, ни числом \ large {\ color {green} e}. Как начать вводить числа на графическом калькуляторе? Как я упоминал ранее, большинство калькуляторов ограничены вычислением логарифмов только с основанием 10 и основанием e. Именно здесь на помощь приходит гоночная модель Formula со сменой базы. Он может преобразовывать логарифм с нестандартным основанием как отношение двух логарифмических операций, которые используют стандартное основание 10 или константу e. Формула изменения базы — это инструкция о том, как переписать или преобразовать данное логарифмическое выражение в виде отношения или доли двух логарифмических операций с использованием любой допустимой базы. Это означает, что если у нас есть логарифм с использованием определенного основания, то мы можем превратить его в эквивалентное отношение или долю двух логарифмических операций, чтобы мы могли выбрать любое основание, которое захотим. Мы можем буквально выбрать любую базу, если она положительна, но не равна \ color {red} 1. Но если мы хотим вычислить или узнать значение логарифма, мы должны выбрать основание-10 или основание-е, так как большинство калькуляторов имеют эти функциональные клавиши. Ключ журнала [log] вычисляет общий логарифм (с основанием 10), а ключ ln [ln] вычисляет натуральный (с основанием e) логарифм. Давайте проанализируем, как формула преобразовала исходный логарифм в эквивалентное выражение в виде отношения двух логарифмических операций. Первые два примера (Пример №1 и №2) являются идеальными учебными задачами, потому что аргумент и основание логарифма могут быть выражены как степени общего числа (положительного числа, не равного 1), которое служит новая база при применении правила изменения базы. Пример 1: Вычислить \ large {\ log {} _48}. Первое, что я понял, это то, что и аргумент, и его основание могут быть выражены как степень двойки.k}} \ right) = k \ cdot {\ log _b} \ left (x \ right)} Вот полное решение. 2}.k}} \ right) = k \ cdot {\ log _b} \ left (x \ right)} Ниже представлено полное решение. Пример 3: Рассчитайте значение \ large {\ log {} _ {\ large {5}} \ left ({12} \ right)}. Округлите ответ до ближайшей тысячной. Это уже не «хорошая» проблема, потому что аргумент и основание логарифма не могут быть выражены как степени общего числа. Другими словами, не существует сценария, в котором мы могли бы выразить 5 и 12 как экспоненциальные числа с одинаковым основанием. Чтобы решить эту проблему, мы можем использовать правило изменения базы, чтобы переписать исходный логарифм как отношение двух логарифмов основания по нашему выбору. У нас есть два варианта: использовать base-10 или base-e. Неважно, какой из них мы выберем, потому что ответ будет одинаковым. Для этой задачи воспользуемся основанием 10. Не забудьте округлить ответ до трех десятичных знаков, потому что нас просят округлить его до ближайшей тысячной. Наш калькулятор должен подтвердить, что наш ответ правильный. Пример 4: Рассчитайте значение \ large {\ log {} _ {\ large {7}} \ left ({9} \ right)}. Округлите ответ до ближайшей сотой. В предыдущем примере мы использовали десятичное основание для вычисления логарифма. На этот раз мы будем использовать натуральное число \ color {red} e в качестве основы выбора при применении формулы замены базы. Обратите внимание, что нам не нужно записывать натуральный логарифм как \ large {{{\ log} _e} \ left (x \ right)}. Мы можем пропустить этот шаг и сразу записать его как \ large {\ ln \ left (x \ right)}.Я добавил это как один из шагов ниже для ясности и акцента. Давайте продолжим и применим правило смены базы, чтобы преобразовать \ large {\ log {} _7 \ left (9 \ right)} как отношение или долю двух операций натурального логарифма. Также не забудьте округлить ответ до двух десятичных знаков, поскольку задача требует, чтобы окончательный ответ выражался с точностью до сотых. Ваш калькулятор должен выдать результат, аналогичный приведенному ниже. Пример 5: Изменить \ large {\ log {} _ {\ large {6}} \ left ({0.1} \ right)} как частное двух натуральных логарифмов. Вычислите его значение и округлите до ближайшей десятой. Эта задача требует, чтобы мы изменили данный логарифм как частное от натуральных логарифмов. Это означает, что у нас нет другого выбора, кроме как использовать натуральное число \ large \ color {red} e в качестве основы, когда мы применяем формулу замены базы. Не забывайте также, что нам велят округлить наш ответ до ближайшей десятой (одного десятичного знака). Вот наше решение: Наш калькулятор согласен с нашим ответом. Пример 6: Измените \ color {blue} \ large {\ log \ left (7 \ right)} как частное от натурального логарифма. Затем вычислите его значение. Округлите ответ до ближайшей десятитысячной. Я допускаю, что, хотя мы можем напрямую решить значение \ color {red} \ log \ left (7 \ right) с помощью калькулятора, поскольку он имеет ключ LOG , эта проблема требует, чтобы мы пошли по длинному пути. Не потому, что это бесполезное занятие нашего времени, но, что более важно, это возможность для нас применить наше твердое понимание формулы смены основы. Помните, что когда вы видите операцию журнала без базы, предполагается, что она имеет базу 10. Поэтому наш самый первый шаг — переписать \ log \ left (7 \ right) как {\ log _ {10}} \ left (7 \ right), чтобы было намного легче увидеть, с какими числами мы имеем дело на этапе смены базы. Это прекрасное чувство, когда калькулятор выводит значение, подтверждающее наш ответ. Пример 7: Измените \ color {blue} \ large \ ln \ left ({13} \ right) как отношение в виде десятичных логарифмов.Затем рассчитайте его стоимость. Округлите ответ до ближайшей десятитысячной. Как и в примере №6, нет необходимости применять формулу изменения базы, потому что мы можем вычислить ее напрямую с помощью калькулятора. Однако цель этой проблемы — продемонстрировать наше глубокое понимание десятичных и натуральных логарифмов и того, как правильно обращаться с формулой. (основание натурального логарифма 2, e, 10, N)
Предложение? обратная связь? Жук ? идея ? Запись в dCode ! Калькулятор логарифмов Log (x) =?
Упрощение логарифмических выражений
Логарифм решателя Log (?) = X
Ответы на вопросы (FAQ)
Какой натуральный логарифм? (Определение)
Как превратить логарифм по основанию N в натуральный логарифм?
Что такое неперианский логарифм?
Что такое десятичный логарифм (log10)?
Что такое двоичный логарифм (log2)?
Почему логарифм может преобразовывать произведение в сумму?
Какие замечательные значения функции логарифма?
Задайте новый вопрос Исходный код
Нужна помощь?
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра! Вопросы / комментарии
— служба поддержки Office
Описание
Синтаксис
Пример
Изменение базовой формулы или правила
Число \ large {\ color {red} {e}}
десятичный логарифм
Натуральный логарифм
Кнопки LOG и LN графического калькулятора
Что такое формула изменения базы ? Примеры формулы замены базы

 Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10.
Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10. expm1(x)
import math
x = 1.0
y = math.expm1(x) # y = 1.718281828459045
y = math.expm1(0.0) # y = 0.0
expm1(x)
import math
x = 1.0
y = math.expm1(x) # y = 1.718281828459045
y = math.expm1(0.0) # y = 0.0 sqrt(x) # y = 9.0
x = -0.0
y = math.sqrt(x) # y = -0.0
x = 2.0
y = math.sqrt(x) # y = 1.4142135623730951
sqrt(x) # y = 9.0
x = -0.0
y = math.sqrt(x) # y = -0.0
x = 2.0
y = math.sqrt(x) # y = 1.4142135623730951