Логарифмы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.
Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов.
Логарифм произведения, сумма логарифмов
Теоретический материал по теме — логарифм произведения.
Пример
Задание. Представить $\log _{5} 6$ в виде суммы логарифмов.
Решение. $\log _{5} 6=\log _{5}(2 \cdot 3)=\log _{5} 2+\log _{5} 3$
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Упростить $\log _{5} 4+\log _{5} 3$
Упростить $\log _{5} 4+\log _{5} 3$
Решение. $\log _{5} 4+\log _{5} 3=\log _{5}(4 \cdot 3)=\log _{5} 12$
Логарифм частного, разность логарифмов
Теоретический материал по теме — логарифм частного.
Пример
Задание. Известно, что $\log _{5} 2=a$, а $\log _{5} 3=b$. Выразить $\log _{5} \frac{2}{3}$ через $a$ и $b$.
Решение. $\log _{5} \frac{2}{3}=\log _{5} 2-\log _{5} 3=a-b$
Пример
Задание. Вычислить значение выражения $\log _{5} 10-\log _{5} 2$
Решение. $\log _{5} 10-\log _{5} 2=\log _{5} \frac{10}{2}=\log _{5} 5=1$
Логарифм степени
Теоретический материал по теме — логарифм степени.
Пример
Задание.
Вычислить $\log _{5} 10-\log _{5} 2=\log _{5} \frac{10}{2}=\log _{5} 5=1$Решение.$\log _{2} \frac{1}{8}+\log _{5} 25=\log _{2} 2^{-3}+\log _{5} 5^{2}=-3 \cdot \log _{2} 2+2 \cdot \log _{5} 5=$
$= -3 + 2 = -1$
Пример
Задание. Второй корень не принадлежит ОДЗ, а значит решение $x=2$ Ответ. $x=2$ Пример Задание. Решить уравнение $\ln (x+1)=\ln (2 x-3)$ Решение. Находим ОДЗ: Решаем уравнение $x+1=2 x-3: x=4 \in$ ОДЗ. Итак, решением исходного логарифмического уравнения
также является это значение. Ответ. $x=4$ Теоретический материал по теме — логарифмические неравенства. Пример Задание. Решить неравенство $\log _{0,5}(x-1)>-1$ Решение. В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$ Ответ. $x \in(1 ; 3)$ Пример Задание. Решить неравенство $\log _{5} 5>\log _{5} x$ Решение. Данное неравенство равносильно системе: Ответ. $x \in(0 ; 5)$ Читать первую тему — формулы и свойства логарифмов,
раздела логарифмы. Факт 1. Заметим, что при выполнении ограничений данные формулы верны в обе стороны!
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что ac = b:
logab=c⇔ac=b(a>0,a≠1,b>0)      
Обратите внимание: логарифм от неположительного числа не определен. Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ. Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу. logabc=logab−logac(a>0,a≠1,b>0,c>0) (6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. Действительно, выражение
loga(f(x)g(x))
определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля. Преобразуя данное выражение в сумму
logaf(x)+logag(x), мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6). И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример: Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной. Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8): Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например,
lg(xy)=lgx+lgy(x>0,y>0). Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e.
Пример 1. Вычислите: lg2 + lg50.
Пример 2. Вычислите: lg125/lg5. {2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$
{2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$Решение логарифмических неравенств
 {-1}$ или $x-1<2 \Rightarrow x<3$
{-1}$ или $x-1<2 \Rightarrow x<3$Логарифмы. Логарифмические формулы. Свойства логарифмов
\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\).
\[\Large{{\color{blue}{\log_a{b}=t\quad\Leftrightarrow\quad
a^t=b }}}\]
Т. {\log_ac}&&a>0, a\ne 1, b>0, c>0\\
&&\\
\textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\
&&\\
\textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\
&&\\
&&\\
{\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\
\textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\
&&\\
\textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\
&&\\ \hline
\end{array}}}\]
{\log_ac}&&a>0, a\ne 1, b>0, c>0\\
&&\\
\textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\
&&\\
\textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\
&&\\
&&\\
{\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\
\textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\
&&\\
\textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\
&&\\ \hline
\end{array}}}\]Логарифмы. Свойства логарифмов. Формулы с логарифмами. Десятичные, натуральные логарифмы, основное логарифмическое тождество
Определение логарифма Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Основное логарифмическое тождество alogab=b(a>0,a≠1)
(2)
Два очевидных следствия определения логарифма logaa=1(a>0,a≠1) (3)
loga1=0(a>0,a≠1) (4)
Логарифм произведения и логарифм частного loga(bc)=logab+logac(a>0,a≠1,b>0,c>0) (5) При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Степень можно выносить за знак логарифма logabp=plogab(a>0,a≠1,b>0) (7) Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Формула перехода к новому основанию logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1) (8) Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:
logab=lgblga=lnblna(a>0,a≠1,b>0)
Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:
logab=lgblga=lnblna(a>0,a≠1,b>0)
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
| alogab=b(a>0,a≠1) |
| logaa=1(a>0,a≠1) |
| loga1=0(a>0,a≠1) |
| loga(bc)=logab+logac(a>0,a≠1,b>0,c>0) |
| logabc=logab−logac(a>0,a≠1,b>0,c>0) |
| logabp=plogab(a>0,a≠1,b>0) |
| logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1) |
| logab=1logba(a>0,a≠1,b>0,b≠1) |
Возможно, вас заинтересуют также:
Логарифм.
 Примеры
ПримерыЛогарифмом числа b по основанию a обозначают выражение . Вычислить логарифм значит найти такой степень x (),при котором выполняется равенство
Основные свойства логарифма
Приведенные свойства необходимо знать, поскольку, на их основе решаются практически все задачи и примеры связаны с логарифмами. Остальные экзотических свойств можно вывести путем математических манипуляций с данными формулами
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
При вычислениях формулы суммы и разности логарифмов (3,4 ) встречаются довольно часто. Остальные несколько сложные, но в ряде задач являются незаменимыми для упрощения сложных выражений и вычисления их значений.
Распространены случаи логарифмов
Одними из распространенных логарифмов такие в которых основание ровное десять, экспоненте или двойке.
Логарифм по основанию десять принято называть десятичным логарифмом и упрощенно обозначать lg(x). 2 (а>0,с>0).
2 (а>0,с>0).
По свойствам 3,5 вычисляем
2.
По свойству разницы логарифмов имеем
3.
Используя свойства 3,5 находим
4. где .
На вид сложное выражение с использованием ряда правил упрощается к виду
——————————————
Нахождение значений логарифмов
Пример 2. Найти х, если
Решение. Для вычисления применим до последнего слагаемого 5 и 13 свойства
Подставляем в запись и скорбим
Поскольку основания равные, то приравниваем выражения
——————————————
Пример 3. Пусть задано значение логарифмов
Вычислить log[a](x), если
Решение: Прологарифмируем переменную, чтобы расписать логарифм через сумму слагаемых
——————————————
На этом знакомство с логарифмами и их свойствами только начинается. Упражняйтесь в вычислениях, обогащайте практические навыки — полученные знания Вам скоро понадобятся для решения логарифмических уравнений. Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме — логарифмические неравенства …
Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме — логарифмические неравенства …
ЛОГАРИФМЫ – свойства, формулы, как решать логарифмы
Логарифм числа b (b > 0) по основанию a (a > 0, a ≠ 1) – показатель степени, в которую нужно возвести число a, чтобы получить b.
Логарифм числа b по основанию 10 можно записать как lg(b), а логарифм по основанию e (натуральный логарифм) – ln(b).
Основное логарифмическое тождество
Основное логарифмическое тождество часто используется при решении задач с логарифмами:
Свойства логарифмов
Существует четыре основных свойства логарифмов.
Пусть a > 0, a ≠ 1, x > 0 и y > 0.
Свойство 1. Логарифм произведения
Логарифм произведения равен сумме логарифмов:
loga(x ⋅ y) = logax + logay
Свойство 2.
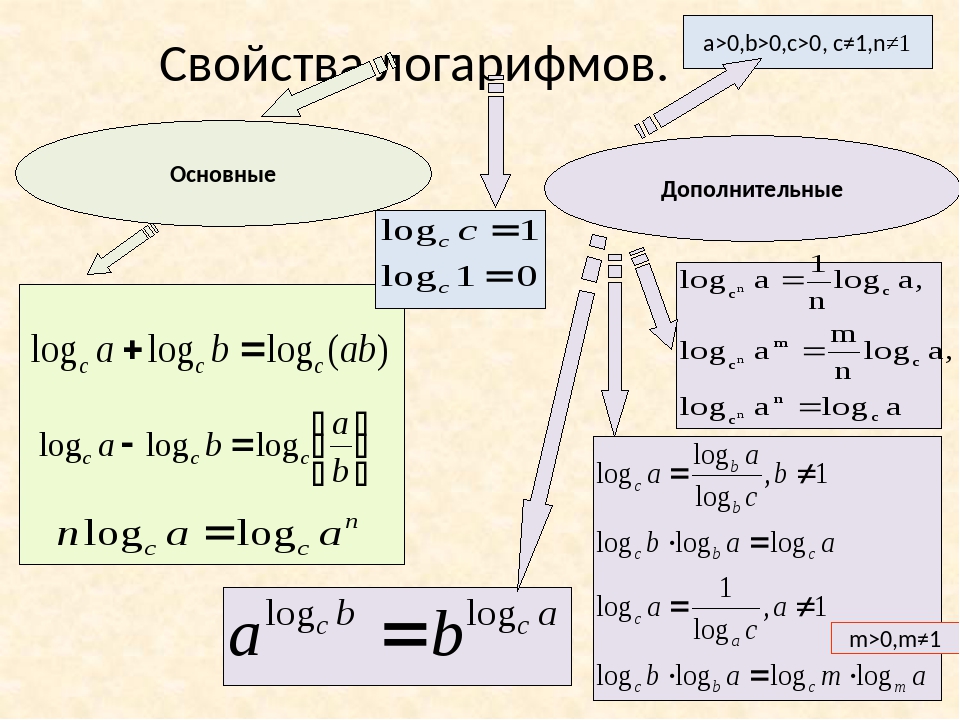 Логарифм частного
Логарифм частногоЛогарифм частного равен разности логарифмов:
loga(x / y) = logax – logay
Свойство 3. Логарифм степени
Логарифм степени равен произведению степени на логарифм:
Если в степени находится основание логарифма, то действует другая формула:
Свойство 4. Логарифм корня
Данной свойство можно получить из свойства логарифм степени, так как корень n-ой степени равен степени 1/n:
loga(x)1/n = 1/n ⋅ log
Формула перехода от логарифма в одном основании к логарифму при другом основании
Данная формула также часто применяется при решении различных заданий на логарифмы:
Частный случай:
Сравнение логарифмов (неравенства)
Пусть у нас есть 2 функции f(x) и g(x) под логарифмами с одинаковыми основаниями и между ними стоит знак неравенства:
Чтобы их сравнить, нужно сначала посмотреть на основание логарифмов a:
- Если a > 0, то f(x) > g(x) > 0
- Если 0 < a < 1, то 0 < f(x) < g(x)
Как решать задачи с логарифмами: примеры
Задания с логарифмами включены в состав ЕГЭ по математике для 11 класса в задании 5 и задании 7, вы можете найти задания с решениями на нашем сайте в соответствующих разделах. Также задания с логарифмами встречаются в банке заданий по математике. Все примеры вы можете найти через поиск по сайту.
Также задания с логарифмами встречаются в банке заданий по математике. Все примеры вы можете найти через поиск по сайту.
Логарифмы свойства и формулы. Формулы логарифмов. Логарифмы примеры решения
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0)       
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Основное логарифмическое тождество a log a b = b (a > 0, a ≠ 1) (2)Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
log a 1 = 0 (a > 0, a ≠ 1) (4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частного log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)Log
a
b
c
=
log
a
b −
log
a
c
(a > 0, a ≠ 1, b > 0, c > 0)
(6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Действительно, выражение
log
a
(f (x) g (x))
определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифма log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
Log a (f (x) 2 = 2 log a f (x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)
Несколько простых примеров с логарифмамиПример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b = b (a > 0, a ≠ 1) |
| log a a = 1 (a > 0, a ≠ 1) |
| log a 1 = 0 (a > 0, a ≠ 1) |
| log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b p = p log a b (a > 0, a ≠ 1, b > 0) |
| log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) |
| log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) |
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Определение
Натуральный логарифм — это функция y = ln x , обратная к экспоненте , x = e y , и являющаяся логарифмом по основанию числа е : ln x = log e x .
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/ x .
Исходя из определения , основанием натурального логарифма является число е :
е
≅ 2,718281828459045… ;
.
График функции y = ln x .
График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .
Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( — ∞ ).
При x → + ∞
пределом натурального логарифма является плюс бесконечность ( + ∞
). При больших x
логарифм возрастает довольно медленно. Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм» .
Обратная функция
Обратной для натурального логарифма является экспонента .
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям :
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z
:
.
Выразим комплексную переменную z через модуль r и аргумент φ :
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ
определен не однозначно. Если положить
,
где n — целое,
то будет одним и тем же числом при различных n
.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения .
Сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов .
Примеры решения логарифмов на основании формул.
Логарифм положительного числа b по основанию a (обозначается log a b) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения log a b = x, что равносильно a x = b, поэтому log a a x = x.
Логарифмы , примеры:
log 2 8 = 3, т.к. 2 3 = 8
log 7 49 = 2, т.к. 7 2 = 49
log 5 1/5 = -1, т.к. 5 -1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
log 10 100 = 2, т.к. 10 2 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828.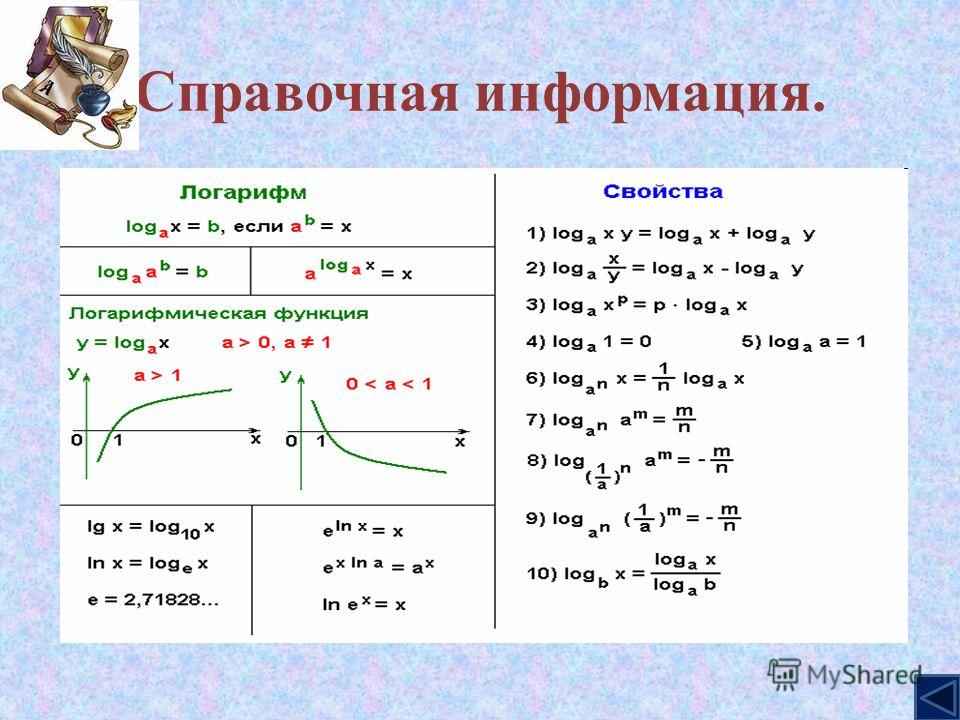 .. — иррациональное число). Обозначается как ln.
.. — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
- Основное логарифмическое тождество
a log a b = b8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9
- Логарифм произведения равен сумме логарифмов
log a (bc) = log a b + log a clog 3 8,1 + log 3 10 = log 3 (8,1*10) = log 3 81 = 4
- Логарифм частного равен разности логарифмов
log a (b/c) = log a b — log a c9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81
- Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа log a b m = mlog a b
Показатель степени основания логарифма log a n b =1/n*log a b
log a n b m = m/n*log a b,
если m = n, получим log a n b n = log a b
log 4 9 = log 2 2 3 2 = log 2 3
- Переход к новому основанию
log a b = log c b/log c a,если c = b, получим log b b = 1
тогда log a b = 1/log b a
log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!
Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!
Если у вас остались вопросы по решению, пишите их в комментариях к статье.
Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Формулы логарифмов
Логарифмом числа b по основанию a называется показатель степени в которую нужно возвести a , чтобы получить b:
c = log a b ⇔ ac = b , причем b > 0, a > 0, a ≠ 1
Свойства логарифма:
a log a b = b
log a 1 = 0
Логарифм произведения:
log a (u ∙ v) = log a u + log a v
Логарифм отношения:
logauvlogaulogav
Логарифм степени и корня:
log a u n = n ∙ log a u
Формула перехода к новому основанию:
logablogcblogac
Формулы, следующие из свойств логарифма:
lognblognalogmblogmalogablog n a ∙ log m b = log m a ∙ log n b
a log n b = b log n a
Сравнение логарифмов:
Решение логарифмических функций – объяснение и примеры
В этой статье мы научимся вычислять и решать логарифмические функции с неизвестными переменными.
Логарифмы и экспоненты — две тесно связанные темы в математике. Поэтому полезно сделать краткий обзор показателей.
Показатель степени — это форма записи многократного умножения числа на себя. Показательная функция имеет вид f (x) = b y , где b > 0 < x и b ≠ 1.Величина x — это число, b — основание, а y — показатель степени или степень.
Например, , 32 = 2 × 2 × 2 × 2 × 2 = 2 2 .
Экспоненциальная функция 2 2 читается как « два, возведенные в степень пяти », или « два, возведенные в степень пять », или « два, возведенные в пятую степень». ”
С другой стороны, логарифмическая функция определяется как обратная функция возведения в степень. Снова рассмотрим экспоненциальную функцию f(x) = b y , где b > 0 < x и b ≠ 1.Мы можем представить эту функцию в логарифмической форме как:
y = log b x
Тогда логарифмическая функция определяется выражением;
f(x) = log b x = y, где b — основание, y — показатель степени, x — аргумент.
Функция f (x) = log b x читается как «логарифмическая база b числа x». Логарифмы полезны в математике, потому что они позволяют нам производить вычисления с очень большими числами.
Как решать логарифмические функции?
Для решения логарифмических функций важно использовать показательные функции в данном выражении.Натуральный бревно или в является обратным e . Это означает, что можно отменить другое, то есть
ln (e x ) = x
e ln x = x
Чтобы решить уравнение с логарифмами, важно знать их свойства.
Свойства логарифмических функций
Свойства логарифмических функций — это просто правила упрощения логарифмов, когда входные данные представлены в виде деления, умножения или возведения в степень логарифмических значений.
Некоторые свойства перечислены ниже.
Правило произведения логарифмов гласит, что логарифм произведения двух чисел, имеющих общее основание, равен сумме индивидуальных логарифмов.
⟹ log a (p q) = log a p + log a q.
Частное правило логарифмов гласит, что логарифм отношения двух чисел с одинаковым основанием равен разности каждого логарифма.
⟹ log a (p/q) = log a p – log a q
Степенное правило логарифмирования гласит, что логарифм числа с рациональным показателем равен произведению показателя степени и его логарифм.
⟹ Log A (P Q ) = Q log A P
3⟹ Log A P = Log x P ⋅ Log A x
⟹ log Q p = log x p / log x q
⟹ log p 1 = 0,
Другие свойства логарифмических функций включают: log A A = 1
7 Логарифмы 1 на любую базу 0 0.
Log A 1 = 0
6
Сравнение экспоненциальной функции и логарифмической функции
Всякий раз, когда вы видите логарифмы в уравнении, вы всегда думаете о том, как отменить логарифм, чтобы решить уравнение. Для этого вы используете экспоненциальную функцию . Обе эти функции взаимозаменяемы.
В следующей таблице показано, как записывать и менять местами экспоненциальные функции и логарифмические функции . В третьем столбце рассказывается о том, как читать обе логарифмические функции.
| Экспоненциальная функция | Логарифмическая функция | READ AS | |
| 8 2 = 64 | 1 Log 8 64 = 2База журнала 8 из 64 | ||
| 10 3 = 1000 | журнал 1000174 | База журнала 10 из 1000170 | |
| 10 0 = 1 | Журнал 1 = 0 | База 10 из 1 | |
| 25 2 = 625 | 625Log 25 625 = 2 | Базы 25 из 625 | |
| 12 2 = 144 | 1 log 12 144 = 2База журнала 12 из 144 |
Давайте воспользуемся этими свойствами для решения нескольких задач, связанных с логарифмическими функциями.
Пример 1
Преобразуйте экспоненциальную функцию 7 2 = 49 в эквивалентную ей логарифмическую функцию.
Решение
Дано 7 2 = 64.
Здесь основание = 7, показатель степени = 2 и аргумент = 49. Следовательно, 7 2 = 64 в логарифмической функции есть;
⟹ log 7 49 = 2
Пример 2
Запишите логарифмический эквивалент 5 3 = 125.
Решение
Основание = 5;
показатель степени = 3;
и аргумент = 125
5 3 = 125 ⟹ Log 5 125 = 3
Пример 3
Решина для X в журнале 3 x = 2
Решение
log 3 x = 2
3 2 = x
⟹ x = 9
Пример 4
Если 2 log x = 4 log 3, то
Solution
2 log x = 4 log 3
Разделите каждую сторону на 2. 2
2
log x = log 9
x = 9
Пример 5 Пример 5 Найти логарифм 1024 до базы 2. Решение 1024 = 2 10 Журнал 2 1024 = 10 Пример 6 Найти значение x в журнал 2 ( x ) = 4
Решение
Переписать логарифмический журнал функций 2 ( x ) = 4 в экспоненциальной форме.
2 4 = x x
9 x
Пример 7
Решите для x В следующих логарифмической функции Log 2 (x — 1) = 5.
Решение
Перепишите логарифм в экспоненциальной форме как;
log 2 (x – 1) = 5 ⟹ x – 1 = 2 5
Теперь найдите x в алгебраическом уравнении.
⟹ x – 1 = 32
x = 33
Пример 8
Найдите значение x в журнале x 900 = 2.
Решение
Запишите логарифм в экспоненциальной форме как;
x 2 = 900
Найдите квадратный корень из обеих частей уравнения, чтобы получить;
x = -30 и 30
Но поскольку основание логарифма никогда не может быть отрицательным или равным 1, поэтому правильный ответ равен 30.
Пример 9 log 2 + log 5
Solution
Используя правило произведения Log b (mn) = log b m + log b n получаем;
⟹ лог. 2 + лог. 5 = лог. (2 * 5) = лог. (10).
Следовательно, x = 10.
Пример 10
решают журнал x (4x — 3) = 2
Раствор
Перепишите логарифм в экспоненциальной форме для получения;
x 2 = 4x – 3
Теперь решите квадратное уравнение.
x 2 = 4x – 3
x 2 – 4x + 3 = 0
(x -1) (x – 3) = 0
x = 1 или 3
Так как основание логарифма равно 1, то единственное решение равно 3.
Логарифм: полное руководство (теория и приложения)
Для подавляющего большинства людей на Земле в старых добрых учебниках по математике есть тема, о которой многие из нас до сих пор даже боятся размышлять, как кажется. возиться с нашим мозгом довольно особым способом. Название? Логарифм — или Логарифм на английском языке, чтобы быть уверенным!
Как бы ужасно это ни звучало, логарифм, кажется, имеет эту отчетливую характеристику метафорического неприятного привкуса во рту.На самом деле, даже для тех, кто сумел обойти его еще в старшей школе, логарифм по-прежнему остается в значительной степени уклончивой концепцией . Синдром «Я могу манипулировать выражениями, ничего не понимая» вырастает, когда дело доходит до логарифмирования.
Действительно, здесь, в Северной Америке, учебная программа начальной школы имеет тенденцию чрезмерно подчеркивать механику за счет базовой теории , оставляя нам огромную задачу по заполнению логарифмического пробела в знаниях, который включает, среди прочего, теорию, лежащую в основе свойств логарифма , и предполагаемое вычислительное использование для обработки чисел с порядком величины , склоняющимся к крайностям.
Итак, имея это в виду, если вы думаете, что, возможно, наконец пришло время укротить этого монстра , который мы называем логарифмом, то мы будем рады поздравить вас с этим очень почетным поступком. А если вы просто хотите заглянуть в кроличью нору, то будет оценен вдвойне как , поскольку, независимо от вашей мотивации, укрощает / размышляет о ! 🙂
Терминология
Учитывая действительное число $x$, одна из задач в элементарной алгебре состоит в том, чтобы выразить $x$ как степень другого числа $b$ (известного как основание ) .{\ гидроразрыва {1} {2}} $).
По этим причинам в контексте определения мощности обычно требуется, чтобы основание $b$ было положительным числом , то есть не равным $1$. Хотя при таком предположении любая степень $b$ обязательно должна быть положительной , также оказывается — при такой установке — что любое положительное число может быть выражено как степень $b$ в уникальном способ.6$. Уже одно это показывает, что $6$ — это логарифм $64$ по основанию $2$.
Хотя при таком предположении любая степень $b$ обязательно должна быть положительной , также оказывается — при такой установке — что любое положительное число может быть выражено как степень $b$ в уникальном способ.6$. Уже одно это показывает, что $6$ — это логарифм $64$ по основанию $2$.
Логарифм $x$ по основанию по основанию $b$ обозначается как $\log_b x$, причем $x$ также называется аргументом логарифма. При рассмотрении в качестве функции $\log_b x$ определяется для всех положительных чисел, если основание $b$ равно действительным (т. е. $\displaystyle b>0, b \ne 1$) .
Для начала отметим, что независимо от значения основания $b$, мы всегда имеем это:
- $\displaystyle \log_b 1 = 0$ (поскольку $0$ — это число, чтобы получить $1$)
- $\displaystyle \log_b b = 1$ (поскольку $1$ — это число $b$, которое нужно увеличить, чтобы получить $b$)
- $\displaystyle \log_b \frac{1 }{b} = -1$ (поскольку $-1$ — это число $b$, которое нужно увеличить, чтобы получить $\displaystyle \frac{1}{b}$)
Поскольку эти результаты почти незамедлительны и достаточно примечательно, мы будем называть их просто тривиальными логарифмическими тождествами .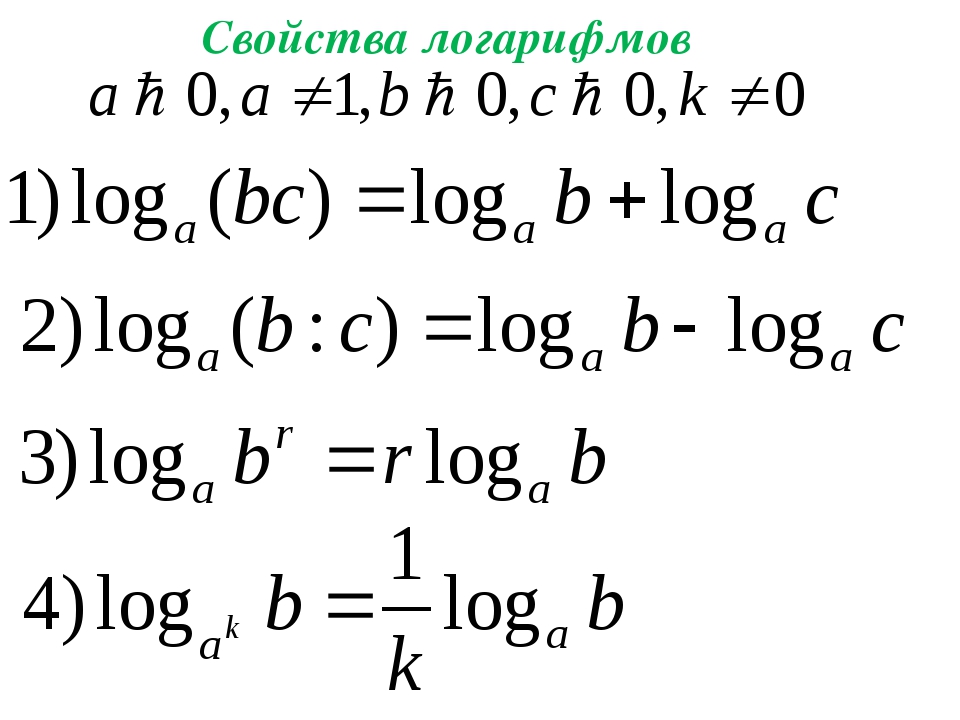 x$, логарифмическая функция по основанию $10$, также известная как десятичный логарифм , обычно обозначается как $\log_{10} x$, $\log x$ или просто $\lg x$ для краткости. Десятичный логарифм представляет для нас большой интерес, в первую очередь из-за распространенности десятичной системы счисления в различных культурах мира.
x$, логарифмическая функция по основанию $10$, также известная как десятичный логарифм , обычно обозначается как $\log_{10} x$, $\log x$ или просто $\lg x$ для краткости. Десятичный логарифм представляет для нас большой интерес, в первую очередь из-за распространенности десятичной системы счисления в различных культурах мира.
Осторожно
Обратите внимание, что в старых научных текстах и некоторых учебниках по высшей математике $\log x$ может также означать — и обычно является — натуральным логарифмом по основанию $e$.
При вычислении десятичного логарифма числа десятичное представление логарифма обычно разбивается на две части: целочисленная составляющая (также известная как характеристика ) и дробная составляющая (также известная как мантисса ). По сути, характеристика сообщает нам цифр цифр исходного числа, а мантисса намекает на то, насколько это число близко к своей следующей степени $10$. Это факты, которые делают десятичный логарифм особенно удобным инструментом для определения порядка величины исключительно большого (или маленького ) числа.x$ функция двоичного логарифма $\log_2 x$ широко используется в области информатики , в первую очередь из-за того, что компьютеры хранят информацию в битах (т.е. цифры, которые принимают $0$ или $1$ возможные значения).
Это факты, которые делают десятичный логарифм особенно удобным инструментом для определения порядка величины исключительно большого (или маленького ) числа.x$ функция двоичного логарифма $\log_2 x$ широко используется в области информатики , в первую очередь из-за того, что компьютеры хранят информацию в битах (т.е. цифры, которые принимают $0$ или $1$ возможные значения).
Как и в случае с основанием $10$, двоичный логарифм можно использовать для определения количества цифр положительного целого числа в двоичном представлении . Кроме того, двоичный логарифм также используется для определения глубины бинарного дерева или даже числа операций , необходимых для определенных компьютерных алгоритмов (это относится к теме, известной как алгоритмическая временная сложность ). ).
Помимо мира компьютеров, двоичный логарифм также используется в теории музыки для осмысления высоты музыкальных нот, основанной на фундаментальном наблюдении, что повышает ноту на октаву увеличивает частоту ноты на удвоить . В результате часто удобно представить музыкальный интервал как двоичный логарифм отношения частот .
В результате часто удобно представить музыкальный интервал как двоичный логарифм отношения частот .
Натуральный логарифм (основание $e$)
В некоторых учебниках, посвященных более строгому развитию трансцендентных функций , логарифмическая функция по основанию $\displaystyle e$ — иначе известная как натуральный логарифм , $\log_e x $ или просто $\ln x$ — иногда определяются как площадь между обратной функцией $\frac{1}{x}$ и осью x от $1$ до $x$ (отсюда термин натуральный ).x$, что приводит к следующему стандартному определению натурального логарифма:
При положительном числе $x$ $\ln x$ обозначает число $e$, которое необходимо увеличить, чтобы стать $x$.
В отличие от числа $10$, которое предпочтительнее из-за преобладания десятичной системы счисления , число $\displaystyle e$ является одной из специальных констант, которая удивительно часто всплывает в различных математических дискурсах — независимо от из выбранная система счисления. В результате математики склонны рассматривать основание $e$ как более натуральных , чем основание $10$, хотя некоторые ученые-прикладники и инженеры в разных случаях расходятся во мнениях… среди научного сообщества, вот интересный отчет из Википедии историческое развитие обозначений логарифмов:
В результате математики склонны рассматривать основание $e$ как более натуральных , чем основание $10$, хотя некоторые ученые-прикладники и инженеры в разных случаях расходятся во мнениях… среди научного сообщества, вот интересный отчет из Википедии историческое развитие обозначений логарифмов:
Поскольку логарифмы с основанием 10 были наиболее полезны для вычислений, инженеры обычно просто писали «log(x)», когда они имели в виду log 10 (х).Математики, с другой стороны, писали «log(x)», когда они имели в виду log e (x) для натурального логарифма. Сегодня встречаются оба обозначения.
Поскольку портативные электронные калькуляторы разрабатываются инженерами, а не математиками, стало обычным использовать обозначения инженеров. Таким образом, запись, в соответствии с которой пишут «ln(x)», когда имеется в виду натуральный логарифм, могла быть еще более популяризирована тем самым изобретением, которое сделало использование «десятичных логарифмов» гораздо менее распространенным, электронными калькуляторами.
Логарифм произвольного основания
Графики логарифмических функций по основанию $2$, $\displaystyle e$ и $10$. Обратите внимание, что двоичный логарифм достигает $1$, когда $x=2$, натуральный логарифм , когда $x=e$, и десятичный логарифм , только когда $x=10$.В дополнение к трем наиболее популярным логарифмическим функциям, представленным ранее, можно также определить логарифм, используя другие допустимых оснований . На практике логарифм обычно используется с целью сжать больших чисел (т.т. е. больше $1$) на меньшие числа, так что больше основание, меньше логарифм.
Однако это только часть истории, поскольку все логарифмические функции, с которыми мы сталкивались до сих пор, имеют основания, превышающие число $1$ (т. е. больших оснований ). На самом деле, в случаях, когда основание строго между 0$ и 1$ (т. е. маленькое основание ), график логарифмической функции будет перевернут вверх дном .Действительно, в отличие от стандартной логарифмической функции, которая на увеличивает с $-\infty$ до $\infty$, логарифмическая функция с малым основанием на самом деле уменьшает с $+\infty$ до $-\infty$ в качестве аргумента увеличивается.
е. маленькое основание ), график логарифмической функции будет перевернут вверх дном .Действительно, в отличие от стандартной логарифмической функции, которая на увеличивает с $-\infty$ до $\infty$, логарифмическая функция с малым основанием на самом деле уменьшает с $+\infty$ до $-\infty$ в качестве аргумента увеличивается.
К счастью, на практике нам редко приходится прибегать к такого рода логарифмическим функциям. Как мы увидим позже с изменением базового правила , каждая пара логарифмических функций представляет собой кратное друг от друга, так что с точки зрения приложений и решений уравнений/неравенств три стандартных логарифма равны.в целом более чем достаточно, чтобы все заработало.
Логарифмическая шкала и ее приложения
Поскольку логарифм позволяет преобразовать экспоненциальную шкалу в линейную шкалу , это стало жизненно важной концепцией, когда дело доходит до сообщения о числовой переменной, величины которой либо растут в геометрической прогрессии, либо уменьшаются экспоненциально.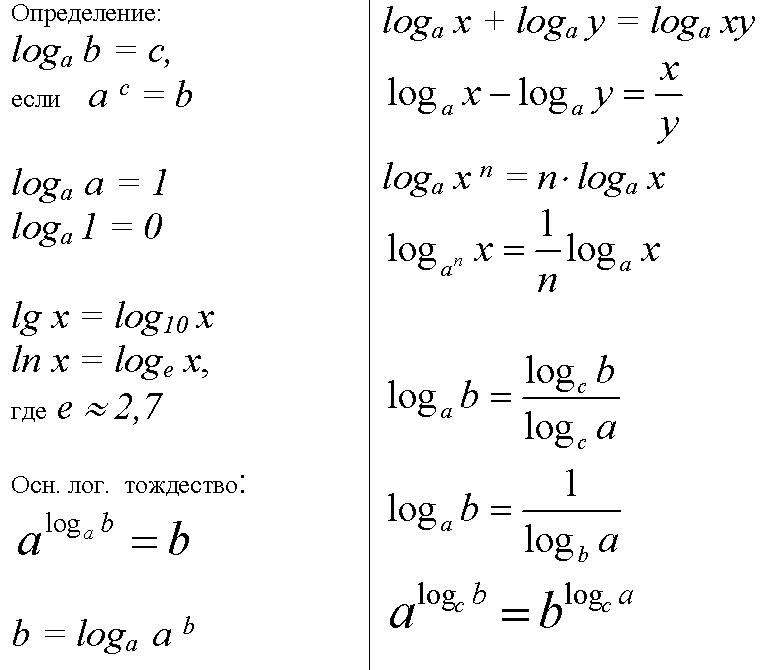 Почему? Потому что, если мы просто возьмем логарифм этой переменной, мы фактически превратим эту переменную в то, что люди называют логарифмической шкалой .
Почему? Потому что, если мы просто возьмем логарифм этой переменной, мы фактически превратим эту переменную в то, что люди называют логарифмической шкалой .
Несмотря на то, что логарифмическая шкала кажется высокотеоретической концепцией, логарифмическая шкала — если принять соответственно — может помочь нам лучше объяснить/понять удивительное количество явлений, обнаруженных в природе . от громкости звука , магнитуды землетрясения до кислотности раствора и высоты музыкального тона :
- В равнотемперированном фортепиано , каждая клавиша на фортепиано может быть представлена как двоичный логарифм ее относительной звуковой частоты, так что каждый раз, когда мы нажимаем более высокую клавишу на фортепиано, мы фактически увеличиваем частоту звука на фиксированный коэффициент ( $\displaystyle \sqrt[12]{2}$, если быть точным).

- В химии кислотность раствора измеряется в pH , который определяется как отрицательный логарифм концентрации ионов водорода . В основном это означает, что при увеличении pH на $1$ концентрация ионов водорода уменьшается в раз в десять раз , что в свою очередь приводит к значительно менее кислому раствору.
- В сейсмологии сила землетрясения может быть определена количественно с использованием шкалы Рихтера , которая по сути является логарифмом амплитуды сейсмических волн (относительно пороговой амплитуды ), так что каждый когда число по шкале Рихтера увеличивается на $1$, сила землетрясения возрастает в раз в десять раз .
- В акустике громкость звука обычно количественно определяется с помощью децибел (дБ), что составляет десятую часть бел (В), последний из которых является логарифмом звуковой мощности.
 (относительно порога слышимости ). На практике это означает, что каждое увеличение на 10 дБ (экв., 1 Б) увеличивает звуковую мощность источника в 9 0 049 десяти раз 90 050 .
(относительно порога слышимости ). На практике это означает, что каждое увеличение на 10 дБ (экв., 1 Б) увеличивает звуковую мощность источника в 9 0 049 десяти раз 90 050 .
Свойства, включающие аргументы
Одна из причин, по которой логарифм был таким мощным вычислительным инструментом в старые времена — до изобретения компьютеров или калькуляторов — заключается в том, что всегда можно использовать определенные свойств логарифма свести сложный аргумент к его отдельным составляющим — и сделать это независимо от рассматриваемого основания. Далее мы приводим пять таких свойств, которые относятся к произведению , обратному , частному , степени и корню логарифма.{\log y} = xy \end{align*}
Далее мы приводим пять таких свойств, которые относятся к произведению , обратному , частному , степени и корню логарифма.{\log y} = xy \end{align*}
Этот факт — то, что логарифм произведения может быть сведен к сумме логарифмов его составляющих — приводит к свойству, обычно известному как Правило продукта .
Правило 1 — Правило произведения для логарифма
Для любых двух положительных чисел $x$, $y$ получаем:
\begin{align*} \log (xy) =\log x + \log y \end{align*}
, где предполагается, что все логарифмы находятся под одним и тем же допустимым основанием $b$.
В частности, когда основание составляет 10 долларов США, Правило произведения можно перевести в следующее утверждение:
Величина произведения равна сумме его отдельных величин.
Например, чтобы измерить приблизительный размер чисел, таких как $365435 \cdot 43223$, мы могли бы взять десятичный логарифм , а затем применить правило продукта , получив следующее:
\begin{align*} \ log (365435 \cdot 43223) & = \log 365435 + \log 43223 \\ & \приблизительно 5. {10})$.
{10})$.
Осторожно
Правило продукта применяется только при выполнении предварительных условий. Например, мы не можем разбить $9$ на $-1$ и $-9$ и утверждать, что $\ln 9 = \ln(-1) + \ln (-9)$.
И поскольку равенство по умолчанию двунаправленное , вместо нарушения произведения с помощью правила произведения слева направо , мы также можем использовать его справа налево , тем самым поворачивая вместо этого сумму логарифмов в произведение.2) = \log x + \log x = 2 \log x\end{align*}
, что служит хорошим напоминанием о том, что любой основанный на логарифмах алгебраический метод — будь то логарифмическое уравнение решает , логарифмическое неравенство решение или логарифмического дифференцирования — следует выполнять с учетом этого потенциального ограничения.
Правило обратной величины
Мы знаем, что каждое положительное число имеет обратное мультипликативное число (т. е. обратное ), так что, возможно, есть также сокращение при нахождении логарифма обратной величины? И здесь снова звучит громкое да .Чтобы понять почему, предположим, что нам дано положительное число $x$, тогда по правилу продукта мы имеем это:
е. обратное ), так что, возможно, есть также сокращение при нахождении логарифма обратной величины? И здесь снова звучит громкое да .Чтобы понять почему, предположим, что нам дано положительное число $x$, тогда по правилу продукта мы имеем это:
\begin{align*} \log \left(x \\cdot \frac{1} {x} \right) & = \log x + \log \left( \frac{1}{x} \right) \end{align*}
С другой стороны, у нас также есть это:
\begin {align*} \log \left(x \cdot \frac{1}{x} \right) & = \log 1 = 0 \end{align*}
Соединяя два уравнения вместе, мы получаем, что:
\begin{align*} \log x + \log \left( \frac{1}{x} \right) & = 0 \end{align*}
Или эквивалентно,
\begin{align*} \log \left( \frac{1}{x} \right) & = – \log x \end{align*}
Сюрприз! Мы только что открыли Правило обратной величины , которое гласит, что для нахождения логарифма обратной величины нам просто нужно инвертировать логарифм исходного числа.
Правило 2 — Правило обратного для логарифма
Для любого положительного числа $x$ имеем:
\begin{align*} \log \left(\frac{1}{x} \right) = -\log x \end{align*}
, где предполагается, что все логарифмы относятся к одному и тому же действительному основанию $b$.
Таким образом, вместо вычисления двоичного логарифма $\displaystyle \frac{1}{512}$ с нуля, мы могли бы повернуть голову вокруг и сделать:
\begin{align*} \log_2 \left ( \frac{1}{512} \right) = -\log_2 512 = -9 \end{align*}
Частное правило
Теперь, когда оба Правило продукта и Взаимное правило в порядке, давайте посмотрим что произойдет, если мы применим их к частному из положительных чисел $x$ и $y$:
\begin{align*} \log \left( \frac{x}{y} \right) & = \log \left( x \cdot \frac{1}{y} \right) \\ & = \log x + \log \left( \frac{1}{y} \right) \\ & = \log x -\log y \end{align*}
Бинго! Мы только что показали, что логарифм частного — это в точности разность между исходными логарифмами — свойство, широко известное как правило частного .
Правило 3 — Правило частных для логарифма
Для любых двух положительных чисел $x$ и $y$ получаем:
\begin{align*} \log \left( \frac{x}{y } \right) =\log x-\log y \end{align*}
, где предполагается, что все логарифмы находятся под одним и тем же действительным основанием $b$.
Например, вместо вычисления натурального логарифма $\displaystyle \frac{2}{e}$ с нуля, мы могли бы применить правило частных и получить это:
\begin{align*} \ln \left( \frac{2}{e}\right) = \ln 2-\ln e = \ln 2-1 \end{align*}
Как и в случае Power Rule , вместо , нарушая частное , мы также можем использовать Правило отношения справа налево , тем самым превращая разность в частное вместо этого.Например:
\begin{align*} \log 45-\log 9 = \log \left( \frac{45}{9} \right) = \log 5 \end{align*}
В базе $10 $, Правило частного можно также перевести в следующее понимание:
Величина частного равна разности отдельных величин.
n \right] = \log x \end{align*}
Соединяя два равенства вместе, мы получаем, что:
\begin{align*} n \log (\sqrt[n]{x}) = \log x \end{align*}
Или эквивалентно,
\begin{align*} \log (\sqrt[n]{x}) = \frac{\log x}{n} \end{align*}
Отлично! Это показывает, что для вычисления логарифма корня из $n$ -го -го достаточно разделить логарифм исходного числа на $n$. Это понимание приводит к еще одному свойству логарифма, известному как . Корневое правило :
Правило 5 — Корневое правило для логарифма
Для любых положительных чисел $x$ и натуральных чисел $n$ мы имеем:
\begin{align*} \log (\sqrt[n ]{x}) = \frac{\log x}{n} \end{align*}
, где предполагается, что все логарифмы находятся под одним и тем же действительным основанием $b$.
Подобно степенному правилу , корневое правило полезно не только своей способностью извлекать корень из логарифма (как в $\displaystyle \log (\sqrt[12]{6}) = \ frac{\log 6}{12}$), но и за его способность создать корень из ничего (как в $\displaystyle \frac{\ln 2}{5}=\ln (\sqrt[ 5]{2})$).
В системе счисления 10$ корневое правило можно интерпретировать следующим образом:
Когда число укореняется, результирующая величина масштабируется точно на степень корня , о котором идет речь.{\pi})\right] \\ & = 3 \log 5 + \frac{\log 15}{4} – 66 \log 10 – \pi \log e \end{align*}
Свойства, включающие основания
ОК. Итак, это было немного свойств, связанных с аргументом логарифма, но что, если вместо этого мы хотим настроить по основанию ? Что ж, мы вас прикрыли и в этом! В дальнейшем мы представим четыре свойства логарифма с учетом оснований для вашего собственного удовольствия. Это правило цепочки , правило смены базы , правило замены базы и взаимозаменяемость базового аргумента .
Цепное правило
Предположим на минуту, что вы освоили все пять свойств логарифма, используемых для сведения аргумента к его простейшим составным частям, но по той или иной причине основание вас раздражает.
Что бы вы сделали?
В нашем случае нам нужно найти альтернативную формулу для вычисления того же логарифма, не прибегая непосредственно к этой базе .
На самом деле, давайте начнем с , немного сузив вопрос: при заданном положительном числе $x$ существует ли способ вычисления $\log x$ (по основанию $b$), используя новое основание $ $? Или еще лучше: что такое выражение , содержащее $a$, такое, что при возведении в него $b$ становится $x$?
Здесь, чтобы найти одно такое выражение, было бы совершенно естественно начать с $\displaystyle \log_a x$ и посмотреть, куда оно нас приведет.{\log a \cdot \log_a x} = x \end{align*}
Бинго! Показатель степени в среднем члене — это именно то, что мы искали — выражение, согласно которому $b$ нужно увеличить, чтобы оно стало $x$! Таким образом, мы можем заключить, что:
\begin{align*} \log x = \log a \cdot \log_a x \end{align*}
По-английски это выглядит так:
Логарифм числа, оценивается как логарифм нового основания , умноженный на логарифм исходного числа по этому новому основанию.
На самом деле это свойство настолько впечатляет, что мы решили окрестить как Цепное правило (не путать с обычным цепным правилом в исчислении).
Правило 6 — Цепное правило для логарифмирования
Для любого положительного числа $x$ и действительного основания $a$ мы имеем следующее:
\begin{align*} \log x = \log a \cdot \log_a x \end{align*}
, где предполагается, что все логарифмы, основание которых не определено явно, находятся под одним и тем же действительным основанием $b$.
Здесь определенно требуется пример, иллюстрирующий его использование: предположим, что нам дали задание определить величину числа $1024$ (т. е. найти $\log_{10} 1024$), но предположим, что вместо этого было бы проще, если бы база была в $2$, тогда мы можем применить цепное правило с $2$ в качестве новой базы , что даст следующее:
\begin{align*} \log_{ 10} 1024 = \log_{10} 2 \cdot \log_2 1024 = \log_{10} 2 \cdot 10 \приблизительно 3,01 \end{align*}
, поэтому величина $1024$ составляет примерно $3.
{3.01}$), что соответствует 4-значному номеру .
На самом деле, это еще не все: на самом деле не имеет значения, какую новую базу мы выберем! База могла быть $3$, $e$ или даже $\pi$, и результат был бы точно таким же!
\begin{align*} \log_{10} 1024 & = \log_{10} 3 \cdot \log_3 1024 \\ & = \log_{10} e \cdot \log_e 1024 \\ & = \log_{10 } \pi \cdot \log_{\pi} 1024 \end{align*}
Правило смены базы
Если вы все еще бродите вокруг, вы помните, что Цепное правило гласит:
\begin {align*} \log x = \log a \cdot \log_a x \end{align*}
Здесь, если мы просто найдем $\log_a x$, мы получим:
\begin{align*} \ log_a x = \frac{\log x}{\log a} \end{align*}
Боже! Еще одна альтернативная формула для логарифма! За исключением того, что на этот раз это (не)известный по-настоящему.Название? Правило смены базы !
Правило 7 — Правило замены основания для логарифма
Для любого положительного числа $x$ и действительного основания $a$ мы имеем следующее:
\begin{align*} \log_a x = \ frac{\log x}{\log a} \end{align*}
где логарифмы, основание которых не определено явно, предполагаются лежащими под одной и той же действительной базой $b$
На первый взгляд, это может показаться простой переформулировкой Цепного правила .
Однако при дальнейшем рассмотрении можно увидеть, что на самом деле это не так: цепное правило превращает логарифм в произведение логарифмов с различными основаниями , в то время как правило смены основания превращает логарифм в частное логарифмов с тем же основанием . Кроме того, цепное правило незначительно облегчает вычисление логарифма по новому основанию, в то время как правило изменения основания фактически полностью устраняет зависимость от старого основания.
На практике правило смены основания в основном используется для вычисления «нестандартного» логарифма путем преобразования его в частное «стандартных логарифмов» (например, $\log_{15} 26 = \frac {\ln 26}{\ln 15} = \frac{\log_2 26}{\log_2 15}$). Однако его также можно использовать в обратном порядке, тем самым объединяя частное логарифмов в один логарифм (например, $\frac{\ln 8}{\ln 2} = \log_2 8 = 3$).
На самом деле, как Цепное правило , так и Правило замены основания обеспечивают унифицированную основу для логарифмов по всем допустимым основаниям, показывая, что каждая логарифмическая функция является кратным отдельно друг от друга.
С появлением компьютеров и калькуляторов Правило смены основания также открывает возможность вычисления логарифма по произвольному основанию, стандартизируя по основанию $e$, или — если научный калькулятор используется — для основания $10$.
Правило замены базы
А теперь давайте повеселимся. Помните, что правило смены базы гласит: фактически предполагается, что «безосновные» логарифмы меньше допустимых оснований $b$.Из любопытства, если мы просто допустим, что это основание равно $a$, мы получим это:
\begin{align*}\log_a x = \frac{\log_a x}{\log_a a} = \log_a x \end {align*}
, что не очень интересно, так как мы в основном идем по кругу. Однако в особом случае, когда $x \ne 1$, мы можем вместо этого взять за основу $x$, получив таким образом следующее тождество:
\begin{align*}\log_a x = \frac{\log_x x}{\log_x a} = \frac{1}{\log_x a}\end{align*}
Впечатляет! Это почти как играть в LEGO® ! И поскольку никто еще не дал ему имя, давайте просто назовем его правилом замены базы .
Правило 8 — Правило замены оснований для логарифма
Для любых двух допустимых оснований $x$ и $a$ мы имеем следующее:
\begin{align*}\log_a x = \frac{1}{ \log_x a}\end{align*}
На английском языке Правило замены основания означает следующее:
Альтернативный способ вычисления логарифма числа по основанию состоит вместо логарифма по основанию под этим числом, а затем взять обратное.
Ужасный каламбур, который мы знаем, но если вы действительно ненавидите работу под определенной базой, правило замены базы предлагает быстрый и грязный способ избавиться от нее. Например:
\begin{align*} \log_{512} 2 = \frac{1}{\log_2 512} = \frac{1}{9}\end{align*}
, что показывает, что психических LEGO может быть таким же увлекательным занятием, как и игра с несколькими десятками кусочков цветного пластика . 🙂
Взаимозаменяемость базовых аргументов
Как правило, мы не хотим возиться с базовыми аргументами и аргументами , меняя их местами.
{\ln 3})\end{align*}
Забавно, правда? Отличное место, чтобы приоткрыть занавес и о свойствах логарифма! 🙂
Как вы, возможно, слышали, как люди неоднократно говорили, что логарифм — по крайней мере, для большинства практических целей — определяется только на положительных действительных чисел. Почему? Потому что число может иметь логарифм только в том случае, если оно выражается как в степени , что, в свою очередь, должно быть положительным — в силу определения действительных экспоненциальных функций .
Однако, как и следовало ожидать, это не устраивает определенную группу из борцов за математическую свободу , для которых следующий вопрос может быть более актуальным:
Можем ли мы что-нибудь сделать, чтобы расширить домен ? логарифмических функций и к другим числам?
Ответ? Да, но не без привязки. Как оказалось, форсирование этого расширения домена неизбежно повлечет за собой болезненные жертвы на многих фронтах, которые включают, помимо прочего, существенную потерю свойств показателя степени и логарифма .
{yi}$ обозначает -единичное комплексное число с углом $y$.{\pi я} = -e$. На самом деле, можно также видеть, что по построению , любая экспонента обязательно является числом с ненулевой длиной (т. е. экспонента всегда ненулевая ).
Переопределение логарифмической функции (основания $e$)
Таким образом, естественная экспоненциальная функция отображает всю комплексную плоскость в ненулевых комплексных чисел, но, возможно, более тонким является тот факт, что любых ненулевых Комплексное число также может быть выражено как степень $e$.{\ theta i} \\ & = \text{комплексное число с длиной и углом } z \\ & = z \end{align*}
Другими словами, мы только что нашли как логарифм $ z$ — $\displaystyle \ln |z|+\theta i$ то есть! Однако обратите внимание на использование « a » вместо « the », поскольку, как упоминалось ранее, это не пройдет гладко…
Во-первых, поскольку комплексное число может иметь несколько эквивалентов углы , определяющие естественную экспоненциальную функцию на всей комплексной плоскости , могут открыть целую банку червей — То есть целую банку бесконечно много комплексных чисел, экспоненты которых почти одинаковы.
{- \pi i} = \dots = -1 \end{align*}
, что показывает, что логарифм $-1$ – или любого другого числа, если уж на то пошло, – плохо определен при текущей настройке.
Естественно, один из способов исправить эту многозначность логарифмирования состоит в том, чтобы ограничить область экспоненциальной функции главной ветвью . То есть множество комплексных чисел, чья мнимая часть лежит в интервале $\displaystyle (-\pi, \pi]$. Ограничив таким образом область определения, мы сможем доказать, что экспоненты различных чисел сами являются различными, что делает натуральную экспоненту обратимой функцией — отображением главной ветви на набор ненулевых комплексных чисел.
Главное отделение — Ограниченная область естественной экспоненциальной функции. Обратите внимание, что линия $y= -\pi$ равна , а не , включенным в график.При такой установке обратная экспоненциальная функция — функция натурального логарифма — отображает набор из ненулевых комплексных чисел в главную ветвь.
{(\ln a)z} \end{align*}
Из конечно, чтобы это определение имело смысл, основание $\displaystyle a$ должно быть ненулевым .Кроме того, база также не должна быть $\displaystyle 1$, иначе мы просто получим константную функцию . По сути, это просто означает, что концепция действительного основания также должна быть обновлена — от положительного действительного числа , которое не является $\displaystyle 1$, до ненулевого комплексного числа , которое не является $\displaystyle 1$. И это большое достижение, если подумать: набор допустимых оснований только что перешел от правой стороны действительной числовой прямой почти ко всей комплексной плоскости !
Свойства логарифма — обновление
Вроде все хорошо. Или это? Под поверхностью свойств логарифма фактически разваливаются:
- Правило продукта не выполняется: $\displaystyle \ln (-1 \cdot -1) = \ln 1 =0$, но $\displaystyle \ln (-1) + \ln (-1) = 2 \pi i$.
2 \right] = \ln 1 = 0$, но $\displaystyle 2 \ln (-1) = 2 \pi i$ .
- Корневое правило не выполняется: Основная теорема алгебры подразумевает, что теперь число может иметь до $n$ $n$ -го -го комплексного корня, поэтому концепция уникального $n$ -го -го корня больше не применимо.
С другой стороны, логарифмических функций произвольного основания теперь могут быть определены — в терминах $\displaystyle \ln z$ — для всех ненулевых комплексных чисел, используя экземпляров то, что ранее было известно как правило смены базы :
\begin{align*} \log_a x \, \stackrel{def}{=} \, \frac{\ln x}{\ln a} \ qquad (x \ne 0, \text{ является допустимой базой}) \end{align*}
В свете этого неудивительно, что полноценное Правило смены базы действительно выполняется для комплексные логарифмы вообще:
\begin{align*} \log_a x & = \frac{\ln x}{\ln a} \\ & = \frac{\frac{\ln x}{\ln b}} {\frac{\ln a}{\ln b}} \\ & = \frac{\log_b x}{\log_b a} \qquad (x \ne 0, a \text{ и } b\text{ допустимых баз})\end{align*}
В частности, в случае, когда $x$ также является допустимой базой , мы получаем, что:
\begin{align*} \log_a x = \frac{\ log_x х} {\log_x a} = \frac{1}{\log_x a} \end{align*}
Что еще за имя? Правило замены базы конечно!
Кроме того, если мы просто начнем с правила смены базы и найдем $\displaystyle \log_b x$, мы получим, что цепное правило также останется:
\begin{ align*} \log_b x = \log_b a \cdot \log_a x \qquad (x \ne 0, a \text{ и } b\text{ являются допустимыми основаниями}) \end{align*}
На самом деле, оказывается, что даже Взаимозаменяемость базового аргумента также сохраняется, но только из-за специального экземпляра «Правила мощности «, который мы встроили в наше определение общей экспоненциальной функции:
\ begin{align*} x ^ {\ log_b y} & = e ^ {\ ln x \ cdot \ log_b y} \\ & = e ^ {\ frac {\ ln x \ cdot \ ln y} {\ ln b} } \\ & = e^{\ln y \cdot \log_b x} \\& =y^{\log_b x} \qquad (x, y \ne 0, b \text{действительное основание}) \end {align*}
Таким образом, хотя все свойства логарифма, включающие аргументов , теряются в процессе, те, которые включают оснований , все m удалось выйти из этого невредимым.
z$ до ветви , мы можем определить логарифм для всех ненулевых комплексных чисел — и сделать это, используя любое действительное основание на свете.
Однако пять свойств логарифма, включающих аргументов (например, Правило произведения , Правило взаимного обращения , Правило частного , Степенное правило , 5 Корневое правило ) будут потеряны в процессе .
Удивительно, но все четыре свойства логарифма, включающие оснований (т. е. Правило смены основания , Цепное правило , Правило замены основания , Взаимозаменяемость аргумента основания06) будут сохранены 90 . Из-за существенной потери в свойствах логарифма, большинство свойств показателя степени также будут разваливаться. Итак, оглядываясь назад, стоит ли прилагать усилия для расширения области логарифмических функций? Черт возьми, думаю, мы позволим вам решить это! 🙂
Ух ты! Кто бы мог подумать, что чистое знакомство с какой-то базовой теорией может завести нас так далеко! Первоначально инструмент для вычисления больших чисел (например,например, превращение произведений или частных в суммы или разности) и для решения показательных уравнений (через свойств логарифма ), логарифм, очевидно, прошел долгий путь, найдя себя в различных областях прикладных наук и чистая математика .
Для ученых-прикладников логарифм, как правило, напоминает такие темы, как вычисление порядка величины (десятичное или двоичное), логарифмические шкалы (т.г., частота в музыкальных нотах , шкала Рихтера , pH , громкость звука ), алгоритмическая сложность и логарифмически-нормальное распределение . Для тех, кто живет в башне из слоновой кости (кто это?), логарифм часто ассоциируется с идеализированными объектами , такими как гармонический ряд , обратная функция и даже простые числа ,
когда мы обдумывали идею включения
комплексных чисел в логарифм, мы обнаружили, что можем не только расширить определение логарифма на отрицательных действительных чисел , но и на любые другие ненулевых комплексных чисел.x) = x$
Trivial Logarithmic : $\displaystyle \log_b 1 = 0$, $\displaystyle \log_b b = 1$, $\displaystyle \log_b \frac{1}{b} = -1$ Десятичный логарифм (основание 10)
$ \ DisplayStyle \ log X $ Характеристика Mantissa Бинарный логарифм (База 2)
$ \ DisplayStyle \ log_2 x $ Количество битов (двоичное представление) Двоичное дерево Количество необходимых операций ( Алгоритм) октавы (музыка) Частота (музыкальные ноты) Натуральный логарифм (база E)
$ \ DisplayStyle \ ln x $ Обратная функция Натуральная показательная функция Harmonic Series $ \ DisplayStyle \ log X $ (нотационная двусмысленность) Logarithm (произвольная база)
Допустимая база База Маленькая база График (Логарифмические функции) Терминология
Линейные масштабы VS. Logarithmic Scale
Экспоненциальный рост / сжимается Приложения
Частота музыкальных нот (теория музыки) : Относительное примечание частоты преобразованы в Двоичный логарифм . Увеличение полутона увеличивает частоту ноты на $\displaystyle \sqrt[12]{2}$. pH (химия) : Концентрация ионов водорода, преобразованная в отрицательных (десятичных) логарифмов. Повышение pH на $1$ снижает кислотность раствора в десятикратном размере . Шкала Рихтера (сейсмология) : Амплитуда относительной сейсмической волны, преобразованная в десятичный логарифм . Одна единица увеличения по шкале Рихтера увеличивает силу землетрясения в раз в десять раз . Децибел (акустика) : относительная звуковая мощность, преобразованная в десятичных логарифмов (с единицей измерения в белах), где 1 бел увеличения увеличивает относительную звуковую мощность в десятикратном . {yi} \quad ( \text{для всех }x, y \in \mathbb{ R})$
Натуральная логарифмическая функция : Для любого ненулевого комплексного числа $ \displaystyle z$, $\ln z \, \stackrel{def}{=} \, \ln |z| + (\arg{z}) i$, где $\displaystyle |z|$ обозначает длину $\displaystyle z$, а $\displaystyle \arg{z}$ главный угол $\ displaystyle z$ в интервале $\displaystyle (-\pi, \pi]$.{(\ln a)z} \quad (a \text{ является допустимым основанием})$ Логарифмическая функция (произвольное основание) : $\displaystyle \log_a x \, \stackrel{def}{= } \, \frac{\ln x}{\ln a} \qquad (x \ne 0, a \text{ является допустимым основанием})$ Свойства логарифма : (т. е. Правило произведения , Правило взаимности , Правило частных , Степенное правило и Корневое правило ).{z_2}}$) осталось. Все другие свойства, которые полагаются на связанные с аргументом свойства логарифма, не работают (например, Common-Exponent Properties , Power Property ). Хорошо. Вот завершение увлекательной темы, известной как логарифм, так что независимо от того, предпочитаете ли вы его реальный или сложный, или предпочитаете алгебраический или прикладной, по крайней мере, теперь нет больше оправданий, чтобы их избегать!
Великолепная Математика и Науки Вики
Шкала Рихтера:
Шкала Рихтерабыла разработана Чарльзом Рихтером в 1935 году для сравнения силы землетрясений.Количество энергии, высвобождаемой при землетрясении, очень велико, поэтому логарифмическая шкала позволяет избежать использования больших чисел.
Для этих расчетов используется формула
.M=log10(II0),M= \log_{10}\left(\frac{I}{I_0}\right),M=log10(I0I),
, где MMM — магнитуда по шкале Рихтера, III — интенсивность измеряемого землетрясения, а I0I_0I0 — интенсивность эталонного землетрясения.
Давайте сделаем небольшой пример, чтобы прояснить, как это работает.
Землетрясение в Сан-Франциско в 1906 году имело магнитуду 8,3 балла по шкале Рихтера.
В то же время в Южной Америке произошло землетрясение магнитудой 4,1, причинившее лишь незначительные разрушения. Во сколько раз сильнее было землетрясение в Сан-Франциско, чем в Южной Америке?
Поскольку магнитуда представляет собой логарифм с основанием 10, число Рихтера на самом деле представляет собой показатель степени, до которого 10 возводят для расчета интенсивности землетрясения. Таким образом, разность магнитуд землетрясений можно рассчитать следующим образом:
М=лог10(108.M \ приблизительно 15848,
10M≈15848,
раза!
Обратите внимание, что вы можете просто вычесть 4,1 из 8,3 и получить тот же результат. Но если ваши учителя математики такие же, как мои, они захотят, чтобы вы использовали логарифмы, и вот как это делается. Причина, по которой вычитание величин работает, заключается в правиле экспоненты для деления экспонент с одним и тем же основанием.
Шкала децибел:
Один децибел — одна десятая бела, назван в честь Александра Грэхема Белла.
.Бел редко используется без префикса деци-, означающего одну десятую.Шкала децибел используется для расчета разницы в интенсивности между двумя звуками:
L=10log10(II0),L=10\log_{10}\left(\frac{I}{I_0}\right),L=10log10(I0I),
, где L LL — громкость звука, измеренная в децибелах, III — интенсивность измеряемого звука, а I0I_0I0 — интенсивность звука на пороге слышимости, равная нулю децибел.
pH\text{pH}Шкала pH:
Шкала pH\text{pH}pH была изобретена в 1910 г.Сорен Соренсон, руководитель лаборатории Carlsberg Beer Company. Буква «H» в слове pH\text{pH}pH обозначает водород, а значение «p» в слове pH\text{pH}pH, хотя и оспаривается, обычно считается означающим силу водорода. Эта шкала используется для измерения кислотности или щелочности воды или водорастворимых веществ, включая почву или дождевую воду, но не ограничиваясь ими. Шкала pH\text{pH}pH колеблется от 1 до 14, где семь — нейтральная точка. Значения ниже 7 указывают на кислотность, при этом 1 является наиболее кислой.
.Значения выше 7 указывают на щелочность, причем 24 является самой щелочной:
pH=-log10[HX+],\text{pH}=-\log_{10}\ce{[H+]},pH=-log10[HX+],
, где pH\text{pH}pH — значение pH\text{pH}pH в диапазоне от 111 до 141414, а [HX+]\ce{[H+]}[HX+] — концентрация ионов водорода.
Работа с экспонентами и логарифмами
Что такое экспонента?
Показатель степени числа говорит сколько раз
до использовать число в умножении.В этом примере: 2 3 = 2 × 2 × 2 = 8
(2 используется 3 раза при умножении, чтобы получить 8)
Что такое логарифм?
Логарифм идет другим путем.
Задает вопрос «какой экспонент произвел это?»:
И отвечает на него так:
В этом примере:
- Показатель степени берет 2 и 3 и дает 8 (2, используется 3 раза при умножении, дает 8)
- Логарифм берет 2 и 8 и дает 3 (2 дает 8 при умножении 3 раз)
Логарифм говорит сколько одного числа нужно умножить, чтобы получить другое число
Таким образом, логарифм фактически дает показатель степени в качестве ответа :
.(Также посмотрите, как связаны экспоненты, корни и логарифмы.)
Совместная работа
Экспоненты и логарифмы хорошо работают вместе, потому что они «отменяют» друг друга (при условии, что основание «а» одинаково):
Это «обратные функции»
Выполнив одно, затем другое, вы вернетесь к тому, с чего начали:
Выполнение a x , затем log a снова дает вам x : Выполнение log a , затем a x снова дает вам x :
Жалко пишут так по другому … это делает вещи странными. Таким образом, может помочь думать о x как о «верхнем» и регистрировать как (x) как «нижнем»:
.идет вверх, затем вниз, возвращает вас снова: вниз(вверх(x)) = x
идет вниз, затем вверх, возвращает вас снова: вверх(вниз(x)) = x
В любом случае, важно то, что:
Логарифмическая функция «отменяется» экспоненциальной функцией.

(и наоборот)
Как в этом примере:
Пример, что такое
x в логарифме 3 (x) = 5Начните с: log 3 (x) = 5
Мы хотим «отменить» журнал 3 , чтобы мы могли получить «x =»
Используйте экспоненциальную функцию (с обеих сторон): И мы это знаем, поэтому:x = 3 5Ответ: х = 243
А также:
Пример: вычислить y в
y=log 4 (1/4)Начните с:y = log 4 (1/4)
Используйте экспоненциальную функцию с обеих сторон:Упростить:4 y = 1/4
Теперь простой трюк: 1/4 = 4 −1
Итак:4 у = 4 −1
Итак: y = −1
Свойства логарифмов
Одна из сильных сторон логарифмов заключается в том, что они могут превратить умножение в сложение .
log a ( m × n ) = log a m + log a n
«логарифм умножения равен сумме логов»
Почему это так? См.
сноску.
Используя это свойство и законы экспонент, мы получаем следующие полезные свойства:
log a (m × n) = log a m + log a n журнал умножения представляет собой сумму журналов бревно a (м/н) = log a m − log a n лог деления разница логов log a (1/n) = −log a n это просто следует из предыдущего правила «деления», потому что log a (1) = 0 log a (m r ) = r (log a m) логарифм m с показателем r равен r, умноженному на логарифм m Помните: основание «а» всегда одинаково!
История: Логарифмы были очень полезны до изобретения калькуляторов.
.. например, вместо умножения двух больших чисел, используя логарифмы, вы могли бы превратить это в сложение (гораздо проще!)
И в помощь были книги, полные таблиц логарифмов.
Давайте повеселимся, используя свойства:
Пример: Упростить
log a ( (x 2 +1) 4 √x )Начните с: log a ( (x 2 +1) 4 √x )
Использовать log a (mn) = log a m + log a n :log a ( (x 2 +1) 4 : 04 ) + log 90
Использовать log a (m r ) = r (log a m) : 4 log a (x 2 +1) + log
a ( √0034)Также √x = x ½ :4 log a (x 2 +1) + log a ( x ½ )
Используйте log a (m r ) = r (log a m ) снова: 4 log a (x 2 +1) + ½ log a x 3 40
Это все, что мы можем упростить.
.. мы ничего не можем сделать с журналом a (x 2 +1).
Ответ: 4 log a (x 2 +1) + ½ log a (x)
Примечание: правила обработки журнала a (m+n) или журнала a (m−n)
отсутствуют.
Мы также можем применить правила логарифмирования «наоборот» для комбинирования логарифмов:
Пример: Превратите это в один логарифм:
log a (5) + log a (x) − log a (2)Начните с: log a (5) + log a (x) − log a (2)
Использовать log a (mn) = log a m + log a n :log a (5x) − log a (2)
Использовать log a (m/n) = log a m − log a n : log a (5x/2)
Ответ: журнал a (5x/2)
Натуральный логарифм и натуральные показательные функции
Когда основание равно e («Число Эйлера» = 2.
718281828459 …) получаем:
- Натуральный логарифм log e (x) , который чаще пишется как ln(x)
- Естественная экспоненциальная функция e x
И та же идея, что одно может «отменить» другое, по-прежнему верна:
ln(e х ) = х
e (ln x) = x
А вот их графики:
Натуральный логарифм
Естественная экспоненциальная функция
График f(x) = ln(x) График f(x) = e x
Проходит через (1,0) и (e,1)
Проходит через (0,1) и (1,e)
Это одна и та же кривая с перевернутыми осями x и y .
Еще одна вещь, чтобы показать вам, что они являются обратными функциями.
На калькуляторе натуральный логарифм — это кнопка «ln».
По возможности всегда старайтесь использовать натуральные логарифмы и натуральную экспоненциальную функцию.
Десятичный логарифм
Когда база равна 10 , вы получаете:
- Десятичный логарифм log 10 (x) , который иногда записывается как log(x)
Инженеры любят его использовать, но в математике он используется редко.
На калькуляторе десятичный логарифм — это кнопка «журнал».
Это удобно, потому что говорит вам, насколько «большим» является десятичное число (сколько раз вам нужно использовать 10 при умножении).
Пример: Расчет журнала
10 100Хорошо, 10 × 10 = 100, поэтому, когда 10 используется 2 раз при умножении, вы получаете 100:
журнал 10 100 = 2
Аналогично log 10 1000 = 3, log 10 10000 = 4 и так далее.
Пример: Расчет журнала
10 369ОК, лучше всего использовать кнопку «журнал» моего калькулятора:
log 10 369 = 2,567…
Замена основания
Что делать, если мы хотим изменить основание логарифма?
Легко! Просто используйте эту формулу:
«х увеличивается, а уменьшается»
Или, по-другому, log b a похоже на «коэффициент преобразования» (та же формула, что и выше):
Итак, теперь мы можем преобразовать любую базу в любую другую базу.
Другое полезное свойство:
Видите, как «x» и «a» меняются местами?
Пример: вычислить 1 / log
8 21 / журнал 8 2 = журнал 2 8
И 2 × 2 × 2 = 8, поэтому, если 2 используется 3 раз при умножении, вы получите 8:
1 / журнал 8 2 = журнал 2 8 = 3
Но мы чаще пользуемся натуральным логарифмом, так что это стоит запомнить:
Пример: Расчет журнала
4 22
В моем калькуляторе нет кнопки « log 4 «.
..
… но у него есть кнопка « ln «, поэтому мы можем использовать ее:
журнал 4 22 = пер. 22 / пер. 4
= 3,09…/1,39…
= 2,23 (до 2 знаков после запятой)
Что означает этот ответ? Это означает, что 4 с показателем степени 2,23 равно 22. Таким образом, мы можем проверить этот ответ:
.Чек: 4 2,23 = 22,01 (достаточно близко!)
Вот еще пример:
Пример: Расчет журнала
5 125журнал 5 125 = пер. 125 / пер. 5
= 4.83…/1,61…
=3 (точно)
Я случайно узнал, что 5 × 5 × 5 = 125 (5 используется 3 раз, чтобы получить 125), поэтому я ожидал ответа 3 , и это сработало!
Использование в реальном мире
Вот несколько примеров использования логарифмов в реальном мире:
Землетрясения
Магнитуда землетрясения имеет логарифмическую шкалу.
В знаменитой «шкале Рихтера» используется следующая формула:
.М = журнал 10 А + В
Где A — амплитуда (в мм), измеренная сейсмографом
, а B — поправочный коэффициент расстоянияВ настоящее время есть более сложные формулы, но они все еще используют логарифмическую шкалу.
Звук
Громкость измеряется в децибелах (дБ для краткости):
Громкость в дБ = 10 log 10 (p × 10 12 )
, где p — звуковое давление.
Кислотный или щелочной
Кислотность (или щелочность) измеряется в pH:
pH = -log 10 [H + ]
, где H + — молярная концентрация растворенных ионов водорода.
Примечание: в химии [ ] означает молярную концентрацию (моль на литр).Дополнительные примеры
Пример: решить 2 log
8 x = log 8 16Начните с: 2 log 8 x = log 8 16
Внесите в журнал цифру «2»: log 8 x 2 = log 8 16
Удалите бревна (они одной базы): x 2 = 16
Решить:x = −4 или +4
Но.
.. но… но… у вас не может быть лог отрицательного числа!
Таким образом, случай −4 не определен.
Ответ: 4
Проверьте: воспользуйтесь калькулятором, чтобы узнать, правильный ли это ответ… также попробуйте вариант «−4».
Пример: Решите e
−w = e 2w+6Начните с:e −w = e 2w+6
Нанесите ln на обе стороны: ln(e −w ) = ln(e 2w+6 )
И ln(e w )=w : −w = 2w+6
Упростить: −3w = 6
Решите: w = 6/−3 = −2
Ответ: w = −2
Проверить: e −(−2) = e 2 и e 2(−2)+6 =e 2
Сноска: почему
log(m × n) = log(m) + log(n) ?Чтобы увидеть , почему , мы будем использовать и:
Сначала преобразуйте m и n в «показатели логарифмов»:
Затем используйте один из законов экспоненты
Наконец, отменить экспоненты.
Это одна из тех умных вещей, которые мы делаем в математике, которую можно описать как «мы не можем сделать это здесь, поэтому давайте пройдемся по там , затем сделаем это, затем вернемся»
БиоМатематика: Логарифмические функции
В этом разделе мы научимся решать уравнения, содержащие показательную или логарифмическая функция. Мы начнем с рассмотрения двух простых уравнений:
(1) 5 e x = 11,
(2) логарифм (2 х ) = 3.
Чтобы решить (1) и (2), нам нужно найти значение (я) x , для которых уравнения истинное утверждение. Важно понимать, что (1) и (2) НЕ верны для всех значения x . Начнем с уравнения (1).
Решение уравнения 1:
5 e x = 11
Как и при решении любого другого уравнения, наша цель — выделить член, включающий x .
.Здесь мы начинаем с деления обеих частей уравнения на 5
Теперь, когда член e x находится сам по себе на одной стороне, мы должны «отменить» экспоненциальную чтобы освободить x . Поскольку наша экспонента имеет основание e , мы берем логарифм по основанию e обе стороны (т.е. натуральный логарифм обеих сторон),
Таким образом, решение уравнения (1) равно
Решение уравнения 2:
log (2 x ) = 3
В этом уравнении член, включающий x , уже изолирован в одной части уравнения.Поэтому мы начнем с «отмены» логарифмической функции по основанию 10 путем возведения в степень обоих стороны уравнения с основанием 10,10 журнал (2 x ) = 2 x = 10 3 = 1000.
Следовательно, мы находим решение уравнения (2) равным
Сейчас попробуем решить еще несколько сложных уравнений.
Хотя эти уравнения могут показаться более сложными, наша цель остается прежней: найдите значение (я) x , которое делает утверждения уравнений верными.
Решение экспоненциальных уравнений с основанием, которого нет в вашем калькуляторе
Решение уравнения 3 :
6 · 2 9+ x = 30
Начнем с выделения термина, включающего x ,
Чтобы найти x , мы должны отменить экспоненту. Несмотря на то, что экспонента по основанию 2, мы будем использовать десятичный логарифм, так как его будет легче получить примерный ответ на нашем калькуляторе,
Используя свойства логарифмов, мы упрощаем приведенное выше уравнение как,
(9 + х ) логарифм (2) = логарифм (5).
Решение x дает,
Вы всегда можете проверить свой ответ, подставив точный ответ, который вы нашли обратно в исходное уравнение.Решение уравнения 4:
3 log 6 (4 + 3 x ) − 2 = 6
Начнем с выделения термина, включающего x ,
Чтобы найти x , нам нужно освободить x из логарифма по основанию 6.Для этого возводим обе части в степень с основанием 6,
.Решение для x у нас есть,
Решение уравнений с экспонентами с разными основаниями
Решение уравнения 5:
3 7−2 x = 4 3+ x
В этом уравнении экспоненты имеют разные основания.
Мы возьмем обычный (по основанию 10) логарифм обеих сторон, чтобы отменить эти экспоненты, и использовать свойства логарифмов,
Перенос терминов размером x в одну сторону и всех остальных терминов в другую,
Факторизация выходов x ,
Теперь мы можем решить уравнение
Решение уравнений с кратными логарифмами
Решение уравнения 6:
2 log 3 (2x) = log 3 (4) + log 3 (3 + 2x)
В этом уравнении следует обратить внимание на две вещи: обе части имеют логарифмы, и одна сторона имеет несколько логарифмов.При работе с несколькими логарифмами на одна сторона, проще всего объединить их в один логарифм, используя в свойства логарифмов.
Однако при этом вам необходимо проверить свои решения. когда вы закончите решать проблему, потому что объединение логарифмов может привести к посторонним решениям.
Начнем с упрощения обеих сторон, используя свойства логарифмы,
Возведение в степень обеих сторон с основанием 3 дает,
Чтобы найти x , мы должны решить квадратное уравнение,
4 х 2 — 8 х — 12 = 0.
Используя квадратичную формулу, решения даются как,
Таким образом, мы находим решения равными x = 3 и x = −1. Поскольку мы объединили логарифмы, мы должны проверить эти решения в исходном уравнении. Проверка
х = 3 дает,2 log 3 (2 · 3) = 2 log 3 (6) ≈ 3.
26,
слева и
log 3 (4) + log 3 (3 + 2 · 3) = log 3 (4) + log 3 (9) ≈ 3,26,
с правой стороны. Эти решения проверяют.
Однако решение x = −1 не проверяет. Если мы попытаемся подставить
x = −1 в исходное уравнение, мы бы,2 лог. 3 (2 · −1),
с левой стороны.Конечно, логарифм отрицательного числа не определен. на вещественной прямой, и мы заключаем, что x = −1 является посторонним решением.
Следовательно, мы заключаем, что решение уравнения (6) равно x = 3,
.
*****
Теперь попробуйте решить некоторые практические задачи с использованием логарифмов и решением логарифмических уравнений.

Проблемы
Формула логарифма: объяснение, формула, примеры решений и важные часто задаваемые вопросы{3} = 1000\], затем \[3 = \log_{10}{1000}\]. Логарифмы с основанием 10 обычно известны как обычные или бриггсовские логарифмы и просто записываются как log n. В этой статье мы обсудим, что такое логарифм, формулы логарифмов, основные формулы логарифмов, правило изменения основания, правила и формулы логарифмов, для чего используется логарифм и т. д. полезны при расширении логарифмов, сокращении логарифмов и решении логарифмических уравнений.Семь правил логарифмирования обсуждаются ниже:
1. Правило произведения
\[\log_{b}{(P \times Q)} = \log_{b}{P} + \log_{b}{Q} \]
Логарифм произведения равен сумме логарифмов факторов.
2. Частное правило
\[\log_{b}{(\frac{P}{Q})} = \log_{b}{P} — \log_{b}{Q}\]
Логарифм отношения двух чисел – это разница между логарифмом числителя и знаменателя.
{Q})} = q \times \log_{b}{P} \]
Приведенное выше свойство правила произведения гласит, что Логарифм положительного числа p в степени q эквивалентен произведению q и log числа p.{\log_{b}{y}}\] = \[y\]
Приведенное выше правило гласит, что возведение логарифма числа в основание логарифма равно числу.
7. Правило тождества
\[\log_{y}{y} = 1 \]
Аргумент логарифма (в скобках) подобен основанию. Поскольку основание равно аргументу, y может быть больше 0, но не может быть равен 0.
Формулы логарифмирования
Ниже приведены некоторые из различных формул логарифмирования, которые помогают решать уравнения логарифмирования.{n})} \]
Сложение и вычитание
Изменение базовой формулы
.
\[\log_{n}{m} = \frac{\log_{d}{m}}{\log_{d}{n}}\]
Решенные примеры
1.
Решить Далее: \[2 \log_{4}{29} \]
Решение:
Дано,
\[2 \log_{4}{29} \]
Используя замену базовой формулы n, мы получаем
\[\log_{b}{x} = \frac{\log_{d}{m}}{\log_{10}{4}}\]
\[2 \log_{4}{29} = \frac{\log_{10}{29}}{\log_{10}{4}}\]
\[2 \log_{4}{29} = 2 \times 2.{4}\] = 10000, поэтому \[\log_{10}{10000} = 4\].
Мы можем представить логарифм произведения как сумму логарифмов, логарифм частного как разность логарифмов и логарифм мощности как произведение, используя эти функции.
Вещественное число Логарифмы видны только в положительных действительных числах; отрицательные и комплексные числа имеют комплексные логарифмы.
Применение логарифмов
Логарифмы имеют широкий спектр применений как в математике, так и за ее пределами.Давайте рассмотрим несколько примеров того, как логарифмы используются в повседневной жизни:
Они используются для расчета магнитуды землетрясения.
Логарифмы используются для расчета уровня шума в децибелах, например звука колокола.
Логарифмы используются в химии для определения кислотности или уровня pH.
Они используются для расчета прироста денег при заданной процентной ставке.
Логарифмы обычно используются для расчета времени, необходимого для распада или экспоненциального развития чего-либо, например роста бактерий или радиоактивного распада.
Их также можно использовать в вычислениях, требующих преобразования умножения в сложение или наоборот.
Вместо простого вычисления мы можем использовать таблицу логарифмов, чтобы получить логарифм целого числа. Прежде чем вычислять логарифм числа, мы должны сначала понять его характеристическую и мантиссу части.
Характеристическая часть — Характеристический компонент — это целая часть числа. Любое число больше единицы имеет положительную характеристику, а если оно на единицу меньше, чем количество цифр слева от десятичной точки в данном целом числе, оно имеет отрицательную характеристику.
Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой.
Часть мантиссы. Часть мантиссы представляет собой десятичную часть логарифмического числа, которая всегда должна быть положительной. Если часть мантиссы имеет отрицательное значение, превратите ее в положительное значение.
Как использовать таблицу журнала?
Ниже показан процесс определения значения журнала числа с помощью таблицы журнала.Во-первых, вы должны понять, как использовать таблицу журнала. Таблица журнала предоставляется как ресурс для определения значений.
Шаг 1: Поймите идею логарифма. Каждая таблица журнала может использоваться только на определенной основе. Логарифмическая база 10 — наиболее часто используемая форма таблицы логарифмов.
Шаг 2: Определите часть характеристики и мантиссы числа. Чтобы получить значение \[\log_{10}{(15.27)}\], например, сначала разделите характеристики и части мантиссы.
Часть характеристики = 15
Часть мантиссы = 27
Шаг 3: Используйте общую таблицу журнала.Теперь используйте строку 15, чтобы проверить столбец 2 и записать соответствующее значение. В результате получается 1818.
Шаг 4: Вычислите среднюю разницу, используя таблицу логарифмов. Проведите пальцем по столбцу средней разницы 7 и строке 15 и запишите соответствующее значение как 20.
Шаг 5: Объедините значения, полученные на шагах 3 и 4. Это равно 1818 + 20 = 1838. В результате значение 1838 представляет часть мантиссы.
Шаг 6. Найдите отличительный признак. Поскольку это число находится в диапазоне от 10 до 100 (от 101 до 102), отличительным признаком должен быть номер 1.
Шаг 7: Наконец, объединив часть характеристики и мантиссы, получим 1,1838.
Пример
Вот пример использования таблицы логарифмов для получения значения логарифмической функции.
Определите значение \[\log_{10}{2,872}\].
Решение:
Шаг 1. Компонент характеристики равен 2, а часть мантиссы равна 872.
Шаг 2. Изучите строки 28 и 7 таблицы. В итоге получается значение 4579.
Шаг 3: Изучите значение средней разницы для строки 28 и среднюю разницу в столбце 2. Значение, связанное со строкой и столбцом, равно 3.
Шаг 4: Сложив числа из шагов 2 и 3, мы получим 4582. Это раздел мантиссы.
Шаг 5: Поскольку количество цифр слева от десятичной части равно единице, характеристическая часть меньше единицы. В результате характеристическая часть будет равна 0
. Шаг 6: Наконец, соедините характеристическую часть и часть мантиссы.В результате получается 0,4582.
В результате log 2,872 = 0,4582
Время викторины
1. Какое из следующих утверждений неверно?
\[\log_{7}{7}\] = 1
\[\log ( 4 + 3) = \log {( 4 \times 3)} \]
\[ \log_{10}{1} = 0 \]
\[\log ( 4 + 5 + 6) = \log{4} + \log{5} + \log{6} \]
2.
Каково значение \[\frac{\log{\sqrt{8}}}{\log{8}}\]?
\[\frac{1}{\sqrt{8}}\]
\[\frac{1}{4}\]
\[\frac{1}{2 }\]
\[\frac{1}{8}\]
Упрощение логарифмов — Математика средней школы
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105Или заполните форму ниже:
.



 (относительно порога слышимости ). На практике это означает, что каждое увеличение на 10 дБ (экв., 1 Б) увеличивает звуковую мощность источника в 9 0 049 десяти раз 90 050 .
(относительно порога слышимости ). На практике это означает, что каждое увеличение на 10 дБ (экв., 1 Б) увеличивает звуковую мощность источника в 9 0 049 десяти раз 90 050 . n \right] = \log x \end{align*}
n \right] = \log x \end{align*}
 Что бы вы сделали?
Что бы вы сделали?
 {3.01}$), что соответствует 4-значному номеру .
{3.01}$), что соответствует 4-значному номеру . Однако при дальнейшем рассмотрении можно увидеть, что на самом деле это не так: цепное правило превращает логарифм в произведение логарифмов с различными основаниями , в то время как правило смены основания превращает логарифм в частное логарифмов с тем же основанием . Кроме того, цепное правило незначительно облегчает вычисление логарифма по новому основанию, в то время как правило изменения основания фактически полностью устраняет зависимость от старого основания.
Однако при дальнейшем рассмотрении можно увидеть, что на самом деле это не так: цепное правило превращает логарифм в произведение логарифмов с различными основаниями , в то время как правило смены основания превращает логарифм в частное логарифмов с тем же основанием . Кроме того, цепное правило незначительно облегчает вычисление логарифма по новому основанию, в то время как правило изменения основания фактически полностью устраняет зависимость от старого основания. С появлением компьютеров и калькуляторов Правило смены основания также открывает возможность вычисления логарифма по произвольному основанию, стандартизируя по основанию $e$, или — если научный калькулятор используется — для основания $10$.
С появлением компьютеров и калькуляторов Правило смены основания также открывает возможность вычисления логарифма по произвольному основанию, стандартизируя по основанию $e$, или — если научный калькулятор используется — для основания $10$.
 {\ln 3})\end{align*}
{\ln 3})\end{align*} {yi}$ обозначает -единичное комплексное число с углом $y$.{\pi я} = -e$. На самом деле, можно также видеть, что по построению , любая экспонента обязательно является числом с ненулевой длиной (т. е. экспонента всегда ненулевая ).
{yi}$ обозначает -единичное комплексное число с углом $y$.{\pi я} = -e$. На самом деле, можно также видеть, что по построению , любая экспонента обязательно является числом с ненулевой длиной (т. е. экспонента всегда ненулевая ). {- \pi i} = \dots = -1 \end{align*}
{- \pi i} = \dots = -1 \end{align*} {(\ln a)z} \end{align*}
{(\ln a)z} \end{align*} 2 \right] = \ln 1 = 0$, но $\displaystyle 2 \ln (-1) = 2 \pi i$ .
2 \right] = \ln 1 = 0$, но $\displaystyle 2 \ln (-1) = 2 \pi i$ . z$ до ветви , мы можем определить логарифм для всех ненулевых комплексных чисел — и сделать это, используя любое действительное основание на свете.
z$ до ветви , мы можем определить логарифм для всех ненулевых комплексных чисел — и сделать это, используя любое действительное основание на свете.
 x) = x$
x) = x$ Logarithmic Scale
Logarithmic Scale  {yi} \quad ( \text{для всех }x, y \in \mathbb{ R})$
{yi} \quad ( \text{для всех }x, y \in \mathbb{ R})$
 В то же время в Южной Америке произошло землетрясение магнитудой 4,1, причинившее лишь незначительные разрушения. Во сколько раз сильнее было землетрясение в Сан-Франциско, чем в Южной Америке?
В то же время в Южной Америке произошло землетрясение магнитудой 4,1, причинившее лишь незначительные разрушения. Во сколько раз сильнее было землетрясение в Сан-Франциско, чем в Южной Америке? Бел редко используется без префикса деци-, означающего одну десятую.Шкала децибел используется для расчета разницы в интенсивности между двумя звуками:
Бел редко используется без префикса деци-, означающего одну десятую.Шкала децибел используется для расчета разницы в интенсивности между двумя звуками: Значения выше 7 указывают на щелочность, причем 24 является самой щелочной:
Значения выше 7 указывают на щелочность, причем 24 является самой щелочной: (Также посмотрите, как связаны экспоненты, корни и логарифмы.)
(Также посмотрите, как связаны экспоненты, корни и логарифмы.) 
 сноску.
сноску. .. например, вместо умножения двух больших чисел, используя логарифмы, вы могли бы превратить это в сложение (гораздо проще!)
.. например, вместо умножения двух больших чисел, используя логарифмы, вы могли бы превратить это в сложение (гораздо проще!) .. мы ничего не можем сделать с журналом a (x 2 +1).
.. мы ничего не можем сделать с журналом a (x 2 +1). 718281828459 …) получаем:
718281828459 …) получаем:

 ..
..
 .. но… но… у вас не может быть лог отрицательного числа!
.. но… но… у вас не может быть лог отрицательного числа!
 Здесь мы начинаем с деления обеих частей уравнения на 5
Здесь мы начинаем с деления обеих частей уравнения на 5

 Мы возьмем
обычный (по основанию 10) логарифм обеих сторон, чтобы отменить эти экспоненты, и
использовать свойства логарифмов,
Мы возьмем
обычный (по основанию 10) логарифм обеих сторон, чтобы отменить эти экспоненты, и
использовать свойства логарифмов, Однако при этом вам необходимо проверить свои решения.
когда вы закончите решать проблему, потому что объединение логарифмов может привести к посторонним решениям.
Однако при этом вам необходимо проверить свои решения.
когда вы закончите решать проблему, потому что объединение логарифмов может привести к посторонним решениям. 26,
26,
 {Q})} = q \times \log_{b}{P} \]
{Q})} = q \times \log_{b}{P} \] Решить Далее: \[2 \log_{4}{29} \]
Решить Далее: \[2 \log_{4}{29} \] 
 Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой.
Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой.

 Каково значение \[\frac{\log{\sqrt{8}}}{\log{8}}\]?
Каково значение \[\frac{\log{\sqrt{8}}}{\log{8}}\]? 
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.