Онлайн урок: Плоскость. Прямая. Луч по предмету Математика 5 класс
Важно отметить, что в начале разбора приходится некоторые понятия принимать как нечто, что не требует определения, к таким понятиям относятся понятия прямой и точки.
Немецкий учений Гильберт как-то сказал на эту тему, что “точкой можно назвать хоть стул”, тем самым говоря, что вся наша модель строится на некоторых условностях.
С этим пониманием приступим к первой теме урока.
Для начала нам нужно понять, что такое поверхность.
Есть много строгих математических формулировок, но они уместны скорее в высших учебных заведениях, пока будет достаточно обиходного понятия поверхности.
Будем понимать под поверхностью непрерывное множество точек, границу, отделяющую геометрическое тело от внешнего пространства.
Представьте себе поверхность рабочего стола, футбольного мяча или любого другого предмета.
Также известно, что некоторые поверхности, например, рабочего стола, плоские.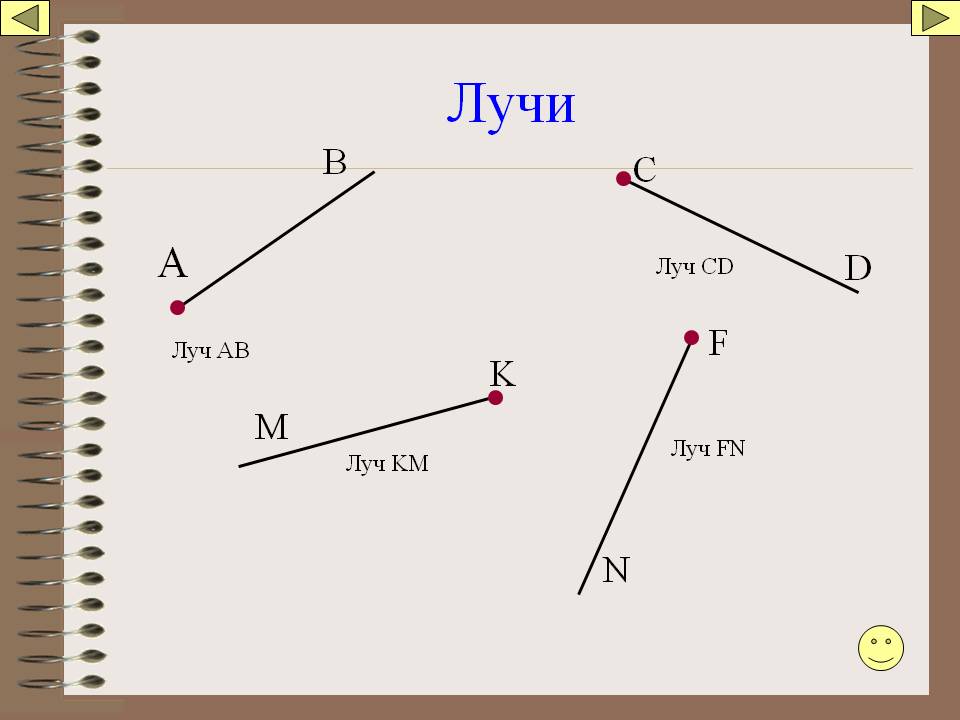
Так мы подходим к понятию плоскости. Плоскость — плоская, бесконечная поверхность.
Плоская в данном случае обозначает, что если через любые две точки, принадлежащие этой плоскости, провести прямую, то она будет лежать в этой плоскости.
В самом деле, если нарисовать две точки на поверхности стола и соединить их прямой, то эта прямая будет лежать в плоскости стола.
Если же отметить две точки на шаре, то (тут нужен некоторый мысленный эксперимент) прямая, соединяющая их, будет проходить внутри шара, а не по его поверхности. Таким образом, поверхность шара не плоская, не является плоскостью.
Сейчас очень важно понять, что плоскость — это некоторое математическое понятие, соответствующее нашим бытовым плоским поверхностям с главным отличием в том, что у плоскости нет края.
Обычно на рисунках плоскость обозначается конечной, в крайнем случае лист бумаги или экран компьютера конечен.
Но это лишь обозначения, сама плоскость бесконечна.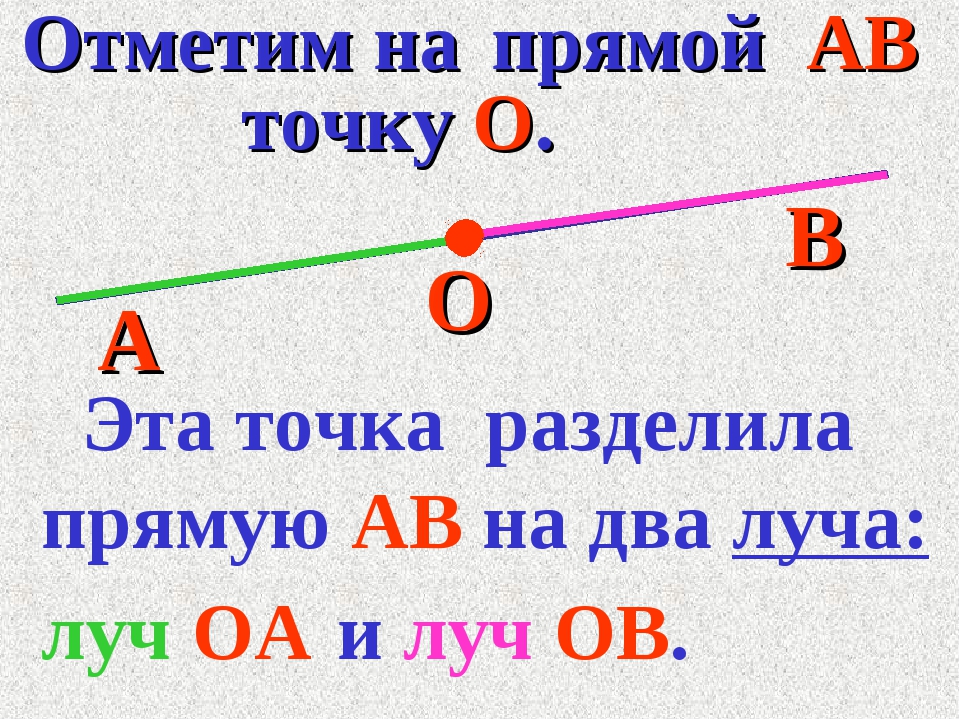
Поверхности и плоскости принято обозначать двумя способами: с помощью трех латинских букв, соответствующих трем точкам плоскости, или одной греческой.
Выше изображена четырехугольная пирамида. В ней можно насчитать 5 плоскостей:
- AEB
- BED
- BDC
- ABC
- AED (которую можно еще записать как AEC, ECD и ADC)
Согласись, две точки слишком мало, чтобы обозначить плоскость: на данном рисунке, например, есть две плоскости, проходящие через точки A и E, а четыре точки уже несут избыточную информацию, поэтому плоскости обозначают тремя точками.
Иногда плоскость обозначают одной строчной греческой буквой, например, так:
кривая, прямая. Отрезок. Луч». (1 класс).
-Отдохнули и можем работать
дальше.
-Ребята, сегодня наша тема урока «Точка. Линия: кривая, прямая. Отрезок. Луч». Как вы думаете, что нам предстоит выяснить на уроке математики? (познакомиться подробнее и узнать, как называются эти фигуры)
Какие ещё задачи мы можем
решить на уроке? ( научимся их различать, чертить)
А кто уже сейчас может дать название этим линиям? ( кривые, прямые)
Это и есть план нашего урока. Давайте работать по нему для достижения целей.
-Откройте учебник на странице 40.
Мы будем с вами учиться распознавать и изображать точку, прямую и кривую линии, отрезок, луч.
Понятие «точка».
— У каждого из вас, на парте есть карандаш и листочек бумаги. Возьмите карандаш и поставьте его на лист (учитель то же самое выполняет на доске мелом).
— что сделал карандаш? (оставил след).
— Этот след и есть точка – геометрическая фигура.
В стране Геометрии жила-была точка. Она
была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто
её не замечал. Так и жила она, пока не попала в гости к линиям. Жила она, пока не попала в гости к линиям.
Её оставил карандаш, когда наступил на лист тетради, и никто
её не замечал. Так и жила она, пока не попала в гости к линиям. Жила она, пока не попала в гости к линиям.
-Посмотрите, какие это линии. (Прямые и кривые)
-На что похожи прямые линии? (похожи на натянутые верёвочки, а верёвочки)
-Сколько прямых линий? (2)
— На что похожи кривые линии? (которые не натянули, – это кривые линии)
— Сколько кривых? (3)
Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»
-Очень интересно сталь точке посмотреть на неё. Сама-то точка малюсенькая. Вышла она, да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На её месте появился луч.
-Он тоже был очень
длинный, но все-таки не такой, как прямая линия. У него появилось начало.
У него появилось начало.
-Испугалась точка: «Что же я наделала?» Хотела она убежать, да как назло наступила опять на луч.
-И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.
-Вот так маленькая точка смогла изменить жизнь больших линий.
-Ребята, какие же геометрические фигуры живут в стране геометрии? (точка, прямая линия, кривая линия, луч, отрезок)
Проверочная работа по математике «Луч и его обозначение» 2 класс
Фамилия______________ Имя___________ Класс_________
№1. Запиши цифрами: двенадцать, двадцать один, сорок три, пятьдесят, пятнадцать, шестьдесят восемь
№2. Запиши по порядку числа от 83 до 76. Обведи все числа, которые больше 80.
№3. 7+8 15-9 17-10 (9+7)-8
6+7 14-6 30+7 17- (12-4)
9+5 13-4 19-9 9+ (12-6)
№4. На одной полке 12 книг, а на второй — на 3 книги
меньше. Сколько книг на второй полке?
На одной полке 12 книг, а на второй — на 3 книги
меньше. Сколько книг на второй полке?
Решение:
Ответ:
№5. Построй луч МК. Отметь точки А и В на луче и точки С и Д вне луча.
___________________________________________________________
Фамилия______________ Имя___________ Класс_________
№1. Запиши цифрами: четырнадцать, сорок один, семьдесят два, сорок, шестнадцать, пятьдесят шесть
№2. Запиши по порядку числа от 64 до 57. Обведи все числа, которые меньше 60.
№3. 9+7 13-8 15-10 (8+5)-7
8+5 16-9 40+3 15- (11-4)
7+4 15-6 17-7 8+(13-5)
№4. В спортивном зале было 9 красных мячей, а синих —
на 3 больше. Сколько синих мячей?
В спортивном зале было 9 красных мячей, а синих —
на 3 больше. Сколько синих мячей?
Решение:
Ответ:
№5. Построй луч ВК. Отметь точки А и М на луче и точки С и Д вне луча.
Презентация к уроку математики по теме «Числовой луч»
библиотека
материалов
Содержание слайдов
Номер слайда 1
Тема: Числовой луч Математика 1 класс УМК «Планета знаний»
Номер слайда 2
Мозговой штурм Вместо точек вставить недостающие фигуры
Номер слайда 3
1 2 3 4 5 Назови линии
Номер слайда 4
Тема урока:
Номер слайда 6
Номер слайда 7
Номер слайда 8
Номер слайда 9
1 см
Номер слайда 10
Номер слайда 11
1 метр
Номер слайда 12
Приборы со шкалой
Номер слайда 13
Рефлексия
Номер слайда 14
МОЛОДЦЫ!
5 класс — прямая, плоскость и луч в 5 классе, урок по математике, презентация
Дата публикации: .
Что такое плоскость? Определение, примеры
Вокруг нас множество примеров плоскостей, например, оконное стекло
Поверхность озера
Лист бумаги
Но все плоскости, о которых мы говорим, имеют границы. В математике же плоскость бесконечна, то есть не имеет границ.
Запомните!
У математической плоскости НЕТ границ. Она простирается безгранично далеко во всех направлениях.
Прямая и её особенности
Нарисуем две точки А и В и соединим их. У нас получился отрезок АВ или ВА (кому как нравится). Продолжим отрезок АВ в оба направлениях. Мы получим прямую АВ или ВА. Запомните!
Прямая не имеет начала и конца. Только границы тетрадного листа или экрана заставляют нас рисовать прямую, как отрезок, на самом деле она бесконечна. Рисуя прямую, нужно мысленно продлевать ее бесконечно.
Принято говорить, что точки А и В лежат на прямой.
В математике прямую обозначают двумя способами.
1. «Прямая АВ»
2. «Прямая с» (маленькая буква)
«Прямая с» (маленькая буква)
1. Если две прямые пересекаются в какой-либо точке, то эта точка является точкой пересечения прямых. В нашем примере прямые а и в пересекаются в точке О. Точка О делит каждую прямую на две части. 2. Через любые две точки можно провести одну единственную прямую.
Луч, Особенности
Если мы отметим на прямой точку, например, точку А, то эта точка разделит прямую на две части или на два луча.
Запомните!
Луч имеет начало, но не имеет конца. Это как луч света от какого-либо источника, который начинается от самого источник света (точки) и уходит в бесконечность.
В нашем примере точка О делит прямую АВ на два луча: луч ОА и луч ОВ. Соответственно, оба луча имеют начало в точке О, но не имеют конца. Они продолжаются до бесконечности.
Переставлять буквы в названии луча нельзя. Первой буквой всегда обозначается начало луча.
Часть I — Лучи
Часть I — ЛучиЛучи
Предположим, что в разрабатываемой нами игре игрок стреляет из ружья в противника. Как определить попала ли в цель пуля, выпущенная из заданной точки в указанном направлении? Один из возможных подходов: моделирование траектории пули с помощью луча и моделирование врага с помощью ограничивающей сферы (bounding sphere). (Ограничивающая сфера — это просто сфера минимального диаметра, в которую помещается весь объект целиком, что позволяет приблизительно представить занимаемый им объем. Более подробно об ограничивающих сферах мы поговорим в главе 11.) Тогда с помощью математических вычислений мы можем определить пересекает ли луч сферу и, если да, то где. В данном разделе мы обсудим математическую модель лучей.
Как определить попала ли в цель пуля, выпущенная из заданной точки в указанном направлении? Один из возможных подходов: моделирование траектории пули с помощью луча и моделирование врага с помощью ограничивающей сферы (bounding sphere). (Ограничивающая сфера — это просто сфера минимального диаметра, в которую помещается весь объект целиком, что позволяет приблизительно представить занимаемый им объем. Более подробно об ограничивающих сферах мы поговорим в главе 11.) Тогда с помощью математических вычислений мы можем определить пересекает ли луч сферу и, если да, то где. В данном разделе мы обсудим математическую модель лучей.
Лучи
Луч описывается путем указания начальной точки и направления. Параметрическая формула луча выглядит следующим образом:
Рис. 14. Луч, заданный начальной точкой p0 и вектором направления u. |
В формуле луча p0 — это начальная точка, u — это вектор, задающий направление луча, а t — это параметр. Подставляя различные значения t, мы сможем получать координаты различных точек луча. Причем для луча значение t должно находиться в диапазоне [0, ∞). Значения меньше нуля приведут к вычислению координат точек, находящихся за лучом (на прямой, частью которой является луч). Фактически, если t принимает значения из диапазона (–∞, ∞), мы получаем линию в трехмерном пространстве.
Пересечение луча и плоскости
Предположим, у нас есть луч p(t) = p0 + tu и плоскость n Ч p + d = 0, и мы хотим определить пересекает ли луч плоскость и, если да, то вычислить координаты точки пересечения. Для этого мы помещаем формулу луча в формулу плоскости и вычисляем такое значение параметра t, которое удовлетворяет уравнению плоскости. Подстановка найденного значения в уравнение луча позволяет вычислить координаты точки пересечения.
Подстановка найденного значения в уравнение луча позволяет вычислить координаты точки пересечения.
Подставляем формулу (9) в формулу плоскости:
Подставляем уравнение луча в формулу плоскости. |
|
|
|
Раскрываем скобки. |
|
|
|
Выносим за скобки переменную. |
|
Решение для t. |
Если значение t не находится в диапазоне [0, ∞), значит луч не пересекает плоскость.
Если значение t находится в диапазоне [0, ∞), точка пересечения находится путем подстановки найденного значения параметра в формулу луча:
Сайт управляется системой uCoz
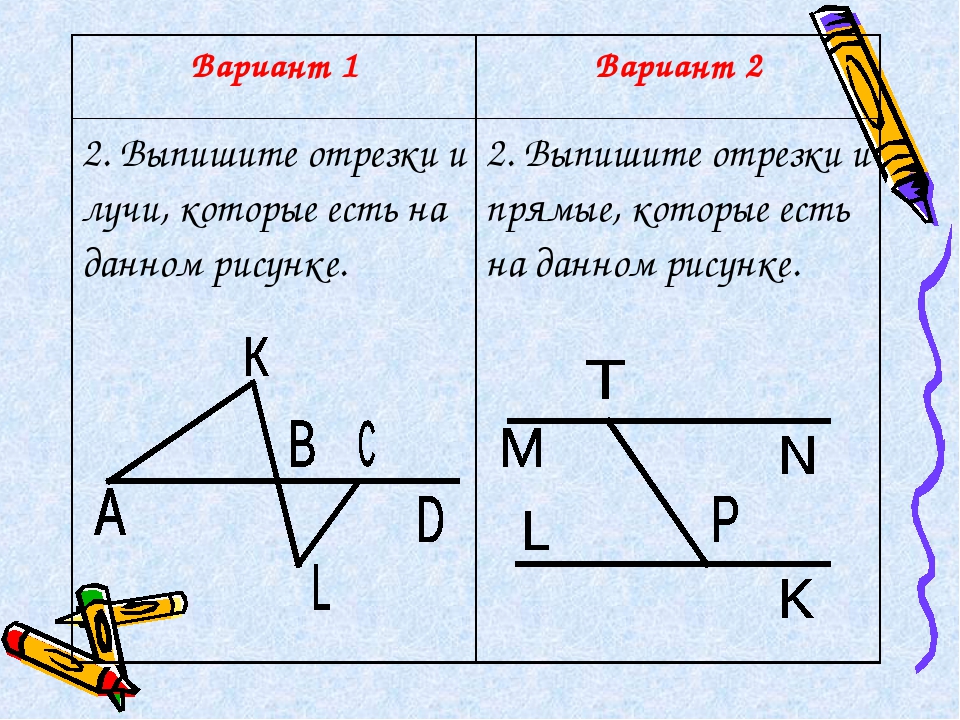
2.
 6: Дополнительная тема — Математическая теория балок
6: Дополнительная тема — Математическая теория балокУравнения равновесия балки с прямоугольным поперечным сечением могут быть элегантным образом выведены из трехмерного уравнения равновесия. При нулевых объемных силах уравнение равновесия в компактной записи имеет вид
.\[ \sigma_{ij,j} = 0 \]
или расширенное обозначение
\[i = 1, \, \sigma_{1j,j} = 0 \rightarrow \sigma_{11,1} + \sigma_{12,2} + \sigma_{13,3} = 0\]
\[i = 2, \, \sigma_{2j,j} = 0 \sigma_{21,1} + \sigma_{22,2} + \sigma_{23,3} = 0\]
\[i = 3, \, \sigma_{3j,j} = 0 \sigma_{31,1} + \sigma_{32,2} + \sigma_{33,3} = 0\]
В инженерных обозначениях полный набор уравнений равновесия, уже заданный уравнениями (2.1.26-2.1.28), это
\[\метка{2.6.5}\]
какая из компонент тензора напряжений выдержит предположение о балке. Рассмотрим балку прямоугольного сечения \((h \times b)\), подвергающуюся плоскому изгибу, рисунок (\(\PageIndex{1}\)).
Балка подвергается нагрузке давлением \(p\) в плоскости \(z = − \frac{h}{2}\). В случае плоского изгиба не должно быть градиента напряжений в направлении \(y\). Следовательно, член \(\frac{\partial \sigma_{xy}}{\partial y} = 0\).Уцелевшие компоненты лежат вне заштрихованного прямоугольника в уравнении \ref{2.6.5} и составляют:
В случае плоского изгиба не должно быть градиента напряжений в направлении \(y\). Следовательно, член \(\frac{\partial \sigma_{xy}}{\partial y} = 0\).Уцелевшие компоненты лежат вне заштрихованного прямоугольника в уравнении \ref{2.6.5} и составляют:
\[\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \sigma_{xz}}{\partial z} = 0 \label{2.6.6}\]
\[\text{Уравнение в направлении Y выполняется одинаково} \label{2.6.7}\]
\[\frac{\partial \sigma_{zx}}{\partial x} + \frac{\partial \sigma_{zz}}{\partial z} = 0 \label{2.6.8}\]
Рисунок \(\PageIndex{1}\): Исчезающие компоненты вектора напряжения.Граничные условия
Граничные условия задаются формулой Коши.Боковые поверхности \(y = \pm \frac{b}{2}\), а также нижняя полка \(z = \frac{h}{2}\) не имеют напряжений. Рассмотрим только верхнюю полку \(z = −\frac{h}{2}\), определяемую единичным вектором нормали \(\boldsymbol{n}[0, 0, −1]\). Предположим, что поперечная нагрузка не приложена, так что распределенная нагрузка направлена вдоль оси \(z\).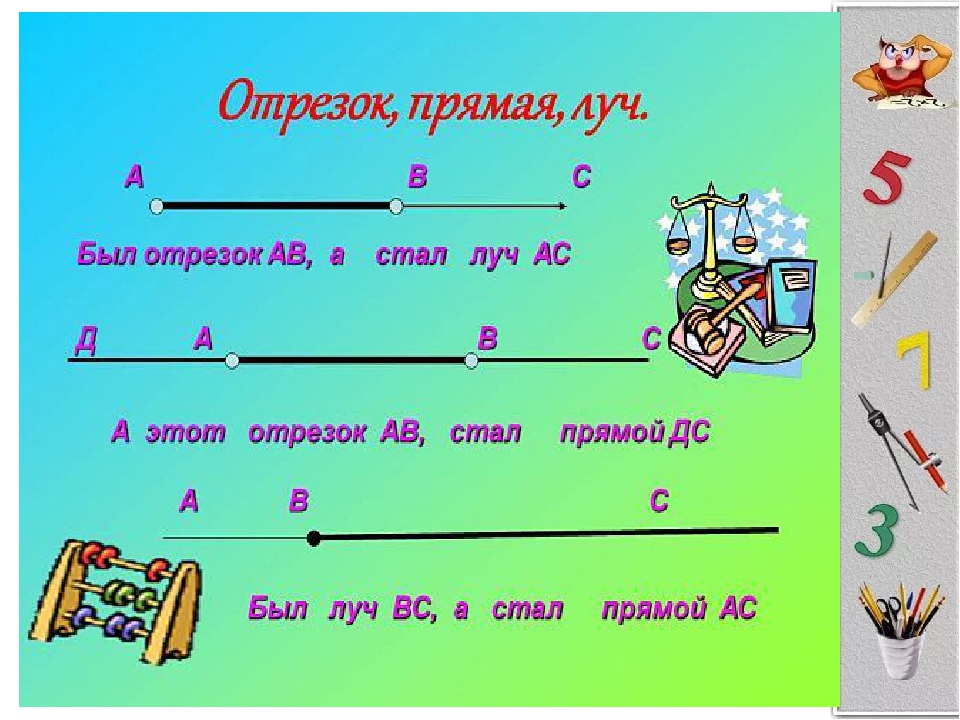 {\frac{h}{2}} \sigma_{xz} dA + b \left[\sigma_{zz }|_{\frac{h}{2}} — \sigma_{zz}|_{-\frac{h}{2}}\right] = 0 \label{2.2} + q(x) = 0\]
{\frac{h}{2}} \sigma_{xz} dA + b \left[\sigma_{zz }|_{\frac{h}{2}} — \sigma_{zz}|_{-\frac{h}{2}}\right] = 0 \label{2.2} + q(x) = 0\]
Это уравнение идентично полученному из принципа виртуальной работы.
BEAM (Будь математиком): Начальная школа: Oxford University Press
Сделайте изучение математики интересным, сложным и приятным с BEAM
Купить или оценить, используя форму заказа серии
BEAM предоставляет ряд основных ресурсов по математике, идеально подходящих для дополнительной практики по ключевым целям национальной учебной программы.
- Сосредоточенные ресурсы для развития решения проблем, рассуждений и беглости речи
- Ресурсы, основанные на исследованиях, разработанные авторами-экспертами, включая Питера Кларка
Серия содержит:
Лучшие ресурсы от BEAM
Говори, решай
Совместная деятельность, требующая, чтобы учащиеся сосредоточились на обсуждении проблем по мере их решения
Результаты поиска
<<Предыдущий Далее>> Показано 1-10 из 123 результатовПродукт | Мы можем это сделать! 3 класс Использование и применение математических задач978-1 |
Продукт | Мы можем это сделать! 6 класс Использование и применение математических задач978-1 |
Продукт | Расскажи, реши — Навыки рассуждения по математике 3 и 4 классы: Навыки рассуждения по математикеКлэр Кинг , Дженни Пеннант , Джеки Уолтерс и Брэкнелл Форест LEA 978-1 2776 Пакет | 07.06.2005 Цена: £40.25 +НДС |
Бесплатная поддержка | BEAM Counting 11-13 Self Checking Grid (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
Бесплатная поддержка | Значки BEAM, подсчитывающие 3–5 дней рождения (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
Бесплатная поддержка | BEAM, подсчитывающий 3-5 кругов животных (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
Бесплатная поддержка | BEAM Counting 3-5 Dot-to-Dot (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
Бесплатная поддержка | BEAM Counting 3-5 Counting Rays (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
Бесплатная поддержка | BEAM Counting 11-13 тюльпанов (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
Бесплатная поддержка | BEAM Счет 3-5 домино (PDF)Скачать бесплатные ресурсы по арифметике для счета, денег и измерения и обработки данных |
(PDF) Экспериментально-математическое моделирование прогиба луча
Теоретическое выражение
Теоретическое выражение для отклонения луча, который был рассчитан с учетом около
приближения и упрощения, имеет форму:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡⎟
⎠
⎠
⎞
⎜
⎝
⎛
—
⎛
⋅
=
2
3
Teorija L
A
4
3
L
L
A
IE
A
IE
L
6
F
,
Y
F
, (1)
, где: C представляет собой постоянную,
F, N, нагрузка,
a, мм – положение нагрузки,
I, мм4 – момент инерции площади поперечного сечения балки,
l, мм – длина балки, l =1000 мм,
E, ГПа, – модуль упругости, E =200 ГПа.
Следующие модели предполагалось:
• Мощность мощности:
3B2B1B
1
IAFCY
⋅ =, (2)
• Модель расширенной мощности с взаимодействиями фактора:
Fi6bai5bfa4b3b2b1b
2
EIAFCY
⋅ + ⋅ + ⋅
⋅⋅ =, (3)
⋅⋅ =, (3)
• Второй заказ полиномиал:
Y
3
= B
0
+ B
1
⋅f + B
2
⋅A + B
3
⋅i + B
11
⋅f
2
+ B
22
⋅A
2
+ B
33
⋅I
2
(4)
(4)
после модели линейности и данных Модели получены применение наименьших квадратных методов:
994119 06843965000445321965000445321,
IAF028750Y
−
⋅= (5)
fi7e22,3ai7e11,62223ai7e11,624603164816246061648,16246 06123,0
2
EIAF14936,19
⋅- + ⋅ — ⋅— ⋅⋅ = (6)
y
3
= 5 , 71711 + 0,004669⋅F-0,03862⋅A-0,0076⋅I — 0,000000048⋅F
2
2
+
+ 0 000102⋅A
2
+0,00000181 ⋅I
2
(7)
Модельные значения прогиба по моделям (5), (6), (7) приведены в табл.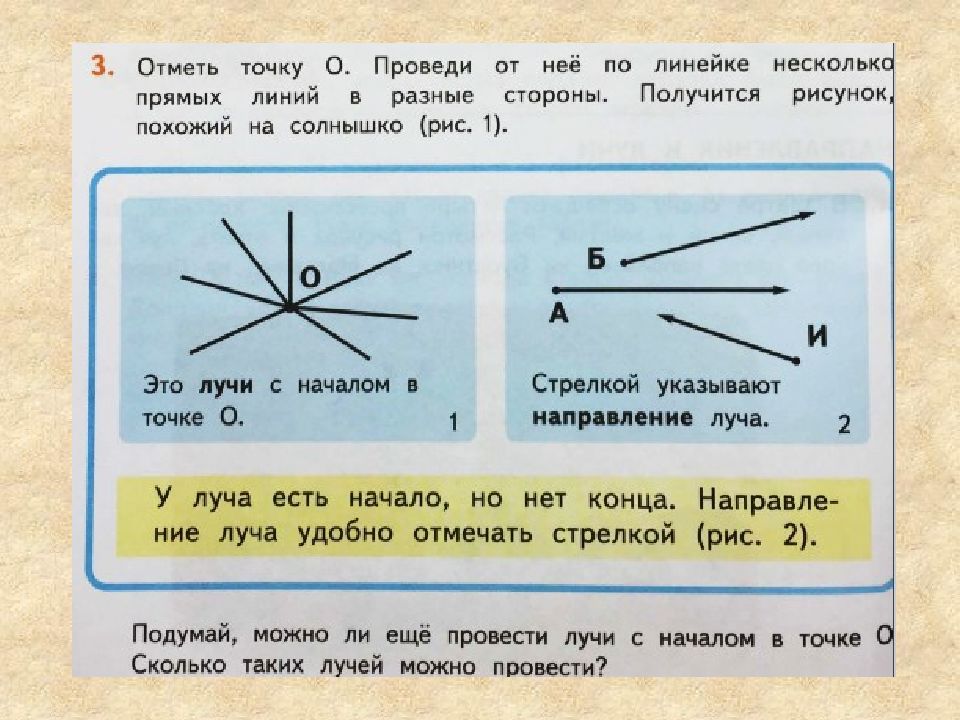 3, а также
3, а также
экспериментальные и теоретические значения (по уравнению ( 1)).
Таблица 3. Экспериментальные, теоретические и модельные значения прогиба
Эксп. Работает
лет. тэор. Модель (5) Модель (6) Модель (7)
1 2.65 2.1578 2.5391 2.9113 4.29
2 4.9625 4.2365 5.0001 4.6368 6.7
3 7.65 6.8817 6.5574 7.4765 8.0687
4 14.275 13.511 12.913 12.890 10.4787
5 0.1975 0.1499 0.1792 0,1825 -2,575
6 0,44 0,2943 0,3529 0,4111 -0,165
7 0.0,4781 0,4628 49 0,4379 1,20375
8 0,95 0,9387 0,9114 1,0676 3,61375
9 1,15 1,2055 1,2008 1,069 1,0125
10 0,85 1,2055 1,2008 1,069 1,0125
11 1,0 1,2055 1,2008 1,069 1,0125
12 1,5 1,2055 1,2008 1,069 1,0125
3. Анализ результатов
Для оценки моделей (5), (6) и (7) был использован статистический анализ данных. Некоторые результаты анализа
показаны в таблице 4 и на рисунках 3 и 4.В таблице 4 приведены значения: коэффициент регрессии
(R), коэффициент детерминации (R2), стандартные ошибки, сумма квадратов регрессии и результаты
F-критерия адекватности модели.
Математическая модель для имитации статических характеристик моста с Т-образной балкой с широкой полкой статические характеристики тавровых мостов точно.При механическом анализе применяются три обобщенные функции перемещений, а определяющие дифференциальные уравнения и естественные граничные условия статических характеристик тавровых балок устанавливаются на основе принципа вариации энергии. В примере анализируется влияние эффекта запаздывания сдвига, различных форм нагрузки и соотношения пролетов на механические свойства тавровых мостов. Поэтому метод данного исследования обогащает и развивает теоретический анализ тавровых балок и играет определенную руководящую роль при проектировании такой конструкции.
1. Введение
Железобетонные тавровые мосты получили широкое распространение в 1970-х и 1980-х годах из-за их простого усилия и удобной конструкции [1–5]. В последние годы сборные железобетонные мосты с Т-образными балками широко используются при строительстве скоростных и железных дорог в Китае, таких как подъездной мост к мосту через реку Циншань Янцзы в Ухане и мост к скоростной автомагистрали Чунцин Чэнкай. Однако с увеличением автомобильного и железнодорожного движения такие конструкции могут серьезно повреждаться, например, появляться трещины на полке и стенке, что снижает их общую жесткость и еще больше ухудшает механические свойства [6–9].Например, в 773 путепроводах и мостах через реку в Пекине большинство мостов с тавровыми балками имеют трещины, коррозию просачивания воды и отслоение бетона. Поэтому уточненный механический анализ тавровых мостов имеет теоретическое и инженерное значение.
Однако с увеличением автомобильного и железнодорожного движения такие конструкции могут серьезно повреждаться, например, появляться трещины на полке и стенке, что снижает их общую жесткость и еще больше ухудшает механические свойства [6–9].Например, в 773 путепроводах и мостах через реку в Пекине большинство мостов с тавровыми балками имеют трещины, коррозию просачивания воды и отслоение бетона. Поэтому уточненный механический анализ тавровых мостов имеет теоретическое и инженерное значение.
В настоящее время ученые проводят интенсивные исследования тавровых мостов, но структурные заболевания остаются серьезными, что показывает, что мостовики до сих пор не понимают механических свойств тавровых мостов. При изучении механических свойств таких структур необходимо учитывать новые механические условия [10–15].Ссылаясь на имеющиеся литературные источники, установлено, что при анализе механических свойств такого рода конструкций не учитываются одновременно напряжения деформации сдвига и запаздывания, условия самоуравновешенности моментов и деформации сдвига Тимошенко, что приводит к ограничению расчетов. Результаты. Поэтому в настоящем исследовании всесторонне рассматриваются различные факторы, такие как сдвиговое запаздывание, коробление, равновесие собственного напряжения, сдвиговое запаздывание и сдвиговая деформация [16–20]. Основные дифференциальные уравнения и естественные граничные условия таврового моста устанавливаются методом вариации энергии.Влияние запаздывания при сдвиге, соотношения пролетов и граничных условий на механические свойства проанализировано на примерах. В соответствии с текущими внешними условиями окружающей среды и характеристиками болезни моста метод, принятый в данной статье, призван обогатить и развить существующую теорию расчета тонкостенных конструкций [21–24] и имеет определенное руководящее значение для проектирования таких конструкций.
Результаты. Поэтому в настоящем исследовании всесторонне рассматриваются различные факторы, такие как сдвиговое запаздывание, коробление, равновесие собственного напряжения, сдвиговое запаздывание и сдвиговая деформация [16–20]. Основные дифференциальные уравнения и естественные граничные условия таврового моста устанавливаются методом вариации энергии.Влияние запаздывания при сдвиге, соотношения пролетов и граничных условий на механические свойства проанализировано на примерах. В соответствии с текущими внешними условиями окружающей среды и характеристиками болезни моста метод, принятый в данной статье, призван обогатить и развить существующую теорию расчета тонкостенных конструкций [21–24] и имеет определенное руководящее значение для проектирования таких конструкций.
2. Управляющее дифференциальное уравнение и естественные граничные условия таврового моста
2.1. Настройка функции продольного деформации полки тавровой балки
Система сил, показанная на рисунке 1, действует на тавровую балку, показанную на рисунке 2. Если пролет конструкции составляет L , то симметричное состояние изгиба представляет собой вертикальное отклонение и вертикальный угол сечения Т-образной балки элементарной теории балки, соответственно, и представляет собой вертикальное отклонение, вызванное сдвиговым эффектом запаздывания Т-образной балки. Тогда продольное смещение полки тавровой балки представляет собой сумму теоретического значения элементарной балки и продольного гистерезисного смещения крыла, вызванного эффектом сдвигового гистерезиса.
Если пролет конструкции составляет L , то симметричное состояние изгиба представляет собой вертикальное отклонение и вертикальный угол сечения Т-образной балки элементарной теории балки, соответственно, и представляет собой вертикальное отклонение, вызванное сдвиговым эффектом запаздывания Т-образной балки. Тогда продольное смещение полки тавровой балки представляет собой сумму теоретического значения элементарной балки и продольного гистерезисного смещения крыла, вызванного эффектом сдвигового гистерезиса.
Продольное перемещение пластины полки тавровой балки определяется следующим образом: где — функция неравномерного распределения полки тавровой балки, и — поправочные коэффициенты полки, удовлетворяющей равновесию собственных напряжений для сдвиговой задержки искривляющее напряжение. Из их, .
Тогда напряжение сдвига полки Т-образной балки будет следующим: где постоянные коэффициенты, полученные для удовлетворения и : .
Продольное смещение стенки тавровой балки определяется следующим образом:
Касательное напряжение полки тавровой балки используется как независимая система напряжений, которая удовлетворяет равновесию собственных напряжений для напряжения деформации сдвига запаздывания. Другими словами, Т-образное сечение будет одновременно удовлетворять балансу самонапряжения сдвига, коробления и изгибающего момента.
Другими словами, Т-образное сечение будет одновременно удовлетворять балансу самонапряжения сдвига, коробления и изгибающего момента.
2.2. Суммарная потенциальная энергия таврового моста
Нормальные и касательные напряжения полки таврового луча выражаются как
Нормальное напряжение стенки таврового луча получается как
Потенциальная энергия деформации таврового моста рассчитывается следующим образом:
Энергии деформации полки и стенки получаются как где .
Энергия деформации сдвига Тимошенко выражается как
Потенциальная энергия нагрузки измеряется как
Тогда общий потенциал системы будет следующим: полки тавровой балки; — изгибающий момент оси x , когда конец балки образует вертикальный угол ; — вертикальная поперечная сила на конце балки и вертикальная распределяющая сила на тавровой балке соответственно; – модули Юнга и сдвига материала тавровой балки соответственно; — площади поперечного сечения полки и стенки тавровой балки соответственно, в которых ; и – момент инерции тавровой балки оси x .
2.3. Дифференциальные уравнения управления и естественные граничные условия тавровых балок
На основе вариационного принципа определяющее дифференциальное уравнение тавровой балки может быть получено как
Естественные граничные условия следующие:
Подставляя дифференциальные уравнения (10) и (11), а вычисляются как где , , , а – постоянные коэффициенты, полученные в соответствии с соответствующими граничными условиями и .
Аналогично, подставив дифференциальное уравнение (12),
Решение его характеристического уравнения .
Таким образом, дифференциальное уравнение (18) рассчитывается как где , , , и – постоянные коэффициенты, полученные в соответствии с соответствующими граничными условиями .
На основе дифференциальных уравнений (10)–(12) механические свойства тавровой балки складываются из двух независимых механических систем, а именно суперпозиции элементарной теории балки и системы теории сдвигового запаздывания.
3.
 Естественные граничные условия, обычно используемые для тавровых балок
Естественные граничные условия, обычно используемые для тавровых балокКонкретные граничные условия элементарной теории балок могут быть получены с использованием уравнений (13) и (14).Обычно используются следующие граничные условия.
3.1. Граничные условия для и
① Равномерная нагрузка: ② Сосредоточенная нагрузка:Для одноопорной тавровой балки, если сила, приложенная между пролетами, включает одну или несколько сосредоточенных сил (рис. 3) и расстояния между соседними силами сосредоточенной силы равны и , индексы и представляют или координаты. Поэтому в k-точке следует ввести следующие непрерывные граничные условия:
Аналогично, граничные условия теории сдвигового запаздывания можно получить, используя уравнения (15) и (16).Обычно используются следующие граничные условия.
3.2. Граничные условия для
① Равномерная сила: ② Сосредоточенная сила: Если сила, приложенная между пролетами, включает в себя одну или несколько сосредоточенных сил (рис. 3) и число в нижнем индексе указывает, находится ли она в системе координат или, то k -точка следует также ввести граничные условия как
3) и число в нижнем индексе указывает, находится ли она в системе координат или, то k -точка следует также ввести граничные условия как
4. Анализ примера таврового моста
Материал и геометрические параметры железобетонной тавровой балки C50 следующие: модуль упругости, модуль сдвига, толщина стенки, толщина пластина крыла, длина пластины крыла и высота тавровой балки.В механическом анализе равномерная сила и сосредоточенная сила , где представляют свободно опертые балочные пролеты или сумму неразрезных балочных пролетов. Сосредоточенная сила приложена к свободно опертой балке в середине пролета или в середине одной из неразрезных балок (рис. 4). Кроме того, напряжение полки тавровой балки и продольный прогиб тавровой балки рассчитываются с использованием формулы вывода в этом исследовании и других алгоритмов (примечание: при расчете методом конечных элементов ANSYS сечение тавровой балки рисуется в соответствии с координатами пересечения тавровой балки на рисунке 2; затем для формирования тела используется функция выдавливания конечного элемента ANSYS; после разделения сетки ячеек моделируются простые или непрерывные граничные условия для наложения соответствующих ограничений на положения тавровых балок для формирования простых или непрерывных граничных условий).
В таблицах 1 и 2 и на рисунке 5 показано следующее: (1) Для свободно опертого таврового моста влияние сосредоточенной нагрузки больше, чем равномерной нагрузки при том же пролете, и чем меньше отношение ширины пролета , тем сильнее эффект запаздывания сдвига. Эффект запаздывания сдвига непрерывных мостов с Т-образной балкой более заметен, чем у просто поддерживаемых мостов с Т-образной балкой. Кроме того, эффект запаздывания сдвига неразрезных тавровых мостов с равномерной нагрузкой больше, чем с сосредоточенными нагрузками.Таким образом, специалисты по мостам должны обратить внимание на этот аспект. (2) С введением равновесия собственных напряжений для деформирующего напряжения сдвигового запаздывания механические свойства тавровых балок разлагаются на независимую элементарную теорию балки и систему теории сдвигового запаздывания, которая является новшеством данного исследования. Пример также показывает, что механические свойства мостов с Т-образными балками накладываются на теоретические значения элементарной балки и расчетные значения теории сдвигового запаздывания.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. Примечание.
Таблицы 3 и 4 и рисунок 6 иллюстрируют следующее: (1) Нормальное напряжение стенки тавровой балки состоит из двух частей, а именно суммы теоретического значения элементарной балки и влияние эффекта сдвигового запаздывания. По мере увеличения эффекта запаздывания сдвига его влияние на нормальное напряжение стенки увеличивается.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание: расчетное сечение является точкой опоры.
Таблица 5 и рисунок 7 иллюстрируют следующее: (1)Вертикальный прогиб Т-образного моста увеличивается из-за влияния эффекта сдвига.Таким образом, эффект запаздывания сдвига снижает вертикальную жесткость Т-образного моста. Таким образом, это исследование имеет теоретическое и практическое значение для инженеров. (2) Точно так же вертикальное отклонение моста с Т-образной балкой по-прежнему является суперпозицией теоретического значения элементарной балки и влияния эффекта запаздывания сдвига, а не отношения связи. существует между ними двумя.
5. Заключение Механическая концепция этого метода ясна, а теоретическая основа надежна благодаря введению равновесия самонапряжения для деформации сдвига.Этот метод обеспечивает большую направляющую роль при проектировании просто опертых балочных или неразрезных тавровых мостов. В частности, механические свойства стенки Т-образных мостов анализируются с использованием метода настоящего исследования. Метод, описанный в данной статье, имеет определенное теоретическое значение и инженерно-практическую ценность. Поэтому есть надежда, что ученые смогут рассмотреть новые механические условия в этой статье и повысить точность расчетов при проектировании или изучении механических свойств Т-образного моста в будущем. Доступность данныхВсе данные, созданные или использованные в ходе исследования, отображаются в представленной статье. Конфликт интересовАвторы заявляют об отсутствии конфликта интересов. Благодарности Авторы выражают благодарность доктору Baoquan Cheng за его техническую поддержку. Проект инновационной исследовательской группы Национального фонда естественных наук Китая (51878323) и Молодежный научный фонд Ланьчжоуского университета Цзяотун (2018037) поддержали это исследование. Произошла ошибка при настройке пользовательского файла cookieПроизошла ошибка при настройке пользовательского файла cookieЭтот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт. Настройка браузера на прием файлов cookieСуществует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
Почему этому сайту требуются файлы cookie?Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня. Что сохраняется в файле cookie? Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется. Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Прогиб балкиБалка – конструктивный элемент, способный выдерживать большие нагрузки при изгибе. В случае малых прогибов форму балки можно описать линейным дифференциальным уравнением четвертого порядка. Рассмотрим вывод этого уравнения. Для изгибающейся балки угол \(d\theta\) возникает между двумя соседними сечениями, отстоящими друг от друга на расстоянии \(dx\) (рис. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Мы можем генерировать точки луча, подставляя в формулу различные значения t, которые должны быть больше или равны нулю
Мы можем генерировать точки луча, подставляя в формулу различные значения t, которые должны быть больше или равны нулю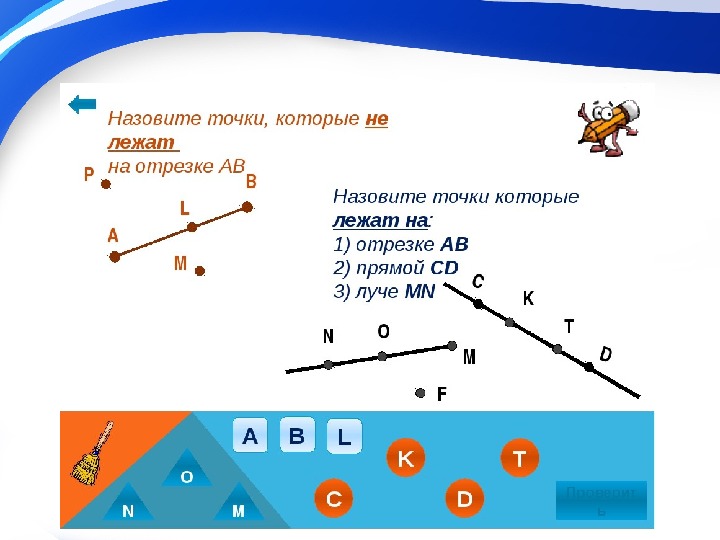 22.2009
22.2009 945
945 585
585 (2) Существующие исследования показывают, что на нормальное напряжение стенки Т-образной балки влияет только элементарная теория балки. Нельзя игнорировать влияние сдвигового запаздывания на нормальное напряжение полотна.Как показано в Таблице 3, эффект запаздывания сдвига увеличивает сжимающее напряжение свободно опертой Т-образной стенки на 33,34%. В таблице 4 эффект запаздывания сдвига увеличивает растягивающее напряжение непрерывного Т-образного полотна на 42,57%. Игнорирование удара, вероятно, приведет к повреждению конструкции; таким образом, эта особенность должна вызывать серьезную озабоченность у архитектора конструкции. (3) Напряжение действует на нейтральную ось теории элементарной балки Т-образного моста из-за эффекта запаздывания сдвига. Как показано в таблице 4, значение напряжения равно .Следовательно, нейтральная ось не является нейтральной осью в реальном смысле. Ось движется вниз.
(2) Существующие исследования показывают, что на нормальное напряжение стенки Т-образной балки влияет только элементарная теория балки. Нельзя игнорировать влияние сдвигового запаздывания на нормальное напряжение полотна.Как показано в Таблице 3, эффект запаздывания сдвига увеличивает сжимающее напряжение свободно опертой Т-образной стенки на 33,34%. В таблице 4 эффект запаздывания сдвига увеличивает растягивающее напряжение непрерывного Т-образного полотна на 42,57%. Игнорирование удара, вероятно, приведет к повреждению конструкции; таким образом, эта особенность должна вызывать серьезную озабоченность у архитектора конструкции. (3) Напряжение действует на нейтральную ось теории элементарной балки Т-образного моста из-за эффекта запаздывания сдвига. Как показано в таблице 4, значение напряжения равно .Следовательно, нейтральная ось не является нейтральной осью в реальном смысле. Ось движется вниз. 2
2 895
895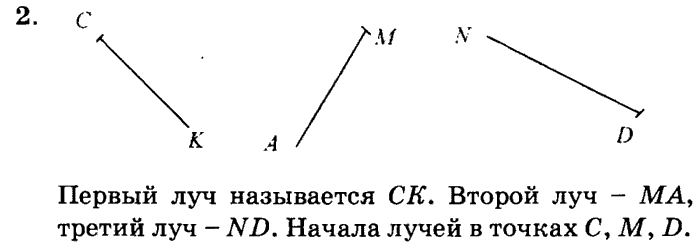 424
424 743
743 Результаты показывают, что на полотна такой структуры действует эффект сдвигового запаздывания, что является основным нововведением данного исследования.
Результаты показывают, что на полотна такой структуры действует эффект сдвигового запаздывания, что является основным нововведением данного исследования.

 date.issued
date.issued Затем они используются для получения мер деформации, за которыми следуют определяющие соотношения. Для линейных теорий балок меры деформации являются линейными функциями градиентов смещения, а напряжения являются линейными функциями мер деформации.Используя эти меры напряжений и деформаций, строится функционал энергии по объему балки, состоящий из кинетической энергии, энергии деформации и потенциальной энергии нагрузок. Уравнение(я) Эйлера, извлеченное из первой вариации этого функционала энергии, равного нулю, дает дифференциальные уравнения, описывающие эволюцию деформирующейся балки. В качестве альтернативы принцип виртуальной работы также можно использовать для получения математических моделей балок. Для линейного упругого поведения с малой деформацией и малой деформацией эти два подхода дают одни и те же математические модели.Энергетические методы или принцип виртуальной работы не могут быть использованы для необратимого процесса, что исключает их использование при наличии механизмов диссипации и памяти.
Затем они используются для получения мер деформации, за которыми следуют определяющие соотношения. Для линейных теорий балок меры деформации являются линейными функциями градиентов смещения, а напряжения являются линейными функциями мер деформации.Используя эти меры напряжений и деформаций, строится функционал энергии по объему балки, состоящий из кинетической энергии, энергии деформации и потенциальной энергии нагрузок. Уравнение(я) Эйлера, извлеченное из первой вариации этого функционала энергии, равного нулю, дает дифференциальные уравнения, описывающие эволюцию деформирующейся балки. В качестве альтернативы принцип виртуальной работы также можно использовать для получения математических моделей балок. Для линейного упругого поведения с малой деформацией и малой деформацией эти два подхода дают одни и те же математические модели.Энергетические методы или принцип виртуальной работы не могут быть использованы для необратимого процесса, что исключает их использование при наличии механизмов диссипации и памяти. В этой диссертации мы исследуем, могут ли используемые в настоящее время математические модели балок для физики обратимых деформаций и с соответствующим кинематическим предположением (i) быть получены с использованием законов сохранения и баланса классической механики сплошной среды или (ii) являются законами сохранения и баланса не -классическая механика сплошных сред, необходимая для их вывода.Чтобы гарантировать, что математические модели для различных теорий балок приводят к деформации, которая находится в термодинамическом равновесии, мы должны установить согласованность теорий балок в отношении сохранения и законов баланса механики сплошной среды, классической или неклассической в сочетании с их соответствующие кинематические предположения. Исследуются используемые в настоящее время математические модели балок Эйлера-Бернулли и Тимошенко, которые являются репрезентативными для большинства математических моделей балок.Затем следуют детали термодинамически согласованных математических моделей балок общего и более высокого порядка, которые свободны от кинематических предположений и других приближений и остаются действительными как для тонких, так и для глубоких балок.
В этой диссертации мы исследуем, могут ли используемые в настоящее время математические модели балок для физики обратимых деформаций и с соответствующим кинематическим предположением (i) быть получены с использованием законов сохранения и баланса классической механики сплошной среды или (ii) являются законами сохранения и баланса не -классическая механика сплошных сред, необходимая для их вывода.Чтобы гарантировать, что математические модели для различных теорий балок приводят к деформации, которая находится в термодинамическом равновесии, мы должны установить согласованность теорий балок в отношении сохранения и законов баланса механики сплошной среды, классической или неклассической в сочетании с их соответствующие кинематические предположения. Исследуются используемые в настоящее время математические модели балок Эйлера-Бернулли и Тимошенко, которые являются репрезентативными для большинства математических моделей балок.Затем следуют детали термодинамически согласованных математических моделей балок общего и более высокого порядка, которые свободны от кинематических предположений и других приближений и остаются действительными как для тонких, так и для глубоких балок. Исследования модельных проблем представлены как для тонких, так и для глубоких балок. Новая формулировка, представленная здесь, обеспечивает термодинамическое равновесие, поскольку она получена с использованием законов сохранения и баланса механики сплошной среды и остается справедливой как для тонких, так и для нетонких балок.Новая формулировка, представленная для термоупругой обратимой механической деформации, распространяется на термовязкоупругие балки с диссипацией и на термовязкоупругие балки с диссипацией и памятью. В каждом случае модельные исследования представлены с использованием используемых в настоящее время математических моделей (когда это возможно), а результаты сравниваются с результатами, полученными с использованием новой термодинамически согласованной формулировки, представленной здесь.
Исследования модельных проблем представлены как для тонких, так и для глубоких балок. Новая формулировка, представленная здесь, обеспечивает термодинамическое равновесие, поскольку она получена с использованием законов сохранения и баланса механики сплошной среды и остается справедливой как для тонких, так и для нетонких балок.Новая формулировка, представленная для термоупругой обратимой механической деформации, распространяется на термовязкоупругие балки с диссипацией и на термовязкоупругие балки с диссипацией и памятью. В каждом случае модельные исследования представлены с использованием используемых в настоящее время математических моделей (когда это возможно), а результаты сравниваются с результатами, полученными с использованием новой термодинамически согласованной формулировки, представленной здесь. rights
rights тип
тип