§ 24. Комбинаторные задачи — Математика. 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. М.: 2014. — 304 с.

Выберите категорию: Все категорииАнглийский языкБиологияВсеобщая историяГеографияДиректору, завучуДоп. образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураМатематикаМузыкаНемецкий языкОБЖОбществознаниеПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФранцузский языкШкольному психологуДругое

Выберите класс: Все классы1 класс2 класс3 класс4 класс5 класс6 класс

Выберите учебник: Все учебникиМатематика, 5 класс, Дорофеев Г.В., Петерсон Л.Г., Изд. «Ювента»Математика, 5 класс, Дорофеев Г.В., Шарыгин И.Ф. и др. / Под ред. Дорофеева Г.В., Шарыгина И.Ф., Изд. «Просвещение»Математика, 5 класс, Козлов В.В., Никитин А.А. и др. / Под ред. Козлова В.В. и Никитина А.А., Изд. «Русское слово»Математика, 5 класс, Муравин Г.К., Муравина О.В., Изд. «ДРОФА»Математика. 5 класс, Башмаков М.И., Изд. АстрельМатематика. 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013. — 280с.Математика. 5 класс. Зубарева И.И., Мордкович А.Г. 14-е изд., испр. и доп. — М.: 2013. — 270Математика. 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. М.: 2014. — 304 с.Математика. 5 класс. Учебник в 2 ч. Козлова С.А., Рубин А.Г. 2-е изд. — М.: 2015. — Ч.1 — 208с., Ч.2 — 208с.Математика. 5 класс. Учебник. Никольский С.М., Потапов М.К. и др. 14-е изд. — М.: 2015. — 272 с.Математика. Арифметика. Геометрия. 5 класс. Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др. 3-е изд. — М.: 2014. — 224 с.Математика. Наглядная геометрия. 5-6 классы. Шарыгин И.Ф., Ерганжиева Л.Н. 2-е изд. — М.: 2015 — 192 с.

Выберите тему: Все темыРаздел I. Натуральные числа и действия над нимиГлава 1. Натуральные числа§ 1. Ряд натуральных чисел§ 2. Цифры. Десятичная запись натуральных чиселКак считали в старинуКак называют «числа-великаны»§ 3. Отрезок. Длина отрезкаОт локтей и ладоней к метрической системе§ 4. Плоскость. Прямая. ЛучО льняной нити и линиях§ 5. Шкала. Координатный луч§ 6. Сравнение натуральных чиселЗадание № 1 «Проверьте себя» в тестовой формеИтоги главы 1Глава 2. Сложение и вычитание натуральных чисел§ 7. Сложение натуральных чисел. Свойства сложения§ 8. Вычитание натуральных чисел§ 9. Числовые и буквенные выражения. ФормулыЯзык, понятный всем§ 10. Уравнение§ 11. Угол. Обозначение углов§ 12. Виды углов. Измерение углов§ 13. Многоугольники. Равные фигуры§ 14. Треугольник и его виды§ 15. Прямоугольник. Ось симметрии фигурыЗадание № 2 «Проверьте себя» в тестовой формеИтоги главы 2Глава 3. Умножение и деление натуральных чисел§ 16. Умножение. Переместительное свойство умножения§ 17. Сочетательное и распределительное свойства умножения§ 18. Деление§ 19. Деление с остатком§ 20. Степень числа§ 21. Площадь. Площадь прямоугольника§ 22. Прямоугольный параллелепипед. Пирамида§ 23. Объём прямоугольного параллелепипеда§ 24. Комбинаторные задачиЗадание № 3 «Проверьте себя» в тестовой формеИтоги главы 3Раздел II. Дробные числа и действия над нимиГлава 4. Обыкновенные дроби§ 25. Понятие обыкновенной дроби«Попасть в дроб軧 26. Правильные и неправильные дроби. Сравнение дробей 1§ 27. Сложение и вычитание дробей с одинаковыми знаменателями§ 28. Дроби и деление натуральных чисел§ 29. Смешанные числаЗадание № 4 «Проверьте себя» в тестовой формеИтоги главы 4Глава 5. Десятичные дроби§ 30. Представление о десятичных дробяхОт шестидесятеричных к десятичным дробям§ 31. Сравнение десятичных дробей§ 32. Округление чисел. Прикидки§ 33. Сложение и вычитание десятичных дробейЗадание № 5 «Проверьте себя» в тестовой форме§ 34. Умножение десятичных дробей§ 35. Деление десятичных дробей§ 36. Среднее арифметическое. Среднее значение величины§ 37. Проценты. Нахождение процентов от числа§ 38. Нахождение числа по его процентамЗадание № 6 «Проверьте себя» в тестовой формеИтоги главы 5Дружим с компьютеромУпражнения для повторения за курс 5 классаИтоговые задания в тестовой форме «Проверьте себя»

Урок закрепления по теме «Решение комбинаторных задач» (5-й класс)

Тип урока: Урок закрепления по теме «решение комбинаторных задач».

Цели урока:

1. систематизирование и обобщение знаний при решении комбинаторных задач, которые сводятся к подсчету всевозможных вариантов перестановки элементов;

2. развитие мыслительной деятельности при практической работе;

3. воспитание навыков самоконтроля и взаимопомощи при работе в группах.

Оборудование: карточки с заданиями, рисунки к игровой ситуации «Волк, коза и капуста», рабочие тетради.

Ход урока

I этап урока. Организационный момент.

Создание проблемной ситуации.

После каникул встретились 5 друзей и обменялись рукопожатиями. Сколько всего было рукопожатий?

Оформление на доске: 12, 13, 14, 15, 23, 24, 25, 34, 35, 45, то есть 10 рукопожатий.

Учитель сообщает тему и цели урока.

II этап урока. Исторические сведения.

В повседневной жизни нередко перед нами возникают проблемы, которые имеют не одно, а несколько различных вариантов решения.

Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число. Такого рода задачи называются комбинаторными. Комбинаторные задачи возникли в глубокой древности. В Древнем Китае несколько тысячелетий назад увлекались составлением логических квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных колебаний длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата и т.д.

Комбинаторные задачи возникали и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Разгадывание шрифтов, древних письменностей.

Сегодня на уроке мы разберем комбинаторные задачи, которые встречаются в школьной жизни.

Задание I группе.

В школе проводятся соревнования «Веселые старты». В качестве призов решили использовать мячи, ракетки, клюшки и шайбы. Сколько различных призов можно составить из этих предметов, если каждому победителю решено давать по 2 разных предмета?

Решение. 1 набор – МР, 2 набор – МК, 3 набор – МШ, Набор – РК, 5 набор – РШ, 6 набор – КШ.

Ответ: 6 наборов призов.

Задание II группе.

Составьте расписание уроков в 1 классе, в котором должно быть 3 урока: русский язык, математика, физкультура. Сколько различных вариантов расписания можно составить на этот день?

Решение.

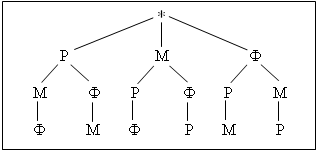
Варианты уроков.

1 – РМФ
2 – РФМ
3 – МРФ
4 – МФР
5 – ФРМ
6 – ФМР

Решения заданий учащиеся вывешивают на плакатах и один учащийся сообщает о ходе рассуждений.

III этап урока. Игровая ситуация.

Сценка «Волк, коза, капуста».

Крестьянину нужно перевезти через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться только крестьянин, а с ним или только волк, или только коза, или только капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевезет свой груз крестьянин?

Решение. Ясно, что приходится начать с козы. Крестьянин, перевезя козу, возвращается и берет волка, которого перевозит на другой берег, где его и оставляет, но зато берет и везет обратно на первый берег козу. Здесь он оставляет ее и перевозит к волку капусту. Вслед затем, возвратившись, он перевозит козу, и переправа оканчивается благополучно.

IV этап урока.

Задание I группе.

В столовой приготовили два разных супа (гороховый и щи), три вторых (котлеты, запеканку, рыбу) и два сока (сливовый и апельсиновый). Сколько различных обедов из трех блюд можно получить в этой столовой?

Решение.

Ввести обозначение:

Г – гороховый суп, Щ – щи, З – запеканка, Р — рыба, К – котлеты, С – сливовый сок, А – апельсиновый сок.

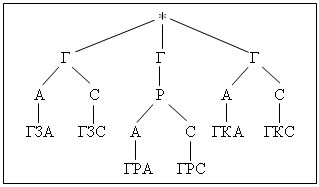
Аналогично:

ЩЗА, ЩЗС, ЩРА, ЩРС, ЩКА, ЩКС.

Ответ. Из двух супов, трех вторых и двух третьих блюд можно составить 12 разных обедов из трех блюд.

Задание II группе.

Марина собрала первый урожай со своей грядки: огурец, репу и морковь – и решила угостить Наташу, Дашу и Катю. Сколькими разными способами можно разделить овощи между тремя девочками, чтобы каждая получила один целый овощ?

Обозначение:

О – огурец, М – морковь, Р –репа.

Решение.

• 1 способ – ОМР,

• 2 способ – ОРМ,

• 3 способ – МОР,

• 4 способ – МРО,

• 5 способ – РОМ,

• 6 способ – РМО.

Ответ. Три овоща можно распределить между тремя девочками 6 способами.

Подведение итогов урока.

Рефлексия. Оцените свою деятельность на уроке. Кому и в чем помог разобраться сегодняшний урок? Достигли ли вы поставленной цели на уроке.

Выставление оценок.

Презентация к уроку (5 класс) на тему: Комбинаторика -1 занятие

Слайд 1

Урок решения комбинаторных задач в 5 классе. Учитель математики МОУ «СОШ №1 г.Суздаля» Плотникова Т.В.

Слайд 2

Математическая разминка 1.Вычисли: а)72:8 б)56:7 в)63:9 +51 *5 +33 :15 -13 :8 *9 :9 *13 +14 +17 -25 ____________ _____________ ____________ 2.Найди пропущенное число: 799 800 11 52 26 170 165 44 83 88 157 159 3.Реши задачи: а)В школьном хоре 41 человек, 36 девочек, а остальные мальчики. Сколько мальчиков в школьном хоре? б)В первой книге 80 страниц, а во второй на 26 страниц меньше. Сколько страниц во второй книге? в)Одна бригада трактористов вспахала 39га земли, что на 12га больше, чем вторая. Сколько гектаров земли вспахала вторая бригада?

Слайд 3

В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: Вперёд поедешь – голову сложишь. Направо поедешь – коня потеряешь. Налево поедешь – меча лишишься. А дальше говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.

Слайд 4

Целый раздел математики, именуемый комбинаторик ой , занят поисками ответов на вопросы: сколько всего комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить. Люди, которые умело владеют техникой решения комбинаторных задач, а следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций. Мы будем относиться к их числу? Тогда, на уроках работайте старательно И успех ваш ждёт обязательно!

Слайд 5

Задача №1 (учебник стр.7 №11): Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2. Решение: (сначала разбираем по учебнику, а затем записываем его в тетради). 1 2 1 1 2 2 1 1 1 1 2 2 2 2 Ответ: 111,112,121,122,211,212,221,222 – восемь чисел. Такой метод решения комбинаторных задач называется деревом выбора (дерево возможных вариантов)

Слайд 6

Задача №2 ( учебник стр.8 № 12): Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. Решение: 7 7 0 7 7 0 0 Ответ: 777,770,707,700 – 4 числа.

Слайд 7

Задача №3 : Запишите все трёхзначные числа, для записи которых используются цифры 5 и 7 . (Решите задачу самостоятельно) Решение: Ответ: 555,557,575,577,755,757,775,777

Слайд 8

Задача №4 (учебник стр.19 №96): В правление фирмы входят 5 человек. Из своего состава правления должно выбрать президента и вице-президента. Сколькими способами это можно сделать? ( Разберите решение задачи по учебнику ) Решение: Президент 1 Вице – президент 2 3 4 5 2 1 3 4 5 3 1 2 4 5 4 1 2 3 4 5 1 2 3 5 Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20. Такой метод решения комбинаторных задач называется правилом умножения.

Слайд 9

Задача №5: В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)? 1. Сколькими способами можно выбрать на дежурство одну девочку? Решение: 10 2.Сколько вариантов выбора мальчика существует для каждой девочки? 15 3.Сколько вариантов выбора двух дежурных существует? 10*15=150 Ответ : 150

Слайд 10

1.Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе. 2.Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок. Домашнее задание:

Слайд 11

До новых встреч с комбинаторными задачами.

План-конспект урока по алгебре (5 класс) на тему: План урока Решение комбинаторных задач

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №25

Открытый урок

 «Решение комбинаторных задач»

в 5 классе

                                     

 Подготовила:  учитель математики

Шабаян Элина Сергеевна

                                                             

ст.Ладожская  

Дата:01.10.2015 г.

Тема: «Решение комбинаторных задач»

Тип урока: урок изучения и первичного закрепления новых знаний

Цель урока: начать формировать умение решать простейшие комбинаторные задачи с помощью «дерева возможных вариантов».

Оборудование: компьютер, экран, проектор, презентация к уроку, раздаточные карточки с заданиями.

Задачи:

1. Образовательные:

К концу урока учащиеся должны уметь:

• выделять комбинаторные задачи из ряда предложенных задач;
• решать простейшие комбинаторные задачи.

2. Воспитательные:

Способствовать:

• формированию познавательного интереса к  предмету; мировоззрения учащихся.
• воспитанию чувства патриотизма; ответственности за качество и результата  выполняемой работы.

3. Развивающие:

Способствовать:

• развитию: речи; творческого мышления;

• совершенствованию операций умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать выводы, выделять существенные признаки.

ХОД УРОКА

I. Организационный момент

Проверка готовности учащихся к уроку.

– Здравствуйте, ребята! Садитесь.

(слайд 1)

— Девиз нашего урока:

Учитесь думать, объяснять,

Учитесь мыслить, рассуждать,

Ведь в математике, друзья,

Без логики никак нельзя!

II. Актуализация знаний.

(слайд 2)

— В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Ребята, с какой проблемой сталкивается добрый молодец на перепутье? (с проблемой выбора дальнейшего пути движения)

— Верно! А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был оптимальный.

— Оказывается, существует  целый раздел математики, который  занят поисками ответов на эти вопросы.  А вот как он называется, мы узнаем, выполнив следующее задание.

— Устный счет. На партах перед вами лежат карточки с примерами. (слайд 3) Запишите ответ к каждому примеру во второй столбец.  Время работы – 3 минуты. Как только закончите, поднимите руку, чтобы я видела. Начали.

— Проверим ответы. (учитель просит 1 ученика зачитать ответы)  

— Кто не согласен?

— Проверим. (слайд 4)

— В третий столбец запишите букву, соответствующую числу. Числа и буквы отражены в таблице на слайде. (слайд 5) В итоге у вас должно получиться слово.

— Какое слово у вас получилось? (комбинаторика) (слайд 6)

— Верно!  (слайд 7) А как вы понимаете, что такое комбинаторика? (ответы учащихся)

Комбинаторика – это раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

— Тема нашего урока называется «Решение комбинаторных задач». Откройте тетради, запишите число и тему урока. (слайд 8)

II. Изучение нового материала.

— Задачи, которые мы сегодня будем решать, помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности.

— И еще сегодня в очередной раз убедимся, что наш мир полон математики, и продолжим исследование на предмет выявления математики вокруг нас.

— Придя в школу, повесив одежду, вы очень часто отправляетесь к расписанию, посмотреть порядок уроков на день. А представьте на миг, что бы стало в школе, если бы не было расписания. Трудно пришлось бы всем: и детям, и учителям.

В помощь тому, кто составляет расписание, решим задачу: (слайд 9)

Задача №1.  В 5А  классе во  вторник 5 уроков: физкультура,  русский язык, литература,  история и математика. Сколько можно составить вариантов расписания на день, зная точно, что математика – первый урок?

Фронтальная работа

— Как бы вы предложили решить эту задачу? (ответы детей)

— Предлагаю вам закодировать названия предметов их начальной буквой: Ф – физкультура, Р – русский язык, Л – литература, И – история, М – математика.

— С какого урока мы начнем составлять расписание? (с математики) (слайд 10)

— Тогда что можно поставить вторым уроком? (физкультуру, русский, литературу или историю).

— Верно! Если вторым уроком будет физкультура, что может располагаться на третьем месте? (литература, русский или история). 

— Если вторым – русский, тогда на третьем? (физ-ра, лит-ра, история)

— Если вторым – литература, то на третьем? (физ-ра, русский, история)

— Если вторым – история, то на третьем? (физ-ра, русский, лит-ра)

— Хорошо. Если третьим уроком будет стоять литература, что будет на четвертом месте? (русский или история).

— Если четвертым уроком будет русский, тогда на 5 месте – какой урок? (история)

— Если четвертым – история, то пятым? (русский)

— А если третий урок – русский, тогда? (четвертым уроком – история или литература) И т.д.

(далее разбираются ответы при условии, что третьим уроком в расписании будет история).

— Заполните до конца данную схему самостоятельно.  Время работы – 2-3 минуты (самостоятельная работа)

— Ребята, посмотрите, что у вас должно было получиться. (смотрят на слайд)

— Сколько возможных вариантов расписания уроков у вас получилось? Подсчитайте.  (24 варианта)

— На что похожа эта схема, если ее перевернуть? (на дерево)

— Верно! Это один из способов решения комбинаторных задач. А называется он «Дерево возможных вариантов».

— Ребята, напишите, какой из вариантов расписания вам больше нравится. (дети пишут в тетради свой вариант расписания уроков)

— А если бы в задаче не было условия, что математика – первый урок, что бы изменилось? (ответ, вариантов расписания было бы намного больше)

— Да, трудно придется тому, кто забудет порядок уроков и, не посмотрев в расписание, захочет правильно заполнить дневник.

— А теперь заглянем на некоторые из этих уроков. И по возможности отыщем на них математические задания.

— Начнем с  истории.

Работа в парах

— Ребята, у вас на партах лежат три полоски разных цветов: красная, белая и синяя. Составьте из них флаг Российской Федерации.

— Проверьте, знаете ли вы флаг нашей страны. (сверяют с изображением на слайде). (слайд 11)

— А знаете ли вы, что означает каждый цвет на флаге?

Значение цветов флага России: белый цвет означает мир, чистоту, непорочность, совершенство; синий – цвет веры и верности, постоянства; красный цвет символизирует энергию, силу, кровь, пролитую за Отечество.

— От перестановок цветных полосок  можно получить другой флаг. Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок?

— Для этого решим следующую задачу: (слайд 12)

Задача №2. Несколько стран решили использовать для своего государственного флага символику в виде 3х горизонтальных полос разных цветов – белый (Б), синий (С), красный (К). Сколько стран могут использовать такую символику при условии, что у каждой страны свой флаг?

— Решите данную задачу с помощью дерева возможных вариантов. (слайд 13)

— Кто желает решить эту задачу на доске? (2 ученика решают с обратной стороны доски)

— Сколько вариантов у вас получилось? (6 вариантов)

— Проверим решения на доске. (ученики открывают доски, показывают свои схемы)

— Ребята, выделите другим цветом путь, в котором зашифрован Российский флаг. (дети у доски выделяют цветным мелом) (слайд 14)

— Какой он по счету на слайде? (четвертый)

— А если бы в условии задачи говорилось не о горизонтальных, а о вертикальных полосках, сколько было бы вариантов флага? (также 6 вариантов)

— Как бы изменился ответ, если в задаче говорилось и о горизонтальных, и о вертикальных полосках? (увеличился в 2 раза, 12 вариантов)

— Поэтому всегда нужно внимательно читать условие задачи.

— Оказывается, есть государства, где флаги имеют такие же цвета. (слайд 15) Посмотрите, два флага имеют горизонтальные полосы, а флаг Франции – вертикальные.

        — Следующий урок – физкультура. (слайд 16)

III. Физминутка

Задание на повторение

 (дети встают, если верное неравенство ученики кивают головой вперёд, если неверно – влево и вправо)

Учитель показывает неравенства на карточках:

а) 67,09>67,99	б) 3,6 = 3,600
в) 51,7	г) 18,605
д) 0,0025	е) 4,85 > 3,192
з) 0,088	ж) 1,782 = 1,786
и) 9,41	к) 27,09

IV. Закрепление изученного

— Настало время перекусить. Мы идем в школьную столовую. (слайд 17)

Задача №3. Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая (ч), кофе (к), булочки (б), печенья (п) и вафель (в)?

      Заполните схему дерева возможных вариантов в соответствии с условием задачи.  (слайд 18)

                                                                                                       

Напитки

Выпечка

— Обменяйтесь тетрадями с соседом по парте. Проверьте друг друга. Сколько завтраков у вас должно получиться? (6 завтраков) (слайд 19)

— Если ваш сосед выполнил задание верно, поставьте «плюс», иначе – «минус». Верните друг другу тетради.

— Ребята, а какой из завтраков вы с удовольствием бы съели? Выделите другим цветом путь наиболее понравившегося варианта.

— Следующий урок – математика.

Самостоятельная работа по учебнику.

— Откройте учебники на с.255. №974(б) (слайд 20)

Сколько трехзначных цифр можно составить из цифр 0, 2, 4 при условии, что цифры не должны повторяться?

Самопроверка. Ответ на слайде. (4 числа) (слайд 21)

— Следующий урок – литература. Внимание, перед вами лежат листочки с текстом отрывка из одного известного произведения. Прочитайте его.

Проказница Мартышка,

Осел,

Козел,

Да косолапый Мишка

Затеяли сыграть в …

Ударили в смычки, дерут, а толку нет.

………………..

«Стой, братцы, стой!» — кричит Мартышка.-

Погодите.

Как музыке идти? Ведь Вы не так сидите!

— Из какого произведения данный отрывок и кто автор? (басня Ивана Андреевича Крылова «Квартет») (слайд 22)

— Какую задачу  можно решить в этой басне? (ответы детей)

V. Подведение итогов

— С чем вы познакомились сегодня на уроке? (с комбинаторными задачами)

— Каким способом вы научились решать такие задачи? («дерево возможных вариантов»)

(слайд 23)

— Итак, ученику приходится встречаться с математикой, практически, постоянно. В частности, вы просчитываете  различные комбинации,

• когда выбираете меню в столовой,
• формулируете свой ответ на уроках,
•  составляете график дежурства по классу,
•  планируете, как провести свои выходные или каникулы и так далее.

VI. Домашнее задание

— Запишите в тетрадь домашнее задание:  по карточке  (слайд 24)

1. Сколькими различными способами могут сесть крыловские музыканты в один ряд?

2. №973(а,б)

3. Придумать свою комбинаторную задачу практического характера.

VII. Рефлексия

— Ребята, нарисуйте дерево возможных эмоций (слайд 25), которые можно испытывать во время урока, в виде различных смайликов. Закрасьте желтым цветом тот смайлик, который соответствовал вашему настроению на уроке.

Презентация к уроку по математике (5 класс): «Решение комбинаторных задач»

Слайд 1

Три пути ведут к знаниям: Путь размышлений- самый благородный, Путь подражания- самый легкий, Путь опыта- самый горький Конфуций

Слайд 2

КОМБИНАТОРИКА

Слайд 3

Практически во всех областях человеческой деятельности приходится заниматься выбором объектов из некоторых множеств и расположением их в том или ином порядке. Например, завучу школы при составлении расписания занятий, диспетчеру при составлении расписания движения транспорта, химику при изучении строения органических молекул, биологу при изучении составов белков и ДНК, специалисту по коммуникациям при организации автоматической телефонной связи, специалисту по защите информации при кодировании и декодировании сообщений и др. Несмотря на внешнее различие перечисленных проблем, математическая модель каждой из них может быть рассмотрена как комбинаторная задача.

Слайд 4

Комбинаторика – раздел математики, в котором изучаются вопросы о том, какие и сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов некоторого конечного множества.

Слайд 5

Какие числа можно записать с помощью цифр 6 и 0 1, 5 и 0 3 и 5

Слайд 6

Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2. № 11

Слайд 7

Запишите все трёхзначные числа, для записи которых употребляются только цифры 0 и 7. Найдите сумму этих чисел и разделите её на 211. № 12

Слайд 8

Сколько трёхзначных чисел можно составить из цифр 3, 5, 7, если в записи числа цифры не будут повторятся? Какое из этих чисел наибольшее и какое наименьшее? № 59

Слайд 9

№ 96

Слайд 10

№ 165 Сколькими способами можно прочитать слово «ЗНАК» на рисунке?

Слайд 11

Сколько трёхзначных чисел можно составить из цифр 2, 4, 6, 8, если в записи числа цифры не будут повторятся? № 228

Слайд 12

№ 388

Слайд 13

Сколько четырёхзначных чисел можно составить из нечётных цифр, если цифры в записи числа не повторяются? № 441

Слайд 14

Код для открывания сейфа состоит из четырёх цифр. Сколько существует различных вариантов кода для этого сейфа? № 598

Слайд 15

Семье, состоящей из бабушки, папы, мамы, дочери и сына, подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи? № 694

Слайд 16

Сколькими способами из 7 бусинок разного цвета можно составить ожерелье (с застежкой)? № 835

Слайд 17

На книжную полку ставят 6 разных книг. Сколькими способами эти книги можно разместить на полке? № 922

Слайд 18

Кодовый замок имеет 6 кнопок. Чтобы его открыть, нужно нажать кнопки в определенной последовательности (набрать код). Сколько существует вариантов кода для этого замка? № 1035

Слайд 19

К полднику в детском саду на четырёхместный стол поставили сок, молоко, какао и компот. Сколькими способами четверо детей могут выбрать себе один из напитков? № 1071