Метод Гаусса, который работает в самых нечеловеческих условиях | Математика не для всех
Даже когда решений бесконечно много или несовместна, а метод Крамера не работает от слова совсем. Сегодня мы с Вами решим систему линейных уравнений, используя метод Гаусса. Поехали!
Метод Гаусса заключается в последовательном исключении неизвестных из уравнений. Наиболее удобно (и так обычно делают при изучении ЛУ в высшей математике) записывать коэффициенты в матричном виде:
Теперь наша задача эквивалентными преобразованиями (исключением одинаковых строк, умножением строк на число, сложением строк) матрицы добиваться исключения переменных из строк, начиная с левого верхнего угла. Например, умножаем первую строку на 2 и складываем со второй, умножаем на три и складываем с третьей. Первую строку оставляем без изменений:
Теперь дальше смотрим на второй столбец и вторую и третью строки. Чтобы исключить вторую переменную из второй строки надо умножить её на 8, третью строку умножить на (-3) и всё полученное добро сложить:
Последняя матрица имеет т. н. ступенчатый вид, значит преобразования закончены. Отметив «ступеньку» получим базисные переменные, которые в итоговом решении должны быть выражены через свободные. Записываем систему уравнений по матрице:
н. ступенчатый вид, значит преобразования закончены. Отметив «ступеньку» получим базисные переменные, которые в итоговом решении должны быть выражены через свободные. Записываем систему уравнений по матрице:
Третью переменную просто выражаем из третьего уравнения. Аналогичные преобразований делаем со второй и третьей строкой, просто подставляя уже известные нам переменные:
Получен ответ в общем виде. Однако, часто бывает необходимо найти в частном виде. Для этого необходимо задаться конкретным набором переменных x4 и x5. Например, если они равны 0, то система имеет решение (1,0,2,0,0).
Карл Фридрих Гаусс. Источник: http://pictures.fanart-central.net/a/AngelusMortis/682157/AngelusMortis-682157-IICIIIXI_Anniversary_Dedication_to_Carl_Friedrich_Gauss.jpgКарл Фридрих Гаусс. Источник: http://pictures.fanart-central.net/a/AngelusMortis/682157/AngelusMortis-682157-IICIIIXI_Anniversary_Dedication_to_Carl_Friedrich_Gauss.jpg
Кстати, во время решения таких систем уравнений может оказаться, что в одной из строк все нули. Впрочем, это совсем другая история! Спасибо за внимание!
Впрочем, это совсем другая история! Спасибо за внимание!
Метод Гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.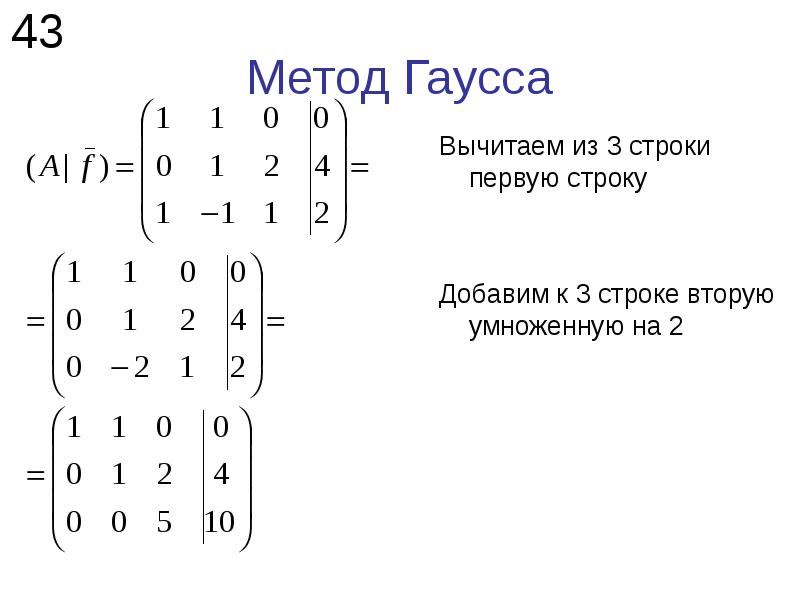
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) строки матрицы можно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) к строке матрицы можно
прибавить другую строку, умноженную на число, отличное от нуля.В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х
 Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную хn. Для этого решаем элементарное уравнение А*хn = В. В примере, приведенном выше, х3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной.
 Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по апробированной методике:
2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг. Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x3 = 23, x3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x
x2 = 3
x1 + x2 – x3 = 1, следовательно x1 + 3 – 1 = 1, x1 = –1
Ответ: x1 = –1, x2 = 3, x3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0. 64 –3 –1
64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х3 = 0,96 или приблизительно 1.
х2 = 3 и х1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Метод гаусса в математике историческая справка
Метод Гаусса в математике
Историческая справка
Гаусс (Gaus)
Карл Фридрих (1777 – 1855
гг.), немецкий математик. Для творчества
Гаусса характерна органическая связь
между теоретической и прикладной
математикой, широта проблематики. Труды
Гаусса оказали большое влияние на
развитие алгебры (доказательство
основной теоремы алгебры), теории чисел
(квадратичные вычеты), дифференциальной
геометрии (внутренняя геометрия
поверхностей), математиче6ской физики
(принцип Гаусса), теории электричества
и магнетизма, геодезии (разработка
метода наименьших квадратов) и многих
разделов астрономии.
Краткая теория
Пусть дана система линейных уравнений
(1)
Коэффициенты a11, 12,…, a1n, …, an1, b2, …, bn считаются заданными.
Вектор — строка í x1, x2, …, xn — называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D = ç A ê = ç aij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи:
Если D¹0, то система (1) имеет единственное решение, которое может быть найдено методом Гаусса.
Если D = 0, то система (1) либо имеет бесконечное множество решений, либо несовместна, т. е. решений нет.
Методические рекомендации
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
(2).
Метод Гаусса решения системы (2) состоит в следующем:
Разделим все члены первого уравнения на , а затем, умножив полученное уравнение на , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное будет исключено, и получится система вида:
(3).
Теперь разделим второе уравнение системы (3) на , умножим полученное уравнение на и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное будет исключено, и получится система треугольного вида:
(4).
Из последнего уравнения системы (4) находим ,подставляя найденное
значение в первое уравнение, находим .
Примеры выполнения заданий
Методом Гаусса решить систему:
.
Решение.
Разделив уравнение (а) на 2, получим систему
.
Вычтем из уравнения (b) уравнение , умноженное на 3, а из уравнения (c) — уравнение , умноженное на 4
.
Разделив уравнение () на -2,5, получим:
.
Вычтем из уравнения () уравнение , умноженное на -3:
.
Из уравнения находим Z = -2.
Подставив это значение в уравнение , получим Y = 0,2 — 0,4Z = 0,2 — 0,4(-2) = 1.
Наконец, подставив значение Z = -2 и Y = 1 в уравнение(a1), находим X = 0,5 — 0,5Y – Z = 0,5 — 0,5 1 — (-2) = 2.
Итак, получаем ответ X = 2, Y = 1, Z = -2.
Проверка:
.
2 Метод Гаусса решения систем линейных уравнений
Рассмотрим квадратную систему
. (1)
У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.
Проведем следующие преобразования системы:
1) поскольку a11¹0, первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1 – 4):
Рекомендуемые файлы
. (2)
Можно доказать, что замена любого уравнения системы новым, получающимся прибавлением к данному уравнению любого другого уравнения системы, умноженного на любое число, является эквивалентным преобразованием системы.
Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде таблицы
. (3)
Прямоугольную таблицу, состоящую из p строк и q столбцов, будем называть матрицей размера p´q:
.
Числа aij называются элементами матрицы. Первый индекс фиксирует номер строки, а второй – номер столбца, в которых стоит данный элемент. Если p = q, то есть число столбцов матрицы равно числу строк, то матрица называется квадратной. Элементы aii образуют главную диагональ матрицы.
Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.
Очевидно, что матрица коэффициентов квадратной системы является квадратной матрицей.
Каждую систему m линейных уравнений с n неизвестными можно представить в виде расширенной матрицы, содержащей m строк и n+1 столбцов. Каждую матрицу можно считать расширенной матрицей или матрицей коэффициентов некоторой системы линейных уравнений. Системе (2) соответствует расширенная матрица
.
Преобразуем эту матрицу следующим образом:
1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
.
Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a33 ¹ 0;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой:
.
Полученная матрица соответствует системе
. (4)
(4)
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.).
Назовем элементарными преобразованиями матрицы следующие преобразования:
1) перемена местами двух строк;
2) умножение строки на число, отличное от нуля;
3) замена строки матрицы суммой этой строки с любой другой строкой, умноженной на некоторое число.
Если матрица A является расширенной матрицей некоторой системы, и путем ряда элементарных преобразований матрица A переводится в матрицу B, являющуюся расширенной матрицей некоторой другой системы, то эти системы эквивалентны.
Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей. Матрица коэффициентов системы (4) – треугольная матрица.
Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна.
Рассмотрим другой пример:
. (5)
Проведем следующие преобразования расширенной матрицы системы:
1) первую строку оставим без изменения;
2) вместо второй строки запишем разность между второй строкой и удвоенной первой;
3) вместо третьей строки запишем разность между третьей строкой и утроенной первой;
4) четвертую строку заменим разностью между четвертой и первой;
5) пятую строку заменим разностью пятой строки и удвоенной первой.
В результате преобразований получим матрицу
.
Оставив без изменения первые две строки этой матрицы, приведем ее элементарными преобразованиями к следующему виду:
.
Если теперь, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки привести к нулю коэффициенты при x3 в четвертой и пятой строках, то после деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получим матрицу
.
Каждая из двух последних строк этой матрицы соответствует уравнению 0x1+0x2+0x3+0x4+0x5 = 0. Это уравнение удовлетворяется любым набором чисел x1, x2, ¼, x5, и его следует удалить из системы. Таким образом, система с только что полученной расширенной матрицей эквивалентна системе с расширенной матрицей вида
. (6)
(6)
Последняя строка этой матрицы соответствует уравнению x3 – 2x4 + 3x5 = –4. Если неизвестным x4 и x5 придать произвольные значения: x4 = r; x5 = s, то из последнего уравнения системы, соответствующей матрице (6), получим x3 = –4 + 2r – 3s. Подставив выражения x3, x4, и x5 во второе уравнение той же системы, получим x2 = –3 + 2r – 2s. Теперь из первого уравнения можно получить x1 = 4 – r + s. Окончательно решение системы представляется в виде
.
Рассмотрим прямоугольную матрицу A, у которой число столбцов m больше, чем число строк n. Если матрицу A можно разделить вертикальной чертой на две матрицы: стоящую слева треугольную матрицу размера m и стоящую справа прямоугольную матрицу, то матрицу A назовем трапециевидной или трапецеидальной. Очевидно, что матрица (6) — трапециевидная матрица.
Очевидно, что матрица (6) — трапециевидная матрица.
Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду
0x1+ 0x2+ ¼0xn = bj (bj ¹ 0),
то система несовместна или противоречива, так как ни один набор чисел x1, x2, ¼, xn не удовлетворяет этому уравнению.
Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к трапецеидальному виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений.
В последней системе можно получить все решения, придавая конкретные числовые значения параметрам r и s.
Те переменные, коэффициенты при которых стоят на главной диагонали трапецеидальной матрицы (это значит, что эти коэффициенты отличны от нуля), называются базисными. В рассмотренном выше примере это неизвестные x1, x2, x3. Остальные неизвестные называются свободными. В рассмотренном выше примере это неизвестные x4, и x5. Свободным неизвестным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.
В рассмотренном выше примере это неизвестные x1, x2, x3. Остальные неизвестные называются свободными. В рассмотренном выше примере это неизвестные x4, и x5. Свободным неизвестным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.
Базисные неизвестные единственным образом выражаются через свободные неизвестные.
Если свободным неизвестным приданы конкретные числовые значения и через них выражены базисные неизвестные, то полученное решение называется частным решением.
Если свободные неизвестные выражены через параметры, то получается решение, которое называется общим решением.
Все бесконечное множество решений системы можно получить, придавая свободным неизвестным любые числовые значения и находя соответствующие значения базисных неизвестных.
Если всем свободным неизвестным приданы нулевые значения, то полученное решение называется базисным.
Одну и ту же систему иногда можно привести к разным наборам базисных неизвестных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда базисными будут неизвестные x1, x2, x4, а свободными – x3 и x5. Рекомендуем читателю самостоятельно привести последнюю систему к такому виду, чтобы свободными неизвестными были x1 и x2, а базисными – x3, x4, x5.
Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы.
Рассмотрим еще одну систему, имеющую бесконечно много решений:
.
Проведем преобразование расширенной матрицы системы по методу Гаусса:
.
Как видно, мы не получили трапецеидальной матрицы, однако последнюю матрицу можно преобразовать, поменяв местами третий и четвертый столбцы:
.
Эта матрица уже является трапецеидальной. У соответствующей ей системы две свободных неизвестных – x3, x5 и три базисных – x1, x2, x4. Решение исходной системы представляется в следующем виде:
.
Приведем пример не имеющей решения системы:
.
Преобразуем матрицу системы по методу Гаусса:
.
Последняя строка последней матрицы соответствует не имеющему решения уравнению 0x1 + 0x2 + 0x3 = 1. Следовательно, исходная система несовместна.
Сформулируем теперь кратко суть метода Гаусса. Полагая, что в системе коэффициент a11 отличен от нуля ( если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1 и переобозначить коэффициенты), преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью эквивалентных преобразований описанным выше способом.
В полученной системе
,
считая, что (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений и переобозначив коэффициенты системы), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
15. Характеристика еженедельника «Эспрессо» — лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
при условии оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:
1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;
2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;
3) если получается система с трапецеидальной матрицей коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.
$$ j = 1 \ точек м, $$
где $ a _ {ji} , a _ {j} $ являются элементами произвольного поля $P$. Без ограничения общности можно считать, что $ a _ {11} \neq 0 $. Метод Гаусса работает следующим образом. Вычитается первое уравнение набора, умноженное на $ a _ {21} / a _ {11} $ почленно из второго уравнения; затем вычитается первое уравнение, умноженное на $ a _ {31} / a _ {11} $ из третьего уравнения; $ \точки, $ затем вычитается первое уравнение, умноженное на $ a _ {m1} / a _ {11} $ от $м$- уравнение.{0} $ для $ U = U _ {i} + U _ {k} $ представляет собой процедуру одновременного исключения двух неизвестных $ x _ {i} $ и $x_{k}$. Например, пусть $ i = 1 $ и $k = 2$. Если также
$$ \Delta _ {12} = \left | \begin{массив}{ll} а _ {11} & _ {21} \\ а _ {12} & _ {22} \\ \конец{массив} \право | \neq 0, $$
тогда строки матрицы
$$ \влево \| \begin{массив}{cccccc} — \Delta _ {23} &\Delta _ {13} &- \Delta _ {12} & 0 &\dots & 0 \\ — \Delta _ {24} &\Delta _ {14} & 0 &- \Delta _ {12} &\dots & 0 \\ \точки &\точки &\точки &\точки &{} &\точки \\ — \Delta _ {2m} &\Delta _ {1m} & 0 & 0 &\dots &- \Delta _ {12} \\ \конец{массив} \право\| , $$
где
$$ \Дельта _ {rs} = \ \влево | \begin{массив}{ll} а _ {r1} & а _ {s1} \\ а _ {r2} & а _ {s2} \\ \конец{массив} \право | , $$
можно использовать для получения $ ( U _ {1} + U _ {2} ) $-
свертка системы $S^{0}$. {0} $
могут быть решены с помощью алгоритмов, являющихся обобщением метода Гаусса.
{0} $
могут быть решены с помощью алгоритмов, являющихся обобщением метода Гаусса.
Ссылки
| [1] | К.Ф. Gauss, «Beiträge zur Theorie der Alexandrischen Gleichungen», Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1876) pp. 71–102 |
| [2] | Курош А.Г., Высшая алгебра, МИР (1972) (Перевод с русского) |
| [3] | К. Фаддеев, В.Н. Фаддеева, «Вычислительные методы линейной алгебры», Freeman (1963) (Перевод с русского) |
| [4] | С.Н. Черников, Lineare Ungleichungen, Deutsch. Verlag Wissenschaft. (1971) (Перевод с русского) |
Существует несколько вариантов этого метода, в основном основанных на соображениях практической реализации (например, методы Краута и Дулиттла) или эффективности (например, метод Холески для симметричных систем).
В западной литературе понятия LU-разложения, прямого исключения и обратной замены часто ассоциируются с методом Гаусса (который также называют методом исключения Гаусса). Рассмотрим частный случай, когда матрица коэффициентов $A$ в системе $ A x = a $ является квадратной матрицей $ ( m = n ) $. Тогда под LU-разложением понимается разложение $A$ в нижне- и верхнетреугольную матрицу $L$ и $U$, т. е. $A = L U $. Под прямой элиминацией и обратной заменой понимаются решения треугольных систем $ L y = a $ и $Ux=y$, соответственно.{2} / 2 $ провалы соответственно.
Для численных целей недостаточно убедиться, что коэффициенты $ a _ {11} $,
и т. д., опорные точки, просто ненулевые, но они наилучшие из возможных; если абсолютно наибольший $ a _ {j} $
используется в качестве опорного, то это называется частичным поворотом. Если в качестве опорного используется абсолютно самый большой элемент во всей матрице (или подматрице на более поздних этапах), это называется полным поворотом.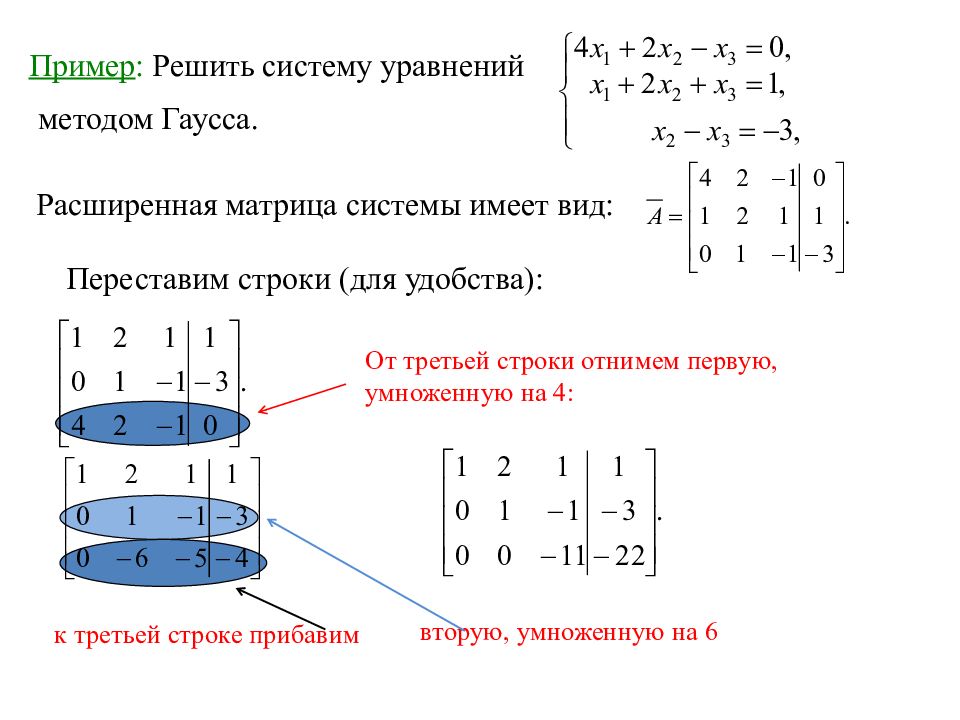 Частичный поворот для возможности LU-разложения в случае, если матрица $ A $
имеет сингулярные ведущие главные подматрицы, равносильные перестановке строк.{2} ) $
сравнения. Можно показать, что с такой стратегией метод численно устойчив (см. Устойчивость вычислительного алгоритма; Устойчивость вычислительного процесса).
Частичный поворот для возможности LU-разложения в случае, если матрица $ A $
имеет сингулярные ведущие главные подматрицы, равносильные перестановке строк.{2} ) $
сравнения. Можно показать, что с такой стратегией метод численно устойчив (см. Устойчивость вычислительного алгоритма; Устойчивость вычислительного процесса).
Отличная книга по численной линейной алгебре — [a1]. Проблема численной устойчивости при исключении Гаусса обсуждается в [a6].
Подпрограммы Fortan можно найти в [a4]; более старую версию Algol см. в [a5].
Ссылки
| [a1] | Г.Х.Голуб, С.Ф. ван Лоан, «Матричные вычисления», Северный Оксфорд, академик. (1983) |
| [a2] | Дж.Х. Уилкинсон, «Алгебраическая проблема собственных значений», Clarendon Press (1965) |
| [a3] | Г. Странг, «Линейная алгебра и ее приложения», акад. Press (1976) |
| [a4] | Х. Донгарра, Дж. Р. Банч, К. Б. Молер, Г. У. Стюарт, «Руководство пользователя LINPACK», SIAM (1978) Донгарра, Дж. Р. Банч, К. Б. Молер, Г. У. Стюарт, «Руководство пользователя LINPACK», SIAM (1978) |
| [a5] | J.H. Wilkinson, C. Reinsch, «Руководство по автоматическим вычислениям», 2. Линейная алгебра , Springer (1971) |
| [a6] | P.A. Bussinger, «Мониторинг численной устойчивости исключения Гаусса» Numer. Мат. , 16 (1971) стр. 360–361 |
Как цитировать эту запись:
Метод Гаусса. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Gauss_method&oldid=47050
Исключение Гаусса Жордана – объяснение и примеры
Метод исключения Гаусса-Жордана представляет собой алгоритм решения линейной системы уравнений.Мы также можем использовать его, чтобы найти обратную обратимую матрицу. Давайте сначала посмотрим на определение:
Исключение Гаусса-Жордана или исключение Гаусса — это алгоритм решения системы линейных уравнений путем представления ее в виде расширенной матрицы, уменьшения ее с помощью операций над строками и представления системы в сокращенной строке. -ступенчатая форма для нахождения значений переменных.
-ступенчатая форма для нахождения значений переменных.
В этом уроке мы подробно рассмотрим метод исключения Гаусса и способы решения системы линейных уравнений методом исключения Гаусса-Жордана.Примеры и практические вопросы будут следовать.
Что такое исключение Гаусса?
Исключение Гаусса — это структурированный метод решения системы линейных уравнений. Таким образом, это алгоритм, который можно легко запрограммировать для решения системы линейных уравнений. Основная цель исключения Гаусса-Жордана:
- представить систему линейных уравнений в расширенной матричной форме
- затем выполнить над ней операции со строками $ 3 $ до сокращенной эшелонированной формы строк (RREF) достигается
- Наконец, мы можем легко распознать решения из RREF
Давайте посмотрим, что такое расширенная матричная форма, $ 3 $ операции над строками, которые мы можем выполнять над матрицей, и уменьшенная ступенчатая форма строки матрицы.
Расширенная матрица
Ниже показана система линейных уравнений:
$ \begin{align*} 2x + 3y &= \,7 \\ x – y &= 4 \end{align*} $
We запишет расширенную матрицу этой системы, используя коэффициенты уравнений и записав ее в стиле , показанном ниже:
$ \left[ \begin{array}{ rr | r } 2 & 3 & 7 \\ 1 & -1 & 4 \end{array} \right] $
Пример использования одновременных уравнений $ 3 $ показан ниже:
$ \begin{align*} 2x + y + z &= \,10 \\ x + 2y + 3z &= 1 \\ – x – y – z &= 2 \end{align*} $
Представление этой системы в виде расширенной матрицы:
$ \left [ \begin{массив}{ ррр | r } 2 & 1 & 1 & 10 \\ 1 & 2 & 3 & 1 \\ – 1 & – 1 & – 1 & 2 \end{array} \right] $
Операции со строками над матрицей
Есть $ 3 $ элементарных операций над строками , которые мы можем выполнять над матрицами.Это не изменит решения системы. Это:
- Перестановка $ 2 $ строк
- Умножение строки на ненулевое ($\neq 0 $) скалярное значение
- Сложение или вычитание скаляра, кратного одной строки, другой строке.

Сокращенная форма со строками
Основная цель метода исключения Гаусса Жордана состоит в том, чтобы использовать $ 3 $ элементарных операций со строками над расширенной матрицей, чтобы привести ее к сокращенной форме со строками (RREF). Говорят, что матрица имеет сокращенную ступенчатую форму строк , также известную как каноническая форма строк , если выполняются следующие $ 4 $ условия:
- строк с нулевыми элементами (все элементы этой строки равны $ 0 $ s) находятся внизу матрицы.
- ведущая запись (первая ненулевая запись в строке) каждой ненулевой строки расположена справа ведущей записи строки непосредственно над ней.
- Первая запись в любой ненулевой строке равна $ 1 $.
- Все записи в столбце, содержащем ведущую запись ($ 1 $), являются нулями.
Как выполнить исключение Гаусса Жордана
В методе исключения Гаусса Жордана нет определенных шагов, но приведенный ниже алгоритм описывает шаги, которые мы выполняем, чтобы получить сокращенную эшелонированную форму расширенной матрицы.
- Поменяйте местами строки так, чтобы все строки с нулевыми элементами находились внизу матрицы.
- Поменять местами строки так, чтобы строка с самой большой крайней левой цифрой находилась в верхней части матрицы.
- Умножьте верхнюю строку на скаляр, который преобразует первую запись верхней строки в $ 1 $ (если первая запись верхней строки равна $ a $, умножьте ее на $ \frac{ 1 }{ a } $, чтобы получить $1$).
- Прибавьте или вычтите кратные числа из верхней строки к другим строкам, чтобы все записи в столбце ведущей записи верхней строки были равны нулю.
- Выполните шаги $ 2–4 $ для следующей крайней левой ненулевой записи , пока все ведущие записи каждой строки не станут $ 1 $.
- Поменяйте местами строки так, чтобы первая запись каждой ненулевой строки находилась справа от первой записи строки непосредственно над ней
На первый взгляд, запомнить шаги не так просто. Это вопрос решения нескольких проблем, пока вы не освоите процесс. Существует также фактор интуиции , который играет БОЛЬШУЮ роль в выполнении метода исключения Гаусса-Жордана.
Существует также фактор интуиции , который играет БОЛЬШУЮ роль в выполнении метода исключения Гаусса-Жордана.
Давайте рассмотрим несколько примеров, чтобы пояснить процесс решения системы линейных уравнений с помощью метода исключения Гаусса-Жордана .
Пример 1
Решите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} { – x } + 2y &= \, { – 6 } \\ { 3x } – 4y &= { 14 } \end{align*} $
Решение
Первым шагом является запись расширенной матрицы системы.Мы покажем это ниже:
$ \left[ \begin{array}{ r r | r } – 1 & 2 & – 6 \\ 3 & -4 & 14 \end{array} \right] $
Теперь наша задача состоит в том, чтобы привести матрицу к приведенной эшелонированной форме строк (RREF), выполнив $ 3 $ элементарные операции со строками.
Расширенная матрица, которая у нас есть:
$ \left[ \begin{array}{ r r | r } – 1 & 2 & – 6 \\ 3 & – 4 & 14 \end{array} \right] $
Шаг 1:
Мы можем умножить первую строку на $ – 1 $, чтобы сделать начальный вход $1$. Ниже показано:
Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 3 & – 4 & 14 \end{array} \right] $
Шаг 2:
Теперь мы можем умножить первую строку на $ 3 $ и вычесть ее из второй ряд. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & -2 & 6 \\ {3 – ( 1 \times 3 ) } & { -4 – ( -2 \times 3 ) } & { 14 – ( 6 \times 3 ) } \end{array} \ right] $
$ = \left[ \begin{array}{ rr | r } 1 & – 2 & 6 \\ 0 & 2 & – 4 \end{array} \right] $
У нас есть $ 0 $ в качестве первой записи второй строки.
Шаг 3:
Чтобы сделать вторую запись второй строки $ 1 $, мы можем умножить вторую строку на $ \ frac { 1 }{ 2 } $. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ { \frac{ 1 }{ 2 } \times 0} & { \frac{ 1 }{ 2 } \times 2 } & { \frac{ 1 }{ 2 } \times – 4} \end{array} \right] $
$ = \left[ \begin{array}{ rr | r } 1 & – 2 & 6 \\ 0 & 1 & – 2 \end{array} \right] $
Шаг 4:
Мы почти у цели!
Вторая запись первой строки должна быть $0 $. Для этого умножаем вторую строку на $2$ и прибавляем к первой строке. Ниже показано:
Для этого умножаем вторую строку на $2$ и прибавляем к первой строке. Ниже показано:
$ \left[ \begin{array}{ r r | r } { 1 + (0 \times 2 ) } & { – 2 + (1 \times 2 ) } & {6 + ( – 2 \times 2 ) } \\ 0 & 1 & – 2 \end{array} \ right] $
$ = \left[ \begin{array}{ rr | r } 1 & 0 & 2 \\ 0 & 1 & – 2 \end{array} \right] $
Это уменьшенный эшелон строк формы . Из расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, 2 \\ 0x + y &= -2 \end{align*} $
$ \begin{align*} x &= \, 2 \\ y &= – 2 \end{align*} $
Таким образом, решением системы уравнений является $ x = 2 $ и $ y = – 2$.
Пример 2Решите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} x + 2y &= \, 4 \\ x – 2y &= 6 \end{ align*} $
Solution
Запишем расширенную матрицу системы уравнений:
$ \left[ \begin{array}{ rr | r } 1 & 2 & 4 \\ 1 & – 2 & 6 \end{array} \right] $
Теперь мы выполняем элементарные операции со строками над этой матрицей, пока не придем к сокращенной ступенчатой форме строк.
Шаг 1:
Умножаем первую строку на $1$ и затем вычитаем ее из второй строки. По сути, это вычитание первой строки из второй строки:
$ \left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 1 – 1 & – 2 – 2 & 6 – 4 \end{массив} \right] $
$ =\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 & – 4 & 2 \end{array} \right] $
Шаг 2:
Умножаем вторую строку на $ -\frac{ 1 }{ 4 }$, чтобы получить вторая запись строки, $ 1 $:
$\left[ \begin{array}{ rr | r } 1 & 2 & 4 \\ 0 \times -\frac{ 1 }{ 4 } & – 4 \times -\frac{ 1 }{ 4 } & 2 \times -\frac{ 1 }{ 4 } \end {массив} \right] $
$ =\left[ \begin{array}{ rr | r } 1 & 2 & 4 \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
Шаг 3:
Наконец, мы умножаем вторую строку на $ – 2 $ и добавьте его в первую строку, чтобы получить уменьшенную форму эшелона строк этой матрицы:
$\left[ \begin{array}{ rr | r } 1+(- 2\times 0) & 2+( — 2 \times 1) & 4 + ( — 2 \times -\frac{ 1 }{ 2 } ) \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
$=\left[ \begin{array}{ rr | r } 1 & 0 & 5 \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
Это сокращенный эшелон строк формы . Из расширенной матрицы мы можем написать два уравнения (решения):
Из расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, 5 \\ 0x+ y &= -\frac{ 1 }{ 2 } \end {align*} $
$ \begin{align*} x &= \, 5 \\ y &= -\frac{ 1 }{ 2 } \end{align*} $
Таким образом, решение системы уравнений есть $ x = 5 $ и $ y = -\frac{ 1 }{ 2 } $.
Практические вопросыРешите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} 2x + y &= \, – 3 \\ – x – y &= 2 \end{align*} $
Решите систему, показанную ниже, используя метод исключения Гаусса-Жордана:
$ \begin{align*} x + 5y &= \, 15 \\ – x + 5y &= 25 \end{align*} $
Ответы
Начнем с записи расширенной матрицы системы уравнений:
$ \left[ \begin{array}{rr | r} 2 & 1 & – 3 \\ – 1 & – 1 & 2 \end{array} \right] $
Теперь мы выполняем элементарные операции со строками, чтобы получить наше решение.

Первый,
Меняем местами знаки во второй строке и меняем строки. Итак, имеем:
$ \left[ \begin{array}{r r | r} 1 & 1 & – 2 \\ 2 & 1 & – 3 \end{array} \right] $
Second,
Вычитаем дважды первую строку из второй строки:
$ \left[ \begin{array}{ рр | r} 1 & 1 & – 2 \\ 2 – ( 2 \times 1 ) & 1 – ( 2 \times 1 ) & – 3 – ( 2 \times – 2 ) \end{array} \right] $
$ = \left[ \begin{массив}{rr | r} 1 & 1 & – 2 \\ 0 & – 1 & 1 \end{array} \right] $
Третий,
Инвертируем вторую строку, чтобы получить:
$ = \left[\begin{array}{rr | r} 1 & 1 & – 2 \\ 0 & 1 & – 1 \end{array} \right] $
Наконец,
Вычитаем вторую строку из первой и получаем:
$ = \left[\begin{ массив}{рр | r} 1 & 0 & – 1 \\ 0 & 1 & – 1 \end{array} \right] $Из этой расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align *} x + 0y &= \, – 1 \\ 0x+ y &= – 1 \end{align*} $
$ \begin{align*} x &= \, – 1 \\ y &= – 1 \ end{align*} $
Таким образом, решением системы уравнений является $ x = – 1 $ и $ y = – 1 $.

- Расширенная матрица системы:
$ \left[\begin{array}{rr|r} 1 & 5 & 15 \\ – 1 & 5 & 25 \end{array} \right] $
Давайте привести эту матрицу к сокращенному ступенчатому виду строк и найти решение системы.
Во-первых,
Отмените первую строку, затем вычтите ее из второй строки, чтобы получить:
$ \left[ \begin{array}{rr|r} 1 & 5 & 15 \\ – 1 – ( – 1 ) & 5 – ( – 5 ) & 25 – ( – 15) \end{array} \right] $
$ =\left[ \begin{array}{rr|r} 1 & 5 & 15 \\ 0 & 10 & 40 \ end{array} \right] $
Second,
Разделите вторую строку на $10$, чтобы получить:
$ \left[\begin{array}{rr | r} 1 & 5 & 15 \\ 0 & 1 & 4 \end{array} \right] $
Затем
Умножьте вторую строку на $ 5 $ и вычтите ее из первой строки, чтобы окончательно получить решение:
$ \left[\begin{массив}{rr | r} 1 – ( 5 \times 0 ) & 5 – ( 5 \times 1 ) & 15 – ( 5 \times 4 ) \\ 0 & 1 & 4 \end{array} \right] $
$ =\left[ \начать{массив}{рр | r} 1 & 0 & – 5 \\ 0 & 1 & 4 \end{array} \right] $
Это сокращенная форма эшелона строк (RREF). Из этой расширенной матрицы мы можем написать два уравнения (решения):
Из этой расширенной матрицы мы можем написать два уравнения (решения):$ \begin{align*} x &= \, – 5 \\ y &= 4 \end{align*} $
Таким образом, решение системы уравнений $ x = – 5 $ и $ y = 4 $.
Исключение Гаусса-Джордана | Блестящая математика и естественные науки вики
Систему уравнений можно представить в нескольких различных матричных формах. Один из способов состоит в том, чтобы реализовать систему как матричное произведение коэффициентов системы и вектор-столбца ее переменных.Квадратная матрица называется матрицей коэффициентов , потому что она состоит из коэффициентов переменных в системе уравнений:
Произведение матриц: 2x+4y+7z=43x+3y+2z=85x+6y+3z=0⟶[247332563][xyz]=[480]. \text{Произведение матриц: }\quad
\begin{массив}{c c c c c c c}
2x & + & 4y & + & 7z & = & 4\\
3x & + & 3y & + & 2z & = & 8\\
5x & + & 6y & + & 3z & = & 0
\конец{массив}
\longrightarrow
\левый[
\begin{массив}{с с с}
2 и 4 и 7\\
3 и 3 и 2\\
5 и 6 и 3
\конец{массив}
\правильно]
\левый[
\начать{массив}{с}
Икс \\
у \\
г
\конец{массив}
\правильно]
= \ влево[
\начать{массив}{с}
4\\
8\
0
\end{массив} \right]. Произведение матриц: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723⎦⎤⎣⎡xyz⎦⎤=⎣⎡480 ⎦⎤.
Произведение матриц: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723⎦⎤⎣⎡xyz⎦⎤=⎣⎡480 ⎦⎤.
Альтернативное представление, называемое расширенной матрицей , создается путем сшивания столбцов матриц вместе и разделения вертикальной чертой. Матрица коэффициентов помещается слева от этой вертикальной черты, а константы в правой части каждого уравнения помещаются справа от вертикальной черты:
Расширенная матрица: 2x+4y+7z=43x+3y+2z=85x+6y+3z=0⟶[247433285630].\text{Дополненная матрица: } \quad \quad \begin{массив}{c c c c c c c} 2x&+&4y&+&7z&=&4\ 3x&+&3y&+&2z&=&8\ 5x&+&6y&+&3z&=&0\ \конец{массив} \longrightarrow \левый[ \begin{массив}{c c c | в} 2 и 4 и 7 и 4 \\ 3 и 3 и 2 и 8 \\ 5 и 6 и 3 и 0 \end{массив}\right]. Расширенная матрица: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723480⎦⎤.
Матрицами, которые представляют эти системы, можно манипулировать таким образом, чтобы обеспечить легко читаемые решения.Эта манипуляция называется сокращением строки. Методы сокращения строк преобразуют матрицу в сокращенную эшелонированную форму строк без изменения решений системы.
Методы сокращения строк преобразуют матрицу в сокращенную эшелонированную форму строк без изменения решений системы.
сокращенная ступенчатая форма строки матрицы AAA (\big((обозначается rref(A)) \text{rref}(A)\big)rref(A)) является матрицей одинаковой размерности, которая удовлетворяет следующему:
- Крайний левый ненулевой элемент в каждой строке равен 1 1 1. Этот элемент называется опорным.
- Любой столбец может иметь не более 1 1 1 точки поворота.Если у столбца есть стержень, то остальные элементы в столбце будут равны 0 0 0.
- Для любых двух столбцов C1C_{1} C1 и C2C_{2}C2, которые имеют сводные значения в строках R1 R_{1} R1 и R2, R_{2}, R2 соответственно, если сводные значения находятся в C1 C_{1 } C1 находится слева от точки поворота в C2 C_{2}C2, тогда R1 R_{1} R1 выше R2 R_{2} R2. Другими словами, для любых двух опорных точек P1 P_{1}P1 и P2P_{2}P2, если P2 P_{2} P2 находится справа от P1 P_{1} P1, то P2 P_{2} P2 ниже P1 P_{1}P1.
- Строки, состоящие только из нулей, находятся внизу матрицы.
Чтобы преобразовать любую матрицу в ее уменьшенную ступенчатую форму строк, выполняется исключение Гаусса-Жордана. Есть три элементарные операции со строками, используемые для получения формы уменьшенного эшелона строк:
- Переключить два ряда.
- Умножить строку на любую ненулевую константу.
- Добавить скалярное число, кратное одной строке, к любой другой строке.
Найдите rref(A) \text{rref}(A)rref(A) методом исключения Гаусса-Жордана, где А=[26-216-4-149].A = \left[ \begin{массив}{c c c} 2 и 6 и -2\\ 1 и 6 и -4 \\ -1 и 4 и 9 \\ \end{массив}\right].A=⎣⎡21−1664−2−49⎦⎤.
Крайний левый элемент в первой строке должен быть равен 1, поэтому первая строка делится на 2:
[26−216−4−149]→Разделить первую строку на 2.[13−116−4−149]. \left[ \begin{массив}{c c c} 2 и 6 и -2\\ 1 и 6 и -4 \\ -1 и 4 и 9 \\ \конец{массив}\справа] \ce{->[\large \text{Разделить первую строку на 2.
}]} \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 1 и 6 и -4 \\ -1 и 4 и 9 \\ \end{массив}\right].⎣⎡21−1664−2−49⎦⎤Разделите первую строку на 2.⎣⎡11−1 364−1−49⎦⎤.
Верхний левый элемент является опорным, поэтому остальные элементы в первом столбце должны быть равны 0. Это можно сделать, вычитая первую строку из второй строки. Кроме того, первую строку можно добавить к третьей строке, чтобы получить необходимые 0 в первом столбце:
[13−116−4−149]→RX2−RX1 и RX3+RX1[13−103−3078]. \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 1 и 6 и -4 \\ -1 и 4 и 9 \\ \конец{массив}\справа] \ce{->[\large R_2 — R_1 \text{ и } R_3 + R_1]} \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 3 и -3 \\ 0 и 7 и 8 \\ \end{массив}\right].⎣⎡11−1364−1−49⎦⎤RX2−RX1 и RX3+RX1⎣⎡100 337−1−38⎦⎤.
Теперь, когда крайний левый столбец равен [100], \left[ \begin{array}{c} 1\\ 0 \\ 0 \\ \end{array}\right], ⎣⎡100⎦⎤, средний элемент можно сделать равным 1, разделив вторую строку на 3:
[13−103−3078]→ Разделить вторую строку на 3 [13−101−1078].
\left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 3 и -3 \\ 0 и 7 и 8 \\ \конец{массив}\справа] \ce{->[\large \text{Поделите вторую строку на 3.}]} \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 1 и -1 \\ 0 и 7 и 8 \\ \end{массив}\right]. ⎣⎡100337−1−38⎦⎤Поделите вторую строку на 3.⎣⎡100 317−1−18⎦⎤.
Верхний и нижний элементы второго столбца можно сделать равными 0 с помощью соответствующих операций над строками:
[13−101−1078]→RX1−3 RX2 и RX3−7 RX2[10201−10015]. \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 1 и -1 \\ 0 и 7 и 8 \\ \конец{массив}\справа] \ce{->[\large R_1 — 3R_2 \text{ и } R_3 — 7R_2]} \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 15 \\ \end{массив}\right].⎣⎡100317−1−18⎦⎤RX1−3RX2 и RX3−7RX2⎣⎡100 0102−115⎦⎤.
Теперь средний столбец [010], \left[ \begin{array}{c} 0 \\ 1\\ 0 \\ \end{array}\right], ⎣⎡010⎦⎤, метод переходит к третьему столбцу путем деления третьей строки на 15:
[10201−10015]→ Разделить третью строку на 15.
[10201−1001]. \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 15 \\ \конец{массив}\справа] \ce{->[\large \text{Поделите третью строку на 15.} ]} \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ \end{массив}\right]. ⎣⎡1000102−115⎦⎤Разделите третью строку на 15.⎣⎡100 0102−11⎦⎤.
На последнем этапе процесса к первой и второй строкам добавляются числа, кратные третьей строке, так что последний столбец становится [001]: \left[ \begin{array}{c} 0 \\ 0 \\ 1\\ \end{массив}\right]: ⎣⎡001⎦⎤:
[10201−1001]→RX1−2 RX3 и RX2+RX3 ⋅ [100010001]. □ \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ \конец{массив}\справа] \ce{->[\large R_1 — 2R_3 \text{ и } R_2 + R_3.]} \left[ \begin{массив}{c c c} 1 и 0 и 0\\ 0 и 1 и 0 \\ 0 и 0 и 1 \\ \end{массив}\right]. \ _\квадратный ⎣⎡1000102−11⎦⎤RX1−2RX3 и RX2+RX3⋅⎣⎡100010001⎦⎤. □
Отправьте свой ответ
A = [14−564022−1] A = \left[ \begin{array}{ccc} 1 и 4 и -5 \\ 6 и 4 и 0 \\ 2&2&-1\ \end{массив} \right] A=⎣⎡162442−50−1⎦⎤
Какова сумма всех записей в rref(A)? \text{rref}(A)?rref(A)?
Примечание : rref(A)\text{rref}(A) rref(A) означает «уменьшенную эшелонированную форму строк» матрицы A. А.А.
А.А.
Соединение с Гауссом | Бред математической мамы
[Кажется, что некоторые люди находят этот пост, ища такие вещи, как «суммирование чисел в последовательности», или «какова сумма всех чисел из…», или «суммирование арифметических последовательностей» и т. д. Я надеюсь, что вы останетесь и прочитаете эту статью, даже если она не даст вам формулы. В нем рассматривается метод нахождения таких сумм на уровне, подходящем примерно для 4-го класса и выше, и вывод формулы на уровне, подходящем для учащихся средней школы.После того, как вы научились выводить формулу, вам не нужно запоминать ее, так как вы можете повторно вывести ее по мере необходимости.]
Вот урок, который я разработал для группы от 10 до 12 лет. Я планирую использовать его при первой встрече с ними в этом году. Сначала я попрошу их подумать, как бы они могли сложить все числа от 1 до 100, и мы поговорим о различных способах, которыми это можно сделать, затем поговорим об истории Гаусса и поиграем с множеством различных видов последовательности. Многим из них я уже показывал прием Гаусса, играя с треугольными числами и т. д.Но я не уверен, что многие его запомнят, и в любом случае этот урок предназначен для того, чтобы вывести их на новый уровень.
Многим из них я уже показывал прием Гаусса, играя с треугольными числами и т. д.Но я не уверен, что многие его запомнят, и в любом случае этот урок предназначен для того, чтобы вывести их на новый уровень.
У них было очень ограниченное знакомство с алгебраическими обозначениями и переменными, поэтому я добавляю информацию в конце, но посмотрим, что из этого получится. Я могу распределить это на два урока; Я не думаю, что им дадут время поиграться с числами и попробовать поиграть с переменными, но я никогда не уверен, сколько времени это займет, так что опять же, посмотрим, как пойдет…
Вот хорошая иллюстрация некоторых других способов сложения таких последовательностей.(Полная статья здесь.) Я надеюсь, что моя группа придумает некоторые из них во время нашего первоначального обсуждения того, как мы можем подойти к суммированию этих чисел.
«Трюк» Юнга Гаусса для нахождения суммы арифметической прогрессии обычно объясняется сложением пар элементов с противоположных концов последовательности, так что все пары имеют одинаковую сумму.
Один из способов представить себе этот процесс — сложить ряд пополам с изгибом шпильки. Другой подход состоит в том, чтобы написать серию дважды, один раз в порядке возрастания и один раз в порядке убывания.Третий метод выбирает только одну пару элементов, обычно первый и последний, чтобы вычислить среднее значение. Наконец, некоторые рассказчики этой истории отмечают, что формула суммирования первых n натуральных чисел также дает n -е треугольное число; на самом деле сумма равна половине площади прямоугольника n на n +1. Брайан Хейс
Добавление арифметических последовательностей путем объединения в пары
Легенда гласит, что когда великий математик Карл Гаусс был маленьким мальчиком, его учитель попросил его сложить все числа от 1 до 100.Гаусс быстро сообразил, что есть быстрый способ сделать это, спаривая числа с каждого конца и умножая их на количество пар.
Мы видим, что эта последовательность содержит несколько пар, каждая из которых в сумме дает 101.
Теперь все, что нам нужно сделать, это выяснить, сколько существует пар. Так как чисел 100, а в каждой паре по 2 числа, то получается 50 пар. Таким образом, нужно добавить 50 101. Прибавив 101 50 раз, мы получим 50 × 101 = 5050. Итак…
1 + 2 + 3 + … + 98 + 99 + 100 = 5050.
Работа в паре – Практика
Используйте метод спаривания, чтобы найти каждую из следующих сумм:
1 + 2 + 3 + … + 28 + 29 + 30
Сколько чисел:_____
Сколько пар:_____
Сумма каждой пары:_____
Общая сумма:_____
1 + 2 + 3 + … + 48 + 49 + 50
Сколько чисел:_____
Сколько пар:_____
Сумма каждой пары:_____
Общая сумма:_____
1 + 2 + 3 + … + 23 + 24 + 25
Сколько чисел:_____
Сколько пар:_____
Сумма каждой пары:_____
Общая сумма:_____
Используйте эту последовательность, чтобы объяснить, почему один и тот же метод работает для последовательностей, содержащих нечетное количество элементов.
(здесь я уберу все «обычные» вопросы для остальных, но все они в рабочем листе для детей.)
2 + 4 + 6 + … + 36 + 38 + 40
11 + 12 + 13 + … + 48 + 49 + 50
5 + 6 + 7 + … + 63 + 64 + 65
1 + 4 + 7 + … + 64 + 67 + 70
Сколько чисел*:_____
*Осторожно, это сложно. Посмотрите, сможете ли вы понять это, найдя закономерность и правило. Объясните, что вы сделали.
Объединение в пары – поиск правил
1 + 2 + 3 + … + (n-2) + (n-1) + n
Сколько чисел:_____
Сколько пар:_____
Сумма каждой пары:_____
Общая сумма:________
2 + 4 + 6 + … + (2n-4) + (2n-2) + 2n
Сколько чисел:_____
Сколько пар:_____
Сумма каждой пары:_____
Общая сумма:________
a + (a+d) + (a+2d) + … + (a+(n-3)d) + (a+(n-2)d) + (a+(n-1)d)
Заполните это Описание: Это последовательность из _____ чисел, начиная с _____ и каждый раз увеличивая на _____.
Сколько чисел:_____
Сколько пар:_____
Сумма каждой пары:_____
Общая сумма:________
Вот ссылка на копию моего рабочего листа. Не стесняйтесь использовать его, если вы сохраните мое уведомление об авторских правах внизу каждой страницы. Если вы найдете это полезным, я был бы рад, если бы вы дали мне знать.
Сопряжение с Гауссом
Связанная запись: Посещение начальной школы Гуанъян (относится к уроку 4-го класса на эту тему — прокрутите вниз)
Последующие действия:
Соединение с Гауссом — продолжение I
Соединение с Гауссом — продолжение II
Нравится:
Нравится Загрузка…
РодственныеКак обычное исключение стало методом исключения Гаусса
https://doi.org/10.1016/j.hm.2010.06.003Get rights and contentAbstract
Ньютон в заметках, которые он предпочел бы не публиковать, описал процесс решение одновременных уравнений, которые более поздние авторы применяли специально к линейным уравнениям. Этот метод, который не рекомендовал Эйлер, который Лежандр называл «обычным», а Гаусс называл «обычным», теперь назван в честь Гаусса: «исключение по Гауссу».Имя Гаусса стало ассоциироваться с элиминацией благодаря принятию профессиональными компьютерами специальной системы обозначений, которую Гаусс разработал для своих собственных вычислений методом наименьших квадратов. Нотация позволяла рассматривать исключение как последовательность арифметических операций, которые неоднократно оптимизировались для ручных вычислений и в конечном итоге описывались матрицами.
Этот метод, который не рекомендовал Эйлер, который Лежандр называл «обычным», а Гаусс называл «обычным», теперь назван в честь Гаусса: «исключение по Гауссу».Имя Гаусса стало ассоциироваться с элиминацией благодаря принятию профессиональными компьютерами специальной системы обозначений, которую Гаусс разработал для своих собственных вычислений методом наименьших квадратов. Нотация позволяла рассматривать исключение как последовательность арифметических операций, которые неоднократно оптимизировались для ручных вычислений и в конечном итоге описывались матрицами.
Zusammenfassung
.Diese Methode — welche Euler nicht empfahl, welche Legendre «ordinaire» nannte, und welche Gauß «gewöhnlich» nannte — wird nun nach Gauß benannt: Gaußsches Eliminationsverfahren. Die Verbindung des Maußschen Namens Mit Elternation Wurde Dadech Hervourcebracht, Dass Professionelle Recner Eine Notivation Übernahmen, Die Gauß Speziell Für Seine Eigenen Berechenun der Kleinsten Quadrate Eersonnen Hatte, Welche Zuließ, DAS ELECHANING ALS EINE Sequenz Von Arithmetischen Rechenoperationen Betrachtet Wurde, Die Wiederholt Für Handrignungen OptimiSiert wurden und schließlich durch Matrizen beschrieben wurden.
2000 MSC
01-08
62J05
62J05
65F05
65F05
65F05
65F05
65F05
ключевые слова
0ключевые слова
00Устранение гауссов
Компьютеры человека
наименьших квадратов
Математическое образование
Рекомендуемые статьи Со ссылками на статьи (0)
Copyright © 2010 Elsevier Inc.
Рекомендуемые статьи
Со ссылками на статьи
Игра на исключение Гаусса: Введение в линейную алгебру | Бретт Берри | Math Hacks
Переход от алгебры к стране матриц 🎉
Подпишитесь на Math Hacks в InstagramC исповедь: я люблю линейную алгебру. Ладно, может, это и не очень похоже на признание, но мне это нравится! Во многом из-за того, что линейная алгебра не похожа на остальную математику, она кажется загадкой.
Это может звучать безумно, но выслушайте меня.
Эта новая земля матриц и векторов может выглядеть и ощущаться пугающей, и на то есть веские причины: новые обозначения, новые правила, новые свойства. Все немного по-другому. Но, возможно, рассматривая это как головоломку, вы сможете преодолеть это новое препятствие в обозначениях.
Все немного по-другому. Но, возможно, рассматривая это как головоломку, вы сможете преодолеть это новое препятствие в обозначениях.
Готовы попробовать?
Я считаю, что лучше всего начать с линейной алгебры с , решая системы уравнений , потому что это то, что вы, вероятно, уже изучили.Помните методы замены и исключения?? Они звонят в колокол? Если нет, вы можете освежить свою память здесь. 🙂
Сегодня мы познакомимся с новым подходом к решению систем уравнений, используя метод под названием Исключение по Гауссу.
Что такое исключение Гаусса??
Исключение Гаусса — это метод, при котором мы переводим наши уравнения в матрицу и используем матрицу для решения системы (т. е. находим решения для каждой переменной, которые делают все уравнения верными).
Сегодня я шаг за шагом проведу вас через упрощенный пример (числа совпадают, так что шагов гораздо меньше!). Если вам нужен более подробный пример, ознакомьтесь с моим руководством на YouTube по исключению Гаусса ниже ⬇
Нажмите здесь, чтобы подписаться на математические приемы на YouTube 🎥 Исключение Гаусса начинается с преобразования наших уравнений в матрицу.
Вот система, которую мы собираемся решить:
Самое первое, что вам нужно понять, это то, что в нашей системе много скрытой информации.Красным цветом я добавлю нули и единицы заполнителя.
Далее мы отделим всю важную числовую информацию от посторонних символов. Теперь, выделенный красным, вы найдете всю важную информацию, с которой мы будем работать:
Нам нужно переписать числовые значения выше в виде матрицы. Мы опустим буквы, знаки равенства и символы сложения (но не символы минус!) и просто напишем числа в точном порядке и в тех строках, в которых они указаны выше.
После этого мы добавим большие квадратные скобки, чтобы сгруппировать их вместе.Это наша матрица:
Как и в любой игре, мы должны соблюдать несколько правил:
- Вы можете поменять местами любые две строки
- Вы можете умножить или разделить любую строку на значение
- Вы можете складывать или вычитать любые две строки вместе
*Примечание: вы можете комбинировать эти правила в любом одном движении.
Не волнуйтесь, если это пока не совсем понятно. Вы увидите, как они работают, когда мы будем работать с нашим примером.
Вы выигрываете, когда ваша матрица выглядит так:
Где символы # представляют собой любые числа, а остальная часть матрицы имеет нули во всех позициях, кроме диагональных. Это называется Эшелонная форма с уменьшенным рядом.
Начните с матрицы, которую вы создали на этапе настройки. Теперь мы собираемся использовать правила, чтобы довести эту матрицу до финиша!
Начальная матрицаХод 1: Поменять местами первую и вторую строки
Есть много разных способов привести эту матрицу в выигрышную форму, но я думаю, что проще всего начать с того, что поменять местами первую и вторую строки.Таким образом, мы получаем 1 в первой позиции первой строки и 0 в первой позиции второй строки.
Шаг 2: прибавьте -2 раза ко второй строке к третьей строке
Одна вещь, которую мы можем сделать, это использовать несколько правил вместе за один шаг. В этом шаге мы умножим -2 на вторую строку и добавим эти продукты в третью строку. Это оставит вторую строку без изменений, но поможет нам получить ноль во второй позиции третьей строки.
В этом шаге мы умножим -2 на вторую строку и добавим эти продукты в третью строку. Это оставит вторую строку без изменений, но поможет нам получить ноль во второй позиции третьей строки.
Ход 3: Разделить третью строку на -3
Далее мы просто разделим третью строку на -3, чтобы получить 1 в третьей позиции третьей строки.
Ход 4: прибавьте -2 раза к третьей строке ко второй строке
Теперь, когда у нас есть все нули в нижнем левом углу, окруженные диагональю 1, мы готовы начать работать над получением нулей в позициях над первой строкой. 1 с.
👉 Но прежде чем мы это сделаем, я хочу сделать небольшое примечание: наша матрица в настоящее время находится в форме эшелона строк. В этой форме вы можете перевести свою матрицу обратно в набор уравнений, если хотите, и легко сможете найти x, y и z.Сегодня мы работаем над преобразованием нашего уравнения в сокращенную -строчную эшелонированную форму, что означает, что мы хотим получить нули в позициях выше единиц.
Часто в линейной алгебре вас будут просить работать до сокращенной формы эшелона строк, поскольку это самая простая форма для чтения ответа.
Хорошо, вернемся к нашей математике. В следующем шаге мы возьмем -2, умноженное на третью строку, и добавим ее ко второй строке, чтобы мы могли получить 0 в третьей позиции строки 2.
Ход 5: добавим третью строку к первой строке
Далее , мы просто добавим третью строку к первой, поскольку -1 + 1 = 0, что поможет нам получить 0 в третьей позиции первой строки.
Ход 6: прибавим -2 раза ко второй строке к первой строке
Наконец, мы добавим -2 раза ко второй строке к первой строке, чтобы получить ноль во второй позиции первой строки.
Осталось только прочитать ответ! Для этого просто переведите свою матрицу обратно в набор уравнений, и вы увидите, что нашли решения для x, y и z.
Отбросив все нулевые члены, вы получите:
Это означает, что точка пересечения в трехмерном пространстве, где пересекаются три плоскости, находится в (-1,2,-3).
Помните, что вы всегда можете проверить свое решение, подставив значения обратно в исходные уравнения.
Все в порядке, вы также можете решать системы 3×3 с хорошей алгеброй 😉
Спасибо, что присоединились ко мне!
— Бретт
для получения обновлений и математического вдохновения следите за Бреттом в социальных сетях:
Instagram | Фейсбук | Twitter
Исключение по Гауссу: метод и примеры — видео и расшифровка урока
Что такое исключение Гаусса?
Возможно, вас интересует второй шаг.Гаусс что теперь? Исключение Гаусса — это процесс использования допустимых операций со строками над матрицей до тех пор, пока она не будет приведена в форму сокращенного эшелона строк. Существует три типа допустимых операций со строками , которые могут выполняться над матрицей.
- OP1 — поменять местами две строки.
- OP2 — умножить все записи строки на ненулевое число.

- OP3 — добавить в целевую строку число, кратное одной строке. (Примечание: целевая строка — это единственная строка, которая изменяется в этом процессе.)
Важно понимать, что это всего лишь правила игры. Как мы применим их в той или иной ситуации, будет зависеть от того, какая матрица нам дана. Имейте в виду, что наша цель состоит в том, чтобы преобразовать матрицу в более простую форму, называемую уменьшенной эшелонированной формой строк (RREF) , используя ряд этих операций со строками.
Сокращенная ступенчатая форма строк
Мы говорим, что матрица находится в сокращенной ступенчатой форме строк, если она удовлетворяет следующим требованиям:
- При чтении слева направо первая ненулевая запись в любой строке равна 1.Это называется ведущей записью строки.
- Начальный элемент строки всегда находится справа от ведущих элементов в строках над ним.
- Любой столбец с ведущей записью имеет нули над и под ним.

Вот пример матрицы в форме RREF (не связанный с нашим примером). Лидирующие записи выделены жирным шрифтом.
Пример исключения Гаусса
Теперь, когда мы знаем правила игры (операции со строками) и цель (RREF), пришло время разработать пример.Предположим, вы знаете, как найти расширенную матрицу матрицы, которую мы только что видели.
1 уже есть в первой позиции входа для строки 1. Нам нужны 0 под ней. Используйте операции OP3. Далее мы используем R 1 для строки 1, R 2 для строки 2 и R 3 для строки 3.
Добавить (-3) Ч 1 к Ч 2. Почему именно эта операция? Суть в том, что R 1 уже имеет 1 на лидирующей позиции.Таким образом, мы можем умножить это на противоположное начальному элементу целевой строки R 2. Когда строки складываются, -3 отменяет 3, чтобы получить 0 в результате.
| (-3) Р 1 | -3 | -6 | -3 | -9 |
| + Р 2 | 3 | 2 | 1 | 3 |
| Результат | 0 | -4 | -2 | -6 |
Результат заменяет R 2, но R 1 фактически не переделывается в самой матрице.
В начальном элементе строки 2 стоит -4. Чтобы вместо этого получить 1, умножьте всю строку на (-1/4). Это ОП2.
Теперь мы снова используем OP3, чтобы сделать все остальные записи равными 0 в том же столбце.
Другая OP2 изменит -4 на 1 в начальном элементе строки 3.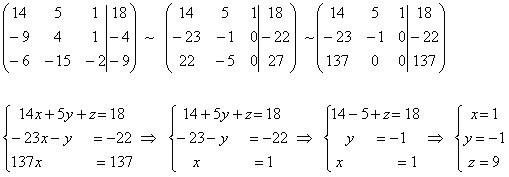
Наконец, используйте OP3, чтобы избавиться от ненулевой записи над первой записью в столбце 3.
Потребовалось некоторое время, но теперь мы поместили матрицу в RREF! Кстати, теперь, когда этапы исключения Гаусса выполнены, мы можем считать решение исходной системы уравнений. Решение находится в последнем столбце: (0, 2, -1).
Краткий обзор урока
Часть процесса решения системы линейных уравнений заключается в использовании исключения Гаусса. Исключение Гаусса — это процесс использования допустимых операций со строками над матрицей до тех пор, пока она не будет приведена в форму сокращенного эшелона строк. Метод включает в себя выбор ряда допустимых операций над строками, которые преобразуют данную матрицу в гораздо более простую форму. Три операции со строками , используемые для решения системы, следующие:
- OP1 — Поменять местами две строки
- OP2 — умножить все записи строки на ненулевое число
- OP3 — добавить несколько строк в целевую строку
Более простая форма называется эшелонированной формой сокращенной строки (RREF) , в которой:
- Первая ненулевая запись в любой строке равна 1.

 Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.


 Из этой расширенной матрицы мы можем написать два уравнения (решения):
Из этой расширенной матрицы мы можем написать два уравнения (решения):
 }]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
1 и 6 и -4 \\
-1 и 4 и 9 \\
\end{массив}\right].⎣⎡21−1664−2−49⎦⎤Разделите первую строку на 2.⎣⎡11−1 364−1−49⎦⎤.
}]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
1 и 6 и -4 \\
-1 и 4 и 9 \\
\end{массив}\right].⎣⎡21−1664−2−49⎦⎤Разделите первую строку на 2.⎣⎡11−1 364−1−49⎦⎤. \left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 3 и -3 \\
0 и 7 и 8 \\
\конец{массив}\справа]
\ce{->[\large \text{Поделите вторую строку на 3.}]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 1 и -1 \\
0 и 7 и 8 \\
\end{массив}\right].
⎣⎡100337−1−38⎦⎤Поделите вторую строку на 3.⎣⎡100 317−1−18⎦⎤.
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 3 и -3 \\
0 и 7 и 8 \\
\конец{массив}\справа]
\ce{->[\large \text{Поделите вторую строку на 3.}]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 1 и -1 \\
0 и 7 и 8 \\
\end{массив}\right].
⎣⎡100337−1−38⎦⎤Поделите вторую строку на 3.⎣⎡100 317−1−18⎦⎤. [10201−1001]. \left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 15 \\
\конец{массив}\справа]
\ce{->[\large \text{Поделите третью строку на 15.} ]}
\left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 1 \\
\end{массив}\right].
⎣⎡1000102−115⎦⎤Разделите третью строку на 15.⎣⎡100 0102−11⎦⎤.
[10201−1001]. \left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 15 \\
\конец{массив}\справа]
\ce{->[\large \text{Поделите третью строку на 15.} ]}
\left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 1 \\
\end{массив}\right].
⎣⎡1000102−115⎦⎤Разделите третью строку на 15.⎣⎡100 0102−11⎦⎤.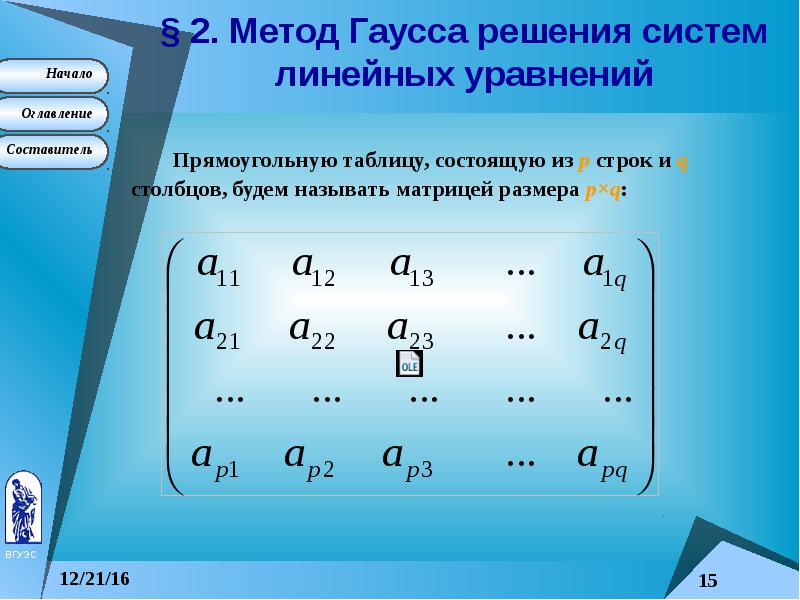 Один из способов представить себе этот процесс — сложить ряд пополам с изгибом шпильки. Другой подход состоит в том, чтобы написать серию дважды, один раз в порядке возрастания и один раз в порядке убывания.Третий метод выбирает только одну пару элементов, обычно первый и последний, чтобы вычислить среднее значение. Наконец, некоторые рассказчики этой истории отмечают, что формула суммирования первых n натуральных чисел также дает n -е треугольное число; на самом деле сумма равна половине площади прямоугольника n на n +1. Брайан Хейс
Один из способов представить себе этот процесс — сложить ряд пополам с изгибом шпильки. Другой подход состоит в том, чтобы написать серию дважды, один раз в порядке возрастания и один раз в порядке убывания.Третий метод выбирает только одну пару элементов, обычно первый и последний, чтобы вычислить среднее значение. Наконец, некоторые рассказчики этой истории отмечают, что формула суммирования первых n натуральных чисел также дает n -е треугольное число; на самом деле сумма равна половине площади прямоугольника n на n +1. Брайан Хейс Часто в линейной алгебре вас будут просить работать до сокращенной формы эшелона строк, поскольку это самая простая форма для чтения ответа.
Часто в линейной алгебре вас будут просить работать до сокращенной формы эшелона строк, поскольку это самая простая форма для чтения ответа.

