Числовая последовательность — Википедия

Последовательность

Числовая последовательность (ранее в русскоязычной математической литературе встречался термин вариа́нта^[1][2], принадлежащий Ш. Мерэ^[1]) — это последовательность элементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Пусть X{\displaystyle X} — это либо множество вещественных чисел R{\displaystyle \mathbb {R} }, либо множество комплексных чисел C{\displaystyle \mathbb {C} }. Тогда последовательность (xn)n=1∞{\displaystyle (x_{n})_{n=1}^{\infty }} элементов множества X{\displaystyle X} называется числовой последовательностью.

• Функция ((−1)n)n=1∞{\displaystyle \left((-1)^{n}\right)_{n=1}^{\infty }} является бесконечной последовательностью целых чисел. Элементы этой последовательности начиная с первого имеют вид ⟨−1,1,−1,1,−1,…⟩{\displaystyle \langle -1,1,-1,1,-1,\ldots \rangle }.
• Функция (1/n)n=1∞{\displaystyle (1/n)_{n=1}^{\infty }} является бесконечной последовательностью рациональных чисел. Элементы этой последовательности начиная с первого имеют вид ⟨1,1/2,1/3,1/4,1/5,…⟩{\displaystyle \langle 1,1/2,1/3,1/4,1/5,\ldots \rangle }.
• Функция, сопоставляющая каждому натуральному числу n⩽12{\displaystyle n\leqslant 12} одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида (xn)n=112{\displaystyle (x_{n})_{n=1}^{12}}. Например, пятым элементом x5{\displaystyle x_{5}} этой последовательности является слово «май».

На множестве всех последовательностей элементов множества X{\displaystyle X} можно определить арифметические и другие операции, если таковые определены на множестве X{\displaystyle X}. Такие операции обычно определяют естественным образом, то есть поэлементно.

Пусть на множестве X{\displaystyle X} определена N{\displaystyle N}-арная операция f{\displaystyle f}: f:XN→X{\displaystyle f\colon X^{N}\rightarrow X} Тогда для элементов x1=(x1n)n=1∞{\displaystyle x_{1}=(x_{1n})_{n=1}^{\infty }}, x2=(x2n)n=1∞{\displaystyle x_{2}=(x_{2n})_{n=1}^{\infty }}, …, xN=(xNn)n=1∞{\displaystyle x_{N}=(x_{Nn})_{n=1}^{\infty }} множества всех последовательностей элементов множества X{\displaystyle X} операция f{\displaystyle f} будет определяться следующим образом: f(x1,x2,⋯,xN)=(f(x1n,x2n,⋯,xNn))n=1∞{\displaystyle f\left(x_{1},x_{2},\cdots ,x_{N}\right)=(f\left(x_{1n},x_{2n},\cdots ,x_{Nn}\right))_{n=1}^{\infty }}

Например, так определяются арифметические операции для числовых последовательностей.

Суммой числовых последовательностей (xn){\displaystyle (x_{n})} и (yn){\displaystyle (y_{n})} называется числовая последовательность (zn){\displaystyle (z_{n})} такая, что zn=xn+yn{\displaystyle z_{n}=x_{n}+y_{n}}.

Разностью числовых последовательностей (xn){\displaystyle (x_{n})} и (yn){\displaystyle (y_{n})} называется числовая последовательность (zn){\displaystyle (z_{n})} такая, что zn=xn−yn{\displaystyle z_{n}=x_{n}-y_{n}}.

Произведением числовых последовательностей xn{\displaystyle x_{n}} и yn{\displaystyle y_{n}} называется числовая последовательность (zn){\displaystyle (z_{n})} такая, что zn=xn⋅yn{\displaystyle z_{n}=x_{n}\cdot y_{n}}.

Частным числовой последовательности xn{\displaystyle x_{n}} и числовой последовательности yn{\displaystyle y_{n}}, все элементы которой отличны от нуля, называется числовая последовательность zn=(xnyn)n=1∞{\displaystyle z_{n}=\left({\frac {x_{n}}{y_{n}}}\right)_{n=1}^{\infty }}. Если в последовательности yn{\displaystyle y_{n}} на позиции k≠1{\displaystyle k\neq 1} всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность zn=(xnyn)n=1k−1{\displaystyle z_{n}=\left({\frac {x_{n}}{y_{n}}}\right)_{n=1}^{k-1}}.

Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.

Подпоследовательность последовательности (xn){\displaystyle (x_{n})} — это последовательность (xnk){\displaystyle (x_{n_{k}})}, где (nk){\displaystyle (n_{k})} — возрастающая последовательность элементов множества натуральных чисел.

Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.

Примеры[править | править код]

• Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.
• Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.

Свойства[править | править код]

• Всякая последовательность является своей подпоследовательностью.
• Для всякой подпоследовательности (xkn){\displaystyle (x_{k_{n}})} верно, что ∀n∈N:kn⩾n{\displaystyle \forall n\in \mathbb {N} \colon k_{n}\geqslant n}.
• Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.
• Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.
• Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.
• Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
• Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.

Предельная точка последовательности[править | править код]

Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности. Для сходящихся числовых последовательностей предельная точка совпадает с пределом.

Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности, для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.

Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.

Верхний предел последовательности — это наибольшая предельная точка этой последовательности.

Нижний предел последовательности — это наименьшая предельная точка этой последовательности.

• Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.

  (xn){\displaystyle (x_{n})} стационарная ⇔(∃N∈N ∀i,j∈N:(i⩾N)∧(j⩾N)⇒(xi=xj)){\displaystyle \Leftrightarrow \left(\exists N\in \mathbb {N} ~\forall i,j\in \mathbb {N} \colon \left(i\geqslant N\right)\land \left(j\geqslant N\right)\Rightarrow \left(x_{i}=x_{j}\right)\right)}

Ограниченные и неограниченные последовательности[править | править код]

В предположении о линейной упорядоченности множества X{\displaystyle X} элементов последовательности можно ввести понятия ограниченных и неограниченных последовательностей.

• Ограниченная сверху последовательность — это последовательность элементов множества X{\displaystyle X}, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

  (xn){\displaystyle (x_{n})} ограниченная сверху ⇔∃M∈X ∀n∈N:xn⩽M{\displaystyle \Leftrightarrow \exists M\in X~\forall n\in \mathbb {N} \colon x_{n}\leqslant M}

• Ограниченная снизу последовательность — это последовательность элементов множества X{\displaystyle X}, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

  (xn){\displaystyle (x_{n})} ограниченная снизу ⇔∃m∈X ∀n∈N:xn⩾m{\displaystyle \Leftrightarrow \exists m\in X~\forall n\in \mathbb {N} \colon x_{n}\geqslant m}

• Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.

  (xn){\displaystyle (x_{n})} ограниченная ⇔∃m,M∈X ∀n∈N:m⩽xn⩽M{\displaystyle \Leftrightarrow \exists m,M\in X~\forall n\in \mathbb {N} \colon m\leqslant x_{n}\leqslant M}

• Неограниченная последовательность — это последовательность, которая не является ограниченной.

  (xn){\displaystyle (x_{n})} неограниченная ⇔∀m,M∈X ∃n∈N:(xn<m)∨(xn>M){\displaystyle \Leftrightarrow \forall m,M\in X~\exists n\in \mathbb {N} \colon \left(x_{n}<m\right)\lor \left(x_{n}>M\right)}

Критерий ограниченности числовой последовательности[править | править код]

Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.

(xn){\displaystyle (x_{n})} ограниченная ⇔∃A∈R ∀n∈N:|xn|⩽A{\displaystyle \Leftrightarrow \exists A\in \mathbb {R} ~\forall n\in \mathbb {N} \colon |x_{n}|\leqslant A}

Свойства ограниченных последовательностей[править | править код]

• Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.
• Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.
• Ограниченная последовательность имеет по крайней мере одну предельную точку.
• У ограниченной последовательности существуют верхний и нижний пределы.
• Для любого наперёд взятого положительного числа ε{\displaystyle \varepsilon } все элементы ограниченной числовой последовательности (xn)n=1∞{\displaystyle \left(x_{n}\right)_{n=1}^{\infty }}, начиная с некоторого номера, зависящего от ε{\displaystyle \varepsilon }, лежат внутри интервала (lim_n→∞⁡xn−ε,lim¯n→∞⁡xn+ε){\displaystyle \left(\varliminf _{n\to \infty }x_{n}-\varepsilon ,\varlimsup _{n\to \infty }x_{n}+\varepsilon \right)}.
• Если за пределами интервала (a,b){\displaystyle \left(a,b\right)} лежит лишь конечное число элементов ограниченной числовой последовательности (xn)n=1∞{\displaystyle \left(x_{n}\right)_{n=1}^{\infty }}, то интервал (lim_n→∞⁡xn,lim¯n→∞⁡xn){\displaystyle \left(\varliminf _{n\to \infty }x_{n},\varlimsup _{n\to \infty }x_{n}\right)} содержится в интервале (a,b){\displaystyle \left(a,b\right)}.
• Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Бесконечно большие и бесконечно малые последовательности[править | править код]

Свойства бесконечно малых последовательностей[править | править код]

Бесконечно малые последовательности отличаются целым рядом замечательных свойств, которые активно используются в математическом анализе, а также в смежных с ним и более общих дисциплинах.

• Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
• Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
• Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
• Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
• Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
• Любая бесконечно малая последовательность ограничена.
• Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.
• Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.
• Если (xn){\displaystyle (x_{n})} — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность (1/xn){\displaystyle (1/x_{n})}, которая является бесконечно малой. Если же (xn){\displaystyle (x_{n})} всё же содержит нулевые элементы, то последовательность (1/xn){\displaystyle (1/x_{n})} всё равно может быть определена, начиная с некоторого номера n{\displaystyle n}, и всё равно будет бесконечно малой.
• Если (αn){\displaystyle (\alpha _{n})} — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность (1/αn){\displaystyle (1/\alpha _{n})}, которая является бесконечно большой. Если же (αn){\displaystyle (\alpha _{n})} всё же содержит нулевые элементы, то последовательность (1/αn){\displaystyle (1/\alpha _{n})} всё равно может быть определена, начиная с некоторого номера n{\displaystyle n}, и всё равно будет бесконечно большой.

Сходящиеся и расходящиеся последовательности[править | править код]

• Сходящаяся последовательность — это последовательность элементов множества X{\displaystyle X}, имеющая предел в этом множестве.
• Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.

Свойства сходящихся последовательностей[править | править код]

• Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
• Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
• Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.
• Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
• Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.
• Если последовательность (xn){\displaystyle (x_{n})} сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность (1/xn){\displaystyle (1/x_{n})}, которая является ограниченной.
• Сумма сходящихся последовательностей также является сходящейся последовательностью.
• Разность сходящихся последовательностей также является сходящейся последовательностью.
• Произведение сходящихся последовательностей также является сходящейся последовательностью.
• Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
• Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.
• Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.
• Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.
• Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к о

Последовательность — Википедия

Материал из Википедии — свободной энциклопедии

Последовательность — такой набор элементов некоторого множества, что:

• для каждого натурального числа можно указать элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.

Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. Если любой конечный набор элементов называют выборкой конечного объёма, то последовательность оказывается выборкой бесконечного объёма.

Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность.

В математике рассматривают различные типы последовательностей:

Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей.

Пусть задано некоторое множество X{\displaystyle X} элементов произвольной природы.

Всякое отображение f:N→X{\displaystyle f\colon \mathbb {N} \to X} множества натуральных чисел N{\displaystyle \mathbb {N} } в заданное множество X{\displaystyle X} называется последовательностью (элементов множества X{\displaystyle X}).

Образ натурального числа n{\displaystyle n}, а именно элемент xn=f(n){\displaystyle x_{n}=f(n)}, называется n{\displaystyle n}-ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.

• Подмножество f[N]{\displaystyle f\left[\mathbb {N} \right]} множества X{\displaystyle X}, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
• Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется
  подпоследовательностью заданной последовательности.

Комментарии[править | править код]

• Не следует смешивать носитель последовательности и саму последовательность! Например, точка a∈X{\displaystyle a\in X} как одноточечное подмножество {a}⊂X{\displaystyle \{a\}\subset X} является носителем стационарной последовательности вида a,a,a,…{\displaystyle a,a,a,\dots }.

• Любое отображение множества N{\displaystyle \mathbb {N} } в себя также является последовательностью.

Последовательности вида

x1,x2,x3,…{\displaystyle x_{1},\quad x_{2},\quad x_{3},\quad \dots }

принято компактно записывать при помощи круглых скобок:

(xn){\displaystyle (x_{n})} или (xn)n=1∞{\displaystyle (x_{n})_{n=1}^{\infty }}

иногда используются фигурные скобки:

{xn}n=1∞{\displaystyle \{x_{n}\}_{n=1}^{\infty }}

Допуская некоторую вольность речи, можно рассматривать и конечные последовательности вида

(xn)n=1N{\displaystyle (x_{n})_{n=1}^{N}},

которые представляют собой образ начального отрезка последовательности натуральных чисел.

Фундаментальная последовательность — Википедия

Материал из Википедии — свободной энциклопедии

Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого ненулевого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии менее, чем заданное.

Последовательность точек {xn}n=1∞{\displaystyle \{x_{n}\}_{n=1}^{\infty }} метрического пространства (X,ρ){\displaystyle (X,\rho )} называется фундаментальной, если она удовлетворяет условию Коши:

для любого ε>0{\displaystyle \varepsilon >0} существует такое натуральное N{\displaystyle N}, что ρ(xn,xm)<ε {\displaystyle \rho (x_{n},x_{m})<\varepsilon \ } для всех n,m>N{\displaystyle n,m>N}.

• Пространство, в котором каждая фундаментальная последовательность сходится к элементу этого же пространства, называется полным.

• Каждая сходящаяся последовательность является фундаментальной, но не каждая фундаментальная последовательность сходится к элементу из своего пространства.
• Метрическое пространство является полным тогда и только тогда, когда всякая система вложенных замкнутых шаров с неограниченно убывающим радиусом имеет непустое пересечение, состоящее из одной точки.
• Если последовательность фундаментальна и содержит сходящуюся подпоследовательность, то сама последовательность сходится.
• Если последовательность фундаментальна, то она ограничена.

• Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, — М.: Наука, 2004. — 7-е изд.
• Шилов Г. Е. Математический анализ. Функции одного переменного. Ч. 3, — М.: Наука, 1970.

Предел числовой последовательности — Википедия

Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, число a{\displaystyle a} называется пределом последовательности {xn}{\displaystyle \{x_{n}\}}, если для любого ε>0{\displaystyle \varepsilon >0} существует номер Nε{\displaystyle N_{\varepsilon }}, зависящий от ε{\displaystyle \varepsilon }, такой, что для любого n>Nε{\displaystyle n>N_{\varepsilon }} выполняется неравенство  |xn−a|<ε{\displaystyle \ |x_{n}-a|<\varepsilon }.

В случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.

Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.^[1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.

Понятие предела последовательности использовалось ещё Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

Число a∈R{\displaystyle a\in \mathbb {R} } называется пределом числовой последовательности {xn}{\displaystyle \{x_{n}\}}, если последовательность {xn−a}{\displaystyle \{x_{n}-a\}} является бесконечно малой, то есть все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

limn→∞xn=a ⇔ ∀ε>0 ∃N(ε)∈N: n⩾N ⇒|xn−a|<ε{\displaystyle \lim _{n\to \infty }x_{n}=a~\Leftrightarrow ~\forall \varepsilon >0~\exists N(\varepsilon )\in \mathbb {N} \colon ~n\geqslant N~\Rightarrow |x_{n}-a|<\varepsilon }

Если число a∈R{\displaystyle a\in \mathbb {R} } является пределом числовой последовательности {xn}{\displaystyle \{x_{n}\}}, то говорят также, что последовательность {xn}{\displaystyle \{x_{n}\}} сходится к a{\displaystyle a}. Если никакое вещественное число не является пределом последовательности {xn}{\displaystyle \{x_{n}\}}, её называют расходящейся.

Для некоторых последовательностей предел полагают равным бесконечности. А именно, говорят, что последовательность {xn}{\displaystyle \{x_{n}\}} стремится к бесконечности, если для любого вещественного числа все члены последовательности, начиная с некоторого, оказываются по модулю больше этого числа. Формально,

limn→∞xn=∞ ⇔ ∀E>0 ∃N(E)∈N: ∀n⩾N⇒|xn|>E{\displaystyle \lim _{n\to \infty }x_{n}=\infty ~\Leftrightarrow ~\forall E>0~\exists N(E)\in \mathbb {N} \colon ~\forall n\geqslant N\Rightarrow |x_{n}|>E}

Кроме того, если все элементы стремящейся к бесконечности последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

limn→∞xn=+∞ ⇔ ∀E>0 ∃N(E)∈N: ∀n⩾N⇒xn>E{\displaystyle \lim _{n\to \infty }x_{n}=+\infty ~\Leftrightarrow ~\forall E>0~\exists N(E)\in \mathbb {N} \colon ~\forall n\geqslant N\Rightarrow x_{n}>E}

Если же элементы стремящейся к бесконечности последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

limn→∞xn=−∞ ⇔ ∀E>0 ∃N(E)∈N: ∀n⩾N⇒xn<−E{\displaystyle \lim _{n\to \infty }x_{n}=-\infty ~\Leftrightarrow ~\forall E>0~\exists N(E)\in \mathbb {N} \colon ~\forall n\geqslant N\Rightarrow x_{n}<-E}

Любая последовательность, стремящаяся к бесконечности — неограниченная. Однако обратное неверно.

Частичный предел последовательности — это предел одной из её подпоследовательностей.

Верхний предел последовательности — это наибольшая из её предельных точек.

Нижний предел последовательности — это наименьшая из её предельных точек.

Тот факт, что последовательность {xn}{\displaystyle \{x_{n}\}} сходится к числу a{\displaystyle a} обозначается одним из следующих способов:

• limn→∞xn=a{\displaystyle \lim _{n\to \infty }x_{n}=a}

или

• xn →n→∞ a{\displaystyle x_{n}~{\xrightarrow[{n\to \infty }]{}}~a}

Существуют определённые особенности для предела последовательностей вещественных чисел.^[2]

Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств.

Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела.

Свойства[править | править код]

Арифметические свойства[править | править код]

• взятия предела числовой последовательности является линейным, то есть проявляет два свойства линейных отображений.
  • Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.

    limn→∞(xn+yn)=limn→∞xn+limn→∞yn{\displaystyle \lim _{n\to \infty }(x_{n}+y_{n})=\lim _{n\to \infty }x_{n}+\lim _{n\to \infty }y_{n}}

  • Однородность. Константу можно выносить из-под знака предела.

    ∀k∈R:limn→∞kxn=klimn→∞xn{\displaystyle \forall k\in \mathbb {R} \colon \lim _{n\to \infty }kx_{n}=k\lim _{n\to \infty }x_{n}}

• Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

  limn→∞(xn⋅yn)=limn→∞xn⋅limn→∞yn{\displaystyle \lim _{n\to \infty }(x_{n}\cdot y_{n})=\lim _{n\to \infty }x_{n}\cdot \lim _{n\to \infty }y_{n}}

• Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.

  limn→∞xnyn=limn→∞xnlimn→∞yn{\displaystyle \lim _{n\to \infty }{\frac {x_{n}}{y_{n}}}={\frac {\lim \limits _{n\to \infty }x_{n}}{\lim \limits _{n\to \infty }y_{n}}}}

Свойства сохранения порядка[править | править код]

• Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.

  ∃N∈N ∀n⩾N:xn⩽a ⇒ limn→∞xn⩽a{\displaystyle \exists N\in \mathbb {N} ~\forall n\geqslant N\colon x_{n}\leqslant a~\Rightarrow ~\lim _{n\to \infty }x_{n}\leqslant a}

• Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.

  ∃N∈N ∀n⩾N:xn⩾a ⇒ limn→∞xn⩾a{\displaystyle \exists N\in \mathbb {N} ~\forall n\geqslant N\colon x_{n}\geqslant a~\Rightarrow ~\lim _{n\to \infty }x_{n}\geqslant a}

• Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.

  ∃N∈N ∀n⩾N:xn<a ⇒ limn→∞xn⩽a{\displaystyle \exists N\in \mathbb {N} ~\forall n\geqslant N\colon x_{n}<a~\Rightarrow ~\lim _{n\to \infty }x_{n}\leqslant a}

• Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.

  ∃N∈N ∀n⩾N:xn>a ⇒ limn→∞xn⩾a{\displaystyle \exists N\in \mathbb {N} ~\forall n\geqslant N\colon x_{n}>a~\Rightarrow ~\lim _{n\to \infty }x_{n}\geqslant a}

• Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.

  ∃N∈N ∀n⩾N:xn⩽yn ⇒ limn→∞xn⩽limn→∞yn{\displaystyle \exists N\in \mathbb {N} ~\forall n\geqslant N\colon x_{n}\leqslant y_{n}~\Rightarrow ~\lim _{n\to \infty }x_{n}\leqslant \lim _{n\to \infty }y_{n}}

• Для числовых последовательностей справедлива теорема о двух милиционерах (принцип двустороннего ограничения).

  ∃N∈N ∀n⩾N:xn⩽zn⩽yn ⇒ limn→∞xn⩽limn→∞zn⩽limn→∞yn{\displaystyle \exists N\in \mathbb {N} ~\forall n\geqslant N\colon x_{n}\leqslant z_{n}\leqslant y_{n}~\Rightarrow ~\lim _{n\to \infty }x_{n}\leqslant \lim _{n\to \infty }z_{n}\leqslant \lim _{n\to \infty }y_{n}}

Другие свойства[править | править код]

• Сходящаяся числовая последовательность имеет только один предел.

  limn→∞xn=a ∧ limn→∞xn=b ⇒ a=b{\displaystyle \lim _{n\to \infty }x_{n}=a~\land ~\lim _{n\to \infty }x_{n}=b~\Rightarrow ~a=b}

• Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.

  ∀n∈N:xn∈[a, b] ⇒ limn→∞xn∈[a, b]{\displaystyle \forall n\in \mathbb {N} \colon x_{n}\in [a,~b]~\Rightarrow ~\lim _{n\to \infty }x_{n}\in [a,~b]}

• Предел последовательности из одного и того же числа равен этому числу.

  limn→∞x=x{\displaystyle \lim _{n\to \infty }x=x}

• Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел.

• У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.

• Если у последовательности xn{\displaystyle x_{n}} существует предел, то последовательность средних арифметических x1+⋯+xnn{\displaystyle {\frac {x_{1}+\dots +x_{n}}{n}}} имеет тот же предел (следствие из теоремы Штольца).

Примеры[править | править код]

• limn→∞1n=limn→∞(−1)nn=0{\displaystyle \lim _{n\to \infty }{\frac {1}{n}}=\lim _{n\to \infty }{\frac {(-1)^{n}}{n}}=0}

• ∀q∈R:limn→∞qnn!=0{\displaystyle \forall q\in \mathbb {R} \colon \lim _{n\to \infty }{\frac {q^{n}}{n!}}=0}

• limn→∞nn=1{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=1}

• limn→∞(1+1n)n=e{\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e}

• ∀a∈R∖{0}:limn→∞a+a+⋯+a⏟n=1+1+4a2{\displaystyle \forall a\in \mathbb {R} \setminus \{0\}\colon \lim _{n\to \infty }\underbrace {\sqrt {a+{\sqrt {a+\cdots +{\sqrt {a}}}}}} _{n}={\frac {1+{\sqrt {1+4a}}}{2}}}

• limn→∞xn=x ⇒ limn→∞∏k=1nxkn=x{\displaystyle \lim _{n\to \infty }x_{n}=x~\Rightarrow ~\lim _{n\to \infty }{\sqrt[{n}]{\prod _{k=1}^{n}x_{k}}}=x}

• ∀n∈N:xn>0 ⇒ limn→∞xn+1xn=limn→∞xnn{\displaystyle \forall n\in \mathbb {N} \colon x_{n}>0~\Rightarrow ~\lim _{n\to \infty }{\frac {x_{n+1}}{x_{n}}}=\lim _{n\to \infty }{\sqrt[{n}]{x_{n}}}}

• limn→∞n=+∞{\displaystyle \lim _{n\to \infty }n=+\infty }

• ∄limn→∞(−1)n{\displaystyle \nexists \lim _{n\to \infty }(-1)^{n}}

Комплексное число a{\displaystyle a} называется пределом последовательности {zn}{\displaystyle \{z_{n}\}}, если для любого положительного числа ε{\displaystyle \varepsilon } можно указать такой номер N=N(ε){\displaystyle N=N(\varepsilon )}, начиная с которого все элементы zn{\displaystyle z_{n}} этой последовательности удовлетворяют неравенству
|zn−a|<ε{\displaystyle |z_{n}-a|<\varepsilon } при n⩾N(ε){\displaystyle n\geqslant N(\varepsilon )}

Последовательность {zn}{\displaystyle \{z_{n}\}}, имеющая предел a{\displaystyle a}, называется сходящейся к числу a{\displaystyle a}, что записывается в виде limn→∞zn=a{\displaystyle \lim \limits _{n\to \infty }z_{n}=a}.

Не у всякой ограниченной последовательности существует предел. Например, если взять в качестве пространства множество вещественных чисел со стандартной топологией, а в качестве xn{\displaystyle x_{n}} последовательность xn=(−1)n{\displaystyle x_{n}=(-1)^{n}}, то у неё не будет предела (однако у неё можно найти верхний и нижний пределы, 1,−1{\displaystyle 1,-1}, то есть пределы её подпоследовательностей — частичные пределы).

Предел последовательности — Википедия

Материал из Википедии — свободной энциклопедии

n	n sin(1/n)
1	0.841471
2	0.958851
…
10	0.998334
…
100	0.999983

С ростом значения n значение функции n sin(1/n) приближается к 1. Говорят, что «предел последовательности n sin(1/n) равен 1».

У этого термина существуют и другие значения, см. Предел.

В математике пределом последовательности элементов метрического пространства или топологического пространства называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементов топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. В метрическом пространстве окрестности определяются через функцию расстояния, поэтому понятие предела формулируется на языке расстояний. Исторически первым было понятие предела числовой последовательности, возникающее в математическом анализе, где оно служит основанием для системы приближений и широко используется при построении дифференциального и интегрального исчислений.

Обозначение: limn→∞xn=a{\displaystyle \lim _{n\to \infty }x_{n}=a}

(читается: предел последовательности икс энное при эн, стремящемся к бесконечности, равен a^[1][2])

Свойство последовательности иметь предел называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательность сходится; в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. В хаусдорфовом пространстве и, в частности, метрическом пространстве^[3], каждая подпоследовательность сходящейся последовательности сходится, и её предел совпадает с пределом исходной последовательности. Другими словами, у последовательности элементов хаусдорфово пространства не может быть двух различных пределов. Может, однако, оказаться, что у последовательности нет предела, но существует подпоследовательность (данной последовательности), которая предел имеет. Если из любой последовательности точек пространства можно выделить сходящуюся подпоследовательность, то, говорят, что данное пространство обладает свойством секвенциальной компактности (или просто компактности, если компактность определяется исключительно в терминах последовательностей).

В топологических пространствах, удовлетворяющих первой аксиоме счётности, понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке. Для произвольных топологических пространств такой последовательности может не существовать.

Пусть дано топологическое пространство T{\displaystyle T} и последовательность {xn}.{\displaystyle \{x_{n}\}.} Тогда, если существует элемент x∈T{\displaystyle x\in T} такой, что

∀U(x)∃N:∀n(n>N)⇒xn∈U(x){\displaystyle \forall U(x)\exists N:\forall n(n>N)\Rightarrow x_{n}\in U(x)},

где U(x){\displaystyle U(x)} — открытое множество, содержащее x{\displaystyle x}, то он называется пределом последовательности xn{\displaystyle x_{n}}. Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент x∈T{\displaystyle x\in T} такой, что

∀ε>0∃N:∀n(n>N)⇒d(xn,x)<ε{\displaystyle \forall \varepsilon >0\exists N:\forall n(n>N)\Rightarrow d(x_{n},x)<\varepsilon },

где d(x,y){\displaystyle d(x,y)} — метрика, то x{\displaystyle x} называется пределом xn{\displaystyle x_{n}}.

• Предел произвольной подпоследовательности называется частным пределом последовательности.

1. ↑ «Знак „lim“ составляет собой первые три буквы латинского слова limes — предел, граница; но читать его следует по-русски: „предел“» (Хинчин А. Я. Краткий курс математического анализа. — М.: ГИТТЛ, 1953. — С. 38. — 624 с.)
2. ↑ «Эта запись читается так: „предел xn{\displaystyle x_{n}} при n{\displaystyle n}, стремящемся к бесконечности, равен a{\displaystyle a}“» (Шипачев В. С. Основы высшей математики / Под ред. акад. А. Н. Тихонова. — М.: Высшая школа, 1989. — С. 121. — 479 с. — ISBN 5-06-000048-6.)
3. ↑ Каждое метрическое пространство является автоматически и хаусдорфовым.

1. Введение в математический анализ. Числовая последовательность.

Числовая последовательность – Функция вида , заданная на множествеN натуральных чисел. Обозначается в виде {x_n}, . Число x₁ называется первым членом (элементом) последовательности, x_n – общим или n-м членом последовательности.

Задается либо формулой общего члена, либо рекуррентной формулой.

Формула общего члена позволяет вычислить любой член последовательности по номеру n (при помощи этой формулы можно сразу вычислить любой член последовательности).

Пример:

Рекуррентная формула определяет правило, по которому можно найти n-ый член последовательности, зная первый и (n-1)-ый члены (при таком способе для нахождения 100-го члена последовательности придётся сначала посчитать 99 предыдущих).

2. Ограниченные и неограниченные последовательности.

Числовая последовательность – Функция вида , заданная на множествеN натуральных чисел. Обозначается в виде {x_n}, . Число x₁ называется первым членом (элементом) последовательности, x_n – общим или n-м членом последовательности.

Последовательность {x_n} называется ограниченной, если существует такое число , что для любого выполняется неравенство . (если, то последовательность —неограниченная).

3. Монотонные последовательности.

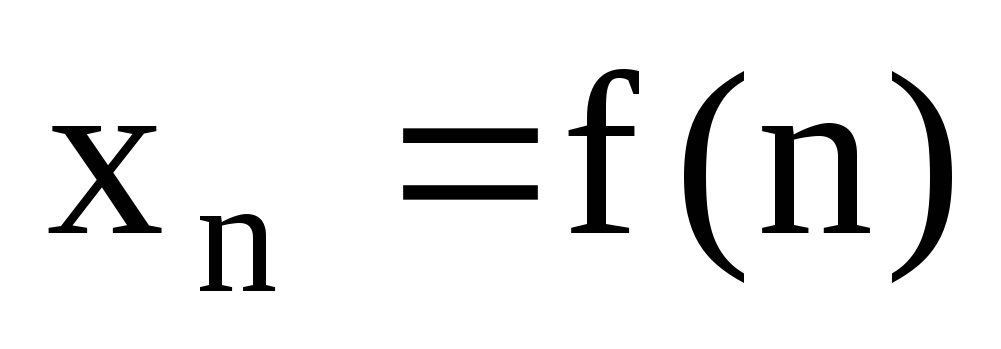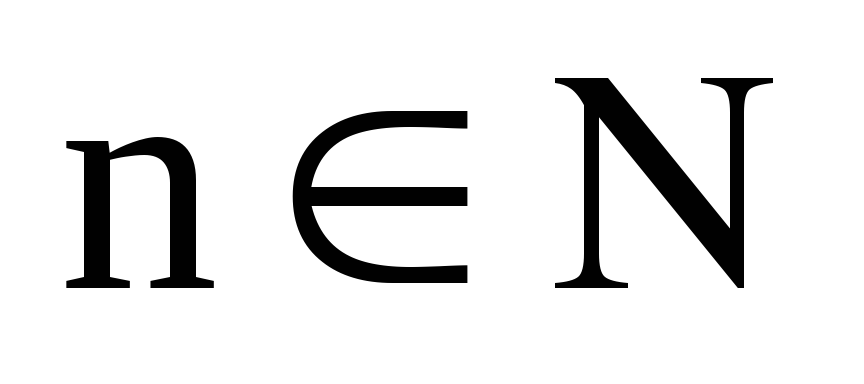Числовая последовательность – Функция вида , заданная на множествеN натуральных чисел. Обозначается в виде {x_n}, . Число x₁ называется первым членом (элементом) последовательности, x_n – общим или n-м членом последовательности.

Последовательность {x_n} называется возрастающей, если для любого выполняется неравенство . (если, то последовательность —убывающая). Если все элементы последовательности {x_n} равны одному и тому же числу с, то ее называют постоянной.

Возрастающие, убывающие и постоянные последовательности – монотонные.

4. Число е.

Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.

Рассмотрим последовательность .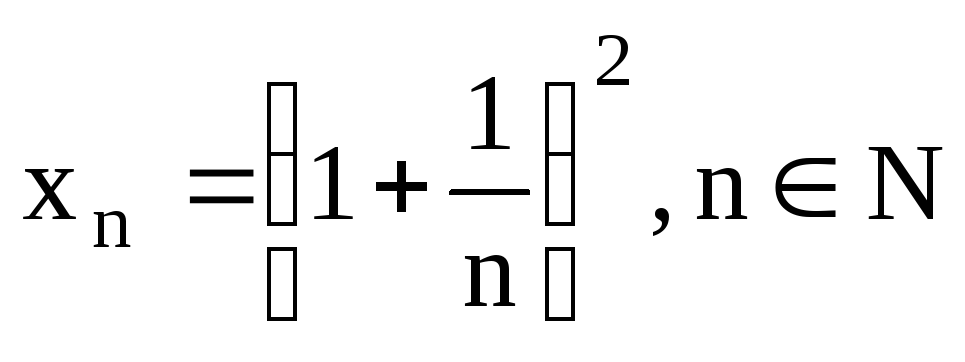

По формуле бинома Ньютона:

Пусть 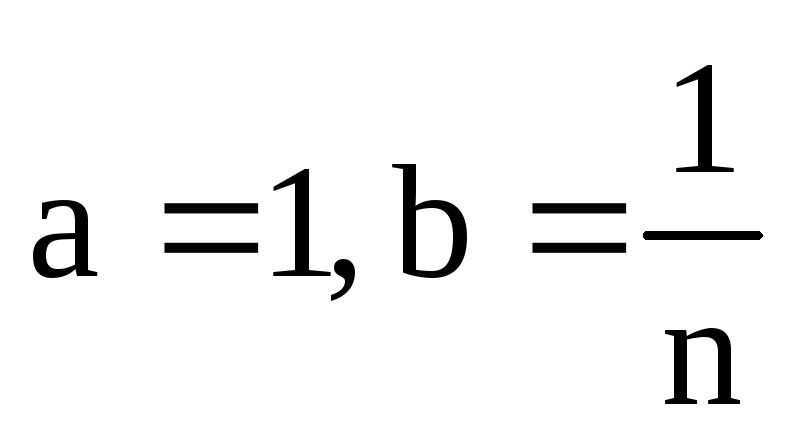, тогда:

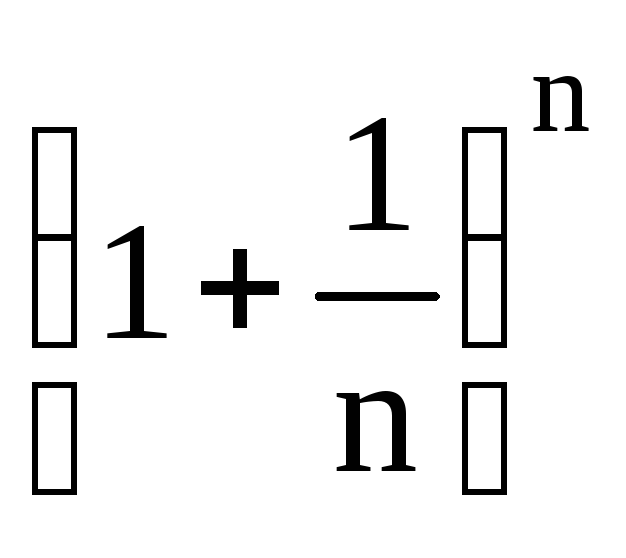— возрастающая последовательность, причём . Заменим в правой части скобки на 1, а факториалы на степени двойки. По формуле суммы членов прогрессии найдём, что:

Последовательность ограничена, при этом для выполняется неравенство:, следовательно на основаниитеоремы Вейерштрасса последовательность имеет предел, обозначаемей буквой е.

.

Число е называется неперовым числом. Число е иррациональное, его приближенное значение равно 2,72 (е = 2,718281828459045…). Число е принято за основание натуральных логарифмов ()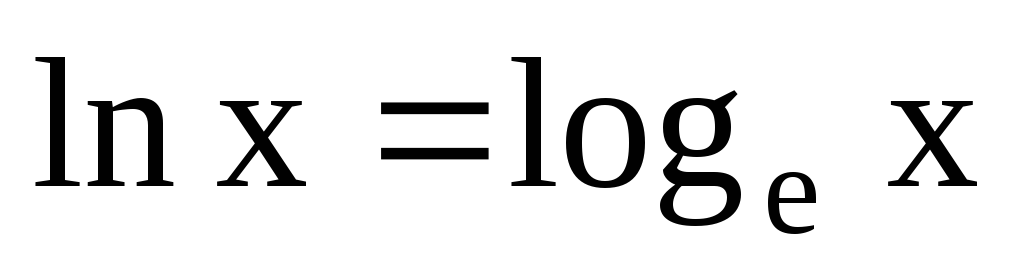

5. Связь натурального и десятичного логарифмов.

За основание натуральных логарифмов принято число е, десятичных – 10. (,)

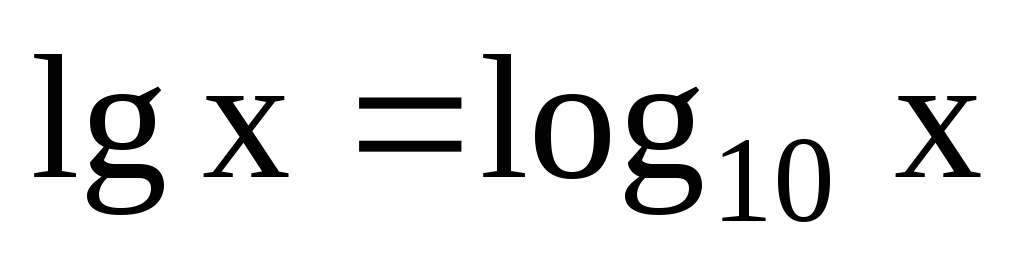По определению логарифма имеем . Прологарифмируем по основанию 10.

Пользуясь десятичными логарифмами, находим , значит, либо

6. Предел функции в точке.

Определение 1 (на “языке последовательностей”, или по Гейне). Пусть функция определена в некоторой окрестности точки, кроме, быть может, самой точки. Число А называется пределом функциив точке(или при), если для любой последовательности допустимых значений аргумента, сходящихся к числу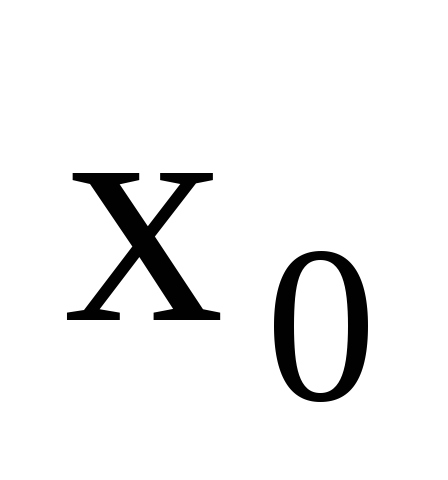(т.е.), последовательность соответствующих значений, сходится к числу А (т.е.).

Определение 2 (на “языке ”, или по Коши). Пусть функция определена в некоторой окрестности точки, кроме, быть может, самой точки. Число А называется пределом функциив точке(или при), если для любого положительногонайдётся такое положительное число, что при всехx, удовлетворяющих неравенству , выполнится неравенство.

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ | Энциклопедия Кругосвет

Содержание статьи

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), x О N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y₁, y₂,…, y_n,…. Значения y₁, y₂, y₃,… называют соответственно первым, вторым, третьим, … членами последовательности.

Например, для функции y = n² можно записать:

y₁ = 1² = 1;

y₂ = 2² = 4;

y₃ = 3² = 9;…y_n = n²;…

Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n-го члена:

y_n = f(n).

Пример. y_n= 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Пример 1. y₁ = 3; y_n = y_n–1 + 4, если n = 2, 3, 4,….

Здесь y₁ = 3; y₂ = 3 + 4 = 7; y₃ = 7 + 4 = 11; ….

Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: y_n = 4n – 1.

Пример 2. y₁ = 1; y₂ = 1; y_n = y_n–2 + y_n–1 , если n = 3, 4,….

Здесь: y₁ = 1; y₂ = 1; y₃ = 1 + 1 = 2; y₄ = 1 + 2 = 3; y₅ = 2 + 3 = 5; y₆ = 3 + 5 = 8;

Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n-е число Фибоначчи выражается через его порядковый номер следующей формулой .

На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n.

Свойства числовых последовательностей.

Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность {y_n} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y₁y₂y₃y_ny_n+1

Определение. Последовательность {y_n} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y₁ > y₂ > y₃ > … > y_n > y_n+1 > … .

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Пример 1. y₁ = 1; y_n = n²– возрастающая последовательность.

Пример 2. y₁ = 1; 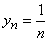– убывающая последовательность.

Пример 3. y₁ = 1; – эта последовательность не является не возрастающей не убывающей.

Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство y_n = y_n+T. Число T называется длиной периода.

Пример. Последовательность периодична с длиной периода T = 2.

Арифметическая прогрессия.

Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

Таким образом, арифметическая прогрессия – это числовая последовательность {a_n}, заданная рекуррентно соотношениями

a₁ = a, a_n = a_n–1 + d (n = 2, 3, 4, …)

(a и d – заданные числа).

Пример. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a₁ = 1, d = 2.

Пример. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a₁ = 20, d = –3.

Нетрудно найти явное (формульное) выражение a_nчерез n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n – 1)d по сравнению с первым членом арифметической прогрессии, т.е.

a_n = a₁ + d(n – 1).

Это формула n-го члена арифметической прогрессии.

Используя явное выражение a_nчерез n, можно доказать следующее свойство арифметической прогрессии: если натуральные числа i, j, k, l таковы, что i + j = k + l, то a_i + a_j= a_k + a_l. Чтобы в этом убедиться, достаточно подставить i, j, k и l вместо n в формулу n-го члена арифметической прогрессии и сложить. Отсюда следует, что если рассматривать первые n членов арифметической прогрессии, то суммы членов, равно отстоящих от концов, будут одинаковы:

a₁ + a_n = a₂ + a_n–1 = a₃ + a_n–2 = … = 2_a1 + (n – 1)d.

Последнее равенство позволяет вычислить сумму первых n членов арифметической прогрессии:

S_n = a₁ + a₂ + … + a_n–1 + a_n.

С этой целью берется еще одна такая же сумма, но слагаемые записывается в обратном порядке:

S_n = a_n + a_n–1 + … + a₂ + a₁.

Далее она складывается почленно с исходной суммой, причем слагаемые сразу попарно группируются. В результате

2S_n = (a₁ + a_n) + (a₂ + a_n–1) + … + (a_n + a₁) = n(2_a1 + (n – 1)d),

откуда . Это формула суммы n членов арифметической прогрессии.

Арифметической прогрессия названа потому, что в ней каждый член, кроме первого, равен среднему арифметическому двух соседних с ним – предыдущего и последующего. Действительно, так как

a_n = a_n–1 + d;

a_n = a_n+1 – d.

Сложение двух последних равенств дает .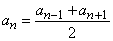

Таким образом, верна следующая теорема (характеристическое свойство арифметической прогрессии). Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.

Пример. При каком значении x числа 3x + 2, 5x – 4 и 11x + 12 образуют конечную арифметическую прогрессию?

Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению

5x – 4 = ((3x + 2) + (11x + 12))/2.

Решение этого уравнения дает x = –5,5. При этом значении x заданные выражения 3x + 2, 5x – 4 и 11x + 12 принимают, соответственно, значения –14,5, –31,5, –48,5. Это – арифметическая прогрессия, ее разность равна –17.

Геометрическая прогрессия.

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.

Таким образом, геометрическая прогрессия – это числовая последовательность {b_n}, заданная рекуррентно соотношениями

b₁ = b, b_n = b_n–1q (n = 2, 3, 4…).

(b и q – заданные числа, b ≠ 0, q ≠ 0).

Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2, q = 3.

Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.

Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.

Геометрическая прогрессия является возрастающей последовательностью, если b1 > 0, q > 1, и убывающей, если b1 > 0, 0 q

Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.

b₁², b₂², b₃², …, b_n2,… является геометрической прогрессией, первый член которой равен b₁², а знаменатель – q².

Формула n-го члена геометрической прогрессии имеет вид

b_n = b₁q^n–1.

Можно получить формулу суммы членов конечной геометрической прогрессии.

Пусть дана конечная геометрическая прогрессия

b₁, b₂, b₃, …, b_n

пусть S_n – сумма ее членов, т.е.

S_n= b₁ + b₂+ b₃ + … + b_n.

Принимается, что q № 1. Для определения S_nприменяется искусственный прием: выполняются некоторые геометрические преобразования выражения S_nq.

Тогда

S_nq = (b₁ + b₂ + b₃+ … + b_n–1 + b_n)q = b₂ + b₃ + b₄ + …+ b_n + b_nq = S_n+ b_nq – b₁.

Таким образом, S_nq = S_n + b_nq – b₁ и, следовательно,

.

Это формула суммы n членов геометрической прогрессии для случая, когда q ≠ 1.

При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае S_n = a₁n.

Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов. Действительно, так как

b_n= b_n-1q;

b_n= b_n+1/q,

следовательно, b_n2= b_n–1 b_n+1 и верна следующая теорема (характеристическое свойство геометрической прогрессии):

числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.

Предел последовательности.

Пусть есть последовательность {c_n} = {1/n}. Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a и b есть число , или . С ростом n все члены геометрической прогрессии убывают и их значение приближается к нулю. В этом случае принято говорить, что при n, стремящемся к бесконечности, данная последовательность сходится и нуль есть ее предел. Записывается это так:

.

Строгое определение предела формулируется следующим образом:

Если существует такое число A, что для любого (сколь угодно малого) положительного числа ε найдется такое натуральное N (вообще говоря, зависящее от ε), что для всех n ≥ N будет выполнено неравенство |a_n – A| {a_n} сходится и A – ее предел.

Обозначается это так: .

В противном случае последовательность называется расходящейся.

Опираясь на это определение, можно, например, доказать наличие предела A = 0 у гармонической последовательности {c_n} = {1/n}. Пусть ε – сколь угодно малое положительное число. Рассматривается разность

.

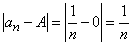Существует ли такое N, что для всех n ≥ N выполняется неравенство 1/N ? Если взять в качестве N любое натуральное число, превышающее 1/ε, то для всех n ≥ N выполняется неравенство 1/n ≤ 1/N ε , что и требовалось доказать.

Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.

Теорема 1. Если последовательность имеет предел, то она ограничена.

Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.

Теорема 3. Если последовательность {a_n} имеет предел A, то последовательности {ca_n}, {a_n + с} и {| a_n|} имеют пределы cA, A + c, |A| соответственно (здесь c – произвольное число).

Теорема 4. Если последовательности {a_n} и {b_n} имеют пределы, равные A и B соответственно, то последовательность {pa_n + qb_n} имеет предел pA + qB.

Теорема 5. Если последовательности {a_n} и {b_n}имеют пределы, равные A и B соответственно, то последовательность {a_nb_n} имеет предел AB.

Теорема 6. Если последовательности {a_n} и {b_n} имеют пределы, равные A и B соответственно, и, кроме того, b_n ≠ 0 и B ≠ 0, то последовательность {a_n / b_n} имеет предел A/B.

Анна Чугайнова