Урок 5. пропорции — Математика — 6 класс
Математика
6 класс
Урок № 5
Пропорции
Перечень рассматриваемых вопросов:
- Понятие пропорции.
- Основное свойство пропорции.
- Как правильно составить пропорцию.
- Как найти неизвестный член пропорции.
Тезаурус
Равенство двух отношений называют пропорцией.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл.

Теоретический материал для самостоятельного изучения
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.
Рассмотрим 3 способа нахождения неизвестного члена пропорции.
1 способ.
2 способ.
Способ 3.
Задача.
Решение:
Ответ:
1) можно;
2) можно;
3) нельзя;
4) нельзя.
Разбор решения заданий тренировочного модуля
№1. Тип задания: сортировка элементов по категориям.
№2. Тип задания: Подстановка элементов в пропуски в тексте.
Найдите неизвестный член пропорции.
Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.
Ответ: 3.
Решение пропорций | Математика
Рассмотрим решение пропорций на конкретных примерах.
Решить уравнения с пропорцией:
1) 25 : x = 10 : 18
Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:
25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.
Ответ: 45.
Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:
Ответ: 13,5.
При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.
Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:
В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Сокращаем 24 и 6 на 6, 10 и 45 — на 5:
Еще раз сокращаем 4 и 2 на 2:
Ответ: 18.
Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.
Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:
Смешанные числа переводим в неправильные дроби:
Ответ: 28.
При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.
Произведение крайних членов пропорции равно произведению средних членов:
Здесь удобно упростить уравнение, разделив обе части на 5:
Ответ: 10,5.
Произведение крайних членов пропорции равно произведению ее средних членов:
Для упрощения вычислений удобно умножить каждую часть уравнения на 10:
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: 1,12.
Отношения и пропорции в математике
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.
Таким образом, сам смысл термина «отношение» был несколько иной, чем термина «деление»: дело в том, что второй означал разделение определенной именованной величины на любое совершенно отвлеченное абстрактное число. В современной математике понятия « деление» и «отношение» по своему смыслу абсолютно идентичны и являются синонимами. Например, и тот, и другой термин с одинаковым успехом применяют для отношения величин, являющихся неоднородными: массы и объема, расстояния и времени и т.п. При этом многие отношения величин однородных принято выражать в процентах.
ПримерВ супермаркете насчитывается четыреста наименований различных товаров. Из них двести произведено на территории Российской Федерации. Определить, каково отношение отечественных товаров к общему числу товаров, продаваемых в супермаркете?
400 – общее число товара
200 – РФ
Ответ: двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов.
200
400 = 0,5 или 50%В математике делимым принято называть предыдущий член отношения, а делителем – последующий член отношения. В приведенном выше примере предыдущим членом являлось число двести, а последующим – число четыреста.
Два равных отношения образуют пропорцию
В современной математике принято считать, что пропорцией является два равным между собой отношения. К примеру, если общее количество наименований товаров, продаваемых в одном супермаркете, – четыреста, а в России из них произведено двести, а те же значения для другого супермаркета составляют шестьсот и триста, то соотношение количества российских товаров к общему их числу, реализовываемых в обеих торговых предприятиях, одинаково:
1.Двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов
200 : 400 = 0,5 или 50%
2.
300 : 600 = 0,5 или 50%
В данном случае имеется пропорция, которую можно записать следующим образом:
Если формулировать это выражение так, как это принято делать в математике, то говорится, что двести относится к четыремстам так же, как триста относится к шестистам. При этом двести и шестьсот называются крайними членами пропорции, а четыреста и триста – средними членами пропорции.
Произведение средних членов пропорции
Согласно одному из законов математики, произведение средних членов любой пропорции равняется произведению ее крайних членов. Если возвратиться к приведенным выше примерам, то проиллюстрировать это можно следующим образом:
Двести умноженное на шестьсот равняется сто двадцать тысяч;
200 × 600 = 120 000
Триста умноженное на четыреста равняется сто двадцать тысяч.
300 × 400 = 120 000
Из этого следует, что любой из крайних членов пропорции равен произведению ее средних членов, деленному на другой крайний член. По тому же самому принципу каждый из средних членов пропорции равен крайних ее членов, деленному на другой средний член.
Если вернуться к приведенному выше примеру пропорции, то:
Двести равняется четыреста умноженное на триста и деленное на шестьсот.
Эти свойства широко используются в практических математических вычислениях тогда, когда требуется найти значение неизвестного члена пропорции при известных значениях трех членов остальных.
Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.
Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины \(4, 2, 8 \) и \(4\) находятся в отношении, если \(\frac{4}{2}=\frac{8}{4}\). Произведение крайних членов пропорции равно произведению средних.
Четыре величины \(4, 2, 8 \) и \(4\) находятся в отношении, если \(\frac{4}{2}=\frac{8}{4}\). Произведение крайних членов пропорции равно произведению средних.
Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.
Если \(\frac{A}{B} = \frac{C}{D}\), то
Пропорция состоит из двух равных отношений. Однако если \(\frac{A}{B}\) не равно \(\frac{C}{D}\), то \(A, B, C, D \) не называются пропорцией.
Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.
\(A, B , C\) находятся в постоянной пропорции, если \(\frac{A}{B} =\frac{C}{D}\)
Если \(A, B ,C \) находятся в постоянном отношении, то \(B\) называется средней в пропорции.
В косвенной пропорции как одно значение увеличивается, так и другое значение уменьшается.
Задача 1. За \(5\) дней и \(12\) человек построили забор. Сколько дней это займет у \(6\) людей?
Сколько дней это займет у \(6\) людей?
Решение.
- \(12\) человек → \(5\) дней
- \(6\) человек → \(x\) дней
- \(\frac{12}{6} = \frac{x}{5}\)
- умножаем крест на крест члены пропорции и сокращаем на \(6\):
\(12*5=6x\)
\(60=6x\)
\(x=10\)
Ответ: \(6\) людей будут работать \(10\) дней, чтобы закончить работу.
Задача 2. Найдите значение \(x\), если \(\frac{2}{5}=\frac{x}{15}\)
Решение:
- \(2*15=5x\)
- \(30 =5x\)
- Делим на 5 обе части равенства: \(\frac{30}{5}=x\), откуда находим
Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?
Решение:\(\)
- \((10+x)(18+x)=(22+x)(38+x)\)
- \(380+48x+2x=396+40x+2x\)
- \(8x=16\)
- \(x=2\)
Задача 4. Найти четвертый член пропорции \(6,10\) и \(12\)
Решение:
\(\frac{6}{10}=\frac{12}{x}\)
6×х = 120
x = 120/6
x = 20
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».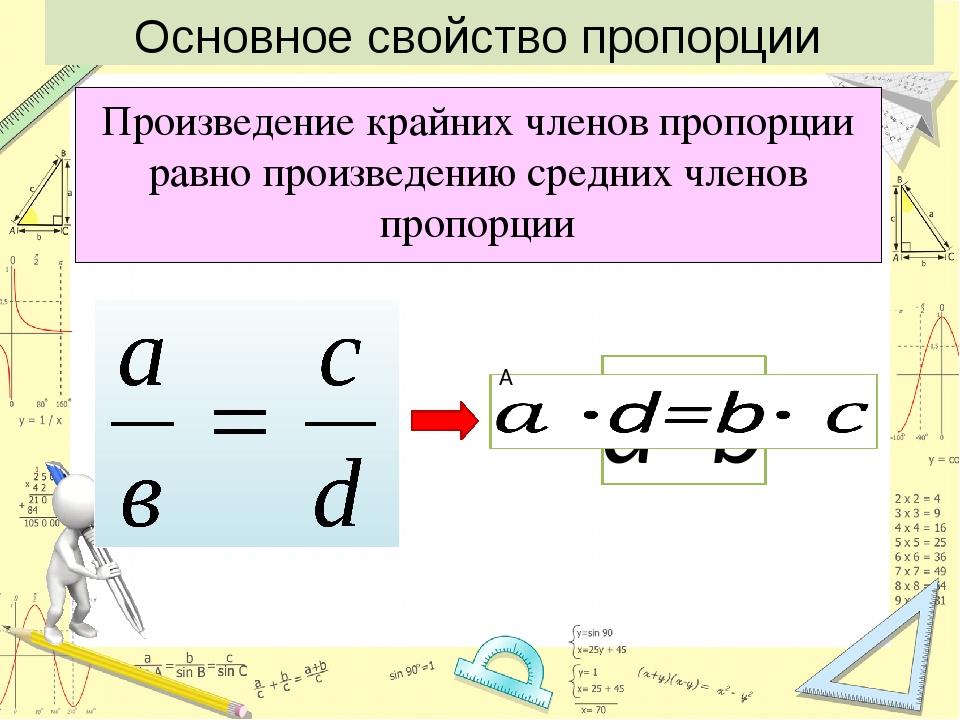 Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Могилёвский государственный университет имени А. А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 4-9 классов. Мой подход в преподавании — не только устранить пробелы в теории, но и привить любовь к предмету, научить самостоятельно, “интуитивно” в нём ориентироваться. Мои ученики успешно сдают выпускные экзамены и пишут республиканские контрольные!
«В математике есть своя красота, как в живописи и поэзии».
Мой подход в преподавании — не только устранить пробелы в теории, но и привить любовь к предмету, научить самостоятельно, “интуитивно” в нём ориентироваться. Мои ученики успешно сдают выпускные экзамены и пишут республиканские контрольные!
«В математике есть своя красота, как в живописи и поэзии».
Репетитор по математике
Донецкий национальный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. Я люблю математику, поскольку математическое мышление помогает вникать в суть вещей и решать повседневные задачи. Математика тренирует память и развивает ум. С радостью помогу ученикам закрепить школьные знания и узнать новое. Научу правильно задавать вопросы, рассуждать и самостоятельно искать решение задач.
Я люблю математику, поскольку математическое мышление помогает вникать в суть вещей и решать повседневные задачи. Математика тренирует память и развивает ум. С радостью помогу ученикам закрепить школьные знания и узнать новое. Научу правильно задавать вопросы, рассуждать и самостоятельно искать решение задач.
Репетитор по математике
Магнитогорский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Я являюсь учителем начальных классов (1-4) и подготовки ребят к школе. Шаг за шагом, проходя все трудности вместе, мы учимся писать, считать и читать. Преподавание в начальной школе очень люблю за возможность объяснить любой материал в ходе творческого задания или игры.
Моя цель — найти к каждому ученику индивидуальный подход. Подобрать тот ключик, который поможет ребенку справиться с возникшими трудностями.
В работе использую технологии развивающего обучения. Применяю методы проблемного обучения. А также словесные, наглядные, практические, объяснительно-иллюстративные методы.
Шаг за шагом, проходя все трудности вместе, мы учимся писать, считать и читать. Преподавание в начальной школе очень люблю за возможность объяснить любой материал в ходе творческого задания или игры.
Моя цель — найти к каждому ученику индивидуальный подход. Подобрать тот ключик, который поможет ребенку справиться с возникшими трудностями.
В работе использую технологии развивающего обучения. Применяю методы проблемного обучения. А также словесные, наглядные, практические, объяснительно-иллюстративные методы.
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Пропорции
Пропорция – это равенство, где с : d = n : m. При этом с, d, n, m являются действительными числами, которые отличные от 0. Числа d и n называются средними членами пропорции, а числа с и m называются крайними членами пропорции.
При этом с, d, n, m являются действительными числами, которые отличные от 0. Числа d и n называются средними членами пропорции, а числа с и m называются крайними членами пропорции.
Для пропорций справедливы несколько следующих утверждений:
- Произведение средних членов пропорции будет равняться произведение крайних членов той же пропорции.
- Крайние члены пропорции всегда можно поменять местами, например, если с : d = n : m, то и m : d = n : c.
- Средние члены пропорции всегда можно поменять местами, например, если c : d = n : m, то и c : n = d : m.
Пропорции довольно часто встречаются в различных математических задачах. При этом, как правило, один или несколько членов пропорции неизвестны. Давайте посмотрим, как же можно найти тот или иной член пропорции, зная значения всех остальных. Для начала, следует усвоить два простых правила:
- Для того, чтобы найти крайний член пропорции, необходимо произведение средних членов поделить на известный крайний член.

- Для того, чтобы найти средний член пропорции, необходимо произведение крайних членов пропорции поделить на известный средний член.
Два равных отношения образуют пропорцию
Основное свойство пропорции
Нахождение членов пропорции
| a | = | bc d |
; | b | = | ad c |
; | c | = | ad b |
; | d | = | bc a |
Пропорции, равносильные между собой
| a b |
= | c d |
; | a c |
= | b d |
; | d b |
= | c a |
; | d c |
= | b a |
Производная пропорция — следствие данной пропорции
| a b |
= | c d |
в виде | ma + nb pa + qb |
= | mc + nd pc + qd |
, |
где m, n, p, q — произвольные числа, причем p и q не равны нулю одновременно.
Открытый урок математики на тему «Пропорции». 6-й класс
Цели: ввести понятие пропорции её членов ; научить чтению пропорции и составлению пропорций из отношений ; закрепить правила деления десятичных дробей, обыкновенных дробей.
Ход урока
1. Организационный момент
Приветствие, проверка готовности учащихся и классной комнаты к уроку, отметка отсутствующих.
2. Устная работа
Вспомним, что такое отношение.
Решим примеры:
1) Выразите отношение 75:100 обыкновенной дробью. И выберите вариант ответа:
2) Сколько процентов числа 200 составляет число 160? (Ответ: 80%.)
Далее спросить у ребят как они решили. Вызвать одного из учеников, чтобы написал на доске.
3) Какой знак действия надо поставить вместо *, чтоб получилось верное равенство:
(Один из учеников объясняет с места).
4) Найдите отношение величин
- 1,5 м и 30 см.
- 1 ч и 15 мин.
После того, как дети решат в тетрадях, учитель записывает решение на доске. Для того, чтобы учащиеся визуально ещё раз увидели и вспомнили, что для нахождения отношения величин, выраженных разными единицами, надо предварительно перейти к одной единице измерения.
3. Изучение нового материала.
1) Найдём значения двух отношений 8 : 4 и 10 : 5. Мы видим , что они равны 8 : 4 = 2 и 10 : 5 = 2, следовательно, можно записать равенство 8 : 4 = 10 : 5.
(Далее пусть дети приведут два , три примера таких равенств.)
Такое равенство отношений называют пропорцией.
Речь учителя:
Пропорция (от лат.(латинский) proportio – соотношение,
соразмерность. Представления о пропорции возникли в ходе практической
деятельности архитекторов и художников древнего мира, применявших при создании
произведений определённые модули и геометрические построения. Системы пропорции
отражающие реально существующие в природе закономерности, нередко были связаны с
мифологическими представлениями о гармонии Вселенной. С древности и по сей день
пропорция – это стандарт красоты. Пропорция в математике – равенство между двумя
отношениями четырёх величин а, в, с, d. В
пластических искусствах – соотношение величин элементов художественного
произведения, а также отдельных элементов и всего произведения в целом. Так же
различают пропорции в архитектуре и пропорции используемые для изображения
человеческого тела и лица.
Системы пропорции
отражающие реально существующие в природе закономерности, нередко были связаны с
мифологическими представлениями о гармонии Вселенной. С древности и по сей день
пропорция – это стандарт красоты. Пропорция в математике – равенство между двумя
отношениями четырёх величин а, в, с, d. В
пластических искусствах – соотношение величин элементов художественного
произведения, а также отдельных элементов и всего произведения в целом. Так же
различают пропорции в архитектуре и пропорции используемые для изображения
человеческого тела и лица.
Принцип пропорции присутствует в работах великих художников и архитекторов от
Витрувия до Ле Корбюзье, от Леонардо да Винчи до Сальвадора Дали. Не только
человек создаёт что- то по свойству пропорции, но и сама природа создала свои
красивые объекты с помощью математики ,с помощью пропорции. Это расположение
семян подсолнечника , элегантная спираль раковины улитки (логарифмическая
спираль) и форма Млечного пути.
Чувствам человека приятны объекты, обладающие правильными пропорциями.
Святой Фома Аквинский (1225–1274).
2) Определение. Ученики записывают в тетрадь. Пропорцией называют равенство двух отношений.
Числа, составляющие пропорцию (8; 4; 10; 5) – члены пропорции.
3) Пропорцию можно записать с помощью букв:
x : a = b : y, или
4) Эти записи читают: «Отношение x к a равно отношению b к y» или «x так относится к a, как b к y».
5) Числа x и y – крайние члены пропорции, а a и b – средние члены.
6) Все члены пропорции не равны нулю:
– всё это учащиеся записывают в тетрадь.
7) Чтобы проверить , верно ли составлена пропорция , вычисляют числовое значение каждого отношения. Если отношения равны , то пропорция составлена верно; если не равны , то пропорция составлена не верно.
Пример: 1) 45 : 5 = 27 : 3 – верно, так как 45 : 5 = 9 и 27 : 3 = 9, 9 = 9. 2) 40 : 8 = 18 : 6
– не верно, так как 40 : 8 = 5, а 18 : 6 = 3. .
.
Далее учащиеся должны составить три пропорции верные и три не верные в своих тетрадях. Записать их примеры пропорции на доске.
4. Закрепление материала
- Устно: a) Прочитайте пропорцию:
18 : 6 = 24 : 8; 30 : 5 = 42 : 7; 36 : 9 = 50 : 10 b) назовите крайние члены пропорции, назовите средние члены пропорции. c) верно ли составлены пропорции? Проверьте. (Спросить с места).
- Составьте четыре пропорции (дети на доске и в тетрадях приводят свои примеры пропорций).
- Далее учитель диктует: запишите пропорции и проверьте верны ли они:
5 так относится к 3 , как 2 к 1,2 ; 0,9 так относится к 1/3, как 45 к 162/3. (После вызвать одного учащегося, чтобы записал результат на доске.) - Решить уравнение:
а) y : 51,6 = 11,2 : 34,4
Решение:
у : 51,6 = 0,3
у = 51,6 * 0,3
у = 15,48
b) 5 : 3 = 5 : х
Решение:
5. Повторение ранее изученного материала:
Повторение ранее изученного материала:
Решить самостоятельно в тетрадях:
У Андрея 6 машинок , а у Миши 4. Во сколько раз у Андрея больше машинок , чем у Миши? Запишите в процентах , сколько машинок у Андрея и сколько у Миши по отношению к общему количеству.
Бригада по плану должна была за месяц засеять 300 га. Но план был выполнен на 120%. Сколько гектар засеяла бригада?
5. Итог.
1. Вопросы: а) Что такое пропорция? б) Как называются числа x и y в пропорции х : a = b : y? в) Как называются числа m и n в пропорции a : m = n : b?
Задание на самоподготовку: выучить из п. 21 первую часть. Решить №№ 776, 778, 781 (а).
Геометрическая Пропорция
370. Но если величины находятся в геометрической пропорции, произведение её крайних членов равно произведению их средних членов.
Если a:b = c:d, ad = bc
Согласно допущению, (Статьи. 341, 359.) $\frac{a}{b } =\frac{c}{d } $
Умножив на bd, (Аксиома 3. ) $\frac{abd}{b } =\frac{cbd}{d } $
) $\frac{abd}{b } =\frac{cbd}{d } $
Упростив дроби, ad = bc.
Так 12:8 = 15:10, поэтому 12*10 = 8*15.
Соотв: Любой множитель может быть перенесён от одной средней величины к другой, без влияния на пропорцию. Если a:mb = x:y, то a:b = mx:y. При этом произведение средних величин в обоих случаях одинаково. И если na:b = x:y, то a:b = x:ny.
371. С другой стороны, если произведение двух величин равно произведению двух других, то четыре величины сформируют пропорцию, где они сгруппированы таким образом, что одна сторона уравнения будет содержать средние члены, а другая — крайние.
Если my = nh, то m:n = h:y, то есть$\frac{m}{n } =\frac{h}{y } $
Таким образом разделив my = nh на ny, мы получим$\frac{my}{ny} =\frac{nh}{ny } $
Упростив дроби, $\frac{m}{n } =\frac{h}{y } $.
Соотв. То же самое должно быть верно по отношению любых множителей, которые образуют две стороны равенства.
Если (a + b).c = (d — m). y, то a + b:d — m = y:c.
y, то a + b:d — m = y:c.
372. Если три величины пропорциональны, то произведение их крайних членов равно квадрату средних. Таким образом одновременно пропорциональны также второй член первой пары и предыдущий член последней. (Статья. 366.) Следовательно они должны быть умножены на себя, то есть возведены в квадрат.
Если a:b = b:c, тогда умножение крайних и средних членов, ac = b2.
Следовательно, среднее пропорциональное двух величин может быть найдено путём извлечения квадратного корня из их произведения.
Если a:x = x:c, то x2 = ac, и x√ac.
373. Из Статьи. 370 следует, что соотношение любого из крайних членов равно произведению средних, разделённых на другой крайний член. И любой из средних членов равен произведению крайних членов, разделённому на другой средний член.
1. Если a:b = c:d, то ad = bc
2. Разделим на d, $a=\frac{bc}{d} $
3. Сначала разделим на c, $b=\frac{ad}{c} $
4. Разделим это на b, $c=\frac{ad}{b} $
Разделим это на b, $c=\frac{ad}{b} $
5. Разделим на a, $d=\frac{bc}{a} $ ; Это значит, что
четвёртый член равен произведению второго и третьего, разделённому на первый.
На этом принципе основаны простые пропорции арифметики, которые часто называют Тройным Правилом. Три числа даны, чтобы найти четвёртое, которое получают путём умножения второго на третье и деления на первое.
374. Утверждение относительно произведений средних и крайних членов предоставляет очень простой и удобный критерий определения того, пропорциональны ли любые четыре величины. Нам только нужно перемножить средние и крайние члены. Если произведения равны, то величины пропорциональны. Если произведения не равны, то величины не пропорциональны.
375. В математических исследованиях, когда даны отношения нескольких величин, то они часто определены в виде пропорции. Но, как правило, необходимо, чтобы эта первая пропорция претерпела ряд трансформаций прежде, чем отчётливо выявится неизвестная величина или утверждение, которое мы хотели доказать. Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.
Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.
В первую очередь очевидно, что любая перемена в расстановке, которая не окажет влияния на эти равенство этих двух произведений, не уничтожит пропорции. Поэтому, если a:b = c:d, то порядок этих величин может варьироваться, что в любом случае приведёт к ad = bc. Отсюда,
376. Если четыре величины пропорциональны, то порядок средних членов, или крайних членов, или членов обоих пар, может быть инвертирован без разрушения пропорции.
Если a:b = c:d,
И 12:8 = 6:4
тогда
1. Инвертируя средние члены,
a:c = b:d
12:6 = 8:4
то есть
Первый относится к третьему
Как второй к четвёртому.
Другими словами, отношение предыдущих членов равно отношению последующих.
Эта инверсия средних членов часто упоминается в геометрии под названием Альтернация.
2. Инвертируя крайние члены,
d:b = c:a
4:8 = 6:12
то есть,
Четвёртый относится ко второму,
Как третий к первому.
3. Инвертируя члены каждой пары,
b:a = d:c
8:12 = 4:6
то есть,
Второй относится к первому,
Как четвёртый к третьему.
Технически это называется Инверсией.
Каждое из этого также может варьироваться, меняя порядок двух пар. (Статья. 365.)
Соотв. Порядок всей пропорции может быть инвертирован.
Если a:b = c:d, то d:c = b:a.
В каждом из данных случаев будет немедленно видно, что вычисляя произведения средних и крайних членов, у нас получается ad = bc, и 12.4 = 8.6.
Если члены только одной из пар инвертированы, то пропорция становится обратной. (Статья 367.)
Если a:b = c:d, то a относится к b, обратно тому, как d относится к c.
377. Разница в расположении не единственная алтернация, которую производят по отношению к членам пропорции. Часто бывает нужным умножить, разделить, возвести в степень и так далее. Во всех случаях искусство ведения исследования заключается в произведении некоторых изменений, при этом сохраняется постоянное равенство между отношением двух первых и двух последних членов. При решении уравнения, мы должны сохранять равенство сторон, так варьируя пропорцию, чтобы сохранить и равенство соотношений. И это достигается либо путём сохранения соотношений теми же, что и при альтернации членов, либо увеличивая или уменьшая одно из соотношений на столько же, как и другое. Большинство последующих доказательств направлены на чёткое выявление этого принципа и ознакомление с ним. Некоторые из утверждений могут быть доказаны более простым способом, возможно, путём умножения крайних и средних членов. Но это не даст ясного понимания природы некоторых изменений в пропорциях.
Было показано, что если оба члена пары умножены или разделены на одинаковую величину, то их соотношение остаётся одинаковым (Статья. 355.) Так умножая предыдущий член (антецедента) проявится в умноженном соотношении, а деление последующего члена (консеквента) — в делении соотношения. (Статья. 352.) и следующие показывают, что умножение консеквента проявится в делении соотношения, а его деление — в произведении соотношения. (Статья. 353.) Так как соотношения в пропорции равны, то если их перемножить или разделить на одинаковую величину, то они всё ещё будут равны (Аксиома. 3.) Одно будет увеличено или уменьшено, так же как и второе. Отсюда,
378. Если четыре величины пропорциональны, два аналогичных или гомологичных члена могут быть умножены или разделены на одну и ту же величину, без нарушения пропорции.
Если аналогичные члены будут умножены или разделены, то их соотношения не поменяются. (Статья, 355.) Если гомологичные члены будут умножены или разделены, оба соотношения одинаково увеличатся или уменьшатся. (Статьи. 352, 353.)
(Статьи. 352, 353.)
Если a:b = c:d, то,
1. Умножая первые два члена, ma:mb = c:d
2. Умножая последние два члена, a:b = mc:md
3. Умножая два первых члена (антецедента), ma:b = mc:d
4. Умножая два последних члена (консеквента), a:mb = c:md
5. Разделив два первых члена, $\frac{a}{m}:\frac{b}{m}=c:d$
6. Разделив два последних члена, $a:b=\frac{c}{m}:\frac{d}{m }$
7. Разделив два антецедента, $\frac{a}{m}:b=\frac{c}{m}:d$ a/m:b = c/m:d
8. Разделив два консеквента, $a:\frac{b}{m}=c:\frac{d}{m}$ a:b/m = c:d/m.
Следствие. 1. Все члены могут быть умножены или разделены на одну и ту же величину.
ma:mb = mc:md, $\frac{a}{m}:\frac{b}{m}=\frac{c}{m}:\frac{d}{m} $.
Следствие. 2. В любом случае, в данной статье умножение консеквентов может быть заменено делением антецедентов той же самой пары, и деление консеквентов — умножением антецедентов. (Статья. 354, след.)
379. Часто бывает необходимо не только изменить члены пропорции и варьировать их расположение, но и сравнить одну пропорцию с другой. Из этого сравнения часто возникает новая пропорция, которая может быть необходима для решения задачи или перехода к доказательству. Один из самых важных случаев, когда сравниваемые два члена одной пропорции такие же как два в другой. Похожие члены могут исчезнуть, и новая пропорция может быть сформирована из оставшихся четырёх членов. Так,
Из этого сравнения часто возникает новая пропорция, которая может быть необходима для решения задачи или перехода к доказательству. Один из самых важных случаев, когда сравниваемые два члена одной пропорции такие же как два в другой. Похожие члены могут исчезнуть, и новая пропорция может быть сформирована из оставшихся четырёх членов. Так,
380. Если два соотношения соответсвтенно равны третьему, то они также равны между собой.
Это не что иное, как 11ая аксиома, применяемая к соотношениям.
1. Если a:b = m:n
И c:d = m:n
тогда a:b = c:d,или a:c = b:d. (Статья.376.)
2. Если a:b = m:n
И m:n = c:d
то a:b = c:d,или a:c = b:d.
След. Если a:b = m:n
m:n > c:d
то a:b > c:d.
Так если соотношение m:n больше, чем c:d, то это показывает, что соотношение a:b, которое равно соотношению m:n, также больше чем соотношение c:d.
381. В этих примерах схожие члены двух пропорций это два первых и два последних. И порядок не важен. Порядок членов может быть изменён разными способами без влияния на равенство соотношений.
И порядок не важен. Порядок членов может быть изменён разными способами без влияния на равенство соотношений.
1. Похожими членами могут быть два антецедента, или два косеквента в каждой пропорции. Таким образом,
Если m:a = n:b
И m:c = n:d
тогда
Чередуем, m:n = a:b
И m:n = c:d
Отсюда a:b = c:d, или a:c = b:d, согласно последнему параграфу.
2. Антецеденты в одной пропорции, могут быть такими же как консеквенты в другой.
Если m:a = n:b
И c:m = d:n
Инветрируя и чередуя a:b = m:n
Чередуя c:d = m:n:
Поэтому a:b, и так далее как ранее.
3. Два гомологичных члена в одной из пропорций могут быть такими же, как два аналогичные члены в другой.
Если a:m = b:n
и c:d = m:n
Чередуя, a:b = m:n
И c:d = m:n
Поэтому, a:b, и так далее.
Всё это примеры равенства между соотношениями в одной пропорции с соотношениями в другой. В геометрии на предположение, к которому они принадлежат обычно ссылаются как на «ex aequo«или «ex aequali» (по справедливости). Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.
Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.
382. Любое число пропорций может быть сравнено аналогичным способом, если два первых или два последних члена в каждой предыдущей пропорции такие же, как два первые и два последние члена в последующей.
Поэтому если a:b = c:d
И c:d = h:l
И h:l = m:n
И m:n = x:y
то a:b = x:y.
То есть два первых члена первой пропорции имеют такое же соотношение, как два последних члена последней пропорции. Это показывает, что соотношение всех пар одинаково.
И если члены не находятся в том же порядке как здесь, но могут быть упрощены к данному виду, применяется тот же самый принцип.
поэтому если a:c = b:d
И c:h = d:l
И h:m = l:n
И m:x = n:y
тогда чередуя
a:b = c:d
c:d = h:l
h:l = m:n
m:n = x:y.
Поэтому a:b = x:y, как и ранее.
Во всех примерах в этой и предшествующих статьях, два члена в одной пропорции, у которых есть равные члены в другой, не являются ни двумя средними членами, ни двумя крайними членами, а одним средним и одним крайним членом, из чего следует, что пропорция однородна и непрерывна.
383. Но если два средних или два крайних члена в одной пропорции такие же, как средние и крайние члены в другой, то оставшиеся четыре члена будут взаимно пропорциональны.
Если a:m = n:b
И c:m = n:d
тогда a:c = $\frac{1}{b}:\frac{1}{d} $, или a:c = d:b
Для ab = mn
И cd = mn
(Статья. 370) Поэтому ab = cd, и a:c = d:b.
В данном примере два средних члена в одной пропорции, такие же как те же в другой. Но принцип будет тем же, если крайние члены не равны или если крайние члены одной пропорции не равны средним членам другой.
Если m:a = b:n
И m:c = d:n
тогда a:c = d:b.
Или if a:m = n:b
И m:c = d:n
тогда a:c = d:b.
Теорема в геометрии, которая применима в данном случае обычно именуется словами «ex aequo perturbate» (по правде запутанная).
384. Другой способ варьировать члены в пропорции это сложение или вычитание.
Если к или от двух гомологичных членов пропорци вычитаются или прибавляются две другие величины, которые находятся в том же соотношении, то пропорция остаётся верной.
Соотношение не меняется, если добавить или отнять от него другое равное соотношение. (Статья. 357.)
Если a:b = c:d
И a:b = m:n
Тогда добавляя или отнимая от a и b, члены с равным соотношением m:n, мы получим
a+m:b+n = c:d, и a-m:b-n = c:d.
И добавляя или отнимая m и n к или от c и d, мы получим,
a:b = c+m:d+n, и a:b = c-m:d-n.
Здесь сложение и вычитание производится к и от аналогичных членов. Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим,
Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим,
a+m:c = b+n:d, и a-m:c = b-n:d.
След. 1. Это добавление может распространяться на любое число равных соотношений.
Таким образом, если
a:b = c:d
a:b = h:l
a:b = m:n
a:b = x:y
Тогда a:b = c+h+m+x:d+l+n+y.
След. 2. Если a:b = c:d
И m:b = n:d
тогда a+m:b = c+n:d.
Чередуем a:c = b:d
И m:n = b:d
таким образом
a+m:c+n = b:d
или a+m:b = c+n:d.
385. Из последней статьи следует, что если в любой пропорции члены прибавляются или отнимаются друг от друга, то,
Если аналогичные и гомологичные члены добавляются или отнимаются от двух других, то пропорция сохраняется верной.
Таким образом, если a:b = c:d, и 12:4 = 6:2, тогда,
1. Добавляя два последних члена к двум первым.
a+c:b+d = a:b 12+6:4+2 = 12:4
и a+c:b+d = c:d 12+6:4+2 = 6:2
или a+c:a = b+d:b 12+6:12 = 4+2:4
и a+c:c = b+d:d 12+6:6 = 4+2:2.
2. Складывая два антецедента с двумя консеквентами.
a+b:b = c+d:d 12+4:4 = 6+2:2
a+b:a = c+d:c, т.д.. 12+4:12 = 6+2:6, т.д..
Это называется Композицией.
3. Отнимая два первых члена от двух последних.
c-a:a = d-b:b
c-a:c = d-b:d, т.д..
4. Отнимая два последних члена от двух первых.
a-c:b-d = a:b
a-c:b-d = c:d, т.д..
5. Отнимая консеквенты от антецедентов.
a-b:b = c-d:d
a:a-b = c:c-d, etc.
Преобразование, показанное в последней форме называется Конверсией.
6. Отнимая антецеденты от консеквентов.
b-a:a = d-c:c
b:b-a = d:d-c, etc.
7. Добывляя и вычитая,
a+b:a-b = c+d:c-d.
То есть сумма первых двух членов относится к их разности, как сумма двух последних к их разности.
След. Если любые сложные величины, расставленые как в предыдущих примерах, пропорциональны, то простые величины, из которых они состоят также пропорциональны.
Таким образом, если a+b:b = c+d:d, то a:b = c:d.
Это называется Делением.
386. Если соответствующие члены двух или более разрядов пропорциональных величин перемножить между собой, то произведение также будет пропорционально.
Это смешанные соотношения (Статья. 347,) или смешанные пропорции. Это нужно уметь отличать от того, что называется композицией, которая является сложением членов соотношения. (Статья 385. 2.)
Если a:b = c:d 12:4 = 6:2
И h:l = m:n 10:5 = 8:4
Тогда ah:bl = cm:dn 120:20 = 48:8.
Исходя из определения пропорции два соотношения первого разряда равны, как и соотношения второго разряда. И умножение соответствующих членов является умножением соотношений, (Статья. 352. соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны.
соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны.
Такое же доказательство применимо к любому числу пропорций.
Если
a:b = c:d
h:l = m:n
p:q = x:y
Тогда ahp:blq = cmx:dny.
Из этого следует, что если члены пропорции перемножить на самих себя, то есть, если они возведены в какую-либо степень, то они всё равно будут пропорциональны.
Если a:b = c:d 2:4 = 6:12
a:b = c:d 2:4 = 6:12
Тогда a2:b2 = c2:d2 4:16 = 36:144
Пропорциональные величины также получаются реверсируя этот процесс, то есть вычисляя корни членов пропорции.
Если a : b:: c : d, тогда √a:√b = √c:√d.
Перемножив средние и крайние члены, ad = bc
И извлекя корень из обеих сторон, √ad = √bc
То есть, (Статья. 254, 371,) √a:√b = √c:√d.
254, 371,) √a:√b = √c:√d.
Отсюда,
387. Если некоторые величины пропорциональны, то продукты их возведения в степень или извлечения корней пропорциональны.
Если a:b = c:d
Тогда an:bn = cn:dn, и m√a:m√b = m√c:m√d.
И m√an:m√bn = m√cn:√dn, то есть, am/n:bm/n = cm/n:dm/n.
388. Если члены одного разряда пропорций разделить на соответствующие члены другого разряда, то частные будут пропорциональны.
Это иногда называют решением соотношений.
Если a:b = c:d 12:6 = 18:9
И h:l = m:n 6:2 = 9:3
Тогда $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $ $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $.
Это просто реверсия процесса в Статье. 386, и может быть доказана похожим образом.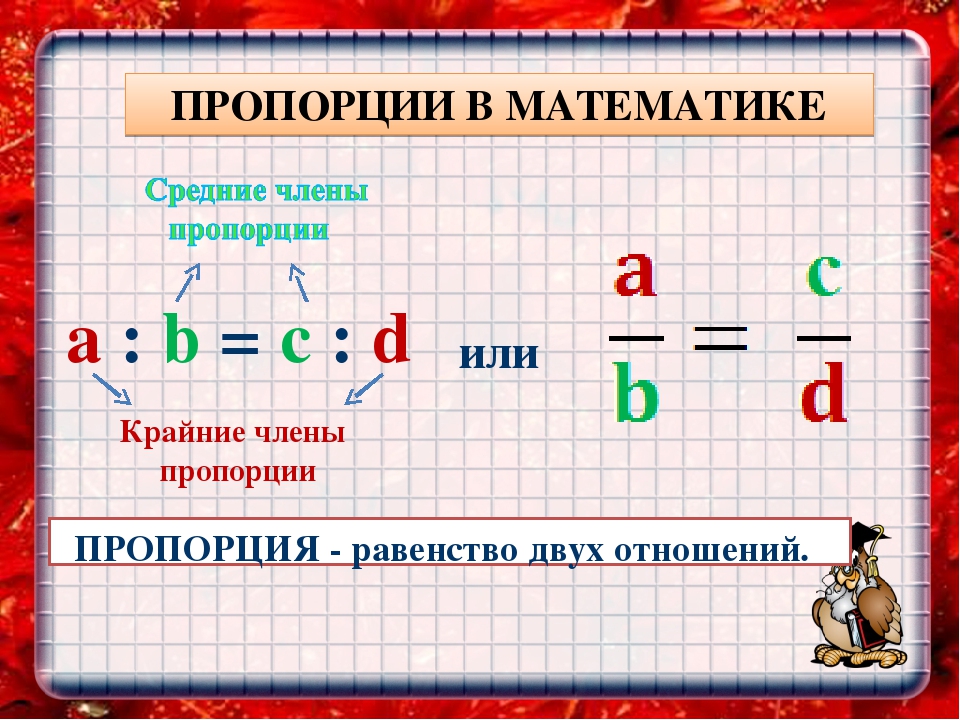
Это нужно уметь различать от того, что в геометрии называется разделением, которое является вычитанием членов соотношения. (Статья. 385. соотв.)
389. В сложных смешанных пропорциях, равные множители или делители двух аналогичных или гомологичных членов могут быть отвергнуты.
Если
a:b = c:d 12:4 = 9:3
b:h = d:l 4:8 = 3:6
h:m = l:n 8:4 = 6:15
Тогда a:m = c:n 12:20 = 9:15.
Это правило может быть применено к случаям, к которым относятся термины «ex aequo» и «ex aequo perturbate«. Смотрите Статьи. 381 и 383. Один из методов может служить для того, чтобы подтвердить другой.
394. Изменения, которые могут быть сделаны в пропорциях без нарушения равенства соотношений, так многочислены, что они стали бы обременительны к запоминанию, если бы их нельзя было бы упростить до нескольких общих принципов. Они обычно получаются,
1. Инвертируя порядок членов, Статья. 376.
376.
2. Умножая или деля на одинаковую величину, Статья. 378.
3. Сравнивая пропорции, в которых есть схожие члены. Статьи. 380, 381, 382, 383.
4. Складывая или отнимая члены одинаковых соотношений, Статьи. 384, 385.
5. Умножая или деля одну пропорцию на другую, Статьи. 386, 387, 388.
6. Возводя в степень или извлекая корни членов, Статья. 387.
391. Когда четыре величины пропорциональны, если первая больше чем вторая, то третья будет больше чем четвёртая; если равны, то равны, а если меньше, то, соответственно, меньше.
Для одинаковых соотношений двух пар, если одно является соотношением равенства, то и второе тоже, и поэтому антецедент в каждой паре равен её консеквенту. (Статья. 345,) Если одно соотношение большего неравенства, то и второе тоже, и поэтому антецедент каждого из них больше чем соответствующий консеквент. А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент.
А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент.
Пусть a:b = c:d; тогда если
a = b, c = d
a > b, c > d
a < b, c < d.
След. 1. Если первый член больше третьего, то тогда второй больше четвёртого, если равен — то равен, если меньше — то, соответсвенно, меньше.
В случае чередования, a:b = c:d становится a:c = b:d, без какого-либо чередования величин. Таким образом, если a = b, c = d, и т.д., как и ранее.
След. 2. Если a:m = c:n
и m:b = n:d
тогда if a = b, c = d, и т.д.
Для равенства соотношений, (Статья. 381. 2.) или смешанных соотношений, (Статьи. 386, 389.)
a:b = c:d. Таким образом, если a = b, c = d, и т.д. как ранее.
След. 3. Если a:m = n:d
и m:b = c:n
тогда if a = b, c = d.
391. b. Если четыре величины пропорциональны, то обратные им величины тоже пропорциональны и наоборот.
Если a:b = c:d, тогда $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $.
Для каждой из этих пропорций, при сокращении получаем ad = bc.
Что такое пропорция — определение, формула, примеры
Пропорция в основном объясняется соотношением и дробями. Дробь, представленная в виде a/b, а отношение a:b, то пропорция утверждает, что два отношения равны. Здесь a и b — любые два целых числа. Соотношение и пропорция являются ключевыми основами для понимания различных концепций в математике, а также в естественных науках.
Пропорция находит применение в решении многих повседневных жизненных проблем, например, в бизнесе, при совершении транзакций или при приготовлении пищи и т. д.Он устанавливает связь между двумя или более величинами и, таким образом, помогает в их сравнении.
Что такое пропорция?
Доля, как правило, называется частью, долей или числом, рассматриваемым в сравнительном отношении к целому. Определение пропорции гласит, что когда два отношения эквивалентны, они пропорциональны. Это уравнение или утверждение, используемое для изображения равенства двух отношений или дробей.
Это уравнение или утверждение, используемое для изображения равенства двух отношений или дробей.
Пропорции — Определение
Пропорция – это математическое сравнение двух чисел.Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же отношении, то говорят, что отношения прямо пропорциональны друг другу. Пропорции обозначаются символом «::» или «=».
Пропорция — Пример
Два отношения называются пропорциональными, если они равны. Например, время, необходимое поезду для прохождения 50 км в час, равно времени, затраченному им на преодоление расстояния 250 км за 5 часов. Например, 50 км/час = 250 км/5 часов.
Продолжение пропорций
Говорят, что любые три величины находятся в непрерывной пропорции , если отношение между первой и второй равно отношению между второй и третьей. Точно так же четыре количества в непрерывной пропорции будут иметь отношение между первым и вторым, равным отношению между третьим и четвертым.
Например, рассмотрим два соотношения: a:b и c:d. Чтобы найти непрерывную пропорцию для двух заданных членов отношения, мы преобразуем их средние значения в один член/число.В общем случае это будет НОК средних, и для данного отношения НОК b и c будет bc. Таким образом, умножив первое отношение на c, а второе отношение на b, мы получим
.- Первое соотношение- ca:bc
- Второе соотношение- bc:bd
Таким образом, непрерывная пропорция для данных отношений может быть записана в виде ca:bc:bd.
Соотношения и пропорции
Отношение — это способ сравнения двух величин одного вида с помощью деления.Формула соотношения для двух чисел a и b задается как a:b или a/b. Умножение и деление каждого члена соотношения на одно и то же число (не ноль) не влияет на отношение.
Когда два или более таких отношения равны, говорят, что они находятся в пропорции .
Четвертая, третья и среднепропорциональная
Если а : b = с : d, то:
- d называется четвертой пропорциональностью a, b, c.

- с называется третьим пропорциональным числам а и b.
- Среднее пропорциональное между a и b равно √(ab).
Советы и рекомендации по пропорциям
- a/b = c/d ⇒ ad = bc
- a/b = c/d ⇒ b/a = d/c
- a/b = c/d ⇒ a/c = b/d
- a/b = c/d ⇒ (a + b)/b = (c + d)/d
- a/b = c/d ⇒ (a – b/b = (c – d)/d
- a/(b + c) = b/(c + a) = c/(a + b) и a + b + c ≠0, тогда a = b = c.
- a/b = c/d ⇒ (a + b)/(a — b) = (c + d)/(c — d), что известно как правило компонендо-дивидендо
- Если оба числа a и b умножить или разделить на одно и то же число в отношении a:b, то полученное соотношение останется таким же, как исходное соотношение.
Формула пропорции с примерами
Формула пропорции — это уравнение, которое можно решить, чтобы получить сравнительные значения. Для решения задач на пропорции мы используем концепцию, согласно которой пропорция — это два отношения, равные друг другу. Мы имеем в виду это в том смысле, что две дроби равны друг другу.
Мы имеем в виду это в том смысле, что две дроби равны друг другу.
Формула соотношения
Предположим, что у нас есть любые две величины (или две сущности) и мы должны найти отношение этих двух, тогда формула отношения определяется как a:b ⇒ a/b , где
- a и b могут быть любыми двумя количествами.
- «а» называется первым термином или предшествующим .
- «b» называется вторым членом или консеквентом .
Например, в соотношении 5:9 представлено 5/9, где 5 предшествует, а 9 последует. 5:9 = 10:18 = 15:27
Формула пропорции
Теперь предположим, что эти два соотношения равны a:b и c:d. Два термина «b» и «c» называются «средними или средними терминами», тогда как термины «a» и «d» известны как «крайние или крайние термины».
a/b = c/d или a:b::c:d. Например, рассмотрим еще один пример числа учащихся в 2-х классах, где соотношение числа девочек и мальчиков равно. Наше первое отношение количества девочек к мальчикам равно 2:5, а другое — 4:8, тогда пропорция может быть записана как: 2:5::4:8 или 2/5 = 4/8. Здесь 2 и 8 — крайние значения, а 5 и 4 — средние значения.
Наше первое отношение количества девочек к мальчикам равно 2:5, а другое — 4:8, тогда пропорция может быть записана как: 2:5::4:8 или 2/5 = 4/8. Здесь 2 и 8 — крайние значения, а 5 и 4 — средние значения.
В зависимости от типа отношения, в котором участвуют два или более количества, пропорция может быть классифицирована по разным типам.Существует два типа пропорций.
- Прямая пропорция
- Обратная пропорция
Прямая пропорция
Этот тип описывает прямую связь между двумя величинами. Проще говоря, если увеличивается одна величина, увеличивается и другая величина, и наоборот. Например, если скорость автомобиля увеличивается, он преодолевает большее расстояние за фиксированный промежуток времени. В обозначениях прямая пропорция записывается как y ∝ x.
Обратная пропорция
Этот тип описывает косвенную связь между двумя величинами. Проще говоря, если одна величина увеличивается, другая величина уменьшается, и наоборот. В обозначениях обратная пропорция записывается как y ∝ 1/x. Например, увеличение скорости автомобиля приведет к преодолению фиксированного расстояния за меньшее время.
В обозначениях обратная пропорция записывается как y ∝ 1/x. Например, увеличение скорости автомобиля приведет к преодолению фиксированного расстояния за меньшее время.
Важные примечания
- Пропорция – это математическое сравнение двух чисел.
- Основные пропорции бывают двух типов: прямые пропорции и обратные пропорции.
- Мы можем применять понятия пропорций к географии, сравнивая количества в физике, диетологии, кулинарии и т. д.
Свойства пропорции
Пропорция устанавливает эквивалентное отношение между двумя отношениями. Свойства пропорции, за которыми следует это отношение:
- Дополнение – Если a : b = c : d, то значение каждого отношения равно a + c : b + d
- Subtrahendo – Если a : b = c : d, то значение каждого отношения равно a – c : b – d
- Дивидендо – Если a : b = c : d, то a – b : b = c – d : d
- Componendo – Если a : b = c : d, то a + b : b = c + d : d
- Alternendo – Если a : b = c : d, то a : c = b: d
- Invertendo – Если a : b = c : d, то b : a = d : c
- Компонендо и дивидендо – Если а : b = с : d, то а + b : а – b = с + d : с – d
Разница между отношением и долей
Соотношение и пропорция являются тесно связанными понятиями. Пропорция означает равное соотношение между двумя или более отношениями. Чтобы понять концепцию отношения и пропорции, просмотрите разницу между соотношением и пропорцией, приведенную здесь.
Пропорция означает равное соотношение между двумя или более отношениями. Чтобы понять концепцию отношения и пропорции, просмотрите разницу между соотношением и пропорцией, приведенную здесь.
| Серийный номер | Соотношение | Пропорция |
| 1 | Соотношение используется для сравнения размеров двух вещей с одинаковыми единицами измерения. | Пропорция используется для выражения отношения двух соотношений. |
| 2 | Выражается двоеточием (:) или косой чертой (/). | Выражается двойным двоеточием (::) или равен символу (=) |
| 3 | Это выражение. | Это уравнение. |
| 4 | Ключевое слово для различения соотношения в задаче — «ко всем». | Ключевое слово для определения пропорции в задаче — «из». |
Доля Связанные темы
Ниже приведен список тем, которые тесно связаны с пропорцией в коммерческой математике. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
Часто задаваемые вопросы о пропорции
Что вы подразумеваете под отношением?
Отношение — это математическое выражение, записанное в форме a:b, которое выражает дробь в форме a/b, где a и b — любые целые числа.Например, дробь 1/3 может быть выражена как 1:3 в форме отношения.
Что такое пропорция в математике?
Пропорция – это математическое сравнение двух чисел. Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же отношении, то говорят, что отношения прямо пропорциональны друг другу. Пропорции обозначаются с помощью символа ‘::’ или ‘=’. Например, 2:5 :: 4:8 или 2/5 = 4/8. Здесь 2 и 8 — крайние значения, а 5 и 4 — средние значения.
Как соотношение и пропорция используются в повседневной жизни?
Соотношения и пропорции используются ежедневно. Соотношения и пропорции используются в деловых операциях при работе с деньгами, сравнении количества по цене при совершении покупок и т. д. Например, у бизнеса может быть коэффициент для суммы прибыли, полученной за продажу определенного продукта, например 5 : 1, в котором говорится, что бизнес получает 2,50 доллара за каждую продажу.
д. Например, у бизнеса может быть коэффициент для суммы прибыли, полученной за продажу определенного продукта, например 5 : 1, в котором говорится, что бизнес получает 2,50 доллара за каждую продажу.
Как узнать, образуют ли два отношения пропорцию?
Если два отношения эквивалентны друг другу, то говорят, что они пропорциональны.Например, соотношения 1:2, 2:4 и 3:6 являются эквивалентными соотношениями.
Как рассчитать пропорцию?
Пропорция рассчитывается по формуле пропорции: a:b::c:d или a:b = c:d. Мы читаем это как «а» для «б», как «с» для «d».
Какие существуют типы пропорций?
В зависимости от типа отношения, в котором участвуют два или более количества, пропорция может быть классифицирована по разным типам. Существует два типа пропорций.
- Прямая пропорция — описывает прямую зависимость между двумя величинами.Проще говоря, если увеличивается одна величина, увеличивается и другая величина, и наоборот.

- Обратная пропорция — описывает косвенную связь между двумя величинами. Проще говоря, если одна величина увеличивается, другая величина уменьшается, и наоборот.
Каковы различные свойства пропорции?
Пропорция устанавливает эквивалентное отношение между двумя отношениями. Свойства пропорции, за которыми следует это отношение:
- Дополнение – Если a : b = c : d, то значение каждого отношения равно a + c : b + d
- Subtrahendo – Если a : b = c : d, то значение каждого отношения равно a – c : b – d
- Дивидендо – Если a : b = c : d, то a – b : b = c – d : d
- Componendo – Если a : b = c : d, то a + b : b = c+d : d
- Alternendo – Если a : b = c : d, то a : c = b: d
- Invertendo – Если a : b = c : d, то b : a = d : c
- Компонендо и дивидендо – Если а : b = с : d, то а + b : а – b = с + d : с – d
Пропорции
Пропорция говорит о том, что два соотношения (или дроби) равны.
Пример:
Итак, 1 из 3 равно 2 из 6
Соотношения одинаковы, поэтому они пропорциональны.
Пример: веревка
Длина веревки и вес пропорциональны.
Когда 20 м веревки весит 1 кг , тогда:
- 40 м этой веревки весит 2 кг
- 200 м этой веревки весит 10 кг
- и т.д.
Итак:
20 1 знак равно 40 2
Размеры
Когда формы «пропорциональны», их относительные размеры одинаковы.
Здесь мы видим, что отношения длины головы к длине тела одинаковы на обоих рисунках. Итак, они пропорциональны . Слишком длинная или короткая голова будет выглядеть плохо! |
Пример. Международные форматы бумаги (такие как A3, A4, A5 и т.
 д.) имеют одинаковые пропорции:
д.) имеют одинаковые пропорции:Таким образом, размер любого изображения или документа можно изменить, чтобы он поместился на любом листе.Очень аккуратный.
Работа с пропорциями
СЕЙЧАС, как нам это использовать?
Пример: вы хотите нарисовать голову собаки… какой длины она должна быть?
Запишем пропорцию с помощью коэффициента 10/20 сверху:
? 42 знак равно 10 20
Сейчас решаем специальным методом:
Умножить на известные углы,
затем разделить на третье число
И получаем это:
? = (42 × 10) / 20
= 420 / 20
= 21
Итак, вы должны нарисовать голову 21 в длину.
Использование пропорций для вычисления процентов
Процент на самом деле является отношением! Говоря «25%», вы фактически говорите «25 на 100»:
25% = 25 100
Мы можем использовать пропорции для решения задач, связанных с процентами.
Хитрость заключается в том, чтобы представить то, что мы знаем, в такой форме:
Часть Целиком = Процент 100
Пример: чему равно 25% от 160?
Процентов 25, целого 160, и мы хотим найти «часть»:
Деталь 160 = 25 100
Умножить известные углы, затем разделить на третье число:
Часть = (160 × 25) / 100
= 4000 / 100
= 40
Ответ: 25% от 160 равно 40.
Примечание: мы могли бы также решить эту проблему, сначала выполнив деление, например:
Деталь = 160 × (25/100)
= 160 × 0,25
= 40
Любой метод работает нормально.
Мы также можем найти Процент:
Пример: сколько составляет 12 долларов в процентах от 80 долларов?
Заполните то, что мы знаем:
12 долларов 80 долларов = Проценты 100
Умножьте известные углы, затем разделите на третье число. На этот раз известными углами являются верхний левый и нижний правый:
На этот раз известными углами являются верхний левый и нижний правый:
Проценты = (12 долл. США × 100) / 80 долл. США
= 1200 / 80
= 15%
Ответ: 12 долларов равно 15% от 80 долларов
Или найди Целое:
Пример: Продажная цена телефона составляла 150 долларов, что составляло всего 80% от обычной цены. Какая была нормальная цена?
Заполните то, что мы знаем:
150 долл. США Целиком = 80 100
Умножить известные углы, затем разделить на третье число:
Всего = (150$ × 100) / 80
= 15000 / 80
= 187.50
Ответ: обычная цена телефона была $187,50
Использование пропорций для решения треугольников
Мы можем использовать пропорции для решения подобных треугольников.
Пример: Какова высота дерева?
Сэм пробовал пользоваться лестницей, рулеткой, веревками и другими вещами, но так и не смог определить высоту дерева.
Но тут у Сэма есть умная идея… похожие треугольники!
Сэм измеряет палку и ее тень (в метрах), а также тень дерева, и вот что у него получается:
Теперь Сэм делает набросок треугольников и записывает отношение высоты к длине для обоих треугольников:
Высота: Длина тени: ч 2.9 м = 2,4 м 1,3 м
Умножить известные углы, затем разделить на третье число:
ч = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 м (с точностью до 0,1)
Ответ: дерево высотой 5,4 м.
И ему даже лестница не понадобилась!
«Высота» могла быть внизу, если она была внизу для ОБОИХ коэффициентов, например:
Попробуем соотношение «длины тени к высоте»:
Длина тени: Высота: 2.9 м ч = 1,3 м 2,4 м
Умножить известные углы, затем разделить на третье число:
ч = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 м (с точностью до 0,1)
Это тот же расчет, что и раньше.
A «Бетон» Пример
Соотношения могут иметь более двух чисел !
Например, бетон получают путем смешивания цемента, песка, камней и воды.
Типичная смесь цемента, песка и камней записывается в виде соотношения, например, 1:2:6.
Мы можем умножить все значения на одну и ту же сумму и все равно получить то же соотношение.
10:20:60 совпадает с 1:2:6
Таким образом, когда мы используем 10 ведер цемента, мы должны использовать 20 ведер песка и 60 камней.
Пример: вы только что засыпали в миксер 12 ведер камней, сколько цемента и сколько песка нужно добавить, чтобы получилась смесь 1:2:6?
Разложим по таблице, чтобы было понятнее:
| Цемент | Песок | Камни | |
|---|---|---|---|
| Необходимое соотношение: | 1 | 2 | 6 |
| У вас есть: | 12 |
У вас есть 12 ведер камней, но соотношение говорит 6.
Все в порядке, просто у вас в два раза больше камней, чем число в соотношении … поэтому вам нужно вдвое больше всего , чтобы сохранить соотношение.
Вот решение:
| Цемент | Песок | Камни | |
|---|---|---|---|
| Необходимое соотношение: | 1 | 2 | 6 |
| У вас есть: | 2 | 4 | 12 |
А соотношение 2:4:12 такое же, как 1:2:6 (поскольку они показывают одинаковые относительные размеры)
Итак, ответ: добавьте 2 ведра цемента и 4 ведра песка. (Вам также понадобится вода и много перемешивания….)
Почему они одинаковые? Ну, соотношение 1:2:6 говорит о том, что :
- В два раза больше песка, чем цемента (1:2:6)
- Камней в 6 раз больше, чем цемента (1:2:6)
В нашем миксе есть:
- В два раза больше песка, чем цемента (2:4:12)
- Камней в 6 раз больше, чем цемента (2:4:12)
Так и должно быть!
Это хорошая вещь о соотношениях. Вы можете сделать суммы больше или меньше, и пока размеры относительных одинаковы, соотношение будет таким же.
Вы можете сделать суммы больше или меньше, и пока размеры относительных одинаковы, соотношение будет таким же.
Соотношения и пропорции — Пропорции
Пропорция просто утверждение, что два отношения равны. можно написать двумя способами: как две равные дроби a/b = c/d; или используя двоеточие, a:b = c:d. Следующее пропорция читается как «двадцать к двадцати пяти, как четыре к пяти».»
В проблемах используя пропорции, мы можем использовать векторные произведения, чтобы проверить, являются ли два отношения равны и составляют пропорцию. Чтобы найти перекрестные произведения пропорции, мы умножаем внешние члены, называемые крайними, и средние члены, называемые Значения.
Здесь, 20 и
5 — крайности, а 25 и 4 — средние. Поскольку перекрестные произведения
оба равны ста, мы знаем, что эти отношения равны и что это
является истинной пропорцией.
Мы также можем использовать перекрестные произведения, чтобы найти недостающий член в пропорции. Вот пример. В фильме ужасов с участием гигантского жука жук был ростом 50 футов. длинная. Однако для жука использовалась модель, которая на самом деле была всего 20 дюймов. длинная. В фильме также использовалась модель здания высотой 30 дюймов. Какого роста здание кажется в фильме?
Сначала напишите
пропорция, используя букву для обозначения отсутствующего термина.Мы находим
перекрестные произведения, умножив 20 на x и 50 на 30. Затем разделите на
найти х. Внимательно изучите этот шаг, потому что это техника, которую мы будем часто использовать.
по алгебре. Мы пытаемся получить наше неизвестное число x слева от
уравнение само по себе. Поскольку x умножается на 20, мы можем использовать «обратное»
умножения, то есть деления, чтобы избавиться от 20. Мы можем разделить оба
стороны уравнения на одно и то же число, не меняя смысла
уравнение. Когда мы разделим обе стороны на 20, мы обнаружим, что здание будет
кажутся ростом 75 футов.
Когда мы разделим обе стороны на 20, мы обнаружим, что здание будет
кажутся ростом 75 футов.
Обратите внимание, что мы используя инверсию умножения на 20, то есть деление на 20, чтобы получить только x на одной стороне.
назад до
Основные или простые пропорции — ChiliMath
Предположим, что есть два отношения a:b и c:d. Их можно записать в виде дробей \Large{a \over b} и \Large{c \over d} соответственно. Теперь, если мы установим эти два соотношения равными друг другу , тогда получится пропорция .
способов написать пропорцию
Пропорция — это утверждение, показывающее, что два соотношения равны. Есть два способа написать пропорцию:
Оба могут быть прочитаны как «a относится к b, как c относится к d».
Далее определим частей пропорции . Эта концепция нужна нам для решения проблем позже.
В форме двоеточия крайними являются два крайних значения, а средними являются два самых внутренних значения.
- ФОРМА Дробей (Стандартная форма)
В форме дроби крайние значения – это значения, попадающие в диагональ, проведенную из верхнего левого угла в нижний правый, а средние значения – это значения, попадающие в диагональ, проведенную из нижнего левого угла в верхний правый.
Познакомившись с определением и частями пропорции, мы можем теперь говорить о свойствах пропорции . Это два полезных свойства , которые можно использовать для решения проблем.
Свойства пропорций
1) Взаимное имущество
Если два отношения равны, то их обратные величины также должны быть равны, пока они существуют.
2) Свойство перекрестного произведения
Произведение крайностей равно произведению средних.
Примеры применения концепции пропорций
Пример 1: Покажите, что приведенная ниже пропорция верна.
Чтобы пропорция была истинной, дроби в обеих частях уравнения должны быть приведены к одному и тому же значению. Дробь в левой части уравнения имеет наибольший общий делитель 5. А дробь в правой части имеет наибольший общий делитель 6.
Так как две дроби с обеих сторон равны после приведения к наименьшему члену, мы можем утверждать, что данная пропорция верна !
Пример 2: Покажите, что приведенная ниже пропорция верна.
Мы также можем показать, верна ли пропорция, используя свойство перекрестного произведения. Проще говоря, если произведение их крайностей (внешних значений) равно произведению средних (внутренних значений), то пропорция верна.
Это показывает, что данная пропорция верна !
Пример 3: Решите приведенную ниже пропорцию.
Эта проблема связана с пропорцией с неизвестным значением. Наша цель — найти значение «x», которое могло бы сделать пропорцию верным утверждением. Мы можем легко решить эту проблему, используя свойство Cross Product.
Мы можем легко решить эту проблему, используя свойство Cross Product.
Вы можете подставить x = 2 обратно в исходную пропорцию и убедиться, что это действительно правильный ответ.
Пример 4: Решите приведенную ниже пропорцию.
Единственное отличие этой задачи от примера №3 состоит в том, что в знаменателе встречается неизвестная переменная «x». Решить эту пропорцию так же просто, как применить свойство перекрестного произведения, а затем решить простое уравнение, которое получается из него.
В качестве альтернативы вы можете сначала применить свойство Reciprocal, чтобы переместить переменную «x» снизу вверх, прежде чем использовать свойство Cross Product. Ответ должен получиться тот же.
Пример 5: Решите приведенную ниже пропорцию.
Это еще одна проблема, с которой вы можете столкнуться при решении пропорций. Формат пропорции использует двоеточие вместо дроби. Чтобы решить это, нам нужно переписать пропорцию в дробной форме, а затем решить это как обычно.
Поскольку a:b = c:d можно записать как \Large{a \over b} = {c \over d}, наша исходная задача принимает вид \Large{{12} \over x} = {4 \over 3 }.
Давайте продолжим и решим это…
Подставьте x = 9 к исходной пропорции, чтобы проверить свой ответ.
Пример 6: Обменный курс между долларом США и индийской рупией составляет 2 к 106 . По этому курсу, сколько долларов США вы бы получили, если бы вы обменяли 901 индийскую рупию?
Нам нужно составить пропорцию, которую мы сможем решить.Мы можем сделать это двумя способами. Один из способов — поместить значения в долларах в числителях, а рупии в знаменателях пропорции. И другой способ — поменять их местами. Любая из настроек должна дать нам один и тот же ответ.
В этом упражнении мы поместим информацию о долларах сверху.
Решите неизвестное значение «x», чтобы получить требуемое значение в долларах.
Это означает, что на момент обмена 17 долларов США эквивалентны 901 индийской рупии .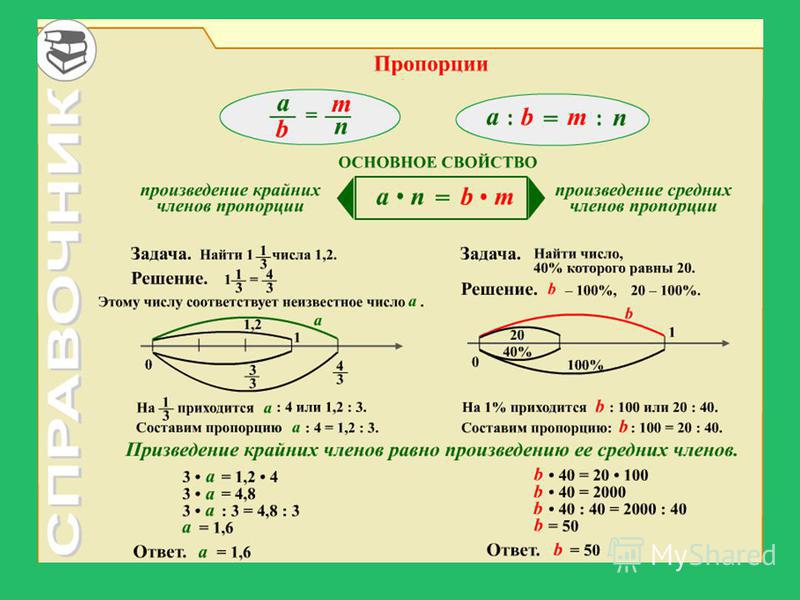
⚠️ Следующий пример представляет собой сложную задачу, потому что он потребует от вас критического мышления и решения многошаговых линейных уравнений с переменными в обеих частях уравнения.
Пример 7: Вы хотите распилить брусок дерева длиной 72 фута на две части так, чтобы отношение более короткой и более длинной части было 2 к 7. Какова их длина?
Пусть «x» будет длиной более короткого куска. Это означает, что «72 — x» будет более длинной частью.См. схему ниже.
Дано, что отношение более короткого куска к более длинному составляет 2:7. Используя всю эту информацию, теперь мы можем настроить пропорцию для определения длин как коротких, так и длинных частей.
Решение приведенной выше пропорции с использованием свойства пропорциональности перекрестного произведения…
Поскольку более короткая часть равна x = 16 футов , это означает, что более длинная часть равна 72 — x = 72 — 16 = 56 футов .
Для проверки нам сказали в задаче, что отношение более короткой части к более длинной равно 2 к 7.Обратите внимание, что когда мы уменьшаем дробь \Large{{16} \over {56}} до наименьшего члена, мы получаем желаемое соотношение.
Практика с рабочими листами
6.3: Введение в пропорцию — Mathematics LibreTexts
В разделе 6.1 мы ввели понятия соотношения и скорости. В этом разделе мы приравниваем эти соотношения в конструкции, называемой пропорцией .
\[\frac{1}{3} = \frac{2}{6}, ~ \frac{15 \text{ миль}}{2 \text{ часов}} = \frac{30 \text{ миль }}{4 \text{ часов}}, \text{ и } \frac{a}{b} = \frac{c}{d}\nonumber \]
сравнивают два соотношения или скорости и представляют собой пропорцию.
читается как «один к трем, как два к шести». Четыре числа, составляющие эту пропорцию, называются членами пропорции и упорядочены естественным образом.
термины a и d являются крайностями; термины b и c являются средними.
\[ \cancel{b} d \left( \frac{a}{\cancel{b}} \right) = b \cancel{d} \left( \frac{c}{\cancel{d}} \right)\nonumber \]
получаем следующий результат.
Это приводит к следующему наблюдению.
Мы можем получить эквивалентный результат, используя метод, называемый скрещиванием умножением .
Решение пропорций
У нас уже есть все инструменты, необходимые для решения пропорций. Начнем с первого примера.
Пример 2
Решите пропорцию для x : \(\frac{3}{4} = \frac{x}{12}\).
Раствор
Перемножить крест-накрест, затем решить полученное уравнение.
\[ \begin{align} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 4 \cdot x = 3 \ cdot 12 ~ & \textcolor{red}{ \text{ Произведения средних и крайних равны.}} \\ 4x = 36 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{4x} {4} = \frac{36}{4} ~ & \textcolor{red}{ \text{ Разделить обе части на 4. }} \\ x = 9 ~ & \textcolor{red}{ \text{ Упростить.} } \end{выровнено}\номер \]
}} \\ x = 9 ~ & \textcolor{red}{ \text{ Упростить.} } \end{выровнено}\номер \]
Чек
Подставьте x в исходную пропорцию на 9 и проверьте.
\[ \begin{align} \frac{3}{4} = \frac{x}{12} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ \frac{3}{4 } = \frac{9}{12} ~ & \textcolor{red}{ \text{ Замените 9 на } x.} \end{aligned}\nonumber \]
Перекрестное умножение.
Таким образом, решение 9 проверяется.
Упражнение
Решите пропорцию для n : \(\frac{2}{3} = \frac{n}{9}\)
- Ответить
6
Пример 3
Решите пропорцию для n : \(\frac{3}{2} = \frac{24}{n}\).
Раствор
Перемножить крест-накрест, затем решить полученное уравнение.
\[ \begin{align} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 3 \cdot n = 2 \ cdot 24 ~ & \textcolor{red}{ \text{ Произведения средних и крайних равны. }} \\ 3n = 48 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{3n} {3} = \frac{48}{3} ~ & \textcolor{red}{ \text{ Разделить обе части на 3.}} \\ n = 16 ~ & \textcolor{red}{ \text{ Упростить.}} \end{выровнено}\номер \]
}} \\ 3n = 48 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{3n} {3} = \frac{48}{3} ~ & \textcolor{red}{ \text{ Разделить обе части на 3.}} \\ n = 16 ~ & \textcolor{red}{ \text{ Упростить.}} \end{выровнено}\номер \]
Чек
Подставьте 16 вместо n в исходную пропорцию и проверьте.
\[ \begin{aligned} \frac{3}{2} = \frac{24}{n} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ \frac{3}{2 } = \frac{24}{16} ~ & \textcolor{red}{ \text{ Замените 16 на } n.} \end{aligned}\nonumber \]
Перекрестное умножение.
Таким образом, решение 16 проверяется.
Упражнение
Решить пропорцию для м : \(\frac{9}{6} = \frac{m}{4}\)
- Ответить
6
Пример 4
Решите пропорцию для x : \(\frac{2x + 1}{15} = \frac{1}{3}\).
Раствор
Перемножить крест-накрест, затем решить полученное уравнение.
\[ \begin{align} \frac{2x+1}{15} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 3(2x+1 ) = 15(1) ~ & \textcolor{red}{ \text{ Произведения f средние и крайние значения равны.}} \\ 6x+3 = 15 ~ & \textcolor{red}{ \begin{aligned} \text{ Слева распределите.} \\ \text{ Справа умножьте.} \end{aligned}} \\ 6x+3-3=15-3 ~ & \textcolor{red}{ \text{ Вычтите 3 из обе стороны.}} \\ 6x=12 ~ & \textcolor{red}{ \text{ Упростить.}} \\ \frac{6x}{6} = \frac{12}{6} ~ & \textcolor{red}{ \ text{ Разделить обе стороны на 6.}} \\ x = 2 ~ & \textcolor{red}{ \text{ Упростить обе стороны.}} \end{aligned}\nonumber \]
Чек
Мы предоставим нашим читателям возможность проверить это решение.
Упражнение
Решите пропорцию для y : \(\frac{6+2y}{18} = \frac{8}{9}\)
- Ответить
5
Приложения
Ряд практических приложений включает в себя решение пропорции.
Пример 5
Если 5 апельсинов стоят 1,15 доллара, сколько будет стоить 15 апельсинов (при равном курсе)?
Раствор
Пусть x представляют стоимость 15 апельсинов. Предполагая, что курс 5 апельсинов по 1,15 доллара равен курсу 15 апельсинов по неизвестной стоимости x , мы устанавливаем следующую пропорцию.
\[ \frac{5}{1.15} = \frac{15}{x}\номер \]
Перекрестное умножение
чтобы получить
\[5x = 17.25.\номер \]
Решить для x .
\[\begin{align} \frac{5x}{5} = \frac{17.25}{5} \\ x = 3.45 \end{align}\nonumber \]
Таким образом, 15 апельсинов стоят 3,45 доллара.
Упражнение
Если 7 яблок стоят 3,15 доллара, сколько будут стоить 10 яблок (при равном курсе)?
- Ответить
4,50 $
Проверка юнитов чрезвычайно важна
При составлении пропорции убедитесь, что оба числителя имеют одинаковые единицы измерения и оба знаменателя имеют одинаковые единицы измерения.
Например, в примере 5 в обоих числителях в качестве единиц измерения используются «апельсины», а в обоих знаменателях — «доллары».
Эта пропорция установлена правильно, потому что оба числителя имеют одинаковые единицы измерения и оба знаменателя имеют одинаковые единицы измерения. С другой стороны, если бы мы установили пропорцию неправильно следующим образом,
быстрая проверка блоков выявляет ошибку; т. е. числители имеют разные единицы измерения, а знаменатели имеют разные единицы измерения.Проверка единиц помогает нам избежать ошибок!
Пример 6
Дилан и Дэвид планируют поход в национальный парк Йосемити. На их карте легенда указывает, что 1,2 сантиметра соответствуют 2 милям. Какова продолжительность их пути, если длина маршрута на карте составляет 10,6 см? Округлите ответ до ближайшей десятой мили.
Раствор
Построим пропорцию в единицах.
\[\frac{1,2 \text{ см}}{2 \text{ми}} = \frac{10. 6 \text{ см}}{x \text{ми}}\номер\]
6 \text{ см}}{x \text{ми}}\номер\]
Обратите внимание, как включение единиц помогает в настройке пропорции. Теперь отбросим единицы измерения и найдем x .
\[ \begin{align} \frac{1.2}{2} = \frac{10.6}{x} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \\ 1.2x = (2)( 10.6) ~ & \textcolor{red}{ \text{ Перекрестное умножение.}} \\ 1.2x = 21.2 ~ & \textcolor{red}{ \text{ Упростить правую часть.}} \\ \frac{1.2x }{1.2} = \frac{21.2}{1.2} ~ & \textcolor{red}{ \text{ Разделите обе части на 1.2.}} \\ x \ приблизительно 17,66 ~ & \textcolor{red}{ \text{ Справа: Разделить.}} \end{aligned}\nonumber \]
Мы перенесли деление на один десятичный знак справа после десятых. Цифра округления — 6, а следующая проверочная цифра — 6. Добавьте 1 к цифре округления и усеките.
С точностью до десятой мили пеший маршрут составляет примерно 17,7 миль.
Упражнение
Элоиза и Сюзанна планируют поездку в Национальный парк Секвойя.На их карте 3 дюйма соответствуют 50 милям. Какова продолжительность их поездки, если размер маршрута составляет \(4 \frac{1}{2}\) дюймов на карте?
Какова продолжительность их поездки, если размер маршрута составляет \(4 \frac{1}{2}\) дюймов на карте?
- Ответить
75 миль
Пример 7
Рецепт приготовления 2 дюжин печенья требует \(1 \frac{3}{4}\) чашек муки, среди прочих ингредиентов. Если пекарь хочет испечь в два раза больше печенья, сколько потребуется муки?
Раствор
Дважды 2 дюжины — это 4 дюжины печенья.Пусть x представляет собой количество муки, необходимое для 4 дюжин печенья. Принимая равноценную норму на 2 дюжины печенья (на 2 дюжины требуется 1 3 4 стакана муки), составим следующую пропорцию. Опять же, использование единиц помогает нам создать правильную пропорцию.
\[\frac{2 \text{ дюжина}}{1 \frac{3}{4} \text{ чашек}} = \frac{4 \text{ дюжина}}{x \text{ чашек}}\nonumber \]
Обратите внимание, как включение единиц помогает в настройке пропорции. Теперь отбросим единицы измерения и найдем x .
\[ \begin{align} \frac{2}{1 \frac{3}{4}} = \frac{4}{x} ~ & \textcolor{red}{ \text{ Исходная пропорция.}} \ \ 2x = 1 \frac{3}{4} \cdot 4 ~ & \textcolor{red}{ \text{ Перекрестное умножение.}} \\ 2x = \frac{7}{4} \cdot 4 ~ & \textcolor {red}{ \text{ Заменить на неправильную дробь.}} \\ 2x = 7 ~ & \textcolor{red}{ \text{ Умножить.}} \end{aligned}\nonumber \]
Разделите обе части уравнения на 2 и закончите.
\[ \begin{aligned} \frac{2x}{2} = \frac{7}{2} ~ & \textcolor{red}{ \text{ Разделите обе стороны на 2.}} \\ x = \frac{7}{2} \end{aligned}\nonumber \]
Замените неправильную дробь на смешанную. Таким образом, для приготовления 4 дюжин печенья потребуется \(3 \frac{1}{2}\) стаканов муки.
Упражнение
Для теста на 3 пиццы требуется \(8 \frac{1}{2}\) чашек муки. Если пекарь хочет испечь 9 пицц, сколько чашек муки потребуется?
- Ответить
\(25 \frac{1}{2}\) чашек
Упражнения
В упражнениях 1-12, что из следующего является истинной пропорцией?
1. \(\frac{9}{7} = \frac{27}{21}, ~ \frac{4}{3} = \frac{9}{7}, ~ \frac{7}{2} = \ frac{8}{9}, ~ \frac{4}{8} = \frac{9}{6}\)
\(\frac{9}{7} = \frac{27}{21}, ~ \frac{4}{3} = \frac{9}{7}, ~ \frac{7}{2} = \ frac{8}{9}, ~ \frac{4}{8} = \frac{9}{6}\)
2. \(\frac{6}{7} = \frac{18}{21}, ~ \frac{2}{3} = \frac{8}{6}, ~ \frac{4}{3 } = \frac{3}{2}, ~ \frac{8}{9} = \frac{3}{8}\)
3. \(\frac{7}{6} = \frac{28}{24}, ~ \frac{5}{6} = \frac{5}{4}, ~ \frac{9}{5 } = \frac{7}{3}, ~ \frac{9}{2} = \frac{8}{9}\)
4. \(\frac{7}{6} = \frac{2}{8}, ~ \frac{4}{5} = \frac{5}{7}, ~ \frac{3}{4 } = \frac{15}{20}, ~ \frac{8}{4} = \frac{8}{7}\)
5.\(\frac{6}{5} = \frac{24}{20}, ~ \frac{7}{3} = \frac{2}{4}, ~ \frac{2}{4} = \ frac{2}{6}, ~ \frac{5}{2} = \frac{2}{8}\)
6. \(\frac{9}{8} = \frac{4}{3}, ~ \frac{5}{7} = \frac{10}{14}, ~ \frac{8}{6 } = \frac{5}{4}, ~ \frac{8}{5} = \frac{2}{6}\)
7. \(\frac{3}{5} = \frac{2}{8}, ~ \frac{3}{7} = \frac{6}{14}, ~ \frac{5}{6 } = \frac{2}{4}, ~ \frac{7}{4} = \frac{5}{9}\)
8. \(\frac{7}{3} = \frac{7}{6}, ~ \frac{4}{7} = \frac{8}{14}, ~ \frac{5}{3 } = \frac{7}{8}, ~ \frac{5}{7} = \frac{6}{9}\)
9. \(\frac{5}{4} = \frac{25}{20}, ~ \frac{9}{3} = \frac{9}{6}, ~ \frac{7}{4} = \ frac{3}{6}, ~ \frac{3}{5} = \frac{9}{4}\)
\(\frac{5}{4} = \frac{25}{20}, ~ \frac{9}{3} = \frac{9}{6}, ~ \frac{7}{4} = \ frac{3}{6}, ~ \frac{3}{5} = \frac{9}{4}\)
10. \(\frac{7}{6} = \frac{6}{9}, ~ \frac{7}{3} = \frac{2}{5}, ~ \frac{6}{7} } = \frac{30}{35}, ~ \frac{4}{7} = \frac{2}{8}\)
11. \(\frac{9}{7} = \frac{4}{3}, ~ \frac{9}{4} = \frac{7}{9}, ~ \frac{3}{5 } = \frac{6}{10}, ~ \frac{3}{9} = \frac{9}{5}\)
12. \(\frac{4}{3} = \frac{8}{7}, ~ \frac{2}{6} = \frac{5}{8}, ~ \frac{7}{2 } = \frac{3}{6}, ~ \frac{9}{4} = \frac{36}{16}\)
В упражнениях 13-36 решите данную пропорцию.
13. \(\frac{17}{3} = \frac{x}{18}\)
14. \(\frac{16}{5} = \frac{x}{20}\)
15. \(\frac{6x + 10}{6} = \frac{11}{3}\)
16. \(\frac{4x + 8}{12} = \frac{5}{3}\)
17. \(\frac{17}{9} = \frac{x}{18}\)
18. \(\frac{8}{9} = \frac{x}{18}\)
19. \(\frac{11}{2} = \frac{x}{8}\)
20. \(\frac{11}{4} = \frac{x}{8}\)
21. \(\frac{7x + 15}{15} = \frac{10}{3}\)
22. \(\frac{7x + 3}{8} = \frac{5}{4}\)
\(\frac{7x + 3}{8} = \frac{5}{4}\)
23.\(\frac{11}{2} = \frac{x}{10}\)
24. \(\frac{19}{6} = \frac{x}{18}\)
25. \(\frac{5x + 8}{12} = \frac{2}{3}\)
26. \(\frac{3x + 12}{6} = \frac{3}{2}\)
27. \(\frac{2}{15} = \frac{24}{x}\)
28. \(\frac{7}{8} = \frac{14}{x}\)
29. \(\frac{3}{16} = \frac{6}{x}\)
30. \(\frac{4}{21} = \frac{12}{x}\)
31. \(\frac{5}{22} = \frac{20}{x}\)
32. \(\frac{3}{22} = \frac{21}{x}\)
33.\(\frac{2x + 10}{6} = \frac{14}{3}\)
34. \(\frac{2x + 9}{9} = \frac{13}{3}\)
35. \(\frac{7}{2} = \frac{21}{x}\)
36. \(\frac{2}{15} = \frac{18}{x}\)
37. Если 13 собачьих костей стоят 1,97 доллара, сколько будет стоить 7 собачьих костей (при условии равного курса)? Округлите ответ до копейки.
38. Если 2 арбуза стоят 3,89 доллара, сколько будет стоить 11 арбузов (при равном курсе)? Округлите ответ до копейки.
39. Если 7 бананов стоят 2,55 доллара, сколько будет стоить 14 бананов (при равном курсе)? Округлите ответ до копейки.
Если 7 бананов стоят 2,55 доллара, сколько будет стоить 14 бананов (при равном курсе)? Округлите ответ до копейки.
40. Если 2 яблока стоят 2,05 доллара, сколько будет стоить 8 яблок (при равном курсе)? Округлите ответ до копейки.
41. Если 13 апельсинов стоят 3,61 доллара, сколько будет стоить 11 апельсинов (при равном курсе)? Округлите ответ до копейки.
42. Если 3 арбуза стоят 1,05 доллара, сколько будет стоить 9 арбузов (при равном курсе)? Округлите ответ до копейки.
43. Если 3 собачьи кости стоят 1,23 доллара, сколько будет стоить 13 собачьих костей (при условии равного курса)? Округлите ответ до копейки.
44. Если 3 арбуза стоят 4,41 доллара, сколько будет стоить 7 арбузов (при равном курсе)? Округлите ответ до копейки.
45. Если 3 яблока стоят 3,24 доллара, сколько будет стоить 13 яблок (при равном курсе)? Округлите ответ до копейки.
46. Если 6 яблок стоят 3,43 доллара, сколько будет стоить 7 яблок (при равном курсе)? Округлите ответ до копейки.
47. Если 4 собачьи кости стоят 1,03 доллара, сколько будет стоить 8 собачьих костей (при равном курсе)? Округлите ответ до копейки.
48. Если 4 апельсина стоят 4,28 доллара, сколько будет стоить 3 апельсина (при равном курсе)? Округлите ответ до копейки.
49. Два рулона. На Гаити две плоские булочки стоят 5 гурдов, около 12 центов. Сколько центов будут стоить 20 рулонов? Ассошиэйтед Пресс-Таймс-Стандарт 18.02.10 Гаитянские лагеря землетрясений превращаются в трущобы.
50. Турбины. В соответствии с предложением, проект Shell Wind Energy состоит из 25 коньковых турбин, которые могут генерировать до 50 мегаватт, что достаточно для снабжения электроэнергией около 1000 домов. Оцените количество турбин на вершине хребта, которые потребуются для снабжения электроэнергией 70 000 домов, приблизительное количество владений в округе Гумбольдт, Калифорния. John Driscoll Times-Standard 24.12.09 Проект ветроэнергетики находится на анализе.
51. Самосвалы. На шоссе 199 США произошел оползень, в результате которого на дорогу упало до 3000 кубических ярдов материала, для вывоза которого, как сообщается, потребовалось около 200 больших самосвалов. Всего за неделю до этого на шоссе 96 упало 40 000 кубических ярдов материала. Оцените количество самосвалов, необходимых для этого спуска, округлив до ближайшего целого числа. Ассошиэйтед Пресс-Таймс-Стандарт 03/09/10 Еще одно шоссе закрыто оползнем.
52. Продажа пиломатериалов. План национального леса Тонгасс площадью 26 000 квадратных миль на Аляске позволяет продавать древесину до 267 миллионов досок в год — этого достаточно почти для 27 000 домов с двумя спальнями, но спрос на древесину намного меньше этого.В 2009 году в лесу было вырублено менее 25 миллионов досок-футов. Представители Лесной службы заявили, что надеются увеличить вырубку в Тонгассе примерно до 100 миллионов досок-футов в год. Ассошиэйтед Пресс-Таймс-Стандарт 18. 02.10 Промышленность проигрывает судебный процесс по вырубке леса на Аляске.
02.10 Промышленность проигрывает судебный процесс по вырубке леса на Аляске.
i) Оцените количество домов с 2 спальнями, которые можно построить из 25 миллионов деревянных досок.
ii) Сколько домов с 2 спальнями можно построить из 100 миллионов деревянных досок?
53. Дорогостоящий разлив. В Австралии штрафы для судов, виновных в разливе нефти, составляют примерно 1,75 млн австралийских долларов, что эквивалентно примерно 1,64 млн долларов США. После того, как нефтяной танкер наскочил на коралловый риф, австралийские власти рассматривают возможность увеличения штрафа до 10 миллионов австралийских долларов. Каким будет новый штраф в долларах США? Округлите ответ до ближайшей сотой доли миллиона долларов. Ассошиэйтед Пресс-Таймс-Стандарт 13.04.10 Корабль, выливший нефть на Большой Барьерный риф, удален.
Часть 4: Пропорции: AMATh268 W16 h343
АМАТх268 — h343
Модуль 4: Пропорции
Перейти к содержанию Приборная доскаАвторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
- Мой Dashboard
- AMATh268 — h343
- Страницы
- Раздел 4: Пропорции
- Главная
- Модули
- Syllabus
- Сотрудники
- Студенческие ресурсы
- Google Drive
- Оценка курса
- Офис 365
- Новости и события
- 3-2-1 Начало работы @RTC (W22)
Пропорции и проценты — GED Math
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
.




