Комбинаторика: основные правила и формулы.

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и  принципы  комбинаторики  используются  в  теории  вероятностей для подсчета  вероятности  случайных  событий и,  соответственно, получения законов распределения случайных величин. Это,  в  свою  очередь,  позволяет  исследовать  закономерности массовых случайных явлений, что является весьма важным для правильного понимания  статистических  закономерностей, проявляющихся в природе и технике.

 

Правила сложения и умножения в комбинаторике

Правило суммы.  Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m  способами.

 

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

 

Правило произведения.  Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k  способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

 Сочетания без повторений. Сочетания с повторениями

 Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

 Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

 Размещения без повторений. Размещения с повторениями

 Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать

и разместить по m различным местам m из n различных предметов?

 

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В  данной  задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким  образом,  задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

 

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими

способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Решение

Можно  считать,  что  опыт  состоит  в 5-кратном выборе  с возращением одной из 3 цифр (1, 3, 7). Таким образом,  число  пятизначных  номеров  определяется  числом  размещений с повторениями из 3 элементов по 5:

.

 Перестановки без повторений. Перестановки с повторениями

 Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом:

сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной  совокупностью  являются 4  буквы слова  «брак» (б, р, а, к). Число  «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква  «м», 4 буквы «и», 3 буквы «c» и 1 буква  «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

ya-znau.ru

Решение более сложных задач по комбинаторике. Видеоурок. Алгебра 11 Класс

Из 2 математиков и 10 экономистов надо составить комиссию из 10 человек. Сколько есть способов сделать это при условии, что в комиссии должен участвовать хотя бы 1 математик?

Решение

Рассмотрим два случая:

1. В комиссии будет один математик.

Существует 2 способа выбрать 1 математика из 2. Из 10 экономистов нужно выбрать 9 человек; количество способов выбрать из 10 человек 9 – это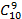

. Следовательно, всего способов:

 

Однако можно посчитать иначе: выбирать не 9 экономистов из 10, а выбрать 1 экономиста из 10, который не попадет в комиссию, то есть:

 

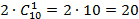
2. В комиссии будет более одного математика, то есть 2.

Существует 1 способ выбрать 2 математиков из 2. Оставшиеся восемь человек комиссии должны быть экономистами. Количество способов выбрать 10 человек 8 – это 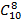. Следовательно, всего способов:

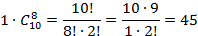
3. Складываем количество способов в первом и во втором случае:

 

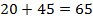
Ответ: 65 способов.

Сколько есть способов составить ожерелье из 5 одинаковых красных бусинок и 2 одинаковых синих бусинок?

Решение

Ожерелье может быть замкнутым и незамкнутым.

1. Если ожерелье замкнутое, то между синими бусинками может находиться или 0, или 1, или 2 красных бусинок (если между синими находятся 3, 4 или 5 красных, то это тоже самое, что и 0, 1, 2, только с другой стороны) (см. Рис. 1). Следовательно, существует три варианта расположения 2 синих и 5 красных бусинок на замкнутом ожерелье.

Рис. 1. Иллюстрация к задаче

2. Если ожерелье незамкнутое (см. Рис. 2), тогда количество вариантов определяется также положением синих бусинок. Количество способов выбрать 2 места из 7 – это .

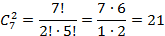
Рис. 2. Иллюстрация к задаче

Ответ: 1. Если ожерелье замкнутое, то существует три способа составить ожерелье; 2. Если ожерелье незамкнутое, то существует 21 способ составить ожерелье.

План города имеет вид прямоугольника 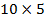 (см. Рис. 3). Его улицы идут строго параллельно сторонам. На каждом перекрестке водитель имеет право ехать либо вправо, либо вверх. Сколько существует различных маршрутов добраться из нижнего левого угла в правый верхний?

Рис. 3. Иллюстрация к задаче

Решение

Движение водителя задается последовательностью движений вправо (П) и вверх (В). Например: если водитель использует схему движения, показанную на рисунке 4, то он 10 раз (10 клеточек) едет вправо (П), а затем 5 раз (5 клеточек) вверх (В):

Рис. 4. Иллюстрация к задаче

Если водитель использует схему движения, показанную на рисунке 5, то он едет 1 раз вверх (В), 1 раз вправо (П), 1 раз В, 1 П, 1 В, 1 П, 1 В, 1 П, 1 В, 6 П:

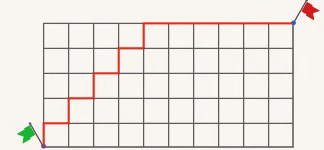
Рис. 5. Иллюстрация к задаче

Таким образом, каждый маршрут водителя задается последовательностью из 15 символов В и П, при этом водитель каждый раз смещается на 10 единиц вправо и на 5 единиц вверх. Следовательно, из 15 символов 5 будут символами В, а 10 будут символами (П). Поэтому для решения задачи необходимо найти количество способов выбрать 5 мест из 15, в которых водитель поедет вверх. Это будет .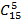

Ответ: 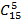 маршрутов.

Даны 2 слова: «интегрирование» и «суперкомпьютер». Вася посчитал, сколько получается слов из слова «интегрирование», если вычеркнуть в нем 2 произвольные буквы (получившиеся слова не обязательно осмысленные). Маша сделала то же самое для слова «суперкомпьютер». У кого слов получилось больше?

Решение

В данных словах одинаковое количество букв (по 14), поэтому вычеркнуть две буквы из каждого из них можно одинаковым количеством способов. Заметим, что при вычеркивании двух букв из слова «суперкомпьютер» все полученные слова будут различны, а при вычеркивании букв РИ и ИР из слова «интегрирование» получается одно и то же слово «интегрование». Поэтому, у Маши получится на одно слово больше.

Количество способов выбрать 2 буквы из 14 – это 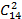, именно столько слов будет у Маши, а у Васи будет  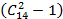слов.

Ответ: больше слов получилось у Маши.

Сколько существует способов рассадить за круглый стол 5 юношей и 5 девушек так, чтобы они чередовались?

Решение

На рисунке 6 изображен стол, на котором для удобства пронумерованы места.

Рис. 6. Иллюстрация к задаче

Предположим, что на месте номер 1 сидит юноша. Тогда все юноши садятся через 1 от этого места (на нечетные места), а девушки – на четные. Количество способов усадить 5 юношей на 5 кресел (количество перестановок) – это 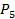, количество способов усадить 5 девушек на 5 кресел – это также 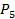. Значит, всего вариантов усадить юношей и девушек – это 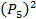. Однако на месте номер 1 может сидеть девушка (на четных – юноши, на нечетных – девушки), тогда окончательный ответ будет в два раза больше, то есть .

 

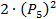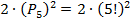
Ответ: 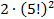 способов.

В стране есть 20 городов, которые соединены между собой 172 авиалиниями. Предположим, что между двумя городами есть только одна авиалиния. Докажите, что из любого города можно попасть в любой город, возможно, с пересадками.

Доказательство

Докажем от противного.

Предположим, что есть города 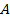 и  такие, что из 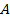 нельзя долететь в . Тогда какой бы мы ни взяли город 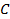, одновременно существовать авиалинии  и 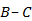 не могут (если существуют обе, можно долететь из  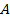в  с пересадкой), и так для любого города из оставшихся 17 (см. Рис. 7).

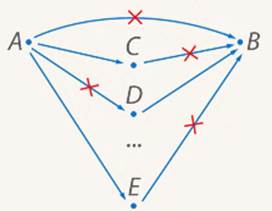
Рис. 7. Иллюстрация к задаче

Следовательно, отсутствует авиалиния 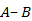 и еще 18 авиалиний, которые связывают другие города либо с городом 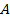, либо с городом , то есть всего отсутствует 19 авиалиний.

В стране 20 городов, следовательно, всего теоретически возможно провести 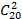 авиалиний.

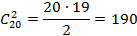
Тогда если из 190 возможных авиалиний 19 отсутствуют, то присутствует всего:

 авиалиния

Однако это противоречит условию:

 

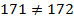
Следовательно, исходное предположение неверно, а из любого города можно попасть в любой.

 

---

Пример

Задача 7

Дано слово «логарифм». Сколько существует способов поменять местами буквы в этом слове так, чтобы в полученном буквосочетании согласные были упорядочены по алфавиту слева направо?

Решение

Например, нам подойдут следующие буквосочетания: ОАИГЛМРФ или ГОАЛИМРФ, или ГЛМАИРОФ. В каждом буквосочетании согласные идут в определенном порядке по алфавиту (ГЛМРФ), следовательно, общее количество вариантов таких буквосочетаний определяется только 3 гласными. Поэтому достаточно определить 3 места из 8 для гласных, после чего все буквы расставляются однозначно. А это будет 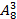 способов.

 

Ответ: 336 способов.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа 10-11 кл. В. 2 ч. Ч. 1: Учебник для общеобразоват. учреждений. – М.: Мнемозина, 2009.

2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа. 

3. М.И. Шабунин, А.А. Прокофьев, Т.А. Олейник, Т.В. Соколова. Алгебра. Начала математического анализа. Профильный уровень: задачник для 10-11 классов. – М.: БИНОМ. Лаборатория знаний, 2009.

4. Мордкович А.Г. Алгебра и начала анализа 10-11 кл. В. 2 ч. Ч. 2: Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1.  Интернет-сайт «Математический тандем» (Источник)

2. Интернет-сайт YouTube (Источник)

3. Интернет-сайт «МатБюро» (Источник)

 

Домашнее задание

1. Глава 20, задания 56, 67, 82 (стр. 382–386) – М.И. Шабунин, А.А. Прокофьев, Т.А. Олейник, Т.В. Соколова. Алгебра. Начала математического анализа. (Источник).

2. У Васи дома живут 4 кота.

а) сколькими способами можно рассадить котов по углам комнаты?
б) сколькими способами можно отпустить гулять котов?
в) сколькими способами Вася может взять на руки двух котов (одного на левую, другого на правую)?

3. Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?

4. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола?

interneturok.ru

Комбинаторика — основные понятия и формулы с примерами

Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.

Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.

Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.

Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников».

Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.

Что такое комбинаторика в математике

Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи.

В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики — на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.

Основные понятия

Их несколько:

1. Элемент – любой объект или явление, входящий в искомое множество.
2. Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
3. Перестановка – элементы во множестве находятся в строго определенном порядке.
4. Размещение – упорядоченные подмножества в исходном множестве.

Правило произведения

Является одним из основных правил при решении таких задач и звучит так:

При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.

Задача №1.

В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?

Ответ прост: 2 * 6 = 12.

Задача №2.

Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?

Решение аналогично: 1 * 2 * 3 * 4 = 24.

Причем левую часть можно записать гораздо проще: 4!

! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).

Задача №3.

Сколько двузначных чисел можно составить из 2 цифр?

Ответ: 2! = 2.

Задача №4.

Сколько десятизначных чисел можно составить из 10 цифр?

10! = 3628800.

Правило суммы

Тоже является базовым правилом комбинаторики.

Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.

В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?

Ответ: 5 + 3 + 7 + 9 = 24.

Сочетания с повторениями и без повторений

Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

Задача №6.

В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?

Решение простое:

Где 4! – комбинация из 4 элементов.

С повторениями чуть сложней, комбинации считаются по такой формуле:

Задача №7.

Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.

В этом случае:

Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

Задача №8.

Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?

Ответ прост:

А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:

Задача №9.

Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.

Решение:

Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

Задача №10.

Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?

Решения, согласно вышеприведенной формуле, следующие:

5! = 120;

6! = 720;

7! = 5040.

А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!

Задача №11.

В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?

Ответ прост: 4! / (3! * 1!) = 4.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) — найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения. Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть — найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Заключение

Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.

1001student.ru

Методы решения комбинаторных задач

При решении многих практических задач приходится использовать комбинации элементов,  выбирать из данной совокупности те, которые имеют определенные свойства, и размещать их в определенном порядке. Такие задачи называются комбинаторными. Раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями, называется комбинаторикой. Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский язык означает – «сочетать», «соединять».

Выбранные группы элементов называют соединениями. Если все элементы соединения разные, то получаем соединения без повторений, которые и рассмотрим ниже.

Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.

Выбор правила	Выбор правила
Правило суммы	Правило произведения
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор объекта либо А, либо В можно осуществить m + n способами.	Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары А и В можно осуществить m · n способами.

Задача 1.

В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?

Решение.

Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).

Ответ: 24.

Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.

Рассмотрим решение нескольких задач на разные виды соединений без повторений.

Задача 2.

Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.

Решение.

Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A₇³ = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.

Ответ: 210.

Задача 3.

Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?

Решение.

На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:

A₁₀⁷ – A₉⁶ = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.

Ответ: 544 320.

Задача 4.

Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?

Решение.

Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит  это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р₈. Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р₅ способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р₈ · Р₅ = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.

Ответ: 8! · 5!

Задача 5. 

В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?

Решение.

Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:

С₁₆⁴ · С₁₂³ = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.

Ответ: 400 400.

Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.

 Остались вопросы? Не знаете, как решать комбинаторные задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru