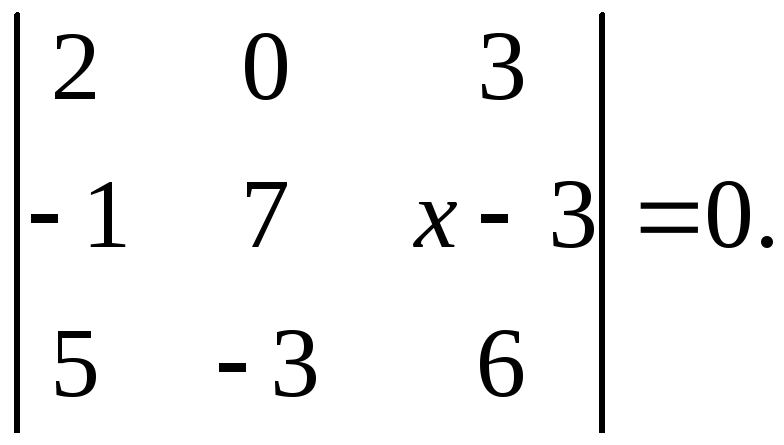Решение матричных уравнений: теория и примеры
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
ax=b,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
A ⋅ X = B
или
X ⋅ A = B,
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того,
чтобы решить матричное уравнение вида A ⋅
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:
.
Как решить матричное уравнение во втором случае? Если дано уравнение
X ⋅ A = B,
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X. То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A.
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
A ⋅ X ⋅ B = C,
является
.
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:
.
Наконец, находим неизвестную матрицу:
Решить матричное уравнение самостоятельно, а затем посмотреть решениеПример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится слева.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A слева. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится справа.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то
есть неизвестная матрица X находится в середине
произведения трёх матриц. Поэтому решение следует искать в виде
. Найдём матрицу, обратную матрице
A.
Поэтому решение следует искать в виде
. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Найдём матрицу, обратную матрице B.
Сначала найдём определитель матрицы B:
.
Найдём алгебраические дополнения матрицы B:
Составим матрицу алгебраических дополнений матрицы B:
.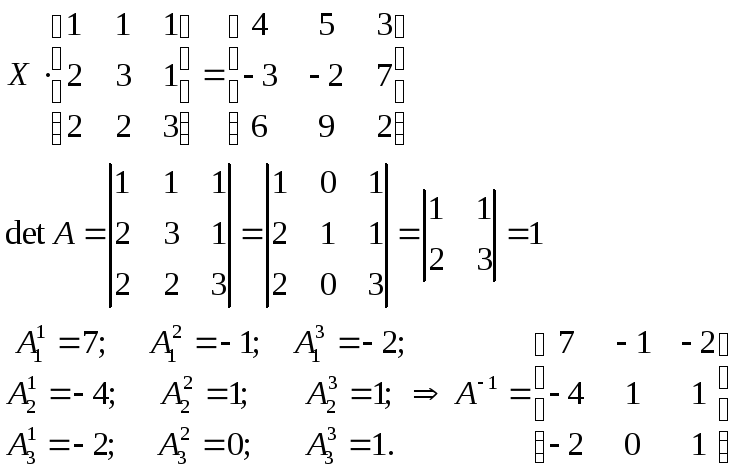 {-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$
{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$
|
Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15). Возможны два случая: 1) матрица А Квадратная невырожденная; 2) матрица А — либо вырожденная, либо прямоугольная. 1) Если А – квадратная и | 2) А – квадратная матрица, но |А| = 0, либо А — прямоугольная матрица. Если матрица А Имеет размерность M´n, а матрица В – Размерность Р´к, то, при M ¹ Р уравнение (14) не имеет решения, а при N ¹ к не имеет решения уравнение (15). Пример 5. Найдите матрицу Х, Если А×Х = В, Где А = , В = . Из примера 5 следует, что матрица А Имеет обратную, поэтому Х = А-1×В. Используя найденную в примере 5 матрицу А-1, Получим Х = × = = . Пример 6. Найдите матрицу Х, Если Х×А = В, где А = , В =. Так как |А| = 0, то для А обратной матрицы нет. По правилам умножения матриц, в матрице В Столько строк, сколько их в матрице Х, И столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х Должно быть два столбца и три строки.
|
Занятие по теме «Матричные уравнения. Вычисление обратной матрицы»
Цель: приобретение базовых знаний в области фундаментального раздела математики “Линейная алгебра”. Проверка усвоения знаний по вычислению обратной матрицы, нахождению алгебраических дополнений, дополнительного минора, вычислению определителей, решению матричных уравнений.
Задачи:
- развитие творческого профессионального мышления;
- развитие познавательной мотивации;
- овладение языком науки, приобретение навыков оперирования понятиями;
- овладение умениями и навыками постановки и решения задач;
- углубление теоретической и практической подготовки;
- развитие инициативы и самостоятельности студентов;
- формирование общих компетенций:
– организация собственной деятельности, исходя из цели и способов ее достижения, определенных руководителем;
– анализ рабочей ситуации, осуществление текущего и итогового контроля, оценка и коррекция собственной деятельности, ответственность за результаты своей работы;
– осуществление поиска информации, необходимой для эффективного выполнения профессиональных задач;
– использование информационно-коммуникационных технологий в профессиональной деятельности;
– работа в команде, эффективное общение с коллегами, руководством.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Учебники: Богомолов Н.В. “Математика”. – М.: Дрофа, 2009.
Омельченко В.П., Э.В. Курбатова. Математика, – Серия: Среднее профессиональное образование. – Ростов-на-Дону “Феникс”,2008-380с.
Индивидуальные карточки с вариантом практической работы.
Структура практического занятия.
1. Организационный этап.
Проверка готовности обучающихся к занятию.
2. Этап подготовки обучающихся к активному усвоению нового материала.
3. Этап усвоения новых знаний.
Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины.
Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
- Изучение теоретического материала по теме “Матричные уравнения. Вычисление обратной матрицы”.
4. Этап проверки понимания обучающимися нового материала.
- Примеры решения типовых заданий.
5. Этап закрепления нового материала.
- Выполнение практической работы по вычислению определителей, выполнению действий над матрицами, решению матричных уравнений.
6. Итоги занятия. Рефлексия.
7. Этап информирования обучающихся о домашнем задании.
Теоретические сведения и методические рекомендации по решению задач.
1. Изложение теоретического материала.
Определение. Квадратная матрица A-1 называется обратной к квадратной матрице A того же порядка, если AA-1 = A-1A = E , где E – единичная матрица.
Утверждение. Квадратная матрица A имеет обратную матрицу тогда и только тогда, когда det A≠ 0 .
Утверждение. Элементы cij обратной матрицы A-1 , если она существует, можно найти по формуле
– алгебраическое дополнение к элементу
aij матрицы
A, ATij – алгебраическое дополнение к элементу
aTij транспонированной матрицы
AT.
Определение. Алгебраическим дополнение Aij элемента aij называется число, равное Aij = (–1)i+jMij.
Определение. Дополнительным минором Mij элемента aij матрицы Ann называется определитель матрицы n-1-го порядка, полученный из матрицы Ann вычеркиванием i-ой строки и j-го столбца.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
, где Мji дополнительный минор элемента аji матрицы А.
Значение определителя: -10 + 6 – 40 = -44.
2. Закрепление теоретического материала, решение типовых задач.
№ 1. Найти матрицу
C = A-1
обратную к A, если
.
Решение. Прежде всего вычислим определитель матрицы A, чтобы убедиться в возможности существования обратной матрицы.
Следовательно, для матрицы A существует обратная матрица.
Воспользуемся формулой, выражающей элементы обратной матрицы через алгебраические дополнения к элементам транспонированной матрицы.
Для AT имеем .
Вычислим последовательно элементы Cij :
С учетом полученных данных, обратная к A матрица имеет вид
№ 2. Решить матричное уравнение A · X = B, где
Решение. Такое матричное уравнение, если определитель матрицы
A отличен от нуля, удобно решать путем умножения обеих частей уравнения слева на матрицу
A-1. В этом случае для искомой матрицы получим
A-1· A · X = A-1 · B
и поскольку A-1· A = E, то
X = A-1· B.
Найдем теперь выражение для A-1 . Детерминант Δ матрицы A равен 4. Пользуясь формулами, определяющими элементы обратной матрицы, имеем
.
Учитывая последнее, для X получим:
.
3. Практическая работа обучающихся.
|
Вариант 1 1. Найти матрицу обратную данной: |
Вариант 2 1. Найти матрицу обратную данной: |
4. Подведение итогов практического занятия.
Рефлексия.
О чем сегодня на занятии шла речь?
Что было новым?
С какими трудностями Вы столкнулись?
Контрольные вопросы:
1. Сформулировать свойства определителя.
2. Какую матрицу называют обратной?
3. При каком условии существует обратная матрица?
4. Что называется алгебраическим дополнением матрицы?
Что называется алгебраическим дополнением матрицы?
5. Что называется минором матрицы?
6. В чем заключается метод построения обратной матрицы с использованием алгебраических дополнений.
5. Домашнее задание.
Учить определения, составить опорную схему конспекта. Выполнить упражнения:
1. Какая из матриц B, C, D является обратной к матрице A, если:
2. При каких λ существует A-1, если:
3. Найти матрицу, обратную данной, если она существует:
Действия с матрицами
Матрицы и действия с ними, определителиСложение матриц
Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц \(A=\{A_{ik}\}\) и \(B=\{B_{ik}\}\), матрица \(A+B\), определяется следующим образом: \((A+B)_{ik}=A_{ik}+B_{ik}\), \(1 \leq i \leq m, 1 \leq k \leq n\). Иными словами: складываются элементы матриц \(A\) и \(B\), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.
Иными словами: складываются элементы матриц \(A\) и \(B\), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , \] \[ B=\left( \begin{array}{ccc} 2 &1 & 0 \\ 1 & 3 & 4 \end{array} \right) , \] тогда \[ A+B=\left( \begin{array}{ccc} 3 & 5 & -1 \\ 4 & -3 & 11 \end{array} \right) . \]
Умножение матрицы на число
Пусть \(A=\{a_{ik}\}\) — матрица типа \((m,n)\), \(\lambda\) — произвольное число. Тогда матрица \(\{\lambda a_{ik}\}\) называется произведением числа \(\lambda \) на матрицу \(A\) и обозначается \(\lambda \cdot A\).
Пример. Пусть
\[
A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array}
\right) ,
\]
тогда
\[
5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array}
\right) . T\) (это выражение занимает меньше места).
T\) (это выражение занимает меньше места).
Элементарные свойства операций с матрицами
Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.
1. Для любых матриц \(A,B,C\) одного типа \((A+B)+C=A+(B+C)\)(ассоциативность сложения).
2. Для любых матриц \(A,B\) одного типа \(A+B=B+A\) (коммутативность сложения).
3. Пусть \((m,n)\)-матрица \(O\) состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа \((m,n)\), \(A+O=A\), \(0\cdot A=O\) для любой матрицы \(A\) того же типа.
4. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1+c_2)A=c_1A+c_2A\).
5. Для любых матриц \(A,B\) одного типа и любого числа \(c\) верно \(c(A+B)=cA+cB\).
6. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1c_2)A=c_1(c_2A)\).
7. Для любой матрицы \(A\) верно \(1\cdot A=A\).
8. Для любых матриц \(A,B\) одного типа \((A+B)^T=A^T+B^T\). na_{im}b_{mk}.
\]
Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
na_{im}b_{mk}.
\]
Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]
В данном случае матрица \(A\) имеет тип (2,3), матрица \(B\) имеет тип (3,2), так что типы матриц согласнованы и в результате умножения \(A\) на \(B\) получим матрицу типа \((2,2)\). Получаем:
\[
AB=\left (
\begin{array}{cc}
1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\
3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5
\end{array}
\right )=
\left( \begin{array}{cc} 9 & 8\\ -21 & 20
\end{array} \right). T\).
T\).
6. Для квадратных матриц \(A,B\) одного типа \(det(AB)=detA \cdot detB\).
7. Рассмотрим квадратную матрицу порядка \(n\), \(E=diag\{1,1,1,…,1\}\). Такая матрица играет выделенную роль в умножении матриц: для любых матриц \(A,B\) имеем \(EA=A\), \(BE=B\). Матрица \(E\) называется единичной матрицей порядка \(n\). Согласно описанным выше результатам, \(detE=1\).
1. Умножить матрицы:
а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]
б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]
2. Вычислить
\[
\left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5. {-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right).
\]
{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right).
\]
Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.
Найти обратную матрицу для матрицы
1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]
2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]
3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]
Матричные уравнения
Матричными уравнениями называются уравнения вида
\[ AX=G, \quad \quad(12)\]
\[ XB=G, \quad \quad(13)\]
\[ AXB=G, \quad \quad(14)\]
где матрицы \(A,B,G\) заданы и требуется построить матрицу \(X\). {-1}.
\]
{-1}.
\]
1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]
2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]
3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]
4. Найти решение матричного уравнения (13), если
\[
B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) ,
G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]
\]
5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]
6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]
21. Матричные уравнения. Теорема существования и единственности решения.
Рассмотрим матричное уравнение вида
где и —
данные матрицы, имеющие одинаковое
количество строк, причем матрица квадратная. Требуется найти матрицу ,
удовлетворяющую уравнению (4.5).
Требуется найти матрицу ,
удовлетворяющую уравнению (4.5).
Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы отличен от нуля, то матричное уравнение (4.5) имеет единственное решение.
В самом деле, подставляя в левую часть равенства (4.5), получаем, т.е. правую часть этого равенства.
Заметим, что решением матричного уравнения служит обратная матрица.
Рассмотрим также матричное уравнение вида
где и — данные матрицы, имеющие одинаковое количество столбцов, причем матрица квадратная. Требуется найти матрицу , удовлетворяющую уравнению (4.6).
Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы отличен от нуля, то уравнение (4.6) имеет единственное решение.
Заметим,
что матрица является
как бы «левым» частным от «деления»
матрицына
матрицу,
поскольку матрицав
(4.5) умножается наслева,
а матрица—
«правым» частным, так как матрицав
(4. 6) умножается насправа.
6) умножается насправа.
Пример 4.5. Даны матрицы
Решить уравнения: а) ; б); в).
Решение. Обратная матрица была найдена в примере 4.2.
а) Решение уравнения находим, умножая обе его части слева на
б) Уравнение не имеет решений, так как матрицы иимеют разное количество столбцов.
в) Решение уравнения находим, умножая обе его части справа на
Пример 4.6. Решить уравнение: , где.
Решение. Преобразуя левую часть уравнения:
приведем его к виду (4.1)
где
Следовательно, . Обратная матрица найдена в примере 4.2:
Значит,
Пример 4.7. Решить уравнение , где
Решение. Обратные матрицы были найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по формуле
Пример 4.8. Решить уравнение , где
Решение. Определитель
матрицы равен
нулю, следовательно, обратная матрица
не существует. Поэтому нельзя использовать
формулу.
Будем искать элементы матрицы.
Подставляя в уравнение, получаем
Определитель
матрицы равен
нулю, следовательно, обратная матрица
не существует. Поэтому нельзя использовать
формулу.
Будем искать элементы матрицы.
Подставляя в уравнение, получаем
Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:
Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные и
Следовательно, решение матричного уравнения имеет вид
где параметры и могут принимать любые значения. Таким образом, данное матричное уравнение имеет бесконечное множество решений.
22. Решение системы линейных уравнений матричным методом. Правило Крамера.
Рассмотрим систему уравнений |
— матрица системы |
—
матрицы-столбцы неизвестных и свободных
членов. |
Очевидно, что , |
тогда АХ=С Такое равенство называется матричным уравнением. Если матрица А системы невырожденная, (det А 0), то это уравнение решается следующим образом: Умножим обе его части на матрицу А-1, обратную матрице А А-1(АХ)=А-1С или, (А-1А) · Х = А-1·С. но так как А-1А=Е, и ЕХ=Х Х=А-1С Например, решим матричным способом систему |
матрица системы |
Не является ли матрица А вырожденной? Найдем ее определитель: А =1·[-1·4 – 1·2] – 1·[2·4 – 2·4] + 2·[2·1 – 4·(-1)] = -6 + 12 = 6 Определитель
не равен нулю, то есть матрица не
вырожденная. А11 = (-1)1+1·М11 = (+1)·[-1·4 – 1·2] = -6 А12 = (-1)1+2·М12 = (-1)·[2·4 – 2·4] = 0 А13 = (-1)1+3·М13 = (+1)·[2·1 – 4·(-1)] = 6 А21 = (-1)2+1·М21 = (-1)·[1·4 – 1·2] = -2 А22 = (-1)2+2·М22 = [1·4 – 2·4] = -4 А23 = (-1)2+3·М23 = (-1)·[1·1 – 4·1] = 3 А31 = (-1)3+1М31 = [1·2 – (-1)·2] = 4 А32 = (-1)3+2·М32 = [(-1)·1·2 – 2·2] = 2 А33 = (-1)3+3·М33 = [1·(-1) – 2·1] = -3 |
Можно
убедиться проверкой в правильности
решения: подставим вектор Х в
первоначальное матричное уравнение. Действительно вектор Х удовлетворяет заданной системе |
Решение систем уравнений методом Крамера Применим теперь наши знания о матрицах к решению систем уравнений первой степени. Рассмотрим систему двух уравнений с двумя неизвестными: |
или коротко или АХ=С |
система записана в матричном виде (как произведение матриц) Решим эту простенькую систему школьными методами. Умножим первое уравнение на а22, а второе на (-а12) и сложим (а11а22 – а21а12)х1 = с1а22 – с2а12 аналогично (а11а22 – а21а12)х2 = с2а11 – с1а21 |
1)
но а11а22 –
а21а12 = —
это определитель матрицы А(det А)
или его еще называют определитель
системы и он составлен из коэффициентов
при неизвестных. |
2) определитель, который получится из det А, если в нем столбец коэффициентов при х1 (первый столбец) заменить на столбец правых частей. Обозначим его Х1 |
3) |
|
Видим, что <=»» font=»»> |
Как вы понимаете, если мы возьмем систему трех уравнений с тремя неизвестными или n уравнений с n неизвестными, то формулы останутся те же: |
Эти
формулы широко известны и называются
формулами Крамера. Возможны 3 случая: 1. 0 Тогда xi= xi/ — решение существует, причем единственное. 2. =0 , а какой-либо из xi 0 , то есть у нас в xi= xi/ производится деление на 0, система не имеет решения (несовместна). 3. =0 и все xi=0 то система имеет бесконечно много решений. Пример: |
Так как второе уравнение получается из первого умножением на 2, то наша система равносильна такой системе. |
Так
получилось, потому что первое и второе
уравнения систем эквивалентны и
фактически мы имеем систему двух
уравнений с тремя неизвестными, то
есть неопределенную систему. получим систему |
Решив ее, найдем 11х=0, х=0, y=1 То есть решение первоначальной системы x=0, y=0, z=0. Если бы мы положили z=1, получили бы еще один ответ и так далее. |
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – наA21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим
каждую из скобок и правую часть этого
уравнения. По теореме о разложении
определителя по элементам 1-го столбца
По теореме о разложении
определителя по элементам 1-го столбца
.
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и .
Наконец несложно заметить, что
Таким образом, получаем равенство: .
Следовательно, .
Аналогично выводятся равенства и , откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Матричный калькулятор онлайн
Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень, умножить матрицу на число, сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a/b, где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.
Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы , очищать содержимое ячеек ) и т.д.
Рис.1
При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.
Рис.2
Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку «A+B «,»A-B» или «A×B».
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.

- Нажмите на кнопку «обратное «.
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «определитель «.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «ранг «.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «псевдообратное «.
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «скелетное разложение «.
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку «решение AX=B».
Учтите, что матрицы и должны иметь равное количество строк .
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Треугольный вид».
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
Для LU(LUP)-разложения:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «LU-разложение».
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «ядро (·)».
Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Ортогонализация Г.-Ш. (·)» или «Ортонормализация Г.-Ш. (·)».
Матричных уравнений
В этом разделе мы представляем очень краткий способ записи системы линейных уравнений: Ax = b. Здесь A — это матрица, а x, b — векторы (обычно разного размера), поэтому сначала мы должны объяснить, как умножить матрицу на вектор.
Когда мы говорим «A — это матрица размера m × n», мы имеем в виду, что A имеет m строк и n столбцов.
Определение
Пусть A — матрица размера m × n со столбцами v1, v2, …, vn:
A = C ||| v1v2 ··· vn ||| D
Произведение A с вектором x в Rn является линейной комбинацией
Ax = C ||| v1v2 ··· vn ||| DEIIGx1x2…xnFJJH = x1v1 + x2v2 + … + xnvn.
Это вектор в Rm.
Чтобы Ax имел смысл, количество записей x должно быть таким же, как количество столбцов A: мы используем записи x как коэффициенты столбцов A в линейной комбинации. Результирующий вектор имеет то же количество записей, что и количество строк A, поскольку каждый столбец A имеет такое же количество записей.
Если A — матрица размера m × n (m строк, n столбцов), то Ax имеет смысл, когда x имеет n элементов.В продукте Ax есть m записей.
Свойства матрично-векторного произведения
Пусть A — матрица размера m × n, пусть u, v — векторы в Rn, и пусть c — скаляр. Тогда:
Определение
Матричное уравнение — это уравнение вида Ax = b, где A — матрица размера m × n, b — вектор в Rm, а x — вектор, коэффициенты которого x1, x2, …, xn неизвестны. .
В этой книге мы изучим два дополнительных вопроса о матричном уравнении Ax = b:
- При конкретном выборе b, каковы все решения Ax = b?
- Каковы все варианты b, чтобы Ax = b было непротиворечивым?
Первый вопрос больше похож на вопросы, к которым вы, возможно, уже привыкли из своих предыдущих курсов алгебры; у вас много практики в решении таких уравнений, как x2−1 = 0 для x.Второй вопрос — это, возможно, новая концепция для вас. Теорема о рангах из раздела 2.9, который является кульминацией этой главы, говорит нам, что эти два вопроса тесно связаны.
Мы будем свободно перемещаться между четырьмя способами написания линейной системы снова и снова до конца книги.
Другой способ вычисления Ax
Приведенное выше определение является полезным способом определения произведения матрицы на вектор, когда дело доходит до понимания взаимосвязи между матричными уравнениями и векторными уравнениями.Здесь мы даем определение, которое лучше подходит для ручных вычислений.
Определение
Вектор-строка — это матрица с одной строкой. Произведение вектора-строки длины n и вектора (столбца) длины n равно
.Aa1a2 ··· anBEIIGx1x2 … xnFJJH = a1x1 + a2x2 + ··· + тревога.
Это скаляр.
Рецепт: правило строки-столбца для умножения матрицы на вектор
Если A — матрица размера m × n со строками r1, r2, …, rm, а x — вектор в Rn, то
Ax = EIIG — r1 —— r2—…— rm — FJJHx = EIIGr1xr2x … rmxFJJH.
Пусть A — матрица со столбцами v1, v2, …, vn:
A = C ||| v1v2 ··· vn ||| D.
Затем
Ax = bhasisolution⇐⇒thereexistx1, x2, …, x означают такие, что AEIIGx1x2 … xnFJJH = b⇐⇒thereexistx1, x2, …, xnsuchthatx1v1 + x2v2 + ··· + xnvn = b⇐⇒visalinearcombination , vn⇐⇒бисинтэппаном столбцов А.
Интервалы и согласованность
Матричное уравнение Ax = b имеет решение тогда и только тогда, когда b находится в промежутке между столбцами A.
Это дает эквивалентность между алгебраическим оператором (Ax = b согласованным) и геометрическим утверждение (b находится в промежутке столбцов A).
Когда решения всегда существуют
Основываясь на этой заметке, у нас есть следующий критерий того, когда Ax = b согласуется для при каждом выборе b.
Теорема
Пусть A — матрица размера m × n (без дополнений). Следующие эквиваленты:
- Ax = b имеет решение для всех b в Rm.
- Пролет столбцов A равен Rm.
- У A есть точка поворота в каждом ряду.
Доказательство
Эквивалентность 1 и 2 устанавливается данным примечанием применительно к каждому b в Rm.
Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, это означает, что 2 и 3 также эквивалентны.) Если A имеет точку поворота в каждой строке, то его сокращенная форма эшелона строк выглядит следующим образом:
C10A0A01A0A0001AD,
и, следовательно, AAbB сводится к этому:
Нет b, который делает его непоследовательным, поэтому всегда есть решение. И наоборот, если A не имеет точки поворота в каждой строке, то его уменьшенная форма эшелона строки выглядит следующим образом:
C10A0A01A0A00000D,
, что может привести к возникновению противоречивой системы после увеличения на b:
Напомним, что эквивалент означает, что для любой данной матрицы A либо все условий приведенной выше теоремы истинны, либо все они ложны.
Будьте внимательны при чтении утверждения приведенной выше теоремы. Первые два условия очень похожи на эту заметку, но логически они сильно различаются из-за квантификатора « для всех b».
Решение матричных уравнений
А матричное уравнение уравнение, в котором переменная обозначает матрица .
Вы можете решить более простые матричные уравнения, используя матрица сложения а также скалярное умножение .
Примеры 1:
Решить для матрицы Икс : Икс + [ 3 2 1 0 ] знак равно [ 6 3 7 — 1 ]
Икс + [ 3 2 1 0 ] — [ 3 2 1 0 ] знак равно [ 6 3 7 — 1 ] — [ 3 2 1 0 ] Икс + [ 0 0 0 0 ] знак равно [ 6 — 3 3 — 2 7 — 1 — 1 — 0 ] Икс знак равно [ 3 1 6 — 1 ]
Примеры 2:
Решить для матрицы Икс : Икс — [ — 9 — 3 6 0 ] знак равно [ 4 0 12 — 10 ]
Икс — [ — 9 — 3 6 0 ] знак равно [ 4 0 12 — 10 ] Икс — [ — 9 — 3 6 0 ] + [ — 9 — 3 6 0 ] знак равно [ 4 0 12 — 10 ] + [ — 9 — 3 6 0 ] Икс — [ 0 0 0 0 ] знак равно [ 4 + ( — 9 ) 0 + ( — 3 ) 12 + 6 — 10 + 0 ] Икс знак равно [ — 5 — 3 18 — 10 ]
Решение систем линейных уравнений с использованием матриц:Матричные уравнения можно использовать для решать системы линейных уравнений используя левую и правую части уравнений.
Примеры 3:
Решите систему уравнений с помощью матриц: { 7 Икс + 5 у знак равно 3 3 Икс — 2 у знак равно 22
7 Икс + 5 у знак равно 3 3 Икс — 2 у знак равно 22 → [ 7 Икс + 5 у 3 Икс — 2 у ] знак равно [ 3 22 ]
Запишите матрицу слева как произведение коэффициентов и переменных.
[ 7 5 3 — 2 ] [ Икс у ] знак равно [ 3 22 ]
↑ ↑ ↑
коэффициент Переменная постоянный матрица матрица матрица
Сначала найдите обратную матрицу коэффициентов.Обратное [ 7 5 3 — 2 ] является
1 7 ( — 2 ) — ( 3 ) ( 5 ) [ — 2 — 5 — 3 7 ] знак равно — 1 29 [ — 2 — 5 — 3 7 ] знак равно [ 2 29 5 29 3 29 — 7 29 ]
Затем умножьте каждую сторону матричного уравнения на обратная матрица .Поскольку матричное умножение нет коммутативной, обратная матрица должна быть слева на каждый сторона матричного уравнения.
[ 2 29 5 29 3 29 — 7 29 ] [ 7 5 3 — 2 ] [ Икс у ] знак равно [ 2 29 5 29 3 29 — 7 29 ] [ 3 22 ]
[ 1 0 0 1 ] [ Икс у ] знак равно [ 4 — 5 ]
В единичная матрица слева подтверждает, что обратная матрица была рассчитана правильно.
[ Икс у ] знак равно [ 4 — 5 ]
Решение ( 4 , — 5 ) .
Решение систем линейных уравнений с использованием матриц
Привет! Эта страница будет иметь смысл только тогда, когда вы немного знаете о системах линейных уравнений и матриц, поэтому, пожалуйста, пойдите и узнайте о них, если вы их еще не знаете!
Пример
Одним из последних примеров систем линейных уравнений был этот:
Пример: Решить
- х + у + г = 6
- 2y + 5z = −4
- 2x + 5y — z = 27
Затем мы решили его, используя метод «исключения»… но мы можем решить это с помощью Матриц!
Использование матриц упрощает жизнь, потому что мы можем использовать компьютерную программу (например, Матричный калькулятор), чтобы выполнять всю «обработку чисел».
Но сначала нам нужно написать вопрос в матричной форме.
в матричной форме?
ОК. Матрица — это массив чисел, верно?
Матрица
Ну, подумайте об уравнениях:
| х | + | y | + | z | = | 6 |
| 2 года | + | 5z | = | −4 | ||
| 2x | + | 5лет | – | z | = | 27 |
Их можно было бы превратить в таблицу чисел вот так:
| 1 | 1 | 1 | = | 6 | ||
| 0 | 2 | 5 | = | −4 | ||
| 2 | 5 | -1 | = | 27 |
Можно даже разделить числа до и после знака «=» на:
| 1 | 1 | 1 | 6 | |
| 0 | 2 | 5 | и | −4 |
| 2 | 5 | -1 | 27 |
Теперь похоже, что у нас есть 2 матрицы.
На самом деле у нас есть третий, это [x y z]:
Почему [x y z] идет туда? Потому что, когда мы умножаем матрицы, левая часть становится:
Это исходная левая часть приведенных выше уравнений (вы можете это проверить).
Матричное решение
Мы можем написать это:
как это:
AX = B
где
- A — это матрица 3×3 коэффициентов x, y и z
- X — это x, y и z и
- B — это 6, −4 и 27
Тогда (как показано на странице инверсии матрицы) решение следующее:
X = A -1 B
Что это значит?
Это означает, что мы можем найти значения x, y и z (матрица X), умножив , инверсную матрицу A , на матрицу B .
Итак, давайте продолжим и сделаем это.
Во-первых, нам нужно найти обратную матрицу A (при условии, что она существует!)
Используя Матричный калькулятор, получаем:
(для упрощения чисел я оставил определитель 1 / вне матрицы)
Затем умножьте A -1 на B (мы снова можем использовать Матричный калькулятор):
И готово! Решение:
х = 5,
у = 3,
г = -2
Как и на странице Системы линейных уравнений.
Довольно изящный и элегантный, человек думает, а компьютер производит вычисления.
Просто для удовольствия … Сделай это снова!
Для удовольствия (и для того, чтобы помочь вам учиться), давайте проделаем все это снова, но сначала поставим матрицу «X».
Я хочу показать вам этот путь, потому что многие думают, что решение, приведенное выше, настолько изящно, что это, должно быть, единственный способ.
Так что решим так:
XA = B
И из-за способа умножения матриц нам нужно настроить матрицы по-другому.Строки и столбцы необходимо поменять местами («транспонировать»):
И XA = B выглядит так:
Матричное решение
Тогда (также показано на странице инверсии матрицы) решение следующее:
X = BA -1
Это то, что мы получаем для A -1 :
На самом деле он похож на инверсию, которую мы получили раньше, но транспонированную (строки и столбцы меняются местами).
Затем умножаем B на A -1 :
И решение то же:
x = 5, y = 3 и z = −2
Это выглядело не так красиво, как предыдущее решение, но оно показывает нам, что существует более одного способа составления и решения матричных уравнений.Только будьте осторожны со строками и столбцами!
Использование матриц для решения систем уравнений
Матричные уравнения
Матрицы можно использовать для компактного написания и работы с системами множественных линейных уравнений.
Цели обучения
Определить, как матрицы могут представлять систему уравнений
Основные выводы
Ключевые моменты
- Если [latex] A [/ latex] является матрицей [latex] m \ times n [/ latex], а [latex] x [/ latex] обозначает вектор-столбец (т.е.е. [латекс] n \ умножить на 1 [/ latex] матрицу) [latex] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex], а [latex] b [/ latex] — это [ latex] m \ times 1 [/ latex] вектор-столбец, тогда матричное уравнение будет: [latex] Ax = b [/ latex].
Ключевые термины
- матрица : прямоугольное расположение чисел или членов, имеющее различное применение, такое как преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.
Матрицы можно использовать для компактного написания и работы с системами уравнений.Как мы узнали в предыдущих разделах, матрицами можно манипулировать так же, как и нормальным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений. Полезно понять, как организовать матрицы для решения этих систем.
Написание системы уравнений с матрицами
Можно решить эту систему, используя метод исключения или замены, но также можно сделать это с помощью матричной операции. Прежде чем приступить к настройке матриц, важно сделать следующее:
- Убедитесь, что все уравнения написаны одинаково, то есть переменные должны быть в одном порядке.
- Убедитесь, что одна часть уравнения — это только переменные и их коэффициенты, а другая сторона — просто константы.
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: [latex] X [/ latex] — это матрица, представляющая переменные системы, а [latex] B [/ latex] — матрица, представляющая константы. Используя матричное умножение, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:
[латекс] \ displaystyle A \ cdot X = B [/ латекс]
Чтобы решить систему линейных уравнений с использованием обратной матрицы, пусть [latex] A [/ latex] будет матрицей коэффициентов, пусть [latex] X [/ latex] будет переменной матрицей, и пусть [latex] B [/ latex ] — постоянная матрица.
Учитывая систему:
[латекс] \ displaystyle \ begin {align} x + 8y & = 7 \\ 2x-8y & = — 3 \ end {align} [/ latex]
Матрица коэффициентов:
[латекс] A = \ begin {bmatrix} 1 & 8 \\ 2 & -8 \ end {bmatrix} [/ latex]
Матрица переменных:
[латекс] \ displaystyle X = \ begin {bmatrix} x \\ y \ end {bmatrix} [/ latex]
Постоянная матрица:
[латекс] \ displaystyle B = \ begin {bmatrix} 7 \\ -3 \ end {bmatrix} [/ latex]
Таким образом, чтобы решить систему [latex] AX = B [/ latex], для [latex] X [/ latex] умножьте обе стороны на обратную величину [latex] A [/ latex], и мы получим решение:
[латекс] \ Displaystyle X = (A ^ {- 1}) B [/ латекс]
Если существует обратный [латекс] \ left (A ^ {- 1} \ right) [/ latex], эта формула решит систему.
Если матрица коэффициентов необратима, система может быть несовместимой и не иметь решения, или быть зависимой и иметь бесконечно много решений.
Матрицы и операции со строками
Две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.
Цели обучения
Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы
Основные выводы
Ключевые моменты
- Операция с элементарной строкой — это любое из следующих действий: переключение строк (перестановка двух строк в матрице), умножение строк (умножение строки матрицы на ненулевую константу) или сложение строк (добавление к одной строке). матрицы до некоторого числа, кратного другой строке).
- Если строки матрицы представляют систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы.
Ключевые термины
- пространство строки : набор всех возможных линейных комбинаций его векторов-строк.
- эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой последовательностью элементарных операций со строкой.
Операции с элементарной строкой (ERO)
В линейной алгебре две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.В качестве альтернативы, две матрицы [latex] m \ times n [/ latex] эквивалентны строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство строки матрицы представляет собой набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы. Две матрицы одинакового размера эквивалентны строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что эквивалентно, матрицы имеют одно и то же нулевое пространство.Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Операция элементарной строки — это любой из следующих трех ходов:
- Переключение строк (перестановка): поменять местами две строки матрицы.
- Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
- Сложение строк (сводная): прибавить к одной строке матрицы несколько значений, кратных другой строке.
Создание эквивалентных матриц с использованием элементарных операций со строками
Поскольку матрица по существу является коэффициентами и константами линейной системы, три операции со строками сохраняют матрицу.Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения, умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных обратных величин, так что переменная сокращается. Наконец, добавление строк аналогично методу исключения, когда для получения переменной выбирается сложение или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод для решения системы уравнений.
Пример 1: Покажите, что эти две матрицы эквивалентны строкам:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \ end {pmatrix} \ quad B = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ латекс]
Начните с [latex] A [/ latex], добавьте вторую строку к первой:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \ end {pmatrix} [/ latex]
Затем умножьте вторую строку на 3 и вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \ end {pmatrix} [/ latex]
Наконец, вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ latex]
Вы можете видеть, что [latex] A = B [/ latex], что мы достигли с помощью серии элементарных операций со строками.
Сокращение строк: решение системы линейных уравнений
В редукторе рядов, линейная система:
[латекс] \ displaystyle x + 3y-2z = 5 \\ 3x + 5y + 6z = 7 \ 2x + 4y + 3z = 8 [/ latex]
Представлен в виде расширенной матрицы:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {pmatrix} [/ latex]
Затем эта матрица модифицируется с использованием операций с элементарными строками до тех пор, пока она не достигнет уменьшенной формы эшелона строк.
Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.
Существует несколько специальных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана. Это вычисление может быть выполнено вручную (с использованием трех типов ERO) или на калькуляторе с использованием матричной функции «rref» (сокращенная форма эшелона строк).
Окончательная матрица представлена в виде уменьшенного ряда строк и представляет систему [латекс] x = -15 [/ latex], [latex] y = 8 [/ latex] [latex] z = 2 [/ latex].
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 0 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {pmatrix} [/ latex]
Упрощение матриц с помощью операций со строками
Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелона строк.
Цели обучения
Используйте операции с элементарными строками, чтобы представить матрицу в упрощенной форме
Основные выводы
Ключевые моменты
- Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк формы эшелона строк такое же, как и у исходной матрицы.
- Существует три типа операций с элементарными строками: поменять местами две строки, умножить строку на ненулевой скаляр и добавить к одной строке скалярное значение, кратное другой.
- На практике обычно не рассматривают системы в терминах уравнений, а вместо этого используют расширенную матрицу (которая также подходит для компьютерных манипуляций).
Ключевые термины
- расширенная матрица : Матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же операций с элементарной строкой для каждой из данных матриц.
С помощью конечной последовательности элементарных операций со строками, называемых исключением по Гауссу, любую матрицу можно преобразовать в форму эшелона строк. Это преобразование необходимо для решения системы линейных уравнений.
Прежде чем углубляться в детали, следует упомянуть несколько ключевых терминов:
- Расширенная матрица : расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же операций с элементарной строкой для каждой из данных матриц.
- Форма верхнего треугольника : Квадратная матрица называется верхней треугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это нижнетреугольная или верхнетреугольная матрица. Матрица, имеющая одновременно верхний и нижний треугольники, является диагональной матрицей.
- Элементарные операции со строками : Поменять местами строки, добавить строки или умножить строки.
Исключение по Гауссу
- Напишите расширенную матрицу для линейных уравнений.
- Используйте элементарные операции со строками в расширенной матрице [latex] [A | b] [/ latex], чтобы преобразовать [latex] A [/ latex] в форму верхнего треугольника. Если на диагонали находится ноль, переключайте строки, пока на его месте не окажется ненулевое значение.
- Используйте обратную замену, чтобы найти решение.
Пример 1: Решите систему методом исключения Гаусса:
[латекс] \ displaystyle 2x + y-z = 8 \\ -3x-y + 2z = -11 \ -2x + y + 2z = -3 [/ latex]
Запишите расширенную матрицу:
[латекс] \ left [\ begin {array} {rrr | r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \ end {array} \ right] [/ latex]
Используйте элементарные операции со строками, чтобы уменьшить матрицу до уменьшенной формы эшелона строк:
[латекс] \ left [\ begin {array} {rrr | r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \ end {array} \ right ] [/ латекс]
Используя элементарные операции со строками для получения сокращенной формы эшелона строк (‘rref’ в калькуляторе), решение системы отображается в последнем столбце: [latex] x = 2, y = 3, z = -1 [/ latex] . {- 1} = \ frac {1} {3 \ cdot -1-1 \ cdot 2} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} = $$
$$ = — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} $$
Следующий шаг — умножить обе части матричного уравнения на обратную матрицу:
$$ — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} \ begin {bmatrix} 3 & 1 \\ 2 & -1 \ end {bmatrix } \ cdot \ begin {bmatrix} x \\ y \\ \ end {bmatrix} = — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} \ begin {bmatrix} 5 \\ 0 \ end {bmatrix} $$
$$ — \ frac {1} {5} \ begin {bmatrix} -5 & 0 \\ 0 & -5 \ end {bmatrix} \ cdot \ begin {bmatrix} x \\ y \ end {bmatrix} = — \ frac {1} {5} \ begin {bmatrix} -5 \\ -10 \ end {bmatrix} $$
$$ \ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix} \ cdot \ begin {bmatrix} x \\ y \ end {bmatrix} = \ begin {bmatrix} 1 \\ 2 \ end { bmatrix} $$
Наше решение — (1,2), самый простой способ проверить, правы ли мы, — это подставить наши значения в наши исходные уравнения.
Видеоурок
Пример выше в видеоформате.
6. Матрицы и линейные уравнения
М. Борна
Мы хотим решить систему одновременных линейных уравнений с помощью матриц:
a 1 x + b 1 y = c 1
a 2 x + b 2 y = c 2
Если допустить
`A = ((a_1, b_1), (a_2, b_2))`, `\ X = ((x), (y)) \` и `\ C = ((c_1), (c_2))`
, затем AX = C . (Впервые мы увидели это в «Умножении матриц»).
Если теперь умножить каждую сторону
AX = C
слева от
А -1 , имеем:
A -1 AX = А -1 С .
Однако мы знаем, что A -1 A = I , матрица идентичности.Получаем
IX = A -1 C .
Но IX = X , поэтому решение системы уравнения задается следующим образом:
X = A -1 C
См. Рамку в верхней части Инверсии матрицы, чтобы узнать больше о том, почему это работает.
Примечание: Мы, , не можем изменить порядок умножения и использовать CA -1 , потому что умножение матриц не коммутативно.
Пример — решение системы с использованием обратной матрицы
Решите систему с помощью матриц.
— x + 5 y = 4
2 x + 5 y = −2
Всегда проверяйте свои решения!
Ответ
У нас:
`A = ((- 1,5), (2,5)),` `\ X = ((x), (y)) \` и `\ C = ((4), (- 2)) `
Чтобы решить эту систему, нам понадобится обратное к A , которое мы запишем как A -1 .-1C` `= ((- 0,333,0,333), (0,133,0,067)) ((4), (- 2))` `= ((- 2), (0,4))`
Этот ответ означает, что мы нашли решение «x = -2» и «y = 0,4».
Решение правильное?
Проверяем в исходной системе уравнений:
`{: (- x + 5y, = 4), (2x + 5y, = — 2):}`
Подставляя x = -2 и y = 0,4, получаем:
`- (- 2) + 5 × (0,4) = 2 + 2 = 4` [Проверяет ОК]
`2 × (−2) + 5 × (0,4)` `= −4 + 2« = −2` [Проверяет ОК]
Итак, решение исходной системы уравнений —
.`х = -2, \ \ у = 0.4`.
Решение 3 × 3 систем Уравнения
Мы можем распространить вышеуказанный метод на системы любого размера. Мы не можем использовать тот же метод для поиска обратных матриц больше 2 × 2.
Мы будем используйте систему компьютерной алгебры, чтобы найти инверсии больше, чем 2 × 2.
Пример — Система 3 × 3 Уравнения
Решите систему матричными методами.
`{: (x + 2y-z = 6), (3x + 5y-z = 2), (- 2x-y-2z = 4):}`
Я уже упоминал? Хорошая идея — всегда проверять свои решения.-1C`
`= ((5.5, -2.5, -1.5), (- 4,2,1), (- 3.5,1.5,0.5)) ((6), (2), (4))`
`= ((22), (- 16), (- 16))`
Чек:
`22 + 2 (-16) — (-16) = 6` [ОК]
`3 (22) + 5 (-16) — (-16) = 2` [ОК]
`-2 (22) — (16) — 2 (-16) = 4` [ОК]
Итак, решение — `x = 22`,` y = -16` и `z = -16`.
Пример — Электронное применение системы 3 × 3 Уравнения
Найдите электрические токи, указанные как решение матричного уравнения (полученного с использованием закона Кирхгофа) возникающие из этой цепи:
`((I_1 + I_2 + I_3), (- 2I_1 + 3I_2), (- 3I_2 + 6I_3)) = ((0), (24), (0))`
(Вы можете изучить, что на самом деле означает решение для этого примера, в этом апплете трехмерных интерактивных систем уравнений.-1 ((0), (24), (0)) `
Используя систему компьютерной алгебры для выполнения обратного и умножения на постоянную матрицу, мы получаем:
`I_1 = -6 \» A «`
`I_2 = 4 \» A «`
`I_3 = 2 \» A «`
Мы видим, что I 1 имеет отрицательное значение, как и следовало ожидать из принципиальной схемы.
Упражнение 1
Найдены следующие уравнения в конкретной электрической цепи. Найдите токи с помощью матрицы методы.-1C`
`= ((0,294,0,353,0,294), (0,118, -0,059,0,118), (0,588, -0,294, -0,412)) ((0), (6), (- 3))`
`= ((1,236), (- 0,708), (- 0,528))`
Следовательно,
`I_A = 1,236 \» A «`,
`I_B = -0,708 \» A «и
`I_C = -0,528 \» A «`
Упражнение 2
Помните эту проблему? Если мы знаем используемые одновременные уравнения, мы сможем решить система с использованием обратных матриц на компьютере.
Уравнения схемы с использованием закона Кирхгофа:
−26 = 72 I 1 — 17 I 3 — 35 Я 4
34 = 122 I 2 — 35 I 3 — 87 Я 7
−4 = 233 I 7 — 87 I 2 — 34 I 3 — 72 I 6
−13 = 149 I 3 — 17 I 1 — 35 I 2 — 28 I 5 — 35 I 6 — 34 Я 7
−27 = 105 I 5 — 28 I 3 — 43 I 4 — 34 I 6
24 = 141 I 6 — 35 I 3 — 34 I 5 — 72 I 7
5 = 105 I 4 — 35 I 1 — 43 Я 5
Каковы отдельные токи, I 1 до I 7 ?
Пользователи телефонов
ПРИМЕЧАНИЕ: Если вы пользуетесь телефоном, вы можете прокрутить любую матрицу шириной на этой странице вправо или влево, чтобы увидеть все выражение. — 1 [(-26), (34), (- 4), (- 13), (- 27), (24), (5)] `
`= [(- 0.-3), (- 0,22243), (- 0,27848), (0,21115), (0,20914)] `
Ответ означает, что токи в этой цепи равны (с точностью до 4 знаков после запятой):
`I_1 = -0,4680 \» A «`
`I_2 = 0,4293 \» A «`
`I_3 = 0,0005 \» A «`
`I_4 = -0,2224 \» A «`
`I_5 = -0,2785 \» A «`
`I_6 = 0,2112 \» A «`
`I_7 = 0.2091 \» A «`
Упражнение 3
Нам нужно 10 л бензина содержащий 2% добавки. У нас есть следующие барабаны:
Бензин без присадок
Бензин с 5% присадкой
Бензин с 6% присадкой
Нам нужно использовать в 4 раза больше чистого бензин в виде 5% присадки к бензину.Сколько нужно каждого?
Всегда проверяйте свои решения!
Ответ
Пусть
x = нет. литров чистого бензина
y = нет. литров 5% бензина
z = нет. литров 6% бензина
Из первого предложения имеем:
`x + y + z = 10`
Второе предложение дает нам:
Мы НЕ получаем присадок из чистого бензина.
Получаем (5% от y ) л добавки из второго барабана.
Получаем (6% от z ) л добавки из третьего барабана.
НАМ НУЖНО 2% из 10 л добавки = 0,2 л = 200 мл.
Так
`0,05y + 0,06z = 0,2`
Умножение на 100 дает:
`5y + 6z = 20`
Второе последнее предложение дает нам:
`x = 4y`
Мы можем записать это как:
`x — 4y = 0`
Это дает нам систему одновременных уравнений:
x + y + z = 10
5 y + 6 z = 20
x — 4 y = 0
Так
`A = ((1,1,1), (0,5,6), (1, -4,0))`, `\ C = ((10), (20), (0))`
Использование Scientific Notebook для обратного:
`((1,1,1), (0,5,6), (1, -4,0)) ^ — 1« = ((0.96, -0,16,0,04), (0,24, -0,04, -0,24), (- 0,2,0.2,0.2)) `
Умножение обратной на матрицу C :
`((0,96, -0,16,0,04), (0,24, -0,04, -0,24), (- 0,2,0,2,0,2)) ((10), (20), (0))` `= ((6,4 ), (1.6), (2)) `
Итак, у нас есть 6,4 л чистого бензина, 1,6 л 5% присадок и 2 л 6% присадок.
Это правильно?
`6.4 + 1.6 + 2 = 10` L [ОК]
`5% xx 1,6 + 6% xx 2 = 200` мл [OK OK]
`4 × 1,6 = 6,4` [ОК]
Упражнение 4
Эта задача статики была представлена ранее в разделе 3: Матрицы.
Из диаграммы получаем следующие уравнения (эти уравнения взяты из теории статики):
Вертикальные силы:
F 1 sin 69,3 ° — F 2 sin 71,1 ° — F 3 sin 56,6 ° + 926 = 0
Горизонтальные силы:
F 1 cos 69,3 ° — F 2 cos 71,1 ° + F 3 cos 56,6 ° = 0
Моменты:
7.80 F 1 sin 69,3 ° — 1,50 F 2 sin 71,1 ° — 5,20 F 3 sin 56,6 ° = 0
С помощью матриц найти силы F 1 , F 2 и F 3 .
Ответ
Запишем первое уравнение так, чтобы постоянный член оказался в правой части:
F 1 sin 69,3 ° — F 2 sin 71,1 ° — F 3 sin 56,6 ° = −926
В матричной форме запишем уравнения как:
`((грех 69.-1 ((- 926), (0), (0)) `
`= ((425,5), (1079,9), (362,2))`
Так
`F_1 = 425,5 \» N «`
`F_2 = 1079.9 \» N «`
`F_3 = 362,2 \» N «`
Это очень просто и быстро в Scientific Ноутбук, Matlab или любая другая система компьютерной алгебры!
Матрицы и системы уравнений
6.1 — Матрицы и системы уравненийОпределение матрицы
- Прямоугольный массив действительных чисел
- м рядов по n столбцов
- Обозначается заглавными буквами
- Первый индекс — строка, второй индекс — столбец
Терминология
- Матрица с m строками и n столбцами называется матрицей порядка m x n .
- Квадратная матрица — это матрица с равным количеством строк и столбцов. Поскольку количество строки и столбцы одинаковы, говорят, что он имеет порядок n .
- Основная диагональ квадратной матрицы — это элементы от верхнего левого угла до нижнего правого угла. матрица.
- Матрица-строка — это матрица, состоящая только из одной строки.
- Матрица столбцов — это матрица, имеющая только один столбец.
- Матрица только с одной строкой или одним столбцом называется вектором.
Преобразование систем линейных уравнений в Матрицы
Каждое уравнение в системе превращается в строку. Каждая переменная в система становится колонной. Переменные отбрасываются, а коэффициенты помещаются в матрицу. Если правая часть включена, это называется расширенной матрицей. Если правая сторона отсутствует, это называется матрицей коэффициентов.
Система линейных уравнений …
х + у - г = 1 3х - 2у + г = 3 4x + y - 2z = 9
становится расширенной матрицей…
| х | y | z | справа | ||
|---|---|---|---|---|---|
| 1 | 1 | –1 | 1 | ||
| 3 | -2 | 1 | 3 | ||
| 4 | 1 | -2 | 9 |
Операции с элементарными строками
Элементарные операции со строками — это операции, которые могут быть выполнены с матрицей, которая даст эквивалентная строка матрица.Если матрица является расширенной матрицей, построенной из системы линейных уравнений, то эквивалентная строка матрица будет иметь то же решение, что и исходная матрица.
При работе с системами линейных уравнений вы могли выполнять три операции. что не повлияет на набор решений.
- Поменять местами два уравнения.
- Умножьте уравнение на ненулевую константу.
- Умножьте уравнение на ненулевую константу и добавьте его к другому уравнению, заменив это уравнение.
Когда система линейных уравнений преобразуется в расширенную матрицу, каждое уравнение становится строка. Итак, теперь есть три элементарные операции со строками, которые производят эквивалент строки матрица.
- Развязка двухрядная
- Умножить строку на ненулевую константу
- Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку.
Формы рядов-эшелонов и сокращенных рядов-эшелонов
Это эквивалентные строкам формы матрицы.Несложно решить систему линейных уравнений когда матрицы находятся в одной из этих форм.
Форма рядов-эшелонов
Матрица находится в виде эшелона строк, когда выполняются следующие условия.
- Если есть строка со всеми нулями, то она находится внизу матрицы.
- Первый ненулевой элемент любой строки — это единица. Этот элемент называется ведущим.
- Первая строка любой строки находится справа от первой строки предыдущей строки.
- Первая строка в строке не обязательно должна быть непосредственно за справа от первой строки предыдущий ряд.
- Матрица в виде строки-эшелона будет иметь нули под ведущими.
- Метод исключения Гаусса переводит матрицу в форму строки-эшелон, а затем выполняется обратная подстановка. требуется, чтобы завершить поиск решений системы.
- Строчная форма матрицы не обязательно уникальна.
Форма ступенчатая уменьшенная
Матрица находится в сокращенной форме строки-эшелона, когда выполняются все условия формы строка-эшелон. и все элементы выше и ниже, ведущие равны нулю.
- Если есть строка со всеми нулями, то она находится внизу матрицы.
- Первый ненулевой элемент любой строки — это единица. Этот элемент называется ведущим.
- Первая строка любой строки находится справа от первой строки предыдущей строки.
- Все элементы выше и ниже ведущего равны нулю.
- Первая строка в строке не обязательно должна быть непосредственно за справа от первой строки предыдущий ряд.
- Матрица в виде эшелона строк будет иметь нули как над, так и под ведущими.
- Метод исключения Гаусса-Джордана переводит матрицу в сокращенную форму строки-эшелона.
- Для завершения поиска решений системы обратная подстановка не требуется.
- Уменьшенная строчно-эшелонированная форма матрицы уникальна.
Исключение по Гауссу
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в эшелонированную форму строки
- Преобразуйте матрицу обратно в систему линейных уравнений
- Используйте обратную замену, чтобы получить все ответы
Гаусс-Джордан Ликвидация
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в сокращенную форму строки-эшелона
- Преобразуйте матрицу обратно в систему линейных уравнений
- Обратной замены не требуется
Поворотный
- Поворот — это процесс, который автоматизирует операции со строками, необходимые для помещения матрицы в рядный эшелон или редуцированный рядный эшелон
- В частности, при повороте элементы выше или ниже ведущей единицы превращаются в нули
Типы решений
Существует три типа решений, которые возможны при решении системы линейных уравнений.
Независимая- Согласованный
- Уникальное решение
- Матрица с сокращенной строкой имеет такое же количество ненулевых строк, что и переменные
- Левая часть обычно представляет собой единичную матрицу, но не обязательно
- Для получения независимого решения должно быть как минимум столько же уравнений, сколько переменных.
| х | y | z | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 2 |
Когда вы конвертируете расширенную матрицу обратно в форму уравнения, вы получаете x = 3, y = 1 и z = 2.
Зависимые- Согласованный
- Множество решений
- Запишите ответ в параметрической форме
- Матрица с сокращенной строкой имеет больше переменных, чем ненулевых строк
- Необязательно должна быть строка нулей, но обычно она есть.
- Это также может произойти, когда уравнений меньше, чем переменных.
| х | y | z | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 0 |
Первое уравнение будет x + 3z = 4.Решение относительно x дает x = 4 — 3z.
Второе уравнение будет y — 2z = 3. Решение для y дает y = 3 + 2z.
Столбец z не очищается (все нули, кроме одно число), поэтому другие переменные будут определены через z. Следовательно, z будет параметром t и решение …
x = 4 — 3t, y = 3 + 2t, z = t
Несоответствие- Нет решения
- Матрица с уменьшенной строкой имеет строку нулей слева, но правая часть не равна нулю.
| х | y | z | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 2 |
Здесь нет решения.
 Если же M = Р , то в уравнении (14) матрица Х Должна иметь К столбцов, а в уравнении (15) она должна иметь Р Строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений.
Если же M = Р , то в уравнении (14) матрица Х Должна иметь К столбцов, а в уравнении (15) она должна иметь Р Строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х = . Тогда Х×А = . Полученная матрица равна матрице В Тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений. Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.
Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х = . Тогда Х×А = . Полученная матрица равна матрице В Тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений. Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.

 Значит, существует
обратная матрица
Значит, существует
обратная матрица
 Обозначим его
Обозначим его  Мы же с Вами займемся
анализом того существует ли решение
и единственно ли оно?
Мы же с Вами займемся
анализом того существует ли решение
и единственно ли оно? Она имеет бесчисленное множество
решений. Положив, например, z=0
Она имеет бесчисленное множество
решений. Положив, например, z=0